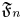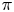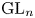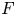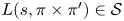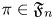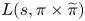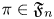1. Introduction and statement of the main result
Let ![]() $\mathbb {A}_F$ be the ring of adèles over a number field
$\mathbb {A}_F$ be the ring of adèles over a number field ![]() $F$ with absolute norm
$F$ with absolute norm ![]() $\mathrm {N}=\mathrm {N}_{F/\mathbb {Q}}$ and absolute discriminant
$\mathrm {N}=\mathrm {N}_{F/\mathbb {Q}}$ and absolute discriminant ![]() $D_F$. Let
$D_F$. Let ![]() $\mathfrak {F}_{n}$ be the set of cuspidal automorphic representations
$\mathfrak {F}_{n}$ be the set of cuspidal automorphic representations ![]() $\pi =\bigotimes _{v} \pi _{v}$ of
$\pi =\bigotimes _{v} \pi _{v}$ of ![]() $\mathrm {GL}_{n}(\mathbb {A}_F)$, where the (restricted) tensor product runs over all places of
$\mathrm {GL}_{n}(\mathbb {A}_F)$, where the (restricted) tensor product runs over all places of ![]() $F$ and
$F$ and ![]() $\pi$ is normalized so that its central character is trivial on the diagonally embedded copy of the positive reals. Let
$\pi$ is normalized so that its central character is trivial on the diagonally embedded copy of the positive reals. Let ![]() $\mathfrak {q}_{\pi }$ be the arithmetic conductor of
$\mathfrak {q}_{\pi }$ be the arithmetic conductor of ![]() $\pi$,
$\pi$, ![]() $C(\pi )\geq 1$ the analytic conductor of
$C(\pi )\geq 1$ the analytic conductor of ![]() $\pi$ (see (3.4)), and
$\pi$ (see (3.4)), and ![]() $\mathfrak {F}_n(Q)=\{\pi \in \mathfrak {F}_n\colon C(\pi )\leq Q\}$. The analytic conductor
$\mathfrak {F}_n(Q)=\{\pi \in \mathfrak {F}_n\colon C(\pi )\leq Q\}$. The analytic conductor ![]() $C(\pi )$ is a useful measure for the arithmetic and spectral complexity of
$C(\pi )$ is a useful measure for the arithmetic and spectral complexity of ![]() $\pi$. Our normalization for the central characters ensures that
$\pi$. Our normalization for the central characters ensures that ![]() $|\mathfrak {F}_n(Q)|$ is finite.
$|\mathfrak {F}_n(Q)|$ is finite.
Given ![]() $\pi \in \mathfrak {F}_n$ and
$\pi \in \mathfrak {F}_n$ and ![]() $\pi '\in \mathfrak {F}_{n'}$, let
$\pi '\in \mathfrak {F}_{n'}$, let ![]() $L(s,\pi \times \pi ')$ be the associated Rankin–Selberg
$L(s,\pi \times \pi ')$ be the associated Rankin–Selberg ![]() $L$-function, and let
$L$-function, and let ![]() $\widetilde {\pi }\in \mathfrak {F}_n$ and
$\widetilde {\pi }\in \mathfrak {F}_n$ and ![]() $\widetilde {\pi }'\in \mathfrak {F}_{n'}$ be the contragredient representations. When
$\widetilde {\pi }'\in \mathfrak {F}_{n'}$ be the contragredient representations. When ![]() $\pi '\in \{\widetilde {\pi },\widetilde {\pi }'\}$, work of Brumley [Reference HumphriesHum19, Appendix] and the authors [Reference Humphries and ThornerHT22] shows that there exists an effectively computable constant
$\pi '\in \{\widetilde {\pi },\widetilde {\pi }'\}$, work of Brumley [Reference HumphriesHum19, Appendix] and the authors [Reference Humphries and ThornerHT22] shows that there exists an effectively computable constant ![]() $c_{1}=c_{1}(n,n')>0$ such that
$c_{1}=c_{1}(n,n')>0$ such that ![]() $L(s,\pi \times \pi ')$ has a ‘standard’ zero-free region of the shape
$L(s,\pi \times \pi ')$ has a ‘standard’ zero-free region of the shape
apart from at most one real simple zero. This is comparable to the classical zero-free region for Dirichlet ![]() $L$-functions. Brumley (see [Reference BrumleyBru06a] and [Reference LapidLap13, Appendix]) established a much narrower zero-free region for all choices of
$L$-functions. Brumley (see [Reference BrumleyBru06a] and [Reference LapidLap13, Appendix]) established a much narrower zero-free region for all choices of ![]() $\pi$ and
$\pi$ and ![]() $\pi '$. The generalized Riemann hypothesis (GRH) asserts that
$\pi '$. The generalized Riemann hypothesis (GRH) asserts that ![]() $L(s,\pi \times \pi ')\neq 0$ for
$L(s,\pi \times \pi ')\neq 0$ for ![]() $\text {Re}(s)>\frac {1}{2}$. Zeros near the line
$\text {Re}(s)>\frac {1}{2}$. Zeros near the line ![]() $\text {Re}(s)=1$ are typically most damaging in applications, but even a zero-free region of the shape
$\text {Re}(s)=1$ are typically most damaging in applications, but even a zero-free region of the shape ![]() $\text {Re}(s)\geq 1-\delta$ for some constant
$\text {Re}(s)\geq 1-\delta$ for some constant ![]() $\delta =\delta (n,n',[F:\mathbb {Q}])>0$ would be sufficient to obtain many spectacular arithmetic consequences.
$\delta =\delta (n,n',[F:\mathbb {Q}])>0$ would be sufficient to obtain many spectacular arithmetic consequences.
Since such strong zero-free regions for Rankin–Selberg ![]() $L$-functions remain out of reach, it is useful to show that zeros near the line
$L$-functions remain out of reach, it is useful to show that zeros near the line ![]() $\text {Re}(s)=1$ must be ‘sparse’. A suitable quantitative formulation can serve as a proxy for a zero-free region of the shape
$\text {Re}(s)=1$ must be ‘sparse’. A suitable quantitative formulation can serve as a proxy for a zero-free region of the shape ![]() $\text {Re}(s)\geq 1-\delta$. Famous consequences of this philosophy include Hoheisel's proof [Reference HoheiselHoh30] that
$\text {Re}(s)\geq 1-\delta$. Famous consequences of this philosophy include Hoheisel's proof [Reference HoheiselHoh30] that ![]() $p_{n+1}-p_n\ll p_n^{1-1/33\,000}$ (where
$p_{n+1}-p_n\ll p_n^{1-1/33\,000}$ (where ![]() $p_n$ is the
$p_n$ is the ![]() $n$th prime) and Linnik's proof [Reference LinnikLin44] that if
$n$th prime) and Linnik's proof [Reference LinnikLin44] that if ![]() $\gcd (a,q)=1$, then there exists an absolute, effectively computable constant
$\gcd (a,q)=1$, then there exists an absolute, effectively computable constant ![]() $B>0$ and a prime
$B>0$ and a prime ![]() $p\leq q^B$ such that
$p\leq q^B$ such that ![]() $p\equiv a\,(\mathrm {mod}\,\,q)$.
$p\equiv a\,(\mathrm {mod}\,\,q)$.
To quantify our notion of ‘sparse’, we define for ![]() $\sigma \geq 0$ and
$\sigma \geq 0$ and ![]() $T\geq 1$ the quantity
$T\geq 1$ the quantity
Note that ![]() $N_{\pi \times \pi '}(\frac {1}{2},T)$ is roughly
$N_{\pi \times \pi '}(\frac {1}{2},T)$ is roughly ![]() $T\log (C(\pi )C(\pi ')T)$ via the argument principle and the functional equation, and GRH can be restated as
$T\log (C(\pi )C(\pi ')T)$ via the argument principle and the functional equation, and GRH can be restated as ![]() $N_{\pi \times \pi '}(\sigma,T)=0$ for all
$N_{\pi \times \pi '}(\sigma,T)=0$ for all ![]() $\sigma >\frac {1}{2}$. The zero density estimate
$\sigma >\frac {1}{2}$. The zero density estimate
follows from work of Soundararajan and Thorner [Reference Soundararajan and ThornerST19, Corollary 2.6]. Therefore, while an arbitrary Rankin–Selberg ![]() $L$-function
$L$-function ![]() $L(s,\pi \times \pi ')$ is not yet known to have the standard zero-free region (1.1), the bound (1.2) ensures that the number of zeros in the region (1.1) is
$L(s,\pi \times \pi ')$ is not yet known to have the standard zero-free region (1.1), the bound (1.2) ensures that the number of zeros in the region (1.1) is ![]() $O_{n,n',[F:\mathbb {Q}]}(1)$.
$O_{n,n',[F:\mathbb {Q}]}(1)$.
Let ![]() $\mathcal {S}\subseteq \mathfrak {F}_n$, and let
$\mathcal {S}\subseteq \mathfrak {F}_n$, and let ![]() $\mathcal {S}(Q)=\{\pi \in \mathcal {S}\colon C(\pi )\leq Q\}$. In this article, we seek a strong averaged form of (1.2), namely
$\mathcal {S}(Q)=\{\pi \in \mathcal {S}\colon C(\pi )\leq Q\}$. In this article, we seek a strong averaged form of (1.2), namely
where ![]() $A=A(n,n',[F:\mathbb {Q}])>0$ is a constant and
$A=A(n,n',[F:\mathbb {Q}])>0$ is a constant and ![]() $\varepsilon >0$. The bound (1.3) follows from the works of Brumley, Thorner, and Zaman under at least one of the following hypotheses:Footnote 1
$\varepsilon >0$. The bound (1.3) follows from the works of Brumley, Thorner, and Zaman under at least one of the following hypotheses:Footnote 1
•
 $\pi '\in \mathfrak {F}_1$ is trivial [Reference Thorner and ZamanTZ21, Theorem 1.2];
$\pi '\in \mathfrak {F}_1$ is trivial [Reference Thorner and ZamanTZ21, Theorem 1.2];•
 $\max \{n,n'\}\leq 4$ (see [Reference Brumley, Thorner and ZamanBTZ22, Theorem 1.3]); or
$\max \{n,n'\}\leq 4$ (see [Reference Brumley, Thorner and ZamanBTZ22, Theorem 1.3]); or•
 $\pi '$ and each
$\pi '$ and each  $\pi \in \mathcal {S}(Q)$ satisfy certain unproven partial progress towards the generalized Ramanujan conjecture (GRC) [Reference Brumley, Thorner and ZamanBTZ22, Hypothesis 1.1 and Theorem 1.3].Footnote 2
$\pi \in \mathcal {S}(Q)$ satisfy certain unproven partial progress towards the generalized Ramanujan conjecture (GRC) [Reference Brumley, Thorner and ZamanBTZ22, Hypothesis 1.1 and Theorem 1.3].Footnote 2
Here, we prove the first completely unconditional zero density estimate of the form (1.3).
Theorem 1.1 Let ![]() $n,n'\geq 1$ and
$n,n'\geq 1$ and ![]() $\varepsilon >0$. Let
$\varepsilon >0$. Let ![]() $\mathcal {S}\subseteq \mathfrak {F}_n$ and
$\mathcal {S}\subseteq \mathfrak {F}_n$ and ![]() $\mathcal {S}(Q)=\{\pi \in \mathcal {S}\colon C(\pi )\leq Q\}$. If
$\mathcal {S}(Q)=\{\pi \in \mathcal {S}\colon C(\pi )\leq Q\}$. If ![]() $0\leq \sigma \leq 1$,
$0\leq \sigma \leq 1$, ![]() $\pi '\in \mathfrak {F}_{n'}$, and
$\pi '\in \mathfrak {F}_{n'}$, and ![]() $Q,T\geq 1$, then
$Q,T\geq 1$, then
 \[ \sum_{\pi\in\mathcal{S}(Q)}N_{\pi\times\pi'}(\sigma,T)\ll_{n,n',[F:\mathbb{Q}],\varepsilon} \big(|\mathcal{S}(Q)|^{4} \big(C(\pi') Q T^{[F:\mathbb{Q}]}\big)^{6.15\max\{n^2,n'n\}}\big)^{1-\sigma+\varepsilon}. \]
\[ \sum_{\pi\in\mathcal{S}(Q)}N_{\pi\times\pi'}(\sigma,T)\ll_{n,n',[F:\mathbb{Q}],\varepsilon} \big(|\mathcal{S}(Q)|^{4} \big(C(\pi') Q T^{[F:\mathbb{Q}]}\big)^{6.15\max\{n^2,n'n\}}\big)^{1-\sigma+\varepsilon}. \]
Theorem 1.1 is non-trivial when
This is important because in applications, it is usually convenient to bound ![]() $Q$ by a power of
$Q$ by a power of ![]() $|\mathcal {S}(Q)|$ or vice versa. When
$|\mathcal {S}(Q)|$ or vice versa. When ![]() $\mathcal {S}=\mathfrak {F}_n$, we have the bounds
$\mathcal {S}=\mathfrak {F}_n$, we have the bounds
The upper bound in (1.5) was proved by Brumley et al. [Reference Brumley, Thorner and ZamanBTZ22, Theorem A.1]. The lower bound in (1.5) follows from work of Brumley and Milićević [Reference Brumley and MilićevićBM18, Theorem 1.1], who computed a constant ![]() $c_{n,F}>0$ such that if
$c_{n,F}>0$ such that if ![]() $\mathfrak {F}_n^*(Q)$ is the subset of
$\mathfrak {F}_n^*(Q)$ is the subset of ![]() $\pi \in \mathfrak {F}_n(Q)$ that are spherical at the archimedean places of
$\pi \in \mathfrak {F}_n(Q)$ that are spherical at the archimedean places of ![]() $F$, then
$F$, then ![]() $|\mathfrak {F}_n^*(Q)|\sim c_{n,F}Q^{n+1}$. (The lower bound in (1.5) reflects the conjectured order of growth; see [Reference Brumley and MilićevićBM18].) Together, Theorem 1.1 and (1.5) imply that
$|\mathfrak {F}_n^*(Q)|\sim c_{n,F}Q^{n+1}$. (The lower bound in (1.5) reflects the conjectured order of growth; see [Reference Brumley and MilićevićBM18].) Together, Theorem 1.1 and (1.5) imply that
Furthermore, if ![]() $n'=n\geq 3$ and
$n'=n\geq 3$ and ![]() $\pi '\in \mathfrak {F}_{n'}$, then Theorem 1.1 and (1.5) together imply that
$\pi '\in \mathfrak {F}_{n'}$, then Theorem 1.1 and (1.5) together imply that
2. Applications
We now describe some applications of Theorem 1.1. In what follows, we write ![]() $f\ll _{\nu }g$,
$f\ll _{\nu }g$, ![]() $f=O_{\nu }(g)$, and
$f=O_{\nu }(g)$, and ![]() $g\gg _{\nu }f$ to denote that there exists a constant
$g\gg _{\nu }f$ to denote that there exists a constant ![]() $c>0$ such that
$c>0$ such that ![]() $|f|\leq c|g|$ in the stated range. The implied constant
$|f|\leq c|g|$ in the stated range. The implied constant ![]() $c$, which is effectively computable unless otherwise stated, will depend at most on
$c$, which is effectively computable unless otherwise stated, will depend at most on ![]() $\nu$,
$\nu$, ![]() $n$,
$n$, ![]() $n'$, and
$n'$, and ![]() $[F:\mathbb {Q}]$. The expression
$[F:\mathbb {Q}]$. The expression ![]() $f\asymp _{\nu } g$ means that
$f\asymp _{\nu } g$ means that ![]() $f\ll _{\nu }g$ and
$f\ll _{\nu }g$ and ![]() $g\ll _{\nu }f$. We use
$g\ll _{\nu }f$. We use ![]() $\varepsilon >0$ to denote an arbitrarily small quantity that depends at most on
$\varepsilon >0$ to denote an arbitrarily small quantity that depends at most on ![]() $n$,
$n$, ![]() $n'$, and
$n'$, and ![]() $[F:\mathbb {Q}]$.
$[F:\mathbb {Q}]$.
2.1 Bounds for Rankin–Selberg  $L$-functions
$L$-functions
It is a classical problem for Dirichlet ![]() $L$-functions to find strong bounds on the critical line
$L$-functions to find strong bounds on the critical line ![]() $\text {Re}(s)=\frac {1}{2}$. The Phragmén–Lindelöf convexity principle shows that if
$\text {Re}(s)=\frac {1}{2}$. The Phragmén–Lindelöf convexity principle shows that if ![]() $q_{\chi}$ is the conductor of a primitive Dirichlet character
$q_{\chi}$ is the conductor of a primitive Dirichlet character ![]() $\chi$, then
$\chi$, then ![]() $L(\tfrac {1}{2},\chi ) \ll q^{1/4}$; improving this bound by replacing
$L(\tfrac {1}{2},\chi ) \ll q^{1/4}$; improving this bound by replacing ![]() $1/4$ with a smaller exponent is known as a subconvex bound. The multiplicative version of the classical large sieve inequality combined with an approximate functional equation shows that for almost all
$1/4$ with a smaller exponent is known as a subconvex bound. The multiplicative version of the classical large sieve inequality combined with an approximate functional equation shows that for almost all ![]() $\chi$, we have the bound
$\chi$, we have the bound ![]() $L(\frac {1}{2},\chi )\ll _{\varepsilon }q_{\chi }^{\varepsilon }$ for all
$L(\frac {1}{2},\chi )\ll _{\varepsilon }q_{\chi }^{\varepsilon }$ for all ![]() $\varepsilon >0$, consistent with the generalized Lindelöf hypothesis (GLH).
$\varepsilon >0$, consistent with the generalized Lindelöf hypothesis (GLH).
For ![]() $\pi \in \mathfrak {F}_2$, GLH predicts that
$\pi \in \mathfrak {F}_2$, GLH predicts that ![]() $L(\tfrac {1}{2},\pi )\ll _{\varepsilon }C(\pi )^{\varepsilon }$. Michel and Venkatesh [Reference Michel and VenkateshMV10] proved that there exists a fixed positive
$L(\tfrac {1}{2},\pi )\ll _{\varepsilon }C(\pi )^{\varepsilon }$. Michel and Venkatesh [Reference Michel and VenkateshMV10] proved that there exists a fixed positive ![]() $\delta >0$ such that
$\delta >0$ such that ![]() $L(\frac {1}{2},\pi )\ll _F C(\pi )^{1/4-\delta }$, the culmination of several decades of research. When
$L(\frac {1}{2},\pi )\ll _F C(\pi )^{1/4-\delta }$, the culmination of several decades of research. When ![]() $F=\mathbb {Q}$, a sharp mean value estimate for Hecke eigenvalues proved by Deshouillers and Iwaniec [Reference Deshouillers and IwaniecDI82], in conjunction with the approximate functional equation, implies the bound
$F=\mathbb {Q}$, a sharp mean value estimate for Hecke eigenvalues proved by Deshouillers and Iwaniec [Reference Deshouillers and IwaniecDI82], in conjunction with the approximate functional equation, implies the bound ![]() $L(\frac {1}{2},\pi )\ll _{\varepsilon } (qT)^{\varepsilon }$ for almost all
$L(\frac {1}{2},\pi )\ll _{\varepsilon } (qT)^{\varepsilon }$ for almost all ![]() $\pi \in \mathfrak {F}_2$ of arithmetic conductor
$\pi \in \mathfrak {F}_2$ of arithmetic conductor ![]() $q$, trivial central character, and archimedean complexity (Laplace eigenvalue or weight squared) lying in the dyadic interval
$q$, trivial central character, and archimedean complexity (Laplace eigenvalue or weight squared) lying in the dyadic interval ![]() $[T,2T]$. Note that in this case,
$[T,2T]$. Note that in this case, ![]() $C(\pi )\asymp qT$.
$C(\pi )\asymp qT$.
For ![]() $\pi \in \mathfrak {F}_n$ with
$\pi \in \mathfrak {F}_n$ with ![]() $n\geq 3$, the best uniform result towards the bound
$n\geq 3$, the best uniform result towards the bound ![]() $L(\frac {1}{2},\pi )\ll _{\varepsilon }C(\pi )^{\varepsilon }$ predicted by GLH is that of Soundararajan and Thorner [Reference Soundararajan and ThornerST19, Corollary 2.7], namely
$L(\frac {1}{2},\pi )\ll _{\varepsilon }C(\pi )^{\varepsilon }$ predicted by GLH is that of Soundararajan and Thorner [Reference Soundararajan and ThornerST19, Corollary 2.7], namely
We mention three results that improve upon (2.1) in an average sense, each having complementary strengths. Jana [Reference JanaJan21, Theorem 6] extended the GLH-on-average bound of Deshouillers and Iwaniec to the family of cuspidal automorphic representations of ![]() $\mathrm {GL}_n(\mathbb {A}_{\mathbb {Q}})$ of arithmetic conductor 1 and growing analytic conductor. Blomer [Reference BlomerBlo23, Corollary 5] proved the corresponding result for the family of cuspidal automorphic representations of
$\mathrm {GL}_n(\mathbb {A}_{\mathbb {Q}})$ of arithmetic conductor 1 and growing analytic conductor. Blomer [Reference BlomerBlo23, Corollary 5] proved the corresponding result for the family of cuspidal automorphic representations of ![]() $\mathrm {GL}_n(\mathbb {A}_{\mathbb {Q}})$ of a large given prime arithmetic conductor
$\mathrm {GL}_n(\mathbb {A}_{\mathbb {Q}})$ of a large given prime arithmetic conductor ![]() $q$, trivial central character, and whose archimedean components are principal series representations confined to a compact subset of the unitary dual. Thorner and Zaman [Reference Thorner and ZamanTZ21, Theorem 1.3] proved that there exists a constant
$q$, trivial central character, and whose archimedean components are principal series representations confined to a compact subset of the unitary dual. Thorner and Zaman [Reference Thorner and ZamanTZ21, Theorem 1.3] proved that there exists a constant ![]() $c_{2} = c_{2}(n,[F:\mathbb {Q}])>0$ such that if
$c_{2} = c_{2}(n,[F:\mathbb {Q}])>0$ such that if ![]() $\varepsilon >0$, then
$\varepsilon >0$, then
Unlike the preceding results, (2.2) is uniform in both the arithmetic conductor and spectral aspects and holds over number fields other than ![]() $\mathbb {Q}$, but the savings over (2.1) is not comparable to GLH on average.
$\mathbb {Q}$, but the savings over (2.1) is not comparable to GLH on average.
Given ![]() $\pi \in \mathfrak {F}_n$ and
$\pi \in \mathfrak {F}_n$ and ![]() $\pi '\in \mathfrak {F}_{n'}$, Soundararajan and Thorner [Reference Soundararajan and ThornerST19, Corollary 2.7] proved when
$\pi '\in \mathfrak {F}_{n'}$, Soundararajan and Thorner [Reference Soundararajan and ThornerST19, Corollary 2.7] proved when ![]() $F=\mathbb {Q}$ that if
$F=\mathbb {Q}$ that if ![]() $C(\pi \times \pi ')$ is the analytic conductor of
$C(\pi \times \pi ')$ is the analytic conductor of ![]() $L(s,\pi \times \pi ')$, then
$L(s,\pi \times \pi ')$, then
As of now, the best general upper bound for ![]() $|L(\tfrac {3}{2},\pi \times \pi ')|^2$ is larger than any fixed power of
$|L(\tfrac {3}{2},\pi \times \pi ')|^2$ is larger than any fixed power of ![]() $\log C(\pi \times \pi ')$ (see [Reference LiLi10, Theorem 2]). The factor of
$\log C(\pi \times \pi ')$ (see [Reference LiLi10, Theorem 2]). The factor of ![]() $|L(\tfrac {3}{2},\pi \times \pi ')|^2$ can be removed under certain partial progress toward GRC. The bound
$|L(\tfrac {3}{2},\pi \times \pi ')|^2$ can be removed under certain partial progress toward GRC. The bound ![]() $L(\frac {1}{2},\pi \times \pi ')\ll _{\varepsilon }C(\pi \times \pi ')^{\varepsilon }$ is predicted by GLH.
$L(\frac {1}{2},\pi \times \pi ')\ll _{\varepsilon }C(\pi \times \pi ')^{\varepsilon }$ is predicted by GLH.
In order to improve (2.3) on average with uniformity in ![]() $\pi$ and
$\pi$ and ![]() $\pi '$, one might first try to mimic the approach that worked well for Dirichlet
$\pi '$, one might first try to mimic the approach that worked well for Dirichlet ![]() $L$-functions and
$L$-functions and ![]() $\mathrm {GL}_2$
$\mathrm {GL}_2$ ![]() $L$-functions using trace formulae, approximate functional equations, the spectral large sieve, Voronoĭ summation, etc. While such methods have seen great success for
$L$-functions using trace formulae, approximate functional equations, the spectral large sieve, Voronoĭ summation, etc. While such methods have seen great success for ![]() $\mathrm {GL}_n\times \mathrm {GL}_{n'}$ with
$\mathrm {GL}_n\times \mathrm {GL}_{n'}$ with ![]() $n,n' \in \{1,2\}$, suitably uniform and flexible versions of these tools do not appear to be available yet in the general setting. The special case where
$n,n' \in \{1,2\}$, suitably uniform and flexible versions of these tools do not appear to be available yet in the general setting. The special case where ![]() $|n-n'|\leq 1$ exhibits some nice structural properties, lending itself to approaches via period integrals that completely avoids the aforementioned tools. To describe work in this direction, let
$|n-n'|\leq 1$ exhibits some nice structural properties, lending itself to approaches via period integrals that completely avoids the aforementioned tools. To describe work in this direction, let ![]() $F=\mathbb {Q}$,
$F=\mathbb {Q}$, ![]() $\mathcal {F}_n\subseteq \mathfrak {F}_n$ be the subset of cuspidal automorphic representations of
$\mathcal {F}_n\subseteq \mathfrak {F}_n$ be the subset of cuspidal automorphic representations of ![]() $\mathrm {GL}_n(\mathbb {A}_{\mathbb {Q}})$ of arithmetic conductor 1, and
$\mathrm {GL}_n(\mathbb {A}_{\mathbb {Q}})$ of arithmetic conductor 1, and ![]() $\mathcal {F}_n(Q)=\{\pi \in \mathcal {F}_n\colon C(\pi )\leq Q\}$. It follows from work of Jana [Reference JanaJan22, Corollary 2.2] that if
$\mathcal {F}_n(Q)=\{\pi \in \mathcal {F}_n\colon C(\pi )\leq Q\}$. It follows from work of Jana [Reference JanaJan22, Corollary 2.2] that if ![]() $\varepsilon >0$,
$\varepsilon >0$, ![]() $\pi '\in \mathcal {F}_n$, and the spectral parameters of
$\pi '\in \mathcal {F}_n$, and the spectral parameters of ![]() $\pi '$ have real part at least
$\pi '$ have real part at least ![]() $- {1}/({n^2+1})$ (which is far stronger than the best known unconditional lower bound
$- {1}/({n^2+1})$ (which is far stronger than the best known unconditional lower bound ![]() $-\frac {1}{2}+ {1}/({n^2+1})$ due to Luo, Rudnick, and Sarnak [Reference Luo, Rudnick and SarnakLRS99]), then
$-\frac {1}{2}+ {1}/({n^2+1})$ due to Luo, Rudnick, and Sarnak [Reference Luo, Rudnick and SarnakLRS99]), then
 \begin{equation} \sum_{\pi\in\mathcal{F}_n(Q)}\bigg|L\bigg(\frac{1}{2},\pi\times\pi'\bigg)\bigg|^2\ll_{\pi',\varepsilon}|\mathcal{F}_n(Q)|^{1+\varepsilon}. \end{equation}
\begin{equation} \sum_{\pi\in\mathcal{F}_n(Q)}\bigg|L\bigg(\frac{1}{2},\pi\times\pi'\bigg)\bigg|^2\ll_{\pi',\varepsilon}|\mathcal{F}_n(Q)|^{1+\varepsilon}. \end{equation}
Therefore, for fixed ![]() $\pi '\in \mathcal {F}_n$, GLH for
$\pi '\in \mathcal {F}_n$, GLH for ![]() $L(\frac {1}{2},\pi \times \pi ')$ holds on average over the
$L(\frac {1}{2},\pi \times \pi ')$ holds on average over the ![]() $\pi \in \mathcal {F}_n$. Using Chebyshev's inequality, we conclude that for all
$\pi \in \mathcal {F}_n$. Using Chebyshev's inequality, we conclude that for all ![]() $\delta >0$, there exists a constant
$\delta >0$, there exists a constant ![]() $c_{\pi ',\delta }>0$ such that
$c_{\pi ',\delta }>0$ such that
See also the work of Blomer [Reference BlomerBlo12, Theorem 2], which proves a variant of (2.4) for families of ‘spectrally close’ Hecke–Maaß newforms on ![]() $\mathrm {SL}_n(\mathbb {Z})$.
$\mathrm {SL}_n(\mathbb {Z})$.
Along the same lines as (2.2), we use (1.6) to prove the following result.
Theorem 2.1 Let ![]() $n,n'\geq 1$ and
$n,n'\geq 1$ and ![]() $Q\geq 1$. If
$Q\geq 1$. If ![]() $\varepsilon >0$ and
$\varepsilon >0$ and ![]() $\pi '\in \mathfrak {F}_{n'}$, then
$\pi '\in \mathfrak {F}_{n'}$, then
Remark 2.2 Given a subset ![]() $\mathcal {S}\subseteq \mathfrak {F}_n$, a similar result can be proved for
$\mathcal {S}\subseteq \mathfrak {F}_n$, a similar result can be proved for ![]() $\pi \in \mathcal {S}(Q)$ using Theorem 1.1. Such a result would depend effectively on
$\pi \in \mathcal {S}(Q)$ using Theorem 1.1. Such a result would depend effectively on ![]() $\delta _{\mathcal {S}}$ in (1.4).
$\delta _{\mathcal {S}}$ in (1.4).
In contrast with Jana's work in (2.5), Theorem 2.1 provides a smaller power-saving improvement over (2.3), but the improvement is uniform in the arithmetic conductor and spectral aspects as well as in ![]() $\pi '$. The exceptional set in Theorem 2.1 is a much smaller than in (2.5). Theorem 2.1 removes the requirements that
$\pi '$. The exceptional set in Theorem 2.1 is a much smaller than in (2.5). Theorem 2.1 removes the requirements that ![]() $n=n'$, that
$n=n'$, that ![]() $q_{\pi }=q_{\pi '}=1$, and that the spectral parameters of
$q_{\pi }=q_{\pi '}=1$, and that the spectral parameters of ![]() $\pi '$ have real part at least
$\pi '$ have real part at least ![]() $- {1}/({n^2+1})$. Finally, Theorem 2.1 is proved over any number field, while [Reference JanaJan22] is only proved over
$- {1}/({n^2+1})$. Finally, Theorem 2.1 is proved over any number field, while [Reference JanaJan22] is only proved over ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
2.2 Effective multiplicity one
Let ![]() $\pi =\bigotimes _v \pi _v$ and
$\pi =\bigotimes _v \pi _v$ and ![]() $\pi '=\bigotimes _v \pi _v'$ be cuspidal automorphic representations in
$\pi '=\bigotimes _v \pi _v'$ be cuspidal automorphic representations in ![]() $\mathfrak {F}_n(Q)$. Under the assumption of GRH for
$\mathfrak {F}_n(Q)$. Under the assumption of GRH for ![]() $L(s,\pi \times \widetilde {\pi })$ and
$L(s,\pi \times \widetilde {\pi })$ and ![]() $L(s,\pi \times \pi ')$ and that
$L(s,\pi \times \pi ')$ and that ![]() $\pi _{\mathfrak {p}}$ and
$\pi _{\mathfrak {p}}$ and ![]() $\pi _{\mathfrak {p}}'$ are tempered for all prime ideals
$\pi _{\mathfrak {p}}'$ are tempered for all prime ideals ![]() $\mathfrak {p} \mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$, it is known that if
$\mathfrak {p} \mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$, it is known that if ![]() $Y=(\log Q)^2$ and
$Y=(\log Q)^2$ and ![]() $\pi _{\mathfrak {p}}\cong \pi _{\mathfrak {p}}'$ for all
$\pi _{\mathfrak {p}}\cong \pi _{\mathfrak {p}}'$ for all ![]() $\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ with
$\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ with ![]() $\mathrm {N}\mathfrak {p}\ll Y$, then
$\mathrm {N}\mathfrak {p}\ll Y$, then ![]() $\pi =\pi '$ (see [Reference Iwaniec and KowalskiIK04, Proposition 5.22]). Brumley [Reference BrumleyBru06a], improving on work of Moreno [Reference MorenoMor85], proved that there exists a constant
$\pi =\pi '$ (see [Reference Iwaniec and KowalskiIK04, Proposition 5.22]). Brumley [Reference BrumleyBru06a], improving on work of Moreno [Reference MorenoMor85], proved that there exists a constant ![]() $B_n>0$ such that this result holds unconditionally with
$B_n>0$ such that this result holds unconditionally with ![]() $Y=Q^{B_n}$. This result makes effective the multiplicity one theorems of Jacquet and Shalika [Reference Jacquet and ShalikaJS81, Theorem 4.8] and Piatetski-Shapiro [Reference Piatetski-ShapiroPia79]. Any fixed
$Y=Q^{B_n}$. This result makes effective the multiplicity one theorems of Jacquet and Shalika [Reference Jacquet and ShalikaJS81, Theorem 4.8] and Piatetski-Shapiro [Reference Piatetski-ShapiroPia79]. Any fixed ![]() $B_n>2n$ suffices [Reference Liu and WangLW09].
$B_n>2n$ suffices [Reference Liu and WangLW09].
When ![]() $n=2$, we have an average result that nearly achieves what GRH predicts. Specifically, let
$n=2$, we have an average result that nearly achieves what GRH predicts. Specifically, let ![]() $\mathfrak {F}_2^{\flat }$ be the subset of
$\mathfrak {F}_2^{\flat }$ be the subset of ![]() $\pi \in \mathfrak {F}_2$ with squarefree conductor and trivial central character, and let
$\pi \in \mathfrak {F}_2$ with squarefree conductor and trivial central character, and let ![]() $\pi '\in \mathfrak {F}_2^{\flat }$. For all
$\pi '\in \mathfrak {F}_2^{\flat }$. For all ![]() $\varepsilon >0$, there exists an effectively computable constant
$\varepsilon >0$, there exists an effectively computable constant ![]() $N_{\varepsilon }>0$, depending at most on
$N_{\varepsilon }>0$, depending at most on ![]() $\varepsilon$ and
$\varepsilon$ and ![]() $[F:\mathbb {Q}]$, such that
$[F:\mathbb {Q}]$, such that
In particular, the implied constant does not depend on ![]() $\pi '$. This was proved by Duke and Kowalski [Reference Duke and KowalskiDK00, Theorem 3] when
$\pi '$. This was proved by Duke and Kowalski [Reference Duke and KowalskiDK00, Theorem 3] when ![]() $F=\mathbb {Q}$ in a stronger form under the assumption of GRC. See Brumley's Ph.D. thesis [Reference BrumleyBru04, Corollary 5.2.2] for a proof that does not use GRC.
$F=\mathbb {Q}$ in a stronger form under the assumption of GRC. See Brumley's Ph.D. thesis [Reference BrumleyBru04, Corollary 5.2.2] for a proof that does not use GRC.
If ![]() $\pi \in \mathfrak {F}_2$ and
$\pi \in \mathfrak {F}_2$ and ![]() $\widetilde {\pi }\in \mathfrak {F}_2$ is the contragredient, then
$\widetilde {\pi }\in \mathfrak {F}_2$ is the contragredient, then ![]() $L(s,\pi \times \widetilde {\pi })=\zeta _F(s)L(s,\pi,\mathrm {Ad})$, where
$L(s,\pi \times \widetilde {\pi })=\zeta _F(s)L(s,\pi,\mathrm {Ad})$, where ![]() $\zeta _F(s)$ is the Dedekind zeta function of
$\zeta _F(s)$ is the Dedekind zeta function of ![]() $F$ and
$F$ and ![]() $\mathrm {Ad}$ is the adjoint square lift from a representation of
$\mathrm {Ad}$ is the adjoint square lift from a representation of ![]() $\mathrm {GL}_2(\mathbb {A}_F)$ to a representation of
$\mathrm {GL}_2(\mathbb {A}_F)$ to a representation of ![]() $\mathrm {GL}_3(\mathbb {A}_F)$. The arguments in [Reference BrumleyBru04, Reference Duke and KowalskiDK00] rely on two key results as follows.
$\mathrm {GL}_3(\mathbb {A}_F)$. The arguments in [Reference BrumleyBru04, Reference Duke and KowalskiDK00] rely on two key results as follows.
(1) Gelbart and Jacquet [Reference Gelbart and JacquetGJ78] proved that if
 $\pi \in \mathfrak {F}_2$, then
$\pi \in \mathfrak {F}_2$, then  $L(s,\pi,\mathrm {Ad})$ is the
$L(s,\pi,\mathrm {Ad})$ is the  $L$-function of an automorphic representation of
$L$-function of an automorphic representation of  $\mathrm {GL}_3(\mathbb {A}_F)$, denoted
$\mathrm {GL}_3(\mathbb {A}_F)$, denoted  $\mathrm {Ad}\,\pi$, complete with a criterion by which one can determine whether
$\mathrm {Ad}\,\pi$, complete with a criterion by which one can determine whether  $\mathrm {Ad}\,\pi$ is cuspidal (and lies in
$\mathrm {Ad}\,\pi$ is cuspidal (and lies in  $\mathfrak {F}_3$).
$\mathfrak {F}_3$).(2) At most
 $O_{\varepsilon }(Q^{1/2+\varepsilon })$ representations
$O_{\varepsilon }(Q^{1/2+\varepsilon })$ representations  $\pi \in \mathfrak {F}_2(Q)$ have the same adjoint lift. In addition, Ramakrishnan (see [Reference Duke and KowalskiDK00, Appendix] and [Reference RamakrishnanRam00]) proved that
$\pi \in \mathfrak {F}_2(Q)$ have the same adjoint lift. In addition, Ramakrishnan (see [Reference Duke and KowalskiDK00, Appendix] and [Reference RamakrishnanRam00]) proved that  $\mathrm {Ad}\colon \mathfrak {F}_2^{\flat }\to \mathfrak {F}_3$ is injective.
$\mathrm {Ad}\colon \mathfrak {F}_2^{\flat }\to \mathfrak {F}_3$ is injective.
In attempting to generalize the strategy of Duke and Kowalski to ![]() $\mathrm {GL}_n$ for
$\mathrm {GL}_n$ for ![]() $n\geq 3$, one encounters some deep open problems. If
$n\geq 3$, one encounters some deep open problems. If ![]() $\pi \in \mathfrak {F}_n$, then for
$\pi \in \mathfrak {F}_n$, then for ![]() $\text {Re}(s)$ sufficiently large,
$\text {Re}(s)$ sufficiently large, ![]() $L(s,\pi \times \widetilde {\pi })$ factors as
$L(s,\pi \times \widetilde {\pi })$ factors as ![]() $\zeta _F(s)L(s,\pi,\mathrm {Ad})$, where
$\zeta _F(s)L(s,\pi,\mathrm {Ad})$, where ![]() $\mathrm {Ad}\,$ is the adjoint square lift from
$\mathrm {Ad}\,$ is the adjoint square lift from ![]() $\mathrm {GL}_{n}$ to
$\mathrm {GL}_{n}$ to ![]() $\mathrm {GL}_{n^2-1}$. Apart from some special cases, the following obstacles arise.
$\mathrm {GL}_{n^2-1}$. Apart from some special cases, the following obstacles arise.
(1) The adjoint lift is not yet known to be automorphic for
 $n\geq 3$, and if it were, there is no known criterion for cuspidality.
$n\geq 3$, and if it were, there is no known criterion for cuspidality.(2) Let
 $\mathcal {H}_n\subseteq \mathfrak {F}_n(Q)$ be the subset of
$\mathcal {H}_n\subseteq \mathfrak {F}_n(Q)$ be the subset of  $\pi \in \mathfrak {F}_n(Q)$ such that
$\pi \in \mathfrak {F}_n(Q)$ such that  $\mathrm {Ad}\,\pi \in \mathfrak {F}_{n^2-1}$. It is not known how many
$\mathrm {Ad}\,\pi \in \mathfrak {F}_{n^2-1}$. It is not known how many  $\pi \in \mathcal {H}_n$ have the same adjoint lift.
$\pi \in \mathcal {H}_n$ have the same adjoint lift.
Despite these setbacks, we can use (1.7) (more specifically, Corollary 7.1) to prove a ![]() $\mathrm {GL}_n$ analogue of (2.6) when
$\mathrm {GL}_n$ analogue of (2.6) when ![]() $\pi '$ depends mildly on
$\pi '$ depends mildly on ![]() $Q$.
$Q$.
Theorem 2.3 Let ![]() $n\geq 3$ and
$n\geq 3$ and ![]() $Q\geq 1$. There exists an absolute, effectively computable constant
$Q\geq 1$. There exists an absolute, effectively computable constant ![]() $c_{3}>0$ such that if
$c_{3}>0$ such that if ![]() $0<\varepsilon <1$ and
$0<\varepsilon <1$ and ![]() $\pi '\in \mathfrak {F}_n((\log Q)^{c_{3}/(n^2 [F:\mathbb {Q}]^2)})$, then
$\pi '\in \mathfrak {F}_n((\log Q)^{c_{3}/(n^2 [F:\mathbb {Q}]^2)})$, then
Remark 2.4 Given a subset ![]() $\mathcal {S}\subseteq \mathfrak {F}_n$, a similar result can be proved for
$\mathcal {S}\subseteq \mathfrak {F}_n$, a similar result can be proved for ![]() $\pi \in \mathcal {S}(Q)$ using Theorem 1.1. Such a result would depend effectively on
$\pi \in \mathcal {S}(Q)$ using Theorem 1.1. Such a result would depend effectively on ![]() $\delta _{\mathcal {S}}$ in (1.4).
$\delta _{\mathcal {S}}$ in (1.4).
The proof is very flexible. For example, if ![]() $\varepsilon >0$ and
$\varepsilon >0$ and ![]() $C(\pi ')\ll _{\varepsilon }Q^{c_{3}\varepsilon ^2/(n^2[F:\mathbb {Q}]^2)}$, then the same proof with minor changes in choices of parameters produces the bound
$C(\pi ')\ll _{\varepsilon }Q^{c_{3}\varepsilon ^2/(n^2[F:\mathbb {Q}]^2)}$, then the same proof with minor changes in choices of parameters produces the bound
While the number of ![]() $\mathfrak {p}$ for which one needs to check that
$\mathfrak {p}$ for which one needs to check that ![]() $\pi _{\mathfrak {p}}\cong \pi _{\mathfrak {p}}'$ is larger, the range of
$\pi _{\mathfrak {p}}\cong \pi _{\mathfrak {p}}'$ is larger, the range of ![]() $C(\pi ')$ is greatly extended, and the threshold
$C(\pi ')$ is greatly extended, and the threshold ![]() $\mathrm {N}\mathfrak {p}\leq Q^{\varepsilon }$ (reminiscent of Vinogradov's conjecture on the size of the least quadratic non-residue) still greatly improves on the unconditional range
$\mathrm {N}\mathfrak {p}\leq Q^{\varepsilon }$ (reminiscent of Vinogradov's conjecture on the size of the least quadratic non-residue) still greatly improves on the unconditional range ![]() $\mathrm {N}\mathfrak {p}\ll _{\varepsilon }Q^{2n+\varepsilon }$ from [Reference Liu and WangLW09].
$\mathrm {N}\mathfrak {p}\ll _{\varepsilon }Q^{2n+\varepsilon }$ from [Reference Liu and WangLW09].
2.3 Automorphic level of distribution
Let ![]() $\Lambda (m)$ be the von Mangoldt function, equal to
$\Lambda (m)$ be the von Mangoldt function, equal to ![]() $\log p$ if
$\log p$ if ![]() $m$ is a power of a prime
$m$ is a power of a prime ![]() $p$ and zero otherwise. The celebrated Bombieri–Vinogradov theorem states that if
$p$ and zero otherwise. The celebrated Bombieri–Vinogradov theorem states that if ![]() $\theta <\frac {1}{2}$ is fixed, then for all
$\theta <\frac {1}{2}$ is fixed, then for all ![]() $A>0$, we have
$A>0$, we have
 \begin{equation} \sum_{q\leq x^{\theta}}~\max_{\gcd(a,q)=1}\max_{y\leq x}\Bigg|\sum_{\substack{m\leq y \\ m\equiv a\,(\mathrm{mod}\,\,q)}}\Lambda(m)-\frac{y}{\varphi(q)}\Bigg|\ll_A\frac{x}{(\log x)^A}. \end{equation}
\begin{equation} \sum_{q\leq x^{\theta}}~\max_{\gcd(a,q)=1}\max_{y\leq x}\Bigg|\sum_{\substack{m\leq y \\ m\equiv a\,(\mathrm{mod}\,\,q)}}\Lambda(m)-\frac{y}{\varphi(q)}\Bigg|\ll_A\frac{x}{(\log x)^A}. \end{equation}
This may be viewed as an average form of GRH for Dirichlet ![]() $L$-functions. As part of his proof [Reference BombieriBom65], Bombieri proved a strong form of the zero density estimate in Theorem 1.1 for Dirichlet
$L$-functions. As part of his proof [Reference BombieriBom65], Bombieri proved a strong form of the zero density estimate in Theorem 1.1 for Dirichlet ![]() $L$-functions. We call any
$L$-functions. We call any ![]() $\theta$ for which (2.7) holds a level of distribution for the primes. Elliott and Halberstam conjectured that any fixed
$\theta$ for which (2.7) holds a level of distribution for the primes. Elliott and Halberstam conjectured that any fixed ![]() $\theta <1$ is a level of distribution for the primes.
$\theta <1$ is a level of distribution for the primes.
Number theorists have proved several interesting extensions and variations of (2.7). For example, Murty and Murty [Reference Murty and MurtyMM87] proved that primes in the Chebotarev density theorem have a positive level of distribution. To describe a different direction for automorphic representations over ![]() $\mathbb {Q}$, we let
$\mathbb {Q}$, we let ![]() $n\geq 2$ and consider
$n\geq 2$ and consider ![]() $\pi \in \mathfrak {F}_{n}$ with conductor
$\pi \in \mathfrak {F}_{n}$ with conductor ![]() $q_{\pi }$. Let
$q_{\pi }$. Let ![]() $\Lambda (m)$ be the von Mangoldt function, and define the numbers
$\Lambda (m)$ be the von Mangoldt function, and define the numbers ![]() $a_{\pi }(m)$ by
$a_{\pi }(m)$ by
 \[ -\frac{L'}{L}(s,\pi)=\sum_{p}\sum_{k=1}^{\infty}\frac{\sum_{j=1}^{n}\alpha_{j,\pi}(p)^k\log p}{p^{ks}}=\sum_{n=1}^{\infty}\frac{a_{\pi}(m)\Lambda(m)}{m^s},\quad \text{Re}(s)>1. \]
\[ -\frac{L'}{L}(s,\pi)=\sum_{p}\sum_{k=1}^{\infty}\frac{\sum_{j=1}^{n}\alpha_{j,\pi}(p)^k\log p}{p^{ks}}=\sum_{n=1}^{\infty}\frac{a_{\pi}(m)\Lambda(m)}{m^s},\quad \text{Re}(s)>1. \]
Note that ![]() $a_{\pi }(p)=\lambda _{\pi }(p)$. For fixed
$a_{\pi }(p)=\lambda _{\pi }(p)$. For fixed ![]() $\theta < {1}/({n^2-2})$, Wong [Reference WongWon20, Theorem 9] proved that if
$\theta < {1}/({n^2-2})$, Wong [Reference WongWon20, Theorem 9] proved that if ![]() $\pi$ satisfies GRC and
$\pi$ satisfies GRC and ![]() $L(s,\pi \times (\widetilde {\pi }\otimes \chi ))$ has no Landau–Siegel zero for all Dirichlet characters
$L(s,\pi \times (\widetilde {\pi }\otimes \chi ))$ has no Landau–Siegel zero for all Dirichlet characters ![]() $\chi$, then for any
$\chi$, then for any ![]() $A>0$,
$A>0$,
 \begin{equation} \sum_{q\leq x^{\theta}}~\max_{\gcd(a,q)=1}\max_{y\leq x}\Bigg|\sum_{\substack{m\leq y \\ \gcd(m,q_{\pi})=1 \\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)-\frac{y}{\varphi(q)}\Bigg|\ll_{A,\pi}\frac{x}{(\log x)^A}. \end{equation}
\begin{equation} \sum_{q\leq x^{\theta}}~\max_{\gcd(a,q)=1}\max_{y\leq x}\Bigg|\sum_{\substack{m\leq y \\ \gcd(m,q_{\pi})=1 \\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)-\frac{y}{\varphi(q)}\Bigg|\ll_{A,\pi}\frac{x}{(\log x)^A}. \end{equation}
This conditionally endows ![]() $L(s,\pi\times\widetilde{\pi})$ with a positive level of distribution
$L(s,\pi\times\widetilde{\pi})$ with a positive level of distribution ![]() $\theta$. The hypotheses for (2.8) hold for
$\theta$. The hypotheses for (2.8) hold for ![]() $\pi$ attached to non-CM holomorphic cuspidal newforms on congruence subgroups of
$\pi$ attached to non-CM holomorphic cuspidal newforms on congruence subgroups of ![]() $\mathrm {SL}_2(\mathbb {Z})$.
$\mathrm {SL}_2(\mathbb {Z})$.
Let ![]() $\pi \in \mathfrak {F}_n$. Using (1.7), we unconditionally endow
$\pi \in \mathfrak {F}_n$. Using (1.7), we unconditionally endow ![]() $L(s,\pi\times\widetilde{\pi})$ with a notion of positive level of distribution. In particular, we avoid recourse to unproven progress toward GRC or the absence of Landau–Siegel zeros.
$L(s,\pi\times\widetilde{\pi})$ with a notion of positive level of distribution. In particular, we avoid recourse to unproven progress toward GRC or the absence of Landau–Siegel zeros.
Theorem 2.5 Let ![]() $F=\mathbb {Q}$ and
$F=\mathbb {Q}$ and ![]() $\pi \in \mathfrak {F}_{n}$. Fix
$\pi \in \mathfrak {F}_{n}$. Fix ![]() $\theta <1/(9n^3)$. If
$\theta <1/(9n^3)$. If ![]() $A>0$, then
$A>0$, then
 \[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x} \Bigg|\sum_{\substack{m\leq y \\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)-\frac{y}{\varphi(q)}\Bigg| \ll_{A,\pi}\frac{x}{(\log x)^A}. \]
\[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x} \Bigg|\sum_{\substack{m\leq y \\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)-\frac{y}{\varphi(q)}\Bigg| \ll_{A,\pi}\frac{x}{(\log x)^A}. \]
The implied constants are ineffective.
Remark 2.6 One can prove an analogue of Theorem 2.5 with ![]() $F\neq \mathbb {Q}$, replacing residue classes modulo
$F\neq \mathbb {Q}$, replacing residue classes modulo ![]() $q$ with ray classes modulo
$q$ with ray classes modulo ![]() $\mathfrak {q}$. We restrict to
$\mathfrak {q}$. We restrict to ![]() $F=\mathbb {Q}$ for notational simplicity.
$F=\mathbb {Q}$ for notational simplicity.
Overview of the paper
In § 3, we recall basic properties of standard ![]() $L$-functions and Rankin–Selberg
$L$-functions and Rankin–Selberg ![]() $L$-functions that we use in our proofs. In § 4, we prove a large sieve inequality for the Dirichlet coefficients of
$L$-functions that we use in our proofs. In § 4, we prove a large sieve inequality for the Dirichlet coefficients of ![]() $L(s,\pi \times \pi ')^{-1}$ and a corollary on mean values of Dirichlet polynomials, which we use in our proof of Theorem 1.1 in § 5. We then prove Theorem 2.1 in § 6, Theorem 2.3 in § 7, and Theorem 2.5 in § 8.
$L(s,\pi \times \pi ')^{-1}$ and a corollary on mean values of Dirichlet polynomials, which we use in our proof of Theorem 1.1 in § 5. We then prove Theorem 2.1 in § 6, Theorem 2.3 in § 7, and Theorem 2.5 in § 8.
3. Properties of  $L$-functions
$L$-functions
We recall some standard facts about ![]() $L$-functions arising from automorphic representations and their Rankin–Selberg convolutions. See [Reference BrumleyBru06a, Reference Godement and JacquetGJ72, Reference Jacquet, Piatetskii-Shapiro and ShalikaJPS83, Reference Mœglin and WaldspurgerMW89, Reference Soundararajan and ThornerST19].
$L$-functions arising from automorphic representations and their Rankin–Selberg convolutions. See [Reference BrumleyBru06a, Reference Godement and JacquetGJ72, Reference Jacquet, Piatetskii-Shapiro and ShalikaJPS83, Reference Mœglin and WaldspurgerMW89, Reference Soundararajan and ThornerST19].
3.1 Standard  $L$-functions
$L$-functions
Given ![]() $\pi \in \mathfrak {F}_n$, let
$\pi \in \mathfrak {F}_n$, let ![]() $\widetilde {\pi }\in \mathfrak {F}_n$ be the contragredient representation and
$\widetilde {\pi }\in \mathfrak {F}_n$ be the contragredient representation and ![]() $\mathfrak {q}_{\pi }$ be the conductor of
$\mathfrak {q}_{\pi }$ be the conductor of ![]() $\pi$. We express
$\pi$. We express ![]() $\pi$ as a restricted tensor product
$\pi$ as a restricted tensor product ![]() $\bigotimes _v \pi _v$ of smooth admissible representations of
$\bigotimes _v \pi _v$ of smooth admissible representations of ![]() $\mathrm {GL}_n(F_v)$, where
$\mathrm {GL}_n(F_v)$, where ![]() $v$ varies over places of
$v$ varies over places of ![]() $F$. When
$F$. When ![]() $v$ is a non-archimedean place corresponding with a prime ideal
$v$ is a non-archimedean place corresponding with a prime ideal ![]() $\mathfrak {p}$, then the local
$\mathfrak {p}$, then the local ![]() $L$-function
$L$-function ![]() $L(s,\pi _{\mathfrak {p}})$ is defined in terms of the Satake parameters
$L(s,\pi _{\mathfrak {p}})$ is defined in terms of the Satake parameters ![]() $A_{\pi }(\mathfrak {p})=\{\alpha _{1,\pi }(\mathfrak {p}),\ldots,\alpha _{n,\pi }(\mathfrak {p})\}$ by
$A_{\pi }(\mathfrak {p})=\{\alpha _{1,\pi }(\mathfrak {p}),\ldots,\alpha _{n,\pi }(\mathfrak {p})\}$ by
 \begin{equation} L(s,\pi_{\mathfrak{p}})=\prod_{j=1}^{n}(1-\alpha_{j,\pi}(\mathfrak{p})\mathrm{N}\mathfrak{p}^{-s})^{-1}=\sum_{k=0}^{\infty}\frac{\lambda_{\pi}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}. \end{equation}
\begin{equation} L(s,\pi_{\mathfrak{p}})=\prod_{j=1}^{n}(1-\alpha_{j,\pi}(\mathfrak{p})\mathrm{N}\mathfrak{p}^{-s})^{-1}=\sum_{k=0}^{\infty}\frac{\lambda_{\pi}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}. \end{equation}
We have ![]() $\alpha _{j,\pi }(\mathfrak {p})\neq 0$ for all
$\alpha _{j,\pi }(\mathfrak {p})\neq 0$ for all ![]() $j$ whenever
$j$ whenever ![]() $\mathfrak {p}\nmid \mathfrak {q}_{\pi }$, and when
$\mathfrak {p}\nmid \mathfrak {q}_{\pi }$, and when ![]() $\mathfrak {p} \mid \mathfrak {q}_{\pi }$, it might be the case that there exist
$\mathfrak {p} \mid \mathfrak {q}_{\pi }$, it might be the case that there exist ![]() $j$ such that
$j$ such that ![]() $\alpha _{j,\pi }(\mathfrak {p})=0$. The standard
$\alpha _{j,\pi }(\mathfrak {p})=0$. The standard ![]() $L$-function
$L$-function ![]() $L(s,\pi )$ associated to
$L(s,\pi )$ associated to ![]() $\pi$ is of the form
$\pi$ is of the form
 \[ L(s,\pi)=\prod_{\mathfrak{p}} L(s,\pi_{\mathfrak{p}})=\sum_{\mathfrak{n}}\frac{\lambda_{\pi}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s}. \]
\[ L(s,\pi)=\prod_{\mathfrak{p}} L(s,\pi_{\mathfrak{p}})=\sum_{\mathfrak{n}}\frac{\lambda_{\pi}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s}. \]
The Euler product and Dirichlet series converge absolutely when ![]() $\text {Re}(s)>1$.
$\text {Re}(s)>1$.
At each archimedean place ![]() $v$ of
$v$ of ![]() $F$, there are
$F$, there are ![]() $n$ Langlands parameters
$n$ Langlands parameters ![]() $\mu _{j,\pi }(v)\in \mathbb {C}$ such that
$\mu _{j,\pi }(v)\in \mathbb {C}$ such that
 \[ L(s,\pi_{\infty}) = \prod_{v|\infty}\prod_{j=1}^{n}\Gamma_{ v}(s+\mu_{j,\pi}(v)),\quad \Gamma_{v}(s):= \begin{cases} \pi^{-s/2}\Gamma(s/2) & \mbox{if}\ F_{ v}=\mathbb{R},\\ 2(2\pi)^{-s}\Gamma(s) & \mbox{if}\ F_{ v}=\mathbb{C}. \end{cases} \]
\[ L(s,\pi_{\infty}) = \prod_{v|\infty}\prod_{j=1}^{n}\Gamma_{ v}(s+\mu_{j,\pi}(v)),\quad \Gamma_{v}(s):= \begin{cases} \pi^{-s/2}\Gamma(s/2) & \mbox{if}\ F_{ v}=\mathbb{R},\\ 2(2\pi)^{-s}\Gamma(s) & \mbox{if}\ F_{ v}=\mathbb{C}. \end{cases} \]
By combining the work in [Reference Blomer and BrumleyBB11, Reference Blomer and BrumleyBB13, Reference Luo, Rudnick and SarnakLRS99, Reference Müller and SpehMS04], we know that there exists
 \begin{equation} 0\leq\theta_n\leq\begin{cases} 0 & \mbox{if}\ n=1,\\ 7/64 & \mbox{if}\ n=2,\\ 5/14 & \mbox{if}\ n=3,\\ 9/22 & \mbox{if}\ n=4,\\ 1/2-1/(n^2+1) & \mbox{if}\ n\geq 5,\end{cases} \end{equation}
\begin{equation} 0\leq\theta_n\leq\begin{cases} 0 & \mbox{if}\ n=1,\\ 7/64 & \mbox{if}\ n=2,\\ 5/14 & \mbox{if}\ n=3,\\ 9/22 & \mbox{if}\ n=4,\\ 1/2-1/(n^2+1) & \mbox{if}\ n\geq 5,\end{cases} \end{equation}such that
GRC asserts that in (3.2), one may take ![]() $\theta _n=0$. We have
$\theta _n=0$. We have ![]() $\mathfrak {q}_{\pi }=\mathfrak {q}_{\widetilde {\pi }}$, and for each
$\mathfrak {q}_{\pi }=\mathfrak {q}_{\widetilde {\pi }}$, and for each ![]() $\mathfrak {p}$ and each
$\mathfrak {p}$ and each ![]() $v$, we have the equalities of sets
$v$, we have the equalities of sets ![]() $\{\alpha _{j,\widetilde {\pi }}(\mathfrak {p})\}=\{\overline { \alpha _{j,\pi }(\mathfrak {p})}\}$ and
$\{\alpha _{j,\widetilde {\pi }}(\mathfrak {p})\}=\{\overline { \alpha _{j,\pi }(\mathfrak {p})}\}$ and ![]() $\{\mu _{j,\widetilde {\pi }}(v)\}=\{\overline {\mu _{j,\pi }(v)}\}$.
$\{\mu _{j,\widetilde {\pi }}(v)\}=\{\overline {\mu _{j,\pi }(v)}\}$.
Let ![]() $r_{\pi }$ be the order of the pole of
$r_{\pi }$ be the order of the pole of ![]() $L(s,\pi )$ at
$L(s,\pi )$ at ![]() $s=1$. The completed
$s=1$. The completed ![]() $L$-function
$L$-function
is entire of order 1, and there exists a complex number ![]() $W(\pi )$ of modulus 1 such that for all
$W(\pi )$ of modulus 1 such that for all ![]() $s\in \mathbb {C}$, we have the functional equation
$s\in \mathbb {C}$, we have the functional equation ![]() $\Lambda (s,\pi )=W(\pi )\Lambda (1-s,\widetilde {\pi })$. Let
$\Lambda (s,\pi )=W(\pi )\Lambda (1-s,\widetilde {\pi })$. Let ![]() $d(v)=1$ if
$d(v)=1$ if ![]() $F_{ v}=\mathbb {R}$ and
$F_{ v}=\mathbb {R}$ and ![]() $d(v)=2$ if
$d(v)=2$ if ![]() $F_{ v}=\mathbb {C}$. The analytic conductor of
$F_{ v}=\mathbb {C}$. The analytic conductor of ![]() $\pi$ (see [Reference Iwaniec and SarnakIS00]) is given by
$\pi$ (see [Reference Iwaniec and SarnakIS00]) is given by
 \begin{equation} C(\pi,t):= D_F^n \mathrm{N}\mathfrak{q}_{\pi}\prod_{v|\infty}\prod_{j=1}^n(3+|it+\mu_{j,\pi}(v)|^{d(v)}),\quad C(\pi):= C(\pi,0). \end{equation}
\begin{equation} C(\pi,t):= D_F^n \mathrm{N}\mathfrak{q}_{\pi}\prod_{v|\infty}\prod_{j=1}^n(3+|it+\mu_{j,\pi}(v)|^{d(v)}),\quad C(\pi):= C(\pi,0). \end{equation}
Since ![]() $\Lambda (s,\pi )$ is entire of order 1, there exist complex numbers
$\Lambda (s,\pi )$ is entire of order 1, there exist complex numbers ![]() $a_{\pi }$ and
$a_{\pi }$ and ![]() $b_{\pi }$ such that
$b_{\pi }$ such that
 \[ \Lambda(s,\pi)=e^{a_{\pi}+b_{\pi}s}\prod_{\Lambda(\rho,\pi)=0}\bigg(1-\frac{s}{\rho}\bigg)e^{s/\rho}. \]
\[ \Lambda(s,\pi)=e^{a_{\pi}+b_{\pi}s}\prod_{\Lambda(\rho,\pi)=0}\bigg(1-\frac{s}{\rho}\bigg)e^{s/\rho}. \]
The zeros ![]() $\rho$ in the above Hadamard product are the non-trivial zeros of
$\rho$ in the above Hadamard product are the non-trivial zeros of ![]() $L(s,\pi )$, and the zeros of
$L(s,\pi )$, and the zeros of ![]() $L(s,\pi )$ that arise as poles of
$L(s,\pi )$ that arise as poles of ![]() $s^{r_{\pi }}L(s,\pi _{\infty })$ are the trivial zeros.
$s^{r_{\pi }}L(s,\pi _{\infty })$ are the trivial zeros.
3.2 Rankin–Selberg  $L$-functions
$L$-functions
Let ![]() $\pi \in \mathfrak {F}_n$ and
$\pi \in \mathfrak {F}_n$ and ![]() $\pi '\in \mathfrak {F}_{n'}$. At each prime ideal
$\pi '\in \mathfrak {F}_{n'}$. At each prime ideal ![]() $\mathfrak {p}$, Jacquet et al. [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPS83] associate to
$\mathfrak {p}$, Jacquet et al. [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPS83] associate to ![]() $\pi _{\mathfrak {p}}$ and
$\pi _{\mathfrak {p}}$ and ![]() $\pi _{\mathfrak {p}}'$ a local Rankin–Selberg
$\pi _{\mathfrak {p}}'$ a local Rankin–Selberg ![]() $L$-function
$L$-function
 \begin{equation} L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')=\prod_{j=1}^{n}\prod_{j'=1}^{n'}(1-\alpha_{j,j',\pi \times\pi'}(\mathfrak{p}) \mathrm{N}\mathfrak{p}^{-s})^{-1}=\sum_{k=0}^{\infty}\frac{\lambda_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}} \end{equation}
\begin{equation} L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')=\prod_{j=1}^{n}\prod_{j'=1}^{n'}(1-\alpha_{j,j',\pi \times\pi'}(\mathfrak{p}) \mathrm{N}\mathfrak{p}^{-s})^{-1}=\sum_{k=0}^{\infty}\frac{\lambda_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}} \end{equation}
and a local conductor ![]() $\mathfrak {q}_{\pi _{\mathfrak {p}}\times \pi _{\mathfrak {p}}'}$. If
$\mathfrak {q}_{\pi _{\mathfrak {p}}\times \pi _{\mathfrak {p}}'}$. If ![]() $\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$, then we have the equality of sets
$\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$, then we have the equality of sets
The Rankin–Selberg ![]() $L$-function
$L$-function ![]() $L(s,\pi \times \pi ')$ associated to
$L(s,\pi \times \pi ')$ associated to ![]() $\pi$ and
$\pi$ and ![]() $\pi '$ and its arithmetic conductor are
$\pi '$ and its arithmetic conductor are
 \[ L(s,\pi\times\pi')=\prod_{\mathfrak{p}}L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')=\sum_{\mathfrak{n}}\frac{\lambda_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s},\quad \mathfrak{q}_{\pi\times\pi'}=\prod_{\mathfrak{p}}\mathfrak{q}_{\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}'}. \]
\[ L(s,\pi\times\pi')=\prod_{\mathfrak{p}}L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')=\sum_{\mathfrak{n}}\frac{\lambda_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s},\quad \mathfrak{q}_{\pi\times\pi'}=\prod_{\mathfrak{p}}\mathfrak{q}_{\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}'}. \]
At an archimedean place ![]() $v$ of
$v$ of ![]() $F$, Jacquet, Piatetski-Shapiro, and Shalika associate
$F$, Jacquet, Piatetski-Shapiro, and Shalika associate ![]() $n'n$ complex Langlands parameters
$n'n$ complex Langlands parameters ![]() $\mu _{j,j',\pi \times \pi '}(v)$ to
$\mu _{j,j',\pi \times \pi '}(v)$ to ![]() $\pi _v$ and
$\pi _v$ and ![]() $\pi _v'$, from which one defines
$\pi _v'$, from which one defines
 \[ L(s,\pi_{\infty}\times\pi_{\infty}') = \prod_{v|\infty}\prod_{j=1}^{n}\prod_{j'=1}^{n'}\Gamma_{ v}(s+\mu_{j,j',\pi\times\pi'}(v)). \]
\[ L(s,\pi_{\infty}\times\pi_{\infty}') = \prod_{v|\infty}\prod_{j=1}^{n}\prod_{j'=1}^{n'}\Gamma_{ v}(s+\mu_{j,j',\pi\times\pi'}(v)). \]
Using the explicit descriptions of ![]() $\alpha _{j,j',\pi \times \pi '}(\mathfrak {p})$ and
$\alpha _{j,j',\pi \times \pi '}(\mathfrak {p})$ and ![]() $\mu _{j,j',\pi \times \pi '}(v)$ in [Reference HumphriesHum19, Reference Soundararajan and ThornerST19], one sees that
$\mu _{j,j',\pi \times \pi '}(v)$ in [Reference HumphriesHum19, Reference Soundararajan and ThornerST19], one sees that
Let ![]() $r_{\pi \times \pi '} = -\mathrm {ord}_{s=1}L(s,\pi \times \pi ')$. By our normalization for the central characters of
$r_{\pi \times \pi '} = -\mathrm {ord}_{s=1}L(s,\pi \times \pi ')$. By our normalization for the central characters of ![]() $\pi$ and
$\pi$ and ![]() $\pi '$, we have that
$\pi '$, we have that ![]() $r_{\pi \times \pi '}=0$ if and only if
$r_{\pi \times \pi '}=0$ if and only if ![]() $\pi \neq \widetilde {\pi }'$, and
$\pi \neq \widetilde {\pi }'$, and ![]() $r_{\pi \times \widetilde {\pi }}=1$ otherwise. The function
$r_{\pi \times \widetilde {\pi }}=1$ otherwise. The function
is entire of order 1, and there exists a complex number ![]() $W(\pi \times \pi ')$ of modulus 1 such that
$W(\pi \times \pi ')$ of modulus 1 such that ![]() $\Lambda (s,\pi \times \pi ')$ satisfies the functional equation
$\Lambda (s,\pi \times \pi ')$ satisfies the functional equation ![]() $\Lambda (s,\pi \times \pi ')=W(\pi \times \pi ')\Lambda (1-s,\widetilde {\pi }\times \widetilde {\pi }')$. As with
$\Lambda (s,\pi \times \pi ')=W(\pi \times \pi ')\Lambda (1-s,\widetilde {\pi }\times \widetilde {\pi }')$. As with ![]() $L(s,\pi )$, the analytic conductor of
$L(s,\pi )$, the analytic conductor of ![]() $L(s,\pi \times \pi ')$ is given by
$L(s,\pi \times \pi ')$ is given by
 \begin{equation} C(\pi\times\pi',t):= D_F^{n'n}\mathrm{N}\mathfrak{q}_{\pi\times\pi'}\prod_{v|\infty}\prod_{j=1}^n \prod_{j'=1}^{n'}(3+|it+\mu_{j,j',\pi\times\pi'}(v)|^{d(v)}),\quad C(\pi\times\pi'):= C(0,\pi\times\pi'). \end{equation}
\begin{equation} C(\pi\times\pi',t):= D_F^{n'n}\mathrm{N}\mathfrak{q}_{\pi\times\pi'}\prod_{v|\infty}\prod_{j=1}^n \prod_{j'=1}^{n'}(3+|it+\mu_{j,j',\pi\times\pi'}(v)|^{d(v)}),\quad C(\pi\times\pi'):= C(0,\pi\times\pi'). \end{equation}The combined work of Bushnell and Henniart [Reference Bushnell and HenniartBH97] and Brumley [Reference HumphriesHum19, Appendix] yields
Since ![]() $\Lambda (s,\pi \times \pi ')$ is entire of order 1, there exist complex numbers
$\Lambda (s,\pi \times \pi ')$ is entire of order 1, there exist complex numbers ![]() $a_{\pi \times \pi '}$ and
$a_{\pi \times \pi '}$ and ![]() $b_{\pi \times \pi '}$ such that the Hadamard factorization
$b_{\pi \times \pi '}$ such that the Hadamard factorization
 \begin{equation} \Lambda(s,\pi\times\pi')=e^{a_{\pi\times\pi'}+b_{\pi\times\pi'}s}\prod_{\Lambda(\rho,\pi\times\pi')=0} \bigg(1-\frac{s}{\rho}\bigg)e^{s/\rho} \end{equation}
\begin{equation} \Lambda(s,\pi\times\pi')=e^{a_{\pi\times\pi'}+b_{\pi\times\pi'}s}\prod_{\Lambda(\rho,\pi\times\pi')=0} \bigg(1-\frac{s}{\rho}\bigg)e^{s/\rho} \end{equation}
holds. The zeros ![]() $\rho$ in (3.11) are the non-trivial zeros of
$\rho$ in (3.11) are the non-trivial zeros of ![]() $L(s,\pi \times \pi ')$, and the zeros of
$L(s,\pi \times \pi ')$, and the zeros of ![]() $L(s,\pi \times \pi ')$ that arise as poles of
$L(s,\pi \times \pi ')$ that arise as poles of ![]() $s^{r_{\pi \times \pi '}}L(s,\pi _{\infty }\times \pi _{\infty }')$ are the trivial zeros.
$s^{r_{\pi \times \pi '}}L(s,\pi _{\infty }\times \pi _{\infty }')$ are the trivial zeros.
It follows from work of Li [Reference LiLi10, Theorem 2] (with minor adjustments when ![]() $F\neq \mathbb {Q}$) that there exists an absolute and effectively computable constant
$F\neq \mathbb {Q}$) that there exists an absolute and effectively computable constant ![]() $c_{4}>0$, which we assume to be sufficiently large for future convenience, such that
$c_{4}>0$, which we assume to be sufficiently large for future convenience, such that
We can change ![]() $\pi '$ to
$\pi '$ to ![]() $\pi '\otimes |\det |^{it}$; at the archimedean places, this has the effect of adding
$\pi '\otimes |\det |^{it}$; at the archimedean places, this has the effect of adding ![]() $it$ to each
$it$ to each ![]() $\mu _{j,j',\pi \times \pi '}(v)$. We then apply functional equation, the Phragmén–Lindelöf convexity principle, and (3.10) to obtain for all
$\mu _{j,j',\pi \times \pi '}(v)$. We then apply functional equation, the Phragmén–Lindelöf convexity principle, and (3.10) to obtain for all ![]() $\sigma \geq 0$
$\sigma \geq 0$
 \begin{align} &\lim_{\sigma_0\to\sigma}\bigg(\frac{\sigma_0+it-1}{\sigma_0+it+1}\bigg)^{r_{\pi\times\pi'}}L(\sigma_0+it,\pi\times\pi')\nonumber\\ &\quad\ll_{\varepsilon} C(\pi\times\pi',t)^{{\max\{1-\sigma,0\}}/{2}+{\varepsilon}/{n'n[F:\mathbb{Q}]}}\nonumber\\ &\quad\ll_{\varepsilon} (C(\pi)^{n'} C(\pi')^n(3+|t|)^{n'n[F:\mathbb{Q}]})^{{\max\{1-\sigma,0\}}/{2}+{\varepsilon}/{n'n[F:\mathbb{Q}]}}. \end{align}
\begin{align} &\lim_{\sigma_0\to\sigma}\bigg(\frac{\sigma_0+it-1}{\sigma_0+it+1}\bigg)^{r_{\pi\times\pi'}}L(\sigma_0+it,\pi\times\pi')\nonumber\\ &\quad\ll_{\varepsilon} C(\pi\times\pi',t)^{{\max\{1-\sigma,0\}}/{2}+{\varepsilon}/{n'n[F:\mathbb{Q}]}}\nonumber\\ &\quad\ll_{\varepsilon} (C(\pi)^{n'} C(\pi')^n(3+|t|)^{n'n[F:\mathbb{Q}]})^{{\max\{1-\sigma,0\}}/{2}+{\varepsilon}/{n'n[F:\mathbb{Q}]}}. \end{align}Lemma 3.1 If ![]() $\pi \in \mathfrak {F}_n$,
$\pi \in \mathfrak {F}_n$, ![]() $X\geq 3$, and
$X\geq 3$, and ![]() $\varepsilon >0$, then
$\varepsilon >0$, then ![]() $\sum _{\mathrm {N}\mathfrak {n}\leq X}\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})/\mathrm {N}\mathfrak {n}\ll _{\varepsilon } C(\pi )^{\varepsilon }\log X$.
$\sum _{\mathrm {N}\mathfrak {n}\leq X}\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})/\mathrm {N}\mathfrak {n}\ll _{\varepsilon } C(\pi )^{\varepsilon }\log X$.
Proof. Since ![]() $\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})\geq 0$ for all
$\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})\geq 0$ for all ![]() $\mathfrak {n}$ by [Reference Hoffstein and RamakrishnanHR95, Lemma a], we observe by (3.12) that
$\mathfrak {n}$ by [Reference Hoffstein and RamakrishnanHR95, Lemma a], we observe by (3.12) that
 \[ \sum_{\mathrm{N}\mathfrak{n}\leq X}\frac{\lambda_{\pi\times\widetilde{\pi}}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}}\leq e \sum_{\mathfrak{n}}\frac{\lambda_{\pi\times\widetilde{\pi}}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log X}}}\ll (\log X)\mathop{\mathrm{Res}}\limits_{s=1}L(s,\pi\times\widetilde{\pi}). \]
\[ \sum_{\mathrm{N}\mathfrak{n}\leq X}\frac{\lambda_{\pi\times\widetilde{\pi}}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}}\leq e \sum_{\mathfrak{n}}\frac{\lambda_{\pi\times\widetilde{\pi}}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log X}}}\ll (\log X)\mathop{\mathrm{Res}}\limits_{s=1}L(s,\pi\times\widetilde{\pi}). \]
The desired bounded now follows from (3.13) with ![]() $\sigma =1$,
$\sigma =1$, ![]() $t=0$, and
$t=0$, and ![]() $\pi '=\widetilde {\pi }$.
$\pi '=\widetilde {\pi }$.
Lemma 3.2 Let ![]() $J\geq 1$ be an integer. For all
$J\geq 1$ be an integer. For all ![]() $j\in \{1,\ldots,J\}$, let
$j\in \{1,\ldots,J\}$, let ![]() $t_j\in \mathbb {R}$;
$t_j\in \mathbb {R}$; ![]() $n_j,n_j'$ be positive integers; and
$n_j,n_j'$ be positive integers; and ![]() $\pi _j\in \mathfrak {F}_{n_j}$ and
$\pi _j\in \mathfrak {F}_{n_j}$ and ![]() $\pi _j'\in \mathfrak {F}_{n_j'}$. Let
$\pi _j'\in \mathfrak {F}_{n_j'}$. Let
 \[ D(s) = \prod_{j=1}^J L(s+it_j,\pi_j\times\widetilde{\pi}_j'),\quad \Delta(s) = \prod_{j=1}^J \Lambda(s+it_j,\pi_j\times\widetilde{\pi}_j'),\quad Q=\prod_{j=1}^J C(\pi_j)^{n_j'}C(\pi_j')^{n_j}. \]
\[ D(s) = \prod_{j=1}^J L(s+it_j,\pi_j\times\widetilde{\pi}_j'),\quad \Delta(s) = \prod_{j=1}^J \Lambda(s+it_j,\pi_j\times\widetilde{\pi}_j'),\quad Q=\prod_{j=1}^J C(\pi_j)^{n_j'}C(\pi_j')^{n_j}. \]
Let ![]() $R=-\mathrm {ord}_{s=1}D(s)$. If
$R=-\mathrm {ord}_{s=1}D(s)$. If ![]() $1<\sigma <2$ and the
$1<\sigma <2$ and the ![]() $\mathfrak {n}$th Dirichlet coefficient of
$\mathfrak {n}$th Dirichlet coefficient of ![]() $- ({D'}/{D})(s)$ is non-negative when
$- ({D'}/{D})(s)$ is non-negative when ![]() $\gcd (\mathfrak {n},\prod _{j=1}^J \mathfrak {q}_{\pi _j}\mathfrak {q}_{\pi _j'})=\mathcal {O}_F$, then
$\gcd (\mathfrak {n},\prod _{j=1}^J \mathfrak {q}_{\pi _j}\mathfrak {q}_{\pi _j'})=\mathcal {O}_F$, then
 \[ \sum_{\Delta(\rho)=0}\text{Re}\bigg(\frac{1}{\sigma-\rho}\bigg) <\frac{R}{\sigma-1} + \sum_{\substack{1\leq j\leq J \\ \pi_j=\pi_j',~t_j\neq 0}}\frac{\sigma-1}{(\sigma-1)^2+t_j^2}+O(\log Q). \]
\[ \sum_{\Delta(\rho)=0}\text{Re}\bigg(\frac{1}{\sigma-\rho}\bigg) <\frac{R}{\sigma-1} + \sum_{\substack{1\leq j\leq J \\ \pi_j=\pi_j',~t_j\neq 0}}\frac{\sigma-1}{(\sigma-1)^2+t_j^2}+O(\log Q). \]
Proof. Let ![]() $1<\sigma <2$ and
$1<\sigma <2$ and
 \[ D_{\infty}(s) = \prod_{j=1}^{J}L(s,(\pi_j)_{\infty}\times(\widetilde{\pi}_j')_{\infty}),\quad \mathfrak{q}_{D}=\prod_{j=1}^{J}\mathfrak{q}_{\pi_j\times\widetilde{\pi}_j'}. \]
\[ D_{\infty}(s) = \prod_{j=1}^{J}L(s,(\pi_j)_{\infty}\times(\widetilde{\pi}_j')_{\infty}),\quad \mathfrak{q}_{D}=\prod_{j=1}^{J}\mathfrak{q}_{\pi_j\times\widetilde{\pi}_j'}. \]
By comparing the logarithmic derivative of ![]() $\Delta (s)$ with the logarithmic derivative of its Hadamard factorization
$\Delta (s)$ with the logarithmic derivative of its Hadamard factorization
 \[ \Delta(s)=e^{a_{D}+b_{D}s}\prod_{\Delta(\rho)=0}\bigg(1-\frac{s}{\rho}\bigg)e^{s/\rho}, \]
\[ \Delta(s)=e^{a_{D}+b_{D}s}\prod_{\Delta(\rho)=0}\bigg(1-\frac{s}{\rho}\bigg)e^{s/\rho}, \]
we find that
 \begin{align*}
&\sum_{\Delta(\rho)=0}\bigg(\frac{1}{\sigma-\rho}+\frac{1}{\rho}\bigg)+ b_{D}\\
&\quad =\frac{D'}{D}(\sigma)+\frac{\log\mathrm{N}\mathfrak{q}_{D}}{2}+\frac{R}{\sigma-1}+\sum_{\substack{1\leq j\leq J\\
\pi_j = \pi_j'}}\bigg(\frac{1}{\sigma+it_j-1}+\frac{1}{\sigma+it_j}\bigg) +\frac{D_{\infty}'}{D_{\infty}}(\sigma).
\end{align*}
\begin{align*}
&\sum_{\Delta(\rho)=0}\bigg(\frac{1}{\sigma-\rho}+\frac{1}{\rho}\bigg)+ b_{D}\\
&\quad =\frac{D'}{D}(\sigma)+\frac{\log\mathrm{N}\mathfrak{q}_{D}}{2}+\frac{R}{\sigma-1}+\sum_{\substack{1\leq j\leq J\\
\pi_j = \pi_j'}}\bigg(\frac{1}{\sigma+it_j-1}+\frac{1}{\sigma+it_j}\bigg) +\frac{D_{\infty}'}{D_{\infty}}(\sigma).
\end{align*}
Since ![]() $\text {Re}(b_{D})=-\sum _{\Delta (\rho )=0}\text {Re}(\rho ^{-1})$ (see [Reference Iwaniec and KowalskiIK04, Proposition 5.7(3)]), we take real parts and obtain
$\text {Re}(b_{D})=-\sum _{\Delta (\rho )=0}\text {Re}(\rho ^{-1})$ (see [Reference Iwaniec and KowalskiIK04, Proposition 5.7(3)]), we take real parts and obtain
 \[ \sum_{\Delta(\rho)=0}\text{Re}\bigg(\frac{1}{\sigma-\rho}\bigg)=\text{Re} \bigg(\frac{D'}{D}(s)+\frac{\log\mathrm{N}\mathfrak{q}_{D}}{2}+\frac{R}{\sigma-1}+\sum_{\substack{1\leq j\leq J \\ \pi_j=\pi_j' \\ t_j\neq 0}}\frac{\sigma-1}{(\sigma-1)^2+t_j^2}+\frac{D_{\infty}'}{D_{\infty}}(s)\bigg)+O(1). \]
\[ \sum_{\Delta(\rho)=0}\text{Re}\bigg(\frac{1}{\sigma-\rho}\bigg)=\text{Re} \bigg(\frac{D'}{D}(s)+\frac{\log\mathrm{N}\mathfrak{q}_{D}}{2}+\frac{R}{\sigma-1}+\sum_{\substack{1\leq j\leq J \\ \pi_j=\pi_j' \\ t_j\neq 0}}\frac{\sigma-1}{(\sigma-1)^2+t_j^2}+\frac{D_{\infty}'}{D_{\infty}}(s)\bigg)+O(1). \]
By (3.3), (3.7), and (3.10), the bound ![]() $\text {Re}( ({D'}/{D})(\sigma ))\ll \log Q$ (respectively,
$\text {Re}( ({D'}/{D})(\sigma ))\ll \log Q$ (respectively, ![]() $ ({D_{\infty }'}/{D_{\infty }})(\sigma )\ll \log Q$) follows from our hypothesis on the Dirichlet coefficients of
$ ({D_{\infty }'}/{D_{\infty }})(\sigma )\ll \log Q$) follows from our hypothesis on the Dirichlet coefficients of ![]() $- ({D'}/{D})(s)$ (respectively, Stirling's formula).
$- ({D'}/{D})(s)$ (respectively, Stirling's formula).
3.3 Rankin–Selberg combinatorics
A partition ![]() $\mu =(\mu _i)_{i=1}^{\infty }$ is a sequence of non-increasing nonnegative integers
$\mu =(\mu _i)_{i=1}^{\infty }$ is a sequence of non-increasing nonnegative integers ![]() $\mu _1\geq \mu _2\geq \cdots$ with only finitely many non-zero entries. For a partition
$\mu _1\geq \mu _2\geq \cdots$ with only finitely many non-zero entries. For a partition ![]() $\mu$, let
$\mu$, let ![]() $\ell (\mu )$ be the number of non-zero
$\ell (\mu )$ be the number of non-zero ![]() $\mu _i$, and let
$\mu _i$, and let ![]() $|\mu |=\sum _{i=1}^{\infty } \mu _i$. For a set
$|\mu |=\sum _{i=1}^{\infty } \mu _i$. For a set ![]() $\{\alpha _{1},\ldots,\alpha _n \}$ of real numbers and a partition
$\{\alpha _{1},\ldots,\alpha _n \}$ of real numbers and a partition ![]() $\mu$ with
$\mu$ with ![]() $\ell (\mu )\leq n$, let
$\ell (\mu )\leq n$, let ![]() $s_{\mu }(\{\alpha _1,\ldots,\alpha _n\})$ be the Schur polynomial
$s_{\mu }(\{\alpha _1,\ldots,\alpha _n\})$ be the Schur polynomial ![]() $\det [(\alpha _{i}^{\lambda (j)+n-j})_{ij}] / \det [(\alpha _{i}^{n-j})_{ij}]$ associated to
$\det [(\alpha _{i}^{\lambda (j)+n-j})_{ij}] / \det [(\alpha _{i}^{n-j})_{ij}]$ associated to ![]() $\mu$. If
$\mu$. If ![]() $|\mu |=0$, then
$|\mu |=0$, then ![]() $s_{\mu }(\{\alpha _1,\ldots,\alpha _n\})$ is identically one. By convention, if
$s_{\mu }(\{\alpha _1,\ldots,\alpha _n\})$ is identically one. By convention, if ![]() $\ell (\mu )>n$, then
$\ell (\mu )>n$, then ![]() $s_{\mu }(\{\alpha _1,\ldots,\alpha _n\})$ is identically zero.
$s_{\mu }(\{\alpha _1,\ldots,\alpha _n\})$ is identically zero.
Let ![]() $\pi \in \mathfrak {F}_n$ and
$\pi \in \mathfrak {F}_n$ and ![]() $\pi '\in \mathfrak {F}_{n'}$. By (3.5), (3.6), and Cauchy's identity [Reference BumpBum13, Theorem 38.1], we have
$\pi '\in \mathfrak {F}_{n'}$. By (3.5), (3.6), and Cauchy's identity [Reference BumpBum13, Theorem 38.1], we have
 \[ \sum_{k=0}^{\infty}\frac{\lambda_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}=L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')=\sum_{\mu}\frac{s_{\mu}(A_{\pi}(\mathfrak{p}))s_{\mu}(A_{\pi'}(\mathfrak{p}))}{\mathrm{N}\mathfrak{p}^{s|\mu|}},\quad \mathfrak{p}\nmid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}, \]
\[ \sum_{k=0}^{\infty}\frac{\lambda_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}=L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')=\sum_{\mu}\frac{s_{\mu}(A_{\pi}(\mathfrak{p}))s_{\mu}(A_{\pi'}(\mathfrak{p}))}{\mathrm{N}\mathfrak{p}^{s|\mu|}},\quad \mathfrak{p}\nmid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}, \]
where the sum ranges over all partitions. This yields
For an integral ideal ![]() $\mathfrak {n}$ with factorization
$\mathfrak {n}$ with factorization ![]() $\mathfrak {n}=\prod _{\mathfrak {p}}\mathfrak {p}^{\mathrm {ord}_{\mathfrak {p}}(\mathfrak {n})}$ (with
$\mathfrak {n}=\prod _{\mathfrak {p}}\mathfrak {p}^{\mathrm {ord}_{\mathfrak {p}}(\mathfrak {n})}$ (with ![]() $\mathrm {ord}_{\mathfrak {p}}(\mathfrak {n})=0$ for all but finitely many
$\mathrm {ord}_{\mathfrak {p}}(\mathfrak {n})=0$ for all but finitely many ![]() $\mathfrak {p}$), the multiplicativity of
$\mathfrak {p}$), the multiplicativity of ![]() $\lambda _{\pi \times \pi '}(\mathfrak {n})$ tells us that if
$\lambda _{\pi \times \pi '}(\mathfrak {n})$ tells us that if ![]() $\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$, then
$\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$, then
where ![]() $(\mu _{\mathfrak {p}})_{\mathfrak {p}}$ denotes a sequence of partitions indexed by prime ideals and
$(\mu _{\mathfrak {p}})_{\mathfrak {p}}$ denotes a sequence of partitions indexed by prime ideals and
Define the numbers ![]() $\mu _{\pi \times \pi '}(\mathfrak {n})$ on unramified prime powers by
$\mu _{\pi \times \pi '}(\mathfrak {n})$ on unramified prime powers by
 \[ \sum_{k=0}^{\infty}\frac{\mu_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}=L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')^{-1}=\prod_{j=1}^{n} \prod_{j'=1}^{n'}(1-\alpha_{j,\pi}(\mathfrak{p})\alpha_{j',\pi'}(\mathfrak{p})\mathrm{N}\mathfrak{p}^{-s}),\quad \mathfrak{p}\nmid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}. \]
\[ \sum_{k=0}^{\infty}\frac{\mu_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}=L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')^{-1}=\prod_{j=1}^{n} \prod_{j'=1}^{n'}(1-\alpha_{j,\pi}(\mathfrak{p})\alpha_{j',\pi'}(\mathfrak{p})\mathrm{N}\mathfrak{p}^{-s}),\quad \mathfrak{p}\nmid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}. \]
By multiplicativity, this defines ![]() $\mu _{\pi \times \pi '}(\mathfrak {n})$ when
$\mu _{\pi \times \pi '}(\mathfrak {n})$ when ![]() $\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$. For a partition
$\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$. For a partition ![]() $\mu =(\mu _i)_{i=1}^{\infty }$, let
$\mu =(\mu _i)_{i=1}^{\infty }$, let ![]() $\mu ^*=(\mu _i^*)_{i=1}^{\infty }$ be the dual partition defined by
$\mu ^*=(\mu _i^*)_{i=1}^{\infty }$ be the dual partition defined by ![]() $\mu _i^*=|\{j\colon \mu _j\geq i\}|$. It follows from the dual Cauchy identity [Reference BumpBum13, Chapter 38] and (3.6) that
$\mu _i^*=|\{j\colon \mu _j\geq i\}|$. It follows from the dual Cauchy identity [Reference BumpBum13, Chapter 38] and (3.6) that
 \[ \sum_{k=0}^{\infty}\frac{\mu_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}=\sum_{\mu}\frac{s_{\mu}(A_{\pi}(\mathfrak{p}))s_{\mu^*}(-A_{\pi'}(\mathfrak{p}))}{\mathrm{N}\mathfrak{p}^{|\mu|s}},\quad \mathfrak{p}\nmid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}, \]
\[ \sum_{k=0}^{\infty}\frac{\mu_{\pi\times\pi'}(\mathfrak{p}^k)}{\mathrm{N}\mathfrak{p}^{ks}}=\sum_{\mu}\frac{s_{\mu}(A_{\pi}(\mathfrak{p}))s_{\mu^*}(-A_{\pi'}(\mathfrak{p}))}{\mathrm{N}\mathfrak{p}^{|\mu|s}},\quad \mathfrak{p}\nmid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}, \]
where ![]() $-A_{\pi '}(\mathfrak {p})=\{-\alpha _{1,\pi '}(\mathfrak {p}),\ldots,-\alpha _{n,\pi '}(\mathfrak {p})\}$. Hence, we have
$-A_{\pi '}(\mathfrak {p})=\{-\alpha _{1,\pi '}(\mathfrak {p}),\ldots,-\alpha _{n,\pi '}(\mathfrak {p})\}$. Hence, we have
Lemma 3.3 If ![]() $\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$, then we have
$\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$, then we have ![]() $|\mu _{\pi \times \pi '}(\mathfrak {n})|\leq \frac {1}{2}(\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})+\lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n}))$.
$|\mu _{\pi \times \pi '}(\mathfrak {n})|\leq \frac {1}{2}(\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})+\lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n}))$.
Proof. We apply the inequality of arithmetic and geometric means to (3.16):
 \[ |\mu_{\pi\times\pi'}(\mathfrak{n})|\leq \frac{1}{2}\bigg(\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg|^2+\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu^*_{\mathfrak{p}}}(-A_{\pi'}(\mathfrak{p}))\bigg|^2\bigg). \]
\[ |\mu_{\pi\times\pi'}(\mathfrak{n})|\leq \frac{1}{2}\bigg(\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg|^2+\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu^*_{\mathfrak{p}}}(-A_{\pi'}(\mathfrak{p}))\bigg|^2\bigg). \]
The first sum equals ![]() $\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})$ by (3.14). For the second sum, note that since
$\lambda _{\pi \times \widetilde {\pi }}(\mathfrak {n})$ by (3.14). For the second sum, note that since ![]() $|\mu |=|\mu ^*|$, we have
$|\mu |=|\mu ^*|$, we have ![]() $(\mu _{\mathfrak {p}})_{\mathfrak {p}}\in \underline {\mu }[\mathfrak {n}]$ if and only if
$(\mu _{\mathfrak {p}})_{\mathfrak {p}}\in \underline {\mu }[\mathfrak {n}]$ if and only if ![]() $(\mu _{\mathfrak {p}}^*)_{\mathfrak {p}}\in \underline {\mu }[\mathfrak {n}]$. Hence, by rearranging, we see that
$(\mu _{\mathfrak {p}}^*)_{\mathfrak {p}}\in \underline {\mu }[\mathfrak {n}]$. Hence, by rearranging, we see that
 \begin{equation} \sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu^*_{\mathfrak{p}}}(-A_{\pi'}(\mathfrak{p}))\bigg|^2= \sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(-A_{\pi'}(\mathfrak{p}))\bigg|^2= \lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n}), \end{equation}
\begin{equation} \sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu^*_{\mathfrak{p}}}(-A_{\pi'}(\mathfrak{p}))\bigg|^2= \sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(-A_{\pi'}(\mathfrak{p}))\bigg|^2= \lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n}), \end{equation}
where the last equality holds because ![]() $\alpha _{j,\pi '}(\mathfrak {p})\overline {\alpha _{j',\pi '}(\mathfrak {p})}=(-\alpha _{j,\pi '}(\mathfrak {p}))\overline {(-\alpha _{j',\pi '}(\mathfrak {p}))}$.
$\alpha _{j,\pi '}(\mathfrak {p})\overline {\alpha _{j',\pi '}(\mathfrak {p})}=(-\alpha _{j,\pi '}(\mathfrak {p}))\overline {(-\alpha _{j',\pi '}(\mathfrak {p}))}$.
4. A new mean value estimate
Our proof of Theorem 1.1 uses the following new mean value estimate for the Dirichlet coefficients of ![]() $L(s,\pi \times \pi ')$ and
$L(s,\pi \times \pi ')$ and ![]() $L(s,\pi \times \pi ')^{-1}$. Let
$L(s,\pi \times \pi ')^{-1}$. Let ![]() $\mathcal {S}\subseteq \mathfrak {F}_n$, and let
$\mathcal {S}\subseteq \mathfrak {F}_n$, and let ![]() $\mathcal {S}(Q)=\{\pi \in \mathcal {S}\colon C(\pi )\leq Q\}$.
$\mathcal {S}(Q)=\{\pi \in \mathcal {S}\colon C(\pi )\leq Q\}$.
Theorem 4.1 Let ![]() $b$ be a complex-valued function supported on the integral ideals of
$b$ be a complex-valued function supported on the integral ideals of ![]() $\mathcal {O}_F$. Let
$\mathcal {O}_F$. Let ![]() $n,n'\geq 1$, and let
$n,n'\geq 1$, and let ![]() $\pi '\in \mathfrak {F}_{n'}$. Let
$\pi '\in \mathfrak {F}_{n'}$. Let ![]() $Q,T\geq 1$,
$Q,T\geq 1$, ![]() $\varepsilon >0$, and
$\varepsilon >0$, and ![]() $x\geq 1$. Both
$x\geq 1$. Both
 \[ \sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\mu_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2\quad\text{and}\quad \sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\lambda_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2 \]
\[ \sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\mu_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2\quad\text{and}\quad \sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\lambda_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2 \]
are
 \[ \ll_{\varepsilon} Q^{\varepsilon}\bigg(\frac{x}{T}+Q^{4n^2\theta_n+n}T^{({1}/{2})n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|\bigg)\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})|b(\mathfrak{n})|^2, \]
\[ \ll_{\varepsilon} Q^{\varepsilon}\bigg(\frac{x}{T}+Q^{4n^2\theta_n+n}T^{({1}/{2})n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|\bigg)\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})|b(\mathfrak{n})|^2, \]
where ![]() $\theta _n\in [0,\frac {1}{2}- {1}/({n^2+1})]$ is the best known exponent towards GRC for
$\theta _n\in [0,\frac {1}{2}- {1}/({n^2+1})]$ is the best known exponent towards GRC for ![]() $\pi \in \mathcal {S}$.
$\pi \in \mathcal {S}$.
Remark 4.2 If ![]() $\pi '= \mathbb{1}$ and
$\pi '= \mathbb{1}$ and ![]() $\mathcal {S}=\mathfrak {F}_n$, then Theorem 4.1 recovers [Reference Thorner and ZamanTZ21, Theorem 1.1]:Footnote 3
$\mathcal {S}=\mathfrak {F}_n$, then Theorem 4.1 recovers [Reference Thorner and ZamanTZ21, Theorem 1.1]:Footnote 3
 \begin{align*}
&\sum_{\pi\in\mathfrak{F}_n(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}]\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)=\mathcal{O}_F
}}\lambda_{\pi}(\mathfrak{n})b(\mathfrak{n})\bigg|^2\\
&\quad\ll_{\varepsilon} Q^{\varepsilon}\bigg(\frac{x}{T}+Q^{4n^2\theta_n+n}T^{({1}/{2})n^2
[F:\mathbb{Q}]+\varepsilon}|\mathfrak{F}_n(Q)|\bigg)\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F}}|b(\mathfrak{n})|^2.
\end{align*}
\begin{align*}
&\sum_{\pi\in\mathfrak{F}_n(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}]\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)=\mathcal{O}_F
}}\lambda_{\pi}(\mathfrak{n})b(\mathfrak{n})\bigg|^2\\
&\quad\ll_{\varepsilon} Q^{\varepsilon}\bigg(\frac{x}{T}+Q^{4n^2\theta_n+n}T^{({1}/{2})n^2
[F:\mathbb{Q}]+\varepsilon}|\mathfrak{F}_n(Q)|\bigg)\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F}}|b(\mathfrak{n})|^2.
\end{align*}
One could try to prove Theorem 4.1 starting with this, replacing ![]() $b(\mathfrak {n})$ with
$b(\mathfrak {n})$ with ![]() $\lambda _{\pi '}(\mathfrak {n})\mu _F(\mathfrak {n})b(\mathfrak {n})$ (where
$\lambda _{\pi '}(\mathfrak {n})\mu _F(\mathfrak {n})b(\mathfrak {n})$ (where ![]() $\mu _F(\mathfrak {n})$ is the
$\mu _F(\mathfrak {n})$ is the ![]() $\mathfrak {n}$th Dirichlet coefficient of
$\mathfrak {n}$th Dirichlet coefficient of ![]() $\zeta _F(s)^{-1}$), and try to recover a version of Theorem 4.1 with
$\zeta _F(s)^{-1}$), and try to recover a version of Theorem 4.1 with ![]() $\mu _{\pi \times \pi '}(\mathfrak {n})$ replaced by
$\mu _{\pi \times \pi '}(\mathfrak {n})$ replaced by ![]() $\lambda _{\pi }(\mathfrak {n})\lambda _{\pi '}(\mathfrak {n})\mu _F(\mathfrak {n})$. Note that
$\lambda _{\pi }(\mathfrak {n})\lambda _{\pi '}(\mathfrak {n})\mu _F(\mathfrak {n})$. Note that ![]() $\mu _{\pi \times \pi '}(\mathfrak {n})=\lambda _{\pi }(\mathfrak {n})\lambda _{\pi '}(\mathfrak {n})\mu _F(\mathfrak {n})$ when
$\mu _{\pi \times \pi '}(\mathfrak {n})=\lambda _{\pi }(\mathfrak {n})\lambda _{\pi '}(\mathfrak {n})\mu _F(\mathfrak {n})$ when ![]() $\mathfrak {n}$ is squarefree and coprime to
$\mathfrak {n}$ is squarefree and coprime to ![]() $\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$. Otherwise, equality is not guaranteed. If one wants to approximate
$\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$. Otherwise, equality is not guaranteed. If one wants to approximate ![]() $L(s,\pi \times \pi ')$ with
$L(s,\pi \times \pi ')$ with ![]() $\sum _{\mathfrak{n}\ {\rm squarefree}}\lambda _{\pi }(\mathfrak {n})\lambda _{\pi '}(\mathfrak {n})\mathrm {N}\mathfrak {n}^{-s}$ and extend into the critical strip when
$\sum _{\mathfrak{n}\ {\rm squarefree}}\lambda _{\pi }(\mathfrak {n})\lambda _{\pi '}(\mathfrak {n})\mathrm {N}\mathfrak {n}^{-s}$ and extend into the critical strip when ![]() $\pi,\pi '\in \mathfrak {F}_n$ and
$\pi,\pi '\in \mathfrak {F}_n$ and ![]() $n\geq 5$, then one must have progress towards GRC well beyond what is known unconditionally [Reference BrumleyBru06b, Reference Duke and KowalskiDK00]. Such progress would then be a hypothesis for Theorem 1.1.
$n\geq 5$, then one must have progress towards GRC well beyond what is known unconditionally [Reference BrumleyBru06b, Reference Duke and KowalskiDK00]. Such progress would then be a hypothesis for Theorem 1.1.
Theorem 4.1 provides the first non-trivial unconditional mean value estimates of large sieve type for the Dirichlet coefficients ![]() $\lambda _{\pi \times \pi '}(\mathfrak {n})$ or
$\lambda _{\pi \times \pi '}(\mathfrak {n})$ or ![]() $\mu _{\pi \times \pi '}(\mathfrak {n})$ for arbitrary
$\mu _{\pi \times \pi '}(\mathfrak {n})$ for arbitrary ![]() $n$ and
$n$ and ![]() $n'$. Theorem 4.1 follows from a more general result, Proposition 4.3, for sequences of products of Schur polynomials evaluated on the set
$n'$. Theorem 4.1 follows from a more general result, Proposition 4.3, for sequences of products of Schur polynomials evaluated on the set ![]() $A_{\pi }(\mathfrak {p})$ of Satake parameters of
$A_{\pi }(\mathfrak {p})$ of Satake parameters of ![]() $\pi$ at
$\pi$ at ![]() $\mathfrak {p}$. We begin with a mean value estimate for the Satake parameters of
$\mathfrak {p}$. We begin with a mean value estimate for the Satake parameters of ![]() $\pi$ as
$\pi$ as ![]() $\pi \in \mathcal {S}$ varies. Let
$\pi \in \mathcal {S}$ varies. Let
be functions that are not identically zero. Their ![]() $\ell ^2$ norms
$\ell ^2$ norms ![]() $\|a\|_2$ and
$\|a\|_2$ and ![]() $\|\alpha \|_2$ are defined by
$\|\alpha \|_2$ are defined by
 \[ \|a\|_2 = \bigg(\sum_{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T}}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}|a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})|^2\bigg)^{1/2},\quad \|\alpha\|_2=\bigg(\sum_{\pi\in\mathcal{S}(Q)}|\alpha(\pi)|^2\bigg)^{1/2}. \]
\[ \|a\|_2 = \bigg(\sum_{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T}}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}|a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})|^2\bigg)^{1/2},\quad \|\alpha\|_2=\bigg(\sum_{\pi\in\mathcal{S}(Q)}|\alpha(\pi)|^2\bigg)^{1/2}. \]
For convenience, we define ![]() $\mathbf {1}_{(\mathfrak {n},\mathfrak {q})}$ to equal one when
$\mathbf {1}_{(\mathfrak {n},\mathfrak {q})}$ to equal one when ![]() $\gcd (\mathfrak {n},\mathfrak {q})=\mathcal {O}_F$ and zero otherwise.
$\gcd (\mathfrak {n},\mathfrak {q})=\mathcal {O}_F$ and zero otherwise.
Proposition 4.3 Let ![]() $x\geq 1$ and
$x\geq 1$ and ![]() $Q,T\geq 1$. Define
$Q,T\geq 1$. Define
 \[ C(Q,T,x):= \sup_{\|a\|_2\neq 0}\frac{1}{\|a\|_2^2}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)=\mathcal{O}_F }}\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})\bigg|^2. \]
\[ C(Q,T,x):= \sup_{\|a\|_2\neq 0}\frac{1}{\|a\|_2^2}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)=\mathcal{O}_F }}\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})\bigg|^2. \]
We have the bound ![]() $C(Q,T,x)\ll _{\varepsilon } Q^{\varepsilon }(T^{-1}x+Q^{4n^2\theta _n+n} T^{ {n^2[F:\mathbb {Q}]}/{2}+\varepsilon }|\mathcal {S}(Q)|)$.
$C(Q,T,x)\ll _{\varepsilon } Q^{\varepsilon }(T^{-1}x+Q^{4n^2\theta _n+n} T^{ {n^2[F:\mathbb {Q}]}/{2}+\varepsilon }|\mathcal {S}(Q)|)$.
Proof. We observe that
 \begin{equation} C(Q,T,x)=\sup_{\|a\|_2=1}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T}}}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})\bigg|^2. \end{equation}
\begin{equation} C(Q,T,x)=\sup_{\|a\|_2=1}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T}}}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})\bigg|^2. \end{equation}
By the duality principle for bilinear forms, (4.2) is bounded by the supremum over the functions ![]() $\alpha \colon \mathcal {S}(Q)\to \mathbb {C}$ such that
$\alpha \colon \mathcal {S}(Q)\to \mathbb {C}$ such that ![]() $\|\alpha \|_2=1$ of
$\|\alpha \|_2=1$ of
 \begin{equation} \sum_{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T}}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]} \bigg|\sum_{\pi\in\mathcal{S}(Q)}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}\alpha(\pi)\bigg|^2. \end{equation}
\begin{equation} \sum_{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T}}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]} \bigg|\sum_{\pi\in\mathcal{S}(Q)}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}\alpha(\pi)\bigg|^2. \end{equation}
Let ![]() $\phi$ be a fixed smooth test function, supported in a compact subset of
$\phi$ be a fixed smooth test function, supported in a compact subset of ![]() $[-2,2]$, such that
$[-2,2]$, such that ![]() $\phi (t)=1$ for
$\phi (t)=1$ for ![]() $t\in [0,1]$ and
$t\in [0,1]$ and ![]() $\phi (t)\in [0,1)$ otherwise. Then (4.3) is at most
$\phi (t)\in [0,1)$ otherwise. Then (4.3) is at most
 \begin{equation} \sum_{\mathfrak{n}}\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg| \sum_{\pi\in\mathcal{S}(Q)}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}\alpha(\pi)\bigg|^2\phi\bigg(T\log\frac{\mathrm{N}\mathfrak{n}}{x}\bigg). \end{equation}
\begin{equation} \sum_{\mathfrak{n}}\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg| \sum_{\pi\in\mathcal{S}(Q)}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}\alpha(\pi)\bigg|^2\phi\bigg(T\log\frac{\mathrm{N}\mathfrak{n}}{x}\bigg). \end{equation}We expand the square, interchange the order of summation, and apply (3.14) to find that (4.4) equals
 \begin{align} &\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}\sum_{\mathfrak{n}}\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in \underline{\mu}[\mathfrak{n}]}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \overline{\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi'}(\mathfrak{p}))\bigg]} \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}\mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi'})}\phi\bigg(T\log\frac{\mathrm{N}\mathfrak{n}}{x}\bigg)\nonumber\\ &\quad =\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}\sum_{\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }\lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n})\phi\bigg(T\log\frac{\mathrm{N}\mathfrak{n}}{x}\bigg). \end{align}
\begin{align} &\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}\sum_{\mathfrak{n}}\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in \underline{\mu}[\mathfrak{n}]}\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] \overline{\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi'}(\mathfrak{p}))\bigg]} \mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi}\!)}\mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi'})}\phi\bigg(T\log\frac{\mathrm{N}\mathfrak{n}}{x}\bigg)\nonumber\\ &\quad =\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}\sum_{\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }\lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n})\phi\bigg(T\log\frac{\mathrm{N}\mathfrak{n}}{x}\bigg). \end{align} Let ![]() $\kappa _{\pi \times \pi '}={\mathrm {Res}}_{s=1}L(s,\pi \times \pi ')\prod _{\mathfrak {p} \mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}}L(s,\pi _{\mathfrak {p}}\times \pi _{\mathfrak {p}}')^{-1}$. Note that
$\kappa _{\pi \times \pi '}={\mathrm {Res}}_{s=1}L(s,\pi \times \pi ')\prod _{\mathfrak {p} \mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}}L(s,\pi _{\mathfrak {p}}\times \pi _{\mathfrak {p}}')^{-1}$. Note that ![]() $\kappa _{\pi \times \pi '}\geq 0$, with equality if and only if
$\kappa _{\pi \times \pi '}\geq 0$, with equality if and only if ![]() $\pi '\neq \widetilde {\pi }$. Since
$\pi '\neq \widetilde {\pi }$. Since ![]() $|\alpha _{j,j',\pi \times \pi '}(\mathfrak {p})|\leq \mathrm {N}\mathfrak {p}$, we have the bound
$|\alpha _{j,j',\pi \times \pi '}(\mathfrak {p})|\leq \mathrm {N}\mathfrak {p}$, we have the bound
 \[ \prod_{\mathfrak{p} \mid \mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}|L(1,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')|^{-1}=\prod_{\mathfrak{p} \mid \mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}\prod_{j=1}^n \prod_{j'=1}^{n'}\bigg|1-\frac{\alpha_{j,j',\pi\times\pi'}(\mathfrak{p})}{\mathrm{N}\mathfrak{p}}\bigg|\leq \prod_{\mathfrak{p} \mid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}2^{n'n}. \]
\[ \prod_{\mathfrak{p} \mid \mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}|L(1,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')|^{-1}=\prod_{\mathfrak{p} \mid \mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}\prod_{j=1}^n \prod_{j'=1}^{n'}\bigg|1-\frac{\alpha_{j,j',\pi\times\pi'}(\mathfrak{p})}{\mathrm{N}\mathfrak{p}}\bigg|\leq \prod_{\mathfrak{p} \mid\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}2^{n'n}. \]
Since ![]() $|\{\mathfrak {p}\colon \mathfrak {p} \mid \mathfrak {n}\}|\ll (\log \mathrm {N}\mathfrak {n})/\!\log \log \mathrm {N}\mathfrak {n}$ (see [Reference WeissWei83, Lemma 1.13b]), it follows from (3.12) that
$|\{\mathfrak {p}\colon \mathfrak {p} \mid \mathfrak {n}\}|\ll (\log \mathrm {N}\mathfrak {n})/\!\log \log \mathrm {N}\mathfrak {n}$ (see [Reference WeissWei83, Lemma 1.13b]), it follows from (3.12) that
Let ![]() $\widehat {\phi }(s)=\int _{\mathbb {R}}\phi (y)e^{sy}\,{{d}y}$. It follows from a standard contour integral calculation using (3.7) and (3.13) that (4.5) equals
$\widehat {\phi }(s)=\int _{\mathbb {R}}\phi (y)e^{sy}\,{{d}y}$. It follows from a standard contour integral calculation using (3.7) and (3.13) that (4.5) equals
 \begin{align}
&\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}
\bigg(\frac{1}{2\pi
iT}\int_{3-i\infty}^{3+i\infty}\frac{L(s,\pi\times\widetilde{\pi}')}{\prod_{\mathfrak{p}
\mid
\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}L(s,\pi_{\mathfrak{p}}\times\widetilde{\pi}_{\mathfrak{p}}')}x^s\widehat{\phi}(s/T)\,ds\bigg)\nonumber\\
&\quad=\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}
\bigg(\kappa_{\pi\times\widetilde{\pi}'}x\frac{\widehat{\phi}({1}/{T})}{T}+\frac{1}{2\pi
iT}\int_{{1}/{4\log(ex)}-i\infty}^{{1}/{4\log(ex)}+i\infty}
\frac{L(s,\pi\times\widetilde{\pi}')x^s\widehat{\phi}(s/T)}{\prod_{\mathfrak{p}
\mid
\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}L(s,\pi_{\mathfrak{p}}\times\widetilde{\pi}_{\mathfrak{p}}')}\,ds\bigg)\nonumber\\
&\quad=\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}\bigg(\kappa_{\pi\times\widetilde{\pi}'}x
\frac{\widehat{\phi}({1}/{T})}{T}+O_{\phi,\varepsilon}(Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2})n^2
[F:\mathbb{Q}]+\varepsilon})\bigg).
\end{align}
\begin{align}
&\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}
\bigg(\frac{1}{2\pi
iT}\int_{3-i\infty}^{3+i\infty}\frac{L(s,\pi\times\widetilde{\pi}')}{\prod_{\mathfrak{p}
\mid
\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}L(s,\pi_{\mathfrak{p}}\times\widetilde{\pi}_{\mathfrak{p}}')}x^s\widehat{\phi}(s/T)\,ds\bigg)\nonumber\\
&\quad=\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}
\bigg(\kappa_{\pi\times\widetilde{\pi}'}x\frac{\widehat{\phi}({1}/{T})}{T}+\frac{1}{2\pi
iT}\int_{{1}/{4\log(ex)}-i\infty}^{{1}/{4\log(ex)}+i\infty}
\frac{L(s,\pi\times\widetilde{\pi}')x^s\widehat{\phi}(s/T)}{\prod_{\mathfrak{p}
\mid
\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}L(s,\pi_{\mathfrak{p}}\times\widetilde{\pi}_{\mathfrak{p}}')}\,ds\bigg)\nonumber\\
&\quad=\sum_{\pi,\pi'\in\mathcal{S}(Q)}\alpha(\pi)\overline{\alpha(\pi')}\bigg(\kappa_{\pi\times\widetilde{\pi}'}x
\frac{\widehat{\phi}({1}/{T})}{T}+O_{\phi,\varepsilon}(Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2})n^2
[F:\mathbb{Q}]+\varepsilon})\bigg).
\end{align}
Recall that ![]() $\kappa _{\pi \times \widetilde {\pi }'}>0$ when
$\kappa _{\pi \times \widetilde {\pi }'}>0$ when ![]() $\pi =\pi '$, and
$\pi =\pi '$, and ![]() $\kappa _{\pi \times \widetilde {\pi }'}=0$ otherwise. Since
$\kappa _{\pi \times \widetilde {\pi }'}=0$ otherwise. Since ![]() $\|\alpha \|_2=1$ and
$\|\alpha \|_2=1$ and ![]() $\phi$ is fixed, it follows from the inequality of arithmetic and geometric means that (4.7) equals
$\phi$ is fixed, it follows from the inequality of arithmetic and geometric means that (4.7) equals
 \begin{align*} &\frac{\widehat{\phi}({1}/{T})}{T}x\sum_{\pi\in\mathcal{S}(Q)}|\alpha(\pi)|^2\kappa_{ \pi\times\widetilde{\pi}'}+O_{\phi}(Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2})n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|)\\ &\quad \ll_{\phi,\varepsilon}\frac{x}{T}\max_{\pi\in\mathcal{S}(Q)}\kappa_{\pi\times\widetilde{\pi}'}+Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2}) n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|. \end{align*}
\begin{align*} &\frac{\widehat{\phi}({1}/{T})}{T}x\sum_{\pi\in\mathcal{S}(Q)}|\alpha(\pi)|^2\kappa_{ \pi\times\widetilde{\pi}'}+O_{\phi}(Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2})n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|)\\ &\quad \ll_{\phi,\varepsilon}\frac{x}{T}\max_{\pi\in\mathcal{S}(Q)}\kappa_{\pi\times\widetilde{\pi}'}+Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2}) n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|. \end{align*}
We estimate the maximum using (4.6), and the desired result follows.
We use Proposition 4.3 to prove Theorem 4.1.
Proof of Theorem 4.1 For the sum involving ![]() $\mu _{\pi \times \pi '}(\mathfrak {n})$, we apply Proposition 4.3 with
$\mu _{\pi \times \pi '}(\mathfrak {n})$, we apply Proposition 4.3 with
 \[ a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}) = b\bigg(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|}\bigg)\mathbf{1}_{(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|},\mathfrak{q}_{\pi'})}\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}^*}(-A_{\pi'}(\mathfrak{p})). \]
\[ a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}) = b\bigg(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|}\bigg)\mathbf{1}_{(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|},\mathfrak{q}_{\pi'})}\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}^*}(-A_{\pi'}(\mathfrak{p})). \]
If ![]() $(\mu _{\mathfrak {p}})_{\mathfrak {p}}\in \underline {\mu }[\mathfrak {n}]$, then by (3.15), we have that
$(\mu _{\mathfrak {p}})_{\mathfrak {p}}\in \underline {\mu }[\mathfrak {n}]$, then by (3.15), we have that ![]() $|\mu _{\mathfrak {p}}|=\mathrm {ord}_{\mathfrak {p}}(\mathfrak {n})$ and
$|\mu _{\mathfrak {p}}|=\mathrm {ord}_{\mathfrak {p}}(\mathfrak {n})$ and
By (3.16), the left-hand side of Proposition 4.3 becomes
 \begin{align*}
&\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)= \mathcal{O}_F }}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}
\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})\bigg|^2\\
&\quad=\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)= \mathcal{O}_F }}b(\mathfrak{n})\mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi'})}
\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in \underline{\mu}[\mathfrak{n}]}
\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))s_{\mu_{\mathfrak{p}}^*}(-A_{\pi'}(\mathfrak{p})\bigg|^2\\
&\quad=\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F }}\mu_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2. \end{align*}
\begin{align*}
&\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)= \mathcal{O}_F }}~\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}
\bigg[\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))\bigg] a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}})\bigg|^2\\
&\quad=\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\!)= \mathcal{O}_F }}b(\mathfrak{n})\mathbf{1}_{(\mathfrak{n},\mathfrak{q}_{\pi'})}
\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in \underline{\mu}[\mathfrak{n}]}
\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi}(\mathfrak{p}))s_{\mu_{\mathfrak{p}}^*}(-A_{\pi'}(\mathfrak{p})\bigg|^2\\
&\quad=\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq xe^{1/T} \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F }}\mu_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2. \end{align*}
Similarly, the right-hand side of Proposition 4.3 becomes
 \[ Q^{\varepsilon}\bigg(\frac{x}{T}+Q^{4n^2\theta_n+n}T^{({1}/{2})n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|\bigg)\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F }}|b(\mathfrak{n})|^2\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}^*}(-A_{\pi'}(\mathfrak{p}))\bigg|^2. \]
\[ Q^{\varepsilon}\bigg(\frac{x}{T}+Q^{4n^2\theta_n+n}T^{({1}/{2})n^2 [F:\mathbb{Q}]+\varepsilon}|\mathcal{S}(Q)|\bigg)\sum_{\substack{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}] \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F }}|b(\mathfrak{n})|^2\sum_{(\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}\in\underline{\mu}[\mathfrak{n}]}\bigg|\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}^*}(-A_{\pi'}(\mathfrak{p}))\bigg|^2. \]
The desired result now follows from (3.17). Apart from the new choice of
 \[ a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}) = b\bigg(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|}\bigg)\mathbf{1}_{(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|},\mathfrak{q}_{\pi'})}\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi'}(\mathfrak{p})), \]
\[ a((\mu_{\mathfrak{p}}\!)_{\mathfrak{p}}) = b\bigg(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|}\bigg)\mathbf{1}_{(\prod_{\mathfrak{p}}\mathrm{N}\mathfrak{p}^{|\mu_{\mathfrak{p}}|},\mathfrak{q}_{\pi'})}\prod_{\mathfrak{p}}s_{\mu_{\mathfrak{p}}}(A_{\pi'}(\mathfrak{p})), \]
the result for the sum involving ![]() $\lambda _{\pi \times \pi '}(\mathfrak {n})$ is handled in the same manner.
$\lambda _{\pi \times \pi '}(\mathfrak {n})$ is handled in the same manner.
Corollary 4.4 Let ![]() $\pi '\in \mathfrak {F}_{n'}$,
$\pi '\in \mathfrak {F}_{n'}$, ![]() $Q,T\geq 1$, and
$Q,T\geq 1$, and ![]() $\varepsilon >0$. If
$\varepsilon >0$. If ![]() $Y\geq e$ and
$Y\geq e$ and
then
 \begin{align*}
\sum_{\pi\in\mathcal{S}(Q)}\int_{-T}^{T}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n} > X \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F
}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}+iv}}\bigg|^2\,dv &\ll_{\varepsilon}
C(\pi')^{\varepsilon}Q^{\varepsilon}\log X,\\
\sum_{\pi\in\mathcal{S}(Q)}\int_{-T}^{T}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\leq
X \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=
\mathcal{O}_F
}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{{1}/{2}+iv}}\bigg|^2
\,dv& \ll_{\varepsilon}
C(\pi')^{\varepsilon}Q^{\varepsilon}X\log X.
\end{align*}
\begin{align*}
\sum_{\pi\in\mathcal{S}(Q)}\int_{-T}^{T}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n} > X \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F
}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}+iv}}\bigg|^2\,dv &\ll_{\varepsilon}
C(\pi')^{\varepsilon}Q^{\varepsilon}\log X,\\
\sum_{\pi\in\mathcal{S}(Q)}\int_{-T}^{T}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\leq
X \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=
\mathcal{O}_F
}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{{1}/{2}+iv}}\bigg|^2
\,dv& \ll_{\varepsilon}
C(\pi')^{\varepsilon}Q^{\varepsilon}X\log X.
\end{align*}
Proof. We prove the first result; the second result is proved completely analogously. A formal generalization of [Reference GallagherGal70, Theorem 1] to number fields tells us that if ![]() $c(\mathfrak {n})$ is a complex-valued function supported on the integral ideals of
$c(\mathfrak {n})$ is a complex-valued function supported on the integral ideals of ![]() $\mathcal {O}_F$ with
$\mathcal {O}_F$ with ![]() $\sum _{\mathfrak {n}}|c(\mathfrak {n})|<\infty$, then
$\sum _{\mathfrak {n}}|c(\mathfrak {n})|<\infty$, then
 \[ \int_{-T}^{T}\bigg|\sum_{\mathfrak{n}}\frac{c(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{it}}\bigg|^2 \,dt\ll T^2 \int_0^{\infty}\bigg|\sum_{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}]}c(\mathfrak{n})\bigg|^2\frac{{d}x}{x}. \]
\[ \int_{-T}^{T}\bigg|\sum_{\mathfrak{n}}\frac{c(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{it}}\bigg|^2 \,dt\ll T^2 \int_0^{\infty}\bigg|\sum_{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}]}c(\mathfrak{n})\bigg|^2\frac{{d}x}{x}. \]
We choose ![]() $b(\mathfrak {n})=\mathrm {N}\mathfrak {n}^{-1- {1}/{\!\log Y}}$ if
$b(\mathfrak {n})=\mathrm {N}\mathfrak {n}^{-1- {1}/{\!\log Y}}$ if ![]() $\mathrm {N}\mathfrak {n}>X$ and
$\mathrm {N}\mathfrak {n}>X$ and ![]() $b(\mathfrak {n})=0$ otherwise, which leads to
$b(\mathfrak {n})=0$ otherwise, which leads to
 \begin{align*}
&\sum_{\pi\in\mathcal{S}(Q)}\int_{-T}^{T}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}
> X \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log
Y}+it}}\bigg|^2\,dt\\ &\quad \ll T^2
\int_0^{\infty}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}]}\mu_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2
\frac{{d}x}{x}. \end{align*}
\begin{align*}
&\sum_{\pi\in\mathcal{S}(Q)}\int_{-T}^{T}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}
> X \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log
Y}+it}}\bigg|^2\,dt\\ &\quad \ll T^2
\int_0^{\infty}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\mathrm{N}\mathfrak{n}\in(x,xe^{1/T}]}\mu_{\pi\times\pi'}(\mathfrak{n})b(\mathfrak{n})\bigg|^2
\frac{{d}x}{x}. \end{align*}
Theorem 4.1 and the fact that ![]() $\lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n})\geq 0$ for all
$\lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n})\geq 0$ for all ![]() $\mathfrak {n}$ imply that the above display is
$\mathfrak {n}$ imply that the above display is
 \begin{align*} &\ll_{\varepsilon}
Q^{\varepsilon}\sum_{\substack{\mathrm{N}\mathfrak{n} > X
\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{2}/{\!\log Y}}}\bigg(1+\frac{Q^{4n^2\theta_n+n}T^{({1}/{2})n^2
[F:\mathbb{Q}]+1+\varepsilon}|\mathcal{S}(Q)|}{\mathrm{N}\mathfrak{n}}\bigg)\\
&\quad \ll_{\varepsilon}
Q^{\varepsilon}\sum_{\mathrm{N}\mathfrak{n} >
X}\frac{\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{2}/{\!\log Y}}}. \end{align*}
\begin{align*} &\ll_{\varepsilon}
Q^{\varepsilon}\sum_{\substack{\mathrm{N}\mathfrak{n} > X
\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{2}/{\!\log Y}}}\bigg(1+\frac{Q^{4n^2\theta_n+n}T^{({1}/{2})n^2
[F:\mathbb{Q}]+1+\varepsilon}|\mathcal{S}(Q)|}{\mathrm{N}\mathfrak{n}}\bigg)\\
&\quad \ll_{\varepsilon}
Q^{\varepsilon}\sum_{\mathrm{N}\mathfrak{n} >
X}\frac{\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{2}/{\!\log Y}}}. \end{align*}
The desired result now follows from Lemma 3.1 and our choices of ![]() $X$ and
$X$ and ![]() $Y$.
$Y$.
5. Proof of Theorem 1.1
Let ![]() $n,n'\geq 1$,
$n,n'\geq 1$, ![]() $\varepsilon >0$,
$\varepsilon >0$, ![]() $T\geq 3$,
$T\geq 3$, ![]() $Q\geq 3$,
$Q\geq 3$, ![]() $\pi \in \mathcal {S}(Q)$, and
$\pi \in \mathcal {S}(Q)$, and ![]() $\pi '\in \mathfrak {F}_{n'}$. Define
$\pi '\in \mathfrak {F}_{n'}$. Define
 \begin{align} &
X:=
C(\pi')^{\varepsilon}Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2})n^2
[F:\mathbb{Q}]+1+\varepsilon}|\mathcal{S}(Q)|,\nonumber\\ &
Y:= \big((C(\pi')^{{n}/{2}}Q^{{n'}/{2}}
(C(\pi')Q)^{2n'n\max\{0,\theta_n+\theta_{n'}-{1}/{2}\}}
|\mathcal{S}(Q)|
T^{{n'n[F:\mathbb{Q}]}/{2}+1})^{1+{\varepsilon}/{4n'n[F:\mathbb{Q}]}}X\big)^{{1}/({3-2\sigma})},\nonumber\\
& L^{\mathrm{ur}}(s,\pi\times\pi'):=
L(s,\pi\times\pi')\prod_{\mathfrak{p} \mid
\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')^{-1},\nonumber\\
& M_X(s,\pi\times\pi'):=
\sum_{\substack{\mathrm{N}\mathfrak{n}\leq X \nonumber\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}
\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s},\nonumber\\
& LM_X(s,\pi\times\pi'):=
L^{\mathrm{ur}}(s,\pi\times\pi') M_X(s,\pi\times\pi').
\end{align}
\begin{align} &
X:=
C(\pi')^{\varepsilon}Q^{4n^2\theta_n+n+\varepsilon}T^{({1}/{2})n^2
[F:\mathbb{Q}]+1+\varepsilon}|\mathcal{S}(Q)|,\nonumber\\ &
Y:= \big((C(\pi')^{{n}/{2}}Q^{{n'}/{2}}
(C(\pi')Q)^{2n'n\max\{0,\theta_n+\theta_{n'}-{1}/{2}\}}
|\mathcal{S}(Q)|
T^{{n'n[F:\mathbb{Q}]}/{2}+1})^{1+{\varepsilon}/{4n'n[F:\mathbb{Q}]}}X\big)^{{1}/({3-2\sigma})},\nonumber\\
& L^{\mathrm{ur}}(s,\pi\times\pi'):=
L(s,\pi\times\pi')\prod_{\mathfrak{p} \mid
\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}L(s,\pi_{\mathfrak{p}}\times\pi_{\mathfrak{p}}')^{-1},\nonumber\\
& M_X(s,\pi\times\pi'):=
\sum_{\substack{\mathrm{N}\mathfrak{n}\leq X \nonumber\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}
\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s},\nonumber\\
& LM_X(s,\pi\times\pi'):=
L^{\mathrm{ur}}(s,\pi\times\pi') M_X(s,\pi\times\pi').
\end{align}
Note that ![]() $\log (C(\pi )C(\pi ')T)\ll \log X\asymp _{\varepsilon } \log Y$. We assume that
$\log (C(\pi )C(\pi ')T)\ll \log X\asymp _{\varepsilon } \log Y$. We assume that ![]() $T\geq 2(\log Y)^2$ since the proof does not change appreciably otherwise. In this section,
$T\geq 2(\log Y)^2$ since the proof does not change appreciably otherwise. In this section, ![]() $\varepsilon$ might vary from line to line, and terms of size
$\varepsilon$ might vary from line to line, and terms of size ![]() $(C(\pi ')QT^{[F:\mathbb {Q}]}|\mathcal {S}(Q)|)^{\varepsilon }$ and polynomials in
$(C(\pi ')QT^{[F:\mathbb {Q}]}|\mathcal {S}(Q)|)^{\varepsilon }$ and polynomials in ![]() $\log (C(\pi ')QT^{[F:\mathbb {Q}]}|\mathcal {S}(Q)|)$ might be bounded by
$\log (C(\pi ')QT^{[F:\mathbb {Q}]}|\mathcal {S}(Q)|)$ might be bounded by ![]() $X^{\varepsilon }$ without mention.
$X^{\varepsilon }$ without mention.
If ![]() $t\in [-T,T]$, then
$t\in [-T,T]$, then
by [Reference Iwaniec and KowalskiIK04, Proposition 5.7]. We observe that the rectangle ![]() $[\sigma,1]\times [-T,T]$ is covered by
$[\sigma,1]\times [-T,T]$ is covered by ![]() $O(T)$ boxes of the form
$O(T)$ boxes of the form ![]() $[\sigma,1]\times [y,y+2(\log Y)^2]$, each containing
$[\sigma,1]\times [y,y+2(\log Y)^2]$, each containing ![]() $O((\log (C(\pi )C(\pi ')T))^3)$ zeros. If we write
$O((\log (C(\pi )C(\pi ')T))^3)$ zeros. If we write ![]() $n_{\pi \times \pi '}$ for the number of such boxes containing at least one zero
$n_{\pi \times \pi '}$ for the number of such boxes containing at least one zero ![]() $\rho$ of
$\rho$ of ![]() $L(s,\pi \times \pi ')$, then
$L(s,\pi \times \pi ')$, then
If ![]() $\pi '=\widetilde {\pi }$, then it suffices to assume that
$\pi '=\widetilde {\pi }$, then it suffices to assume that ![]() $|\rho -1|>1$ since there are
$|\rho -1|>1$ since there are ![]() $O(\log (C(\pi ')QT))$ zeros
$O(\log (C(\pi ')QT))$ zeros ![]() $\rho$ such that
$\rho$ such that ![]() $|\rho -1|\leq 1$.
$|\rho -1|\leq 1$.
Let ![]() $\rho =\beta +i\gamma$ be a zero of
$\rho =\beta +i\gamma$ be a zero of ![]() $L(s,\pi \times \pi ')$, in which case
$L(s,\pi \times \pi ')$, in which case ![]() $LM_X(\rho,\pi \times \pi ')=0$. We compute
$LM_X(\rho,\pi \times \pi ')=0$. We compute
 \begin{align}
e^{-1/Y}&=\frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i\infty}^{1-\beta+{1}/{\!\log Y}+i\infty}(1-LM_X(\rho+w,\pi\times\pi')\Gamma(w)Y^{w}\,dw\nonumber\\
&\quad +\frac{1}{2\pi
i}\int_{{1}/{2}-\beta-i\infty}^{{1}/{2}-\beta+i\infty}LM_X(\rho+w,\pi\times\pi')\Gamma(w)Y^{w}\,dw\nonumber\\
&\quad
+\kappa_{\pi\times\pi'}\Gamma(1-\rho)Y^{1-\rho}\sum_{\substack{\mathrm{N}\mathfrak{n}\leq
X \nonumber\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}}.
\end{align}
\begin{align}
e^{-1/Y}&=\frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i\infty}^{1-\beta+{1}/{\!\log Y}+i\infty}(1-LM_X(\rho+w,\pi\times\pi')\Gamma(w)Y^{w}\,dw\nonumber\\
&\quad +\frac{1}{2\pi
i}\int_{{1}/{2}-\beta-i\infty}^{{1}/{2}-\beta+i\infty}LM_X(\rho+w,\pi\times\pi')\Gamma(w)Y^{w}\,dw\nonumber\\
&\quad
+\kappa_{\pi\times\pi'}\Gamma(1-\rho)Y^{1-\rho}\sum_{\substack{\mathrm{N}\mathfrak{n}\leq
X \nonumber\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}}.
\end{align}
It follows from (3.13) and Lemmas 3.1 and 3.3 that if ![]() $\text {Re}(w) = 1-\beta + {1}/{\!\log Y}$, then
$\text {Re}(w) = 1-\beta + {1}/{\!\log Y}$, then
 \begin{align}
&|1-LM_X(\rho+w,\pi\times\pi')|\nonumber\\ &\quad=
|L^{\mathrm{ur}}(\rho+w,\pi\times\pi')|\cdot|L^{\mathrm{ur}}(\rho+w,\pi\times\pi')^{-1}-M_X(\rho+w,\pi\times\pi')|\nonumber\\
&\quad\ll_{\varepsilon}
C(\pi\times\pi',|\gamma+\text{Im}(w)|+1)^{\varepsilon}\sum_{\substack{\mathrm{N}\mathfrak{n}>X
\nonumber\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{|\mu_{\pi\times\pi'}(\mathfrak{n})|}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}}}\nonumber\\ &\quad\ll_{\varepsilon}
C(\pi\times\pi',|\gamma+\text{Im}(w)|+1)^{\varepsilon}\sum_{\substack{\mathrm{N}\mathfrak{n}>X
\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{\lambda_{\pi\times\widetilde{\pi}}(\mathfrak{n})+\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}}}\nonumber\\ &\quad\ll_{\varepsilon}
C(\pi)^{\varepsilon}C(\pi')^{\varepsilon}(|\gamma+\text{Im}(w)|+1)^{\varepsilon}\log
X. \end{align}
\begin{align}
&|1-LM_X(\rho+w,\pi\times\pi')|\nonumber\\ &\quad=
|L^{\mathrm{ur}}(\rho+w,\pi\times\pi')|\cdot|L^{\mathrm{ur}}(\rho+w,\pi\times\pi')^{-1}-M_X(\rho+w,\pi\times\pi')|\nonumber\\
&\quad\ll_{\varepsilon}
C(\pi\times\pi',|\gamma+\text{Im}(w)|+1)^{\varepsilon}\sum_{\substack{\mathrm{N}\mathfrak{n}>X
\nonumber\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{|\mu_{\pi\times\pi'}(\mathfrak{n})|}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}}}\nonumber\\ &\quad\ll_{\varepsilon}
C(\pi\times\pi',|\gamma+\text{Im}(w)|+1)^{\varepsilon}\sum_{\substack{\mathrm{N}\mathfrak{n}>X
\\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F
}}\frac{\lambda_{\pi\times\widetilde{\pi}}(\mathfrak{n})+\lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}}}\nonumber\\ &\quad\ll_{\varepsilon}
C(\pi)^{\varepsilon}C(\pi')^{\varepsilon}(|\gamma+\text{Im}(w)|+1)^{\varepsilon}\log
X. \end{align}
Therefore, we deduce from Stirling's formula that
 \begin{align*} &\bigg|\frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i\infty}^{1-\beta+{1}/{\!\log Y}+i\infty} (1-LM_X(\rho+w,\pi\times\pi'))\Gamma(w)Y^{w}\,dw\\ &\quad -\frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i(\log Y)^2}^{1-\beta+{1}/{\!\log Y}+ i(\log Y)^2}(1-LM_X(\rho+w,\pi\times\pi'))\Gamma(w)Y^{w}\,dw\bigg|\ll \frac{1}{Y}. \end{align*}
\begin{align*} &\bigg|\frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i\infty}^{1-\beta+{1}/{\!\log Y}+i\infty} (1-LM_X(\rho+w,\pi\times\pi'))\Gamma(w)Y^{w}\,dw\\ &\quad -\frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i(\log Y)^2}^{1-\beta+{1}/{\!\log Y}+ i(\log Y)^2}(1-LM_X(\rho+w,\pi\times\pi'))\Gamma(w)Y^{w}\,dw\bigg|\ll \frac{1}{Y}. \end{align*}
The other terms in (5.2) are handled similarly. Since ![]() $e^{-1/Y}=1+O(1/Y)$, it follows that
$e^{-1/Y}=1+O(1/Y)$, it follows that
 \begin{align} 1&\ll \frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i(\log Y)^2}^{1-\beta+{1}/{\!\log Y}+i(\log Y)^2} (1-LM_X(\rho+w,\pi\times\pi'))\Gamma(w)Y^{w}\,dw\nonumber\\ &\quad +\frac{1}{2\pi i}\int_{{1}/{2}-\beta-i(\log Y)^2}^{{1}/{2}-\beta+i(\log Y)^2} LM_X(\rho+w,\pi\times\pi')\Gamma(w)Y^{w}\,dw+\kappa_{\pi\times\pi'}Y^{1-\sigma}\frac{\log X}{\max\{1,|\gamma|^3\}}. \end{align}
\begin{align} 1&\ll \frac{1}{2\pi i}\int_{1-\beta+{1}/{\!\log Y}-i(\log Y)^2}^{1-\beta+{1}/{\!\log Y}+i(\log Y)^2} (1-LM_X(\rho+w,\pi\times\pi'))\Gamma(w)Y^{w}\,dw\nonumber\\ &\quad +\frac{1}{2\pi i}\int_{{1}/{2}-\beta-i(\log Y)^2}^{{1}/{2}-\beta+i(\log Y)^2} LM_X(\rho+w,\pi\times\pi')\Gamma(w)Y^{w}\,dw+\kappa_{\pi\times\pi'}Y^{1-\sigma}\frac{\log X}{\max\{1,|\gamma|^3\}}. \end{align} Write the first integral in (5.4) as ![]() $I_1$ and the second as
$I_1$ and the second as ![]() $I_2$. A simple optimization calculation shows that if
$I_2$. A simple optimization calculation shows that if ![]() $c\geq 1$ and
$c\geq 1$ and ![]() $c^{-1}\leq |I_1|+|I_2|$, then
$c^{-1}\leq |I_1|+|I_2|$, then ![]() $c^{-1}\leq 2c(|I_1|^2+|I_2|)$. We estimate
$c^{-1}\leq 2c(|I_1|^2+|I_2|)$. We estimate ![]() $|I_1|^2$ using the Cauchy–Schwarz inequality, thus obtaining the bound
$|I_1|^2$ using the Cauchy–Schwarz inequality, thus obtaining the bound
 \begin{align*} 1&\ll (\log Y)^2
Y^{2(1-\sigma)}\int_{\gamma-(\log Y)^2}^{\gamma+(\log
Y)^2}\bigg|1-LM_X\bigg(1+\frac{1}{\log Y}+iv,
\pi\times\pi'\bigg)\bigg|^2\,dv\\ &\quad\,\, +Y^{{1}/{2}-\sigma}\int_{\gamma-(\log
Y)^2}^{\gamma+(\log Y)^2}\bigg|LM_X
\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|\,dv+\kappa_{\pi\times\pi'}Y^{1-\sigma}
\frac{\log X}{\max\{1,|\gamma|^3\}}.
\end{align*}
\begin{align*} 1&\ll (\log Y)^2
Y^{2(1-\sigma)}\int_{\gamma-(\log Y)^2}^{\gamma+(\log
Y)^2}\bigg|1-LM_X\bigg(1+\frac{1}{\log Y}+iv,
\pi\times\pi'\bigg)\bigg|^2\,dv\\ &\quad\,\, +Y^{{1}/{2}-\sigma}\int_{\gamma-(\log
Y)^2}^{\gamma+(\log Y)^2}\bigg|LM_X
\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|\,dv+\kappa_{\pi\times\pi'}Y^{1-\sigma}
\frac{\log X}{\max\{1,|\gamma|^3\}}.
\end{align*}
Since ![]() $T\geq 2(\log Y)^2$ by hypothesis, we conclude that
$T\geq 2(\log Y)^2$ by hypothesis, we conclude that
 \begin{align}
n_{\pi\times\pi'}&\ll (\log Y)^2 Y^{2(1-\sigma)}\int_{-T}^{T}\bigg|1-L\bigg(1+\frac{1}{\log
Y}+iv\bigg)M_X \bigg(1+\frac{1}{\log Y}+iv\bigg)\bigg|^2
\,dv\nonumber\\ &\quad\,\,
+Y^{{1}/{2}-\sigma}\int_{-T}^{T}\bigg|L\bigg(\frac{1}{2}+iv\bigg)M_X\bigg(\frac{1}{2}+iv\bigg)\bigg|\,
dv+\kappa_{\pi\times\pi'}Y^{1-\sigma}\log X+1.
\end{align}
\begin{align}
n_{\pi\times\pi'}&\ll (\log Y)^2 Y^{2(1-\sigma)}\int_{-T}^{T}\bigg|1-L\bigg(1+\frac{1}{\log
Y}+iv\bigg)M_X \bigg(1+\frac{1}{\log Y}+iv\bigg)\bigg|^2
\,dv\nonumber\\ &\quad\,\,
+Y^{{1}/{2}-\sigma}\int_{-T}^{T}\bigg|L\bigg(\frac{1}{2}+iv\bigg)M_X\bigg(\frac{1}{2}+iv\bigg)\bigg|\,
dv+\kappa_{\pi\times\pi'}Y^{1-\sigma}\log X+1.
\end{align}
Note that ![]() $\kappa _{\pi \times \pi '}=0$ unless
$\kappa _{\pi \times \pi '}=0$ unless ![]() $\pi '=\widetilde {\pi }$, which occurs for at most one
$\pi '=\widetilde {\pi }$, which occurs for at most one ![]() $\pi \in \mathcal {S}(Q)$. When
$\pi \in \mathcal {S}(Q)$. When ![]() $\kappa _{\pi \times \pi '}\neq 0$, it satisfies
$\kappa _{\pi \times \pi '}\neq 0$, it satisfies ![]() $\kappa _{\pi \times \pi '}=\kappa _{\pi \times \widetilde {\pi }}\ll _{\varepsilon } C(\pi )^{\varepsilon }$ per (4.6). Therefore, summing (5.5) over
$\kappa _{\pi \times \pi '}=\kappa _{\pi \times \widetilde {\pi }}\ll _{\varepsilon } C(\pi )^{\varepsilon }$ per (4.6). Therefore, summing (5.5) over ![]() $\pi \in \mathcal {S}(Q)$, we find that
$\pi \in \mathcal {S}(Q)$, we find that
 \begin{align} \sum_{\pi\in\mathcal{S}(Q)}N_{\pi\times\pi'}(\sigma,T)&\ll (\log C(\pi)C(\pi')T)^3\sum_{\pi\in\mathcal{S}(Q)}n_{\pi\times\pi'}\nonumber\\ &\ll_{\varepsilon} X^{\varepsilon} \bigg(Y^{2(1-\sigma)}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)} \bigg|1-LM_X\bigg(1+\frac{1}{\log Y}+iv,\pi\times\pi'\bigg)\bigg|^2\,dv\nonumber\\ &\quad\ \ +Y^{{1}/{2}-\sigma}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)} \bigg|LM_X\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|\,dv+Y^{1-\sigma}\bigg). \end{align}
\begin{align} \sum_{\pi\in\mathcal{S}(Q)}N_{\pi\times\pi'}(\sigma,T)&\ll (\log C(\pi)C(\pi')T)^3\sum_{\pi\in\mathcal{S}(Q)}n_{\pi\times\pi'}\nonumber\\ &\ll_{\varepsilon} X^{\varepsilon} \bigg(Y^{2(1-\sigma)}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)} \bigg|1-LM_X\bigg(1+\frac{1}{\log Y}+iv,\pi\times\pi'\bigg)\bigg|^2\,dv\nonumber\\ &\quad\ \ +Y^{{1}/{2}-\sigma}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)} \bigg|LM_X\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|\,dv+Y^{1-\sigma}\bigg). \end{align}For the first integral in (5.6), we deduce from (3.13) that
 \begin{align*} &\bigg|1-LM_X\bigg(1+\frac{1}{\log Y}+it,\pi\times\pi'\bigg)\bigg|^2\\ &\quad=\bigg|L^{\mathrm{ur}}\bigg(1+\frac{1}{\log Y}+it,\pi\times\pi'\bigg)\bigg|^2 \bigg|\frac{1}{L^{\mathrm{ur}}(1+\tfrac{1}{\log Y}+it,\pi\times\pi')}-M_X \bigg(1+\frac{1}{\log Y}+it,\pi\times\pi'\bigg)\bigg|^2\\ &\quad \ll_{\varepsilon} X^{\varepsilon}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}>X \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}}}\bigg|^2. \end{align*}
\begin{align*} &\bigg|1-LM_X\bigg(1+\frac{1}{\log Y}+it,\pi\times\pi'\bigg)\bigg|^2\\ &\quad=\bigg|L^{\mathrm{ur}}\bigg(1+\frac{1}{\log Y}+it,\pi\times\pi'\bigg)\bigg|^2 \bigg|\frac{1}{L^{\mathrm{ur}}(1+\tfrac{1}{\log Y}+it,\pi\times\pi')}-M_X \bigg(1+\frac{1}{\log Y}+it,\pi\times\pi'\bigg)\bigg|^2\\ &\quad \ll_{\varepsilon} X^{\varepsilon}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}>X \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}}}\bigg|^2. \end{align*}
For the second integral in (5.6), it follows from the Cauchy–Schwarz inequality that
 \begin{align*} \int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg|LM_X\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|\,dv &\leq \bigg(\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)} \bigg|L^{\mathrm{ur}}\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|^2 \,dv\bigg)^{{1}/{2}}\\ &\quad \times \bigg(\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\leq X\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{{1}/{2}+iv}}\bigg|^2 \,dv \bigg)^{{1}/{2}}. \end{align*}
\begin{align*} \int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg|LM_X\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|\,dv &\leq \bigg(\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)} \bigg|L^{\mathrm{ur}}\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|^2 \,dv\bigg)^{{1}/{2}}\\ &\quad \times \bigg(\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg|\sum_{\substack{\mathrm{N}\mathfrak{n}\leq X\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{{1}/{2}+iv}}\bigg|^2 \,dv \bigg)^{{1}/{2}}. \end{align*}
We bound the second moment of ![]() $L^{\mathrm {ur}}(\frac {1}{2}+iv,\pi \times \pi ')$ trivially as
$L^{\mathrm {ur}}(\frac {1}{2}+iv,\pi \times \pi ')$ trivially as
 \begin{align*} &\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg|L^{\mathrm{ur}}\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|^2\,dv \\ &\quad \ll_{\varepsilon} (QC(\pi'))^{2n'n\max\{0,\theta_n+\theta_{n'}-{1}/{2}\}+\varepsilon} Q^{{n'}/{2}}C(\pi')^{{n}/{2}}T^{{n'n[F:\mathbb{Q}]}/{2}+1+\varepsilon}|\mathcal{S}(Q)| \ll_{\varepsilon}\frac{Y^{3-2\sigma}}{X} \end{align*}
\begin{align*} &\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg|L^{\mathrm{ur}}\bigg(\frac{1}{2}+iv,\pi\times\pi'\bigg)\bigg|^2\,dv \\ &\quad \ll_{\varepsilon} (QC(\pi'))^{2n'n\max\{0,\theta_n+\theta_{n'}-{1}/{2}\}+\varepsilon} Q^{{n'}/{2}}C(\pi')^{{n}/{2}}T^{{n'n[F:\mathbb{Q}]}/{2}+1+\varepsilon}|\mathcal{S}(Q)| \ll_{\varepsilon}\frac{Y^{3-2\sigma}}{X} \end{align*}
using (3.7) (to bound the ramified Euler factors) and (3.13). In summary, we find that
 \begin{align*} \sum_{\pi\in\mathcal{S}(Q)}N_{\pi\times\pi'}(\sigma,T)& \ll_{\varepsilon} X^{\varepsilon} \bigg(Y^{2(1-\sigma)}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg |\sum_{\substack{\mathrm{N}\mathfrak{n}>X \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'} (\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}+iv}}\bigg|^2\,dv\\ &\quad + Y^{{1}/{2}-\sigma}\bigg(\frac{Y^{3-2\sigma}}{X}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg| \sum_{\substack{\mathrm{N}\mathfrak{n}\leq X\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{{1}/{2}+iv}}\bigg|^2 \,dv\bigg)^{{1}/{2}}+ Y^{1-\sigma}\bigg). \end{align*}
\begin{align*} \sum_{\pi\in\mathcal{S}(Q)}N_{\pi\times\pi'}(\sigma,T)& \ll_{\varepsilon} X^{\varepsilon} \bigg(Y^{2(1-\sigma)}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg |\sum_{\substack{\mathrm{N}\mathfrak{n}>X \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'} (\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{1+{1}/{\!\log Y}+iv}}\bigg|^2\,dv\\ &\quad + Y^{{1}/{2}-\sigma}\bigg(\frac{Y^{3-2\sigma}}{X}\int_{-T}^{T}\sum_{\pi\in\mathcal{S}(Q)}\bigg| \sum_{\substack{\mathrm{N}\mathfrak{n}\leq X\\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F}}\frac{\mu_{\pi\times\pi'}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^{{1}/{2}+iv}}\bigg|^2 \,dv\bigg)^{{1}/{2}}+ Y^{1-\sigma}\bigg). \end{align*}
We bound the two ![]() $v$-integrals using Corollary 4.4 and (5.1), thus obtaining
$v$-integrals using Corollary 4.4 and (5.1), thus obtaining
Theorem 1.1 now follows from (5.1), the bounds for ![]() $\theta _{n}$ and
$\theta _{n}$ and ![]() $\theta _{n'}$ in (3.2), and (1.5).
$\theta _{n'}$ in (3.2), and (1.5).
6. Bounds for Rankin–Selberg  $L$-functions
$L$-functions
In this section, we prove Theorem 2.1. Let ![]() $\pi '\in \mathfrak {F}_{n'}$ and
$\pi '\in \mathfrak {F}_{n'}$ and ![]() $Q\geq 1$. In (1.6), we rescale
$Q\geq 1$. In (1.6), we rescale ![]() $\varepsilon$ to
$\varepsilon$ to ![]() $\varepsilon /72$ and define
$\varepsilon /72$ and define ![]() $\alpha = \varepsilon /(7.2\max \{n,n'\})$ so that
$\alpha = \varepsilon /(7.2\max \{n,n'\})$ so that
Let ![]() $\pi \in \mathfrak {F}_n(Q)$. Proceeding as in the proof of [Reference Soundararajan and ThornerST19, Theorem 1.1], we obtainFootnote 4
$\pi \in \mathfrak {F}_n(Q)$. Proceeding as in the proof of [Reference Soundararajan and ThornerST19, Theorem 1.1], we obtainFootnote 4
 \begin{align*} \log\bigg|L\bigg(\frac{1}{2},\pi\times\pi'\bigg)\bigg|&\leq\bigg (\frac{1}{4}-\frac{\alpha}{10^{9}}\bigg)\log C(\pi\times\pi') +2 \log\bigg|L\bigg(\frac{3}{2},\pi\times\pi'\bigg)\bigg|\\ &\quad\ + \frac{\alpha}{10^{7}} N_{\pi\times\pi'}(1-\alpha,6)+O(1). \end{align*}
\begin{align*} \log\bigg|L\bigg(\frac{1}{2},\pi\times\pi'\bigg)\bigg|&\leq\bigg (\frac{1}{4}-\frac{\alpha}{10^{9}}\bigg)\log C(\pi\times\pi') +2 \log\bigg|L\bigg(\frac{3}{2},\pi\times\pi'\bigg)\bigg|\\ &\quad\ + \frac{\alpha}{10^{7}} N_{\pi\times\pi'}(1-\alpha,6)+O(1). \end{align*}
By (3.12) and (3.13), we find that there exists an effectively computable constant ![]() $c_{5}=c_{5}(n,n',[F:\mathbb {Q}],\varepsilon )>0$ such that if
$c_{5}=c_{5}(n,n',[F:\mathbb {Q}],\varepsilon )>0$ such that if ![]() $C(\pi \times \pi ')\geq c_{5}$, then
$C(\pi \times \pi ')\geq c_{5}$, then
7. Effective multiplicity one on average
In this section, we prove Theorem 2.3. We consider the family of cuspidal automorphic representations ![]() $\mathfrak {F}_n(Q)$ over a number field
$\mathfrak {F}_n(Q)$ over a number field ![]() $F$. Recall our convention that implied constants are allowed to depend on
$F$. Recall our convention that implied constants are allowed to depend on ![]() $n\geq 3$,
$n\geq 3$, ![]() $[F:\mathbb {Q}]$, and
$[F:\mathbb {Q}]$, and ![]() $\varepsilon$ unless specifically mentioned otherwise.
$\varepsilon$ unless specifically mentioned otherwise.
To prove Theorem 2.3, we use Theorem 1.1 to build large zero-free regions for almost all ![]() $L$-functions
$L$-functions ![]() $L(s,\pi \times \pi ')$ with
$L(s,\pi \times \pi ')$ with ![]() $\pi \in \mathfrak {F}_n$ varying. If
$\pi \in \mathfrak {F}_n$ varying. If ![]() $\pi '\in \{\widetilde {\pi },\widetilde {\pi }'\}$, then
$\pi '\in \{\widetilde {\pi },\widetilde {\pi }'\}$, then ![]() $L(s,\pi \times \pi ')$ has the standard zero-free region (1.1) apart from a possible Landau–Siegel zero, which must be both real and simple. In all other cases, only Brumley's much narrower zero-free region is known (see [Reference BrumleyBru06a] and [Reference LapidLap13, Appendix]). We can use Theorem 1.1 to establish a much stronger zero-free region for
$L(s,\pi \times \pi ')$ has the standard zero-free region (1.1) apart from a possible Landau–Siegel zero, which must be both real and simple. In all other cases, only Brumley's much narrower zero-free region is known (see [Reference BrumleyBru06a] and [Reference LapidLap13, Appendix]). We can use Theorem 1.1 to establish a much stronger zero-free region for ![]() $L(s,\pi \times \pi ')$ for all
$L(s,\pi \times \pi ')$ for all ![]() $\pi \in \mathfrak {F}_n(Q)$ with very few exceptions. Here is a simple example.
$\pi \in \mathfrak {F}_n(Q)$ with very few exceptions. Here is a simple example.
Corollary 7.1 Let ![]() $\varepsilon >0$,
$\varepsilon >0$, ![]() $n\geq 3$, and
$n\geq 3$, and ![]() $\pi '\in \mathfrak {F}_n(Q)$. For all
$\pi '\in \mathfrak {F}_n(Q)$. For all ![]() $\pi \in \mathfrak {F}_n(Q)$ with
$\pi \in \mathfrak {F}_n(Q)$ with ![]() $O_{\varepsilon }(Q^{\varepsilon })$ exceptions, the
$O_{\varepsilon }(Q^{\varepsilon })$ exceptions, the ![]() $L$-function
$L$-function ![]() $L(s,\pi \times \pi ')$ is non-zero in the region
$L(s,\pi \times \pi ')$ is non-zero in the region
Proof. This follows from (1.7) (once we rescale ![]() $\varepsilon$ to
$\varepsilon$ to ![]() $\varepsilon /21$) with
$\varepsilon /21$) with ![]() $C(\pi ')\leq Q$,
$C(\pi ')\leq Q$, ![]() $T = \log Q$, and
$T = \log Q$, and ![]() $\sigma = 1-\varepsilon /(20n^2)$.
$\sigma = 1-\varepsilon /(20n^2)$.
For ![]() $\pi _1,\pi _2\in \mathfrak {F}_n$ define the numbers
$\pi _1,\pi _2\in \mathfrak {F}_n$ define the numbers ![]() $\Lambda _{\pi _1\times \pi _2}(\mathfrak {n})$ by the Dirichlet series identity (for
$\Lambda _{\pi _1\times \pi _2}(\mathfrak {n})$ by the Dirichlet series identity (for ![]() $\text {Re}(s)>1$)
$\text {Re}(s)>1$)
 \begin{equation} \sum_{\mathfrak{n}}\frac{\Lambda_{\pi_1\times\pi_2}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s}= -\frac{L'}{L}(s,\pi_1\times\pi_2)= \sum_{\mathfrak{p}} \sum_{k = 1}^{\infty} \frac{\sum_{j=1}^{n}\sum_{j'=1}^{n}\alpha_{j,j',\pi_1\times\pi_2}(\mathfrak{p})^k\log\mathrm{N}\mathfrak{p}}{\mathrm{N}\mathfrak{p}^{ks}}. \end{equation}
\begin{equation} \sum_{\mathfrak{n}}\frac{\Lambda_{\pi_1\times\pi_2}(\mathfrak{n})}{\mathrm{N}\mathfrak{n}^s}= -\frac{L'}{L}(s,\pi_1\times\pi_2)= \sum_{\mathfrak{p}} \sum_{k = 1}^{\infty} \frac{\sum_{j=1}^{n}\sum_{j'=1}^{n}\alpha_{j,j',\pi_1\times\pi_2}(\mathfrak{p})^k\log\mathrm{N}\mathfrak{p}}{\mathrm{N}\mathfrak{p}^{ks}}. \end{equation}Lemma 7.2 Let ![]() $\pi '\in \mathfrak {F}_n$. There exist absolute and effectively computable constants
$\pi '\in \mathfrak {F}_n$. There exist absolute and effectively computable constants ![]() $c_{6}\in (0,1)$,
$c_{6}\in (0,1)$, ![]() $c_{7},c_{8},c_{9},c_{10}\geq 1$, and
$c_{7},c_{8},c_{9},c_{10}\geq 1$, and ![]() $c_{11}\in (0,1)$ such that the following are true.
$c_{11}\in (0,1)$ such that the following are true.
(1) The
 $L$-function
$L$-function  $L(s,\pi '\times \widetilde {\pi }')$ has at most one zero, say
$L(s,\pi '\times \widetilde {\pi }')$ has at most one zero, say  $\beta _1$, in the region
If
$\beta _1$, in the region
If \[ \text{Re}(s)\geq 1- \frac{c_{6}}{\log(C(\pi')^n(|\text{Im}(s)|+e)^{n^2[F:\mathbb{Q}]})}. \]
\[ \text{Re}(s)\geq 1- \frac{c_{6}}{\log(C(\pi')^n(|\text{Im}(s)|+e)^{n^2[F:\mathbb{Q}]})}. \]
 $\beta _1$ exists, then it must be real and simple and satisfy
$\beta _1$ exists, then it must be real and simple and satisfy  $\beta _1\leq 1-C(\pi ')^{-c_{7}n}$.
$\beta _1\leq 1-C(\pi ')^{-c_{7}n}$.(2) If
 $A\geq c_{8}$,
$A\geq c_{8}$,  $\log \log C(\pi ')\geq c_{9}n^4[F:\mathbb {Q}]^2$, and
$\log \log C(\pi ')\geq c_{9}n^4[F:\mathbb {Q}]^2$, and  $x\geq C(\pi ')^{c_{10}A^2n^3[F:\mathbb {Q}]\log (en[F:\mathbb {Q}])}$, then
where
$x\geq C(\pi ')^{c_{10}A^2n^3[F:\mathbb {Q}]\log (en[F:\mathbb {Q}])}$, then
where \[ \sum_{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})=\begin{cases} \dfrac{x}{2}(1-\xi^{\beta_1-1})(1+O(e^{-c_{11}A})) & \mbox{if}\ \beta_1\ \mbox{exists,}\\[8pt] \dfrac{x}{2}(1+O(e^{-c_{11}A})) & \mbox{otherwise,} \end{cases} \]
\[ \sum_{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})=\begin{cases} \dfrac{x}{2}(1-\xi^{\beta_1-1})(1+O(e^{-c_{11}A})) & \mbox{if}\ \beta_1\ \mbox{exists,}\\[8pt] \dfrac{x}{2}(1+O(e^{-c_{11}A})) & \mbox{otherwise,} \end{cases} \]
 $\xi \in [ {x}/{2},x]$ satisfies
$\xi \in [ {x}/{2},x]$ satisfies  $x^{\beta _1}-( {x}/{2})^{\beta _1}=\beta _1 ({x}/{2})\xi ^{\beta _1-1}$ and the implied constants are absolute and effectively computable.
$x^{\beta _1}-( {x}/{2})^{\beta _1}=\beta _1 ({x}/{2})\xi ^{\beta _1-1}$ and the implied constants are absolute and effectively computable.
Proof. This is [Reference Humphries and ThornerHT22, Theorem 2.1] with ![]() $\delta =0$ and
$\delta =0$ and ![]() $x$ replaced with
$x$ replaced with ![]() $x/2$.
$x/2$.
Lemma 7.2 informs the following choices of parameters that we will use throughout the rest of this section. Let ![]() $0<\varepsilon <1$, let
$0<\varepsilon <1$, let ![]() $Q$ be sufficiently large with respect to
$Q$ be sufficiently large with respect to ![]() $\varepsilon$, and let
$\varepsilon$, and let
 \begin{equation} \begin{aligned} & c_{7}\geq \frac{c_{8}^2c_{10}}{3240},\quad A = \sqrt{\frac{3240 c_{7}}{c_{10}\varepsilon}},\quad B= \frac{41n^2}{\varepsilon},\quad x=\frac{1}{2}(\log Q)^B,\\ & \pi\in\mathfrak{F}_n(Q),\quad \pi'\in \mathfrak{F}_n\big(x^{{1}/{A^2c_{10}n^4[F:\mathbb{Q}]^2}}\big)= \mathfrak{F}_n\big((2^{-{\varepsilon}/{41n^2}}\log Q)^{{41}/{3240c_{7}n^2[F:\mathbb{Q}]^2}}\big). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & c_{7}\geq \frac{c_{8}^2c_{10}}{3240},\quad A = \sqrt{\frac{3240 c_{7}}{c_{10}\varepsilon}},\quad B= \frac{41n^2}{\varepsilon},\quad x=\frac{1}{2}(\log Q)^B,\\ & \pi\in\mathfrak{F}_n(Q),\quad \pi'\in \mathfrak{F}_n\big(x^{{1}/{A^2c_{10}n^4[F:\mathbb{Q}]^2}}\big)= \mathfrak{F}_n\big((2^{-{\varepsilon}/{41n^2}}\log Q)^{{41}/{3240c_{7}n^2[F:\mathbb{Q}]^2}}\big). \end{aligned} \end{equation}Corollary 7.3 Under the notation and hypotheses of (7.2), there holds
 \[ \sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }} \Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})\gg_{\varepsilon} x^{1-{2c_{7}}/{A^2c_{10}n^3[F:\mathbb{Q}]^2}}. \]
\[ \sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }} \Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})\gg_{\varepsilon} x^{1-{2c_{7}}/{A^2c_{10}n^3[F:\mathbb{Q}]^2}}. \]
Proof. Let ![]() $\pi,\pi '\in \mathfrak {F}_n(Q)$. In Lemma 7.2, the lower bound on
$\pi,\pi '\in \mathfrak {F}_n(Q)$. In Lemma 7.2, the lower bound on ![]() $C(\pi ')$ only serves to ensure that the implied constants are absolute. This was pertinent in [Reference Humphries and ThornerHT22], but it is not pertinent here. Thus, we may replace the two conditions
$C(\pi ')$ only serves to ensure that the implied constants are absolute. This was pertinent in [Reference Humphries and ThornerHT22], but it is not pertinent here. Thus, we may replace the two conditions ![]() $\log \log C(\pi ')\geq c_{9}n^4[F:\mathbb {Q}]^2$ and
$\log \log C(\pi ')\geq c_{9}n^4[F:\mathbb {Q}]^2$ and ![]() $x\geq C(\pi ')^{A^2 c_{10}n^3[F:\mathbb {Q}]\log (en[F:\mathbb {Q}])}$ with the single condition
$x\geq C(\pi ')^{A^2 c_{10}n^3[F:\mathbb {Q}]\log (en[F:\mathbb {Q}])}$ with the single condition ![]() $C(\pi ')\ll x^{1/(A^2c_{10}n^4[F:\mathbb {Q}]^2)}$. We want to refine Lemma 7.2 so that one only sums over
$C(\pi ')\ll x^{1/(A^2c_{10}n^4[F:\mathbb {Q}]^2)}$. We want to refine Lemma 7.2 so that one only sums over ![]() $\mathfrak {n}$ such that
$\mathfrak {n}$ such that ![]() $\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$. Using (3.3) and (3.7), we find that the contribution to Lemma 7.2(2) arising from
$\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$. Using (3.3) and (3.7), we find that the contribution to Lemma 7.2(2) arising from ![]() $\mathfrak {n}$ such that
$\mathfrak {n}$ such that ![]() $\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})\neq \mathcal {O}_F$ is
$\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})\neq \mathcal {O}_F$ is
 \begin{align*}
\sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})\neq\mathcal{O}_F}}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})&\ll
\sum_{\mathfrak{p} \mid \mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}\ \sum_{{\log(x/2)}/{\!\log\mathrm{N}\mathfrak{p}}< j\leq
{\log x}/{\!\log\mathrm{N}\mathfrak{p}}}\mathrm{N}\mathfrak{p}^{j(1-{2}/({n^2+1}))}\\
&\ll \frac{\log Q}{\log\log Q}x^{1-{2}/({n^2+1})},
\end{align*}
\begin{align*}
\sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\
\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})\neq\mathcal{O}_F}}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})&\ll
\sum_{\mathfrak{p} \mid \mathfrak{q}_{\pi}\mathfrak{q}_{\pi'}}\ \sum_{{\log(x/2)}/{\!\log\mathrm{N}\mathfrak{p}}< j\leq
{\log x}/{\!\log\mathrm{N}\mathfrak{p}}}\mathrm{N}\mathfrak{p}^{j(1-{2}/({n^2+1}))}\\
&\ll \frac{\log Q}{\log\log Q}x^{1-{2}/({n^2+1})},
\end{align*}
which is ![]() $\ll x^{1- {1}/({n^2+1})}$. In the worst case, where
$\ll x^{1- {1}/({n^2+1})}$. In the worst case, where ![]() $\beta _1$ in Lemma 7.2(1) exists, it follows from Lemma 7.2(2) and the above discussion that if
$\beta _1$ in Lemma 7.2(1) exists, it follows from Lemma 7.2(2) and the above discussion that if ![]() $C(\pi ')\ll _{n,[F:\mathbb {Q}]} x^{1/(A^2c_{10}n^3[F:\mathbb {Q}]\log (en[F:\mathbb {Q}]))}$, then
$C(\pi ')\ll _{n,[F:\mathbb {Q}]} x^{1/(A^2c_{10}n^3[F:\mathbb {Q}]\log (en[F:\mathbb {Q}]))}$, then
 \[ \sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq 2x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})\gg x(1-\xi^{\beta_1-1})\gg_{n,[F:\mathbb{Q}]} x\min\{1,(1-\beta_1)\log C(\pi')\}\gg \frac{x\log C(\pi')}{C(\pi')^{c_{7}n}}. \]
\[ \sum_{\substack{x<\mathrm{N}\mathfrak{n}\leq 2x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})\gg x(1-\xi^{\beta_1-1})\gg_{n,[F:\mathbb{Q}]} x\min\{1,(1-\beta_1)\log C(\pi')\}\gg \frac{x\log C(\pi')}{C(\pi')^{c_{7}n}}. \]
The desired result now follows.
Lemma 7.4 Let ![]() $n\geq 3$. Assume the notation and hypotheses in (7.2). Let
$n\geq 3$. Assume the notation and hypotheses in (7.2). Let ![]() $\Phi$ be a fixed smooth function supported on a compact subset of
$\Phi$ be a fixed smooth function supported on a compact subset of ![]() $[\frac {1}{4},2]$ such that
$[\frac {1}{4},2]$ such that ![]() $0\leq \Phi (t)\leq 1$ for all
$0\leq \Phi (t)\leq 1$ for all ![]() $t\in [\frac {1}{4},2]$ and
$t\in [\frac {1}{4},2]$ and ![]() $\Phi (t)=1$ for
$\Phi (t)=1$ for ![]() $t\in (\frac {1}{2},1]$. If
$t\in (\frac {1}{2},1]$. If ![]() $L(s,\pi \times \pi ')$ is entire and does not vanish in the region
$L(s,\pi \times \pi ')$ is entire and does not vanish in the region ![]() $\text {Re}(s)\geq 1-\varepsilon /(20n^2)$ and
$\text {Re}(s)\geq 1-\varepsilon /(20n^2)$ and ![]() $|\text {Im}(s)|\leq \log Q$, then
$|\text {Im}(s)|\leq \log Q$, then
Proof. Writing ![]() $\widehat {\Phi }(s)=\int _0^{\infty }\Phi (t)t^{s-1}\,dt$ for the Mellin transform of
$\widehat {\Phi }(s)=\int _0^{\infty }\Phi (t)t^{s-1}\,dt$ for the Mellin transform of ![]() $\Phi$ (which is an entire function of
$\Phi$ (which is an entire function of ![]() $s$), we observe via Mellin inversion that
$s$), we observe via Mellin inversion that
 \[ \sum_{\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }\Lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n})\Phi(\mathrm{N}\mathfrak{n}/x) = \frac{1}{2\pi i}\int_{2-i\infty}^{2+i\infty}-\frac{(L^{\text{ur}})'}{(L^{\text{ur}})}(s,\pi\times\widetilde{\pi}')\widehat{\Phi}(s)x^s \,ds, \]
\[ \sum_{\gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }\Lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n})\Phi(\mathrm{N}\mathfrak{n}/x) = \frac{1}{2\pi i}\int_{2-i\infty}^{2+i\infty}-\frac{(L^{\text{ur}})'}{(L^{\text{ur}})}(s,\pi\times\widetilde{\pi}')\widehat{\Phi}(s)x^s \,ds, \]
where ![]() $L^{\text {ur}}(s,\pi \times \widetilde {\pi }')=L(s,\pi \times \widetilde {\pi }')\prod _{\mathfrak {p}\mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}}L(s,\pi _{\mathfrak {p}}\times \widetilde {\pi }_{\mathfrak {p}}')^{-1}$. A standard contour integral calculation using the argument principle shows that the above display equals
$L^{\text {ur}}(s,\pi \times \widetilde {\pi }')=L(s,\pi \times \widetilde {\pi }')\prod _{\mathfrak {p}\mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}}L(s,\pi _{\mathfrak {p}}\times \widetilde {\pi }_{\mathfrak {p}}')^{-1}$. A standard contour integral calculation using the argument principle shows that the above display equals
where ![]() $\rho$ ranges over all zeros of
$\rho$ ranges over all zeros of ![]() $L^{\text {ur}}(s,\pi \times \widetilde {\pi }')$.
$L^{\text {ur}}(s,\pi \times \widetilde {\pi }')$.
Since ![]() $\Phi$ is compactly supported and
$\Phi$ is compactly supported and ![]() $\widehat {\Phi }$ is entire, it follows that for any
$\widehat {\Phi }$ is entire, it follows that for any ![]() $R\geq 2$, we have
$R\geq 2$, we have ![]() $|\widehat {\Phi }(s)|\ll _{R}\min \{1,|s|^{-R}e^{\text {Re}(s)}\}$. Note that the reciprocals of the Euler factors of
$|\widehat {\Phi }(s)|\ll _{R}\min \{1,|s|^{-R}e^{\text {Re}(s)}\}$. Note that the reciprocals of the Euler factors of ![]() $L(s,\pi \times \widetilde {\pi }')$ at prime ideals
$L(s,\pi \times \widetilde {\pi }')$ at prime ideals ![]() $\mathfrak {p} \mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ and all of the trivial zeros of
$\mathfrak {p} \mid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ and all of the trivial zeros of ![]() $L(s,\pi \times \widetilde {\pi }')$ have real part no larger than
$L(s,\pi \times \widetilde {\pi }')$ have real part no larger than ![]() $1- {2}/({n^2+1})$ per (3.3) and (3.7). Since for any
$1- {2}/({n^2+1})$ per (3.3) and (3.7). Since for any ![]() $t\in \mathbb {R}$ there are
$t\in \mathbb {R}$ there are ![]() $\ll \log Q+\log (|t|+2)$ zeros
$\ll \log Q+\log (|t|+2)$ zeros ![]() $\rho =\beta +i\gamma$ of
$\rho =\beta +i\gamma$ of ![]() $L^{\text {ur}}(s,\pi \times \widetilde {\pi }')$ that satisfy
$L^{\text {ur}}(s,\pi \times \widetilde {\pi }')$ that satisfy ![]() $0<\beta <1$ and
$0<\beta <1$ and ![]() $|\gamma -t|\leq 1$, we find for any
$|\gamma -t|\leq 1$, we find for any ![]() $T\geq 1$,
$T\geq 1$, ![]() $R\geq 2$, and
$R\geq 2$, and ![]() $\sigma _0\geq 1- {2}/({n^2+1})$ that
$\sigma _0\geq 1- {2}/({n^2+1})$ that
 \begin{equation} \sum_{L^{\text{ur}}(\rho,\pi\times\widetilde{\pi}')=0}\widehat{\Phi}(\rho)x^{\rho}=\sum_{\substack{L^{\text{ur}}(\rho,\pi\times\widetilde{\pi}')=0 \\ \beta\geq \sigma_0 \\ |\gamma|\leq T}}\widehat{\Phi}(\rho)x^{\rho}+O(T^{1-R}\log(QT)x+T\log(QT)x^{\sigma_0}). \end{equation}
\begin{equation} \sum_{L^{\text{ur}}(\rho,\pi\times\widetilde{\pi}')=0}\widehat{\Phi}(\rho)x^{\rho}=\sum_{\substack{L^{\text{ur}}(\rho,\pi\times\widetilde{\pi}')=0 \\ \beta\geq \sigma_0 \\ |\gamma|\leq T}}\widehat{\Phi}(\rho)x^{\rho}+O(T^{1-R}\log(QT)x+T\log(QT)x^{\sigma_0}). \end{equation}
We choose ![]() $T=\log Q=(2x)^{1/B}$ and
$T=\log Q=(2x)^{1/B}$ and ![]() $\sigma _0=1-\varepsilon /(20n^2)$, in which case our hypotheses imply that the sum over zeros on the right-hand side of (7.3) is empty and
$\sigma _0=1-\varepsilon /(20n^2)$, in which case our hypotheses imply that the sum over zeros on the right-hand side of (7.3) is empty and
 \[ \bigg|\sum_{L^{\text{ur}}(\rho,\pi\times\widetilde{\pi}')=0}\widehat{\Phi}(\rho)x^{\rho}\bigg| \ll_{B} x^{1+({2-R})/{B}}+x^{{2}/{B}+\sigma_0}. \]
\[ \bigg|\sum_{L^{\text{ur}}(\rho,\pi\times\widetilde{\pi}')=0}\widehat{\Phi}(\rho)x^{\rho}\bigg| \ll_{B} x^{1+({2-R})/{B}}+x^{{2}/{B}+\sigma_0}. \]
The desired result follows from choosing ![]() $R=\max \{B(1-\sigma _0),3\}$.
$R=\max \{B(1-\sigma _0),3\}$.
Proof of Theorem 2.3 Suppose to the contrary that ![]() $\pi \neq \pi '$ and
$\pi \neq \pi '$ and ![]() $\pi _{\mathfrak {p}}\cong \pi _{\mathfrak {p}}'$ for all
$\pi _{\mathfrak {p}}\cong \pi _{\mathfrak {p}}'$ for all ![]() $\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ with
$\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ with ![]() $\mathrm {N}\mathfrak {p}\leq 2x$. Then
$\mathrm {N}\mathfrak {p}\leq 2x$. Then ![]() $A_{\pi }(\mathfrak {p})=A_{\pi '}(\mathfrak {p})$ for all
$A_{\pi }(\mathfrak {p})=A_{\pi '}(\mathfrak {p})$ for all ![]() $\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ with
$\mathfrak {p}\nmid \mathfrak {q}_{\pi }\mathfrak {q}_{\pi '}$ with ![]() $\mathrm {N}\mathfrak {p}\leq 2x$. By (3.6) and (7.1), it follows that
$\mathrm {N}\mathfrak {p}\leq 2x$. By (3.6) and (7.1), it follows that ![]() $\Lambda _{\pi \times \widetilde {\pi }'}(\mathfrak {n})=\Lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n})$ for all
$\Lambda _{\pi \times \widetilde {\pi }'}(\mathfrak {n})=\Lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n})$ for all ![]() $\mathfrak {n}$ such that
$\mathfrak {n}$ such that ![]() $\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$ and
$\gcd (\mathfrak {n},\mathfrak {q}_{\pi }\mathfrak {q}_{\pi '})=\mathcal {O}_F$ and ![]() $\mathrm {N}\mathfrak {n}\leq x$. Since
$\mathrm {N}\mathfrak {n}\leq x$. Since ![]() $\Lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n})\geq 0$ for all such
$\Lambda _{\pi '\times \widetilde {\pi }'}(\mathfrak {n})\geq 0$ for all such ![]() $\mathfrak {n}$, the same holds for
$\mathfrak {n}$, the same holds for ![]() $\Lambda _{\pi \times \widetilde {\pi }'}(\mathfrak {n})$. It follows that
$\Lambda _{\pi \times \widetilde {\pi }'}(\mathfrak {n})$. It follows that
 \[ \sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F }}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})=\sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n}). \]
\[ \sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})= \mathcal{O}_F }}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})=\sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n}). \]
By (7.2), we have that
Therefore, if ![]() $L(s,\pi \times \widetilde {\pi }')\neq 0$ in the region
$L(s,\pi \times \widetilde {\pi }')\neq 0$ in the region ![]() $\{s\in \mathbb {C}\colon \mathrm {Re}(s)\geq 1-\varepsilon /(20n^2),~|\text {Im}(s)|\leq \log Q\}$, then by Corollary 7.3 and Lemma 7.4, we have that
$\{s\in \mathbb {C}\colon \mathrm {Re}(s)\geq 1-\varepsilon /(20n^2),~|\text {Im}(s)|\leq \log Q\}$, then by Corollary 7.3 and Lemma 7.4, we have that
 \[ x^{1-{2c_{7}}/{A^2c_{10}n^3[F:\mathbb{Q}]^2}}\ll \sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})=\sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n})\ll_{B}x^{1+{2}/{B}-{\varepsilon}/{20n^2}}. \]
\[ x^{1-{2c_{7}}/{A^2c_{10}n^3[F:\mathbb{Q}]^2}}\ll \sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi'\times\widetilde{\pi}'}(\mathfrak{n})=\sum_{\substack{{x}/{2}<\mathrm{N}\mathfrak{n}\leq x \\ \gcd(\mathfrak{n},\mathfrak{q}_{\pi}\mathfrak{q}_{\pi'})=\mathcal{O}_F }}\Lambda_{\pi\times\widetilde{\pi}'}(\mathfrak{n})\ll_{B}x^{1+{2}/{B}-{\varepsilon}/{20n^2}}. \]
This implies that
which contradicts our choices of ![]() $A$ and
$A$ and ![]() $B$ in (7.2). The desired result now follows from Corollary 7.1.
$B$ in (7.2). The desired result now follows from Corollary 7.1.
8. Automorphic level of distribution
In this section, we prove Theorem 2.5. In what follows, let ![]() $F=\mathbb {Q}$. If
$F=\mathbb {Q}$. If ![]() $n=2$, then
$n=2$, then ![]() $L(s,\pi \times \widetilde {\pi })$ is the
$L(s,\pi \times \widetilde {\pi })$ is the ![]() $L$-function of an isobaric automorphic representation of
$L$-function of an isobaric automorphic representation of ![]() $\mathrm {GL}_4(\mathbb {A}_{\mathbb {Q}})$ whose cuspidal constituents have rank at most 3. Since the
$\mathrm {GL}_4(\mathbb {A}_{\mathbb {Q}})$ whose cuspidal constituents have rank at most 3. Since the ![]() $L$-function any Dirichlet character twist of any cuspidal constituents of rank 2 or 3 have no Landau–Siegel zero by [Reference BanksBan97, Reference Hoffstein and RamakrishnanHR95], a stronger result than Theorem 2.5 follows from a minor variation of the proof of [Reference Jiang, Lü, Thorner and WangJLTW23, Theorem 1.1]. Therefore, we may restrict our consideration to
$L$-function any Dirichlet character twist of any cuspidal constituents of rank 2 or 3 have no Landau–Siegel zero by [Reference BanksBan97, Reference Hoffstein and RamakrishnanHR95], a stronger result than Theorem 2.5 follows from a minor variation of the proof of [Reference Jiang, Lü, Thorner and WangJLTW23, Theorem 1.1]. Therefore, we may restrict our consideration to ![]() $n\geq 3$.
$n\geq 3$.
Let ![]() $\pi \in \mathfrak {F}_n$ have arithmetic conductor
$\pi \in \mathfrak {F}_n$ have arithmetic conductor ![]() $q_{\pi }$, and let
$q_{\pi }$, and let ![]() $\chi$ be a primitive Dirichlet character modulo
$\chi$ be a primitive Dirichlet character modulo ![]() $q$. We allow
$q$. We allow ![]() $\pi$ to be fixed, so for notational compactness, we introduce
$\pi$ to be fixed, so for notational compactness, we introduce ![]() $L_{\chi }(s) := L(s,\pi \times (\widetilde {\pi }\otimes \chi ))$ and
$L_{\chi }(s) := L(s,\pi \times (\widetilde {\pi }\otimes \chi ))$ and ![]() $L_1(s):= L(s,\pi \times \widetilde {\pi })$. If
$L_1(s):= L(s,\pi \times \widetilde {\pi })$. If ![]() $q$ and
$q$ and ![]() $q_{\pi }$ are coprime, then
$q_{\pi }$ are coprime, then ![]() $L_{\chi }(s)$ is entire if and only if
$L_{\chi }(s)$ is entire if and only if ![]() $\chi$ is non-trivial, since
$\chi$ is non-trivial, since ![]() $\widetilde {\pi } \otimes \chi \neq \widetilde {\pi }$, which is clear by comparing the arithmetic conductors of
$\widetilde {\pi } \otimes \chi \neq \widetilde {\pi }$, which is clear by comparing the arithmetic conductors of ![]() $q_{\widetilde {\pi } \otimes \chi }$ and
$q_{\widetilde {\pi } \otimes \chi }$ and ![]() $q_{\widetilde {\pi }}$. If
$q_{\widetilde {\pi }}$. If ![]() $\chi$ is trivial, then
$\chi$ is trivial, then ![]() $L_{\chi }(s) = L_1(s)$. We also define
$L_{\chi }(s) = L_1(s)$. We also define ![]() $\Lambda _{\chi }(s):= \Lambda (s,\pi \times (\widetilde {\pi }\otimes \chi ))$ and
$\Lambda _{\chi }(s):= \Lambda (s,\pi \times (\widetilde {\pi }\otimes \chi ))$ and ![]() $\Lambda _1(s):= \Lambda (s,\pi \times \widetilde {\pi })$.
$\Lambda _1(s):= \Lambda (s,\pi \times \widetilde {\pi })$.
8.1 Preliminaries
We define ![]() $a_{\pi }(m)$ and
$a_{\pi }(m)$ and ![]() $a_{\pi \times \widetilde {\pi }}(m)$ by the Dirichlet series identities
$a_{\pi \times \widetilde {\pi }}(m)$ by the Dirichlet series identities
 \[ \sum_{n=1}^{\infty}\frac{a_{\pi}(m)\Lambda(m)}{m^s}=-\frac{L'}{L}(s,\pi),\quad \sum_{n=1}^{\infty}\frac{a_{\pi\times\widetilde{\pi}}(m)\Lambda(m)}{m^s}=-\frac{L'}{L}(s,\pi\times\widetilde{\pi}),\quad\text{Re}(s)>1. \]
\[ \sum_{n=1}^{\infty}\frac{a_{\pi}(m)\Lambda(m)}{m^s}=-\frac{L'}{L}(s,\pi),\quad \sum_{n=1}^{\infty}\frac{a_{\pi\times\widetilde{\pi}}(m)\Lambda(m)}{m^s}=-\frac{L'}{L}(s,\pi\times\widetilde{\pi}),\quad\text{Re}(s)>1. \]
The local calculations in [Reference Luo, Rudnick and SarnakLRS95, Lemma 2.1] show that if ![]() $\chi \,(\mathrm {mod}\,\,q)$ is a primitive Dirichlet character and
$\chi \,(\mathrm {mod}\,\,q)$ is a primitive Dirichlet character and ![]() $\gcd (q,q_{\pi })=1$, then for all primes
$\gcd (q,q_{\pi })=1$, then for all primes ![]() $p$, we have that
$p$, we have that
 \begin{equation} L(s,\pi_p\times(\widetilde{\pi}\otimes\chi)_p) = \prod_{j=1}^n \prod_{j'=1}^{n}(1-\alpha_{j,j',\pi\times\widetilde{\pi}}(p)\chi(p)p^{-s})^{-1}. \end{equation}
\begin{equation} L(s,\pi_p\times(\widetilde{\pi}\otimes\chi)_p) = \prod_{j=1}^n \prod_{j'=1}^{n}(1-\alpha_{j,j',\pi\times\widetilde{\pi}}(p)\chi(p)p^{-s})^{-1}. \end{equation}
It follows from (3.6) and (8.1) that if ![]() $\gcd (m,q_{\pi })=1$, then
$\gcd (m,q_{\pi })=1$, then ![]() $a_{\pi \times (\widetilde {\pi }\otimes \chi )}(m) = |a_{\pi }(m)|^2 \chi (m)$. We now provide a convenient expression for
$a_{\pi \times (\widetilde {\pi }\otimes \chi )}(m) = |a_{\pi }(m)|^2 \chi (m)$. We now provide a convenient expression for ![]() $-L_{\chi }'(s)/L_{\chi }(s)$.
$-L_{\chi }'(s)/L_{\chi }(s)$.
Lemma 8.1 Let ![]() $\pi \in \mathfrak {F}_n$. Let
$\pi \in \mathfrak {F}_n$. Let ![]() $\psi \,(\mathrm {mod}\,\,q)$ be a Dirichlet character with
$\psi \,(\mathrm {mod}\,\,q)$ be a Dirichlet character with ![]() $q$ such that
$q$ such that ![]() $\gcd (q,q_{\pi })=1$ and
$\gcd (q,q_{\pi })=1$ and ![]() $\chi$ be the primitive Dirichlet character that induces
$\chi$ be the primitive Dirichlet character that induces ![]() $\psi$. Let
$\psi$. Let ![]() $\delta (\chi )=1$ if
$\delta (\chi )=1$ if ![]() $\chi$ is trivial and
$\chi$ is trivial and ![]() $\delta (\chi )=0$ otherwise. There exists a function
$\delta (\chi )=0$ otherwise. There exists a function ![]() $H_{\pi }(s;\chi,\psi )$ such that in the region
$H_{\pi }(s;\chi,\psi )$ such that in the region ![]() $\text {Re}(s)\geq 1- {1}/{n^2}$:
$\text {Re}(s)\geq 1- {1}/{n^2}$:
(1)
 $H_{\pi }(s;\chi,\psi )$ is holomorphic;
$H_{\pi }(s;\chi,\psi )$ is holomorphic;(2)
 $|H_{\pi }(s;\chi,\psi )|\ll _{\pi } \log (q(3+|\text {Im}(s)|))$; and
$|H_{\pi }(s;\chi,\psi )|\ll _{\pi } \log (q(3+|\text {Im}(s)|))$; and(3) we have the identity
 \[ \sum_{m=1}^{\infty}\frac{|a_{\pi}(m)|^2\psi(m)\Lambda(m)}{m^s}=\frac{\delta(\chi)}{s-1}-\frac{\Lambda_{\chi}'}{\Lambda_{\chi}}(s) +H_{\pi}(s;\chi,\psi). \]
\[ \sum_{m=1}^{\infty}\frac{|a_{\pi}(m)|^2\psi(m)\Lambda(m)}{m^s}=\frac{\delta(\chi)}{s-1}-\frac{\Lambda_{\chi}'}{\Lambda_{\chi}}(s) +H_{\pi}(s;\chi,\psi). \]
Proof. Suppose first that ![]() $\psi$ is primitive, in which case
$\psi$ is primitive, in which case ![]() $\psi =\chi$ and the function
$\psi =\chi$ and the function ![]() $H_{\pi }(s;\chi,\psi )$ is
$H_{\pi }(s;\chi,\psi )$ is
 \begin{align*} & \frac{\log q_{\pi\times(\widetilde{\pi}\otimes\chi)}}{2}+\frac{L'}{L}(s,\pi_{\infty}\times(\widetilde{\pi}\otimes\chi)_{\infty})+\frac{\delta(\chi)}{s}+\sum_{p \mid q_{\pi}q}\frac{L'}{L}(s,\pi_{p}\times(\widetilde{\pi}'\otimes\chi)_p) \\ &\quad -\sum_{p\mid q_{\pi}q}\sum_{\substack{1\leq j\leq n \\ 1\leq j'\leq n}}\frac{\alpha_{j,\pi}(p)\overline{\alpha_{j',\pi'}(p)}\chi(p)\log p}{p^s-\alpha_{j,\pi}(p)\overline{\alpha_{j',\pi}(p)}\chi(p)}. \end{align*}
\begin{align*} & \frac{\log q_{\pi\times(\widetilde{\pi}\otimes\chi)}}{2}+\frac{L'}{L}(s,\pi_{\infty}\times(\widetilde{\pi}\otimes\chi)_{\infty})+\frac{\delta(\chi)}{s}+\sum_{p \mid q_{\pi}q}\frac{L'}{L}(s,\pi_{p}\times(\widetilde{\pi}'\otimes\chi)_p) \\ &\quad -\sum_{p\mid q_{\pi}q}\sum_{\substack{1\leq j\leq n \\ 1\leq j'\leq n}}\frac{\alpha_{j,\pi}(p)\overline{\alpha_{j',\pi'}(p)}\chi(p)\log p}{p^s-\alpha_{j,\pi}(p)\overline{\alpha_{j',\pi}(p)}\chi(p)}. \end{align*}
This is holomorphic and bounded as claimed for ![]() $\text {Re}(s)\geq 1- {1}/{n^2}$ by (3.7), (3.10), and Stirling's formula. If
$\text {Re}(s)\geq 1- {1}/{n^2}$ by (3.7), (3.10), and Stirling's formula. If ![]() $\psi$ is not primitive and
$\psi$ is not primitive and ![]() $\chi$ is the primitive character that induces
$\chi$ is the primitive character that induces ![]() $\psi$, then in the same region, we have
$\psi$, then in the same region, we have
 \[ \bigg|\sum_{m=1}^{\infty}\frac{|a_{\pi}(m)|^2\psi(m)\Lambda(m)}{m^s}-\sum_{m=1}^{\infty}\frac{|a_{\pi}(m)|^2 \chi(m)\Lambda(m)}{m^s}\bigg|\leq\sum_{p \mid q}\sum_{k\geq 1}\frac{|a_{\pi}(p^k)|^2\log p}{p^{k\,{\text{Re}}(s)}}, \]
\[ \bigg|\sum_{m=1}^{\infty}\frac{|a_{\pi}(m)|^2\psi(m)\Lambda(m)}{m^s}-\sum_{m=1}^{\infty}\frac{|a_{\pi}(m)|^2 \chi(m)\Lambda(m)}{m^s}\bigg|\leq\sum_{p \mid q}\sum_{k\geq 1}\frac{|a_{\pi}(p^k)|^2\log p}{p^{k\,{\text{Re}}(s)}}, \]
which is bounded as desired using (3.7) again.
We use the following zero-free region for ![]() $L_{\chi }(s)$ and Siegel-type bound on any real exceptional zeros. We prove this theorem later.
$L_{\chi }(s)$ and Siegel-type bound on any real exceptional zeros. We prove this theorem later.
Theorem 8.2 Let ![]() $Q\geq 3$ and
$Q\geq 3$ and ![]() $\pi \in \mathfrak {F}_n$. There exists an effectively computable constant
$\pi \in \mathfrak {F}_n$. There exists an effectively computable constant ![]() $c_{12}=c_{12}(\pi )>0$ such that for all primitive Dirichlet characters
$c_{12}=c_{12}(\pi )>0$ such that for all primitive Dirichlet characters ![]() $\chi \,(\mathrm {mod}\,\,q)$ with
$\chi \,(\mathrm {mod}\,\,q)$ with ![]() $q\leq Q$ and
$q\leq Q$ and ![]() ${\gcd (q,q_{\pi })=1}$ with at most one exception, the
${\gcd (q,q_{\pi })=1}$ with at most one exception, the ![]() $L$-function
$L$-function ![]() $L(s,\pi \times (\widetilde {\pi }\otimes \chi ))$ does not vanish in the region
$L(s,\pi \times (\widetilde {\pi }\otimes \chi ))$ does not vanish in the region
If the exceptional character ![]() $\chi _1\,(\mathrm {mod}\,\,q_1)$ exists, then
$\chi _1\,(\mathrm {mod}\,\,q_1)$ exists, then ![]() $L(s,\pi \times (\widetilde {\pi }\otimes \chi _1))$ has at most one zero, say
$L(s,\pi \times (\widetilde {\pi }\otimes \chi _1))$ has at most one zero, say ![]() $\beta _1$, in this region;
$\beta _1$, in this region; ![]() $\beta _1$ is both real and simple; and
$\beta _1$ is both real and simple; and ![]() $\chi _1$ must be quadratic. Moreover, for all
$\chi _1$ must be quadratic. Moreover, for all ![]() $\varepsilon >0$, there exists an ineffective constant
$\varepsilon >0$, there exists an ineffective constant ![]() $c_{\pi }(\varepsilon )>0$ such that
$c_{\pi }(\varepsilon )>0$ such that ![]() $\beta _1\leq 1-c_{\pi }(\varepsilon )q_1^{-\varepsilon }$.
$\beta _1\leq 1-c_{\pi }(\varepsilon )q_1^{-\varepsilon }$.
8.2 Proof of Theorem 2.5
We follow Gallagher's proof of the Bombieri–Vinogradov theorem in [Reference GallagherGal68], with ![]() $n\geq 2$ and
$n\geq 2$ and ![]() $\pi \in \mathfrak {F}_n$ fixed at the onset. Note that the function
$\pi \in \mathfrak {F}_n$ fixed at the onset. Note that the function
 \[ \psi_k(y;q,a):= \frac{1}{k!}\sum_{\substack{m\leq y\\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)\Big(\log\frac{y}{m}\Big)^k \]
\[ \psi_k(y;q,a):= \frac{1}{k!}\sum_{\substack{m\leq y\\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)\Big(\log\frac{y}{m}\Big)^k \]
is monotonically increasing as a function of ![]() $y$ for each
$y$ for each ![]() $k\geq 0$. Thus, if
$k\geq 0$. Thus, if ![]() $0<\lambda \leq 1$, then
$0<\lambda \leq 1$, then
 \[ \frac{1}{\lambda}\int_{e^{-\lambda}y}^{y}\psi_{k-1}(t;q,a)\frac{dt}{t}\leq \psi_{k-1}(y;q,a)\leq \frac{1}{\lambda}\int_{y}^{e^{\lambda}y}\psi_{k-1}(t;q,a)\frac{dt}{t}. \]
\[ \frac{1}{\lambda}\int_{e^{-\lambda}y}^{y}\psi_{k-1}(t;q,a)\frac{dt}{t}\leq \psi_{k-1}(y;q,a)\leq \frac{1}{\lambda}\int_{y}^{e^{\lambda}y}\psi_{k-1}(t;q,a)\frac{dt}{t}. \]
The integrals, which equal ![]() $\psi _k(y;q,a)-\psi _k(e^{-\lambda }y;q,a)$ and
$\psi _k(y;q,a)-\psi _k(e^{-\lambda }y;q,a)$ and ![]() $\psi _k(e^{\lambda }y;q,a)-\psi _k(y;q,a)$, respectively, both have the same asymptotic expansion, namely
$\psi _k(e^{\lambda }y;q,a)-\psi _k(y;q,a)$, respectively, both have the same asymptotic expansion, namely
where ![]() $\varphi$ is Euler's totient function. Thus, we have the bounds
$\varphi$ is Euler's totient function. Thus, we have the bounds
and
 \[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x}|r_{k-1}(y;q,a)|\ll \lambda x\log x+\frac{1}{\lambda}\sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq ex}|r_k(y;q,a)|. \]
\[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x}|r_{k-1}(y;q,a)|\ll \lambda x\log x+\frac{1}{\lambda}\sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq ex}|r_k(y;q,a)|. \]
It follows by induction on ![]() $k$ that
$k$ that
 \[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x}|r_0(y;q,a)|\ll_k \lambda x\log x + \frac{1}{\lambda^{2^k-1}}\sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq ex}|r_k(y;q,a)|. \]
\[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x}|r_0(y;q,a)|\ll_k \lambda x\log x + \frac{1}{\lambda^{2^k-1}}\sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq ex}|r_k(y;q,a)|. \]
Proposition 8.3 If ![]() $\theta <1/(9n^3)$ is fixed and
$\theta <1/(9n^3)$ is fixed and ![]() $k=9n^2+1$, then for any
$k=9n^2+1$, then for any ![]() $B>0$, we have
$B>0$, we have
 \[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq ex}|r_k(y;q,a)|\ll_{\pi,B} \frac{x}{(\log x)^B}. \]
\[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq ex}|r_k(y;q,a)|\ll_{\pi,B} \frac{x}{(\log x)^B}. \]
Proposition 8.3 implies Theorem 2.5 It follows from Proposition 8.3 that
 \[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x}|r_0(y;q,a)|\ll_{\pi,B} \lambda x\log x+\frac{1}{\lambda^{2^k-1}}\frac{x}{(\log x)^B}. \]
\[ \sum_{\substack{q\leq x^{\theta} \\ \gcd(q,q_{\pi}\!)=1}}\max_{\gcd(a,q)=1}\max_{y\leq x}|r_0(y;q,a)|\ll_{\pi,B} \lambda x\log x+\frac{1}{\lambda^{2^k-1}}\frac{x}{(\log x)^B}. \]
To finish, we choose ![]() $B=2^k(A+1)-1$ and
$B=2^k(A+1)-1$ and ![]() $\lambda = (\log x)^{-(B+1)/2^k}$.
$\lambda = (\log x)^{-(B+1)/2^k}$.
8.3 Proof of Proposition 8.3
Let ![]() $\pi \in \mathfrak {F}_n$,
$\pi \in \mathfrak {F}_n$, ![]() $k=9n^2+1$,
$k=9n^2+1$, ![]() $Q= x^{\theta }$ for some fixed
$Q= x^{\theta }$ for some fixed ![]() $0<\theta <1/(9n^3)$, and
$0<\theta <1/(9n^3)$, and ![]() $q\leq Q$. We have the decomposition
$q\leq Q$. We have the decomposition
 \[ \frac{1}{k!}\sum_{\substack{m\leq y \\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)\Big(\log\frac{y}{m}\Big)^k =\frac{1}{k!}\sum_{\psi\,(\mathrm{mod}\,\,q)}\frac{\overline{\psi}(a)}{\varphi(q)}\sum_{\substack{y\leq m}}|a_{\pi}(m)|^2\Lambda(m)\psi(n)\Big(\!\log\frac{y}{m}\Big)^k. \]
\[ \frac{1}{k!}\sum_{\substack{m\leq y \\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m)\Big(\log\frac{y}{m}\Big)^k =\frac{1}{k!}\sum_{\psi\,(\mathrm{mod}\,\,q)}\frac{\overline{\psi}(a)}{\varphi(q)}\sum_{\substack{y\leq m}}|a_{\pi}(m)|^2\Lambda(m)\psi(n)\Big(\!\log\frac{y}{m}\Big)^k. \]
By Lemma 8.1 and Mellin inversion, this equals
 \[
\frac{1}{\varphi(q)}\sum_{\psi\,(\mathrm{mod}\,\,q)}\sum_{\substack{\text{$\chi$
primitive} \\ \text{$\chi$ induces
$\psi$}}}\frac{\overline{\chi}(a)}{2\pi
i}\int_{3-i\infty}^{3+i\infty}\bigg({-}\, \frac{\Lambda_{\chi}'}{\Lambda_{\chi}}(s)+H_{\pi}(s;\chi,\psi)\bigg)\frac{y^s}{s^{k+1}}\,ds.
\]
\[
\frac{1}{\varphi(q)}\sum_{\psi\,(\mathrm{mod}\,\,q)}\sum_{\substack{\text{$\chi$
primitive} \\ \text{$\chi$ induces
$\psi$}}}\frac{\overline{\chi}(a)}{2\pi
i}\int_{3-i\infty}^{3+i\infty}\bigg({-}\, \frac{\Lambda_{\chi}'}{\Lambda_{\chi}}(s)+H_{\pi}(s;\chi,\psi)\bigg)\frac{y^s}{s^{k+1}}\,ds.
\]
Since a primitive character ![]() $\chi \,(\mathrm {mod}\,\,q)$ induces characters to moduli that are a multiple of
$\chi \,(\mathrm {mod}\,\,q)$ induces characters to moduli that are a multiple of ![]() $q$, it follows from the bound
$q$, it follows from the bound ![]() $\sum _{f\leq Q,~q|f}\varphi (f)^{-1}\ll ({\log Q})/{\varphi (q)}$ that
$\sum _{f\leq Q,~q|f}\varphi (f)^{-1}\ll ({\log Q})/{\varphi (q)}$ that
 \begin{align} &\sum_{\substack{q\leq Q \nonumber\\ \gcd(q,q_{\pi}\!)=1}}~\max_{\gcd(a,q)=1}~\max_{y\leq x} \bigg|\frac{1}{k!}\sum_{\substack{m\leq y\\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m) \bigg(\log\frac{y}{m}\bigg)^k- \frac{y}{\varphi(q)}\bigg|\nonumber\\ &\quad \ll \sum_{\substack{q\leq Q \\ \gcd(q,q_{\pi}\!)=1}}\frac{\log Q}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\max_{y\leq x}\bigg|\frac{1}{2\pi i}\int_{3-i\infty}^{3+i\infty}\bigg({-}\,\frac{\Lambda_{\chi}'}{\Lambda_{\chi}}(s)+H_{\pi}(s;\chi,\chi)\bigg) \frac{y^s}{s^{k+1}}\,ds\bigg|. \end{align}
\begin{align} &\sum_{\substack{q\leq Q \nonumber\\ \gcd(q,q_{\pi}\!)=1}}~\max_{\gcd(a,q)=1}~\max_{y\leq x} \bigg|\frac{1}{k!}\sum_{\substack{m\leq y\\ m\equiv a\,(\mathrm{mod}\,\,q)}}|a_{\pi}(m)|^2\Lambda(m) \bigg(\log\frac{y}{m}\bigg)^k- \frac{y}{\varphi(q)}\bigg|\nonumber\\ &\quad \ll \sum_{\substack{q\leq Q \\ \gcd(q,q_{\pi}\!)=1}}\frac{\log Q}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\max_{y\leq x}\bigg|\frac{1}{2\pi i}\int_{3-i\infty}^{3+i\infty}\bigg({-}\,\frac{\Lambda_{\chi}'}{\Lambda_{\chi}}(s)+H_{\pi}(s;\chi,\chi)\bigg) \frac{y^s}{s^{k+1}}\,ds\bigg|. \end{align} Observe that by Lemma 8.1 and our range of ![]() $\theta$, (8.2) equals
$\theta$, (8.2) equals
 \begin{align} & \sum_{\substack{q\leq Q \nonumber\\ \gcd(q,q_{\pi}\!)=1}}\frac{\log Q}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\max_{y\leq x}\bigg|-\sum_{\substack{L_{\chi}(\rho)=0 }}\frac{y^{\rho}}{\rho^{k+1}}+ \frac{1}{2\pi i}\int_{1-{1}/{n^2}-i\infty}^{1-{1}/{n^2}+i\infty}H_{\pi}(s;\chi,\chi)\frac{y^s}{s^{k+1}}\,ds\bigg|\nonumber\\ &\quad \ll_{\pi,B}\log Q \sum_{\substack{q\leq Q \\ \gcd(q,q_{\pi}\!)=1}}\frac{1}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\sum_{\substack{L_{\chi}(\rho)=0 }}\frac{y^{\beta}}{|\rho|^{k+1}}+\frac{x}{(\log x)^B}, \end{align}
\begin{align} & \sum_{\substack{q\leq Q \nonumber\\ \gcd(q,q_{\pi}\!)=1}}\frac{\log Q}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\max_{y\leq x}\bigg|-\sum_{\substack{L_{\chi}(\rho)=0 }}\frac{y^{\rho}}{\rho^{k+1}}+ \frac{1}{2\pi i}\int_{1-{1}/{n^2}-i\infty}^{1-{1}/{n^2}+i\infty}H_{\pi}(s;\chi,\chi)\frac{y^s}{s^{k+1}}\,ds\bigg|\nonumber\\ &\quad \ll_{\pi,B}\log Q \sum_{\substack{q\leq Q \\ \gcd(q,q_{\pi}\!)=1}}\frac{1}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\sum_{\substack{L_{\chi}(\rho)=0 }}\frac{y^{\beta}}{|\rho|^{k+1}}+\frac{x}{(\log x)^B}, \end{align}
where ![]() $\rho =\beta +i\gamma$ ranges over the non-trivial zeros of
$\rho =\beta +i\gamma$ ranges over the non-trivial zeros of ![]() $L_{\chi }(s)$. In light of the bounds
$L_{\chi }(s)$. In light of the bounds ![]() $ {1}/{q} \leq {1}/{\varphi (q)}\ll ({\log (eq)})/{q}$, we dyadically decompose
$ {1}/{q} \leq {1}/{\varphi (q)}\ll ({\log (eq)})/{q}$, we dyadically decompose ![]() $[1,Q]$ into
$[1,Q]$ into ![]() $O(\log Q)$ subintervals and find that (8.3) is
$O(\log Q)$ subintervals and find that (8.3) is
 \begin{equation} \begin{aligned} &
\ll_{\pi,B} x(\log Q)^2\sup_{3\leq R\leq
Q}\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}\frac{1}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$
primitive}}}~\sum_{\substack{\rho=\beta+i\gamma
}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}\\ &
\ll_{\pi,B} x(\log Q)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$
primitive}}}~\sum_{\substack{\rho=\beta+i\gamma
}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}\\ &
\ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\bigg(\frac{x^{\beta_1-1}}{\beta_1^k}+\sum_{\substack{q\leq
R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$ primitive}}}
\sum_{\substack{\rho=\beta+i\gamma\neq\beta_1
}}\frac{x^{\beta-1}}{|\rho|^k}\bigg)+\frac{x}{(\log x)^B}.
\end{aligned} \end{equation}
\begin{equation} \begin{aligned} &
\ll_{\pi,B} x(\log Q)^2\sup_{3\leq R\leq
Q}\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}\frac{1}{\varphi(q)}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$
primitive}}}~\sum_{\substack{\rho=\beta+i\gamma
}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}\\ &
\ll_{\pi,B} x(\log Q)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$
primitive}}}~\sum_{\substack{\rho=\beta+i\gamma
}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}\\ &
\ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\bigg(\frac{x^{\beta_1-1}}{\beta_1^k}+\sum_{\substack{q\leq
R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$ primitive}}}
\sum_{\substack{\rho=\beta+i\gamma\neq\beta_1
}}\frac{x^{\beta-1}}{|\rho|^k}\bigg)+\frac{x}{(\log x)^B}.
\end{aligned} \end{equation}
where ![]() $\beta _1$ is the exceptional zero in Theorem 8.2. The term
$\beta _1$ is the exceptional zero in Theorem 8.2. The term ![]() $x^{\beta _1-1}/\beta _1^k$ is omitted if
$x^{\beta _1-1}/\beta _1^k$ is omitted if ![]() $\beta _1$ does not exist.
$\beta _1$ does not exist.
If ![]() $\beta _1$ exists as in Theorem 8.2 and the supremum is achieved when
$\beta _1$ exists as in Theorem 8.2 and the supremum is achieved when ![]() $R\leq (\log x)^{4B}$, then we apply Theorem 8.2 with
$R\leq (\log x)^{4B}$, then we apply Theorem 8.2 with ![]() $\varepsilon = {1}/{8B}$ and conclude that the contribution from such a zero is absorbed in our error term. If the supremum is achieved when
$\varepsilon = {1}/{8B}$ and conclude that the contribution from such a zero is absorbed in our error term. If the supremum is achieved when ![]() $R>(\log x)^{4B}$, then contribution from
$R>(\log x)^{4B}$, then contribution from ![]() $\beta _1$ is trivially absorbed in our error term. Hence, (8.4) is
$\beta _1$ is trivially absorbed in our error term. Hence, (8.4) is
 \begin{equation} \ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq x^{\theta}}\frac{1}{R} \sum_{\substack{q\leq R \\ \gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\sum_{\substack{\rho=\beta+i\gamma\neq\beta_1 }}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}. \end{equation}
\begin{equation} \ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq x^{\theta}}\frac{1}{R} \sum_{\substack{q\leq R \\ \gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}}\sum_{\substack{\rho=\beta+i\gamma\neq\beta_1 }}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}. \end{equation} Now let us consider the zeros ![]() $\rho$ with
$\rho$ with ![]() $|\rho |<\frac {1}{4}$. The number of such zeros is
$|\rho |<\frac {1}{4}$. The number of such zeros is ![]() $\ll R^2\log R$. From the consideration of the corresponding zeros
$\ll R^2\log R$. From the consideration of the corresponding zeros ![]() $1-\rho$ of
$1-\rho$ of ![]() $L_{\overline {\chi }}(s)$, we deduce that
$L_{\overline {\chi }}(s)$, we deduce that ![]() $|\rho |\gg x^{-1/(4k)}$. Thus, the contribution from these zeros is
$|\rho |\gg x^{-1/(4k)}$. Thus, the contribution from these zeros is ![]() $\ll R x^{ {1}/{4}+ {k}/{4k}}\log R\ll Q x^{ {1}/{2}}\log Q \ll _{B} x(\log x)^{-B}$. Define
$\ll R x^{ {1}/{4}+ {k}/{4k}}\log R\ll Q x^{ {1}/{2}}\log Q \ll _{B} x(\log x)^{-B}$. Define ![]() $T_0=0$ and
$T_0=0$ and ![]() $T_j=2^{j-1}$ for
$T_j=2^{j-1}$ for ![]() $j\geq 1$. The above discussion shows that (8.5) is
$j\geq 1$. The above discussion shows that (8.5) is
 \begin{align} &
\ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$ primitive}}}
\sum_{\substack{\rho=\beta+i\gamma\neq \beta_1 \\
|\rho|>\frac{1}{4}}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log
x)^B}\nonumber\\ & \ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\sum_{j=1}^{\infty}~\sum_{\substack{q\leq
R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$
primitive}}}~\sideset{}{'}\sum_{\substack{\rho=\beta+i\gamma\neq\beta_1
\\ |\rho|\geq\frac{1}{4} \\ T_{j-1}\leq|\gamma|\leq
T_j}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}.
\end{align}
\begin{align} &
\ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$ primitive}}}
\sum_{\substack{\rho=\beta+i\gamma\neq \beta_1 \\
|\rho|>\frac{1}{4}}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log
x)^B}\nonumber\\ & \ll_{\pi,B} x(\log x)^3\sup_{3\leq R\leq
x^{\theta}}\frac{1}{R}\sum_{j=1}^{\infty}~\sum_{\substack{q\leq
R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$
primitive}}}~\sideset{}{'}\sum_{\substack{\rho=\beta+i\gamma\neq\beta_1
\\ |\rho|\geq\frac{1}{4} \\ T_{j-1}\leq|\gamma|\leq
T_j}}\frac{x^{\beta-1}}{|\rho|^k}+\frac{x}{(\log x)^B}.
\end{align}
If ![]() $|\rho |\geq \frac {1}{4}$ and
$|\rho |\geq \frac {1}{4}$ and ![]() $T_{j-1}\leq |\gamma |\leq T_j$, then
$T_{j-1}\leq |\gamma |\leq T_j$, then ![]() $|\rho |\geq \max \{T_{j-1},\frac {1}{4}\}\geq T_j/4$ and
$|\rho |\geq \max \{T_{j-1},\frac {1}{4}\}\geq T_j/4$ and ![]() $|\rho |\gg |\gamma |+3$. Therefore, if
$|\rho |\gg |\gamma |+3$. Therefore, if ![]() $\delta = \min \{1-9n^3\theta,\tfrac {1}{2}\}$, then
$\delta = \min \{1-9n^3\theta,\tfrac {1}{2}\}$, then
 \begin{align*} x^{\beta-1}|\rho|^{-k}&\ll T_j^{-{1}/{2}}(|\gamma|+1)^{-{1}/{2}}x^{-(1-\beta)\delta}(x^{1-\delta}T_j^{k-1})^{-(1-\beta)}\\ &\ll T_j^{-{1}/{2}}(|\gamma|+1)^{-{1}/{2}}x^{-(1-\beta)\delta}(R^{({1-\delta})/{\theta}}T_j^{k-1})^{\beta-1}. \end{align*}
\begin{align*} x^{\beta-1}|\rho|^{-k}&\ll T_j^{-{1}/{2}}(|\gamma|+1)^{-{1}/{2}}x^{-(1-\beta)\delta}(x^{1-\delta}T_j^{k-1})^{-(1-\beta)}\\ &\ll T_j^{-{1}/{2}}(|\gamma|+1)^{-{1}/{2}}x^{-(1-\beta)\delta}(R^{({1-\delta})/{\theta}}T_j^{k-1})^{\beta-1}. \end{align*}
Since ![]() $\rho =\beta +i\gamma \neq \beta _1$, it follows from Theorem 8.2 that
$\rho =\beta +i\gamma \neq \beta _1$, it follows from Theorem 8.2 that
so (8.6) is
 \begin{align*} &\ll_{\pi,B}x(\log x)^3
\sup_{3\leq R\leq x^{\theta}}\frac{e^{-\delta
\eta(x,R)}}{R}\sum_{j=1}^{\infty}T_j^{-{1}/{2}}\\
&\quad\times\sum_{\substack{q\leq
R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$ primitive}}}~\sum_{\substack{\rho=\beta+i\gamma\neq
\beta_1\\ |\gamma|\leq
T_j}}(R^{({1-\delta})/{\theta}}T_j^{k-1})^{\beta-1}+\frac{x}{(\log
x)^B}. \end{align*}
\begin{align*} &\ll_{\pi,B}x(\log x)^3
\sup_{3\leq R\leq x^{\theta}}\frac{e^{-\delta
\eta(x,R)}}{R}\sum_{j=1}^{\infty}T_j^{-{1}/{2}}\\
&\quad\times\sum_{\substack{q\leq
R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q)
\\ \text{$\chi$ primitive}}}~\sum_{\substack{\rho=\beta+i\gamma\neq
\beta_1\\ |\gamma|\leq
T_j}}(R^{({1-\delta})/{\theta}}T_j^{k-1})^{\beta-1}+\frac{x}{(\log
x)^B}. \end{align*}
Define
 \[
N_{\pi}^*(\sigma,T,R)=\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\bmod q \\
\text{$\chi$ primitive}}}|\{\rho=\beta+i\gamma\colon
\beta\geq\sigma,~|\gamma|\leq T,~L_{\chi}(\rho)=0\}|.
\]
\[
N_{\pi}^*(\sigma,T,R)=\sum_{\substack{q\leq R \\
\gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\bmod q \\
\text{$\chi$ primitive}}}|\{\rho=\beta+i\gamma\colon
\beta\geq\sigma,~|\gamma|\leq T,~L_{\chi}(\rho)=0\}|.
\]
By (3.10), there exists an effectively computable constant ![]() $c_{13}=c_{13}(n)>0$ such that
$c_{13}=c_{13}(n)>0$ such that
Thus, by (1.7), we have ![]() $N_{\pi }^*(\sigma,T,R)\ll _{\pi,\varepsilon }(R^n T)^{9n^2(1-\sigma )+\varepsilon }$. Partial summation yields
$N_{\pi }^*(\sigma,T,R)\ll _{\pi,\varepsilon }(R^n T)^{9n^2(1-\sigma )+\varepsilon }$. Partial summation yields
 \begin{align} &\sum_{\substack{q\leq R \nonumber\\ \gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}} \sum_{\substack{\rho=\beta+i\gamma\neq \beta_1\\ |\gamma|\leq T_j}}(R^{({1-\delta})/{\theta}}T_j^{k-1})^{-(1-\beta)}\nonumber\\ &\quad\ll (R^{({1-\delta})/{\theta}}T_j^{k-1})^{-1}N_{\pi}^*(0,T_j,R)+\log(RT_j)\int_0^1 (R^{({1-\delta})/{\theta}}T_j^{k-1})^{-\sigma}N_{\pi}^*(1-\sigma,T_j,R)\,d\sigma\nonumber\\ &\quad\ll_{\pi,\varepsilon} (R T_j)^{\varepsilon}\bigg((R^{({1-\delta})/{\theta}}T_j^{k-1})^{-1}R T_j+ \int_0^1 (R^{({1-\delta})/{\theta}}T_j^{k-1})^{-\sigma}(R^n T_j)^{9n^2\sigma}d\sigma\bigg). \end{align}
\begin{align} &\sum_{\substack{q\leq R \nonumber\\ \gcd(q,q_{\pi}\!)=1}}~\sum_{\substack{\chi\,(\mathrm{mod}\,\,q) \\ \text{$\chi$ primitive}}} \sum_{\substack{\rho=\beta+i\gamma\neq \beta_1\\ |\gamma|\leq T_j}}(R^{({1-\delta})/{\theta}}T_j^{k-1})^{-(1-\beta)}\nonumber\\ &\quad\ll (R^{({1-\delta})/{\theta}}T_j^{k-1})^{-1}N_{\pi}^*(0,T_j,R)+\log(RT_j)\int_0^1 (R^{({1-\delta})/{\theta}}T_j^{k-1})^{-\sigma}N_{\pi}^*(1-\sigma,T_j,R)\,d\sigma\nonumber\\ &\quad\ll_{\pi,\varepsilon} (R T_j)^{\varepsilon}\bigg((R^{({1-\delta})/{\theta}}T_j^{k-1})^{-1}R T_j+ \int_0^1 (R^{({1-\delta})/{\theta}}T_j^{k-1})^{-\sigma}(R^n T_j)^{9n^2\sigma}d\sigma\bigg). \end{align}
Our choices for ![]() $\theta$,
$\theta$, ![]() $k$, and
$k$, and ![]() $\delta$ ensure that (8.7) is
$\delta$ ensure that (8.7) is ![]() $\ll _{\pi,\varepsilon } (R T_j)^{\varepsilon }$. Thus, (8.6) is
$\ll _{\pi,\varepsilon } (R T_j)^{\varepsilon }$. Thus, (8.6) is
 \begin{align}&
\ll_{\pi,B,\varepsilon} x(\log x)^3 \sup_{3\leq R\leq
x^{\theta}}e^{-\delta
\eta_{\pi}(x,R)}\frac{R^{\varepsilon}}{R}\sum_{j=1}^{\infty}T_j^{-{1}/{2}+\varepsilon}+\frac{x}{(\log
x)^B}\nonumber\\ & \ll_{\pi,B,\varepsilon} x(\log x)^3 \sup_{3\leq
R\leq x^{\theta}}e^{-\delta
\eta_{\pi}(x,R)}\frac{R^{\varepsilon}}{R}+\frac{x}{(\log
x)^B}. \end{align}
\begin{align}&
\ll_{\pi,B,\varepsilon} x(\log x)^3 \sup_{3\leq R\leq
x^{\theta}}e^{-\delta
\eta_{\pi}(x,R)}\frac{R^{\varepsilon}}{R}\sum_{j=1}^{\infty}T_j^{-{1}/{2}+\varepsilon}+\frac{x}{(\log
x)^B}\nonumber\\ & \ll_{\pi,B,\varepsilon} x(\log x)^3 \sup_{3\leq
R\leq x^{\theta}}e^{-\delta
\eta_{\pi}(x,R)}\frac{R^{\varepsilon}}{R}+\frac{x}{(\log
x)^B}. \end{align}
A small calculation (cf. [Reference Thorner and ZamanTZ19, § 4]) shows that there is a constant ![]() $c_{14}=c_{14}(\pi )>0$ such that
$c_{14}=c_{14}(\pi )>0$ such that ![]() $e^{-\delta \eta _{\pi }(x,R)}\ll _{\pi,B,\varepsilon } \exp (-c_{14} {\log x}/{\!\log R})+\exp (-c_{14}\sqrt {\log x})$, and Theorem 2.5 follows.
$e^{-\delta \eta _{\pi }(x,R)}\ll _{\pi,B,\varepsilon } \exp (-c_{14} {\log x}/{\!\log R})+\exp (-c_{14}\sqrt {\log x})$, and Theorem 2.5 follows.
8.4 Proof of Theorem 8.2
Although the proof of Theorem 8.2 contains only standard techniques, such zero-free regions for ![]() $L_{\chi }(s)$ are new even in the case when
$L_{\chi }(s)$ are new even in the case when ![]() $\chi$ is trivial. The case when
$\chi$ is trivial. The case when ![]() $\chi$ is trivial was only recently handled unconditionally in [Reference Humphries and ThornerHT22].
$\chi$ is trivial was only recently handled unconditionally in [Reference Humphries and ThornerHT22].
Lemma 8.4 [Reference Humphries and ThornerHT22, Theorem 2.1(1)]
Let ![]() $\pi \in \mathfrak {F}_n$. There exists an absolute and effectively computable constant
$\pi \in \mathfrak {F}_n$. There exists an absolute and effectively computable constant ![]() $c_{15}>0$ such that
$c_{15}>0$ such that ![]() $L_{1}(s)$ has at most one zero, say
$L_{1}(s)$ has at most one zero, say ![]() $\beta _1$, in the region
$\beta _1$, in the region ![]() $\text {Re}(s)\geq 1-c_{15}/\!\log (C(\pi )^n(|\text {Im}(s)|+e)^{n^2})$. If
$\text {Re}(s)\geq 1-c_{15}/\!\log (C(\pi )^n(|\text {Im}(s)|+e)^{n^2})$. If ![]() $\beta _1$ exists, then it must be real and simple, and there exists an absolute and effectively computable constant
$\beta _1$ exists, then it must be real and simple, and there exists an absolute and effectively computable constant ![]() $c_{16}$ such that
$c_{16}$ such that ![]() $\beta _1\leq 1-C(\pi )^{-c_{16}n}$.
$\beta _1\leq 1-C(\pi )^{-c_{16}n}$.
We prove the corresponding result for ![]() $L_{\chi }(s)$. The ideas in [Reference Humphries and ThornerHT22] inform our approach here.
$L_{\chi }(s)$. The ideas in [Reference Humphries and ThornerHT22] inform our approach here.
Lemma 8.5 Let ![]() $\pi \in \mathfrak {F}_{n}$. Let
$\pi \in \mathfrak {F}_{n}$. Let ![]() $\chi \,(\mathrm {mod}\,\,q)$ be a non-trivial primitive Dirichlet character such that
$\chi \,(\mathrm {mod}\,\,q)$ be a non-trivial primitive Dirichlet character such that ![]() $\gcd (q,q_{\pi })=1$. There exists an effectively computable constant
$\gcd (q,q_{\pi })=1$. There exists an effectively computable constant ![]() $c_{17}=c_{17}(n)>0$ such that
$c_{17}=c_{17}(n)>0$ such that ![]() $L_{\chi }(s)$ has at most one zero, say
$L_{\chi }(s)$ has at most one zero, say ![]() $\beta _1$, in the region
$\beta _1$, in the region
If the exceptional zero ![]() $\beta _1$ exists, then it is real and simple, and
$\beta _1$ exists, then it is real and simple, and ![]() $\chi$ is quadratic.
$\chi$ is quadratic.
Proof. Let ![]() $\chi \,(\mathrm {mod}\,\,q)$ be a primitive non-trivial Dirichlet character, let
$\chi \,(\mathrm {mod}\,\,q)$ be a primitive non-trivial Dirichlet character, let ![]() $\psi$ be the primitive character that induces
$\psi$ be the primitive character that induces ![]() $\chi ^2$, and let
$\chi ^2$, and let ![]() $\beta +i\gamma$ be a non-trivial zero of
$\beta +i\gamma$ be a non-trivial zero of ![]() $L_{\chi }(s)$. Define
$L_{\chi }(s)$. Define ![]() $\Pi _{\chi }=\pi \boxplus \pi \otimes \chi |\cdot |^{it}\boxplus \pi \otimes \overline {\chi }|\cdot |^{-it}$, and define
$\Pi _{\chi }=\pi \boxplus \pi \otimes \chi |\cdot |^{it}\boxplus \pi \otimes \overline {\chi }|\cdot |^{-it}$, and define
The factor ![]() $L_1(s)^3$ has a pole of order 3 at
$L_1(s)^3$ has a pole of order 3 at ![]() $s=1$, and the hypothesis that
$s=1$, and the hypothesis that ![]() $\gcd (q,q_{\pi })=1$ ensures that
$\gcd (q,q_{\pi })=1$ ensures that ![]() $L_{\chi }(s+i\gamma )^2 L_{\overline {\chi }}(s-i\gamma )^2$ is entire. If
$L_{\chi }(s+i\gamma )^2 L_{\overline {\chi }}(s-i\gamma )^2$ is entire. If ![]() $\psi$ is complex, then
$\psi$ is complex, then ![]() $L_{\psi }(s+2i\gamma )L_{\overline {\psi }}(s-2i\gamma )$ is entire; otherwise, it has poles of order 1 at
$L_{\psi }(s+2i\gamma )L_{\overline {\psi }}(s-2i\gamma )$ is entire; otherwise, it has poles of order 1 at ![]() $s=1\pm 2i\gamma$. The additional poles when
$s=1\pm 2i\gamma$. The additional poles when ![]() $\psi$ is real require some additional casework when
$\psi$ is real require some additional casework when ![]() $\gamma$ is close to zero. For notational compactness, let
$\gamma$ is close to zero. For notational compactness, let ![]() $\mathcal {Q}_{\gamma }=qC(\pi )(|\gamma |+3)$. Note that
$\mathcal {Q}_{\gamma }=qC(\pi )(|\gamma |+3)$. Note that ![]() $-(D'/D)(s)$ has non-negative Dirichlet coefficients per [Reference Hoffstein and RamakrishnanHR95, Lemma a].
$-(D'/D)(s)$ has non-negative Dirichlet coefficients per [Reference Hoffstein and RamakrishnanHR95, Lemma a].
The functional equation for ![]() $L_{\chi }(s)$ together with the fact that
$L_{\chi }(s)$ together with the fact that ![]() $L(s,\pi \times \widetilde {\pi })$ is a self-dual
$L(s,\pi \times \widetilde {\pi })$ is a self-dual ![]() $L$-function (even if
$L$-function (even if ![]() $L(s,\pi )$ itself is not self-dual) implies that if
$L(s,\pi )$ itself is not self-dual) implies that if ![]() $\rho$ is a zero of
$\rho$ is a zero of ![]() $L_{\chi }(s)$, then
$L_{\chi }(s)$, then ![]() $\overline {\rho }$ is a zero of
$\overline {\rho }$ is a zero of ![]() $L_{\overline {\chi }}(s)$. Thus, we have that
$L_{\overline {\chi }}(s)$. Thus, we have that
Let ![]() $\omega$ denote a non-trivial zero of
$\omega$ denote a non-trivial zero of ![]() $D(s)$,
$D(s)$, ![]() $\delta (\psi )=1$ if
$\delta (\psi )=1$ if ![]() $\psi$ is trivial, and
$\psi$ is trivial, and ![]() $\delta (\psi )=0$ otherwise. We apply Lemma 3.2 and (3.10) to (8.10), concluding that if
$\delta (\psi )=0$ otherwise. We apply Lemma 3.2 and (3.10) to (8.10), concluding that if ![]() $1<\sigma <2$, then
$1<\sigma <2$, then
where ![]() $c_{18}=c_{18}(n)>1$ is a suitable implied constant. Since
$c_{18}=c_{18}(n)>1$ is a suitable implied constant. Since ![]() $\beta <1$ is, by hypothesis, one of the zeros in the sum in (8.12), we have by (8.11) and non-negativity that
$\beta <1$ is, by hypothesis, one of the zeros in the sum in (8.12), we have by (8.11) and non-negativity that
Case 1: Either  $\chi$ is real and
$\chi$ is real and  $|\gamma |\geq {1}/{7c_{22}\log \mathcal {Q}_0}$ or
$|\gamma |\geq {1}/{7c_{22}\log \mathcal {Q}_0}$ or  $\chi$ is complex
$\chi$ is complex
If ![]() $\sigma = 1+ {1}/{5c_{18}\log \mathcal {Q}_{\gamma }}$, then
$\sigma = 1+ {1}/{5c_{18}\log \mathcal {Q}_{\gamma }}$, then
Thus, (8.13) becomes
Upon solving for ![]() $\beta$, we conclude that
$\beta$, we conclude that ![]() $\beta \leq 1- {1}/{136c_{18}\mathcal {Q}_{\gamma }}$.
$\beta \leq 1- {1}/{136c_{18}\mathcal {Q}_{\gamma }}$.
Case 2:  $\chi$ is real and
$\chi$ is real and  $\gamma =0$
$\gamma =0$
We start at (8.12) with ![]() $\delta (\psi )=1$,
$\delta (\psi )=1$, ![]() $\gamma =0$, and
$\gamma =0$, and ![]() $\sigma = 1+ {1}/{3c_{18}\log \mathcal {Q}_0}$. If there are
$\sigma = 1+ {1}/{3c_{18}\log \mathcal {Q}_0}$. If there are ![]() $N$ zeros
$N$ zeros ![]() $\beta$ (with multiplicity) of
$\beta$ (with multiplicity) of ![]() $D(s)$ such that
$D(s)$ such that ![]() $\beta \geq 1- {1}/{96c_{18}\log \mathcal {Q}_0}$, then by (8.12),
$\beta \geq 1- {1}/{96c_{18}\log \mathcal {Q}_0}$, then by (8.12),
It follows that (since ![]() $N$ is an integer)
$N$ is an integer) ![]() $N\leq \lfloor \frac {11}{2}\rfloor =5$. By the bound (8.11),
$N\leq \lfloor \frac {11}{2}\rfloor =5$. By the bound (8.11), ![]() $L_{\chi }(s)$ has at most one real zero
$L_{\chi }(s)$ has at most one real zero ![]() $\beta$, necessarily simple, satisfying
$\beta$, necessarily simple, satisfying ![]() $\beta \geq 1- {1}/{96c_{18}\log \mathcal {Q}_0}$.
$\beta \geq 1- {1}/{96c_{18}\log \mathcal {Q}_0}$.
Case 3:  $\chi$ is quadratic and
$\chi$ is quadratic and  $0<|\gamma |<{1}/{7c_{22}\log \mathcal {Q}_0}$
$0<|\gamma |<{1}/{7c_{22}\log \mathcal {Q}_0}$
We apply Lemma 3.2 to ![]() $L_{1}(s)L_{\chi }(s)$. The only singularity is a simple pole at
$L_{1}(s)L_{\chi }(s)$. The only singularity is a simple pole at ![]() $s=1$. Both
$s=1$. Both ![]() $L_{1}(s)$ and
$L_{1}(s)$ and ![]() $L_{\chi }(s)$ are self-dual, so if
$L_{\chi }(s)$ are self-dual, so if ![]() $\beta +i\gamma$ is a non-trivial zero of
$\beta +i\gamma$ is a non-trivial zero of ![]() $L_1(s)L_{\chi }(s)=0$, then so is
$L_1(s)L_{\chi }(s)=0$, then so is ![]() $\beta -i\gamma$. By (8.1), the
$\beta -i\gamma$. By (8.1), the ![]() $m$th Dirichlet coefficient of
$m$th Dirichlet coefficient of ![]() $- {L_{1}'}/{L_{1}}(s)- {L_{\chi }'}/{L_{\chi }}(s)$ is
$- {L_{1}'}/{L_{1}}(s)- {L_{\chi }'}/{L_{\chi }}(s)$ is ![]() $(1+\chi (m))a_{\pi \times \widetilde {\pi }}(m)\Lambda (m)\geq 0$, so Lemma 3.2 yields
$(1+\chi (m))a_{\pi \times \widetilde {\pi }}(m)\Lambda (m)\geq 0$, so Lemma 3.2 yields
If ![]() $\sigma = 1+ {1}/{2c_{18}\log \mathcal {Q}_{\gamma }}$ and
$\sigma = 1+ {1}/{2c_{18}\log \mathcal {Q}_{\gamma }}$ and ![]() $0<|\gamma |< {1}/{7c_{18}\log \mathcal {Q}_{0}}$ in (8.14), then
$0<|\gamma |< {1}/{7c_{18}\log \mathcal {Q}_{0}}$ in (8.14), then ![]() $\beta \leq 1- {1}/{8c_{18}\log \mathcal {Q}_{\gamma }}$.
$\beta \leq 1- {1}/{8c_{18}\log \mathcal {Q}_{\gamma }}$.
We now prove a Siegel-type bound for ![]() $\beta _1$ in Lemma 8.5 (if it exists) using the ideas of Hoffstein and Lockhart [Reference Hoffstein and LockhartHL94]. This is new for all
$\beta _1$ in Lemma 8.5 (if it exists) using the ideas of Hoffstein and Lockhart [Reference Hoffstein and LockhartHL94]. This is new for all ![]() $\pi \in \mathfrak {F}_n$ with
$\pi \in \mathfrak {F}_n$ with ![]() $n\geq 3$. We begin with an auxiliary calculation. Let
$n\geq 3$. We begin with an auxiliary calculation. Let ![]() $\chi \,(\mathrm {mod}\,\,q)$ and
$\chi \,(\mathrm {mod}\,\,q)$ and ![]() $\chi '\,(\mathrm {mod}\,\,q')$ be distinct non-trivial quadratic Dirichlet characters such that
$\chi '\,(\mathrm {mod}\,\,q')$ be distinct non-trivial quadratic Dirichlet characters such that ![]() $\gcd (q'q,q_{\pi })=1$, and let
$\gcd (q'q,q_{\pi })=1$, and let ![]() $\psi$ be the primitive character that induces
$\psi$ be the primitive character that induces ![]() $\chi '\chi$ (whose conductor is necessarily coprime to
$\chi '\chi$ (whose conductor is necessarily coprime to ![]() $q_{\pi }$). These coprimality restrictions ensure that
$q_{\pi }$). These coprimality restrictions ensure that ![]() $\pi \neq \pi \otimes \chi$,
$\pi \neq \pi \otimes \chi$, ![]() $\pi \neq \pi \otimes \chi '$,
$\pi \neq \pi \otimes \chi '$, ![]() $\pi \neq \pi \otimes \psi$,
$\pi \neq \pi \otimes \psi$, ![]() $q_{\pi \otimes \chi }=q_{\pi }q^n$,
$q_{\pi \otimes \chi }=q_{\pi }q^n$, ![]() $q_{\pi \otimes \chi '}=q_{\pi }(q')^n$, and
$q_{\pi \otimes \chi '}=q_{\pi }(q')^n$, and ![]() $q_{\pi \otimes \psi }=q_{\psi }q^n$. We also have that
$q_{\pi \otimes \psi }=q_{\psi }q^n$. We also have that ![]() $q_{\psi }|q_{\chi }q_{\chi '}$. Let
$q_{\psi }|q_{\chi }q_{\chi '}$. Let
By the above discussion, ![]() $L(s,\Pi ^{\star })$ is holomorphic apart from a simple pole at
$L(s,\Pi ^{\star })$ is holomorphic apart from a simple pole at ![]() $s=1$. It follows from (8.1) that if
$s=1$. It follows from (8.1) that if ![]() $k\geq 1$, then the
$k\geq 1$, then the ![]() $p^k$th Dirichlet coefficient of
$p^k$th Dirichlet coefficient of ![]() $\log L(s,\Pi ^{\star })$ equals
$\log L(s,\Pi ^{\star })$ equals
The non-negativity of ![]() $1+\chi (p^k)+\chi '(p^k)+\psi (p^k)$ follows from the fact that this sum is a Dirichlet coefficient of the Dedekind zeta function of a biquadratic field. Upon exponentiating, we find that the
$1+\chi (p^k)+\chi '(p^k)+\psi (p^k)$ follows from the fact that this sum is a Dirichlet coefficient of the Dedekind zeta function of a biquadratic field. Upon exponentiating, we find that the ![]() $m$th Dirichlet coefficient
$m$th Dirichlet coefficient ![]() $\lambda _{\Pi ^{\star }}(m)$ of
$\lambda _{\Pi ^{\star }}(m)$ of ![]() $L(s,\Pi ^{\star })$ is non-negative.
$L(s,\Pi ^{\star })$ is non-negative.
Lemma 8.6 If ![]() $\pi \in \mathfrak {F}_n$ and
$\pi \in \mathfrak {F}_n$ and ![]() $\chi$ is a primitive non-trivial real Dirichlet character, then
$\chi$ is a primitive non-trivial real Dirichlet character, then ![]() $L_{\chi }(1)>0$ and the Dirichlet coefficients of
$L_{\chi }(1)>0$ and the Dirichlet coefficients of ![]() $L_{1}(s)L_{\chi }(s)$ are non-negative.
$L_{1}(s)L_{\chi }(s)$ are non-negative.
Proof. Let ![]() $K$ be the quadratic field associated to
$K$ be the quadratic field associated to ![]() $\chi$. If
$\chi$. If ![]() $\pi _{\mathrm {BC}}$ is the base change of
$\pi _{\mathrm {BC}}$ is the base change of ![]() $\pi$ to an automorphic representation of
$\pi$ to an automorphic representation of ![]() $\mathrm {GL}_n(\mathbb {A}_K)$, then
$\mathrm {GL}_n(\mathbb {A}_K)$, then ![]() $L(s,\pi _{\mathrm {BC}}\times \widetilde {\pi }_{\mathrm {BC}})=L_{1}(s)L_{\chi }(s)$. Since
$L(s,\pi _{\mathrm {BC}}\times \widetilde {\pi }_{\mathrm {BC}})=L_{1}(s)L_{\chi }(s)$. Since ![]() $L(s,\pi _{\mathrm {BC}}\times \widetilde {\pi }_{\mathrm {BC}})$ is holomorphic on
$L(s,\pi _{\mathrm {BC}}\times \widetilde {\pi }_{\mathrm {BC}})$ is holomorphic on ![]() $\mathbb {C}-\{1\}$ apart from a simple pole at
$\mathbb {C}-\{1\}$ apart from a simple pole at ![]() $s=1$, the same holds for
$s=1$, the same holds for ![]() $L_{1}(s)L_{\chi }(s)$. Since
$L_{1}(s)L_{\chi }(s)$. Since ![]() $\gcd (q,q_{\pi })=1$ (hence,
$\gcd (q,q_{\pi })=1$ (hence, ![]() $L_{\chi }(s)$ is entire), the residue of
$L_{\chi }(s)$ is entire), the residue of ![]() $L(s,\pi _{\mathrm {BC}}\times \widetilde {\pi }_{\mathrm {BC}})$ at
$L(s,\pi _{\mathrm {BC}}\times \widetilde {\pi }_{\mathrm {BC}})$ at ![]() $s=1$, which is positive, equals
$s=1$, which is positive, equals ![]() $L_{\chi }(1)\mathrm {Res}_{s=1}L_{1}(s)$. Since
$L_{\chi }(1)\mathrm {Res}_{s=1}L_{1}(s)$. Since ![]() $\mathrm {Res}_{s=1}L_{1}(s)>0$, it follows that
$\mathrm {Res}_{s=1}L_{1}(s)>0$, it follows that ![]() $L_{\chi }(1)>0$. The Dirichlet coefficients of
$L_{\chi }(1)>0$. The Dirichlet coefficients of ![]() $L_{1}(s)L_{\chi }(s)$ are non-negative per case 3 in the proof of Lemma 8.5.
$L_{1}(s)L_{\chi }(s)$ are non-negative per case 3 in the proof of Lemma 8.5.
Let ![]() $0<\varepsilon <1$, and let
$0<\varepsilon <1$, and let ![]() $\beta \in (1-\varepsilon,1)$. By (3.13) and the above discussion, we have
$\beta \in (1-\varepsilon,1)$. By (3.13) and the above discussion, we have
 \begin{equation} \begin{aligned} L({1}/{2}+it,\Pi^{\star}) & \ll_{\pi,\varepsilon} (q'q)^{{n^2}/{2}+\varepsilon}(3+|t|)^{n^2+\varepsilon},\\ \mathop{\mathrm{Res}}\limits_{s=1-\beta}L(s+\beta,\Pi^{\star})x^s\Gamma(s) & \ll_{\pi,\varepsilon}L_{\chi}(1)(q'q)^{\varepsilon}(1-\beta)^{-1}x^{1-\beta}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} L({1}/{2}+it,\Pi^{\star}) & \ll_{\pi,\varepsilon} (q'q)^{{n^2}/{2}+\varepsilon}(3+|t|)^{n^2+\varepsilon},\\ \mathop{\mathrm{Res}}\limits_{s=1-\beta}L(s+\beta,\Pi^{\star})x^s\Gamma(s) & \ll_{\pi,\varepsilon}L_{\chi}(1)(q'q)^{\varepsilon}(1-\beta)^{-1}x^{1-\beta}. \end{aligned} \end{equation}
If ![]() $x\geq 3$, then since
$x\geq 3$, then since ![]() $\lambda _{\Pi ^{\star }}(1)=1$, we use (8.16) to deduce that
$\lambda _{\Pi ^{\star }}(1)=1$, we use (8.16) to deduce that
 \begin{align} \frac{1}{e}&\leq \sum_{m=1}^{\infty}\frac{\lambda_{\Pi^{\star}}(m)}{m^{\beta}}e^{-{m}/{x}}\nonumber\\ &=\frac{1}{2\pi i}\int_{3-i\infty}^{3+i\infty}L(s+\beta,\Pi^{\star})x^s\Gamma(s)\,ds\nonumber\\ &=\mathop{\mathrm{Res}}\limits_{s=1-\beta}L(s+\beta,\Pi^{\star})x^s\Gamma(s)+L(\beta,\Pi^{\star})+ \frac{1}{2\pi i}\int_{{1}/{2}-\beta-i\infty}^{{1}/{2}-\beta+i\infty}L(s+\beta,\Pi^{\star})x^s\Gamma(s)\,ds\nonumber\\ &\ll_{\pi,\varepsilon}L_{\chi}(1)(q'q)^{\varepsilon}(1-\beta)^{-1}x^{1-\beta}+L(\beta,\Pi^{\star})+(q'q)^{{n^2}/{2}+\varepsilon}x^{{1}/{2}-\beta}. \end{align}
\begin{align} \frac{1}{e}&\leq \sum_{m=1}^{\infty}\frac{\lambda_{\Pi^{\star}}(m)}{m^{\beta}}e^{-{m}/{x}}\nonumber\\ &=\frac{1}{2\pi i}\int_{3-i\infty}^{3+i\infty}L(s+\beta,\Pi^{\star})x^s\Gamma(s)\,ds\nonumber\\ &=\mathop{\mathrm{Res}}\limits_{s=1-\beta}L(s+\beta,\Pi^{\star})x^s\Gamma(s)+L(\beta,\Pi^{\star})+ \frac{1}{2\pi i}\int_{{1}/{2}-\beta-i\infty}^{{1}/{2}-\beta+i\infty}L(s+\beta,\Pi^{\star})x^s\Gamma(s)\,ds\nonumber\\ &\ll_{\pi,\varepsilon}L_{\chi}(1)(q'q)^{\varepsilon}(1-\beta)^{-1}x^{1-\beta}+L(\beta,\Pi^{\star})+(q'q)^{{n^2}/{2}+\varepsilon}x^{{1}/{2}-\beta}. \end{align}Proposition 8.7 Recall the notation and hypotheses of Lemma 8.5. If ![]() $\beta _1$ exists for a primitive character
$\beta _1$ exists for a primitive character ![]() $\chi \,(\mathrm {mod}\,\,q)$ such that
$\chi \,(\mathrm {mod}\,\,q)$ such that ![]() $\gcd (q,q_{\pi })=1$, then for all
$\gcd (q,q_{\pi })=1$, then for all ![]() $\varepsilon >0$, there exists an (ineffective) constant
$\varepsilon >0$, there exists an (ineffective) constant ![]() $c_{\pi }'(\varepsilon )>0$ such that
$c_{\pi }'(\varepsilon )>0$ such that ![]() $L_{\chi }(1)\geq c_{\pi }'(\varepsilon )q^{-\varepsilon }$.
$L_{\chi }(1)\geq c_{\pi }'(\varepsilon )q^{-\varepsilon }$.
Proof. It suffices to take ![]() $0<\varepsilon <1$. Let
$0<\varepsilon <1$. Let ![]() $\chi \,(\mathrm {mod}\,\,q)$ and
$\chi \,(\mathrm {mod}\,\,q)$ and ![]() $\chi '\,(\mathrm {mod}\,\,q')$ be primitive quadratic Dirichlet characters with, let
$\chi '\,(\mathrm {mod}\,\,q')$ be primitive quadratic Dirichlet characters with, let ![]() $\psi$ be the primitive character that induces
$\psi$ be the primitive character that induces ![]() $\chi '\chi$, and recall the definition of
$\chi '\chi$, and recall the definition of ![]() $L(s,\Pi ^{\star })$ from (8.15). Our proof consists of two cases.
$L(s,\Pi ^{\star })$ from (8.15). Our proof consists of two cases.
First, suppose that there exists no primitive quadratic Dirichlet character ![]() $\omega$ such that
$\omega$ such that ![]() $L_{\omega }(s)$ does not vanish for
$L_{\omega }(s)$ does not vanish for ![]() $s\in (1- {\varepsilon }/{2},1)$. It then follows that there exists a constant
$s\in (1- {\varepsilon }/{2},1)$. It then follows that there exists a constant ![]() $c_{19}=c_{19}(\pi )>0$ such that
$c_{19}=c_{19}(\pi )>0$ such that ![]() $L_{1}(s)L_{\chi }(s)\neq 0$ in the interval
$L_{1}(s)L_{\chi }(s)\neq 0$ in the interval ![]() $s\in (1-c_{19}/\!\log q,1)$. Since the Dirichlet coefficients of
$s\in (1-c_{19}/\!\log q,1)$. Since the Dirichlet coefficients of ![]() $L_{1}(s)L_{\chi }(s)$ are non-negative (using Lemma 8.6) and the residue of
$L_{1}(s)L_{\chi }(s)$ are non-negative (using Lemma 8.6) and the residue of ![]() $L_{1}(s)L_{\chi }(s)$ at
$L_{1}(s)L_{\chi }(s)$ at ![]() $s=1$ is
$s=1$ is ![]() $L_{\chi }(1)\mathrm {Res}_{s=1}L_{1}(s)$, it follows from [Reference Hoffstein and LockhartHL94, Proposition 1.1] and (3.13) that
$L_{\chi }(1)\mathrm {Res}_{s=1}L_{1}(s)$, it follows from [Reference Hoffstein and LockhartHL94, Proposition 1.1] and (3.13) that ![]() $L_{\chi }(1){\mathrm {Res}}_{s=1}L_{1}(s)\gg _{\pi }(\log q)^{-1}$. Since each term on the left-hand side is positive (using Lemma 8.6), the desired result follows.
$L_{\chi }(1){\mathrm {Res}}_{s=1}L_{1}(s)\gg _{\pi }(\log q)^{-1}$. Since each term on the left-hand side is positive (using Lemma 8.6), the desired result follows.
Second, suppose that there exists ![]() $\chi '\,(\mathrm {mod}\,\,q')$ and
$\chi '\,(\mathrm {mod}\,\,q')$ and ![]() $\beta \in (1- {\varepsilon }/{2},1)$ such that
$\beta \in (1- {\varepsilon }/{2},1)$ such that ![]() $L_{\chi '}(\beta )=0$. We may assume that
$L_{\chi '}(\beta )=0$. We may assume that ![]() $q'$ is minimal, subject to this condition. Now, let
$q'$ is minimal, subject to this condition. Now, let ![]() $\chi$ be arbitrary. If
$\chi$ be arbitrary. If ![]() $q< q'$, then the minimality of
$q< q'$, then the minimality of ![]() $q'$ ensures that
$q'$ ensures that ![]() $L_{\chi }(s)\neq 0$ for
$L_{\chi }(s)\neq 0$ for ![]() $s\in (1- {\varepsilon }/{2},1)$, and the preceding case implies the desired result. Suppose now that
$s\in (1- {\varepsilon }/{2},1)$, and the preceding case implies the desired result. Suppose now that ![]() $q\geq q'$. If
$q\geq q'$. If ![]() $L_{\chi }(s)$ has no real zero within a distance of
$L_{\chi }(s)$ has no real zero within a distance of ![]() $c_{17}/\!\log (3q'q C(\pi ))$ of
$c_{17}/\!\log (3q'q C(\pi ))$ of ![]() $s=1$, then since
$s=1$, then since ![]() $q\geq q'$,
$q\geq q'$, ![]() $L_{\chi }(s)$ has no real zero within a distance of
$L_{\chi }(s)$ has no real zero within a distance of ![]() $\frac {1}{2}c_{17}/\!\log (3qC(\pi ))$ of
$\frac {1}{2}c_{17}/\!\log (3qC(\pi ))$ of ![]() $s=1$. Again, the desired result follows by the preceding case. Finally, suppose that
$s=1$. Again, the desired result follows by the preceding case. Finally, suppose that ![]() $L_{\chi }(s)$ has a real zero within a distance of
$L_{\chi }(s)$ has a real zero within a distance of ![]() $c_{17}/\!\log (3q'q C(\pi ))$ of
$c_{17}/\!\log (3q'q C(\pi ))$ of ![]() $s=1$. At this stage, we assume that
$s=1$. At this stage, we assume that ![]() $\chi \neq \chi '$.
$\chi \neq \chi '$.
It follows from analysis nearly identical to the second case in Lemma 8.5 (with ![]() $L(s,\Pi ^{\star })$ replacing
$L(s,\Pi ^{\star })$ replacing ![]() $D(s)$) that
$D(s)$) that ![]() $L(s,\Pi ^{\star })$ has at most one real zero within distance
$L(s,\Pi ^{\star })$ has at most one real zero within distance ![]() $c_{17}/\!\log (3q'q C(\pi ))$ from 1. Since we have supposed that
$c_{17}/\!\log (3q'q C(\pi ))$ from 1. Since we have supposed that ![]() $L_{\chi }(s)$ has a real zero within distance
$L_{\chi }(s)$ has a real zero within distance ![]() $c_{17}/\!\log (3q'q C(\pi ))$ of
$c_{17}/\!\log (3q'q C(\pi ))$ of ![]() $s=1$, the above discussion indicates that this is the sole real zero for
$s=1$, the above discussion indicates that this is the sole real zero for ![]() $L(s,\Pi ^{\star })$ within a distance of
$L(s,\Pi ^{\star })$ within a distance of ![]() $c_{17}/\!\log (3q'q C(\pi ))$ of
$c_{17}/\!\log (3q'q C(\pi ))$ of ![]() $s=1$. It follows that the zero
$s=1$. It follows that the zero ![]() $\beta$ of
$\beta$ of ![]() $L_{\chi '}(s)$ must satisfy
$L_{\chi '}(s)$ must satisfy
Since ![]() $L_{\chi '}(\beta )=0$, it follows that
$L_{\chi '}(\beta )=0$, it follows that ![]() $L(\beta,\Pi ^{\star })=0$. Using (8.17), the above bounds on
$L(\beta,\Pi ^{\star })=0$. Using (8.17), the above bounds on ![]() $\beta$, and the fact that
$\beta$, and the fact that ![]() $q\geq q'$, we find that
$q\geq q'$, we find that
Choosing ![]() $x=q^{2n^2}/L_{\chi }(1)^2$ (which is at least 3 by (3.10) and (3.13)) and solving for
$x=q^{2n^2}/L_{\chi }(1)^2$ (which is at least 3 by (3.10) and (3.13)) and solving for ![]() $L_{\chi }(1)$, we find that for all
$L_{\chi }(1)$, we find that for all ![]() $\chi \neq \chi '$ and all
$\chi \neq \chi '$ and all ![]() $0<\varepsilon <1$, there exists a constant
$0<\varepsilon <1$, there exists a constant ![]() $d_{\pi }(\varepsilon )>0$ such that
$d_{\pi }(\varepsilon )>0$ such that ![]() $L_{\chi }(1)\geq d_{\pi }(\varepsilon )q^{-\varepsilon (n^2+2)/(1-\varepsilon )}$. Upon rescaling
$L_{\chi }(1)\geq d_{\pi }(\varepsilon )q^{-\varepsilon (n^2+2)/(1-\varepsilon )}$. Upon rescaling ![]() $\varepsilon$ to
$\varepsilon$ to ![]() $\varepsilon /(n^2+2+\varepsilon )$, we have
$\varepsilon /(n^2+2+\varepsilon )$, we have ![]() $L_{\chi }(1)\geq d_{\pi }(\varepsilon /(n^2+2+\varepsilon ))q^{-\varepsilon }$. As long as
$L_{\chi }(1)\geq d_{\pi }(\varepsilon /(n^2+2+\varepsilon ))q^{-\varepsilon }$. As long as ![]() $\chi \neq \chi '$, the constant
$\chi \neq \chi '$, the constant ![]() $d_{\pi }(\varepsilon /(n^2+2+\varepsilon ))$ is effective. Once we decrease
$d_{\pi }(\varepsilon /(n^2+2+\varepsilon ))$ is effective. Once we decrease ![]() $d_{\pi }(\varepsilon /(n^2+2+\varepsilon ))$ suitably to account for the case where
$d_{\pi }(\varepsilon /(n^2+2+\varepsilon ))$ suitably to account for the case where ![]() $\chi =\chi '$, the claimed result holds for arbitrary
$\chi =\chi '$, the claimed result holds for arbitrary ![]() $\chi$.
$\chi$.
Corollary 8.8 Recall the notation and hypotheses of Lemma 8.5. If ![]() $\beta _1$ exists, then for all
$\beta _1$ exists, then for all ![]() $\varepsilon >0$, there exists an (ineffective) constant
$\varepsilon >0$, there exists an (ineffective) constant ![]() $c_{\pi }(\varepsilon )>0$ such that
$c_{\pi }(\varepsilon )>0$ such that ![]() $\beta _1\leq 1-c_{\pi }(\varepsilon )q^{-\varepsilon }$.
$\beta _1\leq 1-c_{\pi }(\varepsilon )q^{-\varepsilon }$.
Proof. If ![]() $\beta _1$ exists, then there exists
$\beta _1$ exists, then there exists ![]() $\sigma \in [\beta _1,1]$ such that
$\sigma \in [\beta _1,1]$ such that ![]() $L_{\chi }'(\sigma )(1-\beta _1)=L_{\chi }(1)\geq c_{\pi }'( {\varepsilon }/{2})q^{- {\varepsilon }/{2}}$ by Proposition 8.7 and the mean value theorem. The result follows once we establish the bound
$L_{\chi }'(\sigma )(1-\beta _1)=L_{\chi }(1)\geq c_{\pi }'( {\varepsilon }/{2})q^{- {\varepsilon }/{2}}$ by Proposition 8.7 and the mean value theorem. The result follows once we establish the bound ![]() $L_{\chi }'(\sigma )\ll _{\pi,\varepsilon } q^{\frac {\varepsilon }{2}}$ for
$L_{\chi }'(\sigma )\ll _{\pi,\varepsilon } q^{\frac {\varepsilon }{2}}$ for ![]() $\sigma \in [1-b_n/\!\log (3qC(\pi )),1]$, where
$\sigma \in [1-b_n/\!\log (3qC(\pi )),1]$, where ![]() $b_n>0$ is a suitable constant depending at most on
$b_n>0$ is a suitable constant depending at most on ![]() $n$. To prove this, we observe via Cauchy's integral formula that
$n$. To prove this, we observe via Cauchy's integral formula that
in which case the desired bound follows from (3.13).
We show that among the primitive characters ![]() $\chi \,(\mathrm {mod}\,\,q)$ with
$\chi \,(\mathrm {mod}\,\,q)$ with ![]() $q\leq Q$, we encounter very few with the property that
$q\leq Q$, we encounter very few with the property that ![]() $L_{\chi }(s)$ has an exceptional zero.
$L_{\chi }(s)$ has an exceptional zero.
Lemma 8.9 Let ![]() $Q\geq 3$. There exists an effectively computable constant
$Q\geq 3$. There exists an effectively computable constant ![]() $c_{20}=c_{20}(n)>0$ such that there is at most one real non-trivial primitive Dirichlet character
$c_{20}=c_{20}(n)>0$ such that there is at most one real non-trivial primitive Dirichlet character ![]() $\chi _1\,(\mathrm {mod}\,\,q_1)$ with
$\chi _1\,(\mathrm {mod}\,\,q_1)$ with ![]() $q_1\leq Q$ such that
$q_1\leq Q$ such that ![]() $L_{\chi _1}(s)$ has a real zero
$L_{\chi _1}(s)$ has a real zero ![]() $\beta _1$ satisfying
$\beta _1$ satisfying ![]() $\beta _1>1-c_{20}/\!\log (C(\pi )Q)$.
$\beta _1>1-c_{20}/\!\log (C(\pi )Q)$.
Proof. Suppose to the contrary that ![]() $\chi \,(\mathrm {mod}\,\,q)$ and
$\chi \,(\mathrm {mod}\,\,q)$ and ![]() $\chi '\,(\mathrm {mod}\,\,q')$ are two distinct such characters with
$\chi '\,(\mathrm {mod}\,\,q')$ are two distinct such characters with ![]() $q,q'\leq Q$. Let
$q,q'\leq Q$. Let ![]() $\Pi = \pi \boxplus \pi \otimes \chi \boxplus \pi \otimes \chi '$, let
$\Pi = \pi \boxplus \pi \otimes \chi \boxplus \pi \otimes \chi '$, let ![]() $\psi$ be the primitive character that induces
$\psi$ be the primitive character that induces ![]() $\chi '\chi$, and let
$\chi '\chi$, and let
By [Reference Hoffstein and RamakrishnanHR95, Lemma a], the Dirichlet coefficients of ![]() $-(F'/F)(s)$ are non-negative. By Lemma 3.2, there exists a constant
$-(F'/F)(s)$ are non-negative. By Lemma 3.2, there exists a constant ![]() $c_{21}=c_{21}(n)\geq 1$ such that if
$c_{21}=c_{21}(n)\geq 1$ such that if ![]() $\omega$ runs through the nontrivial zeros of
$\omega$ runs through the nontrivial zeros of ![]() $F(s)$ and
$F(s)$ and ![]() $1<\sigma <2$, then
$1<\sigma <2$, then
If ![]() $\sigma =1+ {1}/{2c_{21}\log (C(\pi )Q)}$ and
$\sigma =1+ {1}/{2c_{21}\log (C(\pi )Q)}$ and ![]() $M$ is the number (necessarily an integer) of real zeros (counting multiplicity) of
$M$ is the number (necessarily an integer) of real zeros (counting multiplicity) of ![]() $F(s)$ that are at least
$F(s)$ that are at least ![]() $1- {1}/{14c_{21}\log (C(\pi )Q)}$, then it follows from (8.18) that
$1- {1}/{14c_{21}\log (C(\pi )Q)}$, then it follows from (8.18) that
 \begin{align*} & \frac{M}{1+{1}/{2c_{21}\log(C(\pi)Q)}-(1-{1}/{14c_{21}\log(C(\pi)Q)})} < \frac{3}{(1+{1}/{2c_{21}\log(C(\pi)Q)})-1} \\ & \quad +c_{21}\log(C(\pi)Q).\end{align*}
\begin{align*} & \frac{M}{1+{1}/{2c_{21}\log(C(\pi)Q)}-(1-{1}/{14c_{21}\log(C(\pi)Q)})} < \frac{3}{(1+{1}/{2c_{21}\log(C(\pi)Q)})-1} \\ & \quad +c_{21}\log(C(\pi)Q).\end{align*}
This implies that ![]() $M\leq 3$. However, if
$M\leq 3$. However, if ![]() $L_{\chi }(s)$ and
$L_{\chi }(s)$ and ![]() $L_{\chi '}(s)$ both have real zeros that are larger than
$L_{\chi '}(s)$ both have real zeros that are larger than ![]() $1- {1}/{14c_{21}\log (C(\pi )Q)}$, then
$1- {1}/{14c_{21}\log (C(\pi )Q)}$, then ![]() $F(s)$ has four such zeros, a contradiction. The lemma now follows.
$F(s)$ has four such zeros, a contradiction. The lemma now follows.
Acknowledgements
We thank Gergely Harcos, Rizwanur Khan, and the anonymous referee for helpful comments.
Conflicts of Interest
None.