1. Introduction
Collisions of two or more droplets of one single liquid in a gaseous environment is a common phenomenon whose importance motivated many theoretical (Roisman Reference Roisman2009; Roisman, Berberović & Tropea Reference Roisman, Berberović and Tropea2009), numerical (Sun et al. Reference Sun, Zhang, Law and Wang2015; Li Reference Li2016; Moqaddam, Chikatamarla & Karlin Reference Moqaddam, Chikatamarla and Karlin2016; Huang, Pan & Josserand Reference Huang, Pan and Josserand2019) and experimental (Brenn, Valkovska & Danov Reference Brenn, Valkovska and Danov2001; Brenn & Kolobaric Reference Brenn and Kolobaric2006; Pan, Chou & Tseng Reference Pan, Chou and Tseng2009) studies. Collisions may cause droplets to permanently coalesce and trigger rainfall (Jayaratne & Mason Reference Jayaratne and Mason1964). They may also lead to fragmentation and therefore to the formation of drops with different sizes and trajectories. These phenomena also occur in industrial processes, which produce or employ drops, such as coating, injection, cooling,![]() $\ldots$ (Brenn, Durst & Tropea Reference Brenn, Durst and Tropea1996). The consequences depend on the application, but can be severe. It may alter the delivery of active ingredients from spray-dried particles or modify the intake of pesticide sprayed onto crops. Thus, if not controlled, the collision outcomes must at least be predicted. Results across multiple studies reveal that coalescence, bouncing, reflexive and stretching separations are the four main outcomes of drop–drop (D–D) collisions. Which outcome is obtained depends on the collision parameters and on the liquid drop behaviour characterized by the drop Ohnesorge number
$\ldots$ (Brenn, Durst & Tropea Reference Brenn, Durst and Tropea1996). The consequences depend on the application, but can be severe. It may alter the delivery of active ingredients from spray-dried particles or modify the intake of pesticide sprayed onto crops. Thus, if not controlled, the collision outcomes must at least be predicted. Results across multiple studies reveal that coalescence, bouncing, reflexive and stretching separations are the four main outcomes of drop–drop (D–D) collisions. Which outcome is obtained depends on the collision parameters and on the liquid drop behaviour characterized by the drop Ohnesorge number ![]() $Oh_d=\mu _d/\sqrt {\rho _d \sigma _d D_d}$, which compares the relative importance of the capillary to the viscous contribution. Here,
$Oh_d=\mu _d/\sqrt {\rho _d \sigma _d D_d}$, which compares the relative importance of the capillary to the viscous contribution. Here, ![]() $\mu _d$,
$\mu _d$, ![]() $\rho _d$,
$\rho _d$, ![]() $\sigma _d$ and
$\sigma _d$ and ![]() $D_d$ are the drop liquid viscosity, density, surface tension and the drop diameter, respectively. Note that
$D_d$ are the drop liquid viscosity, density, surface tension and the drop diameter, respectively. Note that ![]() $Oh_d$ is independent from
$Oh_d$ is independent from ![]() $U$, the relative drop velocity. Classically, regime maps are represented for a fixed
$U$, the relative drop velocity. Classically, regime maps are represented for a fixed ![]() $Oh_d$ using the dimensionless impact parameter
$Oh_d$ using the dimensionless impact parameter ![]() $X$, which quantifies the collision eccentricity, and the drop Weber number
$X$, which quantifies the collision eccentricity, and the drop Weber number ![]() $We_d=\rho _d D_d U^2/\sigma _d$, which represents the ratio of inertia over capillarity (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang, Umemura & Law Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Saroka & Ashgriz Reference Saroka and Ashgriz2015).
$We_d=\rho _d D_d U^2/\sigma _d$, which represents the ratio of inertia over capillarity (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang, Umemura & Law Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Saroka & Ashgriz Reference Saroka and Ashgriz2015).
This work focuses on off-centre drop collisions, more precisely on the stretching separation causing the fragmentation of the otherwise permanently merged drop. Despite case-to-case parameters adjustment, the existing models have limited validity ranges (Gotaas et al. Reference Gotaas, Havelka, Jakobsen, Svendsen, Hase, Roth and Weigand2007; Rabe, Malet & Feuillebois Reference Rabe, Malet and Feuillebois2010; Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017; Pan et al. Reference Pan, Huang, Hsieh and Lu2019). More recently, Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021) proposed a new model free of adjustable parameters, but its derivation is empirical and its applicability limited to ![]() $0.02< Oh_d<0.14$. We propose a physical analysis and establish a unique, general and robust model predicting the stretching separation for D–D collisions. It is valid at least for
$0.02< Oh_d<0.14$. We propose a physical analysis and establish a unique, general and robust model predicting the stretching separation for D–D collisions. It is valid at least for ![]() $0.008< Oh_d<0.325$, i.e. over the entire experimentally screened domain. We additionally extend the concept of stretching separation to drops colliding with a continuous jet. These collisions, also called in-air microfluidics, create well-defined liquid structures (Planchette, Hinterbichler & Brenn Reference Planchette, Hinterbichler and Brenn2017a), which can be solidified into fibres or capsules with high precision and throughput (Visser et al. Reference Visser, Kamperman, Karbaat, Lohse and Karperien2018). Yet, studies on drop–jet (D–J) collisions remain rather rare. Chen, Chiu & Lin (Reference Chen, Chiu and Lin2006) investigated the out-of-plane collisions of water drops with a water jet, followed by Planchette et al. (Reference Planchette, Hinterbichler and Brenn2017a, Reference Planchette, Petit, Hinterbichler and Brenn2018), who worked with immiscible liquid pairs on in-plane collisions. In this case, the outcomes were classified according to the fragmentation of either the drops, the jet, both phases or none. While the drop fragmentation limit has been recently well studied (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020a; Baumgartner, Brenn & Planchette Reference Baumgartner, Brenn and Planchette2020b), that of the jet remains poorly explained. We show that the fragmentation of the jet is caused by its excessive stretching and can be predicted by considering the D–J collisions as a succession of off-centre D–D collisions. The article is organized as follows. In the next section, the experimental set-up and problem parameters are presented. Section 3 focuses first on the D–D collisions and then on the D–J collisions. The article ends with the conclusions.
$0.008< Oh_d<0.325$, i.e. over the entire experimentally screened domain. We additionally extend the concept of stretching separation to drops colliding with a continuous jet. These collisions, also called in-air microfluidics, create well-defined liquid structures (Planchette, Hinterbichler & Brenn Reference Planchette, Hinterbichler and Brenn2017a), which can be solidified into fibres or capsules with high precision and throughput (Visser et al. Reference Visser, Kamperman, Karbaat, Lohse and Karperien2018). Yet, studies on drop–jet (D–J) collisions remain rather rare. Chen, Chiu & Lin (Reference Chen, Chiu and Lin2006) investigated the out-of-plane collisions of water drops with a water jet, followed by Planchette et al. (Reference Planchette, Hinterbichler and Brenn2017a, Reference Planchette, Petit, Hinterbichler and Brenn2018), who worked with immiscible liquid pairs on in-plane collisions. In this case, the outcomes were classified according to the fragmentation of either the drops, the jet, both phases or none. While the drop fragmentation limit has been recently well studied (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020a; Baumgartner, Brenn & Planchette Reference Baumgartner, Brenn and Planchette2020b), that of the jet remains poorly explained. We show that the fragmentation of the jet is caused by its excessive stretching and can be predicted by considering the D–J collisions as a succession of off-centre D–D collisions. The article is organized as follows. In the next section, the experimental set-up and problem parameters are presented. Section 3 focuses first on the D–D collisions and then on the D–J collisions. The article ends with the conclusions.
2. Experimental set-up and problem parameters
All D–D and D–J collisions are carried out with the same set-up depicted in figure 1(a). Here and thereafter, subscript ![]() $d$ corresponds to drop liquid properties and parameters while
$d$ corresponds to drop liquid properties and parameters while ![]() $j$ refers to those of the jet. For D–D collisions, two droplet generators (Brenn et al. Reference Brenn, Durst and Tropea1996) are excited with the same frequency
$j$ refers to those of the jet. For D–D collisions, two droplet generators (Brenn et al. Reference Brenn, Durst and Tropea1996) are excited with the same frequency ![]() $f_d$ (
$f_d$ (![]() $5\,{\rm kHz}< f_{d}<24\,{\rm kHz}$), while for D–J collisions, only one (DG1) is activated. An LED stroboscope (illumination) is synchronized with
$5\,{\rm kHz}< f_{d}<24\,{\rm kHz}$), while for D–J collisions, only one (DG1) is activated. An LED stroboscope (illumination) is synchronized with ![]() $f_d$ so that each picture consists of hundreds of superimposed collisions illuminated by short flashes of approximately 100 ns each. The liquids are supplied with two independent pressurized tanks. Two cameras record the collisions in front view (Cam1, observation of the drop and jet deformation, resolution up to 4
$f_d$ so that each picture consists of hundreds of superimposed collisions illuminated by short flashes of approximately 100 ns each. The liquids are supplied with two independent pressurized tanks. Two cameras record the collisions in front view (Cam1, observation of the drop and jet deformation, resolution up to 4 ![]() $\mathrm {\mu }$m per pixel) and orthogonal view (Cam2, in-plane alignment of the trajectories with microtraverses).
$\mathrm {\mu }$m per pixel) and orthogonal view (Cam2, in-plane alignment of the trajectories with microtraverses).

Figure 1. (a) Experimental set-up and problem parameters for (b) D–D and (c) D–J collisions.
Figure 1(b,c) shows the problem parameters associated with D–D and D–J collisions, respectively. All geometrical parameters are extracted from recorded pictures with the public-domain software ImageJ. Here ![]() $D_d$ and
$D_d$ and ![]() $D_j$ stand for the drop and jet diameter, respectively. For D–D collisions,
$D_j$ stand for the drop and jet diameter, respectively. For D–D collisions, ![]() $L_{d,1}$ and
$L_{d,1}$ and ![]() $L_{d,2}$ correspond to the distance between two consecutive drops of each stream. The droplet velocities are given by
$L_{d,2}$ correspond to the distance between two consecutive drops of each stream. The droplet velocities are given by ![]() $\boldsymbol {u}_{d,i}=\boldsymbol {L}_{d,i}\,f_d$. They vary between 3 m s
$\boldsymbol {u}_{d,i}=\boldsymbol {L}_{d,i}\,f_d$. They vary between 3 m s![]() $^{-1}$ and 13 m s
$^{-1}$ and 13 m s![]() $^{-1}$ and provide the relative impact velocity
$^{-1}$ and provide the relative impact velocity ![]() $\boldsymbol {U}=\boldsymbol {u}_{d,2}-\boldsymbol {u}_{d,1}$, which ranges from 1.9 m s
$\boldsymbol {U}=\boldsymbol {u}_{d,2}-\boldsymbol {u}_{d,1}$, which ranges from 1.9 m s![]() $^{-1}$ to 5.4 m s
$^{-1}$ to 5.4 m s![]() $^{-1}$. Practically, we use three liquids: water (W,
$^{-1}$. Practically, we use three liquids: water (W, ![]() $\rho =995$ kg m
$\rho =995$ kg m![]() $^{-3}$,
$^{-3}$, ![]() $\mu =0.98\,{\rm mPa}\,{\rm s}$,
$\mu =0.98\,{\rm mPa}\,{\rm s}$, ![]() $\sigma =72.5\,{\rm mN}\,{\rm m}^{-1}$), an aqueous glycerol solution (G,
$\sigma =72.5\,{\rm mN}\,{\rm m}^{-1}$), an aqueous glycerol solution (G, ![]() $\rho =1125\,{\rm kg}\,{\rm m}^{-3}$,
$\rho =1125\,{\rm kg}\,{\rm m}^{-3}$, ![]() $\mu =5.1\,{\rm mPa}\,{\rm s}$,
$\mu =5.1\,{\rm mPa}\,{\rm s}$, ![]() $\sigma =68.0\,{\rm mN}\,{\rm m}^{-1}$) and one silicone oil (SO,
$\sigma =68.0\,{\rm mN}\,{\rm m}^{-1}$) and one silicone oil (SO, ![]() $\rho =949\,{\rm kg}\,{\rm m}^{-3}$,
$\rho =949\,{\rm kg}\,{\rm m}^{-3}$, ![]() $\mu =18.5\,{\rm mPa}\,{\rm s}$,
$\mu =18.5\,{\rm mPa}\,{\rm s}$, ![]() $\sigma =20.5\,{\rm mN}\,{\rm m}^{-1}$) and vary the drop diameter between 175
$\sigma =20.5\,{\rm mN}\,{\rm m}^{-1}$) and vary the drop diameter between 175 ![]() $\mathrm {\mu }$m and 367
$\mathrm {\mu }$m and 367 ![]() $\mathrm {\mu }$m , covering
$\mathrm {\mu }$m , covering ![]() $0.008 < Oh_d < 0.325$ with
$0.008 < Oh_d < 0.325$ with ![]() $15 < We_d < 265$.
$15 < We_d < 265$.
For D–J collisions, we further introduce the spatial period of the jet ![]() $L_j=|{u}_j|/f_{d}$, where
$L_j=|{u}_j|/f_{d}$, where ![]() ${u}_j$ is the flow-rate equivalent jet velocity (
${u}_j$ is the flow-rate equivalent jet velocity (![]() $3.5\,{\rm m}\,{\rm s}^{-1}<|{u}_j|<11.5\,{\rm m}\,{\rm s}^{-1}$). It is deduced from the measured mass flow rate knowing the liquid density and jet section. The relative impact velocity
$3.5\,{\rm m}\,{\rm s}^{-1}<|{u}_j|<11.5\,{\rm m}\,{\rm s}^{-1}$). It is deduced from the measured mass flow rate knowing the liquid density and jet section. The relative impact velocity ![]() $\boldsymbol {U}=\boldsymbol {u}_{d}-\boldsymbol {u}_{j}$ varies between 3 m s
$\boldsymbol {U}=\boldsymbol {u}_{d}-\boldsymbol {u}_{j}$ varies between 3 m s![]() $^{-1}$ and 8 m s
$^{-1}$ and 8 m s![]() $^{-1}$ and is adjusted to be perpendicular to the jet axis. More precisely, its component parallel to the jet axis obeys
$^{-1}$ and is adjusted to be perpendicular to the jet axis. More precisely, its component parallel to the jet axis obeys ![]() $U_{\|}<0.1U$. There, the drops are always made of the aqueous glycerol solution, while the jet consists of silicone oils. Their density and surface tension are almost constant (
$U_{\|}<0.1U$. There, the drops are always made of the aqueous glycerol solution, while the jet consists of silicone oils. Their density and surface tension are almost constant (![]() $845<\rho <949\,{\rm kg}\,{\rm m}^{-3}$,
$845<\rho <949\,{\rm kg}\,{\rm m}^{-3}$, ![]() $17<\sigma <20.5\,{\rm mN}\,{\rm m}^{-1}$) while their viscosity varies between 1.4 mPa s and 18.5 mPa s. With an interfacial tension of
$17<\sigma <20.5\,{\rm mN}\,{\rm m}^{-1}$) while their viscosity varies between 1.4 mPa s and 18.5 mPa s. With an interfacial tension of ![]() $32\pm 3\,{\rm mN}\,{\rm m}^{-1}$, the jet always totally wets the drops. The jet diameter is equal to
$32\pm 3\,{\rm mN}\,{\rm m}^{-1}$, the jet always totally wets the drops. The jet diameter is equal to ![]() $280\pm 10\,{\mathrm {\mu }{\rm m}}$, resulting in jet Ohnesorge numbers
$280\pm 10\,{\mathrm {\mu }{\rm m}}$, resulting in jet Ohnesorge numbers ![]() $0.02 < Oh_j=\mu _j/\sqrt {\rho _j D_j \sigma _j} < 0.25$. The droplet diameter varies between 190
$0.02 < Oh_j=\mu _j/\sqrt {\rho _j D_j \sigma _j} < 0.25$. The droplet diameter varies between 190 ![]() $\mathrm {\mu }$m and 370
$\mathrm {\mu }$m and 370 ![]() $\mathrm {\mu }$m, leading to diameter ratios
$\mathrm {\mu }$m, leading to diameter ratios ![]() $0.7 < \varDelta =D_{d}/D_j < 1.3$. Further information can also be found in Baumgartner et al. (Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020a,Reference Baumgartner, Brenn and Planchetteb).
$0.7 < \varDelta =D_{d}/D_j < 1.3$. Further information can also be found in Baumgartner et al. (Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020a,Reference Baumgartner, Brenn and Planchetteb).
3. Discussion
While different in nature, D–D and D–J collisions clearly show similarities, encouraging the build of some analogy between the two collision processes, see figure 2(a–d). Before doing so, let us focus on D–D collisions. Our model is based on two ingredients: (i) a fragmentation criterion, which corresponds to a critical value of ![]() $\varPsi _d=\max [H_d(t)/D_d]$, the maximum dimensionless drop extension (see figure 2a,b) and (ii) a function, which describes the variations of
$\varPsi _d=\max [H_d(t)/D_d]$, the maximum dimensionless drop extension (see figure 2a,b) and (ii) a function, which describes the variations of ![]() $\varPsi _d$ with the liquid properties and collision parameters.
$\varPsi _d$ with the liquid properties and collision parameters.

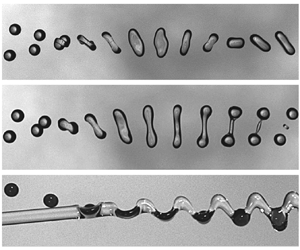
Figure 2. (a–d) Drop and jet trajectories go from left to right. The D–D collision in (a) coalescence (![]() $D_d=341\,{\mathrm {\mu }{\rm m}}$,
$D_d=341\,{\mathrm {\mu }{\rm m}}$, ![]() $X=0.41$,
$X=0.41$, ![]() $We_d=31.5$,
$We_d=31.5$, ![]() $Oh_d=0.033$) and (b) stretching separation (
$Oh_d=0.033$) and (b) stretching separation (![]() $D_d=340\,{\mathrm {\mu }{\rm m}}$,
$D_d=340\,{\mathrm {\mu }{\rm m}}$, ![]() $X=0.61$,
$X=0.61$, ![]() $We_d=31.3$,
$We_d=31.3$, ![]() $Oh_d=0.033$). The D–J collision in (c) drops-in-jet (
$Oh_d=0.033$). The D–J collision in (c) drops-in-jet (![]() $D_d=275\,{\mathrm {\mu }{\rm m}}$,
$D_d=275\,{\mathrm {\mu }{\rm m}}$, ![]() $\tilde {X}=1.64$,
$\tilde {X}=1.64$, ![]() $We_{d}=30$,
$We_{d}=30$, ![]() $Oh_j=0.246$) and (d) capsules (
$Oh_j=0.246$) and (d) capsules (![]() $D_d=292\,{\mathrm {\mu }{\rm m}}$,
$D_d=292\,{\mathrm {\mu }{\rm m}}$, ![]() $\tilde {X}=1.86$,
$\tilde {X}=1.86$, ![]() $We_{d}=48$,
$We_{d}=48$, ![]() $Oh_j=0.246$). (e) Measured temporal evolution of
$Oh_j=0.246$). (e) Measured temporal evolution of ![]() $H_d/D_d$ (symbols) and its fit (dashed line) providing its maximum,
$H_d/D_d$ (symbols) and its fit (dashed line) providing its maximum, ![]() $\varPsi _d$. Collision eccentricity for (f) D–D collisions,
$\varPsi _d$. Collision eccentricity for (f) D–D collisions, ![]() $X=x/D_d$, and (g) D–J collisions,
$X=x/D_d$, and (g) D–J collisions, ![]() $\tilde {X}=2\tilde {x}/D_j$.
$\tilde {X}=2\tilde {x}/D_j$.
First, ![]() $H_d(t)/D_d$ is measured for several instants after the collision and fitted with a third-order polynomial to obtain
$H_d(t)/D_d$ is measured for several instants after the collision and fitted with a third-order polynomial to obtain ![]() $\varPsi _d$, its maximum value with a typical measurement uncertainty of less than
$\varPsi _d$, its maximum value with a typical measurement uncertainty of less than ![]() $3\,\%$, see figure 2(e). Note that the deformation undergone by drops colliding off-centre is not an axisymmetric lamella, as seen for head-on collisions. Thus,
$3\,\%$, see figure 2(e). Note that the deformation undergone by drops colliding off-centre is not an axisymmetric lamella, as seen for head-on collisions. Thus, ![]() $H_d$, the maximal extension is the end-to-end length of a stretched entity and not a maximal diameter. We verify that the separation threshold corresponds to a constant critical value of
$H_d$, the maximal extension is the end-to-end length of a stretched entity and not a maximal diameter. We verify that the separation threshold corresponds to a constant critical value of ![]() $\varPsi _d$ of 3.25 (dashed line in figure 3a), in agreement with the numerical results of Saroka & Ashgriz (Reference Saroka and Ashgriz2015) and the recent experimental findings of Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021). This provides the fragmentation criterion (i). Note that this value remarkably close to
$\varPsi _d$ of 3.25 (dashed line in figure 3a), in agreement with the numerical results of Saroka & Ashgriz (Reference Saroka and Ashgriz2015) and the recent experimental findings of Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021). This provides the fragmentation criterion (i). Note that this value remarkably close to ![]() ${\rm \pi}$, the theoretical one (Rayleigh Reference Rayleigh1892), is obtained by normalizing the critical extension with the initial drop diameter, as done by Saroka & Ashgriz (Reference Saroka and Ashgriz2015); Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021). Assuming a cylindrical shape and using volume conservation leads to a critical value of more than 5, well above the classical result of Plateau–Rayleigh.
${\rm \pi}$, the theoretical one (Rayleigh Reference Rayleigh1892), is obtained by normalizing the critical extension with the initial drop diameter, as done by Saroka & Ashgriz (Reference Saroka and Ashgriz2015); Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021). Assuming a cylindrical shape and using volume conservation leads to a critical value of more than 5, well above the classical result of Plateau–Rayleigh.

Figure 3. D–D collisions: (a) ![]() $\varPsi _d$ as a function of
$\varPsi _d$ as a function of ![]() $We_d$ for
$We_d$ for ![]() $Oh_d=0.033$ and different
$Oh_d=0.033$ and different ![]() $X$. Coalescence (full symbols) and separation (empty symbols). (b)
$X$. Coalescence (full symbols) and separation (empty symbols). (b) ![]() $s_d= \partial \varPsi _d/\partial We_d$ from (a). Inset:
$s_d= \partial \varPsi _d/\partial We_d$ from (a). Inset: ![]() ${\rm log}(s_d/X)$ against
${\rm log}(s_d/X)$ against ![]() ${\rm log}(Oh_d)$ for all experiments (
${\rm log}(Oh_d)$ for all experiments (![]() $Oh_d=0.008$, 0.033, 0.325). (c) Experiments vs model – (3.2). Main graph: our data (
$Oh_d=0.008$, 0.033, 0.325). (c) Experiments vs model – (3.2). Main graph: our data (![]() $Oh_d=0.008$, 0.033, 0.325); inset: data of Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021) (
$Oh_d=0.008$, 0.033, 0.325); inset: data of Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021) (![]() $0.021\leq Oh_d\leq 0.214$,
$0.021\leq Oh_d\leq 0.214$, ![]() $0.24< X<0.55$ and
$0.24< X<0.55$ and ![]() $30\leq We_d \leq 130$).
$30\leq We_d \leq 130$).
We then derive the evolution of ![]() $\varPsi _d$ with the liquid properties and collision parameters, i.e the second ingredient of our approach. We consider a purely geometric contribution
$\varPsi _d$ with the liquid properties and collision parameters, i.e the second ingredient of our approach. We consider a purely geometric contribution ![]() $\varPsi _d|_{We_d\approx 0}$ and an inertial one
$\varPsi _d|_{We_d\approx 0}$ and an inertial one ![]() $\varPsi _d|_{We_d \neq 0}$. The relative velocity
$\varPsi _d|_{We_d \neq 0}$. The relative velocity ![]() $U$ is projected parallel (
$U$ is projected parallel (![]() $\boldsymbol {U}_{ho}$) and normally (
$\boldsymbol {U}_{ho}$) and normally (![]() $\boldsymbol {U}_s$) to the line connecting the two drop centres at contact (see figure 2f). It shows how the merged drop is elongated along
$\boldsymbol {U}_s$) to the line connecting the two drop centres at contact (see figure 2f). It shows how the merged drop is elongated along ![]() $\boldsymbol {U}_s$ in the absence of inertia. This elongation contributes to
$\boldsymbol {U}_s$ in the absence of inertia. This elongation contributes to ![]() $\varPsi _d$ in the form of a purely geometric term
$\varPsi _d$ in the form of a purely geometric term ![]() $\varPsi _d|_{We_d\approx 0}=H_d|_{We_d\approx 0}/D_d$, the normalized length of the red segment in figure 2(f). The latter is a function of the dimensionless impact parameter,
$\varPsi _d|_{We_d\approx 0}=H_d|_{We_d\approx 0}/D_d$, the normalized length of the red segment in figure 2(f). The latter is a function of the dimensionless impact parameter, ![]() $X=x/D_d$, with
$X=x/D_d$, with ![]() $x$, the projection normal to
$x$, the projection normal to ![]() $\boldsymbol {U}$ of the drop-centre-to-drop-centre segment at contact. Geometric considerations give
$\boldsymbol {U}$ of the drop-centre-to-drop-centre segment at contact. Geometric considerations give ![]() $\varPsi _d|_{We_d\approx 0}=(X+1)/\sqrt {1-X^2}$, which can be linearized for
$\varPsi _d|_{We_d\approx 0}=(X+1)/\sqrt {1-X^2}$, which can be linearized for ![]() $0.3< X<0.8$ into
$0.3< X<0.8$ into ![]() $\varPsi _d|_{We_d\approx 0} \approx 2.7X+0.5$. The inertial contribution is obtained by considering that some of the initial kinetic energy (
$\varPsi _d|_{We_d\approx 0} \approx 2.7X+0.5$. The inertial contribution is obtained by considering that some of the initial kinetic energy (![]() ${\rm \pi} \rho _d {D_d}^3 U^2 /24$) is converted into surface energy of the stretched drop (
${\rm \pi} \rho _d {D_d}^3 U^2 /24$) is converted into surface energy of the stretched drop (![]() $\approx \sigma _d {\rm \pi}H_d {D_d}$) providing at first order
$\approx \sigma _d {\rm \pi}H_d {D_d}$) providing at first order ![]() $\varPsi _d|_{We_d \neq 0} \approx f(X, Oh_d) We_d /24$ with
$\varPsi _d|_{We_d \neq 0} \approx f(X, Oh_d) We_d /24$ with ![]() $f(X, Oh_d)$ a function that accounts for the ‘relevant inertia’. Here the relevant inertia causes the merged drop to stretch. Obviously, it corresponds to the inertia of the almost unaffected drop portions that continue on their initial trajectories, see not hatched portions in figure 2(f). Compared with the drops' inertia, that of the almost unaffected portions must be reduced to account for their actual mass (or volume). Neglecting strong distortion, each portion volume is given by
$f(X, Oh_d)$ a function that accounts for the ‘relevant inertia’. Here the relevant inertia causes the merged drop to stretch. Obviously, it corresponds to the inertia of the almost unaffected drop portions that continue on their initial trajectories, see not hatched portions in figure 2(f). Compared with the drops' inertia, that of the almost unaffected portions must be reduced to account for their actual mass (or volume). Neglecting strong distortion, each portion volume is given by ![]() $V=(3X^2-2X^3)V_d$ with
$V=(3X^2-2X^3)V_d$ with ![]() $V_d$ the volume of one drop. The first inertia correction therefore corresponds to a factor
$V_d$ the volume of one drop. The first inertia correction therefore corresponds to a factor ![]() $V/V_d=(3X^2-2X^3)$, which gives after linearization
$V/V_d=(3X^2-2X^3)$, which gives after linearization ![]() $V/V_d \approx (1.4X-0.2)$ and thus a linear variation of
$V/V_d \approx (1.4X-0.2)$ and thus a linear variation of ![]() $f(X, Oh_d)$ with
$f(X, Oh_d)$ with ![]() $X$. This scaling (
$X$. This scaling (![]() $\varPsi _d|_{We_d \neq 0} \propto X We_d$) is specific to off-centre collisions and cannot be extrapolated to head-on impacts. For
$\varPsi _d|_{We_d \neq 0} \propto X We_d$) is specific to off-centre collisions and cannot be extrapolated to head-on impacts. For ![]() $X\lesssim 0.3$, an axisymmetric lamella forms, whose maximal diameter scales as
$X\lesssim 0.3$, an axisymmetric lamella forms, whose maximal diameter scales as ![]() $\sqrt {We_d}$ (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016; Planchette et al. Reference Planchette, Hinterbichler, Liu, Bothe and Brenn2017b). To go further, the viscous losses, i.e. the dependency with
$\sqrt {We_d}$ (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016; Planchette et al. Reference Planchette, Hinterbichler, Liu, Bothe and Brenn2017b). To go further, the viscous losses, i.e. the dependency with ![]() $Oh_d$, must be estimated.
$Oh_d$, must be estimated.
Analytically establishing the quantitative expression of this second correction is rather complex and we decide here to use the numerical findings of Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017). The computed normalized remaining energy is replotted as a function of ![]() $X$ and
$X$ and ![]() $Oh_d$, see Appendix. It provides
$Oh_d$, see Appendix. It provides ![]() $f(X, Oh_d) \approx 0.31 X {Oh}^{-0.18}$, in agreement with the expected linear variation of
$f(X, Oh_d) \approx 0.31 X {Oh}^{-0.18}$, in agreement with the expected linear variation of ![]() $f$ with
$f$ with ![]() $X$. Consequently, we obtain
$X$. Consequently, we obtain ![]() $\varPsi _d|_{We_d \neq 0} \approx (0.31/24) Oh_d^{-0.18} We_d$ and thus the overall theoretical deformation:
$\varPsi _d|_{We_d \neq 0} \approx (0.31/24) Oh_d^{-0.18} We_d$ and thus the overall theoretical deformation:
The constants ![]() $\beta _{d, th}=2.7$ and
$\beta _{d, th}=2.7$ and ![]() $\gamma _{d, th}=0.5$ come from
$\gamma _{d, th}=0.5$ come from ![]() $\varPsi _d|_{We_d \approx 0}$, and
$\varPsi _d|_{We_d \approx 0}$, and ![]() $\alpha _{d, th}= 0.31/24\approx 0.013$ and
$\alpha _{d, th}= 0.31/24\approx 0.013$ and ![]() $m_{th}=-0.18$ originate from
$m_{th}=-0.18$ originate from ![]() $\varPsi _d|_{We_d \neq 0}$ and thus from the estimation of the relevant inertia. Due to the uncertainty of the computed findings, the approximation caused by linearization and the crude estimation of the stretched drop surface energy, we do not expect
$\varPsi _d|_{We_d \neq 0}$ and thus from the estimation of the relevant inertia. Due to the uncertainty of the computed findings, the approximation caused by linearization and the crude estimation of the stretched drop surface energy, we do not expect ![]() $\alpha _{d, th}$ and
$\alpha _{d, th}$ and ![]() $m_{th}$ to be quantitatively well predicted. We nevertheless anticipate a qualitative agreement of (3.1), which we probe by plotting the experimental data
$m_{th}$ to be quantitatively well predicted. We nevertheless anticipate a qualitative agreement of (3.1), which we probe by plotting the experimental data ![]() $\varPsi _{d}$ as a function of
$\varPsi _{d}$ as a function of ![]() $We_d$ for different
$We_d$ for different ![]() $X$. While these curves are obtained for all experiments (
$X$. While these curves are obtained for all experiments (![]() $0.008< Oh_d<0.325$), only those corresponding to
$0.008< Oh_d<0.325$), only those corresponding to ![]() $Oh_d=0.033$ are shown in figure 3(a). Note that the line corresponding to
$Oh_d=0.033$ are shown in figure 3(a). Note that the line corresponding to ![]() $\varPsi _d=3.25$ separates well the coalescence (full symbols) from the separation (empty symbols). In agreement with (3.1),
$\varPsi _d=3.25$ separates well the coalescence (full symbols) from the separation (empty symbols). In agreement with (3.1), ![]() $\varPsi _d$ increases linearly with
$\varPsi _d$ increases linearly with ![]() $We_d$. Saroka & Ashgriz (Reference Saroka and Ashgriz2015), who numerically studied water drop collisions, reported similar variations. Further, for a given
$We_d$. Saroka & Ashgriz (Reference Saroka and Ashgriz2015), who numerically studied water drop collisions, reported similar variations. Further, for a given ![]() $Oh_d$ and fixed
$Oh_d$ and fixed ![]() $X$, the curve slopes
$X$, the curve slopes ![]() $s_d$ are linear in
$s_d$ are linear in ![]() $X$ (figure 3b) as expected by (3.1) (first term). Repeating the experiments with three liquids and thus three
$X$ (figure 3b) as expected by (3.1) (first term). Repeating the experiments with three liquids and thus three ![]() $Oh_d$, we find that
$Oh_d$, we find that ![]() $a_d=s_d/X$ is equal to 0.078 for W (
$a_d=s_d/X$ is equal to 0.078 for W (![]() $Oh_d=0.008$), 0.066 for G (
$Oh_d=0.008$), 0.066 for G (![]() $Oh_d=0.033$) and 0.047 for SO (
$Oh_d=0.033$) and 0.047 for SO (![]() $Oh_d=0.325$), and thus decreases with increasing
$Oh_d=0.325$), and thus decreases with increasing ![]() $Oh_d$. The scaling
$Oh_d$. The scaling ![]() $a_d \propto {Oh_d}^{-0.14}$ (see dashed line in the insert of figure 3b) is reasonably well captured by (3.1), which predicts
$a_d \propto {Oh_d}^{-0.14}$ (see dashed line in the insert of figure 3b) is reasonably well captured by (3.1), which predicts ![]() $a_d \propto {Oh_d}^{-0.18}$.
$a_d \propto {Oh_d}^{-0.18}$.
To obtain a quantitative agreement, the experimental results ![]() $\varPsi _{d}$ are fitted by the model equation
$\varPsi _{d}$ are fitted by the model equation ![]() $\varPsi _{d, mod} = \alpha _{d, mod} Oh_d^{m_{mod}} X We_d + \beta _{d, mod} X + \gamma _{d, mod}$. There,
$\varPsi _{d, mod} = \alpha _{d, mod} Oh_d^{m_{mod}} X We_d + \beta _{d, mod} X + \gamma _{d, mod}$. There, ![]() $m_{mod}$ and
$m_{mod}$ and ![]() $\alpha _{d, mod}$ are only adjusted once, while
$\alpha _{d, mod}$ are only adjusted once, while ![]() $\beta _{d, mod}$ and
$\beta _{d, mod}$ and ![]() $\gamma _{d, mod}$ are taken equal to their theoretical values,
$\gamma _{d, mod}$ are taken equal to their theoretical values, ![]() $\beta _{d, th}$ and
$\beta _{d, th}$ and ![]() $\gamma _{d, th}$, see figure 3(c). We obtain an excellent prediction with
$\gamma _{d, th}$, see figure 3(c). We obtain an excellent prediction with
The discrepancy between ![]() $m_{th}$ and
$m_{th}$ and ![]() $m_{mod}$ (
$m_{mod}$ (![]() $28\,\%$) could originate from the integration by Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017) of the losses over the whole process instead of the first instants, see Appendix for details. The fit also provides
$28\,\%$) could originate from the integration by Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017) of the losses over the whole process instead of the first instants, see Appendix for details. The fit also provides ![]() $\alpha _{d, mod}=0.041$, while the theory gives
$\alpha _{d, mod}=0.041$, while the theory gives ![]() $\alpha _{d, th}=0.013$. The difference (factor 3) can be explained by the crude estimation of the stretched drop surface. All constants being the same, at least for
$\alpha _{d, th}=0.013$. The difference (factor 3) can be explained by the crude estimation of the stretched drop surface. All constants being the same, at least for ![]() $0.008 < Oh_d < 0.325$, (3.2) constitutes a model which is valid over a very wide domain without the need for any adjustment. The agreement is also excellent while using the data of Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021) (inset of figure 3c). This indeed indicates that the stretching separation is not purely inertial as previously reported by Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021). In fact, the authors probed fewer values of
$0.008 < Oh_d < 0.325$, (3.2) constitutes a model which is valid over a very wide domain without the need for any adjustment. The agreement is also excellent while using the data of Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021) (inset of figure 3c). This indeed indicates that the stretching separation is not purely inertial as previously reported by Al-Dirawi et al. (Reference Al-Dirawi, Al-Ghaithi, Sykes, Castrejón-Pita and Bayly2021). In fact, the authors probed fewer values of ![]() $We_d$ over a smaller range of
$We_d$ over a smaller range of ![]() $Oh_d$, which did not allow to identify the variations of
$Oh_d$, which did not allow to identify the variations of ![]() $\partial \varPsi _d/ \partial X$ with
$\partial \varPsi _d/ \partial X$ with ![]() $Oh_d$.
$Oh_d$.
We then predict the separation threshold in the form of an (![]() $X$,
$X$, ![]() $We_d$) relation by fixing in (3.2)
$We_d$) relation by fixing in (3.2) ![]() $\varPsi _{d, mod}$ to its critical value of 3.25. The results are compared to those of the literature, see figure 5(a–c). First of all, for all considered
$\varPsi _{d, mod}$ to its critical value of 3.25. The results are compared to those of the literature, see figure 5(a–c). First of all, for all considered ![]() $Oh_d$, the predicted thresholds (continuous lines) perfectly match the experimental ones (symbols). We further observed a very good agreement to previously proposed models, which involved adjusted parameters while being limited to given values or narrow ranges of
$Oh_d$, the predicted thresholds (continuous lines) perfectly match the experimental ones (symbols). We further observed a very good agreement to previously proposed models, which involved adjusted parameters while being limited to given values or narrow ranges of ![]() $Oh_d$ (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang et al. Reference Jiang, Umemura and Law1992; Gotaas et al. Reference Gotaas, Havelka, Jakobsen, Svendsen, Hase, Roth and Weigand2007; Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017). We recall that with our approach no parameter is adjusted to cover collisions with
$Oh_d$ (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang et al. Reference Jiang, Umemura and Law1992; Gotaas et al. Reference Gotaas, Havelka, Jakobsen, Svendsen, Hase, Roth and Weigand2007; Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017). We recall that with our approach no parameter is adjusted to cover collisions with ![]() $0.008< Oh_d<0.325$.
$0.008< Oh_d<0.325$.
Let us now apply these results to D–J collisions. In former studies (Planchette et al. Reference Planchette, Petit, Hinterbichler and Brenn2018; Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020a,Reference Baumgartner, Brenn and Planchetteb), the spatial period of the jet ![]() $L_j$ was normalized by
$L_j$ was normalized by ![]() $D_j$ and used to build a pseudo-Rayleigh criterion. A critical value of 2 was found to roughly describe the jet fragmentation threshold in the limit of moderate jet viscosity. Here, the analogy with D–D collisions requires the introduction of a new parameter to quantify the eccentricity of the successive collisions. As sketched in figure 2(g), these collisions involve a drop and the jet portions found before and after this drop (lighter grey). Note that the jet portion directly impacted by the drop (hatched) is associated with the drop to form a compound drop. Thus, the distance between the centre of mass of the compound drop and that of the jet portions found before or after is given by
$D_j$ and used to build a pseudo-Rayleigh criterion. A critical value of 2 was found to roughly describe the jet fragmentation threshold in the limit of moderate jet viscosity. Here, the analogy with D–D collisions requires the introduction of a new parameter to quantify the eccentricity of the successive collisions. As sketched in figure 2(g), these collisions involve a drop and the jet portions found before and after this drop (lighter grey). Note that the jet portion directly impacted by the drop (hatched) is associated with the drop to form a compound drop. Thus, the distance between the centre of mass of the compound drop and that of the jet portions found before or after is given by ![]() $\tilde {x}=(L_j+D_d)/4$. This distance is counted twice since each compound drop interacts with two such jet sections. Using
$\tilde {x}=(L_j+D_d)/4$. This distance is counted twice since each compound drop interacts with two such jet sections. Using ![]() $D_j$ for normalization, the equivalent impact parameter reads
$D_j$ for normalization, the equivalent impact parameter reads ![]() $\tilde {X}=(L_j+D_d)/(2D_j)$.
$\tilde {X}=(L_j+D_d)/(2D_j)$.
We record several D–J collisions and define, similarly to ![]() $H_d(t)/D_d$, the dimensionless extension of the jet
$H_d(t)/D_d$, the dimensionless extension of the jet ![]() $H_j(t)/D_j$, which is measured perpendicularly to the final D–J compound trajectory (figure 2c,d). Its temporal evolution is fitted by a third-order polynomial providing its maximum value
$H_j(t)/D_j$, which is measured perpendicularly to the final D–J compound trajectory (figure 2c,d). Its temporal evolution is fitted by a third-order polynomial providing its maximum value ![]() $\varPsi _j=\max (H_j(t)/D_j)$. The procedure and accuracy is similar to that of D–D collisions, see figure 2(e).
$\varPsi _j=\max (H_j(t)/D_j)$. The procedure and accuracy is similar to that of D–D collisions, see figure 2(e).
We first confirm that the jet fragmentation corresponds to a critical value of ![]() $\varPsi _j$, see figure 4(a). Interestingly, this critical value is 3.0, thus remarkably close to that found for the D–D stretching separation and underlines the relevance of our analogy. We then plot for different
$\varPsi _j$, see figure 4(a). Interestingly, this critical value is 3.0, thus remarkably close to that found for the D–D stretching separation and underlines the relevance of our analogy. We then plot for different ![]() $\tilde {X}$, the evolution of
$\tilde {X}$, the evolution of ![]() $\varPsi _j$ with
$\varPsi _j$ with ![]() $We_{d}$ and evidence a linear dependency similar to
$We_{d}$ and evidence a linear dependency similar to ![]() $\varPsi _d$ for D–D collisions. The curve slopes,
$\varPsi _d$ for D–D collisions. The curve slopes, ![]() $s_j$, are again linear in
$s_j$, are again linear in ![]() $\tilde {X}$ (figure 4b) and increase with
$\tilde {X}$ (figure 4b) and increase with ![]() $Oh_j$. For D–J collisions, the relevant Ohnesorge number is that of the jet liquid, since the viscous losses mainly take place in the interstitial jet portions, which are the most stretched. We therefore propose to describe the jet stretching as
$Oh_j$. For D–J collisions, the relevant Ohnesorge number is that of the jet liquid, since the viscous losses mainly take place in the interstitial jet portions, which are the most stretched. We therefore propose to describe the jet stretching as
Here again, ![]() $\alpha _j$,
$\alpha _j$, ![]() $\beta _j$ and
$\beta _j$ and ![]() $\gamma _j$ are constants. The first term accounts for the drop inertia reduced by viscous losses taking place in the jet liquid only. The last two terms correspond to geometrical effects. As shown in figure 4(c), the agreement is again very good. The fit provides
$\gamma _j$ are constants. The first term accounts for the drop inertia reduced by viscous losses taking place in the jet liquid only. The last two terms correspond to geometrical effects. As shown in figure 4(c), the agreement is again very good. The fit provides ![]() $-0.10$ for the exponent
$-0.10$ for the exponent ![]() $n$, close to
$n$, close to ![]() $-0.128$ found for
$-0.128$ found for ![]() $m_{mod}$ and therefore supports the assumption that the viscosity (of drop and jet) plays, despite different geometries, a similar role in both processes (D–D and D–J collisions, respectively). Here
$m_{mod}$ and therefore supports the assumption that the viscosity (of drop and jet) plays, despite different geometries, a similar role in both processes (D–D and D–J collisions, respectively). Here ![]() $\alpha _j$,
$\alpha _j$, ![]() $\beta _j$ and
$\beta _j$ and ![]() $\gamma _j$ are found to be +0.0066, +3.98 and
$\gamma _j$ are found to be +0.0066, +3.98 and ![]() $-5.85$, respectively. The slight deviation observed for D–J could have several origins. First of all, the system centre of mass is approximated by that of the jet, which slightly affects the measurement of the collision inertia. Second, immiscible liquids are used, which modify the flow field and thus the viscous losses. Due to the lack of existing data, (3.3) could not yet be tested against results obtained with miscible liquids. It should definitively be done in future investigations. Finally and despite its similarities, the process itself is different. For D–J collisions, the system is continuous, and mainly shear occurs between the colliding elements. For D–D, the drop pairs constitute a close system, which can rotate around their centre of mass, consuming part of the available inertia.
$-5.85$, respectively. The slight deviation observed for D–J could have several origins. First of all, the system centre of mass is approximated by that of the jet, which slightly affects the measurement of the collision inertia. Second, immiscible liquids are used, which modify the flow field and thus the viscous losses. Due to the lack of existing data, (3.3) could not yet be tested against results obtained with miscible liquids. It should definitively be done in future investigations. Finally and despite its similarities, the process itself is different. For D–J collisions, the system is continuous, and mainly shear occurs between the colliding elements. For D–D, the drop pairs constitute a close system, which can rotate around their centre of mass, consuming part of the available inertia.

Figure 4. D–J collisions: (a) ![]() $\varPsi _j$ against
$\varPsi _j$ against ![]() $We_d$ for different
$We_d$ for different ![]() $\tilde {X}$,
$\tilde {X}$, ![]() $Oh_j=0.246$ and
$Oh_j=0.246$ and ![]() $\varDelta =1.0$. Coalescence (full symbols) and separation (empty symbols); (b)
$\varDelta =1.0$. Coalescence (full symbols) and separation (empty symbols); (b) ![]() $s_j=\partial \varPsi _j/ \partial We_d$ against
$s_j=\partial \varPsi _j/ \partial We_d$ against ![]() $\tilde {X}$ from (a); (c) experiments vs model (3.3) with
$\tilde {X}$ from (a); (c) experiments vs model (3.3) with ![]() $0.021< Oh_j<0.25$ and
$0.021< Oh_j<0.25$ and ![]() $0.7<\varDelta <1.3$.
$0.7<\varDelta <1.3$.
To explain why, in contrast to ![]() $\varPsi _d|_{We_{d}\approx 0}$,
$\varPsi _d|_{We_{d}\approx 0}$, ![]() $\varPsi _j|_{We_{d}\rightarrow 0}=\beta _j Oh_j^n \tilde {X} + \gamma _j$ is a function of
$\varPsi _j|_{We_{d}\rightarrow 0}=\beta _j Oh_j^n \tilde {X} + \gamma _j$ is a function of ![]() $Oh_j$, it is useful to recall that Ohnesorge numbers can be seen as the ratio of a bulk motion time scale,
$Oh_j$, it is useful to recall that Ohnesorge numbers can be seen as the ratio of a bulk motion time scale, ![]() $t_{\mu }=\mu _jD_j/\sigma _j$ (Stone & Leal Reference Stone and Leal1989), and an interfacial time scale,
$t_{\mu }=\mu _jD_j/\sigma _j$ (Stone & Leal Reference Stone and Leal1989), and an interfacial time scale, ![]() $t_{\sigma }=\sqrt {\rho _j {D_j}^3/\sigma _j}$ (Rayleigh Reference Rayleigh1892). At intermediate time scales, when
$t_{\sigma }=\sqrt {\rho _j {D_j}^3/\sigma _j}$ (Rayleigh Reference Rayleigh1892). At intermediate time scales, when ![]() $\varPsi _j$ is measured, the morphology of the compound jet depends on their relative kinetics and therefore on the jet liquid properties via its Ohnesorge number. For high
$\varPsi _j$ is measured, the morphology of the compound jet depends on their relative kinetics and therefore on the jet liquid properties via its Ohnesorge number. For high ![]() $Oh_j$,
$Oh_j$, ![]() $t_{\mu }>t_{\sigma }$, the capillary effects are fast enough to significantly flatten the outer jet surface, leading to small
$t_{\mu }>t_{\sigma }$, the capillary effects are fast enough to significantly flatten the outer jet surface, leading to small ![]() $\varPsi _j|_{We_{d}\rightarrow 0}$. The contrary happens for small
$\varPsi _j|_{We_{d}\rightarrow 0}$. The contrary happens for small ![]() $Oh_j$. We also verify that increasing
$Oh_j$. We also verify that increasing ![]() $L_j$ or
$L_j$ or ![]() $D_d$ as well as decreasing
$D_d$ as well as decreasing ![]() $D_j$ (thus increasing
$D_j$ (thus increasing ![]() $\tilde {X}$) leads – as expected – to greater
$\tilde {X}$) leads – as expected – to greater ![]() $\varPsi _j|_{We_{d}\rightarrow 0}$.
$\varPsi _j|_{We_{d}\rightarrow 0}$.
Note that given the definition of ![]() $\tilde {X}$ and the value of
$\tilde {X}$ and the value of ![]() $\beta _j$,
$\beta _j$, ![]() $\gamma _j$ must be negative to represent separated successive and not overlapping drop collisions. We verify that
$\gamma _j$ must be negative to represent separated successive and not overlapping drop collisions. We verify that ![]() $\varPsi _j|_{We_{j}\rightarrow 0}>1$ in all experiments.
$\varPsi _j|_{We_{j}\rightarrow 0}>1$ in all experiments.
As for D–D collisions, fixing ![]() $\varPsi _{j, mod}$ to 3.0 in (3.3) enables the prediction of the transition between continuous (circles) and fragmented jet (diamonds), see solid lines in figure 5(d–f). The agreement between the model (solid lines) and the experiments (symbols) is very good, significantly better than with the former criterion of
$\varPsi _{j, mod}$ to 3.0 in (3.3) enables the prediction of the transition between continuous (circles) and fragmented jet (diamonds), see solid lines in figure 5(d–f). The agreement between the model (solid lines) and the experiments (symbols) is very good, significantly better than with the former criterion of ![]() $L_j/D_j \approx 2.0$ (horizontal dashed line). It is valid over a wide range of
$L_j/D_j \approx 2.0$ (horizontal dashed line). It is valid over a wide range of ![]() $Oh_j$ (
$Oh_j$ (![]() $0.021 < Oh_j < 0.246$) and for different drop and jet diameters (
$0.021 < Oh_j < 0.246$) and for different drop and jet diameters (![]() $0.7<\varDelta <1.3$) without adjusting any parameter.
$0.7<\varDelta <1.3$) without adjusting any parameter.

Figure 5. (a–c) The D–D collisions: separation transition for ![]() $Oh_d=0.008$ (a),
$Oh_d=0.008$ (a), ![]() $Oh_d=0.033$ (b) and
$Oh_d=0.033$ (b) and ![]() $Oh_d=0.325$ (c) with coalescence (circles) and separation (stars). Solid lines, (3.2) with
$Oh_d=0.325$ (c) with coalescence (circles) and separation (stars). Solid lines, (3.2) with ![]() $\varPsi _{d, mod}=3.25$; dashed lines, Jiang et al. (Reference Jiang, Umemura and Law1992); dash-double-dotted lines, Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017); dotted line, Ashgriz & Poo (Reference Ashgriz and Poo1990); dot-dashed line, Gotaas et al. (Reference Gotaas, Havelka, Jakobsen, Svendsen, Hase, Roth and Weigand2007). (d–f) The D–J collisions: transition between continuous (circles) and fragmented jet (stars) for
$\varPsi _{d, mod}=3.25$; dashed lines, Jiang et al. (Reference Jiang, Umemura and Law1992); dash-double-dotted lines, Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017); dotted line, Ashgriz & Poo (Reference Ashgriz and Poo1990); dot-dashed line, Gotaas et al. (Reference Gotaas, Havelka, Jakobsen, Svendsen, Hase, Roth and Weigand2007). (d–f) The D–J collisions: transition between continuous (circles) and fragmented jet (stars) for ![]() $Oh_j=0.021$ (d),
$Oh_j=0.021$ (d), ![]() $Oh_j=0.073$ (e) and
$Oh_j=0.073$ (e) and ![]() $Oh_j=0.246$ (f). Solid lines: (3.3) with
$Oh_j=0.246$ (f). Solid lines: (3.3) with ![]() $\varPsi _{j, mod}=3.0$. Dashed line (e): former criterion
$\varPsi _{j, mod}=3.0$. Dashed line (e): former criterion ![]() $L_j/D_j=2$.
$L_j/D_j=2$.
4. Conclusions
In conclusion, we have investigated off-centred D–D and D–J collisions and found a universal model for the transition between coalescence and fragmentation caused by stretching separation. Our approach is based on (i) a simple transition criterion based on a critical drop or jet extension of 3.25 or 3.0, and (ii) the evolution of this drop or jet extension with the liquid properties and collision parameters. In contrast to other models of D–D collisions, our model remains valid for a wide range of Ohnesorge numbers – at least over ![]() $0.008< Oh_d<0.325$ – without adjusting any parameter. For D–J collisions, our model is valid at least for
$0.008< Oh_d<0.325$ – without adjusting any parameter. For D–J collisions, our model is valid at least for ![]() $0.02< Oh_j<0.25$ and
$0.02< Oh_j<0.25$ and ![]() $0.7<\varDelta <1.3$ with a precision going far beyond the existing approach based on a critical
$0.7<\varDelta <1.3$ with a precision going far beyond the existing approach based on a critical ![]() $L_j/D_j$. The similarities between the collision morphologies, the fragmentation criterion (
$L_j/D_j$. The similarities between the collision morphologies, the fragmentation criterion (![]() $\varPsi _d=3.25$ and
$\varPsi _d=3.25$ and ![]() $\varPsi _j=3.0$) and the evolution of the maximum drop or jet extension (linear in
$\varPsi _j=3.0$) and the evolution of the maximum drop or jet extension (linear in ![]() $We_d$, linear in
$We_d$, linear in ![]() $X$ or
$X$ or ![]() $\tilde {X}$ and modulated by
$\tilde {X}$ and modulated by ![]() $Oh$ to the power of
$Oh$ to the power of ![]() $m$ or
$m$ or ![]() $n$) underline the universality of our approach and of the so-called stretching separation. It could certainly be successfully applied to further situations, such as miscible D–J collisions and beyond.
$n$) underline the universality of our approach and of the so-called stretching separation. It could certainly be successfully applied to further situations, such as miscible D–J collisions and beyond.
Funding
We would like to thank the Austrian Science Fund (FWF) for the financial support under grant no. P31064-N36.
Declaration of interests
The authors report no conflict of interest.
Appendix. Viscous losses
To estimate the viscous losses taking place in the first part of D–D collisions, we make use of the numerical results of Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017). More precisely, we replot the data of their figure 9. In its original form, it represents the variations of the dissipated energy ![]() $DE$ over the total initial energy
$DE$ over the total initial energy ![]() $TE$ (approximated by the initial kinetic energy) as a function of the impact parameter
$TE$ (approximated by the initial kinetic energy) as a function of the impact parameter ![]() $X$ for different capillary numbers
$X$ for different capillary numbers ![]() $Ca=\mu _dU/\sigma _d$ and Weber numbers:
$Ca=\mu _dU/\sigma _d$ and Weber numbers: ![]() $X \in [0.3, 0.8]$ and
$X \in [0.3, 0.8]$ and ![]() $Oh_d=Ca_d/\sqrt {We_d} \in [0.01, 0.20]$. From these results, we derive the normalized remaining energy (
$Oh_d=Ca_d/\sqrt {We_d} \in [0.01, 0.20]$. From these results, we derive the normalized remaining energy (![]() $1-DE/TE$), which we plot as a function of
$1-DE/TE$), which we plot as a function of ![]() $X$ and a power of
$X$ and a power of ![]() $Oh_d$ (see figure 6). The linear increase with
$Oh_d$ (see figure 6). The linear increase with ![]() $X$ is expected since the region of high dissipation rate grows linearly for decreasing
$X$ is expected since the region of high dissipation rate grows linearly for decreasing ![]() $X$, see Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017). We further choose to use
$X$, see Finotello et al. (Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017). We further choose to use ![]() $Oh_d$ as it is commonly employed to weight the relative importance of viscosity and capillarity, the inertia being here indirectly accounted for via the normalization with the total initial energy, which is approximated by the initial kinetic energy. By doing so, the best fit reveals that the remaining energy, which is left for stretching the ligament between the drops, scales as
$Oh_d$ as it is commonly employed to weight the relative importance of viscosity and capillarity, the inertia being here indirectly accounted for via the normalization with the total initial energy, which is approximated by the initial kinetic energy. By doing so, the best fit reveals that the remaining energy, which is left for stretching the ligament between the drops, scales as ![]() $(1-DE/TE) \propto X Oh_d^{-0.18}$. It is worth noting that Finotello et al. consider the duration of the entire collision process. For low
$(1-DE/TE) \propto X Oh_d^{-0.18}$. It is worth noting that Finotello et al. consider the duration of the entire collision process. For low ![]() $Oh_d$ (
$Oh_d$ (![]() $Oh_d \approx 0.02$, see figure 5(a) of Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017), up to
$Oh_d \approx 0.02$, see figure 5(a) of Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017), up to ![]() $23\,\%$ of the calculated losses arise after
$23\,\%$ of the calculated losses arise after ![]() $\varPsi _d$ has been reached. For larger
$\varPsi _d$ has been reached. For larger ![]() $Oh_d$ (
$Oh_d$ (![]() $Oh_d \approx 0.1$, see figure 5(b) of Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017), these subsequent losses are more limited, in the range of
$Oh_d \approx 0.1$, see figure 5(b) of Finotello et al. Reference Finotello, Padding, Deen, Jongsma, Innings and Kuipers2017), these subsequent losses are more limited, in the range of ![]() $6\,\%$. This may lead to an overestimation of the viscous losses in the case of small
$6\,\%$. This may lead to an overestimation of the viscous losses in the case of small ![]() $Oh_d$ and could explain why in our model, which considers only the first phase of the collision until
$Oh_d$ and could explain why in our model, which considers only the first phase of the collision until ![]() $\varPsi _d$ is reached, an exponent of
$\varPsi _d$ is reached, an exponent of ![]() $-0.128$ in (3.2) provides a better agreement than the value of
$-0.128$ in (3.2) provides a better agreement than the value of ![]() $-0.18$.
$-0.18$.

Figure 6. ![]() $(1-DE/TE)$ – the energy, which is left for droplet stretching – as a function of
$(1-DE/TE)$ – the energy, which is left for droplet stretching – as a function of ![]() $X$ and
$X$ and ![]() $Oh_d$. The dashed line corresponds to
$Oh_d$. The dashed line corresponds to ![]() $1-DE/TE=0.31X{Oh_d}^{-0.18}+0.25$.
$1-DE/TE=0.31X{Oh_d}^{-0.18}+0.25$.
Finally, extrapolating this scaling to head-on collisions shows that approximately ![]() $25\,\%$ of the initial energy remains. While in reasonable agreement with the
$25\,\%$ of the initial energy remains. While in reasonable agreement with the ![]() $35\,\%$ found by Planchette et al. (Reference Planchette, Hinterbichler, Liu, Bothe and Brenn2017b), the comparison is questionable. Off-centre and head-on collisions give rise to different deformation and flow fields, which call for separate modelling. With
$35\,\%$ found by Planchette et al. (Reference Planchette, Hinterbichler, Liu, Bothe and Brenn2017b), the comparison is questionable. Off-centre and head-on collisions give rise to different deformation and flow fields, which call for separate modelling. With ![]() $E_{\mu }$, the viscous losses until maximal extension, and
$E_{\mu }$, the viscous losses until maximal extension, and ![]() $E_k$, the initial kinetic energy, we have
$E_k$, the initial kinetic energy, we have ![]() $E_{\mu }\approx 0.65 E_k$ for
$E_{\mu }\approx 0.65 E_k$ for ![]() $X\approx 0$ and
$X\approx 0$ and ![]() $E_{\mu } \approx (0.75 -0.31 X {Oh_d}^{-0.18})E_k$ for
$E_{\mu } \approx (0.75 -0.31 X {Oh_d}^{-0.18})E_k$ for ![]() $0.3\lesssim X$. How to connect these scalings remains an open question.
$0.3\lesssim X$. How to connect these scalings remains an open question.