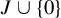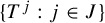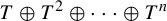Disjoint hypercyclicity, Sidon sets and weakly mixing operators

Abstract

We prove that a finite set of natural numbers J satisfies that $J\cup \{0\}$ is not Sidon if and only if for any operator T, the disjoint hypercyclicity of $\{T^j:j\in J\}$ implies that T is weakly mixing. As an application we show the existence of a non-weakly mixing operator T such that $T\oplus T^2\oplus\cdots \oplus T^n$ is hypercyclic for every n.

1 Introduction

Let X be a Banach space. An operator $T:X\to X$ is said to be hypercyclic if there is a vector $x\in X$ such that its orbit $\mathrm {Orb}_T(x):=\{T^n(x):n\in \mathbb N\}$ is dense in X. Then x is said to be a hypercyclic vector for T. The study of hypercyclic operators has seen lively development in recent decades. See, for example, the books [2, 21] on the subject.

A linear operator is called weakly mixing if $T\oplus T:X\oplus X\to X\oplus X$ is hypercyclic. In the topological setting, it is simple to show examples of hypercyclic maps that are not weakly mixing, for instance, any irrational rotation of the torus. However, in the linear setting, things get more interesting as weak mixing is equivalent to the hypercyclicity criterion, which is the simplest way to prove that a given operator is hypercyclic. Despite its intricate form it is very simple to use. A linear operator is said to satisfy the hypercyclicity criterion if there are dense sets $D_1,D_2\subseteq X$ , a sequence $(n_k)_k$ and applications $S_{n_k}:D_2\to X$ such that:

1. (1) $T^{n_k}(x)\to 0$ for every $x\in D_1$ ;

2. (2) $S_{n_k}(y) \to 0$ and $T^{n_k}S_{n_k}(y)$ for every $y\in D_2$ .

Most common notions in linear dynamics imply or are equivalent to the hypercyclicity criterion. For example, hypercyclic operators having a dense set of vectors with bounded orbits, chaotic operators, and frequently hypercyclic operators are weakly mixing. The existence of a non-weakly mixing but hypercyclic operator was an open question for many years. It was posed by Herrero in the $T\oplus T$ form in 1992 [22] and solved affirmatively by De La Rosa and Read in 2006 [15]. Later on, Bayart and Matheron constructed other examples in spaces such as ${H(\mathbb {C})}$ or $\ell _p$ [1, 3]. A ‘natural’ example of a hypercyclic operator that does not satisfy the hypercyclicity criterion is still unknown.

A natural question that arises is whether the hypercyclicity of $T\oplus T^2\oplus \cdots \oplus T^n$ for every n implies that T is weakly mixing.

Question A. Let T be an operator such that $T\oplus T^2\oplus \cdots \oplus T^n$ is hypercyclic for every n. Does T satisfy the hypercyclicity criterion?

Bayart and Matheron’s construction of a non-weakly mixing but hypercyclic operator invites consideration of disjoint hypercyclic operators. A finite set of operators $\{T_j: j\in J\} $ is called disjoint hypercyclic if there is a vector $x\in X$ such that $\bigoplus _{j\in J} x$ is a hypercyclic vector for $\bigoplus _{j\in J} T_j$ and it is called disjoint transitive if for every non-empty set U and every family of non-empty open sets $\{V_j:j\in J\}$ , there is n such that $U\cap \bigcap _{j\in J} T^{-n}(V)\neq \emptyset $ . The first to study disjoint hypercyclic operators were Bernal-González [4] and Bés and Peris [9]. Since then, the theory of disjoint hypercyclicity has had a huge impact. We now know that there are disjoint hypercyclic operators that are not disjoint transitive [25], there are disjoint weakly mixing operators that fail to satisfy the disjoint hypercyclicity criterion [25], there are disjoint hypercyclic operators in every infinite-dimensional and separable Banach space [26], there are mixing operators that are not disjoint mixing [5], etc.

Thus, the following question is a related Question A.

Question B. Let T be an operator such that $\{T^j: 1\leq j \leq n\}$ is disjoint hypercyclic for every n. Does T satisfy the hypercyclicity criterion? More generally, for which subsets of the natural numbers does it follow that if $\{T^j:j\in J\}$ is disjoint hypercyclic then T is weakly mixing?

The study of these questions leads to a surprising connection with the family of Sidon sets of the natural numbers. In Theorem 3.2 we will give a complete answer to Question A by proving that $J\cup \{0\}$ is Sidon if and only if there is a non-weakly mixing operator T such that $\{T^j:j\in J\}$ is disjoint hypercyclic. As a corollary, we answer Question A by exhibiting a non-weakly mixing operator T such that $T\oplus T^2\oplus \cdots \oplus T^n$ is hypercyclic for every n (Theorem 4.3).

Recall that a subset $A=\{a_i:i\in \mathbb N\}$ of the natural numbers is Sidon if all the sums $a_i+a_j$ for $i\leq j$ are different. The study of Sidon sets has seen considerable development on the last century and is a central task in number theory and additive combinatorics. For instance, in 1941, Erdős and Turán [18] proved that a result of Singer [27] implies that if $S(n)$ denotes the maximal cardinal of a Sidon set contained in $\{1,\ldots ,n\}$ , then the asymptotic behavior of $S(n)$ is $n^{{1}/{2}}$ . They also showed that $S(n)\leq n^{{1}/{2}}+O(n^{{1}/{4}})$ . In 1969, Lindström [23] proved that for all n, $S(n)<n^{{1}/{2}}+n^{{1}/{4}}+1$ , and in 2010, Cilleruelo [14] slightly improved this result by showing that $S(n)<n^{{1}/{2}}+n^{{1}/{4}}+{1}/{2}$ . The question whether $S(n)<n^{{1}/{2}}+o(n^\varepsilon )$ for every $\varepsilon>0$ is still an open problem posed by Erdős [17].

The paper is organized as follows. In §2 we fix notation and recall some facts about weakly mixing operators and disjoint hypercyclic operators. In §3 we answer Question A, by proving that a finite subset $J\subseteq \mathbb N$ satisfies that $J\cup \{0\}$ is not Sidon if and only if for every linear operator T such that $\{T^j:j\in J\}$ is disjoint hypercyclic we have that T is weakly mixing (Theorem 3.2). Moreover, we construct a non-weakly mixing operator T such that $\{T^j:j\in J\}$ is disjoint hypercyclic for every finite set J such that $J\cup \{0\}$ is Sidon (Theorem 3.4). In §4 we answer Question A, and exhibit a non-weakly mixing operator for which $T\oplus T^2\oplus \cdots \oplus T^n$ is hypercyclic for every n. In §5 we study syndetically transitive operators. We prove that a linear operator T is syndetically transitive if and only if $T\oplus S$ is hypercyclic for every weakly mixing operator S (Theorem 5.3) and that a linear operator is piecewise syndetically transitive if and only if $T\oplus S$ is hypercyclic for every syndetically transitive operator S (Theorem 5.4). Finally, we show the existence of a frequently transitive but non-weakly mixing operator (Theorem 5.5), which answers a question of [7, Question 5.12].

2 Preliminaries

Throughout the paper X will denote an infinite-dimensional and separable Fréchet space and $T:X\to X$ will be a linear operator.

Given a linear operator T, $x\in X$ and $U,V$ non-empty open sets, the sets of hitting times $N_T(x,U)$ and $N_T(U,V)$ are defined as

$$ \begin{align*}N_T(x,U):&=\{n\in\mathbb N: T^n(x)\in U\},\\ N_T(U,V):&=\{n\in\mathbb N: T^n(U)\cap V\} .\end{align*} $$

A linear operator is said to be hypercyclic if there is $x\in X$ such that $N_T(x,U)\neq \emptyset $ for every non-empty open set U and transitive if $N_T(U,V)\neq \emptyset $ for every pair of non-empty open sets $U,V$ . Given a hypercyclic vector x and non-empty open sets $U,V$ , then we can write $N_T(U,V)$ as

$$ \begin{align*}N_T(U,V)=N_T(x,V)- N_T(x,U)\!:=\!\{m-n: m\in N_T(x,V),\, n\in N_T(x,U) \text{ and } m\geq n\}. \end{align*} $$

See [2, Lemma 4.5] for a proof of this fact.

A linear operator T is said to be weakly mixing if $T\oplus T$ is hypercyclic. The weak mixing property admits several well-known equivalent formulations. For instance, a nice result due to Bès and Peris [8] shows that T is weakly mixing if and only if T satisfies the hypercyclicity criterion if and only if T is hereditarily hypercyclic. The following characterization [21, Proposition 1.53] of weakly mixing operators will be used repeatedly.

Proposition 2.1. A linear operator is weakly mixing if and only if for every pair of non-empty sets $U,V$ then $N_T(U,U)\cap N_T(U,V)\neq \emptyset $ .

Definition 2.2. A set of operators $\{T_i:X\to X:i\in I\}$ is said to be disjoint hypercyclic (or d-hypercyclic) if there is $x\in X$ such that for every family of non-empty open sets $\{U_i:i\in I\}$ , there is n such that $T_i^n(x)\in U_i$ for every $i\in I$ . In that case we will say that x is a disjoint hypercyclic vector (or d-hypercyclic vector) for $\{T_i:X\to X:i\in I\}$ .

Similarly, there is a notion of d-transitivity.

Definition 2.3. A set of operators $\{T_i:i\in I\}$ is said to be disjoint transitive (or d-transitive) if for every non-empty open set U and every family of non-empty open sets $\{U_i:i\in I\}$ there is n such that $U\cap \bigcap _{i\in I} T_i^{-1}U_i$ is non-empty.

It is not difficult to prove that a set of disjoint transitive operators is a set of disjoint hypercyclic operators with a dense set of d-hypercyclic vectors [9, Proposition 2.3]. However, the converse is false and there are d-hypercyclic operators without a dense set of d-hypercyclic vectors [25, Corollary 3.5].

The next proposition seems to be original. It establishes the equivalence between disjoint hypercyclicity and disjoint transitivity for commuting operators.

Proposition 2.4. Let $\{T_i:1\leq i\leq N\}$ be a set of operators such that $T_1$ commutes with $T_i$ for every $2\leq i\leq N$ . Then $\{T_i:1\leq i\leq N\}$ is disjoint hypercyclic if and only if it is disjoint transitive.

Proof. If $\{T_i:1\leq i\leq N\}$ is disjoint transitive then it is disjoint hypercyclic by [9, Proposition 2.3].

Suppose that $\{T_i:1\leq i\leq N\}$ is disjoint hypercyclic and let $x\in X$ be a disjoint hypercyclic vector for $\{T_i:1\leq i\leq N\}$ . We will prove that, for every $n\in \mathbb N$ , $T_1^n(x)$ is a disjoint hypercyclic vector for $\{T_i:1\leq i\leq N\}$ . Let $n\in \mathbb N$ .

As the operators commute, it follows that

$$ \begin{align*}\mathrm{Orb}_{T_1\oplus \cdots \oplus T_N}\bigg(\bigoplus_{i=1}^N T_1^n(x)\bigg)= \bigoplus_{i=1}^N T_1^n \bigg( \mathrm{Orb}_{T_1\oplus \cdots \oplus T_N}\bigg(\bigoplus_{i=1}^N x\bigg)\bigg).\end{align*} $$

The operator $T_1$ is hypercyclic and hence $T_1^n$ is also hypercyclic [21, Theorem 6.2]. This implies that $Im(\bigoplus _{i=1}^N T_1^n)$ is dense in $\bigoplus _{i=1}^N X$ . On the other hand, $\bigoplus _{i=1}^N \mathrm {Orb}_{T_1\oplus \cdots \oplus T_N}(\bigoplus _{i=1}^N x)$ is also dense in $\bigoplus _{i=1}^N X$ . We conclude that $T_1^n(x)$ is a disjoint hypercyclic vector.

Now consider non-empty open sets U and $V_1,\ldots V_N$ . Since x is a hypercyclic vector for $T_1$ , there is $n_1$ such that $y=T_1^{n_1}(x)\in U$ . We have just proved that y is a d-hypercyclic vector for $\{T_i:1\leq i\leq N\}$ . Thus, there is n such that $T_i^n(y)\in V_i$ for every $1\leq i\leq N$ . It follows that $y\in U\cap \bigcap _{i=1}^N T_i^{-n}V_i.$

3 Disjoint hypercyclicity of powers of an operator and weakly mixing operators

In this section, we prove the main theorem of the paper. It involves a surprising connection between disjoint hypercyclicity, weakly mixing operators and Sidon sets of the natural numbers. We prove that a finite set of natural numbers J satisfies that $J\cup \{0\}$ is not Sidon if and only if for any operator T, the disjoint hypercyclicity of $\{T^j:j\in J\}$ implies that T is weakly mixing (Theorem 3.2). Moreover, we construct a non-weakly mixing operator $T:\ell _1\to \ell _1$ such that $\{T^{j}:j\in J\}$ is disjoint hypercyclic for every finite set J such that $J\cup \{0\}$ is Sidon (Theorem 3.4). This allows us to generalize Theorem 3.2 to infinite sets: an infinite set $S\subseteq \mathbb N$ satisfies that $S\cup \{0\}$ is Sidon if and only if there is a non-weakly mixing operator $T:\ell _1\to \ell _1$ such that for every finite subset $J\subseteq S$ we have that $\{T^j: j\in J\}$ is disjoint hypercyclic (Theorem 3.5).

Definition 3.1. A sequence of integers numbers $(j_k)$ (or a set $J=\{j_k:k\in \mathbb N\}$ ) is said to be Sidon, if all the sums $j_k+j_{k'}$ with $k\le k'$ are different.

In this paper we will only consider Sidon subsets of the non-negative numbers that contain $0$ . Thus, for example, $\{2,4\}$ is Sidon but $\{0,2,4\}$ is not Sidon.

Theorem 3.2. Let $J\subseteq \mathbb N$ be a finite set. Then $J\cup \{0\}$ is Sidon if and only if there exists a non-weakly mixing operator $T:\ell _1\to \ell _1$ such that $\{T^j:j\in J\}$ is disjoint hypercyclic.

The proof is an immediate consequence of Theorems 3.3 and 3.4 below.

Theorem 3.3. Let X be a Banach space, $J\subseteq \mathbb N$ such that $J\cup \{0\}$ is not Sidon and $T:X\to X$ be a linear operator such that { $T^{j}:j\in J\}$ is disjoint hypercyclic. Then T is weakly mixing.

Theorem 3.4. There exists a non-weakly mixing operator $T:\ell _1\to \ell _1$ such that $\{T^{j}: j\in J\}$ is disjoint hypercyclic for every finite set $J\subseteq \mathbb N$ such that $J\cup \{0\}$ is Sidon.

We see in particular that the disjoint hypercyclicity of $\{T,T^j\}$ in $\ell _1$ implies that T is weakly mixing if and only if either $j=1$ or $j=2$ . (But of course $\{T,T\}$ is never disjoint hypercyclic.)

Since a set S is Sidon if and only if every finite subset of S is Sidon, Theorems 3.3 and 3.4 also give a characterization for infinite subsets of the natural numbers.

Theorem 3.5. Let $S\subseteq \mathbb N$ . Then $S\cup \{0\}$ is Sidon if and only if there is a non-weakly mixing operator $T:\ell _1\to \ell _1$ such that for every finite subset $J\subseteq S$ we have that $\{T^j: j\in J\}$ is disjoint hypercyclic.

Proof of Theorem 3.3

Suppose that there are $j_1,j_2,j_3,j_4\in J\cup \{0\},\ 0\leq j_1\leq j_2 \leq j_3\leq ~j_4$ such that $j_1+j_4=j_2+j_3$ .

Let $U,V$ be non-empty open sets. We will prove that $N_T(U,U)\cap N_T(U,V)\neq \emptyset .$ By Proposition 2.1 this implies that T is weakly mixing.

We will divide the proof into three cases.

First case. Suppose that $j_1\neq 0$ and that $j_2<j_3$ . Let $x\in X$ be a disjoint hypercyclic vector for $\{T^{j_i}:1\leq i\leq 4\}$ . Hence, there is $n\in \mathbb N$ such that $T^{j_in}(x)\in U$ for $i\leq 3$ and $T^{j_4n}(x)\in V$ . Therefore, $j_4n-j_2n\in N_T(x,V)-N_T(x,U)=N_T(U,V)$ and, on the other hand, $j_4n-j_2n=j_3n-j_1n\in N_T(x,U)-N_T(x,U)=N_T(U,U)$ .

If $j_1\neq 0$ and $j_2=j_3$ the proof is the same by considering $x\in X$ a disjoint hypercyclic vector for $\{T^{j_1},T^{j_2},T^{j_4}\}$ and $n\in \mathbb N$ such that $T^{j_in}(x)\in U$ for $i\leq 3$ and $T^{j_4n}(x)\in V$ .

Second case. Suppose that $j_1=0$ and that $j_2\neq j_3$ . By Proposition 2.4, the set of disjoint hypercyclic vectors is dense and hence there is a disjoint hypercyclic vector $x\in U$ for $\{T^{j_2},T^{j_3}, T^{j_4}\}$ .

Let $n\in \mathbb N$ such that $T^{j_2n}(x)\in U$ , $T^{j_3n}(x)\in U$ and $T^{j_4n}(x)\in V.$ Therefore, $j_4n-j_3n\in N_T(x,V)-N_T(x,U)= N_T(U,V)$ . On the other hand, $j_4n-j_3n=j_2n\in N_T(U,U)$ , because $x\in U$ and $T^{j2n}(x)\in U.$

Final case. Suppose that $j_1=0$ , $j_2=j_3=j$ and $j_4=2j$ . By Proposition 2.4 there is a disjoint hypercyclic vector $x\in U$ for $\{T^j,T^{2j}\}$ . Let $n\in \mathbb N$ such that $T^{jn}(x)\in U$ and such that $T^{2jn}(x)\in V$ . It follows that $2jn-jn=jn\in N_T(x,V)-N_T(x,U)=N_T(U,V)$ . On the other hand, $jn\in N_T(U,U)$ , because $x\in U$ and $T^{jn}(x)\in U$ .

This implies that $N_T(U,U)\cap N_T(U,V)\ne \emptyset $ and thus T is weakly mixing.

To prove Theorem 3.4 we will use the construction by Bayart and Matheron [3] of a non-weakly mixing and hypercyclic operator. Let us briefly recall their construction.

Bayart and Matheron’s operator is an upper triangular perturbation of a weighted forward shift in $\ell _1$ . For a sparse sequence $(b_n)$ , a sequence $a_n\to \infty $ , weights $w_n$ and a dense sequence of polynomials $(P_n)$ with $\mathrm{deg}(P_n)<b_n$ to be specified, they consider

$$ \begin{align*}\begin{cases} T(e_i)= w_ie_{i+1} \quad\text{if } b_{k-1}\leq i <b_{k}-1;\\[6pt] T^{b_k}(e_1)=P_k(T)(e_1)+ \dfrac{e_{b_k}}{a_k}. \end{cases} \end{align*} $$

Since $\mathrm{deg}(P_n)<b_n$ for every n, it follows that T is an upper triangular operator. In particular, $e_1$ is a cyclic vector for T and hence $\{P(T)(e_1): P \text { is a polynomial}\}$ is dense in $\ell _1$ . Therefore, if ${1}/{(a_n)}\to 0$ and $(P_n)$ is a dense family of polynomials, it follows that $e_1$ is a hypercyclic vector for T. We notice also that $\mathrm{span}(\mathrm {Orb}_T(e_1))=c_{00}$ . The following definition is useful.

Definition 3.6. Let $(P_n)$ be a sequence of polynomials and $(u_n)$ an increasing sequence of positive real numbers. We will say that $(P_n)$ is controlled by $(u_n)$ if for every n, $\mathrm{deg}(P_n)$ and $|P_n|_1$ are both less than $u_n$ .

Definition 3.7. Let $(\Delta _l)$ be a sequence of natural numbers. An increasing sequence of natural numbers ( $b_n$ ) is said to be a ( $\Delta _l$ )-Sidon sequence if the sets of natural numbers

$$ \begin{align*}J_l :=[b_l,b_l+\Delta_l]\cup \bigcup_{k\leq l} [b_l + b_k , b_l + b_k + \Delta_l]\end{align*} $$

are pairwise disjoint.

The following theorem is deduced from the proof of [3, Theorem 1.6].

Theorem 3.8. Let $\Delta _l\to \infty $ and $(b_n)$ be a $(\Delta _l)$ -Sidon sequence. Then there are parameters $w_n$ , $a_n\to \infty $ and $u_n\to \infty $ such that whenever $(P_n)$ is controlled by $(u_n)$ , that is $\mathrm{deg}(P_n)<u_n$ and $|P_n|_1<u_n$ for every n, then the operator T is continuous and not weakly mixing.

Proof of Theorem 3.4

Let $(F_n)_n$ be a collection of finite sets, with $|F_n|=n$ , such that $F_n\cup \{0\}$ is a Sidon set and such that any finite set $F\subset \mathbb N$ such that $F\cup \{0\}$ is Sidon, F is contained in $F_n\cup \{0\}$ for some n. We consider $(j_{n,k})_{0\leq k\le n,n\in \mathbb N}$ such that for every n, $(j_{n,k})_{0\le k\le n}$ forms an increasing enumeration of $F_n\cup \{0\}$ . Thus, it suffices to show the existence of a Bayart–Matheron operator such that for each n, the set of operators $\{T^{j_{n,1}},\dots ,T^{j_{n,n}}\}$ is disjoint hypercyclic.

For a sequence $m_{l,n}$ such that $l\geq n$ (to be defined), we will consider $b_{l,n,k}$ , $1\hspace{-2pt}\leq\hspace{-2pt} k\hspace{-2pt}\leq\hspace{-2pt} n\hspace{-2pt}\leq\hspace{-2pt} l$ , such that $b_{l,n,k}=m_{l,n} j_{n,k}$ . Note that $b_{l,n,k}$ is not defined if $k=0$ .

The order considered for the tuples $(l,n)$ is lexicographic, that is, $(l,n)\leq (l',n')$ if $l<l'$ or if $l=l'$ and $n\le n'$ . The tuples $(l,n,k)$ will also be ordered lexicographically.

We will construct $m_{l,n}$ by induction in $(l,n)$ so that the sets

$$ \begin{align*} J_{l,n,k}:=&\bigg[b_{l,n,k},b_{l,n,k}+\frac{m_{l,n}}{2}\bigg]\\ & \cup \bigg(\bigcup_{(l',n',k')\leq (l,n,k)}\bigg[b_{l,n,k}+ b_{l',n',k'} ,b_{l,n,k}+ b_{l',n',k'}+\frac{m_{l,n}}{2}\bigg]\bigg) \end{align*} $$

with $1\le k\le n\le l$ are pairwise disjoint. If so, it will follow by definition that $(b_{l,n,k})$ is a $\Delta _{l,n,k}$ -Sidon sequence for $\Delta _{l,n,k}=({m_{l,n}})/{2}$ . At each inductive step $(L,N)$ we will construct sets $J_{L,N,k}$ , $1\leq k\leq N$ so that:

1. (i) for $1\leq k\leq N$ , the $J_{L,N,k}$ are pairwise disjoint; and

2. (ii) for every $1\leq k\leq N$ , $1\leq k'\leq N'$ and $(L',N')<(L,N)$ , $J_{L,N,k}$ is disjoint from $J_{L',N',k'}$ .

The first step is straightforward because there is a single set. We put $m_{1,1}=1$ .

Suppose now that we have constructed $m_{1,1},\ldots m_{L,N}$ such all the sets $J_{l,n,k}$ with $(l,n,k)\leq (L,N,N)$ are pairwise disjoint. If $(\tilde L,\tilde N)$ denotes the immediate successor of $(L,N)$ we have to choose $m_{\tilde L, \tilde N}$ such that the $J_{l,n,k}$ are pairwise disjoint for every $(l,n,k)\leq (\tilde L,\tilde N ,\tilde N)$ . To do that, we will choose $m_{\tilde L,\tilde N}$ big enough so that for $k\leq \tilde N$ the minimum of $J_{\tilde L,\tilde N,k}$ is greater than the maximum of $\bigcup _{(l,n,k)\leq (L,N,N)} J_{l,n,k}$ . Then we will use that $(j_{n,k})_k$ is Sidon to show that, for $k\leq \tilde N$ , the $J_{\tilde L,\tilde N,k}$ are pairwise disjoint.

Let $m_{\tilde L,\tilde N}$ such that for every $(l',n')\leq (L,N),$

(1) $$ \begin{align} m_{\tilde L,\tilde N}>2m_{l',n'}j_{n',n'}+\frac{m_{l',n'}}{2}. \end{align} $$

We claim that for every $k\leq \tilde N$ , the set $J_{\tilde L,\tilde N,k}$ is disjoint from $J_{l',n',k'}$ for every $(l',n',k')\leq (L,N,N)$ . Indeed,

$$ \begin{align*} \min J_{\tilde L,\tilde N,k}&= b_{\tilde L,\tilde N,k}= m_{\tilde L,\tilde N}j_{\tilde N,k}\geq m_{\tilde L,\tilde N}j_{\tilde N,1}\\ &> 2m_{l',n'}j_{n',k'}+\frac{m_{l',n'}}{2}= \max J_{l',n',k'}. \end{align*} $$

So, it only remains to prove that $J_{\tilde L,\tilde N,k}$ , with $1\leq k\leq \tilde N$ , are pairwise disjoint.

Suppose otherwise and let $t\in J_{\tilde L,\tilde N,k_1}\cap J_{\tilde L,\tilde N,k_2}$ . Hence, there are $ (L_i',N_i',k_i')\leq (\tilde L,\tilde N,k_i)$ such that for $i=1$ and $i=2$ we have that

$$ \begin{align*} m_{\tilde L,\tilde N}j_{\tilde N,k_i}+m_{L_i',N_i'}j_{N_i',k_i'}\leq t\leq m_{\tilde L,\tilde N}j_{\tilde N,k_i}+m_{L_i',N_i'}j_{N'_i,k_i'} +\frac{m_{\tilde L,\tilde N}}{2}. \end{align*} $$

Note that $k_i'$ may be equal to 0 here. This is the case if $t\in [b_{\tilde L,\tilde N,k_i},b_{\tilde L,\tilde N,k_i}+({m_{\tilde L,\tilde N}})/{2}]$ .

Therefore $j_{\tilde N, k_i}\hspace{-2.3pt}+\hspace{-1.2pt}({m_{L_i',N_i'}})/({m_{\tilde L,\tilde N}})j_{\tilde N,k_i'}\hspace{-1.5pt}\leq\hspace{-1pt} {t}/({m_{\tilde L,\tilde N}})\hspace{-1.2pt}\leq\hspace{-1.3pt} j_{\tilde N,k_i}\hspace{-2.5pt}+\hspace{-1pt}({m_{L_i',N_i'}})/({m_{\tilde L,\tilde N}}) j_{\tilde N,} {}_{k_i'}\hspace{-1.2pt} +\hspace{-1.4pt} \tfrac {1}{2}$ , $i=1,2$ . Applying (1), we obtain that if $(L_i',N_i')<(\tilde L,\tilde N)$ ,

$$ \begin{align*} j_{\tilde N, k_i}\leq \frac{t}{m_{\tilde L,\tilde N}}< j_{\tilde N,k_i} +1. \end{align*} $$

Otherwise, if $(L_i',N_i')=(\tilde L,\tilde N)$ , we obtain

$$ \begin{align*} j_{\tilde N, k_i}+j_{\tilde N,k_i'}\leq \frac{t}{m_{\tilde L,\tilde N}}\leq j_{\tilde N,k_i}+j_{\tilde N,k_i'} +\frac{1}{2}. \end{align*} $$

Thus, for example, if $(L_1',N_1')<(\tilde L,\tilde N)$ and $(L_2',N_2')=(\tilde L,\tilde N)$ , the above inequalities show that $j_{\tilde N, k_1}=\lfloor {t}/({m_{\tilde L,\tilde N}})\rfloor =j_{\tilde N, k_2}+j_{\tilde N, k_2'}$ . This is a contradiction because $\{0,j_{\tilde N,1},\dots ,j_{\tilde N,\tilde N}\}$ is Sidon, $k_1\neq k_2$ and $k_2'\leq k_2$ .

The other cases,

• • $(L_1',N_1')<(\tilde L,\tilde N)$ and $(L_2',N_2')<(\tilde L,\tilde N)$ ,

• • $(L_1',N_1')=(\tilde L,\tilde N)$ and $(L_2',N_2')<(\tilde L,\tilde N)$ ,

• • $(L_1',N_1')=(L_2',N_2')=(\tilde L,\tilde N)$ ,

are similar.

We have proved that the sets $J_{l,n,k}$ , $1\le k\le n\le l$ , are pairwise disjoint and thus $b_{l,n,k}$ is a $\Delta _{l,n,k}$ -Sidon sequence for some $\Delta _{l,n,k}\to \infty $ . Therefore, by Theorem 3.8, there are parameters $w_{l,n,k},{1}/({a_{l,n,k}})\to 0$ and $u_{l,n,k}\to \infty $ such that if $P_{l,n,k}$ is controlled by $u_{l,n,k}$ then T is continuous and not weakly mixing.

We consider a family of polynomials $P_{l,n,k}=P_{l,k}$ controlled by $u_{l,n,k}$ such that for every $n, ( P_{l,1}\oplus P_{l,2}\oplus \cdots \oplus P_{l,n})_{l\geq n}$ is dense in $\bigoplus _{k\leq n} {\mathbb {C}}([x])$ . To construct this sequence of polynomials just consider $v_{l,k}=\min _{n\in [k,l]} \{u_{l,n,k}\}$ and a dense sequence $(Q_l)_l\subset \bigoplus _{k\in \mathbb N} {\mathbb {C}}[x]$ , where $Q_l=([Q_l]_1,[Q_l]_2,\ldots ),$ with the additional property that each $[Q_l]_k$ is controlled by $ v_{l,k}$ whenever $l\geq k$ .

The polynomials $P_{l,k}=[Q_l]_k$ satisfy the desired property.

It remains to show that for every n and k, $e_1\oplus e_1\oplus \cdots \oplus e_1$ is a hypercyclic vector for $T^{j_{n,1}}\oplus T^{j_{n,2}}\oplus \cdots \oplus T^{j_{n,n}}$ . Indeed,

$$ \begin{align*} &(T^{j_{n,1}}\oplus T^{j_{n,2}}\oplus\cdots \oplus T^{j_{n,n}})^{m_{l,n}}(e_1\oplus\cdots \oplus e_1)\\ &\quad= (T^{b_{l,n,1}}\oplus T^{b_{l,n,2}}\oplus\cdots \oplus T^{b_{l,n,n}})(e_1\oplus\cdots \oplus e_1)\\ &\quad=P_{l,1}(T)(e_1)+ {e_{ b_{l,n,1}}}/{ a_{l,n,1}}\oplus \cdots \oplus P_{l,n}(T)(e_1)+ {e_{ b_{l,n,n}}}/{a_{l,n,n}}. \end{align*} $$

Thus $((T^{j_{n,1}}\oplus T^{j_{n,2}}\oplus \cdots \oplus T^{j_{n,n}})^{m_{l,n}}(e_1\oplus \cdots \oplus e_1))_{l\ge n}$ is dense in $\bigoplus _{1\leq k\leq n} \ell _1$ .

Remark 3.9. Our definition of $\Delta _l$ -Sidon set is slightly different from the originally proposed by Bayart and Matheron in [3]. The reason is that their condition is not strong enough to prove Theorem 3.8. Indeed, otherwise, we could, using the same techniques that we used to prove Theorem 3.4, construct a non-weakly mixing operator such that T and $T^2$ are disjoint hypercyclic. These conditions are incompatible since $\{T,T^2\}$ disjoint hypercyclic implies that T is weakly mixing.

4 A non-weakly mixing operator such that T ⊕ T ² ⊕⋯ ⊕ T ⁿ is hypercyclic for every n

In this section, we exhibit a non-weakly mixing operator such that $T\oplus T^2\oplus \cdots \oplus T^n$ is hypercyclic for every n (Theorem 4.3). The operator is the one defined in Theorem 3.4.

To show that the operator satisfies the desired property, we will study a nice relationship between the disjointness hypercyclicity of $\{T^j:j\in J\}$ and the hypercyclicity of $\bigoplus _{k\in K} T^k$ for some subsets $K\subseteq J- J$ .

The next proposition characterizes the hypercyclicity of $\bigoplus _{j=1}^n T_j$ for an n-tuple of hypercyclic operators.

Proposition 4.1. Let $T_1,\ldots T_N$ be hypercyclic operators such that for every ( $N+1$ )-tuple of non-empty open sets $U,V_1,\ldots V_N$ we have that $\bigcap _{i=1}^N N_{T_i}(U,V_i)\neq \emptyset $ . Then $\bigoplus _{i=1}^N T_i$ is hypercyclic.

Proof. Let $U_1,V_1,U_2,V_2\ldots U_N,V_N$ be non-empty open sets.

Put $W_1=U_1$ and $n_1=0$ . By an inductive argument we construct non-empty open sets $W_N\subseteq W_{N-1}\ldots \subseteq W_1\subseteq U_1$ and numbers $n_1,\ldots n_N$ such that for every i, $n_i\in N_{T_{i}}(W_{i-1},U_i)$ and $W_i=W_{i-1}\cap T_i^{-n_i}(U_i)$ .

Since each $T_i$ is hypercyclic we have that each $T^{-n_i} (V_i)$ is a non-empty open set. Let $m\in \bigcap _{i=1}^N N_{T_i} (W_N, T^{-n_i} (V_i))$ . We will show that $m\in \bigcap _{i=1}^N N_{T_i}(U_i,V_i)$ . For $i=1$ it is clear because $W_N\subseteq U_1$ and $T^{-n_1}(V_1)=V_1$ . If $i>1$ , there is $x_i\in W_N$ such that $T_i^m(x_i)\in T_i^{-n_i}(V_i)$ . Hence $T_i^{m+n_i}(x_i)\in V_i$ . Using that $W_N\subseteq W_i\subseteq T_i^{-n_i}(U_i)$ , we see that $T_i^{n_i}(x_i)\in U_i$ . Therefore, $m\in N_{T_i}(U_i,V_i)$ .

In the same way that $\{T^{j}:j\in J\}$ being disjoint hypercyclic implies that $T\oplus T$ is hypercyclic for $J\cup \{0\}$ not Sidon, there are nice relationships between the disjoint hypercyclicity of $\{T^{j}:j\in J\}$ and the hypercyclicity of $\bigoplus _{k\in K} T^{k}$ for some subsets $K\subseteq J-J$ .

Proposition 4.2. Let $J\subseteq \mathbb N$ be a finite set and $\{T^j:j\in J\}$ be disjoint hypercyclic. Let $(j_2^l)_{1\leq l\leq n}\subseteq J$ and $(j_1^l)_{1\leq l\leq n}\subseteq J\cup \{0\}$ such that:

1. (i) $j_2^l\neq j_1^{l'}$ for every $1\leq l,l'\leq n$ ;

2. (ii) $j_2^l\neq j_2^{l'}$ for every $1\leq l< l'\leq n$ ; and

3. (iii) $j_1^l<j_2^l$ for every $1\le l\le n$ .

Then $\bigoplus _{l=1}^n T^{j_2^l-j_1^l}$ is hypercyclic.

Proof. Let U be a non-empty open set and $V_l: 1\leq l\leq n$ be non-empty open sets. We will prove that $\bigcap _{l\leq n} N_{T^{j_2^l-j_1^l}}(U,V_l) $ is non-empty.

By Proposition 2.4 there is a disjoint hypercyclic vector $x\in U$ . Let $m\in \mathbb N$ such that for every $1\leq l\leq n$ , $T^{j^l_2 m}(x)\in V_l$ and $T^{j_1^lm}(x)\in U$ . Therefore, $j_2^lm-j_1^lm\in N_T(x,V_l)-N_T(x,U)=N_T(U,V_l)$ . We conclude that $m\in N_{T^{j_2^l-j_1^l}}(U,V_l)$ for every $1\leq l\leq n$ .

As an application of the above theorems, we now exhibit a non-weakly mixing operator T such that $T\oplus T^2\ldots \oplus T^n$ is hypercyclic for every n.

Theorem 4.3. There exists a non-weakly mixing operator T such that $T\oplus T^2\oplus \cdots \oplus T^n$ is hypercyclic for every n.

Proof. Let T be the operator constructed in Theorem 3.4. Then T is not weakly mixing and $\{T^{j}:j\in J\}$ is disjoint hypercyclic for every finite J such that $J\cup \{0\}$ is Sidon.

Suppose that $J_n=\{k_1,k_1+1,k_2,k_2+2,\dots ,k_n,k_n+n\}$ is a Sidon set. Then Proposition 4.2 implies that $T\oplus T^2\oplus \dots \oplus T^n$ is hypercyclic. Indeed, we may just take $j_2^l=k_l+l$ and $j_1^l=k_l$ for $l=1,\dots , n$ .

If we take $k_1=n+1$ and $k_{j+1}=2(k_j+j)+1$ then it is simple to show that $J_n\cup \{0\}$ is Sidon. Indeed, suppose that $0\leq a_1\leq a_2\leq a_3<a_4$ are elements in $J_n\cup \{0\}$ such that $a_1+a_4=a_2+a_3$ . Notice that, by construction, if $l_1\leq l_2<l_3$ then ${k_{l_1}+l_1+k_{l_2}+l_2<k_{l_3}}$ . This implies that there is $l\leq n$ such that $a_4=k_l+l$ and $a_3=k_l$ . Hence, $l=a_2-a_1$ . It follows that there must be $l'$ such that $a_2=k_{l'}+l'$ and $a_1=k_{l'}$ , because otherwise $a_2-a_1>n+1>l$ . Thus, $l=a_2-a_1=l'$ , which is a contradiction because $a_2<a_4.$

5 Syndetically and frequently transitive operators

In this section we study syndetically and frequently transitive operators. The motivation comes from the facts that syndetically transitive operators satisfy that $T\oplus T^2\oplus \cdots \oplus T^n$ is hypercyclic for every n while frequently hypercyclic operators are syndetically transitive. In Theorem 5.3 we prove that a linear operator T is syndetically transitive if and only if $T\oplus S$ is hypercyclic for every weakly mixing operator S. Analogously, we prove that a linear operator is piecewise syndetically transitive if and only if $T\oplus S$ is hypercyclic for every syndetically transitive operator S. In Theorem 5.5 we show an example of a frequently transitive operator that is not weakly mixing. This answers a question of [7, Question 5.12].

Given a hereditary upward family $F \subseteq \mathcal P(\mathbb N)$ (also called a Furstenberg family) we say that an operator is $\mathcal {F}$ -hypercyclic if there is $x\in X$ for which the sets $N_T (x, U)$ of return times belong to $\mathcal {F}$ , and we say that an operator is $\mathcal {F}$ -transitive if the sets $N_T (U,V)$ belong to $\mathcal {F}$ .

We will consider the following families.

• • A is said to have positive lower density (or $A\in \underline {\mathcal D}$ ) if

  $$ \begin{align*} \underline {d}(A)\!:\!\liminf _n ({\#\{j\leq n:j\in A\}})/{n}>0. \end{align*} $$

• • A is said to be thick, if A contains arbitrary long intervals.

• • A is said to be syndetic if A has bounded gaps.

• • A is said to be piecewise syndetic if A is the intersection of a thick set with a syndetic set. Equivalently, there is b such that A contains arbitrarily large sets with gaps bounded by b.

• • A is said to be thickly syndetic if for every k there is a syndetic set S such that $S+\{0,\ldots k\}\subseteq A$ .

The $\underline {\mathcal D}$ -hypercyclic (transitive) operators are known as frequently hypercyclic (transitive) operators.

Given a family $\mathcal {F}$ , the dual family $\mathcal {F}^*$ is defined as

$$ \begin{align*}\mathcal {F}^*=\{A\subseteq \mathbb N: A\cap F\neq \emptyset \text{ for every } F\in\mathcal {F}\}.\end{align*} $$

The duals of the thick sets (piecewise syndetic sets) are the syndetic sets (thickly syndetic sets).

It is not difficult to prove that there are no thickly or syndetically hypercyclic operators (see Propositions 2 and 3 of [6] for proof of these facts). However, operators can be thickly transitive and syndetically transitive. It is well known that a linear operator is thickly transitive if and only if it is weakly mixing [2, Theorem 4.6] and that if A has positive lower density, then $A- A$ is syndetic [20, Proposition 3.19]. This implies that frequently hypercyclic operators are syndetically transitive. On the other hand, the proof of [2, Theorem 6.31] shows that syndetically transitive operators are weakly mixing. Thus, frequently hypercyclic operators are both syndetically and thickly transitive.

For more on $\mathcal {F}$ -hypercyclicity see [6, 7, 10–13, 19].

It was proved independently in [24, Proposition 4] and [16] that whenever T and S are syndetically and thickly transitive, $T\oplus S$ is syndetically and thickly transitive. (See also Exercises 2.5.4 and 2.5.5 in [21].) In particular, the finite product of syndetically transitive operators is weakly mixing.

Theorem 5.1. Let $f:X\to X$ and $g:Y\to Y$ be syndetically and thickly transitive continuous mappings. Then $f\oplus g$ is syndetically and thickly transitive.

On the other hand, syndetically and transitive operators are thickly syndetically transitive. See [7, Lemma 2.3] for a proof of this result.

Lemma 5.2. Let $f:X\to X$ be a syndetically and thickly transitive mapping. Then f is thickly syndetically transitive.

The intersection of a syndetic set and a thick set is always non-empty. Therefore, if T is syndetically transitive and S is weakly mixing then $T\oplus S$ is hypercyclic. This property characterizes the syndetically transitive operators.

Theorem 5.3. Let T be a linear operator. The following assertions are equivalent.

1. (1) T is syndetically transitive.

2. (2) $T\oplus S$ is weakly mixing for every weakly mixing operator S.

3. (3) $T\oplus S$ is hypercyclic for every weakly mixing operator S.

Proof. $(1)\Rightarrow (2)$ . Since T is a syndetically transitive linear operator, it is thickly transitive. It follows by the above lemma that T is thickly syndetically transitive.

Let $U_1,U_2,V_1,V_2$ be non-empty open sets. Then $N_S(U_2,V_2)$ is thick while $N_T(U_1,V_1)$ is thickly syndetic, that is, for every k, there is a syndetic set A such that $A+\{1,\ldots , k\}\subseteq N_T(U_1,V_1)$ . Let $k\in \mathbb N$ . Then $N_S(U_2,V_2)\cap A+\{1,\ldots , k\}$ contains k consecutive integers.

$(2)\Rightarrow (3)$ . Let S be a weakly mixing operator. Then $T\oplus S$ is weakly mixing. In particular, $T\oplus S$ is hypercyclic.

$(3)\Rightarrow (1)$ . We will prove that if T is not syndetically transitive, then there is a weakly mixing operator S such that $T\oplus S$ is not hypercyclic.

Let T be not syndetically transitive. Hence there are non-empty open sets $U,V$ such that $N_T(U,V)$ is not syndetic. Thus, there is a sequence $(n_k)$ for which $n_{k+1}>n_k+k$ and

$$ \begin{align*}\bigcup_k [n_k,n_k+k]\subseteq N_T(U,V)^c.\end{align*} $$

It suffices to show the existence of a weakly mixing operator S and a non-empty open set W for which

$$ \begin{align*}N_S(W,W)\subseteq \bigcup_k [n_k,n_k+k].\end{align*} $$

Let S be the weighted backward shift on $\ell _2$ given by the weights

$$ \begin{align*}w_n=\begin{cases} 2 &\text{ if } n\in [n_k,n_k+k] \text{ for some } k,\\ 2^{-k} &\text{ if } n=n_k+k+1,\\ 1 &\text{ otherwise}. \end{cases} \end{align*} $$

The weights $(w_n)_n$ are bounded and $\prod _{j=1}^{n_k+k} w_j=2^k$ . These facts imply that $B_w$ is well defined and that $B_w$ is weakly mixing (see [21, Ch. 4]). On the other hand, we notice that if $n\notin \bigcup _k [n_k,n_k+k]$ , then $\prod _{j=1}^n w_j=1$ .

Consider now $W=B(e_1,\varepsilon )$ with $\varepsilon <\tfrac {1}{2}$ and let $n\in N_S(W,W).$ Hence, there is x such that $\|x-e_1\|<\varepsilon $ and $\|S_w^n(x)-e_1\|<\varepsilon .$ Therefore,

$$ \begin{align*}|x_n|<\varepsilon \ \ \text{ and }\ \ \bigg|\prod_{j=1}^n w_j x_n-1\bigg|=|[B_w^n(x)-e_1]_1|<\varepsilon.\end{align*} $$

It follows that $n\in \bigcup _k [n_k,n_k+k].$

The symmetric problem recovers the piecewise syndetically transitive operators.

Theorem 5.4. Let T be a linear operator. The following assertions are equivalent.

1. (1) T is piecewise syndetically transitive.

2. (2) $T\oplus S$ is hypercyclic for every syndetically transitive operator.

Proof. $(1)\Longrightarrow (2)$ . Suppose that T is piecewise syndetically transitive and let S be a syndetically transitive operator. Then S is, by Lemma 5.2, thickly syndetically transitive. By the duality between the piecewise syndetic and the thickly syndetic sets, we obtain that for every tuple of non-empty open sets $U_1,U_2,V_1,V_2$ ,

$$ \begin{align*}N_T(U_1,V_1)\cap N_S(U_2,V_2)\neq \emptyset\end{align*} $$

and hence $T\oplus S$ is hypercyclic.

$(2)\Longrightarrow (1)$ . Suppose that T is not piecewise syndetically transitive. It suffices to show the existence of a syndetically transitive operator S and non-empty open sets $U,V,W$ such that $N_S(W,W)\subseteq N_T(U,V)^c$ .

Since T is not piecewise syndetically transitive there are non-empty open sets $U,V$ such that $N_T(U,V)$ is not piecewise syndetic. By duality, there is a thickly syndetic set A such that $N_T(U,V)\cap A=\emptyset $ . It follows that $N_T(U,V)^c$ is thickly syndetic. Equivalently, we have that for every k, $\{n:[n,n+k]\subseteq N_T(U,V)^c\}$ is syndetic.

Let S be the weighted backward shift on $\ell _2$ given by the weights

$$ \begin{align*}w_n=\begin{cases} 2 &\text{ if } n\in N_T(U,V)^c,\\ 2^{-l} &\text{ if } n\notin N_T(U,V)^c, n-1\in N_T(U,V)^c \text{ and }\\ & l =\max\{j\in\mathbb N:[n-j,n-1] \subseteq N_T(U,V)^c\},\\ 1 &\text{ otherwise}. \end{cases} \end{align*} $$

The weights $w_n$ are bounded and hence S is a well-defined backward shift. Also, for every k, $\{n:[n,n+k+1]\subseteq N_T(U,V)^c\}\subseteq \{n: \prod _{j=1}^n w_j>2^k\}$ . This implies that for every M, $\{n: \prod _{j=1}^n w_j>M\}$ is syndetic and hence S is syndetically transitive [7, Corollary 3.4]. On the other hand, we notice that if $n\notin N_T(U,V)^c$ , then $\prod _{j=1}^n w_j=1$ .

Consider now $W=B(e_1,\varepsilon )$ with $\varepsilon <\tfrac 12$ and let $n\in N_S(W,W)$ . Thus, there is x such that $\|x-e_1\|<\varepsilon $ and $\|S^n(x)-e_1\|<\varepsilon $ . Therefore,

$$ \begin{align*}|x_n|<\varepsilon \quad \text{and}\quad \bigg|\prod_{j=1}^n w_j x_n-1\bigg|=|[B_w^n(x)-e_1]_1|<\varepsilon.\end{align*} $$

It follows that $n\in N_T(U,V)^c.$

Every syndetically transitive linear operator is weakly mixing. It is natural to require the same for the family of sets having positive lower density. The following Theorem answers a question posed in [7, Question 5.12].

Theorem 5.5. There exist a non-weakly mixing operator such that T is frequently transitive.

The proof relies again on the construction of Bayart and Matheron of a non-weakly mixing but hypercyclic operator. The following theorem was proved in [3].

Theorem 5.6. (Bayart and Matheron)

Let $(m_k)$ be a sequence of natural numbers such that $\lim _k ({m_k})/{k}=\infty .$ Then there exist a non-weakly mixing operator T and a vector x such that for every non-empty open set U, $N_T(x,U)\in O(m_k).$

We will need the following lemma, which is number-theoretic.

Lemma 5.7. Let $(n_k)$ be an increasing sequence of natural numbers in $O(n^2)$ . Then the set $\{n_k-n_j:k\geq j\}$ has positive lower density.

Proof. Let $C>0$ such that $n_k\leq Ck^2.$ Notice that $\#\{k\leq K:n_{k+1}-n_{k}\geq 8Ck\}\leq {K}/{2}$ . Indeed, if we suppose otherwise, then we get that

$$ \begin{align*} n_K-n_1=\sum_{l=1}^K n_{l+1}-n_l\geq \sum_{l=1}^{{K}/{2}}8Ck>CK^2, \end{align*} $$

which is a contradiction. Hence, $\#\{k\leq K:n_{k+1}-n_{k}\leq 8Ck\}\geq {K}/{2}$ . This implies that

$$ \begin{align*}\underline d \{n_k-n_j:k\geq j\}\geq \frac{1}{16C}.\end{align*} $$

Proof of Theorem 5.5

Let T be a non-weakly mixing operator and x such that for every non-empty open set U, $N_T(x,U)\in O(n^2)$ . By the above lemma we get that for every non-empty open set U, $N_T(U,U)=N_T(x,U)- N_T(x,U)$ has positive lower density.

Consider now a pair of non-empty open sets $U,V$ . Since T is hypercyclic, there are $U'\subseteq U$ and n such that $T^n(U')\subseteq V$ . Hence $N_T(U',U')+n\subseteq N_T(U,V)$ and therefore $N_T(U,V)$ has positive lower density.

We would like to end this section with an open question related to Theorems 5.3 and 5.4.

Question. Let T be a piecewise syndetically transitive linear operator. Is T weakly mixing?

Remark 5.8. The techniques used in Theorems 3.4 and 5.5 do not provide non-weakly mixing but piecewise syndetically transitive operators. Indeed, Bayart and Matheron’s construction relies on the existence of a $\Delta _l$ -Sidon sequence $b_n$ such that for every non-empty open set U, there is $(b_{n_k})_k$ such that $b_{n_k}\in N(e_1,U)$ for every k. However, the $\Delta _l$ -Sidon structure of $b_n$ implies that the set of differences $\{b_{n}-b_{n'}:n>n'\}$ is not piecewise syndetic. In fact, from this observation and the proof of Theorem 5.6 it follows that given a sequence of natural numbers $(m_k)_k$ with $({m_k})/{k}\to \infty $ , there is $n_k\in O(m_k)$ such that the set of differences $\{n_k-n_{k'}:k>k'\}$ is not piecewise syndetic.