Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-21T01:58:26.264Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula

Part of: Existence theories Real functions Classical measure theory

Published online by Cambridge University Press:  16 April 2024

Elisa Davoli Open the ORCID record for Elisa Davoli [Opens in a new window] ,
Giovanni Di Fratta  and
Valerio Pagliari Open the ORCID record for Valerio Pagliari [Opens in a new window]
Elisa Davoli
Affiliation:
Institute of Analysis and Scientific Computing, TU Wien, Wiedner Hauptstraße 8-10, 1040 Vienna, Austria ([email protected])
Giovanni Di Fratta
Affiliation:
Dipartimento di Matematica e Applicazioni ‘R. Caccioppoli’, Università degli studi di Napoli ‘Federico II’, Via Cintia, Complesso Monte S. Angelo, 80126 Naples, Italy ([email protected])
Valerio Pagliari
Affiliation:
Institute of Analysis and Scientific Computing, TU Wien, Wiedner Hauptstraße 8-10, 1040 Vienna, Austria ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Following the seminal paper by Bourgain, Brezis, and Mironescu, we focus on the asymptotic behaviour of some nonlocal functionals that, for each $u\in L^2(\mathbb {R}^N)$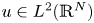, are defined as the double integrals of weighted, squared difference quotients of $u$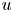. Given a family of weights $\{\rho _{\varepsilon} \}$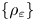, $\varepsilon \in (0,\,1)$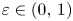, we devise sufficient and necessary conditions on $\{\rho _{\varepsilon} \}$ 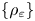for the associated nonlocal functionals to converge as $\varepsilon \to 0$ 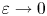to a variant of the Dirichlet integral. Finally, some comparison between our result and the existing literature is provided.

Keywords

nonlocal functionalsBourgain–Brezis–Mironescu formulafractional kernelsGagliardo seminormRadon measures

MSC classification

Primary: 26A33: Fractional derivatives and integrals
Secondary: 28A33: Spaces of measures, convergence of measures 49J45: Methods involving semicontinuity and convergence; relaxation
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 24
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alicandro, R., Ansini, N., Braides, A., Piatnitski, A. and Tribuzio, A.. A variational theory of convolution-type functionals. Springer Briefs on PDEs and Data Science (Springer, 2023).CrossRefGoogle Scholar
Ambrosio, L., De Philippis, G. and Martinazzi, L.. Gamma-convergence of nonlocal perimeter functionals. Manuscr. Math. 134 (2001), 377–403. https://doi.org/10.1007/s00229-010-0399-4CrossRefGoogle Scholar
Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free discontinuity problems, Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, New York, 2000).CrossRefGoogle Scholar
Berendsen, J. and Pagliari, V.. On the asymptotic behaviour of nonlocal perimeters. ESAIM-COCV 25 (2019), 48. https://doi.org/10.1051/cocv/2018038CrossRefGoogle Scholar
Bourgain, J., Brezis, H. and Mironescu, P.. Another look at Sobolev spaces. In Optimal Control and Partial Differential Equations, pp. 439–455 (IOS, Amsterdam, 2001).Google Scholar
Brazke, D., Schikorra, A. and Yung, P. (2021) Bourgain–Brezis–Mironescu convergence via Triebel–Lizorkin spaces. arXiv preprint: 10.48550/ARXIV.2109.04159.Google Scholar
Caffarelli, L., Roquejoffre, J.-M. and Savin, O.. Nonlocal minimal surfaces. Commun. Pure Appl. Math. 63 (2010), 1111–1144. https://doi.org/10.1002/cpa.20331CrossRefGoogle Scholar
Dal Maso, G.. An introduction to Γ-convergence (Birkhäuser, Boston, 1993).CrossRefGoogle Scholar
Dávila, J.. On an open question about functions of bounded variation. Calc. Var. 15 (2002), 519–527. https://doi.org/10.1007/s005260100135CrossRefGoogle Scholar
De Luca, L., Kubin, A. and Ponsiglione, M.. The core-radius approach to supercritical fractional perimeters, curvatures and geometric flows. Nonlinear Anal. 214 (2022), 112585. https://doi.org/10.1016/j.na.2021.112585CrossRefGoogle Scholar
Di Fratta, G. and Slastikov, V.. Curved thin-film limits of chiral Dirichlet energies. Nonlinear Anal. 234 (2023), 113303. https://doi.org/10.1016/j.na.2023.113303CrossRefGoogle Scholar
Foghem, G. and Kaßmann, M. (2022) A general framework for nonlocal Neumann problems. arXiv preprint: 2204.06793.Google Scholar
Leoni, G. and Spector, D.. Characterization of Sobolev and BV spaces. J. Funct. Anal. 261 (2011), 2926–2958. https://doi.org/10.1016/j.jfa.2011.07.018CrossRefGoogle Scholar
Mazón, J., Rossi, J. and Toledo, J.. Nonlocal perimeter, curvature and minimal surfaces for measurable sets (Birkhäuser, Cham, 2019).CrossRefGoogle Scholar
Mengesha, T.. Nonlocal Korn-type characterization of Sobolev vector fields. Commun. Contemp. Math. 14 (2012), 28. https://doi.org/10.1142/S0219199712500289CrossRefGoogle Scholar
Mengesha, T. and Du, Q.. On the variational limit of a class of nonlocal functionals related to peridynamics. Nonlinearity 28 (2015), 3999. https://doi.org/10.1088/0951-7715/28/11/3999CrossRefGoogle Scholar
Pagliari, V.. Halfspaces minimise nonlocal perimeter: a proof via calibrations. Ann. Mat. Pura Appl. 199 (2020), 1685–1696. https://doi.org/10.1007/s10231-019-00937-7CrossRefGoogle Scholar
Ponce, A.. An estimate in the spirit of Poincaré's inequality. J. Eur. Math. Soc. 006 (2004), 1–15. https://doi.org/10.4171/JEMS/1CrossRefGoogle Scholar
Ponce, A.. A new approach to Sobolev spaces and connections to $\Gamma$-convergence. Calc. Var. 19 (2004), 229–255. https://doi.org/10.1007/s00526-003-0195-zCrossRefGoogle Scholar
Rogers, R.. A nonlocal model for the exchange energy in ferromagnetic materials. J. Int. Equ. Appl. 3 (1991), 85–127. https://doi.org/10.1216/jiea/1181075602Google Scholar
Scott, J. and Mengesha, T.. A fractional Korn-type inequality. Discrete Contin. Dyn. Syst. 39 (2019), 3315–3343. https://doi.org/10.3934/dcds.2019137CrossRefGoogle Scholar
Stein, E. and Shakarchi, R.. Fourier analysis, Vol. 1 of Princeton Lectures in Analysis (Princeton University Press, Princeton, NJ, 2003).Google Scholar