Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-28T01:28:46.390Z Has data issue: false hasContentIssue false
  • English
  • Français

New Paradigm of Identifiable General-response Cognitive Diagnostic Models: Beyond Categorical Data

Published online by Cambridge University Press:  01 January 2025

Seunghyun Lee Open the ORCID record for Seunghyun Lee [Opens in a new window]  and
Yuqi Gu Open the ORCID record for Yuqi Gu [Opens in a new window]
Seunghyun Lee
Affiliation:
Columbia University
Yuqi Gu*
Affiliation:
Columbia University
*
Correspondence should be made to Yuqi Gu, Department of Statistics, Columbia University, Room 928 SSW, 1255 Amsterdam Avenue, New York, NY10027, USA. Email: yuqi.gu@columbia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Cognitive diagnostic models (CDMs) are a popular family of discrete latent variable models that model students’ mastery or deficiency of multiple fine-grained skills. CDMs have been most widely used to model categorical item response data such as binary or polytomous responses. With advances in technology and the emergence of varying test formats in modern educational assessments, new response types, including continuous responses such as response times, and count-valued responses from tests with repetitive tasks or eye-tracking sensors, have also become available. Variants of CDMs have been proposed recently for modeling such responses. However, whether these extended CDMs are identifiable and estimable is entirely unknown. We propose a very general cognitive diagnostic modeling framework for arbitrary types of multivariate responses with minimal assumptions, and establish identifiability in this general setting. Surprisingly, we prove that our general-response CDMs are identifiable under Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\textbf{Q}}$$\end{document}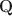-matrix-based conditions similar to those for traditional categorical-response CDMs. Our conclusions set up a new paradigm of identifiable general-response CDMs. We propose an EM algorithm to efficiently estimate a broad class of exponential family-based general-response CDMs. We conduct simulation studies under various response types. The simulation results not only corroborate our identifiability theory, but also demonstrate the superior empirical performance of our estimation algorithms. We illustrate our methodology by applying it to a TIMSS 2019 response time dataset.

Keywords

cognitive diagnostic modeldiagnostic classification modelEM algorithmexponential familygeneral responsesgeneralized linear modelidentifiabilityQ-matrix
Type
Theory and Methods
Information
Psychometrika , Volume 89 , Issue 4 , December 2024 , pp. 1304 - 1336
Copyright
© 2024 The Author(s), under exclusive licence to The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/s11336-024-09983-4.

References

Allman, E. S., Matias, C., Rhodes, J. A. (2009). Identifiability of parameters in latent structure models with many observed variables. The Annals of Statistics, 37 6A3099–3132.CrossRefGoogle Scholar
Casella, G., Berger, R. L. (2021). Statistical inference, Cengage Learning.Google Scholar
Chen, Y., Culpepper, S., Liang, F. (2020). A sparse latent class model for cognitive diagnosis. Psychometrika, 85(1), 121–153.CrossRefGoogle ScholarPubMed
Chen, Y., Culpepper, S. A., Chen, Y., Douglas, J. (2018). Bayesian estimation of the DINA Q matrix. Psychometrika, 83(1), 89–108.CrossRefGoogle ScholarPubMed
Chen, Y., Liu, J., Xu, G., Ying, Z. (2015). Statistical analysis of Q-matrix based diagnostic classification models. Journal of the American Statistical Association, 110(510), 850–866.CrossRefGoogle Scholar
Culpepper, S. A. (2019). An exploratory diagnostic model for ordinal responses with binary attributes: Identifiability and estimation. Psychometrika, 84(4), 921–940.CrossRefGoogle ScholarPubMed
Culpepper, S. A. (2023). A note on weaker conditions for identifying restricted latent class models for binary responses. Psychometrika, 88(1), 158–174.CrossRefGoogle ScholarPubMed
De Boeck, P., Jeon, M. (2019). An overview of models for response times and processes in cognitive tests. Frontiers in Psychology, 10, 102.CrossRefGoogle ScholarPubMed
de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76(2), 179–199.CrossRefGoogle Scholar
de la Torre, J., Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69(3), 333–353.CrossRefGoogle Scholar
Dempster, A. P., Laird, N. M., Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B: Statistical Methodology, 39(1), 1–22.CrossRefGoogle Scholar
DiBello, L. V., Stout, W. F., & Roussos, L. A. (1995). Unified cognitive/psychometric diagnostic assessment likelihood-based classification techniques. Cognitively diagnostic assessment, 361389.Google Scholar
Dunson, D. B. (2000). Bayesian latent variable models for clustered mixed outcomes. Journal of the Royal Statistical Society Series B: Statistical Methodology, 62(2), 355–366.CrossRefGoogle Scholar
Fang, G., Liu, J., Ying, Z. (2019). On the identifiability of diagnostic classification models. Psychometrika, 84(1), 19–40.CrossRefGoogle ScholarPubMed
Fishbein, B., Foy, P., & Yin, L. (2021). TIMSS 2019 user guide for the international database. Hentet fra https://timssandpirls. bc. edu/timss2019/international-database.Google Scholar
Gu, Y., Dunson, D. B. (2023). Bayesian Pyramids: identifiable multilayer discrete latent structure models for discrete data. Journal of the Royal Statistical Society Series B: Statistical Methodology, 85(2), 399–426.CrossRefGoogle Scholar
Gu, Y., Xu, G. (2019). The sufficient and necessary condition for the identifiability and estimability of the DINA model. Psychometrika, 84(2), 468–483.CrossRefGoogle ScholarPubMed
Gu, Y., Xu, G. (2020). Partial identifiability of restricted latent class models. Annals of Statistics, 48(4), 2082–2107.CrossRefGoogle Scholar
Gu, Y., Xu, G. (2021). Sufficient and necessary conditions for the identifiability of the Q\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$Q$$\end{document}-matrix. Statistica Sinica, 31, 449–472.Google Scholar
He, Q., & Von Davier, M. (2016). Analyzing process data from problem-solving items with n-grams: Insights from a computer-based large-scale assessment. In Handbook of research on technology tools for real-world skill development, pages 750–777. IGI Global.CrossRefGoogle Scholar
Henson, R. A., Templin, J. L., Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika, 74, 191–210.CrossRefGoogle Scholar
Junker, B. W., Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25, 258–272.CrossRefGoogle Scholar
Kang, I., Jeon, M., & Partchev, I. (2023). A latent space diffusion item response theory model to explore conditional dependence between responses and response times. Psychometrika, pages 1–35.CrossRefGoogle Scholar
Koller, D., & Friedman, N. (2009). Probabilistic graphical models: principles and techniques. MIT press.Google Scholar
Kruskal, J. B. (1977). Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear Algebra and its Applications, 18(2), 95–138.CrossRefGoogle Scholar
Liu, C-W, Andersson, B., Skrondal, A. (2020). A constrained Metropolis-Hastings Robbins–Monro algorithm for Q matrix estimation in DINA models. Psychometrika, 85(2), 322–357.CrossRefGoogle ScholarPubMed
Liu, R., Heo, I., Liu, H., Shi, D., Jiang, Z. (2023). Applying negative binomial distribution in diagnostic classification models for analyzing count data. Applied Psychological Measurement, 47(1), 64–75.CrossRefGoogle ScholarPubMed
Liu, R., Liu, H., Shi, D., Jiang, Z. (2022). Poisson diagnostic classification models: A framework and an exploratory example. Educational and Psychological Measurement, 82(3), 506–516.CrossRefGoogle Scholar
Lo, S., Andrews, S. (2015). To transform or not to transform: Using generalized linear mixed models to analyse reaction time data. Frontiers in Psychology, 6, 1171.CrossRefGoogle ScholarPubMed
Loeys, T., Rosseel, Y., Baten, K. (2011). A joint modeling approach for reaction time and accuracy in psycholinguistic experiments. Psychometrika, 76, 487–503.CrossRefGoogle Scholar
Ma, C., Ouyang, J., Xu, G. (2023). Learning latent and hierarchical structures in cognitive diagnosis models. Psychometrika, 88(1), 175–207.CrossRefGoogle ScholarPubMed
Magnus, B. E., Thissen, D. (2017). Item response modeling of multivariate count data with zero inflation, maximum inflation, and heaping. Journal of Educational and Behavioral Statistics, 42(5), 531–558.CrossRefGoogle Scholar
Man, K., Harring, J. R. (2019). Negative binomial models for visual fixation counts on test items. Educational and Psychological Measurement, 79(4), 617–635.CrossRefGoogle ScholarPubMed
Man, K., & Harring, J. R. (2022). Detecting preknowledge cheating via innovative measures: A mixture hierarchical model for jointly modeling item responses, response times, and visual fixation counts. Educational and Psychological Measurement, page 00131644221136142.Google Scholar
Maris, E. (1993). Additive and multiplicative models for gamma distributed random variables, and their application as psychometric models for response times. Psychometrika, 58, 445–469.CrossRefGoogle Scholar
Maris, E. (1999). Estimating multiple classification latent class models. Psychometrika, 64(2), 187–212.CrossRefGoogle Scholar
Minchen, N., de la Torre, J. (2018). A general cognitive diagnosis model for continuous-response data. Measurement: Interdisciplinary Research and Perspectives, 16(1), 30–44.Google Scholar
Minchen, N., de la Torre, J., Liu, Y. (2017). A cognitive diagnosis model for continuous response. Journal of Educational and Behavioral Statistics, 42(6), 651–677.CrossRefGoogle Scholar
Molenaar, D., Tuerlinckx, F., van der Maas, H. L. (2015). A bivariate generalized linear item response theory modeling framework to the analysis of responses and response times. Multivariate Behavioral Research, 50(1), 56–74.CrossRefGoogle Scholar
Moustaki, I., Knott, M. (2000). Generalized latent trait models. Psychometrika, 65, 391–411.CrossRefGoogle Scholar
Nelder, J. A., Wedderburn, R. W. (1972). Generalized linear models. Journal of the Royal Statistical Society: Series A (General), 135(3), 370–384.CrossRefGoogle Scholar
Rasch, G. (1993). Probabilistic models for some intelligence and attainment tests. ERIC.Google Scholar
Rupp, A. A., Templin, J., Henson, R. A. (2010). Diagnostic measurement: Theory, methods, and applications, Guilford Press.Google Scholar
Skrondal, A., & Rabe-Hesketh, S. (2004). Generalized latent variable modeling: Multilevel, longitudinal, and structural equation models. Crc Press.CrossRefGoogle Scholar
Sternberg, R. J. (1980). Representation and process in linear syllogistic reasoning. Journal of Experimental Psychology: General, 109(2), 119.CrossRefGoogle Scholar
Sternberg, S. (1969). The discovery of processing stages: Extensions of donders’ method. Acta psychologica, 30, 276–315.CrossRefGoogle Scholar
Tang, X., Wang, Z., He, Q., Liu, J., Ying, Z. (2020). Latent feature extraction for process data via multidimensional scaling. Psychometrika, 85(2), 378–397.CrossRefGoogle ScholarPubMed
Tatsuoka, K. K. (1983). Rule space: an approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement, 20, 345–354.CrossRefGoogle Scholar
Teicher, H. (1967). Identifiability of mixtures of product measures. The Annals of Mathematical Statistics, 38(4), 1300–1302.CrossRefGoogle Scholar
Thissen, D. (1983). Timed testing: An approach using item response theory. In New horizons in testing, pages 179–203. Elsevier.CrossRefGoogle Scholar
van der Linden, W. J. (2006). A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31(2), 181–204.CrossRefGoogle Scholar
van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72(3), 287–308.CrossRefGoogle Scholar
von Davier, M. (2008). A general diagnostic model applied to language testing data. British Journal of Mathematical and Statistical Psychology, 61, 287–307.CrossRefGoogle ScholarPubMed
Wang, C., Xu, G. (2015). A mixture hierarchical model for response times and response accuracy. British Journal of Mathematical and Statistical Psychology, 68(3), 456–477.CrossRefGoogle ScholarPubMed
Wang, S., Zhang, S., Douglas, J., Culpepper, S. (2018). Using response times to assess learning progress: A joint model for responses and response times. Measurement: Interdisciplinary Research and Perspectives, 16(1), 45–58.Google Scholar
Xu, G. (2017). Identifiability of restricted latent class models with binary responses. Annals of Statistics, 45, 675–707.CrossRefGoogle Scholar
Xu, G., Shang, Z. (2018). Identifying latent structures in restricted latent class models. Journal of the American Statistical Association, 113(523), 1284–1295.CrossRefGoogle Scholar
Xu, G., Zhang, S. (2016). Identifiability of diagnostic classification models. Psychometrika, 81(3), 625–649.CrossRefGoogle ScholarPubMed
Yakowitz, S. J., Spragins, J. D. (1968). On the identifiability of finite mixtures. The Annals of Mathematical Statistics, 39(1), 209–214.CrossRefGoogle Scholar
Zhan, P., Jiao, H., Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times. British Journal of Mathematical and Statistical Psychology, 71(2), 262–286.CrossRefGoogle ScholarPubMed
Zhan, P., Liao, M., Bian, Y. (2018). Joint testlet cognitive diagnosis modeling for paired local item dependence in response times and response accuracy. Frontiers in Psychology, 9, 607.CrossRefGoogle ScholarPubMed
Zhan, P., Man, K., Wind, S. A., & Malone, J. (2022). Cognitive diagnosis modeling incorporating response times and fixation counts: Providing comprehensive feedback and accurate diagnosis. Journal of Educational and Behavioral Statistics.CrossRefGoogle Scholar
Supplementary material: File

Lee and Gu supplementary materials

Lee and Gu supplementary materials
Download Lee and Gu supplementary materials(File)
File 673 KB