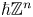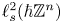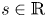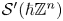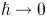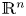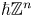1. Introduction
The solvability of the heat equation, as well as the inverse problem for the heat equation where thermal coefficients are constant, time-dependent, or space-dependent, has been studied extensively in many different settings.
For the case of the heat equation with singular potentials in the space variable, we refer to papers [Reference Altybay, Ruzhansky, Sebih and Tokmagambetov1, Reference Chatzakou, Ruzhansky and Tokmagambetov6] for an overview of the known results in different settings. For the case where the time-dependent coefficients are considered, we refer to papers [Reference Duc, Muoi and Anh7, Reference Gulisashvili13–Reference Ljulj, Schmidt, Semin and Tambača16] and [Reference Takahashi and Yanagida27], that apply in settings different from the lattice $\mathbb {Z}^n$![]() . In the particular case of the lattice $\mathbb {Z}^n$
. In the particular case of the lattice $\mathbb {Z}^n$![]() we have paper [Reference Floreanini, Negro, Nieto and Vinet10] where constant coefficients are considered. In the aforesaid setting, the heat equation with constant coefficients reads as the parabolic Anderson model, see e.g. [Reference Chen3] and references therein, and the asymptotic analysis of its solution is a topic of wide interest in the field of stochastic analysis.
we have paper [Reference Floreanini, Negro, Nieto and Vinet10] where constant coefficients are considered. In the aforesaid setting, the heat equation with constant coefficients reads as the parabolic Anderson model, see e.g. [Reference Chen3] and references therein, and the asymptotic analysis of its solution is a topic of wide interest in the field of stochastic analysis.
The setting in the current paper is, for a (small) semi-classical parameter $\hbar >0$![]() , given by
, given by
and clearly includes the $n$![]() -dimensional lattice $\mathbb {Z}^n$
-dimensional lattice $\mathbb {Z}^n$![]() as a special case. For $\alpha >0$
as a special case. For $\alpha >0$![]() , the discrete fractional Laplacian on $\hbar \mathbb {Z}^{n}$
, the discrete fractional Laplacian on $\hbar \mathbb {Z}^{n}$![]() denoted by $(-\mathcal {L}_{\hbar })^{\alpha }$
denoted by $(-\mathcal {L}_{\hbar })^{\alpha }$![]() is defined by
is defined by
where the expansion coefficient $a_{j}^{(\alpha )}$![]() is given by
is given by

For more information on the discrete fractional Laplacian, see § 3.
For the space variable $k \in \hbar \mathbb {Z}^n$![]() in this setting, we analyse the semi-classical analogue of the heat equation in the Euclidean setting, which reads as follows:
in this setting, we analyse the semi-classical analogue of the heat equation in the Euclidean setting, which reads as follows:

where $a=a(t)\geq 0$![]() is the thermal conductivity, $b$
is the thermal conductivity, $b$![]() is a real-valued bounded potential and $f$
is a real-valued bounded potential and $f$![]() is the heat source.
is the heat source.
The first aim of the current paper is to prove the well-posedness of the classical solution of the heat equation as in (1.3) in the semi-classical setting $\hbar \mathbb {Z}^n$![]() . Let us note that in [Reference Dasgupta, Ruzhansky and Tushir8, Reference Dasgupta, Ruzhansky and Tushir9] the authors examine the discrete wave equation with time-dependent coefficients and the discrete Klein–Gordon equation with regular potential and prove that they are well-posed in $\ell ^{2}(\hbar \mathbb {Z}^{n})$
. Let us note that in [Reference Dasgupta, Ruzhansky and Tushir8, Reference Dasgupta, Ruzhansky and Tushir9] the authors examine the discrete wave equation with time-dependent coefficients and the discrete Klein–Gordon equation with regular potential and prove that they are well-posed in $\ell ^{2}(\hbar \mathbb {Z}^{n})$![]() . In this paper, we are extending the well-posedness results in [Reference Dasgupta, Ruzhansky and Tushir8, Reference Dasgupta, Ruzhansky and Tushir9] for our consideration of the Cauchy problem by allowing the initial data to grow polynomially. More precisely, we investigate the well-posedness of the Cauchy problem (1.3) with regular/irregular coefficients as well as the heat source and initial Cauchy data from the space of discrete tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$
. In this paper, we are extending the well-posedness results in [Reference Dasgupta, Ruzhansky and Tushir8, Reference Dasgupta, Ruzhansky and Tushir9] for our consideration of the Cauchy problem by allowing the initial data to grow polynomially. More precisely, we investigate the well-posedness of the Cauchy problem (1.3) with regular/irregular coefficients as well as the heat source and initial Cauchy data from the space of discrete tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() . A special feature in our approach in this article is that we also allow the coefficients $a,\,b$
. A special feature in our approach in this article is that we also allow the coefficients $a,\,b$![]() to be distributions. Particularly, our analysis allows $a,\,b$
to be distributions. Particularly, our analysis allows $a,\,b$![]() to have distributional irregularities; i.e. to have $\delta$
to have distributional irregularities; i.e. to have $\delta$![]() -type terms, while also Heaviside discontinuities e.g. we can take $b(t)=\delta +H(t)$
-type terms, while also Heaviside discontinuities e.g. we can take $b(t)=\delta +H(t)$![]() . Taking into account that the solution $u(t,\,x)$
. Taking into account that the solution $u(t,\,x)$![]() might as well have singularities in $t$
might as well have singularities in $t$![]() , this consideration would lead to foundational mathematical difficulties due to the problem of the impossibility of multiplying distributions, see [Reference Schwartz25]. To overcome this problem we employ the theory of very weak solution as introduced in [Reference Garetto and Ruzhansky12] which allows us to recapture the classical/distributional solution to the Cauchy problem (1.3), provided that the latter exists.
, this consideration would lead to foundational mathematical difficulties due to the problem of the impossibility of multiplying distributions, see [Reference Schwartz25]. To overcome this problem we employ the theory of very weak solution as introduced in [Reference Garetto and Ruzhansky12] which allows us to recapture the classical/distributional solution to the Cauchy problem (1.3), provided that the latter exists.
With the well-posedness of the classical (resp. very weak) solution to the Cauchy problem (1.3) on the lattice $\hbar \mathbb {Z}^n$![]() at our disposal, two natural questions arise:
at our disposal, two natural questions arise:
(1) Can we recapture the classical solution to the heat equation (1.3) when the space variable lies in the Euclidean space $\mathbb {R}^n$
 by allowing $\hbar \rightarrow 0$
by allowing $\hbar \rightarrow 0$ ?
?(2) Can we recapture the very weak solution to (1.3) when the space variable lies in the Euclidean space $\mathbb {R}^n$
 by allowing $\hbar \rightarrow 0$
by allowing $\hbar \rightarrow 0$ ?
?
We will see that both questions are answered in the affirmative, provided additional Sobolev regularity. In particular, we consider the semi-classical limits $\hbar \to 0$![]() for the following cases:
for the following cases:
(A) regular coefficient and Sobolev initial data;
(B) distributional coefficient and Sobolev initial data,
and prove that in both cases we recover the (classical/very weak) solution in the Euclidean setting. The idea of ensuring globally convergence for the solution by adding Sobolev regularity, can be found in the semi-classical limit theorems in [Reference Dasgupta, Ruzhansky and Tushir8, Theorem 1.2] and [Reference Dasgupta, Ruzhansky and Tushir9, Theorem 1.3].
Note that the Cauchy problem (1.3) is the discrete analogue of heat equation with time-dependent coefficients in the Euclidean setting $\mathbb {R}^n$![]() given by:
given by:

where $(-\mathcal {L})^{\alpha }$![]() is the usual fractional Laplacian $(-\mathcal {L})^{\alpha }$
is the usual fractional Laplacian $(-\mathcal {L})^{\alpha }$![]() on $\mathbb {R}^{n}$
on $\mathbb {R}^{n}$![]() defined as a pseudo-differential operator with symbol $|2\pi \xi |^{2\alpha }=[\sum _{l=1}^{n}(2\pi \xi _{l})^{2}]^{\alpha }$
defined as a pseudo-differential operator with symbol $|2\pi \xi |^{2\alpha }=[\sum _{l=1}^{n}(2\pi \xi _{l})^{2}]^{\alpha }$![]() , i.e.:
, i.e.:
Theorems 1.1 and 1.2 state the well-posedness results of the Cauchy problem (1.4) for the above cases in the Euclidean setting $\mathbb {R}^n$![]() .
.
Before presenting the aforementioned results, let us note that, notation-wise, we write $a\in L_{m}^{\infty }([0,\,T])$![]() , if $a\in L^{\infty }([0,\,T])$
, if $a\in L^{\infty }([0,\,T])$![]() is $m$
is $m$![]() -times weakly differentiable with $\partial ^{j}_{t}a\in L^{\infty }([0,\,T])$
-times weakly differentiable with $\partial ^{j}_{t}a\in L^{\infty }([0,\,T])$![]() , for all $j=1,\,\dots,\,m$
, for all $j=1,\,\dots,\,m$![]() . Let us recall the usual Sobolev space $H^{m}(\mathbb {R}^{n})$
. Let us recall the usual Sobolev space $H^{m}(\mathbb {R}^{n})$![]() and its dual $L^{2}_{m}(\mathbb {R}^{n})$
and its dual $L^{2}_{m}(\mathbb {R}^{n})$![]() defined as:
defined as:
and
respectively.
In the sequel, we will be writing $A \lesssim B$![]() whenever there exists a constant $C$
whenever there exists a constant $C$![]() , independent of the appearing parameters, such that $A \leq C B$
, independent of the appearing parameters, such that $A \leq C B$![]() .
.
For the well-posedness of the Cauchy problem (1.4) in case (A) we have the following result:
Theorem 1.1 Let $m\in \mathbb {R}$![]() and $f\in L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$
and $f\in L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$![]() . Assume that $a \in L_1^{\infty }([0,\, T])$
. Assume that $a \in L_1^{\infty }([0,\, T])$![]() satisfies $\inf \nolimits _{t \in [0, T]} a(t)=a_0>0$
satisfies $\inf \nolimits _{t \in [0, T]} a(t)=a_0>0$![]() and $b \in L^{\infty }([0,\, T])$
and $b \in L^{\infty }([0,\, T])$![]() . If the initial Cauchy data $u_{0} \in H^{m}(\mathbb {R}^{n})$
. If the initial Cauchy data $u_{0} \in H^{m}(\mathbb {R}^{n})$![]() , then the Cauchy problem (1.4) has a unique solution $u \in C([0,\,T];H^{m}(\mathbb {R}^{n}))$
, then the Cauchy problem (1.4) has a unique solution $u \in C([0,\,T];H^{m}(\mathbb {R}^{n}))$![]() which satisfies the estimate:
which satisfies the estimate:
for all $t\in [0,\,T]$![]() , where the positive constant $C_{T,a,b}$
, where the positive constant $C_{T,a,b}$![]() is given by
is given by
Similarly, for the well-posedness of the Cauchy problem (1.4) in case (B) we have:
Theorem 1.2 Let a and $b$![]() be distributions with supports included in $[0,\, T]$
be distributions with supports included in $[0,\, T]$![]() such that $a \geq a_0>0$
such that $a \geq a_0>0$![]() for some positive constant $a_0$
for some positive constant $a_0$![]() , and let the source term $f(\cdot,\, x)$
, and let the source term $f(\cdot,\, x)$![]() be a distribution with support included in $[0,\, T]$
be a distribution with support included in $[0,\, T]$![]() , for all $x\in \mathbb {R}^{n}$
, for all $x\in \mathbb {R}^{n}$![]() . Let $m \in \mathbb {R}$
. Let $m \in \mathbb {R}$![]() and $u_{0} \in H^{m}(\mathbb {R}^{n})$
and $u_{0} \in H^{m}(\mathbb {R}^{n})$![]() . Then, the Cauchy problem (1.4) has a unique very weak solution $(u_{\varepsilon })_{\varepsilon }\in L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))^{(0,1]}$
. Then, the Cauchy problem (1.4) has a unique very weak solution $(u_{\varepsilon })_{\varepsilon }\in L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))^{(0,1]}$![]() of order $m$
of order $m$![]() .
.
For more details about the very weak solutions for the Cauchy problem (1.4) in the Euclidean setting, we refer to § 6.
To give a synopsis of the topic of very weak solution, we refer to papers [Reference Muñoz, Ruzhansky and Tokmagambetov17, Reference Ruzhansky and Tokmagambetov22] on Cauchy problems with singular, time-dependent coefficients in the Euclidean setting. The concept of very weak solution with space-dependent coefficients in the general setting of graded Lie groups has been employed in papers [Reference Chatzakou, Ruzhansky and Tokmagambetov4–Reference Chatzakou, Ruzhansky and Tokmagambetov6, Reference Ruzhansky and Taranto23, Reference Ruzhansky and Yessirkegenov24] and [Reference Garetto11] in the Euclidean setting.
To summarize, we are able to: use the notion of very weak solution, as introduced in [Reference Garetto and Ruzhansky12] in the setting of hyperbolic Cauchy problems with distributional coefficients in space; understand distributionally the Cauchy problem (1.3); and prove its well-posedness. Precisely, the following facts will be presented in the sequel:
• The Cauchy problem (1.3) is well-posed in the weighted spaces $\ell ^{2}_{s}(\hbar \mathbb {Z}^n)$
 , for all $s \in \mathbb {R}$
, for all $s \in \mathbb {R}$ and admits a very weak solution even when distributional coefficients $a,\,b$
and admits a very weak solution even when distributional coefficients $a,\,b$ are considered.
are considered.• The very weak solution is unique in the sense of definition 2.5.
• If the coefficients $a,\,b$
 are regular enough so that the Cauchy problem (1.3) has a classical solution, then the very weak solution recaptures the classical one. This fact indicates that the notion of very weak solution as adapted to our setting is consistent with the classical one.
are regular enough so that the Cauchy problem (1.3) has a classical solution, then the very weak solution recaptures the classical one. This fact indicates that the notion of very weak solution as adapted to our setting is consistent with the classical one.• We are able to approximate both the classical and the very weak solution to the heat equation as in (1.3) in the Euclidean setting $\mathbb {R}^n$
 , by the corresponding solution in the semi-classical setting $\hbar \mathbb {Z}^n$
, by the corresponding solution in the semi-classical setting $\hbar \mathbb {Z}^n$ .
.
The structure of the paper is as follows: in § 2 we present our main results. In § 3 we discuss the basics of the Fourier analysis in the case of the lattices $\mathbb {Z}^n$![]() and $\hbar \mathbb {Z}^n$
and $\hbar \mathbb {Z}^n$![]() and of the torus $\mathbb {T}^{n}_{\hbar }$
and of the torus $\mathbb {T}^{n}_{\hbar }$![]() . In addition to this, the functions of spaces and distributions necessary for our analysis are recalled. In § 4 we provide the proofs of the results on the existence and uniqueness of the very weak solution of the problem we consider, as well as the consistency of it with the classical solution. In § 5 we prove the results on the approximation of the (classical/very weak) solution on $\mathbb {R}^n$
. In addition to this, the functions of spaces and distributions necessary for our analysis are recalled. In § 4 we provide the proofs of the results on the existence and uniqueness of the very weak solution of the problem we consider, as well as the consistency of it with the classical solution. In § 5 we prove the results on the approximation of the (classical/very weak) solution on $\mathbb {R}^n$![]() , by the one on $\hbar \mathbb {Z}^n$
, by the one on $\hbar \mathbb {Z}^n$![]() . Finally, in § 6, we make some remarks about the very weak solution in the Euclidean setting.
. Finally, in § 6, we make some remarks about the very weak solution in the Euclidean setting.
2. Main results
In this section, we will present our main results for the well-posedness of the Cauchy problem (1.3) with regular/irregular coefficients and the discrete tempered distributional initial data. We will also present the semi-classical limit theorems for the classical as well as very weak solution.
First, we consider the Cauchy problem (1.3) with discrete tempered distributional initial Cauchy data and the regular coefficients $a \in L_1^{\infty }([0,\, T])$![]() and $b \in L^{\infty }([0,\, T])$
and $b \in L^{\infty }([0,\, T])$![]() . In the light of relation (3.2), proving the well-posedness in the space of weighted spaces $\ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$
. In the light of relation (3.2), proving the well-posedness in the space of weighted spaces $\ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() is sufficient to prove the well-posedness in the space of discrete tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$
is sufficient to prove the well-posedness in the space of discrete tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() .
.
Let us start our exposition of results with the one on the well-posedness theorem (in the classical sense) for the Cauchy problem (1.3):
Theorem 2.1 (Classical solution)
Let $s \in \mathbb {R}$![]() and $f \in L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
and $f \in L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() . Assume that $a \in L_1^{\infty }([0,\, T])$
. Assume that $a \in L_1^{\infty }([0,\, T])$![]() satisfies $\inf \nolimits _{t \in [0, T]} a(t)=a_0>0$
satisfies $\inf \nolimits _{t \in [0, T]} a(t)=a_0>0$![]() and $b \in L^{\infty }([0,\, T])$
and $b \in L^{\infty }([0,\, T])$![]() . If for the initial Cauchy data we have $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {\mathbb {Z}}^{n})$
. If for the initial Cauchy data we have $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {\mathbb {Z}}^{n})$![]() , then the Cauchy problem (1.3) has a unique solution $u \in C([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
, then the Cauchy problem (1.3) has a unique solution $u \in C([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() satisfying the estimate:
satisfying the estimate:
for all $t\in [0,\,T]$![]() and $\hbar >0$
and $\hbar >0$![]() , where the positive constant $C_{T,a,b}$
, where the positive constant $C_{T,a,b}$![]() is given by
is given by
Next, we are considering the Cauchy problem (1.3) with discrete tempered distributional initial Cauchy data and, also allowing the coefficients and the source term to have singularities in the time variable. As we discussed earlier in § 1, in order to deal with such equations where fundamental mathematical difficulties may arise when adapting the classical approach, we have to introduce the notion of a very weak solution. To this end, let us quickly recall the important points for the upcoming analysis.
Let $a\in \mathcal {D}^{\prime }(\mathbb {R})$![]() be a distribution. Using the Friedrichs-mollifier, i.e. a function $\psi \in C_{0}^{\infty }(\mathbb {R}),\, \psi \geq 0$
be a distribution. Using the Friedrichs-mollifier, i.e. a function $\psi \in C_{0}^{\infty }(\mathbb {R}),\, \psi \geq 0$![]() and $\int _{\mathbb {R}} \psi =1$
and $\int _{\mathbb {R}} \psi =1$![]() , we are able to construct families of smooth functions $(a_{\varepsilon })_{\varepsilon }$
, we are able to construct families of smooth functions $(a_{\varepsilon })_{\varepsilon }$![]() by regularizing the distributional coefficient $a$
by regularizing the distributional coefficient $a$![]() as follows:
as follows:
where $\omega (\varepsilon )> 0$![]() and $\omega (\varepsilon )\to 0$
and $\omega (\varepsilon )\to 0$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() . Let us note that since for the purposes of this article, the distributions $a$
. Let us note that since for the purposes of this article, the distributions $a$![]() and $b$
and $b$![]() , as in (1.3), are distributions with domain $[0,\,T]$
, as in (1.3), are distributions with domain $[0,\,T]$![]() , it is enough to consider that $\text {supp}(\psi )\subseteq K$
, it is enough to consider that $\text {supp}(\psi )\subseteq K$![]() , with $K=[0,\,T]$
, with $K=[0,\,T]$![]() throughout this article.
throughout this article.
The notions of moderateness and the negligibility for a net of functions/distributions as follows:
Definition 2.2
(i) A net $(a_{\varepsilon })_{\varepsilon } \in L^{\infty }_{m}(\mathbb {R})^{(0,1]}$
 is said to be $L^{\infty }_{m}$
is said to be $L^{\infty }_{m}$ -moderate if for all $K \Subset \mathbb {R}$
-moderate if for all $K \Subset \mathbb {R}$ , there exist $N \in \mathbb {N}_{0}$
, there exist $N \in \mathbb {N}_{0}$ and $c>0$
and $c>0$ such that
\[ \left\|\partial^{k} a_{\varepsilon}\right\|_{L^{\infty}(K)} \leq c \varepsilon^{{-}N-k},\quad \text{ for all }k=0,1,\dots,m, \]for all $\varepsilon \in (0,\,1]$
such that
\[ \left\|\partial^{k} a_{\varepsilon}\right\|_{L^{\infty}(K)} \leq c \varepsilon^{{-}N-k},\quad \text{ for all }k=0,1,\dots,m, \]for all $\varepsilon \in (0,\,1]$
 .
.(ii) A net $(a_{\varepsilon })_{\varepsilon } \in L^{\infty }_{m}(\mathbb {R})^{(0,1]}$
 is said to be $L^{\infty }_{m}$
is said to be $L^{\infty }_{m}$ -negligible if for all $K \Subset \mathbb {R}$
-negligible if for all $K \Subset \mathbb {R}$ and $q\in \mathbb {N}_{0}$
and $q\in \mathbb {N}_{0}$ , there exists $c>0$
, there exists $c>0$ such that
\[ \left\|\partial^{k} a_{\varepsilon}\right\|_{L^{\infty}(K)} \leq c \varepsilon^{q},\quad \text{ for all }k=0,1,\dots,m, \]for all $\varepsilon \in (0,\,1]$
such that
\[ \left\|\partial^{k} a_{\varepsilon}\right\|_{L^{\infty}(K)} \leq c \varepsilon^{q},\quad \text{ for all }k=0,1,\dots,m, \]for all $\varepsilon \in (0,\,1]$
 .
.(iii) A net $(u_{\varepsilon })_{\varepsilon } \in L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))^{(0,1]}$
 is said to be $L^{2}([0,\, T] ;\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is said to be $L^{2}([0,\, T] ;\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$ -moderate if there exist $N \in \mathbb {N}_{0}$
-moderate if there exist $N \in \mathbb {N}_{0}$ and $c>0$
and $c>0$ such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];\ell^{2}_{s}(\hbar\mathbb{Z}^{n}))} \leq c \varepsilon^{{-}N}, \]for all $\varepsilon \in (0,\,1]$
such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];\ell^{2}_{s}(\hbar\mathbb{Z}^{n}))} \leq c \varepsilon^{{-}N}, \]for all $\varepsilon \in (0,\,1]$
 .
.(iv) A net $(u_{\varepsilon })_{\varepsilon } \in L^{2}([0,\, T] ;\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))^{(0,1]}$
 is said to be $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is said to be $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$ -negligible if for all $q\in \mathbb {N}_{0}$
-negligible if for all $q\in \mathbb {N}_{0}$ there exists $c>0$
there exists $c>0$ such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];\ell^{2}_{s}(\hbar\mathbb{Z}^{n}))} \leq c \varepsilon^{q}, \]for all $\varepsilon \in (0,\,1]$
such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];\ell^{2}_{s}(\hbar\mathbb{Z}^{n}))} \leq c \varepsilon^{q}, \]for all $\varepsilon \in (0,\,1]$
 .
.
We note that the moderateness requirements are natural in the sense that distributions are moderately regularized. Moreover, by the structure theorems for distributions, we have the following inclusion:
Therefore, it is possible that the Cauchy problem (1.3) may not have a solution in the space of compactly supported distributions $\mathcal {E}^{\prime }(\mathbb {R})$![]() but it may exist in the space of $L^{2}$
but it may exist in the space of $L^{2}$![]() -moderate families in some suitable sense.
-moderate families in some suitable sense.
The notion of a very weak solution to the Cauchy problem (1.3) can be viewed as follows:
Definition 2.3 Let $s \in \mathbb {R},\, f \in L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() , and $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}) .$
, and $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}) .$![]() The net $(u_{\varepsilon })_{\varepsilon } \in$
The net $(u_{\varepsilon })_{\varepsilon } \in$![]() $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))^{(0,1]}$
$L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))^{(0,1]}$![]() is a very weak solution of order $s$
is a very weak solution of order $s$![]() of the Cauchy problem (1.3) if there exist
of the Cauchy problem (1.3) if there exist
(1) $L_{1}^{\infty }$
 -moderate regularization $a_{\varepsilon }$
-moderate regularization $a_{\varepsilon }$ of the coefficient $a$
of the coefficient $a$ ;
;(2) $L^{\infty }$
 -moderate regularization $b_{\varepsilon }$
-moderate regularization $b_{\varepsilon }$ of the coefficient $b$
of the coefficient $b$ ; and
; and(3) $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
 -moderate regularization $f_{\varepsilon }$
-moderate regularization $f_{\varepsilon }$ of the source term $f$
of the source term $f$ ,
,
such that $(u_{\varepsilon })_{\varepsilon }$![]() solves the regularized problem:
solves the regularized problem:

for all $\varepsilon \in (0,\,1]$![]() , and is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
, and is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -moderate.
-moderate.
It should be noted that theorem 2.1 provides a unique solution to the regularized Cauchy problem (1.3) that satisfies estimate (2.1).
A distribution $a$![]() is said to be a positive distribution if $\langle a,\, \psi \rangle \geq 0$
is said to be a positive distribution if $\langle a,\, \psi \rangle \geq 0$![]() for all $\psi \in C^{\infty }_{0}(\mathbb {R})$
for all $\psi \in C^{\infty }_{0}(\mathbb {R})$![]() such that $\psi \geq 0$
such that $\psi \geq 0$![]() . Similarly, a distribution $a$
. Similarly, a distribution $a$![]() is said to be a strictly positive distribution if there exists a positive constant $\alpha$
is said to be a strictly positive distribution if there exists a positive constant $\alpha$![]() such that $a-\alpha$
such that $a-\alpha$![]() is a positive distribution in the previous sense. In other words, $a\geq \alpha >0$
is a positive distribution in the previous sense. In other words, $a\geq \alpha >0$![]() in the support of $a$
in the support of $a$![]() , where $a\geq \alpha$
, where $a\geq \alpha$![]() , means that
, means that
Now, we can state the existence theorem for the Cauchy problem (1.3) with distributional coefficients as follows:
Theorem 2.4 (Existence)
Let $a$![]() and $b$
and $b$![]() be distributions with supports contained in $[0,\, T]$
be distributions with supports contained in $[0,\, T]$![]() such that $a\geq a_{0}>0$
such that $a\geq a_{0}>0$![]() for some positive constant $a_{0}$
for some positive constant $a_{0}$![]() , and let the source term $f(\cdot,\,k)$
, and let the source term $f(\cdot,\,k)$![]() be a distribution with support contained in $[0,\,T]$
be a distribution with support contained in $[0,\,T]$![]() , for all $k\in \hbar \mathbb {Z}^{n}$
, for all $k\in \hbar \mathbb {Z}^{n}$![]() . For $s\in \mathbb {R}$
. For $s\in \mathbb {R}$![]() , we assume that the initial Cauchy data $u_0$
, we assume that the initial Cauchy data $u_0$![]() satisfies $u_{0}\in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$
satisfies $u_{0}\in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() . Then, the Cauchy problem (1.3) has a very weak solution $(u_{\varepsilon })_{\varepsilon } \in$
. Then, the Cauchy problem (1.3) has a very weak solution $(u_{\varepsilon })_{\varepsilon } \in$![]() $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))^{(0,1]}$
$L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))^{(0,1]}$![]() of order s.
of order s.
Next, we define the uniqueness of the very weak solution obtained in theorem 2.4 for the Cauchy problem (1.3). This should be regarded as if the family of very weak solution is not ‘significantly’ affected by the negligible changes in the approximations of the coefficients $a,\, b$![]() and of the source term $f$
and of the source term $f$![]() . This can be also regarded as a ‘stability’ property.
. This can be also regarded as a ‘stability’ property.
Strictly speaking, the notion of the uniqueness of the very weak solution for the Cauchy problem (1.3) is formulated as follows:
Definition 2.5 We say that the Cauchy problem (1.3) has a $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -unique very weak solution, if
-unique very weak solution, if
(1) for all $L^{\infty }_{1}$
 -moderate nets $a_{\varepsilon },\,\tilde {a}_{\varepsilon }$
-moderate nets $a_{\varepsilon },\,\tilde {a}_{\varepsilon }$ such that $(a_{\varepsilon }-\tilde {a}_{\varepsilon })_{\varepsilon }$
such that $(a_{\varepsilon }-\tilde {a}_{\varepsilon })_{\varepsilon }$ is $L^{\infty }_{1}$
is $L^{\infty }_{1}$ -negligible;
-negligible;(2) for all $L^{\infty }$
 -moderate nets $b_{\varepsilon },\,\tilde {b}_{\varepsilon }$
-moderate nets $b_{\varepsilon },\,\tilde {b}_{\varepsilon }$ such that $(b_{\varepsilon }-\tilde {b}_{\varepsilon })_{\varepsilon }$
such that $(b_{\varepsilon }-\tilde {b}_{\varepsilon })_{\varepsilon }$ are $L^{\infty }$
are $L^{\infty }$ -negligible; and
-negligible; and(3) for all $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
 -moderate nets $f_{\varepsilon },\,\tilde {f}_{\varepsilon }$
-moderate nets $f_{\varepsilon },\,\tilde {f}_{\varepsilon }$ such that $(f_{\varepsilon }-\tilde {f}_{\varepsilon })_{\varepsilon }$
such that $(f_{\varepsilon }-\tilde {f}_{\varepsilon })_{\varepsilon }$ is
is$L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
 -negligible,
-negligible,
the net $(u_{\varepsilon }-\tilde {u}_{\varepsilon })_{\varepsilon }$![]() is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -negligible, where $(u_{\varepsilon })_{\varepsilon }$
-negligible, where $(u_{\varepsilon })_{\varepsilon }$![]() and $(\tilde {u}_{\varepsilon })_{\varepsilon }$
and $(\tilde {u}_{\varepsilon })_{\varepsilon }$![]() are the families of solution corresponding to the $\varepsilon$
are the families of solution corresponding to the $\varepsilon$![]() -parametrized problems:
-parametrized problems:

and

respectively.
Remark 2.6 The Colombeau algebra $\mathcal {G}(\mathbb {R})$![]() defined as:
defined as:
can also be used to formulate the uniqueness for the Cauchy problem (1.3). For more details about the Colombeau algebra, we refer to [Reference Oberguggenberger18]. The uniqueness of very weak solution in the sense of Colombeau algebra was introduced by Garetto and the third author in [Reference Garetto and Ruzhansky12] and subsequently used in different settings, see e.g. [Reference Ruzhansky and Tokmagambetov21, Reference Ruzhansky and Tokmagambetov22].
The following theorem gives the uniqueness of the very weak solution to the Cauchy problem (1.3) in the sense of definition 2.5.
Theorem 2.7 (Uniqueness)
Let $a$![]() and $b$
and $b$![]() be distributions with supports contained in $[0,\, T]$
be distributions with supports contained in $[0,\, T]$![]() such that $a\geq a_{0}>0$
such that $a\geq a_{0}>0$![]() for some positive constant $a_{0}$
for some positive constant $a_{0}$![]() , and let the source term $f(\cdot,\,k)$
, and let the source term $f(\cdot,\,k)$![]() be a distribution with support contained in $[0,\,T]$
be a distribution with support contained in $[0,\,T]$![]() , for all $k\in \hbar \mathbb {Z}^{n}$
, for all $k\in \hbar \mathbb {Z}^{n}$![]() . For $s \in \mathbb {R}$
. For $s \in \mathbb {R}$![]() , let also $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$
, let also $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() . Then, the very weak solution of the Cauchy problem (1.3) is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
. Then, the very weak solution of the Cauchy problem (1.3) is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -unique.
-unique.
In the following theorem, we prove the consistency results with the classical case:
Theorem 2.8 (Consistency)
Let $s\in \mathbb {R}^{n}$![]() and $f \in L^{2}([0,\, T],\, \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
and $f \in L^{2}([0,\, T],\, \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() . Assume that $a \in L_{1}^{\infty }([0,\, T])$
. Assume that $a \in L_{1}^{\infty }([0,\, T])$![]() satisfies $\inf \nolimits _{t \in [0, T]}a(t)= a_{0}>0$
satisfies $\inf \nolimits _{t \in [0, T]}a(t)= a_{0}>0$![]() and $b \in L^{\infty }([0,\, T])$
and $b \in L^{\infty }([0,\, T])$![]() . Let also $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$
. Let also $u_{0} \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() for any $s \in \mathbb {R}$
for any $s \in \mathbb {R}$![]() . Then, the regularized net $u_\varepsilon$
. Then, the regularized net $u_\varepsilon$![]() converges, as $\varepsilon \rightarrow 0$
converges, as $\varepsilon \rightarrow 0$![]() , in $L^{2}([0,\, T]; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
, in $L^{2}([0,\, T]; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() to the classical solution of the Cauchy problem (1.3).
to the classical solution of the Cauchy problem (1.3).
The following theorem shows that the classical solution of (1.3) in the semi-classical setting $\hbar \mathbb {Z}^n$![]() obtained in theorem 2.1 for $s=0$
obtained in theorem 2.1 for $s=0$![]() , recaptures the classical solution in the Euclidean setting $\mathbb {R}^n$
, recaptures the classical solution in the Euclidean setting $\mathbb {R}^n$![]() as in theorem 1.1, provided the latter exists.
as in theorem 1.1, provided the latter exists.
Theorem 2.9 Let $\alpha \in (0,\,1]$![]() and $s=0$
and $s=0$![]() . Let $u$
. Let $u$![]() and $v$
and $v$![]() be the classical solution of the Cauchy problems (1.3) on $\hbar \mathbb {Z}^n$
be the classical solution of the Cauchy problems (1.3) on $\hbar \mathbb {Z}^n$![]() and (1.4) on $\mathbb {R}^n$
and (1.4) on $\mathbb {R}^n$![]() , respectively. Assume that for the initial Cauchy data we have $u_0 \in H^{m}(\mathbb {R}^{n})$
, respectively. Assume that for the initial Cauchy data we have $u_0 \in H^{m}(\mathbb {R}^{n})$![]() for some $m\geq 4\alpha$
for some $m\geq 4\alpha$![]() . Then, we have the following uniform in $t\in [0,\,T]$
. Then, we have the following uniform in $t\in [0,\,T]$![]() convergence:
convergence:
Remark 2.10 Let us point out that the solution $u,\,v$![]() as in theorem 2.9 are regarded as solution to the Cauchy problems (1.3) and (1.4), respectively, with the same Cauchy data $u_0$
as in theorem 2.9 are regarded as solution to the Cauchy problems (1.3) and (1.4), respectively, with the same Cauchy data $u_0$![]() , source term $f$
, source term $f$![]() and time-dependent coefficients $a,\,b$
and time-dependent coefficients $a,\,b$![]() . The same hypothesis holds true in theorem 2.11 on the convergence of the nets of the very weak solution in the semi-classical and Euclidean settings of the corresponding regularized heat equations.
. The same hypothesis holds true in theorem 2.11 on the convergence of the nets of the very weak solution in the semi-classical and Euclidean settings of the corresponding regularized heat equations.
The analogous to theorem 2.9 statement in the ‘very weak sense’ reads as follows:
Theorem 2.11 Let $\alpha \in (0,\,1]$![]() and $s=0$
and $s=0$![]() . Let $(u_{\varepsilon })_{\varepsilon }$
. Let $(u_{\varepsilon })_{\varepsilon }$![]() and $(v_{\varepsilon })_{\varepsilon }$
and $(v_{\varepsilon })_{\varepsilon }$![]() be the very weak solution of the Cauchy problem (1.3) on $\hbar \mathbb {Z}^n$
be the very weak solution of the Cauchy problem (1.3) on $\hbar \mathbb {Z}^n$![]() and (1.4) on $\mathbb {R}^n$
and (1.4) on $\mathbb {R}^n$![]() , respectively. Assume that for the initial Cauchy data, we have $u_0 \in H^{m}(\mathbb {R}^{n})$
, respectively. Assume that for the initial Cauchy data, we have $u_0 \in H^{m}(\mathbb {R}^{n})$![]() for some $m\geq 4\alpha$
for some $m\geq 4\alpha$![]() . Then, we have the following uniform in $t\in [0,\,T]$
. Then, we have the following uniform in $t\in [0,\,T]$![]() convergence:
convergence:
and pointwise for $\varepsilon \in (0,\,1]$![]() .
.
3. Preliminaries
The Fourier analysis related to the discrete lattice $\mathbb {Z}^{n}$![]() and the torus $\mathbb {T}^{n}$
and the torus $\mathbb {T}^{n}$![]() has been developed by Turunen and the third author in [Reference Ruzhansky and Turunen20]. The pseudo-difference operators and the related symbolic calculus on the weighted sequence space $\ell ^{p}_{s}(\mathbb {Z}^{n})$
has been developed by Turunen and the third author in [Reference Ruzhansky and Turunen20]. The pseudo-difference operators and the related symbolic calculus on the weighted sequence space $\ell ^{p}_{s}(\mathbb {Z}^{n})$![]() have been extensively studied in [Reference Botchway, Gaël Kibiti and Ruzhansky2]. The aim of the section is to recall the preliminaries and important tools related to the discrete lattice $\hbar \mathbb {Z}^{n}$
have been extensively studied in [Reference Botchway, Gaël Kibiti and Ruzhansky2]. The aim of the section is to recall the preliminaries and important tools related to the discrete lattice $\hbar \mathbb {Z}^{n}$![]() and the torus $\mathbb {T}^{n}_{\hbar }$
and the torus $\mathbb {T}^{n}_{\hbar }$![]() that will be necessary for the analysis that we will follow.
that will be necessary for the analysis that we will follow.
3.1 Spaces of functions and distributions on the lattice $\hbar \mathbb {Z}^{n}$
The Schwartz space $\mathcal {S}(\hbar \mathbb {Z}^{n})$![]() on the lattice $\hbar \mathbb {Z}^n$
on the lattice $\hbar \mathbb {Z}^n$![]() is the space of rapidly decreasing functions $\varphi : \hbar \mathbb {Z}^n \rightarrow \mathbb {C}$
is the space of rapidly decreasing functions $\varphi : \hbar \mathbb {Z}^n \rightarrow \mathbb {C}$![]() ; that is, we write $\varphi \in \mathcal {S}(\hbar \mathbb {Z}^{n})$
; that is, we write $\varphi \in \mathcal {S}(\hbar \mathbb {Z}^{n})$![]() if for any $M<\infty$
if for any $M<\infty$![]() there exists a constant $C_{\varphi, M}$
there exists a constant $C_{\varphi, M}$![]() such that
such that
where $|k|$![]() stands for the Euclidean norm of $k \in \hbar \mathbb {Z}^{n}$
stands for the Euclidean norm of $k \in \hbar \mathbb {Z}^{n}$![]() ; i.e. for $k = \hbar (k_{1},\,\ldots,\, k_{n})$
; i.e. for $k = \hbar (k_{1},\,\ldots,\, k_{n})$![]() , we have $|k|=\hbar (\sum \nolimits _{l=1}^{n} k_{l}^{2})^{{1}/{2}}$
, we have $|k|=\hbar (\sum \nolimits _{l=1}^{n} k_{l}^{2})^{{1}/{2}}$![]() . The topology on $\mathcal {S}(\hbar \mathbb {Z}^{n})$
. The topology on $\mathcal {S}(\hbar \mathbb {Z}^{n})$![]() is given by the semi-norms $p_j$
is given by the semi-norms $p_j$![]() , defined as:
, defined as:
The topological dual of $\mathcal {S}(\hbar \mathbb {Z}^{n})$![]() is the space of tempered distributions defined as:
is the space of tempered distributions defined as:
i.e. $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() is the space of all linear continuous functionals on $\mathcal {S}(\hbar \mathbb {Z}^{n})$
is the space of all linear continuous functionals on $\mathcal {S}(\hbar \mathbb {Z}^{n})$![]() of the form
of the form
We note that, in contrast to $\mathcal {S}^{\prime }(\mathbb {R}^{n})$![]() , the tempered distributions in $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$
, the tempered distributions in $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() in the semi-classical setting are pointwise well-defined functions on $\hbar \mathbb {Z}^{n}$
in the semi-classical setting are pointwise well-defined functions on $\hbar \mathbb {Z}^{n}$![]() . Furthermore, a tempered distribution $u: \hbar \mathbb {Z}^n \rightarrow \mathbb {C}$
. Furthermore, a tempered distribution $u: \hbar \mathbb {Z}^n \rightarrow \mathbb {C}$![]() has polynomial growth at infinity, i.e. there exist positive constants $M$
has polynomial growth at infinity, i.e. there exist positive constants $M$![]() and $C_{u, M}$
and $C_{u, M}$![]() such that
such that
For $s \in \mathbb {R}$![]() , one can extend the usual space $\ell ^2(\hbar \mathbb {Z}^n)$
, one can extend the usual space $\ell ^2(\hbar \mathbb {Z}^n)$![]() to the weighted space $\ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$
to the weighted space $\ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() of order $s$
of order $s$![]() as follows: for $f: \hbar \mathbb {Z}^n \rightarrow \mathbb {C}$
as follows: for $f: \hbar \mathbb {Z}^n \rightarrow \mathbb {C}$![]() we write $f \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$
we write $f \in \ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() whenever the following norm is finite:
whenever the following norm is finite:

Clearly, the weighted $\ell ^{2}$![]() -spaces also include $\ell ^{2}(\hbar \mathbb {Z}^{n})$
-spaces also include $\ell ^{2}(\hbar \mathbb {Z}^{n})$![]() as a special case when $s=0$
as a special case when $s=0$![]() .
.
Observe that the weighted space $\ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() is a Hilbert space when endowed with the natural inner product:
is a Hilbert space when endowed with the natural inner product:
where $\overline {v(k)}$![]() stands for the complex conjugate of $v(k)$
stands for the complex conjugate of $v(k)$![]() .
.
Let us point out that the structure of the space of tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() , as well as this of the Schwartz space $\mathcal {S}(\hbar \mathbb {Z}^{n})$
, as well as this of the Schwartz space $\mathcal {S}(\hbar \mathbb {Z}^{n})$![]() , are closely related to the weighted $\ell ^{2}$
, are closely related to the weighted $\ell ^{2}$![]() -spaces. In particular, we have the following useful relations:
-spaces. In particular, we have the following useful relations:
3.2 Space of periodic functions and distributions on the torus $\mathbb {T}_{\hbar }^{n}$
Let us now introduce the torus denoted by $\mathbb {T}_{\hbar }^{n}$![]() that will be useful for the subsequent analysis, especially when the semi-classical limit $\hbar \rightarrow 0$
that will be useful for the subsequent analysis, especially when the semi-classical limit $\hbar \rightarrow 0$![]() is taken. The torus $\mathbb {T}_{\hbar }^{n}$
is taken. The torus $\mathbb {T}_{\hbar }^{n}$![]() can be realized via the identification
can be realized via the identification
Consequently, the space $C^{k}(\mathbb {T}_{\hbar }^{n})$![]() consists of functions that are ${1}/{\hbar }$
consists of functions that are ${1}/{\hbar }$![]() -periodic and $k$
-periodic and $k$![]() -times continuously differentiable functions on torus $\mathbb {T}_{\hbar }^{n}$
-times continuously differentiable functions on torus $\mathbb {T}_{\hbar }^{n}$![]() . The space $C^{\infty }(\mathbb {T}_{\hbar }^{n})$
. The space $C^{\infty }(\mathbb {T}_{\hbar }^{n})$![]() of test functions on the torus $\mathbb {T}_{\hbar }^{n}$
of test functions on the torus $\mathbb {T}_{\hbar }^{n}$![]() can then be defined as:
can then be defined as:

The Fréchet topology on the space of smooth functions $C^{\infty }(\mathbb {T}_{\hbar }^{n})$![]() is given by the semi-norms $p_{j}$
is given by the semi-norms $p_{j}$![]() defined as:
defined as:
The topological dual of $C^{\infty }(\mathbb {T}_{\hbar }^{n})$![]() is the space of periodic distributions defined as:
is the space of periodic distributions defined as:
i.e. it is the space of all linear continuous functionals on $C^{\infty }(\mathbb {T}_{\hbar }^{n})$![]() of the form
of the form
3.3 Related semi-classical Fourier analysis
The Fourier transform operator:
is defined as:
For the inverse Fourier transform operator
we have
implying that the Fourier inversion formula is given by
The Fourier transform $\mathcal {F}_{\hbar \mathbb {Z}^{n}}$![]() can be uniquely extended to the space of tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$
can be uniquely extended to the space of tempered distributions $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() when realized via the distributional duality:
when realized via the distributional duality:
where $u\in \mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() , $\psi \in C^{\infty }(\mathbb {T}_{\hbar }^{n}),$
, $\psi \in C^{\infty }(\mathbb {T}_{\hbar }^{n}),$![]() and $(\iota \circ f)(x)=f(-x)$
and $(\iota \circ f)(x)=f(-x)$![]() .
.
Hence, for the operator $\mathcal {F}_{\hbar \mathbb {Z}^{n}}$![]() we can write in more generality $\mathcal {F}_{\hbar \mathbb {Z}^{n}}:\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})\to \mathcal {D}^{\prime }(\mathbb {T}_{\hbar }^{n})$
we can write in more generality $\mathcal {F}_{\hbar \mathbb {Z}^{n}}:\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})\to \mathcal {D}^{\prime }(\mathbb {T}_{\hbar }^{n})$![]() , and consequently we can define the inverse operator $\mathcal {F}_{\hbar \mathbb {Z}^{n}}^{-1}:\mathcal {D}^{\prime }(\mathbb {T}_{\hbar }^{n})\to \mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$
, and consequently we can define the inverse operator $\mathcal {F}_{\hbar \mathbb {Z}^{n}}^{-1}:\mathcal {D}^{\prime }(\mathbb {T}_{\hbar }^{n})\to \mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() . With the use of the latter, we can define the periodic Sobolev spaces $H^{s}(\mathbb {T}_{\hbar }^{n})$
. With the use of the latter, we can define the periodic Sobolev spaces $H^{s}(\mathbb {T}_{\hbar }^{n})$![]() , for $s\in \mathbb {R}$
, for $s\in \mathbb {R}$![]() as follows:
as follows:

For any $s \in \mathbb {R}$![]() the periodic Sobolev space $H^s(\mathbb {T}^{n}_{\hbar })$
the periodic Sobolev space $H^s(\mathbb {T}^{n}_{\hbar })$![]() is a Hilbert space endowed with the inner product given by
is a Hilbert space endowed with the inner product given by
Clearly, the periodic Sobolev space also includes $L^{2}(\mathbb {T}_{\hbar }^{n})$![]() as a special case when $s=0$
as a special case when $s=0$![]() .
.
We have the following relation between the space of test functions $C^{\infty }(\mathbb {T}_{\hbar }^{n})$![]() and the space of periodic distributions $\mathcal {D}^{\prime }(\mathbb {T}_{\hbar }^{n})$
and the space of periodic distributions $\mathcal {D}^{\prime }(\mathbb {T}_{\hbar }^{n})$![]() and the periodic Sobolev spaces $H^s(\mathbb {T}_{\hbar }^{n})$
and the periodic Sobolev spaces $H^s(\mathbb {T}_{\hbar }^{n})$![]() :
:
Combining the inner product (3.1) and (3.5) with the Fourier transform, we obtain the following Plancherel formula:
3.4 The discrete fractional Laplacian
The discrete fractional Laplacian on the lattice $\hbar \mathbb {Z}^{n}$![]() can be defined by restricting the usual fractional centred difference operators in the Euclidean setting $\mathbb {R}^{n}$
can be defined by restricting the usual fractional centred difference operators in the Euclidean setting $\mathbb {R}^{n}$![]() , see [Reference Ortigueira19, Section 5.4]. For more details about the fractional difference operators on $\mathbb {R}^{n}$
, see [Reference Ortigueira19, Section 5.4]. For more details about the fractional difference operators on $\mathbb {R}^{n}$![]() , we refer to [Reference Samko, Kilbas and Marichev26].
, we refer to [Reference Samko, Kilbas and Marichev26].
Rigorously, for a positive $\alpha >0$![]() and for $u$
and for $u$![]() being a complex-valued grid function on $\hbar \mathbb {Z}^{n}$
being a complex-valued grid function on $\hbar \mathbb {Z}^{n}$![]() , the discrete fractional Laplacian $(-\mathcal {L}_{\hbar })^\alpha$
, the discrete fractional Laplacian $(-\mathcal {L}_{\hbar })^\alpha$![]() is defined by
is defined by
where the generating function $a_j^{(\alpha )}$![]() is given by
is given by

The Fourier transform and the Fourier inversion formula, allow to verify that

Further, using relation (3.8) and the shifting property of the Fourier transform, we can compute the Fourier transform of the discrete fractional Laplacian $(-\mathcal {L}_{\hbar })^{\alpha }$![]() as follows:
as follows:

for all $\xi \in \mathbb {T}_{\hbar }^{n},$![]() and consequently the Fourier transform of fractional Laplacian is
and consequently the Fourier transform of fractional Laplacian is

for all $\xi \in \mathbb {T}_{\hbar }^{n}$![]() . For more details about the construction and other properties of discrete fractional Laplacian on $\hbar \mathbb {Z}^{n}$
. For more details about the construction and other properties of discrete fractional Laplacian on $\hbar \mathbb {Z}^{n}$![]() , see [Reference Dasgupta, Ruzhansky and Tushir9].
, see [Reference Dasgupta, Ruzhansky and Tushir9].
The consistency of formula 3.7 for the discrete fractional Laplacian $(-\mathcal {L}_{\hbar })^{\alpha }$![]() with the usual discrete Laplacian introduced in the monograph [Reference Dasgupta, Ruzhansky and Tushir8], can be understood by explicitly computing the expansion coefficients $a_{j}^{(\alpha )}$
with the usual discrete Laplacian introduced in the monograph [Reference Dasgupta, Ruzhansky and Tushir8], can be understood by explicitly computing the expansion coefficients $a_{j}^{(\alpha )}$![]() , for $\alpha =1$
, for $\alpha =1$![]() and $j\in \mathbb {Z}^{n}$
and $j\in \mathbb {Z}^{n}$![]() . Indeed, it is easy to check that
. Indeed, it is easy to check that
where $v_{l}$![]() is the $l$
is the $l$![]() th basis vector in $\mathbb {Z}^{n}$
th basis vector in $\mathbb {Z}^{n}$![]() , having all zeros except for $1$
, having all zeros except for $1$![]() at the $l$
at the $l$![]() th component. This gives
th component. This gives

which is usual discrete Laplacian on $\hbar \mathbb {Z}^{n}$![]() .
.
4. Proof of the main results
In this section, we give the proofs of all the results presented above in § 2. Before moving on to proving our first result, let us note that the proof of theorem 1.1 in the Euclidean setting $\mathbb {R}^n$![]() follows the same arguments as the ones that are used in the proof of theorem 2.1 in the setting $\hbar \mathbb {Z}^n$
follows the same arguments as the ones that are used in the proof of theorem 2.1 in the setting $\hbar \mathbb {Z}^n$![]() except for using the inner product of $L^{2}_{m}(\mathbb {R}^{n})$
except for using the inner product of $L^{2}_{m}(\mathbb {R}^{n})$![]() instead of $H^{s}(\mathbb {T}_{\hbar }^{n})$
instead of $H^{s}(\mathbb {T}_{\hbar }^{n})$![]() . Therefore, we just prove theorem 2.1 and the proof of theorem 1.1 should be considered verbatim.
. Therefore, we just prove theorem 2.1 and the proof of theorem 1.1 should be considered verbatim.
Proof of theorem 2.1 Taking the Fourier transform of the Cauchy problem (1.3) with respect to $k\in \hbar \mathbb {Z}^{n}$![]() and using (3.9), we obtain:
and using (3.9), we obtain:

where

Define the energy functional for the Cauchy problem (4.1) by
where $(\cdot,\,\cdot )$![]() is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$
is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$![]() given by (3.5). It is easy to check that
given by (3.5). It is easy to check that
Since $a \in L_1^{\infty }([0,\, T])$![]() , there exist two positive constants $a_0$
, there exist two positive constants $a_0$![]() and $a_1$
and $a_1$![]() such that
such that
Combining equations (4.3) and (4.5) together with inequality (4.4), we obtain the following bounds for the energy functional:
Differentiating the energy functional $E(t,\,\xi )$![]() and using (4.1), we obtain:
and using (4.1), we obtain:

Using the hypothesis that $a\in L_{1}^{\infty }([0,\,T])$![]() and $b\in L^{\infty }([0,\,T])$
and $b\in L^{\infty }([0,\,T])$![]() , we obtain:
, we obtain:

If we set $\kappa _{1}=\|a_{t}\|_{L^{\infty }}+2\|a\|_{L^{\infty }}\|b\|_{L^{\infty }}+\|a\|_{L^{\infty }}$![]() and $\kappa _{2}=\|a\|_{L^{\infty }}$
and $\kappa _{2}=\|a\|_{L^{\infty }}$![]() , then putting together (4.6) and (4.7), we obtain:
, then putting together (4.6) and (4.7), we obtain:
Applying the Gronwall's lemma to inequality (4.8), we get:
for all $(t,\,\xi )\in [0,\,T]\times \mathbb {T}_{\hbar }^{n}$![]() . Again combining estimates (4.6) and (4.9), we obtain:
. Again combining estimates (4.6) and (4.9), we obtain:

Further, using the Plancherel formula (3.6), we obtain the required estimate:
where the constant $C_{T,a,b}$![]() is given by
is given by
The uniqueness of the solution follows immediately from the above estimate. This completes the proof.
Thus, we have obtained the well-posedness for the Cauchy problem (1.3) in the weighted spaces $\ell ^{2}_{s}(\hbar \mathbb {Z}^{n})$![]() for all $s\in \mathbb {R}$
for all $s\in \mathbb {R}$![]() and consequently we have distributional well-posedness for the Cauchy problem (1.3) in the space of tempered distribution $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$
and consequently we have distributional well-posedness for the Cauchy problem (1.3) in the space of tempered distribution $\mathcal {S}^{\prime }(\hbar \mathbb {Z}^{n})$![]() . We will now prove the existence of the very weak solution to the Cauchy problem (1.3) in the case of distributional coefficients.
. We will now prove the existence of the very weak solution to the Cauchy problem (1.3) in the case of distributional coefficients.
Proof of theorem 2.4 Consider the regularized Cauchy problem:

where the coefficient $a_{\varepsilon }$![]() is $L^{\infty }_{1}$
is $L^{\infty }_{1}$![]() -moderate, $b_{\varepsilon }$
-moderate, $b_{\varepsilon }$![]() is $L^{\infty }$
is $L^{\infty }$![]() -moderate, and the source term $f_{\varepsilon }$
-moderate, and the source term $f_{\varepsilon }$![]() is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -moderate regularization of the coefficients $a,\,b$
-moderate regularization of the coefficients $a,\,b$![]() and the source term $f$
and the source term $f$![]() , respectively. Taking the Fourier transform with respect to $k\in \hbar \mathbb {Z}^{n}$
, respectively. Taking the Fourier transform with respect to $k\in \hbar \mathbb {Z}^{n}$![]() , we obtain:
, we obtain:

where $\nu ^{2}(\xi )$![]() is given by (4.2). Define the energy functional for the Cauchy problem (4.10) by
is given by (4.2). Define the energy functional for the Cauchy problem (4.10) by
where $(\cdot,\,\cdot )$![]() is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$
is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$![]() . It is easy to check that
. It is easy to check that

Since $a$![]() and $b$
and $b$![]() are distributions, by the structure theorem for compactly supported distributions, there exist $L_{1},\, L_{2} \in \mathbb {N}$
are distributions, by the structure theorem for compactly supported distributions, there exist $L_{1},\, L_{2} \in \mathbb {N}$![]() and $c_{1},\, c_{2}>0$
and $c_{1},\, c_{2}>0$![]() such that
such that
for all $t \in [0,\, T]$![]() , where $\omega (\varepsilon )$
, where $\omega (\varepsilon )$![]() is given by (2.3). Since $a\geq a_{0}>0$
is given by (2.3). Since $a\geq a_{0}>0$![]() , we can write:
, we can write:
where $\tilde {\psi }(x)=\psi (-x),\,x\in \mathbb {R}$![]() and $\tau _{t}\psi (\xi )=\psi (\xi -t),\,\xi \in \mathbb {R}$
and $\tau _{t}\psi (\xi )=\psi (\xi -t),\,\xi \in \mathbb {R}$![]() .
.
Now, applying theorem 2.1 to the Cauchy problem (4.10), we have the following estimate:
where the constant $C_{T,a_{\varepsilon },\,b_{\varepsilon }}$![]() is given by
is given by

where $K_{T}=\max \{1,\,\tilde {a}_{0}^{-1}4T\}$![]() . Combining estimates (4.12) and (4.14) with (4.15) we get:
. Combining estimates (4.12) and (4.14) with (4.15) we get:
for some $c>0$![]() . Putting $(\omega (\varepsilon ))^{-3L_{1}-L_{2}-1}=\log (\varepsilon ^{-1})$
. Putting $(\omega (\varepsilon ))^{-3L_{1}-L_{2}-1}=\log (\varepsilon ^{-1})$![]() , we obtain:
, we obtain:
for all $t\in [0,\,T]$![]() and $\varepsilon \in (0,\,1]$
and $\varepsilon \in (0,\,1]$![]() .
.
Since $(f_{\varepsilon })_{\varepsilon }$![]() is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -moderate regularization of $f$
-moderate regularization of $f$![]() , there exists a positive constants $L_{3}$
, there exists a positive constants $L_{3}$![]() such that
such that
Now, by integrating estimate (4.16) with respect to $t\in [0,\,T]$![]() and then using (4.17), we obtain:
and then using (4.17), we obtain:
Thus, we conclude that $(u_{\varepsilon })_{\varepsilon }$![]() is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -moderate. This completes the proof.
-moderate. This completes the proof.
Therefore, we have established the existence of very weak solution for the Cauchy problem (1.3) with irregular coefficients. We will now prove the uniqueness of the very weak solution of it in the sense of definition 2.5.
Proof of theorem 2.7 Let $(u_{\varepsilon })_{\varepsilon }$![]() and $(\tilde {u}_{\varepsilon })_{\varepsilon }$
and $(\tilde {u}_{\varepsilon })_{\varepsilon }$![]() be the families of solution corresponding to the Cauchy problems (2.6) and (2.7), respectively. Denoting $w_{\varepsilon }:=u_{\varepsilon }-\tilde {u}_{\varepsilon }$
be the families of solution corresponding to the Cauchy problems (2.6) and (2.7), respectively. Denoting $w_{\varepsilon }:=u_{\varepsilon }-\tilde {u}_{\varepsilon }$![]() , we get:
, we get:

where
Since the nets $(\tilde {a}_{\varepsilon }-a_{\varepsilon })_{\varepsilon }$![]() , $(\tilde {b}_{\varepsilon }-b_{\varepsilon })_{\varepsilon }$
, $(\tilde {b}_{\varepsilon }-b_{\varepsilon })_{\varepsilon }$![]() , and $(f_{\varepsilon }-\tilde {f}_{\varepsilon })_{\varepsilon }$
, and $(f_{\varepsilon }-\tilde {f}_{\varepsilon })_{\varepsilon }$![]() are $L^{\infty }_{1}$
are $L^{\infty }_{1}$![]() -negligible, $L^{\infty }$
-negligible, $L^{\infty }$![]() -negligible, and $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
-negligible, and $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -negligible, respectively, it follows that $g_{\varepsilon }$
-negligible, respectively, it follows that $g_{\varepsilon }$![]() is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\,T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -negligible.
-negligible.
Taking the Fourier transform of the Cauchy problem (4.19) with respect to $k\in \hbar \mathbb {Z}^{n}$![]() , we obtain:
, we obtain:

where $\nu ^{2}(\xi )$![]() is given by (4.2). The energy functional for the Cauchy problem (4.21) is given by
is given by (4.2). The energy functional for the Cauchy problem (4.21) is given by
where $(\cdot,\,\cdot )$![]() is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$
is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$![]() . Then, using (4.12), we have the following energy bounds:
. Then, using (4.12), we have the following energy bounds:
Further, we can calculate:

Combining the above estimate with (4.23), we obtain:

Applying the Gronwall's lemma to inequality (4.24), we obtain:

Putting together (4.23) and (4.25), and then using the fact that $\widehat {w}_{\varepsilon }(0,\,\xi )\equiv 0$![]() for all $\varepsilon \in (0,\,1]$
for all $\varepsilon \in (0,\,1]$![]() , we get:
, we get:

where $\kappa _{T}=\max \{1,\,\tilde {a}_{0}^{-1}4T\}$![]() . Combining the above estimate with (4.12), we obtain:
. Combining the above estimate with (4.12), we obtain:
for some $c>0$![]() . Putting $(\omega (\varepsilon ))^{-3L_{1}-L_{2}-1}=\log (\varepsilon ^{-1})$
. Putting $(\omega (\varepsilon ))^{-3L_{1}-L_{2}-1}=\log (\varepsilon ^{-1})$![]() and using the Plancherel formula (3.6), we obtain:
and using the Plancherel formula (3.6), we obtain:
for all $t\in [0,\,T]$![]() . Since $g_{\varepsilon }$
. Since $g_{\varepsilon }$![]() is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -negligible, we obtain:
-negligible, we obtain:
for all $t\in [0,\,T]$![]() . Now, by integrating the above estimate with respect to $t\in [0,\,T]$
. Now, by integrating the above estimate with respect to $t\in [0,\,T]$![]() , we get:
, we get:
Thus, $(u_{\varepsilon }-\tilde {u}_{\varepsilon })_{\varepsilon }$![]() is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
is $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -negligible. This completes the proof.
-negligible. This completes the proof.
Next, we prove that the very weak solution obtained in theorem 2.4 is consistent with the classical solution obtained in theorem 2.1.
Proof of theorem 2.8 Let $\tilde {u}$![]() be the classical solution given by theorem 2.1, that is, $\tilde {u}$
be the classical solution given by theorem 2.1, that is, $\tilde {u}$![]() satisfies the Cauchy problem:
satisfies the Cauchy problem:

and let $(u_{\varepsilon })_{\varepsilon }$![]() be the very weak solution obtained by theorem 2.4, that is, $(u_{\varepsilon })_{\varepsilon }$
be the very weak solution obtained by theorem 2.4, that is, $(u_{\varepsilon })_{\varepsilon }$![]() satisfies the regularized Cauchy problem:
satisfies the regularized Cauchy problem:

Note that by the hypothesis the nets $(a_{\varepsilon }-a)_{\varepsilon },\,(b_{\varepsilon }-b)_{\varepsilon }$![]() , and $(f_{\varepsilon }-f)_{\varepsilon }$
, and $(f_{\varepsilon }-f)_{\varepsilon }$![]() are converging to $0$
are converging to $0$![]() uniformly. Using (4.26) and (4.27), we have
uniformly. Using (4.26) and (4.27), we have

where
$g_{\varepsilon } \in L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() and $g_{\varepsilon }\to 0$
and $g_{\varepsilon }\to 0$![]() in $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
in $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() as $\varepsilon \rightarrow 0$
as $\varepsilon \rightarrow 0$![]() .
.
Combining the Cauchy problem (4.27) and (4.28), we deduce that the net $w_{\varepsilon }:=(\tilde {u}-u_{\varepsilon })$![]() solves the Cauchy problem:
solves the Cauchy problem:

Taking the Fourier transform of the Cauchy problem (4.29) with respect to $k\in \hbar \mathbb {Z}^{n}$![]() , we obtain:
, we obtain:

where $\nu ^{2}(\xi )$![]() is given by (4.2). Define the energy functional for the Cauchy problem (4.30) by
is given by (4.2). Define the energy functional for the Cauchy problem (4.30) by
where $(\cdot,\,\cdot )$![]() is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$
is the inner product in the Sobolev space $H^{s}(\mathbb {T}_{\hbar }^{n})$![]() .
.
Since the coefficients are sufficiently regular, following the lines of theorem 2.1, the next energy estimate holds true:
for some positive constants $\kappa _{1}$![]() and $\kappa _{2}$
and $\kappa _{2}$![]() . Then, using the Gronwall's lemma and the energy bounds similar to (4.6) along with the Plancherel formula (3.6), we obtain the following estimate:
. Then, using the Gronwall's lemma and the energy bounds similar to (4.6) along with the Plancherel formula (3.6), we obtain the following estimate:
$+$![]() for all $t\in [0,\,T]$
for all $t\in [0,\,T]$![]() . Now, by integrating the above estimate with respect to $t\in [0,\,T]$
. Now, by integrating the above estimate with respect to $t\in [0,\,T]$![]() and using the fact that $w_{\varepsilon }(0,\, k)\equiv 0$
and using the fact that $w_{\varepsilon }(0,\, k)\equiv 0$![]() for all $\varepsilon \in (0,\,1]$
for all $\varepsilon \in (0,\,1]$![]() , we get:
, we get:
Since $g_{\varepsilon } \rightarrow 0$![]() in $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
in $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() , we have
, we have
implying also that
Furthermore, the limit is the same for every representation of $u$![]() , since they will differ from $(u_{\varepsilon })_{\varepsilon }$
, since they will differ from $(u_{\varepsilon })_{\varepsilon }$![]() by a $L^{2}([0,\, T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
by a $L^{2}([0,\, T];\ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$![]() -negligible net. This completes the proof.
-negligible net. This completes the proof.
5. Semi-classical limit $\hbar \to 0$
In this section, we will prove the semi-classical limit theorems for the classical solution as well as for the very weak solution.
Proof of theorem 2.9 Consider two Cauchy problems:

and

where $(-\mathcal {L})^{\alpha }$![]() is the usual fractional Laplacian on $\mathbb {R}^{n}$
is the usual fractional Laplacian on $\mathbb {R}^{n}$![]() given by (1.5). We have assumed that $f$
given by (1.5). We have assumed that $f$![]() and $u_0$
and $u_0$![]() in (5.1) are the restrictions in $\hbar \mathbb {Z}^n$
in (5.1) are the restrictions in $\hbar \mathbb {Z}^n$![]() of the corresponding ones in (5.2) defined on $\mathbb {R}^n$
of the corresponding ones in (5.2) defined on $\mathbb {R}^n$![]() . From equations (5.1) and (5.2), denoting $w:=u-v$
. From equations (5.1) and (5.2), denoting $w:=u-v$![]() , we get:
, we get:

Since $w_{0} = 0$![]() , applying theorem 2.1 with $s = 0$
, applying theorem 2.1 with $s = 0$![]() for the Cauchy problem (5.3) and using estimate (2.1), we obtain:
for the Cauchy problem (5.3) and using estimate (2.1), we obtain:

for all $t\in [0,\,T]$![]() , where the constant $C_{T,a,b}$
, where the constant $C_{T,a,b}$![]() is given by
is given by
Now, we will estimate the term $\left \|((-\mathcal {L})^{\alpha }-\hbar ^{-2\alpha }(-\mathcal {L}_{\hbar })^{\alpha })v\right \|^{2}_{L^{2}([0,\,T];\ell ^{2}(\hbar \mathbb {Z}^{n}))}.$![]() Using the Plancherel formula (3.6) for $s=0$
Using the Plancherel formula (3.6) for $s=0$![]() , (3.9) and (3.10), we have
, (3.9) and (3.10), we have

Since $|\cdot |^{\alpha }:\mathbb {R}\to \mathbb {R}$![]() is $\alpha$
is $\alpha$![]() -Hölder continuous for $0<\alpha \leq 1$
-Hölder continuous for $0<\alpha \leq 1$![]() , we have the following inequality:
, we have the following inequality:
and $|x|=\sqrt {x_{1}^{2}+\dots +x_{n}^{2}}$![]() . Now, using the above inequality and the Taylor expansion for $\sin ^{2}(\pi \hbar \xi _{l})$
. Now, using the above inequality and the Taylor expansion for $\sin ^{2}(\pi \hbar \xi _{l})$![]() , we get:
, we get:

where $|\xi |^{4\alpha }=[\sum \nolimits _{l=1}^{n}\xi ^{2}_{l}]^{2\alpha }$![]() and $\theta _{l}\in (0,\,\pi \hbar \xi _{l})$
and $\theta _{l}\in (0,\,\pi \hbar \xi _{l})$![]() or $(\pi \hbar \xi _{l},\,0)$
or $(\pi \hbar \xi _{l},\,0)$![]() depending on the sign of $\xi _{l}$
depending on the sign of $\xi _{l}$![]() . Now, combining estimate (5.6) with (5.5), we get:
. Now, combining estimate (5.6) with (5.5), we get:

whenever $m\geq 4\alpha$![]() . Since $u_{0}\in H^{m}(\mathbb {R}^{n})$
. Since $u_{0}\in H^{m}(\mathbb {R}^{n})$![]() with $m\geq 4\alpha$
with $m\geq 4\alpha$![]() , using theorem 1.1, we have $v\in H^{m}(\mathbb {R}^{n})$
, using theorem 1.1, we have $v\in H^{m}(\mathbb {R}^{n})$![]() with $m\geq 4\alpha$
with $m\geq 4\alpha$![]() . Therefore, using (5.4) and (5.7), we deduce that $\left \|w(t,\,\cdot )\right \|_{\ell ^{2}(\hbar \mathbb {Z}^{n})}\to 0$
. Therefore, using (5.4) and (5.7), we deduce that $\left \|w(t,\,\cdot )\right \|_{\ell ^{2}(\hbar \mathbb {Z}^{n})}\to 0$![]() as $\hbar \to 0.$
as $\hbar \to 0.$![]() Hence, we have
Hence, we have
This finishes the proof of theorem 2.9.
6. Remarks
We conclude the paper with a few remarks related to the very weak solution for the Cauchy problem (1.4) in the Euclidean setting:
(1) For a net $u_\varepsilon =u_\varepsilon (t,\,x)$
 , where $x \in \mathbb {R}^n$
, where $x \in \mathbb {R}^n$ is a variable in the Euclidean space, the definitions of moderateness and negligibility are adapted accordingly from definition (2.2); i.e. the net $(u_\varepsilon )_\varepsilon \in {L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))}$
is a variable in the Euclidean space, the definitions of moderateness and negligibility are adapted accordingly from definition (2.2); i.e. the net $(u_\varepsilon )_\varepsilon \in {L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))}$ is $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$
is $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$ -moderate if there exist $N \in \mathbb {N}_{0}$
-moderate if there exist $N \in \mathbb {N}_{0}$ and $c>0$
and $c>0$ such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];H^{m}(\mathbb{R}^{n}))} \leq c \varepsilon^{{-}N}, \]for all $\varepsilon \in (0,\,1]$
such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];H^{m}(\mathbb{R}^{n}))} \leq c \varepsilon^{{-}N}, \]for all $\varepsilon \in (0,\,1]$
 and is $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$
and is $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$ -negligible if for all $q\in \mathbb {N}_{0}$
-negligible if for all $q\in \mathbb {N}_{0}$ there exists $c>0$
there exists $c>0$ such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];H^{m}(\mathbb{R}^{n}))} \leq c \varepsilon^{q}, \]for all $\varepsilon \in (0,\,1]$
such that
\[ \|u_{\varepsilon}\|_{L^{2}([0,T];H^{m}(\mathbb{R}^{n}))} \leq c \varepsilon^{q}, \]for all $\varepsilon \in (0,\,1]$
 .
.(2) The notion of a very weak solution for the Cauchy problem (1.4) can be adapted from definition 2.3 by simply replacing the $L^{2}([0,\, T] ; \ell ^{2}_{s}(\hbar \mathbb {Z}^{n}))$
 -moderate regularization by the $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$
-moderate regularization by the $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$ -moderate regularization for the source term $f$
-moderate regularization for the source term $f$ and the net $(u_{\varepsilon })_{\varepsilon }.$
and the net $(u_{\varepsilon })_{\varepsilon }.$
(3) The proof of theorem 1.2 will be similar to the proof of theorem 2.4 except for using the inner product of $L^{2}_{m}(\mathbb {R}^{n})$
 instead of $H^{s}(\mathbb {T}_{\hbar }^{n})$
instead of $H^{s}(\mathbb {T}_{\hbar }^{n})$ in (4.11).
in (4.11).(4) The notion of the uniqueness of very weak solution for the Cauchy problem (1.4) can also be formulated by making similar modifications to definition 2.5.
(5) If the coefficients $a,\,b$
 are regular, the very weak solution obtained in theorem 1.2 recaptures the classical solution obtained in theorem 1.1 in the limit $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$
are regular, the very weak solution obtained in theorem 1.2 recaptures the classical solution obtained in theorem 1.1 in the limit $L^{2}([0,\,T];H^{m}(\mathbb {R}^{n}))$ as $\varepsilon \to 0$
as $\varepsilon \to 0$ . More precisely, we have the consistency result similar to theorem 2.8 with the same modifications as above.
. More precisely, we have the consistency result similar to theorem 2.8 with the same modifications as above.
Acknowledgements
The authors thank the anonymous referee for careful reading of the manuscript and for several valuable comments and suggestions leading to the improvement of the manuscript. M. Chatzakou is a postdoctoral fellow of the Research Foundation—Flanders (FWO) under the postdoctoral grant number 12B1223N. A. Dasgupta is supported by Core Research Grant, RP03890G, Science and Engineering Research Board (SERB), DST, India. M. Ruzhansky is supported by the EPSRC Grants EP/R003025 by the FWO Odysseus 1 grant G.0H94.18N: Analysis and Partial Differential Equations and by the Methusalem programme of the Ghent University Special Research Fund (BOF) (grant number 01M01021). A. Tushir is supported by the institute assistantship from the Indian Institute of Technology Delhi, India.
Data
All the data used are provided within the manuscript.
Competing interest
None.