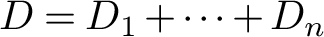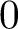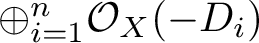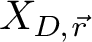1 Introduction
Let X be a smooth projective variety and
![]() $D=D_1+\dotsb +D_n$
a simple normal crossing divisor with nef components
$D=D_1+\dotsb +D_n$
a simple normal crossing divisor with nef components
![]() $D_i$
. We study the relationship between the genus
$D_i$
. We study the relationship between the genus
![]() $0$
local Gromov–Witten theory of
$0$
local Gromov–Witten theory of
![]() $\oplus _{i=1}^n \mathcal O_X(-D_i)$
and the genus
$\oplus _{i=1}^n \mathcal O_X(-D_i)$
and the genus
![]() $0$
orbifold Gromov–Witten theory of the multiroot stack
$0$
orbifold Gromov–Witten theory of the multiroot stack
![]() $X_{D,\vec r}$
. Our main result is a positive answer to [Reference Tseng and You27, Conjecture 1.8]:
$X_{D,\vec r}$
. Our main result is a positive answer to [Reference Tseng and You27, Conjecture 1.8]:
Theorem A (Theorem 2.1)
Let
![]() $\beta $
be a curve class on X with
$\beta $
be a curve class on X with
![]() $d_i:=D_i\cdot \beta>0$
for
$d_i:=D_i\cdot \beta>0$
for
![]() $i\in \{1,\dotsc , n\}$
. For
$i\in \{1,\dotsc , n\}$
. For
![]() $r_i$
pairwise coprime and sufficiently large, the following identity holds on the moduli space
$r_i$
pairwise coprime and sufficiently large, the following identity holds on the moduli space
![]() $\mathsf {K}_{0,m}(X,\beta )$
of stable maps to X:
$\mathsf {K}_{0,m}(X,\beta )$
of stable maps to X:
 $$\begin{align*}\rho_\star \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}\left(X_{D,\vec r},\beta\right)\right]^{\operatorname{virt}} &= \left( \Pi_{i=1}^n (-1)^{d_i-1} \right) \left( \cup_{j=1}^m \operatorname{\mathrm{ev}}_j^\star \left(\cup_{i \in I_j} D_i\right) \right) \\ &\quad \cap \left[\mathsf{K}_{0,m}\left(\oplus_{i=1}^n \mathcal{O}_X(-D_i),\beta\right)\right]^{\operatorname{virt}}, \end{align*}$$
$$\begin{align*}\rho_\star \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}\left(X_{D,\vec r},\beta\right)\right]^{\operatorname{virt}} &= \left( \Pi_{i=1}^n (-1)^{d_i-1} \right) \left( \cup_{j=1}^m \operatorname{\mathrm{ev}}_j^\star \left(\cup_{i \in I_j} D_i\right) \right) \\ &\quad \cap \left[\mathsf{K}_{0,m}\left(\oplus_{i=1}^n \mathcal{O}_X(-D_i),\beta\right)\right]^{\operatorname{virt}}, \end{align*}$$
where
![]() $I_j\subseteq \{1,\dotsc ,n\}$
records the set of divisors which the marking
$I_j\subseteq \{1,\dotsc ,n\}$
records the set of divisors which the marking
![]() $x_j$
is tangent to (see §2.1 for details), and
$x_j$
is tangent to (see §2.1 for details), and
![]() $\rho $
is the morphism forgetting the orbifold structures.
$\rho $
is the morphism forgetting the orbifold structures.
This generalizes the smooth divisor local-logarithmic correspondence [Reference van Garrel, Graber and Ruddat29] to the simple normal crossing setting, by interpreting the orbifold theory of the multiroot stack as an alternative to the logarithmic theory [Reference Tseng and You26].
When D is smooth, Theorem A follows from previous results equating both local and orbifold invariants with relative invariants [Reference Abramovich, Cadman and Wise1, Reference van Garrel, Graber and Ruddat29, Reference Tseng and You28]. For general D, the key observation is that both the local and orbifold theories satisfy a product formula over the space of stable maps to X. Theorem A follows immediately, by bootstrapping from the smooth divisor case. This is another manifestation of the ‘rank reduction’ technique in Gromov–Witten theory [Reference Abramovich and Chen2, Reference Nabijou and Ranganathan22].
1.1 Logarithmic Gromov–Witten theory
Unlike the local and orbifold theories, the logarithmic theory does not satisfy a naive product formula over the space of stable maps to X. This observation was used in [Reference Nabijou and Ranganathan22] to produce counterexamples to the local-logarithmic conjecture. The same reasoning shows that the orbifold invariants also differ from the logarithmic invariants (and it is easy to find counterexamples beyond the maximal contact setting). In fact, Corollary 3.4 equates the orbifold invariants with the so-called naive invariants, introduced in [Reference Nabijou21, §3] and studied in [Reference Nabijou and Ranganathan22]:
Theorem B (Corollary 3.4)
The orbifold invariants of the multiroot stack coincide with the naive invariants, and hence differ from the logarithmic invariants. This holds for arbitrary choices of contact orders.
In summary, there are four genus
![]() $0$
maximal contact theories associated to a simple normal crossings pair: logarithmic, orbifold, naive, and local. They are related as follows:
$0$
maximal contact theories associated to a simple normal crossings pair: logarithmic, orbifold, naive, and local. They are related as follows:

The orbifold, local, and naive theories all coincide up to combinatorial factors. The logarithmic theory differs in a more essential way, though there is an in-principle procedure which relates it to the other three.
Despite the failure of the cycle-level local-logarithmic correspondence, there are many choices of targets and insertions for which the correspondence does hold on the numerical level. This occurs when the insertions kill the correction terms described in [Reference Nabijou and Ranganathan22, Theorem 3.4]. In [Reference Bousseau, Brini and van Garrel7, Reference Bousseau, Brini and van Garrel8, Reference Bousseau, Brini and van Garrel9], numerous instances of the numerical local-logarithmic correspondence are established: for toric varieties, log Calabi–Yau surfaces and orbifold log Calabi–Yau surfaces; in [Reference Nabijou and Ranganathan22, §5], the numerical correspondence is established for product geometries. As a corollary of Theorem A, all of these logarithmic invariants coincide with the corresponding orbifold invariants.
These different theories are approached using very different techniques. Torus localization, in various guises, has been applied to compute both orbifold and local invariants [Reference Klemm and Pandharipande18, Reference Coates, Corti, Iritani and Tseng11, Reference Fan, Tseng and You12]; logarithmic invariants, on the other hand, are typically calculated using tropical correspondence theorems and scattering diagrams [Reference Nishinou and Siebert23, Reference Gross, Pandharipande and Siebert15]. Depending on the context, one technique may be more effective than another. These correspondences provide bridges between different techniques, thus increasing the roster of tools available for computations in Gromov–Witten theory as a whole.
1.2 Relation to previous work
The smooth divisor case of Theorem A follows by combining the orbifold-logarithmic correspondence [Reference Abramovich, Cadman and Wise1, Reference Tseng and You28] with the strong form [Reference Fan and Wu13, Reference Tseng and You27] of the local-logarithmic correspondence [Reference van Garrel, Graber and Ruddat29]. Some cases of Theorem A for normal crossing divisors were numerically verified in [Reference Tseng and You27, §5.2], by computing the J-functions of both sides.
1.3 User’s guide
We provide two approaches to rank reduction. The first (§2) uses the iterative construction of root stacks and the projection formula, and relies on a local-orbifold correspondence for certain smooth orbifold pairs (Theorem 2.2). The second (§3) uses a product formula for orbifold invariants over the space of stable maps to the coarse moduli space (Theorem 3.1). This holds for arbitrary tangency orders but requires a positivity assumption. The identification of orbifold and naive invariants (Corollary 3.4) is an immediate consequence.
2 Rank reduction I: Projection formula
2.1 Geometric setup
Fix a smooth projective variety X and a simple normal crossing divisor
![]() $D=D_1+\dotsb +D_n \subseteq X$
. For a tuple of pairwise coprime and sufficiently large integers
$D=D_1+\dotsb +D_n \subseteq X$
. For a tuple of pairwise coprime and sufficiently large integers
![]() $\vec r = (r_1,\dotsc ,r_n)$
, we form the associated multiroot stack
$\vec r = (r_1,\dotsc ,r_n)$
, we form the associated multiroot stack
Consider m marked points
![]() $x_1,\dotsc ,x_m$
and fix an ordered partition of the index set
$x_1,\dotsc ,x_m$
and fix an ordered partition of the index set
![]() $\{1,\dotsc ,n\}$
into disjoint subsets
$\{1,\dotsc ,n\}$
into disjoint subsets
![]() $I_1,\dotsc ,I_m$
such that
$I_1,\dotsc ,I_m$
such that
![]() $\cap _{i \in I_j} D_i$
is nonempty for each
$\cap _{i \in I_j} D_i$
is nonempty for each
![]() $j \in \{1,\dotsc ,m\}$
. Fix a curve class
$j \in \{1,\dotsc ,m\}$
. Fix a curve class
![]() $\beta \in H_2^+(X)$
such that
$\beta \in H_2^+(X)$
such that
![]() $d_i := D_i \cdot \beta> 0$
for all i.
$d_i := D_i \cdot \beta> 0$
for all i.
We consider a moduli problem of genus
![]() $0$
stable maps relative to
$0$
stable maps relative to
![]() $(X,D)$
, such that the marking
$(X,D)$
, such that the marking
![]() $x_j$
has maximal contact order
$x_j$
has maximal contact order
![]() $d_i$
to each divisor
$d_i$
to each divisor
![]() $D_i$
with
$D_i$
with
![]() $i \in I_j$
. Notice that some of the
$i \in I_j$
. Notice that some of the
![]() $I_j$
may be empty, corresponding to markings with no tangency conditions. Some markings may have positive contact orders along several divisors simultaneously, which implies in particular that they should be mapped to the intersection.
$I_j$
may be empty, corresponding to markings with no tangency conditions. Some markings may have positive contact orders along several divisors simultaneously, which implies in particular that they should be mapped to the intersection.
This moduli problem determines associated discrete data for a moduli problem of orbifold stable maps to the multiroot stack
![]() $\mathcal {X}$
, by taking each marking
$\mathcal {X}$
, by taking each marking
![]() $x_j$
to have twisting index
$x_j$
to have twisting index
 $$\begin{align*}s_j=\prod_{i \in I_j} r_i. \end{align*}$$
$$\begin{align*}s_j=\prod_{i \in I_j} r_i. \end{align*}$$
The twisted sector insertion in
 $$\begin{align*}\mu_{s_j} = \prod_{i \in I_j} \mu_{r_i} \end{align*}$$
$$\begin{align*}\mu_{s_j} = \prod_{i \in I_j} \mu_{r_i} \end{align*}$$
coincides with the tuple of tangency orders, since the twisting indices on source and target are the same [Reference Cadman and Chen10, §2.1]. We denote the associated moduli space by
 $$\begin{align*}\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta) \end{align*}$$
$$\begin{align*}\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta) \end{align*}$$
and let
![]() $\rho $
denote the morphism which forgets the orbifold structures:
$\rho $
denote the morphism which forgets the orbifold structures:
 $$\begin{align*}\rho \colon \mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta) \to \mathsf{K}_{0,m}(X,\beta). \end{align*}$$
$$\begin{align*}\rho \colon \mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta) \to \mathsf{K}_{0,m}(X,\beta). \end{align*}$$
2.2 Local-orbifold correspondence
Our main result is a cycle-level correspondence between the multiroot orbifold theory and the local theory of the associated split vector bundle, proving [Reference Tseng and You27, Conjecture 1.8]:
Theorem 2.1. For
![]() $r_i$
sufficiently large, we have
$r_i$
sufficiently large, we have
 $$\begin{align*}\rho_\star \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta)\right]^{\operatorname{virt}} &= \left( \Pi_{i=1}^n (-1)^{d_i-1} \right) \left( \cup_{j=1}^m \operatorname{\mathrm{ev}}_j^\star \left(\cup_{i \in I_j} D_i\right) \right) \\ & \quad \cap \left[\mathsf{K}_{0,m}\left(\oplus_{i=1}^n \mathcal{O}_X(-D_i),\beta\right)\right]^{\operatorname{virt}}. \end{align*}$$
$$\begin{align*}\rho_\star \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta)\right]^{\operatorname{virt}} &= \left( \Pi_{i=1}^n (-1)^{d_i-1} \right) \left( \cup_{j=1}^m \operatorname{\mathrm{ev}}_j^\star \left(\cup_{i \in I_j} D_i\right) \right) \\ & \quad \cap \left[\mathsf{K}_{0,m}\left(\oplus_{i=1}^n \mathcal{O}_X(-D_i),\beta\right)\right]^{\operatorname{virt}}. \end{align*}$$
The case
![]() $n=1$
follows by combining the smooth divisor local-logarithmic correspondence [Reference van Garrel, Graber and Ruddat29] in its strong form (see [Reference Fan and Wu13, Introduction] or [Reference Tseng and You27, equation (2)]), together with the smooth divisor logarithmic-orbifold correspondence [Reference Abramovich, Cadman and Wise1, Reference Tseng and You28].
$n=1$
follows by combining the smooth divisor local-logarithmic correspondence [Reference van Garrel, Graber and Ruddat29] in its strong form (see [Reference Fan and Wu13, Introduction] or [Reference Tseng and You27, equation (2)]), together with the smooth divisor logarithmic-orbifold correspondence [Reference Abramovich, Cadman and Wise1, Reference Tseng and You28].
Proof. We proceed by induction on n. The base case
![]() $n=1$
was already discussed. For the induction step, consider the root stack
$n=1$
was already discussed. For the induction step, consider the root stack
Letting
![]() $p \colon \mathcal {Z} \to X$
be the morphism to the coarse moduli space and
$p \colon \mathcal {Z} \to X$
be the morphism to the coarse moduli space and
![]() $\mathcal {D}_n=p^{-1} D_n$
, we have
$\mathcal {D}_n=p^{-1} D_n$
, we have
The ordered partition
![]() $(I_1,\dotsc ,I_m)$
of
$(I_1,\dotsc ,I_m)$
of
![]() $\{1,\dotsc ,n\}$
induces a partition
$\{1,\dotsc ,n\}$
induces a partition
![]() $(J_1,\dotsc ,J_m)$
of
$(J_1,\dotsc ,J_m)$
of
![]() ${\{1,\dotsc ,n-1\}}$
by setting
${\{1,\dotsc ,n-1\}}$
by setting
![]() $J_j = I_j \setminus \{ n\}$
. Consider the tower of moduli spaces
$J_j = I_j \setminus \{ n\}$
. Consider the tower of moduli spaces

The induction hypothesis gives
 $$ \begin{align} \varphi_\star \left[\mathsf{K}^{\max}_{0,\left(J_1,\dotsc,J_m\right)}(\mathcal{Z},\beta)\right]^{\operatorname{virt}} &= \left( \Pi_{i=1}^{n-1} (-1)^{d_i-1} \right) \left( \cup_{j=1}^m \operatorname{\mathrm{ev}}_j^\star \left(\cup_{i \in J_j} D_i\right) \right) \nonumber \\ & \quad \cap \left[\mathsf{K}_{0,m}\left(\oplus_{i=1}^{n-1} \mathcal{O}_X(-D_i),\beta\right)\right]^{\operatorname{virt}}, \end{align} $$
$$ \begin{align} \varphi_\star \left[\mathsf{K}^{\max}_{0,\left(J_1,\dotsc,J_m\right)}(\mathcal{Z},\beta)\right]^{\operatorname{virt}} &= \left( \Pi_{i=1}^{n-1} (-1)^{d_i-1} \right) \left( \cup_{j=1}^m \operatorname{\mathrm{ev}}_j^\star \left(\cup_{i \in J_j} D_i\right) \right) \nonumber \\ & \quad \cap \left[\mathsf{K}_{0,m}\left(\oplus_{i=1}^{n-1} \mathcal{O}_X(-D_i),\beta\right)\right]^{\operatorname{virt}}, \end{align} $$
and Theorem 2.2 establishes a local-orbifold correspondence for the smooth orbifold pair
![]() $(\mathcal {Z},\mathcal {D}_n)$
, giving
$(\mathcal {Z},\mathcal {D}_n)$
, giving
 $$ \begin{align} & \psi_{\star} \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta)\right]^{\operatorname{virt}} = (-1)^{d_n-1} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n \cap \left[\mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n),\beta)\right]^{\operatorname{virt}} \nonumber \\ & \quad = (-1)^{d_n-1} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n \cdot \mathrm{e}\left(\mathrm{R}^1 \pi_\star f^\star \mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n)\right) \cap \left[\mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{Z},\beta)\right]^{\operatorname{virt}}, \end{align} $$
$$ \begin{align} & \psi_{\star} \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta)\right]^{\operatorname{virt}} = (-1)^{d_n-1} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n \cap \left[\mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n),\beta)\right]^{\operatorname{virt}} \nonumber \\ & \quad = (-1)^{d_n-1} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n \cdot \mathrm{e}\left(\mathrm{R}^1 \pi_\star f^\star \mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n)\right) \cap \left[\mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{Z},\beta)\right]^{\operatorname{virt}}, \end{align} $$
where
![]() $j_n \in \{1,\dotsc ,m\}$
is the unique index such that
$j_n \in \{1,\dotsc ,m\}$
is the unique index such that
![]() $n \in I_{j_n}$
. Since
$n \in I_{j_n}$
. Since
![]() $\mathcal {D}_n = p^\star D_n$
is pulled back from X, we have
$\mathcal {D}_n = p^\star D_n$
is pulled back from X, we have
 $$ \begin{align*} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n & = \varphi^\star \operatorname{\mathrm{ev}}_{j_n}^\star D_n \\ \mathrm{e}\left(\mathrm{R}^1 \pi_\star f^\star \mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n)\right) & = \varphi^\star \mathrm{e}\left(\mathrm{R}^1 \pi_\star f^\star \mathcal{O}_X(-D_n)\right). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n & = \varphi^\star \operatorname{\mathrm{ev}}_{j_n}^\star D_n \\ \mathrm{e}\left(\mathrm{R}^1 \pi_\star f^\star \mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n)\right) & = \varphi^\star \mathrm{e}\left(\mathrm{R}^1 \pi_\star f^\star \mathcal{O}_X(-D_n)\right). \end{align*} $$
The latter equation follows from the projection formula and the following fact. The pullback
![]() $\varphi ^\star C$
of the universal curve on
$\varphi ^\star C$
of the universal curve on
![]() $\mathsf {K}_{0,m}(X,\beta )$
coincides with the coarsening of the universal curve
$\mathsf {K}_{0,m}(X,\beta )$
coincides with the coarsening of the universal curve
 $$\begin{align*}\mathcal C \to \mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{Z},\beta), \end{align*}$$
$$\begin{align*}\mathcal C \to \mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{Z},\beta), \end{align*}$$
which makes the composite universal map
![]() $\mathcal C\to \mathcal Z\to X$
representable. Therefore the structure sheaves of the universal curves are preserved by push-forward [Reference Abramovich, Olsson and Vistoli4, Theorem 3.1]. The result then follows from equations (1) and (2), the projection formula for
$\mathcal C\to \mathcal Z\to X$
representable. Therefore the structure sheaves of the universal curves are preserved by push-forward [Reference Abramovich, Olsson and Vistoli4, Theorem 3.1]. The result then follows from equations (1) and (2), the projection formula for
![]() $\varphi $
, and the splitting of the obstruction bundle for the local theory of
$\varphi $
, and the splitting of the obstruction bundle for the local theory of
![]() $\oplus _{i=1}^n \mathcal {O}_X(-D_i)$
.
$\oplus _{i=1}^n \mathcal {O}_X(-D_i)$
.
2.3 Local-orbifold correspondence for smooth orbifold pairs
It remains to establish the local-orbifold correspondence for the smooth orbifold pair
![]() $(\mathcal {Z},\mathcal {D}_n)$
, used in the preceding proof.
$(\mathcal {Z},\mathcal {D}_n)$
, used in the preceding proof.
Theorem 2.2. With notation as in the proof of Theorem 2.1, we have
 $$\begin{align*}\psi_\star \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta)\right]^{\operatorname{virt}} = (-1)^{d_n-1} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n \cap \left[\mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n),\beta)\right]^{\operatorname{virt}}. \end{align*}$$
$$\begin{align*}\psi_\star \left[\mathsf{K}^{\max}_{0,\left(I_1,\dotsc,I_m\right)}(\mathcal{X},\beta)\right]^{\operatorname{virt}} = (-1)^{d_n-1} \operatorname{\mathrm{ev}}_{j_n}^\star \mathcal{D}_n \cap \left[\mathsf{K}_{0,\left(J_1,\dotsc,J_m\right)}^{\max}(\mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n),\beta)\right]^{\operatorname{virt}}. \end{align*}$$
We establish this result only in the setting we require, namely when
![]() $\mathcal {Z}$
is a multiroot stack and
$\mathcal {Z}$
is a multiroot stack and
![]() $\mathcal {D}_n$
is a divisor pulled back from the coarse moduli space. The proof adapts the arguments of [Reference van Garrel, Graber and Ruddat29], but subtleties arise due to the twisted sectors of
$\mathcal {D}_n$
is a divisor pulled back from the coarse moduli space. The proof adapts the arguments of [Reference van Garrel, Graber and Ruddat29], but subtleties arise due to the twisted sectors of
![]() $\mathcal {Z}$
, which encode tangencies with respect to the divisors
$\mathcal {Z}$
, which encode tangencies with respect to the divisors
![]() $D_1,\dotsc ,D_{n-1}$
. These complicate a crucial dimension count in the proof (§2.3.3) and also affect the final multiplicity calculation (§2.3.4).
$D_1,\dotsc ,D_{n-1}$
. These complicate a crucial dimension count in the proof (§2.3.3) and also affect the final multiplicity calculation (§2.3.4).
Remark 2.3. It is unclear whether the correspondence holds in greater generality. If the divisor has generic stabilizer, then the dimension count (§2.3.3) can fail, so at best the result must be established via other methods. Moreover, in this case the multiplicity arising from the contribution of the special graph (§2.3.4) is different, hinting that any generalization of the correspondence will in fact require a new formulation.
2.3.1 Setting up the degeneration formula
Let
![]() $\mathfrak {X}$
be the degeneration to the normal cone of
$\mathfrak {X}$
be the degeneration to the normal cone of
![]() $\mathcal {D}_n \subseteq \mathcal {Z}$
, and let M be the degeneration to the normal cone of
$\mathcal {D}_n \subseteq \mathcal {Z}$
, and let M be the degeneration to the normal cone of
![]() $D_n\subseteq X$
.
$D_n\subseteq X$
.
Lemma 2.4.
![]() $\mathfrak {X}$
is the root stack of M along the strict (equivalently, total) transforms of the divisors
$\mathfrak {X}$
is the root stack of M along the strict (equivalently, total) transforms of the divisors
![]() $D_i \times \mathbb {A}^1$
for
$D_i \times \mathbb {A}^1$
for
![]() $i\in \{1,\dotsc ,n-1\}$
.
$i\in \{1,\dotsc ,n-1\}$
.
Proof. The divisors
![]() $D_i \times \mathbb {A}^1$
intersect the blowup center
$D_i \times \mathbb {A}^1$
intersect the blowup center
![]() $D_n\times \{0\}$
transversely, hence the strict and total transforms coincide. Denote these by
$D_n\times \{0\}$
transversely, hence the strict and total transforms coincide. Denote these by
![]() $T_i \subseteq M$
. Each
$T_i \subseteq M$
. Each
![]() $T_i$
admits a root on
$T_i$
admits a root on
![]() $\mathfrak {X}$
, namely the pullback of the rooted divisor
$\mathfrak {X}$
, namely the pullback of the rooted divisor
![]() $\mathcal {D}_i \subseteq \mathcal {Z}$
along the composition
$\mathcal {D}_i \subseteq \mathcal {Z}$
along the composition
![]() $\mathfrak {X} \to \mathcal {Z} \times \mathbb {A}^1 \to \mathcal {Z}$
. By the universal property of the root stack, we obtain a morphism
$\mathfrak {X} \to \mathcal {Z} \times \mathbb {A}^1 \to \mathcal {Z}$
. By the universal property of the root stack, we obtain a morphism
and a local calculation shows that this is an isomorphism.
The general fiber of the family
![]() $\mathfrak {X} \to \mathbb {A}^1$
is
$\mathfrak {X} \to \mathbb {A}^1$
is
The central fiber consists of two components
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() $\mathcal {Y}$
meeting along
$\mathcal {Y}$
meeting along
![]() $\mathcal {D}_n$
. Here
$\mathcal {D}_n$
. Here
![]() $\mathcal {Y}$
is obtained by rooting the bundle
$\mathcal {Y}$
is obtained by rooting the bundle
 $Y=\mathbb {P}_{D_n}\left (\mathrm {N}_{D_n\mid X}\oplus \mathcal {O}_{D_n}\right )$
along the divisors
$Y=\mathbb {P}_{D_n}\left (\mathrm {N}_{D_n\mid X}\oplus \mathcal {O}_{D_n}\right )$
along the divisors
![]() $\pi ^{-1}(D_i \cap D_n)$
for
$\pi ^{-1}(D_i \cap D_n)$
for
![]() $i\in \{1,\dotsc ,n-1\}$
. There is a Cartesian square
$i\in \{1,\dotsc ,n-1\}$
. There is a Cartesian square

where we note that
![]() $\mathcal {D}_n$
is itself a multiroot stack along a simple normal crossing divisor
$\mathcal {D}_n$
is itself a multiroot stack along a simple normal crossing divisor
where
![]() $E_i = D_i \cap D_n \subseteq D_n$
. We let
$E_i = D_i \cap D_n \subseteq D_n$
. We let
![]() $\mathcal {E}_i = E_i/r_i \subseteq \mathcal {D}_n$
be the corresponding gerby divisor.
$\mathcal {E}_i = E_i/r_i \subseteq \mathcal {D}_n$
be the corresponding gerby divisor.
Each connected component of the rigidified inertia stack
![]() $\overline {\mathcal {I}}(\mathcal {D}_n)$
is a rigidification of a closed stratum
$\overline {\mathcal {I}}(\mathcal {D}_n)$
is a rigidification of a closed stratum
![]() $\bigcap _{i\in I}\mathcal {E}_i$
of the divisor
$\bigcap _{i\in I}\mathcal {E}_i$
of the divisor
![]() $\mathcal {E}_1+\dotsb +\mathcal {E}_{n-1} \subseteq \mathcal {D}_n$
(including the stratum
$\mathcal {E}_1+\dotsb +\mathcal {E}_{n-1} \subseteq \mathcal {D}_n$
(including the stratum
![]() $\mathcal {D}_n$
corresponding to the empty intersection). This rigidification is obtained from
$\mathcal {D}_n$
corresponding to the empty intersection). This rigidification is obtained from
![]() $\bigcap _{i\in I} E_i$
by rooting along the intersection with
$\bigcap _{i\in I} E_i$
by rooting along the intersection with
![]() $E_j$
for all
$E_j$
for all
![]() $j\notin I$
. This description of the twisted sectors is crucial for understanding the structure of the degeneration formula later.
$j\notin I$
. This description of the twisted sectors is crucial for understanding the structure of the degeneration formula later.
Finally,
![]() $\mathcal {D}_0\subseteq \mathcal {Y}$
will denote the section of the bundle consisting of its intersection with
$\mathcal {D}_0\subseteq \mathcal {Y}$
will denote the section of the bundle consisting of its intersection with
![]() $\mathcal {Z}$
, and
$\mathcal {Z}$
, and
![]() $\mathcal {D}_\infty \subseteq \mathcal {Y}$
will denote the intersection of the central fiber of
$\mathcal {D}_\infty \subseteq \mathcal {Y}$
will denote the intersection of the central fiber of
![]() $\mathfrak {X}$
with the strict transform
$\mathfrak {X}$
with the strict transform
![]() $\mathfrak {D}$
of
$\mathfrak {D}$
of
![]() $\mathcal {D}_n \times \mathbb {A}^1$
.
$\mathcal {D}_n \times \mathbb {A}^1$
.
Consider
![]() $\mathfrak L=\operatorname {Tot} \mathcal O_{\mathfrak X}(-\mathfrak D)$
. This forms a family of (nonproper) targets over
$\mathfrak L=\operatorname {Tot} \mathcal O_{\mathfrak X}(-\mathfrak D)$
. This forms a family of (nonproper) targets over
![]() $\mathbb {A}^1$
. The general fiber is
$\mathbb {A}^1$
. The general fiber is
![]() $\operatorname {Tot} \mathcal O_{\mathcal Z}(-\mathcal {D}_n)$
and the central fiber is a union of
$\operatorname {Tot} \mathcal O_{\mathcal Z}(-\mathcal {D}_n)$
and the central fiber is a union of
![]() $\mathcal {Z} \times \mathbb A^1$
and
$\mathcal {Z} \times \mathbb A^1$
and
![]() $\operatorname {Tot} \mathcal O_{\mathcal Y}(- \mathcal {D}_\infty )$
.
$\operatorname {Tot} \mathcal O_{\mathcal Y}(- \mathcal {D}_\infty )$
.
We apply the degeneration formula [Reference Abramovich and Fantechi3] to
![]() $\mathfrak {L}$
. The components of the central fiber are indexed by bipartite graphs
$\mathfrak {L}$
. The components of the central fiber are indexed by bipartite graphs
![]() $\Gamma $
. The vertices
$\Gamma $
. The vertices
![]() $v \in \Gamma $
are partitioned into
$v \in \Gamma $
are partitioned into
![]() $\mathcal {Z}$
-vertices and
$\mathcal {Z}$
-vertices and
![]() $\mathcal {Y}$
-vertices, and the associated moduli spaces
$\mathcal {Y}$
-vertices, and the associated moduli spaces
![]() $\mathsf {K}_v$
are spaces of maps to expansions of the rooted pairs
$\mathsf {K}_v$
are spaces of maps to expansions of the rooted pairs
 $$\begin{align*}\left(\mathcal{Z}\times \mathbb{A}^1,\mathcal{D}_n\times\mathbb{A}^1\right) \qquad \text{and} \qquad \left(\mathcal{O}_{\mathcal{Y}}(-\mathcal{D}_\infty),\mathcal{D}_0\times\mathbb{A}^1\right), \end{align*}$$
$$\begin{align*}\left(\mathcal{Z}\times \mathbb{A}^1,\mathcal{D}_n\times\mathbb{A}^1\right) \qquad \text{and} \qquad \left(\mathcal{O}_{\mathcal{Y}}(-\mathcal{D}_\infty),\mathcal{D}_0\times\mathbb{A}^1\right), \end{align*}$$
respectively, as defined in [Reference Abramovich and Fantechi3, §3]. Working with expansions is inconsequential, since the push-forward of the virtual class matches that of the space of maps to the corresponding root stack without expansions [Reference Abramovich, Cadman and Wise1, Theorem 2.2]. We denote the twisting index by
![]() $r_n$
. In the original formulation [Reference Abramovich and Fantechi3, §3.4],
$r_n$
. In the original formulation [Reference Abramovich and Fantechi3, §3.4],
![]() $r_n$
is required to be divisible by all contact orders at the gluing nodes, but by [Reference Tseng and You28] this condition can be removed without affecting the invariants. We assume therefore that
$r_n$
is required to be divisible by all contact orders at the gluing nodes, but by [Reference Tseng and You28] this condition can be removed without affecting the invariants. We assume therefore that
![]() $r_n$
is large and coprime to each of
$r_n$
is large and coprime to each of
![]() $r_1,\dotsc ,r_{n-1}$
.
$r_1,\dotsc ,r_{n-1}$
.
The component
![]() $\mathsf {K}_{\Gamma }$
associated to
$\mathsf {K}_{\Gamma }$
associated to
![]() $\Gamma $
maps to the fiber product
$\Gamma $
maps to the fiber product

with respect to the evaluation maps to the rigidified inertia stack of the join divisor. The virtual class of
![]() $\mathsf {K}_\Gamma $
pushes forward to a multiple of the virtual class with which
$\mathsf {K}_\Gamma $
pushes forward to a multiple of the virtual class with which
![]() $\mathsf {F}_\Gamma $
is endowed by virtue of this diagram; the virtual degree of the morphism
$\mathsf {F}_\Gamma $
is endowed by virtue of this diagram; the virtual degree of the morphism
![]() $\Phi $
is well understood [Reference Abramovich and Fantechi3, Proposition 5.9.1]. Each space
$\Phi $
is well understood [Reference Abramovich and Fantechi3, Proposition 5.9.1]. Each space
![]() $\mathsf {K}_v$
decomposes as a disjoint union of substacks obtained as preimages of connected components of the inertia stack.
$\mathsf {K}_v$
decomposes as a disjoint union of substacks obtained as preimages of connected components of the inertia stack.
After pushing forward to the space of stable maps to
![]() $\mathcal {Z}$
, the degeneration formula gives an equality of classes
$\mathcal {Z}$
, the degeneration formula gives an equality of classes
 $$ \begin{align} \left[\mathsf{K}^{\max}_{0,\left(J_1,\dotsc,J_m\right)}(\mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n),\beta)\right]^{\operatorname{virt}}=\sum_{\Gamma}\dfrac{1}{\lvert E(\Gamma)\rvert !} \cdot \Psi_\star [\mathsf{K}_{\Gamma}]^{\operatorname{virt}}, \end{align} $$
$$ \begin{align} \left[\mathsf{K}^{\max}_{0,\left(J_1,\dotsc,J_m\right)}(\mathcal{O}_{\mathcal{Z}}(-\mathcal{D}_n),\beta)\right]^{\operatorname{virt}}=\sum_{\Gamma}\dfrac{1}{\lvert E(\Gamma)\rvert !} \cdot \Psi_\star [\mathsf{K}_{\Gamma}]^{\operatorname{virt}}, \end{align} $$
where
![]() $\Psi $
is the composition
$\Psi $
is the composition
Let
![]() $j=j_n$
be the index of the marking at which we wish to impose tangency to
$j=j_n$
be the index of the marking at which we wish to impose tangency to
![]() $D_n$
(as in the proof of Theorem 2.1), and cap both sides of equation (4) with
$D_n$
(as in the proof of Theorem 2.1), and cap both sides of equation (4) with
![]() $\operatorname {\mathrm {ev}}_j^\star \mathfrak {D}$
. The left-hand side gives the local invariants of
$\operatorname {\mathrm {ev}}_j^\star \mathfrak {D}$
. The left-hand side gives the local invariants of
![]() $\mathcal {O}_{\mathcal {Z}}(-\mathcal {D}_n)$
capped with
$\mathcal {O}_{\mathcal {Z}}(-\mathcal {D}_n)$
capped with
![]() $\operatorname {\mathrm {ev}}_j^\star \mathcal {D}_n$
. Our aim is to show that all but one of the terms on the right-hand side vanish.
$\operatorname {\mathrm {ev}}_j^\star \mathcal {D}_n$
. Our aim is to show that all but one of the terms on the right-hand side vanish.
2.3.2 First vanishing:
 $\mathcal {Z}$
-vertices
$\mathcal {Z}$
-vertices
Suppose first that there is a
![]() $\mathcal {Z}$
-vertex
$\mathcal {Z}$
-vertex
![]() $v \in \Gamma $
with
$v \in \Gamma $
with
![]() $k>1$
adjacent edges. For each adjacent edge e, the corresponding evaluation map factors (locally) through a specific component of the rigidified inertia stack. Such a component is obtained by rigidifying a (possibly empty) intersection of the divisors
$k>1$
adjacent edges. For each adjacent edge e, the corresponding evaluation map factors (locally) through a specific component of the rigidified inertia stack. Such a component is obtained by rigidifying a (possibly empty) intersection of the divisors
![]() $\mathcal {E}_i$
in
$\mathcal {E}_i$
in
![]() $\mathcal {D}_n$
. We denote this by
$\mathcal {D}_n$
. We denote this by
![]() $\mathcal {E}_e$
. The product of evaluation maps thus takes the form
$\mathcal {E}_e$
. The product of evaluation maps thus takes the form
 $$\begin{align*}\mathsf{K}_v \to \prod_e \left(\mathcal{E}_e \times \mathbb{A}^1\right). \end{align*}$$
$$\begin{align*}\mathsf{K}_v \to \prod_e \left(\mathcal{E}_e \times \mathbb{A}^1\right). \end{align*}$$
However, since the source curve is proper, the map to affine space is constant. This ensures that all the point evaluations agree – that is, the map factors through the closed substack
 $$\begin{align*}\left(\prod_e \mathcal{E}_e \right) \times \mathbb{A}^1 \hookrightarrow \prod_e \left(\mathcal{E}_e \times \mathbb{A}^1\right). \end{align*}$$
$$\begin{align*}\left(\prod_e \mathcal{E}_e \right) \times \mathbb{A}^1 \hookrightarrow \prod_e \left(\mathcal{E}_e \times \mathbb{A}^1\right). \end{align*}$$
We now follow the argument of [Reference van Garrel, Graber and Ruddat29, Lemma 3.1]. There is a Cartesian diagram

The excess intersection formula [Reference Fulton14, Theorem 6.3] gives
 $$\begin{align*}\Delta^!=\operatorname{c}_{k-1}(E)\cap\widetilde\Delta^!, \end{align*}$$
$$\begin{align*}\Delta^!=\operatorname{c}_{k-1}(E)\cap\widetilde\Delta^!, \end{align*}$$
where E is the excess bundle, which in this case [Reference Fulton14, Example 6.3.2] is equal to
 $$\begin{align*}E=\widetilde\Delta^\star \mathrm{N}_{\iota^\prime}/\mathrm{N}_{\iota}, \end{align*}$$
$$\begin{align*}E=\widetilde\Delta^\star \mathrm{N}_{\iota^\prime}/\mathrm{N}_{\iota}, \end{align*}$$
which is clearly trivial if
![]() $k>1$
. It follows that
$k>1$
. It follows that
![]() $\Delta ^!=0$
and so the contribution of
$\Delta ^!=0$
and so the contribution of
![]() $\Gamma $
vanishes.
$\Gamma $
vanishes.
2.3.3 Second vanishing:
 $\mathcal {Y}$
-vertices
$\mathcal {Y}$
-vertices
We conclude that the only graphs which can contribute are those with a single
![]() $\mathcal {Y}$
-vertex. Let
$\mathcal {Y}$
-vertex. Let
![]() $v \in \Gamma $
be such a vertex. This corresponds to a space of expanded maps to the rooted pair
$v \in \Gamma $
be such a vertex. This corresponds to a space of expanded maps to the rooted pair
 $\left (\mathcal {O}_{\mathcal {Y}}(-\mathcal {D}_\infty ),\mathcal {D}_0\times \mathbb {A}^1\right )$
. Recall that
$\left (\mathcal {O}_{\mathcal {Y}}(-\mathcal {D}_\infty ),\mathcal {D}_0\times \mathbb {A}^1\right )$
. Recall that
![]() $\mathcal {Y}$
is a projective bundle over the divisor
$\mathcal {Y}$
is a projective bundle over the divisor
![]() $\mathcal {D}_n$
. Suppose that in the discrete data for
$\mathcal {D}_n$
. Suppose that in the discrete data for
![]() $\mathsf {K}_v$
, either
$\mathsf {K}_v$
, either
-
• the curve class is not a multiple of the fiber class or
-
• there are at least three special points.
This ensures that the corresponding moduli space of stable maps
![]() $\mathsf {K}_v(\mathcal {D}_n)$
to the base of the bundle is well defined. There is a projection
$\mathsf {K}_v(\mathcal {D}_n)$
to the base of the bundle is well defined. There is a projection
and we claim that the virtual class pushes forward to zero along this morphism. Since there is a natural bijection between the twisted sectors in
![]() $\mathcal {Y}$
and the twisted sectors in
$\mathcal {Y}$
and the twisted sectors in
![]() $\mathcal {D}_n$
, the age contributions to the virtual dimensions coincide. From this, one deduces
$\mathcal {D}_n$
, the age contributions to the virtual dimensions coincide. From this, one deduces
and so the claim holds if we show that formula (5) satisfies the virtual push-forward property [Reference Manolache20, Definition 3.1] (we note that this dimension count can fail if
![]() $\mathcal {D}_n$
is allowed to have generic stabilizer). By [Reference Abramovich, Cadman and Wise1, Theorem 2.2], it is equivalent to show that
$\mathcal {D}_n$
is allowed to have generic stabilizer). By [Reference Abramovich, Cadman and Wise1, Theorem 2.2], it is equivalent to show that
satisfies the virtual push-forward property. For this we adapt the arguments of [Reference van Garrel, Graber and Ruddat29, §4]. Let
 $$\begin{align*}s=\Pi_{i=1}^{n} r_i, \qquad t = \Pi_{i=1}^{n-1} r_i=s/r_n. \end{align*}$$
$$\begin{align*}s=\Pi_{i=1}^{n} r_i, \qquad t = \Pi_{i=1}^{n-1} r_i=s/r_n. \end{align*}$$
By representability, the stabilizer groups of the source curve of any stable map to
![]() $\mathcal {Y}_{\mathcal {D}_0,r_n}$
(resp.,
$\mathcal {Y}_{\mathcal {D}_0,r_n}$
(resp.,
![]() $\mathcal {D}_n$
) must have order dividing s (resp., t). We denote the monoids of effective curve classes by
$\mathcal {D}_n$
) must have order dividing s (resp., t). We denote the monoids of effective curve classes by
Now consider the following diagram, involving moduli stacks of prestable twisted curves with homology weights:

in which the morphism
![]() $\nu $
contracts unstable curve components with vertical homology class and coarsens the
$\nu $
contracts unstable curve components with vertical homology class and coarsens the
![]() $r_n$
–twisting (this morphism is the composition of an étale cover followed by a root construction).
$r_n$
–twisting (this morphism is the composition of an étale cover followed by a root construction).
From the short exact sequence of relative tangent bundles associated to the smooth projection
![]() $\mathcal {Y}_{\mathcal {D}_0,r_n} \to \mathcal {D}_n$
, we obtain a compatible triple for the triangle in diagram (6). We note that unlike when the target is a variety, we may have
$\mathcal {Y}_{\mathcal {D}_0,r_n} \to \mathcal {D}_n$
, we obtain a compatible triple for the triangle in diagram (6). We note that unlike when the target is a variety, we may have
 $$\begin{align*}H^1\left(\mathcal{C}, f^\star \mathrm{T}_{\mathcal{Y}_{\mathcal{D}_0,r_n}/\mathcal{D}_n}\right)\neq 0 \end{align*}$$
$$\begin{align*}H^1\left(\mathcal{C}, f^\star \mathrm{T}_{\mathcal{Y}_{\mathcal{D}_0,r_n}/\mathcal{D}_n}\right)\neq 0 \end{align*}$$
if components of
![]() $\mathcal {C}$
are mapped into the rooted divisor. Thus the morphism
$\mathcal {C}$
are mapped into the rooted divisor. Thus the morphism
![]() $\upsilon $
is not typically smooth, but it is always virtually smooth, which is sufficient. The arguments given in [Reference van Garrel, Graber and Ruddat29, Lemma 5.1 and Proposition 5.3] then apply verbatim, showing that the virtual push-forward property holds and the contribution of
$\upsilon $
is not typically smooth, but it is always virtually smooth, which is sufficient. The arguments given in [Reference van Garrel, Graber and Ruddat29, Lemma 5.1 and Proposition 5.3] then apply verbatim, showing that the virtual push-forward property holds and the contribution of
![]() $\Gamma $
vanishes.
$\Gamma $
vanishes.
2.3.4 Contribution of the special graph
We conclude that the only graphs
![]() $\Gamma $
which contribute are those with a single
$\Gamma $
which contribute are those with a single
![]() $\mathcal {Y}$
-vertex
$\mathcal {Y}$
-vertex
![]() $v_1$
with at most two special points and curve class a multiple of the fiber class F. Since
$v_1$
with at most two special points and curve class a multiple of the fiber class F. Since
![]() $v_1$
must contain at least one node as well as the marking
$v_1$
must contain at least one node as well as the marking
![]() $x_{j}$
, we are left with a single graph
$x_{j}$
, we are left with a single graph
![]() $\Gamma $
, consisting of
$\Gamma $
, consisting of
-
• a
 $\mathcal {Z}$
-vertex
$\mathcal {Z}$
-vertex
 $v_0$
supporting all the markings except
$v_0$
supporting all the markings except
 $x_{j}$
and with curve class
$x_{j}$
and with curve class
 $\beta _0=\beta $
; and
$\beta _0=\beta $
; and -
• a
 $\mathcal {Y}$
-vertex
$\mathcal {Y}$
-vertex
 $v_1$
supporting the marking
$v_1$
supporting the marking
 $x_{j}$
and with curve class
$x_{j}$
and with curve class
 $\beta _1=d_n \cdot F$
for
$\beta _1=d_n \cdot F$
for
 $d_n=\mathcal {D}_n\cdot \beta $
.
$d_n=\mathcal {D}_n\cdot \beta $
.
These are connected along a single edge e, and diagram (3) reduces to the following:

Recall that the component
![]() $\mathsf {K}_{\Gamma }$
of the central fiber is virtually finite over the fiber product
$\mathsf {K}_{\Gamma }$
of the central fiber is virtually finite over the fiber product
![]() $\mathsf {F}_{\Gamma }$
. Let
$\mathsf {F}_{\Gamma }$
. Let
be the subset recording those divisors among
![]() $D_1,\dotsc ,D_{n-1}$
which the marking
$D_1,\dotsc ,D_{n-1}$
which the marking
![]() $x_{j}$
is tangent to. This tangency is encoded in twisted sector insertions which are imposed on both the general and central fibers. In
$x_{j}$
is tangent to. This tangency is encoded in twisted sector insertions which are imposed on both the general and central fibers. In
![]() $\mathsf {K}_{v_1}$
these correspond to age constraints with respect to the bundles
$\mathsf {K}_{v_1}$
these correspond to age constraints with respect to the bundles
 $$\begin{align*}\mathcal{O}_{\mathcal{Y}}\left(\pi^{-1}\mathcal{E}_i\right) =\pi^\star \mathcal{O}_{\mathcal{D}_n}(\mathcal{E}_i). \end{align*}$$
$$\begin{align*}\mathcal{O}_{\mathcal{Y}}\left(\pi^{-1}\mathcal{E}_i\right) =\pi^\star \mathcal{O}_{\mathcal{D}_n}(\mathcal{E}_i). \end{align*}$$
Since the curve class is a multiple of a fiber, these bundles have zero degree when pulled back to the source curve. It follows from parity considerations that
![]() $\mathsf {K}_{v_1}$
is empty unless the nodal marking q corresponding to the edge e also carries twisted sector insertions, which are opposite to those at
$\mathsf {K}_{v_1}$
is empty unless the nodal marking q corresponding to the edge e also carries twisted sector insertions, which are opposite to those at
![]() $x_{j}$
. This means we must have
$x_{j}$
. This means we must have
 $$\begin{align*}\operatorname{age}_{q} \pi^\star \mathcal{O}_{\mathcal{D}_n}(\mathcal{E}_i)= 1 - \operatorname{age}_{x_j} \pi^\star \mathcal{O}_{\mathcal{D}_n}(\mathcal{E}_i) \end{align*}$$
$$\begin{align*}\operatorname{age}_{q} \pi^\star \mathcal{O}_{\mathcal{D}_n}(\mathcal{E}_i)= 1 - \operatorname{age}_{x_j} \pi^\star \mathcal{O}_{\mathcal{D}_n}(\mathcal{E}_i) \end{align*}$$
for all
![]() $i \in J_{j}$
. By the inversion of the band in the evaluation maps, we then have the opposite ages for the nodal marking q on
$i \in J_{j}$
. By the inversion of the band in the evaluation maps, we then have the opposite ages for the nodal marking q on
![]() $\mathsf {K}_{v_0}$
. It follows that the vertex
$\mathsf {K}_{v_0}$
. It follows that the vertex
![]() $v_0$
contributes the orbifold invariants of the root stack
$v_0$
contributes the orbifold invariants of the root stack
![]() $\mathcal {Z}_{\mathcal {D}_n,r_n} = \mathcal {X}$
with twisted sector insertions imposing maximal tangency of a single marking q with respect to all divisors
$\mathcal {Z}_{\mathcal {D}_n,r_n} = \mathcal {X}$
with twisted sector insertions imposing maximal tangency of a single marking q with respect to all divisors
![]() $D_i$
for
$D_i$
for
![]() $i \in I_j=J_j \cup \{n\}$
, as required.
$i \in I_j=J_j \cup \{n\}$
, as required.
For the contribution of
![]() $v_1$
, notice that
$v_1$
, notice that
![]() $\operatorname {\mathrm {ev}}_q$
takes values in a component of
$\operatorname {\mathrm {ev}}_q$
takes values in a component of
![]() $\overline {\mathcal {I}}(\mathcal {D}_n)$
which is naturally isomorphic to the rigidification of
$\overline {\mathcal {I}}(\mathcal {D}_n)$
which is naturally isomorphic to the rigidification of
 $$\begin{align*}\bigcap_{i \in J_j} \mathcal{E}_i. \end{align*}$$
$$\begin{align*}\bigcap_{i \in J_j} \mathcal{E}_i. \end{align*}$$
We denote this rigidification by
![]() $\mathcal {E}_{J_j}$
. A direct calculation shows that
$\mathcal {E}_{J_j}$
. A direct calculation shows that
There is a divisorial insertion
![]() $\operatorname {\mathrm {ev}}_j^\star \mathcal {D}_\infty $
on
$\operatorname {\mathrm {ev}}_j^\star \mathcal {D}_\infty $
on
![]() $\mathsf {K}_{v_1}$
, and the contribution of
$\mathsf {K}_{v_1}$
, and the contribution of
![]() $v_1$
can be expressed as the unique
$v_1$
can be expressed as the unique
![]() $m \in \mathbb {Q}$
such that
$m \in \mathbb {Q}$
such that
 $$\begin{align*}(\operatorname{\mathrm{ev}}_q)_\star \left( \operatorname{\mathrm{ev}}_j^\star \mathcal{D}_\infty \cap \left[\mathsf{K}_{v_1}\right]^{\operatorname{virt}} \right)= m\cdot \left[\mathcal{E}_{J_j}\right]. \end{align*}$$
$$\begin{align*}(\operatorname{\mathrm{ev}}_q)_\star \left( \operatorname{\mathrm{ev}}_j^\star \mathcal{D}_\infty \cap \left[\mathsf{K}_{v_1}\right]^{\operatorname{virt}} \right)= m\cdot \left[\mathcal{E}_{J_j}\right]. \end{align*}$$
This can be computed by restricting to the fiber of a general point in
![]() $\mathcal {E}_{J_j}$
. Working locally around this point, the gerbes
$\mathcal {E}_{J_j}$
. Working locally around this point, the gerbes
![]() $\mathcal {E}_i$
become trivial, so that we obtain a space of maps to
$\mathcal {E}_i$
become trivial, so that we obtain a space of maps to
 $$\begin{align*}\mathbb{P}(r_n,1) \times \prod_{i \in J_j} \mathcal{B}\mu_{r_i}. \end{align*}$$
$$\begin{align*}\mathbb{P}(r_n,1) \times \prod_{i \in J_j} \mathcal{B}\mu_{r_i}. \end{align*}$$
The maps to the
![]() $\mathcal {B}\mu _{r_i}$
are uniquely determined, and each has an automorphism factor of
$\mathcal {B}\mu _{r_i}$
are uniquely determined, and each has an automorphism factor of
![]() $1/r_i$
. This cancels with the automorphism factor arising from the Chen–Ruan intersection pairing on the inertia stack of the join divisor [Reference Abramovich and Fantechi3, §5.2.3].
$1/r_i$
. This cancels with the automorphism factor arising from the Chen–Ruan intersection pairing on the inertia stack of the join divisor [Reference Abramovich and Fantechi3, §5.2.3].
We are left with a computation on
![]() $\mathbb {P}(r_n,1)$
. The contribution is a local invariant capped with an insertion of
$\mathbb {P}(r_n,1)$
. The contribution is a local invariant capped with an insertion of
![]() $\operatorname {\mathrm {ev}}_{j}^\star (\infty )$
. The latter insertion can be factored out via the divisor axiom; the obstruction bundle of the local theory is pulled back along the map forgetting a marking, since the structure sheaves of the universal curves are preserved by push-forward along stabilization. The remaining local invariant can be computed by localization. The end result [Reference Johnson, Pandharipande and Tseng17, (21)] is
$\operatorname {\mathrm {ev}}_{j}^\star (\infty )$
. The latter insertion can be factored out via the divisor axiom; the obstruction bundle of the local theory is pulled back along the map forgetting a marking, since the structure sheaves of the universal curves are preserved by push-forward along stabilization. The remaining local invariant can be computed by localization. The end result [Reference Johnson, Pandharipande and Tseng17, (21)] is
 $$\begin{align*}(d_n) \left( \dfrac{(-1)^{d_n-1}}{d_n^2}\right) = \dfrac{(-1)^{d_n-1}}{d_n}, \end{align*}$$
$$\begin{align*}(d_n) \left( \dfrac{(-1)^{d_n-1}}{d_n^2}\right) = \dfrac{(-1)^{d_n-1}}{d_n}, \end{align*}$$
which combines with the gluing factor
![]() $d_n$
appearing in the degeneration formula to complete the proof of Theorem 2.2.□
$d_n$
appearing in the degeneration formula to complete the proof of Theorem 2.2.□
3 Rank reduction II: Relative product formula
Having established the main Theorem 2.1, we now present an alternative approach, also based on the rank-reduction philosophy. While this approach is less general, requiring a positivity assumption, we have chosen to include it because the ‘relative product formula’ it uses provides valuable insight into the geometry of maps to the multiroot stack, and clarifies the relationship to logarithmic invariants. Moreover, the main result does not require the maximal contact assumption.
3.1 Convex embeddings
As before, fix a smooth projective variety X and a simple normal crossing divisor
![]() $D=D_1+\dotsb +D_n \subseteq X$
. To ease notation, we will assume from now on that
$D=D_1+\dotsb +D_n \subseteq X$
. To ease notation, we will assume from now on that
![]() $n=2$
; the extension to the general case follows by induction.
$n=2$
; the extension to the general case follows by induction.
We will assume throughout this section that there exist a simple normal crossing pair
![]() $(P,H=H_1+H_2)$
with P convex and a closed embedding
$(P,H=H_1+H_2)$
with P convex and a closed embedding
![]() $X \hookrightarrow P$
such that
$X \hookrightarrow P$
such that
![]() $D_i = X \cap H_i$
for each i. In this situation we call
$D_i = X \cap H_i$
for each i. In this situation we call
![]() $(X,D)$
a convex embedding. Two important cases encompassed by this definition are
$(X,D)$
a convex embedding. Two important cases encompassed by this definition are
-
(1) X convex and
 $D_i$
arbitrary;
$D_i$
arbitrary; -
(2) X arbitrary and
 $D_i$
very ample.
$D_i$
very ample.
All definitions and proofs will be given first in the case, where X itself is convex, and then extended to convex embeddings via virtual pullback.
3.2 Relative product formula for root stacks
As in §2, we fix discrete data for a moduli problem of genus
![]() $0$
relative stable maps to
$0$
relative stable maps to
![]() $(X,D)$
: a curve class
$(X,D)$
: a curve class
![]() $\beta \in H_2^+(X)$
, a number of marked points m, and specified tangency orders to
$\beta \in H_2^+(X)$
, a number of marked points m, and specified tangency orders to
![]() $D_1$
and
$D_1$
and
![]() $D_2$
at the marked points. Note that we do not require the contact orders to be maximal at this point.
$D_2$
at the marked points. Note that we do not require the contact orders to be maximal at this point.
Choose large coprime integers
![]() $r_1$
and
$r_1$
and
![]() $r_2$
and consider the root stacks
$r_2$
and consider the root stacks
These both have X as their coarse moduli space. For each
![]() $\mathcal {X}_i$
we can set up data for a moduli space of orbifold stable maps, by taking every marking to have twisting index
$\mathcal {X}_i$
we can set up data for a moduli space of orbifold stable maps, by taking every marking to have twisting index
![]() $r_i$
. The twisted sector insertion in
$r_i$
. The twisted sector insertion in
![]() $\mu _{r_i}$
coincides with the tangency order, since the twisting indices on source and target are the same [Reference Cadman and Chen10, §2.1]. Consider now the multiroot stack
$\mu _{r_i}$
coincides with the tangency order, since the twisting indices on source and target are the same [Reference Cadman and Chen10, §2.1]. Consider now the multiroot stack
Just as before, we may construct discrete data for a space of orbifold stable maps to
![]() $\mathcal {X}$
. Markings tangent to both
$\mathcal {X}$
. Markings tangent to both
![]() $D_1$
and
$D_1$
and
![]() $D_2$
will have twisting index
$D_2$
will have twisting index
![]() $r_1r_2$
, and the twisted sector insertion is the unique element of
$r_1r_2$
, and the twisted sector insertion is the unique element of
![]() $\mu _{r_1r_2}$
which maps to the correct pair of tangencies under the canonical isomorphism
$\mu _{r_1r_2}$
which maps to the correct pair of tangencies under the canonical isomorphism
![]() $\mu _{r_1r_2} = \mu _{r_1} \times \mu _{r_2}$
. From now on the discrete data will be suppressed from the notation.
$\mu _{r_1r_2} = \mu _{r_1} \times \mu _{r_2}$
. From now on the discrete data will be suppressed from the notation.
In this section we show that the theory of orbifold stable maps satisfies a relative product formula over the space of maps to the coarse moduli space. To be more precise, we have the following:
Theorem 3.1. There exists a diagram

such that, when X is convex, we have
 $$ \begin{align} \nu_*[\mathsf{K}(\mathcal{X})]^{\operatorname{virt}} = \Delta_{\mathsf{K}(X)}^!\left( [\mathsf{K}(\mathcal{X}_1)]^{\operatorname{virt}} \times [\mathsf{K}(\mathcal{X}_2)]^{\operatorname{virt}} \right)\!. \end{align} $$
$$ \begin{align} \nu_*[\mathsf{K}(\mathcal{X})]^{\operatorname{virt}} = \Delta_{\mathsf{K}(X)}^!\left( [\mathsf{K}(\mathcal{X}_1)]^{\operatorname{virt}} \times [\mathsf{K}(\mathcal{X}_2)]^{\operatorname{virt}} \right)\!. \end{align} $$
Proof. The morphism
![]() $\nu \colon \mathsf {K}(\mathcal {X})\to \mathcal {P}$
is obtained by taking relative coarse moduli spaces (see [Reference Abramovich and Vistoli5, §9] and [Reference Abramovich, Olsson and Vistoli4, Theorem 3.1]). For each i, the partial coarsening
$\nu \colon \mathsf {K}(\mathcal {X})\to \mathcal {P}$
is obtained by taking relative coarse moduli spaces (see [Reference Abramovich and Vistoli5, §9] and [Reference Abramovich, Olsson and Vistoli4, Theorem 3.1]). For each i, the partial coarsening
![]() $\mathcal {C} \to \mathcal {C}_i$
is initial among maps
$\mathcal {C} \to \mathcal {C}_i$
is initial among maps
![]() $\mathcal {C} \to \mathcal {Y}$
through which the map
$\mathcal {C} \to \mathcal {Y}$
through which the map
![]() $\mathcal {C} \to \mathcal {X}_i$
factors and is representable.
$\mathcal {C} \to \mathcal {X}_i$
factors and is representable.
We call a twisted curve an r-curve (for some positive integer r) if the order of every stabilizer group divides r. Since a stable map
![]() $\mathcal {C}_i \to \mathcal {X}_i$
must be representable, it follows that
$\mathcal {C}_i \to \mathcal {X}_i$
must be representable, it follows that
![]() $\mathcal {C}_i$
is an
$\mathcal {C}_i$
is an
![]() $r_i$
-curve.
$r_i$
-curve.
A point of the fiber product
![]() $\mathcal P$
consists of the data of two stable maps
$\mathcal P$
consists of the data of two stable maps
![]() $\mathcal {C}_1 \to \mathcal {X}_1$
and
$\mathcal {C}_1 \to \mathcal {X}_1$
and
![]() $\mathcal {C}_2 \to \mathcal {X}_2$
which induce the same underlying map
$\mathcal {C}_2 \to \mathcal {X}_2$
which induce the same underlying map
![]() $C \to X$
on coarse moduli.
$C \to X$
on coarse moduli.
Lemma 3.2. Suppose that
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are coprime, and let
$r_2$
are coprime, and let
![]() $\mathcal {C}_1,\mathcal {C}_2$
be
$\mathcal {C}_1,\mathcal {C}_2$
be
![]() $r_1$
-,
$r_1$
-,
![]() $r_2$
-curves with the same coarse curve C. Then the normalisation
$r_2$
-curves with the same coarse curve C. Then the normalisation
is a twisted curve.
Proof. If
![]() $p \in C$
is a marking on the coarse curve with local equation z, then the local model for each
$p \in C$
is a marking on the coarse curve with local equation z, then the local model for each
![]() $\mathcal {C}_i$
is given by
$\mathcal {C}_i$
is given by
The fiber product is therefore
![]() $\left [\left (x_1^{r_1}=x_2^{r_2}\right )/\mu _{r_1r_2}\right ]$
. Note that this is not a twisted curve (unless
$\left [\left (x_1^{r_1}=x_2^{r_2}\right )/\mu _{r_1r_2}\right ]$
. Note that this is not a twisted curve (unless
![]() $r_1=1$
or
$r_1=1$
or
![]() $r_2=1$
). On the other hand, since
$r_2=1$
). On the other hand, since
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are coprime, the normalization of the fiber product is given by
$r_2$
are coprime, the normalization of the fiber product is given by
 $$\begin{align*}\left[\mathbb A^1_y/\mu_{r_1r_2}\right], \end{align*}$$
$$\begin{align*}\left[\mathbb A^1_y/\mu_{r_1r_2}\right], \end{align*}$$
where
![]() $y^{r_1}=x_2,y^{r_2}=x_1$
. The computation around a node is entirely analogous except that the base must also be normalized, around the divisor where the node persists.
$y^{r_1}=x_2,y^{r_2}=x_1$
. The computation around a node is entirely analogous except that the base must also be normalized, around the divisor where the node persists.
Remark 3.3. This phenomenon is related to the issue of saturation in logarithmic geometry, via the correspondence between twisted curves and extensions of logarithmic structures [Reference Olsson24]. Indeed, the monoid
![]() $\mathbb {N} e_1 \oplus _{r_1,\mathbb {N},r_2}\mathbb {N} e_2$
is not saturated: in the groupification
$\mathbb {N} e_1 \oplus _{r_1,\mathbb {N},r_2}\mathbb {N} e_2$
is not saturated: in the groupification
![]() $\mathbb {Z}^2/(r_1,-r_2)\cong \mathbb {Z}$
, the image of the generator
$\mathbb {Z}^2/(r_1,-r_2)\cong \mathbb {Z}$
, the image of the generator
![]() $e_1$
is divisible by
$e_1$
is divisible by
![]() $r_2$
:
$r_2$
:
where
![]() $a_1,a_2 \in \mathbb {Z}$
are such that
$a_1,a_2 \in \mathbb {Z}$
are such that
![]() $a_1r_1+a_2r_2=1$
. Similarly the image of
$a_1r_1+a_2r_2=1$
. Similarly the image of
![]() $e_2$
is divisible by
$e_2$
is divisible by
![]() $r_1$
.
$r_1$
.
The twisted curve
![]() $\mathcal {C}$
carries a natural map to
$\mathcal {C}$
carries a natural map to
![]() $\mathcal {X}$
which is clearly representable. We thus have a Cartesian diagram
$\mathcal {X}$
which is clearly representable. We thus have a Cartesian diagram

where the bottom morphism is the normalization. The morphism
![]() $\varphi $
carries a natural perfect obstruction theory. We will now construct a compatible perfect obstruction theory for
$\varphi $
carries a natural perfect obstruction theory. We will now construct a compatible perfect obstruction theory for
![]() $\psi $
. The diagram
$\psi $
. The diagram

is Cartesian. Using the convexity assumption, there is a perfect obstruction theory for
![]() $\Delta $
given by
$\Delta $
given by
 $$ \begin{align} \left(\pi_{0\star}f_0^{\star}\mathrm{T}_X\right)^\vee[1], \end{align} $$
$$ \begin{align} \left(\pi_{0\star}f_0^{\star}\mathrm{T}_X\right)^\vee[1], \end{align} $$
where
![]() $\pi _0$
is the universal coarse curve. This pulls back to a perfect obstruction theory for
$\pi _0$
is the universal coarse curve. This pulls back to a perfect obstruction theory for
![]() $\mathcal {P} \to \mathsf {K}(\mathcal {X}_1)\times _{\mathfrak {M}} \mathsf {K}(\mathcal {X}_2)$
. The latter space carries a perfect obstruction theory over
$\mathcal {P} \to \mathsf {K}(\mathcal {X}_1)\times _{\mathfrak {M}} \mathsf {K}(\mathcal {X}_2)$
. The latter space carries a perfect obstruction theory over
![]() $\mathfrak {M}^{r_1-\operatorname {tw}}\times _{\mathfrak {M}}\mathfrak {M}^{r_2-\operatorname {tw}}$
given by
$\mathfrak {M}^{r_1-\operatorname {tw}}\times _{\mathfrak {M}}\mathfrak {M}^{r_2-\operatorname {tw}}$
given by
 $$ \begin{align} \left(\pi_{1\star}f_1^{\star}\mathrm{T}_{\mathcal{X}_1}\oplus\pi_{2\star}f_2^{\star}\mathrm{T}_{\mathcal{X}_2}\right)^\vee. \end{align} $$
$$ \begin{align} \left(\pi_{1\star}f_1^{\star}\mathrm{T}_{\mathcal{X}_1}\oplus\pi_{2\star}f_2^{\star}\mathrm{T}_{\mathcal{X}_2}\right)^\vee. \end{align} $$
We thus have a triangle with perfect obstruction theories

and wish to build an obstruction theory for
![]() $\psi $
giving a compatible triple. There are natural morphisms
$\psi $
giving a compatible triple. There are natural morphisms
![]() $\mathrm {T}_{\mathcal {X}_i} \to p_i^\star \mathrm {T}_X$
on
$\mathrm {T}_{\mathcal {X}_i} \to p_i^\star \mathrm {T}_X$
on
![]() $\mathcal {X}_i$
. We therefore obtain
$\mathcal {X}_i$
. We therefore obtain
(As in the proof of Theorem 2.1, this follows from the projection formula and the fact that the structure sheaves of the various universal curves are preserved by push-forwards along coarsening maps; see [Reference Abramovich, Olsson and Vistoli4, Theorem 3.1].) Dualizing, shifting, and taking the cone, we obtain
 $$\begin{align*}\left(\pi_{1\star}f_1^{\star}\mathrm{T}_{\mathcal{X}_1}\oplus\pi_{2\star}f_2^{\star}\mathrm{T}_{\mathcal{X}_2}\right)^\vee \to \mathbf{E}_\psi \to \left(\pi_{0\star} f_0^\star \mathrm{T}_X\right)^\vee[1] \xrightarrow{[1]}. \end{align*}$$
$$\begin{align*}\left(\pi_{1\star}f_1^{\star}\mathrm{T}_{\mathcal{X}_1}\oplus\pi_{2\star}f_2^{\star}\mathrm{T}_{\mathcal{X}_2}\right)^\vee \to \mathbf{E}_\psi \to \left(\pi_{0\star} f_0^\star \mathrm{T}_X\right)^\vee[1] \xrightarrow{[1]}. \end{align*}$$
Several applications of the Four Lemma then show that
![]() $\mathbf {E}_\psi $
is a relative perfect obstruction theory for
$\mathbf {E}_\psi $
is a relative perfect obstruction theory for
![]() $\psi $
.
$\psi $
.
Finally, we wish to compare the obstruction theories of
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
in diagram (10). For any root stack
$\varphi $
in diagram (10). For any root stack
![]() $\mathcal {Y}=Y_{D,r}$
with gerby divisor
$\mathcal {Y}=Y_{D,r}$
with gerby divisor
![]() $\mathcal {D}$
, a local computation gives the following exact sequence:
$\mathcal {D}$
, a local computation gives the following exact sequence:
From this we obtain a morphism of short exact sequences

and an application of the snake lemma produces the following exact sequence on
![]() $\mathcal {X}$
:
$\mathcal {X}$
:
Applying
![]() $\pi _\star f^\star $
, we see that the pullback of the perfect obstruction theory for
$\pi _\star f^\star $
, we see that the pullback of the perfect obstruction theory for
![]() $\psi $
coincides with the perfect obstruction theory for
$\psi $
coincides with the perfect obstruction theory for
![]() $\varphi $
in diagram (10). The theorem then follows by the commutativity of virtual pullback and push-forward [Reference Manolache19, Theorem 4.1], since the bottom horizontal arrow in diagram (10) is proper of degree
$\varphi $
in diagram (10). The theorem then follows by the commutativity of virtual pullback and push-forward [Reference Manolache19, Theorem 4.1], since the bottom horizontal arrow in diagram (10) is proper of degree
![]() $1$
.
$1$
.
3.3 Local-orbifold correspondence
With the relative product formula established, we can now give a straightforward proof of Theorem 2.1 in the convex setting.
Proof of Theorem 2.1 for convex targets. Consider again diagram (7). Theorem 3.1 gives the following relation in
![]() $\mathsf {K}(X)$
:
$\mathsf {K}(X)$
:
Specializing to the maximal contact setting, the result immediately follows from the local-orbifold correspondence for smooth divisors and the splitting of the obstruction bundle for the local theory of
![]() $\mathcal {O}_X(-D_1)\oplus \mathcal {O}_X(-D_2)$
.□
$\mathcal {O}_X(-D_1)\oplus \mathcal {O}_X(-D_2)$
.□
This result can be generalized to convex embeddings via virtual pullback methods. This is a fairly routine affair: see for instance [Reference Battistella and Nabijou6, Appendix A]. Since the arguments in §2 already establish the result in full generality, we omit the details here.
3.4 Comparison with naive invariants
Recall from [Reference Nabijou21, Reference Nabijou and Ranganathan22] that for a simple normal crossing pair
![]() $(X,D)$
with X convex, the naive virtual class is defined (in genus
$(X,D)$
with X convex, the naive virtual class is defined (in genus
![]() $0$
) as the product of logarithmic virtual classes
$0$
) as the product of logarithmic virtual classes
 $$\begin{align*}[\mathsf{N}(X\mid D)]^{\operatorname{virt}} := \prod_{i=1}^n (\rho_i)_\star [\mathsf{K}(X\mid D_i)]^{\operatorname{virt}} \end{align*}$$
$$\begin{align*}[\mathsf{N}(X\mid D)]^{\operatorname{virt}} := \prod_{i=1}^n (\rho_i)_\star [\mathsf{K}(X\mid D_i)]^{\operatorname{virt}} \end{align*}$$
inside
![]() $\mathsf {K}(X)$
. We also obtain a refined class on the fiber product
$\mathsf {K}(X)$
. We also obtain a refined class on the fiber product
![]() $\mathsf {N}(X\mid D)$
, but we are mostly interested in its push-forward to
$\mathsf {N}(X\mid D)$
, but we are mostly interested in its push-forward to
![]() $\mathsf {K}(X)$
. This definition extends to arbitrary convex embeddings via virtual pullback. An immediate consequence of Theorem 3.1 is an identification of orbifold and naive invariants.
$\mathsf {K}(X)$
. This definition extends to arbitrary convex embeddings via virtual pullback. An immediate consequence of Theorem 3.1 is an identification of orbifold and naive invariants.
Corollary 3.4. For
![]() $(X,D)$
a convex embedding, the relation
$(X,D)$
a convex embedding, the relation
 $$\begin{align*}\rho_\star\left[\mathsf{K}\left(X_{D,\vec{r}}\right)\right]^{\operatorname{virt}} = [\mathsf{N}(X\mid D)]^{\operatorname{virt}} \end{align*}$$
$$\begin{align*}\rho_\star\left[\mathsf{K}\left(X_{D,\vec{r}}\right)\right]^{\operatorname{virt}} = [\mathsf{N}(X\mid D)]^{\operatorname{virt}} \end{align*}$$
holds inside
![]() $\mathsf {K}(X)$
(for compatible choices of contact orders).
$\mathsf {K}(X)$
(for compatible choices of contact orders).
Given this, the (counter)examples presented in [Reference Nabijou and Ranganathan22, §1] and [Reference Nabijou21, §3.4] show that the orbifold invariants and logarithmic invariants differ in general, and that this defect is not restricted to the maximal contact setting.
The naive spaces provide an alternative perspective for probing the geography and invariants of the multiroot spaces. The iterated blowup construction of [Reference Nabijou and Ranganathan22] gives a method for comparing the logarithmic invariants to the naive/orbifold invariants; see also [Reference Ranganathan25, Reference Herr16] for treatments of related ideas.
Acknowledgments
We are grateful to Dhruv Ranganathan for conversations on related ideas, and comments on a draft manuscript. We also thank Michel van Garrel and Leo Herr for useful discussions. Finally we thank the referee for a thorough reading of the paper and many helpful comments.
The first author is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC-2181/1 - 390900948 (the Heidelberg STRUCTURES Cluster of Excellence). The second author is supported by the Herchel Smith Fund. The third author is supported in part by a Simons Foundation Collaboration Grant. The fourth author is supported by EPSRC grant EP/R013349/1.
Competing Interests
None.