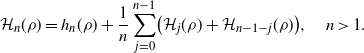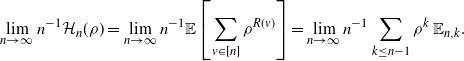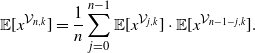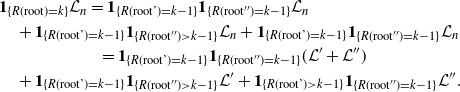In our paper ‘On a random search tree: asymptotic enumeration of vertices by distance from leaves’ (Adv. Appl. Prob. 49 (2017), 850–876), there are a number of typographical errors in mathematical expressions. These errors typically involve calligraphic letters. Below we have listed the correct expressions, with references to the places where the errors occurred in the original paper.
-
1. Page 854, displayed equation (2.4):
Same page, second displayed equation from the bottom: \begin{equation*}\mathcal H_n(\rho)=h_n(\rho)+\frac{1}{n}\sum_{j=0}^{n-1}\bigl(\mathcal H_j(\rho)+\mathcal H_{n-1-j}(\rho)\bigr),\quad n>1.\end{equation*}
\begin{equation*}\mathcal H_n(\rho)=h_n(\rho)+\frac{1}{n}\sum_{j=0}^{n-1}\bigl(\mathcal H_j(\rho)+\mathcal H_{n-1-j}(\rho)\bigr),\quad n>1.\end{equation*}
 \begin{equation*}\mathcal M_j(x):=\sum_{n\ge 1}\Bbb E[\mathcal X_{n,j}]\,x^n=\frac{2^j}{j!}\biggl(\log\frac{1}{1-x}\biggr)^j,\quad j>0.\end{equation*}
\begin{equation*}\mathcal M_j(x):=\sum_{n\ge 1}\Bbb E[\mathcal X_{n,j}]\,x^n=\frac{2^j}{j!}\biggl(\log\frac{1}{1-x}\biggr)^j,\quad j>0.\end{equation*}
-
2. Page 857, proof of Lemma 2.3, first displayed equation:
 \begin{equation*}\lim_{n\to\infty}n^{-1}\mathcal H_n(\rho)=\lim_{n\to\infty} n^{-1} \Bbb E\left[\sum_{v\in [n]}\rho^{R(v)}\right]=\lim_{n\to\infty}n^{-1}\sum_{k\le n-1}\rho^k\, \Bbb E_{n,k}.\end{equation*}
\begin{equation*}\lim_{n\to\infty}n^{-1}\mathcal H_n(\rho)=\lim_{n\to\infty} n^{-1} \Bbb E\left[\sum_{v\in [n]}\rho^{R(v)}\right]=\lim_{n\to\infty}n^{-1}\sum_{k\le n-1}\rho^k\, \Bbb E_{n,k}.\end{equation*}
-
3. Page 860, first displayed equation in proof of Lemma 2.4:
Displayed statement (2.15), last inequality: \begin{equation*}F(x,y)=\sum_{n\ge 0}y^n\Bbb E\left[x^{\mathcal V_{n,k}}\right],\quad \mathcal V_{0,k}:=0.\end{equation*}
\begin{equation*}F(x,y)=\sum_{n\ge 0}y^n\Bbb E\left[x^{\mathcal V_{n,k}}\right],\quad \mathcal V_{0,k}:=0.\end{equation*}
 $>0$
.
$>0$
.
Next displayed equation, last expectation:
 $\Bbb E[x^{\mathcal V_{n-1-j,k}}]$
.
$\Bbb E[x^{\mathcal V_{n-1-j,k}}]$
.Next line:
 $\mathcal V_{n,k}=0$
for
$\mathcal V_{n,k}=0$
for
 $n\le k$
,
$n\le k$
,
 $\mathcal V_{k+1,k}=1\ (\text{resp.\ } 0)$
with probability
$\mathcal V_{k+1,k}=1\ (\text{resp.\ } 0)$
with probability
 $2^k/(k+1)!$
(resp.
$2^k/(k+1)!$
(resp.
 $1-2^k/(k+1)!$
), and for
$1-2^k/(k+1)!$
), and for
 $n>k+1$
,
$n>k+1$
,
 \begin{equation*}\Bbb E[x^{\mathcal V_{n,k}}]=\frac{1}{n}\sum_{j=0}^{n-1} \Bbb E[x^{\mathcal V_{j,k}}]\cdot\Bbb E[x^{\mathcal V_{n-1-j,k}}].\end{equation*}
\begin{equation*}\Bbb E[x^{\mathcal V_{n,k}}]=\frac{1}{n}\sum_{j=0}^{n-1} \Bbb E[x^{\mathcal V_{j,k}}]\cdot\Bbb E[x^{\mathcal V_{n-1-j,k}}].\end{equation*}
-
4. Page 868, bottom line:
 $\mathcal B_k(x)=\mathcal B_{k-1}(x)-\mathcal B_{>k}(x)$
.
$\mathcal B_k(x)=\mathcal B_{k-1}(x)-\mathcal B_{>k}(x)$
. -
5. Page 869, Lemma 4.1 should read as follows:
Lemma 4.1 For all nonnegative integers k, the equalities
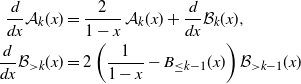 \begin{align*}\frac{d}{dx}\mathcal A_{k}(x)&=\frac{2}{1-x}\, \mathcal A_{k}(x)+\frac{d}{dx}\mathcal B_{k}(x),\\\frac{d}{dx}\mathcal B_{>k}(x)&=2\left(\frac{1}{1-x}-B_{\le k-1}(x)\right)\mathcal B_{>k-1}(x)\end{align*}
\begin{align*}\frac{d}{dx}\mathcal A_{k}(x)&=\frac{2}{1-x}\, \mathcal A_{k}(x)+\frac{d}{dx}\mathcal B_{k}(x),\\\frac{d}{dx}\mathcal B_{>k}(x)&=2\left(\frac{1}{1-x}-B_{\le k-1}(x)\right)\mathcal B_{>k-1}(x)\end{align*}
hold. Here
![]() $\{B_{\le t}(x)\}$
is the sequence determined by the recurrence (3.3),
$\{B_{\le t}(x)\}$
is the sequence determined by the recurrence (3.3),
![]() $B_{\le -1}(x):=0$
, and
$B_{\le -1}(x):=0$
, and
![]() $\mathcal B_{> -1}(x)=\mathcal B_{\ge 0}(x)$
is the generating function of the expected numbers of leaves, that is,
$\mathcal B_{> -1}(x)=\mathcal B_{\ge 0}(x)$
is the generating function of the expected numbers of leaves, that is,
Consequently
-
6. Page 870, second displayed equation from the top:
Proof of Lemma 4.2, first displayed equation: \begin{equation*}f_k=\lim_{x\uparrow 1}(1-x)^2\mathcal A_k(x)=\int_0^1(1-x)^2\frac{d}{dx}\mathcal B_k(x)\,dx=2\int_0^1(1-x)\mathcal B_k(x)\,dx.\end{equation*}
The next line should read as follows: ‘… to the expectation of
\begin{equation*}f_k=\lim_{x\uparrow 1}(1-x)^2\mathcal A_k(x)=\int_0^1(1-x)^2\frac{d}{dx}\mathcal B_k(x)\,dx=2\int_0^1(1-x)\mathcal B_k(x)\,dx.\end{equation*}
The next line should read as follows: ‘… to the expectation of \begin{align*}&\textbf{1}_{\{R(\text{root})=k\}}\mathcal L_n=\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}\mathcal L_n\\&\quad + \textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})>k-1\}}\mathcal L_n+\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}\mathcal L_n\\ &\qquad\qquad\qquad =\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}(\mathcal L'+\mathcal L^{\prime\prime})\\&\quad +\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})>k-1\}}\mathcal L'+\textbf{1}_{\{R(\text{root'})>k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}\mathcal L^{\prime\prime}.\end{align*}
\begin{align*}&\textbf{1}_{\{R(\text{root})=k\}}\mathcal L_n=\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}\mathcal L_n\\&\quad + \textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})>k-1\}}\mathcal L_n+\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}\mathcal L_n\\ &\qquad\qquad\qquad =\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}(\mathcal L'+\mathcal L^{\prime\prime})\\&\quad +\textbf{1}_{\{R(\text{root'})=k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})>k-1\}}\mathcal L'+\textbf{1}_{\{R(\text{root'})>k-1\}}\textbf{1}_{\{R(\text{root}^{\prime\prime})=k-1\}}\mathcal L^{\prime\prime}.\end{align*}
 $\textbf{1}_{\{R(root)=k\}}\mathcal L_n$
conditional on the event “the vertex set of T’ is a given set J of j elements from
$\textbf{1}_{\{R(root)=k\}}\mathcal L_n$
conditional on the event “the vertex set of T’ is a given set J of j elements from
 $[n]\setminus \text{root}$
” is….’ The bottom displayed equation should read as follows:
$[n]\setminus \text{root}$
” is….’ The bottom displayed equation should read as follows:
 \begin{equation*}\Bbb E[\textbf{1}_{\{R(\text{root)=k\}}}\mathcal L_n|J]=g_{j,k-1}p_{n-1-j,>k-1}+g_{n-1-j,>k-1} p_{j, \ge k-1}.\end{equation*}
\begin{equation*}\Bbb E[\textbf{1}_{\{R(\text{root)=k\}}}\mathcal L_n|J]=g_{j,k-1}p_{n-1-j,>k-1}+g_{n-1-j,>k-1} p_{j, \ge k-1}.\end{equation*}
-
7. Page 871, first displayed equation:
The first line of the proof of Theorem 4.1 should read as follows: ‘Consider \begin{equation*}g_{n,k}=\Bbb E[\textbf{1}_{\{R(\text{root})=k\}}\mathcal L_n]=\frac{1}{n}\sum_{j=0}^{n-1}g_{j,k-1} p_{n-1-j,\ge k-1},\end{equation*}
\begin{equation*}g_{n,k}=\Bbb E[\textbf{1}_{\{R(\text{root})=k\}}\mathcal L_n]=\frac{1}{n}\sum_{j=0}^{n-1}g_{j,k-1} p_{n-1-j,\ge k-1},\end{equation*}
 $\mathcal L_{n.k}/V_{n,k}$
, for instance.’
$\mathcal L_{n.k}/V_{n,k}$
, for instance.’
The third display in the proof of Theorem 4.1 should read as follows:
The last line of page 871 should read as follows: ‘… Therefore,
![]() $\mathcal L_{n,k}/V_{n,k}\to f_k/c_k$
….’
$\mathcal L_{n,k}/V_{n,k}\to f_k/c_k$
….’
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.