Growth of a viscoplastic blister underneath an elastic sheet

Abstract

Inspired by geological structures formed by magmatic intrusions that deform the Earth's crust, we investigate the elastohydrodynamic growth of a viscoplastic blister under an elastic sheet resting on a prewetted substrate. By combining experiments, scaling analysis and numerical simulations, we reveal new regimes for the elastoviscoplastic growth dynamics of the blister. The blister height and its apparent radius grow as $h(0,t) \sim t^{5/9}$ and $R(t) \sim t^{2/9}$ if the fluid pressure is set by bending of the sheet, and as $h(0,t) \sim t^{5/13}$ and $R(t) \sim t^{4/13}$ if the fluid pressure is set by stretching of the sheet. A plug-like flow inside the blister dictates its dynamics, whereas the blister takes a self-similar shape given by a balance of the fluid's yield stress and the pressure gradient induced by the deformation of the elastic sheet.

1. Introduction

The intrusion of a liquid underneath an elastic sheet resting on a non-deformable solid has been utilized as a generic model to understand the formation of geological structures such as magmatic sills and laccoliths (Pollard & Johnson 1973; Lister & Kerr 1991; Michaut 2011) and ice sheet relaxation (Lai et al. 2021). In models of e.g. sill and laccolith emplacement, the intruding magma is commonly assumed to be Newtonian, and the solid is assumed to deform by elastic bending and tensile fracturing. However, there is growing evidence that some magmas exhibit highly non-Newtonian behaviour (Balmforth et al. 2000; Caricchi et al. 2007; Cordonnier et al. 2012), such that the magma can transport as plug flow (Morgan et al. 2008). Moreover, rock layers along which magma is emplaced can also exhibit a complex viscoplastic rheological response to magma flow (Scheibert, Galland & Hafver 2017; Galland et al. 2019). To what extent these nonlinear phenomena affect the dynamics of these geophysical systems is still unclear. To model the complex dynamics in geophysical flow, we consider an elastic sheet separated from a rigid substrate by a prewetted layer of viscoplastic fluid, and study the formation of a blister formed as we inject the same viscoplastic fluid in between the elastic sheet and the rigid substrate (see the illustration in figure 1a).

Figure 1. (a) Schematic drawing of the studied system. An incompressible elastic sheet, of Young's modulus $E$, thickness $d$, and Poisson ratio $\nu$, rests on top of the prewetted layer with thickness $h_0$, of yield stress fluid made from a solution of Carbopol mixed with water. A solution of the same Carbopol–water mixture as that in the prewetted layer is injected at a constant flux $Q$ beneath the elastic sheet through a small tube of radius $r_t$. The resulting blister's height profile $h(r,t)$ is measured by tracking a laser line (on top of the sheet). (b) An illustration of the two-dimensional cross-section along the lasing line from the injection point to the edge of the sheet. We define the apparent radius $R(t)$ as the first radial coordinate where the blister height profile matches the prewetted layer thickness, $h(r=R(t),t) = h_0$. The region around this point is referred to as the intrusion tip. Note that the aspect ratio between the fluid depth $h(r,t)$ and the thickness of the elastic sheet $d$ is exaggerated for easier visualization of the intrusion.

Fluid models that account for viscoplasticity have provided a more realistic representation of mud, glacier and magma flows on the Earth's surface (Liu & Mei 1989; Balmforth et al. 2000; Petford 2003). Recently, viscoplastic fluids have also attracted interest in interfacial flows, where they were demonstrated to affect coating, drop spreading, bursting and coalescence (Smit et al. 2019; Jalaal, Stoeber & Balmforth 2021; Sanjay, Lohse & Jalaal 2021; Kern, Sæter & Carlson 2022). For an elastic sheet resting on a solid prewetted by a Newtonian fluid film, it has been shown that the growth dynamics when injecting the same fluid underneath the sheet is determined by a coupling between local effects at the intrusion tip (see figure 1b) and the quasi-static shape of the sheet (Lister, Peng & Neufeld 2013). The dynamic changes, e.g. if there is vapour at the intrusion tip (Wang & Detournay 2018), if there is dry adhesion between the elastic surface and the supporting solid (Hosoi & Mahadevan 2004; Ball & Neufeld 2018; Lister, Skinner & Large 2019), if gravitational effects dominate (Hewitt, Balmforth & De Bruyn 2015), if the ratio of the deformation and the prewetted film thickness changes (Pedersen et al. 2019), if the supporting solid is porous (Chase, Lai & Stone 2021; Lai et al. 2021), or in the case of the effect from thermal fluctuations at small scales (Carlson 2018). The influence of a deformable elastic sheet on the resulting flow has also been demonstrated in the presence of an interface, resulting in e.g. the suppression of viscous fingering in a Hele-Shaw geometry (Pihler-Puzović et al. 2018). This paper looks at another elastohydrodynamic phenomenon, where a working fluid is viscoplastic. Large stresses near the solid surfaces and at the intrusion tip can fluidize the material locally, while the bulk of the viscoplastic liquid forming the blister may remain in a solid-like state. In this paper, we show that having yielded and unyielded regions of the viscoplastic fluid generates growth dynamics distinct from the case of Newtonian fluids.

2. Experimental set-up

Our experiments adapted the design and measurement technique from previous Newtonian elastohydrodynamics studies (Lister et al. 2013; Berhanu et al. 2019). A schematic representation of the experimental system is shown in figure 1(a). An elastic sheet is placed atop a substrate prewetted with a thin film of Carbopol–water mixtures, which have well-characterized rheological properties and minor thixotropic effects (Coussot 2014). A thin elastic sheet covers the Plexiglas plate underneath the liquid film. The dynamics are generated by an influx of the same viscoplastic fluid used to prewet the substrate through an inlet at the centre of the elastic sheet. The sides of the elastic sheets facing the fluid are rough, as Carbopol is known to have significant slip effects on several smooth surfaces (Jalaal, Balmforth & Stoeber 2015).

To avoid clumping, Carbopol 940 (CAS. 9003-01-4) was briefly mixed in deionized water using a Silverson L5M high shear laboratory mixer set to between 300 and 1000 revolutions per minute until the polymer dissolved. 1M NaOH was added to the dissolved solution in an 8 : 1 wt:wt% ratio of 1M NaOH:Carbopol 940. The solution was then gently mixed mechanically using a Kenwood Chef XL Titanium mixer for approximately 10 days. The amount of dissolved Carbopol was controlled to vary the yield stress, and ranged from $0.8\ {\rm g}\ {\rm l}^{-1}$ to $2\ {\rm g}\ {\rm l}^{-1}$, resulting in yield stresses $\tau _0=3.9, 11.3, 31.7, 47.3$ Pa. The Carbopol solutions were characterized using an Anton Paar Rheometer 702 with the striated parallel plate geometry (PP50/P2) to prevent slip. The surface roughness amplitude for the striated plate from Anton Paar was $500 \ \mathrm {\mu }{\rm m}$, with wavelength $1$ mm. Before each measurement, a pre-shear step was included to break and reheal the material's microstructure (Medhi et al. 2020). In figure 2(a), we have plotted the shear stress $\tau _0$ versus the shear rate $\dot {\gamma }$, and fitted the curves with the Herschel–Bulkley model, $\tau = \tau _0 + K \dot {\gamma }^n$. The results of this fit in terms of the yield stress $\tau _0$, consistency index $K$ and flow index $n$ are listed in table 2. Figure 2(b) shows the viscosity curves as a function of the shear rate for the different samples.

Figure 2. (a) Experimental curves (markers) for $\tau$ versus $\dot {\gamma }$, with a Herschel–Bulkley model (line) fitted with the values listed in table 1. (b) Plot of the viscosity $\mu$ versus $\dot {\gamma }$. (c,d) Corresponding measurements of the two highest yield stress fluids, but with smooth and rough walls of elite double (ED) instead of the striated plate geometry.

The prewetted layer was made by pouring the desired amount of Carbopol–water mixture over a surface area corresponding to the area of the elastic sheet, placing the sheet on top of this layer, and then covering it with a rigid plate with uniformly distributed weight $70$ kg for ${\approx }1$ h. Afterwards, excess fluid was removed at the edge of the sheet, and the system was weighed to obtain the deposited Carbopol mass, allowing us to calculate the prewetted film height. The height of the prewetted layer of the Carbopol–water mixture was $h_0 \approx 0.2$ mm in experiments with the two lowest yield stress samples, and $h_0 \approx 0.2\unicode{x2013}0.4$ mm in experiments with the two fluids with the highest yield stress. However, the results were insensitive to the precise value within this range of $h_0$ values.

The elastic sheets were moulded on a coated rough wood plate (Huntonit Classique 1220 HV, product number 231001) using a silicone-based elastomer (Zhermack, Elite Double (ED)), thus ensuring roughness on one side of the sheets. Profilometry measurements of the rough surface were performed on an S Neox optical profiler controlled with the SensoSCAN 6.7 software (Sensofar, Barcelona, Spain). Samples were scanned in confocal mode with white, green, red and blue light with an EPI $20\times$ objective with lateral resolution $0.4 \mathrm {\mu }{\rm m}$. All images were levelled by the least squares method and had filled-in non-measured points (${<}5\,\%$) before analysis. The surface parameters were obtained from image analysis, and all image processing was done using SensoMap Standard 7.4 (Sensofar, Digital Surf's Mountains Technology$\circledR$, Spain). Different roughness parameters measured by the profilometer can be found in table 2. In addition to the elastic sheet on top, made of ED 8, a very thin rough elastic sheet made of ED 32 with thickness $d = 1.7\ \textrm {mm} \pm 0.1\ \textrm {mm}$ was used to cover the Plexiglas plate underneath the prewetted Carbopol layer, to prevent slip at both surfaces. Strong adhesion forces between the Plexiglas and ED 32 render this layer immobile during the experiments. For ED 8, $E = 0.25\ \textrm {MPa}$, and for ED 32, $E = 1.2\ \textrm {MPa}$; both have a Poisson ratio $\nu \approx 0.5$ (Coulais et al. 2015). To study different deformation regimes, two versions of the top sheet of ED 8 were made, with thicknesses $d = 9.5\ {\rm mm} \pm 0.5\ {\rm mm}$ (diameter $D=600$ mm) and $d = 1.5\ {\rm mm} \pm 0.1\ {\rm mm}$ ($D= 400$ mm), resulting in a bending modulus of the sheets $B = {Ed^3}/{12(1-\nu ^2)}= 0.024$ N m and $B= 9.4 \times 10^{-7}$ N m, respectively. In addition, to ensure our roughened elastomer minimized slip, similar measurements of the Carbopol properties as with the striated plates were carried out, but with small circular samples of the elastic sheets as bounding walls. Rough and smooth elastomer layers were tested to characterize how the surface roughness affected the measurements. In figures 2(c) and 2(d), the corresponding curves for the measured shear stress and viscosity versus the shear rate are plotted for Carbopol samples of the highest yield stresses with both smooth and rough ED surfaces. Figures 2(c) and 2(d) measurements suggest that the surface roughness reduces slip effects significantly. However, even with the rough surface configuration, the measured yield stress still deviates from the measurement on the striated plates. We note, however, that the form of the two curves is similar. The discrepancy can be caused by a slip or the custom-built set-up, e.g. a slight non-uniformity in the thickness of the ED samples. To quantify the effects of slip in our experiment, we compare experimental values using rough or smooth sides of the sheets in § 5.2. Otherwise, rough boundaries apply to the results reported.

Table 1. Values for $\tau _0$, $K$ and $n$ after fitting the sample measurements from figure 2(a) with the Herschel–Bulkley model.

Table 2. Different roughness parameters measured by the profilometer. Here, we present the mean, standard deviation (SD) and median values for five different measurements of different samples. Amplitude parameters ($S_a$, $S_q$, $S_z$, $S_{sk}$ and $S_{ku}$) were calculated with advanced software (SensoMap Plus 4.1, Sensofar, Terrassa, Spain). Here, $S_a$ is the average height deviation from the mean plan, $S_q$ is the root mean square value of ordinate values within the defined area, $S_z$ is defined as the sum of the largest peak height value and the largest pit depth value within the defined area, $S_{sk}$ is the surface skewness, and $S_{ku}$ is the surface kurtosis.

Our experiment is conducted by injecting the Carbopol–water mixture through a tube with radius $r_t = 2$ mm, at the centre of the plate at a controlled flux $Q=1.7,3.3,6.7\times 10^{-7}\ {\rm m}^3\ {\rm s}^{-1}$, using two Merck-Millipore-Sigma syringe pumps, injecting a total volume of approximately $180\ {\rm ml}$. A laser line is used to visualize the sheet's deflection $h(r,t)$ as the blister grows in time and space, and we track the profile with a digital camera, imaging with angle $17^{\circ }$ relative to the horizontal plane. The experimental interface profiles are obtained by fitting a Gaussian distribution to the colour intensity along each column of pixels and extracting the mean vertical coordinate. We define the height at the centre of the blister, $h(0,t)$, as the maximum deformation of the profile, and the apparent spreading radius $R(t)$ as described in figure 1(b). For each set of parameters, two experiments were carried out to demonstrate the reproducibility of the results. The error bars correspond to the standard deviation of measurements with the same parameter settings.

3. Theoretical framework

3.1. Mathematical model

To give a theoretical description of the elastohydrodynamics of the viscoplastic intrusion, we assume a small aspect ratio, viscous flow and axial symmetry around the injection point, allowing us to adopt the lubrication theory. To capture the principal viscoplastic effect, we use the Bingham model, which can be combined with the integrated lubrication equations to derive an expression for the vertical yielding line $Y(r,t)$ of the fluid, where the shear stress $|\tau _{rz}|$ equals the yield stress $\tau _0$ (Liu & Mei 1989; Balmforth et al. 2000, 2006):

(3.1)\begin{equation} Y(r,t) = \max \left(0,\frac{h(r,t)}{2} - \frac{\tau_0}{\left|\dfrac{\partial p(r,t)}{\partial r} \right|}\right). \end{equation}

Since we have two solid surfaces, we expect the shear profile $|\tau _{rz}|$ to be symmetric, so it will have another corresponding yielding position along $z(r,t)= h(r,t)-Y(r,t)$. We have a plug flow between the two yielding lines that flows with a constant speed and zero shear rate (Balmforth & Craster 1999). We follow the standard procedure to derive the thin film equation, where the additional term $Y(r,t)$ appears from employing the Bingham model for $|\tau _{rz}| >\tau _0$ (Liu & Mei 1989; Oron, Davis & Bankoff 1997; Balmforth et al. 2000, 2006):

(3.2)\begin{gather} \frac{\partial h(r,t)}{\partial t} = \frac{1}{6\mu r}\,\frac{\partial}{\partial r}\left(r\,Y(r,t)^2(3h(r,t)-2Y(r,t))\,\frac{\partial p(r,t)}{\partial r} \right)+w(r), \end{gather}

(3.3)\begin{gather}p(r,t) = B\,\nabla^4 h(r,t) + \rho g \left(h(r,t)-z\right). \end{gather}

Here, we have introduced $w(r) = ({2Q}/{{\rm \pi} r_t^2})(1- ({r}/{r_t})^2)$ for $r\leq r_t$, which is the Poiseuille flow through the tube with radius $r_t$, allowing us to prescribe the influx $Q$. Note that a no-slip condition has been applied at both solid surfaces, and that $\mu$ is the effective fluid viscosity. The pressure $p(r,t)$ consists of two terms, with the first term representing the elastic bending (Landau et al. 1986), where $\nabla ^4$ is the bi-Laplacian operator in cylindrical coordinates. The second term is the hydrostatic pressure with $g$ the gravitational acceleration and $\rho$ the density of the Carbopol solution, set equal to the water density. Note that the Föppl–von Kármán equations describe the effect of elastic stretching of the sheet, discussed further in § 4.2, but not considered in the numerical simulations of (3.2).

Equation (3.2) has two particularly interesting limits. If $Y(r,t)=h(r,t)/2$, then Newtonian flow is recovered, and the blister grows with a height $\sim t^{8/22}$ (Lister et al. 2013). As $Y(r,t)\rightarrow 0$, we expect a plug flow to form and the flow to be dominated by the effects of $\tau _0$.

3.2. Numerical simulations

The experiments are complemented by numerical solutions of the axisymmetric non-dimensional version of (3.2). The equation is discretized by linear finite elements and an implicit time marching method (Pedersen et al. 2019). We make (3.1) and (3.2) non-dimensional by scaling $h(r,t)$ and $r$ with length scale $L = ({B}/{\tau _0})^{1/3}$, and time $t$ with time scale $T = {B}/{Q\tau _0}$, giving a non-dimensional number $\varPi _1 = {B}/{6\mu Q}$ in front of the first term on the right-hand side of (3.2), which describes the ratio between elastic and viscous forces. In the simulation that includes gravity, we get another non-dimensional number in front of the hydrostatic pressure term, $\varPi _2 = {\rho g B^{1/3}}/{\tau _0^{4/3}}$, representing the ratio between elasto-gravity and the yield stress. We assume that the shear rate will set the effective viscosity in our experiments in the regions where the fluid is yielded, determining the viscous time scale. We estimate the effective viscosity by assuming a parabolic velocity profile for $z > h(r,t) - Y(r,t)$ and $z< Y(r,t)$, and obtain $\dot {\gamma }_{max} \approx ({\partial u}/{\partial z})|_{z=0, z = h} \sim {Q}/{R(t)\,Y(r,t)^2}$. Setting $Q\approx 10^{-7}\ {\rm m}^3\ {\rm s}^{-1}$, $R(t)\approx 10^{-1}\ {\rm m}$ and $Y(r,t)\approx 10^{-4}\ {\rm m}$ gives $\dot {\gamma }_{max} \approx 100 \ {\rm s}^{{-1}}$. This is a conservative estimate for the shear rate, and we therefore assume $\dot {\gamma }\approx 10\unicode{x2013}100\ {\rm s}^{{-1}}$ in the experiments. From the rheological viscosity curves in figure 2, we can then estimate the effective viscosity $\mu \approx 0.1\unicode{x2013}10\ {\rm Pa}\ {\rm s}$, which translates to $\varPi _1\approx 10^2\unicode{x2013}10^4$. We use an adaptive time-stepping routine with a time step limit $\Delta t/T = 9\times 10^{-6}$, and discretization in space $\Delta r/L \in [0.00025\unicode{x2013}0.015]$. We have defined

(3.4)\begin{equation} Y(r,t)=\max\left(\epsilon,h(r,t)/2-\frac{1}{\left|\dfrac{\partial}{\partial r} \nabla^4h(r,t)\right|}\right), \end{equation}

with a regularization parameter $\epsilon = 10^{-6}$ similar to that of Jalaal et al. (2021). We tested that the results are unaffected by this choice of $\epsilon$. The simulations are started with $Y(r,t)=h(r,t)/2$, and the plug flow is introduced gradually until $t/T = 10^{-4}$. We initialize the profile with the shape known from the Newtonian case (Lister et al. 2013), taking the form of a small bump,

(3.5)\begin{equation} \frac{h(r,t = 0)}{L} = \frac{h_0}{L}\left(1-\left(\frac{4r}{L}\right)^2\right)^2\quad {\rm for}\ r/L\leq 1/4, \end{equation}

on top of a prewetted layer $h_0/L =0.007$. As boundary conditions, we set the first three odd derivatives of $h(r,t)$ to vanish at the axis of symmetry,

(3.6)\begin{equation} \frac{\partial h(r=0,t)}{\partial r}=\frac{\partial^3 h(r=0,t)}{\partial r^3}=\frac{\partial^5 h(r=0,t)}{\partial r^5}=0, \end{equation}

and at the edge of the domain,

(3.7)\begin{equation} \frac{\partial h(r=3L,t)}{\partial r}=\frac{\partial^3 h(r=3L,t)}{\partial r^3}=\frac{\partial^5 h(r=3L,t)}{\partial r^5}=0. \end{equation}

Note that in all simulations, the domain's boundary is far from the apparent spreading radius and does not affect the blister dynamics, nor does the choice of the boundary conditions at the edge (as long as they are also satisfied by the initial profile).

4. Scaling analysis

We investigate the dynamics when we have a balance between the driving pressure gradient and the opposing fluid's yield stress force, such that $Y \to 0$ in (3.1). We follow Balmforth et al. (2000), who looked at the gravitational spreading of a viscoplastic dome. An assumption of a quasi-static equilibrium between the hydrostatic pressure gradient and the resisting yield stress leads to Nye's asymptotic solution (Nye 1952), and gravity-driven viscoplastic spreading of the dome: $h(0,t)\sim t^{1/5}$ and $R(t) \sim t^{2/5}$. New scaling laws are described below for the cases when bending or tension in the elastic sheet sets the fluid pressure of the viscoplastic blister.

4.1. Elastic bending regime

We describe the regime where the pressure is dominated by elastic bending, giving $p(r,t) \sim B\,\nabla ^4h(r,t)$. If we scale the height $h(r,t)$ with $h(0,t)$, and the radial direction $r$ with $R(t)$, while assuming unidirectional flow from $r=0$ and outwards in the limit $Y(r,t)\rightarrow 0$, then (3.1) gives ${\partial p(r,t)}/{\partial r} \sim {B\,h(0,t)}/{R(t)^5}\sim 2\tau _0/h(0,t)$. We impose conservation of mass, where the volume $V= \int _0^{R(t)}2{\rm \pi} \, h(r,t)\,r \,{\rm d}r\sim h(0,t)\,R(t)^2 \sim Qt$ is implicit in (3.2). Together, this gives the scaling laws for the blister height $h(0,t)$ and radius $R(t)$:

(4.1)\begin{gather} h(0,t) \sim \left(\frac{4\tau_0^2Q^5}{B^2}\right)^{1/9}t^{5/9} \sim LT^{{-}5/9}t^{5/9}, \end{gather}

(4.2)\begin{gather}R(t) \sim \left(\frac{Q^2B}{2\tau_0}\right)^{1/9}t^{2/9} \sim L T^{{-}2/9}t^{2/9}. \end{gather}

The length scale $L = ({B}/{\tau _0})^{1/3}$ and time scale $T = {B}/{Q\tau _0}$ appear in (4.1) and (4.2), which characterize our system.

In the limit $Y(r,t)\rightarrow 0$, (3.1) reduces to a nonlinear ordinary differential equation (ODE)

(4.3)\begin{align} -\frac{{\rm d}^5 {h}(r)}{{\rm d} r^5} - \frac{2}{r}\,\frac{{\rm d}^4 {h}(r)}{{\rm d} r^4} + \frac{3}{r^2}\,\frac{{\rm d}^3 {h}(r)}{{\rm d} r^3}- \frac{3}{r^3}\,\frac{{\rm d}^2 {h}(r)}{{\rm d} r^2}+\frac{3}{r^4}\,\frac{{\rm d} {h}(r)}{{\rm d} r} = \frac{2 \tau_0}{B\,{h}(r)} \operatorname{sign}({h}(r)-h_{0}), \end{align}

and the height prediction becomes independent of time, i.e. $h(r,t) \to h(r)$. By scaling $h(r)$ and $r$ with $L$, (4.3) becomes parameter-free. Solving this (4.3) for $h(r)$ should therefore yield the same universal shape as obtained when scaling the blister profile with the predicted scaling laws given by (4.1) and (4.2).

From Jalaal et al. (2021), it follows that the sign of the pressure gradient must correspond to the sign of $(h_{0}-h)$. To regularize the step function, we replace it with $\tanh (\varTheta (h_0-h))$ and solve the ODE numerically using $\varTheta = 10^{10}$, which is large enough for the solution to be insensitive to this parameter. We aid the numerical solver by starting with a guess based on a numerical profile from our numerical solution of (3.2). Five boundary conditions are needed to define our problem. We choose three conditions at the centreline, where we pin the height to the maximum height of the simulation profile $h_{max}$, i.e. ${h(0)} = h_{max}$, and set the odd derivatives ${\partial {h}(0)}/{\partial r} = 0$ and ${\partial ^3 {h}(0)}/{\partial r^3} = 0$ at the symmetry axis. Defining $\tilde {R}$ as the radial coordinate corresponding to the minimum value $h_{min}$ of the numerical blister profile $h(r,t)$, we apply the additional two boundary conditions $h(\tilde {R}) = h_{min}$ and ${\partial {h}(\tilde {R})}/{\partial r} = 0$. We solve (4.3) with the solver Solve_bvp retrieved from the scipy package in Python.

4.2. Elastic stretching regime

In order to predict how stretching of the sheet links to fluid pressure, we must consider the Föppl–von Kármán equations for the deformation of an axisymmetric sheet (Landau et al. 1986; Lister et al. 2013; Peng et al. 2015; Pihler-Puzović et al. 2015):

(4.4)\begin{gather} B\,\nabla^4 h(r,t) - \boldsymbol{\nabla}\boldsymbol{\cdot} \left(\varLambda(r,t)\,\boldsymbol{\nabla} h(r,t)\right) = p(r,t), \end{gather}

(4.5)\begin{gather}\frac{1}{r}\,\frac{\partial}{\partial r}\left(r^3\,\frac{\partial \varLambda(r,t)}{\partial r}\right) + \frac{Ed}{2}\left(\frac{\partial h(r,t)}{\partial r}\right)^2 = 0. \end{gather}

Here, $\varLambda (r,t) = {\rm d} \sigma _{rr}$ is the tension in the sheet, where $\sigma$ is the Cauchy stress tensor, and the subscript refers to the radial stress component in the sheet. Equation (4.4) is the momentum balance on the elastic sheet and couples the vertical sheet deflection to the pressure exerted by the fluid, $p(r,t)$. The second equation (4.5) describes the force balance along the radial direction of the sheet and is used to obtain the tension $\varLambda (r,t)$. If we consider intrusion processes where $h(0,t) \gg d$, then the term $p(r,t) \sim ({1}/{r})({\partial }/{\partial r})(r\,\varLambda (r,t)\, {\partial h(r,t)}/{\partial r})$ dominates the pressure. By scaling the pressure gradient with the tension from elastic stretching of the sheet, (3.1) in the limit $Y \to 0$ now gives ${\partial p(r,t)}/{\partial r} \sim {\varLambda (r,t)\, h(0,t)}/{R(t)^3}\sim 2\tau _0/h(0,t)$. From (4.5), we obtain a scaling for the tension in the sheet, $\varLambda (r,t) \sim {Ed}/{2} ({h(0,t)}/{R(t)})^2$. Combining this with conservation of the blister's mass, the regime governed by the balance between the stretching of the elastic sheet and the opposing yield stress reads

(4.6)\begin{gather} h(0,t) \sim \left(\frac{16 \tau_0^2 Q^5}{\left(Ed\right)^2}\right)^{1/13}t^{5/13}\sim L_{\varLambda}T_{\varLambda}^{{-}5/13}t^{5/13}, \end{gather}

(4.7)\begin{gather}R(t) \sim \left(\frac{Ed Q^4}{4 \tau_0}\right)^{1/13}t^{4/13}\sim L_{\varLambda}T_{\varLambda}^{{-}4/13}t^{4/13}. \end{gather}

This scaling yields new length and time scales $L_{\varLambda } = {Ed}/{\tau _0}$ and $T_{\varLambda } = {(Ed)^3}/{\tau _0^3 Q}$ . In the limit as $Y \to 0$, (3.1) becomes

(4.8)\begin{equation} \frac{{\rm d}}{{\rm d}r}\left(\frac{1}{r}\,\frac{{\rm d}}{{\rm d}r}\left (r\,\varLambda(r)\,\frac{{\rm d}h}{{\rm d}r}\right)\right) = \frac{2 \tau_0}{{h}(r)} \operatorname{sign}({h}(r)-h_{0}). \end{equation}

In the case when the stretching of the sheet is isotropic, the equation takes the form similar to an arrested viscoplastic droplet (Jalaal et al. 2021), with $\varLambda$ then interpreted as the surface tension coefficient.

5. Results

5.1. Elastic bending

We use the blister's maximal height $h(0,t)$ as a metric to test the predictions from (4.1) and (4.2). In these experiments, we use the thick membrane ($d=9.5$ mm) with bending stiffness $B = 0.024$ N m. Thus we can consider small deformations compared with the sheet thickness ($h(0,t) \leq d$), similar to those estimated in natural sills and laccoliths (e.g. Castro et al. 2016; Magee et al. 2016), and we expect the elastic bending pressure to dominate the tension in the sheet. The spatiotemporal growths of the blister for two Carbopol solutions, $\tau _0=3.9$ Pa and $47.3$ Pa, are shown in figure 3(a). A distinct effect of $\tau _0$ on the growth of the blister's apparent radius $R(t)$ and its height at the centre $h(0,t)$ is observed.

Figure 3. (a) Experimental profiles $h(r,t)$ of the elastic sheet at $t= 100, 200, 300$ s when injecting a fluid with low ($\tau _0=3.9\ {\rm Pa}$) and high ($\tau _0=47.3\ {\rm Pa}$) yield stresses between the rough surfaces. (b) Plots of the experimental results with the rough surfaces for the blister height $h(0,t)-h_0$ for different yield stresses $\tau _0$ and fluxes $Q$. (c) Results from (b) scaled by the length $L = ({B}/{\tau _0})^{1/3}$ and the time $T = {B}/{Q\tau _0}$ while comparing with the numerical simulations of the non-dimensional version of (3.2). The black dash-dotted line shows the derived scaling law of (4.1), where we have determined $\alpha$ = 0.35.

To explore further the effects of the yield stress and the influx on the dynamics, we vary these parameters systematically while keeping the bending stiffness fixed. Figure 3(b) shows how $h(0,t)$ is affected by $\tau _0$ and $Q$. To see these effects clearly, the experimental data can be rescaled by $h(0,t)/L$ and $t/T$, as shown in figure 3(c). By scaling the data in figure 3(b), we notice that it collapses onto a single curve in figure 3(c), which has a slope in agreement with the proposed scaling law of (4.1).

The results of the numerical simulations based on (3.2) and (3.3) are plotted together with the experimental data in figure 3(c). These results show how the blistering growth is relatively insensitive to the non-dimensional numbers $\varPi _1$ and $\varPi _2$, and recover the scaling law from (4.1). The time shift separating the experiments and the simulations (a factor of $1.33$ in time) can be caused by a combination of small slip effects, the simplified influx condition, or the minimal rheological model that we use to describe the Carbopol solutions (Coussot 2014). As shown in figure 2, the Carbopol solutions are shear-thinning fluids, and our samples are well fitted with a Herschel–Bulkley model using $n\approx 0.4$. In our mathematical model, we neglect this shear-thinning effect, assuming the viscosity to be constant, which serves as a source for error.

Next, we check if the interfacial dynamics of the blister adopts a self-similar shape by using the predicted scaling laws (4.2) and (4.1) to rescale the height profiles. Figures 4(a)–4(d) show the experimental blister's evolution in time for four experiments when injecting fluids of different yield stress. In figures 4(e)–4(h), we scale $h(r,t)/h(0,t)$ with $h(0,t)$ as predicted by (4.1), and $r/R(t)$ with $R(t)$ given by (4.2). It is clear from scaling the experimental blister profiles that they collapse onto what appears to be a universal shape that becomes increasingly apparent as $\tau _0$ increases.

Figure 4. (a–d) Plots of four experimental blister profiles from $t = 136$ s to $t = 376$ s, with time interval $80$ s between each profile, for the different yield stress values with rough surfaces. (e–h) Experimental profiles collapsed into a self-similar shape scaling, with the time $T$ and length $L$ from (4.1) and (4.2).

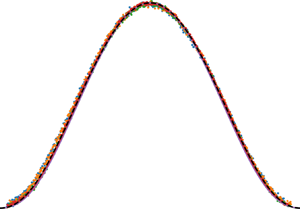
In figure 5(a), we show two numerical profiles at different time instants, and their corresponding yielding lines (dashed lines) from (3.1). A significant part of the fluid volume is between the yielding lines and moves as a plug flow, while the yielded flow with a viscous gradient is limited to narrow regions. For a shear-thinning fluid, the viscosity and the resistance to the flow will decrease in the small pockets close to the boundaries because of the high shear rate. Therefore, including shear-thinning effects in the viscosity could facilitate more fluid flowing radially inside the blister, leading to an even closer agreement with the experiments. We note that despite the simplification in the mathematical model, the simulations capture the elastohydrodynamic growth of the blister well, and the results show consistency concerning the scaling laws from (4.1) and (4.2), and the proposed physical picture based on a plug flow. In figure 5(b), we collapse nine numerical profiles in between these two time instants ($t/T=0.12\unicode{x2013}0.3$) onto the universal shape by scaling the height profiles and the radial coordinate with (4.1) and (4.2), respectively. Apparent time independence of the shape is demonstrated. Furthermore, as shown in figure 5(c), the blister shape predicted by (4.3) is in excellent agreement with the profiles from experiments and the numerical model, normalized with

(5.1a,b)\begin{equation} h_{max} = \frac{(h(0,t)-h_0)T^{5/9}}{Lt^{5/9}}\quad {\rm and}\quad r_{max} =\frac{R(t)\,T^{2/9}}{Lt^{2/9}}. \end{equation}

This suggests that the blister attains the self-similar shape.

Figure 5. (a) Blister profiles extracted from the numerical simulations based on the non-dimensional version of (3.2) with $\varPi _1 = 1000$. Dashed lines for each profile represent the corresponding non-dimensional yield limits $Y(r,t)/L$ and $(h(r,t)-Y(r,t))/L$; plug flow occurs in between the yield lines. (b) Two profiles from (a) collapsed together with nine profiles in between $t/T = 0.12$ and $t/T = 0.3$ by scaling with the time dependence of (4.1) and (4.2), which reveals the time-independent shape. (c) Normalization of our experimental and numerical similarity profiles from figures 4(h) and 5(b) (11 profiles for $t/T\in [0.12\unicode{x2013}0.3]$) by using $h_{max} = (h(0,t)-h_0)T^{5/9}/Lt^{5/9}$ and $r_{max} =R(t)\,T^{2/9}/Lt^{2/9}$, where $L = ({B}/{\tau _0})^{1/3}$ and $T = {B}/{Q\tau _0}$. The self-similar shape is described by the solution of the non-dimensional form of (4.3).

5.2. Elastic bending: slip effect

To address the effect of slip in our experiment, we made a set of experiments with Carbopol–water mixtures of the lowest and highest yield stress on both rough and smooth surfaces, with $B = 0.024\ \textrm {N} \textrm {m}$ of the overlying elastic sheet, and $Q=3.3 \times 10^{-7} \textrm {m}^3\ \textrm {s}^{-1}$. In figure 6(a), we show the results from these experiments in terms of $h(0,t)$ versus time, demonstrating that preventing slip by introducing a rough surface causes a significant increase in the maximum deformation for the high yield stress fluid. Slip decreases the resistance of the fluid along the walls, allowing for faster radial fluid flow in the blister. The effect of slip is less apparent for fluids of lower yield stress. In figure 6(b), we plot the data of figure 6(a) using logarithmic axes, and show that the power law is still recovered when there is slip at the surfaces, implying that only the time shift and not the power-law growth is a consequence of slip. Moreover, this further strengthens our argument that the dynamics is dominated by plug flow.

Figure 6. (a) Comparison of experiments with rough and smooth surfaces of the elastic sheets for two fluids with different yield stress. (b) Results show that slip clearly introduces a time shift with respect to the results on the no-slip surfaces, but that the bending regime discovered in § 4.1 is still recovered. The marker configuration in (a) also applies in (b).

5.3. Elastic stretching

Next, we investigate experimentally the limit when the tension dominates elastic bending, $h(0,t) \gg d$, in the elastic sheet. The thin elastic sheet has thickness $d=1.5$ mm and Young's modulus $E = 0.25$ MPa, giving bending stiffness $B = 9.4\times 10^{-7}\ \textrm {N} \textrm {m}$. The influx $Q = 3.3 \times 10^{-7}\ \textrm {m}^3 \textrm {s}^{-1}$ and the yield stress $\tau _0=47.3$ Pa are also used. The deformation of the sheet in the experiments reaches $h(0,t) \approx 10d$. In figure 7(a), the scaling prediction from tension given by (4.6) is recovered, also demonstrated by the collapse of experimental profiles from figures 7(b) and 7(c), when scaling the vertical and horizontal coordinates with the respective time dependencies from (4.6) and (4.7). The shape of the profiles in figure 7(c) is in close agreement with the shape from the ODE describing an arrested viscoplastic droplet as solved by Jalaal et al. (2021) and discussed in § 4.2, which would hold only if the tension in the sheet is close to isotropic (${\partial \varLambda }/{\partial r} \approx 0$).

Figure 7. (a) Plots of $h(0,t)$ in experiments with rough walls (experimental parameters $d = 1.5$ mm, $E = 0.25$ MPa, $B = 9.4\times 10^{-7}\ \textrm {N}\ \textrm {m}$, $Q = 3.3 \times 10^{-7}\ \textrm {m}^3\ \textrm {s}^{-1}$ and $\tau _0 = 47.3$ Pa), $h(0,t) \gg d$, together with the scaling law in (4.6), where we have determined $\beta = 0.67$. (b) Plots of four experimental blister profiles from $t = 80$ s to $t = 200$ s with time interval $40$ s between each profile. (c) The self-similarity is shown by rescaling the horizontal and vertical axis of the experimental profiles using the scaling laws in (4.7) and (4.6), respectively. The results are non-dimensionalized using $\unicode{x0141} _{\varLambda } = Ed/\tau _0$ and $T_{\varLambda }=(Ed)^3/\tau _0^3Q$.

6. Conclusion

The intrusion of flowing matter with complex rheological properties underneath an elastic layer or inside an elastic matrix appears in many geological processes. Both nonlinear magma plug flow (Morgan et al. 2008) and viscoplastic deformation of magma intrusions in host rocks (Galland et al. 2019) have been documented to play a key role in magma emplacement in the Earth's crust. Our study quantifies the dynamics of a viscoplastic blister's growth underneath an elastic sheet when the pressure is dominated by bending or stretching of the sheet; see table 3. The blister adopts a self-similar quasi-static shape in time that is set by the balance between the pressure gradient induced by the deformation of the elastic sheet and the yield stress of the intruding fluid, independent of the slip in the system. The experimental results have a time shift with respect to the numerical simulations. This time shift could result from our use of the Bingham model, a simplified rheological model that neglects shear-thinning effects, or some remaining slip in our experimental system that would also lead to faster radial growth of the blister. These results point to how the growth of geological structures such as sills and laccoliths may exhibit distinct dynamics from those predicted by a Newtonian model if the intruding fluid can support critical stress before starting to flow. Our work gives a first look at the elastohydrodynamics of a growing viscoplastic blister. Clearly, however, there are many more configurations that remain to be studied, for instance, additional non-Newtonian effects in the bulk and the elastic sheet (Ball & Balmforth 2021), or a combination of the yield stress intrusion model with an elastic fracture toughness at the tip.

Table 3. Summary of the elastoviscoplastic growth regimes of the blister with the influx $Q$, sheet thickness $d$, bending modulus $B$, Young's modulus $E$ and yield stress $\tau _0$.