1 Introduction
When a large number of wind turbines is assembled in a farm, the aggregated effect of wind-turbine energy extraction is strong enough to change the local equilibrium of the atmospheric boundary layer (ABL) (Calaf, Meneveau & Meyers Reference Calaf, Meneveau and Meyers2010). In addition to reduced velocities and enhanced turbulence in the turbine region, large wind farms also induce effects on a regional scale beyond their own boundaries, such as wind farm wakes (Christiansen & Hasager Reference Christiansen and Hasager2005; Fitch et al. Reference Fitch, Olson, Lundquist, Dudhia, Gupta, Michalakes and Barstad2012) and internal boundary layers (Chamorro & Porté-Agel Reference Chamorro and Porté-Agel2011; Newman et al. Reference Newman, Lebron, Meneveau and Castillo2013). As an increasing amount of wind power capacity is being installed each year (GWEC 2015), insight into the complex wind farm–ABL system and its non-local effects forms a key instrument in improving state-of-the-art wind farm operation and design.
For many years, the large-eddy simulation (LES) technique has been the preferred tool for modelling atmospheric turbulence because of its detailed spatial and temporal resolution (see, e.g. Moeng Reference Moeng1984; Mason Reference Mason1989; Mason & Derbyshire Reference Mason and Derbyshire1990; Kosović & Curry Reference Kosović and Curry2000). In recent years, LES has also been applied to study turbulent flow in and around wind turbines and wind farms (see, e.g. Jimenez et al. Reference Jimenez, Crespo, Migoya and Garcia2007, Reference Jimenez, Crespo, Migoya and Garcia2008; Calaf et al. Reference Calaf, Meneveau and Meyers2010; Wu & Porté-Agel Reference Wu and Porté-Agel2011). In the current study, we use large-eddy simulations to study wind farms in conventionally neutral boundary layers (CNBLs), which are often encountered in offshore conditions. Over the sea, shallow CNBLs occur frequently in the presence of strong inversion layers, with boundary-layer heights typically ranging between 200 and 700 m (Brost, Lenschow & Wyngaard Reference Brost, Lenschow and Wyngaard1982; Grant Reference Grant1986; Tjernström & Smedman Reference Tjernström and Smedman1993). Under such conditions, the wind turbines are no longer confined to the inner layer of the boundary layer and outer-layer dynamics become important. To the best of our knowledge, this situation has not been studied before in detail. Of particular interest is the development of an internal boundary layer at the wind farm entrance, and its downwind interaction with the overlying inversion layer. We also investigate the activation and related feedback effects of gravity waves occurring in the free atmosphere above the CNBL. We will show that both effects play an important role in the overall energy extraction of the wind farm, and strongly depend on the height of the CNBL.
The term conventionally neutral atmospheric boundary layer refers to a neutral ABL developing against a stably stratified background (Zilitinkevich & Esau Reference Zilitinkevich and Esau2002). Over land, these conditions are only found during a short transition period after sunset or on cloudy days with very strong winds (Stull Reference Stull1988; Garratt Reference Garratt1992). By contrast, offshore CNBLs occur more often as the surface heat flux tends to be smaller at sea (Businger & Charnock Reference Businger and Charnock1983). CNBLs are also formed by stable internal boundary layers above large lakes or semi-enclosed seas (Csanady Reference Csanady1974; Garratt Reference Garratt1987; Garratt & Ryan Reference Garratt and Ryan1989; Melas Reference Melas1989; Tjernström & Smedman Reference Tjernström and Smedman1993; Smedman, Bergström & Grisogono Reference Smedman, Bergström and Grisogono1997; Lange et al. Reference Lange, Larsen, Højstrup and Barthelmie2004). The vertical structure of the CNBL is illustrated in figure 1 (Allaerts & Meyers Reference Allaerts and Meyers2015). In the free atmosphere, the flow is non-turbulent and the wind speed is perpendicular to the pressure gradient and the Coriolis force. In the boundary layer, the wind speed decreases towards the ground and rotates towards the pressure gradient, as shown in figure 1(b). At the interface, the strong increase in potential temperature limits turbulent gusts and thereby controls the boundary-layer height.

Figure 1. (a) Schematic representation of the conventionally neutral atmospheric boundary layer, showing a three-dimensional view of the profiles of potential temperature and velocity as a function of height, indicating the temperature jump in the capping inversion and the typical Ekman spiral in the boundary layer. Adapted from Allaerts & Meyers (Reference Allaerts and Meyers2015) with the permission of AIP Publishing. (b) Plane view of the horizontal force balance in the free atmosphere and at ground level.
The first LES studies with conventionally neutral conditions considered oceanic bottom boundary layers (McWilliams et al.
Reference McWilliams, Gallacher, Moeng, Wyngaard, Galperin and Orszag1993) or limiting cases in the comparison between shear- and buoyancy-driven ABL flows (Moeng & Sullivan Reference Moeng and Sullivan1994; Sullivan, McWilliams & Moeng Reference Sullivan, McWilliams and Moeng1994). Later, Lin et al. (Reference Lin, McWilliams, Moeng and Sullivan1996) also included an inversion layer when studying coherent structures and dynamics in the neutral boundary layer. However, the actual importance of the capping inversion and the free-atmosphere stratification was only realised when Zilitinkevich & Esau (Reference Zilitinkevich and Esau2002) discovered that the free stream Brunt–Väisälä frequency
![]() $N$
forms a key scaling parameter for the ABL. Since then, a number of authors have used LES to study conventionally neutral conditions. For instance, Zilitinkevich & Esau (Reference Zilitinkevich and Esau2003, Reference Zilitinkevich and Esau2005) and Zilitinkevich, Esau & Baklanov (Reference Zilitinkevich, Esau and Baklanov2007) continued to improve equilibrium height formulations and similarity theory predictions for the CNBL, and Esau (Reference Esau2004a
,Reference Esau
b
) showed the importance of the inversion-layer height for flow properties such as turbulent kinetic energy and surface drag. Further, Taylor & Sarkar (Reference Taylor and Sarkar2007, Reference Taylor and Sarkar2008a
,Reference Taylor and Sarkar
b
) investigated stratification effects in the bottom Ekman layer of the ocean and Pedersen, Gryning & Kelly (Reference Pedersen, Gryning and Kelly2014) recently examined the dynamic evolution of the CNBL towards a statistically steady-state, fully turbulent boundary layer.
$N$
forms a key scaling parameter for the ABL. Since then, a number of authors have used LES to study conventionally neutral conditions. For instance, Zilitinkevich & Esau (Reference Zilitinkevich and Esau2003, Reference Zilitinkevich and Esau2005) and Zilitinkevich, Esau & Baklanov (Reference Zilitinkevich, Esau and Baklanov2007) continued to improve equilibrium height formulations and similarity theory predictions for the CNBL, and Esau (Reference Esau2004a
,Reference Esau
b
) showed the importance of the inversion-layer height for flow properties such as turbulent kinetic energy and surface drag. Further, Taylor & Sarkar (Reference Taylor and Sarkar2007, Reference Taylor and Sarkar2008a
,Reference Taylor and Sarkar
b
) investigated stratification effects in the bottom Ekman layer of the ocean and Pedersen, Gryning & Kelly (Reference Pedersen, Gryning and Kelly2014) recently examined the dynamic evolution of the CNBL towards a statistically steady-state, fully turbulent boundary layer.
Most wind farm boundary-layer studies, however, have focused on neutral pressure-driven boundary layers, in which rotation and stratification effects are absent. Examples are studies of fully developed wind farms by Calaf et al. (Reference Calaf, Meneveau and Meyers2010), Calaf, Parlange & Meneveau (Reference Calaf, Parlange and Meneveau2011), Yang, Kang & Sotiropoulos (Reference Yang, Kang and Sotiropoulos2012), Goit & Meyers (Reference Goit and Meyers2015) and of wind farms with entrance effects and a developing boundary layer by Porté-Agel, Wu & Chen (Reference Porté-Agel, Wu and Chen2013), Wu & Porté-Agel (Reference Wu and Porté-Agel2013, Reference Wu and Porté-Agel2015), Stevens, Gayme & Meneveau (Reference Stevens, Gayme and Meneveau2014a ), Stevens, Graham & Meneveau (Reference Stevens, Graham and Meneveau2014b ), Stevens, Gayme & Meneveau (Reference Stevens, Gayme and Meneveau2015), Nilsson et al. (Reference Nilsson, Ivanell, Hansen, Mikkelsen, Sørensen, Breton and Henningson2015), Goit, Munters & Meyers (Reference Goit, Munters and Meyers2016), Munters, Meneveau & Meyers (Reference Munters, Meneveau and Meyers2016). The main working assumption in these studies is that the wind turbines are located in the inner region of the ABL (i.e. the lower 10 %–15 % of the ABL), so that outer-layer effects such as Coriolis forces and the capping inversion do not directly influence the farm. However, this assumption breaks down for shallow boundary layers in which case the wind turbines reach into the outer layer and external effects start to influence the wind farm flow behaviour (Goit & Meyers Reference Goit and Meyers2013). With respect to wind energy, CNBLs have not been explored much. Abkar & Porté-Agel (Reference Abkar and Porté-Agel2013, Reference Abkar and Porté-Agel2014) investigated the influence of the free-atmosphere stratification on fully developed wind farms and found a decrease in wind farm power extraction for increasing stability in the free atmosphere. Allaerts & Meyers (Reference Allaerts and Meyers2015), on the other hand, focused more on the influence of the inversion layer and related the performance variations to differences in the boundary-layer height. Simulations of developing wind farms under conventionally neutral conditions have only been performed by Churchfield et al. (Reference Churchfield, Lee, Moriarty, Martinez, Leonardi, Vijayakumar and Brasseur2012) and Archer, Mirzaeisefat & Lee (Reference Archer, Mirzaeisefat and Lee2013), both for relatively high inversion layers. None of these studies have simulated atmospheric gravity waves above the inversion layer.
In both wind tunnel experiments (Chamorro, Arndt & Sotiropoulos Reference Chamorro, Arndt and Sotiropoulos2011; Chamorro & Porté-Agel Reference Chamorro and Porté-Agel2011; Markfort, Zhang & Porté-Agel Reference Markfort, Zhang and Porté-Agel2012; Newman et al. Reference Newman, Lebron, Meneveau and Castillo2013) and numerical simulations (of a pressure-driven boundary layer) (Wu & Porté-Agel Reference Wu and Porté-Agel2013), it was shown that an internal boundary layer develops at the entrance of a wind farm. Several studies have argued that the adjustment of the ABL to the increased drag by the wind turbines is comparable to a surface-roughness transition (Crespo et al. Reference Crespo, Frandsen, Gómez-Elvira, Larsen, Petersen, Hjuler Jensen, Rave, Helm and Ehmann1999; Frandsen et al. Reference Frandsen, Barthelmie, Pryor, Rathmann, Larsen, Højstrup and Thøgersen2006). Elliott (Reference Elliott1958) was the first to study the adaptation of the flow close to the ground to a step change in surface roughness. He found that the internal-boundary-layer growth scales with the 0.8 power of the downwind distance, a result that is still commonly used in the wind energy community (see, e.g. Meneveau Reference Meneveau2012). Since then, a considerable amount of literature has been published on this flow transition (see, e.g. Garratt Reference Garratt1990, Reference Garratt1992, for a review). A number of authors have extended the traditional surface-layer approach to meso-scale flows, i.e. including Coriolis effects and the full depth of the ABL, and considered larger downwind fetches (Taylor Reference Taylor1969; Jensen Reference Jensen1978; Wright et al. Reference Wright, Elliott, Ingham and Hewson1998; Hunt et al. Reference Hunt, Orr, Rottman and Capon2004). These studies predicted that the change in surface stress is accompanied by a change in surface wind direction. Taylor (Reference Taylor1969) further showed that the length scales related to the adaptation of the wind direction and the turbulent stress are very different, i.e. the turbulent stress adapts rapidly to the new roughness and spreads up from the surface, whereas the changes in wind direction occur more uniformly across the boundary layer and take place at larger downwind fetches. Moreover, Hunt et al. (Reference Hunt, Orr, Rottman and Capon2004) showed that variations in surface roughness also affect the inversion height and the pressure field. In the current work, we choose a sufficiently large simulation domain to study these effects, and their influence on wind farm power extraction in the context of a wind farm-induced roughness change.
Finally, the inversion layer and the stably stratified free atmosphere above the CNBL facilitate the formation and propagation of atmospheric gravity waves. While these waves are mostly associated with flows over mountain ridges or isolated mountains (Queney Reference Queney1948; Smith Reference Smith1980), Smith (Reference Smith2010) postulated, using a simplified linear model, that gravity waves can also be triggered by very large wind farms. In this respect, the farm can be viewed as a semi-permeable mountain that redirects part of the flow upwards, causing a displacement of the boundary-layer top and thereby generating gravity waves. Although the gravity waves only exist in the inversion layer and the free atmosphere, the associated pressure perturbations are imposed on the boundary layer and modify the wind farm flow. In the current work, the energetic consequences of these gravity waves are investigated by performing a detailed wind farm energy budget analysis. In particular for shallow CNBLs, these gravity waves play an important role in the overall energy budget.
The remainder of this paper is organised as follows. Section 2 first elaborates a number of important numerical aspects. Subsequently, the initialisation of the boundary-layer flow is discussed in § 3 and general trends of developing wind farm boundary layers are shown in § 4. In § 5, the sensitivity of the boundary-layer flow to the inflow conditions is analysed. Conclusions are summarised in § 6.
2 Numerical aspects
The behaviour of developing wind farms under conventionally neutral inflow conditions is studied by performing large-eddy simulations with the SP-Wind solver. This in-house research code was developed in a series of studies by Meyers & Sagaut (Reference Meyers and Sagaut2007), Delport, Baelmans & Meyers (Reference Delport, Baelmans and Meyers2009), Meyers & Meneveau (Reference Meyers and Meneveau2010), Munters et al. (Reference Munters, Meneveau and Meyers2016). The current study is largely based on the SP-Wind version of Allaerts & Meyers (Reference Allaerts and Meyers2015), which includes rotation and stratification effects (see appendix A for a summary of the LES methodology). The specification of boundary conditions is discussed in § 2.1. Further, the wind farm set-up is described in § 2.2, and an overview of the various LES cases is given in § 2.3.
2.1 Boundary conditions
At the top of the domain, non-reflecting boundary conditions are needed so that gravity waves can travel outwards without generating spurious reflections. As it is very difficult to determine appropriate radiation conditions for the highly nonlinear Navier–Stokes equations, wave reflections are alleviated with a simple wave-absorbing layer (see figure 2). In particular, Rayleigh damping is used (Klemp & Lilly Reference Klemp and Lilly1978; Durran & Klemp Reference Durran and Klemp1983), for which the erroneous backward reflection was shown to be less scale dependent than for viscous damping (Israeli & Orszag Reference Israeli and Orszag1981). A cosine profile is chosen for the damping coefficient so that it increases smoothly throughout the damping layer. Boundary conditions still need to be imposed at the top of the domain, for which simple rigid-lid conditions are used, i.e. zero stress and vertical velocity and a fixed potential temperature. At the bottom of the domain, classic wall modelling is applied (see appendix A).

Figure 2. Sketch of the numerical domain, showing the relative positions of the wind farm, the fringe region and Rayleigh damping layer. The vertical scale is exaggerated as the inversion layer occurs at 1 km or less.
In horizontal directions, the pseudo-spectral discretisation implies periodic boundary conditions. In order to prevent turbine-wake effects from being recycled back to the inlet, an artificial ‘fringe region’ is added to the domain in the streamwise direction (see figure 2), in which the flow variables are forced to an unperturbed inflow profile (Spalart & Watmuff Reference Spalart and Watmuff1993; Lundbladh et al.
Reference Lundbladh, Berlin, Skote, Hildings, Choi, Kim and Henningson1999; Nordström, Nordin & Henningson Reference Nordström, Nordin and Henningson1999). Within the fringe region, the masking function of Nordström et al. (Reference Nordström, Nordin and Henningson1999) is used for both the velocity and potential-temperature forcing, and the smoothing parameters
![]() $\unicode[STIX]{x1D6E5}_{s}$
and
$\unicode[STIX]{x1D6E5}_{s}$
and
![]() $\unicode[STIX]{x1D6E5}_{e}$
are set to
$\unicode[STIX]{x1D6E5}_{e}$
are set to
![]() $0.06L_{x}$
. To obtain a fully developed inflow profile with consistent turbulent structures and non-Gaussian statistics, the concurrent-precursor method is applied (Stevens et al.
Reference Stevens, Graham and Meneveau2014b
; Munters et al.
Reference Munters, Meneveau and Meyers2016). This method obtains inflow conditions from a precursor simulation that runs on an independent domain simultaneously with the main domain.
$0.06L_{x}$
. To obtain a fully developed inflow profile with consistent turbulent structures and non-Gaussian statistics, the concurrent-precursor method is applied (Stevens et al.
Reference Stevens, Graham and Meneveau2014b
; Munters et al.
Reference Munters, Meneveau and Meyers2016). This method obtains inflow conditions from a precursor simulation that runs on an independent domain simultaneously with the main domain.
Although extending the fringe region method to non-neutral simulations is straightforward, this method is not widely used for atmospheric flows. Only Inoue, Matheou & Teixeira (Reference Inoue, Matheou and Teixeira2014) have used this technique to model the transition of stratocumulus to shallow cumulus clouds. Nevertheless, the fringe region method, besides providing a desired inflow profile, also absorbs gravity waves leaving through either side of the domain (mathematically, the fringe region is just a Rayleigh damping layer with a time-varying input velocity). In this way, it prevents the formation of non-physical standing wave patterns. Inoue et al. (Reference Inoue, Matheou and Teixeira2014) report that this method is less affected by artificially reflected waves than an inflow–outflow method (Mayor, Spalart & Tripoli Reference Mayor, Spalart and Tripoli2002).
2.2 Wind farm set-up
In the current study, a very large generic wind farm with 180 turbines is considered. The wind turbines have a hub height
![]() $z_{h}=100$
m and diameter
$z_{h}=100$
m and diameter
![]() $D=100$
m, and they are modelled using the actuator disk method (see § A.2). The disk-based thrust coefficient
$D=100$
m, and they are modelled using the actuator disk method (see § A.2). The disk-based thrust coefficient
![]() $C_{T}^{\prime }=4/3$
(Calaf et al.
Reference Calaf, Meneveau and Meyers2010). The wind farm contains 20 rows of turbines so that spatially developing features of various length scales can be investigated. The streamwise spacing is set to
$C_{T}^{\prime }=4/3$
(Calaf et al.
Reference Calaf, Meneveau and Meyers2010). The wind farm contains 20 rows of turbines so that spatially developing features of various length scales can be investigated. The streamwise spacing is set to
![]() $s_{x}D=7.5D$
, which yields a wind farm length of 15 km. In the spanwise direction, nine turbine columns with spanwise spacing
$s_{x}D=7.5D$
, which yields a wind farm length of 15 km. In the spanwise direction, nine turbine columns with spanwise spacing
![]() $s_{y}D=5.33D$
are simulated, giving a width of 4.8 km. Note that, as no fringe region is applied in the spanwise direction and as the wind farm spans the full width of the simulation domain, the current set-up simulates the asymptotic limit of an ‘infinitely’ wide wind farm. This will result in slightly increased wind farm flow blockage and gravity-wave excitation compared to ‘fully finite’ wind farms, where the wind can also flow around the farm in the spanwise direction and waves can expand in three instead of two dimensions. The results of this study therefore reflect the flow behaviour in the middle turbine columns in a very wide wind farm. The large number of turbine columns is chosen to allow fairly large turbulent structures as well as sufficient averaging in the spanwise direction. Moreover, the width of the domain is such that turbulent structures entering the domain at the front (in the lower 80 % of the boundary layer) leave the domain through the back before they are recycled via the spanwise periodic boundary conditions.
$s_{y}D=5.33D$
are simulated, giving a width of 4.8 km. Note that, as no fringe region is applied in the spanwise direction and as the wind farm spans the full width of the simulation domain, the current set-up simulates the asymptotic limit of an ‘infinitely’ wide wind farm. This will result in slightly increased wind farm flow blockage and gravity-wave excitation compared to ‘fully finite’ wind farms, where the wind can also flow around the farm in the spanwise direction and waves can expand in three instead of two dimensions. The results of this study therefore reflect the flow behaviour in the middle turbine columns in a very wide wind farm. The large number of turbine columns is chosen to allow fairly large turbulent structures as well as sufficient averaging in the spanwise direction. Moreover, the width of the domain is such that turbulent structures entering the domain at the front (in the lower 80 % of the boundary layer) leave the domain through the back before they are recycled via the spanwise periodic boundary conditions.
The local wind direction may vary throughout the wind farm due to the combination of flow deceleration and Coriolis effects. Therefore, a simple yaw controller is implemented to keep the rotor disks perpendicular to the incident wind flow. The incident flow angle is measured
![]() $1D$
upwind of the turbine disk so as to ignore the flow deflection in the near vicinity of the turbine. Further, as the effective spanwise width is infinite, incident flow angles can be averaged over each turbine row. Additional averaging of the flow angle by means of a first-order time filter is performed. Since we are only interested in the steady-state yaw angle and not in its dynamics, we take a relatively large time constant of 15 min.
$1D$
upwind of the turbine disk so as to ignore the flow deflection in the near vicinity of the turbine. Further, as the effective spanwise width is infinite, incident flow angles can be averaged over each turbine row. Additional averaging of the flow angle by means of a first-order time filter is performed. Since we are only interested in the steady-state yaw angle and not in its dynamics, we take a relatively large time constant of 15 min.
2.3 Case set-up
Three different LES simulations are performed, among which the height of the undisturbed CNBL upwind of the wind farm is varied. The variable inflow height is thereby achieved by careful selection of initial conditions. Table 1 provides an overview of the numerical set-up of the various LES cases. The parameters specifying the inversion layer are discussed in § 3.1.
Table 1. Overview of the various LES simulations. The size of the numerical domain
![]() $L_{x}\times L_{y}\times L_{z}$
and the number of grid points in horizontal directions
$L_{x}\times L_{y}\times L_{z}$
and the number of grid points in horizontal directions
![]() $N_{x}\times N_{y}$
are equal in all three simulations, i.e. the domain size is
$N_{x}\times N_{y}$
are equal in all three simulations, i.e. the domain size is
![]() $38.4~\text{km}\times 4.8~\text{km}\times 25.0~\text{km}$
and
$38.4~\text{km}\times 4.8~\text{km}\times 25.0~\text{km}$
and
![]() $9.6~\text{km}\times 4.8~\text{km}\times 25.0~\text{km}$
for main and precursor domain, respectively, and the horizontal grid is
$9.6~\text{km}\times 4.8~\text{km}\times 25.0~\text{km}$
for main and precursor domain, respectively, and the horizontal grid is
![]() $1280\times 320$
and
$1280\times 320$
and
![]() $320\times 320$
. The amount of grid points in the vertical direction is divided into the number of equidistant grid points in the lower part of the domain, the number of grid points in the stretched grid part and the grid points in the Rayleigh damping layer.
$320\times 320$
. The amount of grid points in the vertical direction is divided into the number of equidistant grid points in the lower part of the domain, the number of grid points in the stretched grid part and the grid points in the Rayleigh damping layer.

Atmospheric conditions are set to represent an offshore CNBL. All cases are forced with a constant geostrophic wind speed of
![]() $G=12~\text{m}~\text{s}^{-1}$
. The drag of small-scale surface waves on the wind is simply parametrised by a constant surface-roughness length
$G=12~\text{m}~\text{s}^{-1}$
. The drag of small-scale surface waves on the wind is simply parametrised by a constant surface-roughness length
![]() $z_{0}=2\times 10^{-4}$
m (Sullivan et al.
Reference Sullivan, Edson, Hristov and McWilliams2008), and no resolved wave structures are considered. A more detailed representation of the sea surface including wave dynamics could be obtained by, e.g. the dynamic roughness model of Yang, Meneveau & Shen (Reference Yang, Meneveau and Shen2013), but this approach is beyond the scope of this study. The free-atmosphere lapse rate
$z_{0}=2\times 10^{-4}$
m (Sullivan et al.
Reference Sullivan, Edson, Hristov and McWilliams2008), and no resolved wave structures are considered. A more detailed representation of the sea surface including wave dynamics could be obtained by, e.g. the dynamic roughness model of Yang, Meneveau & Shen (Reference Yang, Meneveau and Shen2013), but this approach is beyond the scope of this study. The free-atmosphere lapse rate
![]() $\unicode[STIX]{x1D6FE}$
equals
$\unicode[STIX]{x1D6FE}$
equals
![]() $1~\text{K}~\text{km}^{-1}$
and the temperature of the mixed layer is
$1~\text{K}~\text{km}^{-1}$
and the temperature of the mixed layer is
![]() $\unicode[STIX]{x1D703}_{m}=15\,^{\circ }\text{C}$
, which is also taken as the reference temperature
$\unicode[STIX]{x1D703}_{m}=15\,^{\circ }\text{C}$
, which is also taken as the reference temperature
![]() $\unicode[STIX]{x1D703}_{0}$
. Finally, the Coriolis parameter
$\unicode[STIX]{x1D703}_{0}$
. Finally, the Coriolis parameter
![]() $f_{c}$
is set to
$f_{c}$
is set to
![]() $10^{-4}~\text{s}^{-1}$
, corresponding to a latitude of
$10^{-4}~\text{s}^{-1}$
, corresponding to a latitude of
![]() $\unicode[STIX]{x1D719}=43.43^{\circ }$
.
$\unicode[STIX]{x1D719}=43.43^{\circ }$
.
The size of the numerical domain is to a large extent determined by the presence of atmospheric gravity waves. In the streamwise direction, sufficient spacing between the wind farm and the fringe region is needed to avoid too large distortions of the wind farm-generated gravity-wave field. Inoue et al. (Reference Inoue, Matheou and Teixeira2014) found that the influence of the fringe region is limited to approximately 10 km upwind. For the wind farm length under consideration, we found good results with 10 km upwind and 8.6 km downwind distance between the fringe region and the wind farm (see figure 2). A fringe region of 4.8 km with a damping coefficient
![]() $\unicode[STIX]{x1D706}_{max}$
equal to
$\unicode[STIX]{x1D706}_{max}$
equal to
![]() $0.03~\text{s}^{-1}$
was found sufficient to damp out horizontally propagating gravity waves. Hence, the total domain size in streamwise direction sums up to
$0.03~\text{s}^{-1}$
was found sufficient to damp out horizontally propagating gravity waves. Hence, the total domain size in streamwise direction sums up to
![]() $L_{x}=38.4$
km. In the precursor simulation, a simple ABL without wind turbines is simulated. Accordingly, the streamwise size of the domain can be reduced to save computational costs, and we set
$L_{x}=38.4$
km. In the precursor simulation, a simple ABL without wind turbines is simulated. Accordingly, the streamwise size of the domain can be reduced to save computational costs, and we set
![]() $L_{x}=9.6$
km in the precursor simulation.
$L_{x}=9.6$
km in the precursor simulation.
Under the hydrostatic assumption, the vertical wavelength of gravity waves is given by
![]() $\unicode[STIX]{x1D706}_{z}=2\unicode[STIX]{x03C0}U/N$
, which is approximately 12.8 km under the given atmospheric conditions. Klemp & Lilly (Reference Klemp and Lilly1978) found that the depth of the damping layer should be of the order of one vertical wavelength. We set the depth of the damping layer to 10 km, which corresponds to
$\unicode[STIX]{x1D706}_{z}=2\unicode[STIX]{x03C0}U/N$
, which is approximately 12.8 km under the given atmospheric conditions. Klemp & Lilly (Reference Klemp and Lilly1978) found that the depth of the damping layer should be of the order of one vertical wavelength. We set the depth of the damping layer to 10 km, which corresponds to
![]() $0.78\unicode[STIX]{x1D706}_{z}$
. Further, Durran & Klemp (Reference Durran and Klemp1983) found that ‘the numerical solution is not strongly sensitive to the strength of the damping in the wave-absorbing layer, but it can be very sensitive to changes in the height at which the absorbing layer begins, i.e. the effective height of the upper boundary’. We found reasonably low wave reflection when at least one vertical wavelength fitted into the domain (see § 4.3 for a qualitative discussion on wave reflection). Therefore, the height of the physical domain is set to 15 km. Combined with the Rayleigh damping layer above, the total height of the numerical domain is 25 km (see figure 2). The Rayleigh damping coefficient is set to
$0.78\unicode[STIX]{x1D706}_{z}$
. Further, Durran & Klemp (Reference Durran and Klemp1983) found that ‘the numerical solution is not strongly sensitive to the strength of the damping in the wave-absorbing layer, but it can be very sensitive to changes in the height at which the absorbing layer begins, i.e. the effective height of the upper boundary’. We found reasonably low wave reflection when at least one vertical wavelength fitted into the domain (see § 4.3 for a qualitative discussion on wave reflection). Therefore, the height of the physical domain is set to 15 km. Combined with the Rayleigh damping layer above, the total height of the numerical domain is 25 km (see figure 2). The Rayleigh damping coefficient is set to
![]() $0.0001~\text{s}^{-1}$
. Note that, despite the large vertical extent of the domain, the Boussinesq approximation can still be used as long as the characteristic vertical displacement (of the order of 100 m in our simulations) remains small compared to the density scale height of the atmosphere, which is typically of the order of 10 km (Wyngaard Reference Wyngaard2010).
$0.0001~\text{s}^{-1}$
. Note that, despite the large vertical extent of the domain, the Boussinesq approximation can still be used as long as the characteristic vertical displacement (of the order of 100 m in our simulations) remains small compared to the density scale height of the atmosphere, which is typically of the order of 10 km (Wyngaard Reference Wyngaard2010).
Using SP-Wind, Calaf et al. (Reference Calaf, Meneveau and Meyers2010) and Meyers & Meneveau (Reference Meyers and Meneveau2013) performed sensitivity studies for wind farms with turbine spacing similar to the one considered here (i.e.
![]() $s_{x}\times s_{y}=7.85\times 5.24$
), and they found only small influences of the horizontal resolution when
$s_{x}\times s_{y}=7.85\times 5.24$
), and they found only small influences of the horizontal resolution when
![]() $25~\text{m}\leqslant \unicode[STIX]{x0394}x\leqslant 50~\text{m}$
and
$25~\text{m}\leqslant \unicode[STIX]{x0394}x\leqslant 50~\text{m}$
and
![]() $10~\text{m}\leqslant \unicode[STIX]{x0394}y\leqslant 25~\text{m}$
. Accordingly, the grid resolution is set to 30 m and 15 m in streamwise and spanwise directions, respectively. In the vertical direction, the finite difference scheme requires a finer resolution to accurately resolve turbulent structures. In particular, the inversion layer forms the most stringent region as its strong stability results in fine-scale turbulent motions. These structures should still be resolved in order for LES to provide a good estimate of the turbulent entrainment rate. Taylor & Sarkar (Reference Taylor and Sarkar2008a
) found that the scale of turbulent eddies responsible for entrainment into the boundary layer can be estimated by the Ellison scale, defined as
$10~\text{m}\leqslant \unicode[STIX]{x0394}y\leqslant 25~\text{m}$
. Accordingly, the grid resolution is set to 30 m and 15 m in streamwise and spanwise directions, respectively. In the vertical direction, the finite difference scheme requires a finer resolution to accurately resolve turbulent structures. In particular, the inversion layer forms the most stringent region as its strong stability results in fine-scale turbulent motions. These structures should still be resolved in order for LES to provide a good estimate of the turbulent entrainment rate. Taylor & Sarkar (Reference Taylor and Sarkar2008a
) found that the scale of turbulent eddies responsible for entrainment into the boundary layer can be estimated by the Ellison scale, defined as
using a bar for time averaging and angular brackets for horizontal averaging. From figure 3, showing the Ellison scale for the different simulations, it is found that a vertical resolution of 5 m is sufficient for all simulations to capture the Ellison scale in the inversion layer. The lower 1 km of the domain is therefore equipped with an equidistant grid with 200 grid points (1.5 km with 300 grid points in case S1). Above this equidistant grid and up to a height of 15 km, the grid is stretched with a maximum grid size of 40 m (see table 1 for the amount of grid points in this stretched part). The damping layer at the top of the domain is made up of 50 grid points, with the grid resolution stretching from 40 m to 300 m. Hence, the number of grid points in the vertical direction is 620 (700 in case S1), see table 1. In total, the simulations use approximately 320 million grid cells (360 million for case S1), for the combination of main and precursor domain.

Figure 3. Ellison scale, computed from vertical profiles averaged horizontally and over the last five hours of the spin-up phase, for cases S1 (squares), S2 (circles) and S4 (triangles).
3 Boundary-layer initialisation
The wind farm boundary layer needs to be initialised properly before any flow statistics can be collected over time. This is achieved in two phases, namely the spin-up phase and the wind farm start-up phase.
In the first phase, the precursor domain is simulated starting from average vertical profiles combined with random noise (see § 3.1), and the simulation is progressed in time until a steady-state, fully developed turbulent CNBL is obtained. In the literature, equilibration times for the CNBL are reported to be between 16 and 24 model hours (see, e.g. Zilitinkevich et al.
Reference Zilitinkevich, Esau and Baklanov2007; Pedersen et al.
Reference Pedersen, Gryning and Kelly2014), so the duration of the spin-up phase is set to 20 h. The precursor domain does not contain any wind turbines, so there are no mechanisms to trigger large-scale stationary gravity-wave structures. Gravity waves can still be excited in the precursor domain by turbulent motions near the top of the boundary layer (see, e.g. Taylor & Sarkar Reference Taylor and Sarkar2007), but we found that the amplitude of such waves is at least an order of magnitude smaller than wind farm-induced gravity waves. The effect of these weak gravity waves on the wind farm behaviour will therefore be negligible, which allows us to simulate only the lower 5 km of the domain in this phase, with a damping layer between 1 and 5 km (1.5 for case S1). Furthermore, the wind angle controller of Allaerts & Meyers (Reference Allaerts and Meyers2015) is used during this phase to vary the geostrophic wind angle
![]() $\unicode[STIX]{x1D6FC}$
, such that the flow direction at hub height is aligned with the
$\unicode[STIX]{x1D6FC}$
, such that the flow direction at hub height is aligned with the
![]() $x$
-direction. The control parameters are set to
$x$
-direction. The control parameters are set to
![]() $\unicode[STIX]{x1D6FD}=2~\text{h}^{-1}$
and
$\unicode[STIX]{x1D6FD}=2~\text{h}^{-1}$
and
![]() $\unicode[STIX]{x1D70E}=3.33~\text{min}$
.
$\unicode[STIX]{x1D70E}=3.33~\text{min}$
.
In the second phase, both precursor and main domain are simulated. The precursor simulation now starts from the velocity and potential-temperature fields developed in the spin-up phase, and produces realistic inflow fields for the main domain. This phase is advanced for one hour, corresponding to approximately two and a half wind farm flow-through times, during which the farm goes through its start-up phase, the yaw controller converges to a steady yaw angle and the flow generally adapts to the presence of the wind turbines. By the end of this phase, any transitional effects of the wind farm start-up have died out, and the wind farm boundary layer has reached a statistically stationary state. After these two initialisation phases, flow statistics are collected over a period of two hours, which has been selected as a trade-off between computational cost and statistical convergence. With a turbulent intensity of approximately 4 % (see table 2) and an integral time scale of approximately 500 s (based on the autocorrelation of the disk-averaged velocity), we estimate the statistical error on the time- and column-averaged turbine power to be 1.5 %.
Table 2. Steady-state parameters of the various spin-up cases, including the boundary-layer height
![]() $h$
, the boundary-layer growth
$h$
, the boundary-layer growth
![]() $\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}t$
, the hub-height velocity
$\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}t$
, the hub-height velocity
![]() $M_{hub}$
, the friction velocity
$M_{hub}$
, the friction velocity
![]() $u_{\ast }$
, the geostrophic wind angle
$u_{\ast }$
, the geostrophic wind angle
![]() $\unicode[STIX]{x1D6FC}$
and the turbulent intensity at hub height
$\unicode[STIX]{x1D6FC}$
and the turbulent intensity at hub height
![]() $\mathit{TI}$
.
$\mathit{TI}$
.
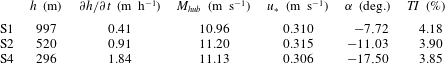
3.1 Initial conditions
Specification of the initial potential-temperature profile for the spin-up phase is very important, because this will have a direct impact on the outcome of the whole simulation as the CNBL is very sensitive to its heating history (Tennekes Reference Tennekes1973). Following Allaerts & Meyers (Reference Allaerts and Meyers2015), the initial potential-temperature profile is specified using an analytical expression that allows control over the inversion parameters (Rampanelli & Zardi Reference Rampanelli and Zardi2004):
where
![]() $\unicode[STIX]{x1D702}$
is a dimensionless height and
$\unicode[STIX]{x1D702}$
is a dimensionless height and
![]() $a$
and
$a$
and
![]() $b$
are tuning parameters related to the inversion characteristics. The properties of the inversion layer are chosen such that the resulting boundary layer is in equilibrium. To this end, the empirical formulation of Csanady (Reference Csanady1974) for the asymptotic depth
$b$
are tuning parameters related to the inversion characteristics. The properties of the inversion layer are chosen such that the resulting boundary layer is in equilibrium. To this end, the empirical formulation of Csanady (Reference Csanady1974) for the asymptotic depth
![]() $h$
of the CNBL is used:
$h$
of the CNBL is used:
where
![]() $u_{\ast }$
is the friction velocity,
$u_{\ast }$
is the friction velocity,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
is the inversion strength and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
is the inversion strength and
![]() $A$
is an empirical parameter estimated to be approximately 500 (Csanady Reference Csanady1974; Tjernström & Smedman Reference Tjernström and Smedman1993). Using typical values of 0.26–
$A$
is an empirical parameter estimated to be approximately 500 (Csanady Reference Csanady1974; Tjernström & Smedman Reference Tjernström and Smedman1993). Using typical values of 0.26–
![]() $0.28~\text{m}~\text{s}^{-1}$
for the friction velocity over sea, we obtain the set of inversion heights and strengths given in table 1.
$0.28~\text{m}~\text{s}^{-1}$
for the friction velocity over sea, we obtain the set of inversion heights and strengths given in table 1.
Initialisation of the velocity follows the approach of Allaerts & Meyers (Reference Allaerts and Meyers2015), i.e. a profile is created by blending a neutral boundary-layer profile below
![]() $h/2$
with the prescribed geostrophic wind velocity above. Random divergence-free perturbations are added to the velocity profile to trigger turbulence. The perturbations have an amplitude of
$h/2$
with the prescribed geostrophic wind velocity above. Random divergence-free perturbations are added to the velocity profile to trigger turbulence. The perturbations have an amplitude of
![]() $0.1G$
and are added below 100 m only, so that the initial ‘non-physical’ random noise does not interact directly with the inversion layer. This initial condition is advanced in time in the first phase, during which the initial random noise evolves into turbulence and fills up the boundary layer under the capping inversion.
$0.1G$
and are added below 100 m only, so that the initial ‘non-physical’ random noise does not interact directly with the inversion layer. This initial condition is advanced in time in the first phase, during which the initial random noise evolves into turbulence and fills up the boundary layer under the capping inversion.
3.2 Initialisation results
Some steady-state parameters are given in table 2 for the various spin-up cases. The height of the inversion layer changes slightly during the spin-up phase, but the total increase remains below 50 m in all cases. Near the end of the first phase, the boundary-layer growth attains a small constant value (less than 2
![]() $\text{m}~\text{h}^{-1}$
), indicating that the boundary layer has reached a quasi-steady state. For comparison, Pedersen et al. (Reference Pedersen, Gryning and Kelly2014) found average growth rates for CNBLs in quasi-steady state between 0.28 and 0.58
$\text{m}~\text{h}^{-1}$
), indicating that the boundary layer has reached a quasi-steady state. For comparison, Pedersen et al. (Reference Pedersen, Gryning and Kelly2014) found average growth rates for CNBLs in quasi-steady state between 0.28 and 0.58
![]() $\text{m}~\text{h}^{-1}$
. Further, the hub-height velocity
$\text{m}~\text{h}^{-1}$
. Further, the hub-height velocity
![]() $M_{hub}$
and the friction velocity
$M_{hub}$
and the friction velocity
![]() $u_{\ast }$
are found to be nearly constant for the different cases, and the geostrophic angle
$u_{\ast }$
are found to be nearly constant for the different cases, and the geostrophic angle
![]() $\unicode[STIX]{x1D6FC}$
increases with decreasing boundary-layer height. The turbulent intensity is defined as
$\unicode[STIX]{x1D6FC}$
increases with decreasing boundary-layer height. The turbulent intensity is defined as
![]() $\mathit{TI}=(\langle \overline{u_{i}^{\prime }u_{i}^{\prime }}\rangle /3)^{1/2}/M_{hub}$
and is approximately 4 % at hub height in every case. For comparison, Bergström (Reference Bergström2009) measured turbulent intensities at Lillgrund in the range 1 to 18 % with an average of 6 % (measured at 65 m), and Barthelmie et al. (Reference Barthelmie, Hansen, Frandsen, Rathmann, Schepers, Schlez, Phillips, Rados, Zervos and Politis2009) reported low turbulent intensities (
$\mathit{TI}=(\langle \overline{u_{i}^{\prime }u_{i}^{\prime }}\rangle /3)^{1/2}/M_{hub}$
and is approximately 4 % at hub height in every case. For comparison, Bergström (Reference Bergström2009) measured turbulent intensities at Lillgrund in the range 1 to 18 % with an average of 6 % (measured at 65 m), and Barthelmie et al. (Reference Barthelmie, Hansen, Frandsen, Rathmann, Schepers, Schlez, Phillips, Rados, Zervos and Politis2009) reported low turbulent intensities (
![]() ${<}8\,\%$
) for the Horns Rev wind farm.
${<}8\,\%$
) for the Horns Rev wind farm.

Figure 4. Vertical profiles, averaged over the horizontal directions and over the last five hours of the spin-up phase, of (a) horizontal velocity magnitude, (b) total shear stress magnitude, (c) horizontal wind direction and (d) potential temperature for cases S1 (squares), S2 (circles) and S4 (triangles).
Figure 4 shows vertical profiles of various flow variables for the different spin-up cases, averaged over the horizontal directions and over the last five hours of the first phase. Note that we normalise figure 4(a,b) with two different velocity scales, i.e. the horizontal velocity profiles are scaled with the geostrophic wind speed
![]() $G$
so that they collapse above the boundary layer, while the stress profiles are non-dimensionalised with the friction velocity
$G$
so that they collapse above the boundary layer, while the stress profiles are non-dimensionalised with the friction velocity
![]() $u_{\ast }$
so that they coincide at the surface. The ratio of
$u_{\ast }$
so that they coincide at the surface. The ratio of
![]() $u_{\ast }/G\approx 0.025$
can be inferred from table 2 given
$u_{\ast }/G\approx 0.025$
can be inferred from table 2 given
![]() $G=12~\text{m}~\text{s}^{-1}$
for all cases. Figure 4(a) shows that all cases develop a supergeostrophic jet near the boundary-layer top with a maximum wind speed of approximately
$G=12~\text{m}~\text{s}^{-1}$
for all cases. Figure 4(a) shows that all cases develop a supergeostrophic jet near the boundary-layer top with a maximum wind speed of approximately
![]() $1.05\,G$
, similar to Pedersen et al. (Reference Pedersen, Gryning and Kelly2014). Further, the vertical profiles of stress and wind direction (see figure 4
b,c) follow the expected trends, i.e. linear (or close to) in the boundary layer and zero or constant above. Finally, the potential-temperature profile in figure 4(d) shows that the general shape of the inversion layer is preserved, and the temperature in the boundary layer increases only very little (less than 0.5 K). Overall, these results demonstrate that the first initialisation phase yields a steady-state, fully turbulent CNBL, which can be used to produce accurate inflow conditions for the developing wind farm.
$1.05\,G$
, similar to Pedersen et al. (Reference Pedersen, Gryning and Kelly2014). Further, the vertical profiles of stress and wind direction (see figure 4
b,c) follow the expected trends, i.e. linear (or close to) in the boundary layer and zero or constant above. Finally, the potential-temperature profile in figure 4(d) shows that the general shape of the inversion layer is preserved, and the temperature in the boundary layer increases only very little (less than 0.5 K). Overall, these results demonstrate that the first initialisation phase yields a steady-state, fully turbulent CNBL, which can be used to produce accurate inflow conditions for the developing wind farm.
Instantaneous contours of the horizontal velocity in the precursor and main domain, obtained at the end of the second initialisation phase of case S1, are shown in figure 5. On the left, figure 5(a,c) show an
![]() $x$
–
$x$
–
![]() $z$
plane (only the lower 2 km of the numerical domain are shown) and an
$z$
plane (only the lower 2 km of the numerical domain are shown) and an
![]() $x$
–
$x$
–
![]() $y$
plane (at
$y$
plane (at
![]() $z_{h}=100$
m) of the precursor domain. In the top view, typical elongated streaks in streamwise direction are visible. The side view, on the other hand, shows that turbulence extends up to the capping inversion, which is located here at approximately 1 km. The flow above the capping inversion is non-turbulent and shear free. Similar cross sections of the main domain are shown in figure 5(b,d), where turbine disk locations are indicated with vertical black lines. The
$z_{h}=100$
m) of the precursor domain. In the top view, typical elongated streaks in streamwise direction are visible. The side view, on the other hand, shows that turbulence extends up to the capping inversion, which is located here at approximately 1 km. The flow above the capping inversion is non-turbulent and shear free. Similar cross sections of the main domain are shown in figure 5(b,d), where turbine disk locations are indicated with vertical black lines. The
![]() $x$
–
$x$
–
![]() $y$
plane through the centre of the rotor disks shows significant turbine-wake meandering, especially from the fourth turbine row onward. Further, a gradually increasing velocity deficit appears throughout the farm. In the side view, the vertical extent of the turbine wakes increases downwind, and the height of the capping inversion appears to increase as well. Behind the farm, the velocity in the boundary layer is lower but more turbulent than upwind, indicating the existence of a long wind farm wake. In conclusion, figure 5 shows that the flow in both the precursor and main domain is fully turbulent, so flow statistics may be collected starting from this state onward.
$y$
plane through the centre of the rotor disks shows significant turbine-wake meandering, especially from the fourth turbine row onward. Further, a gradually increasing velocity deficit appears throughout the farm. In the side view, the vertical extent of the turbine wakes increases downwind, and the height of the capping inversion appears to increase as well. Behind the farm, the velocity in the boundary layer is lower but more turbulent than upwind, indicating the existence of a long wind farm wake. In conclusion, figure 5 shows that the flow in both the precursor and main domain is fully turbulent, so flow statistics may be collected starting from this state onward.

Figure 5. Instantaneous contours of horizontal velocity magnitude, obtained at the end of the second initialisation phase and normalised by the geostrophic wind speed, for case S1; (a,b) an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a turbine column (only the lower 2 km of the numerical domain are shown); (c,d) an
$z$
plane through the middle of a turbine column (only the lower 2 km of the numerical domain are shown); (c,d) an
![]() $x$
–
$x$
–
![]() $y$
plane at turbine hub height
$y$
plane at turbine hub height
![]() $z_{h}=100$
m. The left panel shows the precursor domain (a,c) and the right panel shows the main domain (b,d), where turbine disk locations are indicated with vertical black lines. The bottom panel shows a detailed view of the wind farm entrance region in an
$z_{h}=100$
m. The left panel shows the precursor domain (a,c) and the right panel shows the main domain (b,d), where turbine disk locations are indicated with vertical black lines. The bottom panel shows a detailed view of the wind farm entrance region in an
![]() $x$
–
$x$
–
![]() $y$
plane.
$y$
plane.
4 General behaviour of a developing wind farm in the CNBL
We start by describing the general behaviour of large developing wind farms under conventionally neutral conditions, using the LES results from case S1 averaged over the last two simulation hours. For this case, the inversion layer is located relatively far away from the turbine region, so direct interactions between inner- and outer-layer dynamics are less likely to occur. This allows a first study of the wind farm flow without having to cope with complex interactions between wind turbines and the inversion layer. The flow behaviour in the boundary layer is first examined in § 4.1. After that, the wind farm performance is analysed quantitatively in § 4.2 by looking at the energy budget terms. Finally, atmospheric gravity waves and the corresponding structures in velocity, pressure and potential-temperature fields are discussed in § 4.3.
4.1 Boundary-layer flow behaviour
Contours of the time-averaged horizontal velocity magnitude
![]() $(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
are shown in figure 6 for case S1. The planes are taken at the same locations as in figure 5, i.e. an
$(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
are shown in figure 6 for case S1. The planes are taken at the same locations as in figure 5, i.e. an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a column of turbines and an
$z$
plane through the middle of a column of turbines and an
![]() $x$
–
$x$
–
![]() $y$
plane through the wind-turbine centres. The individual turbine wakes are clearly visible, and we observe strong velocity deficits behind the first and second turbine rows. Further downwind, wake recovery increases and the velocity deficit immediately behind the turbines is smaller. Figure 6(b) further shows that high-speed channels exist between turbine columns in the beginning of the farm. However, these channels gradually decelerate as turbine-wake expansion fills up the spanwise spacing between the turbines.
$y$
plane through the wind-turbine centres. The individual turbine wakes are clearly visible, and we observe strong velocity deficits behind the first and second turbine rows. Further downwind, wake recovery increases and the velocity deficit immediately behind the turbines is smaller. Figure 6(b) further shows that high-speed channels exist between turbine columns in the beginning of the farm. However, these channels gradually decelerate as turbine-wake expansion fills up the spanwise spacing between the turbines.

Figure 6. Contours of time-averaged horizontal velocity magnitude
![]() $(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
, normalised by the geostrophic wind speed, for case S1; (a) an
$(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
, normalised by the geostrophic wind speed, for case S1; (a) an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a turbine column (only the lower 1.5 km of the numerical domain are shown), showing the evolution of the inversion-layer base and top (solid lines) as well as the growth of an internal boundary layer (dashed line); (b) an
$z$
plane through the middle of a turbine column (only the lower 1.5 km of the numerical domain are shown), showing the evolution of the inversion-layer base and top (solid lines) as well as the growth of an internal boundary layer (dashed line); (b) an
![]() $x$
–
$x$
–
![]() $y$
plane at turbine hub height
$y$
plane at turbine hub height
![]() $z_{h}=100$
m (only three of the nine turbine columns are shown). In (a) and (b), the location of the wind-turbine disks are indicated with vertical black lines.
$z_{h}=100$
m (only three of the nine turbine columns are shown). In (a) and (b), the location of the wind-turbine disks are indicated with vertical black lines.
The vertical expansion of wind-turbine wakes and the related velocity deficits can be observed in figure 6(a). The depth of the velocity-deficit region increases with downwind distance, which indicates the growth of an internal boundary layer (IBL). The height of this layer is a useful parameter to quantify the flow development, and it allows comparison between various cases. However, there is often no sharp interface, and several different measures for the IBL height are available in the literature. The simplest approach to estimate the IBL height is based on the horizontal velocity magnitude, i.e.
![]() $h(M)$
is calculated as the height where the ratio of the time-averaged velocity and the inflow velocity at the same height, taken in a plane 2 km upwind reaches a threshold of 97 % (see, e.g. Wu & Porté-Agel Reference Wu and Porté-Agel2013). This estimate is represented by a dashed line in figure 6(a), together with the base and top of the inversion layer (solid lines), showing that the IBL does not interact with the inversion layer located far above.
$h(M)$
is calculated as the height where the ratio of the time-averaged velocity and the inflow velocity at the same height, taken in a plane 2 km upwind reaches a threshold of 97 % (see, e.g. Wu & Porté-Agel Reference Wu and Porté-Agel2013). This estimate is represented by a dashed line in figure 6(a), together with the base and top of the inversion layer (solid lines), showing that the IBL does not interact with the inversion layer located far above.
Figure 7(a) compares
![]() $h(M)$
with two additional estimates
$h(M)$
with two additional estimates
![]() $h(\unicode[STIX]{x1D70F}_{x})$
and
$h(\unicode[STIX]{x1D70F}_{x})$
and
![]() $h(\unicode[STIX]{x1D70F}_{z})$
proposed by Glendening & Lin (Reference Glendening and Lin2002). These estimates are obtained from the vertical profiles of total shear stress (see figure 7(b), showing the vertical shear stress profile at various locations in the farm). The estimate
$h(\unicode[STIX]{x1D70F}_{z})$
proposed by Glendening & Lin (Reference Glendening and Lin2002). These estimates are obtained from the vertical profiles of total shear stress (see figure 7(b), showing the vertical shear stress profile at various locations in the farm). The estimate
![]() $h(\unicode[STIX]{x1D70F}_{x})$
corresponds to the loci where
$h(\unicode[STIX]{x1D70F}_{x})$
corresponds to the loci where
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}/\unicode[STIX]{x2202}x=0$
and marks the place where the shear stress is first influenced by the increased drag of the wind turbines. Alternatively,
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}/\unicode[STIX]{x2202}x=0$
and marks the place where the shear stress is first influenced by the increased drag of the wind turbines. Alternatively,
![]() $h(\unicode[STIX]{x1D70F}_{z})$
is defined as the height where the curvature of the normalised shear stress profile reaches a maximum. Figure 7(a) shows that
$h(\unicode[STIX]{x1D70F}_{z})$
is defined as the height where the curvature of the normalised shear stress profile reaches a maximum. Figure 7(a) shows that
![]() $h(\unicode[STIX]{x1D70F}_{x})>h(\unicode[STIX]{x1D70F}_{z})$
, which corresponds to the findings of Glendening & Lin (Reference Glendening and Lin2002) and which can also be observed in the vertical shear stress profiles in figure 7(b). Further, the estimate
$h(\unicode[STIX]{x1D70F}_{x})>h(\unicode[STIX]{x1D70F}_{z})$
, which corresponds to the findings of Glendening & Lin (Reference Glendening and Lin2002) and which can also be observed in the vertical shear stress profiles in figure 7(b). Further, the estimate
![]() $h(M)$
, based on the horizontal velocity, is lower than both estimates based on the shear stress, which agrees with the observation of Shir (Reference Shir1972) that velocity profiles adapt more slowly than stress profiles.
$h(M)$
, based on the horizontal velocity, is lower than both estimates based on the shear stress, which agrees with the observation of Shir (Reference Shir1972) that velocity profiles adapt more slowly than stress profiles.

Figure 7. (a) IBL height estimates
![]() $h(M)$
(dash-dotted line),
$h(M)$
(dash-dotted line),
![]() $h(\unicode[STIX]{x1D70F}_{z})$
(dashed line) and
$h(\unicode[STIX]{x1D70F}_{z})$
(dashed line) and
![]() $h(\unicode[STIX]{x1D70F}_{x})$
(solid line) for case S1. The estimates
$h(\unicode[STIX]{x1D70F}_{x})$
(solid line) for case S1. The estimates
![]() $h(\unicode[STIX]{x1D70F}_{z})$
and
$h(\unicode[STIX]{x1D70F}_{z})$
and
![]() $h(\unicode[STIX]{x1D70F}_{x})$
have been smoothed with a top-hat filter with width
$h(\unicode[STIX]{x1D70F}_{x})$
have been smoothed with a top-hat filter with width
![]() $2D$
. The thin solid lines represent least-squares fits of the height estimates with a power law, and the theoretical profile of Elliott (Reference Elliott1958) is included (circles). (b) Vertical profiles of total shear stress magnitude for case S1, averaged in time and over a streamwise and spanwise distance of
$2D$
. The thin solid lines represent least-squares fits of the height estimates with a power law, and the theoretical profile of Elliott (Reference Elliott1958) is included (circles). (b) Vertical profiles of total shear stress magnitude for case S1, averaged in time and over a streamwise and spanwise distance of
![]() $2D$
and
$2D$
and
![]() $L_{y}$
, respectively. The profiles have been obtained
$L_{y}$
, respectively. The profiles have been obtained
![]() $1D$
upwind of turbine rows 1, 2, 4, 8, 12, 16 and 20. The corresponding locations are indicated in (a) with vertical dotted lines.
$1D$
upwind of turbine rows 1, 2, 4, 8, 12, 16 and 20. The corresponding locations are indicated in (a) with vertical dotted lines.
Elliott (Reference Elliott1958) observed that the IBL height grows as
with
![]() $z_{0,1}$
and
$z_{0,1}$
and
![]() $z_{0,2}$
the upwind and downwind surface roughness, respectively. This height is included in figure 7(a), using
$z_{0,2}$
the upwind and downwind surface roughness, respectively. This height is included in figure 7(a), using
![]() $z_{0,1}=2\times 10^{-4}\;\text{m}$
and
$z_{0,1}=2\times 10^{-4}\;\text{m}$
and
![]() $z_{0,2}=1.68\;\text{m}$
, where the latter value has been obtained with the wind farm surface-roughness formula of Calaf et al. (Reference Calaf, Meneveau and Meyers2010). Figure 7(a) further includes least-squares fits of the three measures obtained from the LES results using a power law
$z_{0,2}=1.68\;\text{m}$
, where the latter value has been obtained with the wind farm surface-roughness formula of Calaf et al. (Reference Calaf, Meneveau and Meyers2010). Figure 7(a) further includes least-squares fits of the three measures obtained from the LES results using a power law
![]() $h-h_{0}=ax^{p}$
(with
$h-h_{0}=ax^{p}$
(with
![]() $h$
,
$h$
,
![]() $h_{0}$
and
$h_{0}$
and
![]() $x$
in metres). For all three estimates, we find that the exponents are close to the 0.8 power of Elliott (Reference Elliott1958), i.e. 0.75, 0.71 and 0.74 for
$x$
in metres). For all three estimates, we find that the exponents are close to the 0.8 power of Elliott (Reference Elliott1958), i.e. 0.75, 0.71 and 0.74 for
![]() $h(M)$
,
$h(M)$
,
![]() $h(\unicode[STIX]{x1D70F}_{z})$
and
$h(\unicode[STIX]{x1D70F}_{z})$
and
![]() $h(\unicode[STIX]{x1D70F}_{x})$
, respectively. In the remainder of this study, we will quantify the IBL height with
$h(\unicode[STIX]{x1D70F}_{x})$
, respectively. In the remainder of this study, we will quantify the IBL height with
![]() $h(M)$
as this method is also usable when the IBL interferes with the inversion layer (see § 5.1), while the other estimates become intractable.
$h(M)$
as this method is also usable when the IBL interferes with the inversion layer (see § 5.1), while the other estimates become intractable.
Figure 8(a) shows the increase in turbulent kinetic energy
![]() $\unicode[STIX]{x0394}q$
with respect to the inflow in an
$\unicode[STIX]{x0394}q$
with respect to the inflow in an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a turbine column. We observe that the change in turbulent kinetic energy (TKE) starts in the turbine wakes in the lower part of the boundary layer and then spreads upwards with increasing downwind distance. Further, it is also clear that the flow behind the wind farm is significantly more turbulent than the flow upwind, indicating the existence of a wind farm wake.
$z$
plane through the middle of a turbine column. We observe that the change in turbulent kinetic energy (TKE) starts in the turbine wakes in the lower part of the boundary layer and then spreads upwards with increasing downwind distance. Further, it is also clear that the flow behind the wind farm is significantly more turbulent than the flow upwind, indicating the existence of a wind farm wake.

Figure 8. Contours of (a) turbulent kinetic energy increase
![]() $\unicode[STIX]{x0394}q$
and (b) wind veer
$\unicode[STIX]{x0394}q$
and (b) wind veer
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}$
with respect to the inflow, taken in an
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}$
with respect to the inflow, taken in an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a turbine column (only the lower 1.5 km of the numerical domain are shown) and averaged over the last two simulation hours, for case S1. The evolution of the inversion-layer base and top (solid lines) as well as the growth of the IBL (dashed line) are shown. Wind-turbine disk locations are indicated with vertical black lines.
$z$
plane through the middle of a turbine column (only the lower 1.5 km of the numerical domain are shown) and averaged over the last two simulation hours, for case S1. The evolution of the inversion-layer base and top (solid lines) as well as the growth of the IBL (dashed line) are shown. Wind-turbine disk locations are indicated with vertical black lines.
The streamwise mass transport inside the IBL is reduced due to the lower wind speed compared to upwind conditions. The continuity constraint requires this blockage effect to be compensated by either flow acceleration or boundary-layer thickening. Whereas the neutral pressure-driven approach only allows for flow acceleration above the IBL because of the fixed boundary-layer height, we observe a combination of both aspects (see figure 6 b). In fact, as can be seen in the figure, the inversion layer is pushed slightly upward, while at the same time, the flow also slightly accelerates below the inversion layer. We further found that the centre of the inversion layer coincides almost exactly with a streamline (not shown). This finding indicates that the lifting of the inversion layer is only due to the flow divergence and the accompanying displacement of streamlines, and that it is not related to enhanced turbulent mixing. This idea is supported by figure 8(a) showing no increased turbulence in or close to the inversion layer due its location far above the IBL.
The flow deceleration induces a second effect related to the Coriolis force and the horizontal force balance. As the Coriolis force scales linearly with the wind velocity, a slow down of the flow will reduce this force and cause the wind velocity to turn towards the direction of the pressure gradient. In figure 8(b), showing the difference in wind direction with respect to the inflow direction, this deceleration-induced flow rotation is clearly visible. Moreover, comparison with the TKE increase in figure 8(a) shows that the change in the wind direction occurs more uniformly across the boundary layer. Hence, the observation of Taylor (Reference Taylor1969) that the wind direction and turbulent stress adapt very different to a surface-roughness transition also holds for wind farm boundary layers. In the current case, the maximal directional change is approximately
![]() $2^{\circ }$
near the end of the farm. Dörenkämper et al. (Reference Dörenkämper, Witha, Steinfeld, Heinemann and Kühn2015) also observed a slight deviation to the left for a wind farm under stable atmospheric conditions, and attributed this deflection to the decrease in Coriolis force. Other studies reported wind farm wakes turning away from the pressure gradient towards the geostrophic wind direction (Van der Laan et al.
Reference Van der Laan, Hansen, Sørensen and Réthoré2015; Volker et al.
Reference Volker, Badger, Hahmann and Ott2015), and they attributed this effect to turbulent transport of momentum from above. In the current study, however, we find that enhanced turbulent mixing remains limited to the IBL and that the decrease in Coriolis forces dominates the turbulent transport of spanwise momentum, resulting in a wake deflection towards the pressure gradient.
$2^{\circ }$
near the end of the farm. Dörenkämper et al. (Reference Dörenkämper, Witha, Steinfeld, Heinemann and Kühn2015) also observed a slight deviation to the left for a wind farm under stable atmospheric conditions, and attributed this deflection to the decrease in Coriolis force. Other studies reported wind farm wakes turning away from the pressure gradient towards the geostrophic wind direction (Van der Laan et al.
Reference Van der Laan, Hansen, Sørensen and Réthoré2015; Volker et al.
Reference Volker, Badger, Hahmann and Ott2015), and they attributed this effect to turbulent transport of momentum from above. In the current study, however, we find that enhanced turbulent mixing remains limited to the IBL and that the decrease in Coriolis forces dominates the turbulent transport of spanwise momentum, resulting in a wake deflection towards the pressure gradient.
4.2 Energy budget analysis
The gradual flow deceleration and turbine-wake expansion will have an impact on the energy household in both the wind farm and the boundary layer. In order to understand the different processes that deliver energy to the turbines, we look into the kinetic energy budget. The time-averaged kinetic energy equation (per unit mass) can be derived by multiplying the momentum equation (i.e. (A 2)) with
![]() $u_{i}$
and subsequently averaging the equation in time, resulting in
$u_{i}$
and subsequently averaging the equation in time, resulting in
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left[\bar{u}_{j}\overline{E}_{k}+\bar{u}_{i}\overline{u_{i}^{\prime }u_{j}^{\prime }}+\frac{1}{2}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{j}^{\prime }}+\overline{u_{i}\unicode[STIX]{x1D70F}_{ij}^{r}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =-\overline{\frac{u_{i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p^{\star }}{\unicode[STIX]{x2202}x_{i}}}+\frac{g}{\unicode[STIX]{x1D703}_{0}}\overline{u_{3}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}_{0})}+\overline{\unicode[STIX]{x1D70F}_{ij}^{r}S_{ij}}+\overline{u_{i}f_{i}}-\frac{\bar{u}_{i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x_{i}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left[\bar{u}_{j}\overline{E}_{k}+\bar{u}_{i}\overline{u_{i}^{\prime }u_{j}^{\prime }}+\frac{1}{2}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{j}^{\prime }}+\overline{u_{i}\unicode[STIX]{x1D70F}_{ij}^{r}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =-\overline{\frac{u_{i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p^{\star }}{\unicode[STIX]{x2202}x_{i}}}+\frac{g}{\unicode[STIX]{x1D703}_{0}}\overline{u_{3}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}_{0})}+\overline{\unicode[STIX]{x1D70F}_{ij}^{r}S_{ij}}+\overline{u_{i}f_{i}}-\frac{\bar{u}_{i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x_{i}},\end{eqnarray}$$
with
![]() $\overline{E}_{k}=(\bar{u}_{i}\bar{u}_{i}+\overline{u_{i}^{\prime }u_{i}^{\prime }})/2$
and
$\overline{E}_{k}=(\bar{u}_{i}\bar{u}_{i}+\overline{u_{i}^{\prime }u_{i}^{\prime }})/2$
and
![]() $u_{i}^{\prime }=u_{i}-\bar{u}_{i}$
. We are now interested in the variation of the energy budget terms with streamwise distance, i.e. how do the various terms change when going through the farm. In order to average out local oscillations around the turbines, equation (4.2) is integrated for every turbine row over a control volume. In fact, we will consider two different control volumes
$u_{i}^{\prime }=u_{i}-\bar{u}_{i}$
. We are now interested in the variation of the energy budget terms with streamwise distance, i.e. how do the various terms change when going through the farm. In order to average out local oscillations around the turbines, equation (4.2) is integrated for every turbine row over a control volume. In fact, we will consider two different control volumes
![]() $\unicode[STIX]{x1D6FA}^{t}$
and
$\unicode[STIX]{x1D6FA}^{t}$
and
![]() $\unicode[STIX]{x1D6FA}^{b}$
to interpret the results, as indicated in figure 9. The kinetic energy budget for any control volume
$\unicode[STIX]{x1D6FA}^{b}$
to interpret the results, as indicated in figure 9. The kinetic energy budget for any control volume
![]() $\unicode[STIX]{x1D6FA}$
can be written as
$\unicode[STIX]{x1D6FA}$
can be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{\unicode[STIX]{x1D6FA}}\underbrace{\frac{\unicode[STIX]{x2202}\bar{u}_{j}\overline{E}_{m}}{\unicode[STIX]{x2202}x_{j}}}_{\mathscr{D}}\,\text{d}\unicode[STIX]{x1D6FA}-\left[\int _{\unicode[STIX]{x1D6E4}}\left(\underbrace{\bar{u}_{i}\overline{u_{i}^{\prime }u_{1}^{\prime }}+\frac{1}{2}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{1}^{\prime }}+\overline{u_{1}^{\prime }p^{\prime }}/\unicode[STIX]{x1D70C}+\overline{u_{i}\unicode[STIX]{x1D70F}_{i1}^{r}}}_{\mathscr{F}_{x}}\right)\text{d}\unicode[STIX]{x1D6E4}_{x}\right]_{x_{1}}^{x_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\left[\int _{\unicode[STIX]{x1D6E4}}\left(\underbrace{\bar{u}_{i}\overline{u_{i}^{\prime }u_{3}^{\prime }}+\frac{1}{2}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{3}^{\prime }}+\overline{u_{3}^{\prime }p^{\prime }}/\unicode[STIX]{x1D70C}+\overline{u_{i}\unicode[STIX]{x1D70F}_{i3}^{r}}}_{\mathscr{F}_{z}}\right)\,\text{d}\unicode[STIX]{x1D6E4}_{z}\right]_{z_{l}}^{z_{u}}-\int _{\unicode[STIX]{x1D6FA}}\underbrace{\frac{\bar{u}_{i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x_{i}}}_{\mathscr{P}_{\infty }}\,\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{\unicode[STIX]{x1D6FA}}\underbrace{\frac{g}{\unicode[STIX]{x1D703}_{0}}\overline{u_{3}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}_{0})}}_{\mathscr{P}_{\unicode[STIX]{x1D703}}}\,\text{d}\unicode[STIX]{x1D6FA}+\int _{\unicode[STIX]{x1D6FA}}\underbrace{\overline{\unicode[STIX]{x1D70F}_{ij}^{r}S_{ij}}}_{\mathscr{E}}\,\text{d}\unicode[STIX]{x1D6FA}+\int _{\unicode[STIX]{x1D6FA}}\underbrace{\overline{u_{i}f_{i}}}_{\mathscr{P}_{F}}\,\text{d}\unicode[STIX]{x1D6FA}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{\unicode[STIX]{x1D6FA}}\underbrace{\frac{\unicode[STIX]{x2202}\bar{u}_{j}\overline{E}_{m}}{\unicode[STIX]{x2202}x_{j}}}_{\mathscr{D}}\,\text{d}\unicode[STIX]{x1D6FA}-\left[\int _{\unicode[STIX]{x1D6E4}}\left(\underbrace{\bar{u}_{i}\overline{u_{i}^{\prime }u_{1}^{\prime }}+\frac{1}{2}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{1}^{\prime }}+\overline{u_{1}^{\prime }p^{\prime }}/\unicode[STIX]{x1D70C}+\overline{u_{i}\unicode[STIX]{x1D70F}_{i1}^{r}}}_{\mathscr{F}_{x}}\right)\text{d}\unicode[STIX]{x1D6E4}_{x}\right]_{x_{1}}^{x_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\left[\int _{\unicode[STIX]{x1D6E4}}\left(\underbrace{\bar{u}_{i}\overline{u_{i}^{\prime }u_{3}^{\prime }}+\frac{1}{2}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{3}^{\prime }}+\overline{u_{3}^{\prime }p^{\prime }}/\unicode[STIX]{x1D70C}+\overline{u_{i}\unicode[STIX]{x1D70F}_{i3}^{r}}}_{\mathscr{F}_{z}}\right)\,\text{d}\unicode[STIX]{x1D6E4}_{z}\right]_{z_{l}}^{z_{u}}-\int _{\unicode[STIX]{x1D6FA}}\underbrace{\frac{\bar{u}_{i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x_{i}}}_{\mathscr{P}_{\infty }}\,\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{\unicode[STIX]{x1D6FA}}\underbrace{\frac{g}{\unicode[STIX]{x1D703}_{0}}\overline{u_{3}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}_{0})}}_{\mathscr{P}_{\unicode[STIX]{x1D703}}}\,\text{d}\unicode[STIX]{x1D6FA}+\int _{\unicode[STIX]{x1D6FA}}\underbrace{\overline{\unicode[STIX]{x1D70F}_{ij}^{r}S_{ij}}}_{\mathscr{E}}\,\text{d}\unicode[STIX]{x1D6FA}+\int _{\unicode[STIX]{x1D6FA}}\underbrace{\overline{u_{i}f_{i}}}_{\mathscr{P}_{F}}\,\text{d}\unicode[STIX]{x1D6FA}=0,\end{eqnarray}$$

Figure 9. (a) Front view and (b) side view of the computational domain, illustrating the control volumes in the turbine region (
![]() $\unicode[STIX]{x1D6FA}^{t}$
, grey encircled area) and in the layer above (
$\unicode[STIX]{x1D6FA}^{t}$
, grey encircled area) and in the layer above (
![]() $\unicode[STIX]{x1D6FA}^{b}$
, white encircled area) over which the kinetic energy equation is integrated.
$\unicode[STIX]{x1D6FA}^{b}$
, white encircled area) over which the kinetic energy equation is integrated.
where
![]() $p^{\prime }$
is the turbulent fluctuation in
$p^{\prime }$
is the turbulent fluctuation in
![]() $p^{\star }$
and
$p^{\star }$
and
![]() $(x_{1},x_{2},z_{l},z_{u})$
correspond to the boundaries of the control volume. The integrals need to be computed either over the entire control volume (
$(x_{1},x_{2},z_{l},z_{u})$
correspond to the boundaries of the control volume. The integrals need to be computed either over the entire control volume (
![]() $\text{d}\unicode[STIX]{x1D6FA}$
), or over the
$\text{d}\unicode[STIX]{x1D6FA}$
), or over the
![]() $y$
–
$y$
–
![]() $z$
faces (
$z$
faces (
![]() $\text{d}\unicode[STIX]{x1D6E4}_{x}$
) or
$\text{d}\unicode[STIX]{x1D6E4}_{x}$
) or
![]() $x$
–
$x$
–
![]() $y$
faces (
$y$
faces (
![]() $\text{d}\unicode[STIX]{x1D6E4}_{z}$
) of the control volume. There is no transport through the
$\text{d}\unicode[STIX]{x1D6E4}_{z}$
) of the control volume. There is no transport through the
![]() $x$
–
$x$
–
![]() $z$
faces as all control volumes span the full domain width (remember that the domain is periodic in the spanwise direction). We further introduced the total mechanical energy per unit mass as the sum of kinetic energy and pressure, i.e.
$z$
faces as all control volumes span the full domain width (remember that the domain is periodic in the spanwise direction). We further introduced the total mechanical energy per unit mass as the sum of kinetic energy and pressure, i.e.
![]() $\overline{E}_{m}=\overline{E}_{k}+\bar{p}^{\star }/\unicode[STIX]{x1D70C}$
. Note that the mean background pressure
$\overline{E}_{m}=\overline{E}_{k}+\bar{p}^{\star }/\unicode[STIX]{x1D70C}$
. Note that the mean background pressure
![]() $p_{\infty }$
is not included in the mechanical energy as its gradient represents constant meso-scale forcing.
$p_{\infty }$
is not included in the mechanical energy as its gradient represents constant meso-scale forcing.
Equation (4.3) expresses the balance between all energy sources (positive terms) and sinks (negative terms) in a control volume. The term
![]() $\mathscr{D}$
is the divergence of mechanical energy flux and combines the effects of mean-flow energy fluxes and pressure gradients. The terms
$\mathscr{D}$
is the divergence of mechanical energy flux and combines the effects of mean-flow energy fluxes and pressure gradients. The terms
![]() $\mathscr{F}_{x}$
and
$\mathscr{F}_{x}$
and
![]() $\mathscr{F}_{z}$
correspond to the net energy influx due to turbulent transport through the faces of the control volume in streamwise and vertical direction, respectively. These terms are positive (i.e. they act as a source of energy) when turbulence transports more energy in than out of the control volume. The fourth term (
$\mathscr{F}_{z}$
correspond to the net energy influx due to turbulent transport through the faces of the control volume in streamwise and vertical direction, respectively. These terms are positive (i.e. they act as a source of energy) when turbulence transports more energy in than out of the control volume. The fourth term (
![]() $\mathscr{P}_{\infty }$
) is related to the mean background pressure and the fifth term (
$\mathscr{P}_{\infty }$
) is related to the mean background pressure and the fifth term (
![]() $\mathscr{P}_{\unicode[STIX]{x1D703}}$
) represents the conversion between kinetic and potential energy. The last two terms in (4.3) are energy sinks due to turbulent dissipation
$\mathscr{P}_{\unicode[STIX]{x1D703}}$
) represents the conversion between kinetic and potential energy. The last two terms in (4.3) are energy sinks due to turbulent dissipation
![]() $\mathscr{E}$
and wind-turbine power extraction
$\mathscr{E}$
and wind-turbine power extraction
![]() $\mathscr{P}_{F}$
.
$\mathscr{P}_{F}$
.
We first investigate the kinetic energy balance in the turbine region by considering control volumes
![]() $\unicode[STIX]{x1D6FA}^{t}$
extending from
$\unicode[STIX]{x1D6FA}^{t}$
extending from
![]() $0.5s_{x}D$
upwind of the turbine to
$0.5s_{x}D$
upwind of the turbine to
![]() $0.5s_{x}D$
downwind in the streamwise direction. The turbine region is taken between
$0.5s_{x}D$
downwind in the streamwise direction. The turbine region is taken between
![]() $z_{l}=z_{h}-D/2$
and
$z_{l}=z_{h}-D/2$
and
![]() $z_{u}=z_{h}+D/2$
in the vertical direction, so the control volumes have dimensions
$z_{u}=z_{h}+D/2$
in the vertical direction, so the control volumes have dimensions
![]() $s_{x}D\times L_{y}\times D$
and are centred around the rotor disk (see figure 9).
$s_{x}D\times L_{y}\times D$
and are centred around the rotor disk (see figure 9).
For this configuration, figure 10(a) shows the streamwise variation of mechanical energy flux divergence
![]() $\mathscr{D}^{t}$
, vertical energy transport related to turbulence
$\mathscr{D}^{t}$
, vertical energy transport related to turbulence
![]() $\mathscr{F}_{z}^{t}$
, energy dissipation
$\mathscr{F}_{z}^{t}$
, energy dissipation
![]() $\mathscr{E}^{t}$
and wind-turbine power extraction
$\mathscr{E}^{t}$
and wind-turbine power extraction
![]() $\mathscr{P}_{F}$
, scaled with the average power output of the first turbine row (the superscript
$\mathscr{P}_{F}$
, scaled with the average power output of the first turbine row (the superscript
![]() $t$
indicates integration over
$t$
indicates integration over
![]() $\unicode[STIX]{x1D6FA}^{t}$
). The other terms
$\unicode[STIX]{x1D6FA}^{t}$
). The other terms
![]() $(\mathscr{F}_{x}^{t},\mathscr{P}_{\infty }^{t},\mathscr{P}_{\unicode[STIX]{x1D703}}^{t})$
in (4.3) are small compared to these dominant terms (i.e. less than 3 % of the first row power output) and are therefore not shown. First, we observe a large drop in power extraction between the first and second turbine row, typical for aligned wind farms and reported in several studies (see, e.g. Barthelmie et al.
Reference Barthelmie, Hansen, Frandsen, Rathmann, Schepers, Schlez, Phillips, Rados, Zervos and Politis2009; Newman et al.
Reference Newman, Lebron, Meneveau and Castillo2013; Wu & Porté-Agel Reference Wu and Porté-Agel2013; Stevens et al.
Reference Stevens, Graham and Meneveau2014b
). In our simulation, the observed power drop of 63.5 % is more severe than the typical 40 % often documented in the literature. We attribute this larger power deficit to the lower level of turbulent intensity in our simulation. Following the sudden drop, the power increases slightly in the next couple of rows, after which it remains constant throughout the rest of the farm. Overall, the variation in power output from the third turbine row onward is less than 6 % of the power output of the first turbine. Further, the energy dissipation in the turbine region only varies by approximately 3 % throughout the farm (with respect to the power output of the first turbine), except for the first turbine row where the dissipation is lower.
$(\mathscr{F}_{x}^{t},\mathscr{P}_{\infty }^{t},\mathscr{P}_{\unicode[STIX]{x1D703}}^{t})$
in (4.3) are small compared to these dominant terms (i.e. less than 3 % of the first row power output) and are therefore not shown. First, we observe a large drop in power extraction between the first and second turbine row, typical for aligned wind farms and reported in several studies (see, e.g. Barthelmie et al.
Reference Barthelmie, Hansen, Frandsen, Rathmann, Schepers, Schlez, Phillips, Rados, Zervos and Politis2009; Newman et al.
Reference Newman, Lebron, Meneveau and Castillo2013; Wu & Porté-Agel Reference Wu and Porté-Agel2013; Stevens et al.
Reference Stevens, Graham and Meneveau2014b
). In our simulation, the observed power drop of 63.5 % is more severe than the typical 40 % often documented in the literature. We attribute this larger power deficit to the lower level of turbulent intensity in our simulation. Following the sudden drop, the power increases slightly in the next couple of rows, after which it remains constant throughout the rest of the farm. Overall, the variation in power output from the third turbine row onward is less than 6 % of the power output of the first turbine. Further, the energy dissipation in the turbine region only varies by approximately 3 % throughout the farm (with respect to the power output of the first turbine), except for the first turbine row where the dissipation is lower.

Figure 10. Streamwise variation of energy sources and sinks in the turbine region, normalised by the average power extraction of the first turbine row. (a) Dominant energy sources and sinks in (4.3), including mechanical energy flux divergence
![]() $\mathscr{D}^{t}$
(squares), vertical energy transport related to turbulence
$\mathscr{D}^{t}$
(squares), vertical energy transport related to turbulence
![]() $\mathscr{F}_{z}^{t}$
(circles), energy dissipation
$\mathscr{F}_{z}^{t}$
(circles), energy dissipation
![]() $\mathscr{E}^{t}$
(triangles) and wind-turbine power extraction
$\mathscr{E}^{t}$
(triangles) and wind-turbine power extraction
![]() $\mathscr{P}_{F}$
(diamonds); (b) decomposition of the mechanical energy flux divergence
$\mathscr{P}_{F}$
(diamonds); (b) decomposition of the mechanical energy flux divergence
![]() $\mathscr{D}^{t}$
(solid grey line) into energy related to streamwise pressure gradient (squares) and mean-flow kinetic energy transport in streamwise (circles) and vertical (triangles) direction (see (4.4)). In the top right corner, the components in the second part of the wind farm are magnified.
$\mathscr{D}^{t}$
(solid grey line) into energy related to streamwise pressure gradient (squares) and mean-flow kinetic energy transport in streamwise (circles) and vertical (triangles) direction (see (4.4)). In the top right corner, the components in the second part of the wind farm are magnified.
The energy extraction and dissipation are balanced by two different processes. The divergence of mechanical energy flux acts as a first source of energy. As observed in figure 10(a), this term is dominant in the first row but then quickly decreases throughout the farm. More insight can be gained by decomposing this energy source into four terms:
The first two terms refer to the energy delivered or consumed by pressure gradients (excluding the mean background pressure), whereas the last two terms indicate the kinetic energy transported by the mean flow through the boundaries of the control volume. Figure 10(b) shows the mechanical energy divergence and the various components, except for the energy related to the vertical pressure gradient which is negligible. From this figure, it is clear that, for every turbine row, there is more kinetic energy entering the control volume than leaving it through the
![]() $y$
–
$y$
–
![]() $z$
faces, thereby releasing a large amount of energy. However, a considerable amount of this energy leaves the control volume again through the upper or lower face. This is a logical consequence of the vertical mass flux out of the turbine region due to the flow deceleration and the continuity constraint. In other words, these results indicate that, although the flow deceleration releases a lot of energy, not all of this energy is available for power extraction by the wind turbines. Inevitably, part of the kinetic energy leaves the turbine region with the vertical mass flux. Furthermore, it is surprising to see that neither of these components nor the total mechanical energy divergence becomes zero in the farm, though we would expect the streamwise variations to be negligible in a fully developed flow regime. This finding therefore suggests that, with respect to the mean flow, a fully developed regime is nowhere achieved. Figure 10(b) also contains a detailed view of the second half of the wind farm, showing some interesting developments near the end of the farm. First, both streamwise and vertical energy transport change sign in the last few rows, indicating that the wind is flowing downwards and accelerating. Second, there is a streamwise pressure gradient that is delivering energy, although its contribution remains relatively small. As discussed below, this pressure gradient is related to the effect of gravity waves.
$z$
faces, thereby releasing a large amount of energy. However, a considerable amount of this energy leaves the control volume again through the upper or lower face. This is a logical consequence of the vertical mass flux out of the turbine region due to the flow deceleration and the continuity constraint. In other words, these results indicate that, although the flow deceleration releases a lot of energy, not all of this energy is available for power extraction by the wind turbines. Inevitably, part of the kinetic energy leaves the turbine region with the vertical mass flux. Furthermore, it is surprising to see that neither of these components nor the total mechanical energy divergence becomes zero in the farm, though we would expect the streamwise variations to be negligible in a fully developed flow regime. This finding therefore suggests that, with respect to the mean flow, a fully developed regime is nowhere achieved. Figure 10(b) also contains a detailed view of the second half of the wind farm, showing some interesting developments near the end of the farm. First, both streamwise and vertical energy transport change sign in the last few rows, indicating that the wind is flowing downwards and accelerating. Second, there is a streamwise pressure gradient that is delivering energy, although its contribution remains relatively small. As discussed below, this pressure gradient is related to the effect of gravity waves.
The second source of energy that balances energy extraction and dissipation is related to vertical turbulent fluxes transporting kinetic energy from above the wind farm into the turbine region (see figure 10 a). For fully developed wind farms, this energy transport provides almost all the kinetic energy extracted by the turbines (Calaf et al. Reference Calaf, Meneveau and Meyers2010). For the developing case considered here, vertical turbulent energy transport is small at first but becomes the dominant source of energy starting from the third turbine row. From the eighth turbine row onward, this term varies less than 3 % of the power output of the first turbine. This means that, with respect to turbulent stresses and contrary to mean-flow behaviour, the turbulence can be considered fully developed after eight turbine rows.
In summary, figure 10 shows that the energy extracted by the turbines is provided by mean-flow deceleration in the turbine region and vertical turbulent energy transport from above the farm. However, the question then arises as to which processes are balancing the vertical energy transport in the boundary layer. Allaerts & Meyers (Reference Allaerts and Meyers2015) showed that the work by the background pressure gradient is the main source of energy in a fully developed wind farm, but it is unclear whether this conclusion also holds for developing wind farms. To answer this question, the energy budget analysis is repeated for control volumes
![]() $\unicode[STIX]{x1D6FA}^{b}$
extending from
$\unicode[STIX]{x1D6FA}^{b}$
extending from
![]() $z_{l}=z_{h}+D/2$
up to the height of the boundary layer
$z_{l}=z_{h}+D/2$
up to the height of the boundary layer
![]() $z_{u}=h$
(the streamwise and spanwise dimensions are unchanged, see figure 9), and the results are presented in figure 11.
$z_{u}=h$
(the streamwise and spanwise dimensions are unchanged, see figure 9), and the results are presented in figure 11.

Figure 11. Streamwise variation of energy sources and sinks in the layer above the wind farm, normalised by the average power extraction of the first turbine row. (a) Dominant energy sources and sinks in (4.3), including mechanical energy flux divergence
![]() $\mathscr{D}^{b}$
(squares), vertical energy transport related to turbulence
$\mathscr{D}^{b}$
(squares), vertical energy transport related to turbulence
![]() $\mathscr{F}_{z}^{b}$
(circles), energy dissipation
$\mathscr{F}_{z}^{b}$
(circles), energy dissipation
![]() $\mathscr{E}^{b}$
(triangles) and work by the mean background pressure
$\mathscr{E}^{b}$
(triangles) and work by the mean background pressure
![]() $\mathscr{P}_{\infty }^{b}$
(stars); (b) decomposition of the mechanical energy flux divergence
$\mathscr{P}_{\infty }^{b}$
(stars); (b) decomposition of the mechanical energy flux divergence
![]() $\mathscr{D}^{b}$
(solid grey line) into energy related to streamwise pressure gradient (squares) and divergence of the mean-flow kinetic energy flux (circles) (i.e. the sum of the last two terms in (4.4)).
$\mathscr{D}^{b}$
(solid grey line) into energy related to streamwise pressure gradient (squares) and divergence of the mean-flow kinetic energy flux (circles) (i.e. the sum of the last two terms in (4.4)).
The energy balance in the region above the wind farm is governed by mechanical energy divergence
![]() $\mathscr{D}^{b}$
, vertical turbulent transport
$\mathscr{D}^{b}$
, vertical turbulent transport
![]() $\mathscr{F}_{z}^{b}$
, energy dissipation
$\mathscr{F}_{z}^{b}$
, energy dissipation
![]() $\mathscr{E}^{b}$
and work by the mean background pressure
$\mathscr{E}^{b}$
and work by the mean background pressure
![]() $\mathscr{P}_{\infty }^{b}$
(potential energy conversion and streamwise turbulent transport are again small and therefore not shown). Contrary to the results of Allaerts & Meyers (Reference Allaerts and Meyers2015), figure 11(a) shows that the vertical turbulent transport is mainly balanced by the mechanical energy flux divergence
$\mathscr{P}_{\infty }^{b}$
(potential energy conversion and streamwise turbulent transport are again small and therefore not shown). Contrary to the results of Allaerts & Meyers (Reference Allaerts and Meyers2015), figure 11(a) shows that the vertical turbulent transport is mainly balanced by the mechanical energy flux divergence
![]() $\mathscr{D}^{b}$
, and the work by the mean background pressure is only approximately
$\mathscr{D}^{b}$
, and the work by the mean background pressure is only approximately
![]() $0.3\mathscr{D}^{b}$
except above the first few rows. As before, the dominant energy source can be further investigated by decomposing it according to equation (4.4), as shown in figure 11(b). The energy related to the vertical pressure gradient is again negligible, and the last two terms are combined to give the divergence of the mean-flow kinetic energy flux. This mean-flow divergence indicates whether the total kinetic energy of the layer above the farm is increasing or decreasing when advancing in streamwise direction. Negative values thereby correspond to a kinetic energy increase and are mainly related to flow acceleration, whereas positive values are caused by the IBL growth and the accompanying velocity deficit inside it. It appears that the flow acceleration is dominant at the beginning and end of the farm, but the IBL growth dominates in the middle and causes the total kinetic energy to decrease. Finally, we observe that a considerable amount of energy is delivered by a streamwise pressure gradient. This pressure gradient is caused by gravity waves, further discussed in the next section.
$0.3\mathscr{D}^{b}$
except above the first few rows. As before, the dominant energy source can be further investigated by decomposing it according to equation (4.4), as shown in figure 11(b). The energy related to the vertical pressure gradient is again negligible, and the last two terms are combined to give the divergence of the mean-flow kinetic energy flux. This mean-flow divergence indicates whether the total kinetic energy of the layer above the farm is increasing or decreasing when advancing in streamwise direction. Negative values thereby correspond to a kinetic energy increase and are mainly related to flow acceleration, whereas positive values are caused by the IBL growth and the accompanying velocity deficit inside it. It appears that the flow acceleration is dominant at the beginning and end of the farm, but the IBL growth dominates in the middle and causes the total kinetic energy to decrease. Finally, we observe that a considerable amount of energy is delivered by a streamwise pressure gradient. This pressure gradient is caused by gravity waves, further discussed in the next section.
4.3 Wind farm-induced gravity waves
The displacement of the streamlines above the IBL, observed in figure 6(b), excites gravity waves in the inversion layer and the stably stratified free atmosphere. The evidence of these waves is found in figure 12, showing contours of streamwise and vertical velocity, pressure and potential temperature, averaged in time and in spanwise direction, for case S1. Note that the average inflow profile has been subtracted from the time-averaged solution fields of streamwise velocity and potential temperature. The wind farm-induced atmospheric gravity waves create a slanted pattern of alternating positive and negative perturbations in the solution field of every variable. The size and inclination of these structures is the same for every variable, but the exact locations of minima and maxima differ according to the polarisation equations (Nappo Reference Nappo2002). For instance, the streamwise velocity and the pressure are anti-correlated, whereas the potential-temperature perturbations have a
![]() $90^{\circ }$
phase difference with the other variables (e.g.
$90^{\circ }$
phase difference with the other variables (e.g.
![]() $\langle \bar{\unicode[STIX]{x1D703}}\rangle -\unicode[STIX]{x1D703}_{ref}=0$
when
$\langle \bar{\unicode[STIX]{x1D703}}\rangle -\unicode[STIX]{x1D703}_{ref}=0$
when
![]() $\langle \bar{p}^{\star }\rangle$
reaches an extremum, and vice versa). We further observe that the group velocity of these waves forms an angle of approximately
$\langle \bar{p}^{\star }\rangle$
reaches an extremum, and vice versa). We further observe that the group velocity of these waves forms an angle of approximately
![]() $20^{\circ }$
with the horizontal.
$20^{\circ }$
with the horizontal.

Figure 12. Contours of (a) streamwise velocity, (b) vertical velocity, (c) pressure and (d) potential temperature, averaged in time and in spanwise direction, for case S1. The mean inflow profile has been subtracted from the time-averaged solution fields of streamwise velocity and potential temperature to obtain perturbation quantities.
In the vertical velocity field, the wave pattern appears less orderly than in the other wave fields. These distortions are caused by partial wave reflection from the top of the domain and are most obvious in the vertical velocity field. In order to verify the efficiency of the upper boundary condition, the method provided by Taylor & Sarkar (Reference Taylor and Sarkar2007) is used. Based on the intrinsic property that the sign of the vertical group velocity is opposite to the sign of the vertical phase velocity, the wave field can be decomposed into upward and downward propagating waves. As the only source of gravity waves is located near the bottom of the domain, downward propagating waves must be due to reflection from the top. For case S1, the vertical kinetic energy
![]() $(0.5w^{2})$
associated with downward propagating waves is approximately 7.8 % of the energy associated with upward propagating waves, which is similar in order of magnitude to Taylor & Sarkar (Reference Taylor and Sarkar2007). For other cases discussed in the current work (S2 and S4), the reflected energy is 6.2 % and 4.8 %, respectively
$(0.5w^{2})$
associated with downward propagating waves is approximately 7.8 % of the energy associated with upward propagating waves, which is similar in order of magnitude to Taylor & Sarkar (Reference Taylor and Sarkar2007). For other cases discussed in the current work (S2 and S4), the reflected energy is 6.2 % and 4.8 %, respectively
The mechanism triggering the gravity-wave solution can also be appreciated from figure 12. As the wind turbines extract energy from the flow, a momentum deficit accumulates in the wind farm, indicated by the negative velocity perturbation inside the wind farm in figure 12(a). As mentioned before, the continuity constraint results in an upward flow deflection, which appears as a positive vertical velocity above the farm in figure 12(b). This vertical velocity pushes the inversion layer upwards and results in a thickening of the boundary layer. The upward displacement of the inversion layer appears as a negative perturbation in the potential-temperature field (see figure 12 d), as cold air is brought up from below. Finally, similar to stratified flow over topography, the combination of temperature stratification and boundary-layer displacement results in the formation of gravity waves.
Besides the obvious vertically propagating gravity waves in the free atmosphere, we also observe a strong vertical pressure gradient in the inversion layer in figure 12(c). The difference in pressure above and below the inversion is caused by the simple fact that a cold temperature anomaly induces a high pressure anomaly below (Smith Reference Smith2010). As the boundary-layer height increases, the column of cold, heavy air grows taller and results in a higher pressure. The pressure inside the boundary layer is thus the sum of two components related to the vertically propagating waves and to the inversion strength. Figure 12(c) shows that the gravity waves induce a favourable pressure gradient inside the wind farm, similar to the findings of Smith (Reference Smith2010) based on linear gravity-wave theory. The amplitude of the induced pressure gradient is of the same order of magnitude as the background pressure gradient in the streamwise direction, which is of the order of
![]() $10^{-4}~\text{m}~\text{s}^{-2}$
.
$10^{-4}~\text{m}~\text{s}^{-2}$
.
5 Developing wind farms under various inflow conditions
In the current section, we investigate the effects of varying inflow heights on wind farm boundary layers. As before, we first focus on the flow behaviour inside and above the wind farm in § 5.1. Subsequently, wind farm power extraction and energy budget terms of the different cases will be discussed in § 5.2.
5.1 Flow modification under low inversion layers
The difference in flow behaviour resulting from a lower inflow height is illustrated in a qualitative way in figure 13, which shows contours of time-averaged horizontal velocity in an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a turbine column for the various cases (a more quantitative comparison of the three cases follows below in figures 14–16). Inside the farm, the velocity fields appear very similar. However, the shape of the IBL indicates that there are important differences in the boundary-layer flow between the three cases. In the previous section, we found that the IBL does not interact with the inversion layer in the baseline case. Lowering the inflow height results in a collision between the IBL and the inversion at some point in the farm, and the IBL growth is limited further downwind. This event occurs around the twelfth turbine row for case S2, whereas in case S4, the IBL and the inversion already coincide after the second turbine row.
$z$
plane through the middle of a turbine column for the various cases (a more quantitative comparison of the three cases follows below in figures 14–16). Inside the farm, the velocity fields appear very similar. However, the shape of the IBL indicates that there are important differences in the boundary-layer flow between the three cases. In the previous section, we found that the IBL does not interact with the inversion layer in the baseline case. Lowering the inflow height results in a collision between the IBL and the inversion at some point in the farm, and the IBL growth is limited further downwind. This event occurs around the twelfth turbine row for case S2, whereas in case S4, the IBL and the inversion already coincide after the second turbine row.

Figure 13. Contours of time-averaged horizontal velocity magnitude
![]() $(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
in an
$(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
in an
![]() $x$
–
$x$
–
![]() $z$
plane through the middle of a turbine column, normalised by the geostrophic wind speed, for cases (a) S1, (b) S2 and (c) S4. The evolution of the inversion-layer base and top (solid lines) as well as the growth of the IBL height (dashed line) are included. The location of the wind-turbine disks are indicated with vertical black lines.
$z$
plane through the middle of a turbine column, normalised by the geostrophic wind speed, for cases (a) S1, (b) S2 and (c) S4. The evolution of the inversion-layer base and top (solid lines) as well as the growth of the IBL height (dashed line) are included. The location of the wind-turbine disks are indicated with vertical black lines.
The vertical profiles of horizontal velocity magnitude are compared in figure 14 for the three LES cases at various locations in the farm. We observe a clear double logarithmic structure up to the height of the IBL from the fourth turbine row onward. Even though there is a continued decrease in velocity magnitude with downwind distance, we find that the velocity profile in the internal boundary layer becomes self-similar after the tenth turbine row when scaled with the friction velocity of the lower log layer, i.e.
![]() $u_{\ast \mathit{lo}}(x)=[\unicode[STIX]{x1D70F}_{w}(x)/\unicode[STIX]{x1D70C}_{0}]^{1/2}$
. Comparing the different cases, we observe that the strongest decrease in velocity magnitude corresponds to the lowest inflow height. Between the top of the turbine region and the supergeostrophic jet near the boundary-layer top, the IBL separates the velocity profile in two regions with distinct slopes (see, e.g. the profiles of turbine row 2). Due to the IBL growth with streamwise distance, the transition between the two slopes occurs at increasing heights throughout the farm. In case S1, the two regimes are visible in the entire wind farm. In the lower CNBL cases, on the other hand, the log layer above the IBL disappears when the IBL starts interfering with the inversion layer. Finally, above the boundary layer, we observe variations in horizontal velocity with streamwise distance, and this is caused by gravity-wave perturbations.
$u_{\ast \mathit{lo}}(x)=[\unicode[STIX]{x1D70F}_{w}(x)/\unicode[STIX]{x1D70C}_{0}]^{1/2}$
. Comparing the different cases, we observe that the strongest decrease in velocity magnitude corresponds to the lowest inflow height. Between the top of the turbine region and the supergeostrophic jet near the boundary-layer top, the IBL separates the velocity profile in two regions with distinct slopes (see, e.g. the profiles of turbine row 2). Due to the IBL growth with streamwise distance, the transition between the two slopes occurs at increasing heights throughout the farm. In case S1, the two regimes are visible in the entire wind farm. In the lower CNBL cases, on the other hand, the log layer above the IBL disappears when the IBL starts interfering with the inversion layer. Finally, above the boundary layer, we observe variations in horizontal velocity with streamwise distance, and this is caused by gravity-wave perturbations.

Figure 14. Vertical profiles of time-averaged horizontal velocity magnitude
![]() $(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
, normalised by the geostrophic wind speed, for cases S1 (solid lines), S2 (dashed lines) and S4 (dash-dotted lines). The vertical profiles have been averaged over the full spanwise direction and over a streamwise distance
$(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
, normalised by the geostrophic wind speed, for cases S1 (solid lines), S2 (dashed lines) and S4 (dash-dotted lines). The vertical profiles have been averaged over the full spanwise direction and over a streamwise distance
![]() $s_{x}D$
centred around turbine rows 1, 2, 4, 8, 12, 16 and 20. The inflow profile has been obtained between
$s_{x}D$
centred around turbine rows 1, 2, 4, 8, 12, 16 and 20. The inflow profile has been obtained between
![]() $-2.3s_{x}D$
and
$-2.3s_{x}D$
and
![]() $-0.5s_{x}D$
. Vertical dotted lines mark the bottom and top of the turbine region.
$-0.5s_{x}D$
. Vertical dotted lines mark the bottom and top of the turbine region.
Figure 15(a) shows the displacement of the boundary-layer top. In contrast to case S1, the wind farm blockage effect cannot be compensated by an acceleration between the IBL and the inversion layer in case S2 and S4 (see figure 13). Instead, the entire reduction in streamwise mass transport is compensated by the displacement of the boundary-layer top. For the wind farm under consideration, lowering the inversion from 1000 to 300 m raises the maximum displacement from 75 to 97 m. This corresponds to a relative thickening of the boundary layer of 33 % in case S4. Further, we observe that the ascent of the boundary-layer top already starts upwind of the wind farm. On the other hand, the maximum displacement of the boundary-layer top and the onset of its descend always occur before the end of the farm.

Figure 15. Streamwise variation of (a) boundary-layer top displacement and (b) average pressure perturbation for cases S1 (squares), S2 (circles) and S4 (triangles). The vertical dashed lines indicate the start and end of the wind farm. In (b), the pressure prediction based on linear theory (Smith Reference Smith2010) is included (grey).
Figure 15(b) shows the average pressure perturbation in the boundary layer, i.e. averaged over a control volume with dimensions
![]() $s_{x}D\times L_{y}\times h$
with
$s_{x}D\times L_{y}\times h$
with
![]() $h$
the height of the boundary layer. As the pressure perturbations are directly related to the boundary-layer displacement, the pressure also increases for decreasing inflow heights. The general shape of the perturbation is similar in all cases: the pressure increases upwind of the farm, reaches a maximum somewhere inside the farm and then decreases. For case S1, the maximum pressure occurs at the beginning of the farm, creating a favourable pressure gradient throughout the farm. However, the location of the maximum moves downwind with decreasing inflow height, which induces counteracting pressure gradients in the first part of the farm. According to linear theory (Smith Reference Smith2010), the Fourier transformation of the pressure at the top of the boundary layer is given by
$h$
the height of the boundary layer. As the pressure perturbations are directly related to the boundary-layer displacement, the pressure also increases for decreasing inflow heights. The general shape of the perturbation is similar in all cases: the pressure increases upwind of the farm, reaches a maximum somewhere inside the farm and then decreases. For case S1, the maximum pressure occurs at the beginning of the farm, creating a favourable pressure gradient throughout the farm. However, the location of the maximum moves downwind with decreasing inflow height, which induces counteracting pressure gradients in the first part of the farm. According to linear theory (Smith Reference Smith2010), the Fourier transformation of the pressure at the top of the boundary layer is given by
![]() $\hat{p}/\unicode[STIX]{x1D70C}_{0}=(\text{i}N^{2}/m+g^{\prime })\,\hat{\unicode[STIX]{x1D702}}$
, where the first term is the perturbation caused by vertically propagating gravity waves and
$\hat{p}/\unicode[STIX]{x1D70C}_{0}=(\text{i}N^{2}/m+g^{\prime })\,\hat{\unicode[STIX]{x1D702}}$
, where the first term is the perturbation caused by vertically propagating gravity waves and
![]() $g^{\prime }=g\unicode[STIX]{x0394}\unicode[STIX]{x1D703}/\unicode[STIX]{x1D703}_{0}$
is the reduced gravity accounting for the inversion strength. Using the LES data for the boundary-layer displacement
$g^{\prime }=g\unicode[STIX]{x0394}\unicode[STIX]{x1D703}/\unicode[STIX]{x1D703}_{0}$
is the reduced gravity accounting for the inversion strength. Using the LES data for the boundary-layer displacement
![]() $\unicode[STIX]{x1D702}$
, predictions of the pressure perturbation are obtained from linear theory and also included in figure 15(b). The agreement with the actual pressure is remarkably good, both in terms of perturbation magnitude and shape. Linear theory overestimates pressure perturbations from the LES, and the location of the maximum is predicted too far downwind for case S1.
$\unicode[STIX]{x1D702}$
, predictions of the pressure perturbation are obtained from linear theory and also included in figure 15(b). The agreement with the actual pressure is remarkably good, both in terms of perturbation magnitude and shape. Linear theory overestimates pressure perturbations from the LES, and the location of the maximum is predicted too far downwind for case S1.
The growth of the IBL height
![]() $\unicode[STIX]{x0394}h(M)$
of the different cases is compared in figure 16(a) in a double logarithmic scale. In all three cases, the height evolution follows a slope close to 0.8 in the beginning of the farm. In cases S1 and S2, the slope increases slightly from the third turbine row onward, which might be related to outer-layer effects as the theoretical prediction of Elliott (Reference Elliott1958) only holds in the surface layer. Figure 16(a) further shows that the growth rate is reduced when the IBL interferes with the inversion layer in cases S2 and S4.
$\unicode[STIX]{x0394}h(M)$
of the different cases is compared in figure 16(a) in a double logarithmic scale. In all three cases, the height evolution follows a slope close to 0.8 in the beginning of the farm. In cases S1 and S2, the slope increases slightly from the third turbine row onward, which might be related to outer-layer effects as the theoretical prediction of Elliott (Reference Elliott1958) only holds in the surface layer. Figure 16(a) further shows that the growth rate is reduced when the IBL interferes with the inversion layer in cases S2 and S4.

Figure 16. (a) IBL height, shown in a double logarithmic scale, and (b) difference in wind direction at hub height with respect to the inflow wind direction, averaged over the full spanwise direction and over a streamwise distance
![]() $s_{x}D$
centred around each turbine row, for cases S1 (squares), S2 (circles) and S4 (triangles). The dashed line in (a) corresponds to a slope of 0.8. The vertical dashed lines in (b) indicate the start and end of the wind farm.
$s_{x}D$
centred around each turbine row, for cases S1 (squares), S2 (circles) and S4 (triangles). The dashed line in (a) corresponds to a slope of 0.8. The vertical dashed lines in (b) indicate the start and end of the wind farm.
Figure 16(b) shows the difference in wind direction at hub height with respect to the inflow wind direction, averaged over the full spanwise direction and over a streamwise distance
![]() $s_{x}D$
centred around each turbine row. The average wind deviation at hub height increases almost linearly through the farm and reaches a maximum of approximately
$s_{x}D$
centred around each turbine row. The average wind deviation at hub height increases almost linearly through the farm and reaches a maximum of approximately
![]() $1.5^{\circ }$
for case S1. The maximum wind deviation increases to
$1.5^{\circ }$
for case S1. The maximum wind deviation increases to
![]() $2.3^{\circ }$
when lowering the inversion from 1000 m to 500 m, but stays the same when the inflow height is further reduced.
$2.3^{\circ }$
when lowering the inversion from 1000 m to 500 m, but stays the same when the inflow height is further reduced.
5.2 Wind farm power extraction
The wind farm performance in the various cases is presented in figure 17, showing the average turbine power extraction per row. The results have been normalised by the average power (per unit density) of a first row turbine, which was found to be 2.80, 2.79 and 2.73
![]() $[\times 10^{6}~\text{m}^{5}~\text{s}^{-3}]$
in cases S1, S2 and S4, respectively. The general trend in the power extraction per turbine row is very similar among the various cases, but the power deficits are slightly larger for decreasing inflow boundary-layer heights. For example, the turbine power output in case S4 is 6 to 9 percentage points (pp) lower than the power output in the same row in case S1.
$[\times 10^{6}~\text{m}^{5}~\text{s}^{-3}]$
in cases S1, S2 and S4, respectively. The general trend in the power extraction per turbine row is very similar among the various cases, but the power deficits are slightly larger for decreasing inflow boundary-layer heights. For example, the turbine power output in case S4 is 6 to 9 percentage points (pp) lower than the power output in the same row in case S1.

Figure 17. Average power extraction per turbine row, normalised by the first row, for cases S1 (squares), S2 (circles) and S4 (triangles).
The variation of the power deficit with varying inflow height can be further clarified by investigating the dominant energy sources in the turbine region, i.e. the turbulent transport of kinetic energy from above and the mechanical energy divergence, as shown in figure 18(a). For all cases, mechanical energy divergence is large in the beginning of the farm, and vertical turbulent energy transport becomes dominant after a couple of turbine rows. Decreasing the inflow height reduces turbulent energy transport with approximately 12 pp between S1 and S4, whereas the maximum difference in mechanical energy divergence is only 5 pp for these cases. Hence, the difference in wind farm performance is mainly due to the difference in turbulent energy transport. Note also that the mechanical energy divergence stays significant throughout the farm in all cases, i.e. approximately 30 to 35 % of the turbulent flux.

Figure 18. Streamwise variation of energy sources and sinks in the turbine region for cases S1 (squares), S2 (circles) and S4 (triangles), normalised by the average power extraction of the first turbine row. (a) Dominant energy sources of (4.3), including mechanical energy flux divergence
![]() $\mathscr{D}^{t}$
(grey) and vertical energy transport related to turbulence
$\mathscr{D}^{t}$
(grey) and vertical energy transport related to turbulence
![]() $\mathscr{F}_{z}^{t}$
(black); (b) energy related to streamwise pressure gradient (black) and mean-flow kinetic energy transport in streamwise direction (grey) (see (4.4)). In the top right corner, the components in the second part of the wind farm are magnified.
$\mathscr{F}_{z}^{t}$
(black); (b) energy related to streamwise pressure gradient (black) and mean-flow kinetic energy transport in streamwise direction (grey) (see (4.4)). In the top right corner, the components in the second part of the wind farm are magnified.
The small differences in mechanical energy divergence are further explained in figure 18(b), showing terms one and three in (4.4) for the various cases. In accordance with the pressure profiles in figure 15(b), the cases with a lower inflow height experience an energy sink in the first part of the farm due to the counteracting pressure gradient. Further downwind, the induced pressure gradients become favourable and act as a source, as can be seen in the detailed plot in the top right corner. Interestingly, the streamwise mean-flow deceleration increases with decreasing inflow boundary-layer heights due to counteracting pressure gradient and partially due to the higher vertical mass flux (not shown here). This term becomes negative near the end of the farm in all cases, indicating that the wind is flowing downwards and accelerating.
Similar to the analysis in § 4.2, the processes that balance vertical turbulent energy transport can be investigated by looking at the energy budget in the region above the wind farm. The dominant energy terms in this region are shown in figure 19(a). The work by the mean background pressure is highest when the inflow height is high, but remains approximately two to four times smaller than the mechanical energy divergence in all cases. The latter rises sharply in the first few rows and then decreases slowly towards the end of the farm. The initial rise collapses for all cases, whereas the subsequent decrease is strongest for the lowest case.

Figure 19. Streamwise variation of energy sources and sinks in the layer above the wind farm for cases S1 (squares), S2 (circles) and S4 (triangles), normalised by the average power extraction of the first turbine row. (a) Dominant energy sources of (4.3), including mechanical energy flux divergence
![]() $\mathscr{D}^{b}$
(black) and work by the mean background pressure
$\mathscr{D}^{b}$
(black) and work by the mean background pressure
![]() $\mathscr{P}_{\infty }^{b}$
(grey); (b) energy related to streamwise pressure gradient (black) and divergence of the mean-flow kinetic energy flux (grey) (see (4.4)).
$\mathscr{P}_{\infty }^{b}$
(grey); (b) energy related to streamwise pressure gradient (black) and divergence of the mean-flow kinetic energy flux (grey) (see (4.4)).
The decomposition of the mechanical energy divergence into work by streamwise pressure gradients and divergence of mean-flow kinetic energy flux is shown in figure 19(b). Despite the relatively small changes in the mechanical energy divergence, large variations are observed in both contributing terms. Furthermore, the behaviour of both terms is almost reversed, i.e. an increase in work by pressure gradients is mostly accompanied by a decrease in mean-flow divergence and vice versa. This complex interplay can be better understood in terms of the energy flux. Therefore, figure 20 presents the total flux of mechanical energy through the boundary layer and the contributions of kinetic energy and pressure (excluding the mean background pressure). The results are normalised by the flux at the entrance of the farm, and figure 20(b) shows the relative change in both contributions with respect to the inflow. In figure 20(a), the energy flux is nearly constant upwind of the farm which indicates that the boundary layer is in a quasi-equilibrium state. Inside the farm, the total mechanical energy flux decreases monotonically throughout the wind farm as energy is being extracted by wind turbines and dissipated by turbulence. We observe that the relative reduction in energy flux increases for decreasing boundary-layer heights, i.e. a reduction of 11 %, 22 % and 31 % in cases S1, S2 and S4, respectively. Downwind of the farm, the energy flux is considerably lower than upwind, and the flux remains constant or increases slightly.

Figure 20. (a) Total mechanical energy flux in the boundary layer and (b) contributions of kinetic energy (black) and pressure (grey), for cases S1 (squares), S2 (circles) and S4 (triangles). All results are normalised by the total mechanical energy flux at the entrance of the farm, and in (b) the relative change with respect to the inflow (
![]() $x=-10~\text{km}$
) is shown.
$x=-10~\text{km}$
) is shown.
Figure 20(b) shows that the mechanical energy in the boundary layer is not always available in the form of kinetic energy, as part of the energy is contained in the pressure field that is induced by the gravity waves. Moreover, significant conversion between kinetic energy and pressure occurs throughout the boundary layer, even when the total mechanical energy flux remains constant. Upwind of the farm, the kinetic energy flux decreases and causes the pressure to rise. At some point in the farm, the pressure starts to decrease, thereby releasing its energy to the boundary layer. The effect of the pressure gradient is thus to redistribute energy throughout wind farm. This effect is largest for the lowest CNBL case where, at the pressure peak, more than 16 % of the total mechanical energy flux is comprised of pressure contributions, all of which is gathered upwind and in the beginning of the farm and released again in the last rows and in the wind farm wake.
6 Summary and conclusion
The current study set out to analyse how boundary-layer flow adapts to the presence of a large wind farm under conventionally neutral conditions. In particular, we focused on shallow wind farm boundary layers where outer-layer effects are important. Streamwise flow development was obtained by breaking the solver’s periodicity with the concurrent-precursor method, and special care was taken to avoid wave reflection at the domain boundaries. Further, the boundary-layer flow and the wind farm were initialised in several steps in order to represent a realistic, offshore wind farm operating in steady-state conditions. A set of simulations was performed with varying inflow boundary-layer heights, allowing us to study the impact of the boundary-layer depth and the overlying inversion layer on the flow behaviour.
Boundary-layer flow was found to adapt gradually to the increased drag of the wind turbines in the form of an IBL. The observed growth rates were close to Elliott’s 0.8 power law, and interaction with the capping inversion occurred downwind for the two lowest CNBL cases. The wind farm also caused an upward displacement of the inversion layer, which was related to the blockage effect and flow divergence, not to enhanced turbulent mixing. This displacement in turn excited gravity waves in the inversion and in the free atmosphere, which imposed pressure perturbations on the boundary layer.
A detailed analysis of the kinetic energy equation showed that the energy extracted by the turbines is provided by two different processes, i.e. the deceleration of mean flow and the transport of energy from above the farm by turbulent fluxes. With respect to the turbulent stresses, the flow in the wind farm reached a fully developed regime after approximately eight turbine rows. However, streamwise variations in the mean-flow behaviour were observed up till the last turbine row, which suggests that the mean flow did not reach a fully developed regime. Further, it was found that the vertical turbulent energy transport was balanced by mechanical energy divergence in the layer above the wind farm, and that, contrary to the fully developed case, the background pressure gradient was only of minor importance.
The wind farm efficiency was found to be sensitive to the undisturbed boundary-layer height, showing increasing power deficits for decreasing inflow heights. For the wind farm under consideration, lowering the inflow height from 1000 to 300 m increased the power deficits in downwind turbine rows with 6–9 pp. The observed differences were caused by a decrease in turbulent energy transport, while variations in the mechanical energy divergence in the turbine region were less than 5 pp. Further analysis showed that nearly all energy available at turbine level comes from upwind mechanical energy in the boundary layer. This mechanical energy, however, was not always present in the form of kinetic energy as some part was stored in the pressure field induced by gravity waves. Gravity waves thereby tend to redistribute the kinetic energy throughout the farm, and this effect was largest for low boundary-layer heights.
In the current work, we considered the case of a finite length wind farm but with an infinite width. In real wind farms, the blockage effect due to turbine drag will be lower as the wind can flow around the wind farm in the spanwise direction. Therefore, the boundary-layer displacement and excitation of gravity waves found in the current study may be overestimated compared to operational wind farms of finite width. Furthermore, the free atmosphere was assumed to be in steady-state, barotropic conditions with a fixed stratification of
![]() $1~\text{K}~\text{km}^{-1}$
. Allowing for baroclinicity or varying the free-atmosphere stratification will affect gravity-wave properties considerably. As the pressure gradients induced by gravity waves were found to play an important role in the energy budget of the boundary layer, further research is required to determine the effect of gravity waves in fully finite wind farms and subject to various atmospheric conditions. Next to this, equilibrium CNBLs over sea can be even lower than the cases considered in the current study, so that turbines may penetrate the inversion layer. We believe this case is also an interesting topic for further work.
$1~\text{K}~\text{km}^{-1}$
. Allowing for baroclinicity or varying the free-atmosphere stratification will affect gravity-wave properties considerably. As the pressure gradients induced by gravity waves were found to play an important role in the energy budget of the boundary layer, further research is required to determine the effect of gravity waves in fully finite wind farms and subject to various atmospheric conditions. Next to this, equilibrium CNBLs over sea can be even lower than the cases considered in the current study, so that turbines may penetrate the inversion layer. We believe this case is also an interesting topic for further work.
Acknowledgements
The authors acknowledge support from the European Research Council (FP7 – Ideas, grant no. 306471). The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation Flanders (FWO) and the Flemish Government – department EWI.
Appendix A. LES methodology
A.1 Governing equations
In LES of stratified, rotational atmospheric turbulence, the flow is described by transport equations for the three-dimensional filtered velocity and potential-temperature fields,
![]() $\tilde{u} _{i}$
and
$\tilde{u} _{i}$
and
![]() $\tilde{\unicode[STIX]{x1D703}}$
, and the continuity equation for incompressible flow, i.e.
$\tilde{\unicode[STIX]{x1D703}}$
, and the continuity equation for incompressible flow, i.e.
where
![]() $x_{i}$
indicates the streamwise, spanwise and vertical coordinate directions for indices
$x_{i}$
indicates the streamwise, spanwise and vertical coordinate directions for indices
![]() $i=1,2,3$
. The Boussinesq approximation is made to account for buoyancy effects in the momentum equation, with
$i=1,2,3$
. The Boussinesq approximation is made to account for buoyancy effects in the momentum equation, with
![]() $g$
the gravitational acceleration and
$g$
the gravitational acceleration and
![]() $\unicode[STIX]{x1D703}_{0}$
and
$\unicode[STIX]{x1D703}_{0}$
and
![]() $\unicode[STIX]{x1D70C}_{0}$
the temperature and density of the adiabatic base state, respectively. The Coriolis force accounts for rotation effects, with
$\unicode[STIX]{x1D70C}_{0}$
the temperature and density of the adiabatic base state, respectively. The Coriolis force accounts for rotation effects, with
![]() $f_{c}=2\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D719}$
being the Coriolis parameter,
$f_{c}=2\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D719}$
being the Coriolis parameter,
![]() $\unicode[STIX]{x1D6FA}$
the angular velocity of the Earth and
$\unicode[STIX]{x1D6FA}$
the angular velocity of the Earth and
![]() $\unicode[STIX]{x1D719}$
the latitude. Further,
$\unicode[STIX]{x1D719}$
the latitude. Further,
![]() $q_{j}^{R}$
is the subgrid-scale heat flux and
$q_{j}^{R}$
is the subgrid-scale heat flux and
![]() $\unicode[STIX]{x1D70F}_{ij}^{R}$
represents the subgrid-scale stress tensor, of which the anisotropic part
$\unicode[STIX]{x1D70F}_{ij}^{R}$
represents the subgrid-scale stress tensor, of which the anisotropic part
![]() $\unicode[STIX]{x1D70F}_{ij}^{r}=\unicode[STIX]{x1D70F}_{ij}^{R}-\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D70F}_{kk}^{R}/3$
is modelled (see further below). The trace of the subgrid-scale stress tensor is absorbed into the filtered modified pressure, defined as
$\unicode[STIX]{x1D70F}_{ij}^{r}=\unicode[STIX]{x1D70F}_{ij}^{R}-\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D70F}_{kk}^{R}/3$
is modelled (see further below). The trace of the subgrid-scale stress tensor is absorbed into the filtered modified pressure, defined as
![]() $\tilde{p}^{\star }=\tilde{p}-p_{\infty }+\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D70F}_{kk}^{R}/3$
with
$\tilde{p}^{\star }=\tilde{p}-p_{\infty }+\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D70F}_{kk}^{R}/3$
with
![]() $p_{\infty }$
a mean background pressure. Finally,
$p_{\infty }$
a mean background pressure. Finally,
![]() $f_{i}$
represents the force exerted by the wind turbines on the flow (see § A.2).
$f_{i}$
represents the force exerted by the wind turbines on the flow (see § A.2).
The governing equations are solved using the LES code SP-Wind. In SP-Wind, time integration is performed using a classic four-stage fourth-order Runge-Kutta scheme, with a time step based on a Courant–Friedrichs–Lewy number of 0.4. Further, SP-Wind uses pseudo-spectral discretisation schemes in the lateral directions, and a fourth-order energy-conservative finite difference scheme for the vertical direction (Verstappen & Veldman Reference Verstappen and Veldman2003). Allaerts & Meyers (Reference Allaerts and Meyers2015) recently extended the SP-Wind code to include buoyancy effects, allowing simulations of wind farms in various atmospheric boundary-layer types.
The effect of subgrid-scale motions on the resolved flow is modelled using a Smagorinsky type model proposed by Stevens, Moeng & Sullivan (Reference Stevens, Moeng, Sullivan, Kerr and Kimura2000). In this model, the anisotropic part of the subgrid-scale stress tensor and the subgrid-scale heat flux are computed from the resolved flow variables using a mixing length model, i.e.
with
![]() $S_{ij}=0.5(\unicode[STIX]{x2202}\tilde{u} _{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}\tilde{u} _{j}/\unicode[STIX]{x2202}x_{i})$
the filtered rate of strain and
$S_{ij}=0.5(\unicode[STIX]{x2202}\tilde{u} _{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}\tilde{u} _{j}/\unicode[STIX]{x2202}x_{i})$
the filtered rate of strain and
![]() $K_{m}$
and
$K_{m}$
and
![]() $K_{h}$
the eddy coefficients for momentum and heat. Following the
$K_{h}$
the eddy coefficients for momentum and heat. Following the
![]() ${\mathcal{S}}_{\unicode[STIX]{x1D70E}}$
model of Stevens et al. (Reference Stevens, Moeng, Sullivan, Kerr and Kimura2000), the eddy coefficients are given by
${\mathcal{S}}_{\unicode[STIX]{x1D70E}}$
model of Stevens et al. (Reference Stevens, Moeng, Sullivan, Kerr and Kimura2000), the eddy coefficients are given by
Here,
![]() $S=\left(2S_{ij}S_{ij}\right)^{1/2}$
is the characteristic filtered rate of strain,
$S=\left(2S_{ij}S_{ij}\right)^{1/2}$
is the characteristic filtered rate of strain,
![]() $Ri=N^{2}/S^{2}$
is the Richardson number and
$Ri=N^{2}/S^{2}$
is the Richardson number and
![]() $N=[(g/\unicode[STIX]{x1D703}_{0})\,\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}z]^{1/2}$
is the local Brunt–Väisälä frequency. Finally, the characteristic length scale
$N=[(g/\unicode[STIX]{x1D703}_{0})\,\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}z]^{1/2}$
is the local Brunt–Väisälä frequency. Finally, the characteristic length scale
![]() $l$
is defined as the geometric mean of the grid size
$l$
is defined as the geometric mean of the grid size
![]() $\unicode[STIX]{x1D6E5}$
, the stability related length scale
$\unicode[STIX]{x1D6E5}$
, the stability related length scale
![]() $l_{s}=c_{l}\sqrt{e}N^{-1}$
and the theoretical length scale near a wall, i.e.
$l_{s}=c_{l}\sqrt{e}N^{-1}$
and the theoretical length scale near a wall, i.e.
where we use
![]() $n=2$
.
$n=2$
.
At the bottom of the domain, wall stress boundary conditions are specified using classic Monin–Obukhov similarity theory for neutral boundary layers (Moeng Reference Moeng1984):
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70F}_{w1}=-\left(\frac{\unicode[STIX]{x1D705}}{\ln z/z_{0}}\right)^{2}\left(\hat{u} ^{2}+\hat{v}^{2}\right)^{1/2}\hat{u} ,\\ \displaystyle \unicode[STIX]{x1D70F}_{w2}=-\left(\frac{\unicode[STIX]{x1D705}}{\ln z/z_{0}}\right)^{2}\left(\hat{u} ^{2}+\hat{v}^{2}\right)^{1/2}\hat{v},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70F}_{w1}=-\left(\frac{\unicode[STIX]{x1D705}}{\ln z/z_{0}}\right)^{2}\left(\hat{u} ^{2}+\hat{v}^{2}\right)^{1/2}\hat{u} ,\\ \displaystyle \unicode[STIX]{x1D70F}_{w2}=-\left(\frac{\unicode[STIX]{x1D705}}{\ln z/z_{0}}\right)^{2}\left(\hat{u} ^{2}+\hat{v}^{2}\right)^{1/2}\hat{v},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where locally averaged horizontal velocities
![]() $\hat{u}$
and
$\hat{u}$
and
![]() $\hat{v}$
are used to match the average wall stress with the classic log law (Bou-Zeid, Meneveau & Parlange Reference Bou-Zeid, Meneveau and Parlange2005). Further,
$\hat{v}$
are used to match the average wall stress with the classic log law (Bou-Zeid, Meneveau & Parlange Reference Bou-Zeid, Meneveau and Parlange2005). Further,
![]() $\unicode[STIX]{x1D705}$
is the von Kármán constant and
$\unicode[STIX]{x1D705}$
is the von Kármán constant and
![]() $z_{0}$
is the surface-roughness length. No stability corrections are needed in (A 7) as the surface heat flux is set equal to zero.
$z_{0}$
is the surface-roughness length. No stability corrections are needed in (A 7) as the surface heat flux is set equal to zero.
The flow is driven by applying a mean pressure gradient
![]() $\unicode[STIX]{x1D735}p_{\infty }$
, which relates to the geostrophic wind speed
$\unicode[STIX]{x1D735}p_{\infty }$
, which relates to the geostrophic wind speed
![]() $G$
by the geostrophic balance for barotropic conditions,
$G$
by the geostrophic balance for barotropic conditions,
with
![]() $\unicode[STIX]{x1D6FC}$
the angle between the geostrophic velocity vector and the
$\unicode[STIX]{x1D6FC}$
the angle between the geostrophic velocity vector and the
![]() $x$
-direction. In the current study, the LES filtering ‘tilde’ is often omitted to simplify notation.
$x$
-direction. In the current study, the LES filtering ‘tilde’ is often omitted to simplify notation.
A.2 Actuator disk model
Given the large domain sizes required to model entire wind farms, full resolution of the wind-turbine blades is infeasible. Instead, the effect of the turbines on the flow is modelled using a non-rotating actuator disk method (ADM), which has been used by many previous LES studies on wind farms (see, e.g. Calaf et al. Reference Calaf, Meneveau and Meyers2010; Meyers & Meneveau Reference Meyers and Meneveau2010, Reference Meyers and Meneveau2013; Allaerts & Meyers Reference Allaerts and Meyers2015; Goit & Meyers Reference Goit and Meyers2015). This method represents the wind turbines as porous disks exerting a thrust force perpendicular to the rotor plane. The performance of ADM has been investigated by Wu & Porté-Agel (Reference Wu and Porté-Agel2011) and later by Meyers & Meneveau (Reference Meyers and Meneveau2013), and it is generally accepted that ADM provides an accurate representation of the turbine far wake and the wake mixing.
In the actuator disk model, the total thrust force of a turbine is given by
with
![]() $\langle \bar{u}_{\bot }^{T}\rangle _{d}$
the local disk-averaged and time-filtered velocity perpendicular to the turbine disk. The time filter is a one-sided exponential time filter with a time constant of 5 s following Goit & Meyers (Reference Goit and Meyers2015) and Goit et al. (Reference Goit, Munters and Meyers2016). Further,
$\langle \bar{u}_{\bot }^{T}\rangle _{d}$
the local disk-averaged and time-filtered velocity perpendicular to the turbine disk. The time filter is a one-sided exponential time filter with a time constant of 5 s following Goit & Meyers (Reference Goit and Meyers2015) and Goit et al. (Reference Goit, Munters and Meyers2016). Further,
![]() $D$
is the rotor diameter and
$D$
is the rotor diameter and
![]() $C_{T}^{\prime }$
is the disk-based thrust coefficient. The thrust force is distributed uniformly over the disk area and subsequently filtered onto the LES grid by means of a Gaussian convolution filter. Details can be found in Calaf et al. (Reference Calaf, Meneveau and Meyers2010) and Meyers & Meneveau (Reference Meyers and Meneveau2010).
$C_{T}^{\prime }$
is the disk-based thrust coefficient. The thrust force is distributed uniformly over the disk area and subsequently filtered onto the LES grid by means of a Gaussian convolution filter. Details can be found in Calaf et al. (Reference Calaf, Meneveau and Meyers2010) and Meyers & Meneveau (Reference Meyers and Meneveau2010).

























