The rigidity of filtered colimits of n-cluster tilting subcategories

Abstract

Let Λ be an artin algebra and 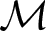$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with 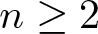$n \geq 2$. From the viewpoint of higher homological algebra, a question that naturally arose in Ebrahimi and Nasr-Isfahani (The completion of d-abelian categories. J. Algebra 645 (2024), 143–163) is when 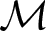$\mathcal{M}$ induces an n-cluster tilting subcategory of Λ-Mod. In this article, we answer this question and explore its connection to Iyama’s question on the finiteness of n-cluster tilting subcategories of Λ-mod. In fact, our theorem reformulates Iyama’s question in terms of the vanishing of Ext and highlights its relation with the rigidity of filtered colimits of 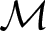$\mathcal{M}$. Also, we show that 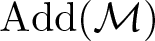${\rm Add}(\mathcal{M})$ is an n-cluster tilting subcategory of Λ-Mod if and only if 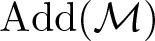${\rm Add}(\mathcal{M})$ is a maximal n-rigid subcategory of Λ-Mod if and only if 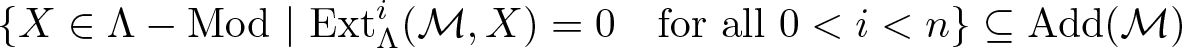$\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace \subseteq {\rm Add}(\mathcal{M})$ if and only if 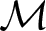$\mathcal{M}$ is of finite type if and only if 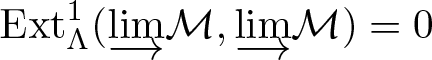${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$. Moreover, we present several equivalent conditions for Iyama’s question which shows the relation of Iyama’s question with different subjects in representation theory such as purity and covering theory.