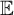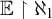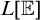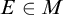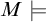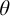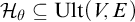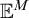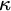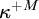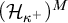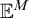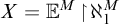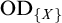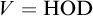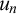THE DEFINABILITY OF THE EXTENDER SEQUENCE $\mathbb {E}$ FROM $\mathbb {E}\upharpoonright \aleph _1$ IN $L[\mathbb {E}]$

Abstract

Let M be a short extender mouse. We prove that if $E\in M$ and $M\models $“E is a countably complete short extender whose support is a cardinal $\theta $ and $\mathcal {H}_\theta \subseteq \mathrm {Ult}(V,E)$”, then E is in the extender sequence $\mathbb {E}^M$ of M. We also prove other related facts, and use them to establish that if $\kappa $ is an uncountable cardinal of M and $\kappa ^{+M}$ exists in M then $(\mathcal {H}_{\kappa ^+})^M$ satisfies the Axiom of Global Choice. We prove that if M satisfies the Power Set Axiom then $\mathbb {E}^M$ is definable over the universe of M from the parameter $X=\mathbb {E}^M\!\upharpoonright \!\aleph _1^M$, and M satisfies “Every set is $\mathrm {OD}_{\{X\}}$”. We also prove various local versions of this fact in which M has a largest cardinal, and a version for generic extensions of M. As a consequence, for example, the minimal proper class mouse with a Woodin limit of Woodin cardinals models “$V=\mathrm {HOD}$”. This adapts to many other similar examples. We also describe a simplified approach to Mitchell–Steel fine structure, which does away with the parameters $u_n$.

1 Introduction

Let M be a premouse. ¹ Write $\mathbb {E}^M$ for the extender sequence of M, not including the active extender $F^M$ of M. Write $\mathbb {E}_+^M=\mathbb {E}^M\ \widehat {\ }\ \left <F^M\right>$ . Write $\left \lfloor M\right \rfloor $ for the universe of M. Write . Write $\mathrm {PS}$ for the Power Set Axiom.

We consider here the following questions:

1. – Given $E\in M$ such that $M\models $ “E is an extender”, is $E\in \mathbb {E}^M$ ?

2. – (Steel) Suppose $M\models \mathrm {ZFC}$ . Does $M\models $ “There is $X\subseteq \aleph _1$ such that $V=\mathrm {HOD}_{\{X\}}$ ”?

3. – Is $\mathbb {E}^M$ definable over $\left \lfloor M\right \rfloor $ , possibly from some (small) parameter?

Throughout the paper, when we write “ $\mathbb {E}^M$ is definable (within some complexity class)”, we literally mean that the class $\{\mathbb {E}^M\!\upharpoonright \!\alpha \mid \alpha <\mathrm {Ord}^M\}$ is so definable. Given a definability class $\Sigma $ , We write $\Sigma ^N(X)$ for the class of relations which are $\Sigma $ -definable over the structure N from parameters in X, or just $\Sigma ^N$ for $\Sigma ^N(\emptyset )$ . As usual, $\Delta _n^N(X)$ denotes $\Sigma _n^N(X)\cap \Pi ^N_n(X)$ .

Answers to certain instances of the above questions have been known for some time. Kunen proved that $L[U]$ satisfies “U is the unique normal measure”, and therefore satisfies “ $V=\mathrm {HOD}$ ”. Recall that $M_n$ is the minimal proper class mouse with n Woodin cardinals. Steel proved [5] that for $n\leq \omega $ , $\mathbb {E}^{M_n}$ is definable over $\left \lfloor M_n\right \rfloor $ without parameters. ² The author proved similar results for larger, sufficiently self-iterable mice in [6] and [11]. The proofs of these earlier results depended on the mice in question being sufficiently self-iterable. But non-meek mice typically fail to have such self-iterability, making it difficult to generalize these kinds of arguments to models with higher large cardinals.

The main result of the paper is the following, Theorem 1.1. It answers Steel’s question above positively, in fact with . ³

Theorem 1.1. Let M be a $(0,\omega _1+1)$ -iterable premouse satisfying $\mathrm {PS}$ and . Then

Therefore if $\left \lfloor M\right \rfloor \models \mathrm {ZFC}$ then $\left \lfloor M\right \rfloor \models $ “” and $M\models \mathrm {ZFC}$ . ⁴

Note that the only large cardinal restriction on the mice involved is the paper’s global assumption that all premice considered have only short extenders on their sequence. This means that we need to deal with mice which are significantly non-self-iterable, for which the earlier arguments mentioned above do not seem to apply.

For the proof, we will use a method which avoids any self-iterability, and is more focused on condensation properties. The first proof we give, in Section 3, will actually yield a more general and local version, in which the mouse can have a largest cardinal, but in which case we must allow somewhat higher complexity in the definition of $\mathbb {E}^M$ from the parameter . We will also give a variant proof in Section 4, which uses the same main idea, but is a little simpler. (However, it does not give all of the information provided by the first proof.) The argument in Section 3 was discovered in 2015, and that in Section 4 in 2019. The argument in Section 4 is used in the preprint [2].

We easily get the following corollary, which does involve some self-iterability:

Corollary 3.15.

Let M be a $(0,\omega _1+1)$ -iterable premouse. Suppose M satisfies $\mathrm {PS}+$ “ is $(\omega ,\omega _1+1)$ -iterable”. Then $\mathbb {E}^M$ is (lightface) $\Delta _2^{\left \lfloor M\right \rfloor }$ -definable and $\left \lfloor M\right \rfloor \models $ “Every set is $\mathrm {OD}$ ”. ⁵

To prove the more local version of Theorem 1.1 we will use certain extender maximality properties of $\mathbb {E}^M$ , Theorems 1.2 and 1.4, which are refinements of results from [6], with similar proofs.

Theorem 1.2 (Steel, Schlutzenberg).

Let M be an $(0,\omega _1+1)$ -iterable premouse. Let $E\in M$ be such that $M\models $ “E is a short, total, countably complete extender”, $\nu _E$ is a cardinal of M and $\mathcal {H}_{\nu _E}^M\subseteq \mathrm {Ult}(M,E)$ . Then (the trivial completion of) E is in $\mathbb {E}^M$ .

Remark 1.3. Steel first proved that $E\in \mathbb {E}^M$ under the assumptions of 1.2 together with the added assumptions that $M\models \mathrm {PS}$ + “ $\nu _E$ is regular” and $\mathrm {Ult}(M,E)|\nu _E=M|\nu _E$ . The author then generalized Steel’s proof to obtain 1.2.

Recall that if $M\models $ “E is a normal measure” then $\nu _E=\mathrm {cr}(E)^{+M}$ , so the requirement that $\mathcal {H}_{\nu _E}^M\subseteq \mathrm {Ult}(M,E)$ holds automatically, and therefore $E\in \mathbb {E}^M$ (given M is iterable).

Theorem 1.4. Let M be a $(0,\omega _1+1)$ -iterable premouse. Let $E,R\in M$ and ${\tau \in \mathrm {Ord}^M}$ be such that $\tau $ is a cardinal of M, R is a premouse, $\rho _\omega ^R=\tau $ and $M\models $ “E is a short extender, $\mathcal {H}_\tau \subseteq \mathrm {Ult}(M,E)$ and $R\triangleleft \mathrm {Ult}(M,E)$ ”. Then $R\triangleleft M$ .

Slightly less general versions of 1.2 and 1.4 were obtained by the author in 2006 [6]. Prior to this, Woodin had conjectured that if M is a mouse, $\kappa $ is uncountable in M and $\kappa ^{+M}<\mathrm {Ord}^M$ , then $L(\mathcal {P}(\kappa )^M)\models \mathrm {AC}$ . Woodin’s conjecture follows immediately from the following corollary (1.5) to the preceding theorems. Steel noticed that 1.5 follows from 1.4 combined with an argument of Woodin’s. ⁶

Corollary 1.5. Let M be a $(0,\omega _1+1)$ -iterable premouse and $\kappa \in \mathrm {Ord}^M$ be such that $M\models $ “ $\kappa $ is uncountable” and $\kappa ^{+M}<\mathrm {Ord}^M$ . Then $M|\kappa ^{+M}$ is definable from parameters over $\mathcal {H}_{\kappa ^{+M}}^M$ .

In Section 5 we also describe a simplification to Mitchell–Steel fine structure of [1], making do without the parameters $u_n$ . One could just use the standard fine structure, but the simplification removes some complications, and we will officially make use of it throughout the paper.

1.1 Conventions and notation

Note that some notation was introduced on page 1.

Most non-standard conventions are as in [9, Section 1.1] or [10, Section 1.1] (and mostly, but not completely, as in [11, Section 1.1]). In particular, premice M have Mitchell–Steel indexing, except that we allow extenders of superstrong type in the extender sequence $\mathbb {E}_+^M$ (see [9, Sections 1.1.2 and 1.1.6], [12, Section 2]), and we adopt a simplified version of the Mitchell–Steel fine structure of [1], which avoids the parameters $u_n$ , as explained in Section 5. By 5.8, this change actually has no impact on the fine structural notions such as standard parameters, k-soundness, etc. In Sections 1–4, when we write $p_k$ (the kth standard parameter), we mean the object defined as $q_k$ in Section 5, as opposed to what is defined as $p_k$ in Section 5. Moreover, we drop the “q-” from the fine structure terminology introduced in Section 5. Because of the change, we use the notation $\mathrm {Hull}_{k+1}^M(X)$ and $\mathrm {cHull}_{k+1}^M(X)$ as defined in 5.1, not as in [11].

For a structure M, $\left \lfloor M\right \rfloor $ denotes the universe of M, and $\mathcal {J}(M)$ denotes the rudimentary closure of $M\cup \{M\}$ .

Let N be a premouse, $\mathbb {E}=\mathbb {E}^N$ and $\mathbb {E}_+=\mathbb {E}_+^N$ . Given $\alpha \leq \mathrm {Ord}^N$ , we write $N|\alpha =(\mathcal {J}_\alpha ^{\mathbb {E}},\mathbb {E}\!\upharpoonright \!\alpha ,\mathbb {E}_+(\alpha ))$ for the initial segment of N of ordinal height $\alpha $ , including its active extender $\mathbb {E}_+(\alpha )$ , and $N||\alpha $ for its passivization $(\mathcal {J}_\alpha ^{\mathbb {E}},\mathbb {E}\!\upharpoonright \!\alpha ,\emptyset )$ . If N is passive, then working inside N, $\mathcal {J}^{\mathbb {E}}$ also denotes N. We write $\mathbb {e}^N=\mathbb {E}\!\upharpoonright \!\omega _1^N$ and .

Let $n<\omega $ . We say that N satisfies $(n+1)$ -condensation iff N is n-sound and whenever H is $(n+1)$ -sound and $\pi :H\to N$ is n-lifting (see [9, Definition 2.1]) and $\rho _{n+1}^H\leq \mathrm {cr}(\pi )$ , then either $H=\mathfrak {C}_{n+1}(N)$ or $H\triangleleft N$ or, letting $\rho =\rho _{n+1}^H$ , $N|\rho $ is active with extender E and $H\triangleleft \mathrm {Ult}(N|\rho ,E)$ (see [9, Theorem 5.2]). We say N satisfies $\omega $ -condensation iff it satisfies $(n+1)$ -condensation for all $n<\omega $ .

Regarding (generalized) solidity, see Definition 2.1 and [9, Section 1.1.3].

We say that N is an $\omega $ -premouse iff N is $\omega $ -sound and $\rho _\omega ^N=\omega $ ; in this case we let $\deg (N)$ denote the least n such that $\rho _{n+1}^N=\omega $ . An $\omega $ -mouse is an $(\omega ,\omega _1+1)$ -iterable $\omega $ -premouse. If N is an $\omega $ -mouse, we write $\Sigma _N$ for the unique $(\omega ,\omega _1+1)$ -strategy for N.

For $\alpha <\mathrm {Ord}^N$ , recall that $\alpha $ is a cutpoint of N iff for all $E\in \mathbb {E}_+^N$ , if $\mathrm {cr}(E)<\alpha $ then $\mathrm {lh}(E)\leq \alpha $ .

For an extender E, $t_E$ and $\tau _E$ denote the Dodd parameter and Dodd projectum of E respectively, if they are defined.

2 Extender maximality

In this section we prove Theorems 1.2 and 1.4. The proofs are refinements of less general results proved in [6]. Toward these proofs, we begin with a lemma which helps us to find sound hulls of premice; the proof is basically as in [11, Lemma 3.1], but here we use the fact that condensation follows from normal iterability in order to reduce our assumptions.

Definition 2.1. Let $k<\omega $ , let H be k-sound, $q\in [\rho _0^H]^{<\omega }$ and $\alpha \in \mathrm {Ord}^H$ . The $(k+1)$ -solidity witness for $(H,q,\alpha )$ , (or just for $(q,\alpha )$ ), is

$$\begin{align*}w^H_{k+1}(q,\alpha)=_{\mathrm{def}}\mathrm{Th}_{k+1}^H(\alpha\cup\{q,\vec{p}_k^H\}). \end{align*}$$

Letting $q=\{q_0,\ldots ,q_{\mathrm {lh}(q)-1}\}$ with $q_i>q_{i+1}$ , the (set of all) $(k+1)$ -solidity witnesses for $(H,q)$ (or just for q) is

$$\begin{align*}w^H_{k+1}(q)=_{\mathrm{def}}\{w_{k+1}^H(q\!\upharpoonright\! i,q_i)\}_{i<\mathrm{lh}(q)},\end{align*}$$

where $q\!\upharpoonright \! i=\{q_0,\ldots ,q_{i-1}\}$ . The (set of all) $(k+1)$ -solidity witnesses for H is

$$\begin{align*}w^H_{k+1}=_{\mathrm{def}} w^H_{k+1}(p_{k+1}^H).\end{align*}$$

Note that in the preceding definition, we are not assuming that the solidity witnesses in consideration are in H.

Definition 2.2. Let $k<\omega $ , let H be $(k+1)$ -sound, $q\in \mathfrak {C}_0(H)$ , $\theta <\rho _0^H$ ,

$$\begin{align*}{\bar{H}}=\mathrm{cHull}_{k+1}^H(\theta\cup\{\vec{p}_k^H,q\}), \end{align*}$$

$\pi :{\bar {H}}\to H$ be the uncollapse and $\pi ({\bar {q}})=q$ . We say that $(\theta ,q)$ is $(k+1)$ -self-solid (for H) iff ${\bar {H}}$ is $k+1$ -sound and $\rho _{k+1}^{\bar {H}}=\theta $ and $p_{k+1}^{\bar {H}}=\bar {q}$ .

Let $x\in \mathfrak {C}_0(H)$ and $r\in [\rho _0^H]^{<\omega }$ . We say that r is an $\mathrm {r}\Sigma _{k+1}^H(\{x\})$ -generator iff for every $\gamma \in r$ , we have

$$\begin{align*}\gamma\notin\mathrm{Hull}_{k+1}^H(\gamma\cup\{\vec{p}_k^H,x,r\backslash\{\gamma\}\}).\end{align*}$$

Lemma 2.3. Let $k<\omega $ and let H be $(k+1)$ -sound and $(k,\omega _1+1)$ -iterable. Let $r\in \mathfrak {C}_0(H)$ and $\theta \leq \rho _{k+1}^H$ be a cardinal of H. Then there is $q\in H$ such that $:$

1. – $(\theta ,q)$ is $(k+1)$ -self-solid for H,

2. – $p_{k+1}^H=q\backslash \min (p_{k+1}^H)$ ,

3. – $r\in \mathrm {Hull}_{k+1}^H(\theta \cup \{\vec {p}_k^H,q\})$ , and

4. – ${\bar {H}}=\mathrm {cHull}_{k+1}^H(\theta \cup \{\vec {p}_k^H,q\})\trianglelefteq H$ .

Proof We may assume H is countable and $\theta <\rho _{k+1}^H$ . We will define $m<\omega $ and

$$\begin{align*}q=(q_0,q_1,\ldots,q_{m-1}),\end{align*}$$

with $q_i>q_{i+1}$ for $i+1<m$ . Let $p=p_{k+1}^H$ . We start with $q\!\upharpoonright \!\mathrm {lh}(p)=p$ . We define $q_i$ for $i\geq \mathrm {lh}(p)$ by induction on i, with $q_i<\rho _{k+1}^H$ . We simultaneously define an H-cardinal $\gamma _i$ , with $\gamma _{\mathrm {lh}(p)}=\rho _{k+1}^H$ and $\theta \leq \gamma _{i}\leq q_{i-1}$ for $i>\mathrm {lh}(p)$ , and

$$\begin{align*}u_i,r\in\mathrm{Hull}_{k+1}^H(\gamma_i\cup\{\vec{p}_k^H,q\!\upharpoonright\! i\}), \end{align*}$$

where $u_i$ is the set of $(k+1)$ -solidity witnesses for $(H,q\!\upharpoonright \! i)$ . Now let $i\geq \mathrm {lh}(p)$ , and let $q\!\upharpoonright \! i$ , $\gamma _i$ be given. If $\gamma _i=\theta $ then we set $m=i$ , so $q=q\!\upharpoonright \! i$ and we are done. So suppose $\gamma _i>\theta $ . Let $\eta <\gamma _i$ be least such that $\eta>\theta $ and $\eta $ is not a cardinal of H and

(1) $$ \begin{align} u_i,r\in H_i=_{\mathrm{def}}\mathrm{Hull}_{k+1}^H((\eta+1)\cup\{\vec{p}_k^H,q\!\upharpoonright\! i\}) \end{align} $$

and

(2) $$ \begin{align} \eta\notin\mathrm{Hull}_{k+1}^H(\eta\cup\{\vec{p}_k^H,q\!\upharpoonright\! i\}). \end{align} $$

Let $q_i=\min (\mathrm {Ord}\backslash H_i)=\gamma _i^{+H}\cap H_i$ and let $\gamma _i=\mathrm {card}^H(q_i)=\mathrm {card}^H(\eta )$ .

Clearly

$$\begin{align*}H_i\subsetneq H_i'=\mathrm{Hull}_{k+1}^H(\gamma_i\cup\{\vec{p}_k^H,q\!\upharpoonright\!(i+1)\}), \end{align*}$$

so it suffices to see that $u_{i+1}\in H_i'$ . Note that the transitive collapse $W_i$ of $H_i$ is (equivalent to) the $(k+1)$ -solidity witness for $(q\!\upharpoonright \! i,q_i)$ , so it suffices to see that $W_i\in H_i'$ . For this, noting that $q_i=\gamma _i^{+W_i}$ , it suffices to see that $W_i\triangleleft H$ , since then $W_i$ is the least segment W of H such that $\mathrm {Ord}^W\geq q_i$ and $\rho _\omega ^W=\gamma _i=\mathrm {lgcd}(H|q_i)$ .

Let $\rho =q_i$ and $\gamma =\gamma _i$ and $W=W_i$ . Let $\pi :W\to H$ be the uncollapse. Then $\pi (p_{k+1}^W\backslash \rho )=q\!\upharpoonright \! i$ and W is $\rho $ -sound and $\mathrm {cr}(\pi )=\rho $ and

$$\begin{align*}\rho>\rho_{k+1}^{W}=\gamma=\mathrm{lgcd}(W|\rho) \end{align*}$$

( $\rho _{k+1}^{W}\geq \gamma $ because $W\in H$ , and $\rho _{k+1}^W<\rho $ because $\eta <\rho $ and by line (1)). So by condensation as stated in [9, Theorem 5.2], either (a) $W\triangleleft H$ or (b) letting $J\triangleleft H$ be least such that $q_i\leq \mathrm {Ord}^J$ and $\rho _\omega ^J=\gamma $ , then $\rho _{k+1}^J=\gamma <\rho _k^J$ and there is a type 1 extender F over J with $\mathrm {cr}(F)=\gamma $ and $W=\mathrm {Ult}_k(J,F)$ . But since $\eta>\gamma $ and because of line (2), we have

$$\begin{align*}\eta\notin\mathrm{Hull}_{k+1}^W((\gamma+1)\cup\{\vec{p}_k^W,p_{k+1}^W\backslash\rho\}), \end{align*}$$

and therefore (b) is false. So $W\triangleleft H$ , as required.

Since $\gamma _{i+1}<\gamma _i$ , the construction terminates successfully.

Finally, the fact that ${\bar {H}}\trianglelefteq H$ (where ${\bar {H}}$ is defined in the statement of the theorem) follows from condensation.

Related calculations also give the following:

Lemma 2.4. Let $k<\omega $ and let H be $(k+1)$ -sound and $(k,\omega _1+1)$ -iterable. Suppose $\rho =\rho _{k+1}^H=\kappa ^{+H}>\omega $ and $\kappa $ is an H-cardinal. For $\gamma <\rho $ let

$$\begin{align*}H_\gamma=\mathrm{Hull}_{k+1}^H(\gamma\cup\{\vec{p}_{k+1}^H\}) \end{align*}$$

and $W_\gamma $ be the transitive collapse of $H_\gamma $ . Then $:$

1. (i) For all sufficiently large $\gamma \in (\kappa ,\rho )$ , either $:$

   1. – $W_\gamma \triangleleft H$ , or

   2. – $\kappa ^{+W_\gamma }=\rho _\omega ^{W_\gamma }=\gamma $ , $H|\gamma $ is active with E ⁷ and $W_\gamma \triangleleft \mathrm {Ult}(H,E)$ .

2. (ii) For cofinally many $\gamma <\rho $ , we have $W_\gamma \triangleleft H$ and $\rho _{k+1}^{W_\gamma }=\kappa $ .

Proof For $\gamma \in (\kappa ,\rho )$ , say that $\gamma $ is a generator iff $\gamma \notin H_\gamma $ . We say that a generator is a limit generator iff it is a limit of generators, and is otherwise a successor generator. Note that the set of generators above $\kappa $ is club in $\rho $ . Let $\gamma>\kappa $ be a generator. Then note that $W_\gamma \in H$ and $\gamma =\kappa ^{+W_\gamma }$ so $\rho _{k+1}^{W_\gamma }\in \{\kappa ,\gamma \}$ ; moreover, if $\gamma $ is a successor generator then $\rho _{k+1}^{W_\gamma }=\kappa $ .

Now let $\eta _0$ be the least generator $\gamma>\kappa $ such that $w_{k+1}^H\in H_\gamma $ . We claim that the conclusion of (i) holds for all generators $\gamma>\eta _0$ . We proceed by induction on $\gamma $ .

First suppose that $\gamma $ is a limit generator. Then by induction, for eventually all successor generators $\gamma '<\gamma $ , we have $W_{\gamma '}\triangleleft H$ and $\gamma '=\kappa ^{+W_{\gamma '}}$ and $W_{\gamma '}$ projects to $\kappa $ . It follows that $W_{\gamma '}\in H_\gamma $ , so $W_{\gamma '}\in W_\gamma $ , which implies that $\rho _{k+1}^{W_{\gamma }}=\gamma $ , and therefore $W_\gamma $ is $(k+1)$ -sound. So the conclusion for $W_\gamma $ follows from $(k+1)$ -condensation.

Now suppose that $\gamma $ is a successor generator. Then there is a largest generator $\eta <\gamma $ , and we have $\kappa <\eta _0\leq \eta <\gamma $ , and $W_\gamma $ projects to $\kappa $ . So using condensation (as stated in [9, Theorem 5.2]) as in the proof of 2.3, we get $W_\gamma \triangleleft H$ .

Part (ii) now easily follows; in fact its conclusion holds for every sufficiently large successor generator.

Remark 2.5. Let M be an m-sound premouse. Recall that a (putative) iteration tree on M is m-maximal given that (i) $\mathcal {T}$ satisfies the monotone length condition

$$\begin{align*}\mathrm{lh}(E^{\mathcal{T}}_\alpha)\leq\mathrm{lh}(E^{\mathcal{T}}_\beta)\text{ for all }\alpha+1<\beta+1<\mathrm{lh}(\mathcal{T}),\end{align*}$$

and for each $\alpha +1<\mathrm {lh}(\mathcal {T})$ , (ii) $\gamma =\mathrm {pred}^{\mathcal {T}}(\alpha +1)$ is least such that $\mathrm {cr}(E^{\mathcal {T}}_\alpha )<\nu (E^{\mathcal {T}}_\gamma )$ , (iii) $M^{*\mathcal {T}}_{\alpha +1}\trianglelefteq M^{\mathcal {T}}_\gamma $ is as large as possible, and (iv) $k=\deg ^{\mathcal {T}}_{\alpha +1}$ is as large as possible subject to the choice of $M^{*\mathcal {T}}_{\alpha +1}$ (with $k\leq \deg ^{\mathcal {T}}_\gamma $ if $M^{*\mathcal {T}}_{\alpha +1}=M^{\mathcal {T}}_\gamma $ ).

Definition 2.6. Let M be an m-sound premouse. An essentially m-maximal tree on M satisfies the requirements of m-maximality, except that we drop the monotone length condition, replacing it with the monotone $\nu $ condition, that is, that

$$\begin{align*}\nu(E^{\mathcal{T}}_\alpha)\leq\nu(E^{\mathcal{T}}_\beta)\text{ for all }\alpha+1<\beta+1<\mathrm{lh}(\mathcal{T}).\end{align*}$$

Remark 2.7. It is easy to see that, for example, $(m,\omega _1+1)$ -iterability is equivalent to essential- $(m,\omega _1+1)$ -iterability.

Definition 2.8. Let $\pi :\mathfrak {C}_0(M)\to \mathfrak {C}_0(N)$ be $\Sigma _0$ -elementary between premice $M,N$ of the same type.

If $M,N$ are passive then $\psi _\pi $ denotes $\pi $ . If $M,N$ are active, $\mu =\mathrm {cr}(F^M)$ and $\kappa =\mathrm {cr}(F^N)$ , then

$$\begin{align*}\psi_\pi:\mathrm{Ult}(M|\mu^{+M},F^M)\to\mathrm{Ult}(N|\kappa^{+N},F^N) \end{align*}$$

denotes the embedding induced by the Shift Lemma from $\pi $ . So in both cases, $\pi \subseteq \psi _\pi $ and $\psi _\pi $ is fully elementary.

Now we say that $\pi $ is:

1. – $\nu $ -low iff $M,N$ are type 3 and $\psi _\pi (\nu ^M)<\nu ^N$ ,

2. – $\nu $ -preserving iff [if $M,N$ are type 3 then $\psi _\pi (\nu ^M)=\nu ^N$ ], and

3. – $\nu $ -high iff $M,N$ are type 3 and $\psi _\pi (\nu ^M)>\nu ^N$ .

Remark 2.9. Suppose $\pi ,M,N$ are as above and $M,N$ are type 3. It is easy to see that if $\pi $ is $\mathrm {r}\Sigma _2$ -elementary then $\pi $ is $\nu $ -preserving, and if $\pi $ is $\mathrm {r}\Sigma _1$ -elementary then $\pi $ is non- $\nu $ -low. Moreover, one can show that if $\pi =\pi _0$ is a $\nu $ -preserving near k-embedding, then the copying construction for k-maximal (or essentially k-maximal) trees with $\pi $ preserves tree order, and for each $\alpha $ , $\pi _\alpha $ is a $\nu $ -preserving near $\deg ^{\mathcal {T}}_\alpha $ -embedding. (Here if $M^{\mathcal {T}}_\alpha $ is type 3 and $\rho _0(M^{\mathcal {T}}_\alpha )<\mathrm {lh}(E^{\mathcal {T}}_\alpha )<\mathrm {Ord}(M^{\mathcal {T}}_\alpha )$ then we copy $E^{\mathcal {T}}_\alpha $ to $E^{\mathcal {U}}_\alpha =\psi _{\pi _\alpha }(E^{\mathcal {T}}_\alpha )$ .)

Definition 2.10. Let M be an active premouse, $F=F^M$ and $\kappa =\mathrm {cr}(F)$ . We say F is of superstrong type iff $i^M_F(\kappa )$ is the largest cardinal of M. We say a premouse N is below superstrong iff no $E\in \mathbb {E}_+^N$ is of superstrong type.

We will primarily be interested in extenders whose support is of form $\sigma \cup t$ where $\sigma \in \mathrm {Ord}$ and t is a finite set of ordinals. However, we do not want to assume explicitly that the “ordinals” in t are in fact wellfounded, and we want to allow that there are other “ordinals” of the ultrapower below “ $\max (t)$ ” which are not themselves in the support. (This can be the case, for example, for an extender of form $E\!\upharpoonright \!(\tau _E\cup t_E)$ .) Toward this we adopt the following terminology:

Definition 2.11. Say a short extender E over $\kappa =\mathrm {cr}(E)$ is standard if it has support $\sigma +n$ for some limit ordinal $\sigma $ and $n<\omega $ , (so $E=\left <E_a\right>_{a\in [\sigma +n]^{<\omega }}$ ), $[\kappa ]^{|a|}\in E_a$ for each $a\in [\sigma +n]^{<\omega }$ , and letting $\mathrm {id}':[\kappa ]^1\to \kappa $ be the function $\mathrm {id}'(\{\alpha \})=\alpha $ , for each $\alpha <\sigma $ , we have $[\{\alpha \},\mathrm {id}']_E=\alpha $ . (We follow the usual conventions regarding how $E_{a\cup b}$ projects to $E_a$ when $a,b\in [\sigma +n]^{<\omega }$ . So for each $\alpha <\sigma $ and $m_0\leq m_1<n$ , $[\{\sigma +m_i\},\mathrm {id}']_E$ represents an “ordinal” $\beta _i$ of the ultrapower and the ultrapower satisfies “ $\alpha <\beta _0<\beta _1$ ”, though we do not assume that $\beta _0,\beta _1$ are in the wellfounded part of the ultrapower.)

In what follows, in the above context, when $n>0$ , we typically write t for $\{\sigma ,\ldots ,\sigma {\kern-1pt}+{\kern-1pt}n{\kern-1pt}-{\kern-1pt}1\}$ , but may also identify t with the finite set $\{[\{\sigma {\kern-1pt}+{\kern-1pt}m\},\mathrm {id}']_E\bigm |m{\kern-1pt}<{\kern-1pt}n\}$ of ordinals of the ultrapower.

We will deduce Theorems 1.2 and 1.4 from the following:

Theorem 2.12. Let N be a $(0,\omega _1+1)$ -iterable premouse, $F\in N$ and $\mu ,\sigma \in \mathrm {Ord}^N$ , $\ell <\omega $ and W be such that $:$

1. – $\sigma $ is an N-cardinal,

2. – F is a standard short N-extender with support $\sigma +\ell $ , weakly amenable to N, coded as a subset of $N|\sigma $ , such that $N\models $ “F is countably complete”,

3. – $W=\mathrm {Ult}_0(N,F)$ , $\mu =\mathrm {cr}(F)<\sigma $ and $\mathcal {H}_\sigma ^N\subseteq W$ .

Then (i) $W|\sigma ^{+W}=N||\sigma ^{+W}$ and if $\ell =0$ then (ii) $F\in \mathbb {E}_+^{N}$ .

Proof We may assume that $N=\mathcal {J}(R)$ where F is definable from parameters over R and $\rho _\omega ^R=\sigma $ . Say that F is $\mathrm {r}\Sigma _{n+1}^R(\{r\})$ . We may also assume inductively that all segments of R satisfy the theorem.

Let $n\ll m<\omega $ and $M=\mathrm {cHull}_{m+1}^R(\{s\})$ where $(\omega ,s)$ is $(m+1)$ -self-solid for R and $r\in \mathrm {rg}(\pi _{MR})$ where $\pi _{MR}:M\to R$ is the uncollapse.

Let $E=(\pi _{MR}^{-1})"F$ . So E is a standard M-extender with support $\tau +\ell $ , where either $\tau <\rho _0^M$ and $\pi _{MR}(\tau )=\sigma $ , or $\tau =\rho _0^M$ and $\rho _0^R=\sigma $ . And E is -definable, M is $(m+1)$ -sound, $n+10< m$ and

$$\begin{align*}\rho_{m+1}^M=\omega<\kappa=\mathrm{cr}(E)<\tau=\rho_{m}^M=\rho_{n+1}^M. \end{align*}$$

Other relevant properties of $(R,F)$ also reflect to $(M,E)$ . Moreover,

(3) $$ \begin{align} U=\mathrm{Ult}_m(M,E)\text{ is wellfounded and }(m,\omega_1+1)\text{-iterable},\end{align} $$

by the countable completeness of F in N and the $(\omega ,\omega _1+1)$ -iterability of R.

Now $\tau <\mathrm {Ord}^M$ . For suppose $\tau =\mathrm {Ord}^M$ . Since $\rho _{n+10}^M=\tau $ , therefore M is passive. If $\tau =\kappa ^{+M}$ (that is, $\kappa $ is the largest cardinal of M), then we have ${U|\kappa ^{+M}=M|\kappa ^{+M}=M}$ (by condensation for M), but then $E\in U$ , which is impossible. So $\tau>\kappa ^{+M}$ . Then $E\!\upharpoonright \!\eta \in M$ for all $\eta <\tau $ (since $\rho _{n+10}^M=\tau $ ), so by induction (with conclusion (i) of the theorem), $U|\tau =M|\tau =M$ , so again, $E\in U$ , a contradiction.

Let $\theta $ be the largest M-cardinal $\leq \tau $ such that $M|\theta =U|\theta $ . ⁸ Let t be $(m,\omega )$ -self-solid for M, and such that letting

$$\begin{align*}\bar{M}=\mathrm{cHull}_m^M(\{t\}) \end{align*}$$

and $\pi :\bar {M}\to M$ be the uncollapse, then $r,s\in \mathrm {rg}(\pi _{MR}\circ \pi )$ , and $\tau \in \mathrm {rg}(\pi )$ if $\tau <\rho _0^M$ , and $\theta \in \mathrm {rg}(\pi )$ if $\theta <\rho _0^M$ . Let $\pi (\bar {t})=t$ , etc., and $\bar {E}=(\pi ^{-1})"E$ , etc. So $\bar {E}$ is defined over $\bar {M}$ from $\bar {t}$ just as E is over M from t, and the relevant properties of $(M,E,U)$ reflect to $(\bar {M},\bar {E},\bar {U})$ , where $\bar {U}=\mathrm {Ult}_{m-1}(\bar {M},\bar {E})$ .

Let $\pi (\bar {\theta })=\theta $ if $\theta <\rho _0^M$ , and otherwise $\bar {\theta }=\rho _0^{\bar {M}}$ . Likewise for $\bar {\tau }$ . So $\bar {\theta },\bar {\tau }$ have the same defining properties with respect to $\bar {M},\bar {U}$ . Define the phalanx (see [11, Section 1.1] for the notation)

$$\begin{align*}\mathfrak{P}=((\bar{M},m-1,\bar{\theta}),(\bar{U},m-1),\bar{\theta}).\end{align*}$$

Claim 1. $\mathfrak {P}$ is $(\omega _1+1)$ -iterable.

Proof We will lift trees on $\mathfrak {P}$ to essentially m-maximal trees on U, which by 2.7 and line (3) suffices. Let $\psi :\bar {U}\to U$ be the Shift Lemma map. Let $\theta '=\sup \pi "\bar {\theta }$ .

Case 1. $\theta '<\theta $ .

Let $\gamma =\mathrm {card}^{M}(\theta ')$ , so $\gamma <\theta $ . Let $t'$ be such that $(\gamma ,t')$ is m-self-solid for M, with

$$\begin{align*}M'=\mathrm{cHull}^{M}_m(\gamma\cup\{t'\})\triangleleft M, \end{align*}$$

and $\widetilde {\pi }:M'\to M$ be the uncollapse, such that $t\in \mathrm {rg}(\widetilde {\pi })$ . Let $\pi ':\bar {M}\to M'$ be ${\pi '=\widetilde {\pi }^{-1}\circ \pi }$ . So

$$\begin{align*}\pi'\!\upharpoonright\!\bar{\theta}=\pi\!\upharpoonright\!\bar{\theta}=\psi\!\upharpoonright\!\bar{\theta}.\end{align*}$$

Note that $\mathrm {Ord}^{M'}<\theta $ , so $M'\triangleleft U$ .

We can use $(\pi ',\psi )$ to lift trees $\mathcal {T}$ on $\mathfrak {P}$ to essentially m-maximal trees $\mathcal {U}$ on U. In case $\theta $ is a limit cardinal of M then everything here is routine (and we actually get m-maximal trees on U). So assume that $\theta =\gamma ^{+M}$ . Most of the details of the copying process are routine, but we explain enough that we can point out how the wrinkles are dealt with. Let $\pi (\bar {\gamma })=\gamma $ . For $\alpha <\mathrm {lh}(\mathcal {T})$ with $\alpha>0$ , let $\mathrm {root}^{\mathcal {T}}_\alpha =0$ if $M^{\mathcal {T}}_\alpha $ is above $\bar {U}$ , and $\mathrm {root}^{\mathcal {T}}_\alpha =-1$ if above $\bar {M}$ . Let $\alpha <\mathrm {lh}(\mathcal {T})$ . If $\mathrm {root}^{\mathcal {T}}_\alpha =0$ then the copy map

$$\begin{align*}\pi_\alpha:M^{\mathcal{T}}_\alpha\to M^{\mathcal{U}}_\alpha \end{align*}$$

is produced routinely. Suppose $\mathrm {root}^{\mathcal {T}}_\alpha =-1$ . If $(-1,\alpha ]_{\mathcal {T}}$ does not drop in model and

$$\begin{align*}\mathrm{cr}(i^{\mathcal{T}}_{\beta\alpha})<i^{\mathcal{T}}_{0\beta}(\bar{\gamma})\text{ for all }\beta\in(-1,\alpha)_{\mathcal{T}} \end{align*}$$

(note this does not include $\beta =-1$ , so we are allowing $\bar {\gamma }=\mathrm {cr}(i^{\mathcal {T}}_{-1,\alpha })$ ), then $[0,\alpha ]_{\mathcal {U}}$ does not drop in model or degree and

$$\begin{align*}\pi_\alpha:M^{\mathcal{T}}_\alpha\to Q_\alpha=i^{\mathcal{U}}_{0\alpha}(M')\triangleleft M^{\mathcal{U}}_\alpha,\end{align*}$$

and $\pi _\alpha $ is an $(m-1)$ -lifting embedding which is produced in the obvious manner via the Shift Lemma. Otherwise, $(0,\alpha ]_{\mathcal {U}}$ drops in model, and $\pi _\alpha :M^{\mathcal {T}}_\alpha \to M^{\mathcal {U}}_\alpha $ , which is again produced in the obvious manner. We copy extenders using these maps. There is a wrinkle when $\mathrm {pred}^{\mathcal {T}}(\alpha +1)=-1$ and $\mathrm {cr}(E^{\mathcal {T}}_\alpha )=\bar {\gamma }$ , so consider this case. We have then $\mathrm {cr}(E^{\mathcal {U}}_\alpha )=\gamma $ . Because

$$\begin{align*}\bar{\gamma}^{+\bar{U}}=\bar{\gamma}^{+\bar{M}}=\bar{\theta}<\mathrm{lh}(E^{\mathcal{T}}_0)\end{align*}$$

and

$$\begin{align*}\gamma^{+U}=\gamma^{+M}=\theta<\mathrm{lh}(E^{\mathcal{U}}_0),\end{align*}$$

we get $M^{*\mathcal {T}}_{\alpha +1}=\bar {M}$ , and $M^{*\mathcal {U}}_{\alpha +1}=U$ (not $M'$ ), and $M'\triangleleft U|\theta $ . Now if $E^{\mathcal {U}}_\alpha $ is not of superstrong type then

$$\begin{align*}\mathrm{lh}(E^{\mathcal{U}}_\alpha)<i^{\mathcal{U}}_{0,\alpha+1}(\gamma)<\mathrm{Ord}^{Q_{\alpha+1}} \end{align*}$$

and

$$\begin{align*}\pi_{\alpha+1}(\mathrm{lh}(E^{\mathcal{T}}_{\alpha}))=\mathrm{lh}(E^{\mathcal{U}}_{\alpha}) \end{align*}$$

and things are standard. However, if $E^{\mathcal {U}}_\alpha $ is of superstrong type, then

$$\begin{align*}Q_{\alpha+1}=i^{\mathcal{U}}_{0,\alpha+1}(M')\triangleleft M^{\mathcal{U}}_{\alpha+1}||\mathrm{lh}(E^{\mathcal{U}}_\alpha),\end{align*}$$

so when we lift $E^{\mathcal {T}}_{\alpha +1}$ , we get $\mathrm {lh}(E^{\mathcal {U}}_{\alpha +1})<\mathrm {lh}(E^{\mathcal {U}}_\alpha )$ . However,

$$\begin{align*}\pi_{\alpha+1}(\lambda(E^{\mathcal{T}}_\alpha))=\lambda(E^{\mathcal{U}}_\alpha).\end{align*}$$

Now we claim that $E^{\mathcal {T}}_\alpha $ is also superstrong, and therefore $\nu (E^{\mathcal {T}}_\alpha )=\lambda (E^{\mathcal {T}}_\alpha )$ and ${\nu (E^{\mathcal {U}}_\alpha )=\lambda (E^{\mathcal {U}}_\alpha )}$ , and then it follows that

$$\begin{align*}\nu(E^{\mathcal{U}}_\alpha)\leq\nu(E^{\mathcal{U}}_{\alpha+1}),\end{align*}$$

as required for the monotone $\nu $ -condition.

So suppose $E^{\mathcal {T}}_\alpha $ is not superstrong. So $\nu (E^{\mathcal {T}}_\alpha )<\lambda (E^{\mathcal {T}}_\alpha )$ , so

$$\begin{align*}\pi_{\alpha+1}(\nu(E^{\mathcal{T}}_\alpha))=\psi_{\pi_\alpha}(\nu(E^{\mathcal{T}}_\alpha))<\lambda(E^{\mathcal{U}}_\alpha)=\nu(E^{\mathcal{U}}_\alpha),\end{align*}$$

which implies that $E^{\mathcal {T}}_\alpha =F(M^{\mathcal {T}}_\alpha )$ and $\pi _\alpha $ is $\nu $ -low. In particular, $\pi _\alpha $ is not $\mathrm {r}\Sigma _1$ -elementary, so is not a near $0$ -embedding. Let $j=\mathrm {root}^{\mathcal {T}}_\alpha \in \{-1,0\}$ . By the proof that the copying construction propagates near embeddings (see [4]), $(j,\alpha ]_{\mathcal {T}}$ does not drop in model, and so $\bar {M},\bar {U}$ are active. But because $\bar {U}=\mathrm {Ult}_{m-1}(\bar {M},\bar {E})$ and

$$\begin{align*}\mathrm{cr}(\bar{E})\leq\bar{\gamma}<\bar{\theta}\leq\lambda(\bar{E}),\end{align*}$$

we have $\bar {\gamma }\neq \mathrm {cr}(F^{\bar {U}})$ , and then similarly, as $\bar {\theta }\leq \lambda (E^{\mathcal {T}}_0)$ , it easily follows that $j={-}1$ . But then $\mathrm {cr}(i^{\mathcal {T}}_{j\alpha })\leq \bar {\gamma }$ and $\bar {\theta }\leq \lambda (E^{\mathcal {T}}_0)$ , so $\bar {\gamma }\neq \mathrm {cr}(F(M^{\mathcal {T}}_\alpha ))$ , contradiction.

So $\nu (E^{\mathcal {T}}_\alpha )\leq \nu (E^{\mathcal {T}}_{\alpha +1})$ , as desired. This is the only situation in which the monotone length condition can fail. We leave the remaining details of the lifting process to the reader.

Case 2. $\pi "\bar {\theta }$ is unbounded in $\theta $ .

In this case we do not see how to produce a single map lifting $\bar {M}$ , and instead produce a sequence of maps. Note that $\theta $ is a limit cardinal of M (by the case hypothesis we have an -singularization of $\theta $ , and if $\theta =\gamma ^{+M}$ this routinely implies that $\rho _m^M<\theta $ , a contradiction), and so $\bar {\theta }$ is a limit cardinal of $\bar {M}$ . For each $\bar {M}$ -cardinal $\gamma <\bar {\theta }$ , let $(M^{\prime }_\gamma ,\sigma _\gamma )$ be such that $M^{\prime }_\gamma \triangleleft M|\theta $ and $\sigma _\gamma :\bar {M}\to M^{\prime }_\gamma $ is a near $(m-1)$ -embedding with

$$\begin{align*}\sigma_\gamma\!\upharpoonright\!\gamma^{+\bar{M}}=\pi\!\upharpoonright\!\gamma^{+\bar{M}}=\psi\!\upharpoonright\!\gamma^{+\bar{M}}\end{align*}$$

and $\rho _m^{M^{\prime }_\gamma }=\sigma _\gamma (\gamma )^{+M}$ ; we get such pairs by taking appropriate hulls much as in the previous case.

Now for each $\gamma $ we have $M^{\prime }_\gamma \triangleleft U$ . So we can use $(\left <\sigma _\gamma \right>_{\gamma <\bar {\theta }},\psi )$ to lift trees on $\mathfrak {P}$ to m-maximal trees on U. This is much as in the previous case, but this time when $\mathrm {cr}(E^{\mathcal {T}}_\alpha )=\gamma <\bar {\theta }$ , then we define $Q_{\alpha +1}=i^{\mathcal {U}}_{0,\alpha +1}(M^{\prime }_\gamma )$ and define $\pi _{\alpha +1}$ via the Shift Lemma from $\sigma _\gamma $ and $\pi _\alpha $ . We get the monotone length condition here, because $\sigma _\gamma (\gamma )^{+}<\mathrm {Ord}^{M^{\prime }_\gamma }$ . The details are left to the reader.

Using the claim, we can now complete the proof. We get a successful comparison $(\mathcal {T},\mathcal {U})$ of $(\bar {M},\mathfrak {P})$ , with $\mathcal {T}$ being $(m-1)$ -maximal. Note that all extenders used in the comparison have length $>\bar {\theta }$ . Standard fine structural arguments show that $b^{\mathcal {U}}$ is above $\bar {U}$ and $b^{\mathcal {T}},b^{\mathcal {U}}$ are non-model-dropping, $M^{\mathcal {T}}_\infty =Q=M^{\mathcal {U}}_\infty $ and $\deg ^{\mathcal {T}}_\infty =m-1=\deg ^{\mathcal {U}}_\infty $ . So $\bar {\theta }\leq \mathrm {cr}(i^{\mathcal {U}})$ , so $\bar {U}|\bar {\theta }^{+\bar {U}}=Q|\bar {\theta }^{+Q}$ , and since $\mathrm {lh}(E^{\mathcal {T}}_0)>\bar {\theta }$ , therefore

(4) $$ \begin{align} \bar{U}|\bar{\theta}^{+\bar{U}}=\bar{M}||\bar{\theta}^{+\bar{U}}.\end{align} $$

But if $\bar {\theta }<\bar {\tau }$ then because $\mathcal {H}_{\bar {\tau }}^{\bar {M}}\subseteq \bar {U}$ , it follows that $\bar {U}|\bar {\theta }^{+\bar {U}}=\bar {M}|\bar {\theta }^{+\bar {M}}$ , which contradicts the choice of $\bar {\theta }$ . So $\bar {\theta }=\bar {\tau }$ , which with line (4) gives the statement of conclusion (i) of the theorem but with $\bar {M}$ instead of N. However, this statement is preserved by $\pi ,\pi _{MR}$ , so part (i) for N follows.

Assuming also that $\ell =0$ , so $\bar {E}$ is generated by $\bar {\tau }$ , then standard arguments show that $\bar {E}$ is just the $(\bar {\kappa },\bar {\tau })$ -extender derived from $i^{\mathcal {T}}$ , and therefore that in fact $\bar {E}\in \mathbb {E}^{\bar {M}}$ . But this reflects back to N, giving part (ii).

Proof of Theorems 1.2 and 1.4

Theorem 2.12 directly implies 1.2. For 1.4 note that we may replace the given extender with a sub-extender derived from a set of form $\tau \cup t$ , where t is a finite set of ordinals, and then appeal to 2.12.

From 1.2 we immediately get:

Corollary 2.13. Let N be a $(0,\omega _1+1)$ -iterable premouse and $\mu ,\delta ,\kappa \in N$ . Then $:$

1. – If $N\models $ “ $\mu $ is a normal measure” then $\mu \in \mathbb {E}^N$ .

2. – If $N\models $ “ $\delta $ is Woodin” then $N\models $ “ $\delta $ is Woodin via extenders in $\mathbb {E}^N$ ”.

3. – If $N\models \mathrm {PS}+$ “ $\kappa $ is strong” then $N\models $ “ $\kappa $ is strong via extenders in $\mathbb {E}^N$ ”.

We next prove a finer variant of Theorem 2.12. However, we do not actually need the variant in later sections of the paper.

Recall the Dodd projectum and parameter $\tau _E$ and $t_E$ of a short extender E (see [3] or [11, Section 2] for background). The most important fact we use in this section regarding this notion is the following:

Fact 2.14 (Steel).

Let M be a $1$ -sound, $(0,\omega _1+1)$ -iterable premouse which is below superstrong. Then every $E\in \mathbb {E}_+^M$ is Dodd-sound.

Remark 2.15. Note that 2.14 and all results in this paper are for mice with Mitchell–Steel indexing. A theorem analogous to 2.14 has been proven by Zeman for mice with Jensen indexing, without the superstrong restriction (see [15]). Further, 2.14 has also been generalized for mice in Mitchell–Steel indexing, to allow extenders of superstrong type in $\mathbb {E}_+^M$ (see [7]). ⁹ With this, Theorem 2.17 should also generalize accordingly in a straightforward manner. However, as of at the time of publication of this paper, [7] is only at the preprint stage, so we have only formally stated 2.17 “below superstrong”.

Note that in 2.17, we allow E itself to ostensibly be of “superstrong type”, but then it follows that $t=\emptyset $ and $E\in \mathbb {E}_+^M$ , so in fact, E is not of such type (because M is assumed to be below superstrong).

Definition 2.16. Let M be a premouse and E a standard short M-extender, with support $\tau +\ell $ where $\tau $ is a limit ordinal and $\ell <\omega $ . Suppose E is weakly amenable (to M). Let $U=\mathrm {Ult}_0(M,E)$ (we don’t assume U is wellfounded). Let $\kappa =\mathrm {cr}(E)$ . We say that E is amenably iff $\tau <\rho _0^M$ and $\tau ^{+U}$ is wellfounded and $U|\tau ^{+U}\subseteq M$ , and the standard coding of E as an amenable subset of $U|\tau ^{+U}$ is . Here the coding consists of tuples $(\xi ,\alpha _\xi ,E_\xi ),$ where $\xi <\kappa ^{+M}$ and $E_\xi $ is the natural coding of the extender fragment

$$\begin{align*}E\!\upharpoonright\!((M|\xi)\times[\tau+\ell]^{<\omega}) \end{align*}$$

as a subset of $M|\tau $ , and $\alpha _\xi $ is the least $\alpha $ such that $E_\xi \in U|(\alpha _\xi +\omega )$ . (By the usual proof (see [1, Section 2]), $E_\xi \in U$ and the $\alpha _\xi $ ’s are cofinal in $\tau ^{+U}$ .) We say that E is explicitly Dodd-solid above $\tau $ iff, letting $j:M\to U$ be the ultrapower map and

$$\begin{align*}t=\{[\{\tau+i\},\mathrm{id}']^{M,0}_E\bigm|i<\ell\},\end{align*}$$

we have $E_j\!\upharpoonright \!(\alpha \cup (t\backslash \{\alpha \}))\in U$ for each $\alpha \in t$ .

Theorem 2.17. Let $m<\omega $ and let M be an $(m+1)$ -sound, $(m,\omega _1+1)$ -iterable premouse which is below superstrong. Let E be a standard short $M^{\mathrm {sq}}$ -extender, with support $\tau +\ell $ where $\tau $ is a limit ordinal and $\ell <\omega $ . Suppose E is weakly amenable to M, $\kappa =\mathrm {cr}(E)<\rho _{m}^M$ , E is amenably , $\tau \leq \rho _{m+1}^M$ and $\tau $ is an M-cardinal with $\mathcal {H}_\tau ^M\subseteq U$ , where $U=\mathrm {Ult}_m(M,E)$ . Then $:$

1. (i) $U|\tau ^{+U}=M||\tau ^{+U}$ and

2. (ii) if E is explicitly Dodd-solid above $\tau $ then $E\in \mathbb {E}_+^M$ .

Proof Let $j:M\to U$ be the ultrapower map. Let t be as in Definition 2.16. So $E\equiv E_j\!\upharpoonright \!\tau \cup t$ , and we will identify these two extenders in what follows.

If $U||\tau =M||\tau $ then let $\theta =\tau $ , and otherwise let $\lambda $ be least such that $U|\lambda \neq M|\lambda $ and let $\theta =\mathrm {card}^M(\lambda )$ . So $\theta $ is an M-cardinal and $\theta \leq \tau $ , and by condensation and weak amenability, $\kappa ^{+M}=\kappa ^{+U} \leq \theta $ . Note that if E is explicitly Dodd-solid above $\tau $ then E is Dodd-sound. (For suppose $\kappa ^{+M}<\tau $ . As $E\!\upharpoonright \!(\tau \cup t)$ is amenably and $\tau \leq \rho _{m+1}^M$ , then $E\!\upharpoonright \!(\alpha \cup t)\in M$ for each $\alpha <\tau $ . But $\mathcal {H}_\tau ^M\subseteq U$ , so $E\!\upharpoonright \!(\alpha \cup t)\in U$ .) Let $e\in [\mathfrak {C}_0(M)]^{<\omega }$ be such that:

1. 1. $\theta ,\tau \in e$ (recall that $\tau <\rho _0^M$ by 2.16).

2. 2. If $\mathfrak {C}_0(M)$ has largest cardinal $\Omega $ then $\Omega \in e$ .

3. 3. The amenable coding of $E\!\upharpoonright \!(\tau \cup t)$ (described in 2.16) is $\mathrm {r}\Sigma _{m+1}^M(\{e\})$ .

4. 4. If $\theta <\tau $ then $\chi \in e$ where $\chi <\tau $ is least such that $U|\chi \neq M|\chi $ .

5. 5. If $\tau ^{+U}<\tau ^{+M}$ then $\tau ^{+U}\in e$ .

6. 6. If $\tau ^{+U}=\tau ^{+M}$ but $U|\tau ^{+U}\neq M||\tau ^{+M}$ then $\lambda \in e$ where $\lambda \in (\tau ,\tau ^{+U}]$ is least such that $U|\lambda \neq M|\lambda $ (note that in fact, $\lambda <\tau ^{+U}$ , because $\tau ^{+U}<\mathrm {Ord}^U$ , because $\kappa ^{+M}\leq \tau <\rho _0^M$ ).

7. 7. If E is explicitly Dodd-solid above $\tau $ then there are $a,f\in e$ such that $a\in [\tau ]^{<\omega }$ and $[a\cup t,f]^{M,m}_E$ is the (finite) set of Dodd-solidity witnesses (for t).

8. 8. ¹⁰ If E is explicitly Dodd-solid above $\tau $ and $\theta =\tau $ and

   $$\begin{align*}\varsigma=\tau^{+U}<\tau^{+M} \end{align*}$$
   and $U|\varsigma =M||\varsigma $ but $M|\varsigma $ is active with an extender F such that $\kappa <\mathrm {cr}(F)$ , then there are $a,f\in e$ with $a\in [\tau ]^{<\omega }$ and such that
   $$\begin{align*}[a\cup t,f]^{M,m}_E=E\!\upharpoonright\!(\mathrm{cr}(F)\cup t).\end{align*}$$

Let q be such that $(\omega ,q)$ is $(m+1)$ -self-solid for M and $e\in \mathrm {rg}(\pi ),$ where ${{\bar {M}}=\mathrm {cHull}_{m+1}^M(\{\vec {p}_m^M,q\})}$ and $\pi :{\bar {M}}\to M$ is the uncollapse (q exists by 2.3).

Let $\pi ({\bar {q}})=q$ , $\pi ({\bar {\theta }})=\theta $ , etc. Also write ${\bar {t}}$ for the preimage of t “in the codes”; but note we did not demand that $t\subseteq \mathrm {Ord}^M$ . So ${\bar {M}}$ is $(m+1)$ -sound with $\rho _{m+1}^{\bar {M}}=\omega $ and ${\bar {q}}=p_{m+1}^{{\bar {M}}}$ . Let ${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$ be defined over ${\bar {M}}$ from ${\bar {e}}$ as $E\!\upharpoonright \!\tau \cup t$ is defined over M from e. Then the usual proof that $\Sigma _1$ -substructures of premice are premice ¹¹ and some similar considerations show that most of the facts reflect to ${\bar {M}},{\bar {E}}$ , etc., and in particular:

1. 1’. ${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$ is a weakly amenable short ${\bar {M}}$ -extender with ${\bar {\kappa }}=\mathrm {cr}({\bar {E}})<\rho _m^{\bar {M}}$ .

Let ${\bar {E}}$ be the short $\bar {M}$ -extender generated by ${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$ and let

$$\begin{align*}{\bar{U}}=\mathrm{Ult}_m({\bar{M}},{\bar{E}}).\end{align*}$$

1. 2’. If M has largest cardinal $\Omega $ then ${\bar {M}}$ has largest cardinal $\bar {\Omega }$ .

2. 3’. ${\bar {\theta }},{\bar {\tau }}$ are ${\bar {M}}$ -cardinals, $\mathcal {H}^{\bar {M}}_{{\bar {\tau }}}\subseteq {\bar {U}}$ and ${\bar {M}}|{\bar {\theta }}={\bar {U}}|{\bar {\theta }}$ .

3. 4’. If $\theta <\tau $ then ${\bar {M}}|{\bar {\theta }}^{+{\bar {M}}}\neq {\bar {U}}|{\bar {\theta }}^{+{\bar {U}}}$ , and $\bar {\chi }$ is least such that ${\bar {M}}|\bar {\chi }\neq {\bar {U}}|\bar {\chi }$ .

4. 5’. If $\theta =\tau $ then:

   1. – If $\tau ^{+U}<\tau ^{+M}$ then ${\bar {\tau }}^{+{\bar {U}}}<{\bar {\tau }}^{+{\bar {M}}}$ and $\pi ({\bar {\tau }}^{+{\bar {U}}})=\tau ^{+U}$ .

   2. – If $\tau ^{+U}=\tau ^{+M}$ then ${\bar {\tau }}^{+{\bar {U}}}={\bar {\tau }}^{+{\bar {M}}}$ .

5. 6’. If $\theta =\tau $ then:

   1. – If $U|\tau ^{+U}=M||\tau ^{+U}$ then ${\bar {U}}|{\bar {\tau }}^{+{\bar {U}}}={\bar {M}}||{\bar {\tau }}^{+{\bar {U}}}$ .

   2. – If $U|\tau ^{+U}\neq M||\tau ^{+U}$ then ${\bar {\tau }}<\bar {\lambda }<{\bar {\tau }}^{+{\bar {U}}}$ and $\bar {\lambda }$ is least such that ${\bar {U}}|\bar {\lambda }\neq {\bar {M}}|\bar {\lambda }$ .

6. 7’. If E is explicitly Dodd-solid above $\tau $ then ${\bar {E}}$ is Dodd-solid with respect to ${\bar {t}}$ . That is, for each $\alpha \in {\bar {t}}$ , we have ${\bar {E}}\!\upharpoonright \!(\alpha \cup ({\bar {t}}\backslash (\alpha +1)))\in {\bar {U}}$ .

7. 8’. If E is explicitly Dodd-solid above $\tau $ and $U,M,\varsigma ,F$ are as in condition 8, then $\bar {\varsigma }={\bar {\tau }}^{+{\bar {U}}}$ and ${\bar {M}}|\bar {\varsigma }$ is active with ${\bar {F}}$ and the Dodd-soundness witness ${\bar {E}}\!\upharpoonright \!(\mathrm {cr}({\bar {F}})\cup {\bar {t}})$ is in ${\bar {U}}$ .

(We do not yet know that ${\bar {U}}$ is wellfounded.) Let ${\bar {j}}:{\bar {M}}\to {\bar {U}}$ be the ultrapower map. Let $\psi :{\bar {U}}\to U$ be the Shift Lemma map. Define the phalanx $\mathfrak {P}=(({\bar {M}},m,{\bar {\theta }}), ({\bar {U}},m), {\bar {\theta }})$ .

Claim 1. ${\bar {U}}$ is wellfounded and $\mathfrak {P}$ is $(\omega _1+1)$ -iterable.

Proof The argument is mostly similar to that in the proof of 2.12. We will lift m-maximal trees $\mathcal {T}$ on $\mathfrak {P}$ to m-maximal trees on M. ¹² For this we will find embeddings from ${\bar {M}}$ and ${\bar {U}}$ into segments of M with appropriate agreement. As before, in one case we only see how to find an infinite sequence of embeddings from $\bar {M}$ into various segments of M, and use of all these together as base copy maps. We will initially find such a system of maps inside U, and then deduce that there is also such a system in M via the elementarity of j. We first make some general observations that will lead to finding the system of embeddings in U.

Let $R\triangleleft M$ . Note that M satisfies condensation with respect to premice embedded into R; in particular, $M\models $ “For every $s<\omega $ and every premouse $S\in R$ such that S is $(s+1)$ -sound and $\pi :S\to R$ is s-lifting and and $\mathrm {cr}(\pi )\geq \rho _{s+1}^S$ , either (i) $S\triangleleft R$ or (ii) $\alpha =_{\mathrm {def}}\mathrm {cr}(\pi )=\rho _{s+1}^S$ and $R|\alpha $ is active and $S\triangleleft \mathrm {Ult}_0(R|\alpha ,F^{R|\alpha })$ ”. Therefore U satisfies the same statement regarding its proper segments.

Let $M_\kappa =\mathrm {cHull}_{m+1}^M(\kappa \cup \{q\})$ . Let $\sigma _\kappa :{\bar {M}}\to M_\kappa $ and $\pi _\kappa :M_\kappa \to M$ be the natural maps and $\pi _\kappa (q_\kappa )=q$ . Note that $M_\kappa $ is sound and $M_\kappa \in M$ . So $\rho _{m+1}^{M_\kappa }=\kappa \leq \mathrm {cr}(\pi _\kappa )$ . By condensation, $M_\kappa \triangleleft M$ .

Now $\tau $ is a U-cardinal with $\kappa <\tau \leq j(\kappa )$ . Working in U, let

$$\begin{align*}U'=\mathrm{cHull}_{m+1}^{j(M_\kappa)}(\tau\cup\{r\}) \end{align*}$$

with $r\in [\mathrm {Ord}^{j(M_\kappa)}]^{<\omega }$ chosen such that $U\models $ “ $(\tau ,r)$ is $(m+1)$ -self-solid for $j(M_\kappa )$ and letting $\varrho _\tau :U'\to j(M_\kappa )$ be the uncollapse, then $j(q_\kappa ),t\in \mathrm {rg}(\varrho _\tau )$ ”. Such an r exists by the elementarity of j and by 2.3. (Note that $U\models $ “ $j(M_\kappa )$ is wellfounded”; the transitive collapse $U'$ is computed inside U, where it is well-defined.) Note that if $\tau =j(\kappa )$ then $t=\emptyset $ and $U'=j(M_\kappa )$ and $r=j(q_\kappa )$ . And if $\tau <j(\kappa )$ then $\rho _{m+1}^{U'}=\tau $ , so $U'\triangleleft j(M_\kappa )$ by condensation in U. In fact, $U'\triangleleft U|\tau ^{+U}$ , and we assumed that $U|\tau ^{+U}$ is wellfounded, so $U'$ is wellfounded.

Let $\psi :{\bar {U}}\to j(M_\kappa )$ be the Shift Lemma map induced by $\sigma _\kappa $ and $\pi $ . That is, given ¹³

$$\begin{align*}x=[a\cup \bar{t},f^{{\bar{M}}}_{\tau,z}]^{\bar{M},m}_{\bar{E}}\in\mathfrak{C}_0({\bar{U}}),\end{align*}$$

where $\tau $ is an $\mathrm {r}\Sigma _m$ term, $z\in \mathfrak {C}_0({\bar {M}})$ and $a\in [\bar {\tau }]^{<\omega }$ , then ¹⁴

$$ \begin{align*} \psi(x)&=[\pi(a)\cup t,f^{M_\kappa}_{\tau,\sigma_\kappa(z)}]^{M,m}_E\\ &=j(f^{M_\kappa}_{\tau,\sigma_\kappa(z)})(\pi(a)\cup t)\\ &=(\tau^{j(M_\kappa)}(j(\sigma_\kappa(z)),\pi(a)\cup t))^U.\end{align*} $$

Now $\mathrm {rg}(\psi )\subseteq \mathrm {rg}(\varrho _\tau )$ , for given x, etc. as above, we have $\pi (a)\subseteq \tau \subseteq \mathrm {rg}(\varrho _\tau )$ , ${t\in \mathrm {rg}(\varrho _\tau )}$ , and $j(\sigma _\kappa (z))\in \mathrm {rg}(\varrho _\tau )$ since

$$\begin{align*}j(\sigma_\kappa(z))\in\mathrm{rg}(j\circ\sigma_\kappa)=(\mathrm{Hull}_{m+1}^{j(M_\kappa)}(\{j(q_\kappa)\}))^U\end{align*}$$

and $j(q_\kappa )\in \mathrm {rg}(\varrho _\tau )$ . So $\psi (x)\in \mathrm {rg}(\varrho _\tau )$ .

So we can define $\psi ':{\bar {U}}\to U'$ by $\psi '=\varrho ^{-1}_\tau \circ \psi $ . Then $\psi '$ is m-lifting, because if $\varphi $ is $\mathrm {r}\Sigma _{m+1}$ and ${\bar {U}}\models \varphi (x)$ then easily

$$\begin{align*}U\models\text{"}j(M_\kappa)\models\varphi(\psi(x))\text{"},\end{align*}$$

so $U\models \text {"}U'\models \varphi (\psi '(x))\text {"}$ , so $U'\models \varphi (\psi '(x))$ . Also $\psi '\!\upharpoonright \!{\bar {\tau }}=\pi \!\upharpoonright \!{\bar {\tau }}$ . And $\psi '$ is c-preserving; if $m=0$ and M has largest cardinal $\Omega $ , this follows easily from commutativity and the fact that we put $\Omega \in \mathrm {rg}(\pi )$ , and if $m=0$ and M has no largest cardinal then it is because then for any M-cardinal $\xi $ , we have $M|\xi \preccurlyeq _1 M$ by condensation, and hence, $\kappa <\max (q)$ (as $\kappa \in \mathrm {rg}(\pi )$ ), and so ${\bar {M}},M_\kappa $ have largest cardinals $\Psi _\omega ,\Psi _\kappa $ respectively, with $\pi (\Psi _\omega )=\pi _\kappa (\Psi _\kappa )=\mathrm {card}^M(\max (q))$ .

For $\eta <\theta $ , let

$$\begin{align*}M_\eta=\mathrm{cHull}_{m+1}^{M}(\eta\cup\{q\}) \end{align*}$$

and $\pi _\eta :M_\eta \to M$ be the uncollapse and $\sigma _\eta :{\bar {M}}\to M_\eta $ the natural map, so ${\pi _\eta \circ \sigma _\eta =\pi }$ . Since $\eta <\theta \leq \tau \leq \rho _{m+1}^M$ , we have $M_\eta \in M$ . Note that if $\eta $ is an M-cardinal then $M_\eta $ is $(m+1)$ -sound with $\eta =\rho _{m+1}^{M_\eta }$ and $p_{m+1}^{M_\eta }=\sigma _\eta ({\bar {q}})\backslash \eta $ , so $M_\eta \triangleleft M|\theta $ .

Now as before, we consider two cases.

Case 1. $\pi "{\bar {\theta }}$ is bounded in $\theta $ . Let $\eta =\sup \pi "{\bar {\theta }}$ . We have $M_\eta $ , etc., as above. Note that either:

1. – $\eta $ is a limit cardinal of M (hence the comments above apply), or

2. – $M||\eta $ has largest cardinal $\xi $ where $\xi $ is an M-cardinal and $\xi \in \mathrm {rg}(\pi )$ , and

   $$\begin{align*}\eta\subseteq\mathrm{Hull}_{m+1}^M(\xi\cup\{q\})=\mathrm{Hull}_{m+1}^M(\eta\cup\{q\}), \end{align*}$$
   because $\mathrm {rg}(\pi )=\mathrm {Hull}_{m+1}^M(\{q\})$ is cofinal in $\eta $ ; therefore, $\rho _{m+1}^{M_\eta }=\xi $ and $p_{m+1}^{M_\eta }=\sigma _\eta ({\bar {q}})\backslash \xi $ .

It follows that $M_\eta $ is sound, and $\mathrm {cr}(\pi _\eta )\geq \eta $ . Since $\eta <\theta \leq \rho _{m+1}^M$ , condensation (see [9, Theorem 5.2]) gives $M_\eta \triangleleft M|\theta $ . Note that $\sigma _\eta \!\upharpoonright \!{\bar {\theta }}=\pi \!\upharpoonright \!{\bar {\theta }}$ and $\sigma _\eta \in M|\theta $ . Since $M|\theta =U|\theta $ , therefore $M_\eta \triangleleft U|\theta $ and $\sigma _\eta \in U|\theta $ . Note that $M_\eta \triangleleft \mathfrak {C}_0(U')$ as $\eta <\tau $ .

Now $\sigma _\eta \!\upharpoonright \!{\bar {\theta }}=\pi \!\upharpoonright \!{\bar {\theta }}=\psi '\!\upharpoonright \!{\bar {\theta }}$ and $\sigma _\eta ,{\bar {U}},U'\in U$ , with ${\bar {U}}\in \mathrm {HC}^U$ , and moreover, $U|(\mathrm {Ord}^{U'})^{+U}$ is wellfounded. So by absoluteness, in U there is some c-preserving m-lifting embedding $\widetilde {\psi }:{\bar {U}}\to U'$ with $\widetilde {\psi }\!\upharpoonright \!{\bar {\theta }}=\sigma _\eta \!\upharpoonright \!{\bar {\theta }}$ .

So $U\models \varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$ , where $\varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$ asserts “There are proper segments $M^*$ and $U^*$ of me, with $M^*\triangleleft \mathfrak {C}_0(U^*)$ , and there are c-preserving m-lifting embeddings

$$\begin{align*}\pi^*:{\bar{M}}\to M^*\text{ and }\psi^*:{\bar{U}}\to U^*\end{align*}$$

such that $\pi ^*\!\upharpoonright \!{\bar {\theta }}=\psi ^*\!\upharpoonright \!{\bar {\theta }}$ and if $\bar {M}|\bar {\theta }$ has largest cardinal $\bar {\xi }$ then $\rho _{m+1}^{M^*}=\pi ^*(\bar {\xi })$ ”.

So by elementarity, $M\models \varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$ . Let $M^*,U^*,\pi ^*,\psi ^*$ witness this in M. These embeddings are enough to copy m-maximal trees on $\mathfrak {P}$ to m-maximal trees on M. Let us point out one detail of the copying process. Suppose $\bar {M}|{\bar {\theta }}$ has largest cardinal $\bar {\xi }$ and let $\xi ^*=\pi ^*(\bar {\xi })$ . Then $\rho _{m+1}^{M^*}=\xi ^*$ and

(5) $$ \begin{align}M|\xi^*\triangleleft M^*\triangleleft U^*|(\xi^*)^{+U^*}=U^*|\psi^*(\bar{\theta}). \end{align} $$

When iterating $\mathfrak {P}$ , extenders G with $\mathrm {cr}(G)=\bar {\xi }$ apply to ${\bar {M}}$ . Let $G^*$ be the lift of G. Then $\mathrm {cr}(G^*)=\xi ^*$ and $G^*$ is $U^*$ -total. From line (5), it follows that we can define a copy map

$$\begin{align*}\mathrm{Ult}_m({\bar{M}},G)\to i^{U^*}_{G^*}(M^*) \end{align*}$$

in the usual manner. Otherwise the copying is routine. ¹⁵

Case 2. $\pi "{\bar {\theta }}$ is unbounded in $\theta $ .

Then $\theta $ is a limit cardinal of M, because $\theta $ is an M-cardinal ${\leq \rho _{m+1}^M}$ and there is an -definable cofinal partial map $\omega \to \sup \pi "{\bar {\theta }}$ . For each M-cardinal $\mu <\theta $ we have $M_\mu ,\sigma _\mu \in M|\theta =U|\theta $ . We have $M_\mu ,\sigma _\mu ,U'\in U|\tau ^{+U}$ .

Let C be the set of ${\bar {M}}$ -cardinals ${<{\bar {\theta }}}$ . Working in U, let T be the tree searching for $\widetilde {\psi },\widetilde {U}$ and a sequence $\left <\widetilde {M}_{{\bar {\mu }}},\widetilde {\sigma }_{{\bar {\mu }}}\right>_{{\bar {\mu }}\in C}$ such that:

1. – $\widetilde {U}\triangleleft U|j(\kappa )^{+U},$

2. – $\widetilde {\psi }:{\bar {U}}\to \widetilde {U}$ is c-preserving m-lifting,

3. – for each ${\bar {\mu }}\in C$ :

   1. – $\widetilde {U}|\widetilde {\psi }({\bar {\mu }})\trianglelefteq \widetilde {M}_{\bar {\mu }}\triangleleft \widetilde {U}$ ,

   2. – $\widetilde {\sigma }_{\bar {\mu }}:{\bar {M}}\to \widetilde {M}_{\bar {\mu }}$ is c-preserving m-lifting,

   3. – $\widetilde {\sigma }_{\bar {\mu }}\!\upharpoonright \!({\bar {\mu }}+1)\subseteq \widetilde {\psi }$ .

We have that $U\models $ “T is illfounded”, because $\psi ',U',\left <M_\mu ,\sigma _\mu \right>_\mu $ exist and $U|\tau ^{+U}$ is wellfounded and models $\mathrm {ZFC}^-$ .

Now $T=j(T^M)$ for some $T^M\in M$ , so $M\models $ “ $T^M$ is illfounded”. But then letting $\widetilde {U},\widetilde {\psi },\left <\widetilde {M}_{\bar {\mu }},\widetilde {\sigma }_{\bar {\mu }}\right>_{{\bar {\mu }}\in C}$ witness this, these objects allow us to lift m-maximal trees on $\mathfrak {P}$ to m-maximal trees on M. (Here when we use an extender G with $\mathrm {cr}(G)={\bar {\gamma }}<{\bar {\theta }}$ , we apply it to ${\bar {M}}$ , and our next lifting map is of the form

$$\begin{align*}\varphi:\mathrm{Ult}_m({\bar{M}},G)\to i(\widetilde{M}_{\bar{\mu}}), \end{align*}$$

where ${\bar {\mu }}={\bar {\gamma }}^{+\bar {M}}$ and where i is the upper ultrapower map, and $\varphi $ is defined as usual using $\widetilde {\sigma }_{{\bar {\mu }}}$ .)

This completes both cases, and hence, the proof that $\mathfrak {P}$ is iterable. $\Box $ (Claim 1)

We have ${\bar {M}}|{\bar {\theta }}={\bar {U}}|{\bar {\theta }}$ . So comparison of $(\mathfrak {P},{\bar {M}})$ uses only extenders indexed above ${\bar {\theta }}$ . So by the claim, there is a successful such comparison $(\mathcal {U},\mathcal {T})$ .

Claim 2. We have $:$

1. 1. $M^{\mathcal {U}}_\infty =M^{\mathcal {T}}_\infty $ , $b^{\mathcal {U}},b^{\mathcal {T}}$ do not drop in model or degree, $b^{\mathcal {U}}$ is above ${\bar {U}}$ and ${i^{\mathcal {U}}\circ {\bar {j}}=i^{\mathcal {T}}}$ .

2. 2. ${\bar {\theta }}={\bar {\tau }}$ , so $\theta =\tau $ .

3. 3. ${\bar {U}}|{\bar {\tau }}^{+{\bar {U}}}={\bar {M}}||{\bar {\tau }}^{+{\bar {U}}}$ , so $U|\tau ^{+U}=M||\tau ^{+M}$ .

4. 4. If E is explicitly Dodd-solid above $\tau $ then ${\bar {E}}\in \mathbb {E}_+^{{\bar {M}}}$ , so $E\in \mathbb {E}_+^M$ .

Proof Because ${\bar {M}}$ is $(m+1)$ -sound and $\rho _{m+1}^{\bar {M}}=\omega $ , standard arguments give part 1.

Part 2: Suppose that ${\bar {\theta }}<{\bar {\tau }}$ . Then since $\mathcal {H}_{\bar {\tau }}^{\bar {M}}\subseteq {\bar {U}}$ , we have ${\bar {\theta }}^{+{\bar {U}}}={\bar {\theta }}^{+{\bar {M}}}$ . But then since $b^{\mathcal {U}}$ is above ${\bar {U}}$ and does not drop,

$$\begin{align*}{\bar{U}}||{\bar{\theta}}^{+{\bar{U}}}=M^{\mathcal{U}}_\infty||{\bar{\theta}}^{+M^{\mathcal{U}}_\infty}= M^{\mathcal{T}}_\infty||{\bar{\theta}}^{+M^{\mathcal{T}}_\infty}={\bar{M}}||{\bar{\theta}}^{+{\bar{U}}}= {\bar{M}}||{\bar{\theta}}^{+{\bar{M}}}, \end{align*}$$

contradicting the choice of $\theta $ (and hence ${\bar {\theta }}$ ).

Part 3: Much as in part 2, but now with ${\bar {\tau }}={\bar {\theta }}$ , so $\mathrm {cr}(i^{\mathcal {U}})\geq {\bar {\tau }}$ . The conclusion that $U|\tau ^{+U}=M||\tau ^{+U}$ follows from the reflection between ${\bar {M}}$ and M discussed earlier.

Part 4: If ${\bar {E}}\in \mathbb {E}^{\bar {M}}$ , note that ${\bar {E}}\in \mathbb {E}(\mathfrak {C}_0({\bar {M}}))$ , since ${\bar {\tau }}<\rho _0^{\bar {M}}$ ; it easily follows then that $E=\pi ({\bar {E}})$ , just by the elementarity of $\pi $ . Similarly if ${\bar {E}}=F^{\bar {M}}$ then $E=F^M$ by elementarity. So we just need to see that ${\bar {E}}\in \mathbb {E}_+^{\bar {M}}$ , assuming that E is explicitly Dodd-solid above $\tau $ .

If $t=\emptyset $ then this follows from the ISC as in the proof of the ISC for pseudo-mice. Suppose instead that E is explicitly Dodd-solid above $\tau $ and $t\neq \emptyset $ . So as discussed earlier, ${\bar {E}}$ is Dodd-solid with respect to ${\bar {t}}$ . Since ${\bar {M}}$ is $1$ -sound and iterable, by 2.14 and as in [11, Section 2], we can analyse the Dodd-structure of the extenders used in $\mathcal {T}$ , decomposing them into Dodd-sound extenders. As there, there is exactly one extender $G=E^{\mathcal {T}}_\alpha $ used along $b^{\mathcal {T}}$ , G has largest generator $\gamma =i^{\mathcal {U}}(\max ({\bar {t}}))$ , and there is a unique $\beta \leq _{\mathcal {T}}\alpha $ such that the Dodd-core D of G is in $\mathbb {E}_+(M^{\mathcal {T}}_\beta )$ . Moreover, $\tau _D\leq {\bar {\tau }}$ , and if $\beta <_{\mathcal {T}}\alpha $ , then letting $\varepsilon +1=\mathrm {succ}^{\mathcal {T}}(\beta ,\alpha )$ , we have $M^{*\mathcal {T}}_{\varepsilon +1}=M^{\mathcal {T}}_\beta |\mathrm {lh}(D)$ and $\deg ^{\mathcal {T}}_{\varepsilon +1}=0$ , and letting $k=i^{*\mathcal {T}}_{\varepsilon +1,\alpha }$ , then $\mathrm {cr}(k)\geq \tau _D$ ,

$$\begin{align*}i^{\mathcal{U}}({\bar{t}})=k(t_D)\backslash{\bar{\tau}} \end{align*}$$

and

$$\begin{align*}{\bar{E}}\!\upharpoonright\!{\bar{\tau}}\cup{\bar{t}}\equiv G\!\upharpoonright\!{\bar{\tau}}\cup k(t_D). \end{align*}$$

Note that $\rho _1(M^{\mathcal {T}}_\beta |\mathrm {lh}(D))\leq \tau _D\leq {\bar {\tau }}$ .

Suppose $D\neq F^{M^{\mathcal {T}}_\beta }$ . Then $\beta =0$ , as otherwise ${\bar {\tau }}<\mathrm {lh}(E^{\mathcal {T}}_0)\leq \rho _1(M^{\mathcal {T}}_\beta |\mathrm {lh}(D))$ , contradiction. So $D\in \mathbb {E}^{{\bar {M}}}$ . Since ${\bar {\tau }}$ is an ${\bar {M}}$ -cardinal, therefore $\tau _D={\bar {\tau }}$ , so

$$\begin{align*}G\!\upharpoonright\!{\bar{\tau}}\cup k(t_D)\equiv D\!\upharpoonright\!\tau_D\cup t_D, \end{align*}$$

so $\bar {E}=D\in \mathbb {E}^{{\bar {M}}}$ , as desired.

Now suppose instead that $D=F^{M^{\mathcal {T}}_\beta }$ . Then again $\beta =0$ , since otherwise ${\bar {\tau }}\leq \lambda (E^{\mathcal {T}}_0)<\tau _D$ , contradiction. So $D=F^{\bar {M}}$ . We claim that $\alpha =0$ , so $G=D$ is Dodd-sound, and it follows then (as in [11]) that $\mathcal {U}$ is trivial and we are done. So suppose $0<_{\mathcal {T}}\alpha $ ; so $(0,\alpha ]_{\mathcal {T}}$ does not drop in model. Let $F^*$ be the first extender used along $(0,\alpha ]_{\mathcal {T}}$ . So ${\bar {\tau }}\leq \nu _{F^*}$ , as ${\bar {\tau }}<\mathrm {lh}(E^{\mathcal {T}}_0)$ and ${\bar {\tau }}$ is an ${\bar {M}}$ -cardinal. Note

$$\begin{align*}{\bar{U}}=\mathrm{Hull}_{m+1}^{M^{\mathcal{T}}_\infty}({\bar{\tau}}\cup k(t_D))=\mathrm{Ult}_m({\bar{M}},G'),\end{align*}$$

where $G'=F^{\mathrm {Ult}_0({\bar {M}},F^*\!\upharpoonright \!{\bar {\tau }})}$ . Therefore ${\bar {U}}$ is the iterate of ${\bar {M}}$ given by the tree $\mathcal {T}'$ which uses exactly two extenders, $E^{\mathcal {T}'}_0=F^*\!\upharpoonright \!{\bar {\tau }}$ and $E^{\mathcal {T}'}_1=G'$ . It follows that $\mathcal {T}=\mathcal {T}'$ , $\mathcal {U}$ is trivial, $E^{\mathcal {T}}_0=F^*$ , $\nu _{E^{\mathcal {T}}_0}={\bar {\tau }}$ , $\tau _D\leq \mathrm {cr}(E^{\mathcal {T}}_0)<{\bar {\tau }}$ and $E^{\mathcal {T}}_1=G=G'$ . So $E^{\mathcal {T}}_0\neq F^{\bar {M}}$ (as ${\bar {\kappa }}=\mathrm {cr}(E^{\mathcal {T}}_1)=\mathrm {cr}(D)$ and $D=F^{\bar {M}}$ ), so $\mathrm {lh}(E^{\mathcal {T}}_0)={\bar {\tau }}^{+{\bar {U}}}=\bar {\varsigma }<{\bar {\tau }}^{+{\bar {M}}}$ , ${\bar {M}}|\bar {\varsigma }$ is active with $E^{\mathcal {T}}_0$ , and ${\bar {\kappa }}<\mathrm {cr}(E^{\mathcal {T}}_0)$ . It follows that $E^{\mathcal {T}}_0={\bar {F}}$ from property 8’ above. But then by that property,

$$\begin{align*}{\bar{E}}\!\upharpoonright\!(\mathrm{cr}(E^{\mathcal{T}}_0)\cup{\bar{t}})\in{\bar{U}}\cap{\bar{M}}.\end{align*}$$

Also ${\bar {t}}=k(t_D\backslash \mathrm {cr}(E^{\mathcal {T}}_0))$ and

$$\begin{align*}D\equiv D\!\upharpoonright\!(\tau_D\cup t_D)\equiv D\!\upharpoonright\!(\mathrm{cr}(E^{\mathcal{T}}_0)\cup (t_D\backslash\mathrm{cr}(E^{\mathcal{T}}_0))) \equiv{\bar{E}}\!\upharpoonright\!(\mathrm{cr}(E^{\mathcal{T}}_0)\cup{\bar{t}}). \end{align*}$$

But then $D\in {\bar {M}}$ , contradiction.

This completes the proof of the theorem.

3 Inductive condensation stack

In this section we prove Theorem 1.1. We first give the proofs of some older results, as their methods are then used in the proof of 1.1. The first is an observation due to Jensen.

Fact 3.1 (Jensen).

Let N be a premouse of height $\kappa>\omega $ , where $\kappa $ is regular. Let P be a sound premouse such that $N\trianglelefteq P$ , $\rho _\omega ^P=\kappa $ , and $\omega $ -condensation holds for P. Let Q be likewise. Then $P\trianglelefteq Q$ or $Q\trianglelefteq P$ .

Proof Suppose not. Taking a hull of V, it is easy to find $\bar {P},\bar {Q}$ such that ${\bar {P}\ntrianglelefteq \bar {Q}\ntrianglelefteq \bar {P}}$ and fully elementary maps $\pi :\bar {P}\to P$ and $\sigma :\bar {Q}\to Q$ and $\bar {\kappa }$ such that

$$\begin{align*}\mathrm{cr}(\pi)=\bar{\kappa}=\mathrm{cr}(\sigma)=\rho_\omega^{\bar{P}}=\rho_\omega^{\bar{Q}}<\kappa \end{align*}$$

and $\pi (\bar {\kappa })=\kappa =\sigma (\bar {\kappa })$ . So by condensation, either:

1. (i) $\bar {P}\trianglelefteq N$ and $\bar {Q}\trianglelefteq N$ , or

2. (ii) $N|\bar {\kappa }$ is active and $\bar {P}\trianglelefteq U$ and $\bar {Q}\trianglelefteq U$ where $U=\mathrm {Ult}(N|\bar {\kappa },F^{N|\bar {\kappa }})$ .

In either case, it follows that either $\bar {P}\trianglelefteq \bar {Q}$ or $\bar {Q}\trianglelefteq \bar {P}$ , a contradiction.

A slight adaptation gives:

Fact 3.2. Let M be a $(0,\omega _1+1)$ -iterable premouse with no largest proper segment. Let $\kappa>\omega $ be a regular cardinal of M. Let $P\in M$ be a sound premouse such that $M|\kappa \trianglelefteq P$ , $\rho _\omega ^P=\kappa $ , and $\omega $ -condensation holds for P. Then $P\triangleleft M$ .

Proof Use the proof above with $Q\trianglelefteq M$ such that $P\in Q$ and $\rho _\omega ^Q=\kappa $ .

A slight refinement of this argument gives:

Fact 3.3. Let M be a $(0,\omega _1+1)$ -iterable premouse. Let $\kappa>\omega $ be a regular cardinal of M. Let $P\in M$ be a $(n+1)$ -sound premouse such that $M|\kappa \trianglelefteq P$ , $\rho _{n+1}^P=\kappa $ , and $(n+1)$ -condensation holds for P. Then $P\triangleleft M$ .

The second ingredient is an argument of Woodin’s, which is used in the proof of Corollary 1.5. Steel noticed that 1.5 follows from Theorem 1.4 combined with Woodin’s argument.

Proof of Corollary 1.5

We have that M is $(0,\omega _1+1)$ -iterable, $\kappa $ is an uncountable cardinal in M and $\kappa ^{+M}<\mathrm {Ord}^M$ . We want to see that $M|\kappa ^{+M}$ is definable from parameters over $\mathcal {H}=(\mathcal {H}_{\kappa ^+})^M$ . There are two cases.

Case 1. M has no cutpoint in $[\kappa ,\kappa ^{+M})$ .

Then there are unboundedly many $\gamma <\kappa ^{+M}$ indexing an M-total extender. So by 1.4, given a premouse $P\in \mathcal {H}$ such that $M|\kappa \trianglelefteq P$ and $\rho _\omega ^P=\kappa $ , we have $P\triangleleft M|\kappa ^{+M}$ iff there is $E\in \mathcal {H}$ such that $P\triangleleft \mathrm {Ult}(M|\kappa ,E)$ and $\mathcal {H}\models $ “E is a countably complete short extender”. This gives a definition of $M|\kappa ^{+M}$ over $\mathcal {H}$ from the parameter $M|\kappa $ , which suffices.

Case 2. Otherwise (M has a cutpoint $\gamma _0\in [\kappa ,\kappa ^{+M})$ ).

The proof in this case is due to Woodin, and was found earlier. Let X be the set of all $H\in \mathrm {HC}^M$ such that there is $P\triangleleft M|\kappa ^{+M}$ and $\pi \in M$ such that $\pi :H\to P$ is elementary. Since $\kappa ^{+M}<\mathrm {Ord}^M$ , we have $X\in M$ and X is essentially a subset of $\omega _1^M$ in M. So $X\in \mathcal {H}$ . Let $P\in M$ be a sound premouse such that $M|\gamma _0\trianglelefteq P$ , $\gamma _0$ is a cutpoint of P and $\rho _\omega ^P\leq \gamma _0$ . We claim that the following are equivalent:

1. (i) $P\triangleleft M$ ,

2. (ii) $\mathcal {H}\models \text {"Every countable elementary submodel of }P\text { is in }X\text {"}$ .

It follows that $M|\kappa ^{+M}$ is definable over $\mathcal {H}$ from the parameter $(X,M|\gamma _0)$ , which suffices. Now (i) implies (ii) by definition. So suppose (ii) holds. Let Q be such that $P\in Q\triangleleft M$ , with $\rho _\omega ^{Q}\leq \gamma _0$ . Working in M, let $Y\preccurlyeq Q$ be countable, with $P\in Y$ . The transitive collapses ${\bar {P}}$ of $Y\cap P$ and ${\bar {Q}}$ of Y are in X, so can be compared in V. But ${\bar {P}}|{\bar {\gamma }}_0={\bar {Q}}|{\bar {\gamma }}_0$ where ${\bar {\gamma }}_0$ is a cutpoint of both ${\bar {P}},{\bar {Q}}$ , and ${\bar {P}},{\bar {Q}}$ are sound and project $\leq {\bar {\gamma }}_0$ . So standard calculations give that ${\bar {P}}\trianglelefteq {\bar {Q}}$ , so $P\trianglelefteq Q$ .

Woodin’s argument above makes use of the parameter X. We can actually replace this parameter with :

Lemma 3.4. Let N be an $(0,\omega _1+1)$ -iterable premouse with no largest proper segment. Let $M\triangleleft N$ and $H\in \mathrm {HC}^N$ and $\pi :H\to M$ be elementary with $\pi \in N$ . Then there is ${\bar {M}}\triangleleft N|\omega _1^N$ and an elementary $\bar {\pi }:H\to {\bar {M}}$ with $\bar {\pi }\in N$ .

Proof Let $M\triangleleft P\triangleleft N$ be such that $\pi \in P$ . Let $q\in [\mathrm {Ord}^P]^{<\omega }$ be such that $(\omega ,q)$ is $1$ -self-solid for P and such that $\pi ,H,M\in \mathrm {Hull}_1^P(\{q\})$ . Let ${\bar {P}}=\mathrm {cHull}_1^P(\{q\})$ . Then by 2.3, ${\bar {P}}\triangleleft N|\omega _1^N$ . Let $\sigma :{\bar {P}}\to P$ be the uncollapse. Then $\sigma (H)=H$ . Let $\sigma (\bar {\pi })=\pi $ and $\sigma ({\bar {M}})=M$ . Then ${\bar {M}}\triangleleft {\bar {P}}$ and $\bar {\pi }:H\to {\bar {M}}$ elementarily, so we are done.

Similarly:

Lemma 3.5. Let N be a $(0,\omega _1+1)$ -iterable premouse. Let $M\triangleleft N$ and $H\in \mathrm {HC}^N$ and $m<\omega $ and $\pi :H\to M$ be an m-lifting ((weak, near) m-embedding respectively) with $\pi \in N$ . Then there is ${\bar {M}}\triangleleft N|\omega _1^N$ and an m-lifting ((weak, near) m-embedding respectively) $\bar {\pi }:H\to {\bar {M}}$ with $\bar {\pi }\in N$ .

Proof Consider the case that $N=\mathcal {J}(M)$ and $\pi :H\to M$ . Then there is $k<\omega $ and $x\in M$ such that $\pi $ is $\mathrm {r}\Sigma _k^M(\{x\})$ . Argue as in the proof of 3.4, but at degree n instead of $1$ , with $n>k+m+5$ .

Woodin’s argument above is abstracted into the following definition:

Definition 3.6. Let M be a $(0,\omega _1+1)$ -iterable premouse satisfying “ $\omega _1$ exists”, with no largest proper segment. Then $\mathrm {css}^M$ (countable substructures) denotes the set of all $H\in \mathrm {HC}^M$ such that for some $Q\triangleleft M$ , there is $\pi \in M$ such that $\pi :H\to Q$ is elementary. (So by 3.4, $\mathrm {css}^M$ is definable over , uniformly in M.) Let $P,Q\in M$ be sound premice. Working in M, say that Q is -verified iff the transitive collapse of every countable elementary substructure of Q is in $\mathrm {css}^M$ , and say that Q is an -lower part premouse iff $P\trianglelefteq Q$ , P is a cutpoint of Q, $\rho _\omega ^Q\leq \mathrm {Ord}^P$ and Q is -verified. The stack of all -lower part premice $Q\in M$ is denoted .

Note that is definable over $\left \lfloor M\right \rfloor $ from ; the fact that it forms a stack follows from the proof of 1.5.

In order to prove Theorem 1.1, it easily suffices to prove that if M is passive, $(0,\omega _1+1)$ -iterable and satisfies $\mathrm {ZFC}^-+$ “ $\omega _1$ exists”, then $\mathbb {E}^M$ is definable over $\left \lfloor M\right \rfloor $ from $\mathbb {E}^M\!\upharpoonright \!\omega _1^M$ , uniformly in M. We will in fact prove a stronger fact, Theorem 3.11, making do with less than $\mathrm {ZFC}^-$ . We may assume that M has a largest cardinal $\theta $ . The proof breaks into different cases, depending on the nature of M above $\theta $ . Clearly the cases are not mutually exclusive (case (i) is in fact subsumed by case (iv)).

Definition 3.7. Let M be a premouse. Let $\kappa <\theta $ be cardinals of M. We say that $\kappa $ is $\mathcal {H}_\theta $ -strong in M iff there is $E\in M$ such that $M\models $ “E is a countably complete short extender” and $\mathrm {cr}(E)=\kappa $ and $\mathcal {H}^M_\theta \subseteq \mathrm {Ult}_0(M,E)$ .

Definition 3.8. A passive premouse M is eventually constructible iff $M=\mathcal {J}_\alpha (R)$ for some $R\triangleleft M$ and $\alpha>0$ .

Remark 3.9. In the theorem statement below, in each case we specify definability classes $\Gamma ,\Lambda $ . The case specification is $\Gamma ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$ , meaning that there is a $\Gamma $ formula $\varphi $ such that for any $(0,\omega _1+1)$ -iterable premouse M satisfying “ $\omega _1$ exists and $\theta $ is the largest cardinal”, the case hypothesis holds of M iff $\left \lfloor M\right \rfloor \models \varphi (M|\theta )$ . In the given case, the definition of $\mathbb {E}^M$ is $\Lambda ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$ . (The definability of the case specification is used in defining $M|\theta $ from over $\left \lfloor M\right \rfloor $ .)

Definition 3.10. Let M be a passive premouse with a largest cardinal $\theta \geq \omega _1^M$ . We say that M is tractable iff either:

1. (i) $\theta $ is regular in M, or

2. (ii) $\theta $ is a cutpoint of M, or

3. (iii) M has no cutpoint in $[\theta ,\mathrm {Ord}^M)$ , or

4. (iv) $\mathrm {cof}^M(\theta )>\omega $ , or

5. (v) $M\models $ “ $\theta $ is not a limit of cardinals which are $\mathcal {H}_\theta $ -strong”, or

6. (vi) , or

7. (vii) and M is eventually constructible.

Theorem 3.11. Let M be a passive $(0,\omega _1+1)$ -iterable premouse satisfying “ $\omega _1$ exists”. Then $:$

1. (a) If M is tractable then $\mathbb {E}^M$ is , uniformly in such M.

2. (b) If $\left \lfloor M\right \rfloor \models \mathrm {PS}$ then $\mathbb {E}^M$ is , uniformly in such M.

3. (c) Suppose that M has largest cardinal $\theta $ and either $:$

   1. (i) $\theta $ is regular in $M;$ and let $(\Gamma ,\Lambda )=(\Pi _1,\Sigma _1)$ , or

   2. (ii) $\theta $ is a cutpoint of $M;$ let $(\Gamma ,\Lambda )=(\Pi _2,\Sigma _2)$ , or

   3. (iii) M has no cutpoint in $[\theta ,\mathrm {Ord}^M);$ let $(\Gamma ,\Lambda )=(\Pi _3,\Sigma _2)$ , or

   4. (iv) $\mathrm {cof}^M(\theta )>\omega ;$ let $(\Gamma ,\Lambda )=(\Pi _1,\Sigma _1)$ , or

   5. (v) $M\models $ “ $\theta $ is not a limit of $\mathcal {H}_\theta $ -strong cardinals” $;$ let $(\Gamma ,\Lambda )=(\Sigma _3,\Sigma _1)$ , or

   6. (vi) ¹⁶ let $(\Gamma ,\Lambda )=(\Pi _5,\Sigma _4)$ , or

   7. (vii) and M is eventually constructible; let $(\Gamma ,\Lambda )=(\Pi _3\wedge \Sigma _3,\Sigma _3)$ .

   Then $\mathbb {E}^M$ is $\Lambda ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$ , and the case specification is $\Gamma ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$ , both uniformly in such M.

Proof of Theorem 3.11

Parts (a) and (b) follow immediately from part (c) by an easy induction on M-cardinals.

Part (c): We split into cases corresponding to hypotheses (i)–(vii). In each case we will give a characterization of $\mathbb {E}^M$ and leave to the reader the verification of the precise degree of definability. Note that for the definability of the case specification, we use 1.2 to determine, for example, whether or not $\theta $ is a cutpoint of M.

Case 1. $\theta $ is regular in M.

By 3.3, working in M, given any premouse P, we have $P\triangleleft M$ iff there is a sound premouse Q and $n<\omega $ such that $P\triangleleft Q$ and $\rho _{n+1}^Q=\theta $ and $M|\theta \trianglelefteq Q$ and Q satisfies $(n+1)$ -condensation. And $\mathbb {E}^M$ is the stack of all structures of the form $\mathcal {S}_m(P)$ for such P and $m<\omega $ .

Case 2. $\theta $ is a cutpoint of M. ¹⁷

Use the proof of Corollary 1.5, or an adaptation thereof if $M=\mathcal {J}(R)$ for some R, combined with 3.4 and 3.5.

Case 3. M has no cutpoint in $[\theta ,\mathrm {Ord}^M)$ .

Use 1.4.

Case 4. $\mathrm {cof}^M(\theta )>\omega $ .

Let $P\in M$ and $n<\omega $ be such that P is a sound premouse, $M|\theta \trianglelefteq P$ , $\rho _{n+1}^P=\theta $ , and P satisfies $(n+1)$ -condensation. We claim that $P\triangleleft M$ ; clearly this suffices. If $\theta $ is regular in M we can use the proof of case (i), so suppose otherwise; in particular, $\theta $ is a limit cardinal of M.

We prove that $P\triangleleft M$ using a phalanx comparison. Let $Q\triangleleft M$ and $x\in Q$ and ${m<\omega }$ be such that P is $\mathrm {r}\Sigma _m^Q(\{x\})$ ; in particular, $\mathrm {Ord}^P\leq \mathrm {Ord}^Q$ . We must show that $P\trianglelefteq Q$ . Suppose not; note that the fact that $P\ntrianglelefteq Q$ is first-order over Q (in the parameter x). So we may assume that $x=\emptyset $ (increasing m if needed). Let $m+n+5<k<\omega $ and let $\bar {Q}=\mathrm {cHull}_{k+1}^Q(\emptyset )$ . Then $\bar {Q}\triangleleft M$ . Let $\bar {P}$ be defined over $\bar {Q}$ as P is over Q. Let $\pi :\bar {Q}\to Q$ be the uncollapse, and $\pi (\bar {\theta })=\theta $ . Then $\bar {P}$ is $(n+1)$ -sound and $\rho _{n+1}^{\bar {P}}=\bar {\theta }$ , $\bar {Q}$ is $\omega $ -sound and $\rho _{k+1}^{\bar {Q}}=\omega $ , $\bar {P}|\bar {\theta }=\bar {Q}|\bar {\theta }$ , $\bar {\theta }$ is a cardinal of both models, and $\bar {P}\ntrianglelefteq \bar {Q}$ .

Define the phalanx $\mathfrak {P}=((\bar {Q},k,\bar {\theta }),(\bar {P},n),\bar {\theta })$ . By the following claim, a standard comparison argument (comparing $\mathfrak {P}$ with $\bar {Q}$ ) shows that $\bar {P}\trianglelefteq \bar {Q}$ , a contradiction, completing the proof.

Claim 1. $\mathfrak {P}$ is $(\omega _1+1)$ -iterable.

Proof Let $\sigma :\bar {P}\to P$ be $\pi \!\upharpoonright \!\bar {P}$ . Then $\sigma \!\upharpoonright \!\bar {\theta }=\pi \!\upharpoonright \!\bar {\theta }$ , and by the choice of k, $\sigma $ is $\Sigma _{n+5}$ -elementary, so

(6) $$ \begin{align}\sigma\text{ is }p_{n+1}\text{-preserving and preserves }(n+1)\text{-solidity witnesses}.\end{align} $$

Let $\eta =\sup \pi "\bar {\theta }$ . Then $\eta <\theta $ because $\mathrm {cof}^M(\theta )>\omega $ . Because $\theta $ is a limit cardinal of M, so is $\eta $ . Let

$$\begin{align*}P'=\mathrm{cHull}_{n+1}^P(\eta\cup\{\vec{p}_{n+1}^P\}) \end{align*}$$

and $\pi ':P'\to P$ be the uncollapse.

We claim $P'$ is $(n+1)$ -sound, $\rho _{n+1}^{P'}=\eta $ and $q=_{\mathrm {def}} p^{P'}_{n+1}=(\pi ')^{-1}(p_{n+1}^P)$ . For

$$\begin{align*}P'=\mathrm{Hull}^{P'}(\eta\cup\{q,\vec{p}_n^{P'}\}), \end{align*}$$

so $\rho _{n+1}^{P'}\leq \eta $ . But $P'|\eta =M|\eta $ and $P'\in M$ , and as $\eta $ is an M-cardinal, therefore $\rho _{n+1}^{P'}=\eta $ and $p_{n+1}^{P'}\leq q$ . But by line (6), $(P',q)$ is $(n+1)$ -solid (and $\pi '$ maps the $(n+1)$ -solidity witnesses of $(P',q)$ to the $(n+1)$ -solidity witnesses of P). Therefore $p_{n+1}^{P'}=q$ and $P'$ is $(n+1)$ -sound, as desired.

So we can apply $(n+1)$ -condensation to $\pi ':P'\to P$ (by hypothesis on P), and note that it follows that $P'\triangleleft M|\theta \trianglelefteq Q\triangleleft M$ .

Let $\sigma ':\bar {P}\to P'$ be the natural factor map. Then $\sigma '$ is a near n-embedding, and $\sigma '\!\upharpoonright \!\bar {\theta }=\pi \!\upharpoonright \!\bar {\theta }$ . Using $(\pi ,\sigma ')$ , one can lift normal trees on $\mathfrak {P}$ to normal trees on Q, completing the proof.

Case 5. $M\models $ “ $\theta $ is not a limit of cardinals which are $\mathcal {H}_\theta $ -strong”.

This is almost the same as the previous case. Everything is identical until defining $\eta $ . Set $\eta =\pi (\bar {\eta })$ where $\bar {\eta }$ is some $\bar {Q}$ -cardinal $\bar {\eta }<\bar {\theta }$ such that $\bar {\eta }>\kappa $ for all $\mathcal {H}_\theta $ -strong cardinals $\kappa $ of M, and the $(n+1)$ -solidity witnesses of $\bar {P}$ are in $\mathrm {Hull}_{n+1}^{\bar {P}}(\bar {\eta }\cup \{\vec {p}_{n+1}^{\bar {P}}\})$ . (Note we may again assume that $\theta $ is singular in M, and hence a limit cardinal of M and $\bar {\theta }$ is a limit cardinal of $\bar {P}$ . We again get that $\eta $ is an M-cardinal, though in this case it might not be a limit cardinal of M.) We get $\sigma '\!\upharpoonright \!(\bar {\eta }+1)=\pi \!\upharpoonright \!(\bar {\eta }+1)$ , which, by the choice of $\bar {\eta }$ , suffices for iterability.

The remaining two cases are more subtle than the previous ones. We (may) now make the:

Assumption 1. $\theta $ is a singular cardinal of M and M has a cutpoint in $[\theta ,\mathrm {Ord}^M)$ .

This must of course be incorporated appropriately into the $\Sigma _4(\{M|\theta \})$ (in case (vi)) and $\Sigma _3(\{M|\theta \})$ (in case (vii)) definitions one forms from the arguments to follow. But given the definability $(\Sigma ,\Lambda )$ established for cases (i) and (iii), this is no problem. (Note here that in case (vii), M does have a cutpoint $\geq \theta $ , so the $\Pi _3$ complexity of asserting the non-existence of a cutpoint is not relevant in this case.)

Case 6. .

Work in M and let P be a premouse. Say that P is good iff P is sound, $M|\theta \trianglelefteq P$ and $\rho _\omega ^P=\theta $ . Say that P is excellent iff P is good, M and have the same universe, and $1$ -condensation holds for every .

By the case hypothesis, M has no largest proper segment, so with Assumption 1, it follows that there are cofinally many excellent $N\triangleleft M$ . Therefore it suffices to prove the following claim:

Claim 1. Let $P,Q\in M$ be excellent. Then either $P\trianglelefteq Q$ or $Q\trianglelefteq P$ .

Proof We may assume $Q\triangleleft M$ and $\mathrm {Ord}^Q$ is a cutpoint of M, so . Define $\left <P_n,Q_n\right>_{n<\omega }$ as follows. Let $P_0=P$ and $Q_0=Q$ . Given $P_n,Q_n$ , let $Q_{n+1}$ be the least $N\triangleleft M$ such that N is good, $Q_n\triangleleft N$ and $P_n\in N$ . Given $P_n,Q_{n+1}$ , let $P_{n+1}$ be the least such that R is good, $P_n\triangleleft R$ and $Q_{n+1}\in R$ .

Let $\widetilde {P}=\mathrm {stack}_{n<\omega }P_n$ and $\widetilde {Q}=\mathrm {stack}_{n<\omega }Q_n$ . Note that $\widetilde {P}$ and $\widetilde {Q}$ have the same universe U (but ostensibly may have different extender sequences). We have $\mathrm {Ord}^U<\mathrm {Ord}^M$ by our case hypothesis, as $\left <P_n,Q_n\right>_{n<\omega }$ is $\Sigma _2^{\left \lfloor M\right \rfloor }(\{P,Q\})$ . ¹⁸ Now $\widetilde {P}$ is definable over U from the parameter P, and likewise $\widetilde {Q}$ over U from Q; in fact,

(Clearly cofinally many segments of $\widetilde {P}$ satisfy the requirements for premice in ; but if R is some premouse satisfying these requirements then working in U, we can run the same proof as before to see that .) Also, U has largest cardinal $\theta $ , so and $M|\mathrm {Ord}^U$ are both passive. So letting $P^+=\mathcal {J}(\widetilde {P})$ and $Q^+=\mathcal {J}(\widetilde {Q})$ , we have and $Q^+\triangleleft M$ and (because $\widetilde {P},\widetilde {Q}$ are definable from parameters over U),

$$\begin{align*}\left\lfloor P^+\right\rfloor=\left\lfloor \mathcal{J}(U)\right\rfloor=\left\lfloor Q^+\right\rfloor. \end{align*}$$

Also because $\mathrm {Ord}^U$ has cofinality $\omega $ , definably over U from parameters, we have

$$\begin{align*}\rho_1^{P^+}=\rho_\omega^{\widetilde{P}}=\theta=\rho_\omega^{\widetilde{Q}}=\rho_1^{Q^+}.\end{align*}$$

We claim that there is an M-cardinal $\gamma <\theta $ such that

(7) $$ \begin{align} H=_{\mathrm{def}}\mathrm{Hull}_1^{P^+}(\gamma\cup p_1^{P^+})\text{ has the same elements as }J=_{\mathrm{def}}\mathrm{Hull}_1^{Q^+}(\gamma\cup p_1^{Q^+}) \end{align} $$

(“ $\mathrm {Hull}$ ” denotes the uncollapsed hull), and the transitive collapses $\bar {P}^+,\bar {Q}^+$ are $1$ -sound and such that $\rho _1^{\bar {P}^+}=\gamma =\rho _1^{\bar {Q}^+}$ . For recalling that $\theta $ is a limit cardinal of M, let $\gamma <\theta $ be an M-cardinal large enough that, defining $H,J$ as above, we have

$$\begin{align*}\widetilde{P},\widetilde{Q},p_1^{P^+},p_1^{Q^+},w_1^{P^+},w_1^{Q^+}\in H\cap J\end{align*}$$

(recall $w_1^{P^+},w_1^{Q^+}$ are the $1$ -solidity witnesses for $P^+,Q^+$ ). Then because $\gamma $ is an M-cardinal and $w_1^{P^+}\in H$ , we easily have that $\rho _1^{\bar {P}^+}=\gamma $ and $\bar {P}^+$ is $1$ -sound, and likewise for $\bar {Q}^+$ . And because

$$\begin{align*}\gamma\cup\{\widetilde{Q},p_1^{Q^+}\}\subseteq H \end{align*}$$

and $P^+,Q^+$ have the same universe, we have $J\subseteq H$ . Similarly $H\subseteq J$ , giving line (7).

By $1$ -condensation for $P^+,Q^+$ (a requirement of excellence), and because ${\rho _1^{\bar {P}^+}=\gamma =\rho _1^{\bar {Q}^+}}$ is an M-cardinal, we have $\bar {P}^+\triangleleft M$ and $\bar {Q}^+\triangleleft M$ . By line (7), $\mathrm {Ord}^{\bar {P}^+}=\mathrm {Ord}^{\bar {Q}^+}$ . Therefore $\bar {P}^+=\bar {Q}^+$ . It easily follows that $\widetilde {P}=\widetilde {Q}$ , giving the claim.

Case 7. and M is eventually constructible.

A simplification of the argument in the previous case shows that the collection of all $R\triangleleft M$ such that $M=\mathcal {J}_\alpha (R)$ for some $\alpha>0$ , is $\Pi _2^{\left \lfloor M\right \rfloor }(\{M|\theta \})$ . Regarding the complexity of the case specification, it is $\Sigma _3^{\left \lfloor M\right \rfloor }$ to assert “M is eventually constructible”, as it is equivalent to

$$\begin{align*}\exists x\ \forall y\ \exists\beta\in\mathrm{Ord}\ [y\in \mathcal{S}_\beta(x)] \end{align*}$$

(M fails to be eventually constructible iff M is closed under sharps).

This completes all cases and hence, the proof of the theorem.

Definition 3.12. Let M be a transitive structure. Let be a premouse with . The inductive condensation stack of M above is the stack of premice in M, extending , satisfying the inductive definition used in the proof of 3.11.

Of course, the inductive condensation stack S could have $\mathrm {Ord}^S<\mathrm {Ord}^M$ . But if M is a $(0,\omega _1+1)$ -iterable tractable premouse and then $M=S$ .

Remark 3.13. In case (iii) of the preceding proof, it appeared that we used 1.4 for extenders E generated by $\theta \cup t$ for some finite set t of generators (in order that we can represent arbitrary segments $R\triangleleft M|\theta ^{+M}$ ). Actually, it suffices to consider only extenders E such that $\nu _E=\theta $ (and $\mathcal {H}_\theta ^M\subseteq \mathrm {Ult}(M,E)$ etc.). For we claim that (under the case hypothesis) there are unboundedly many $\beta <\mathrm {Ord}^M$ such that $M|\beta $ is active with an extender E such that $\nu _E=\theta $ ; clearly this suffices.

For let $Q\triangleleft M$ be such that $\rho _\omega ^Q=\theta $ and let $\alpha $ be least such that $\alpha>\mathrm {Ord}^Q$ and $M|\alpha $ is active with extender F and $\kappa =\mathrm {cr}(F)<\theta $ . We claim that $\nu _F=\theta $ . So suppose that $\theta <\nu _F$ . Easily by the ISC, $\theta $ is the largest cardinal of $M|\alpha $ . So F is type 2. Let $E=F\!\upharpoonright \!\theta $ , let $U_E=\mathrm {Ult}_0(M,E)$ , $U_F=\mathrm {Ult}_0(M,F)$ and $\pi :U_E\to U_F$ the standard factor map. So $\mathrm {cr}(\pi )$ is the least generator $\gamma $ of F with $\gamma \geq \theta $ .

Suppose $\gamma =\theta $ . Then $\theta $ is a limit cardinal of M and $U_E$ , so $\pi (\theta )>\theta ^{+U_F}=\mathrm {lh}(F)$ . By the ISC, $\kappa $ is $\mathcal {H}_\xi $ -strong in $U_E$ for each $\xi <\theta $ . Therefore $\kappa $ is $\mathcal {H}_\xi $ -strong in $U_F$ for each $\xi <\pi (\theta )$ . But then by the ISC, there are unboundedly many $\zeta <\theta ^{+U_F}$ indexing an extender G with $\mathrm {cr}(G)=\kappa $ , and since $Q\triangleleft U_F|\theta ^{+U_F}$ , this contradicts the minimality of F.

So $\gamma>\theta $ . Because $\theta ^{+U_E}=\mathrm {lh}(E)<\mathrm {lh}(F)=\theta ^{+U_F}$ , we have $\gamma =\mathrm {lh}(E)$ and $\pi (\gamma )=\mathrm {lh}(F)$ . But $E\in \mathbb {E}^{U_F}$ , so by reflection, there are unboundedly many $\xi <\mathrm {lh}(E)$ such that $M|\xi $ is active with an extender G with $\mathrm {cr}(G)=\kappa $ , and so the same holds of $\pi (\mathrm {lh}(E))=\mathrm {lh}(F)$ , again contradicting the minimality of F.

Remark 3.14. Let M be passive, $(0,\omega _1+1)$ -iterable, satisfying “ $\omega _1$ exists” and $\theta =\mathrm {lgcd}(M)$ . We sketch, in a further case, the identification of M from parameter $M|\theta $ over $\left \lfloor M\right \rfloor $ . However, here we do not know whether the case specification itself is uniformly definable over $\left \lfloor M\right \rfloor $ as above. Say that M is -bounded iff $\mathrm {Hull}_1^M(\alpha \cup \{x\})$ is bounded in $\mathrm {Ord}^M$ for every $\alpha <\rho _1^M$ and $x\in M$ . Suppose that M is $1$ -sound and $\rho _1^M>\omega $ , and either M is eventually constructible or M is not -bounded. Then M is definable from $M|\theta $ over $\left \lfloor M\right \rfloor $ .

To see this, we argue much as in the last two cases of 3.11. We may make Assumption 1. If M is eventually constructible things are easier (using then either the argument from case (vii) of 3.11 if , or a variant of the argument to follow otherwise), so we leave this case to the reader, and suppose otherwise. So M is closed under sharps and has no largest proper segment. The difference to case (vi) of 3.11 is that now, when we define $\widetilde {P},\widetilde {Q}$ , we might have $\left \lfloor M\right \rfloor =\left \lfloor \widetilde {P}\right \rfloor =\left \lfloor \widetilde {Q}\right \rfloor $ . Let $P\in M$ be good (good defined as before). Say that P is outstanding iff P satisfies the conditions of excellence from before, and letting , then $P^*$ is $1$ -sound, $\rho _1^{P^*}>\omega $ , $P^*$ is not -bounded, $1$ -condensation holds for $P^*$ , and for all $R\trianglelefteq P^*$ , if

$$\begin{align*}\exists\kappa\ \big[\omega<\rho=_{\mathrm{def}}\rho_1^R=\kappa^{+R}\big] \end{align*}$$

then for all sufficiently large $\gamma <\rho $ ,

$$\begin{align*}\mathrm{cHull}_1^R(\gamma\cup p_1^{R})\text{ is }1\text{-sound}\end{align*}$$

(so $1$ -condensation applies to the uncollapse map). By 2.4, all sufficiently large good $Q\triangleleft M$ are outstanding; we take Q such.

Let $P\in M$ be outstanding. We claim $\rho _1^{P^*}=\rho _1^{M}$ . For suppose $\rho _1^{P^*}<\rho _1^M$ . Let $\alpha \in [\rho _1^{P^*},\rho _1^M)$ be large enough that

$$\begin{align*}H=_{\mathrm{def}}\mathrm{Hull}_1^M(\alpha\cup\{p_1^M\}) \end{align*}$$

is unbounded in $\mathrm {Ord}^M$ (using non--boundedness) and $P,p_1^{P^*}\in H$ . Then $P'\in H$ for cofinally many $P'\triangleleft P^*$ . For given $\eta _0,\eta _1\in H\cap \mathrm {Ord}^M$ such that there is a good $P'\triangleleft P^*$ with $\eta _0\leq \mathrm {Ord}^{P'}$ and $P'\in M|\eta _1$ , then the least good $P"\triangleleft P^*$ such that $\eta _0\leq \mathrm {Ord}^{P"}$ , is in H. (Recall that is the stack of all good Q such that $P\trianglelefteq Q$ , P is a cutpoint of Q and all countable elementary substructures of Q in M have transitive collapse . But in order to identify the desired $P"$ , it suffices to restrict attention to all countable elementary substructures of $P"$ in $M|(\eta _1+\omega ^2)$ ; recall here that M is closed under sharps, so $\eta _1+\omega ^2<\mathrm {Ord}^M$ . This is because $P'\in M|\eta _1$ , and we can run the argument which shows that $P'\trianglelefteq P"$ or $P"\trianglelefteq P'$ working in $M_1|(\eta _1+\omega ^2)$ .) It follows that

$$\begin{align*}\mathrm{Hull}_1^{P^*}(\alpha\cup\{p_1^{P^*}\})\subseteq H. \end{align*}$$

But $P^*$ is $1$ -sound and $\left \lfloor P^*\right \rfloor =\left \lfloor M\right \rfloor $ , so $M=H$ , contradicting the fact that $\alpha <\rho _1^M$ . So $\rho _1^M\leq \rho _1^{P^*}$ and the converse is likewise.

The rest is much like the last part of the argument used in case (vi), but we might get $\widetilde {P}=P^*$ and $\widetilde {Q}=M$ , in which case there is a wrinkle. If this occurs, choose $\alpha <\rho _1^M=\rho _1^{P^*}$ such that

$$\begin{align*}P,Q\in\mathrm{Hull}_1^{P^*}(\alpha\cup p_1^{P^*})\text{ has same elements as }\mathrm{Hull}_1^{M}(\alpha\cup p_1^M) \end{align*}$$

by arguing as in the previous paragraph, and such that the transitive collapses $\bar {P},\bar {Q}$ of the hulls are $1$ -sound (using 2.4 and excellence if $\rho _1^M=\kappa ^{+M}$ ). Then by $1$ -condensation we get $\bar {P}=\bar {Q}$ , so $P=Q$ .

Corollary 3.15. Let M be a $(0,\omega _1+1)$ -iterable premouse satisfying either $\mathrm {PS}$ or $\mathrm {ZFC}^-+$ “ $\omega _1$ exists”. Suppose that either $:$

1. (i) is $(\omega ,\omega _1+1)$ -iterable in M, ¹⁹ or

2. (ii) is built by the ²⁰ maximal fully backgrounded $L[\mathbb {E}]$ -construction of M using background extenders $E\in \mathbb {E}^M$ such that $\nu _E$ is an M-cardinal.

Then $:$

1. 1. $\mathbb {E}^M$ is definable over $\left \lfloor M\right \rfloor $ without parameters,

2. 2. $\left \lfloor M\right \rfloor =\mathrm {Hull}^{\left \lfloor M\right \rfloor }(\mathrm {Ord}^M)$ , and

3. 3. if assumption (i) holds and $M\models \mathrm {PS}$ then $\left \lfloor M\right \rfloor =\mathrm {OD}^{\left \lfloor M\right \rfloor }$ . ²¹

Proof If assumption (i) holds, then all three conclusions follow easily from 3.11.

If assumption (ii) holds, by 1.2, if $E\in M$ then [ $E\in \mathbb {E}^M$ and $\nu _E$ is an M-cardinal] iff $M\models \text {"}E$ is a countably complete extender, $\nu _E$ is a cardinal and $\mathcal {H}_{\nu _E}\subseteq \mathrm {Ult}(V,E)$ ”. So the $L[\mathbb {E}]$ -construction using these background extenders is definable over $\left \lfloor M\right \rfloor $ without parameters, so is likewise definable, so conclusions 1 and 2 follow easily from 3.11. ²²

Recall that $M_{\mathrm {wlim}}$ is the least proper class mouse with a Woodin limit of Woodins. Part (ii) of the previous corollary gives:

Corollary 3.16. $\left \lfloor M_{\mathrm {wlim}}\right \rfloor \models $ “ $V=\mathrm {HOD}$ ”.

There are of course many variants of this corollary. Using the background construction of [9] in place of the background construction used above, one gets that $\left \lfloor M\right \rfloor \models $ “ $V=\mathrm {HOD}$ ” where M is, for example, the least proper class mouse with a $\lambda $ which is a limit of Woodins and strong cardinals.

4 Direct condensation stack in $M[G]$

In this section we prove the following theorem, using a variant of the inductive condensation stack:

Theorem 4.1. Let M be a $(0,\omega _1+1)$ -iterable premouse satisfying $\mathrm {PS}$ . Let ${\theta <\mathrm {Ord}^M}$ be a regular cardinal of M and $\mathbb P\in M|\theta $ be a poset. Let G be $(M,\mathbb P)$ -generic. Then $\mathbb {E}^M$ is definable over $M[G]$ from the parameter $M|\theta $ .

Proof Work in $M[G]$ . It suffices to give a definition of $M|\eta ^{+M}$ from the parameter $M|\theta $ , uniformly in M-regular cardinals $\eta \geq \theta $ . Note that the Jensen stack over $M|\eta $ is exactly $M|\eta ^+$ , and this structure satisfies standard condensation facts. (But if $\eta>\theta $ , we don’t have the parameter $M|\eta $ available to refer to.)

Say that a premouse P is excellent iff $M|\theta \trianglelefteq P$ , $\mathrm {Ord}^P=\eta $ , the Jensen stack $P^+$ over P has height $\eta ^+$ , $P^+$ satisfies standard condensation facts, and there is $\mathbb Q\in P|\theta $ and a $(P,\mathbb Q)$ -generic filter h such that $P^+[h]$ has universe $\mathcal {H}_{\eta ^+}$ .

Clearly the following claim completes the proof:

Claim 1. $M|\eta $ is the unique excellent premouse.

Proof Clearly $N=M|\eta $ is excellent, as witnessed by $\mathbb P,g$ .

So let R also be excellent, as witnessed by $\mathbb Q,h$ . Define a sequence $\left <N_n,R_n\right>_{n<\omega }$ as follows. Let $N_0=N$ and $R_0=R$ . Given $N_n,R_n$ , let $N_{n+1}$ be the least $N'$ such that $N_n\triangleleft N'\triangleleft N^+$ and $\rho _\omega ^{N'}=\eta $ and $R_n,h\in N'[g]$ ; then let $R_{n+1}$ be the least $R'$ such that $R_n\triangleleft R'\triangleleft R^+$ and $\rho _\omega ^{R'}=\eta $ and $N_{n+1},g\in R'[h]$ . Let $N_\omega =\mathrm {stack}_{n<\omega }N_n$ and $\widetilde {N}=\mathcal {J}(N_\omega )$ , and $R_\omega ,\widetilde {R}$ likewise. Then $\widetilde {N}\triangleleft N^+$ and $\widetilde {R}\triangleleft R^+$ . Note that $N_\omega [g]$ and $R_\omega [h]$ have the same universe U, and $N_\omega ,R_\omega $ are both definable from parameters over U (via the Jensen stack). Hence, $\mathcal {J}(N_\omega [g])$ and $\mathcal {J}(R_\omega [h])$ and $\widetilde {N}[g]$ and $\widetilde {R}[h]$ all have the same universe $\widetilde {U}=\mathcal {J}(U)$ .

Now $\widetilde {N},\widetilde {R}$ both satisfy standard $1$ -condensation facts. Let $\gamma <\theta $ be a cardinal of the models $N,N[g],R[h],R$ such that $\mathbb P,\mathbb Q$ have cardinality $\leq \gamma $ in $N,R$ respectively.

Subclaim 1.1. For all $x\in \widetilde {U}$ there is $q\in [\mathrm {Ord}^{\widetilde {U}}]^{<\omega }$ such that the hulls $H,H',J,J'$ all contain the same ordinals, where

$$\begin{align*}H=\mathrm{Hull}_1^{\widetilde{N}}(\gamma\cup\{q\}) \text{ and }J=\mathrm{Hull}_1^{\widetilde{R}}(\gamma\cup\{q\}),\end{align*}$$

$$\begin{align*}H'=\mathrm{Hull}_1^{\widetilde{U}}(\gamma\cup\{q,N_\omega,g\}) =\mathrm{Hull}_1^{\widetilde{U}}(\gamma\cup\{q,R_\omega,h\})=J',\end{align*}$$

and moreover, $\mathbb P\in H$ , $\mathbb Q\in J$ , $x\in H'=J'$ , and the transitive collapses $C,D$ of $H,J$ respectively are sound.

Assuming the subclaim, let $\pi :C\to H$ and $\sigma :D\to J$ be the uncollapses. Then by $1$ -condensation, $C\triangleleft N|\theta $ and $D\triangleleft R|\theta $ , and hence $C=D$ (as $N|\theta =R|\theta $ and $\mathrm {Ord}^C=\mathrm {Ord}^D$ ), and $\pi \!\upharpoonright \!\mathrm {Ord}=\sigma \!\upharpoonright \!\mathrm {Ord}$ . But then $\widetilde {N}=\widetilde {R}$ and $N=R$ , as desired.

Proof of Subclaim

Use a simple variant of the proof of 2.3 to choose q, running an algorithm much as there, but simultaneously for both models $\widetilde {N},\widetilde {R}$ , and using the “ $\Sigma _1$ -definability of the $\Sigma _1$ -forcing relation” to see that $H,H'$ contain the same ordinals (and likewise $J,J'$ ), and choosing elements of q large enough to ensure that $H'=J'$ and $\mathbb P\in H$ , etc.

Here are some more details: Given $q\!\upharpoonright \! i$ and $\gamma _i$ much as in the proof of 2.3, first select some $q^{\prime }_i$ satisfying the requirements much as before with respect to $\widetilde {N}$ (hence with $\gamma _i<q^{\prime }_i<(\gamma _i^+)^{\widetilde {U}}$ ), and with $q^{\prime }_i$ large enough that $\mathbb P\cup \{\mathbb P\}\subseteq $ the relevant hulls of $\widetilde {N}$ (note this condition holds trivially unless $\gamma _i<\theta $ ) and $x,N_\omega ,R_\omega ,g,h$ are in the relevant hulls of $\widetilde {U}$ . Then choose $q_i$ with $q^{\prime }_i<q_i<(\gamma _i^+)^{\widetilde {U}}$ and much as before with respect to $\widetilde {R}$ . In this manner it is easy to arrange that $q_i$ works. We leave the rest to the reader.

This completes the proof of the subclaim, claim, and theorem.

Definition 4.2. Let M be a transitive structure satisfying $\mathrm {PS}$ . Work in M. Let P be a premouse with $\mathrm {Ord}^P$ regular. For a regular cardinal $\eta \geq \mathrm {Ord}^P$ , define $\eta $ -excellent premice (relative to $P,\eta $ ) as in the proof above (there we have $P=M|\theta $ ). The direct condensation stack of M above P is the stack S of all $\eta $ -excellent premice, for all such $\eta $ , as far as this is a well-defined stack.

Remark 4.3. As a special case of the previous theorem, we get a shorter proof that if a mouse M satisfies $\mathrm {PS}$ , then $\mathbb {E}^M$ is definable over $\left \lfloor M\right \rfloor $ from the parameter $M|\omega _1^M$ . Note that the proof also easily adapts to the case that M has a largest cardinal $\lambda $ , assuming that $\lambda $ is M-regular. However, for the singular case (most importantly $\mathrm {cof}^M(\lambda )=\omega $ ) we need the earlier methods.

5 A simplified fine structure

In [1], Mitchell–Steel fine structure is introduced, which makes use of the parameters $u_n$ . We introduce a simplified fine structure here which avoids the parameters $u_n$ , and show that in fact, the two fine structures are equivalent: we get the same notions of soundness, the same projecta and standard parameters, etc.

Definition 5.1. Let N be a premouse. Given $X\subseteq N$ , $\mathrm {Hull}_{k+1}^N(X)$ denotes the substructure of N whose elements are those $z\in N$ such that there is $\vec {x}\in X^{<\omega }$ and an $\mathrm {r}\Sigma _{k+1}$ formula $\varphi $ such that z is the unique $z'\in N$ such that $N\models \varphi (\vec {x},z')$ . And $\mathrm {cHull}_{k+1}^N(X)$ denotes its transitive collapse, assuming this is well-defined. Also let $\mathrm {Th}_{k+1}^N(X)$ be the $\mathrm {r}\Sigma _{k+1}$ theory ²³ of N in parameters in X.

Definition 5.2 (Minimal Skolem terms).

Let $\varphi $ be an $\mathrm {r}\Sigma _{k+1}$ formula of $n+1<\omega $ free variables $v_0,\ldots ,v_n$ . The minimal Skolem term associated with $\varphi $ is denoted $\mathrm {m}\tau _\varphi $ , and has n variables $v_1,\ldots ,v_n$ .

Let R be a k-sound premouse with $\rho _k^R>\omega $ . Let $q\in [\rho _0^R]^{<\omega }$ such that (i) if $k>0$ then $R=\mathrm {Hull}_k^R(\rho ^R_k\cup \{q\})$ and (ii) if $q\neq \emptyset $ then $\rho ^R_k\leq \min (q)$ . We define the partial function

$$\begin{align*}\mathrm{m}\tau_{\varphi,q}^R:\mathfrak{C}_0(R)^n\to\mathfrak{C}_0(R). \end{align*}$$

If $k=0$ then $\mathrm {m}\tau _{\varphi ,q}^R$ is just the usual Skolem function associated with $\varphi $ (such that the graph of $\mathrm {m}\tau _\varphi ^R$ is uniformly $\mathrm {r}\Sigma _1^R$ ), with inputs substituting for $v_1,\ldots ,v_n$ and output for $v_0$ . (Note $q=\emptyset $ in this case.)

Suppose $k>0$ . Let $\vec {x}=(x_1,\ldots ,x_n)\in \mathfrak {C}_0(R)^n$ . If $\mathfrak {C}_0(R)\models \neg \exists v_0\ \varphi (v_0,\vec {x})$ , then $\mathrm {m}\tau _{\varphi ,q}^R(\vec {x})$ is undefined.

Suppose $\mathfrak {C}_0(R)\models \exists v_0\ \varphi (v_0,\vec {x})$ . Let $\tau _\varphi $ be the basic Skolem term associated with $\varphi $ (see [1, 2.3.3]). Recall that $\tau _\varphi ^R(\vec {x})$ is the $<_R$ -least y such that $\mathfrak {C}_0(R)\models \varphi (y,\vec {x})$ . For $\beta <\rho _k^R$ , let $(\tau _\varphi )^\beta $ be defined over R as in the proof of [1, 2.10], with q specified above. Let $\beta _0$ be the least $\beta $ such that $(\tau _\varphi )^\beta (\vec {x})$ is defined. Then define

$$\begin{align*}\mathrm{m}\tau_{\varphi,q}^R(\vec{x})=(\tau_\varphi)^{\beta_0}(\vec{x}). \end{align*}$$

Lemma 5.3. The graph of $\mathrm {m}\tau _{\varphi ,q}^R$ is $\mathrm {r}\Sigma _{k+1}^R(\{q\})$ , recursively uniformly in $\varphi ,R,q$ (for $R,q$ as in 5.2).

Given $\mathrm {r}\Sigma _{k+1}$ formulas $\varphi ,\psi _0,\ldots ,\psi _{n-1}$ , with $\varphi $ of n free variables and $\psi _i$ of $n_i+1$ free variables, the relation over $\mathfrak {C}_0(R)$ ,

$$ \begin{align*} \mathfrak{C}_0(R)&\models\varrho(\vec{x}_0,\ldots,\vec{x}_{n-1})\iff \\ & \big(\forall i[\vec{x}_i\in\mathrm{dom}(\mathrm{m}\tau^R_{\psi_i,q})]\big)\wedge \mathfrak{C}_0(R)\models\varphi(\mathrm{m}\tau_{\psi_0,q}(\vec{x}_0),\ldots,\mathrm{m}\tau_{\psi_{n-1},q}(\vec{x}_{n-1} )), \end{align*} $$

is $\mathrm {r}\Sigma _{k+1}(\{q\})$ , uniformly in $R,q$ as in 5.2, and moreover, there is a recursive function passing from $\varphi ,\psi _0,\ldots ,\psi _{n-1}$ to an $\mathrm {r}\Sigma _{k+1}$ formula for $\varrho $ .

Therefore minimal Skolem terms are effectively closed under composition. That is, for example, there is a recursive function passing from formulas $\varphi ,\psi $ , each of two free variables $v_0,v_1$ , to $\varrho $ , of the same free variables, such that for all relevant $R,q$ , we have

$$\begin{align*}\mathrm{m}\tau_{\varrho,q}^R=\mathrm{m}\tau_{\varphi,q}^R\circ\mathrm{m}\tau_{\psi,q}^R.\end{align*}$$

Likewise for compositions involving larger numbers of variables.

Note that the basic Skolem terms referred to in the following lemma were recalled in Definition 5.2.

Lemma 5.4. Let $R,q$ be as in 5.2, $X\subseteq \mathfrak {C}_0(R)$ and

$$ \begin{align*} H_1&=\mathrm{Hull}_{k+1}^R(X\cup\{q\}),\\ H_2&=\big\{\mathrm{m}\tau^R_{\varphi,q}(\vec{x})\bigm|\varphi\text{ is }\mathrm{r}\Sigma_{k+1}\ \&\ \vec{x}\in X^{<\omega}\big\},\\ H_3&=\text{ the closure of }X\cup\{q\}\text{ under the basic } \mathrm{r}\Sigma_{k+1}\text{-Skolem terms.} \end{align*} $$

Then $H_1=H_2=H_3$ .

Proof The main thing is to see that $H_3\subseteq H_2$ . For this, see the proof of [1, 2.10], combined with (for example) the observation that if $\vec {x}\in X^{<\omega }$ and $y\in H_2$ and $R\models \exists z\ \big [z<_R y\wedge \varphi (q,\vec {x},z)\big ]$ , then there is $z\in H_2$ such that $z<_R y$ and $R\models \varphi (q,\vec {x},z)$ ; this is by 5.3. Applying this observation finitely many times shows that $\tau ^R_\varphi (q,\vec {x})\in H_2$ .

Definition 5.5. For $k<\omega $ , the terminology k-u-sound, k-u-universal, etc., mean just what k-sound, k-universal, etc., mean in [1, Section 2]. ²⁴ Let N be a k-u-sound premouse. We define $\rho _k^N=\rho _k(N)$ , $p_k(N)=p_k^N$ , $u_k(N)=u_k^N$ , $\rho _{k+1}^N=\rho _{k+1}(N)$ and $p_{k+1}(N)=p_{k+1}^N$ as in [1, Definition 2.8.1]. We also define $\widetilde {p}_0(N)=\widetilde {p}_0^N=\emptyset $ and if $k>0$ , define $\widetilde {p}_k(N)=\widetilde {p}^N_k=r$ where $p_k^N=(r,u_{k-1}^N)$ . Given $u\in \mathfrak {C}_0(N)$ , $\widetilde {p}\in [\rho _0^N]^{<\omega }$ and $\alpha \in \widetilde {p}$ , define the $(k+1)$ -solidity-witness for $(N,\widetilde {p},u)$ at $\alpha $ , denoted $W_{k+1}^N(\widetilde {p},u,\alpha )$ , by

(8) $$ \begin{align} W_{k+1}^N(\widetilde{p},u,\alpha)=\mathrm{Th}_{k+1}^N(\alpha\cup\{\widetilde{p}\backslash(\alpha+1),u\}).\end{align} $$

We say N is $(k+1)$ -u-solidity-witnessed iff

$$\begin{align*}W_{k+1}^N(\widetilde{p}_{k+1}^N,u_k^N,\alpha)\in N\text{ for each }\alpha\in \widetilde{p}_{k+1}^N.\end{align*}$$

Recall here that in [1, Definition 2.8.2] and [13, Definition 2.15], the adjective $(k+1)$ -solid, as applied to premice N, means something different to $(k+1)$ -u-solidity-witnessed.

Remark 5.6. Recall that $p_{1}^N=(\widetilde {p}_1^N,\emptyset )$ and $\widetilde {p}_1^N\in [\rho _0^N]^{<\omega }$ . Suppose that N is k-sound, $p_k^N=(\widetilde {p}_k^N,u)$ and $s=\widetilde {p}_k^N\in [\rho _{k-1}^N]^{<\omega }$ , $\mathrm {lh}(s)=\ell $ and $b_0,\ldots ,b_{\ell -1}$ are the k-u-solidity witnesses for $(N,s,u)$ (that is, $b_i=W_{k}^N(s,u,\alpha _i)$ for each $i<\ell $ , where $s=\{\alpha _0>\alpha _1>\cdots >\alpha _{\ell -1}\}$ ). Recall that $p_{k+1}^N$ has form $(r,u_k^N)$ where:

1. – if $\rho _{k-1}^N<\rho _0^N$ then $u_k^N=(s,u,b_0,\ldots ,b_{\ell -1},\rho _{k-1}^N)$ , and

2. – if $\rho _{k-1}^N=\rho _0^N$ then $u_k^N=(s,u,b_0,\ldots ,b_{\ell -1})$ .

(Cf. [1, Definition 2.8.1], but note that we are discussing $p_{k+1}$ here, not $p_k$ .)

Definition 5.7. For N a premouse, define $q_k=q_k^N$ , k-q-universality, k-q-solidity and k-q-soundness for $k\in [0,\omega )$ , recursively as follows. The definitions are actually made uniformly in premice N.

Define $q_0^N=\emptyset $ and say that N is $0$ -q-universal, $0$ -q-solid and $0$ -q-sound.

Suppose $q_0,\ldots ,q_k$ have been defined and N is k-q-sound and k-u-sound.

Now if $k\geq 1$ then suppose by induction that

$$\begin{align*}\mathfrak{C}_0(N)=\mathrm{Hull}_k^N(\rho_k^N\cup\{q_k,q_{k-1}\}).\end{align*}$$

Let $q_{k+1}$ be the $<_{\mathrm {lex}}$ -least $q\in [\mathrm {Ord}]^{<\omega }$ such that ²⁵

$$\begin{align*}\mathrm{Th}_{k+1}^N(\rho_{k+1}^N\cup\{q,q_{k}\})\notin\mathfrak{C}_0(N). \end{align*}$$

Define the $(k+1)$ th core $\mathfrak {C}_{k+1}(N)$ of N as

$$\begin{align*}C=\mathfrak{C}_{k+1}(N)=\mathrm{cHull}_{k+1}^N(\rho_{k+1}^N\cup\{q_{k+1},q_k\}) \end{align*}$$

and the $(k+1)$ th core map $\pi :C\to N$ to be the uncollapse map. It will follow from Theorem 5.8 that C is k-q-sound and k-u-sound and if $k\geq 1$ then

$$\begin{align*}\mathfrak{C}_0(C)=\mathrm{Hull}_k^{\mathfrak{C}_0(C)}(\rho_k^C\cup\{q_k^C,q_{k-1}^C\}).\end{align*}$$

So $q_{k+1}^C$ is defined. Say N is $(k+1)$ -q-universal iff $\mathcal {P}(\rho _{k+1}^N)\cap C=\mathcal {P}(\rho _{k+1}^N)\cap N$ .

Given $u\in \mathfrak {C}_0(N)$ and $q\in [\rho _0^N]^{<\omega }$ and $\alpha \in q$ , define $W_{k+1}^N(q,u,\alpha )$ exactly as in line (8) in Definition 5.5, with $\widetilde {p}=q$ . ²⁶

We say $(q,u)$ is $(k+1)$ -solid for N iff $W_{k+1}^N(q,u,\alpha )\in N$ for each $\alpha \in q$ . We say N is $(k+1)$ -q-solid iff $(q_{k+1},q_k)$ is $(k+1)$ -solid for N. ²⁷ We say N is $(k+1)$ -q-sound iff N is $(k+1)$ -q-solid and

$$\begin{align*}N=\mathrm{Hull}_{k+1}^N(\rho_{k+1}^N\cup\{q_{k+1},q_k\}). \end{align*}$$

The theorem below establishes the equivalence between standard Mitchell–Steel fine structure (u-soundness, etc.) and the fine structure introduced here (q-soundness, etc.). In part 3 we show that the parameters provided by $u^N_k$ automatically get into the relevant hulls, so that the direct placement of the $u^N_k$ in those hulls in [1] was superfluous.

Theorem 5.8. Let $k<\omega $ . Let N be a premouse. Then $:$

1. 1. N is k-q-sound iff N is k-u-sound.

If N is k-q-sound and $\omega <\rho _k^N$ then $:$

1. 2. $\widetilde {p}_i^N=q_i^N$ for all $i\leq k$ .

2. 3. Let $X\subseteq N$ , let $C=\mathrm {cHull}_{k+1}^N(X\cup \{q_k^N\})$ and $\pi :C\to N$ be the uncollapse. Then $:$

   1. (i) C is a k-u-sound premouse,

   2. (ii) $\pi $ is a near k-u-embedding ²⁸ $;$ therefore if $\rho _k^C<\rho _0^C$ then $\pi (\rho _k^C)\geq \rho _k^N$ and $\pi "\rho _k^C\subseteq \rho _k^N$ ,

   3. (iii) $\pi (W_i^C(q_i^C,q_{i-1}^C,\alpha ))=W_i^N(q_i^N,q_{i-1}^N,\pi (\alpha ))$ for all $i\in [1,k]$ and ${\alpha \in q_i^C}$ ,

   4. (iv) $\pi (u_k^C)=u_k^N\in H$ .

3. 4. We have $:$

   1. – $\widetilde {p}_{k+1}^N=q_{k+1}^N$ ,

   2. – N is $(k+1)$ -u-solidity-witnessed iff N is $(k+1)$ -q-solid, ²⁹

   3. – N is $(k+1)$ -u-universal iff N is $(k+1)$ -q-universal, and

   4. – N is $(k+1)$ -u-sound iff N is $(k+1)$ -q-sound.

Proof We prove the proposition by induction on k. For $k=0$ it is easy. Assume $k>0$ and the lemma holds at all $k'<k$ . Parts 1 and 2 are trivial by induction (by part 4). So consider part 3. Let $H=\mathrm {rg}(\pi )$ . Note that $X\cup \{q_k^N\}\subseteq H$ and if $\vec {x}\in H$ and $y\in \mathrm {Hull}_{k+1}^N(\{\vec {x}\})$ then $y\in H$ . Now we prove:

Claim 1. Let $i\leq k$ . Then $q_i^N\in H$ and if $i<k$ and $\rho _i^N<\rho _0^N$ then $\rho _i^N\in H$ .

Proof We prove the claim by induction on i. It is trivial for $i=0$ and $i=k$ (since $q_0^N=\emptyset $ and we put $q_k^N\in H$ directly). Suppose $0<i<k$ and the claim holds for all $i'<i$ .

We show $q_i^N\in H$ . So assume $n=\mathrm {lh}(q_i^N)>0$ . Note that $q_i^N$ is the unique ${q\in [\mathrm {Ord}]^{<\omega }}$ such that:

1. (i) $N=\mathrm {Hull}^N_i(\min (q)\cup \{q, q_{i-1}^N\})$ and

2. (ii) $(q,q_{i-1}^N)$ is i-solid for N and

3. (iii) $\mathrm {lh}(q)=n$ .

Now each of the statements (i)–(iii) are $\mathrm {r}\Sigma _{k+1}^N$ assertions of q (in no parameters, but the $\mathrm {r}\Sigma _{k+1}$ formulas used depend on $(\mathrm {lh}(q_0^N),\ldots ,\mathrm {lh}(q_i^N)=n)$ ), and hence, $\{q_i^N\}$ is $\mathrm {r}\Sigma _{k+1}^N$ , so $q_i^N\in H$ . If $i=1$ , this is straightforward. If $i>1$ , then by (another) induction, we can refer to $q_j^N$ for each $j<i$ , since we already know that $\{q_j^N\}$ is $\mathrm {r}\Sigma _{k+1}^N$ . And for $i>1$ , since N is $(i-1)$ -q-sound,

$$\begin{align*}N=\mathrm{Hull}_{i-1}^N(\rho_{i-1}^N\cup\{q_{i-1}^N,q_{i-2}^N\}).\end{align*}$$

So by 5.4, statement (i) just asserts “ $\forall x\in N\ \big [$ there is $\vec {\beta }\in \min (q)^{<\omega }$ and an $\mathrm {r}\Sigma _i$ formula $\varphi $ such that $x=\mathrm {m}\tau _{\varphi ,(q_{i-1}^N,q_{i-2}^N)}(\vec {\beta },q)\big ]$ ”, which is therefore $\mathrm {r}\Sigma _{k+1}^N$ (recall $i<k$ ). So $\{q_i^N\}$ is $\mathrm {r}\Sigma _{k+1}^N$ , as required.

Now if $i<k$ and $\rho _i^N<\rho _0^N$ then by induction, $\rho ^N_i$ is the least $\rho $ with

$$\begin{align*}N=\mathrm{Hull}^N_i(\rho\cup\{q_i^N,q_{i-1}^N\}).\end{align*}$$

So as above and in the proof of 5.4, if $\rho _i^N<\mathrm {Ord}^N$ then $\rho ^N_i\in H$ . ³⁰

Claim 2. If $\varphi $ is $\mathrm {r}\Sigma _{k+1}$ and $\vec {x}\in H$ and $N\models \exists y\ \varphi (\vec {x},y)$ then $\exists y\in H$ such that $N\models \varphi (\vec {x},y)$ .

Proof Let $q=\{q_k^N,q_{k-1}^N\}$ . Since $q\in H$ and $N=\mathrm {Hull}_k^N(\rho _k^N\cup \{q\})$ , 5.4 applies and yields the claim.

We have $H=\mathrm {Hull}^N_i(H)$ for each $i\leq k+1$ . Therefore by induction, C is $(k-1)$ -sound, $\pi $ is a near $(k-1)$ -u-embedding, and so on. Combined with Claim 1, this also gives that if $\rho _{k-1}^C<\rho _0^C$ then $\pi (\rho _{k-1}^C)=\rho _{k-1}^N<\rho _0^N$ , and if $\rho _{k-1}^C=\rho _0^C$ then $\rho _{k-1}^N=\rho _0^N$ . By this and Claim 2 it is straightforward to see that $\pi "\rho _k^C\subseteq \rho _k^N$ and if $\rho _k^C<\rho _0^C$ then $\pi (\rho _k^C)\geq \rho _k^N$ . Moreover,

$$\begin{align*}C=\mathrm{Hull}_k^C(\rho_k^C\cup\{\pi^{-1}(q_k^N),q_{k-1}^C\})\end{align*}$$

and $\pi $ is $\mathrm {r}\Sigma _{k+1}$ elementary. To see that $q_k^C=\pi ^{-1}(q_k^N)$ , we therefore just need that $(\pi ^{-1}(q_k^N),q_{k-1}^C)$ is k-q-solid for C. For this it suffices to know that C has the appropriate generalized solidity witnesses; see [14, Section 1.12]. But this follows from the fact that N has generalized solidity witnesses for $(q_k^N,q_{k-1}^N)$ in $\mathrm {rg}(\pi )$ , which follows from Claim 2.

We have now established that C is k-q-sound, so by induction, C is k-u-sound, giving 3(i). For part 3(ii), it just remains to see that $\pi (p_k^C)=p_k^N$ . (We already know that $C,N$ are k-u-sound, $\pi $ is an $\mathrm {r}\Sigma _{k+1}$ -elementary near $(k-1)$ -u-embedding which preserves $\rho _{k-1}$ , and $\pi "\rho _{k}^C\subseteq \rho _k^N$ .) Recall that $p_k^C=(\widetilde {p}_k^C,u_{k-1}^C)$ and $p_k^N=(\widetilde {p}_k^N,u_{k-1}^N)$ . By induction, we have $\widetilde {p}_k^C=q_k^C$ and $\widetilde {p}_k^N=q_k^N$ , and since $\pi (q_k^C)=q_k^N$ , we have $\pi (\widetilde {p}_k^C)=\widetilde {p}_k^N$ . So we just need $\pi (u_{k-1}^C)=u_{k-1}^N$ . For this, the only condition that remains to be verified is that $\pi $ preserves $(k-1)$ -u-solidity witnesses. But this follows immediately from $\mathrm {r}\Sigma _{k+1}$ -elementarity (in fact $\mathrm {r}\Sigma _k$ -elementarity) together with preservation of the earlier defined objects (from the fine structural recursion). The (full) $\mathrm {r}\Sigma _{k+1}$ -elementarity of $\pi $ and preservation of the $q_i$ ’s for $i\leq k$ similarly gives 3(iii), and part 3(iv) is likewise.

Part 4 follows easily from part 3, according to which, $u_k^N$ is automatically in the relevant hulls.