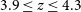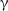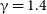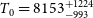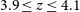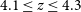1. Introduction
The thermal state of the gas in the intergalactic medium (IGM) is an important characteristic describing the baryonic matter in the Universe (Lidz et al. Reference Lidz2010). Hui & Gnedin (Reference Hui and Gnedin1997) showed that the temperature–density relation of the photoionised IGM in the low-density region can be well approximated by the following equation:
where
![]() $T_{0}$
is the temperature at the mean density,
$T_{0}$
is the temperature at the mean density,
![]() $\Delta$
is the overdensity, and
$\Delta$
is the overdensity, and
![]() $(\unicode{x03B3} - 1)$
is a power-law index.
$(\unicode{x03B3} - 1)$
is a power-law index.
The standard model assumes that the evolution of the IGM has passed through two major reheating events. At first, the reionisation of hydrogen (H i
![]() $\rightarrow$
H ii) occurred, and it is normally assumed that helium is singly ionised (He i
$\rightarrow$
H ii) occurred, and it is normally assumed that helium is singly ionised (He i
![]() $\rightarrow$
He ii) along with H i. This process should be completed at the redshift
$\rightarrow$
He ii) along with H i. This process should be completed at the redshift
![]() $z\sim6$
(Bouwens et al. Reference Bouwens2015). Then, the IGM cooled and is reheated again during the He ii reionisation phase. This process is expected to be completed at the redshift
$z\sim6$
(Bouwens et al. Reference Bouwens2015). Then, the IGM cooled and is reheated again during the He ii reionisation phase. This process is expected to be completed at the redshift
![]() $z\sim2.7$
and can be characterised by three phases (Worseck et al. Reference Worseck2011):
$z\sim2.7$
and can be characterised by three phases (Worseck et al. Reference Worseck2011):
-
1. He iii ‘bubble’ growth around quasars (QSOs) with redshifts
 $z_{\text{em}} \geq 4$
;
$z_{\text{em}} \geq 4$
; -
2. overlap of the He iii zones around more abundant QSOs at
 $z_{\text{reion}} \sim 3$
;
$z_{\text{reion}} \sim 3$
; -
3. gradual reionisation of remaining dense He ii regions.
In recent years, an attention has been paid to characterising the
![]() $T-\rho$
relation of the IGM around
$T-\rho$
relation of the IGM around
![]() $z \sim 3$
(Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000; Rorai et al. Reference Rorai2018; Hiss et al. Reference Hiss2018; Telikova, Balashev, & Shternin Reference Telikova, Balashev and Shternin2018; Telikova et al. Reference Telikova, Shternin and Balashev2019; Walther et al. Reference Walther, Oñorbe and Hennawi2019; Gaikwad et al. Reference Gaikwad, Srianand, Haehnelt and Choudhury2021).
$z \sim 3$
(Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000; Rorai et al. Reference Rorai2018; Hiss et al. Reference Hiss2018; Telikova, Balashev, & Shternin Reference Telikova, Balashev and Shternin2018; Telikova et al. Reference Telikova, Shternin and Balashev2019; Walther et al. Reference Walther, Oñorbe and Hennawi2019; Gaikwad et al. Reference Gaikwad, Srianand, Haehnelt and Choudhury2021).
However, in case of the higher redshifts (
![]() $z > 4$
), absorption features start to become strongly blended (Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011). Due to this, most studies are based on the Ly-
$z > 4$
), absorption features start to become strongly blended (Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011). Due to this, most studies are based on the Ly-
![]() $\unicode{x03B1}$
flux power spectrum (Garzilli, Boyarsky, & Ruchayskiy Reference Garzilli, Boyarsky and Ruchayskiy2017; Iršič et al. 2017; Walther et al. Reference Walther, Oñorbe and Hennawi2019; Boera et al. Reference Boera, Becker, Bolton and Nasir2019). Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011) used the curvature statistic, which does not require the decomposition of the Ly-
$\unicode{x03B1}$
flux power spectrum (Garzilli, Boyarsky, & Ruchayskiy Reference Garzilli, Boyarsky and Ruchayskiy2017; Iršič et al. 2017; Walther et al. Reference Walther, Oñorbe and Hennawi2019; Boera et al. Reference Boera, Becker, Bolton and Nasir2019). Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011) used the curvature statistic, which does not require the decomposition of the Ly-
![]() $\unicode{x03B1}$
forest into individual spectral lines. There is only one study treating the Ly-
$\unicode{x03B1}$
forest into individual spectral lines. There is only one study treating the Ly-
![]() $\unicode{x03B1}$
forest as a superposition of discrete absorption profiles (Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000) at
$\unicode{x03B1}$
forest as a superposition of discrete absorption profiles (Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000) at
![]() $z \sim 4$
.
$z \sim 4$
.
The aim of this work is to study the thermal history of the IGM at
![]() $3.9 \leq z \leq 4.3$
using curvature statistics. Besides, we compare our measurements with the
$3.9 \leq z \leq 4.3$
using curvature statistics. Besides, we compare our measurements with the
![]() $T_{0}$
evolution predicted by widely used spatially homogeneous UVB models of Haardt & Madau (Reference Haardt and Madau2012), Oñorbe, Hennawi, & Lukić (Reference Oñorbe and Hennawi2017), Khaire & Srianand (Reference Khaire and Srianand2019), Puchwein et al. (Reference Puchwein, Haardt, Haehnelt and Madau2019), and Faucher-Giguère (Reference Faucher-Giguère2020). To be more specific, we compare results with the rescaled models, same as in the study by Gaikwad et al. (Reference Gaikwad, Srianand, Haehnelt and Choudhury2021). The results in the aforementioned study are consistent with the relative late He ii reionisation in the models of Oñorbe et al. (Reference Oñorbe and Hennawi2017) and Faucher-Giguère (Reference Faucher-Giguère2020), in which the mid-point of the He ii reionisation is at
$T_{0}$
evolution predicted by widely used spatially homogeneous UVB models of Haardt & Madau (Reference Haardt and Madau2012), Oñorbe, Hennawi, & Lukić (Reference Oñorbe and Hennawi2017), Khaire & Srianand (Reference Khaire and Srianand2019), Puchwein et al. (Reference Puchwein, Haardt, Haehnelt and Madau2019), and Faucher-Giguère (Reference Faucher-Giguère2020). To be more specific, we compare results with the rescaled models, same as in the study by Gaikwad et al. (Reference Gaikwad, Srianand, Haehnelt and Choudhury2021). The results in the aforementioned study are consistent with the relative late He ii reionisation in the models of Oñorbe et al. (Reference Oñorbe and Hennawi2017) and Faucher-Giguère (Reference Faucher-Giguère2020), in which the mid-point of the He ii reionisation is at
![]() $z_{\rm mid} \sim 3$
. On the other hand, in case of the other compared models (Haardt & Madau Reference Haardt and Madau2012; Khaire & Srianand Reference Khaire and Srianand2019; Puchwein et al. Reference Puchwein, Haardt, Haehnelt and Madau2019), we can observe stronger temperature evolution in the redshift range of
$z_{\rm mid} \sim 3$
. On the other hand, in case of the other compared models (Haardt & Madau Reference Haardt and Madau2012; Khaire & Srianand Reference Khaire and Srianand2019; Puchwein et al. Reference Puchwein, Haardt, Haehnelt and Madau2019), we can observe stronger temperature evolution in the redshift range of
![]() $3.8 < z < 4.4$
. Additional impetus could be that even there is good agreement between theory and observations for the temperature evolution of the IGM at
$3.8 < z < 4.4$
. Additional impetus could be that even there is good agreement between theory and observations for the temperature evolution of the IGM at
![]() $\sim$
3, there is still a lack of data at higher redshifts.
$\sim$
3, there is still a lack of data at higher redshifts.
Table 1. List of QSOs whose spectra were used in this study. The S/N ratio was calculated according to Stoehr et al. (Reference Stoehr, Argyle, Bunclark and Lewis2008) for the spectral regions where the absorbers were parameterised.

The article is organised as follows: Section 2 contains the basic information about the observational data used in this work. The curvature method and the summary of the analysis together with the sources of uncertainties are described in Section 3. A description of the used simulations and an explanation of the generation of the simulated spectra are given in Section 4. In Section 5, we present our results and their comparison with the previously published ones and with
![]() $T_{0}$
evolution predicted by widely used spatially homogeneous UVB models. Our conclusions are given in Section 6.
$T_{0}$
evolution predicted by widely used spatially homogeneous UVB models. Our conclusions are given in Section 6.
2. Observations
In this study, we used a sample of QSO spectra (Table 1) obtained by the Ultraviolet and Visual Echelle Spectrograph (UVES) on the VLT/ESO (Murphy et al. Reference Murphy, Kacprzak, Savorgnan and Carswell2019). The UVES Spectral Quasar Absorption Database contain fully reduced, continuum-fitted high-resolution spectra of quasars in the redshift range
![]() $0 < z < 5$
. The spectral data have nominal resolving power
$0 < z < 5$
. The spectral data have nominal resolving power
![]() $R_{\rm nom}\simeq 50000$
and dispersion of
$R_{\rm nom}\simeq 50000$
and dispersion of
![]() $2.5\,\rm km\,s^{-1}\,\rm pixel^{-1}$
. From the whole dataset, we selected only spectra that meet the following criteria:
$2.5\,\rm km\,s^{-1}\,\rm pixel^{-1}$
. From the whole dataset, we selected only spectra that meet the following criteria:
-
1. the sightline partially or fully contains the Ly-
 $\unicode{x03B1}$
forest in the redshift range of
$\unicode{x03B1}$
forest in the redshift range of
 $3.9 \leq z \leq 4.3$
. To be more specific, we focused on the spectral region of rest-frame wavelengths 1050–1180 Å inside the Ly-
$3.9 \leq z \leq 4.3$
. To be more specific, we focused on the spectral region of rest-frame wavelengths 1050–1180 Å inside the Ly-
 $\unicode{x03B1}$
forest. This is the same range used in Palanque-Delabrouille et al. (Reference Palanque-Delabrouille2013), Hiss et al. (Reference Hiss2018), Walther et al. (Reference Walther2018), and Ondro & Gális (Reference Ondro and Gális2021) and is considered a conservative choice for the Ly-
$\unicode{x03B1}$
forest. This is the same range used in Palanque-Delabrouille et al. (Reference Palanque-Delabrouille2013), Hiss et al. (Reference Hiss2018), Walther et al. (Reference Walther2018), and Ondro & Gális (Reference Ondro and Gális2021) and is considered a conservative choice for the Ly-
 $\unicode{x03B1}$
forest region.
$\unicode{x03B1}$
forest region. -
2. the signal-to-noise (S/N) ratio of the spectrum is higher than 10 in the studied spectral region.
We used a sample of 10 QSO spectra, which fulfils above criteria, where the coverage of the analysed QSO spectra is shown in Figure 1.

Figure 1. The coverage of the dataset in which each spectrum represents the Ly-
![]() $\unicode{x03B1}$
redshift range for individual QSOs from our sample.
$\unicode{x03B1}$
redshift range for individual QSOs from our sample.
Note that the Ly-
![]() $\unicode{x03B1}$
absorbers for which
$\unicode{x03B1}$
absorbers for which
![]() (damped Ly-
(damped Ly-
![]() $\unicode{x03B1}$
systems) were identified by eye and excluded from the analysis. In this case, the excluded part of the spectrum was chosen to enclose the region between the points where the damping wings reached a value below 0.9 within the flux error. This value was chosen because the flux only occasionally reaches the continuum value. The spectral intervals with bad pixels were masked and cubically interpolated.
$\unicode{x03B1}$
systems) were identified by eye and excluded from the analysis. In this case, the excluded part of the spectrum was chosen to enclose the region between the points where the damping wings reached a value below 0.9 within the flux error. This value was chosen because the flux only occasionally reaches the continuum value. The spectral intervals with bad pixels were masked and cubically interpolated.
3. Curvature method
In this work, we applied the curvature method to obtain new, robust determinations of the IGM temperature at redshift range of
![]() $3.9 \leq z \leq 4.3$
. The curvature
$3.9 \leq z \leq 4.3$
. The curvature
![]() $\kappa$
is defined as (Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011):
$\kappa$
is defined as (Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011):
where the
![]() $F^{\prime} = {\rm d}F / {\rm d}v$
and
$F^{\prime} = {\rm d}F / {\rm d}v$
and
![]() $F^{\prime\prime} = {\rm d}^{2}F / {\rm d}v^{2}$
are the first and second derivatives of the flux field with respect to velocity, respectively. The greatest advantage of this method is that it does not require the decomposition of the Ly-
$F^{\prime\prime} = {\rm d}^{2}F / {\rm d}v^{2}$
are the first and second derivatives of the flux field with respect to velocity, respectively. The greatest advantage of this method is that it does not require the decomposition of the Ly-
![]() $\unicode{x03B1}$
forest into individual lines. This is useful mainly in the higher redshifts, where absorption features start to become strongly blended.
$\unicode{x03B1}$
forest into individual lines. This is useful mainly in the higher redshifts, where absorption features start to become strongly blended.
Due to the reproducibility, we describe the basic steps of the curvature calculation in Appendix A.
3.1. Sources of uncertainties
As already shown,
![]() $\kappa$
is easy to compute and can be evaluated on a pixel-by-pixel basis (Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011). Before using it, however, several issues need to be addressed, which are described below.
$\kappa$
is easy to compute and can be evaluated on a pixel-by-pixel basis (Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011). Before using it, however, several issues need to be addressed, which are described below.
3.1.1. Noise
The curvature can be affected by the finite S/N of the spectra. To solve this difficulty, Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011) and Boera et al. (Reference Boera, Murphy, Becker and Bolton2014) fitted the b-spline to the flux and then compute the curvature from the fit. In this study, we used the same approach as Gaikwad et al. (Reference Gaikwad, Srianand, Haehnelt and Choudhury2021), and we smoothed the flux using the Gaussian filter of FWHM
![]() $\sim 10$
km s
$\sim 10$
km s
![]() $^{-1}$
. The similar approach was used also in Padmanabhan, Srianand, & Choudhury (Reference Padmanabhan, Srianand and Choudhury2015).
$^{-1}$
. The similar approach was used also in Padmanabhan, Srianand, & Choudhury (Reference Padmanabhan, Srianand and Choudhury2015).
3.1.2. Continuum
In general, for spectra with high-resolution and high
![]() $S/N$
, the continuum is fitted by locally connecting apparent absorption-free spectral regions. However, this approach depends on the average line density, and thus on the redshift. At higher redshifts (typically
$S/N$
, the continuum is fitted by locally connecting apparent absorption-free spectral regions. However, this approach depends on the average line density, and thus on the redshift. At higher redshifts (typically
![]() $z > 4$
), severe blendings make it hard or even impossible to identify the unabsorbed spectral regions. Therefore, a polynomial with typically 3–5 degrees of freedom for the region from Ly-
$z > 4$
), severe blendings make it hard or even impossible to identify the unabsorbed spectral regions. Therefore, a polynomial with typically 3–5 degrees of freedom for the region from Ly-
![]() $\unicode{x03B1}$
to Ly-
$\unicode{x03B1}$
to Ly-
![]() $\unicode{x03B2}$
can be used. This approach can produce the statistical uncertainty of the continuum placement exceeding 7% (Becker, Rauch, & Sargent Reference Becker, Rauch and Sargent2007; Murphy et al. Reference Murphy, Kacprzak, Savorgnan and Carswell2019). To circumvent the continuum issue, we re-normalised both the real data and also the simulations. For each 20 Mpc h
$\unicode{x03B2}$
can be used. This approach can produce the statistical uncertainty of the continuum placement exceeding 7% (Becker, Rauch, & Sargent Reference Becker, Rauch and Sargent2007; Murphy et al. Reference Murphy, Kacprzak, Savorgnan and Carswell2019). To circumvent the continuum issue, we re-normalised both the real data and also the simulations. For each 20 Mpc h
![]() $^{-1}$
section, we divided the flux by the maximum value of smoothed flux in that interval.
$^{-1}$
section, we divided the flux by the maximum value of smoothed flux in that interval.
3.1.3. Metal Lines
It is well known that the Ly-
![]() $\unicode{x03B1}$
forest is contaminated by metal lines, which are a potentially serious source of systematic errors (Boera et al. Reference Boera, Murphy, Becker and Bolton2014). These lines are usually associated with the strong H i absorption. For this reason, we visually inspected the studied spectra to identify damped Ly-
$\unicode{x03B1}$
forest is contaminated by metal lines, which are a potentially serious source of systematic errors (Boera et al. Reference Boera, Murphy, Becker and Bolton2014). These lines are usually associated with the strong H i absorption. For this reason, we visually inspected the studied spectra to identify damped Ly-
![]() $\unicode{x03B1}$
(DLA) and sub-DLA systems, for which the redshifts were determined. In this case, the associated metal lines redward of the Ly-
$\unicode{x03B1}$
(DLA) and sub-DLA systems, for which the redshifts were determined. In this case, the associated metal lines redward of the Ly-
![]() $\unicode{x03B1}$
emission peak of the QSO help with the proper determination of the DLA redshift (see Figure 2). If the redshifts were known, the other metal lines (Table 2) were determined based on their characteristic
$\unicode{x03B1}$
emission peak of the QSO help with the proper determination of the DLA redshift (see Figure 2). If the redshifts were known, the other metal lines (Table 2) were determined based on their characteristic
![]() $\Delta \lambda$
.
$\Delta \lambda$
.

Figure 2. An example of the adopted procedure for rejecting metal lines based on the DLA system at
![]() $z \approx 3.666$
(A) in the spectrum of the quasar QSO J020944 + 051713. The green dashed line and red solid line represent the continuum level and result of the smoothing the flux using the Gaussian filter, respectively. The shaded region (B) demonstrates the excluded part of curvature field (C) due to the contamination of the region by metal absorption (O i 1302).
$z \approx 3.666$
(A) in the spectrum of the quasar QSO J020944 + 051713. The green dashed line and red solid line represent the continuum level and result of the smoothing the flux using the Gaussian filter, respectively. The shaded region (B) demonstrates the excluded part of curvature field (C) due to the contamination of the region by metal absorption (O i 1302).
Table 2. List of metal lines included in our semi-automatic rejection procedure with their oscillator strength f.

References: (1) Morton (Reference Morton1991), (2) Prochaska et al. (Reference Prochaska2001), (3) Howk et al. (Reference Howk, Sembach, Roth and Kruk2000), (4) Tripp et al. (Reference Tripp, Lu and Savage1996), (A1) Schectman et al. (Reference Schectman, Povolny and Curtis1998), (A2) Verner et al. (Reference Verner, Verner and Ferland1996).
It is worth noting that in the case of other metal absorption systems not associated with the DLA, we used the doublet metal lines (typically Si iv, C iv) to determine the redshift of metal absorption systems.
Following these steps, we firstly compute the curvature. Then, based on the determined redshifts, the expected wavelength of the metal lines were calculated. Finally, we excluded a region of the curvature field, which corresponds to the 30 km s
![]() $^{-1}$
in each direction around each potential metal line, so that the metal lines did not affect the results of our analysis.
$^{-1}$
in each direction around each potential metal line, so that the metal lines did not affect the results of our analysis.
3.2. Summary of method
The whole analysis can be summarised as follows:
-
1. We divided the spectra into 20 Mpc h
 $^{-1}$
sections to directly match the box size of the simulated spectra.
$^{-1}$
sections to directly match the box size of the simulated spectra. -
2. The flux field is smoothed using the Gaussian filter of FWHM
 $\sim$
10 km s
$\sim$
10 km s
 $^{-1}$
.
$^{-1}$
. -
3. We re-normalised the flux, which was already normalised by the broader spectral range fit of the continuum, by dividing the flux of each section by the maximum value of the smoothed flux field in that interval.
-
4. The curvature
 $\kappa$
is determined and only pixels, in which the value of the re-normalised flux
$\kappa$
is determined and only pixels, in which the value of the re-normalised flux
 $F^{R}$
falls in the range of
$F^{R}$
falls in the range of
 $0.1 \leq F^{R} \leq 0.9$
are taken into consideration. The lower value was chosen due to the fact that the saturated pixels do not contain any information on the temperature. Using the higher threshold, we exclude the pixels with flux near the continuum.
$0.1 \leq F^{R} \leq 0.9$
are taken into consideration. The lower value was chosen due to the fact that the saturated pixels do not contain any information on the temperature. Using the higher threshold, we exclude the pixels with flux near the continuum. -
5. We masked the metal lines.
-
6. In the case of real QSO spectra, we joint the curvature values from all of the 20 Mpc h
 $^{-1}$
sections and determined the median of the
$^{-1}$
sections and determined the median of the
 $<|\kappa|>$
from the 5000 moving blocks bootstrap realisations.
$<|\kappa|>$
from the 5000 moving blocks bootstrap realisations. -
7. We also applied the same procedure in case of the simulations, which were prepared for the analysis according to the procedure described in the next section. Note that the metal contamination in case of the simulations is not considered.
-
8. Finally, the temperature
 $T(\overline{\Delta})$
is calculated by interpolating the
$T(\overline{\Delta})$
is calculated by interpolating the
 $T(\overline{\Delta}) - \log{<|\kappa|>}$
relation based on the simulations to the value of
$T(\overline{\Delta}) - \log{<|\kappa|>}$
relation based on the simulations to the value of
 $\log{<|\kappa|>}$
determined from the data.
$\log{<|\kappa|>}$
determined from the data.
It is worth noting that all uncertainties in this study correspond to the 2.5th and 97.5th percentiles of distribution based on the bootstrap realisations.
4. Simulations
In this study, we used a part of the THERMALFootnote
a
suite, which consists of
![]() $\sim$
70 Nyx hydrodynamical simulations with different thermal histories on a box size
$\sim$
70 Nyx hydrodynamical simulations with different thermal histories on a box size
![]() $L_{\rm box} = 20$
Mpc h
$L_{\rm box} = 20$
Mpc h
![]() $^{-1}$
and 1024
$^{-1}$
and 1024
![]() $^3$
cells (see details in Oñorbe et al. Reference Oñorbe and Hennawi2017; Hiss et al. Reference Hiss2018; Hiss et al. Reference Hiss, Walther, Oñorbe and Hennawi2019). From the whole dataset, we chose a subset of 38 simulation snapshots at
$^3$
cells (see details in Oñorbe et al. Reference Oñorbe and Hennawi2017; Hiss et al. Reference Hiss2018; Hiss et al. Reference Hiss, Walther, Oñorbe and Hennawi2019). From the whole dataset, we chose a subset of 38 simulation snapshots at
![]() $z = 4.0$
and also at
$z = 4.0$
and also at
![]() $z = 4.2$
, with different combinations of underlying thermal parameters
$z = 4.2$
, with different combinations of underlying thermal parameters
![]() $T_{0}$
,
$T_{0}$
,
![]() $\unicode{x03B3}$
and pressure smoothing scale
$\unicode{x03B3}$
and pressure smoothing scale
![]() $\lambda_{P}$
, which satisfy a spacing threshold:
$\lambda_{P}$
, which satisfy a spacing threshold:
This condition was based on the fact that some of the models have close values of their thermal parameters. This is the similar approach that was used by Walther et al. (Reference Walther, Oñorbe and Hennawi2019). The final subsets of simulations with different combinations of thermal parameters are depicted in Figure 3.

Figure 3. Combinations of
![]() $T_{0}$
,
$T_{0}$
,
![]() $\unicode{x03B3}$
, and
$\unicode{x03B3}$
, and
![]() $\lambda_{\rm P}$
.
$\lambda_{\rm P}$
.
Note that the parameters
![]() $T_0$
and
$T_0$
and
![]() $\unicode{x03B3}$
were determined from the simulations by fitting a power-law temperature–density relation to the distribution of gas cells using linear least squares method as described in Lukić et al. (2015). In order to determine the
$\unicode{x03B3}$
were determined from the simulations by fitting a power-law temperature–density relation to the distribution of gas cells using linear least squares method as described in Lukić et al. (2015). In order to determine the
![]() $\lambda_{P}$
, the approach present in Kulkarni et al. (Reference Kulkarni, Hennawi, Oñorbe, Rorai and Springel2015) was used. The cosmological parameters used in the simulations were based on the results of the Planck mission (Planck Collaboration et al. Reference Planck2014):
$\lambda_{P}$
, the approach present in Kulkarni et al. (Reference Kulkarni, Hennawi, Oñorbe, Rorai and Springel2015) was used. The cosmological parameters used in the simulations were based on the results of the Planck mission (Planck Collaboration et al. Reference Planck2014):
![]() $\Omega_{\Lambda} = 0.6808$
,
$\Omega_{\Lambda} = 0.6808$
,
![]() $\Omega_{\rm m} = 0.3192$
,
$\Omega_{\rm m} = 0.3192$
,
![]() $\sigma_{8} = 0.826$
,
$\sigma_{8} = 0.826$
,
![]() $\Omega_{\rm b} = 0.04964$
,
$\Omega_{\rm b} = 0.04964$
,
![]() $n_{\rm s} = 0.96$
, and
$n_{\rm s} = 0.96$
, and
![]() $h = 0.6704$
.
$h = 0.6704$
.
4.1. Skewer generation
In the next step, for each model that fulfils the aforementioned conditions, we transformed the Ly-
![]() $\unicode{x03B1}$
optical depth
$\unicode{x03B1}$
optical depth
![]() $(\tau)$
skewer into the corresponding flux skewer F according to the equation
$(\tau)$
skewer into the corresponding flux skewer F according to the equation
![]() $F = F_{c} \exp\!({-}A_r \tau)$
, where continuum flux
$F = F_{c} \exp\!({-}A_r \tau)$
, where continuum flux
![]() $F_{c}$
was set up to unity and
$F_{c}$
was set up to unity and
![]() $A_r$
is the scaling factor, which allows us to match the lines of sight to observed mean flux values. Its value can be determined by comparing of the mean flux of the simulations with observational mean flux. In this study, we used the value that corresponds to the mean flux evolution presented in Oñorbe et al. (Reference Oñorbe and Hennawi2017), which is based on accurate measurements of Fan et al. (Reference Fan2006), Becker et al. (Reference Becker, Rauch and Sargent2007), Kirkman et al. (Reference Kirkman, Tytler, Lubin and Charlton2007), Faucher-Giguère et al. (Reference Faucher-Giguère, Prochaska, Lidz, Hernquist and Zaldarriaga2008), and Becker & Bolton (Reference Becker and Bolton2013). It is worth noting that the mean flux normalisation is computed for the full snapshot.
$A_r$
is the scaling factor, which allows us to match the lines of sight to observed mean flux values. Its value can be determined by comparing of the mean flux of the simulations with observational mean flux. In this study, we used the value that corresponds to the mean flux evolution presented in Oñorbe et al. (Reference Oñorbe and Hennawi2017), which is based on accurate measurements of Fan et al. (Reference Fan2006), Becker et al. (Reference Becker, Rauch and Sargent2007), Kirkman et al. (Reference Kirkman, Tytler, Lubin and Charlton2007), Faucher-Giguère et al. (Reference Faucher-Giguère, Prochaska, Lidz, Hernquist and Zaldarriaga2008), and Becker & Bolton (Reference Becker and Bolton2013). It is worth noting that the mean flux normalisation is computed for the full snapshot.
4.2. Modelling noise and resolution
To create mock spectra, we added effects of resolution and noise to the simulated skewers. The magnitude of both effects was adjusted so that the mock spectra corresponded as closely as possible to the observed ones. Note that in case of the real data, we divided the spectra into 20 Mpc h
![]() $^{-1}$
sections to directly match the box size of the simulated spectra and calculate the S/N of each section. Then, we match the S/N of the simulated spectra with the section of the QSO spectra.
$^{-1}$
sections to directly match the box size of the simulated spectra and calculate the S/N of each section. Then, we match the S/N of the simulated spectra with the section of the QSO spectra.
5. Results and discussion
In this section, we present the measured values of the temperature at the mean density by determining the temperature at the characteristic overdensity, which is a tight function of the absolute curvature irrespective of the
![]() $\unicode{x03B3}$
. The final results for the curvature measurements from the real QSO spectra are shown in Figure 4. The results show that there is a small difference between the values of curvature with and without metal correction. However, there is a significant difference of
$\unicode{x03B3}$
. The final results for the curvature measurements from the real QSO spectra are shown in Figure 4. The results show that there is a small difference between the values of curvature with and without metal correction. However, there is a significant difference of
![]() $\log{<|\kappa|>}$
in the case of redshift bin
$\log{<|\kappa|>}$
in the case of redshift bin
![]() $3.9 \leq z \leq 4.1$
compared to study of Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011). It is worth noting that it is problematic to compare these values due to the curvature values depends on the data (noise, resolution) as well as on the method of noise treatment. In a preliminary analysis, we found that the main source of this discrepancy is the noisier dataset we used compared to the study of Becker et al. (Reference Becker, Rauch and Sargent2007).
$3.9 \leq z \leq 4.1$
compared to study of Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011). It is worth noting that it is problematic to compare these values due to the curvature values depends on the data (noise, resolution) as well as on the method of noise treatment. In a preliminary analysis, we found that the main source of this discrepancy is the noisier dataset we used compared to the study of Becker et al. (Reference Becker, Rauch and Sargent2007).

Figure 4. Curvature measurements from the observational QSO spectra.
5.1. Characteristic overdensities
As was shown in Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011), Boera et al. (Reference Boera, Murphy, Becker and Bolton2014), the
![]() $\log{<|\kappa|>}$
follows the tight relation with the gas temperature at the characteristic overdensity (Padmanabhan et al. Reference Padmanabhan, Srianand and Choudhury2015). The method to inferring the characteristic overdensities used in this study can be explained as follows:
$\log{<|\kappa|>}$
follows the tight relation with the gas temperature at the characteristic overdensity (Padmanabhan et al. Reference Padmanabhan, Srianand and Choudhury2015). The method to inferring the characteristic overdensities used in this study can be explained as follows:
-
1. We determined the
 $\log{<|\kappa|>}$
of the simulated spectra for each input model. In this case, the final values of mean absolute curvature corresponds to the median of
$\log{<|\kappa|>}$
of the simulated spectra for each input model. In this case, the final values of mean absolute curvature corresponds to the median of
 ${<|\kappa|>}$
from the 200 mock datasets generated for each input model.
${<|\kappa|>}$
from the 200 mock datasets generated for each input model. -
2. For a given value of
 $\Delta$
, we calculated the
$\Delta$
, we calculated the
 $T(\Delta)$
for each model using the
$T(\Delta)$
for each model using the
 $T_{0}$
and
$T_{0}$
and
 $\unicode{x03B3}$
.
$\unicode{x03B3}$
. -
3. We plotted the values of
 $T(\Delta)$
versus
$T(\Delta)$
versus
 $\log{<|\kappa|>}$
for each input model (Figure 5), and fit the relation using a power-law fit using the least squares method: (4)where A and
$\log{<|\kappa|>}$
for each input model (Figure 5), and fit the relation using a power-law fit using the least squares method: (4)where A and \begin{equation}\log{<|\kappa|>}= - \left( \frac{T(\Delta)}{A} \right) ^{1/\unicode{x03B1}},\end{equation}
\begin{equation}\log{<|\kappa|>}= - \left( \frac{T(\Delta)}{A} \right) ^{1/\unicode{x03B1}},\end{equation}
 $\unicode{x03B1}$
are the free parameters.
$\unicode{x03B1}$
are the free parameters.
-
4. Subsequently, we varied the value of
 $\Delta$
in Equation (4) and determined its value (by varying A and
$\Delta$
in Equation (4) and determined its value (by varying A and
 $\unicode{x03B1}$
), which corresponds to the best-fit.
$\unicode{x03B1}$
), which corresponds to the best-fit.
Note that the value of
![]() $\Delta$
obtained by the aforementioned approach is denote by
$\Delta$
obtained by the aforementioned approach is denote by
![]() $\overline{\Delta}$
and is defined as the ’characteristic overdensity’ associated with the mean curvature (Padmanabhan et al. Reference Padmanabhan, Srianand and Choudhury2015).
$\overline{\Delta}$
and is defined as the ’characteristic overdensity’ associated with the mean curvature (Padmanabhan et al. Reference Padmanabhan, Srianand and Choudhury2015).
To quantify the amount of scatter in Figure 5, we determined the values of the characteristic overdensities and corresponding best-fitting parameters A and
![]() $\unicode{x03B1}$
from the 5000 bootstrap realisations of the curvature values of the input models. These were used for the calculation of
$\unicode{x03B1}$
from the 5000 bootstrap realisations of the curvature values of the input models. These were used for the calculation of
![]() $T(\overline{\Delta})$
and also
$T(\overline{\Delta})$
and also
![]() $T_{0}$
(see below). The final fits in Figure 5 are based on the median values of the
$T_{0}$
(see below). The final fits in Figure 5 are based on the median values of the
![]() $\overline{\Delta}$
and corresponding best-fitting parameters A and
$\overline{\Delta}$
and corresponding best-fitting parameters A and
![]() $\unicode{x03B1}$
.
$\unicode{x03B1}$
.

Figure 5.
![]() $\log{<|\kappa|>}$
as a function of
$\log{<|\kappa|>}$
as a function of
![]() $T(\overline{\Delta})$
for our simulations.
$T(\overline{\Delta})$
for our simulations.
5.2. Temperature at the characteristic overdensity
In the previous part of the study, we determined the free parameters A and
![]() $\unicode{x03B1}$
, which allow us to calculate the
$\unicode{x03B1}$
, which allow us to calculate the
![]() $T(\overline{\Delta})$
from the
$T(\overline{\Delta})$
from the
![]() $\log{<|\kappa|>}$
of the QSO spectra for both redshift bins using Equation (4). It is worth noting that in this case, we combine the values of
$\log{<|\kappa|>}$
of the QSO spectra for both redshift bins using Equation (4). It is worth noting that in this case, we combine the values of
![]() $\overline{\Delta}$
, A and
$\overline{\Delta}$
, A and
![]() $\unicode{x03B1}$
with the
$\unicode{x03B1}$
with the
![]() $\log < |\kappa| >$
of the QSO spectra obtained by bootstrap method. Subsequently, the medians were used as the best estimates of
$\log < |\kappa| >$
of the QSO spectra obtained by bootstrap method. Subsequently, the medians were used as the best estimates of
![]() $T(\overline{\Delta})$
and
$T(\overline{\Delta})$
and
![]() $T_{0}$
(see below). This approach also includes uncertainties which arose during the individual steps implemented in the analysis. The results show that our measurements are in a good agreement with the previous study by Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011) and are depicted in Figure 6.
$T_{0}$
(see below). This approach also includes uncertainties which arose during the individual steps implemented in the analysis. The results show that our measurements are in a good agreement with the previous study by Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011) and are depicted in Figure 6.

Figure 6. Comparison of the temperatures of the intergalactic medium at the optimal overdensity as a function of redshift obtained in this study and previously published ones.
5.3. Temperature at the mean density
We can convert the values of
![]() $T(\overline{\Delta})$
into
$T(\overline{\Delta})$
into
![]() $T_{0}$
using Equation (1), which requires knowing the value of
$T_{0}$
using Equation (1), which requires knowing the value of
![]() $\unicode{x03B3}$
. Under the assumption of
$\unicode{x03B3}$
. Under the assumption of
![]() $\unicode{x03B3} = 1.4$
, motivated by the evolution of this parameter predicted by the various UVB models, we determined the values of temperatures at mean density
$\unicode{x03B3} = 1.4$
, motivated by the evolution of this parameter predicted by the various UVB models, we determined the values of temperatures at mean density
![]() $T_{0} = 7893^{+1417}_{-1226}$
K and
$T_{0} = 7893^{+1417}_{-1226}$
K and
![]() $T_{0} = 8153^{+1224}_{-993}$
K for redshift range of
$T_{0} = 8153^{+1224}_{-993}$
K for redshift range of
![]() $3.9 \leq z \leq 4.1$
and
$3.9 \leq z \leq 4.1$
and
![]() $4.1 \leq z \leq 4.3$
, respectively. All derived value of parameters are listed in Table 3.
$4.1 \leq z \leq 4.3$
, respectively. All derived value of parameters are listed in Table 3.
Table 3. Values of the parameters determined for the investigated redshift ranges (column 1): total numbers of used 20 Mpc h
![]() $^{-1}$
sections (column 2), associated characteristic overdensities (column 3), values of free parameters in Equation (4) (columns 4 and 5), mean absolute curvature values (column 6), temperature measurements at the characteristic overdensity (column 7) and at mean density under the assumption of
$^{-1}$
sections (column 2), associated characteristic overdensities (column 3), values of free parameters in Equation (4) (columns 4 and 5), mean absolute curvature values (column 6), temperature measurements at the characteristic overdensity (column 7) and at mean density under the assumption of
![]() $\unicode{x03B3} = 1.4$
(column 8).
$\unicode{x03B3} = 1.4$
(column 8).

5.4. Comparison with previous studies
The comparison of the results obtained in this study with previously published ones is shown in Figure 7. The derived value of
![]() $T_{0}$
(within uncertainty) is consistent with that published by Walther et al. (Reference Walther, Oñorbe and Hennawi2019) in case of both studied redshift bins. Comparing with the study of Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011), when we rescaled their values assuming
$T_{0}$
(within uncertainty) is consistent with that published by Walther et al. (Reference Walther, Oñorbe and Hennawi2019) in case of both studied redshift bins. Comparing with the study of Becker et al. (Reference Becker, Bolton, Haehnelt and Sargent2011), when we rescaled their values assuming
![]() $\unicode{x03B3} = 1.4$
, we obtained the similar value of
$\unicode{x03B3} = 1.4$
, we obtained the similar value of
![]() $T_{0}$
.
$T_{0}$
.

Figure 7. Comparison of the results obtained in this study with previously published ones and various models. We plotted the
![]() $T_{0}$
and
$T_{0}$
and
![]() $\unicode{x03B3}$
evolution for the UVB models of Haardt & Madau (Reference Haardt and Madau2012), Oñorbe et al. (Reference Oñorbe and Hennawi2017), Khaire & Srianand (Reference Khaire and Srianand2019), Puchwein et al. (Reference Puchwein, Haardt, Haehnelt and Madau2019), and Faucher-Giguère (Reference Faucher-Giguère2020) with red, purple, green, orange, and blue line, respectively. The photoheating rates of the Oñorbe et al. (Reference Oñorbe and Hennawi2017), Puchwein et al. (Reference Puchwein, Haardt, Haehnelt and Madau2019), and Faucher-Giguère (Reference Faucher-Giguère2020) UVB models are scaled by a factors of 0.8, 0.9, and 0.7, respectively.
$\unicode{x03B3}$
evolution for the UVB models of Haardt & Madau (Reference Haardt and Madau2012), Oñorbe et al. (Reference Oñorbe and Hennawi2017), Khaire & Srianand (Reference Khaire and Srianand2019), Puchwein et al. (Reference Puchwein, Haardt, Haehnelt and Madau2019), and Faucher-Giguère (Reference Faucher-Giguère2020) with red, purple, green, orange, and blue line, respectively. The photoheating rates of the Oñorbe et al. (Reference Oñorbe and Hennawi2017), Puchwein et al. (Reference Puchwein, Haardt, Haehnelt and Madau2019), and Faucher-Giguère (Reference Faucher-Giguère2020) UVB models are scaled by a factors of 0.8, 0.9, and 0.7, respectively.
In case of the bin which corresponds to the higher redshift (
![]() $z = 4.2$
), our results correspond to the results presented by Garzilli et al. (Reference Garzilli, Boyarsky and Ruchayskiy2017) and Boera et al. (Reference Boera, Becker, Bolton and Nasir2019). Note that due to similarity of our results and ones of the aforementioned study, the points in the Figure 7, which corresponds to the Boera et al. (Reference Boera, Becker, Bolton and Nasir2019) are overlapped with our values.
$z = 4.2$
), our results correspond to the results presented by Garzilli et al. (Reference Garzilli, Boyarsky and Ruchayskiy2017) and Boera et al. (Reference Boera, Becker, Bolton and Nasir2019). Note that due to similarity of our results and ones of the aforementioned study, the points in the Figure 7, which corresponds to the Boera et al. (Reference Boera, Becker, Bolton and Nasir2019) are overlapped with our values.
5.5. Comparison with models
We also compared the obtained results with predictions of five widely used UVB models with rescaled H i, He i, and He ii photoheating rates as presented in the study of Gaikwad et al. (Reference Gaikwad, Srianand, Haehnelt and Choudhury2021). Based on the measurement of the thermal state of the IGM in the redshift range of
![]() $2 \leq z \leq 4$
determined using various statistics available in the literature (i.e. flux power spectrum, wavelet statistics, curvature statistics, and b-parameter probability distribution function) the authors found a good match between the shape of the observed
$2 \leq z \leq 4$
determined using various statistics available in the literature (i.e. flux power spectrum, wavelet statistics, curvature statistics, and b-parameter probability distribution function) the authors found a good match between the shape of the observed
![]() $T_{0}$
and
$T_{0}$
and
![]() $\unicode{x03B3}$
evolution and that predicted by the UVB models with scaled photoheating rates.
$\unicode{x03B3}$
evolution and that predicted by the UVB models with scaled photoheating rates.
The rescaled models, as were presented in the aforementioned study, together with our results are showed in Figure 7. In the case of the lower redshift bin, the determined value of
![]() $T_{0}$
is lower that predicted by the UVB models. On the other hand, in the case of the higher redshift bin, the determined value of
$T_{0}$
is lower that predicted by the UVB models. On the other hand, in the case of the higher redshift bin, the determined value of
![]() $T_{0}$
corresponds (within the error) with that predicted by the models of Oñorbe et al. (Reference Oñorbe and Hennawi2017) and Faucher-Giguère (Reference Faucher-Giguère2020). It can be concluded that these results are consistent with the relatively late He ii reionisation in the aforementioned models.
$T_{0}$
corresponds (within the error) with that predicted by the models of Oñorbe et al. (Reference Oñorbe and Hennawi2017) and Faucher-Giguère (Reference Faucher-Giguère2020). It can be concluded that these results are consistent with the relatively late He ii reionisation in the aforementioned models.
6. Conclusions
In this study, we applied the curvature method on a sample of 10 QSO spectra obtained by the Ultraviolet and Visual Echelle Spectrograph on the VLT/ESO to obtained the value of IGM temperature at a mean density. The main results could be summarised as follows:
-
1. Adopting the assumption of
 $\unicode{x03B3} = 1.4$
, we determined the values of IGM temperatures at mean density
$\unicode{x03B3} = 1.4$
, we determined the values of IGM temperatures at mean density
 $T_{0} = 7893^{+1417}_{-1226}$
K and
$T_{0} = 7893^{+1417}_{-1226}$
K and
 $T_{0} = 8153^{+1224}_{-993}$
K for redshift range of
$T_{0} = 8153^{+1224}_{-993}$
K for redshift range of
 $3.9 \leq z \leq 4.1$
and
$3.9 \leq z \leq 4.1$
and
 $4.1 \leq z \leq 4.3$
, respectively.
$4.1 \leq z \leq 4.3$
, respectively. -
2. The value of
 $T_0$
that we derived from our
$T_0$
that we derived from our
 $T(\overline{\Delta})$
starts to be largely independent of
$T(\overline{\Delta})$
starts to be largely independent of
 $\unicode{x03B3}$
, with increasing z, because we have measured the temperature close to the mean density.
$\unicode{x03B3}$
, with increasing z, because we have measured the temperature close to the mean density. -
3. Although the results show no strong temperature evolution over the studied redshift range, our measurements are consistent with the relatively late He ii reionisation presented in the Oñorbe et al. (Reference Oñorbe and Hennawi2017) and Faucher-Giguère (Reference Faucher-Giguère2020) models.
Acknowledgement
This research is based on the data products created from observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere. The authors would also like to thank Jose Oñorbe, Prakash Gaikwad, and George Becker for the fruitful discussion and to the anonymous referee for carefully reading our manuscript and for insightful comments and suggestions that improved the quality of this work.
Data Availability
The data underlying this article will be shared on reasonable request to the corresponding author.
Appendix A. Steps of the curvature calculation
For the purpose of reproducibility, in this section, we describe the basic steps of the curvature calculation, which include the first and second derivatives and the Gaussian filter.
Appendix A.1. First and second derivative
Firstly, we create the new array in which the first and second values correspond to the first value of re-normalized flux. Similarly, the last two values correspond to the last value of the re-normalized flux array (see Figure A.1).

Figure A.1. Input and output arrays for the derivative calculation.
Then, for the derivative calculation we used the centered difference approximations:
Appendix A.2. Gaussian filter
As was mentioned before, the curvature method can be affected by the finite S/N of the spectra. To solve this difficulty, we smoothed the flux using the Gaussian filter according to the following algorithm.
Algorithm 1: An algorithm for a Gaussian filter