Crystal structure of deracoxib, C₁₇H₁₄F₃N₃O₃S

Abstract

The crystal structure of deracoxib has been solved and refined using synchrotron X-ray powder diffraction data, and optimized using density functional theory techniques. Deracoxib crystallizes in space group Pbca (#61) with a = 9.68338(11), b = 9.50690(5), c = 38.2934(4) Å, V = 3525.25(3) ų, and Z = 8. The molecules stack in layers parallel to the ab-plane. N–H⋯O hydrogen bonds link the molecules along the b-axis, in chains with the graph set C1,1(4), as well as more-complex patterns. N–H⋯N hydrogen bonds link the layers. The powder pattern has been submitted to ICDD for inclusion in the Powder Diffraction File™ (PDF®).

I. INTRODUCTION

Deracoxib (sold under the brand name Deramaxx) is a selective cyclooxygenase 2 inhibitor, used in veterinary medicine for the control of pain and inflammation associated with osteoarthritis in dogs. Deracoxib is also used after canine dental procedures and is not recommended for use in cats. The systematic name (CAS Registry Number 169590-41-4) is 4-[3-(difluoromethyl)-5-(3-fluoro-4-methoxyphenyl)pyrazol-1-yl]benzenesulfonamide. A two-dimensional molecular diagram is shown in Figure 1.

Figure 1. The 2D molecular structure of deracoxib.

We are unaware of any published powder diffraction data on deracoxib. This work was carried out as part of a project (Kaduk et al., 2014) to determine the crystal structures of large-volume commercial pharmaceuticals, and include high-quality powder diffraction data for them in the Powder Diffraction File (Gates-Rector and Blanton, 2019).

II. EXPERIMENTAL AND REFINEMENTS

Deracoxib was a commercial reagent, purchased from TargetMol (Batch #113281), and was used as-received. The white powder was packed into a 1.5 mm diameter Kapton capillary and rotated during the measurement at ~50 Hz. The powder pattern was measured at 295 K at beamline 11-BM (Antao et al., 2008; Lee et al., 2008; Wang et al., 2008) of the Advanced Photon Source at Argonne National Laboratory using a wavelength of 0.458208(2) Å from 0.5 to 50° 2θ with a step size of 0.001° and a counting time of 0.1 s step⁻¹. The high-resolution powder diffraction data were collected using twelve silicon crystal analyzers that allow for high angular resolution, high precision, and accurate peak positions. A mixture of silicon (NIST SRM 640c) and alumina (NIST SRM 676a) standards (ratio Al₂O₃:Si = 2:1 by weight) was used to calibrate the instrument and refine the monochromatic wavelength used in the experiment.

The pattern was indexed using JADE Pro 8.1 (MDI, 2021) on a high-quality primitive orthorhombic unit cell with a = 9.71606, b = 9.54339, c = 38.43565 Å, V = 3563.91 Å³, and Z = 8. The suggested space group was Pbca, which was confirmed by successful solution and refinement of the structure. A reduced cell search in the Cambridge Structural Database (Groom et al., 2016) combined with only C, H, F, N, O, and S elements, yielded no hits.

A deracoxib molecule was downloaded from PubChem (Kim et al., 2019) as Conformer3D_CID_3058754.sdf. It was converted to a *.mol2 file using Mercury (Macrae et al., 2020) and to a Fenske-Hall Z-matrix using Open Babel (O'Boyle et al., 2011). The structure was solved using FOX (Favre-Nicolin and Černý, 2002) using sinθ/λ _max = 0.32 Å⁻¹ (2θ _max = 16.9°).

Rietveld refinement was carried out using GSAS-II (Toby and Von Dreele, 2013). Only the 1.0–25.0° portion of the pattern was included in the refinement (d _min = 1.058 Å). The region 1.50–2.12°, which contained a peak from the Kapton capillary, was excluded from the refinement. All non-H bond distances and angles were subjected to restraints, based on a Mercury/Mogul Geometry Check (Bruno et al., 2004; Sykes et al., 2011). The Mogul average and standard deviation for each quantity were used as the restraint parameters. The restraints contributed 4.2% to the final χ ². The hydrogen atoms were included in calculated positions, which were recalculated during the refinement using Materials Studio (Dassault, 2021). The U _iso were grouped by chemical similarity. The U _iso for the H atoms were fixed at 1.3× the U _iso of the heavy atoms to which they are attached. A second-order spherical harmonic model was included in the refinement. The texture index was 1.032(0). The peak profiles were described using the generalized microstrain model. The background was modeled using a 6-term shifted Chebyshev polynomial, plus a peak at 5.81° 2θ to model the scattering from the Kapton capillary and any amorphous component.

The final refinement of 106 variables using 23 413 observations and 72 restraints yielded the residuals R _wp = 0.0589 and GOF = 1.26. The largest peak (1.09 Å from C19) and hole (1.01 Å from C17) in the difference Fourier map were 0.19(5) and −0.23(5) eÅ⁻³, respectively. The largest errors in the difference plot (Figure 2) are in the shapes of some of the strong low-angle peaks.

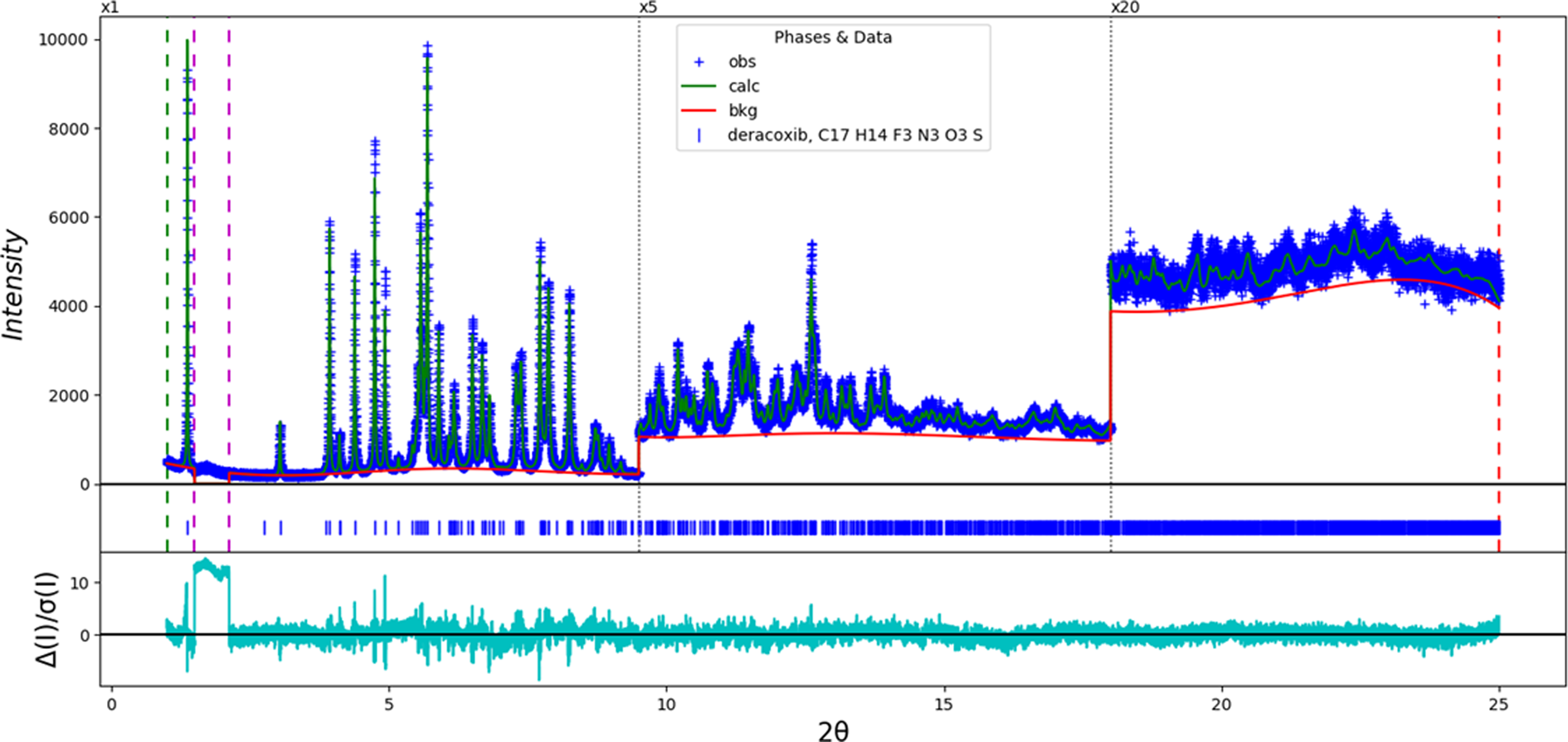
Figure 2. The Rietveld plot for the refinement of deracoxib. The blue crosses represent the observed data points, and the green line is the calculated pattern. The cyan curve is the normalized error plot, and the red line is the background curve. The vertical scale has been multiplied by a factor of 5× for 2θ > 9.5° and by 20× for 2θ > 18.0°. The two vertical magenta dashed lines indicate the excluded region 1.50–2.12° 2θ, which contains a peak from the Kapton capillary.

The structure of deracoxib was optimized using VASP (Kresse and Furthmüller, 1996) (fixed experimental unit cell) through the MedeA graphical interface (Materials Design, 2016). The calculation was carried out on 16 2.4 GHz processors (each with 4 GB RAM) of a 64-processor HP Proliant DL580 Generation 7 Linux cluster at North Central College. The calculation used the GGA-PBE functional, a plane wave cutoff energy of 400.0 eV, and a k-point spacing of 0.5 Å⁻¹ leading to a 2 × 2 × 1 mesh, and took ~17 h. A single-point density functional theory calculation (fixed experimental cell) and population analysis were carried out using CRYSTAL17 (Dovesi et al., 2018). The basis sets for the H, C, N, and O atoms in the calculation were those of Gatti et al. (1994), and those for F and S were those of Peintinger et al. (2013). The calculations were run on a 3.5 GHz PC using 8 k-points and the B3LYP functional, and took ~3.1 h.

III. RESULTS AND DISCUSSION

The root-mean-square (rms) Cartesian displacement between the Rietveld-refined and DFT-optimized structures of deracoxib is 0.070 Å (Figure 3). The excellent agreement provides strong evidence that the structure is correct (van de Streek and Neumann, 2014). This discussion concentrates on the DFT-optimized structure. The asymmetric unit (with atom numbering) is illustrated in Figure 4. The best view of the crystal structure is down the a-axis (Figure 5). The molecules stack in layers parallel to the ab-plane.

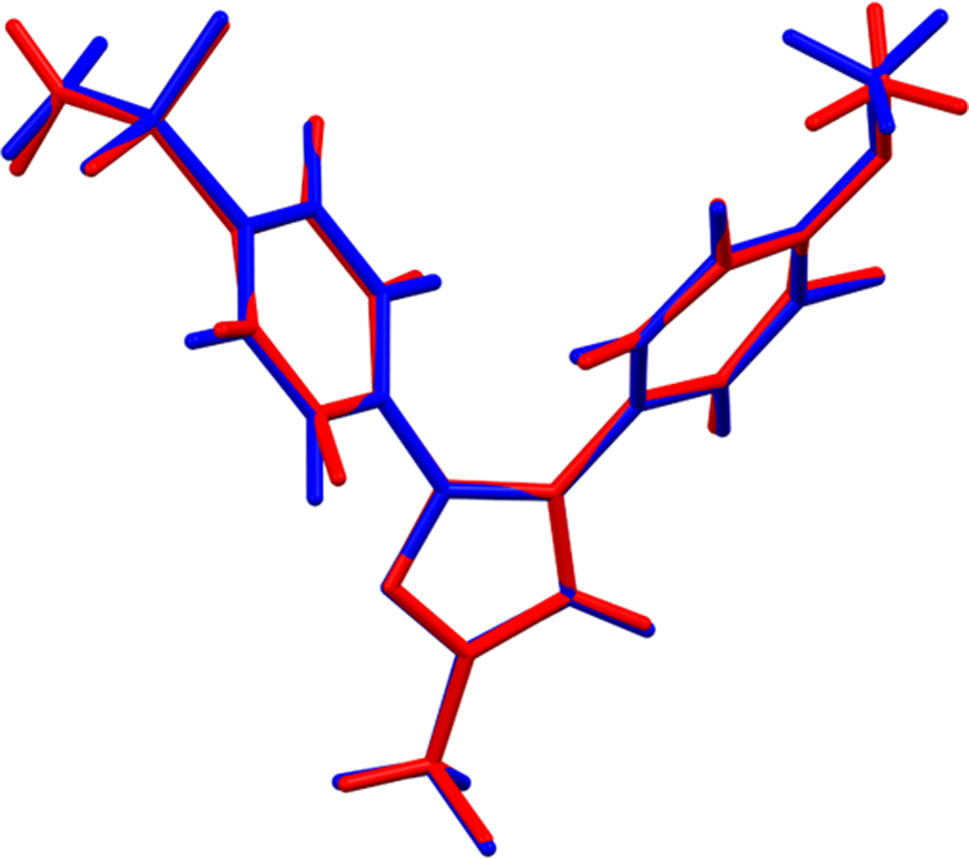
Figure 3. Comparison of the Rietveld-refined (red) and VASP-optimized (blue) structures of deracoxib. The rms Cartesian displacement is 0.070 Å. Image generated using Mercury (Macrae et al., 2020).

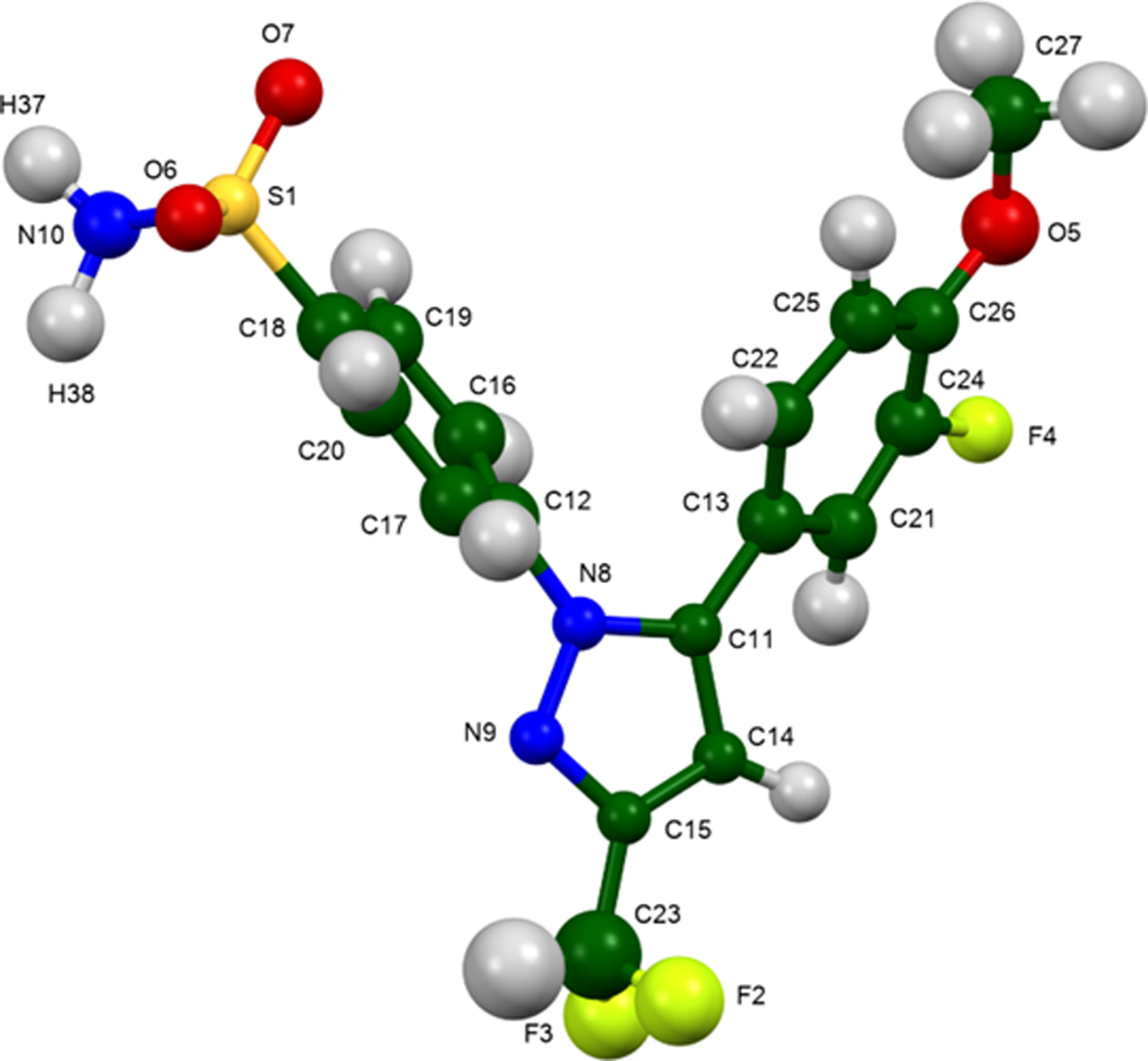
Figure 4. The asymmetric unit of deracoxib, with the atom numbering. The atoms are represented by 50% probability spheroids/ellipsoids. Image generated using Mercury (Macrae et al., 2020).

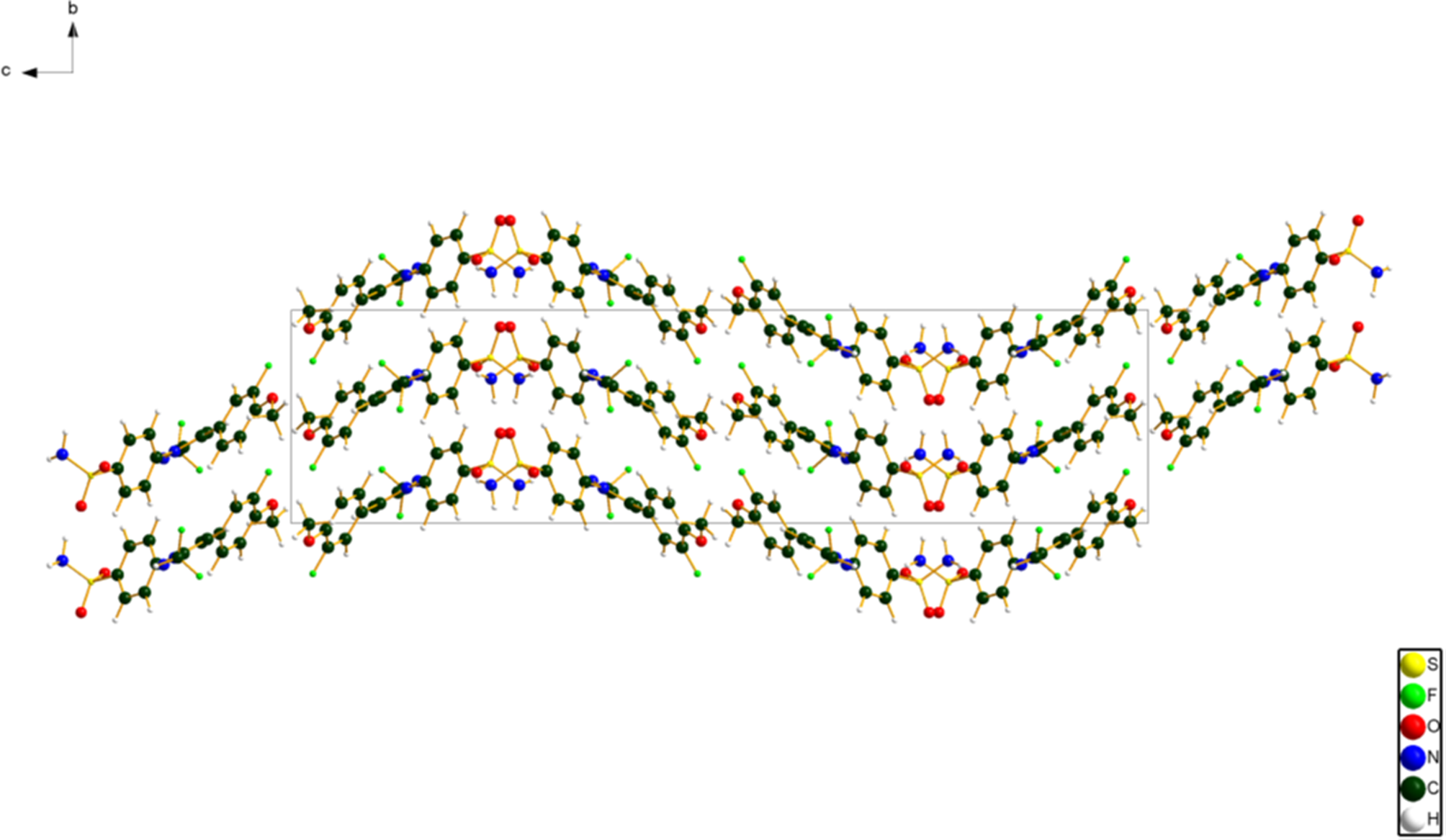
Figure 5. The crystal structure of deracoxib, viewed down the a-axis. Image generated using Diamond (Crystal Impact, 2022).

All of the bond distances and angles fall within the normal ranges indicated by a Mercury/Mogul Geometry Check (Macrae et al., 2020). The quantum chemical geometry optimization of the deracoxib molecule (DFT/B3LYP/6-31G*/water) using Spartan ‘18 (Wavefunction, 2020) indicated that the observed conformation is very close to a local minimum in energy. A conformational analysis (MMFF force field) indicates that the minimum-energy conformation is 5.9 kcal mol⁻¹ lower in energy, and has a different orientation of the phenyl ring containing the sulfonamide group (~180° rotation). Intermolecular interactions, thus, affect the solid-state conformation.

Analysis of the contributions to the total crystal energy of the structure using the Forcite module of Materials Studio (Dassault, 2021) suggests that the intramolecular deformation energy is dominated by angle deformation terms. The intermolecular energy is dominated by van der Waals and electrostatic attractions, which in this force field analysis also include hydrogen bonds. The hydrogen bonds are better analyzed using the results of the DFT calculation.

There are three traditional hydrogen bonds in the structure (Table I), between the amino group H37–N10–H38 and the sulfonyl group O6–S1–O7, as well as the ring nitrogen atom N9. The energies of the N–H⋯O hydrogen bonds were calculated using the correlation of Wheatley and Kaduk (2019). The N–H⋯O hydrogen bonds link the molecules along the b-axis, in chains with the graph set (Etter, 1990; Bernstein et al., 1995; Shields et al., 2000) C1,1(4), as well as more-complex patterns. The N–H⋯N hydrogen bonds link the layers. Several intramolecular and intermolecular C–H⋯O and C–H⋯N hydrogen bonds contribute to the crystal energy.

TABLE I. Hydrogen bonds (CRYSTAL17) in deracoxib.

^a Intramolecular.

The volume enclosed by the Hirshfeld surface of the deracoxib molecule (Figure 6; Hirshfeld, 1977; Turner et al., 2017) is 433.26 Å³, 98.32% of 1/8 the unit cell volume. The packing density is thus fairly typical. The only significant close contacts (red in Figure 6) involve the hydrogen bonds. The volume/non-hydrogen atom is 16.3 Å³.

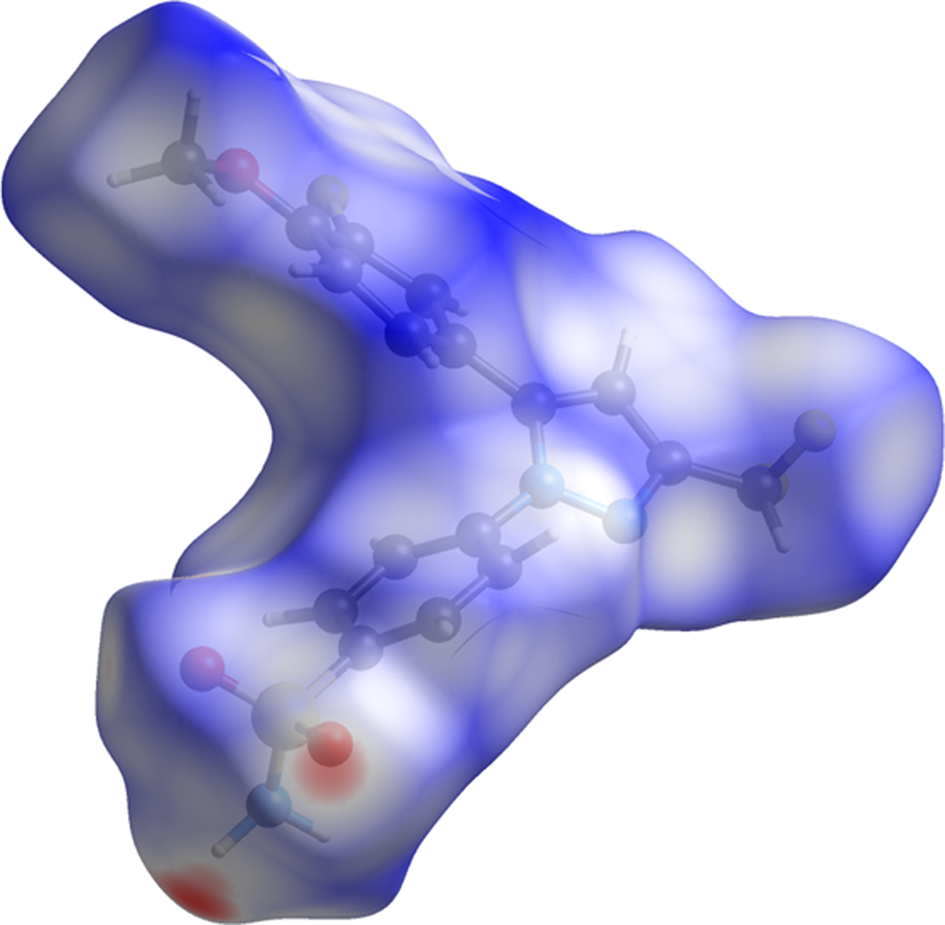
Figure 6. The Hirshfeld surface of deracoxib. Intermolecular contacts longer than the sums of the van der Waals radii are colored blue, and contacts shorter than the sums of the radii are colored red. Contacts equal to the sums of radii are white.

The Bravais–Friedel–Donnay–Harker (Bravais, 1866; Friedel, 1907; Donnay and Harker, 1937) morphology suggests that we might expect platy morphology for deracoxib, with {001} as the major faces. A second-order spherical harmonic model was included in the refinement. The texture index was 1.032(0), indicating that preferred orientation was small in this rotated capillary specimen.

IV. DEPOSITED DATA

The powder pattern of deracoxib from this synchrotron data set has been submitted to ICDD for inclusion in the Powder Diffraction File. The Crystallographic Information Framework (CIF) files containing the results of the Rietveld refinement (including the raw data) and the DFT geometry optimization were deposited with the ICDD. The data can be requested at [email protected].