1 Introduction
Among the various unsolved problems of plasma physics, controlled thermonuclear fusion remains the most challenging one, both with respect to its complexity and to the forthcoming critical energy transition. All projections of future energy consumption converge towards a doubling, at the very least, of the world’s energy demand by the end of this century. Today’s consumption is approximately
![]() $10^{20}~\text{J}~\text{yr}^{-1}$
. Given the increasing evidence of the dramatic impact of oil and coal energy sources on our environment, thermonuclear fusion and advanced nuclear fission are the only energy sources providing a straightforward development path toward a long term, sustainable, post-industrial society for which the energy demand is foreseen to, at least, double.
$10^{20}~\text{J}~\text{yr}^{-1}$
. Given the increasing evidence of the dramatic impact of oil and coal energy sources on our environment, thermonuclear fusion and advanced nuclear fission are the only energy sources providing a straightforward development path toward a long term, sustainable, post-industrial society for which the energy demand is foreseen to, at least, double.
Nuclear fission, in particular with the deployment of fourth generation fast breeders, has the potential to ensure a soft energy transition. However, the management of nuclear fuel cycle remains an open problem. Further to nuclear fusion, plasma physics and technologies could provide novel and unique solutions in this context as well. Indeed, plasmas offer a wide range of possibilities for isotope and mass separation (Grossman & Shepp Reference Grossman and Shepp1991; Timofeev Reference Timofeev2007, Reference Timofeev2014; Gueroult, Hobbs & Fisch Reference Gueroult, Hobbs and Fisch2015). However, despite experimental demonstrations in the form of plasma centrifugation (Krishnan, Geva & Hirshfield Reference Krishnan, Geva and Hirshfield1981; Hole & Simpson Reference Hole and Simpson1999), ion cyclotron resonance (Dawson et al. Reference Dawson, Kim, Arnush, Fried, Gould, Heflinger, Kennel, Romesser, Stenzel and Wong1976; Dolgolenko & Muromkin Reference Dolgolenko and Muromkin2009) and the historical calutron configuration; plasma isotope and mass separation are not to date used at industrial scale. In this respect, plasma separation remains an unsolved problem of plasma physics.
Plasma separation could be particularly useful for reprocessing burned nuclear fuel and ashes, with the objective of closing the nuclear cycle (Timofeev Reference Timofeev2007; Gueroult & Fisch Reference Gueroult and Fisch2014). Two choices can be made with nuclear energy. First, an open cycle, where the downloaded burned fuel is not reprocessed. Second, a closed cycle, where reprocessing provides new fuel, both as fissile and fertile materials, and reduces the volume of high-level waste, particularly through the separation of minor actinides (Timofeev Reference Timofeev2007; Gueroult & Fisch Reference Gueroult and Fisch2014).
It is commonly accepted that closing the nuclear cycle with the fourth generation of fast breeders would increase the energy extracted from uranium by a factor of approximately 50 to 60.
Closed cycle reprocessing is generally based on hot chemistry with a large number of steps in large-scale facilities. Besides the inventory problem associated with the large number of steps, particularly for minor actinides, huge volumes of organic solvent and acids are used for extraction. In addition, large volumes of nuclear waste are transported, for separation and then storage, through the countries who made the closed cycle choice (France, Japan, China, Russia and the UK). In contrast, plasma separation has the potential to offer efficient reprocessing in a single step. A small footprint plasma based facility located near each nuclear power station, providing in situ efficient reprocessing, hence appears particularly attractive for the development of advanced nuclear energy.
Each
![]() $^{235}\text{U}$
fission releases an energy of the order of
$^{235}\text{U}$
fission releases an energy of the order of
![]() $200$
MeV, and the ratio
$200$
MeV, and the ratio
![]() $^{235}\text{U}/^{238}\text{U}$
is of the order of a few per cent. Each nucleus in the irradiated nuclear fuel to be processed is thus associated with an energy deposited in the reactor core of the order of a few MeV. Plasma reprocessing cost can be roughly estimated based on the following assumptions. First, each atom of the burned fuel will have to be ionised. This ionisation cost is a few tens of eV per atom. Second, an electron temperature of the order of
$^{235}\text{U}/^{238}\text{U}$
is of the order of a few per cent. Each nucleus in the irradiated nuclear fuel to be processed is thus associated with an energy deposited in the reactor core of the order of a few MeV. Plasma reprocessing cost can be roughly estimated based on the following assumptions. First, each atom of the burned fuel will have to be ionised. This ionisation cost is a few tens of eV per atom. Second, an electron temperature of the order of
![]() $10$
eV has to be maintained to ensure suitable plasma parameters. Third, a selected minority of ions have to be accelerated or heated to be separated. Corresponding energy losses are expected to be up to a few
$10$
eV has to be maintained to ensure suitable plasma parameters. Third, a selected minority of ions have to be accelerated or heated to be separated. Corresponding energy losses are expected to be up to a few
![]() $100$
eV per selected ion. Fourth, the background ion temperature will be brought from room temperature to a fraction of an eV. Summing up these contributions, an energy cost of a few keV per atom seems like a safe upper bound for the whole plasma process. With these estimates, the power requirement to achieve a closed fuel cycle with plasma separation technologies will be below one per cent of the reactor power, far below the projected gain of 50–60.
$100$
eV per selected ion. Fourth, the background ion temperature will be brought from room temperature to a fraction of an eV. Summing up these contributions, an energy cost of a few keV per atom seems like a safe upper bound for the whole plasma process. With these estimates, the power requirement to achieve a closed fuel cycle with plasma separation technologies will be below one per cent of the reactor power, far below the projected gain of 50–60.
In addition to this favourable basic power balance, estimates of plasma processing throughput are consistent with the need of a typical fission reactor. Typical ion current density in plasmas is given by the relation
![]() $nC_{s}$
where
$nC_{s}$
where
![]() $C_{s}$
is the ion acoustic velocity,
$C_{s}$
is the ion acoustic velocity,
![]() $C_{s}\sim 10^{5}~\text{cm}~\text{s}^{-1}$
and
$C_{s}\sim 10^{5}~\text{cm}~\text{s}^{-1}$
and
![]() $n$
the plasma density. In advanced helicons and Electron Cyclotron Resonance (ECR) plasma sources, plasma density can be as large as
$n$
the plasma density. In advanced helicons and Electron Cyclotron Resonance (ECR) plasma sources, plasma density can be as large as
![]() $10^{12}{-}10^{13}~\text{cm}^{-3}$
. The continuous processing of a beam with cross-section
$10^{12}{-}10^{13}~\text{cm}^{-3}$
. The continuous processing of a beam with cross-section
![]() $S\sim 10^{3}~\text{cm}^{2}$
during one year, that is to say
$S\sim 10^{3}~\text{cm}^{2}$
during one year, that is to say
![]() $\unicode[STIX]{x1D70F}\sim 10^{7}$
s, is thus equivalent to approximately
$\unicode[STIX]{x1D70F}\sim 10^{7}$
s, is thus equivalent to approximately
![]() $nC_{s}S\unicode[STIX]{x1D70F}\sim 10^{28}$
nuclei. This is to be compared with the
$nC_{s}S\unicode[STIX]{x1D70F}\sim 10^{28}$
nuclei. This is to be compared with the
![]() $10^{24}$
nuclei contained in
$10^{24}$
nuclei contained in
![]() $1$
kg of irradiated fuel. Based on these simple estimates, about
$1$
kg of irradiated fuel. Based on these simple estimates, about
![]() $10^{4}$
kg of irradiated fuel can be processed per year. Interestingly, this is about the amount of burned fuel downloaded from a typical reactor per year.
$10^{4}$
kg of irradiated fuel can be processed per year. Interestingly, this is about the amount of burned fuel downloaded from a typical reactor per year.
Among the numerous separation mechanisms one can envision in a magnetised plasma column, classical electric field-driven centrifugation (Ohkawa & Miller Reference Ohkawa and Miller2002; Rax et al. Reference Rax, Fruchtman, Gueroult and Fisch2015), advanced magnetic centrifugal mass filter (Fetterman & Fisch Reference Fetterman and Fisch2011a ; Gueroult & Fisch Reference Gueroult and Fisch2012; Gueroult, Rax & Fisch Reference Gueroult, Rax and Fisch2014), ion cyclotron resonances (Dawson et al. Reference Dawson, Kim, Arnush, Fried, Gould, Heflinger, Kennel, Romesser, Stenzel and Wong1976; Dolgolenko & Muromkin Reference Dolgolenko and Muromkin2009), auto-resonant ion cyclotron resonance (Rax, Robiche & Fisch Reference Rax, Robiche and Fisch2007) and wave-driven centrifugation (Fetterman & Fisch Reference Fetterman and Fisch2009, Reference Fetterman and Fisch2011c ) have been proposed and deemed promising for isotope and mass separation. In this study, after briefly reviewing rotating plasma separation schemes in the next section, we identify and analyse a new scheme: the use of a rotating magnetic field for isotope and mass separation in a plasma column.
That a rotating magnetic field should drag a fluid plasma rotation is a direct consequence of the Alfvén frozen in law, but (i) the dynamics at the single particle level is far more complex than a simple rotation (Soldatenkov Reference Soldatenkov1966; Fisch & Watanabe Reference Fisch and Watanabe1982; Hugrass & Jones Reference Hugrass and Jones1983), and (ii) each choice of different driving external currents, for the very same magnetic field, provide new classes of orbits. This unexplored versatility offers several pathways for optimisation. In § 2, the different possible methods for spinning a magnetised plasma for the purpose of mass separation are reviewed. Moving on to rotating magnetic fields, in § 3, three different rotating vector potentials providing the same magnetic field are introduced. The associated, external or internal, currents are analysed and shown to be physically realisable. Then in §§ 4–6 we present an analysis of the orbital stability for these three rotating configurations. The relative advantages and drawbacks of these configurations for plasma mass separation are discussed in § 7. Finally, § 8 gives a summary of these new results pertaining to one of the most challenging unsolved problem of plasma physics: isotope and mass separation in rotating plasmas.
2 Angular momentum conversion and rotating plasmas for mass separation
To assess the originality of rotating magnetic fields for isotope and mass separation, let us briefly review the principles of other rotating plasma configurations. As per usual in plasma physics, the analysis of the physical processes must be performed both at the macroscopic fluid level and at the microscopic single particle level. Isotope separation with rotating plasmas offers a clear illustration of this rule. At the fluid level the description can be reduced to a uniform rotation with a steady state vorticity. On the other hand, at the single particle level, the orbits always display more complex behaviours than a simple rotation, leading to the occurrence of orbital instabilities. These instabilities can in turn be put at work for mass discrimination. The macroscopic averaging of these mass-dependent complex orbits is responsible for the emerging simple uniform rotation at the fluid level. In this study we will concentrate on a microscopic analysis and on the identification of orbital instabilities under various rotating fields configurations.
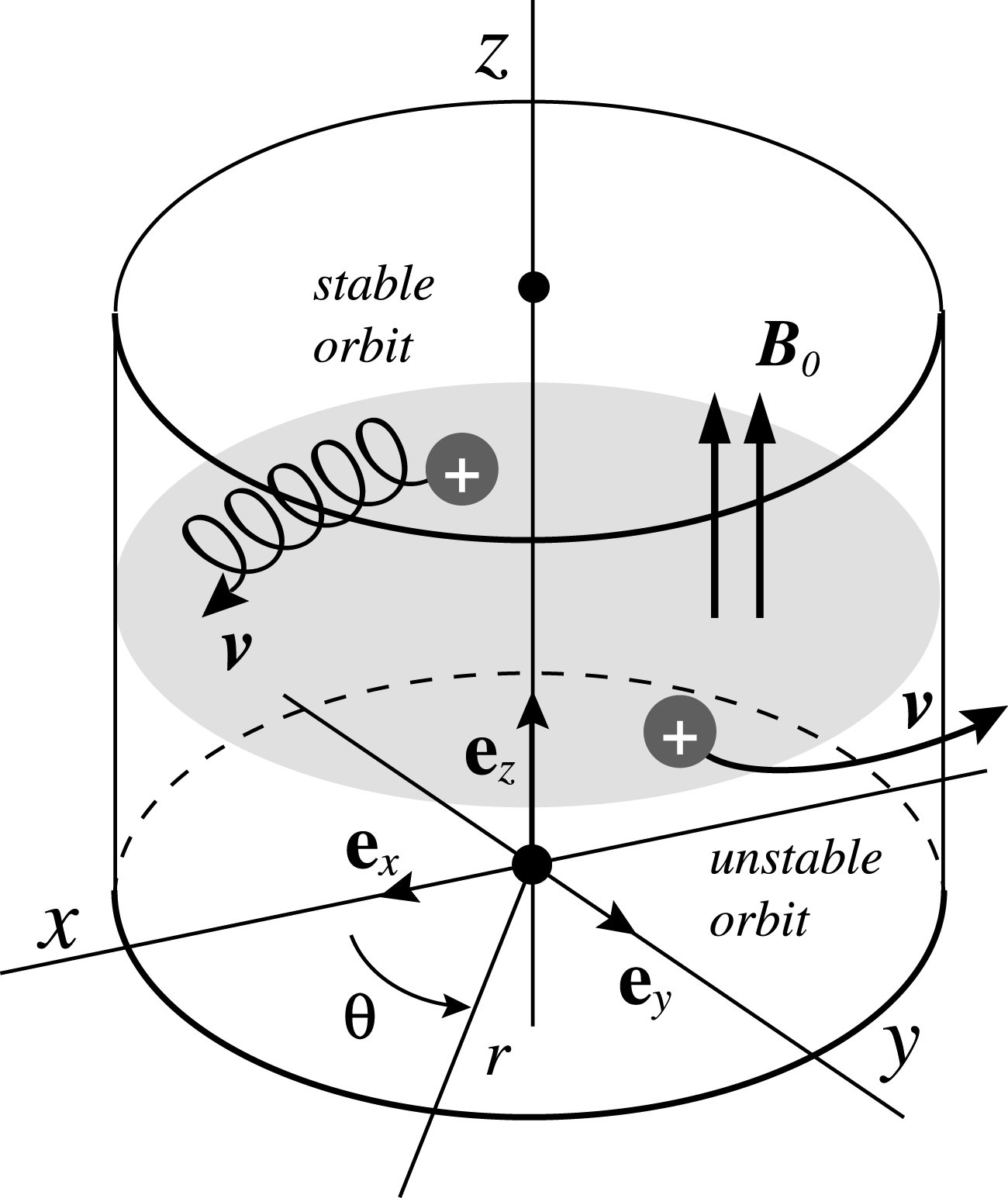
Figure 1. Classical axially magnetised plasma configuration for mass separation. The azimuthal rotation can be induced through any angular momentum deposition process around the
![]() $z$
axis.
$z$
axis.
The Brillouin limit associated with the rigid body rotation of a magnetised plasma column has been explored both theoretically and experimentally for nuclear waste management. Consider an ion, with mass
![]() $m$
and charge
$m$
and charge
![]() $q$
, interacting with a static radial linear electric field
$q$
, interacting with a static radial linear electric field
![]() $\boldsymbol{E}$
and an axial uniform magnetic field
$\boldsymbol{E}$
and an axial uniform magnetic field
![]() $\boldsymbol{B}_{0}$
$\boldsymbol{B}_{0}$
as depicted in figure 1. Here,
![]() $[\boldsymbol{e}_{x},\boldsymbol{e}_{y},\boldsymbol{e}_{z}]$
is a Cartesian basis and
$[\boldsymbol{e}_{x},\boldsymbol{e}_{y},\boldsymbol{e}_{z}]$
is a Cartesian basis and
![]() $[x,y,z]$
is the associated Cartesian coordinates. In this configuration, ion orbits are radially confined if the Brillouin condition (Rax et al.
Reference Rax, Fruchtman, Gueroult and Fisch2015),
$[x,y,z]$
is the associated Cartesian coordinates. In this configuration, ion orbits are radially confined if the Brillouin condition (Rax et al.
Reference Rax, Fruchtman, Gueroult and Fisch2015),
is fulfilled. For
![]() $\unicode[STIX]{x1D6FA}_{c}<\sqrt{2}\unicode[STIX]{x1D6FA}_{E}$
ions are ejected radially from the plasma column. As the cyclotron frequency is given by
$\unicode[STIX]{x1D6FA}_{c}<\sqrt{2}\unicode[STIX]{x1D6FA}_{E}$
ions are ejected radially from the plasma column. As the cyclotron frequency is given by
![]() $\unicode[STIX]{x1D6FA}_{c}=qB_{0}/m$
and
$\unicode[STIX]{x1D6FA}_{c}=qB_{0}/m$
and
![]() $\unicode[STIX]{x1D6FA}_{E}\sim 1/\sqrt{m}$
, for a given configuration, the heavy elements are expelled from a rotating plasma mixture and the light ones remain confined. It is to be noted that this simple configuration can be used in another way if we sustain an electrostatic potential with two radial minima rather than one with a parabolic potential associated with a linear field (Gueroult et al.
Reference Gueroult, Rax and Fisch2014). Beside these two simple
$\unicode[STIX]{x1D6FA}_{E}\sim 1/\sqrt{m}$
, for a given configuration, the heavy elements are expelled from a rotating plasma mixture and the light ones remain confined. It is to be noted that this simple configuration can be used in another way if we sustain an electrostatic potential with two radial minima rather than one with a parabolic potential associated with a linear field (Gueroult et al.
Reference Gueroult, Rax and Fisch2014). Beside these two simple
![]() $E$
cross
$E$
cross
![]() $B$
configurations, more sophisticated fields configurations have been identified and analysed for isotope processing. The auto-resonant interaction (Rax et al.
Reference Rax, Robiche and Fisch2007) between an ion beam with axial velocity
$B$
configurations, more sophisticated fields configurations have been identified and analysed for isotope processing. The auto-resonant interaction (Rax et al.
Reference Rax, Robiche and Fisch2007) between an ion beam with axial velocity
![]() $V$
and the helical magnetic field associated with the vector potential
$V$
and the helical magnetic field associated with the vector potential
![]() $\boldsymbol{A}$
,
$\boldsymbol{A}$
,
also provides a very efficient separation process if the periodic transverse field, with local wave vector
![]() $k(z)$
, is tapered according to the cyclotron auto-resonance relation
$k(z)$
, is tapered according to the cyclotron auto-resonance relation
Here,
![]() $\text{J}_{n}$
is the ordinary Bessel function of order
$\text{J}_{n}$
is the ordinary Bessel function of order
![]() $n$
. Such a tapered helical wiggler configuration ensures that the resonant conversion of the linear momentum
$n$
. Such a tapered helical wiggler configuration ensures that the resonant conversion of the linear momentum
![]() $mV$
, along
$mV$
, along
![]() $z$
, into an angular momentum, around
$z$
, into an angular momentum, around
![]() $z$
, is only efficient for a given mass, and inefficient for all other masses.
$z$
, is only efficient for a given mass, and inefficient for all other masses.
In between the simple radial
![]() $E$
cross axial
$E$
cross axial
![]() $B$
configurations, and this complex tapered helical wiggler configuration, a variety of electric and magnetic geometries and topologies have been studied, and should be explored in order to solve the open problem of plasma isotope and mass separations. Another very elegant and efficient way to sustain plasma rotation was recently identified and analysed (Fetterman & Fisch Reference Fetterman and Fisch2011c
): angular momentum injection through resonant waves–particle interactions. A cylindrical plasma wave whose electric (and/or magnetic) potential
$B$
configurations, and this complex tapered helical wiggler configuration, a variety of electric and magnetic geometries and topologies have been studied, and should be explored in order to solve the open problem of plasma isotope and mass separations. Another very elegant and efficient way to sustain plasma rotation was recently identified and analysed (Fetterman & Fisch Reference Fetterman and Fisch2011c
): angular momentum injection through resonant waves–particle interactions. A cylindrical plasma wave whose electric (and/or magnetic) potential
![]() $\unicode[STIX]{x1D6F7}$
varies according to
$\unicode[STIX]{x1D6F7}$
varies according to
with
![]() $r^{2}=x^{2}+y^{2}$
and
$r^{2}=x^{2}+y^{2}$
and
![]() $\unicode[STIX]{x1D703}$
the polar coordinates (as illustrated in figure 1),
$\unicode[STIX]{x1D703}$
the polar coordinates (as illustrated in figure 1),
![]() $l$
an integer and
$l$
an integer and
![]() $\unicode[STIX]{x1D719}(r)$
an appropriate solution of the radial Maxwell equations, interacting with a cylindrical plasma column, is able to transfer to magnetised particles (i) energy, (ii) axial linear momentum along
$\unicode[STIX]{x1D719}(r)$
an appropriate solution of the radial Maxwell equations, interacting with a cylindrical plasma column, is able to transfer to magnetised particles (i) energy, (ii) axial linear momentum along
![]() $z$
, and (iii) azimuthal angular momentum around
$z$
, and (iii) azimuthal angular momentum around
![]() $z$
. For this transfer to happen, the velocity
$z$
. For this transfer to happen, the velocity
![]() $V=\text{d}z/\text{d}t$
of the particles must satisfy the Doppler shifted cyclotron resonance condition,
$V=\text{d}z/\text{d}t$
of the particles must satisfy the Doppler shifted cyclotron resonance condition,
![]() $kV=n\unicode[STIX]{x1D6FA}_{c}+\unicode[STIX]{x1D714}$
where
$kV=n\unicode[STIX]{x1D6FA}_{c}+\unicode[STIX]{x1D714}$
where
![]() $n$
is any integer. If an amount of energy
$n$
is any integer. If an amount of energy
![]() $\unicode[STIX]{x1D6FF}W$
is transferred from this wave to the particles, an amount of axial linear momentum
$\unicode[STIX]{x1D6FF}W$
is transferred from this wave to the particles, an amount of axial linear momentum
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{P}=m\unicode[STIX]{x1D6FF}V\boldsymbol{e}_{z}$
and an amount of angular momentum
$\unicode[STIX]{x1D6FF}\boldsymbol{P}=m\unicode[STIX]{x1D6FF}V\boldsymbol{e}_{z}$
and an amount of angular momentum
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{L}$
appear in the plasma,
$\unicode[STIX]{x1D6FF}\boldsymbol{L}$
appear in the plasma,
The plasma column will respond to this linear momentum deposition through a
![]() $z$
acceleration and to this angular momentum deposition through a rotation. The energy deposition profile
$z$
acceleration and to this angular momentum deposition through a rotation. The energy deposition profile
![]() $\unicode[STIX]{x1D6FF}W(r)$
, the collisional dissipation and the plasma column inertia tensor will determine the value of the angular velocity.
$\unicode[STIX]{x1D6FF}W(r)$
, the collisional dissipation and the plasma column inertia tensor will determine the value of the angular velocity.
The frozen in law with a transverse rotating magnetic field
![]() $\boldsymbol{b}(t)$
$\boldsymbol{b}(t)$
provides yet another original mechanism to spin a magnetised plasma column around the
![]() $z$
axis. The potential of such a configuration for mass separation will be presented and analysed here. Compared to current generation applications (see, for example, Fisch & Watanabe (Reference Fisch and Watanabe1982)) for which
$z$
axis. The potential of such a configuration for mass separation will be presented and analysed here. Compared to current generation applications (see, for example, Fisch & Watanabe (Reference Fisch and Watanabe1982)) for which
![]() $\unicode[STIX]{x1D6FA}$
is chosen such that
$\unicode[STIX]{x1D6FA}$
is chosen such that
![]() $\unicode[STIX]{x1D714}_{ci}<\unicode[STIX]{x1D6FA}<\unicode[STIX]{x1D714}_{ce}$
to drive an azimuthal electron current, the regime envisioned here is the one for which the entire plasma column (both ions and electrons) rotates, with zero or limited associated azimuthal current. The realisation of this new configuration for mass separation is not straightforward because a magnetised plasma column will always accept a radial static electric field
$\unicode[STIX]{x1D714}_{ci}<\unicode[STIX]{x1D6FA}<\unicode[STIX]{x1D714}_{ce}$
to drive an azimuthal electron current, the regime envisioned here is the one for which the entire plasma column (both ions and electrons) rotates, with zero or limited associated azimuthal current. The realisation of this new configuration for mass separation is not straightforward because a magnetised plasma column will always accept a radial static electric field
![]() $\boldsymbol{E}(x,y)$
strictly perpendicular to the static magnetic field
$\boldsymbol{E}(x,y)$
strictly perpendicular to the static magnetic field
![]() $\boldsymbol{B}_{0}$
or a plasma wave belonging to one of its dispersion branches, but it will always screen out a time varying magnetic field
$\boldsymbol{B}_{0}$
or a plasma wave belonging to one of its dispersion branches, but it will always screen out a time varying magnetic field
![]() $\boldsymbol{b}(t)$
. The screening length depends on collisionality and is in between the collisionless and diffusive limits
$\boldsymbol{b}(t)$
. The screening length depends on collisionality and is in between the collisionless and diffusive limits
![]() $\unicode[STIX]{x1D706}_{L}=c/\unicode[STIX]{x1D714}_{pe}$
and
$\unicode[STIX]{x1D706}_{L}=c/\unicode[STIX]{x1D714}_{pe}$
and
![]() $\unicode[STIX]{x1D706}_{K}=(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D714})^{-1/2}$
, which are respectively the London and Kelvin characteristic lengths. Here,
$\unicode[STIX]{x1D706}_{K}=(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D714})^{-1/2}$
, which are respectively the London and Kelvin characteristic lengths. Here,
![]() $\unicode[STIX]{x1D714}_{pe}$
is the plasma frequency,
$\unicode[STIX]{x1D714}_{pe}$
is the plasma frequency,
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $\unicode[STIX]{x1D707}_{0}$
is the vacuum permittivity,
$\unicode[STIX]{x1D707}_{0}$
is the vacuum permittivity,
![]() $\unicode[STIX]{x1D70E}$
is the plasma electric conductivity and
$\unicode[STIX]{x1D70E}$
is the plasma electric conductivity and
![]() $\unicode[STIX]{x1D714}$
is the wave frequency. Since the potential of this type of rotating plasma configuration for mass separation and nuclear waste management has never been explored, we will analyse the orbit at the single particle level, for various schemes, to evaluate the potential for mass separation.
$\unicode[STIX]{x1D714}$
is the wave frequency. Since the potential of this type of rotating plasma configuration for mass separation and nuclear waste management has never been explored, we will analyse the orbit at the single particle level, for various schemes, to evaluate the potential for mass separation.
To conclude this discussion, let us summarise, and illustrate in figure 2, an emerging classification of the physical processes aimed at rotating an axially magnetised plasma for the purpose of isotope and mass separations: (i) the
![]() $E$
cross
$E$
cross
![]() $B$
drift with a linear radial electric field (see figure 2
a), (ii) the use of the frozen in law with a rotating magnetic field
$B$
drift with a linear radial electric field (see figure 2
a), (ii) the use of the frozen in law with a rotating magnetic field
![]() $\boldsymbol{b}(t)$
(see figure 2
b), (iii) direct angular momentum absorption from a cylindrical plasma wave displaying a high content of angular momentum (see figure 2
c). In this paper, we will consider three basic types of rotating magnetic fields configurations leading to the same rotating magnetic field
$\boldsymbol{b}(t)$
(see figure 2
b), (iii) direct angular momentum absorption from a cylindrical plasma wave displaying a high content of angular momentum (see figure 2
c). In this paper, we will consider three basic types of rotating magnetic fields configurations leading to the same rotating magnetic field
![]() $\boldsymbol{b}(t)$
and focus the analysis on the stability of ion orbits for the purpose of isotope and mass separation. We will demonstrate that, for appropriate field strength and frequency, two neighbouring masses display completely different behaviours, one performing a stable multi-periodic oscillation near the
$\boldsymbol{b}(t)$
and focus the analysis on the stability of ion orbits for the purpose of isotope and mass separation. We will demonstrate that, for appropriate field strength and frequency, two neighbouring masses display completely different behaviours, one performing a stable multi-periodic oscillation near the
![]() $z$
axis and the other being expelled radially far from the
$z$
axis and the other being expelled radially far from the
![]() $z$
axis.
$z$
axis.
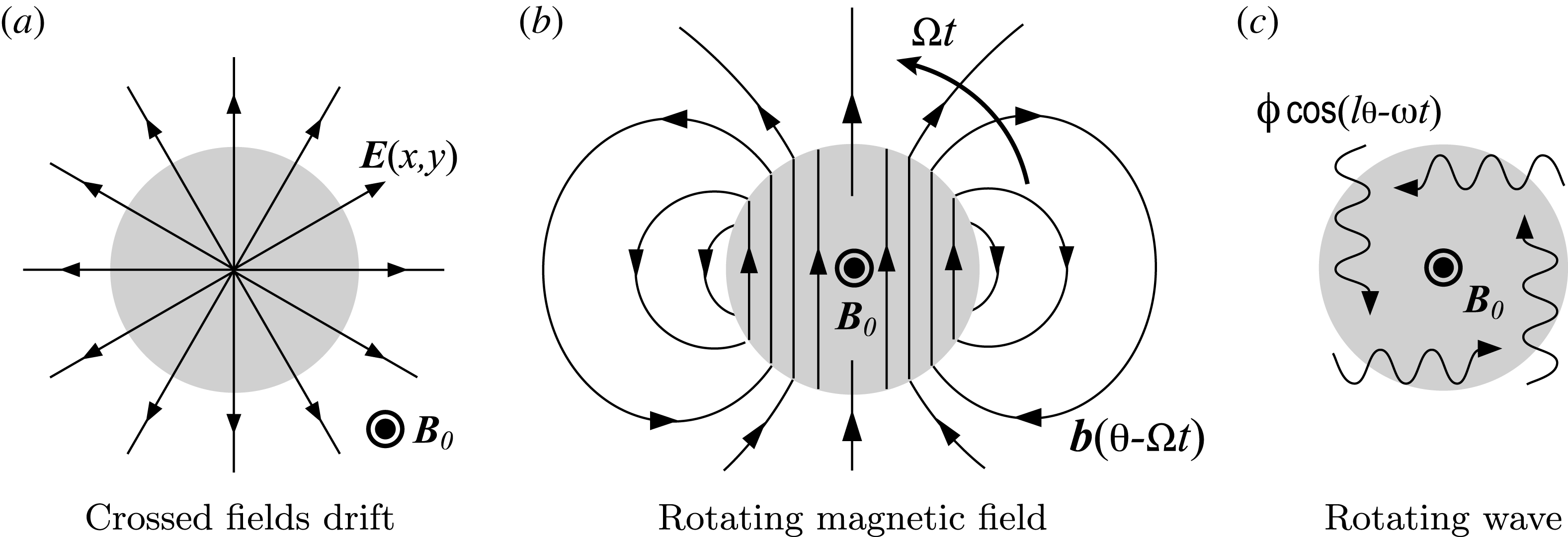
Figure 2. Angular momentum injection in an axially magnetised plasma column, (a)
![]() $\boldsymbol{E}(x,y)$
crossed fields drift, (b) rotating
$\boldsymbol{E}(x,y)$
crossed fields drift, (b) rotating
![]() $\boldsymbol{b}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FA}t)$
magnetic field, (c) rotating cylindrical
$\boldsymbol{b}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FA}t)$
magnetic field, (c) rotating cylindrical
![]() $\unicode[STIX]{x1D719}\cos (l\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)$
wave.
$\unicode[STIX]{x1D719}\cos (l\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)$
wave.
3 The three basic rotating fields configurations
Plasma interaction with rotating magnetic fields has been investigated in the past for the purpose of thermonuclear confinement (Soldatenkov Reference Soldatenkov1966; Hugrass & Jones Reference Hugrass and Jones1983), current generation (Fisch & Watanabe Reference Fisch and Watanabe1982) and plasma acceleration (Shinohara et al. Reference Shinohara, Nishida, Tanikawa, Hada, Funaki and Shamrai2014), but the potential for separation technologies has never been considered.
Consider a homogeneous magnetic field
![]() $\boldsymbol{b}(t)$
rotating at an angular velocity
$\boldsymbol{b}(t)$
rotating at an angular velocity
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
This magnetic field can be derived from any linear combination of the following vector potentials: (i)
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{a}$
or (ii)
$\boldsymbol{A}_{a}$
or (ii)
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{c}$
or (iii)
$\boldsymbol{A}_{c}$
or (iii)
![]() $\boldsymbol{A}_{c}$
and
$\boldsymbol{A}_{c}$
and
![]() $\boldsymbol{A}_{a}$
.
$\boldsymbol{A}_{a}$
.
To each of these three magnetic vector potentials corresponds a different electric field
![]() $\boldsymbol{E}=-\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t$
. For completeness, these electric fields read
$\boldsymbol{E}=-\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t$
. For completeness, these electric fields read
The rotating magnetic field configuration is thus not unique and must be viewed as a two-dimensional vector space, but the orbit in a given combination of
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{a}$
is not a simple combination of the orbit in
$\boldsymbol{A}_{a}$
is not a simple combination of the orbit in
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{a}$
. This is a simple consequence, as it will become clear, of the fact that the determinant of the sum of two matrices is different from the sum of their determinants. It is worth noting that most of the plasma literature on rotating magnetic fields for thermonuclear confinement or current generation is restricted to
$\boldsymbol{A}_{a}$
. This is a simple consequence, as it will become clear, of the fact that the determinant of the sum of two matrices is different from the sum of their determinants. It is worth noting that most of the plasma literature on rotating magnetic fields for thermonuclear confinement or current generation is restricted to
![]() $\boldsymbol{A}_{s}$
, while the simplest configuration is arguably the one described by
$\boldsymbol{A}_{s}$
, while the simplest configuration is arguably the one described by
![]() $\boldsymbol{A}_{c}$
, which corresponds to two phased coils. These three vector potentials,
$\boldsymbol{A}_{c}$
, which corresponds to two phased coils. These three vector potentials,
![]() $\boldsymbol{A}_{s}$
,
$\boldsymbol{A}_{s}$
,
![]() $\boldsymbol{A}_{a}$
and
$\boldsymbol{A}_{a}$
and
![]() $\boldsymbol{A}_{c}$
, cannot be reduced to the same function through a gauge transformation and these different expressions are associated with different boundary conditions, that is to say with different external and plasma currents.
$\boldsymbol{A}_{c}$
, cannot be reduced to the same function through a gauge transformation and these different expressions are associated with different boundary conditions, that is to say with different external and plasma currents.
![]() $\boldsymbol{A}_{s}$
is the most popular expression and can be produced with an axial surface current on a cylinder aligned along
$\boldsymbol{A}_{s}$
is the most popular expression and can be produced with an axial surface current on a cylinder aligned along
![]() $z$
. The current amplitudes are proportional to
$z$
. The current amplitudes are proportional to
![]() $\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FA}t)$
where
$\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FA}t)$
where
![]() $\unicode[STIX]{x1D703}$
is the polar angle around the
$\unicode[STIX]{x1D703}$
is the polar angle around the
![]() $z$
axis.
$z$
axis.
![]() $\boldsymbol{A}_{a}$
is the vector potential describing the vicinity of the electric node of an
$\boldsymbol{A}_{a}$
is the vector potential describing the vicinity of the electric node of an
![]() $l=1$
standing surface Alfvén wave along a cylindrical plasma column, where
$l=1$
standing surface Alfvén wave along a cylindrical plasma column, where
![]() $l$
is the Fourier mode number associated with
$l$
is the Fourier mode number associated with
![]() $\exp jl\unicode[STIX]{x1D703}$
. Finally,
$\exp jl\unicode[STIX]{x1D703}$
. Finally,
![]() $\boldsymbol{A}_{c}$
is the vector potential describing the classical synchronous rotating field generated by two coils whose axes are oriented along
$\boldsymbol{A}_{c}$
is the vector potential describing the classical synchronous rotating field generated by two coils whose axes are oriented along
![]() $x$
and
$x$
and
![]() $y$
and whose currents are out of phase by an angle
$y$
and whose currents are out of phase by an angle
![]() $\unicode[STIX]{x03C0}/2$
.
$\unicode[STIX]{x03C0}/2$
.
These three field configurations
![]() $\boldsymbol{A}_{s}$
,
$\boldsymbol{A}_{s}$
,
![]() $\boldsymbol{A}_{a}$
and
$\boldsymbol{A}_{a}$
and
![]() $\boldsymbol{A}_{c}$
provide a convenient and tractable theoretical framework to illustrate mass separation effects in rotating magnetic fields. However, these configurations only describe an idealised plasma. Practically, various effects could limit the range of plasma parameters and device dimensions for which the simple picture derived in this paper will hold true. Although the full study of these practical effects is beyond the scope of this paper, possible challenges towards the implementation of these three configurations are briefly discussed for completeness in the remaining of this section.
$\boldsymbol{A}_{c}$
provide a convenient and tractable theoretical framework to illustrate mass separation effects in rotating magnetic fields. However, these configurations only describe an idealised plasma. Practically, various effects could limit the range of plasma parameters and device dimensions for which the simple picture derived in this paper will hold true. Although the full study of these practical effects is beyond the scope of this paper, possible challenges towards the implementation of these three configurations are briefly discussed for completeness in the remaining of this section.
First,
![]() $\boldsymbol{A}_{a}$
appears a priori to be the best candidate since it is a normal mode of a plasma mixture. As a result, it does not suffer from plasma screening. However, the main limitation of this configuration stems from the fact that
$\boldsymbol{A}_{a}$
appears a priori to be the best candidate since it is a normal mode of a plasma mixture. As a result, it does not suffer from plasma screening. However, the main limitation of this configuration stems from the fact that
![]() $\boldsymbol{A}_{a}$
only describes the local field of a standing wave in the vicinity of an electric node of this wave. The full structure of the vector potential of a surface Alfvén wave, with wave vector
$\boldsymbol{A}_{a}$
only describes the local field of a standing wave in the vicinity of an electric node of this wave. The full structure of the vector potential of a surface Alfvén wave, with wave vector
![]() $k_{A}$
along a plasma cylinder, is given by
$k_{A}$
along a plasma cylinder, is given by
![]() $\boldsymbol{A}_{a}^{\ast }$
,
$\boldsymbol{A}_{a}^{\ast }$
,
A full analysis of ion orbit stability would thus require considering
![]() $\boldsymbol{A}_{a}^{\ast }$
in lieu of the idealised vector potential
$\boldsymbol{A}_{a}^{\ast }$
in lieu of the idealised vector potential
![]() $\boldsymbol{A}_{a}$
used in this study.
$\boldsymbol{A}_{a}$
used in this study.
Then,
![]() $\boldsymbol{A}_{c}$
is to be considered because of the simplicity of the forcing currents configuration. However, since it is not a normal mode of the plasma, penetration of the rotating field within the plasma column will depend on plasma parameters, and
$\boldsymbol{A}_{c}$
is to be considered because of the simplicity of the forcing currents configuration. However, since it is not a normal mode of the plasma, penetration of the rotating field within the plasma column will depend on plasma parameters, and
![]() $\boldsymbol{A}_{c}$
only describes the asymptotic limit corresponding to instantaneous field penetration. Field penetration for similar coil configurations has been shown to be a strong function of two dimensionless parameters (Milroy Reference Milroy1999): (i) the plasma column radius
$\boldsymbol{A}_{c}$
only describes the asymptotic limit corresponding to instantaneous field penetration. Field penetration for similar coil configurations has been shown to be a strong function of two dimensionless parameters (Milroy Reference Milroy1999): (i) the plasma column radius
![]() $a$
normalised by the Kelvin characteristic length
$a$
normalised by the Kelvin characteristic length
![]() $\unicode[STIX]{x1D706}_{K}$
and (ii) the electron cyclotron frequency – computed for the rotating magnetic field – normalised by the electron–ion collision frequency. For large devices (
$\unicode[STIX]{x1D706}_{K}$
and (ii) the electron cyclotron frequency – computed for the rotating magnetic field – normalised by the electron–ion collision frequency. For large devices (
![]() $a\gg \unicode[STIX]{x1D706}_{K}$
), electron–ion collisionality has to be sufficiently small to ensure fast field penetration. For mass separation purposes, this would translate into a trade-off between plasma density, plasma dimensions and magnetic field intensity.
$a\gg \unicode[STIX]{x1D706}_{K}$
), electron–ion collisionality has to be sufficiently small to ensure fast field penetration. For mass separation purposes, this would translate into a trade-off between plasma density, plasma dimensions and magnetic field intensity.
Similarly,
![]() $\boldsymbol{A}_{s}$
is not a normal mode of the plasma column. In this configuration, electron screening is expected to take place because the inductive electric field
$\boldsymbol{A}_{s}$
is not a normal mode of the plasma column. In this configuration, electron screening is expected to take place because the inductive electric field
![]() $-\unicode[STIX]{x2202}\boldsymbol{A}_{s}/\unicode[STIX]{x2202}t$
is along the static field lines. For collisionless plasmas, one can solve Maxwell–Faraday and Maxwell–Ampere equations taking into account the response of the plasma electrons (mass
$-\unicode[STIX]{x2202}\boldsymbol{A}_{s}/\unicode[STIX]{x2202}t$
is along the static field lines. For collisionless plasmas, one can solve Maxwell–Faraday and Maxwell–Ampere equations taking into account the response of the plasma electrons (mass
![]() $m_{e}$
, charge
$m_{e}$
, charge
![]() $q_{e}$
) along
$q_{e}$
) along
![]() $z$
to find the screened vector potential
$z$
to find the screened vector potential
![]() $\boldsymbol{A}_{s}^{\ast }$
inside the plasma,
$\boldsymbol{A}_{s}^{\ast }$
inside the plasma,
Here
![]() $k_{p}^{-1}=\unicode[STIX]{x1D706}_{p}$
is the London length, or inertial skin depth, defined as
$k_{p}^{-1}=\unicode[STIX]{x1D706}_{p}$
is the London length, or inertial skin depth, defined as
![]() $\unicode[STIX]{x1D706}_{p}^{2}=m_{e}c^{2}\unicode[STIX]{x1D700}_{0}/nq_{e}^{2}$
(
$\unicode[STIX]{x1D706}_{p}^{2}=m_{e}c^{2}\unicode[STIX]{x1D700}_{0}/nq_{e}^{2}$
(
![]() $c$
is the velocity of light and
$c$
is the velocity of light and
![]() $\unicode[STIX]{x1D700}_{0}$
the permittivity of vacuum). For plasma density
$\unicode[STIX]{x1D700}_{0}$
the permittivity of vacuum). For plasma density
![]() $n\sim 10^{12}~\text{cm}^{-3}$
, the inertial skin depth is of the order of a centimetre. The rotating magnetic field will display a homogeneous structure near the
$n\sim 10^{12}~\text{cm}^{-3}$
, the inertial skin depth is of the order of a centimetre. The rotating magnetic field will display a homogeneous structure near the
![]() $z$
axis, and an inhomogeneous one near the edge since
$z$
axis, and an inhomogeneous one near the edge since
![]() $\cosh (x/\unicode[STIX]{x1D706}_{p})=1+x^{2}/2{\unicode[STIX]{x1D706}_{p}}^{2}+O(x^{4}/{\unicode[STIX]{x1D706}_{p}}^{4})$
and
$\cosh (x/\unicode[STIX]{x1D706}_{p})=1+x^{2}/2{\unicode[STIX]{x1D706}_{p}}^{2}+O(x^{4}/{\unicode[STIX]{x1D706}_{p}}^{4})$
and
![]() $\cosh (y/\unicode[STIX]{x1D706}_{p})=1+y^{2}/2{\unicode[STIX]{x1D706}_{p}}^{2}+O(y^{4}/{\unicode[STIX]{x1D706}_{p}}^{4})$
. As a result, the effect of plasma screening on the orbit stability will mainly be important at the edge. Here again, a full analysis of ion orbit stability would require using
$\cosh (y/\unicode[STIX]{x1D706}_{p})=1+y^{2}/2{\unicode[STIX]{x1D706}_{p}}^{2}+O(y^{4}/{\unicode[STIX]{x1D706}_{p}}^{4})$
. As a result, the effect of plasma screening on the orbit stability will mainly be important at the edge. Here again, a full analysis of ion orbit stability would require using
![]() $\boldsymbol{A}_{s}^{\ast }$
rather than the idealised vector potential
$\boldsymbol{A}_{s}^{\ast }$
rather than the idealised vector potential
![]() $\boldsymbol{A}_{s}$
.
$\boldsymbol{A}_{s}$
.
Let us conclude this discussion of possible limitations with a practical observation. For minor actinides separation (Gueroult & Fisch Reference Gueroult and Fisch2014), if we choose to expel the heavy part, the core will be cleaned up and the edge will be a mix of light and heavy ions. However, the study of the stability diagram, taking into account the nonlinear coupling terms associated with electron screening (
![]() $\boldsymbol{A}_{s}^{\ast }$
in lieu of
$\boldsymbol{A}_{s}^{\ast }$
in lieu of
![]() $\boldsymbol{A}_{s}$
), will make it possible to modify the separation strategy using well-identified nonlinear stability boundaries. This identification is left for a future study, and so is the identification of the optimum combination of
$\boldsymbol{A}_{s}$
), will make it possible to modify the separation strategy using well-identified nonlinear stability boundaries. This identification is left for a future study, and so is the identification of the optimum combination of
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{c}$
, both from the standpoint of orbits and from the standpoint of field penetration in the plasma. However, we note in passing that a
$\boldsymbol{A}_{c}$
, both from the standpoint of orbits and from the standpoint of field penetration in the plasma. However, we note in passing that a
![]() $1/1$
combination of these vectors gives
$1/1$
combination of these vectors gives
![]() $\boldsymbol{A}_{a}$
, which is a natural mode of the plasma. As a result, there is clearly a synergy for penetration between these vacuum modes.
$\boldsymbol{A}_{a}$
, which is a natural mode of the plasma. As a result, there is clearly a synergy for penetration between these vacuum modes.
In the following three sections, in order to address the open problem of mass separation with rotating magnetic fields, we will compare ion orbits in the combination of an axial static magnetic field
![]() $\boldsymbol{B}_{0}$
and a transverse rotating magnetic field
$\boldsymbol{B}_{0}$
and a transverse rotating magnetic field
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{A}$
,
$\unicode[STIX]{x1D735}\times \boldsymbol{A}$
,
for the ideal potential vectors
![]() $\boldsymbol{A}=\boldsymbol{A}_{a}$
(§ 4),
$\boldsymbol{A}=\boldsymbol{A}_{a}$
(§ 4),
![]() $\boldsymbol{A}=\boldsymbol{A}_{c}$
(§ 5) and finally
$\boldsymbol{A}=\boldsymbol{A}_{c}$
(§ 5) and finally
![]() $\boldsymbol{A}=\boldsymbol{A}_{s}$
(§ 6). To analyse the orbits we will consider Newton’s equations for an ion with mass
$\boldsymbol{A}=\boldsymbol{A}_{s}$
(§ 6). To analyse the orbits we will consider Newton’s equations for an ion with mass
![]() $m$
, charge
$m$
, charge
![]() $q$
and velocity
$q$
and velocity
![]() $\boldsymbol{V}$
,
$\boldsymbol{V}$
,
and calculate the stability diagram in the (
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
,
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
,
![]() $\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
) space as
$\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
) space as
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
![]() $\unicode[STIX]{x1D6FA}_{c}$
and
$\unicode[STIX]{x1D6FA}_{c}$
and
![]() $\unicode[STIX]{x1D714}_{c}$
are the three control parameters of these innovative separation schemes. In the last sections, on the basis of these stability diagrams, we will consider the potential for mass separation. To simplify the forthcoming studies, we define the control parameters
$\unicode[STIX]{x1D714}_{c}$
are the three control parameters of these innovative separation schemes. In the last sections, on the basis of these stability diagrams, we will consider the potential for mass separation. To simplify the forthcoming studies, we define the control parameters
![]() $u$
and
$u$
and
![]() $v$
and the normalised eigenfrequency
$v$
and the normalised eigenfrequency
![]() $w$
as follows,
$w$
as follows,
where
![]() $\unicode[STIX]{x1D714}$
, through a factor
$\unicode[STIX]{x1D714}$
, through a factor
![]() $\exp j\unicode[STIX]{x1D714}t$
, will be the generic pulsation of the ion periodic motion. The position of
$\exp j\unicode[STIX]{x1D714}t$
, will be the generic pulsation of the ion periodic motion. The position of
![]() $w$
in the complex plane, as a function of (
$w$
in the complex plane, as a function of (
![]() $u$
,
$u$
,
![]() $v$
), will decide of the stability, or the instability, of the orbit.
$v$
), will decide of the stability, or the instability, of the orbit.
4 Orbital stability with a surface Alfvén standing wave
Consider a standing low-frequency wave along a magnetised plasma column belonging to the Alfvénic branch of the dispersion relation, the vector potential for an
![]() $l=1$
surface wave is given by
$l=1$
surface wave is given by
![]() $\boldsymbol{A}_{a}$
in the vicinity of an electric node. Then, let us write down the dynamics of an ion, with mass
$\boldsymbol{A}_{a}$
in the vicinity of an electric node. Then, let us write down the dynamics of an ion, with mass
![]() $m$
and charge
$m$
and charge
![]() $q$
, on a Cartesian set of axis where
$q$
, on a Cartesian set of axis where
![]() $z$
is oriented along the static magnetic field
$z$
is oriented along the static magnetic field
![]() $\boldsymbol{B}_{0}$
:
$\boldsymbol{B}_{0}$
:
We recognise a total time derivative in the first and second equation, so the order of the first two equations can be lowered. We introduce the fixed guiding centres
![]() $(x_{g},y_{g})$
of the transverses oscillations and rewrite these two equations
$(x_{g},y_{g})$
of the transverses oscillations and rewrite these two equations
We move from the laboratory frame
![]() $(x,y)$
to a rotating frame
$(x,y)$
to a rotating frame
![]() $(X,Y)$
through the transformation
$(X,Y)$
through the transformation
and we get the following set of relations describing the dynamics in this rotating frame
A normal mode analysis can be performed as these equations are linear and the coefficients are constant. Thus, we define the amplitudes
![]() $(\boldsymbol{X}_{0},Y_{0},\boldsymbol{z}_{0})$
of the multi-periodic motion,
$(\boldsymbol{X}_{0},Y_{0},\boldsymbol{z}_{0})$
of the multi-periodic motion,
Introducing the control parameters
![]() $(u,v)$
and the normalised eigenfrequency
$(u,v)$
and the normalised eigenfrequency
![]() $w=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}$
, the characteristic equation, resulting from the nullity of the characteristic determinant, displays the simple form
$w=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}$
, the characteristic equation, resulting from the nullity of the characteristic determinant, displays the simple form
For stability, the discriminant
![]() $D_{2}(u,v)$
of the associated algebraic second-order equation with unknown
$D_{2}(u,v)$
of the associated algebraic second-order equation with unknown
![]() $w^{2}$
must be positive and the two real roots must be positive and different. Two numbers are strictly positive if and only if their sum and product are strictly positive, so the stability condition,
$w^{2}$
must be positive and the two real roots must be positive and different. Two numbers are strictly positive if and only if their sum and product are strictly positive, so the stability condition,
![]() $\unicode[STIX]{x1D714}=w\unicode[STIX]{x1D6FA}_{c}$
real, in the
$\unicode[STIX]{x1D714}=w\unicode[STIX]{x1D6FA}_{c}$
real, in the
![]() $(u,v)$
plane reduces to
$(u,v)$
plane reduces to
The shaded regions in figure 3 are associated with unstable orbits and the contour lines indicate the value of
![]() $D_{2}(u,v)$
which is proportional to the square of the growth rate of the exponential instability of the unconfined orbits.
$D_{2}(u,v)$
which is proportional to the square of the growth rate of the exponential instability of the unconfined orbits.

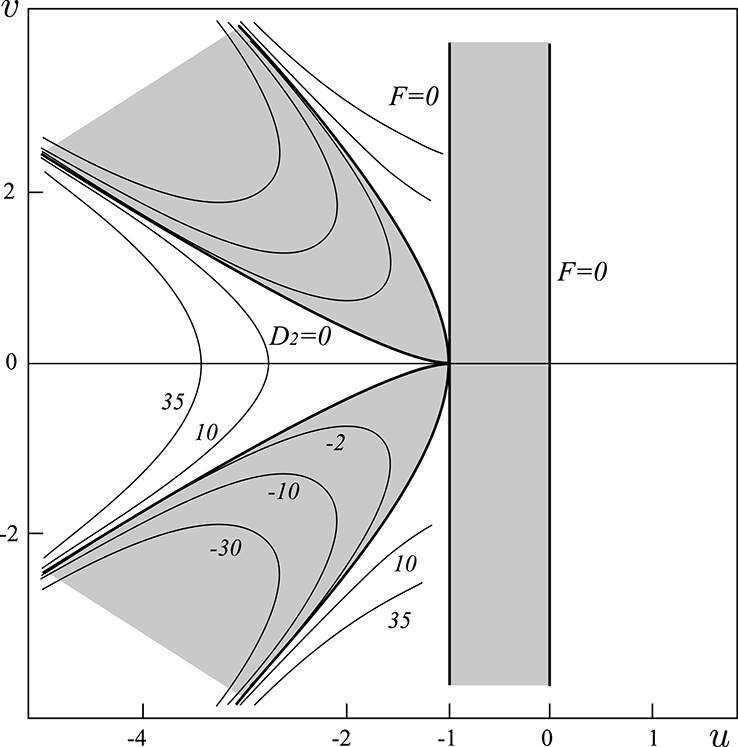
Figure 3. Stability regions,
![]() $D_{2}>0$
,
$D_{2}>0$
,
![]() $F>0$
, in the
$F>0$
, in the
![]() $u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
and
$u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
and
![]() $v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
plane, for ion orbits in a surface Alfvén standing wave, the contour lines are labelled with the value of
$v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
plane, for ion orbits in a surface Alfvén standing wave, the contour lines are labelled with the value of
![]() $D_{2}(u,v)$
.
$D_{2}(u,v)$
.
5 Orbital stability with dephased orthogonal coils
Let us consider two solenoidal coils whose axes are oriented along
![]() $x$
and
$x$
and
![]() $y$
, in the vicinity of the origin
$y$
, in the vicinity of the origin
![]() $x=y=z=0$
, the superposition of their vector potentials is given by
$x=y=z=0$
, the superposition of their vector potentials is given by
![]() $\boldsymbol{A}_{c}$
. The dynamics of an ion on a Cartesian set of axis, where
$\boldsymbol{A}_{c}$
. The dynamics of an ion on a Cartesian set of axis, where
![]() $z$
is oriented along the static magnetic field
$z$
is oriented along the static magnetic field
![]() $\boldsymbol{B}_{0}$
, is given by the solutions of
$\boldsymbol{B}_{0}$
, is given by the solutions of
Then we move from the laboratory frame
![]() $(x,y)$
to a rotating frame
$(x,y)$
to a rotating frame
![]() $(X,Y)$
through the transformation
$(X,Y)$
through the transformation
in order to obtain the following set of equations
The
![]() $\unicode[STIX]{x1D6FA}^{2}$
factors are associated with the centrifugal force and the
$\unicode[STIX]{x1D6FA}^{2}$
factors are associated with the centrifugal force and the
![]() $2\unicode[STIX]{x1D6FA}$
terms with the Coriolis one. A classical normal mode analysis, with the amplitudes
$2\unicode[STIX]{x1D6FA}$
terms with the Coriolis one. A classical normal mode analysis, with the amplitudes
![]() $(\boldsymbol{X}_{0},\boldsymbol{Y}_{0},\boldsymbol{z}_{0})$
and the eigenfrequency
$(\boldsymbol{X}_{0},\boldsymbol{Y}_{0},\boldsymbol{z}_{0})$
and the eigenfrequency
![]() $\unicode[STIX]{x1D714}=w\unicode[STIX]{x1D6FA}_{c}$
,
$\unicode[STIX]{x1D714}=w\unicode[STIX]{x1D6FA}_{c}$
,
leads to the characteristic equation for the normalised eigenfrequency
![]() $w=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}$
$w=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}$
For stability, both the discriminant
![]() $D_{3}(u,v)$
of the associated algebraic third-order equation with unknown
$D_{3}(u,v)$
of the associated algebraic third-order equation with unknown
![]() $w^{2}$
and the three real roots must be positive. Three real numbers are strictly positive if, and only if, their sum, product and sum of double products are strictly positive, this reduces the stability condition,
$w^{2}$
and the three real roots must be positive. Three real numbers are strictly positive if, and only if, their sum, product and sum of double products are strictly positive, this reduces the stability condition,
![]() $\unicode[STIX]{x1D714}$
real, to the relations:
$\unicode[STIX]{x1D714}$
real, to the relations:
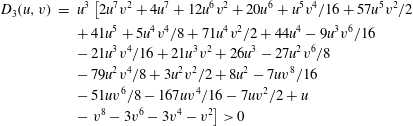 $$\begin{eqnarray}\displaystyle D_{3}(u,v) & = & \displaystyle u^{3}\left[2u^{7}v^{2}+4u^{7}+12u^{6}v^{2}+20u^{6}+u^{5}v^{4}/16+57u^{5}v^{2}/2\right.\nonumber\\ \displaystyle & & \displaystyle +\,41u^{5}+5u^{4}v^{4}/8+71u^{4}v^{2}/2+44u^{4}-9u^{3}v^{6}/16\nonumber\\ \displaystyle & & \displaystyle -\,21u^{3}v^{4}/16+21u^{3}v^{2}+26u^{3}-27u^{2}v^{6}/8\nonumber\\ \displaystyle & & \displaystyle -\,79u^{2}v^{4}/8+3u^{2}v^{2}/2+8u^{2}-7uv^{8}/16\nonumber\\ \displaystyle & & \displaystyle -\,51uv^{6}/8-167uv^{4}/16-7uv^{2}/2+u\nonumber\\ \displaystyle & & \displaystyle -\left.v^{8}-3v^{6}-3v^{4}-v^{2}\right]>0\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{3}(u,v) & = & \displaystyle u^{3}\left[2u^{7}v^{2}+4u^{7}+12u^{6}v^{2}+20u^{6}+u^{5}v^{4}/16+57u^{5}v^{2}/2\right.\nonumber\\ \displaystyle & & \displaystyle +\,41u^{5}+5u^{4}v^{4}/8+71u^{4}v^{2}/2+44u^{4}-9u^{3}v^{6}/16\nonumber\\ \displaystyle & & \displaystyle -\,21u^{3}v^{4}/16+21u^{3}v^{2}+26u^{3}-27u^{2}v^{6}/8\nonumber\\ \displaystyle & & \displaystyle -\,79u^{2}v^{4}/8+3u^{2}v^{2}/2+8u^{2}-7uv^{8}/16\nonumber\\ \displaystyle & & \displaystyle -\,51uv^{6}/8-167uv^{4}/16-7uv^{2}/2+u\nonumber\\ \displaystyle & & \displaystyle -\left.v^{8}-3v^{6}-3v^{4}-v^{2}\right]>0\end{eqnarray}$$
The shaded regions displayed in figure 4 are associated with unstable orbits in the (
![]() $u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
,
$u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
,
![]() $v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
) plane, the ion orbits remain confined and periodic outside these regions.
$v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
) plane, the ion orbits remain confined and periodic outside these regions.

Figure 4. Stability regions,
![]() $D_{3}>0$
,
$D_{3}>0$
,
![]() $F>0$
, in the
$F>0$
, in the
![]() $u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
and
$u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
and
![]() $v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
plane, for ion orbits in a rotating field generated by dephased orthogonal coils.
$v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
plane, for ion orbits in a rotating field generated by dephased orthogonal coils.
6 Orbital stability with squirrel cage axial currents
In the previous configuration, we have considered surface currents on two cylinders with axes perpendicular to the
![]() $z$
axis. Here, we consider axial surface currents on a cylinder whose axis is along the
$z$
axis. Here, we consider axial surface currents on a cylinder whose axis is along the
![]() $z$
axis. These squirrel cage axial currents are along
$z$
axis. These squirrel cage axial currents are along
![]() $z$
and distributed according to the relation
$z$
and distributed according to the relation
![]() $\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FA}t)$
so that the resulting vector potential is given by
$\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FA}t)$
so that the resulting vector potential is given by
![]() $\boldsymbol{A}_{s}$
. The dynamics of an ion is described by
$\boldsymbol{A}_{s}$
. The dynamics of an ion is described by
Moving from the laboratory frame
![]() $(x,y)$
to a rotating frame
$(x,y)$
to a rotating frame
![]() $(X,Y)$
,
$(X,Y)$
,
we end up with the set of equations
The
![]() $\unicode[STIX]{x1D6FA}^{2}$
factors are associated with the centrifugal force and the
$\unicode[STIX]{x1D6FA}^{2}$
factors are associated with the centrifugal force and the
![]() $2\unicode[STIX]{x1D6FA}$
terms with the Coriolis one. Introducing
$2\unicode[STIX]{x1D6FA}$
terms with the Coriolis one. Introducing
![]() $Y_{g}$
, a constant of integration, a normal mode analysis with the eigenvectors
$Y_{g}$
, a constant of integration, a normal mode analysis with the eigenvectors
![]() $(\boldsymbol{X}_{0},\boldsymbol{Y}_{0},\boldsymbol{z}_{0})$
,
$(\boldsymbol{X}_{0},\boldsymbol{Y}_{0},\boldsymbol{z}_{0})$
,
leads to the characteristic equation for the normalised eigenfrequency
![]() $w=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}$
,
$w=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}$
,
For stability, both the discriminant of the associated algebraic second-order equation with unknown
![]() $w^{2}$
and the two real roots must be positive. This discriminant is given by
$w^{2}$
and the two real roots must be positive. This discriminant is given by
![]() $(1+2u)^{2}(1+2v^{2})+v^{4}$
and is obviously always positive, so the stability condition (two numbers are strictly positive if, and only if, their sum and product are strictly positive) reduces to
$(1+2u)^{2}(1+2v^{2})+v^{4}$
and is obviously always positive, so the stability condition (two numbers are strictly positive if, and only if, their sum and product are strictly positive) reduces to
![]() $HF>0$
, where
$HF>0$
, where
![]() $H=0$
is an hyperbola and
$H=0$
is an hyperbola and
![]() $F=0$
is a set of two vertical lines
$F=0$
is a set of two vertical lines
The eigenfrequencies
![]() $\unicode[STIX]{x1D714}$
of the periodic stables orbits (
$\unicode[STIX]{x1D714}$
of the periodic stables orbits (
![]() $HF>0$
) and of the growth rate
$HF>0$
) and of the growth rate
![]() $\unicode[STIX]{x1D6FE}$
of the unstable escaping orbits (
$\unicode[STIX]{x1D6FE}$
of the unstable escaping orbits (
![]() $HF<0$
, shaded regions in figure 5), are given by the expressions:
$HF<0$
, shaded regions in figure 5), are given by the expressions:
In figure 5 the contour lines indicate the value of
![]() $HF$
which is proportional, for the escaping orbits, to the growth rate of the exponential instability.
$HF$
which is proportional, for the escaping orbits, to the growth rate of the exponential instability.

Figure 5. Stability regions,
![]() $HF>0$
, in the
$HF>0$
, in the
![]() $u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
and
$u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{c}$
and
![]() $v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
plane, for ion orbits in a rotating field generated by squirrel cage axial currents; the contour lines are labelled with the value of
$v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
plane, for ion orbits in a rotating field generated by squirrel cage axial currents; the contour lines are labelled with the value of
![]() $HF$
.
$HF$
.
7 Principles of isotope separation with a rotating magnetic field
On the basis of figures 3, 4 and 5, we reach the important conclusion that the stability diagram of ion orbits in the (
![]() $u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}$
,
$u=\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}$
,
![]() $v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
) plane is very sensitive to the currents driving the fields for the very same magnetic field configuration
$v=\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}_{c}$
) plane is very sensitive to the currents driving the fields for the very same magnetic field configuration
![]() $\unicode[STIX]{x1D714}_{c}\cos \unicode[STIX]{x1D6FA}t~\boldsymbol{e}_{x}$
+
$\unicode[STIX]{x1D714}_{c}\cos \unicode[STIX]{x1D6FA}t~\boldsymbol{e}_{x}$
+
![]() $\unicode[STIX]{x1D714}_{c}\sin \unicode[STIX]{x1D6FA}t~\boldsymbol{e}_{y}$
+
$\unicode[STIX]{x1D714}_{c}\sin \unicode[STIX]{x1D6FA}t~\boldsymbol{e}_{y}$
+
![]() $\unicode[STIX]{x1D6FA}_{c}~\boldsymbol{e}_{z}$
. This sensitivity is due to the fact that, even if a superposition principle can be established in the rotating frame, the determinant of the sum of two matrices is different from the sum of their determinants, so the characteristic equation is expected to be very different for every new linear combination of the three basic potentials
$\unicode[STIX]{x1D6FA}_{c}~\boldsymbol{e}_{z}$
. This sensitivity is due to the fact that, even if a superposition principle can be established in the rotating frame, the determinant of the sum of two matrices is different from the sum of their determinants, so the characteristic equation is expected to be very different for every new linear combination of the three basic potentials
![]() $\boldsymbol{A}_{s}$
,
$\boldsymbol{A}_{s}$
,
![]() $\boldsymbol{A}_{a}$
and
$\boldsymbol{A}_{a}$
and
![]() $\boldsymbol{A}_{c}$
, despite an interaction with the same rotating magnetic field.
$\boldsymbol{A}_{c}$
, despite an interaction with the same rotating magnetic field.
This sensitivity to the electric part of the field offers opportunities to design dedicated configurations, but here, rather than addressing this optimisation issue, we will focus the study on the most simple diagram associated with squirrel cage currents along
![]() $z$
, analysed and described in § 6.
$z$
, analysed and described in § 6.
The case
![]() $\boldsymbol{A}_{s}$
has been investigated within the context of thermonuclear confinement and current generation but not for mass separation. In these studies, other normalised control parameters have been defined, different from
$\boldsymbol{A}_{s}$
has been investigated within the context of thermonuclear confinement and current generation but not for mass separation. In these studies, other normalised control parameters have been defined, different from
![]() $(u,v)$
, and the emphasis was put on confined orbits. Here, for the purpose of studying the potential for mass separation, the choice of
$(u,v)$
, and the emphasis was put on confined orbits. Here, for the purpose of studying the potential for mass separation, the choice of
![]() $u$
and
$u$
and
![]() $v$
is not only new, but particularly appropriate because
$v$
is not only new, but particularly appropriate because
![]() $v$
is a structural parameter of the separator independent of the ion mass,
$v$
is a structural parameter of the separator independent of the ion mass,
and
![]() $u$
is a linear function of the mass. If we define the reference mass
$u$
is a linear function of the mass. If we define the reference mass
![]() $m^{\ast }$
of the separator,
$m^{\ast }$
of the separator,
![]() $m^{\ast }=qB_{0}$
/
$m^{\ast }=qB_{0}$
/
![]() $\unicode[STIX]{x1D6FA}$
, then:
$\unicode[STIX]{x1D6FA}$
, then:
The
![]() $(u,v)$
plane can thus be viewed as an
$(u,v)$
plane can thus be viewed as an
![]() $(m,b)$
plane. It is straightforward to understand that the various masses
$(m,b)$
plane. It is straightforward to understand that the various masses
![]() $m$
of an ion mixture, with lower and upper bounds
$m$
of an ion mixture, with lower and upper bounds
![]() $m_{1}<m_{2}$
, will be distributed along a horizontal segment
$m_{1}<m_{2}$
, will be distributed along a horizontal segment
![]() $v=b/B_{0}$
in between
$v=b/B_{0}$
in between
On the basis of this picture, illustrated in figure 6, the squirrel cage currents configuration
![]() $\boldsymbol{A}_{s}$
offers two different strategies for mass separation: (i) we can confine the heavy part of the mass spectrum and expel the light one (figure 6
b) or (ii) confine the light part and expel the heavy one (figure 6
a). These two choices are associated with the fact that we have two choices for rotation
$\boldsymbol{A}_{s}$
offers two different strategies for mass separation: (i) we can confine the heavy part of the mass spectrum and expel the light one (figure 6
b) or (ii) confine the light part and expel the heavy one (figure 6
a). These two choices are associated with the fact that we have two choices for rotation
![]() $\pm \unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
for a given static field
$\pm \unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
for a given static field
![]() $B_{0}\boldsymbol{e}_{z}$
, or two choices for the static field
$B_{0}\boldsymbol{e}_{z}$
, or two choices for the static field
![]() $\pm B_{0}\boldsymbol{e}_{z}$
for a given angular velocity
$\pm B_{0}\boldsymbol{e}_{z}$
for a given angular velocity
![]() $\unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
. For the case (b), in order to understand the separation process, the reference
$\unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
. For the case (b), in order to understand the separation process, the reference
![]() $m^{\ast }$
is to be supplemented by
$m^{\ast }$
is to be supplemented by
as the curved boundary of the instability zone is given by the relation
![]() $m=m^{\ast \ast }(b)$
. This principle of mass and isotope separation is the same for all the stability boundaries of figures 3–5 identified during the studies of the three basic cases
$m=m^{\ast \ast }(b)$
. This principle of mass and isotope separation is the same for all the stability boundaries of figures 3–5 identified during the studies of the three basic cases
![]() $\boldsymbol{A}_{s}$
,
$\boldsymbol{A}_{s}$
,
![]() $\boldsymbol{A}_{a}$
and
$\boldsymbol{A}_{a}$
and
![]() $\boldsymbol{A}_{c}$
.
$\boldsymbol{A}_{c}$
.

Figure 6. Principles of rotating fields mass separation for a mass spectrum
![]() $m_{1}<m<m_{2}$
: (a) the light part is confined and the heavy one expelled or (b) the heavy part of the spectrum is confined and the light one expelled.
$m_{1}<m<m_{2}$
: (a) the light part is confined and the heavy one expelled or (b) the heavy part of the spectrum is confined and the light one expelled.
8 Conclusions
Despite these original promising conclusions, innovative mass separation with a rotating magnetic field remains an open problem of plasma physics and further studies are clearly needed.
This study was not intended to converge towards the final design of a mass separator for burned nuclear fuel management, but was aimed at advocating rotating plasma devices as promising candidates for closing the nuclear fuel cycle in next generation nuclear power plants (Fetterman & Fisch Reference Fetterman and Fisch2011b ; Timofeev Reference Timofeev2014). In addition to a short review of existing concepts and results given in section two, new classes of field configurations and plasma processes for this strategic purpose were uncovered in this paper, and a rotating plasma driven by a rotating magnetic field was identified as a new candidate to solve the unsolved problem of plasma mass separation.
We showed that for a given rotating magnetic field
![]() $\boldsymbol{b}(t)$
there is an infinite number of associated inductive electric fields or vector potentials which cannot be reduced to a smaller set through a gauge transformation. These vector potentials can be obtained through any linear combination of:
$\boldsymbol{b}(t)$
there is an infinite number of associated inductive electric fields or vector potentials which cannot be reduced to a smaller set through a gauge transformation. These vector potentials can be obtained through any linear combination of:
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{a}$
, or
$\boldsymbol{A}_{a}$
, or
![]() $\boldsymbol{A}_{s}$
and
$\boldsymbol{A}_{s}$
and
![]() $\boldsymbol{A}_{c}$
, or
$\boldsymbol{A}_{c}$
, or
![]() $\boldsymbol{A}_{c}$
and
$\boldsymbol{A}_{c}$
and
![]() $\boldsymbol{A}_{a}$
. An analysis of the orbital stability diagram for each of these basic fields was carried out, each of them presenting drawbacks and advantages with respect to the others. In light of this stability analysis, the general principles of mass separation using a rotating magnetic field were introduced using the field configuration
$\boldsymbol{A}_{a}$
. An analysis of the orbital stability diagram for each of these basic fields was carried out, each of them presenting drawbacks and advantages with respect to the others. In light of this stability analysis, the general principles of mass separation using a rotating magnetic field were introduced using the field configuration
![]() $\boldsymbol{A}_{s}$
as an illustration.
$\boldsymbol{A}_{s}$
as an illustration.
The Alfvén standing wave field
![]() $\boldsymbol{A}_{a}$
seems to be a very promising candidate for mass separation since it is a normal mode of the plasma and does not suffer from plasma screening. However, this result is weakened by the fact that
$\boldsymbol{A}_{a}$
seems to be a very promising candidate for mass separation since it is a normal mode of the plasma and does not suffer from plasma screening. However, this result is weakened by the fact that
![]() $\boldsymbol{A}_{a}$
is restricted to the vicinity of an electric node of the standing wave.
$\boldsymbol{A}_{a}$
is restricted to the vicinity of an electric node of the standing wave.
Although the two orthogonal dephased coils field
![]() $\boldsymbol{A}_{c}$
is probably the most widely used field configuration in synchronous and asynchronous rotating electric devices, the stability diagram associated with this configuration displays less opportunities for mass separation than the other two basic fields. Furthermore, the field penetration problem remains to be addressed in this configuration.
$\boldsymbol{A}_{c}$
is probably the most widely used field configuration in synchronous and asynchronous rotating electric devices, the stability diagram associated with this configuration displays less opportunities for mass separation than the other two basic fields. Furthermore, the field penetration problem remains to be addressed in this configuration.
Finally, the squirrel cage axial currents configuration
![]() $\boldsymbol{A}_{s}$
exhibits the simplest stability diagram. Although screening effects are expected to disturb the stability diagram in this configuration, preliminary analysis seems to indicate that these effects could be overcome for typical processing plasma densities and dimensions. In addition, the nonlinearity brought by screening effects could, in some cases, be advantageous to design advanced separation schemes.
$\boldsymbol{A}_{s}$
exhibits the simplest stability diagram. Although screening effects are expected to disturb the stability diagram in this configuration, preliminary analysis seems to indicate that these effects could be overcome for typical processing plasma densities and dimensions. In addition, the nonlinearity brought by screening effects could, in some cases, be advantageous to design advanced separation schemes.
Further to these open questions, yet another challenge in the way of developing large-scale plasma separation lies in the extraction of ions after they have been separated. This question has been considered for other rotating plasma separators, but not answered in a fully satisfactory manner to date.
To conclude, we identified, described and analysed the principles, main advantages and drawbacks of a new kind of rotating plasma separator based on a rotating magnetic field. This new concept is free of the Doppler shift broadening which hinders classical ion cyclotron isotope separation methods (Dawson et al. Reference Dawson, Kim, Arnush, Fried, Gould, Heflinger, Kennel, Romesser, Stenzel and Wong1976; Dolgolenko & Muromkin Reference Dolgolenko and Muromkin2009). Preliminary estimates suggest that rotating plasma separators could both satisfy the throughput requirement and be energetically attractive for spent fuel reprocessing applications. This novel approach could be extremely valuable for advanced closed nuclear fuel cycles. However, several challenges such as optimisation, screening and extraction remain to be addressed in order to design an industrial isotope and mass separator.
Acknowledgement
This work is dedicated to Professor N. J. Fisch, on the occasion of his 65th birthday, whose seminal contributions to numerous fields of plasma physics inspired these developments.