On the strong stability of ergodic iterations

Abstract

We revisit processes generated by iterated random functions driven by a stationary and ergodic sequence. Such a process is called strongly stable if a random initialization exists for which the process is stationary and ergodic, and for any other initialization the difference of the two processes converges to zero almost surely. Under some mild conditions on the corresponding recursive map, without any condition on the driving sequence we show the strong stability of iterations. Several applications are surveyed such as generalized autoregression and queuing. Furthermore, new results are deduced for Langevin-type iterations with dependent noise and for multitype branching processes.

1. Introduction

We are studying stochastic processes defined by iterating random functions. For a measurable function $F\,:\, \mathbb{R}^d\times \mathbb{R}^k\to \mathbb{R}^d$ , consider the following iteration: set $X_n=X_n(v)$ such that $X_{0}=v$ , with a vector $v\in\mathbb{R}^d$ , and let

(1) \begin{equation}X_{n+1}=F(X_{n},Z_{n+1}),\end{equation}

where the driving sequence $\{Z_i\}_{1}^{\infty}$ is a stochastic process with values in $\mathbb{R}^{k}$ .

In the standard setup, $\{Z_i\}_{1}^{\infty}$ is independent and identically distributed (i.i.d.) and so $\{X_i(v)\}_{0}^{\infty}$ is a homogeneous Markov process [17, 31]. Furthermore, (1) is called a forward iteration. If, in (1), $Z_1,\ldots ,Z_n$ is replaced by $Z_n,\ldots ,Z_1$ , then the resulting iteration $\tilde X_n$ is called the backward iteration [40, 41]. Clearly, $X_n$ and $\tilde X_n$ have the same distribution for each n.

In the present paper the main role is played by another type of iteration, called negative iteration, defined as follows. For a $k\le 0$ , let the random double array $X^{(k)}_n=X^{(k)}_n(0)$ , $k\le n$ , be defined such that $X^{(k)}_{k}=0$ and

(2) \begin{equation} X^{(k)}_{n+1}=F\big(X^{(k)}_n,Z_{n+1}\big),\quad n\ge k,\end{equation}

i.e. the iteration starts at negative time k with initial vector 0. This iteration scheme is also often used and appears, e.g., in [9, 10, 16, 17, 19, 20, 25, 26, 31].

Under mild conditions, [17] proved that the backward iteration $\tilde X_n$ is almost surely (a.s.) convergent to a random vector V with a distribution $\nu$ , which implies that the forward iteration $X_n$ has the limit distribution $\nu$ . As in the standard setup of Markov chains, if $X_0$ has distribution $\nu$ (and it is independent from the driving sequence $\{Z_i\}_{1}^{\infty}$ ), then $X_n$ will be a stationary Markov process.

More general schemes have also been considered, where $\{Z_i\}_{1}^{\infty}$ is merely stationary and ergodic [16, 19, 31]. In [9, 10, 20] such processes are treated under the name ‘stochastically recursive sequences’. We remark for later use that, by the Doob–Kolmogorov theorem, a stationary sequence $\{Z_i\}_{1}^{\infty}$ can always be completed to a sequence $\{Z_i\}_{-\infty}^{\infty}$ , defined on the whole integer lattice $\mathbb{Z}=\{0,\pm 1,\pm 2,\ldots\}$ . We assume henceforth that this completion has been carried out.

In [13] the stationary process $\{X^{\prime}_i\}_{-\infty}^{\infty}$ was called a weak solution of the iteration if there exists a $\{Z^{\prime}_i\}_{-\infty}^{\infty}$ such that $(X^{\prime}_i,Z^{\prime}_i)$ satisfies the recursion (1), and $\{Z_i\}_{-\infty}^{\infty}$ and $\{Z^{\prime}_i\}_{-\infty}^{\infty}$ have the same distribution. $\{X_i\}_{-\infty}^{\infty}$ is called a strong solution if it is stationary and $(X_i,Z_i)$ satisfies the recursion (1).

In this paper, we study the strong solutions. Using the almost sure limit of the negative iteration we construct such solutions under mild conditions. Actually, we investigate the following novel concept of strong stability.

Definition 1. The class of random processes $\{X_n(v), v\in\mathbb{R}^d\}$ is called strongly stable if:

1. (i) there exists a random vector $V^*$ such that $\{X_i(V^*)\}_{0}^{\infty}$ is stationary and ergodic;

2. (ii) for any random vector V, $X_n(V)-X_n(V^*)\to 0$ a.s.

Note that in this definition the random initial vector V may depend on the entire trajectory of $\{Z_i\}_{1}^{\infty}$ . As a result, the concept of strong stability may seem overly demanding. Furthermore, for integer-valued processes it follows from (ii) that there is a random index $\tau$ such that, for all $n>\tau$ , we have $X_n(V)=X_n(V^*)$ . In other words, $\{X_i(V)\}_{0}^{\infty}$ is forward coupled with $\{X_i(V^*)\}_{0}^{\infty}$ . This stronger notion of stability was introduced in [35] and also discussed in [21]. Traditional proofs establishing the existence of a unique limiting distribution for Markov chains on Polish spaces under Doeblin’s minorization condition involve representing transitions through iterated i.i.d. random maps and a coupling argument [5]. In this way, it can be shown that the iteration starting from any possibly random initial value is forward coupled with its stationary counterpart.

The aim of this paper is to show the strong stability of $\{X_n(v), v\in\mathbb{R}^d\}$ in great generality for several relevant models and important applications. As in [16], under some mild conditions on the function F we show that the almost sure limiting process $X_n^*=\lim_{k\to -\infty}X^{(k)}_n$ exists and is stationary and ergodic; [13] had similar results in the particular case of monotonic F, see (10).

Our main results are stated and proved in Section 2. Generalized autoregressions, queuing systems, and generalized Langevin dynamics are surveyed in Sections 3, 4, and 5, respectively. Section 6 treats multi-type generalized Galton–Watson processes. Finally, Section 7 discusses open problems.

2. Iterated ergodic function systems

Defining $F_n(x)\,:\!=\,F(x,Z_{n})$ , $n\in\mathbb{Z}$ , we can write

\begin{equation*} X_n^{(k)}(v)=F_n \circ \cdots \circ F_{k+1}(v),\quad k\le 0,\,\,n\geq k,\end{equation*}

where the empty composition is defined as the identity function.

In the following, $|\cdot|$ refers to the standard Euclidean norm on $\mathbb{R}^{d}$ . For a function $g\,:\,\mathbb{R}^{d}\to\mathbb{R}^{d}$ , set

\begin{equation*} \|g\|=\sup_{x\ne y}\frac{|g(x)-g(y)|}{|x-y|}.\end{equation*}

The following theorem is an extension of [17, Theorem 5.1] and [31, Theorem 6.2]. It is contained in [19, Theorem 3] (except for proving (ii)). We provide a proof for completeness.

Theorem 1. Assume that $\{Z_i\}_{-\infty}^{\infty}$ is a stationary and ergodic sequence. Suppose that

1. (i) $\mathbb{E}\{ (\log \|F_1\|)^+\}<\infty$ , and

2. (ii) for some n,

   (3) \begin{equation} \mathbb{E}\{ \log \|F_n \circ \cdots \circ F_1\|\}<0. \end{equation}

Then the class $\{X_n(v), v\in\mathbb{R}^d\}$ is strongly stable.

Notice that (3) is a sort of long-run contraction condition here.

Proof. For the stationary and ergodic process $\mathbf{Z}=\{Z_i\}_{-\infty}^{\infty}$ , let $f_n$ , $n=1,2,\ldots$ , be vector-valued functions such that $f_i(T^i\mathbf{Z})=X_i(0)$ , where T stands for the shift transformation. Let’s calculate $f_n(\mathbf{Z})$ . If the process $\{X^{(k)}_n\}$ is defined in (2), then $f_n(\mathbf{Z})=X^{(-n)}_{0}(0)$ , i.e. $X^{(-n)}_{0}(0)$ is the value of the process at time 0, when the process started at negative time $-n$ with the 0 vector. We show that, under the conditions (i) and (ii),

(4) \begin{equation} X^{(-n)}_{0}(0) \text{ is a.s. convergent to a random vector } V^*. \end{equation}

It will be clear that $V^{*}=f(\mathbf{Z})$ for some suitable functional f, so we will in fact show that

(5) \begin{equation} f_n(\mathbf{Z})\to f(\mathbf{Z})\text{ a.s.} \end{equation}

As for (4), we show that this sequence is a.s. a Cauchy sequence, i.e. even

\begin{equation*} \sum_{n=1}^{\infty}\big|X^{(-n)}_{0}(0)-X^{(-n-1)}_{0}(0)\big|<\infty \end{equation*}

holds a.s. Notice that iterating (2) yields

\begin{equation*} X^{(-n-1)}_{-n}(0) = F(X^{(-n-1)}_{-n-1}(0),Z_{-n}) = F(0,Z_{-n}) = X^{(-n)}_{-n}(F(0,Z_{-n})), \end{equation*}

So

\begin{align*} X^{(-n)}_{0}(0)-X^{(-n-1)}_{0}(0) & = X^{(-n)}_{0}(0)-X^{(-n)}_{0}(F(0,Z_{-n})) \\ & = F_{0} \circ \cdots \circ F_{-n+1}(0-F(0,Z_{-n})). \end{align*}

Thus, $\big|X^{(-n)}_{0}(0)-X^{(-n-1)}_{0}(0)\big| \le \|F_{0} \circ \cdots \circ F_{-n+1} \|\cdot |F(0,Z_{-n})|$ . We will show that the ergodicity of $\{Z_i\}_{-\infty}^{\infty}$ together with (i) and (ii) implies

(6) \begin{equation} \sum_{n=1}^{\infty}\|F_{0} \circ \cdots \circ F_{-n+1} \|\cdot |F(0,Z_{-n})|<\infty \end{equation}

a.s., and so (4) is verified.

In the following, the key ingredient is [19, Proposition 2], which is an extension of Fűrstenberg and Kesten [22]. To prove (6), note that by [19, Proposition 2], the condition (3) implies that the sequence

\begin{equation*} E_n \,:\!=\, \frac 1n \mathbb{E}\{\log \Vert F_{0} \circ \cdots \circ F_{-n+1} \Vert \} \to E,\quad n\to\infty, \end{equation*}

with $E<0$ such that

(7) \begin{equation} \frac 1n \log \Vert F_{0} \circ \cdots \circ F_{-n+1} \Vert \to E \end{equation}

a.s. Note that E is called the Lyapunov exponent. Next, we argue as in [31, Proposition 6.1]. We have $\Vert F_{0}\circ\cdots\circ F_{-n+1}\Vert = \exp\{n(1/n)\log\Vert F_{0}\circ\cdots\circ F_{-n+1}\Vert\}$ . The limit in (7) implies that there are random integer $n_0$ and $a>0$ such that, for all $n\ge n_0$ ,

\begin{equation*} \frac 1n \log \Vert F_{0} \circ \cdots \circ F_{-n+1} \Vert \le -a < 0. \end{equation*}

Thus,

\begin{equation*} \sum_{n=n_0}^{\infty}\|F_{0} \circ \cdots \circ F_{-n+1} \|\cdot |F(0,Z_{-n})| \le \sum_{n=n_0}^{\infty}|F(0,Z_{-n})|{\mathrm{e}}^{-na}. \end{equation*}

Since $\lambda\ln^{+}|F(0,Z_{-1})|$ is integrable for all $\lambda>0$ , it follows that

$$\sum_{n=1}^{\infty}\mathbb{P} (\lambda\ln |F(0,Z_{-1})|>n)<\infty.$$

Applying this observation for $\lambda\,:\!=\,2/\alpha$ , the Borel–Cantelli lemma implies that $|F(0,Z_{-1})|<{\mathrm{e}}^{na/2}$ holds except for finitely many n a.s., which implies that $\sum_{n=n_0}^{\infty}|F(0,Z_{-n})|{\mathrm{e}}^{-na}<\infty$ a.s.

Because $X_i(V^*)=f(T^i\mathbf{Z})$ , $\{X_i(V^*)\}_{0}^{\infty}$ is stationary and ergodic so Definition 1(i) is proved. Furthermore,

\begin{equation*} \|X_n(V)-X_n(V^*)\| \le \|F_{n} \circ \cdots \circ F_{1} \|\cdot |V-V^*| \to 0 \end{equation*}

a.s., as before. Thus, Definition 1(ii) is verified, too.

Theorem 1 applies, in particular, under the one-step contraction condition (8) in the following result.

Proposition 1. Assume that $\{Z_i\}_{-\infty}^{\infty}$ is a stationary and ergodic sequence such that the distribution of $Z_{1}$ is denoted by $\mu$ . Suppose that $\int |F(0,z)|\mu({\mathrm{d}} z)<\infty$ , and $|F(x,z)-F(x^{\prime},z)|\le K_z |x-x^{\prime}|$ with

(8) \begin{equation} \mathbb{E}\{ \log K_{Z_1}\}<0. \end{equation}

Then the class $\{X_n(v), v\in\mathbb{R}^d\}$ is strongly stable.

Proof. This proposition is an easy consequence of Theorem 1, since

\begin{align*} \mathbb{E}\{ \log \|F_n \circ \cdots \circ F_1\|\} \le \mathbb{E}\{ \log (\|F_n\| \cdots \| F_1\|)\} & = n\mathbb{E}\{ \log \| F_1\|\} \\ & \le n\mathbb{E}\{ \log K_{Z_1}\} < 0.\end{align*}

Definition 2. We say that the class of strongly stable random processes $\{X_n(v), v\in\mathbb{R}^d\}$ satisfies the strong law of large numbers (SLLN) if $\mathbb{E}\{V^*\}$ is well-defined and finite, and, for any $v\in\mathbb{R}^d$ , $\lim_n (1/n) \sum^{n}_{i=1} X_{i}(v)=\mathbb{E}\{V^*\}$ a.s.

Remark 1. Under the conditions of Theorem 1, if $V^*$ has a well-defined and finite expectation $\mathbb{E}\{V^*\}$ then we have the SLLN:

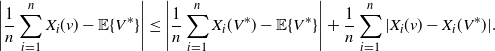\begin{equation*} \Bigg|\frac 1n \sum^{n}_{i=1} X_{i}(v)-\mathbb{E}\{V^*\}\Bigg| \le \Bigg|\frac 1n \sum^{n}_{i=1} X_{i}(V^*)-\mathbb{E}\{V^*\}\Bigg| + \frac 1n \sum^{n}_{i=1} |X_{i}(v)- X_{i}(V^*)|. \end{equation*}

By Birkhoff’s ergodic theorem, the first term on the right-hand side tends to 0 a.s., while the almost sure convergence of the second term follows from Theorem 1(ii).

Remark 2. Now we discuss some conditions guaranteeing $\mathbb{E}\{|V^{*}|\}<\infty$ . By Fatou’s lemma and the triangle inequality, we can write

$$ \mathbb{E} \{|V^*|\} \le \liminf_{n\to\infty}\mathbb{E}\big\{\big|X_0^{(-n)}(0)\big|\big\} \le \sum_{k=0}^{\infty} \mathbb{E} \Big\{\Big| X_0^{(-k)}(0) - X_0^{(-k+1)}(0)\Big|\Big\}, $$

which we can estimate further and obtain

$$ \mathbb{E} \{|V^*|\} \le \sum_{k=0}^{\infty} \mathbb{E} \{\lVert F_{0}\circ\cdots\circ F_{-k+1}\rVert\cdot | F(0,Z_{-k})|\}. $$

For the sake of simplicity, assume for the moment that $z\mapsto |F(0,z)|$ is bounded by some constant C. By stationarity, it is enough to investigate $\mathbb{E} \{\lVert F_{k}\circ\cdots\circ F_{1}\rVert\}$ . Here, either we can prescribe a ‘contractivity in the long run’-type condition like

(9) \begin{equation} \limsup_{k\to\infty}\mathbb{E}^{1/k} \{\lVert F_{k}\circ\cdots\circ F_{1}\rVert\}<1, \end{equation}

and then the nth-root test gives the desired result (i.e., $\mathbb{E}\{|V^{*}|\}<\infty$ ), or, by Hölder’s inequality, we can write

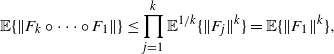$$ \mathbb{E} \{\lVert F_{k}\circ\cdots\circ F_{1}\rVert\} \le \prod_{j=1}^{k} \mathbb{E}^{1/k}\{\lVert F_{j}\rVert^k\} = \mathbb{E} \{\lVert F_{1}\rVert^k\}, $$

and thus we have

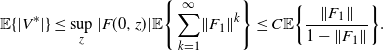$$ \mathbb{E} \{|V^*|\} \le \sup_{z}|F(0,z)| \mathbb{E}\Bigg\{\sum_{k=1}^{\infty}\lVert F_{1}\rVert^k\Bigg\} \leq C\mathbb{E}\bigg\{\frac{\lVert F_{1}\rVert}{1-\lVert F_{1}\rVert}\bigg\}. $$

We should assume here that $\lVert F_{1}\rVert<1$ a.s.; moreover, $\mathbb{E}\{{\lVert F_{1}\rVert}/({1-\lVert F_{1}\rVert})\}<\infty$ and hence this approach looks much more restrictive than requiring (9).

As pointed out in [47], the long-time contractivity condition (9) is stronger than (3) in Theorem 1 or, equivalently, (7). On the other hand, in the i.i.d. case, (9) reduces to $\mathbb{E}\{\lVert F_1\rVert\}<1$ . If $\mathbb{E}\{\lVert F_1\rVert\}<1$ fails in the i.i.d. case then $E[V^{*}]=\infty$ can easily happen; see the example in Remark 3.

Remark 3. Concerning the SLLN, we should have to verify that $\mathbb{E}\big\{\sup_n\big|X^{(-n)}_{0}(0)\big|\big\}<\infty$ . Note that $X^{(0)}_{0}(0)=0$ , and thus

\begin{equation*} \sup_n\big|X^{(-n)}_{0}(0)\big| \le \sum_{k=1}^{\infty}\Big|X^{(-k+1)}_{0}(0)-X^{(-k)}_{0}(0)\Big|. \end{equation*}

One possibility would be to check that

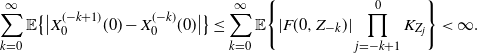\begin{equation*} \sum_{k=0}^{\infty}\mathbb{E}\big\{\big|X^{(-k+1)}_{0}(0)-X^{(-k)}_{0}(0)\big|\big\} \le \sum_{k=0}^{\infty}\mathbb{E}\Bigg\{|F(0,Z_{-k})|\prod_{j=-k+1}^0K_{Z_j}\Bigg\} < \infty. \end{equation*}

Here is a counterexample, however, to show that this is not true in general. Let $d=k=1$ and $\{Z_i\}_{i\in\mathbb{Z}}$ be i.i.d. such that $\mathbb{P} \{Z_0={\mathrm{e}}^{-2}\}=\frac23$ and $\mathbb{P} \{Z_0={\mathrm{e}}^2\}=\frac13$ . Put $X_{0}=v>0$ and $X_{n+1}=Z_{n+1}\cdot X_{n}$ . Clearly, $K_{Z_0}=Z_0$ with $\mathbb{E} \{\log K_{Z_0}\}=-\frac23<0$ and so the conditions of Proposition 1 are satisfied. Furthermore, $\mathbb{E}\{K_{Z_0}\} = \mathbb{E}\{Z_{1}\} = \frac23{\mathrm{e}}^{-2}+\frac13{\mathrm{e}}^2>1$ . By independence,

\begin{equation*} \mathbb{E}\{X_{n+1}\} = \mathbb{E}\{Z_{n+1}\}\cdot \mathbb{E}\{X_{n}\} = \mathbb{E}\{Z_{1}\}^{n+1}\cdot v = \big(\tfrac23{\mathrm{e}}^{-2}+\tfrac13{\mathrm{e}}^2\big)^{n+1}\cdot v \to \infty \end{equation*}

as $n\to\infty$ . Therefore, $\mathbb{E}\{V^*\}=\infty$ .

Next, the contraction condition of Theorem 1 is replaced by a monotonicity assumption. We denote by $\mathcal{F}_{t}$ the sigma-algebra generated by $Z_{j}$ , $-\infty<j\le t$ . Furthermore, we use the notation $\mathbb{R}^d_+$ for the positive orthant endowed with the usual coordinatewise partial ordering, i.e., $x\le y$ for $x,y\in\mathbb{R}^d$ when each coordinate of x is less than or equal to the corresponding coordinate of y. In what follows, $|x|_p=[|x_1|^p+\cdots+|x_d|^p]^{1/p}$ stands for the usual $l_p$ -norm on $\mathbb{R}^d$ .

Proposition 2. Assume that $\{Z_i\}_{-\infty}^{\infty}$ is a stationary and ergodic sequence, and $F\,:\,\mathbb{R}^d_+\times\mathbb{R}^k\to\mathbb{R}^d_+$ is monotonic in its first argument:

(10) \begin{equation} F(x,z)\le F(x^{\prime},z) \quad \text{if } x\le x^{\prime}. \end{equation}

For a fixed $1\le p <\infty$ , suppose that there exist a constant $0\leq \rho<1$ and $K>0$ such that

(11) \begin{equation} \mathbb{E}[|F(x,Z_{1})|_p\mid \mathcal{F}_{0}]\leq \rho |x|_p+K \end{equation}

a.s. for all $x\in\mathbb{R}^d$ , and

(12) \begin{equation} \mathbb{E}[|F(0,Z_0)|_p]<\infty. \end{equation}

Then, the class $\{X_n(v),v\in\mathbb{R}^d\}$ is strongly stable. Furthermore, the SLLN is satisfied.

Notice that (11) also implies, for all t,

(13) \begin{equation} \mathbb{E}[|F(x,Z_{t+1})|_p\mid \mathcal{F}_{t}]\leq \rho |x|_p+K\end{equation}

a.s. for all $x\in\mathbb{R}_+^d$ . [9, 21, 40] studied the monotonic iteration under the fairly restrictive condition that the range of the iteration is a bounded set.

Proof. This proposition extends the Foster–Lyapunov stability argument to a non-Markovian setup. We apply the notations in the proof of Theorem 1 such that we verify the condition (5) or, equivalently, check (4). Since $F_n({\cdot})\,:\!=\,F(\cdot,Z_n)\,:\,\mathbb{R}_+^d\to\mathbb{R}_+^d$ , $n\in\mathbb{Z}$ , are order-preserving maps and $F(0,Z_{-n})\ge 0$ ,

\begin{align*} X^{(-n-1)}_{0}(0)-X^{(-n)}_{0}(0) & = X^{(-n)}_{0}(F(0,Z_{-n}))-X^{(-n)}_{0}(0) \\ & = F_0\circ\cdots\circ F_{-n+1}(F(0,Z_{-n}))-F_0\circ\cdots\circ F_{-n+1}(0) \end{align*}

is non-negative, therefore $\big(X^{(-n)}_{0}(0)\big)_{n\in\mathbb{N}}$ is monotonically increasing and so (4) is verified.

As for Theorem 1(i), we need that $V^*=\lim_{n\to\infty} X^{(-n)}_{0}(0)$ takes finite values a.s., which would follow from $\mathbb{E}\big\{\sup_n\big|X^{(-n)}_{0}(0)\big|_p\big\}<\infty$ . It is easily seen that $x\le y$ implies $|x|_p\le |y|_p$ for $x,y\in\mathbb{R}_+^d$ , and therefore, by the Beppo Levi theorem and the monotonicity of $X^{(-n)}_{0}(0)$ , $n\in\mathbb{N}$ , $\mathbb{E}\big\{\sup_n\big|X^{(-n)}_{0}(0)\big|_p\big\} = \sup_n\mathbb{E}\big\{\big|X^{(-n)}_{0}(0)\big|_p\big\}$ . From (13) we get that

$$ \mathbb{E}\big[\big|X_{i+1}^{(-n)}(0)\big|_p\mid\mathcal{F}_{i}\big] = \mathbb{E}\big[\big|F(X_i^{(-n)}(0),Z_{i+1})\big|_p\mid\mathcal{F}_{i}\big] \leq \rho\big|X_i^{(-n)}(0)\big|_p+K, \quad i\geq -n. $$

Iterating this leads to

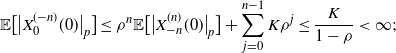$$ \mathbb{E}\big[\big|X^{(-n)}_{0}(0)\big|_p\big]\leq \rho^{n}\mathbb{E}\big[\big|X_{-n}^{(n)}(0)\big|_p\big] + \sum_{j=0}^{n-1} K\rho^{j}\leq \frac{K}{1-\rho}<\infty; $$

hence, $\sup_n\mathbb{E}\big\{\big|X^{(-n)}_{0}(0)\big|_p\big\}$ is finite, which completes the proof.

Remark 4. Proposition 2 holds with an analogous proof if we replace (13) by

$$\mathbb{E}[|F(x,Z_{t+1})|_p\mid \mathcal{F}_{t}]\leq \rho(t) |x|_p+K,$$

where $\rho(t)$ , $t\in\mathbb{Z}$ , is a stationary process adapted to $\mathcal{F}_{t}$ and $\limsup_{n\to\infty}\mathbb{E}^{1/n}\{\rho(1)\cdots$ $\rho(n)\}<1$ .

3. Generalized autoregression

In this section, $\| A\|$ will denote the operator norm of a matrix A. Several authors investigated the iteration of matrix recursion. Set $X_n=X_n(v)$ such that $X_{0}=v$ , and

(14) \begin{equation} X_{n+1}=A_{n+1}X_{n}+B_{n+1},\quad n\ge 0,\end{equation}

where $\{(A_n,B_n)\}$ are i.i.d., $A_n$ is a $d\times d$ matrix, and $B_n$ is a d-dimensional vector. In this section we study a more general case of (14) where the sequence $\{(A_n,B_n)\}$ is stationary and ergodic. The minimal sufficient condition for the existence of a stationary solution for (14) was proved in [12]. In the i.i.d. case, [11] showed that those conditions are indeed minimal.

For the stationary and ergodic case, we now reprove the sufficiency part of [11, Theorem 2.5].

Proposition 3. Assume that $\{(A_n,B_n)\}$ is stationary and ergodic such that $\mathbb{E} \{\log^{+}\Vert A_{0}\Vert\}<\infty$ and $\mathbb{E}\{ \log^{+}|B_{0}|\} <\infty $ . If

(15) \begin{equation} \mathbb{E}\{\log ||A_{0}\cdots A_{-n}||\}<0 \end{equation}

for some n, then the class $\{X_n(v), v\in\mathbb{R}^d\}$ is strongly stable.

Proof. Since $\Vert A_{n}A_{n-1}\cdots A_{1}\Vert$ corresponds to $\Vert F_{n}\circ\cdots\circ F_{1}\Vert$ , we can verify the conditions of Theorem 1 easily: (15) implies (ii) and the integrability conditions of Proposition 1 imply (i).

Remark 5. Note that the argument above showed up first in [22], which proved that if $\mathbb{E} \{\log^{+}\Vert A_{0}\Vert\}<\infty$ , then $\lim_n (1/n) \log \Vert A_{n}A_{n-1}\cdots A_{1} \Vert = E$ a.s., where E stands for the Lyapunov exponent.

In the rest of this section we recall results about a similar iteration which are based on negative iterations (though they cannot be treated by our results in this paper). Let us consider the stochastic gradient method for least-squares regression, when there are given observation sequences of random, symmetric, and positive semi-definite $d\times d$ matrices $A_{n}$ and random d-dimensional vectors $V_{n}$ such that $A = \mathbb{E}(A_{n})$ and $V = \mathbb{E}(V_{n})$ $(n=0,\pm 1,\pm 2,\ldots )$ . If $A^{-1}$ exists then the aim is to estimate $\vartheta = A^{-1}V.$ For this reason, a stochastic gradient algorithm with constant gain is introduced. Set $X_{0}=v$ , and

(16) \begin{equation} X_{n+1}=X_{n}-\lambda (A_{n+1}X_{n}-V_{n+1}),\quad n\ge 0,\end{equation}

followed by an averaging, $\bar X_{n}= (1/n) \sum^{n}_{i=1} X_{i}$ .

If $\lambda$ depends on n, then $\bar X_{n}$ is called an averaged stochastic approximation introduced in [39, 45, 46]. If the sequence $\{(A_{n},V_{n})\}_{-\infty}^{\infty}$ is i.i.d., then they proved the optimal rate of convergence of $\bar X_{n}$ to $\vartheta$ .

The case of dependent $\{(A_{n},V_{n})\}_{-\infty}^{\infty}$ was studied in [26]. Assume that the sequence $\{(A_{n},V_{n})\}_{-\infty}^{\infty}$ is stationary and ergodic such that $\mathbb{E} \Vert A_{n} \Vert<\infty$ , $\mathbb{E} | V_{n}| <\infty$ , and A is positive definite. Then there is a $\lambda _{0}>0$ such that, for all $0<\lambda <\lambda _{0}$ , there exists a stationary and ergodic process $\{X_n^*\}_{-\infty}^{\infty}$ satisfying the recursion (16) and $\lim_n (X_n-X_n^*)=0$ a.s. Moreover, $\lim_n \bar X_n=\vartheta+\delta_{\lambda}$ a.s. with an asymptotic bias vector $\delta_{\lambda}$ . In [26] there is a 3-dependent example of $\{(A_{n},V_{n})\}_{-\infty}^{\infty}$ , where $\delta_{\lambda}\ne 0$ . Furthermore, under a suitable mixing condition on $\{(A_{n},V_{n})\}_{-\infty}^{\infty}$ , $|\delta_{\lambda}|$ is of order $\sqrt{\lambda}$ .

4. Lindley process

We recall some results from queuing theory. They do not follow from arguments of the present paper but they are also based on negative iterations and hence provide one more illustration of the usefulness of this technique.

For $d=k=1$ , consider the following iteration. Set $X_n=X_n(v)$ such that $X_{0}=v\geq 0$ , and $X_{n+1}=(X_{n}+Z_{n+1})^+$ . The next proposition is an extension of the concept of strong stability. Let $\{X^{\prime}_i\}_{0}^{\infty}$ be a stationary and ergodic sequence. Recall that $\{X_i\}_{0}^{\infty}$ is forward coupled with $\{X^{\prime}_i\}_{0}^{\infty}$ if there is a random index $\tau$ such that, for all $n>\tau$ , $X^{\prime}_n=X_n$ .

Proposition 4. Assume that $\{Z_i\}_{-\infty}^{\infty}$ is a stationary and ergodic sequence with $\mathbb{E}\{Z_1\}<0$ . Put $V^*=\sup_{j\le 0}(Z_j+\cdots +Z_0)^+$ and $X^{\prime}_n=X_n(V^*)$ . Then $\{X^{\prime}_i\}_{0}^{\infty}$ is stationary and ergodic, and $\{X_i\}_{0}^{\infty}$ is forward coupled with $\{X^{\prime}_i\}_{0}^{\infty}$ .

As an application of Proposition 4 consider the extension of the G/G/1 queuing model. Let $X_n$ be the waiting time of the nth arrival, $S_n$ be the service time of the nth arrival, and $T_{n+1}$ be the inter-arrival time between the $(n+1)$ th and nth arrivals. Then, we get the recursion $X_{n+1}=(X_{n}-T_{n+1}+S_n)^+$ .

The generalized G/G/1, where either the arrival times, or the service times, or both are not memoryless, was studied in [25, 37]; see also [2, 3, 9, 13, 23].

Proposition 4 implies that if $\{ Z_{i}\}\,:\!=\,\{S_{i-1}-T_i\}_{-\infty}^{\infty}$ is a stationary and ergodic sequence with $\mathbb{E}\{S_0\}<\mathbb{E}\{T_1\}$ , then $\{X_i\}_{0}^{\infty}$ is forward coupled with a stationary and ergodic $\{X^{\prime}_i\}_{0}^{\infty}$ .

5. The Langevin iteration

For a measurable function $H\,:\,\mathbb{R}^d\times \mathbb{R}^m\to \mathbb{R}^d$ , the Langevin iteration is defined as follows. Set $X_n=X_n(v)$ such that $X_{0}=v$ , and

(17) \begin{equation} X_{n+1}=X_{n}-\lambda H(X_n,Y_n)+\sqrt{2\lambda}N_{n+1},\quad n\ge 0,\end{equation}

where $\{Y_i\}_{-\infty}^{\infty}$ and $\{N_i\}_{-\infty}^{\infty}$ are random sequences. In the literature of stochastic approximation $ \lambda >0 $ is called the step size, while in machine learning it is called the learning rate.

The simplest case is where the sequences $N_n$ and $Y_n$ are independent, $Y_n$ is i.i.d., and $N_n$ is i.i.d. standard d-dimensional Gaussian. This algorithm was introduced in [50] and later analyzed by a large corpus of literature which we cannot review here. It is called ‘stochastic gradient Langevin dynamics’ and it can be used for sampling from high-dimensional, not necessarily log-concave, distributions and for finding the global minimum of high-dimensional functionals. In this context, $Y_n$ represents a data sequence (obtained, for instance, by averaging a big dataset over randomly chosen minibatches), and $N_n$ is artificially added noise to guarantee that the process does not get stuck near local minima.

The case where the data sequence $Y_n$ may be a dependent stationary process (but $N_n$ is still i.i.d. standard Gaussian) has been treated less extensively: see [4, 15] for the convex and [14] for the non-convex settings.

Another stream of literature, starting from [30], concentrated on stochastic differential equations driven by colored Gaussian noise. The discrete-time case of difference equations was treated in [49]. This setting corresponds to the case where in (17), $Y_n$ is constant and $N_n$ is a dependent Gaussian sequence.

We know of no studies so far that allowed both $Y_n$ and $N_n$ to be only stationary. We manage to establish strong stability in this case, under reasonable assumptions.

Defining $F(x,z)=x-\lambda H(x,y)+\sqrt{2\lambda}u$ , $z=(y,u)$ , and $Z_{i+1}\,:\!=\,(Y_i,N_{i+1})$ , Proposition 1 implies the following result.

Corollary 1. Assume that the sequence $\{(Y_i,N_{i+1})\}_{-\infty}^{\infty}$ is stationary and ergodic, and that, for a $\lambda _{0}>0$ and for all $0<\lambda <\lambda _{0}$ , $\mathbb{E}|{-}\lambda H(0,Y_1)+\sqrt{2\lambda}N_{2}|<\infty$ and

\begin{align*} |x-\lambda H(x,z)-(x^{\prime}-\lambda H(x^{\prime},z))|\le K_z|x-x^{\prime}| \end{align*}

with (8). Then, for all $0<\lambda <\lambda _{0}$ , the class $\{X_n(v), v\in\mathbb{R}^d\}$ is strongly stable.

Remark 6. Next, we prove the convergence of the iterative scheme (17) assuming only that H satisfies

(18) \begin{equation} \langle\partial_1 H (x,y)v,v\rangle \ge m (y) | v |^2 \quad \text{and} \quad |\partial_1 H (x,y)| \le M(y) \end{equation}

with measurable $m,M\,:\,\mathbb{R}^{m}\to [0,\infty)$ . (This is a parametric form of the usual strong convexity condition. We can replace it by a so-called dissipativity condition and hence extend the analysis beyond the convex case. However, this direction requires a different technology.) We introduce $g(t)=H(t x^{\prime}+(1-t)x,y)$ , and thus we can write

$$ |F(x,y)-F(x^{\prime},y)|^2 =| x-x^{\prime}|^2 - 2\lambda\langle x-x^{\prime},g(0)-g(1)\rangle + \lambda^2 |g(0)-g(1)|^2, $$

where $g(0)-g(1) = \int_0^1 \partial_1 H (t x^{\prime} + (1-t)x,y)(x-x^{\prime})\,\mathrm{d}t$ . Using (18), we estimate $|g(0)-g(1)|\le M_y |x-x^{\prime}|$ and $\langle x-x^{\prime},g(0)-g(1)\rangle\ge m_y|x-x^{\prime}|^2$ , and arrive at

$$ |F(x,y)-F(x^{\prime},y)| \le (1+\lambda^2 M_y^2 -2\lambda m_y)^{1/2}|x-x^{\prime}|. $$

In (18), without loss of generality, we can assume that $\mathbb{E}(m_{Z_1})<\infty$ . Furthermore, requiring $\mathbb{E}(M_y^2)<\infty$ , we can set $\lambda$ such that the conditions of Proposition 1, i.e. (8), are satisfied. It is also not restrictive to assume that $\mathbb{E}(m_{Z_1})^2<\mathbb{E}(M_{Z_1}^2)$ . Since $K_{Z_1} = (1+\lambda^2 M_{Z_1}^2 -2\lambda m_{Z_1})^{1/2}$ , Jensen’s inequality implies that

$$\mathbb{E}(K_{Z_1})\le(1+\lambda^2 \mathbb{E} (M_{Z_1}^2) -2\lambda \mathbb{E}(m_{Z_1}))^{1/2} < 1$$

whenever $\lambda<{2\mathbb{E}(m_{Z_1})}/{\mathbb{E} (M_{Z_1}^2)}$ .

Remark 7. Strong convexity is a usual assumption in the stochastic gradient Langevin dynamics literature [4, 15, 18]. Remark 6 shows that our results cover this case. It would, however, be nice to weaken this condition to dissipativity (see [14, 36]). It seems that such a generalization requires much more advanced techniques; see, e.g., [49].

Remark 8. Note that the iteration (16) in Section 3 is a special case of the Langevin iteration (17) such that $H(X_{n},A_{n+1})=A_{n+1}X_{n}$ , with the difference that for this, only convexity holds and not strong convexity. In a least-squares regression setup it is important that $A_n$ is assumed positive semi-definite only and not necessarily positive definite.

6. Generalized multi-type Galton–Watson process

We follow the notation of [33]. A d-type Galton–Watson branching process with immigration (GWI process) $\mathbf{X}_n = ( X_{n,1} , \ldots, X_{n,d} )$ , $n \in \mathbb{Z}_+$ , is defined as

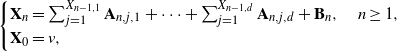\begin{align*} \begin{cases} \mathbf{X}_n = \sum_{j=1}^{X_{n-1,1}} \mathbf{A}_{n,j,1}+ \cdots + \sum_{j=1}^{X_{n-1,d}} \mathbf{A}_{n,j,d} + \mathbf{B}_n , \quad n \geq 1 , \\ \mathbf{X}_0 = v , \end{cases}\end{align*}

where $v\in\mathbb{N}^{d}$ and $\{ \mathbf{A}_{n,j,i},\mathbf{B}_n\,:\, n, j \in \mathbb{N} , \, i \in \{1,\ldots,d\} \}$ are random vectors with non-negative integer coordinates. Here, $X_{n,i}$ is the number of i-type individuals in the nth generation of a population, $\mathbf{A}_{n,j,i}$ is the vector of the number of offspring produced by the jth individual of type i belonging to the $(n-1)$ th generation, and $\mathbf{B}_n$ is the vector of the number of immigrants.

Let $\mathbf{C}_n\,:\!=\,\{\mathbf{A}_{n,j,i}\,:\, j \in \mathbb{N} , \, i \in \{1,\ldots,d\} \}$ . In the standard setup the families of random variables $\{\mathbf{C}_n\,:\, n \in \mathbb{N}\}$ and $\{\mathbf{B}_n\,:\, n \in \mathbb{N}\}$ are independent and $(\mathbf{C}_n,\mathbf{B}_n)$ , $n \in \mathbb{N}$ , is a sequence of independent vectors. The process $\{\mathbf{X}_n\,:\, n \in \mathbb{N}\}$ is called homogeneous when $(\mathbf{C}_n,\mathbf{B}_n)$ , $n \in \mathbb{N}$ , are identically distributed, otherwise it is inhomogeneous. In this section we study the generalization of the homogeneous case, when $\{ Z_{n}\,:\!=\,(\mathbf{C}_n,\mathbf{B}_n)\,:\, n \in \mathbb{N} \}$ is a stationary and ergodic process. As before, we extend this stationary process to the timeline $\mathbb{Z}$ . We furthermore assume for each i that $\mathbf{A}_{1,j,i}$ has, for each $j\in\mathbb{N}$ , the same conditional law with respect to $\mathcal{F}_{0}$ .

Note that the state space of $Z_{n}$ is $\mathbb{R}^{\mathbb{N}}$ . It can easily be checked that all the arguments of our paper also apply for such state spaces.

Homogeneous multi-type GWI processes were introduced and studied in [42, 43]. In [42], a necessary and sufficient condition is given for the existence of a stationary distribution in the subcritical case. A complete answer is given by [32]. Also, [38] gives a sufficient condition for the existence of a stationary distribution, and in a special case shows that the limiting distribution is a multivariate Poisson process with independent components.

Branching process models are extensively used in various parts of the natural sciences, in biology, epidemiology, physics, and computer science, among other subjects. In particular, multi-type GWI processes were used to determine the asymptotic mean and covariance matrix of deleterious and mutant genes in a stationary population in [24], and in a non-stationary population in [34]. Another rapidly developing area where multi-type GWI processes can be applied is the theory of polling systems: [44] pointed out that a large variety of polling models can be described as a multi-type GWI process. [1, 6, 7, 44, 48] investigated several communication protocols applied in info-communication networks with differentiated services. There are different quality of service requirements, e.g. some of them are delay sensitive (telephone, online video, etc.), while others tolerate some delay (email, internet, downloading files, etc.). Thus, the services are grouped into service classes such that each class has its own transmission protocol, like priority queuing. In the papers mentioned above the d-type Galton–Watson process has been used, where the process was defined either by the sizes of the active user populations of the d service classes, or by the length of the d priority queues. For the general theory and applications of multi-type Galton–Watson processes we refer to [29, 38].

Define the random row vectors $m_i\,:\!=\,\mathbb{E}[\mathbf{A}_{1,1;i}\mid\mathcal{F}_0]$ , $i=1,\ldots,d$ , where $\mathcal{F}_{t}$ is the sigma-algebra generated by $Z_{j}$ , $-\infty<j\leq t$ . Note that, by our assumptions, $m_{i}$ has the same law as $\mathbb{E}[\mathbf{A}_{n+1,j;i}\mid\mathcal{F}_n]$ for each n and j. For $x\in\mathbb{R}^d$ we will use the $\ell_1$ -norm $|x|_1\,:\!=\,\sum_{j=1}^d |x_i|$ , where $x_i$ is the ith coordinate of x.

Proposition 5. If

(19) \begin{equation} \max_{1\leq i\leq d}|m_i|_1\leq\varrho \end{equation}

almost surely for some constant $\varrho<1$ and $\mathbb{E}\{|\mathbf{B}_{1}|_{1}\}<\infty$ , then $\mathbf{X}_{t}=\mathbf{X}_{t}(v)$ is strongly stable and the SLLN holds.

Proof. Define $F(x,z)\,:\!=\,\sum_{j=1}^d\sum_{i=1}^{x_j}z_{i;j} +z_0$ , where $z_{i;j}\in\mathbb{N}^{d}$ , $i\in\mathbb{N}$ , $1\leq j\leq d$ , $z_{0}\in\mathbb{N}^{d}$ . Note that this iteration is monotone. As already defined, the stationary process will be $Z_n=((\mathbf{A}_{n,i;j})_{1\leq j\leq d,i\in\mathbb{N}},\mathbf{B}_n)$ .

Let us check (11) with $p=1$ :

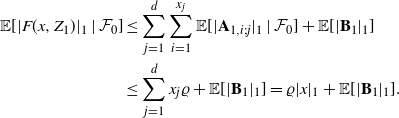\begin{align*} \mathbb{E}[|F(x,Z_1)|_1\mid\mathcal{F}_0] & \leq \sum_{j=1}^d\sum_{i=1}^{x_j}\mathbb{E}[|\mathbf{A}_{1,i;j}|_1\mid\mathcal{F}_0] + \mathbb{E}[|\mathbf{B}_1|_1]\\& \leq \sum_{j=1}^d x_j\varrho + \mathbb{E}[|\mathbf{B}_1|_1] = \varrho |x|_1+\mathbb{E}[|\mathbf{B}_1|_1]. \end{align*}

Note also that $\mathbb{E}[|F(0,Z_{1})|]=\mathbb{E}[|\mathbf{B}_{1}|_{1}]<\infty$ , as required by (12). We may conclude the required result from Proposition 2.

Remark 9. In the case where the sequence $\mathbf{A}_{n,\cdot;\cdot}$ , $n\in\mathbb{N}$ , is i.i.d., we have $m_i=\mathbb{E}[\mathbf{A}_{1,1;i}\mid\mathcal{F}_0]=\mathbb{E}[\mathbf{A}_{1,1;i}]$ . In that case, the standard assumption is that the matrix M composed from row vectors $m_i$ satisfies

(20) \begin{equation} \varrho(M)<1, \end{equation}

where $\varrho(M)$ denotes the spectral radius [33]. Our (19) is stronger than (20). In arguments for i.i.d. $\mathbf{A}_{n,\cdot;\cdot}$ , the general case (20) can be easily reduced to (19). However, it is not clear to us how to do so in the current, non-independent, setting. Perhaps the techniques of [16, Theorem 4] could be adapted.

7. Open problems

The study of iterated random functions driven by stationary and ergodic sequences, particularly their strong stability, opens several intriguing avenues for future research. While we have established foundational results and explored various applications, there remain numerous questions that merit further investigation. Addressing these open problems could not only deepen our understanding of the underlying theoretical framework but also expand its applicability to broader contexts. Below, we outline several key areas where additional research could be highly beneficial, identifying specific challenges and potential directions for future work.

For instance, Theorem 1 implies weak convergence of the laws of the process $X_{n}$ . A particularly intriguing question is under what conditions we could strengthen this to, e.g., convergence in total variation. Furthermore, it is also not uninteresting whether we could relax the contractivity condition (3) to some kind of dissipativity condition. This was done in [49] only for a particular class of Gaussian infinite moving average processes $Z_{n}$ , using heavy technicalities. As for the strong law of large numbers, the condition deduced in Remark 2 to ensure $\mathbb{E}\{|V^\ast|\}<\infty$ also looks too restrictive. Can this assumption be weakened in a reasonable way?

The Lindley iteration is addressed in [17, Theorem 4.1] when $\{Z_i\}_{-\infty}^{\infty}$ is i.i.d., noting that the condition $\mathbb{E}\{Z_1\}<0$ can be weakened to

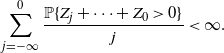\begin{align*}\sum_{j=-\infty}^0\frac{\mathbb{P}\{Z_j+\cdots+Z_0>0\} }{j}<\infty.\end{align*}

We hypothesize that this observation is valid for the ergodic case as well.

In Section 5, we studied Langevin iteration driven by stationary and ergodic noise under the strong convexity assumption. It would be desirable to replace this with a dissipativity condition, thereby extending the analysis beyond the convex case.

The limit distribution of the inhomogeneous Galton–Watson processes, which means that the driving processes are independent but not identically distributed, was studied in [27, 28]. A challenging research problem is how to weaken the independence. Finally, we conjecture that the condition (19) we imposed on the expected number of offspring in the Galton–Watson process could certainly be relaxed with more sophisticated arguments.