1 Introduction
Incipient yield of dense assemblies of granular materials and their subsequent flows pose many modelling challenges. In slow-flow problems, stress does not depend on the rate of deformation in the flow regions or only weakly so (Schofield & Wroth Reference Schofield and Wroth1968). Initially dense assemblies of particles exhibit dilation upon shear deformation, while loose assemblies compact (Reynolds Reference Reynolds1885; Schofield & Wroth Reference Schofield and Wroth1968). Furthermore, much of the deformation is often localized in dynamic shear bands separating non-deforming or weakly deforming regions; the particle volume fraction and velocity fields manifest sharp variations across the shear layer (Desrues et al. Reference Desrues, Chambon, Mokni and Mazerolle1996). These shear bands can form near boundaries (walls) or in the interior of the flow domain.
There is a long history of modelling the order-zero dependence of stress on rate of deformation and the dilation or compaction upon deformation through a combination of yield function and flow rule, which are two essential components of plasticity theories (Schofield & Wroth Reference Schofield and Wroth1968). Such models permit discontinuous changes in the velocity field, corresponding to shear bands of zero thickness. In reality, however, the width of the shear bands is of the order of ten particle diameters. How the standard plasticity models should be augmented to predict both the finite size of the shear band and the flow behaviour inside it has been studied by many research groups.
Additive models (Johnson & Jackson Reference Johnson and Jackson1987) which combine the (frictional) stress transmitted through enduring contact between particles in an assembly (modelled via classical plasticity theory) and the inertial stress resulting from the fluctuating motion of particles (modelled via kinetic theory of granular flows) have been used previously to investigate flows in the so-called intermediate regime (where both collisional and frictional stresses are important). Flow in the shear band was hypothesized to fall into this regime. Savage (Reference Savage1998) went further and modified the plasticity theory capturing the effects of strain rate fluctuations on yield via its standard deviation  $\unicode[STIX]{x1D716}$ and proposed a relation between
$\unicode[STIX]{x1D716}$ and proposed a relation between  $\unicode[STIX]{x1D716}$ and the local granular temperature. In these models, granular inertia is central to the formation of shear layers. However, shear bands do form even at extremely slow flows where inertial effects are no more than a minor perturbation. This consideration has led to the search for models that do not include the granular temperature and also preserve the order-zero dependence on rate. Dsouza & Nott (Reference Dsouza and Nott2020) summarize the literature on such models, which introduce non-locality to generate a non-zero length scale for the shear layer. However, these models focus on the velocity profile in the shear band but ignore dilation (e.g. Bouzid et al. Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Henann & Kamrin Reference Henann and Kamrin2013).
$\unicode[STIX]{x1D716}$ and the local granular temperature. In these models, granular inertia is central to the formation of shear layers. However, shear bands do form even at extremely slow flows where inertial effects are no more than a minor perturbation. This consideration has led to the search for models that do not include the granular temperature and also preserve the order-zero dependence on rate. Dsouza & Nott (Reference Dsouza and Nott2020) summarize the literature on such models, which introduce non-locality to generate a non-zero length scale for the shear layer. However, these models focus on the velocity profile in the shear band but ignore dilation (e.g. Bouzid et al. Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Henann & Kamrin Reference Henann and Kamrin2013).
2 Overview
Dsouza & Nott (Reference Dsouza and Nott2020) present a model that (a) does not introduce new variables such as fluidity (Henann & Kamrin Reference Henann and Kamrin2013), (b) does not require particle inertia and (c) allows for dilation in the shear layer. Although this model shows promising comparison with computational results obtained through discrete element method (DEM) simulations, loose ends remain which warrant further investigation.
While the standard plasticity theory assumes that the yield function and the flow rule can be expressed strictly in terms of local stress and particle volume fraction, Dsouza & Nott (Reference Dsouza and Nott2020) begin with a postulate that the dynamic response of the assembly at any location is affected by the state of the particle assembly in the neighbourhood of the location under consideration, for which there is ample experimental support. This provides a mechanism to introduce non-locality into the model, which could be thought of as a consequence of dynamic force chains that arise in dense flows. To be precise, the authors make the following postulates: (a) the local deviatoric rate of deformation and the local rate of dilation are determined by the local average deviatoric stress and the local average of the derivative of the yield function with pressure, respectively, instead of their local values as in classical plasticity theory and (b) the critical pressure at any location is affected not only by the local particle volume fraction (as in classical plasticity theory) but also by its spatial variation in the averaging region. Savage (Reference Savage1998) posited that strain rate variations affect the local stress, while Dsouza & Nott (Reference Dsouza and Nott2020) postulate the opposite, namely that the spatial distribution of stress in a neighbourhood around the point of interest affects the local strain rate, which is equally, if not more, reasonable. They then assume that the spatial variations are only gradual, estimate the integrals involved in the local average via Taylor series and arrive at (2.9) in their paper, which is a non-local extension of the standard plasticity theory. This extension removes the Hadamard ill-posedness associated with classical plasticity models.
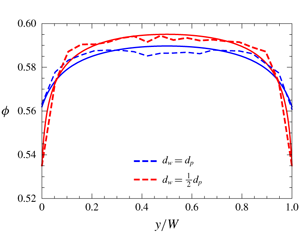
This model does not introduce any new variable such as fluidity which requires its own evolution equation and boundary conditions. Instead, it introduces the radius of the averaging region  $\ell$ as a new parameter, which is set to ten particle diameters. Dsouza & Nott (Reference Dsouza and Nott2020) show that this model can be used to fit the DEM results from simple shear flows with and without gravity in the shear direction by adjusting the values of the wall slip coefficient and the ratio of wall and bulk friction coefficients. The figure by the title of this article, taken from Dsouza & Nott (Reference Dsouza and Nott2020), compares the predictions of their model for wall-bounded shear flows in the absence of gravity with the corresponding DEM results for two different sets of bumpy walls. In this figure the ordinate refers to particle volume fraction and the abscissa is the scaled position in the gap. The solid lines show model predictions while the dashed lines refer to DEM results. The bumpier wall produces more dilation near the wall. As the authors acknowledge, the need to fit these parameters is unsatisfactory, but it is encouraging that the same set of fitting parameters apply equally in the presence and absence of gravity, suggesting that predictive models or simple calibration rules can be developed in the future for these parameters.
$\ell$ as a new parameter, which is set to ten particle diameters. Dsouza & Nott (Reference Dsouza and Nott2020) show that this model can be used to fit the DEM results from simple shear flows with and without gravity in the shear direction by adjusting the values of the wall slip coefficient and the ratio of wall and bulk friction coefficients. The figure by the title of this article, taken from Dsouza & Nott (Reference Dsouza and Nott2020), compares the predictions of their model for wall-bounded shear flows in the absence of gravity with the corresponding DEM results for two different sets of bumpy walls. In this figure the ordinate refers to particle volume fraction and the abscissa is the scaled position in the gap. The solid lines show model predictions while the dashed lines refer to DEM results. The bumpier wall produces more dilation near the wall. As the authors acknowledge, the need to fit these parameters is unsatisfactory, but it is encouraging that the same set of fitting parameters apply equally in the presence and absence of gravity, suggesting that predictive models or simple calibration rules can be developed in the future for these parameters.
In their example of simple shear with gravity, Dsouza & Nott (Reference Dsouza and Nott2020) observed dilation and shear flow in the vicinity of a sliding top plate, with an essentially static region forming near the bottom stationary boundary. This type of flow behaviour is well known. Their model could fit the simulation results only if the boundary condition first suggested for the bottom plate was enforced at an intermediate elevation, which was found to be a distance  $\ell$ away from the top plate in the two cases they present. It is reasonable to anticipate that this location will change with applied normal stress and/or the buoyant weight of particles (perhaps scaled with the critical state pressure to form proper dimensionless groups). The model can be used to make predictions only once a robust criterion to locate the boundary between deforming and non-deforming regions in terms of local variables has been developed and validated.
$\ell$ away from the top plate in the two cases they present. It is reasonable to anticipate that this location will change with applied normal stress and/or the buoyant weight of particles (perhaps scaled with the critical state pressure to form proper dimensionless groups). The model can be used to make predictions only once a robust criterion to locate the boundary between deforming and non-deforming regions in terms of local variables has been developed and validated.
3 Future
Dsouza & Nott (Reference Dsouza and Nott2020) have subjected the model to a limited set of tests thus far and more work is needed to fully assess the model. Specifically, they have only considered steady, simple shear flows, where the divergence of the velocity  $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ field is zero; thus, the components of the model that include
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ field is zero; thus, the components of the model that include  $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ (see equation (2.9c) in their paper) remain untested. They suggest dilation-driven secondary flows (Krishnaraj & Nott Reference Krishnaraj and Nott2016) and oscillatory shear where the assemblies undergo repeated dilation and compaction (Sun & Sundaresan Reference Sun and Sundaresan2011) as worthwhile tests. These would indeed be a key to understanding the merits and limitations of the model.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ (see equation (2.9c) in their paper) remain untested. They suggest dilation-driven secondary flows (Krishnaraj & Nott Reference Krishnaraj and Nott2016) and oscillatory shear where the assemblies undergo repeated dilation and compaction (Sun & Sundaresan Reference Sun and Sundaresan2011) as worthwhile tests. These would indeed be a key to understanding the merits and limitations of the model.
Sun & Sundaresan (Reference Sun and Sundaresan2011) studied, through DEM simulations, oscillatory shear of granular assemblies where shear reversal led to collapse of force chains and their gradual re-emergence in a different orientation. They found that the dynamics of shear reversal on stress could be quantified in terms of the fabric tensor  $\unicode[STIX]{x1D63C}$ and the contact coordination number
$\unicode[STIX]{x1D63C}$ and the contact coordination number  $Z$. They then proposed a local model for the evolution of
$Z$. They then proposed a local model for the evolution of  $\unicode[STIX]{x1D63C}$ and
$\unicode[STIX]{x1D63C}$ and  $Z$. It would be interesting to explore if the model proposed by Dsouza & Nott (Reference Dsouza and Nott2020) (their equation (2.9)) can capture the spontaneous occurrence of dilation and compaction in dynamic flows without further modification (although it is difficult to see how it can without introducing additional microstructural variables). If it were able to do so, it would not only demonstrate that a complex model accounting for the dynamics of microstructure evolution is not required to capture dilatancy and its effects but also tie these outcomes to non-locality of flow. If not, analysis of a model that integrates non-locality and the dynamics of microstructure evolution would be of interest as a natural next step.
$Z$. It would be interesting to explore if the model proposed by Dsouza & Nott (Reference Dsouza and Nott2020) (their equation (2.9)) can capture the spontaneous occurrence of dilation and compaction in dynamic flows without further modification (although it is difficult to see how it can without introducing additional microstructural variables). If it were able to do so, it would not only demonstrate that a complex model accounting for the dynamics of microstructure evolution is not required to capture dilatancy and its effects but also tie these outcomes to non-locality of flow. If not, analysis of a model that integrates non-locality and the dynamics of microstructure evolution would be of interest as a natural next step.
In summary, the non-local extension of the standard plasticity model proposed by Dsouza & Nott (Reference Dsouza and Nott2020) is based on readily understandable averaging, and it leads to a well-posed model. It allows for dilatancy across the shear layer and the initial tests of the model are promising. Much additional work remains to be done to fully test and refine the model as well as to develop a criterion to locate the boundary between deforming and non-deforming regions in terms of local variables.



1 Introduction
Incipient yield of dense assemblies of granular materials and their subsequent flows pose many modelling challenges. In slow-flow problems, stress does not depend on the rate of deformation in the flow regions or only weakly so (Schofield & Wroth Reference Schofield and Wroth1968). Initially dense assemblies of particles exhibit dilation upon shear deformation, while loose assemblies compact (Reynolds Reference Reynolds1885; Schofield & Wroth Reference Schofield and Wroth1968). Furthermore, much of the deformation is often localized in dynamic shear bands separating non-deforming or weakly deforming regions; the particle volume fraction and velocity fields manifest sharp variations across the shear layer (Desrues et al. Reference Desrues, Chambon, Mokni and Mazerolle1996). These shear bands can form near boundaries (walls) or in the interior of the flow domain.
There is a long history of modelling the order-zero dependence of stress on rate of deformation and the dilation or compaction upon deformation through a combination of yield function and flow rule, which are two essential components of plasticity theories (Schofield & Wroth Reference Schofield and Wroth1968). Such models permit discontinuous changes in the velocity field, corresponding to shear bands of zero thickness. In reality, however, the width of the shear bands is of the order of ten particle diameters. How the standard plasticity models should be augmented to predict both the finite size of the shear band and the flow behaviour inside it has been studied by many research groups.
Additive models (Johnson & Jackson Reference Johnson and Jackson1987) which combine the (frictional) stress transmitted through enduring contact between particles in an assembly (modelled via classical plasticity theory) and the inertial stress resulting from the fluctuating motion of particles (modelled via kinetic theory of granular flows) have been used previously to investigate flows in the so-called intermediate regime (where both collisional and frictional stresses are important). Flow in the shear band was hypothesized to fall into this regime. Savage (Reference Savage1998) went further and modified the plasticity theory capturing the effects of strain rate fluctuations on yield via its standard deviation $\unicode[STIX]{x1D716}$ and proposed a relation between
$\unicode[STIX]{x1D716}$ and proposed a relation between  $\unicode[STIX]{x1D716}$ and the local granular temperature. In these models, granular inertia is central to the formation of shear layers. However, shear bands do form even at extremely slow flows where inertial effects are no more than a minor perturbation. This consideration has led to the search for models that do not include the granular temperature and also preserve the order-zero dependence on rate. Dsouza & Nott (Reference Dsouza and Nott2020) summarize the literature on such models, which introduce non-locality to generate a non-zero length scale for the shear layer. However, these models focus on the velocity profile in the shear band but ignore dilation (e.g. Bouzid et al. Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Henann & Kamrin Reference Henann and Kamrin2013).
$\unicode[STIX]{x1D716}$ and the local granular temperature. In these models, granular inertia is central to the formation of shear layers. However, shear bands do form even at extremely slow flows where inertial effects are no more than a minor perturbation. This consideration has led to the search for models that do not include the granular temperature and also preserve the order-zero dependence on rate. Dsouza & Nott (Reference Dsouza and Nott2020) summarize the literature on such models, which introduce non-locality to generate a non-zero length scale for the shear layer. However, these models focus on the velocity profile in the shear band but ignore dilation (e.g. Bouzid et al. Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Henann & Kamrin Reference Henann and Kamrin2013).
2 Overview
Dsouza & Nott (Reference Dsouza and Nott2020) present a model that (a) does not introduce new variables such as fluidity (Henann & Kamrin Reference Henann and Kamrin2013), (b) does not require particle inertia and (c) allows for dilation in the shear layer. Although this model shows promising comparison with computational results obtained through discrete element method (DEM) simulations, loose ends remain which warrant further investigation.
While the standard plasticity theory assumes that the yield function and the flow rule can be expressed strictly in terms of local stress and particle volume fraction, Dsouza & Nott (Reference Dsouza and Nott2020) begin with a postulate that the dynamic response of the assembly at any location is affected by the state of the particle assembly in the neighbourhood of the location under consideration, for which there is ample experimental support. This provides a mechanism to introduce non-locality into the model, which could be thought of as a consequence of dynamic force chains that arise in dense flows. To be precise, the authors make the following postulates: (a) the local deviatoric rate of deformation and the local rate of dilation are determined by the local average deviatoric stress and the local average of the derivative of the yield function with pressure, respectively, instead of their local values as in classical plasticity theory and (b) the critical pressure at any location is affected not only by the local particle volume fraction (as in classical plasticity theory) but also by its spatial variation in the averaging region. Savage (Reference Savage1998) posited that strain rate variations affect the local stress, while Dsouza & Nott (Reference Dsouza and Nott2020) postulate the opposite, namely that the spatial distribution of stress in a neighbourhood around the point of interest affects the local strain rate, which is equally, if not more, reasonable. They then assume that the spatial variations are only gradual, estimate the integrals involved in the local average via Taylor series and arrive at (2.9) in their paper, which is a non-local extension of the standard plasticity theory. This extension removes the Hadamard ill-posedness associated with classical plasticity models.
This model does not introduce any new variable such as fluidity which requires its own evolution equation and boundary conditions. Instead, it introduces the radius of the averaging region $\ell$ as a new parameter, which is set to ten particle diameters. Dsouza & Nott (Reference Dsouza and Nott2020) show that this model can be used to fit the DEM results from simple shear flows with and without gravity in the shear direction by adjusting the values of the wall slip coefficient and the ratio of wall and bulk friction coefficients. The figure by the title of this article, taken from Dsouza & Nott (Reference Dsouza and Nott2020), compares the predictions of their model for wall-bounded shear flows in the absence of gravity with the corresponding DEM results for two different sets of bumpy walls. In this figure the ordinate refers to particle volume fraction and the abscissa is the scaled position in the gap. The solid lines show model predictions while the dashed lines refer to DEM results. The bumpier wall produces more dilation near the wall. As the authors acknowledge, the need to fit these parameters is unsatisfactory, but it is encouraging that the same set of fitting parameters apply equally in the presence and absence of gravity, suggesting that predictive models or simple calibration rules can be developed in the future for these parameters.
$\ell$ as a new parameter, which is set to ten particle diameters. Dsouza & Nott (Reference Dsouza and Nott2020) show that this model can be used to fit the DEM results from simple shear flows with and without gravity in the shear direction by adjusting the values of the wall slip coefficient and the ratio of wall and bulk friction coefficients. The figure by the title of this article, taken from Dsouza & Nott (Reference Dsouza and Nott2020), compares the predictions of their model for wall-bounded shear flows in the absence of gravity with the corresponding DEM results for two different sets of bumpy walls. In this figure the ordinate refers to particle volume fraction and the abscissa is the scaled position in the gap. The solid lines show model predictions while the dashed lines refer to DEM results. The bumpier wall produces more dilation near the wall. As the authors acknowledge, the need to fit these parameters is unsatisfactory, but it is encouraging that the same set of fitting parameters apply equally in the presence and absence of gravity, suggesting that predictive models or simple calibration rules can be developed in the future for these parameters.
In their example of simple shear with gravity, Dsouza & Nott (Reference Dsouza and Nott2020) observed dilation and shear flow in the vicinity of a sliding top plate, with an essentially static region forming near the bottom stationary boundary. This type of flow behaviour is well known. Their model could fit the simulation results only if the boundary condition first suggested for the bottom plate was enforced at an intermediate elevation, which was found to be a distance $\ell$ away from the top plate in the two cases they present. It is reasonable to anticipate that this location will change with applied normal stress and/or the buoyant weight of particles (perhaps scaled with the critical state pressure to form proper dimensionless groups). The model can be used to make predictions only once a robust criterion to locate the boundary between deforming and non-deforming regions in terms of local variables has been developed and validated.
$\ell$ away from the top plate in the two cases they present. It is reasonable to anticipate that this location will change with applied normal stress and/or the buoyant weight of particles (perhaps scaled with the critical state pressure to form proper dimensionless groups). The model can be used to make predictions only once a robust criterion to locate the boundary between deforming and non-deforming regions in terms of local variables has been developed and validated.
3 Future
Dsouza & Nott (Reference Dsouza and Nott2020) have subjected the model to a limited set of tests thus far and more work is needed to fully assess the model. Specifically, they have only considered steady, simple shear flows, where the divergence of the velocity $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ field is zero; thus, the components of the model that include
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ field is zero; thus, the components of the model that include  $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ (see equation (2.9c) in their paper) remain untested. They suggest dilation-driven secondary flows (Krishnaraj & Nott Reference Krishnaraj and Nott2016) and oscillatory shear where the assemblies undergo repeated dilation and compaction (Sun & Sundaresan Reference Sun and Sundaresan2011) as worthwhile tests. These would indeed be a key to understanding the merits and limitations of the model.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$ (see equation (2.9c) in their paper) remain untested. They suggest dilation-driven secondary flows (Krishnaraj & Nott Reference Krishnaraj and Nott2016) and oscillatory shear where the assemblies undergo repeated dilation and compaction (Sun & Sundaresan Reference Sun and Sundaresan2011) as worthwhile tests. These would indeed be a key to understanding the merits and limitations of the model.
Sun & Sundaresan (Reference Sun and Sundaresan2011) studied, through DEM simulations, oscillatory shear of granular assemblies where shear reversal led to collapse of force chains and their gradual re-emergence in a different orientation. They found that the dynamics of shear reversal on stress could be quantified in terms of the fabric tensor $\unicode[STIX]{x1D63C}$ and the contact coordination number
$\unicode[STIX]{x1D63C}$ and the contact coordination number  $Z$. They then proposed a local model for the evolution of
$Z$. They then proposed a local model for the evolution of  $\unicode[STIX]{x1D63C}$ and
$\unicode[STIX]{x1D63C}$ and  $Z$. It would be interesting to explore if the model proposed by Dsouza & Nott (Reference Dsouza and Nott2020) (their equation (2.9)) can capture the spontaneous occurrence of dilation and compaction in dynamic flows without further modification (although it is difficult to see how it can without introducing additional microstructural variables). If it were able to do so, it would not only demonstrate that a complex model accounting for the dynamics of microstructure evolution is not required to capture dilatancy and its effects but also tie these outcomes to non-locality of flow. If not, analysis of a model that integrates non-locality and the dynamics of microstructure evolution would be of interest as a natural next step.
$Z$. It would be interesting to explore if the model proposed by Dsouza & Nott (Reference Dsouza and Nott2020) (their equation (2.9)) can capture the spontaneous occurrence of dilation and compaction in dynamic flows without further modification (although it is difficult to see how it can without introducing additional microstructural variables). If it were able to do so, it would not only demonstrate that a complex model accounting for the dynamics of microstructure evolution is not required to capture dilatancy and its effects but also tie these outcomes to non-locality of flow. If not, analysis of a model that integrates non-locality and the dynamics of microstructure evolution would be of interest as a natural next step.
In summary, the non-local extension of the standard plasticity model proposed by Dsouza & Nott (Reference Dsouza and Nott2020) is based on readily understandable averaging, and it leads to a well-posed model. It allows for dilatancy across the shear layer and the initial tests of the model are promising. Much additional work remains to be done to fully test and refine the model as well as to develop a criterion to locate the boundary between deforming and non-deforming regions in terms of local variables.
Declaration of interests
The author reports no conflict of interest.