Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-08T00:15:57.416Z Has data issue: false hasContentIssue false
  • English
  • Français

ILL-POSEDNESS FOR THE COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH THE VELOCITY IN 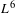$L^{6}$ FRAMEWORK

Part of: Equations of mathematical physics and other areas of application Parabolic equations and systems

Published online by Cambridge University Press:  29 June 2017

Jiecheng Chen  and
Renhui Wan
Jiecheng Chen
Affiliation:
Department of Mathematics, Zhejiang Normal University, Jinhua 321004, China ([email protected])
Renhui Wan
Affiliation:
School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, China ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Ill-posedness for the compressible Navier–Stokes equations has been proved by Chen et al. [On the ill-posedness of the compressible Navier–Stokes equations in the critical Besov spaces, Revista Mat. Iberoam.31 (2015), 1375–1402] in critical Besov space 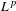$L^{p}$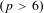$(p>6)$ framework. In this paper, we prove ill-posedness with the initial data satisfying

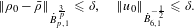$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{0}-\bar{\unicode[STIX]{x1D70C}}\Vert _{{\dot{B}}_{p,1}^{\frac{3}{p}}}\leqslant \unicode[STIX]{x1D6FF},\quad \Vert u_{0}\Vert _{{\dot{B}}_{6,1}^{-\frac{1}{2}}}\leqslant \unicode[STIX]{x1D6FF}. & & \displaystyle \nonumber\end{eqnarray}$$
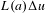To accomplish this goal, we require a norm inflation coming from the coupling term $L(a)\unicode[STIX]{x1D6E5}u$ instead of 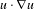$u\cdot \unicode[STIX]{x1D6FB}u$ and construct a new decomposition of the density.

Keywords

Navier–Stokes equationsill-posednessBesov space

MSC classification

Primary: 35Q35: PDEs in connection with fluid mechanics 35K55: Nonlinear parabolic equations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 829 - 854
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The original version of this article was submitted without an identified corresponding author. A notice detailing this has been published and the error rectified in the online PDF and HTML copies.

*

Author for correspondence.

References

Bahouri, H., Chemin, J.-Y. and Danchin, R., Fourier analysis and nonlinear partial differential equations, in Grundlehren der Mathematischen Wissenschaften (Springer, Heidelberg, 2011).Google Scholar
Bourgain, J. and Pavlović, N., Ill-posedness of the Navier–Stokes equations in a critical space in 3D, J. Func. Anal. 255 (2008), 2233–2247.Google Scholar
Charve, F. and Danchin, R., A global existence result for the compressible Navier–Stokes equations in the critical L p framework, Arch. Ration. Mech. Anal. 198 (2010), 233–271.Google Scholar
Chemin, J.-Y. and Lerner, N., Flow of non-Lipschitz vector-fields and Navier–Stokes equations, J. Differential Equations 121 (1995), 314–328.Google Scholar
Chen, Q., Miao, C. and Zhang, Z., Well-posedness in critical spaces for the compressible Navier–Stokes equations with density dependent viscosities, Rev. Mat. Iberoam. 26 (2010), 915–946.Google Scholar
Chen, Q., Miao, C. and Zhang, Z., Global well-posedness for compressible Navier–Stokes equations with highly oscillating initial velocity, Comm. Pure Appl. Math. 63 (2010), 1173–1224.Google Scholar
Chen, Q., Miao, C. and Zhang, Z., On the ill-posedness of the compressible Navier–Stokes equations in the critical Besov spaces, Rev. Mat. Iberoam. 31 (2015), 1375–1402.Google Scholar
Chikami, N. and Danchin, R., On the well-posedness of the full compressible Navier–Stokes system in critical Besov space, J. Differential Equations 258 (2015), 3435–3467.Google Scholar
Danchin, R., Global existence in critical spaces for compressible Navier–Stokes equations, Invent. Math. 141 (2000), 579–614.Google Scholar
Danchin, R., Global existence in critical spaces for flows of compressible viscous and heat-conductive gases, Arch. Ration. Mech. Anal. 160 (2001), 1–39.Google Scholar
Danchin, R., Local theory in critical spaces for compressible viscous and heat-conductive gases, Comm. Partial Differential Equations 26 (2001), 1183–1233.Google Scholar
Danchin, R., Well-posedness in critical spaces for barotropic viscous fluids with truly not constant density, Comm. Partial Differential Equations 32 (2007), 1373–1397.Google Scholar
Danchin, R., A Lagrangian approach for the compressible Navier–Stokes equations, Ann. Inst. Fourier 64 (2014), 753–791.Google Scholar
Feireisl, E., Dynamics of Viscous Vompressible Fluids (Oxford University Press, Oxford, 2004).Google Scholar
Fujita, H. and Kato, T., On the Navier–Stokes initial value problem I, Arch. Ration. Mech. Anal. 16 (1964), 269–315.Google Scholar
Germain, P., Multipliers, paramultipliers, and weak-strong uniqueness for the Navier–Stokes equations, J. Differential Equations 226 (2006), 373–428.Google Scholar
Germain, P., The second iterate for the Navier–Stokes equation, J. Funct. Anal. 255 (2008), 2248–2264.Google Scholar
Huang, X., Li, J. and Xin, Z., Global well-posedness of classical solutions with large oscillations and vacuum to the three dimensional isentropic compressible Navier–Stokes equations, Comm. Pure Appl. Math. 65 (2012), 549–585.Google Scholar
Kato, T. and Ponce, G., Commutator estimates and the Euler and Navier–Stokes equations, Comm. Pure Appl. Math. 41 (1988), 891–907.Google Scholar
Lions, P.-L., Mathematical Topics in Fluid Mechanics. Vol. 2. Compressible Models, Oxford Lecture Series in Mathematics and its Applications, Volume 10, (Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1998).Google Scholar
Matsumura, A. and Nishida, T., The initial value problem for the equations of motion of compressible viscous and heat-conductive fluids, Proc. Japan Acad. Ser. A Math. Sci. 55 (1979), 337–342.Google Scholar
Nash, J., Le problème de Cauchy pour les équations différentielles d’un fluide général, Bull. Soc. Math. France 90 (1962), 487–497.Google Scholar
Sun, Y., Wang, C. and Zhang, Z., A Beale–Kato–Majda Blow-up criterion for the 3-D compressible Navier–Stokes equations, J. Math. Pures Appl. 95 (2011), 36–47.Google Scholar
Sun, Y., Wang, C. and Zhang, Z., A Beale–Kato–Majda criterion for three dimensional compressible viscous heat-conductive flows, Arch. Ration. Mech. Anal. 201 (2011), 727–742.Google Scholar
Vasseur, A. F. and Yu, C., Existence of global weak solutions for 3D degenerate compressible Navier–Stokes equations, Invent. Math. 206 (2016), 935–974.Google Scholar
Wang, B., Ill-posedness for the Navier–Stokes equations in critical Besov spaces Ḃ ∞, q -1 , Adv. Math. 208 (2015), 350–372.Google Scholar
Wang, C., Wang, W. and Zhang, Z., Global well-posedness of compressible Navier–Stokes equations for some classes of large initial data, Arch. Ration. Mech. Anal. 213 (2014), 171–214.Google Scholar
Xin, Z., Blowup of smooth solutions to the compressible Navier–Stokes equation with compact density, Comm. Pure Appl. Math. 51 (1998), 229–240.Google Scholar
Yoneda, T., Ill-posedness of the 3D Navier–Stokes equations in a generalized Besov space near BMO -1 , J. Funct. Anal 258 (2010), 3376–3387.Google Scholar
Zhang, T., Global solutions of compressible Navier–Stokes equations with a density-dependent viscosity coefficient, J. Math. Phys 52 (2011), 043510.Google Scholar