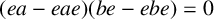1 Introduction
In [Reference Cojuhari and Gardner2], we studied connections between radicals and corners, subrings of the form
![]() $eAe$
where e is an idempotent of a ring A, including corner-hereditary radical classes, the radical classes
$eAe$
where e is an idempotent of a ring A, including corner-hereditary radical classes, the radical classes
![]() $\mathcal {R}$
satisfying the condition
$\mathcal {R}$
satisfying the condition
and corner-strict
![]() $\mathcal {R}$
, those satisfying
$\mathcal {R}$
, those satisfying
In [Reference Cojuhari and Gardner3], we investigated relative versions of these notions: hereditariness or strictness for corners defined by idempotents of some specified kind, for example, left semicentral idempotents. We also examined radical classes defined by the presence or absence of idempotents of various kinds.
In the present paper we revisit some of these concerns in the context of q-central idempotents as defined by Lam [Reference Lam5] for rings with identity. The q-central property is weaker than that of being left or right semicentral, but it is easily seen that all radical classes are hereditary for corners defined by q-central idempotents e since the map
is a homomorphism (endomorphism) of the ring A containing e precisely when e is q-central.
We also investigate the property HPC (hereditary for phantom corners) of radical classes
![]() $\mathcal {R}$
such that (in the notation of the Peirce decomposition)
$\mathcal {R}$
such that (in the notation of the Peirce decomposition)
This property also has relative forms such as HPC for left semicentral idempotents.
In [Reference Cojuhari and Gardner3], it was shown that normal radicals have HPC and all radical classes have HPC for left or right semicentral idempotents. Here, we show that all radical classes have HPC for what we call Peirce trivial idempotents (definition in the next section).
Now Peirce trivial is a stronger property than q-central and we have been unable to determine whether or not every radical class has HPC for q-central idempotents. However, in the final section, we present the first example (to our knowledge) of a radical class which lacks HPC.
Our notation and terminology are generally standard. Unexplained notions from radical theory can be found in [Reference Gardner and Wiegandt4]. Note though that as usual, we denote classes by upper case script rather than lower case Greek letters. The symbols
![]() $\lhd $
,
$\lhd $
,
![]() $<_l$
and
$<_l$
and
![]() $<_r$
denote ideals, left ideals and right ideals, respectively. The following notation is used for particular radical classes:
$<_r$
denote ideals, left ideals and right ideals, respectively. The following notation is used for particular radical classes:
2 q-central idempotents
Lam [Reference Lam5] calls an idempotent e of a ring A with identity q-central if it satisfies the condition
(Such idempotents are called inner-Peirce-trivial in [Reference Anh, Birkenmeier and van Wyk1].) The paper [Reference Lam5] contains several characterisations of q-central idempotents, some of which are related to the Peirce decomposition and can be extended without difficulty from rings with identity to rings in general.
The condition
![]() $eA(1-e)Ae = 0$
is equivalent to
$eA(1-e)Ae = 0$
is equivalent to
The two factors here are terms in the Peirce decomposition and we shall use the nonunital analogue of the second equation in our definition of q-central idempotents.
We first recall the Peirce decomposition. If e is an idempotent in a ring A, let
 $$ \begin{align*} A_{11} = eAe;& \quad A_{12} = \{ea - eae: a\in A\};\\ A_{21} = \{ae - eae: a\in A\};&\quad A_{22} = \{a-ea - ae + eae: a\in A\}. \end{align*} $$
$$ \begin{align*} A_{11} = eAe;& \quad A_{12} = \{ea - eae: a\in A\};\\ A_{21} = \{ae - eae: a\in A\};&\quad A_{22} = \{a-ea - ae + eae: a\in A\}. \end{align*} $$
Then A is the abelian group direct sum of
![]() $A_{11}$
,
$A_{11}$
,
![]() $A_{12}$
,
$A_{12}$
,
![]() $A_{21}$
and
$A_{21}$
and
![]() $A_{22}$
, and the multiplicative relationships between
$A_{22}$
, and the multiplicative relationships between
![]() $A_{11}$
,
$A_{11}$
,
![]() $A_{12}$
,
$A_{12}$
,
![]() $A_{21}$
and
$A_{21}$
and
![]() $A_{22}$
ensure the partial matrix ring
$A_{22}$
ensure the partial matrix ring
![]() $\big [\begin {smallmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end {smallmatrix} \big ]$
is well defined, and, moreover, is isomorphic to A. Both the additive representation and the matrix form can be called the Peirce decomposition of A with respect to e. In what follows, we shall always use the
$\big [\begin {smallmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end {smallmatrix} \big ]$
is well defined, and, moreover, is isomorphic to A. Both the additive representation and the matrix form can be called the Peirce decomposition of A with respect to e. In what follows, we shall always use the
![]() $A_{ij}$
notation (
$A_{ij}$
notation (
![]() $i,j = 1, 2$
) to describe Peirce decomposition and our use of the same notation for all idempotents should not be seriously ambiguous.
$i,j = 1, 2$
) to describe Peirce decomposition and our use of the same notation for all idempotents should not be seriously ambiguous.
We define an idempotent e of a ring A to be q-central if
This is a good point to show the relationship between q-central idempotents and some other types of idempotents. We have the following characterisation:
 $$ \begin{align*} q\text{-central}:&\ A_{12}A_{21} = 0;\\ \text{left semicentral}:&\ A_{12} = 0;\\ \text{right semicentral}:&\ A_{21} = 0;\\ \text{central}:&\ A_{12}=0 \text{ and } A_{21} = 0. \end{align*} $$
$$ \begin{align*} q\text{-central}:&\ A_{12}A_{21} = 0;\\ \text{left semicentral}:&\ A_{12} = 0;\\ \text{right semicentral}:&\ A_{21} = 0;\\ \text{central}:&\ A_{12}=0 \text{ and } A_{21} = 0. \end{align*} $$
It will be observed that
and
Indeed, the motivation in [Reference Lam5] for the term ‘q-central’ is that it is a weakening of ‘semicentral’ and could thus be thought of as ‘quarter-central’.
The next few results contain further characterisations of q-central idempotents, analogous to unital results in [Reference Anh, Birkenmeier and van Wyk1, Reference Lam5].
Theorem 2.1. For an idempotent e in a ring A, the following are equivalent:
-
(i) e is q-central;
-
(ii) the map
 $ A \to eAe: a \mapsto eae$
is a ring homomorphism;
$ A \to eAe: a \mapsto eae$
is a ring homomorphism; -
(iii)
 $eabe = eaebe \text { for all } a, b \in A$
.
$eabe = eaebe \text { for all } a, b \in A$
.
Proof. Since
![]() $eae \cdot ebe = eaebe$
, items (ii) and (iii) are equivalent.
$eae \cdot ebe = eaebe$
, items (ii) and (iii) are equivalent.
(i)
![]() $\Rightarrow $
(ii). For all
$\Rightarrow $
(ii). For all
![]() $a, b \in A$
,
$a, b \in A$
,
This argument is reversible, so also (ii)
![]() $\Rightarrow $
(i).
$\Rightarrow $
(i).
Adapting the terminology used in [Reference Anh, Birkenmeier and van Wyk1] for rings with identity, we say that an idempotent e in a ring A is Peirce trivial if
In rings with identity, e is Peirce trivial if and only if e and
![]() $1-e$
are both q-central.
$1-e$
are both q-central.
Theorem 2.2. For an idempotent e in a ring A, the following conditions are equivalent:
-
(i) e is q-central;
-
(ii)
 $A_{12} $
is a right ideal of A;
$A_{12} $
is a right ideal of A; -
(iii)
 $A_{21} $
is a left ideal of A.
$A_{21} $
is a left ideal of A.
Proof. (i)
![]() $\Leftrightarrow $
(ii). We have
$\Leftrightarrow $
(ii). We have
Hence,
![]() $A_{12}$
is a right ideal if and only if
$A_{12}$
is a right ideal if and only if
![]() $ A_{12}A_{21} \subseteq A_{12}$
. However,
$ A_{12}A_{21} \subseteq A_{12}$
. However,
![]() $A_{11} \cap A_{12} = 0$
so
$A_{11} \cap A_{12} = 0$
so
![]() $A_{12}$
is a right ideal if and only if
$A_{12}$
is a right ideal if and only if
![]() $A_{12}A_{21} =0$
, that is, e is q-central.
$A_{12}A_{21} =0$
, that is, e is q-central.
Similarly, (i)
![]() $\Leftrightarrow $
(iii).
$\Leftrightarrow $
(iii).
There is an analogous result for Peirce trivial idempotents.
Theorem 2.3. For an idempotent e in a ring A, the following are equivalent:
-
(i) e is Peirce trivial;
-
(ii)
 $A_{12} \lhd A$
;
$A_{12} \lhd A$
; -
(iii)
 $A_{21} \lhd A$
;
$A_{21} \lhd A$
; -
(iv)
 $A_{12} + A_{21} \lhd A$
;
$A_{12} + A_{21} \lhd A$
; -
(v)
 $A_{12} + A_{21}$
is an ideal of square zero.
$A_{12} + A_{21}$
is an ideal of square zero.
Proof. (i)
![]() $ \Rightarrow $
(ii) and (iii). Since e is Peirce trivial,
$ \Rightarrow $
(ii) and (iii). Since e is Peirce trivial,
Thus,
and since
![]() $A_{12}$
is a right ideal,
$A_{12}$
is a right ideal,
![]() $A_{12} \lhd A$
. Similarly,
$A_{12} \lhd A$
. Similarly,
![]() $A_{21} \lhd A.$
$A_{21} \lhd A.$
Clearly, (ii) and (iii)
![]() $\Rightarrow $
(iv).
$\Rightarrow $
(iv).
(iv)
![]() $\Rightarrow $
(i). If
$\Rightarrow $
(i). If
![]() $A_{12} + A_{21} \lhd A$
, then
$A_{12} + A_{21} \lhd A$
, then
However,
![]() $A_{12}A_{21} \subseteq A_{11}$
, so
$A_{12}A_{21} \subseteq A_{11}$
, so
![]() $A_{12}A_{21} =0$
. Similarly,
$A_{12}A_{21} =0$
. Similarly,
![]() $A_{21}A_{12} = 0$
, so e is Peirce trivial.
$A_{21}A_{12} = 0$
, so e is Peirce trivial.
Finally, if
![]() $A_{12} + A_{21} \lhd A$
, then
$A_{12} + A_{21} \lhd A$
, then
so (iv)
![]() $\Rightarrow $
(v).
$\Rightarrow $
(v).
Using Theorems 2.1, 2.2 and 2.3, we can see that for semiprime rings, all our centrality properties coincide. For if e is a q-central idempotent of a semiprime ring A, then
![]() $A_{12}$
and
$A_{12}$
and
![]() $A_{21}$
are one-sided ideals of square zero, so that
$A_{21}$
are one-sided ideals of square zero, so that
![]() $A_{12} = 0 = A_{21}$
and e is therefore central.
$A_{12} = 0 = A_{21}$
and e is therefore central.
3 Connections with radicals
Our first result is almost immediate.
Theorem 3.1. Every radical class
![]() $\mathcal {R}$
is hereditary, but not necessarily very hereditary, for corners defined by q-central idempotents.
$\mathcal {R}$
is hereditary, but not necessarily very hereditary, for corners defined by q-central idempotents.
Proof. If
![]() $e\in A \in \mathcal {R}$
and e is a q-central idempotent, then
$e\in A \in \mathcal {R}$
and e is a q-central idempotent, then
![]() $eAe$
is a homomorphic image of A and hence is in
$eAe$
is a homomorphic image of A and hence is in
![]() $\mathcal {R}$
. By [Reference Cojuhari and Gardner3, Theorem 2.1], radical classes need not be very hereditary for corners defined by semicentral idempotents and hence for q-central idempotents.
$\mathcal {R}$
. By [Reference Cojuhari and Gardner3, Theorem 2.1], radical classes need not be very hereditary for corners defined by semicentral idempotents and hence for q-central idempotents.
Theorem 3.2 (See [Reference Cojuhari and Gardner3, Proposition 2.3]).
If
![]() $\mathcal {S}$
is the semisimple class corresponding to a radical class
$\mathcal {S}$
is the semisimple class corresponding to a radical class
![]() $\mathcal {R}$
containing all nilpotent rings, then
$\mathcal {R}$
containing all nilpotent rings, then
![]() $\mathcal {S}$
is hereditary for corners defined by q-central idempotents and hence
$\mathcal {S}$
is hereditary for corners defined by q-central idempotents and hence
![]() $\mathcal {R}$
in strict for such corners.
$\mathcal {R}$
in strict for such corners.
Proof. All rings in
![]() $\mathcal {S}$
are semiprime, so q-central = central for idempotents in rings in
$\mathcal {S}$
are semiprime, so q-central = central for idempotents in rings in
![]() $\mathcal {S}$
. The result now follows from [Reference Cojuhari and Gardner3, Theorem 2.1] and [Reference Cojuhari and Gardner2, Corollary 3.10].
$\mathcal {S}$
. The result now follows from [Reference Cojuhari and Gardner3, Theorem 2.1] and [Reference Cojuhari and Gardner2, Corollary 3.10].
Proposition 3.3. Any nonzero q-central idempotent in a prime ring is an identity.
Proof. Let e be a nonzero q-central idempotent in a prime ring A. Then as A is semiprime, e is central, so that
![]() $A=eAe \oplus I$
for an ideal I. Since A is prime and
$A=eAe \oplus I$
for an ideal I. Since A is prime and
![]() $e \neq 0$
, we have
$e \neq 0$
, we have
![]() $I=0$
and thus e is an identity for
$I=0$
and thus e is an identity for
![]() $eAe = A$
.
$eAe = A$
.
In [Reference Cojuhari and Gardner3], we studied radical classes defined by the presence or absence of idempotents of various kinds. This we shall now do for q-central idempotents, first showing that these satisfy some conditions considered in [Reference Cojuhari and Gardner3, page 4795]:
-
I(i) if e is a q-central idempotent of A and
 $I \lhd A$
, then
$I \lhd A$
, then
 $e+I$
is q-central in
$e+I$
is q-central in
 $A/I$
;
$A/I$
; -
I(ii) if
 $e \in I \lhd A$
and e is a q-central idempotent in A, then e is a q-central idempotent in I;
$e \in I \lhd A$
and e is a q-central idempotent in A, then e is a q-central idempotent in I; -
I(iii) if
 $e \in I \lhd A$
and e is a q-central idempotent in I, then e is a q-central idempotent in A.
$e \in I \lhd A$
and e is a q-central idempotent in I, then e is a q-central idempotent in A.
Items
![]() $I(i)$
and
$I(i)$
and
![]() $I(ii)$
are easily verified. If e is a q-central idempotent in I, then for all
$I(ii)$
are easily verified. If e is a q-central idempotent in I, then for all
![]() $a, b \in A$
, we have
$a, b \in A$
, we have
![]() $eabe = e(ea)(be)e = e(ea)e \cdot e (be) e = eae \cdot ebe$
.
$eabe = e(ea)(be)e = e(ea)e \cdot e (be) e = eae \cdot ebe$
.
By [Reference Cojuhari and Gardner3, Theorem 3.3], we have the following result.
Theorem 3.4. Let
![]() $\mathcal {R}_q$
be the class of rings of which every nonzero homomorphic image has a nonzero q-central idempotent. Then
$\mathcal {R}_q$
be the class of rings of which every nonzero homomorphic image has a nonzero q-central idempotent. Then
![]() $\mathcal {R}_q$
is a radical class and by items
$\mathcal {R}_q$
is a radical class and by items
![]() $I(i)$
,
$I(i)$
,
![]() $I(ii)$
and
$I(ii)$
and
![]() $I(iii)$
, its semi-simple class is
$I(iii)$
, its semi-simple class is
Our definition of
![]() $\mathcal {R}_q$
is analogous to the definitions, in [Reference Cojuhari and Gardner3, Examples 3.6 and 3.7], of
$\mathcal {R}_q$
is analogous to the definitions, in [Reference Cojuhari and Gardner3, Examples 3.6 and 3.7], of
![]() $\mathcal {R}_c$
(respectively
$\mathcal {R}_c$
(respectively
![]() $\mathcal {R}_{lsc}$
) as the class of rings, each nonzero homomorphic image of which has a nonzero central (respectively left semicentral) idempotent.
$\mathcal {R}_{lsc}$
) as the class of rings, each nonzero homomorphic image of which has a nonzero central (respectively left semicentral) idempotent.
Let
![]() $\mathcal {R}^{(q)} = \{ A:$
no homomorphic image of A has a nonzero q-central idempotent
$\mathcal {R}^{(q)} = \{ A:$
no homomorphic image of A has a nonzero q-central idempotent
![]() $\}$
. By [Reference Cojuhari and Gardner3, Theorem 3.8], and using items
$\}$
. By [Reference Cojuhari and Gardner3, Theorem 3.8], and using items
![]() $I(i)$
–
$I(i)$
–
![]() $I(iii)$
, we have the following result.
$I(iii)$
, we have the following result.
Theorem 3.5. The class
![]() $\mathcal {R}^{(q)}$
is a radical class and is the upper radical class defined by the class of subdirectly irreducible rings whose hearts contain nonzero q-central idempotents.
$\mathcal {R}^{(q)}$
is a radical class and is the upper radical class defined by the class of subdirectly irreducible rings whose hearts contain nonzero q-central idempotents.
By Proposition 3.3, a q-central idempotent of a heart must be an identity. Thus, using [Reference Cojuhari and Gardner3, Example 3.10] gives the following corollary.
Corollary 3.6.
![]() $\mathcal {R}^{(q)} = \mathcal {G}\ ( = \mathcal {R}^{(lsc)} = \mathcal {R}^{(c)})$
, where
$\mathcal {R}^{(q)} = \mathcal {G}\ ( = \mathcal {R}^{(lsc)} = \mathcal {R}^{(c)})$
, where
![]() $\mathcal {R}^{(c)}$
and
$\mathcal {R}^{(c)}$
and
![]() $\mathcal {R}^{(lsc)}$
are the analogues of
$\mathcal {R}^{(lsc)}$
are the analogues of
![]() $\mathcal {R}^{(q)}$
for central and left semicentral idempotents, respectively.
$\mathcal {R}^{(q)}$
for central and left semicentral idempotents, respectively.
In [Reference Cojuhari and Gardner3], we saw that
![]() $\mathcal {R}_c$
is the lower radical class defined by the rings with identity (Example 3.6) and
$\mathcal {R}_c$
is the lower radical class defined by the rings with identity (Example 3.6) and
![]() $\mathcal {R}_{lsc}$
is the lower radical class defined by all rings with left identities (Example 3.7). It could be interesting to find a characterisation of
$\mathcal {R}_{lsc}$
is the lower radical class defined by all rings with left identities (Example 3.7). It could be interesting to find a characterisation of
![]() $\mathcal {R}_q$
as a lower radical class (or even as an upper radical class). The best we can do at present is to find an upper radical class which is an upper bound of
$\mathcal {R}_q$
as a lower radical class (or even as an upper radical class). The best we can do at present is to find an upper radical class which is an upper bound of
![]() $\mathcal {R}_q$
.
$\mathcal {R}_q$
.
Proposition 3.7. If e is a nonzero q-central idempotent of a ring A, then A has a prime ideal I such that
![]() $e+I$
is an identity for
$e+I$
is an identity for
![]() $A/I$
.
$A/I$
.
Proof. Since A contains a nonzero idempotent element, it is not a prime radical ring. Now,
Hence, there is a prime ideal I for which
![]() $e\notin I$
. Then,
$e\notin I$
. Then,
![]() $A/I$
is a prime ring and
$A/I$
is a prime ring and
![]() $e+I$
is a q-central idempotent of an
$e+I$
is a q-central idempotent of an
![]() $A/I$
by item
$A/I$
by item
![]() $I(i)$
, so by Proposition 3.3,
$I(i)$
, so by Proposition 3.3,
![]() $e+I$
is an identity for
$e+I$
is an identity for
![]() $A/I$
.
$A/I$
.
Corollary 3.8. With the hypothesis of Proposition 3.7, A has a maximal ideal M such that
![]() $e+M$
is an identity of
$e+M$
is an identity of
![]() $A/M$
.
$A/M$
.
Proof. In Proposition 3.7,
![]() $A/I$
has a maximal ideal
$A/I$
has a maximal ideal
![]() $K/I$
such that
$K/I$
such that
![]() $A/K \cong (A/I)(K/I)$
has
$A/K \cong (A/I)(K/I)$
has
![]() $e+K$
as an identity. (Let
$e+K$
as an identity. (Let
![]() $K/I$
be maximal with respect to exclusion of
$K/I$
be maximal with respect to exclusion of
![]() $e+I$
.)
$e+I$
.)
The Brown–McCoy radical class
![]() $\mathcal {G}$
is hereditary, so its upper radical class
$\mathcal {G}$
is hereditary, so its upper radical class
![]() $U(\mathcal {G})$
is
$U(\mathcal {G})$
is
Theorem 3.9. We have
![]() $\mathcal {R}_q \subseteq U(\mathcal {G})$
.
$\mathcal {R}_q \subseteq U(\mathcal {G})$
.
Proof. If
![]() $A \in \mathcal {R}_q$
and B is a nonzero homomorphic image of A, then B has a nonzero q-central idempotent and hence, by Corollary 3.8, a homomorphic image which is a simple ring with identity. However, then
$A \in \mathcal {R}_q$
and B is a nonzero homomorphic image of A, then B has a nonzero q-central idempotent and hence, by Corollary 3.8, a homomorphic image which is a simple ring with identity. However, then
![]() $B \notin \mathcal {G}$
, so
$B \notin \mathcal {G}$
, so
![]() $A \in U(\mathcal {G})$
.
$A \in U(\mathcal {G})$
.
The containment in Theorem 3.9 is proper, as we shall see in Section 5. This section will also contain a counterexample to the converse of Proposition 3.7, that is, if a prime, even simple prime, factor ring has an identity which lifts to an idempotent, the latter need not be q-central.
4 The phantom corners problem
In [Reference Cojuhari and Gardner3, page 4194], we defined, for a radical class
![]() $\mathcal {R}$
, the property
$\mathcal {R}$
, the property
This can be relativised in the obvious way. For example, normal radical classes have HPC and all radical classes have HPC for left or right semicentral idempotents [Reference Cojuhari and Gardner3, pages 4794–4795].
We now examine HPC for q-central idempotents. Note that as all radical classes are hereditary for q-central idempotents, HPC for q-central idempotents requires that
![]() $A_{22} \in \mathcal {R}$
for all
$A_{22} \in \mathcal {R}$
for all
![]() $A \in \mathcal {R}$
and for all q-central idempotents.
$A \in \mathcal {R}$
and for all q-central idempotents.
Proposition 4.1. Every radical class
![]() $\mathcal {R}$
has HPC for Peirce trivial idempotents.
$\mathcal {R}$
has HPC for Peirce trivial idempotents.
Proof. Let
![]() $\mathcal {R}$
be a radical class and e a Peirce trivial idempotent of a ring
$\mathcal {R}$
be a radical class and e a Peirce trivial idempotent of a ring
![]() $A \in \mathcal {R}$
. By Theorem 2.3,
$A \in \mathcal {R}$
. By Theorem 2.3,
![]() $A_{12} + A_{21} \lhd A$
and so
$A_{12} + A_{21} \lhd A$
and so
![]() $A_{11} \oplus A_{12} \cong A/(A_{12} + A_{21}) \in \mathcal {R}$
, whence
$A_{11} \oplus A_{12} \cong A/(A_{12} + A_{21}) \in \mathcal {R}$
, whence
![]() $A_{22} \in \mathcal {R}$
.
$A_{22} \in \mathcal {R}$
.
We have been unable to determine whether all radical classes have HPC for all q-central idempotents, but there are affirmative answers in the presence of certain hypotheses.
Proposition 4.2. Every left or right hereditary radical class has HPC for q-central idempotents.
Proof. Let
![]() $\mathcal {R}$
be a left-hereditary radical class and e a q-central idempotent of a ring
$\mathcal {R}$
be a left-hereditary radical class and e a q-central idempotent of a ring
![]() $A \in \mathcal {R}$
. Then the map
$A \in \mathcal {R}$
. Then the map
is a ring homomorphism. Its kernel as a homomorphism of abelian groups is
![]() $ \big [\begin {smallmatrix} 0 & A_{12} \\ A_{21} & A_{22} \end {smallmatrix} \big ],$
so this is an ideal. Now,
$ \big [\begin {smallmatrix} 0 & A_{12} \\ A_{21} & A_{22} \end {smallmatrix} \big ],$
so this is an ideal. Now,
so
![]() $\big [\begin {smallmatrix} 0 & A_{12} \\ 0 & A_{22} \end {smallmatrix}\big ] \in \mathcal {R}$
. Since
$\big [\begin {smallmatrix} 0 & A_{12} \\ 0 & A_{22} \end {smallmatrix}\big ] \in \mathcal {R}$
. Since
and
we have
![]() $A_{22} \in \mathcal {R}$
as required. For the right hereditary case, use
$A_{22} \in \mathcal {R}$
as required. For the right hereditary case, use
![]() $\big [\begin {smallmatrix} 0 & 0 \\ A_{21} & A_{22} \end {smallmatrix}\big ]. $
$\big [\begin {smallmatrix} 0 & 0 \\ A_{21} & A_{22} \end {smallmatrix}\big ]. $
Remark 4.3.
-
(i) The requirement that
 $\mathcal {R}$
be left or right hereditary is weaker than the requirement that it be normal.
$\mathcal {R}$
be left or right hereditary is weaker than the requirement that it be normal. -
(ii) Whether
 $\mathcal {N}$
is normal or not depends on the Köthe problem, but
$\mathcal {N}$
is normal or not depends on the Köthe problem, but
 $\mathcal {N}$
is certainly left and right hereditary.
$\mathcal {N}$
is certainly left and right hereditary. -
(iii) Radical classes which are left or right hereditary are corner hereditary for all idempotents by [Reference Cojuhari and Gardner2, Proposition 3.1].
Proposition 4.4. If a radical class
![]() $\mathcal {R}$
contains all nilpotent rings, that is, if
$\mathcal {R}$
contains all nilpotent rings, that is, if
![]() $ \mathcal {B} \subseteq \mathcal {R}$
, then
$ \mathcal {B} \subseteq \mathcal {R}$
, then
![]() $\mathcal {R}$
has HPC for q-central idempotents.
$\mathcal {R}$
has HPC for q-central idempotents.
Proof. Let e be a q-central idempotent of
![]() $A \in \mathcal {R}$
. Then
$A \in \mathcal {R}$
. Then
![]() $A_{12}$
(respectively
$A_{12}$
(respectively
![]() $A_{21}$
) is a nilpotent right (respectively left) ideal of A by Theorem 2.2, so
$A_{21}$
) is a nilpotent right (respectively left) ideal of A by Theorem 2.2, so
![]() $A_{12} + A_{21} \subseteq \mathcal {B}(A)$
. Hence,
$A_{12} + A_{21} \subseteq \mathcal {B}(A)$
. Hence,
 $$ \begin{align*} A/ \mathcal{B}(A) =&\ (A_{11} + A_{12} + A_{21} + A_{22} ) / \mathcal{B}(A) \\ = &\ (A_{11} + A_{22} + \mathcal{B}(A) ) / \mathcal{B}(A) \\ \cong &\ (A_{11} + A_{22} ) / ( (A_{11} + A_{22} ) \cap \mathcal{B}(A) ). \end{align*} $$
$$ \begin{align*} A/ \mathcal{B}(A) =&\ (A_{11} + A_{12} + A_{21} + A_{22} ) / \mathcal{B}(A) \\ = &\ (A_{11} + A_{22} + \mathcal{B}(A) ) / \mathcal{B}(A) \\ \cong &\ (A_{11} + A_{22} ) / ( (A_{11} + A_{22} ) \cap \mathcal{B}(A) ). \end{align*} $$
Now,
as
![]() $\mathcal {B}$
is strongly hereditary, while
$\mathcal {B}$
is strongly hereditary, while
so
whence
![]() $A_{22} \in \mathcal {R}.$
$A_{22} \in \mathcal {R}.$
Remark 4.5.
-
(i) Although
 $\mathcal {B} \subseteq \mathcal {G}$
,
$\mathcal {B} \subseteq \mathcal {G}$
,
 $\mathcal {G}$
is neither left nor right hereditary.
$\mathcal {G}$
is neither left nor right hereditary. -
(ii) The radical class
 $\mathcal {T}$
is left and right hereditary, but
$\mathcal {T}$
is left and right hereditary, but
 $\mathcal {B} \nsubseteq \mathcal {T}$
.
$\mathcal {B} \nsubseteq \mathcal {T}$
. -
(iii) The results just proved show that if
 $\mathcal {R}$
and
$\mathcal {R}$
and
 $\mathcal {U}$
are radical classes,
$\mathcal {U}$
are radical classes,
 $\mathcal {R}$
is left or right hereditary and
$\mathcal {R}$
is left or right hereditary and
 $\mathcal {B} \subseteq \mathcal {U}$
, then
$\mathcal {B} \subseteq \mathcal {U}$
, then
 $\mathcal {R} \cap \mathcal {U}$
has HPC for q-central idempotents. For instance,
$\mathcal {R} \cap \mathcal {U}$
has HPC for q-central idempotents. For instance,
 $\mathcal {T} \cap \mathcal {G}$
has HPC for q-central idempotents.
$\mathcal {T} \cap \mathcal {G}$
has HPC for q-central idempotents.
5 A useful ring
In this section, we shall study the partial matrix ring
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
. We do not know whether all radical classes have HPC for q-central idempotents. In fact, we do not have any examples of radical classes without HPC, global or specialised. The next result gives an example of nonsatisfaction of HPC.
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
. We do not know whether all radical classes have HPC for q-central idempotents. In fact, we do not have any examples of radical classes without HPC, global or specialised. The next result gives an example of nonsatisfaction of HPC.
Theorem 5.1. The upper radical class
![]() $U(\{2\mathbb {Z} \})$
defined by
$U(\{2\mathbb {Z} \})$
defined by
![]() $\{2\mathbb {Z}\}$
is strict and corner-hereditary but does not satisfy HPC.
$\{2\mathbb {Z}\}$
is strict and corner-hereditary but does not satisfy HPC.
Proof. As all accessible subrings of
![]() $2\mathbb {Z}$
are ideals,
$2\mathbb {Z}$
are ideals,
![]() $U(\{2\mathbb {Z} \})$
is the class of rings which do not have nonzero homomorphisms to
$U(\{2\mathbb {Z} \})$
is the class of rings which do not have nonzero homomorphisms to
![]() $\{2\mathbb {Z}\}$
. Since
$\{2\mathbb {Z}\}$
. Since
we see that
![]() $U(\{ 2\mathbb {Z}\}) $
is strict.
$U(\{ 2\mathbb {Z}\}) $
is strict.
All rings with identity are in
![]() $U(\{ 2\mathbb {Z} \}) $
; in particular, all corners of all rings are in
$U(\{ 2\mathbb {Z} \}) $
; in particular, all corners of all rings are in
![]() $U(\{ 2\mathbb {Z} \} ) $
which is therefore corner-hereditary.
$U(\{ 2\mathbb {Z} \} ) $
which is therefore corner-hereditary.
We now consider the Peirce ring
![]() $\big [\begin {smallmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end {smallmatrix}\big ]$
of
$\big [\begin {smallmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end {smallmatrix}\big ]$
of
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
. Let
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
. Let
![]() $e = \big [\begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix}\big ]$
. Then,
$e = \big [\begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix}\big ]$
. Then,
 $$ \begin{align*} A_{11} = e \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right] e = \left[\begin{array}{cc} \mathbb{Z} & 0 \\ 0 & 0 \end{array}\right].\end{align*} $$
$$ \begin{align*} A_{11} = e \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right] e = \left[\begin{array}{cc} \mathbb{Z} & 0 \\ 0 & 0 \end{array}\right].\end{align*} $$
Also, for all m, n, x,
![]() $y \in \mathbb {Z}$
,
$y \in \mathbb {Z}$
,
It follows that
![]() $A_{12} = \big [\begin {smallmatrix} 0 & \mathbb {Z} \\ 0 & 0 \end {smallmatrix}\big ].$
Similar calculations complete the demonstration that
$A_{12} = \big [\begin {smallmatrix} 0 & \mathbb {Z} \\ 0 & 0 \end {smallmatrix}\big ].$
Similar calculations complete the demonstration that
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
itself is the Peirce decomposition matrix ring of our ring.
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
itself is the Peirce decomposition matrix ring of our ring.
Let
![]() $ f: \big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \to 2\mathbb {Z}$
be a ring homomorphism. Then as noted above,
$ f: \big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \to 2\mathbb {Z}$
be a ring homomorphism. Then as noted above,
![]() $f(A_{11})=0.$
Now,
$f(A_{11})=0.$
Now,
so
![]() $f(A_{12})=f(A_{11})f(A_{12})=0$
and
$f(A_{12})=f(A_{11})f(A_{12})=0$
and
![]() $f(A_{21})=f(A_{21})f(A_{11})=0.$
Finally,
$f(A_{21})=f(A_{21})f(A_{11})=0.$
Finally,
![]() $A_{21}A_{12}=A_{22}$
, so
$A_{21}A_{12}=A_{22}$
, so
Thus,
![]() $f=0$
and
$f=0$
and
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
is in
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
is in
![]() $U(\{ 2\mathbb {Z} \}) $
as is its corner
$U(\{ 2\mathbb {Z} \}) $
as is its corner
However,
![]() $A_{22} = \big [\begin {smallmatrix} 0 & 0 \\ 0 & 2\mathbb {Z} \end {smallmatrix}\big ] \cong 2\mathbb {Z} \notin U(\{ 2\mathbb {Z} \} ).$
$A_{22} = \big [\begin {smallmatrix} 0 & 0 \\ 0 & 2\mathbb {Z} \end {smallmatrix}\big ] \cong 2\mathbb {Z} \notin U(\{ 2\mathbb {Z} \} ).$
Proposition 5.2. The ring
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
has no nonzero q-central idempotents.
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
has no nonzero q-central idempotents.
Proof. The idempotents are the matrices
![]() $ \big [\begin {smallmatrix} 1 & 0 \\ z & 0 \end {smallmatrix}\big ] $
and
$ \big [\begin {smallmatrix} 1 & 0 \\ z & 0 \end {smallmatrix}\big ] $
and
![]() $ \big [\begin {smallmatrix} 1 & w \\ 0 & 0 \end {smallmatrix}\big ] $
, where
$ \big [\begin {smallmatrix} 1 & w \\ 0 & 0 \end {smallmatrix}\big ] $
, where
![]() $ z \in 2\mathbb {Z}$
and
$ z \in 2\mathbb {Z}$
and
![]() $ w \in \mathbb {Z}$
. The case
$ w \in \mathbb {Z}$
. The case
![]() $z = 0\ (= w)$
gives
$z = 0\ (= w)$
gives
![]() $ \big [\begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix}\big ] $
, which we shall continue to call e. We shall prove that none of these idempotents is q-central by testing their ‘multiplicative property’ on the matrices
$ \big [\begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix}\big ] $
, which we shall continue to call e. We shall prove that none of these idempotents is q-central by testing their ‘multiplicative property’ on the matrices
![]() $ \big [\begin {smallmatrix} 0 & 1 \\ 2 & 0 \end {smallmatrix}\big ] $
,
$ \big [\begin {smallmatrix} 0 & 1 \\ 2 & 0 \end {smallmatrix}\big ] $
,
![]() $ \big [\begin {smallmatrix} 0 & 1 \\ 2 & 2 \end {smallmatrix}\big ] $
and their product
$ \big [\begin {smallmatrix} 0 & 1 \\ 2 & 2 \end {smallmatrix}\big ] $
and their product
![]() $ \big [\begin {smallmatrix} 2 & 2 \\ 0 & 2 \end {smallmatrix}\big ] $
.
$ \big [\begin {smallmatrix} 2 & 2 \\ 0 & 2 \end {smallmatrix}\big ] $
.
Now, for all (even) z,
 $$ \begin{align*} \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] & \cdot \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 2 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] \\ & = \bigg[\begin{array}{cc} z & 0 \\ z^2 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} z & 0 \\ z^2 & 0 \end{array}\bigg] = \bigg[\begin{array}{cc} z^2 & 0 \\ z^3 & 0 \end{array}\bigg], \end{align*} $$
$$ \begin{align*} \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] & \cdot \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 2 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & 0 \\ z & 0 \end{array}\bigg] \\ & = \bigg[\begin{array}{cc} z & 0 \\ z^2 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} z & 0 \\ z^2 & 0 \end{array}\bigg] = \bigg[\begin{array}{cc} z^2 & 0 \\ z^3 & 0 \end{array}\bigg], \end{align*} $$
while
Since the equation
![]() $z^2 = 2 + 2z$
has no even integer solutions, the products are unequal.
$z^2 = 2 + 2z$
has no even integer solutions, the products are unequal.
Also, for all w,
 $$ \begin{align*} \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg] & \cdot \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 2 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg]\\ &= \bigg[\begin{array}{cc} 2w & 2w^2 \\ 0 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 2w & 2w^2 \\ 0 & 0 \end{array}\bigg] = \bigg[\begin{array}{cc} 4w^2 & 4w^3 \\ 0 & 0 \end{array}\bigg], \end{align*} $$
$$ \begin{align*} \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg] & \cdot \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 0 & 1 \\ 2 & 2 \end{array}\bigg] \bigg[\begin{array}{cc} 1 & w \\ 0 & 0 \end{array}\bigg]\\ &= \bigg[\begin{array}{cc} 2w & 2w^2 \\ 0 & 0 \end{array}\bigg] \bigg[\begin{array}{cc} 2w & 2w^2 \\ 0 & 0 \end{array}\bigg] = \bigg[\begin{array}{cc} 4w^2 & 4w^3 \\ 0 & 0 \end{array}\bigg], \end{align*} $$
while
However, the equation
![]() $ 2 = 4w^2$
has no integer solutions, so again the products are unequal.
$ 2 = 4w^2$
has no integer solutions, so again the products are unequal.
This proves that
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
has no nonzero q-central idempotents.
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
has no nonzero q-central idempotents.
Corollary 5.3.
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \notin \mathcal {R}_q. $
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \notin \mathcal {R}_q. $
Proposition 5.4.
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \in U(\mathcal {G}). $
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \in U(\mathcal {G}). $
Proof (outline).
The calculations involved in showing this result are lengthy, so we content ourselves with an outline. We have
and
which maps onto
![]() $\mathbb {Z}_2$
. Hence,
$\mathbb {Z}_2$
. Hence,
One shows that the ideals of
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
have the form
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
have the form
![]() $ \big [\begin {smallmatrix} p\mathbb {Z} & q\mathbb {Z} \\ 2r\mathbb {Z} & 2s\mathbb {Z} \end {smallmatrix}\big ] $
, where p, q, r,
$ \big [\begin {smallmatrix} p\mathbb {Z} & q\mathbb {Z} \\ 2r\mathbb {Z} & 2s\mathbb {Z} \end {smallmatrix}\big ] $
, where p, q, r,
![]() $s \in \mathbb {Z}$
, and there are certain relationships between p, q, r and s. It then turns out that each
$s \in \mathbb {Z}$
, and there are certain relationships between p, q, r and s. It then turns out that each
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] / \big [\begin {smallmatrix} p\mathbb {Z} & q\mathbb {Z} \\ 2r\mathbb {Z} & 2s\mathbb {Z} \end {smallmatrix}\big ]$
can be mapped onto
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] / \big [\begin {smallmatrix} p\mathbb {Z} & q\mathbb {Z} \\ 2r\mathbb {Z} & 2s\mathbb {Z} \end {smallmatrix}\big ]$
can be mapped onto
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] / \big [\begin {smallmatrix} 2\mathbb {Z} & 2\mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
or something similar and hence is not in
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] / \big [\begin {smallmatrix} 2\mathbb {Z} & 2\mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
or something similar and hence is not in
![]() $\mathcal {G}$
. Since no nonzero homomorphic image of
$\mathcal {G}$
. Since no nonzero homomorphic image of
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
is in
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
is in
![]() $\mathcal {G}$
, we have
$\mathcal {G}$
, we have
![]() $ \big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \in U(\mathcal {G}).$
$ \big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \in U(\mathcal {G}).$
By Theorem 3.9,
![]() $\mathcal {R}_q \subseteq U(\mathcal {G})$
. The next corollary follows from Proposition 5.4 and Corollary 5.3.
$\mathcal {R}_q \subseteq U(\mathcal {G})$
. The next corollary follows from Proposition 5.4 and Corollary 5.3.
Corollary 5.5. We have
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \in U(\mathcal {G}) \backslash \mathcal {R}_q$
, so
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ] \in U(\mathcal {G}) \backslash \mathcal {R}_q$
, so
![]() $ \mathcal {R}_q \subsetneqq U(\mathcal {G})$
.
$ \mathcal {R}_q \subsetneqq U(\mathcal {G})$
.
Our final result shows that the converse to Proposition 3.7 is false.
Proposition 5.6. If a simple factor ring has an identity which lifts to an idempotent, the latter need not be q-central.
Proof. The ring
and under this homomorphism,
![]() $\big [\begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix} \big ] \mapsto 1.$
However,
$\big [\begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix} \big ] \mapsto 1.$
However,
![]() $\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
has no nonzero q-central idempotents.
$\big [\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ 2\mathbb {Z} & 2\mathbb {Z} \end {smallmatrix}\big ]$
has no nonzero q-central idempotents.
In [Reference Cojuhari and Gardner2, Corollary 3.12], we showed that if a radical class
![]() $\mathcal {R}$
is very corner hereditary, then both
$\mathcal {R}$
is very corner hereditary, then both
![]() $\mathcal {R}$
and its semisimple class
$\mathcal {R}$
and its semisimple class
![]() $\mathcal {S}$
are corner-hereditary. The status of the converse is unknown. We can get a partial converse using material from this section.
$\mathcal {S}$
are corner-hereditary. The status of the converse is unknown. We can get a partial converse using material from this section.
Proposition 5.7. Let
![]() $\mathcal {R}$
be a radical class with semi-simple class
$\mathcal {R}$
be a radical class with semi-simple class
![]() $\mathcal {S}$
and suppose
$\mathcal {S}$
and suppose
![]() $\mathcal {R}$
contains all rings with identity. If
$\mathcal {R}$
contains all rings with identity. If
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
![]() $\mathcal {S}$
are both corner-hereditary, then
$\mathcal {S}$
are both corner-hereditary, then
![]() $\mathcal {R}$
is very corner-hereditary.
$\mathcal {R}$
is very corner-hereditary.
Proof. Let e be an idempotent in a ring A. Then
![]() $eAe \in \mathcal {R}$
. As
$eAe \in \mathcal {R}$
. As
![]() $\mathcal {S}$
is corner-hereditary,
$\mathcal {S}$
is corner-hereditary,
![]() $\mathcal {R}$
is corner strict by [Reference Cojuhari and Gardner2, Corollary 3.10], so
$\mathcal {R}$
is corner strict by [Reference Cojuhari and Gardner2, Corollary 3.10], so
![]() $eAe \subseteq \mathcal {R}(A)$
. However, then
$eAe \subseteq \mathcal {R}(A)$
. However, then
![]() $\mathcal {R}(eAe) = eAe = eAe \cap \mathcal {R}(A)$
, so
$\mathcal {R}(eAe) = eAe = eAe \cap \mathcal {R}(A)$
, so
![]() $\mathcal {R}$
is very corner-hereditary.
$\mathcal {R}$
is very corner-hereditary.
Example 5.8. As
![]() $U(2\mathbb {Z})$
is the upper radical class defined by the set of subrings of
$U(2\mathbb {Z})$
is the upper radical class defined by the set of subrings of
![]() $2\mathbb {Z}$
, which is strongly hereditary, the corresponding semi-simple class is strongly hereditary and hence corner-hereditary. All corners of all rings are in
$2\mathbb {Z}$
, which is strongly hereditary, the corresponding semi-simple class is strongly hereditary and hence corner-hereditary. All corners of all rings are in
![]() $\mathcal {R}$
, so
$\mathcal {R}$
, so
![]() $\mathcal {R}$
is corner-hereditary. It follows that
$\mathcal {R}$
is corner-hereditary. It follows that
![]() $U(2\mathbb {Z})$
is very corner-hereditary.
$U(2\mathbb {Z})$
is very corner-hereditary.