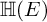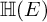1 Introduction
This work is a contribution to the study of distinguished complex representations for Galois symmetric spaces over a non-archimedean local field. It may be viewed as a continuation of [Reference Broussous and Courtès6] where the authors prove a particular case of Prasad’s conjecture on the distinction of the Steinberg representation ([Reference Prasad15], Conjecture 3, p. 77). However, even though the Bruhat-Tits building will be used here as a geometrical tool as in [Reference Broussous and Courtès6], our fundamental techniques will be that of integration of matrix coefficients, in the spirit of [Reference Broussous5].
We restrict ourselves to the easy case where the symmetric space is of the form
![]() ${\mathbb H}(E)/{\mathbb H}(F)$
, where
${\mathbb H}(E)/{\mathbb H}(F)$
, where
![]() $E/F$
is a quadratic unramified extension of non-archimedean local fields and
$E/F$
is a quadratic unramified extension of non-archimedean local fields and
![]() $\mathbb H$
a connected simple group defined and split over F. For simplicity sake, we shall assume that
$\mathbb H$
a connected simple group defined and split over F. For simplicity sake, we shall assume that
![]() $\mathbb H$
is simply connected. Indeed, in that case, the set of Iwahori subgroups of
$\mathbb H$
is simply connected. Indeed, in that case, the set of Iwahori subgroups of
![]() ${\mathbb H}(E)$
identifies with the set of chambers in the Bruhat-Tits building of
${\mathbb H}(E)$
identifies with the set of chambers in the Bruhat-Tits building of
![]() ${\mathbb H}(E)$
, and this makes our calculations less technical. However, our arguments should adapt easily to the non-simply connected case.
${\mathbb H}(E)$
, and this makes our calculations less technical. However, our arguments should adapt easily to the non-simply connected case.
Recall that a smooth complex representation
![]() $(\pi ,{\mathcal {V}} )$
of
$(\pi ,{\mathcal {V}} )$
of
![]() ${\mathbb H} (E)$
is said to be
${\mathbb H} (E)$
is said to be
![]() ${\mathbb H} (F)$
-distinguished if the intertwining space
${\mathbb H} (F)$
-distinguished if the intertwining space
![]() $\mathrm {Hom}_{{\mathbb H} (F)} \, ({\mathcal {V}} ,{\mathbb {C}} )$
is non-zero, where
$\mathrm {Hom}_{{\mathbb H} (F)} \, ({\mathcal {V}} ,{\mathbb {C}} )$
is non-zero, where
![]() ${\mathbb {C}}$
is a complex line with the trivial action of
${\mathbb {C}}$
is a complex line with the trivial action of
![]() ${\mathbb H} (F)$
. In this article, we study the distinction of Iwahori-spherical irreducible representations (i.e., representations
${\mathbb H} (F)$
. In this article, we study the distinction of Iwahori-spherical irreducible representations (i.e., representations
![]() $(\pi ,{\mathcal {V}} )$
such that
$(\pi ,{\mathcal {V}} )$
such that
![]() ${\mathcal {V}}^I\not = 0$
), where I is some fixed Iwahori subgroup of
${\mathcal {V}}^I\not = 0$
), where I is some fixed Iwahori subgroup of
![]() ${\mathbb H} (E)$
. If
${\mathbb H} (E)$
. If
![]() $(\pi ,{\mathcal {V}} )$
is such a representation, the Iwahori-Hecke algebra
$(\pi ,{\mathcal {V}} )$
is such a representation, the Iwahori-Hecke algebra
![]() ${\mathcal H}_{\mathrm {I}}$
of
${\mathcal H}_{\mathrm {I}}$
of
![]() ${\mathbb H} (E)$
relative to I acts on
${\mathbb H} (E)$
relative to I acts on
![]() $M={\mathcal {V}}^I$
via an irreducible representation
$M={\mathcal {V}}^I$
via an irreducible representation
![]() $(r,M)$
.
$(r,M)$
.
Our first result is the following.
Theorem 1.1 (Theorem 4.1).
Let
![]() $(\pi ,{\mathcal {V}} )$
be an Iwahori-spherical irreducible representation of
$(\pi ,{\mathcal {V}} )$
be an Iwahori-spherical irreducible representation of
![]() ${\mathbb H} (E)$
. Let J be any
${\mathbb H} (E)$
. Let J be any
![]() $\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of
$\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of
![]() ${\mathbb H}(E)$
. Then the obvious restriction map
${\mathbb H}(E)$
. Then the obvious restriction map
![]() $\mathrm {Hom}_{{\mathbb H} (F)}\, ({\mathcal {V}} ,{\mathbb {C}} )\longrightarrow \mathrm {Hom}_{{\mathbb {C}}}\, ({\mathcal {V}}^J ,{\mathbb {C}} )$
is injective.
$\mathrm {Hom}_{{\mathbb H} (F)}\, ({\mathcal {V}} ,{\mathbb {C}} )\longrightarrow \mathrm {Hom}_{{\mathbb {C}}}\, ({\mathcal {V}}^J ,{\mathbb {C}} )$
is injective.
As a consequence, if
![]() $\Lambda \in \mathrm {Hom}_{{\mathbb H} (F)} ({\mathcal {V}} ,{\mathbb {C}} )$
is non-zero, then for any
$\Lambda \in \mathrm {Hom}_{{\mathbb H} (F)} ({\mathcal {V}} ,{\mathbb {C}} )$
is non-zero, then for any
![]() $\mathrm {Gal}(E/F)$
-stable Iwahori subgroup J of
$\mathrm {Gal}(E/F)$
-stable Iwahori subgroup J of
![]() ${\mathbb H} (E)$
, there exists a vector
${\mathbb H} (E)$
, there exists a vector
![]() $v\in {\mathcal {V}}^J$
such that
$v\in {\mathcal {V}}^J$
such that
![]() $\Lambda (v)\not = 0$
.
$\Lambda (v)\not = 0$
.
The proofs of these results are based on a transitivity property of the action of
![]() ${\mathbb H} (F)$
on the set of chambers of the Bruhat-Tits building of
${\mathbb H} (F)$
on the set of chambers of the Bruhat-Tits building of
![]() ${\mathbb H} (E)$
, which was a crucial ingredient of [Reference Broussous and Courtès6].
${\mathbb H} (E)$
, which was a crucial ingredient of [Reference Broussous and Courtès6].
We next assume, moreover, that
![]() $(\pi ,{\mathcal {V}} )$
is a discrete series representation. Using the fact due to Zhang [Reference Zhang19] that
$(\pi ,{\mathcal {V}} )$
is a discrete series representation. Using the fact due to Zhang [Reference Zhang19] that
![]() ${\mathbb H} (E )/{\mathbb H} (F)$
is a very strongly discrete symmetric space, we establish a second result.
${\mathbb H} (E )/{\mathbb H} (F)$
is a very strongly discrete symmetric space, we establish a second result.
Theorem 1.2 (Theorem 5.3).
Let
![]() $(\pi ,{\mathcal {V}} )$
be an irreducible Iwahori-spherical discrete series representation of
$(\pi ,{\mathcal {V}} )$
be an irreducible Iwahori-spherical discrete series representation of
![]() ${\mathbb H} (E)$
. Let J be some
${\mathbb H} (E)$
. Let J be some
![]() $\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of
$\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of
![]() ${\mathbb H} (E)$
and
${\mathbb H} (E)$
and
![]() $\nu $
denote a Haar measure on
$\nu $
denote a Haar measure on
![]() ${\mathbb H} (F)$
.
${\mathbb H} (F)$
.
Then
![]() $(\pi ,{\mathcal {V}} )$
is
$(\pi ,{\mathcal {V}} )$
is
![]() ${\mathbb H} (F)$
-distinguished if, and only if, there exist
${\mathbb H} (F)$
-distinguished if, and only if, there exist
![]() $v\in {\mathcal {V}}^J$
,
$v\in {\mathcal {V}}^J$
,
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}^J}$
, such that
${\tilde v}\in {\tilde {{\mathcal {V}}}^J}$
, such that
 $$ \begin{align*}\int_{{\mathbb H} (F)} c_{v,{\tilde v}}(h)\, d\nu (h)\not= 0, \end{align*} $$
$$ \begin{align*}\int_{{\mathbb H} (F)} c_{v,{\tilde v}}(h)\, d\nu (h)\not= 0, \end{align*} $$
where
![]() $\tilde {{\mathcal {V}}}$
is the contragredient representation and
$\tilde {{\mathcal {V}}}$
is the contragredient representation and
![]() $c_{v, {\tilde v}}$
is the coefficient of
$c_{v, {\tilde v}}$
is the coefficient of
![]() $\pi $
attached to v and
$\pi $
attached to v and
![]() $\tilde v$
.
$\tilde v$
.
To turn the previous theorem into an effective criterion, we use the notion of generalized Poincaré series attached to an Iwahori-Hecke algebra introduced by Gyoja [Reference Gyoja11]. Let
![]() $(W,S)$
be a Coxeter system with associated Hecke algebra
$(W,S)$
be a Coxeter system with associated Hecke algebra
![]() ${\mathcal H}$
. Let
${\mathcal H}$
. Let
![]() $S_i$
,
$S_i$
,
![]() $i=1,...,m$
be the intersections of the conjugacy classes of W with S. For each representation
$i=1,...,m$
be the intersections of the conjugacy classes of W with S. For each representation
![]() $(r,M)$
of
$(r,M)$
of
![]() ${\mathcal H}$
, Gyoja attaches a power series
${\mathcal H}$
, Gyoja attaches a power series
![]() $L(t_1 ,...,t_m ,r)\in \mathrm {End}(M)\otimes _{\mathbb {C}} {\mathbb {C}} [[t_1 ,...,t_m ]]$
. Now assume that
$L(t_1 ,...,t_m ,r)\in \mathrm {End}(M)\otimes _{\mathbb {C}} {\mathbb {C}} [[t_1 ,...,t_m ]]$
. Now assume that
![]() ${\mathcal H}={\mathcal H}_{\mathrm {I}}$
is the Iwahori-Hecke algebra of
${\mathcal H}={\mathcal H}_{\mathrm {I}}$
is the Iwahori-Hecke algebra of
![]() ${\mathbb H} (E)$
relative to I and
${\mathbb H} (E)$
relative to I and
![]() $(r,M)$
is the representation associated to the
$(r,M)$
is the representation associated to the
![]() ${\mathcal H}_{\mathrm {I}}$
-module
${\mathcal H}_{\mathrm {I}}$
-module
![]() ${\mathcal {V}}^I$
, for a representation
${\mathcal {V}}^I$
, for a representation
![]() $(\pi , {\mathcal {V}} )$
of
$(\pi , {\mathcal {V}} )$
of
![]() ${\mathbb H} (E)$
.
${\mathbb H} (E)$
.
Theorem 1.3 (Theorem 7.1).
Let
![]() $(\pi ,{\mathcal {V}} )$
be an irreducible Iwahori-spherical discrete series representation of
$(\pi ,{\mathcal {V}} )$
be an irreducible Iwahori-spherical discrete series representation of
![]() ${\mathbb H} (E)$
. Then
${\mathbb H} (E)$
. Then
![]() $\pi $
is
$\pi $
is
![]() ${\mathbb H} (F)$
-distinguished if, and only if,
${\mathbb H} (F)$
-distinguished if, and only if,
![]() $L(1/q_o ,...,1/q_o ,r)\in \mathrm {End} (M)$
is non-zero, where
$L(1/q_o ,...,1/q_o ,r)\in \mathrm {End} (M)$
is non-zero, where
![]() $q_o$
is the size of the residue field of F.
$q_o$
is the size of the residue field of F.
Our last result is concerned with the case where the discrete series
![]() $(\pi ,{\mathcal {V}} )$
corresponds to a degree
$(\pi ,{\mathcal {V}} )$
corresponds to a degree
![]() $1$
character of
$1$
character of
![]() ${\mathcal H}_{\mathrm {I}}$
. Those representations were classified by A. Borel in [Reference Borel2]. It is by using techniques borrowed from loc. cit that we prove the following: the value of
${\mathcal H}_{\mathrm {I}}$
. Those representations were classified by A. Borel in [Reference Borel2]. It is by using techniques borrowed from loc. cit that we prove the following: the value of
![]() $L (t_1 ,...,t_m ,r)$
occuring in Theorem 1.3 can be calculated using a Macdonald’s Poincaré series (cf. [Reference Macdonald14]). Using Macdonald’s formulas, we obtain the following:
$L (t_1 ,...,t_m ,r)$
occuring in Theorem 1.3 can be calculated using a Macdonald’s Poincaré series (cf. [Reference Macdonald14]). Using Macdonald’s formulas, we obtain the following:
Theorem 1.4 (Theorem 7.4).
Let
![]() $(\pi ,{\mathcal {V}} )$
be an irreducible Iwahori-spherical discrete series representation of
$(\pi ,{\mathcal {V}} )$
be an irreducible Iwahori-spherical discrete series representation of
![]() ${\mathbb H} (E)$
such that
${\mathbb H} (E)$
such that
![]() ${\mathcal {V}}^I$
is
${\mathcal {V}}^I$
is
![]() $1$
-dimensional. If
$1$
-dimensional. If
![]() ${\mathbb H}$
is not of type
${\mathbb H}$
is not of type
![]() $G_2$
, then
$G_2$
, then
![]() $\pi $
is
$\pi $
is
![]() ${\mathbb H} (F)$
-distinguished if, and only if, it is the Steinberg representation. If
${\mathbb H} (F)$
-distinguished if, and only if, it is the Steinberg representation. If
![]() ${\mathbb H}$
has type
${\mathbb H}$
has type
![]() $G_2$
, there are two representations satisfying the assumptions of the theorem: the Steinberg representation and another one; they are both
$G_2$
, there are two representations satisfying the assumptions of the theorem: the Steinberg representation and another one; they are both
![]() ${\mathbb H} (F)$
-distinguished.
${\mathbb H} (F)$
-distinguished.
In other words, the Steinberg representation of
![]() ${\mathbb H} (E)$
is the unique representation satisfying the assumption of the theorem and which is
${\mathbb H} (E)$
is the unique representation satisfying the assumption of the theorem and which is
![]() ${\mathbb H} (F)$
-distinguished, except in type
${\mathbb H} (F)$
-distinguished, except in type
![]() $G_2$
where there is another one.
$G_2$
where there is another one.
The case of the Steinberg representation (originally D. Prasad’s conjecture) was already established in [Reference Broussous and Courtès6] (where
![]() ${\mathbb H}$
is not necessarily assumed simply connected) and in characteristic
${\mathbb H}$
is not necessarily assumed simply connected) and in characteristic
![]() $0$
, Prasad’s conjecture was entirely proved by Beuzart-Plessis [Reference Beuzart-Plessis1].
$0$
, Prasad’s conjecture was entirely proved by Beuzart-Plessis [Reference Beuzart-Plessis1].
Macdonald’s formulas [Reference Macdonald14] allow only to calculate Gyoja L-functions
![]() $L(t_1 ,...,t_m ,r)$
when r is a degree
$L(t_1 ,...,t_m ,r)$
when r is a degree
![]() $1$
character; this is why we are not able to give a classification of distinguished discrete series representations when
$1$
character; this is why we are not able to give a classification of distinguished discrete series representations when
![]() $\mathrm {dim}\, {\mathcal {V}}^I>1$
.
$\mathrm {dim}\, {\mathcal {V}}^I>1$
.
In [Reference Prasad16], Dipendra Prasad states a conjecture predicting the distinction of irreducible smooth complex representations in the case of a general Galois symmetric space
![]() ${\mathbb H} (E)/{\mathbb H} (F)$
(Conjecture 2 of loc. cit.). An irreducible smooth representation
${\mathbb H} (E)/{\mathbb H} (F)$
(Conjecture 2 of loc. cit.). An irreducible smooth representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathbb H} (E)$
conjecturally has a Langlands parameter
${\mathbb H} (E)$
conjecturally has a Langlands parameter
![]() $\phi _\pi $
:
$\phi _\pi $
:
![]() $W_E \times \mathrm {SL}_2 ({\mathbb {C}} )\longrightarrow {}^L G$
, where the Langlands dual
$W_E \times \mathrm {SL}_2 ({\mathbb {C}} )\longrightarrow {}^L G$
, where the Langlands dual
![]() ${}^L G$
is a semidirect product
${}^L G$
is a semidirect product
![]() $W_E\ltimes \widehat {G}$
,
$W_E\ltimes \widehat {G}$
,
![]() $\widehat {G}$
being the complex dual of
$\widehat {G}$
being the complex dual of
![]() $G={\mathbb H} (E)$
. Roughly speaking, the point of Prasad’s conjecture is to relate the
$G={\mathbb H} (E)$
. Roughly speaking, the point of Prasad’s conjecture is to relate the
![]() ${\mathbb H} (F)$
-distinction of
${\mathbb H} (F)$
-distinction of
![]() $\pi $
to properties of the parameter
$\pi $
to properties of the parameter
![]() $\varphi _\pi $
. A precise formulation of this conjecture in our case may be stated as follows (this formulation as well as the two following remarks are due to Prasad himself).
$\varphi _\pi $
. A precise formulation of this conjecture in our case may be stated as follows (this formulation as well as the two following remarks are due to Prasad himself).
Conjecture 1.5 (Prasad).
Let
![]() $E/F$
be a quadratic unramified extension of non-archimedean local fields. Let
$E/F$
be a quadratic unramified extension of non-archimedean local fields. Let
![]() ${\mathbb H}$
be a simply connected split simple group over F if
${\mathbb H}$
be a simply connected split simple group over F if
![]() $-1$
belongs to the Weyl group of
$-1$
belongs to the Weyl group of
![]() ${\mathbb H}$
, and the unique quasi-split (but not split) group over F which splits over E otherwise. (This ensures that the opposition group
${\mathbb H}$
, and the unique quasi-split (but not split) group over F which splits over E otherwise. (This ensures that the opposition group
![]() $H^{\mathrm {op}}$
of
$H^{\mathrm {op}}$
of
![]() $H={\mathbb H} (F)$
, defined in [Reference Prasad16], is split over F.) A Iwahori-spherical discrete series representation
$H={\mathbb H} (F)$
, defined in [Reference Prasad16], is split over F.) A Iwahori-spherical discrete series representation
![]() $\pi $
of
$\pi $
of
![]() $G={\mathbb H} (E)$
has, by the work of Kazhdan-Lusztig, cf. [Reference Kazhdan and Lusztig13], an
$G={\mathbb H} (E)$
has, by the work of Kazhdan-Lusztig, cf. [Reference Kazhdan and Lusztig13], an
![]() $\mathrm {L}$
-parameter
$\mathrm {L}$
-parameter
![]() $\phi : W_E \times \mathrm {SL}_2({\mathbb {C}} ) \rightarrow {}^LG$
which on
$\phi : W_E \times \mathrm {SL}_2({\mathbb {C}} ) \rightarrow {}^LG$
which on
![]() $W_E$
factors through an unramified extension of E. Assume that the group of connected components of the centralizer of the corresponding unipotent element in
$W_E$
factors through an unramified extension of E. Assume that the group of connected components of the centralizer of the corresponding unipotent element in
![]() $\widehat {G}$
is an elementary abelian
$\widehat {G}$
is an elementary abelian
![]() $2$
-group (which is known to be the case for all groups of type
$2$
-group (which is known to be the case for all groups of type
![]() $B_n,C_n,D_n$
). Then
$B_n,C_n,D_n$
). Then
![]() $\pi $
is distinguished by
$\pi $
is distinguished by
![]() $H= {\mathbb H} (F)$
if and only if
$H= {\mathbb H} (F)$
if and only if
-
1. The restriction of
 $\phi $
to
$\phi $
to
 $W_E$
is trivial,
$W_E$
is trivial, -
2. The representation
 $\pi $
is generic. (Under condition (1), genericity should not depend on the choice of the Whittaker datum.)
$\pi $
is generic. (Under condition (1), genericity should not depend on the choice of the Whittaker datum.)
Further, if the conditions (1) and (2) are satisfied, then
![]() $\mathrm {dim} \, \mathrm {Hom}_{H}\, (\pi , {\mathbb {C}} )$
is the order of the centralizer of
$\mathrm {dim} \, \mathrm {Hom}_{H}\, (\pi , {\mathbb {C}} )$
is the order of the centralizer of
![]() $\phi (\mathrm {SL}_2({\mathbb {C}} ))$
in
$\phi (\mathrm {SL}_2({\mathbb {C}} ))$
in
![]() $ \hat {G}$
, which by assumption, is a finite elementary abelian 2-group.
$ \hat {G}$
, which by assumption, is a finite elementary abelian 2-group.
Remark 1. We relate the above conjecture to that in [Reference Prasad16]. In the present case,
![]() $W_F \times \mathrm {SL}_2({\mathbb {C}} )$
and
$W_F \times \mathrm {SL}_2({\mathbb {C}} )$
and
![]() $W_E\times \mathrm {SL}_2({\mathbb {C}})$
can be replaced by
$W_E\times \mathrm {SL}_2({\mathbb {C}})$
can be replaced by
![]() $\langle \mathrm {Fr}^{\mathbb Z} \rangle \times \mathrm {SL}_2({\mathbb {C}} )$
and
$\langle \mathrm {Fr}^{\mathbb Z} \rangle \times \mathrm {SL}_2({\mathbb {C}} )$
and
![]() $\langle \mathrm {Fr}^{2\mathbb Z} \rangle \times \mathrm {SL}_2({\mathbb {C}})$
, where
$\langle \mathrm {Fr}^{2\mathbb Z} \rangle \times \mathrm {SL}_2({\mathbb {C}})$
, where
![]() $\mathrm {Fr}$
is a Frobenius element of
$\mathrm {Fr}$
is a Frobenius element of
![]() $W_F$
. Because of the hypothesis in the conjecture,
$W_F$
. Because of the hypothesis in the conjecture,
![]() $\pi _0 (Z_{\widehat {G}}(\phi ( \mathrm {SL}_2({\mathbb {C}} ))))$
being an elementary abelian
$\pi _0 (Z_{\widehat {G}}(\phi ( \mathrm {SL}_2({\mathbb {C}} ))))$
being an elementary abelian
![]() $2$
-group,
$2$
-group,
![]() $\langle \mathrm {Fr}^{2\mathbb Z} \rangle $
must land inside the connected component of identity of
$\langle \mathrm {Fr}^{2\mathbb Z} \rangle $
must land inside the connected component of identity of
![]() $Z_{\widehat {G}}(\phi (\mathrm {SL}_2({\mathbb {C}} )))$
. Hence, by the discreteness of the parameter
$Z_{\widehat {G}}(\phi (\mathrm {SL}_2({\mathbb {C}} )))$
. Hence, by the discreteness of the parameter
![]() $\phi $
,
$\phi $
,
![]() $Z_{\widehat {G}}(\phi (\mathrm {SL}_2({\mathbb {C}} )))$
must be finite and therefore an elementary abelian
$Z_{\widehat {G}}(\phi (\mathrm {SL}_2({\mathbb {C}} )))$
must be finite and therefore an elementary abelian
![]() $2$
-group, and the image of
$2$
-group, and the image of
![]() $\langle \mathrm {Fr}^{2\mathbb Z} \rangle $
under
$\langle \mathrm {Fr}^{2\mathbb Z} \rangle $
under
![]() $\phi $
must be trivial, which is the conclusion in part (1) of the conjecture. Further, the natural map from the component group of a lifted parameter
$\phi $
must be trivial, which is the conclusion in part (1) of the conjecture. Further, the natural map from the component group of a lifted parameter
![]() $\tilde {\phi }$
for
$\tilde {\phi }$
for
![]() $H^{\mathrm {op}}$
to the component group for
$H^{\mathrm {op}}$
to the component group for
![]() $\phi $
is clearly an isomorphism. Hence, by the conjecture of [Reference Prasad16], the only
$\phi $
is clearly an isomorphism. Hence, by the conjecture of [Reference Prasad16], the only
![]() $\pi $
corresponding to the trivial character of the component group can be distinguished, which is the conclusion in part (2) of the conjecture.
$\pi $
corresponding to the trivial character of the component group can be distinguished, which is the conclusion in part (2) of the conjecture.
Remark 2. Here is the example of
![]() $G_2$
, which appears in this work but for which the hypothesis in the conjecture above does not hold. There is a discrete series representation
$G_2$
, which appears in this work but for which the hypothesis in the conjecture above does not hold. There is a discrete series representation
![]() $\pi $
of
$\pi $
of
![]() $G_2 (E)$
which has a one dimensional fixed vector for an Iwahori subgroup, which by Reeder [Reference Reeder17], page 480, corresponds to a subregular unipotent element with component group isomorphic to
$G_2 (E)$
which has a one dimensional fixed vector for an Iwahori subgroup, which by Reeder [Reference Reeder17], page 480, corresponds to a subregular unipotent element with component group isomorphic to
![]() $S_3$
with the representation of the component group, the
$S_3$
with the representation of the component group, the
![]() $2$
-dimensional irreducible representation
$2$
-dimensional irreducible representation
![]() $\rho $
of
$\rho $
of
![]() $S_3$
. It is thus a non-generic representation of
$S_3$
. It is thus a non-generic representation of
![]() $G_2$
which is distinguished by
$G_2$
which is distinguished by
![]() $G_2(F)$
(by Theorem 7.4 of this paper). In this case, the representation
$G_2(F)$
(by Theorem 7.4 of this paper). In this case, the representation
![]() $\rho $
of
$\rho $
of
![]() $S_3$
has a fixed vector under any transposition in
$S_3$
has a fixed vector under any transposition in
![]() $S_3$
, thus confirming the general conjecture of [Reference Prasad16] in an example with a non-abelian component group.
$S_3$
, thus confirming the general conjecture of [Reference Prasad16] in an example with a non-abelian component group.
It would be nice to check Prasad’s conjecture in our case. In this aim, one would have to determine the Galois parameters of our representations, which are not known in general.
The article is organized as follows. After introducing the general notation in §1, in §2 we recall the models of Iwahori-spherical representations introduced in [Reference Borel2] and explain how to deduce a very simple formula for the Iwahori-spherical coefficients. The bound on the dimension of the space of
![]() ${\mathbb H} (F)$
-invariant linear forms is given in §3, and the fact that test-vectors can be chosen Iwahori-spherical is proved in §4. In §5, we recall the definition of Gyoja’s generalized Poincaré series, and we give Macdonald’s formulas. Finally, §6 is devoted to establishing the numerical criterion in terms of Gyoja’s Poincaré series values and to applying it to the case of degree
${\mathbb H} (F)$
-invariant linear forms is given in §3, and the fact that test-vectors can be chosen Iwahori-spherical is proved in §4. In §5, we recall the definition of Gyoja’s generalized Poincaré series, and we give Macdonald’s formulas. Finally, §6 is devoted to establishing the numerical criterion in terms of Gyoja’s Poincaré series values and to applying it to the case of degree
![]() $1$
characters of the Iwahori-Hecke algebra.
$1$
characters of the Iwahori-Hecke algebra.
I warmly thank Nadir Matringe and Dipendra Prasad for their help in writing this article. I am grateful to the referee whose comments helped me to improve the content of the manuscript.
2 Notation
Throughout the article, we use the following notation.
If X is a set, we denote by
![]() $\vert X\vert $
its cardinal. If a group
$\vert X\vert $
its cardinal. If a group
![]() $\Gamma $
acts on X and
$\Gamma $
acts on X and
![]() $\Gamma '$
is a subset of
$\Gamma '$
is a subset of
![]() $\Gamma $
,
$\Gamma $
,
![]() $X^{\Gamma '}$
denotes the subset of those
$X^{\Gamma '}$
denotes the subset of those
![]() $x\in X$
that are fixed by
$x\in X$
that are fixed by
![]() $\Gamma '$
.
$\Gamma '$
.
We let F denote a non-archimedean, non-discrete, locally compact field. We denote by
![]() ${\mathfrak o}_F$
its ring of integers, by
${\mathfrak o}_F$
its ring of integers, by
![]() ${\mathfrak p}_F$
the maximal ideal of
${\mathfrak p}_F$
the maximal ideal of
![]() ${\mathfrak o}_F$
, and we set
${\mathfrak o}_F$
, and we set
![]() $k_F ={\mathfrak o}_F /{\mathfrak p}_F$
(residue field),
$k_F ={\mathfrak o}_F /{\mathfrak p}_F$
(residue field),
![]() $q_0 =\vert k_F\vert =p^r$
, p being the characteristic of
$q_0 =\vert k_F\vert =p^r$
, p being the characteristic of
![]() $k_F$
(residue characteristic).
$k_F$
(residue characteristic).
We fix an unramified quadratic extension
![]() $E/F$
and use the obvious pieces of notation
$E/F$
and use the obvious pieces of notation
![]() ${\mathfrak o}_E$
,
${\mathfrak o}_E$
,
![]() ${\mathfrak p}_E$
,
${\mathfrak p}_E$
,
![]() $k_E$
. We denote by
$k_E$
. We denote by
![]() $\theta $
the generator of the Galois group
$\theta $
the generator of the Galois group
![]() $\mathrm {Gal}(E/F)$
. We set
$\mathrm {Gal}(E/F)$
. We set
![]() $q =\vert k_E\vert $
, so that
$q =\vert k_E\vert $
, so that
![]() $q=q_0^2$
.
$q=q_0^2$
.
We fix a connected simple F-algebraic group
![]() $\mathbb H$
assumed to be split over F and simply connected, and we write
$\mathbb H$
assumed to be split over F and simply connected, and we write
![]() $H={\mathbb H}(F)$
for the locally compact group of its F-rationnal points. We denote by
$H={\mathbb H}(F)$
for the locally compact group of its F-rationnal points. We denote by
![]() ${\mathbb G}=\mathrm {Res}_{E/F}{\mathbb H}$
the F-algebraic group obtained by Weil’s restriction of scalars. It is semisimple and simply connected. We set
${\mathbb G}=\mathrm {Res}_{E/F}{\mathbb H}$
the F-algebraic group obtained by Weil’s restriction of scalars. It is semisimple and simply connected. We set
![]() $G={\mathbb G}(F)={\mathbb H}(E)$
.
$G={\mathbb G}(F)={\mathbb H}(E)$
.
The Galois group
![]() $\mathrm {Gal}(E/F)$
acts on
$\mathrm {Gal}(E/F)$
acts on
![]() $\mathbb G$
by F-rational automorphisms of algebraic group. We still denote by
$\mathbb G$
by F-rational automorphisms of algebraic group. We still denote by
![]() $\theta $
the action of
$\theta $
the action of
![]() $\theta $
on
$\theta $
on
![]() $\mathbb G$
and G so that
$\mathbb G$
and G so that
![]() ${\mathbb H} = {\mathbb G}^\theta $
and
${\mathbb H} = {\mathbb G}^\theta $
and
![]() $H=G^\theta $
. The pair
$H=G^\theta $
. The pair
![]() $(G,H)$
(or the G-set
$(G,H)$
(or the G-set
![]() $G/H$
) is called a (Galois) reductive symmetric space.
$G/H$
) is called a (Galois) reductive symmetric space.
We let
![]() $X_F$
(resp.
$X_F$
(resp.
![]() $X_E$
) denote the Bruhat-Tits building of
$X_E$
) denote the Bruhat-Tits building of
![]() $\mathbb H$
over F (resp. over E). Recall that
$\mathbb H$
over F (resp. over E). Recall that
![]() $X_E$
identifies canonically with the Bruhat-Tits building of
$X_E$
identifies canonically with the Bruhat-Tits building of
![]() $\mathrm {Res}_{E/F}({\mathbb H})$
over F. As simplicial complexes
$\mathrm {Res}_{E/F}({\mathbb H})$
over F. As simplicial complexes
![]() $X_F$
and
$X_F$
and
![]() $X_E$
have dimension d, the F-rank of
$X_E$
have dimension d, the F-rank of
![]() $\mathbb H$
. As a particular case of building functorialities, there is an injection j:
$\mathbb H$
. As a particular case of building functorialities, there is an injection j:
![]() $X_F\longrightarrow X_E$
satisfying the following properties:
$X_F\longrightarrow X_E$
satisfying the following properties:
-
(a) j is
 $\mathrm {Gal}(E/F)\ltimes H$
-equivariant,
$\mathrm {Gal}(E/F)\ltimes H$
-equivariant, -
(b) the image of j is
 $X_E^{\mathrm {Gal}(E/F)}$
,
$X_E^{\mathrm {Gal}(E/F)}$
, -
(c) j is simplicial and maps chambers to chambers.
We identify
![]() $X_F$
as a subsimplicial complex of
$X_F$
as a subsimplicial complex of
![]() $X_E$
, viewing j as an inclusion.
$X_E$
, viewing j as an inclusion.
We fix a maximal F-split torus
![]() $\mathbb T$
of
$\mathbb T$
of
![]() $\mathbb H$
and set
$\mathbb H$
and set
![]() $T_F = {\mathbb T}(F)$
,
$T_F = {\mathbb T}(F)$
,
![]() $T_E ={\mathbb T}(E)$
. We denote by
$T_E ={\mathbb T}(E)$
. We denote by
![]() $\Phi =\Phi ({\mathbb T}, {\mathbb H})$
the root system of
$\Phi =\Phi ({\mathbb T}, {\mathbb H})$
the root system of
![]() $\mathbb T$
in
$\mathbb T$
in
![]() $\mathbb H$
. Let
$\mathbb H$
. Let
![]() $W^{\mathrm {Aff}}_F = N_{H} ({T} )/T_F^o$
be the affine Weyl group of H relative to
$W^{\mathrm {Aff}}_F = N_{H} ({T} )/T_F^o$
be the affine Weyl group of H relative to
![]() $\mathbb T$
, where
$\mathbb T$
, where
![]() $N_{ H} ( T_F )$
is the normalizer of
$N_{ H} ( T_F )$
is the normalizer of
![]() $\mathbb T$
in H and
$\mathbb T$
in H and
![]() $T_F^o$
the maximal compact subgroup of
$T_F^o$
the maximal compact subgroup of
![]() $T_F$
. The group
$T_F$
. The group
![]() $W^{\mathrm {Aff}}_E$
is defined in the same way, and the inclusion
$W^{\mathrm {Aff}}_E$
is defined in the same way, and the inclusion
![]() $N_H (T_F )\subset N_G (T_E )$
induces an isomorphism of groups
$N_H (T_F )\subset N_G (T_E )$
induces an isomorphism of groups
![]() $W_F^{\mathrm {Aff}} \simeq W_E^{\mathrm {Aff}}$
. In the sequel, we abbreviate
$W_F^{\mathrm {Aff}} \simeq W_E^{\mathrm {Aff}}$
. In the sequel, we abbreviate
![]() $W^{\mathrm {Aff}} =W_F^{\mathrm {Aff}}=W_E^{\mathrm {Aff}}$
.
$W^{\mathrm {Aff}} =W_F^{\mathrm {Aff}}=W_E^{\mathrm {Aff}}$
.
Let
![]() ${\mathcal A}_F$
(resp.
${\mathcal A}_F$
(resp.
![]() ${\mathcal A}_E$
) denote the appartment of
${\mathcal A}_E$
) denote the appartment of
![]() $X_F$
(resp.
$X_F$
(resp.
![]() $X_E$
) associated to
$X_E$
) associated to
![]() $\mathbb T$
. It follows from the construction of j that
$\mathbb T$
. It follows from the construction of j that
![]() ${\mathcal A}_F ={\mathcal A}_E$
. Fix a chamber
${\mathcal A}_F ={\mathcal A}_E$
. Fix a chamber
![]() $C_o$
of
$C_o$
of
![]() ${\mathcal A}_F$
, and let
${\mathcal A}_F$
, and let
![]() $I^o_F$
(resp.
$I^o_F$
(resp.
![]() $I_E^o$
) denote the Iwahori subgroup of H (resp. the
$I_E^o$
) denote the Iwahori subgroup of H (resp. the
![]() $\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of G) fixing
$\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of G) fixing
![]() $C_o$
. Since
$C_o$
. Since
![]() $\mathbb H$
is simply connected, these Iwahori subgroups are the (global) fixators of
$\mathbb H$
is simply connected, these Iwahori subgroups are the (global) fixators of
![]() $C_o$
. Let
$C_o$
. Let
![]() $S\subset W_F^{\mathrm {Aff}}$
be the set of involutions corresponding to reflections in
$S\subset W_F^{\mathrm {Aff}}$
be the set of involutions corresponding to reflections in
![]() ${\mathcal A}_F$
relative to the walls of
${\mathcal A}_F$
relative to the walls of
![]() $C_o$
. Then, since
$C_o$
. Then, since
![]() ${\mathbb H}$
is simply connected,
${\mathbb H}$
is simply connected,
![]() $(I_F^o ,N_H (T_F ))$
(resp.
$(I_F^o ,N_H (T_F ))$
(resp.
![]() $(I_E^o ,N_G (T_E ))$
) is a Tits system (or BN-pair) in H (resp. in G) with Coxeter system
$(I_E^o ,N_G (T_E ))$
) is a Tits system (or BN-pair) in H (resp. in G) with Coxeter system
![]() $(W^{\mathrm {Aff}},S)$
. We denote by l the length function of W relative to the generative subset S. Recall that
$(W^{\mathrm {Aff}},S)$
. We denote by l the length function of W relative to the generative subset S. Recall that
Recall that the vertices of
![]() $X_E$
are naturally labelled by the elements of S. Since the action of G preserves the labelling, it suffices to define the labels of vertices of
$X_E$
are naturally labelled by the elements of S. Since the action of G preserves the labelling, it suffices to define the labels of vertices of
![]() $C_o$
. Then if
$C_o$
. Then if
![]() $s\in S$
, the vertex fixed by the standard maximal parahoric subgroup
$s\in S$
, the vertex fixed by the standard maximal parahoric subgroup
![]() $I_E^o\langle S\backslash \{ s\}\rangle I_E^o$
has label s (here,
$I_E^o\langle S\backslash \{ s\}\rangle I_E^o$
has label s (here,
![]() $\langle S\backslash \{ s\}\rangle $
is the subgroup of
$\langle S\backslash \{ s\}\rangle $
is the subgroup of
![]() $W_E^{\mathrm {Aff}}$
generated by
$W_E^{\mathrm {Aff}}$
generated by
![]() $S\backslash \{ s\}$
). If C is a chamber of
$S\backslash \{ s\}$
). If C is a chamber of
![]() $X_E$
, the wall of C which does not contain the unique vertex of type s is said to be of type s. If C and D are two chambers of
$X_E$
, the wall of C which does not contain the unique vertex of type s is said to be of type s. If C and D are two chambers of
![]() $X_E$
, we write
$X_E$
, we write
![]() $D\sim _s C$
if D and C are adjacent and if the wall
$D\sim _s C$
if D and C are adjacent and if the wall
![]() $D\cap C$
is of type s.
$D\cap C$
is of type s.
We let
![]() ${\mathcal H}_{\mathrm {I}}$
denote the Iwahori-Hecke algebra of G relative to our choice
${\mathcal H}_{\mathrm {I}}$
denote the Iwahori-Hecke algebra of G relative to our choice
![]() $I_E^o$
of Iwahori subgroup. Recall that as a complex vector space,
$I_E^o$
of Iwahori subgroup. Recall that as a complex vector space,
![]() ${\mathcal H}_{\mathrm {I}}$
is the set of complex functions of G which are bi-invariant by
${\mathcal H}_{\mathrm {I}}$
is the set of complex functions of G which are bi-invariant by
![]() $I_E^o$
and have compact support. It is endowed with the convolution product defined by
$I_E^o$
and have compact support. It is endowed with the convolution product defined by
 $$ \begin{align*}u\star v (g)=\int_G u(gx^{-1})v(x)\, d\mu (x)=\sum_{x\in I_E^o \backslash G} u(gx^{-1})v(x), \ g\in G, \ u,v\in {\mathcal H}_{\mathrm{I}}, \end{align*} $$
$$ \begin{align*}u\star v (g)=\int_G u(gx^{-1})v(x)\, d\mu (x)=\sum_{x\in I_E^o \backslash G} u(gx^{-1})v(x), \ g\in G, \ u,v\in {\mathcal H}_{\mathrm{I}}, \end{align*} $$
where
![]() $\mu $
is the Haar measure on G normalized by
$\mu $
is the Haar measure on G normalized by
![]() $\mu (I_E^o )=1$
. Recall that
$\mu (I_E^o )=1$
. Recall that
![]() $(e_w )_{w\in W^{\mathrm {Aff}}}$
is a
$(e_w )_{w\in W^{\mathrm {Aff}}}$
is a
![]() ${\mathbb {C}}$
-basis of
${\mathbb {C}}$
-basis of
![]() ${\mathcal H}_{\mathrm {I}}$
, where for
${\mathcal H}_{\mathrm {I}}$
, where for
![]() $w\in W^{\mathrm {Aff}}$
,
$w\in W^{\mathrm {Aff}}$
,
![]() $e_w$
denotes the caracteristic function of
$e_w$
denotes the caracteristic function of
![]() $I_E^o wI_E^o$
. Recall that we have the classical relations
$I_E^o wI_E^o$
. Recall that we have the classical relations
 $$ \begin{align*} (e_s +1)\star (e_s -q)=0, \ s\in S\\ e_w \star e_{w'} = e_{ww'}\ \mathrm{if}\ l(ww')=l(w)+l(w'), \ w, \ w'\in W^{\mathrm{Aff}} \end{align*} $$
$$ \begin{align*} (e_s +1)\star (e_s -q)=0, \ s\in S\\ e_w \star e_{w'} = e_{ww'}\ \mathrm{if}\ l(ww')=l(w)+l(w'), \ w, \ w'\in W^{\mathrm{Aff}} \end{align*} $$
and that the
![]() $e_s$
,
$e_s$
,
![]() $s\in S$
generate
$s\in S$
generate
![]() ${\mathcal H}_{\mathrm {I}}$
as an algebra.
${\mathcal H}_{\mathrm {I}}$
as an algebra.
If
![]() $f\in {\mathcal H}_{\mathrm {I}}$
, we define
$f\in {\mathcal H}_{\mathrm {I}}$
, we define
![]() $\check {f}$
by
$\check {f}$
by
![]() $\check {f} (x)=f( x^{-1} )$
,
$\check {f} (x)=f( x^{-1} )$
,
![]() $x\in G$
. The map
$x\in G$
. The map
![]() $f\mapsto \check {f}$
is an automorphism of the vector space
$f\mapsto \check {f}$
is an automorphism of the vector space
![]() ${\mathcal H}_{\mathrm {I}}$
satisfying
${\mathcal H}_{\mathrm {I}}$
satisfying
![]() $ (f\star g)\check {} =\check {g} \star \check {f}$
,
$ (f\star g)\check {} =\check {g} \star \check {f}$
,
![]() $f,g\in {\mathcal H}_{\mathrm {I}}$
. If
$f,g\in {\mathcal H}_{\mathrm {I}}$
. If
![]() $(r,M)$
is a complex representation of
$(r,M)$
is a complex representation of
![]() ${\mathcal H}_{\mathrm {I}}$
, we define its contragredient
${\mathcal H}_{\mathrm {I}}$
, we define its contragredient
![]() $({\tilde r}, {\tilde M})$
in the dual
$({\tilde r}, {\tilde M})$
in the dual
![]() ${\tilde M}$
of M by
${\tilde M}$
of M by
![]() ${\tilde r}(f)={}^t r(\check {f} )$
,
${\tilde r}(f)={}^t r(\check {f} )$
,
![]() $f\in {\mathcal H}_{\mathrm {I}}$
, where
$f\in {\mathcal H}_{\mathrm {I}}$
, where
![]() ${}^t$
denotes the transposition.
${}^t$
denotes the transposition.
In this article, representations of G, H or
![]() ${\mathcal H}_{\mathrm {I}}$
are always assumed to be in complex vector spaces. If
${\mathcal H}_{\mathrm {I}}$
are always assumed to be in complex vector spaces. If
![]() $(\pi ,{\mathcal {V}} )$
is a smooth representation of G,
$(\pi ,{\mathcal {V}} )$
is a smooth representation of G,
![]() $({\tilde \pi }, {\tilde {{\mathcal {V}}} })$
denotes its contragredient (i.e., its smooth dual). If W is a complex vector space,
$({\tilde \pi }, {\tilde {{\mathcal {V}}} })$
denotes its contragredient (i.e., its smooth dual). If W is a complex vector space,
![]() $W^* =\mathrm {Hom}_{\mathbb {C}} (W,{\mathbb {C}})$
denotes its algebraic dual.
$W^* =\mathrm {Hom}_{\mathbb {C}} (W,{\mathbb {C}})$
denotes its algebraic dual.
3 Iwahori-spherical representations: models and coefficients
In this section, we abbreviate
![]() $I=I_E^o$
.
$I=I_E^o$
.
Let
![]() $\mathcal S (G)$
denote the abelian category of smooth representations of G and
$\mathcal S (G)$
denote the abelian category of smooth representations of G and
![]() $\mathcal S (G)_{\mathrm {I}}$
denote the full subcategory of those representations
$\mathcal S (G)_{\mathrm {I}}$
denote the full subcategory of those representations
![]() $(\pi , {\mathcal {V}} )$
that are generated by the fixed vector set
$(\pi , {\mathcal {V}} )$
that are generated by the fixed vector set
![]() ${\mathcal {V}}^I$
. Let
${\mathcal {V}}^I$
. Let
![]() ${\mathcal H}_{\mathrm {I}}\mathrm {-Mod}$
denote the category of left
${\mathcal H}_{\mathrm {I}}\mathrm {-Mod}$
denote the category of left
![]() ${\mathcal H}_{\mathrm {I}}$
-modules. If
${\mathcal H}_{\mathrm {I}}$
-modules. If
![]() $(\pi ,{\mathcal {V}} )$
is an object of
$(\pi ,{\mathcal {V}} )$
is an object of
![]() $\mathcal S (G)_{\mathrm {I}}$
, then
$\mathcal S (G)_{\mathrm {I}}$
, then
![]() ${\mathcal {V}}^I$
is naturally a left
${\mathcal {V}}^I$
is naturally a left
![]() ${\mathcal H}_{\mathrm {I}}$
-module, so that we have a well-defined functor
${\mathcal H}_{\mathrm {I}}$
-module, so that we have a well-defined functor
It is now a well-known fact ([Reference Borel2],[Reference Casselman8]) that
![]() $\mathbf M$
is an equivalence of categories; in other words, the trivial character of I is a type for G in the sense of [Reference Bushnell and Kutzko7]. Moreover, if
$\mathbf M$
is an equivalence of categories; in other words, the trivial character of I is a type for G in the sense of [Reference Bushnell and Kutzko7]. Moreover, if
![]() $(\pi ,{\mathcal {V}} )$
is admissible, we have
$(\pi ,{\mathcal {V}} )$
is admissible, we have
![]() $\mathbf M ({\tilde {{\mathcal {V}}}} )= \mathbf M ({\mathcal {V}} )\, \tilde {}$
: the functor commutes with the operation of taking the contragredient.
$\mathbf M ({\tilde {{\mathcal {V}}}} )= \mathbf M ({\mathcal {V}} )\, \tilde {}$
: the functor commutes with the operation of taking the contragredient.
A pseudo-inverse
![]() $\mathbf V$
for
$\mathbf V$
for
![]() $\mathbf M$
may be constructed as follows (cf. [Reference Borel2]§4). Let us fix a left
$\mathbf M$
may be constructed as follows (cf. [Reference Borel2]§4). Let us fix a left
![]() ${\mathcal H}_{\mathrm {I}}$
-module M viewed as a representation
${\mathcal H}_{\mathrm {I}}$
-module M viewed as a representation
![]() $(r,M)$
of
$(r,M)$
of
![]() ${\mathcal H}_{\mathrm {I}}$
. Let
${\mathcal H}_{\mathrm {I}}$
. Let
![]() $C_c (G/I)$
be the space of functions on G which are right I-invariant and have compact support. This is naturally a right
$C_c (G/I)$
be the space of functions on G which are right I-invariant and have compact support. This is naturally a right
![]() ${\mathcal H}_{\mathrm {I}}$
-module and a smooth representation of G (by left translation) and both structures are compatible. Hence, we may form the tensor product
${\mathcal H}_{\mathrm {I}}$
-module and a smooth representation of G (by left translation) and both structures are compatible. Hence, we may form the tensor product
![]() ${\mathbf V}(M) := C_c (G/I)\otimes _{{\mathcal H}_{\mathrm {I}}} M$
. Of course, we have an isomorphism of left
${\mathbf V}(M) := C_c (G/I)\otimes _{{\mathcal H}_{\mathrm {I}}} M$
. Of course, we have an isomorphism of left
![]() ${\mathcal H}_{\mathrm {I}}$
-modules
${\mathcal H}_{\mathrm {I}}$
-modules
![]() $M\simeq {\mathbf V}(M)^I$
; it is explicitly given by
$M\simeq {\mathbf V}(M)^I$
; it is explicitly given by
![]() $m\mapsto e_1 \otimes m$
.
$m\mapsto e_1 \otimes m$
.
We shall need two other functorial constructions
![]() $\mathbf P$
,
$\mathbf P$
,
![]() ${\mathbf P}^o$
, considered by Borel in loc. cit. §2. If
${\mathbf P}^o$
, considered by Borel in loc. cit. §2. If
![]() $(r,M)$
is a representation of
$(r,M)$
is a representation of
![]() ${\mathcal H}_{\mathrm {I}}$
, we set
${\mathcal H}_{\mathrm {I}}$
, we set
where
![]() $C(G/I ,M)$
denotes the space of M-valued functions on G which are right I-invariant. This space is acted upon by G via left translation, but the obtained representation of G is not smooth in general; we denote by
$C(G/I ,M)$
denotes the space of M-valued functions on G which are right I-invariant. This space is acted upon by G via left translation, but the obtained representation of G is not smooth in general; we denote by
![]() ${\mathbf P}(M)\subset {\mathbf P}^o (M)$
the subspace of smooth vectors. By [Reference Borel2] Proposition 2.4, the map
${\mathbf P}(M)\subset {\mathbf P}^o (M)$
the subspace of smooth vectors. By [Reference Borel2] Proposition 2.4, the map
is an isomorphism of vector spaces. Moreover, for
![]() $m\in M$
, the element
$m\in M$
, the element
![]() $f_m\in {\mathbf P}(M)^I$
mapped onto m by
$f_m\in {\mathbf P}(M)^I$
mapped onto m by
![]() $\nu _o$
is the function
$\nu _o$
is the function
![]() $f_e$
on G mapping any element of
$f_e$
on G mapping any element of
![]() $IwI$
,
$IwI$
,
![]() $w\in W^{\mathrm {Aff}}$
, to
$w\in W^{\mathrm {Aff}}$
, to
![]() $q_w^{-1}\, r(\check {e_w}).m$
, symbolically written by Borel as
$q_w^{-1}\, r(\check {e_w}).m$
, symbolically written by Borel as
The tensor product
![]() $C_c (G/I)\otimes _{{\mathcal H}_{\mathrm {I}}} M$
may be viewed as the quotient of
$C_c (G/I)\otimes _{{\mathcal H}_{\mathrm {I}}} M$
may be viewed as the quotient of
![]() $C_c (G/I)\otimes _{\mathbb {C}} M$
by the G-invariant subspace generated by
$C_c (G/I)\otimes _{\mathbb {C}} M$
by the G-invariant subspace generated by
![]() $(f\star u)\otimes m-f\otimes r(u).m$
,
$(f\star u)\otimes m-f\otimes r(u).m$
,
![]() $f\in C_c (G/I)$
,
$f\in C_c (G/I)$
,
![]() $u\in {\mathcal H}_{\mathrm {I}}$
,
$u\in {\mathcal H}_{\mathrm {I}}$
,
![]() $m\in M$
. We may identify
$m\in M$
. We may identify
![]() $C_c (G/I)\otimes _{\mathbb {C}} M$
with the space
$C_c (G/I)\otimes _{\mathbb {C}} M$
with the space
![]() $C_c (G/I,M)$
of M-valued functions on G which are right I-invariant. The bilinear G-invariant map
$C_c (G/I,M)$
of M-valued functions on G which are right I-invariant. The bilinear G-invariant map
 $$ \begin{align} {\mathbf P}^o ({\tilde M})\times C_c (G/I,M)\longrightarrow {\mathbb{C}}, \ (f,g)\mapsto \sum_{x\in G/I} \langle f(x), g(x)\rangle_M \end{align} $$
$$ \begin{align} {\mathbf P}^o ({\tilde M})\times C_c (G/I,M)\longrightarrow {\mathbb{C}}, \ (f,g)\mapsto \sum_{x\in G/I} \langle f(x), g(x)\rangle_M \end{align} $$
induces a well-defined G-invariant bilinear map
whence a G-intertwining operator
where
![]() $*$
denotes an algebraic dual. From [Reference Borel2] Proposition 2.6, we have the following.
$*$
denotes an algebraic dual. From [Reference Borel2] Proposition 2.6, we have the following.
Proposition 3.1. Let
![]() $(r,M)$
be a representation of
$(r,M)$
be a representation of
![]() ${\mathcal H}_{\mathrm {I}}$
. Then the intertwining operator
${\mathcal H}_{\mathrm {I}}$
. Then the intertwining operator
![]() $\psi _M\ :\ {\mathbf P}^o ({\tilde M})\longrightarrow {\mathbf V}(M)^*$
is an isomorphism and restricts to an isomorphism
$\psi _M\ :\ {\mathbf P}^o ({\tilde M})\longrightarrow {\mathbf V}(M)^*$
is an isomorphism and restricts to an isomorphism
![]() ${\mathbf P} ({\tilde M})\simeq {\mathbf V}(M)\tilde {}$
.
${\mathbf P} ({\tilde M})\simeq {\mathbf V}(M)\tilde {}$
.
Observe that if M is finite dimensional,
![]() ${\mathbf V}(M)$
is admissible and we have
${\mathbf V}(M)$
is admissible and we have
![]() ${\mathbf V}(M)\tilde {} \simeq {\mathbf V}({\tilde M})$
. So exchanging the roles of M and
${\mathbf V}(M)\tilde {} \simeq {\mathbf V}({\tilde M})$
. So exchanging the roles of M and
![]() $\tilde M$
, we obtain
$\tilde M$
, we obtain
![]() ${\mathbf P}(M)\simeq {\mathbf V}(M)$
as G-modules.
${\mathbf P}(M)\simeq {\mathbf V}(M)$
as G-modules.
Let
![]() $(r,M)$
be a finite dimensional representation of
$(r,M)$
be a finite dimensional representation of
![]() ${\mathcal H}_{\mathrm {I}}$
, and set
${\mathcal H}_{\mathrm {I}}$
, and set
![]() $(\pi ,{\mathcal {V}} )={\mathbf V}(r,M)$
. We make the canonical identifications
$(\pi ,{\mathcal {V}} )={\mathbf V}(r,M)$
. We make the canonical identifications
![]() ${\mathcal {V}}^I =M$
and
${\mathcal {V}}^I =M$
and
![]() ${\tilde {{\mathcal {V}}}}^I ={\tilde M}$
. Recall that for
${\tilde {{\mathcal {V}}}}^I ={\tilde M}$
. Recall that for
![]() $m\in M$
and
$m\in M$
and
![]() ${\tilde m}\in {\tilde M}$
, the corresponding coefficient
${\tilde m}\in {\tilde M}$
, the corresponding coefficient
![]() $c_{m,{\tilde m}}$
of
$c_{m,{\tilde m}}$
of
![]() ${\mathcal {V}}$
is the complex function on G defined by
${\mathcal {V}}$
is the complex function on G defined by
Let us observe that by construction,
![]() $c_{m,{\tilde m}}$
is I-bi-invariant.
$c_{m,{\tilde m}}$
is I-bi-invariant.
Corollary 3.2. For
![]() $m\in M$
,
$m\in M$
,
![]() ${\tilde m}\in {\tilde M}$
,
${\tilde m}\in {\tilde M}$
,
![]() $w\in W^{\mathrm {Aff}}$
, the value of
$w\in W^{\mathrm {Aff}}$
, the value of
![]() $c_{m,{\tilde m}}$
on
$c_{m,{\tilde m}}$
on
![]() $IwI$
is
$IwI$
is
![]() $q_w^{-1}\langle {\tilde m}, r({e}_w ) .m\rangle _M$
.
$q_w^{-1}\langle {\tilde m}, r({e}_w ) .m\rangle _M$
.
Proof. The vector
![]() $m\in {\mathcal {V}}$
corresponds to the function
$m\in {\mathcal {V}}$
corresponds to the function
![]() $v_m\in C_c (G/I ,M)$
which has support I and constant value m on I. The linear form
$v_m\in C_c (G/I ,M)$
which has support I and constant value m on I. The linear form
![]() $\tilde m$
corresponds to the function
$\tilde m$
corresponds to the function
![]() ${f_{\tilde m}\in C(G/I,{\tilde M})}$
whose value on
${f_{\tilde m}\in C(G/I,{\tilde M})}$
whose value on
![]() $IwI$
,
$IwI$
,
![]() $w\in W^{\mathrm {Aff}}$
, is given by
$w\in W^{\mathrm {Aff}}$
, is given by
![]() $q_w^{-1}\, {\tilde r}(\check {e}_w).m$
. Applying the pairing formula (2), for
$q_w^{-1}\, {\tilde r}(\check {e}_w).m$
. Applying the pairing formula (2), for
![]() $w\in W^{\mathrm {Aff}}$
, we have
$w\in W^{\mathrm {Aff}}$
, we have
![]() $c_{m,{\tilde m}}(w) = \langle q_w^{-1}\, {\tilde r}(\check {e}_w ).{\tilde m},m\rangle _M = q_w^{-1}\, \langle {\tilde m}, r(e_w ).m\rangle $
, as required.
$c_{m,{\tilde m}}(w) = \langle q_w^{-1}\, {\tilde r}(\check {e}_w ).{\tilde m},m\rangle _M = q_w^{-1}\, \langle {\tilde m}, r(e_w ).m\rangle $
, as required.
We now describe a geometric model for the space
![]() ${\mathbf P}^o ({\tilde M})$
for a given representation
${\mathbf P}^o ({\tilde M})$
for a given representation
![]() $(r,M)$
of
$(r,M)$
of
![]() ${\mathcal H}_{\mathrm {I}}$
. We let
${\mathcal H}_{\mathrm {I}}$
. We let
![]() $\mathrm {Ch (X_E)}$
denote the G-set of chambers of
$\mathrm {Ch (X_E)}$
denote the G-set of chambers of
![]() $X_E$
and
$X_E$
and
![]() ${\mathcal {F}} \mathrm {(Ch (X_E), {\tilde M})}$
the space of
${\mathcal {F}} \mathrm {(Ch (X_E), {\tilde M})}$
the space of
![]() $\tilde {M}$
-valued functions on
$\tilde {M}$
-valued functions on
![]() $\mathrm {Ch (X_E)}$
. We let
$\mathrm {Ch (X_E)}$
. We let
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde {M}})_r}$
denote the subspace of
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde {M}})_r}$
denote the subspace of
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde {M}})}$
formed of those functions f satisfying for all
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde {M}})}$
formed of those functions f satisfying for all
![]() $C\in \mathrm {Ch (X_E)}$
and for all
$C\in \mathrm {Ch (X_E)}$
and for all
![]() $s\in S$
:
$s\in S$
:
Since G acts on
![]() $\mathrm {Ch (X_E )}$
by preserving the labelling of vertices,
$\mathrm {Ch (X_E )}$
by preserving the labelling of vertices,
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r}$
is a G-subspace of
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r}$
is a G-subspace of
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})}$
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})}$
Proposition 3.3. The spaces
![]() ${\mathbf P}^o ({\tilde M})$
and
${\mathbf P}^o ({\tilde M})$
and
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r}$
are isomorphic as G-modules.
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r}$
are isomorphic as G-modules.
Proof. Since G acts transitively on
![]() $\mathrm {Ch (X_E)}$
and the global stabilizer of
$\mathrm {Ch (X_E)}$
and the global stabilizer of
![]() $C_o$
is I, we may identify
$C_o$
is I, we may identify
![]() $C (G/I ,{\tilde M})$
with
$C (G/I ,{\tilde M})$
with
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})}$
. Since
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})}$
. Since
![]() $\{ e_s \; \ s\in S\}$
generates
$\{ e_s \; \ s\in S\}$
generates
![]() ${\mathcal H}_{\mathrm {I}}$
as an algebra, a function
${\mathcal H}_{\mathrm {I}}$
as an algebra, a function
![]() $f\in C(G/I ,{\tilde M})$
is in
$f\in C(G/I ,{\tilde M})$
is in
![]() ${\mathbf P}^o ({\tilde M})$
if and only if
${\mathbf P}^o ({\tilde M})$
if and only if
![]() $f\star e_s ={\tilde r}(e_s ).f$
, for all
$f\star e_s ={\tilde r}(e_s ).f$
, for all
![]() $s\in S$
. It follows that
$s\in S$
. It follows that
![]() ${\mathbf P}^o ({\tilde M})$
identifies with the space of functions f:
${\mathbf P}^o ({\tilde M})$
identifies with the space of functions f:
![]() $\mathrm {Ch (X_E )\longrightarrow {\tilde M}}$
satisfying
$\mathrm {Ch (X_E )\longrightarrow {\tilde M}}$
satisfying
![]() $f\star e_s = {\tilde r}(e_s ).f$
. Now our result follows from [Reference Borel2] §4 Equation (6):
$f\star e_s = {\tilde r}(e_s ).f$
. Now our result follows from [Reference Borel2] §4 Equation (6):
4 Multiplicities
We continue to abbreviate
![]() $I=I_E^o$
, a fixed
$I=I_E^o$
, a fixed
![]() $\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of G.
$\mathrm {Gal}(E/F)$
-stable Iwahori subgroup of G.
We fix an irreducible Iwahori-spherical representation
![]() $(\pi , {\mathcal {V}} )$
of G. It is of the form
$(\pi , {\mathcal {V}} )$
of G. It is of the form
![]() ${\mathbf V}(M)$
, for some irreducible representation
${\mathbf V}(M)$
, for some irreducible representation
![]() $(r,M)$
of
$(r,M)$
of
![]() ${\mathcal H}_{\mathrm {I}}$
. The aim of this section is to give a bound for the dimension of the intertwining space
${\mathcal H}_{\mathrm {I}}$
. The aim of this section is to give a bound for the dimension of the intertwining space
![]() $\mathrm {Hom}_H \, ({\mathcal {V}} ,{\mathbb {C}} )$
, where
$\mathrm {Hom}_H \, ({\mathcal {V}} ,{\mathbb {C}} )$
, where
![]() ${\mathbb {C}}$
is acted upon via the trivial representation of H.
${\mathbb {C}}$
is acted upon via the trivial representation of H.
We shall prove the following.
Theorem 4.1. The obvious restriction map
![]() $\mathrm {Hom}_H (\pi ,{\mathbb {C}} )\longrightarrow \mathrm {Hom}_{\mathbb {C}} (\pi ^I ,{\mathbb {C}} )$
is injective. In particular, we have
$\mathrm {Hom}_H (\pi ,{\mathbb {C}} )\longrightarrow \mathrm {Hom}_{\mathbb {C}} (\pi ^I ,{\mathbb {C}} )$
is injective. In particular, we have
By Propositions 3.1 and 3.3, we have an isomorphism of vector spaces:
Through this isomorphism, the restriction map
![]() $\mathrm {Hom}_H (\pi ,{\mathbb {C}} )\longrightarrow \mathrm {Hom}_{\mathbb {C}} (\pi ^I ,{\mathbb {C}} )$
corresponds to the map
$\mathrm {Hom}_H (\pi ,{\mathbb {C}} )\longrightarrow \mathrm {Hom}_{\mathbb {C}} (\pi ^I ,{\mathbb {C}} )$
corresponds to the map
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H \longrightarrow {\tilde M}}$
,
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H \longrightarrow {\tilde M}}$
,
![]() $f\longrightarrow f(C_o )$
. Indeed, recall that
$f\longrightarrow f(C_o )$
. Indeed, recall that
![]() $\pi ={\mathbf V}(M)$
, where
$\pi ={\mathbf V}(M)$
, where
![]() ${\mathbf V}(M)$
is the image of
${\mathbf V}(M)$
is the image of
![]() $C_c (G/I,M)\simeq C_c (G/I) \otimes M$
in the quotient
$C_c (G/I,M)\simeq C_c (G/I) \otimes M$
in the quotient
![]() $C_c (G/I)\otimes _{{\mathcal H}_{\mathrm {I}}} M$
. Then
$C_c (G/I)\otimes _{{\mathcal H}_{\mathrm {I}}} M$
. Then
![]() $\pi ^I \simeq M$
corresponds to the images
$\pi ^I \simeq M$
corresponds to the images
![]() ${\bar v}_m$
,
${\bar v}_m$
,
![]() $m\in M$
, where
$m\in M$
, where
![]() $v_m \in C_c (G/I,M)$
is the function with support I and value m. For
$v_m \in C_c (G/I,M)$
is the function with support I and value m. For
![]() $f\in \mathrm { Hom}_H (\pi ,{\mathbb {C}} )\simeq {\mathbf P}^o ( {\tilde M})^H$
and
$f\in \mathrm { Hom}_H (\pi ,{\mathbb {C}} )\simeq {\mathbf P}^o ( {\tilde M})^H$
and
![]() $m\in \pi ^I \simeq M$
, we have
$m\in \pi ^I \simeq M$
, we have
 $$ \begin{align*}f({\bar v}_m)= \sum_{x\in G/I}\langle f(xC_o ),v_m (x)\rangle_{M} = f(C_0) (m). \end{align*} $$
$$ \begin{align*}f({\bar v}_m)= \sum_{x\in G/I}\langle f(xC_o ),v_m (x)\rangle_{M} = f(C_0) (m). \end{align*} $$
Hence, we are reduced to proving the following result.
Proposition 4.2. A map
![]() $f\in {\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H}$
is entirely determined by the value
$f\in {\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H}$
is entirely determined by the value
![]() $f(C_o )$
(i.e., the mapping
$f(C_o )$
(i.e., the mapping
![]() ${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H \longrightarrow {\tilde M}}$
,
${\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H \longrightarrow {\tilde M}}$
,
![]() $f\mapsto f(C_o )$
is injective).
$f\mapsto f(C_o )$
is injective).
To prove the proposition, we use the same tool that allowed us to establish the multiplicity
![]() $1$
property of the main result of [Reference Broussous and Courtès6] (Theorem 2):
$1$
property of the main result of [Reference Broussous and Courtès6] (Theorem 2):
Proposition 4.3 (François Courtès).
Let d be a non-negative integer and C be a chamber of
![]() $X_E$
at combinatorial distance d from
$X_E$
at combinatorial distance d from
![]() $X_F$
. Let
$X_F$
. Let
![]() $D^+$
be a chamber of
$D^+$
be a chamber of
![]() $X_E$
, adjacent to C and at combinatorial distance
$X_E$
, adjacent to C and at combinatorial distance
![]() $d+1$
from
$d+1$
from
![]() $X_F$
. Consider the wall
$X_F$
. Consider the wall
![]() $A=D^+ \cap C$
. The set
$A=D^+ \cap C$
. The set
![]() ${\mathcal C}_A$
of chambers of
${\mathcal C}_A$
of chambers of
![]() $X_E$
containing A splits into two subsets: the set
$X_E$
containing A splits into two subsets: the set
![]() ${\mathcal C}_A^+$
(resp.
${\mathcal C}_A^+$
(resp.
![]() ${\mathcal C}_A^-$
) formed of those chambers at combinatorial distance
${\mathcal C}_A^-$
) formed of those chambers at combinatorial distance
![]() $d+1$
(resp. d) from
$d+1$
(resp. d) from
![]() $X_F$
.
$X_F$
.
Then the stabilizer
![]() $H_A$
of A in H acts transitively of
$H_A$
of A in H acts transitively of
![]() ${\mathcal C}_A^+$
et
${\mathcal C}_A^+$
et
![]() ${\mathcal C}_A^-$
. Moreover, we have
${\mathcal C}_A^-$
. Moreover, we have
 $$ \begin{align*}(\vert {\mathcal C}_A^-\vert ,\vert {\mathcal C}_A^+\vert )=\left\{ \begin{array}{@{}l} (1,q_o^2 )\\ \mathrm{or}\\ (q_o +1 ,q_o^2 -q_o ). \end{array} \right. \end{align*} $$
$$ \begin{align*}(\vert {\mathcal C}_A^-\vert ,\vert {\mathcal C}_A^+\vert )=\left\{ \begin{array}{@{}l} (1,q_o^2 )\\ \mathrm{or}\\ (q_o +1 ,q_o^2 -q_o ). \end{array} \right. \end{align*} $$
Proof. This follows from [Reference Broussous and Courtès6] Proposition A1 and the proof of [Reference Courtès9] Theorem 6.1.
Proof of Proposition 4.2
. Let
![]() $f\in {\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H}$
. For a non-negative integer d, we let
$f\in {\mathcal {F}} \mathrm {(Ch (X_E ),{\tilde M})_r^H}$
. For a non-negative integer d, we let
![]() $\mathrm {Ch (X_E )_d}$
denote the set of chambers in
$\mathrm {Ch (X_E )_d}$
denote the set of chambers in
![]() $X_E$
at combinatorial distance from
$X_E$
at combinatorial distance from
![]() $X_F$
less than or equal to d. In particular,
$X_F$
less than or equal to d. In particular,
![]() $\mathrm {Ch (X_E )}_0 =\mathrm {Ch (X_F)}$
, the set of chambers in
$\mathrm {Ch (X_E )}_0 =\mathrm {Ch (X_F)}$
, the set of chambers in
![]() $X_F$
. We prove by induction on d that for all
$X_F$
. We prove by induction on d that for all
![]() $d\geqslant 0$
, the restriction of f to
$d\geqslant 0$
, the restriction of f to
![]() $\mathrm {Ch (X_E)_d}$
depends only on
$\mathrm {Ch (X_E)_d}$
depends only on
![]() $f(C_o )$
.
$f(C_o )$
.
Our assertion holds for
![]() $d=0$
since H acts transitively on
$d=0$
since H acts transitively on
![]() $\mathrm {Ch (X_F)}$
. Assume it holds for an integer
$\mathrm {Ch (X_F)}$
. Assume it holds for an integer
![]() $d\geqslant 0$
. Let D be a chamber a combinatorial distance
$d\geqslant 0$
. Let D be a chamber a combinatorial distance
![]() $d+1$
from
$d+1$
from
![]() $X_F$
. By definition, there exists a chamber C adjacent to D and at combinatorial distance d from
$X_F$
. By definition, there exists a chamber C adjacent to D and at combinatorial distance d from
![]() $X_F$
. Use the notation
$X_F$
. Use the notation
![]() $A=D\cap C$
,
$A=D\cap C$
,
![]() ${\mathcal C}_A^-$
and
${\mathcal C}_A^-$
and
![]() ${\mathcal C}_A^+$
as in Proposition 4.3. Let s be the type of A. By Relation 3, we have
${\mathcal C}_A^+$
as in Proposition 4.3. Let s be the type of A. By Relation 3, we have
 $$ \begin{align} {\tilde r}(e_s ).f(C)=\sum_{E\in {\mathcal C}_A^- \backslash \{ C\}} f(E) +\sum_{E\in {\mathcal C}_A^+} f(E) = (\vert {\mathcal C}_A^- \vert -1)f(C) +\vert {\mathcal C}_A^+\vert f(D), \end{align} $$
$$ \begin{align} {\tilde r}(e_s ).f(C)=\sum_{E\in {\mathcal C}_A^- \backslash \{ C\}} f(E) +\sum_{E\in {\mathcal C}_A^+} f(E) = (\vert {\mathcal C}_A^- \vert -1)f(C) +\vert {\mathcal C}_A^+\vert f(D), \end{align} $$
where we used the fact that H acts transitively on
![]() ${\mathcal C}_A^+$
and
${\mathcal C}_A^+$
and
![]() ${\mathcal C}_A^-$
, and that f is H-invariant. Hence, we have
${\mathcal C}_A^-$
, and that f is H-invariant. Hence, we have
 $$ \begin{align} f(D) =\frac{1}{\vert {\mathcal C}_A^+ \vert} {\tilde r}\left( e_s -(\vert {\mathcal C}_A^-\vert -1)\, e_1 \right). f(C) \end{align} $$
$$ \begin{align} f(D) =\frac{1}{\vert {\mathcal C}_A^+ \vert} {\tilde r}\left( e_s -(\vert {\mathcal C}_A^-\vert -1)\, e_1 \right). f(C) \end{align} $$
so that
![]() $f(D)$
depend only on
$f(D)$
depend only on
![]() $f(C_o )$
, as required.
$f(C_o )$
, as required.
Theorem 4.1 has the following nice consequence.
Theorem 4.4. Let
![]() $(\pi , {\mathcal {V}} )$
be an irreducible Iwahori-spherical representation satisfying
$(\pi , {\mathcal {V}} )$
be an irreducible Iwahori-spherical representation satisfying
![]() $\mathrm {dim}\, {\mathcal {V}}^I =1$
. Then
$\mathrm {dim}\, {\mathcal {V}}^I =1$
. Then
![]() $\pi $
has the multiplicity
$\pi $
has the multiplicity
![]() $1$
property
$1$
property
5 Test vectors
Let us fix an irreducible square integrable (or discrete series) representation
![]() $(\pi ,{\mathcal {V}} )$
of G. By definition, for
$(\pi ,{\mathcal {V}} )$
of G. By definition, for
![]() $v\in {\mathcal {V}}$
and
$v\in {\mathcal {V}}$
and
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, the coefficient
${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, the coefficient
![]() $c_{v,{\tilde v}}$
:
$c_{v,{\tilde v}}$
:
![]() $g\mapsto \langle {\tilde v}, \pi (g).v\rangle _{\mathcal {V}}$
,
$g\mapsto \langle {\tilde v}, \pi (g).v\rangle _{\mathcal {V}}$
,
![]() $g\in G$
, lies in
$g\in G$
, lies in
![]() $L^2 (G)$
. Fix a Haar measure
$L^2 (G)$
. Fix a Haar measure
![]() $\nu $
on H.
$\nu $
on H.
Proposition 5.1. For all
![]() $v\in {\mathcal {V}}$
,
$v\in {\mathcal {V}}$
,
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, the integral
${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, the integral
is absolutely convergent.
Proof. Indeed, by [Reference Gurevich and Offen10] Corollary 1.2, a Galois symmetric space as
![]() $G/H$
is strongly discrete: the restriction to H of a coefficient of an irreducible discrete series representation of G lies in
$G/H$
is strongly discrete: the restriction to H of a coefficient of an irreducible discrete series representation of G lies in
![]() $L^1 (H)$
.
$L^1 (H)$
.
Following Zhang [Reference Zhang19], for
![]() $v\in {\mathcal {V}}$
and
$v\in {\mathcal {V}}$
and
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, we set
${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, we set
Then
![]() $\mathcal L$
:
$\mathcal L$
:
![]() ${\mathcal {V}}\times {\tilde {{\mathcal {V}}}}\longrightarrow {\mathbb {C}}$
is a bi-H-invariant bilinear form. For
${\mathcal {V}}\times {\tilde {{\mathcal {V}}}}\longrightarrow {\mathbb {C}}$
is a bi-H-invariant bilinear form. For
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, we set
${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, we set
By construction,
![]() ${\mathcal L}_{\tilde v}\in \mathrm {Hom}_H\, ({\mathcal {V}} ,{\mathbb {C}} )$
for all
${\mathcal L}_{\tilde v}\in \mathrm {Hom}_H\, ({\mathcal {V}} ,{\mathbb {C}} )$
for all
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, and we set
${\tilde v}\in {\tilde {{\mathcal {V}}}}$
, and we set
![]() ${\mathcal H}(\pi ) = \{ {\mathcal L}_{\tilde v} \; \ {\tilde v}\in {\tilde {{\mathcal {V}}}}\}\subset \mathrm {Hom}_H \, ({\mathcal {V}} ,{\mathbb {C}} )$
.
${\mathcal H}(\pi ) = \{ {\mathcal L}_{\tilde v} \; \ {\tilde v}\in {\tilde {{\mathcal {V}}}}\}\subset \mathrm {Hom}_H \, ({\mathcal {V}} ,{\mathbb {C}} )$
.
By [Reference Zhang19] Proposition 3.2,
![]() $G/H$
is very strongly discrete in the sense of loc. cit. Definition 1.3; this means that the linear form
$G/H$
is very strongly discrete in the sense of loc. cit. Definition 1.3; this means that the linear form
is well defined and continuous, where
![]() ${\mathcal C}(G)$
denotes the Harish-Chandra’s Schwartz space of G (cf. loc. cit. §2). As a consequence, by loc. cit. Theorem 1.4, we have the following result.
${\mathcal C}(G)$
denotes the Harish-Chandra’s Schwartz space of G (cf. loc. cit. §2). As a consequence, by loc. cit. Theorem 1.4, we have the following result.
Theorem 5.2 (Zhang).
We have the equality
![]() ${\mathcal H}(\pi )=\mathrm {Hom}_H \, ({\mathcal {V}} ,{\mathbb {C}} )$
(i.e., any H-invariant linear form on
${\mathcal H}(\pi )=\mathrm {Hom}_H \, ({\mathcal {V}} ,{\mathbb {C}} )$
(i.e., any H-invariant linear form on
![]() ${\mathcal {V}}$
is obtained by integration on H against a smooth linear form on
${\mathcal {V}}$
is obtained by integration on H against a smooth linear form on
![]() ${\mathcal {V}}$
).
${\mathcal {V}}$
).
The following result relates the distinction of
![]() $\pi $
to the integral of a bi-I-invariant coefficient.
$\pi $
to the integral of a bi-I-invariant coefficient.
Theorem 5.3. The discrete series representation
![]() $(\pi ,{\mathcal {V}} )$
is H-distinguished if, and only if, there exist
$(\pi ,{\mathcal {V}} )$
is H-distinguished if, and only if, there exist
![]() $v\in {\mathcal {V}}^I$
and
$v\in {\mathcal {V}}^I$
and
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}^I$
such that
${\tilde v}\in {\tilde {{\mathcal {V}}}}^I$
such that
![]() $\displaystyle \int _{H}c_{v,{\tilde v}}(h)\, d\nu (h)\not = 0$
.
$\displaystyle \int _{H}c_{v,{\tilde v}}(h)\, d\nu (h)\not = 0$
.
Proof. One implication in Theorem 5.3 being obvious, let us assume that
![]() $(\pi , {\mathcal {V}} )$
is H-distinguished, and let us fix a non-zero
$(\pi , {\mathcal {V}} )$
is H-distinguished, and let us fix a non-zero
![]() $\Lambda \in \mathrm {Hom}_H ({\mathcal {V}} ,{\mathbb {C}} )$
. By Theorem 5.2, there exists
$\Lambda \in \mathrm {Hom}_H ({\mathcal {V}} ,{\mathbb {C}} )$
. By Theorem 5.2, there exists
![]() ${\tilde v}_1\in {\tilde {{\mathcal {V}}}}$
such that
${\tilde v}_1\in {\tilde {{\mathcal {V}}}}$
such that
![]() $\Lambda ={\mathcal L}_{{\tilde v}_1}$
. By Theorem 4.1, pick
$\Lambda ={\mathcal L}_{{\tilde v}_1}$
. By Theorem 4.1, pick
![]() $v\in {\mathcal {V}}^I$
such that
$v\in {\mathcal {V}}^I$
such that
![]() $\Lambda (v)={\mathcal L}(v,{\tilde v}_1 )\not = 0$
. The map
$\Lambda (v)={\mathcal L}(v,{\tilde v}_1 )\not = 0$
. The map
![]() ${\tilde \Lambda }$
:
${\tilde \Lambda }$
:
![]() ${\tilde v}\mapsto {\mathcal L}(v,{\tilde v})$
is a non-zero element of
${\tilde v}\mapsto {\mathcal L}(v,{\tilde v})$
is a non-zero element of
![]() $\mathrm {Hom}_H \, ({\tilde {{\mathcal {V}}}},{\mathbb {C}} )$
. Applying Theorem 4.1 again to
$\mathrm {Hom}_H \, ({\tilde {{\mathcal {V}}}},{\mathbb {C}} )$
. Applying Theorem 4.1 again to
![]() $({\tilde \pi },{\tilde {{\mathcal {V}}}})$
, there exists
$({\tilde \pi },{\tilde {{\mathcal {V}}}})$
, there exists
![]() ${\tilde v}\in {\tilde {{\mathcal {V}}}}^I$
such that
${\tilde v}\in {\tilde {{\mathcal {V}}}}^I$
such that
![]() ${\mathcal L}(v,{\tilde v})\not = 0$
, and we are done.
${\mathcal L}(v,{\tilde v})\not = 0$
, and we are done.
6 Generalized Poincaré series
Recall that we abbreviate
![]() $W=W_F^{\mathrm {Aff}}=W_E^{\mathrm {Aff}}$
.
$W=W_F^{\mathrm {Aff}}=W_E^{\mathrm {Aff}}$
.
The Poincaré series of the Coxeter system
![]() $(W,S)$
is the formal power series
$(W,S)$
is the formal power series
![]() $W(t)=\displaystyle \sum _{w\in W} t^{l(w)}\in \mathbb Z [[t]]$
. This is the generating function of the length of elements of W. It is known ([Reference Bott3],[Reference Steinberg18]) to be a rational function of t. We shall need a generalization of the Poincaré series due to Macdonald and Gyoja.
$W(t)=\displaystyle \sum _{w\in W} t^{l(w)}\in \mathbb Z [[t]]$
. This is the generating function of the length of elements of W. It is known ([Reference Bott3],[Reference Steinberg18]) to be a rational function of t. We shall need a generalization of the Poincaré series due to Macdonald and Gyoja.
We let
![]() $S_1$
,
$S_1$
,
![]() $...$
,
$...$
,
![]() $S_m$
be the non-empty intersections of S with the conjugacy classes of W. By [Reference Bourbaki4] Proposition 5, page 16, for
$S_m$
be the non-empty intersections of S with the conjugacy classes of W. By [Reference Bourbaki4] Proposition 5, page 16, for
![]() $w\in W$
the number of elements of
$w\in W$
the number of elements of
![]() $S_i$
occurring in a reduced expression of w depends only on w, we denote it by
$S_i$
occurring in a reduced expression of w depends only on w, we denote it by
![]() $l_i (w)$
. We have
$l_i (w)$
. We have
![]() $l(w) = l_1 (w)+\cdots +l_m (w)$
. Let
$l(w) = l_1 (w)+\cdots +l_m (w)$
. Let
![]() $t_1$
,
$t_1$
,
![]() $...$
,
$...$
,
![]() $t_m$
be indeterminates. For
$t_m$
be indeterminates. For
![]() $w\in W$
, we write
$w\in W$
, we write
![]() ${\mathbf t}=(t_1 ,...,t_m )$
and
${\mathbf t}=(t_1 ,...,t_m )$
and
![]() ${\mathbf t}^{l(w)} := t_1^{l_1 (w)} \cdots t_m^{l_m (w)}$
.
${\mathbf t}^{l(w)} := t_1^{l_1 (w)} \cdots t_m^{l_m (w)}$
.
By [Reference Borel2] §3.3, the
![]() $S_i$
,
$S_i$
,
![]() $i=1,...,m$
are the connected components of the subgraph of the Coxeter graph
$i=1,...,m$
are the connected components of the subgraph of the Coxeter graph
![]() $\mathrm {Cox}(W,S)$
obtained by erasing the multiple edges. The number m is so given as follows:
$\mathrm {Cox}(W,S)$
obtained by erasing the multiple edges. The number m is so given as follows:
![]() $m=1$
if G is of type
$m=1$
if G is of type
![]() $A_n$
(
$A_n$
(
![]() $n\geqslant 2$
),
$n\geqslant 2$
),
![]() $D_n$
(
$D_n$
(
![]() $n\geqslant 3$
) and
$n\geqslant 3$
) and
![]() $E_i$
(
$E_i$
(
![]() $i=6,7,8$
),
$i=6,7,8$
),
![]() $m=2$
if G is of type
$m=2$
if G is of type
![]() $A_1$
,
$A_1$
,
![]() $B_n$
(
$B_n$
(
![]() $n\geqslant 3$
),
$n\geqslant 3$
),
![]() $G_2$
and
$G_2$
and
![]() $F_4$
,
$F_4$
,
![]() $m=3$
if G is of type
$m=3$
if G is of type
![]() $C_n$
(
$C_n$
(
![]() $n\geqslant 2$
).
$n\geqslant 2$
).
Remark. There is a mistake in loc. cit.. Indeed, Borel claims that
![]() $m=2$
when G is of type
$m=2$
when G is of type
![]() $B_2 =C_2$
.
$B_2 =C_2$
.
We choose the indexing in
![]() $(t_i )_{i=1,..,m}$
as in [Reference Gyoja11], pages 173, 174.
$(t_i )_{i=1,..,m}$
as in [Reference Gyoja11], pages 173, 174.
Following Gyoja [Reference Gyoja11], for a representation
![]() $(r,M)$
of
$(r,M)$
of
![]() ${\mathcal H}_{\mathrm {I}}$
, define an element of
${\mathcal H}_{\mathrm {I}}$
, define an element of
![]() $\mathrm {End}_{\mathbb {C}} (M)\otimes _{\mathbb {C}} {\mathbb {C}} [[t_1 ,...,t_m ]]$
by
$\mathrm {End}_{\mathbb {C}} (M)\otimes _{\mathbb {C}} {\mathbb {C}} [[t_1 ,...,t_m ]]$
by
Theorem 6.1 ([Reference Gyoja11] Theorem 1.8, page 90).
In any basis of M, the matrix components of
![]() $L({\mathbf t},r)$
are rational functions of
$L({\mathbf t},r)$
are rational functions of
![]() $t_1$
,
$t_1$
,
![]() $...$
,
$...$
,
![]() $t_m$
.
$t_m$
.
When
![]() $(r,M)$
is the trivial representation of
$(r,M)$
is the trivial representation of
![]() ${\mathcal H}_{\mathrm {I}}$
, we set
${\mathcal H}_{\mathrm {I}}$
, we set
![]() $W ({\mathbf t})=L({\mathbf t},r)$
, that is
$W ({\mathbf t})=L({\mathbf t},r)$
, that is
![]() $W({\mathbf t}) = \displaystyle \sum _{w\in W} {\mathbf t}^{l(w)}$
. This rational function has been computed by Macdonald ([Reference Macdonald14] Theorem 3.3). When
$W({\mathbf t}) = \displaystyle \sum _{w\in W} {\mathbf t}^{l(w)}$
. This rational function has been computed by Macdonald ([Reference Macdonald14] Theorem 3.3). When
![]() $m=1$
, then
$m=1$
, then
![]() $W({\mathbf t})= W(t)$
is the ordinary Poincaré series, and Bott’s formula gives
$W({\mathbf t})= W(t)$
is the ordinary Poincaré series, and Bott’s formula gives
 $$ \begin{align*}W(t) = \prod_{i=1,..,l} \frac{1-t_i^{m_i +1}}{(1-t_i)(1-t_i^{m_i})}, \end{align*} $$
$$ \begin{align*}W(t) = \prod_{i=1,..,l} \frac{1-t_i^{m_i +1}}{(1-t_i)(1-t_i^{m_i})}, \end{align*} $$
where
![]() $m_1$
,
$m_1$
,
![]() $...$
,
$...$
,
![]() $m_l$
are the exponents of the spherical Coxeter group attached to W (cf. [Reference Bourbaki4] Chap. V, §6, Définition 2).
$m_l$
are the exponents of the spherical Coxeter group attached to W (cf. [Reference Bourbaki4] Chap. V, §6, Définition 2).
If
![]() $m=2$
, the formulas are the following.
$m=2$
, the formulas are the following.
Type
![]() $A_1$
,
$A_1$
,
![]() $W(t_1 ,t_2 )=\displaystyle \frac {(1+t_1 )(1+t_2 )}{1-t_1 t_2 }$
.
$W(t_1 ,t_2 )=\displaystyle \frac {(1+t_1 )(1+t_2 )}{1-t_1 t_2 }$
.
Type
![]() $B_n$
(
$B_n$
(
![]() $n\geqslant 3$
),
$n\geqslant 3$
),
 $\displaystyle W(t_1 ,t_2 )=\frac {1-t_1^n }{(1-t_1 )^n}\, \prod _{i=1}^{n-1} (1-t_1^{2i})\, \prod _{i=0}^{n-1} \frac { 1+t_1^i t_2}{1-t_1^{n-1+i}t_2}$
.
$\displaystyle W(t_1 ,t_2 )=\frac {1-t_1^n }{(1-t_1 )^n}\, \prod _{i=1}^{n-1} (1-t_1^{2i})\, \prod _{i=0}^{n-1} \frac { 1+t_1^i t_2}{1-t_1^{n-1+i}t_2}$
.
Type
![]() $G_2$
,
$G_2$
,
 $\displaystyle W (t_1 ,t_2 )=\frac {(1+t_1 )(1+t_1 +t_1^2 )(1+t_2 )(1+t_1 t_2 +t_1^2 t_2^2 )}{(1-t_1^2 t_2 )(1-t_1^3 t_2^2 )}$
.
$\displaystyle W (t_1 ,t_2 )=\frac {(1+t_1 )(1+t_1 +t_1^2 )(1+t_2 )(1+t_1 t_2 +t_1^2 t_2^2 )}{(1-t_1^2 t_2 )(1-t_1^3 t_2^2 )}$
.
Type
![]() $F_4$
,
$F_4$
,
![]() $W(t_1 ,t_2 )=$
$W(t_1 ,t_2 )=$
 $$ \begin{align*}\left( \prod_{i=1}^3 \frac{(1-t_1^{i+1})(1+t_1^i t_2 )(1-t_2^i )}{(1-t_1 )(1-t_2 )}\right) \, \frac{(1+t_1 t_2^2 )(1+t_1^2 t_2^2 )(1+t_1^3 t_2^3 )}{(1-t_1^3 t_2^2 )(1-t_1^4 t_2^3 )(1-t_1^5 t_2^3 )(1-t_1^6 t_2^5 )} . \end{align*} $$
$$ \begin{align*}\left( \prod_{i=1}^3 \frac{(1-t_1^{i+1})(1+t_1^i t_2 )(1-t_2^i )}{(1-t_1 )(1-t_2 )}\right) \, \frac{(1+t_1 t_2^2 )(1+t_1^2 t_2^2 )(1+t_1^3 t_2^3 )}{(1-t_1^3 t_2^2 )(1-t_1^4 t_2^3 )(1-t_1^5 t_2^3 )(1-t_1^6 t_2^5 )} . \end{align*} $$
Finally, for
![]() $m=3$
, we have the following formula.
$m=3$
, we have the following formula.
Type
![]() $C_n$
(
$C_n$
(
![]() $n\geqslant 2$
),
$n\geqslant 2$
),
 $\displaystyle W(t_1 ,t_2 ,t_3 ) = \prod _{i=0}^{n-1} \frac {(1-t_1^{i+1})(1+t_1^i t_2 )(1+t_1^i t_3 )}{(1-t_1 )(1-t_1^{n-1+i} t_2 t_3 )}$
.
$\displaystyle W(t_1 ,t_2 ,t_3 ) = \prod _{i=0}^{n-1} \frac {(1-t_1^{i+1})(1+t_1^i t_2 )(1+t_1^i t_3 )}{(1-t_1 )(1-t_1^{n-1+i} t_2 t_3 )}$
.
Remark. These formulas are taken from [Reference Macdonald14], page 173.
7 A numerical criterion with application to degree
 $1$
characters
$1$
characters
Let
![]() $(\pi ,{\mathcal {V}} )$
be an irreducible discrete series representation of G, and let us assume that it is Iwahori-spherical:
$(\pi ,{\mathcal {V}} )$
be an irreducible discrete series representation of G, and let us assume that it is Iwahori-spherical:
![]() ${\mathcal {V}}^I\not = 0$
. Let
${\mathcal {V}}^I\not = 0$
. Let
![]() $(r,M)$
denote the representation of
$(r,M)$
denote the representation of
![]() ${\mathcal H}_{\mathrm {I}}$
in
${\mathcal H}_{\mathrm {I}}$
in
![]() $M={\mathcal {V}}^I$
. The following result is a numerical criterion to decide whether or not
$M={\mathcal {V}}^I$
. The following result is a numerical criterion to decide whether or not
![]() $(\pi ,{\mathcal {V}} )$
is H-distinguished.
$(\pi ,{\mathcal {V}} )$
is H-distinguished.
Theorem 7.1.
(a) The representation
![]() $\pi $
is H-distinguished if, and only if, the endomorphism
$\pi $
is H-distinguished if, and only if, the endomorphism
![]() $L({\mathbf t}_o ,r)\in \mathrm {End}_{\mathbb {C}} (M)$
is non-zero, where
$L({\mathbf t}_o ,r)\in \mathrm {End}_{\mathbb {C}} (M)$
is non-zero, where
![]() ${\mathbf t}_o =\displaystyle (\frac {1}{q_o},...,\frac {1}{q_o})$
.
${\mathbf t}_o =\displaystyle (\frac {1}{q_o},...,\frac {1}{q_o})$
.
(b) We have
![]() $\mathrm {dim}\, \mathrm {Hom}_H \, (\pi ,{\mathbb {C}} )\geqslant \mathrm {rank}\, L({\mathbf t}_o ,r)$
.
$\mathrm {dim}\, \mathrm {Hom}_H \, (\pi ,{\mathbb {C}} )\geqslant \mathrm {rank}\, L({\mathbf t}_o ,r)$
.
Proof. (a) We abbreviate
![]() $J=I_F^o$
. Recall that
$J=I_F^o$
. Recall that
![]() $JwJ\subset IwI$
, for all
$JwJ\subset IwI$
, for all
![]() $w\in W$
. Let
$w\in W$
. Let
![]() $\nu $
the Haar measure on H normalized by
$\nu $
the Haar measure on H normalized by
![]() $\nu (J)=1$
. Let
$\nu (J)=1$
. Let
![]() $m\in M$
and
$m\in M$
and
![]() ${\tilde m}\in {\tilde M}$
. We first calculate the integral
${\tilde m}\in {\tilde M}$
. We first calculate the integral
![]() $\displaystyle \int _H c_{m,{\tilde m}} (h)\, d\nu (h)$
. By the Bruhat-Tits decomposition
$\displaystyle \int _H c_{m,{\tilde m}} (h)\, d\nu (h)$
. By the Bruhat-Tits decomposition
![]() $\displaystyle H=\sqcup _{w\in W} JwJ$
, we have
$\displaystyle H=\sqcup _{w\in W} JwJ$
, we have
 $$ \begin{align} \int_{H} c_{m,{\tilde m}} (h)\, d\nu (h) & = \sum_{w\in W} \int_{JwJ} c_{m,{\tilde m}}(h)\, d\nu (h) \end{align} $$
$$ \begin{align} \int_{H} c_{m,{\tilde m}} (h)\, d\nu (h) & = \sum_{w\in W} \int_{JwJ} c_{m,{\tilde m}}(h)\, d\nu (h) \end{align} $$
 $$ \begin{align} & = \frac{\nu (JwJ)}{q^{l(w)}} \sum_{w\in W} \langle {\tilde m}, r(e_w ).m\rangle_M \end{align} $$
$$ \begin{align} & = \frac{\nu (JwJ)}{q^{l(w)}} \sum_{w\in W} \langle {\tilde m}, r(e_w ).m\rangle_M \end{align} $$
 $$ \begin{align} & = \frac{q_o^{l(w)}}{q^{l(w)}} \sum_{w\in W}\langle {\tilde m}, r(e_w ).m\rangle_M \end{align} $$
$$ \begin{align} & = \frac{q_o^{l(w)}}{q^{l(w)}} \sum_{w\in W}\langle {\tilde m}, r(e_w ).m\rangle_M \end{align} $$
 $$ \begin{align} & = \langle {\tilde m} ,\sum_{w\in W}r(e_w )\left( \frac{1}{q_o}\right)^{l(w)} .m\rangle_M \end{align} $$
$$ \begin{align} & = \langle {\tilde m} ,\sum_{w\in W}r(e_w )\left( \frac{1}{q_o}\right)^{l(w)} .m\rangle_M \end{align} $$
where in (9), we used Corollary 3.2 and where we set
![]() ${\mathbf t}_o = \displaystyle (\frac {1}{q_o},...,\frac {1}{q_o})$
.
${\mathbf t}_o = \displaystyle (\frac {1}{q_o},...,\frac {1}{q_o})$
.
By Proposition 5.3,
![]() $\pi $
is H-distinguished if and only if there exist
$\pi $
is H-distinguished if and only if there exist
![]() $m\in M$
and
$m\in M$
and
![]() ${\tilde m}\in {\tilde M}$
such that
${\tilde m}\in {\tilde M}$
such that
![]() $\displaystyle \int _{H} c_{m,{\tilde m}}(h)\, d\nu (h)\not = 0$
. Thanks to the last calculation, this is indeed equivalent to
$\displaystyle \int _{H} c_{m,{\tilde m}}(h)\, d\nu (h)\not = 0$
. Thanks to the last calculation, this is indeed equivalent to
![]() $L({\mathbf t}_o ,r)\not = 0$
, as required.
$L({\mathbf t}_o ,r)\not = 0$
, as required.
(b) It follows from (a), using the notation of §5, that for
![]() $m\in M$
and
$m\in M$
and
![]() ${\tilde m}\in {\tilde M}$
, we have
${\tilde m}\in {\tilde M}$
, we have
![]() ${\mathcal L}_{\tilde m}(m)=\langle {\tilde m}, L({\mathbf t}_o ,r)\rangle _M$
. Let us put
${\mathcal L}_{\tilde m}(m)=\langle {\tilde m}, L({\mathbf t}_o ,r)\rangle _M$
. Let us put
![]() $s=\mathrm {rank}\, L({\mathbf t}_o ,r)$
. Then there exist
$s=\mathrm {rank}\, L({\mathbf t}_o ,r)$
. Then there exist
![]() ${\tilde m}_1$
,
${\tilde m}_1$
,
![]() $...$
,
$...$
,
![]() ${\tilde m}_s\in {\tilde M}$
such that the
${\tilde m}_s\in {\tilde M}$
such that the
![]() $({\mathcal L}_{{\tilde m}_i})_{\mid M}$
,
$({\mathcal L}_{{\tilde m}_i})_{\mid M}$
,
![]() $i=1,...,s$
, are linearly independent. It follows that the
$i=1,...,s$
, are linearly independent. It follows that the
![]() ${\mathcal M}_{{\tilde m}_i}\in \mathrm {Hom}_H \, (\pi ,{\mathbb {C}} )$
,
${\mathcal M}_{{\tilde m}_i}\in \mathrm {Hom}_H \, (\pi ,{\mathbb {C}} )$
,
![]() $i=1,...,s$
, are linearly independent, and we are done.
$i=1,...,s$
, are linearly independent, and we are done.
We now assume that the discrete series representation
![]() $(\pi ,{\mathcal {V}} )$
satisfies
$(\pi ,{\mathcal {V}} )$
satisfies
![]() $\mathrm {dim}\, M = \mathrm {dim}\, {\mathcal {V}}^I =1$
, so that we may view r as an algebra homomorphism
$\mathrm {dim}\, M = \mathrm {dim}\, {\mathcal {V}}^I =1$
, so that we may view r as an algebra homomorphism
![]() ${\mathcal H}_{\mathrm {I}} \longrightarrow {\mathbb {C}}$
. Such discrete series were classified in [Reference Borel2] §5 by A. Borel. We recall this classification.
${\mathcal H}_{\mathrm {I}} \longrightarrow {\mathbb {C}}$
. Such discrete series were classified in [Reference Borel2] §5 by A. Borel. We recall this classification.
The character r is constant on each
![]() $\{ e_s \; \ s\in S_i\}$
,
$\{ e_s \; \ s\in S_i\}$
,
![]() $i=1,...,m$
and because of the quadratic relations, we have
$i=1,...,m$
and because of the quadratic relations, we have
![]() $r(e_s )\in \{ -1 ,q\}$
,
$r(e_s )\in \{ -1 ,q\}$
,
![]() $s\in S$
. Following Borel loc. cit, for
$s\in S$
. Following Borel loc. cit, for
![]() $i=1,...,m$
, we set
$i=1,...,m$
, we set
 $$ \begin{align*}\epsilon_i =\left\{ \begin{array}{rl} 1 & \mathrm{if}\ r(e_s )=q\\ -1 & \mathrm{if}\ r(e_s )=-1 \end{array} \right. \end{align*} $$
$$ \begin{align*}\epsilon_i =\left\{ \begin{array}{rl} 1 & \mathrm{if}\ r(e_s )=q\\ -1 & \mathrm{if}\ r(e_s )=-1 \end{array} \right. \end{align*} $$
so that the representation
![]() $\pi $
is entirely characterized by the m-uple
$\pi $
is entirely characterized by the m-uple
![]() $(\epsilon _1 ,...,\epsilon _m )$
; we write
$(\epsilon _1 ,...,\epsilon _m )$
; we write
![]() $\pi = \pi (\epsilon _1 ,...,\epsilon _m )$
. Recall that
$\pi = \pi (\epsilon _1 ,...,\epsilon _m )$
. Recall that
![]() ${\mathbf S}{\mathbf t}_G = \pi (-1,..,-1 )$
is the Steinberg representation of G.
${\mathbf S}{\mathbf t}_G = \pi (-1,..,-1 )$
is the Steinberg representation of G.
Proposition 7.2 (Borel [Reference Borel2] §5.8).
The discrete series representations of G of the form
![]() $\pi (\epsilon _1 ,...,\epsilon _m )$
are the Steinberg representation and
$\pi (\epsilon _1 ,...,\epsilon _m )$
are the Steinberg representation and
![]() $\pi (-1,1)$
for types
$\pi (-1,1)$
for types
![]() $B_n$
(
$B_n$
(
![]() $n\geqslant 3$
),
$n\geqslant 3$
),
![]() $F_4$
,
$F_4$
,
![]() $G_2$
,
$G_2$
,
![]() $\pi (-1,-1,1)$
,
$\pi (-1,-1,1)$
,
![]() $\pi (-1,1,-1)$
for types
$\pi (-1,1,-1)$
for types
![]() $C_2$
,
$C_2$
,
![]() $C_3$
,
$C_3$
,
![]() $\pi (-1,-1,1)$
,
$\pi (-1,-1,1)$
,
![]() $\pi (-1,1,-1)$
,
$\pi (-1,1,-1)$
,
![]() $\pi (-1,1,1)$
for type
$\pi (-1,1,1)$
for type
![]() $C_n$
(
$C_n$
(
![]() $n\geqslant 4$
).
$n\geqslant 4$
).
Lemma 7.3. Assume that
![]() $\pi (\epsilon _1 ,...,\epsilon _m )$
is a discrete series representations of G. We have
$\pi (\epsilon _1 ,...,\epsilon _m )$
is a discrete series representations of G. We have
![]() $L({\mathbf t}_o ,r)= W(\epsilon _1 q_o^{\epsilon _i},...,\epsilon _m q_o^{\epsilon _m})$
. In particular,
$L({\mathbf t}_o ,r)= W(\epsilon _1 q_o^{\epsilon _i},...,\epsilon _m q_o^{\epsilon _m})$
. In particular,
![]() $\pi (\epsilon _1 ,...,\epsilon _m )$
is H-distinguished if, and only if,
$\pi (\epsilon _1 ,...,\epsilon _m )$
is H-distinguished if, and only if,
![]() $W(\epsilon _1 q_o^{\epsilon _i},...,\epsilon _m q_o^{\epsilon _m}) \not = 0$
.
$W(\epsilon _1 q_o^{\epsilon _i},...,\epsilon _m q_o^{\epsilon _m}) \not = 0$
.
Proof. Observe that for
![]() $i=1,...,m$
and
$i=1,...,m$
and
![]() $s\in S_i$
, we have
$s\in S_i$
, we have
![]() $r(e_s )= \epsilon _i q_{o}^{\epsilon _i +1}$
, so that for
$r(e_s )= \epsilon _i q_{o}^{\epsilon _i +1}$
, so that for
![]() $w\in W$
, we have
$w\in W$
, we have
 $\displaystyle r(e_w ) = \prod _{i=1}^m (\epsilon _i q_o^{\epsilon _i +1})^{l_i (w)}$
. Hence, we have
$\displaystyle r(e_w ) = \prod _{i=1}^m (\epsilon _i q_o^{\epsilon _i +1})^{l_i (w)}$
. Hence, we have
 $$ \begin{align*} L({\mathbf t}_o ,r) &= \sum_{w\in W} r(e_w ) (\frac{1}{q_o})^{l(w)}\\ &= \sum_{w\in W}\prod_{i=1}^m (\epsilon_i \frac{q_o^{\epsilon_i +1}}{q_o})^{l_i (w)}\\ & = W( \epsilon_i q_o^{\epsilon_i}, ..., \epsilon_i q_o^{\epsilon_i}) \end{align*} $$
$$ \begin{align*} L({\mathbf t}_o ,r) &= \sum_{w\in W} r(e_w ) (\frac{1}{q_o})^{l(w)}\\ &= \sum_{w\in W}\prod_{i=1}^m (\epsilon_i \frac{q_o^{\epsilon_i +1}}{q_o})^{l_i (w)}\\ & = W( \epsilon_i q_o^{\epsilon_i}, ..., \epsilon_i q_o^{\epsilon_i}) \end{align*} $$
as required.
We may now state the main result of this article.
Theorem 7.4. The discrete series representation
![]() $\pi (\epsilon _1 ,...,\epsilon _m )$
is H-distinguished if and only if it is a Steinberg representation, or if H is of type
$\pi (\epsilon _1 ,...,\epsilon _m )$
is H-distinguished if and only if it is a Steinberg representation, or if H is of type
![]() $G_2$
and
$G_2$
and
![]() $(\epsilon _1 ,\epsilon _2 )=(-1 ,1)$
. When it is distinguished, it has the multiplicity
$(\epsilon _1 ,\epsilon _2 )=(-1 ,1)$
. When it is distinguished, it has the multiplicity
![]() $1$
property
$1$
property
![]() $\displaystyle \mathrm {dim}\, \mathrm {Hom}_H\, (\pi (\epsilon _1 ,...,\epsilon _m ),{\mathbb {C}} ) = 1$
.
$\displaystyle \mathrm {dim}\, \mathrm {Hom}_H\, (\pi (\epsilon _1 ,...,\epsilon _m ),{\mathbb {C}} ) = 1$
.
Proof. The multiplicity
![]() $1$
property follows from Theorem 4.1. The first assertion is proved by a case-by-case calculation based on Macdonald’s formulas given in §6. Note that in the case of the Steinberg representation, the distinction property was originally D. Prasad’s conjecture ([Reference Prasad15] Conjecture 3, p. 77) and was proved in [Reference Broussous and Courtès6] (cf. [Reference Beuzart-Plessis1] for a proof of Prasad’s conjecture in the general case).
$1$
property follows from Theorem 4.1. The first assertion is proved by a case-by-case calculation based on Macdonald’s formulas given in §6. Note that in the case of the Steinberg representation, the distinction property was originally D. Prasad’s conjecture ([Reference Prasad15] Conjecture 3, p. 77) and was proved in [Reference Broussous and Courtès6] (cf. [Reference Beuzart-Plessis1] for a proof of Prasad’s conjecture in the general case).
Competing interest
None.