Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T13:04:24.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Time-varying risk behavior and prior investment outcomes: Evidence from Italy

Published online by Cambridge University Press:  01 January 2023

Andrea Lippi ,
Laura Barbieri ,
Mariacristina Piva  and
Werner De Bondt
Laura Barbieri*
Affiliation:
Department of Economics and Social Sciences, Università Cattolica del Sacro Cuore, Via Emilia Parmense, 84, 29122, Piacenza, Italy
Mariacristina Piva*
Affiliation:
Department of Economic Policy, Università Cattolica del Sacro Cuore, Via Emilia Parmense, 84, 29122, Piacenza, Italy
Werner De Bondt*
Affiliation:
Driehaus College of Business, DePaul University, 1 E. Jackson Blvd., Chicago, IL, 60604, U.S.A.
*
†E-mail: [email protected]
‡E-mail: [email protected]
§E-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Risk behavior can be capricious and may vary from month to month. We study 62 clients of a private bank in Northern Italy. The individuals are of special interest for several reasons. As active traders, they manage the value-at-risk (VaR) of a portion of their wealth portfolios. In addition, they act alone, i.e., without input from a financial adviser. Based on VaR-statistics, we find that, in general, the subjects become more risk-averse after suffering losses and more risk-seeking after experiencing gains. The monthly gains and losses that alter investor risk behavior represent true changes in wealth but are “on paper” only, i.e., not immediately realized. Our results allow several interpretations, but they are not at odds with a house money effect, or the possibility that overconfident investors trade on illusions. Rapidly shifting risk behavior in fast response to unstable circumstances weakens individual risk tolerance as a deep parameter and key construct of finance theory.

Keywords

risk attitudegains perceptionlosses perceptiondecision making
Type
Research Article
Information
Judgment and Decision Making , Volume 13 , Issue 5 , September 2018 , pp. 471 - 483
Creative Commons
Creative Common License - CCCreative Common License - BY
The authors license this article under the terms of the Creative Commons Attribution 3.0 License.
Copyright
Copyright © The Authors [2018] This is an Open Access article, distributed under the terms of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

“There are two times in a man’s life when he should not speculate. When he can’t afford it, and when he can.” Mark Twain, Pudd’nhead Wilson’s New Calendar, 1897

Speculative gambling is risky business. While Mark Twain counsels against investment bets, no matter what, his words admit that people’s changing fortunes often have a bearing on what they decide to do.

Understanding how prior gains and losses affect risk attitudes is a significant question in the study of intertemporal choice. Research in this field has produced various perplexing results. Some experimental studies suggest that individuals often become more willing to gamble following gains (Reference Thaler and JohnsonThaler & Johnson, 1990). Other studies propose either that individuals become more risk-seeking after losses (Reference Langer and WeberLanger & Weber, 2008) or, the opposite, more risk-averse (Reference Shiv, Loewenstein, Bechara, Damasio and DamasioShiv et al., 2005; Reference Liu, Tsai, Wang and ZhuLiu et al., 2010).Footnote 1 Here, we investigate the degree to which the experience of gains and losses influences subsequent asset allocation choices made by a sample of clients of an Italian private bank. Thus, we look at the risk behavior of real-world investors, the paper gains or losses in their portfolios, and their monthly asset allocation changes during the year 2015.Footnote 2

As it happens, supervisory authorities in Italy and elsewhere require banks and other financial intermediaries to identify the risk profile of each client — commonly on a scale that runs between “no-risk” and “risk-seeking”. The level of hazard assumed by an investor’s portfolio is supposed to correspond to his or her risk profile. This is why financial service firms assess a value-at-risk (VaR) measure which determines the maximum amount of potential loss and its probability within a specific time frame. Banks and financial intermediaries gather information about clients through forms approved by supervisory authorities. The questionnaires list demographic and financial characteristics such as age, gender, level of education, work experience, financial knowledge and wealth. These characteristics determine the level of VaR that is suitable for a given investor.Footnote 3 Banks and financial intermediaries must check whether the VaR of a particular portfolio matches its owner’s risk profile. The portfolio VaR fluctuates over time as an investor modifies his or her asset allocation, but it can never be allowed to exceed the investor’s VaR.

We examine monthly asset allocation changes made by clients of an Italian private bank. The bank in question considers six levels of VaR: 0 represents “no-risk”; 1, “low-risk”; 2, “prudent balanced risk”; 3, “balanced risk”; 4, “aggressive balanced risk”; and 5 “high-risk”. The greater the loss a specific investor is able to tolerate, the higher the VaR is permitted to be. To repeat, VaR itself assesses the level of risk of the portfolio. This aspect of our study is noteworthy since — as far as we know, without exception — past empirical research on investor trading assesses only the risks and returns associated with individual transactions.

Portfolio allocation decisions are often altered by an investor’s advisor (see, e.g., Reference Foerster, Linnainmaa, Melzer and PreviteroFoerster et al., 2017). Evidently, the fact that advisors guide investors makes it difficult to interpret the findings of an analysis like the one already outlined. That is why we opt for a much smaller sample comprised only of investors who act on their own (i.e., without experienced advisors) and who all qualify for the highest level of VaR.

Our paper contributes to the literature on dynamic choice under risk and uncertainty. How do past gains and/or losses influence the level of downside risk assumed by investors? Section 2 summarizes past research and “what we know” about risk behavior. Sections 3 presents our data collection effort. Section 4 presents the main hypothesis and the methods that are used. Section 5 discusses the results. Section 6 concludes.

2 Theory and literature

A central feature of prospect theory and its successor, cumulative prospect theory, is that people are not consistently risk-averse (Reference Kahneman and TverskyKahneman & Tversky, 1979; Reference Tversky and KahnemanTversky & Kahneman, 1981; Reference Tversky and KahnemanTversky & Kahneman, 1992). Rather, people are risk-seeking in the domain of losses and risk-averse in the domain of gains, with gains and losses defined relative to a target or reference point. Also, individuals feel the pain of a loss more acutely than the pleasure of an equal-sized gain. These basic insights are corroborated by many experimental studies of risky decision making.Footnote 4 Kahneman even dismisses as a “myth” the widespread belief among finance experts that the task of an advisor is to find a portfolio that fits the investor’s attitude to risk. The fundamental problem with individual risk tolerance, Kahneman submits, is that “there is no such thing” (2009, p. 1).Footnote 5

Reference Thaler and JohnsonThaler and Johnson (1990) demonstrate that people tend to assume higher risk immediately following a previous gain. This psychological tendency is labeled the house money effect. It is supported by the further laboratory experiments of Reference Battalio, Kagel and JiranyakulBattalio et al. (1990), Reference Keasey and MoonKeasey and Moon (1996), and Reference Ackert, Charupat, Church and DeavesAckert et al. (2006). Reference Franken, Georgieva, Muris and DijksterhuisFranken et al. (2006) study the Iowa Gambling Task of Reference Bechara, Tranel and DamasioBechara et al. (2000), which involves repeated choices among four decks of cards, two of which have negative expected value because they lead to large but infrequent losses. Young adults who experienced gains make more gainful and safer choices afterward than people who were subjected to losses. Then again, in an adaptation of Franken et al., Reference Rosi, Cavallini, Gamboz and RussoRosi et al. (2016) find that previous episodes makes no difference. As mentioned, Reference ImasImas (2016) shows that many individuals with paper losses accept more risk but that, once a loss is realized, they take less risk. Imas also replicates selected findings of Reference Shiv, Loewenstein and BecharaShiv et al. (2005), Reference Weber and ZuchelWeber and Zuchel (2005), and Reference Langer and WeberLanger and Weber (2008).

Besides theory and laboratory-type experiments, there is limited empirical evidence. However, Reference Malmendier and NagelMalmendier and Nagel (2011) and Reference Bucciol and ZarriBucciol and Zarri (2015) look at the long-lasting effects on risk attitudes of traumatic experiences such as the Great Depression. Weber et al. (2012) use repeated surveys of British investors to study their risk taking during (and closely after) the 2008 financial crisis. Reference Frino, Grant and JohnstoneFrino et al. (2008) consider the behavior of futures traders in Australia. Reference Liu, Tsai, Wang and ZhuLiu et al. (2010) look at market-makers in the Taiwan Futures Exchange. Gains earned during morning hours appear to produce above average risk-taking during afternoon trading. In addition, Reference Hsu and ChowHsu and Chow (2013) study individual investors in Taiwan. After substantial gains, investors assume greater risks. Hsu and Chow notice that, as time goes by, the house money effect slowly weakens. Lastly, Reference Lien and ZhengLien and Zheng (2015) look at slot machinge gambling.Footnote 6

Clearly, it is difficult to tell what defines a gain or loss for a specific investor or to predict frames (Reference FischhoffFischhoff, 1983; Reference BarberisBarberis, 2013). For instance, investors may consider gains and losses in overall wealth, or in the value of their securities, or in the value of a certain asset. If we focus on a specific stock, a return that is positive may be considered a gain, or a return that exceeds the risk-free rate. Timing poses a further problem. Does the investor fixate on weekly, monthly, annual or lifetime gains and losses? This is the problem of choice bracketing Broad bracketing, which allows people to con¬sider all the consequences of their actions, often leads to superior decisions (Reference Read, Lowenstein and RabinRead et al., 1999).

Numerous studies attempt to connect risk preferences with demographic factors such as age, gender and education.Footnote 7 As a rule, risk tolerance strengthens with a higher level of schooling, e.g., a university education (Reference Riley and ChowRiley & Chow, 1992; Reference Halek and EisenhauerHalek & Eisenhauer, 2001; Reference Hartog, Ferrer-i-Carbonell and JonkerHartog et al., 2002; Reference Dwyer, Gilkeson and ListDwyer et al., 2002).

Generally, women are more risk-averse (e.g., Reference Bajtelsmit and BernasekBajtelsmit & Bernasek, 1996; Reference Powell and AnsicPowell & Ansic, 1997; Reference Byrnes, Miller and SchaferByrnes et al., 1999; Reference Schubert, Brown, Gysler and BrachingerSchubert et al., 1999; Reference Eckel and GrossmanEckel & Grossman, 2008; Reference Lusardi and MitchellLusardi & Mitchell, 2008; Reference Croson and GneezyCroson & Gneezy, 2009) while men are more overconfident than women (e.g., Reference Barber and OdeanBarber & Odean, 2000; Reference Croson and GneezyCroson & Gneezy, 2009; Reference Eckel and GrossmanEckel & Grossman, 2008).

With respect to age, the evidence is more ambiguous. For example, Reference Mikels and ReedMikels and Reed (2009), Reference Nielsen, Knutson and CarstensenNielsen et al. (2008), and Reference Albert and DuffyAlbert and Duffy (2012) find that, compared to young adults, the elderly are more risk-averse for losses. Reference Lauriola and LevinLauriola and Levin (2001), and Reference Weller, Levin and DenburgWeller et al. (2011) indicate that the same is true for gains. On the other hand, Reference Mather, Mazar, Gorlick, Lighthall, Burgeno, Schoeke and ArielyMather et al. (2012) suggest that aging instigates risk-seeking in the domain of losses, and Reference Samanez-Larkin, Gibbs, Khanna, Nilsen, Carstensen and KnutsonSamanez-Larkin et al. (2007) and Reference Thomas and MillarThomas and Millar (2012) find no link, either for losses or gains, between risk attitudes and growing older. If measured by the ratio of risky assets to total wealth, risk tolerance may rise with age (Reference Wang and HannaWang & Hanna, 1997). Regarding the link between age and the fraction of equity in investment portfolios (“the risky share”), there is no consensus.Footnote 8

As a final point, we note that past gains and losses may also guide financial decisions for the reason that they change people’s beliefs, e.g., about their power to generate precise return forecasts or to control risk. Reference Moore and HealyMoore & Healy (2008) discuss various aspects of overconfidence. The experiments of Reference Nosić and WeberNosić & Weber (2010) imply that poor calibration encourages aggressive risk-taking. Reference MerkleMerkle (2017) reports related empirical findings.Footnote 9 Clearly, outcomes that validate a person’s beliefs or actions elevate confidence. People may fantasize that success primarily reflects personal ability. Self-assessments of competence correlate with self-assurance (Reference Graham, Campbell and HaiGraham et al., 2009). That many people hold inflated views of themselves, and are also unaware of it (Reference Kruger and DunningKruger & Dunning (1999).

3 Data

A private bank provided us with access to data. We are not allowed to disclose its name, but we can reveal that the bank is located in Northern Italy and that it is one of the five market leaders in financial planning, operating across Italy through a network of more than 1,000 financial advisers. As shown on http://www.assoreti.it, the website of the Associazione delle Società per la Consulenza agli Investimenti, the customers of banks such as ours typically have portfolios invested primarily, if not exclusively, in mutual funds, managed portfolios, insurance and pension funds. A fraction of clients, about 1 percent, use a part of their portfolio, usually between 5% and 10%, for direct investment in shares and/or bonds. With reference to this portion of the portfolio, managed autonomously, some clients adopt a buy-and-hold approach, i.e., they buy securities and hold them over extended periods of time. Others perform trading operations.

We created a data set using several criteria. First, we only consider investors with a total portfolio at the bank worth, on average, about €300,000 and with a portfolio that has two parts. The first piece, representing roughly 90% of its value, is administered with the supervision of a personal financial adviser. The second piece, corresponding to roughly 10%, is managed by the investor on his/her own via home banking. We label this part the “trading portfolio”. It is the main object of our study. Second, we study investors’ asset allocation decisions related to their trading portfolios during the calendar year 2015. In particular, we analyze data for clients who adjust their trading portfolios — at least once a month — but do not refashion the overall strategy of the total portfolio during 2015. This element is essential since, in some cases, financial advisers suggest specific asset allocation modifications, and clients may well apply the advice to their trading portfolios. To repeat, in order to be able to observe portfolio revisions made by clients in complete autonomy, we include only investors who never alter the asset allocation of the total portfolio under management but who do modify the trading portfolio.

Third, we exclude bank clients who add or withdraw funds (say, for consumption purposes) from their trading portfolio between January and December 2015. This makes it much easier for them to calculate and to mentally grasp monthly percentage returns and monetary gains or losses (in Euro).

Finally, we exclude clients who, for whatever reason, are not permitted by bank rules and procedures to raise their portfolio VaR into category 5, i.e., the maximum. Overall, our panel data set comprises data for 62 investors. For each, we have statistics regarding age, gender, level of education, the value of the trading portfolio, monthly gains and losses, and variations in portfolio risk exposure, i.e., the private bank’s estimates of the VaR of the trading portfolio. Our data are snapshots of portfolio value and VaR at the end of each month between January and December 2015.Footnote 10 We note that the subjects in the sample have access to the same information and, of course, much more. On a bank website, they can inspect the composition of their trading portfolio, the account balance, and the VaR at any time, and as often as they wish. (The VaR is calculated around-the-clock.)Footnote 11

4 Hypothesis and Methods

Monthly changes in VaR are the dependent variable in the analysis that follows. In effect, we pretend that, at every month’s end, each individual subject faces a “decision point” where the performance of the trading portfolio over the most recent month is evaluated. At that time, the investor may resolve to vigorously correct the strategy. Only substantial adjustments would lead to a category change in VaR that becomes detectible, straightaway, over the current month. The main predictors of ΔVaR that we employ below are either a gain/loss dummy variable for changes in value of the trading portfolio during the prior month (priorGLD) (gain=1) or the percentage portfolio return (multiplied by 100) for the prior month (priorRET).

To be fully clear, consider an investor who at the beginning of month #1 has a trading portfolio of €100 (V1) invested in stocks and bonds with a VaR equal to 3. During the month, the investor performs at least one transaction that may modify the asset allocation within the trading portfolio and may produce a gain or a loss. Imagine that at the end of month #1 (which is also the start of month #2), the trading portfolio asset allocation is changed in terms of stocks and bonds so as to achieve a VaR equal to 4 and the value of the portfolio value is now €110 (V2). In this example, the investor obtains a gain of V2−V1 and records an increase in VaR from 3 to 4, so that the ΔVaR is +1. See Figure 1.

Figure 1: Overview of the data and the hypothesis.

The main hypothesis tested below is that paper investment gains that are earned over an initial period embolden individuals to accept more risk during a later period. Conversely, current paper losses cause people to diminish risk afterward. We check whether changes in the VaR-category of the trading portfolio during month t (ΔVaR) are predicted by investor-specific portfolio gains or losses during month t − 1.Footnote 12

At first glance, the hypothesis appears to challenge prospect theory since we propose that achievement promotes adventure and failure invites prudence. This is false. We relate present changes in risk behavior (observed through fluctuations in VaR) to past returns. The time dynamics are key. Vis-à-vis decision-making under risk, not only future risk and return matter to investors, but so does history.

Our customized data set and empirical methods intend to reproduce a natural experiment, i.e., a study in which nature, i.e., factors outside our control, exposes clusters of individuals to dissimilar experimental and control conditions. Importantly, the process that governs exposures resembles random assignment. To repeat, we have access to portfolio values and VaRs at the end of each month between January and December 2015. This makes 62 investors ×11 months = 682 observations of ΔVaR, priorGLD, and priorRET. Since we relate changes in risk to prior month returns, the first set of 62 ΔVaRs that may be analyzed are for March 2015. The last set is for December 2015. All in all, we are able to examine investor behavior at 620 decision points which occur at the end of February 2015 through the end of November 2015 as subjects come to grips with the monthly performance of their trading portfolios.Footnote 13

Since we have panel data, we estimate random-effects ordered logit regressions with changes in portfolio risk levels (ΔVaR) as a categorical dependent variable.Footnote 14 Age, gender, education, and the total value of the trading portfolio at the end of the previous month serve as control variables. The main regression is:

Likewise, we run the same regression with priorGLD substituting for priorRET. We also conduct a string of robustness tests.

5 Results

The main result is that, as hypothesized, the subjects become more risk-averse after suffering losses and more risk-seeking after experiencing gains, from month to month. Relevant details for this result are in Section 5.2. Section 5.1 provides basic descriptive statistics.

5.1 Descriptive statistics

Tables 1, 2 and 3 offer descriptive statistics for 62 private bank clients. Hereafter, we briefly state — and further illustrate — the main facts in these tables.

The mean VaR across 682 monthly observations was 2.90. The 2015 age of the individuals in the sample varied between 35 and 65 years. On average, the subjects were 47 years old. Sixteen (26%) were women; 44% were university-educated. (Women were equally distributed between education levels.)

The mean trading portfolio balance, across investors and months, was €30,952. The minimum was €20,204 (investor #14, female, with a high-school education, age 55, and an average monthly VaR of 2.00) while the maximum was €46,125 (#25, male, high-school educated, 57, VaR 3.00).

The largest recorded loss in portfolio value between January and December 2015 was €13,000 (an 11-month return of −38.2% for #37, male, high-school educated, 41, VaR 2.92); the largest recorded gain came to €9,000 (a return of 32.1% for #33, female, university-educated, 40, VaR 2.42). The median investor lost €150.

Panel B in Table 1 shows data similar to panel A but for subsamples arranged by age, gender, education, and the monthly average trading portfolio balance. On average, older investors ran portfolios with somewhat lower VaRs but the difference is not large. Compared to the men, the women in the sample managed portfolios that were about €4,000 smaller with VaRs that were much lower. (Note the t- and Mann-Whitney U-tests.) Subjects with a university degree were on average 5½ years younger than high-school graduates. Larger portfolios displayed higher VaRs.

Table 1: Descriptive statistics for 62 private bank clients. Panel A describes bank client age (in years), the value of the trading portfolio (Value, average of 12 monthly observations, in Euro), the change in portfolio value between end January and end December 2015 (ΔValue), and the value-at-risk category (1 to 5). Panel B shows means for subsamples of (1) men (M) and women (F), individuals (2) who are standard- or high-educated (LE and HE), (3) young or old, relative to the median sample age (Y and O), and hold (3) small or large trading portfolios, relative to the value of the median portfolio (SM and LG). We run t-tests for differences in means and Mann-Whitney U tests. The null hypothesis is that the sample means are equal. * (**) indicates statistical significance at the 5 (1) % level for t-tests; + (++) does the same for nonparametric tests.

Some of the relationships thus far discussed are also visible in Table 2, a correlation matrix.

It shows that the current monthly returns earned by individual investors (RET), these same returns for the previous month (measured either by priorRET and priorGLD, the gain/loss dummy), the VaRs and ΔVaRs are all strongly positively correlated.

Table 2: Pearson pairwise correlations, calculated for the 620 observations that correspond to the ordered logistic regressions estimated later in Table 5. Variables are measured monthly (at the end of month t) except Value, priorGLD and priorRET which are measured with respect to month t−1. ΔVaR is the portfolio value-at-risk category (1 through 5, with 5 indicating high risk) at the end of current month minus the value-at-risk at the beginning of the current month. VaR is the value-at-risk at the end of the current month. Age is measured in years. Gender is a dummy variable (female=1) and so is Education (high education=1). Value denotes portfolio value (in Euros) at the end of the previous month (which is the start of the current month). priorGLD is a dummy variable equal to one if the portfolio gained in value during the previous month. priorRET denotes the portfolio return during the previous month. RET is the portfolio return during the current month.

Table 3 shows some of the data month-by-month.

Table 3: Portfolio VaRs, values, gains and losses, by month. Panel A shows VaRs by month, averaged across 62 subjects; the monthly fraction of subjects who raise or cut VaR; monthly cross-sectional averages of portfolio values, and of the ratios of the smallest and the largest portfolios relative to the mean portfolio. Panel B shows mean, minimum and maximum returns by month (in percent). In addition, it lists the fraction of all portfolios that rise in value during the month; the average gain or loss (in Euros) across all portfolios; and the matching monthly cross-sectional average of the absolute changes in value (in Euros).

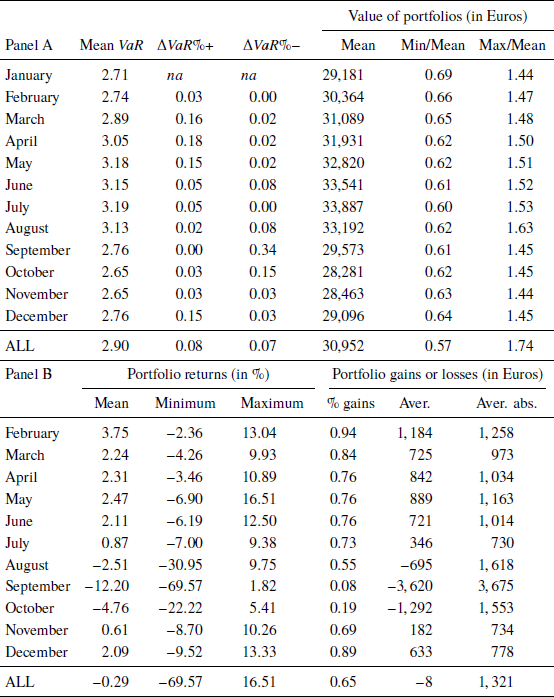
Between January and August 2015, the average portfolio was rising in value. This was followed by big negative shocks in September and October. The same pattern emerges in the monthly VaRs, averaged across bank clients. Also, in all months but September, there were some subjects who increased the value-at-risk of their portfolios; in all months but July, some decreased VaR. About 2/3’s of all monthly observations are gains; 8% are associated with increases in ΔVaR, 7% with decreases in ΔVaR, and 85% cause no change in value-at-risk.

The simple average monthly portfolio return was minus 29 basis points, equivalent to a loss of €8. In terms of this investigation, the averages are deceptive, however. The absolute monthly change in portfolio value, averaged across individuals, is €1,321; the same statistic calculated for two-month periods is €2,294, and it is €3,202 for three-month periods. Figure 2 is a histogram with all one-month gains and losses for all subjects between February to November 2015. Evidently, most monthly value changes are modest, and cannot be expected to prompt changes in risk-taking, but a considerable number are very large relative to the size of the portfolio. As seen in Table 3, the cruelest monthly shock was a loss of €16,000 in September (−69.57% for #28, female, 41, high-school educated, VaR 2.83); the best result was a gain of €7,100 in May (+16.51% for #1, male, 35, university-educated, VaR 4.50).

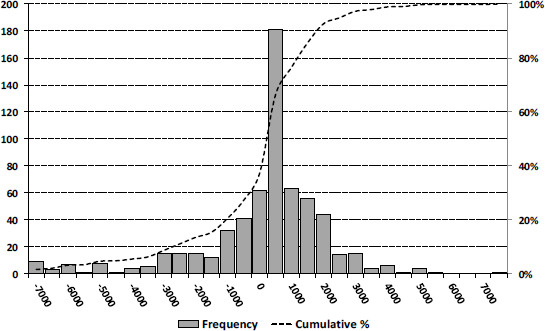
Figure 2: Trading portfolio gains or losses in Euro (62 investors, 10 decision points each, February-November 2015).

5.2 Tallying VaR transitions and regression evidence

In a simple analysis, we regressed the change in VaR category on whether the previous month showed a gain or a loss, for each subject. Of the regression coefficients, 39 were positive, 2 were negative, and 21 were 0. This difference suggests that changes of the last month affect risk taking in the present month.

For a more complete analysis, Table 4 (panel A) presents the transition matrix describing the frequency with which investors move their portfolios from one VaR category to another.

Table 4: Monthly transitions between VaR categories. Panel A shows frequencies for 25 different types of VaR transitions as well as the number of of portfolio gains and losses (over the previous month) associated with specific VaR transitions (during the current month). In total, there are 620 decision points that lead to 98 VaR transitions to a different category. Panel B lists equivalent percentages totaling to 100 percent. Panel C shows the average Euro gain or loss for all transitions of a given type.

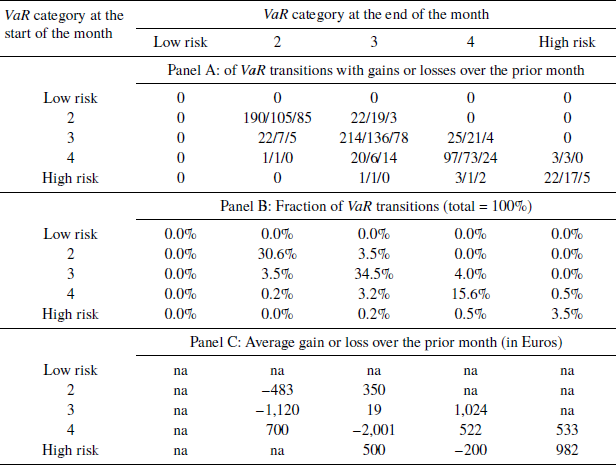
Each cell lists the total number of cases, the number of cases associated with portfolio gains during the previous month, and the ones associated with losses during that month. Panel B shows the fraction of VaR transitions of different types, and panel C lists the matching average €gain or loss, averaged across all observations for the matrix cell.

Since the largest percentages are on the main diagonal of panel B, Table 4 indicates that investors tend to preserve the status-quo level of VaR. Values outside the diagonal and other than zero represent the changes in VaR which we want to explain. The average ΔVaR is close to zero, and this remains true even if we exclude the 85% of cases on the diagonal. Some individuals changed VaR as often as three or four times during 2015. Others never did.

The main insight derived from Table 4 is that VaR increases (from 2 to 3, from 3 to 4, and from 4 to 5) are allied with a high proportion of gains and high average €gains during the previous month. VaR decreases (from 3 to 2, from 4 to 3, and from 5 to 4) are coupled with a high proportion of losses and high average €losses.Footnote 15 This agrees with our main hypothesis.

Figure 3 presents a different route to the same destination. There, all past one-month gains or losses, previously shown in Figure 2, are sorted into quintiles and, for each quintile, we find the fraction of all VaR increases and all VaR decreases associated with it. The results are crystal clear. Nearly half of all VaR decreases accompany the 20% of months with the worst portfolio performance. Also, roughly 70% of all VaR increases follow months with portfolio value changes in the top 40%. Lastly, the middle quintile shows less than proportional VaR increases and decreases. If past gains or losses did not bring about changes in risk-taking, all bars in Figure 3 should have been of the same height.

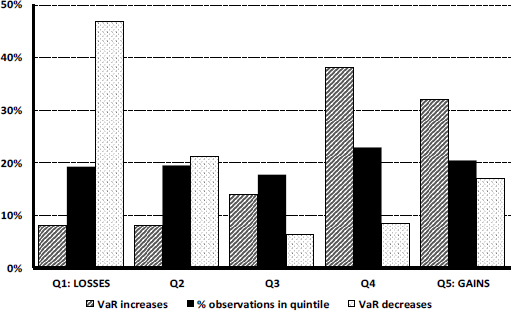
Figure 3: Fraction of all bank-recorded VaR increases or decreases by quantile of gains or losses over the prior month (620 decision points).

Table 5 displays the regression results for the full sample and various subsamples.

Table 5: Which factors cause variation in Value-at-Risk?

We estimate random-effect ordered logistic regressions. The dependent variable is Δ VaR. The predictor variables are Age (in years), Gender (female=1), Education (high education=1), the value of the portfolio at the beginning of the month (in thousands of Euros), a gain/loss dummy (PriorGLD, gain=1) for the change in portfolio value during the prior month, and the portfolio return during the prior month (PriorRET, in percent). The regressions are for the full sample and for subsamples. *** is p<.01; **, p<.05; *, p<.10. S.E., clustered by individual investor, are in parentheses.

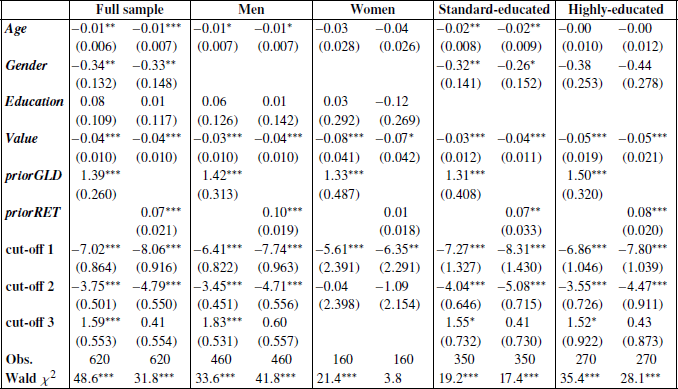
The cut-off points in the table are auxiliary parameters that separate the four categories of the dependent variable (ΔVaR) is +1, 0, −1, or −2). Equality tests strongly reject the null hypothesis that the cut-off points are equal — confirming the relevance of the four categories. For the sample as a whole, the results indicate that, except for education, all variables contribute in a significant way. The results are fairly uniform across subsamples.Footnote 16 Older subjects are less likely to appear in the top category, i.e., their risk appetite is lower. The same applies to women, and to clients with somewhat more abundant portfolios.

6 Conclusion

In the financial industry, and also in finance theory, the assessment of investor risk profiles is normally seen as a elementary step toward identifying asset portfolios that are most appropriate to serve client needs. Past studies find that risk tolerance varies with demographic factors that change slowly over time or not at all. Here, we offer direct evidence that risk preferences and/or beliefs about one’s ability to manage risk and return evolve from month to month and in direct response to recent portfolio performance. This is shown for a sample of genuine investors who act on their own without external advisory influence. All told, fast-changing circumstances predict fast-changing risk attitudes.

If correct and characteristic of the behavior of important segments of the financial community, our empirical findings appear to offer some circuitous support for modern asset pricing theory in the manner of Reference Campbell and CochraneCampbell and Cochrane (1999) and others. The fact that we study active traders likely helps to explain why our results are so markedly different from the inertia reported by Reference Brunnermeier and NagelBrunnermeier and Nagel (2008) who, based on data from the Panel of Income Dynamics, report that most U.S. households do not adjust the share of their portfolios invested in risky assets following wealth changes, and who find in favor of constant relative risk aversion.Footnote 17

Our chief result, however, is that, for the Italian bank clients in our sample, past portfolio performance — which, as we have seen, can be quite erratic — predicts short-term variations in risk-taking quantified by value at risk. The house money effect of Reference Thaler and JohnsonThaler and Johnson (1990) is not discarded by our data set, and neither is the alternate view that fluctuations in self-confidence, feeding an illusion of control, is the main culprit. However, the tests do appear to challenge Reference ImasImas (2016).

The investors that we study are amateurs, not experts. Our analysis agrees with the Dunning-Kruger effect (Reference Kruger and DunningKruger & Dunning, 1999). Intuitively, it is plausible that amateurs look at past performance, even if not realized, to divine the future, especially when they act alone without highly trained assistance. Success builds confidence; failure undermines it.Footnote 18 The switches from less risk tolerance to more, and vice versa, on the basis of near past performance also lead us straightforwardly to Bandura’s concept of self-efficacy. The beliefs that people hold about their capabilities, e.g., the presence or lack of mastery, affect the quality of their functioning. Self-efficacy has a bearing on thought patterns, emotional arousal, and behavior (Reference BanduraBandura, 1982). The findings in this article suggest to us that quite a few investors (i) may eventually come to doubt their own skills, (ii) may no longer put in much effort, and (iii) do not truly learn from experience. As their self-efficacy erodes, they may have a sense of futility, perhaps apathy.Footnote 19 Of course, we recognize that these last sentences are highly speculative, and necessitate much more investigation. The results may also have some limited practical/regulatory use. Italian banks and financial intermediaries are required to monitor the level of risk of their clients’ portfolios so as to avoid excessive loss exposure and potential discontent. Financial advisers who observe unusual trading and fluctuations in risk-taking may use our findings for didactic purposes, leading clients to be more sensible in their investments and thereby also building more fruitful advisory relationships.

Footnotes

An earlier version of this manuscript was presented at the international conference on Wealth Management: Behavioral Finance held in Piacenza (Italy) in May 2017. We are grateful to Rosa Mayoral, our discussant, for comments. Werner De Bondt also thanks Richard and Inese Driehaus for generous financial support.

1 The evidence on intertemporal choice and risk-taking is multifaceted. For instance, Reference Weber and ZuchelWeber and Zuchel (2005) show that manipulations of the presentation format can induce both types of behavior. In a later study of myopic loss aversion, Reference Langer and WeberLanger and Weber (2008) find a strong interaction effect between how long an investor is bound by his initial decision and feedback frequency. Reference Andrade and IyerAndrade and Iyer (2009) find that people may intend to bet less after a loss but end up betting more because they underestimated how the negative emotion linked to the loss would affect later decisions.

2 The distinction between realized capital gains or losses and paper gains or losses is meaningful. The former are generated when money is transferred between accounts (e.g., the sale of an asset that fell in price) but the latter do not generate any associated cash flows. In an informative article that starts with a useful synopsis of prior work, Reference ImasImas (2016) finds that, following realized losses, individuals tend to avoid risk but, if they sit on paper losses, they are inclined to take on greater risk. We thank a referee for telling us about Imas’s work.

3 There are various ways to calculate VaR. See, e.g., Reference HoltonHolton (2014). Each Italian bank is free to choose its own preferred method. The method of choice has to be approved by the Commissione Nazionale per le Società e la Borsa (Consob), however. The bank that provided data for this study uses Monte Carlo methods. Note that VaR is a view of risk that emphasizes downward risk and the wish for financial security. For more discussion of the diverse concepts of portfolio risk applied in financial economics, see Reference Shefrin and StatmanShefrin and Statman (2000).

4 Still, various complexities result in further choice paradoxes examined by Reference Battalio, Kagel and JiranyakulBattalio et al. (1990), Reference BirnbaumBirnbaum (2008), Reference Callen, Isaqzadeh, Long and SprengerCallen et al. (2014) and others.

5 How prospect theory works in practice further depends on its editing phase. The framing of the decision problem is all-important. On one view, at some point in time, each individual investor opens a separate mental account for every distinctly identifiable portfolio (even as his/her total wealth may be spread over quite a few portfolios). Within each account, risk is managed in isolation, perhaps with the aim of reaching a given target or, at a minimum, in order to preserve the status-quo (Reference Kahneman and TverskyKahneman & Tversky, 1979; Reference Kahneman and TverskyKahneman & Tversky, 1984; Reference Tversky and KahnemanTversky & Kahneman, 1981). Therefore, capital preservation, and risk control, may be more urgent for large size portfolios.

6 The final causes of the house money effect remain unclear. People often contrast outcomes to mental simulations of what may have been or what may come to pass. Salient counterfactuals set off emotions, positive or negative, such as regret. For instance, past trauma and recollection of fear bolster cautiousness (Reference Callen, Isaqzadeh, Long and SprengerCallen et al., 2014; Reference Cameron and ShahCameron & Shah, 2015). Reference Strahilevitz, Odean and BarberStrahilevitz et al. (2011) study this type of reinforcement learning with trading data from two brokerage firms. Many investors avoid stocks for which past purchases ended in losses. Conversely, Reference Kaustia and KnüpferKaustia and Knupfer (2008) report that people are more likely to subscribe to initial public offerings of equity if their past personal experience with IPOs was positive. More generally, Reference Arkes, Joyner, Pezzo, Nash, Siegel-Jacobs and StoneArkes et al. (1994) argue that unexpected gains may be put in a windfall (“fun money”) account outside usual financial plans, or in no account at all, and that the surprise element itself explains why people bet more. The issue is related to the subtleties of reference point adaptation which may be quicker and more complete for gains than for losses (Reference Arkes, Hirshleifer, Jiang and LimArkes et al., 2008).

7 Wide-ranging literature reviews of financial risk-taking, surveying both experimental and empirical studies, include Reference Roszkowski and CordellRoszkowski (2001) and Reference Grable and XiaoGrable (2008).

8 Reference Poterba, Samwick, Ogura, Tachibanaki and WisePoterba & Samwick (2001) find that the risky share increases with age. While the age profile for financial ownership is hump-shaped, the share of risky assets tends to be flat (Reference Guiso, Haliassos and JappelliGuiso et al., 2002). According to Reference Fagereng, Gottlieb and GuisoFagereng et al. (2013), the hump-shaped pattern peaks around retirement. But Reference Foerster, Linnainmaa, Melzer and PreviteroFoerster et al. (2017) say that the risky share peaks around age 40 and falls as retirement approaches.

9 Related empirical studies in financial economics include Reference Blume and FriendBlume & Friend (1975), Reference OdeanOdean (1999), Reference Barber and OdeanBarber & Odean (2000), and Reference Grinblatt and KeloharjuGrinblatt & Keloharju (2009). Reference De BondtDe Bondt (1998) offers a brief survey.

10 We do not know the exact composition of the trading portfolios but we do know that they typically include a variety of financial instruments (e.g., stocks, bonds, commodities, derivatives, funds, ETFs and various insurance products).

11 Investors also have continuous access to the same data for the full portfolio. The website does not separately indicate recent changes in VaR. If the VaR were to exceed the maximum allowed level for a given client, the bank directly contacts that client so as to enforce relevant regulations and to avoid a mishap. However, the maximum allowed VaR for the investors in our sample (VaR=5) is the maximum allowed under Italian law. Therefore, these subjects may adjust the riskiness of their portfolio as they wish without interference from the bank.

12 It would seem that only sizeable past value changes can cause VaR to cross a threshold. As stated earlier, there are six VaR categories. In only two instances (out of 620 decision points) did a portfolio jump two VaR categories in adjacent months. Thus, nearly all one-month ΔVaRs were +1, 0 or −1. (This also explains our later use of ordered logit regressions.)

13 Accordingly, the analysis does not employ the 62 VaR estimates for February 2015 and the 62 gains or losses for December 2015. This rule does not apply to some of the descriptive statistics.

14 Although it may be of interest to compare the random and fixed effect estimates, there is no unanimity in the literature on how to implement a fixed effect estimator for an ordered logit model (see Baetschmann et al., 2015). The results reported below appear to be robust despite significant effort on our part to do away with them.

15 Broadly similar patterns are visible in matrices (equivalent to Table 4) for subsamples of men, women, high-school and university-educated subjects.

16 In addition, we run regressions, not shown in Table 5, with dummy variables controlling for the month of the year; with gain/loss dummies and/or returns measured over the previous two months, or over the previous three months; with a gain/loss dummy and the return for the current month included; and with Value left out of the regression. None of these variations destroy the apparent explanatory power of past performance for later ΔVaR.

17 Yet, risk-aversion intensified in the aftermath of the 2008 financial crisis, and many investors abruptly divested their stock holdings. Reference Guiso, Sapienza and ZingalesGuiso et al. (2018) list four possible channels but favor a fear-based explanation with possibly long-lasting effects as suggested by Reference Malmendier and NagelMalmendier and Nagel (2011).

18 Kahneman cheerfully extends this logic to business and financial professionals. In a lengthy article published in the New York Times Magazine (October 19, 2011), he writes that overconfidence and the illusion of skill are “sincere”, “not only an individual aberration”, and “deeply ingrained in the culture of the [financial] industry.” The biases arise, he says, “because people are often blind to their own blindness.”

19 According to Reference BanduraBandura (1982), the quality of performance depends, in general, on whether people approach life with devoted effort and realistic goals. Easy success with little energy can lead them to expect too much and get disappointed. In this sense, failure is an opportunity to build resilience. The research literature set in motion by Bandura’s ideas since the late 1970s is immense. One noteworthy example is the study by Reference Caprara, Fida, Vecchione, Del Bove, Vecchio, Barbaranelli and BanduraCaprara et al. (2008) on the academic achievement of Italian high-school students.

References

Ackert, L., Charupat, N., Church, B., & Deaves, R. (2006). An experimental examination of the house money effect in a multi-period setting. Experimental Economics, 9(1), 5–16.CrossRefGoogle Scholar
Albert, S., & Duffy, J. (2012). Differences in risk aversion between young and older adults. Neuroscience and Neuroeconomics, 1, 3–9.CrossRefGoogle Scholar
Andrade, E. B., & Iyer, G. (2009). Planned versus actual betting in sequential gambles. Journal of Marketing Research, 46(3), 372–383.CrossRefGoogle Scholar
Arkes, H. R., Hirshleifer, D., Jiang, D., & Lim, S. (2008). Reference point adaptation: Tests in the domain of security trading. Organizational Behavior and Human Decision Processes, 105(1), 67–81.CrossRefGoogle Scholar
Arkes, H. R., Joyner, C. A., Pezzo, M. V., Nash, J. G., Siegel-Jacobs, K., & Stone, E. (1994). The psychology of windfall gains. Organizational Behavior and Human Decision Processes, 59(3), 331–347.CrossRefGoogle Scholar
Baetschmann, G., Staub, K. E., & Winkelmann, R. (2011). Consistent estimation of the fixed effects ordered logit model, Discussion Paper #5443, Forschungsinstitut zur Zukunft der Arbeit (www.econstor.eu).Google Scholar
Bajtelsmit, V., & Bernasek, A. (1996). Why do women invest differently than men? Financial Counseling and Planning, 7(1), 1–10.Google Scholar
Bandura, A. (1982). Self-efficacy mechanism in human agency. American Psychologist, 37(2), 112–147.CrossRefGoogle Scholar
Barber, B., & Odean, T. (2000). Trading is hazardous to your wealth: The common stock investment performance of individual investors. Journal of Finance, 55(2), 773–806.CrossRefGoogle Scholar
Barber, B., & Odean, T. (2001). Boys will be boys: Gender, overconfidence and common stock investment. Quarterly Journal of Economics, 116(1), 261–292.CrossRefGoogle Scholar
Barberis, N. C. (2013). Thirty years of Prospect Theory in Economics: A review and assessment. Journal of Economic Perspective, 27(1), 173–196.CrossRefGoogle Scholar
Battalio, R., Kagel, J., & Jiranyakul, K. (1990). Testing between alternative models of choice under uncertainty: Some initial results. Journal of Risk and Uncertainty, 3(1), 25–50.CrossRefGoogle Scholar
Bechara, A., Tranel, D., & Damasio, H. (2000). Characterizations of the decision-making deficit of patients with ventromedial prefrontal cortext lesions. Brain, 123(11), 2189–2202.CrossRefGoogle Scholar
Birnbaum, M. H. (2008). New paradoxes of risky decision making. Psychological Review, 115(2), 463–501.CrossRefGoogle ScholarPubMed
Blume, M., & Friend, I. (1975). The asset structure of individual portfolios and some implications for utility functions. Journal of Finance, 30(2), 585–603.CrossRefGoogle Scholar
Brunnermeier, M. K., & Nagel, S. (2008). Do wealth fluctuations generate time-varying risk aversion? Micro-evidence on individuals’ asset allocation. American Economic Review, 98(3), 713–736.CrossRefGoogle Scholar
Bucciol, A., & Zarri, L. (2015). The shadow of the past: Financial risk taking and negative life events. Journal of Economic Psychology, 48, 1–16.CrossRefGoogle Scholar
Byrnes, J., Miller, D., & Schafer, W. (1999). Gender differences in risk taking: A meta analysis. Psychological Bulletin, 125(3), 367–383.CrossRefGoogle Scholar
Callen, M., Isaqzadeh, M, Long, D. J., & Sprenger, C. (2014). Violence and risk preference: Experimental evidence from Afghanistan. American Economic Review, 104(1), 123–148.CrossRefGoogle Scholar
Cameron, L., & Shah, M. (2015). Risk-taking behavior in the wake of natural disasters. Journal of Human Resources, 50(2), 484–515.CrossRefGoogle Scholar
Campbell, J. Y., & Cochrane, J. H. (1999). By force of habit: A consumption-based explanation of aggregate stock market behavior. Journal of Political Economy, 107(2), 205–251.CrossRefGoogle Scholar
Caprara, G. V., Fida, R., Vecchione, M., Del Bove, G., Vecchio, G. M., Barbaranelli, C., & Bandura, A. (2008). Longitudinal analysis of the role of perceived self-efficacy for self-regulated learning in academic continuance and achievement. Journal of educational psychology, 100(3), 525–534.CrossRefGoogle Scholar
Cardak, B., & Wilkins, R. (2009). The determinants of household risky asset holdings: Australian evidence on background risk and other factors. Journal of Banking and Finance, 33(5), 850–860.CrossRefGoogle Scholar
Croson, R., & Gneezy, U. (2009). Gender differences in preferences. Journal of Economic Literature, 47(2), 448–474.CrossRefGoogle Scholar
De Bondt, W. F. M. 1998. A portrait of the individual investor. European Economic review, 42(3–5), 831–844.CrossRefGoogle Scholar
Dwyer, P. D., Gilkeson, J. H., & List, J. A. (2002). Gender differences in revealed risk taking: Evidence from mutual fund investors. Economics Letters, 76(2), 151–158.CrossRefGoogle Scholar
Eckel, C., & Grossman, P. (2008). Forecasting risk attitudes: an experimental study using actual and forecast gamble choices. Journal of Economic Behavior and Organization, 68(1, 1–17.CrossRefGoogle Scholar
Everson, H., & Tobias, S. (1998). The ability of estimate knowledge and performance in college: A metacognitive analysis. Instructional Science, 26(1–2), 65–79.CrossRefGoogle Scholar
Fagereng, A., Gottlieb, C. & Guiso, L. (2013). Asset market participation and portfolio choice over the life-cycle. EUI Working Paper ECO 2013/07.CrossRefGoogle Scholar
Fan, E., & Zhao, R. (2009). Health status and portfolio choice: Causality or heterogeneity? Journal of Banking and Finance, 33(6), 1079–1088.CrossRefGoogle Scholar
Fischhoff, B. (1983). Predicting frames. Journal of Experimental Psychology: Learning, Memory, and Cognition, 9(1), 103–116.Google Scholar
Foerster, S., Linnainmaa, J. T., Melzer, B. T., & Previtero, A. (2017). Retail financial advice: Does one size fit all? Journal of Finance, 72(4), 1441–1482.CrossRefGoogle Scholar
Franken, I., Georgieva, I., Muris, P., & Dijksterhuis, A. (2006). The rich get richer and the poor get poorer: On risk aversion in behavioral decision-making. Judgment and Decision Making, 1(2), 153–158.CrossRefGoogle Scholar
Frino, A., Grant, J., & Johnstone, D. (2008). The house money effect and local traders on the Sydney Futures Exchange. Pacific-Basin Finance Journal, 16(1), 8–25.CrossRefGoogle Scholar
Grable, J. E. (2008). Risk tolerance. In Xiao, J. J. (Ed), Handbook of Consumer Finance Research (pp. 3–19). New York: Springer.CrossRefGoogle Scholar
Graham, J., Campbell, R., & Hai, H. (2009). Investor competence, trading frequency, and home bias. Management Science, 55(7), 1094–1106.CrossRefGoogle Scholar
Grinblatt, M., & Keloharju, M. (2009). Sensation seeking, overconfidence, and trading activity. Journal of Finance, 64(2), 549–578.CrossRefGoogle Scholar
Guiso, L., Haliassos, M. & Jappelli, T. (2002), Household Portfolios. Cambridge, Massachusetts: The MIT Press.CrossRefGoogle Scholar
Guiso, L., Sapienza, P. & Zingales, L. (2018). Time-varying risk aversion. Journal of Financial Economics, 128(3), 403–421.CrossRefGoogle Scholar
Halek, M., & Eisenhauer, J. G. (2001). Demography of risk aversion. The Journal of Risk and Insurance, 68(1), 1–24.CrossRefGoogle Scholar
Hartog, J., Ferrer-i-Carbonell, A., & Jonker, N. (2002). Linking measured risk aversion to individual characteristics. Kyklos, 55(1), 3–26.CrossRefGoogle Scholar
Hinz, R., McCarthy, D., & Turner, J. (1997). Are women more conservative investors? Gender differences in participant-directed pension investments. In Gordon, M. S., Mitchell, O. S. & Twinney, M. M. (Eds.), Positioning Pensions for the Twenty-first Century (pp.45–66). Philadelphia: University of Pennsylvania Press.Google Scholar
Holton, G. A. (2014). Value-at-Risk: Theory and practice, e-book at urlhttp://value-at-risk.net (2nd ed.).Google Scholar
Hsu, Y. L., & Chow, E. (2013). The house money effect on investment risk taking: Evidence from Taiwan. Pacific-Basin Finance Journal, 21(1), 1102–1115.CrossRefGoogle Scholar
Imas, A. (2016). The realization effect: Risk-taking after realized versus paper losses. American Economic Review, 106(8), 2086–2109.CrossRefGoogle Scholar
Kahneman, D. (2009). The myth of risk attitudes. Journal of Portfolio Management, 36(1), 1–1.CrossRefGoogle Scholar
Kahneman, D., Knetsch, J., & Thaler, R. H. (1991). The endowment effect, loss aversion, and status quo bias. Journal of Economic Perspectives, 5(1), 193–206.CrossRefGoogle Scholar
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.CrossRefGoogle Scholar
Kahneman, D., & Tversky, A. (1984). Choices, values and frames. American Psychologist, 39(4), 341–350.CrossRefGoogle Scholar
Kaustia, M., & Knüpfer, S. (2008). Do investors overweight personal experience? Evidence from IPO subscriptions. Journal of Finance, 63(6), 2679–2702.CrossRefGoogle Scholar
Keasey, K., & Moon, P. (1996). Gambling with the house money in capital expenditure decisions: An experimental analysis. Economics Letters, 50(1), 105–110.CrossRefGoogle Scholar
Kruger, J., & Dunning, D. (1999). Unskilled and unaware of it: How difficulties in recognizing one’s own incompetence lead to inflated self-assessments. Journal of Personality and Social Psychology, 77(6), 1121–1134.CrossRefGoogle ScholarPubMed
Langer, T., & Weber, M. (2008). Does commitment or feedback influence myopic loss aversion? Journal of Economic Behavior and Organization, 67(3–4), 810–819.CrossRefGoogle Scholar
Lauriola, M., & Levin, I. (2001). Personality traits and risky decision-making in a controlled experimental task: An exploratory study. Personality and Individual Differences, 31(2), 215–226.CrossRefGoogle Scholar
Lien, J. W., & Zheng, J. (2015). Deciding when to quit: Reference-dependence over slot machine outcomes, American Economic Review, 105(5), 366–370.CrossRefGoogle Scholar
Liu, Y.-J., Tsai, C.-L., Wang, M.-C., & Zhu, N. (2010). Prior consequences and subsequent risk taking: New field evidence from the Taiwan Futures Exchange. Management Science, 56(4), 606–620.CrossRefGoogle Scholar
Lusardi, A., & Mitchell, O. (2008). Planning and financial literacy: How do women fare? American Economic Review, 98(2), 413–417.CrossRefGoogle Scholar
Malmendier, U., & Nagel, S. (2011). Depression babies: Do macroeconomic experiences affect risk taking? Quarterly Journal of Economics, 126(1), 373–416.CrossRefGoogle Scholar
Mather, M., Mazar, N., Gorlick, M. A., Lighthall, N. R., Burgeno, J., Schoeke, A., & Ariely, D. (2012). Risk preferences and aging: The certainty effect in older adults’ decision making. Psychology and Aging, 27(4), 801–816.CrossRefGoogle ScholarPubMed
Merkle, C. (2017). Financial overconfidence over time: Foresight, hindsight, and insight of investors. Journal of Banking & Finance, 84(C), 68–87.CrossRefGoogle Scholar
Mikels, J., & Reed, A. (2009). Monetary losses do not loom large in later life: Age differences in the framing effect. Journal of Gerontology: Psychological Science and Social Science, 64B(4), 457–460.CrossRefGoogle Scholar
Moore, D., & Healy, P. (2008). The trouble with overconfidence. Psychological Review, 115(2), 502–517.CrossRefGoogle ScholarPubMed
Nielsen, L., Knutson, B., & Carstensen, L. (2008). Affect dynamics, affective forecasting, and aging. Emotion, 8(3), 318–330.CrossRefGoogle ScholarPubMed
Nosić, A., & Weber, M. (2010). How riskily do I invest? The role of risk attitudes, risk perceptions, and overconfidence. Decision Analysis, 7(3), 282–301.CrossRefGoogle Scholar
Novemsky, N., & Kahneman, D. (2005). The boundaries of loss aversion. Journal of Marketing Research, 42(2), 119–128.CrossRefGoogle Scholar
Odean, T. (1999). Do investors trade too much? American Economic Review, 89(5), 1279–1298.CrossRefGoogle Scholar
Poterba, J. M. & Samwick, A. A. (2001). Household portfolio allocation over the life cycle. In Ogura, S., Tachibanaki, T., & Wise, D. A. (Eds.), Aging Issues in the United States and Japan (pp. 65–103). Chicago: University Of Chicago Press.CrossRefGoogle Scholar
Powell, M., & Ansic, D. (1997). Gender differences in risk behaviour in financial decision-making. An experimental analysis. Journal of Economic Psychology, 18(6), 605–628.CrossRefGoogle Scholar
Read, D., Lowenstein, G., & Rabin, M. (1999). Choice bracketing. Journal of Risk and Uncertainty, 19(1–3), 171–197.CrossRefGoogle Scholar
Riley, W. B., & Chow, K. V. (1992). Asset allocation and individual risk aversion. Financial Analysts Journal, 48(6), 32–37.CrossRefGoogle Scholar
Rosi, A., Cavallini, E., Gamboz, N., & Russo, R. (2016). On the generality of the effect of experiencing prior gains and losses on the Iowa Gambling Task: A study on young and old adults. Judgment and Decision Making, 11(2), 185–196.CrossRefGoogle Scholar
Roszkowski, M. (2001). Risk tolerance in financial decisions. In Cordell, D. M. (Ed.), Fundamentals of Financial Planning, 5th ed. (pp. 237–298). Bryn Mawr: The American College.Google Scholar
Samanez-Larkin, G., Gibbs, S., Khanna, K., Nilsen, L., Carstensen, L., & Knutson, B. (2007). Anticipation of monetary gain but not monetary loss in healthy older adults. Nature Neuroscience, 10(6), 787–791.CrossRefGoogle Scholar
Schubert, R., Brown, M., Gysler, M., & Brachinger, H. (1999). Financial decision-making: Are women really more risk-averse? American Economic Review, 89(2), 381–385.CrossRefGoogle Scholar
Shefrin, H., & M. Statman, M. (2000). Behavioral portfolio theory. Journal of Financial and Quantitative Analysis, 35(2), 127–151.CrossRefGoogle Scholar
Shiv, B., Loewenstein, G., & Bechara, A. (2005). The dark side of emotion in decision-making: When individuals with decreased emotional reactions make more advantageous decisions. Cognitive Brain Research, 23(1), 85–92.CrossRefGoogle ScholarPubMed
Shiv, B., Loewenstein, G., Bechara, A., Damasio, H., & Damasio, A. R. (2005). Investment behavior and the negative side of emotion. Psychological Science, 16(6), 435–439.CrossRefGoogle ScholarPubMed
Strahilevitz, M. A., Odean, T., & Barber, B. M. (2011). Once burned, twice shy: How naïve learning, counterfactuals, and regret affect the repurchase of stocks previously sold. Journal of Marketing Research, 48(SPL), S102–S120.CrossRefGoogle Scholar
Thaler, R. H., & Johnson, E. J. (1990). Gambling with the house money and trying to break even: Effects of prior outcomes on risky choice. Management Science, 36(6), 643–660.CrossRefGoogle Scholar
Thomas, A., & Millar, P. (2012). Reducing the framing effect in older and younger adults by encouraging analytical processing. Journal of Gerontology: Psychological Science and Social Science, 67B(2), 139–149.CrossRefGoogle Scholar
Tversky, A., & Kahneman, D. (1981). The framing of decisions and the psychology of choice. Science, 211(4481), 453–458.CrossRefGoogle ScholarPubMed
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5(4), 297–323.CrossRefGoogle Scholar
Wang, H., & Hanna, S. (1997). Does risk tolerance decrease with age? Financial Counseling and Planning, 8(2), 27–31.Google Scholar
Weber, M., & Zuchel, H. (2005). How do prior outcomes affect risk attitude? Comparing escalation of commitment and house-money effect. Decision Analysis, 2(1), 30–43.CrossRefGoogle Scholar
Weber, M., Weber, E. U., & Nosic, A. (2013). Who takes risks when and why: Determinants of changes in investor risk taking. Review of Finance, 17, 847–883.CrossRefGoogle Scholar
Weller, J., Levin, I., & Denburg, N. (2011). Trajectory of risky decision making for potential gains and losses for ages 5 to 85. Journal of Behavioral Decision Making, 24(4), 331–344.CrossRefGoogle Scholar
Figure 0

Figure 1: Overview of the data and the hypothesis.

Figure 1

Table 1: Descriptive statistics for 62 private bank clients. Panel A describes bank client age (in years), the value of the trading portfolio (Value, average of 12 monthly observations, in Euro), the change in portfolio value between end January and end December 2015 (ΔValue), and the value-at-risk category (1 to 5). Panel B shows means for subsamples of (1) men (M) and women (F), individuals (2) who are standard- or high-educated (LE and HE), (3) young or old, relative to the median sample age (Y and O), and hold (3) small or large trading portfolios, relative to the value of the median portfolio (SM and LG). We run t-tests for differences in means and Mann-Whitney U tests. The null hypothesis is that the sample means are equal. * (**) indicates statistical significance at the 5 (1) % level for t-tests; + (++) does the same for nonparametric tests.

Figure 2

Table 2: Pearson pairwise correlations, calculated for the 620 observations that correspond to the ordered logistic regressions estimated later in Table 5. Variables are measured monthly (at the end of month t) except Value, priorGLD and priorRET which are measured with respect to month t−1. ΔVaR is the portfolio value-at-risk category (1 through 5, with 5 indicating high risk) at the end of current month minus the value-at-risk at the beginning of the current month. VaR is the value-at-risk at the end of the current month. Age is measured in years. Gender is a dummy variable (female=1) and so is Education (high education=1). Value denotes portfolio value (in Euros) at the end of the previous month (which is the start of the current month). priorGLD is a dummy variable equal to one if the portfolio gained in value during the previous month. priorRET denotes the portfolio return during the previous month. RET is the portfolio return during the current month.

Figure 3

Table 3: Portfolio VaRs, values, gains and losses, by month. Panel A shows VaRs by month, averaged across 62 subjects; the monthly fraction of subjects who raise or cut VaR; monthly cross-sectional averages of portfolio values, and of the ratios of the smallest and the largest portfolios relative to the mean portfolio. Panel B shows mean, minimum and maximum returns by month (in percent). In addition, it lists the fraction of all portfolios that rise in value during the month; the average gain or loss (in Euros) across all portfolios; and the matching monthly cross-sectional average of the absolute changes in value (in Euros).

Figure 4

Figure 2: Trading portfolio gains or losses in Euro (62 investors, 10 decision points each, February-November 2015).

Figure 5

Table 4: Monthly transitions between VaR categories. Panel A shows frequencies for 25 different types of VaR transitions as well as the number of of portfolio gains and losses (over the previous month) associated with specific VaR transitions (during the current month). In total, there are 620 decision points that lead to 98 VaR transitions to a different category. Panel B lists equivalent percentages totaling to 100 percent. Panel C shows the average Euro gain or loss for all transitions of a given type.

Figure 6

Figure 3: Fraction of all bank-recorded VaR increases or decreases by quantile of gains or losses over the prior month (620 decision points).

Figure 7

Table 5: Which factors cause variation in Value-at-Risk?We estimate random-effect ordered logistic regressions. The dependent variable is Δ VaR. The predictor variables are Age (in years), Gender (female=1), Education (high education=1), the value of the portfolio at the beginning of the month (in thousands of Euros), a gain/loss dummy (PriorGLD, gain=1) for the change in portfolio value during the prior month, and the portfolio return during the prior month (PriorRET, in percent). The regressions are for the full sample and for subsamples. *** is p<.01; **, p<.05; *, p<.10. S.E., clustered by individual investor, are in parentheses.

Supplementary material: File

Lippi et al.supplementary material

Lippi et al.supplementary material
Download Lippi et al.supplementary material(File)
File 64.1 KB