Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-02T21:19:54.341Z Has data issue: false hasContentIssue false
  • English
  • Français

The evolution of large-scale motions in turbulent pipe flow

Published online by Cambridge University Press:  19 August 2015

Leo H. O. Hellström ,
Bharathram Ganapathisubramani  and
Alexander J. Smits
Leo H. O. Hellström*
Affiliation:
Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Bharathram Ganapathisubramani
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Alexander J. Smits
Affiliation:
Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A dual-plane snapshot proper orthogonal decomposition (POD) analysis of turbulent pipe flow at a Reynolds number of 104 000 is presented. The high-speed particle image velocimetry data were simultaneously acquired in two planes, a cross-stream plane (2D–3C) and a streamwise plane (2D–2C) on the pipe centreline. 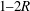The cross-stream plane analysis revealed large structures with a spatio-temporal extent of $1{-}2R$, where 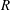$R$ is the pipe radius. The temporal evolution of these large-scale structures is examined using the time-shifted correlation of the cross-stream snapshot POD coefficients, identifying the low-energy intermediate modes responsible for the transition between the large-scale modes. By conditionally averaging based on the occurrence/intensity of a given cross-stream snapshot POD mode, a complex structure consisting of wall-attached and -detached large-scale structures is shown to be associated with the most energetic modes. There is a pseudo-alignment of these large structures, which together create structures with a spatio-temporal extent of approximately 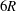$6R$, which appears to explain the formation of the very-large-scale motions previously observed in pipe flow.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 701 - 715
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry, Cambridge Aerospace Series, vol. 30. Cambridge University Press.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Bailey, S. C. C., Hultmark, M., Smits, A. J. & Schultz, M. P. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.Google Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Citriniti, J. H. & George, W. K. 2000 Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 418, 137–166.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
van Doorne, C. W. H. & Westerweel, J. 2007 Measurement of laminar, transitional and turbulent pipe flow using stereoscopic-PIV. Exp. Fluids 42, 259–279.Google Scholar
Duggleby, A. & Paul, M. R. 2010 Computing the Karhunen–Loéve dimension of an extensively chaotic flow field given a finite amount of data. Comput. Fluids 39 (9), 1704–1710.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Ganapathisubramani, B., Longmire, E. K., Marusic, I. & Pothos, S. 2005 Dual-plane PIV technique to determine the complete velocity gradient tensor in a turbulent boundary layer. Exp. Fluids 39 (2), 222–231.Google Scholar
Glauser, M. N. & George, W. K. 1987 Orthogonal decomposition of the axisymmetric jet mixing layer including azimuthal dependence. In Advances in Turbulence, pp. 357–366. Springer.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Hambleton, W., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.Google Scholar
Hellström, L. H. O., Sinha, A. & Smits, A. J. 2011 Visualizing the very-large-scale motions in turbulent pipe flow. Phys. Fluids 23, 011703.Google Scholar
Hellström, L. H. O. & Smits, A. J. 2014 The energetic motions in turbulent pipe flow. Phys. Fluids 26 (12), 125102.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the 2nd Midwestern Conference on Fluid Mechanics, Ohio State University.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Tutkun, M., Johansson, P. B. V. & George, W. K. 2008 Three-component vectorial proper orthogonal decomposition of axisymmetric wake behind a disk. AIAA J. 46 (5), 1118–1134.Google Scholar