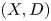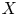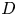BCOV invariant and blow-up

Abstract

Bershadsky, Cecotti, Ooguri and Vafa constructed a real-valued invariant for Calabi–Yau manifolds, which is now called the BCOV invariant. In this paper, we extend the BCOV invariant to such pairs $(X,D)$, where $X$ is a compact Kähler manifold and $D$ is a pluricanonical divisor on $X$ with simple normal crossing support. We also study the behavior of the extended BCOV invariant under blow-ups. The results in this paper lead to a joint work with Fu proving that birational Calabi–Yau manifolds have the same BCOV invariant.

Introduction

In this paper, we consider a real-valued invariant for Calabi–Yau manifolds equipped with Ricci flat metrics, which is now called the BCOV torsion. The BCOV torsion was introduced by Bershadsky, Cecotti, Ooguri and Vafa [BCOV93, BCOV94] as the stringy genus-one partition function of $N=2$ superconformal field theory. Their work extended the mirror symmetry conjecture of Candelas, de la Ossa, Green and Parkes [COGP91]. Fang and Lu [FL05] used BCOV torsion to study the moduli space of Calabi–Yau manifolds.

The BCOV torsion is an invariant on the B-side. Its mirror on the A-side is conjecturally the genus-one Gromov–Witten invariant. Though genus $\geqslant 2$ Gromov–Witten invariants have been intensively studied recently, there is no rigorously defined genus $\geqslant 2$ invariant on the B-side.

The BCOV invariant is a real-valued invariant for Calabi–Yau manifolds, which could be viewed as a normalization of the BCOV torsion. Fang, Lu and Yoshikawa [FLY08] constructed the BCOV invariant for Calabi–Yau threefolds and established the asymptotics of the BCOV invariant (of Calabi–Yau threefolds) for one-parameter normal crossings degenerations. They also confirmed the (B-side) genus-one mirror symmetry conjecture of Bershadsky, Cecotti, Ooguri and Vafa [BCOV93, BCOV94] for quintic threefolds.

Eriksson, Freixas i Montplet and Mourougane [EFM21] constructed the BCOV invariant for Calabi–Yau manifolds of arbitrary dimension and established the asymptotics of the BCOV invariant for one-parameter normal crossings degenerations. In another paper [EFM22], they confirmed the (B-side) genus-one mirror symmetry conjecture of Bershadsky, Cecotti, Ooguri and Vafa [BCOV93, BCOV94] for Calabi–Yau hypersurfaces of arbitrary dimension, which is compatible with the results of Zinger [Zin08, Zin09] on the A-side.

For a Calabi–Yau manifold $X$, we denote by $\tau (X)$ the logarithm of the BCOV invariant of $X$ defined in [EFM21].

Yoshikawa [Yos06, Conjecture 2.1] conjectured that for a pair of birational projective Calabi–Yau threefolds $(X,X')$, we have $\tau (X') = \tau (X)$. Eriksson, Freixas i Montplet and Mourougane [EFM21, Conjecture B] conjectured the following higher-dimensional analogue.

Conjecture 0.1 For a pair of birational projective Calabi–Yau manifolds $(X,X')$, we have

(0.1)\begin{equation} \tau(X') = \tau(X) . \end{equation}

Let $X$ and $X'$ be projective Calabi–Yau threefolds defined over a field $L$. Let $T$ be a finite set of embeddings $L\hookrightarrow \mathbb{C}$. For $\sigma \in T$, we denote by $X_\sigma$ (respectively, $X_\sigma '$) the base change of $X$ (respectively, $X'$) to $\mathbb{C}$ via the embedding $\sigma$. We denote by $D^b(X_\sigma )$ (respectively, $D^b(X_\sigma ')$) the bounded derived category of coherent sheaves on $X_\sigma$ (respectively, $X_\sigma '$). Maillot and Rössler [MR12, Theorem 1.1] showed that if one of the following conditions holds:

1. (a) there exists $\sigma \in T$ such that $X_\sigma$ and $X_\sigma '$ are birational;

2. (b) there exists $\sigma \in T$ such that $D^b(X_\sigma )$ and $D^b(X_\sigma ')$ are equivalent;

then there exist a positive integer $n$ and a non-zero element $\alpha \in L$ such that

(0.2)\begin{equation} \tau(X_\sigma') - \tau(X_\sigma) = \frac{1}{n} \log |\sigma(\alpha)| \quad \text{for all } \sigma\in T . \end{equation}

Although a result of Bridgeland [Bri02, Theorem 1.1] showed that condition (a) implies condition (b), Maillot and Rössler gave separate proofs for conditions (a) and (b).

Let $X$ be a Calabi–Yau threefold. Let $Z \hookrightarrow X$ be a $(-1,-1)$-curve. Let $X'$ be the Atiyah flop of $X$ along $Z$, which is also a Calabi–Yau threefold. We assume that both $X$ and $X'$ are compact and Kähler. The current author [Zha22, Corollary 0.5] showed that

(0.3)\begin{equation} \tau(X') = \tau(X) . \end{equation}

In other words, Conjecture 0.1 holds for three-dimensional Atiyah flops. The proof of (0.3) consists of two key ingredients:

1. (i) we extend the BCOV invariant from Calabi–Yau manifolds to certain ‘Calabi–Yau pairs’, more precisely, we consider manifolds equipped with smooth reduced canonical divisors;

2. (ii) we study the behavior of the extended BCOV invariant under blow-ups.

To fully confirm Conjecture 0.1 following this strategy, it is necessary to further extend the BCOV invariant as well as the blow-up formula. This is exactly the purpose of this paper. We consider pairs consisting of a compact Kähler manifold and a canonical divisor with rational coefficients on the manifold with simple normal crossing support and without component of multiplicity $\leqslant -1$. We construct the BCOV invariant of such pairs and establish a blow-up formula for our BCOV invariant.

In the joint work with Fu [FZ20], we use the results in this paper together with a factorization theorem of Abramovich, Karu, Matsuki and Włodarczyk [AKMW02, Theorem 0.3.1] to confirm Conjecture 0.1 in full generality.

Let us now give more detail about the matter of this paper.

BCOV torsion. We use the notation in (0.23) and (0.24). Let $X$ be an $n$-dimensional compact Kähler manifold. Let $H^\bullet _\mathrm {dR}(X)$ be the de Rham cohomology of $X$. Let $H^k_\mathrm {dR}(X) = \bigoplus _{p+q=k}H^{p,q}(X)$ be the Hodge decomposition. Set

(0.4)\begin{equation} \begin{aligned} & \lambda_p(X) = \det H^{p,\bullet}(X) = \bigotimes_{q=0}^n \big(\!\det H^{p,q}(X) \big)^{(-1)^q} \quad \text{for } p=0,\ldots,n ,\\ & \lambda_\mathrm{tot}(X) = \bigotimes_{k=1}^{2n} \big(\!\det H^k_\mathrm{dR}(X)\big)^{(-1)^kk} = \bigotimes_{p=1}^n \big(\lambda_p(X)\otimes\overline{\lambda_p(X)}\big)^{(-1)^pp} . \end{aligned} \end{equation}

Let $H^\bullet _\mathrm {Sing}(X,\mathbb{C} )$ be the singular cohomology of $X$ with coefficients in $\mathbb{C}$. We identify $H^k_\mathrm {dR}(X)$ with $H^k_\mathrm {Sing}(X,\mathbb{C} )$ (see (1.121)). For $k=0,\ldots,2n$, let

(0.5)\begin{equation} \sigma_{k,1},\ldots,\sigma_{k,b_k} \in \mathrm{Im}\big(H^k_\mathrm{Sing}(X,\mathbb{Z}) \rightarrow H^k_\mathrm{Sing}(X,\mathbb{R})\big) \subseteq H^k_\mathrm{dR}(X) \end{equation}

be a basis of the lattice. Set

(0.6)\begin{equation} \sigma_X = \bigotimes_{k=1}^{2n} (\sigma_{k,1}\wedge\cdots\wedge\sigma_{k,b_k})^{(-1)^kk} \in \lambda_\mathrm{tot}(X) , \end{equation}

which is well-defined up to $\pm 1$.

Let $\omega$ be a Kähler form on $X$. Let $\lVert \cdot \rVert _{\lambda _p(X),\omega }$ be the Quillen metric (see § 1.4) on $\lambda _p(X)$ associated with $\omega$. Let $\lVert \cdot \rVert _{\lambda _\mathrm {tot}(X),\omega }$ be the metric on $\lambda _\mathrm {tot}(X)$ induced by $\lVert \cdot \rVert _{\lambda _p(X),\omega }$ via (0.4). Set

(0.7)\begin{equation} \tau_\mathrm{BCOV}(X,\omega) = \log \lVert\sigma_X\rVert_{\lambda_\mathrm{tot}(X),\omega} , \end{equation}

which we call the unnormalized BCOV invariant of $(X,\omega )$.

BCOV invariant. For a compact complex manifold $X$ and a divisor $D$ on $X$, we denote

(0.8)\begin{equation} D = \sum_{j=1}^l m_j D_j , \end{equation}

where $m_j\in \mathbb {Z}\backslash \{0\}$, $D_1,\ldots,D_l \subseteq X$ are mutually distinct and irreducible. We call $D$ a divisor with simple normal crossing support if $D_1,\ldots,D_l$ are smooth and transversally intersect. Let $d$ be a non-zero integer. We assume that $D$ is of simple normal crossing support and $m_j\neq -d$ for $j=1,\ldots,l$. For $J\subseteq \{1,\ldots,l\}$, we denote

(0.9)\begin{equation} \begin{aligned} & w_d^J = \prod_{j\in J} \frac{-m_j}{m_j+d} ,\quad D_J = X \cap \bigcap_{j\in J} D_J ,\\ & w_d^\emptyset = 1 ,\quad D_\emptyset = X . \end{aligned} \end{equation}

See [FZ20, § 4] for an interpretation of this construction.

Now let $X$ be a compact Kähler manifold. Let $K_X$ be the canonical line bundle over $X$. Let $K_X^d$ be the $d$th tensor power of $K_X$. Let $\gamma \in \mathscr {M}(X,K_X^d)$ be an invertible element.

Definition 0.2 We call $(X,\gamma )$ a $d$-Calabi–Yau pair if:

1. (i) $\mathrm {div}(\gamma ) = \sum _{j=1}^l m_j D_j$ is of simple normal crossing support;

2. (ii) $m_j\neq -d$ for $j=1,\ldots,l$.

Here are some examples of $d$-Calabi–Yau pairs.

1. (a) If $X$ is a compact Kähler Calabi–Yau manifold and $0 \neq \gamma \in H^0(X,K_X^d)$, then $(X,\gamma )$ is a $d$-Calabi–Yau pair.

2. (b) If $(X,\gamma )$ is a $d$-Calabi–Yau pair with $d>0$ and $Y \subseteq X$ transversally intersects with $\mathrm {div}(\gamma )$ in the sense of Definition 1.1, then $(\mathrm {Bl}_YX,f^*\gamma )$ is a $d$-Calabi–Yau pair, where $f: \mathrm {Bl}_YX \rightarrow X$ is the blow-up along $Y$.

Now we assume that $(X,\gamma )$ is a $d$-Calabi–Yau pair. Let $w_d^J$ and $D_J$ be as in (0.9). Let $\omega$ be a Kähler form on $X$. Recall that $\tau _\mathrm {BCOV}(\cdot,\cdot )$ was constructed in (0.7). The BCOV invariant of $(X,\gamma )$ is defined as

(0.10)\begin{equation} \tau_d(X,\gamma) = \sum_{J\subseteq\{1,\ldots,l\}} w_d^J \tau_\mathrm{BCOV}(D_J,\omega|_{D_J}) + \text{correction terms} , \end{equation}

where the correction terms are Bott–Chern-type integrations (see Definition 3.2 and (3.10)). We construct $\tau _d(X,\gamma )$ and show that it is independent of $\omega$.

We can further extend our construction to canonical divisors with rational coefficients. We consider a pair $(X,D)$, where $X$ is an $n$-dimensional compact Kähler manifold, $D$ is a canonical divisor with rational coefficients on $X$ such that:

1. (i) $D$ is of simple normal crossing support;

2. (ii) each component of $D$ is of multiplicity $>-1$.

Definition 0.3 Let $d$ be a positive integer such that $dD$ is a divisor with integer coefficients. Let $\gamma$ be a meromorphic section of $K_X^d$ such that $\mathrm {div}(\gamma ) = dD$. We define

(0.11)\begin{equation} \tau(X,D) = \tau_d(X,\gamma) + \frac{\chi_d(X,dD)}{12} \log \bigg( (2\pi)^{-n} \int_{X\backslash|D|} |\gamma\bar{\gamma}|^{1/d} \bigg) , \end{equation}

where $\chi _d(\cdot,\cdot )$ is defined in Definition 1.3, $|D|$ is defined in (0.25), $|\gamma \bar {\gamma }|^{1/d}$ is the unique positive volume form on $X\backslash |D|$ whose $d$th tensor power equals $i^{n^2d}\gamma \bar {\gamma }$. By Propositions 3.3, 3.4, the BCOV invariant $\tau (X,D)$ is well-defined, i.e. independent of $d$ and $\gamma$.

Our BCOV invariant differs from the one defined in [EFM21] by a topological invariant. More precisely, if $X$ is a Calabi–Yau manifold, the logarithm of the BCOV invariant of $X$ defined in [EFM21] is equal to

(0.12)\begin{equation} \tau(X,\emptyset) + \frac{\log(2\pi)}{2} \sum_{k=0}^{2n} (-1)^k k(n-k) b_k(X) , \end{equation}

where $b_k(X)$ is the $k$th Betti number of $X$. The sum of Betti numbers in (0.12) comes from our choice of the $L^2$-metric (see (1.70)) and the identification between singular cohomology and de Rham cohomology (see (1.121)).

Curvature formula. Let $\pi : \mathscr {X} \rightarrow S$ be a holomorphic submersion. We assume that $\pi$ is locally Kähler in the sense of [BGS88b, Definition 1.25], i.e. for any $s\in S$, there exists an open subset $s\in U \subseteq S$ such that $\pi ^{-1}(U)$ is Kähler. For $s\in S$, we denote $X_s = \pi ^{-1}(s)$. Let

(0.13)\begin{equation} \big(\gamma_s\in\mathscr{M}(X_s,K_{X_s}^d)\big)_{s\in S} \end{equation}

be a holomorphic family. We assume that $(X_s,\gamma _s)$ is a $d$-Calabi–Yau pair for any $s\in S$. We assume that there exist $l\in \mathbb {N}$, $m_1,\ldots,m_l\in \mathbb {Z}\backslash \{0,-d\}$ and $(D_{j,s}\subseteq X_s)_{j\in \{1,\ldots,l\}, s\in S}$ such that

(0.14)\begin{equation} \mathrm{div}(\gamma_s) = \sum_{j=1}^l m_j D_{j,s} \quad \text{for } s\in S . \end{equation}

For $J\subseteq \{1,\ldots,l\}$ and $s\in S$, let $D_{J,s} \subseteq X_s$ be as in (0.9) with $X$ replaced by $X_s$ and $D_j$ replaced by $D_{j,s}$. We assume that $(D_{J,s})_{s\in S}$ is a smooth holomorphic family for each $J$.

Let $\tau _d(X,\gamma )$ be the function $s\mapsto \tau _d(X_s,\gamma _s)$ on $S$. Let $w_d^J$ be as in (0.9). Let $H^\bullet (D_J)$ be the variation of Hodge structure associated with $(D_{J,s})_{s\in S}$. Let $\omega _{H^\bullet (D_J)}\in \Omega ^{1,1}(S)$ be its Hodge form (see [Zha22, § 1.2]).

Theorem 0.4 The following identity holds:

(0.15)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \tau_d(X,\gamma) = \sum_{J\subseteq\{1,\ldots,l\}} w_d^J \omega_{H^\bullet(D_J)} . \end{equation}

Blow-up formula. Let $(X,\gamma )$ be a $d$-Calabi–Yau pair in the sense of Definition 0.2 with $d>0$.

Let $Y \subseteq X$ be a connected complex submanifold such that $Y,D_1,\ldots,D_l$ transversally intersect (in the sense of Definition 1.1). We assume that $m_j > 0$ for $j$ satisfying $Y \subseteq D_j$. Let $r$ be the codimension of $Y\subseteq X$. Let $q$ be the number of $D_j$ containing $Y$. Then we have $q\leqslant r$. Without loss of generality, we assume that

(0.16)\begin{equation} Y \subseteq D_j \quad \text{for } j=1,\ldots,q ; \quad Y \nsubseteq D_j \quad \text{for } j=q+1,\ldots,l . \end{equation}

Let $f: X' \rightarrow X$ be the blow-up along $Y$. Let $D_j' \subseteq X'$ be the strict transformation of $D_j \subseteq X$. Set $E = f^{-1}(Y)$. Let $f^*\gamma \in \mathscr {M}(X',K_{X'})$ be the pull-back of $\gamma$. We denote $D'=\mathrm {div}(f^*\gamma )$. We denote

(0.17)\begin{equation} m_0 = m_1 + \cdots + m_q + rd -d . \end{equation}

We have (cf. [MM07, Proposition 2.1.11])

(0.18)\begin{equation} D' = m_0 E + \sum_{j=1}^l m_j D_j' . \end{equation}

Hence, $(X',f^*\gamma )$ is a $d$-Calabi–Yau pair.

Set

(0.19)\begin{equation} D_Y = \sum_{j=q+1}^l m_j (D_j \cap Y) ,\quad D_E = \sum_{j=1}^l m_j (D_j' \cap E) . \end{equation}

Then $D_Y$ (respectively, $D_E$) is a divisor on $Y$ (respectively, $E$) with simple normal crossing support.

We identify $\mathbb{C} \mathrm {P}^r$ with $\mathbb{C} ^r \cup \mathbb{C} \mathrm {P}^{r-1}$. Let $(z_1,\ldots,z_r)\in \mathbb{C} ^r$ be the coordinates. Let $\gamma _{r,m_1,\ldots,m_q}\in \mathscr {M}(\mathbb{C} \mathrm {P}^r,K_{\mathbb{C} \mathrm {P}^r}^d)$ be such that

(0.20)\begin{equation} \gamma_{r,m_1,\ldots,m_q} |_{\mathbb{C}^r} = ( dz_1\wedge\cdots\wedge dz_r )^d \prod_{j=1}^q z_j^{m_j} . \end{equation}

Let $H_k \subseteq \mathbb{C} \mathrm {P}^r$ be the closure of $\{z_k=0\} \subseteq \mathbb{C} ^r$. Let $H_\infty = \mathbb{C} \mathrm {P}^{r-1} \subseteq \mathbb{C} \mathrm {P}^r$. We have

(0.21)\begin{equation} \mathrm{div}(\gamma_{r,m_1,\ldots,m_q}) = -(m_1+\cdots+m_q + rd + d) H_\infty + \sum_{j=1}^q m_j H_j . \end{equation}

Thus, $(\mathbb{C} \mathrm {P}^r,\gamma _{r,m_1,\ldots,m_q})$ is a $d$-Calabi–Yau pair.

Theorem 0.5 The following identities hold:

(0.22)\begin{equation} \begin{aligned} \chi_d(X',f^*\gamma) - \chi_d(X,\gamma) & = 0 ,\\ \tau_d(X',f^*\gamma) - \tau_d(X,\gamma) & = \chi_d(E,D_E) \tau_d(\mathbb{C}\mathrm{P}^1,\gamma_{1,m_0}) \\ & \quad - \chi_d(Y,D_Y) \tau_d(\mathbb{C}\mathrm{P}^r,\gamma_{r,m_1,\ldots,m_q}) , \end{aligned} \end{equation}

where $\chi _d(\cdot,\cdot )$ is given by Definition 1.3.

The proof of Theorem 0.5 is based on:

1. (i) the deformation to the normal cone introduced by Baum, Fulton and MacPherson [BFM75, § 1.5];

2. (ii) the immersion formula for Quillen metrics due to Bismut and Lebeau [BL91];

3. (iii) the submersion formula for Quillen metrics due to Berthomieu and Bismut [BB94];

4. (iv) the blow-up formula for Quillen metrics due to Bismut [Bis97];

5. (v) the relation between the holomorphic torsion and the de Rham torsion established by Bismut [Bis04].

We remark that the Quillen metric can be extended to orbifolds, and the immersion formula and the submersion formula still hold (see [Ma05, Ma21]).

Notation. For a complex vector space $V$, we denote

(0.23)\begin{equation} \det V = \Lambda^{\dim V} V , \end{equation}

which is a complex line. For a complex line $\lambda$, we denote by $\lambda ^{-1}$ the dual of $\lambda$. For a graded complex vector space $V^\bullet = \bigoplus _{k=0}^m V^k$, we denote

(0.24)\begin{equation} \det V^\bullet = \bigotimes_{k=0}^m (\det V^k)^{(-1)^k} . \end{equation}

For a complex manifold $X$ and a divisor $D = m_1 D_1 + \cdots + m_l D_l$ on $X$, where $m_1,\ldots,m_l\in \mathbb {Z}\backslash \{0\}$, $D_1,\ldots,D_l$ are mutually distinct and irreducible, we denote

(0.25)\begin{equation} |D| = D_1 \cup \cdots \cup D_l \subseteq X , \end{equation}

which we call the support of $D$.

For a complex manifold $X$, we denote by $\Omega ^{p,q}(X)$ the vector space of $(p,q)$-forms on $X$. We denote by $\mathscr {O}_X$ the analytic coherent sheaf of holomorphic functions on $X$. We denote by $\Omega ^p_X$ the analytic coherent sheaf of holomorphic $p$-forms on $X$. For a complex vector bundle $E$ over $X$, we denote by $\Omega ^{p,q}(X,E)$ the vector space of $(p,q)$-forms on $X$ with values in $E$. We denote by $\mathscr {M}(X,E)$ the vector space of meromorphic sections of $E$. We denote by $\mathscr {O}_X(E)$ the analytic coherent sheaf of holomorphic sections of $E$. For an analytic coherent sheaf $\mathscr {F}$ on $X$, we denote by $H^q(X,\mathscr {F})$ the $q$th cohomology of $\mathscr {F}$. We denote $H^q(X,E) = H^q(X,\mathscr {O}_X(E))$. We denote $H^{p,q}(X) = H^q(X,\Omega ^p_X)$. We denote by $H^k_\mathrm {dR}(X)$ the $k$th de Rham cohomology of $X$ with coefficients in $\mathbb{C}$. If $X$ is a compact Kähler manifold, we identify $H^{p,q}(X)$ with a vector subspace of $H^{p+q}_\mathrm {dR}(X)$ via the Hodge decomposition.

1. Preliminaries

1.1 Divisor with simple normal crossing support

For $I\subseteq \{1,\ldots,n\}$, we denote

(1.1)\begin{equation} \mathbb{C}^n_I = \{ (z_1,\ldots,z_n)\in \mathbb{C}^n : z_i = 0 \text{ for } i\in I \} \subseteq \mathbb{C}^n . \end{equation}

Let $X$ be an $n$-dimensional complex manifold.

Definition 1.1 For closed complex submanifolds $Y_1,\ldots,Y_l \subseteq X$, we say that $Y_1,\ldots,Y_l$ transversally intersect if for any $x\in X$, there exists a holomorphic local chart $\mathbb{C} ^n \supseteq U \xrightarrow {\varphi } X$ such that:

1. (i) $0\in U$ and $\varphi (0) = x$;

2. (ii) for each $k$, either $\varphi ^{-1}(Y_k) = \emptyset$ or $\varphi ^{-1}(Y_k) = U \cap \mathbb{C} ^n_{I_k}$ for certain $I_k\subseteq \{1,\ldots,n\}$.

Let $D$ be a divisor on $X$. We denote

(1.2)\begin{equation} D = \sum_{j=1}^l m_j D_j , \end{equation}

where $m_j\in \mathbb {Z}\backslash \{0\}$, $D_1,\ldots,D_l \subseteq X$ are mutually distinct and irreducible.

Definition 1.2 We call $D$ a divisor with simple normal crossing support if $D_1,\ldots,D_l$ are smooth and transversally intersect.

For $J\subseteq \{1,\ldots,l\}$, let $w_d^J$ and $D_J$ be as in (0.9), let $\chi (D_J)$ be the topological Euler characteristic of $D_J$.

Definition 1.3 If $D$ is a divisor with simple normal crossing support, we define

(1.3)\begin{equation} \chi_d(X,D) = \sum_{J\subseteq\{1,\ldots,l\}} w_d^J \chi(D_J) . \end{equation}

Moreover, if there is a meromorphic section $\gamma$ of a holomorphic line bundle over $X$ such that $\mathrm {div}(\gamma ) = D$, we define

(1.4)\begin{equation} \chi_d(X,\gamma) = \chi_d(X,D) . \end{equation}

Now we assume that $D$ is a divisor with simple normal crossing support. Let $L$ be a holomorphic line bundle over $X$ together with $\gamma \in \mathscr {M}(X,L)$ such that

(1.5)\begin{equation} \mathrm{div}(\gamma) = D . \end{equation}

Let $\gamma ^{-1}\in \mathscr {M}(X,L^{-1})$ be the inverse of $\gamma$.

We denote by $(T^*X\oplus \overline {T^*X})^{\otimes k}$ the $k$th tensor power of $T^*X\oplus \overline {T^*X}$. We denote

(1.6)\begin{equation} E^\pm_k = (T^*X\oplus\overline{T^*X})^{\otimes k} \otimes L^{\pm 1} . \end{equation}

In particular, we have $E_0^{\pm } = L^{\pm 1}$. Let $\nabla ^{E^\pm _k}$ be a connection on $E^\pm _k$.

Let $L_j$ be the normal line bundle of $D_j \hookrightarrow X$.

Definition 1.4 We define $\mathrm {Res}_{D_j}(\gamma )\in \mathscr {M}(D_j,L \otimes L_j^{-m_j})$ as follows:

(1.7) \begin{equation} \mathrm{Res}_{D_j}(\gamma) = \left\{\begin{array}{@{}ll} \dfrac{1}{m_j!}\Big(\nabla^{E^+_{m_j-1}} \cdots \nabla^{E^+_0} \gamma\Big) \Big|_{D_j} & \text{if } m_j > 0 ,\\ \dfrac{1}{|m_j|!} \Big(\Big(\nabla^{E^-_{|m_j|-1}} \cdots \nabla^{E^-_0} \gamma^{-1}\Big) \Big|_{D_j} \Big)^{-1} & \text{if } m_j < 0 . \end{array} \right. \end{equation}

Here $\mathrm {Res}_{D_j}(\gamma )$ is independent of $(\nabla ^{E^\pm _k})_{k\in \mathbb {N}}$.

For $j \in \{1,\ldots,l\}$, we have

(1.8)\begin{equation} \mathrm{div}\big(\mathrm{Res}_{D_j}(\gamma)\big) = \sum_{k\in\{1,\ldots,l\}\backslash\{j\}} m_k ( D_j \cap D_k ) . \end{equation}

For distinct $j,k \in \{1,\ldots,l\}$, we have

(1.9)\begin{align} & \mathrm{Res}_{D_j \cap D_k}\big(\mathrm{Res}_{D_j}(\gamma)\big) = \mathrm{Res}_{D_j \cap D_k}\big(\mathrm{Res}_{D_k}(\gamma)\big) \nonumber\\ & \quad \in \mathscr{M}(D_j \cap D_k,L \otimes L_j^{-m_j} \otimes L_k^{-m_k}) . \end{align}

1.2 Some characteristic classes

For an $(m\times m)$-matrix $A$, we define

(1.10)\begin{equation} \mathrm{ch}(A) = \operatorname{Tr}[e^A] ,\quad \mathrm{Td}(A) = \det\bigg(\frac{A}{\operatorname{Id}-e^{-A}}\bigg) ,\quad c(A) = \det(\operatorname{Id}+A) . \end{equation}

We have

(1.11)\begin{equation} c(tA) = 1 + \sum_{k=1}^m t^kc_k(A) , \end{equation}

where $c_k(A)$ is the $k$th elementary symmetric polynomial of the eigenvalues of $A$.

Let $V$ be an $m$-dimensional complex vector space. Let $R\in \mathrm {End}(V)$. Let $V^*$ be the dual of $V$. Let $R^*\in \mathrm {End}(V^*)$ be the dual of $R$. For $r=1,\ldots,m$, we construct $R_r\in \mathrm {End}(\Lambda ^rV^*)$ by induction,

(1.12)\begin{equation} R_1 = -R^* ,\quad R_r = R_1 \wedge \operatorname{Id}_{\Lambda^{r-1}V^*} + \operatorname{Id}_{V^*} \wedge R_{r-1} . \end{equation}

We use the convention $\Lambda ^0V^* = \mathbb{C}$ and $R_0 = 0$.

Let $\lambda _1,\ldots,\lambda _m$ be the eigenvalues of $R$. For $p\in \mathbb {N}$ and $F$ a polynomial of $\lambda _1,\ldots,\lambda _m$, we denote by $\{F\}^{[p]}$ the component of $F$ of degree $p$.

Proposition 1.5 The following identities hold:

(1.13)\begin{equation} \begin{aligned} \mathrm{Td}(R) \bigg( \sum_{r=0}^m (-1)^r \mathrm{ch}(R_r) \bigg) & = c_m(R) ,\\ \bigg\{ \mathrm{Td}(R) \bigg( \sum_{r=1}^m (-1)^r r \mathrm{ch}(R_r) \bigg) \bigg\}^{[\leqslant m]} & = -c_{m-1}(R) + \frac{m}{2}c_m(R) ,\\ \bigg\{ \mathrm{Td}(R) \bigg( \sum_{r=2}^m (-1)^r r(r-1) \mathrm{ch}(R_r) \bigg) \bigg\}^{[m]} & = \frac{1}{6}(c_1c_{m-1})(R) + \frac{m(3m-5)}{12}c_m(R) . \end{aligned} \end{equation}

Proof. Note that the eigenvalues of $R_r$ are given by $((-1)^r \lambda _{j_1}\cdots \lambda _{j_r})_{1 \leqslant j_1 < \cdots < j_r \leqslant m}$, we have

(1.14)\begin{equation} \mathrm{Td}(R) = \prod_{j=1}^m \frac{\lambda_j}{1-e^{-\lambda_j}} ,\quad \sum_{r=0}^m (-1)^r t^r \mathrm{ch}(R_r) = \prod_{j=1}^m (1-te^{-\lambda_j}) . \end{equation}

Taking $t=1$ in (1.14), we obtain the first identity in (1.13).

Taking the derivative of the second identity in (1.14) at $t=1$, we obtain

(1.15)\begin{equation} \sum_{r=0}^m (-1)^r r \mathrm{ch}(R_r) = - \bigg(\sum_{j=1}^m \frac{e^{-\lambda_j}}{1-e^{-\lambda_j}}\bigg) \prod_{j=1}^m (1-e^{-\lambda_j}) . \end{equation}

From the first identity in (1.14), (1.15) and the identity

(1.16)\begin{equation} \frac{e^{-\lambda_j}}{1-e^{-\lambda_j}} = \lambda_j^{-1} - \frac{1}{2} + \frac{1}{12}\lambda_j + \cdots , \end{equation}

we obtain the second identity in (1.13).

Taking the second derivative of the second identity in (1.14) at $t=1$, we obtain

(1.17)\begin{equation} \sum_{r=0}^m (-1)^r r(r-1) \mathrm{ch}(R_r) = \bigg( \bigg(\sum_{j=1}^m \frac{e^{-\lambda_j}}{1-e^{-\lambda_j}}\bigg)^2 - \sum_{j=1}^m \bigg(\frac{e^{-\lambda_j}}{1-e^{-\lambda_j}}\bigg)^2 \bigg) \prod_{j=1}^m (1-e^{-\lambda_j}) . \end{equation}

From the first identity in (1.14), (1.16) and (1.17), we obtain the third identity in (1.13). This completes the proof.

For an $(m\times m)$-matrix $A$, we define

(1.18)\begin{equation} \mathrm{Td}'(A) = \frac{\partial}{\partial t} \mathrm{Td}(A+t\operatorname{Id}) \bigg|_{t=0} . \end{equation}

Proposition 1.6 We have

(1.19)\begin{equation} \begin{aligned} \bigg\{ \mathrm{Td}'(R) \bigg( \sum_{r=0}^m (-1)^r \mathrm{ch}(R_r) \bigg) \bigg\}^{[m]} & = \frac{m}{2}c_m(R) ,\\ \bigg\{ \mathrm{Td}'(R) \bigg( \sum_{r=0}^m (-1)^r r \mathrm{ch}(R_r) \bigg) \bigg\}^{[m]} & = \frac{1}{12}(c_1c_{m-1})(R) + \frac{m^2}{4}c_m(R). \end{aligned} \end{equation}

Proof. Let $c_k'$ be as in (1.18) with $\mathrm {Td}$ replaced by $c_k$. We have

(1.20)\begin{equation} c_1'(R) = m ,\quad c_2'(R) = (m-1)c_1(R) . \end{equation}

On the other hand, we have

(1.21)\begin{equation} \big\{\mathrm{Td}(R)\big\}^{[\leqslant 2]} = 1 + \tfrac{1}{2}c_1(R) + \tfrac{1}{12}\big(c_1^2(R)+c_2(R)\big) . \end{equation}

By (1.20) and (1.21), we have

(1.22)\begin{equation} \bigg\{\frac{\mathrm{Td}'(R)}{\mathrm{Td}(R)}\bigg\}^{[\leqslant 1]} = \frac{m}{2} - \frac{1}{12}c_1(R) . \end{equation}

From (1.13) and (1.22), we obtain (1.19). This completes the proof.

1.3 Chern form and Bott–Chern form

Let $S$ be a compact Kähler manifold. We denote

(1.23)\begin{equation} \begin{aligned} Q^S & = \bigoplus_{p=0}^{\dim S} \Omega^{p,p}(S) ,\\ Q^{S,0} & = \bigoplus_{p=1}^{\dim S} \big(\partial\Omega^{p-1,p}(S)+\bar{\partial}\Omega^{p,p-1}(S)\big) \subseteq Q^S . \end{aligned} \end{equation}

Let $E$ be a holomorphic vector bundle over $S$. Let $g^E$ be a Hermitian metric on $E$. Let $R^E \in \Omega ^{1,1}(S,\mathrm {End}(E))$ be the curvature of the Chern connection on $(E,g^E)$. Recall that $c(\cdot )$ was defined in (1.10). The total Chern form of $(E,g^E)$ is defined by

(1.24)\begin{equation} c(E,g^E) = c\bigg(-\frac{R^E}{2\pi i}\bigg) \in Q^S . \end{equation}

The total Chern class of $E$ is defined by

(1.25)\begin{equation} c(E) = \big[c(E,g^E)\big]\in H^\mathrm{even}_\mathrm{dR}(S) , \end{equation}

which is independent of $g^E$.

Let $E'\subseteq E$ be a holomorphic subbundle. Let $E''=E/E'$. We have a short exact sequence of holomorphic vector bundles over $S$,

(1.26)\begin{equation} 0 \rightarrow E' \xrightarrow{\alpha} E \xrightarrow{\beta} E'' \rightarrow 0 , \end{equation}

where $\alpha$ (respectively, $\beta$) is the canonical embedding (respectively, projection). We have

(1.27)\begin{equation} c(E) = c(E')c(E'') . \end{equation}

Let $g^{E'}$ be a Hermitian metric on $E'$. Let $g^{E''}$ be a Hermitian metric on $E''$. The Bott–Chern form [BGS88a, § 1f)]

(1.28)\begin{equation} \tilde{c}(g^{E'},g^E,g^{E''})\in Q^S/Q^{S,0} \end{equation}

is such that

(1.29)\begin{align} \frac{\bar{\partial}\partial}{2\pi i} \tilde{c}(g^{E'},g^E,g^{E''}) & = c(E,g^E) - c(E' \oplus E'',g^{E'} \oplus g^{E''}) \nonumber\\ & = c(E,g^E) - c(E',g^{E'})c(E'',g^{E''}) . \end{align}

Let $\alpha ^*g^E$ be the Hermitian metric on $E'$ induced by $g^E$ via the embedding $\alpha : E'\rightarrow E$. Let $\beta _*g^E$ be the quotient Hermitian metric on $E''$ induced by $g^E$ via the surjection $\beta : E\rightarrow E''$. We denote

(1.30)\begin{equation} \tilde{c}(E',E,g^E) = \tilde{c}(\alpha^*g^E,g^E,\beta_*g^E) . \end{equation}

Let $\beta ^*g^{E''}$ be the Hermitian pseudometric on $E$ induced by $g^{E''}$ via the surjection $\beta : E\rightarrow E''$. For $\varepsilon >0$, set

(1.31)\begin{equation} g^E_\varepsilon = g^E + \frac{1}{\varepsilon} \beta^*g^{E''} . \end{equation}

We equip $Q^S \subseteq \Omega ^{\bullet,\bullet }(S)$ with the compact-open topology. We equip $Q^S/Q^{S,0}$ with the quotient topology.

Proposition 1.7 As $\varepsilon \rightarrow 0$,

(1.32)\begin{equation} c(E,g^E_\varepsilon) \rightarrow c(E',\alpha^*g^E)c(E'',g^{E''}) ,\quad \tilde{c}(E',E,g^E_\varepsilon) \rightarrow 0 . \end{equation}

Proof. We follow the proof of [BGS88a, Theorem 1.29].

Let $\mathrm {pr}: S \times \mathbb{C} \rightarrow S$ be the canonical projection. Let

(1.33)\begin{equation} \tilde{\alpha}: \mathrm{pr}^* E' \rightarrow \mathrm{pr}^* E \end{equation}

be the pull-back of $\alpha : E' \rightarrow E$. Let $(s,z)\in S\times \mathbb{C}$ be coordinates. Let $\sigma \in H^0(S\times \mathbb{C},\mathbb{C} )$ be the holomorphic function $\sigma (s,z) = z$. Let

(1.34)\begin{equation} \tilde{\sigma}: \mathrm{pr}^* E' \rightarrow \mathrm{pr}^* E' \end{equation}

be the multiplication by $\sigma$. Set

(1.35)\begin{equation} \mathcal{E}' = \mathrm{pr}^* E' ,\quad \mathcal{E} = \mathrm{Coker} ( \tilde{\alpha} \oplus \tilde{\sigma}: \mathrm{pr}^* E' \rightarrow \mathrm{pr}^* E \oplus \mathrm{pr}^* E' ) . \end{equation}

We get a short exact sequence of holomorphic vector bundles over $S\times \mathbb{C}$,

(1.36)\begin{equation} 0 \rightarrow \mathcal{E}' \rightarrow \mathcal{E} \rightarrow \mathcal{E}'' \rightarrow 0 , \end{equation}

where $\mathcal {E}' \rightarrow \mathcal {E}$ is induced by the embedding $0 \oplus \operatorname {Id}_{\mathrm {pr}^* E'} : \mathrm {pr}^* E' \hookrightarrow \mathrm {pr}^* E \oplus \mathrm {pr}^* E'$, and $\mathcal {E} \rightarrow \mathcal {E}'' := \mathrm {Coker}(\mathcal {E}'\rightarrow \mathcal {E})$ is the canonical projection. For $z\in \mathbb{C}$, let

(1.37)\begin{equation} 0 \rightarrow \mathcal{E}_z' \rightarrow \mathcal{E}_z \rightarrow \mathcal{E}_z'' \rightarrow 0 \end{equation}

be the restriction of (1.36) to $S\times \{z\}$. For $z\neq 0$, let

(1.38)\begin{equation} \phi_z: E \rightarrow \mathcal{E}_z = \mathrm{Coker} ( \alpha \oplus z \operatorname{Id}_{E'}: E' \rightarrow E \oplus E' ) \end{equation}

be the isomorphism induced by the embedding $\operatorname {Id}_E \oplus 0: E \hookrightarrow E \oplus E'$. We obtain a commutative diagram

(1.39)

where the vertical maps are induced by $\phi _z$. Let

(1.40)\begin{equation} \phi_0: E' \oplus E'' \rightarrow \mathcal{E}_0 = \mathrm{Coker} ( \alpha \oplus 0 : E' \rightarrow E \oplus E' ) = E'' \oplus E' \end{equation}

be the obvious isomorphism. We obtain a commutative diagram

(1.41)

where the vertical maps are induced by $\phi _0$.

We can construct a Hermitian metric $g^\mathcal {E}$ on $\mathcal {E}$ such that

(1.42)\begin{equation} \phi_z^* g^\mathcal{E} = |z|^2 g^E + \beta^* g^{E''} \quad \text{for } z \neq 0 ,\quad \phi_0^* g^\mathcal{E} = \alpha^*g^E \oplus g^{E''} . \end{equation}

To show that $g^\mathcal {E}$ is a smooth metric, we consider the metric $g^{\mathrm {pr}^* E \oplus \mathrm {pr}^* E'}$ on $\mathrm {pr}^* E \oplus \mathrm {pr}^* E'$ defined by

(1.43)\begin{equation} g^{\mathrm{pr}^* E \oplus \mathrm{pr}^* E'}|_{S\times\{z\}} = (1+|z|^2)(g^E \oplus \alpha^*g^E) . \end{equation}

We can directly verify that $g^\mathcal {E}$ is the quotient metric induced by $g^{\mathrm {pr}^* E \oplus \mathrm {pr}^* E'}$ via the canonical projection $\mathrm {pr}^* E \oplus \mathrm {pr}^* E' \rightarrow \mathcal {E}$.

By (1.39) and (1.42), for $\varepsilon = |z|^2 > 0$, we have

(1.44)\begin{equation} c(\mathcal{E}_z,g^{\mathcal{E}_z}) = c(E,g^E_\varepsilon) ,\quad \tilde{c}(\mathcal{E}_z',\mathcal{E}_z,g^{\mathcal{E}_z}) = \tilde{c}(E',E,g^E_\varepsilon) . \end{equation}

By [BGS88a, Theorem 1.29 iii)], (1.41) and (1.42), we have

(1.45)\begin{equation} c(\mathcal{E}_0,g^{\mathcal{E}_0}) = c(E',\alpha^*g^E)c(E'',g^{E''}) ,\quad \tilde{c}(\mathcal{E}_0',\mathcal{E}_0,g^{\mathcal{E}_0}) = 0 . \end{equation}

On the other hand, by [BGS88a, Theorem 1.29 ii)], we have

(1.46)\begin{equation} \lim_{z\rightarrow 0} c(\mathcal{E}_z,g^{\mathcal{E}_z}) = c(\mathcal{E}_0,g^{\mathcal{E}_0}) ,\quad \lim_{z\rightarrow 0} \tilde{c}(\mathcal{E}_z',\mathcal{E}_z,g^{\mathcal{E}_z}) = \tilde{c}(\mathcal{E}_0',\mathcal{E}_0,g^{\mathcal{E}_0}) . \end{equation}

From (1.44)–(1.46), we obtain (1.32). This completes the proof.

Remark 1.8 We can also prove Proposition 1.7 by applying the arguments in [BB94, (4.67)–(4.70) and (4.75)–(4.81)], which show that the connection of $E$ converges to a triangular $2\times 2$ matrix with diagonal elements given by the connections of $E'$ and $E''$ as $\varepsilon \rightarrow 0$. Though [BB94, (4.67)–(4.70) and (4.75)–(4.81)] work with tangent bundles, the argument equally holds in our case (because the connections under consideration are Chern connections).

Let $F \subseteq E$ be a holomorphic subbundle. Set $F' = \alpha ^{-1}(F) \subseteq E'$, $F'' = \beta (F) \subseteq E''$.

Proposition 1.9 If $F'=E'$, as $\varepsilon \rightarrow 0$,

(1.47)\begin{equation} \tilde{c}(F,E,g^E_\varepsilon) \rightarrow c(E',\alpha^*g^E) \tilde{c}(F'',E'',g^{E''}) . \end{equation}

If $F''=E''$, as $\varepsilon \rightarrow 0$,

(1.48)\begin{equation} \tilde{c}(F,E,g^E_\varepsilon) \rightarrow c(E'',g^{E''}) \tilde{c}(F',E',\alpha^*g^E) . \end{equation}

Proof. We use the notation from the proof of Proposition 1.7. Set

(1.49)\begin{equation} \mathcal{F} = \mathrm{Coker} ( \tilde{\alpha} \oplus \tilde{\sigma}|_{\mathrm{pr}^* F'} : \mathrm{pr}^* F' \rightarrow \mathrm{pr}^* F \oplus \mathrm{pr}^* F' ) \subseteq \mathcal{E} . \end{equation}

For $z\in \mathbb{C}$, let $\mathcal {F}_z$ be the restriction of $\mathcal {F}$ to $S\times \{z\}$.

For $z\neq 0$, we have $\phi _z(F) = \mathcal {F}_z \subseteq \mathcal {E}_z$. By (1.42), for $\varepsilon = |z|^2 > 0$, we have

(1.50)\begin{equation} \tilde{c}(\mathcal{F}_z,\mathcal{E}_z,g^{\mathcal{E}_z}\!) = \tilde{c}(F,E,g^E_\varepsilon). \end{equation}

We have $\phi _0(F) = F' \oplus F'' \subseteq E' \oplus E'' = \mathcal {E}_0$. By (1.42), we have

(1.51)\begin{equation} \tilde{c}(\mathcal{F}_0,\mathcal{E}_0,g^{\mathcal{E}_0}) = \tilde{c}(F'\oplus F'',E' \oplus E'',\alpha^*g^E \oplus g^{E''}) . \end{equation}

By [BGS88a, Theorem 1.29], we have

(1.52)\begin{equation} \begin{aligned} & \tilde{c}(F'\oplus F'',E' \oplus E'',\alpha^*g^E \oplus g^{E''}) = c(E',\alpha^*g^E) \tilde{c}(F'',E'',g^{E''}) \quad \text{if } F' = E' ,\\ & \tilde{c}(F'\oplus F'',E' \oplus E'',\alpha^*g^E \oplus g^{E''}) = c(E'',g^{E''})\tilde{c}(F',E',\alpha^*g^E) \quad \text{if } F'' = E'' . \end{aligned} \end{equation}

On the other hand, by [BGS88a, Theorem 1.29 ii)], we have

(1.53)\begin{equation} \lim_{z\rightarrow 0} \tilde{c}(\mathcal{F}_z,\mathcal{E}_z,g^{\mathcal{E}_z}) = \tilde{c}(\mathcal{F}_0,\mathcal{E}_0,g^{\mathcal{E}_0}) . \end{equation}

From (1.50)–(1.53), we obtain (1.47) and (1.48). This completes the proof.

Recall that $\mathrm {Td}(\cdot )$ was defined in (1.10). The Bott–Chern form [BGS88a, § 1f)]

(1.54)\begin{equation} \widetilde{\mathrm{Td}}(g^{E'},g^E,g^{E''}) \in Q^S/Q^{S,0} \end{equation}

is such that

(1.55)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \widetilde{\mathrm{Td}}(g^{E'},g^E,g^{E''}) = \mathrm{Td}(E,g^E) - \mathrm{Td}(E',g^{E'})\mathrm{Td}(E'',g^{E''}) . \end{equation}

Proposition 1.10 Propositions 1.7 and 1.9 hold with $c(\cdot )$ replaced by $\mathrm {Td}(\cdot )$.

Recall that $\mathrm {ch}(\cdot )$ was defined in (1.10). The Bott–Chern form [BGS88a, § 1f)]

(1.56)\begin{equation} \widetilde{\mathrm{ch}}(g^{E'},g^E,g^{E''}) \in Q^S/Q^{S,0} \end{equation}

is such that

(1.57)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \widetilde{\mathrm{ch}}(g^{E'},g^E,g^{E''}) = \mathrm{ch}(E',g^{E'}) - \mathrm{ch}(E,g^E) + \mathrm{ch}(E'',g^{E''}) . \end{equation}

For another Hermitian metric $\hat {g}^E$ on $E$, let

(1.58)\begin{equation} \widetilde{\mathrm{ch}}(\hat{g}^E,g^E) \in Q^S/Q^{S,0} \end{equation}

be the Bott–Chern form [BGS88a, § 1f)] such that

(1.59)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \widetilde{\mathrm{ch}}(\hat{g}^E,g^E) = \mathrm{ch}(E,\hat{g}^E) - \mathrm{ch}(E,g^E) . \end{equation}

The following proposition is a direct consequence of the construction of the Bott–Chern form [BGS88a, § 1f)].

Proposition 1.11 For another Hermitian metric $\hat {g}^E$ (respectively, $\hat {g}^{E'}$, $\hat {g}^{E''}$) on $E$ (respectively, $E'$, $E''$), we have

(1.60)\begin{equation} \widetilde{\mathrm{ch}}(\hat{g}^{E'},\hat{g}^E,\hat{g}^{E''}) = \widetilde{\mathrm{ch}}(g^{E'},g^E,g^{E''}) + \widetilde{\mathrm{ch}}(\hat{g}^{E'},g^{E'}) - \widetilde{\mathrm{ch}}(\hat{g}^E,g^E) + \widetilde{\mathrm{ch}}(\hat{g}^{E''},g^{E''}) . \end{equation}

For $a,b>0$, we have

(1.61)\begin{equation} \widetilde{\mathrm{ch}}(a g^E,bg^E) = \mathrm{ch}(E,g^E) (\log b - \log a) . \end{equation}

For $(g^E_t)_{t\in \mathbb {R}}$ a smooth family of Hermitian metrics on $E$, the map $t \mapsto \widetilde {\mathrm {ch}}(g^E_t,g^E_0)$ is continuous. In particular, we have

(1.62)\begin{equation} \widetilde{\mathrm{ch}}(g^E_t,g^E_0) \rightarrow 0 \quad \text{as } t \rightarrow 0 . \end{equation}

Let $E^*$ be the dual of $E$. Following [BB94, § 1a)], for $p=0,\ldots,\dim E$ and $s=0,\ldots,p-1$, set

(1.63)\begin{align} I^p_s = \big\{ u \in \Lambda^pE^* : u(v_1,\ldots,v_p) = 0 \text{ for any } v_1,\ldots,v_{s+1} \in E', v_{s+2},\ldots,v_p \in E \big\} . \end{align}

For convenience, we denote $I^p_p = \Lambda ^pE^*$ and $I^p_{-1} = 0$. We obtain a filtration

(1.64)\begin{equation} \Lambda^pE^* = I^p_p \hookleftarrow I^p_{p-1} \hookleftarrow \cdots \hookleftarrow I^p_{-1} = 0 . \end{equation}

For $r=0,\ldots,\dim E''$ and $s=0,\ldots,\dim E'$, we denote $E_{r,s} = \Lambda ^s{E'}^* \otimes \Lambda ^r{E''}^*$. We have a short exact sequence of holomorphic vector bundles over $S$,

(1.65)\begin{equation} 0 \rightarrow I^{r+s}_{s-1} \rightarrow I^{r+s}_s \rightarrow E_{r,s} \rightarrow 0 . \end{equation}

Recall that $g^E_\varepsilon$ was defined in (1.31). Let $g^{\Lambda ^pE^*}_\varepsilon$ be the Hermitian metric on $\Lambda ^pE^*$ induced by $g^E_\varepsilon$. Let $g^{I^{r+s}_s}_\varepsilon$ be the restriction of $g^{\Lambda ^pE^*}_\varepsilon$ to $I^{r+s}_s$. Let $g^{E_{r,s}}_\varepsilon$ be the quotient metric on $E_{r,s}$ induced by $g^{I^{r+s}_s}_\varepsilon$ via the surjection $I^{r+s}_s \rightarrow E_{r,s}$.

Similarly to Proposition 1.7, we have the following proposition.

Proposition 1.12 As $\varepsilon \rightarrow 0$,

(1.66)\begin{equation} \widetilde{\mathrm{ch}}\Big(g^{I^{r+s}_{s-1}}_\varepsilon, g^{I^{r+s}_s}_\varepsilon,g^{E_{r,s}}_\varepsilon\Big) \rightarrow 0 . \end{equation}

Proof. Let $0 \rightarrow \mathcal {E}' \rightarrow \mathcal {E} \rightarrow \mathcal {E}'' \rightarrow 0$ be as in (1.36). Let $\mathcal {I}^p_s \subseteq \Lambda ^p\mathcal {E}^*$ be as in (1.63) with $E$ replaced by $\mathcal {E}$ and $E'$ replaced by $\mathcal {E}'$. We denote $\mathcal {E}_{r,s} = \Lambda ^s{\mathcal {E}'}^* \otimes \Lambda ^r{\mathcal {E}''}^*$. We have a short exact sequence of holomorphic vector bundles over $S\times \mathbb{C}$,

(1.67)\begin{equation} 0 \rightarrow \mathcal{I}^{r+s}_{s-1} \rightarrow \mathcal{I}^{r+s}_s \rightarrow \mathcal{E}_{r,s} \rightarrow 0 . \end{equation}

Proceeding in the same way as in the proof of Proposition 1.7 with (1.36) replaced by (1.67), we obtain (1.66). This completes the proof.

1.4 Quillen metric

Let $X$ be an $n$-dimensional compact Kähler manifold. Let $E$ be a holomorphic vector bundle over $X$. Let $\bar {\partial }^E$ be the Dolbeault operator on

(1.68)\begin{equation} \Omega^{0,\bullet}(X,E) = {\mathscr{C}^\infty}\big(X,\Lambda^\bullet(\overline{T^*X})\otimes E\big) . \end{equation}

For $q=0,\ldots,n$, we have $H^q(X,E) = H^q(\Omega ^{0,\bullet }(X,E),\bar {\partial }^E)$. Set

(1.69)\begin{equation} \lambda(E) = \det H^\bullet(X,E) := \bigotimes_{q=0}^n \big(\!\det H^q(X,E)\big)^{(-1)^q} . \end{equation}

Let $g^{TX}$ be a Kähler metric on $TX$. Let $g^E$ be a Hermitian metric on $E$. Let $\langle \cdot,\cdot \rangle _{\Lambda ^\bullet (\overline {T^*X})\otimes E}$ be the Hermitian product on $\Lambda ^\bullet (\overline {T^*X})\otimes E$ induced by $g^{TX}$ and $g^E$. Let $dv_X$ be the Riemannian volume form on $X$ induced by $g^{TX}$. For $s_1,s_2\in \Omega ^{0,\bullet }(X,E)$, set

(1.70)\begin{equation} \langle s_1,s_2 \rangle = (2\pi)^{-n} \int_X \langle s_1,s_2 \rangle_{\Lambda^\bullet(\overline{T^*X})\otimes E}\, dv_X , \end{equation}

which we call the $L^2$-product.

Let $\bar {\partial }^{E,*}$ be the formal adjoint of $\bar {\partial }^E$ with respect to the Hermitian product (1.70). The Kodaira Laplacian on $\Omega ^{0,\bullet }(X,E)$ is defined by

(1.71)\begin{equation} \square^E = \bar{\partial}^E\bar{\partial}^{E,*} + \bar{\partial}^{E,*}\bar{\partial}^E . \end{equation}

Let $\square ^E_q$ be the restriction of $\square ^E$ to $\Omega ^{0,q}(X,E)$.

By the Hodge theorem, we have

(1.72)\begin{equation} \mathrm{Ker}(\square^E_q) = \{s\in\Omega^{0,q}(X,E): \bar{\partial}^Es=0,\bar{\partial}^{E,*}s=0\} . \end{equation}

Still by the Hodge theorem, the following map is bijective:

(1.73)\begin{equation} \begin{aligned} \mathrm{Ker}(\square^E_q) & \rightarrow H^q(X,E) \\ s & \mapsto [s] . \end{aligned} \end{equation}

Let $|\cdot |_{\lambda (E)}$ be the $L^2$-metric on $\lambda (E)$ induced by the metric (1.70) via (1.69) and (1.73).

Let $\mathrm {Sp}(\square ^E_q)$ be the spectrum of $\square ^E_q$, which is a multiset.¹ For $z\in \mathbb{C}$ with $\mathrm {Re}(z)>n$, set

(1.74)\begin{equation} \theta(z) = \sum_{q=1}^n (-1)^{q+1}q \sum_{\lambda\in\mathrm{Sp}(\square^E_q),\lambda\neq 0} \lambda^{-z} . \end{equation}

By [See67], the function $\theta (z)$ extends to a meromorphic function of $z\in \mathbb{C}$, which is holomorphic at $z=0$.

The following definition is due to Quillen [Qui85] and Bismut, Gillet and Soulé [BGS88b, § 1d)].

Definition 1.13 The Quillen metric on $\lambda (E)$ is defined by

(1.75)\begin{equation} \lVert\cdot\rVert_{\lambda(E)} = \exp\big(\tfrac{1}{2}\theta'(0)\big) |\cdot|_{\lambda(E)} . \end{equation}

Remark 1.14 Denote $\chi (X,E) = \sum _{q=0}^n (-1)^q \dim H^q(X,E)$. For $a>0$, if we replace $g^E$ by $ag^E$, then $\lVert \cdot \rVert _{\lambda (E)}$ is replaced by $a^{\chi (X,E)/2}\lVert \cdot \rVert _{\lambda (E)}$.

1.5 Analytic torsion form

Let $\pi : X \rightarrow Y$ be a holomorphic submersion between Kähler manifolds with compact fiber $Z$.

Let $E$ be a holomorphic vector bundle over $X$. Let $R^\bullet \pi _*E$ be the derived direct image of $E$, which is a graded analytic coherent sheaf on $Y$. We assume that $R^\bullet \pi _*E$ is a graded holomorphic vector bundle. Let $H^\bullet (Z,E)$ be the fiberwise cohomology. More precisely, its fiber at $y\in Y$ is given by $H^\bullet (Z_y,E|_{Z_y})$. We have a canonical identification $R^\bullet \pi _*E = H^\bullet (Z,E)$. We have the Grothendieck–Riemann–Roch formula,

(1.76)\begin{equation} \mathrm{ch}(H^\bullet(Z,E)) := \sum_j (-1)^j \mathrm{ch}(H^j(Z,E)) = \int_Z \mathrm{Td}(TZ) \mathrm{ch}(E) \in H^\mathrm{even}_\mathrm{dR}(Y) .\end{equation}

Let $\omega \in \Omega ^{1,1}(X)$ be a Kähler form. Let $g^{TZ}$ be the Hermitian metric on $TZ$ associated with $\omega$. Let $g^E$ be a Hermitian metric on $E$. Let $g^{H^\bullet (Z,E)}$ be the $L^2$-metric on $H^\bullet (Z,E)$ associated with $g^{TZ}$ and $g^E$ via (1.73).

We use the notation in (1.23). Let $\mathrm {ch}(H^\bullet (Z,E),g^{H^\bullet (Z,E)}) \in Q^Y$ be the Chern character form of $(H^\bullet (Z,E),g^{H^\bullet (Z,E)})$. We introduce $\mathrm {Td}(TZ,g^{TZ}) \in Q^X$ and $\mathrm {ch}(E,g^E) \in Q^X$ in the same way.

Bismut and Köhler [BK92, Definition 3.8] defined the analytic torsion forms. The analytic torsion form associated with $(\pi : X \rightarrow Y, \omega, E, g^E)$ is a differential form on $Y$, which we denote by $T(\omega,g^E)$. Moreover, we have

(1.77)\begin{equation} T(\omega,g^E) \in Q^Y . \end{equation}

We sometimes view $T(\omega,g^E)$ as an element in $Q^Y/Q^{Y,0}$. By [BK92, Theorem 3.9], we have

(1.78)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} T(\omega,g^E) = \mathrm{ch}\big(H^\bullet(Z,E),g^{H^\bullet(Z,E)}\big) - \int_Z \mathrm{Td}(TZ,g^{TZ}) \mathrm{ch}(E,g^E) . \end{equation}

The identity (1.78) is a refinement of the Grothendieck–Riemann–Roch formula (1.76).

For $y\in Y$, let $\theta _y(z)$ be as in (1.74) with $(X,g^{TX},E,g^E)$ replaced by $(Z_y,g^{TZ_y},E|_{Z_y},g^E|_{Z_y})$. Let $\theta '(0)$ be the function $y \mapsto \theta _y'(0)$ on $Y$. By the construction of the analytic torsion forms, we have

(1.79)\begin{equation} \big\{T(\omega,g^E)\big\}^{(0,0)} = \theta'(0) \in {\mathscr{C}^\infty}(Y), \end{equation}

where $\{\cdot \}^{(0,0)}$ means the component of degree $(0,0)$.

Let $F$ be a holomorphic vector bundle over $Y$. Let $\pi ^*F$ be its pull-back via $\pi$, which is a holomorphic vector bundle over $X$. Let $g^F$ be a Hermitian metric on $F$. Let $g^{E\otimes \pi ^*F}$ be the Hermitian metric on $E\otimes \pi ^*F$ induced by $g^E$ and $g^F$. Let

(1.80)\begin{equation} T(\omega,g^{E\otimes\pi^*F}) \in Q^Y \end{equation}

be the analytic torsion form associated with $(\pi : X \rightarrow Y, \omega, E\otimes \pi ^*F, g^{E\otimes \pi ^*F})$.

The following proposition is a direct consequence of the construction of the analytic torsion forms.

Proposition 1.15 The following identity holds in $Q^Y/Q^{Y,0}$:

(1.81)\begin{equation} T(\omega,g^{E\otimes\pi^*F}) = \mathrm{ch}(F,g^F) T(\omega,g^E) . \end{equation}

For $p=0,\ldots,\dim Z$, let $g^{\Lambda ^p(T^*Z)}$ be the metric on $\Lambda ^p(T^*Z)$ induced by $g^{TZ}$. Let

(1.82)\begin{equation} T(\omega,g^{\Lambda^p(T^*Z)}) \in Q^Y \end{equation}

be the analytic torsion form associated with $(\pi : X \rightarrow Y, \omega, \Lambda ^p(T^*Z), g^{\Lambda ^p(T^*Z)})$.

Theorem 1.16 (Bismut [Bis04, Theorem 4.15])

The following identity holds in $Q^Y/Q^{Y,0}$,

(1.83)\begin{equation} \sum_{p=0}^{\dim Z} (-1)^p T(\omega,g^{\Lambda^p(T^*Z)}) = 0 . \end{equation}

1.6 Properties of the Quillen metric

In this subsection, we state several results describing the behavior of the Quillen metric under submersion, resolution, immersion and blow-up.

Submersion. Let $\pi : X \rightarrow Y$, $Z$, $E$ and $H^\bullet (Z,E)$ be as in § 1.5. We assume that $X$ and $Y$ are compact. We further assume that the Leray spectral sequence for $E$ and $\pi$ degenerates at $E_2$, i.e.

(1.84)\begin{equation} H^q(X,E) \simeq \bigoplus_{j+k = q} H^j(Y,H^k(Z,E)) \quad \text{for } q = 0,\ldots,\dim X . \end{equation}

We denote

(1.85) \begin{align} \det H^\bullet(Y,H^\bullet(Z,E)) & = \bigotimes_{k=0}^{\dim Z} \big(\!\det H^\bullet\big(Y,H^k(Z,E)\big)\big)^{(-1)^k} \nonumber\\ & = \bigotimes_{j=0}^{\dim Y} \bigotimes_{k=0}^{\dim Z} \big(\!\det H^j\big(Y,H^k(Z,E)\big)\big)^{(-1)^{j+k}} . \end{align}

Let

(1.86)\begin{equation} \sigma \in \det H^\bullet(X,E) \otimes \big(\!\det H^\bullet\big(Y,H^\bullet(Z,E)\big)\big)^{-1} \end{equation}

be the canonical section induced by (1.84).

Let $\omega _X\in \Omega ^{1,1}(X)$ and $\omega _Y\in \Omega ^{1,1}(Y)$ be Kähler forms. For $\varepsilon >0$, set

(1.87)\begin{equation} \omega_\varepsilon = \omega_X + \frac{1}{\varepsilon}\pi^*\omega_Y . \end{equation}

Let $g^E$ be a Hermitian metric on $E$.

Let $g^{TX}_\varepsilon$ be the metric on $TX$ associated with $\omega _\varepsilon$. Let

(1.88)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X,E),\varepsilon} \end{equation}

be the Quillen metric on $\det H^\bullet (X,E)$ associated with $g^{TX}_\varepsilon$ and $g^E$. Let $g^{TY}$ be the metric on $TY$ associated with $\omega _Y$. Let $g^{TZ}$ be the metric on $TZ$ associated with $\omega _X|_Z$. Let $g^{H^\bullet (Z,E)}$ be the $L^2$-metric on $H^\bullet (Z,E)$ associated with $g^{TZ}$ and $g^E$. For $k=0,\ldots,\dim Z$, let

(1.89)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(Y,H^k(Z,E))} \end{equation}

be the Quillen metric on $\det H^\bullet (Y,H^k(Z,E))$ associated with $g^{TY}$ and $g^{H^k(Z,E)}$. Let

(1.90)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(Y,H^\bullet(Z,E))} \end{equation}

be the metric on $\det H^\bullet (Y,H^\bullet (Z,E))$ induced by the Quillen metrics (1.89) via (1.85). Let $\lVert \sigma \rVert _\varepsilon$ be the norm of $\sigma$ with respect to the metrics (1.88) and (1.90).

We use the notation in (1.23). Let $\mathrm {Td}(TY,g^{TY}) \in Q^Y$ be the Todd form of $(TY,g^{TY})$. Let

(1.91)\begin{equation} T(\omega,g^E) \in Q^Y \end{equation}

be the analytic torsion form (see § 1.5) associated with $(\pi : X \rightarrow Y, \omega _X, E, g^E)$.

Recall that $\mathrm {Td}'(\cdot )$ was defined by (1.18).

Theorem 1.17 (Berthomieu and Bismut [BB94, Theorem 3.2])

As $\varepsilon \rightarrow 0$,

(1.92)\begin{equation} \log \lVert\sigma\rVert^2_\varepsilon + \int_Y \mathrm{Td}'(TY) \int_Z \mathrm{Td}(TZ)\mathrm{ch}(E) \log \varepsilon \rightarrow \int_Y \mathrm{Td}(TY,g^{TY}) T(\omega,g^E) . \end{equation}

Resolution. Let $X$ be a compact Kähler manifold. Let

(1.93)\begin{equation} 0 \rightarrow E^0 \rightarrow E^1 \rightarrow E^2 \rightarrow 0 \end{equation}

be a short exact sequence of holomorphic vector bundles over $X$. Let

(1.94)\begin{equation} \sigma \in \bigotimes_{k=0}^2 \big(\!\det H^\bullet(X,E^k)\big)^{(-1)^{k+1}} \end{equation}

be the canonical section induced by the long exact sequence induced by (1.93).

Let $g^{TX}$ be a Kähler metric on $TX$. For $k=0,1,2$, let $g^{E^k}$ be a Hermitian metric on $E^k$. Let

(1.95)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X,E^k)} \end{equation}

be the Quillen metric on $\det H^\bullet (X,E^k)$ associated with $g^{TX}$ and $g^{E^k}$. Let $\lVert \sigma \rVert$ be the norm of $\sigma$ with respect to the metrics (1.95).

We use the notation in (1.23). Let $\mathrm {Td}(TX,g^{TX}) \in Q^X$ be the Todd form of $(TX,g^{TX})$. Let $\mathrm {ch}(E^k,g^{E^k}) \in Q^X$ be the Chern character form of $(E^k,g^{E^k})$. Let

(1.96)\begin{equation} \widetilde{\mathrm{ch}}(g^{E^\bullet}) \in Q^X/Q^{X,0} \end{equation}

be the Bott–Chern form [BGS88a, § 1f)] such that

(1.97)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \widetilde{\mathrm{ch}}(g^{E^\bullet}) = \sum_{k=0}^2 (-1)^k \mathrm{ch}(E^k,g^{E^k}) . \end{equation}

Theorem 1.18 (Bismut, Gillet and Soulé [BGS88b, Theorem 1.23])

The following identity holds:

(1.98)\begin{equation} \log \lVert\sigma\rVert^2 = \int_X \mathrm{Td}(TX,g^{TX}) \widetilde{\mathrm{ch}}(g^{E^\bullet}). \end{equation}

Immersion. Let $X$ be a compact Kähler manifold. Let $Y \subseteq X$ be a complex submanifold of codimension one. Let $i: Y \hookrightarrow X$ be the canonical embedding. Let $F$ be a holomorphic vector bundle over $Y$. Let $v: E_1 \rightarrow E_0$ be a map between holomorphic vector bundles over $X$ which, together with a restriction map $r: E_0|_Y \rightarrow F$, provides a resolution of $i_*\mathscr {O}_Y(F)$. More precisely, we have an exact sequence of analytic coherent sheaves on $X$,

(1.99)\begin{equation} 0 \rightarrow \mathscr{O}_X(E_1) \xrightarrow{v} \mathscr{O}_X(E_0) \xrightarrow{r} i_*\mathscr{O}_Y(F) \rightarrow 0 . \end{equation}

Let

(1.100)\begin{equation} \sigma \in \big(\!\det H^\bullet(X,E_1)\big)^{-1} \otimes \det H^\bullet(X,E_0) \otimes \big(\!\det H^\bullet(Y,F)\big)^{-1} \end{equation}

be the canonical section induced by the long exact sequence induced by (1.99).

Let $\omega \in \Omega ^{1,1}(X)$ be a Kähler form. For $k=0,1$, let $g^{E_k}$ be a Hermitian metric on $E_k$. Let $g^F$ be a Hermitian metric on $F$. Assume that there is an open neighborhood $Y \subseteq U \subseteq X$ such that $v|_{X\backslash U}$ is isometric, i.e.

(1.101)\begin{equation} g^{E_1}|_{X\backslash U} = v^*g^{E_0}|_{X\backslash U} . \end{equation}

Let $g^{TX}$ be the metric on $TX$ associated with $\omega$. For $k=0,1$, let

(1.102)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X,E_k)} \end{equation}

be the Quillen metric on $\det H^\bullet (X,E_k)$ associated with $g^{TX}$ and $g^{E_k}$. Let $g^{TY}$ be the metric on $TY$ associated with $\omega |_Y$. Let

(1.103)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(Y,F)} \end{equation}

be the Quillen metric on $\det H^\bullet (Y,F)$ associated with $g^{TY}$ and $g^F$. Let $\lVert \sigma \rVert$ be the norm of $\sigma$ with respect to the metrics (1.102) and (1.103).

The following theorem is a direct consequence of the immersion formula due to Bismut and Lebeau [BL91, Theorem 0.1] and the anomaly formula due to Bismut, Gillet and Soulé [BGS88b, Theorem 1.23].

Theorem 1.19 We have

(1.104)\begin{equation} \log \lVert\sigma\rVert^2 = \alpha(U,\omega|_U,v|_U,g^{E_\bullet}|_U,r,g^F), \end{equation}

where $\alpha (U,\omega |_U,v|_U,r|_U,g^{E_\bullet },g^F)$ is a real number determined by

(1.105)\begin{equation} U ,\quad \omega|_U ,\quad v|_U: E_1|_U \rightarrow E_0|_U ,\quad g^{E_\bullet}|_U ,\quad r: E_0|_Y \rightarrow F ,\quad g^F . \end{equation}

More precisely, given

(1.106)\begin{equation} \tilde{Y} \subseteq \tilde{U} \subseteq \tilde{X} , \quad \tilde{\omega} ,\quad \tilde{v}: \tilde{E}_1 \rightarrow \tilde{E}_0 ,\quad \tilde{r}: \tilde{E}_0 |_{\tilde{Y}} \rightarrow \tilde{F} ,\quad g^{\tilde{E}_\bullet} ,\quad g^{\tilde{F}} \end{equation}

satisfying the same properties that

(1.107)\begin{equation} Y \subseteq U \subseteq X ,\quad \omega ,\quad v: E_1 \rightarrow E_0 ,\quad r: E_0 |_Y \rightarrow F ,\quad g^{E_\bullet} ,\quad g^F \end{equation}

satisfy, if there is a biholomorphic map $U \rightarrow \tilde {U}$ inducing an isomorphism between the restrictions of the data above to $U$ and $\tilde {U}$, then

(1.108)\begin{equation} \log \lVert\sigma\rVert^2 = \log \lVert\tilde{\sigma}\rVert^2 , \end{equation}

where

(1.109)\begin{equation} \tilde{\sigma} \in \big(\!\det H^\bullet(\tilde{X},\tilde{E}_1)\big)^{-1} \otimes \det H^\bullet(\tilde{X},\tilde{E}_0) \otimes \big(\!\det H^\bullet(\tilde{Y},\tilde{F})\big)^{-1} \end{equation}

is the canonical section, and $\lVert \tilde {\sigma }\rVert$ is its norm with respect to the Quillen metrics.

Remark 1.20 The real number $\alpha (U,\omega |_U,v|_U,r|_U,g^{E_\bullet },g^F)$ depends continuously on the input data.

Blow-up. Let $X$ be a compact Kähler manifold. Let $Y \subseteq X$ be a complex submanifold of codimension $r \geqslant 2$. Let $f: X' \rightarrow X$ be the blow-up along $Y$. Let $E$ be a holomorphic vector bundle over $X$. Let $f^*E$ be the pull-back of $E$ via $f$, which is a holomorphic vector bundle over $X'$. Applying spectral sequence, we obtain a canonical identification

(1.110)\begin{equation} H^\bullet(X',f^*E) = H^\bullet(X,E) . \end{equation}

Let

(1.111)\begin{equation} \sigma \in \big(\!\det H^\bullet(X,E)\big)^{-1} \otimes \det H^\bullet(X',f^*E) \end{equation}

be the canonical section induced by (1.110).

Let $\omega \in \Omega ^{1,1}(X)$ and $\omega '\in \Omega ^{1,1}(X')$ be Kähler forms. Assume that there are open neighborhoods $Y \subseteq U \subseteq X$ and $f^{-1}(Y) \subseteq U' \subseteq X'$ such that

(1.112)\begin{equation} f^{-1}(U) = U' ,\quad f^*( \omega|_{X\backslash U} ) = \omega'|_{X'\backslash U'} . \end{equation}

For the existence of such $\omega$ and $\omega '$, see the proof of [Voi02, Proposition 3.24]. Let $g^E$ be a Hermitian metric on $E$.

Let $g^{TX}$ be the metric on $TX$ associated with $\omega$. Let

(1.113)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X,E)} \end{equation}

be the Quillen metric on $\det H^\bullet (X,E)$ associated with $g^{TX}$ and $g^E$. Let $g^{TX'}$ be the metric on $TX'$ associated with $\omega '$. Let

(1.114)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X',f^*E)} \end{equation}

be the Quillen metric on $\det H^\bullet (X',f^*E)$ associated with $g^{TX'}$ and $f^*g^E$. Let $\lVert \sigma \rVert$ be the norm of $\sigma$ with respect to the metrics (1.113) and (1.114).

The following theorem is a direct consequence of the blow-up formula due to Bismut [Bis97, Theorem 8.10].

Theorem 1.21 We have

(1.115)\begin{equation} \log \lVert\sigma\rVert^2 = \alpha(U,\omega|_U,U',\omega'|_{U'},E|_U,g^E|_U) , \end{equation}

where $\alpha (U,\omega |_U,U',\omega '|_{U'},E|_U,g^E|_U)$ is a real number determined by

(1.116)\begin{equation} U ,\quad \omega|_U ,\quad U' ,\quad \omega'|_{U'} ,\quad E|_U ,\quad g^E|_U . \end{equation}

Remark 1.22 The real number $\alpha (U,\omega |_U,U',\omega '|_{U'},E|_U,g^E|_U)$ depends continuously on the input data.

1.7 Topological torsion and BCOV torsion

Let $X$ be an $n$-dimensional compact Kähler manifold. For $p=0,\ldots,n$, set

(1.117)\begin{equation} \lambda_p(X) = \det H^{p,\bullet}(X) := \bigotimes_{q=0}^n\, (\det H^{p,q}(X))^{(-1)^q} . \end{equation}

Set

(1.118)\begin{align} \eta(X) = \det H^\bullet_\mathrm{dR}(X) & := \bigotimes_{k=0}^{2n} \big(\!\det H^k_\mathrm{dR}(X)\big)^{(-1)^k} \nonumber\\ & = \bigotimes_{p=0}^n \big(\lambda_p(X)\big)^{(-1)^p} . \end{align}

Set

(1.119)\begin{equation} \begin{aligned} \lambda(X) & = \bigotimes_{0\leqslant p,q\leqslant n} \big(\!\det H^{p,q}(X) \big)^{(-1)^{p+q}p} = \bigotimes_{p=1}^n \big(\lambda_p(X)\big)^{(-1)^pp} ,\\ \lambda_\mathrm{tot}(X) & = \bigotimes_{k=1}^{2n} \big(\!\det H^k_\mathrm{dR}(X)\big)^{(-1)^kk} = \lambda(X) \otimes \overline{\lambda(X)} . \end{aligned} \end{equation}

The identities in (1.119) appeared in [Kat14]. They were applied to the theory of BCOV invariant by Eriksson, Freixas i Montplet and Mourougane [EFM21].

For $\mathbb {A} = \mathbb {Z},\mathbb {R},\mathbb{C}$, we denote by $H^\bullet _\mathrm {Sing}(X,\mathbb {A})$ the singular cohomology of $X$ with coefficients in $\mathbb {A}$. For $k=0,\ldots,2n$, let

(1.120)\begin{equation} \sigma_{k,1},\ldots,\sigma_{k,b_k} \in \mathrm{Im}\big(H^k_\mathrm{Sing}(X,\mathbb{Z}) \rightarrow H^k_\mathrm{Sing}(X,\mathbb{R})\big) \end{equation}

be a basis of the lattice. We fix a square root of $i$. In what follows, the choice of square root is irrelevant. We identify $H^k_\mathrm {dR}(X)$ with $H^k_\mathrm {Sing}(X,\mathbb{C} )$ as follows:

(1.121)\begin{equation} \begin{aligned} H^k_\mathrm{dR}(X) & \rightarrow H^k_\mathrm{Sing}(X,\mathbb{C}) \\ [\alpha] & \mapsto \bigg[\mathfrak{a} \mapsto (2\pi i)^{-k/2} \int_\mathfrak{a}\alpha\bigg], \end{aligned} \end{equation}

where $\alpha$ is a closed $k$-form on $X$ and $\mathfrak {a}$ is a $k$-chain in $X$. Then $\sigma _{k,1},\ldots,\sigma _{k,b_k}$ form a basis of $H^k_\mathrm {dR}(X)$. Set

(1.122)\begin{equation} \begin{aligned} & \sigma_k = \sigma_{k,1}\wedge\cdots\wedge\sigma_{k,b_k} \in \det H^k_\mathrm{dR}(X) ,\\ & \epsilon_X = \bigotimes_{k=0}^{2n} \sigma_k^{(-1)^k} \in \eta(X) ,\quad \sigma_X = \bigotimes_{k=1}^{2n} \sigma_k^{(-1)^kk} \in \lambda_\mathrm{tot}(X) , \end{aligned} \end{equation}

which are well-defined up to $\pm 1$.

Let $\omega$ be a Kähler form on $X$. Let $\lVert \cdot \rVert _{\lambda _p(X),\omega }$ be the Quillen metric on $\lambda _p(X)$ associated with $\omega$. Let $\lVert \cdot \rVert _{\eta (X)}$ be the metric on $\eta (X)$ induced by $\lVert \cdot \rVert _{\lambda _p(X),\omega }$ via (1.118). The same calculation as in [Zha22, Theorem 2.1] together with the first identity in Proposition 1.5 shows that $\lVert \cdot \rVert _{\eta (X)}$ is independent of $\omega$.

Definition 1.23 We define

(1.123)\begin{equation} \tau_\mathrm{top}(X) = \log \lVert\epsilon_X\rVert_{\eta(X)} . \end{equation}

Indeed $\lVert \cdot \rVert _{\eta (X)}$ is the classical Ray–Singer metric up to a normalization. Later, we use this fact to show that $\tau _\mathrm {top}(X) = 0$.

Let $\lVert \cdot \rVert _{\lambda (X),\omega }$ be the metric on $\lambda (X)$ induced by $\lVert \cdot \rVert _{\lambda _p(X),\omega }$ via the first identity in (1.119). Let $\lVert \cdot \rVert _{\lambda _\mathrm {tot}(X),\omega }$ be the metric on $\lambda _\mathrm {tot}(X)$ induced by $\lVert \cdot \rVert _{\lambda (X),\omega }$ via the second identity in (1.119).

Definition 1.24 We define

(1.124)\begin{equation} \tau_\mathrm{BCOV}(X,\omega) = \log \lVert\sigma_X\rVert_{\lambda_\mathrm{tot}(X),\omega} . \end{equation}

For $p=0,\ldots,n$, let $g^{\Lambda ^p(T^*X)}_\omega$ be the metric on $\Lambda ^p(T^*X)$ induced by $\omega$. Let $g^{\Omega ^{p,q}(X)}_\omega$ be the $L^2$-metric on $\Omega ^{p,q}(X)$. More precisely, $g^{\Omega ^{p,q}(X)}_\omega$ is defined by (1.70) with $(E,g^E)$ replaced by $(\Lambda ^p(T^*X),g^{\Lambda ^p(T^*X)}_\omega )$. Let $g^{H^{p,q}(X)}_\omega$ be the $L^2$-metric on $H^{p,q}(X)$. More precisely, $g^{H^{p,q}(X)}_\omega$ is induced by $g^{\Omega ^{p,q}(X)}_\omega$ via the Hodge theorem. Let $|\cdot |_{\eta (X),\omega }$ be the metric on $\eta (X)$ induced by $(g^{H^{p,q}(X)}_\omega )_{0\leqslant p,q\leqslant n}$ via (1.117) and (1.118).

Proposition 1.25 The following identity holds,

(1.125)\begin{equation} \tau_\mathrm{top}(X) = \log |\epsilon_X|_{\eta(X),\omega} = 0 . \end{equation}

Proof. Let $\square _p$ be as in (1.71) with $( \Omega ^{0,\bullet }(X,E), \bar {\partial }^E, g^E )$ replaced by $( \Omega ^{p,\bullet }(X), \bar {\partial }, g^{\Lambda ^p(T^*X)}_\omega )$. Let $\square _{p,q}$ be the restriction of $\square _p$ to $\Omega ^{p,q}(X)$. Let $\theta _p(z)$ be as in (1.74) with $\square ^E_q$ replaced by $\square _{p,q}$. By Definition 1.13, 1.23, the first equality in (1.125) is equivalent to

(1.126)\begin{equation} \sum_{p=0}^n (-1)^p \theta_p'(0) = 0 , \end{equation}

which was indicated in [Bis04, p. 1304].

Denote by $\mathrm {covol}(H^k_\mathrm {Sing}(X,\mathbb {Z}),\omega )$ the covolume of $\mathrm {Im}(H^k_\mathrm {Sing}(X,\mathbb {Z}) \rightarrow H^k_\mathrm {Sing}(X,\mathbb {R}))$ with respect to the metric induced by $\bigoplus _{p+q=k} g^{H^{p,q}(X)}_\omega$ via (1.121). We have

(1.127)\begin{equation} |\epsilon_X|_{\eta(X),\omega} = \prod_{k=0}^{2n} \big( \mathrm{covol}(H^k_\mathrm{Sing}(X,\mathbb{Z}),\omega) \big)^{(-1)^k} . \end{equation}

On the other hand, by [EFM21, Remark 5.5(ii)], we have

(1.128)\begin{equation} \mathrm{covol}\big(H^k_\mathrm{Sing}(X,\mathbb{Z}),\omega\big) \mathrm{covol}\big(H^{2n-k}_\mathrm{Sing}(X,\mathbb{Z}),\omega\big) = 1 . \end{equation}

Here we remark that, due to the normalization in (1.70) and (1.121), the covolume in the sense of [EFM21, Remark 5.5(ii)] equals $(2\pi )^{(n-k)b_k/2}\mathrm {covol}(H^k_\mathrm {Sing}(X,\mathbb {Z}),\omega )$, where $b_k$ is the $k$th Betti number of $X$. From (1.127) and (1.128), we obtain $|\epsilon _X|_{\eta (X),\omega } = 1$, which is equivalent to the second equality in (1.125). This completes the proof.

2. Several properties of the BCOV torsion

2.1 Kähler metric on projective bundle

For a complex vector space $V$, we denote by $\mathbb {P}(V)$ the set of complex lines in $V$. Then $\mathbb {P}(V)$ is complex manifold.

Let $Y$ be an $m$-dimensional compact Kähler manifold. Let $N$ be a holomorphic vector bundle over $Y$ of rank $n$. Let $\mathbb {1}$ be the trivial line bundle over $Y$. Set

(2.1)\begin{equation} X = \mathbb{P}(N\oplus\mathbb{1}) . \end{equation}

Let $\pi : X \rightarrow Y$ be the canonical projection. For $y\in Y$, we denote $Z_y = \pi ^{-1}(y)$, which is isomorphic to $\mathbb{C} \mathrm {P}^n$. Let $\omega _{\mathbb{C} \mathrm {P}^n}$ be the Kähler form on $\mathbb{C} \mathrm {P}^n$ associated with the Fubini–Study metric. More precisely, $-i\omega _{\mathbb{C} \mathrm {P}^n}$ is equal to the curvature of the tautological line bundle over $\mathbb{C} \mathrm {P}^n$ equipped with the standard metric.

Lemma 2.1 There exists a Kähler form $\omega$ on $X$ such that for any $y\in Y$, there exists an isomorphism $\phi _y: \mathbb{C} \mathrm {P}^n \rightarrow Z_y$ such that $\phi _y^*(\omega |_{Z_y}) = \omega _{\mathbb{C} \mathrm {P}^n}$.

Here $(\phi _y)_{y\in Y}$ is merely a set of maps parameterized by $y\in Y$. It is not even required to depend continuously on $y$.

Proof. We refer the reader to the proof of [Voi02, Proposition 3.18].

Let $s\in \{1,\ldots,n\}$. We assume that there are holomorphic line bundles $L_1,\ldots,L_s$ over $Y$ together with a surjection between holomorphic vector bundles,

(2.2)\begin{equation} N \rightarrow L_1 \oplus \cdots \oplus L_s . \end{equation}

For $k=1,\ldots,s$, let $N \rightarrow L_k$ be the composition of (2.2) and the canonical projection $L_1 \oplus \cdots \oplus L_s \rightarrow L_k$. Set

(2.3)\begin{equation} N_k = \mathrm{Ker}(N\rightarrow L_k) \subseteq N ,\quad X_k = \mathbb{P}(N_k\oplus\mathbb{1}) \subseteq X ,\quad X_0 = \mathbb{P}(N) \subseteq X . \end{equation}

Let $[\xi _0:\cdots :\xi _n]$ be homogenous coordinates on $\mathbb{C} \mathrm {P}^n$. For $k=0,\ldots,n$, we denote ${H_k = \{\xi _k = 0 \} \subseteq \mathbb{C} \mathrm {P}^n}$.

Lemma 2.2 There exists a Kähler form $\omega$ on $X$ such that for any $y\in Y$, there exists an isomorphism $\phi _y: \mathbb{C} \mathrm {P}^n \rightarrow Z_y$ such that $\phi _y^*(\omega |_{Z_y}) = \omega _{\mathbb{C} \mathrm {P}^n}$ and $\phi _y^{-1}(X_k \cap Z_y) = H_k$ for $k=0,\ldots,s$.

Proof. Let $N^*$ be the dual of $N$. We have $L_1^{-1}\oplus \cdots \oplus L_s^{-1} \hookrightarrow N^*$. Let $g^{N^*}$ be a Hermitian metric on $N^*$ such that $L_1^{-1},\ldots,L_s^{-1}\subseteq N^*$ are mutually orthogonal. Let $g^N$ be the dual metric on $N$. Now, proceeding in the same way as in the proof of [Voi02, Proposition 3.18], we obtain $\omega$ satisfying the desired properties. This completes the proof.

2.2 Behavior under adiabatic limit

We use the notation in § 2.1. By Lemma 2.1, there exists a Kähler form $\omega _X$ on $X$ such that for any $y\in Y$, there exists an isomorphism $\phi _y: \mathbb{C} \mathrm {P}^n\rightarrow Z_y$ such that

(2.4)\begin{equation} \phi_y^*(\omega_X|_{Z_y}) = \omega_{\mathbb{C}\mathrm{P}^n} . \end{equation}

Let $\omega _{Z_y} = \omega _X|_{Z_y}$. Note that $(Z_y,\omega _{Z_y})_{y\in Y}$ are mutually isometric, we omit the index $y$ as long as there is no confusion. Let $\omega _Y$ be a Kähler form on $Y$. For $\varepsilon >0$, set

(2.5)\begin{equation} \omega_\varepsilon = \omega_X + \frac{1}{\varepsilon} \pi^*\omega_Y . \end{equation}

We denote

(2.6)\begin{equation} (c_1c_{m-1})(Y) = \int_Y c_1(TY)c_{m-1}(TY) . \end{equation}

Let $\chi (\cdot )$ be the topological Euler characteristic. Recall that $\tau _\mathrm {BCOV}(\cdot,\cdot )$ was defined in Definition 1.24.

Theorem 2.3 As $\varepsilon \rightarrow 0$,

(2.7)\begin{align} & \tau_\mathrm{BCOV}(X,\omega_\varepsilon) - \tfrac{1}{12} \chi(Z) \big( m \chi(Y) + (c_1c_{m-1})(Y) \big) \log \varepsilon \nonumber\\ & \quad \rightarrow \chi(Z) \tau_\mathrm{BCOV}(Y,\omega_Y) + \chi(Y) \tau_\mathrm{BCOV}(Z,\omega_Z) . \end{align}

Proof. The proof consists of several steps.

Recall that $\eta (\cdot )$ was constructed in (1.118) and $\lambda _\mathrm {tot}(\cdot )$ was constructed in (1.119).

Step 1. We construct two canonical sections of

(2.8)\begin{equation} \lambda_\mathrm{tot}(X) \otimes \big(\lambda_\mathrm{tot}(Y)\big)^{-\chi(Z)} \otimes \big(\eta(Y)\big)^{-n\chi(Z)} . \end{equation}

For $p=0,\ldots,m+n$ and $s=0,\ldots,p-1$, set

(2.9)\begin{equation} I^p_s = \big\{ u \in \Lambda^p(T^*X) : u(v_1,\ldots,v_p) = 0 \text{ for any } v_1,\ldots,v_{s+1} \in TZ, v_{s+2},\ldots,v_p \in TX \big\} .\end{equation}

For convenience, we denote $I^p_p = \Lambda ^p(T^*X)$ and $I^p_{-1} = 0$. We obtain a filtration

(2.10)\begin{equation} \Lambda^p(T^*X) = I^p_p \hookleftarrow I^p_{p-1} \hookleftarrow \cdots \hookleftarrow I^p_{-1} = 0 . \end{equation}

For $r=0,\ldots,m$ and $s=0,\ldots,n$, we denote

(2.11)\begin{equation} E_{r,s} = \Lambda^s(T^*Z) \otimes \pi^*\Lambda^r(T^*Y) . \end{equation}

We have a short exact sequence of holomorphic vector bundles over $X$,

(2.12)\begin{equation} 0 \rightarrow I^{r+s}_{s-1} \rightarrow I^{r+s}_s \rightarrow E_{r,s} \rightarrow 0 . \end{equation}

Let

(2.13)\begin{equation} \alpha_{r,s} \in \big(\!\det H^\bullet(X,I^{r+s}_{s-1})\big)^{-1} \otimes \det H^\bullet(X,I^{r+s}_s) \otimes \big(\!\det H^\bullet(X,E_{r,s})\big)^{-1} . \end{equation}

be the canonical section induced by the long exact sequence induced by (2.12).

Let $H^{\bullet,\bullet }(Z)$ be the fiberwise cohomology. As $Z \simeq \mathbb{C} \mathrm {P}^n$, we have

(2.14)\begin{equation} H^{p,p}(Z) = \mathbb{C} \quad\text{for } p = 0,\ldots, n ,\quad H^{p,q}(Z) = 0 \quad\text{for } p \neq q . \end{equation}

Applying spectral sequence while using (2.11) and (2.14), we obtain

(2.15)\begin{equation} H^q(X,E_{r,s}) \simeq H^{r,q-s}\big(Y,H^{s,s}(Z)\big) := H^{q-s}\big(Y,\Lambda^r(T^*Y) \otimes H^{s,s}(Z)\big) . \end{equation}

Let

(2.16)\begin{equation} \beta_{r,s} \in \det H^\bullet(X,E_{r,s}) \otimes \big(\!\det H^{r,\bullet}\big(Y,H^{s,s}(Z)\big) \big)^{-(-1)^s} \end{equation}

be the canonical section induced by (2.15).

We have a generator of lattice,

(2.17)\begin{equation} \delta_s \in H^{2s}_\mathrm{Sing}(\mathbb{C}\mathrm{P}^n,\mathbb{Z}) \subseteq H^{2s}_\mathrm{Sing}(\mathbb{C}\mathrm{P}^n,\mathbb{R}) \subseteq H^{2s}_\mathrm{Sing}(\mathbb{C}\mathrm{P}^n,\mathbb{C}) . \end{equation}

We identify $H^{2s}_\mathrm {Sing}(\mathbb{C} \mathrm {P}^n,\mathbb{C} )$ with $H^{2s}_\mathrm {dR}(\mathbb{C} \mathrm {P}^n) = H^{s,s}(\mathbb{C} \mathrm {P}^n)$ (see (1.121)). Since $H^{s,s}(Z) = H^{s,s}(\mathbb{C} \mathrm {P}^n) = H^{2s}_\mathrm {Sing}(\mathbb{C} \mathrm {P}^n,\mathbb{C} )$ is a trivial line bundle over $Y$, we have an isomorphism (cf. [GH94, p. 607])

(2.18)\begin{equation} \begin{aligned} H^{r,\bullet}(Y) & \rightarrow H^{r,\bullet}\big(Y,H^{s,s}(Z)\big) = H^{r,\bullet}(Y) \otimes H^{s,s}(\mathbb{C}\mathrm{P}^n)\\ u & \mapsto u \otimes \delta_s . \end{aligned} \end{equation}

Let

(2.19)\begin{equation} \gamma_{r,s} \in \big(\!\det H^{r,\bullet}\big(Y,H^{s,s}(Z)\big) \big)^{(-1)^s} \otimes \big(\!\det H^{r,\bullet}(Y) \big)^{-(-1)^s} \end{equation}

be the canonical section induced by (2.18). By (2.13), (2.16) and (2.19), we have

(2.20)\begin{equation} \alpha_{r,s} \otimes \beta_{r,s} \otimes \gamma_{r,s} \in \big(\!\det H^\bullet(X,I^{r+s}_{s-1})\big)^{-1} \otimes \det H^\bullet(X,I^{r+s}_s) \otimes \big(\!\det H^{r,\bullet}(Y) \big)^{-(-1)^s} .\end{equation}

Recall that $\lambda (\cdot )$ was defined in (1.119). By (1.119) and (2.10), we have

(2.21)\begin{align} \lambda(X) & = \bigotimes_{p=1}^{m+n} \big(\!\det H^\bullet\big(X,\Lambda^p(T^*X)\big)\big)^{(-1)^pp} \nonumber\\ & = \bigotimes_{p=1}^{m+n} \big(\!\det H^\bullet(X,I^p_p)\big)^{(-1)^pp} \nonumber\\ & = \bigotimes_{r=0}^m \bigotimes_{s=0}^n \big( \big(\!\det H^\bullet(X,I^{r+s}_{s-1})\big)^{-1} \otimes \det H^\bullet(X,I^{r+s}_s) \big)^{(-1)^{r+s}(r+s)}. \end{align}

On the other hand, by (1.118), (1.119) and the identities

(2.22)\begin{equation} n+1 = \chi(Z) ,\quad \sum_{s=0}^n s = \frac{n(n+1)}{2} = \frac{n}{2}\chi(Z) , \end{equation}

we have

(2.23)\begin{equation} \bigotimes_{r=0}^m \bigotimes_{s=0}^n \big(\!\det H^{r,\bullet}(Y) \big)^{(-1)^r(r+s)} = \big(\lambda(Y)\big)^{\chi(Z)} \otimes \big(\eta(Y)\big)^{n\chi(Z)/2} . \end{equation}

By (2.20), (2.21) and (2.23), we have

(2.24)\begin{equation} \prod_{r=0}^m \prod_{s=0}^n ( \alpha_{r,s}\otimes\beta_{r,s}\otimes\gamma_{r,s} )^{(-1)^{r+s}(r+s)} \in \lambda(X) \otimes \big(\lambda(Y)\big)^{-\chi(Z)} \otimes \big(\eta(Y)\big)^{-n\chi(Z)/2} .\end{equation}

By (1.119) and (2.24), we have

(2.25)\begin{align} &\prod_{r=0}^m \prod_{s=0}^n ( \alpha_{r,s}\otimes\beta_{r,s}\otimes\gamma_{r,s} )^{(-1)^{r+s}(r+s)} \otimes \overline{ \prod_{r=0}^m \prod_{s=0}^n ( \alpha_{r,s}\otimes\beta_{r,s}\otimes\gamma_{r,s} )^{(-1)^{r+s}(r+s)} } \nonumber\\ &\quad \in \lambda_\mathrm{tot}(X) \otimes \big(\lambda_\mathrm{tot}(Y)\big)^{-\chi(Z)} \otimes \big(\eta(Y)\big)^{-n\chi(Z)} , \end{align}

where $\bar {\cdot }$ is the conjugation.

Let $\sigma _X \in \lambda _\mathrm {tot}(X)$, $\sigma _Y \in \lambda _\mathrm {tot}(Y)$ and $\epsilon _Y \in \eta (Y)$ be as in (1.122). Obviously, we have

(2.26)\begin{equation} \sigma_X \otimes \sigma_Y^{-\chi(Z)} \otimes \epsilon_Y^{-n\chi(Z)} \in \lambda_\mathrm{tot}(X) \otimes \big(\lambda_\mathrm{tot}(Y)\big)^{-\chi(Z)} \otimes \big(\eta(Y)\big)^{-n\chi(Z)} . \end{equation}

Step 2. We show that

(2.27)\begin{align} &\prod_{r=0}^m \prod_{s=0}^n ( \alpha_{r,s}\otimes\beta_{r,s}\otimes\gamma_{r,s} )^{(-1)^{r+s}(r+s)} \otimes \overline{ \prod_{r=0}^m \prod_{s=0}^n ( \alpha_{r,s}\otimes\beta_{r,s}\otimes\gamma_{r,s} )^{(-1)^{r+s}(r+s)} } \nonumber\\ &\quad = \pm \sigma_X \otimes \sigma_Y^{-\chi(Z)} \otimes \epsilon_Y^{-n\chi(Z)}. \end{align}

Let $\mathbb {Z}(-1)$ be the inverse of the Tate twist, which is a Hodge structure of pure weight two. For $j\in \mathbb {N}$, we denote by $\mathbb {Z}(-j)$ its $j$th tensor power. We have canonical identifications of Hodge structures,

(2.28)\begin{equation} \begin{aligned} H^{2j}_\mathrm{Sing}(\mathbb{C}\mathrm{P}^n,\mathbb{Z}) & = \mathbb{Z}(-j) \quad \text{for } j = 0,\ldots,n ,\\ H^k_\mathrm{Sing}(X,\mathbb{Z}) & = \bigoplus_{j=0}^n H^{k-2j}_\mathrm{Sing}(Y,\mathbb{Z}) \otimes H^{2j}_\mathrm{Sing}(\mathbb{C}\mathrm{P}^n,\mathbb{Z}) \\ & = \bigoplus_{j=0}^n H^{k-2j}_\mathrm{Sing}(Y,\mathbb{Z}) \otimes \mathbb{Z}(-j) . \end{aligned} \end{equation}

Complexifying (2.28) and applying Hodge decomposition, we obtain

(2.29)\begin{equation} \begin{aligned} & H^{j,j}(\mathbb{C}\mathrm{P}^n) = \mathbb{C} \quad \text{for } j = 0,\ldots,n ,\\ & H^{p,q}(X) = \bigoplus_{j=0}^n H^{p-j,q-j}(Y) \otimes H^{j,j}(\mathbb{C}\mathrm{P}^n) = \bigoplus_{j=0}^n H^{p-j,q-j}(Y) . \end{aligned} \end{equation}

We use the identifications in (2.28) and (2.29) until the end of Step 2.

Claim. For complex vector spaces $A$ and $B$, the canonical identification $\det A \otimes \det B \otimes (\det (A \oplus B))^{-1} = \mathbb{C}$ is such that the canonical section of $\det A \otimes \det B \otimes (\det (A \oplus B))^{-1}$ is identified with $1\in \mathbb{C}$.

Recall that $I^{r+s}_s$ was defined in (2.9) and $E_{r,s}$ was defined in (2.11). We have

(2.30)\begin{equation} H^q(X,I^{r+s}_s) = \bigoplus_{j=0}^s H^{r+s-j,q-j}(Y) ,\quad H^q(X,E_{r,s}) = H^{r,q-s}(Y) . \end{equation}

By (2.30), we have

(2.31)\begin{equation} H^\bullet(X,I^{r+s}_s) = H^\bullet(X,I^{r+s}_{s-1}) \oplus H^\bullet(X,E_{r,s}). \end{equation}

Applying the claim in the last paragraph to (2.31), we obtain

(2.32)\begin{equation} \big(\!\det H^\bullet(X,I^{r+s}_{s-1})\big)^{-1} \otimes \det H^\bullet(X,I^{r+s}_s) \otimes \big(\!\det H^\bullet(X,E_{r,s})\big)^{-1} = \mathbb{C} , \quad \alpha_{r,s} = 1 . \end{equation}

A similar argument shows that

(2.33)\begin{equation} \begin{aligned} \det H^\bullet(X,E_{r,s}) \otimes \big(\!\det H^{r,\bullet}\big(Y,H^{s,s}(Z)\big) \big)^{-(-1)^s} = \mathbb{C} , \quad \beta_{r,s} = 1 , \\ \big(\!\det H^{r,\bullet}\big(Y,H^{s,s}(Z)\big) \big)^{(-1)^s} \otimes \big(\!\det H^{r,\bullet}(Y) \big)^{-(-1)^s} = \mathbb{C} , \quad \gamma_{r,s} = 1 . \end{aligned} \end{equation}

Using (1.119), (1.121) and (2.28), we can show that

(2.34)\begin{equation} \begin{aligned} \lambda_\mathrm{tot}(X) \otimes \big(\lambda_\mathrm{tot}(Y)\big)^{-\chi(Z)} \otimes \big(\eta(Y)\big)^{-n\chi(Z)} & = \mathbb{C} ,\\ \sigma_X \otimes \sigma_Y^{-\chi(Z)} \otimes \epsilon_Y^{-n\chi(Z)} & = \pm 1 . \end{aligned} \end{equation}

From (2.32)–(2.34), we obtain (2.27).

Step 3. We introduce several Quillen metrics.

• • Let $g^{TX}_\varepsilon$ be the metric on $TX$ induced by $\omega _\varepsilon$.

• • Let $g^{\Lambda ^p(T^*X)}_\varepsilon$ be the metric on $\Lambda ^p(T^*X)$ induced by $g^{TX}_\varepsilon$.

• • Let $g^{I^p_s}_\varepsilon$ be the metric on $I^p_s$ induced by $g^{\Lambda ^p(T^*X)}_\varepsilon$ via (2.10).

• • Let $g^{TY}$ be the metric on $TY$ induced by $\omega _Y$.

• • Let $g^{\Lambda ^r(T^*Y)}$ be the metric on $\Lambda ^r(T^*Y)$ induced by $g^{TY}$.

• • Let $g^{TZ}$ be the metric on $TZ$ induced by $\omega _Z = \omega _\varepsilon |_Z$.

• • Let $g^{\Lambda ^s(T^*Z)}$ be the metric on $\Lambda ^s(T^*Z)$ induced by $g^{TZ}$.

• • Let $g^{E_{r,s}}$ be the metric on $E_{r,s}$ induced by $g^{\Lambda ^r(T^*Y)}$ and $g^{\Lambda ^s(T^*Z)}$ via (2.11).

Let

(2.35)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X,I^p_s),\varepsilon} \end{equation}

be the Quillen metric on $\det H^\bullet (X,I^p_s)$ associated with $g^{TX}_\varepsilon$ and $g^{I^p_s}_\varepsilon$. Let

(2.36)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X,E_{r,s}),\varepsilon} \end{equation}

be the Quillen metric on $\det H^\bullet (X,E_{r,s})$ associated with $g^{TX}_\varepsilon$ and $g^{E_{r,s}}$. Recall that $\alpha _{r,s}$ was defined by (2.13). Let $\lVert \alpha _{r,s}\rVert _\varepsilon$ be the norm of $\alpha _{r,s}$ with respect to the metrics (2.35) and (2.36).

• • Let $g^{\Omega ^{s,s}(Z)}$ be the $L^2$-metric on $\Omega ^{s,s}(Z)$ induced by $g^{TZ}$ (see (1.70)).

• • Let $g^{H^{s,s}(Z)}$ be the metric on $H^{s,s}(Z)$ induced by $g^{\Omega ^{s,s}(Z)}$ via the Hodge theorem.

Let

(2.37)\begin{equation} \lVert\cdot\rVert_{\det H^{r,\bullet}(Y,H^{s,s}(Z))} \end{equation}

be the Quillen metric on $\det H^{r,\bullet }(Y,H^{s,s}(Z)) = \det H^\bullet (Y,\Lambda ^r(T^*Y)\otimes H^{s,s}(Z))$ associated with $g^{TY}$ and $g^{\Lambda ^r(T^*Y)} \otimes g^{H^{s,s}(Z)}$. Recall that $\beta _{r,s}$ was defined by (2.16). Let $\lVert \beta _{r,s}\rVert _\varepsilon$ be the norm of $\beta _{r,s}$ with respect to the metrics (2.36) and (2.37). Let

(2.38)\begin{equation} \lVert\cdot\rVert_{\det H^{r,\bullet}(Y)} \end{equation}

be the Quillen metric on $\det H^{r,\bullet }(Y) = \det H^\bullet (Y,\Lambda ^r(T^*Y))$ associated with $g^{TY}$ and $g^{\Lambda ^r(T^*Y)}$. Recall that $\gamma _{r,s}$ was defined by (2.19). Let $\lVert \gamma _{r,s}\rVert$ be the norm of $\gamma _{r,s}$ with respect to the metrics (2.37) and (2.38).

By (1.119) and (2.10), we have

(2.39)\begin{equation} \sigma_X \in \lambda_\mathrm{tot}(X) = \bigotimes_{p=1}^{m+n} \big(\!\det H^\bullet(X,I^p_p)\big)^{(-1)^pp} \otimes \overline{\bigotimes_{p=1}^{m+n} \big(\!\det H^\bullet(X,I^p_p)\big)^{(-1)^pp}} . \end{equation}

Let $\lVert \sigma _X\rVert _\varepsilon$ be the norm of $\sigma _X$ with respect to the metrics (2.35) with $s=p$. By (1.118) and (1.119), we have

(2.40)\begin{equation} \begin{aligned} & \epsilon_Y \in \eta(Y) = \bigotimes_{r=0}^m \big(\!\det H^{r,\bullet}(Y)\big)^{(-1)^r} ,\\ & \sigma_Y \in \lambda_\mathrm{tot}(Y) = \bigotimes_{r=1}^m \big(\!\det H^{r,\bullet}(Y)\big)^{(-1)^rr} \otimes \overline{\bigotimes_{r=1}^m \big(\!\det H^{r,\bullet}(Y)\big)^{(-1)^rr}} . \end{aligned} \end{equation}

Let $\lVert \epsilon _Y\rVert$ be the norm of $\epsilon _Y$ with respect to the metrics (2.38). Let $\lVert \sigma _Y\rVert$ be the norm of $\sigma _Y$ with respect to the metrics (2.38). By (2.27), we have

(2.41)\begin{align} & \sum_{r=0}^m \sum_{s=0}^n (-1)^{r+s}(r+s) \big( \log\lVert\alpha_{r,s}\rVert^2_\varepsilon + \log\lVert\beta_{r,s}\rVert^2_\varepsilon + \log\lVert\gamma_{r,s}\rVert^2 \big) \nonumber\\ &\quad = \log\lVert\sigma_X\rVert_\varepsilon - \chi(Z) \log\lVert\sigma_Y\rVert - n \chi(Z) \log\lVert\epsilon_Y\rVert . \end{align}

On the other hand, by Definition 1.23 and Proposition 1.25, we have

(2.42)\begin{equation} \log\lVert\epsilon_Y\rVert = 0 . \end{equation}

By Definition 1.24, (2.41) and (2.42), we have

(2.43) \begin{align} \tau_\mathrm{BCOV}(X,\omega_\varepsilon) &= \chi(Z) \tau_\mathrm{BCOV}(Y,\omega_Y) \nonumber\\ &\quad + \sum_{r=0}^m \sum_{s=0}^n (-1)^{r+s}(r+s) \big( \log\lVert\alpha_{r,s}\rVert^2_\varepsilon + \log\lVert\beta_{r,s}\rVert^2_\varepsilon + \log\lVert\gamma_{r,s}\rVert^2 \big) . \end{align}

Step 4. We estimate $\log \lVert \alpha _{r,s}\rVert ^2_\varepsilon$.

Recall that $I^{r+s}_s$ was defined in (2.9), $E_{r,s}$ was defined in (2.11), $g^{I^{r+s}_s}_\varepsilon$ and $g^{E_{r,s}}$ were defined at the beginning of Step 3. Let $g^{E_{r,s}}_\varepsilon$ be quotient metric on $E_{r,s}$ induced by $g^{I^{r+s}_s}_\varepsilon$ via the surjection $I^{r+s}_s \rightarrow E_{r,s}$ in (2.12). Note that $g^{I^{r+s}_s}_\varepsilon$ is induced by $\omega _\varepsilon$. By (2.5), as $\varepsilon \rightarrow 0$,

(2.44)\begin{equation} \varepsilon^{-r} g^{E_{r,s}}_\varepsilon \rightarrow g^{E_{r,s}} . \end{equation}

We use the notation from (1.23). Let

(2.45)\begin{equation} \tilde{T}_{r,s,\varepsilon} = \widetilde{\mathrm{ch}}\Big( g^{I^{r+s}_{s-1}}_\varepsilon, g^{I^{r+s}_s}_\varepsilon, g^{E_{r,s}}_\varepsilon \Big) \in Q^X/Q^{X,0} \end{equation}

be the Bott–Chern form (1.56) with $0\rightarrow E' \rightarrow E \rightarrow E'' \rightarrow 0$ replaced by (2.12) and $(g^{E'},g^E,g^{E''})$ replaced by $( g^{I^{r+s}_{s-1}}_\varepsilon, g^{I^{r+s}_s}_\varepsilon, g^{E_{r,s}}_\varepsilon )$. Let

(2.46)\begin{equation} T_{r,s,\varepsilon} = \widetilde{\mathrm{ch}}\Big( g^{I^{r+s}_{s-1}}_\varepsilon, g^{I^{r+s}_s}_\varepsilon, g^{E_{r,s}} \Big) \in Q^X/Q^{X,0} \end{equation}

be the Bott–Chern form (1.56) with $0\rightarrow E' \rightarrow E \rightarrow E'' \rightarrow 0$ replaced by (2.12) and $(g^{E'},g^E,g^{E''})$ replaced by $( g^{I^{r+s}_{s-1}}_\varepsilon, g^{I^{r+s}_s}_\varepsilon, g^{E_{r,s}} )$. By Proposition 1.11 and (2.44), as $\varepsilon \rightarrow 0$,

(2.47) \begin{align} T_{r,s,\varepsilon} - \tilde{T}_{r,s,\varepsilon} - \mathrm{ch}(E_{r,s},g^{E_{r,s}}) r \log \varepsilon = \widetilde{\mathrm{ch}}(g^{E_{r,s}},g^{E_{r,s}}_\varepsilon) - \mathrm{ch}(E_{r,s},g^{E_{r,s}}) r \log \varepsilon \rightarrow 0 . \end{align}

On the other hand, by Proposition 1.12, as $\varepsilon \rightarrow 0$,

(2.48)\begin{equation} \tilde{T}_{r,s,\varepsilon} \rightarrow 0 . \end{equation}

By (2.47) and (2.48), as $\varepsilon \rightarrow 0$,

(2.49)\begin{equation} T_{r,s,\varepsilon} - \mathrm{ch}(E_{r,s},g^{E_{r,s}}) r \log \varepsilon \rightarrow 0 . \end{equation}

Applying Theorem 1.18 to the short exact sequence (2.12), we obtain

(2.50)\begin{equation} \log \lVert\alpha_{r,s}\rVert_\varepsilon^2 = \int_X \mathrm{Td}(TX,g^{TX}_\varepsilon) T_{r,s,\varepsilon} . \end{equation}

By Proposition 1.10, as $\varepsilon \rightarrow 0$,

(2.51)\begin{equation} \mathrm{Td}(TX,g^{TX}_\varepsilon) \rightarrow \pi^*\mathrm{Td}(TY,g^{TY}) \mathrm{Td}(TZ,g^{TZ}) . \end{equation}

On the other hand, by the Grothendieck–Riemann–Roch formula (1.76), (2.11) and (2.14), we have

(2.52)\begin{align} & \int_X \pi^*\mathrm{Td}(TY,g^{TY}) \mathrm{Td}(TZ,g^{TZ}) \mathrm{ch}(E_{r,s},g^{E_{r,s}})\nonumber\\ &\quad = \int_Y \mathrm{Td}(TY) \mathrm{ch}\big(H^\bullet(Z,E_{r,s})\big) \nonumber\\ &\quad = \int_Y \mathrm{Td}(TY) \mathrm{ch}\big(\Lambda^r(T^*Y)\big) \mathrm{ch}\big(H^{s,\bullet}(Z)\big) \nonumber\\ &\quad = (-1)^s \int_Y \mathrm{Td}(TY) \mathrm{ch}\big(\Lambda^r(T^*Y)\big) . \end{align}

By (2.49)–(2.52), as $\varepsilon \rightarrow 0$,

(2.53)\begin{equation} \log \lVert\alpha_{r,s}\rVert_\varepsilon^2 - (-1)^s r \int_Y \mathrm{Td}(TY) \mathrm{ch}\big(\Lambda^r(T^*Y)\big) \log \varepsilon \rightarrow 0. \end{equation}

By Proposition 1.5, (2.22) and (2.53), as $\varepsilon \rightarrow 0$,

(2.54)\begin{align} & \sum_{r=0}^m \sum_{s=0}^n (-1)^{r+s}(r+s) \log\lVert\alpha_{r,s}\rVert^2_\varepsilon \nonumber\\ & \quad - \bigg( \frac{m(3m+3n+1)}{12}\chi(Y) + \frac{1}{6}(c_1c_{m-1})(Y) \bigg) \chi(Z) \log \varepsilon \rightarrow 0 . \end{align}

Step 5. We estimate $\log \lVert \beta _{r,s}\rVert ^2_\varepsilon$.

Let

(2.55)\begin{equation} T_{r,s}\in Q^Y \end{equation}

be the Bismut–Köhler analytic torsion form (see § 1.5) associated with $( \pi : X \rightarrow Y, \omega _X, E_{r,s}, g^{E_{r,s}} )$. Applying Theorem 1.17 with $E=E_{r,s}$, as $\varepsilon \rightarrow 0$,

(2.56) \begin{align} \log \lVert\beta_{r,s}\rVert_\varepsilon^2 + \int_Y \mathrm{Td}'(TY) \int_Z \mathrm{Td}(TZ) \mathrm{ch}(E_{r,s}) \log\varepsilon\rightarrow \int_Y \mathrm{Td}(TY,g^{TY}) T_{r,s}. \end{align}

Similarly to (2.52), we have

(2.57) \begin{align} \int_Y \mathrm{Td}'(TY) \int_Z \mathrm{Td}(TZ) \mathrm{ch}(E_{r,s}) = (-1)^s \int_Y \mathrm{Td}'(TY)\mathrm{ch}\big(\Lambda^r(T^*Y)\big). \end{align}

Applying Proposition 1.15 with $E = E_{0,s}$ and $F = \Lambda ^r(T^*Y)$, we obtain

(2.58)\begin{equation} T_{r,s} = \mathrm{ch}\big(\Lambda^r(T^*Y),g^{\Lambda^r(T^*Y)}\big)T_{0,s} \text{ modulo } Q^{Y,0} . \end{equation}

By (2.56)–(2.58), as $\varepsilon \rightarrow 0$,

(2.59)\begin{align} & \log \lVert\beta_{r,s}\rVert_\varepsilon^2 + (-1)^s \int_Y \mathrm{Td}'(TY)\mathrm{ch}\big(\Lambda^r(T^*Y)\big) \log\varepsilon \nonumber\\ & \quad \rightarrow \int_Y \mathrm{Td}(TY,g^{TY}) \mathrm{ch}\big(\Lambda^r(T^*Y),g^{\Lambda^r(T^*Y)}\big)T_{0,s} . \end{align}

On the other hand, by Theorem 1.16, we have

(2.60)\begin{equation} \sum_{s=0}^n (-1)^s T_{0,s} = 0 \text{ modulo } Q^{Y,0} . \end{equation}

By Propositions 1.5, 1.6, (2.22), (2.59) and (2.60), as $\varepsilon \rightarrow 0$,

(2.61) \begin{align} &\sum_{r=0}^m \sum_{s=0}^n (-1)^{r+s}(r+s) \log\lVert\beta_{r,s}\rVert^2_\varepsilon+ \bigg( \frac{m(m+n)}{4}\chi(Y) + \frac{1}{12}(c_1c_{m-1})(Y) \bigg) \chi(Z) \log \varepsilon\nonumber\\ &\quad \rightarrow \int_Y c_m(TY,g^{TY}) \sum_{s=0}^n (-1)^s s T_{0,s} \nonumber\\ &\quad = \int_Y c_m(TY,g^{TY}) \sum_{s=0}^n (-1)^s s \{ T_{0,s} \}^{(0,0)}, \end{align}

where $\{\cdot \}^{(0,0)}$ means the component of degree $(0,0)$.

Step 6. We calculate $\log \lVert \gamma _{r,s}\rVert ^2$.

Recall that $H^{s,s}(Z)$ is a trivial line bundle over $Y$. Recall that $g^{H^{s,s}(Z)}$ was constructed in the paragraph above (2.37). By our assumption (2.4), $g^{H^{s,s}(Z)}$ is a constant metric. Recall that $\delta _s \in H^{s,s}(Z)$ was constructed in (2.17). Let $|\delta _s|$ be the norm of $\delta _s$ with respect to $g^{H^{s,s}(Z)}$, which is a constant function on $Y$. In the following, we do not distinguish between a constant function and its value. We denote $\chi _r(Y) = \sum _{q=0}^m (-1)^q \dim H^{r,q}(Y)$. By Remark 1.14, we have

(2.62)\begin{equation} \log\lVert\gamma_{r,s}\rVert^2 = (-1)^s \chi_r(Y) \log |\delta_s|^2 . \end{equation}

Let $\epsilon _Z \in \eta (Z)$ be as in (1.122). We have

(2.63)\begin{equation} \epsilon_Z = \pm \bigotimes_{s=0}^n \delta_s . \end{equation}

Let $|\epsilon _Z|$ be the norm of $\epsilon _Z$ with respect to the metrics $g^{H^{s,s}(Z)}$. By Proposition 1.25 and (2.63), we have

(2.64)\begin{equation} \sum_{s=0}^n \log |\delta_s|^2 = \log |\epsilon_Z|^2 = 0 . \end{equation}

Let $\sigma _Z \in \lambda _\mathrm {tot}(Z)$ be as in (1.122). We have

(2.65)\begin{equation} \sigma_Z = \pm \bigotimes_{s=1}^n \delta_s^{2s} . \end{equation}

Let $|\sigma _Z|$ be the norm of $\sigma _Z$ with respect to the metrics $g^{H^{s,s}(Z)}$. By (2.65), we have

(2.66)\begin{equation} \sum_{s=0}^n s \log |\delta_s|^2 = \log | \sigma_Z | . \end{equation}

By (2.62), (2.64), (2.66) and the identity $\sum _{r=0}^m (-1)^r \chi _r(Y) = \chi (Y)$, we have

(2.67)\begin{equation} \sum_{r=0}^m \sum_{s=0}^n (-1)^{r+s}(r+s) \log\lVert\gamma_{r,s}\rVert^2 = \chi(Y) \log | \sigma_Z |. \end{equation}

Step 7. We conclude.

By (2.43), (2.54), (2.61) and (2.67), as $\varepsilon \rightarrow 0$,

(2.68) \begin{align} & \tau_\mathrm{BCOV}(X,\omega_\varepsilon) - \frac{1}{12} \chi(Z) \big( m \chi(Y) + (c_1c_{m-1})(Y) \big) \log \varepsilon \nonumber\\ & \quad \rightarrow \chi(Z) \tau_\mathrm{BCOV}(Y,\omega_Y) + \chi(Y) \log |\sigma_Z | \nonumber\\ & \qquad + \int_Y c_m(TY,g^{TY}) \sum_{s=0}^n (-1)^s s \{T_{0,s}\}^{(0,0)} . \end{align}

Let $\theta _s(z)$ be as in (1.74) with $(X,\omega )$ replaced by $(Z,\omega _Z)$ and $(E,g^E)$ replaced by $(\Lambda ^s(T^*Z),g^{\Lambda ^s(T^*Z)})$. By Definition 1.13, 1.24, we have

(2.69)\begin{equation} \tau_\mathrm{BCOV}(Z,\omega_Z) = \log | \sigma_Z | + \sum_{s=0}^n (-1)^s s \theta_s'(0) . \end{equation}

By (2.4), all the terms in (2.69) are constant functions on $Y$. By (1.79), we have

(2.70)\begin{equation} \{ T_{0,s} \}^{(0,0)} = \theta_s'(0) . \end{equation}

From (2.68)–(2.70), we obtain (2.7). This completes the proof.

Remark 2.4 The key ingredient in the proof of Theorem 2.3 is [BB94, Theorem 3.2], which is a consequence of [BB94, Theorem 3.1]. Of course, we can replace [BB94, Theorem 3.2] by [BB94, Theorem 3.1] in our proof to obtain a formula for $\tau _\mathrm {BCOV}(X,\omega _X)$. However, because [BB94, Theorem 3.1] involves a Bott–Chern form, the formula obtained will be far from clean.

2.3 Behavior under blow-ups

The following lemma is direct consequence of Bott formula [Bot57] (see also [OSS11, p. 5]).

Lemma 2.5 Let $L$ be the holomorphic line bundle of degree one over $\mathbb{C} \mathrm {P}^n$. For $k=1,\ldots,n$ and $s =1,\ldots,k$, we have

(2.71)\begin{equation} H^\bullet\big(\mathbb{C}\mathrm{P}^n,\Lambda^k(T^*\mathbb{C}\mathrm{P}^n) \otimes L^s \big) = 0 . \end{equation}

Let $X$ be an $n$-dimensional compact Kähler manifold. Let $Y\subseteq X$ be a closed complex submanifold. Let $f: X' \rightarrow X$ be the blow-up along $Y$. Let $Y \subseteq U \subseteq X$ be an open neighborhood of $Y$. Set $U' = f^{-1}(U)$. Let $\omega$ be a Kähler form on $X$. Let $\omega '$ be a Kähler form on $X'$ such that

(2.72)\begin{equation} \omega'|_{X'\backslash U'} = f^*(\omega|_{X\backslash U}) . \end{equation}

For the existence of such $\omega '$, see the proof of [Voi02, Proposition 3.24].

Theorem 2.6 We have

(2.73)\begin{equation} \tau_\mathrm{BCOV}(X',\omega') - \tau_\mathrm{BCOV}(X,\omega) = \alpha(U,U',\omega|_U,\omega'|_{U'}) , \end{equation}

where $\alpha (U,U',\omega |_U,\omega '|_{U'})$ is a real number determined by $U$, $U'$, $\omega |_U$ and $\omega '|_{U'}$.

Proof. The proof consists of several steps.

Step 0. We introduce several pieces of notation.

We denote $D = f^{-1}(Y)$. Let $i: D \hookrightarrow X'$ be the canonical embedding. Let $\mathscr {I} \subseteq \mathscr {O}_{X'}$ be the ideal sheaf associated with $D$. More precisely, for open subset $U \subseteq X'$, we have

(2.74)\begin{equation} \mathscr{I}(U) = \{ \theta \in \mathscr{O}_{X'}(U) : \theta|_{U \cap D} = 0 \} . \end{equation}

For $p=0,\ldots,n$, there exist holomorphic vector bundles over $X'$ linked by holomorphic maps

(2.75)\begin{equation} f^*\Lambda^p(T^*X) = F^p_p \rightarrow F^p_{p-1} \rightarrow \cdots \rightarrow F^p_0 = \Lambda^p(T^*X') \end{equation}

such that for $s=0,\ldots,p-1$,

• • the induced map $\mathscr {O}_{X'}(F^p_{s+1}) \rightarrow \mathscr {O}_{X'}(F^p_s)$ is injective;

• • we have $\mathscr {I} \otimes \mathscr {O}_{X'}(F^p_s) \hookrightarrow \mathscr {O}_{X'}(F^p_{s+1}) \hookrightarrow \mathscr {O}_{X'}(F^p_s)$.

Set

(2.76)\begin{equation} \mathscr{G}^p_s = \mathscr{O}_{X'}(F^p_s)/\mathscr{O}_{X'}(F^p_{s+1}) . \end{equation}

Then we have a commutative diagram of analytic coherent sheaves on $X'$,

(2.77)

where the first row is exact. Now we briefly explain the existence of these $F^p_s$. We have

(2.78)\begin{equation} \mathscr{I}^{\otimes p} \otimes \mathscr{O}_{X'}\big(\Lambda^p(T^*X')\big) \hookrightarrow \mathscr{O}_{X'}\big(f^*\Lambda^p(T^*X)\big) \hookrightarrow \mathscr{O}_{X'}\big(\Lambda^p(T^*X')\big) . \end{equation}

For $s=0,\ldots,p$, let $\mathscr {F}^p_s$ be the sub-sheaf of $\mathscr {O}_{X'}(\Lambda ^p(T^*X'))$ generated by $\mathscr {I}^{\otimes s} \otimes \mathscr {O}_{X'}(\Lambda ^p(T^*X'))$ and $\mathscr {O}_{X'}(f^*\Lambda ^p(T^*X))$. Then the desired properties hold with $\mathscr {O}_{X'}(F^p_s)$ replaced by $\mathscr {F}^p_s$. It remains to show that each $\mathscr {F}^p_s$ is given by a holomorphic vector bundle. Let $r$ be the codimension of $Y\hookrightarrow X$. Let $N_Y$ be the normal bundle of $Y\hookrightarrow X$. Let $\pi : D = \mathbb {P}(N_Y) \rightarrow Y$ be the canonical projection. Let $(y_0,y_1,\ldots,y_{n-r},z_1,\ldots,z_{r-1}) \in \mathbb{C} ^n$ be local coordinates on a neighborhood of $x \in D$ such that:

• • $(y_1,\ldots,y_{n-r})$ are the coordinates on $Y$;

• • $(z_1,\ldots,z_{r-1})$ are the coordinates on the fiber of $\pi : D \rightarrow Y$;

• • $D \subseteq X'$ is given by the equation $y_0 = 0$.

Then the image of $\mathscr {O}_{X'}(f^*T^*X) \hookrightarrow \mathscr {O}_{X'}(T^*X')$ is generated by

(2.79)\begin{equation} dy_0 , dy_1 , \ldots , dy_{n-r} , y_0\,dz_1 , \ldots , y_0\,dz_{r-1} . \end{equation}

As a consequence, the image of $\mathscr {F}^p_s \hookrightarrow \mathscr {O}_{X'}(\Lambda ^p(T^*X'))$ is generated by

(2.80)\begin{equation} y_0^{\min\{s,|J|\}} \bigotimes_{i\in I}\, dy_i \otimes \bigotimes_{j\in J } \,dz_j \end{equation}

with $I \subseteq \{0,1,\ldots,n-r\}$ and $J \subseteq \{1,\ldots,r-1\}$ satisfying $|I|+|J|=p$. Each term in (2.80) yields a holomorphic line bundle. Hence, $\mathscr {F}^p_s$ is given by a holomorphic vector bundle, which we denote by $F^p_s$.

Let $TD \rightarrow \pi ^* TY$ be the derivative of $\pi$. Set

(2.81)\begin{equation} T^VD = \mathrm{Ker}(TD \rightarrow \pi^* TY) \subseteq TD \subseteq TX'|_D . \end{equation}

Set

(2.82)\begin{align} I^p_s = \big\{\alpha \in \Lambda^p(T^*X')|_D : \alpha (v_1,\ldots,v_p) = 0 \text{ for any } v_1,\ldots,v_{s+1}\in T^VD, v_{s+2},\ldots,v_p\in TX'|_D \} .\end{align}

We obtain a filtration of holomorphic vector bundles over $D$,

(2.83)\begin{equation} \Lambda^p(T^*X')|_D = I^p_p \supseteq I^p_{p-1} \supseteq \cdots \supseteq I^p_0 . \end{equation}

Let $N_D$ be the normal line bundle of $D\hookrightarrow X'$. From the calculation in local coordinates, we see that

(2.84)\begin{equation} \mathscr{G}^p_s = i_*\mathscr{O}_D\big(N_D^{-s} \otimes (I^p_p/I^{p}_s)\big) \quad \text{for } s=0,\ldots,p-1 . \end{equation}

For convenience, we denote

(2.85)\begin{equation} G^p_s = N_D^{-s} \otimes (I^p_p/I^{p}_s) . \end{equation}

Then we obtain a short exact sequence

(2.86)\begin{equation} 0 \rightarrow \mathscr{O}_{X'}(F^p_{s+1}) \rightarrow \mathscr{O}_{X'}(F^p_s) \rightarrow i_*\mathscr{O}_D(G^p_s) \rightarrow 0 . \end{equation}

Step 1. We show that

(2.87)\begin{equation} \begin{aligned} H^q(D,G^p_0) & = \bigoplus_{k=1}^{r-1} H^{k,k}(\mathbb{C}\mathrm{P}^{r-1}) \otimes H^{p-k,q-k}(Y) ,\\ H^q(D,G^p_s) & = 0 \quad \text{for } s = 1,\ldots,p-1 . \end{aligned} \end{equation}

Set

(2.88)\begin{align} J^p_s = \big\{\alpha \in \Lambda^p(T^*D) : \alpha (v_1,\ldots,v_p) = 0 \text{ for any } v_1,\ldots,v_{s+1}\in T^VD, v_{s+2},\ldots,v_p\in TD \big\} .\end{align}

Let $\phi : \Lambda ^p(T^*X')|_D \rightarrow \Lambda ^p(T^*D)$ be the canonical projection. By (2.82) and (2.88), we have

(2.89)\begin{equation} J^p_s = \phi(I^p_s) \subseteq \Lambda^p(T^*D) . \end{equation}

By (2.83) and (2.89), we have a filtration of holomorphic vector bundles over $D$,

(2.90)\begin{equation} \Lambda^p(T^*D) = J^p_p \supseteq J^p_{p-1} \supseteq \cdots \supseteq J^p_0 . \end{equation}

We also have

(2.91)\begin{equation} J^p_k/J^p_{k-1} = \pi^*\big(\Lambda^{p-k}(T^*Y)\big) \otimes \Lambda^k(T^{V,*}D) , \end{equation}

and a short exact sequence of holomorphic vector bundles over $D$,

(2.92)\begin{equation} 0 \rightarrow N_D^{-1} \otimes J^{p-1}_k \rightarrow I^p_k \rightarrow J^p_k \rightarrow 0 . \end{equation}

Combining (2.91) and (2.92), we obtain a short exact sequence,

(2.93)\begin{align} 0 & \rightarrow N_D^{-1}\otimes\pi^*\big(\Lambda^{p-k-1}(T^*Y)\big) \otimes \Lambda^k(T^{V,*}D) \rightarrow I^p_k/I^p_{k-1} \nonumber\\ & \rightarrow \pi^*\big(\Lambda^{p-k}(T^*Y)\big) \otimes \Lambda^k(T^{V,*}D) \rightarrow 0 . \end{align}

By (2.85) and (2.93), $G^p_s$ admits a filtration with factors

(2.94)\begin{equation} \big( N_D^{-s-\epsilon}\otimes\pi^*\big(\Lambda^{p-k-\epsilon}(T^*Y)\big) \otimes \Lambda^k(T^{V,*}D) \big)_{\epsilon = 0,1, k = s+1,\ldots,p} . \end{equation}

We remark that $\pi : D \rightarrow Y$ is a $\mathbb{C} \mathrm {P}^{r-1}$-bundle and the restriction of $N_D^{-1}$ to the fiber of $\pi : D \rightarrow Y$ is a holomorphic line bundle of degree one. Applying spectral sequence while using Lemma 2.5, we see that the cohomology of the holomorphic vector bundles in (2.94) vanishes unless $\epsilon = s = 0$. Hence, we obtain the second identity in (2.87). This argument also shows that

(2.95)\begin{equation} H^q(D,G^p_0) = H^q(D,I^p_p/I^p_0) = H^q(D,J^p_p/J^p_0) . \end{equation}

Using spectral sequence and (2.91), we obtain

(2.96)\begin{equation} H^q(D,J^p_k/J^p_{k-1}) = H^{k,k}(\mathbb{C}\mathrm{P}^{r-1}) \otimes H^{p-k,q-k}(Y). \end{equation}

On the other hand, it is classical that

(2.97)\begin{equation} H^q(D,J^p_p) = H^q\big(D,\Lambda^p(T^*D)\big) = \bigoplus_{k=0}^{r-1} H^{k,k}(\mathbb{C}\mathrm{P}^{r-1}) \otimes H^{p-k,q-k}(Y) . \end{equation}

From (2.95)–(2.97), we obtain the first identity in (2.87).

Set

(2.98)\begin{equation} \lambda(G^\bullet_0) = \bigotimes_{p=1}^n\big(\!\det H^\bullet(D,G^p_0)\big)^{(-1)^pp} ,\quad \lambda_\mathrm{tot}(G^\bullet_0) = \lambda(G^\bullet_0) \otimes \overline{\lambda(G^\bullet_0)} . \end{equation}

Recall that $\lambda _\mathrm {tot}(X)$ was defined in (1.119).

Step 2. We construct two canonical sections of

(2.99)\begin{equation} \big(\lambda_\mathrm{tot}(X)\big)^{-1} \otimes \lambda_\mathrm{tot}(X') \otimes \big(\lambda_\mathrm{tot}(G^\bullet_0)\big)^{-1} \end{equation}

and show that they coincide up to $\pm 1$.

Let

(2.100)\begin{equation} \mu_{p,s} \in \big(\!\det H^\bullet(X',F^p_{s+1}) \big)^{-1} \otimes \det H^\bullet(X',F^p_s) \otimes \big(\!\det H^\bullet(D,G^p_s)\big)^{-1} \end{equation}

be the canonical section induced by the long exact sequence induced by (2.86). Indeed, by (2.87), we have

(2.101)\begin{equation} \mu_{p,s} \in \big(\!\det H^\bullet(X',F^p_{s+1}) \big)^{-1} \otimes \det H^\bullet(X',F^p_s) \quad \text{for } s \neq 0 . \end{equation}

Set

(2.102)\begin{align} \mu_p &= \bigotimes_{s=0}^{p-1} \mu_{p,s} \in \big(\!\det H^\bullet(X',F^p_p) \big)^{-1} \otimes \det H^\bullet(X',F^p_0) \otimes \big(\!\det H^\bullet(D,G^p_0)\big)^{-1} \nonumber\\ & = \big(\!\det H^\bullet(X',f^*\Lambda^p(T^*X)) \big)^{-1} \otimes \det H^{p,\bullet}(X') \otimes \big(\!\det H^\bullet(D,G^p_0)\big)^{-1} . \end{align}

We remark that $f_*\mathscr {O}_{X'} = \mathscr {O}_X$ and $R^{>0}f_*\mathscr {O}_{X'} = 0$. Using spectral sequence, we obtain a canonical identification

(2.103)\begin{equation} H^{p,\bullet}(X) = H^\bullet\big(X',f^*\Lambda^p(T^*X)\big) . \end{equation}

Let

(2.104)\begin{equation} \nu_p \in \big(\!\det H^{p,\bullet}(X) \big)^{-1} \otimes \det H^\bullet\big(X',f^*\Lambda^p(T^*X)\big) \end{equation}

be the canonical section induced by (2.103).

By (2.102) and (2.104), we have

(2.105)\begin{equation} \mu_p \otimes \nu_p \in \big(\!\det H^{p,\bullet}(X) \big)^{-1} \otimes \det H^{p,\bullet}(X') \otimes \big(\!\det H^\bullet(D,G^p_0)\big)^{-1} . \end{equation}

By (1.119), (2.98) and (2.105), we have

(2.106)\begin{equation} \bigotimes_{p=1}^n (\mu_p \otimes \nu_p)^{(-1)^pp} \in \big(\lambda(X)\big)^{-1} \otimes \lambda(X') \otimes \big(\lambda(G^\bullet_0)\big)^{-1} , \end{equation}

and

(2.107) \begin{align} \bigotimes_{p=1}^n (\mu_p \otimes \nu_p)^{(-1)^pp} \otimes \overline{\bigotimes_{p=1}^n (\mu_p \otimes \nu_p)^{(-1)^pp}} \in \big(\lambda_\mathrm{tot}(X)\big)^{-1} \otimes \lambda_\mathrm{tot}(X') \otimes \big(\lambda_\mathrm{tot}(G^\bullet_0)\big)^{-1} . \end{align}

We have the Hodge decomposition

(2.108)\begin{equation} H^j_\mathrm{dR}(Y) = \bigoplus_{p+q=j} H^{p,q}(Y) . \end{equation}

Let $b_k$ be the $k$th Betti number of $Y$. By (2.87), (2.98) and (2.108), we have

(2.109)\begin{equation} \lambda_\mathrm{tot}(G^\bullet_0) = \bigotimes_{k=1}^{r-1} \bigotimes_{j=2k}^{2k+2n-2r} \Big( \big(\!\det H^{2k}_\mathrm{dR}(\mathbb{C}\mathrm{P}^{r-1})\big)^{b_{j-2k}} \otimes \det H^{j-2k}_\mathrm{dR}(Y) \Big)^{(-1)^jj} . \end{equation}

Let

(2.110)\begin{equation} \delta_j\in H^j_\mathrm{Sing}(\mathbb{C}\mathrm{P}^{r-1},\mathbb{Z}) \subseteq H^j_\mathrm{Sing}(\mathbb{C}\mathrm{P}^{r-1},\mathbb{C}) = H^j_\mathrm{dR}(\mathbb{C}\mathrm{P}^{r-1}) \end{equation}

be a generator of $H^j_\mathrm {Sing}(\mathbb{C} \mathrm {P}^{r-1},\mathbb {Z})$. Let

(2.111)\begin{equation} \tau_{j,1},\ldots,\tau_{j,b_j}\in \mathrm{Im}\big( H^j_\mathrm{Sing}(Y,\mathbb{Z}) \rightarrow H^j_\mathrm{Sing}(Y,\mathbb{R}) \big) \subseteq H^j_\mathrm{dR}(Y) \end{equation}

be a basis of the lattice. We denote $\tau _j = \tau _{j,1}\wedge \cdots \wedge \tau _{j,b_j} \in \det H^j_\mathrm {dR}(Y)$. Set

(2.112)\begin{equation} \sigma_{G^\bullet_0} = \bigotimes_{k=1}^{r-1} \bigotimes_{j=2k}^{2k+2n-2r} ( \delta_{2k}^{b_{j-2k}} \otimes \tau_{j-2k} )^{(-1)^jj} \in \lambda_\mathrm{tot}(G^\bullet_0) . \end{equation}

Let $\sigma _X \in \lambda _\mathrm {tot}(X)$ and $\sigma _{X'} \in \lambda _\mathrm {tot}(X')$ be as in (1.122). Obviously, we have

(2.113)\begin{equation} \sigma_X^{-1} \otimes \sigma_{X'} \otimes \sigma_{G^\bullet_0}^{-1} \in \big(\lambda_\mathrm{tot}(X)\big)^{-1} \otimes \lambda_\mathrm{tot}(X') \otimes \big(\lambda_\mathrm{tot}(G^\bullet_0)\big)^{-1} . \end{equation}

We have a canonical identification (cf. [Voi02, Théorème 7.31])

(2.114)\begin{equation} H^j_\mathrm{Sing}(X',\mathbb{Z}) = H^j_\mathrm{Sing}(X,\mathbb{Z}) \oplus \bigoplus_{k=1}^{r-1} H^{2k}_\mathrm{Sing}(\mathbb{C}\mathrm{P}^{r-1},\mathbb{Z}) \otimes H^{j-2k}_\mathrm{Sing}(Y,\mathbb{Z}) , \end{equation}

which induces an isomorphism of Hodge structures. Similarly to Step 2 in the proof of Theorem 2.3, using (2.114), we can show that

(2.115)\begin{equation} \bigotimes_{p=1}^n (\mu_p \otimes \nu_p)^{(-1)^pp} \otimes \overline{\bigotimes_{p=1}^n (\mu_p \otimes \nu_p)^{(-1)^pp}} = \pm \sigma_X^{-1} \otimes \sigma_{X'} \otimes \sigma_{G^\bullet_0}^{-1} . \end{equation}

Step 3. We introduce Quillen metrics.

Let $g^{TX}$ be the metric on $TX$ induced by $\omega$. Let $g^{\Lambda ^p(T^*X)}$ be the metric on $\Lambda ^p(T^*X)$ induced by $g^{TX}$. Let

(2.116)\begin{equation} \lVert\cdot\rVert_{\det H^{p,\bullet}(X)} \end{equation}

be the Quillen metric on $\det H^{p,\bullet }(X) = \det H^\bullet (X,\Lambda ^p(T^*X))$ associated with $g^{TX}$ and $g^{\Lambda ^p(T^*X)}$.

Let $g^{TX'}$ be the metric on $TX'$ induced by $\omega '$. Let $g^{\Lambda ^p(T^*X')}$ be the metric on $\Lambda ^p(T^*X')$ induced by $g^{TX'}$. Let

(2.117)\begin{equation} \lVert\cdot\rVert_{\det H^{p,\bullet}(X')} \end{equation}

be the Quillen metric on $\det H^{p,\bullet }(X') = \det H^\bullet (X',\Lambda ^p(T^*X'))$ associated with $g^{TX'}$ and $g^{\Lambda ^p(T^*X')}$.

Let

(2.118)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X',f^*\Lambda^p(T^*X))} \end{equation}

be the Quillen metric on $\det H^\bullet (X',f^*\Lambda ^p(T^*X))$ associated with $g^{TX'}$ and $f^*g^{\Lambda ^p(T^*X)}$.

Let $g^{TD}$ and $g^{N_D}$ be the metrics on $TD$ and $N_D$ induced by $g^{TX'}$. Let $g^{I^p_s}$ be the metric on $I^p_s$ induced by $g^{\Lambda ^p(T^*X')}$ via (2.83). Let $g^{G^p_s}$ be the metric on $G^p_s$ induced by $g^{N_D}$ and $g^{I^p_s}$ via (2.85). Let

(2.119)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(D,G^p_s)} \end{equation}

be the Quillen metric on $\det H^\bullet (D,G^p_s)$ associated with $g^{TD}$ and $g^{G^p_s}$. By the second identity in (2.87), we have a canonical identification $\det H^\bullet (D,G^p_s) = \mathbb{C}$ for $s\neq 0$. However, the metric (2.119) with $s\neq 0$ is not necessarily the standard metric on $\mathbb{C}$.

We remark that

(2.120)\begin{align} \Lambda^p(T^*X')|_{X'\backslash U'} & = F^p_s |_{X'\backslash U'} \nonumber\\ & = f^*\Lambda^p(T^*X)|_{X'\backslash U'} \quad \text{for } s=0,\ldots,p . \end{align}

We equip $F^p_s$ with Hermitian metric $g^{F^p_s}$ such that

(2.121) \begin{equation} \begin{gathered} g^{F^p_0} = g^{\Lambda^p(T^*X')} ,\quad g^{F^p_p} = f^*g^{\Lambda^p(T^*X)} ,\\ g^{F^p_{s+1}}|_{X'\backslash U'} = g^{F^p_s}|_{X'\backslash U'} \quad \text{for } s = 0,\ldots,p-1 . \end{gathered} \end{equation}

Our assumption (2.72) implies $g^{\Lambda ^p(T^*X')}|_{X'\backslash U'} = f^*(g^{\Lambda ^p(T^*X)}|_{X\backslash U})$, which guarantees the existence of $g^{F^p_s}$ satisfying (2.121). Let

(2.122)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X',F^p_s)} \end{equation}

be the Quillen metric on $\det H^\bullet (X',F^p_s)$ associated with $g^{TX'}$ and $g^{F^p_s}$. We remark that $H^\bullet (X',F^p_0) = H^{p,\bullet }(X')$ and

(2.123)\begin{equation} \lVert\cdot\rVert_{\det H^\bullet(X',F^p_0)} = \lVert\cdot\rVert_{\det H^{p,\bullet}(X')} . \end{equation}

Recall that $\mu _{p,s}$ was defined in (2.100). Let $\lVert \mu _{p,s}\rVert$ be the norm of $\mu _{p,s}$ with respect to the metrics (2.119) and (2.122).

Recall that $\nu _p$ was defined in (2.104). Let $\lVert \nu _p\rVert$ be the norm of $\nu _p$ with respect to the Quillen metrics (2.116) and (2.118).

Recall that $\sigma _{G^\bullet _0}$ was defined in (2.112). By (2.98) and the second identity in (2.87), we can and do view $\sigma _{G^\bullet _0}$ as the section of

(2.124)\begin{equation} \lambda_\mathrm{tot}(G^\bullet_\bullet) := \bigotimes_{p=1}^n \bigotimes_{s=0}^{p-1} \big(\!\det H^\bullet(D,G^p_s)\big)^{(-1)^pp} \otimes \overline{\bigotimes_{p=1}^n \bigotimes_{s=0}^{p-1} \big(\!\det H^\bullet(D,G^p_s)\big)^{(-1)^pp}} . \end{equation}

Let $\lVert \sigma _{G^\bullet _0}\rVert _{\lambda _\mathrm {tot}(G^\bullet _\bullet )}$ be the norm of $\sigma _{G^\bullet _0}\in \lambda _\mathrm {tot}(G^\bullet _\bullet )$ with respect to the metrics (2.119).

Let $\lVert \sigma _X\rVert _{\lambda _\mathrm {tot}(X)}$ be the norm of $\sigma _X$ with respect to the metrics (2.116). Let $\lVert \sigma _{X'}\rVert _{\lambda _\mathrm {tot}(X')}$ be the norm of $\sigma _{X'}$ with respect to the metrics (2.117). By (2.102) and (2.115), we have

(2.125)\begin{align} & \log \lVert\sigma_{X'}\rVert_{\lambda_\mathrm{tot}(X')} - \log \lVert\sigma_X\rVert_{\lambda_\mathrm{tot}(X)} - \log \lVert\sigma_{G^\bullet_0}\rVert_{\lambda_\mathrm{tot} (G^\bullet_\bullet)} \nonumber\\ &\quad = \sum_{p=1}^n (-1)^pp \bigg( \log \lVert\nu_p\rVert^2 + \sum_{s=0}^{p-1} \log \lVert\mu_{p,s}\rVert^2 \bigg) . \end{align}

By Definition 1.24 and (2.125), we have

(2.126) \begin{align} &\tau_\mathrm{BCOV}(X',\omega') - \tau_\mathrm{BCOV}(X,\omega)\nonumber\\ &\quad= \log \lVert\sigma_{G^\bullet_0}\rVert_{\lambda_\mathrm{tot}(G^\bullet_\bullet)} +\sum_{p=1}^n (-1)^pp \bigg( \log \lVert\nu_p\rVert^2 + \sum_{s=0}^{p-1} \log \lVert\mu_{p,s}\rVert^2 \bigg) . \end{align}

Step 4. We conclude.

For ease of notation, we denote

(2.127)\begin{equation} \alpha_{p,s} = \log \lVert\mu_{p,s}\rVert^2 . \end{equation}

Applying Theorem 1.19 to the short exact sequence (2.86) while using the second line in (2.121), we see that $\alpha _{p,s}$ is determined by $( U', \omega '|_{U'}, g^{F^p_s}|_{U'}, g^{F^p_{s+1}}|_{U'} )$. We denote

(2.128)\begin{equation} \alpha_p = \sum_{s=0}^{p-1} \alpha_{p,s} . \end{equation}

We remark that for $s = 1,\ldots,p-1$, the contributions of the metric $\lVert \cdot \rVert _{\det H^\bullet (X',F^p_s)}$ (see (2.122)) to $\alpha _{p,s-1}$ and $\alpha _{p,s}$ cancel with each other. Thus, $\alpha _p$ is independent of $(g^{F^p_s})_{s=1,\ldots,p-1}$. Hence, $\alpha _p$ is determined by $( U', \omega '|_{U'}, g^{F^p_0}|_{U'}, g^{F^p_p}|_{U'} )$. Now, applying the first line in (2.121), we see that $\alpha _p$ is determined by $(U, U', \omega |_U, \omega '|_{U'})$.

For ease of notation, we denote

(2.129)\begin{equation} \beta_p = \log \lVert\nu_p\rVert^2 , \end{equation}

Applying Theorem 1.21 with $E = \Lambda ^p(T^*X)$ while using (2.72), we see that $\beta _p$ is determined by $(U, U', \omega |_U, \omega '|_{U'})$.

By (2.126)–(2.129), we have

(2.130) \begin{align} \tau_\mathrm{BCOV}(X',\omega') - \tau_\mathrm{BCOV}(X,\omega) = \log \lVert\sigma_{G^\bullet_0}\rVert_{\lambda_\mathrm{tot}(G^\bullet_\bullet)} + \sum_{p=1}^n (-1)^pp ( \alpha_p + \beta_p).\end{align}

Here:

• • the section $\sigma _{G^\bullet _0}\in \lambda _\mathrm {tot}(G^\bullet _\bullet )$ is determined by $D\subseteq U'$ and its normal bundle;

• • the Quillen metric $\lVert \cdot \rVert _{\lambda _\mathrm {tot}(G^\bullet _\bullet )}$ is determined by $\omega '|_{U'}$;

• • the real number $\alpha _p$ is determined by $(U, U', \omega |_U, \omega '|_{U'})$;

• • the real number $\beta _p$ is determined by $(U, U', \omega |_U, \omega '|_{U'})$.

In conclusion, the right-hand side of (2.130) is determined by $(U, U', \omega |_U, \omega '|_{U'})$. This completes the proof.

Let $\pi : \mathscr {U} \rightarrow \mathbb{C}$ be a holomorphic submersion between complex manifolds. Let $\mathscr {Y} \subseteq \mathscr {U}$ be a closed complex submanifold. We assume that $\pi |_\mathscr {Y}: \mathscr {Y} \rightarrow \mathbb{C}$ is a holomorphic submersion with compact fiber. For $z\in \mathbb{C}$, we denote $U_z = \pi ^{-1}(z)$ and $Y_z = U_z \cap \mathscr {Y}$. Assume that for any $z\in \mathbb{C}$, $U_z$ can be extended to a compact Kähler manifold. More precisely, there exist a compact Kähler manifold $X_z$ and a holomorphic embedding $i_z: U_z \hookrightarrow X_z$ whose image is open. Here $\{ X_z : z\in \mathbb{C} \}$ is just a set of complex manifolds parameterized by $\mathbb{C}$. The topology of $X_z$ may vary as $z$ varies. We identify $U_z$ with $i_z(U_z)\subseteq X_z$. Let $f_z: X_z' \rightarrow X_z$ be the blow-up along $Y_z$. Set $U_z' = f_z^{-1}(U_z) \subseteq X_z'$. Let

(2.131)\begin{equation} \big(\omega_z\in\Omega^{1,1}(X_z)\big)_{z\in \mathbb{C}} ,\quad \big(\omega_z'\in\Omega^{1,1}(X_z')\big)_{z\in \mathbb{C}} \end{equation}

be Kähler forms. We assume that $(\omega _z|_{U_z})_{z\in \mathbb{C} }$ and $(\omega _z'|_{U_z'})_{z\in \mathbb{C} }$ are smooth families. We further assume that

(2.132)\begin{equation} \omega_z'|_{X_z'\backslash U_z'} = f_z^*(\omega_z|_{X_z\backslash U_z}) \quad \text{for } z\in \mathbb{C}. \end{equation}

Theorem 2.7 The function $z \mapsto \tau _\mathrm {BCOV}(X_z',\omega _z') - \tau _\mathrm {BCOV}(X_z,\omega _z)$ is continuous.

Proof. We proceed in the same way as in the proof of Theorem 2.6. Each object constructed becomes a function of $z\in \mathbb{C}$. In particular, the identity (2.130) becomes

(2.133) \begin{align} \tau_\mathrm{BCOV}(X_z',\omega_z') - \tau_\mathrm{BCOV}(X_z,\omega_z) = \log \lVert\sigma_{G^\bullet_0}\rVert_{\lambda_\mathrm{tot}(G^\bullet_\bullet),z} + \sum_{p=1}^n (-1)^pp ( \alpha_{p,z} + \beta_{p,z} ). \end{align}

From Remarks 1.20 and 1.22 and the last paragraph in the proof of Theorem 2.6, we see that each term on the right-hand side of (2.133) is a continuous function of $z$. This completes the proof.

3. BCOV invariant

3.1 Several meromorphic sections

Let $X$ be a compact complex manifold. Let $K_X$ be the canonical line bundle of $X$. Let $d$ be a non-zero integer. Let $K_X^d$ be the $d$th tensor power of $K_X$. We assume that there is an invertible element $\gamma \in \mathscr {M}(X,K_X^d)$. We denote

(3.1)\begin{equation} \mathrm{div}(\gamma) = D = \sum_{j=1}^l m_j D_j , \end{equation}

where $m_j\in \mathbb {Z}\backslash \{0\}$, $D_1,\ldots,D_l \subseteq X$ are mutually distinct and irreducible. We assume that $D$ is of simple normal crossing support (see Definition 1.2).

For $J\subseteq \{1,\ldots,l\}$, let $D_J \subseteq X$ be as in (0.9). For $j\in J\subseteq \{1,\ldots,l\}$, let $L_{J,j}$ be the normal line bundle of $D_J \hookrightarrow D_{J\backslash \{j\}}$. Set

(3.2)\begin{equation} K_J = K_X^d|_{D_J} \otimes \bigotimes_{j\in J} L_{J,j}^{-m_j} = K_{D_J}^d \otimes \bigotimes_{j\in J} L_{J,j}^{-m_j-d} , \end{equation}

which is a holomorphic line bundle over $D_J$. In particular, we have $K_\emptyset = K_X^d$.

Recall that $\mathrm {Res}_\cdot (\cdot )$ was defined in Definition 1.4. By (1.9), there exist

(3.3)\begin{equation} \big(\gamma_J \in \mathscr{M}(D_J,K_J)\big)_{J \subseteq\{1,\ldots,l\}} \end{equation}

such that

(3.4)\begin{equation} \gamma_\emptyset = \gamma ,\quad \gamma_J = \mathrm{Res}_{D_J}(\gamma_{J\backslash\{j\}}) \quad \text{for } j\in J\subseteq\{1,\ldots,l\} . \end{equation}

By (1.8), we have

(3.5)\begin{equation} \mathrm{div}(\gamma_J) = \sum_{j\notin J} m_j D_{J\cup\{j\}} . \end{equation}

3.2 Construction of BCOV invariant

We use the notation from § 3.1. We further assume that $X$ is Kähler and $m_j\neq -d$ for $j=1,\ldots,l$. Then $(X,\gamma )$ is a $d$-Calabi–Yau pair (see Definition 0.2).

Let $\omega$ be a Kähler form on $X$. Let $|\cdot |_{K_{D_J},\omega }$ be the metric on $K_{D_J}$ induced by $\omega$. Let $|\cdot |_{L_{J,j},\omega }$ be the metric on $L_{J,j}$ induced by $\omega$. Let $|\cdot |_{K_J,\omega }$ be the metric on $K_J$ induced by $|\cdot |_{K_{D_J},\omega }$ and $|\cdot |_{L_{J,j},\omega }$ via (3.2).

We use the notation from (1.23). For $J\subseteq \{1,\ldots,l\}$, let $|J|$ be the number of elements in $J$, let $g^{TD_J}_\omega$ be the metric on $TD_J$ induced by $\omega$, let $c_k(TD_J,g^{TD_J}_\omega ) \in Q^{D_J}$ be $k$th Chern form of $(TD_J,g^{TD_J}_\omega )$. Let $n = \dim X$. Set

(3.6)\begin{equation} a_J(\gamma,\omega) = \frac{1}{12} \int_{D_J} c_{n-|J|}\big(TD_J,g^{TD_J}_\omega\big) \log |\gamma_J|^{2/d}_{K_J,\omega} . \end{equation}

We consider the short exact sequence of holomorphic vector bundles over $D_J$,

(3.7)\begin{equation} 0 \rightarrow TD_J \rightarrow TD_{J\backslash\{j\}}|_{D_J} \rightarrow L_{J,j} \rightarrow 0 . \end{equation}

Let

(3.8)\begin{equation} \tilde{c}\Big(TD_J,TD_{J\backslash\{j\}}|_{D_J}, g^{TD_{J\backslash\{j\}}}_\omega|_{D_J}\Big) \in Q^{D_J}/Q^{D_J,0} \end{equation}

be the Bott–Chern form (1.30) with $0\rightarrow E' \rightarrow E \rightarrow E''$ replaced by (3.7) and $g^E$ replaced by $g^{TD_{J\backslash \{j\}}}_\omega |_{D_J}$. Set

(3.9)\begin{equation} b_{J,j}(\omega) = \frac{1}{12} \int_{D_J} \tilde{c}\Big(TD_J,TD_{J\backslash\{j\}}|_{D_J}, g^{TD_{J\backslash\{j\}}}_\omega|_{D_J}\Big). \end{equation}

Let $w_d^J$ be as in (0.9). Recall that $\tau _\mathrm {BCOV}(\cdot,\cdot )$ was defined in Definition 1.24. For ease of notation, we denote $\tau _\mathrm {BCOV}(D_J,\omega ) = \tau _\mathrm {BCOV}(D_J,\omega |_{D_J})$. We define

(3.10)\begin{equation} \tau_d(X,\gamma,\omega) = \sum_{J \subseteq\{1,\ldots,l\}} w_d^J \bigg( \tau_\mathrm{BCOV}(D_J,\omega) - a_J(\gamma,\omega) - \sum_{j\in J} \frac{m_j+d}{d} b_{J,j}(\omega) \bigg) . \end{equation}

Theorem 3.1 The real number $\tau _d(X,\gamma,\omega )$ is independent of $\omega$.

Proof. Let $(\omega _s)_{s\in \mathbb{C} \mathrm {P}^1}$ be a smooth family of Kähler forms on $X$ parameterized by $\mathbb{C} \mathrm {P}^1$. It is sufficient to show that $\tau _d(X,\gamma,\omega _s)$ is independent of $s$.

We view the terms involved in (3.10) as smooth functions on $\mathbb{C} \mathrm {P}^1$, i.e.

(3.11)\begin{equation} \begin{aligned} & \tau_d(X,\gamma,\omega): s \mapsto \tau_d(X,\gamma,\omega_s) ,\\ & \tau_\mathrm{BCOV}(D_J,\omega): s \mapsto \tau_\mathrm{BCOV} (D_J,\omega_s) ,\quad \text{etc} . \end{aligned} \end{equation}

We view $TD_J$ and $L_{J,j}$ as holomorphic vector bundles over $D_J \times \mathbb{C} \mathrm {P}^1$. Let $g^{TD_J}_\omega$ and $g^{L_{J,j}}_\omega$ be metrics on $TD_J$ and $L_{J,j}$ induced by $(\omega _s)_{s\in \mathbb{C} \mathrm {P}^1}$. More precisely, the restrictions $g^{TD_J}_\omega |_{D_J\times \{s\}}$ and $g^{L_{J,j}}_\omega |_{D_J\times \{s\}}$ are induced by $\omega _s$. By [Zha22, Theorem 1.6], we have

(3.12)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \tau_\mathrm{BCOV}(D_J,\omega) = \frac{1}{12} \int_{D_J} c_{n-|J|}(TD_J,g^{TD_J}_\omega) c_1(TD_J,g^{TD_J}_\omega). \end{equation}

Similarly to [Zha22, (2.9)], by the Poincaré–Lelong formula, (3.2), (3.5) and (3.6), we have

(3.13)\begin{align} \frac{\bar{\partial}\partial}{2\pi i} a_J(\gamma,\omega) & = \frac{1}{12d} \int_{D_J} c_{n-|J|}(TD_J,g^{TD_J}_\omega) \big( - c_1(K_J,|\cdot|_{K_J,\omega}) + \delta_{\mathrm{div}(\gamma_J)} \big) \nonumber\\ & = \frac{1}{12} \int_{D_J} c_{n-|J|}(TD_J,g^{TD_J}_\omega) c_1(TD_J,g^{TD_J}_\omega) \nonumber\\ &\quad +\sum_{j\in J} \frac{m_j+d}{12d} \int_{D_J} c_{n-|J|}(TD_J,g^{TD_J}_\omega) c_1(L_{J,j},|\cdot|_{L_{J,j},\omega}) \nonumber\\ &\quad + \sum_{j\notin J} \frac{m_j}{12d} \int_{D_{J\cup\{j\}}} c_{n-|J|}(TD_J,g^{TD_J}_\omega) . \end{align}

Similarly to [Zha22, (2.10)], by (1.29), (1.30) and (3.9), we have

(3.14)\begin{align} \frac{\bar{\partial}\partial}{2\pi i} b_{J,j}(\omega) & = \frac{1}{12} \int_{D_J} c_{n-|J|+1}\Big(TD_{J\backslash\{j\}}, g^{TD_{J\backslash\{j\}}}_\omega\Big)\nonumber\\ & \quad - \frac{1}{12} \int_{D_J} c_{n-|J|}\big(TD_J,g^{TD_J}_\omega\big)c_1 \big(L_{J,j},g^{L_{J,j}}_\omega\big). \end{align}

By (3.12)–(3.14), we have

(3.15) \begin{align} & \frac{\bar{\partial}\partial}{2\pi i} \bigg( \tau_\mathrm{BCOV}(D_J,\omega) - a_J(\gamma,\omega) - \sum_{k\in J} \frac{m_j+d}{d} b_{J,j}(\omega) \bigg) \nonumber\\ & \quad = - \sum_{j\in J} \frac{m_j+d}{12d} \int_{D_J} c_{n-|J|+1}\Big(TD_{J\backslash\{j\}}, g^{TD_{J\backslash\{j\}}}_\omega\Big) - \sum_{j\notin J} \frac{m_j}{12d} \int_{D_{J\cup\{j\}}} c_{n-|J|}\big(TD_J,g^{TD_J}_\omega\big) . \end{align}

From (0.9), (3.10) and (3.15), we obtain $\bar {\partial }\partial \tau _d(X,\gamma,\omega ) = 0$. Hence, $s\mapsto \tau _d(X,\gamma,\omega _s)$ is constant on $\mathbb{C} \mathrm {P}^1$. This completes the proof.

Definition 3.2 The BCOV invariant of $(X,\gamma )$ is defined by

(3.16)\begin{equation} \tau_d(X,\gamma) = \tau_d(X,\gamma,\omega) . \end{equation}

By Theorem 3.1, $\tau _d(X,\gamma )$ is well-defined.

Proposition 3.3 For a non-zero integer $r$, let $\gamma ^r\in \mathscr {M}(X,K_X^{rd})$ be the $r$th tensor power of $\gamma$. Then $(X,\gamma ^r)$ is a $rd$-Calabi–Yau pair and

(3.17)\begin{equation} \tau_{rd}(X,\gamma^r) = \tau_d(X,\gamma) . \end{equation}

Proof. Once we replace $\gamma$ by $\gamma ^r$, each $\gamma _J$ is replaced by $\gamma _J^r$. We can directly verify that

(3.18)\begin{equation} \tau_{rd}(X,\gamma^r,\omega) = \tau_d(X,\gamma,\omega) . \end{equation}

From Definition 3.2 and (3.18), we obtain (3.17). This completes the proof.

Recall that $\chi _d(\cdot,\cdot )$ was defined in Definition 1.3.

Proposition 3.4 For $z\in \mathbb{C} ^*$, we have

(3.19)\begin{equation} \tau_d(X,z\gamma) = \tau_d(X,\gamma) - \frac{\chi_d(X,D)}{12}\log|z|^{2/d} . \end{equation}

Proof. Once we replace $\gamma$ by $z\gamma$, each $\gamma _J$ is replaced by $z\gamma _J$. By (3.6), we have

(3.20)\begin{equation} a_J(z\gamma,\omega) - a_J(\gamma,\omega) = \frac{\chi(D_J)}{12} \log |z|^{2/d} . \end{equation}

By Definition 1.3, (3.10) and (3.20), we have

(3.21)\begin{equation} \tau_d(X,z\gamma,\omega) - \tau_d(X,\gamma,\omega) = - \frac{\chi_d(X,D)}{12} \log |z|^{2/d} . \end{equation}

From Definition 3.2 and (3.21), we obtain (3.19). This completes the proof.

Proof of Theorem 0.4 As $\pi : \mathscr {X} \rightarrow S$ is locally Kähler, for any $s_0\in S$, there exist an open subset $s_0\in U \subseteq S$ and a Kähler form $\omega$ on $\pi ^{-1}(U)$. For $s\in U$, we denote $\omega _s = \omega |_{X_s}$. Similarly to the proof of Theorem 3.1, we view the terms involved in (3.10) as smooth functions on $U$.

Though the fibration $\pi ^{-1}(U) \rightarrow U$ is not necessarily trivial, the identities (3.13) and (3.14) still hold. On the other hand, by [Zha22, Theorem 1.6], we have

(3.22)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \tau_\mathrm{BCOV}(D_J,\omega) = \omega_{H^\bullet(D_J)} + \frac{1}{12} \int_{D_J} c_{n-|J|}\big(TD_J,g^{TD_J}_\omega\big) c_1\big(TD_J,g^{TD_J}_\omega\big) . \end{equation}

By (0.9), (3.10), (3.13), (3.14) and (3.22), we have

(3.23)\begin{equation} \frac{\bar{\partial}\partial}{2\pi i} \tau_d(X,\gamma,\omega)\bigg|_U = \sum_{J\subseteq\{1,\ldots,l\}} w_d^J \omega_{H^\bullet(D_J)} . \end{equation}

From Definition 3.2 and (3.23), we obtain (0.15). This completes the proof.

3.3 BCOV invariant of projective bundle

Let $Y$ be a compact Kähler manifold. Let $N$ be a holomorphic vector bundle of rank $r\geqslant 2$ over $Y$. Let $\mathbb {1}$ be the trivial line bundle over $Y$. Set

(3.24)\begin{equation} X = \mathbb{P}(N\oplus\mathbb{1}) . \end{equation}

Let $\pi : X \rightarrow Y$ be the canonical projection.

Let $q\in \{0,\ldots,r\}$. Let $(L_k)_{k=1,\ldots,q}$ be holomorphic line bundles over $Y$. We assume that there is a surjection between holomorphic vector bundles

(3.25)\begin{equation} N \rightarrow L_1 \oplus \cdots \oplus L_q . \end{equation}

Let $N^*$ be the dual of $N$. Taking the dual of (3.25), we obtain

(3.26)\begin{equation} L_1^{-1} \oplus \cdots \oplus L_q^{-1} \hookrightarrow N^* . \end{equation}

Let $d,m_1,\ldots,m_q$ be positive integers. Let

(3.27)\begin{equation} \gamma_Y \in \mathscr{M}\big(Y,(K_Y\otimes \det N^*)^d \otimes L_1^{-m_1} \otimes \cdots \otimes L_q^{-m_q}\big) \end{equation}

be an invertible element. We assume that

• • $\mathrm {div}(\gamma _Y)$ is of simple normal crossing support;

• • $\mathrm {div}(\gamma _Y)$ does not possess component of multiplicity $-d$.

Denote $m = m_1+\cdots +m_q$. Let $S^mN^*$ be the $m$th symmetric tensor power of $N^*$. By (3.26) and (3.27), we have

(3.28)\begin{equation} \gamma_Y \in \mathscr{M}\big(Y,(K_Y\otimes \det N^*)^d \otimes S^m N^*\big) . \end{equation}

Let $\mathcal {N}$ be the total space of $N$. We have

(3.29)\begin{equation} X = \mathcal{N} \cup \mathbb{P}(N) ,\quad K_X|_\mathcal{N} = \pi^* ( K_Y\otimes \det N^* ) . \end{equation}

We may view a section of $S^mN^*$ as a function on $\mathcal {N}$. By (3.28) and (3.29), $\gamma _Y$ may be viewed as an element of $\mathscr {M}(\mathcal {N},K_X^d)$. Let

(3.30)\begin{equation} \gamma_X\in\mathscr{M}(X,K_X^d) \end{equation}

be such that $\gamma _X|_\mathcal {N} = \gamma _Y$.

For $j = 1,\ldots,q$, let $N\rightarrow L_j$ be the composition of the map (3.25) and the canonical projection $L_1 \oplus \cdots \oplus L_q \rightarrow L_j$. Set

(3.31)\begin{equation} N_j = \mathrm{Ker}(N\rightarrow L_j) ,\quad X_j = \mathbb{P}(N_j\oplus\mathbb{1}) \subseteq X ,\quad X_\infty = \mathbb{P}(N) \subseteq X . \end{equation}

We denote

(3.32)\begin{equation} \mathrm{div}(\gamma_Y) = \sum_{j=q+1}^l m_j Y_j , \end{equation}

where $Y_j\subseteq Y$ are mutually distinct and irreducible. For $j=q+1,\ldots,l$, set

(3.33)\begin{equation} X_j = \pi^{-1}(Y_j) \subseteq X . \end{equation}

Denote

(3.34)\begin{equation} m_\infty = - m_1 - \cdots - m_q - rd - d . \end{equation}

Note that:

• • $X$ is locally the product of an open subset of $Y$ and $\mathbb{C} \mathrm {P}^r$;

• • $\gamma _X$ is locally the product of a $d$-canonical section on an open subset of $Y$ and $\gamma _{r,m_1,\ldots,m_q}$ defined in (0.20);

we have

(3.35)\begin{equation} \mathrm{div}(\gamma_X) = \pi^* \mathrm{div}(\gamma_Y) + m_\infty X_\infty + \sum_{j=1}^q m_j X_j = m_\infty X_\infty + \sum_{j=1}^l m_j X_j , \end{equation}

which is of simple normal crossing support. Hence, $(X,\gamma _X)$ is a $d$-Calabi–Yau pair.

For $y\in Y$, we denote $Z_y = \pi ^{-1}(y)$. Let $K_{Y,y}$ be the fiber of $K_Y$ at $y\in Y$. We have

(3.36)\begin{equation} K_X|_{Z_y} = K_{Z_y} \otimes \pi^* K_{Y,y} . \end{equation}

For $y\in Y \backslash \bigcup _{j=q+1}^l Y_j$, there exist $\gamma _{Z_y}\in \mathscr {M}(Z_y,K_{Z_y}^d)$ and $\eta _y\in K_{Y,y}^d$ such that

(3.37)\begin{equation} \gamma_X|_{Z_y} = \gamma_{Z_y} \otimes \pi^* \eta_y . \end{equation}

Then $(Z_y,\gamma _{Z_y})$ is a $d$-Calabi–Yau pair, which is independent of $y$ up to isomorphism. We may omit the index $y$ as long as there is no confusion. We remark that $(Z,\gamma _Z)$ is isomorphic to $(\mathbb{C} \mathrm {P}^r,\gamma _{r,m_1,\ldots,m_q})$ constructed in the paragraph containing (0.20).

Recall that $\chi _d(\cdot,\cdot )$ was defined in Definition 1.3.

Lemma 3.5 The following identity holds:

(3.38)\begin{equation} \chi_d(Z,\gamma_Z) = 0 . \end{equation}

Proof. Set

(3.39)\begin{equation} f(t) = t^{r-q} \prod_{j \in \{1,\ldots,q,\infty\}} \bigg( t - \frac{m_j}{m_j+d} \bigg) . \end{equation}

For $J \subseteq \{1,\ldots,q,\infty \}$, let $w_d^J$ be as in (0.9). By (1.3), (1.4) and the fact that $\chi (\mathbb{C} \mathrm {P}^k) = k+1$, we have

(3.40)\begin{equation} \chi_d(Z,\gamma_Z) = \sum_{J \subseteq \{1,\ldots,q,\infty\}} w_d^J (r+1-|J|) = f'(1) . \end{equation}

On the other hand, we have

(3.41)\begin{align} \frac{f'(1)}{f(1)} & = r - q + \sum_{j \in \{1,\ldots,q,\infty\}} \bigg( 1 - \frac{m_j}{m_j+d} \bigg)^{-1} \nonumber\\ & = \frac{m_1 + \cdots + m_q + m_\infty}{d} + r + 1 . \end{align}

From (3.34), (3.40) and (3.41), we obtain (3.38). This completes the proof.

Theorem 3.6 The following identity holds:

(3.42)\begin{equation} \tau_d(X,\gamma_X) = \chi_d(Y,\gamma_Y) \tau_d(Z,\gamma_Z) . \end{equation}

Proof. The proof consists of several steps.

Step 0. We introduce several pieces of notation.

We denote $A = \{q+1,\ldots,l\}$ and $B = \{1,\ldots,q,\infty \}$. For $I\subseteq A$ and $J\subseteq B$, set

(3.43) \begin{equation} \begin{gathered} Y_I = Y \cap \bigcap_{j\in I} Y_j ,\quad X_{I,J} = X \cap \bigcap_{j\in I \cup J} X_j ,\\ X_I = X_{I,\emptyset} ,\quad X_J = X_{\emptyset,J} . \end{gathered} \end{equation}

For $y\in Y$ and $J\subseteq B$, set

(3.44)\begin{equation} Z_{J,y} = Z_y \cap X_J . \end{equation}

Note that $Z_{J,y}$ is independent of $y$ up to isomorphism, we may omit the index $y$ as long as there is no confusion. We remark that $\pi |_{X_{I,J}}: X_{I,J} \rightarrow Y_I$ is a fibration with fiber $Z_J$.

Let $\omega _X$ be a Kähler form on $X$ such that Lemma 2.2 holds. Let $\omega _Y$ be a Kähler form on $Y$. For $\varepsilon >0$, set

(3.45)\begin{equation} \omega_\varepsilon = \omega_X + \frac{1}{\varepsilon}\pi^*\omega_Y . \end{equation}

For $I\subseteq A$, $J\subseteq B$ and $j \in (A \cup B) \backslash (I \cup J)$, let $a_{I,J}(\gamma _X,\omega _\varepsilon )$ and $b_{I,J,j}(\omega _\varepsilon )$ be as in (3.6) and (3.9) with $(X,\gamma,\omega )$ replaced by $(X,\gamma _X,\omega _\varepsilon )$ and $J$ replaced by $I \cup J$. Let $w_d^I$ be as in (0.9) with $J$ replaced by $I$. By Definition 3.2, (0.9) and (3.10), we have

(3.46)\begin{align} \tau_d(X,\gamma_X) & = \sum_{I\subseteq A} \sum_{J\subseteq B} w_d^I w_d^J \tau_\mathrm{BCOV}(X_{I,J},\omega_\varepsilon) \nonumber\\ & \quad - \sum_{I\subseteq A} \sum_{J\subseteq B} w_d^I w_d^J a_{I,J}(\gamma_X,\omega_\varepsilon) \nonumber\\ & \quad - \sum_{I\subseteq A} \sum_{J\subseteq B} \sum_{j\in I \cup J} w_d^I w_d^J \frac{m_j+d}{d} b_{I,J,j}(\omega_\varepsilon) . \end{align}

Step 1. We estimate $\tau _\mathrm {BCOV}(X_{I,J},\omega _\varepsilon )$.

For $y\in Y$, we denote $\omega _{Z_y} = \omega _X|_{Z_y}$. As $\omega _X$ satisfies Lemma 2.2, for any $J\subseteq B$, $(Z_{J,y},\omega _{Z_y}|_{Z_{J,y}})_{y\in Y}$ are mutually isometric. We may omit the index $y$ as long as there is no confusion. For ease of notation, we denote

(3.47)\begin{equation} \tau_\mathrm{BCOV}(Y_I,\omega_Y) = \tau_\mathrm{BCOV}(Y_I,\omega_Y|_{Y_I}) ,\quad \tau_\mathrm{BCOV}(Z_J,\omega_Z) = \tau_\mathrm{BCOV}(Z_J,\omega_Z|_{Z_J}) . \end{equation}

For $I\subseteq A$ and $J\subseteq B$, by Theorem 2.3, as $\varepsilon \rightarrow 0$,

(3.48)\begin{align} & \tau_\mathrm{BCOV}(X_{I,J},\omega_\varepsilon) - \frac{\chi(Z_J)}{12} \big( \dim(Y_I)\chi(Y_I) + c_1c_{\dim(Y_I)-1}(Y_I) \big) \log \varepsilon \nonumber\\ & \quad \rightarrow \chi(Z_J) \tau_\mathrm{BCOV}(Y_I,\omega_Y) + \chi(Y_I) \tau_\mathrm{BCOV}(Z_J,\omega_Z) . \end{align}

On the other hand, by Lemma 3.5, (1.3) and (1.4), we have

(3.49)\begin{equation} \sum_{I\subseteq A} w_d^I \chi(Y_I) = \chi_d(Y,\gamma_Y) ,\quad \sum_{J\subseteq B} w_d^J \chi(Z_J) = 0 . \end{equation}

By (3.48) and (3.49), as $\varepsilon \rightarrow 0$,

(3.50) \begin{align} \sum_{I\subseteq A} \sum_{J\subseteq B} w_d^I w_d^J \tau_\mathrm{BCOV}(X_{I,J},\omega_\varepsilon)\rightarrow \chi_d(Y,\gamma_Y) \sum_{J\subseteq B} w_d^J \tau_\mathrm{BCOV}(Z_J,\omega_Z). \end{align}

Step 2. We estimate $a_{I,J}(\gamma _X,\omega _\varepsilon )$.

For $I\subseteq A$ and $J\subseteq B$, let $K_{I,J}$ be as in (3.2) with $(X,\gamma )$ replaced by $(X,\gamma _X)$ and $J$ replaced by $I\cup J$. Then $K_{I,J}$ is a holomorphic line bundle over $X_{I,J}$. Let

(3.51)\begin{equation} \gamma_{I,J} \in \mathscr{M}(X_{I,J},K_{I,J}) \end{equation}

be as in (3.4) with $(X,\gamma )$ replaced by $(X,\gamma _X)$ and $J$ replaced by $I\cup J$.

Let $U\subseteq Y$ be a small open subset. Set $\mathcal {U} = \pi ^{-1}(U)$. Recall that $\gamma _Z \in \mathscr {M}(Z,K_Z^d)$ was constructed in the paragraph containing (3.36). We fix an identification $\mathcal {U} = U \times Z$ such that there exists $\eta \in \mathscr {M}(U,K_Y^d)$ satisfying

(3.52)\begin{equation} \gamma_X|_\mathcal{U} = \mathrm{pr}_1^*\eta \otimes \mathrm{pr}_2^*\gamma_Z , \end{equation}

where $\mathrm {pr}_1: U \times Z \rightarrow U$ and $\mathrm {pr}_2: U \times Z \rightarrow Z$ are canonical projections.

For $I\subseteq A$, let $K_I$ be as in (3.2) with $(X,\gamma )$ replaced by $(U,\eta )$. Then $K_I$ is a holomorphic line bundle over $U \cap Y_I$. Let

(3.53)\begin{equation} \eta_I \in \mathscr{M}(U \cap Y_I,K_I) \end{equation}

be as in (3.4) with $(X,\gamma )$ replaced by $(U,\eta )$. For $J\subseteq B$, let $K_J$ be as in (3.2) with $(X,\gamma )$ replaced by $(Z,\gamma _Z)$. Then $K_J$ is a holomorphic line bundle over $Z_J$. Let

(3.54)\begin{equation} \gamma_J \in \mathscr{M}(Z_J,K_J) \end{equation}

be as in (3.4) with $(X,\gamma )$ replaced by $(Z,\gamma _Z)$. By the constructions of $K_{I,J}$ and $\gamma _{I,J}$ in the paragraph containing (3.51), we have

(3.55)\begin{equation} K_{I,J}|_{\mathcal{U}\cap X_{I,J}} = \mathrm{pr}_1^* K_I \otimes \mathrm{pr}_2^* K_J ,\quad \gamma_{I,J}|_{\mathcal{U}\cap X_{I,J}} = \mathrm{pr}_1^*\eta_I \otimes \mathrm{pr}_2^*\gamma_J . \end{equation}

For $I\subseteq A$ and $J\subseteq B$, let $g^{TX_{I,J}}_\varepsilon$ (respectively, $g^{TY_I}$, $g^{TZ_J}$) be the metric on $TX_{I,J}$ (respectively, $TY_I$, $TZ_J$) induced by $\omega _\varepsilon$ (respectively, $\omega _Y$, $\omega _Z$), let $|\cdot |_{K_{I,J},\varepsilon }$ (respectively, $|\cdot |_{K_I}$, $|\cdot |_{K_J}$) be the norm on $K_{I,J}$ (respectively, $K_I$, $K_J$) induced by $\omega _\varepsilon$ (respectively, $\omega _Y$, $\omega _Z$) in the same way as in the paragraph above (3.6). We denote

(3.56)\begin{equation} a_{I,J}(\mathcal{U},\gamma_X,\omega_\varepsilon) = \frac{1}{12} \int_{\mathcal{U}\cap X_{I,J}} c(TX,g^{TX}_{\varepsilon}) \log |\gamma_{I,J}|_{K_{I,J},\varepsilon}^{2/d} . \end{equation}

Recall that $\omega _\varepsilon$ was defined in (3.45). As $g^{TX_{I,J}}_\varepsilon$ is induced by $\omega _\varepsilon$, by Proposition 1.7, as $\varepsilon \rightarrow 0$.

(3.57)\begin{equation} c\big(TX_{I,J},g^{TX_{I,J}}_\varepsilon\big) \rightarrow c\big(TZ_J,g^{TZ_J}\big)\pi^*c(TY_I,g^{TY_I}) . \end{equation}

Recall that $\eta _I$, $\gamma _J$ and $\gamma _{I,J}$ are linked by (3.55). As $|\cdot |_{K_{I,J},\varepsilon }$ is induced by $\omega _\varepsilon$, as $\varepsilon \rightarrow 0$,

(3.58) \begin{align} \log |\gamma_{I,J}|_{K_{I,J},\varepsilon}^2 - \bigg(\dim(Y)d + \sum_{j\in I} m_j \bigg) \log\varepsilon \rightarrow \log |\gamma_J|_{K_J}^2 + \log |\eta_I|_{K_I}^2. \end{align}

Let $a_J(\gamma _Z,\omega _Z)$ be as in (3.6) with $(X,\gamma,\omega )$ replaced by $(Z,\gamma _Z,\omega _Z)$. More precisely,

(3.59)\begin{equation} a_J(\gamma_Z,\omega_Z) = \frac{1}{12} \int_{Z_J} c\big(TZ_J,g^{TZ_J}\big) \log|\gamma_Z|_{K_J}^{2/d} . \end{equation}

By (3.56)–(3.59), as $\varepsilon \rightarrow 0$,

(3.60)\begin{align} & a_{I,J}(\mathcal{U},\gamma_X,\omega_\varepsilon) - \frac{\chi(Z_J)}{12} \bigg(\dim(Y) + \frac{1}{d}\sum_{j\in I} m_j \bigg) \log\varepsilon \int_{U\cap Y_I} c(TY_I,g^{TY_I}) \nonumber\\ &\quad \rightarrow \frac{\chi(Z_J)}{12} \int_{U\cap Y_I} c(TY_I,g^{TY_I}) \log|\eta_I|_{K_I}^{2/d} + a_J(\gamma_Z,\omega_Z) \int_{U\cap Y_I} c(TY_I,g^{TY_I}) . \end{align}

By (3.49) and (3.60), as $\varepsilon \rightarrow 0$,

(3.61) \begin{align} \sum_{I\subseteq A} \sum_{J\subseteq B} w_d^I w_d^J a_{I,J}(\mathcal{U},\gamma_X,\omega_\varepsilon) \rightarrow \sum_{J\subseteq B} w_d^J a_J(\gamma_Z,\omega_Z) \sum_{I\subseteq A} w_d^I \int_{U\cap Y_I} c(TY_I,g^{TY_I}) . \end{align}

The left-hand side of (3.61) yields a measure on $X$,

(3.62)\begin{equation} \mu_\varepsilon : \mathcal{U} \mapsto \sum_{I\subseteq A} \sum_{J\subseteq B} w_d^I w_d^J a_{I,J}(\mathcal{U},\gamma_X,\omega_\varepsilon) , \end{equation}

The right-hand side of (3.61) yields a measure on $Y$,

(3.63)\begin{equation} \nu : U \mapsto \sum_{J\subseteq B} w_d^J a_J(\gamma_Z,\omega_Z) \sum_{I\subseteq A} w_d^I \int_{U\cap Y_I} c(TY_I,g^{TY_I}) . \end{equation}

The convergence in (3.61) is equivalent to the following: as $\varepsilon \rightarrow 0$,

(3.64)\begin{equation} \pi_*\mu_\varepsilon \rightarrow \nu . \end{equation}

By (3.49) and (3.62)–(3.64), as $\varepsilon \rightarrow 0$,

(3.65) \begin{align} \sum_{I\subseteq A} \sum_{J\subseteq B} w_d^I w_d^J a_{I,J}(\gamma_X,\omega_\varepsilon) = \mu_\varepsilon(X) \rightarrow \nu(Y) = \chi_d(Y,\gamma_Y) \sum_{J\subseteq B} w_d^J a_J(\gamma_Z,\omega_Z). \end{align}

Step 3. We estimate $b_{I,J,j}(\omega _\varepsilon )$.

First we consider the case $j\in I$. We denote $I'=I\backslash \{j\}$. By (3.9), we have

(3.66)\begin{equation} b_{I,J,j}(\omega_\varepsilon) = \frac{1}{12} \int_{X_{I,J}} \tilde{c}\Big(TX_{I,J},TX_{I',J}|_{X_{I,J}}, g^{TX_{I',J}}_\varepsilon|_{X_{I,J}}\Big). \end{equation}

By Proposition 1.9, as $\varepsilon \rightarrow 0$,

(3.67) \begin{align} \tilde{c}\Big(TX_{I,J},TX_{I',J}|_{X_{I,J}}, g^{TX_{I',J}}_\varepsilon|_{X_{I,J}}\Big)\rightarrow c\big(TZ_J,g^{TZ_J}\big) \pi^*\tilde{c}\Big(TY_I,TY_{I'}|_{Y_I},g^{TY_{I'}}|_{Y_I}\Big) . \end{align}

By (3.66) and (3.67), as $\varepsilon \rightarrow 0$,

(3.68)\begin{equation} b_{I,J,j}(\omega_\varepsilon) \rightarrow \frac{\chi(Z_J) }{12} \int_{Y_I} \tilde{c}\Big(TY_I,TY_{I'}|_{Y_I},g^{TY_{I'}}|_{Y_I}\Big) . \end{equation}

By (3.49) and (3.68), as $\varepsilon \rightarrow 0$,

(3.69)\begin{equation} \sum_{I\subseteq A} \sum_{J\subseteq B} \sum_{j\in I} w_d^I w_d^J \frac{m_j+d}{d} b_{I,J,j}(\omega_\varepsilon) \rightarrow 0 . \end{equation}

Now we consider the case $j\in J$. We denote $J'=J\backslash \{j\}$. By (3.9), we have

(3.70)\begin{equation} b_{I,J,j}(\omega_\varepsilon) = \frac{1}{12} \int_{X_{I,J}} \tilde{c}\Big(TX_{I,J},TX_{I,J'}|_{X_{I,J}}, g^{TX_{I,J'}}_\varepsilon|_{X_{I,J}}\Big). \end{equation}

By Proposition 1.9, as $\varepsilon \rightarrow 0$,

(3.71) \begin{align} \tilde{c}\Big(TX_{I,J},TX_{I,J'}|_{X_{I,J}}, g^{TX_{I,J'}}_\varepsilon|_{X_{I,J}}\Big) \rightarrow \tilde{c}\Big(TZ_J,TZ_{J'}|_{Z_J}, g^{TZ_{J'}}|_{Z_J}\Big) \pi^*c (TY_I,g^{TY_I}) . \end{align}

Let $b_{J,j}(\omega _Z)$ be as in (3.9) with $(X,\gamma,\omega )$ replaced by $(Z,\gamma _Z,\omega _Z)$. More precisely,

(3.72)\begin{equation} b_{J,j}(\omega_Z) = \frac{1}{12} \int_{Z_J} \tilde{c}\Big(TZ_J,TZ_{J'}|_{Z_J},g^{TZ_{J'}}|_{Z_J}\Big) . \end{equation}

By (3.70)–(3.72), as $\varepsilon \rightarrow 0$,

(3.73)\begin{equation} b_{I,J,j}(\omega_\varepsilon) \rightarrow \chi(Y_I) b_{J,j}(\omega_Z) . \end{equation}

By (3.49) and (3.73), as $\varepsilon \rightarrow 0$,

(3.74) \begin{align} \sum_{I\subseteq A} \sum_{J\subseteq B} \sum_{j\in J} w_d^I w_d^J \frac{m_j+d}{d} b_{I,J,j}(\omega_\varepsilon) \rightarrow \chi_d(Y,\gamma_Y) \sum_{J\subseteq B} \sum_{j\in J} w_d^J \frac{m_j+d}{d} b_{J,j}(\omega_Z) . \end{align}

Step 4. We conclude.

Taking $\varepsilon \rightarrow 0$ on the right-hand side of (3.46) and applying (3.50), (3.65), (3.69) and (3.74), we obtain

(3.75)\begin{equation} \tau_d(X,\gamma_X) = \chi_d(Y,\gamma_Y) \sum_{J\subseteq B} w_d^J \bigg( \tau_\mathrm{BCOV}(Z_J,\omega_Z) - a_J(\gamma_Z,\omega_Z) - \sum_{j\in J} \frac{m_j+d}{d} b_{J,j}(\omega_Z) \bigg) .\end{equation}

On the other hand, by Definition 3.2 and (3.10), we have

(3.76)\begin{equation} \tau(Z,\gamma_Z) = \sum_{J\subseteq B} w_d^J \bigg( \tau_\mathrm{BCOV}(Z_J,\omega_Z) - a_J(\gamma_Z,\omega_Z) - \sum_{j\in J} \frac{m_j+d}{d} b_{J,j}(\omega_Z) \bigg) . \end{equation}

From (3.75) and (3.76), we obtain (3.42). This completes the proof.

3.4 Proof of Theorem 0.5

Now we are ready to prove Theorem 0.5.

Proof of Theorem 0.5 The proof consists of several steps.

Step 1. Following [BFM75, § 1.5], we introduce a deformation to the normal cone.

Let $\mathscr {X} \rightarrow X\times \mathbb{C}$ be the blow-up along $Y \times \{0\}$. Let $\Pi : \mathscr {X} \rightarrow \mathbb{C}$ be the composition of the canonical projections $\mathscr {X} \rightarrow X\times \mathbb{C}$ and $X\times \mathbb{C} \rightarrow \mathbb{C}$. For $z\in \mathbb{C} ^*$, we denote

(3.77)\begin{equation} X_z = \Pi^{-1}(z) . \end{equation}

Let $\mathbb {1}$ be the trivial line bundle over $Y$. Recall that $N_Y$ is the normal bundle of $Y \hookrightarrow X$. Recall that $X'$ is the blow-up of $X$ along $Y$. The variety $\Pi ^{-1}(0)$ consists of two irreducible components: $\Pi ^{-1}(0) = \Sigma _1 \cup \Sigma _2$ with $\Sigma _1 \simeq \mathbb {P}(N_Y\oplus \mathbb {1})$ and $\Sigma _2 \simeq X'$. We denote

(3.78)\begin{equation} X_0 = \Sigma_1 . \end{equation}

For $j=1,\ldots, l$, let $\mathscr {D}_j\subseteq \mathscr {X}$ be the closure of $D_j\times \mathbb{C} ^*\subseteq \mathscr {X}$. For $z\in \mathbb{C}$, we denote

(3.79)\begin{equation} D_{j,z} = \mathscr{D}_j \cap X_z . \end{equation}

Let $\mathscr {Y}\subseteq \mathscr {X}$ be the closure of $Y\times \mathbb{C} ^*\subseteq \mathscr {X}$. For $z\in \mathbb{C}$, we denote

(3.80)\begin{equation} Y_z = \mathscr{Y} \cap X_z . \end{equation}

See Figure 1.

Figure 1. Deformation to the normal cone.

Let $g^{TX}$ be a Hermitian metric on $TX$. Let $d(\cdot,\cdot ): X \times X \rightarrow \mathbb {R}$ be the geodesic distance associated with $g^{TX}$. For $x\in X$, we denote

(3.81)\begin{equation} d_Y(x) = \inf_{y\in Y} d(x,y) . \end{equation}

For $z\in \mathbb{C} ^*$, set

(3.82)\begin{equation} U_z =\{ x \in X : d_Y(x)<|z| \} \times \{z\} \subseteq X_z . \end{equation}

We identify the fiber of $\mathbb {1}$ with $\mathbb{C}$. For $v\in N_Y$ and $s\in \mathbb{C}$ such that $(v,s)\neq (0,0)$, we denote by $[v:s]$ the image of $(v,s)$ in $\mathbb {P}(N_Y\oplus \mathbb {1})$. Let $|\cdot |$ be the norm on $N_Y$ induced by $g^{TX}$. Set

(3.83)\begin{equation} U_0 =\{ [v:s] \in \mathbb{P}(N_Y\oplus\mathbb{1}) : |v|<|s| \}\subseteq X_0 . \end{equation}

For $\varepsilon >0$ small enough, we have smooth families

(3.84)\begin{equation} (U_z)_{|z|<\varepsilon} ,\quad (Y_z)_{|z|<\varepsilon} ,\quad (U_z\cap D_{j,z})_{|z|<\varepsilon} \quad \text{with } j=1,\ldots,l . \end{equation}

We remark that $Y_z \subseteq U_z$ for $z\in \mathbb{C}$.

Let $\mathscr {F}: \mathscr {X}' \rightarrow \mathscr {X}$ be the blow-up along $\mathscr {Y}$. For $z\in \mathbb{C}$, we denote

(3.85)\begin{equation} X_z' = \mathscr{F}^{-1}(X_z) . \end{equation}

Set

(3.86)\begin{equation} f_z = \mathscr{F}|_{X_z'} : X_z' \rightarrow X_z , \end{equation}

which is the blow-up along $Y_z$. For $z\in \mathbb{C}$, set

(3.87)\begin{equation} D_{0,z}' = f_z^{-1}(Y_z) \subseteq X_z' . \end{equation}

For $z\in \mathbb{C}$ and $j=1,\ldots,l$, let $D_{j,z}' \subseteq X_z'$ be the strict transformation of $D_{j,z}\subseteq X_z$.

For $z\in \mathbb{C}$, set

(3.88)\begin{equation} U_z' = f_z^{-1}(U_z) . \end{equation}

For $\varepsilon >0$ small enough, we have smooth families

(3.89)\begin{equation} (U_z')_{|z|<\varepsilon} ,\quad (U_z'\cap D_{j,z}')_{|z|<\varepsilon} \quad \text{with } j=0,\ldots,l . \end{equation}

We remark that $D_{0,z}' \subseteq U_z'$ for $z\in \mathbb{C}$.

Step 2. We introduce a family of meromorphic pluricanonical sections.

Denote

(3.90)\begin{equation} m = m_1 + \cdots + m_q , \end{equation}

which is the vanishing order of $\gamma$ on $Y$. Recall that $r$ is the codimension of $Y\hookrightarrow X$. Recall that $\gamma \in \mathscr {M}(X,K_X^d)$. For $z\neq 0$, we identify $X_z$ with $X$ in the obvious way. For $z\neq 0$, set

(3.91)\begin{equation} \gamma_z = z^{-m-rd} \gamma \in \mathscr{M}(X_z,K_{X_z}^d) . \end{equation}

There is a unique $\gamma _0 \in \mathscr {M}(X_0,K_{X_0}^d)$ such that for $\varepsilon >0$ small enough,

(3.92)\begin{equation} (\gamma_z|_{U_z})_{|z|<\varepsilon} \end{equation}

is a smooth family. Now we briefly explain the existence of $\gamma _0$. We take a holomorphic local chart

(3.93)\begin{equation} \varphi: \mathbb{C}^n \supseteq V \rightarrow X \end{equation}

such that:

• • $0\in V$ and $\varphi (0) \in Y$;

• • $\varphi ^{-1}(Y) = \{(z_1,\ldots,z_n)\in V : z_1 = \cdots = z_r = 0 \}$;

• • $\varphi ^*\gamma = \theta (z_1,\ldots,z_n) z_1^{m_1}\cdots z_q^{m_q} (dz_1\wedge \cdots \wedge dz_n)^d$, where $\theta$ is a holomorphic function on $V$ such that $\theta (0,\ldots,0,z_{r+1},\ldots,z_n) \neq 0$ for generic $z_{r+1},\ldots,z_n$.

For $z\neq 0$, let $\varphi _z: V \rightarrow X_z$ be the composition of $\varphi : V \rightarrow X$ and the identification $X = X_z$. We take a holomorphic local chart

(3.94)\begin{equation} \phi: \mathbb{C}^n \times \{z\in\mathbb{C} : |z|<\varepsilon \} \supseteq W \rightarrow \mathscr{X} \end{equation}

such that for $0<|z|<\varepsilon$:

• • $\phi (z_1,\ldots,z_n,z) \in \varphi _z(V) \subseteq X_z$;

• • $\varphi _z^{-1}(\phi (z_1,\ldots,z_n,z)) = (zz_1,\ldots,zz_r,z_{r+1},\ldots,z_n)$.

Then a direct calculation yields

(3.95) \begin{align} z^{-m-rd} \phi^*\gamma & = \theta(zz_1,\ldots,zz_r,z_{r+1},\ldots,z_n) z_1^{m_1}\cdots z_q^{m_q} (dz_1\wedge\cdots\wedge dz_n)^d \nonumber\\ & \rightarrow \theta(0,\ldots,0,z_{r+1},\ldots,z_n) z_1^{m_1}\cdots z_q^{m_q} (dz_1\wedge\cdots\wedge dz_n)^d \end{align}

as $z \rightarrow 0$. Moreover, the calculation above shows that the hypothesis in § 3.3 holds with $(X,\gamma _X)$ replaced by $(X_0,\gamma _0)$. In particular, $(X_0,\gamma _0)$ is a $d$-Calabi–Yau pair.

Step 3. We introduce a family of Kähler forms.

Let $\mathscr {U} \subseteq \mathscr {X}$ be such that $\mathscr {U} \cap X_z = U_z$ for any $z\in \mathbb{C}$. Then $\mathscr {U}$ is an open subset of $\mathscr {X}$. Set $\mathscr {U}' = \mathscr {F}^{-1}(\mathscr {U}) \subseteq \mathscr {X}'$. We have $\mathscr {U}' \cap X_z' = U_z'$ for any $z\in \mathbb{C}$.

Let $\omega$ be a Kähler form on $\mathscr {X}$. Let $\omega '$ be a Kähler form on $\mathscr {X}'$ such that

(3.96)\begin{equation} \omega'|_{\mathscr{X}'\backslash\mathscr{U}'} = \mathscr{F}^* ( \omega|_{\mathscr{X}\backslash\mathscr{U}} ) . \end{equation}

For $z\in \mathbb{C}$, set

(3.97)\begin{equation} \omega_z = \omega|_{X_z} ,\quad \omega_z' = \omega'|_{X_z'} . \end{equation}

By (3.86), (3.96) and (3.97), we have

(3.98)\begin{equation} \omega_z'|_{X_z'\backslash U_z'} = f_z^*(\omega_z|_{X_z\backslash U_z}) \quad \text{for } z\in \mathbb{C} . \end{equation}

For $\varepsilon >0$ small enough, we have smooth families

(3.99)\begin{equation} (\omega_z|_{U_z})_{|z|<\varepsilon} ,\quad (\omega_z'|_{U_z'})_{|z|<\varepsilon} . \end{equation}

Step 4. We show that the function $z \mapsto \tau _d(X_z',f_z^*\gamma _z) - \tau _d(X_z,\gamma _z)$ is continuous at $z=0$.

Denote

(3.100)\begin{equation} m_0 = m_1 + \cdots + m_q + (r-1)d . \end{equation}

For $z\in \mathbb{C}$, by (3.79), (3.86), (3.87) and (3.92), we have

(3.101)\begin{equation} \mathrm{div}(\gamma_z) = \sum_{j=1}^l m_j D_{j,z} ,\quad \mathrm{div}(f_z^*\gamma_z) = \sum_{j=0}^l m_j D_{j,z}' . \end{equation}

Here $D_{j,0}$ and $D_{j,0}'$ may be empty for certain $j$. Let $(D_{J,z})_{J\subseteq \{1,\ldots,l\}}$ be as in (0.9) with $X$ replaced by $X_z$ and $D_j$ replaced by $D_{j,z}$. Let $(D_{J,z}')_{J\subseteq \{0,\ldots,l\}}$ be as in (0.9) with $X$ replaced by $X_z'$ and $D_j$ replaced by $D_{j,z}'$. By Definition 3.2 and (3.10), we have

(3.102) \begin{align} &\tau_d(X_z',f_z^*\gamma_z) - \tau_d(X_z,\gamma_z)\nonumber\\ & \quad = \sum_{0\in J\subseteq\{0,\ldots,l\}} w_d^J \bigg( \tau_\mathrm{BCOV}(D_{J,z}',\omega_z') - a_J(f_z^*\gamma_z,\omega_z') - \sum_{j\in J}\frac{m_j+d}{d} b_{J,j}(\omega_z') \bigg) \nonumber\\ & \qquad - \sum_{J\subseteq\{1,\ldots,l\}} w_d^J \big( a_J(f_z^*\gamma_z,\omega_z') - a_J(\gamma_z,\omega_z) \big) \nonumber\\ & \qquad - \sum_{J\subseteq\{1,\ldots,l\}} \sum_{j\in J} w_d^J \frac{m_j+d}{d} \big( b_{J,j}(\omega_z') - b_{J,j}(\omega_z) \big) \nonumber\\ & \qquad + \sum_{J\subseteq\{1,\ldots,l\}} w_d^J \big( \tau_\mathrm{BCOV}(D_{J,z}',\omega_z') - \tau_\mathrm{BCOV}(D_{J,z},\omega_z) \big). \end{align}

For $0\in J\subseteq \{0,\ldots,l\}$, we have $D_{J,z}' \subseteq U_z'$. Thus,

(3.103)\begin{equation} (D_{J,z}')_{z\in\mathbb{C}} \end{equation}

is a smooth family. Hence, the first summation in (3.102) is continuous at $z=0$.

For $J\subseteq \{1,\ldots,l\}$, we denote

(3.104)\begin{equation} D_{J,z} = D_{J,z}^\mathrm{in} \sqcup D_{J,z}^\mathrm{ex} \end{equation}

such that each irreducible component of $D_{J,z}^\mathrm {in}$ (respectively, $D_{J,z}^\mathrm {ex}$) lies in (respectively, does not lie in) $Y_z$. As $D_{J,z}^\mathrm {in} \subseteq Y_z \subseteq U_z$, the family

(3.105)\begin{equation} (D_{J,z}^\mathrm{in})_{z\in\mathbb{C}} \end{equation}

is smooth. On the other hand, we have

(3.106)\begin{equation} D_{J,z}^\mathrm{ex} = f_z(D_{J,z}'). \end{equation}

Moreover, the map $f_z|_{D_{J,z}'}: D_{J,z}' \rightarrow D_{J,z}^\mathrm {ex}$ is the blow-up along $D_{J,z}^\mathrm {ex} \cap Y_z$.

Recall that

(3.107)\begin{equation} K_J ,\quad \gamma_J ,\quad g^{TD_J}_\omega ,\quad |\cdot|_{K_J,\omega} \end{equation}

were constructed in §§ 3.1 and 3.2 for a $d$-Calabi–Yau pair $(X,\gamma )$ together with a Kähler form $\omega$ on $X$. Let

(3.108)\begin{equation} K_{J,z} ,\quad \gamma_{J,z} ,\quad g^{TD_{J,z}}_{\omega_z} ,\quad |\cdot|_{K_{J,z},\omega_z} \end{equation}

be as in (3.107) with $(X,\gamma )$ replaced by $(X_z,\gamma _z)$ and $\omega$ replaced by $\omega _z$. Let

(3.109)\begin{equation} K_{J,z}' ,\quad \gamma_{J,z}' ,\quad g^{TD_{J,z}'}_{\omega_z'} ,\quad |\cdot|_{K_{J,z}',\omega_z'} \end{equation}

be as in (3.107) with $(X,\gamma )$ replaced by $(X_z',f_z^*\gamma _z)$ and $\omega$ replaced by $\omega _z'$. By (3.6), (3.98), (3.104) and (3.106), for $J\subseteq \{1,\ldots,l\}$, we have

(3.110)\begin{align} a_J(f_z^*\gamma_z,\omega_z') - a_J(\gamma_z,\omega_z) & = \frac{1}{12} \int_{D_{J,z}' \cap U_z'} c_{n-|J|}\Big(TD_{J,z}',g^{TD_{J,z}'}_{\omega_z'}\Big) \log |\gamma_{J,z}'|^{2/d}_{K_{J,z}',\omega_z'} \nonumber\\ & \quad - \frac{1}{12} \int_{D_{J,z}^\mathrm{ex} \cap U_z } c_{n-|J|}\Big(TD_{J,z},g^{TD_{J,z}}_{\omega_z}\Big) \log |\gamma_{J,z}|^{2/d}_{K_{J,z},\omega_z} \nonumber\\ & \quad - \frac{1}{12} \int_{D_{J,z}^\mathrm{in}} c_{n-|J|}\Big(TD_{J,z},g^{TD_{J,z}}_{\omega_z}\Big) \log |\gamma_{J,z}|^{2/d}_{K_{J,z},\omega_z} . \end{align}

By (3.89), each integration in (3.110) depends continuously on $z$. Thus, the second summation in (3.102) is continuous at $z=0$. The same argument shows that the third summation in (3.102) is continuous at $z=0$.

By (3.104), we have the obvious identity

(3.111)\begin{align} & \tau_\mathrm{BCOV}(D_{J,z}',\omega_z') - \tau_\mathrm{BCOV}(D_{J,z},\omega_z) \nonumber\\ &\quad = \tau_\mathrm{BCOV}(D_{J,z}',\omega_z') - \tau_\mathrm{BCOV}(D_{J,z}^\mathrm{ex},\omega_z) - \tau_\mathrm{BCOV}(D_{J,z}^\mathrm{in},\omega_z). \end{align}

As the families in (3.99) are smooth, by Theorem 2.7 and (3.98), the function $z\mapsto \tau _\mathrm {BCOV}(D_{J,z}',\omega _z') - \tau _\mathrm {BCOV}(D_{J,z}^\mathrm {ex},\omega _z)$ is continuous at $z=0$. As the families in (3.99) and (3.105) are smooth, the function $z\mapsto \tau _\mathrm {BCOV}(D_{J,z}^\mathrm {in},\omega _z)$ is continuous at $z=0$. Hence, the fourth summation in (3.102) is continuous at $z=0$.

Step 5. We conclude.

By Step 4, we have

(3.112)\begin{equation} \lim_{z\rightarrow 0} \big( \tau(X_z',f_z^*\gamma_z) - \tau(X_z,\gamma_z) \big) = \tau(X_0',f_0^*\gamma_0)-\tau(X_0,\gamma_0) . \end{equation}

On the other hand, by Proposition 3.4 and (3.91), for $z\neq 0$, we have

(3.113)\begin{equation} \begin{aligned} \tau_d(X_z,\gamma_z) & = \tau_d(X,\gamma) - \frac{\chi_d(X,\gamma)}{12} \log|z|^{-2(m+rd)/d} ,\\ \tau_d(X_z',f_z^*\gamma_z) & = \tau(X',f^*\gamma) - \frac{\chi_d(X',f^*\gamma)}{12} \log|z|^{-2(m+rd)/d} . \end{aligned} \end{equation}

Note that $(m+rd)/d>0$, by (3.112) and (3.113), we have

(3.114)\begin{equation} \begin{aligned} \chi_d(X',f^*\gamma) - \chi_d(X,\gamma) & = 0 ,\\ \tau_d(X',f^*\gamma) - \tau_d(X,\gamma) & = \tau_d(X_0',f_0^*\gamma_0) - \tau_d(X_0,\gamma_0) . \end{aligned} \end{equation}

Note that $X_0$ is a $\mathbb{C} \mathrm {P}^r$-bundle over $Y_0 \simeq Y$, by Theorem 3.6, we have

(3.115)\begin{equation} \tau_d(X_0,\gamma_0) = \chi_d(Y,D_Y) \tau_d\big(\mathbb{C}\mathrm{P}^r,\gamma_{r,m_1,\ldots,m_q}\big) . \end{equation}

Recall that $E = f^{-1}(Y)$. Note that $X_0'$ is a $\mathbb{C} \mathrm {P}^1$-bundle over $D_{0,0}' \simeq E$, by Theorem 3.6, we have

(3.116)\begin{equation} \tau_d(X_0',f_0^*\gamma_0) = \chi_d(E,D_E) \tau_d\big(\mathbb{C}\mathrm{P}^1,\gamma_{1,m_0}\big) . \end{equation}

From (3.114)–(3.116), we obtain (0.22). This completes the proof.