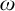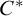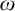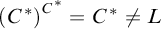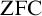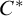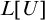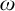1 Introduction
The model
![]() $C^{*}$
, introduced by Kennedy, Magidor, and Väänänen in [Reference Kennedy, Magidor and Väänänen5], is the model of sets constructible using the logic
$C^{*}$
, introduced by Kennedy, Magidor, and Väänänen in [Reference Kennedy, Magidor and Väänänen5], is the model of sets constructible using the logic
![]() $\mathcal {L}(Q_{\omega }^{\mathrm {cf}})$
—first order logic augmented with the “cofinality
$\mathcal {L}(Q_{\omega }^{\mathrm {cf}})$
—first order logic augmented with the “cofinality
![]() $\omega $
” quantifier. To be precise, for a regular cardinal
$\omega $
” quantifier. To be precise, for a regular cardinal
![]() $\kappa $
we define a logic
$\kappa $
we define a logic
![]() $\mathcal {L}(Q_{\kappa }^{\mathrm {cf}})$
where we add to the syntax of first order logic a quantifier
$\mathcal {L}(Q_{\kappa }^{\mathrm {cf}})$
where we add to the syntax of first order logic a quantifier
![]() $Q_{\kappa }^{\mathrm {cf}}$
whose semantics are given by
$Q_{\kappa }^{\mathrm {cf}}$
whose semantics are given by
 $$\begin{align*}\mathcal{M}\vDash Q_{\kappa}^{\mathrm{cf}}xy\varphi\left(x,y,\bar{b}\right)\iff\underset{{\textstyle \text{is a linear order of cofinality } \kappa}.}{\left\{ \left(c,d\right)\in M^{2}\mid\mathcal{M}\vDash\varphi\left(c,d,\bar{b}\right)\right\} } \end{align*}$$
$$\begin{align*}\mathcal{M}\vDash Q_{\kappa}^{\mathrm{cf}}xy\varphi\left(x,y,\bar{b}\right)\iff\underset{{\textstyle \text{is a linear order of cofinality } \kappa}.}{\left\{ \left(c,d\right)\in M^{2}\mid\mathcal{M}\vDash\varphi\left(c,d,\bar{b}\right)\right\} } \end{align*}$$
This logic, first introduced by Shelah [Reference Shelah10], is a proper extension of first order logic, which is fully compact. Using this logic we construct inner models of set theory, akin to Gödel’s constructible universe L:
Definition 1.1.
![]() $C_{\kappa }^{*}$
, the class of
$C_{\kappa }^{*}$
, the class of
![]() $\mathcal {L}(Q_{\kappa }^{\mathrm {cf}})$
-constructible sets, is defined by induction:
$\mathcal {L}(Q_{\kappa }^{\mathrm {cf}})$
-constructible sets, is defined by induction:
 $$ \begin{align*} L^{\prime}_{0} & =\varnothing,\\ L^{\prime}_{\alpha+1} & =\operatorname{Def}_{\mathcal{L}(Q_{\kappa}^{\mathrm{cf}})}\left(L^{\prime}_{\alpha}\right),\\ L_{\beta}' & =\bigcup_{\alpha<\beta}L_{\alpha}'\,\,\,\text{for limit } \beta,\\ C_{\kappa}^{*} & =\bigcup_{\alpha\in \mathbf{Ord}}L^{\prime}_{\alpha}, \end{align*} $$
$$ \begin{align*} L^{\prime}_{0} & =\varnothing,\\ L^{\prime}_{\alpha+1} & =\operatorname{Def}_{\mathcal{L}(Q_{\kappa}^{\mathrm{cf}})}\left(L^{\prime}_{\alpha}\right),\\ L_{\beta}' & =\bigcup_{\alpha<\beta}L_{\alpha}'\,\,\,\text{for limit } \beta,\\ C_{\kappa}^{*} & =\bigcup_{\alpha\in \mathbf{Ord}}L^{\prime}_{\alpha}, \end{align*} $$
where for any logic
![]() $\mathcal {L}$
extending first-order logic and a set M,
$\mathcal {L}$
extending first-order logic and a set M,
We focus on the case
![]() $\kappa =\omega $
and denote
$\kappa =\omega $
and denote
![]() $C^{*}:=C_{\omega }^{*}$
. As shown in [Reference Kennedy, Magidor and Väänänen5],
$C^{*}:=C_{\omega }^{*}$
. As shown in [Reference Kennedy, Magidor and Väänänen5],
![]() $C^{*}$
is a model of
$C^{*}$
is a model of
![]() $\mathrm {ZFC}$
, and in fact it is the same as
$\mathrm {ZFC}$
, and in fact it is the same as
![]() $L[\mathbf {Ord}_{\omega }]$
where
$L[\mathbf {Ord}_{\omega }]$
where
![]() $\mathbf {Ord}_{\omega }=\{\alpha \in \mathbf { Ord}\mid \mathrm {cf}\left (\alpha \right )=\omega \}$
. Like in the case of L, one can phrase the formula “
$\mathbf {Ord}_{\omega }=\{\alpha \in \mathbf { Ord}\mid \mathrm {cf}\left (\alpha \right )=\omega \}$
. Like in the case of L, one can phrase the formula “
![]() $V=C^{*}$
”, i.e.,
$V=C^{*}$
”, i.e.,
![]() $\forall x\exists \alpha (x\in L^{\prime }_{\alpha })$
where
$\forall x\exists \alpha (x\in L^{\prime }_{\alpha })$
where
![]() $L^{\prime }_{\alpha }$
is the
$L^{\prime }_{\alpha }$
is the
![]() $\alpha $
th level in the construction of
$\alpha $
th level in the construction of
![]() $C^{*}$
. Unlike L, however, it is not always true that
$C^{*}$
. Unlike L, however, it is not always true that
![]() $C^{*}\vDash V=C^{*}$
, which is equivalent to the question whether
$C^{*}\vDash V=C^{*}$
, which is equivalent to the question whether
![]() $\left (C^{*}\right )^{C^{*}}=C^{*}$
. This is clearly the case if
$\left (C^{*}\right )^{C^{*}}=C^{*}$
. This is clearly the case if
![]() $V=L$
, so the interesting question is whether this can hold with
$V=L$
, so the interesting question is whether this can hold with
![]() $C^{*}\ne L$
. In Section 2 we show that this is consistent relative to the consistency of
$C^{*}\ne L$
. In Section 2 we show that this is consistent relative to the consistency of
![]() $\mathrm {ZFC}$
. Next we investigate the possibilities of
$\mathrm {ZFC}$
. Next we investigate the possibilities of
![]() $C^{*}\nvDash V=C^{*}$
. In such a case, it makes sense to define recursively the iterated
$C^{*}\nvDash V=C^{*}$
. In such a case, it makes sense to define recursively the iterated
![]() $C^{*}$
s:
$C^{*}$
s:
 $$ \begin{align*} C^{*0} & =V,\\ C^{*\left(\alpha+1\right)} & =\left(C^{*}\right)^{C^{*\alpha}}\,\text{ for any } \alpha,\\ C^{*\alpha} & =\bigcap_{\beta<\alpha}C^{*\beta}\,\,\text{ for limit } \alpha. \end{align*} $$
$$ \begin{align*} C^{*0} & =V,\\ C^{*\left(\alpha+1\right)} & =\left(C^{*}\right)^{C^{*\alpha}}\,\text{ for any } \alpha,\\ C^{*\alpha} & =\bigcap_{\beta<\alpha}C^{*\beta}\,\,\text{ for limit } \alpha. \end{align*} $$
This type of construction was first investigated by McAloon [Reference McAloon8] regarding
![]() $\mathrm {HOD}$
, the class of hereditarily ordinal definable sets, where he showed that it is equiconsistent with
$\mathrm {HOD}$
, the class of hereditarily ordinal definable sets, where he showed that it is equiconsistent with
![]() $\mathrm {ZFC}$
that there is a strictly decreasing sequence of iterated
$\mathrm {ZFC}$
that there is a strictly decreasing sequence of iterated
![]() $\mathrm {HOD}^{\mathrm{s}}$
of length
$\mathrm {HOD}^{\mathrm{s}}$
of length
![]() $\omega $
, and the intersection of the sequence can be either a model of
$\omega $
, and the intersection of the sequence can be either a model of
![]() $\mathrm {ZFC}$
or of
$\mathrm {ZFC}$
or of
![]() $\mathrm {ZF+\neg AC}$
. Harrington also showed (in unpublished notes; cf. [Reference Zadrożny14]) that the intersection might not even be a model of
$\mathrm {ZF+\neg AC}$
. Harrington also showed (in unpublished notes; cf. [Reference Zadrożny14]) that the intersection might not even be a model of
![]() $\mathrm {ZF}$
. Jech [Reference Jech4] used forcing with Suslin trees to show that it is possible to have a strictly decreasing sequence of iterated
$\mathrm {ZF}$
. Jech [Reference Jech4] used forcing with Suslin trees to show that it is possible to have a strictly decreasing sequence of iterated
![]() $\mathrm {HOD}^{\mathrm{s}}$
of any arbitrary ordinal length, and later Zadrożny [Reference Zadrożny13] improved this to an
$\mathrm {HOD}^{\mathrm{s}}$
of any arbitrary ordinal length, and later Zadrożny [Reference Zadrożny13] improved this to an
![]() $\mathbf {Ord}$
length sequence. In [Reference Zadrożny14] Zadrożny generalized McAloon’s method and gave a more flexible framework for coding sets by forcing, which he used to give another proof of this result.
$\mathbf {Ord}$
length sequence. In [Reference Zadrożny14] Zadrożny generalized McAloon’s method and gave a more flexible framework for coding sets by forcing, which he used to give another proof of this result.
![]() $\mathrm {HOD}$
can be described also as the model constructed using second order logic (as shown by Myhill and Scott [Reference Myhill, Scott and Scott9]), so it is natural to ask which of the results for
$\mathrm {HOD}$
can be described also as the model constructed using second order logic (as shown by Myhill and Scott [Reference Myhill, Scott and Scott9]), so it is natural to ask which of the results for
![]() $\mathrm {HOD}$
apply to other such models, specifically to
$\mathrm {HOD}$
apply to other such models, specifically to
![]() $C^{*}$
. In Section 3 we show that unlike the case of
$C^{*}$
. In Section 3 we show that unlike the case of
![]() $\mathrm {HOD}$
, without large cardinals we can only have finite decreasing sequences of iterated
$\mathrm {HOD}$
, without large cardinals we can only have finite decreasing sequences of iterated
![]() $C^{*\mathrm{s}}$
, and that the existence of an inner model with a measurable cardinal is equivalent to the existence of an inner model with a strictly decreasing
$C^{*\mathrm{s}}$
, and that the existence of an inner model with a measurable cardinal is equivalent to the existence of an inner model with a strictly decreasing
![]() $C^*$
sequence of length
$C^*$
sequence of length
![]() $\omega $
.
$\omega $
.
2 Relative consistency of “
 $V=C^{*} \ne L$
”
$V=C^{*} \ne L$
”
In this section we follow the method of Zadrożny [Reference Zadrożny14] to obtain the following result:
Theorem 2.1. If
![]() $\mathrm {ZFC}$
is consistent then so is
$\mathrm {ZFC}$
is consistent then so is
![]() $\mathrm {ZFC}+V=C^{*}\ne L\,+$
$\mathrm {ZFC}+V=C^{*}\ne L\,+$
![]() $2^{\aleph _{0}}=\aleph _{1}$
.
$2^{\aleph _{0}}=\aleph _{1}$
.
The ideaFootnote
1
of Zadrożny’s proofs, which are based on results of McAloon’s [Reference McAloon7, Reference McAloon8], is to add a generic object (to make
![]() $V\ne L$
), code it using some other generic object, then code the coding, and so on, iterating until we catch our tail. Our coding tool will be the modified Namba forcing of [Reference Kennedy, Magidor and Väänänen5, Section 6], which adds a countable cofinal sequence to any element of some countable sequence of regular cardinals
$V\ne L$
), code it using some other generic object, then code the coding, and so on, iterating until we catch our tail. Our coding tool will be the modified Namba forcing of [Reference Kennedy, Magidor and Väänänen5, Section 6], which adds a countable cofinal sequence to any element of some countable sequence of regular cardinals
![]() $>\aleph _{1}$
(and only to them).
$>\aleph _{1}$
(and only to them).
Definition 2.2. Suppose
![]() $S=\left \langle \lambda _{n}\mid n<\omega \right \rangle $
is a sequence of regular cardinals
$S=\left \langle \lambda _{n}\mid n<\omega \right \rangle $
is a sequence of regular cardinals
![]() $>\omega _{1}$
such that every
$>\omega _{1}$
such that every
![]() $\lambda _{n}$
occurs infinitely many times in the sequence. Let
$\lambda _{n}$
occurs infinitely many times in the sequence. Let
![]() $\left \langle B_{n}\mid n<\omega \right \rangle $
be a partition of
$\left \langle B_{n}\mid n<\omega \right \rangle $
be a partition of
![]() $\omega $
into infinite sets. The modified Namba forcing with respect to S is defined as follows. Conditions are trees T with
$\omega $
into infinite sets. The modified Namba forcing with respect to S is defined as follows. Conditions are trees T with
![]() $\omega $
levels, consisting of finite sequences of ordinals, such that if
$\omega $
levels, consisting of finite sequences of ordinals, such that if
![]() $\left (\alpha _{0},\dots ,\alpha _{i}\right )\in T$
and
$\left (\alpha _{0},\dots ,\alpha _{i}\right )\in T$
and
![]() $i\in B_{n}$
then:
$i\in B_{n}$
then:
-
1.
 $\alpha _{i}<\lambda _{n}$
.
$\alpha _{i}<\lambda _{n}$
. -
2.
 $\left |\left \{ \beta \mid \left (\alpha _{0},\dots ,\alpha _{i-1},\beta \right )\in T\right \} \right |\in \left \{ 1,\lambda _{n}\right \} $
.
$\left |\left \{ \beta \mid \left (\alpha _{0},\dots ,\alpha _{i-1},\beta \right )\in T\right \} \right |\in \left \{ 1,\lambda _{n}\right \} $
. -
3. For every m there are
 $\alpha _{i+1},\dots ,\alpha _{k-1}$
such that
$\alpha _{i+1},\dots ,\alpha _{k-1}$
such that
 $k\in B_{m}$
and
$k\in B_{m}$
and
 $\left |\left \{ \beta \mid \left (\alpha _{0},\dots ,\alpha _{k-1},\beta \right )\in T\right \} \right |=\lambda _{m}$
.
$\left |\left \{ \beta \mid \left (\alpha _{0},\dots ,\alpha _{k-1},\beta \right )\in T\right \} \right |=\lambda _{m}$
.
A condition
![]() $T'$
extends another condition T,
$T'$
extends another condition T,
![]() $T'\leq T$
, if
$T'\leq T$
, if
![]() $T'\subseteq T$
.
$T'\subseteq T$
.
If
![]() $\left \langle T_{n}\mid n<\omega \right \rangle $
is a generic sequence of conditions, then the stems of the trees
$\left \langle T_{n}\mid n<\omega \right \rangle $
is a generic sequence of conditions, then the stems of the trees
![]() $T_{n}$
form a sequence
$T_{n}$
form a sequence
![]() $\left \langle \alpha _{n}\mid n<\omega \right \rangle $
such that
$\left \langle \alpha _{n}\mid n<\omega \right \rangle $
such that
![]() $\left \langle \alpha _{i}\mid i\in B_{n}\right \rangle $
is cofinal in
$\left \langle \alpha _{i}\mid i\in B_{n}\right \rangle $
is cofinal in
![]() $\lambda _{n}$
. Thus, in the generic extension
$\lambda _{n}$
. Thus, in the generic extension
![]() $\mathrm {cf}\left (\lambda _{n}\right )=\omega $
for all
$\mathrm {cf}\left (\lambda _{n}\right )=\omega $
for all
![]() $n<\omega $
, and KMV show that these are the only regular cardinals that change their cofinality to
$n<\omega $
, and KMV show that these are the only regular cardinals that change their cofinality to
![]() $\omega $
. Furthermore, it is shown that revised countable support iterations of this forcing preserves
$\omega $
. Furthermore, it is shown that revised countable support iterations of this forcing preserves
![]() $\omega _{1}$
.
$\omega _{1}$
.
In [Reference Kennedy, Magidor and Väänänen5, Theorem 6.7], these tools are used to produce a model of
![]() $\mathrm {ZFC}+V=C^{*}\ne L\,+ 2^{\aleph _{0}}=\aleph _{2}$
, but this requires an inaccessible cardinal (as proven there as well). Here we show that we can get a model of
$\mathrm {ZFC}+V=C^{*}\ne L\,+ 2^{\aleph _{0}}=\aleph _{2}$
, but this requires an inaccessible cardinal (as proven there as well). Here we show that we can get a model of
![]() $\mathrm {ZFC}+V=C^{*}\ne L$
from
$\mathrm {ZFC}+V=C^{*}\ne L$
from
![]() $\mathrm {ZFC}$
alone, and this model will satisfy
$\mathrm {ZFC}$
alone, and this model will satisfy
![]() $2^{\aleph _{0}}=\aleph _{1}$
. These two results covers all possibilities, since in [Reference Kennedy, Magidor and Väänänen5, Corollary to Theorem 5.20], it is shown that the statement
$2^{\aleph _{0}}=\aleph _{1}$
. These two results covers all possibilities, since in [Reference Kennedy, Magidor and Väänänen5, Corollary to Theorem 5.20], it is shown that the statement
![]() $V=C^{*}$
implies that
$V=C^{*}$
implies that
![]() $2^{\aleph _{0}}\in \left \{ \aleph _{1},\aleph _{2}\right \} $
, and for any
$2^{\aleph _{0}}\in \left \{ \aleph _{1},\aleph _{2}\right \} $
, and for any
![]() $\kappa>\aleph _{0} \ 2^{\kappa }=\kappa ^{+}$
.
$\kappa>\aleph _{0} \ 2^{\kappa }=\kappa ^{+}$
.
We say that a set X is nice if it is a countable set of ordinals which does not contain any of its limit points, and such that
![]() $L[X]$
agrees with L on
$L[X]$
agrees with L on
![]() $\omega _{1}$
and on regular cardinals starting from
$\omega _{1}$
and on regular cardinals starting from
![]() $\aleph _{\sup X+2}$
. Note that if
$\aleph _{\sup X+2}$
. Note that if
![]() $S\in L$
is a countable sequence of regular L cardinals
$S\in L$
is a countable sequence of regular L cardinals
![]() $> \aleph _{1}$
, and X is generic for the modified Namba forcing corresponding to S, then X is nice as the size of the forcing is
$> \aleph _{1}$
, and X is generic for the modified Namba forcing corresponding to S, then X is nice as the size of the forcing is
![]() $\leq \aleph _{\sup X+1}$
(we assume GCH, at least starting from this point). Assume
$\leq \aleph _{\sup X+1}$
(we assume GCH, at least starting from this point). Assume
![]() $V=L\left [A_{0}\right ]$
where
$V=L\left [A_{0}\right ]$
where
![]() $A_{0}$
is nice. Set
$A_{0}$
is nice. Set
![]() $\mathbb {P}_{0}=\left \{ 1\right \} $
, and inductively we assume that
$\mathbb {P}_{0}=\left \{ 1\right \} $
, and inductively we assume that
![]() $\mathbb {P}_{n}$
forces the existence of a nice set of ordinals
$\mathbb {P}_{n}$
forces the existence of a nice set of ordinals
![]() $A_{n}$
, denote
$A_{n}$
, denote
![]() $\xi _{n}=\sup A_{n}$
and we set
$\xi _{n}=\sup A_{n}$
and we set
![]() $\mathbb {P}_{n+1}=\mathbb {P}_{n}*\dot {\mathbb {Q}}_{n+1}$
where
$\mathbb {P}_{n+1}=\mathbb {P}_{n}*\dot {\mathbb {Q}}_{n+1}$
where
![]() $\dot {\mathbb {Q}}_{n+1}$
is the modified Namba forcing to add a Namba sequence
$\dot {\mathbb {Q}}_{n+1}$
is the modified Namba forcing to add a Namba sequence
![]() $E_{\alpha }$
to each
$E_{\alpha }$
to each
![]() $\aleph _{\xi _{n}+\alpha +2}^{L}$
such that
$\aleph _{\xi _{n}+\alpha +2}^{L}$
such that
![]() $\alpha \in A_{n}$
(note that by niceness,
$\alpha \in A_{n}$
(note that by niceness,
![]() $\aleph _{\xi _{n}+\alpha +2}^{L}$
is still a regular uncountable cardinal in
$\aleph _{\xi _{n}+\alpha +2}^{L}$
is still a regular uncountable cardinal in
![]() $V^{\mathbb {P}_{n}}$
). We can require that
$V^{\mathbb {P}_{n}}$
). We can require that
![]() $E_{\alpha }\subseteq \left (\aleph _{\xi _{n}+\alpha +1}^{L},\aleph _{\xi _{n}+\alpha +2}^{L}\right )$
, so that
$E_{\alpha }\subseteq \left (\aleph _{\xi _{n}+\alpha +1}^{L},\aleph _{\xi _{n}+\alpha +2}^{L}\right )$
, so that
![]() $A_{n+1}:=\bigcup \left \{ E_{\alpha }\mid \alpha \in A_{n}\right \} $
does not contain any of its limit points, and as we noted, it is nice.
$A_{n+1}:=\bigcup \left \{ E_{\alpha }\mid \alpha \in A_{n}\right \} $
does not contain any of its limit points, and as we noted, it is nice.
![]() $\mathbb {P}_{\omega }$
is the full support (which is in our case also the revised countable support) iteration. Let
$\mathbb {P}_{\omega }$
is the full support (which is in our case also the revised countable support) iteration. Let
![]() $G\subseteq \mathbb {P}_{\omega }$
generic, and denote
$G\subseteq \mathbb {P}_{\omega }$
generic, and denote
![]() $A=\bigcup _{n<\omega }A_{n}$
. By the properties of the modified Namba forcing, for any
$A=\bigcup _{n<\omega }A_{n}$
. By the properties of the modified Namba forcing, for any
![]() $\gamma $
,
$\gamma $
,
![]() $V\left [G\right ]\vDash \mathrm {cf}\left (\aleph _{\gamma +2}^{L}\right )=\omega $
iff
$V\left [G\right ]\vDash \mathrm {cf}\left (\aleph _{\gamma +2}^{L}\right )=\omega $
iff
![]() $\gamma =\xi _{n}+\alpha $
for
$\gamma =\xi _{n}+\alpha $
for
![]() $\alpha \in A_{n}$
.
$\alpha \in A_{n}$
.
Remark 2.3.
-
1.
 $\xi _{n+1}=\aleph _{\xi _{n}\cdot 2}^{L}$
, so inductively depends only
$\xi _{n+1}=\aleph _{\xi _{n}\cdot 2}^{L}$
, so inductively depends only
 $A_{0}$
and not on the generics.
$A_{0}$
and not on the generics.
 $\xi _{\omega }:=\sup A$
satisfies
$\xi _{\omega }:=\sup A$
satisfies
 $\xi _{\omega }=\aleph _{\xi _{\omega }}^{L}$
and is of cofinality
$\xi _{\omega }=\aleph _{\xi _{\omega }}^{L}$
and is of cofinality
 $\omega $
.
$\omega $
. -
2. From
 $\operatorname {otp}(A_{0})$
and A we can inductively reconstruct each
$\operatorname {otp}(A_{0})$
and A we can inductively reconstruct each
 $A_{n}$
–
$A_{n}$
–
 $A_{0}$
is the first
$A_{0}$
is the first
 $\operatorname {otp}(A_{0})$
elements of A, and if we know
$\operatorname {otp}(A_{0})$
elements of A, and if we know
 $A_{n}$
, then
$A_{n}$
, then
 $A_{n+1}$
are the first
$A_{n+1}$
are the first
 $\operatorname {otp}(A_{n})\cdot \omega $
elements of A above
$\operatorname {otp}(A_{n})\cdot \omega $
elements of A above
 $\sup A_{n}$
.
$\sup A_{n}$
. -
3. Hence for each n,
 $\operatorname {otp}(A_{n})=\operatorname {otp}(A_{0})\cdot \omega ^{n}$
.
$\operatorname {otp}(A_{n})=\operatorname {otp}(A_{0})\cdot \omega ^{n}$
. -
4. If
 $\alpha \in A_{n}$
, then
$\alpha \in A_{n}$
, then
 $E_{\alpha }=A\cap \left (\aleph _{\xi _{n}+\alpha +1}^{L},\aleph _{\xi _{n}+\alpha +2}^{L}\right )$
.
$E_{\alpha }=A\cap \left (\aleph _{\xi _{n}+\alpha +1}^{L},\aleph _{\xi _{n}+\alpha +2}^{L}\right )$
.
Proposition 2.4.
![]() $\left (C^{*}\right )^{V\left [G\right ]}=L\left [A\right ]=V\left [G\right ]$
.
$\left (C^{*}\right )^{V\left [G\right ]}=L\left [A\right ]=V\left [G\right ]$
.
Proof By the properties of the modified Namba forcing, at each stage of the iteration the only cardinals of
![]() $L\left [A_{0}\right ]$
receiving cofinality
$L\left [A_{0}\right ]$
receiving cofinality
![]() $\omega $
are the ones in
$\omega $
are the ones in
![]() $A_{n}$
. The whole iteration will also add new
$A_{n}$
. The whole iteration will also add new
![]() $\omega $
sequences to
$\omega $
sequences to
![]() $\sup A$
, but this already had cofinality
$\sup A$
, but this already had cofinality
![]() $\omega $
as we noted earlier. So
$\omega $
as we noted earlier. So
![]() $V[G]\vDash \mathrm {cf}\left (\gamma \right )=\omega $
iff either
$V[G]\vDash \mathrm {cf}\left (\gamma \right )=\omega $
iff either
![]() $V\vDash \mathrm {cf}\left (\gamma \right )=\omega $
or there is n s.t.
$V\vDash \mathrm {cf}\left (\gamma \right )=\omega $
or there is n s.t.
![]() $V\vDash \mathrm {cf}\left (\gamma \right )=\aleph _{\xi _{n}+\alpha +2}^{L}$
for
$V\vDash \mathrm {cf}\left (\gamma \right )=\aleph _{\xi _{n}+\alpha +2}^{L}$
for
![]() $\alpha \in A_{n}$
. And on the other hand, if
$\alpha \in A_{n}$
. And on the other hand, if
![]() $\alpha \in A$
then
$\alpha \in A$
then
![]() $V\left [G\right ]\vDash \mathrm {cf}\left (\aleph _{\xi _{n}+\alpha +2}^{L}\right )=\omega $
. So
$V\left [G\right ]\vDash \mathrm {cf}\left (\aleph _{\xi _{n}+\alpha +2}^{L}\right )=\omega $
. So
(where
![]() $\xi _{-1}=0$
); hence
$\xi _{-1}=0$
); hence
![]() $L\left [A\right ]\subseteq \left (C^{*}\right )^{V\left [G\right ]}$
.
$L\left [A\right ]\subseteq \left (C^{*}\right )^{V\left [G\right ]}$
.
As we noted, for every
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $E_{\alpha }$
can be reconstructed from A and
$E_{\alpha }$
can be reconstructed from A and
![]() $\alpha $
, so
$\alpha $
, so
![]() $\left \langle E_{\alpha }\mid \alpha \in A\right \rangle $
is in
$\left \langle E_{\alpha }\mid \alpha \in A\right \rangle $
is in
![]() $L\left [A\right ]$
. G can be reconstructed from this sequence; hence
$L\left [A\right ]$
. G can be reconstructed from this sequence; hence
![]() $V\left [G\right ]\subseteq L\left [A\right ]\subseteq \left (C^{*}\right )^{V\left [G\right ]}$
, so the equality follows.
$V\left [G\right ]\subseteq L\left [A\right ]\subseteq \left (C^{*}\right )^{V\left [G\right ]}$
, so the equality follows.
To finish the proof of Theorem 2.1, we start with a model of
![]() $V=L$
+ “there is no inaccessible cardinal,” and take, e.g.,
$V=L$
+ “there is no inaccessible cardinal,” and take, e.g.,
![]() $A_{0}=\omega $
. Then
$A_{0}=\omega $
. Then
![]() $L[A]$
will satisfy
$L[A]$
will satisfy
![]() $V=C^{*}\ne L$
, and
$V=C^{*}\ne L$
, and
![]() $2^{\aleph _{0}}=\aleph _{1}$
will still hold since by [Reference Kennedy, Magidor and Väänänen5, Theorem 6.7], violating CH in a model of
$2^{\aleph _{0}}=\aleph _{1}$
will still hold since by [Reference Kennedy, Magidor and Väänänen5, Theorem 6.7], violating CH in a model of
![]() $V=C^{*}$
requires an inaccessible cardinal.Footnote
2
$V=C^{*}$
requires an inaccessible cardinal.Footnote
2
3 Iterating
 $C^{*}$
$C^{*}$
Theorem 3.1. If
![]() $\mathrm {ZFC}$
is consistent then so is the existence of a model with a decreasing
$\mathrm {ZFC}$
is consistent then so is the existence of a model with a decreasing
![]() $C^{*}$
-sequence of any given finite length.
$C^{*}$
-sequence of any given finite length.
Proof Going back to the proof of Theorem 2.1, we note that for any n,
 $$\begin{align*}\left(C^{*}\right)^{L\left[\bigcup_{k=0}^{n+1}A_{k}\right]}=L\left[\bigcup_{k=0}^{n}A_{k}\right]: \end{align*}$$
$$\begin{align*}\left(C^{*}\right)^{L\left[\bigcup_{k=0}^{n+1}A_{k}\right]}=L\left[\bigcup_{k=0}^{n}A_{k}\right]: \end{align*}$$
![]() $A_{n}$
can be computed from
$A_{n}$
can be computed from
![]() $A_{n+1}$
using the cofinality-
$A_{n+1}$
using the cofinality-
![]() $\omega $
quantifier, which gives
$\omega $
quantifier, which gives
![]() $\supseteq $
, and on the other hand, from
$\supseteq $
, and on the other hand, from
![]() $\bigcup _{k=0}^{n}A_{k}$
we know exactly which ordinals will have cofinality
$\bigcup _{k=0}^{n}A_{k}$
we know exactly which ordinals will have cofinality
![]() $\omega $
in
$\omega $
in
![]() $L\left [\bigcup _{k=0}^{n+1}A_{k}\right ]$
, which gives
$L\left [\bigcup _{k=0}^{n+1}A_{k}\right ]$
, which gives
![]() $\subseteq $
. So by starting, e.g., from
$\subseteq $
. So by starting, e.g., from
![]() $A_{0}=\omega $
,
$A_{0}=\omega $
,
![]() $L\left [\bigcup _{k=0}^{n}A_{k}\right ]$
has the decreasing
$L\left [\bigcup _{k=0}^{n}A_{k}\right ]$
has the decreasing
![]() $C^{*}$
chain
$C^{*}$
chain
 $$\begin{align*}L\left[\bigcup_{k=0}^{n}A_{k}\right]=C^{*0}\supsetneq C^{*1}\supsetneq\cdots\supsetneq C^{*n}=L. \end{align*}$$
$$\begin{align*}L\left[\bigcup_{k=0}^{n}A_{k}\right]=C^{*0}\supsetneq C^{*1}\supsetneq\cdots\supsetneq C^{*n}=L. \end{align*}$$
We now show that without large cardinals this is best possible.
Lemma 3.2. Let
![]() $E=\left \{ \alpha <\omega _{2}^{V}\mid \mathrm {cf}\left (\alpha \right )=\omega \right \} $
.
$E=\left \{ \alpha <\omega _{2}^{V}\mid \mathrm {cf}\left (\alpha \right )=\omega \right \} $
.
-
1. If
 $0^{\sharp }$
does not exist, then
$0^{\sharp }$
does not exist, then
 $C^{*}=L\left [E\right ]$
.
$C^{*}=L\left [E\right ]$
. -
2. If there is no inner model with a measurable cardinal, then
 $C^{*}=K\left [E\right ]$
where K is the Dodd–Jensen core model.
$C^{*}=K\left [E\right ]$
where K is the Dodd–Jensen core model.
Proof 1. Clearly
![]() $E\in C^{*}$
so
$E\in C^{*}$
so
![]() $L\left [E\right ]\subseteq C^{*}$
. Let
$L\left [E\right ]\subseteq C^{*}$
. Let
![]() $\alpha \in \mathbf {Ord}$
. If
$\alpha \in \mathbf {Ord}$
. If
![]() $\mathrm {cf}\left (\alpha \right )\geq \omega _{2}^{V}$
then also
$\mathrm {cf}\left (\alpha \right )\geq \omega _{2}^{V}$
then also
![]() $L\vDash \mathrm {cf}\left (\alpha \right )\geq \omega _{2}^{V}$
so in particular
$L\vDash \mathrm {cf}\left (\alpha \right )\geq \omega _{2}^{V}$
so in particular
![]() $L\vDash \mathrm {cf}\left (\alpha \right )>\omega $
. If
$L\vDash \mathrm {cf}\left (\alpha \right )>\omega $
. If
![]() $\mathrm {cf}\left (\alpha \right )<\omega _{2}^{V}$
, let
$\mathrm {cf}\left (\alpha \right )<\omega _{2}^{V}$
, let
![]() $A\subseteq \alpha $
be cofinal, so
$A\subseteq \alpha $
be cofinal, so
![]() $\left |A\right |\leq \aleph _{1}$
. By the covering theorem, there is
$\left |A\right |\leq \aleph _{1}$
. By the covering theorem, there is
![]() $B\in L$
,
$B\in L$
,
![]() $A\subseteq B\subseteq \alpha $
s.t.
$A\subseteq B\subseteq \alpha $
s.t.
![]() $\left |B\right |=\aleph _{1}+\left |A\right |=\aleph _{1}$
. Let
$\left |B\right |=\aleph _{1}+\left |A\right |=\aleph _{1}$
. Let
![]() $\bar {\alpha }=\operatorname {otp}(B)$
, so
$\bar {\alpha }=\operatorname {otp}(B)$
, so
![]() $\bar {\alpha }<\omega _{2}^{V}$
, and
$\bar {\alpha }<\omega _{2}^{V}$
, and
![]() $\mathrm {cf}\left (\alpha \right )=\mathrm {cf}\left (\bar {\alpha }\right )$
, so
$\mathrm {cf}\left (\alpha \right )=\mathrm {cf}\left (\bar {\alpha }\right )$
, so
![]() $\mathrm {cf}\left (\alpha \right )=\omega $
iff
$\mathrm {cf}\left (\alpha \right )=\omega $
iff
![]() $\bar {\alpha }\in E$
.
$\bar {\alpha }\in E$
.
To summarize, we get that for every
![]() $\alpha $
, in
$\alpha $
, in
![]() $L\left [E\right ]$
we can determine whether
$L\left [E\right ]$
we can determine whether
![]() $\mathrm {cf}\left (\alpha \right )=\omega $
or not, so
$\mathrm {cf}\left (\alpha \right )=\omega $
or not, so
![]() $C^{*}\subseteq L\left [E\right ]$
.
$C^{*}\subseteq L\left [E\right ]$
.
2. The proof is exactly the same, noting that
![]() $K\subseteq C^{*}$
by [Reference Kennedy, Magidor and Väänänen5, Theorem 5.5], and that our assumption implies the covering theorem holds for K.
$K\subseteq C^{*}$
by [Reference Kennedy, Magidor and Väänänen5, Theorem 5.5], and that our assumption implies the covering theorem holds for K.
Theorem 3.3. If there is no inner model with a measurable cardinal, then there is
![]() $k<\omega $
such that
$k<\omega $
such that
![]() $C^{*k}=C^{*(k+1)}$
.
$C^{*k}=C^{*(k+1)}$
.
Proof By applying Lemma 3.2 clause 2 inside each
![]() $C^{*n}$
, for every n we have
$C^{*n}$
, for every n we have
![]() $C^{*(n+1)}=K\left [E_{n}\right ]$
where
$C^{*(n+1)}=K\left [E_{n}\right ]$
where
The sequence
![]() $\left \langle \left (\omega _{1}^{C^{*n}},\omega _{2}^{C^{*n}}\right )\mid n<\omega \right \rangle $
is non-increasing in both coordinates; hence it stabilizes. Let k be such that
$\left \langle \left (\omega _{1}^{C^{*n}},\omega _{2}^{C^{*n}}\right )\mid n<\omega \right \rangle $
is non-increasing in both coordinates; hence it stabilizes. Let k be such that
![]() $(\omega _{1}^{C^{*k}},\omega _{2}^{C^{*k}})=(\omega _{1}^{C^{*(k+1)}},\omega _{2}^{C^{*(k+1)}})$
, and we claim that
$(\omega _{1}^{C^{*k}},\omega _{2}^{C^{*k}})=(\omega _{1}^{C^{*(k+1)}},\omega _{2}^{C^{*(k+1)}})$
, and we claim that
![]() $C^{*(k+1)}=C^{*(k+2)}$
. To simplify notation we assume w.l.o.g.
$C^{*(k+1)}=C^{*(k+2)}$
. To simplify notation we assume w.l.o.g.
![]() $k=0$
, i.e.,
$k=0$
, i.e.,
![]() $\omega _{i}^{C^{*}}=\omega _{i}^{V}$
for
$\omega _{i}^{C^{*}}=\omega _{i}^{V}$
for
![]() $i=1,2$
(so we can omit the superscript) and we want to show that
$i=1,2$
(so we can omit the superscript) and we want to show that
![]() $\left (C^{*}\right )^{C*}=C^{*}$
. We have
$\left (C^{*}\right )^{C*}=C^{*}$
. We have
 $$ \begin{align*} C^{*} & =K\left[\left\{ \alpha<\omega_{2}\mid V\vDash\mathrm{cf}\left(\alpha\right)=\omega\right\} \right]=K\left[E_{0}\right],\\ \left(C^{*}\right)^{C*} & =K\left[\left\{ \alpha<\omega_{2}\mid C^{*}\vDash\mathrm{cf}\left(\alpha\right)=\omega\right\} \right]=K\left[E_{1}\right]. \end{align*} $$
$$ \begin{align*} C^{*} & =K\left[\left\{ \alpha<\omega_{2}\mid V\vDash\mathrm{cf}\left(\alpha\right)=\omega\right\} \right]=K\left[E_{0}\right],\\ \left(C^{*}\right)^{C*} & =K\left[\left\{ \alpha<\omega_{2}\mid C^{*}\vDash\mathrm{cf}\left(\alpha\right)=\omega\right\} \right]=K\left[E_{1}\right]. \end{align*} $$
Clearly
![]() $E_{1}\subseteq E_{0}$
. On the other hand, if
$E_{1}\subseteq E_{0}$
. On the other hand, if
![]() $\alpha \in \omega _{2}\mathord {\smallsetminus } E_{1}$
, this means that
$\alpha \in \omega _{2}\mathord {\smallsetminus } E_{1}$
, this means that
![]() $C^{*}\vDash \mathrm {cf}\left (\alpha \right )=\omega _{1}$
, and since
$C^{*}\vDash \mathrm {cf}\left (\alpha \right )=\omega _{1}$
, and since
![]() $\omega _{1}^{C^{*}}=\omega _{1}$
, we get that also
$\omega _{1}^{C^{*}}=\omega _{1}$
, we get that also
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\omega _{1}$
, so
$V\vDash \mathrm {cf}\left (\alpha \right )=\omega _{1}$
, so
![]() $\alpha \in \omega _{2}\mathord {\smallsetminus } E_{0}$
, thus
$\alpha \in \omega _{2}\mathord {\smallsetminus } E_{0}$
, thus
![]() $E_{1}=E_{0}$
, and our claim is proved.
$E_{1}=E_{0}$
, and our claim is proved.
Our next goal is to show that this is precisely the consistency strength of a decreasing sequence:
Theorem 3.4. If there is an inner model with a measurable cardinal, then there is an inner model in which the sequence
![]() $\left \langle C^{*n}\mid n<\omega \right \rangle $
is strictly decreasing.
$\left \langle C^{*n}\mid n<\omega \right \rangle $
is strictly decreasing.
We work in
![]() $L[U]$
where U is a normal ultrafilter on
$L[U]$
where U is a normal ultrafilter on
![]() $\kappa $
, and denote by
$\kappa $
, and denote by
![]() $M_{\alpha }$
the
$M_{\alpha }$
the
![]() $\alpha $
th iterate of
$\alpha $
th iterate of
![]() $L[U]$
by U,
$L[U]$
by U,
![]() $j_{\alpha ,\beta }:M_{\alpha }\to M_{\beta }$
the elementary embedding,
$j_{\alpha ,\beta }:M_{\alpha }\to M_{\beta }$
the elementary embedding,
![]() $\kappa _{\alpha }=j_{0,\alpha }(\kappa )$
and
$\kappa _{\alpha }=j_{0,\alpha }(\kappa )$
and
![]() $U^{(\alpha )}=j_{0,\alpha }(U)$
.
$U^{(\alpha )}=j_{0,\alpha }(U)$
.
In [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16] the authors show that if
![]() $V=L[U]$
then
$V=L[U]$
then
![]() $C^{*}=M_{\omega ^{2}}\left [E\right ]$
where
$C^{*}=M_{\omega ^{2}}\left [E\right ]$
where
![]() $E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
. We improve this by showing that
$E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
. We improve this by showing that
![]() $C^{*}$
is unchanged after adding a Prikry sequence to
$C^{*}$
is unchanged after adding a Prikry sequence to
![]() $\kappa $
, and then investigate the
$\kappa $
, and then investigate the
![]() $C^{*}$
-chain of
$C^{*}$
-chain of
![]() $L[U]$
. First we prove two useful lemmas.
$L[U]$
. First we prove two useful lemmas.
Lemma 3.5.
![]() $E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
is generic over
$E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
is generic over
![]() $M_{\omega ^{2}}$
for the Prikry forcing on
$M_{\omega ^{2}}$
for the Prikry forcing on
![]() $\kappa _{\omega ^{2}}$
defined from the ultrafilter
$\kappa _{\omega ^{2}}$
defined from the ultrafilter
![]() $U^{(\omega ^{2})}\in M_{\omega ^{2}}$
.
$U^{(\omega ^{2})}\in M_{\omega ^{2}}$
.
Proof We use Mathias’s characterization of Prikry forcing:
Fact 3.6 (Mathias, cf. [Reference Mathias6]).
Let M be a transitive model of
![]() $\mathrm {ZFC}$
, U a normal ultrafilter on
$\mathrm {ZFC}$
, U a normal ultrafilter on
![]() $\kappa $
, then
$\kappa $
, then
![]() $S\subseteq \kappa $
of order type
$S\subseteq \kappa $
of order type
![]() $\omega $
is generic over M for the Prikry forcing defined from U iff for any
$\omega $
is generic over M for the Prikry forcing defined from U iff for any
![]() $X\in U$
,
$X\in U$
,
![]() $S\mathord {\smallsetminus } X$
is finite.
$S\mathord {\smallsetminus } X$
is finite.
So we need to show that for any
![]() $X\in U^{(\omega ^{2})}$
,
$X\in U^{(\omega ^{2})}$
,
![]() $E\mathord {\smallsetminus } X$
is finite. The ultrafilter
$E\mathord {\smallsetminus } X$
is finite. The ultrafilter
![]() $U^{(\omega ^{2})}$
is defined by
$U^{(\omega ^{2})}$
is defined by
![]() $X\in U^{(\omega ^{2})}$
iff
$X\in U^{(\omega ^{2})}$
iff
![]() $\exists \alpha <\omega ^{2}\ \left \{ \kappa _{\beta }\mid \alpha \leq \beta <\omega ^{2}\right \} \subseteq X$
. For
$\exists \alpha <\omega ^{2}\ \left \{ \kappa _{\beta }\mid \alpha \leq \beta <\omega ^{2}\right \} \subseteq X$
. For
![]() $X\in U^{(\omega ^{2})}$
, choose some
$X\in U^{(\omega ^{2})}$
, choose some
![]() $\alpha <\omega ^{2}$
such that
$\alpha <\omega ^{2}$
such that
![]() $\left \{ \kappa _{\beta }\mid \alpha \leq \beta <\omega ^{2}\right \} \subseteq X$
, then
$\left \{ \kappa _{\beta }\mid \alpha \leq \beta <\omega ^{2}\right \} \subseteq X$
, then
![]() $E\mathord {\smallsetminus }\alpha =\left \{ \kappa _{\omega \cdot n}\mid \omega \cdot n<\alpha \right \} $
, and since
$E\mathord {\smallsetminus }\alpha =\left \{ \kappa _{\omega \cdot n}\mid \omega \cdot n<\alpha \right \} $
, and since
![]() $\kappa _{\omega ^{2}}=\sup \left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
, this set is finite. Hence
$\kappa _{\omega ^{2}}=\sup \left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
, this set is finite. Hence
![]() $E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
satisfies the characterization.
$E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
satisfies the characterization.
Lemma 3.7. For any
![]() $\beta <\kappa $
and any
$\beta <\kappa $
and any
![]() $\alpha $
,
$\alpha $
,
![]() $M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
iff
$M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
iff
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
.
$V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
.
Proof
![]() $\kappa $
is regular in V; thus it is regular in every
$\kappa $
is regular in V; thus it is regular in every
![]() $M_{\beta }$
which is an inner model of V. If
$M_{\beta }$
which is an inner model of V. If
![]() $M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
, then there is a cofinal
$M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
, then there is a cofinal
![]() $\kappa $
-sequence in
$\kappa $
-sequence in
![]() $\alpha $
(in both
$\alpha $
(in both
![]() $M_{\beta }$
and V), and since
$M_{\beta }$
and V), and since
![]() $\kappa $
is regular we get
$\kappa $
is regular we get
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
. If
$V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
. If
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
, then the same argument rules out
$V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
, then the same argument rules out
![]() $M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )<\kappa $
. So the only case left to rule out is
$M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )<\kappa $
. So the only case left to rule out is
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\kappa \ \land \ M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )>\kappa $
. If
$V\vDash \mathrm {cf}\left (\alpha \right )=\kappa \ \land \ M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )>\kappa $
. If
![]() $\beta =\gamma +1$
, then
$\beta =\gamma +1$
, then
![]() $M_{\beta }$
is contained in
$M_{\beta }$
is contained in
![]() $M_{\gamma }$
and closed under
$M_{\gamma }$
and closed under
![]() $\kappa $
-sequences in it, so they agree on cofinality
$\kappa $
-sequences in it, so they agree on cofinality
![]() $\kappa $
, and by induction we get that they agree with V as well. So assume
$\kappa $
, and by induction we get that they agree with V as well. So assume
![]() $\beta $
is limit and let
$\beta $
is limit and let
![]() $\left \langle \alpha _{\eta }\mid \eta <\kappa \right \rangle $
be a cofinal sequence in
$\left \langle \alpha _{\eta }\mid \eta <\kappa \right \rangle $
be a cofinal sequence in
![]() $\alpha $
. By definition of the limit ultrapower, each
$\alpha $
. By definition of the limit ultrapower, each
![]() $\alpha _{\eta }$
is of the form
$\alpha _{\eta }$
is of the form
![]() $j_{\bar {\beta },\beta }(\bar {\alpha }_{\eta })$
for some
$j_{\bar {\beta },\beta }(\bar {\alpha }_{\eta })$
for some
![]() $\bar {\beta }<\beta $
. We can also assume that each such
$\bar {\beta }<\beta $
. We can also assume that each such
![]() $\bar {\beta }$
is large enough so that
$\bar {\beta }$
is large enough so that
![]() $\alpha \in \operatorname {Range}(j_{\bar {\beta },\beta })$
. Since
$\alpha \in \operatorname {Range}(j_{\bar {\beta },\beta })$
. Since
![]() $\beta <\kappa $
, there is some
$\beta <\kappa $
, there is some
![]() $\bar {\beta }$
fitting
$\bar {\beta }$
fitting
![]() $\kappa $
many
$\kappa $
many
![]() $\alpha _{\eta }$
s, so without loss of generality we can assume
$\alpha _{\eta }$
s, so without loss of generality we can assume
![]() $\bar {\beta }$
fits all of them. We can assume
$\bar {\beta }$
fits all of them. We can assume
![]() $\bar {\beta }>0$
so
$\bar {\beta }>0$
so
![]() $\kappa $
is a fixed point of
$\kappa $
is a fixed point of
![]() $j_{\bar {\beta },\beta }$
. If
$j_{\bar {\beta },\beta }$
. If
![]() $\bar {\alpha }=\sup \left \{ \bar {\alpha }_{\eta }\mid \eta <\kappa \right \} $
Footnote
3
then, since
$\bar {\alpha }=\sup \left \{ \bar {\alpha }_{\eta }\mid \eta <\kappa \right \} $
Footnote
3
then, since
![]() $\alpha =\sup \left \{ j_{\bar {\beta },\beta }(\bar {\alpha }_{\eta })\mid \eta <\kappa \right \} $
and
$\alpha =\sup \left \{ j_{\bar {\beta },\beta }(\bar {\alpha }_{\eta })\mid \eta <\kappa \right \} $
and
![]() $\alpha \in \operatorname {Range}(j_{\bar {\beta },\beta })$
, we must have that
$\alpha \in \operatorname {Range}(j_{\bar {\beta },\beta })$
, we must have that
![]() $\alpha =j_{\bar {\beta },\beta }(\bar {\alpha })$
.
$\alpha =j_{\bar {\beta },\beta }(\bar {\alpha })$
.
![]() $\bar {\alpha }$
is of cofinality
$\bar {\alpha }$
is of cofinality
![]() $\kappa $
in V, so by the induction hypothesis also in
$\kappa $
in V, so by the induction hypothesis also in
![]() $M_{\bar {\beta }}$
, hence by elementarity
$M_{\bar {\beta }}$
, hence by elementarity
![]() $M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
.
$M_{\beta }\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
.
Proposition 3.8. If
![]() $V=L[U]$
where U is a measure on
$V=L[U]$
where U is a measure on
![]() $\kappa $
, G is generic for Prikry forcing on
$\kappa $
, G is generic for Prikry forcing on
![]() $\kappa $
, then
$\kappa $
, then
![]() $\left (C^{*}\right )^{V\left [G\right ]}=\left (C^{*}\right )^{V}$
.
$\left (C^{*}\right )^{V\left [G\right ]}=\left (C^{*}\right )^{V}$
.
Proof After forcing with Prikry forcing, the only change of cofinalities is that
![]() $\kappa $
becomes of cofinality
$\kappa $
becomes of cofinality
![]() $\omega $
. So
$\omega $
. So
![]() $V\left [G\right ]\vDash \mathrm {cf}\left (\alpha \right )=\omega $
iff
$V\left [G\right ]\vDash \mathrm {cf}\left (\alpha \right )=\omega $
iff
![]() $V\vDash \mathrm {cf}\left (\alpha \right )\in \left \{ \omega ,\kappa \right \} $
. We now follow the proof of [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16].
$V\vDash \mathrm {cf}\left (\alpha \right )\in \left \{ \omega ,\kappa \right \} $
. We now follow the proof of [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16].
Consider
![]() $M_{\omega ^{2}}$
, the
$M_{\omega ^{2}}$
, the
![]() $\omega ^{2}$
iterate of V, and let
$\omega ^{2}$
iterate of V, and let
![]() $E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
. As we noted above, by [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16] we know that
$E=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
. As we noted above, by [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16] we know that
![]() $\left (C^{*}\right )^{V}=M_{\omega ^{2}}\left [E\right ]$
, so it is enough to show that also
$\left (C^{*}\right )^{V}=M_{\omega ^{2}}\left [E\right ]$
, so it is enough to show that also
![]() $\left (C^{*}\right )^{V[G]}=M_{\omega ^{2}}\left [E\right ]$
.
$\left (C^{*}\right )^{V[G]}=M_{\omega ^{2}}\left [E\right ]$
.
Fix an ordinal
![]() $\alpha $
. As in the proof of [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16],
$\alpha $
. As in the proof of [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16],
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\omega $
iff
$V\vDash \mathrm {cf}\left (\alpha \right )=\omega $
iff
![]() $M_{\omega ^{2}}\left [E\right ]\vDash \mathrm {cf}\left (\alpha \right )\in \left \{ \omega \right \} \cup E\cup \left \{ \sup E\right \} $
. Regarding cofinality
$M_{\omega ^{2}}\left [E\right ]\vDash \mathrm {cf}\left (\alpha \right )\in \left \{ \omega \right \} \cup E\cup \left \{ \sup E\right \} $
. Regarding cofinality
![]() $\kappa $
–by Lemma 3.7,
$\kappa $
–by Lemma 3.7,
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
iff
$V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
iff
![]() $M_{\omega ^{2}}\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
. As we noted,
$M_{\omega ^{2}}\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
. As we noted,
![]() $M_{\omega ^{2}}=L[u']$
where
$M_{\omega ^{2}}=L[u']$
where
![]() $u' $
is a measure on
$u' $
is a measure on
![]() $\kappa _{\omega ^{2}}$
and by Lemma 3.5, E is Prikry generic over it; hence, since cofinality
$\kappa _{\omega ^{2}}$
and by Lemma 3.5, E is Prikry generic over it; hence, since cofinality
![]() $\kappa $
is unaffected by Prikry forcing on
$\kappa $
is unaffected by Prikry forcing on
![]() $\kappa _{\omega ^{2}}$
, we get
$\kappa _{\omega ^{2}}$
, we get
![]() $V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
iff
$V\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
iff
![]() $M_{\omega ^{2}}\left [E\right ]\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
. Putting these facts together, in
$M_{\omega ^{2}}\left [E\right ]\vDash \mathrm {cf}\left (\alpha \right )=\kappa $
. Putting these facts together, in
![]() $M_{\omega ^{2}}\left [E\right ]$
we can detect whether
$M_{\omega ^{2}}\left [E\right ]$
we can detect whether
![]() $V\vDash \mathrm {cf}\left (\alpha \right )\in \left \{ \omega ,\kappa \right \} $
, so we know whether
$V\vDash \mathrm {cf}\left (\alpha \right )\in \left \{ \omega ,\kappa \right \} $
, so we know whether
![]() $V\left [G\right ]\vDash \mathrm {cf}\left (\alpha \right )=\omega $
; hence we can construct
$V\left [G\right ]\vDash \mathrm {cf}\left (\alpha \right )=\omega $
; hence we can construct
![]() $\left (C^{*}\right )^{V\left [G\right ]}$
inside
$\left (C^{*}\right )^{V\left [G\right ]}$
inside
![]() $M_{\omega ^{2}}\left [E\right ]$
.
$M_{\omega ^{2}}\left [E\right ]$
.
The other direction of the proof is almost the same as in [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16]: E is the set of ordinals in the interval
![]() $(\kappa ,\kappa _{\omega ^{2}})$
which have cofinality
$(\kappa ,\kappa _{\omega ^{2}})$
which have cofinality
![]() $\omega $
in
$\omega $
in
![]() $V\left [G\right ]$
and are regular in the core model,Footnote
4
which is contained in any
$V\left [G\right ]$
and are regular in the core model,Footnote
4
which is contained in any
![]() $C^{*}$
, so
$C^{*}$
, so
![]() $E\in \left (C^{*}\right )^{V\left [G\right ]}$
, and from E one can define
$E\in \left (C^{*}\right )^{V\left [G\right ]}$
, and from E one can define
![]() $M_{\omega ^{2}}$
, so
$M_{\omega ^{2}}$
, so
![]() $M_{\omega ^{2}}[E]\subseteq \left (C^{*}\right )^{V\left [G\right ]}$
.
$M_{\omega ^{2}}[E]\subseteq \left (C^{*}\right )^{V\left [G\right ]}$
.
Now we can analyze the
![]() $C^{*}$
-chain of
$C^{*}$
-chain of
![]() $V=L[U]$
. We stick to the notation
$V=L[U]$
. We stick to the notation
![]() $C^{*\alpha }$
, starting from
$C^{*\alpha }$
, starting from
![]() $C^{*0}=L[U]=M_{0}$
, with
$C^{*0}=L[U]=M_{0}$
, with
![]() $M_{\alpha }$
being the
$M_{\alpha }$
being the
![]() $\alpha $
th iterate of
$\alpha $
th iterate of
![]() $L[U]$
and
$L[U]$
and
![]() $\kappa _{\alpha }$
the
$\kappa _{\alpha }$
the
![]() $\alpha $
th image of the measurable cardinal. So by [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16] we have
$\alpha $
th image of the measurable cardinal. So by [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16] we have
![]() $C^{*1}=M_{\omega ^{2}}\left [E_{1}\right ]$
for
$C^{*1}=M_{\omega ^{2}}\left [E_{1}\right ]$
for
![]() $E_{1}=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
. As we noted earlier
$E_{1}=\left \{ \kappa _{\omega \cdot n}\mid n<\omega \right \} $
. As we noted earlier
![]() $M_{\omega ^{2}}$
is also of the form
$M_{\omega ^{2}}$
is also of the form
![]() $L[U']$
for the measurable
$L[U']$
for the measurable
![]() $\kappa _{\omega ^{2}}$
, and by Lemma 3.5,
$\kappa _{\omega ^{2}}$
, and by Lemma 3.5,
![]() $E_{1}$
is Prikry generic over it, so by Proposition 3.8,
$E_{1}$
is Prikry generic over it, so by Proposition 3.8,
which is again the
![]() $\omega ^{2}$
th iterate of
$\omega ^{2}$
th iterate of
![]() $M_{\omega ^{2}}$
, i.e.,
$M_{\omega ^{2}}$
, i.e.,
![]() $M_{\omega ^{2}+\omega ^{2}}$
, plus the corresponding sequence–
$M_{\omega ^{2}+\omega ^{2}}$
, plus the corresponding sequence–
![]() $E_{2}=\left \{ \kappa _{\omega ^{2}+\omega \cdot n}\mid n<\omega \right \} $
. So
$E_{2}=\left \{ \kappa _{\omega ^{2}+\omega \cdot n}\mid n<\omega \right \} $
. So
![]() $C^{*2}=M_{\omega ^{2}\cdot 2}\left [E_{2}\right ]$
. We can continue inductively, and get the following:
$C^{*2}=M_{\omega ^{2}\cdot 2}\left [E_{2}\right ]$
. We can continue inductively, and get the following:
Theorem 3.9. If
![]() $V=L[U]$
then for every
$V=L[U]$
then for every
![]() $1\leq m<\omega \ C^{*m}=M_{\omega ^{2}\cdot m}\left [E_{m}\right ]$
where
$1\leq m<\omega \ C^{*m}=M_{\omega ^{2}\cdot m}\left [E_{m}\right ]$
where
![]() $M_{\alpha }$
is the
$M_{\alpha }$
is the
![]() $\alpha $
th iterate of V,
$\alpha $
th iterate of V,
![]() $\kappa _{\alpha }$
the
$\kappa _{\alpha }$
the
![]() $\alpha $
th image of the measurable cardinal, and
$\alpha $
th image of the measurable cardinal, and
![]() $E_{m}=\left \{ \kappa _{\omega ^{2}\cdot (m-1)+\omega \cdot n}\mid n<\omega \right \} $
.
$E_{m}=\left \{ \kappa _{\omega ^{2}\cdot (m-1)+\omega \cdot n}\mid n<\omega \right \} $
.
To see that this gives us a strictly decreasing sequence of models, consider the following. For every m,
![]() $\kappa _{\omega ^{2}\cdot m}$
is the single measurable in
$\kappa _{\omega ^{2}\cdot m}$
is the single measurable in
![]() $M_{\omega ^{2}\cdot m}$
, by which we iterate, so it remains regular in all subsequent models, in particular in
$M_{\omega ^{2}\cdot m}$
, by which we iterate, so it remains regular in all subsequent models, in particular in
![]() $M_{\omega ^{2}\cdot (m+1)}$
. Since
$M_{\omega ^{2}\cdot (m+1)}$
. Since
![]() $E_{m+1}$
is Prikry generic for
$E_{m+1}$
is Prikry generic for
![]() $\kappa _{\omega ^{2}\cdot (m+1)}$
which is larger than
$\kappa _{\omega ^{2}\cdot (m+1)}$
which is larger than
![]() $\kappa _{\omega ^{2}\cdot m}$
, the latter remains regular in
$\kappa _{\omega ^{2}\cdot m}$
, the latter remains regular in
![]() $M_{\omega ^{2}\cdot (m+1)}[E_{m+1}]$
, while in
$M_{\omega ^{2}\cdot (m+1)}[E_{m+1}]$
, while in
![]() $M_{\omega ^{2}\cdot m}[E_{m}]$
it is singular, so indeed
$M_{\omega ^{2}\cdot m}[E_{m}]$
it is singular, so indeed
This concludes the proof of Theorem 3.4.
To analyze
![]() $\left (C^{*\omega }\right )^{L[U]}$
, we will use the following theorem, due to Bukovský [Reference Bukovský1, Reference Bukovský2] and Dehornoy [Reference Dehornoy3]:
$\left (C^{*\omega }\right )^{L[U]}$
, we will use the following theorem, due to Bukovský [Reference Bukovský1, Reference Bukovský2] and Dehornoy [Reference Dehornoy3]:
Fact 3.10. If
![]() $\kappa $
is measurable,
$\kappa $
is measurable,
![]() $M_{\alpha }$
is the
$M_{\alpha }$
is the
![]() $\alpha $
th iterate of V by a normal ultrafilter on
$\alpha $
th iterate of V by a normal ultrafilter on
![]() $\kappa $
, and
$\kappa $
, and
![]() $\kappa _{\alpha }$
is the
$\kappa _{\alpha }$
is the
![]() $\alpha $
th image of
$\alpha $
th image of
![]() $\kappa $
, then for any limit ordinal
$\kappa $
, then for any limit ordinal
![]() $\lambda $
exactly one of the following holds:
$\lambda $
exactly one of the following holds:
-
1. If
 $\exists \alpha <\lambda $
s.t.
$\exists \alpha <\lambda $
s.t.
 $M_{\alpha }\vDash \mathrm {cf}\left (\lambda \right )>\omega $
then
$M_{\alpha }\vDash \mathrm {cf}\left (\lambda \right )>\omega $
then
 $\bigcap _{\alpha <\lambda }M_{\alpha }=M_{\lambda }.$
$\bigcap _{\alpha <\lambda }M_{\alpha }=M_{\lambda }.$
-
2. If
 $\lambda =\alpha +\omega $
for some
$\lambda =\alpha +\omega $
for some
 $\alpha $
, then
$\alpha $
, then
 $\left \langle \kappa _{\alpha +n}\mid n<\omega \right \rangle $
is Prikry generic over
$\left \langle \kappa _{\alpha +n}\mid n<\omega \right \rangle $
is Prikry generic over
 $M_{\lambda }$
and
$M_{\lambda }$
and
 $\bigcap _{\alpha <\lambda }M_{\alpha }=M_{\lambda }\left [\left \langle \kappa _{\alpha +n}\mid n<\omega \right \rangle \right ].$
$\bigcap _{\alpha <\lambda }M_{\alpha }=M_{\lambda }\left [\left \langle \kappa _{\alpha +n}\mid n<\omega \right \rangle \right ].$
-
3. Otherwise,
 $\bigcap _{\alpha <\lambda }M_{\alpha }$
is a quasi-generic extension of
$\bigcap _{\alpha <\lambda }M_{\alpha }$
is a quasi-generic extension of
 $M_{\lambda }$
, hence satisfies
$M_{\lambda }$
, hence satisfies
 $\mathrm {ZF}$
, but doesn’t satisfy
$\mathrm {ZF}$
, but doesn’t satisfy
 $\mathrm {AC}$
.
$\mathrm {AC}$
.
Corollary 3.11. If
![]() $V=L[U]$
then
$V=L[U]$
then
![]() $C^{*\omega }=\bigcap _{\alpha <\omega ^{3}}M_{\alpha }$
and it satisfies
$C^{*\omega }=\bigcap _{\alpha <\omega ^{3}}M_{\alpha }$
and it satisfies
![]() $\mathrm {ZF}$
but not
$\mathrm {ZF}$
but not
![]() $\mathrm {AC}$
.
$\mathrm {AC}$
.
Proof By definition and our previous calculation,
and for each
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $E_{m} \notin M_{\omega ^{2}\cdot (m+1)} [E_{m+1}]$
so
$E_{m} \notin M_{\omega ^{2}\cdot (m+1)} [E_{m+1}]$
so
Since
![]() $\omega ^{3}$
is of cofinality
$\omega ^{3}$
is of cofinality
![]() $\omega $
but not of the form
$\omega $
but not of the form
![]() $\alpha +\omega $
, the conclusion follows from Fact 3.10 clause 3.
$\alpha +\omega $
, the conclusion follows from Fact 3.10 clause 3.
4 Conclusion and open questions
We summarize what is now known in terms of equiconsistency:
-
1.
 $\mathrm {ZFC}$
is equiconsistent with
$\mathrm {ZFC}$
is equiconsistent with
 $V=C^{*}\ne L\,+ \ 2^{\aleph _{0}}=\aleph _{1}$
.
$V=C^{*}\ne L\,+ \ 2^{\aleph _{0}}=\aleph _{1}$
. -
2. Existence of an inaccessible cardinal is equiconsistent with
 $V=C^{*}+$
$V=C^{*}+$
 $2^{\aleph _{0}}=\aleph _{2}$
.
$2^{\aleph _{0}}=\aleph _{2}$
. -
3. Existence of a measurable cardinal is equiconsistent with
 $\forall n<\omega (C^{*n}\supsetneq C^{*(n+1)})$
and
$\forall n<\omega (C^{*n}\supsetneq C^{*(n+1)})$
and
 $C^{*\omega }\vDash \mathrm {ZF+\neg AC}$
.
$C^{*\omega }\vDash \mathrm {ZF+\neg AC}$
.
Compared to the results regarding
![]() $\mathrm {HOD}$
, the following questions remain open:
$\mathrm {HOD}$
, the following questions remain open:
Question 4.1.
-
1. Is it possible, under any large cardinal hypothesis, that
 $\forall n<\omega $
$\forall n<\omega $
 $C^{*n}\supsetneq C^{*(n+1)}$
and
$C^{*n}\supsetneq C^{*(n+1)}$
and
 $C^{*\omega }\vDash \mathrm {ZFC}$
? More generally, for which ordinals
$C^{*\omega }\vDash \mathrm {ZFC}$
? More generally, for which ordinals
 $\alpha $
can we get a decreasing
$\alpha $
can we get a decreasing
 $C^{*}$
sequence of length
$C^{*}$
sequence of length
 $\alpha $
?
$\alpha $
? -
2. Is it possible, under any large cardinal hypothesis, that
 $\forall n<\omega $
$\forall n<\omega $
 $C^{*n}\supsetneq C^{*(n+1)}$
and
$C^{*n}\supsetneq C^{*(n+1)}$
and
 $C^{*\omega }\nvDash \mathrm {ZF}$
?
$C^{*\omega }\nvDash \mathrm {ZF}$
?
A natural first attempt towards answering the first question would be to try and work in a model with more measurable cardinals. However, it seems that it would require at least measurably many measurables: in a forthcoming paper [Reference Ya’ar12], we generalize [Reference Kennedy, Magidor and Väänänen5, Theorem 5.16] and our Proposition 3.8 and show the following:
Theorem 4.2. Assume
![]() $V=L\left [\mathcal {U}\right ]$
where
$V=L\left [\mathcal {U}\right ]$
where
![]() $\mathcal {U}=\left \langle U_{\gamma }\mid \gamma <\chi \right \rangle $
is a sequence of measures on the increasing measurables
$\mathcal {U}=\left \langle U_{\gamma }\mid \gamma <\chi \right \rangle $
is a sequence of measures on the increasing measurables
![]() $\left \langle \kappa ^{\gamma }\mid \gamma <\chi \right \rangle $
where
$\left \langle \kappa ^{\gamma }\mid \gamma <\chi \right \rangle $
where
![]() $\chi <\kappa ^{0}$
. Iterate V according to
$\chi <\kappa ^{0}$
. Iterate V according to
![]() $\mathcal {U}$
where each measurable is iterated
$\mathcal {U}$
where each measurable is iterated
![]() $\omega ^{2}$
many times, to obtain
$\omega ^{2}$
many times, to obtain
![]() $\left \langle M_{\alpha }^{\gamma }\mid \gamma <\chi ,\alpha \leq \omega ^{2}\right \rangle $
, with iteration points
$\left \langle M_{\alpha }^{\gamma }\mid \gamma <\chi ,\alpha \leq \omega ^{2}\right \rangle $
, with iteration points
![]() $\left \langle \kappa _{\alpha }^{\gamma }\mid \gamma <\chi ,\alpha \leq \omega ^{2}\right \rangle $
, and set
$\left \langle \kappa _{\alpha }^{\gamma }\mid \gamma <\chi ,\alpha \leq \omega ^{2}\right \rangle $
, and set
![]() $M^{\chi }$
as the directed limit of this iteration. Let G be generic over V for the forcing adding a Prikry sequence to every
$M^{\chi }$
as the directed limit of this iteration. Let G be generic over V for the forcing adding a Prikry sequence to every
![]() $\kappa ^{\gamma }$
. Set for every
$\kappa ^{\gamma }$
. Set for every
![]() $\gamma <\chi \ E^{\gamma }=\left \langle \kappa _{\omega \cdot n}^{\gamma }\mid 1\leq n<\omega \right \rangle $
and
$\gamma <\chi \ E^{\gamma }=\left \langle \kappa _{\omega \cdot n}^{\gamma }\mid 1\leq n<\omega \right \rangle $
and
![]() $\hat {E}^{\gamma }=\left \langle \kappa _{\omega \cdot n}^{\gamma }\mid 0\leq n<\omega \right \rangle $
then
$\hat {E}^{\gamma }=\left \langle \kappa _{\omega \cdot n}^{\gamma }\mid 0\leq n<\omega \right \rangle $
then
 $$ \begin{align*} \left(C^{*}\right)^{V} & =M^{\chi}\left[\left\langle E^{\gamma}\mid\gamma<\chi\right\rangle \right],\\\left(C^{*}\right)^{V\left[G\right]} & =M^{\chi}[\langle \hat{E}^{\gamma}\mid\gamma<\chi\rangle ]. \end{align*} $$
$$ \begin{align*} \left(C^{*}\right)^{V} & =M^{\chi}\left[\left\langle E^{\gamma}\mid\gamma<\chi\right\rangle \right],\\\left(C^{*}\right)^{V\left[G\right]} & =M^{\chi}[\langle \hat{E}^{\gamma}\mid\gamma<\chi\rangle ]. \end{align*} $$
So, if
![]() $V=L\left [\mathcal {U}\right ]$
as above,
$V=L\left [\mathcal {U}\right ]$
as above,
![]() $C^{*}$
is of the form
$C^{*}$
is of the form
![]() $L\left [\mathcal {U}_{1}\right ]\left [G_{1}\right ]$
for some sequence of measures and a sequence of Prikry sequences on its measures, and so
$L\left [\mathcal {U}_{1}\right ]\left [G_{1}\right ]$
for some sequence of measures and a sequence of Prikry sequences on its measures, and so
![]() $C^{*2}$
is again of that form, where we iterated the measures in
$C^{*2}$
is again of that form, where we iterated the measures in
![]() $\mathcal {U} \ \omega ^{2}\cdot 2$
many times and add Prikry sequences. So again, as we’ve done here, we’ll get that
$\mathcal {U} \ \omega ^{2}\cdot 2$
many times and add Prikry sequences. So again, as we’ve done here, we’ll get that
![]() $C^{*\omega }$
is the intersection of the models
$C^{*\omega }$
is the intersection of the models
![]() $M_{\omega ^{2}\cdot n}^{\chi }$
where we iterated each measure
$M_{\omega ^{2}\cdot n}^{\chi }$
where we iterated each measure
![]() $\omega ^{2}\cdot n$
times. This is due to the facts that changing the order of iteration between the measures doesn’t change the final result, and that the Prikry sequences “fall out” during the intersection. Now, we don’t have a complete analysis of intersections of iterations by more than one measure, but Dehornoy proves the following more general fact:
$\omega ^{2}\cdot n$
times. This is due to the facts that changing the order of iteration between the measures doesn’t change the final result, and that the Prikry sequences “fall out” during the intersection. Now, we don’t have a complete analysis of intersections of iterations by more than one measure, but Dehornoy proves the following more general fact:
Fact 4.3 [Reference Dehornoy3, Section 5.3, Proposition 3].
For every
![]() $\alpha $
let
$\alpha $
let
![]() $N_{\alpha }$
be the
$N_{\alpha }$
be the
![]() $\alpha $
th iteration of V by some measure. Assume
$\alpha $
th iteration of V by some measure. Assume
![]() $\lambda $
is such that for every
$\lambda $
is such that for every
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $N_{\alpha }\vDash \mathrm {cf}(\lambda )=\omega $
but there is no
$N_{\alpha }\vDash \mathrm {cf}(\lambda )=\omega $
but there is no
![]() $\rho $
such that
$\rho $
such that
![]() $\lambda =\rho +\omega $
. Then if M is a transitive inner model of
$\lambda =\rho +\omega $
. Then if M is a transitive inner model of
![]() $\mathrm {ZFC}$
containing
$\mathrm {ZFC}$
containing
![]() $\bigcap _{\alpha <\lambda }N_{\alpha }$
, then there is some
$\bigcap _{\alpha <\lambda }N_{\alpha }$
, then there is some
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $N_{\alpha }\subseteq M$
.
$N_{\alpha }\subseteq M$
.
So, if we take
![]() $N_{\alpha }$
to be the iteration of V by the first measure in
$N_{\alpha }$
to be the iteration of V by the first measure in
![]() $\mathcal {U}$
, we get that
$\mathcal {U}$
, we get that
![]() $C^{*\omega }$
contains
$C^{*\omega }$
contains
![]() $\bigcap _{\alpha <\omega ^{3}}N_{\alpha }$
, but doesn’t contain any
$\bigcap _{\alpha <\omega ^{3}}N_{\alpha }$
, but doesn’t contain any
![]() $N_{\alpha }$
for
$N_{\alpha }$
for
![]() $\alpha <\omega ^{3}$
, so
$\alpha <\omega ^{3}$
, so
![]() $C^{*\omega }$
cannot satisfy
$C^{*\omega }$
cannot satisfy
![]() $\mathrm {AC}$
.
$\mathrm {AC}$
.
Furthermore, a recent result by Welch [Reference Welch11] shows that under the assumption that
![]() $O^{k}$
(O-kukri) doesn’t exist, i.e., there is no elementary embedding of an inner model with a proper class of measurables to itself (and in particular no measurable limit of measurables), the characterization
$O^{k}$
(O-kukri) doesn’t exist, i.e., there is no elementary embedding of an inner model with a proper class of measurables to itself (and in particular no measurable limit of measurables), the characterization
![]() $\left (C^{*}\right )^{V}=M^{\chi }\left [\left \langle E^{\gamma }\mid \gamma <\chi \right \rangle \right ]$
holds for any
$\left (C^{*}\right )^{V}=M^{\chi }\left [\left \langle E^{\gamma }\mid \gamma <\chi \right \rangle \right ]$
holds for any
![]() $\chi \leq \mathbf {Ord}$
, and it seems likely that the analysis of the iterated
$\chi \leq \mathbf {Ord}$
, and it seems likely that the analysis of the iterated
![]() $C^{*}$
will be the same as well. Hence a different approach, or larger cardinals, would be required to answer this question.
$C^{*}$
will be the same as well. Hence a different approach, or larger cardinals, would be required to answer this question.
A different line of inquiry stems from the following fact:
Fact 4.4 [Reference Kennedy, Magidor and Väänänen5].
If there is a proper class of Woodin cardinals then the theory of
![]() $C^{*}$
is unchanged by forcing.
$C^{*}$
is unchanged by forcing.
So the question whether
![]() $C^{*}\vDash V=C^{*}$
cannot be changed under forcing in the presence of class many Woodin cardinals. If the sequence of
$C^{*}\vDash V=C^{*}$
cannot be changed under forcing in the presence of class many Woodin cardinals. If the sequence of
![]() $C^{*\alpha }$
is definable (perhaps up to some ordinal) then this will also be in the theory of
$C^{*\alpha }$
is definable (perhaps up to some ordinal) then this will also be in the theory of
![]() $C^{*}$
(note that on the face of it even the sequence up to
$C^{*}$
(note that on the face of it even the sequence up to
![]() $\omega $
may not be definable).
$\omega $
may not be definable).
Question 4.5. What can be deduced on the sequence of iterated
![]() $C^{*}$
from a proper class of Woodin cardinals?
$C^{*}$
from a proper class of Woodin cardinals?
Acknowledgments
I would like to thank my advisor, Prof. Menachem Magidor, for his guidance and support without which this work would not have been possible. I would also like to thank the anonymous referee for their comments and suggestions.