1. Introduction
Despite their ephemeral nature and apparent fragility, soap bubbles and soap films can withstand large stresses. As first shown by Courbin & Stone (Reference Courbin and Stone2006) and later by Gilet & Bush (Reference Gilet and Bush2009), soap films act as non-linear vertical springs (liquid trampolines) capable of repelling a drop or a particle approaching at low velocity. For more violent impacts, they deform so much that they let the incoming object pass without rupturing (Pan & Law Reference Pan and Law2007; Fell et al. Reference Fell, Sokuler, Lembach, Eibach, Liu, Bonaccurso, Auernhammer and Butt2013). They capture instead a fraction of the particle kinetic energy (Le Goff et al. Reference Le Goff, Courbin, Stone and Quéré2008), making foams capable of stopping projectiles. The transition between bouncing and crossing is governed by the Weber number, which compares the surface energy of the film with the kinetic energy of the particle (Gilet & Bush Reference Gilet and Bush2009). Using this criterion, soap films can be used as liquid sieves, trapping the small and slow objects while allowing the larger and faster ones to pass (Stogin et al. Reference Stogin, Gockowski, Feldstein, Claure, Wang and Wong2018).
Soap films are usually modelled quasi-statically, considering only the effect of surface tension forces: they are often considered and studied as real-life minimal surfaces (Courant Reference Courant1940; Almgren & Taylor Reference Almgren and Taylor1976; Goldstein et al. Reference Goldstein, Moffatt, Pesci and Ricca2010). In presence of a drop or a particle, the expected minimal surface is a catenoid, a geometry that matches relatively well the shape of a film deformed by an impacting object (Gilet & Bush Reference Gilet and Bush2009; Chen et al. Reference Chen, Perera, Jackson, Hallmark and Davidson2019). Experimentally, the weight of the liquid contained in a soap film is not expected to significantly affect its geometry as long as the film dimension does not exceed a characteristic length
![]() $\ell \sim {\gamma }/{(\rho g e)}$
, where
$\ell \sim {\gamma }/{(\rho g e)}$
, where
![]() $\gamma$
is the surface tension of the film,
$\gamma$
is the surface tension of the film,
![]() $e$
its thickness,
$e$
its thickness,
![]() $\rho$
the density of the liquid and
$\rho$
the density of the liquid and
![]() $g$
gravity (Cohen et al. Reference Cohen, Darbois-Texier, Reyssat, Snoeijer, Quéré and Clanet2017). For a film of thickness
$g$
gravity (Cohen et al. Reference Cohen, Darbois-Texier, Reyssat, Snoeijer, Quéré and Clanet2017). For a film of thickness
![]() $e$
= 10
$e$
= 10
![]() $\mu$
m, the length
$\mu$
m, the length
![]() $\ell$
is equal to
$\ell$
is equal to
![]() $30$
cm, which is larger than the films usually studied. Here, we consider the dynamics of a millimetre-sized marble trapped in a 10 centimetre-wide horizontal soap film. For this problem, we evidence in contrast the key role of the intrinsic weight of the film, whose deformation is at the origin of the particle motion. We also focus on the drag force experienced by a bead and evidence the almost equal contributions of air and the film.
$30$
cm, which is larger than the films usually studied. Here, we consider the dynamics of a millimetre-sized marble trapped in a 10 centimetre-wide horizontal soap film. For this problem, we evidence in contrast the key role of the intrinsic weight of the film, whose deformation is at the origin of the particle motion. We also focus on the drag force experienced by a bead and evidence the almost equal contributions of air and the film.
2. Experiment
A soap film with dimensions
![]() $2L \times 2L$
(with 3.3 cm
$2L \times 2L$
(with 3.3 cm
![]() $\leqslant L \leqslant$
5 cm) is produced by dipping a square frame in a soap solution consisting of 5.6 g L–1 of sodium dodecyl sulfate (SDS), 50 mg L–1 of dodecanol in a water–glycerol mixture (15 % of glycerol in volume). The concentration of SDS is more than two times the critical micellar concentration (CMC
$\leqslant L \leqslant$
5 cm) is produced by dipping a square frame in a soap solution consisting of 5.6 g L–1 of sodium dodecyl sulfate (SDS), 50 mg L–1 of dodecanol in a water–glycerol mixture (15 % of glycerol in volume). The concentration of SDS is more than two times the critical micellar concentration (CMC
![]() $_{\textit{SDS}}$
= 2.37 g L–1), and the surface tension of the film is equal to
$_{\textit{SDS}}$
= 2.37 g L–1), and the surface tension of the film is equal to
![]() $\gamma$
= 33.2
$\gamma$
= 33.2
![]() $\pm$
0.1 mN m–1. Glycerol is used to reduce evaporation so that a film lasts 1–3 min before rupture. To ensure the repeatability of the experiments, the frame is removed from the bath at a constant velocity
$\pm$
0.1 mN m–1. Glycerol is used to reduce evaporation so that a film lasts 1–3 min before rupture. To ensure the repeatability of the experiments, the frame is removed from the bath at a constant velocity
![]() $V_{\textit{motor}}$
using a motorised stage. The thickness
$V_{\textit{motor}}$
using a motorised stage. The thickness
![]() $e$
of the film is calibrated as a function of
$e$
of the film is calibrated as a function of
![]() $V_{\textit{motor}}$
, by puncturing the film and following the growth of the hole with a high-speed camera (Phantom Miro LAB3a10) at 6000 f.p.s. The opening velocity
$V_{\textit{motor}}$
, by puncturing the film and following the growth of the hole with a high-speed camera (Phantom Miro LAB3a10) at 6000 f.p.s. The opening velocity
![]() $V$
is related to
$V$
is related to
![]() $e$
by the Taylor–Culick law:
$e$
by the Taylor–Culick law:
![]() $e = 2 \gamma/ (\rho V^2)$
(Taylor Reference Taylor1959; Culick Reference Culick1960), with
$e = 2 \gamma/ (\rho V^2)$
(Taylor Reference Taylor1959; Culick Reference Culick1960), with
![]() $\rho \simeq 1042$
kg m–
$\rho \simeq 1042$
kg m–
![]() $^3$
the density of the soap solution. The film thickness
$^3$
the density of the soap solution. The film thickness
![]() $e$
is thus varied in a controlled manner between 3 and 25
$e$
is thus varied in a controlled manner between 3 and 25
![]() $\mu$
m, with an error of 15 %. In almost all experiments,
$\mu$
m, with an error of 15 %. In almost all experiments,
![]() $V_{\textit{motor}}$
= 20 cm s–1 and a film thickness
$V_{\textit{motor}}$
= 20 cm s–1 and a film thickness
![]() $e$
=
$e$
=
![]() $9.8 \pm 1.4$
$9.8 \pm 1.4$
![]() $\mu$
m is expected. Approximately 10 s after the film fabrication, a millimetre-sized particle (Silibeads from Sigmund Lindner) with radius
$\mu$
m is expected. Approximately 10 s after the film fabrication, a millimetre-sized particle (Silibeads from Sigmund Lindner) with radius
![]() $R_b$
(250
$R_b$
(250
![]() $\mu$
m
$\mu$
m
![]() $\leqslant R_{{b}} \leqslant$
750
$\leqslant R_{{b}} \leqslant$
750
![]() $\mu$
m), mass
$\mu$
m), mass
![]() $m_{{b}}$
and density
$m_{{b}}$
and density
![]() $\rho _b$
(2580 kg m–
$\rho _b$
(2580 kg m–
![]() $^3$
$^3$
![]() $\leqslant \rho _b \leqslant$
9200 kg m–
$\leqslant \rho _b \leqslant$
9200 kg m–
![]() $^3$
) is deposited in the film, a few centimetres from the centre (figure 1
a). The particle is initially wet by the soap solution, so that it is held in the film after its release. It is thus surrounded by a meniscus whose height and width increase with time as the liquid in the film is drained towards the bead by capillary suction (Aradian, Raphaël & de Gennes Reference Aradian, Raphaël and de Gennes2001; Guo et al. Reference Guo, Xu, Qian, Di, Doi and Tong2019). For a given extension
$^3$
) is deposited in the film, a few centimetres from the centre (figure 1
a). The particle is initially wet by the soap solution, so that it is held in the film after its release. It is thus surrounded by a meniscus whose height and width increase with time as the liquid in the film is drained towards the bead by capillary suction (Aradian, Raphaël & de Gennes Reference Aradian, Raphaël and de Gennes2001; Guo et al. Reference Guo, Xu, Qian, Di, Doi and Tong2019). For a given extension
![]() $R$
of the meniscus (relative to the centre of the particle), the shape of the meniscus is fully determined using the model of Orr, Scriven & Rivas (Reference Orr, Scriven and Rivas1975) (see figure 5
a in Appendix A). The volume and mass of the meniscus can thus be calculated exactly.
$R$
of the meniscus (relative to the centre of the particle), the shape of the meniscus is fully determined using the model of Orr, Scriven & Rivas (Reference Orr, Scriven and Rivas1975) (see figure 5
a in Appendix A). The volume and mass of the meniscus can thus be calculated exactly.
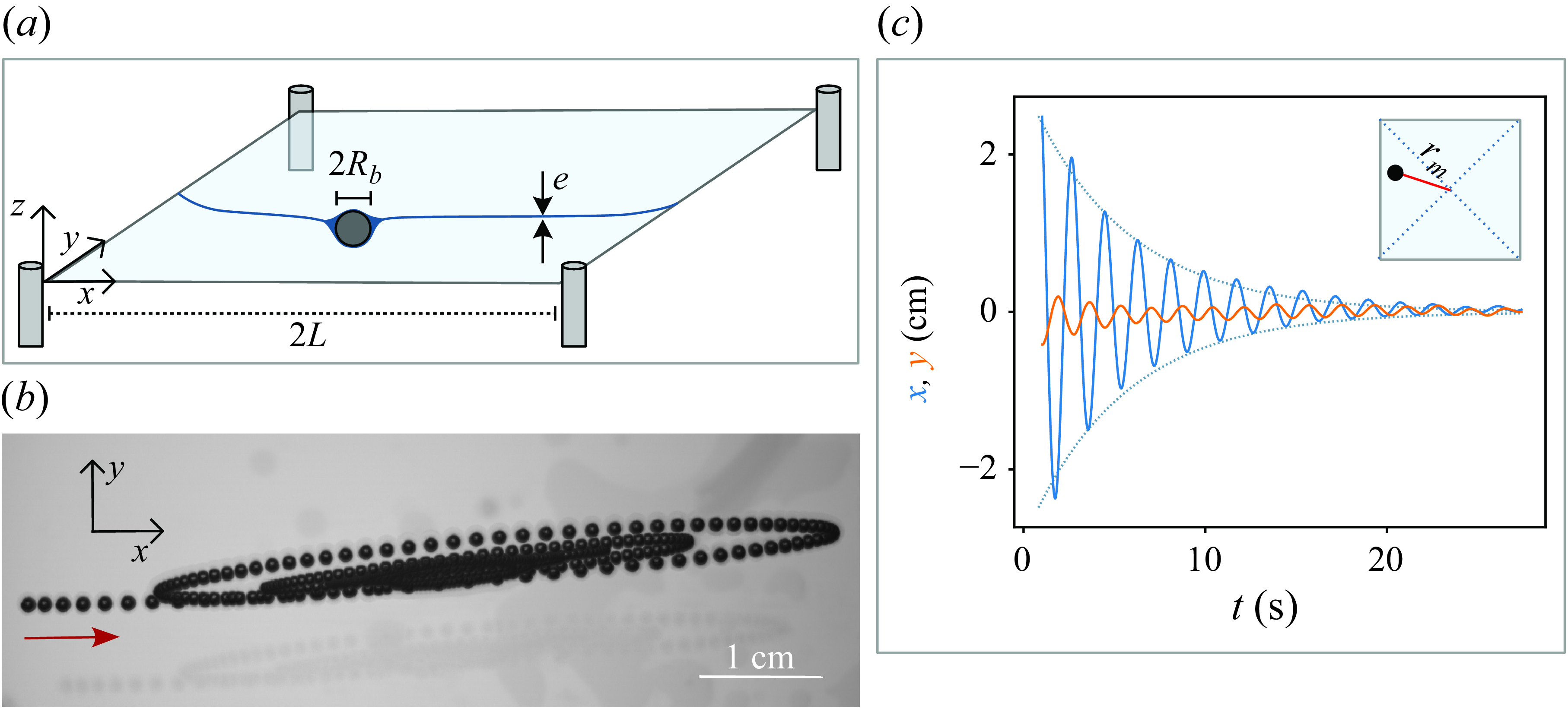
Figure 1. (a) A bead with radius
![]() $R_{{b}}$
is deposited in a square soap film of size 2L
$R_{{b}}$
is deposited in a square soap film of size 2L
![]() $\sim$
10 cm and thickness
$\sim$
10 cm and thickness
![]() $e \sim$
10
$e \sim$
10
![]() $\mu$
m. (b) Top view. Chronophotography showing the trajectory of a bead of mass
$\mu$
m. (b) Top view. Chronophotography showing the trajectory of a bead of mass
![]() $m_{{b}}$
= 3.7 mg (effective mass
$m_{{b}}$
= 3.7 mg (effective mass
![]() $m$
= 4.41 mg) and radius
$m$
= 4.41 mg) and radius
![]() $R_b$
= 0.5 mm within the film, as seen from the top. Two different images of the particle are separated by 20 ms. (c) Position (
$R_b$
= 0.5 mm within the film, as seen from the top. Two different images of the particle are separated by 20 ms. (c) Position (
![]() $x,y$
) of the particle relative to the centre of the film as a function of time
$x,y$
) of the particle relative to the centre of the film as a function of time
![]() $t$
. It follows closely what is expected from a damped harmonic oscillator, with a pseudo-pulsation
$t$
. It follows closely what is expected from a damped harmonic oscillator, with a pseudo-pulsation
![]() $\omega = 3.4 \pm 0.1$
s
$\omega = 3.4 \pm 0.1$
s
![]() $^{-1}$
, and an exponentially decaying envelop (dotted line)
$^{-1}$
, and an exponentially decaying envelop (dotted line)
![]() $A\,e^{-t/\tau }$
, with
$A\,e^{-t/\tau }$
, with
![]() $A = 2.9 \pm 0.1$
cm and
$A = 2.9 \pm 0.1$
cm and
![]() $\tau = 5.4 \pm 0.2$
s.
$\tau = 5.4 \pm 0.2$
s.
Figure 1(b) illustrates the motion of a particle with radius
![]() $R_b$
= 0.5 mm and mass
$R_b$
= 0.5 mm and mass
![]() $m_b = 3.7$
mg after its release in the film without initial velocity. The bead spontaneously slides towards the centre of the film, following a very flattened spiral trajectory (see also supplementary movie 1 at https://doi.org/10.1017/jfm.2025.157). The positions
$m_b = 3.7$
mg after its release in the film without initial velocity. The bead spontaneously slides towards the centre of the film, following a very flattened spiral trajectory (see also supplementary movie 1 at https://doi.org/10.1017/jfm.2025.157). The positions
![]() $x$
and
$x$
and
![]() $y$
of the particle, relative to the film centre, are plotted in blue and orange in figure 1(c) as a function of time
$y$
of the particle, relative to the film centre, are plotted in blue and orange in figure 1(c) as a function of time
![]() $t$
. They exhibit damped harmonic oscillations with a nearly identical period but different amplitudes, due to the nature of the trajectory. The position of the particle along the primary direction of the spiral is fitted by a damped sinusoidal function of the form
$t$
. They exhibit damped harmonic oscillations with a nearly identical period but different amplitudes, due to the nature of the trajectory. The position of the particle along the primary direction of the spiral is fitted by a damped sinusoidal function of the form
![]() $A \exp (-t/\tau )\sin (\omega t+\phi )$
, with
$A \exp (-t/\tau )\sin (\omega t+\phi )$
, with
![]() $A$
and
$A$
and
![]() $\phi$
two constants. In figure 1(c), the pseudo-pulsation is
$\phi$
two constants. In figure 1(c), the pseudo-pulsation is
![]() $\omega = 3.4 \pm 0.1$
s
$\omega = 3.4 \pm 0.1$
s
![]() $^{-1}$
and the characteristic time of the exponential envelope (shown with a dotted line) is
$^{-1}$
and the characteristic time of the exponential envelope (shown with a dotted line) is
![]() $\tau = 5.4 \pm 0.2$
s. Damped oscillations are observed for all the particles that were tested (e.g. see supplementary movies 2 and 3). Their presence indicate that, at the dominant order, the particle is (i) driven by a spring-like force
$\tau = 5.4 \pm 0.2$
s. Damped oscillations are observed for all the particles that were tested (e.g. see supplementary movies 2 and 3). Their presence indicate that, at the dominant order, the particle is (i) driven by a spring-like force
![]() $\boldsymbol {F} = -k(\boldsymbol {x}+\boldsymbol {y}) = -k\boldsymbol {r_{{m}}}$
(with
$\boldsymbol {F} = -k(\boldsymbol {x}+\boldsymbol {y}) = -k\boldsymbol {r_{{m}}}$
(with
![]() $k$
the spring constant and
$k$
the spring constant and
![]() $\boldsymbol {r_{{m}}}$
the radial distance between the bead and the film centres) and (ii) slowed down by a viscous drag force
$\boldsymbol {r_{{m}}}$
the radial distance between the bead and the film centres) and (ii) slowed down by a viscous drag force
![]() $\boldsymbol {F}_{\textit{friction}} = -\alpha \boldsymbol {v}$
(with
$\boldsymbol {F}_{\textit{friction}} = -\alpha \boldsymbol {v}$
(with
![]() $\alpha$
the friction coefficient and
$\alpha$
the friction coefficient and
![]() $\boldsymbol {v}$
the particle velocity). The friction coefficient
$\boldsymbol {v}$
the particle velocity). The friction coefficient
![]() $\alpha = {2m}/{\tau }$
and the spring constant
$\alpha = {2m}/{\tau }$
and the spring constant
![]() $k = m [\omega^2 + (1/\tau^2)]$
are deduced from
$k = m [\omega^2 + (1/\tau^2)]$
are deduced from
![]() $\omega$
and
$\omega$
and
![]() $\tau$
using a damped harmonic oscillator model. Here
$\tau$
using a damped harmonic oscillator model. Here
![]() $m$
is the effective mass of the moving object, taking into account the added mass of the meniscus around the particle.
$m$
is the effective mass of the moving object, taking into account the added mass of the meniscus around the particle.
With the reflective lighting used here (where the soap film acts as a mirror reflecting light to the camera), the meniscus appears as a darker area surrounding the particle in the top-view images. Its size
![]() $R$
increases over the course of the oscillations from
$R$
increases over the course of the oscillations from
![]() $R = 2.05\,R_{{b}}$
(relative to the centre of the particle) at
$R = 2.05\,R_{{b}}$
(relative to the centre of the particle) at
![]() $t = 0$
to
$t = 0$
to
![]() $3.63\,R_{{b}}$
after 30 s in figure 1(b). The curve
$3.63\,R_{{b}}$
after 30 s in figure 1(b). The curve
![]() $R(t)$
is presented in figure 5(b) (Appendix A). The density of the particles being significantly higher than that of the film, the meniscus growth causes a modest variation of the effective mass
$R(t)$
is presented in figure 5(b) (Appendix A). The density of the particles being significantly higher than that of the film, the meniscus growth causes a modest variation of the effective mass
![]() $m$
with time: in figure 1(b) (and later in figure 5
b),
$m$
with time: in figure 1(b) (and later in figure 5
b),
![]() $m$
varies from
$m$
varies from
![]() $1.08\,m_{{b}}$
at
$1.08\,m_{{b}}$
at
![]() $t = 0$
to
$t = 0$
to
![]() $1.24\,m_{{b}}$
at t = 30 s. Experimentally,
$1.24\,m_{{b}}$
at t = 30 s. Experimentally,
![]() $\alpha$
and
$\alpha$
and
![]() $k$
are calculated from a fit over the duration of the oscillations: the value obtained is therefore a time average between the start and end of the oscillations. For this reason, we also use an average effective mass
$k$
are calculated from a fit over the duration of the oscillations: the value obtained is therefore a time average between the start and end of the oscillations. For this reason, we also use an average effective mass
![]() $m$
for the moving object. In practise,
$m$
for the moving object. In practise,
![]() $m$
is measured at a time
$m$
is measured at a time
![]() $t = 2.5 \tau$
, corresponding to half of the oscillation duration (green dotted line in Appendix A, figure 5
b). As shown later in figure 5(c),
$t = 2.5 \tau$
, corresponding to half of the oscillation duration (green dotted line in Appendix A, figure 5
b). As shown later in figure 5(c),
![]() $m$
is typically 20 % higher than the mass
$m$
is typically 20 % higher than the mass
![]() $m_{{b}}$
of the particle alone.
$m_{{b}}$
of the particle alone.
In the rest of the paper, we systematically take into account the added mass of the meniscus and use the effective mass
![]() $m$
for the particle.
$m$
for the particle.
To model the particle dynamics, we first study in § 3 the film deformation, which is then used in § 4 to model the spring force. In § 5, we finally characterise the friction force.
3. Film deformation by a static particle
The film deformation is observed from the side using a back-light illumination. The light source (a square LED light of width 50 cm and height 25 cm) is placed 2 m away from the film, and a vertical plate with a slit of height 1 cm is positioned a few centimetres in front of the frame. This set-up ensures that the incident light rays on the film are almost parallel, with a variation of incident angles smaller than 3 degrees. The soap film, consisting of two parallel interfaces, does not deflect the light. However, a large majority of the light intensity is reflected when the film is illuminated by a grazing light: a darker area is then visible on the camera sensor, corresponding to the projection of the film shape in the
![]() $(y,z)$
plane. The frame used here is a nylon wire of diameter 120
$(y,z)$
plane. The frame used here is a nylon wire of diameter 120
![]() $\mu$
m held between four vertical posts. It appears as a fuzzy grey line of width 220
$\mu$
m held between four vertical posts. It appears as a fuzzy grey line of width 220
![]() $\mu$
m. It is shown (in absence of a film) in the inset of figure 2(a) (red rectangle), with the same scale and position as the rest of the picture.
$\mu$
m. It is shown (in absence of a film) in the inset of figure 2(a) (red rectangle), with the same scale and position as the rest of the picture.
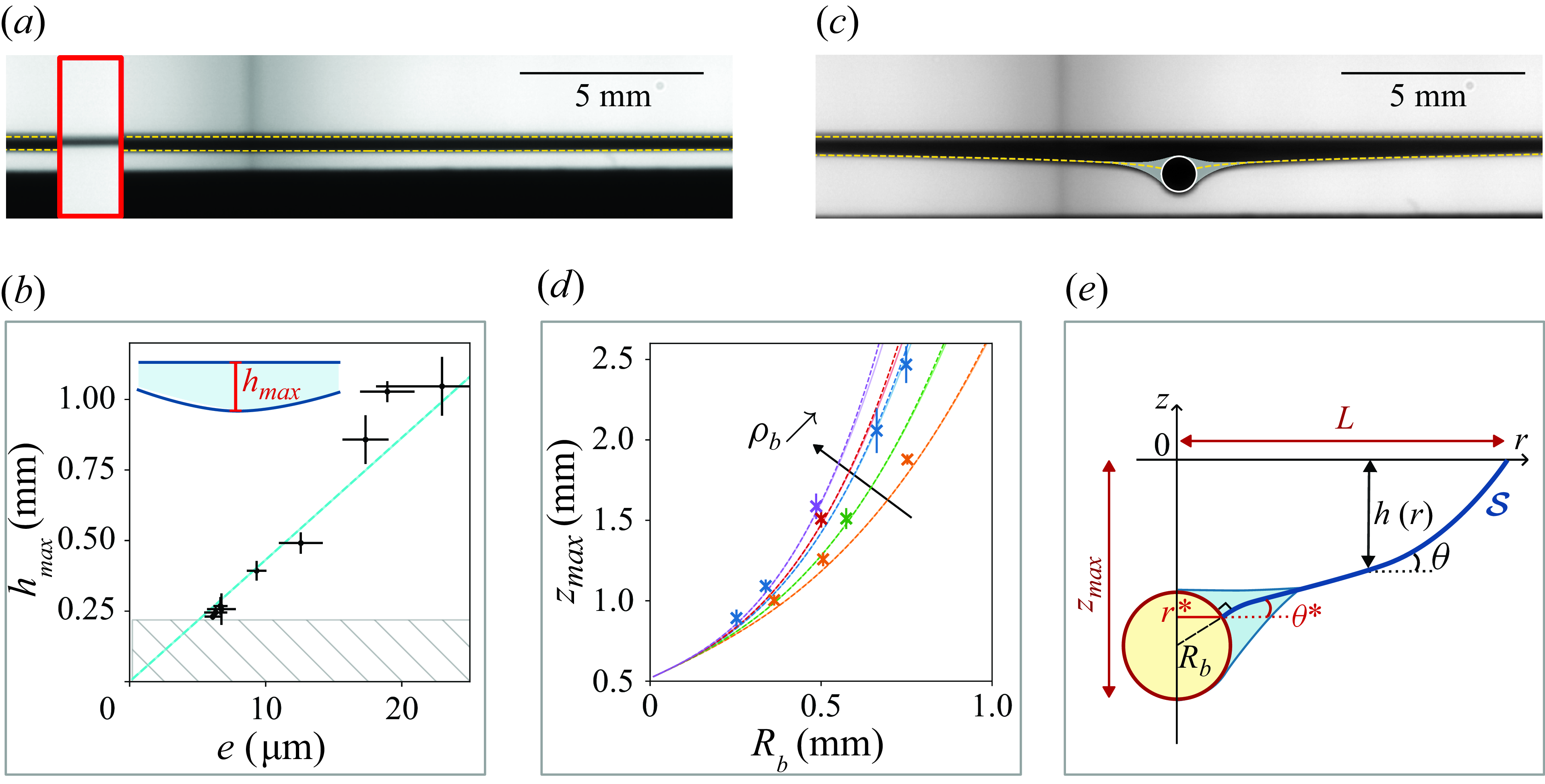
Figure 2. (a) Side-view image of a soap film attached to a frame of size
![]() $2L$
= 6.7 cm, evidencing the film deformation under its weight. The dotted line is the full numerical solution of the film shape. The inset (in red) is a picture of the frame without the film. (b) Maximum deformation
$2L$
= 6.7 cm, evidencing the film deformation under its weight. The dotted line is the full numerical solution of the film shape. The inset (in red) is a picture of the frame without the film. (b) Maximum deformation
![]() $h_{\textit{max}}$
of the film as a function of its thickness
$h_{\textit{max}}$
of the film as a function of its thickness
![]() $e$
. The hatched area is a region where
$e$
. The hatched area is a region where
![]() $h_{\textit{max}}$
cannot be measured. Equation (3.3) is shown with a continuous line; the numerical solution is a perfectly superposed dotted line. (c) Deformation of the film in the presence of a marble of radius
$h_{\textit{max}}$
cannot be measured. Equation (3.3) is shown with a continuous line; the numerical solution is a perfectly superposed dotted line. (c) Deformation of the film in the presence of a marble of radius
![]() $R_{{b}}$
= 0.5 mm (with theoretical position shown with a white circle). The dotted line is the numerical solution of the film shape; the meniscus shape is added in grey. (d) Maximum deformation
$R_{{b}}$
= 0.5 mm (with theoretical position shown with a white circle). The dotted line is the numerical solution of the film shape; the meniscus shape is added in grey. (d) Maximum deformation
![]() $z_{\textit{max}}$
as a function of
$z_{\textit{max}}$
as a function of
![]() $R_{{b}}$
. The experiments are shown with crosses, for varying
$R_{{b}}$
. The experiments are shown with crosses, for varying
![]() $\rho _{{b}}$
: 2580 kg m–
$\rho _{{b}}$
: 2580 kg m–
![]() $^3$
(orange), 4100 kg m–
$^3$
(orange), 4100 kg m–
![]() $^3$
(green), 6300 kg m–
$^3$
(green), 6300 kg m–
![]() $^3$
(blue), 7100 kg m–
$^3$
(blue), 7100 kg m–
![]() $^3$
(red) and 9200 kg m–
$^3$
(red) and 9200 kg m–
![]() $^3$
(purple) and compared with 3.4 (continuous lines). The numerical solution is shown with a dotted line. The best fit is obtained for
$^3$
(purple) and compared with 3.4 (continuous lines). The numerical solution is shown with a dotted line. The best fit is obtained for
![]() $e = 12$
$e = 12$
![]() $\mu$
m. (e) Notations used to model the film shape.
$\mu$
m. (e) Notations used to model the film shape.
Figure 2(a) shows an image of a film of size
![]() $2L$
= 6.7 cm obtained with this method (the black area below the film is the edge of the slit). The dark region induced by the reflection of the ray lights on the film is
$2L$
= 6.7 cm obtained with this method (the black area below the film is the edge of the slit). The dark region induced by the reflection of the ray lights on the film is
![]() $393\pm 35$
$393\pm 35$
![]() $\mu$
m thick: it is much larger than the film thickness (
$\mu$
m thick: it is much larger than the film thickness (
![]() $e$
= 10
$e$
= 10
![]() $\mu$
m) or the apparent frame diameter (red inset), indicating that the film is deflected. In figure 2(b), the maximum deflection of the film
$\mu$
m) or the apparent frame diameter (red inset), indicating that the film is deflected. In figure 2(b), the maximum deflection of the film
![]() $h_{\textit{max}}$
is measured for various film thicknesses
$h_{\textit{max}}$
is measured for various film thicknesses
![]() $e$
, obtained by puncturing the film. The error bars show the standard deviation of 10 experiments, and the hatched area indicates the region where the film shadow is smaller than the apparent diameter of the frame. The amplitude of the deflection
$e$
, obtained by puncturing the film. The error bars show the standard deviation of 10 experiments, and the hatched area indicates the region where the film shadow is smaller than the apparent diameter of the frame. The amplitude of the deflection
![]() $h_{\textit{max}}$
increases linearly with
$h_{\textit{max}}$
increases linearly with
![]() $e$
; it reaches 1 mm for the thicker films (
$e$
; it reaches 1 mm for the thicker films (
![]() $e$
= 23
$e$
= 23
![]() $\mu$
m). Figure 2(c) is a picture of the film of figure 2(a), now holding a marble of radius
$\mu$
m). Figure 2(c) is a picture of the film of figure 2(a), now holding a marble of radius
![]() $R_{{b}} = 0.5$
mm and density
$R_{{b}} = 0.5$
mm and density
![]() $\rho _b$
= 9200 kg m–
$\rho _b$
= 9200 kg m–
![]() $^3$
(which theoretical position is highlighted by a white circle). The marble induces an additional deformation of the order of the initial film deflection. To characterise it, we plot in figure 2(d) the maximum deflection
$^3$
(which theoretical position is highlighted by a white circle). The marble induces an additional deformation of the order of the initial film deflection. To characterise it, we plot in figure 2(d) the maximum deflection
![]() $z_{\textit{max}}$
measured as the distance between the top of the film and the bottom of the marble. We vary both the bead radius
$z_{\textit{max}}$
measured as the distance between the top of the film and the bottom of the marble. We vary both the bead radius
![]() $R_{{b}}$
and its density
$R_{{b}}$
and its density
![]() $\rho _b$
. The crosses are the experimental measurements, and the dotted lines show (3.4). The deflection
$\rho _b$
. The crosses are the experimental measurements, and the dotted lines show (3.4). The deflection
![]() $z_{\textit{max}}$
increases both with
$z_{\textit{max}}$
increases both with
![]() $R_{{b}}$
and
$R_{{b}}$
and
![]() $\rho _b$
, with an offset of 530
$\rho _b$
, with an offset of 530
![]() $\mu$
m for
$\mu$
m for
![]() $R_{{b}} = 0$
associated with the film deformation in absence of a particle.
$R_{{b}} = 0$
associated with the film deformation in absence of a particle.
The film geometry is determined using an axisymmetric model, thus assuming a circular frame. The film height is noted
![]() $h(r)$
with
$h(r)$
with
![]() $r$
the distance to the centre of the film in cylindrical coordinates, in the (
$r$
the distance to the centre of the film in cylindrical coordinates, in the (
![]() $x,y$
) plane of the frame. The film is identified with the surface
$x,y$
) plane of the frame. The film is identified with the surface
![]() $\mathcal{S}$
given by
$\mathcal{S}$
given by
![]() $z=h(r)$
(see figure 2(e) for a definition of the variables). Close to the bead, the two film interfaces separate to form a meniscus: in that region,
$z=h(r)$
(see figure 2(e) for a definition of the variables). Close to the bead, the two film interfaces separate to form a meniscus: in that region,
![]() $\mathcal{S}$
(shown as a dark blue line in figure 2
e) is the midsurface between the two interfaces. As the particle is entirely wet,
$\mathcal{S}$
(shown as a dark blue line in figure 2
e) is the midsurface between the two interfaces. As the particle is entirely wet,
![]() $\mathcal{S}$
is perpendicular to the solid along the contact line, located at
$\mathcal{S}$
is perpendicular to the solid along the contact line, located at
![]() $r = r^* = R_{{b}}\cos \theta ^*$
, with
$r = r^* = R_{{b}}\cos \theta ^*$
, with
![]() $\theta ^*$
the angle between the normal to the particle and the horizontal at the contact line. Here
$\theta ^*$
the angle between the normal to the particle and the horizontal at the contact line. Here
![]() $\theta ^*$
is given by the vertical equilibrium between the surface tension force and the particle’s weight:
$\theta ^*$
is given by the vertical equilibrium between the surface tension force and the particle’s weight:
![]() $2 \times 2 \pi \gamma r^* \sin \theta ^* = mg$
so that
$2 \times 2 \pi \gamma r^* \sin \theta ^* = mg$
so that
![]() $\sin (2\theta ^*) = {mg}/{(2\pi \gamma R_{{b}})}$
. The condition
$\sin (2\theta ^*) = {mg}/{(2\pi \gamma R_{{b}})}$
. The condition
![]() $\sin (2\theta ^*) \leqslant 1$
sets the criteria at which a particle of mass
$\sin (2\theta ^*) \leqslant 1$
sets the criteria at which a particle of mass
![]() $m$
(density
$m$
(density
![]() $\rho _b$
) and radius
$\rho _b$
) and radius
![]() $R_{{b}}$
can be held within the soap film. For
$R_{{b}}$
can be held within the soap film. For
![]() $\rho _{{b}} = 6300$
kg m–
$\rho _{{b}} = 6300$
kg m–
![]() $^3$
, the critical bead radius predicted by the theory is
$^3$
, the critical bead radius predicted by the theory is
![]() $R_{{c,th}} = 0.90$
mm. This is consistent with our experimental observations, where 0.75
$R_{{c,th}} = 0.90$
mm. This is consistent with our experimental observations, where 0.75
![]() $\lt R_c\lt$
1.05 mm.
$\lt R_c\lt$
1.05 mm.
The film shape
![]() $h(r)$
is determined by the force balance on a film element, projected on its normal, where the Laplace pressure due to the two curved liquid interfaces
$h(r)$
is determined by the force balance on a film element, projected on its normal, where the Laplace pressure due to the two curved liquid interfaces
![]() $2\gamma \kappa$
(with
$2\gamma \kappa$
(with
![]() $\kappa$
the local curvature of the film) balances that of the weight of the film
$\kappa$
the local curvature of the film) balances that of the weight of the film
![]() $\rho g e \cos \theta$
(with
$\rho g e \cos \theta$
(with
![]() $\theta$
the angle between the tangent to the film and the horizontal, or equivalently between the normal to the film and the horizontal). The equation
$\theta$
the angle between the tangent to the film and the horizontal, or equivalently between the normal to the film and the horizontal). The equation
![]() $\kappa = \rho g e \cos \theta /(2\gamma )$
is solved numerically using the same parametrisation as Cohen et al. (Reference Cohen, Darbois-Texier, Reyssat, Snoeijer, Quéré and Clanet2017), and the predicted film shape is shown with dotted lines in figures 2(a) and 2(c). It matches well the film distortion, with the film thickness as an adjustable parameter. The best fit is obtained for
$\kappa = \rho g e \cos \theta /(2\gamma )$
is solved numerically using the same parametrisation as Cohen et al. (Reference Cohen, Darbois-Texier, Reyssat, Snoeijer, Quéré and Clanet2017), and the predicted film shape is shown with dotted lines in figures 2(a) and 2(c). It matches well the film distortion, with the film thickness as an adjustable parameter. The best fit is obtained for
![]() $e = 11$
$e = 11$
![]() $\mu$
m, which corresponds to the film calibration:
$\mu$
m, which corresponds to the film calibration:
![]() $e = 9.8 \pm 1.4$
$e = 9.8 \pm 1.4$
![]() $\mu$
m. In our experiments,
$\mu$
m. In our experiments,
![]() $\|\boldsymbol {\nabla } h\| \sim h_{\textit{max}}/L \simeq 10^{-2}\,\ll \,1$
, meaning that the problem can be simplified to a small deflection situation and solved analytically. The curvature of the film is then
$\|\boldsymbol {\nabla } h\| \sim h_{\textit{max}}/L \simeq 10^{-2}\,\ll \,1$
, meaning that the problem can be simplified to a small deflection situation and solved analytically. The curvature of the film is then
![]() $\kappa = \Delta h$
and
$\kappa = \Delta h$
and
![]() $\cos \theta \simeq 1$
so that
$\cos \theta \simeq 1$
so that
![]() $h(r)$
is the solution of
$h(r)$
is the solution of
For a particle placed at the centre of the film, (3.1) is solved with the following constraints: (i) the film is attached to the frame, so that
![]() $h = 0$
in
$h = 0$
in
![]() $r = L$
and (ii) it is attached to the particle in
$r = L$
and (ii) it is attached to the particle in
![]() $r = r^* = R_{{b}}\cos \theta ^* = R_{{b}}$
. For small deflections, the attachment condition simplifies to
$r = r^* = R_{{b}}\cos \theta ^* = R_{{b}}$
. For small deflections, the attachment condition simplifies to
![]() ${\mathrm {d} h}/{\mathrm {d} r}|_{r = R_{\textrm {b}}} = \theta ^* = {mg}/{(4 \pi \gamma R_{{b}})}$
. The physical boundary condition of a
${\mathrm {d} h}/{\mathrm {d} r}|_{r = R_{\textrm {b}}} = \theta ^* = {mg}/{(4 \pi \gamma R_{{b}})}$
. The physical boundary condition of a
![]() $\pi /2$
contact angle between the mid plane of the film and the bead is replaced in this limit by a condition of contact along the bead diameter at a free angle; an approximation that we will keep in the following models. The film shape is then
$\pi /2$
contact angle between the mid plane of the film and the bead is replaced in this limit by a condition of contact along the bead diameter at a free angle; an approximation that we will keep in the following models. The film shape is then
with the approximation that
![]() $\rho \pi R_{{b}}^2 e \ll m$
. Due to the linearity of (3.1),
$\rho \pi R_{{b}}^2 e \ll m$
. Due to the linearity of (3.1),
![]() $h(r)$
is the sum of a logarithmic deformation caused by the particle mass and a parabolic deformation due to the film mass. The maximum deflection of the film is then deduced directly from (3.2):
$h(r)$
is the sum of a logarithmic deformation caused by the particle mass and a parabolic deformation due to the film mass. The maximum deflection of the film is then deduced directly from (3.2):
Equation 3.3 is shown with a continuous line in figure 2(b): the small deflection approximation perfectly overlaps the complete numerical solution of the problem (dotted line). It also fits the experimental measurements without an adjustable parameter. A good fit between (3.4) (continuous line) and the experiments is also observed in figure 2(d). A small difference between the linearised solution and the complete numerical solution (dotted lines) is visible for the largest
![]() $R_{{b}}$
, but it remains much smaller than the experimental error bars. Here, the best fitting parameter is
$R_{{b}}$
, but it remains much smaller than the experimental error bars. Here, the best fitting parameter is
![]() $e$
= 12
$e$
= 12
![]() $\mu$
m, a value close to the calibration of the film thickness.
$\mu$
m, a value close to the calibration of the film thickness.
4. Film force on a bead
The force exerted by the film on the bead can be decomposed into two components. The vertical component,
![]() $F_{\perp }$
, holds the particle in the film by counterbalancing its weight:
$F_{\perp }$
, holds the particle in the film by counterbalancing its weight:
![]() $F_{\perp } = mg$
. The in-plane component,
$F_{\perp } = mg$
. The in-plane component,
![]() $F$
, drives the motion of the particle (figure 1
b). In the following, we focus the characteristics of the in-plane force,
$F$
, drives the motion of the particle (figure 1
b). In the following, we focus the characteristics of the in-plane force,
![]() $F$
.
$F$
.
The force
![]() $F$
is first measured in static conditions, by tilting the frame at an angle
$F$
is first measured in static conditions, by tilting the frame at an angle
![]() $\beta$
. Here,
$\beta$
. Here,
![]() $\beta$
is kept small enough (below one degree) that, in the absence of a particle, the film retains its parabolic shape. When the frame is tilted, the particle stabilises at a position
$\beta$
is kept small enough (below one degree) that, in the absence of a particle, the film retains its parabolic shape. When the frame is tilted, the particle stabilises at a position
![]() $r_{{m}}$
where the film force
$r_{{m}}$
where the film force
![]() $F$
balances the projection of the weight of the particle in the (
$F$
balances the projection of the weight of the particle in the (
![]() $x,y$
) plane
$x,y$
) plane
![]() $m g \sin \beta$
(see the inset of figure 3
a). In figure 3(a), the equilibrium position
$m g \sin \beta$
(see the inset of figure 3
a). In figure 3(a), the equilibrium position
![]() $r_{{m}}$
is plotted as a function of the tilt angle
$r_{{m}}$
is plotted as a function of the tilt angle
![]() $\sin \beta$
for three beads with effective mass
$\sin \beta$
for three beads with effective mass
![]() $m$
= 0.75 mg (blue),
$m$
= 0.75 mg (blue),
![]() $m$
= 2.05 mg (orange) and
$m$
= 2.05 mg (orange) and
![]() $m$
= 5.04 mg (green). The equilibrium position of the particle does not depend on
$m$
= 5.04 mg (green). The equilibrium position of the particle does not depend on
![]() $m$
, as evidenced by the collapse of the data. In addition,
$m$
, as evidenced by the collapse of the data. In addition,
![]() $r_{{m}}$
increases linearly with
$r_{{m}}$
increases linearly with
![]() $\sin \beta$
, which indicates that the in-plane film force on the bead,
$\sin \beta$
, which indicates that the in-plane film force on the bead,
![]() $F = mg\sin \beta$
, is linear in the domain where it is measured (75 % of the width of the frame). This is consistent with the particle dynamics in a horizontal frame, where a linear spring force
$F = mg\sin \beta$
, is linear in the domain where it is measured (75 % of the width of the frame). This is consistent with the particle dynamics in a horizontal frame, where a linear spring force
![]() $F = k r_{{m}}$
is deduced from damped harmonic oscillations. In figure 3(b), the spring coefficient
$F = k r_{{m}}$
is deduced from damped harmonic oscillations. In figure 3(b), the spring coefficient
![]() $k$
is plotted as a function of the effective mass
$k$
is plotted as a function of the effective mass
![]() $m$
. Here,
$m$
. Here,
![]() $k$
is determined from tilting the film (blue dots) and from the particle oscillations (red dots). In both cases,
$k$
is determined from tilting the film (blue dots) and from the particle oscillations (red dots). In both cases,
![]() $k$
increases linearly with
$k$
increases linearly with
![]() $m$
(which is varied by a factor
$m$
(which is varied by a factor
![]() $\simeq$
20 between 0.5 mg and 13.4 mg). Note that two different frames are used in these experiments (a nylon wire frame of size
$\simeq$
20 between 0.5 mg and 13.4 mg). Note that two different frames are used in these experiments (a nylon wire frame of size
![]() $2L = 6.7$
cm for the blue points and a 2 mm thick frame with
$2L = 6.7$
cm for the blue points and a 2 mm thick frame with
![]() $2L = 10$
cm for the red points), so that the exact values of
$2L = 10$
cm for the red points), so that the exact values of
![]() $k$
cannot be directly compared.
$k$
cannot be directly compared.
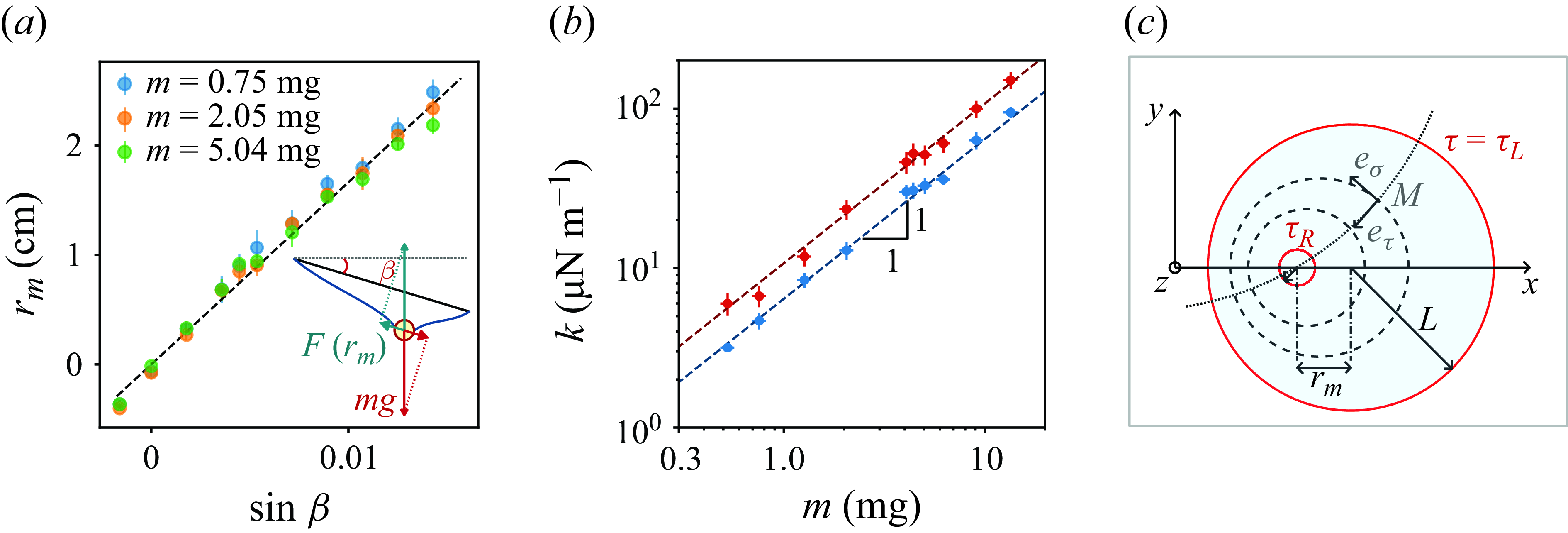
Figure 3. (a) Equilibrium position
![]() $r_{{m}}$
of the particle as a function of the tilt angle
$r_{{m}}$
of the particle as a function of the tilt angle
![]() $\sin \beta$
. The experiments are shown with dots (blue,
$\sin \beta$
. The experiments are shown with dots (blue,
![]() $m=0.75$
mg; orange,
$m=0.75$
mg; orange,
![]() $m=2.05$
mg; green,
$m=2.05$
mg; green,
![]() $m=5.04$
mg); the error bars are the standard deviation of 10 measurements. The dotted line shows (4.1), with fitting parameter
$m=5.04$
mg); the error bars are the standard deviation of 10 measurements. The dotted line shows (4.1), with fitting parameter
![]() $e=8.0$
$e=8.0$
![]() $\mu$
m. The inset is a schematic of the tilted frame experiment. (b) Spring constant
$\mu$
m. The inset is a schematic of the tilted frame experiment. (b) Spring constant
![]() $k$
as a function of the effective mass
$k$
as a function of the effective mass
![]() $m$
(static measurements in blue, dynamic measurements in red). Equation (4.1) is shown with dotted lines, with fitting parameter
$m$
(static measurements in blue, dynamic measurements in red). Equation (4.1) is shown with dotted lines, with fitting parameter
![]() $e = 8.9$
$e = 8.9$
![]() $\mu$
m for the static experiment (blue) and
$\mu$
m for the static experiment (blue) and
![]() $e = 14.2$
$e = 14.2$
![]() $\mu$
m for the dynamic experiment (red). In both cases, the fitting parameter matches the film thickness calibration (two different frames are used). (c) In bipolar coordinates, any point M of the plane has coordinates
$\mu$
m for the dynamic experiment (red). In both cases, the fitting parameter matches the film thickness calibration (two different frames are used). (c) In bipolar coordinates, any point M of the plane has coordinates
![]() $(\sigma ,\tau ,z)$
with an orthonormal basis
$(\sigma ,\tau ,z)$
with an orthonormal basis
![]() $(\mathbf {e}_\sigma ,\mathbf {e}_\tau ,\mathbf {e}_z)$
. The iso-
$(\mathbf {e}_\sigma ,\mathbf {e}_\tau ,\mathbf {e}_z)$
. The iso-
![]() $\tau$
curves are non-intersecting circles: the circular frame is defined by
$\tau$
curves are non-intersecting circles: the circular frame is defined by
![]() $\tau = \tau _L$
and the equator of the particle is
$\tau = \tau _L$
and the equator of the particle is
![]() $\tau = \tau _R$
(both shown in red).
$\tau = \tau _R$
(both shown in red).
To model this spring force, the film-shape equation (3.1) has to be solved for a particle off-centred by a distance
![]() $r_{{m}}$
. Due to the linearity of (3.1), the film deformation
$r_{{m}}$
. Due to the linearity of (3.1), the film deformation
![]() $h$
is the superposition of (i) the deformation caused by the weight of the film
$h$
is the superposition of (i) the deformation caused by the weight of the film
![]() $h_{1} = \rho ge(r^2 - L^2)/(8\gamma)$
, as previously determined (3.2) and (ii) the deformation
$h_{1} = \rho ge(r^2 - L^2)/(8\gamma)$
, as previously determined (3.2) and (ii) the deformation
![]() $h_{2}$
of a weightless film subjected only to the weight of an off-centred particle. We start by calculating the force that the deformation
$h_{2}$
of a weightless film subjected only to the weight of an off-centred particle. We start by calculating the force that the deformation
![]() $h_{1}$
alone would create. In this limit, the film shape does not depend on the bead position and its surface energy is constant. The particle is held by the film at a height
$h_{1}$
alone would create. In this limit, the film shape does not depend on the bead position and its surface energy is constant. The particle is held by the film at a height
![]() $z = h_{1}(r_{{m}})$
: it is thus in a potential well of equation
$z = h_{1}(r_{{m}})$
: it is thus in a potential well of equation
![]() $E_{} = mgz$
. This produces a horizontal spring force of amplitude
$E_{} = mgz$
. This produces a horizontal spring force of amplitude
![]() $F_{1} = \lvert - \partial E_{}/\partial r_m \rvert$
:
$F_{1} = \lvert - \partial E_{}/\partial r_m \rvert$
:
Interestingly, the force
![]() $F_{1}$
alone reproduces remarkably well the experimental data. First, similarly to what is expected of a particle in a tilted bowl, the equilibrium position of the bead varies linearly with the tilt angle
$F_{1}$
alone reproduces remarkably well the experimental data. First, similarly to what is expected of a particle in a tilted bowl, the equilibrium position of the bead varies linearly with the tilt angle
![]() $\sin \beta$
and does not depend on the mass of the particle. In figure 3(a),
$\sin \beta$
and does not depend on the mass of the particle. In figure 3(a),
![]() $r_m$
= f(
$r_m$
= f(
![]() $\sin \beta$
) is fitted by a linear curve of slope
$\sin \beta$
) is fitted by a linear curve of slope
![]() $4\gamma /(\rho g e)$
, as expected from (4.1), with
$4\gamma /(\rho g e)$
, as expected from (4.1), with
![]() $e$
= 8.0
$e$
= 8.0
![]() $\mu$
m as a fitting parameter (dotted line). More importantly, (4.1) reproduces the linearity of
$\mu$
m as a fitting parameter (dotted line). More importantly, (4.1) reproduces the linearity of
![]() $F$
with the effective mass
$F$
with the effective mass
![]() $m$
for both static and dynamic experiments, as evidenced in figure 3(b). The best fit is
$m$
for both static and dynamic experiments, as evidenced in figure 3(b). The best fit is
![]() $e$
= 8.9
$e$
= 8.9
![]() $\mu$
m for the static measurements and
$\mu$
m for the static measurements and
![]() $e$
= 14.2
$e$
= 14.2
![]() $\mu$
m for the dynamic experiments. Both values match the film thickness calibration with the two different frames:
$\mu$
m for the dynamic experiments. Both values match the film thickness calibration with the two different frames:
![]() $e$
= 9.8
$e$
= 9.8
![]() $\pm$
1.4
$\pm$
1.4
![]() $\mu$
m for the blue points and
$\mu$
m for the blue points and
![]() $e$
= 14.6
$e$
= 14.6
![]() $\pm$
2.3
$\pm$
2.3
![]() $\mu$
m for the red points. Experimentally, the particle moves as if it were trapped in a parabolic well only determined only by the mass of the film. The catenoid-like film deformation induced by the particle does not impact its dynamics, even if
$\mu$
m for the red points. Experimentally, the particle moves as if it were trapped in a parabolic well only determined only by the mass of the film. The catenoid-like film deformation induced by the particle does not impact its dynamics, even if
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are of the same order of magnitude (figures 2
b and 2
d).
$h_2$
are of the same order of magnitude (figures 2
b and 2
d).
To understand this apparent discrepancy, we calculate the force
![]() $F_2$
due to
$F_2$
due to
![]() $h_2$
only (corresponding to the limit of a particle in a weightless film). Here
$h_2$
only (corresponding to the limit of a particle in a weightless film). Here
![]() $F_2$
is found by solving the film-shape equation
$F_2$
is found by solving the film-shape equation
![]() $\Delta h_{2} = 0$
for an off-centred particle in the small deflection limit. The boundary conditions are
$\Delta h_{2} = 0$
for an off-centred particle in the small deflection limit. The boundary conditions are
![]() $h_{2} = 0$
at the frame and
$h_{2} = 0$
at the frame and
![]() $h_{2} = h_R$
at the equator of the particle (
$h_{2} = h_R$
at the equator of the particle (
![]() $h_R = f(r_{{m}})$
is the vertical position of the centre of the particle, calculated later). In this problem, a relevant coordinate system are bipolar coordinates (
$h_R = f(r_{{m}})$
is the vertical position of the centre of the particle, calculated later). In this problem, a relevant coordinate system are bipolar coordinates (
![]() $\sigma , \tau , z$
), shown in figure 3(c). In bipolar coordinates, the circular frame is expressed simply as the iso-
$\sigma , \tau , z$
), shown in figure 3(c). In bipolar coordinates, the circular frame is expressed simply as the iso-
![]() $\tau$
curve
$\tau$
curve
![]() $\tau = \tau _L$
and the equator of the particle as
$\tau = \tau _L$
and the equator of the particle as
![]() $\tau = \tau _R$
(see Appendix B). Solving the film equation in bipolar coordinates becomes straightforward, and gives
$\tau = \tau _R$
(see Appendix B). Solving the film equation in bipolar coordinates becomes straightforward, and gives
![]() $h_2 = h_R {(\tau - \tau _L)}/{(\tau _R - \tau _L)}$
. The film deformation is associated with the surface energy
$h_2 = h_R {(\tau - \tau _L)}/{(\tau _R - \tau _L)}$
. The film deformation is associated with the surface energy
![]() $E_{\gamma } = E_0 + 2\pi \gamma h_R^2/(\tau _R - \tau _L)$
where
$E_{\gamma } = E_0 + 2\pi \gamma h_R^2/(\tau _R - \tau _L)$
where
![]() $E_0$
is the surface energy of the flat film in the absence of a particle. The force
$E_0$
is the surface energy of the flat film in the absence of a particle. The force
![]() $F_2$
is calculated from the total energy
$F_2$
is calculated from the total energy
![]() $E_{} = E_{\gamma } + mg h_R$
of the system {particle
$E_{} = E_{\gamma } + mg h_R$
of the system {particle
![]() $+$
film}. First, the vertical equilibrium of the particle imposes
$+$
film}. First, the vertical equilibrium of the particle imposes
![]() $\partial E_{}/\partial h_R = 0$
, which gives the vertical position of the particle
$\partial E_{}/\partial h_R = 0$
, which gives the vertical position of the particle
![]() $h_R = - {mg(\tau _R - \tau _L)}/{(4\pi \gamma )}$
. Using the expression of
$h_R = - {mg(\tau _R - \tau _L)}/{(4\pi \gamma )}$
. Using the expression of
![]() $h_R$
,
$h_R$
,
![]() $E$
writes
$E$
writes
![]() $E = E_0 - {(mg)^2 (\tau _R - \tau _L)}/{(8\pi \gamma )}$
. When expressed in cylindrical coordinates,
$E = E_0 - {(mg)^2 (\tau _R - \tau _L)}/{(8\pi \gamma )}$
. When expressed in cylindrical coordinates,
![]() $E$
is a harmonic (see Appendix B), but it is harmonic in the limit
$E$
is a harmonic (see Appendix B), but it is harmonic in the limit
![]() $r_{{m}} \ll L$
:
$r_{{m}} \ll L$
:
![]() $E \simeq E_1 + {(mg)^2 r_{{m}}^2}/{(8\pi \gamma L^2)}$
, where
$E \simeq E_1 + {(mg)^2 r_{{m}}^2}/{(8\pi \gamma L^2)}$
, where
![]() $E_1 = E_0 - (mg)^2/(8 \pi \gamma) \ln(L/R)$
is the surface energy of the film when the marble is centred. Finally, the amplitude of the film force
$E_1 = E_0 - (mg)^2/(8 \pi \gamma) \ln(L/R)$
is the surface energy of the film when the marble is centred. Finally, the amplitude of the film force
![]() $F_2$
is calculated as
$F_2$
is calculated as
![]() $F_2 = \lvert - \partial E/\partial r_{{m}} \rvert$
, which writes
$F_2 = \lvert - \partial E/\partial r_{{m}} \rvert$
, which writes
The film force (
![]() $F_2$
) increases quadratically with the mass
$F_2$
) increases quadratically with the mass
![]() $m$
of the particles, which differs from the experiments where
$m$
of the particles, which differs from the experiments where
![]() $F \propto m$
(figure 3
b). This confirms that
$F \propto m$
(figure 3
b). This confirms that
![]() $F_1$
dominates: the key factor in the particle dynamics is the deformation of the film under its weight.
$F_1$
dominates: the key factor in the particle dynamics is the deformation of the film under its weight.
This is understood by calculating the ratio of the two forces
![]() ${F_1}/{F_2} = {\rho \pi L^2 e}/{m}$
, which is the exact ratio of the masses of the film and the particle. In our experiment, the mass of the film
${F_1}/{F_2} = {\rho \pi L^2 e}/{m}$
, which is the exact ratio of the masses of the film and the particle. In our experiment, the mass of the film
![]() $m_{\!f{\kern-1pt}i{\kern-1pt}lm}$
is close to 35 mg: it is 3–100 times higher than the particle mass, explaining why
$m_{\!f{\kern-1pt}i{\kern-1pt}lm}$
is close to 35 mg: it is 3–100 times higher than the particle mass, explaining why
![]() $F_1$
dominates. By keeping the same film size, and in the limit of small, dense particles such as those used here (
$F_1$
dominates. By keeping the same film size, and in the limit of small, dense particles such as those used here (
![]() $R_{{b}} \ll L$
and
$R_{{b}} \ll L$
and
![]() $\rho _b \gt \rho$
) the condition
$\rho _b \gt \rho$
) the condition
![]() $F_1 \gt F_2$
is almost always verified. Taking, for example,
$F_1 \gt F_2$
is almost always verified. Taking, for example,
![]() $\rho _b$
= 5000 kg m–
$\rho _b$
= 5000 kg m–
![]() $^3$
, the maximum bead mass that can be held by the film is
$^3$
, the maximum bead mass that can be held by the film is
![]() $m_{\textit{max}}$
= 19 mg (see § 3), which is still smaller than the mass of the film. However, the force
$m_{\textit{max}}$
= 19 mg (see § 3), which is still smaller than the mass of the film. However, the force
![]() $F_2$
is expected to dominate when reducing the film size
$F_2$
is expected to dominate when reducing the film size
![]() $L$
: for a particle of mass
$L$
: for a particle of mass
![]() $m = 5$
mg, it happens for
$m = 5$
mg, it happens for
![]() $L \lt 1.8$
cm. Experimentally, we could not test this limit due to edge effects (the bead is attracted towards the frame by capillarity at distances of the order of 5 mm).
$L \lt 1.8$
cm. Experimentally, we could not test this limit due to edge effects (the bead is attracted towards the frame by capillarity at distances of the order of 5 mm).
5. Friction in a soap film
We finally focus on the friction force
![]() $\boldsymbol {F}_{\textit{friction}} =- \alpha \boldsymbol {v}$
(with
$\boldsymbol {F}_{\textit{friction}} =- \alpha \boldsymbol {v}$
(with
![]() $\boldsymbol {v}$
the particle velocity) experienced by the particle during its motion. The friction coefficient
$\boldsymbol {v}$
the particle velocity) experienced by the particle during its motion. The friction coefficient
![]() $\alpha$
is deduced from the characteristic time
$\alpha$
is deduced from the characteristic time
![]() $\tau$
of the exponential envelope of
$\tau$
of the exponential envelope of
![]() $x(t)$
and
$x(t)$
and
![]() $y(t)$
(figure 1
c), using a damped harmonic oscillator model. Due to the extending meniscus around the particle (see figure 5 in Appendix A), we expect
$y(t)$
(figure 1
c), using a damped harmonic oscillator model. Due to the extending meniscus around the particle (see figure 5 in Appendix A), we expect
![]() $\alpha$
to vary with time as the effective radius of the particle increases. Experimentally, this variation is small enough not to significantly perturb exponential fit. In figure 4(a),
$\alpha$
to vary with time as the effective radius of the particle increases. Experimentally, this variation is small enough not to significantly perturb exponential fit. In figure 4(a),
![]() $\alpha$
is plotted as a function of the radius
$\alpha$
is plotted as a function of the radius
![]() $R_b$
of the particle; the different colours correspond to different particle densities
$R_b$
of the particle; the different colours correspond to different particle densities
![]() $\rho _b$
. The friction coefficient is extremely small:
$\rho _b$
. The friction coefficient is extremely small:
![]() $\alpha \simeq 1$
$\alpha \simeq 1$
![]() $\mu$
Pa s m for a millimetre-sized particle. This is of the order of the drag experienced by Leidenfrost droplets (Quéré Reference Quéré2013) and 10 times smaller than the friction of a particle floating at the surface of a bath of bulk viscosity
$\mu$
Pa s m for a millimetre-sized particle. This is of the order of the drag experienced by Leidenfrost droplets (Quéré Reference Quéré2013) and 10 times smaller than the friction of a particle floating at the surface of a bath of bulk viscosity
![]() $\eta$
, where
$\eta$
, where
![]() $\alpha \simeq 3 \pi \eta R \simeq 10$
$\alpha \simeq 3 \pi \eta R \simeq 10$
![]() $\mu$
Pa s m (Danov, Dimova & Pouligny Reference Danov, Dimova and Pouligny2000).
$\mu$
Pa s m (Danov, Dimova & Pouligny Reference Danov, Dimova and Pouligny2000).
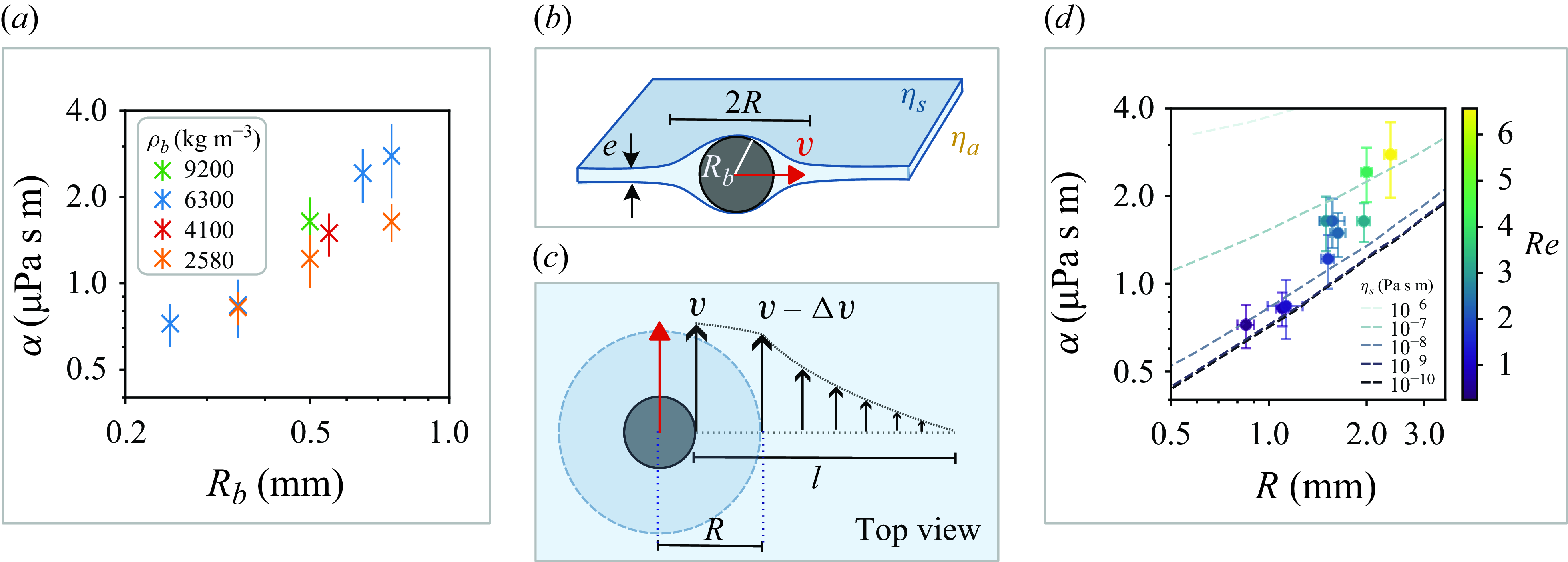
Figure 4. (a) Translational drag coefficient
![]() $\alpha$
as a function of the radius
$\alpha$
as a function of the radius
![]() $R_{{b}}$
of the particle, for varying marble densities. (b) Side view of a particle immersed in a soap film. (c) Top view. The limit of the meniscus surrounding the particle is shown with a dotted blue line. The arrows evidence the shear flow in the meniscus and the film. (d) Comparison between model and experiments for the drag coefficient
$R_{{b}}$
of the particle, for varying marble densities. (b) Side view of a particle immersed in a soap film. (c) Top view. The limit of the meniscus surrounding the particle is shown with a dotted blue line. The arrows evidence the shear flow in the meniscus and the film. (d) Comparison between model and experiments for the drag coefficient
![]() $\alpha$
as a function of the effective radius
$\alpha$
as a function of the effective radius
![]() $R$
of the moving object (particle + meniscus). The colour code shows the Reynolds number (in air) for each experiment. The dotted lines show the theory for varying surface viscosities
$R$
of the moving object (particle + meniscus). The colour code shows the Reynolds number (in air) for each experiment. The dotted lines show the theory for varying surface viscosities
![]() $\eta _s$
, from 10
$\eta _s$
, from 10
![]() $^{-6}$
Pa s m (light grey) to 10
$^{-6}$
Pa s m (light grey) to 10
![]() $^{-10}$
Pa s m (black). The curves for 10
$^{-10}$
Pa s m (black). The curves for 10
![]() $^{-9}$
Pa s m and 10
$^{-9}$
Pa s m and 10
![]() $^{-10}$
Pa s m are almost perfectly superimposed.
$^{-10}$
Pa s m are almost perfectly superimposed.
To understand and model the friction coefficient
![]() $\alpha$
, one must first consider the flow (in the film and in the air) induced by the translation at a velocity
$\alpha$
, one must first consider the flow (in the film and in the air) induced by the translation at a velocity
![]() $v$
of a particle trapped in the film (figure 4
b).
$v$
of a particle trapped in the film (figure 4
b).
In the film, the total flow is the sum of the flow towards the bead by capillary suction (with characteristic velocity
![]() $v_{c}$
) and the flow induced by the translation of the particle. The value of
$v_{c}$
) and the flow induced by the translation of the particle. The value of
![]() $v_{c}$
is first estimated from the variation
$v_{c}$
is first estimated from the variation
![]() $\Delta \Omega \simeq 4 R_{{b}}^3$
of the meniscus volume in the duration
$\Delta \Omega \simeq 4 R_{{b}}^3$
of the meniscus volume in the duration
![]() $\Delta t \simeq 30$
s of an experiment (see figure 5
b). It gives
$\Delta t \simeq 30$
s of an experiment (see figure 5
b). It gives
![]() $v_{c} = (\Delta \Omega /\Delta t) \times 1/(e 2\pi R) \simeq 500$
$v_{c} = (\Delta \Omega /\Delta t) \times 1/(e 2\pi R) \simeq 500$
![]() $\mu$
m s–
$\mu$
m s–
![]() $^1$
, which is more than 10 times smaller than
$^1$
, which is more than 10 times smaller than
![]() $v$
. The flow induced by capillary suction is therefore negligible compared with the flow induced by the motion of the bead.
$v$
. The flow induced by capillary suction is therefore negligible compared with the flow induced by the motion of the bead.
Due to the mobility of the interfaces, the velocity field induced by the motion of the particle is dominated by in-plane flows, which are invariant along the
![]() $z$
-direction. Figure 4(b) is a sketch from the top of the experiment, where the velocity profile
$z$
-direction. Figure 4(b) is a sketch from the top of the experiment, where the velocity profile
![]() $v = v_{\theta }(r)$
of the in-plane flow perpendicular to the direction of motion of the particle is shown with black arrows. Here, the shear happens over a characteristic distance
$v = v_{\theta }(r)$
of the in-plane flow perpendicular to the direction of motion of the particle is shown with black arrows. Here, the shear happens over a characteristic distance
![]() $l$
of the order of a few times
$l$
of the order of a few times
![]() $R_{\textrm {b}}$
(Stone & Ajdari Reference Stone and Ajdari1998). If we now focus on the viscous dissipation associated with the in-plane flow, a two-dimensional (2-D) apparent viscosity term appears:
$R_{\textrm {b}}$
(Stone & Ajdari Reference Stone and Ajdari1998). If we now focus on the viscous dissipation associated with the in-plane flow, a two-dimensional (2-D) apparent viscosity term appears:
![]() $\eta ^{2D} = 2\eta _s + \eta e$
, which is the sum of (i) the surface viscosity
$\eta ^{2D} = 2\eta _s + \eta e$
, which is the sum of (i) the surface viscosity
![]() $\eta _s$
associated with the shearing of the 2-D surfactant-rich layers at the two-liquid–air interfaces and (ii) the liquid bulk viscosity integrated over the thickness
$\eta _s$
associated with the shearing of the 2-D surfactant-rich layers at the two-liquid–air interfaces and (ii) the liquid bulk viscosity integrated over the thickness
![]() $e$
of the film,
$e$
of the film,
![]() $\eta e$
. The measurement of the surface viscosity of interfaces populated by soluble surfactants such as SDS has demonstrated to be particularly challenging (Stevenson Reference Stevenson2005). However, a carefully designed experiment of Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014) gave an upper bound
$\eta e$
. The measurement of the surface viscosity of interfaces populated by soluble surfactants such as SDS has demonstrated to be particularly challenging (Stevenson Reference Stevenson2005). However, a carefully designed experiment of Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014) gave an upper bound
![]() $\eta _s \lt 0.01$
$\eta _s \lt 0.01$
![]() $\mu$
Pa s m. Here,
$\mu$
Pa s m. Here,
![]() $\eta e$
is systematically higher than this value: in a first approximation, we therefore consider that
$\eta e$
is systematically higher than this value: in a first approximation, we therefore consider that
![]() $\eta ^{2D} \simeq \eta e$
. The validity of this assumption, and the impact of
$\eta ^{2D} \simeq \eta e$
. The validity of this assumption, and the impact of
![]() $\eta _s$
on the friction is discussed later.
$\eta _s$
on the friction is discussed later.
An important parameter for the friction is the presence of the meniscus surrounding the particle. It creates a region of characteristic size
![]() $R$
(see figure 5
a in Appendix A) where the film thickness is
$R$
(see figure 5
a in Appendix A) where the film thickness is
![]() $\sim R_{{b}}$
, which is 100 times thicker than the rest of the film. To evaluate the impact of the presence of a thicker zone on the in-plane flows, we calculate the velocity
$\sim R_{{b}}$
, which is 100 times thicker than the rest of the film. To evaluate the impact of the presence of a thicker zone on the in-plane flows, we calculate the velocity
![]() $v-\Delta v$
of the fluid in the film at the boundary between the meniscus (dark blue in figure 4
c) and the film (light blue) using a scaling law analysis. For simplicity, we consider that the film thickness is uniform in the meniscus and suddenly decreases from
$v-\Delta v$
of the fluid in the film at the boundary between the meniscus (dark blue in figure 4
c) and the film (light blue) using a scaling law analysis. For simplicity, we consider that the film thickness is uniform in the meniscus and suddenly decreases from
![]() $R_{{b}}$
to
$R_{{b}}$
to
![]() $e$
at the boundary, i.e. at a distance
$e$
at the boundary, i.e. at a distance
![]() $R - R_{{b}} \sim R_{{b}}$
from the equator of the particle. This induces a jump of the 2-D viscosity, from
$R - R_{{b}} \sim R_{{b}}$
from the equator of the particle. This induces a jump of the 2-D viscosity, from
![]() $\eta ^{2D} \sim \eta R_{{b}}$
in the meniscus to
$\eta ^{2D} \sim \eta R_{{b}}$
in the meniscus to
![]() $\eta ^{2D}\sim \eta e$
in the film. The continuity of the surface stress
$\eta ^{2D}\sim \eta e$
in the film. The continuity of the surface stress
![]() $\sigma ^{2D} = \eta ^{2D} (\partial v/\partial r)$
(the shear stress integrated over the film thickness) then gives
$\sigma ^{2D} = \eta ^{2D} (\partial v/\partial r)$
(the shear stress integrated over the film thickness) then gives
![]() $\Delta v$
. Using the notations of figure 4(b),
$\Delta v$
. Using the notations of figure 4(b),
![]() $\sigma ^{2D}$
scales as
$\sigma ^{2D}$
scales as
![]() $(\eta R_{{b}}) \Delta v/R_{{b}}$
in the meniscus, and
$(\eta R_{{b}}) \Delta v/R_{{b}}$
in the meniscus, and
![]() $(\eta e) (v- \Delta v)/l$
in the film. Equating these two terms gives
$(\eta e) (v- \Delta v)/l$
in the film. Equating these two terms gives
![]() $\Delta v \sim (e/l) \, v$
and
$\Delta v \sim (e/l) \, v$
and
![]() $v - \Delta v \sim (1-e/l)v \simeq 0.99 v$
, meaning that the meniscus moves with the particle at a velocity
$v - \Delta v \sim (1-e/l)v \simeq 0.99 v$
, meaning that the meniscus moves with the particle at a velocity
![]() $v$
. In addition, in the absence of a velocity gradient, there is no viscous dissipation in the meniscus. From the outside, the particle and its meniscus thus form a larger object with effective radius
$v$
. In addition, in the absence of a velocity gradient, there is no viscous dissipation in the meniscus. From the outside, the particle and its meniscus thus form a larger object with effective radius
![]() $R$
and effective mass
$R$
and effective mass
![]() $m$
. Similarly to what is done for
$m$
. Similarly to what is done for
![]() $m$
, the characteristic dimension
$m$
, the characteristic dimension
![]() $R$
is measured for each experiment at a time
$R$
is measured for each experiment at a time
![]() $t = 2.5 \tau$
corresponding to half of the duration of the oscillations.
$t = 2.5 \tau$
corresponding to half of the duration of the oscillations.
The translation of the particle and the meniscus also induce a shear flow in the surrounding air. The Reynolds number associated with this motion writes
![]() $Re = \rho _a R v/\eta _a$
, with, respectively,
$Re = \rho _a R v/\eta _a$
, with, respectively,
![]() $\rho _a$
and
$\rho _a$
and
![]() $\eta _a$
the density and viscosity of air. We take the characteristic velocity
$\eta _a$
the density and viscosity of air. We take the characteristic velocity
![]() $v$
as the average maximum velocity of the particle over the duration of the oscillations. Experimentally,
$v$
as the average maximum velocity of the particle over the duration of the oscillations. Experimentally,
![]() $Re$
varies between 0.25 for the smallest (and slowest) particle and 6.5 for the larger one. The smallest particles thus induce a Stokes flow in the air, while for the largest particles, a visco-inertial boundary layer starts to develop. Inertial effects are expected to impact the friction: for a sphere translating in air, the friction coefficient is increased by 50 % at
$Re$
varies between 0.25 for the smallest (and slowest) particle and 6.5 for the larger one. The smallest particles thus induce a Stokes flow in the air, while for the largest particles, a visco-inertial boundary layer starts to develop. Inertial effects are expected to impact the friction: for a sphere translating in air, the friction coefficient is increased by 50 % at
![]() $Re$
= 6 compared with the Stokes drag (Munson, Young & Okiishi Reference Munson, Young and Okiishi1995).
$Re$
= 6 compared with the Stokes drag (Munson, Young & Okiishi Reference Munson, Young and Okiishi1995).
In the following, we propose to model the friction in the (simpler) situation of
![]() $Re \lt 1$
. In this regime, the relative contributions of the film and the surrounding air to the viscous dissipation are given by the Boussinesq number
$Re \lt 1$
. In this regime, the relative contributions of the film and the surrounding air to the viscous dissipation are given by the Boussinesq number
![]() $Bo = {(\eta e + 2 \eta _s)}/{(\eta _a R)}$
. For a characteristic film thickness
$Bo = {(\eta e + 2 \eta _s)}/{(\eta _a R)}$
. For a characteristic film thickness
![]() $e$
= 10
$e$
= 10
![]() $\mu$
m,
$\mu$
m,
![]() $Bo \simeq 2$
: a value close to one, meaning that the bulk film and air both contribute to the friction. This configuration has been rarely considered in the literature, which is generally focused on the
$Bo \simeq 2$
: a value close to one, meaning that the bulk film and air both contribute to the friction. This configuration has been rarely considered in the literature, which is generally focused on the
![]() $Bo \ll 1$
limit (the drag of an object in a three-dimensional fluid) and
$Bo \ll 1$
limit (the drag of an object in a three-dimensional fluid) and
![]() $Bo \gg 1$
(an inclusion trapped in a viscous membrane). We propose here to base our analysis on the prediction of Hughes, Pailthorpe & White (Reference Hughes, Pailthorpe and White1981), who solved numerically the translational drag coefficient
$Bo \gg 1$
(an inclusion trapped in a viscous membrane). We propose here to base our analysis on the prediction of Hughes, Pailthorpe & White (Reference Hughes, Pailthorpe and White1981), who solved numerically the translational drag coefficient
![]() $\alpha$
of a non-protruding cylindrical inclusion in a membrane for any arbitrary Boussinesq number. They show that, for an inclusion of radius
$\alpha$
of a non-protruding cylindrical inclusion in a membrane for any arbitrary Boussinesq number. They show that, for an inclusion of radius
![]() $R$
, the friction coefficient writes
$R$
, the friction coefficient writes
![]() $\alpha = 8\pi \eta _a R \Lambda _T(Bo)$
with
$\alpha = 8\pi \eta _a R \Lambda _T(Bo)$
with
![]() $\Lambda _T(Bo)$
a numerical coefficient decreasing when the Boussinesq number increases. In our system, however, the particle with radius
$\Lambda _T(Bo)$
a numerical coefficient decreasing when the Boussinesq number increases. In our system, however, the particle with radius
![]() $R_{{b}} \gg e$
protrudes strongly from the film. To account for this, we consider in a first approximation that the friction of the marble and meniscus in a soap film is equal to the friction of a disk of radius
$R_{{b}} \gg e$
protrudes strongly from the film. To account for this, we consider in a first approximation that the friction of the marble and meniscus in a soap film is equal to the friction of a disk of radius
![]() $R$
in a membrane surrounded by air (Hughes et al. Reference Hughes, Pailthorpe and White1981) to which we add the difference between the friction of a sphere of size
$R$
in a membrane surrounded by air (Hughes et al. Reference Hughes, Pailthorpe and White1981) to which we add the difference between the friction of a sphere of size
![]() $R$
in air (
$R$
in air (
![]() $\alpha = 6 \pi \eta _a R$
) and that of an infinitely thin disk moving in its plane direction (
$\alpha = 6 \pi \eta _a R$
) and that of an infinitely thin disk moving in its plane direction (
![]() $\alpha = 32\eta _a R/3$
) (Happel & Brenner Reference Happel and Brenner1983). This gives the following expression for
$\alpha = 32\eta _a R/3$
) (Happel & Brenner Reference Happel and Brenner1983). This gives the following expression for
![]() $\alpha$
:
$\alpha$
:
In figure 4(d), the experimental measurement of
![]() $\alpha$
is plotted as a function of the effective radius of the moving object
$\alpha$
is plotted as a function of the effective radius of the moving object
![]() $R$
. The colour code indicates the Reynolds number in air, varying from
$R$
. The colour code indicates the Reynolds number in air, varying from
![]() $Re$
= 0 (dark blue) to
$Re$
= 0 (dark blue) to
![]() $Re$
= 6.5 (yellow). The dotted lines are the theoretical prediction for varying surface viscosities
$Re$
= 6.5 (yellow). The dotted lines are the theoretical prediction for varying surface viscosities
![]() $\eta _s$
, varied logarithmically between 10
$\eta _s$
, varied logarithmically between 10
![]() $^{-10}$
(black) and 10
$^{-10}$
(black) and 10
![]() $^{-6}$
(light grey). For the smallest particles (
$^{-6}$
(light grey). For the smallest particles (
![]() $R \lt 2$
mm and
$R \lt 2$
mm and
![]() $Re \lt 1$
), the measured friction coefficient
$Re \lt 1$
), the measured friction coefficient
![]() $\alpha$
matches the prediction of (5.1), for a surface viscosity
$\alpha$
matches the prediction of (5.1), for a surface viscosity
![]() $\eta _s \leqslant 10^{-8}$
Pa s m. These values of the surface viscosity agree perfectly with the previous measurement of Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014), who also gave 10
$\eta _s \leqslant 10^{-8}$
Pa s m. These values of the surface viscosity agree perfectly with the previous measurement of Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014), who also gave 10
![]() $^{-8}$
Pa s m as an upper boundary for the surface viscosity. As the Reynolds number increases, the experiments deviate from the theoretical curve: the friction coefficient
$^{-8}$
Pa s m as an upper boundary for the surface viscosity. As the Reynolds number increases, the experiments deviate from the theoretical curve: the friction coefficient
![]() $\alpha$
is higher than that expected from a model based on purely viscous flows. An increase of
$\alpha$
is higher than that expected from a model based on purely viscous flows. An increase of
![]() $\alpha$
is coherent with inertial effects; however, there is no simple way to simply model it as the friction coefficient results from a complex interplay between the flow in the film and in air (Hughes et al. Reference Hughes, Pailthorpe and White1981).
$\alpha$
is coherent with inertial effects; however, there is no simple way to simply model it as the friction coefficient results from a complex interplay between the flow in the film and in air (Hughes et al. Reference Hughes, Pailthorpe and White1981).
6. Conclusion
To conclude, we measured and modelled the forces that apply to a millimetre-sized particle trapped in a soap film, by focusing on both the static position of the bead and its motion. We show that the gravitational distortion of the film under its own weight – of only a few hundreds of micrometres – is the key to understanding the bead dynamics. Indeed, in our experiment, the component of the force due to the film weight systematically dominates over the force induced by the weight of the particle. This is expected as long as the mass of the film is larger than the mass of the particle, which happens for solid particles of size
![]() $R \ll L$
. Counter-intuitively, decreasing the size of the film while keeping the same ratio between the particle radius and the film width
$R \ll L$
. Counter-intuitively, decreasing the size of the film while keeping the same ratio between the particle radius and the film width
![]() $L/R \simeq$
100 will only increase the relative importance of the film weight. For example, for a 10
$L/R \simeq$
100 will only increase the relative importance of the film weight. For example, for a 10
![]() $\mu$
m particle trapped on an 1 mm
$\mu$
m particle trapped on an 1 mm
![]() $^2$
horizontal film,
$^2$
horizontal film,
![]() $F_1/F_2 \gt 10$
even for very thin films of
$F_1/F_2 \gt 10$
even for very thin films of
![]() $e \simeq 100$
nm.
$e \simeq 100$
nm.
In the second part, we focus on the drag force experienced by the particle, and we propose a model in the limit of low Reynolds number in air (
![]() $Re \lt 1$
). In this regime, the particle is submitted to the viscous friction of air and to that of the film, with an almost equal contribution. A simplified model based on the work of Hughes et al. (Reference Hughes, Pailthorpe and White1981) matches exactly our measurements for the smallest particles. A deviation is observed as the Reynolds number (and the size of the particle) increase, which we interpret as the effect of the inertia of the air. Interestingly, the match between the theory and the experiments is valid for all surface viscosities
$Re \lt 1$
). In this regime, the particle is submitted to the viscous friction of air and to that of the film, with an almost equal contribution. A simplified model based on the work of Hughes et al. (Reference Hughes, Pailthorpe and White1981) matches exactly our measurements for the smallest particles. A deviation is observed as the Reynolds number (and the size of the particle) increase, which we interpret as the effect of the inertia of the air. Interestingly, the match between the theory and the experiments is valid for all surface viscosities
![]() $\eta _s \leqslant 10^{-8}$
Pa s m: a mismatch of at least 50 % is expected for
$\eta _s \leqslant 10^{-8}$
Pa s m: a mismatch of at least 50 % is expected for
![]() $\eta _s \geqslant 10^{-7}$
Pa s m. This suggests that our experiment should be sensitive to surface viscosities as low as
$\eta _s \geqslant 10^{-7}$
Pa s m. This suggests that our experiment should be sensitive to surface viscosities as low as
![]() $10^{-8}$
Pa s m, which is as sensitive as the most precise interfacial rheology set-ups, for example controlled microrheological probes at the surface of a bath (Zell et al. Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014). We expect our model to remain valid when reducing the size of the probe, which opens interesting perspectives on the possibility of using small particles as probes to explore in-situ the rheological properties of soap film.
$10^{-8}$
Pa s m, which is as sensitive as the most precise interfacial rheology set-ups, for example controlled microrheological probes at the surface of a bath (Zell et al. Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014). We expect our model to remain valid when reducing the size of the probe, which opens interesting perspectives on the possibility of using small particles as probes to explore in-situ the rheological properties of soap film.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2025.157.
Acknowledgements
The authors thank D. van der Meer for the initial discussions on the topic, and M. Taoufiki and H. Delrieu for preliminary experiments.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Meniscus characterisation
A particle trapped in a soap film is surrounded by a meniscus which extends with time by capillary suction. Figure 5 characterises the shape of the meniscus, and presents its growth dynamics in a typical experiment. The presence of the meniscus increases the effective mass
![]() $m$
of the moving object, which is taken into account in the calculation of the forces.
$m$
of the moving object, which is taken into account in the calculation of the forces.
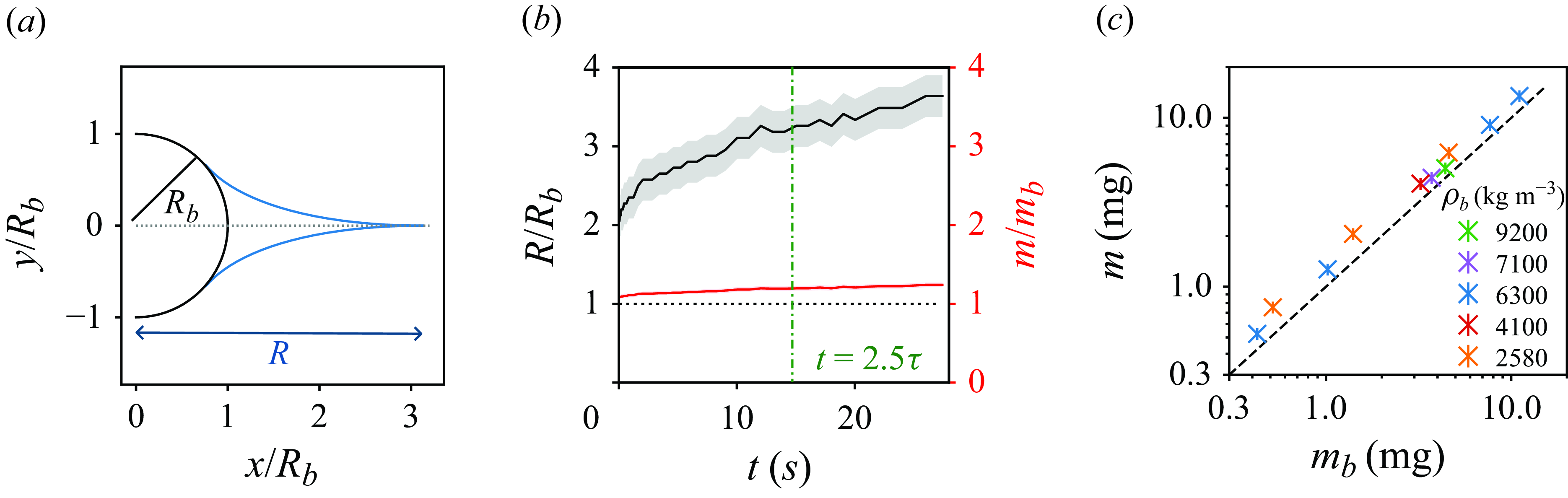
Figure 5. (a) Shape of a meniscus with an extension
![]() $R = 3R_{{b}}$
around a particle, calculated based on Orr et al. (Reference Orr, Scriven and Rivas1975). The position of the interface is normalised by the particle radius
$R = 3R_{{b}}$
around a particle, calculated based on Orr et al. (Reference Orr, Scriven and Rivas1975). The position of the interface is normalised by the particle radius
![]() $R_b$
. (b) Normalised extension
$R_b$
. (b) Normalised extension
![]() $R/R_{{b}}$
of the meniscus (black line) and mass
$R/R_{{b}}$
of the meniscus (black line) and mass
![]() $m/m_{{b}}$
(red line) as a function of time
$m/m_{{b}}$
(red line) as a function of time
![]() $t$
, for a particle of radius
$t$
, for a particle of radius
![]() $R_b = 0.5$
mm and mass
$R_b = 0.5$
mm and mass
![]() $m_b$
= 3.7 mg. The black dotted line evidences the limit
$m_b$
= 3.7 mg. The black dotted line evidences the limit
![]() $R = R_{{b}}$
and
$R = R_{{b}}$
and
![]() $m = m_{{b}}$
. The vertical green line evidences the time
$m = m_{{b}}$
. The vertical green line evidences the time
![]() $t = 2.5 \tau$
at which the characteristic size
$t = 2.5 \tau$
at which the characteristic size
![]() $R$
and mass
$R$
and mass
![]() $m$
are measured. Here
$m$
are measured. Here
![]() $t = 2.5 \tau$
is half of the duration of the oscillations. (c) Total mass
$t = 2.5 \tau$
is half of the duration of the oscillations. (c) Total mass
![]() $m$
of the particle and its meniscus, measured at a time
$m$
of the particle and its meniscus, measured at a time
![]() $t = 2.5 \tau$
, as a function of the mass
$t = 2.5 \tau$
, as a function of the mass
![]() $m_{{b}}$
of the particle alone. The dotted line shows the limit
$m_{{b}}$
of the particle alone. The dotted line shows the limit
![]() $m = m_{{b}}$
.
$m = m_{{b}}$
.
Appendix B. Calculation of the film-mediated force in bipolar coordinates
We want to determine the energy of the system consisting of a particle of radius
![]() $R_{{b}}$
off-centred by
$R_{{b}}$
off-centred by
![]() $r_m$
in a circular soap film of radius
$r_m$
in a circular soap film of radius
![]() $L$
. In bipolar coordinates, any point
$L$
. In bipolar coordinates, any point
![]() $M$
has coordinates (
$M$
has coordinates (
![]() $\sigma, \tau, z$
). The iso-
$\sigma, \tau, z$
). The iso-
![]() $\tau$
curves are circles of radius
$\tau$
curves are circles of radius
![]() $c/|\sinh \tau |$
, centred in (
$c/|\sinh \tau |$
, centred in (
![]() $x = c\coth \tau$
,
$x = c\coth \tau$
,
![]() $y = 0$
), with
$y = 0$
), with
![]() $c$
a constant, and the iso-
$c$
a constant, and the iso-
![]() $\sigma$
curves are circles of radius
$\sigma$
curves are circles of radius
![]() $c/|\sin\sigma|$
, centred in (
$c/|\sin\sigma|$
, centred in (
![]() $x = 0$
,
$x = 0$
,
![]() $y = c\cot\sigma$
). One needs to find the constant
$y = c\cot\sigma$
). One needs to find the constant
![]() $c$
so that the frame position is expressed simply as
$c$
so that the frame position is expressed simply as
![]() $\tau = \tau _L$
and the edge of the particle is
$\tau = \tau _L$
and the edge of the particle is
![]() $\tau = \tau _R$
(as shown in figure 3
c). We can restrict
$\tau = \tau _R$
(as shown in figure 3
c). We can restrict
![]() $\tau _L$
and
$\tau _L$
and
![]() $\tau _R$
to be positive, and by construction of the bipolar coordinates,
$\tau _R$
to be positive, and by construction of the bipolar coordinates,
![]() $\tau _R \gt \tau _L$
. The relation between
$\tau _R \gt \tau _L$
. The relation between
![]() $\tau _L$
,
$\tau _L$
,
![]() $\tau _R$
,
$\tau _R$
,
![]() $c$
and the dimensions of the problem
$c$
and the dimensions of the problem
![]() $L$
,
$L$
,
![]() $R_{{b}}$
and
$R_{{b}}$
and
![]() $r_m$
is solved by inverting the three relations
$r_m$
is solved by inverting the three relations
![]() $r_m = c(\coth {\tau _L} - \coth {\tau _R})$
$r_m = c(\coth {\tau _L} - \coth {\tau _R})$
![]() $(r_m \gt 0)$
,
$(r_m \gt 0)$
,
![]() $L = c/\sinh {\tau _L}$
and
$L = c/\sinh {\tau _L}$
and
![]() $R_{{b}} = c/\sinh {\tau _R}$
. In particular,
$R_{{b}} = c/\sinh {\tau _R}$
. In particular,
In bipolar coordinates,
![]() $\Delta h = (\cosh \tau - \cos \sigma )^2 (\partial ^2 h/\partial \sigma ^2 + \partial ^2 h/\partial \tau ^2)/c^2$
(Happel & Brenner Reference Happel and Brenner1983). The film-shape equation
$\Delta h = (\cosh \tau - \cos \sigma )^2 (\partial ^2 h/\partial \sigma ^2 + \partial ^2 h/\partial \tau ^2)/c^2$
(Happel & Brenner Reference Happel and Brenner1983). The film-shape equation
![]() $\Delta h_2 = 0$
is then solved with the boundary conditions
$\Delta h_2 = 0$
is then solved with the boundary conditions
![]() $h(\tau _L) = 0$
and
$h(\tau _L) = 0$
and
![]() $h(\tau _R) = h_R$
, giving a simple solution:
$h(\tau _R) = h_R$
, giving a simple solution:
![]() $h_2 = h_R (\tau - \tau _L)/{(\tau _R - \tau _L)}$
. In the small deflection limit, the surface energy associated with the film deformation is
$h_2 = h_R (\tau - \tau _L)/{(\tau _R - \tau _L)}$
. In the small deflection limit, the surface energy associated with the film deformation is
![]() $E_{\gamma } \simeq E_0 + \gamma \iint (\nabla h)^2 {\rm d}S$
. A small surface element is
$E_{\gamma } \simeq E_0 + \gamma \iint (\nabla h)^2 {\rm d}S$
. A small surface element is
![]() $dS= {c^2 \mathrm {d}\sigma \,\mathrm {d}\tau }/{(\cosh {\tau } - \cos {\sigma })^2}$
while
$dS= {c^2 \mathrm {d}\sigma \,\mathrm {d}\tau }/{(\cosh {\tau } - \cos {\sigma })^2}$
while
![]() $\boldsymbol{\nabla } h = (\cosh {\tau }-\cos {\sigma }) ( \mathbf {e}_{\sigma } {\partial h}/{\partial \sigma } + \mathbf {e}_{\tau } {\partial h}/{\partial \tau } )/c$
. Using the expression of
$\boldsymbol{\nabla } h = (\cosh {\tau }-\cos {\sigma }) ( \mathbf {e}_{\sigma } {\partial h}/{\partial \sigma } + \mathbf {e}_{\tau } {\partial h}/{\partial \tau } )/c$
. Using the expression of
![]() $h_2$
, the film energy is
$h_2$
, the film energy is
The total energy
![]() $E$
of the film and particle is
$E$
of the film and particle is
![]() $E = E_{\gamma } + mgh_R$
. The vertical equilibrium of the particle imposes
$E = E_{\gamma } + mgh_R$
. The vertical equilibrium of the particle imposes
![]() $\partial E_{}/\partial h_R = 0$
, which gives
$\partial E_{}/\partial h_R = 0$
, which gives
![]() $h_R = -{mg(\tau _R - \tau _L)}/{(4\pi \gamma) }$
and
$h_R = -{mg(\tau _R - \tau _L)}/{(4\pi \gamma) }$
and
![]() $E = E_0 - {(mg)^2 (\tau _R - \tau _L)}/{(8\pi \gamma )}$
. Using (B1), and in the limit
$E = E_0 - {(mg)^2 (\tau _R - \tau _L)}/{(8\pi \gamma )}$
. Using (B1), and in the limit
![]() $R_{{b}} \ll L$
,
$R_{{b}} \ll L$
,
![]() $E$
finally writes
$E$
finally writes
 \begin{align} E = E_0 - \frac {(mg)^2}{8\pi \gamma }\left [ \ln \frac {L}{R_{\textrm {b}}} + \ln \left (1-\frac {r_m^2}{L^2} + \sqrt {1-2\frac {r_m^2}{L^2}}\right ) - \ln \left (1+\frac {r_m^2}{L^2} + \sqrt {1-2\frac {r_m^2}{L^2}}\right ) \right ] . \end{align}
\begin{align} E = E_0 - \frac {(mg)^2}{8\pi \gamma }\left [ \ln \frac {L}{R_{\textrm {b}}} + \ln \left (1-\frac {r_m^2}{L^2} + \sqrt {1-2\frac {r_m^2}{L^2}}\right ) - \ln \left (1+\frac {r_m^2}{L^2} + \sqrt {1-2\frac {r_m^2}{L^2}}\right ) \right ] . \end{align}



















































































