Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-05-02T00:46:22.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts

Part of: Theory of computing Algebraic geometry: Foundations Topological dynamics

Published online by Cambridge University Press:  15 February 2024

TULLIO CECCHERINI-SILBERSTEIN Open the ORCID record for TULLIO CECCHERINI-SILBERSTEIN [Opens in a new window] ,
MICHEL COORNAERT  and
XUAN KIEN PHUNG Open the ORCID record for XUAN KIEN PHUNG [Opens in a new window]
TULLIO CECCHERINI-SILBERSTEIN*
Affiliation:
Dipartimento di Ingegneria, Università del Sannio, 82100 Benevento, Italy
MICHEL COORNAERT
Affiliation:
Université de Strasbourg, CNRS, IRMA UMR 7501, F-67000 Strasbourg, France (e-mail: [email protected])
XUAN KIEN PHUNG
Affiliation:
Département d’Informatique et de Recherche Opérationnelle, Université de Montréal, Montréal, Québec H3T 1J4, Canada Département de Mathématiques et de Statistique, Université de Montréal, Montréal, Québec, H3T 1J4, Canada (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a group and let V be an algebraic variety over an algebraically closed field K. Let A denote the set of K-points of V. We introduce algebraic sofic subshifts 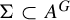${\Sigma \subset A^G}$ and study endomorphisms 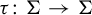$\tau \colon \Sigma \to \Sigma $. We generalize several results for dynamical invariant sets and nilpotency of 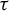$\tau $ that are well known for finite alphabet cellular automata. Under mild assumptions, we prove that 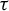$\tau $ is nilpotent if and only if its limit set, that is, the intersection of the images of its iterates, is a singleton. If moreover G is infinite, finitely generated and 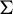$\Sigma $ is topologically mixing, we show that 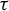$\tau $ is nilpotent if and only if its limit set consists of periodic configurations and has a finite set of alphabet values.

Keywords

algebraic varietyalgebraic cellular automatonalgebraic sofic subshiftnilpotencylimit set

MSC classification

Primary: 37B15: Cellular automata 14A10: Varieties and morphisms
Secondary: 37B10: Symbolic dynamics 37B20: Notions of recurrence 14A15: Schemes and morphisms 68Q80: Cellular automata
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 10 , October 2024 , pp. 2859 - 2900
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aanderaa, S. and Lewis, H. R.. Linear sampling and the $\forall \exists \forall$ case of the decision problem. J. Symb. Log. 39 (1974), 519–548.10.2307/2272894CrossRefGoogle Scholar
Aubrun, N., Barbieri, S. and Sablik, M.. A notion of effectiveness for subshifts on finitely generated groups. Theoret. Comput. Sci. 661 (2017), 35–55.10.1016/j.tcs.2016.11.033CrossRefGoogle Scholar
Ax, J.. Injective endomorphisms of varieties and schemes. Pacific J. Math. 31 (1969), 1–7.10.2140/pjm.1969.31.1CrossRefGoogle Scholar
Ballier, A.. Propriété structurelle, combinatoires et logiques des pavages. PhD Thesis, Aix-Marseille Université, 2009.Google Scholar
Ballier, A., Durand, B. and Jeandel, E.. Structural aspects of tilings. STACS 2008: 25th International Symposium on Theoretical Aspects of Computer Science (Leibniz International Proceedings in Informatics, 1). Schloss Dagstuhl - Leibniz Center for Informatics (LZI), Wadern, 2008, pp. 61–72.Google Scholar
Bartholdi, L. and Salo, V.. Simulations and the lamplighter group. Groups Geom. Dyn. 16 (2022), 1461–1514.10.4171/GGD/692CrossRefGoogle Scholar
Berger, R.. The undecidability of the domino problem. Mem. Amer. Math. Soc. 66 (1966), 72.Google Scholar
Boyle, M., Buzzi, J. and Gómez, R.. Almost isomorphism for countable state Markov shifts. J. Reine Angew. Math. 592 (2006), 23–47.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Induction and restriction of cellular automata. Ergod. Th. & Dynam. Sys. 29 (2009), 371–380.10.1017/S0143385708080437CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Cellular Automata and Groups (Springer Monographs in Mathematics). Springer-Verlag, Berlin, 2010.10.1007/978-3-642-14034-1CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. On algebraic cellular automata. J. Lond. Math. Soc. (2) 84 (2011), 541–558.10.1112/jlms/jdr016CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Surjunctivity and reversibility of cellular automata over concrete categories. Trends in Harmonic Analysis (Springer INdAM Series, 3). Ed. Picardello, M. A.. Springer, Milan, 2013, pp. 91–133.10.1007/978-88-470-2853-1_6CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Exercises in Cellular Automata and Groups (Springer Monographs in Mathematics). Springer, Cham, 2023.10.1007/978-3-031-10391-9CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Coornaert, M. and Phung, X. K.. On injective endomorphisms of symbolic schemes. Comm. Algebra 47 (2019), 4824–4852.10.1080/00927872.2019.1602872CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Coornaert, M. and Phung, X. K.. On the Garden of Eden theorem for endomorphisms of symbolic algebraic varieties. Pacific J. Math. 306 (2020), 31–66.10.2140/pjm.2020.306.31CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Coornaert, M. and Phung, X. K.. On linear shifts of finite type and their endomorphisms. J. Pure Appl. Algebra 226 (2022), Paper no. 106962, 27 pp.10.1016/j.jpaa.2021.106962CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Coornaert, M. and Phung, X. K.. First-order model theory and Kaplansky’s stable finiteness conjecture. Preprint, 2023, arXiv:2310.09451.Google Scholar
Culik, K., Pachl, J. and Yu, S.. On the limit sets of cellular automata. SIAM J. Comput. 18 (1989), 831–842.10.1137/0218057CrossRefGoogle Scholar
Cyr, V., Franks, J. and Kra, B.. The spacetime of a shift endomorphism. Trans. Amer. Math. Soc. 371 (2019), 461–488.10.1090/tran/7254CrossRefGoogle Scholar
Gromov, M.. Endomorphisms of symbolic algebraic varieties. J. Eur. Math. Soc. (JEMS) 1 (1999), 109–197.10.1007/pl00011162CrossRefGoogle Scholar
Grothendieck, A.. Éléments de géométrie algébrique. I. Le langage des schémas. Publ. Math. Inst. Hautes Études Sci. 4 (1960), 5–228.10.1007/BF02684778CrossRefGoogle Scholar
Grothendieck, A.. Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I. Publ. Math. Inst. Hautes Études Sci. 20 (1964), 5–259.10.1007/BF02684747CrossRefGoogle Scholar
Grothendieck, A.. Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III. Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.10.1007/BF02684343CrossRefGoogle Scholar
Guillon, P. and Richard, G.. Nilpotency and limit sets of cellular automata. Mathematical Foundations of Computer Science 2008 (Lecture Notes in Computer Science, 5162). Eds. Ochmański, E. and Tyszkiewicz, J.. Springer, Berlin, 2008, pp. 375–386.10.1007/978-3-540-85238-4_30CrossRefGoogle Scholar
Kari, J.. The nilpotency problem of one-dimensional cellular automata. SIAM J. Comput. 21 (1992), 571–586.10.1137/0221036CrossRefGoogle Scholar
Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9 (1989), 691–735.10.1017/S0143385700005290CrossRefGoogle Scholar
Kitchens, B. P.. Expansive dynamics on zero-dimensional groups. Ergod. Th. & Dynam. Sys. 21 (1987), 249–261.10.1017/S0143385700003989CrossRefGoogle Scholar
Kitchens, B. P.. Symbolic Dynamics. One-Sided, Two-Sided and Countable State Markov Shifts (Universitext). Springer-Verlag, Berlin, 1998.Google Scholar
Lima, Y. and Sarig, M.. Symbolic dynamics for three-dimensional flows with positive topological entropy. J. Eur. Math. Soc. (JEMS) 21 (2019), 199–256.10.4171/jems/834CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511626302CrossRefGoogle Scholar
Liu, Q.. Algebraic Geometry and Arithmetic Curves (Oxford Graduate Texts in Mathematics, 6). Oxford University Press, Oxford, 2002; translated from the French by R. Erné, Oxford Science Publications.10.1093/oso/9780198502845.001.0001CrossRefGoogle Scholar
Meyerovitch, T. and Salo, V.. On pointwise periodicity in tilings, cellular automata, and subshifts. Groups Geom. Dyn. 13 (2019), 549–578.10.4171/ggd/497CrossRefGoogle Scholar
Milne, J. S.. Algebraic Groups: The Theory of Group Schemes of Finite Type Over a Field (Cambridge Studies in Advanced Mathematics, 170). Cambridge University Press, Cambridge, 2017.10.1017/9781316711736CrossRefGoogle Scholar
Milnor, J.. On the entropy geometry of cellular automata. Complex Systems 2 (1988), 357–385.Google Scholar
Moore, E. F.. Machine Models of Self-Reproduction (Proceedings of Symposia in Applied Mathematics, 14). American Mathematical Society, Providence, 1963, pp. 17–34.Google Scholar
Myhill, J.. The converse of Moore’s Garden-of-Eden theorem. Proc. Amer. Math. Soc. 14 (1963), 685–686.Google Scholar
Osipenko, G.. Dynamical Systems, Graphs, and Algorithms (Lecture Notes in Mathematics, 1889). Springer-Verlag, Berlin, 2007. Appendix A by N. B. Ampilova and Appendix B by D. Fundinger.Google Scholar
Ovchinnikov, A., Pogudin, G. and Scanlon, T.. Effective difference elimination and Nullstellensatz. J. Eur. Math. Soc. (JEMS) 22(8) (2020), 2419–2452.10.4171/jems/968CrossRefGoogle Scholar
Phung, X. K.. On sofic groups, Kaplansky’s conjectures, and endomorphisms of pro-algebraic groups. J. Algebra 562 (2020), 537–586.10.1016/j.jalgebra.2020.05.037CrossRefGoogle Scholar
Phung, X. K.. Weakly surjunctive groups and symbolic group varieties. Preprint, 2021, arXiv:2111.13607.Google Scholar
Phung, X. K.. LEF-groups and endomorphisms of symbolic varieties. Preprint, 2021, arXiv:2112.00603.Google Scholar
Phung, X. K.. On Dynamical Finiteness Properties of Algebraic Group Shifts. Israel J. Math. 252(1) (2022), 355–398.10.1007/s11856-022-2351-1CrossRefGoogle Scholar
Phung, X. K.. Shadowing for families of endomorphisms of generalized group shifts. Discrete Contin. Dyn. Syst. 42(1) (2022), 285–299.10.3934/dcds.2021116CrossRefGoogle Scholar
Phung, X. K.. On linear non-uniform cellular automata: duality and dynamics. Preprint, 2022, arXiv:2208.13069.Google Scholar
Phung, X. K.. On images of subshifts under embeddings of symbolic varieties. Ergod. Th. & Dynam. Sys. 43(9) (2023), 3131–3149.10.1017/etds.2022.48CrossRefGoogle Scholar
Phung, X. K.. A geometric generalization of Kaplansky’s direct finiteness conjecture. Proc. Amer. Math. Soc. 151 (2023), 2863–2871.10.1090/proc/16333CrossRefGoogle Scholar
Phung, X. K.. On symbolic group varieties and dual surjunctivity. Groups Geom. Dyn. doi:10.4171/GGD/749. Published online 9 November 2023.CrossRefGoogle Scholar
Phung, X. K.. Stable finiteness of twisted group rings and noisy linear cellular automata. Canad. J. Math. doi:10.4153/S0008414X23000329. Published online 22 May 2023.Google Scholar
Robinson, R.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.10.1007/BF01418780CrossRefGoogle Scholar
Salo, V.. On nilpotency and asymptotic nilpotency of cellular automata. Cellular Automata and Discrete Complex Systems and 3rd Int. Symp. Journées Automates Cellulaires, AUTOMATA & JAC 2012 (La Marana, Corsica, 201) (Electronic Proceedings in Theoretical Computer Science, 90). Ed. E. Formenti. (Open Publishing Association, 2012), pp. 86–96.Google Scholar
Salo, V.. Strict asymptotic nilpotency in cellular automata. Cellular Automata and Discrete Complex Systems (Lecture Notes in Computer Science, 10248). Eds. Dennunzio, A., Formenti, E., Manzoni, L. and Porreca, A. E.. Springer, Cham, 2017, pp. 3–15.10.1007/978-3-319-58631-1_1CrossRefGoogle Scholar
Sarig, M.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19 (1999), 1565–1593.10.1017/S0143385799146820CrossRefGoogle Scholar
Sarig, M.. Symbolic dynamics for surface diffeomorphisms with positive entropy. J. Amer. Math. Soc. 26 (2013), 341–426.10.1090/S0894-0347-2012-00758-9CrossRefGoogle Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128). Birkhäuser Verlag, Basel, 1995.Google Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer-Verlag, New York, 1987; with the collaboration of A. Fathi and R. Langevin, translated from the French by J. Christy.10.1007/978-1-4757-1947-5CrossRefGoogle Scholar
Tomašić, I. and Wibmer, M.. Difference Galois theory and dynamics. Adv. Math. 402 (2022), 108328.10.1016/j.aim.2022.108328CrossRefGoogle Scholar
Vakil, R.. MATH 216: Foundations of algebraic geometry. Class Notes, 2010. Available at https://api.semanticscholar.org/CorpusID:124268419.Google Scholar
von Neumann, J.. Theory of Self-Reproducing Automata. Ed. A. W. Burks. University of Illinois Press, Champaign, IL, 1966.Google Scholar
Wibmer, M.. Finiteness properties of affine difference algebraic groups. Int. Math. Res. Not. IMRN 2022(1) (2022), 506–555.10.1093/imrn/rnaa177CrossRefGoogle Scholar
Wolfram, S.. Universality and complexity in cellular automata. Phys. D 10 (1984), 1–35.10.1016/0167-2789(84)90245-8CrossRefGoogle Scholar
Wolfram, S.. A New Kind of Science. Wolfram Media, Inc., Champaign, IL, 2002.Google Scholar