Optimized wavelet-domain filtering under noisy and reverberant conditions

Abstract

The paper addresses a robust wavelet-based speech enhancement for automatic speech recognition in reverberant and noisy conditions. We propose a novel scheme in improving the speech, late reflection, and noise power estimates from the observed contaminated signal. The improved estimates are used to calculate the Wiener gain in filtering the late reflections and additive noise. In the proposed scheme, optimization of the wavelet family and its parameters is conducted using an acoustic model (AM). In the offline mode, the optimal wavelet family is selected separately for the speech, late reflections, and background noise based on the AM likelihood. Then, the parameters of the selected wavelet family are optimized specifically for each signal subspace. As a result we can use a wavelet sensitive to the speech, late reflection, and the additive noise, which can independently and accurately estimate these signals directly from an observed contaminated signal. For speech recognition, the most suitable wavelet is identified from the pre-stored wavelets, and wavelet-domain filtering is conducted to the noisy and reverberant speech signal. Experimental evaluations using real reverberant data demonstrate the effectiveness and robustness of the proposed method.

I. INTRODUCTION

In a real-world enclosed environment, the speech signal is reflected and arrives at different time delays when observed by the microphone. This effect is considered as a form of a contamination due to channel distortion, and commonly known as reverberation. The degree of reverberation depends on the reverberation time T ₆₀, which dictates the severity of distortion. Speech contamination is one of the most common problems in automatic speech recognition (ASR) applications. In the perspective of ASR, any form of contamination of the speech signal at runtime (test condition) is a mismatch to the acoustic model (AM) (training condition). The mismatch may result in the degradation of the ASR performance. Thus, speech enhancement is one of the most important topics in robust ASR. In this paper, we focus primarily on the topic of dereverberation for ASR; since background noise is always present in a real environment, we address enhancement in reverberant and noisy condition, and extend our dereverberation framework to include denoising effect.

The scheme of decomposition of the reverberant signal into early and late reflections [1] simplifies the treatment of reverberation. In this scheme, the late reflection is treated as additive noise, and the seminal works [2–5] in denoising has been adopted. We expanded multi-band spectral subtraction (SS) so that the multi-band weighting parameters are optimized based on the criterion of the ASR [6]. Similarly, the Wiener filtering (WF) approach can be employed to the same dereverberation scheme. Originally adopted from athe denoising work in [7], it can be extended to suppress the late reflection by filtering the reverberant signal with the Wiener gain. Although the filtering-based methods (e.g. SS and Wiener) work well, they share a common problem: power estimation of the contaminant (i.e. late reflection and background noise) and the desired signal (i.e. speech). This problem is inherent to the filtering-based methods [2–5]. In real scenario, both the contaminant and the speech signals are not available separately, instead, we need to deal with a composite signal, and extracting independent power estimates for each of these is not simple. Since the filtering-based methods depend primarily on power estimation, inaccurate estimates result in artifacts in the recovered signal. This impacts the ASR performance in general, as it manifests as another form of mismatch to the recognizer. Power estimation is improved through popular methods in the seminal works [8–11] coupled with the deployment of voice activity detector (VAD).

In this paper, we address the problem through optimal wavelet-domain filtering. WF is adopted as the enhancement platform, but instead of operating in the frequency domain, we perform filtering in the wavelet domain. Wavelets offer more flexibility in signal representation. A proper choice of wavelet allows us to track the power of the signal of interest directly from the observed contaminated signal. This mechanism results to a more accurate instantaneous (frame-wise) power estimates. This is not possible using traditional VAD relying on a priori information regarding speech/non-speech frames. Specifically, in this paper, we present a method in optimizing the wavelets based on the ASR criterion. We note that the ASR is a complex system and operates independently from speech enhancement (i.e. dereverberation) module. By setting the optimization criterion used in the dereverberation as a function of the AM used by the ASR, we can expect that the dereverberation method is optimized to improving ASR performance. Our previous work in [12,13] addressed a very limited optimization which only covers wavelet parameter tuning. In the proposed method, optimization is more comprehensive via wavelet family selection and parameter optimization not covered in [12,13]. Thus, optimization of the wavelet family and parameters is conducted using AM likelihood (Section III) for each signal of interest (i.e. speech, late reflection, and additive background noise). Since characteristics of these signals are different, optimizing the wavelet for each corresponding signal improves signal representation and power estimation for effective speech enhancement in ASR.

The paper is organized as follows. In Section II we present the enhancement concept of our proposed method which includes the formulation of the reverberant model and its expansion to include background noise, theory of WF in the wavelet domain, and the synergy between enhancement and the ASR system. Section III describes the optimization via wavelet family selection and wavelet parameter tuning. Then, the method of estimating the reverberation time T ₆₀ and the identification of the noise profiles using Gaussian mixture model (GMM) is discussed in Section IV. The experimental setup and ASR performance are presented in Section V. Finally, we conclude the paper in Section VI.

II. ENHANCEMENT CONCEPT

In this section, we present the concept of our enhancement approach by introducing the reverberant model we adopted from [1]. The formulation of the Wiener filter in the frequency domain together with its expansion to the wavelet domain is presented. Lastly, the wavelet optimization based on acoustic likelihood criterion is discussed.

A) Model for dereverberation

The reverberant spectra R(f, w) (short-term spectrum, w: window frame, f: frequency) is given as

(1)$${R}(f,w) \approx {S}(f,w)H(f,w),$$

where S(f, w) and H(f, w) are the clean speech signal and the room impulse response (RIR), respectively. The RIR h can be expressed with early h _E and late h _L components of the RIR as follows:

(2)$${h}_{E}{(t)} =\left\{{\matrix{ h(t) \quad {t} \lt \Gamma, \cr 0 \quad {\rm otherwise,} \cr } } \right.$$

(3)$${h}_{L}{(t)} =\left\{{\matrix{ h(t + \Gamma) \quad {t} \ge \Gamma, \cr 0 \quad {\rm otherwise,} \cr } } \right.$$

Equations (2) and (3) characterize both the short and long-period effects of the reverberant signal. From equation (1), the reverberant speech model R(f, w) is expressed as

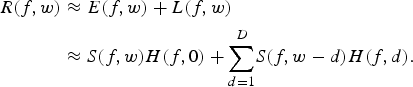(4)$$\eqalign{{R}(f,w) & \approx E(f,w) + L(f,w) \cr & \approx {S}(f,w)H(f,0) + {\sum\limits_{d=1}^{D}} {S}(f,w-d)H(f,d).}$$

The first term is referred to as the early reflection denoted as E(f, w), where H(f, 0) is the RIR effect to the speech signal S(f, w). It is due to the direct-path signal contaminated with some reflections that occur at earlier time (short period). The second term L(f, w), is attributed by late reflection, which can be viewed as smearing of the clean speech by H(f, d) which corresponds to the d frame-shift effect of the RIR. D is the number of frames over which the reverberation (smearing) has an effect. Since the late reflection spans over frames, it can be treated as long-period noise [14,15]. In real environments, it is safe to assume that some additive noise may be present. Although our main focus in this paper is about dereverberation, we include a simple additive noise mitigation scheme, since we experiment using real data and the presence of noise impacts the dereverberation mechanism in [6,14].

In general, removing contaminants especially the effects of late reflection and background noise is a difficult task. Since the dereverberation concept in this paper was originally inspired from denoising [2–5], the treatment of noise together with the effects of reverberation is possible as long as the following assumptions are adopted:

• • Decomposition of reverberation into early and late reflection.

• • Additive property of late reflection and noise.

• • Statistical independence and uncorrelatedness of the signals (i.e. speech, late reflection, and additive noise).

Following equation (4), we can include the effects of the additive background noise B(f, w) and the observed contaminated signal O(f, w) becomes

(5)$$\eqalign{{O}(f,w)&\approx R(f,w) + B(f,w)\cr & \approx E(f,w) + L(f,w) +B(f,w).}$$

In equation (5), we assume that the early reflection, late reflection and background noise are uncorrelated and statistically independent. However, this assumption may not hold true; thus, we show later an optimization process aimed to further strengthen the assumption in the wavelet domain. From here, we refer to the combined effects of the late reflection and the background noise as contaminant. Speech is enhanced by suppressing L(f, w) and B(f, w). Consequently, the recovered early reflection is processed via Cepstral Mean Normalization (CMN) [6] prior to the ASR. From this point onward, we assume that processing is conducted in framewise manner, dropping the index w.

B) WF in the wavelet domain

WF is an enhancement method based on the stochastic filter theory. Enhancement of the contaminated signal is based on the choice of the coefficients of the Wiener filter [16], and by imposing a criterion that minimizes the minimum mean square error (MMSE) between the desired and observed signals, the enhanced signal resembles that of the desired signal in the MMSE sense. Consider the conventional Wiener filter in Fig. 1 (top), the recovered early reflection ê can be expressed as

Fig. 1. Overview of the enhancement model.

(6)$$\hat{e}(t) = o(t) * w(t),$$

where w(t) is the Wiener filter impulse response. By applying the Wiener–Khinchine relation

(7)$${E}^{2}(f)=\cal{FT}\{R_{ee}(\nu)\},$$

the autocorrelation function R _ee is replaced in terms of power spectra [7]. Thus, we can formulate the Wiener filter gain in terms of the frequency domain as

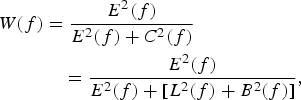(8)$$\eqalign{{W}(f)&={E^{2}(f)\over E^{2}(f)+C^{2}(f)}\cr & \quad ={E^{2}(f)\over E^{2}(f)+[L^{2}(f)+B^{2}(f)]},}$$

where E ²(f) and C ²(f) are the power of early reflection and the contaminant, respectively. The contaminant signal is composed of the late reflection and background noise ($L^{2}(f)+B^{2}(f)$). By maximizing the discriminative property between the subspaces E and C, and by a proper wavelet choice Ψ (Section III), equation (8) can be expanded in the wavelet domain as

(9)$${W}(\Psi)={E^{2}(\Psi_E)\over E^{2}(\Psi_E)+[L^{2}(\Psi_L)+B^{2}(\Psi_B)]},$$

where E ²(Ψ_E), L ²(Ψ_L), and B ²(Ψ_B) are the early reflection, late reflection and background noise power, respectively. The wavelet domain Ψ_E, Ψ_L, and Ψ_B are the corresponding wavelets that enhances the discriminative property among subspaces E, L, and B (Section III). In the context of fast wavelet transform, we define κ from equation (9) at band m as

(10)$${\kappa}_{m}={E^{2}_{m} \over E^{2}_{m}+L^{2}_{m}+B^{2}_{m}},$$

where band m denotes the level of the wavelet decomposition. In reality, we are interested in recovering the clean speech and not the early reflection. Although these two are not strictly the same (i.e. waveform-wise), they are almost the “same” as far as the ASR is concerned. We have concurred through experiments in [6] that the ASR is robust to the early reflection when processed with CMN; interestingly, recognition performance for CMN-processed signal using clean AM is comparable with that of clean speech signal. This means that the ASR makes no distinction between clean speech and CMN-processed early reflection. The CMN is able to compensate the mismatch caused by short-term smearing of the speech signal. By exploiting this behavior of the ASR, we can replace E ²(Ψ_E) with S ²(Ψ_S) in equation (9). Thus, we can rewrite equations (9) and (10) as

(11)$${W}(\Psi)= {{S^{2}(\Psi_S)}\over{S^{2}(\Psi_S)+L^{2}(\Psi_L)+B^{2}(\Psi_B)}}$$

and

(12)$${\kappa}_{m}={S^{2}_{m}\over S^{2}_{m}+L^{2}_{m}+B^{2}_{m}}.$$

This assumption was also confirmed in [614,15]. The ASR-inspired WF is implemented in the wavelet domain after wavelet decomposition as shown in Fig. 1 (bottom). First, the early reflection is recovered by weighting the observed contaminated signal with Weiner gain as

(13)$$\hat{E}_{m}=\kappa_m \cdot O_{m},$$

then, the enhanced speech is recovered after CMN processing expressed as,

(14)$$\hat{S}_{m}=\rm{CMN}(\hat{E}_{m}).$$

The time-domain speech can be recovered through inverse wavelet transform (IWT). It is obvious that the enhancement ability of the system is dependent on the Wiener gain, which is a function of the power estimates of the signals of interest. Unfortunately, there is no straightforward solution to power estimation. The observed signal at the microphone is a composite signal, which makes it difficult to estimate the speech power and the contaminant power (late reflection and background noise) independently and accurately. Conventionally, a VAD is used to improve power estimation as presented in [7,17]. The contaminant power is estimated from the non-speech parts of the utterance. With the presumption that contaminant frames are of low-power as opposed to the composite signal which includes the speech. The speech power can be estimated by subtracting the observed signal with the contaminant estimate. Although this method works, estimation tends to be inaccurate especially with shorter utterances that do not have sufficient non-speech frames. Moreover, since the VAD method needs several frames for improved power estimation performance, it is difficult to calculate instantaneous power at a particular frame, resulting to poor performance in tracking the contaminant signal.

Speech enhancement performance relies primarily on the effectiveness of the contaminant power estimate, specifically for filtering-based methods. It is imperative to address the power estimation problem. In this paper, the expansion of WF to the wavelet domain presents a viable alternative in improving the power estimation (Section III).

C) Optimization via AM criterion

Speech enhancement and ASR are independent and complex processes. Originally, speech enhancement was developed to suppress noise and improve speech intelligibility for human listening, later it has been adopted for robust ASR application. However, human and machine perceive speech differently, and by simply cascading these two processes may not be effective [18]. Improvement in perceptual objective or subjective measures does not necessarily translate to improving ASR performance. As mentioned earlier, enhancement also introduces artifacts which may be detrimental to model-based ASR systems. Since there are many factors affecting ASR performance, it is appropriate to design an ASR-inspired speech enhancement method, and adopt the ASR criterion in the enhancement process. One of the most important features of the proposed method is the intricate link between the enhancement process and the ASR system.

The basic hidden Markov model (HMM)-based ASR system employs AM λ and language model in decoding speech to a word sequence. λ is obtained usually by maximum likelihood estimation

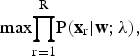(15)$$\rm{max} {\prod_{r=1}^{R}} P({\bf x}_{r}|{\bf w};\lambda),$$

where w is the word sequence. x_r is the rth training utterance. Since equation (15) is an integral part of an ASR system, it is desirable to adopt this in the speech enhancement process. In conjunction with equation (15), we define the likelihood criterion score

(16)$$L({\bf x},\lambda)= p({\bf x}|\lambda),$$

to measure the similarity between the signal x and the AM λ. For speech enhancement, x becomes the enhanced speech while λ is the AM used by the ASR. For computational efficiency, we adopt a GMM instead of a HMM to compute the AM likelihood. The likelihood score L increases when there is a good match between x and λ. This is a potent measure that relates the enhanced speech with the AM used by the ASR system. We note that w is purposely removed in equation (16) since we are only interested in the acoustic part of speech enhancement. Equation (16) will be extensively used throughout this paper for the wavelet optimization process (i.e. in Section III) used in our proposed dereverberation scheme.

III. WAVELET OPTIMIZATION FOR ENHANCEMENT

In this section, we discuss the optimization of the wavelet family and parameters using AM, which is the major contribution of this paper. A wavelet is generally expressed as

(17)$$\Psi(\upsilon,\tau,t)={1\over \sqrt{\upsilon}} \Psi \left( {t-\tau \over \upsilon} \right),$$

where t denotes time, υ and τ are the scaling and shifting parameters, respectively. $\Psi \lpar [{t-\tau}]/{\upsilon}\rpar $ is often referred to as a mother wavelet. Assuming that we deal with real-valued signal, the wavelet transform (WT) is defined as

(18)$$F(\upsilon,\tau)=\int z(t)\Psi(\upsilon,\tau,t)dt,$$

where $F(\upsilon,\tau)$ is a wavelet coefficient and z(t) is a time-domain function. With a proper choice of wavelet family coupled with a training algorithm, τ and υ are optimized, so that the wavelet captures the characteristics of the signal of interest. The resulting wavelet is sensitive to detecting the presence of the said signal. Specifically, in the wavelet filtering method, we are interested in detecting the power of speech, noise, and late reflection, given the observed signal at the microphone. Thus, we optimize the wavelet to detect these signals separately.

A) Wavelet family selection

LIKELIHOOD CRITERION

There exist different types of wavelets, bearing different waveforms (e.g. Daubechies and Morlet) referred to as wavelet family (f), and it is desirable to find an optimal match between the signal of interest and the corresponding wavelet family. We note that a particular wavelet family has a unique characteristic (i.e. waveform and frequency response) and may not be appropriate to represent a particular signal of interest. For example, Daubechies wavelet has the property which is more suitable to represent a speech signal than representing a background noise. We develop a process to quantify the distinction of which wavelet family is best suited for the signal of interest. The process is achieved by selecting a wavelet family Ψ among (f=1:F) denoted as $\Psi^{(f=1:F)}$ that best represents the signal of interest for speech S, late reflection L, and background noise B using the likelihood criterion given as

(19)$$\psi_{S} = \arg\max_{f}p({\bf s}(\Psi^{(f)})|\lambda_S),$$

(20)$$\psi_{L} = \arg\max_{f}p({\bf l}(\Psi^{(f)})|\lambda_L),$$

and

(21)$$\psi_{B}= \arg\max_{f}p({\bf b}(\Psi^{(f)})|\lambda_B),$$

where ${\bf s}(\Psi^{(f)})$, ${\bf l}(\Psi^{(f)}),$ and ${\bf b}(\Psi^{(f)})$ are the speech, late reflection, and background noise processed with the wavelet family Ψ^(f). λ_S, λ_L, and λ_B are AMs trained from clean speech, late reflection, and background noise database, respectively, using Mel-frequency cepstrum coefficients (MFCC) features. Equations (19)–(21) calculate the likelihood scores for the clean speech, late reflection, and background noise when decomposed using different wavelet family (f=1:F) against the corresponding AM. Thus, the corresponding wavelet family that results to the best decomposition of the signal of interest is selected based on the likelihood criterion.

LIKELIHOOD RATIO CRITERION

The likelihood criterion in Section III-A searches for the correspondence between the signal of interest and the collection of wavelet families. In this subsection, we introduce another optimization criteria focusing on the late reflection and background noise, so they are better separated from the speech signal.

In particular we search for the corresponding wavelet that maximizes the likelihood ratio between the speech model λ_S and the corresponding signal, given as

(22)$$\psi_{L}= \arg\max{p({\bf l}(\psi_L)|\lambda_L)\over p({\bf l}(\psi_L)|\lambda_S)}$$

and

(23)$$\psi_{B}= \arg\max{p({\bf b}(\psi_B)|\lambda_B)\over p({\bf b}(\psi_B)|\lambda_S)}$$

Then, equation (11) becomes

(24)$${W}(\psi)={S^{2}(\psi_{S})\over S^{2}(\psi_{S})+L^{2}(\psi_{L})+B^{2}(\psi_{B})}.$$

B) Wavelet parameter optimization

A wavelet family is characterized by its parameters (i.e. scaling v and shifting τ) as described in equation (18) which can significantly impact its response. Thus, we perform wavelet parameter optimization after the optimized wavelet family selection discussed in Section III-A. Optimizing both v and τ will further refine the optimization process. The process of optimizing the wavelet parameters for each corresponding signal in the form of training as shown in Fig. 2 is discussed as follows:

Fig. 2. Wavelet parameter optimization scheme for speech, late reflection and background noise.

SPEECH

Figure 2 (Top) shows the process of tuning the wavelet parameters for the speech signal. To conform with the model in Fig. 1 (bottom), the clean speech estimate ŝ is synthesized by generating the early reflection using the the early components h _E of the RIR. The RIR can be synthetically generated as described in [6]. The RIR can be set as a function of reverberation time $T_{60}^{(j)}$ based on room acoustics model in [19]. Thus, physical measurement inside the room is not required. The theory behind the use of synthetic RIR stems from the fact that the HMM's description of speech is of low resolution compared with the RIR, with respect to time and frequency. Thus, for ASR applications, it may be sufficient to use an approximation of it [20]. And, its effectiveness in ASR is verified in [6]. Moreover, we have devised a method to effectively identify the early h _E and late h _L reflections boundary of the RIR in [6]. Thus, for a particular reverberation time j (i.e. $T_{60}^{(j)}$); $h_{E}^{(j)}$ and $h_{L}^{(j)}$ are readily available.

The early reflection estimate ê is generated using the speech database and the corresponding early reflection coefficient h _E of the RIR. Then, CMN is applied resulting to ŝ. Wavelet coefficients $\hat{S}(\upsilon,\tau)$ is extracted through equation (18) using the optimized wavelet family in Section III-A. Likelihood scores are computed using the clean speech AM λ_S, a GMM of 256 components. λ_S is a text-independent model which captures the statistical information of the speech subspace. A greedy search process is iterated by adjusting υ and τ. The corresponding υ=a and τ=α that result in the highest score are selected. Since we are interested in the speech subspace in general, optimizing a single wavelet to capture the general speech characteristics is sufficient.

ADDITIVE BACKGROUND NOISE

The same procedure is applied to the additive background noise as shown in Fig. 2: (Bottom), except for the creation of multiple noise profiles (i), representing different types of background noise. After decomposing the time domain signal b ⁽ⁱ⁾ through wavelet decomposition to $B(\upsilon,\tau)^{(i)}$, likelihood scores are computed using the corresponding noise model $\lambda_{B^{(i)}}$ (same model structure as that of λ_S). This model is trained using a noise database. The corresponding υ=p ⁽ⁱ⁾ and τ=$\bi{\beta^{(i)}}$ that maximize the likelihood score are stored and associated with the corresponding noise profile.

The noise database is originally composed of different background noise recordings referred to as base noise (i.e. Mall, Hall, Crowd, Office, Vacuum, and Computer). To generalize to a variety of noise characteristics, additional entries are made by combining different types of the base noise. First, a simple piece-wise combination is performed and the resulting noise combination is further combined in the next level. To remove redundancy and suppress the increase of the entries, we measure the correlation of the resulting combinations and select the ones that are less correlated with existing noise entries. Thus, the expanded noise database referred to as noise profiles will provide more degree of freedom in characterizing various noise distributions. More detailed explanation regarding noise profiles is found in [12].

LATE REFLECTION

In the case of the late reflection, wavelet parameter tuning is shown in Fig. 2: (Middle). The late reflection l ^(j) for the corresponding reverberation time j (i.e. $T_{60}^{(j)}$) is generated using the clean speech database and the predetermined late reflection coefficients $h_{l}^{(j)}$ of the RIR. The late reflection boundary is predetermined experimentally as discussed in [6,21]. Next, wavelet coefficients $L(\upsilon,\tau)^{(j)}$ are extracted through WD. In order to make $L(\upsilon,\tau)^{(j)}$ void of speech characteristics, thresholding is applied to $L(\upsilon,\tau)^{(j)}$. Speech energy is characterized with high coefficient values [17,22] and thresholding sets these coefficients to zero as,

(25)$$\bar{L}(\upsilon,\tau)^{(j)}=\left\{\matrix{0, \quad \quad \quad \quad \quad \mid L (\upsilon,\tau)^{(j)} \mid \gt \rm{thr,} \cr L(\upsilon,\tau)^{(j)}, \quad \quad \mid L(\upsilon,\tau)^{(j)} \mid \leq \hbox{thr}, \cr }\right.$$

thr is calculated similar to that in [22]. The thresholded signal $\bar{L}{(\upsilon,\tau)}^{(j)}$ is evaluated against a late reflection model $\lambda_{\bar{L}^{(j)}}$. D templates for every reverberation time $T_{60}^{(j)}$ are to be optimized for both scale ($\upsilon_{1},\ldots\upsilon_{D}$)^(j) and shift ($\tau_{1},\ldots,\tau_{D}$)^(j). These correspond to D preceding frames (refer to equation (4)) that cause smearing to the current frame of interest. We note that the effect of smearing is not constant, thus D templates are created and experimentally identified. The parameters υ and τ are adjusted and the corresponding υ=\{e ₁, \ldots, e _D\}^(j) and τ=\{ξ₁, \ldots, ξ_D\}^(j) that result in the highest likelihood score are selected. We note that $\lambda_{\bar{L}^{(j)}}$ is trained using the synthetically generated late reflection data (during training) with thresholding applied.

C) Optimized wavelet-domain WF

The general expression of the conventional Wiener gain (un-optimized) at band m is expressed as

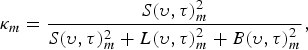$$\kappa_{m} = {S(\upsilon,\tau)^2_{m}\over S(\upsilon,\tau)^2_{m}+{{L(\upsilon,\tau)}^2_{m}}+{B(\upsilon,\tau)}^2_{m}},$$

where $S(\upsilon,\tau)^{2}_{m}$, $L(\upsilon,\tau)^{2}_{m}$, and $B(\upsilon,\tau)^{2}_{m}$ are the wavelet power estimates for the clean speech, late reflection, and background noise, respectively. Using the optimized values for υ and τ as described in Section III-B, we can compute the respective power estimates directly from the observed contaminated signal $O(\upsilon,\tau)_{m}$. Thus, the speech power estimate becomes

(26)$${S(\upsilon,\tau)^2_{m}}\approx{{O(a,\alpha)}^2_{m}},$$

the background noise power estimate ${B(\upsilon,\tau)}^{2}_{m}$ as

(27)$${B(\upsilon,\tau)^2_{m}}\approx{{O(p^{(i)},\beta^{(i)})}^2_{m}},$$

and the late reflection estimate ${L(\upsilon,\tau)}^{2}_{m}$ as

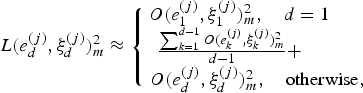(28)$$L(e^{(j)}_d,\xi^{(j)}_d)^{2}_{m} \approx \left\{ \matrix{O(e^{(j)}_1,\xi^{(j)}_1)^{2}_{m}, \quad d =1 \quad \quad \cr {\sum_{k=1}^{d-1} O (e^{(j)}_k,\xi^{(j)}_k)^{2}_{m}\over{d-1} }+ \quad\quad \quad \cr O(e^{(j)}_d,\xi^{(j)}_d)^{2}_{m}, \quad \rm{otherwise} ,\cr} \right.$$

WF is conducted by weighting the contaminated wavelet coefficient $O(\upsilon,\tau)_{m}$ with the Wiener gain as

(29)$${O}(\upsilon,\tau)_{m}(\rm enhanced) = O(\upsilon,\tau)_{m}. \kappa^{}_{m}.$$

In equation (29), the Wiener weight κ_m dictates the degree of suppression of the contaminant to the observed signal at band m. If the contaminant power estimate is greater than the estimate of the speech power, then κ_m for that band may be set to zero or a small value. This attenuates the effect of contamination. On the other hand, if the power of the clean speech estimate is greater, the Wiener gain will emphasize its effect. Equation (29) is further processed with CMN prior to input to the ASR system.

IV. IDENTIFYING NOISE PROFILE AND REVERBERATION TIME

In Fig. 3 (Top A) we show the training of GMMs μ. Each GMM is composed of 256 mixture components. In this work, we experimentally set the step size of T ₆₀ to 20 ms. covering from 100  to 600 ms (each step size corresponds as a discrete entry (j). We use the RIR generator in [6] to synthetically create reverberant data x ^(j). In the case of the noise profiles in (Bottom A), we generated different background noise entry x ⁽ⁱ⁾ through synthetic superimposition using the speech database and the noise profiles. GMM architecture and training mechanism is the same as that used in the reverberant GMMs where $\mu_{b}^{(i)}$ GMMs are trained for each noise profile i.

Fig. 3. Noise profile and reverberation time identification.

The reverberation time (j) has a corresponding optimized wavelet parameters \{e ₁, \ldots, e _D\}^(j) and \{ξ₁, \ldots, ξ_D\}^(j) while the noise profile (i) has (p ⁽ⁱ⁾, β⁽ⁱ⁾). During ASR use, it is necessary to identify the profile that corrupts the speech signal to retrieve the appropriate parameters. To identify reverberation time (j), a GMM-based classifier is employed in Fig. 3 (Top B) using the pre-trained reverberant models $\mu_{T_{60}}^{(j)}$. Subsequently, the profile (j) that leads to the best likelihood is selected. The same procedure is applied to the identification of noise profile (i) shown in (Bottom B).

V. EXPERIMENTAL EVALUATIONS

Experimental setup

TRAINING

We evaluate the proposed method in large vocabulary continuous speech recognition (LVCSR). The training database is the Japanese Newspaper Article Sentence (JNAS) corpus with a total of approximately 60 h of speech. The test set is composed of 200 sentences uttered by 50 speakers. The vocabulary size is 20 K and the language model is a standard word trigram model. Speech is processed using 25 ms-frame with 10 ms shift. The features used are 12-order MFCCs, ΔMFCCs, and ΔPower. The AM is a phonetically tied mixture (PTM) HMMs with 8256 Gaussians in total.

TESTING

For testing, we used seven types of noise in the NAIST database [23]: mall, hall, crowd, office, vacuum cleaner, and computer noise. As a result of combining different types of noise from the noise database, 20 noise profiles are generated. We considered reverberation time T ₆₀ of 400 and 600 ms. with SNR of 20, 10, and 0 dB.

WAVELET FAMILY

In our work, we considered several wavelet families as shown in [24,25]. Based on our experiments, the Daubechies wavelet was selected to better represent the speech signal. In the case of different noise types, the Symlet, Coiflet, and Meyer wavelets were selected in most cases. Lastly, the Gaussian derivative wavelets was selected for the late reflection. Wavelet selection is based primarily on the likelihood score between the actual signal and the AM, respectively. Hence, a noise type recorded at a particular environment condition may have a unique wavelet.

B) Noise and late reflection tracking performance

The advantage of optimizing the wavelets in estimating the signal of interest is shown in Fig. 4. In this experiment, noise and late reflection were super-imposed to the speech to synthesize the model in equation (5). The contaminant power was variably adjusted along the time axis to recreate a varying effect of contamination (i.e. amplitude). For simplicity, only the amplitude variability is shown. We note that for the oracle, we used the actual contaminant data for the power measurement while the observed signal (composite) is used for others. In this graph, the power envelope estimated using the proposed optimized wavelet parameter closely tracks the actual power of the contaminant. Obviously, the proposed wavelet optimization outperforms the other power estimation techniques.

Fig. 4. Combined noise and late reflection power tracking.

C) GMM classification performance

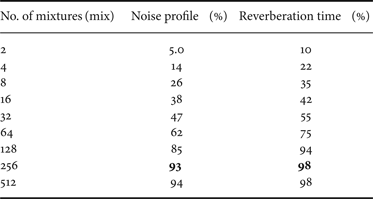
The identification of the noise profile (i) and reverberation time (j) during recognition is vital in selecting the optimal wavelets. The overall performance of the proposed method depends on the accurate identification of these two. Given an observed reverberant and noisy data, we show in Table 1 the classification rate of the GMM classifier as a function of Gaussian mixtures. We have dyadically increased the mixture size in each training from 2 up to 512. With a smaller mixture, the classifier is unable to discriminate the the inherent characteristics of noise profiles and T ₆₀, resulting to poor identification rate. As the mixture size is increased, the identification rate improves and saturates at 256 mixtures. This means that with a sufficient mixtures, the classifier is capable of resolving signal characteristics. We have found out that the identification of the noise profile and the reverberation time as discussed in Section IV works well even with only a few frames of data.

Table 1. GMM classification performance.

D) Comparing ASR performance with other methods

We compare the proposed method against the following methods:

• • A) No processing: Reverberant and noisy data processed with reverberant and noisy model;

• • B) Based on LP residual signals: Reference technique based on Linear Prediction-based (LP) dereverberation analysis [26];

• • C) Improved wavelet-based speech enhancement: Technique that incorporates VAD and contaminant-specific profiles for improved contaminant power estimation and improved performance [9,17];

• • D) Wavelet extrema clustering: Technique based on linear predictive coding (LPC) in the wavelet domain [27];

• • E) Multi-band SS: Technique that employs suppression of the late reflection; optimization criterion is based on MMSE [21];

• • F) Multi-band SS (ASR-optimized): Technique that suppresses the late reflection and at the same time maximizes the AM likelihood [6];

• • G) Wavelet filtering (un-optimized): Technique that employs WF in the wavelet domain\enlargethispage{7.5pt} [7,14,28];

• • H) Optimized wavelet filtering (Proposed method): Wavelet filtering is optimized using the AM.

While (C), (D), and (G) are wavelet-based techniques, (B), (E), and (F) are implemented in domains other than the wavelet. For the methods in (B)–(G), processing using the ETSI advanced front-end (AFE) [29] is applied to mitigate the effects of background noise.

The summary of the recognition performance comparing the proposed method and other existing methods described is shown in Fig. 5. In this figure, we show the word accuracy for reverberation time T ₆₀ = 400 and 600 ms. Each of the reverberant condition is also corrupted with background noise with SNRs 0 , 10,  and 20 dB, respectively. Recognition performance is averaged over all types of noise (i.e. Mall, Hall, Crowd, Office, Vacuum cleaner, and Computer noise).

Fig. 5. ASR performance in word accuracy (averaged over all types of noise: Mall, Hall, Crowd, Office, Vacuum cleaner, and Computer noise.

The results in Fig. 5 show that the proposed method outperforms existing wavelet-based methods in (C), (D), and (G). The main difference between the proposed method and these methods is the nature in which the wavelets are employed. While the latter indiscriminately use the same generic wavelet to represent both the contaminant and the desired signal, the proposed method uses a wavelet suitable for each of the signal via optimization in Section III-B. This results to an improved correspondence between the wavelet and the signal of interest.

The SS methods in (E) and (F) are based on Fourier transform processing. For these methods, the same basis function is used to process all of the signals of interest, while the proposed method in (H) employs wavelets that are optimized for a particular signal via training in Section III-C. Moreover, in the methods (E) and (F) there is no mechanism of improving the discrimination property among signal subspaces. As a result, the proposed method outperforms methods (E) and (F). The LP-based dereverberation scheme (B) is also based on the Fourier transform principle and this method is not tuned to the ASR. Moreover, it is very sensitive to the effects of the background noise. We note that at the very severe condition (T60=600 ms and SNR=0 dB), word accuracy becomes negative due to a large number of insertion errors together with substitution errors for unprocessed speech.

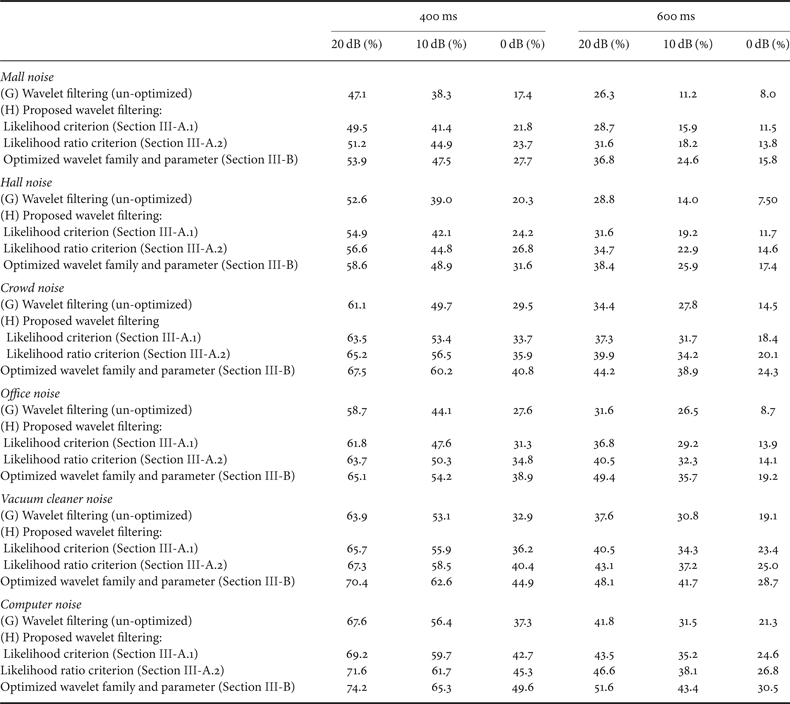
E) Effectiveness of the proposed wavelet optimization

In Table 2, we show the detailed recognition performance in word accuracy, when optimizing the wavelet family based on the likelihood criterion (Section II-A.1) and the likelihood ratio criterion (Section III-A.2). The former only deals with the correspondence matching between the wavelet family and the signal of interest, while the latter includes a mechanism to improve the subspace{} discrimination among the signals of interest. In this table, we also show the effect of the proposed method (H) which includes both maximizing the likelihood ratio criterion (Section III-A.2) and optimizing the wavelet parameter (Section III-B). The existing wavelet-based filtering method (un-optimized) [7,14] (G) is also provided. The effectiveness of the proposed method is confirmed in Table 2. For reference, both methods (C) and (G) use the Daubechies wavelet while method (D) uses a Quadratic spline wavelet.

Table 2. Performance in word accuracy (%) attributed to the series of optimization.

F) Robustness to new noise types

The notion of expanding the original base noise into noise profiles is to find a representative of an unknown noise. We investigate the robustness of the proposed method in the event that a particular noise during testing is not covered in the noise profile database. To simulate this scenario, we held out the base noise together with its derivatives and compare its performance when it is not being held-out. The noise types that were excluded constitute as a new set of test data representing the new noise type. The comparative results are shown in Fig. 6. The difference in word accuracy between held-out (open test) and noise-enrolled, averaged over 20, 10, and 0 dB is negligible as shown in the figure, which means that the system is robust to noises that may not be present during enrolment. This may be attributed to the expansion of the noise database (i.e. noise profiles). The combination of different types of base noise as discussed in [12] has generated some noise profiles similar in characteristics to that of the held-out noise types. This renders the system to be robust. Moreover, the ability to select appropriate wavelet for different noise-types may have a positive impact as well.

Fig. 6. Robustness to noise that are not enrolled in the profile database (averaged results of 20, 10, and 0 dB SNR).

VI. CONCLUSION

In this paper, we have presented the methods of optimizing the wavelet family and parameters using AM. The resulting optimized wavelets effectively estimate the power of the clean speech, late reflection, and background noise, respectively, from a contaminant signal. Thus, WF in the wavelet domain is improved. Since the optimization process is carried out using the AM, the enhanced speech signal is more likely to improve recognition performance. Currently, we deal with simple additive background noise since our method is primarily focused on dereverberation. In the future, we will further investigate a more sophisticated treatment of both dereverberation and denoising (combined); including the convolutive effect of noise. Further investigation in enhancing the current contaminant model to effectively address both reverberation and background noise will be a challenging task in our future work. Lastly, since the proposed method is a waveform enhancement technique, it can also be employed to train deep neural network-based ASR systems.