Do the Right Thing: Experimental evidence that preferences for moral behavior, rather than equity or efficiency per se, drive human prosociality

Abstract

Decades of experimental research show that some people forgo personal gains to benefit others in unilateral anonymous interactions. To explain these results, behavioral economists typically assume that people have social preferences for minimizing inequality and/or maximizing efficiency (social welfare). Here we present data that cannot be explained by these standard social preference models. We use a “Trade-Off Game” (TOG), where players unilaterally choose between an equitable option and an efficient option. We show that simply changing the labelling of the options to describe the equitable versus efficient option as morally right completely reverses the correlation between behavior in the TOG and play in a separate Dictator Game (DG) or Prisoner’s Dilemma (PD): people who take the action framed as moral in the TOG, be it equitable or efficient, are much more prosocial in the DG and PD. Rather than preferences for equity and/or efficiency per se, our results suggest that prosociality in games such as the DG and PD are driven by a generalized morality preference that motivates people to do what they think is morally right.

1 Introduction

Humans regularly pay costs to benefit others. This prosocial (or “cooperative”) behavior is central to the success of our personal relationships and the functioning of our societies, and is more important than ever in the face of global-level challenges like resource conservation and climate change. Thus a great deal of research across the natural and social sciences has sought to understand what motivates people to be prosocial.

One answer to this question is offered by work demonstrating myriad long-run benefits that accrue from helping others: if I pay a cost to give you a benefit today, you may be more willing to help me in the future, as may others who observe my action (Axelrod & Hamilton, 1981; Dal Bó, 2005; Fudenberg & Maskin, 1986; Nowak, 2006; Nowak & Sigmund, 2005; Rand & Nowak, 2013; Trivers, 1971). Thus, in situations where there are future consequences for current actions. pure self-interest can often motivate prosocial behavior (e.g., Dreber, Fudenberg, and Rand (2014).

However, people are sometimes willing to be prosocial even when doing so is not self-interested. For example, decades of research show that many people will pay costs to benefit strangers in one-shot anonymous laboratory experiments (Camerer, 2003; Dawes & Thaler, 1988), and recent work has shown that prosocial behaviors in different economic games are typically correlated, both in the same session and over time (Capraro, Smyth, Mylona & Niblo, 2014; Capraro, Jordan & Rand, 2014; Peysakhovich, Nowak & Rand, 2014; Reigstad, Strømland & Tinghög, 2017). This suggests the existence of stable individual differences in prosociality, what has been dubbed a “cooperative phenotype” (Peysakhovich et al., 2014). To explain these observations, behavioral economists typically employ social preference models (Camerer, 2003; Camerer & Fehr, 2004). These models argue that people care about more than just their own material payoffs.

Widely used social preference models, especially for analyzing unilateral giving decisions, focus exclusively on outcomes. They assume that people get psychological benefits (utility) from the payoffs of others (i.e., are “altruistic” or care about efficiency, the total payoff of all players) (Charness & Rabin, 2002; Engelmann & Strobel, 2004); and/or incur psychological costs (disutility) from when payoffs are unequal between themselves and others (i.e., are “inequity averse”) (Bolton & Ockenfels, 2000; Fehr & Schmidt, 1999). (There are also reciprocity-based social preference models where people get utility from rewarding positive actions and punishing negative actions [e.g., Dufwenberg & Kirchsteiger, 2004; Falk & Fischbacher, 2006; Rabin, 1993)], but these theories do not make clear predictions about behavior in unilateral decisions, which are our focus; thus we restrict our attention to purely outcome-based preferences related to efficiency and inequity.)

These social preference models based on efficiency and inequity have helped to organize a great deal of experimental data on prosociality in economic games. In these games, such as the Prisoner’s Dilemma (PD) and the Dictator Game (DG), subjects choose between selfish options that maximize their own payoff and prosocial options that increase the other’s payoff and/or reduce inequity. By stipulating that people vary in the weights placed on efficiency and inequity in their utility functions, one can account for variation in behavior in these games.

Despite their success and widespread use, however, many scholars have argued that human prosociality is not, in fact, driven by outcome-based preferences. An alternative on which we focus here is the idea of a generalized morality preference – that is, the proposal that people vary in the utility they get from “doing the right thing” broadly, instead of caring specifically about efficiency and inequity (e.g., Alger & Weibull, 2013; Baron, 2008; Bicchieri, 2005; Brekke, Kverndokk & Nyborg, 2003; Eriksson, Strimling, Andersson & Lindholm, 2017; Huck, Kübler & Weibull, 2012; Jordan, Mullen & Murnighan, 2011; Krupka & Weber, 2013; López-Pérez, 2008; Mazar, Amir, & Ariely, 2008; Sachdeva, Iliev & Medin, 2009; Weber, Kopelman & Messick, 2004). A variety of sources – which sometimes, but not always, include the extent of efficiency or inequity – influence which action is “right” in a given situation.

Here, we present new experimental evidence showing the limitations of outcome-based social preference models of equity and efficiency concerns, and supporting a generalized morality preference account. We do so by leveraging individual differences in prosociality in canonical games (the Prisoner’s Dilemma, PD, and Dictator Game, DG). Specifically, we examine the correlation between an individual’s prosociality in these games and their play in a “Trade-Off Game” (TOG) which pits equity against efficiency – and, critically, how this correlation varies with the framing of the TOG.

In the TOG, players unilaterally determine the payoffs of themselves and two others, and can choose between an option that is more equitable (all three people earn 13 Monetary Units (MUs)) and an option that is more efficient (the player receives 15 MUs, while the other two people receive 13 MUs and 23 MUs respectively).

If a stable outcome-based preference for efficiency/altruism drives cooperation in the PD and giving in the DG, then people who are more prosocial in the PD and DG should be more likely to choose the efficient option in the TOG. Conversely, if a stable outcome-based preference for inequity aversion drives cooperation in the PD and giving in the DG, then people who are more prosocial in the PD and DG should be more likely to choose the equitable option in the TOG. In either case, these correlations should not be influenced by how the TOG is framed.

The predictions of a general morality preference, however, are different. Because neither option in the TOG is clearly more prosocial than the other, having a morality preference should not lead to a consistent, clearly defined favoring of one option over the other. Instead, play should be heavily influenced by the framing (despite the irrelevance of beliefs): subjects should be much more likely to choose the option which is presented as the morally appropriate. As a result, if a general morality preference drives prosociality in the PD and DG, then people who are more prosocial in the PD and DG should choose whichever TOG option is presented as morally right, regardless of whether it is more equitable or efficient.

In this paper, we present six experiments testing these diverging predictions. The results cannot be explained by standard social preference models based on preferences over outcomes, but they are consistent with the predictions of the general morality preference account.

2 Study 1

In Study 1, we examine how framing affects play in the TOG, as well as the relationship between TOG play and play in a PD. To do so, we compare two different TOG frames designed to suggest that one choice versus the other is morally appropriate – and thereby to resolve the ambiguity that the equity/efficiency trade-offs creates about what the “right thing to do” is in the TOG. That is to say, we purposely create an experimenter demand effect — i.e., provide “cues about what constitutes appropriate behavior” (Zizzo, 2010) – for either the equitable or efficient TOG choice, and observe the impact on TOG behavior and cross-game correlation in play.

Experimenter demand effects are typically seen as problematic because experimenters are usually trying to assess how subjects respond to the details of their design (e.g., the payoffs in an economic game). Thus, injecting cues about which option is appropriate creates an undesirable alternative source of variation in behavior, which is particularly problematic when the choice suggested by the demand effect is the same as the one hypothesized to be caused by the experimental manipulation (in which case one cannot tell if the result is due to the manipulation or the demand effect). This is not, however, a problem for the experiments we present in this paper. On the contrary, what we are seeking to study is precisely the effect of giving information about the appropriateness of different options. The demand effect is our manipulation, rather than being a confound.

2.1 Subjects

We recruit N = 498 subjects living in the US at the time of the experiment using the online labor market Amazon Mechanical Turk (AMT)¹.

2.2 Procedure

Subjects are randomly assigned to one of four conditions. In the PD-Give condition, subjects first play the Prisoner’s dilemma (PD), and then play the Trade-Off game (TOG) in the “give frame”. In the PD, subjects are given $0.10 and asked whether they want to “keep it” or “hand it over” to the other subject. In the latter case, the other subject would earn $0.20. Subjects are informed that the subject they are matched with is simultaneously facing the same decision. In the TOG in the “give frame”, subjects in the role of Player A are grouped with two other subjects (Player B and Player C) and told that all three players start with $0.13. Subjects can choose “to be nice” in which case they gain $0.02 and player B gains $0.10, or “not to be nice”, in which case nothing happens and all three players remain with $0.13. Subjects are aware that Player B and Player C are not making any decision. In the PD-Equalize condition, subjects first play the PD and then play the TOG in the “equalize frame”. The “equalize frame” of the TOG is economically identical to the “give frame”, but the names of the strategies are switched: subjects in the role of Player A are told that they start with $0.15, player B starts with $0.23, and player C starts with $0.13, and that they can choose “to be nice” by giving up $0.02 in order “to restore equality” or “not to be nice”, in which case nothing happens. The Give-PD and the Equalize-PD conditions are identical to the PD-Give and PD-Equalize conditions, respectively, apart from the order in which the games are played. Our main analyses collapse over game order, which does not interact with TOG framing (see the Supplementary Information, SI). In this and in the following experiments, standard comprehension questions are asked right after presenting the instructions of the Prisoner’s dilemma and the Dictator game. Subjects failing any comprehension question are automatically excluded from the survey. After the data are collected, bonuses are computed and paid, on top of the participation fee ($0.50). No deception is used. Full experimental instructions are reported in the Appendix.

2.3 Results

As predicted by our account, but not the equity and efficiency preferences account, the frame has a dramatic impact on TOG play: under the Equalize frame, 47.2% of players choose the equitable option, compared to only 5.6% under the Give frame, χ²(1, N=498)=110.4, p<.001. Furthermore, the frame also reverses the relationship between one’s play in the PD and the TOG (Figure 1; positive interaction between frame [0=Give, 1=Equalize] and TOG choice [0=Efficient, 1=Equitable] when predicting PD cooperation using logistic regression: b=2.42, p=.003, see the supplement, Table S1, for regression details). Under the Equalize frame, subjects that choose the equitable option are much more likely to cooperate (49.1%) in the PD than subjects that choose the efficient option (22.7%), χ²(1, N=250)=19.1, p<.001. Under the Give frame, however, the opposite is true (equitable option, 14.5%C; efficient option, 36.3%C; χ²(1, N=248)=2.8, p=.09).

Figure 1: Results of Study 1 (N=498): Subjects who make the nice choice in the Trade-Off Game, whichever that is, cooperate more in the Prisoner’s Dilemma. We plot average cooperation in the Prisoner’s Dilemma as a function of the choice made in each of the two frames of the Trade-Off Game. Error bars represent +/- 1 SEM. Subjects making the “nice” choice in the Trade-Off Game, whichever that is, cooperate more in the Prisoner’s Dilemma than subjects who make the “non-nice” choice. Since the nice choice in the Equalize frame is economically equivalent to the non-nice choice in the Give frame, this correlation cannot be explained by outcome-based preferences and suggests that a substantial proportion of cooperators is motivated by a preference for “being nice”.

3 Study 2

Study 2 seeks to replicate Study 1’s result regarding the frame’s effect on TOG play, and to show that the frame also reverses the relationship between TOG play and play in a DG where the subject unilaterally chooses how much of 10 MU to transfer to a passive recipient. Unlike the PD, beliefs about the other player’s actions have no role in the DG (since the recipient takes no action). Thus any change in the relationship between DG and TOG play induced by the frame cannot be attributed to beliefs.

3.1 Subjects

We recruit N = 379 subjects living in the US at the time of the experiment on AMT.

3.2 Procedure

Study 2 differs from Study 1 only in that the PD is replaced by a Dictator game (DG). In the DG, subjects are given $0.10 and are asked how much, if any, to give to another subject who is given nothing. The other subject is given no choice and only gets what the first subject decides to give.

3.3 Results

As in Study 1, TOG play is dramatically altered by the frame in Study 2: under the Equalize frame, 49.2% of players choose the equitable option, compared to only 9.3% under the Give frame, χ²(1, N=379)=73.6, p<.001. And, as with the PD of Study 1, in Study 2 the frame reverses the relationship between one’s play in the DG and the TOG (Figure 2; positive interaction between frame [0=Give, 1=Equalize] and TOG choice [0=Efficient, 1=Equitable] when predicting amount transferred in the DG using linear regression: b=.342, p<.001, see SI, Table S2 for regression details). Under the Equalize frame, subjects that choose the equitable option transfer substantially more in the DG (40.1% of the endowment) than subjects that choose the efficient option (18.7% of the endowment), t(183)=6.6, p<.001. Under the Give frame, however, the opposite is true (equitable option, 17.2%; efficient option, 30.0%; t(192)=2.05, p=.04).

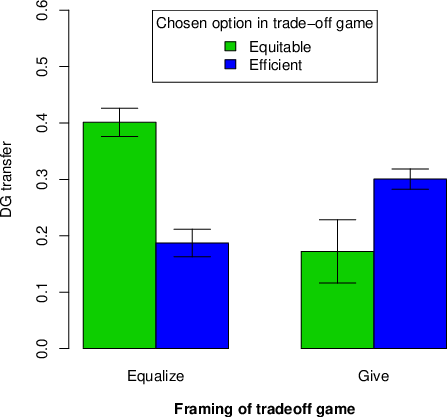
Figure 2: Results of Study 2 (N=379): Subjects who make the nice choice in the Trade-Off Game, whichever that is, give more in the Dictator Game. We plot average giving in the Dictator Game as a function of the choice made in each of the two frames of the Trade-Off Game. Error bars represent +/- 1 SEM. Subjects making the “nice” choice in the Trade-Off Game, whichever that is, give more in the Dictator Game than subjects who make the “non-nice” choice. Again, since the nice choice in the Equalize frame is economically equivalent to the non-nice choice in the Give frame, this correlation cannot be explained by outcome-based preferences and suggests that a substantial proportion of DG giving is motivated by a preference for “being nice”.

4 Study 3

In Study 3, we investigate whether our results are robust to modifying the framing of the TOG. Instead of telling subjects that they can either choose to be nice or not (by choosing either the equitable or efficient option, depending on condition), in Study 3 we compare a Fair frame (where the equitable option is referred to as “more fair” and the efficient option “less fair”) with a Generous frame (where the efficient option is referred to as “more generous” and the equitable option “less generous”). As in Study 2, we pair the TOG with a DG.

4.1 Subjects

We recruit N = 263 subjects living in the US at the time of the experiment on AMT.

4.2 Procedure

Study 3 differs from Study 2 only in that the frame of the TOG is modified. In the “give frame”, the equitable choice is termed “less generous choice” and the efficient choice is termed “more generous choice”. In the “equalize frame”, the equitable choice is termed “more fair choice” and the efficient choice is termed “less fair choice”.

4.3 Results

Once again, we see major differences in TOG play based on the frame: under the Fair frame, 55.3% of players choose the equitable option, compared to only 22.9% under the Generous frame, χ²(1, N=263)=29.0, p<.001. And once again, the frame reverses the relationship between one’s play in the DG and the TOG (Figure 3; positive interaction between frame [0=Generous, 1=Fair] and TOG choice [0=Efficient, 1=Equitable] when predicting amount transferred in the DG using linear regression: b=.340, p<.001, see SI, Table S3 for regression details). Under the Fair frame, subjects that choose the equitable option transfer substantially more in the DG (36.7% of the endowment) than subjects that choose the efficient option (18.6% of the endowment), t(130)=4.1, p<.001. Under the Generous frame, however, the opposite is true (equitable option, 14.3%; efficient option, 30.3%; t(129)=3.05, p=.003).

Figure 3: Results of Study 3 (N=263): Subjects who make the positively framed choice in the Trade-Off Game, whichever that is, give more in the Dictator Game. We plot average giving in the Dictator Game as a function of the choice made in each of the two frames the Trade-Off game. Error bars represent +/- 1 SEM. Subjects making the positively framed choice (more generous or more fair) in the Trade-Off Game, whichever that is, give more in the Dictator Game than subjects who make the negatively framed choice (less generous or less fair, respectively). Thus, the findings from the earlier studies generalize beyond the nice vs non-nice framing used previously.

5 Study 4

We would like to argue that these framing effects are the result of changes in subjects’ perception of which TOG option is the morally correct choice. To provide more direct evidence for this claim, in Study 4 we recruit subjects to read the instructions for each game (in random order), and indicate which option they think is the morally right choice.

5.1 Subjects

We recruit N=369 subjects living in the US at the time of the experiment on AMT.

5.2 Procedure

Subjects are presented with the rules of the PD, the DG, and the TOG (both frames), in random order. For each of these games, they are asked to tell what they think is the morally right thing to do.

5.3 Results

Unsurprisingly, 80.7% of subjects select cooperation in the PD, and 88.8% of them select giving half in the DG. Turning to the TOG, the responses are consistent with our proposal: the frame reverses subjects’ perceptions of what is morally right, χ²(1, N=369)=148.6, p<.001. Subjects exposed to the Equalize frame overwhelmingly (76.8%) rate the equitable option as the morally right TOG choice, whereas subjects exposed to the Give frame overwhelmingly (86.4%) rate the efficient option as the morally right TOG choice.

6 Study 5

In Study 5 we recruit subjects to rule out the alternative explanation that the frame is operating by changing subjects’ perceptions of the descriptive social norm (i.e., what they think other people would do (Cialdini & Trost, 1998)), rather than their perceptions of what is morally right (i.e., what they think they should do). To do so, we have subjects again play a TOG and a DG, but this time cross the Equalize versus Give frame of the TOG with a descriptive social norm manipulation in which subjects are shown the TOG choices of five previous subjects. In the Equitable Norm condition, they are shown four subjects who chose the equitable option and one subject who chose the efficient option. In the Efficient Norm condition, they are shown four subjects who chose the efficient option, and one subject who chose the equitable option.

6.1 Subjects

We recruit N=496 subjects living in the US at the time of the experiment on AMT.

6.2 Procedure

Study 5 implements a 2x2 design in which, after the DG, we manipulate the framing of the TOG (as in the Studies 1 and 2) and the descriptive norm. The descriptive norm is manipulated by telling subjects that we recorded the choices of five subjects who played before them and only one of them did make or did not make the nice choice.

6.3 Results

Both in terms of TOG play, and the relationship between play in the TOG and the DG, we see that the frame has a large effect while the descriptive social norm information has little effect. In the TOG, subjects are more likely to choose the equitable option under the Equalize frame, regardless of the descriptive norm (although the effect is somewhat weaker under the Efficient Norm condition; logistic regression shows a significant positive interaction between frame [0=Give, 1=Equalize] and norm [0=Efficient, 1=Equitable], b=.89, p=.049, see SI, Table S4). With the Equitable Norm, 65.9% of players choose the equitable option under the Equalize frame, compared to only 11.7% under the Give frame, χ²(1, N=254)=78.6, p<.001. With the Efficient Norm, 53.6% of subjects choose the equitable option under the Equalize frame, compared to only 16.2% under the Give frame, χ²(1, N=242)=36.8, p<.001. See SI, Figure S1.

Predicting DG transfer using linear regression, there is a significant positive interaction between frame [0=Give, 1=Equalize] and TOG choice [0=Efficient, 1=Equitable] (b=.470, p<.001), as in the earlier studies; but no significant interaction between Norm and TOG choice nor any higher-order interactions (p>.3 for all); see Figure 4 and SI, Table S5. Thus, regardless of the descriptive norm information, it is the case that under the Equalize frame, subjects who choose the equitable TOG option give more in the DG than those who choose the efficient option; and under the Give frame, the opposite is true. Study 5 therefore demonstrates that the effects observed in Studies 1-3 were not driven by the frame creating an implicit descriptive social norm.

Figure 4: Results of Study 5 (N=496): Manipulating descriptive norm in the Trade-Off Game has virtually no effect on the correlation between play in the Trade-Off Game and play in the Dictator Game. We plot average giving in the Dictator Game as a function of the choice made in each condition of the Trade-Off game (“frame” stands for the framing of the TOG, and “norm” stands for the salient norm; for instance, “norm = Equitable” means that subjects are informed that we have recorded the responses of five subjects who played before them and four of them have chosen the equitable option). Error bars represent +/- 1 SEM. Subjects making the nice choice in the Trade-Off Game give more in the Dictator Game, independently of the frame of the Trade-Off Game and independently of the descriptive norm.

7 Study 6

In the previous studies, the choice framed as nice in the TOG – be it efficient or equitable – is always the active choice, as is the prosocial action in the DG and in the PD. Thus, it is possible that the correlation between choosing the nice option in the TOG game and being prosocial in the PD/DG is driven by a preference for action, rather than a preference for morality. To rule out this potential alternative explanation, Study 6 re-explores the correlation between the DG and the TOG, but this time using a take frame in the DG: now the active choice in the DG (taking) is selfish, whereas the passive choice (not taking) is prosocial. Thus, if the results of the previous studies were driven by preferences for action, then in this study we would see a reversal of the correlation, such that the prosocial choice in the DG would be correlated with the non-nice choice in the TOG. Conversely, if, as we argue, our results were instead driven by preferences for being moral, then we would find the same pattern as in the previous studies, with the prosocial choice in the DG being correlated with the nice choice in the TOG.

7.1 Subjects

We recruit N=275 subjects living in the US at the time of the experiment on AMT.

7.2 Procedure

Subjects are randomly divided in two conditions: the DGtake-Equalize condition and the DGtake-Give condition, similar to those in Study 2. The only difference regards the instructions of the DG. While in Study 2 subjects played the DG in the standard “Give frame”, here subjects play the DG in the “Take frame”: they are told that they are paired with another person and that both of them start with $0.05, and that they could take any amount between 0$0.00 and $0.05 from the other person. The other person has no choice and only gets the amount of money unclaimed by the first subject.

7.3 Results

The results are consistent with Study 2. Play in the TOG is dramatically altered by the frame: under the Equalize frame, 48.2% of players choose the equitable option, compared to only 13.9% under the Give frame, χ²(1, N=275)=37.5, p<.001. And the TOG frame reverses the relationship between one’s play in the DG and the TOG in the same way as in Study 2 (Figure 5; significant positive interaction between Equalize frame and equitable TOG choice when predicting amount unclaimed in the DG using linear regression: b=.431, p<.001, see SI, Table A6 for regression details). Under the Equalize frame, subjects that choose the equitable option leaved more money unclaimed in the DG (39.6% of the endowment) compared to subjects that choose the efficient option (14.2% of the endowment), t(137)=7.35, p<.001. Under the Give frame, however, the opposite is true (equitable option, 8.9% unclaimed; efficient option, 26.7% unclaimed; t(134)=3.09, p=.001). Thus, these results confirm our interpretation that the previous findings are driven by preferences for morality, rather than preferences for action.

Figure 5: Results of Study 6 (N=275): Manipulating the active choice in the DG has virtually no effect on the correlation between play in the Trade-Off Game and play in the Dictator Game. We plot average amount unclaimed in the Dictator Game in the “Take-frame” as a function of the choice made in each condition of Trade-Off game condition. Error bars represent +/- 1 SEM. Subjects making the nice choice in the Trade-Off Game unclaim more in the Dictator Game, independently of the frame of the Trade-Off Game.

8 Discussion

Decades of experimental research have shown that people sometimes forgo personal gains for the benefit of others, and they do so even in unilateral one-shot anonymous interactions. The standard approach in behavioral economics to understanding this pure prosocial behavior, which cannot be explained by material self-interest, has been to assume that people have social preferences for minimizing social inequities and/or for maximizing social welfare (Bolton & Ockenfels, 2000; Camerer & Fehr, 2004; Charness & Rabin, 2002; Dufwenberg & Kirchsteiger, 2004; Engelmann & Strobel, 2004; Falk & Fischbacher, 2006; Fehr & Schmidt, 1999; Rabin, 1993).

Across six experiments, we present results that are inconsistent with equity or efficient preferences per se determining behavior (and, more generally, with any outcome-based utility function). Instead of making outcome-based evaluations of all available options, we observe that prosocial people tend to choose the option that is presented as being morally right in the given situation, be it equitable or efficient. We argue that these results support the idea of a general morality preference.

The idea that people are motivated to be moral is not new. The drive to appear moral to oneself has received considerable attention in the psychological literature (e.g., Baron, 2008; Bicchieri, 2005; Jordan, Mullen & Murnighan, 2011; Mazar, Amir & Ariely, 2008; Sachdeva, Iliev & Medin, 2009). Several formal models in the economics literature have incorporated such ideas, as opposed to preferences for equity or efficiency per se (Alger & Weibull, 2013; Brekke, Kverndokk, & Nyborg, 2003; Huck, Kübler & Weibull, 2012). Importantly, however, our results cannot be explained by any of these particular models. For example, Brekke et al. (2003) assume that people are motivated to be socially responsible and to adhere to their individual “moral ideal”. On the contrary, again, our results show that the moral ideal is not individual and can be very easily manipulated. Huck et al. (2012) assume that people choose according to a utility function that is the sum between their material payoff and a “social payoff”, which, in turn, is a function of the economic externalities. Thus, the model by Huck et al. (2012) employs an outcome-dependent utility function. On the contrary, our findings cannot be explained by outcome-dependent utility functions. Finally, the model by Alger and Weibull (2013) regards symmetric interactions and thus it does not make clear predictions in our case. Thus, our results push the boundary of extant theories of morality preferences.

Our critique is also distinct from the reciprocity-based argument that intentions matter as well as outcomes (Dufwenberg & Kirchsteiger, 2004; Falk & Fischbacher, 2006; Rabin, 1993), as we largely focus on unilateral decisions where the other parties take no actions and thus have no relevant intentions. Our results are also inconsistent with norms-based preferences where one’s aversion to norm-breaking is contingent on others also following the norm. For example, López-Pérez (2008) proposes a model in which people gain utility from choosing appropriate actions, but this utility is discounted by the extent to which they expect others to act selfishly and choose inappropriate actions. They in particular focus on an “E-norm” in which people determine which actions are appropriate based on some fixed weighting of equity and efficiency. Neither the E-norm nor their more general model fit our data, because Study 5 demonstrates that learning that other people have not chosen the “nice” option has very little effect on subjects’ behavior: that is, the effects we observe are not driven by “descriptive norms” (beliefs about the actions of others). Instead, our experiments demonstrate a causal impact of perceived morality (an “injunctive norm”) on prosocial behavior.

Prior work on injunctive norms has shown a correlation between an action’s perceived appropriateness and its likelihood of being chosen (Krupka & Weber, 2013). Although these results are consistent with our general morality preference account, their correlational nature limits the level of support they can provide. For example, the observed correlation could be the result of people justifying the action they want to choose by saying that it is appropriate. Or, both choices and appropriateness judgements could be driven by other unobserved variables, including outcome-based preferences that are implemented via heuristics/bounded rationality (and thus do not perfectly respond to outcomes, e.g., Capraro, Jordan & Rand, 2014) or descriptive social norms (i.e., perceptions of the frequency of others’ actions). Our experiments, in contrast, manipulate the perceived injunctive norm by varying which option is framed as morally right. We thereby demonstrate a clear, unambiguous causal effect of perceived morality on behavior. Even more importantly, we not only examine how average behavior in a specific game varies as a function of the details of the setup (as in Krupka and Weber (2013), but also investigate individual differences in play across games. In doing so, we show that people who cooperate in the PD and give in the DG typically choose the TOG action which is framed as morally right (be it equitable or efficient). Thus, we show that a preference for moral action is central to the basic phenomenon of prosocial behavior in canonical games, rather than just being important for explaining deviations from outcome-based preferences in non-standard game setups.

Our morality preference proposal obviously raises the question of what action is seen as morally right in any given scenario (prior modeling work has either side-stepped this question entirely and just measured perceived appropriateness empirically, e.g., Krupka & Weber, 2013, or has assumed that judgements of rightness are driven by a fixed preference for equity versus efficiency, e.g., López-Pérez, 2008, an assumption which our data show is incorrect). Based on our experiments, we of course cannot provide an exhaustive characterization of morality – and, most likely, morality judgments are driven at least in part by necessarily-imprecise heuristics and emotions (Capraro et al., 2014; Greene, Sommerville, Nystrom, Darley & Cohen, 2001; Haidt, 2001; Rand, 2016).

Finally, our data bear on the debate about the basis of framing effects in economic games. A long literature has demonstrated that payoff-irrelevant social frames can alter behavior in economic games. For example, people cooperate more in a standard PD that is titled the “Community game” compared to one titled the “Wall Street game” (Liberman, Samuels & Ross, 2004). Some have argued that such framing effects can be accounted for using stable preferences for efficiency and equity, once you take into account the fact that the frames can change peoples’ beliefs about the actions of others (Ellingsen, Johannesson, Mollerstrom & Munkhammar, 2012). Support for this position comes from evidence that frames typically have a substantial effect only in multi-lateral games where there is uncertainty about other players’ actions, such as the standard simultaneous PD or Public Goods Game (Dufwenberg, Gächter & Hennig-Schmidt, 2011; Ellingsen et al., 2012; Engel & Rand, 2014; Goerg, Rand & Walkowitze, 2017; Liberman et al., 2004), but not in games where there is no uncertainty about the others actions, such as the asynchronous PD (Ellingsen et al., 2012) or the DG where the other party takes no action (Chowdhury, Jeon & Saha, 2016; Dreber, Ellingsen, Johannesson & Rand, 2013; Goerg et al., 2017; Grossman & Eckel, 2015). Contradicting this account, however, are the results of Krupka and Weber (2013) who do find framing effects in a DG, as well as Eriksson, Strimling, Andersson & Lindholm (2017) and Larrick & Blount (1997), who find framing effects for the second mover in the Ultimatum Game. Our results on behavior in the TOG, where the frame has a dramatic effect on behavior despite it being a unilateral decision, provide further evidence that beliefs alone cannot account for framing effects in economic games.

In sum, we have presented six experiments which demonstrate a causal effect of perceived morality on prosocial behavior, and show that responding to this manipulation predicts prosociality in the PD and DG. Our results cannot be accounted for by the standard approach to understanding prosocial behavior in behavioral economics: it cannot be the case that people’s prosocial behavior is driven per se by preferences regarding inequity and efficiency (or, more generally, any outcome-based preferences). Instead, the data suggest that people have a stable preference for doing what they understand to be the morally right thing in a given situation – a preference which cannot be cleanly expressed using a purely outcome-based utility function.