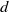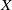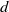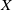The operad of Latin hypercubes

Abstract

We show that the sets of $d$-dimensional Latin hypercubes over a non-empty set $X$, with $d$ running over the positive integers, determine an operad which is isomorphic to a sub-operad of the endomorphism operad of $X$. We generalise this to categories with finite products, and then further to internal versions for certain Cartesian closed monoidal categories with pullbacks.

1. Introduction

There are several variants of the definition of Latin hypercubes in the literature – see the discussions and references in [1, §4] and [8, Section 1]. In order to define the version, we will be considering here, we fix the following notation and conventions. Categories are assumed to be essentially small. Let $X$ be an object in a category $\mathcal {C}$ with finite products and let $d$ be a positive integer. The product $X^d$ of $d$ copies of $X$ in $\mathcal {C}$ is equipped with $d$ canonical projections $\pi ^d_i : X^d\to X$ , characterised by the universal property that for any object $Y$ and morphisms $\eta _i : Y\to X$ , with $1\leq i\leq d$ , there is a unique morphism $\eta : Y\to X^d$ satisfying $\eta _i = \pi ^d_i\circ \eta$ for $1 \leq i\leq d$ . In that case we write $\eta =$ $(\eta _i)_{1\leq i\leq d}$ . Applied to $X^{d+1}$ instead of $Y$ and any subset of $d$ of the $d+1$ canonical projections $\pi ^{d+1}_j$ yields for every $s$ such that $1\leq s \leq d+1$ a unique morphism $\tau ^{d+1}_s : X^{d+1} \to X^d$ satisfying $\pi ^{d+1}_i = \pi ^d_i\circ \tau ^{d+1}_s$ for $1\leq i\leq s-1$ , and $\pi ^{d+1}_i = \pi ^d_{i-1}\circ \tau ^{d+1}_s$ for $s+1 \leq i\leq d+1$ . With the notation above, this is equivalent to

\begin{equation*}\tau ^{d+1}_s= (\pi ^{d+1}_1,..,\pi ^{d+1}_{s-1}, \pi ^{d+1}_{s+1},..,\pi ^{d+1}_{d+1}). \end{equation*}

If $X$ is a non-empty set, then $X^{d+1}$ is the Cartesian product of $d+1$ copies of $X$ , and we have

\begin{equation*}\tau ^{d+1}_s(x_1,x_2,..,x_{d+1})= (x_1,..,x_{s-1}, x_{s+1},..,x_{d+1}),\end{equation*}

where $x_i\in X$ for $1\leq i\leq d+1$ . That is, $\tau ^{d+1}_s$ is the projection from $X^{d+1}$ to $X^d$ which discards the coordinate $s$ in $X^{d+1}$ .

Definition 1.1. Let $\mathcal {C}$ be a category with finite products, let $X$ be an object in $\mathcal {C}$ , and let $d$ be a positive integer. A Latin hypercube of dimension $d$ over $X$ is a morphism $\lambda : L \to X^{d+1}$ in $\mathcal {C}$ such that $\tau ^{d+1}_s\circ \lambda : L \to X^d$ is an isomorphism in $\mathcal {C}$ , for $1\leq s\leq d+1$ .

The morphism $\lambda$ in this Definition is necessarily a monomorphism. Two Latin hypercubes $\lambda : L\to X^{d+1}$ and $\lambda ' : L'\to X^{d+1}$ are called isomorphic if there is an isomorphism $\alpha : L\to L'$ such that $\lambda =\lambda '\circ \alpha$ . In that case $\alpha$ is unique since $\lambda '$ is a monomorphism.

A Latin hypercube of dimension $d$ over a non-empty set $X$ is uniquely isomorphic to a Latin hypercube given by a subset $L$ of $X^{d+1}$ with the property that for any choice of $d$ of the $d+1$ coordinates of an element in $X^{d+1}$ there is a unique element in the remaining coordinate such that the resulting element belongs to $L$ . In particular, we can identify a Latin hypercube of dimension $d$ over a non-empty set uniquely, up to unique isomorphism, as the graph of the map $f : X^d\to X$ satisfying $(x_1,x_2,..,x_d, f(x_1,x_2,..,x_d))\in L$ for all $(x_1,x_2,..,x_d)\in X^d$ . In this way, Latin hypercubes of dimension $d$ can be identified with a subset, denoted $\mathcal {L}(X^d,X)$ , of the set $\mathrm {Map}(X^d,X)$ of all maps from $X^d$ to $X$ . Any map in $\mathcal {L}(X^d,X)$ is clearly surjective. The following result shows that the subsets $\mathcal {L}(X^d,X)$ of $\mathrm {Map}(X^d,X)$ with $d\in \mathbb {N}$ determine an operad. We refer to [6] or [7, Part II, §1.2] for basic terminology on operads.

Theorem 1.2. Let $X$ be a non-empty set. There is a sub-operad $\mathcal {L}$ of the endomorphism operad $\mathcal {E}$ of $X$ such that $\mathcal {L}(d)=$ $\mathcal {L}(X^d,X)$ , for all $d\in \mathbb {N}$ .

This is not the most general version in which this result can be stated. Theorem1.2 admits a generalisation to categories with finite products, which we will describe in Theorem3.4, and a further generalisation, in Theorem4.5, to certain Cartesian closed monoidal categories in which $\mathcal {L}$ can be identified with a sub-operad of an internal endomorphism operad. We have chosen to state and prove this result first in the context of non-empty sets in order to not distract from the elementary nature of the proof. Operads were first introduced for topological spaces, and Theorem1.2 holds verbatim for non-empty compactly generated topological spaces (this is a special case of Theorem4.5; see Remark 4.8).

Remark 1.3. As pointed out in [8], if $d=1$ , then a Latin hypercube over a non-empty set $X$ is a subset of $X^2$ of the form $\{(x,\sigma (x))\}_{x\in X}$ for some permutation $\sigma$ of $X$ , and hence Latin hypercubes of dimension $1$ over $X$ correspond to the elements of the symmetric group $\mathfrak {S}_X$ of permutations of $X$ , so they form themselves a group. This group structure is encoded as the structural map $-\circ _1 -$ on $\mathcal {L}(1)$ of the operad $\mathcal {L}$ .

Remark 1.4. Let $X$ be an object in a category $\mathcal {C}$ with finite products and let $d$ be a positive integer. The group $\mathrm {Aut}_{\mathcal {C}}(X)\wr \mathfrak {S}_{d+1}$ acts on $X^{d+1}$ , hence on the class of Latin hypercubes of dimension $d$ over $X$ , with the base group of $d+1$ copies of $\mathrm {Aut}_{\mathcal {C}}(X)$ acting by composing $\lambda$ with a $(d+1)$ -tuple of automorphisms of $X^{d+1}$ and $\mathfrak {S}_{d+1}$ acting on $X^{d+1}$ by permuting the $d+1$ canonical projections $\pi ^{d+1}_i : X^{d+1}\to X$ . This action induces an action of $\mathrm {Aut}_{\mathcal {C}}(X)\wr \mathfrak {S}_{d+1}$ on the isomorphism classes of Latin hypercubes of dimension $d$ over $X$ , which for $\mathcal {C}$ the category of sets is the standard notion of paratopism.

Remark 1.5. Let $X$ be an object in a category $\mathcal {C}$ with finite products and let $d$ be a positive integer. The canonical projections $\pi ^{d}_i : X^{d}\to$ $X$ are split surjective, with section the diagonal morphism $\delta : X\to$ $X^{d}$ defined as the unique morphism such that $\pi ^{d}_i\circ \delta =$ $\mathrm {Id}_X$ , for $1\leq i\leq d$ . Let $\lambda : L\to X^{d+1}$ be a Latin hypercube. The $d+1$ components $\lambda _i=$ $\pi ^{d+1}_i\circ \lambda : L\to X$ of $\lambda$ are split epimorphisms. Indeed, if we choose $s\neq i$ , with $1\leq i,s\leq d+1$ , then $\pi ^{d+1}_i$ factors through $\tau ^{d+1}_s$ ; more precisely, $\pi ^{d+1}_i\circ \lambda = \pi ^{d}_j\circ \tau ^{d+1}_s\circ \lambda$ where $j=i$ if $i\lt s$ , and $j=i-1$ if $i\gt s$ . Since $\tau ^{d+1}_s\circ \lambda$ is an isomorphism and $\pi ^d_j$ a split epimorphism, it follows that their composition is a split epimorphism, and hence so is $\pi ^{d+1}_i\circ \lambda$ .

2. Proof of Theorem 1.2

The endomorphism operad $\mathcal {E}$ of a non-empty set $X$ consists of the sets $\mathcal {E}(n) = \mathrm {Map}(X^n,X)$ for any positive integer $n$ , together with strutural maps

\begin{equation*}-\circ _i - : \,\mathrm {Map}(X^n,X) \times \mathrm {Map}(X^m,X) \to \mathrm {Map}(X^{n+m-1},X)\end{equation*}

given by

\begin{equation*}(f \circ _i g)(x_1,x_2,\ldots, x_{n+m-1}) = f(x_1,..,x_{i-1}, g(x_i,..,x_{i+m-1}), x_{i+m},..,x_{n+m-1})\end{equation*}

for all positive integers $n$ , $m$ , $i$ , such that $1\leq i\leq n$ , all $x_1,x_2,..,x_{n+m-1}\in X$ , and all maps $f\in \mathrm {Map}(X^n,X)$ and $g\in \mathrm {Map}(X^m,X)$ . The sets $\mathcal {E}(n)=\mathrm {Map}(X^n,X)$ are equipped with the action of $\mathfrak {S}_n$ on the $n$ coordinates of $X^n$ , and the identity map $\mathrm {Id}_X\in$ $\mathcal {E}(1)=\mathrm {Map}(X,X)$ is the unit element of this operad. For the associativity properties of the maps $-\circ _i -$ and their compatibility with the symmetric group actions on the sets $\mathrm {Map}(X^n,X)$ , see for instance [6, Definition 1.2] or [7, Part II,§1.2]. The main step for the proof of Theorem1.2 is the following Lemma.

Lemma 2.1. Let $X$ be a non-empty set, and let $d$ , $e$ , $i$ be positive integers such that $1\leq i\leq d$ . Let $f\in \mathcal {L}(X^d,X)$ and $g\in \mathcal {L}(X^e,X)$ . Then $f\circ _i g\in$ $\mathcal {L}(X^{d+e-1},X)$ .

Proof. In order to show that $f\circ _i g$ belongs to $\mathcal {L}(X^{d+e-1},X)$ we need to show that for any $c\in X$ and an arbitrary choice of $d+e-2$ of the $d+e-1$ elements $x_1,x_2,..,x_{d+e-1}\in X$ the remaining of these elements is uniquely determined by the equation

(1) \begin{equation} f(x_1,..,x_{i-1}, g(x_i,..,x_{i+e-1}), x_{i+e},..,x_{d+e-1}) = c. \end{equation}

Let $s$ be an integer such that $1\leq s\leq d+e-1$ . Fix elements $x_1,x_2,..,x_{s-1}, x_{s+1},..,x_{d+e-1}, c \in$ $X$ .

Consider first that case where $s\leq i-1$ or $s\geq i+e$ . Then, setting $y=g(x_i,..,x_{i+e-1})$ , the Equation 1 becomes

(2) \begin{equation} f(x_1,..,x_{i-1},y,x_{i+e},..,x_{d+e-1}) = c. \end{equation}

All entries but the entry $x_s$ in this equation are fixed. Since $f\in \mathcal {L}(X^d,X)$ it follows that there is a unique choice for $x_s\in X$ such that Equation 2 holds, and hence a unique choice for $x_s\in X$ such that Equation 1 holds.

Consider the remaining case where $i\leq s \leq i+e-1$ . Then in particular the elements $x_1,..,x_{i-1}, x_{i+e},..,x_{d+e-1}$ are fixed in $X$ . Since $f\in \mathcal {L}(X^d,X)$ it follows that there is a unique $y\in X$ such that Equation 2 holds. Thus for Equation 1 to hold, we must have

(3) \begin{equation} g(x_i,..,x_{i+e-1}) = y. \end{equation}

In this equation all but $x_s$ have been chosen. Since $g\in \mathcal {L}(X^e,X)$ it follows that there is a unique choice $x_s\in X$ such that Equation 3 holds. In all cases, there is a unique choice of $x_s$ such that Equation 1 holds. This shows that $f\circ _i g$ belongs to $\mathcal {L}(X^{d+e-1},X)$ and completes the proof.

Proof of Theorem 1.2. Let $d\in \mathbb {N}$ . A map $f\in \mathcal {E}(d)=$ $\mathrm {Map}(X^d,X)$ belongs to $\mathcal {L}(d)=\mathcal {L}(X^d,X)$ if and only if the set

\begin{equation*}L = \{(x_1,x_2,..,x_d, f(x_1,x_2,..,x_d))\ |\ x_1,x_2,..,x_d \in X\}\end{equation*}

is a Latin hypercube in $X^{d+1}$ . Equivalently, $f$ belongs to $\mathcal {L}(d)$ if and only for every $c\in X$ and an arbitrary choice of $d-1$ of the $d$ entries $x_1,..,x_d\in X$ the remaining entry is uniquely determined by the equation $f(x_1,x_2,..,x_d)=c$ . The action of $\mathfrak {S}_d$ on $\mathrm {Map}(X^d,X)$ by permuting the $d$ coordinates of $X^d$ clearly preserves the subset $\mathcal {L}(d)$ , and $\mathrm {Id}_X$ belongs to $\mathcal {L}(1)$ . In order to prove Theorem1.2, it remains to show that the sets $\mathcal {L}(d)$ are closed under the operations $-\circ _i-$ . This is done in Lemma2.1 above, and this concludes the proof.

Remark 2.2. We could have very slightly simplified the proof of Lemma 2.1 by observing that thanks to the symmetric group actions on the coordinates of Latin hypercubes (cf. Remark 1.4) it would have been sufficient in the proof of Lemma 2.1 to consider the map $f\circ _{d} g$ and a single $s$ in the distinction into the two cases for $s$ . That is, it would have been sufficient in the last part of the proof of Lemma 2.1 to consider the cases where either $1=s\leq d-1$ or $s=d$ . We will make use of this observation in the proof of the more general Theorem 3.4 below.

Remark 2.3. The proof of Theorem 1.2, as written, involves choices of elements in the set $X$ . In Section  3 below we will rewrite this proof in such a way that it extends to categories with finite products.

3. On Latin hypercubes in Cartesian monoidal categories

In this section, we extend Theorem1.2 to categories with finite products. Given an object $X$ in a category $\mathcal {C}$ with finite products, a positive integer $n$ , and a morphism $\lambda : L \to X^n$ in $\mathcal {C}$ , we denote as at the beginning by $\lambda _i=$ $\pi ^n_i\circ \lambda$ the composition of $\lambda$ with the $i$ -th canonical projection $\pi ^n_i : X^n\to X$ , where $1\leq i\leq n$ . The morphism $\lambda$ is uniquely determined by the $\lambda _i$ , and we will write abusively $\lambda =$ $(\lambda _i)_{1\leq i\leq n}$ whenever convenient. If $\sigma \in$ $\mathfrak {S}_n$ , then $\sigma$ induces an automorphism $\hat \sigma$ on $X^n$ given by $\hat \sigma _i=\pi ^n_{\sigma ^{-1}(i)}$ ; that is, $\hat \sigma$ permutes the coordinates of $X^n$ . This yields a group homomorphism $\mathfrak {S}_n \to \mathrm {Aut}_{\mathcal {C}}(X^n)$ . We write ${^\sigma {\lambda }}=$ $\hat \sigma \circ \lambda$ . We extend the earlier notation $\mathcal {L}_{\mathcal {C}}(X^d,X)$ in the obvious way.

Definition 3.1. Let $\mathcal {C}$ be a category with finite products. Let $d$ be a positive integer. We denote by $\mathcal {L}_{\mathcal {C}}(X^d,X)$ the subset of $\mathrm {Hom}_{\mathcal {C}}(X^d,X)$ consisting of all morphisms $f : X^d\to X$ such that the morphism $(\mathrm {Id}_{X^d}, f) : X^d \to X^d\times X = X^{d+1}$ is a Latin hypercube.

We first identify canonical representatives in isomorphism classes of Latin hypercubes.

Proposition 3.2. Let $\mathcal {C}$ be a category with finite products, let $X$ be an object in $\mathcal {C}$ , and let $d$ , $s$ be positive integers such that $1\leq s\leq d+1$ . Let $\lambda : L\to X^{d+1}$ be a Latin hypercube. Then there is a unique Latin hypercube $\iota : X^d \to X^{d+1}$ such that $\tau ^{d+1}_{s}\circ \iota = \mathrm {Id}_{X^d}$ and such that $\iota \circ \alpha =\lambda$ for some isomorphism $\alpha : L \to X^d$ . In that case we have $\alpha =$ $\tau ^{d+1}_{s}\circ \lambda : L \to X^d$ .

Proof. By the definition of Latin hypercubes, the morphism $\alpha = \tau ^{d+1}_{s}\circ \lambda : L\to$ $X^d$ is an isomorphism. Then setting $\iota = \lambda \circ \alpha ^{-1}$ implies immediately that $\alpha$ determines an isomorphism between the Latin hypercubes $\lambda : L\to X^{d+1}$ and $\iota : X^d\to X^{d+1}$ . We need to show that $\alpha$ and $\iota$ are unique subject to these properties. Let $\iota ' : X^d\to X^{d+1}$ a Latin hypercube and $\alpha ' : L\to X^d$ an isomorphism such that $\tau ^{d+1}_{s}\circ \iota '=$ $\mathrm {Id}_{X^d}$ and such that $\iota '\circ \alpha '= \lambda$ . Composing this equality with $\tau ^{d+1}_{s}$ yields

\begin{equation*}\alpha ' = \mathrm {Id}_{X^d}\circ \alpha ' = \tau ^{d+1}_{s}\circ \iota '\circ \alpha ' = \tau ^{d+1}_{s}\circ \lambda = \alpha \end{equation*}

This implies $\iota '=\lambda \circ \alpha ^{-1}=\iota$ , whence the uniqueness of $\iota$ and $\alpha$ as stated. The result follows.

Applied with $s=d+1$ , Proposition 3.2 implies that – as earlier in the category of sets –- the morphisms in $\mathcal {L}_{\mathcal {C}}(X^d,X)$ parametrise the isomorphism classes of $d$ -dimensional Latin hypercubes over $X$ .

Corollary 3.3. Let $\mathcal {C}$ be a category with finite products, let $X$ be an object in $\mathcal {C}$ , and let $d$ be a positive integer. Any Latin hypercube of dimension $d$ over $X$ is uniquely isomorphic to a Latin hypercube of the form $\iota : X^d\to X^{d+1}$ such that $\iota$ is a section of the morphism $\tau ^{d+1}_{d+1}$ discarding the coordinate $d+1$ . Any such morphism $\iota$ is then uniquely determined by its last component $f = \iota _{d+1} = \pi ^{d+1}_{d+1}\circ \iota : X^d\to X$ . In particular, the set $\mathcal {L}_{\mathcal {C}}(X^d,X)$ parametrises the isomorphism classes of $d$ -dimensional Latin hypercubes over $X$ .

We show now that the sets $\mathcal {L}_{\mathcal {C}}(X^d,X)$ form an operad, together with the structural maps $-\circ _i -$ defined as follows. Let $f\in$ $\mathcal {L}_{\mathcal {C}}(X^d,X)$ and $g\in$ $\mathcal {L}_{\mathcal {C}}(X^e,X)$ , where $d$ , $e$ are positive integers. For $1\leq i \leq d$ , the structural map

\begin{equation*}-\circ _i - : \,\mathrm {Hom}_{\mathcal {C}}(X^d,X) \times \mathrm {Hom}_{\mathcal {C}}(X^e,X) \to \mathrm {Hom}_{\mathcal {C}}(X^{d+e-1},X)\end{equation*}

sends $(f, g)$ to the morphism

\begin{equation*}f \circ (\mathrm {Id}_{X^{i-1}}\times g \times \mathrm {Id}_{X^{d-i}})\end{equation*}

where we identify $X^{i-1}\times X^e\times X^{d-i}=X^{d+e-1}$ for the domain of this morphism and where we identify $X^{i-1}\times X\times X^{d-i}=$ $X^d$ for the codomain of $ \mathrm {Id}_{X^{i-1}}\times g \times \mathrm {Id}_{X^{d-i}}$ . One checks that if $X$ is a set, this coincides with the earlier definition of $f\circ _i g$ .

Theorem 3.4. Let $X$ be an object in a category $\mathcal {C}$ with finite products. There is a sub-operad $\mathcal {L}$ of the endomorphism set operad $\mathcal {E}$ of $X$ such that $\mathcal {L}(d)=$ $\mathcal {L}_{\mathcal {C}}(X^d,X)$ , for all $d\in \mathbb {N}$ . In particular, for any positive integers $d$ , $e$ , $i$ such that $1\leq i\leq d$ , and any morphisms $f\in$ $\mathcal {L}_{\mathcal {C}}(X^d,X)$ and $g\in$ $\mathcal {L}_{\mathcal {C}}(X^e,X)$ we have $f\circ _i g \in \mathcal {L}_{\mathcal {C}}(X^{d+e-1},X)$ .

Proof. The proof amounts to rewriting the proof of Theorem1.2, including the statement and proof of Lemma 2.1, in such a way that all steps remain valid for the Cartesian products in $\mathcal {C}$ . In order to keep this readable, we mention in each step what this corresponds to in the case where $X$ is a non-empty set (and by considering coordinates, one easily translates this to statements in $\mathcal {C}$ ).

Let $f\in$ $\mathcal {L}_{\mathcal {C}}(X^d,X)$ and $g\in$ $\mathcal {L}_{\mathcal {C}}(X^e,X)$ , where $d$ , $e$ are positive integers. That is, the morphisms

\begin{equation*}(\mathrm {Id}_{X^d}, f) \,:\, X^d \to X^{d+1}, \end{equation*}

\begin{equation*}(\mathrm {Id}_{X^e},g) \,:\, X^e \to X^{e+1}\end{equation*}

are Latin hypercubes. As in the proof of Theorem1.2, the unitality and symmetric group actions are obvious, and we only need to show, analogously to Lemma 2.1, that $(\mathrm {Id}_{X^{d+e-1}}, f\circ _i g)$ is a Latin hypercube. That is, we need to show that for $1\leq s\leq d+e-1$ and $1\leq i\leq d$ , the composition $\tau ^{d+e}_s \circ (\mathrm {Id}_{X^{d+e-1}}, f\circ _i g)$ is an automorphism of $X^{d+e-1}$ . As pointed out in Remark 2.2, since we may permute coordinates, it suffices to do this for $i=d$ and in the two cases where either $1=s\leq d-1$ or $s=d$ .

We consider first the case $1=s\leq d-1$ , so $d\geq 2$ . We need to show that the morphism

\begin{equation*}\tau ^{d+e}_1\circ (\mathrm {Id}_{X^{d+e-1}}, f\circ _d g)\end{equation*}

is an automorphism of $X^{d+e-1}$ . If $X$ is a set, then this automorphism is given by the assignment

\begin{equation*}(x_1,x_2,..,x_{d+e-1}) \mapsto (x_2,..,x_{d+e-1}, f(x_1,..,x_{d-1},g(x_d,..,x_{d+e-1}))).\end{equation*}

First, the morphism $\tau ^d_1\circ (\mathrm {Id}_{X^d}, f)$ is an automorphism of $X^d$ because $(\mathrm {Id}_{X^d},f)$ is a Latin hypercube. We note that if $X$ is a non-empty set, then the morphism $\tau ^d_1\circ (\mathrm {Id}_{X^d}, f)$ is given by the assignment

\begin{equation*}(x_1,..,x_d) \mapsto (x_2,..,x_d, f(x_1,..,x_d)).\end{equation*}

Compose this with the automorphism $\hat \sigma$ induced by the cyclic permutation $\sigma =$ $(1,2,..,d)$ on coordinates. The resulting automorphism

\begin{equation*}\hat \sigma \circ \tau ^d_1\circ (\mathrm {Id}_{X^d},f)\end{equation*}

is, for $X$ a set, given by the assignment

\begin{equation*}(x_1,..,x_d) \mapsto (f(x_1,..,x_d),x_2,..,x_d)\end{equation*}

The Cartesian product of this automorphism with $-\times \mathrm {Id}_{X^{e-1}}$ yields an automorphism of $X^{d+e-1}$ , which for $X$ a set corresponds to

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (f(x_1,..,x_d),x_2,..,x_{d+e-1}))\end{equation*}

Again permuting cyclically, the coordinates yields an automorphism of $X^{d+e-1}$ which we will denote by $\alpha$ , which, if $X$ is a set, corresponds to

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (x_2,..,x_{d+e-1}, f(x_1,..,x_d)).\end{equation*}

Using the fact that $\tau ^e_1\circ (\mathrm {Id}_{X^e}, g)$ is an automorphism of $X^e$ , combined with cyclically permuting coordinates, we obtain an automorphism $\gamma$ of $X^e$ , which corresponds to the assignment

\begin{equation*}(x_d,..,x_{d+e-1}) \mapsto (g(x_d,..,x_{d+e-1}), x_{d+1},..,x_{d+e-1}).\end{equation*}

Then $\beta = \mathrm {Id}_{X^{d-1}}\times \eta$ is the automorphism of $X^{d+e-1}$ which corresponds to

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (x_1,..,x_{d-1}, g(x_d,..,x_{d+e-1}), x_{d+1},..,x_{d+e-1}).\end{equation*}

Similarly, $\gamma =\mathrm {Id}_{X^{d-1}}\times \eta \times \mathrm {Id}_X$ is an automorphism of $X^{d+e-1}$ . Now $\alpha \circ \beta$ is an automorphism of $X^{d+e-1}$ corresponding to

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (x_2,..,x_{d-1},g(x_d,..,x_{d+e-1}),x_{d+1},..,x_{d+e-1}, f(x_1,..,x_{d-1}, g(x_d,..,x_{d+e-1}))).\end{equation*}

Thus the automorphism $\gamma ^{-1}\circ \alpha \circ \beta$ of $X^{d+e-1}$ coincides with the morphism $\tau ^{d+e}_1\circ (\mathrm {Id}_{X^{d+e-1}}, f\circ _d g)$ . This proves the result in the case $1=s\leq d-1$ .

Consider next the case $s=d$ . We need to show that the morphism $\tau ^{d+e}_d\circ (\mathrm {Id}_{X^{d+e-1}}, f\circ _d g)$ is an automorphism of $X^{d+e-1}$ . If $X$ is a set, then this automorphism is given by the assignment

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (x_1,..,x_{d-1},x_{d+1},..,x_{d+e-1}, f(x_1,..,x_{d-1},g(x_d,..,x_{d+e-1}))).\end{equation*}

As before, by using the automorphism $\tau ^e_1\circ (\mathrm {Id}_{X^e}, g)$ , cyclically permuting the coordinates and then applying $\mathrm {Id}_{X^{d-1}}\times -$ we obtain anautomorphism $\delta$ of $X^{d+e-1}$ , which for $X$ a set corresponds to

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (x_1,..,x_{d-1}, g(x_d,..,x_{d+e-1}), x_{d+1},..,x_{d+e-1}).\end{equation*}

Similarly, applying $-\times \mathrm {Id}_{X^{e-1}}$ to the automorphism $\tau ^d_d\circ (\mathrm {Id}_{X^d}, f)$ yields an automorphism $\epsilon$ of $X^{d+e-1}$ , which for $X$ a set corresponds to

\begin{equation*}(x_1,..,x_{d+e-1}) \mapsto (x_1,..,x_{d-1}, f(x_1,..,x_d), x_{d+1},..,x_{d+e-1}).\end{equation*}

Thus $\epsilon \circ \delta$ is the automorphism of $X^{d+e-1}$ which for $X$ a set corresponds to

\begin{equation*}(x_1,\ldots, x_{d+e-1}) \mapsto (x_1,..,x_{d-1},x_{d+1},..,x_{d+e-1}, (f\circ _d g)(x_1,..,x_{d+e-1})),\end{equation*}

and this is indeed the automorphism $\tau ^{d+e-1}_d\circ (\mathrm {Id}_{X^{d+e-1}}, f\circ _d g)$ . This proves the second case, and the result follows.

4. On Latin hypercubes in closed Cartesian monoidal categories

A monoidal category $\mathcal {C}$ with unit object $\unicode {x1D7D9}$ is closed if $\mathcal {C}$ has an internal Hom, denoted $\mathbf {Hom}$ . That is, $\mathbf {Hom} : \mathcal {C}^{\mathrm {op}}\times \mathcal {C}\to \mathcal {C}$ is a bifunctor such that for any object $X$ in $\mathcal {C}$ the functor $X\times -$ on $\mathcal {C}$ is left adjoint to the functor $\mathbf {Hom}(X,-)$ . This adjunction yields in particular natural bijections $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9}, \mathbf {Hom}(X,Y))\cong$ $\mathrm {Hom}_{\mathcal {C}}(X,Y)$ and natural isomorphisms $\mathbf {Hom}(\unicode {x1D7D9}, X)\cong$ $X$ ; see Kelly [3] and [5] for more background material. Following [4], endomorphism operads can be defined over objects in certain closed symmetric monoidal categories. For the definition of Latin hypercubes we need in addition that $\mathcal {C}$ is Cartesian monoidal; that is, the monoidal product is a product in the category $\mathcal {C}$ . In that case the unit object $\unicode {x1D7D9}$ is a terminal object in $\mathcal {C}$ . In what follows we say that a morphism $\hat \alpha$ between Hom objects in $\mathcal {C}$ lifts a map $\alpha$ if $\alpha$ is the image of $\hat \alpha$ under the functor $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ modulo canonical identifications.

In order to show that the morphism sets $\mathcal {L}_{\mathcal {C}}(X^d,X)$ lift to internal objects whenever $\mathcal {C}$ has pullbacks, we will need, from [5, Exercise 5, page 213], the fact that automorphism groups of objects lift to internal objects. We have a pullback diagram

where $\delta$ sends $\sigma \in \mathrm {Aut}_{\mathcal {C}}(X)$ to $(\sigma, \sigma ^{-1})$ , where $\mu (\alpha, \beta )=$ $(\beta \circ \alpha, \alpha \circ \beta )$ for any $\alpha$ , $\beta \in$ $\mathrm {Hom}_{\mathcal {C}}(X,X)$ , and where the right vertical map sends $\mathrm {Id}_{\unicode {x1D7D9}}$ to $(\mathrm {Id}_X,\mathrm {Id}_X)$ . The lower horizontal map $\mu$ commutes with the involution on $\mathrm {Hom}_{\mathcal {C}}(X,X)\times \mathrm {Hom}_{\mathcal {C}}(X,X)$ given by exchanging coordinates. The map $\mu$ and the right vertical map lift to maps on internal Hom objects, and hence, if $\mathcal {C}$ has pullbacks, then the above diagram lifts to a pullback diagram in $\mathcal {C}$ of the form

4.1.

Composing $\iota$ with the canonical involution on $\mathbf {Hom}(X,X)\times \mathbf {Hom}(X,X)$ commutes with $\nu$ , does not change $\iota$ , while it changes $(\gamma, \gamma ')$ to $(\gamma ',\gamma )$ . The universal property of pullbacks implies that there is a unique automorphism $\epsilon$ of the object $\mathbf {Aut}(X)$ of order $2$ with the property that $(\gamma ',\gamma )=$ $(\gamma, \gamma ')\circ \epsilon$ . This automorphism lifts the bijection given by taking inverses in the group $\mathrm {Aut}_{\mathcal {C}}(X)$ . Since $\iota$ is trivially a monomorphism, it follows that $(\gamma, \gamma ')$ is a monomorphism. If $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ is faithful, hence reflects monomorphism, then both $\gamma$ and $\gamma '$ are monomorphisms, since they lift inclusion maps. The following result shows that there are internal objects lifting the morphism sets $\mathcal {L}_{\mathcal {C}}(X^d,X)$ .

Theorem 4.2. Let $\mathcal {C}$ be a Cartesian closed monoidal category with pullbacks. Let $X$ be an object in $\mathcal {C}$ , and let $d$ be a positive integer. There is an object $\mathbf {L}(X^d,X)$ in $\mathcal {C}$ , determined uniquely up to unique isomorphism, such that we have a canonical isomorphism $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},\mathbf {L}(X^d,X))\cong$ $\mathcal {L}_{\mathcal {C}}(X^d,X)$ , and such that there is a canonical morphism $\mathbf {L}(X^d,X) \to \mathbf {Hom}(X^d,X)$ in $\mathcal {C}$ which lifts the inclusion $\mathcal {L}_{\mathcal {C}}(X^d,X) \to \mathrm {Hom}_{\mathcal {C}}(X^d,X)$ . If in addition the functor $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ faithful, then the canonical morphism $\mathbf {L}(X^d,X) \to \mathbf {Hom}(X^d,X)$ is a monomorphism.

We will need the following characterisation of the morphism sets $\mathcal {L}_{\mathcal {C}}(X^d,X)$ in a category with finite products.

Lemma 4.3. Let $\mathcal {C}$ be a category with finite products, let $X$ be an object in $\mathcal {C}$ , and let $d$ be a positive integer. We have a pullback diagram of sets

where $\gamma =$ $(\gamma _i : \mathrm {Hom}_{\mathcal {C}}(X^d,X)\to \mathrm {Hom}_{\mathcal {C}}(X^d,X^d))_{1\leq i\leq d}$ is defined by

\begin{equation*}\gamma _i(\lambda )=\tau ^{d+1}_i \circ (\mathrm {Id}_{X^d},\lambda )\end{equation*}

for $1\leq i\leq d$ and $\lambda \in \mathrm {Hom}_{\mathcal {C}}(X^d, X)$ , and where $\iota$ is the product of $d$ copies of the inclusion $\mathrm {Aut}_{\mathcal {C}}(X^d)\to$ $\mathrm {Hom}_{\mathcal {C}}(X^d,X^d)$ .

Proof. Let $\lambda \in$ $\mathrm {Hom}_{\mathcal {C}}(X^d,X)$ . By definition, we have $\lambda \in \mathcal {L}_{\mathcal {C}}(X^d, X)$ if and only if $\gamma _i\in$ $\mathrm {Aut}_{\mathcal {C}}(X^d)$ for $1\leq i\leq d$ . This is clearly equivalent to the assertion that the diagram in the statement is a pullback diagram.

Proof of Theorem 4.2 . As described in the diagram 4.1, appplied with $X^d$ instead of $X$ , there is a morphism $\mathbf {Aut}(X^d) \to \mathbf {Hom}(X^d,X^d)$ which lifts the inclusion $\mathrm {Aut}_{\mathcal {C}}(X^d)\to$ $\mathrm {Hom}_{\mathcal {C}}(X^d,X^d)$ . Both maps $\gamma$ and $\iota$ in the diagram from Lemma 4.3 lift to morphisms $\hat \gamma$ and $\hat \iota$ between the relevant internal Hom objects, and hence, by the assumptions on $\mathcal {C}$ , there is a pullback diagram in $\mathcal {C}$ of the form

4.4.

The functor $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ from $\mathcal {C}$ to the category of sets preserves pullbacks, hence sends this pullback diagram to a diagram isomorphic to that in Lemma 4.3. It follows in particular that $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9}, \mathbf {L}(X^d,X))\cong$ $\mathcal {L}_{\mathcal {C}}(X^d,X)$ . The uniqueness statement follows from the fact that pullbacks are unique up to unique isomorphism. If the functor $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ is faithful, then this functor reflects monomorphisms, whence the last statement follows.

Theorem 4.5. Let $\mathcal {C}$ be a Cartesian closed monoidal category with pullbacks. Suppose that the functor $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ is faithful. Suppose in addition that for any two objects $Y,$ Z $@@$ in $\mathcal {C}$ and any morphism $\zeta : Z \to \mathbf {Hom}(Y,Y)$ , if the map $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},\zeta )$ factors through the inclusion $\mathrm {Aut}_{\mathcal {C}}(Y)\to$ $\mathrm {Hom}_{\mathcal {C}}(Y,Y)$ , then the morphism $\zeta$ factors through the morphism $\mathbf {Aut}(Y) \to$ $ \mathbf {Hom}(Y,Y)$ . Let $X$ be an object in $\mathcal {C}$ . For any positive integer $d$ the morphism $\mathbf {L}(X^d,X) \to \mathbf {Hom}(X^d,X)$ is a monomorphism, and, with $d$ running over $\mathbb {N}$ , these monomorphisms form a sub-operad of the internal endomorphism operad of $X$ in $\mathcal {C}$ .

Proof. Note that since we assume $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ to be faithful (hence reflecting monomorphisms), it follows that the morphism $\mathbf {L}(X^d,X)\to$ $\mathbf {Hom}(X^d,X)$ from Theorem4.2 is a monomorphism, for any positive integer $d$ . Furthermore, as in the proofs of Theorems1.2, 3.4, showing the unitality and compatibility with symmetric group actions is straightforward. What remains to be proved is that the maps $- \circ _i -$ of the endomorphism operad induce maps on the subobjects $\mathbf {L}(X^d,X)$ of the internal Hom objects $\mathbf {Hom}(X^d,X)$ . Let $d$ , $e$ , $i$ be positive integers such that $1\leq i\leq d$ . The map

\begin{equation*} - \circ _i - : \mathrm {Hom}_{\mathcal {C}}(X^d,X) \times \mathrm {Hom}_{\mathcal {C}}(X^e,X) \to \mathrm {Hom}_{\mathcal {C}}(X^{d+e-1},X)\end{equation*}

sends $(f,g)$ to $f\circ (\mathrm {Id}_{X^{i-1}} \times g \times \mathrm {Id}_{X^{d-i}})$ . Since this involves composition and products only, this map lifts to a map of internal Hom objects

\begin{equation*} \mathbf {Hom}(X^d,X) \times \mathbf {Hom}(X^e,X) \to \mathbf {Hom}(X^{d+e-1}, X).\end{equation*}

At the level of morphism sets it follows from Theorem3.4 that we have a commutative diagram 4.6.

where the vertical maps are inclusions. We need to show that this diagram lifts to the internal Hom objects and relevant subobjects. We note that the vertical maps in the diagram 4.6 lift by Theorem 4.2, and the top horizontal map lifts by the discussion preceding the diagram 4.6. What we need to show is that the bottom horizontal map in diagram 4.6 lifts as well.

Since $\mathbf {L}(X^{d+e-1},X)$ is defined via a pullback diagram 4.4 (with $d+e-1$ instead of $d$ ), we need to show that there is a commutative diagram of the form

4.7.

Combining Lemma 4.3 (with $d+e-1$ instead of $d$ ) and diagram 4.6 yields a commutative diagram

The top horizontal and two vertical maps in this diagram lift to maps as in the diagram 4.7. The hypothesis on lifting maps through morphisms of the form $\mathbf {Aut}(Y)\to$ $\mathbf {Hom}(Y,Y)$ applied to the $d+e-1$ components on the right side of the diagram 4.7 shows the existence of the lower horizontal map making the diagram 4.7 commutative. The uniqueness of such a map follows from the fact that the right vertical map is a monomorphism, where we use that the functor $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ is faithful.

Remark 4.8. We do not know whether the hypothesis on lifting morphisms $Z\to \mathbf {Hom}(Y,Y)$ through $\mathbf {Aut}(Y)\to$ $\mathbf {Hom}(Y,Y)$ is indeed needed for Theorem 4.5 to hold. This hypothesis holds in the category of compactly generated topological spaces. It is easy to see that this hypothesis holds if $\mathbf {Aut}(Y) \to$ $\mathbf {Hom}(Y,Y)$ is a regular monomorphism (these are monomorphisms which are an equaliser of a pair of parallel morphisms), assuming as before that $\mathrm {Hom}_{\mathcal {C}}(\unicode {x1D7D9},-)$ is faithful.

5. Latin hypercubes in terms of pullback diagrams and further remarks

Definition 1.1 describes Latin hypercubes of dimension $d$ over a non-empty set $X$ as subsets of $X^{d+1}$ instead as the graph of a function $X^d\to X$ . We describe the composition maps $-\circ _i -$ in terms of these subsets as pullbacks.

Proposition 5.1. Let $X$ be a non-empty set, and let $d$ , $e$ , $i$ be positive integers such that $1\leq i\leq d$ . Let $L\subset X^{d+1}$ and $M\subseteq X^{e+1}$ be Latin hypercubes over $X$ of dimension $d$ and $e$ , respectively. Let $f : X^d\to X$ and $g : X^e \to X$ be the maps whose graphs are $L$ and $M$ , respectively. Denote by $L\circ _i M\subseteq X^{d+e}$ the Latin hypercube over $X$ of dimension $d+e-1$ which is the graph of the map $f\circ _i g : X^{d+e-1}\to X$ .

An element $(x_1,x_2,..,x_{d+e})\in$ $X^{d+e}$ belongs to $L\circ _i\,M$ if and only if there is an element $z\in X$ such that $(x_1,..,x_{i-1},z,x_{e+i},..,x_{d+e})\in$ $L$ and such that $(x_i,..,x_{e+i-1},z)\in$ $M$ . Then $z$ is uniquely determined by the elements $x_1$ , $x_2$ ,.., $x_{d+e}$ . Equivalently, we have a pullback diagram of the form

where $\lambda _i$ is the restriction to $L$ of the canonical projection $\pi ^{d+1}_i : X^{d+1}\to X$ onto the coordinate $i$ , where $\mu _{e+1}$ is the restriction to $M$ of the canonical projection $\pi ^{e+1}_{e+1} : X^{e+1}\to X$ onto the coordinate $e+1$ , and where

\begin{equation*}\alpha (x_1,x_2,..,x_{d+e}) = (x_1,..,x_{i-1},z,x_{e+i},..,x_{d+e}),\end{equation*}

\begin{equation*}\beta (x_1,x_2,..,x_{d+e}) = (x_i,..,x_{i+e-1},z).\end{equation*}

Proof. Note that $L\circ _i M$ is indeed a Latin hypercube by Theorem1.2. We have

\begin{equation*}(x_1,x_2,..,x_{d+e})\in L\circ _i M\end{equation*}

if and only if

\begin{equation*}x_{d+e} = (f\circ _i g)(x_1,x_2,..,x_{d+e-1}) = f(x_1,..,x_{i-1}, g(x_i,..,x_{i+e-1}),x_{i+e},..,x_{d+e-1}).\end{equation*}

Since $z=g(x_i,..,x_{e+i-1})$ is the unique element in $X$ such that $(x_i,..,x_{i+e-1},z)\in M$ and the unique element such that $(x_1,..,x_{i-1},z,x_{i+e},..,x_{d+e})\in L$ , the first statement follows. The second statement follows from the fact that $z$ is uniquely determined by the coordinates $x_i$ , $1\leq i \leq d+e$

It is well known that for a Latin hypercube of dimension $d\geq 2$ over a non-empty set $X$ , fixing one of the coordinates in $X^{d+1}$ yields a Latin hypercube of dimension $d-1$ (this was implicitly used in the proof of Theorem1.2). This can be extended to Cartesian monoidal categories with pullbacks. We will need the following Lemma to show this.

Lemma 5.2. Let $\mathcal {C}$ be a Cartesian monoidal category. Let $X$ be an object in $\mathcal {C}$ and let $d$ , $s$ be positive integers such that $s\leq d$ and $d\geq 2$ . Let $c :\unicode {x1D7D9}\to X$ be a morphism in $\mathcal {C}$ . Denote by $\mathrm {Id}_{X^d}\times c : X^d\to X^{d+1}$ the unique morphism satisfying $\tau ^{d+1}_{d+1} \circ (\mathrm {Id}_{X^d}\times c) =$ $\mathrm {Id}_{X^d}$ and $\pi ^{d+1}_{d+1} \circ (\mathrm {Id}_{X^d}\times c) =$ $t\times c$ , where $t$ is the unique morphism $X^d\to \unicode {x1D7D9}$ , and where we identify $X^d=X^d\times \unicode {x1D7D9}$ and $X=\unicode {x1D7D9}\times X$ . The diagram

is a pullback diagram.

Proof. By permuting the coordinates it suffices to show this for $s=d$ . Let $Z$ be an object in $\mathcal {C}$ , and let $u : Z\to X^{d+1}$ and $v : Z\to X^{d-1}$ be morphisms such that

\begin{equation*}\tau ^{d+1}_d\circ u= (\mathrm {Id}_{X^{d-1}}\circ c)\circ v.\end{equation*}

We need to show that there is a unique morphism $w : Z\to X^d$ satisfying $u=(\mathrm {Id}_{X^d}\times c)\circ w$ and $v = \tau ^d_d\circ w$ . By checking on coordinates one sees that $w = (v,u_d) : Z\to X^{d-1}\times X=X^d$ is the unique morphism with this property, where as before $u_d=$ $\pi ^{d+1}_d\circ u$ .

Proposition 5.3. Let $\mathcal {C}$ be a Cartesian monoidal category with pullbacks. Let $d$ be an integer such that $d\geq 2$ . Let $\lambda : L\to X^{d+1}$ be a morphism in $\mathcal {C}$ . Suppose that the morphism $\lambda : L \to X^{d+1}$ is a Latin hypercube. Then the morphism $\tau ^{d+1}_{d+1}\circ \lambda : L\to X^d$ is an isomorphism, and for every morphism $c : \unicode {x1D7D9} \to X$ and every pullback diagram of the form

the morphism $\lambda _c : L_c \to X^d$ is a Latin hypercube.

Proof. The morphism $\tau ^{d+1}_{d+1}\circ \lambda$ is an isomorphism as part of the definition of a Latin hypercube. Let $c : \unicode {x1D7D9} \to X$ be a morphism, and let $s$ be an integer such that $1\leq s\leq d$ . Consider a pullback diagram as in the statement. We need to show that $\tau ^d_s\circ \lambda _c : L_c \to X^{d-1}$ is an isomorphism. Since $s\leq d$ and $d\geq 2$ we can complete the diagram in the statement to a commutative diagram

The right square is a pullback diagram by Lemma 5.2. Since the left square is a pullback diagram, the pasting law for pullbacks implies that the outer rectangle is a pullback diagram as well. Since the lower horizontal morphism in the outer rectangle is an isomorphism, so is the upper horizontal morphism (we use here that pullbacks preserve isomorphisms).

We conclude this note with some further remarks.

Remark 5.4. The notion of transversals can be adapted to the situation of Definition 1.1 as follows. Given an object $X$ in a category with finite products and a positive integer $d$ , a transversal in $X^{d+1}$ is a morphism $\sigma : X\to X^{d+1}$ such that $\sigma _i=\pi ^{d+1}_i\circ \sigma$ is an automorphism of $X$ , for $1\leq i\leq d+1$ . The morphism $\sigma$ is obviously a monomorphism. We say that such a transversal is contained in a Latin hypercube $\lambda : L\to X^{d+1}$ if there is a morphism $\iota : X\to L$ such that $\lambda \circ \iota =$ $\sigma$ . In that case, $\iota$ is necessarily a monomorphism as well. If $X$ is a non-empty set, then a transversal $\sigma$ can be identified with the subset $\sigma (X)$ of $X^{d+1}$ . If $X$ is finite and has an abelian group structure, and if $T\subseteq X^{d+1}$ is a transversal, then we have a version of the $\Delta$ -Lemma [9, Lemma2.1] as follows. Denote by $\alpha : X^{d+1}\to X$ the alternating sum map $\alpha (x_1,x_2,..,x_{d+1})=\sum _{i=1}^{d+1} (-1)^{i-1}x_i$ and by $t$ the sum of all involutions in $X$ . Since the sum of all elements in $X$ is equal to the sum $t$ of all involutions in $X$ , an elementary calculation shows that

\begin{equation*}\sum _{x \in T} \ \ \alpha (x) = \begin{cases} 0 & \text {if}\ d \ \text {is odd} \\ t & \text {if}\ d\ \text {is even.} \end{cases} \end{equation*}

If $X=\mathbb {Z}/n\mathbb {Z}$ for some positive integer $n$ , then $t=0$ if $n$ is odd, and $t=$ $\frac {n}{2} + n\mathbb {Z}$ if $n$ is even.

Remark 5.5. Adapting another well-known notion for Latin squares going back to Bose [2], the graph of a Latin hypercube $L\subseteq X^{d+1}$ of dimension $d\geq 1$ over a non-empty set $X$ is the simple graph $\Gamma (L)$ with vertex set $L$ , with an edge between two elements in $L$ if the two elements have $d-1$ coordinates at which they coincide. Being a Latin hypercube implies that if one fixes $d-1$ coordinates of an element in $L$ , then the remaining two coordinates determine each other. In particular, if two elements of $L$ coincide at $d$ coordinates, then these two elements are equal. If $|X|=n$ is finite, then $\Gamma (L)$ has $n^d$ vertices and valency $\binom {d+1}{2} (n-1)$ ; indeed, the neighbours of $(x_1,x_2,..,x_{d+1})\in L$ are obtained by first choosing a two-element subset $\{i_1,i_2\}$ of $\{1,2,..,d+1\}$ and then replacing $x_{i_1}$ by any of the $n-1$ values different from $x_{i_1}$ and replacing $x_{i_2}$ by the unique element such that the resulting $d+1$ -tuple belongs to $L$ . Adjacent vertices have $n-2 + 2 (d-1)=$ $n+2d-4$ common neighbours; indeed, two distinct elements of the form $(x_1,x_2,x_3,..,x_{d+1})$ , $(x_1',x_2',x_3,..,x_{d+1})$ in $L$ have the $n-2$ common neighbours of the form $(y_1,y_2,x_3,..,x_{d+1})$ with $y_1\neq x_1, x'_1$ (so necessarily $y_2\neq x_2,x'_2$ ), and in addition the $2(d-1)$ common neighbours of the form $(x_1,x'_2,x_3,..,y_j,..,x_{d+1})$ , $(x'_1,x_2, x_3,..,z_j,..,x_{d+1})$ in $L$ where $3\leq j\leq d+1$ and $y_j$ , $z_j$ are the uniquely determined elements by the remaining coordinates. If $d\geq 3$ , then the length of the shortest path between non-adjacent vertices depends on the number of common coordinates.

Remark 5.6. Latin hypercubes of a fixed dimension $d$ over objects in a category $\mathcal {C}$ with finite products form themselves a category. Let $X$ , $Y$ be objects in $\mathcal {C}$ . Let $\lambda : X^d\to X^{d+1}$ and $\mu : Y^d \to Y^{d+1}$ be Latin hypercubes. A morphism from $\mu$ to $\lambda$ is a morphism $\iota : Y\to X$ such that $\lambda \circ \iota ^{\times d} =$ $\iota ^{\times (d+1)}\circ \mu$ . Here $\iota ^{\times d} : Y^d\to X^d$ is the morphism obtained by taking $d$ times the product of $\iota$ ; similarly for $d+1$ . Note though that the notion of isomorphism in this category is different from the notion of isomorphism considered in the Introduction, where we regard Latin hypercubes of dimension $d$ over $X$ as objects in the under-category of $X^{d+1}$ . For a Latin hypercube $\lambda : X^d\to X^{d+1}$ of the form $\lambda = (\mathrm {Id}_{X^d}, f)$ for some morphism $f : X^d\to X$ , one checks easily that an automorphism of this Latin hypercube in the category defined here is an automorphism $\iota \in \mathrm {Aut}_{\mathcal {C}}(X)$ satisfying $\iota \circ f=$ $f\circ \iota ^{\times d}$ .