1 Introduction
The macroscopic Navier–Stokes equations allow one to describe Newtonian fluids with constant transport coefficients (e.g. viscosity). Non-Newtonian systems, where the transport coefficients can depend on the state variables mass, momentum or energy densities, feature phenomena such as shear thickening, shear-band formation, clustering or plastic deformations related to creep/relaxation (Berger et al.
Reference Berger, Azema, Douce and Radjai2015; Mari et al.
Reference Mari, Seto, Morris and Denn2015; Roy, Luding & Weinhart Reference Roy, Luding and Weinhart2017; Nicolas et al.
Reference Nicolas, Ferrero, Martens and Barrat2018). How can we understand those phenomena that originate from the meso-scale, which is intermediate between atoms/particles and the hydrodynamic scale?
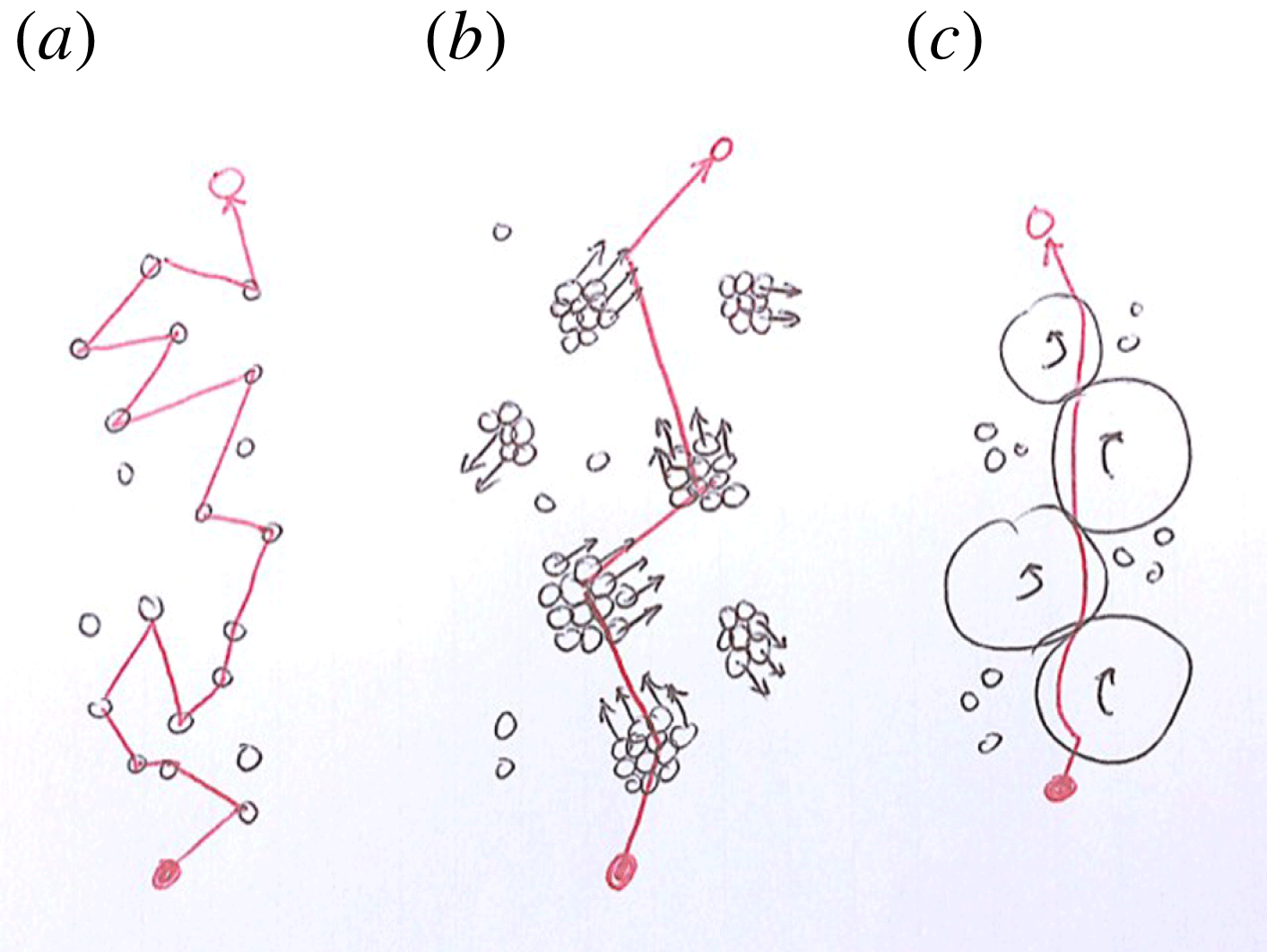
Each transport coefficient is related to the propagation and evolution of one (or more) of these quantities. For simple fluids (Hansen & McDonald Reference Hansen and McDonald1986), it is possible to bridge between the (macroscopic) hydrodynamic and the (microscopic) atomistic scales; as an example, the diffusion coefficient quantifies mass transport mediated by microscopic fluctuations, see figure 1(a). In the case of low density gases, the macroscopic equations and the transport coefficients can be obtained using the Boltzmann kinetic equation as a starting point. For moderate densities, the Enskog equation gives a good description of dense gases (or fluids) of hard atoms (Hansen & McDonald Reference Hansen and McDonald1986) or of particles including the effects of dissipation (Pöschel & Luding Reference Pöschel and Luding2001), reaching out (empirically) towards realistic systems (Luding Reference Luding2009).
Figure 1. Sketch of three modes of mass transport: (a) diffusion, (b) convection via clusters and (c) ‘rotection’, i.e. rotations of clusters mediating convection in dense shear flow as found by Macaulay & Rognon (Reference Macaulay and Rognon2019).
One interesting phenomenon caused by dissipation at low and moderate densities, occurring at a scale considerably larger than the particles, is the so-called clustering (hydrodynamic) instability (Luding Reference Luding2009; Gonzalez, Thornton & Luding Reference Gonzalez, Thornton and Luding2014): in an initially homogeneous system, large-scale structures form in the presence of strong enough dissipation for a given system size and density, see figure 1(b). The associated large time of (free) motion between collisions of clusters, allows mass, momentum and energy to be transported much faster with the clusters, which changes mixing from diffusive to ballistic (https://www2.msm.ctw.utwente.nl/sluding/pictures/cooling.html).
Among many realistic material properties, friction typically enhances dissipation and thus clustering, whereas rotations of particles (due to frictional contacts) can help to randomise the system. Charges or cohesion are other practically relevant material properties: repulsive forces, with potential energy scale
 $\unicode[STIX]{x1D719}>0$
, suppress structure formation since collisions become less probable, so that dissipation is reduced. In contrast, attractive forces, with cohesive (surface) energy
$\unicode[STIX]{x1D719}>0$
, suppress structure formation since collisions become less probable, so that dissipation is reduced. In contrast, attractive forces, with cohesive (surface) energy
 $\unicode[STIX]{x1D719}<0$
, can enhance structure formation by favouring collisions, enhancing dissipation and keeping particles together. Both forces can be unified into one framework and the onset of structure formation can be predicted by hydrodynamic stability analysis in a phase diagram with parameters dissipation and repulsion/cohesion (Gonzalez et al.
Reference Gonzalez, Thornton and Luding2014). The relevant dimensionless number is the relative strength of the interaction potential energy to the fluctuations of kinetic energy,
$\unicode[STIX]{x1D719}<0$
, can enhance structure formation by favouring collisions, enhancing dissipation and keeping particles together. Both forces can be unified into one framework and the onset of structure formation can be predicted by hydrodynamic stability analysis in a phase diagram with parameters dissipation and repulsion/cohesion (Gonzalez et al.
Reference Gonzalez, Thornton and Luding2014). The relevant dimensionless number is the relative strength of the interaction potential energy to the fluctuations of kinetic energy,
 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}/T_{g}$
. The denominator,
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}/T_{g}$
. The denominator,
 $T_{g}$
, is the widely accepted ‘granular temperature’ that quantifies the microscopic fluctuations of kinetic energy, very much in analogy to the temperature in molecular systems. Cohesion becomes relevant for large enough
$T_{g}$
, is the widely accepted ‘granular temperature’ that quantifies the microscopic fluctuations of kinetic energy, very much in analogy to the temperature in molecular systems. Cohesion becomes relevant for large enough
 $|\unicode[STIX]{x1D6E4}|$
, which can occur either for strong interaction energy,
$|\unicode[STIX]{x1D6E4}|$
, which can occur either for strong interaction energy,
 $|\unicode[STIX]{x1D719}|$
, or when
$|\unicode[STIX]{x1D719}|$
, or when
 $T_{g}$
is sufficiently small.
$T_{g}$
is sufficiently small.
Since cluster-mediated mass transport requires some free space, one remaining question is: how is cohesion influencing the transport properties in very dense systems?
2 Overview: sticky ‘rotection’
In their recent paper, Macaulay & Rognon (Reference Macaulay and Rognon2019) explain enhanced diffusion in rather dense, sheared, cohesive granular systems by large-scale structures (agglomerates) formed by sufficiently strong cohesion (Roy et al.
Reference Roy, Luding and Weinhart2017). In the absence of cohesion, clusters in sheared flows were reported already as early as 1986 (Drake Reference Drake1990), but those have a rather short lifetime. Such meso-scale structures are considered as one of the major hurdles towards connecting the microscopic (particle) world with a purely macroscopic, hydrodynamic view on granular flows (Drake Reference Drake1990).
The understanding of convective transport mediated by rotations of substructures in the system was first used as an explanation for the unusually strong heat transport in some geophysical systems (Griffani et al.
Reference Griffani, Rognon, Metzger and Einav2013). Building on earlier work, Macaulay & Rognon (Reference Macaulay and Rognon2019) gain complementary insights from simulations on the convective mass transport mediated by the rotations of the intermediate-scale substructures. Their stochastic, meso-scale theory is an important piece of a bigger puzzle regarding the rich rheology in granular and other complex fluids.
How big are these cohesion induced clusters? And how long do they persist?
If the clusters have too short a lifetime, like in most cohesionless systems, they will not contribute significantly to the transport properties of the system and diffusion will remain mostly dominated by the particle size
 $d$
and their fluctuation velocity, so that the diffusion coefficient of the grains is
$d$
and their fluctuation velocity, so that the diffusion coefficient of the grains is
 $D_{T}\propto dv_{g}$
, where
$D_{T}\propto dv_{g}$
, where
 $v_{g}\propto \sqrt{T_{g}}$
. In contrast, when clusters are permanent, diffusion will be fully dominated by their size and fluctuation velocities,
$v_{g}\propto \sqrt{T_{g}}$
. In contrast, when clusters are permanent, diffusion will be fully dominated by their size and fluctuation velocities,
 $v_{c}$
, so that the diffusion coefficient of the clusters is
$v_{c}$
, so that the diffusion coefficient of the clusters is
 $D_{c}\propto d_{c}v_{c}$
, with corresponding ‘cluster temperature’
$D_{c}\propto d_{c}v_{c}$
, with corresponding ‘cluster temperature’
 $v_{c}\propto \sqrt{T_{c}}$
. Clusters, clumps or granules transport mass and momentum in one direction, but after a short while their direction of motion changes, giving rise to rather slow, random, diffusive transport on large time scales.
$v_{c}\propto \sqrt{T_{c}}$
. Clusters, clumps or granules transport mass and momentum in one direction, but after a short while their direction of motion changes, giving rise to rather slow, random, diffusive transport on large time scales.
Macaulay and Rognon report a stochastic meso-scale model for the case of clusters having such a lifetime that they constructively contribute to transport (Macaulay & Rognon Reference Macaulay and Rognon2019). In particular rotective transport of mass (convection by rotations) can be realised by particles rotating with a cluster (without displacement of the clusters themselves), see figure 1(c). However, in order to make this a ballistic, convective transport mode for particles, the clusters must give up their existence after a certain time,
 $\unicode[STIX]{x1D6F9}$
, so that these same particles can move further with a newly formed structure, in the same direction as before – and so on – over several cluster lifetimes.
$\unicode[STIX]{x1D6F9}$
, so that these same particles can move further with a newly formed structure, in the same direction as before – and so on – over several cluster lifetimes.
This behaviour could be called super-diffusive, or turbulent-like, but one can also see it as convection through coherent handover and rotations of intermittent meso-scale structures in the flow. Macaulay & Rognon (Reference Macaulay and Rognon2019) demonstrate convection by rotation (i.e. rotection), with a diffusion coefficient
 $D\propto l_{c}^{2}\dot{\unicode[STIX]{x1D6FE}}^{2}\unicode[STIX]{x1D6F9}$
, under shear rate
$D\propto l_{c}^{2}\dot{\unicode[STIX]{x1D6FE}}^{2}\unicode[STIX]{x1D6F9}$
, under shear rate
 $\dot{\unicode[STIX]{x1D6FE}}$
, for a wide range of cohesive strengths, if the cluster size,
$\dot{\unicode[STIX]{x1D6FE}}$
, for a wide range of cohesive strengths, if the cluster size,
 $l_{c}$
, is correlated with a finite but limited lifetime,
$l_{c}$
, is correlated with a finite but limited lifetime,
 $\unicode[STIX]{x1D6F9}$
. After rotective transport over several cluster sizes, during several lifetimes, this new mode of transport becomes random and thus diffusive again. Open questions remaining are: what is the proper cluster temperature,
$\unicode[STIX]{x1D6F9}$
. After rotective transport over several cluster sizes, during several lifetimes, this new mode of transport becomes random and thus diffusive again. Open questions remaining are: what is the proper cluster temperature,
 $T_{c}$
, and what is the control parameter replacing or complementing the energy ratio
$T_{c}$
, and what is the control parameter replacing or complementing the energy ratio
 $\unicode[STIX]{x1D6E4}$
?
$\unicode[STIX]{x1D6E4}$
?
3 Future: multi-scale fluids
From the conceptual perspective, the present results by Macaulay & Rognon (Reference Macaulay and Rognon2019) deepen our understanding of multi-scale problems in general by considering also the fluctuations and physics at intermediate length scales. This might require an additional ‘meso-scale temperature’ that quantifies the fluctuation kinetics of meso-structures, clusters, clumps or agglomerates – involving their lifetimes, sizes and interactions, representing novel (possibly multiple) scale(s) in between the micro- and macro-scales.
In the presence of strong enough cohesion, the existence of enduring agglomerates is a fact used in wet granulation processes to make stable, bigger granules with much better processing and flow properties than the usually fine, sticky primary particles. Experimentally, the dependence of (dry) macroscopic cohesion on the particle size was recently studied (Shi et al.
Reference Shi, Mohanty, Chakravarty, Cabiscol, Morgeneyer, Zetzener, Ooi, Kwade, Luding and Magnanimo2018) without reference to typical clusters and their sizes in such flows, since it was not possible to look inside the limestone powder used.
The new insights into the enhanced mass transport by rotection, i.e. convection enhanced by rotations in cohesive systems with meso-scale structures, are potentially relevant to understand and improve mixing in many industrial systems. The omnipresent segregation could then be counterbalanced by enhanced mixing triggered by the right amount of cohesion – neither too weak, nor too strong. This could reduce the costs of many products and improve the quality of materials and processes. But what is the right amount of cohesion? And how to keep cohesion that enhances mixing on the meso-scale under control is a practical problem yet unsolved.
1 Introduction
The macroscopic Navier–Stokes equations allow one to describe Newtonian fluids with constant transport coefficients (e.g. viscosity). Non-Newtonian systems, where the transport coefficients can depend on the state variables mass, momentum or energy densities, feature phenomena such as shear thickening, shear-band formation, clustering or plastic deformations related to creep/relaxation (Berger et al. Reference Berger, Azema, Douce and Radjai2015; Mari et al. Reference Mari, Seto, Morris and Denn2015; Roy, Luding & Weinhart Reference Roy, Luding and Weinhart2017; Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018). How can we understand those phenomena that originate from the meso-scale, which is intermediate between atoms/particles and the hydrodynamic scale?
Each transport coefficient is related to the propagation and evolution of one (or more) of these quantities. For simple fluids (Hansen & McDonald Reference Hansen and McDonald1986), it is possible to bridge between the (macroscopic) hydrodynamic and the (microscopic) atomistic scales; as an example, the diffusion coefficient quantifies mass transport mediated by microscopic fluctuations, see figure 1(a). In the case of low density gases, the macroscopic equations and the transport coefficients can be obtained using the Boltzmann kinetic equation as a starting point. For moderate densities, the Enskog equation gives a good description of dense gases (or fluids) of hard atoms (Hansen & McDonald Reference Hansen and McDonald1986) or of particles including the effects of dissipation (Pöschel & Luding Reference Pöschel and Luding2001), reaching out (empirically) towards realistic systems (Luding Reference Luding2009).
Figure 1. Sketch of three modes of mass transport: (a) diffusion, (b) convection via clusters and (c) ‘rotection’, i.e. rotations of clusters mediating convection in dense shear flow as found by Macaulay & Rognon (Reference Macaulay and Rognon2019).
One interesting phenomenon caused by dissipation at low and moderate densities, occurring at a scale considerably larger than the particles, is the so-called clustering (hydrodynamic) instability (Luding Reference Luding2009; Gonzalez, Thornton & Luding Reference Gonzalez, Thornton and Luding2014): in an initially homogeneous system, large-scale structures form in the presence of strong enough dissipation for a given system size and density, see figure 1(b). The associated large time of (free) motion between collisions of clusters, allows mass, momentum and energy to be transported much faster with the clusters, which changes mixing from diffusive to ballistic (https://www2.msm.ctw.utwente.nl/sluding/pictures/cooling.html).
Among many realistic material properties, friction typically enhances dissipation and thus clustering, whereas rotations of particles (due to frictional contacts) can help to randomise the system. Charges or cohesion are other practically relevant material properties: repulsive forces, with potential energy scale $\unicode[STIX]{x1D719}>0$
, suppress structure formation since collisions become less probable, so that dissipation is reduced. In contrast, attractive forces, with cohesive (surface) energy
$\unicode[STIX]{x1D719}>0$
, suppress structure formation since collisions become less probable, so that dissipation is reduced. In contrast, attractive forces, with cohesive (surface) energy
 $\unicode[STIX]{x1D719}<0$
, can enhance structure formation by favouring collisions, enhancing dissipation and keeping particles together. Both forces can be unified into one framework and the onset of structure formation can be predicted by hydrodynamic stability analysis in a phase diagram with parameters dissipation and repulsion/cohesion (Gonzalez et al.
Reference Gonzalez, Thornton and Luding2014). The relevant dimensionless number is the relative strength of the interaction potential energy to the fluctuations of kinetic energy,
$\unicode[STIX]{x1D719}<0$
, can enhance structure formation by favouring collisions, enhancing dissipation and keeping particles together. Both forces can be unified into one framework and the onset of structure formation can be predicted by hydrodynamic stability analysis in a phase diagram with parameters dissipation and repulsion/cohesion (Gonzalez et al.
Reference Gonzalez, Thornton and Luding2014). The relevant dimensionless number is the relative strength of the interaction potential energy to the fluctuations of kinetic energy,
 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}/T_{g}$
. The denominator,
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}/T_{g}$
. The denominator,
 $T_{g}$
, is the widely accepted ‘granular temperature’ that quantifies the microscopic fluctuations of kinetic energy, very much in analogy to the temperature in molecular systems. Cohesion becomes relevant for large enough
$T_{g}$
, is the widely accepted ‘granular temperature’ that quantifies the microscopic fluctuations of kinetic energy, very much in analogy to the temperature in molecular systems. Cohesion becomes relevant for large enough
 $|\unicode[STIX]{x1D6E4}|$
, which can occur either for strong interaction energy,
$|\unicode[STIX]{x1D6E4}|$
, which can occur either for strong interaction energy,
 $|\unicode[STIX]{x1D719}|$
, or when
$|\unicode[STIX]{x1D719}|$
, or when
 $T_{g}$
is sufficiently small.
$T_{g}$
is sufficiently small.
Since cluster-mediated mass transport requires some free space, one remaining question is: how is cohesion influencing the transport properties in very dense systems?
2 Overview: sticky ‘rotection’
In their recent paper, Macaulay & Rognon (Reference Macaulay and Rognon2019) explain enhanced diffusion in rather dense, sheared, cohesive granular systems by large-scale structures (agglomerates) formed by sufficiently strong cohesion (Roy et al. Reference Roy, Luding and Weinhart2017). In the absence of cohesion, clusters in sheared flows were reported already as early as 1986 (Drake Reference Drake1990), but those have a rather short lifetime. Such meso-scale structures are considered as one of the major hurdles towards connecting the microscopic (particle) world with a purely macroscopic, hydrodynamic view on granular flows (Drake Reference Drake1990).
The understanding of convective transport mediated by rotations of substructures in the system was first used as an explanation for the unusually strong heat transport in some geophysical systems (Griffani et al. Reference Griffani, Rognon, Metzger and Einav2013). Building on earlier work, Macaulay & Rognon (Reference Macaulay and Rognon2019) gain complementary insights from simulations on the convective mass transport mediated by the rotations of the intermediate-scale substructures. Their stochastic, meso-scale theory is an important piece of a bigger puzzle regarding the rich rheology in granular and other complex fluids.
How big are these cohesion induced clusters? And how long do they persist?
If the clusters have too short a lifetime, like in most cohesionless systems, they will not contribute significantly to the transport properties of the system and diffusion will remain mostly dominated by the particle size $d$
and their fluctuation velocity, so that the diffusion coefficient of the grains is
$d$
and their fluctuation velocity, so that the diffusion coefficient of the grains is
 $D_{T}\propto dv_{g}$
, where
$D_{T}\propto dv_{g}$
, where
 $v_{g}\propto \sqrt{T_{g}}$
. In contrast, when clusters are permanent, diffusion will be fully dominated by their size and fluctuation velocities,
$v_{g}\propto \sqrt{T_{g}}$
. In contrast, when clusters are permanent, diffusion will be fully dominated by their size and fluctuation velocities,
 $v_{c}$
, so that the diffusion coefficient of the clusters is
$v_{c}$
, so that the diffusion coefficient of the clusters is
 $D_{c}\propto d_{c}v_{c}$
, with corresponding ‘cluster temperature’
$D_{c}\propto d_{c}v_{c}$
, with corresponding ‘cluster temperature’
 $v_{c}\propto \sqrt{T_{c}}$
. Clusters, clumps or granules transport mass and momentum in one direction, but after a short while their direction of motion changes, giving rise to rather slow, random, diffusive transport on large time scales.
$v_{c}\propto \sqrt{T_{c}}$
. Clusters, clumps or granules transport mass and momentum in one direction, but after a short while their direction of motion changes, giving rise to rather slow, random, diffusive transport on large time scales.
Macaulay and Rognon report a stochastic meso-scale model for the case of clusters having such a lifetime that they constructively contribute to transport (Macaulay & Rognon Reference Macaulay and Rognon2019). In particular rotective transport of mass (convection by rotations) can be realised by particles rotating with a cluster (without displacement of the clusters themselves), see figure 1(c). However, in order to make this a ballistic, convective transport mode for particles, the clusters must give up their existence after a certain time, $\unicode[STIX]{x1D6F9}$
, so that these same particles can move further with a newly formed structure, in the same direction as before – and so on – over several cluster lifetimes.
$\unicode[STIX]{x1D6F9}$
, so that these same particles can move further with a newly formed structure, in the same direction as before – and so on – over several cluster lifetimes.
This behaviour could be called super-diffusive, or turbulent-like, but one can also see it as convection through coherent handover and rotations of intermittent meso-scale structures in the flow. Macaulay & Rognon (Reference Macaulay and Rognon2019) demonstrate convection by rotation (i.e. rotection), with a diffusion coefficient $D\propto l_{c}^{2}\dot{\unicode[STIX]{x1D6FE}}^{2}\unicode[STIX]{x1D6F9}$
, under shear rate
$D\propto l_{c}^{2}\dot{\unicode[STIX]{x1D6FE}}^{2}\unicode[STIX]{x1D6F9}$
, under shear rate
 $\dot{\unicode[STIX]{x1D6FE}}$
, for a wide range of cohesive strengths, if the cluster size,
$\dot{\unicode[STIX]{x1D6FE}}$
, for a wide range of cohesive strengths, if the cluster size,
 $l_{c}$
, is correlated with a finite but limited lifetime,
$l_{c}$
, is correlated with a finite but limited lifetime,
 $\unicode[STIX]{x1D6F9}$
. After rotective transport over several cluster sizes, during several lifetimes, this new mode of transport becomes random and thus diffusive again. Open questions remaining are: what is the proper cluster temperature,
$\unicode[STIX]{x1D6F9}$
. After rotective transport over several cluster sizes, during several lifetimes, this new mode of transport becomes random and thus diffusive again. Open questions remaining are: what is the proper cluster temperature,
 $T_{c}$
, and what is the control parameter replacing or complementing the energy ratio
$T_{c}$
, and what is the control parameter replacing or complementing the energy ratio
 $\unicode[STIX]{x1D6E4}$
?
$\unicode[STIX]{x1D6E4}$
?
3 Future: multi-scale fluids
From the conceptual perspective, the present results by Macaulay & Rognon (Reference Macaulay and Rognon2019) deepen our understanding of multi-scale problems in general by considering also the fluctuations and physics at intermediate length scales. This might require an additional ‘meso-scale temperature’ that quantifies the fluctuation kinetics of meso-structures, clusters, clumps or agglomerates – involving their lifetimes, sizes and interactions, representing novel (possibly multiple) scale(s) in between the micro- and macro-scales.
In the presence of strong enough cohesion, the existence of enduring agglomerates is a fact used in wet granulation processes to make stable, bigger granules with much better processing and flow properties than the usually fine, sticky primary particles. Experimentally, the dependence of (dry) macroscopic cohesion on the particle size was recently studied (Shi et al. Reference Shi, Mohanty, Chakravarty, Cabiscol, Morgeneyer, Zetzener, Ooi, Kwade, Luding and Magnanimo2018) without reference to typical clusters and their sizes in such flows, since it was not possible to look inside the limestone powder used.
The new insights into the enhanced mass transport by rotection, i.e. convection enhanced by rotations in cohesive systems with meso-scale structures, are potentially relevant to understand and improve mixing in many industrial systems. The omnipresent segregation could then be counterbalanced by enhanced mixing triggered by the right amount of cohesion – neither too weak, nor too strong. This could reduce the costs of many products and improve the quality of materials and processes. But what is the right amount of cohesion? And how to keep cohesion that enhances mixing on the meso-scale under control is a practical problem yet unsolved.