A unified approach to characterize and conserve adaptive and neutral genetic diversity in subdivided populations

Summary

As extinction of local domestic breeds and of isolated subpopulations of wild species continues, and the resources available for conservation programs are limited, prioritizing subpopulations for conservation is of high importance to halt the erosion of genetic diversity observed in endangered species. Current approaches usually only take neutral genetic diversity into account. However, adaptation of subpopulations to different environments also contributes to the diversity found in the species. This paper introduces two notions of adaptive variation. The adaptive diversity in a trait is the excess of variance found in genotypic values relative to the variance that would have been expected in the absence of selection. The adaptivity coverage of a set of subpopulations quantifies how well the subpopulations could adapt to a large range of environments within a limited time span. Additionally, genome-based notions of neutral diversities were obtained that correspond to well known pedigree-based definitions. The values of subpopulations for conservation of adaptivity coverage were compared with their conservation values for adaptive diversity and neutral diversities using simulated data. Conservation values for adaptive diversity and neutral diversities were only slightly correlated, but the values for conservation of adaptivity coverage showed a reasonable correlation with both kinds if the time span was chosen appropriately. Hence, maintaining adaptivity coverage is a promising approach to prioritize subpopulations for conservation decisions.

1. Introduction

Geneticists are increasingly aware of the erosion of genetic diversity in livestock populations and wild species, and the need for genetic conservation to halt this erosion (Oldenbroek, 2007). Most populations are subdivided, either into subspecies living in different fragments of habitats and zoos in the case of wild animals, or into breeds in the case of domestic species (Toro & Caballero, 2005). Conservation of the genetic diversity found in subdivided populations not only facilitates adaptation of the species to changing environments, but it also enables identification of useful alleles segregating in endangered livestock populations and subsequent introgression into commercial breeds. If resources available for conservation are limited, an important issue is to prioritize subpopulations (hereinafter also refered to as ‘breeds’) for conservation plans. Given a total budget for conservation, the allocation of resources to a variety of conservation options affects the probabilities of breeds going extinct. The entire set of different possibilities to allocate resources is called the decision space (Simianer, 2005). If CV(K) is a function measuring the conservation value (CV) of a set K of breeds, then the decision A, which is of interest, minimizes the expected conservation value E _A(CV) of the breeds going extinct. Thus, besides estimating extinction probabilities (Reist-Marti et al., 2003; Bennewitz & Meuwissen, 2005a ) and computational challenges, the problem of decision making in livestock conservation is to find an appropriate function CV measuring the CV of a set of breeds. The CV of a set of breeds can be defined with respect to a given measure Div of diversity via the core set approach. Each breed b is assumed to have a particular genetic contribution c _b to a hypothetical subdivided population C with diversity Div(C). Population C is called the core set (Eding et al., 2002). The diversity Div(S) of a set S of breeds is the maximum diversity that could be achieved within a core set by optimum contributions of the breeds if only breeds from S are allowed to have nonzero contributions. It can be used to define the CV of breeds K as the relative decrease of the diversity that would occur if the breeds K become extinct. Note that minimizing the expected CV of the breeds going extinct is equivalent to maximizing expected diversity of the breeds that survive, which was studied by Simianer et al. (2003).

In the classical approach the objective is maximizing neutral diversity of the core set, i.e. genetic diversity arising from random genetic drift and new neutral mutations. Various measures for neutral genetic diversity are known. The most commonly used measure is the gene diversity (NGD) of Nei (1973), defined as the probability that two alleles randomly chosen from the population are different. It is also called expected heterozygosity. Maximization of gene diversity is equivalent to minimizing the average kinships and to maximizing the expected additive variance of a neutral trait in a hypothetical synthetic population that could be obtained by random mating within the core set. However, random crossing of conserved populations is not advisable because this synthetic population could have lost the adaptations of the ancestral populations. Therefore, Bennewitz & Meuwissen (2005b ) proposed maximizing the expected sampling variance of the genotypic values of a neutral trait in the core set itself, i.e. without mating individuals across the breeds included in the core set.

The choice of breeds for conservation should not only be based on neutral diversity, but the diversity in traits that arose from adaptations to different environments should also be maintained. The variation found between the genomes of individuals that is a result of selection is termed adaptive genetic variation (Schoville et al., 2012). Various statistical methods have been proposed to detect alleles contributing to the adaptive genetic variation, e.g. by detecting correlations between particular alleles and environmental factors (Manel et al., 2010). Outlier-detection methods are used to identify genomic regions under divergent or convergent selection without requiring measurement of environmental factors, e.g. by identifying outlier loci with extreme F _ST values (Antao et al., 2008; Toro et al., 2009). Bonin et al. (2006) defined a set of adaptive loci of a subdivided population as the set of all loci whose F _ST values were significantly higher than expected under a chosen model of evolution for at least one pair of subpopulations. They defined the adaptive index of a subpopulation as the percentage of adaptive loci with allele frequencies significantly different from those in all other populations. However, the genetic architecture of complex traits may not allow for classifying loci as adaptive or neutral based on their F _ST values because it is well known that a substantial proportion of the genetic variance is often explained by many quantitative trait loci (QTLs) with small effect (e.g. Hill, 2010; Wellmann & Bennewitz, 2011). These QTLs with small effect are not likely to have significant F _ST values (Kemper et al., 2014). Although methods have been proposed for detecting the presence of adaptive diversity (AD), to our knowledge a clear definition of the AD itself is still missing in the literature. Neutral and non-neutral diversity of subdivided populations are expected to be correlated owing to linkage disequilibrium or hitch-hiking effects (Toro et al., 2006), but this correlation may be small, so conservation of neutral diversity may not automatically conserve AD and vice versa. Thus, objective functions are needed that conserve both kinds of diversities simultaneously. A requirement for this is a clear definition of AD.

The aim of this paper is to introduce neutral and adaptive diversity measures based on the same quantitative genetic framework. The neutral diversity measures are extensions of the concepts of Bennewitz & Meuwissen (2005b ), Caballero & Toro (2002) and Eding et al. (2002). The AD measure is derived by applying these concepts to specific traits. The AD in a trait measures how much the variance of the trait values exceeds the variance that would have been expected in the absence of selection. In order to consider multiple traits simultaneously, the concept of adaptivity coverage (AC) was introduced. A high AC of a set of breeds indicates that breeds from the set can be well adapted to a large range of environments within a limited time span. The behaviour of the different measures with respect to the CVs of different breeds was evaluated by a computer simulation study.

2. Methods

In this section we define the adaptive and neutral diversities and provide formulas for computing them for core sets. A core set C is defined here as a large hypothetical population that is obtained by random mating within breeds but without crossing the breeds. Every subpopulation b has a specific contribution to the core set. Let ${\bf c} \in {{\opf R}} ^B $ be the vector with genetic contributions of all B subpopulations to the core set. Let C _N denote a random subset of the core set consisting of N individuals. A precise definition of the core set is given in the supplementary material (available online). The CV of a set of breeds can be defined with respect to a given measure Div of diversity as follows. Take Div(C) to be the diversity of core set C. For a set S of breeds let Div(S) denote the maximum diversity that could be achieved within a core set by optimum contributions of the breeds if only breeds from S are allowed to have nonzero contributions. This definition ensures that Div(K) ⩽ Div(S) if ${\rm K} \subset {\rm S} \subseteq {\rm B}$ , where B = {1, . . . ,B} is the set of breeds. The diversity of a set of breeds can be used to define the conservation value CV _Div (K) of the breeds K as the relative decrease of the diversity that would occur if the breeds become extinct. That is, ${\rm CV}_{Div} ({\rm K}) = \displaystyle{{Div({\rm B}) - Div({\rm B\backslash K})} \over {Div({\rm B})}}$ This approach is elaborated for different diversity measures. In the following, ${\rm S} \subseteq {\rm B}$ denotes an arbitrary subset of breeds, and ${\rm K} \subset {\rm B}$ is a set of breeds for which the CV is to be determined. By contrast, C _N is not a set of breeds but a set of individuals from different breeds.

(i) Total trait diversity

For trait t we define the total trait diversity (TTD) in C _N as the sampling variance of the genotypic values. That is,

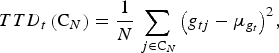$$TTD_t \left( {{\rm C}_N} \right) = \displaystyle{1 \over N}\sum\limits_{\,j \in {\rm C}_N} {\left( {g_{tj} - \mu _{g_t}} \right)} ^2, $$

where g _tj is the genotypic value of individual j for trait t, and $\mu _{g_t}$ is the average genotypic value of all individuals from C _N . For a purely additive trait t we have

(1) $$TTD_t \left( {\rm C} \right) = {\bf c}^T {\bf V}_{{\bf A}_{\bf t}} + {\bf c}^T \left( {\displaystyle{1 \over 2}\left( {\bar{\bf g}_t^2 {\bf 1}^T - 2{\bar{\bf g}}_t {\bar{\bf g}}_t^T + {\bf 1}{\bar{\bf g}}_t^{2T}} \right)} \right){\bf c},$$

where the left summand accounts for within population diversity and the right summand accounts for between population diversity. The vector ${\bar{\bf g}}_t \in {\opf R} ^B $ contains the average genotypic values of the subpopulations, $\bar{\bf g}_t^2 = \left( {{\bar{\bf g}}_{t1}^2,{\cdots\,}, {\bar{\bf g}}_{tB}^2} \right)^T $ contains the squared average genotypic values and ${\bf V}_{{\bf A}_{\bf t}} \in {{\opf R}} ^B $ is the vector with the additive variances of the subpopulations. A proof of eqn (1) can be found in the supplementary material.

Additive variances and average genotypic values can be computed from QTLs effects. The average genotypic value in subpopulation b is

$$\bar g_{tb} = \left( {2{\bf p}_b - 2{\bf p}_0} \right)^T {\bf a}_t, $$

where ${\bf a}_t \in {{\opf R}} ^M $ is the vector with true SNP effects (a _tm  = 0 if SNP m is not a QTL), ${\bf p}_b \in {{\opf R}} ^M $ contains the frequencies of the 1-alleles of the SNP in subpopulation b, and M is the number of biallelic SNPs in the subdivided population. The SNPs are assumed to include the true QTL. The vector ${\bf p}_0 \in {{\opf R}} ^M $ may be chosen arbitrarily since the definition of TTD shows that adding a constant to all genotypic values does not change the value of the function. If linkage disequilibrium between QTLs is neglegted, then the additive variance of breed b is

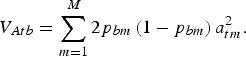$$V_{Atb} = \sum\limits_{m = 1}^M {2p_{bm} \left( {1 - p_{bm}} \right)} \,a_{tm}^2. $$

(ii) Neutral trait diversity

For a given trait t we define the neutral trait diversity (NTD) in C _N as the expected total trait diversity of a hypothetical randomly chosen neutral trait that has the same distribution of QTLs effects (for new mutations) as the trait under consideration. That is,

$$NTD_t \left( {{\rm C}_N} \right) = E\left( {\displaystyle{1 \over N}\sum\limits_{\,j \in {\rm C}_N} {\left( {g_{tj} - \mu _{g_t}} \right)^2 \left\vert {{\rm C}_N} \right.}} \right),$$

where the SNP effects are random. Every SNP is a QTL with equal probability p _QTL and the QTL effects are independent and identically distributed with variance $\sigma _{a_t} ^2 $ and mean 0. Since the absence of selection is assumed, $\sigma _{a_t} ^2 $ is equal to the variance of the additive effects of new mutant QTL alleles.

NTD can be computed from a marker-based kinship matrix f with components f _bl that fulfil the following two conditions:

1. A) (1 − f _bb )V _t  = E(V _Atb ),

2. B) $\displaystyle{{f_{bb}+ f_{ll}} \over 2} - f_{bl} = \alpha \displaystyle{{E\left( {\left( {{\bar g}_{tb} - {\bar g}_{tl}} \right)^2} \right)} \over {V_t}} $

for all breeds b,l, and some constants V _t and α. That is, the average kinship within a breed determines the expected additive variance of the trait in the breed, and $\Delta _{bl} = \sqrt {\displaystyle{{f_{bb} + f_{ll}} \over 2} - f_{bl}}$ is proportional to the expected difference of the population means of breeds b and l for a neutral trait. In particular, the marker-based kinship between two breeds is always smaller than the average kinship within the breeds. In this case we have

(2) $$NTD_t \left( {\rm C} \right) = V_t {\bf c}^T \left( {{\bf 1} - {\bf F}} \right) + \displaystyle{{V_t} \over {4\alpha}} {\bf c}^T \left( {{\bf F1}^T - 2{\bf f} + {\bf 1F}^T} \right){\bf c},$$

where the vector F = diag(f) contains for every breed the average kinships of individuals from this breed. The left summand accounts for within population diversity and the right summand accounts for between population diversity. The formula is derived in the supplementary material. Note that eqn (2) corresponds to the formula of Bennewitz & Meuwissen (2005b ) if $\alpha = \displaystyle {1\over4}$ is used, so in the remaining part of the paper we choose $\alpha = \displaystyle {1\over4}$ . But unlike their formula, this formula is not based on pedigree kinships but on actual genotypes, so it accounts for actual mutations. Explicit formulas for computing the marker-based kinship between breeds b and l and the scaling parameter V _t are

$$f_{bl} = \displaystyle{{2 - \kappa} \over 2} + \displaystyle{\kappa \over {2M}}\left( {2{\bf p}_b - {\bf 1}} \right)^T \left( {2{\bf p}_l - {\bf 1}} \right), \quad {\rm and}$$

$$V_t = \displaystyle{{\sigma _{a_t} ^2 p_{QTL} M} \over \kappa} ,$$

where $\kappa \gt 0$ can be choosen arbitrarily. For $\kappa = 1$ the kinships are defined in the interval [0, 1] and f _bl is equal to Nei's gene identity between populations b and l. Thus, 1 – f _bl is Nei's distance between breeds. For $\kappa = 2$ the kinships are defined in the interval [−1,1], but within breed kinships f _bb are positive. In this case, V _t can be interpreted as the maximum additive variance that could be obtained in a synthetic random mating population by bringing all SNP segregating in the core set to frequency 0·5. In the following $\kappa = 2$ is used. In this case the kinship matrix is

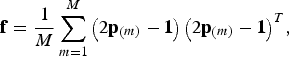$${\bf f} = \displaystyle{1 \over M}\sum\limits_{m = 1}^M {\left( {2{\bf p}_{\left( m \right)} - {\bf 1}} \right)\left( {2{\bf p}_{\left( m \right)} - {\bf 1}} \right)^T}, $$

where the vector ${\bf p}_{(m)} \in {{\opf R}} ^B $ contains the frequencies of SNP m in all populations, and M is the total number of SNPs in the breeds. Note that f = cov((2p  − 1)a) for a random vector ${\bf a}\sim N_M \left( {{\bf 0},\,\displaystyle{1 \over M}{\bf I}} \right)$ , so f is a covariance matrix.

For NTD, the CV of a set ${\rm K} \subset {\rm B}$ of breeds is defined as the relative decrease of the achievable NTD that would occur if the breeds become extinct. That is,

(3) $${\rm CV}_{NTD} \left( {\rm K} \right) = \displaystyle{{NTD_t \left( {\rm B} \right) - NTD_t \left( {{\rm B}\backslash {\rm K}} \right)} \over {NTD_t \left( {\rm B} \right)}},$$

where NTD _t (S) is the maximum NTD that can be achieved under the side constraint that only breeds from S could have positive contributions to the core set. With eqn (2) it can be seen that CV _NTD (K) does not depend on the trait t under consideration and V _t  = 1 can be assumed for computing it.

(iii) Neutral gene diversity

Conserved breeds should not only show a high diversity in trait values, but the gene diversity should also be large. The neutral gene diversity (NGD) is the gene diversity of Nei (1973), i.e. the probability that two alleles at the same locus randomly chosen from the core set are different. In the supplementary material it is shown that NGD can be computed as

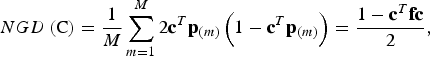(4) $$NGD\left( {\rm C} \right) = \displaystyle{1 \over M}\sum\limits_{m = 1}^M {2{\bf c}^T} {\bf p}_{(m)} \left( {1 - {\bf c}^T {\bf p}_{(m)}} \right) = \displaystyle{{1 - {\bf c}^T {\bf fc}} \over 2},$$

where c ^T p _(m) is the frequency of SNP m in the core set C. Note that NGD(C) is proportional to the expected additive variance of a neutral trait in the admixed population that would be obtained from the core set by random mating, so this equation corresponds to the formula of Eding et al. (2002). But unlike their formula, this formula does not refer to a historic base population as allele frequencies are fixed parameters.

For NGD the CV of a set K of breeds is defined as the relative decrease of the maximum achievable gene diversity if the breeds become extinct. That is,

(5) $${\rm CV}_{NGD} \left( {\rm K} \right) = \displaystyle{{NGD\left( {\rm B} \right) - NGD\left( {{\rm B}\backslash {\rm K}} \right)} \over {NGD\left( {\rm B} \right)}}.$$

The CV of breeds K for neutral diversity is defined as

(6) $${\rm CV}_{ND_\lambda} ({\rm K}) = \lambda {\rm CV}_{NTD} ({\rm K}) + \left( {1 - \lambda} \right){\rm CV}_{NGD} ({\rm K}),$$

where $\lambda \in \left[ {0,1} \right]$ is the weight given to the NTD. Note that λ > 0 ensures that the CV of a breed for neutral diversity is positive if it would be required for achieving the maximum NTD in the core set. Accordingly, λ < 1 ensures that the CV of a breed for neutral diversity is positive if it would be required for achieving the maximum NGD in the core set.

(iv) Adaptive diversity

The AD of trait t measures how much the total diversity of the genotypic values of the trait exceeds the neutral diversity. That is,

$$AD_t ({\rm C}) = TTD_t ({\rm C}) - NTD_t ({\rm C})$$

$$\hskip-3.5pt = {\bf c}^T\left( {{\bf V}_{{\bf At}} - V_t \left( {{\bf 1} - {\bf F}} \right)} \right) + {\bf c}^T \!\left( {\displaystyle{1 \over 2}\!\left( {\bar{\bf g}_t^2 1^T \!\!-\! 2{\bar{\bf g}}_t {\bar{\bf g}}_t^T \!+\! {\bf 1\bar g}_t^{2T}} \right) \!- \!V_t \left( {{\bf F1}\!^T \!-\! 2{\bf f} \!+\! {\bf 1F}^T} \right)} \!\right){\bf c}.$$

If all breeds are adapted to the same environment, then the total diversity of the trait may be smaller than the total diversity of a neutral trait, so AD may be negative.

The importance of the breeds K for conservation of the AD in trait t is defined as the relative decrease of the maximum AD in trait t if the breeds K become extinct. That is,

(7) $${\rm CV}_{AD_t} ({\rm K}) = \displaystyle{{AD_t ({\rm B}) - AD_t ({\rm B\backslash K})} \over {TTD_t ({\rm B})}},$$

Note that TTD was used as the denominator and not AD because AD can be negative.

Usually more than one trait is recorded and a measure for the overall importance of a set ${\rm K} \subset {\rm B}$ of breeds for conservation of AD is of interest. For overall AD the CV of a set K of breeds is defined as

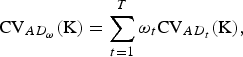(8) $${\rm CV}_{AD_\omega} ({\rm K}) = \sum\limits_{t = 1}^T {\omega _t} {\rm CV}_{AD_t} ({\rm K}),$$

where ω _t  ⩾ 0 and $\sum\nolimits_t {\omega _t} = 1$ is assumed, and the traits are assumed to be uncorrelated in order to avoide double counting of traits.

The CV of the breeds with respect to overall diversity (OD) is defined as

(9) $${\rm CV}_{OD} ({\rm K}) = \gamma {\rm CV}_{AD_\omega} ({\rm K}) + \left( {1 - \gamma} \right){\rm CV}_{ND_\lambda} ({\rm K}),$$

where $\gamma \in \left[ {0,1} \right]$ is the weight given to adaptive diversities.

(v) Adaptivity coverage

For motivating the definition of AC, we assume that for every new environment that may provide a niche for a breed in the future there is a total merit index, such that selecting for the total merit index adapts the breed to this environment. If we randomly choose an environment that might become relevant in the future, we would like that at least one breed could achieve a high index value after adapting it for a limited time span to the new environment. A high AC of a set of breeds should indicate that breeds from the set can be well adapted to a large range of environments within a limited time span.

More precisely, we would like that for any putative selection index e there exists a conserved breed b that could be adapted to this new breeding goal within only a few generations. Today, the average total merit of breed b with respect to index e is ${\bf e}^T {\bar{\bf g}}_{(b)} $ , where ${\bar{\bf g}}_{(b)} \in {{\opf R}} ^T $ contains the average genotypic values of breed b for all traits. The breeder's equation states that the response to selection after n generations is $ni\sqrt {h_b^2 ({\bf e})V_{Ab} ({\bf e})} $ , where h _b ²(e) is the heritability in the index for breed b, V _Ab (e) is the additive variance in the index for breed b, and i is the selection intensity (Falconer & Mackay, 1996). Thus, after improving the breed n generations, the average total merit index of the breed would be ${\bf e}^T {\bar{\bf g}}_{(b)} + ni\sqrt {h_b^2 ({\bf e})V_{Ab} ({\bf e})} $ . Given that the breed with the highest achievable total merit index would be chosen, the total merit of the breed after improving it n generations is

$$TM_{\rm B} ({\bf e}) = \mathop {\max} \limits_{b \in {\rm B}} \left( {{\bf e}^T {\bar{\bf g}}_{(b)} + ni\sqrt {h_b^2 ({\bf e})V_{Ab} ({\bf e})}} \right)\comma $$

Note that the additive variance in the index for breed b is

$$V_{Ab} ({\bf e}) = \sum\limits_{m = 1}^M {2p_{bm}} (1 - p_{bm} ){({\bf e}^T {\bf a}_{(m)} )^2}, $$

where ${\bf a}_{(m)} \in {{\opf R}} ^T $ contains the additive effects of SNP m for all traits. The heritability in the index is

$$h_b^2 ({\bf e}) = \displaystyle{{V_{Ab} ({\bf e})} \over {V_{Ab} ({\bf e}) + {\bf e}^T {\bf \sum} _{\bf E} {\bf e}}},$$

where ${\bf \sum} _{\bf E} \in {{\opf R}} ^{T \times T} $ is the covariance matrix of the errors.

The AC realized by a set B of breeds is the weighted average of these total merits TM _B(e), weighted by the importances f(e) placed to the respective breeding goals e. That is,

$$AC_{ni} ({\rm B}) = E_{\bf e} \left(TM_{\rm B} ({\bf e}) \right) = \int\limits_{\open{R}}^T f ({\bf e})TM_{\rm B} ({\bf e})d{\bf e},$$

where f is a density such that f(e) is the importance being placed to the putative breeding goal e. Note that the present adaptivity coverage AC ₀ does not depend on the additive variances preserved in the breeds, whereas the long-term AC (ni >> 10) heavily depends on within breed genetic variances.

Of particular importance to quantify CV of a set K of breeds is the loss of AC that would occur if the breeds would become extinct. It is defined as

(10) $${\rm CV}_{AC_{ni}} ({\rm K}) = \displaystyle{{AC_{ni} ({\rm B}) - AC_{ni} ({\rm B\backslash K})} \over {AC_{ni} ({\rm B})}}.$$

Table 1 gives an overview on the different possibilities considered for measuring CV of a set of breeds.

Table 1. Possibilities for measuring conservation values

Symbols used for conservation values (top) and subscripts (bottom).

CV, conservation value.

3. Materials

The methods were applied to a simulated data set in order to compare the CV of breeds with respect to different objective functions and to explore correlations between CV for different criteria. We simulated five populations with different effective size N _e and different selection intensities (see Fig. 1). The ancestral population was split into population 1 and population 3 in generation 1000. Both populations had N _e  = 100. The ancestral population had N _e  = 200 until generation 1000 because domesticated species typically had larger N _e in former times. Population 2 with N _e  = 50 was derived from population 1 in generation 1050. In the same generation, population 4 with N _e  = 50 was obtained from population 3. Population 5 with N _e  = 50 was obtained from population 4 in generation 1085. All populations were evaluated in generation 1100.

Fig. 1. History and effective size Ne of the simulated populations. Populations 2, 3 and 4 were selected for different traits (indicated by the bold lines). Population 5 was selected for a short time for the same traits as population 4. Selection intensity for population 4 was larger than for populations 2 and 3.

Only populations 2, 3 and 4 were selected by truncation selection within males in the last 25 generations. We simulated five traits. Population 2 was selected for trait 1, population 3 for traits 2 and 3, and population 4 was selected for traits 4 and 5 (see Fig. 2). The selection index e of a population was e _t  = 0 for neutral traits, and e _t  ~ N(0,1) for the selected traits.

Fig. 2. Development of the trait means for all traits and breeds in the last 100 generations for one replicate. Behind the population number, the legend shows the index weight of the breed for the respective trait in the last generation.

The total population size N was larger than N _e for the selected populations. For these populations the total population size was obtained by solving $N_e = \displaystyle{{4N_m N_f} \over {N_m + N_f}} = N\displaystyle{{2p} \over {p + 1}}$ , where N _f  = 0·5N is the number of females, N _m  = p0·5N is the number of males, and p is the portion of males used for breeding. Note that the formula ignores selection and that fertility is inherited, so the true effective sizes were slightly smaller than estimated here. The portion of males suitable for breeding was 0·8 for population 2, 0·7 for population 3 and 0·6 for population 4. Thus, 100, 56, 121, 67 and 50 individuals from the respective breed were included in the analysis.

The individuals had 30 chromosomes with a length of 1 Morgan. The expected number of new mutations per individual was nMut = 10. Only polymorphisms were included in the simulation, not monomorphic alleles. New mutations were inserted at a random position in the genome. Mutant alleles were coded as 1, the remaining alleles were coded as 0. About 22 000 polymorphisms were present in the last generation, but some of them were divergently fixed within populations. Each new mutation created a biallelic allele (SNP), which was a QTL with probability pQTL = 1/nMut = 0·1. The additive QTLs effects of new mutant QTL were normally distributed and independent with mean 0 and variance 1. The traits were purely additive. Normally distributed errors with variance 75 were added to the genotypic values, resulting in traits with heritabilities between 0·75 and 0·80 in the final generation. Heritabilities were large, so trait records should be interpreted as estimated breeding values rather than phenotypic records. That is, livestock populations were simulated in which selection is based on breeding values.

Computing adaptive and neutral diversities of sets of breeds are quadratic programming problems. For solving quadratic programming problems under the side constraints c^T 1 = 1, and c _b ⩾0, we used the method ipop in the R-package kernlab, followed by a hill climbing step in order to ensure convergence. For computing CV with respect to neutral diversity we used λ = 0·5, so both neutral diversity measures had equal weight. For computing CV for overall AD, the weight given to trait t was $\omega _t \propto \displaystyle{{\max \left( {{\bar{\bf g}}_t} \right) - \min \left( {{\bar{\bf g}}_t} \right)} \over {\sqrt {V_t}}} $ , so traits that were under divergent selection in the past had a large weight. For computing CV with respect to OD we used γ = 0·2, so a small weight was given to the AD. This was done because CV for neutral diversity is affected only a little by removing single breeds, so for larger values of γ, CV for OD would be affected only very little by the neutral diversity. Adaptive coverage (AC) was computed from a sequence of simulated i.i.d. random numbers TM _B(e), where e ~ N _T (0,diag( ω )) was assumed, i.e. e has a multivariate normal distribution.

4. Results

Table 2 shows CV of all breeds with respect to the different criteria. Each cell contains for one breed b and one criterion D the conservation value CV _D ({b}) of the breed, i.e. the relative decrease of objective function D that would occur if only breed b is going extinct. The standard deviations of the CV are given in parentheses (estimated from ten replicates). A high standard deviation indicates that the current CV of a breed is strongly affected by historic random processes (genetic drift and random index weights). If for a particular criterion all values in the row are small, then the objective function cannot be diminished considerably by removing only one breed.

Table 2. Conservation value of each breed with respect to different criteria

The average conservation value of each breed and its standard deviation (estimated from ten replicates) for all criteria. If all breeds have a small conservation value for a particular criterion, then the objective function cannot be decreased considerably by removing only one breed. The meaning of the criteria is summarized in Table 1. AC, adaptivity coverage; AD, adaptive diversity; ND, neutral diversity; NGD, neutral gene diversity; NTD, neutral trait diversity; OD, overall diversity.

For conservation of AD in a trait, particular breeds can be of high importance. For example, breed 3 has high CV for AD in traits 2 and 3, which are the traits that were under selection in this breed. In most cases only two breeds were important for conservation of AD of a particular trait. This is not visible in the table as the table contains the averages over the replicates. These two breeds were the breed with lowest yield and the breed with highest yield. One of the two breeds can be of much higher importance for conservation than the other, which occurs if the yield of this breed deviates more from the yields of the other breeds. If the range of genotypic values is small relative to the additive variance, then more than two breeds may have nonzero but small CV for AD in the trait. Removing single breeds can also considerably decrease overall AD. This is the case for breed 3 that has been under relatively strong selection on traits that were not selected in other breeds.

Recall that the AC is the expected total merit the best breed would have after improving it n generations towards a new randomly chosen breeding goal. As it is not known which total merit indexes will be important in the future, a normal distribution was assumed for the distribution of the index values. The table shows that the CV for AC depends on the time horizon considered. If the breeds are expected to be adapted immediately (ni = 0), AC is simply the expected genotypic value of the best breed with respect to the randomly chosen index. In this case, the CVs for AC are very similar to the CVs for AD. However, if breeders are willing to select their breeds for a long time in order to adapt them to new environments (ni ⩾ 50), then all breeds are similarly suited and removing single breeds from the core set could not decrease the AC considerably. In this case, the breed with the largest additive variance has the largest CV for AC.

For conservation of neutral diversities, no single breed is of high importance as neutral diversities could not be decreased considerably by removing only one breed.

For every replicate and every pair of criteria, the correlation between the CV of the five breeds was calculated. Table 3 shows the average correlations, averaged over ten replicates. The CV of all criteria are positively correlated because Pop5 has very low CV with respect to all critera. The CV for OD has a high correlation with the CV for AC (r > 0·86) when 0 ⩽ni ⩽10 was used, even though AC is not part of the formula that was used for computing CV for OD.

Table 3. Average correlations between conservation values with respect to the different criteria

For every replicate and every pair of criteria, the correlation between the conservation values of the five breeds was calculated. The average correlations, estimated from ten replicates, are shown in the table. AC, adaptivity coverage; AD, adaptive diversity; NGD, neutral gene diversity; NTD, neutral trait diversity; OD, overall diversity.

CV for AC was highly correlated with CV for AD (r ⩾ 0·95) when 0 ⩽ni ⩽2 was used, but it was only slightly correlated with the CV for neutral diversities (r ⩽ 0·28). This shows that AD and AC are similar properties of the population if the ni chosen is small. With increasing ni, the correlation between CV for AC and CV for AD decreases and the correlation between CV for AC and CV for NGD increases. For intermediate values (ni ≈ 10), CV for AC showed a reasonable correlation with CV for AD (r = 0·82) and CV for NGD (r = 0·55). The CV for OD also showed a reasonable correlation with CV for AD (r = 0·90) and CV for NGD (r = 0·53).

Table 4 shows, above the diagonal, the expected differences Δ _bl of the trait means for a neutral standardized trait. The diagonal contains the average marker-based kinships f _bb within breeds, and below the diagonal the marker-based kinships f _bl between the different breeds are shown. The largest expected difference in the trait means was found between Pop2 and Pop4. This was expected because these populations were split early and both populations had low effective sizes, resulting in high genetic drift. The smallest expected difference of the trait means was found between Pop4 and Pop5 as their most recent common ancestors lived only 15 generations ago. Populations split 100 generations ago had a kinship of approximately 0·595 regardless of their effective sizes. Populations split 50 generations ago had a kinship of 0·671 and the two populations split 15 generations ago had a kinship of 0·766. The kinship between individuals from the same breed depended on the historic effective size of the breed. For populations with an effective size of 100 it was 0·744, whereas for populations with an effective size of 50 it was around 0·800.

Table 4. Marker-based kinships and expected trait mean differences

The table shows above the diagonal the expected differences Δ _bl of the population means for a neutral standardized trait. The diagonal contains the average marker-based kinships f _bb within breeds, and below the diagonal the marker-based kinships f _bl between different breeds are shown. Only SNPs with minor allele frequency >0·01 were included. The standard deviation of kinships for different replicates was 0·005 at most.

5. Discussion

Measures for adaptive and neutral diversity in subdivided populations were introduced. They were used to evaluate the potential of AC as a novel approach to quantify the CVs of breeds. A linear combination of CVs for ADs and neutral diversities (CV for OD) was considered an alternative. The behaviour of these methods for the assessment of the CVs of breeds were evaluated using simulated data. CV for AC and CV for OD both turned out to be suitable parameters for quantifying CV of breeds, but the CV for AC has the advantage of being a meaningful parameter that could be estimated from real data, whereas the CV for OD is a linear combination of several parameters that need to be weighted somewhat arbitrarily.

The neutral diversities defined in eqns (2) and (4) correspond to the formulas of Bennewitz & Meuwissen (2005b ) and Eding et al. (2002), respectively. Whereas their definitions are based on pedigree-based kinships and require definition of a reference population, these formulas are based on actual genotypes. Since genotypes are known, no random Mendelian segregation is included in the model (except for creating the core set), so the formulas account for recent mutations and do not require historic base population definition. Although eqns (2) and (4) look identical with the corresponding formulas of Bennewitz & Meuwissen (2005b ) and Eding et al. (2002), the kinship matrix and the scale parameter V _t have different definitions in this paper. Defining neutral diversity as NTD provides a natural way for weighting within population diversity vs. between population diversity. The weight given to within population diversity can crucially affect conservation decisions (Toro & Caballero, 2005).

In the remaining part of this section, characteristics of breeds with extreme CVs are discussed, possibilities for improving the diversity measures are surveyed and possibilities for increasing the CV of a breed are discussed.

(i) Breeds with extreme conservation values

(a) Adaptivity coverage and adaptive diversity

Economically important breeds are usually strongly selected for particular traits. However, since these traits are of economic importance, there usually exist related breeds that are also selected for these traits. This situation is reflected in Populations 4 and 5, whereby Population 4 represents an economically important breed and Population 5 represents a closely related breed that has been selected for the same traits but has had a smaller selection response. The results for Population 5 suggest that breeds that have been selected for the same traits as economically important breeds are of little importance for maintenance of AC or AD because their trait values are intermediate between extensive breeds (reflected by Population 1) and economically important breeds. Economically important breeds (Pop 4) are needed for maintenance of AD in the traits for which they have been selected (traits 4 and 5). However, a hypothetical extinction of these breeds would decrease AD only a little as long as other breeds survive that have also been selected for these traits. By contrast, breeds that have been selected for exotic traits (reflected by Pop 3) are of larger importance for conservation of AD, given that there are no other breeds that have also been selected for these traits. Although very extensive breeds (Pop 1) also have extreme trait values, they are of minor importance for maintenance of AD as long as for every trait there exists a nonendangered breed that has not been selected for the trait, although Pop1 combines all these traits into one breed.

(b) Neutral gene diversity

The breeds with highest importance for the maintenance of NGD were the breeds with largest historic effective size (Pop1 and Pop3). Breeds with lowest importance were the breeds with a small historic effective size that are closely related with other breeds from the core set. They are of little importance for conservation of NGD because if they are going extinct, the closely related breeds would ensure that their alleles would not get lost.

(c) Neutral trait diversity

Of high importance for conservation of NTD are populations with low effective size that have been separated from other populations a long time ago (Pop 2). This is because these populations have undergone the strongest genetic drift, which might have resulted in unique phenotypes. However, it is questionable whether unique phenotypes resulting from random genetic drift facilitate adaptations to environments that could become important in the future.

Thus, the results suggest that breeds with small historic effective size that are closely related with intensely selected breeds and are selected for the same traits (Pop 5) have the smallest CV. The highest CV have breeds with a large historic effective size that have been selected for exotic traits and are not closely related with other breeds from the core set (Pop 3). Both, the CV for AC and the CV for OD were able to identify these breeds (Table 2).

(ii) Possible modifications and extensions

(a) Overall diversity

A crucial issue are the weights given to the different components contributing to CV for OD. The optimum weights are unknown. The weight λ for NTD in the formula for CV _OD may be chosen smaller because eqn (2) shows that NTD is maximized if the total population is split into many breeds with low kinships between breeds, but with high kinships between individuals of the same breed. Thus, maximization of NTD diminishes the within population diversity. But diminishing within population diversity may be undesirable because a low within population diversity causes large inbreeding coefficients and this could cause inbreeding depression. On the other hand, however, incorporation of NTD gives extra weight to populations with small effective size, which may have unique phenotypes due to random genetic drift. Therefore, the formula for CV _OD needs to account for NTD.

(b) Adaptivity coverage

The current definition of AC accounts only for a limited number T of traits that have been observed, and these traits are typically observed because they were expected to be under selection. Consequently, CV for AC is only slightly correlated with CV for NTD. However, there also exists a large number of neutral unobserved traits that were neutral in the past but might be important in the future. The definition could be extended to account for these traits by letting a _(m) be a vector with additional components, where the first T components contain the additive effects of the observed traits and one or more additional components contain random additive effects of unobserved neutral traits. Consequently, ${\bar{\bf g}}_{(b)} $ would be a vector of the same length, where the first T components contain the known average genotypic values of the observed traits for breed b and the additional components would contain random average genotypic values of one or more unobserved traits. This modification could cause the CV for AC to be more strongly correlated with the CV for NTD.

(iii) Increasing conservation values

It may be noted that the CV of a breed can vary over time. The CV of one breed may change if another breed is going extinct. Moreover, the CV of a breed for AD may be increased with selection programs that increase adaptation of the breed to particular niches, and the CV of a breed for neutral genetic diversity may be increased by accumulation of haplotypes that are not observed in other breeds. A pedigree-based method for the latter was proposed by Wellmann et al. (2012). Accumulation of these haplotypes would also cause genetic drift that may result in unique phenotypes, which would also increase the CV of the breed for NTD.

(iv) Application to real data sets

The conservation criteria were analyzed using simulated data, which reflected a typical phylogeny of subdivided livestock populations. Important attributes and correlations of the criteria could be worked out this way. An interesting application is the allocation of resources to a variety of conservation options in order to minimize the CV of the breeds going extinct. For allocation decision A let p _A (K) be the probability that the set K contains exactly the breeds going extinct within a given time horizon. The expected CV of the breeds going extinct $E_{\rm A} (CV) = \sum\nolimits_{{\rm K} \subset {\rm B}} {p_{\rm A}} ({\rm K})CV({\rm K})$ should be minimized. This requires estimatimation of the extinction probabilities of the breeds and estimatimation of the function CV(K) measuring the CV of a set of breeds. To estimate the function CV(K), trait records would be required for traits that might be relevant in the future. Factor analysis can then be applied to define underlying uncorrelated traits to which this methodology can be applied. The most promising approach is to define CV(K) as the CV for AC. In this case, additive variances, heritabilities and average genotypic values of the subpopulations would be needed. Alternatively CV(K) could be defined as the CV for OD, which requires appropriate choice of weighting parameters. One approach is to choose γ, λ and ω such that the correlation between CV for OD and CV for AC (with 2 ⩽ni ⩽10) is maximized. CV for NTD and CV for NGD enter the equation, which can be estimated from SNP data of the individuals. Computing CV for AD from real data would require an estimate of V _t , which is difficult to obtain in practice and only by making a lot of assumptions. This could be avoided by substituting CV for AD with CV for TTD in the equation for computation of CV for OD and by reducing the weight given to CV for NTD. We expect that this would result in similar CVs, especially if the selection intensities of the traits were reasonably high in the past.

R.W. was partially supported by the German Academic Exchange Service.