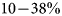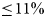Deriving seasonal and annual surface mass balance for debris-covered glaciers from flow-corrected satellite stereo DEM time series

Abstract

Glaciers in High-Mountain Asia are experiencing varying rates and patterns of mass loss due to a complex interplay between glacier surface processes, local conditions and climate forcing. Spatially distributed surface mass balance (SMB) estimates can provide valuable insight into these drivers, but observations are currently limited in both space and time. We used very-high-resolution optical stereo images acquired by commercial satellites to prepare time series of digital elevation models (DEMs), and derived contemporaneous surface velocity and elevation change products for six debris-covered glaciers in Nepal. We developed new methods to produce flow-corrected Lagrangian SMB maps to isolate local surface ablation signals with enough detail to study individual ice cliffs. Our results show reduced ablation under thick debris cover and enhanced ablation over ice cliffs. Ablating ice cliffs were responsible for $10\!-\!38\%$ of the total ablation over debris-covered areas, even though they covered $\leq \!11\%$ of the total area. Seasonal SMB products reveal the timing and patterns of summer accumulation and ablation, underscoring the importance of snow avalanches for low-elevation debris-covered glaciers in the region. Our approach can be applied to other glaciers with repeat high-resolution DEM coverage and extended for regional analyses of SMB on seasonal to interannual timescales.

1. Introduction

Glacier and snow melt in High-Mountain Asia (HMA) provide essential water resources to one of the most densely populated regions in the world (e.g. Immerzeel and others, 2020). Current glacier mass loss in High-Mountain Asia accounts for $\sim \!8\%$ of the total land ice sea level rise contribution (excluding the ice sheets) (Hugonnet and others, 2021). The majority of glaciers in High-Mountain Asia are losing mass (e.g. Maurer and others, 2019; Shean and others, 2020; Hugonnet and others, 2021) as global and regional temperatures continue to rise (e.g. Hansen and others, 2006; Lalande and others, 2021). This mass loss is projected to continue in the future (e.g. Kraaijenbrink and others, 2017; Huss and Hock, 2018; Rounce and others, 2020a), with a recent study suggesting that even if global temperature is limited to $1.5^\circ$C above pre-industrial levels, 46% of current glacier mass in High-Mountain Asia will be lost by 2100 (Rounce and others, 2023).

Supraglacial debris modifies the fundamental relationship between climate and glacier surface mass balance (SMB). However, the effects of debris cover on SMB are still poorly understood, especially at fine spatial scales. Debris covers approximately 30% of the ablation area of High-Mountain Asia glaciers (e.g. Scherler and others, 2018; Herreid and Pellicciotti, 2020), with significant surface heterogeneity and short-scale variations in debris thickness and properties (i.e. lithology, grain size). Thicker debris cover effectively insulates the underlying ice and reduces ablation (potentially by more than 50% for debris thickness $\gtrsim$10 cm), while thin debris cover can decrease surface albedo and enhance ablation (e.g. Östrem, 1959; Mihalcea and others, 2006; Nicholson and Benn, 2006; Kraaijenbrink and others, 2017).

The presence and spatial distribution of exposed, steep ice cliffs (e.g. Sakai and others, 2002) and supraglacial ponds (e.g. Sakai and others, 2000) further complicates relationships between debris thickness and ablation rates (e.g. Benn and others, 2012; Racoviteanu and others, 2022). Exposed ice cliffs generally have higher ablation rates as they intercept outgoing longwave radiation from surrounding debris (e.g. Buri and others, 2016), which is especially true for south-facing cliffs that also directly receive incoming shortwave radiation (e.g. Buri and Pellicciotti, 2018). Supraglacial ponds absorb additional heat due to their low albedo (e.g. Miles and others, 2018a), which increases local ablation and sustains ice cliffs around their edges (e.g. Benn and others, 2001; Watson and others, 2017b; Steiner and others, 2019; Kneib and others, 2022). Despite their importance, studying these features has proven difficult with available coarse satellite observations due to their small size and transient nature (e.g. Brun and others, 2018; Anderson and others, 2021a).

Most geodetic glacier mass-balance measurement approaches involve analysis of surface elevation differences between co-registered medium- to high-resolution digital elevation models (DEMs) using a fixed Eulerian grid (e.g. Brun and others, 2017; Shean and others, 2020; Hugonnet and others, 2021). While this simplifies analysis, local elevation change signals (e.g. ice cliff retreat) are obscured in an Eulerian reference frame due to ice flow and advection of rough surface features (e.g. Thompson and others, 2016). Furthermore, Eulerian measurements inherently capture surface elevation change due to both vertical ice flow (emergence from flux divergence) and SMB (e.g. Cuffey and Paterson, 2010; Berthier and Vincent, 2012; Miles and others, 2021; Zeller and others, 2022). Understanding the relative contributions of these two components is challenging, especially for coarse products with limited vertical accuracy/precision over shorter time intervals. As a result, geodetic mass balance is typically computed using aggregated Eulerian elevation change rates spanning longer time periods (i.e. decades).

Isolating the surface mass-balance component from observed elevation change is essential for understanding glacier sensitivity to climate forcing (e.g. Miles and others, 2021) and calibrating glacier mass-balance models (e.g. Huss and Hock, 2015; Zekollari and Huybrechts, 2018; Rounce and others, 2020a; Schuster and others, 2023). These glacier evolution models are often used to understand the drivers of current glacier change and produce policy-relevant projections of glacier change under different emission scenarios. While models can be calibrated for individual glaciers using in situ measurements (e.g. automated weather station data, ablation stakes), many regional models continue to rely on annualized glacier-wide average mass-balance estimates from long-term geodetic elevation change measurements (e.g. Kraaijenbrink and others, 2017; Rounce and others, 2020a). Reliance on a single observation for calibration can lead to model overparameterization (e.g. Rounce and others, 2020b), which is a major source of uncertainty in projections at the individual glacier scale (Rounce and others, 2020a). Additionally, most glacier evolution models do not account for spatially variable ablation rates due to ice cliffs and melt ponds on debris-covered glaciers (e.g. Ferguson and Vieli, 2021; Racoviteanu and others, 2022). A notable exception is the study conducted by Kraaijenbrink and others (2017), which included melt enhancement factors for supraglacial ponds in their mass-balance model, but did not explicitly discuss their influence on modeled melt rates.

Isolating the seasonal components of SMB (i.e. summer and winter balance) is also needed to better understand the timing and magnitude of glacier meltwater runoff and associated contributions to river discharge. High-resolution, distributed seasonal mass-balance observations would fill a major gap in existing calibration data used by glacier evolution models and improve their seasonal predictive capabilities. Unfortunately, many of the issues mentioned above for geodetic mass-balance calculations are exacerbated for shorter seasonal time periods.

1.1. Previous work involving glacier surface mass-balance estimation from DEMs

Several recent studies isolated the SMB component of mountain glacier elevation change over seasonal to decadal time periods using remote-sensing observations (Table 1). In most cases, remotely sensed elevation and velocity observations were combined with ice thickness estimates from models and/or ice-penetrating radar (IPR) surveys to estimate the SMB using the continuity equation (e.g. Hubbard and others, 2000).

Table 1. Summary of recent work involving glacier surface mass-balance estimates derived from remote-sensing observations

Gridded glacier surface elevation measurements were derived from stereo/SfM processing of the image source(s) listed, and horizontal surface velocity measurements were derived from feature tracking of orthoimages or shaded relief maps for the source(s) listed.

^a Vincent and others (2016).

^b Seasonal glacier-wide mass balance only.

^c Farinotti and others (2019).

^d DEM derived from interpolation of digitized 1957 contour map (Das and others, 2014).

^e Estimated from DEM slope and surface velocity using Shallow Ice Approximation (SIA).

^f Combination of Consensus estimates and OGGM (Maussion and others, 2019) model output, calibrated using IPR transects (Pelto and others, 2020).

^g Interpolated from IPR transects (Zekollari and others, 2013; Langhammer and others, 2019).

^h Flux divergence was determined using three methods: (1) stake measurements at specific points, (2) by adjusting the surface elevation change profile obtained from annual DEM differencing with the long-term modeled surface mass-balance profile, and (3) by correcting the surface elevation change products for the winter period using end-of-winter IPR-derived snow depth and modeled firn compaction rates.

These studies show that DEMs derived from Unoccupied Aerial Vehicle (UAV), Structure-from-Motion (SfM) and Airborne Laser Scanning (ALS) surveys with centimeter-scale geolocation accuracy and sub-meter-scale spatial resolution can provide useful seasonal and annual SMB measurements. Though DEMs derived from currently available very-high-resolution satellite stereo images cannot match this accuracy and resolution, they offer much greater spatial coverage, and large archives spanning the past few decades offer the potential to scale these methods for remote and inaccessible regions. Aside from early work by Brun and others (2018), to our knowledge, flow-corrected satellite stereo DEMs have not previously been used to study the seasonal mass balance of large, fast-flowing (>10  m a⁻¹) debris-covered glaciers.

1.2. Study objectives

We developed methods to estimate glacier SMB from very-high-resolution satellite stereo images. We used these methods and the resulting high-resolution SMB products to address two main research questions in the monsoon-dominated regions of the Central Himalayas:

1. (1) How do surface features (e.g. local debris thickness variations, and ice cliffs) influence debris-covered glacier ablation rates?

2. (2) What are the spatial patterns of seasonal accumulation and ablation over debris-covered glaciers?

We highlight several results that offer new insights into these questions, consider the current limitations of our methods and summarize the future potential to scale for regional analysis.

2. Study sites

We focus our study on debris-covered glaciers located in the Central Himalayan mountain range in Nepal. The region is tectonically active (e.g. Nakata, 1989), with high rates of uplift (e.g. Lavé and Avouac, 2001) and erosion (e.g. Marc and others, 2019), which provides an abundant supply of loose rock material with variable particle sizes to sustain debris-covered glaciers (e.g. McCarthy and others, 2022; Racoviteanu and others, 2022). The regional climate is heavily influenced by the Indian summer monsoon from June to September (e.g. Webster and others, 1998; Wang and Lin, 2002), which typically involves heavy rain at lower elevations, and snow accumulation at high elevations (e.g. Ageta and Higuchi, 1984; Perry and others, 2020). The monsoon season coincides with the boreal summer extending from May to October, followed by a cold and dry winter from November to March (e.g. Stumm and others, 2021; Pelto and others, 2021). Glaciers in the region are generally classified as ‘summer accumulation type’, and they are more sensitive to summer air temperature than the more conventional ‘winter accumulation type’ glaciers found in most mid- to high-latitude regions (e.g. Naito, 2011; Sakai and Fujita, 2017).

We identified six well-documented debris-covered glaciers in Nepal as study sites: Ngozumpa, Khumbu, Changri Nup and Imja Lhotse Shar glaciers in the Sagarmatha National Park, and Langtang and Lirung glaciers in the Langtang National Park (Fig. 1, Table 2). These glaciers vary in size (2–70 km²), debris cover thickness and extent (partially to fully debris-covered) and geometry (single trunk to multiple tributaries), allowing us to test our methods and analyze results for a representative set of the wide range of debris-covered glaciers in the region.

Figure 1. Context map for the study area in Nepal, Central Himalayas. Lower panels show the ESRI World Imagery satellite basemap for Langtang National Park (red) and Sagarmatha National Park (blue) with yellow outlines for the six study glaciers from the Randolph Glacier Inventory (RGI) v6.0. Note that for the Changri Nup Glacier complex, we only consider the Black Changri Nup Glacier (dashed red line).

Table 2. Glacier area, elevation (height above WGS84 ellipsoid) and debris cover metrics for the six debris-covered glaciers considered in this study

^a Randolph Glacier Inventory (RGI) v6.0 identifier (Pfeffer and others, 2014; RGI Consortium, 2017).

^b From RGI v6.0.

^c From RGI v6.0.

^d Computed using debris cover extents from Scherler and others (2018).

^e 5th, 16th, 50th, 84th, 95th percentile of debris thickness products from Rounce and others (2021).

3. Data

3.1. Very-high-resolution optical stereo images, DEMs and velocity maps

We obtained archived cloud-free Level-1B Maxar WorldView-01/02/03 and GeoEye-01 panchromatic stereo images with ground sample distance (GSD) of ~0.3–0.5 m for our study sites. These in-track stereo images were collected between December 2012 and December 2017 (Table S1).

3.1.1. Stereo DEM generation

We used v3.0.1-alpha (Alexandrov and others, 2022) of the NASA Ames Stereo Pipeline (Shean and others, 2016; Beyer and others, 2018) to prepare DEMs for each in-track stereo pair listed in Table S1. We followed the ‘map-project’ workflow of Shean and others (2016), orthorectifying input stereo images to a common resolution and extent using a smoothed, gap-filled version of the 8-m HiMAT DEM composite (Shean and others, 2020). We used the ‘fine-quality’ stereo processing settings outlined in Bhushan and Shean (2021) to resolve meter-scale surface features. The output DEMs were posted at 2 m resolution in the Universal Transverse Mercator (UTM) Zone 45N projection (EPSG:32645), with heights relative to the WGS84 ellipsoid.

We performed a relative co-registration step to align all DEMs for each site over non-glacierized, static surfaces using the Iterative Closest Point (ICP) point-to-plane algorithm (Pomerleau and others, 2013) implemented in ASP. We used the resulting transformation matrices to update the corresponding camera models for each stereo pair (following Bhushan and others, 2021) and prepared orthorectified images with improved geolocation accuracy for subsequent analysis.

3.1.2. Surface velocity map generation

We prepared horizontal surface velocity products for each glacier by tracking moving features in pairs of shaded relief maps. Unlike the original panchromatic images, the shaded relief maps are unaffected by changes in surface albedo (e.g. surface snow cover) and illumination. Using shaded relief maps also allows our workflow to be adapted for other high-resolution DEM products distributed without corresponding very-high-resolution orthoimages (e.g. ArcticDEM (Porter and others, 2018), REMA (Howat and others, 2019), EarthDEM (Porter and others, 2022)).

We used the ‘combined shading’ algorithm implemented in the gdaldem hillshade utility to prepare shaded relief maps for all co-registered 2 m DEM products. This approach uses a combination of local slopes and oblique shading to enhance detail over a broader range of slope and aspect values than traditional hillshade algorithms. Pairs of shaded relief maps were processed using the ASP parallel_stereo program in correlator mode. Dense image correlation was performed using the More Global Matching (MGM, Facciolo and others (2015)) algorithm with a 9 × 9 px kernel, and subpixel refinement was achieved by fitting a 4th order polynomial to the initial disparity values using a 15 × 15 px SGM_poly4 kernel (Miclea and others, 2015).

The resulting dense, 2-D disparity maps were then filtered using a two-stage procedure: a median filter (41 × 41 px kernel) to remove outliers, followed by an adaptive moving-average smoothing filter (maximum kernel size 25 × 25 px, ASP scale factor 0.50). This smoothing operation reduced noise in the disparity products stemming from DEM artifacts (e.g. Kraaijenbrink and others, 2016a), local ice cliff backwasting (e.g. Rounce and others, 2018) and surface feature changes unrelated to glacier flow (e.g. surface pond expansion). We found the default filtering approach to be too aggressive for the relatively slow Lirung Glacier (~4 m a⁻¹), so we used a smaller median filter (15 × 15 px kernel) to remove outliers while also preserving viable disparity measurements.

The filtered disparity values (units of pixels) were converted to surface velocity values in m a⁻¹ based on the spatial resolution and temporal baseline of the input DEMs. Residual data gaps in the velocity maps were filled with a 51 × 51 px NaN-aware Gaussian kernel, followed by a final manual quality control review to mask any lingering artifacts.

3.2. Ice thickness estimates

Accurate, spatially distributed ice thickness estimates are essential for many glaciological applications, including computing flux divergence. Ideally, one would use dense grids of ice thickness measurements derived from in situ measurements (e.g. IPR; Sharp and others, 1993; Hubbard and others, 2000; Van Tricht and others, 2021a). However, such measurements are sparse and limited to only a few glaciers in High-Mountain Asia (e.g. Pritchard and others, 2020; Welty and others, 2020).

We used ice thickness estimates prepared by Farinotti and others (2019), a consensus product derived from four different approaches based on Glen's flow law and the shallow ice approximation. To estimate ice thickness, these four approaches either invert the SMB gradient to match the volumetric change in ice flux (e.g. Huss and Farinotti, 2012; Maussion and others, 2019), or rely on empirical relationships between observed surface slope and characteristic basal shear stress (e.g. Frey and others, 2014; Fürst and others, 2017). Figure S1 shows maps of consensus ice thickness estimates and the per-pixel standard deviation of the four input ice thickness model outputs for our study glaciers. Several previous studies show that the consensus ice thickness products can provide reasonable estimates of flux divergence for individual glaciers (e.g. Miles and others, 2021; Pelto and others, 2021; Steiner and others, 2021; Mishra and others, 2022).

3.3. Debris-cover extent and thickness

We utilized gridded debris thickness products from Rounce and others (2021) to examine the effect of debris thickness on ice ablation for our study glaciers. The debris thickness products were derived using thermal infrared images from Landsat-8, and a combination of sub-debris ablation and surface temperature inversion models for glacier areas identified as debris-covered by Scherler and others (2018). The uncertainty of the debris thickness estimates varies as a function of the observed debris thickness, with higher uncertainty expected for thicker debris (see Fig. S5 and Table S4 in Rounce and others, 2021).

4. Methods

To assess the influence of surface features on ice ablation over annual time scales (Objective 1), we analyzed DEM pairs with temporal baselines of approximately 1 or 2 years (Table S1), ensuring that our observations included at least one full summer and winter season. Ngozumpa Glacier had the longest temporal baseline between DEM observations (2.08 years), while Langtang Glacier had the shortest (0.87 years). To assess patterns of seasonal accumulation and ablation (Objective 2), we computed elevation change from DEM pairs with shorter temporal baselines spanning the summer and winter seasons for Black Changri Nup and Lirung Glacier (Table S1).

We now describe the detailed methodology used to prepare and validate our SMB estimates. We begin with a theoretical framework, and then outline each step in our data processing and analysis workflow, including Lagrangian SMB calculation, uncertainty propagation, ice cliff delineation and aggregation.

4.1. Theory: isolating surface mass balance from elevation change with Lagrangian specification

Assuming a constant, incompressible ice column density beneath the seasonal snow layer (e.g. Zeller and others, 2022), fixed bed elevation, negligible firn compaction and negligible englacial and basal mass balance, the Eulerian specification for the surface elevation change of an ice column (${\partial h\over \partial t}$, units of m a⁻¹) can be defined by the continuity equation (Equation 8.77 in Cuffey and Paterson, 2010):

(1)$${\partial h\over \partial t} = {\dot{b}\over \rho} - \nabla\cdot( H\overline{{\boldsymbol u}}) $$

where h is the surface elevation above datum (m), $\dot {b}$ is the specific SMB rate (${\rm {kg\over m^{2}.yr}}$), which is equal to the net mass change per unit area added by accumulation and/or removed by ablation, ρ is the bulk density of the material added or removed from the surface (kg m⁻³), H is the ice thickness (m), and ${\boldsymbol {\bar u}}$ is the column-averaged horizontal velocity vector (m a⁻¹). The $\nabla \cdot ( H\bar {{\boldsymbol u}})$ term represents the ice flux divergence, which accounts for the vertical elevation change due to ice flow (m a⁻¹) into or out of the ice column. Flux divergence is typically negative for compressional flow, resulting in thickening of the ice column and emergence. Negative flux divergence is generally expected over the ablation area, downstream of icefalls or upstream of bed obstacles which are large relative to the local ice thickness. Flux divergence is positive for extensional flow, resulting in thinning of the ice column and submergence. Positive flux divergence is expected in the accumulation area, upstream of icefalls and downstream of bed obstacles.

Remote-sensing observations can directly measure the surface elevation change rate (${\partial h\over \partial t}$) and horizontal surface velocity vector (u_s). The latter can be used to estimate the column-averaged horizontal velocity:

(2)$${\boldsymbol {\bar u}} = {\rm f}{\boldsymbol u_{\rm s}}$$

where f is the ratio of the depth-averaged horizontal velocity and the horizontal surface velocity. Assuming Glen's flow law with exponent n = 3 and negligible basal sliding, f ≈ 0.8 (Eq. 8.36 in Cuffey and Paterson, 2010; Cogley and others, 2011), and we use this constant throughout our study.

Substituting Eqn (2) into Eqn (1) and rearranging, we obtain an equation for SMB as a function of surface elevation change rate, horizontal surface velocity and ice thickness:

(3)$${\dot{b}\over \rho} = {\partial h\over \partial t} + {\rm f}\nabla\cdot( H{\boldsymbol u_{\rm s}}) $$

The Eulerian surface elevation change rate (${\partial h\over \partial t}$) includes signals due to advection of short-scale surface roughness (e.g. boulders, ice cliffs, crevasses) superimposed on long-wavelength signals from SMB and ice flux divergence. This phenomenon manifests as alternating positive and negative elevation change signals, with magnitude and spatial scale dependent on feature dimensions, orientation and displacement distance.

To remove these apparent elevation change signals, we calculate the Lagrangian specification for surface elevation change (${{\rm D}h\over {\rm D}t}$, m a⁻¹), effectively following individual surface features using known horizontal displacements from surface velocity observations and measuring local surface elevation change. The Lagrangian surface elevation change rate (${{\rm D}h\over {\rm D}t}$) is related to the Eulerian surface elevation change rate (${\partial h\over \partial t}$) by the material derivative equation:

(4)$${{\rm D}h\over {\rm D}t} = {\partial h\over \partial t} + {\boldsymbol u_{\rm s}}\cdot{\nabla h}$$

The term ${\boldsymbol u_{\rm s}}\cdot {\nabla h}$ in Eqn (4) accounts for the expected elevation change due to slope-parallel flow – the elevation decrease of a surface feature as it moves downslope, independent of local surface thinning or thickening due to SMB or flux divergence.

Rearranging Eqn (4) and substituting into Eqn (3), we obtain an equation for the Lagrangian SMB rate (${\dot {b}\over \rho }$) in m a⁻¹ as a function of the slope-corrected Lagrangian elevation change rate and flux divergence:

(5)$${\dot{b}\over \rho} = {{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot{\nabla h} + {\rm f}\nabla\cdot( H{\boldsymbol u_{\rm s}}) $$

For the remainder of the manuscript, we refer to ${\partial h\over \partial t}$ as Eulerian elevation change rate, ${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$ as slope-corrected Lagrangian elevation change rate, and ${\dot {b}\over \rho }$ as Lagrangian SMB rate. Unless otherwise specified, all values are reported in units of m a⁻¹.

4.1.1. Density considerations and assumptions

We chose to preserve the density (ρ) term in the denominator of our final definition for the Lagrangian SMB rate (${\dot {b}\over \rho }$), so that all terms have comparable units of meters per year (m a⁻¹). Given our study objectives, this approach avoids the need of spatially variable surface material density in the accumulation areas, which are not well constrained. Our Lagrangian SMB rate estimates can be interpreted as meters ice equivalent (i.e. m a⁻¹) over ablation areas, as the material density will be equal to the density of glacier ice (e.g. Van Tricht and others, 2021b) and can be used to directly estimate ice ablation rates. Using common density values for glacier ice (900–917 kg m⁻³; e.g. Cogley and others, 2011; Huss, 2013; Kääb and others, 2012), our Lagrangian SMB rate products can be converted to SMB estimates in ${{\rm kg}\over {\rm m}^{2}.{\rm yr}}$ over ablation areas.

To assess the spatial patterns of seasonal accumulation, we also present the same Lagrangian SMB rate estimates over the limited portions of accumulation areas with available product coverage. Conversion to ${{\rm kg}\over {\rm m}^{2}.{\rm yr}}$ in accumulation areas is more complicated, as bulk density of surface snow and firn may vary spatially (e.g. Zeller and others, 2022). We assume that the firn column represents a small fraction of the total ice thickness, and assume a constant ice column density over time. This condition allows us to assume negligible firn compaction rates during the study period (Cogley and others, 2011) which is true near the equilibrium line altitude and over the lower accumulation areas, where we have valid product coverage. With higher accumulation rates at higher elevations, a more sophisticated density treatment might be necessary to modify our equation and the underlying assumptions (e.g. Zeller and others, 2022) for improved Lagrangian SMB estimates. In summary, although Lagrangian SMB rate products contain valuable information over accumulation areas, interpretation can be challenging – we offer additional discussion in Section 6.5.5.

4.2. Lagrangian surface mass-balance calculation

For each pair of DEMs, we used the corresponding filtered horizontal surface displacement product (Section 3.1.2) to back-project elevation pixels in the second DEM to their expected initial position in the first DEM grid (e.g. Van Tricht and others, 2021b; Shean and others, 2019). We subtracted the first DEM elevation value from the corresponding second DEM elevation value at each pixel and divided by the time interval to measure the local Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t}$), effectively removing any apparent elevation change signals due to advection of rough surface features. This approach maintains the direct per-pixel correspondence between ${{\rm D}h\over {\rm D}t}$ and u_s values for the same observation period, which is essential for continuity and detailed analysis of surface features.

The choice of back-projecting pixels in the second DEM to their initial locations or forward-projecting pixels in the first DEM to their final locations before subtraction will not impact the ${{\rm D}h\over {\rm D}t}$ magnitude for short time intervals, but it will determine the location where the ${{\rm D}h\over {\rm D}t}$ value is assigned. Our study includes Lhotse Shar Glacier which calves into the Imja Lake, so we used the back-projection approach to preserve ${{\rm D}h\over {\rm D}t}$ values near the terminus.

4.2.1. Slope-parallel elevation change

Using the same displacement product, we forward-projected pixels from the first DEM to their expected final position on the second DEM acquisition date. We sampled the first DEM at this final expected location. We then subtracted this elevation value from the initial elevation value in the first DEM to obtain the expected slope-parallel elevation change, and divided by the time interval to obtain the ‘expected slope-parallel elevation change rate’ ${\boldsymbol u_{\rm s}}\cdot {\nabla h}$ (m a⁻¹).

Our approach to estimate ${\boldsymbol u_{\rm s}}\cdot {\nabla h}$ differs from those used by Brun and others (2018) and Van Tricht and others (2021b), which combine horizontal surface velocity measurements from one time period and surface elevation gradient (slope) measurements from a non-contemporaneous DEM (e.g. SRTM from February 2001, or a DEM composite from observations over an extended period). Any real surface elevation change between the periods when u_s and $\nabla h$ were measured will introduce errors in the resulting slope-corrected Lagrangian elevation change rate measurements. Our approach more accurately captures the true surface gradients during the observation period when we have contemporaneous surface velocity and elevation change measurements.

4.2.2. Flux divergence

We computed ice flux for each pixel in the first DEM grid coordinate system as the product of the column-averaged horizontal velocity vector and the ice thickness from the Farinotti and others (2019) consensus product (Section 3.2). The flux divergence (${\rm f}\nabla \cdot ( H{\boldsymbol u}_{\rm s}$)) was then computed from the spatial gradients of this ice flux product using the numpy gradient operator (central difference, except near array boundaries).

4.2.3. Length scale considerations and ice-thickness-dependent smoothing

Ice flow is primarily governed by surface slope and longitudinal driving stress over length scales that are proportional to several times the local ice thickness (e.g. Kamb and Echelmeyer, 1986; Cuffey and Paterson, 2010; Alley and others, 2018). Therefore, we must use appropriate length scales when computing the expected slope-parallel elevation change and flux divergence, rather than the original DEM resolution. Previous studies used either a fixed distance between flux gates (e.g. Bisset and others, 2020; Miles and others, 2021) or a constant multiplicative factor l of 2–8 times the local ice thickness to compute longitudinal stress or flux divergence for mountain glaciers (Dehecq and others, 2019; Van Tricht and others, 2021b; Armstrong and others, 2022; Van Wyk de Vries and others, 2022).

We used a value of l = 5 times the local ice thickness to assign the spatially variable kernel width for a custom 2-D Gaussian filter, and then used this filter to smooth the expected slope-parallel elevation change rate and flux divergence products (Fig. 2). This empirically derived choice of l reduced artifacts while preserving physically meaningful signals in these products for our study glaciers.

Figure 2. Example of our adaptive smoothing filter, which removes artifacts while preserving signals with the physically appropriate length scales expected for ice flow. (a) Initial expected slope-parallel elevation change rate for Langtang Glacier before filtering. Note artifacts due to short-scale surface roughness. (b) Local ice thickness values from the Farinotti and others (2019) consensus product are used to determine the spatially variable (c) Gaussian smoothing kernel width (and height). (d) Final expected slope-parallel elevation change rate (${\boldsymbol u_{\rm s}}\cdot {\nabla h}$) after filtering. Green outline shows RGI v6.0 glacier extent.

4.2.4. Annual Lagrangian surface mass-balance rate

The final Lagrangian SMB rate (${\dot {b}\over \rho }$) was calculated from the Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t}$), and the smoothed expected slope-parallel elevation change rate (${\boldsymbol u_{\rm s}}\cdot {\nabla h}$) and flux divergence (${\rm f}\nabla \cdot ( H{\boldsymbol u_{\rm s}})$) products using Eqn (5).

4.2.5. Seasonal Lagrangian surface mass balance

For the seasonal products, we report Lagrangian SMB (${b\over \rho }$) with units of meters. Note the absence of a dot, as this is not a rate. This approach is more appropriate for observed seasonal elevation change over the shorter ~4–6 month intervals, rather than the annualized rates for the longer ~1–2 year intervals. The flux divergence was calculated using seasonal velocity products derived from the same DEMs used to compute the seasonal Lagrangian ${{\rm D}h\over {\rm D}t}$.

4.2.6. Evaluation

To ensure that our slope-parallel flow correction and adaptive smoothing approaches did not violate mass conservation principles, we compared several metrics before and after each correction and filtering step, assuming they should be equal. To ensure that our thickness-dependent Gaussian smoothing filter conserved mass, we compared the mean flux divergence (${\rm f}\nabla \cdot ( H{\boldsymbol u_{\rm s}})$) before and after filtering, and the mean expected slope-parallel elevation change rate (${\boldsymbol u_{\rm s}}\cdot {\nabla h}$) before and after filtering. To ensure that our Lagrangian framework conserved mass, we compared the mean Eulerian ${{\rm d}h\over {\rm d}t}$ and mean slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ for the common area with valid coverage in both products.

In principle, a similar comparison can be performed between the mean Eulerian ${{\rm d}h\over {\rm d}t}$ and the mean Lagrangian SMB rate to validate the flux divergence correction, assuming both products have complete spatial coverage over the glacier. However, the Lagrangian SMB rate maps typically have data gaps over accumulation areas and more continuous coverage over ablation areas, where we expect non-zero flux divergence due to net emergence. Despite this limitation, we performed this additional validation test for Black Changri Nup and Lirung Glaciers, where both products have near-complete coverage.

4.3. Uncertainty estimates

Estimating the uncertainty of our final Lagrangian SMB rate products is complicated by the variety of input datasets with spatially variable error and the lack of available in situ measurements. Several processing steps (e.g. feature tracking to derive horizontal surface velocity, flow correction of elevation change rates) and some of our simplifying assumptions (e.g. contribution of basal sliding to observed surface velocity) can introduce additional error.

Despite these challenges, we conservatively estimate the Lagrangian SMB uncertainty ($\sigma _{{\dot {b}\over \rho }}$) as the combined uncertainty of the two main components in Eqn 5 for each pixel on the glacier:

(6)$$\sigma_{{\dot{b}\over \rho}} = \sqrt{( \sigma_{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot{\nabla h}}) ^2 + ( \sigma_{{\rm f}\nabla\cdot( H{\boldsymbol u_{\rm s}}) }) ^2}$$

where uncertainty of the ice flux (Hfu_s) is:

(7)$$\sigma_{( H{\rm f}{\boldsymbol u_{\rm s}}) } = H{\rm f}{\boldsymbol u_{\rm s}}\sqrt{\left({{\sigma_{H}\over H}}\right)^2 + \left({\sigma_{{\boldsymbol u_{\rm s}}}\over {{\boldsymbol u_{\rm s}}}}\right)^2},\; $$

and the uncertainty of the ice flux divergence (${\rm f}\nabla \cdot ( H{\boldsymbol u_{\rm s}})$) is:

(8)$$\sigma_{{\rm f}\nabla\cdot( H{\boldsymbol u_{\rm s}}) } = \sqrt{\left({\partial\sigma_{( H{\rm f}{u_{x}}) }\over \partial{x}}\right)^2 + \left({\partial\sigma_{( H{\rm f}{u_{y}}) }\over \partial{y}}\right)^2}$$

To estimate $\sigma _{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$, we computed the systematic and random error of the slope-corrected Lagrangian elevation change rate products (${{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$) as the median and normalized median absolute deviation (NMAD) of residuals over non-glacierized, static surfaces, where we assume zero elevation change. The combined $\sigma _{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$ is the root sum of the squared median and NMAD values. The same approach involving observed errors over static surfaces was used to estimate the uncertainty of the surface velocity products ($\sigma _{{\boldsymbol u_{\rm s}}}$). While these $\sigma _{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$ and $\sigma _{{\boldsymbol u_{\rm s}}}$ values were estimated over terrain around the glacier, we assume that they capture similar uncertainty for the same products over the glacier surface. Finally, we estimated ice thickness uncertainty (σ _H) as the per-pixel weighted standard deviation of four ice thickness grids used to derive the consensus ice thickness estimates (Farinotti and others, 2019). The resulting grids capture the spatial variability of ice thickness uncertainty for each glacier (Fig. S1). We substituted the uncertainty estimates for these components into Eqns (6)–(8) to obtain the Lagrangian SMB uncertainty ($\sigma _{{\dot {b}\over \rho }}$) for each of our study glaciers.

4.4. Identifying areas affected by ice cliff ablation and retreat

Several methods to map ice cliffs on debris-covered glaciers have been proposed in recent years, with varying degrees of success. These methods typically use either differences in optical multispectral image surface reflectance values (e.g. Kraaijenbrink and others, 2016b; Steiner and others, 2019; Anderson and others, 2021a; Kneib and others, 2021a) or surface slope and roughness values from a high-resolution DEM (e.g. Reid and Brock, 2014; Herreid and Pellicciotti, 2018; King and others, 2020). Methods using surface reflectance values are limited by image view and solar illumination angles, as near-nadir imagery presents challenges for observing vertical cliffs. High-resolution satellite images orthorectified using outdated and/or coarse DEMs often have geolocation error and ‘smearing’ artifacts near steep features such as ice cliffs. Image-based techniques can also fail to identify ice cliffs covered by a very thin layer of debris. Methods based on DEM slope and surface roughness struggle to differentiate ice cliffs from other steep surfaces, such as moraines or debris cones. Additionally, DEMs from satellite stereo images can fail to reconstruct steep ice cliff faces, especially when the face is oriented away from one or both of the satellite view angles.

To avoid complications around ice cliff mapping, we limited our analysis to a subset of ‘ablating ice cliffs’, which we define as ice cliffs with high observed ablation rates. Our semi-automated identification approach takes advantage of the fact that ice cliffs are typically steep surfaces that melt at higher rates than their surroundings.

We segmented features with local slopes greater than 10° in both input DEMs and at least 15 connected pixels. We then used the observed slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ elevation change values to remove steep, but unchanging surface features that should not be classified as ablating ice cliffs. Modeled ice cliff melt rates for glaciers in the region (Rounce and others, 2021; Miles and others, 2022) typically exceed 3–7 m a⁻¹. Based on these results and our own manual mapping efforts, we used a conservative maximum ${{\rm D}h\over {\rm D}t}-{\boldsymbol u_{\rm s}}\cdot {\nabla h}$ threshold of −2.5 m a⁻¹ to isolate ablating ice cliffs. We then performed a manual review of corresponding orthoimages to identify and remove any remaining misclassified features.

In summary, while we do not attempt to map every ice cliff on our study glaciers (an inherently subjective and tedious process), our approach allows us to objectively isolate areas that were affected by ablation and retreat of ice cliffs, and then measure local elevation change over these areas.

4.5. Elevation-dependent aggregation and ice-cliff metrics

We computed the median, NMAD and interquartile range (IQR) of all valid pixels within 50 m elevation bins for the following products: Eulerian elevation change rate (${{\rm d}h\over {\rm d}t}$), Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t}$), slope-corrected Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$), Lagrangian SMB rate (${\dot {b}\over \rho }$), debris thickness, area affected by ablating ice cliffs (A _icecliff) and debris-covered area (A _debris, excluding ice cliffs). All the area estimates were derived in map-view.

We computed the percent of the total debris-covered area affected by ablating ice cliffs in each bin as:

(9)$$A_{\rm{icecliff}}\% = {A_{\rm{icecliff}}\over A_{\rm{icecliff}} + A_{\rm{debris}}} \cdot 100$$

Next, we isolated the median Lagrangian SMB rate over areas affected by ablating ice cliffs (${\dot {b}}_{\rm{icecliff}}$, dropping ρ divisor for simplicity) and debris-covered surfaces (${\dot {b}}_{\rm{debris}}$, excluding areas affected by ablating ice cliffs) for each bin. We also computed the percent contribution of ablating ice cliffs to total ablation in debris-covered areas:

(10)$$\dot{b}_{\rm{icecliff}}\% = {\dot{b}_{\rm{icecliff}}A_{\rm{icecliff}}\over \dot{b}_{\rm{icecliff}}A_{\rm{icecliff}} + \dot{b}_{\rm{debris}}A_{\rm{debris}}} \cdot 100$$

for bins with negative median Lagrangian SMB rate (ablation). Finally, we computed summary statistics for each glacier as the area-weighted average of these metrics for all bins within the debris-covered area.

5. Results

5.1. Surface velocity and flux divergence

The velocity products derived from shaded relief maps resolve detailed spatial velocity variations over the study glaciers (Figs 3c, S2c–S6c). In general, the glaciers have maximum surface velocity over steep icefalls. Velocity is less than 5 m a⁻¹ over the lower debris-covered ablation areas for all glaciers except the Lhotse Shar Glacier, which terminates in Imja Lake. Residual data gaps occur over accumulation areas and some areas of fast flow due to a lack of texture (e.g. snow-covered surfaces) and/or loss of coherence between the two shaded relief maps, especially over longer time intervals.

Figure 3. Subset of data products over Imja Lhotse Shar Glacier for the ~1-year period between 2 October 2015 and 29 October 2016: (a) panchromatic WV-01 orthoimage from 2 October 2015, (b) color shaded relief map for the 2 October 2015 DEM, (c) horizontal surface velocity (u_s), (d) flux divergence (${\rm f}\nabla \cdot ( H{\boldsymbol u_{\rm s}})$) with 1 m contours, (e) Eulerian elevation change rate (${{\rm d}h\over {\rm d}t}$), (f) Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t}$), (g) slope-corrected Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$) and (h) Lagrangian SMB rate (${\dot {b}\over \rho }$) obtained by adding flux divergence (panel d) to slope-corrected Lagrangian elevation change rate (panel g). Red outlines in panel a show location of subregions in Figure 4. Note the reduction of noise and artifacts in the Lagrangian products (f–h) and higher ablation rates in panel h where the flux divergence is more negative (positive emergence velocity).

All study glaciers have negative flux divergence (positive emergence velocity) over the majority of their debris-covered ablation areas (Figs 3d, S2d–S6d). Some local areas of positive flux divergence are observed near tributary confluence zones or along margins where the flow direction changes. Maximum emergence velocities are observed a few kilometers downstream from the areas with fastest horizontal glacier flow. All glaciers except Lhotse Shar have near-zero flux divergence over their lower debris-covered ablation areas, indicating that emergence is limited over near-stagnant areas.

5.2. Annual surface mass balance

The slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ maps (Figs 3g, S2g–S2 g) do not contain the artifacts related to advection of short-scale surface features and roughness observed in the Eulerian ${{\rm d}h\over {\rm d}t}$ maps (Figs 3e, S2e–S2e). The slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ maps also resolve local ablation signals over steep ice cliffs in debris-covered ablation areas (Fig. 4).

Figure 4. Detail of orthoimages and Lagrangian SMB rate maps over (a, b) Imja Lhotse Shar Glacier (see Fig. 3 for context), and (c) Khumbu Glacier (see Fig. S4 for context). Green outlines show areas affected by ablating ice cliffs using the methodology described in Section 4.4. Red arrows denote the median flow direction in the area. Note high ablation rates over ice cliffs (all panels), and spatial variability of ablation rates across the boundary between exposed ice and debris-covered ice with relatively thin debris in panel a. Also note positive elevation change due to pond filling and small positive/negative signals due to relative displacement of large boulders in panel c.

The Lagrangian SMB rate map for Imja Lhotse Shar Glacier (Fig. 3h) shows ablation signals over the northern tributary and near the calving front that were compensated by negative flux divergence (Fig. 3d) and thus not apparent in the Eulerian ${{\rm d}h\over {\rm d}t}$ map (Fig. 3e). Near the base of the northeastern tributary icefall (upper edge of valid coverage), we observe positive Lagrangian SMB rates indicating surface accumulation (Fig. 3h). Isolated positive Lagrangian SMB rates are also observed over melt ponds and near the confluence of Lhotse Shar and Imja Glacier.

The Eulerian and Lagrangian products appear similar over the relatively slow-moving Black Changri Nup (Fig. S3) and Lirung Glaciers (Fig. S5). The Lagrangian SMB rate products show relatively low ablation rates over the stagnant, debris-covered areas of the lower Ngozumpa, Khumbu, Langtang and Lirung Glaciers, which highlights the relatively high local ablation rates associated with ice cliffs in these same areas (Figs S2, S4–S6). Relatively high ablation rates are also observed farther upglacier on these same four glaciers, with local rates exceeding 4 m a⁻¹ over both clean and debris-covered ice. However, for Black Changri Nup Glacier, the ablation rates are consistently larger (1–2 m a⁻¹) over the majority of the debris-covered surface near the terminus (Fig. S3). At Lirung Glacier, very high ablation rates (3 to >20 m a⁻¹) are observed over the large ice cliff approximately 1 km from the terminus defined by the RGI v6.0 outline (Fig. S5).

The observed uncertainty for our surface velocity ($\sigma _{{\boldsymbol u_{\rm s}}}$) and slope-corrected Lagrangian elevation change rate ($\sigma _{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$) products ranges between 0.54–1.60 and 0.30–1.03 m a⁻¹ respectively (Table S4, Fig. S7). In general, the Lagrangian SMB uncertainty ($\sigma _{{\dot {b}\over \rho }}$) estimates are relatively low (<1 m a⁻¹) for stagnant, low elevation debris-covered ablation areas, with higher values (>1 to 2 m a⁻¹) over actively flowing regions (Fig. 5). The higher $\sigma _{{\dot {b}\over \rho }}$ estimates are largely driven by larger $\sigma _{{\rm f}\nabla \cdot ( H{\boldsymbol u_{\rm s}}) }$ estimates over fast-flowing areas with relatively thin ice (Fig. S7). The $\sigma _{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$ estimates for Langtang Glacier are notably higher than the other study glaciers (Fig. S7). This increased error is likely caused by the shorter time interval and relatively large residual DEM errors, potentially due to co-registration issues for the snow-covered 22 February 2015 DEM.

Figure 5. Lagrangian surface mass-balance rate (${\dot {b}\over \rho }$) and uncertainty ($\sigma _{{\dot {b}\over \rho }}$) estimates for the six study glaciers. See Figure S7 for additional details.

5.3. Evaluation

Our adaptive smoothing approach performed well at all study glaciers, with negligible pre- and post-filter differences (computed over the same set of valid pixels) for both the average flux divergence and expected slope-parallel elevation change products (Table S2). Similarly, the observed differences between the glacier-wide average of Eulerian ${{\rm d}h\over {\rm d}t}$ and slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ estimates were also negligible for our study glaciers (Table S3).

The Lagrangian SMB rate maps covered almost the entire Lirung and Black Changri Nup Glaciers due to their relatively small size and large debris-covered ablation areas. This enabled additional evaluation of the Eulerian ${{\rm d}h\over {\rm d}t}$ and final Lagrangian SMB rate products, with observed differences of 0.15 and 0.03 m a⁻¹ for these two glaciers, respectively. The slightly larger difference over Lirung Glacier can be attributed to its unique state, where the current RGI polygon extent suggests that the active portion of the glacier is disconnected from its accumulation area. In this case, the observed difference represents the mean emergence velocity for Lirung Glacier, which is close to the value of 0.16 ± 0.1 m a⁻¹ reported by Miles and others (2018a). Overall, these comparisons provide confidence that our Lagrangian framework properly conserves mass.

Figure 6 shows profiles for the full set of elevation change (${{\rm d}h\over {\rm d}t}$, ${{\rm D}h\over {\rm D}t}$, ${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$) and SMB (${\dot {b}\over \rho }$) rate products for each of the study glaciers. As observed in the map products, the uncorrected Lagrangian ${{\rm D}h\over {\rm D}t}$ measurements appear more negative than the corresponding Eulerian ${{\rm d}h\over {\rm d}t}$ measurements, underscoring the importance of the expected slope-parallel elevation change correction (Section 4.2). The resulting slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ measurements show good agreement with corresponding Eulerian ${{\rm d}h\over {\rm d}t}$ measurements. We also observe a notable reduction in the spread of elevation change values within each bin in the slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ products, especially for fast-flowing glaciers, due to the removal of artifacts related to advection of short-scale roughness. After correcting for estimated flux divergence, the final Lagrangian SMB rates generally appear more negative in the low to mid-elevation bins, and more positive in the high-elevation bins for glaciers with valid measurements in the accumulation area.

Figure 6. Elevation change profiles for the six study glaciers, showing the median values of each gridded product within 50 m elevation bins. Each plot includes Eulerian elevation change rate (${{\rm d}h\over {\rm d}t}$; red lines), Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t}$; blue lines), slope-corrected Lagrangian elevation change rate (${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$; black lines) and final Lagrangian SMB rate (${\dot {b}\over \rho }$; green lines). The Eul. ${{\rm d}h\over {\rm d}t}$ and Lag. ${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$ profiles show good agreement at all glaciers, confirming that our correction approach conserves mass. The shaded area around the Eul. ${{\rm d}h\over {\rm d}t}$ and Lag. ${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$ profiles represents the NMAD of values within each elevation bin, which includes real spatial variability. Note the reduced spread of the Lag. ${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}$ products (which remove artifacts due to advection of short-scale roughness) for all glaciers except Lirung and Black Changri Nup, where the flow velocity is relatively slow and we do not expect to see large differences.

5.4. Surface mass-balance profiles

To investigate how debris thickness and elevation affect SMB, we compared profiles of the binned Lagrangian SMB rate, debris thickness and glacier hypsometry for each glacier (Fig. 7). Debris is generally thicker at lower elevations and thinner at higher elevations for all study glaciers, with some local variations (Fig. 8). We generally observe a pattern of more negative Lagrangian SMB rates at higher elevations for all six study glaciers (Fig. 8b), though there are some notable differences. For example, we observe an abrupt transition to more negative values in elevation bins ~ 200 and 400 m above the termini of the Langtang and Ngozumpa Glaciers, respectively. Lirung Glacier is entirely debris-covered with no tributaries (Figs S5, 7a), and the Lagrangian SMB rates become more negative at higher elevations, with the most negative values approximately 300 m above the terminus. There is also a decrease in median debris thickness across bins with the highest ablation rates.

Figure 7. Aggregated Lagrangian SMB rate (top panel), debris thickness (middle panel) and hypsometry of valid pixels in the Lagrangian SMB rate products (bottom panel) over 50 m elevation bins for the six study glaciers. Shaded area around the Lagrangian SMB rate curve represents the median SMB uncertainty for each elevation bin (see Section 4.3, Fig. 5). The box plots show the median and interquartile range of debris thickness in each bin. The area-weighted average of the Lagrangian SMB rate for bins with valid data is printed in the lower right corner for each glacier. Note the location of the most negative SMB values at mid-elevations, not at the glacier terminus, where debris is thicker. See maps in Figures 3, S2–S6 for context. Figure S8 shows the same plots with logarithmic scale.

Figure 8. Debris thickness, Lagrangian SMB rate and ice cliff ablation rate aggregated over 50 m elevation bins for the six study glaciers. See Section 4.5 and Figure 7 for additional details. (a) Median debris thickness, (b) median Lagrangian SMB rate (${{\dot {b}\over \rho }}$), (c) median Lagrangian SMB rate (${{\dot {b}\over \rho }}$) aggregated separately for debris-covered areas (transparent lines) and areas affected by ablating ice cliffs (solid lines), (d) percent of the total debris-covered area affected by ablating ice cliffs ($A_{\rm{icecliff}}\%$), and (e) the percent contribution of ablating ice cliffs to total ablation in debris-covered areas ($\dot {b}_{\rm{icecliff}}$%). Note larger $\dot {b}_{\rm{icecliff}}$% values for bins with thicker debris and higher $A_{\rm{icecliff}}\%$.

5.5. Contribution of ablating ice cliffs to surface mass balance

The Lagrangian SMB rates are considerably more negative over ice cliffs compared to surrounding debris-covered ice for all study glaciers (Fig. 8c). The corresponding bin values for percent contribution of ablating ice cliffs to total ablation in debris-covered area ($\dot {b}_{\rm{icecliff}}$%) range from as low as $\leq 5\%$ to $\geq 50\%$ (Fig. 8e). Generally, the $\dot {b}_{\rm{icecliff}}$% values decrease with elevation, and covary with debris thickness and total debris-covered area affected by ablating ice cliffs (Fig. 8). For instance, at an elevation range between ~5000 and 5200 m over Ngozumpa, Imja Lhotse Shar and Khumbu Glaciers, debris thickness is similar, but the ($\dot {b}_{\rm{icecliff}}$%) for Khumbu and Imja Lhotse Shar Glacier is approximately twice that of Ngozumpa Glacier, as the debris-covered area affected by ablating ice cliffs is higher for these two glaciers.

When the binned values are aggregated over the entire debris-covered ablation area of each glacier, the ablating ice cliffs account for 9.8–37.9% of the total ablation, even though they only occupy 3.6–10.8% of the total debris-covered area (Table 3).

Table 3. Summary statistics for ice cliff area (A _icecliff), percent of the total debris-covered area affected by ablating ice cliffs ($A_{\rm{icecliff}}\%$) and percent contribution of ablating ice cliffs to total ablation in debris-covered areas ($\dot {b}_{\rm{icecliff}}$%) for the six study glaciers

5.6. Seasonal surface mass balance

The seasonal Lagrangian SMB maps over Black Changri Nup Glacier document the spatial patterns of accumulation and ablation during both the summer and winter seasons (Fig. 9). During the winter period (November 2015 to April 2016), except for prominent negative signals over ice cliffs, we observe near-zero Lagrangian SMB over most of the debris-covered portions of the glacier (left panel of Fig. 9b). During the summer period (April 2016 to October 2016), most of the debris-covered surfaces have negative Lagrangian SMB, with greater ablation over ice cliffs (right panel of Fig. 9b). This summer ablation pattern is consistent with expectations for typical mountain glaciers. At elevations higher than 5600 m, however, we observe atypical patterns, with negative Lagrangian SMB during winter and positive Lagrangian SMB during summer (Figs 9b,c). This observation is corroborated by the end of winter orthoimage, which shows a reduction in snow cover from the preceding end of summer orthoimage (center panel of Fig. 9a). We also observe more snow cover at higher elevations in the subsequent end-of-summer orthoimage (right panel of Fig. 9a).

Figure 9. Seasonal orthoimages and Lagrangian SMB maps for Black Changri Nup Glacier. (a) Panchromatic Maxar WorldView-02/03 orthoimages acquired at end of summer (2 November 2015), end of winter (22 April 2016) and end of the following summer (25 October 2016). Note the reduction in snow cover at the end of the winter period and the increase in snow cover extent at the end of the summer 2016. Green outline shows glacier extent from Brun and others (2018). (b) Seasonal Lagrangian SMB (${{b\over \rho }}$ with units of m, not m a⁻¹ as in previous figures, see Section 4.2.3) for the winter period (2 November 2015 to 22 April 2016) and the summer period (22 April 2016 to 25 October 2016). (c) Profiles showing the median of seasonal Lagrangian SMB in 50 m elevation bins during summer (pink) and winter (blue), with shading showing the NMAD for each bin. Bottom panel shows glacier hypsometry from the end of summer DEM (2 November 2015). Note the atypical seasonal balance gradients above 5600 m, with apparent accumulation during summer and ablation during winter.

The high-resolution orthoimages and seasonal elevation change maps for Lirung Glacier (Fig. 10) capture deposition from avalanche event(s) triggered by the 25 April 2015 Gorkha Earthquake (Ragettli and others, 2016). We were unable to prepare contemporaneous velocities from the shaded relief maps for these periods, as the avalanche deposits obscured the surface features needed for coherent feature tracking. We therefore limited our analysis to the Eulerian elevation change products, without any additional corrections. We observe a large positive elevation change over the upper glacier during the winter period (22 January 2015 to 8 May 2015), with maximum local deposit thickness of ~30–55 m (left panel in Fig. 10b). We observe a large decrease in surface elevation over this same area during the following ~8 months (8 May 2015 to 29 December 2015), likely due to ablation and compaction of the avalanche deposits (right panel in Fig. 10b). The 29 December 2015 orthoimage from the end of this period shows that the entire glacier surface was covered in debris (right panel in Fig. 10a). However, the annual elevation change map for the full ~1-year period (22 January 2015 to 29 December 2015) shows a large area with residual positive elevation change of $\gtrsim \!10\!-\!30$ m, indicative of net accumulation (Fig. 10c). The maximum magnitude of expected elevation change due to flux divergence over these areas during the ~1-year period between 6 November 2016 and 22 December 2017 is only ~±1 m a⁻¹ (Fig. S5d), an order of magnitude smaller than the observed seasonal elevation change.

Figure 10. Seasonal orthoimage and surface elevation change products over Lirung Glacier capturing accumulation due to avalanche event(s) triggered by the 25 April 2015 Gorkha Earthquake. (a) Panchromatic Maxar WorldView-01/03 orthoimage time series (see Table 2) before the avalanche (22 January 2015), a few weeks after the avalanche (8 May 2015) and after the subsequent ablation season (29 December 2015). (b) Eulerian elevation change maps for the two periods, capturing the avalanche deposits (left, 22 January 2015 to 8 May 2015) and subsequent ablation and compaction of the avalanche deposits during the ablation season (right, 8 May 2015 to 29 December 2015). (c) Annual elevation change map spanning the full period (22 January 2015 to 29 December 2015). Green outline shows RGI v6 glacier extent. Note the ~30–55 m thick deposit, and net positive annual elevation change following the ablation season, when the glacier once again appears covered with debris.

6. Discussion

6.1. Lagrangian surface mass-balance products

Ablation rates over debris-covered glaciers are expected to be highly heterogeneous due to the spatial variation of debris thickness and distribution of relevant surface features (ice cliffs, supraglacial streams and melt ponds), though detailed observations of these surface features and their evolution are limited. Our results show that slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ products derived from contemporaneous high-resolution elevation change and surface velocity products can measure local ablation rates over steep ice cliffs (e.g. Fig. 4). The Lagrangian specification is essential to remove anomalous elevation change signals due to advection of rough surface features (like ice cliffs) for actively flowing ice (>5 m a⁻¹ surface velocity for our study glaciers). Isolated positive signals near some ice cliffs in the slope-corrected Lagrangian ${{\rm D}h\over {\rm D}t}$ and Lagrangian SMB rate products (e.g. Fig. 4) are most likely due to infilling of adjacent supraglacial ponds and/or debris redistribution, as observed in recent studies of other debris-covered glaciers (e.g. Westoby and others, 2020; Mishra and others, 2022).

Our velocity products and associated flux divergence products offer comparable resolution to previous studies involving UAV datasets (e.g. Van Tricht and others, 2021b). The flux divergence maps prepared with our adaptive smoothing approach preserve important spatial variability that is removed by other approaches that average flux divergence over large bins or the entire ablation area (e.g. Brun and others, 2018; Mishra and others, 2022). The spatial resolution of our smoothed flux divergence varies with local ice thickness, which approximates the physical controls on longitudinal driving stress and surface slopes. Some isolated areas with larger, potentially anomalous flux divergence values may be explained by some combination of real variations in the bed and observed surface topography (e.g. near icefalls, confluence of glacier tributaries), residual errors in ice thickness estimates and/or residual errors in surface velocity measurements.

6.2. Controls on ablation rates

The Lagrangian SMB rates observed near the terminus of all six studied glaciers were less negative than rates further upstream. This phenomenon can be explained by the thick debris cover in these areas that effectively offsets the higher ablation rates expected for the warmer air temperatures at lower elevations, as noted in previous studies (e.g. Östrem, 1959; Nicholson and Benn, 2006; Rounce and McKinney, 2014). With decreasing debris thickness upstream, the Lagrangian SMB rates become more negative despite cooler air temperatures, resulting in an inversion of the mass-balance gradient over low- to mid-elevation bins (Figs S5, 8).

Our results support the notion that debris thickness is a major control over ice ablation rates, in line with previous studies (e.g. Anderson and others, 2021a; Zhao and others, 2023). We note that the debris thickness estimates and our Lagrangian SMB rate estimates are not entirely independent, as the debris thickness estimation method (Rounce and others, 2021) included a calibration step based on long-term elevation change measurements (Shean and others, 2020) from the 2000 to 2018 period, which overlaps with the 2012–2017 period of this study. However, given the independence of the underlying DEM observations, this temporal overlap is not a concern.

Our analysis also demonstrates that while ablating ice cliffs affect a small percentage of the debris-covered area (4–11%), they account for a large percentage of total ablation (10–38%) for our study glaciers (Table 3). While this relationship has been observed in previous work for individual glaciers, to our knowledge, this is the first detailed observational analysis using consistent methodology for multiple glaciers. We did not observe a clear relationship between the observed Lagrangian SMB rate and elevation for areas affected by ablating ice cliffs (Fig. 8c), which is most likely due to the fact that the energy available for ice cliff ablation depends on local radiative forcing (Buri and others, 2021). However, the percent contribution of ablating ice cliffs to total ablation (Fig. 8e) does display some elevation dependence, which is most likely related to elevation-dependent differences in debris thickness and ice dynamics (i.e. surface velocity variations that influence ice cliff formation and evolution; e.g. Watson and others, 2017a).

For relatively slow, stagnant ice with thick debris cover, we expect to see fewer but more persistent ice cliffs, sustained mainly by surrounding supraglacial ponds (e.g. Buri and Pellicciotti, 2018; Kneib and others, 2022). Sub-debris ablation rates over these stagnant regions will be low, which increases the relative contribution of ice cliffs to total ablation. This phenomenon is clearly demonstrated at Lirung Glacier, where the large terminal ice cliff can account for ~60% of the total ablation in its elevation bin (Figs S5, 8).

For actively flowing (>5 m a⁻¹) ice, multiple transitions between compressional and extensional flow are expected to produce more dynamic ice cliffs which grow and disappear relatively quickly (e.g. Benn and others, 2012; Kraaijenbrink and others, 2016b; Anderson and others, 2021b). This phenomenon can be attributed to higher crevasse density (Reid and Brock, 2014), more rugged surface topography that exposes steep ice faces due to thinner debris cover, and higher rates of debris redistribution (Anderson and others, 2021b). In these areas, even though the size and location of the ice cliffs will evolve with time, the number of ice cliffs is expected to be relatively high (e.g. Kneib and others, 2022), again resulting in a considerable contribution of ice cliffs to total ablation, especially at high elevations where sub-debris ablation rates are low (Fig. 8) due to cooler air temperatures (Buri and others, 2021).

6.3. Comparison with previously published results

Our estimates for Lagrangian SMB rate and the percent contribution of ablating ice cliffs to total ablation in debris-covered areas ($\dot {b}_{\rm{icecliff}}$%) are consistent with existing estimates for the same glaciers prepared using independent methods and/or data sources. While these comparisons are limited to select glaciers and time periods, they offer additional validation for our methodology, and greater confidence when applying our approach to study other glaciers in the region.

Buri and others (2021) estimated the contribution of ice cliffs to total ablation in debris-covered areas using energy balance models for four glaciers in Langtang National park. Their estimates for Lirung and Langtang Glacier, 11 ± 5 and $21\pm 4\%$, respectively, are similar to our estimates of 10 and 24% for the same glaciers. They manually identified ice cliffs, and their reported ice cliff area (A _icecliff) was 0.018 ± 0.0047 km² for Lirung Glacier and 0.31 ± 0.081 km² for Langtang Glacier (Table 1 in Buri and others, 2021) – considerably lower than our estimates for area affected by ablating ice cliffs of 0.05 and 0.98 km², respectively (Table 3). This discrepancy in ice cliff area is likely due to the methodological differences and real temporal changes in ice cliff distribution. For instance, Steiner and others (2019) and Buri and others (2021) used a conservative approach for ice cliff mapping, favoring large cliffs that could be delineated in high-resolution (~1.5 m GSD) SPOT-6 satellite images with high confidence. Additionally, ice cliff area evolves on seasonal (Steiner and others, 2019) to annual timescales (Kneib and others, 2021b), especially for smaller ice cliffs. Despite these differences, the fact that our estimates for percent contribution are similar to those of Buri and others (2021) suggests that larger ice cliffs dominate the total ice cliff contribution to ablation for these glaciers.

Thompson and others (2016) prepared DEMs for Ngozumpa Glacier using the same very-high-resolution stereo image pairs from December 2012 and January 2015 (Table S1). They estimated an ice cliff contribution to total ablation in debris-covered areas of $39\%$, though they did not correct for flux divergence and their analysis was limited to slow-flowing (<5 m a⁻¹) regions. Our Lagrangian framework allowed us to extend this analysis to the entire debris-covered surface of Ngozumpa Glacier, where we estimate a smaller contribution of ablating ice cliffs to total ablation in debris-covered areas of $31\%$.

Brun and others (2018) estimated a mean SMB rate of −1.10 ± 0.27 m a⁻¹ over the entire debris-covered portion of the Black Changri Nup Glacier for the period spanning 23 November 2015 to 16 November 2016, and −1.20 ± 0.36  m a⁻¹ for the period spanning 22 November 2015 to 13 November 2016, using DEMs derived from UAV and Pleiades-HR images, respectively. These values agree very well with our mean Lagrangian SMB rate estimate of −1.18 m a⁻¹ over the debris-covered portion of the Black Changri Nup Glacier from the same period (15 November 2015 to 25 October 2016). Over the same area, Brun and others (2018) estimated an emergence velocity of 0.33 ± 0.11 m a⁻¹ using IPR-derived ice thickness transects, agreeing closely with the mean flux divergence of −0.31 m a⁻¹ derived in this study. Additionally, Brun and others (2018) estimated that ice cliffs contributed up to $24\pm 5\%$ of the total ablation in debris-covered areas, which is similar to our estimate of 22%, even though the two studies used different methods for ice-cliff delineation.

6.4. Seasonal surface mass balance

Our seasonal case studies for Black Changri Nup (median elevation of 5468 m, Table 2) and Lirung Glacier (4255 m) document the distinctive accumulation and ablation patterns of debris-covered glaciers at different elevations in the Central Himalayas.

We observed significant accumulation and increased snow cover during the summer period for the high-elevation Black Changri Nup Glacier (right panel in Fig. 9b). Wagnon and others (2013) reported mean monthly temperatures of ~3−4°C during summer (June–August) at the Pyramid Base station (~5035 m) between 2003 and 2012. This suggests that summer temperatures should be at or below freezing at elevations higher than ~5650 m for a standard adiabatic lapse rate of 6.5°C km⁻¹. The Black Changri Nup accumulation area is located above ~5600 m, which should allow for sustained snow accumulation during the summer monsoon season.

In contrast, we observe ablation and decreased snow cover during the winter period for the Black Changri Nup Glacier (left panel in Fig. 9b), which is consistent with traditional glaciological measurements for the nearby debris-free Mera Glacier (Wagnon and others, 2013). The large negative Lagrangian SMB observed at higher elevations during winter can potentially be explained by some combination of snow sublimation (e.g. Litt and others, 2019; Mandal and others, 2022), snow redistribution due to stronger winds at higher altitudes (e.g. Wagnon and others, 2013; Huintjes and others, 2015) and/or snow and firn compaction. We are confident that these are real signals, but some component may also be related to the underestimation of submergence velocities due to local errors in the ice thickness and surface velocity estimates.

While these results for a summer-accumulation type glacier are intriguing, our preliminary seasonal observations only span 1 year, and 2015 may not be representative of typical seasonal SMB. Notably, our methods can be applied to other glaciers where multiple very-high-resolution stereo images have been acquired in a single year, which can improve our understanding of seasonal accumulation and ablation patterns for glaciers in the region. Future comparisons with available weather station and climate reanalysis data during our observation period could potentially offer additional insights to guide further interpretation.

Snow avalanches also represent an important seasonal accumulation source for many debris-covered glaciers, especially those with accumulation areas at lower elevations. We documented a large late winter accumulation signal at Lirung Glacier due to snow avalanche(s) triggered by the Gorkha Earthquake. The large volume of these snow avalanche deposits can be explained by the anomalously high snow accumulation on surrounding peaks during the preceding 2014–15 winter (Fujita and others, 2017). Future systematic very-high-resolution stereo image tasking campaigns can potentially document the timing, magnitude and evolution (potentially isolating compaction vs ablation) of large avalanche deposits on Lirung Glacier or others in the region to better understand their contribution to glacier SMB in the Central Himalayas and other regions of High-Mountain Asia.

6.5. Limitations and considerations for future work

The primary focus of our study was to develop a processing workflow and analysis framework, knowing that future improvements in ice thickness, surface velocity and density products will improve the accuracy of our results. Our methodology involves several advancements including high-resolution DEM processing, contemporaneous surface velocity and elevation difference calculation, and a thickness-dependent smoothing approach for flow correction. However, we also identified several limitations of our approach and areas for future improvement, including the need for more in situ reference measurements (e.g. ice thickness, flux divergence, SMB, firn thickness and density) which we discuss in the following sections.

6.5.1. Surface velocity measurements

The contemporaneous velocity and DEM products are essential to maintain feature correspondence and track individual ice cliffs over debris-covered ablation areas. Our approach involving shaded relief maps to compute horizontal surface displacements can fail in fast-flowing areas (e.g. icefalls) due to feature decorrelation over longer timescales and a lack of surface texture (e.g. snow-covered accumulation areas; Section 3.1.2, 5.1). One potential solution is to create composite ice velocity products, using short baseline pairs of complementary optical (e.g. Chapter 4 in Altena and Kääb, 2020; Bhushan, 2023) or Synthetic Aperture Radar images (e.g. Lei and others, 2022) from the same time period to fill these data gaps.

6.5.2. Flux divergence, ice thickness and basal sliding

We derived flux divergence using modeled estimates of ice thickness and some simplifying assumptions (Section 4.1). The ice thickness estimates could be calibrated and/or validated using in situ ice thickness measurements (e.g. Pritchard and others, 2020), which would reduce the flux divergence uncertainty.

We made common assumptions about the relative contributions of deformation and basal sliding to observed surface velocity. It is possible that basal sliding is non-negligible for some areas of our study glaciers (e.g. Kraaijenbrink and others, 2016a), which could warrant a spatially and temporally variable f scaling parameter to estimate column-averaged velocity. However, we expect the magnitude of elevation change uncertainty to exceed any uncertainty introduced by f variation, as demonstrated in Van Tricht and others (2021b) and Armstrong and others (2022). Future studies exploring seasonal glacier velocity variability (e.g. Chapter 4 in Armstrong and others, 2017; Bhushan, 2023) and connections between glacier surface hydrology and basal conditions (e.g. Benn and others, 2017; Miles and others, 2018b) should improve our understanding of the relative contribution of basal sliding to glacier flow for these debris-covered glaciers.

6.5.3. Uncertainty propagation

While our uncertainty estimation approach for the elevation change and surface velocity products follows standard geodetic glacier mass-balance community practices, we now discuss potential limitations and challenges. For one, the same set of non-glacierized, static control surfaces were used for calibration (co-registration) and uncertainty estimation. Also, while global statistics (e.g. median, NMAD) computed over static surfaces are robust to outliers, they may not be directly representative of the true errors in the same products over glacier surfaces, which can have characteristically different surface slope and roughness distributions (e.g. Hugonnet and others, 2022; Zheng and others, 2023; Guillet and Bolch, 2023). To examine the assumption of uniform uncertainty across static and glacier surfaces, we assessed observed residuals over static areas as a function of terrain predictors (e.g. surface slope and elevation). We did not observe any distinct relationship between observed residual error magnitude and the range of surface elevation and slope values for our study glaciers. Finally, there are coherent patterns of $\sigma _{{{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\cdot {\nabla h}}$ residuals (Fig. S7) that appear to be real elevation change signals over moraines, hillslopes, lakes and seasonal snow, suggesting that some of these surfaces should not be considered ‘static’. Their inclusion likely resulted in a small overestimate of errors for glacier surfaces.

Our adaptive smoothing approach reduces the random errors in the flux divergence products inherited from the velocity and ice thickness products. However, residual systematic bias could introduce errors when averaging over large areas (e.g. SMB for the entire ablation area, as in Van Tricht and others, 2021b). Quantifying the accuracy improvement offered by our adaptive smoothing approach and isolating the relative contribution of ice thickness bias to flux divergence uncertainty is difficult without spatially distributed reference flux divergence and SMB measurements.

Finally, our forward uncertainty propagation approach likely overestimates uncertainty, especially over slow-flowing areas where the ${\sigma _{{\boldsymbol u_{\rm s}}}\over {\boldsymbol u_{\rm s}}}$ term is large. Future work involving probabilistic uncertainty estimation approaches such as bootstrapping or Monte Carlo methods (e.g. Miles and others, 2021) may provide more representative estimates and better understanding of sensitivity to errors in each component.

6.5.4. Ice cliff delineation and ablation rates

We identified areas affected by retreat and ablation of ice cliffs using empirically derived thresholds for surface slope and observed ablation rates (Section 4.4). While our ice cliff ablation metrics are consistent with published results (Section 6.3), we acknowledge that our approach preferentially identifies areas with steeper ice cliffs experiencing high ablation rates, while potentially excluding ice cliffs with lower ablation rates. The percent contribution of ablating ice cliffs to total ablation metric (Eqn (10)) is less sensitive to this delineation approach, as it captures the total volume of ablation associated with ice cliffs, which is dominated by losses from large ice cliffs (e.g. Brun and others, 2018).

We evaluated the accuracy of our approach to identify areas affected by ablating and retreating ice cliffs, and the associated sensitivity to our maximum ${{\rm D}h\over {\rm D}t}- {\boldsymbol u_{\rm s}}\nabla {h}$ threshold, for Black Changri Nup Glacier. To accomplish this, we prepared a control inventory by manually mapping ice cliffs using very-high-resolution orthoimages, shaded relief maps and surface slope maps. We then compared the control inventory with inventories derived using a maximum ${{\rm D}h\over {\rm D}t}- {\boldsymbol u_{\rm s}}\nabla {h}$ threshold of between −3.5 and −1.6 m a⁻¹, with 0.1 m a⁻¹ interval. We defined true positives as pixels that were classified as ice cliffs by both approaches, false positives as pixels that were classified as ice cliffs by the threshold approach but not the manual approach, false negatives as pixels that were classified as ice cliffs by the manual approach but not the threshold approach, and true negatives as pixels that were correctly classified as non-ice cliffs by both approaches. We computed the Sørensen–Dice coefficient and other accuracy metrics from the confusion matrix for the range of ${{\rm D}h\over {\rm D}t} - {\boldsymbol u_{\rm s}}\nabla {h}$ thresholds. We found that higher threshold values (closer to −1.6 m a⁻¹) resulted in more false positives, and lower threshold values (closer to −3.5 m a⁻¹) resulted in more false negatives. The maximum Sørensen–Dice coefficient of 0.57 occurred for thresholds between −2.1 and −2.6 m a⁻¹, which supports our decision to use a conservative −2.5 m a⁻¹ threshold to identify areas affected by ablating ice cliffs for all of our study glaciers.

As noted previously, all approaches to delineate ice cliffs have limitations (Section 4.4), but future studies could employ a combination of approaches using additional datasets (orthoimages, DEMs, elevation change products) and temporal consistency checks to increase confidence. Approaches involving convolutional neural networks for segmentation are also promising, assuming adequate manually prepared training datasets are available. Future work could also explore the M3C2 approach (Lague and others, 2013) to compute surface-normal elevation change for ice cliffs, rather than vertical elevation change, to produce more robust ablation estimates over steeper ice cliffs (e.g. Mishra and others, 2022; Kneib and others, 2023).

6.5.5. Density considerations

In principle, we could have made common assumptions about the density and spatial distribution of ice, firn and snow to estimate mass change and SMB with units of m w.e. a⁻¹ for our study glaciers. However, as discussed in Section 4.1 and many previous studies (e.g. Sold and others, 2013; Huss, 2013; Belart and others, 2017; Florentine and others, 2019; Pelto and others, 2019; Berthier and others, 2023), these values are poorly constrained for mountain glaciers, especially those in High-Mountain Asia, and they display considerable spatial and temporal variability.

With this in mind, we chose to report Lagrangian SMB rate in m a⁻¹, and offer guidance for interpretation and conversion to m w.e. a⁻¹. In practice, a constant ice density of ~900 kg m⁻³ is appropriate for most of the observed change over ablation areas, and multiplying the Lagrangian SMB rate values by 900  kg m⁻³ will provide ablation rates in ${{\rm kg}\over {\rm m}^{2}.{\rm yr}}$. The mass-balance estimates in ${\rm{kg\over m^{2}.yr}}$ can be divided by density of water (assumed to be 1000  kg m⁻³) to obtain measurements in units of m w.e. a⁻¹. While our product coverage is relatively limited over the accumulation areas of our study glaciers, following Zeller and others (2022), we recommend that a constant bulk density of between 400 and 750 kg m⁻³ could be used to convert our Lagrangian SMB rate products to m w.e. a⁻¹ depending on material type (e.g. snow vs firn) and observation period (seasonal vs annual). Future site-specific in situ observations of seasonal snow density could provide improved bulk density constraints for SMB conversion over accumulation areas.

Our approach assumes a constant density of ice when computing the flux divergence for a column with thickness H (e.g. Miles and others, 2021). We expect a slightly lower column-averaged density (i.e. ~850 to <900 vs 900 to 917 kg m⁻³) in accumulation areas due to firn (e.g. Pelto and Menounos, 2021), which would reduce the effective ice thickness and likely the magnitude of the flux divergence component in Eqn (5). As a result, our final Lagrangian SMB rate estimates may have a small positive bias in accumulation areas, though this bias should be well within our estimated uncertainty (Fig. 5).

Our theoretical framework assumes a constant column-averaged density over time (Eqn (5)), thereby neglecting the effects of firn densification. Firn compaction should introduce a small negative bias in our final Lagrangian SMB rate estimates over accumulation areas. However, we expect lower accumulation areas (i.e. closer to the equilibrium line, where we typically have valid product coverage) to have thin firn and low densification rates, such that any bias would be within the range of our estimated uncertainty (Figs 5, S7). Finally, changes in firn densification rates over seasonal time intervals could also introduce bias (Huss, 2013), but this effect is not directly quantifiable without a well-calibrated firn model.

In general, calibration and validation of firn models for mountain glaciers remains a major challenge, and there are few in situ measurements available for these remote debris-covered glaciers (e.g. Stumm and others, 2021). As firn models for glaciers in High-Mountain Asia continue to improve (e.g. Kronenberg and others, 2022, 2021), our open-source code can be adapted to incorporate spatially and temporally variable snow and firn density, ultimately improving estimates of Lagrangian SMB rates in upper accumulation areas.

6.5.6. Implications for glacier model calibration

Many glacier mass-balance models rely on specific SMB rates in m w.e. a⁻¹ over the full glacier for calibration. At present, we do not provide these estimates for accumulation areas due to issues around missing data and not as well constrained surface material density, as discussed in the previous section. However, our high-resolution SMB estimates over ablation areas can be directly used for model calibration on seasonal to annual timescales. Our annual observations capture the spatially varying effects of debris thickness and ice cliffs on ablation rates with unprecedented detail for six debris-covered glaciers in Nepal. These results and associated data products can improve calibration of glacier mass-balance models for the region, and in turn, coupled glacio-hydrologic models (e.g. Khadka and others, 2020; Srivastava and Azam, 2022), and land surface models (e.g. Buri and others, 2023). With further improvements in density handling over accumulation areas, our distributed seasonal SMB estimates will improve the calibration of temperature and precipitation correction factors in glacier mass-balance models (e.g. Rounce and others, 2020a; Schuster and others, 2023). Our methods can be extended to include a larger sample of representative glaciers in High-Mountain Asia and other regions of the world, which would improve global glacier modeling efforts, including prognostic models for debris-covered glacier evolution in the coming century.

7. Conclusions

We developed a workflow to generate flow-corrected Lagrangian SMB measurements using contemporaneous glacier surface elevation and surface velocity observations derived from very-high-resolution commercial satellite stereo images. The resulting high-resolution Lagrangian SMB rate products capture the detailed spatial patterns of surface ablation for six debris-covered glaciers in the Central Himalayas.

Our processing workflow includes a slope-parallel flow correction using contemporaneous DEM and velocity products, and a novel ice-thickness-dependent smoothing filter that removes artifacts while preserving signals with physically meaningful length scales. We evaluated our approach using mass conservation checks between the Eulerian and Lagrangian products and independent published SMB estimates for the same glaciers and time periods. Our conservative forward uncertainty calculation framework allowed us to evaluate the relative contribution of different input products to the final Lagrangian SMB rate uncertainty estimates. We found that flux divergence uncertainty dominated total uncertainty over most of the glacier surface, especially for relatively fast-flowing, thin ice.

Our Lagrangian SMB rate products document local ablation rates for debris-covered areas and surface features such as ice cliffs. We analyzed the elevation-dependent relationship between debris thickness and observed ablation rates for our study glaciers, reaffirming that local debris thickness exerts important control on ice ablation rates. Ice cliffs also increase ablation rates over both stagnant and actively flowing debris-covered ice. Our results showed that ice cliffs are responsible for 10–38% of the total ablation in debris-covered areas for these glaciers, even though they occupy $< \!11\%$ by area.

We documented the atypical timing and patterns of seasonal accumulation and ablation for two of our study glaciers. The high-elevation Black Changri Nup Glacier had limited winter accumulation rates and relatively high summer accumulation rates, which highlights the importance of summer snow accumulation for glaciers in the high-elevation Sagarmatha (Everest) region. We also documented the emplacement and evolution of ~30−55 m thick winter snow avalanche deposits over the low-elevation, completely debris-covered Lirung Glacier. These results suggest that avalanche runout represents an important accumulation mechanism for lower elevation glaciers in monsoon-dominated regions of High-Mountain Asia.

Our methodology can be applied to large archives of very-high-resolution stereo images (e.g. Maxar WorldView-01/02/03, Shean and others (2020), Pléiades-HR/NEO, Berthier and others (2014), Planet SkySat, Bhushan and others (2021)) and derived high-resolution DEM products (e.g. ArcticDEM, REMA, EarthDEM), providing new opportunities to study glacier SMB processes on a regional scale. Future work can potentially offer solutions to current limitations related to data gaps over accumulation areas, ice thickness uncertainty, poorly constrained density estimates and residual elevation change uncertainty related to systematic DEM artifacts and co-registration errors. Ultimately, high-resolution SMB observations like those presented here will improve our understanding of debris-covered glacier surface processes, offer improved calibration data for glacier mass-balance models, and enhance our overall understanding of the past and future behavior of High-Mountain Asia glaciers in a changing climate.