1 Introduction
Rotation powered pulsars are wonderfully complex systems that convert mechanical (rotational) energy to electromagnetic energy with high efficiency. Relativistic pair plasmas mediate this conversion and determine both the location and amount of dissipation, primarily in the form of particle acceleration and radiation, self-consistently with the structure of the global magnetosphere. Although pulsars were first discovered by their radio pulsations, an understanding of their underlying physics is probably the most difficult at radio wavelengths due to the coherent nature of the radio pulsations, combined with the fact that they represent a very small fraction (
![]() ${\sim}10^{-5}$
) of the rotational energy loss. On the other hand, pulsations in the high-energy
${\sim}10^{-5}$
) of the rotational energy loss. On the other hand, pulsations in the high-energy
![]() ${\it\gamma}$
-ray band consume a much higher fraction (up to nearly 100 %) of spin-down power and have proven to be powerful probes of particle acceleration and magnetosphere structure.
${\it\gamma}$
-ray band consume a much higher fraction (up to nearly 100 %) of spin-down power and have proven to be powerful probes of particle acceleration and magnetosphere structure.
Pulsations at
![]() ${\it\gamma}$
-ray energies (
${\it\gamma}$
-ray energies (
![]() ${>}30~\text{MeV}$
) were discovered in 1972 (Albats, Frye & Zych Reference Albats, Frye and Zych1972), but only 6
${>}30~\text{MeV}$
) were discovered in 1972 (Albats, Frye & Zych Reference Albats, Frye and Zych1972), but only 6
![]() ${\it\gamma}$
-ray pulsars were known until the launch of the Fermi Gamma-Ray Space Telescope in 2008. Due to its superior sensitivity and resolution (Atwood et al.
Reference Atwood, Bagagli, Baldini, Bellazzini, Barbiellini, Belli, Borden, Brez, Brigida and Caliandro2007), Fermi has been able to detect a large number of
${\it\gamma}$
-ray pulsars were known until the launch of the Fermi Gamma-Ray Space Telescope in 2008. Due to its superior sensitivity and resolution (Atwood et al.
Reference Atwood, Bagagli, Baldini, Bellazzini, Barbiellini, Belli, Borden, Brez, Brigida and Caliandro2007), Fermi has been able to detect a large number of
![]() ${\it\gamma}$
-ray pulsars (more than 200 at present), enough to observe the emission (regions of dissipation) from many different viewing directions. Most importantly, more precise measurements of the
${\it\gamma}$
-ray pulsars (more than 200 at present), enough to observe the emission (regions of dissipation) from many different viewing directions. Most importantly, more precise measurements of the
![]() ${\it\gamma}$
-ray spectra were able to firmly establish the location of the emission in the outer parts of the magnetosphere. Since this site is near and/or beyond the pulsar light cylinder, where the corotation velocity equals the speed of light, the structure of the magnetic field as it is being distorted and swept back by currents can be explored. Because the accelerated highly relativistic particles follow trajectories nearly along the magnetic field lines, and their
${\it\gamma}$
-ray spectra were able to firmly establish the location of the emission in the outer parts of the magnetosphere. Since this site is near and/or beyond the pulsar light cylinder, where the corotation velocity equals the speed of light, the structure of the magnetic field as it is being distorted and swept back by currents can be explored. Because the accelerated highly relativistic particles follow trajectories nearly along the magnetic field lines, and their
![]() ${\it\gamma}$
-ray emission is beamed along their momentum direction, modelling the high-energy emission as a function of pulse phase is very sensitive to field structure.
${\it\gamma}$
-ray emission is beamed along their momentum direction, modelling the high-energy emission as a function of pulse phase is very sensitive to field structure.
In parallel with the observational
![]() ${\it\gamma}$
-ray pulsar revolution (see Caraveo Reference Caraveo2014 for a detailed account), our theoretical understanding of the pulsar magnetosphere through numerical simulations has also been evolving (see Grenier & Harding (Reference Grenier and Harding2015), for a recent review). The first solution of a global pulsar magnetosphere was the vacuum retarded dipole (VRD) (Deutsch Reference Deutsch1955), which was used as the background field structure of emission and light curve modelling even though it was not a realistic model of a real pulsar, where currents play a significant role in the global field structure (Goldreich & Julian Reference Goldreich and Julian1969). It was not until 1999 (Contopoulos, Kazanas & Fendt Reference Contopoulos, Kazanas and Fendt1999) that the aligned (magnetic and rotation axes parallel) force-free magnetosphere (where the electric field parallel to the magnetic field,
${\it\gamma}$
-ray pulsar revolution (see Caraveo Reference Caraveo2014 for a detailed account), our theoretical understanding of the pulsar magnetosphere through numerical simulations has also been evolving (see Grenier & Harding (Reference Grenier and Harding2015), for a recent review). The first solution of a global pulsar magnetosphere was the vacuum retarded dipole (VRD) (Deutsch Reference Deutsch1955), which was used as the background field structure of emission and light curve modelling even though it was not a realistic model of a real pulsar, where currents play a significant role in the global field structure (Goldreich & Julian Reference Goldreich and Julian1969). It was not until 1999 (Contopoulos, Kazanas & Fendt Reference Contopoulos, Kazanas and Fendt1999) that the aligned (magnetic and rotation axes parallel) force-free magnetosphere (where the electric field parallel to the magnetic field,
![]() $\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}$
, vanishes) was solved. The solution for the oblique force-free pulsar magnetosphere appeared in 2006 (Spitkovsky Reference Spitkovsky2006), showing that the currents produced a greater sweepback of the magnetic field near the light cylinder. Although the force-free solutions were thought to be much closer to actual pulsar magnetospheres they did not, by definition, include any particle accelerationFootnote
1
. Dissipative magnetosphere solutions, that assumed a macroscopic conductivity, were later developed by several groups (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li, Spitkovsky & Tchekhovskoy Reference Li, Spitkovsky and Tchekhovskoy2012a
). These models have accelerating electric fields that are self-consistent with a prescribed conductivity distribution, so that the model radiation was for the first time consistent with the magnetic field structure (Kalapotharakos, Harding & Kazanas Reference Kalapotharakos, Harding and Kazanas2014). The dissipative MHD models are still not a true pulsar model since they do not model the source of particles (that provide the conductivity) self-consistently. Thus has begun the modelling of pulsar magnetospheres using particle-in-cell codes (see Cerutti, this volume) that can potentially treat the source(s) of charge self-consistently. However, these models are still in an early stage and reaching
$\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}$
, vanishes) was solved. The solution for the oblique force-free pulsar magnetosphere appeared in 2006 (Spitkovsky Reference Spitkovsky2006), showing that the currents produced a greater sweepback of the magnetic field near the light cylinder. Although the force-free solutions were thought to be much closer to actual pulsar magnetospheres they did not, by definition, include any particle accelerationFootnote
1
. Dissipative magnetosphere solutions, that assumed a macroscopic conductivity, were later developed by several groups (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li, Spitkovsky & Tchekhovskoy Reference Li, Spitkovsky and Tchekhovskoy2012a
). These models have accelerating electric fields that are self-consistent with a prescribed conductivity distribution, so that the model radiation was for the first time consistent with the magnetic field structure (Kalapotharakos, Harding & Kazanas Reference Kalapotharakos, Harding and Kazanas2014). The dissipative MHD models are still not a true pulsar model since they do not model the source of particles (that provide the conductivity) self-consistently. Thus has begun the modelling of pulsar magnetospheres using particle-in-cell codes (see Cerutti, this volume) that can potentially treat the source(s) of charge self-consistently. However, these models are still in an early stage and reaching
![]() ${\it\gamma}$
-ray emitting particle energies is not yet possible.
${\it\gamma}$
-ray emitting particle energies is not yet possible.
This article will review what we can learn about the pulsar magnetosphere structure and plasma through modelling
![]() ${\it\gamma}$
-ray light curves and comparing with or fitting Fermi data.
${\it\gamma}$
-ray light curves and comparing with or fitting Fermi data.
2 Fermi observations of
 ${\it\gamma}$
-ray pulsars
${\it\gamma}$
-ray pulsars
The Fermi satellite carries two instruments, the large area telescope (LAT) sensitive to energies from 20 MeV to over 300 GeV and the
![]() ${\it\gamma}$
-ray burst monitor (GBM), with all-sky sensitivity at lower energies. The LAT is the main instrument for pulsar detection, since the vast majority have their spectral power peak around a GeV. In survey mode, which has been the default mode of operation, the LAT sees the entire sky every 3 h and has detected pulsars over the whole Galaxy as well as in the Large Magellanic Cloud.
${\it\gamma}$
-ray burst monitor (GBM), with all-sky sensitivity at lower energies. The LAT is the main instrument for pulsar detection, since the vast majority have their spectral power peak around a GeV. In survey mode, which has been the default mode of operation, the LAT sees the entire sky every 3 h and has detected pulsars over the whole Galaxy as well as in the Large Magellanic Cloud.
2.1 Rotating neutron star model
Rotation powered pulsars are highly magnetized neutron stars that lose their rotational kinetic energy through the emission of magnetic dipole radiation. According to this basic model, the rate of rotational energy loss
![]() ${\dot{E}}_{d}$
of a pulsar with surface polar magnetic field strength
${\dot{E}}_{d}$
of a pulsar with surface polar magnetic field strength
![]() $B_{d}$
, moment of inertia
$B_{d}$
, moment of inertia
![]() $I$
, radius
$I$
, radius
![]() $R$
and rotation rate,
$R$
and rotation rate,
![]() ${\it\Omega}$
, is given by
${\it\Omega}$
, is given by
Since
![]() ${\it\Omega}=2{\rm\pi}/P$
and
${\it\Omega}=2{\rm\pi}/P$
and
![]() $\dot{{\it\Omega}}$
, where
$\dot{{\it\Omega}}$
, where
![]() $P$
is the spin period, are observed, the magnetic field strength at the poles can be derived by
$P$
is the spin period, are observed, the magnetic field strength at the poles can be derived by
assuming values for
![]() $I$
and
$I$
and
![]() $R$
. The rotating dipole model requires very surface magnetic field strengths, of order
$R$
. The rotating dipole model requires very surface magnetic field strengths, of order
![]() $10^{12}$
G, to produce the observed spin-down rates. The pulsar characteristic age
$10^{12}$
G, to produce the observed spin-down rates. The pulsar characteristic age
![]() ${\it\tau}=P/2{\dot{P}}$
, from integration of (2.1) assuming that the birth period
${\it\tau}=P/2{\dot{P}}$
, from integration of (2.1) assuming that the birth period
![]() $P_{0}$
is much smaller than the present period, gives an estimate of the spin-down lifetime but can differ from the true pulsar age if
$P_{0}$
is much smaller than the present period, gives an estimate of the spin-down lifetime but can differ from the true pulsar age if
![]() $P_{0}\sim P$
. The magnetic field of the pulsar can corotate with the neutron star out to the light cylinder,
$P_{0}\sim P$
. The magnetic field of the pulsar can corotate with the neutron star out to the light cylinder,
![]() $R_{lc}=c/{\it\Omega}$
, the cylindrical radius at which the rotation velocity equals the speed of light. Near and beyond
$R_{lc}=c/{\it\Omega}$
, the cylindrical radius at which the rotation velocity equals the speed of light. Near and beyond
![]() $R_{lc}$
, corotation breaks down and the magnetic field is distorted from a dipole by displacement and/or real currents (see §§ 3 and 4).
$R_{lc}$
, corotation breaks down and the magnetic field is distorted from a dipole by displacement and/or real currents (see §§ 3 and 4).
The light cylinder divides the pulsar magnetosphere into regions of open field lines that do not close inside
![]() $R_{lc}$
and closed field lines that close inside
$R_{lc}$
and closed field lines that close inside
![]() $R_{lc}$
. The boundary of open and closed field regions is the last closed field line whose footpoints at the neutron star surface have polar angle
$R_{lc}$
. The boundary of open and closed field regions is the last closed field line whose footpoints at the neutron star surface have polar angle
for a static dipole field. The open field region is the site of particle acceleration and radiation in the magnetosphere.
2.2
 ${\it\gamma}$
-ray pulsar populations
${\it\gamma}$
-ray pulsar populations
Figure 1 shows the observed populations of both radio and
![]() ${\it\gamma}$
-ray pulsars on a plot of their spin periods,
${\it\gamma}$
-ray pulsars on a plot of their spin periods,
![]() $P$
, versus their period derivatives,
$P$
, versus their period derivatives,
![]() ${\dot{P}}$
. There are about 2500 known radio pulsars to date, which far outnumber the
${\dot{P}}$
. There are about 2500 known radio pulsars to date, which far outnumber the
![]() ${\it\gamma}$
-ray pulsars. The difference in numbers is likely due to the difference in sensitivity of radio and
${\it\gamma}$
-ray pulsars. The difference in numbers is likely due to the difference in sensitivity of radio and
![]() ${\it\gamma}$
-ray telescopes, driven by the much higher rate of source photons at the lower frequencies. Fermi has detected three main populations of
${\it\gamma}$
-ray telescopes, driven by the much higher rate of source photons at the lower frequencies. Fermi has detected three main populations of
![]() ${\it\gamma}$
-ray pulsars: young radio-loud, young radio-faint and millisecond pulsars (MSPs). Most of the young radio-loud and millisecond
${\it\gamma}$
-ray pulsars: young radio-loud, young radio-faint and millisecond pulsars (MSPs). Most of the young radio-loud and millisecond
![]() ${\it\gamma}$
-ray pulsars were discovered by folding
${\it\gamma}$
-ray pulsars were discovered by folding
![]() ${\it\gamma}$
-ray photons using a radio ephemeris, while all of the young radio faint and a few of the millisecond
${\it\gamma}$
-ray photons using a radio ephemeris, while all of the young radio faint and a few of the millisecond
![]() ${\it\gamma}$
-ray pulsars were discovered through blind search methods (Atwood et al.
Reference Atwood, Ziegler, Johnson and Baughman2006; Pletsch et al.
Reference Pletsch, Guillemot and Fehrmann2012). After their discovery by
${\it\gamma}$
-ray pulsars were discovered through blind search methods (Atwood et al.
Reference Atwood, Ziegler, Johnson and Baughman2006; Pletsch et al.
Reference Pletsch, Guillemot and Fehrmann2012). After their discovery by
![]() ${\it\gamma}$
-ray blind search, a few of the young radio-faint pulsars were found to be weak radio pulsars and all of the MSPs are radio loud. It is thought that radio loudness or faintness is not an intrinsic property of the pulsar but rather a function of our viewing angle to a radio beam that is much smaller than the
${\it\gamma}$
-ray blind search, a few of the young radio-faint pulsars were found to be weak radio pulsars and all of the MSPs are radio loud. It is thought that radio loudness or faintness is not an intrinsic property of the pulsar but rather a function of our viewing angle to a radio beam that is much smaller than the
![]() ${\it\gamma}$
-ray beam (see § 3). A large number of new MSPs have been discovered through targeted radio searches in the error boxes of Fermi point sources with no known counterparts at other wavelengths (Ray et al.
Reference Ray, Abdo, Parent, Bhattacharya, Bhattacharyya, Camilo, Cognard, Theureau, Ferrara and Harding2012). The pulsations are very difficult to find by
${\it\gamma}$
-ray beam (see § 3). A large number of new MSPs have been discovered through targeted radio searches in the error boxes of Fermi point sources with no known counterparts at other wavelengths (Ray et al.
Reference Ray, Abdo, Parent, Bhattacharya, Bhattacharyya, Camilo, Cognard, Theureau, Ferrara and Harding2012). The pulsations are very difficult to find by
![]() ${\it\gamma}$
-ray blind search, but when radio timing solutions for these new MSPs became available, the
${\it\gamma}$
-ray blind search, but when radio timing solutions for these new MSPs became available, the
![]() ${\it\gamma}$
-ray pulsations were found by folding with the radio ephemerides. To date, 71 radio MSPs have been discovered by this method, 64 with
${\it\gamma}$
-ray pulsations were found by folding with the radio ephemerides. To date, 71 radio MSPs have been discovered by this method, 64 with
![]() ${\it\gamma}$
-ray pulsations.
${\it\gamma}$
-ray pulsations.
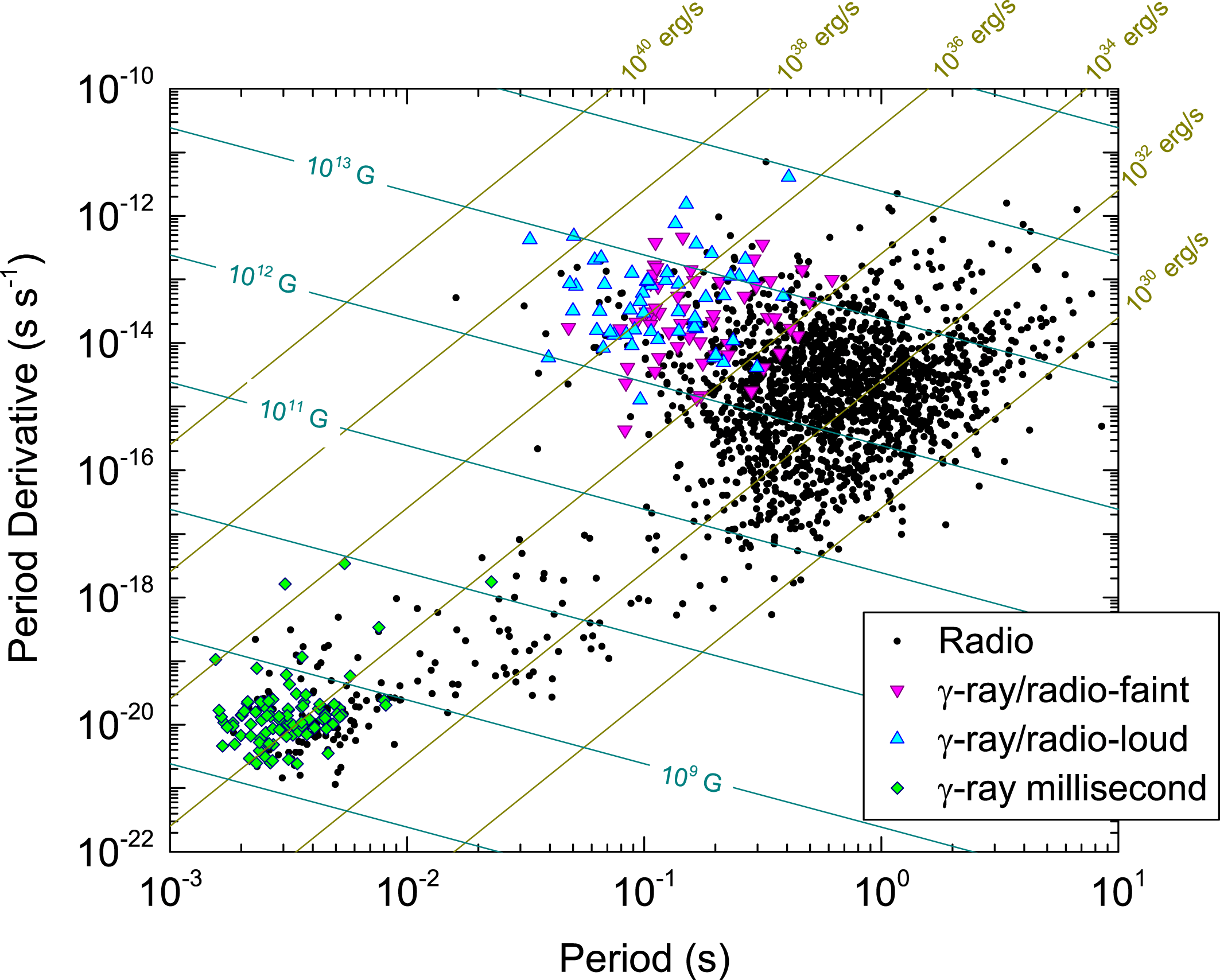
Figure 1. Plot of period versus period derivative for the presently known radio pulsars (from http://www.atnf.csiro.au/people/pulsar/psrcat/) and
![]() ${\it\gamma}$
-ray pulsars detected by Fermi (from https://confluence.slac.stanford.edu/display/GLAMCOG/Public+List+of+LAT-Detected+Gamma-Ray+Pulsars). Lines of constant dipole spin-down luminosity,
${\it\gamma}$
-ray pulsars detected by Fermi (from https://confluence.slac.stanford.edu/display/GLAMCOG/Public+List+of+LAT-Detected+Gamma-Ray+Pulsars). Lines of constant dipole spin-down luminosity,
![]() ${\dot{E}}_{d}$
(brown) and surface magnetic field strength (blue) are superposed.
${\dot{E}}_{d}$
(brown) and surface magnetic field strength (blue) are superposed.
Lines of constant dipole spin-down power,
![]() ${\dot{E}}_{d}=4{\rm\pi}^{2}I{\dot{P}}/P^{3}$
, where
${\dot{E}}_{d}=4{\rm\pi}^{2}I{\dot{P}}/P^{3}$
, where
![]() $I$
is the neutron star moment of inertia and dipole magnetic field strength,
$I$
is the neutron star moment of inertia and dipole magnetic field strength,
![]() $B_{d}\propto (P{\dot{P}})^{1/2}$
are also shown in figure 1. All of the
$B_{d}\propto (P{\dot{P}})^{1/2}$
are also shown in figure 1. All of the
![]() ${\it\gamma}$
-ray pulsars have higher
${\it\gamma}$
-ray pulsars have higher
![]() ${\dot{E}}_{d}$
(
${\dot{E}}_{d}$
(
![]() ${>}10^{33}~\text{erg}~\text{s}^{-1}$
), than the full radio pulsar population. This may also be a selection effect since
${>}10^{33}~\text{erg}~\text{s}^{-1}$
), than the full radio pulsar population. This may also be a selection effect since
![]() ${\it\gamma}$
-ray luminosity increases with
${\it\gamma}$
-ray luminosity increases with
![]() ${\dot{E}}_{d}$
(see Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013). The main cluster of pulsars have surface dipole magnetic field strengths in the range
${\dot{E}}_{d}$
(see Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013). The main cluster of pulsars have surface dipole magnetic field strengths in the range
![]() $B_{d}=10^{11}$
–
$B_{d}=10^{11}$
–
![]() $10^{14}$
G and ages
$10^{14}$
G and ages
![]() ${\it\tau}<10^{8}$
years. Extending downward and to the left in figure 1 are the MSPs, that are much older, have much shorter spin periods, and much lower field strengths
${\it\tau}<10^{8}$
years. Extending downward and to the left in figure 1 are the MSPs, that are much older, have much shorter spin periods, and much lower field strengths
![]() $B_{d}\sim 10^{8}$
–
$B_{d}\sim 10^{8}$
–
![]() $10^{11}$
G. They have been spun up to millisecond periods by accretion from a binary companion in a low-mass X-ray binary phase of their evolution and are thought to be recycled from the young binary pulsar population. A much higher fraction of radio MSPs are
$10^{11}$
G. They have been spun up to millisecond periods by accretion from a binary companion in a low-mass X-ray binary phase of their evolution and are thought to be recycled from the young binary pulsar population. A much higher fraction of radio MSPs are
![]() ${\it\gamma}$
-ray pulsars (nearly 50 %) than are young radio pulsars (
${\it\gamma}$
-ray pulsars (nearly 50 %) than are young radio pulsars (
![]() ${\sim}$
4 %). This can be understood by noting that most all of the radio MSP population has
${\sim}$
4 %). This can be understood by noting that most all of the radio MSP population has
![]() ${\dot{E}}_{d}>10^{33}~\text{erg}~\text{s}^{-1}$
, a level that seems to be a limit for Fermi detection of
${\dot{E}}_{d}>10^{33}~\text{erg}~\text{s}^{-1}$
, a level that seems to be a limit for Fermi detection of
![]() ${\it\gamma}$
-ray pulsations, whereas most of the young radio pulsar population lies below this level.
${\it\gamma}$
-ray pulsations, whereas most of the young radio pulsar population lies below this level.
2.3 Observed
 ${\it\gamma}$
-ray light curves
${\it\gamma}$
-ray light curves
Light curves of
![]() ${\it\gamma}$
-ray pulsars show a wide variety of shapes, from narrow double peaks separated up to half a period in phase to more closely spaced or merging double peaks to broad single peaks (see the Second Fermi Catalog of
${\it\gamma}$
-ray pulsars show a wide variety of shapes, from narrow double peaks separated up to half a period in phase to more closely spaced or merging double peaks to broad single peaks (see the Second Fermi Catalog of
![]() ${\it\gamma}$
-Ray Pulsars, Abdo et al. (Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013), for a detailed discussion). In the vast majority of cases, the radio peaks are not in phase with any of the
${\it\gamma}$
-Ray Pulsars, Abdo et al. (Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013), for a detailed discussion). In the vast majority of cases, the radio peaks are not in phase with any of the
![]() ${\it\gamma}$
-ray peaks. The different populations of
${\it\gamma}$
-ray peaks. The different populations of
![]() ${\it\gamma}$
-ray pulsars generally all show the same full variety of light curves, even though their intrinsic spin properties vary over a large range. For the radio-loud pulsars, there is a distinct pattern that as the
${\it\gamma}$
-ray pulsars generally all show the same full variety of light curves, even though their intrinsic spin properties vary over a large range. For the radio-loud pulsars, there is a distinct pattern that as the
![]() ${\it\gamma}$
-ray peak separation
${\it\gamma}$
-ray peak separation
![]() ${\it\Delta}$
decreases, the phase lag between the first
${\it\Delta}$
decreases, the phase lag between the first
![]() ${\it\gamma}$
-ray peak and the main radio peak
${\it\gamma}$
-ray peak and the main radio peak
![]() ${\it\delta}$
increases. For single-peak
${\it\delta}$
increases. For single-peak
![]() ${\it\gamma}$
-ray light curves, the radio phase lag is the largest. As discussed in §§ 3–5, this correlation is very strong evidence that the
${\it\gamma}$
-ray light curves, the radio phase lag is the largest. As discussed in §§ 3–5, this correlation is very strong evidence that the
![]() ${\it\gamma}$
-ray emission originates from the outer magnetosphere if the radio emission originates near the magnetic poles. The distribution of
${\it\gamma}$
-ray emission originates from the outer magnetosphere if the radio emission originates near the magnetic poles. The distribution of
![]() ${\it\Delta}$
increases toward a maximum at
${\it\Delta}$
increases toward a maximum at
![]() ${\it\Delta}\sim 0.5$
and does not show any correlation with
${\it\Delta}\sim 0.5$
and does not show any correlation with
![]() ${\dot{E}}_{d}$
(Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013) or period (Pierbattista et al.
Reference Pierbattista, Harding, Gonthier and Grenier2016).
${\dot{E}}_{d}$
(Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013) or period (Pierbattista et al.
Reference Pierbattista, Harding, Gonthier and Grenier2016).
The double-peaked
![]() ${\it\gamma}$
-ray light curves often show emission above background, or bridge emission between the main peaks. The double-peaked
${\it\gamma}$
-ray light curves often show emission above background, or bridge emission between the main peaks. The double-peaked
![]() ${\it\gamma}$
-ray light curves very often show an evolution where the ratio of the first to the second peak decreases with increasing energy. Interestingly, the
${\it\gamma}$
-ray light curves very often show an evolution where the ratio of the first to the second peak decreases with increasing energy. Interestingly, the
![]() ${\it\gamma}$
-ray light curves with peak separations
${\it\gamma}$
-ray light curves with peak separations
![]() ${\it\Delta}\sim 0.5$
do not show this energy evolution, probably since this is a symmetric case where identification of first and second peaks is ambiguous. A group of pulsars show emission above background at phases outside of the main
${\it\Delta}\sim 0.5$
do not show this energy evolution, probably since this is a symmetric case where identification of first and second peaks is ambiguous. A group of pulsars show emission above background at phases outside of the main
![]() ${\it\gamma}$
-ray peaks (Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013). Such off-peak emission is more often seen in the young radio-faint pulsars and the MSPs.
${\it\gamma}$
-ray peaks (Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013). Such off-peak emission is more often seen in the young radio-faint pulsars and the MSPs.
MSPs show the widest variety of
![]() ${\it\gamma}$
-ray light curves (see figure 2). Most MSP light curves are similar to those of young pulsars where the
${\it\gamma}$
-ray light curves (see figure 2). Most MSP light curves are similar to those of young pulsars where the
![]() ${\it\gamma}$
-ray peaks lag the radio peaks. For a subset of
${\it\gamma}$
-ray peaks lag the radio peaks. For a subset of
![]() ${\it\gamma}$
-ray MSPs, the
${\it\gamma}$
-ray MSPs, the
![]() ${\it\gamma}$
-ray peak(s) lead the radio peaks, this type of light curve being exclusive to MSPs. For another group of MSPs (plus the Crab pulsar and PSR B0540-69), the
${\it\gamma}$
-ray peak(s) lead the radio peaks, this type of light curve being exclusive to MSPs. For another group of MSPs (plus the Crab pulsar and PSR B0540-69), the
![]() ${\it\gamma}$
-ray peak(s) are aligned with one or more of the radio peaks.
${\it\gamma}$
-ray peak(s) are aligned with one or more of the radio peaks.

Figure 2. Millisecond pulsar
![]() ${\it\gamma}$
-ray light curve types – (a):
${\it\gamma}$
-ray light curve types – (a):
![]() ${\it\gamma}$
-ray peaks (black) lag the radio peak (red), (b):
${\it\gamma}$
-ray peaks (black) lag the radio peak (red), (b):
![]() ${\it\gamma}$
-ray and radio peaks are aligned in phase, (c):
${\it\gamma}$
-ray and radio peaks are aligned in phase, (c):
![]() ${\it\gamma}$
-ray peaks lead the radio peaks. From Abdo et al. (Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013).
${\it\gamma}$
-ray peaks lead the radio peaks. From Abdo et al. (Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013).
2.4 Spectra
The broadband spectral energy distribution of all but a few
![]() ${\it\gamma}$
-ray pulsars peaks in the range 1–10 GeV and pulsars consequently emit most of their power in pulsed emission in the
${\it\gamma}$
-ray pulsars peaks in the range 1–10 GeV and pulsars consequently emit most of their power in pulsed emission in the
![]() ${\it\gamma}$
-ray band. The
${\it\gamma}$
-ray band. The
![]() ${\it\gamma}$
-ray spectra are power laws with subexponential cutoffs,
${\it\gamma}$
-ray spectra are power laws with subexponential cutoffs,
![]() $E^{-{\it\Gamma}}\exp [-(E/E_{c})^{b}]$
, where
$E^{-{\it\Gamma}}\exp [-(E/E_{c})^{b}]$
, where
![]() ${\it\Gamma}$
is the spectral index,
${\it\Gamma}$
is the spectral index,
![]() $E_{c}$
is the cutoff energy and
$E_{c}$
is the cutoff energy and
![]() $b$
is a parameter that measures how sharply the spectrum turns over. The index
$b$
is a parameter that measures how sharply the spectrum turns over. The index
![]() ${\it\Gamma}$
lies in the range
${\it\Gamma}$
lies in the range
![]() ${\sim}$
0.5–2,
${\sim}$
0.5–2,
![]() $E_{c}$
lies in a small range from 1 to 7 GeV, and
$E_{c}$
lies in a small range from 1 to 7 GeV, and
![]() $b\leqslant 1$
, indicating that the spectral cutoffs are more gradual than a pure exponential. The spectral index
$b\leqslant 1$
, indicating that the spectral cutoffs are more gradual than a pure exponential. The spectral index
![]() ${\it\Gamma}$
seems to be correlated with
${\it\Gamma}$
seems to be correlated with
![]() ${\dot{E}}_{d}$
, increasing with increasing
${\dot{E}}_{d}$
, increasing with increasing
![]() ${\dot{E}}_{d}$
, while
${\dot{E}}_{d}$
, while
![]() $E_{c}$
has an increasing trend with the magnetic field strength at the light cylinder,
$E_{c}$
has an increasing trend with the magnetic field strength at the light cylinder,
![]() $B_{LC}=4{\rm\pi}^{2}(1.5I_{0}{\dot{P}}/P^{5}c^{3})^{1/2}$
. The correlation of
$B_{LC}=4{\rm\pi}^{2}(1.5I_{0}{\dot{P}}/P^{5}c^{3})^{1/2}$
. The correlation of
![]() ${\it\Gamma}$
and
${\it\Gamma}$
and
![]() ${\dot{E}}_{d}$
is also observed in phase-resolved spectra of MSPs (Renault, Grenier & Harding Reference Renault, Grenier and Harding2016) and indicates an additional spectral component becoming important at high
${\dot{E}}_{d}$
is also observed in phase-resolved spectra of MSPs (Renault, Grenier & Harding Reference Renault, Grenier and Harding2016) and indicates an additional spectral component becoming important at high
![]() ${\dot{E}}_{d}$
, possibly from electron–position pairs.
${\dot{E}}_{d}$
, possibly from electron–position pairs.
3 Light curve modelling – vacuum retarded dipole
The solution for a rotating, magnetized and perfectly conducting star in a vacuum (Deutsch Reference Deutsch1955) appeared well before pulsars were discovered in 1967. Even though Goldreich & Julian (Reference Goldreich and Julian1969) pointed out shortly after that a magnetized neutron star cannot be surrounded by a vacuum (see § 4) the VRD solution was adopted for pulsar radiation modelling for many years. The VRD solution was analytic, easy to use and the only available solution for a global pulsar magnetosphere. The VRD magnetic field is very close to dipole near the stellar surface but near the light cylinder the field lines are swept back into a toroidal pattern by displacement currents. A quadrupole electric field is induced by the rotating magnetic field which is very strong near the stellar surface but falls off quickly with distance. The sweepback of magnetic field lines distorts the polar cap (defined by the footpoints of the last open field lines) and shifts it in the trailing direction (Dyks & Harding Reference Dyks and Harding2004).
3.1 Accelerator gap models
Pulsar
![]() ${\it\gamma}$
-ray light curves strongly depend not only on the magnetic field structure but also on the distribution of emission in the magnetosphere. Since the energies of the
${\it\gamma}$
-ray light curves strongly depend not only on the magnetic field structure but also on the distribution of emission in the magnetosphere. Since the energies of the
![]() ${\it\gamma}$
-ray emitting particles are so high (
${\it\gamma}$
-ray emitting particles are so high (
![]() ${\it\gamma}\sim 10^{7}$
), they lose most of their energy within a very small distance, so that the emission zones are practically equivalent to the acceleration zones. A number of pulsar acceleration models have been developed that assume boundary conditions that are sensibly motivated but do not come from a global magnetosphere model. These models determine the accelerating electric field (
${\it\gamma}\sim 10^{7}$
), they lose most of their energy within a very small distance, so that the emission zones are practically equivalent to the acceleration zones. A number of pulsar acceleration models have been developed that assume boundary conditions that are sensibly motivated but do not come from a global magnetosphere model. These models determine the accelerating electric field (
![]() $E_{\Vert }$
) in a localized region where force-free conditions break down because the charge densities are not high enough to screen the local
$E_{\Vert }$
) in a localized region where force-free conditions break down because the charge densities are not high enough to screen the local
![]() $E_{\Vert }$
. The parallel electric field can be found by solving Poisson’s equation,
$E_{\Vert }$
. The parallel electric field can be found by solving Poisson’s equation,
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{E}=-4{\rm\pi}({\it\rho}-{\it\rho}_{GJ})$
, where
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{E}=-4{\rm\pi}({\it\rho}-{\it\rho}_{GJ})$
, where
![]() ${\it\rho}$
is the actual charge density and
${\it\rho}$
is the actual charge density and
![]() ${\it\rho}_{GJ}=-{\it\bf\Omega}\boldsymbol{\cdot }\boldsymbol{B}/2{\rm\pi}c$
is the Goldreich–Julian charge density, the minimum needed to screen the
${\it\rho}_{GJ}=-{\it\bf\Omega}\boldsymbol{\cdot }\boldsymbol{B}/2{\rm\pi}c$
is the Goldreich–Julian charge density, the minimum needed to screen the
![]() $E_{\Vert }$
. In the case of an orthogonal rotator, magnetic inclination angle
$E_{\Vert }$
. In the case of an orthogonal rotator, magnetic inclination angle
![]() ${\it\alpha}=90^{\circ }$
, the polar cap is divided into two regions of opposite
${\it\alpha}=90^{\circ }$
, the polar cap is divided into two regions of opposite
![]() ${\it\rho}_{GJ}$
. One important limitation of VRD models is that particle trajectories that follow magnetic field lines cannot be modelled beyond the light cylinder since the particle velocities would exceed the speed of light.
${\it\rho}_{GJ}$
. One important limitation of VRD models is that particle trajectories that follow magnetic field lines cannot be modelled beyond the light cylinder since the particle velocities would exceed the speed of light.
Such models have been developed near the stellar surface at the polar caps (PC model). In the case where particles are freely extracted from the neutron star surface, or space-charge limited flow (SCLF), the
![]() ${\it\rho}$
is assumed to equal
${\it\rho}$
is assumed to equal
![]() ${\it\rho}_{GJ}$
at the stellar surface but will decrease with
${\it\rho}_{GJ}$
at the stellar surface but will decrease with
![]() $r$
faster than
$r$
faster than
![]() ${\it\rho}_{GJ}$
, leaving a charge deficit to create an
${\it\rho}_{GJ}$
, leaving a charge deficit to create an
![]() $E_{\Vert }$
(Arons & Scharlemann Reference Arons and Scharlemann1979; Harding & Muslimov Reference Harding and Muslimov1998). The accelerated primary particles radiate
$E_{\Vert }$
(Arons & Scharlemann Reference Arons and Scharlemann1979; Harding & Muslimov Reference Harding and Muslimov1998). The accelerated primary particles radiate
![]() ${\it\gamma}$
-rays that can create electron–positron pairs by one-photon pair production in the strong magnetic field (Sturrock Reference Sturrock1971) which screen the
${\it\gamma}$
-rays that can create electron–positron pairs by one-photon pair production in the strong magnetic field (Sturrock Reference Sturrock1971) which screen the
![]() $E_{\Vert }$
above a pair formation front (PFF) at a radius of 100–1000 cm. If forces are large enough to trap charges in the neutron star crust, then
$E_{\Vert }$
above a pair formation front (PFF) at a radius of 100–1000 cm. If forces are large enough to trap charges in the neutron star crust, then
![]() ${\it\rho}=0$
at the surface and a vacuum gap develops with a large
${\it\rho}=0$
at the surface and a vacuum gap develops with a large
![]() $E_{\Vert }$
(Ruderman & Sutherland Reference Ruderman and Sutherland1975). In the vacuum gap case, external
$E_{\Vert }$
(Ruderman & Sutherland Reference Ruderman and Sutherland1975). In the vacuum gap case, external
![]() ${\it\gamma}$
-rays create pairs and cause the gap the break down through an avalanche of radiation and further pair creation. In both cases, the screening of
${\it\gamma}$
-rays create pairs and cause the gap the break down through an avalanche of radiation and further pair creation. In both cases, the screening of
![]() $E_{\Vert }$
by pairs limits the accelerating voltage to
$E_{\Vert }$
by pairs limits the accelerating voltage to
![]() ${\sim}$
10
${\sim}$
10
![]() $^{13}$
eV, a quantity that is very weakly dependent on
$^{13}$
eV, a quantity that is very weakly dependent on
![]() $P$
and
$P$
and
![]() ${\dot{P}}$
(Harding & Muslimov Reference Harding and Muslimov1998) since it is the particle energy necessary to initiate pair cascades.
${\dot{P}}$
(Harding & Muslimov Reference Harding and Muslimov1998) since it is the particle energy necessary to initiate pair cascades.
The PFF height above the neutron star surface is a function of magnetic colatitude
![]() ${\it\theta}$
, forming very near the surface for small
${\it\theta}$
, forming very near the surface for small
![]() ${\it\theta}$
but rising to increasing height as
${\it\theta}$
but rising to increasing height as
![]() ${\it\theta}\rightarrow {\it\theta}_{PC}$
, where
${\it\theta}\rightarrow {\it\theta}_{PC}$
, where
![]() ${\it\theta}_{PC}=({\it\Omega}R/c)$
is the colatitude of the last open field line of a dipole field. At
${\it\theta}_{PC}=({\it\Omega}R/c)$
is the colatitude of the last open field line of a dipole field. At
![]() ${\it\theta}_{PC}$
, it is assumed that
${\it\theta}_{PC}$
, it is assumed that
![]() $E_{\Vert }=0$
since the closed field boundary is perfectly conducting. Particles accelerating near this boundary do not gain enough energy to produce pairs before the magnetic field drops, forming a narrow zone where the
$E_{\Vert }=0$
since the closed field boundary is perfectly conducting. Particles accelerating near this boundary do not gain enough energy to produce pairs before the magnetic field drops, forming a narrow zone where the
![]() $E_{\Vert }$
is smaller but unscreened (Arons Reference Arons1983). In this ‘slot gap’ (SG) model, particles continue accelerating to high altitudes near the light cylinder, producing high energy emission from curvature radiation (Muslimov & Harding Reference Muslimov and Harding2004a
). The gap width depends on
$E_{\Vert }$
is smaller but unscreened (Arons Reference Arons1983). In this ‘slot gap’ (SG) model, particles continue accelerating to high altitudes near the light cylinder, producing high energy emission from curvature radiation (Muslimov & Harding Reference Muslimov and Harding2004a
). The gap width depends on
![]() $B_{d}$
and
$B_{d}$
and
![]() $P$
, increasing for smaller
$P$
, increasing for smaller
![]() $B_{d}$
and larger
$B_{d}$
and larger
![]() $P$
.
$P$
.
Because of this dependence of SG width, older and slower pulsars and those with very low
![]() $B_{d}$
with low or no pair multiplicity have SGs filling the whole open field. In this case, the
$B_{d}$
with low or no pair multiplicity have SGs filling the whole open field. In this case, the
![]() $E_{\Vert }$
is unscreened throughout the entire open field volume and particles can accelerate on all open field lines up to and beyond the light cylinder (Muslimov & Harding Reference Muslimov and Harding2004b
). In this pair-starved polar cap (PSPC, figure 3) model the resulting emission pattern is quite different from that of the narrow gap models, showing large regions of emission surrounding the polar caps at low altitude, distorted to earlier phases by aberration at large altitudes.
$E_{\Vert }$
is unscreened throughout the entire open field volume and particles can accelerate on all open field lines up to and beyond the light cylinder (Muslimov & Harding Reference Muslimov and Harding2004b
). In this pair-starved polar cap (PSPC, figure 3) model the resulting emission pattern is quite different from that of the narrow gap models, showing large regions of emission surrounding the polar caps at low altitude, distorted to earlier phases by aberration at large altitudes.

Figure 3. (a,c,e,g): Sky maps of emission (luminosity per sold angle) at several magnetic inclination angles
![]() ${\it\alpha}$
for polar cap (PC) at
${\it\alpha}$
for polar cap (PC) at
![]() ${\it\alpha}=45^{\circ }$
, two-pole caustic (TPC) at
${\it\alpha}=45^{\circ }$
, two-pole caustic (TPC) at
![]() ${\it\alpha}=70^{\circ }$
, outer gap (OG) at
${\it\alpha}=70^{\circ }$
, outer gap (OG) at
![]() ${\it\alpha}=70^{\circ }$
and pair-starved polar cap (Sky map) geometry at
${\it\alpha}=70^{\circ }$
and pair-starved polar cap (Sky map) geometry at
![]() ${\it\alpha}=60^{\circ }$
. (b,d,f,h): light curves at particular observer angles
${\it\alpha}=60^{\circ }$
. (b,d,f,h): light curves at particular observer angles
![]() ${\it\zeta}$
. Adapted from Seyffert (Reference Seyffert2014), Johnson et al. (Reference Johnson, Venter, Harding, Guillemot, Smith, Kramer, Çelik, den Hartog, Ferrara and Hou2014).
${\it\zeta}$
. Adapted from Seyffert (Reference Seyffert2014), Johnson et al. (Reference Johnson, Venter, Harding, Guillemot, Smith, Kramer, Çelik, den Hartog, Ferrara and Hou2014).
Another potential particle acceleration site is the outer gap (OG) (Cheng, Ho & Ruderman Reference Cheng, Ho and Ruderman1986; Romani Reference Romani1996), a region of reduced plasma density that develops above the null-charge surface,
![]() ${\it\rho}_{GJ}=0$
, where charges of one sign flowing out of the magnetosphere along magnetic field lines cannot be replaced from below since those charges are of opposite sign. In the OG,
${\it\rho}_{GJ}=0$
, where charges of one sign flowing out of the magnetosphere along magnetic field lines cannot be replaced from below since those charges are of opposite sign. In the OG,
![]() $E_{\Vert }$
can accelerate particles that produce curvature radiation photons that interact with X-rays, either from the hot polar caps or the OG, to create pairs. The pairs screen the OG inside some magnetic colatitude and also radiate synchrotron radiation to produce tertiary pairs. In OG models the high-energy emission extends very close to the light cylinder in order to produce the observed double-peaked
$E_{\Vert }$
can accelerate particles that produce curvature radiation photons that interact with X-rays, either from the hot polar caps or the OG, to create pairs. The pairs screen the OG inside some magnetic colatitude and also radiate synchrotron radiation to produce tertiary pairs. In OG models the high-energy emission extends very close to the light cylinder in order to produce the observed double-peaked
![]() ${\it\gamma}$
-ray light curves.
${\it\gamma}$
-ray light curves.
3.2 Sky map emission features and magnetospheric structure
Although the accelerator gap models described above assume a static dipole field geometry, three-dimensional (3-D) models to simulate their emission at different observer angles have been developed using the VRD field structure. The emission patterns, or sky maps of observer angle
![]() ${\it\zeta}$
versus rotation phase
${\it\zeta}$
versus rotation phase
![]() ${\it\phi}$
, associated with each of the models produces observable signatures from different parts of the magnetospheric structure. A robust feature of the modelled 3-D emission is the bright caustics, formed by radiation along the trailing edge of the last open field lines where phase delays due to the field line curvature cancel those due to aberration and photon travel time (Morini Reference Morini1983; Dyks, Harding & Rudak Reference Dyks, Harding and Rudak2004). Photons emitted along these field lines all arrive at a distant observer at the same phase and the loci of these points form bright lines in the sky map. The caustics are the lines marked B and C in the sky maps shown in figure 3. A different type of caustic is formed by overlapping field lines from opposite poles and are the lines marked by O. Figure 3 shows sky maps of emission for geometric representations of the OG model and SG model, known as two-pole caustic (TPC) geometry (Dyks & Rudak Reference Dyks and Rudak2003). An observer will see only one slice through the sky map at constant
${\it\phi}$
, associated with each of the models produces observable signatures from different parts of the magnetospheric structure. A robust feature of the modelled 3-D emission is the bright caustics, formed by radiation along the trailing edge of the last open field lines where phase delays due to the field line curvature cancel those due to aberration and photon travel time (Morini Reference Morini1983; Dyks, Harding & Rudak Reference Dyks, Harding and Rudak2004). Photons emitted along these field lines all arrive at a distant observer at the same phase and the loci of these points form bright lines in the sky map. The caustics are the lines marked B and C in the sky maps shown in figure 3. A different type of caustic is formed by overlapping field lines from opposite poles and are the lines marked by O. Figure 3 shows sky maps of emission for geometric representations of the OG model and SG model, known as two-pole caustic (TPC) geometry (Dyks & Rudak Reference Dyks and Rudak2003). An observer will see only one slice through the sky map at constant
![]() ${\it\zeta}$
, forming the light curve. In the TPC sky map, the black circles at
${\it\zeta}$
, forming the light curve. In the TPC sky map, the black circles at
![]() ${\it\phi}=0,0.5$
and 1.0 are the magnetic polar caps. The faint lines marked N arise from the distortions in the polar cap due to field line sweepback at which field lines are bunched together (see figure 4 and Dyks & Harding Reference Dyks and Harding2004).
${\it\phi}=0,0.5$
and 1.0 are the magnetic polar caps. The faint lines marked N arise from the distortions in the polar cap due to field line sweepback at which field lines are bunched together (see figure 4 and Dyks & Harding Reference Dyks and Harding2004).

Figure 4. Polar cap rim shapes for vacuum retarded dipole (blue) and force free (red) for different magnetic inclination angles
![]() ${\it\alpha}$
. For
${\it\alpha}$
. For
![]() ${\it\alpha}=90^{\circ }$
, polar cap rims are also shown for two different values of finite conductivity,
${\it\alpha}=90^{\circ }$
, polar cap rims are also shown for two different values of finite conductivity,
![]() ${\it\sigma}=0.08{\it\Omega}$
(purple) and
${\it\sigma}=0.08{\it\Omega}$
(purple) and
![]() $24{\it\Omega}$
(green). The magnetic pole is at 0, the standard polar cap radius is at 1.0 and the rotation axis is toward the top.
$24{\it\Omega}$
(green). The magnetic pole is at 0, the standard polar cap radius is at 1.0 and the rotation axis is toward the top.
The emission seen by a single observer at
![]() ${\it\zeta}$
will be an intensity (or flux) pattern as a function of rotation phase, or a light curve. Examples of light curves are shown in figure 3 (b,d,f,h) with the different features resulting from the emission sky maps. In the OG emission geometry, an observer sees emission associated with only one magnetic pole, since the gap forms above the null-charge surface, which is at
${\it\zeta}$
will be an intensity (or flux) pattern as a function of rotation phase, or a light curve. Examples of light curves are shown in figure 3 (b,d,f,h) with the different features resulting from the emission sky maps. In the OG emission geometry, an observer sees emission associated with only one magnetic pole, since the gap forms above the null-charge surface, which is at
![]() ${\it\zeta}=90^{\circ }$
. Emission in the sky map from the two poles is cut off below this line. The first peak in the OG light curve peaks come from either the O or C caustic, depending on
${\it\zeta}=90^{\circ }$
. Emission in the sky map from the two poles is cut off below this line. The first peak in the OG light curve peaks come from either the O or C caustic, depending on
![]() ${\it\zeta}$
, while the second peak always comes from the C caustic. In the TPC emission geometry, an observer sees emission from both poles, since there is emission below and above the null-charge surface. The first light curve peak comes from the B caustic from one pole and the second peak comes from the C caustic from the other pole, as in the OG geometry. The O or C caustic that produces the first OG peak, causes a bump on the trailing edge of the first TPC peak. The N (‘notch’) feature produces a small bump following the second peak. For
${\it\zeta}$
, while the second peak always comes from the C caustic. In the TPC emission geometry, an observer sees emission from both poles, since there is emission below and above the null-charge surface. The first light curve peak comes from the B caustic from one pole and the second peak comes from the C caustic from the other pole, as in the OG geometry. The O or C caustic that produces the first OG peak, causes a bump on the trailing edge of the first TPC peak. The N (‘notch’) feature produces a small bump following the second peak. For
![]() ${\it\alpha}\lesssim 45^{\circ }$
, the B caustic fades and both TPC peaks come from the O or C caustics, as in the OG model, but the faint B caustic can produce a bump on the leading edge of the first TPC peak. All TPC light curves show emission outside the main peak at all phases, or off-peak emission, unlike the OG geometry where there is no emission outside the peaks.
${\it\alpha}\lesssim 45^{\circ }$
, the B caustic fades and both TPC peaks come from the O or C caustics, as in the OG model, but the faint B caustic can produce a bump on the leading edge of the first TPC peak. All TPC light curves show emission outside the main peak at all phases, or off-peak emission, unlike the OG geometry where there is no emission outside the peaks.
The radio emission is thought to come from lower altitudes and a cone beam centred on the magnetic pole, and/or a core component at the pole, has been used to model the emission geometry (Rankin Reference Rankin1983; Gonthier, Van Guilder & Harding Reference Gonthier, Van Guilder and Harding2004). The cone beam may be emitted at some height above the neutron star surface, shifting the radio peak forward in phase due to aberration and retardation. In this geometry, the radio peak would arrive earlier in phase than the
![]() ${\it\gamma}$
-ray peaks of the OG and TPC model light curves. This is most often seen in the observed Fermi light curves. However, the
${\it\gamma}$
-ray peaks of the OG and TPC model light curves. This is most often seen in the observed Fermi light curves. However, the
![]() ${\it\gamma}$
-ray peaks of the PSPC model, originating at higher altitude, would lead the radio peak since the
${\it\gamma}$
-ray peaks of the PSPC model, originating at higher altitude, would lead the radio peak since the
![]() ${\it\gamma}$
-ray emission will undergo a larger degree of aberration and retardation (see figure 3). This is seen in a small number of MSPs (figure 2), but not in any of the young pulsar population. The PC model
${\it\gamma}$
-ray emission will undergo a larger degree of aberration and retardation (see figure 3). This is seen in a small number of MSPs (figure 2), but not in any of the young pulsar population. The PC model
![]() ${\it\gamma}$
-ray peak(s) should be roughly aligned in phase with the radio peak(s) at phase 0 and 0.5. Aligned
${\it\gamma}$
-ray peak(s) should be roughly aligned in phase with the radio peak(s) at phase 0 and 0.5. Aligned
![]() ${\it\gamma}$
-ray and radio peaks are observed for a number of MSPs (Guillemot et al.
Reference Guillemot, Johnson, Venter, Kerr, Pancrazi, Livingstone, Janssen, Jaroenjittichai, Kramer and Cognard2012) and two young pulsars with small
${\it\gamma}$
-ray and radio peaks are observed for a number of MSPs (Guillemot et al.
Reference Guillemot, Johnson, Venter, Kerr, Pancrazi, Livingstone, Janssen, Jaroenjittichai, Kramer and Cognard2012) and two young pulsars with small
![]() $P$
, the Crab pulsar and PSR B0540-69 (Ackermann et al.
Reference Ackermann, Albert, Baldini, Ballet, Barbiellini, Barbieri, Bastieri, Bellazzini, Bissaldi and Bonino2015). Because of the light curve shapes, the preferred interpretation is not that the
$P$
, the Crab pulsar and PSR B0540-69 (Ackermann et al.
Reference Ackermann, Albert, Baldini, Ballet, Barbiellini, Barbieri, Bastieri, Bellazzini, Bissaldi and Bonino2015). Because of the light curve shapes, the preferred interpretation is not that the
![]() ${\it\gamma}$
-ray emission is from the PC but that the radio emission comes from high altitudes in the magnetosphere where caustic peaks are formed, similar to and in phase with the
${\it\gamma}$
-ray emission is from the PC but that the radio emission comes from high altitudes in the magnetosphere where caustic peaks are formed, similar to and in phase with the
![]() ${\it\gamma}$
-ray peaks (Venter, Johnson & Harding Reference Venter, Johnson and Harding2012). There are small secondary
${\it\gamma}$
-ray peaks (Venter, Johnson & Harding Reference Venter, Johnson and Harding2012). There are small secondary
![]() ${\it\gamma}$
-ray peaks in phase with either a radio peak or the opposite magnetic pole, that could possibly be emission from PC cascades.
${\it\gamma}$
-ray peaks in phase with either a radio peak or the opposite magnetic pole, that could possibly be emission from PC cascades.
3.3 Geometric light curve models
As Fermi began to accumulate a variety of
![]() ${\it\gamma}$
-ray pulsar light curves, there were a number of studies fitting model light curves in the OG, TPC and PC geometry to those observed, using VRD geometry. Watters et al. (Reference Watters, Romani, Weltevrede and Johnston2009) and Romani & Watters (Reference Romani and Watters2010) produced an atlas of model light curves for OG and TPC models with different gap widths, documenting the properties of the light curves, such as the incidence of different peak numbers and peak separations, to compare with Fermi light curves. They concluded that the OG model best reproduced the light curves of the bright pulsars they fit and the observed peak separation
${\it\gamma}$
-ray pulsar light curves, there were a number of studies fitting model light curves in the OG, TPC and PC geometry to those observed, using VRD geometry. Watters et al. (Reference Watters, Romani, Weltevrede and Johnston2009) and Romani & Watters (Reference Romani and Watters2010) produced an atlas of model light curves for OG and TPC models with different gap widths, documenting the properties of the light curves, such as the incidence of different peak numbers and peak separations, to compare with Fermi light curves. They concluded that the OG model best reproduced the light curves of the bright pulsars they fit and the observed peak separation
![]() ${\it\Delta}$
radio lag
${\it\Delta}$
radio lag
![]() ${\it\delta}$
correlation. This result indicates that at least within the VRD geometry, most of the observed
${\it\delta}$
correlation. This result indicates that at least within the VRD geometry, most of the observed
![]() ${\it\gamma}$
-ray is coming from the outer magnetosphere near the light cylinder. Venter, Harding & Guillemot (Reference Venter, Harding and Guillemot2009) produced similar atlases of OG and TPC models, and also of PSPC and radio cone emission, in VRD geometry and fit light curves of the 8 MSPs with detected
${\it\gamma}$
-ray is coming from the outer magnetosphere near the light cylinder. Venter, Harding & Guillemot (Reference Venter, Harding and Guillemot2009) produced similar atlases of OG and TPC models, and also of PSPC and radio cone emission, in VRD geometry and fit light curves of the 8 MSPs with detected
![]() ${\it\gamma}$
-ray emission during the first year of Fermi. They found that OG or TPC models best fit the light curves of 6 of the MSPs while PSPC models were preferred for 2 MSPs. Johnson et al. (Reference Johnson, Venter, Harding, Guillemot, Smith, Kramer, Çelik, den Hartog, Ferrara and Hou2014) fit all 40 MSPs from the Fermi Second Pulsar Catalog (2PC, Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013) using model OG, TPC and PSPC
${\it\gamma}$
-ray emission during the first year of Fermi. They found that OG or TPC models best fit the light curves of 6 of the MSPs while PSPC models were preferred for 2 MSPs. Johnson et al. (Reference Johnson, Venter, Harding, Guillemot, Smith, Kramer, Çelik, den Hartog, Ferrara and Hou2014) fit all 40 MSPs from the Fermi Second Pulsar Catalog (2PC, Abdo et al.
Reference Abdo, Ajello, Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Belfiore and Bellazzini2013) using model OG, TPC and PSPC
![]() ${\it\gamma}$
-ray light curves simultaneously with radio cone and core beam light curves. Among this group of MSPs, most had light curves in which the
${\it\gamma}$
-ray light curves simultaneously with radio cone and core beam light curves. Among this group of MSPs, most had light curves in which the
![]() ${\it\gamma}$
-ray peaks lagged the radio peak in phase (Class I), for 6 MSPs the
${\it\gamma}$
-ray peaks lagged the radio peak in phase (Class I), for 6 MSPs the
![]() ${\it\gamma}$
-ray and radio peaks were aligned in phase (Class II) and for 6 MSPs the
${\it\gamma}$
-ray and radio peaks were aligned in phase (Class II) and for 6 MSPs the
![]() ${\it\gamma}$
-ray peak led the radio peak (Class III). The Class I light curves could be fit with either OG or TPC models (but often not both), the Class II light curves were best fit with OG and TPC models for both
${\it\gamma}$
-ray peak led the radio peak (Class III). The Class I light curves could be fit with either OG or TPC models (but often not both), the Class II light curves were best fit with OG and TPC models for both
![]() ${\it\gamma}$
-ray and radio emission and Class III light curves were best fit with PSPC models. Pierbattista et al. (Reference Pierbattista, Harding, Grenier, Johnson, Caraveo, Kerr and Gonthier2015), used model light curves for PC, TPC, OG and one-pole-caustic (OPC) geometries, where the OPC model uses the same geometry as the OG model but with a different gap width dependence. They fit the
${\it\gamma}$
-ray and radio emission and Class III light curves were best fit with PSPC models. Pierbattista et al. (Reference Pierbattista, Harding, Grenier, Johnson, Caraveo, Kerr and Gonthier2015), used model light curves for PC, TPC, OG and one-pole-caustic (OPC) geometries, where the OPC model uses the same geometry as the OG model but with a different gap width dependence. They fit the
![]() ${\it\gamma}$
-ray light curves of all the young pulsars in the 2PC, jointly fitting the
${\it\gamma}$
-ray light curves of all the young pulsars in the 2PC, jointly fitting the
![]() ${\it\gamma}$
-ray and radio light curves for the radio-loud pulsars. They found that the outer magnetosphere models, TPC, OG and OPC, best fit the observed light curves. However, none of the models by themselves best fit all the light curves, indicating that either the VRD field geometry and/or the emission geometry of any one model could explain some subset of the observations (Venter & Harding Reference Venter and Harding2014). All of these studies are able to constrain the magnetic inclination
${\it\gamma}$
-ray and radio light curves for the radio-loud pulsars. They found that the outer magnetosphere models, TPC, OG and OPC, best fit the observed light curves. However, none of the models by themselves best fit all the light curves, indicating that either the VRD field geometry and/or the emission geometry of any one model could explain some subset of the observations (Venter & Harding Reference Venter and Harding2014). All of these studies are able to constrain the magnetic inclination
![]() ${\it\alpha}$
and viewing angles
${\it\alpha}$
and viewing angles
![]() ${\it\zeta}$
for each pulsar sometimes to within several degrees. However, a strong caveat is that the fits for individual models are not statistically good, with
${\it\zeta}$
for each pulsar sometimes to within several degrees. However, a strong caveat is that the fits for individual models are not statistically good, with
![]() ${\it\chi}_{red}^{2}$
often several hundred for the bright pulsars. Only the comparative goodness of fit is meaningful; a preferred model is one with a
${\it\chi}_{red}^{2}$
often several hundred for the bright pulsars. Only the comparative goodness of fit is meaningful; a preferred model is one with a
![]() ${\it\chi}^{2}$
lower by more than
${\it\chi}^{2}$
lower by more than
![]() $3{\it\sigma}$
compared to the
$3{\it\sigma}$
compared to the
![]() ${\it\chi}^{2}$
of other models.
${\it\chi}^{2}$
of other models.
As well as the VRD geometry, Breed et al. (Reference Breed, Venter, Harding, Johnson, Engelbrecht and Karataglidis2015, Reference Breed, Venter, Harding and Johnson2016) explored sky maps and model light curves for magnetic field models with offset dipoles (Harding & Muslimov Reference Harding and Muslimov2011). Since these field models were formulated using a static dipole, Breed et al. modelled OG and TPC geometric emission for offset dipoles with the static dipole and with centred dipoles in the VRD, concentrating on fits to the bright Vela pulsar. Additionally, they explored light curves for non-uniform emission in an SG model using an
![]() $E_{\Vert }$
distribution that had been derived for the offset dipole. They found that modulation of the emissivity by
$E_{\Vert }$
distribution that had been derived for the offset dipole. They found that modulation of the emissivity by
![]() $E_{\Vert }$
can have a greater effect on the
$E_{\Vert }$
can have a greater effect on the
![]() ${\it\gamma}$
-ray light curves than magnetic field geometry alone. Additional light curve modelling for particular pulsars were carried out for OG models of the Crab (Takata, Chang & Cheng Reference Takata, Chang and Cheng2007; Hirotani Reference Hirotani2008) using VRD field structure and for annular gap models for Vela (Du et al.
Reference Du, Han, Qiao and Chou2011), the Crab (Du, Qiao & Wang Reference Du, Qiao and Wang2012) and several MSPs (Du, Qiao & Chen Reference Du, Qiao and Chen2013) using static dipole field structure.
${\it\gamma}$
-ray light curves than magnetic field geometry alone. Additional light curve modelling for particular pulsars were carried out for OG models of the Crab (Takata, Chang & Cheng Reference Takata, Chang and Cheng2007; Hirotani Reference Hirotani2008) using VRD field structure and for annular gap models for Vela (Du et al.
Reference Du, Han, Qiao and Chou2011), the Crab (Du, Qiao & Wang Reference Du, Qiao and Wang2012) and several MSPs (Du, Qiao & Chen Reference Du, Qiao and Chen2013) using static dipole field structure.
4 Light curve modelling – force-free magnetospheres
In their classic paper, Goldreich & Julian (Reference Goldreich and Julian1969) showed that the electric force is many orders of magnitude larger than gravitational force at the neutron star surface of the VRD so that particles should be pulled from the star to fill the magnetosphere with charges to potentially screen the
![]() $E_{\Vert }$
. A pulsar magnetosphere should therefore be closer to a force free than a vacuum solution.
$E_{\Vert }$
. A pulsar magnetosphere should therefore be closer to a force free than a vacuum solution.
4.1 Force free versus VRD magnetic field structure
Numerical solutions for the oblique force-free magnetospheres were first developed by Spitkovsky (Reference Spitkovsky2006), solving the time-dependent Maxwell’s equations and imposing the condition
![]() $E_{\Vert }=0$
. Plasma pressure and inertial forces are neglected since in a pulsar magnetosphere the magnetic field pressure dominates, except in the current sheet, which is not well resolved in these simulations. Figure 5 shows simulated magnetic field lines for near VRD and force-free (FF) magnetospheres. The presence of charges and currents have a significant effect on the structure of the pulsar magnetosphere. The main effect of the current is to create a toroidal magnetic field component that opens more field lines. Near the neutron star surface, the toroidal field is small compared to the dipole field, but the toroidal component grows with radius until it becomes comparable to the poloidal field at the light cylinder. As a result, the poloidal magnetic field lines straighten in the poloidal plane and become asymptotically monopolar beyond the light cylinder. The extra toroidal component from the current, in addition to the toroidal component from the displacement current in the VRD, increases the field line sweepback. In the FF magnetosphere, a current sheet forms along the spin equator, that is a flat plane for an aligned rotator but begins to undulate for an oblique rotator. The amplitude of undulation increases with increasing obliquity and for
$E_{\Vert }=0$
. Plasma pressure and inertial forces are neglected since in a pulsar magnetosphere the magnetic field pressure dominates, except in the current sheet, which is not well resolved in these simulations. Figure 5 shows simulated magnetic field lines for near VRD and force-free (FF) magnetospheres. The presence of charges and currents have a significant effect on the structure of the pulsar magnetosphere. The main effect of the current is to create a toroidal magnetic field component that opens more field lines. Near the neutron star surface, the toroidal field is small compared to the dipole field, but the toroidal component grows with radius until it becomes comparable to the poloidal field at the light cylinder. As a result, the poloidal magnetic field lines straighten in the poloidal plane and become asymptotically monopolar beyond the light cylinder. The extra toroidal component from the current, in addition to the toroidal component from the displacement current in the VRD, increases the field line sweepback. In the FF magnetosphere, a current sheet forms along the spin equator, that is a flat plane for an aligned rotator but begins to undulate for an oblique rotator. The amplitude of undulation increases with increasing obliquity and for
![]() ${\it\alpha}=90^{\circ }$
the current sheet completely surrounds the neutron star. The current in the FF magnetosphere changes with magnetic colatitude across the open field lines, with current flowing out of one region of the polar cap and returning over another region. The shape of the outflowing and return current regions change with
${\it\alpha}=90^{\circ }$
the current sheet completely surrounds the neutron star. The current in the FF magnetosphere changes with magnetic colatitude across the open field lines, with current flowing out of one region of the polar cap and returning over another region. The shape of the outflowing and return current regions change with
![]() ${\it\alpha}$
. For small
${\it\alpha}$
. For small
![]() ${\it\alpha}$
, the current flows out near the magnetic poles and returns through the current sheet and near the last open field lines to the neutron star. For large
${\it\alpha}$
, the current flows out near the magnetic poles and returns through the current sheet and near the last open field lines to the neutron star. For large
![]() ${\it\alpha}$
, the current flows out over one side of the polar cap and returns over the other side.
${\it\alpha}$
, the current flows out over one side of the polar cap and returns over the other side.

Figure 5. Simulated pulsar magnetospheres shown in the magnetic field poloidal plane for two different values of finite conductivity
![]() ${\it\sigma}$
and a force-free model, at different inclination angles
${\it\sigma}$
and a force-free model, at different inclination angles
![]() ${\it\alpha}$
. Each plot shows projections of the magnetic field lines on the poloidal plane and charge density
${\it\alpha}$
. Each plot shows projections of the magnetic field lines on the poloidal plane and charge density
![]() ${\it\rho}$
in colour (a,c,e). For the finite
${\it\rho}$
in colour (a,c,e). For the finite
![]() ${\it\sigma}$
models, the parallel electric field
${\it\sigma}$
models, the parallel electric field
![]() $E_{\Vert }$
is shown in colour (b,d). Adapted from Kalapotharakos et al. (Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
).
$E_{\Vert }$
is shown in colour (b,d). Adapted from Kalapotharakos et al. (Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
).
The outer boundary of the open field volume defines the polar cap when the last open field lines are traced back to their foot points on the neutron star surface. Figure 4 shows the polar cap rims for different magnetic inclination angles in the VRD and FF cases. The polar cap rim for the VRD field is distorted and displaced relative to the dipole axis toward the trailing edge, the amount of shift increasing with
![]() ${\it\alpha}$
. The VRD cap size also increases with
${\it\alpha}$
. The VRD cap size also increases with
![]() ${\it\alpha}$
. The polar cap rim for the FF field is both enlarged, because of the larger open field volume, and more shifted to the trailing edge, due to the greater degree of sweepback relative to the VRD. Both of these effects also increase with
${\it\alpha}$
. The polar cap rim for the FF field is both enlarged, because of the larger open field volume, and more shifted to the trailing edge, due to the greater degree of sweepback relative to the VRD. Both of these effects also increase with
![]() ${\it\alpha}$
.
${\it\alpha}$
.
4.2 Force free versus VRD
 ${\it\gamma}$
-ray light curves
${\it\gamma}$
-ray light curves
Following the numerical solutions for oblique FF pulsar magnetospheres (Spitkovsky Reference Spitkovsky2006), the field structure was used together with the emission geometries discussed in § 3 to model
![]() ${\it\gamma}$
-ray light curves. Since the FF solutions assume
${\it\gamma}$
-ray light curves. Since the FF solutions assume
![]() $E_{\Vert }=0$
and thus no acceleration or emission, these models are not self-consistent. Nevertheless, the FF field structure is likely to be closer to that of young pulsars with dense pair plasma production at least at their polar caps. Romani & Watters (Reference Romani and Watters2010) used an approximation to various magnetic field geometries from VRD to FF, with OG and TPC emission regions, to fit the
$E_{\Vert }=0$
and thus no acceleration or emission, these models are not self-consistent. Nevertheless, the FF field structure is likely to be closer to that of young pulsars with dense pair plasma production at least at their polar caps. Romani & Watters (Reference Romani and Watters2010) used an approximation to various magnetic field geometries from VRD to FF, with OG and TPC emission regions, to fit the
![]() ${\it\gamma}$
-ray light curves of the brightest pulsars. They found that the OG emission models and a field geometry close to FF provided the best fits, although they did not consider the radio lags or perform joint
${\it\gamma}$
-ray light curves of the brightest pulsars. They found that the OG emission models and a field geometry close to FF provided the best fits, although they did not consider the radio lags or perform joint
![]() ${\it\gamma}$
-ray and radio light curve fits. Bai & Spitkovsky (Reference Bai and Spitkovsky2010) produced model light curves in FF magnetic fields using OG and TPC emission regions extending up to the light cylinder, as well as ‘separatrix’ model emission extending along the last open field line from the neutron star surface to beyond the light cylinder, taking advantage of the possibility of following particle trajectories past the light cylinder in the inertial (non-rotating) observers frame (IOF). In the IOF, the particle velocity, which is a sum of the drift velocity and the velocity parallel to the
${\it\gamma}$
-ray and radio light curve fits. Bai & Spitkovsky (Reference Bai and Spitkovsky2010) produced model light curves in FF magnetic fields using OG and TPC emission regions extending up to the light cylinder, as well as ‘separatrix’ model emission extending along the last open field line from the neutron star surface to beyond the light cylinder, taking advantage of the possibility of following particle trajectories past the light cylinder in the inertial (non-rotating) observers frame (IOF). In the IOF, the particle velocity, which is a sum of the drift velocity and the velocity parallel to the
![]() $B$
field, stays below
$B$
field, stays below
![]() $c$
for FF geometry and the particle trajectories become asymptotically straight lines at
$c$
for FF geometry and the particle trajectories become asymptotically straight lines at
![]() $r\gg R_{LC}$
. The magnetic field lines are swept back at just the right rate to counteract the superluminal drift velocity, so that the particles move forward along the expanding and spiralling field lines but radially outward. In the force-free magnetosphere, the drift velocity keeps the particle trajectory along the
$r\gg R_{LC}$
. The magnetic field lines are swept back at just the right rate to counteract the superluminal drift velocity, so that the particles move forward along the expanding and spiralling field lines but radially outward. In the force-free magnetosphere, the drift velocity keeps the particle trajectory along the
![]() $B$
field lines, whereas in a dissipative magnetosphere (see § 5) particles can drift across field lines. Bai & Spitkovsky (Reference Bai and Spitkovsky2010) identified a ‘sky map stagnation’ (SMS) caustic that forms near the last open field lines near and outside the light cylinder as particle trajectories along those field lines stagnate to travel radially outwards, so that their radiation is seen in phase by an inertial (non-rotating) observer. The SMS caustic can dominate the TPC and OG caustics, that form for emission inside the light cylinder, to produce the main
$B$
field lines, whereas in a dissipative magnetosphere (see § 5) particles can drift across field lines. Bai & Spitkovsky (Reference Bai and Spitkovsky2010) identified a ‘sky map stagnation’ (SMS) caustic that forms near the last open field lines near and outside the light cylinder as particle trajectories along those field lines stagnate to travel radially outwards, so that their radiation is seen in phase by an inertial (non-rotating) observer. The SMS caustic can dominate the TPC and OG caustics, that form for emission inside the light cylinder, to produce the main
![]() ${\it\gamma}$
-ray peaks at somewhat different locations. For the assumed uniform emission, the phase lag with respect to the magnetic pole of the FF
${\it\gamma}$
-ray peaks at somewhat different locations. For the assumed uniform emission, the phase lag with respect to the magnetic pole of the FF
![]() ${\it\gamma}$
-ray peaks are larger than those in the VRD field.
${\it\gamma}$
-ray peaks are larger than those in the VRD field.
Petri (Reference Petri2011) proposed a model for high-energy emission from the current sheet, modelling
![]() ${\it\gamma}$
-ray light curves assuming that the emission comes from a specific radius range and that the emissivity is uniform in azimuth. This model can produce double-peaked profiles with different peak separation, but the phase lag with respect to the magnetic pole of the
${\it\gamma}$
-ray light curves assuming that the emission comes from a specific radius range and that the emissivity is uniform in azimuth. This model can produce double-peaked profiles with different peak separation, but the phase lag with respect to the magnetic pole of the
![]() ${\it\gamma}$
-ray peaks is too large to explain the observed radio lags, as is the case for the separatrix model.
${\it\gamma}$
-ray peaks is too large to explain the observed radio lags, as is the case for the separatrix model.
Harding et al. (Reference Harding, DeCesar, Miller, Kalapotharakos and Contopoulos2011) and DeCesar (Reference DeCesar2013) produced atlases of TPC and OG emission models in FF and VRD field geometry to compare the light curve features. They also found larger radio phase lags of the
![]() ${\it\gamma}$
-ray peaks in the FF geometry but the TPC and OG light curve peaks come from different caustics that form inside the light cylinder. They concluded that the larger radio phase lags of the FF geometry for both TPC/OG and SMS caustics were caused by the larger backward shift of the open field volume for the FF field due to the higher degree of field line sweep back as well as the larger open field volume (see figure 4). The FF phase lags are larger than those observed in
${\it\gamma}$
-ray peaks in the FF geometry but the TPC and OG light curve peaks come from different caustics that form inside the light cylinder. They concluded that the larger radio phase lags of the FF geometry for both TPC/OG and SMS caustics were caused by the larger backward shift of the open field volume for the FF field due to the higher degree of field line sweep back as well as the larger open field volume (see figure 4). The FF phase lags are larger than those observed in
![]() ${\it\gamma}$
-ray light curves, indicating that either the distribution of emission is non-uniform or the field structure is not close to FF. The
${\it\gamma}$
-ray light curves, indicating that either the distribution of emission is non-uniform or the field structure is not close to FF. The
![]() ${\it\gamma}$
-ray peaks in FF geometry are also wider than those in the VRD field, due again to the larger open volume in the FF case.
${\it\gamma}$
-ray peaks in FF geometry are also wider than those in the VRD field, due again to the larger open volume in the FF case.
5 Dissipative magnetospheres
Real pulsar magnetospheres must lie somewhere between the VRD, which has high accelerating
![]() $E_{\Vert }$
but no charges or currents, and the FF magnetosphere which has charges and currents but no
$E_{\Vert }$
but no charges or currents, and the FF magnetosphere which has charges and currents but no
![]() $E_{\Vert }$
. In other words, pulsar magnetospheres must have at least some regions of finite conductivity to allow dissipation in the form of particle acceleration and radiation. Dissipative magnetospheres have only recently been simulated (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li et al.
Reference Li, Spitkovsky and Tchekhovskoy2012a
) and their properties explored. These simulations adopt a macroscopic conductivity parameter,
$E_{\Vert }$
. In other words, pulsar magnetospheres must have at least some regions of finite conductivity to allow dissipation in the form of particle acceleration and radiation. Dissipative magnetospheres have only recently been simulated (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li et al.
Reference Li, Spitkovsky and Tchekhovskoy2012a
) and their properties explored. These simulations adopt a macroscopic conductivity parameter,
![]() ${\it\sigma}$
, that relates the current to the
${\it\sigma}$
, that relates the current to the
![]() $E_{\Vert }$
through an Ohm’s law prescription. Although the simulations of Li et al. (Reference Li, Spitkovsky and Tchekhovskoy2012a
), who define their prescription in the fluid rest frame where the
$E_{\Vert }$
through an Ohm’s law prescription. Although the simulations of Li et al. (Reference Li, Spitkovsky and Tchekhovskoy2012a
), who define their prescription in the fluid rest frame where the
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
field are parallel, and Kalapotharakos et al. (Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
), who adopt a simpler prescription in the IOF, make different assumptions for Ohm’s Law, this is unlikely to make much difference except very near the current sheet.
$\boldsymbol{B}$
field are parallel, and Kalapotharakos et al. (Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
), who adopt a simpler prescription in the IOF, make different assumptions for Ohm’s Law, this is unlikely to make much difference except very near the current sheet.
5.1 Field structure of dissipative magnetospheres
The most important difference between FF and dissipative magnetospheres is the presence of a non-zero
![]() $E_{\Vert }$
which enables acceleration of charges. The introduction of a finite conductivity allows simulation of magnetospheres that range from VRD (
$E_{\Vert }$
which enables acceleration of charges. The introduction of a finite conductivity allows simulation of magnetospheres that range from VRD (
![]() ${\it\sigma}=0$
) to FF (
${\it\sigma}=0$
) to FF (
![]() ${\it\sigma}\rightarrow \infty$
). Figure 5 shows the magnetic field and
${\it\sigma}\rightarrow \infty$
). Figure 5 shows the magnetic field and
![]() $E_{\Vert }$
distribution for magnetospheres with a range of
$E_{\Vert }$
distribution for magnetospheres with a range of
![]() ${\it\sigma}$
from near VRD to FF. As
${\it\sigma}$
from near VRD to FF. As
![]() ${\it\sigma}$
increases, the charge density and current density increase while the
${\it\sigma}$
increases, the charge density and current density increase while the
![]() $E_{\Vert }$
decreases, the poloidal field lines become more radial, and the current sheet gets stronger. The open field volume increases with increasing
$E_{\Vert }$
decreases, the poloidal field lines become more radial, and the current sheet gets stronger. The open field volume increases with increasing
![]() ${\it\sigma}$
, enlarging the polar cap and the field lines become more swept back, shifting the polar cap towards the trailing edge (see figure 4). The Poynting flux, or spin-down luminosity, is seen to increase with increasing
${\it\sigma}$
, enlarging the polar cap and the field lines become more swept back, shifting the polar cap towards the trailing edge (see figure 4). The Poynting flux, or spin-down luminosity, is seen to increase with increasing
![]() ${\it\sigma}$
and with increasing inclination angle (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li et al.
Reference Li, Spitkovsky and Tchekhovskoy2012a
).
${\it\sigma}$
and with increasing inclination angle (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li et al.
Reference Li, Spitkovsky and Tchekhovskoy2012a
).
5.2 Light curve modelling in dissipative magnetospheres
Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Contopoulos2012a
) modelled
![]() ${\it\gamma}$
-ray light curves in dissipative magnetospheres using both simple geometric OG and TPC emission models as well as emission from test particles accelerated in the
${\it\gamma}$
-ray light curves in dissipative magnetospheres using both simple geometric OG and TPC emission models as well as emission from test particles accelerated in the
![]() $E_{\Vert }$
of the simulation. The geometric model light curves, shown in figure 6, display a progression with increasing conductivity, from zero (VRD) through higher
$E_{\Vert }$
of the simulation. The geometric model light curves, shown in figure 6, display a progression with increasing conductivity, from zero (VRD) through higher
![]() ${\it\sigma}$
, to FF, of increasing phase lag with respect to the magnetic pole and increasing peak width. This behaviour can be directly traced to the increase and backward shift of the open field volume with increasing
${\it\sigma}$
, to FF, of increasing phase lag with respect to the magnetic pole and increasing peak width. This behaviour can be directly traced to the increase and backward shift of the open field volume with increasing
![]() ${\it\sigma}$
. Since the peaks are caustics formed along the trailing edge field lines, the shift of this boundary toward the trailing edge causes the increasing phase lag of the peaks with respect to the magnetic pole. The phase lags for OG geometry are larger than those for TPC geometry. The gap widths are assumed to be the same fraction of the open field volume, causing an increase in peak width with increasing
${\it\sigma}$
. Since the peaks are caustics formed along the trailing edge field lines, the shift of this boundary toward the trailing edge causes the increasing phase lag of the peaks with respect to the magnetic pole. The phase lags for OG geometry are larger than those for TPC geometry. The gap widths are assumed to be the same fraction of the open field volume, causing an increase in peak width with increasing
![]() ${\it\sigma}$
. Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Contopoulos2012a
) also modelled light curve of curvature radiation emitted by particles accelerated in the
${\it\sigma}$
. Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Contopoulos2012a
) also modelled light curve of curvature radiation emitted by particles accelerated in the
![]() $E_{\Vert }$
fields of the simulation for increasing
$E_{\Vert }$
fields of the simulation for increasing
![]() ${\it\sigma}$
. These light curves generally show phase lags and widths of the peaks that are much larger than for the geometric models.
${\it\sigma}$
. These light curves generally show phase lags and widths of the peaks that are much larger than for the geometric models.

Figure 6. Geometric LCs for slot gap (a,c,e,g) (TPC) and outer gap (b,d,f,h) emission in VRD (black), FF (purple) solutions for different viewing angles
![]() ${\it\zeta}$
, and resistive magnetospheres with
${\it\zeta}$
, and resistive magnetospheres with
![]() ${\it\sigma}=0.08{\it\Omega}$
(red) and
${\it\sigma}=0.08{\it\Omega}$
(red) and
![]() ${\it\sigma}=1.5{\it\Omega}$
(green) for pulsar inclination angle
${\it\sigma}=1.5{\it\Omega}$
(green) for pulsar inclination angle
![]() ${\it\alpha}=90^{\circ }$
. From Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Contopoulos2012a
).
${\it\alpha}=90^{\circ }$
. From Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Contopoulos2012a
).
Kalapotharakos et al. (Reference Kalapotharakos, Harding and Kazanas2014) further explored emission location and light curves from dissipative magnetospheres, finding that for low (uniform) conductivity through the magnetosphere the emission is concentrated in lobes above the polar caps. As
![]() ${\it\sigma}$
increases the emission moves outward with the low-altitude component fading and more emission appearing near the light cylinder. At very high
${\it\sigma}$
increases the emission moves outward with the low-altitude component fading and more emission appearing near the light cylinder. At very high
![]() ${\it\sigma}$
, all the emission is concentrated near the equatorial current sheet outside the light cylinder. The light curves are very broad at low
${\it\sigma}$
, all the emission is concentrated near the equatorial current sheet outside the light cylinder. The light curves are very broad at low
![]() ${\it\sigma}$
, narrowing significantly with increasing
${\it\sigma}$
, narrowing significantly with increasing
![]() ${\it\sigma}$
. The emission concentrates near the current sheet because the
${\it\sigma}$
. The emission concentrates near the current sheet because the
![]() $E_{\Vert }$
is proportional to the current, which is highest near the current sheet. Comparing the model light curves (figure 7) and their peak separation
$E_{\Vert }$
is proportional to the current, which is highest near the current sheet. Comparing the model light curves (figure 7) and their peak separation
![]() ${\it\Delta}$
versus radio lag
${\it\Delta}$
versus radio lag
![]() ${\it\delta}$
with that of Fermi pulsars, they found the best agreement for a conductivity distribution with infinite
${\it\delta}$
with that of Fermi pulsars, they found the best agreement for a conductivity distribution with infinite
![]() ${\it\sigma}$
(force free) inside the light cylinder and high but finite
${\it\sigma}$
(force free) inside the light cylinder and high but finite
![]() ${\it\sigma}$
outside the light cylinder (FF inside-dissipative outside, FIDO models). For this type of model, the phase lags of the peaks are smaller than those for the geometric models with uniform emissivity in azimuth, and are in very good agreement with the Fermi
${\it\sigma}$
outside the light cylinder (FF inside-dissipative outside, FIDO models). For this type of model, the phase lags of the peaks are smaller than those for the geometric models with uniform emissivity in azimuth, and are in very good agreement with the Fermi
![]() ${\it\Delta}$
versus
${\it\Delta}$
versus
![]() ${\it\delta}$
distribution (see figure 8). The distribution of
${\it\delta}$
distribution (see figure 8). The distribution of
![]() $E_{\Vert }$
in dissipative magnetospheres with high
$E_{\Vert }$
in dissipative magnetospheres with high
![]() ${\it\sigma}$
is not uniform near the current sheet, but is highest at azimuthal angles that connect to the leading edge of the polar caps.
${\it\sigma}$
is not uniform near the current sheet, but is highest at azimuthal angles that connect to the leading edge of the polar caps.

Figure 7. Skymaps of high-energy luminosity per solid angle
![]() $\text{d}L/\text{d}{\it\omega}$
at different inclination angles
$\text{d}L/\text{d}{\it\omega}$
at different inclination angles
![]() ${\it\alpha}$
(a) and light curves at observer angles
${\it\alpha}$
(a) and light curves at observer angles
![]() ${\it\zeta}$
(b), for a dissipative MHD magnetosphere model, FIDO, having infinite conductivity (force free) inside the light cylinder and a finite conductivity outside. From Kalapotharakos et al. (Reference Kalapotharakos, Harding and Kazanas2014).
${\it\zeta}$
(b), for a dissipative MHD magnetosphere model, FIDO, having infinite conductivity (force free) inside the light cylinder and a finite conductivity outside. From Kalapotharakos et al. (Reference Kalapotharakos, Harding and Kazanas2014).

Figure 8. Distribution of peak separations in the
![]() ${\it\gamma}$
-ray light-curves versus the phase lag between the radio and
${\it\gamma}$
-ray light-curves versus the phase lag between the radio and
![]() ${\it\gamma}$
-ray peaks, for detected Fermi pulsars (black) and the FIDO model (coloured ellipses). From Kalapotharakos et al. (Reference Kalapotharakos, Harding and Kazanas2014).
${\it\gamma}$
-ray peaks, for detected Fermi pulsars (black) and the FIDO model (coloured ellipses). From Kalapotharakos et al. (Reference Kalapotharakos, Harding and Kazanas2014).
5.3 Spectral modelling and energetics in dissipative magnetospheres
The simulated magnetospheres with finite conductivity also make it possible to constrain the macroscopic properties of the plasma by comparing model and observed
![]() ${\it\gamma}$
-ray spectra. Brambilla et al. (Reference Brambilla, Kalapotharakos, Harding and Kazanas2015) modelled the phase-averaged and phase-resolved
${\it\gamma}$
-ray spectra. Brambilla et al. (Reference Brambilla, Kalapotharakos, Harding and Kazanas2015) modelled the phase-averaged and phase-resolved
![]() ${\it\gamma}$
-ray spectra of eight of the brightest Fermi pulsars using dissipative magnetospheres with the FIDO conductivity distribution. From a range of models with varying magnetic inclination angle
${\it\gamma}$
-ray spectra of eight of the brightest Fermi pulsars using dissipative magnetospheres with the FIDO conductivity distribution. From a range of models with varying magnetic inclination angle
![]() ${\it\alpha}$
and conductivity
${\it\alpha}$
and conductivity
![]() ${\it\sigma}$
outside the light cylinder, they found parameters that best matched the light curves and phase-resolved spectra of each of the pulsars. They found that the FIDO models could generally match the observed pattern and values of the spectral indices and cutoff energies
${\it\sigma}$
outside the light cylinder, they found parameters that best matched the light curves and phase-resolved spectra of each of the pulsars. They found that the FIDO models could generally match the observed pattern and values of the spectral indices and cutoff energies
![]() $E_{c}$
of the pulsars. The FIDO model can also explain the energy dependence of the observed light curves, notably the observed trend of the strength of the first peak relative to the second peak decreasing with increasing energy due a higher
$E_{c}$
of the pulsars. The FIDO model can also explain the energy dependence of the observed light curves, notably the observed trend of the strength of the first peak relative to the second peak decreasing with increasing energy due a higher
![]() $E_{c}$
of the second peak spectrum, although this behaviour does not occur for all geometries. In the FIDO model, the emission that forms the second peak lies closer to the current sheet where the
$E_{c}$
of the second peak spectrum, although this behaviour does not occur for all geometries. In the FIDO model, the emission that forms the second peak lies closer to the current sheet where the
![]() $E_{\Vert }$
is higher. The eight pulsars were best matched with different values of
$E_{\Vert }$
is higher. The eight pulsars were best matched with different values of
![]() ${\it\sigma}$
, and trends of
${\it\sigma}$
, and trends of
![]() ${\it\sigma}$
increasing with increasing
${\it\sigma}$
increasing with increasing
![]() ${\dot{E}}_{d}$
and decreasing age are apparent. Such trends would be theoretically expected if the magnetospheric conductivity comes from electron–positron pairs produced by cascades near the polar caps (Daugherty & Harding Reference Daugherty and Harding1982; Timokhin & Arons Reference Timokhin and Arons2013), in outer gaps (Cheng et al.
Reference Cheng, Ho and Ruderman1986) or in the current sheet. The pair cascades produce higher multiplicity for younger pulsars with higher
${\dot{E}}_{d}$
and decreasing age are apparent. Such trends would be theoretically expected if the magnetospheric conductivity comes from electron–positron pairs produced by cascades near the polar caps (Daugherty & Harding Reference Daugherty and Harding1982; Timokhin & Arons Reference Timokhin and Arons2013), in outer gaps (Cheng et al.
Reference Cheng, Ho and Ruderman1986) or in the current sheet. The pair cascades produce higher multiplicity for younger pulsars with higher
![]() ${\dot{E}}_{d}$
. What is not yet understood is how the pair cascade multiplicity and location determines the conductivity.
${\dot{E}}_{d}$
. What is not yet understood is how the pair cascade multiplicity and location determines the conductivity.
Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Brambilla2016) studied models with a
![]() ${\it\sigma}$
distribution that was non-uniform outside the light cylinder (as opposed to the FIDO models with uniform
${\it\sigma}$
distribution that was non-uniform outside the light cylinder (as opposed to the FIDO models with uniform
![]() ${\it\sigma}$
outside the light cylinder), with regions of low
${\it\sigma}$
outside the light cylinder), with regions of low
![]() ${\it\sigma}$
near the current sheet and infinite
${\it\sigma}$
near the current sheet and infinite
![]() ${\it\sigma}$
outside these regions. Such a configuration would be expected if dense pair plasma screened the
${\it\sigma}$
outside these regions. Such a configuration would be expected if dense pair plasma screened the
![]() $E_{\Vert }$
outside the gaps. By relating the model
$E_{\Vert }$
outside the gaps. By relating the model
![]() $E_{\Vert }$
to the observed spectral cutoff energies, expected if accelerating particles were in the curvature radiation reaction regime, they were able to find a relation between
$E_{\Vert }$
to the observed spectral cutoff energies, expected if accelerating particles were in the curvature radiation reaction regime, they were able to find a relation between
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() ${\dot{E}}_{d}$
for the Fermi pulsars. Then using this relation and the dependence of
${\dot{E}}_{d}$
for the Fermi pulsars. Then using this relation and the dependence of
![]() $E_{\Vert }$
on
$E_{\Vert }$
on
![]() ${\it\sigma}$
in the model simulations, they determined the
${\it\sigma}$
in the model simulations, they determined the
![]() ${\it\gamma}$
-ray luminosities of young pulsars as a function of
${\it\gamma}$
-ray luminosities of young pulsars as a function of
![]() ${\dot{E}}_{d}$
. As shown in figure 9, the model
${\dot{E}}_{d}$
. As shown in figure 9, the model
![]() $L_{{\it\gamma}}$
versus
$L_{{\it\gamma}}$
versus
![]() ${\dot{E}}_{d}$
depends on inclination angle
${\dot{E}}_{d}$
depends on inclination angle
![]() ${\it\alpha}$
and can account for the large observed dispersion of
${\it\alpha}$
and can account for the large observed dispersion of
![]() $L_{{\it\gamma}}$
at each
$L_{{\it\gamma}}$
at each
![]() ${\dot{E}}_{d}$
but lies somewhat below the data points. A possible explanation for the lower model
${\dot{E}}_{d}$
but lies somewhat below the data points. A possible explanation for the lower model
![]() $L_{{\it\gamma}}$
could be that the flux of radiating charges is higher than the assumed Goldreich–Julian flux.
$L_{{\it\gamma}}$
could be that the flux of radiating charges is higher than the assumed Goldreich–Julian flux.
Figure 9. Log of
![]() ${\it\gamma}$
-ray luminosity
${\it\gamma}$
-ray luminosity
![]() $L_{{\it\gamma}}$
versus log of spin-down power
$L_{{\it\gamma}}$
versus log of spin-down power
![]() ${\dot{E}}_{d}$
for young Fermi pulsars (black) and predictions for dissipative magnetosphere models with different magnetic inclination angle
${\dot{E}}_{d}$
for young Fermi pulsars (black) and predictions for dissipative magnetosphere models with different magnetic inclination angle
![]() ${\it\alpha}$
. From Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Brambilla2016).
${\it\alpha}$
. From Kalapotharakos et al. (Reference Kalapotharakos, Harding, Kazanas and Brambilla2016).
5.4 Magnetosphere state changes
Magnetosphere simulations have the potential to explain a wide array of transient and time-dependent phenomena observed in rotation powered pulsars. These include spin-down state changes observed at radio (Lyne et al.
Reference Lyne, Hobbs, Kramer, Stairs and Stappers2010), X-ray (Marshall et al.
Reference Marshall, Guillemot, Harding, Martin and Smith2015) and
![]() ${\it\gamma}$
-ray (Allafort et al.
Reference Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Bellazzini, Bonamente, Bottacini and Brandt2013) wavelengths, intermittent pulsars (Kramer et al.
Reference Kramer, Lyne, O’Brien, Jordan and Lorimer2006), and multifrequency mode switching in radio and X-ray (Hermsen et al.
Reference Hermsen, Hessels, Kuiper, van Leeuwen, Mitra, de Plaa, Rankin, Stappers, Wright and Basu2013). Intermittent pulsars show radio pulsations that turn on and off completely (or are at least not detectable) on several month time scales, with different spin frequency derivatives
${\it\gamma}$
-ray (Allafort et al.
Reference Allafort, Baldini, Ballet, Barbiellini, Baring, Bastieri, Bellazzini, Bonamente, Bottacini and Brandt2013) wavelengths, intermittent pulsars (Kramer et al.
Reference Kramer, Lyne, O’Brien, Jordan and Lorimer2006), and multifrequency mode switching in radio and X-ray (Hermsen et al.
Reference Hermsen, Hessels, Kuiper, van Leeuwen, Mitra, de Plaa, Rankin, Stappers, Wright and Basu2013). Intermittent pulsars show radio pulsations that turn on and off completely (or are at least not detectable) on several month time scales, with different spin frequency derivatives
![]() $\dot{{\it\nu}}$
in on and off states. The ratio of
$\dot{{\it\nu}}$
in on and off states. The ratio of
![]() $\dot{{\it\nu}}_{on}/\dot{{\it\nu}}_{off}\sim 1.5{-}2.5$
in the three sources that have been so far discovered. It was suggested (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li, Spitkovsky & Tchekhovskoy Reference Li, Spitkovsky and Tchekhovskoy2012b
) that the on and off states are states with high and low conductivity
$\dot{{\it\nu}}_{on}/\dot{{\it\nu}}_{off}\sim 1.5{-}2.5$
in the three sources that have been so far discovered. It was suggested (Kalapotharakos et al.
Reference Kalapotharakos, Kazanas, Harding and Contopoulos2012b
; Li, Spitkovsky & Tchekhovskoy Reference Li, Spitkovsky and Tchekhovskoy2012b
) that the on and off states are states with high and low conductivity
![]() ${\it\sigma}$
which, as dissipative model simulations have shown, have different Poynting flux, implying different
${\it\sigma}$
which, as dissipative model simulations have shown, have different Poynting flux, implying different
![]() $\dot{{\it\nu}}$
, since
$\dot{{\it\nu}}$
, since
![]() ${\dot{E}}_{d}=4{\rm\pi}^{2}I{\dot{P}}/P^{3}$
. The models can easily produce the observed
${\dot{E}}_{d}=4{\rm\pi}^{2}I{\dot{P}}/P^{3}$
. The models can easily produce the observed
![]() $\dot{{\it\nu}}_{on}/\dot{{\it\nu}}_{off}$
ratios depending on
$\dot{{\it\nu}}_{on}/\dot{{\it\nu}}_{off}$
ratios depending on
![]() ${\it\alpha}$
, the ratios actually constraining
${\it\alpha}$
, the ratios actually constraining
![]() ${\it\alpha}$
for those pulsars. The changes in conductivity could possibly result from transitions between different modes of pair production. In fact the three intermittent pulsars all lie along the theoretical line in the
${\it\alpha}$
for those pulsars. The changes in conductivity could possibly result from transitions between different modes of pair production. In fact the three intermittent pulsars all lie along the theoretical line in the
![]() $P$
–
$P$
–
![]() ${\dot{P}}$
diagram dividing the regime of pair cascades initiated by curvature radiation and inverse Compton scattering (Harding & Muslimov Reference Harding and Muslimov2002). The other observed
${\dot{P}}$
diagram dividing the regime of pair cascades initiated by curvature radiation and inverse Compton scattering (Harding & Muslimov Reference Harding and Muslimov2002). The other observed
![]() $\dot{{\it\nu}}$
state changes are relatively smaller than those of intermittent pulsars indicate smaller changes of
$\dot{{\it\nu}}$
state changes are relatively smaller than those of intermittent pulsars indicate smaller changes of
![]() ${\it\sigma}$
. The mode switching observed in a number of radio pulsars occurs on faster time scales, on the order of hours to days, and could also result from transitions between pair cascade modes. Many of the mode-switching pulsars lie near and below the cascade mode transition line. Alternatively, changes in the global magnetospheric configuration could change the global currents that affect the polar cap pair cascades (Timokhin & Arons Reference Timokhin and Arons2013), causing changes in the polar cap potential drop and multiplicity.
${\it\sigma}$
. The mode switching observed in a number of radio pulsars occurs on faster time scales, on the order of hours to days, and could also result from transitions between pair cascade modes. Many of the mode-switching pulsars lie near and below the cascade mode transition line. Alternatively, changes in the global magnetospheric configuration could change the global currents that affect the polar cap pair cascades (Timokhin & Arons Reference Timokhin and Arons2013), causing changes in the polar cap potential drop and multiplicity.
6 Summary
We have reviewed the flurry of activity and excitement that has followed the discovery of the large numbers and different types of
![]() ${\it\gamma}$
-ray pulsars by Fermi, that opened up the observational study of pulsar magnetospheres and launched a theoretical drive to develop increasingly sophisticated magnetosphere simulations. This review has covered the development of vacuum, force-free and dissipative MHD magnetosphere models and the light curve modelling using these. The important result of the
${\it\gamma}$
-ray pulsars by Fermi, that opened up the observational study of pulsar magnetospheres and launched a theoretical drive to develop increasingly sophisticated magnetosphere simulations. This review has covered the development of vacuum, force-free and dissipative MHD magnetosphere models and the light curve modelling using these. The important result of the
![]() ${\it\gamma}$
-ray light curve modelling is the finding that the main part of the emission comes from the outer magnetosphere, near and/or beyond the light cylinder. This was first apparent from fitting simplified emission models with VRD and FF field geometry. The dissipative magnetosphere models, that were for the first time able to simulate accelerating electric fields that are self-consistent with the magnetic fields of the magnetosphere, confirmed this earlier finding. Most importantly, the dissipative models provide a physical reason for the emission geometry – that the
${\it\gamma}$
-ray light curve modelling is the finding that the main part of the emission comes from the outer magnetosphere, near and/or beyond the light cylinder. This was first apparent from fitting simplified emission models with VRD and FF field geometry. The dissipative magnetosphere models, that were for the first time able to simulate accelerating electric fields that are self-consistent with the magnetic fields of the magnetosphere, confirmed this earlier finding. Most importantly, the dissipative models provide a physical reason for the emission geometry – that the
![]() $E_{\Vert }$
and emission is highest in regions where the current is highest. For magnetospheres with high conductivity, this region is near the current sheet.
$E_{\Vert }$
and emission is highest in regions where the current is highest. For magnetospheres with high conductivity, this region is near the current sheet.
The recent development of PIC simulations (Chen & Beloborodov Reference Chen and Beloborodov2014; Philippov & Spitkovsky Reference Philippov and Spitkovsky2014) is the logical next step that has the potential to build self-consistent pulsar magnetospheres by modelling the pair cascades simultaneously with the global field structure. Such simulations could identify the physical nature and distribution of the conductivity. This effort is just beginning and the light curve modelling using the PIC codes is in its early stages (Cerutti, Philippov, Spitkovsky Reference Cerutti, Philippov and Spitkovsky2016). The article by Cerutti in this volume will review the progress in using PIC simulations.
Acknowledgements
I would like to thank my collaborators M. Breed, G. Brambilla, M. DeCesar, I. Grenier, T. Johnson, K. Kalapotharakos, D. Kazanas, A. Muslimov, M. Pierbattista, B. Seyffert, and C. Venter, and E. Ferrara for help with the Fermi pulsar data. I also acknowledge support from the Fermi Guest Investigator Program.