Large-scale characteristics of the distribution of blowing-snow sublimation

Abstract

To consider the large-scale characteristics of blowing-snow sublimation and its importance in the hydrological cycle in the cryosphere, we investigated the sublimation of blowing snow particles on a global scale using the global datasets of the European Centre for Medium-RangeWeather Forecasts (ECMWF) re-analysis data and the International Satellite Land Surface Climatology Project (ISLSCP) Initiative I data for 1987. The sublimation fluxes of blowing snow particles were estimated globally with 2.5^˚ resolution at 6 hour intervals. We found that the sublimation of blowing snow particles occurs more widely in the Northern Hemisphere than in the Southern Hemisphere, does not increase monotonously with latitude, and becomes more active in the polar coast regions and highlands, although the annual mean sublimation fluxes of the Northern and Southern Hemispheres are almost equal. In addition, we confirmed the characteristic seasonal changes in the area of sublimation in the Northern Hemisphere. Although we need to incorporate continuous parameters from systematic ground-based studies of the structure of blowing snow in specific fields to reduce uncertainty regarding the characteristics of blowing snow, our results point to a need to review the current understanding of the hydrological cycle.

Introduction

The sublimation of blowing snow particles is a significant process in the hydrological cycle of snow-covered plains and other regions in which most of the winter snowfall is relocated by wind (Dyunin, 1967; Tabler and Schmidt, 1972; Male, 1980; Schmidt, 1982). Thorpe and Mason (1966) performed sublimation process experiments on ice spheres, and process-based blowing snow models that incorporate sublimation have been developed (Pomeroy and others, 1993; Déry and others, 1998; Liston and Sturm, 1998; Déry and Yau, 1999; Bintanja, 2000; Xiao and others, 2000; Sugiura, 2006). Although several field studies have examined blowing-snow sublimation on a point or basin scale (Tabler, 1975; Pomeroy and others, 1997; Bintanja, 1998; Liston and Sturm, 1998; Mann and others, 2000; King and others, 2001), it is necessary to clarify the large-scale characteristics of the sublimation of blowing snow particles to better understand blowing-snow sublimation as a subprocess in the hydrological cycle of the entire cryosphere. To consider the large-scale characteristics and importance of blowing-snow sublimation in the hydrological cycle in the cryosphere, we investigated the sublimation of blowing snow particles on a global scale using global datasets and determined its distribution.

Dataset and Methods of Analysis

To focus our effort on global snow conditions on the land and sea using a combination of datasets that provide as fine a resolution as possible, we selected the European Centre for Medium-Range Weather Forecasts (ECMWF) re-analysis (ERA) data for 1987 and the International Satellite Land Surface Climatology Project (ISLSCP) Initiative I datasets for 1987. The elements of the ERA data for 1987 that were necessary to apply our calculation method were wind velocity at a height of 10 m, air temperature at a height of 2 m, skin temperature, and snow depth archived on a 2.5^˚×2.5^˚ grid at 6 hour intervals. For the ISLSCP Initiative I datasets for 1987, the sea-ice concentration archived on a 1^˚×1^˚ grid at 1 month intervals was used for the calculation.

The sublimation flux of blowing snow particles, S (kgm^–2 s^–1), which equals 8.6×10⁴ S (mm d^–1), was calculated for every 2.5^˚×2.5^˚ grid at 6 hour intervals. The monthly and annual mean sublimation fluxes of blowing snow particles were obtained. The sublimation flux of blowing snow particles, S, was defined as

(1)

where fS is the main parameter used to estimate the sublimation flux of blowing snow particles, fOF, f _ST and f _SD are a step function of blowing-snow occurrence, skin temperature and snow depth, respectively, and f _WF is a weighting function to compensate for the difference between the ECMWF and ISLSCP gridscales.

Here f _S was defined as

(2)

(3)

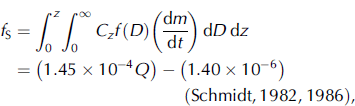
and

(4)

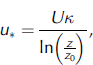
where C_z is the number of particles in a unit volume of air at z (m^–3), f(D) is a distribution function of particle diameter D, m is the mass of a snow particle (kg), t is time (s), z is height (m), Q is the snow transport rate (kgm^–1 s^–1), u* is the friction velocity (m s^–1), U is the wind velocity at a height of 10m (m s^–1), κ is von Kármán’s constant (0.4), and z ₀ is roughness (0.001 m).

Because a strong dependence of the sublimation flux of blowing snow particles on the snow transport rate is expected, we used Equation (2) to describe the sublimation flux of blowing snow particles as a function of the snow transport rate.

Much effort has been made to estimate the snow transport rate as a function of wind velocity for several regions (Fig. 1; Khrgian in 1934, Ivanov in 1951 and Mel’nik in 1952 (according to Dyunin, 1963); Dyunin, 1963; Komarov, 1963; Budd and others, 1966; Kobayashi and others, 1969; Takeuchi, 1980; Tabler, 1991; Sugiura and others, 1998). There is considerable variation in the estimated snow transport rate because of differences in conditions such as topography, distance from the fetch, and temperature. Because differences in the particle collection efficiency of the instruments, most of which capture particles directly, would cause variation in the estimated snow transport rate, Sugiura and others (1998) conducted wind tunnel experiments using an optical snow particle counter without capturing particles directly, and calculated the snow transport rate as a function of the friction velocity. The

Fig. 1. The snow transport rate as a function of wind velocity at a height of 1 m and a roughness of 0.001 m. 1. Khrgian in 1934 from Dyunin (1963); 2. Ivanov in 1951 from Dyunin (1963); 3. Mel’nik in 1952 from Dyunin (1963); 4. Dyunin (1963); 5. Komarov (1963); 6. Budd and others (1966); 7. Kobayashi and others (1969); 8 and 9. Takeuchi (1980); 10. Tabler (1991); 11. Sugiura and others (1998).

validity of the snow particle counter is confirmed by field observations (Sato and others, 1993).We used the relation of Sugiura and others (1998), which gives a value that is close to the average of numerous observations (Fig. 1).

Here, f _OF was defined as

(5)

(6)

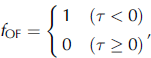
where AT is air temperature at a height of 2 m (^˚C). Nishimura and Maeno (1987) estimated the blowing-snow occurrence, τ, using data for several regions, including Hokkaido, Japan, (Sato, 1962) Syowa station, Antarctica, (Oura and others, 1967; JMA, 1984), Mizuho station, Antarctica, (Ohata and others, 1981) and cold wind-tunnel experiments (Maeno, 1986a, b) with an accuracy of 80.7%. For example, if the air temperature at a height of 2m is 0 or –30^˚C, blowing snow occurs at 10m wind velocities of 10.4 or 8.6 ms^–1, respectively.

Here f _ST was defined as

(7)

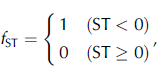
where ST is skin temperature (^˚C). If U = 20ms^–1 and AT = +30^˚C, Equation (5) outputs f _OF = 1. In this case, blowing snow occurs. Therefore, we took Equation (7) into consideration so that blowing snow might not occur.

Here f _SD was defined as

(8)

where SD is snow depth (m) and SI is the sea-ice concentration (%).

Here f _WF was defined as:

(9)

where i is the number of 1^˚×1^˚ grids in a 2.5×2.5^˚ grid and I is a constant for normalization. Because the ECMWF and ISLSCP gridscales are 2.5^˚×2.5^˚ and 1^˚×1˚ , respectively, a weighting of W was used to account for the different coverage according to grid area.

Results And Discussion

We calculated the annual mean sublimation flux of blowing snow particles (Table 1). Although the coverage percentage of land and sea differs in the two hemispheres, the estimated annual mean sublimation flux was similar in the Northern and Southern Hemispheres.

We also determined the latitude distribution of the annual mean sublimation flux of blowing snow particles with a 2.5^˚ latitude spacing (Fig. 2). The annual mean sublimation flux does not increase monotonously with latitude, and ranges from 0 to 2.2×10^–6 kgm^–2 s^–1 (= 1.9×10^–1mmd^–1). The maximum is at 70^˚ S, which corresponds to the coast of Antarctica. Similarly, significant sublimation occurs along the Arctic Ocean coast between 70^˚ and 80^˚ N.

Fig. 2. Latitude distribution of the annual mean sublimation flux of blowing snow particles at 2.5^˚ latitude spacing.

The longitude distribution of the annual mean sublimation flux of blowing snow particles with a 2.5^˚ longitude spacing is shown in Figure 3. The annual mean sublimation flux fluctuates with longitude, and ranges from 1.4×10^–7 (= 1.2×10^–2mmd^–1) to 5.2×10^–7 kgm^–2 s^–1 (= 4.5×10^–2mmd^–1), with a 3.8 times difference between the maximum and minimum in the Western Hemisphere. The longitude distribution of the annual mean sublimation flux depends on the coverage rates of land and sea in the longitude zone.

Fig. 3. Longitude distribution of the annual mean sublimation flux of blowing snow particles at 2.5^˚ longitude spacing.

The spatial distribution of the annual mean sublimation flux of blowing snow particles on a global scale (2.5^˚×2.5^˚ grid) is shown in Figure 4. It is clear that sublimation in the Northern Hemisphere occurs over a wider range up to 30˚N latitude, which includes high-elevation regions such as the Tibetan Plateau, in comparison with the Southern Hemisphere. This is because snow in the Northern Hemisphere covers a wider area than in the Southern Hemisphere on a 2.5^˚×2.5^˚ gridscale. In addition, it is clear that sublimation becomes more active on the high-latitude coasts, such as the coast of Antarctica, the coast of the Arctic Ocean, Bering Strait, Hudson Bay, Baffin Basin, Davis Strait, Greenland and, noteworthily, the Sea of Okhotsk which is close to the mid-latitudes. Sublimation is moderately active in west Siberia and the Tibetan Plateau because of strong wind.

Fig. 4. Spatial distribution of the annual mean sublimation flux of blowing snow particles in each 2.5^˚×2.5^˚ grid on a global scale.

The annual mean sublimation flux of the Northern Hemisphere was similar to that of the Southern Hemisphere, although the area of blowing-snow sublimation is considerably wider in the Northern Hemisphere (Table 1). One explanation may be that the area of active sublimation is distributed at high latitudes in both hemispheres, and the sublimation flux of the mid-latitudes in the Northern Hemisphere is not intense.

The annual mean sublimation flux at the boundary grid between sea ice and the sea in both hemispheres is lower than that of the grids entirely covered by sea ice (Fig. 4). This boundary grid overlaps the sea and sea ice and may be associated with the low sea-ice concentration. Based on Equations (8) and (9), blowing snow develops fully in the grid in proportion to the sea-ice concentration, even if the sea-ice concentration is low. Blowing snow develops according to the distance from the fetch. Therefore, it is thought that the actual sublimation flux at the grid with low sea-ice concentration is lower because of the short distance from the fetch.

Table 1. Annual mean sublimation flux

The spatial distribution of the monthly mean sublimation flux of blowing snow particles in each 2.5^˚×2.5^˚ grid on a global scale is shown in Figure 5. The area of sublimation on the Eurasian and North American continents characteristically moves to high or low latitudes according to the season, whereas sublimation on the Antarctic coast occurs throughout the year in contrast to that in the Antarctic interior.

Fig. 5. Spatial distribution of the monthly mean sublimation flux of blowing snow particles in each 2.5^˚×2.5˚ grid on a global scale.

Liston and Sturm (1998) estimated the total winter sublimation of blowing snow particles at a snow water equivalent depth using a numerical snow-transport model based on physical quantities (SnowTran-3D) with a 20×20m grid spacing, a 1 day time-step, and 4 years of climate observations from September through April for the winters 1986/87, 1987/88, 1988/89 and 1989/90 at the 2×3 km Imnavait Creek domain in the foothills north of the Brooks Range, Arctic Alaska, USA. The domain-averaged, winter-only total, and snow water equivalent quantities were tabulated. Using 0.038 m of the total winter sublimation data for the 1986/87 winter (8 months from September 1986 through April 1987) from Liston and Sturm (1998), the mean sublimation in snow water equivalent depth was calculated (0.16mmd^–1). Our value for the mean sublimation in snow water equivalent depth for the corresponding 4 months from January 1987 through April 1987 at the corresponding grid is lower (2.1×10^–3mmd^–1). Although only Liston and Sturm’s (1998) study of a particular region over 1 year can be compared with our study and our calculation is rough, it is important to consider the difference. The snow transport rate in Equations (3) and (4) increases with wind velocity to the power of 3.96, not linearly. The ECMWF 2.5^˚×2.5^˚ grid, corresponding to the Imnavait Creek domain, comprises tundra, a hill and part of the Brooks Range. It is difficult for a large grid to describe the wind velocity distribution accurately over such an uneven surface. Consequently, fine-scale grid datasets allow more accurate estimation of the sublimation flux, and the estimated sublimation flux in high-altitude regions may increase and be emphasized more. In addition, no sublimation occurs below a threshold wind velocity derived from Equations (5) and (6), although the threshold shear velocity given by Liston and Sturm (1998) is 0.25 ms^–1, which equals a 10 m wind velocity of 7.2 ms^–1 and is weaker than the value obtained from Equations (5) and (6). Furthermore, because Equation (2) was obtained under the condition of a vertical height limit of the integration such as a height of 1 m from the snow surface (Schmidt, 1982), it might underestimate the amount of sublimation.

In addition to these uncertainties associated with our analyses, another uncertainty is the formation of a near-saturated air layer. The observed relative humidity within the blowing-snow layer at Halley, Antarctica, reaches near-saturation with respect to ice quite rapidly at the onset of a blowing-snow episode as the air becomes saturated (Mann and others, 2000). This further limits sublimation. As Mann and others (2000) discussed, the air surrounding the particles may reach near-saturation during transport across snow cover with long fetches and low ambient temperature. Finally, parameters describing the relationship between the occurrence frequency of blowing snow and the actual conditions of the snowpack on sea ice and vegetation, in addition to the formation of a near-saturated air layer, are needed for specific field observations based on systematic ground-based studies.

We have given a condensed account of blowing-snow sublimation. Our results show that the hydrological cycle of the polar coast regions and highlands in the cryosphere is characterized by blowing-snow sublimation. The general hydrological cycle is given as:

(10)

where P is precipitation, E is evapotranspiration, R is runoff and S is storage. The blowing-snow sublimation has been estimated as 33% of the total winter P by Tabler (1975) in Wyoming, USA, 20% of the total winter P by Pomeroy and others (1997) at Inuvik, Canada, 9–22% of the total winter P by Liston and Sturm (1998) at the Imnavait Creek domain, 10–20% of the total annual S by Bintanja (1998) at D-10, a costal Antarctic location, 10% of the total annual S by King and others (2001) at Halley, and 4% of the total winter S by Mann and others (2000) at Halley. As has been suggested, blowing-snow sublimation is enhanced in the polar coast regions and highlands. The annual total sublimation at Halley is smaller than that at the costal Antarctic location. This is consistent with our results and suggests that evapotranspiration, E, in the polar coast regions and highlands should take account of blowing-snow sublimation. Future continuous work might reduce the uncertainty of various error sources in hydrological-cycle estimates for the polar coast regions and highlands.

Conclusion

The large-scale distribution of the sublimation of blowing snow particles can be calculated using global datasets (ECMWF and ISLSCP for 1987). The sublimation of blowing snow particles in the Northern Hemisphere occurs over a wider range than in the Southern Hemisphere, but the annual mean sublimation flux is similar in both hemispheres. The annual mean sublimation flux does not increase monotonously with latitude, and sublimation is more active on the polar coast. The latitude of the sublimation area in the Northern Hemisphere characteristically changes greatly with the seasons. The polar coast regions and highlands are important for the hydrological cycle of the cryosphere. The reduction of the uncertainty of parameters describing the characteristics of blowing snow would require the incorporation of parameters based on systematic ground-based studies of the structure of blowing snow in specific fields, especially the relationship between the frequency of occurrence of blowing snow and the actual conditions of snow on sea ice and vegetation, in addition to the formation of a near-saturated air layer.