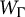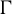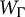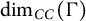A new upper bound for the asymptotic dimension of RACGs

Abstract

Let $W_{\Gamma} $ be the right-angled Coxeter group with defining graph $\Gamma $. We show that the asymptotic dimension of $W_{\Gamma} $ is smaller than or equal to $\mathrm{dim}_{CC}(\Gamma )$, the clique-connected dimension of the graph. We generalize this result to graph products of finite groups.

1 Introduction

Coxeter groups touch upon a number of areas of mathematics, such as representation theory, combinatorics, topology, and geometry. They are often considered as a playground for many open problems in geometric group theory.

It is known by an isometric embedding theorem of Januszkiewicz (see [10]) that Coxeter groups have finite asymptotic dimension. In particular, Januszkiewicz’s theorem shows that for any Coxeter group $W_{\Gamma} $ with defining graph $\Gamma $ , we have the following upper bound: $\mathrm{asdim}W_{\Gamma} \leq \sharp V(\Gamma )$ . A lower bound for the asymptotic dimension of Coxeter groups was given by Dranishnikov in [6], $\mathrm{vcd}(W_{\Gamma} ) \leq \mathrm{asdim} W_{\Gamma} $ .

Right-angled Coxeter groups (RACGs) are the simplest examples of Coxeter groups; in these, the only relations between distinct generators are commuting relations. In other words, RACGs are the Coxeter groups defined by RAAGs (Right-angled Artin groups). Dranishnikov proved (see [5]) that the asymptotic dimension of RACGs is bounded from above by the dimension of their Davis complex.

Question Is possible to determine the asymptotic dimension of a RACG from its defining graph?

In many cases, Dranishnikov’s bound is far from being optimal. For example, if the defining graph $\Gamma $ is a clique with n vertices, then by Dranishnikov’s result, we have that $\mathrm{asdim} W_{\Gamma }\leq n$ , however, $\mathrm{asdim} W_{\Gamma }=0$ . The aim of this paper is to provide a new upper bound for the asymptotic dimension of RACGs treating some of the cases in which Dranishnikov’s bound fails to be optimal. The main result of this paper and its corollaries make some progress toward the previous question.

We prove the following theorem.

Theorem 1.1 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . Then

$$ \begin{align*}\mathrm{asdim} W_{\Gamma} \leq \mathrm{dim}_{CC} (\Gamma).\end{align*} $$

If $\Gamma $ is not connected, then $\mathrm{asdim} W_{\Gamma} \leq \max \lbrace 1, \mathrm{dim}_{CC} (\Gamma ) \rbrace .$

The clique-connected dimension of a finite graph, $\mathrm{dim}_{CC}(\Gamma )$ (see Section 2.1), can be described as an index showing how connected is the graph modulo cliques. For example, if $\Gamma $ is a clique, then $\mathrm{dim}_{CC}(\Gamma )=0$ . In the case of $\Gamma $ being a clique, we have that $W_{\Gamma} $ is finite, so $\mathrm{asdim} W_{\Gamma} = \mathrm{dim}_{CC}(\Gamma )$ . We will further show that if $\mathrm{dim}_{CC}(\Gamma )\leq 2$ , then $\mathrm{asdim} W_{\Gamma} = \mathrm{dim}_{CC}(\Gamma )$ (see Proposition 6.2).

Since there are cases where the dimension of the Davis complex $\Sigma (W_{\Gamma} )$ is smaller than $\mathrm{dim}_{CC}(\Gamma )$ and other cases where $\mathrm{dim}_{CC}(\Gamma )< \mathrm{dim} \Sigma (W_{\Gamma} )$ , we have as a corollary in the following theorem.

Theorem 1.2 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . Then

$$ \begin{align*}\mathrm{asdim} W_{\Gamma} \leq \min \lbrace \mathrm{dim}_{CC} (\Gamma), \mathrm{dim}\Sigma(W_{\Gamma}) \rbrace.\end{align*} $$

If $\Gamma $ is not connected, then $\mathrm{asdim} W_{\Gamma} \leq \max \lbrace 1, \min \lbrace \mathrm{dim}_{CC} (\Gamma ) , \mathrm{dim}\Sigma (W_{\Gamma} ) \rbrace \rbrace .$

As a corollary of Theorem 1.1, we prove the following proposition.

Proposition 1.3 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . If $\mathrm{dim}_{CC}(\Gamma )\leq 2$ , then $\mathrm{asdim} W_{\Gamma} = \mathrm{dim}_{CC}(\Gamma )$ .

Let $\Gamma $ be a simplicial graph. We label every vertex v of the graph by a vertex group $G_v$ . The graph product $\mathbb {GP}(\Gamma ,G_v)_{v\in V(\Gamma )}$ is the free product of the vertex groups modulo the relations $xyx^{-1}y^{-1}$ , where $x \in G_v$ , $y \in G_w$ , and $v, w$ are connected by an edge.

We generalize Theorem 1.1 to the following theorem.

Theorem 1.4 Let $\Gamma $ be a finite connected simplicial graph along with a finite collection of finite vertex groups. Then

$$ \begin{align*}\mathrm{asdim}\, \mathbb{GP}(\Gamma,G_v)_{v\in V(\Gamma)} \leq \mathrm{dim}_{CC} (\Gamma).\end{align*} $$

If $\Gamma $ is not connected, then $\mathrm{asdim}\, \mathbb {GP}(\Gamma ,G_v)_{v\in V(\Gamma )} \leq \max \lbrace 1, \mathrm{dim}_{CC} (\Gamma ) \rbrace .$

The paper is organized as follows: In Section 2, we start with some basic definitions and some preliminary results that are used in the rest of the paper. Section 3 contains some important lemmas, for example, we show that $\mathrm{dim}_{CC}(\ast )$ is “monotone” in the following sense: if $\Gamma ^{\prime }$ is a full subgraph of $\Gamma $ , then $\mathrm{dim}_{CC}(\Gamma ^{\prime }) \leq \mathrm{dim}_{CC}(\Gamma )$ . In Section 4, we prove that the clique-connected dimension is increasing in some cases. In Section 5, we prove the main theorems of the paper. Finally, in Section 6, we present some corollaries of the main results.

2 Preliminaries

The asymptotic dimension $\mathrm{asdim}X$ of a metric space X is defined as follows: $\mathrm{asdim}X \leq n$ if and only if for every $R> 0,$ there exists a uniformly bounded covering $\mathcal {U}$ of X such that the R-multiplicity of $\mathcal {U}$ is smaller than or equal to $n+1$ (i.e., every R-ball in X intersects at most $n+1$ elements of $\mathcal {U}$ ). There are many equivalent ways to define the asymptotic dimension of a metric space. It turns out that the asymptotic dimension of an infinite tree is $1$ and the asymptotic dimension of $\mathbb {E}^{n}$ is n.

By finite simplicial labeled graph, we mean a finite simplicial graph $\Gamma $ such that every edge $[a,b]$ is labeled by a natural number $m_{ab}>1$ . The Coxeter group associated with $\Gamma $ is the group $W_{\Gamma} $ given by the following presentation:

$$ \begin{align*} W_{\Gamma}= \langle V(\Gamma) \vert a^2=e &\textrm{ for all }a \in V(\Gamma)\textrm{ and } \underbrace{ab \ldots}_{m_{ab}}= \underbrace{ba \ldots}_{m_{ab}} \textrm{ when }a, b\\& \textrm{ are connected by an edge } \rangle. \end{align*} $$

A Coxeter group is called RACG if $m_{ab}=2$ when a, b are connected by an edge.

We say a simplicial graph is complete or equivalently a clique if any two vertices are connected by an edge. An n-clique is the complete graph on n vertices. We recall that the full subgraph defined by a subset V of the vertices of a graph $\Gamma $ is a subgraph of $\Gamma $ formed from V and from all of the edges that have both endpoints in the subset V. If G is a subgraph of $\Gamma $ , we denote by $FS^{\Gamma }(G)$ the full subgraph of $\Gamma $ defined by $V(G)$ . The simplicial closure of $\Gamma $ is the flag complex $SC(\Gamma )$ defined by $\Gamma $ .

We recall the definition of a parabolic subgroup of a Coxeter group. Let $\Gamma $ be a finite simplicial labeled graph, and let $W_{\Gamma} $ be the Coxeter group associated with $\Gamma $ . Let X be a subset of $V(\Gamma )$ , we denote by $\Gamma _X$ the full subgraph of $\Gamma $ formed from X, and by $G_{X}$ the subgroup of $W_{\Gamma} $ generated by X (we see X as a subset of the natural generating set of $W_{\Gamma} $ ). We consider the graph $\Gamma _X$ as a labeled graph inheriting its labeling from $\Gamma $ . It is known that $G_X$ is a Coxeter group, it is actually equal to $W_{\Gamma _{X}}$ , the Coxeter group associated with $\Gamma _{X}$ (see [7]). The subgroup $G_X=W_{\Gamma _{X}}$ is called standard parabolic subgroup of $W_{\Gamma} $ .

The following theorem is proved by Dranishnikov in [5].

Theorem 2.1 For any finitely generated groups A and B with a common finitely generated subgroup C, we have:

$$ \begin{align*} \mathrm{asdim} A \ast_C B \leq \max \lbrace \mathrm{asdim} A, \mathrm{asdim} B, \mathrm{asdim} C + 1 \rbrace. \end{align*} $$

The following theorem is a generalization of Theorem 2.1. It was proved by the author in [13].

Theorem 2.2 Let $(\mathbb {G}, Y)$ be a finite graph of groups with vertex groups $\lbrace G_{v} \mid v \in Y^{0} \rbrace $ and edge groups $\lbrace G_{e} \mid e \in Y^{1}_{+} \rbrace $ . Then the following inequality holds:

$$ \begin{align*} \mathrm{asdim}\,\pi_{1}(\mathbb{G},Y,\mathbb{T}) \leq \max\nolimits_{v \in Y^{0} ,e \in Y^{1}_{+}} \lbrace \mathrm{asdim} G_{v}, \mathrm{asdim}\,G_{e} +1 \rbrace. \end{align*} $$

We also need a theorem for free products from [2] (see also [1]).

Theorem 2.3 Let A, B be two finitely generated groups. Then

$$ \begin{align*} \mathrm{asdim}\,A \ast B = \max \lbrace \mathrm{asdim} A, \mathrm{asdim} B, 1 \rbrace. \end{align*} $$

2.1 $\mathrm{dim}_{CC}(\ast )$

Let $\Gamma $ be a connected simplicial graph. We say that a finite subset S of $V(\Gamma )$ is a vertex cut of $\Gamma $ if $FS^{\Gamma} (S)$ separates the graph (i.e., $\Gamma \setminus FS^{\Gamma} (S)$ contains at least two connected components) and no proper subset of S does that.

Definition 2.1 Let $\Gamma $ be a simplicial graph, and let $ \mathcal {C}_{\Gamma }= \lbrace C_1 , \ldots ,C_i , \ldots \rbrace $ be a collection of distinct cliques of $\Gamma $ . We say $\mathcal {C}_{\Gamma }$ is a clique twin of $\Gamma $ if the following conditions are satisfied:

(i) Each $C_i$ is a maximal clique in $\Gamma $ , i.e., there is no other clique in $\Gamma $ containing $C_i$ .

(ii) If C is a clique of $\Gamma $ , then there is a clique in $\mathcal {C}_{\Gamma} $ containing C.

We note that the last condition can be replaced by the following:

$\cup _{C_i \in \mathcal {C}_{\Gamma} } SC(C_i) = SC(\Gamma )$ .

Observe that a clique twin of a graph $\Gamma $ is actually a “covering” of $\Gamma $ with maximal cliques. We further observe, that if a clique twin exists, then it is equal to the set of the maximal cliques of the graph.

Definition 2.2 Let $\Gamma $ be a simplicial graph which has at least one clique twin $ \mathcal {C}_{\Gamma }$ . We set

$$ \begin{align*} m_C (\Gamma)= \min \lbrace \sharp \mathcal{C}_{\Gamma} \vert\textrm{ where } \mathcal{C}_{\Gamma}\textrm{ is a clique twin of } \Gamma \rbrace. \end{align*} $$

Definition 2.3 Let $\Gamma $ be a connected simplicial graph. We set

$$ \begin{align*} CC (\Gamma)= \min \lbrace m_C (FS^{\Gamma}(S)) \vert\textrm{ where }S\textrm{ is a vertex cut of } \Gamma \rbrace. \end{align*} $$

To treat the case when the set on the right-hand side is empty, we insist that $\min \lbrace \varnothing \rbrace = 0.$ The number $CC(\Gamma )$ “measures” how connected is the graph $\Gamma $ modulo its cliques. If S is a vertex cut of $\Gamma $ such that $CC (\Gamma )= m_C (FS^{\Gamma} (S))$ , we say that S is a minimal vertex cut of $\Gamma $ .

Observe that we can generalize the previous definition to all simplicial graphs, by setting $CC(\Gamma )= \min \lbrace CC(E) \mid E$ is a component of $ \Gamma \rbrace $ . Finally, we can define $\mathrm{dim}_{CC}(\ast )$ .

Definition 2.4 Let $\Gamma $ be a simplicial graph. We set

$$ \begin{align*} \mathrm{dim}_{CC} (\Gamma)= \sup \lbrace CC (G) \vert\textrm{ where }G\textrm{ is a full subgraph of } \Gamma \rbrace. \end{align*} $$

The clique-connected dimension $\mathrm{dim}_{CC}(\Gamma )$ “measures” how connected is the graph $\Gamma $ modulo its cliques by taking into account all the full subgraphs of $\Gamma $ .

3 Basic lemmas

Lemma 3.1 (Existence of clique twins)

Let $\Gamma $ be a finite simplicial graph. Then there exists at least one clique twin of $\Gamma $ .

Proof We use induction on the number of vertices of the graph. Obviously, the lemma is true if the graph is just a vertex. We assume the lemma is true for any graph with less than $N+1$ vertices. Let $\Gamma $ be a finite simplicial graph with $N+1$ vertices.

If the graph is disconnected the lemma follows by the inductive hypothesis and the fact that the clique twins of the components of the graph forms a clique twin of $\Gamma $ .

So we assume that the graph is connected. We choose an arbitrary vertex say v and we consider the graph $\Gamma _v = \Gamma \setminus v$ . By inductive hypothesis, there exists a clique twin $\mathcal {C}_{\Gamma _v}$ of $\Gamma _v$ . Since the graph is connected the link of v in $\Gamma $ is non-empty ( $lk_{\Gamma} (v) \neq \varnothing $ ). We enumerate the vertices of the link, $lk_{\Gamma} (v)=\lbrace v_1, v_2 , \ldots ,v_k \rbrace $ . For every C in $\mathcal {C}_{\Gamma _v}$ , we set:

$$ \begin{align*} \overline{C}= \textrm{ either } C\textrm{ (if }C \cup v&\textrm{ doesn't define a clique of }\Gamma),\textrm{ or the clique defined }\\ &\textrm{by }C\textrm{ and }v\textrm{ (otherwise)}. \end{align*} $$

For every $v_i$ in $lk_{\Gamma} (v)$ , we define:

$$ \begin{align*} \mathcal{C}_i \textrm{ to be the collection of all maximal cliques in }\Gamma\textrm{ containing both }v\textrm{ and }v_i. \end{align*} $$

Observe then that the union $\mathcal {C}_{\Gamma} = (\cup _i \mathcal {C}_i ) \cup \lbrace \overline {C} \vert C \in \mathcal {C}_{\Gamma _v} \rbrace $ satisfies the conditions of Definition 2.1, so it is a clique twin of $\Gamma $ .

We will see that every finite graph has a unique clique twin. The proof of the previous lemma actually give us a description of how to construct the clique twin of every graph.

Lemma 3.2 Let $\Gamma $ be a connected finite simplicial graph. Then $\Gamma $ is a clique if and only if $CC(\Gamma )=0=\mathrm{dim}_{CC}(\Gamma )$ .

Proof We assume that $\Gamma $ is a clique, then obviously, there is no vertex cut of $\Gamma $ . So by Definition 2.3 we have that $CC(\Gamma )=0$ .

We now prove the other direction, so we assume that $CC(\Gamma )=0$ . If $\Gamma $ is not a clique there exist two vertices $a,b$ such that they are not connected by an edge, then $V(\Gamma )\setminus \lbrace a,b \rbrace $ separate the graph. Obviously, then we may find a vertex cut S of $\Gamma $ , so by Lemma 3.1 $CC(\Gamma )>0.$

Lemma 3.3 (Uniqueness of clique twins) Let $\Gamma $ be a simplicial graph. If $\Gamma $ has a clique twin, then it is unique.

Proof It follows from the observation that if a clique twin exists, then it is equal to the set of the maximal cliques of the graph.

Let $\Gamma $ be a simplicial graph, and let $\mathcal {C}_{\Gamma} $ be its clique twin. We note that, if no element of $\mathcal {C}_{\Gamma} $ is a vertex and every two distinct elements have at most one common vertex, then the clique twin is a maximal-clique partition of $\Gamma $ (see [12] for definition).

Lemma 3.4 (Monotonicity of $\mathrm{dim}_{CC}(\ast )$ ) Let $\Gamma $ be a simplicial graph, and let G be a full subgraph of $\Gamma $ . Then

$$ \begin{align*} \mathrm{dim}_{CC}(G) \leq \mathrm{dim}_{CC}(\Gamma). \end{align*} $$

Proof Since G is a full subgraph of $\Gamma $ we have that every full subgraph of G is also a full subgraph of $\Gamma $ . The lemma follows by the definition of $\mathrm{dim}_{CC}$ .

If G is not full subgraph the previous lemma is not true. The reader may notice some similarities between the proof of the following lemma and the paper [4].

Lemma 3.5 Let $\Gamma $ be a connected simplicial graph such that $CC(\Gamma ) \geq 2$ . Then $CC(G) \leq 1$ , for every G, proper full subgraph of $\Gamma $ if and only if $\Gamma $ is a k-cycle ( $k \geq 4$ ).

Proof Suppose that $CC(G) \leq 1$ , for every G, proper full subgraph of $\Gamma $ . Let S be a vertex cut of $\Gamma $ such that $m_C(FS^{\Gamma} (S)) \geq 2$ , and let $\mathcal {C}_S= \lbrace C_1, \ldots , C_k \rbrace $ be the clique twin of $FS^{\Gamma} (S)$ .

Let $E_1 , E_2$ be two of the components of $\Gamma \setminus FS^{\Gamma }(S)$ . Observe that there are vertices $v_1 , v_2 \in FS^{\Gamma }(S)$ such that they are not connected by an edge in $\Gamma $ . Obviously, they belong to distinct cliques. We may assume that $v_1 \in C_1 \setminus C_2$ and $v_2 \in C_2 \setminus C_1$ . We note that for every $s\in S$ and every component $E_i$ , there exists an edge connecting s with $E_i$ (it follows from the fact that S is a vertex cut of the graph). Thus, there exist edge paths $p_i \subseteq E_i \cup C_1 \cup C_2$ connecting $v_1$ with $v_2$ such that $p_i \cap (C_1 \cup C_2) = \lbrace v_1, v_2 \rbrace $ . We may assume that these paths have the minimum possible length.

Observe that the length of these edge paths is at least two. Trivially, the union $p_1 \cup p_2$ is k-cycle, where $k \geq 4$ .

It remains to show that $p_1 \cup p_2$ is a full subgraph of $\Gamma $ . Indeed, it follows from the choice of $v_1$ and $v_2$ , the fact that $p_1$ , $p_2$ are of minimum length and that $p_1 \setminus (C_1 \cup C_2) $ , $p_2 \setminus (C_1 \cup C_2)$ belong to distinct components of $\Gamma \setminus FS^{\Gamma }(S)$ .

Obviously, $CC(p_1 \cup p_2)=2$ . By the hypothesis of lemma, we conclude that $\Gamma = p_1 \cup p_2$ .

We assume that $\Gamma $ is a k-cycle ( $k \geq 4$ ). Let G be a proper full subgraph of $\Gamma $ . Then there is a vertex v of $\Gamma $ such that G is a full subgraph of $\Gamma \setminus v$ . We observe that if we remove a vertex from $\Gamma $ , then the resulting graph $\Gamma ^\prime $ is a concatenation of edges. Trivially, $CC(\Gamma ^\prime )=1$ and $CC(G) \leq 1$ for every G full subgraph of $\Gamma ^\prime $ .

4 An increasing property of $\mathrm{dim}_{CC}(\ast )$

Lemma 3.4 will play a vital role to prove our main theorem but it is not enough for a complete proof; we need something stronger. The main result of this paper is an interesting increasing property of $\mathrm{dim}_{CC}(\ast )$ . We will show that $ \mathrm{dim}_{CC}(G) < \mathrm{dim}_{CC}(\Gamma ) $ , for some full subgraphs G of $\Gamma $ .

Lemma 4.1 Let $\Gamma $ be a finite simplicial graph, and let G be a full subgraph of $\Gamma $ . Then $m_C (G) \leq m_C (\Gamma )$ .

Proof By Lemma 3.3, there exists unique clique twins $\mathcal {C}_G$ of G and $\mathcal {C}_{\Gamma} $ of $\Gamma $ . By condition (ii) of definition of clique twins, we observe that for every $C_G \in \mathcal {C}_G$ , there exists a $C_{\Gamma } \in \mathcal {C}_{\Gamma }$ containing $C_G$ . Since G is a full subgraph of $\Gamma $ , this correspondence is 1–1 meaning there are no two distinct cliques of $\mathcal {C}_G$ contained in the same clique of $\mathcal {C}_{\Gamma }$ . Thus, $m_C (G) =\sharp \mathcal {C}_G \leq \sharp \mathcal {C}_{\Gamma} = m_C (\Gamma )$ .

Proposition 4.2 Let $\Gamma $ be a finite simplicial graph. Then

$$ \begin{align*} CC(\Gamma)< m_C (\Gamma). \end{align*} $$

Proof It is suffices to show the proposition for connected graphs. If $\Gamma $ is a clique, then the proposition holds. We assume that the graph is not a clique. We denote by $\mathcal {C}_{\Gamma} $ the unique clique twin of $\Gamma $ .

Since $\Gamma $ is connected, there exists at least two cliques of $\mathcal {C}_{\Gamma} $ intersecting each other. Let $C_1$ be a clique of $\mathcal {C}_{\Gamma} $ such that there exists another element of $\mathcal {C}_{\Gamma} $ intersecting $C_1$ . Let F be a subclique of $C_1$ of maximal cardinality such that there exists $C_2 \in \mathcal {C}_{\Gamma} $ and $C_1 \cap C_2=F$ .

We set $C_i^c=C_i \setminus F$ ( $i=1,2$ ) and $\Gamma ^\prime = \Gamma \setminus (C_1^c \cup C_2^c)$ . Obviously, all of them are full subgraphs of $\Gamma $ .

Claim 1: $\Gamma ^\prime $ separates $\Gamma $ .

If not, then there exists an edge $e=[v_1,v_2]$ , where $v_i \in C_i^c$ . But then the clique $F^\prime =FS^{\Gamma} (F \cup v_1) \subseteq C_1$ has strictly larger cardinality from F, and the clique $C_3=FS^{\Gamma} (F^\prime \cup v_2) $ intersects $\Gamma $ on $F^\prime $ , which is a contradiction by the choice of F.

Claim 2: $m_C(\Gamma ^\prime ) < m_C(\Gamma )$ .

We denote by $\mathcal {C}_{\Gamma ^\prime }$ , the unique clique twin of $\Gamma ^\prime $ . Observe that distinct elements of $\mathcal {C}_{\Gamma ^\prime }$ belong to distinct elements of $\mathcal {C}_{\Gamma }$ . Thus, if the claim is not true (i.e., $\mid \mathcal {C}_{\Gamma ^\prime } \mid =\mid \mathcal {C}_{\Gamma } \mid $ ), there are distinct elements $B_1, B_2 \in \mathcal {C}_{\Gamma ^\prime }$ such that $B_i \subseteq C_i$ ( $i=1,2$ ). By the definition of $\Gamma ^{\prime }$ , we have that $B_i \subseteq F$ , but both $B_1$ and $B_2$ are maximal in $\Gamma ^\prime $ , thus $B_1=F=B_2$ , which is a contradiction.

By Claim 1 and the fact that $\Gamma $ is finite, there exists a vertex cut $S \subseteq \Gamma ^\prime $ . Then $CC(\Gamma ) \leq m_C(FS^{\Gamma} (S)) \leq m_C(\Gamma ^\prime ) < m_C(\Gamma ).$

Proposition 4.3 Let $\Gamma $ be a connected finite simplicial graph, and let S be a minimal vertex cut of $\Gamma $ . Then

$$ \begin{align*}CC(FS^{\Gamma}(S))< CC (\Gamma).\end{align*} $$

Proof By Proposition 4.2, we have that $CC(FS^{\Gamma} (S))< m_C(FS^{\Gamma} (S)) = CC(\Gamma )$ .

The next theorem is the main result of this section.

Theorem 4.4 Let $\Gamma $ be a connected finite simplicial graph, and let S be a minimal vertex cut of $\Gamma $ . Then, for every full subgraph G of $FS^{\Gamma} (S)$ , we have the following:

$$ \begin{align*}\mathrm{dim}_{CC}(G)< \mathrm{dim}_{CC} (\Gamma).\end{align*} $$

In particular, $\mathrm{dim}_{CC}(FS^{\Gamma} (S))< \mathrm{dim}_{CC} (\Gamma ).$

Proof Let H be a full subgraph of G, observe that H is a full subgraph of $\Gamma $ as well. By Proposition 4.2 and Lemma 4.1, we have that $CC(H)< m_C (H) \leq m_C(G) \leq m_C(FS^{\Gamma} (S))=CC (\Gamma ) $ . Thus $CC(H)<CC(\Gamma )$ .

5 Asymptotic dimension of RACGs

Theorem 5.1 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . Then $W_{\Gamma }$ is the fundamental group of a graph of groups such that $\mathrm{asdim}(G_v) \leq \mathrm{dim}_{CC}(\Gamma )$ for every vertex group and $\mathrm{asdim}(G_e) < \mathrm{dim}_{CC}(\Gamma )$ for every edge group. In particular,

$$ \begin{align*}\mathrm{asdim} W_{\Gamma} \leq \mathrm{dim}_{CC} (\Gamma).\end{align*} $$

If $\Gamma $ is not connected, then $\mathrm{asdim} W_{\Gamma} \leq \max \lbrace 1, \mathrm{dim}_{CC} (\Gamma ) \rbrace .$

Proof We will use induction on $\sharp V(\Gamma )$ . If $\sharp V(\Gamma )=1$ , the theorem is obviously true. We assume that for any graph with $\sharp V(\Gamma )< N+1$ , the theorem holds. Let $\Gamma $ be a graph such that $\sharp V(\Gamma )= N+1$ .

By Theorem 2.3, it is enough to prove the inequality only for RACGs with connected defining graphs. So we assume that the graph is connected. If the graph $\Gamma $ is a clique, then by Lemma 3.2, the theorem holds. So we further assume that the graph is not a clique. Since the graph is not a clique, there is a subset of its vertices separating it, thus, there is at least one vertex cut of $\Gamma $ . Let S be a minimal vertex cut of the graph, and let $E_1, \ldots , E_k$ be the connected components of $\Gamma \setminus FS^{\Gamma} (S)$ . Observe that since S is a vertex cut, we have that for every vertex s of S and every component $E_i$ , there exists at least one edge connecting them. We set $\overline {E_i}=FS^{\Gamma} (E_i \cup S)$ , observe that $\overline {E_i}$ is a connected full subgraph of $\Gamma $ ; and thus, by lemma 3.4, $\mathrm{dim}_{CC}(\overline {E}_i) \leq \mathrm{dim}_{CC}(\Gamma )$ . By the inductive hypothesis $\mathrm{asdim} W_{\overline {E}_i} \leq \mathrm{dim}_{CC}(\overline {E}_i)$ , so

(1) $$ \begin{align} \mathrm{asdim} W_{\overline{E}_i} \leq \mathrm{dim}_{CC}(\Gamma), \end{align} $$

where $ W_{\overline {E}_i} $ is the parabolic subgroup of $W_{\Gamma} $ defined by $\overline {E}_i$ (of course, $W_{\overline {E}_i}$ is RACG). Using Theorem 4.4, we have $\mathrm{dim}_{CC}(FS^{\Gamma} (S)) < \mathrm{dim}_{CC}(\Gamma )$ . We distinguish two cases.

Case 1: $FS^{\Gamma} (S)$ is connected.

By the inductive hypothesis $\mathrm{asdim} W_{FS^{\Gamma} (S)} \leq \mathrm{dim}_{CC}(FS^{\Gamma} (S))$ , then

(2) $$ \begin{align} \mathrm{asdim} W_{FS^{\Gamma} (S)} < \mathrm{dim}_{CC}(\Gamma), \end{align} $$

where $ W_{FS^{\Gamma} (S)} $ is the parabolic subgroup of $W_{\Gamma} $ defined by $FS^{\Gamma} (S)$ (of course, $W_{FS^{\Gamma} (S)}$ is RACG).

Finally, observe that $W_{\Gamma} $ can be obtained from $W_{\overline {E}_i}$ after a finite sequence of amalgamated product over $W_{FS^{\Gamma} (S)} $ . To be more precise,

(3) $$ \begin{align} W_{\Gamma} = (W_{\overline{E}_1 } \underset{W_{FS^{\Gamma} (S)}}{\ast} W_{\overline{E}_2}) \underset{W_{FS^{\Gamma} (S)}}{\ast} \ldots W_{\overline{E}_k}. \end{align} $$

In other words, $W_{\Gamma }$ is the fundamental group of a graph of groups with vertex groups $W_{\overline {E}_i }$ and $W_{FS^{\Gamma} (S)}$ , and edge groups isomorphic to $W_{FS^{\Gamma} (S)}$ . Applying Theorems 2.1 or 2.2, we conclude that $\mathrm{asdim} W_{\Gamma} \leq \mathrm{dim}_{CC} (\Gamma ).$

Case 2: $FS^{\Gamma} (S)$ is not connected.

By equality (3), we observe that to complete the proof of the theorem, it’s enough to show that $\mathrm{asdim} W_{FS^{\Gamma} (S)}< \mathrm{dim}_{CC} (\Gamma )$ .

Let $C_1,\ldots ,C_\lambda $ be the connected components of $FS^{\Gamma} (S)$ ( $\lambda \geq 2$ ). Without loss of generality, we may assume that the $\mathrm{dim}_{CC}(C_i) \leq \mathrm{dim}_{CC}(C_\lambda )$ , for any i. By the inductive hypothesis $\mathrm{asdim} W_{C_i} \leq \mathrm{dim}_{CC}(C_\lambda )$ . So, by Theorem 2.3,

(4) $$ \begin{align} \mathrm{asdim} W_{FS^{\Gamma} (S)}= \max \lbrace 1, \mathrm{dim}_{CC}(C_\lambda) \rbrace. \end{align} $$

We distinguish two subcases.

Case 2(a): $\mathrm{dim}_{CC}(C_\lambda ) \geq 1$ .

Then $\mathrm{asdim} W_{FS^{\Gamma} (S)}= \mathrm{dim}_{CC}(C_\lambda ) $ . Since $\mathrm{dim}_{CC}(C_\lambda ) \leq \mathrm{dim}_{CC}({FS^{\Gamma} (S)}) < \mathrm{dim}_{CC}(\Gamma )$ , we conclude that $\mathrm{asdim} W_{FS^{\Gamma} (S)}< \mathrm{dim}_{CC}(\Gamma )$ .

Case 2(b): $\mathrm{dim}_{CC}(C_\lambda ) =0$ .

Then $\mathrm{asdim} W_{FS^{\Gamma} (S)}= 1$ . Since S is a minimal vertex cut, and $FS^{\Gamma} (S)$ is not connected, we obtain that $\mathrm{dim}_{CC}(\Gamma ) \geq 2$ . Thus, $\mathrm{asdim} W_{FS^{\Gamma} (S)}< \mathrm{dim}_{CC}(\Gamma )$ .

We observe that the previous theorem is also true for Coxeter groups such that every clique in their defining graph defines a finite Coxeter subgroup. As a corollary of Theorem 5.1, we have the following theorem.

Theorem 5.2 Let $W_{\Gamma} $ be the RACG with defining graph $\Gamma $ . Then

$$ \begin{align*}\mathrm{asdim} W_{\Gamma} \leq \min \lbrace \mathrm{dim}_{CC} (\Gamma), \mathrm{dim}\Sigma(W_{\Gamma}) \rbrace.\end{align*} $$

If $\Gamma $ is not connected, then $\mathrm{asdim} W_{\Gamma} \leq \max \lbrace 1, \min \lbrace \mathrm{dim}_{CC} (\Gamma ) , \mathrm{dim}\Sigma (W_{\Gamma} ) \rbrace \rbrace .$

5.1 Graph products of finite groups

We recall the definition of graph products of groups. Let $\Gamma $ be a simplicial graph. We label every vertex v of the graph by a vertex group $G_v$ . The graph product $\mathbb {GP}(\Gamma ,G_v)_{v\in V(\Gamma )}$ is the free product of the vertex groups modulo the relations $xyx^{-1}y^{-1}$ , where $x \in G_v$ , $y \in G_w$ , and $v, w$ are connected by an edge.

Graph products generalize free products, direct products, RAAGs, and RACGs.

We set $G=\mathbb {GP}(\Gamma ,G_v)_{v\in V(\Gamma )}$ . For a full subgraph X of $\Gamma $ , we define the graph product $G \mid _X$ as $\mathbb {GP}(X,G_v)_{v\in V(X)}$ .

Theorem 5.3 Let $\Gamma $ be a finite connected simplicial graph along with a finite collection of finite vertex groups. Then

$$ \begin{align*}\mathrm{asdim}\, \mathbb{GP}(\Gamma,G_v)_{v\in V(\Gamma)} \leq \mathrm{dim}_{CC} (\Gamma).\end{align*} $$

If $\Gamma $ is not connected, then $\mathrm{asdim}\, \mathbb {GP}(\Gamma ,G_v)_{v\in V(\Gamma )} \leq \max \lbrace 1, \mathrm{dim}_{CC} (\Gamma ) \rbrace .$

Proof The proof of this theorem is almost identical to the proof of Theorem 5.1. We only need the fact that if X is a full subgraph of $\Gamma $ , then $G \mid _X$ is a subgroup of $\mathbb {GP}(\Gamma ,G_v)_{v\in V(\Gamma )}$ (see [9]). The subgroups $G \mid _X$ are the analogs of the parabolic subgroups of RACGs.

6 Corollaries of the main result

Proposition 6.1 Let $\Gamma $ be a simplicial graph such that $\mathrm{dim}_{CC}(\Gamma ) \geq 2$ . Then the RACG $W_{\Gamma} $ defined by $\Gamma $ contains a one-ended parabolic subgroup.

Proof $\Gamma $ contains a full subgraph G such that $CC(G) \geq 2$ . We assume that G is a minimal full subgraph of $\Gamma $ such that $CC(G) \geq 2$ . Trivially, G is connected. Since G is minimal, we have that $CC(G^\prime ) \leq 1$ for every $G^\prime $ proper full subgraph of G, so by Lemma 3.5, G is a k-cycle ( $k \geq 4$ ).

By Theorem 8.7.2 of [3], we have that the parabolic subgroup $W_G$ of $W_{\Gamma} $ defined by G is one-ended.

Proposition 6.2 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . If $\mathrm{dim}_{CC}(\Gamma )\leq 2$ , then $\mathrm{asdim} W_{\Gamma} = \mathrm{dim}_{CC}(\Gamma )$ .

Proof If $\mathrm{dim}_{CC}(\Gamma )=0$ , then $\Gamma $ is a clique, so $W_{\Gamma} $ is finite. Then $\mathrm{asdim} W_{\Gamma} =0$ .

If $\mathrm{dim}_{CC}(\Gamma )=1$ , then by Theorem 5.1, we have $\mathrm{asdim} W_{\Gamma} \leq 1$ . By Lemma 3.2, $\Gamma $ is not a clique; and thus, there are two vertices $a,b$ which are not connected by an edge. This means that $W_{\Gamma} $ contains $\mathbb {Z}_2 \ast \mathbb {Z}_2$ as a parabolic subgroup, so $\mathrm{asdim} W_{\Gamma} = 1$ .

If $\mathrm{dim}_{CC}(\Gamma )=2$ , then by Theorem 5.1, we have $\mathrm{asdim} W_{\Gamma} \leq 2$ . By Proposition 6.1, we have that there exists an one-ended parabolic subgroup $W_G$ of $W_{\Gamma} $ . Then, by the main theorem of [8], we obtain that $2 \leq \mathrm{asdim} W_G$ . So $\mathrm{asdim} W_{\Gamma} = 2$ .

Corollary 1 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . Then $W_{\Gamma} $ is finite if and only if $\mathrm{dim}_{CC}(\Gamma )=0$ .

Proof Suppose that $W_{\Gamma} $ is finite. Then $\Gamma $ is a clique, indeed, otherwise $W_{\Gamma} $ contains $\mathbb {Z}_2 \ast \mathbb {Z}_2$ as a parabolic subgroup, so $\mathrm{asdim}W_{\Gamma}>0$ . Which is a contradiction. Since $\Gamma $ is not a clique, by Lemma 3.2, we obtain $\mathrm{dim}_{CC}(\Gamma )=0$ .

The other direction follows by the previous proposition.

When $\Gamma $ is connected and has clique-connected dimension one, the graph looks like a “thick” tree.

Proposition 6.3 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . Then $W_{\Gamma} $ is virtually free if and only if $\mathrm{dim}_{CC}(\Gamma )=1$ .

Proof We assume that $W_{\Gamma} $ is virtually free. If $\mathrm{dim}_{CC}(\Gamma ) \geq 2$ , then, by Proposition 6.1, $W_{\Gamma} $ contains an one-ended parabolic subgroup. Since one-ended groups have asymptotic dimension at least two (see [8]), we have that $\mathrm{asdim}W_{\Gamma} \geq 2$ . By the fact that the asymptotic dimension of virtually free groups is one (see [8]), we have a contradiction.

If $\mathrm{dim}_{CC}(\Gamma ) =0$ , then $\Gamma $ is a clique. In that case, $W_{\Gamma} $ is finite, which is a contradiction.

Suppose that $\mathrm{dim}_{CC}(\Gamma )=1$ , then, by Proposition 6.2, we have $\mathrm{asdim} W_{\Gamma} = 1$ . Applying Gentimis’ theorem for virtually free groups (see [8]), we conclude that $W_{\Gamma} $ is virtually free.

Remark 1 It is known by Lohrey and Senizergues (see [11]) that a RACG is virtually free if and only if its defining graph $\Gamma $ is chordal (i.e., does not contain k-cycles as a full subgraph for $k \geq 4$ ). We note that, in their paper, they consider finite groups as virtually free groups.

Remark 2 It is easy to see that a graph $\Gamma $ is chordal if and only if $\mathrm{dim}_{CC}(\Gamma ) \leq 1$ . Indeed, if a graph $\Gamma $ is chordal and $\mathrm{dim}_{CC}(\Gamma )\geq 2$ , then there exists a full subgraph $\Gamma ^{\prime }$ such that $CC(\Gamma ^{\prime })\geq 2$ . Thus, by Lemma 3.5, we have a contradiction.

Now, suppose that $\mathrm{dim}_{CC}(\Gamma ) \leq 1$ and that $\Gamma $ is connected (w.l.o.g). Since cliques are complete graphs, we further assume that $\Gamma $ is not a clique. By Lemma 3.2, we have that $\mathrm{dim}_{CC}(\Gamma ) = 1$ . Then, by the definition of the clique-connected dimension and the fact that $CC(k$ -cycle $)=2$ ( $k\geq 4$ ), we have that $\Gamma $ is chordal. This proves our statement.

One can also show the fact in Remark 2 by using Theorem 2.1 from [4], and the observation that vertex cuts are minimal vertex separators in the sense of Dirac (see [4]).

As a corollary of Proposition 6.3, we obtain the following proposition.

Proposition 6.4 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . Then $\mathrm{asdim}(W_{\Gamma} ) \geq 2$ if and only if $\mathrm{dim}_{CC}(\Gamma )\geq 2$ .

Proof We suppose that $\mathrm{asdim}(W_{\Gamma} ) \geq 2$ , then, by Theorem 5.1, we have that $\mathrm{dim}_{CC}(\Gamma )\geq 2$ .

Conversely, we assume that $\mathrm{dim}_{CC}(\Gamma ) \geq 2$ , then, by the previous proposition and the fact that the only groups having asymptotic dimension one are the virtually free groups (see [8]), we have that $\mathrm{asdim}(W_{\Gamma} ) \neq 1$ . Obviously, $\mathrm{asdim}(W_{\Gamma} ) \neq 0$ , otherwise we have a contradiction by Corollary 1.

Observe that Proposition 6.3 and Corollary 1 can be rephrased as follows:

$$ \begin{align*} \textrm{Corollary 1: } \mathrm{asdim}W_{\Gamma}=0\textrm{ if and only if }\mathrm{dim}_{CC}(\Gamma)=0. \end{align*} $$

$$ \begin{align*} \textrm{Proposition 6.3: } \mathrm{asdim}W_{\Gamma}=1\textrm{ if and only if }\mathrm{dim}_{CC}(\Gamma)=1. \end{align*} $$

We know, by Proposition 6.2, that if $\mathrm{dim}_{CC}(\Gamma )=2$ , then $\mathrm{asdim}W_{\Gamma} =2$ . One may ask whether the converse is true. We note that by the previous proposition if $\mathrm{asdim}(W_{\Gamma} ) = 2$ , then $\mathrm{dim}_{CC}(\Gamma )\geq 2$ .

Question Is there any connected graph such that the RACG defined by the graph has asymptotic dimension two while the clique-connected dimension of the graph is greater than two?

The answer is yes. We will construct a graph X with clique-connected dimension equal to three while $\mathrm{asdim}W_X=2$ . Let $X_1$ , $X_2$ , and $X_3$ be 4-cycles with vertices $\lbrace v_1^1,\ldots ,v^1_4 \rbrace , \lbrace v_1^2,\ldots ,v^2_4\rbrace $ , and $\lbrace v_1^3,\ldots ,v^3_4 \rbrace $ . We join the vertices $v^i_j,v^{i+1}_j$ with edges. The resulting graph X has clique-connected dimension equal to three. The graph X is actually the 1-skeleton of a cube complex, thus $\mathrm{Sim}(X)=2$ .

By $\mathrm{Sim}(\Gamma )$ , we denote the number of vertices of a maximal clique of $\Gamma $ . It turns out that the dimension of the Davis complex of $W_{\Gamma} $ is equal to $\mathrm{Sim}(\Gamma )$ . Using the Dranishnikov’s upper bound (see [5]) and the fact that $W_{X}$ is one ended, we obtain that $\mathrm{asdim}W_{X}=2$ .

Thus, an analog of Corollary 1 and Proposition 6.3 for asymptotic dimension two doesn’t exist. However, we have the following proposition.

Proposition 6.5 Let $W_{\Gamma} $ be the RACG with connected defining graph $\Gamma $ . If $\mathrm{asdim}W_{\Gamma} =2$ , then there exists a full subgraph G of $\Gamma $ such that $\mathrm{dim}_{CC}(G)=2$ and $\mathrm{asdim}W_G =2$ .

Proof By Theorem 5.1, $\mathrm{dim}_{CC}(\Gamma )\geq 2$ . By the proof of Proposition 6.1, $\Gamma $ contains a k-cycle G as a full subgraph ( $k \geq 4 $ ). Trivially, $\mathrm{dim}_{CC}(G)=2$ .