Coat colour in mouse populations selected for weight gain: support for hitchhiking, not pleiotropy

Summary

With many molecular markers in many species, research efforts in quantitative genetics have focused on dissecting these traits and understanding the importance of factors such as correlated response due to hitchhiking or pleiotropy. Here, in an examination of long-term selection experiments in mice, the evidence strongly supports the primary importance of hitchhiking on the coat colour loci brown and dilute in mice selected for high weight gain. First, the amount of observed change in coat colour allele frequency could not be explained by genetic drift alone, implying that selection was of high importance. Second, the allele frequency changes included reversals in the direction change, but there were still positive correlations in the early generations with differences in weight gain between the phenotypes. Third, the correlation between the change in allele frequencies and phenotypic difference in weight gain declined over time, consistent with the decay expected from linkage associations. Fourth, the changes at both loci in a short-term selection experiment for low weight gain were in the opposite direction than the changes in the contemporaneous related population selected for high weight gain.

Introduction

Determining the genetic basis of complex traits is the focus of extensive recent research using molecular genomic markers (Flint & Mackay, 2009). Before genomic examination was possible, long-term selection experiments and related crosses were used to characterize and estimate the amount of genetic response and the types of genetic variation important for quantitative traits (Comstock, 1996; Falconer & Mackay, 1996; Lynch & Walsh, 1998). These experiments statistically evaluated the importance of pleiotropy, epistasis, dominance and linkage as well as the genetic architecture, the number of genes and their effects influencing quantitative traits. For example, the role of various causes of the ultimate cessation of the response to directional selection, such as loss of genetic variation, negative genetic correlation with fitness traits and overdominance (heterozygote advantage), was of particular interest.

When there was polymorphism for visible traits in long-term selection experiments, potential insight into the relative significance of hitchhiking (linked gene effects) and pleiotropy on correlated response was possible. In general, associations between characters can be ephemeral, as that caused by linkage disequilibrium between genes influencing traits, or more persistent as that resulting from pleiotropic effects. Given selection for a particular trait, if the association with another trait is due to pleiotropy, then the response should be more constant, predictable and long term than if the association results from linkage associations which could decay and change over time.

The visible traits that were segregating in the mouse populations examined here were the coat colour genes brown (with recessive allele b) and dilute (with recessive allele d). The brown (b) gene is now known as Tryp1 or Tyrosinase-related protein and codes for a melanosomal protein on chromosome 4 in the mouse (Bennett & Lamoreux, 2003). The homologous gene in humans is known as TRYP1, is located on chromosome 9, and variants can cause oculocutaneous albinism type 3 (OCA3). Interestingly, blond hair in Melanesians and colour polymorphism in a free-living population of sheep are caused by variants at the TRYP1 locus (Gratten et al., 2007; Kenny et al., 2012). The dilute (d) gene is now known as Myo5a or Myosin Va and codes for the melanosome transport molecule on chromosome 9 in the mouse (Bennett & Lamoreux, 2003). The homologous gene in humans is known as MY05A, is located on chromosome 15, and variants can cause Griselli syndrome. Interestingly, one of the first inbred mouse stains was called DBA, named because it was homozygous at the coat colour mutations dilute (d), brown (b) and agouti (a) (Steingrimsson et al., 2006). C. C. Little began inbreeding this line in 1909 and it has been widely used in many research areas including cardiovascular biology, neurobiology, sensorineural research and quantitative genetics research discussed below.

In early studies, mice homozygous for both the recessive mutant brown and dilute phenotypes were observed to have larger body size than wild-type mice (Feldman, 1935; Green, 1935; Castle et al., 1936; Castle, 1941). This effect could be attributed to pleiotropy where the coat colour genes directly influenced body weight or to linkage associations where the coat colour genes are associated by linkage to genes (quantitative trait loci (QTLs)) affecting body weight. For example, Castle et al. (1936) measured body weight for different backcrosses for both brown (bb) and dilute (dd) and their black (Bb) and non-dilute (Dd) sibs and found that larger size was associated with mice having the recessive phenotypes, implying a pleiotropic effect. Subsequently, MacArthur (1949) carried out a two-way selection experiment for body weight and found that his high line was mostly bbdd and his low line mostly BBDD, consistent with the findings of Castle et al. (1936).

On the other hand, Green (1935) measured body size in brown and heterozygous black mice and found that body size differences between colour phenotypes varied between different backcrosses and suggested that these effects were caused by different linkages between the brown locus and genes affecting body weight. Butler (1954) crossed MacArthur's high line with two different inbred lines homozygous for the non-dilute allele and found that non-dilute mice were larger in the F₂ and backcrosses. Based on these results and other related ones, Butler (1954) suggested that differential linkage between the dilute locus and genes affecting body size was the source of these effects.

Ralph Comstock and his colleagues and students (Rahnefeld et al., 1963) carried out long-term selection experiments for post-weaning weight gain (18–42 days of age) in mice from 1957 to 1976. These experiments were funded by the National Science Foundation at the University of Minnesota to determine with statistical tools the type of gene action, such as dominance and epistasis, the basis for plateaued response to selection and the number of genes influencing weight gain in mice. In addition, the selected populations were segregating for these two coat colour loci (marker loci). In an analysis of the first part of these experiments (Hedrick & Comstock, 1968), it appeared that linkage associations between the coat colour genes and genes influencing weight gain were significant and that pleiotropy for weight gain by the coat colour genes was less likely.

Keightly & Bulfield (1993) examined populations selected for large or small body size which were started from crosses of inbred lines that differed at the brown and dilute loci (one of the lines they used was a DBA strain). The frequency of the b allele increased over 20 generations in the six large select lines (0·65) and decreased in the six small select lines (0·09), while the frequency of the d allele declined in the large select lines (0·15) and increased in the small selection lines (0·84). Keightly & Bulfield (1993) and Heath (1995) concluded that these effects were the result of linkage of the coat colour alleles to body size QTLs rather than a direct pleiotropic effect of the coat colour alleles on body size. Heath (1995) analysed these data and estimated that there was a QTL 10 cM from dilute with an effect on body weight of 0·40 g. On the other hand, Heath (1995) estimated that there was a QTL 45 cM from brown with an effect on body weight of 1·70 g, but that it was ‘difficult to draw any firm conclusions … about the QTL linked to brown.’ Finally, from examination of 927 F₂ individuals, Morris et al. (1999) identified QTLs for body weight on chromosomes 4 and 9, consistent with previous findings of linkage of QTLs with brown and dilute genes (on chromosomes 4 and 9).

Recently, there has been renewed interest in the extent of pleiotropy for quantitative traits. For example, Stearns (2010) reviewed the history of the concept of pleiotropy and provided a prospective for pleiotropy in genomics today. Subsequently, Wagner & Zhang (2011) provided a theoretical context for pleiotropy for quantitative traits and suggested that universal pleiotropy (every gene influences every trait) was not empirically supported. In contrast, Hill & Zhang (2012) stated that the evaluation of the nature of pleiotropy is highly dependent upon statistical assumptions and that the extent of pleiotropy is not necessarily limited. In addition, genome-wide studies for complex diseases and traits in humans have found abundant evidence of pleiotropy (e.g. Sivakumaran et al., 2011). More specifically, considering pleiotropic effects of coat colour genes on weight in mice, there is evidence that the gene agouti influences obesity (Klebig et al., 1995) and that Mc4r (a G protein-coupled receptor related to the colour gene Mc1r) also has impacts on obesity (Ste. Marie et al., 2000).

Here, data are examined from the remainder of the generations of the selection experiments carried out by R. Comstock and his colleagues and assessed whether the data from the total experiments are consistent with an explanation based mainly on linkage associations of the coat colour variants with loci influencing weight gain or on pleiotropy. In addition, the potential role of genetic drift in the variation of allele frequencies over time and in generating linkage disequilibrium between the coat colour loci is examined.

Methods

The populations of mice examined here originated at different times by crossing the same two unrelated inbred lines (Rahnefeld et al., 1963). The two inbred lines had been maintained by full-sib mating for 25 or more generations and were fixed for the mutant brown and dilute alleles (genotype bbdd) and the black and non-dilute alleles (genotype BBDD), respectively. As a result, the initial allele frequency in the selection populations was 0·5 for the coat colour alleles and any other alleles that differed between the lines. Also, because the selected populations were the result of a cross between lines, there was the maximum linkage disequilibrium possible in the initial generation. The two inbred lines were similar in weight gain. The F₂ and F₃ generations of the selection lines were produced by mating random individuals within the F₁ and F₂ generations, respectively. Selection for a post-weaning growth rate began in the F₃, which was designated as generation 1 for each of the populations. The selection criterion was individual post-weaning weight gain from 18 to 42 days and the selected mice were randomly mated with the restriction that no brother–sister matings were permitted (some other efforts were made to minimize inbreeding within the lines; Rahnefeld et al., 1963). The first selection line S for increased weight gain was started in 1957 and the second one S′ was started 15 generations later in 1961. Two other similar short-term selection populations, S″ and S″′, and one low selection population, were started at different times later, and will be discussed only briefly here.

The number of litters per generation in a selection population was ordinarily 40 or more with 20 or more males used with each male mated with two or more females. The numbers were generally greater than these values and never fell short of these values by more than a very few individuals or litters. The effective population size when there are different numbers of female and male parents can be estimated as

(1)$$N_{\rm e} \equals {{4N_{\rm f} N_{\rm m} } \over {N_{\rm f} \plus N_{\rm m} }}\comma $$

where N _f and N _m are the numbers of female and male parents (Wright, 1931; Hedrick, 2011). Given that N _f = 40 and that N _m = 20, then an estimate of N _e is approximately 53, or perhaps somewhat more if there were more parents and litters and if other efforts to minimize inbreeding increased N _e. For example, for 10 generations in the early part of the S population, the mean number of male parents was 21·4 and the mean number of female parents was 65·2, giving N _e = 64·4 for this period. On average for the S and S′ populations, 331 and 347 progeny per generation were scored and measured. Therefore, as basic numbers for the calculations and examinations below, it was assumed that there were 60 effective parents that produced 300 progeny per generation. Deviations from the number of parents were examined in relevant situations to determine the impact of other values.

Mice coat colour in progeny of each generation was classified as either black (B-D-), silver-grey (B-dd), brown (bbD-), or dilute brown (bbdd). Different colours of mice can be seen in Silvers (1979) which is also online at http://www.informatics.jax.org/wksilvers/. The frequency of the recessive allele b in each generation was estimated as

(2a)$$p_{b} \equals \left( {{{N_{bb} } \over N}} \right)^{\setnum{1}\sol \setnum{2}} \comma $$

where N_bb and N are the numbers of bb homozygotes and the total number of individuals scored (the frequency of allele B was p_B). The frequency of the recessive d allele in each generation was estimated as

(2b)$$q_{d} \equals \left( {{{N_{dd} } \over N}} \right)^{\setnum{1}\sol \setnum{2}} \comma $$

where N_dd is the numbers of dd homozygotes (the frequency of allele D was q_D).

To examine whether genetic drift could result in the observed changes in allele frequency, simulations were carried out where in each generation a given number of diploid offspring was generated with phenotypes as indicated and the allele frequencies were estimated as described above. From these individuals, a given number of individuals were randomly selected as parents for the next generation. The change in the estimated allele frequency was calculated for each generation and the average absolute value of the allele frequency change was determined. Simulations were run for 70 generations to mimic the S population and only simulated populations that were polymorphic for 70 generations were used. In all cases, the replicate–generation numbers used to calculate the mean average absolute allele frequency change were at least 500 000.

A general measure of linkage disequilibrium between two loci (here for the two coat colour loci) is

(3a)$$D \equals x_{bd} \minus p_{b} q_{d} \comma $$

where x_bd is the frequency of gamete bd and is estimated as

$$x_{bd} \equals \left( {{{N_{bbdd} } \over N}} \right)^{\setnum{1}\sol \setnum{2}} .$$

Linkage disequilibrium was estimated using the standardized measure of Lewontin (1964)

(3b)$$D\prime \equals {D \over {D_{\max } }}\comma $$

where D _max is the maximum D possible for a given set of allele frequencies at the two loci. That is, D _max is equal either to the lesser of p_Bq_d or p_bq_D if D is positive or to the lesser of p_Bq_D or p_bq_d if D is negative. Linkage disequilibrium significance was tested with the likelihood ratio statistic

(4)$$Q \equals {{4ND^{\setnum{2}} } \over {p_{B} \lpar 2 \minus p_{B} \rpar q_{D} \lpar 2 \minus q_{D} \rpar }}\comma $$

which is approximately χ² distributed with one degree of freedom (Hill, 1974).

In addition, the probability using Fisher's exact test that the level of linkage disequilibrium as extreme as that observed was calculated (Lewontin, 1995; Weir, 1996). In this case, the number of phenotypes of the four classes, B-D-, B-dd, bbD- and bbdd, and the marginal numbers of the four phenotypic classes, B-, bb, D- and dd, are as given in Table 1. The probability of an array with these numbers of phenotypes, given the marginal numbers of phenotypes in Table 1, is

(5)$$\eqalign{\tab{\Pr \lpar N_{B \hbox{-} D\hbox{-}} \comma N_{B \hbox{-} dd} \comma N_{bbD \hbox{-} } \comma N_{bbdd} \left\vert {N_{B\hbox{-} } \comma N_{D\hbox{-} } } \right.\rpar }\cr\tab\quad \equals{{N_{B\hbox{-} } \exclam N_{bb} \exclam N_{D \hbox{-} } \exclam N_{dd} \exclam } \over {N_{B\hbox{-} D\hbox{-} } \exclam N_{B\hbox{-} dd} \exclam N_{bbD\hbox{-} } \exclam N_{bbdd} \exclam N\exclam }}.}$$

All possible samples with the same marginal totals were generated and the probability and the amount of linkage disequilibrium for each sample calculated. The cumulative probability of observing a given array by chance is then calculated by summarizing the probabilities for all the samples with linkage disequilibrium greater than, or equal to, that in the observed sample.

Table 1. Symbols indicating the numbers of the four phenotypic classes for the two coat colour loci and the marginal numbers for each locus

Finally, simulations were run designed to mimic the populations with a given number of offspring in each generation in which the linkage disequilibrium was measured and a given number of parents for the next generation. In these simulations, no linkage was assumed between the two loci and linkage disequilibrium was generated from genetic drift resulting from the limited number of parents in each generation. Simulations were run for 70 generations as for population S, only replicates that were polymorphic for all generations were used, and at least 5000 values of each combination of the number of offspring and parents were generated. The amount of linkage disequilibrium was estimated both using the phenotype frequencies in the offspring, as in the actual data, and using the gametic frequencies known from the simulations.

To examine the effect of artificial selection for weight gain on allele frequency change in the coat colour loci, first the average weight gain of mice with the recessive phenotype (bb or dd) minus the average weight gain of mice with the dominant phenotype (B- or D-) was calculated. Second, the estimated change in allele frequency for the recessive allele between the generation in which the weight gain was measured and the next generation was calculated and then the correlation coefficient between these two values was calculated. For example, a positive correlation coefficient indicates that overall a higher weight gain of the recessive phenotype results in an increase in the recessive allele and that a lower weight gain of the recessive phenotype results in a decrease in the recessive allele.

Results

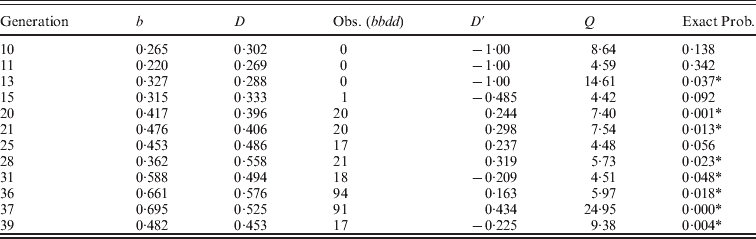
As a background to illustrate the effectiveness of the selection regimes, Fig. 1 gives the weight gain for populations S and S′ over the course of the two experiments. Population S reached a plateau in generations 47–60 with an average weight gain of 20·4 g, nearly double the initial weight gain of 11·0 g (Comstock & Enfield, 1981). In other words, even though the two lines crossed to form the initial population had similar low weight gains, selection resulted in a large increase in weight gain, implying considerable genetic variation in the initial population. Although populations S and S′ were started 15 generations apart (nearly 4 years), the responses for the shared generations were similar. For example, the mean weight gain for the last ten generations (36–45) of population S′ was 20·4, the same average as that for the plateau level observed in the S population.

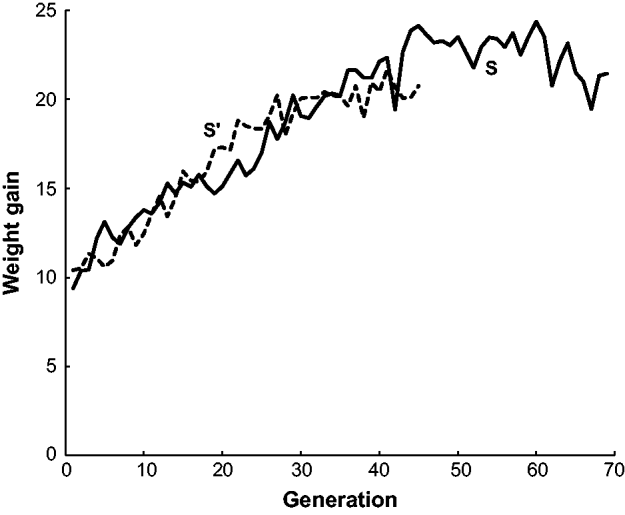
Fig. 1. The mean post-weaning weight gain from 18 to 42 days for mice in two long-term selection populations, S and S′, for high weight gain.

As further background information for these experiments, the estimate of heritability of weight gain in the narrow sense over the first 17 generations of selection for line S was about 0·25 for both males and females (Rahnefeld et al., 1963). Using the selective response for weight gain estimated during the same period and a theoretical approach, the estimate of the number of genes contributing to the response, assuming multiplicative gene action and no epistasis, was large and greater than 100 (Comstock & Enfield, 1981).

The estimated frequency of the b allele at the brown locus over the 70 generations of line S and the 45 generations of line S′ are given in Fig. 2. Both populations initially declined in frequency from 0·5 to around 0·2 in generation 10. The frequency of b in S stayed at around this level for the remaining 60 generations. On the other hand, the frequency of b in S′ increased to nearly 0·7 in generation 36 and then declined to 0·26 in the last generation 45. In other words, S′ appeared to have two reversals in allele frequency from the initial decline while S had none. Neither population appeared to be approaching fixation at the termination of the experiment. There are also data from two other short-generation populations, S″ and S″′, not given in Fig. 2. In generations 1–3 of S″, the frequency of b was close to 0·5 and then in generations 4–6 increased to around 0·6. In generations 1–3 of S″′, the frequency of b was close 0·5 but in generations 4 and 5 declined to nearly 0·3.

Fig. 2. The estimated frequency of the brown (b) allele for mice in two long-term selection populations, S and S′, for high weight gain.

The estimated frequency of the d allele at the dilute locus is given for lines S and S′ in Fig. 3. There is little change in both populations in the first few generations but then d increases in S to 0·78 in generation 31 and then declines to around 0·2 at the end of the experiment. On the other hand, S′ initially declines to below 0·3, then increases to nearly 0·6, and then declines to nearly 0·3 at the end of the experiment. This pattern for d is similar to the two reversals in b allele frequency also observed in S′. Although both populations declined in frequency by the end of the experiments neither appeared to be approaching fixation. In generations 1 and 2 of S″, the frequency of d was close to 0·5 and then in generations 4–6 decreased to around 0·3. In generations 2–5 of S″′, the frequency of d declined to 0·4.

Fig. 3. The estimated frequency of the dilute (d) allele for mice in two long-term selection populations, S and S′, for high weight gain.

Are these changes consistent with that expected by chance? Hedrick & Comstock (1968) demonstrated that in the first part of these experiments there were significant reversals in the direction of allele frequency change, suggesting that the early changes were the result of genes influencing weight gain linked to the coat colour genes. Here, let us examine if genetic drift generated by the limited number of parents could generate the changes observed over the total period of the populations.

The left side of Table 2 gives the observed average absolute change in allele frequency for populations S and S′ for both loci. Overall, these observed values do not differ very much and the mean of the four values is 0·053. Simulations were done to determine if this level of average change could be generated by a limited number of parents (small effective population size). The right side of Table 2 gives these average values for four different numbers of parents. All of these theoretically generated values are less than that observed. From the way each generation of the populations were set up with 20 males mated to two or more females, and efforts made to reduce inbreeding, it is unlikely that the effective population size is below 50. However, even with N _e = 40, the amount of change per generation (0·044) is below that observed (0·053). In other words, it seems unlikely that all of the variation observed in allele frequency over time was generated by genetic drift and suggests that selection was important causing changes in allele frequency.

Table 2. The observed absolute average change in allele frequency for loci b and d in populations S and S′ (Δp_b or Δq_d) and the simulated absolute average change in allele frequency (Δp) for different effective population sizes (number of parents)

The estimated linkage disequilibrium as measured by D′ between the unlinked b and d loci is given in Fig. 4. Generations where there is significant disequilibrium using the likelihood ratio statistic between the loci are indicated by either solid circles (S) or solid squares (S′). There were very similar percentages of generations with significant disequilibrium for the S population (18 of 70 or 26%) and for the S′ population (12 of 45 generations or 27%). For both populations, the percentage of significant values greatly exceeded the 5% significance level expected.

Fig. 4. The estimated amount of linkage disequilibrium between the brown (b) and dilute (d) alleles using the measure D′ of Lewontin (1964) where the generations with significant linkage disequilibrium are indicated by solid circles for population S and solid squares for population S′.

D′<0 generally occurred when there was a deficiency of bbdd individuals compared with linkage equilibrium expectations and sometimes no bbdd individuals were present which gives D′ = − 1. D′>0 values generally occurred when there was an excess of bbdd individuals compared with expectations or in a few cases where there was a deficiency of bbD-individuals. For population S, 14 of the 18 significant linkage disequilibrium values had D′ < 0 and most of these had either 0 or 1 bbdd individuals. Population S′ had equal numbers of significant D′ < 0 and D′ > 0 values. Most of the D′ < 0 values occurred in the early generations when bbdd individuals were missing and the D′ > 0 values occurred in later generations from an excess of bbdd individuals over expectations.

The generations in populations S and S′ for which there was significant linkage disequilibrium using the likelihood ratio statistic and the exact probability of observing this level of linkage disequilibrium are given in Appendix Tables A1 and A2 along with some other data about these generations. For both populations, the generations with exact probabilities less than 0·05 were subsets of the generations significant using the likelihood ratio statistic. For population S, there were 10 generations (14·3%) that had exact probabilities less than 0·05. That is, 8 of the generations that had significant linkage disequilibrium using the likelihood ratio statistic had exact probabilities greater than 0·05. For example, generation 11 had Q = 6·86 but Pr = 0·102. In this case, D′ = 1 because no bbD- were observed while 4·1 were expected. Generation 18 had Q = 10·93 but Pr = 0·126. In this case, D′ = − 1 because no bbdd were observed while 1·8 were expected. For population S′, there were 8 generations (17·8%) that had exact probabilities less than 0·05 (four of the generations with significant linkage disequilibrium with the likelihood ratio statistic had exact probabilities greater than 0·05). For all generations, the mean observed value of the likelihood ratio statistic was 2·82 and 3·01 for populations S and S′, respectively.

In order to examine the potential impact of the method of linkage disequilibrium estimation on increasing the observed level of linkage disequilibrium, simulation results using the phenotypic approach above was compared with that estimated from the known simulated gametic frequencies (remember gametic numbers are not available from the actual populations but only from these simulations). Table 3 gives these estimates for three different numbers of parents. For 60 parents, the minimum expected number, the phenotypic and gametic approaches gave very similar average Q values (1·44 and 1·48) and percentage of significant Q values (10·3 and 10·2%). Note that the proportion of significant Q values is greater than the 0·05 level expected, but less than that observed in the two populations, even when using the exact probabilities. Note also that the mean value of the likelihood ratio statistic from the simulations for 60 parents was much less than the mean observed value of the statistic.

Table 3. Simulation results with 300 offspring per generation and different numbers of parents for the amount of linkage disequilibrium estimated by Q and the proportion of significant Q values (>3·84) using the number of different phenotypes, as in the experiment, and using the number of gametes in the offspring

By looking at the effect of different numbers of parents, we can determine the impact of genetic drift on the level of linkage disequilibrium. For 80 and 100 effective parents, the level of Q and the proportion of significant Q values was less than that for 60 parents. For example, when there were 100 parents using the number of phenotypes, the percentage of significant Q values declined from 10·3% for 60 parents to 8·3% for 100, indicating that genetic drift does generate some of the observed linkage disequilibrium.

To examine the potential effect of artificial selection changing the frequency of the two coat colour loci, the correlation between the weight gain difference between recessive and dominant phenotypes and the change in recessive allele frequencies is given in Table 4. The first period in populations S (generation 1–33) and S′ (generations 1–18) are from Hedrick & Comstock (1968) where they observed a strong positive correlation for both loci in both populations and the correlation for the b locus in population S and for the d locus in population S′ were significant even though there were reversals in allele frequencies. However, in the second part of the experiments examined here, generations 34–69 in population S and generations 19–42 in population S′, the correlations in all four locus-population combinations were lower and none were statistically significant. Over all the generations, the correlations were non-significant for both loci for population S and for locus b in population S′ while the correlation was still significant for locus d in population S′, presumably because of the strong effect of the early generations.

Table 4. Correlation between the change in allele frequency and the difference in weight gain between dominant and recessive phenotypes for the brown and dilute loci observed in Hedrick & Comstock (1968) (generations 1–33 in populations S and generations 1–18 in population S′) and for the rest of the generations examined here

** P < 0.01.

A population selected for low weight gain was initiated from the S population in generation 8 for six generations. The pattern of allele frequency change for the coat colour loci in this population was different from the simultaneous S population selected for high weight gain (Table 5). In fact in these generations, the b allele declined while in the population selected for low weight gain it increased (the average difference in frequency between these lines was 0·123). A similar, but not as extreme, pattern occurred for the d allele with higher frequencies in the high population line and lower frequencies in the low selected population. In other words, the changes in the populations selected in the opposite direction for weight gain were also opposite in the change in coat colour allele frequency supporting the effect of selection on weight gain on the frequency of the coat colour alleles.

Table 5. The observed frequencies of alleles b and d in contemporaneous generations of population S selected for high weight gain and a population selected for low weight gain originated from generation 7 of population S

Discussion

There is a history of experiments that have shown an association of coat colour alleles at the brown and dilute genes with body weight or weight gain. Overall, there is strong evidence that the patterns of change in populations segregating for these variants and the phenotypic values in experimental crosses are influenced by selective differences. Some early studies suggested that this association was the result of pleiotropic effects of the mutants on body weight but more recent examination suggests that QTLs with linked associations are more consistent with the data although it is not possible to completely exclude pleiotropic effects. Most of these studies used crosses between inbred or differentiated lines to initiate their experiments so that high linkage disequilibrium between the coat colour mutants and alleles at any genes (QTLs) that were different between the parental lines was initially expected.

In experiments examined over time, the pattern of change in allele frequency for the coat colour alleles varied between replicate populations, over time within the populations and over different studies. For example, although both populations S and S′ examined here selected for high weight gain initially had reduced frequency of the b allele, the pattern of change after the first 10 generations was different with the S′ population increasing greatly in allele frequency and S having a low frequency throughout the experiment. The two populations diverged at the d allele early in the experiment and had reversals in allele frequency at different times. These patterns would be unlikely if pleiotropy were the most important factor influencing allele frequency change. In the similar experiments examined by Keightly & Bulfield (1993) and Heath (1995), the b allele increased in frequency in populations selected for high body weight (and decreased in lines selected for low body weight) and the d allele declined in frequency in populations selected for high body weight (and increased in lines selected for low body weight). A likely explanation for the dissimilarities in the two experiments was that the inbred lines used to establish these populations were different so that different associations of linked QTLs with the mutant alleles occurred.

Several other findings point to the importance of selection at linked QTLs, relative to pleiotropy, influencing the change in coat colour allele frequency in populations selected for size. First, the amount of change in allele frequency found in populations S and S′ was too great to be explained only by genetic drift, suggesting that selection was an important factor. Second, the association of allele frequency change with differences in weight gain was highest in the first part of the experiment with S and S′ and was lower in the last part of the experiment, consistent with the expected decay in association for linked variants. On the other hand, if pleiotropy was important, then these associations would not be expected to decline over time and if there were pleiotropic differences, then fixation or loss of the mutants might be expected by the end of the long-term experiments. The average frequency of b for populations S and S′ was 0·243 and the average frequency for d was 0·284 at the end of the experiments, suggesting some selection against both mutants, but both coat colour mutants were still segregating at a substantial frequency. Finally, Heath (1995) found that the patterns observed in the Keightly & Bulfield (1993) crosses were consistent with linked QTLs for both the b and d alleles and not with pleiotropy (for pleiotropy, the QTLs would map to the same map location as the mutants), although the QTL linked to the d allele appeared more closely linked than the QTL linked to the b allele.

A significant difference between the experiments reported here and those examined by Keightly & Bulfield (1993) and Heath (1995) was that after 20 generations, four of their six low populations were fixed for b, two of their six high populations were fixed for d and two of their six low populations were fixed for the D allele. In other words, in 8 of 24 cases (33%) their populations had become fixed by generation 20. On the other hand, after 70 generations in population S and 45 generations in populations S′ neither population appeared close to fixation for either the b or d alleles. Part of the difference may be the effective population size and genetic drift in the situations. Keightly & Bulfield (1993) estimated that the effective population size within their lines was about 23 while a reasonable general estimate for S and S′ was around 60, several times larger. In addition, assuming that there were QTLs initially in strong linkage disequilibrium, and then their impact on allele frequency change would be greatest in the early generations before the linkage disequilibrium had decayed and where genetic drift may have augmented selective changes.

The observed number of generations with significant linkage disequilibrium was much higher than the expectation. To provide an evaluation of this, several potential factors were examined using simulations that might have contributed. First, some of the high proportion of generations with significant linkage disequilibrium is reduced if exact probabilities are used instead of the likelihood ratio statistic. Second, the method of estimating using phenotype numbers instead of gametic numbers (not available from the experimental populations) has little effect on the proportion of significant linkage disequilibrium values, except when the number of parents is high. Finally, genetic drift because of a limited number of effective parents can increase the proportion of significant linkage disequilibrium values. Taking these factors into consideration, it does not seem necessary to invoke some further factors, such as selection, to generate what at first appeared to be a high level of linkage disequilibrium between the two loci.

Examination of the coat colour loci over these long-term experiments provides more support for the hypothesis that associations generated by linkage of QTLs to the coat colour loci were more important than pleiotropic effects. Overall, the length and size of these experiments are generally unequalled today (with some exceptions, e.g., Renne et al. 2003; Dudley & Lambert, 2004), and the analysis of these data provides important insights into selection for quantitative traits.