1. INTRODUCTION
Functional abstraction allows a person to take a step back and view a system based on the system's functionality or its purpose, where the purpose is what the system is trying to achieve and not how the systems works. However, we have noted a tendency with students to focus on the details without recognizing the overall purpose of the system (i.e., they miss the forest for the trees). Systems thinking introduces a holistic view that recognizes that the whole system is taken to be more than the sum of its parts and that the parts are interrelated and connected (Senge Reference Senge1990; Frank, Reference Frank2000; Caulfield & Maj, Reference Caulfield and Maj2001; Sireli & Mengers, Reference Sireli and Mengers2009; Valerdi & Rouse, Reference Valerdi and Rouse2010; Chan, Reference Chan2015). It requires both conceptual (abstract) and technical (concrete) thinking, where the conceptual thinking is the core to understanding the system while any technical understandings of the system only contributes to a greater conceptual understanding of the system as a whole (Richmond, Reference Richmond1991). This conceptual or abstract thinking directly correlates to and resides in thinking of a system in terms of its function(s) and whether that is of the system as a whole, its subsystems, or its components. Consequently, we posit that students' systems thinking ability may be developed through learning function abstraction.
When it comes to function abstraction in engineering design, there is little literature that recognizes and classifies its role in systems thinking for students. Students themselves are novices in being able to take a systems thinking approach to a problem, which causes much of the literature about systems thinking to be beyond the scope of their abilities. Consequently, we must acknowledge that directly assessing systems thinking is a nuanced endeavor, and herein, we are presenting initial work toward this endeavor through identification of the characteristics of systems thinking that students are beginning to use when abstracting functions.
In this study, we seek to understand the difference in systems thinking between sophomore engineering students who were taught function enumeration and functional modeling versus sophomore engineering students who were only taught function enumeration. Specifically, we are benchmarking the learning outcomes of two different modeling approaches. While we do not focus on a product for benchmarking, like the glue gun presented in Summers et al. (Reference Summers, Eckert and Goel2017), we do present quantified metrics for model comparison. We used the Functional Modeling Skill Quiz (FunSkills; Linsey et al., Reference Linsey, Viswanathan and Gadwal2010), as well as a validated rubric in order to understand potential differences. The rubric was used to assess function correctness as well as to classify enumerated functions as high level, low level, interface, or ambiguous. The correctness of a function was assessed using three criteria: contains a verb–noun pair, realistic and relevant to the system, and does not act on or contain the system itself. A partially correct function meets some but not all of these criteria, and an incorrect function does not meet any of these criteria, deeming it not suitable for a functional or black box model of the system. Both a correct and a partially correct function can fall into the following categories: high level, low level, interface, or ambiguous, which are defined as the follows: a high-level function is suitable for creating a black box model of the system; a low-level function serves to decompose a black box model and is internal to the system; an interface function connects with entities that are external to the system; and an ambiguous function reasonably fits into multiple prior categories. Figure 1 demonstrates where these function categories might be located in a function model. These function categories coupled with the correctness of functions provides insight into the ability for students to abstract functionality.

Fig. 1. Example of where high-level, low-level, ambiguous, and interface functions correspond to in a functional model.
The underlying premise of this approach is that students who are able to recognize both the forest (high-level functions) and the trees (low-level functions) have a more developed systems thinking ability than those who miss one or the other. Consequently, we posit that while an ability to identify the high-level functions touches upon the ability for students to abstract in systems thinking, identification of interface and low-level functions demonstrates an increased holistic understanding of an engineered system and corresponds to additional abstraction ability (i.e., systems thinking). This paper demonstrates the process for implementing the FunSkills Quiz, discusses the development and validation of the design rubric, provides analyzed student responses, and discusses our findings.
2. BACKGROUND
A system is a network of components and processes that are interconnected to an overarching goal. The more complex a system becomes, then the more cognitively challenging it is for humans to comprehend due to both the properties and the processes occurring at the numerous levels within a system (Goel, Reference Goel2013). In order to create a more cognitively approachable system, the system can be represented by a functional model. Functional modeling is inherently based on decomposing a system into subsystems by identifying functions at various levels of abstraction and then connecting these function abstractions in order to create a holistic representation. Understanding this relationship between function and a system is not without its challenges, especially with more complex systems. This relationship is further strained from the variety of views or definitions of function and the different views of functional modeling approaches. By exploring these different views and definitions, we can begin to identify the link between function, functional models, and systems thinking.
The link between function and systems thinking is first captured in the literature that considers the definition and meaning behind the term function and the different views or classifications of function. Function can be defined as doing something, as transforming an input to an output, as being the purpose of the device, as the relationship between inputs and outputs of a given task-performing system, or as what the components of a system do (Miles, Reference Miles1972; Keuneke, Reference Keuneke1991; Pahl & Beitz, Reference Pahl and Beitz1996; Chittaro & Kumar, Reference Chittaro and Kumar1998; Srinivasan et al., Reference Srinivasan, Chakrabarti and Lindemann2012). Vermaas (Reference Vermaas2013) even looks at the ambiguity in defining function and analyzes different ways of responding to this multidefined term by either creating a single meaning or embracing the coexisting definitions. Even so, function becomes more complicated in that it can be viewed in a variety of ways as well. Chandrasekaran and Josephson (Reference Chandrasekaran and Josephson2000) identify two views of function where one is centered on the environment and the other is centered on the device. The environment-centric view refers to the impact that the device has on the environment, whereas the device-centric view focuses on the features of the device itself. There is also Chakrabarti (Reference Chakrabarti1998), who views function in two ways, where the first views function as being on the same level of abstraction with an intended behavior and the second views function at a higher level regarding the purpose of a system. Moreover, researchers have allocated functions into different classifications; for example, primary and carrier flows (Pahl & Beitz, Reference Pahl and Beitz1996; Nagel et al., Reference Nagel, Bohm, Stone and McAdams2007). Deng (Reference Deng2002) utilizes two types of function, purpose and action, where purpose functions pervade higher levels of abstraction in design and action functions remain specific to a particular design. In addition, Crilly (Reference Crilly2010) analyzes the numerous classifications of functions and developed a 7 × 7 matrix that classifies functions into seven categories (physical, status, technical, social, ideological, aesthetic, and nonaesthetic) by looking at the purpose, effect, or means and then classifying functions into another set of seven categories (proper, system, design, use, service, manifest, and latent) by examining selection, intention, and recognition of the function. The matrix was crafted in order to represent the variety of function classes and combinations. Evidently, function ironically has a versatile function or purpose depending on the context for which it is to be used. Still, the variety of definitions and views involve different levels of abstraction that can be related to the continuum from conceptual (abstract) to technical (concrete) in systems thinking. Depending on the view or definition of function that a designer adopts, this alters the way a designer will look at and think about a system, which then leads to various ways to represent a system.
The variety of function definitions and views has initiated functional modeling approaches that can also be viewed in different ways. For instance, a group of researchers determined that one could classify functional modeling approaches into three ontologies: device, process, and functional concept (Kitamura & Mizoguchi, Reference Kitamura and Mizoguchi2003; Erden et al., Reference Erden, Komoto, Tvan Beek, D'Amelio, Echavarria and Tomiyama2008) . The device ontology encompasses Pahl et al. (Reference Pahl, Beitz, Schulz, Jarecki and Wallace2007) models, which are the foundation of this work, where a system is represented by black boxes having input and outputs. Then the process ontology looks at process and not individual components, whereas the functional concept ontology focuses on the ultimate and final purpose of the device and its components. These different ontological viewpoints impact how a designer views a system and then translates and represents that system into a functional model. Regardless of the viewpoint, though, functional modeling approaches are one way to “bridge the gap between the high-level requirements and the low-level details” (Erden et al., Reference Erden, Komoto, Tvan Beek, D'Amelio, Echavarria and Tomiyama2008). Thereby, functional modeling approaches allow for a constant interaction between the high-level requirements and the low-level details. In systems thinking, this interaction is essential for fostering the holistic view of a system, where the designer is able to identify and understand both the high-level and the low-level aspects to a system. For example, the holistic view of a coffee maker would include high-level requirements for generating hot water and filtering coffee while the low-level details refer to understanding the equations, theory, and application behind heat transfer and fluid dynamics so as to transfer and heat the water. Because functional modeling can bridge the gap between the high-level and the low-level aspects of the system, this indicates that functional modeling should support and enhance one's ability to apply systems thinking for solving problems. Chakrabarti et al. (Reference Chakrabarti, Srinivasan, Ranjan and Lindemann2013) speak to this fundamental challenge of viewing systems from multiple functional perspectives and levels, arguing for a common definition of function as a potential solution for representing engineered system.
Furthermore, the challenge to bridge the gap between high-level and low-level aspects to a system can be seen in artificial intelligence (AI) research. In AI research, the goal is to first develop an understanding of the human mind and cognition and then to use what is learned in order to design an intelligent agent (Goel & Davies, Reference Goel, Davies, Sternberg and Kauffman2011; Langley, Reference Langley2012). The focus of AI research is on knowledge content and the representation of this knowledge (Goel, Reference Goel2013). In order to build representations, AI researchers may build function models for their work. Eckert (Reference Eckert2013) points out, however, that there are many challenges with designers' interaction with their models. For one, she states that while designers are regularly in contact with their models, they neglect to understand the model being built and what can come from the model. This lends itself to the need for designers to have a more holistic view of their system where they can understand the parts of the model despite what the model can do and what can come from the model. Even so, Eckert (Reference Eckert2013) refers to experiments where participants pursued more abstract functional models but neglected to understand the system fully and connects this struggle to the participants' inability to connect components of a product family to what should be included in the functional model. AI researchers are apparently recognizing a need for designers to understand their systems and also the function of their systems more fully.
2.1. Functional modeling
Functional modeling presents a graphical description of what a system should do based on customer needs, target specifications, objectives, and constraints. Flow-based functional models stemming from the Pahl and Beitz methodology are perhaps the more common forms of functional models in engineering design. Models are generated at two levels of abstraction: a black box model and a subfunctional model. Black box functional models are stand-alone functional models abstracting a high-level transformation intended for the product to complete and are generated based on the system design requirements. A functional model decomposes the overall functional black box into specific flow transformations of material, energy, and signal. Flow transformations define the operations required of the system such that the identified input flows do become the identified output flows through the operation of the system.
The roots of flow-based functional modeling can be traced back to the field of value analysis (Rodenacker, Reference Rodenacker1971; Miles, Reference Miles1972). From these early representations of functions in value analysis, researchers have continued work to effectively and accurately describe functionality (Roth, Reference Roth1981; Koller, Reference Koller1985; Hundal, Reference Hundal1990; Little et al., Reference Little, Wood and McAdams1997; Szykman et al., Reference Szykman, Racz and Sriram1999; Stone & Wood, 2000; Hirtz et al., Reference Hirtz, Stone, McAdams, Szykman and Wood2002; Pahl et al., Reference Pahl, Beitz, Schulz, Jarecki and Wallace2007). In engineering design, a functional model is often a description of a product in terms of the elementary functions and flows that are required to achieve the product's overall function or purpose. A graphical form of a functional model is represented by a collection of subfunctions connected by the flows on which they operate (Kurfman et al., Reference Kurfman, Stone, van Wie, Wood and Otto2000). This structure is a way for a designer to abstract an engineered system based on how the engineered system is meant to “work” without having to consider the specific form or components required.
2.2. Teaching and assessing function
There is little literature that strictly focuses on teaching and assessing functional modeling. Still, there are traces of teaching function and functional modeling. For example, Stone and Wood (2000) outline how to use a common language taxonomy for creating functional models. While the purpose of this common language may not have originally been pedagogical, in practice it can provide a conduit for teaching students to uniformly abstract functionality of engineered system, and based on this common language taxonomy, Nagel et al. (Reference Nagel, Bohm, Cole and Shepard2012) developed an algorithmic approach to teaching functionality. This approach uses a series of grammar rules to assemble function chains from a list of enumerated functions that are desired for the final product. Function chains are then aggregated into a complete functional model that represents a system or product. Creating a functional model consists of three primary steps: developing a black box model, developing function chains from black box input and output flows, and aggregating function chains into a functional model. To assess students' abilities to identify functions, generate functions for a system, and create a functional model of a system, Linsey et al. (Reference Linsey, Viswanathan and Gadwal2010) created and validated the FunSkills Quiz. FunSkills was designed to determine differences between the impact of high-complexity design problems and lower complexity design problems on functional modeling skills. Since development, FunSkills has been implemented on a range of students from undergraduates with no functional modeling experience to graduate students with more extensive training in functional modeling. To evaluate student-generated functional models, Nagel et al. (Reference Nagel, Bohm and Linsey2016) developed and validated an 18-question rubric that assesses functional models on their adherence to standard modeling practices. The rubric has been used to evaluate functional models generated by novice modelers ranging from sophomore level through graduate.
Teaching function and functional modeling approaches presents a unique challenge to many organizations. Eckert (Reference Eckert2013) points out the difficulty in teaching and then applying functional models. Teaching functional modeling approaches requires using step-by-step instruction and small examples. Challenges arise, however, when designers are given complex, real-life scenarios and must rely more on their own personal experience. Another challenge arises when “applying and formulating concepts of internal and cross-boundary functions” (Ernst Eder, Reference Ernst Eder2014). In a study of professional engineers, Eckert et al. (Reference Eckert, Alink, Ruckpaul and Albers2011) found that professional engineers either utilized formal definitions that they had been previously exposed to or they resorted to terms that they associated with their everyday language. This demonstrates not only a challenge with respect to teaching and assessing function but also a challenge with linking functional expression to systems thinking.
2.3. Systems thinking
Originally coined by Barry Richmond, the term systems thinking was left as a loose concept involving a “continuum of activities” that ranged from understanding the overall system and the relationships to the equations and simulations of the system (Richmond, Reference Richmond1991). This continuum, however, neglected to clearly articulate all that systems thinking entails or to provide a fully articulated definition of systems thinking. Recognizing the importance of system thinking, researchers have taken the effort to further articulate and advance the field of systems thinking, thus leading to many overlapping definitions and characteristics pertaining to systems thinking. Some definitions include the following by Kordova et al. (Reference Kordova, Ribnikov and Frank2015), Chan (Reference Chan2015), and Camelia et al. (Reference Camelia, Ferris and Cropley2015):
-
• Kordova et al. (Reference Kordova, Ribnikov and Frank2015) describe systems thinking as “a concept that reflects thinking about the issue as a whole, emphasizing the interrelationships among its components, rather than the components themselves.”
-
• Chan (Reference Chan2015) describes systems thinking as “conceptualizing real world phenomenon as models. A model is a set of interrelated concepts, expressed in a language that captures some aspects of the reality of interest.”
-
• Camelia et al. (Reference Camelia, Ferris and Cropley2015) define systems thinking as a “bridge between theory and practice, and between the abstract, intellectual domains and the concrete, practical domains.”
Although there are more definitions than these, it is apparent that systems thinking ranges from abstract to concrete thinking. As a single definition of systems thinking is nonexistent, this begs the question of how do you measure systems thinking if it is not clearly defined. In response, researchers have sought to identify characteristics of systems thinking. For example, Valerdi and Rouse (Reference Valerdi and Rouse2010) outline systems thinking competencies as the abilities to define the universe and overall system appropriately, see relationships and things holistically, comprehend the complexity of the system, communicate among disciplines, and utilize a broad range of concepts and tools. Stave and Hopper (Reference Stave and Hopper2007) completed an extensive literature review of 100 articles on systems thinking, largely based in systems dynamics, which led them to identify five characteristics of systems thinking, which included holistic thinking, interconnections and feedback, dynamic behavior, system in terms of causing its own behavior, and system structure.
With respect to function in systems thinking, most systems thinking literature agrees that the function of a system is at least a necessary consideration, but generally the application of function is not explicitly prescribed. Derro and Williams (Reference Derro and Williams2009) note among their competencies for problem solving and systems thinking are “the ability to find connections and patterns across the system” and “thinking systemically.” Both of which could reasonably include function as a primary component or a tool for a systems thinker. Similar themes run in the variety of definitions for systems thinking. In addition, Frank (Reference Frank2006) examined three different studies involving professional engineers and undergraduate engineering students in order to understand the participants' levels of systems thought or capacity for systems thinking. If a participant corresponded to having a high capacity for systems thinking, then he or she does not need to look at the system components in order to be able to articulate aspects of the system such as function, behavior, and emergent properties. This shows that there is a clear place for the application of function as a central tool in a systems thinker's arsenal.
3. EXPERIMENT
Building on the literature, we define systems thinking as being able to consider a system holistically while also understanding the relationships and interfaces within a system and at the system's boundaries. A student's ability to enumerate functions was used as the exemplar of a student's systems thinking ability. This study uses a slightly modified version of FunSkills (Linsey et al., Reference Linsey, Viswanathan and Gadwal2010) to assess students' ability to enumerate functions of two systems. Some of the original questions on hierarchical functions were not applicable for the current study. FunSkills provides two noted advantages: the lack of reliance of a common taxonomy, and the aforementioned instrument validation.
A between-subject controlled experiment was designed to test students' ability to abstract engineered systems functionally. Student participants were from one of two treatment groups: modeling group students, who were taught functional modeling and function enumeration, and enumeration group students, who were only taught function enumeration. Students in the enumeration group were instructed in how to identify the function or purpose of a system and were also taught to identify the system, subsystems, and components of a system. The students in the modeling group were given the same instruction as the function enumeration group but were also given additional instruction in how to create functional models. Functional modeling is a method that is used to visually represent system functions and how they interact to produce a desired output based on system boundaries, where function enumeration is simply the list of all functions that may be associated with a system of interest.
3.1. Hypothesis
If functional modeling does further develop systems thinking among students, then it would be expected that by asking students to identify functions for a given product, the students who are taught functional modeling will list fewer high-level functions than those students who are only taught functional enumeration. This is because students who are taught functional modeling have been trained through functional modeling to identify low-level and interface functions in addition to high-level functions, and through identification of low-level and interface functions, the number of high-level functions would decrease when asked to provide a limited sample of exemplar functions as is requested in FunSkills.
If students who are taught functional modeling are conjectured to be able to identify other functions, then it would be expected that they would list more low-level functions than those not taught functional modeling. In conjunction with this reasoning, students who are taught functional modeling are also expected to identify more interface functions than those who are not taught functional modeling. In addition, we expect that students who are taught functional modeling will be able to better identify functions for a system, and therefore students who were taught functional modeling will list fewer incorrect functions for a system than those who are not taught functional modeling.
Functional modeling instructs students to understand a system at both the surface level (high level) along with the interactions and subfunction levels of the system (interface and low level). In our study, the only instructions that the students who were not taught functional modeling received on systems hierarchy were on systems decomposition through identification of subsystems and components. For the students who were not taught functional modeling, we believe that as they were not taught to recognize low-level functions and interface functions, and consequently, they will resort to more high-level functions or functions that are incorrect when prompted to enumerate four functions for an engineered system.
Following this logic, four hypotheses are explored in this research:
-
1. High-level functions: The modeling group will list fewer high-level functions than the enumeration group.
-
2. Low-level functions: The modeling group will list more low-level functions than the enumeration group.
-
3. Interface functions: The modeling group will list more interface functions than the Enumeration group.
-
4. Incorrect functions: The modeling group will list fewer incorrect functions than the enumeration group.
3.2. Assessment instrument
To assess a student's ability to abstract systems using function, the FunSkills Quiz was used. The FunSkills Quiz in its entire form is a combination of free-response, open-ended questions and questions requiring a yes/no response. For this study, just two questions (Question 2 and Question 3), both free response, open-ended questions, were used. Question 2 requires the enumeration of potential function statements for a system based on an image of a nail clipper and Question 3 requires the enumeration of functions from design objectives of an imaginary dorm room product/system. Questions 2 and 3 are provided as Figure 2 and Figure 3, respectively. No pre- or posttests were conducted for the student groups regarding their general knowledge of the systems (nail clipper and cleaning system) in the questionnaire. It is assumed that based on geographical location and culture that the students would be familiar with the systems. Nevertheless, students were given a picture of the nail clipper to provide a clear representation of the system. In addition, the cleaning system is purely fictional, where the students would deduce functionality via the described customer needs.

Fig. 2. Question 2: enumeration of potential function statements for a system.

Fig. 3. Question 3: enumeration of functions from design objectives.
3.3. Participants
In this study, data collection occurred across four sections of a sophomore design course taught in an engineering program (~450 students) at a comprehensive university (~20,000 students) on the East Coast of the United States.
Seventy-nine students across all four sections of the sophomore design course provided consent to use their FunSkills Quiz results in this research. No incentives were provided to the participants. All sophomore engineering students were of similar background with their only prior engineering course having been two introductory engineering courses completed during the prior academic year. Students did not learn functional abstraction during their first year in the engineering program, so for all students, this would have been their first introduction to function. All students were enrolled in a nondiscipline-specific engineering program on track to earn a bachelor of science in engineering.
There is no expected difference between students from different sections. Students could choose to take either a 9:30 a.m. or a 12:05 p.m. section of design on Tuesday or a 9:30 a.m. or 12:05 p.m. section of design on Thursday. Students' choice in mathematics and science (physics or chemistry) class is the primary impact on their design course section. For example, if students make the choice for lunch or afternoon design, they take morning science or math. Based on student background and course enrollment logistics, there is no reason to believe that one class is composed of stronger students than another. Tuesday sections were assigned to the modeling group while Thursday sections were assigned to the experimental group. The design counterbalances classes at different times of the day.
3.4. Procedure
Students in the modeling group were taught about systems abstractions, function enumeration, and functional modeling including generating a black box model and a subfunctional model, while students in the enumeration group were taught the same information about systems abstractions as well as function enumeration but were not taught functional modeling. All classes met for 100 min.
The system abstraction content taught to all students included identifying a system boundary, subsystems, components, and flows. For students in both the enumeration group and the modeling groups, an engineered system was used as an example during class with a discussion on system breakdown and perspective being the driving factors for system abstraction choices (~30 min). For students in the enumeration group, a natural system was also used as an example, and students worked in-class examples as groups to understand the process (~60 min). For the modeling group, no additional system abstraction content was taught using this technique.
The function enumeration content taught to all students included a discussion that function is a translation of design objectives; is composed of a verb–noun pair; describes what a system, subsystem, or component does; and is form independent (~5 min). Examples of a bicycle, music player, lawn mower, electric motor, and toothbrush were used during class for both groups. For these example systems, students identified functions for the system during class, and student responses were discussed (~5 min). No further discussion of function was provided for the enumeration group.
Students in the modeling group were provided with the algorithmic approach (Nagel et al. Reference Nagel, Bohm, Cole and Shepard2012) to generating a functional modeling during the class period. Students were talked through an example functional model during the lecture portion of the course (~20 min), and during the active learning portion of the course, students, as teams of four, worked through an example functional model during class (~40 min). All students were provided with a step-by-step example, and students were provided the following four steps annotated with an example black box and/or functional model developed to a level appropriate for each step.
-
Step 1. Generate a black box model for the product being designed considering the input flows, output flows, and the overall functionality of the product. Flows and function should be identified from the customer needs for the product.
-
Step 2. Follow the functional basis (Hirtz et al., Reference Hirtz, Stone, McAdams, Szykman and Wood2002) or a similar approach for the generation of the function–flow pairs. Generate function chains for flows identified at the black box level. Follow the material, energy, and signal flow convention from Step 1 when generating function chains. Add flows to represent the importation and exportation of materials, energies, and signals into the functional system.
-
Step 3. Aggregate function chains. Add flows to represent the importation and exportation of materials, energies, and signals into the functional system.
-
Step 4. Verify that all input functions identified in the black box model transition to all output flows in the black box model.
Students in the modeling group generated black box and functional models first independently as a homework assignment for a bicycle (provided in Nagel et al., Reference Nagel, Bohm, Linsey and Riggs2015). Feedback was provided by the course instructor on student submissions as a grade and written comments at the start of class 2 weeks following the initial functional modeling instruction. Following receipt of feedback, as a second homework assignment, students then worked as teams to generate a second functional model for the course project, a human-powered vehicle for a person with a disability.
Students in the enumeration group generated abstracted systems following the approach learned during class for a bicycle. Feedback was provided by the course instructor on student submissions as a grade and written comments. A team assignment was not provided.
The FunSkills Quiz was given to both the enumeration group and the modeling group 6 weeks following the initial instruction of functional modeling in the modeling group. The quiz was administered at the start of the class period, and the time given to the students was not restricted. The topic of the quiz was not known to the students prior to class; however, students likely anticipated a quiz at the start of class as most class periods started with a short quiz during the semester.
4. RUBRIC ITERATIONS
The importance of Questions 2 and 3 in FunSkills is that these questions allowed the students the freedom to fabricate their own functions for the given design problems. In other words, both asked students to simply enumerate functions for the system. Students were not prompted to identify high-level, low-level, or interface functions, nor were students explicitly taught about high-level, low-level, or interface functions. Consequently, students' enumeration of high-level, low-level, and interface functions was based simply on their prior system decomposition, enumeration, and/or modeling knowledge.
4.1. Rubric development
To evaluate the students' enumerated functions, a universal rubric was designed to evaluate the students' abilities to create “good” functions. However, a good function is not enough to begin building a formalized rubric. The goal was to answer two questions. What makes a student's response a good function? What is meant by a good function?
4.1.1. Rubric development: Phase 1
The first iteration of this rubric, presented by Nagel et al. (Reference Nagel, Bohm and Linsey2016), provided preliminary results for identifying correct, incorrect, high-level, and low-level functions. Although there was interrater agreement for assessing correct and incorrect, interrater agreement was not obtained for high-level and low-level functions. The rubric presented herein was modified significantly from this original iteration to include a three-level scale for correctness (correct, partially correct, and incorrect). Definitions for high-level, low-level, interface, and ambiguous functions were developed and refined to allow for repeatable assessment of student enumerated functions.
4.1.2. Rubric development: Phase 2
To improve specifically upon the results presented by Nagel et al. (Reference Nagel, Bohm and Linsey2016) and improve the interrater agreement on high- and low-level functions, two evaluators who had initially evaluated the data set presented the basic rubric that they originally agreed to use for evaluating the student responses. A third evaluator used the Phase 1 rubric that was also used in Nagel et al. (Reference Nagel, Bohm and Linsey2016) and evaluated a random sample of the collected data in order to establish familiarity, compare results, and identify areas for improvement. The third evaluator identified areas of confusion and contention in the rubric, such as the need to further designate correctness and the categories to two components of the rubric and also to create clearer definitions. These areas of confusion became the basis for developing the definitions of high- and low-level functions. Three experts, plus one graduate student and one undergraduate student, both with experience in creating and analyzing functional models, discussed and refined the definitions of high- and low-level functions as well as correct and incorrect functions. Using these revised definitions, the third evaluator checked the ability to apply these definitions to another random sample of student responses. The sole purpose of this evaluation was so that the evaluator could provide feedback on the new definitions and rubric. Based on the evaluator's feedback, the definitions for high- and low-level functions were once again revised, and the two evaluators proceeded to evaluate the data from the East Coast university and count the total correct, incorrect, high-level, and low-level functions for each student. As a check, this was then compared to the total scores of similar data using the same FunSkills Quiz that was collected at another university. Disagreements on the high- and low-level functions in Question 3 were still identified.
4.1.3. Rubric development: Phase 3
To arrive at agreement, the differences between the scores from each evaluator were marked and discussed in order to identify reasoning behind the differences between the evaluators' decisions. From these conversations, the following additional guiding questions for high-level functions were added to the assessment process:
-
1. Can you create a logical and useful model for an objective, intent, or common use of the object described with all pertinent flows and sufficient functional detail? (Note that it does not necessarily have to capture ALL the intents, objectives, or common use, but it must completely capture one.)
-
2. Do/can you use [Object] to function? If so, you can likely satisfy (Question 1), and it is a high-level function.
The guiding questions demonstrated that the current categories of high-level and low-level functions along with correct and incorrect would not adequately represent systems thinking attributes nor adequately capture all of the functions that students would list. Systems thinking recognizes that there is a spectrum from low level to high level, whereas the current categories were classifying functions into low level or high level and correct or incorrect. On top of that, the current definitions were causing confusion and required further clarity and articulation. Adjustments to definitions and new categories would be necessary in order to fully classify the functions. A new level to the scale for correctness was developed: partially correct. In addition, two new categories were developed: interface and ambiguous. The result is a 3-point scale for correctness: correct, partially correct, and incorrect, and a method for categorizing correct and partially correct functions based on high level, low level, interface, and ambiguous. The correctness and the categories have the following definitions:
-
1. Correctness:
-
a. Incorrect functions are not evaluated into categories, while partially correct and correct functions should be.
-
b. A correct function should be
-
• a verb–noun pair,
-
• realistic and relevant to the system, and
-
• should not act on or contain the system itself.
-
-
c. A partially correct function: if evaluators can interpret the answer as a function or see, in their eyes, overwhelming functional thought, it should be considered as a function.
-
-
2. Categories:
-
a. High-level functions (black box) are functions suitable for creating a black box model of the system.
-
b. Interface functions are functions that likely interface with entities external to the system.
-
c. Low-level functions (internal) are functions that serve to decompose a black box model.
-
d. Ambiguous functions are functions that could reasonably fit into multiple categories.
-
To test the revised rubric and to evaluate the results of the FunSkills quizzes, the undergraduate research student and the graduate student used the rubric to score Questions 2 and 3 of 20 of FunSkills for both correctness (correct, partially correct, and incorrect) and for function categorization (high, interface, low, and ambiguous) resulting in a total of 80 assessed functions. Following this evaluation, the raters identified that the definition of partially correct and incorrect functions required additional clarity; the definitions were adjusted to include ratios of correct function characteristics. The evaluators reassessed their 20 FunSkills quizzes prior to calculating interrater agreement. The interrater agreement using a Cohen κ was found to be 0.688 for the correctness of functions (Table 1), 0.8 for category responses to Question 2 (Table 2), and 0.785 for category responses to Question 3 (Table 3). According to McHugh (Reference McHugh2012), a Cohen κ value of 0.61–0.80 is substantial agreement. Therefore, in this additional evaluation, we were able to achieve substantial agreement in all three areas using the same rubric.
Table 1. Cohen κ values for two raters on Question 2

aNot assuming the null hypothesis.
bUsing the asymptotic standard error assuming the null hypothesis.
Table 2. Cohen κ values for two raters on Question 3

aNot assuming the null hypothesis.
bUsing the asymptotic standard error assuming the null hypothesis.
Table 3. Cohen κ values for two raters on the frequency of correct functions

aNot assuming the null hypothesis.
bUsing the asymptotic standard error assuming the null hypothesis.
4.2. Final rubric
The final rubric was composed and is described herein.
4.2.1. Scoring Sheet: FunSkills Quiz
Functions are evaluated for correctness, which is a frequency metric. Functions should be assessed as correct, partially correct, or incorrect based on the following definitions:
-
1. A correct function is where clear functional thought is given. A correct function
-
a. is a verb–noun pair,
-
b. is realistic and relevant to the system, and
-
c. does not act on or contain the system itself.
-
An example of a correct function is “cut nails” or “wash hands.”
-
2. A partially correct function is where some functional thought is given. A partially correct function matches 2/3 of the qualifications for the correct function. An example of a partially correct function is “blade cuts.”
-
3. An incorrect function is where no functional thought is given. An incorrect function matches 0/3 or 1/3 of the qualifications for the correct function. These functions are not suitable for a functional model or black box model of the system. An example of an incorrect function is “must be easy to use.”
For correct or partially correct functions, each function is categorized as high level, low level, interface, or ambiguous. Definitions for each category follow:
-
4. High-level functions (black box): functions suitable for creating a black box model of the system. A high-level function satisfies the following:
-
a. Could you use the function to create a logical and useful model that captures an objective, intent, or common use of the object and all pertinent flows with sufficient functional detail? (Note that it does not necessarily have to capture ALL the intents, objectives, or common use, but it must completely capture one.)
-
b. Do/can you use [Object] to [Function]?
If so, it is likely a high-level function. For example, “cut nail” or “wash hands.”
-
-
5. Interface functions: functions that likely interface with entities external to the system. An interface function satisfies the following:
-
a. Does the function transfer an energy, material, or signal (EMS) flow across the system boundary?
-
b. Does/could the function accept an external flow of EMS and export an intermediate flow into the model?
-
c. Does/could the function accept an intermediate flow and export a black box-level EMS flow?
If so it is likely an interface function. For example, “import hand” or “dispense soap.”
-
-
6. Low-level functions (internal): functions that serve to decompose a black box model. A low-level function satisfies the following:
-
a. Does the function address a single transformation within a larger process?
-
b. Could it be used to decompose a black box model?
If so it is likely a low-level function. For example, “convert human E. to mechanical E.” and “guide hands.”
-
-
7. Ambiguous functions: functions that could reasonably fit into multiple categories. An ambiguous function could reasonably fit into multiple categories. For example, “apply soap” or “move object.”
4.3. Rubric application
The application of the FunSkill rubric is divided into two rounds of assessment for each question. First, the evaluator reviews the student's four responses to Question 2 based on correctness, which is outlined by the criteria in the rubric. The evaluator notes the number of correct functions (3/3 characteristics of a function), the number of partially correct functions (2/3 characteristics of a function), and the number of incorrect functions (1/3 or 0/3 characteristics of a function). The total number of correct, partially correct, and incorrect functions should equal four.
Second, once correctness has been scored, the evaluator proceeds to the second round, where he or she is to assign each correct and partially correct function to a category by following the rubric guidelines. The number of high-level, low-level, interface, and ambiguous functions is tallied for Question 2, and the total of these should be equal to the number of correct and partially correct functions found in the first round. The evaluator then repeats this process for Question 3 of the quiz.
To demonstrate, a student responds with four functions for Question 2. The rater assesses that one function is correct, one function achieves two-thirds of the rubric qualifications for a correct function, and the other two functions do not achieve any rubric qualifications for a correct function and are thereby incorrect. In turn, the rater inputs a 1 into the partially correct column of Table 4, a 2 into the Incorrect column, and a 1 into the correct column. Of these four functions provided, two functions, the correct and partially correct functions, are then further evaluated into categories and scored. In this example, the rater assesses one function to be a high-level function and the other to be an ambiguous function.
Table 4. Example of the application of the FunSkills Rubric to an example

5. RESULTS
When comparing the modeling group to the enumeration group (Fig. 4), the results from Questions 2 and 3 of the FunSkills Quiz were combined since both questions were asking the students to generate functions. Figures 5 to 9 show the box-and-whisker plots for the number of correct, ambiguous, interface, low-level, and high-level functions combined for Questions 2 and 3. The nonparametric statistical Mann–Whitney U test was implemented because the outcome variable was a on scale of 0 to 4. A Mann–Whitney U test compares the median ranks rather than the averages. It is used when you have interval scale data or if the data fails to meet the assumptions required for a t test of normal distribution and equal variances. A Mann–Whitney U is the nonparametric equivalent of a t test. In addition, the data is not normally distributed, and the variances are not necessarily equal.

Fig. 4. Mean number of functions per group by function type.
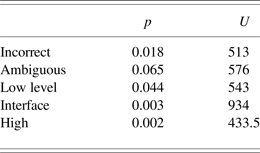
As shown in Figure 4 and Table 5 the number of high-level functions produced by the modeling group was significantly lower than the enumeration group (Mann–Whitney U = 433.5, p = 0.002). Furthermore, the students who were taught functional modeling also produced significantly more interface and low-level functions (Mann–Whitney U = 934.0, p = 0.003; Mann–Whitney U = 543.0, p = 0.044). This supports our first three hypotheses that students would list more low-level and interface functions and fewer high-level functions when taught functional modeling, due to their ability to begin to see the system more holistically. Moreover, for incorrect functions, there was statistically significant difference in the functions that were incorrect between the two groups of students (Mann–Whitney, U = 513.0, p = 0.018). As such, this endorses the final hypothesis that more incorrect functions would be generated by students who did not receive training in functional modeling. Overall, these results do indicate that students who are taught functional models are able to generate a variety of functions that are both appropriate for a system and describe more than just the high-level function of a system. This ultimately demonstrates that teaching functional modeling is more effective than just enumerating function.
Table 5. Mann–Whitney U for the total number of function in each function category
The box-and-whiskers plots (Figs. 5–9) provide an additional aid to showing how the student responses compare according to the spread and median of the data. For high-level functions, the median for the enumeration group was two high-level functions, whereas the modeling group had a median of zero. In addition, the middle 50% of the data set for the enumeration group is in the four to six count region whereas the middle 50% of the data set for the modeling group is in the two to four count region. Still, the modeling group does span from one to eight counts, which demonstrates that they are using high-level functions, but just at a lower count, a result that is not surprising considering students were prompted for a discrete number of functions. Furthermore, the low-level functions have a similar bottom 50% of the data for both conditions. The modeling group, however, has a higher upper value for the top 50% of the data, which shows that students who were taught functional modeling are using more low-level functions. A similar finding is shown in the interface function box-and-whisker plot. In this case, though, the third quartile spans from three counts down to the median of the modeling group, which is also the upper bound of the enumeration group. Clearly, students who were taught functional modeling articulated more interface functions in their responses. Finally, the box-and-whisker plots, which show the incorrect functions data, highlight that the enumeration group has a larger portion residing in higher counts, which demonstrates the impact that teaching functional modeling has on a student's abilities to generate functions.

Fig. 5. Box-and-whisker plot comparing high-level functions between the students who were taught functional modeling and those only taught function enumeration.

Fig. 6. Box-and-whisker plot comparing low-level functions between the students who were taught functional modeling and those only taught function enumeration.

Fig. 7. Box-and-whisker plot comparing interface functions between the students who were taught functional modeling and those only taught function enumeration.

Fig. 8. Box-and-whisker plot comparing ambiguous functions between the students who were taught functional modeling and those only taught function enumeration.

Fig. 9. Box-and-whisker plot comparing incorrect functions between the students who were taught functional modeling and those only taught function enumeration.
6. DISCUSSION
In our data we were able to identify that students who received functional modeling instruction did not list as many high-level functions as those students who only received function enumeration instruction. We posit that this is because students who are learning functional modeling are also gaining the ability to see the holistic view of the system so as to understand the interfaces and relationships between the parts of a system. In turn, these students are able to start recognizing functions that are at lower levels of the system. Because of this, they will have both high-level and low-level functions in their minds when they are asked to generate function for a given design problem. From the FunSkill Quiz questions, we asked them to generate four functions for both Questions 2 and 3. Because the students who were taught functional modeling also understood lower level functions, this took away from the amount of higher level functions that they were able to transcribe onto the page. Alternatively, students who were taught only function enumeration were not trained in the ability to identify lower level functions. Thus, when asked the same questions, they were able to generate high-level functions. As such, this resulted in more high-level functions for students who were taught function enumeration than those taught functional modeling.
Students in the modeling group also understood lower level functions; our results confirm that they were able to list more low-level functions than students who were taught only function enumeration. The low-level functions are indicative of the internal details and subsystems of a system and understanding the processes or relationships within a system. Functional models are one method that allows students to create a representation that decomposes a system and then identifies connections within the system. Even though the quiz questions did not explicitly ask for subfunctions, students within the functional modeling condition still generated low-level functions.
Not only was the modeling group able to answer with low-level functions, but they were also able to identify more interface functions than the enumeration group. The interface functions are the functions that interacted with the external system. This indicates that the students are able to recognize system boundaries and how the system interacts with its environment. This integrates into systems thinking since students are not isolating their system. The students are thinking of the system in terms of its environment and surroundings.
Moreover, the modeling group recorded less incorrect functions than the enumeration group. This indicates that students who are learning functional modeling are developing the ability to correctly identify functions for a system. Being able to correctly identify functions is very important for numerous functional modeling approaches and for a variety of disciplines and fields (i.e., engineering design, product development, and systems engineering). Function is utilized across a vast and versatile number of fields. It is even used as a means to create a common language across disciplines. Therefore, if a student is able to begin to correctly identify functions, then this is the beginning for what can lead to a versatile and applicable systems thinking skill set.
7. LIMITATIONS
For Questions 2 and 3 of the FunSkills Quiz, the students are prompted to generate only four lines for the given system. Although the reason for this was to capture the initial thoughts of the students, this does not necessarily consider that a student who lists high-level functions may have knowledge of low-level or other functions for the systems. While it is assumed that students would put forth the functions that they presume to most accurately suit the system, the current method does not fully capture what the students understand about a system. Future revisions to the quiz will aim to provide students with the opportunity to generate more functions for the systems. In addition, students are not directly taught or prompted to identify high-level, low-level, and interface functions, which limits the ability to ask them specifically to generate high-level, low-level, or interface functions. Finally, an assumption was made that due to the cultural background of the student population, students from both groups would understand both the fingernail clipper and the washing station for a dormitory room. While no evidence was noted in the results that students did not understand these two systems, the possibility of misunderstanding remains.
This work sought to demonstrate the means for how teaching function can correspond to how students are utilizing systems thinking. While the design rubric is aimed at capturing the systems thinking of the students, the results of this work simply indicate that there is a link between systems thinking and teaching function. The lack of literature on the relationship between function and systems thinking provides some difficulty in establishing a more thorough rubric. Nevertheless, this work seeks to initiate the conversation on how students are utilizing systems thinking and how this depends on the way that they are taught and understand function.
8. CONCLUSIONS
In a Reference Nagel and Bohm2011 ASME IDETC conference paper examining approaches to teaching function, Nagel and Bohm asked “How do you quantitatively determine the value that functional modeling and their related approaches bring to the design process?” and posed several research questions that must be answered before such a determination could be made. The work and resulting data and analysis presented in this paper is a first step in beginning to answer the questions of “quantitatively determining” the value of learning to think in terms of function. While analysis of the different groups in this work shows that students who learn functional modeling are able to identify more low-level and interface functions than students who only learn function enumeration, the data does still not conclusively demonstrate the benefits of learning functional modeling in the design process.
Existing research in systems engineering regarding systems thinking recognizes that the identification of function is an important aspect of having a holistic view of a system. The leap presented in this work proposes that not only the recognition of function but also the level of detail of function recognition is critical in systems thinking. That is, to say that a pair of fingernail clippers “convert human energy to mechanical energy” or “import human energy” is much more insightful than saying that they simply “clip nails.” Future work involves structuring a set of assessments, metrics, and design problems in order to determine how functional modeling skills (or level of skill) impact the quality of a particular design problem.
To build on these results and further explore the impact that teaching functional modeling has on engineering students' design abilities, we will examine how teaching function enumeration and functional modeling have a longitudinal impact on students as the progress from their sophomore to senior year. This will help us to understand the impact and retention of functional modeling and help to validate and refine the rubric that was presented in this paper. Further future work is needed to expand on understanding and investigating the intersection between function and function modeling with systems thinking.
ACKNOWLEDGMENTS
This work is supported by the National Science Foundation through Grants 1525449, 1525170, and 1525284. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of National Science Foundation.
Julie S. Linsey is an Associate Professor in the George W. Woodruff School of Mechanical Engineering at the Georgia Institute of Technology. She founded and leads the Innovation, Design Reasoning, and Engineering Education Methods (IDREEM) Lab. Julie received her PhD in mechanical engineering at the University of Texas at Austin. Dr. Linsey's research area is design cognition, including systematic methods and tools for innovative design with a particular focus on concept generation and design by analogy. The goal of her research is to discover new knowledge about how engineers think and leverage this knowledge into design methods and tools to improve engineering design. She has authored over 100 technical publications including over 30 journal papers, six book chapters, and she holds two patents.
Robert L. Nagel is an Associate Professor in the Department of Engineering at James Madison University. Since joining James Madison University, he codeveloped the department's six-course engineering design sequence. He is currently Lead Instructor of the two-course, client-based sophomore design experience, where students design and construct human-powered vehicles for individuals with cerebral palsy. Robert's research interests are in engineering design and design education. He has performed research with the United States Army Chemical Corps, General Motors Research and Development Center, and the United States Air Force Academy. Dr. Nagel is currently investigating the impact of functional modeling on students' ability to understand, represent, and design systems as well as studying the impact of student engagement in University MakerSpaces on students' design self-efficacy and student retention.
Matthew Bohm is an Associate Professor of mechanical and industrial engineering at Florida Polytechnic University. He was previously an Assistant Professor of mechanical engineering at the University of Louisville, where he was primarily responsible for overseeing the Mechanical Engineering Department's capstone design program; a Visiting Researcher at Oregon State University; and a Lecturer for the Department of Interdisciplinary Engineering at Missouri University of Science and Technology, where he was responsible for coordinating and teaching design and mechanics related courses. Dr. Bohm received his PhD at the Missouri University of Science and Technology. Matt's research examines the intersection of three distinct areas: engineering education, engineering design, and big data.
Megan E. Tomko is a PhD graduate student in the George W. Woodruff School of Mechanical Engineering at the Georgia Institute of Technology under the guidance of Dr. Julie Linsey. She completed one semester in her graduate studies at James Madison University with Dr. Robert Nagel as her advisor. Her BS degree in mechanical engineering is from the University of Pittsburgh, where she also worked as a Field Telecommunications Intern for three consecutive summers at EQT, a natural gas company headquartered in Pittsburgh. Megan's research interests are in identifying ways to teach students how to become better designers and learners through creative and nontraditional means.
Jacob T. Nelson is an undergraduate student pursuing a BS in engineering from the Department of Engineering at James Madison University. He has worked with Dr. Robert Nagel on research into functional modeling and its applications in the identification of failure modes, and in the effect teaching function has on students. Jacob has worked on several design projects, primarily of a mechanical nature, and is preparing to start his 2-year capstone project, focusing on the application of systems abstraction to the engineering design process.
















