1 Introduction
1.1 Background
Suppose that
![]() $P$
and
$P$
and
![]() $N$
are compact smooth
$N$
are compact smooth
![]() $n$
-manifolds, possibly with boundary. Let
$n$
-manifolds, possibly with boundary. Let
![]() $E^{\operatorname{sm}}(P,N)$
be the space of smooth (
$E^{\operatorname{sm}}(P,N)$
be the space of smooth (
![]() $C^{\infty }$
) embeddings from
$C^{\infty }$
) embeddings from
![]() $P$
into the interior of
$P$
into the interior of
![]() $N$
. The manifold calculus of Goodwillie and Weiss produces a tower of fibrations
$N$
. The manifold calculus of Goodwillie and Weiss produces a tower of fibrations
and compatible maps
![]() $E^{\operatorname{sm}}(P,N)\rightarrow E_{j}^{\operatorname{sm}}(P,N)$
. If we assume that
$E^{\operatorname{sm}}(P,N)\rightarrow E_{j}^{\operatorname{sm}}(P,N)$
. If we assume that
![]() $P$
admits a handle decomposition with handles of index at most
$P$
admits a handle decomposition with handles of index at most
![]() $n-3$
, then the maps
$n-3$
, then the maps
![]() $E^{\operatorname{sm}}(P,N)\rightarrow E_{j}^{\operatorname{sm}}(P,N)$
have connectivity given by a linear function of
$E^{\operatorname{sm}}(P,N)\rightarrow E_{j}^{\operatorname{sm}}(P,N)$
have connectivity given by a linear function of
![]() $j$
with positive slope, so in this case the tower strongly converges [Reference Goodwillie and Weiss8], [Reference Goodwillie and Klein7]. Furthermore,
$j$
with positive slope, so in this case the tower strongly converges [Reference Goodwillie and Weiss8], [Reference Goodwillie and Klein7]. Furthermore,
![]() $E_{1}^{\operatorname{sm}}(P,N)$
has the homotopy type of the space of smooth immersions from
$E_{1}^{\operatorname{sm}}(P,N)$
has the homotopy type of the space of smooth immersions from
![]() $P$
to
$P$
to
![]() $N$
. For
$N$
. For
![]() $j\geqslant 2$
, the layers of the tower, that is, the homotopy fibers of the maps
$j\geqslant 2$
, the layers of the tower, that is, the homotopy fibers of the maps
![]() $E_{j}^{\operatorname{sm}}(P,N)\rightarrow E_{j-1}^{\operatorname{sm}}(P,N)$
, have an explicit description in terms of configuration spaces.
$E_{j}^{\operatorname{sm}}(P,N)\rightarrow E_{j-1}^{\operatorname{sm}}(P,N)$
, have an explicit description in terms of configuration spaces.
In essence, the strong convergence result relies on the following schematic passage:
where
![]() $E^{\operatorname{bl}}(P,N)$
is the space of smooth block embeddings of
$E^{\operatorname{bl}}(P,N)$
is the space of smooth block embeddings of
![]() $P$
in
$P$
in
![]() $N$
and
$N$
and
![]() $E^{\operatorname{pd}}(P,N)$
is the corresponding space of Poincaré embeddings. Convergence is proved by establishing certain higher excision statements, which are known as “multiple disjunction” results for spaces of smooth embeddings. One achieves such results by first proving analogous ones for spaces of Poincaré embeddings. The Poincaré statements were proved in [Reference Goodwillie and Klein6] using homotopy theory. One then lifts the Poincaré statements to the block setting using surgery theory. The final step is to lift the block statements to the smooth ones using concordance theory. Given the method of proof, it seems appropriate to ask:
$E^{\operatorname{pd}}(P,N)$
is the corresponding space of Poincaré embeddings. Convergence is proved by establishing certain higher excision statements, which are known as “multiple disjunction” results for spaces of smooth embeddings. One achieves such results by first proving analogous ones for spaces of Poincaré embeddings. The Poincaré statements were proved in [Reference Goodwillie and Klein6] using homotopy theory. One then lifts the Poincaré statements to the block setting using surgery theory. The final step is to lift the block statements to the smooth ones using concordance theory. Given the method of proof, it seems appropriate to ask:
Question 1.1. Is there an analogue of Goodwillie–Weiss manifold calculus in the Poincaré duality space setting?
More precisely, suppose now that
![]() $P$
and
$P$
and
![]() $N$
are Poincaré spaces of dimension
$N$
are Poincaré spaces of dimension
![]() $n$
(possibly with boundary). One then has a space of Poincaré embeddings
$n$
(possibly with boundary). One then has a space of Poincaré embeddings
![]() $E^{\operatorname{pd}}(P,N)$
and we wish to construct a Goodwillie–Weiss calculus for it. Unfortunately, we do not know how to proceed. The problem here is that the set-up of [Reference Weiss22] does not properly translate over: in the manifold case one considers the poset of subsets of the interior of
$E^{\operatorname{pd}}(P,N)$
and we wish to construct a Goodwillie–Weiss calculus for it. Unfortunately, we do not know how to proceed. The problem here is that the set-up of [Reference Weiss22] does not properly translate over: in the manifold case one considers the poset of subsets of the interior of
![]() $P$
which are diffeomorphic to finite collections of open balls. This poset has good properties because a manifold is locally Euclidean. In the Poincaré case there does not seem to be a sensible replacement for this, as Poincaré spaces are not necessarily locally well-behaved.
$P$
which are diffeomorphic to finite collections of open balls. This poset has good properties because a manifold is locally Euclidean. In the Poincaré case there does not seem to be a sensible replacement for this, as Poincaré spaces are not necessarily locally well-behaved.
A related but perhaps more accessible question is
Question 1.2. Is there a version of the Goodwillie–Weiss tower in the Poincaré embedding case?
We propose to attack Question (1.2) from a point-of-view arising out of the surgery school in conjunction with one of the other functor calculi: Goodwillie’s homotopy functor calculus.
To simplify the presentation, we will only consider the case when
![]() $N=D^{n}$
is an
$N=D^{n}$
is an
![]() $n$
-disk, and we will assume that
$n$
-disk, and we will assume that
![]() $P$
is “sectioned” in the sense defined below. We will see that a certain space
$P$
is “sectioned” in the sense defined below. We will see that a certain space
of “unlinked” Poincaré embeddings of
![]() $P$
in
$P$
in
![]() $D^{n}$
does have a tower associated with it. A point in this space consists of a Poincaré embedding of
$D^{n}$
does have a tower associated with it. A point in this space consists of a Poincaré embedding of
![]() $P$
in
$P$
in
![]() $D^{n}$
together with a choice of Null homotopy of the “link” of the embedding. We will also see that the tower associated with this space strongly converges under mild hypotheses, and its first stage coincides with the space of “Poincaré immersions” of
$D^{n}$
together with a choice of Null homotopy of the “link” of the embedding. We will also see that the tower associated with this space strongly converges under mild hypotheses, and its first stage coincides with the space of “Poincaré immersions” of
![]() $P$
in
$P$
in
![]() $D^{n}$
. Furthermore, we will identify the homotopy fibers of the canonical map
$D^{n}$
. Furthermore, we will identify the homotopy fibers of the canonical map
![]() $\mathfrak{L}E^{\operatorname{pd}}(P,D^{n})\rightarrow E^{\operatorname{pd}}(P,D^{n})$
as spaces of “unlinkings” of
$\mathfrak{L}E^{\operatorname{pd}}(P,D^{n})\rightarrow E^{\operatorname{pd}}(P,D^{n})$
as spaces of “unlinkings” of
![]() $P$
in
$P$
in
![]() $D^{n}$
.
$D^{n}$
.
In what follows we simplify notation by setting
1.2 Sectioned Poincaré spaces
Our goal will be to say something sensible about the embeddings of the following class of Poincaré spaces:
Definition 1.3. A sectioning of a Poincaré space
![]() $P$
with boundary
$P$
with boundary
![]() $\unicode[STIX]{x2202}P$
is a triple
$\unicode[STIX]{x2202}P$
is a triple
in which
-
∙
 $K$
is a cofibrant space;
$K$
is a cofibrant space; -
∙
 $f:\!K\overset{\simeq }{\rightarrow }P$
is a homotopy equivalence;
$f:\!K\overset{\simeq }{\rightarrow }P$
is a homotopy equivalence; -
∙
 $s:\!K\rightarrow \unicode[STIX]{x2202}P$
is a map such that the composition coincides with
$s:\!K\rightarrow \unicode[STIX]{x2202}P$
is a map such that the composition coincides with $$\begin{eqnarray}K\overset{s}{\rightarrow }\unicode[STIX]{x2202}P\rightarrow P\end{eqnarray}$$
$$\begin{eqnarray}K\overset{s}{\rightarrow }\unicode[STIX]{x2202}P\rightarrow P\end{eqnarray}$$
 $f$
.
$f$
.
We refer to
![]() $\unicode[STIX]{x1D709}$
as sectioning data. For the sake of brevity, we will say that
$\unicode[STIX]{x1D709}$
as sectioning data. For the sake of brevity, we will say that
![]() $P$
is sectioned when the sectioning data are understood.
$P$
is sectioned when the sectioning data are understood.
Example 1.4. Let
![]() $D^{1}=[-1,1]$
be the 1-disk. If
$D^{1}=[-1,1]$
be the 1-disk. If
![]() $Q$
is a Poincaré space, possibly with boundary
$Q$
is a Poincaré space, possibly with boundary
![]() $\unicode[STIX]{x2202}Q$
, then
$\unicode[STIX]{x2202}Q$
, then
![]() $Q\times D^{1}$
is sectioned by means of the homotopy equivalence
$Q\times D^{1}$
is sectioned by means of the homotopy equivalence
![]() $Q\times \{-1\}\subset Q\times D^{1}$
and the inclusion
$Q\times \{-1\}\subset Q\times D^{1}$
and the inclusion
![]() $Q\times \{-1\}\subset \unicode[STIX]{x2202}(Q\times D^{1})$
.
$Q\times \{-1\}\subset \unicode[STIX]{x2202}(Q\times D^{1})$
.
Example 1.5. Suppose
![]() $\unicode[STIX]{x1D702}$
is a
$\unicode[STIX]{x1D702}$
is a
![]() $(j-1)$
-spherical fibration over a Poincaré space
$(j-1)$
-spherical fibration over a Poincaré space
![]() $Q$
of dimension
$Q$
of dimension
![]() $d$
having empty boundary. Let
$d$
having empty boundary. Let
![]() $S(\unicode[STIX]{x1D702})$
be its total space. Suppose
$S(\unicode[STIX]{x1D702})$
be its total space. Suppose
![]() $\unicode[STIX]{x1D702}$
comes equipped with a section
$\unicode[STIX]{x1D702}$
comes equipped with a section
![]() $s:\!Q\rightarrow S(\unicode[STIX]{x1D702})$
. Let
$s:\!Q\rightarrow S(\unicode[STIX]{x1D702})$
. Let
![]() $D(\unicode[STIX]{x1D702})$
be the mapping cylinder of
$D(\unicode[STIX]{x1D702})$
be the mapping cylinder of
![]() $\unicode[STIX]{x1D702}$
, and let
$\unicode[STIX]{x1D702}$
, and let
![]() $f:\!Q\rightarrow D(\unicode[STIX]{x1D702})$
be the inclusion. Then
$f:\!Q\rightarrow D(\unicode[STIX]{x1D702})$
be the inclusion. Then
![]() $\unicode[STIX]{x1D709}:=(Q,f,s)$
is sectioning data for the
$\unicode[STIX]{x1D709}:=(Q,f,s)$
is sectioning data for the
![]() $(n+j)$
-dimensional Poincaré space
$(n+j)$
-dimensional Poincaré space
![]() $D(\unicode[STIX]{x1D709})$
.
$D(\unicode[STIX]{x1D709})$
.
Definition 1.6. (Generalized Thom Space)
If
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}=(K,f,s)$
, then we define
$\unicode[STIX]{x1D709}=(K,f,s)$
, then we define
that is, the mapping cone of the map
![]() $s:\!K\rightarrow \unicode[STIX]{x2202}P$
. This is a based space.
$s:\!K\rightarrow \unicode[STIX]{x2202}P$
. This is a based space.
The justification for this notation/terminology is that the spherical fibration case in Example 1.5 gives the Thom space in the usual sense.
Lemma 1.7. Assume that
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}=(K,f,s)$
and
$\unicode[STIX]{x1D709}=(K,f,s)$
and
![]() $\unicode[STIX]{x2202}P\rightarrow P$
is a cofibration. Then there is a preferred weak homotopy equivalence
$\unicode[STIX]{x2202}P\rightarrow P$
is a cofibration. Then there is a preferred weak homotopy equivalence
That is,
![]() $P^{\unicode[STIX]{x1D709}}$
is a preferred desuspension of
$P^{\unicode[STIX]{x1D709}}$
is a preferred desuspension of
![]() $P/\unicode[STIX]{x2202}P$
.
$P/\unicode[STIX]{x2202}P$
.
Proof. One has a commutative diagram
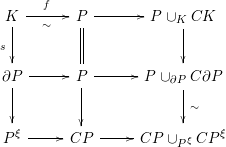
in which
![]() $CX$
denotes the cone on a space
$CX$
denotes the cone on a space
![]() $X$
. The rows and columns of the diagram form homotopy cofiber sequences (cf. 2.1; the null homotopies in this case are evident). The space in the upper right corner is contractible so the map
$X$
. The rows and columns of the diagram form homotopy cofiber sequences (cf. 2.1; the null homotopies in this case are evident). The space in the upper right corner is contractible so the map
![]() $P\cup _{\unicode[STIX]{x2202}P}C\unicode[STIX]{x2202}P\rightarrow CP\cup _{P^{\unicode[STIX]{x1D709}}}CP^{\unicode[STIX]{x1D709}}$
is a weak equivalence. The domain of this map is identified with
$P\cup _{\unicode[STIX]{x2202}P}C\unicode[STIX]{x2202}P\rightarrow CP\cup _{P^{\unicode[STIX]{x1D709}}}CP^{\unicode[STIX]{x1D709}}$
is a weak equivalence. The domain of this map is identified with
![]() $P/\unicode[STIX]{x2202}P$
up to a preferred weak equivalence (given by collapsing
$P/\unicode[STIX]{x2202}P$
up to a preferred weak equivalence (given by collapsing
![]() $CP$
to a point) and the codomain is identified with
$CP$
to a point) and the codomain is identified with
![]() $\unicode[STIX]{x1D6F4}P^{\unicode[STIX]{x1D709}}$
.◻
$\unicode[STIX]{x1D6F4}P^{\unicode[STIX]{x1D709}}$
.◻
In particular, the lemma gives a preferred isomorphism of singular homology groups
![]() $\tilde{H}_{k-1}(P^{\unicode[STIX]{x1D709}})\cong H_{k}(P,\unicode[STIX]{x2202}P)$
.
$\tilde{H}_{k-1}(P^{\unicode[STIX]{x1D709}})\cong H_{k}(P,\unicode[STIX]{x2202}P)$
.
1.3 Homotopy codimension
A Poincaré space
![]() $P$
of dimension
$P$
of dimension
![]() $n$
is said to have homotopy codimension
$n$
is said to have homotopy codimension
![]() ${\geqslant}j$
if the map
${\geqslant}j$
if the map
![]() $\unicode[STIX]{x2202}P\rightarrow P$
is
$\unicode[STIX]{x2202}P\rightarrow P$
is
![]() $(j-1)$
-connected.
$(j-1)$
-connected.
Example 1.8. Let
![]() $\unicode[STIX]{x1D702}:\!S(\unicode[STIX]{x1D702})\rightarrow Q$
be a
$\unicode[STIX]{x1D702}:\!S(\unicode[STIX]{x1D702})\rightarrow Q$
be a
![]() $(j-1)$
-spherical fibration over a Poincaré space without boundary. Then
$(j-1)$
-spherical fibration over a Poincaré space without boundary. Then
![]() $D(\unicode[STIX]{x1D702})$
has homotopy codimension
$D(\unicode[STIX]{x1D702})$
has homotopy codimension
![]() ${\geqslant}j$
.
${\geqslant}j$
.
Example 1.9. If
![]() $P$
is a compact smooth manifold, possibly with boundary, which admits a handle decomposition whose handles all have index
$P$
is a compact smooth manifold, possibly with boundary, which admits a handle decomposition whose handles all have index
![]() ${\leqslant}k$
, then the homotopy codimension of
${\leqslant}k$
, then the homotopy codimension of
![]() $P$
is
$P$
is
![]() ${\geqslant}n-k$
.
${\geqslant}n-k$
.
Example 1.10. Suppose
![]() $P$
is an
$P$
is an
![]() $n$
-dimensional Poincaré space,
$n$
-dimensional Poincaré space,
![]() $n-k\geqslant 3$
. Then
$n-k\geqslant 3$
. Then
![]() $P$
has homotopy codimension
$P$
has homotopy codimension
![]() ${\geqslant}n-k$
if the map
${\geqslant}n-k$
if the map
![]() $\unicode[STIX]{x2202}P\rightarrow P$
is
$\unicode[STIX]{x2202}P\rightarrow P$
is
![]() $2$
-connected and
$2$
-connected and
![]() $P$
has the weak homotopy type of a CW complex of dimension
$P$
has the weak homotopy type of a CW complex of dimension
![]() ${\leqslant}k$
. This is a consequence of duality, the relative Hurewicz theorem and a result of Wall [Reference Wall20, Theorem E].
${\leqslant}k$
. This is a consequence of duality, the relative Hurewicz theorem and a result of Wall [Reference Wall20, Theorem E].
We will assume the following throughout the paper.
Hypothesis 1.11. The Poincaré space
![]() $P$
has homotopy codimension
$P$
has homotopy codimension
![]() ${\geqslant}3$
.
${\geqslant}3$
.
1.4 Poincaré embeddings
We recall the notion of codimension zero Poincaré embedding (see e.g., [Reference Klein13], [Reference Goodwillie and Klein6]). We will restrict ourselves to the case when the ambient space is an
![]() $n$
-disk.
$n$
-disk.
A Poincaré embedding of a Poincaré space
![]() $P$
of dimension
$P$
of dimension
![]() $n$
in
$n$
in
![]() $D^{n}$
consists of a “complement” space
$D^{n}$
consists of a “complement” space
![]() $C$
equipped with a (gluing data) map
$C$
equipped with a (gluing data) map
making
![]() $C$
into an
$C$
into an
![]() $n$
-dimensional Poincaré space with boundary
$n$
-dimensional Poincaré space with boundary
![]() $\unicode[STIX]{x2202}P\amalg S^{n-1}$
. Furthermore, we require the homotopy pushout of
$\unicode[STIX]{x2202}P\amalg S^{n-1}$
. Furthermore, we require the homotopy pushout of
to have the weak homotopy type of
![]() $D^{n}$
, that is, it is required to be weakly contractible. The set of all such Poincaré embeddings comes equipped with a topology (cf. Section 3).
$D^{n}$
, that is, it is required to be weakly contractible. The set of all such Poincaré embeddings comes equipped with a topology (cf. Section 3).
We denote this space by
![]() $E(P,D^{n})$
. We typically specify a Poincaré embedding by writing its complement, that is, we write
$E(P,D^{n})$
. We typically specify a Poincaré embedding by writing its complement, that is, we write
![]() $C\in E(P,D^{n})$
.
$C\in E(P,D^{n})$
.
1.5 Unstable normal invariants
Assume
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Definition 1.12. An unstable normal invariant for
![]() $P$
is a based map
$P$
is a based map
such that
is a fundamental class for
![]() $P$
.
$P$
.
Remark 1.13. The stable version of the normal invariant appeared in the context of surgery theory [Reference Novikov16]. Applications of unstable normal invariants to embedding theory were investigated in [Reference Williams23], [Reference Ricther18] and [Reference Klein13].
Proposition 1.14. Assume
![]() $P$
is sectioned. Then an unstable normal invariant for
$P$
is sectioned. Then an unstable normal invariant for
![]() $P$
gives rise to a Poincaré embedding of
$P$
gives rise to a Poincaré embedding of
![]() $P$
in
$P$
in
![]() $D^{n}$
.
$D^{n}$
.
Proof. The proof harkens back to a construction of Browder [Reference Browder2]. Let
![]() $\unicode[STIX]{x1D709}$
be the sectioning data. Set
$\unicode[STIX]{x1D709}$
be the sectioning data. Set
![]() $C:=P^{\unicode[STIX]{x1D709}}$
. We have an evident map
$C:=P^{\unicode[STIX]{x1D709}}$
. We have an evident map
where on the second wedge summand we use
![]() $\unicode[STIX]{x1D6FC}$
. Let
$\unicode[STIX]{x1D6FC}$
. Let
![]() $\unicode[STIX]{x2202}P\rightarrow P^{\unicode[STIX]{x1D709}}$
be the evident map. Consider the composite
$\unicode[STIX]{x2202}P\rightarrow P^{\unicode[STIX]{x1D709}}$
be the evident map. Consider the composite
It follows from [Reference Klein11, Lemma 2.3] that this map gives
![]() $C$
the structure of a Poincaré space with boundary
$C$
the structure of a Poincaré space with boundary
![]() $\unicode[STIX]{x2202}P\amalg S^{n-1}$
and defines a Poincaré embedding of
$\unicode[STIX]{x2202}P\amalg S^{n-1}$
and defines a Poincaré embedding of
![]() $P$
in
$P$
in
![]() $D^{n}$
. (Note: since
$D^{n}$
. (Note: since
![]() $(P,\unicode[STIX]{x2202}P)$
is
$(P,\unicode[STIX]{x2202}P)$
is
![]() $2$
-connected and
$2$
-connected and
![]() $P\cup _{\unicode[STIX]{x2202}P}C$
is
$P\cup _{\unicode[STIX]{x2202}P}C$
is
![]() $\infty$
-connected, it follows that
$\infty$
-connected, it follows that
![]() $C$
is
$C$
is
![]() $1$
-connected. So Poincaré duality for
$1$
-connected. So Poincaré duality for
![]() $C$
only needs to be verified with constant
$C$
only needs to be verified with constant
![]() $\mathbb{Z}$
coefficients.)◻
$\mathbb{Z}$
coefficients.)◻
Notation 1.15. If
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}$
, then the space of its unstable normal invariants will be denoted by
$\unicode[STIX]{x1D709}$
, then the space of its unstable normal invariants will be denoted by
This is to be topologized as a subspace of the
![]() $(n-1)$
-fold based loop space
$(n-1)$
-fold based loop space
![]() $\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
.
$\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
.
Remark 1.16. The subspace
![]() $\unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}\subset \unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
is a collection of connected components: the Hurewicz map gives a (homotopy) Cartesian square
$\unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}\subset \unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
is a collection of connected components: the Hurewicz map gives a (homotopy) Cartesian square
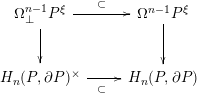
where
![]() $H_{n}(P,\unicode[STIX]{x2202}P)^{\times }$
is the set of fundamental classes of
$H_{n}(P,\unicode[STIX]{x2202}P)^{\times }$
is the set of fundamental classes of
![]() $P$
. This set is nonempty if and only if
$P$
. This set is nonempty if and only if
![]() $P$
is orientable. If
$P$
is orientable. If
![]() $P$
is connected and orientable then
$P$
is connected and orientable then
![]() $H_{n}(P,\unicode[STIX]{x2202}P)^{\times }$
has precisely two elements.
$H_{n}(P,\unicode[STIX]{x2202}P)^{\times }$
has precisely two elements.
The proof of Proposition 1.14 yields a map
which we henceforth call the Browder construction.
1.6 The link; the first main result
We continue to assume that
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}=(K,f,s)$
. Given a point
$\unicode[STIX]{x1D709}=(K,f,s)$
. Given a point
![]() $C\in E(P,D^{n})$
, we have a weak map
$C\in E(P,D^{n})$
, we have a weak map
Using the basepoint of
![]() $S^{n-1}$
we obtain a preferred basepoint for
$S^{n-1}$
we obtain a preferred basepoint for
![]() $C$
. Let
$C$
. Let
be the homotopy class of the weak map (2), where
![]() $P_{+}$
is
$P_{+}$
is
![]() $P$
with a disjoint basepoint. We call
$P$
with a disjoint basepoint. We call
![]() $\ell _{0}(C)$
the link of the Poincaré embedding. The next example motivates the terminology.
$\ell _{0}(C)$
the link of the Poincaré embedding. The next example motivates the terminology.
Example 1.17. Let
![]() $f:\!M^{p}\rightarrow D^{2p+1}$
be a smooth framed embedding, where
$f:\!M^{p}\rightarrow D^{2p+1}$
be a smooth framed embedding, where
![]() $M$
is connected. This means that
$M$
is connected. This means that
![]() $f$
admits a preferred extension to a smooth embedding
$f$
admits a preferred extension to a smooth embedding
![]() $F:\!M^{p}\times D^{p+1}\rightarrow D^{2p+1}$
. By Alexander duality and the Hurewicz isomorphism we have a preferred isomorphism
$F:\!M^{p}\times D^{p+1}\rightarrow D^{2p+1}$
. By Alexander duality and the Hurewicz isomorphism we have a preferred isomorphism
![]() $H_{p}(D^{2p+1}\setminus f(M^{p}))\cong \mathbb{Z}$
. Let
$H_{p}(D^{2p+1}\setminus f(M^{p}))\cong \mathbb{Z}$
. Let
![]() $\ast \in S^{p}$
be the basepoint. Then the homology class induced by
$\ast \in S^{p}$
be the basepoint. Then the homology class induced by
is the self-linking number of
![]() $f$
.
$f$
.
Theorem A. Assume
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}$
. Given a Poincaré embedding
$\unicode[STIX]{x1D709}$
. Given a Poincaré embedding
![]() $C\in E(P,D^{n})$
, then the homotopy fiber of the Browder construction (1) taken at
$C\in E(P,D^{n})$
, then the homotopy fiber of the Browder construction (1) taken at
![]() $C$
is non-empty if and only if the link
$C$
is non-empty if and only if the link
![]() $\ell _{0}(C)$
is trivial.
$\ell _{0}(C)$
is trivial.
Furthermore, if the link is trivial, then the Browder construction sits in a homotopy fiber sequence
where the homotopy fiber is taken at
![]() $C$
and
$C$
and
![]() $F_{\ast }(\unicode[STIX]{x1D6F4}(P_{+}),C)$
is the function space of based maps
$F_{\ast }(\unicode[STIX]{x1D6F4}(P_{+}),C)$
is the function space of based maps
![]() $\unicode[STIX]{x1D6F4}(P_{+})\rightarrow C$
.
$\unicode[STIX]{x1D6F4}(P_{+})\rightarrow C$
.
Remarks 1.18. (1). The null homotopy yielding the homotopy fiber sequence will made explicit in the proof of Theorem A.
(2). Theorem A answers a question posed to me by Sylvain Cappell about how far the Browder construction is from being a homotopy equivalence.
(3). Let
![]() $Q$
be a Poincaré space of dimension
$Q$
be a Poincaré space of dimension
![]() $n-1$
and homotopy codimension
$n-1$
and homotopy codimension
![]() ${\geqslant}n-k\geqslant 4$
, but not necessarily sectioned. Then as in Example (1.4),
${\geqslant}n-k\geqslant 4$
, but not necessarily sectioned. Then as in Example (1.4),
![]() $Q\times D^{1}$
is sectioned with generalized Thom space
$Q\times D^{1}$
is sectioned with generalized Thom space
![]() $Q/\unicode[STIX]{x2202}Q$
.
$Q/\unicode[STIX]{x2202}Q$
.
The “decompression” map
![]() $E(Q,D^{n-1})\rightarrow E(Q\times D^{1},D^{n})$
(cf. (8) below) factors as
$E(Q,D^{n-1})\rightarrow E(Q\times D^{1},D^{n})$
(cf. (8) below) factors as
in which the first map is given by the Pontryagin–Thom construction, and the second is the one of Theorem A. The results of [Reference Klein13] imply that the first map is
![]() $(2n-3k-6)$
-connected.
$(2n-3k-6)$
-connected.
(4). The map
![]() $F_{\ast }(\unicode[STIX]{x1D6F4}(P_{+}),C)\rightarrow \unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}$
can be described as an orbit map of an “action” of
$F_{\ast }(\unicode[STIX]{x1D6F4}(P_{+}),C)\rightarrow \unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}$
can be described as an orbit map of an “action” of
![]() $\unicode[STIX]{x1D6FA}F_{\ast }(P_{+},P^{\unicode[STIX]{x1D709}})$
on
$\unicode[STIX]{x1D6FA}F_{\ast }(P_{+},P^{\unicode[STIX]{x1D709}})$
on
![]() $\unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}$
: fix an unstable normal invariant
$\unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}$
: fix an unstable normal invariant
![]() $\unicode[STIX]{x1D6FC}:\!S^{n-1}\rightarrow P^{\unicode[STIX]{x1D709}}$
. Then the Browder construction applied to
$\unicode[STIX]{x1D6FC}:\!S^{n-1}\rightarrow P^{\unicode[STIX]{x1D709}}$
. Then the Browder construction applied to
![]() $\unicode[STIX]{x1D6FC}$
gives a Poincaré embedding with complement
$\unicode[STIX]{x1D6FC}$
gives a Poincaré embedding with complement
![]() $C=P^{\unicode[STIX]{x1D709}}$
.
$C=P^{\unicode[STIX]{x1D709}}$
.
Let
![]() $c:\!P^{\unicode[STIX]{x1D709}}\rightarrow P^{\unicode[STIX]{x1D709}}\vee \unicode[STIX]{x1D6F4}(P_{+})$
be the Barratt–Puppe coaction map for the based cofiber sequence
$c:\!P^{\unicode[STIX]{x1D709}}\rightarrow P^{\unicode[STIX]{x1D709}}\vee \unicode[STIX]{x1D6F4}(P_{+})$
be the Barratt–Puppe coaction map for the based cofiber sequence
![]() $P_{+}\rightarrow (\unicode[STIX]{x2202}P)_{+}\rightarrow P^{\unicode[STIX]{x1D709}}$
. Given
$P_{+}\rightarrow (\unicode[STIX]{x2202}P)_{+}\rightarrow P^{\unicode[STIX]{x1D709}}$
. Given
![]() $\unicode[STIX]{x1D719}\in F_{\ast }(\unicode[STIX]{x1D6F4}(P_{+}),P^{\unicode[STIX]{x1D709}})=\unicode[STIX]{x1D6FA}F_{\ast }(P_{+},P^{\unicode[STIX]{x1D709}})$
, we obtain a new normal invariant
$\unicode[STIX]{x1D719}\in F_{\ast }(\unicode[STIX]{x1D6F4}(P_{+}),P^{\unicode[STIX]{x1D709}})=\unicode[STIX]{x1D6FA}F_{\ast }(P_{+},P^{\unicode[STIX]{x1D709}})$
, we obtain a new normal invariant
![]() $\unicode[STIX]{x1D719}\star \unicode[STIX]{x1D6FC}$
by taking the composition
$\unicode[STIX]{x1D719}\star \unicode[STIX]{x1D6FC}$
by taking the composition
Then the operation
![]() $\unicode[STIX]{x1D719}\mapsto \unicode[STIX]{x1D719}\star \unicode[STIX]{x1D6FC}$
yields the desired description.
$\unicode[STIX]{x1D719}\mapsto \unicode[STIX]{x1D719}\star \unicode[STIX]{x1D6FC}$
yields the desired description.
Example 1.19. (Embeddings of the
 $n$
-disk)
$n$
-disk)
Let
![]() $P=D^{n}$
where
$P=D^{n}$
where
![]() $n\geqslant 3$
. Then
$n\geqslant 3$
. Then
![]() $P$
is sectioned by the basepoint of
$P$
is sectioned by the basepoint of
![]() $S^{n-1}$
. In this case, Theorem A gives a homotopy fiber sequence
$S^{n-1}$
. In this case, Theorem A gives a homotopy fiber sequence
where
![]() $F_{n-1}$
is the space of based self homotopy equivalences of
$F_{n-1}$
is the space of based self homotopy equivalences of
![]() $S^{n-1}$
. In fact,
$S^{n-1}$
. In fact,
![]() $E(D^{n},D^{n})\simeq G_{n}$
, the unbased self homotopy equivalences of
$E(D^{n},D^{n})\simeq G_{n}$
, the unbased self homotopy equivalences of
![]() $S^{n-1}$
. Furthermore, the above homotopy fiber sequence is principal and with respect to the identifications is just a shift to the left of the evident fibration
$S^{n-1}$
. Furthermore, the above homotopy fiber sequence is principal and with respect to the identifications is just a shift to the left of the evident fibration
![]() $F_{n-1}\rightarrow G_{n}\rightarrow S^{n-1}$
.
$F_{n-1}\rightarrow G_{n}\rightarrow S^{n-1}$
.
Example 1.20. (Disjoint unions of
 $n$
-disks)
$n$
-disks)
Assume
![]() $n\geqslant 3$
. Let
$n\geqslant 3$
. Let
![]() $T$
be a finite set and let
$T$
be a finite set and let
![]() $P=D^{n}\times T$
. Then
$P=D^{n}\times T$
. Then
![]() $P$
is sectioned by choosing a basepoint
$P$
is sectioned by choosing a basepoint
![]() $\ast \in S^{n-1}$
. Theorem A gives in this case a homotopy fiber sequence
$\ast \in S^{n-1}$
. Theorem A gives in this case a homotopy fiber sequence
For each
![]() $x\in T$
we have a projection map
$x\in T$
we have a projection map
![]() $p_{x}:\!S^{n-1}\wedge T_{+}\rightarrow S^{n-1}$
. The condition for a based map
$p_{x}:\!S^{n-1}\wedge T_{+}\rightarrow S^{n-1}$
. The condition for a based map
![]() $f:\!S^{n-1}\rightarrow S^{n-1}\wedge T_{+}$
to be a normal invariant is that every composite
$f:\!S^{n-1}\rightarrow S^{n-1}\wedge T_{+}$
to be a normal invariant is that every composite
![]() $p_{x}\circ f$
should lie in
$p_{x}\circ f$
should lie in
![]() $F_{n-1}$
.
$F_{n-1}$
.
Since
![]() $S^{n-1}\wedge T_{+}$
is a finite wedge of spheres, the Hilton–Milnor theorem implies that the homotopy groups of the two spaces on the left of (4) can be expressed explicitly in terms of the homotopy groups of spheres.
$S^{n-1}\wedge T_{+}$
is a finite wedge of spheres, the Hilton–Milnor theorem implies that the homotopy groups of the two spaces on the left of (4) can be expressed explicitly in terms of the homotopy groups of spheres.
For example, if
![]() $n$
is even, then these two spaces are rationally equivalent to generalized Eilenberg–Mac Lane spaces with finitely generated homotopy groups that only occur in even degrees. These rational homotopy groups can be explicitly computed in terms of a Hall basis for the free Lie algebra on
$n$
is even, then these two spaces are rationally equivalent to generalized Eilenberg–Mac Lane spaces with finitely generated homotopy groups that only occur in even degrees. These rational homotopy groups can be explicitly computed in terms of a Hall basis for the free Lie algebra on
![]() $|T|$
-generators (see e.g., [Reference Boardman and Steer1, Theorem 4.7]). For parity reasons, the long exact homotopy sequence of rational homotopy groups splits into short exact sequences
$|T|$
-generators (see e.g., [Reference Boardman and Steer1, Theorem 4.7]). For parity reasons, the long exact homotopy sequence of rational homotopy groups splits into short exact sequences
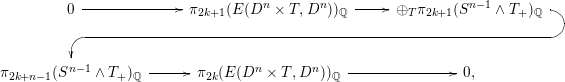
where we are assuming
![]() $k>0$
(this is not a serious restriction: it can be shown that
$k>0$
(this is not a serious restriction: it can be shown that
![]() $\unicode[STIX]{x1D70B}_{0}(E(D^{n}\times T,D^{n}))$
is a set of cardinality
$\unicode[STIX]{x1D70B}_{0}(E(D^{n}\times T,D^{n}))$
is a set of cardinality
![]() $2^{|T|}$
and
$2^{|T|}$
and
![]() $\unicode[STIX]{x1D70B}_{1}(E(D^{n}\times T,D^{n}))$
is the direct sum of
$\unicode[STIX]{x1D70B}_{1}(E(D^{n}\times T,D^{n}))$
is the direct sum of
![]() $|T|$
copies of the cyclic group of order two). From this we immediately obtain a crude bound for the rank of the rational homotopy groups of
$|T|$
copies of the cyclic group of order two). From this we immediately obtain a crude bound for the rank of the rational homotopy groups of
![]() $E(D^{n}\times T,D^{n})$
. To obtain finer information would require explicit knowledge of the curved arrow in the diagram.
$E(D^{n}\times T,D^{n})$
. To obtain finer information would require explicit knowledge of the curved arrow in the diagram.
1.7 Unlinked embeddings; the second main result
Definition 1.21. Assume
![]() $P$
is sectioned. The space of unlinked embeddings
$P$
is sectioned. The space of unlinked embeddings
consists of those points
![]() $C\in E(P,D^{n})$
such that the gluing data
$C\in E(P,D^{n})$
such that the gluing data
comes equipped with a factorization
where the first map is evident.
It is clear that the Browder construction (1) factors as
We call the map
the refined Browder construction.
Theorem B. The refined Browder construction (6) is a homotopy equivalence.
Remarks 1.22. (1). Theorem B is essentially a “space-ification” of a result Williams [Reference Williams23, Theorem A(i)] who considered a version of the map (6) on the level of path components. However, there are some minor differences:
-
∙ Williams restricts himself to sectioned Poincaré spaces of the type appearing in Example 1.5.
-
∙ Williams studies Poincaré embeddings in the
 $n$
-sphere rather than in the
$n$
-sphere rather than in the
 $n$
-disk. This distinction does not appear on the level of path components.
$n$
-disk. This distinction does not appear on the level of path components. -
∙ Williams equips his Poincaré spaces and their embeddings with orientations. His unstable normal invariants are of degree one.
The disadvantage with the
![]() $n$
-sphere is that Williams’ result does not extend to higher homotopy groups without modifying the domain of the refined Browder construction: the correct replacement is the space of “fiberwise unstable normal invariants over
$n$
-sphere is that Williams’ result does not extend to higher homotopy groups without modifying the domain of the refined Browder construction: the correct replacement is the space of “fiberwise unstable normal invariants over
![]() $S^{n}$
” (cf. [Reference Klein13]). Another disadvantage is that Williams has to work much harder than we do to prove his result.
$S^{n}$
” (cf. [Reference Klein13]). Another disadvantage is that Williams has to work much harder than we do to prove his result.
(2). Let
![]() $Q$
be as in Remark 1.18(1). Then Theorem B implies that the decompression map
$Q$
be as in Remark 1.18(1). Then Theorem B implies that the decompression map
is
![]() $(2n-3k-4)$
-connected.
$(2n-3k-4)$
-connected.
1.8 Poincaré Immersions
The space of (Poincaré) immersions
![]() $I(P,D^{n})$
is defined to be the homotopy colimit of the diagram
$I(P,D^{n})$
is defined to be the homotopy colimit of the diagram
where
![]() $P_{j}=P\times D^{j}$
. Note by construction
$P_{j}=P\times D^{j}$
. Note by construction
We view this as a reasonable definition, since the analogous statement is valid in the case of smooth block embeddings.
We will exhibit below a homotopy equivalence
where the right-hand side denotes the space of stable normal invariants of
![]() $P$
: this is the space whose points are stable maps
$P$
: this is the space whose points are stable maps
![]() $\unicode[STIX]{x1D6FC}:\!S^{n}\rightarrow P/\unicode[STIX]{x2202}P$
such that
$\unicode[STIX]{x1D6FC}:\!S^{n}\rightarrow P/\unicode[STIX]{x2202}P$
such that
![]() $\unicode[STIX]{x1D6FC}_{\ast }([S^{n}])\in H_{n}(P,\unicode[STIX]{x2202}P)$
is a fundamental class. We topologize this as a subspace of
$\unicode[STIX]{x1D6FC}_{\ast }([S^{n}])\in H_{n}(P,\unicode[STIX]{x2202}P)$
is a fundamental class. We topologize this as a subspace of
![]() $\unicode[STIX]{x1D6FA}^{n}Q(P/\unicode[STIX]{x2202}P):=\unicode[STIX]{x1D6FA}^{n}\unicode[STIX]{x1D6FA}^{\infty }\unicode[STIX]{x1D6F4}^{\infty }(P/\unicode[STIX]{x2202}P)$
.
$\unicode[STIX]{x1D6FA}^{n}Q(P/\unicode[STIX]{x2202}P):=\unicode[STIX]{x1D6FA}^{n}\unicode[STIX]{x1D6FA}^{\infty }\unicode[STIX]{x1D6F4}^{\infty }(P/\unicode[STIX]{x2202}P)$
.
Remark 1.23. Assuming
![]() $I(P,D^{n})$
is non-empty, we will also exhibit (Lemma 3.4) a homotopy equivalence
$I(P,D^{n})$
is non-empty, we will also exhibit (Lemma 3.4) a homotopy equivalence
where
![]() $G$
is the topological monoid of stable self-equivalences of the sphere. The equivalence depends on choosing a basepoint in
$G$
is the topological monoid of stable self-equivalences of the sphere. The equivalence depends on choosing a basepoint in
![]() $I(P,D^{n})$
.
$I(P,D^{n})$
.
Remark 1.24. Assume
![]() $P$
is orientable. The Spivak normal fibration of
$P$
is orientable. The Spivak normal fibration of
![]() $P$
is an orientable stable spherical fibration
$P$
is an orientable stable spherical fibration
![]() $\unicode[STIX]{x1D709}$
over
$\unicode[STIX]{x1D709}$
over
![]() $P$
that is equipped with a stable map
$P$
that is equipped with a stable map
![]() $\unicode[STIX]{x1D6FC}:\!S^{n}\rightarrow P^{\unicode[STIX]{x1D709}}/(\unicode[STIX]{x2202}P)^{\unicode[STIX]{x1D709}}$
representing a fundamental class for
$\unicode[STIX]{x1D6FC}:\!S^{n}\rightarrow P^{\unicode[STIX]{x1D709}}/(\unicode[STIX]{x2202}P)^{\unicode[STIX]{x1D709}}$
representing a fundamental class for
![]() $P$
by means of the Thom isomorphism. The data
$P$
by means of the Thom isomorphism. The data
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D6FC})$
are well-defined up to contractible choice [Reference Spivak19], [Reference Klein12].
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D6FC})$
are well-defined up to contractible choice [Reference Spivak19], [Reference Klein12].
Note that if
![]() $\unicode[STIX]{x1D709}$
is fiber homotopically trivial, then
$\unicode[STIX]{x1D709}$
is fiber homotopically trivial, then
![]() $\unicode[STIX]{x1D6FC}$
amounts to a stable normal invariant for
$\unicode[STIX]{x1D6FC}$
amounts to a stable normal invariant for
![]() $P$
. Furthermore,
$P$
. Furthermore,
![]() $I(P,D^{n})$
is identified with the space of fiber homotopy trivializations
$I(P,D^{n})$
is identified with the space of fiber homotopy trivializations
![]() $\unicode[STIX]{x1D709}$
(in particular, it is non-empty if and only if
$\unicode[STIX]{x1D709}$
(in particular, it is non-empty if and only if
![]() $\unicode[STIX]{x1D709}$
trivializable). The fiber homotopy triviality of
$\unicode[STIX]{x1D709}$
trivializable). The fiber homotopy triviality of
![]() $\unicode[STIX]{x1D709}$
is the Poincaré analog of stable parallelizability.
$\unicode[STIX]{x1D709}$
is the Poincaré analog of stable parallelizability.
1.9 A tower for unlinked embeddings; the third main result
We introduce some notation. If
![]() $V$
is an orthogonal representation of a group
$V$
is an orthogonal representation of a group
![]() $G$
, we let
$G$
, we let
![]() $S^{V}$
be the based
$S^{V}$
be the based
![]() $G$
-sphere given by the one-point compactification of
$G$
-sphere given by the one-point compactification of
![]() $V$
. If
$V$
. If
![]() $V$
and
$V$
and
![]() $W$
are two orthogonal representations, then we write
$W$
are two orthogonal representations, then we write
![]() $V+W$
for the direct sum and
$V+W$
for the direct sum and
![]() $nV$
will denote the direct sum of
$nV$
will denote the direct sum of
![]() $n$
-copies of
$n$
-copies of
![]() $V$
. If
$V$
. If
![]() $W\subset V$
is an orthogonal sub-representation, then we let
$W\subset V$
is an orthogonal sub-representation, then we let
![]() $V-W$
be its orthogonal complement. Let
$V-W$
be its orthogonal complement. Let
![]() $1$
denote the trivial representation of rank one. Let
$1$
denote the trivial representation of rank one. Let
![]() $\unicode[STIX]{x1D6F4}_{j}$
be the symmetric group on the standard basis for
$\unicode[STIX]{x1D6F4}_{j}$
be the symmetric group on the standard basis for
![]() $\mathbb{R}^{j}$
. Then we obtain the standard representation of
$\mathbb{R}^{j}$
. Then we obtain the standard representation of
![]() $\unicode[STIX]{x1D6F4}_{j}$
on
$\unicode[STIX]{x1D6F4}_{j}$
on
![]() $\mathbb{R}^{j}$
. The diagonal gives an embedding of the trivial representation
$\mathbb{R}^{j}$
. The diagonal gives an embedding of the trivial representation
![]() $1$
inside the standard representation. Let
$1$
inside the standard representation. Let
![]() $V_{j}$
be denote its orthogonal complement. Call this the reduced standard representation; it has rank
$V_{j}$
be denote its orthogonal complement. Call this the reduced standard representation; it has rank
![]() $j-1$
. For example,
$j-1$
. For example,
![]() $V_{2}$
is the rank one sign representation.
$V_{2}$
is the rank one sign representation.
If
![]() $X$
is a based (cofibrant) space and
$X$
is a based (cofibrant) space and
![]() $E$
is a (fibrant) spectrum, then we let
$E$
is a (fibrant) spectrum, then we let
![]() $F_{\ast }(X,E)$
be the (stable) function spectrum whose
$F_{\ast }(X,E)$
be the (stable) function spectrum whose
![]() $j$
th space is given by the based maps
$j$
th space is given by the based maps
![]() $X\rightarrow E_{j}$
. If
$X\rightarrow E_{j}$
. If
![]() $X$
and
$X$
and
![]() $E$
are equipped with
$E$
are equipped with
![]() $G$
-actions then
$G$
-actions then
![]() $F_{\ast }(X,E)$
inherits a
$F_{\ast }(X,E)$
inherits a
![]() $G$
-action by conjugation. In particular, one can consider the homotopy orbit spectrum
$G$
-action by conjugation. In particular, one can consider the homotopy orbit spectrum
![]() $F_{\ast }(X,E)_{hG}$
and its associated infinite loop space
$F_{\ast }(X,E)_{hG}$
and its associated infinite loop space
![]() $\unicode[STIX]{x1D6FA}^{\infty }F_{\ast }(X,E)_{hG}$
, the latter which will be denoted by
$\unicode[STIX]{x1D6FA}^{\infty }F_{\ast }(X,E)_{hG}$
, the latter which will be denoted by
![]() $F_{\ast }^{\operatorname{st}}(X,E)_{hG}$
.
$F_{\ast }^{\operatorname{st}}(X,E)_{hG}$
.
Let
![]() ${\mathcal{W}}_{j}$
denote the
${\mathcal{W}}_{j}$
denote the
![]() $j$
-coefficient spectrum of the identity functor from based spaces to based spaces in the sense of the calculus of homotopy functors [Reference Johnson10]. In particular,
$j$
-coefficient spectrum of the identity functor from based spaces to based spaces in the sense of the calculus of homotopy functors [Reference Johnson10]. In particular,
![]() ${\mathcal{W}}_{j}$
is a spectrum with
${\mathcal{W}}_{j}$
is a spectrum with
![]() $\unicode[STIX]{x1D6F4}_{j}$
-action which is unequivariantly weak equivalent to a wedge of
$\unicode[STIX]{x1D6F4}_{j}$
-action which is unequivariantly weak equivalent to a wedge of
![]() $(j-1)!$
copies of the
$(j-1)!$
copies of the
![]() $(1-j)$
-sphere.
$(1-j)$
-sphere.
Theorem C. Assume
![]() $P$
is sectioned and assume that the homotopy codimension of
$P$
is sectioned and assume that the homotopy codimension of
![]() $P$
is
$P$
is
![]() ${\geqslant}n-k\geqslant 3$
. Then there is a tower of fibrations
${\geqslant}n-k\geqslant 3$
. Then there is a tower of fibrations
equipped with compatible maps
such that
-
∙ the map
 $\unicode[STIX]{x1D719}_{j}$
is
$\unicode[STIX]{x1D719}_{j}$
is
 $(2-n+(j+1)(n-k-2))$
-connected; in particular, the induced map is a weak equivalence;
$(2-n+(j+1)(n-k-2))$
-connected; in particular, the induced map is a weak equivalence; $$\begin{eqnarray}\mathfrak{L}E(P,D^{n})\rightarrow \lim _{j\rightarrow \infty }\mathfrak{L}E_{j}(P,D^{n})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{L}E(P,D^{n})\rightarrow \lim _{j\rightarrow \infty }\mathfrak{L}E_{j}(P,D^{n})\end{eqnarray}$$
-
∙ there is a preferred homotopy equivalence
 $$\begin{eqnarray}\mathfrak{L}E_{1}(P,D^{n})\simeq I(P,D^{n});\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{L}E_{1}(P,D^{n})\simeq I(P,D^{n});\end{eqnarray}$$
-
∙ if
 $j\geqslant 2$
and
$j\geqslant 2$
and
 $x\in \mathfrak{L}E_{j-1}(P,D^{n})$
is a point, then there is an obstruction which is trivial if and only if the homotopy fiber of the map
$x\in \mathfrak{L}E_{j-1}(P,D^{n})$
is a point, then there is an obstruction which is trivial if and only if the homotopy fiber of the map $$\begin{eqnarray}\ell _{j-1}(x)\in \unicode[STIX]{x1D70B}_{0}(F_{\ast }(P_{+}^{\times j},{\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}+1})_{h\unicode[STIX]{x1D6F4}_{j}})\end{eqnarray}$$
$$\begin{eqnarray}\ell _{j-1}(x)\in \unicode[STIX]{x1D70B}_{0}(F_{\ast }(P_{+}^{\times j},{\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}+1})_{h\unicode[STIX]{x1D6F4}_{j}})\end{eqnarray}$$
 $\mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n})$
at
$\mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n})$
at
 $x$
is non-empty;
$x$
is non-empty;
-
∙ if
 $\ell _{j-1}(x)$
is trivial, then there is a homotopy fiber sequence where the displayed homotopy fiber is taken at
$\ell _{j-1}(x)$
is trivial, then there is a homotopy fiber sequence where the displayed homotopy fiber is taken at $$\begin{eqnarray}F_{\ast }^{\operatorname{st}}((P^{\times j})_{+},{\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}})_{h\unicode[STIX]{x1D6F4}_{j}}\rightarrow \mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n}).\end{eqnarray}$$
$$\begin{eqnarray}F_{\ast }^{\operatorname{st}}((P^{\times j})_{+},{\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}})_{h\unicode[STIX]{x1D6F4}_{j}}\rightarrow \mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n}).\end{eqnarray}$$
 $x$
.
$x$
.
Remarks 1.25. (1). The first part of Theorem C implies that if
![]() $(j+1)k+2j\leqslant jn$
and
$(j+1)k+2j\leqslant jn$
and
![]() $\mathfrak{L}E_{j}(P,D^{n})$
is non-empty, then
$\mathfrak{L}E_{j}(P,D^{n})$
is non-empty, then
![]() $\mathfrak{L}E(P,D^{n})$
is also non-empty.
$\mathfrak{L}E(P,D^{n})$
is also non-empty.
(2). It follows from the last two parts of the theorem that the map
![]() $\mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n})$
is
$\mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n})$
is
![]() $(2-n+j(n-k-2))$
-connected.
$(2-n+j(n-k-2))$
-connected.
(3). Modulo torsion, a transfer argument shows that the class
![]() $\ell _{j-1}(x)$
is detected in the singular cohomology group
$\ell _{j-1}(x)$
is detected in the singular cohomology group
![]() $H^{s}(P^{\times j};\mathbb{Q}^{(j-1)!})$
, where
$H^{s}(P^{\times j};\mathbb{Q}^{(j-1)!})$
, where
![]() $s=(n-2)(j-1)+1$
.
$s=(n-2)(j-1)+1$
.
(4). The layers of the tower depend only on the homotopy type of
![]() $P$
and in particular do not depend on the choice of sectioning data.
$P$
and in particular do not depend on the choice of sectioning data.
Outline.
The material of Section 2 is mostly language. The literate reader can skip it and refer back to it as needed. In Section 3 we provide constructions of the Poincaré embedding space, its unlinked variant and the space of Poincaré immersions. We prove Theorems A and B in Section 4. In Section 5 we prove Theorem C. The final section, Appendix A, is conjectural: it poses a connection between the tower of Theorem C and the Goodwillie–Weiss tower for smooth embeddings.
2 Preliminaries
2.1 Spaces
Our ground category is
![]() $T$
, the category of compactly generated weak Hausdorff spaces. A non-empty space
$T$
, the category of compactly generated weak Hausdorff spaces. A non-empty space
![]() $X$
is
$X$
is
![]() $r$
-connected if
$r$
-connected if
![]() $\unicode[STIX]{x1D70B}_{j}(X,x)$
is trivial for
$\unicode[STIX]{x1D70B}_{j}(X,x)$
is trivial for
![]() $j\leqslant r$
, for all base points
$j\leqslant r$
, for all base points
![]() $x\in X$
. The empty space is
$x\in X$
. The empty space is
![]() $(-2)$
-connected and every non-empty space is
$(-2)$
-connected and every non-empty space is
![]() $(-1)$
-connected. A map
$(-1)$
-connected. A map
![]() $X\rightarrow Y$
of non-empty spaces is
$X\rightarrow Y$
of non-empty spaces is
![]() $r$
-connected if each of its homotopy fibers is
$r$
-connected if each of its homotopy fibers is
![]() $(r-1)$
-connected (every map of non-empty spaces is
$(r-1)$
-connected (every map of non-empty spaces is
![]() $(-1)$
-connected; a weak homotopy equivalence is an
$(-1)$
-connected; a weak homotopy equivalence is an
![]() $\infty$
-connected map).
$\infty$
-connected map).
For unbased spaces
![]() $X$
and
$X$
and
![]() $Y$
we let
$Y$
we let
![]() $F(X,Y)$
be the unbased function space and if
$F(X,Y)$
be the unbased function space and if
![]() $X$
and
$X$
and
![]() $Y$
are based we let
$Y$
are based we let
![]() $F_{\ast }(X,Y)$
be the based function space. When we write
$F_{\ast }(X,Y)$
be the based function space. When we write
![]() $[X,Y]$
, we mean homotopy classes of based maps
$[X,Y]$
, we mean homotopy classes of based maps
![]() $X^{\text{c}}\rightarrow Y$
, where
$X^{\text{c}}\rightarrow Y$
, where
![]() $X^{\text{c}}$
is a cofibrant replacement for
$X^{\text{c}}$
is a cofibrant replacement for
![]() $X$
. When
$X$
. When
![]() $X$
and
$X$
and
![]() $Y$
are based, then the based homotopy classes are to be written as
$Y$
are based, then the based homotopy classes are to be written as
![]() $[X,Y]_{\ast }$
. We use the usual notation for the smash product:
$[X,Y]_{\ast }$
. We use the usual notation for the smash product:
![]() $X\wedge Y$
, and the iterated smash product of
$X\wedge Y$
, and the iterated smash product of
![]() $j$
-copies of
$j$
-copies of
![]() $X$
is denoted
$X$
is denoted
![]() $X^{[j]}$
.
$X^{[j]}$
.
We equip
![]() $T$
with the Quillen model category structure given by the Serre fibrations, Serre cofibrations and weak homotopy equivalences [Reference Quillen17], [Reference Hovey9, Theorem 2.4.23]. Note that
$T$
with the Quillen model category structure given by the Serre fibrations, Serre cofibrations and weak homotopy equivalences [Reference Quillen17], [Reference Hovey9, Theorem 2.4.23]. Note that
![]() $T$
is enriched over itself. We let
$T$
is enriched over itself. We let
![]() $T_{\ast }$
denote the model category of based spaces.
$T_{\ast }$
denote the model category of based spaces.
A commutative square of spaces
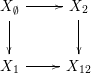
is homotopy co-Cartesian if the map
is a weak equivalence, where the domain of this map is given by the homotopy pushout of the diagram obtained from the square by removing its terminal vertex. In the special case when
![]() $X_{2}$
is contractible, we abuse notation and refer to
$X_{2}$
is contractible, we abuse notation and refer to
![]() $X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
as a homotopy cofiber sequence. This is the same as equipping the composition
$X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
as a homotopy cofiber sequence. This is the same as equipping the composition
![]() $X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
with a preferred choice of null homotopy such that the induced map
$X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
with a preferred choice of null homotopy such that the induced map
![]() $X_{2}\cup _{X_{\emptyset }}CX_{\emptyset }\rightarrow X_{12}$
is required to be a weak equivalence.
$X_{2}\cup _{X_{\emptyset }}CX_{\emptyset }\rightarrow X_{12}$
is required to be a weak equivalence.
Similarly, the above square is homotopy Cartesian if the map from
![]() $X_{\emptyset }$
to the homotopy pullback of
$X_{\emptyset }$
to the homotopy pullback of
![]() $X_{1}\rightarrow X_{12}\leftarrow X_{2}$
is a weak equivalence. When
$X_{1}\rightarrow X_{12}\leftarrow X_{2}$
is a weak equivalence. When
![]() $X_{2}$
is contractible, we refer to
$X_{2}$
is contractible, we refer to
![]() $X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
as a homotopy fiber sequence. The latter is equivalent to describing a null homotopy of the composition
$X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
as a homotopy fiber sequence. The latter is equivalent to describing a null homotopy of the composition
![]() $X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
such that the map from
$X_{\emptyset }\rightarrow X_{1}\rightarrow X_{12}$
such that the map from
![]() $X_{\emptyset }$
to the homotopy fiber of the map
$X_{\emptyset }$
to the homotopy fiber of the map
![]() $X_{1}\rightarrow X_{12}$
is a weak equivalence.
$X_{1}\rightarrow X_{12}$
is a weak equivalence.
In each of these notions, when the null homotopy is understood, we typically omit it from the notation to avoid clutter.
2.2 Factorization categories
Fix a map of spaces
![]() $f:A\rightarrow B$
. Define a category
$f:A\rightarrow B$
. Define a category
whose objects are spaces
![]() $X$
and a factorization
$X$
and a factorization
![]() $A\rightarrow X\rightarrow B$
by continuous maps. A morphism
$A\rightarrow X\rightarrow B$
by continuous maps. A morphism
![]() $X\rightarrow X^{\prime }$
is a map of spaces that is compatible with the factorizations. When
$X\rightarrow X^{\prime }$
is a map of spaces that is compatible with the factorizations. When
![]() $f$
is understood, we usually write this category as
$f$
is understood, we usually write this category as
![]() $T(A\rightarrow B)$
.
$T(A\rightarrow B)$
.
Here are some important special cases:
Example 2.1. Let
![]() $A=B$
and use the identity map. Then
$A=B$
and use the identity map. Then
![]() $T(B\rightarrow B)$
is the category of spaces which contain
$T(B\rightarrow B)$
is the category of spaces which contain
![]() $B$
as a retract.
$B$
as a retract.
Example 2.2. Let
![]() $A=\emptyset$
be the empty space. Then
$A=\emptyset$
be the empty space. Then
![]() $T(\emptyset \rightarrow B)$
is the category of spaces over
$T(\emptyset \rightarrow B)$
is the category of spaces over
![]() $B$
.
$B$
.
Example 2.3. Let
![]() $B=\ast$
be the one-point space. Then
$B=\ast$
be the one-point space. Then
![]() $T(A\rightarrow \ast )$
is the category of spaces under
$T(A\rightarrow \ast )$
is the category of spaces under
![]() $A$
.
$A$
.
The forgetful functor
![]() $T(A\rightarrow B)\rightarrow T$
induces a model structure on
$T(A\rightarrow B)\rightarrow T$
induces a model structure on
![]() $T(A\rightarrow B)$
by declaring a morphism to be a cofibration, fibration or weak equivalence if and only if it is one in
$T(A\rightarrow B)$
by declaring a morphism to be a cofibration, fibration or weak equivalence if and only if it is one in
![]() $T$
[Reference Quillen17, 2.8, Proposition 6]. This model structure is enriched over
$T$
[Reference Quillen17, 2.8, Proposition 6]. This model structure is enriched over
![]() $T$
. The category of weak equivalences is denoted by
$T$
. The category of weak equivalences is denoted by
Remark 2.4. We use the notation
![]() $|{\mathcal{C}}|$
for the realization (of the nerve) of a small category
$|{\mathcal{C}}|$
for the realization (of the nerve) of a small category
![]() ${\mathcal{C}}$
. The functor
${\mathcal{C}}$
. The functor
![]() ${\mathcal{C}}\mapsto |{\mathcal{C}}|$
enables one to transfer homotopical properties of spaces over to small categories. For example, we declare a functor
${\mathcal{C}}\mapsto |{\mathcal{C}}|$
enables one to transfer homotopical properties of spaces over to small categories. For example, we declare a functor
![]() $f:\!{\mathcal{C}}\rightarrow {\mathcal{D}}$
to be
$f:\!{\mathcal{C}}\rightarrow {\mathcal{D}}$
to be
![]() $r$
-connected if and only if it is so upon taking realization. Likewise, it makes sense to ask whether a commutative square of small categories is homotopy Cartesian.
$r$
-connected if and only if it is so upon taking realization. Likewise, it makes sense to ask whether a commutative square of small categories is homotopy Cartesian.
In this paper the categories
![]() ${\mathcal{C}}$
that we will want to apply realization to are full subcategories of
${\mathcal{C}}$
that we will want to apply realization to are full subcategories of
![]() $wT(A\rightarrow B)$
– but they are not small. This is not a major dilemma; for a discussion of the options on how to deal with the matter, see [Reference Goodwillie and Klein6, p. 766].
$wT(A\rightarrow B)$
– but they are not small. This is not a major dilemma; for a discussion of the options on how to deal with the matter, see [Reference Goodwillie and Klein6, p. 766].
2.3 Spectra
The spectra appearing in this paper are formed from objects of
![]() $T_{\ast }$
. For us, a spectrum will be a sequence of based spaces
$T_{\ast }$
. For us, a spectrum will be a sequence of based spaces
![]() $E_{j}$
and (structure) maps
$E_{j}$
and (structure) maps
![]() $\unicode[STIX]{x1D6F4}E_{j}\rightarrow E_{j+1}$
. We say that
$\unicode[STIX]{x1D6F4}E_{j}\rightarrow E_{j+1}$
. We say that
![]() $E$
is cofibrant if each of the spaces
$E$
is cofibrant if each of the spaces
![]() $E_{j}$
is cofibrant and each structure map is a cofibration.
$E_{j}$
is cofibrant and each structure map is a cofibration.
![]() $E$
is fibrant if each adjoint
$E$
is fibrant if each adjoint
![]() $E_{j}\rightarrow \unicode[STIX]{x1D6FA}E_{j+1}$
is a weak equivalence.
$E_{j}\rightarrow \unicode[STIX]{x1D6FA}E_{j+1}$
is a weak equivalence.
A map of spectra
![]() $f:\!E\rightarrow E^{\prime }$
is a collection of maps
$f:\!E\rightarrow E^{\prime }$
is a collection of maps
![]() $f_{j}:\!E_{j}\rightarrow E_{j}^{\prime }$
that are compatible with the structure maps. Any spectrum
$f_{j}:\!E_{j}\rightarrow E_{j}^{\prime }$
that are compatible with the structure maps. Any spectrum
![]() $E$
has a fibrant replacement, which is a spectrum
$E$
has a fibrant replacement, which is a spectrum
![]() $E^{\text{f}}$
equipped with a natural map of spectra
$E^{\text{f}}$
equipped with a natural map of spectra
![]() $E\rightarrow E^{\text{f}}$
, where
$E\rightarrow E^{\text{f}}$
, where
![]() $E_{j}^{\text{f}}:=\operatorname{colim}_{k}\unicode[STIX]{x1D6FA}^{k}(S^{j}\wedge E_{k})$
. The map
$E_{j}^{\text{f}}:=\operatorname{colim}_{k}\unicode[STIX]{x1D6FA}^{k}(S^{j}\wedge E_{k})$
. The map
![]() $f:\!E\rightarrow E^{\prime }$
is a (stable) weak equivalence if the associated map
$f:\!E\rightarrow E^{\prime }$
is a (stable) weak equivalence if the associated map
![]() $E^{\text{f}}\rightarrow (E^{\prime })^{\text{f}}$
is such that for each
$E^{\text{f}}\rightarrow (E^{\prime })^{\text{f}}$
is such that for each
![]() $j$
the map of based spaces
$j$
the map of based spaces
![]() $E_{j}^{\text{f}}\rightarrow (E^{\prime })_{j}^{\text{f}}$
is a weak equivalence. If
$E_{j}^{\text{f}}\rightarrow (E^{\prime })_{j}^{\text{f}}$
is a weak equivalence. If
![]() $E$
is a spectrum, we write
$E$
is a spectrum, we write
![]() $\unicode[STIX]{x1D6FA}^{\infty }E$
for the associated infinite loop space given by the zeroth space of its fibrant replacement. If
$\unicode[STIX]{x1D6FA}^{\infty }E$
for the associated infinite loop space given by the zeroth space of its fibrant replacement. If
![]() $X$
is a based space, then we let
$X$
is a based space, then we let
![]() $\unicode[STIX]{x1D6F4}^{\infty }X$
be its suspension spectrum whose
$\unicode[STIX]{x1D6F4}^{\infty }X$
be its suspension spectrum whose
![]() $j$
th space is
$j$
th space is
![]() $S^{j}\wedge X$
. For it to have the correct homotopy type we should assume that
$S^{j}\wedge X$
. For it to have the correct homotopy type we should assume that
![]() $X$
is cofibrant. The zeroth space of
$X$
is cofibrant. The zeroth space of
![]() $\unicode[STIX]{x1D6F4}^{\infty }X$
is denoted
$\unicode[STIX]{x1D6F4}^{\infty }X$
is denoted
![]() $Q(X)$
.
$Q(X)$
.
Given a based space
![]() $X$
and a spectrum
$X$
and a spectrum
![]() $E$
we can form
$E$
we can form
![]() $X\wedge E$
which is the spectrum whose
$X\wedge E$
which is the spectrum whose
![]() $j$
th space is
$j$
th space is
![]() $X\wedge E_{j}$
. This has the correct homotopy type if both
$X\wedge E_{j}$
. This has the correct homotopy type if both
![]() $X$
and
$X$
and
![]() $E$
are cofibrant. Similarly we can form the functions
$E$
are cofibrant. Similarly we can form the functions
![]() $F_{\ast }(X,E)$
which is the spectrum whose
$F_{\ast }(X,E)$
which is the spectrum whose
![]() $j$
th space is
$j$
th space is
![]() $F_{\ast }(X,E_{j})$
. This has the correct homotopy type when
$F_{\ast }(X,E_{j})$
. This has the correct homotopy type when
![]() $X$
is cofibrant and
$X$
is cofibrant and
![]() $E$
is fibrant (when
$E$
is fibrant (when
![]() $E$
fails to be fibrant, we will implicitly replace it by its fibrant model). The associated stable function space is
$E$
fails to be fibrant, we will implicitly replace it by its fibrant model). The associated stable function space is
![]() $\unicode[STIX]{x1D6FA}^{\infty }F_{\ast }(X,E)$
. We will typically be sloppy and omit the
$\unicode[STIX]{x1D6FA}^{\infty }F_{\ast }(X,E)$
. We will typically be sloppy and omit the
![]() $\unicode[STIX]{x1D6FA}^{\infty }$
from the notation. Thus,
$\unicode[STIX]{x1D6FA}^{\infty }$
from the notation. Thus,
![]() $F_{\ast }(X,E)$
can mean either the spectrum or its associated infinite loop space. If
$F_{\ast }(X,E)$
can mean either the spectrum or its associated infinite loop space. If
![]() $X$
is unbased then we set
$X$
is unbased then we set
![]() $F(X,E)=F_{\ast }(X_{+},E)$
where
$F(X,E)=F_{\ast }(X_{+},E)$
where
![]() $X_{+}=X\amalg \ast$
. If
$X_{+}=X\amalg \ast$
. If
![]() $X$
and
$X$
and
![]() $Y$
are based spaces, then a stable map
$Y$
are based spaces, then a stable map
![]() $X\rightarrow Y$
is an element of the stable function space
$X\rightarrow Y$
is an element of the stable function space
![]() $F_{\ast }(X,\unicode[STIX]{x1D6F4}^{\infty }Y)$
, that is, a point of the function space
$F_{\ast }(X,\unicode[STIX]{x1D6F4}^{\infty }Y)$
, that is, a point of the function space
![]() $F_{\ast }(X,Q(Y))$
, where
$F_{\ast }(X,Q(Y))$
, where
![]() $Q(Y)=\unicode[STIX]{x1D6FA}^{\infty }\unicode[STIX]{x1D6F4}^{\infty }Y$
. We let
$Q(Y)=\unicode[STIX]{x1D6FA}^{\infty }\unicode[STIX]{x1D6F4}^{\infty }Y$
. We let
![]() $\{X,Y\}_{\ast }$
denote the stable homotopy classes of maps from
$\{X,Y\}_{\ast }$
denote the stable homotopy classes of maps from
![]() $X$
to
$X$
to
![]() $Y$
; this is the same as
$Y$
; this is the same as
![]() $\unicode[STIX]{x1D70B}_{0} (F_{\ast }(X,Q(Y))$
when
$\unicode[STIX]{x1D70B}_{0} (F_{\ast }(X,Q(Y))$
when
![]() $X$
and
$X$
and
![]() $Y$
are cofibrant.
$Y$
are cofibrant.
Smash products of spectra are barely used in this paper, and are confined to the proof of Theorem C. It is for this reason that we are content to work in the above category of spectra. The reader is free to use a more modern approach.
2.4 Spectra with group action
Fix a discrete group
![]() $G$
. We say that a spectrum
$G$
. We say that a spectrum
![]() $E$
has a
$E$
has a
![]() $G$
-action if each
$G$
-action if each
![]() $E_{j}$
has the structure of a based
$E_{j}$
has the structure of a based
![]() $G$
-space and each structure map
$G$
-space and each structure map
![]() $\unicode[STIX]{x1D6F4}E_{j}\rightarrow E_{j+1}$
is equivariant, where
$\unicode[STIX]{x1D6F4}E_{j}\rightarrow E_{j+1}$
is equivariant, where
![]() $G$
acts trivially on the suspension coordinate. A map
$G$
acts trivially on the suspension coordinate. A map
![]() $E\rightarrow E^{\prime }$
of spectra with
$E\rightarrow E^{\prime }$
of spectra with
![]() $G$
-action is just a map of underlying spectra which is
$G$
-action is just a map of underlying spectra which is
![]() $G$
-equivariant. A map of spectra is a weak equivalence if it is when considered as a map of spectra without action. We say that
$G$
-equivariant. A map of spectra is a weak equivalence if it is when considered as a map of spectra without action. We say that
![]() $E$
is fibrant if its underlying spectrum (without action) is. Call a based
$E$
is fibrant if its underlying spectrum (without action) is. Call a based
![]() $G$
-space
$G$
-space
![]() $X$
$X$
![]() $G$
-cofibrant if it is built up from the basepoint by attaching free
$G$
-cofibrant if it is built up from the basepoint by attaching free
![]() $G$
-cells along equivariant maps; a free
$G$
-cells along equivariant maps; a free
![]() $G$
-cell has the form
$G$
-cell has the form
![]() $D^{n}\times G$
.
$D^{n}\times G$
.
If
![]() $X$
is a
$X$
is a
![]() $G$
-space and
$G$
-space and
![]() $E$
is a spectrum with
$E$
is a spectrum with
![]() $G$
-action, then
$G$
-action, then
![]() $G$
acts diagonally on
$G$
acts diagonally on
![]() $X\wedge E$
. We write
$X\wedge E$
. We write
![]() $X\wedge _{G}E$
for the orbit spectrum. This has the correct homotopy type if
$X\wedge _{G}E$
for the orbit spectrum. This has the correct homotopy type if
![]() $X$
and
$X$
and
![]() $E$
are both
$E$
are both
![]() $G$
-cofibrant. The homotopy orbits of
$G$
-cofibrant. The homotopy orbits of
![]() $G$
acting on
$G$
acting on
![]() $E$
is the spectrum
$E$
is the spectrum
where
![]() $EG$
the universal contractible
$EG$
the universal contractible
![]() $G$
-space. This has the correct homotopy type of the underlying spectrum of
$G$
-space. This has the correct homotopy type of the underlying spectrum of
![]() $E$
is cofibrant.
$E$
is cofibrant.
2.5 Poincaré spaces
The Poincaré spaces of this paper are orientable. An orientable Poincaré space of dimension
![]() $d$
consists of a homotopy finite space
$d$
consists of a homotopy finite space
![]() $P$
for which there exists a fundamental class
$P$
for which there exists a fundamental class
![]() $[P]\in H_{d}(P;\mathbb{Z})$
such that the cap product
$[P]\in H_{d}(P;\mathbb{Z})$
such that the cap product
is an isomorphism in all degrees for any locally constant sheaf
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
If
![]() $\unicode[STIX]{x1D70B}:\!\tilde{P}\rightarrow P$
is a choice of universal cover, then the cap product is an isomorphism for all
$\unicode[STIX]{x1D70B}:\!\tilde{P}\rightarrow P$
is a choice of universal cover, then the cap product is an isomorphism for all
![]() ${\mathcal{M}}$
if and only if it is an isomorphism for the locally constant sheaf
${\mathcal{M}}$
if and only if it is an isomorphism for the locally constant sheaf
![]() $\unicode[STIX]{x1D6EC}$
whose stalk at
$\unicode[STIX]{x1D6EC}$
whose stalk at
![]() $x\in P$
is given by the free abelian group with basis
$x\in P$
is given by the free abelian group with basis
![]() $\unicode[STIX]{x1D70B}^{-1}(x)$
(cf. [Reference Wall21, Lemma 1.1]).
$\unicode[STIX]{x1D70B}^{-1}(x)$
(cf. [Reference Wall21, Lemma 1.1]).
Poincaré spaces
![]() $P$
with boundary
$P$
with boundary
![]() $\unicode[STIX]{x2202}P$
, also known as Poincaré pairs, are defined similarly, where now
$\unicode[STIX]{x2202}P$
, also known as Poincaré pairs, are defined similarly, where now
![]() $[P]\in H_{d}(P,\unicode[STIX]{x2202}P;\mathbb{Z})$
, the cap product
$[P]\in H_{d}(P,\unicode[STIX]{x2202}P;\mathbb{Z})$
, the cap product
is an isomorphism, and the class
![]() $[\unicode[STIX]{x2202}P]\in H_{d-1}(\unicode[STIX]{x2202}P;\mathbb{Z})$
, obtained by applying the boundary homomorphism to
$[\unicode[STIX]{x2202}P]\in H_{d-1}(\unicode[STIX]{x2202}P;\mathbb{Z})$
, obtained by applying the boundary homomorphism to
![]() $[P]$
, equips
$[P]$
, equips
![]() $\unicode[STIX]{x2202}P$
the structure of a Poincaré space of dimension
$\unicode[STIX]{x2202}P$
the structure of a Poincaré space of dimension
![]() $d-1$
(this assumes in particular that
$d-1$
(this assumes in particular that
![]() $\unicode[STIX]{x2202}P$
is homotopy finite). We will be relaxed about language and refer to a Poincaré space with or without boundary simply as a Poincaré space.
$\unicode[STIX]{x2202}P$
is homotopy finite). We will be relaxed about language and refer to a Poincaré space with or without boundary simply as a Poincaré space.
We will also sometimes omit the condition that the map
![]() $\unicode[STIX]{x2202}P\rightarrow P$
is an inclusion. The definition of a Poincaré space still makes sense in this instance since we can replace any map by its mapping cylinder inclusion.
$\unicode[STIX]{x2202}P\rightarrow P$
is an inclusion. The definition of a Poincaré space still makes sense in this instance since we can replace any map by its mapping cylinder inclusion.
3 Poincaré embeddings
Let
![]() $P$
be a Poincaré space of dimension
$P$
be a Poincaré space of dimension
![]() $n$
. We will assume here that
$n$
. We will assume here that
![]() $\unicode[STIX]{x2202}P\rightarrow P$
is a cofibration. An (interior) Poincaré embedding of
$\unicode[STIX]{x2202}P\rightarrow P$
is a cofibration. An (interior) Poincaré embedding of
![]() $P$
in
$P$
in
![]() $D^{n}$
consists of a space
$D^{n}$
consists of a space
![]() $C$
and a map
$C$
and a map
![]() $\unicode[STIX]{x2202}P\amalg S^{n-1}\rightarrow C$
such that
$\unicode[STIX]{x2202}P\amalg S^{n-1}\rightarrow C$
such that
-
∙
 $C$
is a Poincaré space with boundary
$C$
is a Poincaré space with boundary
 $\unicode[STIX]{x2202}P\amalg S^{n-1}$
;
$\unicode[STIX]{x2202}P\amalg S^{n-1}$
; -
∙ the amalgamated union
is weakly contractible. $$\begin{eqnarray}P\cup _{\unicode[STIX]{x2202}P}C\end{eqnarray}$$
$$\begin{eqnarray}P\cup _{\unicode[STIX]{x2202}P}C\end{eqnarray}$$
In what follows we set
Then
is an object. Let
be the full subcategory whose objects give Poincaré embeddings of
![]() $P$
in
$P$
in
![]() $D^{n}$
. The space of Poincaré embeddings of
$D^{n}$
. The space of Poincaré embeddings of
![]() $P$
in
$P$
in
![]() $D^{n}$
is then defined as the realization
$D^{n}$
is then defined as the realization
This is an open and closed subspace of
![]() $|wT(A\rightarrow \ast )|$
.
$|wT(A\rightarrow \ast )|$
.
Remark 3.1. The version of the Poincaré embedding space appearing here is slightly different from the one in [Reference Goodwillie and Klein6, Definition 2.8]. There it is defined to be the homotopy fiber of the functor
given by “gluing in
![]() $P$
,” where for a Poincaré space
$P$
,” where for a Poincaré space
![]() $\unicode[STIX]{x2202}$
without boundary, the category
$\unicode[STIX]{x2202}$
without boundary, the category
![]() ${\mathcal{I}}(\unicode[STIX]{x2202})$
has objects Poincaré spaces
${\mathcal{I}}(\unicode[STIX]{x2202})$
has objects Poincaré spaces
![]() $X$
with
$X$
with
![]() $\unicode[STIX]{x2202}$
as boundary, and morphisms are weak homotopy equivalences
$\unicode[STIX]{x2202}$
as boundary, and morphisms are weak homotopy equivalences
![]() $X\rightarrow X^{\prime }$
which restrict to the identity on
$X\rightarrow X^{\prime }$
which restrict to the identity on
![]() $\unicode[STIX]{x2202}$
. In the definition of [Reference Goodwillie and Klein6, Definition 2.8], the homotopy fiber of (7) is taken at
$\unicode[STIX]{x2202}$
. In the definition of [Reference Goodwillie and Klein6, Definition 2.8], the homotopy fiber of (7) is taken at
![]() $D^{n}\in {\mathcal{I}}(S^{n-1})$
. Our definition here amounts to taking a certain open and closed subspace of
$D^{n}\in {\mathcal{I}}(S^{n-1})$
. Our definition here amounts to taking a certain open and closed subspace of
![]() ${\mathcal{I}}(A)$
rather than a homotopy fiber. This definition is equivalent to the one in [Reference Goodwillie and Klein6] because the component of
${\mathcal{I}}(A)$
rather than a homotopy fiber. This definition is equivalent to the one in [Reference Goodwillie and Klein6] because the component of
![]() $D^{n}\in {\mathcal{I}}(S^{n-1})$
is contractible.
$D^{n}\in {\mathcal{I}}(S^{n-1})$
is contractible.
The decompression functor
is defined by mapping
![]() $C\in {\mathcal{E}}(P,D^{n})$
to its unreduced suspension
$C\in {\mathcal{E}}(P,D^{n})$
to its unreduced suspension
![]() $SC$
. On realizations it defines the decompression map
$SC$
. On realizations it defines the decompression map
3.1 Unlinked embeddings
If
![]() $P$
is sectioned, then we set
$P$
is sectioned, then we set
There is then a cofiber sequence
![]() $P_{+}\rightarrow A\rightarrow A^{\prime }$
. The map
$P_{+}\rightarrow A\rightarrow A^{\prime }$
. The map
![]() $A\rightarrow A^{\prime }$
induces a (forgetful) functor
$A\rightarrow A^{\prime }$
induces a (forgetful) functor
Definition 3.2. The space of unlinked embeddings
![]() $\mathfrak{L}E(P,D^{n})$
is the realization of the full subcategory
$\mathfrak{L}E(P,D^{n})$
is the realization of the full subcategory
consisting of objects
![]() $C$
which become Poincaré embeddings when considered in
$C$
which become Poincaré embeddings when considered in
![]() $wT(A\rightarrow \ast )$
.
$wT(A\rightarrow \ast )$
.
Unraveling the definition, we see that an unlinked embedding consists of a space
![]() $C$
and a map
$C$
and a map
![]() $P^{\unicode[STIX]{x1D709}}\vee S^{n-1}\rightarrow C$
such that the composition
$P^{\unicode[STIX]{x1D709}}\vee S^{n-1}\rightarrow C$
such that the composition
defines a Poincaré embedding of
![]() $P$
in
$P$
in
![]() $D^{n}$
.
$D^{n}$
.
By definition, there is a homotopy Cartesian square
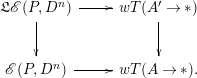
3.2 Poincaré Immersions
Recall
![]() $P_{j}:=P\times D^{j}$
. The immersion space
$P_{j}:=P\times D^{j}$
. The immersion space
![]() $I(P,D^{n})$
is defined as the homotopy colimit of the sequence of decompression maps
$I(P,D^{n})$
is defined as the homotopy colimit of the sequence of decompression maps
Lemma 3.3. There is a homotopy equivalence
Proof. The Browder construction gives a factorization of the filtration defining
![]() $I(P,D^{n})$
as
$I(P,D^{n})$
as
The homotopy colimit of the odd terms appearing in the sequence yields
![]() $I(P,D^{n})$
by definition, whereas the homotopy colimit of the even terms gives the space of stable normal invariants
$I(P,D^{n})$
by definition, whereas the homotopy colimit of the even terms gives the space of stable normal invariants
since
![]() $\unicode[STIX]{x1D6FA}^{n+j}(P_{j}/\unicode[STIX]{x2202}P_{j})=\unicode[STIX]{x1D6FA}^{n+j}\unicode[STIX]{x1D6F4}^{j}(P/\unicode[STIX]{x2202}P)$
.◻
$\unicode[STIX]{x1D6FA}^{n+j}(P_{j}/\unicode[STIX]{x2202}P_{j})=\unicode[STIX]{x1D6FA}^{n+j}\unicode[STIX]{x1D6F4}^{j}(P/\unicode[STIX]{x2202}P)$
.◻
Lemma 3.4. (Smale–Hirsch for Poincaré Spaces)
If
![]() $I(P,D^{n})$
is non-empty and equipped with a basepoint, then there is preferred weak homotopy equivalence
$I(P,D^{n})$
is non-empty and equipped with a basepoint, then there is preferred weak homotopy equivalence
where the right side denotes the function space of unbased maps from
![]() $P$
to the topological monoid of stable self equivalences of the sphere.
$P$
to the topological monoid of stable self equivalences of the sphere.
Remark 3.5. The corresponding statement in the smooth case is that the smooth immersions of
![]() $P$
to
$P$
to
![]() $D^{n}$
is weak equivalent to the function space
$D^{n}$
is weak equivalent to the function space
![]() $F(P,O_{n})$
, where
$F(P,O_{n})$
, where
![]() $O_{n}$
is the group of orthogonal
$O_{n}$
is the group of orthogonal
![]() $n\times n$
matrices. Note that the smooth version depends on
$n\times n$
matrices. Note that the smooth version depends on
![]() $n$
.
$n$
.
To obtain a smooth statement which does not depend on
![]() $n$
, one should replace the smooth immersion space by its block analogue. In this instance one obtains a weak equivalence to the function space
$n$
, one should replace the smooth immersion space by its block analogue. In this instance one obtains a weak equivalence to the function space
![]() $F(P,O)$
.
$F(P,O)$
.
Proof of Lemma 3.4.
If
![]() $I(P,D^{n})$
is non-empty then the Spivak fibration for
$I(P,D^{n})$
is non-empty then the Spivak fibration for
![]() $P$
is trivializable, implying that
$P$
is trivializable, implying that
![]() $P/\unicode[STIX]{x2202}P$
is
$P/\unicode[STIX]{x2202}P$
is
![]() $n$
-dual to
$n$
-dual to
![]() $P_{+}$
. By S-duality, we have a weak equivalence
$P_{+}$
. By S-duality, we have a weak equivalence
Restricting to stable normal invariants on the right corresponds to replacing
![]() $Q(S^{0})$
on the left by its units, namely
$Q(S^{0})$
on the left by its units, namely
![]() $G$
. The result now follows by Lemma 3.3.◻
$G$
. The result now follows by Lemma 3.3.◻
4 Proof of Theorems A and B
Consider the following situation: fix a map of based spaces
and let
![]() $Y$
denote its reduced mapping cone. Consider the forgetful functor
$Y$
denote its reduced mapping cone. Consider the forgetful functor
Let
![]() $Z\in wT(X\rightarrow \ast )$
be an object; in particular,
$Z\in wT(X\rightarrow \ast )$
be an object; in particular,
![]() $Z$
has the structure of a based space. The map
$Z$
has the structure of a based space. The map
![]() $X\rightarrow Z$
factors through
$X\rightarrow Z$
factors through
![]() $Y$
precisely when the composition
$Y$
precisely when the composition
is null homotopic. In what follows we fix based null homotopy
![]() $CA\rightarrow Z$
.
$CA\rightarrow Z$
.
Lemma 4.1. With these assumptions, there is a homotopy fiber sequence
where the displayed fiber is taken at the basepoint
![]() $Z\in |wT(X\rightarrow \ast )|$
.
$Z\in |wT(X\rightarrow \ast )|$
.
Proof. By [Reference Goodwillie and Klein6, Proposition 2.14], the homotopy fiber of
![]() $|wT(Y\rightarrow \ast )|\rightarrow |wT(X\rightarrow \ast )|$
taken at
$|wT(Y\rightarrow \ast )|\rightarrow |wT(X\rightarrow \ast )|$
taken at
![]() $Z$
identified up to preferred weak equivalence with the function space of liftings/extensions
$Z$
identified up to preferred weak equivalence with the function space of liftings/extensions
We employ the notation
for this space. The given extension equips
![]() $F_{X}(Y,Z)$
with a basepoint and the restriction map
$F_{X}(Y,Z)$
with a basepoint and the restriction map
![]() $F_{X}(Y,Z)\rightarrow F_{A}(CA,Z)$
is a homeomorphism. Let
$F_{X}(Y,Z)\rightarrow F_{A}(CA,Z)$
is a homeomorphism. Let
![]() $\unicode[STIX]{x1D70C}:\!CA\rightarrow Z$
be the given null homotopy. The cofiber sequence
$\unicode[STIX]{x1D70C}:\!CA\rightarrow Z$
be the given null homotopy. The cofiber sequence
![]() $A\rightarrow A\rightarrow CA$
has a coaction map
$A\rightarrow A\rightarrow CA$
has a coaction map
![]() $\unicode[STIX]{x1D6FF}:\!CA\rightarrow CA\vee \unicode[STIX]{x1D6F4}A$
. Given a map
$\unicode[STIX]{x1D6FF}:\!CA\rightarrow CA\vee \unicode[STIX]{x1D6F4}A$
. Given a map
![]() $g:\!\unicode[STIX]{x1D6F4}A\rightarrow Z$
, we form
$g:\!\unicode[STIX]{x1D6F4}A\rightarrow Z$
, we form
Then
![]() $g\mapsto \unicode[STIX]{x1D70C}\star g$
defines a weak equivalence
$g\mapsto \unicode[STIX]{x1D70C}\star g$
defines a weak equivalence
![]() $F_{\ast }(\unicode[STIX]{x1D6F4}A,Z)\simeq F_{A}(CA,Z)$
.◻
$F_{\ast }(\unicode[STIX]{x1D6F4}A,Z)\simeq F_{A}(CA,Z)$
.◻
Proof of Theorem B.
Recall that
![]() $A=\unicode[STIX]{x2202}P\amalg S^{n-1}$
and
$A=\unicode[STIX]{x2202}P\amalg S^{n-1}$
and
![]() $A^{\prime }=P^{\unicode[STIX]{x1D709}}\vee S^{n-1}$
. Consider the full subcategory
$A^{\prime }=P^{\unicode[STIX]{x1D709}}\vee S^{n-1}$
. Consider the full subcategory
with objects
![]() $C$
such that the composite
$C$
such that the composite
is a weak homotopy equivalence. We claim there is a homotopy equivalence
To see this, note that
![]() $wT(A^{\prime }\rightarrow \ast ;\sim P^{\unicode[STIX]{x1D709}})$
is the right fiber taken at
$wT(A^{\prime }\rightarrow \ast ;\sim P^{\unicode[STIX]{x1D709}})$
is the right fiber taken at
![]() $P^{\unicode[STIX]{x1D709}}\in wT(\ast \rightarrow \ast )$
of the forgetful functor
$P^{\unicode[STIX]{x1D709}}\in wT(\ast \rightarrow \ast )$
of the forgetful functor
and by [Reference Goodwillie and Klein6, Proposition 2.19] we may identify this right fiber with
![]() $\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
. This gives the claim.
$\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
. This gives the claim.
We restrict our attention to the full subcategory
of those objects
![]() $C$
such that the weak map
$C$
such that the weak map
![]() $S^{n-1}\rightarrow C\overset{{\sim}}{\leftarrow }P^{\unicode[STIX]{x1D709}}$
corresponds to an unstable normal invariant. This additional constraint yields a homotopy equivalence
$S^{n-1}\rightarrow C\overset{{\sim}}{\leftarrow }P^{\unicode[STIX]{x1D709}}$
corresponds to an unstable normal invariant. This additional constraint yields a homotopy equivalence
The refined Browder construction defines a functor
On the other hand, the identity defines a functor
It is tautological that these functors are inverses to each other. ◻
Proof of Theorem A.
By Theorem B it suffices to consider the map
We will make use of the cofiber sequence
If
![]() $C\in {\mathcal{E}}(P,D^{n})$
is an object, then clearly the obstruction to lifting it to an object of
$C\in {\mathcal{E}}(P,D^{n})$
is an object, then clearly the obstruction to lifting it to an object of
![]() $\mathfrak{L}{\mathcal{E}}(P,D^{n})$
up to weak equivalence is that the composite
$\mathfrak{L}{\mathcal{E}}(P,D^{n})$
up to weak equivalence is that the composite
is null homotopic. This proves the first part. Now suppose a null homotopy
![]() $P_{+}\rightarrow C$
has been chosen. Using Lemma 4.1, we have a homotopy fiber sequence
$P_{+}\rightarrow C$
has been chosen. Using Lemma 4.1, we have a homotopy fiber sequence
One completes the proof using the homotopy Cartesian square (9).◻
5 Proof of Theorem C
5.1 Principal fibrations
We recall a basic result about principal fibrations from [Reference Klein14, Lemma 6.1]. Suppose
![]() $p:\!E\rightarrow Z$
is a fibration. We say that
$p:\!E\rightarrow Z$
is a fibration. We say that
![]() $p$
is principal if there exists a commutative homotopy Cartesian square of spaces
$p$
is principal if there exists a commutative homotopy Cartesian square of spaces
such that
![]() $C$
is contractible. Note that the property of being a principal fibration is preserved under base changes. Choose a basepoint for
$C$
is contractible. Note that the property of being a principal fibration is preserved under base changes. Choose a basepoint for
![]() $C$
. This gives a basepoint for
$C$
. This gives a basepoint for
![]() $B$
.
$B$
.
Suppose that
![]() $Z$
is connected. If
$Z$
is connected. If
![]() $p:\!E\rightarrow Z$
is principal, there is an “action”
$p:\!E\rightarrow Z$
is principal, there is an “action”
![]() $\unicode[STIX]{x1D6FA}B\times E\rightarrow E$
. If there exists a section
$\unicode[STIX]{x1D6FA}B\times E\rightarrow E$
. If there exists a section
![]() $Z\rightarrow E$
, one can combine it with this action to produce a map of fibrations
$Z\rightarrow E$
, one can combine it with this action to produce a map of fibrations
![]() $\unicode[STIX]{x1D6FA}B\times Z\rightarrow E$
covering the identity map of
$\unicode[STIX]{x1D6FA}B\times Z\rightarrow E$
covering the identity map of
![]() $Z$
. This implies that
$Z$
. This implies that
![]() $p$
is weak fiber homotopically trivial. Let
$p$
is weak fiber homotopically trivial. Let
![]() $\operatorname{sec}(p)$
denote the space of sections of
$\operatorname{sec}(p)$
denote the space of sections of
![]() $p$
. Then we have shown
$p$
. Then we have shown
Lemma 5.1. Assume
![]() $p:\!E\rightarrow Z$
is principal. Assume that
$p:\!E\rightarrow Z$
is principal. Assume that
![]() $\operatorname{sec}(p)$
is non-empty and comes equipped with basepoint. Then there is a preferred weak equivalence
$\operatorname{sec}(p)$
is non-empty and comes equipped with basepoint. Then there is a preferred weak equivalence
![]() $\operatorname{sec}(p)\simeq F(Z,\unicode[STIX]{x1D6FA}B)$
.
$\operatorname{sec}(p)\simeq F(Z,\unicode[STIX]{x1D6FA}B)$
.
Let
![]() $p:\!E\rightarrow Z$
be a principal fibration and suppose that
$p:\!E\rightarrow Z$
be a principal fibration and suppose that
![]() $A\rightarrow Y$
is a cofibration. Then given a lifting problem
$A\rightarrow Y$
is a cofibration. Then given a lifting problem
we let
![]() $\operatorname{lifts}(f|p)$
be the solution space: the space of maps
$\operatorname{lifts}(f|p)$
be the solution space: the space of maps
![]() $Y\rightarrow E$
of
$Y\rightarrow E$
of
![]() $f$
making the diagram commute.
$f$
making the diagram commute.
Corollary 5.2. If
![]() $\operatorname{lifts}(f|p)$
is non-empty then a choice of lift determines a weak equivalence
$\operatorname{lifts}(f|p)$
is non-empty then a choice of lift determines a weak equivalence
![]() $\operatorname{lifts}(f|p)\simeq F_{\ast }(Y/A,\unicode[STIX]{x1D6FA}B)$
.
$\operatorname{lifts}(f|p)\simeq F_{\ast }(Y/A,\unicode[STIX]{x1D6FA}B)$
.
Proof. Observe that
![]() $f^{\ast }E\rightarrow Y$
is principal. Furthermore
$f^{\ast }E\rightarrow Y$
is principal. Furthermore
![]() $\operatorname{lifts}(f|p)\cong \operatorname{sec}(f^{\ast }E\rightarrow Y)$
. Hence if
$\operatorname{lifts}(f|p)\cong \operatorname{sec}(f^{\ast }E\rightarrow Y)$
. Hence if
![]() $\operatorname{lifts}(f|p)$
is nonempty we can identify
$\operatorname{lifts}(f|p)$
is nonempty we can identify
![]() $f^{\ast }E$
with the trivial fibration
$f^{\ast }E$
with the trivial fibration
![]() $\unicode[STIX]{x1D6FA}B\times Y\rightarrow Y$
once a basepoint lift has been chosen. With respect to the identification, the given map
$\unicode[STIX]{x1D6FA}B\times Y\rightarrow Y$
once a basepoint lift has been chosen. With respect to the identification, the given map
![]() $A\rightarrow f^{\ast }E$
corresponds to the inclusion
$A\rightarrow f^{\ast }E$
corresponds to the inclusion
![]() $\ast \times A\rightarrow \unicode[STIX]{x1D6FA}B\times Y$
.
$\ast \times A\rightarrow \unicode[STIX]{x1D6FA}B\times Y$
.
Hence,
![]() $\operatorname{lifts}(f|p)$
is then identified up to weak equivalence with the space of sections of the trivial fibration
$\operatorname{lifts}(f|p)$
is then identified up to weak equivalence with the space of sections of the trivial fibration
![]() $\unicode[STIX]{x1D6FA}B\times Y\rightarrow Y$
which are fixed on
$\unicode[STIX]{x1D6FA}B\times Y\rightarrow Y$
which are fixed on
![]() $A$
. But this is just
$A$
. But this is just
![]() $F_{\ast }(Y/A,\unicode[STIX]{x1D6FA}B)$
.◻
$F_{\ast }(Y/A,\unicode[STIX]{x1D6FA}B)$
.◻
5.2 The Goodwillie tower of the identity
Let
![]() $\mathbb{I}:\!\mathbf{Top}_{\ast }\rightarrow \mathbf{Top}_{\ast }$
be the identity functor. We recall some of the basic properties of its Goodwillie tower. (cf. [Reference Goodwillie3], [Reference Goodwillie4], [Reference Goodwillie5], [Reference Johnson10]).
$\mathbb{I}:\!\mathbf{Top}_{\ast }\rightarrow \mathbf{Top}_{\ast }$
be the identity functor. We recall some of the basic properties of its Goodwillie tower. (cf. [Reference Goodwillie3], [Reference Goodwillie4], [Reference Goodwillie5], [Reference Johnson10]).
Theorem 5.3. There is a tower of fibrations of homotopy functors on based spaces
and compatible natural transformations
![]() $X\rightarrow P_{j}\mathbb{I}(X)$
such that
$X\rightarrow P_{j}\mathbb{I}(X)$
such that
-
∙ if
 $X$
is
$X$
is
 $1$
-connected, then the natural map is a weak equivalence.
$1$
-connected, then the natural map is a weak equivalence. $$\begin{eqnarray}X\rightarrow \lim _{j}P_{j}\mathbb{I}(X)\end{eqnarray}$$
$$\begin{eqnarray}X\rightarrow \lim _{j}P_{j}\mathbb{I}(X)\end{eqnarray}$$
-
∙ There is a natural weak equivalence
 $P_{1}\mathbb{I}(X)\simeq Q(X)$
;
$P_{1}\mathbb{I}(X)\simeq Q(X)$
; -
∙ For
 $j\geqslant 2$
, the fibration is principal (cf. [Reference Goodwillie5, Lemma 2.2]);
$j\geqslant 2$
, the fibration is principal (cf. [Reference Goodwillie5, Lemma 2.2]); $$\begin{eqnarray}P_{j}\mathbb{I}(X)\rightarrow P_{j-1}\mathbb{I}(X)\end{eqnarray}$$
$$\begin{eqnarray}P_{j}\mathbb{I}(X)\rightarrow P_{j-1}\mathbb{I}(X)\end{eqnarray}$$
-
∙ the
 $j$
th layer
$j$
th layer
 $L_{j}\mathbb{I}(X):=\text{fib}(P_{j}\mathbb{I}(X)\rightarrow P_{j-1}\mathbb{I}(X))$
is naturally weak equivalent to the functor where the spectrum with
$L_{j}\mathbb{I}(X):=\text{fib}(P_{j}\mathbb{I}(X)\rightarrow P_{j-1}\mathbb{I}(X))$
is naturally weak equivalent to the functor where the spectrum with $$\begin{eqnarray}X\mapsto \unicode[STIX]{x1D6FA}^{\infty }({\mathcal{W}}_{j}\wedge _{h\unicode[STIX]{x1D6F4}_{j}}X^{[j]});\end{eqnarray}$$
$$\begin{eqnarray}X\mapsto \unicode[STIX]{x1D6FA}^{\infty }({\mathcal{W}}_{j}\wedge _{h\unicode[STIX]{x1D6F4}_{j}}X^{[j]});\end{eqnarray}$$
 $\unicode[STIX]{x1D6F4}_{j}$
-action
$\unicode[STIX]{x1D6F4}_{j}$
-action
 ${\mathcal{W}}_{j}$
is as in [Reference Johnson10].
${\mathcal{W}}_{j}$
is as in [Reference Johnson10].
5.3 The spaces
 $E_{j}(P,D^{n})$
$E_{j}(P,D^{n})$
Recall that
![]() $P$
is sectioned by
$P$
is sectioned by
![]() $\unicode[STIX]{x1D709}$
. We fix the natural identification
$\unicode[STIX]{x1D709}$
. We fix the natural identification
![]() $P_{1}\mathbb{I}(X)\simeq Q(X)$
. Then we have a map
$P_{1}\mathbb{I}(X)\simeq Q(X)$
. Then we have a map
Note that the source of this map is identified with a collection of components of the target.
Definition 5.4. The space
![]() $\mathfrak{L}E_{j}(P,D^{n})$
is defined to be the union of path components of
$\mathfrak{L}E_{j}(P,D^{n})$
is defined to be the union of path components of
![]() $\unicode[STIX]{x1D6FA}^{n-1}P_{j}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
given by taking the pullback of the diagram
$\unicode[STIX]{x1D6FA}^{n-1}P_{j}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
given by taking the pullback of the diagram
Proof of Theorem C.
It is a consequence of the definition that there is a tower of fibrations
By definition
![]() $\mathfrak{L}E_{1}(P,D^{n})\cong \unicode[STIX]{x1D6FA}_{\bot }^{n-1}Q(P^{\unicode[STIX]{x1D709}})$
and by Lemma 3.3,
$\mathfrak{L}E_{1}(P,D^{n})\cong \unicode[STIX]{x1D6FA}_{\bot }^{n-1}Q(P^{\unicode[STIX]{x1D709}})$
and by Lemma 3.3,
![]() $\unicode[STIX]{x1D6FA}_{\bot }^{n-1}Q(P^{\unicode[STIX]{x1D709}})\simeq I(P,D^{n})$
. Moreover, the square
$\unicode[STIX]{x1D6FA}_{\bot }^{n-1}Q(P^{\unicode[STIX]{x1D709}})\simeq I(P,D^{n})$
. Moreover, the square

is homotopy Cartesian. The lower right corner of this diagram is identified with
![]() $Q(P^{\unicode[STIX]{x1D709}})$
. Since that map
$Q(P^{\unicode[STIX]{x1D709}})$
. Since that map
![]() $\unicode[STIX]{x2202}P\rightarrow P$
is at least
$\unicode[STIX]{x2202}P\rightarrow P$
is at least
![]() $2$
-connected, it follows that the section
$2$
-connected, it follows that the section
![]() $K\rightarrow \unicode[STIX]{x2202}P$
is at least
$K\rightarrow \unicode[STIX]{x2202}P$
is at least
![]() $1$
-connected. Hence,
$1$
-connected. Hence,
![]() $P^{\unicode[STIX]{x1D709}}$
is
$P^{\unicode[STIX]{x1D709}}$
is
![]() $1$
-connected and the upper right corner of diagram is identified with
$1$
-connected and the upper right corner of diagram is identified with
![]() $\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
. Substituting these identifications, we obtain a homotopy Cartesian square
$\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
. Substituting these identifications, we obtain a homotopy Cartesian square
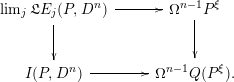
Clearly, if we replace the upper left corner by the space of unstable normal invariants
![]() $\unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}$
the square remains homotopy Cartesian, since a point of
$\unicode[STIX]{x1D6FA}_{\bot }^{n-1}P^{\unicode[STIX]{x1D709}}$
the square remains homotopy Cartesian, since a point of
![]() $\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
yields an unstable normal invariant if and only if the associated point of
$\unicode[STIX]{x1D6FA}^{n-1}P^{\unicode[STIX]{x1D709}}$
yields an unstable normal invariant if and only if the associated point of
![]() $\unicode[STIX]{x1D6FA}^{n-1}Q(P^{\unicode[STIX]{x1D709}})$
yields a stable normal invariant. It follows that the map
$\unicode[STIX]{x1D6FA}^{n-1}Q(P^{\unicode[STIX]{x1D709}})$
yields a stable normal invariant. It follows that the map
is a weak equivalence. Therefore, the composite map
is also a weak equivalence.
We next identify the layers of the tower (11) whenever they are non-empty. The fiber of the map
![]() $\unicode[STIX]{x1D6FA}^{n-1}P_{j}\mathbb{I}(P^{\unicode[STIX]{x1D709}})\rightarrow \unicode[STIX]{x1D6FA}^{n-1}P_{j-1}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
at any basepoint is just the lifting space
$\unicode[STIX]{x1D6FA}^{n-1}P_{j}\mathbb{I}(P^{\unicode[STIX]{x1D709}})\rightarrow \unicode[STIX]{x1D6FA}^{n-1}P_{j-1}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
at any basepoint is just the lifting space
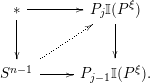
If this lifting space is non-empty, then Corollary 5.2 says that after making a choice of lift, the space of all such lifts is identified with the stable function space
We need to rewrite this stable function space up to homotopy in the requisite form. First identify it as the zeroth space of the homotopy orbit spectrum
The plan is to rewrite the latter in terms of
![]() $P_{+}$
using Spanier–Whitehead duality. Assuming that
$P_{+}$
using Spanier–Whitehead duality. Assuming that
![]() $I(P,D^{n})$
is non-empty guarantees that
$I(P,D^{n})$
is non-empty guarantees that
![]() $P^{\unicode[STIX]{x1D709}}$
is
$P^{\unicode[STIX]{x1D709}}$
is
![]() $(n-1)$
-dual to
$(n-1)$
-dual to
![]() $P_{+}$
. We can write this as
$P_{+}$
. We can write this as
where
![]() $D(P_{+})$
is the
$D(P_{+})$
is the
![]() $0$
-dual of
$0$
-dual of
![]() $P_{+}$
, that is,
$P_{+}$
, that is,
![]() $F_{\ast }(P_{+},S)$
, where
$F_{\ast }(P_{+},S)$
, where
![]() $S$
denotes the sphere spectrum. If we smash this identification with itself
$S$
denotes the sphere spectrum. If we smash this identification with itself
![]() $j$
-times, we obtain an equivariant weak equivalence of spectra with
$j$
-times, we obtain an equivariant weak equivalence of spectra with
![]() $\unicode[STIX]{x1D6F4}_{j}$
-action
$\unicode[STIX]{x1D6F4}_{j}$
-action
Substituting this into (15), and doing some minor rewriting, we obtain the spectrum
The zeroth space of this spectrum is thus identified with the homotopy fibers of
![]() $\mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n})$
whenever these are non-empty.
$\mathfrak{L}E_{j}(P,D^{n})\rightarrow \mathfrak{L}E_{j-1}(P,D^{n})$
whenever these are non-empty.
Lastly, we need to exhibit the obstruction
![]() $\ell _{j-1}$
. According to [Reference Goodwillie5, Lemma 2.2] there is a
$\ell _{j-1}$
. According to [Reference Goodwillie5, Lemma 2.2] there is a
![]() $j$
-homogeneous functor
$j$
-homogeneous functor
![]() $X\mapsto R_{j}\mathbb{I}(X)$
and a homotopy Cartesian square
$X\mapsto R_{j}\mathbb{I}(X)$
and a homotopy Cartesian square
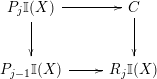
where
![]() $C$
is contractible. By the classification of
$C$
is contractible. By the classification of
![]() $j$
-homogeneous functors [Reference Goodwillie5], [Reference Goodwillie3, p. 5], we infer
$j$
-homogeneous functors [Reference Goodwillie5], [Reference Goodwillie3, p. 5], we infer
for a some spectrum with
![]() $\unicode[STIX]{x1D6F4}_{j}$
-action
$\unicode[STIX]{x1D6F4}_{j}$
-action
![]() ${\mathcal{V}}_{j}$
. Furthermore, the map
${\mathcal{V}}_{j}$
. Furthermore, the map
is a weak equivalence of
![]() $j$
-homogenous functors. It follows that there is a weak equivalence of spectra with
$j$
-homogenous functors. It follows that there is a weak equivalence of spectra with
![]() $\unicode[STIX]{x1D6F4}_{j}$
-action
$\unicode[STIX]{x1D6F4}_{j}$
-action
Consequently, setting
![]() $X=P^{\unicode[STIX]{x1D709}}$
, we have a homotopy Cartesian square
$X=P^{\unicode[STIX]{x1D709}}$
, we have a homotopy Cartesian square
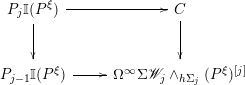
in which
![]() $C$
is contractible. Hence, the obstruction up to homotopy to a lifting a based map
$C$
is contractible. Hence, the obstruction up to homotopy to a lifting a based map
![]() $x:\!S^{n-1}\rightarrow P_{j-1}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
to a based map
$x:\!S^{n-1}\rightarrow P_{j-1}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
to a based map
![]() $S^{n-1}\rightarrow P_{j}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
is given by the homotopy class of the composition
$S^{n-1}\rightarrow P_{j}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
is given by the homotopy class of the composition
In particular, if
![]() $x\in E_{j-1}(P,D^{n})\subset \unicode[STIX]{x1D6FA}^{n-1}P_{j-1}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
is a point, then we define
$x\in E_{j-1}(P,D^{n})\subset \unicode[STIX]{x1D6FA}^{n-1}P_{j-1}\mathbb{I}(P^{\unicode[STIX]{x1D709}})$
is a point, then we define
![]() $\ell _{j-1}(x)$
to be the homotopy class of (16). Then
$\ell _{j-1}(x)$
to be the homotopy class of (16). Then
![]() $\ell _{j-1}(x)$
a priori lies in the abelian group
$\ell _{j-1}(x)$
a priori lies in the abelian group
Again by duality, we can rewrite the latter up to canonical isomorphism as
Acknowledgements
I learned about unstable normal invariants many years ago in discussions with Bill Richter and Bruce Williams. Most of the research for this paper was done while I visited the Mathematics Institute at the University of Copenhagen in the Summer of 2014.
Appendix A. Relationship with manifold calculus
It is legitimate to ask what the tower of Theorem C has to do with the Goodwillie–Weiss manifold calculus [Reference Weiss22]. Here is one possible scenario: suppose that
![]() $Q$
is a compact smooth
$Q$
is a compact smooth
![]() $(n-1)$
-manifold—which we assume admits a handle decomposition with handles of index at most
$(n-1)$
-manifold—which we assume admits a handle decomposition with handles of index at most
![]() $k\leqslant n-4$
. We consider the forgetful/decompression map
$k\leqslant n-4$
. We consider the forgetful/decompression map
from the space of smooth embeddings of
![]() $Q$
in
$Q$
in
![]() $D^{n}$
to the space of unlinked Poincaré embeddings of
$D^{n}$
to the space of unlinked Poincaré embeddings of
![]() $Q\times D^{1}$
in
$Q\times D^{1}$
in
![]() $D^{n}$
.
$D^{n}$
.
Conjecture A.1. The map (A1) induces a map of towers from the Goodwillie–Weiss tower for
![]() $E^{\operatorname{sm}}(Q,D^{n-1})$
to the tower of Theorem C for
$E^{\operatorname{sm}}(Q,D^{n-1})$
to the tower of Theorem C for
![]() $\mathfrak{L}E(Q\times D^{1},D^{n})$
.
$\mathfrak{L}E(Q\times D^{1},D^{n})$
.
Remark A.2. By Theorem B we can identify the map with the Pontryagin–Thom construction
from a space of smooth embeddings to the space of unstable normal invariants, the latter which is collection of components of
![]() $\unicode[STIX]{x1D6FA}^{n-1}(Q/\unicode[STIX]{x2202}Q)$
. Recall that the tower of Theorem C is arises from the Goodwillie tower of the identity functor
$\unicode[STIX]{x1D6FA}^{n-1}(Q/\unicode[STIX]{x2202}Q)$
. Recall that the tower of Theorem C is arises from the Goodwillie tower of the identity functor
![]() $\mathbb{I}$
applied to the based space
$\mathbb{I}$
applied to the based space
![]() $Q/\unicode[STIX]{x2202}Q$
. The conjecture therefore concerns how the manifold calculus tower for the embedding functor relates to the homotopy calculus for the functor
$Q/\unicode[STIX]{x2202}Q$
. The conjecture therefore concerns how the manifold calculus tower for the embedding functor relates to the homotopy calculus for the functor
![]() $\mathbb{I}$
.
$\mathbb{I}$
.
We will give some evidence for the conjecture on the level of layers. In what follows we shall assume that the reader is familiar with [Reference Weiss22]. Here is some notation: suppose
![]() $T$
is a finite set. We write
$T$
is a finite set. We write
for the configuration space of the injective functions from
![]() $T$
to the interior of
$T$
to the interior of
![]() $Q$
. This has a free action of
$Q$
. This has a free action of
![]() $\unicode[STIX]{x1D6F4}_{T}$
, the symmetric group of automorphisms of
$\unicode[STIX]{x1D6F4}_{T}$
, the symmetric group of automorphisms of
![]() $T$
. In the case when
$T$
. In the case when
![]() $T=\text{}\underline{j}=\{1,\ldots ,j\}$
, we write
$T=\text{}\underline{j}=\{1,\ldots ,j\}$
, we write
![]() ${\mathcal{P}}(Q,j):={\mathcal{P}}(Q,\text{}\underline{j})$
. Let
${\mathcal{P}}(Q,j):={\mathcal{P}}(Q,\text{}\underline{j})$
. Let
the orbit space of the action of
![]() $\unicode[STIX]{x1D6F4}_{T}$
on
$\unicode[STIX]{x1D6F4}_{T}$
on
![]() ${\mathcal{P}}(Q,T)$
; this is the configuration space of (unordered) subsets of the interior of
${\mathcal{P}}(Q,T)$
; this is the configuration space of (unordered) subsets of the interior of
![]() $Q$
of cardinality
$Q$
of cardinality
![]() $|T|$
. Similarly, we write
$|T|$
. Similarly, we write
![]() $\binom{Q}{j}:=\binom{Q}{\text{}\underline{j}}$
.
$\binom{Q}{j}:=\binom{Q}{\text{}\underline{j}}$
.
The quotient map
![]() $\unicode[STIX]{x1D70B}:\!{\mathcal{P}}(Q,j)\rightarrow \binom{Q}{j}$
is a principal covering space with respect to the group
$\unicode[STIX]{x1D70B}:\!{\mathcal{P}}(Q,j)\rightarrow \binom{Q}{j}$
is a principal covering space with respect to the group
![]() $\unicode[STIX]{x1D6F4}_{j}$
; we let
$\unicode[STIX]{x1D6F4}_{j}$
; we let
![]() $i:\!\binom{Q}{j}\rightarrow B\unicode[STIX]{x1D6F4}_{j}$
denote its classifying map. Then
$i:\!\binom{Q}{j}\rightarrow B\unicode[STIX]{x1D6F4}_{j}$
denote its classifying map. Then
![]() $i\circ \unicode[STIX]{x1D70B}$
is the constant map to the basepoint. Let
$i\circ \unicode[STIX]{x1D70B}$
is the constant map to the basepoint. Let
![]() $c:\!Q^{\times j}\rightarrow B\unicode[STIX]{x1D6F4}_{j}$
be the constant map. Then
$c:\!Q^{\times j}\rightarrow B\unicode[STIX]{x1D6F4}_{j}$
be the constant map. Then
![]() $c$
restricted to
$c$
restricted to
![]() ${\mathcal{P}}(Q,j)$
is
${\mathcal{P}}(Q,j)$
is
![]() $i\circ \unicode[STIX]{x1D70B}$
. There is an inclusion
$i\circ \unicode[STIX]{x1D70B}$
. There is an inclusion
![]() ${\mathcal{P}}(Q,j)\subset Q^{\times j}$
whose complement is the diagonal
${\mathcal{P}}(Q,j)\subset Q^{\times j}$
whose complement is the diagonal
![]() $\unicode[STIX]{x1D6E5}\subset Q^{\times j}$
.
$\unicode[STIX]{x1D6E5}\subset Q^{\times j}$
.
The evidence we give for Conjecture A.1 is a diagram
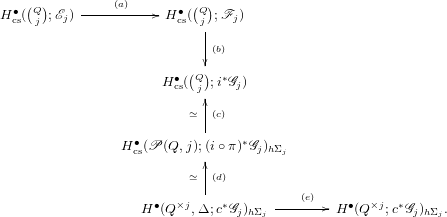
We first summarize what the maps of the diagram are about and thereafter we give some of the details. For
![]() $j\geqslant 2$
, the source of (a) is the
$j\geqslant 2$
, the source of (a) is the
![]() $j$
th layer for the manifold calculus tower of the smooth embedding space
$j$
th layer for the manifold calculus tower of the smooth embedding space
![]() $E^{\operatorname{sm}}(Q,D^{n-1})$
. The target of (a) is the
$E^{\operatorname{sm}}(Q,D^{n-1})$
. The target of (a) is the
![]() $j$
th layer for the manifold calculus tower of, in the terminology of [Reference Weiss22, Definition 2.2], the good cofunctor
$j$
th layer for the manifold calculus tower of, in the terminology of [Reference Weiss22, Definition 2.2], the good cofunctor
![]() ${\mathcal{O}}\mapsto \unicode[STIX]{x1D6FA}^{n-1}\unicode[STIX]{x1D6F4}^{n-1}{\mathcal{O}}^{+}$
, where
${\mathcal{O}}\mapsto \unicode[STIX]{x1D6FA}^{n-1}\unicode[STIX]{x1D6F4}^{n-1}{\mathcal{O}}^{+}$
, where
![]() ${\mathcal{O}}\subset Q$
varies over the open subsets of the interior of
${\mathcal{O}}\subset Q$
varies over the open subsets of the interior of
![]() $Q$
and
$Q$
and
![]() ${\mathcal{O}}^{+}$
denotes one-point compactification. The map (a) is induced by the Pontryagin–Thom construction. The map (b) is a kind of stabilization map. The equivalence (c) is a version of the Adams isomorphism (which is valid since the source and target in this case are infinite loop spaces) and the equivalence (d) is excision. The map (e) is a relaxation of constraints. The target of (e) coincides with the
${\mathcal{O}}^{+}$
denotes one-point compactification. The map (a) is induced by the Pontryagin–Thom construction. The map (b) is a kind of stabilization map. The equivalence (c) is a version of the Adams isomorphism (which is valid since the source and target in this case are infinite loop spaces) and the equivalence (d) is excision. The map (e) is a relaxation of constraints. The target of (e) coincides with the
![]() $j$
th layer of the tower of Theorem C for
$j$
th layer of the tower of Theorem C for
![]() $\mathfrak{L}E(Q\times D^{1},D^{n})$
.
$\mathfrak{L}E(Q\times D^{1},D^{n})$
.
We now proceed to give more detail. In the above,
![]() ${\mathcal{E}}_{j}$
and
${\mathcal{E}}_{j}$
and
![]() ${\mathcal{F}}_{j}$
are fibrations over
${\mathcal{F}}_{j}$
are fibrations over
![]() $\binom{Q}{j}$
, and
$\binom{Q}{j}$
, and
![]() ${\mathcal{G}}_{j}$
is a fibration over
${\mathcal{G}}_{j}$
is a fibration over
![]() $B\unicode[STIX]{x1D6F4}_{j}$
. The notation
$B\unicode[STIX]{x1D6F4}_{j}$
. The notation
![]() $H^{\bullet }(B;{\mathcal{U}})$
refers to the space of sections of a fibration
$H^{\bullet }(B;{\mathcal{U}})$
refers to the space of sections of a fibration
![]() ${\mathcal{U}}\rightarrow B$
(which we feel compelled to indicate as “unstable” cohomology), and similarly,
${\mathcal{U}}\rightarrow B$
(which we feel compelled to indicate as “unstable” cohomology), and similarly,
![]() $H_{\text{cs}}^{\bullet }(B;{\mathcal{U}})$
refers to the space of sections with compact support relative to a given fixed section; these are the sections which agree with the given one outside a compact subset of
$H_{\text{cs}}^{\bullet }(B;{\mathcal{U}})$
refers to the space of sections with compact support relative to a given fixed section; these are the sections which agree with the given one outside a compact subset of
![]() $B$
.
$B$
.
The fibration
![]() ${\mathcal{E}}_{j}\rightarrow \binom{Q}{j}$
may be described as follows: if
${\mathcal{E}}_{j}\rightarrow \binom{Q}{j}$
may be described as follows: if
![]() $T\in \binom{Q}{j}$
, then we form the
$T\in \binom{Q}{j}$
, then we form the
![]() $j$
-cube of spaces
$j$
-cube of spaces
The total homotopy fiber of (A2) is the fiber at
![]() $T$
of the fibration
$T$
of the fibration
![]() ${\mathcal{E}}_{j}\rightarrow \binom{Q}{j}$
(we will leave it to the reader to provide the topology on
${\mathcal{E}}_{j}\rightarrow \binom{Q}{j}$
(we will leave it to the reader to provide the topology on
![]() ${\mathcal{E}}_{j}$
as well as on
${\mathcal{E}}_{j}$
as well as on
![]() ${\mathcal{F}}_{j}$
). By [Reference Weiss22, sum. 4.2] we know that
${\mathcal{F}}_{j}$
). By [Reference Weiss22, sum. 4.2] we know that
![]() $H_{\text{cs}}^{\bullet }(\binom{Q}{j};{\mathcal{E}}_{j})$
is the
$H_{\text{cs}}^{\bullet }(\binom{Q}{j};{\mathcal{E}}_{j})$
is the
![]() $j$
th layer of the Goodwillie–Weiss tower for the space of smooth embeddings
$j$
th layer of the Goodwillie–Weiss tower for the space of smooth embeddings
![]() $E^{\operatorname{sm}}(Q,D^{n-1})$
when
$E^{\operatorname{sm}}(Q,D^{n-1})$
when
![]() $j\geqslant 2$
.
$j\geqslant 2$
.
The fibration
![]() ${\mathcal{F}}_{j}\rightarrow \binom{Q}{j}$
has fiber at
${\mathcal{F}}_{j}\rightarrow \binom{Q}{j}$
has fiber at
![]() $T$
given by the total homotopy fiber of the
$T$
given by the total homotopy fiber of the
![]() $j$
-cube
$j$
-cube
The map
![]() ${\mathcal{E}}_{j}\rightarrow {\mathcal{F}}_{j}$
is induced by the Pontryagin–Thom construction
${\mathcal{E}}_{j}\rightarrow {\mathcal{F}}_{j}$
is induced by the Pontryagin–Thom construction
![]() ${\mathcal{P}}(D^{n-1},U)\rightarrow \unicode[STIX]{x1D6FA}^{n-1}\unicode[STIX]{x1D6F4}^{n-1}(U_{+})$
with respect to the trivial framing. This induces the map (a). The map (a) is
${\mathcal{P}}(D^{n-1},U)\rightarrow \unicode[STIX]{x1D6FA}^{n-1}\unicode[STIX]{x1D6F4}^{n-1}(U_{+})$
with respect to the trivial framing. This induces the map (a). The map (a) is
![]() $(2n-3k-5)$
-connected [Reference Klein13].
$(2n-3k-5)$
-connected [Reference Klein13].
The fibration
![]() ${\mathcal{G}}_{j}\rightarrow B\unicode[STIX]{x1D6F4}_{j}$
arises as follows: take the unreduced Borel construction of
${\mathcal{G}}_{j}\rightarrow B\unicode[STIX]{x1D6F4}_{j}$
arises as follows: take the unreduced Borel construction of
![]() $\unicode[STIX]{x1D6F4}_{j}$
acting on
$\unicode[STIX]{x1D6F4}_{j}$
acting on
![]() ${\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}}$
. This gives a fibered spectrum
${\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}}$
. This gives a fibered spectrum
Then
![]() ${\mathcal{G}}_{j}$
is the fiberwise zeroth space of (A4), i.e,
${\mathcal{G}}_{j}$
is the fiberwise zeroth space of (A4), i.e,
![]() ${\mathcal{G}}_{j}$
is the unreduced Borel construction of
${\mathcal{G}}_{j}$
is the unreduced Borel construction of
![]() $\unicode[STIX]{x1D6F4}_{j}$
acting on
$\unicode[STIX]{x1D6F4}_{j}$
acting on
![]() $\unicode[STIX]{x1D6FA}^{\infty }({\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}})$
. The fibration
$\unicode[STIX]{x1D6FA}^{\infty }({\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}})$
. The fibration
![]() $i^{\ast }{\mathcal{G}}_{j}\rightarrow \binom{Q}{j}$
is obtained by taking the base change of
$i^{\ast }{\mathcal{G}}_{j}\rightarrow \binom{Q}{j}$
is obtained by taking the base change of
![]() ${\mathcal{G}}_{j}$
along
${\mathcal{G}}_{j}$
along
![]() $i$
.
$i$
.
The source of (c) is the homotopy orbits of
![]() $\unicode[STIX]{x1D6F4}_{j}$
acting on the section space with compact supports of the fibration
$\unicode[STIX]{x1D6F4}_{j}$
acting on the section space with compact supports of the fibration
![]() $(i\circ \unicode[STIX]{x1D70B})^{\ast }{\mathcal{G}}_{j}\rightarrow {\mathcal{P}}(Q,j)$
. Here we are using the observation that this last map is
$(i\circ \unicode[STIX]{x1D70B})^{\ast }{\mathcal{G}}_{j}\rightarrow {\mathcal{P}}(Q,j)$
. Here we are using the observation that this last map is
![]() $\unicode[STIX]{x1D6F4}_{j}$
-equivariant (
$\unicode[STIX]{x1D6F4}_{j}$
-equivariant (
![]() $\unicode[STIX]{x1D6F4}_{j}$
-acts on
$\unicode[STIX]{x1D6F4}_{j}$
-acts on
![]() $(i\circ \unicode[STIX]{x1D70B})^{\ast }{\mathcal{G}}_{j}$
because it is a trivial fibration over
$(i\circ \unicode[STIX]{x1D70B})^{\ast }{\mathcal{G}}_{j}$
because it is a trivial fibration over
![]() ${\mathcal{P}}(Q,j)$
whose fiber
${\mathcal{P}}(Q,j)$
whose fiber
![]() $\unicode[STIX]{x1D6FA}^{\infty }({\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}})$
comes equipped with a
$\unicode[STIX]{x1D6FA}^{\infty }({\mathcal{W}}_{j}\wedge S^{(n-1)V_{j}})$
comes equipped with a
![]() $\unicode[STIX]{x1D6F4}_{j}$
-action). As already mentioned, the map (c) is a homotopy equivalence by the Adams isomorphism [Reference May15, Section 2] and the map (d) is an equivalence by excision. The map (e) is the map which forgets that a section is fixed along the diagonal; it is
$\unicode[STIX]{x1D6F4}_{j}$
-action). As already mentioned, the map (c) is a homotopy equivalence by the Adams isomorphism [Reference May15, Section 2] and the map (d) is an equivalence by excision. The map (e) is the map which forgets that a section is fixed along the diagonal; it is
![]() $((j-1)(n-2)-k-1)$
-connected.
$((j-1)(n-2)-k-1)$
-connected.
The map (b) is induced by a map
![]() ${\mathcal{F}}_{j}\rightarrow i^{\ast }{\mathcal{G}}_{j}$
which on the level of fibers at
${\mathcal{F}}_{j}\rightarrow i^{\ast }{\mathcal{G}}_{j}$
which on the level of fibers at
![]() $T$
arises from the natural map
$T$
arises from the natural map
which induces map of
![]() $j$
-cubes. As noted above, the total homotopy fiber of the source is identified with the fiber of
$j$
-cubes. As noted above, the total homotopy fiber of the source is identified with the fiber of
![]() ${\mathcal{F}}_{j}$
at
${\mathcal{F}}_{j}$
at
![]() $T$
. The total homotopy fiber of the target cube can be obtained by replacing the
$T$
. The total homotopy fiber of the target cube can be obtained by replacing the
![]() $j$
th stage
$j$
th stage
![]() $P_{j}\mathbb{I}$
in the above with the
$P_{j}\mathbb{I}$
in the above with the
![]() $j$
-layer in the tower for
$j$
-layer in the tower for
![]() $\mathbb{I}$
. An analysis which we omit shows that total homotopy fiber of the target is identified with the fiber of
$\mathbb{I}$
. An analysis which we omit shows that total homotopy fiber of the target is identified with the fiber of
![]() $i^{\ast }{\mathcal{G}}_{j}$
at
$i^{\ast }{\mathcal{G}}_{j}$
at
![]() $T$
.
$T$
.
In fact, the Hilton–Milnor theorem shows that the map
![]() ${\mathcal{F}}_{j}\rightarrow i^{\ast }{\mathcal{G}}_{j}$
is
${\mathcal{F}}_{j}\rightarrow i^{\ast }{\mathcal{G}}_{j}$
is
![]() $((j+1)(n-2)+2-n)$
-connected. By subtracting the handle dimension of
$((j+1)(n-2)+2-n)$
-connected. By subtracting the handle dimension of
![]() $Q^{\times j}$
(i.e.,
$Q^{\times j}$
(i.e.,
![]() $jk$
) we infer that (b) is
$jk$
) we infer that (b) is
![]() $j(n-k-2)$
-connected.
$j(n-k-2)$
-connected.
Finally, observe that the connectivity of each of the maps (b) and (e) is a linear function of
![]() $j$
with positive slope. Thus the map (a) is the only map of the diagram which does not tend to weak equivalence as
$j$
with positive slope. Thus the map (a) is the only map of the diagram which does not tend to weak equivalence as
![]() $j$
gets large.
$j$
gets large.


