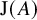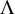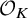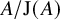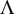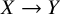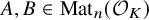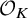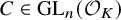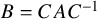1 Introduction
Let K be a number field with ring of integers
![]() $\mathcal {O}_{K}$
. Let A be a finite-dimensional K-algebra, and let
$\mathcal {O}_{K}$
. Let A be a finite-dimensional K-algebra, and let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}_{K}$
-order in A. A
$\mathcal {O}_{K}$
-order in A. A
![]() $\Lambda $
-lattice is a (left)
$\Lambda $
-lattice is a (left)
![]() $\Lambda $
-module that is finitely generated and torsion-free over
$\Lambda $
-module that is finitely generated and torsion-free over
![]() $\mathcal {O}_{K}$
. We will consider the following problem.
$\mathcal {O}_{K}$
. We will consider the following problem.
Problem (
 $\mathsf {IsIsomorphic}$
)
$\mathsf {IsIsomorphic}$
)
Given two
![]() $\Lambda $
-lattices X and Y, decide whether X and Y are isomorphic, and if so, return an isomorphism
$\Lambda $
-lattices X and Y, decide whether X and Y are isomorphic, and if so, return an isomorphism
![]() $X \to Y$
.
$X \to Y$
.
A
![]() $\Lambda $
-lattice contained in A is said to be full if it contains a K-basis of A. We will show that
$\Lambda $
-lattice contained in A is said to be full if it contains a K-basis of A. We will show that
![]() $\mathsf {IsIsomorphic}$
is polynomial-time reducible (see §5) to the following problem.
$\mathsf {IsIsomorphic}$
is polynomial-time reducible (see §5) to the following problem.
Problem (
 $\mathsf {IsPrincipal}$
)
$\mathsf {IsPrincipal}$
)
Given a full
![]() $\Lambda $
-lattice X in A, decide whether there exists
$\Lambda $
-lattice X in A, decide whether there exists
![]() $\alpha \in X$
such that
$\alpha \in X$
such that
![]() $X = \Lambda \alpha $
, and if so, return such an element
$X = \Lambda \alpha $
, and if so, return such an element
![]() $\alpha $
.
$\alpha $
.
Let
![]() $\operatorname {\mathrm {J}}(A)$
denote the Jacobson radical of A. Note that the quotient algebra
$\operatorname {\mathrm {J}}(A)$
denote the Jacobson radical of A. Note that the quotient algebra
![]() $\overline {A} := A/{\operatorname {\mathrm {J}}(A)}$
is semisimple. Let
$\overline {A} := A/{\operatorname {\mathrm {J}}(A)}$
is semisimple. Let
![]() $h : A \rightarrow \overline {A}$
denote the canonical projection map, and let
$h : A \rightarrow \overline {A}$
denote the canonical projection map, and let
![]() $\overline {\Lambda } = h(\Lambda )$
. We will show that the problem
$\overline {\Lambda } = h(\Lambda )$
. We will show that the problem
![]() $\mathsf {IsPrincipal}$
for a full
$\mathsf {IsPrincipal}$
for a full
![]() $\Lambda $
-lattice X in A is polynomial-time reducible to the problem
$\Lambda $
-lattice X in A is polynomial-time reducible to the problem
![]() $\mathsf {IsPrincipal}$
for the full
$\mathsf {IsPrincipal}$
for the full
![]() $\overline {\Lambda }$
-lattice
$\overline {\Lambda }$
-lattice
![]() $\overline {X}$
in
$\overline {X}$
in
![]() $\overline {A}$
, where
$\overline {A}$
, where
![]() $\overline {X}=h(X)$
.
$\overline {X}=h(X)$
.
Let
 $$\begin{align*}A/{\operatorname{\mathrm{J}}(A)} \simeq \bigoplus_{i=1}^{r} A_{i} \end{align*}$$
$$\begin{align*}A/{\operatorname{\mathrm{J}}(A)} \simeq \bigoplus_{i=1}^{r} A_{i} \end{align*}$$
be the Wedderburn decomposition. Each simple component
![]() $A_{i}$
is isomorphic to a matrix ring
$A_{i}$
is isomorphic to a matrix ring
![]() $\mathrm {Mat}_{n_i}(D_i)$
, where
$\mathrm {Mat}_{n_i}(D_i)$
, where
![]() $D_i$
is a skew field extension of K. Let
$D_i$
is a skew field extension of K. Let
![]() $K_{i}$
denote the centre of
$K_{i}$
denote the centre of
![]() $D_{i}$
. In order to make progress on the above problems, we impose the following hypothesis.
$D_{i}$
. In order to make progress on the above problems, we impose the following hypothesis.
-
(H) Each component
 $A_{i}$
of the Wedderburn decomposition
$A_{i}$
of the Wedderburn decomposition
 $A/{\operatorname {\mathrm {J}}(A)} \simeq \bigoplus _{i=1}^{r} A_{i}$
is isomorphic to a matrix ring over a field.
$A/{\operatorname {\mathrm {J}}(A)} \simeq \bigoplus _{i=1}^{r} A_{i}$
is isomorphic to a matrix ring over a field.
In the above notation, this is equivalent to the assertion that
![]() $D_{i}=K_{i}$
for each i.
$D_{i}=K_{i}$
for each i.
Under hypothesis (H), we give algorithms that solve both
![]() $\mathsf {IsIsomorphic}$
and
$\mathsf {IsIsomorphic}$
and
![]() $\mathsf {IsPrincipal}$
. Moreover, we give the first complexity analysis of these problems and thus prove the following result. For precise definitions and statements, we refer the reader to §5 and §8.
$\mathsf {IsPrincipal}$
. Moreover, we give the first complexity analysis of these problems and thus prove the following result. For precise definitions and statements, we refer the reader to §5 and §8.
Theorem. The problem
![]() $\mathsf {IsIsomorphic}$
for lattices over orders in algebras satisfying hypothesis (H) reduces in probabilistic polynomial time to
$\mathsf {IsIsomorphic}$
for lattices over orders in algebras satisfying hypothesis (H) reduces in probabilistic polynomial time to
-
(a)
 $\mathsf {Wedderburn}$
, the problem of computing explicitly the Wedderburn decomposition,
$\mathsf {Wedderburn}$
, the problem of computing explicitly the Wedderburn decomposition, -
(b)
 $\mathsf {Factor}$
, the problem of factoring integers,
$\mathsf {Factor}$
, the problem of factoring integers, -
(c)
 $\mathsf {IsPrincipal}$
in the special case of rings of integers of number fields,
$\mathsf {IsPrincipal}$
in the special case of rings of integers of number fields, -
(d)
 $\mathsf {UnitGroup}$
, the computation of unit groups for rings of integers of number fields,
$\mathsf {UnitGroup}$
, the computation of unit groups for rings of integers of number fields, -
(e)
 $\mathsf {Primitive}$
, the computation of primitive elements in finite fields and
$\mathsf {Primitive}$
, the computation of primitive elements in finite fields and -
(f)
 $\mathsf {DLog}$
, the computation of discrete logarithms in finite fields.
$\mathsf {DLog}$
, the computation of discrete logarithms in finite fields.
A number of articles have considered
![]() $\mathsf {IsIsomorphic}$
,
$\mathsf {IsIsomorphic}$
,
![]() $\mathsf {IsPrincipal}$
or closely related problems in special cases. In particular, [Reference Bley and EndresBE05] applies in the case that A is commutative and semisimple; [Reference Bley and WilsonBW09] applies to group rings
$\mathsf {IsPrincipal}$
or closely related problems in special cases. In particular, [Reference Bley and EndresBE05] applies in the case that A is commutative and semisimple; [Reference Bley and WilsonBW09] applies to group rings
![]() $\mathcal {O}_{K}[G]$
, where G is a finite group, but only decides whether two lattices are both locally free and stably isomorphic; and [Reference Dembélé and DonnellyDD08, Reference Kirschmer and VoightKV10, Reference PagePag14] apply to maximal or Eichler orders in quaternion algebras. The series of articles [Reference BleyBle97, Reference Bley and JohnstonBJ08, Reference Bley and JohnstonBJ11, Reference Hofmann and JohnstonHJ20] consider progressively more general situations, culminating in a solution to
$\mathcal {O}_{K}[G]$
, where G is a finite group, but only decides whether two lattices are both locally free and stably isomorphic; and [Reference Dembélé and DonnellyDD08, Reference Kirschmer and VoightKV10, Reference PagePag14] apply to maximal or Eichler orders in quaternion algebras. The series of articles [Reference BleyBle97, Reference Bley and JohnstonBJ08, Reference Bley and JohnstonBJ11, Reference Hofmann and JohnstonHJ20] consider progressively more general situations, culminating in a solution to
![]() $\mathsf {IsIsomorphic}$
when A is semisimple, but they all involve a very expensive enumeration step, which in many cases renders the algorithm impractical. We refer the reader to the introduction of [Reference Hofmann and JohnstonHJ20] for a more detailed overview. By contrast, Algorithm 8.3 replaces this enumeration step by a new method combining results of [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Reference Bley and WilsonBW09] with an idea of Husert [Reference HusertHus17].
$\mathsf {IsIsomorphic}$
when A is semisimple, but they all involve a very expensive enumeration step, which in many cases renders the algorithm impractical. We refer the reader to the introduction of [Reference Hofmann and JohnstonHJ20] for a more detailed overview. By contrast, Algorithm 8.3 replaces this enumeration step by a new method combining results of [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Reference Bley and WilsonBW09] with an idea of Husert [Reference HusertHus17].
The original motivation for the study of these problems comes from the Galois module structure of rings of integers. Let
![]() $L/K$
be a finite Galois extension of number fields, and let
$L/K$
be a finite Galois extension of number fields, and let
![]() $G=\mathrm {Gal}(L/K)$
. An interesting but difficult problem is to determine whether
$G=\mathrm {Gal}(L/K)$
. An interesting but difficult problem is to determine whether
![]() $\mathcal {O}_{L}$
is free over its so-called associated order
$\mathcal {O}_{L}$
is free over its so-called associated order
![]() $\mathcal {A}_{L/K} = \{ \alpha \in K[G] \mid \alpha \mathcal {O}_{L} \subseteq \mathcal {O}_{L} \}$
and, if so, to determine an explicit generator. We refer the reader to §10 and to the introduction of [Reference Hofmann and JohnstonHJ20] for a more detailed overview of this question and related problems.
$\mathcal {A}_{L/K} = \{ \alpha \in K[G] \mid \alpha \mathcal {O}_{L} \subseteq \mathcal {O}_{L} \}$
and, if so, to determine an explicit generator. We refer the reader to §10 and to the introduction of [Reference Hofmann and JohnstonHJ20] for a more detailed overview of this question and related problems.
The main application of
![]() $\mathsf {IsPrincipal}$
in the present article is to the following problem.
$\mathsf {IsPrincipal}$
in the present article is to the following problem.
Problem (
 $\mathsf {IsSimilar}$
)
$\mathsf {IsSimilar}$
)
Given a number field K with ring of integers
![]() $\mathcal {O}=\mathcal {O}_{K}$
, an integer
$\mathcal {O}=\mathcal {O}_{K}$
, an integer
![]() $n \in \mathbb {Z}_{>0}$
and two matrices
$n \in \mathbb {Z}_{>0}$
and two matrices
![]() $A,B \in \mathrm {Mat}_{n}(\mathcal {O})$
, determine whether A and B are similar over
$A,B \in \mathrm {Mat}_{n}(\mathcal {O})$
, determine whether A and B are similar over
![]() $\mathcal {O}$
, and if so, return a conjugating matrix
$\mathcal {O}$
, and if so, return a conjugating matrix
![]() $C \in \mathrm {GL}_{n}(\mathcal {O})$
such that
$C \in \mathrm {GL}_{n}(\mathcal {O})$
such that
![]() $B= CAC^{-1}$
.
$B= CAC^{-1}$
.
As a special case, this problem includes the so-called conjugacy problem for
![]() $\mathrm {GL}_{n}(\mathcal {O})$
. A number of authors have considered the problem
$\mathrm {GL}_{n}(\mathcal {O})$
. A number of authors have considered the problem
![]() $\mathsf {IsSimilar}$
(or special cases), including Latimer–MacDuffee [Reference Latimer and MacDuffeeLM33], Sarkisyan [Reference SarkisyanSar79], Grunewald [Reference GrunewaldGru80], Husert [Reference HusertHus17] and Marseglia [Reference MarsegliaMar20]. Eick–O’Brien and the second named author of the present article gave the first practical algorithm that solves this problem in full generality [Reference Eick, Hofmann and O’BrienEHO19]. We refer the reader to §9.4 and §9.5 for a more detailed discussion of these results.
$\mathsf {IsSimilar}$
(or special cases), including Latimer–MacDuffee [Reference Latimer and MacDuffeeLM33], Sarkisyan [Reference SarkisyanSar79], Grunewald [Reference GrunewaldGru80], Husert [Reference HusertHus17] and Marseglia [Reference MarsegliaMar20]. Eick–O’Brien and the second named author of the present article gave the first practical algorithm that solves this problem in full generality [Reference Eick, Hofmann and O’BrienEHO19]. We refer the reader to §9.4 and §9.5 for a more detailed discussion of these results.
In §9, we give an efficient algorithm that solves
![]() $\mathsf {IsSimilar}$
in full generality and a complexity analysis showing that it is polynomial-time reducible to standard problems in algorithmic algebraic number theory, including the principal ideal problem in certain rings of integers and the computation of their unit groups (see Algorithm 9.13 and Theorem 9.14). As a corollary we obtain the following result (see Corollary 9.15 and Remark 5.1).
$\mathsf {IsSimilar}$
in full generality and a complexity analysis showing that it is polynomial-time reducible to standard problems in algorithmic algebraic number theory, including the principal ideal problem in certain rings of integers and the computation of their unit groups (see Algorithm 9.13 and Theorem 9.14). As a corollary we obtain the following result (see Corollary 9.15 and Remark 5.1).
Theorem. The problem
![]() $\mathsf {IsSimilar}$
reduces in probabilistic subexponential time to the problems
$\mathsf {IsSimilar}$
reduces in probabilistic subexponential time to the problems
![]() $\mathsf {IsPrincipal}$
and
$\mathsf {IsPrincipal}$
and
![]() $\mathsf {UnitGroup}$
for rings of integers of number fields.
$\mathsf {UnitGroup}$
for rings of integers of number fields.
We first adapt ideas of Faddeev [Reference FaddeevFad66] to recast
![]() $\mathsf {IsSimilar}$
in terms of lattices over orders in a certain K-algebra satisfying hypothesis (H). We then show how to explicitly compute the Jacobson radical of this K-algebra as well as the Wedderburn decomposition of the semisimple quotient from the rational canonical forms of the input matrices. Thus, we show that
$\mathsf {IsSimilar}$
in terms of lattices over orders in a certain K-algebra satisfying hypothesis (H). We then show how to explicitly compute the Jacobson radical of this K-algebra as well as the Wedderburn decomposition of the semisimple quotient from the rational canonical forms of the input matrices. Thus, we show that
![]() $\mathsf {IsSimilar}$
is reducible to
$\mathsf {IsSimilar}$
is reducible to
![]() $\mathsf {IsPrincipal}$
. In particular, Algorithm 9.13 avoids any expensive enumeration step. For a detailed comparison with other algorithms and implementations, including explicit examples and timings, we refer the reader to §9.5. As these comparisons and our complexity analysis suggest, the implementation of Algorithm 9.13 in the computer algebra package Hecke [Reference Fieker, Hart, Hofmann and JohanssonFHHJ17] vastly outperforms implementations of other algorithms.
$\mathsf {IsPrincipal}$
. In particular, Algorithm 9.13 avoids any expensive enumeration step. For a detailed comparison with other algorithms and implementations, including explicit examples and timings, we refer the reader to §9.5. As these comparisons and our complexity analysis suggest, the implementation of Algorithm 9.13 in the computer algebra package Hecke [Reference Fieker, Hart, Hofmann and JohanssonFHHJ17] vastly outperforms implementations of other algorithms.
2 Preliminaries on lattices and orders
For further background on lattices and orders, we refer the reader to [Reference ReinerRei03, §4, §8]. Henceforth, all rings considered will be associative and unital.
Let R be an Noetherian integral domain with field of fractions K. To avoid trivialities, we assume that
![]() $R \neq K$
. An R-lattice is a finitely generated torsion-free module over R. Since R is Noetherian, any R-submodule of an R-lattice is again an R-lattice. For any finite-dimensional K-vector space V, an R-lattice in V is a finitely generated R-submodule M in V. We define a K-vector subspace of V by
$R \neq K$
. An R-lattice is a finitely generated torsion-free module over R. Since R is Noetherian, any R-submodule of an R-lattice is again an R-lattice. For any finite-dimensional K-vector space V, an R-lattice in V is a finitely generated R-submodule M in V. We define a K-vector subspace of V by
and say that M is a full R-lattice in V if
![]() $K M=V$
. We may identify
$K M=V$
. We may identify
![]() $KM$
with
$KM$
with
![]() $K \otimes _{R} M$
.
$K \otimes _{R} M$
.
Now, let A be a finite-dimensional K-algebra. Then A is both left and right Artinian and Noetherian. An R-order in A is a subring
![]() $\Lambda $
of A (so in particular has the same unit element as A) such that
$\Lambda $
of A (so in particular has the same unit element as A) such that
![]() $\Lambda $
is a full R-lattice in A. Note that
$\Lambda $
is a full R-lattice in A. Note that
![]() $\Lambda $
is both left and right Noetherian, since
$\Lambda $
is both left and right Noetherian, since
![]() $\Lambda $
is finitely generated over R. A left
$\Lambda $
is finitely generated over R. A left
![]() $\Lambda $
-lattice X is a left
$\Lambda $
-lattice X is a left
![]() $\Lambda $
-module that is also an R-lattice; in this case,
$\Lambda $
-module that is also an R-lattice; in this case,
![]() $KX$
may be viewed as a left A-module.
$KX$
may be viewed as a left A-module.
Henceforth, all modules (resp. lattices) will be assumed to be left modules (resp. lattices) unless otherwise stated. Two
![]() $\Lambda $
-lattices are said to be isomorphic if they are isomorphic as
$\Lambda $
-lattices are said to be isomorphic if they are isomorphic as
![]() $\Lambda $
-modules. The following two lemmas generalise [Reference Hofmann and JohnstonHJ20, Lemma 2.1].
$\Lambda $
-modules. The following two lemmas generalise [Reference Hofmann and JohnstonHJ20, Lemma 2.1].
Lemma 2.1. Let S be a Noetherian integral domain such that
![]() $R \subseteq S \subsetneq K$
. Let
$R \subseteq S \subsetneq K$
. Let
![]() $\Gamma $
be an S-order in A. Let V be a finitely generated A-module. For any R-lattice M in V, the set
$\Gamma $
be an S-order in A. Let V be a finitely generated A-module. For any R-lattice M in V, the set
is a
![]() $\Gamma $
-lattice in V containing M.
$\Gamma $
-lattice in V containing M.
Proof. That
![]() $M \subseteq \Gamma M$
is clear. Note that K is the field of fractions of both R and S. Write
$M \subseteq \Gamma M$
is clear. Note that K is the field of fractions of both R and S. Write
![]() $M = \langle v_{1}, \ldots , v_{l} \rangle _{R}$
and
$M = \langle v_{1}, \ldots , v_{l} \rangle _{R}$
and
![]() $\Gamma = \langle w_{1}, \ldots , w_{m} \rangle _{S}$
. An easy calculation shows that
$\Gamma = \langle w_{1}, \ldots , w_{m} \rangle _{S}$
. An easy calculation shows that
and hence
![]() $\Gamma M$
is an S-lattice in V. Moreover, it is straightforward to see that
$\Gamma M$
is an S-lattice in V. Moreover, it is straightforward to see that
![]() $\Gamma M$
is also a
$\Gamma M$
is also a
![]() $\Gamma $
-module and therefore is a
$\Gamma $
-module and therefore is a
![]() $\Gamma $
-lattice in V.
$\Gamma $
-lattice in V.
Lemma 2.2. Let S be a Noetherian integral domain such that
![]() $R \subseteq S \subsetneq K$
. Let
$R \subseteq S \subsetneq K$
. Let
![]() $\Lambda $
be an R-order in A, let
$\Lambda $
be an R-order in A, let
![]() $\Gamma $
be an S-order in A and suppose that
$\Gamma $
be an S-order in A and suppose that
![]() $\Lambda \subseteq \Gamma $
. Let
$\Lambda \subseteq \Gamma $
. Let
![]() $f \colon X \to Y$
be a homomorphism of
$f \colon X \to Y$
be a homomorphism of
![]() $\Lambda $
-lattices. Then the following hold.
$\Lambda $
-lattices. Then the following hold.
-
(a) There exists a unique homomorphism of A-modules
 $f^{A} \colon KX \to KY$
extending f.
$f^{A} \colon KX \to KY$
extending f. -
(b) There exists a unique homomorphism of
 $\Gamma $
-lattices
$\Gamma $
-lattices
 $f^{\Gamma }\colon \Gamma X \to \Gamma Y$
extending f.
$f^{\Gamma }\colon \Gamma X \to \Gamma Y$
extending f. -
(c) If f is injective (resp. surjective), then
 $f^{A}$
and
$f^{A}$
and
 $f^{\Gamma }$
are injective (resp. surjective).
$f^{\Gamma }$
are injective (resp. surjective).
Proof. This is straightforward. The key points are to (a) extend f to
![]() $KX$
using K-linearity; (b) restrict
$KX$
using K-linearity; (b) restrict
![]() $f^{A}$
to
$f^{A}$
to
![]() $\Gamma X$
; (c) (injectivity) check that
$\Gamma X$
; (c) (injectivity) check that
![]() $\ker (f)$
is a full R-lattice in
$\ker (f)$
is a full R-lattice in
![]() $\ker (f^{A})$
and (c) (surjectivity) use the definitions of
$\ker (f^{A})$
and (c) (surjectivity) use the definitions of
![]() $K Y$
and
$K Y$
and
![]() $\Gamma Y$
.
$\Gamma Y$
.
We will often use the following result without explicit mention.
Lemma 2.3. Let
![]() $\Lambda $
be an R-order in A, and let X be a
$\Lambda $
be an R-order in A, and let X be a
![]() $\Lambda $
-lattice such that
$\Lambda $
-lattice such that
![]() $\dim _{K} KX = \dim _{K} A$
. Let
$\dim _{K} KX = \dim _{K} A$
. Let
![]() $\alpha \in X$
. Then
$\alpha \in X$
. Then
![]() $X=\Lambda \alpha $
if and only if
$X=\Lambda \alpha $
if and only if
![]() $\alpha $
is a free generator of X over
$\alpha $
is a free generator of X over
![]() $\Lambda $
.
$\Lambda $
.
Proof. Suppose
![]() $X = \Lambda \alpha $
. Then the map
$X = \Lambda \alpha $
. Then the map
![]() $f : \Lambda \rightarrow X$
given by
$f : \Lambda \rightarrow X$
given by
![]() $f(\lambda ) = \lambda \alpha $
is a surjective homomorphism of
$f(\lambda ) = \lambda \alpha $
is a surjective homomorphism of
![]() $\Lambda $
-lattices. By Lemma 2.2 f extends uniquely to a surjective map
$\Lambda $
-lattices. By Lemma 2.2 f extends uniquely to a surjective map
![]() $f^{A} : A \rightarrow KX$
. The hypotheses imply that
$f^{A} : A \rightarrow KX$
. The hypotheses imply that
![]() $f^{A}$
is injective, thus f is an isomorphism and so
$f^{A}$
is injective, thus f is an isomorphism and so
![]() $\alpha $
is a free generator of X over
$\alpha $
is a free generator of X over
![]() $\Lambda $
. The converse is trivial.
$\Lambda $
. The converse is trivial.
3 Reduction steps for the lattice isomorphism problem
Let R be a Noetherian integral domain with field of fractions K and assume that
![]() $R \neq K$
. Let
$R \neq K$
. Let
![]() $\Lambda $
be an R-order in a finite-dimensional K-algebra A.
$\Lambda $
be an R-order in a finite-dimensional K-algebra A.
3.1 Reduction to the free rank
 $1$
case via homomorphism groups
$1$
case via homomorphism groups
Let X and Y be
![]() $\Lambda $
-lattices. Let
$\Lambda $
-lattices. Let
![]() $V=KX$
and
$V=KX$
and
![]() $W=KY$
, which we regard as A-modules. We have
$W=KY$
, which we regard as A-modules. We have
where
![]() $f|_{X}$
denotes the restriction of f to a map
$f|_{X}$
denotes the restriction of f to a map
![]() $f \colon X \to Y$
. This follows from the fact that every element in
$f \colon X \to Y$
. This follows from the fact that every element in
![]() $\mathrm {Hom}_{\Lambda }(X, Y)$
extends uniquely to an element in
$\mathrm {Hom}_{\Lambda }(X, Y)$
extends uniquely to an element in
![]() $\mathrm {Hom}_{A}(V, W)$
(see Lemma 2.2). Since a map
$\mathrm {Hom}_{A}(V, W)$
(see Lemma 2.2). Since a map
![]() $f \in \mathrm {Hom}_{A}(V,W)$
is also R-linear, we have
$f \in \mathrm {Hom}_{A}(V,W)$
is also R-linear, we have
![]() $f(X) \subseteq Y$
if and only if
$f(X) \subseteq Y$
if and only if
![]() $f \in \mathrm {Hom}_{R}(X,Y)$
. Therefore,
$f \in \mathrm {Hom}_{R}(X,Y)$
. Therefore,
Since X and Y are finitely generated over R, so is
![]() $\mathrm {Hom}_{R}(X,Y)$
. Therefore,
$\mathrm {Hom}_{R}(X,Y)$
. Therefore,
![]() $\mathrm {Hom}_{\Lambda }(X,Y)$
is a full R-lattice in
$\mathrm {Hom}_{\Lambda }(X,Y)$
is a full R-lattice in
![]() $\mathrm {Hom}_{A}(V,W)$
. Similarly,
$\mathrm {Hom}_{A}(V,W)$
. Similarly,
![]() $\mathrm {End}_{\Lambda }(Y)$
is a full R-lattice in
$\mathrm {End}_{\Lambda }(Y)$
is a full R-lattice in
![]() $\mathrm {End}_{A}(W)$
.
$\mathrm {End}_{A}(W)$
.
In fact,
![]() $\mathrm {End}_{\Lambda }(Y)$
is an R-order in
$\mathrm {End}_{\Lambda }(Y)$
is an R-order in
![]() $\mathrm {End}_{A}(W)$
and
$\mathrm {End}_{A}(W)$
and
![]() $\mathrm {Hom}_{\Lambda }(X,Y)$
is a (left)
$\mathrm {Hom}_{\Lambda }(X,Y)$
is a (left)
![]() $\mathrm {End}_{\Lambda }(Y)$
-lattice in
$\mathrm {End}_{\Lambda }(Y)$
-lattice in
![]() $\mathrm {Hom}_{A}(V,W)$
via postcomposition. The following result underpins the main results of the present article; it is a straightforward generalisation of [Reference Hofmann and JohnstonHJ20, Proposition 3.7].
$\mathrm {Hom}_{A}(V,W)$
via postcomposition. The following result underpins the main results of the present article; it is a straightforward generalisation of [Reference Hofmann and JohnstonHJ20, Proposition 3.7].
Proposition 3.1. Two
![]() $\Lambda $
-lattices X and Y are isomorphic if and only if
$\Lambda $
-lattices X and Y are isomorphic if and only if
-
(a) the
 $\mathrm {End}_{\Lambda }(Y)$
-lattice
$\mathrm {End}_{\Lambda }(Y)$
-lattice
 $\mathrm {Hom}_{\Lambda }(X, Y)$
is free of rank
$\mathrm {Hom}_{\Lambda }(X, Y)$
is free of rank
 $1$
, and
$1$
, and -
(b) every (any) free generator of
 $\mathrm {Hom}_{\Lambda }(X, Y)$
over
$\mathrm {Hom}_{\Lambda }(X, Y)$
over
 $\mathrm {End}_{\Lambda }(Y)$
is an isomorphism.
$\mathrm {End}_{\Lambda }(Y)$
is an isomorphism.
Proof. If (a) and (b) hold, then it is clear that X and Y are isomorphic. Suppose conversely that X and Y are isomorphic. Fix an isomorphism
![]() $\varphi \in \mathrm {Hom}_{\Lambda }(X, Y)$
. Then for any
$\varphi \in \mathrm {Hom}_{\Lambda }(X, Y)$
. Then for any
![]() $g \in \mathrm {Hom}_{\Lambda }(X, Y)$
, we have
$g \in \mathrm {Hom}_{\Lambda }(X, Y)$
, we have
![]() $h_{g} := g \circ \varphi ^{-1} \in \mathrm {End}_{\Lambda }(Y)$
and so
$h_{g} := g \circ \varphi ^{-1} \in \mathrm {End}_{\Lambda }(Y)$
and so
![]() $g = h_{g} \circ \varphi $
. Hence,
$g = h_{g} \circ \varphi $
. Hence,
![]() $\varphi $
is a generator of
$\varphi $
is a generator of
![]() $\mathrm {Hom}_{\Lambda }(X, Y)$
over
$\mathrm {Hom}_{\Lambda }(X, Y)$
over
![]() $\mathrm {End}_{\Lambda }(Y)$
and by Lemma 2.3 it is in fact a free generator. Thus, (a) holds. Now, let f be any free generator of
$\mathrm {End}_{\Lambda }(Y)$
and by Lemma 2.3 it is in fact a free generator. Thus, (a) holds. Now, let f be any free generator of
![]() $\mathrm {Hom}_{\Lambda }(X, Y)$
over
$\mathrm {Hom}_{\Lambda }(X, Y)$
over
![]() $\mathrm {End}_{\Lambda }(Y)$
. Then there exists
$\mathrm {End}_{\Lambda }(Y)$
. Then there exists
![]() $\theta \in \mathrm {Aut}_{\Lambda }(Y)=\mathrm {End}_{\Lambda }(Y)^{\times }$
such that
$\theta \in \mathrm {Aut}_{\Lambda }(Y)=\mathrm {End}_{\Lambda }(Y)^{\times }$
such that
![]() $f = \theta \circ \varphi $
, and hence f is an isomorphism. Thus, (b) holds.
$f = \theta \circ \varphi $
, and hence f is an isomorphism. Thus, (b) holds.
We now state and prove a closely related ‘folklore’ result that appears to be well known but whose proof is difficult to locate in the literature. We include this result for completeness, and it will not be applied in the present article. For any full R-lattice M in A, we define
![]() $\mathcal {O}_{r}(M) = \{ \mu \in A \mid M\mu \subseteq M \}$
. This is an R-order in A and is called the right order of M in A (see [Reference ReinerRei03, §8]). The following result may be viewed as a corollary of Proposition 3.1, but it is easier to give a direct proof.
$\mathcal {O}_{r}(M) = \{ \mu \in A \mid M\mu \subseteq M \}$
. This is an R-order in A and is called the right order of M in A (see [Reference ReinerRei03, §8]). The following result may be viewed as a corollary of Proposition 3.1, but it is easier to give a direct proof.
Proposition 3.2. Let X and Y be full
![]() $\Lambda $
-lattices in A. Then
$\Lambda $
-lattices in A. Then
![]() $C := \{ \lambda \in A \mid X\lambda \subseteq Y \}$
is a full
$C := \{ \lambda \in A \mid X\lambda \subseteq Y \}$
is a full
![]() $\mathcal {O}_{r}(X)$
-lattice in A. Moreover, X and Y are isomorphic if and only if
$\mathcal {O}_{r}(X)$
-lattice in A. Moreover, X and Y are isomorphic if and only if
-
(a) there exists
 $\alpha \in A^{\times }$
such that
$\alpha \in A^{\times }$
such that
 $C=\mathcal {O}_{r}(X) \alpha $
, and
$C=\mathcal {O}_{r}(X) \alpha $
, and -
(b) we have
 $Y=XC$
.
$Y=XC$
.
Furthermore, when this is the case,
![]() $Y=X\alpha $
.
$Y=X\alpha $
.
Proof. Set
![]() $\mathcal {O}:=\mathcal {O}_{r}(X)$
. Clearly, C is both an R-module and an
$\mathcal {O}:=\mathcal {O}_{r}(X)$
. Clearly, C is both an R-module and an
![]() $\mathcal {O}$
-module. Since X and Y are both full R-lattices in A, there exist nonzero
$\mathcal {O}$
-module. Since X and Y are both full R-lattices in A, there exist nonzero
![]() $r,s \in R$
such that
$r,s \in R$
such that
![]() $Ys \subseteq X$
and
$Ys \subseteq X$
and
![]() $Xr \subseteq Y$
(see [Reference ReinerRei03, §4]). Thus,
$Xr \subseteq Y$
(see [Reference ReinerRei03, §4]). Thus,
![]() $\mathcal {O}r \subseteq C \subseteq \mathcal {O}s^{-1}$
, where
$\mathcal {O}r \subseteq C \subseteq \mathcal {O}s^{-1}$
, where
![]() $\mathcal {O}r$
and
$\mathcal {O}r$
and
![]() $\mathcal {O}s^{-1}$
are both full R-lattices in A. Hence, C is a full R-lattice and therefore a full
$\mathcal {O}s^{-1}$
are both full R-lattices in A. Hence, C is a full R-lattice and therefore a full
![]() $\mathcal {O}$
-lattice in A.
$\mathcal {O}$
-lattice in A.
Suppose (a) and (b) hold. Then
![]() $Y=XC=X(\mathcal {O}\alpha ) = (X\mathcal {O})\alpha = X \alpha $
. Hence, X and Y are isomorphic since
$Y=XC=X(\mathcal {O}\alpha ) = (X\mathcal {O})\alpha = X \alpha $
. Hence, X and Y are isomorphic since
![]() $\alpha \in A^{\times }$
. Suppose conversely that
$\alpha \in A^{\times }$
. Suppose conversely that
![]() $f: X \rightarrow Y$
is a
$f: X \rightarrow Y$
is a
![]() $\Lambda $
-isomorphism. Then by Lemma 2.2 f extends uniquely to an A-isomorphism
$\Lambda $
-isomorphism. Then by Lemma 2.2 f extends uniquely to an A-isomorphism
![]() $f^{A} : A \rightarrow A$
and hence is given by right multiplication by an element
$f^{A} : A \rightarrow A$
and hence is given by right multiplication by an element
![]() $\alpha \in A^{\times }$
. Thus,
$\alpha \in A^{\times }$
. Thus,
![]() $Y = X\alpha $
. Moreover,
$Y = X\alpha $
. Moreover,
![]() $C = \{ \lambda \in A \mid X\lambda \subseteq X\alpha \} = \mathcal {O} \alpha $
and
$C = \{ \lambda \in A \mid X\lambda \subseteq X\alpha \} = \mathcal {O} \alpha $
and
![]() $Y = X\alpha = (X\mathcal {O})\alpha = X(\mathcal {O}\alpha ) \,{=}\, XC$
.
$Y = X\alpha = (X\mathcal {O})\alpha = X(\mathcal {O}\alpha ) \,{=}\, XC$
.
3.2 An alternative approach via localisation
We give an alternative version of Proposition 3.1 that uses localisation. This will be useful later for understanding the relation of some of our results to other results in the literature. For a nonzero prime ideal
![]() $\mathfrak {p}$
of R, we let
$\mathfrak {p}$
of R, we let
![]() $R_{\mathfrak {p}}$
denote the localisation (not completion) of R at
$R_{\mathfrak {p}}$
denote the localisation (not completion) of R at
![]() $\mathfrak {p}$
. We define the localisation
$\mathfrak {p}$
. We define the localisation
![]() $M_{\mathfrak {p}}$
of M at
$M_{\mathfrak {p}}$
of M at
![]() $\mathfrak {p}$
to be
$\mathfrak {p}$
to be
![]() $R_{\mathfrak {p}}M$
and note that this is an
$R_{\mathfrak {p}}M$
and note that this is an
![]() $R_{\mathfrak {p}}$
-lattice in
$R_{\mathfrak {p}}$
-lattice in
![]() $KM$
. The localisation
$KM$
. The localisation
![]() $\Lambda _{\mathfrak {p}}$
is an
$\Lambda _{\mathfrak {p}}$
is an
![]() $R_{\mathfrak {p}}$
-order in A, and localising a
$R_{\mathfrak {p}}$
-order in A, and localising a
![]() $\Lambda $
-lattice X at
$\Lambda $
-lattice X at
![]() $\mathfrak {p}$
yields a
$\mathfrak {p}$
yields a
![]() $\Lambda _{\mathfrak {p}}$
-lattice
$\Lambda _{\mathfrak {p}}$
-lattice
![]() $X_{\mathfrak {p}}$
. Two
$X_{\mathfrak {p}}$
. Two
![]() $\Lambda $
-lattices X and Y are said to be locally isomorphic if the
$\Lambda $
-lattices X and Y are said to be locally isomorphic if the
![]() $\Lambda _{\mathfrak {p}}$
-lattices
$\Lambda _{\mathfrak {p}}$
-lattices
![]() $X_{\mathfrak {p}}$
and
$X_{\mathfrak {p}}$
and
![]() $Y_{\mathfrak {p}}$
are isomorphic for all maximal ideals
$Y_{\mathfrak {p}}$
are isomorphic for all maximal ideals
![]() $\mathfrak {p}$
of R.
$\mathfrak {p}$
of R.
Proposition 3.3. Two
![]() $\Lambda $
-lattices X and Y are isomorphic if and only if
$\Lambda $
-lattices X and Y are isomorphic if and only if
-
(a) X and Y are locally isomorphic, and
-
(b) the
 $\mathrm {End}_{\Lambda }(Y)$
-lattice
$\mathrm {End}_{\Lambda }(Y)$
-lattice
 $\mathrm {Hom}_{\Lambda }(X, Y)$
is free of rank
$\mathrm {Hom}_{\Lambda }(X, Y)$
is free of rank
 $1$
.
$1$
.
Furthermore, when this is the case, every free generator of
![]() $\mathrm {Hom}_{\Lambda }(X, Y)$
over
$\mathrm {Hom}_{\Lambda }(X, Y)$
over
![]() $\mathrm {End}_{\Lambda }(Y)$
is an isomorphism.
$\mathrm {End}_{\Lambda }(Y)$
is an isomorphism.
Proof. If X and Y are isomorphic, then (a) clearly holds and (b) holds by Proposition 3.1. Suppose conversely that (a) and (b) hold. Let f be a free generator of
![]() $\mathrm {Hom}_{\Lambda }(X, Y)$
over
$\mathrm {Hom}_{\Lambda }(X, Y)$
over
![]() $\mathrm {End}_{\Lambda }(Y)$
. Let
$\mathrm {End}_{\Lambda }(Y)$
. Let
![]() $\mathfrak {p}$
be a maximal ideal of R. Then there exists an isomorphism
$\mathfrak {p}$
be a maximal ideal of R. Then there exists an isomorphism
![]() $g_{\mathfrak {p}} \in \mathrm {Hom}_{\Lambda _{\mathfrak {p}}}(X_{\mathfrak {p}}, Y_{\mathfrak {p}})$
. Moreover, f extends to a free generator
$g_{\mathfrak {p}} \in \mathrm {Hom}_{\Lambda _{\mathfrak {p}}}(X_{\mathfrak {p}}, Y_{\mathfrak {p}})$
. Moreover, f extends to a free generator
![]() $f_{\mathfrak {p}}$
of
$f_{\mathfrak {p}}$
of
![]() $\mathrm {Hom}_{\Lambda _{\mathfrak {p}}}(X_{\mathfrak {p}}, Y_{\mathfrak {p}})$
over
$\mathrm {Hom}_{\Lambda _{\mathfrak {p}}}(X_{\mathfrak {p}}, Y_{\mathfrak {p}})$
over
![]() $\mathrm {End}_{\Lambda _{\mathfrak {p}}}(Y_{\mathfrak {p}})$
, and so there exists
$\mathrm {End}_{\Lambda _{\mathfrak {p}}}(Y_{\mathfrak {p}})$
, and so there exists
![]() $h_{\mathfrak {p}} \in \mathrm {End}_{\Lambda _{\mathfrak {p}}}(Y_{\mathfrak {p}})$
such that
$h_{\mathfrak {p}} \in \mathrm {End}_{\Lambda _{\mathfrak {p}}}(Y_{\mathfrak {p}})$
such that
![]() $g_{\mathfrak {p}} = h_{\mathfrak {p}} \circ f_{\mathfrak {p}}$
. Note that
$g_{\mathfrak {p}} = h_{\mathfrak {p}} \circ f_{\mathfrak {p}}$
. Note that
![]() $h_{\mathfrak {p}}$
is surjective and thus is in fact an automorphism of
$h_{\mathfrak {p}}$
is surjective and thus is in fact an automorphism of
![]() $Y_{\mathfrak {p}}$
by [Reference Curtis and ReinerCR81, (5.8)]. Therefore,
$Y_{\mathfrak {p}}$
by [Reference Curtis and ReinerCR81, (5.8)]. Therefore,
![]() $f_{\mathfrak {p}}$
is an isomorphism. Since this is true for all choices of
$f_{\mathfrak {p}}$
is an isomorphism. Since this is true for all choices of
![]() $\mathfrak {p}$
, we have that f itself is an isomorphism by [Reference Curtis and ReinerCR81, (4.2)(ii)].
$\mathfrak {p}$
, we have that f itself is an isomorphism by [Reference Curtis and ReinerCR81, (4.2)(ii)].
3.3 Reduction to the case of lattices in semisimple algebras
Let
![]() $\operatorname {\mathrm {J}}(A)$
denote the Jacobson radical of A, and note that
$\operatorname {\mathrm {J}}(A)$
denote the Jacobson radical of A, and note that
![]() $\overline {A} := A/{\operatorname {\mathrm {J}}(A)}$
is a semisimple K-algebra by [Reference Curtis and ReinerCR81, (5.19)]. Let
$\overline {A} := A/{\operatorname {\mathrm {J}}(A)}$
is a semisimple K-algebra by [Reference Curtis and ReinerCR81, (5.19)]. Let
![]() $h : A \rightarrow \overline {A}$
denote the canonical projection map. For an element
$h : A \rightarrow \overline {A}$
denote the canonical projection map. For an element
![]() $a \in A$
, write
$a \in A$
, write
![]() $\overline {a}$
for
$\overline {a}$
for
![]() $h(a)$
, and for a subset
$h(a)$
, and for a subset
![]() $S \subseteq A$
, write
$S \subseteq A$
, write
![]() $\overline {S}$
for
$\overline {S}$
for
![]() $h(S)$
. Then
$h(S)$
. Then
![]() $\overline {\Lambda }$
is an R-order in
$\overline {\Lambda }$
is an R-order in
![]() $\overline {A}$
. The following result may be viewed as a variant of [Reference FaddeevFad66, Theorem 3].
$\overline {A}$
. The following result may be viewed as a variant of [Reference FaddeevFad66, Theorem 3].
Theorem 3.4. Let X be a full
![]() $\Lambda $
-lattice in A. Then
$\Lambda $
-lattice in A. Then
![]() $\overline {X}$
is a full
$\overline {X}$
is a full
![]() $\overline {\Lambda }$
-lattice in
$\overline {\Lambda }$
-lattice in
![]() $\overline {A}$
. Moreover, the following statements hold for
$\overline {A}$
. Moreover, the following statements hold for
![]() $\alpha \in X$
.
$\alpha \in X$
.
-
(a) If
 $X = \Lambda \alpha $
, then
$X = \Lambda \alpha $
, then
 $\overline {X} = \overline {\Lambda } \overline {\alpha }$
.
$\overline {X} = \overline {\Lambda } \overline {\alpha }$
. -
(b) If
 $\overline {X} = \overline {\Lambda } \overline {\alpha }$
, then either
$\overline {X} = \overline {\Lambda } \overline {\alpha }$
, then either
 $X = \Lambda \alpha $
or
$X = \Lambda \alpha $
or
 $X \ne \Lambda \beta $
for all
$X \ne \Lambda \beta $
for all
 $\beta \in X$
.
$\beta \in X$
.
Proof. The first claim and part (a) are both clear. Suppose that
![]() $\overline {X} = \overline {\Lambda } \overline {\alpha }$
and that there exists
$\overline {X} = \overline {\Lambda } \overline {\alpha }$
and that there exists
![]() $\beta \in X$
such that
$\beta \in X$
such that
![]() $X=\Lambda \beta $
. Since
$X=\Lambda \beta $
. Since
![]() $\alpha \in X=\Lambda \beta $
, there exists
$\alpha \in X=\Lambda \beta $
, there exists
![]() $\varepsilon \in \Lambda $
such that
$\varepsilon \in \Lambda $
such that
![]() $\alpha = \varepsilon \beta $
. Hence,
$\alpha = \varepsilon \beta $
. Hence,
![]() $\overline {\alpha } = \overline {\varepsilon }\overline {\beta }$
, and since each of
$\overline {\alpha } = \overline {\varepsilon }\overline {\beta }$
, and since each of
![]() $\overline {\alpha }$
and
$\overline {\alpha }$
and
![]() $\overline {\beta }$
is a free generator of
$\overline {\beta }$
is a free generator of
![]() $\overline {X}$
over
$\overline {X}$
over
![]() $\overline {\Lambda }$
, we must have
$\overline {\Lambda }$
, we must have
![]() $\overline {\varepsilon } \in \overline {\Lambda }^{\times }$
. Let
$\overline {\varepsilon } \in \overline {\Lambda }^{\times }$
. Let
![]() $\eta \in \Lambda $
such that
$\eta \in \Lambda $
such that
![]() $\overline {\eta }=\overline {\varepsilon }^{-1}$
. Then
$\overline {\eta }=\overline {\varepsilon }^{-1}$
. Then
![]() $\varepsilon \eta = 1 + \rho $
, where
$\varepsilon \eta = 1 + \rho $
, where
![]() $\rho \in \operatorname {\mathrm {J}}(A)$
. Moreover,
$\rho \in \operatorname {\mathrm {J}}(A)$
. Moreover,
![]() $\rho = \varepsilon \eta - 1 \in \Lambda $
. Since A is Artinian,
$\rho = \varepsilon \eta - 1 \in \Lambda $
. Since A is Artinian,
![]() $\operatorname {\mathrm {J}}(A)$
is a nilpotent ideal (see [Reference Curtis and ReinerCR81, (5.15)]), and so
$\operatorname {\mathrm {J}}(A)$
is a nilpotent ideal (see [Reference Curtis and ReinerCR81, (5.15)]), and so
![]() $\rho $
is a nilpotent element. Therefore,
$\rho $
is a nilpotent element. Therefore,
where the alternating sum is finite. Hence,
![]() $\varepsilon \in \Lambda ^{\times }$
and so
$\varepsilon \in \Lambda ^{\times }$
and so
![]() $\Lambda \alpha = \Lambda \varepsilon \beta = \Lambda \beta = X$
.
$\Lambda \alpha = \Lambda \varepsilon \beta = \Lambda \beta = X$
.
4 A necessary and sufficient condition for freeness
Let K be a number field with ring of integers
![]() $\mathcal {O}=\mathcal {O}_{K}$
, and let A be a finite-dimensional semisimple K-algebra. Let
$\mathcal {O}=\mathcal {O}_{K}$
, and let A be a finite-dimensional semisimple K-algebra. Let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}$
-order in A. By [Reference ReinerRei03, (10.4)] there exists a (not necessarily unique) maximal
$\mathcal {O}$
-order in A. By [Reference ReinerRei03, (10.4)] there exists a (not necessarily unique) maximal
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\mathcal {M}$
in A containing
$\mathcal {M}$
in A containing
![]() $\Lambda $
.
$\Lambda $
.
Lemmas 4.1 and 4.2, as well as part of Proposition 4.3, are based on [Reference HusertHus17, §1.6].
Lemma 4.1. Let
![]() $\mathfrak {c}, \mathfrak {d}, \mathfrak {f}$
be left ideals of
$\mathfrak {c}, \mathfrak {d}, \mathfrak {f}$
be left ideals of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\mathfrak {c} \subseteq \mathfrak {d}$
. Then
$\mathfrak {c} \subseteq \mathfrak {d}$
. Then
![]() $ \mathfrak {d} \cap (\mathfrak {c} + \mathfrak {f}) = \mathfrak {c} + (\mathfrak {d} \cap \mathfrak {f}) $
.
$ \mathfrak {d} \cap (\mathfrak {c} + \mathfrak {f}) = \mathfrak {c} + (\mathfrak {d} \cap \mathfrak {f}) $
.
Proof. We follow the proof of [Reference HusertHus17, Lemma 1.37]. If
![]() $c \in \mathfrak {c}$
and
$c \in \mathfrak {c}$
and
![]() $f \in \mathfrak {f}$
with
$f \in \mathfrak {f}$
with
![]() $c+f \in \mathfrak {d}$
, then
$c+f \in \mathfrak {d}$
, then
![]() $f \in \mathfrak {d}$
since
$f \in \mathfrak {d}$
since
![]() $c \in \mathfrak {d}$
. Hence,
$c \in \mathfrak {d}$
. Hence,
![]() $c+f \in \mathfrak {c} + (\mathfrak {d} \cap \mathfrak {f})$
. Therefore,
$c+f \in \mathfrak {c} + (\mathfrak {d} \cap \mathfrak {f})$
. Therefore,
![]() $\mathfrak {d} \cap (\mathfrak {c} + \mathfrak {f}) \subseteq \mathfrak {c} + (\mathfrak {d} \cap \mathfrak {f})$
. For the reverse inclusion, note that both
$\mathfrak {d} \cap (\mathfrak {c} + \mathfrak {f}) \subseteq \mathfrak {c} + (\mathfrak {d} \cap \mathfrak {f})$
. For the reverse inclusion, note that both
![]() $\mathfrak {c}$
and
$\mathfrak {c}$
and
![]() $\mathfrak {d} \cap \mathfrak {f}$
are contained in
$\mathfrak {d} \cap \mathfrak {f}$
are contained in
![]() $\mathfrak {d} \cap (\mathfrak {c} + \mathfrak {f})$
, and thus the same is true for their sum.
$\mathfrak {d} \cap (\mathfrak {c} + \mathfrak {f})$
, and thus the same is true for their sum.
An ideal of a ring will be said to be proper if the containment is strict. Henceforth, let
![]() $\mathfrak {f}$
be any proper full two-sided ideal of
$\mathfrak {f}$
be any proper full two-sided ideal of
![]() $\mathcal {M}$
that is contained in
$\mathcal {M}$
that is contained in
![]() $\Lambda $
. For
$\Lambda $
. For
![]() $\eta \in \mathcal {M}$
we write
$\eta \in \mathcal {M}$
we write
![]() $\overline {\eta }$
for its image in
$\overline {\eta }$
for its image in
![]() $\mathcal {M} / \mathfrak {f}$
.
$\mathcal {M} / \mathfrak {f}$
.
Lemma 4.2. Let X be a left ideal of
![]() $\Lambda $
. If
$\Lambda $
. If
![]() $X + \mathfrak {f} = \Lambda $
and
$X + \mathfrak {f} = \Lambda $
and
![]() $\beta \in \mathcal {M}$
such that
$\beta \in \mathcal {M}$
such that
![]() $\mathcal {M}X = \mathcal {M}\beta $
, then
$\mathcal {M}X = \mathcal {M}\beta $
, then
![]() $\overline {\beta } \in (\mathcal {M}/\mathfrak {f})^{\times }$
and
$\overline {\beta } \in (\mathcal {M}/\mathfrak {f})^{\times }$
and
![]() $\mathcal {M}X \cap \Lambda = X$
.
$\mathcal {M}X \cap \Lambda = X$
.
Proof. We adapt the proof of [Reference HusertHus17, Lemma 1.38]. Clearly,
![]() $\mathfrak {f}X \subseteq \mathcal {M}X \cap \mathfrak {f}$
. We now show the reverse inclusion. Let
$\mathfrak {f}X \subseteq \mathcal {M}X \cap \mathfrak {f}$
. We now show the reverse inclusion. Let
![]() $\gamma \in \mathcal {M} X \cap \mathfrak {f}$
. Then we write
$\gamma \in \mathcal {M} X \cap \mathfrak {f}$
. Then we write
![]() $\gamma = \lambda \beta $
with
$\gamma = \lambda \beta $
with
![]() $\lambda \in \mathcal {M}$
and we have
$\lambda \in \mathcal {M}$
and we have
 $$ \begin{align*} X + \mathfrak{f} = \Lambda &\implies \mathcal{M}(X + \mathfrak{f}) = \mathcal{M} \\ & \implies \mathcal{M}\beta + \mathfrak{f} = \mathcal{M} \\ & \implies \overline{\beta} \in (\mathcal{M} / \mathfrak{f})^{\times} \\ &\implies \overline{\lambda} = \overline{\gamma} \overline{\beta}^{-1} = \overline{0} (\overline{\beta})^{-1} = \overline{0} \textrm{ in } \mathcal{M}/\mathfrak{f}\\ & \implies \lambda \in \mathfrak{f} \\ &\implies \gamma=\lambda\beta \in \mathfrak{f}\beta = \mathfrak{f}\mathcal{M}\beta = \mathfrak{f}\mathcal{M} X = \mathfrak{f} X. \end{align*} $$
$$ \begin{align*} X + \mathfrak{f} = \Lambda &\implies \mathcal{M}(X + \mathfrak{f}) = \mathcal{M} \\ & \implies \mathcal{M}\beta + \mathfrak{f} = \mathcal{M} \\ & \implies \overline{\beta} \in (\mathcal{M} / \mathfrak{f})^{\times} \\ &\implies \overline{\lambda} = \overline{\gamma} \overline{\beta}^{-1} = \overline{0} (\overline{\beta})^{-1} = \overline{0} \textrm{ in } \mathcal{M}/\mathfrak{f}\\ & \implies \lambda \in \mathfrak{f} \\ &\implies \gamma=\lambda\beta \in \mathfrak{f}\beta = \mathfrak{f}\mathcal{M}\beta = \mathfrak{f}\mathcal{M} X = \mathfrak{f} X. \end{align*} $$
Therefore,
![]() $\mathfrak {f}X = \mathcal {M}X \cap \mathfrak {f}$
. Moreover, we have
$\mathfrak {f}X = \mathcal {M}X \cap \mathfrak {f}$
. Moreover, we have
where the second equality holds by Lemma 4.1.
Define
to be the map induced by the canonical projection, where the codomain is the collection of left cosets of
![]() $ (\Lambda / \mathfrak {f} )^{\times }$
in
$ (\Lambda / \mathfrak {f} )^{\times }$
in
![]() $(\mathcal {M} / \mathfrak {f} )^{\times }$
. Note that
$(\mathcal {M} / \mathfrak {f} )^{\times }$
. Note that
![]() $(\Lambda /\mathfrak {f})^{\times }$
is a subgroup of
$(\Lambda /\mathfrak {f})^{\times }$
is a subgroup of
![]() $(\mathcal {M}/\mathfrak {f})^{\times }$
but is not necessarily a normal subgroup, and so
$(\mathcal {M}/\mathfrak {f})^{\times }$
but is not necessarily a normal subgroup, and so
![]() $\pi $
is only a map of sets in general.
$\pi $
is only a map of sets in general.
Part of the following result is a variant of [Reference HusertHus17, Theorem 1.39].
Proposition 4.3. Let X be a left ideal of
![]() $\Lambda $
. Suppose that
$\Lambda $
. Suppose that
![]() $X + \mathfrak {f} = \Lambda $
and that there exists
$X + \mathfrak {f} = \Lambda $
and that there exists
![]() $\beta \in \mathcal {M}$
such that
$\beta \in \mathcal {M}$
such that
![]() $\mathcal {M}X = \mathcal {M}\beta $
. Let
$\mathcal {M}X = \mathcal {M}\beta $
. Let
![]() $u \in \mathcal {M}^{\times }$
, and let
$u \in \mathcal {M}^{\times }$
, and let
![]() $\alpha = u \beta $
. Then
$\alpha = u \beta $
. Then
![]() $\overline {\alpha }, \overline {\beta }, \overline {u} \in (\mathcal {M}/\mathfrak {f})^{\times }$
and the following are equivalent:
$\overline {\alpha }, \overline {\beta }, \overline {u} \in (\mathcal {M}/\mathfrak {f})^{\times }$
and the following are equivalent:
-
(a)
 $X = \Lambda \alpha $
,
$X = \Lambda \alpha $
, -
(b)
 $\Lambda \alpha + \mathfrak {f} = \Lambda $
,
$\Lambda \alpha + \mathfrak {f} = \Lambda $
, -
(c)
 $\overline {\alpha } \in (\Lambda /\mathfrak {f})^{\times }$
,
$\overline {\alpha } \in (\Lambda /\mathfrak {f})^{\times }$
, -
(d)
 $\pi (\overline {\beta }) = \pi (\overline {u^{-1}})$
,
$\pi (\overline {\beta }) = \pi (\overline {u^{-1}})$
, -
(e)
 $\alpha \in X$
and X is locally free over
$\alpha \in X$
and X is locally free over
 $\Lambda $
.
$\Lambda $
.
Proof. Lemma 4.2 and the definitions of u and
![]() $\alpha $
imply that
$\alpha $
imply that
![]() $\overline {\alpha }, \overline {\beta }, \overline {u} \in (\mathcal {M}/\mathfrak {f})^{\times }$
. It is clear that (b)
$\overline {\alpha }, \overline {\beta }, \overline {u} \in (\mathcal {M}/\mathfrak {f})^{\times }$
. It is clear that (b)
![]() $\Leftrightarrow $
(c). Since
$\Leftrightarrow $
(c). Since
![]() $\beta = u^{-1} \alpha $
, that (c)
$\beta = u^{-1} \alpha $
, that (c)
![]() $\Leftrightarrow $
(d) follows from the definition of
$\Leftrightarrow $
(d) follows from the definition of
![]() $\pi $
. Since
$\pi $
. Since
![]() $X + \mathfrak {f} = \Lambda $
, we also have (a)
$X + \mathfrak {f} = \Lambda $
, we also have (a)
![]() $\Rightarrow $
(b). Assume (b) holds. By two applications of Lemma 4.2, we have
$\Rightarrow $
(b). Assume (b) holds. By two applications of Lemma 4.2, we have
where the first equality uses the hypothesis that
![]() $X + \mathfrak {f} = \Lambda $
and the last equality uses the assumption that (b) holds; thus (a) holds. Therefore, (a)
$X + \mathfrak {f} = \Lambda $
and the last equality uses the assumption that (b) holds; thus (a) holds. Therefore, (a)
![]() $\Leftrightarrow $
(b). Finally, a special case of [Reference Bley and JohnstonBJ08, Proposition 2.1] shows that (a)
$\Leftrightarrow $
(b). Finally, a special case of [Reference Bley and JohnstonBJ08, Proposition 2.1] shows that (a)
![]() $\Leftrightarrow $
(e).
$\Leftrightarrow $
(e).
Much of the following notation is adopted from [Reference Bley, Boltje, Hess, Pauli and PohstBB06] and [Reference Hofmann and JohnstonHJ20]. Denote the centre of a ring R by
![]() $Z(R)$
. Let
$Z(R)$
. Let
![]() $C=Z(A)$
, and let
$C=Z(A)$
, and let
![]() $\mathcal {O}_{C}$
be the integral closure of
$\mathcal {O}_{C}$
be the integral closure of
![]() $\mathcal {O}$
in C. Let
$\mathcal {O}$
in C. Let
![]() $\mathfrak {g} = \mathfrak {f} \cap C$
, and note that this is a proper full ideal of
$\mathfrak {g} = \mathfrak {f} \cap C$
, and note that this is a proper full ideal of
![]() $\mathcal {O}_{C}$
. Let
$\mathcal {O}_{C}$
. Let
![]() $e_{1}, \ldots , e_{r}$
be the primitive idempotents of C and set
$e_{1}, \ldots , e_{r}$
be the primitive idempotents of C and set
![]() $A_{i} = Ae_{i}$
. Then
$A_{i} = Ae_{i}$
. Then
is a decomposition of A into indecomposable two-sided ideals (see [Reference Curtis and ReinerCR81, (3.22)]). Each
![]() $A_{i}$
is a simple K-algebra with identity element
$A_{i}$
is a simple K-algebra with identity element
![]() $e_{i}$
. The centres
$e_{i}$
. The centres
![]() $K_{i} := Z(A_{i})$
are finite field extensions of K via
$K_{i} := Z(A_{i})$
are finite field extensions of K via
![]() $K \rightarrow K_{i}$
,
$K \rightarrow K_{i}$
,
![]() $\alpha \mapsto \alpha e_{i}$
, and we have K-algebra isomorphisms
$\alpha \mapsto \alpha e_{i}$
, and we have K-algebra isomorphisms
![]() $A_{i} \cong \mathrm {Mat}_{n_{i}}(D_{i})$
, where
$A_{i} \cong \mathrm {Mat}_{n_{i}}(D_{i})$
, where
![]() $D_{i}$
is a skew field with
$D_{i}$
is a skew field with
![]() $Z(D_{i}) \cong K_{i}$
(see [Reference Curtis and ReinerCR81, (3.28)]). The Wedderburn decomposition (1) induces decompositions
$Z(D_{i}) \cong K_{i}$
(see [Reference Curtis and ReinerCR81, (3.28)]). The Wedderburn decomposition (1) induces decompositions
where
![]() $\mathcal {O}_{K_i}$
denotes the ring of algebraic integers of
$\mathcal {O}_{K_i}$
denotes the ring of algebraic integers of
![]() $K_{i}$
. By [Reference ReinerRei03, (10.5)] we have
$K_{i}$
. By [Reference ReinerRei03, (10.5)] we have
![]() $e_{1}, \ldots , e_{r} \in \mathcal {M}$
and each
$e_{1}, \ldots , e_{r} \in \mathcal {M}$
and each
![]() $\mathcal {M}_{i}:=\mathcal {M}e_{i}$
is a maximal
$\mathcal {M}_{i}:=\mathcal {M}e_{i}$
is a maximal
![]() $\mathcal {O}$
-order (and thus a maximal
$\mathcal {O}$
-order (and thus a maximal
![]() $\mathcal {O}_{K_{i}}$
-order) in
$\mathcal {O}_{K_{i}}$
-order) in
![]() $A_{i}$
. Moreover, each
$A_{i}$
. Moreover, each
![]() $\mathfrak {f}_{i}:=\mathfrak {f} e_{i}$
is a full two-sided ideal of
$\mathfrak {f}_{i}:=\mathfrak {f} e_{i}$
is a full two-sided ideal of
![]() $\mathcal {M}_{i}$
, each
$\mathcal {M}_{i}$
, each
![]() $\mathfrak {g}_{i} := \mathfrak {g} e_{i}$
is a nonzero integral ideal of
$\mathfrak {g}_{i} := \mathfrak {g} e_{i}$
is a nonzero integral ideal of
![]() $\mathcal {O}_{K_{i}}$
and we have decompositions
$\mathcal {O}_{K_{i}}$
and we have decompositions
The reduced norm map
![]() $\mathrm {nr} : A \rightarrow C$
is defined componentwise (see [Reference ReinerRei03, §9]) and restricts to a group homomorphism
$\mathrm {nr} : A \rightarrow C$
is defined componentwise (see [Reference ReinerRei03, §9]) and restricts to a group homomorphism
![]() $\mathrm {nr} : \mathcal {M}^{\times } \rightarrow \mathcal {O}_{C}^{\times }$
.
$\mathrm {nr} : \mathcal {M}^{\times } \rightarrow \mathcal {O}_{C}^{\times }$
.
Lemma 4.4. There exists a surjective group homomorphism
![]() $\overline {\mathrm {nr}}: (\mathcal {M}/\mathfrak {f})^{\times } \longrightarrow (\mathcal {O}_{C}/\mathfrak {g})^{\times }$
that fits into the commutative diagram
$\overline {\mathrm {nr}}: (\mathcal {M}/\mathfrak {f})^{\times } \longrightarrow (\mathcal {O}_{C}/\mathfrak {g})^{\times }$
that fits into the commutative diagram

where the vertical maps are induced by the canonical projections.
Proof. The decompositions (1), (2) and (3) and the componentwise definition of the reduced norm mean that we can and do assume without loss of generality that
![]() $r=1$
, that is, A is simple,
$r=1$
, that is, A is simple,
![]() $\mathcal {M}=\mathcal {M}_{1}$
,
$\mathcal {M}=\mathcal {M}_{1}$
,
![]() $\mathfrak {f}=\mathfrak {f}_{1}$
,
$\mathfrak {f}=\mathfrak {f}_{1}$
,
![]() $\mathfrak {g}=\mathfrak {g}_{1}$
and
$\mathfrak {g}=\mathfrak {g}_{1}$
and
![]() $C=K=K_{1}$
. Let
$C=K=K_{1}$
. Let
![]() $\mathfrak {p}$
be a prime ideal of
$\mathfrak {p}$
be a prime ideal of
![]() $\mathcal {O}_{K}$
dividing
$\mathcal {O}_{K}$
dividing
![]() $\mathfrak {g}$
, and let
$\mathfrak {g}$
, and let
![]() $K_{\mathfrak {p}}$
denote the completion (not localisation) of K at
$K_{\mathfrak {p}}$
denote the completion (not localisation) of K at
![]() $\mathfrak {p}$
. If M is an
$\mathfrak {p}$
. If M is an
![]() $\mathcal {O}_{K}$
-module or an
$\mathcal {O}_{K}$
-module or an
![]() $\mathcal {O}_{K}$
-algebra, then we write
$\mathcal {O}_{K}$
-algebra, then we write
![]() $\widehat {M}_{\mathfrak {p}} := M \otimes _{\mathcal {O}_{K}} {\mathcal {O}_{K_{\mathfrak {p}}}}$
. By [Reference ReinerRei03, (7.6),(11.6)],
$\widehat {M}_{\mathfrak {p}} := M \otimes _{\mathcal {O}_{K}} {\mathcal {O}_{K_{\mathfrak {p}}}}$
. By [Reference ReinerRei03, (7.6),(11.6)],
![]() $\widehat {\mathcal {M}}_{\mathfrak {p}}$
is a maximal
$\widehat {\mathcal {M}}_{\mathfrak {p}}$
is a maximal
![]() $\mathcal {O}_{K_{\mathfrak {p}}}$
-order in the central simple
$\mathcal {O}_{K_{\mathfrak {p}}}$
-order in the central simple
![]() $K_{\mathfrak {p}}$
-algebra
$K_{\mathfrak {p}}$
-algebra
![]() $A \otimes _{K} K_{\mathfrak {p}}$
. Let
$A \otimes _{K} K_{\mathfrak {p}}$
. Let
![]() $\mathrm {nr}_{\mathfrak {p}} : \widehat {\mathcal {M}}_{\mathfrak {p}}^{\times } \rightarrow \mathcal {O}_{K_{\mathfrak {p}}}^{\times }$
denote the restriction of the reduced norm map. Then by [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Corollary 2.4], we have that
$\mathrm {nr}_{\mathfrak {p}} : \widehat {\mathcal {M}}_{\mathfrak {p}}^{\times } \rightarrow \mathcal {O}_{K_{\mathfrak {p}}}^{\times }$
denote the restriction of the reduced norm map. Then by [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Corollary 2.4], we have that
![]() $\mathrm {nr}_{\mathfrak {p}}(1+\widehat {\mathfrak {f}}_{\mathfrak {p}})=1+\widehat {\mathfrak {g}}_{\mathfrak {p}}$
and
$\mathrm {nr}_{\mathfrak {p}}(1+\widehat {\mathfrak {f}}_{\mathfrak {p}})=1+\widehat {\mathfrak {g}}_{\mathfrak {p}}$
and
![]() $\mathrm {nr}_{\mathfrak {p}}(\widehat {\mathcal {M}}_{\mathfrak {p}}^{\times })=\mathcal {O}_{K_{\mathfrak {p}}}^{\times }$
. Hence, we have a commutative diagram
$\mathrm {nr}_{\mathfrak {p}}(\widehat {\mathcal {M}}_{\mathfrak {p}}^{\times })=\mathcal {O}_{K_{\mathfrak {p}}}^{\times }$
. Hence, we have a commutative diagram

where
![]() $\overline {\mathrm {nr}}_{\mathfrak {p}}$
is induced by the other two vertical maps and is surjective by the snake lemma.
$\overline {\mathrm {nr}}_{\mathfrak {p}}$
is induced by the other two vertical maps and is surjective by the snake lemma.
The Chinese remainder theorem gives canonical isomorphisms
Let
![]() $\overline {\mathrm {nr}} = \prod _{\mathfrak {p} \mid \mathfrak {g}} \overline {\mathrm {nr}}_{\mathfrak {p}}$
, and observe that the desired result now follows since the reduced norm map commutes with completion by [Reference ReinerRei03, (9.29)].
$\overline {\mathrm {nr}} = \prod _{\mathfrak {p} \mid \mathfrak {g}} \overline {\mathrm {nr}}_{\mathfrak {p}}$
, and observe that the desired result now follows since the reduced norm map commutes with completion by [Reference ReinerRei03, (9.29)].
Let
![]() $\mathrm {SL}(\mathcal {M})=\ker (\mathrm {nr}: \mathcal {M}^{\times } \rightarrow \mathcal {O}_{C}^{\times })$
and
$\mathrm {SL}(\mathcal {M})=\ker (\mathrm {nr}: \mathcal {M}^{\times } \rightarrow \mathcal {O}_{C}^{\times })$
and
![]() $\mathrm {SL}(\mathcal {M}/\mathfrak {f})=\ker (\overline {\mathrm {nr}})$
. (Note that in the literature the set
$\mathrm {SL}(\mathcal {M}/\mathfrak {f})=\ker (\overline {\mathrm {nr}})$
. (Note that in the literature the set
![]() $\mathrm {SL}(\mathcal {M})$
, which is the group of units of reduced norm one, is sometimes also denoted by
$\mathrm {SL}(\mathcal {M})$
, which is the group of units of reduced norm one, is sometimes also denoted by
![]() $\mathcal {M}^1$
.) Then by Lemma 4.4 and the definitions, we have the following commutative diagram
$\mathcal {M}^1$
.) Then by Lemma 4.4 and the definitions, we have the following commutative diagram

where the rows are exact and the vertical maps are induced by the canonical projections. Note that all the maps are group homomorphisms, apart from
![]() $\pi $
, which is only a map of sets in general.
$\pi $
, which is only a map of sets in general.
Theorem 4.5. Let X be a left ideal of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $X + \mathfrak {f} = \Lambda $
. Suppose that there exists
$X + \mathfrak {f} = \Lambda $
. Suppose that there exists
![]() $\beta \in \mathcal {M}$
such that
$\beta \in \mathcal {M}$
such that
![]() $\mathcal {M}X = \mathcal {M}\beta $
. Then the following statements hold.
$\mathcal {M}X = \mathcal {M}\beta $
. Then the following statements hold.
-
(a) If X is free over
 $\Lambda $
, then
$\Lambda $
, then
 $\pi _{2}(\overline {\mathrm {nr}}(\overline {\beta }))$
is in the image of
$\pi _{2}(\overline {\mathrm {nr}}(\overline {\beta }))$
is in the image of
 $\pi _{2} \circ f_{2}$
.
$\pi _{2} \circ f_{2}$
. -
(b) If
 $f_{1}$
is surjective, then the converse of (a) holds. More precisely, if
$f_{1}$
is surjective, then the converse of (a) holds. More precisely, if
 $u \in \mathcal {M}^\times $
and
$u \in \mathcal {M}^\times $
and
 $\overline {a} \in (\Lambda /\mathfrak {f})^{\times }$
satisfy
$\overline {a} \in (\Lambda /\mathfrak {f})^{\times }$
satisfy
 $\overline {\mathrm {nr}}(\overline {\beta }) = \overline {\mathrm {nr}}(\overline {u}) \overline {\mathrm {nr}}(\overline {a})$
, then for any
$\overline {\mathrm {nr}}(\overline {\beta }) = \overline {\mathrm {nr}}(\overline {u}) \overline {\mathrm {nr}}(\overline {a})$
, then for any
 $v \in \mathrm {SL}(\mathcal {M})$
with
$v \in \mathrm {SL}(\mathcal {M})$
with
 $f_{1}(v)=\overline {\beta }\overline { a}^{-1}\overline {u}^{-1}$
, we have
$f_{1}(v)=\overline {\beta }\overline { a}^{-1}\overline {u}^{-1}$
, we have
 $X = \Lambda \alpha $
, where
$X = \Lambda \alpha $
, where
 $\alpha := (vu)^{-1}\beta $
.
$\alpha := (vu)^{-1}\beta $
.
Proof. (a) Suppose that X is free over
![]() $\Lambda $
. Then there exists
$\Lambda $
. Then there exists
![]() $\alpha \in X$
such that
$\alpha \in X$
such that
![]() $X=\Lambda \alpha $
. Thus,
$X=\Lambda \alpha $
. Thus,
![]() $\mathcal {M}\beta = \mathcal {M}X=\mathcal {M}(\Lambda \alpha )=\mathcal {M}\alpha $
, and so there exists
$\mathcal {M}\beta = \mathcal {M}X=\mathcal {M}(\Lambda \alpha )=\mathcal {M}\alpha $
, and so there exists
![]() $u \in \mathcal {M}^{\times }$
such that
$u \in \mathcal {M}^{\times }$
such that
![]() $\alpha = u\beta $
. Hence,
$\alpha = u\beta $
. Hence,
![]() $\pi (\overline {\beta }) = \pi (\overline {u^{-1}})$
by Proposition 4.3. In other words, there exists
$\pi (\overline {\beta }) = \pi (\overline {u^{-1}})$
by Proposition 4.3. In other words, there exists
![]() $a \in \Lambda $
such that
$a \in \Lambda $
such that
![]() $\overline {a} \in (\Lambda /\mathfrak {f})^{\times }$
and
$\overline {a} \in (\Lambda /\mathfrak {f})^{\times }$
and
![]() $\overline {\beta }=\overline {u^{-1}}\overline {a}$
. Thus,
$\overline {\beta }=\overline {u^{-1}}\overline {a}$
. Thus,
and so
![]() $\pi _{2}(\overline {\mathrm {nr}}(\overline {\beta }))=\pi _{2}(f_{2}(\mathrm {nr}(u^{-1})))$
.
$\pi _{2}(\overline {\mathrm {nr}}(\overline {\beta }))=\pi _{2}(f_{2}(\mathrm {nr}(u^{-1})))$
.
(b) Suppose that
![]() $f_1$
is surjective and
$f_1$
is surjective and
![]() $\pi _{2}(\overline {\mathrm {nr}}(\overline {\beta }))$
is in the image of
$\pi _{2}(\overline {\mathrm {nr}}(\overline {\beta }))$
is in the image of
![]() $\pi _{2} \circ f_{2}$
. Then there exist
$\pi _{2} \circ f_{2}$
. Then there exist
![]() $u,a$
and v as in (b), and so
$u,a$
and v as in (b), and so
![]() $\pi (\overline {\beta })= \pi (\overline {vu})$
. Hence, by Proposition 4.3 we have
$\pi (\overline {\beta })= \pi (\overline {vu})$
. Hence, by Proposition 4.3 we have
![]() $X = \Lambda \alpha $
where
$X = \Lambda \alpha $
where
![]() $\alpha := (vu)^{-1}\beta $
.
$\alpha := (vu)^{-1}\beta $
.
5 Preliminaries on complexity
We briefly recall the conventions that we will use for the complexity analysis of our algorithms. For details we refer the reader to Lenstra [Reference LenstraLen92] or Cohen [Reference CohenCoh93, §1.1].
Let l be the size of the input data measured by the number of required bits. Then an algorithm is polynomial time if the running time is
![]() $O(P(l))$
for a polynomial P. An algorithm is subexponential time if there exists
$O(P(l))$
for a polynomial P. An algorithm is subexponential time if there exists
![]() $0 \le a < 1$
and
$0 \le a < 1$
and
![]() $b \in \mathbb {R}_{>0}$
such that the running time is
$b \in \mathbb {R}_{>0}$
such that the running time is
![]() $O(\exp (b \cdot l^a(\log l)^{a-1}))$
.
$O(\exp (b \cdot l^a(\log l)^{a-1}))$
.
A probabilistic algorithm may call a random number generator. In this case we say that the algorithm is probabilistic polynomial time if the expected running time is
![]() $O(P(l))$
for a polynomial P. We adopt the same convention for probabilistic subexponential time algorithms.
$O(P(l))$
for a polynomial P. We adopt the same convention for probabilistic subexponential time algorithms.
Given two computational problems
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $\mathsf {B}$
, a (probabilistic) polynomial-time reduction from
$\mathsf {B}$
, a (probabilistic) polynomial-time reduction from
![]() $\mathsf {A}$
to
$\mathsf {A}$
to
![]() $\mathsf {B}$
is an algorithm that solves
$\mathsf {B}$
is an algorithm that solves
![]() $\mathsf {A}$
using a polynomial number of calls to an oracle solving
$\mathsf {A}$
using a polynomial number of calls to an oracle solving
![]() $\mathsf {B}$
and is (probabilistic) polynomial time outside of those calls to the oracle.
$\mathsf {B}$
and is (probabilistic) polynomial time outside of those calls to the oracle.
Let K be a number field with ring of integers
![]() $\mathcal {O} = \mathcal {O}_K$
. We follow the convention of [Reference LenstraLen92] for representing our input data. In some more detail, if
$\mathcal {O} = \mathcal {O}_K$
. We follow the convention of [Reference LenstraLen92] for representing our input data. In some more detail, if
![]() $V = K^{n}$
is an n-dimensional vector space over K, we represent an
$V = K^{n}$
is an n-dimensional vector space over K, we represent an
![]() $\mathcal {O}$
-module
$\mathcal {O}$
-module
![]() $M \subseteq V$
by a pseudobasis of M, that is, by elements
$M \subseteq V$
by a pseudobasis of M, that is, by elements
![]() $v_1,\dotsc ,v_k \in V$
and fractional
$v_1,\dotsc ,v_k \in V$
and fractional
![]() $\mathcal {O}$
-ideals
$\mathcal {O}$
-ideals
![]() $\mathfrak a_1,\dotsc ,\mathfrak a_k$
such that
$\mathfrak a_1,\dotsc ,\mathfrak a_k$
such that
![]() $M = \mathfrak a_1 v_1 \oplus \dotsb \oplus \mathfrak a_k v_k$
for some
$M = \mathfrak a_1 v_1 \oplus \dotsb \oplus \mathfrak a_k v_k$
for some
![]() $k \leq n$
. A K-algebra A of dimension d is represented as a d-dimensional vector space together with the K-linear multiplication map
$k \leq n$
. A K-algebra A of dimension d is represented as a d-dimensional vector space together with the K-linear multiplication map
![]() $A \otimes _K A \to A$
, which is represented using
$A \otimes _K A \to A$
, which is represented using
![]() $d^{3}$
elements of K. Given a finite-dimensional K-algebra A, an
$d^{3}$
elements of K. Given a finite-dimensional K-algebra A, an
![]() $\mathcal {O}$
-order of A is represented using a pseudobasis. An n-dimensional A-module V is represented as a vector space over K together with d matrices in
$\mathcal {O}$
-order of A is represented using a pseudobasis. An n-dimensional A-module V is represented as a vector space over K together with d matrices in
![]() $\mathrm {Mat}_{n}(K)$
, one for each basis element of A describing the action on elements of V. Given an
$\mathrm {Mat}_{n}(K)$
, one for each basis element of A describing the action on elements of V. Given an
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\Lambda $
, a
$\Lambda $
, a
![]() $\Lambda $
-lattice is represented by an
$\Lambda $
-lattice is represented by an
![]() $\mathcal {O}$
-submodule of a finite-dimensional A-module, invariant under the action of
$\mathcal {O}$
-submodule of a finite-dimensional A-module, invariant under the action of
![]() $\Lambda $
.
$\Lambda $
.
We will be mainly interested in solving the following two problems.
Problem (
 $\mathsf {IsIsomorphic}$
)
$\mathsf {IsIsomorphic}$
)
Given a finite-dimensional K-algebra A, an
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\Lambda $
in A and two
$\Lambda $
in A and two
![]() $\Lambda $
-lattices X and Y, decide whether X and Y are isomorphic, and if so, return an isomorphism
$\Lambda $
-lattices X and Y, decide whether X and Y are isomorphic, and if so, return an isomorphism
![]() $X \to Y$
.
$X \to Y$
.
Problem (
 $\mathsf {IsPrincipal}$
)
$\mathsf {IsPrincipal}$
)
Given a finite-dimensional K-algebra A, an
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\Lambda $
in A and a full
$\Lambda $
in A and a full
![]() $\Lambda $
-lattice X in A, decide whether there exists
$\Lambda $
-lattice X in A, decide whether there exists
![]() $\alpha \in X$
such that
$\alpha \in X$
such that
![]() $X = \Lambda \alpha $
, and if so, return such an element
$X = \Lambda \alpha $
, and if so, return such an element
![]() $\alpha $
.
$\alpha $
.
Under the assumption that A satisfies hypothesis (H), we will reduce these questions to well-studied problems in algorithmic number theory. These include
![]() $\mathsf {IsPrincipal}$
in the case where
$\mathsf {IsPrincipal}$
in the case where
![]() $A = K$
and
$A = K$
and
![]() $\Lambda =\mathcal {O}$
, as well as the following problems:
$\Lambda =\mathcal {O}$
, as well as the following problems:
-
○
 $\mathsf {Factor}$
: Given an ideal or element of the ring of integers
$\mathsf {Factor}$
: Given an ideal or element of the ring of integers
 $\mathcal {O}_{F}$
of a number field F, determine its factorisation into prime ideals.
$\mathcal {O}_{F}$
of a number field F, determine its factorisation into prime ideals. -
○
 $\mathsf {Primitive}$
: Given a finite field
$\mathsf {Primitive}$
: Given a finite field
 $\mathbb {F}_{q}$
, determine
$\mathbb {F}_{q}$
, determine
 $\alpha \in \mathbb {F}_{q}^{\times }$
such that
$\alpha \in \mathbb {F}_{q}^{\times }$
such that
 $\mathbb {F}_{q}^{\times } = \langle \alpha \rangle $
.
$\mathbb {F}_{q}^{\times } = \langle \alpha \rangle $
. -
○
 $\mathsf {DLog}$
: Given a finite field
$\mathsf {DLog}$
: Given a finite field
 $\mathbb {F}_{q}$
and
$\mathbb {F}_{q}$
and
 $\alpha , \beta \in \mathbb {F}_{q}^{\times }$
with
$\alpha , \beta \in \mathbb {F}_{q}^{\times }$
with
 $\mathbb {F}_{q}^{\times } = \langle \alpha \rangle $
, determine
$\mathbb {F}_{q}^{\times } = \langle \alpha \rangle $
, determine
 $n \in \mathbb {Z}_{\geq 0}$
such that
$n \in \mathbb {Z}_{\geq 0}$
such that
 $\alpha ^{n} = \beta $
.
$\alpha ^{n} = \beta $
. -
○
 $\mathsf {UnitGroup}$
: Given the ring of integers
$\mathsf {UnitGroup}$
: Given the ring of integers
 $\mathcal {O}_{F}$
of a number field F, determine a system of fundamental units for
$\mathcal {O}_{F}$
of a number field F, determine a system of fundamental units for
 $\mathcal {O}_{F}^{\times }$
.
$\mathcal {O}_{F}^{\times }$
.
We will use the following standard convention and notation to denote variations and instances of computational problems. For example, for an
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\Lambda $
, we denote by
$\Lambda $
, we denote by
![]() $\mathsf {IsIsomorphic}_{\Lambda }$
the set of instances of
$\mathsf {IsIsomorphic}_{\Lambda }$
the set of instances of
![]() $\mathsf {IsIsomorphic}$
restricted to
$\mathsf {IsIsomorphic}$
restricted to
![]() $\Lambda $
-lattices. Similarly, we use
$\Lambda $
-lattices. Similarly, we use
![]() $\mathsf {IsPrincipal}_\Lambda $
for the set of instances of
$\mathsf {IsPrincipal}_\Lambda $
for the set of instances of
![]() $\mathsf {IsPrincipal}$
for
$\mathsf {IsPrincipal}$
for
![]() $\Lambda $
-lattices. Moreover, given a
$\Lambda $
-lattices. Moreover, given a
![]() $\Lambda $
-lattice X, we use
$\Lambda $
-lattice X, we use
![]() $\mathsf {IsPrincipal}(X)$
to denote the instance of
$\mathsf {IsPrincipal}(X)$
to denote the instance of
![]() $\mathsf {IsPrincipal}$
for the lattice X. Note that in this case we still consider
$\mathsf {IsPrincipal}$
for the lattice X. Note that in this case we still consider
![]() $\Lambda $
part of the input.
$\Lambda $
part of the input.
Remark 5.1. Currently, the following complexity statements are known.
-
(a) The problem
 $\mathsf {Factor}_{\mathbb {Z}}$
can be solved in probabilistic subexponential time ([Reference Lenstra and PomeranceLP92, Theorem 10.5]). Given an ideal I of the ring of integers
$\mathsf {Factor}_{\mathbb {Z}}$
can be solved in probabilistic subexponential time ([Reference Lenstra and PomeranceLP92, Theorem 10.5]). Given an ideal I of the ring of integers
 $\mathcal {O}_{F}$
of a number field F, the prime ideals of
$\mathcal {O}_{F}$
of a number field F, the prime ideals of
 $\mathcal {O}_{F}$
lying above the rational prime factors of
$\mathcal {O}_{F}$
lying above the rational prime factors of
 $\mathrm {Norm}_{F/\mathbb {Q}}(I)$
can be determined in probabilistic polynomial time ([Reference CohenCoh93, §6.2]); hence, there is a probabilistic polynomial-time reduction from
$\mathrm {Norm}_{F/\mathbb {Q}}(I)$
can be determined in probabilistic polynomial time ([Reference CohenCoh93, §6.2]); hence, there is a probabilistic polynomial-time reduction from
 $\mathsf {Factor}$
to
$\mathsf {Factor}$
to
 $\mathsf {Factor}_{\mathbb {Z}}$
. Since
$\mathsf {Factor}_{\mathbb {Z}}$
. Since
 $\mathsf {Primitive}(\mathbb {F}_q)$
is probabilistic polynomial-time reducible to
$\mathsf {Primitive}(\mathbb {F}_q)$
is probabilistic polynomial-time reducible to
 $\mathsf {Factor}(q-1)$
, the same holds for
$\mathsf {Factor}(q-1)$
, the same holds for
 $\mathsf {Primitive}$
. Moreover,
$\mathsf {Primitive}$
. Moreover,
 $\mathsf {DLog}$
can be solved in subexponential time; see [Reference OdlyzkoOdl00] and the references therein. While it is conjectured that
$\mathsf {DLog}$
can be solved in subexponential time; see [Reference OdlyzkoOdl00] and the references therein. While it is conjectured that
 $\mathsf {IsPrincipal}$
and
$\mathsf {IsPrincipal}$
and
 $\mathsf {UnitGroup}$
can also be solved in subexponential time, so far this has been established only under additional hypotheses and heuristics, including the generalised Riemann hypothesis (GRH); see [Reference BuchmannBuc90, Reference BiasseBia14, Reference Biasse and FiekerBF14].
$\mathsf {UnitGroup}$
can also be solved in subexponential time, so far this has been established only under additional hypotheses and heuristics, including the generalised Riemann hypothesis (GRH); see [Reference BuchmannBuc90, Reference BiasseBia14, Reference Biasse and FiekerBF14]. -
(b) There exist quantum polynomial-time algorithms for solving each of the problems
 $\mathsf {Factor}_{\mathbb {Z}}$
,
$\mathsf {Factor}_{\mathbb {Z}}$
,
 $\mathsf {DLog}$
,
$\mathsf {DLog}$
,
 $\mathsf {Primitive}$
([Reference ShorSho97, §5, §6]),
$\mathsf {Primitive}$
([Reference ShorSho97, §5, §6]),
 $\mathsf {UnitGroup}$
([Reference Eisenträger, Hallgren, Kitaev and SongEHKS14, Theorem 1.2]) and
$\mathsf {UnitGroup}$
([Reference Eisenträger, Hallgren, Kitaev and SongEHKS14, Theorem 1.2]) and
 $\mathsf {IsPrincipal}$
for rings of integers of number fields ([Reference Biasse and SongBS16, Theorem 1.3]).
$\mathsf {IsPrincipal}$
for rings of integers of number fields ([Reference Biasse and SongBS16, Theorem 1.3]).
Our approach to solving
![]() $\mathsf {IsIsomorphic}$
and
$\mathsf {IsIsomorphic}$
and
![]() $\mathsf {IsPrincipal}$
for noncommutative algebras A satisfying hypothesis (H) relies crucially on the solution of the following two subproblems.
$\mathsf {IsPrincipal}$
for noncommutative algebras A satisfying hypothesis (H) relies crucially on the solution of the following two subproblems.
Problem (
 $\mathsf {Wedderburn}$
)
$\mathsf {Wedderburn}$
)
Given a number field K and a finite-dimensional semisimple K-algebra A satisfying hypothesis (H), determine number fields
![]() $K_{i}$
, integers
$K_{i}$
, integers
![]() $r, n_{i} \in \mathbb {Z}_{>0}$
and an explicit isomorphism
$r, n_{i} \in \mathbb {Z}_{>0}$
and an explicit isomorphism
![]() $A \cong \prod _{i=1}^{r} \mathrm {Mat}_{n_i}(K_i)$
.
$A \cong \prod _{i=1}^{r} \mathrm {Mat}_{n_i}(K_i)$
.
Problem (
 $\mathsf {SplittingMatrixAlgebra}$
)
$\mathsf {SplittingMatrixAlgebra}$
)
Given a number field K and a split central simple K-algebra A, determine an isomorphism
![]() $A \cong \mathrm {Mat}_{n}(K)$
for some
$A \cong \mathrm {Mat}_{n}(K)$
for some
![]() $n \in \mathbb {Z}_{>0}$
.
$n \in \mathbb {Z}_{>0}$
.
Remark 5.2. For a finite-dimensional semisimple K-algebra A, an explicit decomposition
![]() $A \cong \prod _{i=1}^{r} A_{i}$
into simple K-algebras
$A \cong \prod _{i=1}^{r} A_{i}$
into simple K-algebras
![]() $A_{i}$
, as well as the centre
$A_{i}$
, as well as the centre
![]() $K_{i}$
of each
$K_{i}$
of each
![]() $A_{i}$
, can be computed in polynomial time by [Reference Friedl and RonyaiFR85, 1.5 B]. Thus,
$A_{i}$
, can be computed in polynomial time by [Reference Friedl and RonyaiFR85, 1.5 B]. Thus,
![]() $\mathsf {Wedderburn}$
reduces to
$\mathsf {Wedderburn}$
reduces to
![]() $\mathsf {SplittingMatrixAlgebra}$
. The decision problem of checking whether
$\mathsf {SplittingMatrixAlgebra}$
. The decision problem of checking whether
![]() $A_{i} \cong \mathrm {Mat}_{n_{i}}(K_{i})$
for some
$A_{i} \cong \mathrm {Mat}_{n_{i}}(K_{i})$
for some
![]() $n_{i} \in \mathbb {Z}_{>0}$
is polynomial-time reducible to the computation of (the discriminant of) a maximal order in
$n_{i} \in \mathbb {Z}_{>0}$
is polynomial-time reducible to the computation of (the discriminant of) a maximal order in
![]() $A_{i}$
by [Reference Nebe and SteelNS09, Corollary 3.4], hence to
$A_{i}$
by [Reference Nebe and SteelNS09, Corollary 3.4], hence to
![]() $\mathsf {Factor}$
by [Reference Ivanyos and RónyaiIR93, Corollary 5.3]. The problem of finding an explicit isomorphism appears to be a much harder problem. In [Reference Ivanyos, Rónyai and SchichoIRS12, Theorem 1] it was shown that for algebras of bounded dimension over a fixed number field,
$\mathsf {Factor}$
by [Reference Ivanyos and RónyaiIR93, Corollary 5.3]. The problem of finding an explicit isomorphism appears to be a much harder problem. In [Reference Ivanyos, Rónyai and SchichoIRS12, Theorem 1] it was shown that for algebras of bounded dimension over a fixed number field,
![]() $\mathsf {SplittingMatrixAlgebra}$
is probabilistic polynomial-time reducible to the problem of computing a maximal order, hence to
$\mathsf {SplittingMatrixAlgebra}$
is probabilistic polynomial-time reducible to the problem of computing a maximal order, hence to
![]() $\mathsf {Factor}$
.
$\mathsf {Factor}$
.
6 Complexity of algorithms related to orders and their lattices
Let K be a number field with ring of integers
![]() $\mathcal {O} = \mathcal {O}_{K}$
. The aim of this section is to establish the complexity of certain algorithms related to
$\mathcal {O} = \mathcal {O}_{K}$
. The aim of this section is to establish the complexity of certain algorithms related to
![]() $\mathcal {O}$
-orders and their lattices. These algorithms have already appeared in the literature, either implicitly or explicitly, but with either no or only partial analysis of their complexity.
$\mathcal {O}$
-orders and their lattices. These algorithms have already appeared in the literature, either implicitly or explicitly, but with either no or only partial analysis of their complexity.
6.1 Computing maximal orders
Let A be a finite-dimensional semisimple K-algebra, and let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}$
-order in A. Let
$\mathcal {O}$
-order in A. Let
![]() $d = \dim _{K}A$
and let
$d = \dim _{K}A$
and let
![]() $\mathrm {tr} \colon A \rightarrow K$
denote the reduced trace map (see [Reference Curtis and ReinerCR81, §7D]). Following [Reference Curtis and ReinerCR81, §26A], we define
$\mathrm {tr} \colon A \rightarrow K$
denote the reduced trace map (see [Reference Curtis and ReinerCR81, §7D]). Following [Reference Curtis and ReinerCR81, §26A], we define
![]() $\mathrm {Disc}(\Lambda )$
to be the ideal of
$\mathrm {Disc}(\Lambda )$
to be the ideal of
![]() $\mathcal {O}$
generated by all elements
$\mathcal {O}$
generated by all elements
By applying a result of [Reference Friedl and RonyaiFR85], the following is straightforward to deduce from the results of [Reference FriedrichsFri00].
Proposition 6.1. Let
![]() $\Lambda $
and A be as above. Then the problem of computing a maximal
$\Lambda $
and A be as above. Then the problem of computing a maximal
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\mathcal {M}$
in A containing
$\mathcal {M}$
in A containing
![]() $\Lambda $
is probabilistic polynomial-time reducible to
$\Lambda $
is probabilistic polynomial-time reducible to
![]() $\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
.
$\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
.
Proof. Let
![]() $\mathfrak {p}$
be a maximal ideal of
$\mathfrak {p}$
be a maximal ideal of
![]() $\mathcal {O}$
dividing
$\mathcal {O}$
dividing
![]() $\mathrm {Disc}(\Lambda )$
, and write
$\mathrm {Disc}(\Lambda )$
, and write
![]() $v_{\mathfrak {p}}(-)$
for the
$v_{\mathfrak {p}}(-)$
for the
![]() $\mathfrak {p}$
-adic valuation. It follows from [Reference FriedrichsFri00, (3.17)] that the computation of an order
$\mathfrak {p}$
-adic valuation. It follows from [Reference FriedrichsFri00, (3.17)] that the computation of an order
![]() $\Lambda ^{(\mathfrak {p})}$
such that
$\Lambda ^{(\mathfrak {p})}$
such that
![]() $v_{\mathfrak {p}}([\Lambda ^{(\mathfrak {p})} : \Lambda ]_{\mathcal {O}})$
is maximal reduces in polynomial time to the problem of computing the maximal two-sided ideals of an order containing
$v_{\mathfrak {p}}([\Lambda ^{(\mathfrak {p})} : \Lambda ]_{\mathcal {O}})$
is maximal reduces in polynomial time to the problem of computing the maximal two-sided ideals of an order containing
![]() $\mathfrak {p}$
. Now, fix an order
$\mathfrak {p}$
. Now, fix an order
![]() $\Gamma $
. Then the maximal two-sided ideals of
$\Gamma $
. Then the maximal two-sided ideals of
![]() $\Gamma $
containing
$\Gamma $
containing
![]() $\mathfrak {p}$
are the preimages of the maximal two-sided ideals under the canonical projection
$\mathfrak {p}$
are the preimages of the maximal two-sided ideals under the canonical projection
![]() $\Gamma \to (\Gamma /\mathfrak {p}\Gamma )/{\operatorname {\mathrm {J}}(\Gamma /\mathfrak {p}\Gamma )}$
(see [Reference FriedrichsFri00, (5.23)]). As a decomposition of this
$\Gamma \to (\Gamma /\mathfrak {p}\Gamma )/{\operatorname {\mathrm {J}}(\Gamma /\mathfrak {p}\Gamma )}$
(see [Reference FriedrichsFri00, (5.23)]). As a decomposition of this
![]() $(\mathcal {O}/\mathfrak {p})$
-algebra into simple components and therefore the maximal two-sided ideals can be found in probabilistic polynomial time by [Reference Friedl and RonyaiFR85, 1.5 B], an order
$(\mathcal {O}/\mathfrak {p})$
-algebra into simple components and therefore the maximal two-sided ideals can be found in probabilistic polynomial time by [Reference Friedl and RonyaiFR85, 1.5 B], an order
![]() $\Lambda ^{(\mathfrak {p})}$
can be determined in probabilistic polynomial time. By [Reference FriedrichsFri00, (3.19)] the order
$\Lambda ^{(\mathfrak {p})}$
can be determined in probabilistic polynomial time. By [Reference FriedrichsFri00, (3.19)] the order
![]() $\sum _{\mathfrak {p}} \Lambda ^{(\mathfrak {p})}$
is maximal, where
$\sum _{\mathfrak {p}} \Lambda ^{(\mathfrak {p})}$
is maximal, where
![]() $\mathfrak {p}$
runs over the maximal ideals of
$\mathfrak {p}$
runs over the maximal ideals of
![]() $\mathcal {O}$
dividing
$\mathcal {O}$
dividing
![]() $\mathrm {Disc}(\Lambda )$
. Therefore, the computation of a maximal order
$\mathrm {Disc}(\Lambda )$
. Therefore, the computation of a maximal order
![]() $\mathcal {M}$
containing
$\mathcal {M}$
containing
![]() $\Lambda $
reduces in probabilistic polynomial time to
$\Lambda $
reduces in probabilistic polynomial time to
![]() $\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
.
$\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
.
6.2 Nice maximal orders
Let
![]() $n \in \mathbb {Z}_{>0}$
, and let
$n \in \mathbb {Z}_{>0}$
, and let
![]() $A = \mathrm {Mat}_{n}(K)$
be a full matrix algebra. For a nonzero fractional ideal
$A = \mathrm {Mat}_{n}(K)$
be a full matrix algebra. For a nonzero fractional ideal
![]() $\mathfrak {a}$
of
$\mathfrak {a}$
of
![]() $\mathcal {O}$
, let
$\mathcal {O}$
, let
 $$\begin{align*}\mathcal{M}_{\mathfrak a, n} := \left( \begin{array}{cccc} \mathcal{O} & \ldots & \mathcal{O} & \mathfrak{a}^{-1} \\ \vdots & \ddots & \vdots & \vdots \\ \mathcal{O} & \ldots & \mathcal{O} & \mathfrak{a}^{-1} \\ \mathfrak{a} & \ldots & \mathfrak{a} & \mathcal{O} \end{array} \right) \end{align*}$$
$$\begin{align*}\mathcal{M}_{\mathfrak a, n} := \left( \begin{array}{cccc} \mathcal{O} & \ldots & \mathcal{O} & \mathfrak{a}^{-1} \\ \vdots & \ddots & \vdots & \vdots \\ \mathcal{O} & \ldots & \mathcal{O} & \mathfrak{a}^{-1} \\ \mathfrak{a} & \ldots & \mathfrak{a} & \mathcal{O} \end{array} \right) \end{align*}$$
denote the
![]() $\mathcal {O}$
-order in A consisting of all
$\mathcal {O}$
-order in A consisting of all
![]() $n \times n$
matrices
$n \times n$
matrices
![]() $(x_{ij})_{1 \leq i,j \leq n}$
, where
$(x_{ij})_{1 \leq i,j \leq n}$
, where
![]() $x_{11}$
ranges over all elements of
$x_{11}$
ranges over all elements of
![]() $\mathcal {O}$
, …,
$\mathcal {O}$
, …,
![]() $x_{1n}$
ranges over all elements of
$x_{1n}$
ranges over all elements of
![]() $\mathfrak {a}^{-1}$
and so on. (In the case
$\mathfrak {a}^{-1}$
and so on. (In the case
![]() $n=1$
, we take
$n=1$
, we take
![]() $\mathcal {M}_{\mathfrak a, n}=\mathcal {O}$
.) We say that a maximal
$\mathcal {M}_{\mathfrak a, n}=\mathcal {O}$
.) We say that a maximal
![]() $\mathcal {O}$
-order in A is nice if it is equal to
$\mathcal {O}$
-order in A is nice if it is equal to
![]() $\mathcal {M}_{\mathfrak a, n}$
for some choice of
$\mathcal {M}_{\mathfrak a, n}$
for some choice of
![]() $\mathfrak {a}$
. By [Reference ReinerRei03, (27.6)] every maximal
$\mathfrak {a}$
. By [Reference ReinerRei03, (27.6)] every maximal
![]() $\mathcal {O}$
-order in A is conjugate to a nice maximal order.
$\mathcal {O}$
-order in A is conjugate to a nice maximal order.
Lemma 6.2. There exists a probabilistic polynomial-time algorithm that, given a maximal
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\mathcal {M}$
in
$\mathcal {M}$
in
![]() $A=\mathrm {Mat}_{n}(K)$
, determines a nonzero fractional ideal
$A=\mathrm {Mat}_{n}(K)$
, determines a nonzero fractional ideal
![]() $\mathfrak {a}$
of
$\mathfrak {a}$
of
![]() $\mathcal {O}$
and
$\mathcal {O}$
and
![]() $S \in \mathrm {GL}_{n}(K)$
such that
$S \in \mathrm {GL}_{n}(K)$
such that
![]() $S\mathcal {M} S^{-1} = \mathcal {M}_{\mathfrak a, n}$
.
$S\mathcal {M} S^{-1} = \mathcal {M}_{\mathfrak a, n}$
.
Proof. The algorithm is presented in [Reference Bley and JohnstonBJ08, §5] and works by reducing the problem to the computation of a Steinitz form of an
![]() $\mathcal {O}$
-lattice of rank n, which can be performed in probabilistic polynomial time by Corollary A.3.
$\mathcal {O}$
-lattice of rank n, which can be performed in probabilistic polynomial time by Corollary A.3.
6.3 Norm equations and principal ideals
Let
![]() $r \in \mathbb {Z}_{>0}$
, and let
$r \in \mathbb {Z}_{>0}$
, and let
![]() $A = \prod _{i=1}^{r} \mathrm {Mat}_{n_i}(K_i)$
, where
$A = \prod _{i=1}^{r} \mathrm {Mat}_{n_i}(K_i)$
, where
![]() $K_{i}$
is a finite field extension of K and
$K_{i}$
is a finite field extension of K and
![]() $n_{i} \in \mathbb {Z}_{>0}$
for each i. In particular, A is a finite-dimensional semisimple K-algebra satisfying hypothesis (H). Let C be the centre of A, which we can and do identify with
$n_{i} \in \mathbb {Z}_{>0}$
for each i. In particular, A is a finite-dimensional semisimple K-algebra satisfying hypothesis (H). Let C be the centre of A, which we can and do identify with
![]() $\prod _{i=1}^{r} K_{i}$
. Let
$\prod _{i=1}^{r} K_{i}$
. Let
![]() $\mathcal {M}$
be a maximal
$\mathcal {M}$
be a maximal
![]() $\mathcal {O}$
-order in A, and let
$\mathcal {O}$
-order in A, and let
![]() $\mathcal {O}_{C} = \mathcal {M} \cap C = \prod _{i=1}^{r} {\mathcal {O}_{K_{i}}}$
.
$\mathcal {O}_{C} = \mathcal {M} \cap C = \prod _{i=1}^{r} {\mathcal {O}_{K_{i}}}$
.
Lemma 6.3. The reduced norm map
![]() $\mathrm {nr} \colon \mathcal {M}^\times \to \mathcal {O}_C^\times $
is surjective. Moreover, there exists a probabilistic polynomial-time algorithm that given
$\mathrm {nr} \colon \mathcal {M}^\times \to \mathcal {O}_C^\times $
is surjective. Moreover, there exists a probabilistic polynomial-time algorithm that given
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $a \in \mathcal {O}_C^\times $
determines
$a \in \mathcal {O}_C^\times $
determines
![]() $\alpha \in \mathcal M^\times $
such that
$\alpha \in \mathcal M^\times $
such that
![]() $\mathrm {nr}(\alpha ) = a$
.
$\mathrm {nr}(\alpha ) = a$
.
Proof. By decomposing
![]() $\mathcal {M}$
using the central primitive idempotents of A, it suffices to consider the case
$\mathcal {M}$
using the central primitive idempotents of A, it suffices to consider the case
![]() $A = \mathrm {Mat}_{n}(K)$
, in which we must have
$A = \mathrm {Mat}_{n}(K)$
, in which we must have
![]() $\mathcal {O}_{C} = \mathcal {O}$
. Then the reduced norm map
$\mathcal {O}_{C} = \mathcal {O}$
. Then the reduced norm map
![]() $\mathrm {nr}: A \rightarrow K$
is just the usual determinant map. Moreover, using Lemma 6.2, we can and do assume that
$\mathrm {nr}: A \rightarrow K$
is just the usual determinant map. Moreover, using Lemma 6.2, we can and do assume that
![]() $\mathcal {M} = \mathcal {M}_{\mathfrak a, n}$
is a nice maximal order. Since
$\mathcal {M} = \mathcal {M}_{\mathfrak a, n}$
is a nice maximal order. Since
![]() $\alpha = \operatorname {diag}(a,1,\dotsc ,1) \in \mathcal {M}_{\mathfrak a, n}^{\times }$
satisfies
$\alpha = \operatorname {diag}(a,1,\dotsc ,1) \in \mathcal {M}_{\mathfrak a, n}^{\times }$
satisfies
![]() $\mathrm {nr}(\alpha ) = a$
, the claim follows.
$\mathrm {nr}(\alpha ) = a$
, the claim follows.
An algorithm for solving the principal ideal problem for
![]() $\mathcal {M}$
-lattices was given in [Reference Bley and JohnstonBJ08, §5]. We now analyse its complexity.
$\mathcal {M}$
-lattices was given in [Reference Bley and JohnstonBJ08, §5]. We now analyse its complexity.
Proposition 6.4. The problem
![]() $\mathsf {IsPrincipal}_{\mathcal {M}}$
is probabilistic polynomial-time reducible to one instance of
$\mathsf {IsPrincipal}_{\mathcal {M}}$
is probabilistic polynomial-time reducible to one instance of
![]() $\mathsf {IsPrincipal}_{\mathcal O_{K_i}}{}$
for each
$\mathsf {IsPrincipal}_{\mathcal O_{K_i}}{}$
for each
![]() $i = 1,\dotsc ,r$
.
$i = 1,\dotsc ,r$
.
Proof. By decomposing
![]() $\mathcal {M}$
using the central primitive idempotents of A, it suffices to consider the case
$\mathcal {M}$
using the central primitive idempotents of A, it suffices to consider the case
![]() $A = \mathrm {Mat}_{n}(K)$
, in which we must have
$A = \mathrm {Mat}_{n}(K)$
, in which we must have
![]() $\mathcal {O}_{C} = \mathcal {O}$
. Let X be a full
$\mathcal {O}_{C} = \mathcal {O}$
. Let X be a full
![]() $\mathcal {M}$
-lattice in A. Let
$\mathcal {M}$
-lattice in A. Let
![]() $e_{11} \in A$
be the matrix with the top-left entry equal to
$e_{11} \in A$
be the matrix with the top-left entry equal to
![]() $1$
and all other entries equal to
$1$
and all other entries equal to
![]() $0$
. Using Lemma 6.2, we can and do assume that
$0$
. Using Lemma 6.2, we can and do assume that
![]() $\mathcal {M} = \mathcal {M}_{\mathfrak a, n}$
is a nice maximal order. By [Reference Bley and JohnstonBJ08, Corollary 5.4], it is sufficient to check whether the Steinitz class of the
$\mathcal {M} = \mathcal {M}_{\mathfrak a, n}$
is a nice maximal order. By [Reference Bley and JohnstonBJ08, Corollary 5.4], it is sufficient to check whether the Steinitz class of the
![]() $\mathcal {O}$
-module
$\mathcal {O}$
-module
![]() $e_{11}X$
is equal to
$e_{11}X$
is equal to
![]() $[\mathfrak a^{-1}]$
, which amounts to testing whether a certain ideal of
$[\mathfrak a^{-1}]$
, which amounts to testing whether a certain ideal of
![]() $\mathcal {O}$
is principal.
$\mathcal {O}$
is principal.
6.4 Computing isomorphisms between localised lattices
Let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}$
-order in a finite-dimensional K-algebra A. Given two
$\mathcal {O}$
-order in a finite-dimensional K-algebra A. Given two
![]() $\Lambda $
-lattices X and Y and a maximal ideal
$\Lambda $
-lattices X and Y and a maximal ideal
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathcal {O}$
, we wish to determine whether there exists an isomorphism
$\mathcal {O}$
, we wish to determine whether there exists an isomorphism
![]() $X_{\mathfrak p} \cong Y_{\mathfrak {p}}$
of
$X_{\mathfrak p} \cong Y_{\mathfrak {p}}$
of
![]() $\Lambda _{\mathfrak {p}}$
-lattices and to compute such an isomorphism if so. By computing an isomorphism we mean computing a
$\Lambda _{\mathfrak {p}}$
-lattices and to compute such an isomorphism if so. By computing an isomorphism we mean computing a
![]() $\Lambda $
-morphism
$\Lambda $
-morphism
![]() $f\colon X \to Y$
such that its localisation
$f\colon X \to Y$
such that its localisation
![]() $f_{\mathfrak p} \colon X_{\mathfrak p} \to Y_{\mathfrak p}$
is an isomorphism.
$f_{\mathfrak p} \colon X_{\mathfrak p} \to Y_{\mathfrak p}$
is an isomorphism.
We first consider the case where X is a full
![]() $\Lambda $
-lattice in A and
$\Lambda $
-lattice in A and
![]() $Y = \Lambda $
, for which an algorithm was presented in [Reference Bley and WilsonBW09, §4.2] (although the algorithm was presented only in the context of semisimple algebras, the semisimplicity hypothesis is in fact unnecessary). We now outline the algorithm and analyse its complexity.
$Y = \Lambda $
, for which an algorithm was presented in [Reference Bley and WilsonBW09, §4.2] (although the algorithm was presented only in the context of semisimple algebras, the semisimplicity hypothesis is in fact unnecessary). We now outline the algorithm and analyse its complexity.
Proposition 6.5. There exists a probabilistic polynomial-time algorithm that, given A,
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathfrak {p}$
as above and a full
$\mathfrak {p}$
as above and a full
![]() $\Lambda $
-lattice X in A, decides whether
$\Lambda $
-lattice X in A, decides whether
![]() $X_{\mathfrak p}$
is free over
$X_{\mathfrak p}$
is free over
![]() $\Lambda _{\mathfrak {p}}$
and, if so, returns
$\Lambda _{\mathfrak {p}}$
and, if so, returns
![]() $\alpha \in X$
such that
$\alpha \in X$
such that
![]() $X_{\mathfrak {p}} = \Lambda _{\mathfrak {p}} \alpha $
.
$X_{\mathfrak {p}} = \Lambda _{\mathfrak {p}} \alpha $
.
Proof. Consider the finitely generated
![]() $\mathcal {O}/\mathfrak {p}$
-algebra
$\mathcal {O}/\mathfrak {p}$
-algebra
![]() $R_{\mathfrak {p}} := \Lambda /\mathfrak {p} \Lambda \cong \Lambda _{\mathfrak {p}} / \mathfrak {p} \Lambda _{\mathfrak {p}}$
. It follows from [Reference Friedl and RonyaiFR85, 1.5 A] that the Jacobson radical
$R_{\mathfrak {p}} := \Lambda /\mathfrak {p} \Lambda \cong \Lambda _{\mathfrak {p}} / \mathfrak {p} \Lambda _{\mathfrak {p}}$
. It follows from [Reference Friedl and RonyaiFR85, 1.5 A] that the Jacobson radical
![]() $J_{\mathfrak {p}} = \operatorname {\mathrm {J}}(R_{\mathfrak {p}})$
can be determined in polynomial time. Let
$J_{\mathfrak {p}} = \operatorname {\mathrm {J}}(R_{\mathfrak {p}})$
can be determined in polynomial time. Let
![]() $\overline {R}_{\mathfrak {p}} = R_{\mathfrak {p}}/J_{\mathfrak {p}}$
. By Lemma 2.3 and Nakayama’s lemma,
$\overline {R}_{\mathfrak {p}} = R_{\mathfrak {p}}/J_{\mathfrak {p}}$
. By Lemma 2.3 and Nakayama’s lemma,
![]() $X_{\mathfrak {p}}$
is free over
$X_{\mathfrak {p}}$
is free over
![]() $\Lambda _{\mathfrak {p}}$
if and only if
$\Lambda _{\mathfrak {p}}$
if and only if
![]() $\overline {X}_{\mathfrak {p}} := (X/\mathfrak {p}X)/J_{\mathfrak {p}}(X/\mathfrak {p}X) \cong (X_{\mathfrak {p}}/\mathfrak {p}X_{\mathfrak {p}})/J_{\mathfrak {p}}(X_{\mathfrak {p}}/\mathfrak {p}X_{\mathfrak {p}})$
is free of rank
$\overline {X}_{\mathfrak {p}} := (X/\mathfrak {p}X)/J_{\mathfrak {p}}(X/\mathfrak {p}X) \cong (X_{\mathfrak {p}}/\mathfrak {p}X_{\mathfrak {p}})/J_{\mathfrak {p}}(X_{\mathfrak {p}}/\mathfrak {p}X_{\mathfrak {p}})$
is free of rank
![]() $1$
over
$1$
over
![]() $\overline {R}_{\mathfrak {p}}$
. Using algorithms of Friedl–Rónyai [Reference Friedl and RonyaiFR85, 1.5 B] and Ronyai [Reference RonyaiRon87, Theorem 6.2], one can determine an isomorphism of
$\overline {R}_{\mathfrak {p}}$
. Using algorithms of Friedl–Rónyai [Reference Friedl and RonyaiFR85, 1.5 B] and Ronyai [Reference RonyaiRon87, Theorem 6.2], one can determine an isomorphism of
![]() $\overline {R}_{\mathfrak {p}}$
with a product of matrix algebras over finite fields
$\overline {R}_{\mathfrak {p}}$
with a product of matrix algebras over finite fields
![]() $k_{i}$
in probabilistic polynomial time. The final steps are just linear algebra over finite fields.
$k_{i}$
in probabilistic polynomial time. The final steps are just linear algebra over finite fields.
The following algorithm without the complexity statement was given in [Reference Hofmann and JohnstonHJ20, §8.4].
Corollary 6.6. There exists a probabilistic polynomial-time algorithm that, given A,
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathfrak {p}$
as above and
$\mathfrak {p}$
as above and
![]() $\Lambda $
-lattices X and Y, decides whether
$\Lambda $
-lattices X and Y, decides whether
![]() $X_{\mathfrak {p}}$
and
$X_{\mathfrak {p}}$
and
![]() $Y_{\mathfrak {p}}$
are isomorphic as
$Y_{\mathfrak {p}}$
are isomorphic as
![]() $\Lambda _{\mathfrak {p}}$
-lattices and, if so, returns
$\Lambda _{\mathfrak {p}}$
-lattices and, if so, returns
![]() $f \in \mathrm {Hom}_\Lambda (X, Y)$
such that the localisation
$f \in \mathrm {Hom}_\Lambda (X, Y)$
such that the localisation
![]() $f_{\mathfrak {p}} \colon X_{\mathfrak {p}} \to Y_{\mathfrak {p}}$
is an isomorphism.
$f_{\mathfrak {p}} \colon X_{\mathfrak {p}} \to Y_{\mathfrak {p}}$
is an isomorphism.
Proof. We use Proposition 6.5 together with the reduction to the free rank
![]() $1$
case given by Proposition 3.1. Both
$1$
case given by Proposition 3.1. Both
![]() $\mathrm {End}_{\Lambda }(Y)$
and
$\mathrm {End}_{\Lambda }(Y)$
and
![]() $\mathrm {Hom}_{\Lambda }(X, Y)$
can be determined as described in [Reference Hofmann and JohnstonHJ20, §7.3] using pseudo-Hermite normal form and pseudo-Smith normal form computations, which are probabilistic polynomial time by [Reference Biasse, Fieker and HofmannBFH17, Theorem 34, Proposition 43]. Using Proposition 6.5 one can determine in probabilistic polynomial time whether the
$\mathrm {Hom}_{\Lambda }(X, Y)$
can be determined as described in [Reference Hofmann and JohnstonHJ20, §7.3] using pseudo-Hermite normal form and pseudo-Smith normal form computations, which are probabilistic polynomial time by [Reference Biasse, Fieker and HofmannBFH17, Theorem 34, Proposition 43]. Using Proposition 6.5 one can determine in probabilistic polynomial time whether the
![]() $(\mathrm {End}_\Lambda (Y))_{\mathfrak {p}}$
-lattice
$(\mathrm {End}_\Lambda (Y))_{\mathfrak {p}}$
-lattice
![]() $(\mathrm {Hom}_\Lambda (X, Y))_{\mathfrak {p}}$
is free of rank
$(\mathrm {Hom}_\Lambda (X, Y))_{\mathfrak {p}}$
is free of rank
![]() $1$
. If not, then
$1$
. If not, then
![]() $X_{\mathfrak {p}}$
and
$X_{\mathfrak {p}}$
and
![]() $Y_{\mathfrak {p}}$
are not isomorphic over
$Y_{\mathfrak {p}}$
are not isomorphic over
![]() $\Lambda _{\mathfrak {p}}$
. If so, then the algorithm returns a free generator
$\Lambda _{\mathfrak {p}}$
. If so, then the algorithm returns a free generator
![]() $f \in \mathrm {Hom}_\Lambda (X, Y)$
of
$f \in \mathrm {Hom}_\Lambda (X, Y)$
of
![]() $(\mathrm {Hom}_\Lambda (X, Y))_{\mathfrak {p}}$
over
$(\mathrm {Hom}_\Lambda (X, Y))_{\mathfrak {p}}$
over
![]() $(\mathrm {End}_\Lambda (Y))_{\mathfrak {p}}$
. Then
$(\mathrm {End}_\Lambda (Y))_{\mathfrak {p}}$
. Then
![]() $X_{\mathfrak {p}} \cong Y_{\mathfrak {p}}$
over
$X_{\mathfrak {p}} \cong Y_{\mathfrak {p}}$
over
![]() $\Lambda _{\mathfrak {p}}$
if and only if the localisation
$\Lambda _{\mathfrak {p}}$
if and only if the localisation
![]() $f_{\mathfrak {p}} \colon X_{\mathfrak {p}} \to Y_{\mathfrak {p}}$
is an isomorphism.
$f_{\mathfrak {p}} \colon X_{\mathfrak {p}} \to Y_{\mathfrak {p}}$
is an isomorphism.
Remark 6.7. Given two
![]() $\Lambda $
-lattices X and Y, Corollary 6.6 can be used to decide if X and Y are in the same genus, that is, whether
$\Lambda $
-lattices X and Y, Corollary 6.6 can be used to decide if X and Y are in the same genus, that is, whether
![]() $X_{\mathfrak {p}}$
and
$X_{\mathfrak {p}}$
and
![]() $Y_{\mathfrak {p}}$
are isomorphic
$Y_{\mathfrak {p}}$
are isomorphic
![]() $\Lambda _{\mathfrak {p}}$
-lattices for every nonzero prime ideal
$\Lambda _{\mathfrak {p}}$
-lattices for every nonzero prime ideal
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathcal {O}$
. Note that a necessary condition is that
$\mathcal {O}$
. Note that a necessary condition is that
![]() $KX$
and
$KX$
and
![]() $KY$
are isomorphic as A-modules. By [Reference Chistov, Ivanyos and KarpinskiCIK97, Corollary 3] there is a polynomial-time algorithm that decides whether
$KY$
are isomorphic as A-modules. By [Reference Chistov, Ivanyos and KarpinskiCIK97, Corollary 3] there is a polynomial-time algorithm that decides whether
![]() $KX$
and
$KX$
and
![]() $KY$
are isomorphic as A-modules and, if so, computes an isomorphism; hence, the problem reduces to the case
$KY$
are isomorphic as A-modules and, if so, computes an isomorphism; hence, the problem reduces to the case
![]() $KX = KY$
. In this situation, X and Y are in the same genus if and only if
$KX = KY$
. In this situation, X and Y are in the same genus if and only if
![]() $X_{\mathfrak {p}}$
and
$X_{\mathfrak {p}}$
and
![]() $Y_{\mathfrak {p}}$
are isomorphic
$Y_{\mathfrak {p}}$
are isomorphic
![]() $\Lambda _{\mathfrak {p}}$
-lattices for the finitely many prime ideals
$\Lambda _{\mathfrak {p}}$
-lattices for the finitely many prime ideals
![]() $\mathfrak {p}$
dividing the module index
$\mathfrak {p}$
dividing the module index
![]() $[X : Y]_{\mathcal {O}}$
(see [Reference FröhlichFrö67, §3]). Hence, checking whether X and Y are in the same genus is polynomial-time reducible to
$[X : Y]_{\mathcal {O}}$
(see [Reference FröhlichFrö67, §3]). Hence, checking whether X and Y are in the same genus is polynomial-time reducible to
![]() $\mathsf {Factor}([X : Y]_{\mathcal {O}})$
.
$\mathsf {Factor}([X : Y]_{\mathcal {O}})$
.
6.5 Finding a suitable choice of locally free left ideal
Let A be a finite-dimensional semisimple K-algebra, and let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}$
-order in A. By [Reference ReinerRei03, (10.4)] there exists a (not necessarily unique) maximal
$\mathcal {O}$
-order in A. By [Reference ReinerRei03, (10.4)] there exists a (not necessarily unique) maximal
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\mathcal {M}$
in A containing
$\mathcal {M}$
in A containing
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mathfrak {f}$
be any proper full two-sided ideal of
$\mathfrak {f}$
be any proper full two-sided ideal of
![]() $\mathcal {M}$
that is contained in
$\mathcal {M}$
that is contained in
![]() $\Lambda $
. The following result without the complexity statements is a consequence of a special case of the argument given in [Reference Bley and JohnstonBJ11, §5.1].
$\Lambda $
. The following result without the complexity statements is a consequence of a special case of the argument given in [Reference Bley and JohnstonBJ11, §5.1].
Proposition 6.8. Given A,
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathfrak {f}$
as above and a full
$\mathfrak {f}$
as above and a full
![]() $\Lambda $
-lattice X in A, the problem of determining whether X is locally free over
$\Lambda $
-lattice X in A, the problem of determining whether X is locally free over
![]() $\Lambda $
and, if so, computing an element
$\Lambda $
and, if so, computing an element
![]() $\xi \in A^{\times }$
such that
$\xi \in A^{\times }$
such that
![]() $X \xi \subseteq \Lambda $
and
$X \xi \subseteq \Lambda $
and
![]() $X\xi + \mathfrak {f} = \Lambda $
, is probabilistic polynomial-time reducible to
$X\xi + \mathfrak {f} = \Lambda $
, is probabilistic polynomial-time reducible to
![]() $\mathsf {Factor}(\mathcal {O} \cap \mathfrak {f})$
.
$\mathsf {Factor}(\mathcal {O} \cap \mathfrak {f})$
.
Proof. Let
![]() $\mathrm {MaxSpec}(\mathcal {O})$
denote the set of all maximal ideals of
$\mathrm {MaxSpec}(\mathcal {O})$
denote the set of all maximal ideals of
![]() $\mathcal {O}$
. Let
$\mathcal {O}$
. Let
![]() $\mathfrak {S}= \{ \mathfrak {p}_{1}, \ldots , \mathfrak {p}_{n} \}$
be the subset consisting of ideals that divide
$\mathfrak {S}= \{ \mathfrak {p}_{1}, \ldots , \mathfrak {p}_{n} \}$
be the subset consisting of ideals that divide
![]() $\mathcal {O} \cap \mathfrak {f}$
(note that this is a proper nonzero ideal of
$\mathcal {O} \cap \mathfrak {f}$
(note that this is a proper nonzero ideal of
![]() $\mathcal {O}$
), and let
$\mathcal {O}$
), and let
![]() $\mathfrak {T} = \mathrm {MaxSpec}(\mathcal {O}) \setminus \mathfrak {S}$
. Observe that, for every
$\mathfrak {T} = \mathrm {MaxSpec}(\mathcal {O}) \setminus \mathfrak {S}$
. Observe that, for every
![]() $\mathfrak {p} \in \mathfrak {T}$
, we have
$\mathfrak {p} \in \mathfrak {T}$
, we have
![]() $\mathfrak {f}_{\mathfrak {p}} = \Lambda _{\mathfrak {p}}=\mathcal {M}_{\mathfrak {p}}$
, and so
$\mathfrak {f}_{\mathfrak {p}} = \Lambda _{\mathfrak {p}}=\mathcal {M}_{\mathfrak {p}}$
, and so
![]() $X_{\mathfrak {p}}$
is free over
$X_{\mathfrak {p}}$
is free over
![]() $\Lambda _{\mathfrak {p}}$
by [Reference ReinerRei03, (18.10)]. Moreover, for each i, checking whether
$\Lambda _{\mathfrak {p}}$
by [Reference ReinerRei03, (18.10)]. Moreover, for each i, checking whether
![]() $X_{\mathfrak {p}_i}$
is free over
$X_{\mathfrak {p}_i}$
is free over
![]() $\Lambda _{\mathfrak {p}_i}$
and, if so, computing
$\Lambda _{\mathfrak {p}_i}$
and, if so, computing
![]() $\omega _{i} \in X$
such that
$\omega _{i} \in X$
such that
![]() $X_{\mathfrak {p}_i} = \Lambda _{\mathfrak {p}_i} \omega _{i}$
, can be performed in probabilistic polynomial time by Proposition 6.5. In particular, if this step is completed successfully, then X is locally free over
$X_{\mathfrak {p}_i} = \Lambda _{\mathfrak {p}_i} \omega _{i}$
, can be performed in probabilistic polynomial time by Proposition 6.5. In particular, if this step is completed successfully, then X is locally free over
![]() $\Lambda $
.
$\Lambda $
.
By [Reference CohenCoh00, Proposition 1.3.11], elements
![]() $\beta _{1}, \ldots , \beta _{n} \in \mathcal {O}$
such that for each i, we have
$\beta _{1}, \ldots , \beta _{n} \in \mathcal {O}$
such that for each i, we have
can be computed in polynomial time. For each i, let
![]() $\nu _i \in \mathcal {O} \setminus \mathfrak {p}_i$
be an element such that
$\nu _i \in \mathcal {O} \setminus \mathfrak {p}_i$
be an element such that
![]() $X \omega _i^{-1} \nu _i \subseteq \Lambda $
. Then
$X \omega _i^{-1} \nu _i \subseteq \Lambda $
. Then
![]() $X\xi \subseteq \Lambda $
, where
$X\xi \subseteq \Lambda $
, where
![]() $\xi := \sum _{i=1}^{n} \beta _{i} \omega _{i}^{-1} \nu _{i}$
. By construction we have
$\xi := \sum _{i=1}^{n} \beta _{i} \omega _{i}^{-1} \nu _{i}$
. By construction we have
![]() $(X \xi )_{\mathfrak {p}_{i}} = \Lambda _{\mathfrak {p}_{i}}$
for each i. Moreover,
$(X \xi )_{\mathfrak {p}_{i}} = \Lambda _{\mathfrak {p}_{i}}$
for each i. Moreover,
![]() $\mathfrak {f}_{\mathfrak {p}} = \Lambda _{\mathfrak {p}}$
for all
$\mathfrak {f}_{\mathfrak {p}} = \Lambda _{\mathfrak {p}}$
for all
![]() $\mathfrak {p} \in \mathfrak {T}$
. Therefore,
$\mathfrak {p} \in \mathfrak {T}$
. Therefore,
![]() $(X\xi + \mathfrak {f})_{\mathfrak {p}} = \Lambda _{\mathfrak {p}}$
for all
$(X\xi + \mathfrak {f})_{\mathfrak {p}} = \Lambda _{\mathfrak {p}}$
for all
![]() $\mathfrak {p} \in \mathrm {MaxSpec}(\mathcal {O})$
, and so
$\mathfrak {p} \in \mathrm {MaxSpec}(\mathcal {O})$
, and so
![]() $X\xi + \mathfrak {f} = \Lambda $
by [Reference ReinerRei03, (4.21)].
$X\xi + \mathfrak {f} = \Lambda $
by [Reference ReinerRei03, (4.21)].
6.6 Computing generators of
 $(\Lambda /\mathfrak {f})^{\times }$
and
$(\Lambda /\mathfrak {f})^{\times }$
and
 $K_{1}(\Lambda /\mathfrak f)$
$K_{1}(\Lambda /\mathfrak f)$
We first recall some definitions from algebraic K-theory and refer the reader to [Reference Curtis and ReinerCR87, §40] for more details. For any ring R, the Whitehead group
![]() $K_{1}(R)$
is defined as
$K_{1}(R)$
is defined as
![]() $\mathrm {GL}(R)/[\mathrm {GL}(R),\mathrm {GL}(R)]$
, where
$\mathrm {GL}(R)/[\mathrm {GL}(R),\mathrm {GL}(R)]$
, where
![]() $\mathrm {GL}(R) = \varinjlim \mathrm {GL}_n(R)$
and
$\mathrm {GL}(R) = \varinjlim \mathrm {GL}_n(R)$
and
![]() $\mathrm {GL}_n(R)$
embeds into
$\mathrm {GL}_n(R)$
embeds into
![]() $\mathrm {GL}_{n + 1}(R)$
via
$\mathrm {GL}_{n + 1}(R)$
via
 $$\begin{align*}\alpha \mapsto \begin{pmatrix} \alpha & 0 \\ 0 & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\alpha \mapsto \begin{pmatrix} \alpha & 0 \\ 0 & 1 \end{pmatrix}. \end{align*}$$
In particular, there is a canonical map
![]() $R^\times \to \mathrm {GL}(R) \to K_1(R)$
.
$R^\times \to \mathrm {GL}(R) \to K_1(R)$
.
Now, assume the notation and setting of §6.5. Since
![]() $\Lambda /\mathfrak {f}$
is of finite cardinality, it is semilocal, and so the canonical map
$\Lambda /\mathfrak {f}$
is of finite cardinality, it is semilocal, and so the canonical map
is surjective by [Reference Curtis and ReinerCR87, (40.31)]. We consider the problems of computing generators of
![]() $(\Lambda /\mathfrak {f})^{\times }$
and of
$(\Lambda /\mathfrak {f})^{\times }$
and of
![]() $K_{1}(\Lambda /\mathfrak f)$
, where the latter task means computing elements
$K_{1}(\Lambda /\mathfrak f)$
, where the latter task means computing elements
![]() $x_1,\dotsc ,x_n \in (\Lambda /\mathfrak {f})^{\times }$
such that their images generate
$x_1,\dotsc ,x_n \in (\Lambda /\mathfrak {f})^{\times }$
such that their images generate
![]() $K_1(\Lambda /\mathfrak f)$
.
$K_1(\Lambda /\mathfrak f)$
.
An algorithm for computing generators of
![]() $K_1(\Lambda /\mathfrak {f})$
is described in [Reference Bley, Boltje, Hess, Pauli and PohstBB06, §3.4–3.7]. With minor modifications, this algorithm also computes a generating set of
$K_1(\Lambda /\mathfrak {f})$
is described in [Reference Bley, Boltje, Hess, Pauli and PohstBB06, §3.4–3.7]. With minor modifications, this algorithm also computes a generating set of
![]() $(\Lambda /\mathfrak f)^\times $
. In this subsection, we will analyse the complexity of both these algorithms. To treat both cases simultaneously, for a ring R we let
$(\Lambda /\mathfrak f)^\times $
. In this subsection, we will analyse the complexity of both these algorithms. To treat both cases simultaneously, for a ring R we let
![]() $\mathrm {G}(R)$
denote either
$\mathrm {G}(R)$
denote either
![]() $K_{1}(R)$
or
$K_{1}(R)$
or
![]() $R^{\times }$
.
$R^{\times }$
.
Let C denote the centre of A, and let
![]() $\mathcal {O}_{C}$
be the integral closure of
$\mathcal {O}_{C}$
be the integral closure of
![]() $\mathcal {O}$
in C. Let
$\mathcal {O}$
in C. Let
![]() $\mathfrak {g} = \mathfrak {f} \cap C$
, and note that this is a proper full ideal of
$\mathfrak {g} = \mathfrak {f} \cap C$
, and note that this is a proper full ideal of
![]() $\mathcal {O}_{C}$
and of
$\mathcal {O}_{C}$
and of
![]() $\Lambda \cap \mathcal {O}_{C} = \Lambda \cap C$
. Let
$\Lambda \cap \mathcal {O}_{C} = \Lambda \cap C$
. Let
be the prime ideal decomposition of
![]() $\mathfrak {g}$
in
$\mathfrak {g}$
in
![]() $\mathcal {O}_{C}$
, where the set
$\mathcal {O}_{C}$
, where the set
of prime ideals of
![]() $\mathcal {O}_{C}$
is defined by the decomposition. Set
$\mathcal {O}_{C}$
is defined by the decomposition. Set
, a set of prime ideals of
![]() $\Lambda \cap \mathcal {O}_{C}$
. For each
$\Lambda \cap \mathcal {O}_{C}$
. For each
consider the ideal

We write
for the set of ideals
![]() $\mathfrak {q}$
. Then by [Reference Bley and EndresBE05, Proposition 3.2]
$\mathfrak {q}$
. Then by [Reference Bley and EndresBE05, Proposition 3.2]
is the unique primary decomposition of
![]() $\mathfrak {g}$
when considered as an ideal of
$\mathfrak {g}$
when considered as an ideal of
![]() $\Lambda \cap \mathcal {O}_{C}$
. Moreover, by [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Lemma 3.5], we have
$\Lambda \cap \mathcal {O}_{C}$
. Moreover, by [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Lemma 3.5], we have
and by the Chinese remainder theorem we obtain an isomorphism
This induces a decomposition
Thus, given
, it suffices to compute generators of
![]() $\mathrm {G}(\Lambda /(\mathfrak {q}\Lambda + \mathfrak {f}))$
for each
$\mathrm {G}(\Lambda /(\mathfrak {q}\Lambda + \mathfrak {f}))$
for each
.
Now, fix
![]() , and let
, and let
![]() be the associated prime ideal of
be the associated prime ideal of
![]() $\Lambda \cap \mathcal {O}_{C}$
for some
$\Lambda \cap \mathcal {O}_{C}$
for some
![]() . As shown in [Reference Bley, Boltje, Hess, Pauli and PohstBB06, §3.7], we have an exact sequence
. As shown in [Reference Bley, Boltje, Hess, Pauli and PohstBB06, §3.7], we have an exact sequence
We consider the problems of computing generators for the first and third terms in this sequence. Let
![]() $d := \dim _{K} A$
.
$d := \dim _{K} A$
.
Lemma 6.9. Given
![]() $\Lambda $
,
$\Lambda $
,
![]() $\mathfrak {f}$
and
$\mathfrak {f}$
and
![]() $\mathfrak p$
as above, the problem of computing generators of
$\mathfrak p$
as above, the problem of computing generators of
is probabilistic polynomial-time reducible to at most d instances of the problem
![]() $\mathsf {Primitive}$
for extensions of
$\mathsf {Primitive}$
for extensions of
![]() $\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. The number of generators is at most
$\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. The number of generators is at most
![]() $d([K : \mathbb {Q}]+2)$
.
$d([K : \mathbb {Q}]+2)$
.
Proof. Let k denote the finite field
![]() $\mathcal {O}/(\mathfrak {p} \cap \mathcal {O})$
. Let
$\mathcal {O}/(\mathfrak {p} \cap \mathcal {O})$
. Let
![]() $R = \Lambda /(\mathfrak {p} \Lambda + \mathfrak {f})$
, and note that this is annihilated by
$R = \Lambda /(\mathfrak {p} \Lambda + \mathfrak {f})$
, and note that this is annihilated by
![]() $\mathfrak {p} \cap \mathcal {O}$
. Thus, R is a k-algebra such that
$\mathfrak {p} \cap \mathcal {O}$
. Thus, R is a k-algebra such that
![]() $\dim _{k} R \leq d$
. In particular, R is Artinian, so its Jacobson radical
$\dim _{k} R \leq d$
. In particular, R is Artinian, so its Jacobson radical
![]() $J = \operatorname {\mathrm {J}}(R)$
is nilpotent by [Reference Curtis and ReinerCR81, (5.15)]. Since we have a decreasing filtration
$J = \operatorname {\mathrm {J}}(R)$
is nilpotent by [Reference Curtis and ReinerCR81, (5.15)]. Since we have a decreasing filtration
![]() $J \supseteq J^2 \supseteq \cdots \supseteq J^d$
and
$J \supseteq J^2 \supseteq \cdots \supseteq J^d$
and
![]() $\dim _k(J) \le d-1$
, we obtain
$\dim _k(J) \le d-1$
, we obtain
![]() $J^{d}=0$
. By [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Lemma 3.6] and the same reasoning as in [Reference Bley, Boltje, Hess, Pauli and PohstBB06, §3.7], we have an exact sequence
$J^{d}=0$
. By [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Lemma 3.6] and the same reasoning as in [Reference Bley, Boltje, Hess, Pauli and PohstBB06, §3.7], we have an exact sequence
We first discuss the computation of generators for
![]() $1 + J$
. To this end, let
$1 + J$
. To this end, let
![]() $l \in \mathbb {Z}_{\geq 0}$
be minimal subject to the condition
$l \in \mathbb {Z}_{\geq 0}$
be minimal subject to the condition
![]() $J^{2^l} = 0$
and note that
$J^{2^l} = 0$
and note that
![]() $2^{l} \leq 2d$
. Consider the filtration
$2^{l} \leq 2d$
. Consider the filtration
Generators of J can be determined in polynomial time using the algorithms of [Reference Friedl and RonyaiFR85, 1.5 A]. For each
![]() $i = 0,\dotsc ,l-1$
, the map
$i = 0,\dotsc ,l-1$
, the map
![]() $\overline {x} \mapsto \overline {x-1}$
induces an isomorphism
$\overline {x} \mapsto \overline {x-1}$
induces an isomorphism
of abelian groups, and so it follows that we can find generators of
![]() $1 + J$
in polynomial time. For each
$1 + J$
in polynomial time. For each
![]() $i = 0, \dotsc , l - 1$
the number of generators of
$i = 0, \dotsc , l - 1$
the number of generators of
![]() $J^{2^i}/J^{2^{i + 1}}$
is bounded by
$J^{2^i}/J^{2^{i + 1}}$
is bounded by
![]() $\dim _k(J^{2^i}/J^{2^{i+1}}) [K : \mathbb {Q}]$
. Now, summing over
$\dim _k(J^{2^i}/J^{2^{i+1}}) [K : \mathbb {Q}]$
. Now, summing over
![]() $i = 0,\dotsc ,l-1$
shows that
$i = 0,\dotsc ,l-1$
shows that
![]() $1 + J$
is generated by at most
$1 + J$
is generated by at most
![]() $\dim _k(J) [K : \mathbb {Q}] \leq (d-1) [K : \mathbb {Q}]$
elements.
$\dim _k(J) [K : \mathbb {Q}] \leq (d-1) [K : \mathbb {Q}]$
elements.
Using algorithms of [Reference Friedl and RonyaiFR85, 1.5 B] and [Reference RonyaiRon87, Theorem 6.2], one can determine an isomorphism
![]() $R/J \cong \prod _{1 \leq i \leq r} \mathrm {Mat}_{n_{i}}(k_{i})$
with a product of matrix algebras over finite fields
$R/J \cong \prod _{1 \leq i \leq r} \mathrm {Mat}_{n_{i}}(k_{i})$
with a product of matrix algebras over finite fields
![]() $k_{i}$
in probabilistic polynomial time. Since
$k_{i}$
in probabilistic polynomial time. Since
this problem reduces to the computation of each
![]() $\operatorname {\mathrm {G}}(\mathrm {Mat}_{n_i}(k_i))$
, which we claim is generated by at most
$\operatorname {\mathrm {G}}(\mathrm {Mat}_{n_i}(k_i))$
, which we claim is generated by at most
![]() $2$
elements. If
$2$
elements. If
![]() $\operatorname {\mathrm {G}}{} = K_1$
, then the claim follows from the fact that the canonical maps
$\operatorname {\mathrm {G}}{} = K_1$
, then the claim follows from the fact that the canonical maps
![]() $k_{i}^{\times } \to K_{1}(k_{i}) \to K_1(\mathrm {Mat}_{n_i}(k_i))$
are isomorphisms. If
$k_{i}^{\times } \to K_{1}(k_{i}) \to K_1(\mathrm {Mat}_{n_i}(k_i))$
are isomorphisms. If
![]() $\operatorname {\mathrm {G}}{} = (-)^\times $
, then the claim follows from [Reference TaylorTay87], where it is shown that given a primitive element of
$\operatorname {\mathrm {G}}{} = (-)^\times $
, then the claim follows from [Reference TaylorTay87], where it is shown that given a primitive element of
![]() $k_i$
one can write down directly a two element generating set of
$k_i$
one can write down directly a two element generating set of
![]() $\mathrm {GL}_{n_i}(k_i)$
. Since
$\mathrm {GL}_{n_i}(k_i)$
. Since
![]() $\dim _{k}(R/J) \leq d$
we have
$\dim _{k}(R/J) \leq d$
we have
![]() $r \leq d$
and
$r \leq d$
and
![]() $[k_i : k] \leq d$
for each i. Finally, note that
$[k_i : k] \leq d$
for each i. Finally, note that
![]() $\mathcal {O}/(\mathcal {O}\cap \mathfrak {p}) = \mathcal {O} / (\mathcal {O}\cap \mathfrak {P})$
since
$\mathcal {O}/(\mathcal {O}\cap \mathfrak {p}) = \mathcal {O} / (\mathcal {O}\cap \mathfrak {P})$
since
![]() $\mathcal {O}\subseteq \Lambda $
implies
$\mathcal {O}\subseteq \Lambda $
implies
![]() $\mathcal {O}\cap \mathfrak {p}= \mathcal {O}\cap \mathfrak {P}\cap \Lambda = \mathcal {O}\cap \mathfrak {P}$
. In particular,
$\mathcal {O}\cap \mathfrak {p}= \mathcal {O}\cap \mathfrak {P}\cap \Lambda = \mathcal {O}\cap \mathfrak {P}$
. In particular,
![]() $G(R/J)$
is generated by at most
$G(R/J)$
is generated by at most
![]() $2r \leq 2d$
elements.
$2r \leq 2d$
elements.
Lemma 6.10. Given
![]() $\Lambda $
,
$\Lambda $
,
![]() $\mathfrak {f}$
,
$\mathfrak {f}$
,
![]() $\mathfrak {p}$
and
$\mathfrak {p}$
and
![]() $\mathfrak {q}$
as above, we set
$\mathfrak {q}$
as above, we set
Then there exists a polynomial-time algorithm that returns m elements of
![]() $\Lambda $
whose classes generate
$\Lambda $
whose classes generate
![]() $(1 + \mathfrak {p} \Lambda + \mathfrak {f})/(1 + \mathfrak {q} \Lambda + \mathfrak {f})$
. If
$(1 + \mathfrak {p} \Lambda + \mathfrak {f})/(1 + \mathfrak {q} \Lambda + \mathfrak {f})$
. If
![]() $e_{\mathfrak {p}} = 1$
; we have
$e_{\mathfrak {p}} = 1$
; we have
![]() $m=0$
. If
$m=0$
. If
![]() $e_{\mathfrak {p}}> 1$
, the number m of generators is bounded by
$e_{\mathfrak {p}}> 1$
, the number m of generators is bounded by
![]() $d (1+\log _2(e_{\mathfrak {p}})) [K:\mathbb {Q}]$
.
$d (1+\log _2(e_{\mathfrak {p}})) [K:\mathbb {Q}]$
.
Proof. If
![]() $e_{\mathfrak {p}}=1$
, we clearly have
$e_{\mathfrak {p}}=1$
, we clearly have
![]() $\mathfrak {p} = \mathfrak {q}$
, and so
$\mathfrak {p} = \mathfrak {q}$
, and so
![]() $m=0$
. If
$m=0$
. If
![]() $e_{\mathfrak {p}}> 1$
, we let
$e_{\mathfrak {p}}> 1$
, we let
![]() $l \in \mathbb {Z}_{>0}$
be minimal subject to the condition
$l \in \mathbb {Z}_{>0}$
be minimal subject to the condition
![]() $\mathfrak {p}^{2^l} \subseteq \mathfrak {q}$
. Then there exists a filtration
$\mathfrak {p}^{2^l} \subseteq \mathfrak {q}$
. Then there exists a filtration
For each
![]() $i = 0,\dotsc ,l-1$
, the map
$i = 0,\dotsc ,l-1$
, the map
![]() $\overline {x} \mapsto \overline {x-1}$
induces an isomorphism
$\overline {x} \mapsto \overline {x-1}$
induces an isomorphism
 $$\begin{align*}\frac{1 + (\mathfrak{q} + \mathfrak{p}^{2^i})\Lambda + \mathfrak{f}} {1 + (\mathfrak{q} + \mathfrak{p}^{2^{i+1}})\Lambda + \mathfrak{f}} \longrightarrow \frac{(\mathfrak{q} + \mathfrak{p}^{2^i})\Lambda + \mathfrak{f}}{(\mathfrak{q} + \mathfrak{p}^{2^{i+1}})\Lambda + \mathfrak{f}} \end{align*}$$
$$\begin{align*}\frac{1 + (\mathfrak{q} + \mathfrak{p}^{2^i})\Lambda + \mathfrak{f}} {1 + (\mathfrak{q} + \mathfrak{p}^{2^{i+1}})\Lambda + \mathfrak{f}} \longrightarrow \frac{(\mathfrak{q} + \mathfrak{p}^{2^i})\Lambda + \mathfrak{f}}{(\mathfrak{q} + \mathfrak{p}^{2^{i+1}})\Lambda + \mathfrak{f}} \end{align*}$$
of abelian groups. Hence, any
![]() $\mathbb {Z}$
-basis of the right-hand side yields generators of the left-hand side. It remains to bound l. For every
$\mathbb {Z}$
-basis of the right-hand side yields generators of the left-hand side. It remains to bound l. For every
![]() with
with
![]() $\mathfrak {P} \cap \Lambda = \mathfrak {p}$
, the inclusion
$\mathfrak {P} \cap \Lambda = \mathfrak {p}$
, the inclusion
![]() $\mathfrak {p}^{e_{\mathfrak {p}}} = (\mathfrak {P} \cap \Lambda )^{e_{\mathfrak {p}}} \subseteq \mathfrak {P}^{e_{\mathfrak {p}}} \cap \Lambda \subseteq \mathfrak {P}^{e_{\mathfrak {P}}} \cap \Lambda $
holds. Hence,
$\mathfrak {p}^{e_{\mathfrak {p}}} = (\mathfrak {P} \cap \Lambda )^{e_{\mathfrak {p}}} \subseteq \mathfrak {P}^{e_{\mathfrak {p}}} \cap \Lambda \subseteq \mathfrak {P}^{e_{\mathfrak {P}}} \cap \Lambda $
holds. Hence,
![]() $\mathfrak {p}^{e_{\mathfrak {p}}} \subseteq \mathfrak {q}$
and therefore
$\mathfrak {p}^{e_{\mathfrak {p}}} \subseteq \mathfrak {q}$
and therefore
![]() $2^{l} \leq 2e_{\mathfrak {p}}$
, which gives
$2^{l} \leq 2e_{\mathfrak {p}}$
, which gives
![]() $l \leq 1 + \log _{2}(e_{\mathfrak {p}})$
.
$l \leq 1 + \log _{2}(e_{\mathfrak {p}})$
.
Since any quotient
![]() $((\mathfrak {q} + \mathfrak {p}^{2^i})\Lambda + \mathfrak {f}) / ((\mathfrak {q} + \mathfrak {p}^{2^{i+1}})\Lambda + \mathfrak {f})$
is generated by at most
$((\mathfrak {q} + \mathfrak {p}^{2^i})\Lambda + \mathfrak {f}) / ((\mathfrak {q} + \mathfrak {p}^{2^{i+1}})\Lambda + \mathfrak {f})$
is generated by at most
![]() $d [K : \mathbb {Q}]$
elements, the quotient
$d [K : \mathbb {Q}]$
elements, the quotient
![]() $(1 + \mathfrak {p} \Lambda + \mathfrak {f})/(1 + \mathfrak {q} \Lambda + \mathfrak {f})$
is generated by at most
$(1 + \mathfrak {p} \Lambda + \mathfrak {f})/(1 + \mathfrak {q} \Lambda + \mathfrak {f})$
is generated by at most
![]() $(1 + \log _{2}(e_{\mathfrak {p}})) d [K : \mathbb {Q}]$
elements.
$(1 + \log _{2}(e_{\mathfrak {p}})) d [K : \mathbb {Q}]$
elements.
Proposition 6.11. Given
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathfrak {f}$
as above, the problem of computing generators of
$\mathfrak {f}$
as above, the problem of computing generators of
![]() $(\Lambda /\mathfrak {f})^{\times }$
and
$(\Lambda /\mathfrak {f})^{\times }$
and
![]() $K_{1}(\Lambda /\mathfrak {f})$
is probabilistic polynomial-time reducible to the factorisation of
$K_{1}(\Lambda /\mathfrak {f})$
is probabilistic polynomial-time reducible to the factorisation of
![]() $\mathfrak {g} := \mathfrak {f} \cap \mathcal {O}_{C}$
as an ideal of
$\mathfrak {g} := \mathfrak {f} \cap \mathcal {O}_{C}$
as an ideal of
![]() $\mathcal {O}_{C}$
and, for each prime ideal divisor
$\mathcal {O}_{C}$
and, for each prime ideal divisor
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\mathfrak {g}$
, at most d instances of
$\mathfrak {g}$
, at most d instances of
![]() $\mathsf {Primitive}$
for extensions of
$\mathsf {Primitive}$
for extensions of
![]() $\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. The number of generators is bounded by
$\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. The number of generators is bounded by
![]() $5 d [ K:\mathbb {Q}]\log _2|\mathcal {O}_C/\mathfrak {g}|$
.
$5 d [ K:\mathbb {Q}]\log _2|\mathcal {O}_C/\mathfrak {g}|$
.
Proof. Using the factorisation of
![]() $\mathfrak {g} = \mathfrak {f} \cap \mathcal {O}_{C}$
, one can determine the sets of ideals
$\mathfrak {g} = \mathfrak {f} \cap \mathcal {O}_{C}$
, one can determine the sets of ideals
,
and
in polynomial time. Since
, the claim follows from the reduction to the computation of
![]() $\mathrm {G}(\Lambda /(\mathfrak {q}\Lambda + \mathfrak {f}))$
for each
$\mathrm {G}(\Lambda /(\mathfrak {q}\Lambda + \mathfrak {f}))$
for each
discussed at the beginning of the section, the exact sequence (5), Lemmas 6.9 and 6.10 and the following computation

The inequality
![]() $(*)$
is a consequence of
$(*)$
is a consequence of
which, in turn, is immediate from
.
Remark 6.12. In the setup above, we start with a proper full two-sided ideal
![]() $\mathfrak {f}$
of
$\mathfrak {f}$
of
![]() $\mathcal {M}$
contained in
$\mathcal {M}$
contained in
![]() $\Lambda $
and set
$\Lambda $
and set
![]() $\mathfrak {g} := \mathfrak {f} \cap C$
. Under hypothesis (H) on A, we may instead start with a proper full ideal
$\mathfrak {g} := \mathfrak {f} \cap C$
. Under hypothesis (H) on A, we may instead start with a proper full ideal
![]() $\mathfrak {g}$
of
$\mathfrak {g}$
of
![]() $\mathcal {O}_{C}$
such that
$\mathcal {O}_{C}$
such that
![]() $\mathfrak {g}\mathcal {M}$
is contained in
$\mathfrak {g}\mathcal {M}$
is contained in
![]() $\Lambda $
and then set
$\Lambda $
and then set
![]() $\mathfrak {f} := \mathfrak {g}\mathcal {M}$
. In this situation, we then have
$\mathfrak {f} := \mathfrak {g}\mathcal {M}$
. In this situation, we then have
![]() $\mathfrak {g} = \mathfrak {f} \cap \mathcal {O}_C$
by [Reference ReinerRei03, (27.6)].
$\mathfrak {g} = \mathfrak {f} \cap \mathcal {O}_C$
by [Reference ReinerRei03, (27.6)].
7 Lifting units of reduced norm one
Let K be a number field with ring of integers
![]() $\mathcal {O} = {\mathcal {O}_K}$
. Let
$\mathcal {O} = {\mathcal {O}_K}$
. Let
![]() $r \in \mathbb {Z}_{>0}$
, and let
$r \in \mathbb {Z}_{>0}$
, and let
![]() $A = \prod _{i=1}^{r} \mathrm {Mat}_{n_i}(K_i)$
, where
$A = \prod _{i=1}^{r} \mathrm {Mat}_{n_i}(K_i)$
, where
![]() $K_{i}$
is a finite field extension of K and
$K_{i}$
is a finite field extension of K and
![]() $n_{i} \in \mathbb {Z}_{>0}$
for each i. In particular, A is a finite-dimensional semisimple K-algebra satisfying hypothesis (H). Let C be the centre of A, which we can and do identify with
$n_{i} \in \mathbb {Z}_{>0}$
for each i. In particular, A is a finite-dimensional semisimple K-algebra satisfying hypothesis (H). Let C be the centre of A, which we can and do identify with
![]() $\prod _{i=1}^{r} K_{i}$
. In this situation, the reduced norm map
$\prod _{i=1}^{r} K_{i}$
. In this situation, the reduced norm map
![]() $\mathrm {nr} \colon A \rightarrow C$
is equal to the product of maps
$\mathrm {nr} \colon A \rightarrow C$
is equal to the product of maps
![]() $\det : \mathrm {Mat}_{n_i}(K_i) \rightarrow K_{i}$
.
$\det : \mathrm {Mat}_{n_i}(K_i) \rightarrow K_{i}$
.
Let
![]() $\mathcal {M}$
be a maximal
$\mathcal {M}$
be a maximal
![]() $\mathcal {O}$
-order in A, and let
$\mathcal {O}$
-order in A, and let
![]() $\mathcal {O}_{C} = \mathcal {M} \cap C = \prod _{i=1}^{r} {\mathcal {O}_{K_{i}}}$
. Then
$\mathcal {O}_{C} = \mathcal {M} \cap C = \prod _{i=1}^{r} {\mathcal {O}_{K_{i}}}$
. Then
![]() $\mathrm {nr}$
restricts to a group homomorphism
$\mathrm {nr}$
restricts to a group homomorphism
![]() $\mathrm {nr} \colon \mathcal {M}^{\times } \rightarrow \mathcal {O}_{C}^{\times }$
, which is surjective since A satisfies the Eichler condition relative to
$\mathrm {nr} \colon \mathcal {M}^{\times } \rightarrow \mathcal {O}_{C}^{\times }$
, which is surjective since A satisfies the Eichler condition relative to
![]() $\mathcal {O}$
(see [Reference Curtis and ReinerCR87, (45.4), (45.6)]). Let
$\mathcal {O}$
(see [Reference Curtis and ReinerCR87, (45.4), (45.6)]). Let
![]() $\mathfrak {g}$
be a proper full ideal of
$\mathfrak {g}$
be a proper full ideal of
![]() $\mathcal {O}_C$
, and let
$\mathcal {O}_C$
, and let
![]() $\mathfrak {f} = \mathfrak {g}\mathcal {M}$
. Then by Lemma 4.4 there exists a commutative diagram of groups
$\mathfrak {f} = \mathfrak {g}\mathcal {M}$
. Then by Lemma 4.4 there exists a commutative diagram of groups

where the rows are exact,
![]() $\mathrm {SL}(\mathcal {M})$
and
$\mathrm {SL}(\mathcal {M})$
and
![]() $\mathrm {SL}(\mathcal {M}/\mathfrak {f})$
are defined by the exactness of these rows, and the vertical maps are induced by the canonical projections. Note that this is consistent with diagram (4), but we do not require an order
$\mathrm {SL}(\mathcal {M}/\mathfrak {f})$
are defined by the exactness of these rows, and the vertical maps are induced by the canonical projections. Note that this is consistent with diagram (4), but we do not require an order
![]() $\Lambda $
for the above setup.
$\Lambda $
for the above setup.
The aim of this section is to show that, under the above assumptions on A and
![]() $\mathfrak {f}$
, the map
$\mathfrak {f}$
, the map
![]() $f_{1}$
is surjective, and there exists a polynomial-time algorithm that given an element of
$f_{1}$
is surjective, and there exists a polynomial-time algorithm that given an element of
![]() $\mathrm {SL}(\mathcal {M}/\mathfrak {f})=\mathrm {SL}(\mathcal {M}/\mathfrak {g}\mathcal {M})$
returns a preimage under
$\mathrm {SL}(\mathcal {M}/\mathfrak {f})=\mathrm {SL}(\mathcal {M}/\mathfrak {g}\mathcal {M})$
returns a preimage under
![]() $f_{1}$
.
$f_{1}$
.
7.1 Lifting unimodular matrices
We first consider the case where
![]() $A = \mathrm {Mat}_{n}(K)$
and
$A = \mathrm {Mat}_{n}(K)$
and
![]() $\mathcal {M} = \mathrm {Mat}_{n}(\mathcal {O})$
for some
$\mathcal {M} = \mathrm {Mat}_{n}(\mathcal {O})$
for some
![]() $n \in \mathbb {Z}_{>0}$
. In this situation, we have
$n \in \mathbb {Z}_{>0}$
. In this situation, we have
![]() $\mathcal {O}=\mathcal {O}_{C}$
and
$\mathcal {O}=\mathcal {O}_{C}$
and
![]() $\mathcal {M}/\mathfrak {f} = \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {g})$
. Moreover, both the maps
$\mathcal {M}/\mathfrak {f} = \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {g})$
. Moreover, both the maps
![]() $\mathrm {nr}$
and
$\mathrm {nr}$
and
![]() $\overline {\mathrm {nr}}$
in diagram (6) are just the usual determinant maps,
$\overline {\mathrm {nr}}$
in diagram (6) are just the usual determinant maps,
![]() $\mathrm {SL}(\mathcal {M}) = \mathrm {SL}_{n}(\mathcal {O})$
, and
$\mathrm {SL}(\mathcal {M}) = \mathrm {SL}_{n}(\mathcal {O})$
, and
![]() $\mathrm {SL}(\mathcal {M}/\mathfrak {f}) = \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
. Thus,
$\mathrm {SL}(\mathcal {M}/\mathfrak {f}) = \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
. Thus,
![]() $f_{1}$
is the canonical map
$f_{1}$
is the canonical map
![]() $f_{1} : \mathrm {SL}_{n}(\mathcal {O}) \rightarrow \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
. Note that this map is trivial when
$f_{1} : \mathrm {SL}_{n}(\mathcal {O}) \rightarrow \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
. Note that this map is trivial when
![]() $n=1$
, so we henceforth suppose that
$n=1$
, so we henceforth suppose that
![]() $n \geq 2$
.
$n \geq 2$
.
We use the following notation for a commutative ring R. Given
![]() $1 \leq i, j \leq n$
with
$1 \leq i, j \leq n$
with
![]() $i \neq j$
, and
$i \neq j$
, and
![]() $r \in R$
, we denote by
$r \in R$
, we denote by
![]() $e_{ij}(r) \in \mathrm {SL}_{n}(R)$
the matrix with ones on the diagonal and entry r at position
$e_{ij}(r) \in \mathrm {SL}_{n}(R)$
the matrix with ones on the diagonal and entry r at position
![]() $(i, j)$
. We refer to these matrices as elementary matrices. Let
$(i, j)$
. We refer to these matrices as elementary matrices. Let
![]() $\mathrm {E}_{n}(R)$
denote the subgroup of
$\mathrm {E}_{n}(R)$
denote the subgroup of
![]() $\mathrm {SL}_{n}(R)$
generated by all elementary matrices.
$\mathrm {SL}_{n}(R)$
generated by all elementary matrices.
Since
![]() $\mathcal {O}/\mathfrak {g}$
is semilocal,
$\mathcal {O}/\mathfrak {g}$
is semilocal,
![]() $\mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g}) = \mathrm {E}_{n}(\mathcal {O}/\mathfrak {g})$
by [Reference BassBas68, Chapter V, Corollary 9.2]. Thus, every element of
$\mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g}) = \mathrm {E}_{n}(\mathcal {O}/\mathfrak {g})$
by [Reference BassBas68, Chapter V, Corollary 9.2]. Thus, every element of
![]() $\mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
can be expressed as a product of elementary matrices, and every such matrix can easily be lifted to an elementary matrix in
$\mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
can be expressed as a product of elementary matrices, and every such matrix can easily be lifted to an elementary matrix in
![]() $\mathrm {SL}_{n}(\mathcal {O})$
. This immediately implies the theoretical part of Corollary 7.6 below. However, we will need a constructive proof that then translates into an efficient algorithm.
$\mathrm {SL}_{n}(\mathcal {O})$
. This immediately implies the theoretical part of Corollary 7.6 below. However, we will need a constructive proof that then translates into an efficient algorithm.
We will show that, given the factorisation of
![]() $\mathfrak {g}$
, there exists a polynomial-time algorithm for lifting unimodular matrices over
$\mathfrak {g}$
, there exists a polynomial-time algorithm for lifting unimodular matrices over
![]() $\mathcal {O}/\mathfrak {g}$
to
$\mathcal {O}/\mathfrak {g}$
to
![]() $\mathcal {O}$
. The idea is to reduce to the local case and then apply the Chinese remainder theorem.
$\mathcal {O}$
. The idea is to reduce to the local case and then apply the Chinese remainder theorem.
For any matrix M, let
![]() $M^{t}$
denote its transpose. A vector
$M^{t}$
denote its transpose. A vector
![]() $\mathbf {v} = (v_{1}, \ldots , v_{n})^{t}$
of elements of a commutative ring R is said to be unimodular if
$\mathbf {v} = (v_{1}, \ldots , v_{n})^{t}$
of elements of a commutative ring R is said to be unimodular if
![]() $\sum _{i=1}^{n} R v_{i} = R$
. In the following we denote by
$\sum _{i=1}^{n} R v_{i} = R$
. In the following we denote by
![]() $\mathfrak {q} = \mathfrak {p}^l$
,
$\mathfrak {q} = \mathfrak {p}^l$
,
![]() $l \in \mathbb {Z}_{>0}$
, the power of a nonzero prime ideal of
$l \in \mathbb {Z}_{>0}$
, the power of a nonzero prime ideal of
![]() $\mathcal {O}$
. Note that
$\mathcal {O}$
. Note that
![]() $\mathcal {O}/\mathfrak {q}$
is a local ring.
$\mathcal {O}/\mathfrak {q}$
is a local ring.
Lemma 7.1. There exists a polynomial-time algorithm that given a unimodular vector
![]() $\mathbf {v} \in (\mathcal {O}/\mathfrak {q})^{n}$
returns elementary matrices
$\mathbf {v} \in (\mathcal {O}/\mathfrak {q})^{n}$
returns elementary matrices
![]() $E_{1},\dotsc ,E_{k} \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
such that
$E_{1},\dotsc ,E_{k} \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
such that
![]() $E_{1} \dotsm E_{k} \mathbf {v} = (x,0,\dotsc ,0)^{t}$
for some
$E_{1} \dotsm E_{k} \mathbf {v} = (x,0,\dotsc ,0)^{t}$
for some
![]() $x \in (\mathcal {O}/\mathfrak {q})^{\times }$
.
$x \in (\mathcal {O}/\mathfrak {q})^{\times }$
.
Proof. Write
![]() $\mathbf {v} = (v_1,\dotsc ,v_n)^t$
. Note that as
$\mathbf {v} = (v_1,\dotsc ,v_n)^t$
. Note that as
![]() $\mathcal {O}/\mathfrak {q}$
is local;
$\mathcal {O}/\mathfrak {q}$
is local;
![]() $\mathbf {v}$
being unimodular implies that there exists
$\mathbf {v}$
being unimodular implies that there exists
![]() $1 \leq i \leq n$
such that
$1 \leq i \leq n$
such that
![]() $v_i \in (\mathcal {O}/\mathfrak {q})^\times $
.
$v_i \in (\mathcal {O}/\mathfrak {q})^\times $
.
Case 1: If
![]() $v_1 \in (\mathcal {O}/\mathfrak {q})^\times $
, then
$v_1 \in (\mathcal {O}/\mathfrak {q})^\times $
, then
![]() $e_{21}(-v_1^{-1}v_2) \dotsm e_{n1}(-v_1^{-1}v_n) \mathbf {v}$
has the required form.
$e_{21}(-v_1^{-1}v_2) \dotsm e_{n1}(-v_1^{-1}v_n) \mathbf {v}$
has the required form.
Case 2: If
![]() $v_i \in (\mathcal {O}/\mathfrak {q})^\times $
with
$v_i \in (\mathcal {O}/\mathfrak {q})^\times $
with
![]() $1 < i \leq n$
, then after multiplying
$1 < i \leq n$
, then after multiplying
![]() $\mathbf {v}$
by
$\mathbf {v}$
by
![]() $e_{1i}(1) e_{i1}(-1) e_{1i}(1)$
on the left, the first entry will be invertible and we are in the first case.
$e_{1i}(1) e_{i1}(-1) e_{1i}(1)$
on the left, the first entry will be invertible and we are in the first case.
Lemma 7.2. There exists a polynomial-time algorithm that given a matrix
![]() $V \in \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {q})$
returns elementary matrices
$V \in \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {q})$
returns elementary matrices
![]() $E_{1},\dotsc ,E_{k} \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
such that
$E_{1},\dotsc ,E_{k} \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
such that
![]() $E_{1} \dotsm E_{k} V$
is upper triangular. If V is lower triangular, then
$E_{1} \dotsm E_{k} V$
is upper triangular. If V is lower triangular, then
![]() $E_{1} \dotsm E_{k} V$
is diagonal.
$E_{1} \dotsm E_{k} V$
is diagonal.
Proof. The first part follows by repeatedly applying Lemma 7.1 to V and submatrices of V. If V is lower triangular, then we are always in Case 1 of the proof of Lemma 7.1 and thus easily see that the resulting matrix is diagonal.
As we will see below, the previous results allow us to transform unimodular matrices into diagonal matrices. Thus, it remains to consider unimodular diagonal matrices.
Lemma 7.3. There exists a polynomial-time algorithm that given
![]() $V = \operatorname {diag}(v_1,\dotsc ,v_n) \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
with
$V = \operatorname {diag}(v_1,\dotsc ,v_n) \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
with
![]() $\prod _{1 \leq i \leq n} v_i = 1$
returns elementary matrices
$\prod _{1 \leq i \leq n} v_i = 1$
returns elementary matrices
![]() $E_{1}, \dotsc , E_{k} \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
such that
$E_{1}, \dotsc , E_{k} \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {q})$
such that
![]() $E_1 \dotsm E_k V$
is the
$E_1 \dotsm E_k V$
is the
![]() $n \times n$
identity matrix.
$n \times n$
identity matrix.
Proof. From [Reference RosenbergRos94, 2.1.3 Corollary] it follows that a diagonal matrix with diagonal
![]() $(1,\dotsc ,1,v,v^{-1},1,\dotsc ,1)$
with
$(1,\dotsc ,1,v,v^{-1},1,\dotsc ,1)$
with
![]() $v \in (\mathcal {O}/\mathfrak {q})^\times $
is the product of six elementary matrices since
$v \in (\mathcal {O}/\mathfrak {q})^\times $
is the product of six elementary matrices since
 $$\begin{align*}\begin{pmatrix} v & 0 \\ 0 & v^{-1} \end{pmatrix} = \begin{pmatrix} 1 & v \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ -v^{-1} & 1 \end{pmatrix} \begin{pmatrix} 1 & v \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} v & 0 \\ 0 & v^{-1} \end{pmatrix} = \begin{pmatrix} 1 & v \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ -v^{-1} & 1 \end{pmatrix} \begin{pmatrix} 1 & v \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix}. \end{align*}$$
Hence, we can left-multiply V with
![]() $6(n - 1)$
elementary matrices to obtain
$6(n - 1)$
elementary matrices to obtain
![]() $(1,1,\dotsc ,1)^t$
.
$(1,1,\dotsc ,1)^t$
.
Proposition 7.4. There exists a polynomial-time algorithm that given a matrix
![]() $V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {q})$
returns elementary matrices
$V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {q})$
returns elementary matrices
![]() $E_1,\dotsc ,E_k, F_1,\dotsc ,F_l \in \mathrm {Mat}_n(\mathcal {O}/\mathfrak {q})$
such that
$E_1,\dotsc ,E_k, F_1,\dotsc ,F_l \in \mathrm {Mat}_n(\mathcal {O}/\mathfrak {q})$
such that
![]() $E_1\dotsm E_k V F_1\dotsc F_l$
is the
$E_1\dotsm E_k V F_1\dotsc F_l$
is the
![]() $n \times n$
identity matrix.
$n \times n$
identity matrix.
Proof. Using Lemma 7.2 there exist elementary matrices
![]() $E_1, \dotsc ,E_{k'}$
such that
$E_1, \dotsc ,E_{k'}$
such that
![]() $U := E_1\dotsm E_{k'} V$
is an upper triangular matrix. Using Lemma 7.2 again, this time applied to the lower diagonal matrix
$U := E_1\dotsm E_{k'} V$
is an upper triangular matrix. Using Lemma 7.2 again, this time applied to the lower diagonal matrix
![]() $U^t$
, we can find elementary matrices
$U^t$
, we can find elementary matrices
![]() $F_1,\dotsc ,F_l$
such that
$F_1,\dotsc ,F_l$
such that
![]() $D = UF_1\dotsm F_l$
is a diagonal matrix. Finally, invoking Lemma 7.3 yields elementary matrices
$D = UF_1\dotsm F_l$
is a diagonal matrix. Finally, invoking Lemma 7.3 yields elementary matrices
![]() $\tilde E_1,\dotsc ,\tilde E_{\tilde k}$
such that
$\tilde E_1,\dotsc ,\tilde E_{\tilde k}$
such that
![]() $\tilde E_1\dotsm \tilde E_{\tilde k} D$
is the
$\tilde E_1\dotsm \tilde E_{\tilde k} D$
is the
![]() $n \times n$
identity matrix.
$n \times n$
identity matrix.
Corollary 7.5. There exists a polynomial-time algorithm that given the factorisation of
![]() $\mathfrak {g}$
and a matrix
$\mathfrak {g}$
and a matrix
![]() $V \in \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
returns elementary matrices
$V \in \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
returns elementary matrices
![]() $E_1,\dotsc ,E_k \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {g})$
such that
$E_1,\dotsc ,E_k \in \mathrm {Mat}_{n}(\mathcal {O}/\mathfrak {g})$
such that
![]() $V = E_1\dotsm E_k$
.
$V = E_1\dotsm E_k$
.
Proof. In the case that
![]() $\mathfrak {g}$
is a prime ideal power, this follows from Proposition 7.4. Now, let
$\mathfrak {g}$
is a prime ideal power, this follows from Proposition 7.4. Now, let
![]() $\mathfrak {g} = \mathfrak {q}_{1}\dotsm \mathfrak {q}_{m}$
be the product of m coprime prime ideal powers, and consider a matrix
$\mathfrak {g} = \mathfrak {q}_{1}\dotsm \mathfrak {q}_{m}$
be the product of m coprime prime ideal powers, and consider a matrix
![]() $V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {g})$
. For each
$V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {g})$
. For each
![]() $1 \leq i \leq m$
we can determine in polynomial time a factorisation of
$1 \leq i \leq m$
we can determine in polynomial time a factorisation of
![]() $V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {q}_i)$
into elementary matrices. The result follows by observing that the canonical map
$V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {q}_i)$
into elementary matrices. The result follows by observing that the canonical map
 $$\begin{align*}\mathrm{E}_n(\mathcal{O}/\mathfrak{g}) \to \prod_{i=1}^m \mathrm{E}_n(\mathcal{O}/\mathfrak{q}_i) \end{align*}$$
$$\begin{align*}\mathrm{E}_n(\mathcal{O}/\mathfrak{g}) \to \prod_{i=1}^m \mathrm{E}_n(\mathcal{O}/\mathfrak{q}_i) \end{align*}$$
is an isomorphism by the Chinese remainder theorem which can be made effective in polynomial time ([Reference CohenCoh00, Proposition 1.3.11]).
Since we can trivially lift elementary matrices along the canonical map
![]() $f_{1}: \mathrm {SL}_{n}(\mathcal {O}) \to \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {\mathfrak {g}})$
, the same is true for arbitrary matrices in
$f_{1}: \mathrm {SL}_{n}(\mathcal {O}) \to \mathrm {SL}_{n}(\mathcal {O}/\mathfrak {\mathfrak {g}})$
, the same is true for arbitrary matrices in
![]() $\mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
.
$\mathrm {SL}_{n}(\mathcal {O}/\mathfrak {g})$
.
Corollary 7.6. There exists a polynomial-time algorithm that given the factorisation of
![]() $\mathfrak {g}$
and a matrix
$\mathfrak {g}$
and a matrix
![]() $V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {g})$
returns
$V \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {g})$
returns
![]() $U \in \mathrm {SL}_n(\mathcal {O})$
such that
$U \in \mathrm {SL}_n(\mathcal {O})$
such that
![]() $f_{1}(U) = V$
.
$f_{1}(U) = V$
.
7.2 Lifting norm one units for nice maximal orders
We now consider the case in which
![]() $A = \mathrm {Mat}_{n}(K)$
and
$A = \mathrm {Mat}_{n}(K)$
and
![]() $\mathcal {M} = \mathcal {M}_{\mathfrak a,n}$
is a nice maximal order as defined in §6.2, where
$\mathcal {M} = \mathcal {M}_{\mathfrak a,n}$
is a nice maximal order as defined in §6.2, where
![]() $\mathfrak {a}$
is a nonzero fractional ideal of
$\mathfrak {a}$
is a nonzero fractional ideal of
![]() $\mathcal {O}$
and
$\mathcal {O}$
and
![]() $n \in \mathbb {Z}_{\geq 2}$
. (As in §7.1, the case
$n \in \mathbb {Z}_{\geq 2}$
. (As in §7.1, the case
![]() $n=1$
is trivial.) Some of the ideas used here are based on [Reference Bley and JohnstonBJ08, §6].
$n=1$
is trivial.) Some of the ideas used here are based on [Reference Bley and JohnstonBJ08, §6].
Let
![]() $\mathfrak {b}$
be an integral ideal of
$\mathfrak {b}$
be an integral ideal of
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
![]() $\mathfrak {b} + \mathfrak {g} = \mathcal {O}$
and
$\mathfrak {b} + \mathfrak {g} = \mathcal {O}$
and
![]() $\mathfrak {a} = \xi \mathfrak {b}$
for some
$\mathfrak {a} = \xi \mathfrak {b}$
for some
![]() $\xi \in K^{\times }$
. Such an ideal
$\xi \in K^{\times }$
. Such an ideal
![]() $\mathfrak {b}$
and element
$\mathfrak {b}$
and element
![]() $\xi $
can be computed in probabilistic polynomial time, as shown in Corollary A.2. Let
$\xi $
can be computed in probabilistic polynomial time, as shown in Corollary A.2. Let
![]() $b \in \mathfrak b, y \in \mathfrak {g}$
such that
$b \in \mathfrak b, y \in \mathfrak {g}$
such that
![]() $b + y = 1$
, and let
$b + y = 1$
, and let
![]() $R=\mathcal {O}/\mathfrak {g}$
. Then we have an isomorphism
$R=\mathcal {O}/\mathfrak {g}$
. Then we have an isomorphism
![]() $\mathcal {O}/\mathfrak {g} \rightarrow \mathfrak {a}/\mathfrak {a}\mathfrak {g}$
of R-modules defined by
$\mathcal {O}/\mathfrak {g} \rightarrow \mathfrak {a}/\mathfrak {a}\mathfrak {g}$
of R-modules defined by
![]() $z + \mathfrak {g} \mapsto zb\xi + \mathfrak {a}\mathfrak {g}$
, with the inverse map given by
$z + \mathfrak {g} \mapsto zb\xi + \mathfrak {a}\mathfrak {g}$
, with the inverse map given by
![]() $x + \mathfrak {a}\mathfrak {g} \mapsto \xi ^{-1}x + \mathfrak {g}$
. The first of these maps induces an isomorphism
$x + \mathfrak {a}\mathfrak {g} \mapsto \xi ^{-1}x + \mathfrak {g}$
. The first of these maps induces an isomorphism
![]() $\theta _{1} : R^{\oplus n} \rightarrow R^{\oplus n-1} \oplus \mathfrak {a}/\mathfrak {a}\mathfrak {g}$
of R-modules, and the second map induces an inverse
$\theta _{1} : R^{\oplus n} \rightarrow R^{\oplus n-1} \oplus \mathfrak {a}/\mathfrak {a}\mathfrak {g}$
of R-modules, and the second map induces an inverse
![]() $\theta _{2}$
. Define
$\theta _{2}$
. Define
![]() $n \times n$
diagonal matrices
$n \times n$
diagonal matrices
![]() $\Phi _{1} = \operatorname {diag}(1, \ldots , 1, \xi ^{-1})$
and
$\Phi _{1} = \operatorname {diag}(1, \ldots , 1, \xi ^{-1})$
and
![]() $\Phi _{2} = \operatorname {diag}(1, \ldots , 1, b\xi )$
. Then we have maps
$\Phi _{2} = \operatorname {diag}(1, \ldots , 1, b\xi )$
. Then we have maps
These maps are not multiplicative in general. However, since
![]() $\theta _{1}$
and
$\theta _{1}$
and
![]() $\theta _{2}$
are mutually inverse isomorphisms, we see that
$\theta _{2}$
are mutually inverse isomorphisms, we see that
![]() $\psi _{1}$
and
$\psi _{1}$
and
![]() $\psi _{2}$
induce mutually inverse isomorphisms
$\psi _{2}$
induce mutually inverse isomorphisms
Lemma 7.7. Let
![]() $\overline {E} \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {g})$
be an elementary matrix. Then
$\overline {E} \in \mathrm {SL}_n(\mathcal {O}/\mathfrak {g})$
be an elementary matrix. Then
![]() $\overline {\psi }_{1}(\overline {E})$
can be lifted to an element
$\overline {\psi }_{1}(\overline {E})$
can be lifted to an element
![]() $U \in \mathcal {M}^\times $
with
$U \in \mathcal {M}^\times $
with
![]() $\mathrm {nr}(U) = 1$
.
$\mathrm {nr}(U) = 1$
.
Proof. For
![]() $V \in \mathrm {Mat}_n(\mathcal {O})$
we write
$V \in \mathrm {Mat}_n(\mathcal {O})$
we write
 $$\begin{align*}\def\arraystretch{1.2} V = \left( \begin{array}{c|c}V_1 & x \\ \hline y & d \end{array} \right) \end{align*}$$
$$\begin{align*}\def\arraystretch{1.2} V = \left( \begin{array}{c|c}V_1 & x \\ \hline y & d \end{array} \right) \end{align*}$$
with
![]() $V_1 \in \mathrm {Mat}_{n-1}(\mathcal {O}), x,y^t \in \mathcal {O}^{n-1}$
and
$V_1 \in \mathrm {Mat}_{n-1}(\mathcal {O}), x,y^t \in \mathcal {O}^{n-1}$
and
![]() $d \in \mathcal {O}$
. Then
$d \in \mathcal {O}$
. Then
 $$\begin{align*}\def\arraystretch{1.2} \psi_{1}(V) = \left( \begin{array}{c|c}V_1 & \xi^{-1}x \\ \hline \xi b y & bd \end{array} \right). \end{align*}$$
$$\begin{align*}\def\arraystretch{1.2} \psi_{1}(V) = \left( \begin{array}{c|c}V_1 & \xi^{-1}x \\ \hline \xi b y & bd \end{array} \right). \end{align*}$$
Let
![]() $I_m \in \mathrm {Mat}_m(\mathcal {O})$
denote the identity matrix.
$I_m \in \mathrm {Mat}_m(\mathcal {O})$
denote the identity matrix.
Case 1: If
 $\def \arraystretch {1.2} \overline {E} = \left ( \begin {array}{c|c} e_{ij}(\bar a) & 0 \\ \hline 0 & 1 \end {array} \right ) $
with
$\def \arraystretch {1.2} \overline {E} = \left ( \begin {array}{c|c} e_{ij}(\bar a) & 0 \\ \hline 0 & 1 \end {array} \right ) $
with
![]() $a \in \mathcal {O}$
, then
$a \in \mathcal {O}$
, then
 $\def \arraystretch {1.2} \overline {\psi }_1(\overline {E}) = \left ( \begin {array}{c|c} e_{ij}(\bar a) & 0 \\ \hline 0 & \bar b \end {array} \right ) $
and a lift is given by
$\def \arraystretch {1.2} \overline {\psi }_1(\overline {E}) = \left ( \begin {array}{c|c} e_{ij}(\bar a) & 0 \\ \hline 0 & \bar b \end {array} \right ) $
and a lift is given by
 $$\begin{align*}\left( \begin{array}{c|c} e_{ij}(a) & 0 \\ \hline 0 & 1 \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{c|c} e_{ij}(a) & 0 \\ \hline 0 & 1 \end{array} \right). \end{align*}$$
Case 2: If
 $\def \arraystretch {1.2} \overline {E} = \left ( \begin {array}{c|c} \overline {I}_{n-1} & \bar x \\ \hline 0 & 1 \end {array} \right ) $
with
$\def \arraystretch {1.2} \overline {E} = \left ( \begin {array}{c|c} \overline {I}_{n-1} & \bar x \\ \hline 0 & 1 \end {array} \right ) $
with
![]() $\bar x^t = (0,\ldots ,0,\bar a, 0, \ldots , 0), a \in \mathcal {O}$
, then
$\bar x^t = (0,\ldots ,0,\bar a, 0, \ldots , 0), a \in \mathcal {O}$
, then
 $\def \arraystretch {1.2} \overline {\psi }_{1}(\overline {E}) = \left ( \begin {array}{c|c} \overline {I}_{n-1} & \overline {\xi ^{-1} x}\\ \hline 0 & \bar b \end {array} \right ) $
and a lift is given by
$\def \arraystretch {1.2} \overline {\psi }_{1}(\overline {E}) = \left ( \begin {array}{c|c} \overline {I}_{n-1} & \overline {\xi ^{-1} x}\\ \hline 0 & \bar b \end {array} \right ) $
and a lift is given by
 $$\begin{align*}\left( \begin{array}{c|c} I_{n-1} & {\xi^{-1} x}\\ \hline 0 & 1 \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{c|c} I_{n-1} & {\xi^{-1} x}\\ \hline 0 & 1 \end{array} \right). \end{align*}$$
Note that in this case
![]() $\xi ^{-1}a \in \mathfrak {b}\mathfrak {a}^{-1} \subseteq \mathfrak {a}^{-1}$
.
$\xi ^{-1}a \in \mathfrak {b}\mathfrak {a}^{-1} \subseteq \mathfrak {a}^{-1}$
.
Case 3: If
 $\overline {E} = \left ( \begin {array}{c|c} \overline {I}_{n-1} & 0 \\ \hline \bar y & 1 \end {array} \right )$
with
$\overline {E} = \left ( \begin {array}{c|c} \overline {I}_{n-1} & 0 \\ \hline \bar y & 1 \end {array} \right )$
with
![]() $\bar y = (0,\ldots ,0,\bar a, 0, \ldots , 0), a \in \mathcal {O}$
, then
$\bar y = (0,\ldots ,0,\bar a, 0, \ldots , 0), a \in \mathcal {O}$
, then
 $\def \arraystretch {1.2} \psi _{1}(\overline {E}) = \left ( \begin {array}{c|c} \overline {I}_{n-1} & 0 \\ \hline \overline {\xi by} & \bar b \end {array} \right )$
and a lift is given by
$\def \arraystretch {1.2} \psi _{1}(\overline {E}) = \left ( \begin {array}{c|c} \overline {I}_{n-1} & 0 \\ \hline \overline {\xi by} & \bar b \end {array} \right )$
and a lift is given by
 $$\begin{align*}\left( \begin{array}{c|c} I_{n-1} & 0 \\ \hline \xi by & 1 \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{c|c} I_{n-1} & 0 \\ \hline \xi by & 1 \end{array} \right). \end{align*}$$
Here we note that
![]() $\xi ba \in \xi \mathfrak {b} = \mathfrak {a}$
.
$\xi ba \in \xi \mathfrak {b} = \mathfrak {a}$
.
Proposition 7.8. For
![]() $A = \mathrm {Mat}_{n}(K)$
let
$A = \mathrm {Mat}_{n}(K)$
let
![]() $\mathcal {M} = \mathcal {M}_{\mathfrak a,n} \subseteq A$
be a nice maximal order. Then there exists a probabilistic polynomial-time algorithm that given the factorisation of
$\mathcal {M} = \mathcal {M}_{\mathfrak a,n} \subseteq A$
be a nice maximal order. Then there exists a probabilistic polynomial-time algorithm that given the factorisation of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $V \in \mathrm {SL}(\mathcal {M}/\mathfrak {g}\mathcal {M})$
returns
$V \in \mathrm {SL}(\mathcal {M}/\mathfrak {g}\mathcal {M})$
returns
![]() $U \in \mathrm {SL}(\mathcal {M})$
with
$U \in \mathrm {SL}(\mathcal {M})$
with
![]() $f_{1}(U) = V$
.
$f_{1}(U) = V$
.
Proof. By Corollary 7.5 we can find elementary matrices
![]() $E_1,\dotsc ,E_r \in \mathrm {Mat}_n(\mathcal {O}/\mathfrak {g})$
with
$E_1,\dotsc ,E_r \in \mathrm {Mat}_n(\mathcal {O}/\mathfrak {g})$
with
![]() $\overline {\psi }_2(V) = E_1\dotsm E_r$
. Applying
$\overline {\psi }_2(V) = E_1\dotsm E_r$
. Applying
![]() $\overline {\psi }_{1}$
we obtain
$\overline {\psi }_{1}$
we obtain
![]() $V = \overline {\psi }_1(E_1)\dotsm \overline {\psi }_1(E_r)$
. Moreover, by Lemma 7.7, each of the matrices
$V = \overline {\psi }_1(E_1)\dotsm \overline {\psi }_1(E_r)$
. Moreover, by Lemma 7.7, each of the matrices
![]() $\overline {\psi }_1(E_i)$
can be lifted to a matrix
$\overline {\psi }_1(E_i)$
can be lifted to a matrix
![]() $U_i \in \mathcal {M}^\times $
with
$U_i \in \mathcal {M}^\times $
with
![]() $\mathrm {nr}(U_{i}) = 1$
. Thus, we can and do take
$\mathrm {nr}(U_{i}) = 1$
. Thus, we can and do take
![]() $U := \prod _{i}U_{i}$
.
$U := \prod _{i}U_{i}$
.
7.3 Lifting norm one units in maximal orders
We now consider an arbitrary maximal order
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $A = \prod _{i=1}^{r}\mathrm {Mat}_{n_{i}}(K_{i})$
.
$A = \prod _{i=1}^{r}\mathrm {Mat}_{n_{i}}(K_{i})$
.
Theorem 7.9. The map
![]() $f_{1} \colon \mathrm {SL}(\mathcal {M}) \to \mathrm {SL}(\mathcal {M}/\mathfrak {g} \mathcal {M})$
is surjective. Moreover, there exists a probabilistic polynomial-time algorithm that given the factorisation of
$f_{1} \colon \mathrm {SL}(\mathcal {M}) \to \mathrm {SL}(\mathcal {M}/\mathfrak {g} \mathcal {M})$
is surjective. Moreover, there exists a probabilistic polynomial-time algorithm that given the factorisation of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $V \in \mathrm {SL}(\mathcal {M}/\mathfrak {g} \mathcal {M})$
returns an element
$V \in \mathrm {SL}(\mathcal {M}/\mathfrak {g} \mathcal {M})$
returns an element
![]() $U \in \mathrm {SL}(\mathcal {M})$
with
$U \in \mathrm {SL}(\mathcal {M})$
with
![]() $f_{1}(U) = V$
.
$f_{1}(U) = V$
.
Proof. By decomposing
![]() $\mathcal {M}$
using the central primitive idempotents, it is sufficient to consider the case
$\mathcal {M}$
using the central primitive idempotents, it is sufficient to consider the case
![]() $A = \mathrm {Mat}_{n}(K)$
. By Lemma 6.2, we can and do assume that
$A = \mathrm {Mat}_{n}(K)$
. By Lemma 6.2, we can and do assume that
![]() $\mathcal {M} = \mathcal {M}_{\mathfrak a, n}$
is a nice maximal order. Thus, the result follows from Proposition 7.8.
$\mathcal {M} = \mathcal {M}_{\mathfrak a, n}$
is a nice maximal order. Thus, the result follows from Proposition 7.8.
8 Isomorphism testing and the principal ideal problem
Let K be a number field with ring of integers
![]() $\mathcal {O} = {\mathcal {O}_K}$
, and let A be a finite-dimensional K-algebra satisfying hypothesis (H). Let
$\mathcal {O} = {\mathcal {O}_K}$
, and let A be a finite-dimensional K-algebra satisfying hypothesis (H). Let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}$
-order in A. In this section, we present the main algorithm for solving the isomorphism problem
$\mathcal {O}$
-order in A. In this section, we present the main algorithm for solving the isomorphism problem
![]() $\mathsf {IsIsomorphic}$
for lattices over
$\mathsf {IsIsomorphic}$
for lattices over
![]() $\Lambda $
.
$\Lambda $
.
We begin with two straightforward reductions which together show that it suffices to consider the problem
![]() $\mathsf {IsPrincipal}$
in the case that A is semisimple. Note that these reductions are valid when A is an arbitrary finite-dimensional K-algebra that does not necessarily satisfy hypothesis (H).
$\mathsf {IsPrincipal}$
in the case that A is semisimple. Note that these reductions are valid when A is an arbitrary finite-dimensional K-algebra that does not necessarily satisfy hypothesis (H).
Proposition 8.1. The problem
![]() $\mathsf {IsIsomorphic}$
is polynomial-time reducible to
$\mathsf {IsIsomorphic}$
is polynomial-time reducible to
![]() $\mathsf {IsPrincipal}$
. More precisely, for
$\mathsf {IsPrincipal}$
. More precisely, for
![]() $\Lambda $
-lattices X and Y, the problem
$\Lambda $
-lattices X and Y, the problem
![]() $\mathsf {IsIsomorphic}$
is polynomial-time reducible to
$\mathsf {IsIsomorphic}$
is polynomial-time reducible to
![]() $\mathsf {IsPrincipal}$
for an
$\mathsf {IsPrincipal}$
for an
![]() $\mathrm {End}_\Lambda (Y)$
-lattice in
$\mathrm {End}_\Lambda (Y)$
-lattice in
![]() $\mathrm {End}_A(KY)$
.
$\mathrm {End}_A(KY)$
.
Proof. Let X and Y be two
![]() $\Lambda $
-lattices. By [Reference Chistov, Ivanyos and KarpinskiCIK97, Corollary 3] we can check in polynomial time whether the A-modules
$\Lambda $
-lattices. By [Reference Chistov, Ivanyos and KarpinskiCIK97, Corollary 3] we can check in polynomial time whether the A-modules
![]() $KX$
and
$KX$
and
![]() $KY$
are isomorphic and, if so, compute an isomorphism
$KY$
are isomorphic and, if so, compute an isomorphism
![]() $f \colon KY \to KX$
. Then
$f \colon KY \to KX$
. Then
![]() $\Phi \colon \mathrm {Hom}_A(KX, KY) \to \mathrm {End}_A(KY), \, g \mapsto g \circ f$
is an isomorphism of
$\Phi \colon \mathrm {Hom}_A(KX, KY) \to \mathrm {End}_A(KY), \, g \mapsto g \circ f$
is an isomorphism of
![]() $\mathrm {End}_A(KY)$
-modules. Recall from §3.1 that we consider
$\mathrm {End}_A(KY)$
-modules. Recall from §3.1 that we consider
![]() $\mathrm {Hom}_\Lambda (X, Y)$
as a subset of
$\mathrm {Hom}_\Lambda (X, Y)$
as a subset of
![]() $\mathrm {Hom}_A(KX, KY)$
. Thus, by Proposition 3.1, the
$\mathrm {Hom}_A(KX, KY)$
. Thus, by Proposition 3.1, the
![]() $\Lambda $
-lattices X and Y are isomorphic if and only if the full
$\Lambda $
-lattices X and Y are isomorphic if and only if the full
![]() $\mathrm {End}_\Lambda (Y)$
-lattice
$\mathrm {End}_\Lambda (Y)$
-lattice
![]() $\Phi (\mathrm {Hom}_\Lambda (X, Y))$
in
$\Phi (\mathrm {Hom}_\Lambda (X, Y))$
in
![]() $\mathrm {End}_A(KY)$
is free of rank
$\mathrm {End}_A(KY)$
is free of rank
![]() $1$
and for every (any) free generator
$1$
and for every (any) free generator
![]() $\alpha $
the morphism
$\alpha $
the morphism
![]() $\alpha \circ f^{-1} \colon X \to Y$
is an isomorphism.
$\alpha \circ f^{-1} \colon X \to Y$
is an isomorphism.
Let
![]() $\operatorname {\mathrm {J}}(A)$
denote the Jacobson radical of A, and recall that
$\operatorname {\mathrm {J}}(A)$
denote the Jacobson radical of A, and recall that
![]() $\overline {A} := A/{\operatorname {\mathrm {J}}(A)}$
is a semisimple K-algebra by [Reference Curtis and ReinerCR81, (5.19)]. For any full
$\overline {A} := A/{\operatorname {\mathrm {J}}(A)}$
is a semisimple K-algebra by [Reference Curtis and ReinerCR81, (5.19)]. For any full
![]() $\Lambda $
-lattice X in A, let
$\Lambda $
-lattice X in A, let
![]() $\overline {X}$
denote its image under the canonical projection map
$\overline {X}$
denote its image under the canonical projection map
![]() $A \rightarrow \overline {A}$
. Note that
$A \rightarrow \overline {A}$
. Note that
![]() $\overline {\Lambda }$
is an
$\overline {\Lambda }$
is an
![]() $\mathcal {O}$
-order in
$\mathcal {O}$
-order in
![]() $\overline {A}$
.
$\overline {A}$
.
Proposition 8.2. The problem
![]() $\mathsf {IsPrincipal}$
for an arbitrary finite-dimensional K-algebra is polynomial-time reducible to
$\mathsf {IsPrincipal}$
for an arbitrary finite-dimensional K-algebra is polynomial-time reducible to
![]() $\mathsf {IsPrincipal}$
for a finite-dimensional semisimple K-algebra. More precisely, for a full
$\mathsf {IsPrincipal}$
for a finite-dimensional semisimple K-algebra. More precisely, for a full
![]() $\Lambda $
-lattice X in A, the problem
$\Lambda $
-lattice X in A, the problem
![]() $\mathsf {IsPrincipal}$
is polynomial-time reducible to the problem
$\mathsf {IsPrincipal}$
is polynomial-time reducible to the problem
![]() $\mathsf {IsPrincipal}$
for the full
$\mathsf {IsPrincipal}$
for the full
![]() $\overline {\Lambda }$
-lattice
$\overline {\Lambda }$
-lattice
![]() $\overline {X}$
in
$\overline {X}$
in
![]() $\overline {A}$
.
$\overline {A}$
.
Proof. The Jacobson radical of A can be computed in polynomial time by [Reference Friedl and RonyaiFR85, 1.5 A]. The result then follows from Theorem 3.4.
The main algorithm of the present article is as follows.
Algorithm 8.3. Suppose that A is semisimple and satisfies hypothesis (H). Let X be a full
![]() $\Lambda $
-lattice in A. The following steps solve
$\Lambda $
-lattice in A. The following steps solve
![]() $\textsf {IsPrincipal}(X)$
, that is, they determine whether there exists
$\textsf {IsPrincipal}(X)$
, that is, they determine whether there exists
![]() $\alpha \in X$
such that
$\alpha \in X$
such that
![]() $X=\Lambda \alpha $
and, if so, return such an element
$X=\Lambda \alpha $
and, if so, return such an element
![]() $\alpha $
.
$\alpha $
.
-
(1) Determine the centre C of A, the decomposition
 $A = \prod _{i} A_i$
into simple K-algebras
$A = \prod _{i} A_i$
into simple K-algebras
 $A_i$
and, for each i, an isomorphism
$A_i$
and, for each i, an isomorphism
 $A_i \cong \mathrm {Mat}_{n_i}(K_i)$
.
$A_i \cong \mathrm {Mat}_{n_i}(K_i)$
. -
(2) Compute a maximal
 $\mathcal {O}$
-order
$\mathcal {O}$
-order
 $\mathcal {M}$
in A containing
$\mathcal {M}$
in A containing
 $\Lambda $
and its centre
$\Lambda $
and its centre
 $\mathcal {O}_{C} := \mathcal {M} \cap C$
.
$\mathcal {O}_{C} := \mathcal {M} \cap C$
. -
(3) Compute the central primitive idempotents
 $e_{i}$
and the components
$e_{i}$
and the components
 $\mathcal {M}_{i}:=\mathcal {M} e_{i}$
.
$\mathcal {M}_{i}:=\mathcal {M} e_{i}$
. -
(4) Compute the central conductor
 $\mathfrak {g} := \{ x \in C \mid x\mathcal {M} \subseteq \Lambda \}$
of
$\mathfrak {g} := \{ x \in C \mid x\mathcal {M} \subseteq \Lambda \}$
of
 $\Lambda $
in
$\Lambda $
in
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $\mathfrak {f} := \mathfrak {g}\mathcal {M}$
.
$\mathfrak {f} := \mathfrak {g}\mathcal {M}$
. -
(5) Check whether
 $\mathcal {M}X$
is free over
$\mathcal {M}X$
is free over
 $\mathcal {M}$
, and if so, compute
$\mathcal {M}$
, and if so, compute
 $\beta $
such that
$\beta $
such that
 $\mathcal {M} X = \mathcal {M} \beta $
.
$\mathcal {M} X = \mathcal {M} \beta $
. -
(6) Check whether X is locally free over
 $\Lambda $
.
$\Lambda $
. -
(7) Replace X by
 $X \xi $
, where
$X \xi $
, where
 $\xi \in A^\times $
is such that
$\xi \in A^\times $
is such that
 $X\xi \subseteq \Lambda $
and
$X\xi \subseteq \Lambda $
and
 $X\xi + \mathfrak {f} = \Lambda $
.
$X\xi + \mathfrak {f} = \Lambda $
. -
(8) Compute a set of generators for
 $\left ( \Lambda / \mathfrak {f}\right )^\times $
.
$\left ( \Lambda / \mathfrak {f}\right )^\times $
. -
(9) Let
 $\overline {\mathrm {nr}} \colon \left ( \mathcal {M} / \mathfrak {f}\right )^\times \longrightarrow \left ( \mathcal {O}_C/\mathfrak {g} \right )^{\times }$
be the map of Lemma 4.4. Compute
$\overline {\mathrm {nr}} \colon \left ( \mathcal {M} / \mathfrak {f}\right )^\times \longrightarrow \left ( \mathcal {O}_C/\mathfrak {g} \right )^{\times }$
be the map of Lemma 4.4. Compute
 $\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
as an abstract abelian group and compute
$\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
as an abstract abelian group and compute
 $\overline {\mathrm {nr}}\left ( (\Lambda / \mathfrak {f})^\times \right )$
as a subgroup of
$\overline {\mathrm {nr}}\left ( (\Lambda / \mathfrak {f})^\times \right )$
as a subgroup of
 $\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
.
$\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
. -
(10) Let
 $\pi _{2}$
and
$\pi _{2}$
and
 $f_2$
be the maps defined in the commutative diagram (4). Decide whether
$f_2$
be the maps defined in the commutative diagram (4). Decide whether
 $\overline {\mathrm {nr}}(\overline \beta )$
is in the image of
$\overline {\mathrm {nr}}(\overline \beta )$
is in the image of
 $\pi _2\circ f_2$
, and if so, compute
$\pi _2\circ f_2$
, and if so, compute
 $\bar a \in \left ( \Lambda / \mathfrak {f}\right )^\times $
and
$\bar a \in \left ( \Lambda / \mathfrak {f}\right )^\times $
and
 $u \in \mathcal {M}^\times $
such that
$u \in \mathcal {M}^\times $
such that
 $\overline {\mathrm {nr}}(\overline {\beta a}) = \overline {\mathrm {nr}}(\bar u)$
.
$\overline {\mathrm {nr}}(\overline {\beta a}) = \overline {\mathrm {nr}}(\bar u)$
. -
(11) Compute
 $v \in \mathrm {SL}(\mathcal {M})$
such that
$v \in \mathrm {SL}(\mathcal {M})$
such that
 $\overline {\beta a u^{-1}} = \overline v$
.
$\overline {\beta a u^{-1}} = \overline v$
.
If any of steps (5), (6) or (10) fail, then X is not free over
![]() $\Lambda $
. If all these steps succeed, then
$\Lambda $
. If all these steps succeed, then
![]() $X = \Lambda \alpha $
where
$X = \Lambda \alpha $
where
![]() $\alpha := (vu)^{-1}\beta $
.
$\alpha := (vu)^{-1}\beta $
.
Proof of correctness of Algorithm 8.3
Failure of steps (5) or (6) immediately implies that X is not free over
![]() $\Lambda $
. Otherwise, we use the local bases computed in step (6) to replace X by
$\Lambda $
. Otherwise, we use the local bases computed in step (6) to replace X by
![]() $X\xi $
in step (7), as described in Proposition 6.8 and its proof. After successful completion of steps (1) to (7), we then can and do assume that X is a locally free full
$X\xi $
in step (7), as described in Proposition 6.8 and its proof. After successful completion of steps (1) to (7), we then can and do assume that X is a locally free full
![]() $\Lambda $
-lattice in A such that
$\Lambda $
-lattice in A such that
![]() $X+\mathfrak {f} = \Lambda $
and
$X+\mathfrak {f} = \Lambda $
and
![]() $\mathcal {M} X = \mathcal {M}\beta $
. These are the assumptions needed for Theorem 4.5. Moreover, since A is semisimple and satisfies hypothesis (H), the map
$\mathcal {M} X = \mathcal {M}\beta $
. These are the assumptions needed for Theorem 4.5. Moreover, since A is semisimple and satisfies hypothesis (H), the map
![]() $f_1$
in diagram (4) is surjective by Theorem 7.9, and so Theorem 4.5 (b) can be applied. Hence, X is free over
$f_1$
in diagram (4) is surjective by Theorem 7.9, and so Theorem 4.5 (b) can be applied. Hence, X is free over
![]() $\Lambda $
if and only if
$\Lambda $
if and only if
![]() $\overline {\mathrm {nr}}(\overline \beta )$
is contained in the image of
$\overline {\mathrm {nr}}(\overline \beta )$
is contained in the image of
![]() $\pi _2\circ f_2$
. This is precisely what is checked in step (10). In addition, the second part of Theorem 4.5 (b) implies that
$\pi _2\circ f_2$
. This is precisely what is checked in step (10). In addition, the second part of Theorem 4.5 (b) implies that
![]() $X = \Lambda \alpha $
with
$X = \Lambda \alpha $
with
![]() $\alpha $
as at the end of Algorithm 8.3.
$\alpha $
as at the end of Algorithm 8.3.
The following result analyses the complexity of Algorithm 8.3, and further details on each step are given in the proof.
Theorem 8.4. Let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $\mathcal {O}$
-order in a finite-dimensional semisimple K-algebra A satisfying hypothesis (H), and let
$\mathcal {O}$
-order in a finite-dimensional semisimple K-algebra A satisfying hypothesis (H), and let
![]() $K_{1}, \ldots , K_{r}$
be the simple components of the centre of A. Let
$K_{1}, \ldots , K_{r}$
be the simple components of the centre of A. Let
![]() $\mathcal {M}$
be any choice of maximal
$\mathcal {M}$
be any choice of maximal
![]() $\mathcal {O}$
-order in A containing
$\mathcal {O}$
-order in A containing
![]() $\Lambda $
, and let
$\Lambda $
, and let
![]() $\mathfrak {h} = [\mathcal {M} : \Lambda ]_{\mathcal {O}}$
be the module index of
$\mathfrak {h} = [\mathcal {M} : \Lambda ]_{\mathcal {O}}$
be the module index of
![]() $\Lambda $
in
$\Lambda $
in
![]() $\mathcal {M}$
. Then for a full
$\mathcal {M}$
. Then for a full
![]() $\Lambda $
-lattice X in A, Algorithm 8.3 reduces the problem
$\Lambda $
-lattice X in A, Algorithm 8.3 reduces the problem
![]() $\mathsf {IsPrincipal}(X)$
in probabilistic polynomial time to
$\mathsf {IsPrincipal}(X)$
in probabilistic polynomial time to
-
(a)
 $\mathsf {Wedderburn}(A)$
, the computation of the Wedderburn decomposition of A,
$\mathsf {Wedderburn}(A)$
, the computation of the Wedderburn decomposition of A, -
(b)
 $\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
, the factorisation of the discriminant of
$\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
, the factorisation of the discriminant of
 $\Lambda $
,
$\Lambda $
, -
(c) for each i with
 $1 \leq i \leq r$
, one instance of
$1 \leq i \leq r$
, one instance of
 $\mathsf {IsPrincipal}_{\mathcal O_{K_i}}$
,
$\mathsf {IsPrincipal}_{\mathcal O_{K_i}}$
, -
(d) for each i with
 $1 \leq i \leq r$
,
$1 \leq i \leq r$
,
 $\mathsf {UnitGroup}(\mathcal O_{K_i})$
,
$\mathsf {UnitGroup}(\mathcal O_{K_i})$
, -
(e) for each prime ideal divisor
 $\mathfrak {p}$
of
$\mathfrak {p}$
of
 $\mathfrak {h}$
, the problem
$\mathfrak {h}$
, the problem
 $\mathsf {DLog}$
for extensions of
$\mathsf {DLog}$
for extensions of
 $\mathcal {O}/\mathfrak {p}$
and
$\mathcal {O}/\mathfrak {p}$
and -
(f) for each prime ideal divisor
 $\mathfrak {p}$
of
$\mathfrak {p}$
of
 $\mathfrak {h}$
, the problem
$\mathfrak {h}$
, the problem
 $\mathsf {Primitive}$
for extensions of
$\mathsf {Primitive}$
for extensions of
 $\mathcal {O}/\mathfrak {p}$
.
$\mathcal {O}/\mathfrak {p}$
.
Note that
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathfrak {h}$
are not part of the input and
$\mathfrak {h}$
are not part of the input and
![]() $\mathfrak {h}$
is only needed for the above complexity statement. Moreover,
$\mathfrak {h}$
is only needed for the above complexity statement. Moreover,
![]() $\mathfrak {h}$
does not depend on the choice of
$\mathfrak {h}$
does not depend on the choice of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. In the following, the steps refer to those of Algorithm 8.3. Let
![]() $\mathcal {M}$
be the maximal order computed in step (2), and let
$\mathcal {M}$
be the maximal order computed in step (2), and let
![]() $\mathfrak {f}$
be the ideal computed in step (4). Before analysing the steps, we make the following observations. By [Reference ReinerRei03, (25.3)],
$\mathfrak {f}$
be the ideal computed in step (4). Before analysing the steps, we make the following observations. By [Reference ReinerRei03, (25.3)],
![]() $\mathrm {Disc}(\mathcal {M})$
is independent of the choice of
$\mathrm {Disc}(\mathcal {M})$
is independent of the choice of
![]() $\mathcal {M}$
. Moreover, by [Reference Curtis and ReinerCR81, (26.3)(iii)], we have
$\mathcal {M}$
. Moreover, by [Reference Curtis and ReinerCR81, (26.3)(iii)], we have
![]() $\mathrm {Disc}(\Lambda ) = \mathfrak {h}^{2} \mathrm {Disc}(\mathcal {M})$
, and so
$\mathrm {Disc}(\Lambda ) = \mathfrak {h}^{2} \mathrm {Disc}(\mathcal {M})$
, and so
![]() $\mathrm {Disc}(\Lambda )$
and
$\mathrm {Disc}(\Lambda )$
and
![]() $\mathfrak {h}$
are also independent of the choice of
$\mathfrak {h}$
are also independent of the choice of
![]() $\mathcal {M}$
. Since
$\mathcal {M}$
. Since
![]() $\mathfrak {h}\mathcal {M} \subseteq \Lambda $
, we have
$\mathfrak {h}\mathcal {M} \subseteq \Lambda $
, we have
![]() $\mathfrak {h} \subseteq \mathfrak {g}$
for any choice of
$\mathfrak {h} \subseteq \mathfrak {g}$
for any choice of
![]() $\mathcal {M}$
. Therefore,
$\mathcal {M}$
. Therefore,
![]() $\mathrm {Disc}(\Lambda ) \subseteq \mathfrak {h}\subseteq \mathfrak {g}$
and
$\mathrm {Disc}(\Lambda ) \subseteq \mathfrak {h}\subseteq \mathfrak {g}$
and
![]() $\mathfrak {h}\Lambda \subseteq \mathfrak {f}$
. In particular,
$\mathfrak {h}\Lambda \subseteq \mathfrak {f}$
. In particular,
![]() $\mathsf {Factor}(\mathcal {O} \cap \mathfrak {f})$
and
$\mathsf {Factor}(\mathcal {O} \cap \mathfrak {f})$
and
![]() $\mathsf {Factor}(\mathfrak {g})$
reduce in polynomial time to
$\mathsf {Factor}(\mathfrak {g})$
reduce in polynomial time to
![]() $\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
.
$\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
.
Step (1) is an instance of
![]() $\mathsf {Wedderburn}$
. In step (2), the problem of computing a maximal
$\mathsf {Wedderburn}$
. In step (2), the problem of computing a maximal
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\mathcal {M}$
in A containing
$\mathcal {M}$
in A containing
![]() $\Lambda $
reduces in probabilistic polynomial time to
$\Lambda $
reduces in probabilistic polynomial time to
![]() $\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
by Proposition 6.1. It is then trivial to determine
$\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
by Proposition 6.1. It is then trivial to determine
![]() $\mathcal {O}_C = \mathcal {M} \cap C$
. Step (3) can be easily performed using the isomorphisms
$\mathcal {O}_C = \mathcal {M} \cap C$
. Step (3) can be easily performed using the isomorphisms
![]() $A_i \cong \mathrm {Mat}_{n_i}(K_i)$
from step (1). In step (4), the central conductor
$A_i \cong \mathrm {Mat}_{n_i}(K_i)$
from step (1). In step (4), the central conductor
![]() $\mathfrak {g}$
can be computed as the intersection
$\mathfrak {g}$
can be computed as the intersection
![]() $(\mathcal {M} : \Lambda )_l \cap C$
, where
$(\mathcal {M} : \Lambda )_l \cap C$
, where
![]() $(\mathcal {M} : \Lambda )_l := \{ x \in \mathcal {M} \mid x\mathcal {M} \subseteq \Lambda \}$
is the left conductor of
$(\mathcal {M} : \Lambda )_l := \{ x \in \mathcal {M} \mid x\mathcal {M} \subseteq \Lambda \}$
is the left conductor of
![]() $\Lambda $
into
$\Lambda $
into
![]() $\mathcal {M}$
. As the left conductor can be determined using a pseudo-Hermite normal form computation (see [Reference FriedrichsFri00, (2.16)]), this step can also be performed in polynomial time. Step (5) is probabilistic polynomial-time reducible to one instance of
$\mathcal {M}$
. As the left conductor can be determined using a pseudo-Hermite normal form computation (see [Reference FriedrichsFri00, (2.16)]), this step can also be performed in polynomial time. Step (5) is probabilistic polynomial-time reducible to one instance of
![]() $\mathsf {IsPrincipal}_{\mathcal O_{K_i}}$
for each
$\mathsf {IsPrincipal}_{\mathcal O_{K_i}}$
for each
![]() $1 \leq i \leq r$
, by Proposition 6.4. Steps (6) and (7) are probabilistic polynomial-time reducible to
$1 \leq i \leq r$
, by Proposition 6.4. Steps (6) and (7) are probabilistic polynomial-time reducible to
![]() $\mathsf {Factor}(\mathcal {O} \cap \mathfrak {f})$
by Proposition 6.8.
$\mathsf {Factor}(\mathcal {O} \cap \mathfrak {f})$
by Proposition 6.8.
Step (8): Proposition 6.11 shows that this is probabilistic polynomial-time reducible to
![]() $\mathsf {Factor}(\mathfrak {g})$
and for each prime ideal divisor
$\mathsf {Factor}(\mathfrak {g})$
and for each prime ideal divisor
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\mathfrak {g}$
at most d instances of
$\mathfrak {g}$
at most d instances of
![]() $\mathsf {Primitive}$
in extensions of
$\mathsf {Primitive}$
in extensions of
![]() $\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. Now, for each prime ideal
$\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. Now, for each prime ideal
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {g} \cap \mathcal {O}$
, there are at most d prime ideals
$\mathfrak {g} \cap \mathcal {O}$
, there are at most d prime ideals
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\mathcal {O}_C$
satisfying
$\mathcal {O}_C$
satisfying
![]() $\mathfrak {P} \cap \mathcal {O} = \mathfrak {p}$
. Finally, note that
$\mathfrak {P} \cap \mathcal {O} = \mathfrak {p}$
. Finally, note that
![]() $\mathfrak {g} \cap \mathcal {O}$
divides
$\mathfrak {g} \cap \mathcal {O}$
divides
![]() $\mathfrak {h}$
.
$\mathfrak {h}$
.
Step (9): It follows from [Reference CohenCoh00, Algorithms 4.2.2 and 4.2.17] that the computation of generators and the structure of
![]() $\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
as an abelian group is polynomial-time reducible to
$\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
as an abelian group is polynomial-time reducible to
![]() $\mathsf {Factor}(\mathfrak {g})$
and for each prime ideal divisor
$\mathsf {Factor}(\mathfrak {g})$
and for each prime ideal divisor
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\mathfrak {g}$
one instance of
$\mathfrak {g}$
one instance of
![]() $\mathsf {Primitive}$
in an extension
$\mathsf {Primitive}$
in an extension
![]() $\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. Estimating the number of prime ideal divisors as in the previous paragraph shows that this part contributes d instances of
$\mathcal {O}/(\mathcal {O}\cap \mathfrak {P})$
of degree at most d. Estimating the number of prime ideal divisors as in the previous paragraph shows that this part contributes d instances of
![]() $\mathsf {Primitive}$
in (e). Let
$\mathsf {Primitive}$
in (e). Let
![]() $V = \{\bar a_1, \ldots , \bar a_m\}$
be a set of generators of
$V = \{\bar a_1, \ldots , \bar a_m\}$
be a set of generators of
![]() $\left ( \Lambda / \mathfrak {f} \right )^\times $
. Let e denote the exponent of
$\left ( \Lambda / \mathfrak {f} \right )^\times $
. Let e denote the exponent of
![]() $\left ( \mathcal {O}_C / \mathfrak {g} \right )^\times $
, and let
$\left ( \mathcal {O}_C / \mathfrak {g} \right )^\times $
, and let
![]() $\mathcal {G} := \prod _{i=1}^m \mathbb {Z} / e\mathbb {Z} \cdot \bar a_i$
be the
$\mathcal {G} := \prod _{i=1}^m \mathbb {Z} / e\mathbb {Z} \cdot \bar a_i$
be the
![]() $\mathbb {Z}/e\mathbb {Z}$
-free abelian group on V. Let
$\mathbb {Z}/e\mathbb {Z}$
-free abelian group on V. Let
![]() $\overline \nu \colon \mathcal {G} \rightarrow \left ( \mathcal {O}_C / \mathfrak {g} \right )^\times $
be the homomorphism induced by
$\overline \nu \colon \mathcal {G} \rightarrow \left ( \mathcal {O}_C / \mathfrak {g} \right )^\times $
be the homomorphism induced by
![]() $\bar a_i \mapsto \overline {\mathrm {nr}}(\bar a_i)$
. Then
$\bar a_i \mapsto \overline {\mathrm {nr}}(\bar a_i)$
. Then
![]() $\mathrm {im}(\bar \nu ) = \overline {\mathrm {nr}}\left ( (\Lambda / \mathfrak {f})^\times \right )$
and we apply algorithms for finite abelian groups (see [Reference CohenCoh00, §4.1]) to compute the image. For this we have to solve the discrete logarithm in
$\mathrm {im}(\bar \nu ) = \overline {\mathrm {nr}}\left ( (\Lambda / \mathfrak {f})^\times \right )$
and we apply algorithms for finite abelian groups (see [Reference CohenCoh00, §4.1]) to compute the image. For this we have to solve the discrete logarithm in
![]() $(\mathcal {O}_C/\mathfrak {g})^\times $
for each of the m generators
$(\mathcal {O}_C/\mathfrak {g})^\times $
for each of the m generators
![]() $\bar a_1, \ldots , \bar a_m$
. By Proposition 6.11, the number m is bounded by
$\bar a_1, \ldots , \bar a_m$
. By Proposition 6.11, the number m is bounded by
![]() $5d[K:\mathbb {Q}]\log _2|\mathcal {O}_C/\mathfrak {g}|$
. Thus, the claim in part (f) follows from
$5d[K:\mathbb {Q}]\log _2|\mathcal {O}_C/\mathfrak {g}|$
. Thus, the claim in part (f) follows from
 $$ \begin{align*} |\mathcal{O}_C/\mathfrak{g}| & \leq |\mathcal{O}_C/\mathfrak{h}\mathcal{O}_C| = \prod_{i=1}^{r} |\mathcal{O}_{K_i}/\mathfrak{h}\mathcal{O}_{K_i}| = \prod_{i=1}^{r} \mathrm{N}_{K_i/\mathbb{Q}}(\mathfrak{h}\mathcal{O}_{K_i}) = \prod_{i=1}^{r} \mathrm{N}_{K/\mathbb{Q}}(\mathfrak{h})^{[K_i:K]} \\ &= \mathrm{N}_{K/\mathbb{Q}}(\mathfrak{h})^{[C:K]} \leq \mathrm{N}_{K/\mathbb{Q}}(\mathfrak{h})^d. \end{align*} $$
$$ \begin{align*} |\mathcal{O}_C/\mathfrak{g}| & \leq |\mathcal{O}_C/\mathfrak{h}\mathcal{O}_C| = \prod_{i=1}^{r} |\mathcal{O}_{K_i}/\mathfrak{h}\mathcal{O}_{K_i}| = \prod_{i=1}^{r} \mathrm{N}_{K_i/\mathbb{Q}}(\mathfrak{h}\mathcal{O}_{K_i}) = \prod_{i=1}^{r} \mathrm{N}_{K/\mathbb{Q}}(\mathfrak{h})^{[K_i:K]} \\ &= \mathrm{N}_{K/\mathbb{Q}}(\mathfrak{h})^{[C:K]} \leq \mathrm{N}_{K/\mathbb{Q}}(\mathfrak{h})^d. \end{align*} $$
Note that solving the discrete logarithm in
![]() $(\mathcal {O}_C/\mathfrak {g})^\times $
requires solving the discrete logarithm problem in
$(\mathcal {O}_C/\mathfrak {g})^\times $
requires solving the discrete logarithm problem in
![]() $(\mathcal {O}_C/\mathfrak {P})^\times $
for all prime ideals
$(\mathcal {O}_C/\mathfrak {P})^\times $
for all prime ideals
![]() $\mathfrak {P}$
dividing
$\mathfrak {P}$
dividing
![]() $\mathfrak {g}$
. As in step (8), for each prime ideal
$\mathfrak {g}$
. As in step (8), for each prime ideal
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {g}\cap \mathcal {O}$
there are at most d prime ideals
$\mathfrak {g}\cap \mathcal {O}$
there are at most d prime ideals
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\mathcal {O}_C$
with
$\mathcal {O}_C$
with
![]() $\mathfrak {P} \cap \mathcal {O} = \mathfrak {p}$
and for each of those prime ideals
$\mathfrak {P} \cap \mathcal {O} = \mathfrak {p}$
and for each of those prime ideals
![]() $\mathcal {O}_C/\mathfrak {P}$
is an extension of
$\mathcal {O}_C/\mathfrak {P}$
is an extension of
![]() $\mathcal {O}/\mathfrak {p}$
of degree at most d.
$\mathcal {O}/\mathfrak {p}$
of degree at most d.
Step (10): The reduced norm map
![]() $\mathrm {nr} \colon \mathcal {M}^\times \rightarrow \mathcal {O}_C^\times $
is surjective by Lemma 6.3. The computation of
$\mathrm {nr} \colon \mathcal {M}^\times \rightarrow \mathcal {O}_C^\times $
is surjective by Lemma 6.3. The computation of
![]() $\mathcal {O}_C^\times $
is performed componentwise and thus reduces to
$\mathcal {O}_C^\times $
is performed componentwise and thus reduces to
![]() $\mathsf {UnitGroup}(\mathcal O_{K_i})$
for
$\mathsf {UnitGroup}(\mathcal O_{K_i})$
for
![]() $1 \leq i \leq r$
. We then determine the image of the canonical projection
$1 \leq i \leq r$
. We then determine the image of the canonical projection
![]() $\mathcal {O}_C^\times \rightarrow \left ( \mathcal {O}_C/\mathfrak {g} \right )^\times / \mathrm {im}(\bar \nu )$
as an abstract subgroup of
$\mathcal {O}_C^\times \rightarrow \left ( \mathcal {O}_C/\mathfrak {g} \right )^\times / \mathrm {im}(\bar \nu )$
as an abstract subgroup of
![]() $ \left ( \mathcal {O}_C/\mathfrak {g} \right )^\times / \mathrm {im}(\bar \nu )$
. This again requires an instance of solving the discrete logarithm in
$ \left ( \mathcal {O}_C/\mathfrak {g} \right )^\times / \mathrm {im}(\bar \nu )$
. This again requires an instance of solving the discrete logarithm in
![]() $\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
for each of the generators of
$\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times $
for each of the generators of
![]() $\mathcal {O}_C^\times $
. By Dirichlet’s unit theorem the number of these generators can be bounded by d. Applying standard algorithms for finite abelian groups it is then straightforward to decide whether
$\mathcal {O}_C^\times $
. By Dirichlet’s unit theorem the number of these generators can be bounded by d. Applying standard algorithms for finite abelian groups it is then straightforward to decide whether
![]() $\overline {\mathrm {nr}}(\bar \beta )$
is contained in the image of
$\overline {\mathrm {nr}}(\bar \beta )$
is contained in the image of
![]() $\mathcal {O}_C^\times \rightarrow {\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times } /{\mathrm {im}(\bar \nu )}$
and, if so, to compute
$\mathcal {O}_C^\times \rightarrow {\left ( \mathcal {O}_C/\mathfrak {g} \right )^\times } /{\mathrm {im}(\bar \nu )}$
and, if so, to compute
![]() $\epsilon \in \mathcal {O}_C^\times $
,
$\epsilon \in \mathcal {O}_C^\times $
,
![]() $a \in \left (\Lambda / \mathfrak {f}\right )^\times $
such that
$a \in \left (\Lambda / \mathfrak {f}\right )^\times $
such that
![]() $\bar \epsilon \equiv \overline {\beta a} \pmod {\mathfrak {g}}$
. An element
$\bar \epsilon \equiv \overline {\beta a} \pmod {\mathfrak {g}}$
. An element
![]() $u \in \mathcal {M}^\times $
such that
$u \in \mathcal {M}^\times $
such that
![]() $\mathrm {nr}(u) = \epsilon $
can be found using Lemma 6.3 in probabilistic polynomial time. Note that this step requires one more instance of solving the discrete logarithm in
$\mathrm {nr}(u) = \epsilon $
can be found using Lemma 6.3 in probabilistic polynomial time. Note that this step requires one more instance of solving the discrete logarithm in
![]() $(\mathcal {O}_C/\mathfrak {g})^{\times }$
, which was already analysed in step (9).
$(\mathcal {O}_C/\mathfrak {g})^{\times }$
, which was already analysed in step (9).
Step (11): As the factorisation of
![]() $\mathfrak {g}$
is known, this can be done in probabilistic polynomial time by Theorem 7.9.
$\mathfrak {g}$
is known, this can be done in probabilistic polynomial time by Theorem 7.9.
We now consider the case in which we allow certain precomputations that only depend on the order
![]() $\Lambda $
and not on the
$\Lambda $
and not on the
![]() $\Lambda $
-lattice X.
$\Lambda $
-lattice X.
Corollary 8.5. Fix an
![]() $\mathcal {O}$
-order
$\mathcal {O}$
-order
![]() $\Lambda $
in a finite-dimensional semisimple K-algebra A satisfying hypothesis (H), and let
$\Lambda $
in a finite-dimensional semisimple K-algebra A satisfying hypothesis (H), and let
![]() $K_{1}, \ldots , K_{r}$
be the simple components of the centre of A. Then for a full
$K_{1}, \ldots , K_{r}$
be the simple components of the centre of A. Then for a full
![]() $\Lambda $
-lattice X in A, the problem
$\Lambda $
-lattice X in A, the problem
![]() $\mathsf {IsPrincipal}(X)$
reduces in probabilistic polynomial to
$\mathsf {IsPrincipal}(X)$
reduces in probabilistic polynomial to
![]() $\mathsf {IsPrincipal}$
for
$\mathsf {IsPrincipal}$
for
![]() $\mathcal {O}_{K_i}$
,
$\mathcal {O}_{K_i}$
,
![]() $1 \leq i \leq r$
, and
$1 \leq i \leq r$
, and
![]() $\mathsf {DLog}$
.
$\mathsf {DLog}$
.
Proof. In Algorithm 8.3 we may consider all steps which do not depend on X as precomputations. Then for each lattice X only steps (5), (6), (7), (10) and (11) have to be performed. The claim follows as in the proof of Theorem 8.4.
Remark 8.6. In Theorem 8.4 better results can be obtained by describing the complexity in terms of the central conductor
![]() $\mathfrak {g}$
(which depends not only on the order
$\mathfrak {g}$
(which depends not only on the order
![]() $\Lambda $
but also on the maximal order computed during the algorithm) instead of
$\Lambda $
but also on the maximal order computed during the algorithm) instead of
![]() $\mathfrak {h}$
. More precisely, (e) and (f) can be replaced by
$\mathfrak {h}$
. More precisely, (e) and (f) can be replaced by
(e
 $'$
) for each prime ideal divisor
$'$
) for each prime ideal divisor
 $\mathfrak {P}$
of
$\mathfrak {P}$
of
 $\mathfrak {g}$
, the problem
$\mathfrak {g}$
, the problem
 $\mathsf {DLog}$
for extensions of
$\mathsf {DLog}$
for extensions of
 $\mathcal {O}/ (\mathcal {O} \cap \mathfrak {P})$
,
$\mathcal {O}/ (\mathcal {O} \cap \mathfrak {P})$
,(f
 $'$
) for each prime ideal divisor
$'$
) for each prime ideal divisor
 $\mathfrak {P}$
of
$\mathfrak {P}$
of
 $\mathfrak {g}$
, the problem
$\mathfrak {g}$
, the problem
 $\mathsf {Primitive}$
for extensions of
$\mathsf {Primitive}$
for extensions of
 $\mathcal {O} / (\mathcal {O} \cap \mathfrak {P})$
.
$\mathcal {O} / (\mathcal {O} \cap \mathfrak {P})$
.
Remark 8.7. By Remark 5.2, in Theorem 8.4, (a) can be replaced by
(a
 $'$
)
$'$
)
 $\mathsf {SplittingMatrixAlgebra}(A_i)$
for
$\mathsf {SplittingMatrixAlgebra}(A_i)$
for
 $1 \leq i \leq r$
, where
$1 \leq i \leq r$
, where
 $A = \bigoplus _{i=1}^r A_i$
is the decomposition into simple K-algebras.
$A = \bigoplus _{i=1}^r A_i$
is the decomposition into simple K-algebras.
Note that we have formulated Theorem 8.4 using
![]() $\mathsf {Wedderburn}$
since for certain families of algebras, one can directly solve
$\mathsf {Wedderburn}$
since for certain families of algebras, one can directly solve
![]() $\mathsf {Wedderburn}$
in polynomial time (which would not necessarily be true after passing to the simple components). This happens, for example, for certain algebras of the form
$\mathsf {Wedderburn}$
in polynomial time (which would not necessarily be true after passing to the simple components). This happens, for example, for certain algebras of the form
![]() $A/{\operatorname {\mathrm {J}}(A)}$
that appear in the similarity problem for matrices over rings of integers of number fields (see §9.3).
$A/{\operatorname {\mathrm {J}}(A)}$
that appear in the similarity problem for matrices over rings of integers of number fields (see §9.3).
Remark 8.8. In view of Remarks 5.1 and 5.2, as well as the reductions of Propositions 8.1 and 8.2, the problems
![]() $\mathsf {IsPrincipal}_{\Lambda }$
and
$\mathsf {IsPrincipal}_{\Lambda }$
and
![]() $\mathsf {IsIsomorphic}_{\Lambda }$
for orders
$\mathsf {IsIsomorphic}_{\Lambda }$
for orders
![]() $\Lambda $
in finite-dimensional K-algebras A satisfying hypothesis (H) reduces
$\Lambda $
in finite-dimensional K-algebras A satisfying hypothesis (H) reduces
-
(a) in probabilistic subexponential time to
 $\mathsf {UnitGroup}$
and
$\mathsf {UnitGroup}$
and
 $\mathsf {IsPrincipal}$
for rings of integers of number fields, and
$\mathsf {IsPrincipal}$
for rings of integers of number fields, and
 $\mathsf {Wedderburn}$
or
$\mathsf {Wedderburn}$
or
 $\mathsf {SplittingMatrixAlgebra}$
,
$\mathsf {SplittingMatrixAlgebra}$
, -
(b) in quantum polynomial time to
 $\mathsf {Wedderburn}$
or
$\mathsf {Wedderburn}$
or
 $\mathsf {SplittingMatrixAlgebra}$
.
$\mathsf {SplittingMatrixAlgebra}$
.
9 Application: similarity of matrices over rings of integers
After proving some general results on the similarity of matrices over commutative rings, we will give an application of Algorithm 8.3 to the similarity problem for matrices over rings of integers of number fields.
9.1 Similarity of matrices over commutative rings
Let R be a commutative ring, and let
![]() $n \in \mathbb {Z}_{>0}$
. Recall that two matrices
$n \in \mathbb {Z}_{>0}$
. Recall that two matrices
![]() $A,B \in \mathrm {Mat}_{n}(R)$
are said to be similar over R if there exists a conjugating matrix
$A,B \in \mathrm {Mat}_{n}(R)$
are said to be similar over R if there exists a conjugating matrix
![]() $C \in \mathrm {GL}_{n}(R)$
such that
$C \in \mathrm {GL}_{n}(R)$
such that
![]() $B=CAC^{-1}$
.
$B=CAC^{-1}$
.
We will adopt the setup of Faddeev [Reference FaddeevFad66]. For
![]() $A,B \in \mathrm {Mat}_{n}(R)$
we define
$A,B \in \mathrm {Mat}_{n}(R)$
we define
Note that
![]() $C_{R}(B)$
is an R-algebra and that
$C_{R}(B)$
is an R-algebra and that
![]() $C_{R}(A,B)$
is a (left)
$C_{R}(A,B)$
is a (left)
![]() $C_{R}(B)$
-module.
$C_{R}(B)$
-module.
Lemma 9.1. Suppose there exists
![]() $C \in \mathrm {GL}_{n}(R)$
such that
$C \in \mathrm {GL}_{n}(R)$
such that
![]() $B=CAC^{-1}$
. Then the maps
$B=CAC^{-1}$
. Then the maps
 $$ \begin{align*} \theta_{C} : C_R(B) \longrightarrow C_R(A,B), \quad & X \longmapsto XC,\\ \theta_{C^{-1}} : C_R(A, B) \longrightarrow C_R(B), \quad & X \longmapsto XC^{-1}, \end{align*} $$
$$ \begin{align*} \theta_{C} : C_R(B) \longrightarrow C_R(A,B), \quad & X \longmapsto XC,\\ \theta_{C^{-1}} : C_R(A, B) \longrightarrow C_R(B), \quad & X \longmapsto XC^{-1}, \end{align*} $$
are mutually inverse
![]() $C_{R}(B)$
-module isomorphisms.
$C_{R}(B)$
-module isomorphisms.
Proof. If
![]() $X \in C_{R}(B)$
, then
$X \in C_{R}(B)$
, then
![]() $B(XC)=XBC=X(CAC^{-1})C=(XC)A$
and so
$B(XC)=XBC=X(CAC^{-1})C=(XC)A$
and so
![]() $XC \in C_{R}(A,B)$
. Hence, the map
$XC \in C_{R}(A,B)$
. Hence, the map
![]() $\theta _{C}$
is well defined. Similarly, the map
$\theta _{C}$
is well defined. Similarly, the map
![]() $\theta _{C}^{-1}$
is also well defined and it is clear that
$\theta _{C}^{-1}$
is also well defined and it is clear that
![]() $\theta _{C}$
and
$\theta _{C}$
and
![]() $\theta _{C^{-1}}$
are mutually inverse.
$\theta _{C^{-1}}$
are mutually inverse.
Proposition 9.2. Two matrices
![]() $A,B \in \mathrm {Mat}_n(R)$
are similar over R if and only if
$A,B \in \mathrm {Mat}_n(R)$
are similar over R if and only if
-
(a) the
 $C_R(B)$
-module
$C_R(B)$
-module
 $C_R(A, B)$
is free of rank
$C_R(A, B)$
is free of rank
 $1$
, and
$1$
, and -
(b) every (any) free generator C of
 $C_R(A, B)$
over
$C_R(A, B)$
over
 $C_{R}(B)$
is in
$C_{R}(B)$
is in
 $\mathrm {GL}_n(R)$
.
$\mathrm {GL}_n(R)$
.
Furthermore, when this is the case, C as in part (b) satisfies
![]() $B=CAC^{-1}$
.
$B=CAC^{-1}$
.
Proof. Suppose that (a) and (b) hold, and let C be a free generator of
![]() $C_{R}(A, B)$
over
$C_{R}(A, B)$
over
![]() $C_{R}(B)$
. In particular,
$C_{R}(B)$
. In particular,
![]() $C \in C_{R}(A,B) \cap \mathrm {GL}_{n}(R)$
, and it easily follows that
$C \in C_{R}(A,B) \cap \mathrm {GL}_{n}(R)$
, and it easily follows that
![]() $B=CAC^{-1}$
. Suppose conversely that there exists
$B=CAC^{-1}$
. Suppose conversely that there exists
![]() $C \in \mathrm {GL}_{n}(R)$
such that
$C \in \mathrm {GL}_{n}(R)$
such that
![]() $B=CAC^{-1}$
. Then
$B=CAC^{-1}$
. Then
![]() $\theta _{C}$
is an isomorphism by Lemma 9.1, and so C is a free generator of
$\theta _{C}$
is an isomorphism by Lemma 9.1, and so C is a free generator of
![]() $C_{R}(A,B)$
over
$C_{R}(A,B)$
over
![]() $C_{R}(B)$
. Thus, (a) holds. Now, let D be any free generator of
$C_{R}(B)$
. Thus, (a) holds. Now, let D be any free generator of
![]() $C_{R}(A,B)$
over
$C_{R}(A,B)$
over
![]() $C_{R}(B)$
. Then there exists
$C_{R}(B)$
. Then there exists
![]() $E \in C_{R}(B)^{\times } \subseteq \mathrm {GL}_{n}(R)$
such that
$E \in C_{R}(B)^{\times } \subseteq \mathrm {GL}_{n}(R)$
such that
![]() $D=EC$
and so
$D=EC$
and so
![]() $D \in \mathrm {GL}_{n}(R)$
. Thus, (b) holds.
$D \in \mathrm {GL}_{n}(R)$
. Thus, (b) holds.
The following result was proven by Faddeev [Reference FaddeevFad66, Theorem 2] in the case
![]() $R=\mathbb {Z}$
, though it was expressed in terms of ideals rather than modules. Moreover, Guralnick [Reference GuralnickGur80, Theorem 6] observed that the proof works for any integral domain. We include a short proof for the convenience of the reader and for comparison as per Remark 9.4.
$R=\mathbb {Z}$
, though it was expressed in terms of ideals rather than modules. Moreover, Guralnick [Reference GuralnickGur80, Theorem 6] observed that the proof works for any integral domain. We include a short proof for the convenience of the reader and for comparison as per Remark 9.4.
Proposition 9.3. Suppose that R is an integral domain. Two matrices
![]() $A,B \in \mathrm {Mat}_n(R)$
are similar over R if and only if
$A,B \in \mathrm {Mat}_n(R)$
are similar over R if and only if
-
(a) the
 $C_R(B)$
-module
$C_R(B)$
-module
 $C_R(A, B)$
is free of rank
$C_R(A, B)$
is free of rank
 $1$
, and
$1$
, and -
(b) for every maximal ideal
 $\mathfrak {p}$
of R, the matrices A and B are similar over
$\mathfrak {p}$
of R, the matrices A and B are similar over
 $R_{\mathfrak {p}}$
.
$R_{\mathfrak {p}}$
.
Furthermore, when this is the case, any free generator C of
![]() $C_R(A, B)$
over
$C_R(A, B)$
over
![]() $C_{R}(B)$
satisfies
$C_{R}(B)$
satisfies
![]() $B=CAC^{-1}$
.
$B=CAC^{-1}$
.
Proof. Suppose that
![]() $A,B \in \mathrm {Mat}_n(R)$
are similar over R. Then (b) clearly holds and (a) holds by Proposition 9.2. Suppose conversely that (a) and (b) hold. Let C be a free generator of
$A,B \in \mathrm {Mat}_n(R)$
are similar over R. Then (b) clearly holds and (a) holds by Proposition 9.2. Suppose conversely that (a) and (b) hold. Let C be a free generator of
![]() $C_{R}(A,B)$
over
$C_{R}(A,B)$
over
![]() $C_{R}(B)$
. Let
$C_{R}(B)$
. Let
![]() $\mathfrak {p}$
be a maximal ideal of R. Then there exists
$\mathfrak {p}$
be a maximal ideal of R. Then there exists
![]() $C_{\mathfrak {p}} \in \mathrm {GL}_{n}(R_{\mathfrak {p}})$
such that
$C_{\mathfrak {p}} \in \mathrm {GL}_{n}(R_{\mathfrak {p}})$
such that
![]() $B=C_{\mathfrak {p}}AC_{\mathfrak {p}}^{-1}$
and so
$B=C_{\mathfrak {p}}AC_{\mathfrak {p}}^{-1}$
and so
![]() $C_{\mathfrak {p}} \in C_{R_{\mathfrak {p}}}(A,B)$
. Since C is also a free generator of
$C_{\mathfrak {p}} \in C_{R_{\mathfrak {p}}}(A,B)$
. Since C is also a free generator of
![]() $C_{R_{\mathfrak {p}}}(A,B)$
over
$C_{R_{\mathfrak {p}}}(A,B)$
over
![]() $C_{R_{\mathfrak {p}}}(B)$
, there exists
$C_{R_{\mathfrak {p}}}(B)$
, there exists
![]() $D_{\mathfrak {p}} \in C_{R_{\mathfrak {p}}}(B)$
such that
$D_{\mathfrak {p}} \in C_{R_{\mathfrak {p}}}(B)$
such that
![]() $C_{\mathfrak {p}} = D_{\mathfrak {p}} C$
. Then
$C_{\mathfrak {p}} = D_{\mathfrak {p}} C$
. Then
![]() $\det (D_{\mathfrak {p}})\det (C)=\det (C_{\mathfrak {p}}) \in R_{\mathfrak {p}}^{\times }$
and so
$\det (D_{\mathfrak {p}})\det (C)=\det (C_{\mathfrak {p}}) \in R_{\mathfrak {p}}^{\times }$
and so
![]() $\det (C) \in R_{\mathfrak {p}}^{\times }$
. Moreover, by [Reference Curtis and ReinerCR81, (4.2)(iv)], we have
$\det (C) \in R_{\mathfrak {p}}^{\times }$
. Moreover, by [Reference Curtis and ReinerCR81, (4.2)(iv)], we have
![]() $R = \cap _{\mathfrak {p}} R_{\mathfrak {p}}$
which implies that
$R = \cap _{\mathfrak {p}} R_{\mathfrak {p}}$
which implies that
![]() $R^{\times } = \cap _{\mathfrak {p}} R_{\mathfrak {p}}^{\times }$
, where in both cases the intersection ranges over all maximal ideals
$R^{\times } = \cap _{\mathfrak {p}} R_{\mathfrak {p}}^{\times }$
, where in both cases the intersection ranges over all maximal ideals
![]() $\mathfrak {p}$
of R. Therefore,
$\mathfrak {p}$
of R. Therefore,
![]() $\det (C) \in R^{\times }$
and so
$\det (C) \in R^{\times }$
and so
![]() $C \in \mathrm {GL}_{n}(R)$
. In particular,
$C \in \mathrm {GL}_{n}(R)$
. In particular,
![]() $C \in C_{R}(A,B) \cap \mathrm {GL}_{n}(R)$
, and it easily follows that
$C \in C_{R}(A,B) \cap \mathrm {GL}_{n}(R)$
, and it easily follows that
![]() $B=CAC^{-1}$
.
$B=CAC^{-1}$
.
Remark 9.4. Propositions 9.2 and 9.3 and their proofs are analogues of Propositions 3.1 and 3.3, respectively. Indeed, in the case that R is a Noetherian integral domain, the former can be deduced from the latter, though it is easier to give more direct proofs of more general results. Moreover, as well as having weaker hypotheses, Proposition 9.2 is better suited to algorithmic applications than Proposition 9.3.
9.2 The similarity problem in terms of modules over polynomial rings
Let R be a commutative ring, and let
![]() $n \in \mathbb {Z}_{>0}$
. Let
$n \in \mathbb {Z}_{>0}$
. Let
![]() $R[x]$
be a polynomial ring in one variable over R. For
$R[x]$
be a polynomial ring in one variable over R. For
![]() $A \in \mathrm {Mat}_{n}(R)$
, we define
$A \in \mathrm {Mat}_{n}(R)$
, we define
![]() $T_{R}(A)$
to be the
$T_{R}(A)$
to be the
![]() $R[x]$
-module
$R[x]$
-module
![]() $R^{n}$
with the action
$R^{n}$
with the action
![]() $x v = Av$
for
$x v = Av$
for
![]() $v \in R^{n}$
.
$v \in R^{n}$
.
Lemma 9.5. Let
![]() $A,B,C \in \mathrm {Mat}_{n}(R)$
. Define
$A,B,C \in \mathrm {Mat}_{n}(R)$
. Define
![]() $\psi _{A,B,C} : T_{R}(A) \rightarrow T_{R}(B)$
by
$\psi _{A,B,C} : T_{R}(A) \rightarrow T_{R}(B)$
by
![]() $v \mapsto Cv$
. Then
$v \mapsto Cv$
. Then
![]() $C \in C_{R}(A,B)$
if and only if
$C \in C_{R}(A,B)$
if and only if
![]() $\psi _{A,B,C}$
is an
$\psi _{A,B,C}$
is an
![]() $R[x]$
-module homomorphism. In particular, we have canonical isomorphisms
$R[x]$
-module homomorphism. In particular, we have canonical isomorphisms
-
(a)
 $C_{R}(A,B) \cong \mathrm {Hom}_{R[x]}(T_{R}(A),T_{R}(B))$
of R-modules;
$C_{R}(A,B) \cong \mathrm {Hom}_{R[x]}(T_{R}(A),T_{R}(B))$
of R-modules; -
(b)
 $C_{R}(A) \cong \mathrm {End}_{R[x]}(T_{R}(A))$
of R-algebras.
$C_{R}(A) \cong \mathrm {End}_{R[x]}(T_{R}(A))$
of R-algebras.
Proof. The function
![]() $\psi _{A,B,C}$
is an
$\psi _{A,B,C}$
is an
![]() $R[x]$
-module homomorphism if and only if
$R[x]$
-module homomorphism if and only if
![]() $C(Av) = B(Cv)$
for all
$C(Av) = B(Cv)$
for all
![]() $v \in R^{n}$
, which in turn is equivalent to
$v \in R^{n}$
, which in turn is equivalent to
![]() $C \in C_{R}(A,B)$
. This gives the first claim; the remaining claims now follow easily.
$C \in C_{R}(A,B)$
. This gives the first claim; the remaining claims now follow easily.
The following result is well known and is an easy consequence of Lemma 9.5.
Lemma 9.6. Let
![]() $A,B,C \in \mathrm {Mat}_{n}(R)$
. Then the following are equivalent:
$A,B,C \in \mathrm {Mat}_{n}(R)$
. Then the following are equivalent:
-
(a)
 $C \in C_{R}(A,B) \cap \mathrm {GL}_{n}(R)$
,
$C \in C_{R}(A,B) \cap \mathrm {GL}_{n}(R)$
, -
(b)
 $C \in \mathrm {GL}_{n}(R)$
and
$C \in \mathrm {GL}_{n}(R)$
and
 $B=CAC^{-1}$
,
$B=CAC^{-1}$
, -
(c)
 $\psi _{A,B,C}$
is an
$\psi _{A,B,C}$
is an
 $R[x]$
-module isomorphism.
$R[x]$
-module isomorphism.
In particular, A and B are similar over R if and only if
![]() $T_R(A) \cong T_R(B)$
as
$T_R(A) \cong T_R(B)$
as
![]() $R[x]$
-modules.
$R[x]$
-modules.
9.3 Jacobson radicals of certain endomorphism algebras
Let F be a field. We now explicitly compute the Jacobson radical
![]() $\operatorname {\mathrm {J}}(\mathrm {End}_{F[x]}(V))$
of
$\operatorname {\mathrm {J}}(\mathrm {End}_{F[x]}(V))$
of
![]() $\mathrm {End}_{F[x]}(V)$
for a finitely generated
$\mathrm {End}_{F[x]}(V)$
for a finitely generated
![]() $F[x]$
-module V. The motivating application is Proposition 9.11 below.
$F[x]$
-module V. The motivating application is Proposition 9.11 below.
Lemma 9.7. Let
![]() $f \in F[x]$
be an irreducible polynomial, and let
$f \in F[x]$
be an irreducible polynomial, and let
![]() $j,k \in \mathbb {Z}_{>0}$
. Let
$j,k \in \mathbb {Z}_{>0}$
. Let
-
(a) If
 $j \leq k$
then
$j \leq k$
then
 $\mathrm {im}(\lambda ) \subseteq f^{k-j}\cdot \left ( F[x]/(f^k) \right )$
.
$\mathrm {im}(\lambda ) \subseteq f^{k-j}\cdot \left ( F[x]/(f^k) \right )$
. -
(b) For any choice of
 $j,k$
we have
$j,k$
we have
 $\mathrm {im}(\lambda \circ \mu ) \subseteq f^{|k-j|} \cdot \left ( F[x]/(f^k) \right )$
.
$\mathrm {im}(\lambda \circ \mu ) \subseteq f^{|k-j|} \cdot \left ( F[x]/(f^k) \right )$
.
Proof. Suppose
![]() $j \leq k$
. We have
$j \leq k$
. We have
![]() $\lambda (x+(f^{j})) = y + (f^{k})$
for some
$\lambda (x+(f^{j})) = y + (f^{k})$
for some
![]() $y \in F[x]$
. Then
$y \in F[x]$
. Then
so
![]() $f^{j}y \in (f^{k})$
and hence
$f^{j}y \in (f^{k})$
and hence
![]() $y \in (f^{k-j})$
. Thus, (a) follows from the fact that the image of
$y \in (f^{k-j})$
. Thus, (a) follows from the fact that the image of
![]() $\lambda $
is uniquely determined by the image of
$\lambda $
is uniquely determined by the image of
![]() $x+(f^j)$
. Part (b) follows easily from (a).
$x+(f^j)$
. Part (b) follows easily from (a).
Proposition 9.8. Let
![]() $f \in F[x]$
be an irreducible polynomial. Let
$f \in F[x]$
be an irreducible polynomial. Let
![]() $m \in \mathbb {Z}_{>0}$
, let
$m \in \mathbb {Z}_{>0}$
, let
![]() $d_{1}, \ldots , d_{m} \in \mathbb {Z}_{\geq 0}$
and let
$d_{1}, \ldots , d_{m} \in \mathbb {Z}_{\geq 0}$
and let
![]() $V = \bigoplus _{j = 1}^{m} (F[x]/(f^j))^{d_{j}}$
. Then we have a canonical isomorphism
$V = \bigoplus _{j = 1}^{m} (F[x]/(f^j))^{d_{j}}$
. Then we have a canonical isomorphism
 $$ \begin{align} \mathrm{End}_{F[x]}(V) \cong E := \bigoplus_{j=1}^{m} \bigoplus_{k=1}^{m} e_{jk} \mathrm{Hom}_{F[x]}((F[x]/(f^k))^{d_k}, (F[x]/(f^j))^{d_j}), \end{align} $$
$$ \begin{align} \mathrm{End}_{F[x]}(V) \cong E := \bigoplus_{j=1}^{m} \bigoplus_{k=1}^{m} e_{jk} \mathrm{Hom}_{F[x]}((F[x]/(f^k))^{d_k}, (F[x]/(f^j))^{d_j}), \end{align} $$
where the right-hand side denotes the
![]() $m \times m$
‘matrix ring’ with
$m \times m$
‘matrix ring’ with
![]() $(j,k)$
-th entries in
$(j,k)$
-th entries in
![]() $\mathrm {Hom}_{F[x]}((F[x]/(f^k))^{d_k}, (F[x]/(f^j))^{d_j})$
. For
$\mathrm {Hom}_{F[x]}((F[x]/(f^k))^{d_k}, (F[x]/(f^j))^{d_j})$
. For
![]() $1 \leq j,k \leq m$
, define
$1 \leq j,k \leq m$
, define
![]() $\gamma _{jk}=f$
if
$\gamma _{jk}=f$
if
![]() $j=k$
and
$j=k$
and
![]() $\gamma _{jk}=1$
otherwise. Then the isomorphism
$\gamma _{jk}=1$
otherwise. Then the isomorphism
![]() $\mathrm {End}_{F[x]}(V) \cong E$
induces isomorphisms
$\mathrm {End}_{F[x]}(V) \cong E$
induces isomorphisms
 $$ \begin{align} \operatorname{\mathrm{J}}(\mathrm{End}_{F[x]}(V)) \cong I := \bigoplus_{j=1}^{m} \bigoplus_{k=1}^{m} e_{jk} \gamma_{jk} \mathrm{Hom}_{F[x]}((F[x]/(f^k))^{d_k}, (F[x]/(f^j))^{d_j}), \text{ and } \end{align} $$
$$ \begin{align} \operatorname{\mathrm{J}}(\mathrm{End}_{F[x]}(V)) \cong I := \bigoplus_{j=1}^{m} \bigoplus_{k=1}^{m} e_{jk} \gamma_{jk} \mathrm{Hom}_{F[x]}((F[x]/(f^k))^{d_k}, (F[x]/(f^j))^{d_j}), \text{ and } \end{align} $$
 $$ \begin{align} \mathrm{End}_{F[x]}(V)/{\operatorname{\mathrm{J}}(\mathrm{End}_{F[x]}(V))} \cong E/I \cong \prod_{j = 1}^{m} \mathrm{Mat}_{d_j}(F[x]/(f)). \end{align} $$
$$ \begin{align} \mathrm{End}_{F[x]}(V)/{\operatorname{\mathrm{J}}(\mathrm{End}_{F[x]}(V))} \cong E/I \cong \prod_{j = 1}^{m} \mathrm{Mat}_{d_j}(F[x]/(f)). \end{align} $$
Proof. The decomposition (7) follows from standard properties of Homs and direct sums. It follows from Lemma 9.7 (b) that I is a two-sided ideal of E. Moreover, it is straightforward to check that
![]() $E/I$
is canonically isomorphic to the right-hand side of equation (9). Thus,
$E/I$
is canonically isomorphic to the right-hand side of equation (9). Thus,
![]() $E/I$
is Artinian semisimple and so
$E/I$
is Artinian semisimple and so
![]() $\operatorname {\mathrm {J}}(E/I) =0$
by [Reference Curtis and ReinerCR81, (5.18)]. Hence,
$\operatorname {\mathrm {J}}(E/I) =0$
by [Reference Curtis and ReinerCR81, (5.18)]. Hence,
![]() $\operatorname {\mathrm {J}}(E) \subseteq I$
by [Reference Curtis and ReinerCR81, (5.6)(ii)]. Lemma 9.7 (a) and the definition of
$\operatorname {\mathrm {J}}(E) \subseteq I$
by [Reference Curtis and ReinerCR81, (5.6)(ii)]. Lemma 9.7 (a) and the definition of
![]() $\gamma _{jk}$
implies that each element
$\gamma _{jk}$
implies that each element
![]() $\lambda = (\lambda _{jk}) \in I$
is an upper triangular matrix in the sense that for
$\lambda = (\lambda _{jk}) \in I$
is an upper triangular matrix in the sense that for
![]() $j \ge k$
the image of
$j \ge k$
the image of
![]() $\lambda _{jk}$
is contained in
$\lambda _{jk}$
is contained in
![]() $f \cdot F[x]/(f^{j})$
. Hence, for
$f \cdot F[x]/(f^{j})$
. Hence, for
![]() $\mu = (\mu _{jk}) \in I^{m}$
the image of each
$\mu = (\mu _{jk}) \in I^{m}$
the image of each
![]() $\mu _{jk}$
is contained in
$\mu _{jk}$
is contained in
![]() $f \cdot F[x]/(f^{j})$
. It follows that
$f \cdot F[x]/(f^{j})$
. It follows that
![]() $I^{m^2} = 0$
, and thus I is nilpotent. Thus, since E is Artinian,
$I^{m^2} = 0$
, and thus I is nilpotent. Thus, since E is Artinian,
![]() $I \subseteq \operatorname {\mathrm {J}}(E)$
by [Reference Curtis and ReinerCR81, (5.15)]. Therefore,
$I \subseteq \operatorname {\mathrm {J}}(E)$
by [Reference Curtis and ReinerCR81, (5.15)]. Therefore,
![]() $\operatorname {\mathrm {J}}(E)=I$
, as claimed.
$\operatorname {\mathrm {J}}(E)=I$
, as claimed.
Corollary 9.9. Let
![]() $r \in \mathbb {Z}_{>0}$
, and let
$r \in \mathbb {Z}_{>0}$
, and let
![]() $V = \bigoplus _{i=1}^{r} V_{i}$
, where
$V = \bigoplus _{i=1}^{r} V_{i}$
, where
![]() $V_{i} = \bigoplus _{j = 1}^{m_{i}} (F[x]/(f_{i}^{j}))^{d_{i,j}}$
for some
$V_{i} = \bigoplus _{j = 1}^{m_{i}} (F[x]/(f_{i}^{j}))^{d_{i,j}}$
for some
![]() $m_{i} \in \mathbb {Z}_{>0}$
,
$m_{i} \in \mathbb {Z}_{>0}$
,
![]() $d_{i,j} \in \mathbb {Z}_{\geq 0}$
, and some distinct monic irreducible polynomials
$d_{i,j} \in \mathbb {Z}_{\geq 0}$
, and some distinct monic irreducible polynomials
![]() $f_{i} \in F[x]$
. Then there are canonical isomorphisms
$f_{i} \in F[x]$
. Then there are canonical isomorphisms
 $$\begin{align*}\mathrm{End}_{F[x]}(V) \cong \prod_{i=1}^{r} \mathrm{End}_{F[x]}(V_{i}) \cong \prod_{i=1}^{r} \bigoplus_{j=1}^{m_{i}} \bigoplus_{k=1}^{m_{i}} e_{jk} \mathrm{Hom}_{F[x]}((F[x]/(f_{i}^{k}))^{d_{i,k}}, (F[x]/(f_{i}^{j}))^{d_{i,j}}) \end{align*}$$
$$\begin{align*}\mathrm{End}_{F[x]}(V) \cong \prod_{i=1}^{r} \mathrm{End}_{F[x]}(V_{i}) \cong \prod_{i=1}^{r} \bigoplus_{j=1}^{m_{i}} \bigoplus_{k=1}^{m_{i}} e_{jk} \mathrm{Hom}_{F[x]}((F[x]/(f_{i}^{k}))^{d_{i,k}}, (F[x]/(f_{i}^{j}))^{d_{i,j}}) \end{align*}$$
and
 $$\begin{align*}\mathrm{End}_{F[x]}(V)/{\operatorname{\mathrm{J}}(\mathrm{End}_{F[x]}(V))} \cong \prod_{i=1}^{r} \prod_{j = 1}^{m_{i}} \mathrm{Mat}_{d_{i, j}}(F[x]/(f_{i})). \end{align*}$$
$$\begin{align*}\mathrm{End}_{F[x]}(V)/{\operatorname{\mathrm{J}}(\mathrm{End}_{F[x]}(V))} \cong \prod_{i=1}^{r} \prod_{j = 1}^{m_{i}} \mathrm{Mat}_{d_{i, j}}(F[x]/(f_{i})). \end{align*}$$
In particular, if F is a number field, then
![]() $\mathrm {End}_{F[x]}(V)$
satisfies hypothesis (H).
$\mathrm {End}_{F[x]}(V)$
satisfies hypothesis (H).
Proof. The desired result follows from Proposition 9.8 together with the observation that
![]() $\mathrm {Hom}_{F[x]}(V_i, V_j) = 0$
for
$\mathrm {Hom}_{F[x]}(V_i, V_j) = 0$
for
![]() $i \neq j$
.
$i \neq j$
.
Proposition 9.10. Let
![]() $n \in \mathbb {Z}_{>0}$
, and let
$n \in \mathbb {Z}_{>0}$
, and let
![]() $A \in \mathrm {Mat}_{n}(F)$
.
$A \in \mathrm {Mat}_{n}(F)$
.
-
(a) The minimal polynomial of A is squarefree if and only if
 $C_{F}(A)$
is semisimple.
$C_{F}(A)$
is semisimple. -
(b) The minimal polynomial of A is equal to the characteristic polynomial of A if and only if
 $C_{F}(A)/{\operatorname {\mathrm {J}}(C_{F}(A))}$
is isomorphic to a finite product of fields.
$C_{F}(A)/{\operatorname {\mathrm {J}}(C_{F}(A))}$
is isomorphic to a finite product of fields. -
(c) The characteristic polynomial of A is squarefree if and only if
 $C_{F}(A)$
is isomorphic to a finite product of fields.
$C_{F}(A)$
is isomorphic to a finite product of fields. -
(d) If A is nilpotent, then
 $C_{F}(A)/{\operatorname {\mathrm {J}}(C_{F}(A))}$
is isomorphic to
$C_{F}(A)/{\operatorname {\mathrm {J}}(C_{F}(A))}$
is isomorphic to
 $\prod _{j = 1}^{m} \mathrm {Mat}_{d_{j}}(F)$
for some
$\prod _{j = 1}^{m} \mathrm {Mat}_{d_{j}}(F)$
for some
 $m, d_{1}, \ldots , d_{m} \in \mathbb {Z}_{>0}$
.
$m, d_{1}, \ldots , d_{m} \in \mathbb {Z}_{>0}$
.
Proof. Let
![]() $f \in F[x]$
denote the characteristic polynomial of A. It is a standard result in linear algebra that there is an isomorphism of
$f \in F[x]$
denote the characteristic polynomial of A. It is a standard result in linear algebra that there is an isomorphism of
![]() $F[x]$
-modules
$F[x]$
-modules
where
![]() $g_{1}, \ldots , g_{s} \in F[x]$
are the invariant factors of A and
$g_{1}, \ldots , g_{s} \in F[x]$
are the invariant factors of A and
![]() $g_{1} \mid g_{2} \mid \cdots \mid g_{s}$
. Thus,
$g_{1} \mid g_{2} \mid \cdots \mid g_{s}$
. Thus,
![]() $g_{s}$
is the minimal polynomial of A and
$g_{s}$
is the minimal polynomial of A and
![]() $f=g_{1}\cdots g_{s}$
. Moreover, by Lemma 9.5 (b), there is a canonical isomorphism
$f=g_{1}\cdots g_{s}$
. Moreover, by Lemma 9.5 (b), there is a canonical isomorphism
![]() $C_{F}(A) \cong \mathrm {End}_{F[x]}(V)$
of F-algebras, where
$C_{F}(A) \cong \mathrm {End}_{F[x]}(V)$
of F-algebras, where
![]() $V:=T_{F}(A)$
. Let
$V:=T_{F}(A)$
. Let
![]() $f_{1}, \ldots , f_{r} \in F[x]$
denote the distinct monic irreducible factors of f. Then there exists a decomposition
$f_{1}, \ldots , f_{r} \in F[x]$
denote the distinct monic irreducible factors of f. Then there exists a decomposition
![]() $V= \bigoplus _{i=1}^{r} V_{i}$
and isomorphisms
$V= \bigoplus _{i=1}^{r} V_{i}$
and isomorphisms
![]() $V_{i} \cong \bigoplus _{j = 1}^{m_i} F[x]/(f_{i}^{j})^{d_{i,j}}$
for some
$V_{i} \cong \bigoplus _{j = 1}^{m_i} F[x]/(f_{i}^{j})^{d_{i,j}}$
for some
![]() $m_{i} \in \mathbb {Z}_{>0}$
and
$m_{i} \in \mathbb {Z}_{>0}$
and
![]() $d_{i,j} \in \mathbb {Z}_{\geq 0}$
. (a) Observe that
$d_{i,j} \in \mathbb {Z}_{\geq 0}$
. (a) Observe that
![]() $g_{s}$
is squarefree if and only if each
$g_{s}$
is squarefree if and only if each
![]() $g_{k}$
is squarefree if and only if
$g_{k}$
is squarefree if and only if
![]() $m_{i}=1$
for
$m_{i}=1$
for
![]() $i=1,\ldots ,r$
. By Corollary 9.9, this in turn is equivalent to the triviality of
$i=1,\ldots ,r$
. By Corollary 9.9, this in turn is equivalent to the triviality of
![]() $\operatorname {\mathrm {J}}(\mathrm {End}_{F[x]}(V))$
, which is equivalent to the semisimplicity of
$\operatorname {\mathrm {J}}(\mathrm {End}_{F[x]}(V))$
, which is equivalent to the semisimplicity of
![]() $\mathrm {End}_{F[x]}(V)$
by [Reference Curtis and ReinerCR81, (5.18)]. (b) Observe that
$\mathrm {End}_{F[x]}(V)$
by [Reference Curtis and ReinerCR81, (5.18)]. (b) Observe that
![]() $g_{s}=f$
if and only if
$g_{s}=f$
if and only if
![]() $s=1$
if and only if
$s=1$
if and only if
![]() $d_{i,1}=1$
for
$d_{i,1}=1$
for
![]() $i=1,\ldots ,r$
. By Corollary 9.9, this in turn holds if and only if
$i=1,\ldots ,r$
. By Corollary 9.9, this in turn holds if and only if
![]() $\mathrm {End}_{F[x]}(V)/{\operatorname {\mathrm {J}}(\mathrm {End}_{F[x]}(V))}$
is isomorphic to a finite product of fields. (c) This follows from the previous two parts, once one obverses that if f is squarefree then it must be equal to
$\mathrm {End}_{F[x]}(V)/{\operatorname {\mathrm {J}}(\mathrm {End}_{F[x]}(V))}$
is isomorphic to a finite product of fields. (c) This follows from the previous two parts, once one obverses that if f is squarefree then it must be equal to
![]() $g_{s}$
. (d) If A is nilpotent, then f is some power of x, and so
$g_{s}$
. (d) If A is nilpotent, then f is some power of x, and so
![]() $r=1$
and
$r=1$
and
![]() $f_{1}=x$
. Thus the claim follows from Proposition 9.8 and the canonical isomorphism
$f_{1}=x$
. Thus the claim follows from Proposition 9.8 and the canonical isomorphism
![]() $F[x]/(x) \cong F$
.
$F[x]/(x) \cong F$
.
Proposition 9.11. Let K be a number field, let
![]() $n \in \mathbb {Z}_{>0}$
, and let
$n \in \mathbb {Z}_{>0}$
, and let
![]() $A \in \mathrm {Mat}_{n}(K)$
. Let f be the characteristic polynomial of A, and let
$A \in \mathrm {Mat}_{n}(K)$
. Let f be the characteristic polynomial of A, and let
![]() $f=f_{1}^{n_{1}} \cdots f_{r}^{n_{r}}$
be its factorisation, where
$f=f_{1}^{n_{1}} \cdots f_{r}^{n_{r}}$
be its factorisation, where
![]() $f_{1}, \ldots , f_{r} \in K[x]$
are distinct monic irreducible polynomials and
$f_{1}, \ldots , f_{r} \in K[x]$
are distinct monic irreducible polynomials and
![]() $n_{i} \in \mathbb {Z}_{>0}$
for each i. Let
$n_{i} \in \mathbb {Z}_{>0}$
for each i. Let
![]() $K_{i}=K[x]/(f_{i})$
for
$K_{i}=K[x]/(f_{i})$
for
![]() $i=1,\ldots ,r$
. Then there exists a polynomial-time algorithm that computes the factorisation of f, computes
$i=1,\ldots ,r$
. Then there exists a polynomial-time algorithm that computes the factorisation of f, computes
![]() $C_{K}(A)$
and
$C_{K}(A)$
and
![]() $\operatorname {\mathrm {J}}(C_K(A))$
and computes an explicit homomorphism of K-algebras
$\operatorname {\mathrm {J}}(C_K(A))$
and computes an explicit homomorphism of K-algebras
 $$\begin{align*}\rho \colon C_K(A) \longrightarrow C_K(A)/{\operatorname{\mathrm{J}}(C_K(A))} \stackrel{\cong}{\longrightarrow} \prod_{i=1}^{r} \prod_{j = 1}^{m_{i}} \mathrm{Mat}_{d_{i,j}}(K_i) \end{align*}$$
$$\begin{align*}\rho \colon C_K(A) \longrightarrow C_K(A)/{\operatorname{\mathrm{J}}(C_K(A))} \stackrel{\cong}{\longrightarrow} \prod_{i=1}^{r} \prod_{j = 1}^{m_{i}} \mathrm{Mat}_{d_{i,j}}(K_i) \end{align*}$$
for some
![]() $m_{i} \in \mathbb {Z}_{>0}$
and
$m_{i} \in \mathbb {Z}_{>0}$
and
![]() $d_{i,j} \in \mathbb {Z}_{\geq 0}$
such that
$d_{i,j} \in \mathbb {Z}_{\geq 0}$
such that
![]() $\sum _{j=1}^{m_{i}} jd_{i,j} = n_{i}$
for each i. In particular, this solves
$\sum _{j=1}^{m_{i}} jd_{i,j} = n_{i}$
for each i. In particular, this solves
![]() $\mathsf {Wedderburn}$
for
$\mathsf {Wedderburn}$
for
![]() $C_K(A)/{\operatorname {\mathrm {J}}(C_K(A))}$
, which satisfies hypothesis (H).
$C_K(A)/{\operatorname {\mathrm {J}}(C_K(A))}$
, which satisfies hypothesis (H).
Proof. Assume the setup and notation of the proof of Proposition 9.10 with
![]() $F=K$
. The isomorphism of (10) is obtained when computing the rational canonical form, which can be performed in polynomial time (see [Reference VillardVil93, Theorem 4]). Moreover, polynomials in
$F=K$
. The isomorphism of (10) is obtained when computing the rational canonical form, which can be performed in polynomial time (see [Reference VillardVil93, Theorem 4]). Moreover, polynomials in
![]() $K[x]$
can be factored in polynomial time by the algorithm of [Reference LenstraLen83, (4.5) Theorem]. Thus, we can explicitly compute a decomposition
$K[x]$
can be factored in polynomial time by the algorithm of [Reference LenstraLen83, (4.5) Theorem]. Thus, we can explicitly compute a decomposition
![]() $T_{K}(A) = \bigoplus _{i=1}^{r} V_{i}$
and isomorphisms
$T_{K}(A) = \bigoplus _{i=1}^{r} V_{i}$
and isomorphisms
![]() $V_{i} \cong \bigoplus _{j = 1}^{m_i} (K[x]/(f_{i}^{j}))^{d_{i,j}}$
for some
$V_{i} \cong \bigoplus _{j = 1}^{m_i} (K[x]/(f_{i}^{j}))^{d_{i,j}}$
for some
![]() $m_{i} \in \mathbb {Z}_{>0}$
and
$m_{i} \in \mathbb {Z}_{>0}$
and
![]() $d_{i,j} \in \mathbb {Z}_{\geq 0}$
. Note that, for each i, we have
$d_{i,j} \in \mathbb {Z}_{\geq 0}$
. Note that, for each i, we have
![]() $\sum _{j=1}^{m_{i}} jd_{i,j} = n_{i}$
since
$\sum _{j=1}^{m_{i}} jd_{i,j} = n_{i}$
since
![]() $f=g_{1}\cdots g_{s}$
. Since
$f=g_{1}\cdots g_{s}$
. Since
![]() $C_K(A)$
is canonically isomorphic to
$C_K(A)$
is canonically isomorphic to
![]() $\mathrm {End}_{K[x]}(T_{K}(A))$
by Lemma 9.5 (b), the desired result now follows from Corollary 9.9.
$\mathrm {End}_{K[x]}(T_{K}(A))$
by Lemma 9.5 (b), the desired result now follows from Corollary 9.9.
9.4 An algorithm for determining similarity and computing a conjugating matrix
We now consider the following problem.
Problem (IsSimilar)
Given a number field K with ring of integers
![]() $\mathcal {O}=\mathcal {O}_{K}$
, an integer
$\mathcal {O}=\mathcal {O}_{K}$
, an integer
![]() $n \in \mathbb {Z}_{>0}$
and two matrices
$n \in \mathbb {Z}_{>0}$
and two matrices
![]() $A,B \in \mathrm {Mat}_{n}(\mathcal {O})$
, determine whether A and B are similar over
$A,B \in \mathrm {Mat}_{n}(\mathcal {O})$
, determine whether A and B are similar over
![]() $\mathcal {O}$
, and if so, return a conjugating matrix
$\mathcal {O}$
, and if so, return a conjugating matrix
![]() $C \in \mathrm {GL}_{n}(\mathcal {O})$
such that
$C \in \mathrm {GL}_{n}(\mathcal {O})$
such that
![]() $B= CAC^{-1}$
.
$B= CAC^{-1}$
.
Let
![]() $n \in \mathbb {Z}_{>0}$
, and let
$n \in \mathbb {Z}_{>0}$
, and let
![]() $A,B \in \mathrm {Mat}_{n}(\mathbb {Z})$
. Assume that there exists
$A,B \in \mathrm {Mat}_{n}(\mathbb {Z})$
. Assume that there exists
![]() $D \in \mathrm {GL}_{n}(\mathbb {Q})$
such that
$D \in \mathrm {GL}_{n}(\mathbb {Q})$
such that
![]() $B=DAD^{-1}$
. Thus, A and B have the same minimal polynomial
$B=DAD^{-1}$
. Thus, A and B have the same minimal polynomial
![]() $f \in \mathbb {Z}[x]$
, and so the
$f \in \mathbb {Z}[x]$
, and so the
![]() $\mathbb {Z}[x]$
-modules
$\mathbb {Z}[x]$
-modules
![]() $T_{\mathbb {Z}}(A)$
and
$T_{\mathbb {Z}}(A)$
and
![]() $T_{\mathbb {Z}}(B)$
are in fact
$T_{\mathbb {Z}}(B)$
are in fact
![]() $\mathbb {Z}[x]/(f)$
-lattices. In view of Lemma 9.6, this implies that
$\mathbb {Z}[x]/(f)$
-lattices. In view of Lemma 9.6, this implies that
![]() $\mathsf {IsSimilar}$
over
$\mathsf {IsSimilar}$
over
![]() $\mathbb {Z}$
can be reduced to the problem of determining whether the
$\mathbb {Z}$
can be reduced to the problem of determining whether the
![]() $\mathbb {Z}[x]/(f)$
-lattices
$\mathbb {Z}[x]/(f)$
-lattices
![]() $T_{\mathbb {Z}}(A)$
and
$T_{\mathbb {Z}}(A)$
and
![]() $T_{\mathbb {Z}}(B)$
are isomorphic and, if so, of computing an isomorphism between them.
$T_{\mathbb {Z}}(B)$
are isomorphic and, if so, of computing an isomorphism between them.
Using this observation, Sarkisyan [Reference SarkisyanSar79] and Grunewald [Reference GrunewaldGru80] independently showed that the conjugacy problem over
![]() $\mathbb {Z}$
for arbitrary pairs of matrices is decidable. Moreover, Applegate and Onishi [Reference Appelgate and OnishiAO81, Reference Appelgate and OnishiAO82] considered the cases of
$\mathbb {Z}$
for arbitrary pairs of matrices is decidable. Moreover, Applegate and Onishi [Reference Appelgate and OnishiAO81, Reference Appelgate and OnishiAO82] considered the cases of
![]() $2 \times 2$
and
$2 \times 2$
and
![]() $3 \times 3$
matrices, and Behn and Van der Merwe [Reference Behn and Van der MerweBVdM02] also considered the
$3 \times 3$
matrices, and Behn and Van der Merwe [Reference Behn and Van der MerweBVdM02] also considered the
![]() $2 \times 2$
case.
$2 \times 2$
case.
In the case that the characteristic polynomial of A (and B) is squarefree (and thus the minimal and characteristic polynomials coincide), the above approach via
![]() $\mathbb {Z}[x]/(f)$
-lattices is equivalent to a classical result of Latimer–MacDuffee [Reference Latimer and MacDuffeeLM33]. This last result was recently generalised in the dissertation of Husert [Reference HusertHus17] to the case where the minimal polynomial is squarefree but the characteristic polynomial is arbitrary. See Proposition 9.10 for properties of the
$\mathbb {Z}[x]/(f)$
-lattices is equivalent to a classical result of Latimer–MacDuffee [Reference Latimer and MacDuffeeLM33]. This last result was recently generalised in the dissertation of Husert [Reference HusertHus17] to the case where the minimal polynomial is squarefree but the characteristic polynomial is arbitrary. See Proposition 9.10 for properties of the
![]() $\mathbb {Q}$
-algebra
$\mathbb {Q}$
-algebra
![]() $C_{\mathbb {Q}}(A)$
in both of these special cases.
$C_{\mathbb {Q}}(A)$
in both of these special cases.
For a discussion of practical algorithms that have been implemented on a computer, see §9.5.
Proposition 9.12. Let R be a Noetherian integral domain with field of fractions
![]() $K \neq R$
. Let
$K \neq R$
. Let
![]() $n \in \mathbb {Z}_{>0}$
, and let
$n \in \mathbb {Z}_{>0}$
, and let
![]() $A,B \in \mathrm {Mat}_{n}(R)$
. Suppose that
$A,B \in \mathrm {Mat}_{n}(R)$
. Suppose that
![]() $D \in \mathrm {GL}_{n}(K)$
satisfies
$D \in \mathrm {GL}_{n}(K)$
satisfies
![]() $B=DAD^{-1}$
. Then A and B are similar over R if and only if
$B=DAD^{-1}$
. Then A and B are similar over R if and only if
-
(a) the
 $C_R(B)$
-lattice
$C_R(B)$
-lattice
 $C_R(A, B)D^{-1}$
in
$C_R(A, B)D^{-1}$
in
 $C_{K}(B)$
is free of rank
$C_{K}(B)$
is free of rank
 $1$
, and
$1$
, and -
(b) every (any) free generator
 $C'$
of
$C'$
of
 $C_R(A, B)D^{-1}$
over
$C_R(A, B)D^{-1}$
over
 $C_{R}(B)$
satisfies
$C_{R}(B)$
satisfies
 $C'D \in \mathrm {GL}_n(R)$
.
$C'D \in \mathrm {GL}_n(R)$
.
Furthermore, when this is the case,
![]() $B=CAC^{-1}$
, where
$B=CAC^{-1}$
, where
![]() $C:=C'D$
.
$C:=C'D$
.
Proof. By Lemma 9.1 the map
![]() $\theta _{D^{-1}} : C_{K}(A,B) \rightarrow C_{K}(B)$
,
$\theta _{D^{-1}} : C_{K}(A,B) \rightarrow C_{K}(B)$
,
![]() $X \mapsto XD^{-1}$
is an isomorphism of
$X \mapsto XD^{-1}$
is an isomorphism of
![]() $C_{K}(B)$
-modules. Hence, the desired result follows from Proposition 9.2.
$C_{K}(B)$
-modules. Hence, the desired result follows from Proposition 9.2.
The main algorithm of this section is as follows.
Algorithm 9.13. Let K be a number field with ring of integers
![]() $\mathcal {O}=\mathcal {O}_{K}$
, let
$\mathcal {O}=\mathcal {O}_{K}$
, let
![]() $n \in \mathbb {Z}_{>0}$
and let
$n \in \mathbb {Z}_{>0}$
and let
![]() $A, B \in \mathrm {Mat}_{n}(\mathcal {O})$
. The following steps solve
$A, B \in \mathrm {Mat}_{n}(\mathcal {O})$
. The following steps solve
![]() $\textsf {IsSimilar}$
for A and B, that is, they determine whether A and B are similar over
$\textsf {IsSimilar}$
for A and B, that is, they determine whether A and B are similar over
![]() $\mathcal {O}$
, and if so, return an element
$\mathcal {O}$
, and if so, return an element
![]() $C \in \mathrm {GL}_{n}(\mathcal {O})$
such that
$C \in \mathrm {GL}_{n}(\mathcal {O})$
such that
![]() $B = CAC^{-1}$
.
$B = CAC^{-1}$
.
-
(1) Check whether A and B are similar over K, and if so, compute
 $D \in \mathrm {GL}_{n}(K)$
such that
$D \in \mathrm {GL}_{n}(K)$
such that
 $B = DAD^{-1}$
. If not, then A and B are not similar over
$B = DAD^{-1}$
. If not, then A and B are not similar over
 $\mathcal {O}$
.
$\mathcal {O}$
. -
(2) Compute
 $C_{K}(B)$
,
$C_{K}(B)$
,
 $\operatorname {\mathrm {J}}(C_K(B))$
and an explicit homomorphism of K-algebras where the
$\operatorname {\mathrm {J}}(C_K(B))$
and an explicit homomorphism of K-algebras where the $$\begin{align*}\rho \colon C_K(B) \longrightarrow C_K(B)/{\operatorname{\mathrm{J}}(C_K(B))} \stackrel{\cong}{\longrightarrow} \prod_{i=1}^{t} \mathrm{Mat}_{d_i}(K_i), \end{align*}$$
$$\begin{align*}\rho \colon C_K(B) \longrightarrow C_K(B)/{\operatorname{\mathrm{J}}(C_K(B))} \stackrel{\cong}{\longrightarrow} \prod_{i=1}^{t} \mathrm{Mat}_{d_i}(K_i), \end{align*}$$
 $K_{i}$
’s are (not necessarily distinct) finite field extensions of K.
$K_{i}$
’s are (not necessarily distinct) finite field extensions of K.
-
(3) Check whether
 $\rho (C_{\mathcal {O}}(A, B)D^{-1})$
is a free
$\rho (C_{\mathcal {O}}(A, B)D^{-1})$
is a free
 $\rho (C_{\mathcal {O}}(B))$
-lattice, and if so, compute a generator
$\rho (C_{\mathcal {O}}(B))$
-lattice, and if so, compute a generator
 $E \in \rho (C_{\mathcal {O}}(A, B)D^{-1})$
. If not, then A and B are not similar over
$E \in \rho (C_{\mathcal {O}}(A, B)D^{-1})$
. If not, then A and B are not similar over
 $\mathcal {O}$
.
$\mathcal {O}$
. -
(4) Compute
 $C' \in C_{\mathcal {O}}(A, B)D^{-1}$
such that
$C' \in C_{\mathcal {O}}(A, B)D^{-1}$
such that
 $\rho (C')=E$
.
$\rho (C')=E$
. -
(5) Check whether
 $C := C'D \in \mathrm {GL}_n(\mathcal {O})$
. If so, then
$C := C'D \in \mathrm {GL}_n(\mathcal {O})$
. If so, then
 $B=CAC^{-1}$
. If not, then A and B are not similar over
$B=CAC^{-1}$
. If not, then A and B are not similar over
 $\mathcal {O}$
.
$\mathcal {O}$
.
Proof of correctness of Algorithm 9.13
If all steps succeed, then
![]() $C \in C_{\mathcal {O}}(A, B) \cap \mathrm {GL}_{n}(\mathcal {O})$
and it easily follows that
$C \in C_{\mathcal {O}}(A, B) \cap \mathrm {GL}_{n}(\mathcal {O})$
and it easily follows that
![]() $B=CAC^{-1}$
. It remains to show that if any of steps (1), (3) or (5) fail, then A and B are not similar over
$B=CAC^{-1}$
. It remains to show that if any of steps (1), (3) or (5) fail, then A and B are not similar over
![]() $\mathcal {O}$
. If step (1) fails, then this is clear. If step (3) fails, then Theorem 3.4 (a) implies that
$\mathcal {O}$
. If step (1) fails, then this is clear. If step (3) fails, then Theorem 3.4 (a) implies that
![]() $C_{\mathcal {O}}(A, B)D^{-1}$
is not free over
$C_{\mathcal {O}}(A, B)D^{-1}$
is not free over
![]() $C_{\mathcal {O}}(B)$
, and the result follows from Proposition 9.12 (a). Finally, suppose that step (5) fails, that is,
$C_{\mathcal {O}}(B)$
, and the result follows from Proposition 9.12 (a). Finally, suppose that step (5) fails, that is,
![]() $C \notin \mathrm {GL}_{n}(\mathcal {O})$
. If
$C \notin \mathrm {GL}_{n}(\mathcal {O})$
. If
![]() $C'$
is not a free generator of
$C'$
is not a free generator of
![]() $C_{\mathcal {O}}(A, B)D^{-1}$
over
$C_{\mathcal {O}}(A, B)D^{-1}$
over
![]() $C_{\mathcal {O}}(B)$
, then Theorem 3.4 (b) implies that
$C_{\mathcal {O}}(B)$
, then Theorem 3.4 (b) implies that
![]() $C_{\mathcal {O}}(A, B)D^{-1}$
is not free over
$C_{\mathcal {O}}(A, B)D^{-1}$
is not free over
![]() $C_{\mathcal {O}}(B)$
, and again the result follows from Proposition 9.12 (a). If
$C_{\mathcal {O}}(B)$
, and again the result follows from Proposition 9.12 (a). If
![]() $C'$
is a free generator of
$C'$
is a free generator of
![]() $C_{\mathcal {O}}(A, B)D^{-1}$
over
$C_{\mathcal {O}}(A, B)D^{-1}$
over
![]() $C_{\mathcal {O}}(B)$
, then the result follows from Proposition 9.12 (b).
$C_{\mathcal {O}}(B)$
, then the result follows from Proposition 9.12 (b).
The following result analyses the complexity of Algorithm 9.13, and further details on each step are given in the proof.
Theorem 9.14. Let K be a number field with ring of integers
![]() $\mathcal {O}=\mathcal {O}_{K}$
, let
$\mathcal {O}=\mathcal {O}_{K}$
, let
![]() $n \in \mathbb {Z}_{>0}$
and let
$n \in \mathbb {Z}_{>0}$
and let
![]() $A, B \in \mathrm {Mat}_{n}(\mathcal {O})$
. Let
$A, B \in \mathrm {Mat}_{n}(\mathcal {O})$
. Let
![]() $f_{1}, \ldots , f_{r} \in K[x]$
be the distinct monic irreducible factors of the characteristic polynomial of B. For
$f_{1}, \ldots , f_{r} \in K[x]$
be the distinct monic irreducible factors of the characteristic polynomial of B. For
![]() $i=1,\ldots ,r$
let
$i=1,\ldots ,r$
let
![]() $K_{i}=K[x]/(f_{i})$
. Let
$K_{i}=K[x]/(f_{i})$
. Let
![]() $\Lambda $
be the image of
$\Lambda $
be the image of
![]() $C_{\mathcal {O}}(B)$
under the projection
$C_{\mathcal {O}}(B)$
under the projection
![]() $C_K(B) \to C_K(B)/{\operatorname {\mathrm {J}}(C_K(B))}$
. Let
$C_K(B) \to C_K(B)/{\operatorname {\mathrm {J}}(C_K(B))}$
. Let
![]() $\mathcal {M}$
be any choice of maximal
$\mathcal {M}$
be any choice of maximal
![]() $\mathcal {O}$
-order in
$\mathcal {O}$
-order in
![]() $C_K(B)/\operatorname {\mathrm {J}}(C_K(B))$
containing
$C_K(B)/\operatorname {\mathrm {J}}(C_K(B))$
containing
![]() $\Lambda $
, and let
$\Lambda $
, and let
![]() $\mathfrak {h} = [\mathcal {M} : \Lambda ]_{\mathcal {O}}$
be the module index of
$\mathfrak {h} = [\mathcal {M} : \Lambda ]_{\mathcal {O}}$
be the module index of
![]() $\Lambda $
in
$\Lambda $
in
![]() $\mathcal {M}$
. Then Algorithm 9.13 reduces the problem
$\mathcal {M}$
. Then Algorithm 9.13 reduces the problem
![]() $\mathsf {IsSimilar}$
for A and B in probabilistic polynomial time to
$\mathsf {IsSimilar}$
for A and B in probabilistic polynomial time to
-
(a)
 $\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
, the factorisation of the discriminant of
$\mathsf {Factor}(\mathrm {Disc}(\Lambda ))$
, the factorisation of the discriminant of
 $\Lambda $
,
$\Lambda $
, -
(b) for each i with
 $1 \leq i \leq r$
, one instance of
$1 \leq i \leq r$
, one instance of
 $\mathsf {IsPrincipal}_{\mathcal O_{K_i}}$
,
$\mathsf {IsPrincipal}_{\mathcal O_{K_i}}$
, -
(c) for each i with
 $1 \leq i \leq r$
,
$1 \leq i \leq r$
,
 $\mathsf {UnitGroup}(\mathcal O_{K_i})$
,
$\mathsf {UnitGroup}(\mathcal O_{K_i})$
, -
(d) for each prime ideal divisor
 $\mathfrak {p}$
of
$\mathfrak {p}$
of
 $\mathfrak {h}$
, the problem
$\mathfrak {h}$
, the problem
 $\mathsf {DLog}$
for extensions of
$\mathsf {DLog}$
for extensions of
 $\mathcal {O}/\mathfrak {p}$
and
$\mathcal {O}/\mathfrak {p}$
and -
(e) for each prime ideal divisor
 $\mathfrak {p}$
of
$\mathfrak {p}$
of
 $\mathfrak {h}$
, the problem
$\mathfrak {h}$
, the problem
 $\mathsf {Primitive}$
for extensions of
$\mathsf {Primitive}$
for extensions of
 $\mathcal {O}/\mathfrak {p}$
.
$\mathcal {O}/\mathfrak {p}$
.
Note that
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathfrak {h}$
are not part of the input and
$\mathfrak {h}$
are not part of the input and
![]() $\mathfrak {h}$
is only needed for the above complexity statement. Moreover,
$\mathfrak {h}$
is only needed for the above complexity statement. Moreover,
![]() $\mathfrak {h}$
does not depend on the choice of
$\mathfrak {h}$
does not depend on the choice of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. In the following, the steps refer to those of Algorithm 9.13. Step (1) can be performed in polynomial time by [Reference Chistov, Ivanyos and KarpinskiCIK97, Theorem 2], and step (2) can be performed in polynomial time by Proposition 9.11. Steps (4) and (5) are straightforward and can both be performed in polynomial time. Step (3) can be performed using Algorithm 8.3, and so the desired result now follows from Theorem 8.4 after noting that
![]() $\mathsf {Wedderburn}(C_K(B)/{\operatorname {\mathrm {J}}(C_K(B)))}$
was already performed in step (2).
$\mathsf {Wedderburn}(C_K(B)/{\operatorname {\mathrm {J}}(C_K(B)))}$
was already performed in step (2).
We also record the following two consequences of Remark 8.8.
Corollary 9.15. The problem
![]() $\mathsf {IsSimilar}$
reduces in probabilistic subexponential time to the problems
$\mathsf {IsSimilar}$
reduces in probabilistic subexponential time to the problems
![]() $\mathsf {IsPrincipal}$
and
$\mathsf {IsPrincipal}$
and
![]() $\mathsf {UnitGroup}$
for rings of integers of number fields.
$\mathsf {UnitGroup}$
for rings of integers of number fields.
Corollary 9.16. There exists a polynomial quantum algorithm for solving
![]() $\mathsf {IsSimilar}$
.
$\mathsf {IsSimilar}$
.
9.5 Implementation of the algorithm
The algorithm for solving the principal ideal problem for orders in algebras satisfying hypothesis (H), and its application to the similarity problem has been implemented using the computer algebra package Hecke [Reference Fieker, Hart, Hofmann and JohanssonFHHJ17] (also available in Oscar [OSC22]) and is included from version 0.13 onwards. The implementation works for arbitrary pairs of matrices in
![]() $\mathrm {Mat}_{n}(\mathbb {Z})$
. We now give a brief comparison with other algorithms and implementations, all of which are for pairs of matrices in
$\mathrm {Mat}_{n}(\mathbb {Z})$
. We now give a brief comparison with other algorithms and implementations, all of which are for pairs of matrices in
![]() $\mathrm {Mat}_{n}(\mathbb {Z})$
, subject to certain further restrictions in cases (a)–(c). Recall that in Proposition 9.10 the restrictions in (b) and (c) are rephrased in terms of the algebra
$\mathrm {Mat}_{n}(\mathbb {Z})$
, subject to certain further restrictions in cases (a)–(c). Recall that in Proposition 9.10 the restrictions in (b) and (c) are rephrased in terms of the algebra
![]() $C_{\mathbb {Q}}(A)$
.
$C_{\mathbb {Q}}(A)$
.
-
(a) The algorithm of Opgenorth–Plesken–Schulz [Reference Opgenorth, Plesken and SchulzOPS98] solves the similarity problem for pairs of matrices of finite order.
-
(b) The algorithm of Husert [Reference HusertHus17] solves the similarity problem for pairs of matrices, both of which are either nilpotent or have squarefree minimal polynomial. However, the implementation is restricted to nilpotent matrices and matrices with irreducible minimal polynomial.
-
(c) The algorithm of Marseglia [Reference MarsegliaMar20] solves the similarity problem for pairs of matrices with squarefree characteristic polynomial (this condition implies that the minimal and characteristic polynomials coincide).
-
(d) The algorithm of Eick–O’Brien and the second named author of the present article [Reference Eick, Hofmann and O’BrienEHO19] is based on ideas of Grunewald [Reference GrunewaldGru80] and solves the similarity problem for arbitrary pairs of matrices.
All of the above algorithms (a)–(d) have been implemented in Magma [Reference Bosma, Cannon and PlayoustBCP97], but no formal complexity analysis has been given for any of them. However, we can compare these with our algorithm using timings and heuristic reasoning. All timings in the examples below were performed using a single core of a 3.40 GHz Intel E5-2643 processor and under the assumption of GRH. Magma V2.23-3 was used to run algorithms (a)–(d).
For random pairs of matrices of a given rational canonical form, our algorithm dramatically outperforms (a) and the algorithm for nilpotent matrices of (b). In the latter case this is not surprising since the algorithm in question requires an exhaustive search among candidates within a large search space. In the case of matrices with squarefree minimal polynomial, the bottleneck of algorithm (b) is a final enumeration over a set
![]() $\Lambda /\mathfrak {f}$
, which our algorithm avoids by means of the results of §6.6 (in particular, see Proposition 6.11). In cases where the set
$\Lambda /\mathfrak {f}$
, which our algorithm avoids by means of the results of §6.6 (in particular, see Proposition 6.11). In cases where the set
![]() $\Lambda /\mathfrak {f}$
is large, our algorithm dramatically outperforms that of (b).
$\Lambda /\mathfrak {f}$
is large, our algorithm dramatically outperforms that of (b).
Example 9.17. Consider the two matrices
 $$\begin{align*}A = \left(\begin{smallmatrix} 0&1&0&0&0&0\\ -5336100&0&0&0&0&0\\ 0&0&0&1&0&0\\ 0&0&-5336100&0&0&0\\ 0&0&0&0&0&1\\ 0&0&0&0&-5336100&0 \end{smallmatrix}\right), \quad B = \left(\begin{smallmatrix} 0&1&5&0&53361000&0\\ -5336100&0&40&-5&0&-53361000\\ 0&0&-8&1&0&0\\ 0&0&-5336164&8&0&0\\ 0&0&0&0&0&1\\ 0&0&0&0&-5336100&0 \end{smallmatrix}\right), \end{align*}$$
$$\begin{align*}A = \left(\begin{smallmatrix} 0&1&0&0&0&0\\ -5336100&0&0&0&0&0\\ 0&0&0&1&0&0\\ 0&0&-5336100&0&0&0\\ 0&0&0&0&0&1\\ 0&0&0&0&-5336100&0 \end{smallmatrix}\right), \quad B = \left(\begin{smallmatrix} 0&1&5&0&53361000&0\\ -5336100&0&40&-5&0&-53361000\\ 0&0&-8&1&0&0\\ 0&0&-5336164&8&0&0\\ 0&0&0&0&0&1\\ 0&0&0&0&-5336100&0 \end{smallmatrix}\right), \end{align*}$$
both with irreducible minimal polynomial
![]() $f = x^2 + 5336100$
and characteristic polynomial
$f = x^2 + 5336100$
and characteristic polynomial
![]() $f^3$
. The algorithm of (b) requires an enumeration over a set of size
$f^3$
. The algorithm of (b) requires an enumeration over a set of size
![]() $2357947691 \approx 10^9$
, thus rendering it impractical for this example. However, the implementation of our algorithm requires 6 seconds to recognise that A and B are similar over
$2357947691 \approx 10^9$
, thus rendering it impractical for this example. However, the implementation of our algorithm requires 6 seconds to recognise that A and B are similar over
![]() $\mathbb {Z}$
and to find a conjugating matrix. Note that
$\mathbb {Z}$
and to find a conjugating matrix. Note that
![]() $C_{\mathbb {Q}}(A) \cong \mathrm {Mat}_3(K)$
, where
$C_{\mathbb {Q}}(A) \cong \mathrm {Mat}_3(K)$
, where
![]() $K = \mathbb {Q}[x]/(x^2 + 5336100)$
.
$K = \mathbb {Q}[x]/(x^2 + 5336100)$
.
Algorithm (c) is more restricted than (b) in that it requires the matrices in question to have squarefree characteristic polynomial. However, in contrast to the squarefree minimal polynomial case of (b), it avoids a final enumeration step, and thus it performs as well as our algorithm in this special case.
We have compared the implementation of our algorithm with that of algorithm (d) for a variety of different examples and found that in all cases the former outperformed the latter, often dramatically. However, we should mention that as a by-product, given a matrix
![]() $A \in \mathrm {Mat}_{n}(\mathbb {Z})$
, algorithm (d) can be used to determine generators of the arithmetic group
$A \in \mathrm {Mat}_{n}(\mathbb {Z})$
, algorithm (d) can be used to determine generators of the arithmetic group
![]() $C_{\mathbb {Z}}(A)^{\times } = \{ X \in \mathrm {GL}_{n}(\mathbb {Z}) \mid XA = AX \}$
. Various examples in [Reference Eick, Hofmann and O’BrienEHO19] as well as the overall strategy of finding candidates in large search spaces suggest that algorithm (d) has at least exponential complexity. We now review some of these examples from [Reference Eick, Hofmann and O’BrienEHO19] and show how our algorithm fares in comparison.
$C_{\mathbb {Z}}(A)^{\times } = \{ X \in \mathrm {GL}_{n}(\mathbb {Z}) \mid XA = AX \}$
. Various examples in [Reference Eick, Hofmann and O’BrienEHO19] as well as the overall strategy of finding candidates in large search spaces suggest that algorithm (d) has at least exponential complexity. We now review some of these examples from [Reference Eick, Hofmann and O’BrienEHO19] and show how our algorithm fares in comparison.
Example 9.18 [Reference Eick, Hofmann and O’BrienEHO19, 6.3.2]
Consider the two matrices
 $$\begin{align*}A = \left( \begin{smallmatrix} -3 & -1 & 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -5 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -3 & -1 & 3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -5 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -3 & -1 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -5 & 0 & 1 \end{smallmatrix} \right) , \quad B = \left(\begin{smallmatrix} 13 & -15 & 16 & 24 & -16 & -7 & -35 & 15 & 0 \\ -3 & 44 & -40 & -71 & 62 & 28 & 157 & -76 & 16 \\ 18 & -15 & -3 & -7 & -31 & 6 & -226 & 129 & -52 \\ -69 & 72 & -55 & -78 & 86 & 18 & 355 & -186 & 48 \\ -75 & 98 & -82 & -124 & 117 & 35 & 406 & -206 & 46 \\ -45 & 19 & -21 & -22 & 10 & 1 & 49 & -25 & -3 \\ 24 & -66 & 53 & 89 & -89 & -31 & -289 & 147 & -37 \\ 30 & -78 & 61 & 102 & -104 & -35 & -348 & 178 & -45 \\ 24 & 11 & -8 & -23 & 26 & 14 & 58 & -29 & 11 \end{smallmatrix} \right), \end{align*}$$
$$\begin{align*}A = \left( \begin{smallmatrix} -3 & -1 & 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -5 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -3 & -1 & 3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -5 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -3 & -1 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -5 & 0 & 1 \end{smallmatrix} \right) , \quad B = \left(\begin{smallmatrix} 13 & -15 & 16 & 24 & -16 & -7 & -35 & 15 & 0 \\ -3 & 44 & -40 & -71 & 62 & 28 & 157 & -76 & 16 \\ 18 & -15 & -3 & -7 & -31 & 6 & -226 & 129 & -52 \\ -69 & 72 & -55 & -78 & 86 & 18 & 355 & -186 & 48 \\ -75 & 98 & -82 & -124 & 117 & 35 & 406 & -206 & 46 \\ -45 & 19 & -21 & -22 & 10 & 1 & 49 & -25 & -3 \\ 24 & -66 & 53 & 89 & -89 & -31 & -289 & 147 & -37 \\ 30 & -78 & 61 & 102 & -104 & -35 & -348 & 178 & -45 \\ 24 & 11 & -8 & -23 & 26 & 14 & 58 & -29 & 11 \end{smallmatrix} \right), \end{align*}$$
both with irreducible minimal polynomial
![]() $f = x^3 + 2x^2 + 13x - 1$
and characteristic polynomial
$f = x^3 + 2x^2 + 13x - 1$
and characteristic polynomial
![]() $f^{3}$
. As these are not equal, algorithm (c) cannot be applied in this situation. Moreover, algorithm (d) fails to run in reasonable time because the search space is too large. However, the implementation of our algorithm requires 10 seconds to recognise that A and B are similar over
$f^{3}$
. As these are not equal, algorithm (c) cannot be applied in this situation. Moreover, algorithm (d) fails to run in reasonable time because the search space is too large. However, the implementation of our algorithm requires 10 seconds to recognise that A and B are similar over
![]() $\mathbb {Z}$
and to find a conjugating matrix. Note that
$\mathbb {Z}$
and to find a conjugating matrix. Note that
![]() $C_{\mathbb {Q}}(A) \cong \mathrm {Mat}_3(K)$
, where
$C_{\mathbb {Q}}(A) \cong \mathrm {Mat}_3(K)$
, where
![]() $K = \mathbb {Q}[x]/(f)$
.
$K = \mathbb {Q}[x]/(f)$
.
Example 9.19 [Reference Eick, Hofmann and O’BrienEHO19, 6.3.3]
Consider the two matrices
 $$\begin{align*}A = \left(\begin{smallmatrix} 13 & 67 & 6 & 0 & 0 & -1 \\ 0 & 1 & 3 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ -270 & -1350 & 0 & 1 & 2 & 20 \\ -135 & -675 & 0 & 0 & 1 & 10 \\ -27 & -135 & 0 & 0 & 0 & 2 \end{smallmatrix}\right), \quad B = \left(\begin{smallmatrix} 13 & 79 & 0 & 0 & 1 & -76 \\ 0 & 1 & 0 & 0 & 0 & 3 \\ -270 & -1620 & 1 & 2 & -20 & 1620 \\ -135 & -810 & 0 & 1 & -10 & 810 \\ 27 & 162 & 0 & 0 & 2 & -162 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{smallmatrix} \right), \end{align*}$$
$$\begin{align*}A = \left(\begin{smallmatrix} 13 & 67 & 6 & 0 & 0 & -1 \\ 0 & 1 & 3 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ -270 & -1350 & 0 & 1 & 2 & 20 \\ -135 & -675 & 0 & 0 & 1 & 10 \\ -27 & -135 & 0 & 0 & 0 & 2 \end{smallmatrix}\right), \quad B = \left(\begin{smallmatrix} 13 & 79 & 0 & 0 & 1 & -76 \\ 0 & 1 & 0 & 0 & 0 & 3 \\ -270 & -1620 & 1 & 2 & -20 & 1620 \\ -135 & -810 & 0 & 1 & -10 & 810 \\ 27 & 162 & 0 & 0 & 2 & -162 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{smallmatrix} \right), \end{align*}$$
both with minimal and characteristic polynomial equal to
![]() $(x - 1)^{4}(x^2 - 15x - 1)$
. As this is not squarefree, algorithms (b) and (c) cannot be applied in this situation. Again, the search space for a certain subproblem is too large, making the computation infeasible for algorithm (d). However, the implementation of our algorithm finds a conjugating matrix in less than one second. Note that
$(x - 1)^{4}(x^2 - 15x - 1)$
. As this is not squarefree, algorithms (b) and (c) cannot be applied in this situation. Again, the search space for a certain subproblem is too large, making the computation infeasible for algorithm (d). However, the implementation of our algorithm finds a conjugating matrix in less than one second. Note that
![]() $\dim _{\mathbb {Q}}(C_{\mathbb {Q}}(A)) = 6$
and
$\dim _{\mathbb {Q}}(C_{\mathbb {Q}}(A)) = 6$
and
where
![]() $K = \mathbb {Q}[x]/(x^2 - 15x - 1)$
.
$K = \mathbb {Q}[x]/(x^2 - 15x - 1)$
.
Example 9.20. Consider the two matrices
 $$\begin{align*}A = \left(\begin{smallmatrix} 1 & -4 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -3 & -6 & 0 \\ 0 & 0 & 0 & 1 & 2 & 0 \\ -4 & 16 & -3 & 0 & -5 & -6 \\ 0 & 0 & -37 & 0 & -9 & -55 \end{smallmatrix}\right), \quad B = \left(\begin{smallmatrix} -88 & -4 & 0 & -66 & -51 & 32 \\ -2683 & 225 & 326 & -2670 & 1755 & 634 \\ -2607 & -666 & -332 & -525 & -6747 & 2835 \\ 14 & 0 & 0 & 13 & 2 & 0 \\ 523 & 38 & -3 & 330 & 440 & -325 \\ 285 & 74 & 37 & 54 & 749 & -314 \end{smallmatrix}\right), \quad \end{align*}$$
$$\begin{align*}A = \left(\begin{smallmatrix} 1 & -4 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -3 & -6 & 0 \\ 0 & 0 & 0 & 1 & 2 & 0 \\ -4 & 16 & -3 & 0 & -5 & -6 \\ 0 & 0 & -37 & 0 & -9 & -55 \end{smallmatrix}\right), \quad B = \left(\begin{smallmatrix} -88 & -4 & 0 & -66 & -51 & 32 \\ -2683 & 225 & 326 & -2670 & 1755 & 634 \\ -2607 & -666 & -332 & -525 & -6747 & 2835 \\ 14 & 0 & 0 & 13 & 2 & 0 \\ 523 & 38 & -3 & 330 & 440 & -325 \\ 285 & 74 & 37 & 54 & 749 & -314 \end{smallmatrix}\right), \quad \end{align*}$$
both with minimal and characteristic polynomial
![]() $(x - 1)^2 (x^4 + 58x^3 + 88x^2 + 176x + 1)$
. As this is not squarefree, algorithms (b) and (c) cannot be applied in this situation. Moreover, the implementation of algorithm (d) requires approximately one hour to find a conjugating matrix. By contrast, the implementation of our algorithm finds such a matrix in less than one second. Note that
$(x - 1)^2 (x^4 + 58x^3 + 88x^2 + 176x + 1)$
. As this is not squarefree, algorithms (b) and (c) cannot be applied in this situation. Moreover, the implementation of algorithm (d) requires approximately one hour to find a conjugating matrix. By contrast, the implementation of our algorithm finds such a matrix in less than one second. Note that
![]() $\dim _{\mathbb {Q}}(C_{\mathbb {Q}}(A)) = 6$
and
$\dim _{\mathbb {Q}}(C_{\mathbb {Q}}(A)) = 6$
and
where
![]() $K = \mathbb {Q}[x]/(x^4 + 58x^3 + 88x^2 + 176x + 1)$
.
$K = \mathbb {Q}[x]/(x^4 + 58x^3 + 88x^2 + 176x + 1)$
.
10 Application: Galois module structure of rings of integers
An important motivation for Algorithm 8.3 and its predecessors is the investigation of the Galois module structure of rings of integers. We only briefly recall the problem here and refer the reader to the introduction of [Reference Hofmann and JohnstonHJ20] for a more detailed overview.
Let
![]() $L/K$
be a finite Galois extension of number fields, and let
$L/K$
be a finite Galois extension of number fields, and let
![]() $G=\mathrm {Gal}(L/K)$
. The classical normal basis theorem says that
$G=\mathrm {Gal}(L/K)$
. The classical normal basis theorem says that
![]() $L \cong K[G]$
as
$L \cong K[G]$
as
![]() $K[G]$
-modules. A much more difficult problem is that of determining whether the ring of integers
$K[G]$
-modules. A much more difficult problem is that of determining whether the ring of integers
![]() $\mathcal {O}_{L}$
is free over its so-called associated order
$\mathcal {O}_{L}$
is free over its so-called associated order
![]() $\mathcal {A}_{L/K} = \{ \alpha \in K[G] \mid \alpha \mathcal {O}_{L} \subseteq \mathcal {O}_{L} \}$
. Note that if a prime
$\mathcal {A}_{L/K} = \{ \alpha \in K[G] \mid \alpha \mathcal {O}_{L} \subseteq \mathcal {O}_{L} \}$
. Note that if a prime
![]() $\mathfrak {p}$
of K is (at most) tamely ramified in
$\mathfrak {p}$
of K is (at most) tamely ramified in
![]() $L/K$
or is such that the localised associated order
$L/K$
or is such that the localised associated order
![]() $\mathcal {A}_{L/K, \mathfrak {p}}$
is maximal, then the localisation
$\mathcal {A}_{L/K, \mathfrak {p}}$
is maximal, then the localisation
![]() $\mathcal {O}_{L,\mathfrak {p}}$
is necessarily free over
$\mathcal {O}_{L,\mathfrak {p}}$
is necessarily free over
![]() $\mathcal {A}_{L/K, \mathfrak {p}}$
. In particular,
$\mathcal {A}_{L/K, \mathfrak {p}}$
. In particular,
![]() $\mathcal {O}_{L}$
is locally free over
$\mathcal {O}_{L}$
is locally free over
![]() $\mathcal {A}_{L/K}$
if and only if
$\mathcal {A}_{L/K}$
if and only if
![]() $\mathcal {O}_{L,\mathfrak {p}}$
is free over
$\mathcal {O}_{L,\mathfrak {p}}$
is free over
![]() $\mathcal {A}_{L/K, \mathfrak {p}}$
for every prime
$\mathcal {A}_{L/K, \mathfrak {p}}$
for every prime
![]() $\mathfrak {p}$
of K that is wildly ramified in
$\mathfrak {p}$
of K that is wildly ramified in
![]() $L/K$
. In this situation, one can consider the class
$L/K$
. In this situation, one can consider the class
![]() $[\mathcal {O}_{L}]$
in the locally free class group
$[\mathcal {O}_{L}]$
in the locally free class group
![]() $\mathrm {Cl}(\mathcal {A}_{L/K})$
. Moreover, if
$\mathrm {Cl}(\mathcal {A}_{L/K})$
. Moreover, if
![]() $K[G]$
satisfies hypothesis (H), then every order in
$K[G]$
satisfies hypothesis (H), then every order in
![]() $K[G]$
has the so-called locally free cancellation property (this follows from Jacobinski’s cancellation theorem [Reference Curtis and ReinerCR87, (51.24)]), and so
$K[G]$
has the so-called locally free cancellation property (this follows from Jacobinski’s cancellation theorem [Reference Curtis and ReinerCR87, (51.24)]), and so
![]() $\mathcal {O}_{L}$
is free over
$\mathcal {O}_{L}$
is free over
![]() $\mathcal {A}_{L/K}$
if and only if it is locally free and the class
$\mathcal {A}_{L/K}$
if and only if it is locally free and the class
![]() $[\mathcal {O}_{L}]$
is the trivial element of
$[\mathcal {O}_{L}]$
is the trivial element of
![]() $\mathrm {Cl}(\mathcal {A}_{L/K})$
.
$\mathrm {Cl}(\mathcal {A}_{L/K})$
.
For an abstract finite group
![]() $\Gamma $
, we say that
$\Gamma $
, we say that
![]() $L/K$
is a
$L/K$
is a
![]() $\Gamma $
-extension if it is a Galois extension such that
$\Gamma $
-extension if it is a Galois extension such that
![]() $\mathrm {Gal}(L/K) \cong \Gamma $
. Let
$\mathrm {Gal}(L/K) \cong \Gamma $
. Let
![]() $\Gamma =S_{4} \times C_{2}$
, the direct product of the symmetric group on
$\Gamma =S_{4} \times C_{2}$
, the direct product of the symmetric group on
![]() $4$
letters and the cyclic group of order
$4$
letters and the cyclic group of order
![]() $2$
. Since
$2$
. Since
 $$\begin{align*}\mathbb{Q}[\Gamma] \cong \prod_{i=1}^{4} \mathbb{Q} \times \prod_{j=1}^{2} \mathrm{Mat}_2(\mathbb{Q}) \times \prod_{k=1}^{4} \mathrm{Mat}_3(\mathbb{Q}), \end{align*}$$
$$\begin{align*}\mathbb{Q}[\Gamma] \cong \prod_{i=1}^{4} \mathbb{Q} \times \prod_{j=1}^{2} \mathrm{Mat}_2(\mathbb{Q}) \times \prod_{k=1}^{4} \mathrm{Mat}_3(\mathbb{Q}), \end{align*}$$
the algebra
![]() $\mathbb {Q}[\Gamma ]$
satisfies hypothesis (H). Using the methods of [Reference Fieker, Hofmann and SircanaFHS19], we have constructed wildly ramified
$\mathbb {Q}[\Gamma ]$
satisfies hypothesis (H). Using the methods of [Reference Fieker, Hofmann and SircanaFHS19], we have constructed wildly ramified
![]() $\Gamma $
-extensions of
$\Gamma $
-extensions of
![]() $\mathbb {Q}$
of small discriminant. The wildly ramified
$\mathbb {Q}$
of small discriminant. The wildly ramified
![]() $\Gamma $
-extension of minimal discriminant is
$\Gamma $
-extension of minimal discriminant is
![]() $L_1 := K_1(\sqrt {92})$
, where
$L_1 := K_1(\sqrt {92})$
, where
![]() $K_1$
is the
$K_1$
is the
![]() $S_4$
-extension of
$S_4$
-extension of
![]() $\mathbb {Q}$
defined by
$\mathbb {Q}$
defined by
 $$ \begin{align*} x^{24} + 2 x^{22} + 27 x^{20} + 112 x^{18} + 585 x^{16} &+ 338 x^{14} + 5767 x^{12} \\ &\ \quad+ 4362 x^{10} + 1417 x^{8} - 76 x^{6} - 29 x^{4} - 6 x^{2} + 1 \in \mathbb{Q}[x]. \end{align*} $$
$$ \begin{align*} x^{24} + 2 x^{22} + 27 x^{20} + 112 x^{18} + 585 x^{16} &+ 338 x^{14} + 5767 x^{12} \\ &\ \quad+ 4362 x^{10} + 1417 x^{8} - 76 x^{6} - 29 x^{4} - 6 x^{2} + 1 \in \mathbb{Q}[x]. \end{align*} $$
The field
![]() $L_1$
has discriminant
$L_1$
has discriminant
![]() $2^{84} \cdot 23^{24}$
and is wildly ramified at
$2^{84} \cdot 23^{24}$
and is wildly ramified at
![]() $2$
. Moreover, the associated order
$2$
. Moreover, the associated order
![]() $\mathcal {A}_{L_1/\mathbb {Q}}$
has index
$\mathcal {A}_{L_1/\mathbb {Q}}$
has index
![]() $2^{43} \cdot 3^{3}$
in a maximal order
$2^{43} \cdot 3^{3}$
in a maximal order
![]() $\mathcal {M}$
satisfying
$\mathcal {M}$
satisfying
![]() $\mathcal {A}_{L_1/\mathbb {Q}} \subseteq \mathcal {M} \subseteq \mathbb {Q}[\mathrm {Gal}(L_{1}/\mathbb {Q})]$
(note that this index is independent of the choice of
$\mathcal {A}_{L_1/\mathbb {Q}} \subseteq \mathcal {M} \subseteq \mathbb {Q}[\mathrm {Gal}(L_{1}/\mathbb {Q})]$
(note that this index is independent of the choice of
![]() $\mathcal {M}$
). Using Algorithm 8.3 we have checked that
$\mathcal {M}$
). Using Algorithm 8.3 we have checked that
![]() $\mathcal {O}_{L_1}$
is free over
$\mathcal {O}_{L_1}$
is free over
![]() $\mathcal {A}_{L_1/\mathbb {Q}}$
and have also obtained an explicit generator (unfortunately, the coefficients are too large to reproduce in print). The algorithms of [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Reference Bley and WilsonBW09] show that
$\mathcal {A}_{L_1/\mathbb {Q}}$
and have also obtained an explicit generator (unfortunately, the coefficients are too large to reproduce in print). The algorithms of [Reference Bley, Boltje, Hess, Pauli and PohstBB06, Reference Bley and WilsonBW09] show that
![]() $\mathrm {Cl}(\mathcal {A}_{L_1/\mathbb {Q}}) \cong C_{2}$
. However, the algorithm of [Reference Bley and WilsonBW09] for solving the discrete logarithm problem in a locally free class group is restricted to the case in which the order in question is a group ring or a maximal order, and so this approach does not allow us to determine
$\mathrm {Cl}(\mathcal {A}_{L_1/\mathbb {Q}}) \cong C_{2}$
. However, the algorithm of [Reference Bley and WilsonBW09] for solving the discrete logarithm problem in a locally free class group is restricted to the case in which the order in question is a group ring or a maximal order, and so this approach does not allow us to determine
![]() $[\mathcal {O}_{L_1}]$
in
$[\mathcal {O}_{L_1}]$
in
![]() $\mathrm {Cl}(\mathcal {A}_{L_1/\mathbb {Q}})$
.
$\mathrm {Cl}(\mathcal {A}_{L_1/\mathbb {Q}})$
.
We have performed the same computation using Algorithm 8.3 described above for all wildly ramified
![]() $\Gamma $
-extensions
$\Gamma $
-extensions
![]() $L/\mathbb {Q}$
with
$L/\mathbb {Q}$
with
![]() $\lvert \mathrm {Disc}(L) \rvert \leq 60^{48}$
. For
$\lvert \mathrm {Disc}(L) \rvert \leq 60^{48}$
. For
![]() $686$
out of these
$686$
out of these
![]() $2600$
extensions,
$2600$
extensions,
![]() $\mathcal {O}_{L}$
is locally free over
$\mathcal {O}_{L}$
is locally free over
![]() $\mathcal {A}_{L/\mathbb {Q}}$
, and in all of these cases,
$\mathcal {A}_{L/\mathbb {Q}}$
, and in all of these cases,
![]() $\mathcal {O}_{L}$
is in fact free over
$\mathcal {O}_{L}$
is in fact free over
![]() $\mathcal {A}_{L/\mathbb {Q}}$
. It would be interesting to find a proof of, or counterexample to, the assertion that the same phenomenon holds without the restriction on
$\mathcal {A}_{L/\mathbb {Q}}$
. It would be interesting to find a proof of, or counterexample to, the assertion that the same phenomenon holds without the restriction on
![]() $\lvert \mathrm {Disc}(L) \rvert $
.
$\lvert \mathrm {Disc}(L) \rvert $
.
A Weak approximation in probabilistic polynomial time
Let K be a number field with ring of integers
![]() $\mathcal {O} = {\mathcal {O}_K}$
. Let
$\mathcal {O} = {\mathcal {O}_K}$
. Let
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {b}$
be nonzero integral ideals of
$\mathfrak {b}$
be nonzero integral ideals of
![]() $\mathcal {O}$
. A classical result (see [Reference CohenCoh00, Corollary 1.3.9]) asserts that there exists a deterministic algorithm for computing
$\mathcal {O}$
. A classical result (see [Reference CohenCoh00, Corollary 1.3.9]) asserts that there exists a deterministic algorithm for computing
![]() $x \in K^{\times }$
such that
$x \in K^{\times }$
such that
![]() $x \mathfrak {a}$
is integral and coprime to
$x \mathfrak {a}$
is integral and coprime to
![]() $\mathfrak {b}$
. If the factorisation of
$\mathfrak {b}$
. If the factorisation of
![]() $\mathfrak {b}$
, or equivalently, of
$\mathfrak {b}$
, or equivalently, of
![]() $\mathrm {N}(\mathfrak {b})$
, is given, the algorithm runs in polynomial time. There also exists a probabilistic algorithm [Reference CohenCoh00, Algorithm 1.3.14], which does not require the factorisation of
$\mathrm {N}(\mathfrak {b})$
, is given, the algorithm runs in polynomial time. There also exists a probabilistic algorithm [Reference CohenCoh00, Algorithm 1.3.14], which does not require the factorisation of
![]() $\mathfrak {b}$
or
$\mathfrak {b}$
or
![]() $\mathrm {N}(\mathfrak {b})$
, but is not polynomial time. The aim of this section is to combine the deterministic and probabilistic variants to obtain a probabilistic polynomial-time algorithm. The approach is based on the following general form of the constructive weak approximation theorem, which relies on ideas of [Reference BelabasBel04, Algorithm 6.15]. For a nonzero prime ideal
$\mathrm {N}(\mathfrak {b})$
, but is not polynomial time. The aim of this section is to combine the deterministic and probabilistic variants to obtain a probabilistic polynomial-time algorithm. The approach is based on the following general form of the constructive weak approximation theorem, which relies on ideas of [Reference BelabasBel04, Algorithm 6.15]. For a nonzero prime ideal
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathcal {O}$
, let
$\mathcal {O}$
, let
![]() $v_{\mathfrak {p}}(-)$
denote the
$v_{\mathfrak {p}}(-)$
denote the
![]() $\mathfrak {p}$
-adic valuation.
$\mathfrak {p}$
-adic valuation.
Proposition A.1. There exists a probabilistic polynomial-time algorithm that given nonzero integral ideals
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {b}$
of
$\mathfrak {b}$
of
![]() $\mathcal {O}$
returns an element
$\mathcal {O}$
returns an element
![]() $x \in \mathfrak {a}$
with
$x \in \mathfrak {a}$
with
![]() $v_{\mathfrak {p}}(x) = v_{\mathfrak {p}}(\mathfrak {a})$
for all prime ideals
$v_{\mathfrak {p}}(x) = v_{\mathfrak {p}}(\mathfrak {a})$
for all prime ideals
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {b}$
.
$\mathfrak {b}$
.
Proof. We adapt the proofs of [Reference BelabasBel04, Lemmas 6.14, 6.16], taking into account [Reference BelabasBel04, Remark 6.17 (2)]. For the rest of the proof, we fix a positive constant
![]() $0<C<1$
. Let
$0<C<1$
. Let
![]() $a = \min (\mathfrak {a} \cap \mathbb {Z}_{>0})$
, let
$a = \min (\mathfrak {a} \cap \mathbb {Z}_{>0})$
, let
![]() $b = \min (\mathfrak {b} \cap \mathbb {Z}_{>0})$
and let
$b = \min (\mathfrak {b} \cap \mathbb {Z}_{>0})$
and let
![]() $d=[K:\mathbb {Q}]$
. Note that if
$d=[K:\mathbb {Q}]$
. Note that if
![]() $a=1$
or
$a=1$
or
![]() $b=1$
or
$b=1$
or
![]() $d=1$
, then we can just take
$d=1$
, then we can just take
![]() $x=a$
. Thus, we can and do assume that
$x=a$
. Thus, we can and do assume that
![]() $a, b,d \geq 2$
. We define
$a, b,d \geq 2$
. We define
![]() $y \in \mathbb {R}$
by the equality
$y \in \mathbb {R}$
by the equality
![]() $Cy\log (y) = d \log (b)$
. Then
$Cy\log (y) = d \log (b)$
. Then
![]() $y>2$
and we observe that y is polynomially bounded in terms of d and
$y>2$
and we observe that y is polynomially bounded in terms of d and
![]() $\log (b)$
. Hence, we can determine the set
$\log (b)$
. Hence, we can determine the set
in polynomial time. We define ideals
Then
![]() $\mathfrak {a} = \mathfrak {a}_0\mathfrak {a}_1$
and
$\mathfrak {a} = \mathfrak {a}_0\mathfrak {a}_1$
and
![]() $\mathfrak {b} = \mathfrak {b}_0\mathfrak {b}_1$
with integral ideals
$\mathfrak {b} = \mathfrak {b}_0\mathfrak {b}_1$
with integral ideals
![]() $\mathfrak {a}_1, \mathfrak {b}_1$
such that
$\mathfrak {a}_1, \mathfrak {b}_1$
such that
which can be computed in polynomial time. We write
![]() $b = b_0 b_1$
with
$b = b_0 b_1$
with
Since the factorisations of
![]() $\mathfrak {a}_{0}$
and
$\mathfrak {a}_{0}$
and
![]() $\mathfrak {b}_{0}$
are known, using the deterministic polynomial-time algorithm [Reference CohenCoh00, Proposition 1.3.8] we can find
$\mathfrak {b}_{0}$
are known, using the deterministic polynomial-time algorithm [Reference CohenCoh00, Proposition 1.3.8] we can find
![]() $x_0 \in \mathcal {O}$
with
$x_0 \in \mathcal {O}$
with
![]() $x_0 \in \mathfrak a_0$
and
$x_0 \in \mathfrak a_0$
and
![]() $v_{\mathfrak p}(x_0) = v_{\mathfrak p}(\mathfrak a_0)$
for all
$v_{\mathfrak p}(x_0) = v_{\mathfrak p}(\mathfrak a_0)$
for all
![]() $\mathfrak p$
dividing
$\mathfrak p$
dividing
![]() $\mathfrak b_0$
.
$\mathfrak b_0$
.
We now show that we can find an element
![]() $x_{1} \in \mathfrak {a}_{1}$
with
$x_{1} \in \mathfrak {a}_{1}$
with
![]() $v_{\mathfrak {p}}(x_1) = v_{\mathfrak {p}}(\mathfrak {a}_{1})$
for all
$v_{\mathfrak {p}}(x_1) = v_{\mathfrak {p}}(\mathfrak {a}_{1})$
for all
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {b}_{1}$
in probabilistic polynomial time. For the rest of the proof, we will refer to such elements as good elements. We will prove that a positive proportion (independent of
$\mathfrak {b}_{1}$
in probabilistic polynomial time. For the rest of the proof, we will refer to such elements as good elements. We will prove that a positive proportion (independent of
![]() $\mathfrak a$
and
$\mathfrak a$
and
![]() $\mathfrak b$
) of elements of the finite abelian group
$\mathfrak b$
) of elements of the finite abelian group
![]() $\mathfrak a_1/\mathfrak a_1\mathfrak b_1$
are good. For a prime ideal
$\mathfrak a_1/\mathfrak a_1\mathfrak b_1$
are good. For a prime ideal
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {b}_1$
, let
$\mathfrak {b}_1$
, let
![]() $A_{\mathfrak {p}}$
denote the set
$A_{\mathfrak {p}}$
denote the set
![]() $\mathfrak {a}_1 \mathfrak {p}/\mathfrak {a}_1 \mathfrak {b}_1$
. Then, for a set of prime ideals T dividing
$\mathfrak {a}_1 \mathfrak {p}/\mathfrak {a}_1 \mathfrak {b}_1$
. Then, for a set of prime ideals T dividing
![]() $\mathfrak {b}_1$
, we have
$\mathfrak {b}_1$
, we have
 $$\begin{align*}\Bigl\lvert \bigcap_{\mathfrak{p} \in T} A_{\mathfrak{p}} \Bigr\rvert = \mathrm{N}(\mathfrak b_1)/\prod_{\mathfrak p \in T}\mathrm{N}(\mathfrak{p}). \end{align*}$$
$$\begin{align*}\Bigl\lvert \bigcap_{\mathfrak{p} \in T} A_{\mathfrak{p}} \Bigr\rvert = \mathrm{N}(\mathfrak b_1)/\prod_{\mathfrak p \in T}\mathrm{N}(\mathfrak{p}). \end{align*}$$
From the inclusion-exclusion principle it follows that
 $$\begin{align*}\Bigl\lvert \bigcup_{\mathfrak{p} \mid \mathfrak{b}_1 } A_{\mathfrak{p}} \Bigr\rvert = \mathrm{N}(\mathfrak{b}_1) \left( 1 - \prod_{\mathfrak{p} \mid \mathfrak{b}_1} \left(1 - \frac{1}{\mathrm{N}(\mathfrak{p})}\right) \right). \end{align*}$$
$$\begin{align*}\Bigl\lvert \bigcup_{\mathfrak{p} \mid \mathfrak{b}_1 } A_{\mathfrak{p}} \Bigr\rvert = \mathrm{N}(\mathfrak{b}_1) \left( 1 - \prod_{\mathfrak{p} \mid \mathfrak{b}_1} \left(1 - \frac{1}{\mathrm{N}(\mathfrak{p})}\right) \right). \end{align*}$$
By definition, the lift of
![]() $x \in \mathfrak {a}_1/\mathfrak {a}_1\mathfrak {b}_1$
is good if and only if
$x \in \mathfrak {a}_1/\mathfrak {a}_1\mathfrak {b}_1$
is good if and only if
![]() $x \not \in \bigcup _{\mathfrak {p} \mid \mathfrak {b}_1} A_{\mathfrak {p}}$
. Hence, the probability that (the lift) of a random element of
$x \not \in \bigcup _{\mathfrak {p} \mid \mathfrak {b}_1} A_{\mathfrak {p}}$
. Hence, the probability that (the lift) of a random element of
![]() $\mathfrak {a}_1/\mathfrak {a}_1\mathfrak {b}_1$
is good is
$\mathfrak {a}_1/\mathfrak {a}_1\mathfrak {b}_1$
is good is
 $$\begin{align*}\prod_{\mathfrak p \mid \mathfrak b_1}\left( 1 - \frac{1}{\mathrm{N}(\mathfrak p)} \right). \end{align*}$$
$$\begin{align*}\prod_{\mathfrak p \mid \mathfrak b_1}\left( 1 - \frac{1}{\mathrm{N}(\mathfrak p)} \right). \end{align*}$$
Now, set
![]() $C_1 := d \log (b_1)/(y \log (y)) \leq C$
. Since there are at most
$C_1 := d \log (b_1)/(y \log (y)) \leq C$
. Since there are at most
![]() $d \log _y(b_1)$
prime ideals
$d \log _y(b_1)$
prime ideals
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {b}_1$
, each satisfying
$\mathfrak {b}_1$
, each satisfying
![]() $\mathrm {N}(\mathfrak {p}) \geq y$
, we have
$\mathrm {N}(\mathfrak {p}) \geq y$
, we have
 $$ \begin{align*} \textstyle{\prod_{\mathfrak p \mid \mathfrak b_1}(1 - 1/\mathrm{N}(\mathfrak p))} \geq (1 - 1/y)^{d \log_y(b_1)} & \geq \exp(-1/y-1/y^{2})^{d \log_y(b_1)} = \exp(-C_1 - C_1/y) \\ &\geq \exp(-C(1+1/y)) \geq \exp(-3 C/2). \end{align*} $$
$$ \begin{align*} \textstyle{\prod_{\mathfrak p \mid \mathfrak b_1}(1 - 1/\mathrm{N}(\mathfrak p))} \geq (1 - 1/y)^{d \log_y(b_1)} & \geq \exp(-1/y-1/y^{2})^{d \log_y(b_1)} = \exp(-C_1 - C_1/y) \\ &\geq \exp(-C(1+1/y)) \geq \exp(-3 C/2). \end{align*} $$
Here the second inequality follows from
![]() $1 - x \geq \exp (-x - x^2)$
for
$1 - x \geq \exp (-x - x^2)$
for
![]() $0 \leq x \leq 1/2$
. Thus, we can find a good element in probabilistic polynomial time.
$0 \leq x \leq 1/2$
. Thus, we can find a good element in probabilistic polynomial time.
Now, given
![]() $x_i \in \mathfrak a_i$
with
$x_i \in \mathfrak a_i$
with
![]() $v_{\mathfrak p}(x_i) = v_{\mathfrak p}(\mathfrak a_i)$
for all primes
$v_{\mathfrak p}(x_i) = v_{\mathfrak p}(\mathfrak a_i)$
for all primes
![]() $\mathfrak p$
dividing
$\mathfrak p$
dividing
![]() $\mathfrak b_i$
, we proceed as follows. For
$\mathfrak b_i$
, we proceed as follows. For
![]() $i=0,1$
let
$i=0,1$
let
![]() $\mathfrak {c}_i$
be the largest divisor of
$\mathfrak {c}_i$
be the largest divisor of
![]() $\mathfrak {b}_i$
which is coprime to
$\mathfrak {b}_i$
which is coprime to
![]() $\mathfrak {a}$
. Note that each
$\mathfrak {a}$
. Note that each
![]() $\mathfrak {c}_i$
can be determined in polynomial time by using only ideal sums and ideal division. Moreover, if
$\mathfrak {c}_i$
can be determined in polynomial time by using only ideal sums and ideal division. Moreover, if
![]() $\mathfrak {p}$
is a prime ideal with
$\mathfrak {p}$
is a prime ideal with
![]() $\mathfrak {p} \mid \mathfrak {b}_i$
and
$\mathfrak {p} \mid \mathfrak {b}_i$
and
![]() $\mathfrak {p} \nmid \mathfrak {a}$
, then
$\mathfrak {p} \nmid \mathfrak {a}$
, then
![]() $\mathfrak {p} \mid \mathfrak {c}_i$
. Since
$\mathfrak {p} \mid \mathfrak {c}_i$
. Since
![]() $\mathfrak {a}_0^2\mathfrak {c}_0 + \mathfrak {a}_1^2\mathfrak {c}_1 = \mathcal {O}$
, we can determine elements
$\mathfrak {a}_0^2\mathfrak {c}_0 + \mathfrak {a}_1^2\mathfrak {c}_1 = \mathcal {O}$
, we can determine elements
![]() $e_i \in \mathfrak {a}_i^2\mathfrak {c}_i$
with
$e_i \in \mathfrak {a}_i^2\mathfrak {c}_i$
with
![]() $e_0 + e_1 = 1$
in polynomial time. We now prove that the element
$e_0 + e_1 = 1$
in polynomial time. We now prove that the element
satisfies
![]() $v_{\mathfrak {p}} (x) = v_{\mathfrak {p}}(\mathfrak {a})$
for all
$v_{\mathfrak {p}} (x) = v_{\mathfrak {p}}(\mathfrak {a})$
for all
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {b}$
.
$\mathfrak {b}$
.
Case 1:
![]() $\mathfrak {p} \nmid \mathfrak {a}$
. Assume that
$\mathfrak {p} \nmid \mathfrak {a}$
. Assume that
![]() $\mathfrak {p} \mid \mathfrak {b}_1$
. Then
$\mathfrak {p} \mid \mathfrak {b}_1$
. Then
![]() $\mathfrak {p} \mid \mathfrak {c}_1$
and hence
$\mathfrak {p} \mid \mathfrak {c}_1$
and hence
![]() $e_1 \in \mathfrak {p}$
,
$e_1 \in \mathfrak {p}$
,
![]() $e_0 \not \in \mathfrak {p}$
. Moreover,
$e_0 \not \in \mathfrak {p}$
. Moreover,
 $$ \begin{align*} v_{\mathfrak{p}}(e_0x_1) &= v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(x_1) = v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(\mathfrak{a}_1) = v_{\mathfrak{p}}(e_0) = 0, \\ v_{\mathfrak{p}}(e_1x_0) &= v_{\mathfrak{p}}(e_1) + v_{\mathfrak{p}}(x_0) \ge v_{\mathfrak{p}}(e_1)> 0. \end{align*} $$
$$ \begin{align*} v_{\mathfrak{p}}(e_0x_1) &= v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(x_1) = v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(\mathfrak{a}_1) = v_{\mathfrak{p}}(e_0) = 0, \\ v_{\mathfrak{p}}(e_1x_0) &= v_{\mathfrak{p}}(e_1) + v_{\mathfrak{p}}(x_0) \ge v_{\mathfrak{p}}(e_1)> 0. \end{align*} $$
Hence,
![]() $v_{\mathfrak {p}}(x) = \min (v_{\mathfrak {p}}(e_0x_1), v_{\mathfrak {p}}(e_1x_0)) = 0 = v_{\mathfrak {p}}(\mathfrak {a})$
. The subcase
$v_{\mathfrak {p}}(x) = \min (v_{\mathfrak {p}}(e_0x_1), v_{\mathfrak {p}}(e_1x_0)) = 0 = v_{\mathfrak {p}}(\mathfrak {a})$
. The subcase
![]() $\mathfrak {p} \mid \mathfrak {b}_0$
is similar.
$\mathfrak {p} \mid \mathfrak {b}_0$
is similar.
Case 2:
![]() $\mathfrak {p} \mid \mathfrak {a}$
. Assume that
$\mathfrak {p} \mid \mathfrak {a}$
. Assume that
![]() $\mathfrak {p} \mid \mathfrak {b}_1$
. Then
$\mathfrak {p} \mid \mathfrak {b}_1$
. Then
![]() $\mathfrak {p} \not \in S$
and hence
$\mathfrak {p} \not \in S$
and hence
![]() $\mathfrak {p} \nmid \mathfrak {a}_0$
. It follows that
$\mathfrak {p} \nmid \mathfrak {a}_0$
. It follows that
![]() $\mathfrak {p}\mid \mathfrak {a}_1$
, and hence
$\mathfrak {p}\mid \mathfrak {a}_1$
, and hence
![]() $e_0 \not \in \mathfrak {p}, e_1 \in \mathfrak {p}$
. Moreover,
$e_0 \not \in \mathfrak {p}, e_1 \in \mathfrak {p}$
. Moreover,
 $$ \begin{align*} v_{\mathfrak{p}}(e_0x_1) &= v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(x_1) = v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(\mathfrak{a}_1) = v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(\mathfrak{a}) = v_{\mathfrak{p}}(\mathfrak{a}), \\ v_{\mathfrak{p}}(e_1x_0) &= v_{\mathfrak{p}}(e_1) + v_{\mathfrak{p}}(x_0) \ge v_{\mathfrak{p}}(e_1) \ge 2v_{\mathfrak{p}}(\mathfrak{a}_1)> v_{\mathfrak{p}}(\mathfrak{a}_1) = v_{\mathfrak{p}}(\mathfrak{a}). \end{align*} $$
$$ \begin{align*} v_{\mathfrak{p}}(e_0x_1) &= v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(x_1) = v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(\mathfrak{a}_1) = v_{\mathfrak{p}}(e_0) + v_{\mathfrak{p}}(\mathfrak{a}) = v_{\mathfrak{p}}(\mathfrak{a}), \\ v_{\mathfrak{p}}(e_1x_0) &= v_{\mathfrak{p}}(e_1) + v_{\mathfrak{p}}(x_0) \ge v_{\mathfrak{p}}(e_1) \ge 2v_{\mathfrak{p}}(\mathfrak{a}_1)> v_{\mathfrak{p}}(\mathfrak{a}_1) = v_{\mathfrak{p}}(\mathfrak{a}). \end{align*} $$
Hence,
![]() $v_{\mathfrak {p}}(x) = \min (v_{\mathfrak {p}}(e_0x_1), v_{\mathfrak {p}}(e_1x_0)) = v_{\mathfrak {p}}(\mathfrak {a})$
. The subcase
$v_{\mathfrak {p}}(x) = \min (v_{\mathfrak {p}}(e_0x_1), v_{\mathfrak {p}}(e_1x_0)) = v_{\mathfrak {p}}(\mathfrak {a})$
. The subcase
![]() $\mathfrak {p} \mid \mathfrak {b}_0$
is similar.
$\mathfrak {p} \mid \mathfrak {b}_0$
is similar.
Corollary A.2. There exists a probabilistic polynomial-time algorithm that given nonzero integral ideals
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {b}$
of
$\mathfrak {b}$
of
![]() $\mathcal {O}$
returns an element
$\mathcal {O}$
returns an element
![]() $x \in K^{\times }$
such that
$x \in K^{\times }$
such that
![]() $x \mathfrak {a}$
is integral and coprime to
$x \mathfrak {a}$
is integral and coprime to
![]() $\mathfrak {b}$
.
$\mathfrak {b}$
.
Proof. We need to find an element
![]() $x \in \mathfrak {a}^{-1}$
such that
$x \in \mathfrak {a}^{-1}$
such that
![]() $v_{\mathfrak {p}}(x) = v_{\mathfrak {p}}(\mathfrak {a}^{-1})$
for all prime ideals
$v_{\mathfrak {p}}(x) = v_{\mathfrak {p}}(\mathfrak {a}^{-1})$
for all prime ideals
![]() $\mathfrak {p}$
dividing
$\mathfrak {p}$
dividing
![]() $\mathfrak {b}$
. Setting
$\mathfrak {b}$
. Setting
![]() $a = \min (\mathfrak a \cap \mathbb {Z}_{>0})$
to be the minimum of
$a = \min (\mathfrak a \cap \mathbb {Z}_{>0})$
to be the minimum of
![]() $\mathfrak a$
, this is equivalent to
$\mathfrak a$
, this is equivalent to
![]() $v_{\mathfrak p}(ax) = v_{\mathfrak p}(a\mathfrak a^{-1})$
for all
$v_{\mathfrak p}(ax) = v_{\mathfrak p}(a\mathfrak a^{-1})$
for all
![]() $\mathfrak p$
dividing
$\mathfrak p$
dividing
![]() $\mathfrak b$
. As
$\mathfrak b$
. As
![]() $a \mathfrak a^{-1}$
is integral, the result follows from Proposition A.1 applied to
$a \mathfrak a^{-1}$
is integral, the result follows from Proposition A.1 applied to
![]() $a\mathfrak {a}^{-1}$
and
$a\mathfrak {a}^{-1}$
and
![]() $\mathfrak {b}$
.
$\mathfrak {b}$
.
Corollary A.3. There exists a probabilistic polynomial-time algorithm that, given a generating set of an
![]() $\mathcal {O}$
-lattice
$\mathcal {O}$
-lattice
![]() $M \subseteq K^{n}$
of rank n, determines a Steinitz form of M, that is, elements
$M \subseteq K^{n}$
of rank n, determines a Steinitz form of M, that is, elements
![]() $w_1,\dotsc ,w_n \in K^{n}$
and a fractional ideal
$w_1,\dotsc ,w_n \in K^{n}$
and a fractional ideal
![]() $\mathfrak {a}$
of
$\mathfrak {a}$
of
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
Proof. A pseudo-Hermite normal form can be determined in probabilistic polynomial time by [Reference Biasse, Fieker and HofmannBFH17, Theorem 34]. The reduction to the Steinitz form is described in [Reference CohenCoh00, Lemma 1.2.20] and requires the computation of coprime representatives of ideal classes. Thus, the claim follows from Corollary A.2.
Acknowledgements
The authors wish to thank Nigel Byott, Fabio Ferri, Claus Fieker and Jürgen Klüners for useful conversations and are grateful for numerous helpful comments and corrections from Nigel Byott, Gunter Malle, Stefano Marseglia and an anonymous referee. The second named author was supported by Project II.2 of SFB-TRR 195 ‘Symbolic Tools in Mathematics and Their Application’ of the German Research Foundation (DFG).
Conflicts of Interest
None.
Data availability statement
The source code for Hecke is available at https://github.com/thofma/Hecke.jl.