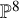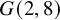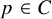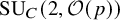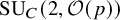1 Introduction
A century ago, Arthur Coble proved that there exists a unique quartic hypersurface
![]() $\mathcal {C}$
in
$\mathcal {C}$
in
![]() ${\mathbb {P}}^7$
that is singular exactly along the three-dimensional Kummer variety, image of the Jacobian of a nonhyperelliptic genus
${\mathbb {P}}^7$
that is singular exactly along the three-dimensional Kummer variety, image of the Jacobian of a nonhyperelliptic genus
![]() $3$
curve C via the
$3$
curve C via the
![]() $|2\Theta |$
-linear system ([Reference CobleCob61]; see also [Reference BeauvilleBea03, Reference KollárKol23]). This remarkable hypersurface is now named after him, and its many very special features have been studied by several algebraic geometers. For example,
$|2\Theta |$
-linear system ([Reference CobleCob61]; see also [Reference BeauvilleBea03, Reference KollárKol23]). This remarkable hypersurface is now named after him, and its many very special features have been studied by several algebraic geometers. For example,
![]() $\mathcal {C}$
is projectively self-dual [Reference PaulyPau02], it has close relationships with the
$\mathcal {C}$
is projectively self-dual [Reference PaulyPau02], it has close relationships with the
![]() $\Theta $
-geometry of the curve (e.g., a Schottky–Jung configuration of Kummer surfaces of Prym varieties [Reference van Geemen and PreviatovGP92], etc.) and with moduli of configurations of points in the projective space [Reference Alzati and BolognesiAB15].
$\Theta $
-geometry of the curve (e.g., a Schottky–Jung configuration of Kummer surfaces of Prym varieties [Reference van Geemen and PreviatovGP92], etc.) and with moduli of configurations of points in the projective space [Reference Alzati and BolognesiAB15].
Probably, the most striking property is, however, that
![]() $\mathcal {C}$
is the image, via the theta map, of the moduli space of semistable rank two vector bundles on C with trivial determinant. This was first remarked by Narasimhan and Ramanan in the seminal paper [Reference Narasimhan and RamananNR87]. In particular, since the theta map is an embedding for rank two bundles with trivial determinant [Reference BeauvilleBea88], we can identify
$\mathcal {C}$
is the image, via the theta map, of the moduli space of semistable rank two vector bundles on C with trivial determinant. This was first remarked by Narasimhan and Ramanan in the seminal paper [Reference Narasimhan and RamananNR87]. In particular, since the theta map is an embedding for rank two bundles with trivial determinant [Reference BeauvilleBea88], we can identify
![]() $\mathcal {C}$
with the moduli space
$\mathcal {C}$
with the moduli space
![]() $\operatorname {\mathrm {SU}}_C(2)$
itself.
$\operatorname {\mathrm {SU}}_C(2)$
itself.
In rank two, there is, up to isomorphism, only one other moduli space
![]() $\operatorname {\mathrm {SU}}_C(2,L)$
of rank two vector bundles on C, obtained by fixing the determinant to be any given line bundle L of odd degree (up to noncanonical isomorphisms, L is irrelevant). Contrary to
$\operatorname {\mathrm {SU}}_C(2,L)$
of rank two vector bundles on C, obtained by fixing the determinant to be any given line bundle L of odd degree (up to noncanonical isomorphisms, L is irrelevant). Contrary to
![]() ${\mathcal {C}}$
, this moduli space is smooth and we can wonder what could be an analogue of the Coble quartic. The main results of this paper answer this natural question.
${\mathcal {C}}$
, this moduli space is smooth and we can wonder what could be an analogue of the Coble quartic. The main results of this paper answer this natural question.
In order to achieve this, we will use the theory of theta representations [Reference VinbergVin76], in the way this was initiated in [Reference Gruson, Sam and WeymanGSW13] as a complex addition to arithmetic invariant theory. In our setting, the main point is that starting from the
![]() $\operatorname {\mathrm {GL}}_8$
-module
$\operatorname {\mathrm {GL}}_8$
-module
![]() $\wedge ^4{\mathbb {C}}^8$
one can easily construct the Coble quartics in terms of Pfaffian loci. From this point of view, the curve C defined by a general element of
$\wedge ^4{\mathbb {C}}^8$
one can easily construct the Coble quartics in terms of Pfaffian loci. From this point of view, the curve C defined by a general element of
![]() $\wedge ^4{\mathbb {C}}^8$
is not immediately visible, but certain deep properties of the quartic
$\wedge ^4{\mathbb {C}}^8$
is not immediately visible, but certain deep properties of the quartic
![]() ${\mathcal {C}}$
become easy to establish. For example, we give in Theorem 3.4 a short, self-contained proof of the self-duality of
${\mathcal {C}}$
become easy to establish. For example, we give in Theorem 3.4 a short, self-contained proof of the self-duality of
![]() ${\mathcal {C}}$
. Then we switch from
${\mathcal {C}}$
. Then we switch from
![]() ${\mathbb {P}}^7$
to the Grassmannian
${\mathbb {P}}^7$
to the Grassmannian
![]() $G(2,8)$
and observe that also in this Grassmannian, there exist natural Pfaffian loci corresponding to skew forms of rank at most
$G(2,8)$
and observe that also in this Grassmannian, there exist natural Pfaffian loci corresponding to skew forms of rank at most
![]() $4$
and
$4$
and
![]() $6$
, respectively of codimension
$6$
, respectively of codimension
![]() $6$
and
$6$
and
![]() $1$
:
$1$
:
Here, v is a general element in
![]() $\wedge ^4 {\mathbb {C}}^8$
and Q is a quadric section of the Grassmannian that is singular exactly along the six-dimensional smooth locus D (the notation
$\wedge ^4 {\mathbb {C}}^8$
and Q is a quadric section of the Grassmannian that is singular exactly along the six-dimensional smooth locus D (the notation
![]() $D_{Z_i}(v)$
will be explained in Section 4.2). The connection with the Coble quartic comes from the fact that D parametrizes a family of lines on it, some of the so-called Hecke lines. We deduce (Theorem 4.8 later on):
$D_{Z_i}(v)$
will be explained in Section 4.2). The connection with the Coble quartic comes from the fact that D parametrizes a family of lines on it, some of the so-called Hecke lines. We deduce (Theorem 4.8 later on):
Theorem 1.1.
![]() $D\simeq \operatorname {\mathrm {SU}}_C(2,L)$
for L of odd degree.
$D\simeq \operatorname {\mathrm {SU}}_C(2,L)$
for L of odd degree.
Consequently, the moduli space, which is smooth, comes up with a natural hypersurface of which it is the singular locus, contrary to the even case for which the moduli space is singular and uniquely determined by its singular locus, which is the Kummer. We extend the unicity statement by proving (Theorem 5.1 later on):
Theorem 1.2. Q is the only quadratic section of the Grassmannian that is singular along D.
Because of this property, Q really deserves to be called a Coble quadric. Moreover, exactly as the Coble quartic, we show this hypersurface is self-dual in a suitable sense (Theorem 5.15). As a matter of fact, for each point
![]() $p\in C$
, there is an embedding
$p\in C$
, there is an embedding
(see [Reference BeauvilleBea91]), and we show that at least for the generic p, there exists a unique quadric section of the Grassmannian that is singular along the moduli space (Theorem 5.14).
Remarkably, we found other instances of this phenomenon: For example, an eightfold inside the flag variety
![]() $Fl(1,7,8)$
whose singular locus is an abelian threefold, essentially the Jacobian of the curve (see Remark 3.7).
$Fl(1,7,8)$
whose singular locus is an abelian threefold, essentially the Jacobian of the curve (see Remark 3.7).
The paper is organized as follows. In section 2, we recall a few classical results about lines on moduli spaces of vector bundles on curves and more specifically about lines in the Coble quartic. In section 3, we explain how the Coble quartic, the Kummer threefold and the associated Jacobian can be constructed from a skew-symmetric four-form in eight variables, and we give a short proof of the self-duality of the quartic. In section 4, we explain how this point of view allows to understand the lines in the Coble quartic in terms of orbital degeneracy loci [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Reference Benedetti, Filippini, Manivel and TanturriBFMT20b], and we deduce Theorem 1 (see Theorem 21). The resulting description as a relative Pfaffian locus makes it clear that the odd moduli space is the singular locus of a special quadratic section of the Grassmannian
![]() $G(2,8)$
. In order to prove that this special quadric is unique, we need to study the square of the ideal of the Grassmannian
$G(2,8)$
. In order to prove that this special quadric is unique, we need to study the square of the ideal of the Grassmannian
![]() $G(2,6)$
in its Plücker embedding. Going back to the relative setting we deduce Theorem 2 (see Theorem 27). We finally complete the picture by explaining why and how the special quadric is also self-dual.
$G(2,6)$
in its Plücker embedding. Going back to the relative setting we deduce Theorem 2 (see Theorem 27). We finally complete the picture by explaining why and how the special quadric is also self-dual.
2 Lines in the Coble quartic
Throughout the text, we will denote by
![]() $\mathrm {U}_C(r,d)$
the moduli space of semistable vector bundles on a curve C of rank r and determinant of degree d. If L is a degree d line bundle on C, we will denote by
$\mathrm {U}_C(r,d)$
the moduli space of semistable vector bundles on a curve C of rank r and determinant of degree d. If L is a degree d line bundle on C, we will denote by
![]() $\operatorname {\mathrm {SU}}_C(r,L)$
the subvariety of
$\operatorname {\mathrm {SU}}_C(r,L)$
the subvariety of
![]() $U_C(r,d)$
parametrizing vector bundles of determinant L; moreover,
$U_C(r,d)$
parametrizing vector bundles of determinant L; moreover,
![]() $\operatorname {\mathrm {SU}}_C(r):=\operatorname {\mathrm {SU}}_C(r,{\mathcal {O}}_C)$
. Since all the moduli spaces
$\operatorname {\mathrm {SU}}_C(r):=\operatorname {\mathrm {SU}}_C(r,{\mathcal {O}}_C)$
. Since all the moduli spaces
![]() $\operatorname {\mathrm {SU}}(r,L)$
are (noncanonically) isomorphic when the degree of L is fixed, we will also denote their isomorphism class by
$\operatorname {\mathrm {SU}}(r,L)$
are (noncanonically) isomorphic when the degree of L is fixed, we will also denote their isomorphism class by
![]() $\operatorname {\mathrm {SU}}_C(r,d)$
; it depends only on d modulo r. Finally, we will denote by
$\operatorname {\mathrm {SU}}_C(r,d)$
; it depends only on d modulo r. Finally, we will denote by
![]() $\mathrm {U}_C(r,d)^{\mathrm {eff}}$
the moduli space of vector bundles with effective determinant. When
$\mathrm {U}_C(r,d)^{\mathrm {eff}}$
the moduli space of vector bundles with effective determinant. When
![]() $d=1$
, this moduli space fibers over the curve C with fiber over c isomorphic to
$d=1$
, this moduli space fibers over the curve C with fiber over c isomorphic to
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
.
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
.
2.1 Covering families of rational curves in
 $\operatorname {\mathrm {SU}}_C(2)$
$\operatorname {\mathrm {SU}}_C(2)$
Rational curves in the moduli spaces
![]() $\operatorname {\mathrm {SU}}_C(r,d)$
were extensively studied; see, for example, [Reference Narasimhan and RamananNR75, Reference Oxbury, Pauly and PreviatoOPP98, Reference HwangHwa00, Reference Hwang and RamananHR04, Reference SunSun05, Reference Mok and SunMS09, Reference PalPal16]. Restricting to
$\operatorname {\mathrm {SU}}_C(r,d)$
were extensively studied; see, for example, [Reference Narasimhan and RamananNR75, Reference Oxbury, Pauly and PreviatoOPP98, Reference HwangHwa00, Reference Hwang and RamananHR04, Reference SunSun05, Reference Mok and SunMS09, Reference PalPal16]. Restricting to
![]() $g=3$
,
$g=3$
,
![]() $r=2$
and
$r=2$
and
![]() $d=0$
, the results of [Reference Mustopa and Teixidor i BigasMTiB20] show that there exist two different families of covering lines, that is, families of rational curves of degree one with respect to the Theta embedding
$d=0$
, the results of [Reference Mustopa and Teixidor i BigasMTiB20] show that there exist two different families of covering lines, that is, families of rational curves of degree one with respect to the Theta embedding
passing through a general point of the moduli space. We will denote these two families by
![]() ${\mathcal {F}}_H$
and
${\mathcal {F}}_H$
and
![]() ${\mathcal {F}}_R$
and consider them as subvarieties of the Grassmannain
${\mathcal {F}}_R$
and consider them as subvarieties of the Grassmannain
![]() $G(2,V_8)$
. In the sequel, we describe these two covering families in some detail. They are both of dimension six but behave very differently; we will illustrate this by showing how different are the corresponding variety of minimal rational tangents(VMRTs), which in our case, since we deal with lines, are just the spaces of lines through a fixed general point.
$G(2,V_8)$
. In the sequel, we describe these two covering families in some detail. They are both of dimension six but behave very differently; we will illustrate this by showing how different are the corresponding variety of minimal rational tangents(VMRTs), which in our case, since we deal with lines, are just the spaces of lines through a fixed general point.
2.2 Hecke lines
Before going through the body of this section, we need to recall the following
Definition 2.1. A vector bundle V on C is called
![]() $(k,\ell )$
-semistable (resp.
$(k,\ell )$
-semistable (resp.
![]() $(k,\ell )$
-stable) if for any proper subbundle
$(k,\ell )$
-stable) if for any proper subbundle
![]() $W\subset V$
we have
$W\subset V$
we have
A generic Hecke line can be described by choosing a point
![]() $c\in C$
and a rank two vector bundle F on C with determinant
$c\in C$
and a rank two vector bundle F on C with determinant
![]() $\det (F)={\mathcal {O}}_C(c)$
. Then the bundles E that fit into an exact sequence
$\det (F)={\mathcal {O}}_C(c)$
. Then the bundles E that fit into an exact sequence
are parametrized by
![]() ${\mathbb {P}} (F_c^\vee )\simeq {\mathbb {P}}^1$
. They have trivial determinant and are all stable when F is
${\mathbb {P}} (F_c^\vee )\simeq {\mathbb {P}}^1$
. They have trivial determinant and are all stable when F is
![]() $(1,0)$
-semistable in the sense of [Reference Mok and SunMS09, Definition 2.5]. For vector bundles of rank two and degree one, this condition is equivalent to stability, hence also to semistability. The resulting curve in
$(1,0)$
-semistable in the sense of [Reference Mok and SunMS09, Definition 2.5]. For vector bundles of rank two and degree one, this condition is equivalent to stability, hence also to semistability. The resulting curve in
![]() $\operatorname {\mathrm {SU}}_C(2)$
is a line and such lines are called Hecke lines. Note that dualizing, we get an exact sequence
$\operatorname {\mathrm {SU}}_C(2)$
is a line and such lines are called Hecke lines. Note that dualizing, we get an exact sequence
so a Hecke line parametrizes all the possible extensions of
![]() ${\mathcal {O}}_c$
by
${\mathcal {O}}_c$
by
![]() $F^\vee $
.
$F^\vee $
.
By [Reference PalPal16, Remark 5.3], a general Hecke line defines a vector bundle
![]() ${\mathcal {E}}$
of rank
${\mathcal {E}}$
of rank
![]() $2$
over
$2$
over
![]() $C\times {\mathbb {P}}^1$
fitting into an exact sequence
$C\times {\mathbb {P}}^1$
fitting into an exact sequence
where
![]() $p_1$
and
$p_1$
and
![]() $p_2$
are the projections of
$p_2$
are the projections of
![]() $C \times {\mathbb {P}}^1$
onto the two factors C and
$C \times {\mathbb {P}}^1$
onto the two factors C and
![]() ${\mathbb {P}}^1$
. An easy consequence is that, since
${\mathbb {P}}^1$
. An easy consequence is that, since
![]() ${\mathcal {E}}^\vee $
admits a unique jumping line at c, this point can be uniquely recovered from the Hecke line. (Beware this is only true for general Hecke lines.)
${\mathcal {E}}^\vee $
admits a unique jumping line at c, this point can be uniquely recovered from the Hecke line. (Beware this is only true for general Hecke lines.)
We will denote by
![]() ${\mathcal {F}}_H$
the family of Hecke lines in
${\mathcal {F}}_H$
the family of Hecke lines in
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C)$
, considered as a subvariety of the space
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C)$
, considered as a subvariety of the space
![]() $G(2,V_8)$
of lines in
$G(2,V_8)$
of lines in
![]() ${\mathbb {P}}(V_8)$
.
${\mathbb {P}}(V_8)$
.
Remark 2.2. Although a Hecke line does not always define a unique point in C, once we have fixed such a point c there is a well-defined morphism from
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
to
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
to
![]() ${\mathcal {F}}_H$
. By the previous observations, the resulting morphism from
${\mathcal {F}}_H$
. By the previous observations, the resulting morphism from
![]() $\tilde {\mathcal {F}}_H:=\mathrm {U}_C(2,1)^{\mathrm {eff}}$
to
$\tilde {\mathcal {F}}_H:=\mathrm {U}_C(2,1)^{\mathrm {eff}}$
to
![]() ${\mathcal {F}}_H$
is birational.
${\mathcal {F}}_H$
is birational.
Conversely, Hecke lines passing through a general point
![]() $[E]$
of
$[E]$
of
![]() $\operatorname {\mathrm {SU}}_C(2,K_C)$
(we make this choice of determinant just for convenience) are obtained by choosing a projection
$\operatorname {\mathrm {SU}}_C(2,K_C)$
(we make this choice of determinant just for convenience) are obtained by choosing a projection
![]() $E{\rightarrow } E_c{\rightarrow }{\mathcal {O}}_c$
, where
$E{\rightarrow } E_c{\rightarrow }{\mathcal {O}}_c$
, where
![]() $E_c$
denotes the fiber of the vector bundle E at the point
$E_c$
denotes the fiber of the vector bundle E at the point
![]() $c\in C$
. So they are parametrized by (the image in
$c\in C$
. So they are parametrized by (the image in
![]() ${\mathcal {F}}_H$
of) the total space of the projective bundle
${\mathcal {F}}_H$
of) the total space of the projective bundle
![]() ${\mathbb {P}}(E^\vee )$
over C. The tangent map of this morphism sends
${\mathbb {P}}(E^\vee )$
over C. The tangent map of this morphism sends
![]() ${\mathbb {P}}(E^\vee )$
to the tangent space of the moduli space at
${\mathbb {P}}(E^\vee )$
to the tangent space of the moduli space at
![]() $[E]$
, which is the projectivization of
$[E]$
, which is the projectivization of
since
![]() $K_C\simeq \det (E)$
. Here,
$K_C\simeq \det (E)$
. Here,
![]() $ \mathcal {E}nd_0(E)$
denotes the vector bundle of traceless endomorphisms of E. This implies (see [Reference HwangHwa00, Reference Hwang and RamananHR04] for more general statements):
$ \mathcal {E}nd_0(E)$
denotes the vector bundle of traceless endomorphisms of E. This implies (see [Reference HwangHwa00, Reference Hwang and RamananHR04] for more general statements):
Proposition 2.3. The VMRT of the family
![]() ${\mathcal {F}}_H$
of Hecke lines at a general point
${\mathcal {F}}_H$
of Hecke lines at a general point
![]() $[E]$
of the moduli space is the image of the ruled surface
$[E]$
of the moduli space is the image of the ruled surface
![]() ${\mathbb {P}}(E^\vee )$
by the linear system
${\mathbb {P}}(E^\vee )$
by the linear system
![]() $|{\mathcal {O}}_E(2)|$
. In particular this surface contains no line.
$|{\mathcal {O}}_E(2)|$
. In particular this surface contains no line.
Equivalently, the latter claim means that a general Hecke line is not contained in any larger linear space contained in
![]() $\operatorname {\mathrm {SU}}_C(2)$
, although such larger linear spaces do exist.
$\operatorname {\mathrm {SU}}_C(2)$
, although such larger linear spaces do exist.
2.3 Lines in the ruling
For each line bundle
![]() $L\in \operatorname {\mathrm {Pic}}^1(C)$
, consider the rank two vector bundles E obtained as extensions of the form
$L\in \operatorname {\mathrm {Pic}}^1(C)$
, consider the rank two vector bundles E obtained as extensions of the form
Such extensions are parametrized by
![]() ${\mathbb {P}}_L:={\mathbb {P}} (\operatorname {\mathrm {Ext}}^1(K_C\otimes L^\vee ,L))\simeq {\mathbb {P}}^3$
. Hence, we obtain a ruling of
${\mathbb {P}}_L:={\mathbb {P}} (\operatorname {\mathrm {Ext}}^1(K_C\otimes L^\vee ,L))\simeq {\mathbb {P}}^3$
. Hence, we obtain a ruling of
![]() $\operatorname {\mathrm {SU}}_C(2)$
by a family of
$\operatorname {\mathrm {SU}}_C(2)$
by a family of
![]() ${\mathbb {P}}^3$
s parametrized by
${\mathbb {P}}^3$
s parametrized by
![]() $\operatorname {\mathrm {Pic}}^1(C)$
, which we denote by
$\operatorname {\mathrm {Pic}}^1(C)$
, which we denote by
![]() ${\mathbb {P}}({\mathcal {R}}){\rightarrow } \operatorname {\mathrm {Pic}}^1(C)$
.
${\mathbb {P}}({\mathcal {R}}){\rightarrow } \operatorname {\mathrm {Pic}}^1(C)$
.
Note that
![]() ${\mathbb {P}}_L$
intersects the Kummer threefold along a copy
${\mathbb {P}}_L$
intersects the Kummer threefold along a copy
![]() $C_L$
of C [Reference Oxbury, Pauly and PreviatoOPP98, 1.1]. According to [Reference Oxbury, Pauly and PreviatoOPP98, Theorem 1.3], a line in
$C_L$
of C [Reference Oxbury, Pauly and PreviatoOPP98, 1.1]. According to [Reference Oxbury, Pauly and PreviatoOPP98, Theorem 1.3], a line in
![]() ${\mathbb {P}}_L$
is a Hecke line if and only if it meets
${\mathbb {P}}_L$
is a Hecke line if and only if it meets
![]() $C_L$
.
$C_L$
.
Moreover, by [Reference Oxbury, Pauly and PreviatoOPP98, Proposition 1.2], two spaces
![]() ${\mathbb {P}}_L$
and
${\mathbb {P}}_L$
and
![]() ${\mathbb {P}}_M$
are always distinct for
${\mathbb {P}}_M$
are always distinct for
![]() $L\ne M$
and, for sufficiently general choices of L and M, they are disjoint. When they meet, their intersection is a single point, or a line; the latter case happens exactly when
$L\ne M$
and, for sufficiently general choices of L and M, they are disjoint. When they meet, their intersection is a single point, or a line; the latter case happens exactly when
![]() $K_C-L-M$
is effective. In particular, if a line is contained in
$K_C-L-M$
is effective. In particular, if a line is contained in
![]() ${\mathbb {P}}_L\cap {\mathbb {P}}_M$
, it must be a bisecant to both
${\mathbb {P}}_L\cap {\mathbb {P}}_M$
, it must be a bisecant to both
![]() $C_L$
and
$C_L$
and
![]() $C_M$
.
$C_M$
.
Now, consider the family
![]() ${\mathcal {F}}_R$
of lines contained in the
${\mathcal {F}}_R$
of lines contained in the
![]() ${\mathbb {P}}^3$
s of the ruling. By what we have just recalled,
${\mathbb {P}}^3$
s of the ruling. By what we have just recalled,
![]() ${\mathcal {F}}_R$
is the birational image in
${\mathcal {F}}_R$
is the birational image in
![]() $G(2,V_8)$
of the quadric bundle
$G(2,V_8)$
of the quadric bundle
![]() $G(2,{\mathcal {R}})$
over
$G(2,{\mathcal {R}})$
over
![]() $\operatorname {\mathrm {Pic}}^1(C)$
.
$\operatorname {\mathrm {Pic}}^1(C)$
.
Proposition 2.4. The VMRT at a general point of
![]() $\operatorname {\mathrm {SU}}_C(2)$
, of the family
$\operatorname {\mathrm {SU}}_C(2)$
, of the family
![]() ${\mathcal {F}}_R$
of lines in its ruling, is the disjoint union of eight planes in
${\mathcal {F}}_R$
of lines in its ruling, is the disjoint union of eight planes in
![]() ${\mathbb {P}}^5$
.
${\mathbb {P}}^5$
.
Proof. It follows from [Reference PaulyPau02, Section 4.1] that the map
![]() ${\mathbb {P}}({\mathcal {R}}){\longrightarrow } \operatorname {\mathrm {SU}}_C(2)$
is generically finite of degree
${\mathbb {P}}({\mathcal {R}}){\longrightarrow } \operatorname {\mathrm {SU}}_C(2)$
is generically finite of degree
![]() $8$
. This means that eight
$8$
. This means that eight
![]() ${\mathbb {P}}^3$
s of the ruling pass through a general point
${\mathbb {P}}^3$
s of the ruling pass through a general point
![]() $[E]$
of
$[E]$
of
![]() $\operatorname {\mathrm {SU}}_C(2)$
, and for each of them the lines passing through
$\operatorname {\mathrm {SU}}_C(2)$
, and for each of them the lines passing through
![]() $[E]$
are parametrized by a projective plane. Finally, these projective planes are disjoint, again by [Reference Oxbury, Pauly and PreviatoOPP98, Proposition 1.2].
$[E]$
are parametrized by a projective plane. Finally, these projective planes are disjoint, again by [Reference Oxbury, Pauly and PreviatoOPP98, Proposition 1.2].
For future use, we record the following easy consequence.
Corollary 2.5. Any plane in
![]() $\operatorname {\mathrm {SU}}_C(2,K_C)$
passing through a general point is contained in a unique
$\operatorname {\mathrm {SU}}_C(2,K_C)$
passing through a general point is contained in a unique
![]() ${\mathbb {P}}^3$
of the ruling.
${\mathbb {P}}^3$
of the ruling.
3 Four-forms and orbital degeneracy loci
In this section, we recall the definitions of some orbital degeneracy loci closely connected to the geometry of
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C)$
, for C a general curve of genus
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C)$
, for C a general curve of genus
![]() $3$
. In particular, we recall how to recover the Coble quartic from a general four-form in eight variables. Using this description, we give a short proof of the self-duality statement of [Reference PaulyPau02]. Our references for orbital degeneracy loci (sometimes abbreviated as ODL) are [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Reference Benedetti, Filippini, Manivel and TanturriBFMT20b]. All the results in this section are contained either in [Reference PaulyPau02] or in [Reference Gruson, Sam and WeymanGSW13]; our contribution consists in a new interpretation in terms of ODL and in the technique employed in the proof of the self-duality statement, which does not rely anymore on [Reference PaulyPau02].
$3$
. In particular, we recall how to recover the Coble quartic from a general four-form in eight variables. Using this description, we give a short proof of the self-duality statement of [Reference PaulyPau02]. Our references for orbital degeneracy loci (sometimes abbreviated as ODL) are [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Reference Benedetti, Filippini, Manivel and TanturriBFMT20b]. All the results in this section are contained either in [Reference PaulyPau02] or in [Reference Gruson, Sam and WeymanGSW13]; our contribution consists in a new interpretation in terms of ODL and in the technique employed in the proof of the self-duality statement, which does not rely anymore on [Reference PaulyPau02].
Notation. We will denote by
![]() $V_n$
and
$V_n$
and
![]() $U_i$
complex vector spaces of dimension n and i, respectively (usually
$U_i$
complex vector spaces of dimension n and i, respectively (usually
![]() $V_n$
will be fixed and
$V_n$
will be fixed and
![]() $U_i$
will be a variable subspace of
$U_i$
will be a variable subspace of
![]() $V_n$
). We will also denote by
$V_n$
). We will also denote by
![]() $G(i,V_n)$
the Grassmannian of i-dimensional subspaces of
$G(i,V_n)$
the Grassmannian of i-dimensional subspaces of
![]() $V_n$
and by
$V_n$
and by
![]() $Fl(i_1,\ldots ,i_k,V_n)$
the flag variety of flags of subspaces of
$Fl(i_1,\ldots ,i_k,V_n)$
the flag variety of flags of subspaces of
![]() $V_n$
of dimensions
$V_n$
of dimensions
![]() $i_1<\cdots <i_k$
. Over the flag variety, we will denote by
$i_1<\cdots <i_k$
. Over the flag variety, we will denote by
![]() ${\mathcal {U}}_{i_j}$
the rank-
${\mathcal {U}}_{i_j}$
the rank-
![]() $i_j$
tautological bundle; over the Grassmannian, we will denote by
$i_j$
tautological bundle; over the Grassmannian, we will denote by
![]() ${\mathcal {U}}$
the tautological bundle and by
${\mathcal {U}}$
the tautological bundle and by
![]() ${\mathcal {Q}}$
the universal quotient bundle.
${\mathcal {Q}}$
the universal quotient bundle.
3.1 A simple construction of the Coble quartic
In this section, we recall some results from [Reference Gruson, Sam and WeymanGSW13]. The starting point is a general four-form in eight variables,
![]() $v\in \wedge ^4V_8\simeq \wedge ^4V_8^\vee $
, where
$v\in \wedge ^4V_8\simeq \wedge ^4V_8^\vee $
, where
![]() $V_8$
denotes a complex eight-dimensional vector space. Recall that this is a theta-representation, being part of a
$V_8$
denotes a complex eight-dimensional vector space. Recall that this is a theta-representation, being part of a
![]() ${\mathbb {Z}}_2$
-grading of the exceptional Lie algebra
${\mathbb {Z}}_2$
-grading of the exceptional Lie algebra
The action of the so-called theta-group, which here is
![]() $\operatorname {\mathrm {SL}}(V_8)$
, behaves very much as the action of the adjoint group on a simple complex Lie algebra. In particular, one has Jordan decompositions, and the GIT-quotient
$\operatorname {\mathrm {SL}}(V_8)$
, behaves very much as the action of the adjoint group on a simple complex Lie algebra. In particular, one has Jordan decompositions, and the GIT-quotient
for some finite complex reflection group W acting on what is called a Cartan subspace
![]() ${\mathfrak h}$
of the theta-representation. We will make this Cartan subspace explicit later on. For now, we just need to know that it coincides with the seven-dimensional representation of the Weyl group of
${\mathfrak h}$
of the theta-representation. We will make this Cartan subspace explicit later on. For now, we just need to know that it coincides with the seven-dimensional representation of the Weyl group of
![]() $E_7$
. As a consequence, the choice of v determines uniquely a nonhyperelliptic curve C of genus three (a plane quartic) with a marked flex point [Reference Gruson, Sam and WeymanGSW13, Remark 6.1].
$E_7$
. As a consequence, the choice of v determines uniquely a nonhyperelliptic curve C of genus three (a plane quartic) with a marked flex point [Reference Gruson, Sam and WeymanGSW13, Remark 6.1].
We will construct from our general
![]() $v\in \wedge ^4V_8$
a collection of geometric objects defined as orbital degeneracy loci. The main point of this approach is that it allows us to reduce to simpler representations. Typically, the Borel–Weil theorem gives an isomorphism
$v\in \wedge ^4V_8$
a collection of geometric objects defined as orbital degeneracy loci. The main point of this approach is that it allows us to reduce to simpler representations. Typically, the Borel–Weil theorem gives an isomorphism
where
![]() ${\mathcal {Q}}$
denotes the rank seven quotient vector bundle on
${\mathcal {Q}}$
denotes the rank seven quotient vector bundle on
![]() ${\mathbb {P}}(V_8)$
. At the price of passing to a relative setting over
${\mathbb {P}}(V_8)$
. At the price of passing to a relative setting over
![]() ${\mathbb {P}}(V_8)$
, this reduces the study of
${\mathbb {P}}(V_8)$
, this reduces the study of
![]() $\wedge ^4V_8$
to that of three-forms in seven variables.
$\wedge ^4V_8$
to that of three-forms in seven variables.
But then the situation is much simpler because if
![]() $V_7$
is a seven-dimensional complex vector space,
$V_7$
is a seven-dimensional complex vector space,
![]() $\wedge ^3V_7^\vee \cong \wedge ^4 V_7$
has finitely many orbits under the action of
$\wedge ^3V_7^\vee \cong \wedge ^4 V_7$
has finitely many orbits under the action of
![]() $\operatorname {\mathrm {GL}}(V_7)$
. Each orbit closure Y allows to associate to
$\operatorname {\mathrm {GL}}(V_7)$
. Each orbit closure Y allows to associate to
![]() $v\in \wedge ^4V_8$
the locus
$v\in \wedge ^4V_8$
the locus
![]() $D_Y(v)\subset {\mathbb {P}}(V_8)$
of points x where the image of v lies in the corresponding
$D_Y(v)\subset {\mathbb {P}}(V_8)$
of points x where the image of v lies in the corresponding
![]() $Y_x\subset \wedge ^3{\mathcal {Q}}^\vee (1)_x$
(this is exactly how orbital degeneracy loci are defined). By the general results of [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a], for v general the main properties of Y will be transferred to
$Y_x\subset \wedge ^3{\mathcal {Q}}^\vee (1)_x$
(this is exactly how orbital degeneracy loci are defined). By the general results of [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a], for v general the main properties of Y will be transferred to
![]() $D_Y(v)$
, starting from its codimension. We can therefore focus on the orbit closures in
$D_Y(v)$
, starting from its codimension. We can therefore focus on the orbit closures in
![]() $\wedge ^3V_7^\vee $
of codimension at most seven. Remarkably, there are only three such orbit closures (not counting the whole space), that we can index by their codimension:
$\wedge ^3V_7^\vee $
of codimension at most seven. Remarkably, there are only three such orbit closures (not counting the whole space), that we can index by their codimension:
![]() $Y_1$
is a hypersurface of degree
$Y_1$
is a hypersurface of degree
![]() $7$
,
$7$
,
![]() $Y_4$
is its singular locus,
$Y_4$
is its singular locus,
![]() $Y_7$
is the singular locus of
$Y_7$
is the singular locus of
![]() $Y_4$
. The corresponding orbital degeneracy loci have been described in [Reference Gruson, Sam and WeymanGSW13, 6.1, 6.2].
$Y_4$
. The corresponding orbital degeneracy loci have been described in [Reference Gruson, Sam and WeymanGSW13, 6.1, 6.2].
Proposition 3.1. For v general, the threefold
![]() ${\mathrm {Kum}_C}:=D_{Y_4}(v)$
is the Kummer variety of a nonhyperelliptic genus three curve C. It is the singular locus of the quartic hypersurface
${\mathrm {Kum}_C}:=D_{Y_4}(v)$
is the Kummer variety of a nonhyperelliptic genus three curve C. It is the singular locus of the quartic hypersurface
![]() ${\mathcal {C}}:=D_{Y_1}(v)$
. Its singular locus is the finite set
${\mathcal {C}}:=D_{Y_1}(v)$
. Its singular locus is the finite set
![]() ${\mathrm {Kum}_C}[2]:=D_{Y_7}(v)$
.
${\mathrm {Kum}_C}[2]:=D_{Y_7}(v)$
.
Since the Coble quartic can be characterized as the unique quartic hypersurface that is singular along the Kummer threefold [Reference BeauvilleBea91, Proposition 3.1], we can immediately deduce that it coincides with
![]() $D_{Y_1}(v)$
.
$D_{Y_1}(v)$
.
3.2 Kempf collapsings
A nice feature of our orbital degeneracy loci is the following. It turns out that the orbit closures they are associated to, although singular, admit nice resolutions of singularities by Kempf collapsings, which are birational contractions from total spaces of homogeneous vector bundles on flag manifolds. These homogeneous vector bundles are typically nonsemisimple, making them more difficult to handle. Nevertheless, these collapsings allow to describe the corresponding orbital degeneracy loci in terms of zero loci of sections of vector bundles.
In the cases we are interested in, we obtain the following descriptions, where
![]() $U_k$
stands for a k-dimensional subspace of
$U_k$
stands for a k-dimensional subspace of
![]() $V_8$
. For
$V_8$
. For
![]() $A,B$
subspaces of a vector space V, we will denote by
$A,B$
subspaces of a vector space V, we will denote by
![]() $(\wedge ^p A) \wedge (\wedge ^q B) \subset \wedge ^{p+q}V$
the linear subspace spanned by the elements of the form
$(\wedge ^p A) \wedge (\wedge ^q B) \subset \wedge ^{p+q}V$
the linear subspace spanned by the elements of the form
![]() $a_1\wedge \cdots \wedge a_p \wedge b_1 \wedge \cdots \wedge b_q$
with
$a_1\wedge \cdots \wedge a_p \wedge b_1 \wedge \cdots \wedge b_q$
with
![]() $a_1,\ldots ,a_p \in A$
and
$a_1,\ldots ,a_p \in A$
and
![]() $b_1,\ldots ,b_q\in B$
. For vector subbundles
$b_1,\ldots ,b_q\in B$
. For vector subbundles
![]() $\mathcal {A},\mathcal {B}$
of a the trivial bundle
$\mathcal {A},\mathcal {B}$
of a the trivial bundle
![]() $V \otimes {\mathcal {O}}$
, we use the same convention to define
$V \otimes {\mathcal {O}}$
, we use the same convention to define
![]() $(\wedge ^p \mathcal {A}) \wedge (\wedge ^q \mathcal {B})$
in
$(\wedge ^p \mathcal {A}) \wedge (\wedge ^q \mathcal {B})$
in
![]() $\wedge ^{p+q} V \otimes {\mathcal {O}}$
.
$\wedge ^{p+q} V \otimes {\mathcal {O}}$
.
Proposition 3.2. Let
![]() $v\in \wedge ^4 V_8$
be a generic element. The Coble quartic
$v\in \wedge ^4 V_8$
be a generic element. The Coble quartic
![]() ${\mathcal {C}}$
associated to v can be described as
${\mathcal {C}}$
associated to v can be described as
The corresponding Kummer threefold
![]() ${\mathrm {Kum}_C}$
is
${\mathrm {Kum}_C}$
is
The singular locus
![]() ${\mathrm {Kum}_C}[2]$
of
${\mathrm {Kum}_C}[2]$
of
![]() ${\mathrm {Kum}_C}$
is
${\mathrm {Kum}_C}$
is
These results follow from a combination of [Reference Gruson, Sam and WeymanGSW13, Section 6] and [Reference Kraskiewicz and WeymanKW13, Section 3]. Let us clarify the statement for instance for
![]() ${\mathrm {Kum}_C}$
, the explanations for the other loci being similar. In [Reference Gruson, Sam and WeymanGSW13, Section 6], it is shown that
${\mathrm {Kum}_C}$
, the explanations for the other loci being similar. In [Reference Gruson, Sam and WeymanGSW13, Section 6], it is shown that
![]() ${\mathrm {Kum}_C}:=D_{Y_4}(v)$
is the Kummer threefold. In [Reference Kraskiewicz and WeymanKW13, Section 3] it is proved that
${\mathrm {Kum}_C}:=D_{Y_4}(v)$
is the Kummer threefold. In [Reference Kraskiewicz and WeymanKW13, Section 3] it is proved that
![]() $Y_4\subset \wedge ^4 V_7 $
is desingularized by a the total space of the vector bundle
$Y_4\subset \wedge ^4 V_7 $
is desingularized by a the total space of the vector bundle
over the flag variety
![]() $Fl(1,5,V_7)$
. Here, we denoted by
$Fl(1,5,V_7)$
. Here, we denoted by
![]() ${\mathcal {U}}_1$
and
${\mathcal {U}}_1$
and
![]() ${\mathcal {U}}_5$
, respectively, the rank one and rank five tautological vector bundles on
${\mathcal {U}}_5$
, respectively, the rank one and rank five tautological vector bundles on
![]() $Fl(1,5,V_7)$
. The projection from the total space of
$Fl(1,5,V_7)$
. The projection from the total space of
![]() ${\mathcal {W}}$
to
${\mathcal {W}}$
to
![]() $Y_4\subset \wedge ^4 V_7$
is given by the composition of the inclusion of
$Y_4\subset \wedge ^4 V_7$
is given by the composition of the inclusion of
![]() ${\mathcal {W}}$
inside
${\mathcal {W}}$
inside
![]() $\wedge ^4 V_7 \otimes {\mathcal {O}}_{Fl(1,5,V_7)}$
with the projection to
$\wedge ^4 V_7 \otimes {\mathcal {O}}_{Fl(1,5,V_7)}$
with the projection to
![]() $\wedge ^4 V_7$
. For v general, this desingularization
$\wedge ^4 V_7$
. For v general, this desingularization
![]() $\operatorname {\mathrm {Tot}}({\mathcal {W}})\to Y_4$
of
$\operatorname {\mathrm {Tot}}({\mathcal {W}})\to Y_4$
of
![]() $Y_4$
can be relativized to obtain a desingularization of
$Y_4$
can be relativized to obtain a desingularization of
![]() $D_{Y_4}(v)$
, as explained in [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Section 2]. For this, we simply consider the flag bundle
$D_{Y_4}(v)$
, as explained in [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Section 2]. For this, we simply consider the flag bundle
![]() $Fl(1,5,{\mathcal {Q}})$
: By the previous discussion, any point of
$Fl(1,5,{\mathcal {Q}})$
: By the previous discussion, any point of
![]() $x=[U_1]\in D_{Y_4}(v)$
must be the image of a flag
$x=[U_1]\in D_{Y_4}(v)$
must be the image of a flag
![]() $\bar {U}_1 \subset \bar {U}_5\subset {\mathcal {Q}}_x=V_8/U_1$
such that
$\bar {U}_1 \subset \bar {U}_5\subset {\mathcal {Q}}_x=V_8/U_1$
such that
![]() $v \; \mathrm {mod} \; U_1$
belongs to
$v \; \mathrm {mod} \; U_1$
belongs to
![]() $\wedge ^4 \bar {U}_5+ \wedge ^2 \bar {U}_5\wedge \bar {U}_1 \wedge {\mathcal {Q}}_x\subset \wedge ^4{\mathcal {Q}}_x$
. This flag originates from a flag
$\wedge ^4 \bar {U}_5+ \wedge ^2 \bar {U}_5\wedge \bar {U}_1 \wedge {\mathcal {Q}}_x\subset \wedge ^4{\mathcal {Q}}_x$
. This flag originates from a flag
![]() $(U_1\subset U_2\subset U_6\subset V_8)$
(such that
$(U_1\subset U_2\subset U_6\subset V_8)$
(such that
![]() $\bar {U}_1=U_2/U_1$
, etc.), and we can rewrite the previous condition as asking that
$\bar {U}_1=U_2/U_1$
, etc.), and we can rewrite the previous condition as asking that
![]() $x=[U_1]$
belongs to the projection of
$x=[U_1]$
belongs to the projection of
This is the zero locus of a global section of a globally generated bundle, obtained as a quotient of the trivial bundle with fiber
![]() $\wedge ^4V_8$
. For v general, this section is general, so
$\wedge ^4V_8$
. For v general, this section is general, so
![]() $Z(v)$
is smooth. Moreover, the projection
$Z(v)$
is smooth. Moreover, the projection
![]() $Z(v)\to D_{Y_4}(v)\subset {\mathbb {P}}(V_8)$
, obtained by just forgetting
$Z(v)\to D_{Y_4}(v)\subset {\mathbb {P}}(V_8)$
, obtained by just forgetting
![]() $U_2$
and
$U_2$
and
![]() $U_6$
, is birational.
$U_6$
, is birational.
3.3 Self-duality of the Coble quartic
Because of the natural isomorphism
![]() $\wedge ^4V_8\simeq \wedge ^4V_8^\vee $
(defined up to scalar or, more precisely, up to the choice of a volume form on
$\wedge ^4V_8\simeq \wedge ^4V_8^\vee $
(defined up to scalar or, more precisely, up to the choice of a volume form on
![]() $V_8$
), the same constructions can be performed in the dual projective space
$V_8$
), the same constructions can be performed in the dual projective space
![]() ${\mathbb {P}}(V_8^\vee )$
. This is related to the remarkable fact that the Coble quartic is projectively self-dual [Reference PaulyPau02]. Let us show how this duality statement easily follows from our approach in terms of orbital degeneracy loci.
${\mathbb {P}}(V_8^\vee )$
. This is related to the remarkable fact that the Coble quartic is projectively self-dual [Reference PaulyPau02]. Let us show how this duality statement easily follows from our approach in terms of orbital degeneracy loci.
First, consider a general point
![]() $[U_1]$
of
$[U_1]$
of
![]() ${\mathcal {C}}=D_{Y_1}(v)$
. As we have seen in the previous section, there exists (a unique)
${\mathcal {C}}=D_{Y_1}(v)$
. As we have seen in the previous section, there exists (a unique)
![]() $U_4\supset U_1$
such that v belongs to
$U_4\supset U_1$
such that v belongs to
![]() $(\wedge ^2 U_4) \wedge (\wedge ^2 V_8) +\wedge ^3 V_8\wedge U_1$
. Reducing modulo
$(\wedge ^2 U_4) \wedge (\wedge ^2 V_8) +\wedge ^3 V_8\wedge U_1$
. Reducing modulo
![]() $(\wedge ^2 U_4) \wedge (\wedge ^2 V_8)$
, we get
$(\wedge ^2 U_4) \wedge (\wedge ^2 V_8)$
, we get
In general,
![]() $\bar {v}$
is nonzero and defines a hyperplane in
$\bar {v}$
is nonzero and defines a hyperplane in
![]() $V_8/U_4$
, that is, a hyperplane
$V_8/U_4$
, that is, a hyperplane
![]() $U_7$
of
$U_7$
of
![]() $V_8$
, containing
$V_8$
, containing
![]() $U_4$
. Note that this exactly means that
$U_4$
. Note that this exactly means that
Lemma 3.3.
![]() ${\mathbb {P}}(U_7)$
is the tangent hyperplane to
${\mathbb {P}}(U_7)$
is the tangent hyperplane to
![]() ${\mathcal {C}}$
at
${\mathcal {C}}$
at
![]() $[U_1]$
.
$[U_1]$
.
Proof. Let
![]() $\tilde {{\mathcal {C}}}$
denote the variety of flags
$\tilde {{\mathcal {C}}}$
denote the variety of flags
![]() $(U_1\subset U_4)$
such that v belongs to
$(U_1\subset U_4)$
such that v belongs to
We know that the projection
![]() $\tilde {{\mathcal {C}}}{\longrightarrow }{\mathcal {C}}$
is birational. Moreover, as a subvariety of the flag manifold
$\tilde {{\mathcal {C}}}{\longrightarrow }{\mathcal {C}}$
is birational. Moreover, as a subvariety of the flag manifold
![]() $Fl(1,4,V_8)$
,
$Fl(1,4,V_8)$
,
![]() $\tilde {{\mathcal {C}}}$
is the zero-locus of the section of the vector bundle
$\tilde {{\mathcal {C}}}$
is the zero-locus of the section of the vector bundle
![]() $\wedge ^4V_8/{\mathcal {F}} (U_1,U_4)$
defined by v since such a section vanishes exactly when
$\wedge ^4V_8/{\mathcal {F}} (U_1,U_4)$
defined by v since such a section vanishes exactly when
![]() $v\in {\mathcal {F}}(U_1,U_4)\subset \wedge ^4 V_8$
. Let
$v\in {\mathcal {F}}(U_1,U_4)\subset \wedge ^4 V_8$
. Let
![]() $\mathfrak {p}(U_1,U_4)$
denote the stabilizer of the flag
$\mathfrak {p}(U_1,U_4)$
denote the stabilizer of the flag
![]() $(U_1\subset U_4)$
inside
$(U_1\subset U_4)$
inside
![]() $\mathfrak {gl}(V_8)$
. The tangent space to
$\mathfrak {gl}(V_8)$
. The tangent space to
![]() $Fl(1,4,V_8)$
at the corresponding point is the quotient
$Fl(1,4,V_8)$
at the corresponding point is the quotient
![]() $\mathfrak {gl}(V_8)/\mathfrak {p}(U_1,U_4)$
, and the tangent space to
$\mathfrak {gl}(V_8)/\mathfrak {p}(U_1,U_4)$
, and the tangent space to
![]() $\tilde {{\mathcal {C}}}$
is the image, in this quotient, of the space of endomorphisms
$\tilde {{\mathcal {C}}}$
is the image, in this quotient, of the space of endomorphisms
![]() $X\in \mathfrak {gl}(V_8)$
such that
$X\in \mathfrak {gl}(V_8)$
such that
![]() $X(v)$
belongs to
$X(v)$
belongs to
![]() ${\mathcal {F}}(U_1,U_4)$
, as follows from the normal exact sequence
${\mathcal {F}}(U_1,U_4)$
, as follows from the normal exact sequence
The tangent space to
![]() ${\mathcal {C}}$
is then the image of this space inside
${\mathcal {C}}$
is then the image of this space inside
![]() $\mathfrak {gl}(V_8)/\mathfrak {p}(U_1)\simeq \operatorname {\mathrm {Hom}}(U_1,V_8/U_1)$
, where
$\mathfrak {gl}(V_8)/\mathfrak {p}(U_1)\simeq \operatorname {\mathrm {Hom}}(U_1,V_8/U_1)$
, where
![]() $\mathfrak {p}(U_1)$
denotes the stabilizer of the line
$\mathfrak {p}(U_1)$
denotes the stabilizer of the line
![]() $U_1$
.
$U_1$
.
So our claim will follow, if we can check that any
![]() $X\in \mathfrak {gl}(V_8)$
such that
$X\in \mathfrak {gl}(V_8)$
such that
![]() $X(v)$
belongs to
$X(v)$
belongs to
![]() ${\mathcal {F}}(U_1,U_4)$
, must send
${\mathcal {F}}(U_1,U_4)$
, must send
![]() $U_1$
into the hyperplane
$U_1$
into the hyperplane
![]() $U_7$
. But (3.1) implies, once we apply X, that
$U_7$
. But (3.1) implies, once we apply X, that
If
![]() $X(v)$
belongs to
$X(v)$
belongs to
![]() ${\mathcal {F}}(U_1,U_4)$
, it has to vanish modulo
${\mathcal {F}}(U_1,U_4)$
, it has to vanish modulo
![]() $U_4$
. So
$U_4$
. So
![]() $\wedge ^3 U_7\wedge X(U_1)$
must also vanish modulo
$\wedge ^3 U_7\wedge X(U_1)$
must also vanish modulo
![]() $U_4$
, which is the case only if
$U_4$
, which is the case only if
![]() $X(U_1)\subset U_7$
.
$X(U_1)\subset U_7$
.
Recall that once we fix a volume form on
![]() $V_8$
, we get an isomorphism of
$V_8$
, we get an isomorphism of
![]() $\wedge ^4V_8$
with
$\wedge ^4V_8$
with
![]() $\wedge ^4V_8^\vee $
. We will denote by
$\wedge ^4V_8^\vee $
. We will denote by
![]() $v^\vee $
the image of v. (Strictly speaking, it is uniquely defined only up to scalar, but this is irrelevant in our constructions.) To make things clearer, we will denote by
$v^\vee $
the image of v. (Strictly speaking, it is uniquely defined only up to scalar, but this is irrelevant in our constructions.) To make things clearer, we will denote by
![]() ${\mathcal {C}}(v)$
the Coble quartic defined by v in
${\mathcal {C}}(v)$
the Coble quartic defined by v in
![]() ${\mathbb {P}}(V_8)$
and by
${\mathbb {P}}(V_8)$
and by
![]() ${\mathcal {C}}(v^\vee )$
the Coble quartic defined by
${\mathcal {C}}(v^\vee )$
the Coble quartic defined by
![]() $v^\vee $
in
$v^\vee $
in
![]() ${\mathbb {P}}(V_8^\vee )$
.
${\mathbb {P}}(V_8^\vee )$
.
Theorem 3.4. The projective dual of
![]() ${\mathcal {C}}(v)$
is
${\mathcal {C}}(v)$
is
![]() ${\mathcal {C}}(v^\vee )$
.
${\mathcal {C}}(v^\vee )$
.
Proof. For
![]() $[U_1]$
a general point of
$[U_1]$
a general point of
![]() ${\mathcal {C}}$
, we have a flag
${\mathcal {C}}$
, we have a flag
![]() $(U_1\subset U_4\subset U_7)$
such that v belongs to
$(U_1\subset U_4\subset U_7)$
such that v belongs to
![]() $(\wedge ^2 U_4) \wedge (\wedge ^2 V_8) +\wedge ^3 U_7\wedge U_1$
. Choose an adapted basis
$(\wedge ^2 U_4) \wedge (\wedge ^2 V_8) +\wedge ^3 U_7\wedge U_1$
. Choose an adapted basis
![]() $e_1,\ldots , e_8$
so that
$e_1,\ldots , e_8$
so that
![]() $e_1$
generates
$e_1$
generates
![]() $U_1$
, etc. The condition means that v is a linear combination of elementary tensors
$U_1$
, etc. The condition means that v is a linear combination of elementary tensors
![]() $e_i\wedge e_j\wedge e_k\wedge e_\ell $
with
$e_i\wedge e_j\wedge e_k\wedge e_\ell $
with
![]() $i,j\le 4$
, and of
$i,j\le 4$
, and of
![]() $e_5\wedge e_6\wedge e_7\wedge e_1$
.
$e_5\wedge e_6\wedge e_7\wedge e_1$
.
Now, recall that if the chosen volume form on
![]() $V_8$
is
$V_8$
is
![]() $e_1\wedge \cdots \wedge e_8$
, and
$e_1\wedge \cdots \wedge e_8$
, and
![]() $e_1^\vee ,\ldots , e_8^\vee $
is the dual basis of
$e_1^\vee ,\ldots , e_8^\vee $
is the dual basis of
![]() $e_1,\ldots , e_8$
, then the isomorphism of
$e_1,\ldots , e_8$
, then the isomorphism of
![]() $\wedge ^4V_8$
with
$\wedge ^4V_8$
with
![]() $\wedge ^4V_8^\vee $
sends the elementary tensor
$\wedge ^4V_8^\vee $
sends the elementary tensor
![]() $e_i\wedge e_j\wedge e_k\wedge e_\ell $
to
$e_i\wedge e_j\wedge e_k\wedge e_\ell $
to
![]() $\pm e_p^\vee \wedge e_q^\vee \wedge e_r^\vee \wedge e_s^\vee $
, where
$\pm e_p^\vee \wedge e_q^\vee \wedge e_r^\vee \wedge e_s^\vee $
, where
![]() $\{i,j,k,l\} \cap \{p,q,r,s\}=\emptyset $
.
$\{i,j,k,l\} \cap \{p,q,r,s\}=\emptyset $
.
As a consequence,
![]() $v^\vee $
will be a linear combination of elementary tensors
$v^\vee $
will be a linear combination of elementary tensors
![]() $e_p^\vee \wedge e_q^\vee \wedge e_r^\vee \wedge e_s^\vee $
with
$e_p^\vee \wedge e_q^\vee \wedge e_r^\vee \wedge e_s^\vee $
with
![]() $p,q\ge 5$
, and
$p,q\ge 5$
, and
![]() $e_2^\vee \wedge e_3^\vee \wedge e_4^\vee \wedge e_8^\vee $
. In other words,
$e_2^\vee \wedge e_3^\vee \wedge e_4^\vee \wedge e_8^\vee $
. In other words,
This is exactly the condition that ensures that
![]() $[U_7^\perp ]$
belongs to
$[U_7^\perp ]$
belongs to
![]() ${\mathcal {C}}(v^\vee )$
. Thanks to the previous lemma, we deduce that
${\mathcal {C}}(v^\vee )$
. Thanks to the previous lemma, we deduce that
![]() ${\mathcal {C}}(v)^\vee \subset {\mathcal {C}}(v^\vee )$
. Moreover, the symmetry between
${\mathcal {C}}(v)^\vee \subset {\mathcal {C}}(v^\vee )$
. Moreover, the symmetry between
![]() $U_1$
and
$U_1$
and
![]() $U_7^\perp $
implies that in general,
$U_7^\perp $
implies that in general,
![]() $U_1$
can be recovered from
$U_1$
can be recovered from
![]() $U_7$
exactly as
$U_7$
exactly as
![]() $U_7$
is constructed from
$U_7$
is constructed from
![]() $U_1$
, which means that
$U_1$
, which means that
![]() ${\mathcal {C}}(v)^\vee $
is birationally equivalent to
${\mathcal {C}}(v)^\vee $
is birationally equivalent to
![]() ${\mathcal {C}}(v)$
. Finally, since
${\mathcal {C}}(v)$
. Finally, since
![]() ${\mathcal {C}}(v)^\vee $
and
${\mathcal {C}}(v)^\vee $
and
![]() ${\mathcal {C}}(v^\vee )$
are both irreducible hypersurfaces, they must be equal.
${\mathcal {C}}(v^\vee )$
are both irreducible hypersurfaces, they must be equal.
The previous discussion shows that it is natural to define the variety
![]() ${\mathcal {C}}(v,v^\vee )\subset Fl(1,4,7,V_8)$
parametrizing the flags
${\mathcal {C}}(v,v^\vee )\subset Fl(1,4,7,V_8)$
parametrizing the flags
![]() $(U_1\subset U_4\subset U_7\subset V_8) $
satisfying condition (3.1). This is a smooth variety dominating birationally both
$(U_1\subset U_4\subset U_7\subset V_8) $
satisfying condition (3.1). This is a smooth variety dominating birationally both
![]() ${\mathcal {C}}(v)$
and
${\mathcal {C}}(v)$
and
![]() ${\mathcal {C}}(v^\vee )$
; there is a diagram
${\mathcal {C}}(v^\vee )$
; there is a diagram

One recovers that way the constructions explained is [Reference PaulyPau02, section 3.3]. We used the suggestive notation
![]() $d{\mathcal {C}}$
for the Gauss map, which sends a smooth point of
$d{\mathcal {C}}$
for the Gauss map, which sends a smooth point of
![]() ${\mathcal {C}}(v)$
to its tangent hyperplane, given by the differential of the cubic’s equation.
${\mathcal {C}}(v)$
to its tangent hyperplane, given by the differential of the cubic’s equation.
3.4 The Cartan subspace
Recall that a Cartan subspace for the
![]() ${\mathbb {Z}}_2$
-graded Lie algebra
${\mathbb {Z}}_2$
-graded Lie algebra
![]() ${\mathfrak e}_7=\mathfrak {sl}(V_8)\oplus \wedge ^4V_8$
is a maximal subspace of
${\mathfrak e}_7=\mathfrak {sl}(V_8)\oplus \wedge ^4V_8$
is a maximal subspace of
![]() $\wedge ^4V_8$
, made of elements of
$\wedge ^4V_8$
, made of elements of
![]() ${\mathfrak e}_6$
which are semisimple and commute [Reference VinbergVin76]. Among other nice properties, a general element of
${\mathfrak e}_6$
which are semisimple and commute [Reference VinbergVin76]. Among other nice properties, a general element of
![]() $\wedge ^4V_8$
is
$\wedge ^4V_8$
is
![]() $\operatorname {\mathrm {SL}}(V_8)$
-conjugate to (finitely many) elements of any given Cartan subspace.
$\operatorname {\mathrm {SL}}(V_8)$
-conjugate to (finitely many) elements of any given Cartan subspace.
An explicit Cartan subspace of
![]() $\wedge ^4V_8$
is worked out in [Reference OedingOed22, (3.1)]. It coincides with the space of Heisenberg invariants provided in [Reference Ren, Sam, Schrader and SturmfelsRSSS13, Remark 4.2]. Here is a list of seven generators, for a given basis
$\wedge ^4V_8$
is worked out in [Reference OedingOed22, (3.1)]. It coincides with the space of Heisenberg invariants provided in [Reference Ren, Sam, Schrader and SturmfelsRSSS13, Remark 4.2]. Here is a list of seven generators, for a given basis
![]() $e_1,\ldots , e_8$
of
$e_1,\ldots , e_8$
of
![]() $V_8$
:
$V_8$
:
 $$ \begin{align*}\begin{array}{rcl} h_1 & = & e_1\wedge e_2\wedge e_3\wedge e_4 +e_5\wedge e_6\wedge e_7\wedge e_8 ,\\ h_2 & = & e_1\wedge e_3\wedge e_5\wedge e_7 +e_6\wedge e_8\wedge e_2\wedge e_4 ,\\ h_3 & = & e_1\wedge e_5\wedge e_6\wedge e_2 +e_8\wedge e_4\wedge e_3\wedge e_7 ,\\ h_4 & = & e_1\wedge e_6\wedge e_8\wedge e_3 +e_4\wedge e_5\wedge e_7\wedge e_2 ,\\ h_5 & = & e_1\wedge e_8\wedge e_4\wedge e_5 +e_7\wedge e_2\wedge e_6\wedge e_3 ,\\ h_6 & = & e_1\wedge e_4\wedge e_7\wedge e_6 +e_2\wedge e_3\wedge e_8\wedge e_5 ,\\ h_7 & = & e_1\wedge e_7\wedge e_2\wedge e_8 +e_3\wedge e_5\wedge e_4\wedge e_6. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{rcl} h_1 & = & e_1\wedge e_2\wedge e_3\wedge e_4 +e_5\wedge e_6\wedge e_7\wedge e_8 ,\\ h_2 & = & e_1\wedge e_3\wedge e_5\wedge e_7 +e_6\wedge e_8\wedge e_2\wedge e_4 ,\\ h_3 & = & e_1\wedge e_5\wedge e_6\wedge e_2 +e_8\wedge e_4\wedge e_3\wedge e_7 ,\\ h_4 & = & e_1\wedge e_6\wedge e_8\wedge e_3 +e_4\wedge e_5\wedge e_7\wedge e_2 ,\\ h_5 & = & e_1\wedge e_8\wedge e_4\wedge e_5 +e_7\wedge e_2\wedge e_6\wedge e_3 ,\\ h_6 & = & e_1\wedge e_4\wedge e_7\wedge e_6 +e_2\wedge e_3\wedge e_8\wedge e_5 ,\\ h_7 & = & e_1\wedge e_7\wedge e_2\wedge e_8 +e_3\wedge e_5\wedge e_4\wedge e_6. \end{array}\end{align*} $$
Combinatorially, each of these generators is given by a pair of complementary fourtuples of indices in
![]() $\{1,\ldots ,8\}$
. Each of these
$\{1,\ldots ,8\}$
. Each of these
![]() $14$
fourtuples shares a pair of indices with any other distinct, not complementary fourtuple. This is the property that ensures the commutation in
$14$
fourtuples shares a pair of indices with any other distinct, not complementary fourtuple. This is the property that ensures the commutation in
![]() ${\mathfrak e}_6$
, since the Lie bracket of
${\mathfrak e}_6$
, since the Lie bracket of
![]() ${\mathfrak e}_6$
, restricted to
${\mathfrak e}_6$
, restricted to
![]() $\wedge ^4V_8$
, is given by the unique (up to scalar)
$\wedge ^4V_8$
, is given by the unique (up to scalar)
![]() $\mathfrak {sl}_8$
-equivariant morphism
$\mathfrak {sl}_8$
-equivariant morphism
where
![]() $S_{21111110}$
denotes the Schur functor corresponding to the partition
$S_{21111110}$
denotes the Schur functor corresponding to the partition
![]() $(2,1,1,1,1,1,1,0)$
. If we start with two elementary tensors given by fourtuples with a common pair of indices, we can include them into
$(2,1,1,1,1,1,1,0)$
. If we start with two elementary tensors given by fourtuples with a common pair of indices, we can include them into
![]() $\wedge ^4U_6$
for some codimension two subspace
$\wedge ^4U_6$
for some codimension two subspace
![]() $U_6\subset V_8$
. But then the Lie bracket factors through
$U_6\subset V_8$
. But then the Lie bracket factors through
![]() $S_{21111110}U_6=\{0\}$
, so it has to vanish.
$S_{21111110}U_6=\{0\}$
, so it has to vanish.
Each pair of indices in
![]() $\{1,\ldots ,8\}$
belongs to three of the
$\{1,\ldots ,8\}$
belongs to three of the
![]() $14$
fourtuples. For any triple
$14$
fourtuples. For any triple
![]() $(ijk)$
among
$(ijk)$
among
![]() $h_i$
,
$h_i$
,
![]() $h_j$
and
$h_j$
and
![]() $h_k$
share four disjoint pairs (for example
$h_k$
share four disjoint pairs (for example
![]() $h_1$
,
$h_1$
,
![]() $h_2$
and
$h_2$
and
![]() $h_4$
share
$h_4$
share
![]() $(13), (24), (57), (68)$
). These seven triples always meet in exactly one index, so they are in correspondence with the lines in a Fano plane. One can find more on this in [Reference ManivelMan06, Section 4].
$(13), (24), (57), (68)$
). These seven triples always meet in exactly one index, so they are in correspondence with the lines in a Fano plane. One can find more on this in [Reference ManivelMan06, Section 4].
A nice consequence of this description is the following
Proposition 3.5.
![]() ${\mathcal {C}}(v)$
and
${\mathcal {C}}(v)$
and
![]() ${\mathcal {C}}(v^\vee )$
are isomorphic.
${\mathcal {C}}(v^\vee )$
are isomorphic.
Proof. Since our v is general, we may suppose up to the action of
![]() $\operatorname {\mathrm {SL}}(V_8)$
that v belongs to our Cartan subspace above, given in terms of the basis
$\operatorname {\mathrm {SL}}(V_8)$
that v belongs to our Cartan subspace above, given in terms of the basis
![]() $e_1, \ldots , e_8$
of
$e_1, \ldots , e_8$
of
![]() $V_8$
. Denote the dual basis by
$V_8$
. Denote the dual basis by
![]() $e_1^\vee , \ldots , e_8^\vee $
, and choose the volume form
$e_1^\vee , \ldots , e_8^\vee $
, and choose the volume form
![]() $e_1^\vee \wedge \cdots \wedge e_8^\vee $
on
$e_1^\vee \wedge \cdots \wedge e_8^\vee $
on
![]() $V_8$
. Then the induced isomorphism from
$V_8$
. Then the induced isomorphism from
![]() $\wedge ^4V_8$
to
$\wedge ^4V_8$
to
![]() $\wedge ^4V^\vee _8$
sends
$\wedge ^4V^\vee _8$
sends
![]() $e_I=e_{i_1}\wedge e_{i_2}\wedge e_{i_3} \wedge e_{i_4}$
to
$e_I=e_{i_1}\wedge e_{i_2}\wedge e_{i_3} \wedge e_{i_4}$
to
![]() $\epsilon _{I,J}e_J$
, where J is the complement of I in
$\epsilon _{I,J}e_J$
, where J is the complement of I in
![]() $\{1,\ldots , 8\}$
and
$\{1,\ldots , 8\}$
and
![]() $\epsilon _{I,J}$
is the sign of the permutation
$\epsilon _{I,J}$
is the sign of the permutation
![]() $(i_1,\ldots , i_4,j_1,\ldots , j_4)$
.
$(i_1,\ldots , i_4,j_1,\ldots , j_4)$
.
Now, observe that for each i,
![]() $h_i$
is of the form
$h_i$
is of the form
![]() $e_K+e_L$
for two complementary sets of indices K and L. Moreover, one can check that
$e_K+e_L$
for two complementary sets of indices K and L. Moreover, one can check that
![]() $\epsilon _{K,L}$
is always equal to
$\epsilon _{K,L}$
is always equal to
![]() $1$
. This implies that
$1$
. This implies that
![]() $h_i^\vee =e^\vee _K+e^\vee _L$
has exactly the same expression as
$h_i^\vee =e^\vee _K+e^\vee _L$
has exactly the same expression as
![]() $h_i$
in terms of the dual basis. In other words the map
$h_i$
in terms of the dual basis. In other words the map
![]() $v\mapsto v^\vee $
, when restricted to our Cartan subspace, is essentially the identity, and the claim follows.
$v\mapsto v^\vee $
, when restricted to our Cartan subspace, is essentially the identity, and the claim follows.
3.5 The abelian threefold
Remarkably, one can construct the abelian threefold whose Kummer variety is
![]() ${\mathrm {Kum}_C}$
by considering another orbital degeneracy locus. The idea is to use the flag variety
${\mathrm {Kum}_C}$
by considering another orbital degeneracy locus. The idea is to use the flag variety
![]() $Fl(1,7,V_8)$
, the incidence correspondence in
$Fl(1,7,V_8)$
, the incidence correspondence in
![]() ${\mathbb {P}}(V_8)\times {\mathbb {P}}(V_8^\vee )$
parametrizing flags
${\mathbb {P}}(V_8)\times {\mathbb {P}}(V_8^\vee )$
parametrizing flags
![]() $(U_1\subset U_7)$
. The rank six quotient bundle
$(U_1\subset U_7)$
. The rank six quotient bundle
![]() ${\mathcal {N}}={\mathcal {U}}_7/{\mathcal {U}}_1$
allows to realize the space of four-forms as
${\mathcal {N}}={\mathcal {U}}_7/{\mathcal {U}}_1$
allows to realize the space of four-forms as
Exactly as before, this allows to associate to any
![]() $\operatorname {\mathrm {GL}}(V_6)$
-orbit closure Y in
$\operatorname {\mathrm {GL}}(V_6)$
-orbit closure Y in
![]() $\wedge ^3V_6$
an orbital degeneracy locus
$\wedge ^3V_6$
an orbital degeneracy locus
![]() $D_Y(v)\subset Fl(1,7,V_8)$
. Here,
$D_Y(v)\subset Fl(1,7,V_8)$
. Here,
![]() $V_6$
is a six-dimensional vector space. In particular, the cone
$V_6$
is a six-dimensional vector space. In particular, the cone
![]() $Y_{10}$
over the Grassmannian
$Y_{10}$
over the Grassmannian
![]() $G(3,V_6)$
yields, for v generic, a smooth threefold
$G(3,V_6)$
yields, for v generic, a smooth threefold
![]() ${\mathrm {A}_C}:=D_{Y_{10}}(v)$
. In similar terms as for the other orbital degeneracy loci, this threefold is
${\mathrm {A}_C}:=D_{Y_{10}}(v)$
. In similar terms as for the other orbital degeneracy loci, this threefold is
Proposition 3.6.
![]() ${\mathrm {A}_C}$
is a torsor over an abelian threefold, and the projection to
${\mathrm {A}_C}$
is a torsor over an abelian threefold, and the projection to
![]() ${\mathbb {P}}(V_8)$
is a double cover of
${\mathbb {P}}(V_8)$
is a double cover of
![]() ${\mathrm {Kum}_C}$
.
${\mathrm {Kum}_C}$
.
Proof. This is [Reference Gruson, Sam and WeymanGSW13, Proposition 6.12].
Over a point of
![]() ${\mathrm {A}_C}$
, given by a flag
${\mathrm {A}_C}$
, given by a flag
![]() $U_1\subset U_7$
, the four-form v defines a decomposable tensor in
$U_1\subset U_7$
, the four-form v defines a decomposable tensor in
![]() $\wedge ^3(U_7/U_1)$
. This tensor is never zero if v is general and therefore defines a four-dimensional space
$\wedge ^3(U_7/U_1)$
. This tensor is never zero if v is general and therefore defines a four-dimensional space
![]() $U_4$
such that
$U_4$
such that
![]() $U_1\subset U_4\subset U_7$
. Hence, a rank-four vector bundle
$U_1\subset U_4\subset U_7$
. Hence, a rank-four vector bundle
![]() ${\mathcal {U}}_4$
on
${\mathcal {U}}_4$
on
![]() ${\mathrm {A}_C}$
, a subbundle of the trivial bundle
${\mathrm {A}_C}$
, a subbundle of the trivial bundle
![]() $V_8\otimes {\mathcal {O}}_{\mathrm {A}_C}$
.
$V_8\otimes {\mathcal {O}}_{\mathrm {A}_C}$
.
Remark 3.7. The proper orbit closures of the
![]() $\operatorname {\mathrm {GL}}(V_6)$
-action on
$\operatorname {\mathrm {GL}}(V_6)$
-action on
![]() $\wedge ^3V_6$
are, apart from the cone over the Grassmannian, a quartic hypersurface and the codimension five locus of partially decomposable tensors. In our relative setting, the quartic induces a hypersurface of bidegree
$\wedge ^3V_6$
are, apart from the cone over the Grassmannian, a quartic hypersurface and the codimension five locus of partially decomposable tensors. In our relative setting, the quartic induces a hypersurface of bidegree
![]() $(2,2)$
in
$(2,2)$
in
![]() ${\mathbb {P}}(V_8)\times {\mathbb {P}}(V_8^\vee )$
, whose singular locus is an eightfold that is singular exactly along
${\mathbb {P}}(V_8)\times {\mathbb {P}}(V_8^\vee )$
, whose singular locus is an eightfold that is singular exactly along
![]() ${\mathrm {A}_C}$
. So once again we get a very interesting singular hypersurface. It would be very nice to find a modular interpretation of these loci.
${\mathrm {A}_C}$
. So once again we get a very interesting singular hypersurface. It would be very nice to find a modular interpretation of these loci.
4 Lines from alternating forms
In this section, we will identify the two covering families of lines in
![]() $\operatorname {\mathrm {SU}}_C(2)$
in terms of orbital degeneracy loci; this will give a very explicit description of these families in terms of existence of special flags of vector spaces. As a consequence of this, we will obtain Theorem 4.8, in which we identify the moduli space
$\operatorname {\mathrm {SU}}_C(2)$
in terms of orbital degeneracy loci; this will give a very explicit description of these families in terms of existence of special flags of vector spaces. As a consequence of this, we will obtain Theorem 4.8, in which we identify the moduli space
![]() $\operatorname {\mathrm {SU}}_C(2,L)$
, for L of odd degree, with an orbital degeneracy locus in
$\operatorname {\mathrm {SU}}_C(2,L)$
, for L of odd degree, with an orbital degeneracy locus in
![]() $G(2,V_8)$
associated to
$G(2,V_8)$
associated to
![]() $v\in \wedge ^4 V_8$
.
$v\in \wedge ^4 V_8$
.
4.1 The ruling and its lines
Recall the definition of the abelian threefold
![]() ${\mathrm {A}_C}$
from Equation (3.2). Our next result relates it to the ruling described in section 2.3.
${\mathrm {A}_C}$
from Equation (3.2). Our next result relates it to the ruling described in section 2.3.
Proposition 4.1. The family
![]() ${\mathbb {P}}({\mathcal {U}}_4)$
over
${\mathbb {P}}({\mathcal {U}}_4)$
over
![]() ${\mathrm {A}_C}$
coincides with the ruling
${\mathrm {A}_C}$
coincides with the ruling
![]() ${\mathbb {P}}({\mathcal {R}})$
over
${\mathbb {P}}({\mathcal {R}})$
over
![]() $\operatorname {\mathrm {Pic}}^1(C)$
of the moduli space
$\operatorname {\mathrm {Pic}}^1(C)$
of the moduli space
![]() $\operatorname {\mathrm {SU}}_C(2)$
.
$\operatorname {\mathrm {SU}}_C(2)$
.
Proof. We need to prove that for any flag
![]() $(U_1\subset U_7)$
in
$(U_1\subset U_7)$
in
![]() ${\mathrm {A}_C}$
, defining the four-plane
${\mathrm {A}_C}$
, defining the four-plane
![]() $U_4$
, the linear space
$U_4$
, the linear space
![]() ${\mathbb {P}}(U_4)$
is contained in
${\mathbb {P}}(U_4)$
is contained in
![]() ${\mathcal {C}}$
. If we can show that
${\mathcal {C}}$
. If we can show that
![]() ${\mathcal {C}}$
is even covered by this family of
${\mathcal {C}}$
is even covered by this family of
![]() ${\mathbb {P}}^3$
s, we will be done since the ruling is unique. So let us prove these two statements.
${\mathbb {P}}^3$
s, we will be done since the ruling is unique. So let us prove these two statements.
Lemma 4.2. The image of
![]() ${\mathbb {P}}({\mathcal {U}}_4)$
in
${\mathbb {P}}({\mathcal {U}}_4)$
in
![]() ${\mathbb {P}}(V_8)$
is contained in the Coble quartic.
${\mathbb {P}}(V_8)$
is contained in the Coble quartic.
Proof. Consider a point of
![]() ${\mathrm {A}_C}$
and the associated flag
${\mathrm {A}_C}$
and the associated flag
![]() $U_1\subset U_4\subset U_7$
. By the very definition of
$U_1\subset U_4\subset U_7$
. By the very definition of
![]() ${\mathrm {A}_C}$
, this means we can write
${\mathrm {A}_C}$
, this means we can write
for some vectors
![]() $e_1\in U_1$
and
$e_1\in U_1$
and
![]() $e_2,e_3,e_4\in U_4$
, with
$e_2,e_3,e_4\in U_4$
, with
![]() $w\in \wedge ^3V_8$
,
$w\in \wedge ^3V_8$
,
![]() $e_8\in V_8$
and
$e_8\in V_8$
and
![]() $v'\in \wedge ^4U_7$
. Under the generality hypothesis we can suppose that
$v'\in \wedge ^4U_7$
. Under the generality hypothesis we can suppose that
![]() $U_4=\langle e_1,e_2,e_3,e_4\rangle $
, and it suffices to check that
$U_4=\langle e_1,e_2,e_3,e_4\rangle $
, and it suffices to check that
![]() $U^{\prime }_1={\mathbb {C}} e_2$
defines a point of
$U^{\prime }_1={\mathbb {C}} e_2$
defines a point of
![]() ${\mathcal {C}}$
.
${\mathcal {C}}$
.
Modulo
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, the tensor w is a three-form in six variables. Since the secants of the Grassmannian
$e_2$
, the tensor w is a three-form in six variables. Since the secants of the Grassmannian
![]() $G(3,6)$
in its Plücker embedding fill up the ambient projective space, generically we can write
$G(3,6)$
in its Plücker embedding fill up the ambient projective space, generically we can write
![]() $w=a\wedge b\wedge c+d\wedge e\wedge f$
modulo
$w=a\wedge b\wedge c+d\wedge e\wedge f$
modulo
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, for some vectors
$e_2$
, for some vectors
![]() $a,b,c,d,e,f$
. Modulo
$a,b,c,d,e,f$
. Modulo
![]() $e_1$
and
$e_1$
and
![]() $e_2$
again,
$e_2$
again,
![]() $v'$
is a four-form in only five variables, so it defines a hyperplane that will cut the three-dimensional space
$v'$
is a four-form in only five variables, so it defines a hyperplane that will cut the three-dimensional space
![]() $\langle a,b,c\rangle $
in codimension one, say along
$\langle a,b,c\rangle $
in codimension one, say along
![]() $\langle a,b\rangle $
, and similarly it will cut
$\langle a,b\rangle $
, and similarly it will cut
![]() $\langle d,e,f\rangle $
in codimension one, say along
$\langle d,e,f\rangle $
in codimension one, say along
![]() $\langle d,e\rangle $
. In other words, we may suppose that modulo
$\langle d,e\rangle $
. In other words, we may suppose that modulo
![]() $e_1$
and
$e_1$
and
![]() $e_2$
,
$e_2$
,
![]() $v'=a\wedge b\wedge d\wedge e$
. But then, modulo
$v'=a\wedge b\wedge d\wedge e$
. But then, modulo
![]() $e_2$
we get
$e_2$
we get
So v belongs to
![]() $(\wedge ^2U^{\prime }_4)\wedge (\wedge ^2V_8)+\wedge ^3V_8\wedge U^{\prime }_1$
if
$(\wedge ^2U^{\prime }_4)\wedge (\wedge ^2V_8)+\wedge ^3V_8\wedge U^{\prime }_1$
if
![]() $U^{\prime }_4=\langle e_1,e_2,a,d\rangle .$
The existence of such a space
$U^{\prime }_4=\langle e_1,e_2,a,d\rangle .$
The existence of such a space
![]() $U^{\prime }_4\supset U^{\prime }_1$
is precisely the required condition for
$U^{\prime }_4\supset U^{\prime }_1$
is precisely the required condition for
![]() $U^{\prime }_1$
to belong to
$U^{\prime }_1$
to belong to
![]() ${\mathcal {C}}$
, so we are done.
${\mathcal {C}}$
, so we are done.
Lemma 4.3. The family
![]() ${\mathbb {P}}({\mathcal {U}}_4)$
covers the Coble quartic.
${\mathbb {P}}({\mathcal {U}}_4)$
covers the Coble quartic.
Proof. This can be done by a Chern class computation, being equivalent to the fact that the degree of
![]() ${\mathbb {P}}({\mathcal {U}}_4)$
with respect to the relative hyperplane class does not vanish. Notice that by Equation (3.2),
${\mathbb {P}}({\mathcal {U}}_4)$
with respect to the relative hyperplane class does not vanish. Notice that by Equation (3.2),
![]() ${\mathrm {A}_C}$
can be considered as a subvariety of
${\mathrm {A}_C}$
can be considered as a subvariety of
![]() $Fl(1,4,7,V_8)$
. Even more, it is the zero locus in the flag manifold of the section
$Fl(1,4,7,V_8)$
. Even more, it is the zero locus in the flag manifold of the section
![]() $\overline {v}$
of the rank
$\overline {v}$
of the rank
![]() $19$
vector bundle
$19$
vector bundle
over
![]() $Fl(1,4,7,V_8)$
defined by v. Since this section is general, the class of
$Fl(1,4,7,V_8)$
defined by v. Since this section is general, the class of
![]() ${\mathrm {A}_C}$
in the Chow ring of the flag manifold is the top Chern class of
${\mathrm {A}_C}$
in the Chow ring of the flag manifold is the top Chern class of
![]() ${\mathcal {G}}$
. So the degree we are looking for is
${\mathcal {G}}$
. So the degree we are looking for is
 $$ \begin{align*}\int_{{\mathbb{P}}({\mathcal{U}}_4)}c_1({\mathcal{U}}_1^\vee)^6=\int_{{\mathrm{A}_C}}s_3({\mathcal{U}}_4^\vee)=\int_{Fl(1,4,7,V_8)}c_{19}({\mathcal{G}})s_3({\mathcal{U}}_4^\vee)=32,\end{align*} $$
$$ \begin{align*}\int_{{\mathbb{P}}({\mathcal{U}}_4)}c_1({\mathcal{U}}_1^\vee)^6=\int_{{\mathrm{A}_C}}s_3({\mathcal{U}}_4^\vee)=\int_{Fl(1,4,7,V_8)}c_{19}({\mathcal{G}})s_3({\mathcal{U}}_4^\vee)=32,\end{align*} $$
as can be computed using [Reference Grayson and StillmanGS, Schubert2 package]. This implies the claim.
Remark.
![]() $32$
is the expected number: Since the Coble hypersurface has degree
$32$
is the expected number: Since the Coble hypersurface has degree
![]() $4$
, we recover the fact that exactly
$4$
, we recover the fact that exactly
![]() $8 {\mathbb {P}}^3$
s of the ruling pass through a general point of the quartic, as recalled in the proof of Proposition 2.4.
$8 {\mathbb {P}}^3$
s of the ruling pass through a general point of the quartic, as recalled in the proof of Proposition 2.4.
The previous statement allows to reconstruct the curve C purely in terms of the four-form and its associated orbital degeneracy loci. Indeed, we have recalled that a
![]() ${\mathbb {P}}^3$
of the ruling meets the Kummer threefold along a copy of the curve.
${\mathbb {P}}^3$
of the ruling meets the Kummer threefold along a copy of the curve.
Corollary 4.4. For any point of
![]() ${\mathrm {A}_C}$
, with associated flag
${\mathrm {A}_C}$
, with associated flag
![]() $(U_1\subset U_4\subset U_7)$
, the intersection of
$(U_1\subset U_4\subset U_7)$
, the intersection of
![]() ${\mathbb {P}} (U_4)$
with
${\mathbb {P}} (U_4)$
with
![]() ${\mathrm {Kum}_C}$
is a copy of the curve C.
${\mathrm {Kum}_C}$
is a copy of the curve C.
And of course we also recover the family of lines in the ruling as a quadric bundle. Indeed, the same arguments as in section 2.3 yield:
Corollary 4.5. The total space of the fiber bundle
![]() $G(2,{\mathcal {U}}_4)$
over
$G(2,{\mathcal {U}}_4)$
over
![]() ${\mathrm {A}_C}$
maps birationally to the family
${\mathrm {A}_C}$
maps birationally to the family
![]() ${\mathcal {F}}_R$
in
${\mathcal {F}}_R$
in
![]() $G(2,V_8)$
.
$G(2,V_8)$
.
4.2 Hecke lines from alternating forms
In the previous section, we have defined some ODL
![]() $D_{Y_i}(v)$
from orbits inside the space of three-forms in seven variables (i.e., in the notation of the previous sections, inside
$D_{Y_i}(v)$
from orbits inside the space of three-forms in seven variables (i.e., in the notation of the previous sections, inside
![]() $\wedge ^3 V_7$
). We will use a similar construction to obtain ODL inside the Grassmannian
$\wedge ^3 V_7$
). We will use a similar construction to obtain ODL inside the Grassmannian
![]() $G(2,V_8)$
. The Borel–Weil theorem gives an isomorphism
$G(2,V_8)$
. The Borel–Weil theorem gives an isomorphism
where
![]() ${\mathcal {Q}}$
denotes the rank six quotient vector bundle on
${\mathcal {Q}}$
denotes the rank six quotient vector bundle on
![]() $G(2,V_8)$
. Thus, in this case, we need to look at two-forms in six variables.
$G(2,V_8)$
. Thus, in this case, we need to look at two-forms in six variables.
If
![]() $V_6$
is as before a six-dimensional complex vector space,
$V_6$
is as before a six-dimensional complex vector space,
![]() $\wedge ^4 V_6^\vee \simeq \wedge ^2 V_6$
has only two proper
$\wedge ^4 V_6^\vee \simeq \wedge ^2 V_6$
has only two proper
![]() $\operatorname {\mathrm {GL}}(V_6)$
-orbit closures, that we will index by their codimension: the Pfaffian cubic hypersurface
$\operatorname {\mathrm {GL}}(V_6)$
-orbit closures, that we will index by their codimension: the Pfaffian cubic hypersurface
![]() $Z_1$
and its singular locus
$Z_1$
and its singular locus
![]() $Z_6$
, that is the cone over the Grassmannian
$Z_6$
, that is the cone over the Grassmannian
![]() $G(2,V_6)$
. These allow us to construct inside
$G(2,V_6)$
. These allow us to construct inside
![]() $G(2,V_8)$
the two orbital degeneracy loci
$G(2,V_8)$
the two orbital degeneracy loci
![]() $D_{Z_1}(v)$
and
$D_{Z_1}(v)$
and
![]() $D_{Z_6}(v)$
.
$D_{Z_6}(v)$
.
Let us first consider
![]() $D_{Z_6}(v)$
, which can also be defined by
$D_{Z_6}(v)$
, which can also be defined by
Lemma 4.6.
![]() $D_{Z_6}(v)$
is a smooth Fano sixfold of even index.
$D_{Z_6}(v)$
is a smooth Fano sixfold of even index.
Proof. By definition,
![]() $D_{Z_6}(v)$
is the projection in
$D_{Z_6}(v)$
is the projection in
![]() $G(2,V_8)$
of the locus
$G(2,V_8)$
of the locus
![]() $Z_6(v)$
in
$Z_6(v)$
in
![]() $Fl(2,6,V_8)$
parametrizing flags
$Fl(2,6,V_8)$
parametrizing flags
![]() $(U_2\subset U_6\subset V_8)$
such that v belongs to the
$(U_2\subset U_6\subset V_8)$
such that v belongs to the
![]() $56$
-dimensional space
$56$
-dimensional space
![]() $\wedge ^3 V_8\wedge U_2+\wedge ^4 U_6$
. Taking the quotient of
$\wedge ^3 V_8\wedge U_2+\wedge ^4 U_6$
. Taking the quotient of
![]() $\wedge ^4V_8$
by the latter, we get a rank
$\wedge ^4V_8$
by the latter, we get a rank
![]() $14$
vector bundle
$14$
vector bundle
![]() ${\mathcal {P}}$
on
${\mathcal {P}}$
on
![]() $Fl(2,6,V_8)$
, generated by global sections since it is a quotient of a trivial bundle. Moreover, v defines a generic section of this bundle, and
$Fl(2,6,V_8)$
, generated by global sections since it is a quotient of a trivial bundle. Moreover, v defines a generic section of this bundle, and
![]() $Z_6(v)$
is the zero-locus of this section, hence it is smooth. Since
$Z_6(v)$
is the zero-locus of this section, hence it is smooth. Since
![]() $Fl(2,6,V_8)$
has dimension
$Fl(2,6,V_8)$
has dimension
![]() $20$
,
$20$
,
![]() $Z_6(v)$
has dimension
$Z_6(v)$
has dimension
![]() $6$
and its canonical bundle is given by the adjunction formula. A straightforward computation yields
$6$
and its canonical bundle is given by the adjunction formula. A straightforward computation yields
On the other hand, for any
![]() $[U_2]\in G(2,V_8)$
, the quotient of
$[U_2]\in G(2,V_8)$
, the quotient of
![]() $\wedge ^4V_8$
by
$\wedge ^4V_8$
by
![]() $\wedge ^3 V_8\wedge U_2$
is isomorphic to
$\wedge ^3 V_8\wedge U_2$
is isomorphic to
![]() $\wedge ^4(V_8/U_2)\simeq \wedge ^2(V_8/U_2)^\vee \otimes \det (V_8/U_2)$
. This is a space of skew-symmetric forms in six dimensions, and the existence of
$\wedge ^4(V_8/U_2)\simeq \wedge ^2(V_8/U_2)^\vee \otimes \det (V_8/U_2)$
. This is a space of skew-symmetric forms in six dimensions, and the existence of
![]() $U_6$
exactly means that v defines a skew-symmetric form in
$U_6$
exactly means that v defines a skew-symmetric form in
![]() $\wedge ^2(V_8/U_2)^\vee \otimes \det (V_8/U_2)$
whose rank is at most two. In fact, the rank must be exactly two, since for v generic, a simple dimension count shows that the rank can never be zero. In particular, the projection of
$\wedge ^2(V_8/U_2)^\vee \otimes \det (V_8/U_2)$
whose rank is at most two. In fact, the rank must be exactly two, since for v generic, a simple dimension count shows that the rank can never be zero. In particular, the projection of
![]() $Z_6(v)$
to
$Z_6(v)$
to
![]() $D_{Z_6}(v)$
is an isomorphism.
$D_{Z_6}(v)$
is an isomorphism.
More than that, the kernel of our two-form on
![]() $V_8/U_2$
is
$V_8/U_2$
is
![]() $U_6/U_2$
, so we get a nondegenerate skew-symmetric form on the quotient
$U_6/U_2$
, so we get a nondegenerate skew-symmetric form on the quotient
![]() $V_8/U_6$
, which is therefore identified with its dual. To be precise, since the skew-symmetric form has values in
$V_8/U_6$
, which is therefore identified with its dual. To be precise, since the skew-symmetric form has values in
![]() $\det (V_8/U_2)$
, we get an isomorphism
$\det (V_8/U_2)$
, we get an isomorphism
![]() $V_8/U_6\simeq (V_8/U_6)^\vee \otimes \det (V_8/U_2)$
. Taking determinants, we deduce that
$V_8/U_6\simeq (V_8/U_6)^\vee \otimes \det (V_8/U_2)$
. Taking determinants, we deduce that
![]() $\det (U_2)^2\simeq \det (U_6)^2$
; in other words, the line bundle
$\det (U_2)^2\simeq \det (U_6)^2$
; in other words, the line bundle
![]() ${\mathcal {L}}=\det ({\mathcal {U}}_6)\otimes \det ({\mathcal {U}}_2)^\vee $
is
${\mathcal {L}}=\det ({\mathcal {U}}_6)\otimes \det ({\mathcal {U}}_2)^\vee $
is
![]() $2$
-torsion on
$2$
-torsion on
![]() $Z_6(v)$
.
$Z_6(v)$
.
But then we can rewrite the canonical bundle as
Note that
![]() $\det ({\mathcal {U}}_2)^\vee \otimes \det ({\mathcal {U}}_6)^\vee $
is very ample on
$\det ({\mathcal {U}}_2)^\vee \otimes \det ({\mathcal {U}}_6)^\vee $
is very ample on
![]() $Fl(2,6,V_8)$
since it defines its canonical Plücker type embedding. Since
$Fl(2,6,V_8)$
since it defines its canonical Plücker type embedding. Since
![]() ${\mathcal {L}}$
is torsion, we deduce that
${\mathcal {L}}$
is torsion, we deduce that
![]() $Z_6(v)$
is Fano. But then its Picard group is torsion free, so
$Z_6(v)$
is Fano. But then its Picard group is torsion free, so
![]() ${\mathcal {L}}$
is actually trivial. So finally
${\mathcal {L}}$
is actually trivial. So finally
![]() $K_{Z_6(v)}=\det ({\mathcal {U}}_2)^2$
, hence the index is even.
$K_{Z_6(v)}=\det ({\mathcal {U}}_2)^2$
, hence the index is even.
The previous discussion shows that
![]() $D_{Z_6}(v)$
is a Pfaffian locus defined by a skew-symmetric map
$D_{Z_6}(v)$
is a Pfaffian locus defined by a skew-symmetric map
![]() $\psi _v : {\mathcal {Q}}{\rightarrow } {\mathcal {Q}}^\vee (1)$
associated with v. The restriction of
$\psi _v : {\mathcal {Q}}{\rightarrow } {\mathcal {Q}}^\vee (1)$
associated with v. The restriction of
![]() $\psi _v$
to
$\psi _v$
to
![]() $D_{Z_6}(v)$
has constant rank, hence its Kernel
$D_{Z_6}(v)$
has constant rank, hence its Kernel
![]() $\operatorname {\mathrm {Ker}} (\psi _v)$
is a rank four vector bundle on
$\operatorname {\mathrm {Ker}} (\psi _v)$
is a rank four vector bundle on
![]() $D_{Z_6}(v)$
, that coincides with
$D_{Z_6}(v)$
, that coincides with
![]() $({\mathcal {U}}_6/{\mathcal {U}}_2)|_{D_{Z_6}(v)}$
and fits into an exact sequence
$({\mathcal {U}}_6/{\mathcal {U}}_2)|_{D_{Z_6}(v)}$
and fits into an exact sequence
Let us set once and for all the more compact notation
![]() $D:=D_{Z_6}(v)$
and
$D:=D_{Z_6}(v)$
and
![]() $G:=G(2,V_8)$
. The exact sequence (4.1) allows to describe the normal bundle
$G:=G(2,V_8)$
. The exact sequence (4.1) allows to describe the normal bundle
![]() ${\mathcal {N}}_{D/G}$
as follows.
${\mathcal {N}}_{D/G}$
as follows.
Lemma 4.7. We have isomorphisms
![]() ${\mathcal {N}}_{D/G}\simeq \wedge ^2\operatorname {\mathrm {Ker}}(\psi _v)^\vee (1)$
and
${\mathcal {N}}_{D/G}\simeq \wedge ^2\operatorname {\mathrm {Ker}}(\psi _v)^\vee (1)$
and
![]() ${\mathcal {N}}_{D/G}^\vee \simeq {\mathcal {N}}_{D/G}(-2)$
.
${\mathcal {N}}_{D/G}^\vee \simeq {\mathcal {N}}_{D/G}(-2)$
.
We will use this information later on. Our next goal is to prove the following theorem.
Theorem 4.8. For a generic
![]() $v\in \wedge ^4 V_8$
, the orbital degeneracy locus
$v\in \wedge ^4 V_8$
, the orbital degeneracy locus
![]() $D_{Z_6}(v)$
is isomorphic to the moduli space
$D_{Z_6}(v)$
is isomorphic to the moduli space
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
of semistable rank two vector bundles on C with fixed determinant
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
of semistable rank two vector bundles on C with fixed determinant
![]() ${\mathcal {O}}_C(c)$
, for a certain point
${\mathcal {O}}_C(c)$
, for a certain point
![]() $c\in C$
.
$c\in C$
.
Remark 4.9. Such embeddings defined by Hecke lines are studied in [Reference BeauvilleBea91, section 3.4], and there is one, denoted
![]() $\varphi _p$
in loc. cit., for each choice of a point p on the curve C. Here, we only get one of these embeddings, in agreement with the already mentioned fact that v does not only determine a genus three curve but a marked point on this curve.
$\varphi _p$
in loc. cit., for each choice of a point p on the curve C. Here, we only get one of these embeddings, in agreement with the already mentioned fact that v does not only determine a genus three curve but a marked point on this curve.
Remark 4.10. An interesting consequence is that we know a minimal resolution of the structure sheaf of
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
inside the Grassmannian
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
inside the Grassmannian
![]() $G(2,V_8)$
. From this resolution, it is easy to check that the intersection with a general copy of
$G(2,V_8)$
. From this resolution, it is easy to check that the intersection with a general copy of
![]() $G(2,6)$
inside
$G(2,6)$
inside
![]() $G(2,V_8)$
is a K3 surface of genus
$G(2,V_8)$
is a K3 surface of genus
![]() $13$
. This kind of description is used in [Reference Kanemitsu and MukaiKM23] to provide a new model for the general such K3 surface.
$13$
. This kind of description is used in [Reference Kanemitsu and MukaiKM23] to provide a new model for the general such K3 surface.
Let us begin by showing that
![]() $D_{Z_6}(v)$
defines a six-dimensional family of Hecke lines.
$D_{Z_6}(v)$
defines a six-dimensional family of Hecke lines.
Proposition 4.11. Let
![]() $[U_2]\in D_{Z_6}(v)$
, then
$[U_2]\in D_{Z_6}(v)$
, then
![]() ${\mathbb {P}}(U_2)\subset {\mathbb {P}}(V_8)$
is a line in
${\mathbb {P}}(U_2)\subset {\mathbb {P}}(V_8)$
is a line in
![]() ${\mathcal {C}}$
.
${\mathcal {C}}$
.
Proof. Let
![]() $[U_1]\in {\mathbb {P}}(U_2)$
be a point in the line. By definition of
$[U_1]\in {\mathbb {P}}(U_2)$
be a point in the line. By definition of
![]() $D_{Z_6}(v)$
, one can write
$D_{Z_6}(v)$
, one can write
for some
![]() $u_2\in U_2$
, some trivector
$u_2\in U_2$
, some trivector
![]() $v'$
and some vectors
$v'$
and some vectors
![]() $a,b,c,d$
. The trivector
$a,b,c,d$
. The trivector
![]() $v'$
is a trivector in six variables; therefore, it can in general be written as
$v'$
is a trivector in six variables; therefore, it can in general be written as
![]() $e\wedge f\wedge g + h\wedge i\wedge l$
for some vectors
$e\wedge f\wedge g + h\wedge i\wedge l$
for some vectors
![]() $e,f,g,h,i,l$
since the secant variety of
$e,f,g,h,i,l$
since the secant variety of
![]() $G(3,6)$
is the whole Plücker space. Now, modulo
$G(3,6)$
is the whole Plücker space. Now, modulo
![]() $U_2$
,
$U_2$
,
![]() $\dim (\langle a,b,c,d \rangle \cap \langle e,f,g \rangle )\geq 1$
and
$\dim (\langle a,b,c,d \rangle \cap \langle e,f,g \rangle )\geq 1$
and
![]() $\dim (\langle a,b,c,d \rangle \cap \langle h,i,l \rangle )\geq 1$
. Thus, we can suppose that
$\dim (\langle a,b,c,d \rangle \cap \langle h,i,l \rangle )\geq 1$
. Thus, we can suppose that
![]() $a=e$
and
$a=e$
and
![]() $b=h$
. But then if we let
$b=h$
. But then if we let
![]() $U_4=\langle U_2,a,b \rangle ,$
it is straightforward to check that
$U_4=\langle U_2,a,b \rangle ,$
it is straightforward to check that
![]() $( v\ \mod U_1) \in (\wedge ^2 U_4)\wedge (\wedge ^2 V_8)$
. This ensures that
$( v\ \mod U_1) \in (\wedge ^2 U_4)\wedge (\wedge ^2 V_8)$
. This ensures that
![]() $[U_1]$
belongs to
$[U_1]$
belongs to
![]() ${\mathcal {C}}$
.
${\mathcal {C}}$
.
The point-line incidence variety of the family of lines parametrized by
![]() $D_{Z_6}(v)$
is given by the projective bundle
$D_{Z_6}(v)$
is given by the projective bundle
![]() ${\mathbb {P}}({\mathcal {U}}_2)\to D_{Z_6}(v)$
.
${\mathbb {P}}({\mathcal {U}}_2)\to D_{Z_6}(v)$
.
Proposition 4.12. The family of lines parametrized by
![]() $D_{Z_6}(v)$
covers
$D_{Z_6}(v)$
covers
![]() ${\mathcal {C}}$
.
${\mathcal {C}}$
.
Proof. This is again a Chern class computation. Indeed, by irreducibility of the varieties in play, it is sufficient to check that, if
![]() ${\mathcal {U}}_1^\vee $
denotes the relative dual tautological line bundle of
${\mathcal {U}}_1^\vee $
denotes the relative dual tautological line bundle of
![]() ${\mathbb {P}}({\mathcal {U}}_2)\to D_{Z_6}(v)$
, then
${\mathbb {P}}({\mathcal {U}}_2)\to D_{Z_6}(v)$
, then
![]() $c_1({\mathcal {U}}_1^\vee )^6\neq 0$
; indeed
$c_1({\mathcal {U}}_1^\vee )^6\neq 0$
; indeed
![]() ${\mathcal {U}}_1^\vee $
is the pullback to
${\mathcal {U}}_1^\vee $
is the pullback to
![]() ${\mathbb {P}}({\mathcal {U}}_2)$
of
${\mathbb {P}}({\mathcal {U}}_2)$
of
![]() ${\mathcal {O}}_{{\mathbb {P}}(V_8)}(1)$
. This implies that the image of
${\mathcal {O}}_{{\mathbb {P}}(V_8)}(1)$
. This implies that the image of
![]() ${\mathbb {P}}({\mathcal {U}}_2)$
inside
${\mathbb {P}}({\mathcal {U}}_2)$
inside
![]() ${\mathbb {P}}(V_8)$
has dimension at least six and is thus the Coble quartic
${\mathbb {P}}(V_8)$
has dimension at least six and is thus the Coble quartic
![]() ${\mathcal {C}}$
by Proposition 4.11. Notice that one can work directly on
${\mathcal {C}}$
by Proposition 4.11. Notice that one can work directly on
![]() $Z_6(v)$
since it is isomorphic to
$Z_6(v)$
since it is isomorphic to
![]() $D_{Z_6}(v)$
. Since
$D_{Z_6}(v)$
. Since
![]() $Z_6(v)$
can be constructed as the zero locus of a section of a vector bundle inside the flag variety
$Z_6(v)$
can be constructed as the zero locus of a section of a vector bundle inside the flag variety
![]() $Fl(2,4,V_8)$
, we can verify that
$Fl(2,4,V_8)$
, we can verify that
![]() $c_1({\mathcal {U}}_1^\vee )^6\neq 0$
with [Reference Grayson and StillmanGS] by constructing the coordinate ring of the zero locus
$c_1({\mathcal {U}}_1^\vee )^6\neq 0$
with [Reference Grayson and StillmanGS] by constructing the coordinate ring of the zero locus
![]() $Z_6(v)$
and of the projective bundle
$Z_6(v)$
and of the projective bundle
![]() ${\mathbb {P}}({\mathcal {U}}_2)$
over it, similarly to what we did in the proof of Lemma 4.3.
${\mathbb {P}}({\mathcal {U}}_2)$
over it, similarly to what we did in the proof of Lemma 4.3.
Proposition 4.13. The lines parametrized by
![]() $D_{Z_6}(v)$
are Hecke lines.
$D_{Z_6}(v)$
are Hecke lines.
Proof. Suppose by contradiction that the lines parametrized by
![]() $D_{Z_6}(v)$
are not Hecke. Since they form a covering family, they must be lines in the ruling, that is,
$D_{Z_6}(v)$
are not Hecke. Since they form a covering family, they must be lines in the ruling, that is,
![]() $D_{Z_6}(v)\subset {\mathcal {F}}_R$
. Now, recall that
$D_{Z_6}(v)\subset {\mathcal {F}}_R$
. Now, recall that
![]() ${\mathcal {F}}_R$
is a birational image of the quadric bundle
${\mathcal {F}}_R$
is a birational image of the quadric bundle
![]() $G(2,{\mathcal {U}}_4)$
over
$G(2,{\mathcal {U}}_4)$
over
![]() ${\mathrm {A}_C}$
. The preimage of
${\mathrm {A}_C}$
. The preimage of
![]() $D_{Z_6}(v)$
in
$D_{Z_6}(v)$
in
![]() $G(2,{\mathcal {U}}_4)$
is rationally connected, being birationally equivalent to the Fano manifold
$G(2,{\mathcal {U}}_4)$
is rationally connected, being birationally equivalent to the Fano manifold
![]() $D_{Z_6}(v)$
. But then its projection to
$D_{Z_6}(v)$
. But then its projection to
![]() ${\mathrm {A}_C}$
must be constant. Since the fibers of this projection are only four-dimensional, while the dimension of
${\mathrm {A}_C}$
must be constant. Since the fibers of this projection are only four-dimensional, while the dimension of
![]() $D_{Z_6}(v)$
is six, we get a contradiction.
$D_{Z_6}(v)$
is six, we get a contradiction.
Proof of Theorem 4.8.
Recall that the family
![]() ${\mathcal {F}}_H$
of Hecke lines has dimension seven, so
${\mathcal {F}}_H$
of Hecke lines has dimension seven, so
![]() $D_{Z_6}(v)$
cannot be the whole family. In fact,
$D_{Z_6}(v)$
cannot be the whole family. In fact,
![]() ${\mathcal {F}}_H$
has a rational map
${\mathcal {F}}_H$
has a rational map
![]() $\eta $
to C, and by the same argument as above, the fact that
$\eta $
to C, and by the same argument as above, the fact that
![]() $D_{Z_6}(v)$
is Fano ensures that its image in
$D_{Z_6}(v)$
is Fano ensures that its image in
![]() ${\mathcal {F}}_H$
is contained in a fiber of
${\mathcal {F}}_H$
is contained in a fiber of
![]() $\eta $
, over some point
$\eta $
, over some point
![]() $c\in C$
. But then the morphism from
$c\in C$
. But then the morphism from
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
to
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
to
![]() ${\mathcal {F}}_H$
is birational onto its image
${\mathcal {F}}_H$
is birational onto its image
![]() $D_{Z_6}(v)$
. Since
$D_{Z_6}(v)$
. Since
![]() $\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
has Picard rank one [Reference RamananRam73], this morphism must be an isomorphism.
$\operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
has Picard rank one [Reference RamananRam73], this morphism must be an isomorphism.
5 A Coble type quadric hypersurface
The aim of this section is to show that the Coble quadric hypersurface in
![]() $G(2,V_8)$
deserves its name in the sense that it is singular along the moduli space and it is uniquely determined by this property. So the section is mainly devoted to the proof of Theorem 5.1. In the last part, we also prove a self-duality statement concerning this hypersurface which is analogous to the self-duality of the Coble quartic in
$G(2,V_8)$
deserves its name in the sense that it is singular along the moduli space and it is uniquely determined by this property. So the section is mainly devoted to the proof of Theorem 5.1. In the last part, we also prove a self-duality statement concerning this hypersurface which is analogous to the self-duality of the Coble quartic in
![]() ${\mathbb {P}}(V_8)$
.
${\mathbb {P}}(V_8)$
.
5.1 The relative Pfaffian
As we have seen, the fact that
![]() $D_{Z_6}(v)$
is defined as a Pfaffian locus in
$D_{Z_6}(v)$
is defined as a Pfaffian locus in
![]() $G(2,V_8)$
implies that it is the singular locus of a Pfaffian hypersurface, defined as the first degeneracy locus
$G(2,V_8)$
implies that it is the singular locus of a Pfaffian hypersurface, defined as the first degeneracy locus
![]() $D_{Z_1}(v)$
of the skew-symmetric morphism
$D_{Z_1}(v)$
of the skew-symmetric morphism
![]() ${\mathcal {Q}}{\longrightarrow } {\mathcal {Q}}^\vee (1)$
defined by v.
${\mathcal {Q}}{\longrightarrow } {\mathcal {Q}}^\vee (1)$
defined by v.
Theorem 5.1. The hypersurface
![]() $D_{Z_1}(v)$
of
$D_{Z_1}(v)$
of
![]() $G(2,V_8)$
is a quadratic section of the Grassmannian. It is the unique quadratic section that is singular along
$G(2,V_8)$
is a quadratic section of the Grassmannian. It is the unique quadratic section that is singular along
![]() $D_{Z_6}(v)$
.
$D_{Z_6}(v)$
.
Remark 5.2. Starting from a genus three curve C and its Kummer threefold embedded in
![]() ${\mathbb {P}}^7$
by the linear system
${\mathbb {P}}^7$
by the linear system
![]() $|2\Theta |$
, the original observation of Coble was that there exists a unique Heisenberg-invariant quartic
$|2\Theta |$
, the original observation of Coble was that there exists a unique Heisenberg-invariant quartic
![]() ${\mathcal {C}}$
that is singular along the Kummer. Beauville proved much later that the Heisenberg-invariance hypothesis was actually not necessary [Reference BeauvilleBea03]. In our context, the curve and its Heisenberg group are not easily available (although there are connections between the latter and the Weyl group
${\mathcal {C}}$
that is singular along the Kummer. Beauville proved much later that the Heisenberg-invariance hypothesis was actually not necessary [Reference BeauvilleBea03]. In our context, the curve and its Heisenberg group are not easily available (although there are connections between the latter and the Weyl group
![]() $W(E_7)$
of the theta-representation
$W(E_7)$
of the theta-representation
![]() $\wedge ^4V_8$
), so we do not use any Heisenberg-invariance hypothesis.
$\wedge ^4V_8$
), so we do not use any Heisenberg-invariance hypothesis.
5.1.1 Structure of the proof of Theorem 5.1
Recall that D stands for
![]() $D_{Z_6}(v)$
and G for
$D_{Z_6}(v)$
and G for
![]() $G(2,V_8)$
. That
$G(2,V_8)$
. That
![]() $D_{Z_1}(v)$
is a quadratic section of G follows from the fact that it is defined by a rank six Pfaffian, obtained as the image of v by the cubic morphism
$D_{Z_1}(v)$
is a quadratic section of G follows from the fact that it is defined by a rank six Pfaffian, obtained as the image of v by the cubic morphism
In order to prove that this is the only quadratic section that is singular along D, recall that the conormal bundle of D in the Grassmannian G is the quotient of the ideal sheaf
![]() ${\mathcal {I}}_D$
by its square
${\mathcal {I}}_D$
by its square
![]() ${\mathcal {I}}^2_D$
. Twisting by
${\mathcal {I}}^2_D$
. Twisting by
![]() ${\mathcal {O}}_G(2)$
and taking cohomology, we get an exact sequence
${\mathcal {O}}_G(2)$
and taking cohomology, we get an exact sequence
Observe that
![]() $H^0(G,{\mathcal {I}}_D(2))$
parametrizes quadratic sections of G (up to scalar) that contain D, while, since D is smooth,
$H^0(G,{\mathcal {I}}_D(2))$
parametrizes quadratic sections of G (up to scalar) that contain D, while, since D is smooth,
![]() $H^0(G,{\mathcal {I}}^2_D(2))$
parametrizes quadratic sections that are singular along D. Our claim is that the latter space is one-dimensional. This will be proved in three steps: First, compute the dimension of the space of quadrics containing D; second, bound
$H^0(G,{\mathcal {I}}^2_D(2))$
parametrizes quadratic sections that are singular along D. Our claim is that the latter space is one-dimensional. This will be proved in three steps: First, compute the dimension of the space of quadrics containing D; second, bound
![]() $H^0(D,{\mathcal {N}}_{D/G}^\vee (2))$
from below; third, prove that
$H^0(D,{\mathcal {N}}_{D/G}^\vee (2))$
from below; third, prove that
![]() $H^1(G,{\mathcal {I}}^2_D(2))$
vanishes. These results are contained in Lemmas 5.3, 5.6, 5.11. From the fact that
$H^1(G,{\mathcal {I}}^2_D(2))$
vanishes. These results are contained in Lemmas 5.3, 5.6, 5.11. From the fact that
![]() $H^1({\mathcal {I}}_D^2(2))=0$
, the exact sequence
$H^1({\mathcal {I}}_D^2(2))=0$
, the exact sequence
knowing that
![]() $h^0({\mathcal {I}}_D(2))=71$
and
$h^0({\mathcal {I}}_D(2))=71$
and
![]() $h^0({\mathcal {N}}_{D/G})\ge 70$
, will allow us to conclude that
$h^0({\mathcal {N}}_{D/G})\ge 70$
, will allow us to conclude that
![]() $h^0({\mathcal {I}}_D^2(2))\le 1$
and the proof will be complete.
$h^0({\mathcal {I}}_D^2(2))\le 1$
and the proof will be complete.
5.1.2 Quadrics containing the moduli space
Let us count the quadric sections of
![]() $G=G(2,V_8)$
that contain the moduli space
$G=G(2,V_8)$
that contain the moduli space
![]() $D\simeq \operatorname {\mathrm {SU}}_C(2,L)$
.
$D\simeq \operatorname {\mathrm {SU}}_C(2,L)$
.
Lemma 5.3.
![]() $h^0(G,{\mathcal {I}}_D(2))=71.$
$h^0(G,{\mathcal {I}}_D(2))=71.$
Proof. Let us first recall the classical minimal resolution of the ideal I generated by submaximal Pfaffians of a generic skew-symmetric matrix of size
![]() $6$
; in other words, the ideal of the cone over the Grassmannian
$6$
; in other words, the ideal of the cone over the Grassmannian
![]() $G(2,V_6)$
inside
$G(2,V_6)$
inside
![]() $\wedge ^2V_6$
. As usual, we will use the notation
$\wedge ^2V_6$
. As usual, we will use the notation
![]() $S_\lambda $
, for
$S_\lambda $
, for
![]() $\lambda $
a partition, in order to indicate the corresponding Schur functor. Letting
$\lambda $
a partition, in order to indicate the corresponding Schur functor. Letting
![]() $S={\mathbb {C}}[\wedge ^2V_6]$
, this resolution is the following [Reference WeymanWey03, (6.4.6)]:
$S={\mathbb {C}}[\wedge ^2V_6]$
, this resolution is the following [Reference WeymanWey03, (6.4.6)]:

Since D is a Pfaffian locus of the expected dimension, given by a skew-symmetric map
![]() ${\mathcal {Q}}{\rightarrow }{\mathcal {Q}}^\vee (1)$
, we deduce the following free resolution of its twisted ideal sheaf (we used identifications like
${\mathcal {Q}}{\rightarrow }{\mathcal {Q}}^\vee (1)$
, we deduce the following free resolution of its twisted ideal sheaf (we used identifications like
![]() $S_{332222}{\mathcal {Q}}^\vee =\wedge ^2{\mathcal {Q}}^\vee (-2)$
):
$S_{332222}{\mathcal {Q}}^\vee =\wedge ^2{\mathcal {Q}}^\vee (-2)$
):

Note that this resolution is self-dual, up to twist. Moreover, using the Bott–Borel–Weil theorem one can check that all the factors are acyclic homogeneous vector bundles, with two exceptions:
![]() $\wedge ^4{\mathcal {Q}}$
has a nonzero space of sections, isomorphic to
$\wedge ^4{\mathcal {Q}}$
has a nonzero space of sections, isomorphic to
![]() $\wedge ^4V_8$
; and
$\wedge ^4V_8$
; and
![]() $S^2{\mathcal {Q}}^\vee (-1)$
, which is one of the two irreducible factors of
$S^2{\mathcal {Q}}^\vee (-1)$
, which is one of the two irreducible factors of
![]() $\Omega _G^2$
, has a one dimensional cohomology group in degree two. We end up with a canonical exact sequence
$\Omega _G^2$
, has a one dimensional cohomology group in degree two. We end up with a canonical exact sequence
and our claim follows.
Remark 5.4. Being defined by a cubic Pfaffian, the equation of the hypersurface
![]() $D_{Z_1}(v)$
must be a cubic
$D_{Z_1}(v)$
must be a cubic
![]() $\operatorname {\mathrm {SL}}(V_8)$
-covariant of v in
$\operatorname {\mathrm {SL}}(V_8)$
-covariant of v in
![]() $\wedge ^4V_8$
, taking values in
$\wedge ^4V_8$
, taking values in
![]() $H^0({\mathcal {O}}_G(2))\simeq S_{22}V_8$
. In fact, it is a
$H^0({\mathcal {O}}_G(2))\simeq S_{22}V_8$
. In fact, it is a
![]() $\operatorname {\mathrm {GL}}(V_8)$
-covariant, that by homogeneity with respect to
$\operatorname {\mathrm {GL}}(V_8)$
-covariant, that by homogeneity with respect to
![]() $V_8$
, must take its values in
$V_8$
, must take its values in
![]() $S_{22}V_8\otimes \det (V_8)$
. One can check that the latter module has multiplicity one inside
$S_{22}V_8\otimes \det (V_8)$
. One can check that the latter module has multiplicity one inside
![]() $S^3(\wedge ^4V_8)$
, so this covariant is unique up to scalar. For example, it can be obtained as the composition
$S^3(\wedge ^4V_8)$
, so this covariant is unique up to scalar. For example, it can be obtained as the composition
 $$ \begin{align*} S^3(\wedge^4V_8)\hookrightarrow &S^3(\wedge^2V_8\otimes \wedge^2V_8)\to S^3(\wedge^2V_8)\otimes S^3(\wedge^2V_8)\to S^3(\wedge^2V_8)\otimes \wedge^6V_8 \to \\ &\to S^3(\wedge^2V_8)\otimes \wedge^2V_8^\vee\otimes\det(V_8) \to S^2(\wedge^2V_8)\otimes\det(V_8) \to S_{22}V_8\otimes\det(V_8). \end{align*} $$
$$ \begin{align*} S^3(\wedge^4V_8)\hookrightarrow &S^3(\wedge^2V_8\otimes \wedge^2V_8)\to S^3(\wedge^2V_8)\otimes S^3(\wedge^2V_8)\to S^3(\wedge^2V_8)\otimes \wedge^6V_8 \to \\ &\to S^3(\wedge^2V_8)\otimes \wedge^2V_8^\vee\otimes\det(V_8) \to S^2(\wedge^2V_8)\otimes\det(V_8) \to S_{22}V_8\otimes\det(V_8). \end{align*} $$
Following the natural morphisms involved in these arrows, this would allow to give an explicit formula for an equation of the quadratic hypersurface
![]() $D_{Z_1}(v)$
in terms of the coefficients of v (this was done in [Reference Ren, Sam, Schrader and SturmfelsRSSS13] for the Coble quartic itself). It would suffice to do this when v belongs to our preferred Cartan subspace; this is in principle a straightforward computation but the resulting formulas would be huge.
$D_{Z_1}(v)$
in terms of the coefficients of v (this was done in [Reference Ren, Sam, Schrader and SturmfelsRSSS13] for the Coble quartic itself). It would suffice to do this when v belongs to our preferred Cartan subspace; this is in principle a straightforward computation but the resulting formulas would be huge.
Remark 5.5. The embedding of
![]() $\wedge ^4V_8$
inside
$\wedge ^4V_8$
inside
![]() $H^0(G,{\mathcal {I}}_D(2))$
in Equation (5.1) is given by the derivatives of
$H^0(G,{\mathcal {I}}_D(2))$
in Equation (5.1) is given by the derivatives of
![]() $D_{Z_1}(v)$
with respect to v, that is, can be obtained by polarizing the cubic morphism discussed in the previous remark. On the other hand, modulo these derivatives, (4) shows that there is a uniquely defined ‘non-Pfaffian’ quadric vanishing on D. This non-Pfaffian quadric comes from the contribution of
$D_{Z_1}(v)$
with respect to v, that is, can be obtained by polarizing the cubic morphism discussed in the previous remark. On the other hand, modulo these derivatives, (4) shows that there is a uniquely defined ‘non-Pfaffian’ quadric vanishing on D. This non-Pfaffian quadric comes from the contribution of
![]() $S^2{\mathcal {Q}}^\vee (-1)$
in the resolution of
$S^2{\mathcal {Q}}^\vee (-1)$
in the resolution of
![]() ${\mathcal {I}}_D(2)$
. Since in this resolution, these two terms are connected one to the other through three morphisms having respective degree two, one and two with respect to v, the non-Pfaffian quadric must be given by a quintic covariant in v. And indeed, a computation with Lie [Reference van Leeuwen, Cohen and LisservLCL92] shows that
${\mathcal {I}}_D(2)$
. Since in this resolution, these two terms are connected one to the other through three morphisms having respective degree two, one and two with respect to v, the non-Pfaffian quadric must be given by a quintic covariant in v. And indeed, a computation with Lie [Reference van Leeuwen, Cohen and LisservLCL92] shows that
A special line in this space of covariants is generated by the cubic covariant defining the Pfaffian quadric, twisted by the invariant quadratic form (defined by the wedge product). The quotient is our non-Pfaffian quadric. As before, we could in principle compute it explicitly by constructing a specific covariant. One way to construct such a covariant is to observe that
Taking the square of the resulting morphism, we can define a quartic covariant
hence the desired quintic covariant.
5.1.3 The normal bundle of D in
 $G(2,V_8)$
$G(2,V_8)$
Let us now bound from below the dimension of
![]() $H^0(D,{\mathcal {N}}_{D/G}^\vee (2))$
. By Lemma 4.7, this space is isomorphic with
$H^0(D,{\mathcal {N}}_{D/G}^\vee (2))$
. By Lemma 4.7, this space is isomorphic with
![]() $H^0({\mathcal {N}}_{D/G})$
, which parametrizes infinitesimal deformations of D inside G. Some of these deformations must be induced by the deformation of
$H^0({\mathcal {N}}_{D/G})$
, which parametrizes infinitesimal deformations of D inside G. Some of these deformations must be induced by the deformation of
![]() $[v]$
inside
$[v]$
inside
![]() ${\mathbb {P}}(\wedge ^4V_8)$
, which should provide
${\mathbb {P}}(\wedge ^4V_8)$
, which should provide
![]() $69$
parameters. But recall that the family
$69$
parameters. But recall that the family
![]() ${\mathcal {F}}_H$
of Hecke lines inside
${\mathcal {F}}_H$
of Hecke lines inside
![]() $SU_C(2)$
is a subvariety of
$SU_C(2)$
is a subvariety of
![]() $G(2,V_8)$
, birationally fibered over the curve C, with one fiber isomorphic to
$G(2,V_8)$
, birationally fibered over the curve C, with one fiber isomorphic to
![]() $D\simeq \operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
for some point
$D\simeq \operatorname {\mathrm {SU}}_C(2,{\mathcal {O}}_C(c))$
for some point
![]() $c\in C$
. So we expect one extra deformation of D to be obtained by deforming c in the curve C. That these deformations are independent is essentially the content of
$c\in C$
. So we expect one extra deformation of D to be obtained by deforming c in the curve C. That these deformations are independent is essentially the content of
Lemma 5.6.
![]() $h^0(D,{\mathcal {N}}_{D/G})\ge 70.$
$h^0(D,{\mathcal {N}}_{D/G})\ge 70.$
Proof. The locus in
![]() $\wedge ^4 V_6\simeq \wedge ^2V_6^\vee $
corresponding to skew-symmetric forms of rank at most
$\wedge ^4 V_6\simeq \wedge ^2V_6^\vee $
corresponding to skew-symmetric forms of rank at most
![]() $2$
is desingularized by the total space of
$2$
is desingularized by the total space of
![]() $\wedge ^4 {\mathcal {U}}_4 $
over the Grassmannian
$\wedge ^4 {\mathcal {U}}_4 $
over the Grassmannian
![]() $G(4,V_6)$
[Reference WeymanWey03, (6.4.2)]. As a consequence of this and of [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Proposition 2.3], the Pfaffian locus D is desingularized by the zero locus
$G(4,V_6)$
[Reference WeymanWey03, (6.4.2)]. As a consequence of this and of [Reference Benedetti, Filippini, Manivel and TanturriBFMT20a, Proposition 2.3], the Pfaffian locus D is desingularized by the zero locus
![]() $Z:=Z_6(v)$
inside
$Z:=Z_6(v)$
inside
![]() $Fl(2,6,V_8)$
of a (general) section of the bundle
$Fl(2,6,V_8)$
of a (general) section of the bundle
![]() ${\mathcal {V}}=\wedge ^4 (V_8/{\mathcal {U}}_2)/\wedge ^4 ({\mathcal {U}}_6/{\mathcal {U}}_2)$
. This bundle is an extension of irreducible bundles
${\mathcal {V}}=\wedge ^4 (V_8/{\mathcal {U}}_2)/\wedge ^4 ({\mathcal {U}}_6/{\mathcal {U}}_2)$
. This bundle is an extension of irreducible bundles
By dimension count, Z is in fact isomorphic to D via the natural projection. Under this isomorphism and by Lemma 4.7,
![]() ${\mathcal {N}}_{D/G}$
can be identified with the restriction of
${\mathcal {N}}_{D/G}$
can be identified with the restriction of
![]() ${\mathcal {N}}:=\wedge ^2 ({\mathcal {U}}_6/{\mathcal {U}}_2)\otimes \det (V_8/{\mathcal {U}}_6)$
to Z. In order to compute the cohomology of this restriction, we can tensorize with
${\mathcal {N}}:=\wedge ^2 ({\mathcal {U}}_6/{\mathcal {U}}_2)\otimes \det (V_8/{\mathcal {U}}_6)$
to Z. In order to compute the cohomology of this restriction, we can tensorize with
![]() ${\mathcal {N}}$
the Koszul complex
${\mathcal {N}}$
the Koszul complex
![]() $\wedge ^\bullet {\mathcal {V}}^\vee $
of the global section of
$\wedge ^\bullet {\mathcal {V}}^\vee $
of the global section of
![]() ${\mathcal {V}}$
, whose zero locus is
${\mathcal {V}}$
, whose zero locus is
![]() $Z\subset Fl(2,6,V_8)$
. This gives the following resolution of
$Z\subset Fl(2,6,V_8)$
. This gives the following resolution of
![]() ${\mathcal {N}}_{D/G}$
by locally free sheaves on
${\mathcal {N}}_{D/G}$
by locally free sheaves on
![]() $Fl(2,6,V_8)$
$Fl(2,6,V_8)$
By applying the Bott–Borel–Weil theorem we can compute the cohomology groups of the bundles
![]() $\wedge ^k {\mathcal {V}}^\vee \otimes {\mathcal {N}}$
, for all
$\wedge ^k {\mathcal {V}}^\vee \otimes {\mathcal {N}}$
, for all
![]() $k \ge 0$
. Those that do not vanish are the following:
$k \ge 0$
. Those that do not vanish are the following:
 $$ \begin{gather*} H^0(\wedge^0 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\wedge^4 V_8, \\H^0(\wedge^1 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^2(\wedge^3 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}} , \;\; H^3(\wedge^3 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}}^2, \\H^4(\wedge^4 {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^5(\wedge^4 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\wedge^4 V_8,\\H^4(\wedge^5 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\mathfrak{sl}(V_8)\oplus {\mathbb{C}}^3, \quad H^5(\wedge^5 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\mathfrak{sl}(V_8)\oplus {\mathbb{C}}^4 , \quad H^6(\wedge^5 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^6(\wedge^7 {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^7(\wedge^7 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^8(\wedge^9 {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^9(\wedge^9 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^{12}(\wedge^{13} {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^{13}(\wedge^{13} {\mathcal{V}}^\vee \otimes {\mathcal{N}})= {\mathbb{C}}. \end{gather*} $$
$$ \begin{gather*} H^0(\wedge^0 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\wedge^4 V_8, \\H^0(\wedge^1 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^2(\wedge^3 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}} , \;\; H^3(\wedge^3 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}}^2, \\H^4(\wedge^4 {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^5(\wedge^4 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\wedge^4 V_8,\\H^4(\wedge^5 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\mathfrak{sl}(V_8)\oplus {\mathbb{C}}^3, \quad H^5(\wedge^5 {\mathcal{V}}^\vee \otimes {\mathcal{N}})=\mathfrak{sl}(V_8)\oplus {\mathbb{C}}^4 , \quad H^6(\wedge^5 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^6(\wedge^7 {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^7(\wedge^7 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^8(\wedge^9 {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^9(\wedge^9 {\mathcal{V}}^\vee \otimes {\mathcal{N}})={\mathbb{C}},\\H^{12}(\wedge^{13} {\mathcal{V}}^\vee \otimes {\mathcal{N}})= H^{13}(\wedge^{13} {\mathcal{V}}^\vee \otimes {\mathcal{N}})= {\mathbb{C}}. \end{gather*} $$
A direct consequence is that
![]() $\chi ({\mathcal {N}}_{D/G})=70$
. Moreover, observe that
$\chi ({\mathcal {N}}_{D/G})=70$
. Moreover, observe that
Since these groups give the first page of the spectral sequence in cohomology induced by the Koszul complex of
![]() ${\mathcal {O}}_{Z}$
twisted by
${\mathcal {O}}_{Z}$
twisted by
![]() ${\mathcal {N}}$
, this implies that
${\mathcal {N}}$
, this implies that
![]() $H^i({\mathcal {N}}_{D/G})=0$
for
$H^i({\mathcal {N}}_{D/G})=0$
for
![]() $i>1$
. Therefore,
$i>1$
. Therefore,
![]() $h^0({\mathcal {N}}_{D/G})=\chi ({\mathcal {N}}_{D/G})+h^1({\mathcal {N}}_{D/G})\ge 70$
.
$h^0({\mathcal {N}}_{D/G})=\chi ({\mathcal {N}}_{D/G})+h^1({\mathcal {N}}_{D/G})\ge 70$
.
5.1.4 An affine module M
As usual
![]() $V_6$
denotes a six-dimensional vector space. Let S be the coordinate ring of
$V_6$
denotes a six-dimensional vector space. Let S be the coordinate ring of
![]() $\wedge ^2 V_6$
. The ideal I of the cone over
$\wedge ^2 V_6$
. The ideal I of the cone over
![]() $G(2,V_6)$
is generated by the submaximal Pfaffians of the generic skew-symmetric matrix of size
$G(2,V_6)$
is generated by the submaximal Pfaffians of the generic skew-symmetric matrix of size
![]() $6$
; the
$6$
; the
![]() $\operatorname {\mathrm {GL}}(6)$
-module generated by these submaximal Pfaffians is
$\operatorname {\mathrm {GL}}(6)$
-module generated by these submaximal Pfaffians is
![]() $\wedge ^4V_6^\vee \subset S^2(\wedge ^2V_6^\vee )$
. The square of I is then generated by the symmetric square of this module. The module decomposes [Reference van Leeuwen, Cohen and LisservLCL92] as
$\wedge ^4V_6^\vee \subset S^2(\wedge ^2V_6^\vee )$
. The square of I is then generated by the symmetric square of this module. The module decomposes [Reference van Leeuwen, Cohen and LisservLCL92] as
The first component is
![]() $\wedge ^2V_6^\vee \otimes \det V_6^\vee $
and must be interpreted as parametrizing quartics that are multiples of linear forms by the Pfaffian cubic. The ideal they generate is
$\wedge ^2V_6^\vee \otimes \det V_6^\vee $
and must be interpreted as parametrizing quartics that are multiples of linear forms by the Pfaffian cubic. The ideal they generate is
![]() $S_+I_{P}$
, where
$S_+I_{P}$
, where
![]() $S_+\subset S$
is the irrelevant ideal, and
$S_+\subset S$
is the irrelevant ideal, and
![]() $I_P$
denotes the ideal of the Pfaffian hypersurface.
$I_P$
denotes the ideal of the Pfaffian hypersurface.
Consider the exact sequence
The quotient module M is generated by
![]() $S_{2222}V_6^\vee $
. According to [Reference Grayson and StillmanGS], the minimal resolution
$S_{2222}V_6^\vee $
. According to [Reference Grayson and StillmanGS], the minimal resolution
![]() $R_\bullet $
of M has the Betti numbers of Table 1.
$R_\bullet $
of M has the Betti numbers of Table 1.
Table 1 Betti table of M.

The minimal resolution is
![]() $\operatorname {\mathrm {GL}}_6$
-equivariant, and it is not difficult to write it in terms of Schur functors. Indeed, we know that the quartic generators are parametrized by
$\operatorname {\mathrm {GL}}_6$
-equivariant, and it is not difficult to write it in terms of Schur functors. Indeed, we know that the quartic generators are parametrized by
![]() $S_{2222}V_6^\vee $
, so the first syzygy module must be contained in
$S_{2222}V_6^\vee $
, so the first syzygy module must be contained in
![]() $S_{2222}V_6^\vee \otimes \wedge ^2V_6^\vee $
, and it turns out that there is a unique
$S_{2222}V_6^\vee \otimes \wedge ^2V_6^\vee $
, and it turns out that there is a unique
![]() $\operatorname {\mathrm {GL}}_6$
-module of the correct dimension inside this tensor product. Proceeding inductively, we arrive at the following conclusion: The minimal
$\operatorname {\mathrm {GL}}_6$
-module of the correct dimension inside this tensor product. Proceeding inductively, we arrive at the following conclusion: The minimal
![]() $\operatorname {\mathrm {GL}}_6$
-equivariant resolution of the S-module M has the following shape:
$\operatorname {\mathrm {GL}}_6$
-equivariant resolution of the S-module M has the following shape:

Here, vertical arrows have degree one and diagonal arrows have degree two. Notice that the complex in bold reproduces the resolution of the Pfaffian ideal I itself.
Remark 5.7. As J. Weyman observed, one could also obtain this resolution by considering the natural resolution of the Pfaffian hypersurface given by the total space of the vector bundle
![]() $\wedge ^2{\mathcal {U}}$
over the Grassmannian
$\wedge ^2{\mathcal {U}}$
over the Grassmannian
![]() $G(4,V_6)$
. The morphism
$G(4,V_6)$
. The morphism
![]() $\pi $
from
$\pi $
from
![]() $\operatorname {\mathrm {Tot}}(\wedge ^2{\mathcal {U}})$
to
$\operatorname {\mathrm {Tot}}(\wedge ^2{\mathcal {U}})$
to
![]() $\wedge ^2V_6$
is a resolution of singularities, and one can check that M is the push-forward by
$\wedge ^2V_6$
is a resolution of singularities, and one can check that M is the push-forward by
![]() $\pi $
of the module given by the pull-back of the line bundle
$\pi $
of the module given by the pull-back of the line bundle
![]() ${\mathcal {O}}(2)$
from the Grassmannian. Applying the geometric technique from [Reference WeymanWey03], one can extract the minimal resolution of M from the collection of
${\mathcal {O}}(2)$
from the Grassmannian. Applying the geometric technique from [Reference WeymanWey03], one can extract the minimal resolution of M from the collection of
![]() $\operatorname {\mathrm {GL}}(V_6)$
-modules given by
$\operatorname {\mathrm {GL}}(V_6)$
-modules given by
 $$ \begin{align*}F_i = \bigoplus_{j\ge 0} H^j(G(4,V_6),{\mathcal{O}}(2)\otimes\wedge^{i+j}(\wedge^2{\mathcal{U}})^\perp).\end{align*} $$
$$ \begin{align*}F_i = \bigoplus_{j\ge 0} H^j(G(4,V_6),{\mathcal{O}}(2)\otimes\wedge^{i+j}(\wedge^2{\mathcal{U}})^\perp).\end{align*} $$
Here,
![]() $(\wedge ^2{\mathcal {U}})^\perp $
is the kernel of the natural projection
$(\wedge ^2{\mathcal {U}})^\perp $
is the kernel of the natural projection
![]() $\wedge ^2V_6^\vee \to \wedge ^2{\mathcal {U}} ^\vee $
. The bundle
$\wedge ^2V_6^\vee \to \wedge ^2{\mathcal {U}} ^\vee $
. The bundle
![]() $(\wedge ^2{\mathcal {U}})^\perp $
is not semisimple but is an extension of
$(\wedge ^2{\mathcal {U}})^\perp $
is not semisimple but is an extension of
![]() ${\mathcal {O}}(-1)$
by
${\mathcal {O}}(-1)$
by
![]() ${\mathcal {U}}^\vee \otimes Q^\vee $
. Remarkably, it is the contribution of
${\mathcal {U}}^\vee \otimes Q^\vee $
. Remarkably, it is the contribution of
![]() ${\mathcal {O}}(-1)$
that reproduces the minimal resolution of I (twisted) inside that of M.
${\mathcal {O}}(-1)$
that reproduces the minimal resolution of I (twisted) inside that of M.
5.1.5 Relativizing M
Now, we want to use these results in the relative setting. Since
![]() $\wedge ^4 {\mathcal {Q}}$
is a vector bundle on
$\wedge ^4 {\mathcal {Q}}$
is a vector bundle on
![]() $G(2,V_8)$
which is locally isomorphic to
$G(2,V_8)$
which is locally isomorphic to
![]() $\wedge ^2 V_6$
, we can relativize the construction of I and
$\wedge ^2 V_6$
, we can relativize the construction of I and
![]() $I_P$
and M. For convenience, let us restrict to the complement
$I_P$
and M. For convenience, let us restrict to the complement
![]() ${\mathcal {X}}$
of the zero section inside the total space of this vector bundle. We get sheaves of
${\mathcal {X}}$
of the zero section inside the total space of this vector bundle. We get sheaves of
![]() ${\mathcal {O}}_{{\mathcal {X}}}$
-modules and ideals that we denote, respectively, by
${\mathcal {O}}_{{\mathcal {X}}}$
-modules and ideals that we denote, respectively, by
![]() ${\mathcal {I}}', {\mathcal {I}}^{\prime }_P, {\mathcal {M}}'$
. Note that, since we avoid the zero section, we get an exact sequence
${\mathcal {I}}', {\mathcal {I}}^{\prime }_P, {\mathcal {M}}'$
. Note that, since we avoid the zero section, we get an exact sequence
Then we consider
![]() $v\in \wedge ^4V_8$
as a general section of
$v\in \wedge ^4V_8$
as a general section of
![]() $\wedge ^4 {\mathcal {Q}}$
, that we interpret as a morphism from
$\wedge ^4 {\mathcal {Q}}$
, that we interpret as a morphism from
![]() $G=G(2,V_8)$
to the total space of
$G=G(2,V_8)$
to the total space of
![]() $\wedge ^4 {\mathcal {Q}}$
. By the definition of orbital degeneracy loci [Reference Benedetti, Filippini, Manivel and TanturriBFMT20b, Definition 2.1], the ideal of
$\wedge ^4 {\mathcal {Q}}$
. By the definition of orbital degeneracy loci [Reference Benedetti, Filippini, Manivel and TanturriBFMT20b, Definition 2.1], the ideal of
![]() $D_{Z_1}(v)$
is
$D_{Z_1}(v)$
is
![]() ${\mathcal {I}}_P:={\mathcal {I}}^{\prime }_P\otimes {\mathcal {O}}_G$
and the ideal of
${\mathcal {I}}_P:={\mathcal {I}}^{\prime }_P\otimes {\mathcal {O}}_G$
and the ideal of
![]() $D=D_{Z_6}(v)$
is
$D=D_{Z_6}(v)$
is
![]() ${\mathcal {I}}_D:={\mathcal {I}}'\otimes {\mathcal {O}}_G$
. Let us also denote
${\mathcal {I}}_D:={\mathcal {I}}'\otimes {\mathcal {O}}_G$
. Let us also denote
![]() ${\mathcal {M}}={\mathcal {M}}'\otimes {\mathcal {O}}_G$
. Of course, these tensor products are taken over
${\mathcal {M}}={\mathcal {M}}'\otimes {\mathcal {O}}_G$
. Of course, these tensor products are taken over
![]() ${\mathcal {O}}_{{\mathcal {X}}}$
.
${\mathcal {O}}_{{\mathcal {X}}}$
.
Lemma 5.8. There is an exact sequence
Proof. By the right exactness of tensor product, here by
![]() ${\mathcal {O}}_G$
, we get an exact sequence
${\mathcal {O}}_G$
, we get an exact sequence
But the map
![]() ${\mathcal {I}}_P \subset {\mathcal {I}}_D^2$
(which expresses the fact that D is contained in the singular locus of the Pfaffian hypersurface) clearly remains an injection, and we are done.
${\mathcal {I}}_P \subset {\mathcal {I}}_D^2$
(which expresses the fact that D is contained in the singular locus of the Pfaffian hypersurface) clearly remains an injection, and we are done.
In order to control
![]() ${\mathcal {M}}$
, we will now consider the complex of vector bundles induced by the resolution we constructed for M. We can deduce a resolution of
${\mathcal {M}}$
, we will now consider the complex of vector bundles induced by the resolution we constructed for M. We can deduce a resolution of
![]() ${\mathcal {M}}'$
and then tensor out again by
${\mathcal {M}}'$
and then tensor out again by
![]() ${\mathcal {O}}_G$
. In order to prove that we get a resolution of
${\mathcal {O}}_G$
. In order to prove that we get a resolution of
![]() ${\mathcal {M}}$
(the resolution given just below), we need to check that the Tor-sheaves of
${\mathcal {M}}$
(the resolution given just below), we need to check that the Tor-sheaves of
![]() ${\mathcal {O}}_{\mathcal {X}}$
-modules
${\mathcal {O}}_{\mathcal {X}}$
-modules
![]() $\mathcal {T}or_i({\mathcal {M}}',{\mathcal {O}}_G)$
vanish for
$\mathcal {T}or_i({\mathcal {M}}',{\mathcal {O}}_G)$
vanish for
![]() $i>0$
. All the Tor-sheaves we compute in the sequel will also be for
$i>0$
. All the Tor-sheaves we compute in the sequel will also be for
![]() ${\mathcal {O}}_{\mathcal {X}}$
-modules.
${\mathcal {O}}_{\mathcal {X}}$
-modules.

Lemma 5.9. For any
![]() $i>0$
,
$i>0$
,
-
1.
 $\mathcal {T}or_i({\mathcal {I}}^{\prime }_P,{\mathcal {O}}_G)=0,$
$\mathcal {T}or_i({\mathcal {I}}^{\prime }_P,{\mathcal {O}}_G)=0,$
-
2.
 $\mathcal {T}or_i({\mathcal {O}}_{\mathcal {X}}/{\mathcal {I}}',{\mathcal {O}}_G)=0,$
$\mathcal {T}or_i({\mathcal {O}}_{\mathcal {X}}/{\mathcal {I}}',{\mathcal {O}}_G)=0,$
-
3.
 $\mathcal {T}or_i({\mathcal {I}}'/{\mathcal {I}}^{\prime 2},{\mathcal {O}}_G)=0,$
$\mathcal {T}or_i({\mathcal {I}}'/{\mathcal {I}}^{\prime 2},{\mathcal {O}}_G)=0,$
-
4.
 $\mathcal {T}or_i({\mathcal {M}}',{\mathcal {O}}_G)=0.$
$\mathcal {T}or_i({\mathcal {M}}',{\mathcal {O}}_G)=0.$
Proof. (1) is obvious since
![]() ${\mathcal {I}}^{\prime }_P$
is locally free. (2) is a consequence of the generic perfection theorem (see [Reference Eagon and NorthcottEN67]), since I and therefore
${\mathcal {I}}^{\prime }_P$
is locally free. (2) is a consequence of the generic perfection theorem (see [Reference Eagon and NorthcottEN67]), since I and therefore
![]() ${\mathcal {I}}'$
is perfect, and D has the expected dimension. (3) is a consequence of (2) because
${\mathcal {I}}'$
is perfect, and D has the expected dimension. (3) is a consequence of (2) because
![]() ${\mathcal {I}}'/{\mathcal {I}}^{\prime 2}$
is a locally free
${\mathcal {I}}'/{\mathcal {I}}^{\prime 2}$
is a locally free
![]() ${\mathcal {O}}_{\mathcal {X}}/{\mathcal {I}}'$
-module (recall that since we have a generality assumption the singular locus is avoided). Finally, to prove (4) observe first that, by the long exact sequence of Tor,
${\mathcal {O}}_{\mathcal {X}}/{\mathcal {I}}'$
-module (recall that since we have a generality assumption the singular locus is avoided). Finally, to prove (4) observe first that, by the long exact sequence of Tor,
![]() $\mathcal {T}or_i({\mathcal {I}}',{\mathcal {O}}_G)=\mathcal {T}or_ {i+1}({\mathcal {O}}_{\mathcal {X}}/{\mathcal {I}}',{\mathcal {O}}_G)=0$
for any
$\mathcal {T}or_i({\mathcal {I}}',{\mathcal {O}}_G)=\mathcal {T}or_ {i+1}({\mathcal {O}}_{\mathcal {X}}/{\mathcal {I}}',{\mathcal {O}}_G)=0$
for any
![]() $i>0$
. Because of (3) this implies that
$i>0$
. Because of (3) this implies that
![]() $\mathcal {T}or_i({\mathcal {I}}^{\prime 2},{\mathcal {O}}_G)=0$
for any
$\mathcal {T}or_i({\mathcal {I}}^{\prime 2},{\mathcal {O}}_G)=0$
for any
![]() $i>0$
. Then we can use the exact sequence of Lemma 5.8 to deduce that
$i>0$
. Then we can use the exact sequence of Lemma 5.8 to deduce that
![]() $\mathcal {T}or_i({\mathcal {M}}',{\mathcal {O}}_G)=0$
when
$\mathcal {T}or_i({\mathcal {M}}',{\mathcal {O}}_G)=0$
when
![]() $i>1$
and that there is an exact sequence
$i>1$
and that there is an exact sequence
By Lemma 5.8,
![]() $\mathcal {T}or_1({\mathcal {M}}',{\mathcal {O}}_G)$
vanishes as well, and we are done.
$\mathcal {T}or_1({\mathcal {M}}',{\mathcal {O}}_G)$
vanishes as well, and we are done.
Lemma 5.10.
![]() ${\mathcal {M}}(2)$
is acyclic.
${\mathcal {M}}(2)$
is acyclic.
Proof. Twist the previous resolution of
![]() ${\mathcal {M}}$
by
${\mathcal {M}}$
by
![]() ${\mathcal {O}}(2)$
, and deduce from the Bott–Borel–Weil theorem that all the bundles in the twisted resolution are acyclic. This implies the claim.
${\mathcal {O}}(2)$
, and deduce from the Bott–Borel–Weil theorem that all the bundles in the twisted resolution are acyclic. This implies the claim.
Lemma 5.11.
![]() $H^i({\mathcal {I}}_D^2(2))=0$
for any
$H^i({\mathcal {I}}_D^2(2))=0$
for any
![]() $i>0$
.
$i>0$
.
This concludes the proof of Theorem 5.1. Note the following consequence: D has nonobstructed deformations.
Corollary 5.12.
![]() $h^0({\mathcal {N}}_{D/G})=70$
and
$h^0({\mathcal {N}}_{D/G})=70$
and
![]() $h^i({\mathcal {N}}_{D/G})=0$
for any
$h^i({\mathcal {N}}_{D/G})=0$
for any
![]() $i>0$
.
$i>0$
.
5.2 Deforming the Pfaffian hypersurface
We already observed that, varying v in
![]() $\wedge ^4V_8$
, we only get a codimension one family of deformations of D. The missing dimension is provided by the choice of the point on the curve C, but this is invisible in our constructions. We will nevertheless prove that the special quadric section of the Grassmannian deforms.
$\wedge ^4V_8$
, we only get a codimension one family of deformations of D. The missing dimension is provided by the choice of the point on the curve C, but this is invisible in our constructions. We will nevertheless prove that the special quadric section of the Grassmannian deforms.
Lemma 5.13. For a generic point
![]() $p\in C$
and the associated embedding
$p\in C$
and the associated embedding
![]() $\varphi _p: \operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p)) \hookrightarrow G(2,V_8)$
(see Remark 4.9), there exists at most one quadric hypersurface
$\varphi _p: \operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p)) \hookrightarrow G(2,V_8)$
(see Remark 4.9), there exists at most one quadric hypersurface
![]() $Q_p$
in the Grassmannian that is singular along
$Q_p$
in the Grassmannian that is singular along
![]() $\operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p))$
.
$\operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p))$
.
Proof. Such a quadric corresponds to a line in
![]() $H^0(G(2,V_8), {\mathcal {I}}^2_{\operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p))}(2))$
and we have computed in the proof of Theorem 5.1 that this space has dimension one for certain special points p. By semicontinuity, this dimension remains smaller or equal to one for p generic.
$H^0(G(2,V_8), {\mathcal {I}}^2_{\operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p))}(2))$
and we have computed in the proof of Theorem 5.1 that this space has dimension one for certain special points p. By semicontinuity, this dimension remains smaller or equal to one for p generic.
Theorem 5.14. For the generic embedding
![]() $\varphi _p$
, there exists a unique quadric hypersurface of
$\varphi _p$
, there exists a unique quadric hypersurface of
![]() $G(2,V_8)$
that is singular along
$G(2,V_8)$
that is singular along
![]() $\operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p))$
.
$\operatorname {\mathrm {SU}}_C(2,\mathcal {O}_C(p))$
.
Proof. Let us consider the embedding
![]() $Q=D_{Z_1}(v)\hookrightarrow G$
from Theorem 5.1. Let
$Q=D_{Z_1}(v)\hookrightarrow G$
from Theorem 5.1. Let
![]() $H^{\prime }_{Q/G}$
be the so-called ‘locally trivial Hilbert scheme’ parametrizing locally trivial deformations of
$H^{\prime }_{Q/G}$
be the so-called ‘locally trivial Hilbert scheme’ parametrizing locally trivial deformations of
![]() $Q\subset G$
, as defined in [Reference Greuel and KarrasGK89, 2.2]. Remark that the construction of [Reference Greuel and KarrasGK89] is done for finite singularities, but their arguments, as the authors underline in the introduction, go through for arbitrary singularities because of [Reference Flenner and KosarewFK87]. Let
$Q\subset G$
, as defined in [Reference Greuel and KarrasGK89, 2.2]. Remark that the construction of [Reference Greuel and KarrasGK89] is done for finite singularities, but their arguments, as the authors underline in the introduction, go through for arbitrary singularities because of [Reference Flenner and KosarewFK87]. Let
where
![]() $\mathcal {T}^1_Q$
denotes the first cotangent sheaf of Q (as defined, for instance, in [Reference SernesiSer06, Section 1.1.3]). In order that the locally trivial Hilbert scheme be smooth at Q, by [Reference Greuel and KarrasGK89, Prop. 2.3], we need that
$\mathcal {T}^1_Q$
denotes the first cotangent sheaf of Q (as defined, for instance, in [Reference SernesiSer06, Section 1.1.3]). In order that the locally trivial Hilbert scheme be smooth at Q, by [Reference Greuel and KarrasGK89, Prop. 2.3], we need that
![]() $H^1(Q,\mathcal {N}^{\prime }_{Q/G})=0$
. If this happens, then
$H^1(Q,\mathcal {N}^{\prime }_{Q/G})=0$
. If this happens, then
![]() $h^0(Q,\mathcal {N}^{\prime }_{Q/G})=\dim (H^{\prime }_{Q/G})$
and we will show that this equals 70. By [Reference SernesiSer06, Section 4.7.1], we have an exact sequence
$h^0(Q,\mathcal {N}^{\prime }_{Q/G})=\dim (H^{\prime }_{Q/G})$
and we will show that this equals 70. By [Reference SernesiSer06, Section 4.7.1], we have an exact sequence
Hence,
![]() $\mathcal {N}^{\prime }_{Q/G}$
coincides with the image of
$\mathcal {N}^{\prime }_{Q/G}$
coincides with the image of
![]() $T_{G/Q}$
inside
$T_{G/Q}$
inside
![]() ${\mathcal {N}}_{Q/G}$
, which is exactly the (twisted) Jacobian ideal
${\mathcal {N}}_{Q/G}$
, which is exactly the (twisted) Jacobian ideal
![]() ${\mathcal {J}}_{Q/G}(2)$
restricted to Q. In turn, the Jacobian ideal of the Pfaffian locus of
${\mathcal {J}}_{Q/G}(2)$
restricted to Q. In turn, the Jacobian ideal of the Pfaffian locus of
![]() $6\times 6$
matrices is exactly the ideal of
$6\times 6$
matrices is exactly the ideal of
![]() $4\times 4$
skew-symmetric minors. This implies that
$4\times 4$
skew-symmetric minors. This implies that
![]() ${\mathcal {J}}_{Q/G}(2)$
is the twisted ideal
${\mathcal {J}}_{Q/G}(2)$
is the twisted ideal
![]() ${\mathcal {I}}_D(2)/{\mathcal {I}}_Q(2)$
of D inside
${\mathcal {I}}_D(2)/{\mathcal {I}}_Q(2)$
of D inside
![]() ${\mathcal {O}}_Q(2)={\mathcal {O}}_Q(Q)$
. Let us therefore consider the exact sequence
${\mathcal {O}}_Q(2)={\mathcal {O}}_Q(Q)$
. Let us therefore consider the exact sequence
By Lemma 5.3, we have
![]() $h^0(G,{\mathcal {I}}_D(2))=71$
and in the proof of the same lemma we showed that
$h^0(G,{\mathcal {I}}_D(2))=71$
and in the proof of the same lemma we showed that
![]() $h^i(G,{\mathcal {I}}_D(2))=0$
, for
$h^i(G,{\mathcal {I}}_D(2))=0$
, for
![]() $i>0$
. On the other hand, we have
$i>0$
. On the other hand, we have
![]() ${\mathcal {I}}_Q(2)={\mathcal {O}}_G$
. Via the long cohomology exact sequence associated to sequence (5.2), we deduce that
${\mathcal {I}}_Q(2)={\mathcal {O}}_G$
. Via the long cohomology exact sequence associated to sequence (5.2), we deduce that
![]() $h^0(G,{\mathcal {J}}_{Q/G}(2))=70$
and
$h^0(G,{\mathcal {J}}_{Q/G}(2))=70$
and
![]() $h^i(G,{\mathcal {J}}_{Q/G}(2))=0$
for
$h^i(G,{\mathcal {J}}_{Q/G}(2))=0$
for
![]() $i>0.$
Hence
$i>0.$
Hence
![]() $H^{\prime }_{Q/G}$
is smooth of dimension 70 at
$H^{\prime }_{Q/G}$
is smooth of dimension 70 at
![]() $[Q]$
. We have a natural map between Hilbert schemes
$[Q]$
. We have a natural map between Hilbert schemes
where
![]() $H_D$
is the component of the Hilbert scheme of
$H_D$
is the component of the Hilbert scheme of
![]() $G(2,V_8)$
that contains the point
$G(2,V_8)$
that contains the point
![]() $[D]$
defined by D. Both spaces have dimension
$[D]$
defined by D. Both spaces have dimension
![]() $70$
and are smooth, respectively, at
$70$
and are smooth, respectively, at
![]() $[Q]$
and
$[Q]$
and
![]() $[D]$
by Corollary 5.12. In order to show that
$[D]$
by Corollary 5.12. In order to show that
![]() $\sigma $
is dominant, it is enough to check that the induced morphism of tangent spaces is dominant. This is true because
$\sigma $
is dominant, it is enough to check that the induced morphism of tangent spaces is dominant. This is true because
![]() $H^0(G,{\mathcal {J}}_{Q/G}(2))$
and
$H^0(G,{\mathcal {J}}_{Q/G}(2))$
and
![]() $H^0({\mathcal {N}}_{D/G})$
are both dominated by
$H^0({\mathcal {N}}_{D/G})$
are both dominated by
![]() $H^0({\mathcal {I}}_D(2))$
, and the morphism from
$H^0({\mathcal {I}}_D(2))$
, and the morphism from
![]() ${\mathcal {I}}_D(2)$
to
${\mathcal {I}}_D(2)$
to
![]() ${\mathcal {N}}_{D/G}$
factorizes through
${\mathcal {N}}_{D/G}$
factorizes through
![]() ${\mathcal {J}}_{Q/G}(2)$
. This concludes the proof.
${\mathcal {J}}_{Q/G}(2)$
. This concludes the proof.
5.3 Grassmannian self-duality
Exactly as we constructed the singular quadric hypersurface
![]() $D_{Z_1}(v)\subset G(2,V_8)$
, there is another hypersurface
$D_{Z_1}(v)\subset G(2,V_8)$
, there is another hypersurface
![]() $D_{Z_1}(v^\vee )\subset G(2,V_8^\vee )=G(6,V_8)$
. Because of Proposition 3.5, these two hypersurfaces are projectively isomorphic since they are constructed from lines contained in isomorphic Coble quartics. But one should also expect some projective duality statement analogous to Theorem 3.4. Of course, we cannot refer to classical projective duality since we want to consider
$D_{Z_1}(v^\vee )\subset G(2,V_8^\vee )=G(6,V_8)$
. Because of Proposition 3.5, these two hypersurfaces are projectively isomorphic since they are constructed from lines contained in isomorphic Coble quartics. But one should also expect some projective duality statement analogous to Theorem 3.4. Of course, we cannot refer to classical projective duality since we want to consider
![]() $D_{Z_1}(v)$
and
$D_{Z_1}(v)$
and
![]() $D_{Z_1}(v^\vee )$
really as hypersurfaces in Grassmannians, not as subvarieties of the ambient projective spaces. It turns out that a version of projective duality in this setting (and for certain other ambient varieties than Grassmannians) was once proposed in [Reference ChaputCha07] (that remained unpublished). We will refer to it as Grassmannian duality.
$D_{Z_1}(v^\vee )$
really as hypersurfaces in Grassmannians, not as subvarieties of the ambient projective spaces. It turns out that a version of projective duality in this setting (and for certain other ambient varieties than Grassmannians) was once proposed in [Reference ChaputCha07] (that remained unpublished). We will refer to it as Grassmannian duality.
The idea is the following. Consider, say, a hypersurface H in
![]() $G(2,V_8)$
(or any Grassmannian, but let us restrict to the case we are interested in). At a smooth point
$G(2,V_8)$
(or any Grassmannian, but let us restrict to the case we are interested in). At a smooth point
![]() $h=[U_2]$
of H, the tangent space to H is a hyperplane in
$h=[U_2]$
of H, the tangent space to H is a hyperplane in
![]() $T_hG(2,V_8)=\operatorname {\mathrm {Hom}}(U_2,V_8/U_2)$
or, equivalently, a line in the dual space
$T_hG(2,V_8)=\operatorname {\mathrm {Hom}}(U_2,V_8/U_2)$
or, equivalently, a line in the dual space
![]() $\operatorname {\mathrm {Hom}}(V_8/U_2,U_2)$
. If this line is generated by a surjective morphism, the kernel of this morphism is a four-dimensional subspace of
$\operatorname {\mathrm {Hom}}(V_8/U_2,U_2)$
. If this line is generated by a surjective morphism, the kernel of this morphism is a four-dimensional subspace of
![]() $V_8/U_2$
. Equivalently, this defines a six-dimensional space
$V_8/U_2$
. Equivalently, this defines a six-dimensional space
![]() $U_6$
such that
$U_6$
such that
![]() $U_2\subset U_6\subset V_8$
. We get in this way a rational map from H to
$U_2\subset U_6\subset V_8$
. We get in this way a rational map from H to
![]() $G(6,V_8)$
, and we can define the Grassmannian dual
$G(6,V_8)$
, and we can define the Grassmannian dual
![]() $H^\vee $
as the image of this rational map. For more details, see [Reference ChaputCha07, section 1.6]. Chaput has a remarkable biduality theorem generalizing the classical statement, according to which duality for subvarieties of Grassmannians is an involution [Reference ChaputCha07, Theorem 2.1].
$H^\vee $
as the image of this rational map. For more details, see [Reference ChaputCha07, section 1.6]. Chaput has a remarkable biduality theorem generalizing the classical statement, according to which duality for subvarieties of Grassmannians is an involution [Reference ChaputCha07, Theorem 2.1].
So this Grassmannian duality is perfectly natural, and we have:
Theorem 5.15.
![]() $D_{Z_1}(v)\simeq D_{Z_1}(v^\vee )$
is Grassmannian self-dual.
$D_{Z_1}(v)\simeq D_{Z_1}(v^\vee )$
is Grassmannian self-dual.
Proof. Suppose that
![]() $U_2$
belongs to
$U_2$
belongs to
![]() $D_{Z_1}(v)$
. By definition, this means that there exists
$D_{Z_1}(v)$
. By definition, this means that there exists
![]() $U_4\supset U_2$
(unique in general) such that
$U_4\supset U_2$
(unique in general) such that
If we mod out by
![]() $ \wedge ^2U_4$
, we get a tensor in
$ \wedge ^2U_4$
, we get a tensor in
![]() $U_2\otimes \wedge ^3(V_8/U_4)\simeq U_2\otimes (V_8/U_4)^\vee $
, that is, a morphism from
$U_2\otimes \wedge ^3(V_8/U_4)\simeq U_2\otimes (V_8/U_4)^\vee $
, that is, a morphism from
![]() $V_8/U_4$
to
$V_8/U_4$
to
![]() $U_2$
. Generically, this morphism has full rank, and its kernel defines some
$U_2$
. Generically, this morphism has full rank, and its kernel defines some
![]() $U_6\supset U_4$
. So we get a flag
$U_6\supset U_4$
. So we get a flag
![]() $(U_2\subset U_4\subset U_6)$
such that
$(U_2\subset U_4\subset U_6)$
such that
Lemma 5.16.
![]() $U_6$
defines a point of
$U_6$
defines a point of
![]() $D_{Z_1}(v^\vee )$
.
$D_{Z_1}(v^\vee )$
.
Proof. Using adapted basis, one checks that condition (5.3) implies that
In particular,
![]() $v^\vee $
mod
$v^\vee $
mod
![]() $U_6^\perp $
has rank at most four.
$U_6^\perp $
has rank at most four.
Lemma 5.17.
![]() $U_6$
defines a point of
$U_6$
defines a point of
![]() $D_{Z_1}(v)^\vee $
.
$D_{Z_1}(v)^\vee $
.
Proof. Using a basis of
![]() $V_8$
adapted to the flag
$V_8$
adapted to the flag
![]() $(U_2\subset U_4\subset U_6)$
, we can rewrite relation (5.3) in the form
$(U_2\subset U_4\subset U_6)$
, we can rewrite relation (5.3) in the form
where
![]() $U_2=\langle e_1,e_2\rangle $
and
$U_2=\langle e_1,e_2\rangle $
and
![]() $U_6=\langle e_1,\ldots ,e_6\rangle $
. We can describe infinitesimal deformations of
$U_6=\langle e_1,\ldots ,e_6\rangle $
. We can describe infinitesimal deformations of
![]() $U_2$
by some infinitesimal deformations of the vectors in the adapted basis, say
$U_2$
by some infinitesimal deformations of the vectors in the adapted basis, say
![]() $e_i\mapsto e_i+\epsilon \delta _i$
, and we must keep a similar relation. Modding out by
$e_i\mapsto e_i+\epsilon \delta _i$
, and we must keep a similar relation. Modding out by
![]() $U_4$
, we only remain with the relation
$U_4$
, we only remain with the relation
which we can simply rewrite as
![]() $\delta _{18}=\delta _{27}$
. This relation describes the tangent hyperplane to
$\delta _{18}=\delta _{27}$
. This relation describes the tangent hyperplane to
![]() $D_{Z_1}(v)$
at
$D_{Z_1}(v)$
at
![]() $U_2$
, as a hyperplane in
$U_2$
, as a hyperplane in
![]() $\operatorname {\mathrm {Hom}}(U_2,V_8/U_2)$
, orthogonal to the morphism
$\operatorname {\mathrm {Hom}}(U_2,V_8/U_2)$
, orthogonal to the morphism
![]() $e_8^*\otimes e_1-e_7^*\otimes e_2$
. The kernel of this morphism is
$e_8^*\otimes e_1-e_7^*\otimes e_2$
. The kernel of this morphism is
![]() $U_6/U_2$
, and we are done.
$U_6/U_2$
, and we are done.
These two lemmas together imply that
![]() $D_{Z_1}(v^\vee )$
coincides with the Grassmannian dual to
$D_{Z_1}(v^\vee )$
coincides with the Grassmannian dual to
![]() $D_{Z_1}(v)$
. The proof of the theorem is complete.
$D_{Z_1}(v)$
. The proof of the theorem is complete.
Note that we can resolve the singularities of
![]() $D_{Z_1}(v)$
by considering flags
$D_{Z_1}(v)$
by considering flags
![]() $(U_2\subset U_4)$
as before, which gives a subvariety
$(U_2\subset U_4)$
as before, which gives a subvariety
![]() $\tilde {D}_{Z_1}(v)\subset Fl(2,4,V_8)$
. By considering the flags
$\tilde {D}_{Z_1}(v)\subset Fl(2,4,V_8)$
. By considering the flags
![]() $(U_2\subset U_4\subset U_6)$
as in the proof of the previous statement, we obtain a subvariety
$(U_2\subset U_4\subset U_6)$
as in the proof of the previous statement, we obtain a subvariety
![]() $D_{Z_1}(v,v^\vee )\subset Fl(2,4,6,V_8)$
that resolves simultaneously the singularities of
$D_{Z_1}(v,v^\vee )\subset Fl(2,4,6,V_8)$
that resolves simultaneously the singularities of
![]() $D_{Z_1}(v)$
and
$D_{Z_1}(v)$
and
![]() $D_{Z_1}(v^\vee )$
. As for the Coble quartic, we get a diagram
$D_{Z_1}(v^\vee )$
. As for the Coble quartic, we get a diagram

The birational map
![]() $\tilde {D}_{Z_1}(v)\dashrightarrow \tilde {D}_{Z_1}(v^\vee )$
must be a flop, resolved by two symmetric contractions.
$\tilde {D}_{Z_1}(v)\dashrightarrow \tilde {D}_{Z_1}(v^\vee )$
must be a flop, resolved by two symmetric contractions.
Question. Is there a modular interpretation of
![]() $D_{Z_1}(v)$
as for the Coble quartic and of this diagram?
$D_{Z_1}(v)$
as for the Coble quartic and of this diagram?
Remark 5.18. Our framework excludes the hyperelliptic genus three curves, but there should be a very similar story for these curves. In fact, consider a general pencil of quadrics in
![]() ${\mathbb {P}}^7={\mathbb {P}}(V_8)$
. The eight singular members of the pencil define such a hyperelliptic curve C. It is a special case of the results of [Reference Desale and RamananDR77] that the moduli space
${\mathbb {P}}^7={\mathbb {P}}(V_8)$
. The eight singular members of the pencil define such a hyperelliptic curve C. It is a special case of the results of [Reference Desale and RamananDR77] that the moduli space
![]() $\operatorname {\mathrm {SU}}_C(2,L)$
, for L of odd degree, can be identified with the biorthogonal Grassmannian, that is the subvariety of
$\operatorname {\mathrm {SU}}_C(2,L)$
, for L of odd degree, can be identified with the biorthogonal Grassmannian, that is the subvariety of
![]() $G(2,V_8)$
parametrizing subspaces that are isotropic with respect to any quadric in the pencil. On the other hand, the even moduli space
$G(2,V_8)$
parametrizing subspaces that are isotropic with respect to any quadric in the pencil. On the other hand, the even moduli space
![]() $\operatorname {\mathrm {SU}}_C(2)$
is a double cover of the six-dimensional quadric
$\operatorname {\mathrm {SU}}_C(2)$
is a double cover of the six-dimensional quadric
![]() ${\mathbb {Q}}^6$
, branched over a quartic section which is singular along a copy of the Kummer threefold of the curve. One expects this quartic to be of Coble type in the sense that it should be the unique quartic section of
${\mathbb {Q}}^6$
, branched over a quartic section which is singular along a copy of the Kummer threefold of the curve. One expects this quartic to be of Coble type in the sense that it should be the unique quartic section of
![]() ${\mathbb {Q}}^6$
that is singular along the Kummer of C. It should also be self-dual in a suitable sense, and the whole story should be related to the representation theory of
${\mathbb {Q}}^6$
that is singular along the Kummer of C. It should also be self-dual in a suitable sense, and the whole story should be related to the representation theory of
![]() $\mathrm {Spin}_8$
. We plan to explore these topics in future work.
$\mathrm {Spin}_8$
. We plan to explore these topics in future work.
Acknowledgements
We warmly thank Christian Pauly, Sasha Kuznetsov and Jerzy Weyman for useful discussions. Special thanks also to Shigeru Mukai and Akihiro Kanemitsu for sharing the results of [Reference Kanemitsu and MukaiKM23].
Competing interest
The authors have no competing interest to declare.
Funding statement
All authors were partially supported by FanoHK ANR-20-CE40-0023. D.F. and V.B. were partially supported by SupToPhAG/EIPHI ANR-17-EURE-0002, Région Bourgogne-Franche-Comté, Feder Bourgogne and Bridges ANR-21-CE40-0017.