DECOMPOSITION OF THE JACOBIAN OF SOME TWISTS OF A GENUS $2$ CURVE

Abstract

Cardona and Lario [‘Twists of the genus 2 curve 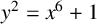$y^2 = x^6+1$’, J. Number Theory 209 (2020), 195–211] gave a complete classification of the twists of the curve 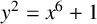$y^2 = x^6+1$. In this paper, we study the twists of the curve whose automorphism group is defined over a biquadratic extension of the rationals. If the twists are of type B or C in the Cardona–Lario classification, we find a pair of elliptic curves whose product is isogenous with the Jacobian of the twist.

1. Introduction

Given a curve defined over a field, its twist is another curve that becomes isomorphic to the given curve over the algebraic closure. For example, an elliptic curve over a field k whose defining equation is $ y^2 = f(x) $ is isomorphic to a curve defined by the equation $Dy^2 = f(x)$ over $k(\sqrt {D})$ . This is called a quadratic twist of the elliptic curve. In the case of a generic elliptic curve (that is, its j-invariant is not equal to $0, 1728$ ), every twist is a quadratic twist.

For a curve of genus $\geq 2$ , the notion of the quadratic twist of an elliptic curve can be generalised to the hyperelliptic twist. A hyperelliptic twist of a curve $y^2 = f(x)$ has an affine equation $Dy^2 = f(x)$ for some $D \in k^\times /(k^\times )^2$ . We denote by $X^{(D)}$ the hyperelliptic twist of the curve X. Again, X and $X^{(D)}$ become isomorphic over $k(\sqrt {D})$ . Since the automorphism group of a hyperelliptic curve can be larger than that of an elliptic curve, there are also nonhyperelliptic twists in the genus $2$ case. The automorphism group of the genus $2$ curve is one of

$$ \begin{align*} C_2, \quad V_4, \quad D_8, \quad D_{12}, \quad C_{10}, \quad \widetilde{S_4}, \quad 2D_{12}, \end{align*} $$

where $C_n$ is the cyclic group of order n, $D_n$ is the dihedral group of order n, $V_4$ is the Klein $4$ group, $\widetilde {S_4}\cong \operatorname {\mathrm {GL}}_2(\mathbb {F}_3)$ is a double cover of the symmetric group $S_4$ and $2D_{12}$ is a double cover of $D_{12}$ . The classification of isomorphism classes of curves whose automorphism group is $D_8, D_{12}, \widetilde {S}_4$ and $ 2D_{12}$ is studied by Cardona and his collaborators [1–3].

We consider twists of a genus $2$ curve defined over $\mathbb {Q}$ whose automorphism group is isomorphic to $2D_{12}$ . There is only one such $\overline {\mathbb {Q}}$ -isomorphism class, and a representative is given by the equation $y^2 = x^6+1$ . From [2], the classification of the $\mathbb {Q}$ -isomorphism class of the curve $y^2 = x^6+1$ is given by two steps: first, the classification of the possible Galois module structures on $2D_{12}$ ; second, the classification of the curves whose automorphism group has the given Galois module structure.

For nonhyperelliptic twists, we consider twists whose automorphism group has the Galois module structure defined over a biquadratic extension of $\mathbb {Q}$ . From [2, Section 7]:

1. (i) the biquadratic extension of $\mathbb {Q}$ should have $\mathbb {Q}(\sqrt {-3})$ as a subfield;

2. (ii) let $\mathbb {Q}(\sqrt {d}, \sqrt {-3})$ be the biquadratic extension. Then, there are six types $A, B, \ldots , E, G$ (see (2.2) and the discussion following Definition 2.5) so that any twist whose automorphism group is $\mathbb {Q}(\sqrt {d}, \sqrt {-3})$ is one of $V_4^A, \ldots , V_4^E, V_4^G$ (type F does not appear when the base field is $\mathbb {Q}$ );

3. (iii) if two curves of the same type also have the same biquadratic extension, then they are hyperelliptic twists of each other.

In short, the $\mathbb {Q}$ -isomorphism class of a twist is determined by three parameters: a type in $\{ A, B, \ldots , E, G \}$ , the defining field of the automorphism group $\mathbb {Q}(\sqrt {d}, \sqrt {-3})$ and a hyperelliptic twist.

Types B and C are relatively simple because, in this case, the parameter d has no additional restrictions. We give a concrete decomposition of twists of these types.

Theorem 1.1. Let $X/\mathbb {Q}$ be a twist of type $V_4^B$ or $V_4^C$ . Then, there are $d, D \in \mathbb {Q}^\times /(\mathbb {Q}^\times )^2$ such that the Jacobian of X is isogenous to $E_0^{(-D)}\times E_0^{(-dD)}$ or $E_0^{(D)} \times E_0^{(dD)}$ where $E_0^m$ for $m\in\mathbb{Q}^\times$ is the elliptic curve given by $my^2=x^3+1$ .

The main tool is a computation of L-factors of twists of $y^2 = x^6+1$ which is done by Fité and Sutherland [5]. In Section 2, we recall previous results on the twists of the curve $y^2 = x^6+1$ . In Section 3, we study some properties of our twist families. In Section 4, we give a proof of the main theorem.

2. Preliminaries

In this section, we recall the classification [2] of twists of the curve $y^2 = x^6+1$ , with an emphasis on the biquadratic case, and some previous results of [5].

For a curve X over a field k, we say that another curve $X'$ over k is a twist of X if $X'$ becomes isomorphic to X over the algebraic closure $\overline {k}$ of k. The set of k-isomorphism classes of X is denoted by $\operatorname {\mathrm {Twist}}(X/k)$ . In what follows, we abbreviate $\operatorname {\mathrm {Aut}}_{\overline {k}}(X):=\operatorname {\mathrm {Aut}}_{\overline {k}}(X_{\overline {k}})$ . It is well known (see, for example, [6, Theorem X.2.2]) that there is a canonical bijection

From now on, let $X_0/\mathbb {Q}$ denote the genus $2$ curve defined by the equation $ y^2 = x^6+1$ . We recall that $\operatorname {\mathrm {Aut}}_{\overline {\mathbb {Q}}}(X_0)$ is isomorphic to $2D_{12}$ as an abstract group. Following [2], we use a group presentation

$$ \begin{align*} A := \langle{U, V, -1 : (-1)^2 = U^2 = V^6 = 1, (UV)^2 = (VU)^2 = -1, -1 \in Z(A)}\rangle, \end{align*} $$

which is isomorphic to $2D_{12}$ as a group. Its automorphism group is isomorphic to $C_2 \times D_{12}$ . We specify the elements of $\operatorname {\mathrm {Aut}}(A)$ as follows: $\iota , \jmath $ are two central involutions, s the noncentral involution, t the automorphism of order $3$ with relation $ts = st^2$ (see [2, Section 3]).

Suppose that X is a twist of $X_0$ . Then $\operatorname {\mathrm {Aut}}_{\overline {\mathbb {Q}}}(X)$ is also isomorphic to $2D_{12}$ as a group, so we first consider possible $G_{\mathbb {Q}}$ -module structures on A. Since giving a $G_{\mathbb {Q}}$ -structure on A is equivalent to giving a morphism $G_{\mathbb {Q}} \to \operatorname {\mathrm {Aut}}(A)$ , we concentrate on the latter. Let K be the field of definition of the $G_{\mathbb {Q}}$ -structure on A so that

for a certain subgroup H in $C_2 \times D_{12}$ . Then, a $G_{\mathbb {Q}}$ -structure on A is determined by $K, H$ and a group isomorphism between H and $\operatorname {\mathrm {Gal}}(K/\mathbb {Q})$ . To describe the extension $K/\mathbb {Q}$ , we need to define some subfields of K. We consider subgroups of H, which are

$$ \begin{align*} H \cap \langle \iota, s, t \rangle, \quad H \cap \langle \iota, \jmath, t \rangle, \quad H \cap \langle \jmath, s, t \rangle. \end{align*} $$

They are index $1$ or $2$ , so induce a quadratic or trivial extension of $\mathbb {Q}$ . We denote them by

(2.1) $$ \begin{align} K_1 = \mathbb{Q}(\sqrt{u}), \quad K_2 = \mathbb{Q}(\sqrt{v}), \quad K_3 = \mathbb{Q}(\sqrt{v'}). \end{align} $$

In other words, we define $u, v, v' \in \mathbb {Q}^\times /(\mathbb {Q}^\times )^2$ determined by a $G_{\mathbb {Q}}$ -action on A.

Since we only consider a biquadratic extension $K/\mathbb {Q}$ , the subgroup H is isomorphic to $V_4$ . We recall that there are seven subgroups of $C_2 \times 2D_{12}$ isomorphic to $V_4$ :

(2.2) $$ \begin{align} \langle \iota, \jmath \rangle, \quad \langle \iota, s \rangle, \quad \langle \jmath, s \rangle \quad \langle \iota\jmath, s \rangle, \quad \langle \iota, \jmath s \rangle, \quad \langle \jmath, \iota s \rangle, \quad \langle \iota s, \jmath s \rangle. \end{align} $$

They correspond to the type $V_4^{\bullet }$ for $\bullet \in \{ A, \ldots , G \}$ (see [2, Table 3]). To describe a specific isomorphism (in $6=|\operatorname {\mathrm {Aut}}(V_4)|$ -choices) between $\operatorname {\mathrm {Gal}}(K/\mathbb {Q})$ and H, it suffices to give quadratic subfields of K corresponding to the generators of H. For instance, we consider $V_4^A$ , which corresponds to $\langle \iota , \jmath \rangle \leq \operatorname {\mathrm {Aut}}(A)$ . Then an isomorphism between $\operatorname {\mathrm {Gal}}(K/\mathbb {Q})$ and $\langle \iota , \jmath \rangle $ can be described by $K^{\langle \iota \rangle }, K^{\langle \jmath \rangle }$ , which are quadratic extensions of $\mathbb {Q}$ .

We next describe a constraint for our $G_{\mathbb {Q}}$ -module A.

Lemma 2.1 [4, Ch. 1].

If $X/k$ is of genus $2$ , then there is an injection $\operatorname {\mathrm {Aut}}_{\overline {k}}(X)\hookrightarrow \operatorname {\mathrm {GL}}_2(\overline {k})$ of $G_k$ -groups.

By Lemma 2.1, we only consider $G_{\mathbb {Q}}$ -subgroups of $\operatorname {\mathrm {GL}}_2(\overline {\mathbb {Q}})$ whose underlying groups are isomorphic to $2D_{12}$ . To get a more explicit condition using the parameters in (2.1), we introduce the following definition.

Definition 2.2. If $u,v \in \mathbb {Q}$ satisfy $(u, -3v) = 1 \in \mathrm {Br}_2(\mathbb {Q})$ , then by [2, Remark 1],

$$ \begin{align*} x^2 + \frac{3}{v}y^2 = u \end{align*} $$

has solutions in $\mathbb {Q}^\times $ . Once solutions $\alpha ,\beta \in \mathbb {Q}^\times $ are chosen, we define constants

$$ \begin{align*} z = 4 \alpha^3 - 3u\alpha, \quad s = \frac{u^2 - 2\alpha^2u + \alpha z}{3\beta}. \end{align*} $$

Theorem 2.3 [2, Theorem 2].

Let A be a $G_{\mathbb {Q}}$ -group with underlying group isomorphic to $2D_{12}$ , K the defining field of the $G_{\mathbb {Q}}$ -module structure on A which is a biquadratic extension of $\mathbb {Q}$ , $K_i$ the subfield of K defined by (2.1) for $i=1, 2, 3$ , and $u, v, v'$ elements in $\mathbb {Q}^\times /(\mathbb {Q}^\times )^2$ also defined by (2.1). Then A can be embedded in $\operatorname {\mathrm {GL}}_2(\overline {\mathbb {Q}})$ if and only if $(u, -3v) = 1 \in \mathrm {Br}_2(\mathbb {Q})$ and $v' \equiv -3v \pmod {\mathbb {Q}^{\times 2}}$ . In this case, $A \cong \langle U, V, -1 \rangle $ , where

$$ \begin{align*} U = \frac{1}{\sqrt{u}} \begin{pmatrix} \alpha & \beta \\ {3\beta}/{v} & -\alpha \end{pmatrix}, \quad V = \frac{\sqrt{-3}}{2} \begin{pmatrix} 1 & {\sqrt{v}}/{3} \\ -{1}/{\sqrt{v}} & 1 \end{pmatrix}, \quad -1 = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \end{align*} $$

and the field of definition is $K = \mathbb {Q}(\sqrt {u}, \sqrt {v}, \sqrt {-3})$ .

In particular, the biquadratic extension K should include $\mathbb {Q}(\sqrt {-3})$ . Using these parameters, we can give a concrete defining equation of a twist.

Theorem 2.4 [2, Propositions 3 and 4].

For a $G_{\mathbb {Q}}$ -group A embedded in $\operatorname {\mathrm {GL}}_2(\overline {\mathbb {Q}})$ and isomorphic to $2D_{12}$ as an abstract group, there is a twist with defining equation

$$ \begin{align*} y^2 = 27zx^6 - 162svx^5 - 135vzx^4 + 180sv^2x^3 + 45v^2zx^2 - 18sv^3x - v^3z, \end{align*} $$

whose automorphism group is $G_{\mathbb {Q}}$ -isomorphic to A. Furthermore, two twists, whose automorphism group is $G_{\mathbb {Q}}$ -isomorphic to A, differ by a hyperelliptic twist.

Together with a classification of hyperelliptic twists [2, Proposition 6], we obtain the complete classification of twists of $X_0$ , whose automorphism group is defined over K.

Definition 2.5. A twist $X/k$ of $X_0/k$ is said to be of biquadratic type if the defining field of $\operatorname {\mathrm {Aut}}_{\overline {k}}(X)$ is a biquadratic extension of k.

We note that this terminology works well with [2] since the twists of biquadratic type are twists of type $V_4^\bullet $ for $\bullet \in \{ A, B, \ldots , G \}$ in [2].

We also have a complete classification of twists of biquadratic type. The classification is given in two steps. First, we specify the $G_{\mathbb {Q}}$ -module structure on $2D_{12}$ by describing the quadratic subfields (2.1). After that, Theorem 2.4 gives a twist whose automorphism group is isomorphic to a given $G_{\mathbb {Q}}$ -module, and any other twists with the same conditions are the hyperelliptic twists of the given twist. By [2, Section 7], we give $K_i$ (and hence, a $G_{\mathbb {Q}}$ -module structure on $2D_{12}$ ) for each type $V_4^\bullet $ , $\bullet \in \{ A, B, \ldots , G \}$ . Here is a summary of [2, Section 7]:

• • if $(d, -3) = 1 \in \operatorname {\mathrm {Br}}_2(\mathbb {Q})$ , there is the twist of type $V_4^A$ with $u = d, v=1$ ;

• • there is the twist of type $V_4^B$ with $u = 1, v=d$ ;

• • there is the twist of type $V_4^C$ with $u = d, v=-3$ ;

• • if $(d, d) = 1 \in \operatorname {\mathrm {Br}}_2(\mathbb {Q})$ , there is the twist of type $V_4^D$ with $u = d, v=-3u$ ;

• • if $(d, -3d) = 1 \in \operatorname {\mathrm {Br}}_2(\mathbb {Q})$ , there is the twist of type $V_4^E$ with $u = d, v=d$ ;

• • there is no twist of the form $V_4^F$ ;

• • if $(-3d, -3) = 1 \in \operatorname {\mathrm {Br}}_2(\mathbb {Q})$ , there is the twist of type $V_4^G$ with $u = -3, v=d$ .

We recall that $K_1 = \mathbb {Q}(\sqrt {u}), K_2 = \mathbb {Q}(\sqrt {v})$ and $K_3 = \mathbb {Q}(\sqrt {v'})$ .

Remark 2.6. We emphasise that the word ‘biquadratic’ in ‘biquadratic type’ is not the same as in the ‘quadratic’ twists of elliptic curves. In the case of elliptic curves, the only twists come from a character of order $2, 3, 4, 6$ (see [6, Example X.2.4]). They are usually called quadratic, cubic, quartic and sextic twists of elliptic curves, referring to the minimal field defining $\phi : C^{\prime }_{\overline {k}} \to C_{\overline {k}}$ . For example, the map $ \phi (x, y) := (\kern-1pt\sqrt [3]{A^2}x, Ay) $ that gives a $\overline {\mathbb {Q}}$ -isomorphism between $E_A : y^2 = x^3 + A^2$ and $E_1 : y^2 = x^3 + 1$ is defined over $\mathbb {Q}(\kern-1.5pt\sqrt [3]{A})$ . This is a cubic extension of $\mathbb {Q}$ when A is a cube-free integer, so it is called a cubic twist.

The following definitions come from [5].

Definition 2.7. Let $X'/k$ be a twist of X and let $\phi : X^{\prime }_{\overline {k}} \to X_{\overline {k}}$ be a $\overline {k}$ -isomorphism. We use the following notation:

1. (1) $L_\phi $ is the defining field of the isomorphism $\phi $ ;

2. (2) K is the defining field of $\operatorname {\mathrm {Aut}}_{\overline {k}}(X')$ ;

3. (3) L is the compositum of the defining fields of $\overline {k}$ -isomorphisms from $X'$ to X.

We note that $K, L$ depend on $X'$ and $L_\phi $ further depends on the choice of $\phi $ . In the above example concerning $E_A$ and $E_1$ , there are other choices of $\phi $ making $L_0 = \mathbb {Q}(\zeta _3\!\sqrt [3]{A})$ or $\mathbb {Q}(\zeta _3^2\sqrt [3]{A})$ . However, $K = \mathbb {Q}(\zeta _3)$ and $L = KL_0 = \mathbb {Q}(\zeta _3, \sqrt [3]{A})$ for any choice of $\phi $ . Hence a quadratic, cubic, quartic and sextic twist on an elliptic curve indicates the degree of $L_{\phi }$ , and the word ‘biquadratic’ in the phrase ‘twists of biquadratic type’ means the extension of $K/\mathbb {Q}$ .

Lemma 2.8 [5, Lemmas 4.2 and 4.3 and Proposition 4.6].

The following statements hold for a twist X of $X_0$ .

1. (1) K is the defining field of endomorphisms of $\operatorname {\mathrm {Jac}}(X_{\overline {\mathbb {Q}}})$ .

2. (2) The following extensions of K coincide:

   1. (a) L as in Definition 2.7;

   2. (b) the compositum of K and $L_{\phi }$ for any $\overline {\mathbb {Q}}$ -isomorphism $\phi : X \to X_0$ ;

   3. (c) the defining field of all homomorphisms from $\operatorname {\mathrm {Jac}}(X_0)_{\overline {\mathbb {Q}}}$ to $\operatorname {\mathrm {Jac}}(X)_{\overline {\mathbb {Q}}}$ .

3. (3) $[L : K] \leq 2$ .

3. Twist families of biquadratic type

In this section, we give a concrete parametrisation of twist types $V_4^B$ and $V_4^C$ . Then we prove that L is a subfield of $K(i)$ in both cases.

3.1. Type C

For $V_4^C$ , we have $u = d$ , $v = -3$ . According to Definition 2.2, $ x^2-y^2=d$ has solutions in $\mathbb {Q}^\times $ . We choose (with $d\neq \pm 1$ )

$$ \begin{align*} \alpha=\frac{d+1}{2},\quad\beta=\frac{d-1}{2} \end{align*} $$

so that the defining equation in Theorem 2.4 becomes $y^2 = f_d(x)$ , where

(3.1) $$ \begin{align} f_d(x) =54(d^3 + 1) x^6 & + 324( d^3 - 1) x^5 + 810(d^3 + 1) x^4 + 1080(d^3 - 1) x^3 \notag \\ &+ 810(d^3 + 1) x^2 + 324(d^3 - 1) x + 54( d^3 + 1). \end{align} $$

Let $X_d^C$ be the twist defined by the equation $y^2 = f_d(x)$ . Then, the field K of $X_d^C$ is $\mathbb {Q}(\sqrt {d}, \sqrt {-3})$ since $u = d$ and $v = -3$ . Also, by Theorem 2.4, $\{X_d^C\}$ is the one-parameter twist such that:

• • none of the elements is a hyperelliptic twist of another element;

• • every twist of type $V_4^C$ is a hyperelliptic twist of $\{X_d^C\}$ .

Hence, one can say that this family is a family of twists orthogonal to the hyperelliptic twists. This is the first motivation of our paper.

The polynomial $f_d(x)$ in (3.1) factors into

$$ \begin{align*} &54( (d+1)x^2 + 2(d-1)x + d + 1) \\ &\quad \times ((d^2-d+1) x^4 + 4 (d^2 - 1) x^3 + (6 d^2 + 2 d + 6) x^2 + 4 (d^2 - 1) x + d^2 - d + 1). \end{align*} $$

We further suppose that $d \neq 0$ and set $\delta _C = (1+\sqrt {-3})/2d$ . Then the zeros are

$$ \begin{align*} \frac{-(d-1) \pm 2\sqrt{-d}}{d+1}, \quad -\frac{1-\sqrt{\delta_C}}{1+\sqrt{\delta_C}}, \quad -\frac{1+\sqrt{\delta_C}}{1-\sqrt{\delta_C}}, \quad -\frac{1-\sqrt{\overline{\delta_C}}}{1+\sqrt{\overline{\delta_C}}}, \quad -\frac{1+\sqrt{\overline{\delta_C}}}{1-\sqrt{\overline{\delta_C}}}. \end{align*} $$

Lemma 3.1. Let d be a nonsquare rational number and let $L_d$ be the splitting field of the quartic factor of $f_d(x)$ , that is,

$$ \begin{align*} (d^2-d+1) x^4 + 4 (d^2 - 1) x^3 + (6 d^2 + 2 d + 6) x^2 + 4 (d^2 - 1) x + d^2 - d + 1. \end{align*} $$

Then, $L_d$ is a biquadratic extension of $\mathbb {Q}$ satisfying $L_d \subset K(i)$ when $d \neq \pm 1, \pm 3$ .

Proof. One can easily compute that

$$ \begin{align*} \sqrt{\delta_C \overline{\delta_C}} = \frac{1}{d} \in \mathbb{Q}, \quad \bigg(\sqrt{\delta_C} + \sqrt{\overline{\delta_C}}\bigg)^2 = \delta_C + \overline{\delta_C} + 2\sqrt{\delta_C\overline{\delta_C}} \in \mathbb{Q} \end{align*} $$

and

$$ \begin{align*} \frac{\displaystyle\frac{1 - \sqrt{\delta_C}}{1 + \sqrt{\delta_C}} -1 }{\displaystyle\frac{1 - \sqrt{\delta_C}}{1 + \sqrt{\delta_C}} +1} = -\sqrt{\delta_C}. \end{align*} $$

Hence,

$$ \begin{align*} L_d = \mathbb{Q} \bigg({\frac{1-\sqrt{\delta_C}}{1+\sqrt{\delta_C}}, \frac{1-\sqrt{\overline{\delta_C}}}{1+\sqrt{\overline{\delta_C}}}}\bigg) = \mathbb{Q} \bigg(\frac{1-\sqrt{\delta_C}}{1+\sqrt{\delta_C}}\bigg) = \mathbb{Q}(\sqrt{\delta_C}). \end{align*} $$

We note that each root of the quartic part of $f_d$ is not in $\mathbb {Q}$ because

$$ \begin{align*} \frac{1-\sqrt{\delta_C}}{1 + \sqrt{\delta_C}} = -1 + \frac{2}{1 + \sqrt{\delta_C}} \not\in \mathbb{Q}, \quad \sqrt{\delta_C} \not\in \mathbb{Q}, \quad \delta_C \not\in\mathbb{Q}. \end{align*} $$

Hence, if the quartic part is reducible, then it is a product of two quadratics over $\mathbb {Q}$ . So in this case, $L_d \supset \mathbb {Q}(\sqrt {-3})$ is a biquadratic extension of $\mathbb {Q}$ .

Otherwise, the discriminant of the quartic is ${2^{16}\cdot 3^2 \cdot d^6}/{(d^2-d+1)^6}$ and the resolvent of the quartic is

$$ \begin{align*} &x^3 + \frac{-6d^2 - 2d - 6}{d^2 - d + 1} \cdot x^2 + \frac{12d^4 + 8d^3 - 44d^2 + 8d + 12}{d^4 - 2d^3 + 3d^2 - 2d + 1} \cdot x \\ &\qquad+ \frac{-8d^4 - 16d^3 + 104d^2 - 16d - 8}{d^4 - 2d^3 + 3d^2 - 2d + 1}\\ &\quad=\bigg(x + \frac{-2d^2 - 10d - 2}{d^2 - d + 1}\bigg) \cdot (x - 2) \cdot \bigg(x + \frac{-2d^2 + 6d - 2}{d^2 - d + 1}\bigg). \end{align*} $$

Hence, $L_d$ is again a biquadratic extension of $\mathbb {Q}$ , since the discriminant is square and the resolvent is reducible.

We can say that $L_d = \mathbb {Q}(\sqrt {-3}, \sqrt {t})$ for some $t \in \mathbb {Q}^\times /(\mathbb {Q}^\times )^2$ since $\sqrt {-3} \in L_d$ . Then, $K(\sqrt {\delta _C}) = \mathbb {Q}(\sqrt {-3}, \sqrt {d}, \sqrt {t})$ should be a triquadratic extension containing $\mathbb {Q}(\sqrt {\delta _C})$ or $\mathbb {Q}(\sqrt {\delta _C})$ itself. However,

$$ \begin{align*} \sqrt{d}\sqrt{\delta_C} = \sqrt{ \frac{1 + \sqrt{-3}}{2} } = \frac{i}{\frac{1+\sqrt{-3}}{2}} \in K(\sqrt{\delta_C}), \end{align*} $$

which implies that $i \in K(\sqrt {\delta _C})$ . Hence, when $d \neq \pm 3$ , $K(\sqrt {\delta _C}) = \mathbb {Q}(\sqrt {-3}, i, \sqrt {d} )$ and $\mathbb {Q}(\sqrt {\delta _C}) \subset K(i)$ .

3.2. Type B

For $V_4^B$ , we have $u=1$ and $v=d$ . According to Definition 2.2, $x^2+({3}/{d})y^2=1$ has solutions in $\mathbb {Q}^\times $ . We choose (with $d\neq \pm 3$ )

$$ \begin{align*} \alpha = \frac{d-3}{d+3}, \quad \beta = \frac{2d}{d+3}, \end{align*} $$

so that the defining equation in Theorem 2.4 becomes of the form $y^2 = f_d(x)$ , where

$$ \begin{align*} f_d(x) &= 27 \frac{(d - 3)(d^2 - 42d + 9)}{(d + 3)^3} \bigg( x^2 + \frac{{4d}}{{d - 3}}x - \frac{{1}}{{3}}d \bigg) \\ &\quad \times \bigg( x^4 + \frac{{32d^2 - 96d}}{{d^2 - 42d + 9}}x^3 + \frac{{-\frac{{14}}{{3}}d^3 + 68d^2 - 42d}}{{d^2 - 42d + 9}}x^2 + \frac{{-\frac{{32}}{{3}}d^3 + 32d^2}}{{d^2 - 42d + 9}}x + \frac{{1}}{{9}}d^2 \bigg). \end{align*} $$

As before, we denote by $X_d^B$ the twist $y^2 = f_d(x)$ . Then the family $\{X_d^B\}$ has the same properties as the family $\{X_d^C\}$ discussed in the previous section.

The zeros of the quadratic factors of $f_d$ are

$$ \begin{align*} \frac{-6d \pm (d+3)\sqrt{3d}}{3(d-3)}, \end{align*} $$

and the zeros of the quartic factor are

$$ \begin{align*} -\frac{1}{2}\Bigg({\delta_B \pm \sqrt{\delta_B^2 + \frac{4d}{3}} }\Bigg), \quad -\frac{1}{2}\Bigg({\overline{\delta_B} \pm \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}} }\Bigg), \end{align*} $$

where

$$ \begin{align*} \delta_B := \frac{-16d^2 + 48d + 2(d+3)^2 \sqrt{d}}{d^2-42d+9}, \quad \overline{\delta_B} := \frac{-16d^2 + 48d - 2(d+3)^2 \sqrt{d}}{d^2-42d+9}. \end{align*} $$

The defining fields of zeros of the quadratic and the quartic are

$$ \begin{align*} \mathbb{Q}(\sqrt{3d}), \quad \mathbb{Q}\Bigg(\sqrt{d}, \sqrt{\delta_B^2 + \frac{4d}{3}}, \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}}\Bigg). \end{align*} $$

The latter is denoted by $L_d$ , which is the splitting field of the quartic part of $f_d$ .

Lemma 3.2. In the above settings, $L_d = \mathbb {Q}(\sqrt {d}, \sqrt {3})$ when $d\neq \pm 3$ is a nonsquare rational number.

Proof. The quartic part of $f_d$ is

$$ \begin{align*} &x^4 + \frac{32d^2 - 96d}{d^2 - 42d + 9} x^3 + \frac{-\frac{14}{3}d^3 + 68d^2 - 42d}{d^2 - 42d + 9} x^2 + \frac{-\frac{32}{3}d^3 + 32d^2}{d^2 - 42d + 9} x + \frac{1}{9}d^2. \end{align*} $$

Since

$$ \begin{align*} \sqrt{\delta_B^2 + \frac{4d}{3}} \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}} = \frac{16}{3} \frac{d(d+3)^2}{(d^2 - 42 d + 9)} \in \mathbb{Q}, \end{align*} $$

we have

$$ \begin{align*} L_d = \mathbb{Q}\Bigg(\sqrt{d}, \sqrt{\delta_B^2 + \frac{4d}{3}}, \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}}\Bigg) = \mathbb{Q}\Bigg({\sqrt{\delta_B^2 + \frac{4d}{3}}}\Bigg). \end{align*} $$

However,

$$ \begin{align*} \Bigg({\sqrt{\delta_B^2 + \frac{4d}{3}} + \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}}}\Bigg)^2 &= \delta_B^2 + \overline{\delta_B}^2 +\frac{8d}{3} + \sqrt{\delta_B^2 + \frac{4d}{3}} \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}} \in \mathbb{Q}, \end{align*} $$

which means that

$$ \begin{align*} \mathbb{Q}\Bigg({\sqrt{\delta_B^2 + \frac{4d}{3}} + \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}}}\Bigg) \subset \mathbb{Q} \Bigg({\sqrt{\delta_B^2 + \frac{4d}{3}} }\Bigg) \end{align*} $$

is a quadratic subfield. Since

$$ \begin{align*} \Bigg({\sqrt{\delta_B^2 + \frac{4d}{3}} + \sqrt{\overline{\delta_B}^2 + \frac{4d}{3}}}\Bigg)^2 = \Bigg({\frac{8}{3} \frac{(d-3)(d+3)}{d^2 - 42d + 9}\sqrt{3d}}\Bigg)^2, \end{align*} $$

we can conclude that $L_d \supset \mathbb {Q}(\sqrt {d}, \sqrt {3})$ .

Next, we claim that each zero of the quartic is not rational. Suppose that

$$ \begin{align*} \delta_B\pm\sqrt{\delta_B^2+\frac{4d}{3}}\in\mathbb{Q}. \end{align*} $$

Then there is a rational number a such that

$$ \begin{align*} \sqrt{\delta_B^2+\frac{4d}{3}}=a\mp\frac{2(d+3)^2}{d^2-42d+9}\sqrt{d}. \end{align*} $$

Taking the squares of both sides,

$$ \begin{align*} \frac{16d(d+3)^2(d^2+30d+9)}{3(d^2-42d+9)^2} & \mp\frac{64(d-3)d(d+3)^2}{(d^2-42d+9)^2}\sqrt{d} \\ =a^2+\frac{4d(d+3)^4}{(d^2-42d+9)^2} & \mp\frac{4a(d+3)^2}{(d^2-42d+9)}\sqrt{d}. \end{align*} $$

Comparing the coefficients of $\sqrt {d}$ ,

$$ \begin{align*} a=\frac{16d(d-3)}{d^2-42d+9}. \end{align*} $$

Substituting this yields

$$ \begin{align*} \frac{16d(d+3)^2(d^2+30d+9)}{3(d^2-42d+9)^2}=\frac{16^2d^2(d-3)^2}{(d^2-42d+9)^2}+\frac{4d(d+3)^4}{(d^2-42d+9)^2}. \end{align*} $$

This is equivalent to

$$ \begin{align*} \tfrac{4}{3} (d^2 - 42d + 9)^2 = 0, \end{align*} $$

which does not have a solution in $\mathbb {Q}$ . To deal with the other case:

$$ \begin{align*} \overline{\delta}_B\pm\sqrt{\overline{\delta}_B^2+\frac{4d}{3}}\in\mathbb{Q}, \end{align*} $$

it suffices to replace $\sqrt {d}$ by $-\sqrt {d}$ in the above computation. Therefore, we arrive at the same conclusion. Hence, if the quartic part of f is reducible over $\mathbb {Q}$ , it is a product of two quadratics, which means that $L_d$ is a biquadratic extension of $\mathbb {Q}$ .

Suppose that the quartic part is irreducible over $\mathbb {Q}$ . Its discriminant is

$$ \begin{align*} \frac{2^{16}}{3^4} \frac{d^6 (d + 3)^{12}}{(d^2 - 42d + 9)^{6}}, \end{align*} $$

which is a square, and its resolvent is

$$ \begin{align*} \bigg(x + \frac{\frac{{-2}}{{3}}d^3 - 36d^2 - 6d}{d^2 - 42d + 9} \bigg) \cdot \bigg(x + \frac{{2}}{{3}}d \bigg) \cdot \bigg(x + \frac{\frac{{14}}{{3}}d^3 - 4d^2 + 42d }{d^2 - 42d + 9}\bigg), \end{align*} $$

which is reducible. Hence, $L_d$ is also a biquadratic extension of $\mathbb {Q}$ . Consequently, we have $L_d = \mathbb {Q}(\sqrt {d}, \sqrt {3})$ in both cases.

3.3. Computation of the number field L

Proposition 3.3. Let $X_d : y^2 = f_d(x)$ be a twist of type $V_4^{\bullet }$ with $\bullet \in \{ A, B, \ldots , G \}$ and $K = \mathbb {Q}(\sqrt {d}, \sqrt {-3})$ . Suppose that $f_d(x)$ is decomposed in $K(i)$ . Then, L is $K(i)$ or K.

Proof. By Lemma 2.1, every isomorphism from $X_0$ to $X_d$ can be represented by a linear fractional transformation on x. More precisely, an isomorphism is given by

$$ \begin{align*} x \to \frac{mx + n}{px + q}, \quad y \to \frac{(mq-pn)y}{(px+q)^3} \end{align*} $$

with $mq-pn \neq 0$ . Let $\gamma _i$ denote the zeros of $f_d$ . Since the zeros of $x^6+1$ are $\pm i, \pm i\zeta _3, \pm i\zeta _3^2$ , at least one of the linear fractional transformations that satisfy

$$ \begin{align*} \gamma_{k_1} \to i, \quad \gamma_{k_2} \to -i, \quad \gamma_{k_3} \to i\zeta_3 \end{align*} $$

for $k_i \in \{ 1, \ldots , 6 \}$ is the isomorphism from $C_1$ to $C_d$ , which is defined over (possibly a subfield of) $\mathbb {Q}(i, \zeta _3, \gamma _1, \ldots , \gamma _6)$ .

Let $L_{\phi }$ be the defining field of this isomorphism so that $L_{\phi } \subset \mathbb {Q}(i, \zeta _3, \gamma _1, \ldots , \gamma _6)$ . By assumption, $\mathbb {Q}(\gamma _1, \ldots , \gamma _6)$ and also $\mathbb {Q}(i, \zeta _3, \gamma _1, \ldots , \gamma _6)$ are subfields of $K(i)$ . Therefore,

$$ \begin{align*} L = \left\{ \begin{array}{@{}ll} K & \textrm{if } L_{\phi} \subset K, \\ K(i) & \textrm{otherwise}, \end{array} \right. \end{align*} $$

since $L_{\phi }K = L$ by Lemma 2.8.

Corollary 3.4. Let $X_d$ be a twist of type $V_4^B$ or $V_4^C$ . Then, L is $K(i)$ or K.

Proof. This is a direct consequence of Lemmas 3.1, 3.2 and Proposition 3.3.

4. Proof of the main theorem

4.1. Proof for type $B, C$

Let E be an elliptic curve. Then, its L-function is a product of L-factors, $L_p(E/\mathbb {Q}, s) = (1 - a_p(E) p^{-s} + p^{1 - 2s})^{-1}$ , where E has good reduction at p. Here, $a_p(E)$ is the trace of the Frobenius which is in the interval $[-2\sqrt {p}, 2\sqrt {p}]$ . Similarly,

$$ \begin{align*} L_p(X/\mathbb{Q}, s) = (1 + a_{p, 1}(X)p^{-s} + a_{p, 2}(X)p^{-2s} + a_{p, 1}(X)p^{1-3s} + p^{2-4s} )^{-1}, \end{align*} $$

when X is a curve of genus $2$ and has good reduction at p. For an elliptic curve E and a genus $2$ curve X, we denote by $E^{(D)}$ and $X^{(D)}$ the respective hyperelliptic twists given by the field $\mathbb {Q}(\sqrt {D})$ . It is also well known that

$$ \begin{align*} L_p(E^{(D)}/\mathbb{Q}, s) = (1 - a_p(E) \chi_D(p) p^{-s} + p^{1 - 2s})^{-1}, \end{align*} $$

where $\chi _D$ is the quadratic character attached to the field extension $\mathbb {Q}(\sqrt {D})/\mathbb {Q}$ .

Table 1 The L-factors of $J_d$ corresponding to $I(p)$ .

Let $X_d^B$ and $X_d^C$ be the twists of $X_0$ of biquadratic type $B, C$ studied in the previous section. We denote by $J_0, J_d^B, J_d^C$ their Jacobians, by $X_0^{(D)}, X_d^{B, (D)}, X_d^{C, (D)}$ the hyperelliptic twists and by $J_0^{(D)}, J_d^{B, (D)}, J_d^{C, (D)}$ the Jacobians of the hyperelliptic twists. Finally, we denote by $E_0$ the elliptic curve over $\mathbb {Q}$ defined by the equation $y^2 = x^3 + 1$ .

We also recall some notation from [5, Section 4]. Let $M = \mathbb {Q}(\sqrt {-3})$ . The definition of $L, K$ which depends on the choice of the twist X of $X_0$ is given by Definition 2.7. For a number field F, the residue degree at p in $F/\mathbb {Q}$ is denoted by $f_F(p)$ . We define $ I(p) = I(p, C) := (f_L(p), f_K(p), f_M(p))$ .

Proposition 4.1. Let $X_d^{\bullet }$ be a twist of $X_0$ with $\bullet \in \{ B, C \}$ , and let p be a prime greater than $3$ , where $X_d^{\bullet }$ have good reduction at p. Table 1 gives the L-factors for $J_d^{\bullet }$ (with $a_p = a_{p}(E_0)$ ).

Proof. This is an application of [5, Proposition 4.9] in our cases, but we note that [5] uses a normalisation $a_{p, i}(J)/p^{{i}/{2}}$ and $a_1(E)(p) = -a_p(E_0)$ . (For example, the L-factor of an elliptic curve is $1 + a_1(E)(p)T + T^2$ in [5, page 555].)

By Corollary 3.4, $L = K(i)$ or $L = K$ . By [5, Proposition 4.9], the possible values of $I(p)$ are

$$ \begin{align*} (1, 1, 1), \quad (2, 1, 1), \quad (2, 2, 1), \quad (4, 2, 1), \quad (2,2,2), \quad (4, 2, 2), \end{align*} $$

and $I(p)$ determines $a_{p, 1}$ and $a_{p, 2}$ . When $L=K(i)$ , which is a triquadratic field, the first entry of $I(p)$ cannot be $4$ . This gives the first three columns of Table 1 and the last one can be easily computed.

When $L = K$ , the only possible value of $I(p)$ is one of $(1,1,1)$ , $(2, 2, 1)$ and $(2, 2, 2)$ . The other results are not changed.

We note that each entry of the fourth column in Table 1 can be factorised, namely $(1 - a_pp^{-s} + p^{1-2s})^2$ , $(1 + a_pp^{-s} + p^{1-2s})^2$ , $(1 - a_pp^{-s} + p^{1-2s})(1 + a_pp^{-s} + p^{1-2s})$ and $(1 + p^{1-2s})^2$ .

Suppose that $L = K(i)$ . Since there is no rational prime whose residue degree is $4$ in a biquadratic extension, the conditions on $I(p)$ are:

• • $I(p) = (1, 1, 1)$ if and only if p totally splits in L;

• • $I(p) = (2, 1, 1)$ if and only if p is inert in $\mathbb {Q}(i)$ and totally splits in K;

• • $I(p) = (2, 2, 1)$ if and only if p is inert in $\mathbb {Q}(\sqrt {d})$ and splits in $\mathbb {Q}(\sqrt {-3})$ ;

• • $I(p) = (2, 2, 2)$ if and only if p is inert in $\mathbb {Q}(\sqrt {-3})$ .

Let us define

$$ \begin{align*} &S_1 = \{ p : I(p) = (1, 1, 1) \}, \quad S_2 = \{ p : I(p) = (2, 1, 1) \}, \\ & S_3 = \{ p : I(p) = (2, 2, 1) \}, \quad S_4 = \{ p : I(p) = (2, 2, 2) \}. \end{align*} $$

It follows that half of the primes are in $S_4$ , $\tfrac 14$ in $S_3$ and $\tfrac 18$ in each of $S_2, S_1$ .

When $L = K$ , a rational prime is an element of $S_1$ , $S_3$ or $S_4$ . Also in this case:

• • $p \in S_1$ if and only if p totally splits in $L=K$ ;

• • $p \in S_3$ if and only if p is inert in $\mathbb {Q}(\sqrt {d})$ and splits in $\mathbb {Q}(\sqrt {-3})$ ;

• • $p \in S_4$ if and only if p is inert in $\mathbb {Q}(\sqrt {-3})$ .

Hence, in this case, half of the primes are in $S_4$ and $\tfrac 14$ in each of $S_3, S_1$ .

Proof of Theorem 1.1.

We first consider the case $L = K(i)$ . By Proposition 4.1,

$$ \begin{align*} L(J_d^{\bullet}/\mathbb{Q}, s)^{-1} &\sim \prod_{p \in S_1} ({ 1 - a_pp^{-s} + p^{1-2s} })^2 \prod_{p \in S_2} ({ 1 + a_pp^{-s} + p^{1-2s} })^2\\ &\quad \times \prod_{p \in S_3} (1 - a_pp^{-s} + p^{1-2s})(1 + a_p p^{-s} + p^{1-2s}) \prod_{p \in S_4} (1 + p^{1-2s})^2, \end{align*} $$

where $\bullet \in \{ B, C \}$ . Here, $\sim $ means that the quantities are the same at unramified primes. We consider L-functions of $E_0^{(-1)} \times E_0^{(-d)}$ . Note that $p\equiv 2\pmod {3}$ if and only if p is inert in $\mathbb {Q}(\sqrt {-3})$ . Since $a_p = 0$ when $p \equiv 2 \pmod {3}$ ,

$$ \begin{align*} L(E_0^{(D)}/\mathbb{Q}, s)^{-1} &= \prod_p (1 - a_p\chi_{D}(p)p^{-s} + p^{1 - 2s} ) \\ &= \prod_{p \in S_1} (1 - a_p\chi_{D}(p)p^{-s} + p^{1 - 2s} ) \prod_{p \in S_2} (1 - a_p\chi_{D}(p)p^{-s} + p^{1 - 2s} )\\ &\quad \times \prod_{p \in S_3} (1 - a_p\chi_{D}(p)p^{-s} + p^{1 - 2s} ) \prod_{p \in S_4} (1 + p^{1 - 2s} ). \end{align*} $$

We have $\chi _{-1}(p) = \chi _{-d}(p) = 1$ for a prime in $S_1$ and $\chi _{-1}(p) = -1, \chi _{-d}(p) = 1$ for a prime in $S_2$ . In $S_3$ , there are two subclasses of primes:

$$ \begin{align*} S_{3, 1} := \{ p \in S_3 : p \textrm{ splits in } \mathbb{Q}(i) \}, \quad S_{3, 2} := \{ p \in S_3 : p \textrm{ is inert in } \mathbb{Q}(i) \}. \end{align*} $$

Since $p \in S_3$ if and only if $\chi _d(p) = -1$ , we have $\chi _{-d}(p)=\chi _{-1}(p)\chi _d(p)=-\chi _{-1}(p)$ . Hence, for a prime $p \in S_3$ , p is in $S_{3, 1}$ if and only if $\chi _{-1}(p) = 1$ and p is in $S_{3, 2}$ if and only if $\chi _{-d}(p) = 1$ . Consequently, $L(E_0^{(-1)}/\mathbb {Q}, s)^{-1}$ is given by

$$ \begin{align*} \prod_{p \in S_1 \cup S_{3, 1}} (1 - a_pp^{-s} + p^{1 - 2s} ) \prod_{p \in S_2 \cup S_{3, 2}} (1 + a_pp^{-s} + p^{1 - 2s} ) \prod_{p \in S_4} (1 + p^{1 - 2s} ) \end{align*} $$

and $L(E_0^{(-d)}/\mathbb {Q}, s)^{-1}$ is given by

$$ \begin{align*} \prod_{p \in S_1 \cup S_{3, 2}} (1 - a_pp^{-s} + p^{1 - 2s} ) \prod_{p \in S_2 \cup S_{3, 1}} (1 + a_pp^{-s} + p^{1 - 2s} ) \prod_{p \in S_4} (1 + p^{1 - 2s} ). \end{align*} $$

Therefore, $L(J_d^{\bullet }/\mathbb {Q}, s) \sim L(E_0^{(-1)}/\mathbb {Q}, s)L(E_0^{(-d)}/\mathbb {Q}, s),$ which means that $J_d^{\bullet }$ is isogenous to $E_0^{(-1)} \times E_{0}^{(-d)}$ over $\mathbb {Q}$ . When $L = K$ , the same argument shows that $J_d^\bullet $ is isogenous to $E_0 \times E_0^{(d)}$ .

Let $\rho _{J, \ell }$ be the $\ell $ -adic Galois representation attached to the abelian variety J. It is well known that $\rho _{J^{(D)}, \ell } \sim \rho _{J, \ell } \otimes \chi _D$ and $J_1$ is isogenous to $J_2$ if and only if $\rho _{J_1} \sim \rho _{J_2}$ (see [6, Section III.7]). Hence, for $\bullet \in \{ B, C \}$ ,

$$ \begin{align*} \rho_{J_d^{\bullet, (D)}, \ell} & \sim \rho_{J_d^\bullet, \ell} \otimes \chi_D \sim \rho_{E_0^{(-1)} \times E_0^{(-d)}} \otimes \chi_D = ({\rho_{E_0^{(-1)}} \oplus \rho_{E_0^{(-d)}} }) \otimes \chi_D \\ & = ({ \rho_{E_0^{(-1)}} \otimes \chi_D }) \oplus ({ \rho_{E_0^{(-d)}} \otimes \chi_D }) = \rho_{E_0^{(-D)}} \oplus \rho_{E_0^{(-dD)}}. \end{align*} $$

This proves the result.

We give two remarks on Theorem 1.1. Some values of d are naturally excluded in the family $\{X_d^B\}$ or $\{X_d^C\}$ since they do not define a twist of biquadratic type. Also, Theorem 1.1 shows that two curves in the family $\{X_d^B\}$ (or $\{X_d^C\}$ ), where $d \in \mathbb {Q}^\times /(\mathbb {Q}^\times )^2$ , are not isogenous.

4.2. Remarks for other types

In this section, we give some remarks on the other types $A, D, E$ and G. Compared with the types B and C, there are two main obstacles.

1. (i) The Brauer group condition becomes nontrivial.

2. (ii) For each integer d, we have to find a solution $x,y\in \mathbb {Q}$ of

   (4.1) $$ \begin{align} x^2+\frac{3y^2}{v(d)}=u(d). \end{align} $$
   In practice, we should express x and y as rational functions in d.

Note that when we deal with types B and C, we have easy solutions for obstacle (ii).

In some cases, we may restrict d to make obstacle (i) simpler. However, even in this case, obstacle (ii) may remain nontrivial. In the following examples, we numerically verify the expected nonsimplicity for some small d by finding explicit solutions $(\alpha , \beta )$ of (4.1).

Example 4.2. The Brauer group condition $(d, -3) = 1 \in \operatorname {\mathrm {Br}}_2(\mathbb {Q})$ for type A is equivalent to $d \equiv 1 \pmod {3}$ when d is prime. In this case, $(\alpha , \beta )$ is a solution of

$$ \begin{align*} x^2 + 3y^2 = d. \end{align*} $$

For example, we have $(\alpha , \beta ) = (2, 1)$ when $d = 7$ . With the calculations of previous sections, we find the list of $(\alpha , \beta )$ and $f_d$ for primes $d < 70$ shown in Table 2.

Table 2 The solutions $(\alpha,\beta)$ associated to d and the resulting $f_d$ for type A.

By computing the discriminant of each quadratic divisor of $f_d$ , we have $L_d = \mathbb {Q}(\sqrt {3d})$ , which is a subfield of $K(i)$ . By Proposition 3.3, $L = K$ or $L = K(i)$ . Hence, the proof of Proposition 4.1, and Theorem 1.1 also works. Consequently, $J_d^A$ is not simple for primes $d < 70$ satisfying the Brauer group condition.

Example 4.3. In the case of type D and prime d, the Brauer group condition gives $d \equiv 1 \pmod {4}$ . Since numerical computation is too complicated, we omit a detailed description as in the previous example. For such primes $d < 70$ , the factorisation of $f_d(x)$ over $\mathbb {Q}(i)$ shows that $L_d$ is a quartic extension of $\mathbb {Q}$ whose unique intermediate field is $\mathbb {Q}(i)$ . By the proof of Proposition 3.3, $L_{\phi }$ is a subfield of $L_d(i) = L_d$ . Hence, L is a subfield of $L_dK$ with $[L:K] \leq 2$ . Therefore, we can conclude that $L = K$ or $K(i)$ . This implies that $J_d^D$ is not simple for primes $d < 70$ .

Example 4.4. For type E, the Brauer group condition makes the prime $d \equiv 1 \pmod {12}$ . Analogous computation shows that $f_d$ has three quadratic factors over $\mathbb {Q}(\sqrt {3})$ and $L_d$ is a quartic extension whose quadratic subfield is $\mathbb {Q}(\sqrt {3})$ . By the same argument as for type D, we have checked that $J_d^E$ is not simple for primes $d < 190$ .

Example 4.5. In the case of type G, a simple computation shows that $d = -p$ with $p \equiv 1 \pmod {3}$ satisfies the Brauer group condition. This case may require more effort to find explicit $\alpha , \beta $ .