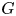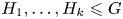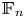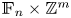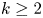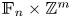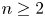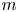Intersection configurations in free and free times free-abelian groups

Abstract

In this paper, we study intersection configurations – which describe the behaviour of multiple (finite) intersections of subgroups with respect to finite generability – in the realm of free and free times free-abelian (FTFA) groups. We say that a configuration is realizable in a group $G$ if there exist subgroups $H_1,\ldots, H_k \leqslant G$ realizing it. It is well known that free groups ${\mathbb {F}_{n}}$ satisfy the Howson property: the intersection of any two finitely generated subgroups is again finitely generated. We show that the Howson property is indeed the only obstruction for multiple intersection configurations to be realizable within nonabelian free groups. On the contrary, FTFA groups ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ are well known to be non-Howson. We also study multiple intersections within FTFA groups, providing an algorithm to decide, given $k\geq 2$ finitely generated subgroups, whether their intersection is again finitely generated and, in the affirmative case, compute a ‘basis’ for it. We finally prove that any intersection configuration is realizable in an FTFA group ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, for $n\geq 2$ and large enough $m$. As a consequence, we exhibit finitely presented groups where every intersection configuration is realizable.

1. Introduction

The behaviour of subgroup intersections with respect to finite generability has a long and interesting history in the context of nonabelian groups. Although finitely generated free groups $\mathbb {F}_{n}$ contain non-(finitely generated) subgroups, in the 1950s Howson proved that the intersection of two (and hence, finitely many) finitely generated subgroups of $\mathbb {F}_{n}$ is again finitely generated; see [9]. In acknowledgement of this initial result, a group is said to satisfy the Howson property (or to be Howson, for short) if the intersection of any two finitely generated subgroups is again finitely generated. As a generalization, Baumslag proved in [1] the preservation of the Howson property under free products: if $G_1$ and $G_2$ satisfy the Howson property then so does $G_1 *G_2$. However, the same statement fails dramatically when replacing the free product by the apparently tame direct product: the result below is folklore (it appears in [3] attributed to Moldavanski, and as the solution to Exercise 23.8(3) in [2]).

Proposition 1.1 The group ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, for $n\geq 2$ and $m\geq 1$, does not satisfy the Howson property.

Proof. In $\mathbb {F}_{2} \times \mathbb {Z} =\langle x,y \mid \, \rangle \times \langle t \mid \, \rangle$, consider the (two-generated, free) subgroups $H=\langle x,y \rangle$ and $H'=\langle xt, y \rangle$. Clearly,

\begin{align*} H\cap H' & =\{ w(x,y) \mid w\in \mathbb{F}_{2}\} \cap \{ w(xt,y) \mid w\in \mathbb{F}_{2}\} \\ & = \{ w(x,y) \mid w\in \mathbb{F}_{2}\} \cap \{ w(x,y)\mathrm{t}^{|w|_x} \mid w\in \mathbb{F}_{2}\} \\ & = \{ w(x,y)\mathrm{t}^0 \mid w\in \mathbb{F}_{2},\, |w|_x =0 \} \\ & =\langle x^{{-}k} y x^{k} , k\in \mathbb{Z} \rangle =\langle\!\langle y\rangle\!\rangle_{\mathbb{F}_{2}}, \end{align*}

where $|w|_x$ is the total $x$-exponent of $w$ (i.e. the first coordinate of the image $\mathbf {w} = (w)\rho \in \mathbb {Z}^2$ of $w \in \mathbb {F}_{2}$ under the abelianization map $\rho \colon \mathbb {F}_{2}\xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^2$ with the obvious bases). It is well known that the normal closure $\langle \! \langle \hspace {1pt} y \hspace {1pt} \rangle \! \rangle$ of $y$ in $\mathbb {F}_{2}$ is not finitely generated, hence $\mathbb {F}_{2} \times \mathbb {Z}$ does not satisfy the Howson property. Since, for all $n\geq 2$ and $m\geq 1$, the group $\mathbb {F}_{2} \times \mathbb {Z}$ embeds in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, this last one does not satisfy the Howson property either.

We remark that the subgroups $H$ and $H'$ in the previous counterexample are both isomorphic to $\mathbb {F}_{2}$. Quite interestingly, the above is a situation where two free groups of rank 2 have a non-(finitely generated), of course free, intersection. This does not contradict the Howson property for free groups, but rather indicates that there is no free subgroup of $\mathbb {F}_{2} \times \mathbb {Z}$ containing both $H$ and $H'$.

The behaviour of intersections within free times free-abelian groups (FTFA groups, for short) was studied in detail in [6, 8], where the authors solved the so-called Subgroup Intersection Problem (SIP, for short) within this family of groups.

Theorem 1.2 [6]

The $\mathsf {SIP}$ for ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ is computable.

The SIP is the special case of the multiple subgroup intersection problem for $k=2$ subgroups:

Definition 1.3 The multiple subgroup intersection problem for a group $G$, $\mathsf {MSIP}(G)$, consists in, given finite sets of generators for finitely many subgroups $H_1,\ldots,H_k\leqslant _{\mathsf {fg}} G$, deciding whether the intersection ${H_1\cap \cdots \cap H_k}$ is again finitely generated and, in the affirmative case, computing a set of generators for it.

In the present paper, we investigate the multiple versions of both the Howson property for free groups, and the SIP for FTFA groups (solved in the theorem above for two subgroups). We emphasize that $\mathsf {MSIP}({\mathbb {F}_{n}} \times \mathbb {Z}^m)$ does not follow directly by induction from $\mathsf {SIP}({\mathbb {F}_{n}} \times \mathbb {Z}^m)$ (using the recurrence $H_1\cap \cdots \cap H_k =(H_1\cap \cdots \cap H_{k-1}) \cap H_k$) because it could very well happen that some of the intermediate intersections, even all of them, are not finitely generated, whereas $H_1, \ldots,H_k$ and $H_1\cap \cdots \cap H_k$ are all finitely generated. Instead, we need to build a procedure dealing directly with the total intersection $H_1\cap \cdots \cap H_k$, but without going through the intermediate ones.

At the beginning of § 2 we briefly survey the algebraic proof for theorem 1.2, before delving into the more involved multiple variant of this problem. Then, we set up the machinery needed to study multiple intersections within ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, which allows us to extend $\mathsf {SIP}({\mathbb {F}_{n}} \times \mathbb {Z}^m)$ to $\mathsf {MSIP}({\mathbb {F}_{n}} \times \mathbb {Z}^m)$ (see theorem 2.10) and prove some technical statements (remarkably, theorem 2.14) crucial to derive our main results in later sections.

On the contrary recall that, since ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ is not Howson (for $n \geq 2$ and $m\geq 1$), for each pair of subgroups of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, there are two possibilities for their intersection: either it is finitely generated, or it is not. When we consider $k\geq 2$ subgroups, many different combinations of finitely generated and non-(finitely generated) partial intersections may arise. In § 3 we introduce the notion of intersection configuration as a compact way to describe all the possible intersection situations (in terms of finite generability) between finitely many subgroups.

In § 4 we take advantage of our analysis of multiple intersections to deduce obstructions for these $k$-intersection configurations to be realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$. In particular, we see that, despite their very flexible character (described in [8]) not every intersection configuration is realizable in (a fixed) ${\mathbb {F}_{n}} \times \mathbb {Z}^m$.

As a natural continuation, in § 5 we use some results from § 2 to show that every $k$-configuration is realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ for a large enough $m$. That is, for $\mathcal {I} \subseteq \mathcal {P}([k])\setminus \{ \varnothing \}$, there exists a large enough $m\geq 0$ and subgroups $H_1, H_2, \ldots,H_k$ of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ satisfying the following: for every nonempty $I\subseteq \{1,\ldots,k\}$, the intersection $H_I=\bigcap _{\, i\in I} H_i$ is finitely generated if and only if $I \in \mathcal {I}$ (see theorem 5.5 below for details). We deduce the existence of finitely presented groups where all such configurations are realizable; we call them intersection-saturated groups.

Finally, in § 6, we study the free case ($m=0$): such a $k$-configuration is realizable in ${\mathbb {F}_{n}}$, $n\geq 2$, if and only if, for every nonempty $I,J\subseteq \{1,\ldots,k\}$, $H_{I\cup J}=H_I\cap H_J$ is required to be finitely generated whenever $H_I$ and $H_J$ are so; that is, the Howson property is the only obstacle to realize arbitrary $k$-configurations in a free ambient group; see theorem 6.7.

General notation and conventions

The set of natural numbers, denoted by $\mathbb {N}$, is assumed to contain 0, and we specify conditions on this set using subscripts; for example, we denote by $\mathbb {N}_{\geq 1}$ the set of strictly positive integers. For $k \in \mathbb {N}_{\geq 1}$, we write $[k]=\{n\in \mathbb {N} \mid 1 \leq n \leq k\}$.

We use lowercase boldface font ($\mathbf {a}, \mathbf {b}, \mathbf {c},\ldots$) to denote elements of the free-abelian group $\mathbb {Z}^m$ (usually thought as horizontal vectors); and uppercase boldface font ($\mathbf {A},\mathbf {B},\mathbf {C},\ldots$) to denote matrices, which – as homomorphisms in general – are assumed to act on the right. That is, we denote by $(x)\varphi$ (or simply by $x \varphi$) the image of the element $x$ by the map $\varphi$, and we denote by $\varphi \psi$ the composition $A \xrightarrow[]{\varphi} B \xrightarrow[]{\psi} C$. In order to distinguish from inverse maps, we denote by $S\varphi ^{\boldsymbol {\leftarrow }}$ the set of preimages in $A$ of the set $S\subseteq B$ under the map $\varphi$.

Throughout the paper, we write $H \leqslant G$ (resp., $H\leqslant _{\mathsf {fg}} G$ and $H\leqslant _{\mathsf {fi}} G$) to express that $H$ is a subgroup (resp., a finitely generated subgroup, and a finite index subgroup) of $G$, reserving the symbol $\leq$ for inequalities among real numbers. We use the abbreviations ‘f.g.’ to mean ‘finitely generated’ and ‘non-f.g.’ to mean ‘non-(finitely generated)’; and we refer to the difference between finite generability and non-(finite generability) of a subgroup as the character of the subgroup.

Finally, the symbol $\infty$ denotes the countable infinity (i.e. $\infty =\aleph _0$), and we denote by $\mathbb {Z}^{\infty }$ the direct sum of countably many copies of $\mathbb {Z}$, i.e. $\mathbb {Z}^{\infty }=\bigoplus _{n\geq 1} \mathbb {Z}$ (where elements always have finite support). More specific notation and terminology are set forth in the corresponding sections.

2. Multiple intersections in FTFA groups

We call free times free-abelian (FTFA) groups the groups admitting a presentation of the form

(2.1)\begin{equation} {\mathbb{F}_{n}} \times \mathbb{Z}^m =\left\langle \, x_1,\ldots,x_n,t_1,\ldots,t_m\, \mid t_it_j = t_jt_i, t_ix_k=x_kt_i \, \right\rangle, \end{equation}

where $n,m \geq 0$. We write $X=\{x_1,\ldots,x_n\}$ the set of (freely independent) generators of a free group ${\mathbb {F}_{n}}$ of rank $n$, and $T=\{t_1,\ldots,t_m\}$ the set of (commuting and linearly independent) generators of a free-abelian group $\mathbb {Z}^m$ of rank $m$; of course, each of the $x_i$'s also commutes with each of the $t_j$'s. Note that these groups $G = {\mathbb {F}_{n}} \times \mathbb {Z}^m$ fit in the middle of a short exact sequence of the form

which obviously splits; that is, there exists a homomorphism $\sigma \colon {\mathbb {F}_{n}} \to G$ such that $\sigma \pi =\operatorname {id}_{{\mathbb {F}_{n}}}$ (called a section of $\pi$).

As is customary with this kind of groups, we shall refer to the elements in $G = {\mathbb {F}_{n}} \times \mathbb {Z}^m$ by using their normal forms (with vectors on the right), which we write multiplicatively as $u\mathrm {t}^\mathbf {a}$, where $u=u(x_1,\ldots,x_n) \in {\mathbb {F}_{n}}$ is called the free part of $u\mathrm {t}^\mathbf {a}$, and $\mathbf {a}=(a_1, \ldots,a_m)\in \mathbb {Z}^m$ is called the abelian part of $u\mathrm {t}^\mathbf {a}$ (the meta-symbol $\mathrm {t}$ is just a mnemonic way to encapsulate the standard additive notation for $\mathbb {Z}^m$ into a multiplicative one, i.e. $\mathrm {t}^\mathbf {a}=t_1^{a_1} \cdots t_m^{a_m}$). Note that then, $(u\mathrm {t}^\mathbf {a})(v\mathrm {t}^\mathbf {b})=uv \, \mathrm {t}^\mathbf {a+b}$.

We denote by $\pi \colon {\mathbb {F}_{n}} \times \mathbb {Z}^m \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow {\mathbb {F}_{n}}$, $u\mathrm {t}^\textbf {a}\mapsto u$ and by $\tau \colon {\mathbb {F}_{n}} \times \mathbb {Z}^m \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^m$, $u\mathrm {t}^\textbf {a}\mapsto \textbf {a}$, the natural projections to the free part ${\mathbb {F}_{n}}$ and to the free-abelian part $\mathbb {Z}^m$ (now in additive notation), respectively. Clearly, both maps are group homomorphisms.

It is not difficult to see that every subgroup $H \leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ is of the form $H=H\pi \sigma \times (H \cap \mathbb {Z}^m)$, where $\sigma$ is a section of $\pi$, $\mathrm {rk} (H\pi \sigma ) =\mathrm {rk} (H \pi )\in [0,\infty ]$, and the rank of $L_H =H\cap \mathbb {Z}^m$ is at most $m$. An immediate (but important for us) consequence is stated below.

Remark 2.1 A subgroup $H\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ is finitely generated if and only if its projection $H \pi$ (to the free part) is finitely generated.

Next, we introduce (abelian) completions, a concept playing an important role in this kind of groups.

Definition 2.2 Let $H$ be a subgroup of $G ={\mathbb {F}_{n}} \times \mathbb {Z}^m$, let $\sigma$ be a section of $\pi _{|H}$, let $w\in \mathbb {F}_n$, and let $\mathbf {a} \in \mathbb {Z}^m$. If $w \mathrm {t}^{\mathbf {a}} \in H$ then we say that $\mathbf {a}$ completes $w$ into $H$. More precisely, the $\sigma$-completion of $w$ in $H$, denoted by $\mathbf {c}_{H,\sigma }(w)$, is the empty set if $w\not \in H\pi$, and equals to $w\sigma \tau \in \mathbb {Z}^m$ otherwise. Similarly, the (full) completion of $w$ in $H$ is $C_{H}(w)=(w\pi _{|H}^{{\boldsymbol {\leftarrow }}}) \tau =\{ \mathbf {a} \in \mathbb {Z}^m \mid w\mathrm {t}^{\mathbf {a}} \in H \}$. That is, $C_{H}(w)$ is the full set of vectors completing $w$ into $H$.

It is straightforward to see that $C_{H}(w)$ is either empty or a coset of the subgroup $L_{H}=H\cap \mathbb {Z}^m$.

Lemma 2.3 Let $H$ be a subgroup of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, and let $w\in {\mathbb {F}}$. Then,

(2.2)\begin{equation} C_{H}(w) = \bigg\{\! \begin{array}{@{}ll} \varnothing & \text{if } w\notin H \pi, \\ \mathbf{c}_{H,\sigma}(w) + L_{H} & \text{if } w \in H \pi \,, \end{array} \end{equation}

where $\sigma$ is any section of $\pi _{|H}$.

As defined in [6], a basis of a subgroup $H\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ is a subset of $H$ of the form

(2.3)\begin{equation} \mathcal{B} = \left\{ u_1\mathrm{t}^\mathbf{a_1}, u_2\mathrm{t}^\mathbf{a_2},\ldots ; \mathrm{t}^\mathbf{b_1},\ldots, \mathrm{t}^\mathbf{b_s} \right\}\,, \end{equation}

where $\{u_1, u_2, \ldots \}$ is a (finite or infinite) free basis of $H\pi \leqslant \mathbb {F}_{n}$, $\mathbf {a_1}, \mathbf {a_2},\ldots \in \mathbb {Z}^m$ are integral vectors, and $\{\mathrm {t}^\mathbf {b_1}, \ldots,\mathrm {t}^\mathbf {b_s}\}$ is a free-abelian basis of the intersection $L_H =H\cap \mathbb {Z}^m$; we use a semicolon as a notational device to separate the purely abelian elements in $\mathcal {B}$. In [6, Sect. 1] it is shown that every subgroup $H\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ admits such a basis (computable from any given set of generators in the finitely generated case). We use the terms free basis, free-abelian basis and just basis, depending on whether we refer to a basis for the free part, the free-abelian part or the whole FTFA group, respectively.

We denote $r=\mathrm {rk}(H\pi )$ and $s=\mathrm {rk}(L_H)$. Note that $0\leq r\leq \infty$, while $0\leq s\leq m$, with the first dots in equation (2.3) representing countably many elements in the case $r=\infty$. Note that, then, $H\simeq \mathbb {F}_{\!r} \times \mathbb {Z}^s$, and $H$ is finitely generated if and only if $r<\infty$. Finally, we introduce some more notation for later use: let $\rho _H\colon H\pi \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r}$ be the abelianization map (not to be confused with the restriction to $H$ of the global abelianization map $\mathbb {F}_{n} \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^n$), and let $A_H\colon \mathbb {Z}^r\to \mathbb {Z}^m$ be the so-called completion homomorphism, sending the canonical $j$-th vector to $\mathbf {a_j}$.

When $r=\mathrm {rk} (H\pi )<\infty$, we write

\[ \mathbf{A}_H=\left( \!\begin{array}{@{}c@{}} \mathbf{a_1} \\ \vdots \\ \mathbf{a_r} \end{array}\!\right) \in M_{r\times m}(\mathbb{Z}), \quad \quad \mathbf{L}_H =\left( \!\begin{array}{@{}c@{}} \mathbf{b_1} \\ \vdots \\ \mathbf{b_s} \end{array}\!\right) \in M_{s\times m}(\mathbb{Z}), \]

called the completion matrix of $H$ (w.r.t. $\mathcal {B}$), and the matrix of $L_H$ (w.r.t. $\mathcal {B}$), respectively; note that $\mathbf {A}_H$ is the matrix of the completion homomorphism $A_H$ w.r.t. the canonical bases, and that the row space of $\mathbf {L}_H$ (i.e. the subspace of $\mathbb {Z}^m$ generated by the rows of $\mathbf {L}_H$) is precisely $L_H$.

Below, we see that full completions are easily computable from any given finite basis for the subgroup.

Corollary 2.4 If $\mathcal {B} =\big \{ u_1\mathrm {t}^\mathbf {a_1}, u_2 \mathrm {t}^{\mathbf {a_2}},\ldots ;\mathrm {t}^\mathbf {b_1},\ldots, \mathrm {t}^\mathbf {b_s} \big \}$ is a basis of $H\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ then, for every $w\in H\pi$, $C_{H}(w)=w\rho _H A_H +\langle \mathbf {b_1}, \ldots,\mathbf {b_s} \rangle$.

Proof. Let $\sigma$ be the section of $\pi _{\mid H}$ given by $\mathcal {B}$; namely, $\sigma \colon H\pi \to H$, $u_i \mapsto u_i \mathrm {t}^{\mathbf {a_i}}$. Then, applying lemma 2.3 to $\sigma$ we have that, for every $w\in H\pi$, $C_{H}(w)=w\sigma \tau +L_{H}=w\rho _H A_H +\langle \mathbf {b_1}, \ldots, \mathbf {b_s} \rangle$, since $\sigma \tau =\rho _H A_H \colon H\pi \to \mathbb {Z}^m$, $u_i\mapsto \mathbf {a_i}$.

In [6], Delgado and Ventura studied intersections between two finitely generated subgroups of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ given by respective bases (alternatively, see [5, 8] for a geometric description of the subgroups of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ and their intersections in the spirit of Stallings automata). We briefly summarize the main results here, with the goal of generalizing them to the case of finitely many, say $k\geq 2$, arbitrary subgroups $H_1,\ldots,H_k\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$.

Consider two subgroups $H_1,H_2\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ and take (finite or infinite) bases for them:

\begin{align*} H_1 & = \langle u_1 \mathrm{t}^\mathbf{a_1}, u_2 \mathrm{t}^\mathbf{a_2},\ldots ; \mathrm{t}^\mathbf{b_1},\ldots,\mathrm{t}^\mathbf{b_{s_1}}\rangle, \\ H_2 & = \langle v_1 \mathrm{t}^\mathbf{a'_1}, v_2 \mathrm{t}^\mathbf{a'_2},\ldots ; \mathrm{t}^\mathbf{b'_1},\ldots,\mathrm{t}^\mathbf{b'_{s_2}} \rangle, \end{align*}

where $\{u_1, u_2, \ldots \}$ and $\{v_1,v_2,\ldots \}$ are (finite or infinite) sets of freely independent elements in ${\mathbb {F}_{n}}$, $\mathbf {a_i}, \mathbf {a'_i}, \mathbf {b_i}, \mathbf {b'_i}\in \mathbb {Z}^m$, and $\{\mathrm {t}^\mathbf {b_1},\ldots,\mathrm {t}^\mathbf {b_{s_1}}\}$ and $\{ \mathrm {t}^\mathbf {b'_1}, \ldots, \mathrm {t}^\mathbf {b'_{s_2}}\}$ are free-abelian bases for $L_1=H_1\cap \mathbb {Z}$ and $L_2=H_2\cap \mathbb {Z}$, respectively. Observe that $(H_1\cap H_2)\pi \leqslant H_1\pi \cap H_2\pi$, with the equality not being true in general: $H_1\pi \cap H_2\pi$ is the set of elements from $\mathbb {F}_{n}$ admitting completions both in $H_1$ and in $H_2$, while $(H_1\cap H_2)\pi$ is the set of elements from $\mathbb {F}_{n}$ which admit a common completion in both $H_1$ and $H_2$. In [6], the diagram in figure 1 was used in order to describe the key subgroup $(H_1\cap H_2)\pi$.

Figure 1. Intersection diagram for $H_1 \cap H_2$.

Here, $\iota _1$ and $\iota _2$ are the natural inclusions; $\rho _1$, $\rho _2$ and $\rho$ are the corresponding abelianization maps with respect to the chosen bases in the domains and codomains (not to be confused with the restrictions of the global abelianization $\mathbb {F}_{n} \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^n$); $P_1$ and $P_2$ are the abelianizations of $\iota _1$ and $\iota _2$ (note that, although $\iota _1$ and $\iota _2$ are injective, $P_1$ and $P_2$ may very well not be so); and $A_1$ and $A_2$ are the completion homomorphisms, sending the $i$-th canonical vector to $\mathbf {a_i}$ and to $\mathbf {a'_i}$, respectively. In general, the ranks $r_1=\mathrm {rk}(H_1\pi )$, $r_2=\mathrm {rk}(H_2\pi )$ and $r=\mathrm {rk}(H_1\pi \cap H_2\pi )$ may be finite or infinite, with the restriction coming from the Howson property for free groups: $r$ is finite whenever $r_1$ and $r_2$ are so. Finally, $R$ is the linear map given by $R=P_1A_1-P_2A_2$. Using this scheme, Delgado–Ventura [6] proved the following result, announced there for finitely generated subgroups $H_1$, $H_2$, but valid in full generality with essentially the same proof; see also [8, Section 4] for a more detailed (geometric) analysis of this and related facts.

Proposition 2.5 [6]

For any two subgroups $H_1,H_2\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ (and using the above notation), $(H_1 \cap H_2) \pi =(L_1 +L_2)R^{{\boldsymbol {\leftarrow }}} \rho ^{{\boldsymbol {\leftarrow }}}$, which is a normal subgroup of $H_1 \pi \cap H_2\pi$.

It is well known that, for $r<\infty$, a normal subgroup $N \trianglelefteq \mathbb {F}_{\!r}$ is finitely generated if and only if either $N=\{ 1 \}$ or $N\leqslant _{\mathsf {fi}} \mathbb {F}_{\!r}$; whereas, a normal subgroup $N \trianglelefteq \mathbb {F}_{\!\infty }$ is finitely generated if and only if $N= \{ 1 \}$. From this observation and proposition 2.5, we can immediately deduce the following characterization for the finite generability of the intersection of two arbitrary subgroups of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, fully in abelian terms; see [8, Lemma 4.17] for details.

Corollary 2.6 [6]

For any two subgroups $H_1,H_2\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ (and using the above notation), $H_1 \cap H_2$ is finitely generated if and only if either (i) $r=0,1$; or (ii) $2\leq r<\infty$ and $(L_1 +L_2)R^{{\boldsymbol {\leftarrow }}} \leqslant _{\mathsf {fi}} \mathbb {Z}^r$.

Remark 2.7 Note that if $r=\mathrm {rk}(H_1\pi \cap H_2\pi ) = \infty$ then $(H_1 \cap H_2) \pi$ is never finitely generated, since $(H_1 \cap H_2) \pi = (L_1 +L_2)R^{{\boldsymbol {\leftarrow }}} \rho ^{{\boldsymbol {\leftarrow }}} \geqslant [\mathbb {F}_{\!\infty }, \mathbb {F}_{\!\infty }] \neq \{ 1 \}$ and hence is a nontrivial normal subgroup of $\mathbb {F}_{\!\infty }$, thus not being finitely generated.

When $H_1$ and $H_2$ are finitely generated, each of $r_1,r_2$ and $r$ are finite and the homomorphisms $P_1,P_2,A_1,A_2$ and $R$ can be represented by their corresponding matrices (w.r.t. chosen bases), denoted by $\mathbf {P_1}, \mathbf {P_2}, \mathbf {A_1}, \mathbf {A_2}$ and $\mathbf {R}= \mathbf {P_1} \mathbf {A_1}-\mathbf {P_2}\mathbf {A_2}$, respectively (where $\mathbf {A_1}=\mathbf {A}_{H_1}$ and $\mathbf {A_2}=\mathbf {A}_{H_2}$ are the corresponding completion matrices). In this finitely generated case, all the conditions in corollary 2.6 are algorithmically checkable and theorem 1.2 follows.

Let us now extend the previous set-up to finitely many arbitrary subgroups $H_1, \ldots, H_k\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$ instead of two. In order to study the subgroup intersection $H_1\cap \cdots \cap H_k$, we first fix a basis for each subgroup, say

(2.4)\begin{equation} H_i =\langle u_{i,1}\mathrm{t}^\mathbf{a_{i,1}}, u_{i,2}\mathrm{t}^\mathbf{a_{i,2}}, \ldots ; \mathrm{t}^\mathbf{b_{i,1}}, \ldots ,\mathrm{t}^\mathbf{b_{i,s_i}}\rangle, \end{equation}

for every $i=1,\ldots,k$; here, the ranks $r_i=\mathrm {rk}(H_i\pi )$ and $r=\mathrm {rk}(H_1\pi \cap \cdots \cap H_k\pi )$ may be finite or infinite (again, with the dots above representing countably many elements in the infinite case). Let us consider the following notation, which is summarized in figure 2. We denote:

1. (i) the abelianization maps by $\rho _i \colon H_i\pi \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r_i}$, for $i=1,\ldots,k$; also $\rho \colon \bigcap _{j=1}^k H_j\pi \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r}$;

2. (ii) the inclusion maps by $\iota _i \colon \bigcap _{j=1}^k H_j\pi \hookrightarrow H_i\pi$, for $i=1,\ldots,k$;

3. (iii) the abelianization of the inclusion maps $\iota _i$ by $P_i \colon \mathbb {Z}^r \rightarrow \mathbb {Z}^{r_i}$, for $i=1,\ldots,k$;

4. (iv) the completion homomorphisms by $A_i\colon \mathbb {Z}^{r_i}\to \mathbb {Z}^m$ (mapping the canonical $j$-th vector to $\mathbf {a_{i,j}}\in \mathbb {Z}^m$, for $i=1,\ldots,k$ and $j\geq 1$); and

5. (v) the intersections of the subgroups $H_i$ with the free-abelian part as $L_i =H_i\cap \mathbb {Z}^m=\langle \mathbf {b_{i,1}},\ldots, \mathbf {b_{i,s_i}} \rangle$, where $0\leq s_i=\mathrm {rk}(L_i)\leq m$, and call $\mathbf {L_i}$ the $s_i \times m$ integral matrix having $\mathbf {b_{i,j}}$ as $j$-th row, $i=1,\ldots,k$.

Figure 2. Intersection diagram for $\bigcap _{j=1}^{k} H_j$.

In the $k=2$ scenario, proposition 2.5 crucially reduces the finite generability of the intersection of two subgroups of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ to an abelian condition, which is easily decidable in the finitely generated case. The lemma below is a first necessary ingredient to generalize the aforementioned reduction to multiple intersections.

Lemma 2.8 Let $\mathbf {p_1},\ldots, \mathbf {p_k} \in \mathbb {Z}^m$, and $L_1,\ldots, L_k \leqslant \mathbb {Z}^{m}$. Then, the integral affine varieties $\mathbf {p_1}+L_1, \ldots,\mathbf {p_k}+L_k$ intersect nontrivially (i.e. $\bigcap _{j=1}^{k} (\mathbf {p_j}+L_j) \neq \varnothing$) if and only if

\[ \big( \mathbf{p_2}-\mathbf{p_1} \mid \mathbf{p_3}-\mathbf{p_2} \mid \cdots \mid \mathbf{p_k}-\mathbf{p_{k-1}}) \in \mathrm{Im} (\mathbf{L}), \]

where

\[ \mathbf{L}=\left(\begin{array}{@{}rrrcc@{}} \mathbf{L}_1 & & & & \\ - \mathbf{L}_2 & \mathbf{L_2} & & & \\ & -\mathbf{L_3} & \mathbf{L_3} & & \\ & & \hspace{-5pt}\ddots & \hspace{-1pt} \ddots & \\ & & & -\mathbf{L_{k-1}} & \mathbf{L_{k-1}} \\ & & & & -\mathbf{L_{k}} \end{array}\right)\in M_{(\sum _j s_j )\times (k-1)m} (\mathbb{Z}), \]

and, for each $i=1,\ldots,k$, $\mathbf {L_i}$ is a $s_i\times m$ integral matrix with row space $L_i$.

Proof. Observe that $\bigcap _{j=1}^{k} (\mathbf {p_j}+L_j) \neq \varnothing$ if and only if $\mathbf {p_1}+\boldsymbol {\ell _1}= \mathbf {p_2}+\boldsymbol {\ell _2}=\cdots =\mathbf {p_k}+\boldsymbol {\ell _k}$, for some $\boldsymbol {\ell _1}\in L_1$, $\boldsymbol {\ell _2}\in L_2$, $\ldots$, $\boldsymbol {\ell _k}\in L_k$. But this is the same as the existence of $\boldsymbol {\ell _1}\in L_1$, $\boldsymbol {\ell _2}\in L_2$, $\ldots$, $\boldsymbol {\ell _k}\in L_k$ such that $\mathbf {p_2}-\mathbf {p_1}= \boldsymbol {\ell _1}-\boldsymbol {\ell _2}$, $\mathbf {p_3}-\mathbf {p_2} =\boldsymbol {\ell _2}-\boldsymbol {\ell _3}$, $\ldots$, $\mathbf {p_{k}}-\mathbf {p_{k-1}} =\boldsymbol {\ell _{k-1}}-\boldsymbol {\ell _{k}}$. Or, equivalently, the existence of $\mathbf {a_1}\in \mathbb {Z}^{s_1}$, $\mathbf {a_2}\in \mathbb {Z}^{s_2}$, $\ldots$, $\mathbf {a_k}\in \mathbb {Z}^{s_k}$ such that

\[ \left. \begin{array}{rc@{}} \mathbf{p_2}-\mathbf{p_1} = \mathbf{a_1}\mathbf{L_1}- \mathbf{a_2}\mathbf{L_2} & = (\mathbf{a_1} \mid \mathbf{a_2}) \left( \begin{array}{c} \phantom{-}\mathbf{L_1}\\ - \mathbf{L_2} \end{array}\right) \\ & \vdots \\ \mathbf{p_k}-\mathbf{p_{k-1}} = \mathbf{a_{k-1}}\mathbf{L_{k-1}}- \mathbf{a_k}\mathbf{L_k} & = (\mathbf{a_{k-1}} \mid \mathbf{a_k}) \left( \begin{array}{c} \mathbf{L_{k-1}}\\ - \mathbf{L_k} \end{array}\right) \end{array} \right\} \]

Putting these conditions together, this is the same as saying that there exists $\mathbf {a}\in \mathbb {Z}^{{\Sigma _j s_j}}$ such that

\[(\mathbf{p_2}-\mathbf{p_1} \mid \mathbf{p_3}-\mathbf{p_2} \mid \cdots \mid \mathbf{p_k}-\mathbf{p_{k-1}}) =\mathbf{a} \mathbf{L} \in \mathrm{Im} (\mathbf{L}).\]

□

Let us now combine lemma 2.8 with the characterization coming from the above diagram to obtain the multiple version of proposition 2.5 and, as a consequence, the decidability of the multiple SIP for free-abelian times free groups. In order to do so it is convenient to define the stack homomorphism as

(2.5)\begin{equation} \begin{array}{rcl} R=(R_2, \ldots ,R_k)\colon \mathbb{Z}^r & \to \mathbb{Z}^m\oplus \stackrel{(k-1)}{\ldots} \oplus \mathbb{Z}^m=\mathbb{Z}^{(k-1)m} \\ w & \mapsto (wR_2, \ldots ,wR_k), \end{array} \end{equation}

where $R_i=P_iA_i-P_{i-1}A_{i-1}\colon$ $\mathbb {Z}^r \to \mathbb {Z}^m$, $i=2, \ldots,k$. Note that, for the case $k=2$, $R=R_2 \colon \mathbb {Z}^r \to \mathbb {Z}^{(2-1)m}=\mathbb {Z}^m$, $w\mapsto w(P_2A_2-P_1A_1)$ agrees with the homomorphism $R$ used in proposition 2.5 and corollary 2.6.

The introduced scheme and notation (see figure 2 and equation (2.5)) together with lemma 2.8 allows us to describe the projection $(H_1 \cap \cdots \cap H_k) \pi$ in a particularly convenient way, which unveils its character (and hence that of the intersection $H_1 \cap \cdots \cap H_k$).

Theorem 2.9 For any $k\geq 2$ subgroups $H_1, \ldots, H_k\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$, we have that $(H_1\cap \cdots \cap H_k)\pi =(\mathrm {Im} (\mathbf {L})) R^{{\boldsymbol {\leftarrow }}}\rho ^{{\boldsymbol {\leftarrow }}}$, which is a normal subgroup of $H_1\pi \cap \cdots \cap H_k\pi$. In particular, $H_1\cap \cdots \cap H_k$ is finitely generated if and only if one of the following conditions holds:

1. (i) $r=0,1$;

2. (ii) $2\leq r<\infty$ and $\mathrm {rk} ((\mathrm {Im} (\mathbf {L})) R^{{\boldsymbol {\leftarrow }}})=r$;

where $r = \mathrm {rk}(H_1 \pi \cap \cdots \cap H_k \pi )$.

Proof. Consider a basis for each of the given subgroups, $H_i =\langle u_{i,1}\mathrm {t}^\mathbf {a_{i,1}}, u_{i,2}\mathrm {t}^\mathbf {a_{i,2}}, \ldots ; \mathrm {t}^\mathbf {b_{i,1}}, \ldots,\mathrm {t}^\mathbf {b_{i,s_i}}\rangle$, $i=1,\ldots,k$, and keep all the notation introduced above (see figure 2 and equation (2.5)). Then,

\begin{align*} & (H_1 \cap \cdots \cap H_k)\pi\nonumber\\ & \quad= \big\{w \in \textstyle{\bigcap_{j=1}^{k} H_j\pi \mid w\text{ has a common completion into $H_1, \ldots ,H_k$}} \big\} \\ & \quad= \{w \in \textstyle{\bigcap_{j=1}^{k} H_j\pi \mid (w\iota_1 \rho_1 A_1 +L_1) \cap \cdots \cap(w\iota_k \rho_k A_k +L_k) \neq \varnothing} \} \\ & \quad= \{w \in \textstyle{\bigcap_{j=1}^{k} H_j\pi \mid (w\rho P_1 A_1 +L_1) \cap \cdots \cap(w\rho P_k A_k +L_k) \neq \varnothing} \} \\ & \quad= \{w \in \textstyle{\bigcap_{j=1}^{k} H_j\pi \mid w\rho R\in \mathrm{Im} (\mathbf{L})} \} \\ & \quad= \big(\mathrm{Im} (\mathbf{L})\big) R^{{\boldsymbol{\leftarrow}}} \rho^{{\boldsymbol{\leftarrow}}}, \end{align*}

where the second equality follows from corollary 2.4, the third one from the commutativity of the diagram in figure 2, and the fourth one from lemma 2.8. Note that, then, $(H_1 \cap \cdots \cap H_k)\pi$ is a normal subgroup of $H_1\pi \cap \cdots \cap H_k\pi$.

In particular, if $r=0,1$ (i.e. if $H_1 \pi \cap \cdots \cap H_k \pi \simeq \mathbb {F}_{\!r}$ is cyclic) then the projection $(H_1 \cap \cdots \cap H_k)\pi$ is cyclic and hence $H_1 \cap \cdots \cap H_k$ is necessarily finitely generated. Otherwise (i.e. if $2\leq r\leq \infty$), $(H_1 \cap \cdots \cap H_k)\pi$ contains the (nontrivial) commutator $[\mathbb {F}_{\!r}, \mathbb {F}_{\!r}]$ and so, it is nontrivial. This implies that, when $r=\infty$, $(H_1 \cap \cdots \cap H_k )\pi$ is never finitely generated; whereas, for $2\leq r<\infty$:

\begin{align*} H_1 \cap \cdots \cap H_k \text{ is finitely generated} & \Leftrightarrow\, (H_1 \cap \cdots \cap H_k)\pi \text{ is finitely generated} \\ & \Leftrightarrow\, \big(\mathrm{Im} (\mathbf{L})\big) R^{{\boldsymbol{\leftarrow}}} \rho^{{\boldsymbol{\leftarrow}}} \text{ is finitely generated}\\ & \Leftrightarrow\, |\mathbb{F}_{\!r} : \big(\mathrm{Im} (\mathbf{L})\big) R^{{\boldsymbol{\leftarrow}}} \rho^{{\boldsymbol{\leftarrow}}}| < \infty\\ & \,\Leftrightarrow\, |\mathbb{Z}^r : \big(\mathrm{Im} (\mathbf{L})\big) R^{{\boldsymbol{\leftarrow}}}| < \infty \\ & \,\Leftrightarrow\, \mathrm{rk}((\mathrm{Im} (\mathbf{L})) R^{{\boldsymbol{\leftarrow}}} )=r, \end{align*}

where we have used (i) remark 2.1, in the first equivalence; (ii) the fact that $(H_1 \cap \cdots \cap H_k)\pi = (\mathrm {Im} (\mathbf {L})) R^{{\boldsymbol {\leftarrow }}} \rho ^{{\boldsymbol {\leftarrow }}}$, in the second equivalence; (iii) that a nontrivial normal subgroup of a finitely generated free group is finitely generated if and only if it has finite index, in the third equivalence; (iv) that the abelianization map $\rho \colon \mathbb {F}_{\!r} \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^r$ is surjective, in the fourth equivalence; and (v) that a subgroup of $\mathbb {Z}^r$ is of finite index if and only if it has maximum rank, in the fifth equivalence.

Putting together the obtained conditions, we reach the claimed result.

Finally, let's see that, as a consequence of theorem 2.9, when all the input subgroups are finitely generated (i.e. when $r_1,\ldots,r_k<\infty$ and so, $r<\infty$), we can decide algorithmically whether $H_1\cap \cdots \cap H_k$ is finitely generated and, in case it is, compute a basis for it. This generalizes theorem 1.2 to multiple intersections.

Theorem 2.10 The multiple subgroup intersection problem for FTFA groups is computable. That is, there exists an algorithm which, on input a finite number of (finite sets of generators for) subgroups $H_1, \ldots, H_k\leqslant _{\mathsf {fg}} {\mathbb {F}_{n}} \times \mathbb {Z}^m$, decides whether the intersection $H_1\cap \cdots \cap H_k$ is finitely generated and, in the affirmative case, computes a basis for it.

Proof. The result is obvious for $k=0,1$, so we assume $k \geq 2$. In theorem 2.9, we have reduced the finite generability of the intersection $H_1\cap \cdots \cap H_k$ down to explicit linear algebra conditions, which are clearly verifiable using standard techniques. Hence, the decision problem is computable.

Finally, let us assume that $H_1\cap \cdots \cap H_k$ is finitely generated, and let us see how to compute a basis for it. It is clear that if $(H_1\cap \cdots \cap H_k)\pi =\{1\}$ then we can easily compute a (free-abelian) basis for $H_1 \cap \cdots \cap H_k =L_1\cap \cdots \cap L_k\leqslant \mathbb {Z}^m$.

Otherwise, $1\leq r=\mathrm {rk} (H_1\pi \cap \cdots \cap H_k\pi )=\mathrm {rk} ( (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}})<\infty$ and so, $|\mathbb {Z}^r : (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}|=\ell <\infty$. With a standard linear algebra procedure, we can compute a set $\{\mathbf {c_1},\ldots,\mathbf {c_\ell }\}$ of coset representatives of $(\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}$ in $\mathbb {Z}^r$, namely

\[ \mathbb{Z}^r =\big(\mathbf{c_1}+(\mathrm{Im} (\mathbf{L})) \mathbf{R^{{\boldsymbol{\leftarrow}}}} \big)\sqcup \cdots \sqcup \big(\mathbf{c_\ell}+(\mathrm{Im} (\mathbf{L})) \mathbf{R^{{\boldsymbol{\leftarrow}}}}\big). \]

Then, we can use pull-backs of Stallings’ automata (see [7, 10]) to compute a free basis $\{v_1, \ldots, v_r\}$ for $H_1\pi \cap \cdots \cap H_k\pi$, and choose respective arbitrary $\rho$-preimages in $H_1\pi \cap \cdots \cap H_k\pi$, say $z_1,\ldots,z_\ell$, of $\mathbf {c_1},\ldots,\mathbf {c_\ell }$, in order to obtain a set of right coset representatives of $(H_1 \cap \cdots \cap H_k)\pi = (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}\rho ^{{\boldsymbol {\leftarrow }}}$ in $H_1\pi \cap \cdots \cap H_k\pi$:

(2.6)\begin{equation} H_1\pi \cap \cdots \cap H_k\pi=\big( (H_1 \cap \cdots \cap H_k)\pi \big)z_1 \sqcup \cdots \sqcup \big( (H_1 \cap \cdots \cap H_k)\pi \big) z_\ell. \end{equation}

Finally, we build the Schreier digraph for $(H_1 \cap \cdots \cap H_k)\pi \leqslant _{\mathsf {fi}} H_1\pi \cap \cdots \cap H_k\pi$ with respect to $\{v_1, \ldots, v_r \}$ (which coincides with the Cayley graph of the finite abelian group

\[ \big( H_1\pi \cap \cdots \cap H_k\pi \big)/ (H_1 \cap \cdots \cap H_k)\pi \simeq \mathbb{Z}^r/ (\mathrm{Im} (\mathbf{L})) \mathbf{R^{{\boldsymbol{\leftarrow}}}} \]

with respect to the set of generators $\{v_1\rho, \ldots,v_r\rho \}$), and compute the desired basis for $H_1\cap \cdots \cap H_k$ in the following way:

1. (1) Take the cosets $( (H_1 \cap \cdots \cap H_k)\pi )z_i =( (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}\rho ^{{\boldsymbol {\leftarrow }}} ) z_i$, $i=1,\ldots,\ell$, from (2.6) as vertices, and with no edges.

2. (2) For every vertex $( (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}\rho ^{{\boldsymbol {\leftarrow }}}) z_i$, $i=1,\ldots,\ell$, and every letter $v_j$, $j=1,\ldots,r$, add an edge labelled $v_j$ from $( (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}\rho ^{{\boldsymbol {\leftarrow }}}) z_i$ to the vertex $( (\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}\rho ^{{\boldsymbol {\leftarrow }}}) z_iv_j$; we can algorithmically identify this vertex among the available ones by repeatedly solving the membership problem for $\mathrm {Im} (\mathbf {L})$, which is just solving a system of linear equations, i.e.

   \begin{align*} \big( (\mathrm{Im} (\mathbf{L})) \mathbf{R^{{\boldsymbol{\leftarrow}}}}\rho^{{\boldsymbol{\leftarrow}}}\big) z_iv_j =\big( (\mathrm{Im} (\mathbf{L})) \mathbf{R^{{\boldsymbol{\leftarrow}}}}\rho^{{\boldsymbol{\leftarrow}}}\big) z_{i'} & \Leftrightarrow z_iv_jz_{i'}^{{-}1}\in (\mathrm{Im} (\mathbf{L})) \mathbf{R^{{\boldsymbol{\leftarrow}}}}\rho^{{\boldsymbol{\leftarrow}}} \\ & \Leftrightarrow\ (z_iv_jz_{i'}^{{-}1}) \rho \mathbf{R}\in \mathrm{Im} (\mathbf{L})\,. \end{align*}
   Once we have run over all $i=1,\ldots,\ell$ and all $j=1,\ldots,r$, we have fully computed the Schreier graph $\Gamma :=\Gamma ( (H_1 \cap \cdots \cap H_k)\pi, H_1\pi \cap \cdots \cap H_k\pi, \{v_1,\,{\ldots}\,,v_r\}\!)$, of the finite index subgroup $(H_1\cap\cdots\cap H_k)\pi\,{\leqslant _{\mathsf {fi}}}\, H_1\pi \cap\cdots \cap H_k\pi$ with respect to the free basis $\{v_1, \ldots,v_r\}$ of $H_1\pi \cap \cdots \cap H_k\pi$.

3. (3) Select a maximal tree $T$ in $\Gamma$ and, for every edge $e\in E\Gamma \setminus ET$, read the label $u_e$ (a word on the $v_i$'s) of the closed path $T[\odot, \iota e]eT[\tau e, \odot ]$, where $\odot$ denotes the vertex corresponding to the trivial coset $(H_1 \cap \cdots \cap H_k)\pi$, and $T[p,p']$ denotes the $T$-geodesic from vertex $p$ to vertex $p'$. It is well known that the elements obtained in this way, say $\{u_1, \ldots,u_q\}$, form a free basis for $(\mathrm {Im} (\mathbf {L})) \mathbf {R^{{\boldsymbol {\leftarrow }}}}\rho ^{{\boldsymbol {\leftarrow }}} =(H_1 \cap \cdots \cap H_k)\pi$.

4. (4) Finally, solving $q$ (compatible) systems of linear equations, we can effectively compute vectors $\mathbf {a_1}, \ldots,\mathbf {a_q}\in \mathbb {Z}^m$ such that $u_1\mathrm {t}^\mathbf {a_1}, \ldots,u_q\mathrm {t}^\mathbf {a_q} \in H_1 \cap \cdots \cap H_k$ (see lemma 2.3); and a free-abelian basis $\{ \mathrm {t}^\mathbf {b_1}, \ldots,\mathrm {t}^\mathbf {b_s}\}$ for $L_{H_1\cap \cdots \cap H_k}=L_1\cap \cdots \cap L_k$.

By construction, the set $\{u_1\mathrm {t}^\mathbf {a_1}, \ldots,u_q \mathrm {t}^\mathbf {a_q};\, \mathrm {t}^\mathbf {b_1},\ldots,\mathrm {t}^\mathbf {b_s}\}$ is the required basis for ${H_1 \cap \cdots \cap H_k}$.

To finish this section, we prove theorem 2.14, a result which will be of central importance for the arguments in the later sections, but we think it is also of independent interest. We emphasize that it is a fairly sensitive result as slight modifications of it turn out to be false; see examples 2.16 and 2.17.

Proposition 2.11 Let $M', M''\leqslant \mathbb {F}_{n}$ be two subgroups of $\mathbb {F}_{n}$ in free-factor position, i.e. such that $\langle M',M'' \rangle =M'*M''$. Then, for any $H'_1,\ldots,H'_k\leqslant M'\leqslant \mathbb {F}_{n}$ and $H''_1,\ldots,H''_k\leqslant M''\leqslant \mathbb {F}_{n}$,

(2.7)\begin{equation} \bigcap\nolimits_{j=1}^k \langle H'_j, H''_j\rangle = \Big\langle\, \bigcap\nolimits_{j=1}^k H'_j,\, \bigcap\nolimits_{j=1}^k H''_j \,\Big\rangle . \end{equation}

Proof. For $k=1$ there is nothing to prove. And, by a straightforward induction on $k$, it is enough to prove the result for $k=2$, i.e.

(2.8)\begin{equation} \langle H'_1, H''_1\rangle \cap \langle H'_2, H''_2\rangle =\langle H'_1\cap H'_2, H''_1\cap H''_2 \rangle. \end{equation}

The inclusion to the left is obvious. For the converse, take an element $w\in \langle H'_1,H''_1 \rangle \cap \langle H'_2,H''_2 \rangle =(H'_1*H''_1 )\cap (H'_2*H''_2)$ and consider its normal form in these two free products, $w=u'_1u''_1\cdots u'_pu''_p$ with $u'_i\in H'_1$ and $u''_i\in H''_1$, and $w=v'_1v''_1\cdots v'_qv''_q$ with $v'_i\in H'_2$ and $v''_i\in H''_2$. Since $H'_1,H'_2\leqslant M'$ and $H''_1,H''_2\leqslant M''$, both are also valid normal forms for $w$ as an element from $M'*M''$. Hence, they must coincide: $p=q$, $u'_i=v'_i$, and $u''_i=v''_i$. This means that $u'_i=v'_i\in H'_1\cap H'_2$ and $u''_i=v''_i\in H''_1\cap H''_2$ and so, $w\in \langle H'_1\cap H'_2 , H''_1\cap H''_2 \rangle$, as required.

As an alternative proof, fix free bases $\mathcal {B}'$ and $\mathcal {B}''$ for $M'$ and $M''$, and it is clear that, for $i=1,2$, the Stallings automaton $\Gamma _i$ for $H'_i*H''_i$ with respect to the free basis $\mathcal {B}'\sqcup \mathcal {B}''$ of $M'*M''$ is just $\Gamma '_i*\Gamma ''_i$, the disjoint union of the Stallings automaton $\Gamma '_i$ for $H'_i$ with respect to $\mathcal {B}'$ and the Stallings automaton $\Gamma ''_i$ for $H''_i$ with respect to $\mathcal {B}''$, after identifying their basepoints (see [7, 11]). Since the labels at the edges in $\Gamma '_1$ and $\Gamma '_2$ (which belong to $\mathcal {B}'$), and in $\Gamma ''_1$ and $\Gamma ''_2$ (which belong to $\mathcal {B}''$) are completely disjoint, the pull-back of $\Gamma _1=\Gamma '_1*\Gamma ''_1$ and $\Gamma _2=\Gamma '_2*\Gamma ''_2$ will be the disjoint union of the pull-backs of $\Gamma '_1$ and $\Gamma '_2$, and of $\Gamma ''_1$ and $\Gamma ''_2$, after identifying their basepoints. Hence, $(H'_1*H''_1 )\cap (H'_2*H''_2)=(H'_1\cap H'_2)*(H''_1\cap H''_2)=\langle H'_1\cap H'_2, H''_1\cap H''_2 \rangle$, as required.

In order to transfer some behaviours of free products (in ${\mathbb {F}_{n}}$) and direct sums (in $\mathbb {Z}^m$) to ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, we introduce the terminology and notation below.

Definition 2.12 We say that two subgroups $M',M''$ of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ are strongly complementary if their projections to the free part are in free-factor position and their projections to the free-abelian part are in direct sum position. If so, we say that $\langle M',M'' \rangle$ is the strongly complementary product (s.c.-product) of $M'$ and $M''$, and we write $\langle M',M'' \rangle =M'\circledast M''$; that is,

\[ \langle M',M'' \rangle = M'\circledast M'' \ \Leftrightarrow\ \left\{\begin{array}{@{}ll} \langle M'\pi,M''\pi \rangle= M'\pi * M''\pi\leqslant \mathbb{F}_{n}, \text{ and} \\ \langle M'\tau,M''\tau \rangle= M'\tau \oplus M''\tau\leqslant \mathbb{Z}^m. \end{array} \right. \]

Remark 2.13 Note that, in general, $L_{M'}=M'\cap \mathbb {Z}^m \leqslant M'\tau$ and $L_{M''}=M''\cap \mathbb {Z}^m \leqslant M''\tau$ and so the condition $\langle M'\tau, M''\tau \rangle = M'\tau \oplus M''\tau$ implies (but it is stronger than) $\langle L_{M'}, L_{M''} \rangle = L_{M'} \oplus L_{M''}$.

Note also that, if $M'$ and $M''$ are strongly complementary, a basis for $M'\circledast M''$ can be obtained by just taking the (disjoint) union of a basis for $M'$ and a basis for $M''$; in particular, $M'\circledast M''$ is finitely generated if and only if $M'$ and $M''$ are so. Accordingly, we define the external s.c.-product of two FTFA groups to be

\[ (\mathbb{F}_{\!n'} \times \mathbb{Z}^{m'}) \circledast (\mathbb{F}_{\!n''} \times \mathbb{Z}^{m''}) = (\mathbb{F}_{\!n'} * \mathbb{F}_{\!n''}) \times (\mathbb{Z}^{m'} \oplus \mathbb{Z}^{m''}) \,\simeq\, \mathbb{F}_{\!n'+n''} \times \mathbb{Z}^{m'+ m''}. \]

In particular, s.c.-products agglutinate both free products and direct sums in the corresponding factors; that is, if $M',M''\leqslant {\mathbb {F}_{n}}$ then $M'\circledast M''=M'*M''$; and if $M',M''\leqslant \mathbb {Z}^m$ then $M'\circledast M''=M'\oplus M''$.

Also, given arbitrary groups $A,B,C,D$, and homomorphisms $\alpha \colon A \to C$ and $\beta \colon B \to D$, we define the three homomorphisms $\alpha *\beta \colon A*B\to C*D$, $\alpha \oplus \beta \colon A\oplus B\to C\oplus D$ and $\alpha \circledast \beta \colon A*B\to C\oplus D$ in the natural ways, each mapping $a\in A$ to $a\alpha$, and $b\in B$ to $b\beta$ into the corresponding codomain.

Theorem 2.14 Let $H'_1,\ldots,H'_k\leqslant \mathbb {F}_{\!n'}\times \mathbb {Z}^{m'} = G'$ and $H''_1,\ldots,H''_k\leqslant \mathbb {F}_{\!n''}\times \mathbb {Z}^{m''}=G''$ be $k\geq 2$ subgroups of $G'$ and $G''$, respectively. Write $r'=\mathrm {rk}( \bigcap _{j=1}^k H'_j\pi )$, $r''=\mathrm {rk}( \bigcap _{j=1}^k H''_j\pi )$, and consider $\langle H'_1, H''_1 \rangle,\ldots,\langle H'_k, H''_k \rangle \leqslant G' \circledast G'' = (\mathbb {F}_{\!n'}*\mathbb {F}_{\!n''})\times (\mathbb {Z}^{m'}\oplus \mathbb {Z}^{m''})$. Then, if $\min (r',r'')\neq 1$:

(2.9)\begin{equation} \bigcap\nolimits_{j=1}^k \langle H'_j, H''_j \rangle \text{ is f.g.} \ \Leftrightarrow \text{both } \bigcap\nolimits_{j=1}^k H'_j \quad \text{and}\quad \bigcap\nolimits_{j=1}^k H''_j \text{ are f.g.} \end{equation}

Proof. Contrary to what happens in the free ambient (e.g. in proposition 2.11), the claimed property does not seem to pass through induction over $k$. Hence, we need to use the precise description obtained in theorem 2.9 (instead of just using proposition 2.5 inductively) in order to analyse the multiple intersections $\bigcap _{j=1}^k H'_j$ and $\bigcap _{j=1}^k H''_j$, and to compare them to $\bigcap _{j=1}^k \langle H'_j, H''_j\rangle$.

Consider general subgroups $H'_1,\ldots,H'_k \leqslant G'$ and $H''_1,\ldots,H''_k \leqslant G''$ (with no extra assumptions, at the moment, on $r'$ and $r''$) and fix a basis for each of them, say:

\begin{align*} H'_i & = \big\langle u'_{i,1} \mathrm{t}^\mathbf{a'_{i,1}}, u'_{i,2} \mathrm{t}^\mathbf{a'_{i,2}},\ldots ; \mathrm{t}^\mathbf{b'_{i,1}},\ldots ,\mathrm{t}^\mathbf{b'_{i,s'_i}}\big\rangle \,\leqslant\, \mathbb{F}_{\!n'}\times \mathbb{Z}^{m'}=G', \\ H''_i & = \big\langle u''_{i,1} \mathrm{t}^\mathbf{a''_{i,1}}, u''_{i,2} \mathrm{t}^\mathbf{a''_{i,2}},\ldots ; \mathrm{t}^\mathbf{b''_{i,1}},\ldots ,\mathrm{t}^\mathbf{b''_{i,s''_i}}\big\rangle \,\leqslant\, \mathbb{F}_{\!n''}\times \mathbb{Z}^{m''}=G'', \end{align*}

where, for every $i=1,\ldots,k$ and every $j$, $u'_{i,j}\in \mathbb {F}_{\!n'}$, $u''_{i,j}\in \mathbb {F}_{\!n''}$, $\mathbf {a'_{i,j}}, \mathbf {b'_{i,j}}\in \mathbb {Z}^{m'}$ and $\mathbf {a''_{i,j}}, \mathbf {b''_{i,j}}\in \mathbb {Z}^{m''}$. For $i=1,\ldots,k$, we write $r'_i=\mathrm {rk}(H'_i\pi )$, $r''_i=\mathrm {rk}(H''_i\pi )$, $s'_i=\mathrm {rk}(L'_i)\leq m'$ and $s''_i=\mathrm {rk}(L''_i)\leq m''$, where $L'_i=H'_i\cap \mathbb {Z}^{m'}$ and $L''_i=H''_i\cap \mathbb {Z}^{m''}$.

With the data from the basis for $H'_i$, $i=1,\ldots,k$, we adapt the intersection diagram (figure 2) and notation adding primes everywhere; i.e. the abelianization maps are $\rho '_i \colon H'_i\pi \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r'_i}$ and $\rho '\colon \bigcap _{j=1}^k H'_j\pi \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r'}$; the inclusion maps are $\iota '_i \colon \bigcap _{j=1}^k H'_j\pi \hookrightarrow H'_i\pi$; the abelianization of the $\iota '_i$'s are ${P'_i \colon \mathbb {Z}^{r'} \rightarrow \mathbb {Z}^{r'_i}}$; the completion homomorphisms are $A'_i\colon \mathbb {Z}^{r'_i}\to \mathbb {Z}^{m'}$; $L'_i =H'_i\cap \mathbb {Z}^{m'}=\langle \mathbf {b'_{i,1}},\ldots, \mathbf {b'_{i,s'_i}} \rangle$; $\mathbf {L'_i}$ is the $s'_i \times m'$ integral matrix having $\mathbf {b'_{i,j}}$ as $j$-th row, $i=1,\ldots,k$; $\mathbf {L'}$ is the $(\sum _{j=1}^k s'_j )\times (k-1)m'$ integral matrix from lemma 2.8; and the stack homomorphism is

(2.10)\begin{equation} \begin{array}{rcl} R'\colon \mathbb{Z}^{r'} & \to & \mathbb{Z}^{m'}\oplus \stackrel{_{(k-1)}}{\ldots} \oplus \mathbb{Z}^{m'} \\ w & \mapsto & (wR'_2,\ldots ,wR'_k) , \end{array} \end{equation}

where $R'_i=P'_iA'_i-P'_{i-1}A'_{i-1}$, for $i=2,\ldots,k$.

In this situation, theorem 2.9 characterizes when the intersection $H'_1\cap \cdots \cap H'_k$ is finitely generated:

(2.11)\begin{align} H'_1\cap \cdots \cap H'_k \quad \text{is f.g.} \quad \Leftrightarrow \quad \left\{ \begin{array}{@{}l} r'=0,1, \quad \text{or} \\ 2\leq r'<\infty\quad \text{and}\quad (\mathrm{Im} (\mathbf{L'}))(R'){^{{\boldsymbol{\leftarrow}}}} \leqslant_{\mathsf{fi}} \mathbb{Z}^{r'}. \end{array}\right. \end{align}

In the exact same manner, we construct the intersection diagram for $H''_1\cap \cdots \cap H''_k$; the notation being exactly the same as in the previous paragraph, replacing primes by double primes everywhere. Repeating the previous argument, we have:

(2.12)\begin{align} H''_1\cap \cdots \cap H''_k \quad \text{is f.g.} \quad \Leftrightarrow \quad \left\{ \begin{array}{@{}l} r''=0,1, \quad \text{or} \\ 2\leq r''<\infty\quad \text{and}\quad (\mathrm{Im} (\mathbf{L''}))(R''){^{{\boldsymbol{\leftarrow}}}} \leqslant_{\mathsf{fi}} \mathbb{Z}^{r''}. \end{array} \right. \end{align}

Now, consider the combined subgroups $H_1=\langle H'_1, H''_1\rangle, \ldots,H_k=\langle H'_k, H''_k\rangle$, all of them viewed as subgroups of $G =G'\circledast G''=(\mathbb {F}_{\!n'}*\mathbb {F}_{\!n''})\times (\mathbb {Z}^{m'}\oplus \mathbb {Z}^{m''})$. The key point is to observe that the intersection diagram for $H_1\cap \cdots \cap H_k$ is just the $\circledast$-juxtaposition of the previous two (primed and double primed) diagrams. In fact, for $i=1,\ldots,k$, since $H'_i$ and $H''_i$ are contained in the strongly complementary subgroups $\mathbb {F}_{\!n'}\times \mathbb {Z}^{m'}$ and $\mathbb {F}_{\!n''}\times \mathbb {Z}^{m''}$ of $(\mathbb {F}_{\!n'}*\mathbb {F}_{\!n''})\times (\mathbb {Z}^{m'}\oplus \mathbb {Z}^{m''})$ and hence they are strongly complementary as well, we can obtain a basis for $H_i=H'_i\circledast H''_i$ by taking the disjoint union of the bases we already have for $H'_i$ and for $H''_i$, namely:

\begin{align*} H_i=H'_i \circledast H''_i = \big\langle \{ u'_{i,1} \mathrm{t}^\mathbf{a'_{i,1}}, u'_{i,2} \mathrm{t}^\mathbf{a'_{i,2}},\ldots \}\cup\{ u''_{i,1} \mathrm{t}^\mathbf{a''_{i,1}}, u''_{i,2} \mathrm{t}^\mathbf{a''_{i,2}},\ldots \}; \mathrm{t}^\mathbf{b'_{i,1}},\ldots ,\mathrm{t}^\mathbf{b'_{i,s'_i}} ,\\ \mathrm{t}^\mathbf{b''_{i,1}},\ldots ,\mathrm{t}^\mathbf{b''_{i,s''_i}} \big\rangle, \end{align*}

Now, by proposition 2.11:

\begin{align*} H_1\pi \cap \cdots \cap H_k\pi & = \langle H'_1 \pi, H''_1\pi \rangle \cap \cdots \cap \langle H'_k \pi, H''_k \pi\rangle\\ & = (H'_1 \pi \cap \cdots \cap H'_k\pi)*(H''_1 \pi \cap \cdots \cap H''_k\pi). \end{align*}

Hence, the intersection diagram for $H_1\pi \cap \cdots \cap H_k\pi$ consists of (for $i=1,\ldots,k$):

1. (i) the abelianization map $\rho _i\colon H_i\pi = H'_i\pi *H''_i\pi \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r'_i}\oplus \mathbb {Z}^{r''_i}=\mathbb {Z}^{r_i}$ is $\rho _i=\rho '_i\circledast \rho ''_i$, where $r_i=r'_i+r''_i$; and $\rho \colon \bigcap _{j=1}^{k} H_j\pi =(\bigcap _{j=1}^{k} H'_j \pi )*(\bigcap _{j=1}^{k} H''_j \pi ) \xrightarrow {\ }\mathrel {\mkern -14mu}\rightarrow \mathbb {Z}^{r'}\oplus \mathbb {Z}^{r''}=\mathbb {Z}^{r}$ is $\rho =\rho '\circledast \rho ''$, where $r=r'+r''$;

2. (ii) the natural inclusion map $\iota _i \colon \bigcap _{j=1}^{k} H_j \pi = (\bigcap _{j=1}^{k} H'_j \pi )*(\bigcap _{j=1}^{k} H''_j \pi ) \hookrightarrow H_i =H'_i\pi * H''_i\pi$ is $\iota _i =\iota '_i *\iota ''_i$;

3. (iii) the abelianization of $\iota _i$, $P_i\colon \mathbb {Z}^r =\mathbb {Z}^{r'}\oplus \mathbb {Z}^{r''} \to \mathbb {Z}^{r'_i}\oplus \mathbb {Z}^{r''_i}=\mathbb {Z}^{r_i}$, is $P_i=P'_i \oplus P''_i$;

4. (iv) the completion homomorphism $A_i\colon \mathbb {Z}^{r_i}=\mathbb {Z}^{r'_i}\oplus \mathbb {Z}^{r''_i} \to \mathbb {Z}^{m'}\oplus \mathbb {Z}^{m''}=\mathbb {Z}^{m}$ is $A_i=A'_i \oplus A''_i$;

5. (v) $L_i =H_i\cap (\mathbb {Z}^{m'}\oplus \mathbb {Z}^{m''})=\langle \mathbf {b'_{i,1}},\ldots,\mathbf {b'_{i,s'_i}}, \mathbf {b''_{i,1}},\ldots,\mathbf {b''_{i,s''_i}} \rangle =L'_i\oplus L''_i$, where $s_i=\mathrm {rk}(L_i)= s'_i+s''_i\leq m'+m''=m$ and, accordingly, $\mathbf {L_i}$ is the $s_i\times m$ integral matrix $\mathbf {L_i} =(\!\begin{smallmatrix} \mathbf {L'_i} & \\ & \mathbf {L''_i} \end{smallmatrix}\!)$.

Figure 3 summarizes the combined situation so far.

Figure 3. Intersection diagram for $\bigcap _{j=1}^{k} ( H'_j \circledast H''_j )$.

Then, for $i=2,\ldots,k$, the homomorphisms $R_i \colon \mathbb {Z}^{r'} \oplus \mathbb {Z}^{r''} \to \mathbb {Z}^{m'}\oplus \mathbb {Z}^{m''}$ are given by

\begin{align*} R_i & = P_iA_i-P_{i-1}A_{i-1} \\ & = (P'_i \oplus P''_i)(A'_i\oplus A''_i)-(P'_{i-1}\oplus P''_{i-1})(A'_{i-1}\oplus A''_{i-1}) \\ & = (P'_iA'_i \oplus P''_iA''_i)-(P'_{i-1}A'_{i-1}\oplus P''_{i-1}A''_{i-1}) \\ & = (P'_iA'_i-P'_{i-1}A'_{i-1})\oplus (P''_iA''_i-P''_{i-1}A''_{i-1}) \\ & = R'_i\oplus R''_i \end{align*}

and, using them, we build the combined stack homomorphism:

\[ \begin{array}{rcl} R=(R_2,\ldots ,R_k) \colon \mathbb{Z}^r=\mathbb{Z}^{r'}\oplus \mathbb{Z}^{r''} & \to & (\mathbb{Z}^{m'} \oplus \mathbb{Z}^{m''})\, \oplus \stackrel{_{(k-1)}}{\ldots} \oplus \, (\mathbb{Z}^{m'} \oplus \mathbb{Z}^{m''}). \\ \mathbf{w} = (\mathbf{w'}, \mathbf{w''}) & \mapsto & (\underbrace{\mathbf{w'}R'_2, \mathbf{w''}R''_2}_{\mathbf{w} R_2}, \ldots ,\underbrace{\mathbf{w'}R'_k, \mathbf{w''}R''_k}_{\mathbf{w}R_k}) \end{array} \]

Finally, the combined matrix $\mathbf {L}$ takes the form:

(2.13)\begin{equation} \mathbf{L}=\left(\begin{array}{@{}rrrcc@{}} \mathbf{L_1} & & & & \\ - \mathbf{L_2} & \mathbf{L_2} & & & \\ & -\mathbf{L_3} & \mathbf{L_3} & & \\ & & \ddots & \ddots & \\ & & & -\mathbf{L_{k-1}} & \mathbf{L_{k-1}} \\ & & & & -\mathbf{L_{k}} \end{array}\right)\in M_{(\sum_j s_j )\times (k-1)m} (\mathbb{Z}). \end{equation}

Now, applying theorem 2.9 to the combined situation, we have $(H_1\cap\cdots\cap H_k)\pi{=} (\mathrm {Im} (\mathbf {L}))R^{{\boldsymbol {\leftarrow }}} \rho ^{{\boldsymbol {\leftarrow }}}$ is a normal subgroup of $H_1\pi \cap \cdots \cap H_k\pi$ and,

(2.14)\begin{equation} H_1\cap \cdots \cap H_k \quad \text{is f.g.} \quad \Leftrightarrow \quad \left\{ \begin{array}{@{}l} r=0,1, \quad \text{or} \\ 2\leq r<\infty\quad \text{and}\quad (\mathrm{Im} (\mathbf{L}))R{^{{\boldsymbol{\leftarrow}}}} \leqslant_{\mathsf{fi}} \mathbb{Z}^{r}. \end{array} \right. \end{equation}

Furthermore, at this point we claim that

(2.15)\begin{equation} \big( \mathrm{Im} (\mathbf{L}) \big)R^{{\boldsymbol{\leftarrow}}} =(\mathrm{Im} (\mathbf{L}'))(R')^{{\boldsymbol{\leftarrow}}} \oplus (\mathrm{Im} (\mathbf{L}''))(R'')^{{\boldsymbol{\leftarrow}}} \leqslant \mathbb{Z}^{r'}\oplus \mathbb{Z}^{r''} = \mathbb{Z}^r. \end{equation}

To see this, observe that $(\mathbf {w'}, \mathbf {w''})\in ( \mathrm {Im} (\mathbf {L}) )R^{{\boldsymbol {\leftarrow }}}$ if and only if

(2.16)\begin{equation} (\mathbf{w'}, \mathbf{w''})R = (\mathbf{w'}R'_2, \mathbf{w''}R''_2, \ldots ,\mathbf{w'}R'_k, \mathbf{w''}R''_k) \,\in\, \mathrm{Im} (\mathbf{L}), \end{equation}

that is, if and only if there exist integral vectors $\mathbf {c'_1}, \mathbf {c''_1}, \ldots,\mathbf {c'_k}, \mathbf {c''_k}$ of the corresponding sizes such that

(2.17)\begin{equation} (\mathbf{w'}R'_2, \mathbf{w''}R''_2, \ldots ,\mathbf{w'}R'_k, \mathbf{w''}R''_k) = (\mathbf{c'_1}, \mathbf{c''_1}, \ldots ,\mathbf{c'_k}, \mathbf{c''_k})\mathbf{L}. \end{equation}

But, due to the form (2.13) of the matrix $\mathbf {L}$, this is equivalent to

\[ \bigg\{ \! \begin{array}{@{}l} (\mathbf{w'}R'_2, \ldots ,\mathbf{w'}R'_k) = (\mathbf{c'_1}, \ldots ,\mathbf{c'_k})\mathbf{L'} ,\quad \text{and} \\ (\mathbf{w''}R''_2, \ldots ,\mathbf{w''}R''_k) = (\mathbf{c''_1}, \ldots ,\mathbf{c''_k})\mathbf{L''}, \end{array} \]

which is the same as saying that $\mathbf {w'}R'\in \mathrm {Im} (\mathbf {L'})$ and $\mathbf {w''}R''\in \mathrm {Im} (\mathbf {L''})$ (independently). Therefore, $(\mathbf {w'}, \mathbf {w''})\in ( \mathrm {Im} (\mathbf {L}) )R^{{\boldsymbol {\leftarrow }}}$ if and only if $\mathbf {w'}\in ( \mathrm {Im} (\mathbf {L}') )(R')^{{\boldsymbol {\leftarrow }}}$ and $\mathbf {w''}\in ( \mathrm {Im} (\mathbf {L}'') )(R'')^{{\boldsymbol {\leftarrow }}}$, as claimed.

Finally, let us make use of the hypothesis $\min (r',r'')\neq 1$; by symmetry, we can assume $1\neq r'\leq r''$. Taking into account that $r=r'+r''$, we prove (2.9) by relating equivalences (2.11) and (2.12) with (2.14), and by distinguishing the different possibilities for $r'$ and $r''$:

1. (a) if $r'= 0$ (i.e. if $\bigcap _{j=1}^k H'_j\pi = \{ 1 \}$) then $r = r''$, $\bigcap _{j=1}^k H_j \pi = \bigcap _{j=1}^k H''_j \pi$, $\mathbb {Z}^r =\mathbb {Z}^{r''}$, $P_i=P''_i$, and $R_i=R''_i$; moreover, equation (2.16) takes the form $\mathbf {w''} R=(\mathbf {w''}R''_2, \ldots, \mathbf {w''}R''_k)\,\in \, \mathrm {Im} (\mathbf {L''})$, and hence, $R=R''$. Therefore, $( \bigcap _{j=1}^{k} H_j ) \pi = \mathrm {Im}(\mathbf {L}) R^{{\boldsymbol {\leftarrow }}} \rho ^{{\boldsymbol {\leftarrow }}} = \mathrm {Im}(\mathbf {L''}) (R'')^{{\boldsymbol {\leftarrow }}} (\rho '')^{{\boldsymbol {\leftarrow }}} = ( \bigcap _{j=1}^{k} H''_j ) \pi$ and equivalence (2.9) holds trivially.

2. (b) if $r'\geq 2$ then $r\geq 2$ and, by (2.15), $(\mathrm {Im} (\mathbf {L}))R{^{{\boldsymbol {\leftarrow }}}} \leqslant _{\mathsf {fi}} \mathbb {Z}^{r}$ if and only if $(\mathrm {Im} (\mathbf {L'}))(R'){^{{\boldsymbol {\leftarrow }}}} \leqslant _{\mathsf {fi}} \mathbb {Z}^{r'}$ and $(\mathrm {Im} (\mathbf {L''}))(R''){^{{\boldsymbol {\leftarrow }}}} \leqslant _{\mathsf {fi}} \mathbb {Z}^{r''}$. So, equivalence (2.9) holds.

This completes the proof.

Remark 2.15 In order to understand the intersection of $k\geq 2$ subgroups we have used theorem 2.9, with the technical hypothesis $\min (r',r'')\neq 1$ to avoid the exceptional behaviour shown in the example below, where the equivalence (2.9) fails in the cases $r'=\mathrm {rk}( \bigcap _{j=1}^k H'_j\pi )=1$ and $r''=\mathrm {rk}( \bigcap _{j=1}^k H''_j\pi )\geq 1$. However, note that in the degenerated case $k=1$ there is no intersection to consider and equivalence (2.9) follows immediately from $G'$ and $G''$ being strongly complementary in $G'\circledast G''$, without any assumption on $r'$ or $r''$.

Example 2.16 Let $n\geq 1$, $G'=\mathbb {F}_{\!1}\times \mathbb {Z}^1=\langle x\mid - \rangle \times \langle t\mid - \rangle$ and $G''=\mathbb {F}_{n}\times \mathbb {Z}^0=\langle y_1,\ldots,y_{n} \mid -\rangle$, and take the subgroups $H'_1=\langle x\rangle$ and $H'_2=\langle x\mathrm {t}\rangle$ of $G'$; and $H''_1 =H''_2 =\langle y_1,\ldots,y_{n}\rangle$ of $G''$. Note that $r'=\mathrm {rk}(H'_1\pi \cap H'_2\pi )=1$ and $r''=\mathrm {rk}(H''_1\pi \cap H''_2\pi )=n\geq 1$. Consider then $H_1=\langle H'_1, H''_1 \rangle =\langle x,y_1,\ldots,y_{n} \rangle$ and $H_2=\langle H'_2, H''_2 \rangle =\langle x t, y_1,\ldots,y_n \rangle$, both as subgroups of $G'\circledast G''=\langle x,y_1,\ldots,y_{n} \mid -\rangle \times \langle \mathrm {t} \mid - \rangle =\mathbb {F}_{\!n+1}\times \mathbb {Z}$.

Clearly, $H'_1 \cap H'_2=\{1\}$ and $H''_1\cap H''_2 =\langle y_1,\ldots,y_{n} \rangle$ are both finitely generated, whereas ${H_1 \cap H_2} =\langle x,y_1,\ldots,y_{n}\rangle \cap \langle x\mathrm {t}, y_1,\ldots,y_{n}\rangle =\{w(x,y_1,\ldots,y_{n}) \mid |w|_x =0\}=\langle \! \langle \hspace {1pt} y_1,\ldots,y_{n} \hspace {1pt} \rangle \! \rangle _{\langle x,y_1,\ldots,y_{n} \rangle }$ is not. Hence, equivalence (2.9) can fail whenever $\min (r',r'') = 1$ and theorem 2.14 is as general as possible.

Moreover, observe that adding an extra freely independent letter, say $z$, to $G'$, $H'_1$ and $H'_2$ (and so, forcing $r'=2$ instead of $r'=1$) spoils the counterexample because then $H'_1 \cap H'_2$ becomes $\langle \! \langle \hspace {1pt} z \hspace {1pt} \rangle \! \rangle _{\langle x,z \rangle }$, which is not finitely generated any more.

It is worth mentioning that the proof of theorem 2.14 is a bit delicate, in consonance with the fact that the statement is quite sensible to slight modifications. For example, an equality like (2.7) (from which theorem 2.14 would follow immediately) is not true in the FTFA case, even in the strongly complementary situation; see the example below. This forced us to prove theorem 2.14 directly, adding the complication that the statement does not pass well through induction on $k$ and so, forcing us to work with the multiple intersection situation (theorem 2.9) instead of the easier $k=2$ case (proposition 2.5).

Example 2.17 Consider in $\mathbb {F}_{\!4}\times \mathbb {Z}^2=\langle x_1,x_2,x_3,x_4 \mid -\rangle \times \langle t_1, t_2 \mid [t_1, t_2]\rangle$, the strongly complementary subgroups ${M'=\langle x_1,x_2,\mathrm {t}^\mathbf {(1,0)} \rangle }$ and $M''=\langle x_3,x_4,\mathrm {t}^\mathbf {(0,1)} \rangle$, and the respective subgroups

\begin{align*} H'_1 & =\langle x_1,x_2 \rangle, \quad H'_2=\langle x_1\mathrm{t}^\mathbf{(1,0)}, x_2 \rangle \,\leqslant\, M', \\ H''_1 & =\langle x_3,x_4 \rangle, \quad H''_2=\langle x_3\mathrm{t}^\mathbf{(0,1)}, x_4 \rangle \,\leqslant\, M'', \end{align*}

clearly satisfying $r'=\mathrm {rk}(H'_1\pi \cap H'_2\pi )=2$ and $r''=\mathrm {rk}(H''_1\pi \cap H''_2\pi )=2$. It is well known that $H'_1\cap H'_2=\langle x_1^{-i} x_2x_1^{i} , i\in \mathbb {Z} \rangle$ and $H''_1\cap H''_2=\langle x_3^{-i} x_4 x_3^{i} , i\in \mathbb {Z} \rangle$ are not finitely generated; see proposition 1.1. Hence,

\[ \langle H'_1 \cap H'_2, H''_1\cap H''_2 \rangle=(H'_1 \cap H'_2)*(H''_1\cap H''_2)=\langle x_1^{{-}i} x_2 x_1^{i}, x_3^{{-}i} x_4 x_3^{i} \mid i\in \mathbb{Z} \rangle \]

and a quick look at its Stallings automaton tells us that this subgroup does not contain the element $x_3^{-1} x_2 x_3$ while, clearly, $x_3^{-1} x_2x_3\in \langle H'_1, H''_1 \rangle =\langle x_1, x_2, x_3, x_4 \rangle$ and $x_3^{-1} x_2 x_3\in \langle H'_2, H''_2 \rangle =\langle x_1\mathrm {t}^\mathbf {(1,0)}, x_2, x_3\mathrm {t}^\mathbf {(0,1)}, x_4 \rangle$. Thus, proposition 2.11 is not true in the FTFA context, even in the strongly complementary situation. Note, however, that this example satisfies the less demanding statement from theorem 2.14, namely the subgroups $H'_1\cap H'_2$, $H''_1\cap H''_2$, and

\begin{align*} \langle H'_1, H''_1 \rangle\cap \langle H'_2, H''_2 \rangle & = \langle x_1, x_2, x_3, x_4 \rangle \cap \langle x_1\mathrm{t}^\mathbf{(1,0)}, x_2, x_3\mathrm{t}^\mathbf{(0,1)}, x_4 \rangle \\ & = \{w(x_1, x_2, x_3, x_4)\mid |w|_{x_1}=|w|_{x_3}=0\} \end{align*}

are all of the same character: not finitely generated.

3. Intersection configurations

In this section, we introduce some basic terminology, in order to conveniently state our next results. The first notion is that of $k$-configuration.

Definition 3.1 Let $k\in \mathbb {N}_{\geq 1}$. A $k$-configuration is a map $\chi$ from ${\mathcal {P}}([k])\setminus \{\varnothing \}$ to the binary set $\{0, 1\}$, i.e.

\[ \chi\colon {\mathcal{P}}([k])\setminus \{\varnothing\} \to \{0, 1\}. \]

Note that this is just a fancy way to specify a family of nonempty subsets of $[k]$. That is, $\chi$ is just the indicator function $\chi_{\mathcal {I}}^{_{(k)}}$ of the inclusion $\mathcal {I} = (1)\chi^{{\boldsymbol {\leftarrow }}} \subseteq \mathcal {P}([k])\setminus \{\varnothing \}$; then we say that $\mathcal {I}$ is the support, and $k$ is the dimension of $\chi$. In particular, the $k$-configuration $\mathsf {0}^{_{(k)}}_{\phantom {a}}=\chi_{\varnothing }^{_{(k)}}$ (sending every nonempty set of indices to $0$) is called the zero $k$-configuration. The one $k$-configuration $\mathsf {1}^{_{(k)}}_{\phantom {a}}=\chi_{\mathcal {P}([k])\setminus \{\varnothing \}}^{_{(k)}}$ is defined accordingly. When $\mathcal {I}=\{I\}$ (i.e. only one nonempty subset $I\subseteq [k]$ goes to $1$), we write $\chi_{\{\hspace {-1pt}I\hspace {-1pt}\}}^{_{(k)}}=\chi_{I}^{_{(k)}}$ and we say that it is an almost- $\mathsf {0}$ $k$-configuration. If the ambient is clear (or does not affect the ongoing argument) we usually omit any reference to it and simply write $\chi_{\mathcal {I}}^{_{(k)}}= {\chi }_{\scriptstyle {\mathcal {I}}}$, $\mathsf {0}^{_{(k)}}_{\phantom {a}}=\mathsf {0}$, $\mathsf {1}^{_{(k)}}_{\phantom {a}}=\mathsf {1}$, etc.

A convenient way to visualize $k$-configurations is as 2-coloured, oriented, $k$-dimensional hypercube digraphs, where white vertices correspond to nonempty subsets of $[k]$ going to $0$, black vertices correspond to nonempty subsets of $[k]$ going to $1$, and arcs (directed edges) denote inclusion into a subset with exactly one more element. In our representation, the top vertex corresponds to the empty subset (which is excluded in definition 3.1 and will be ignored in the graphical representation), and the bottom vertex corresponds to the total subset $I=[k]$.

Note that, with this interpretation, the family of subsets containing (resp., not containing) a given index $i\in [1,k]$ is a maximal hyperface of the hypercube.

Example 3.2 The lattice of subsets of $[k]$ with $k=3$ can be represented as shown in figure 4.

Figure 4. Lattice of subsets of $[3] = \{1,2,3\}$.

Now, colouring in white (resp., black) the vertices mapping to $0$ (resp., $1$) by $\chi$ provides the desired representation for the $3$-configurations (see figure 5).

Figure 5. From left to right, a random $3$-configuration, the $\mathsf {0}$ $3$-configuration, and two almost-$\mathsf {0}$ $3$-configurations.

Now, we introduce a couple of ways to build new configurations from older ones.

Definition 3.3 Given two $k$-configurations $\chi = {\chi }_{\scriptstyle {\mathcal {I}}}, \chi '={\chi }_{\scriptstyle {\mathcal {I}'}}$, we define their join as the new $k$-configuration ${\chi }_{\scriptstyle {\mathcal {I}}} \vee {\chi }_{\scriptstyle {\mathcal {I}'}} = {\chi }_{\scriptstyle {\mathcal {I} \cup \mathcal {I}'}}$. That is (see figure 6),

\[ \begin{array}{rcl} \chi\vee \chi' \colon \mathcal{P}([k])\setminus \{\varnothing\} & \to & \{0, 1\} \\ I & \mapsto & \left\{ \begin{array}{@{}lcl} 0 & & \text{if } (I)\chi=(I)\chi'=0, \\ 1 & & \text{otherwise.} \end{array}\right. \end{array} \]

Figure 6. Schematic representation for ${\chi }_{\scriptstyle {\{\{1\},\{1,2\}\}}} \vee {\chi }_{\scriptstyle {\{1,2\}}} ={\chi }_{\scriptstyle {\{\{1\},\{1,2\}\}}}$.

Definition 3.4 Given two $k$-configurations $\chi, \chi '$ and $\delta \in \{0,1\}$, we define the $\delta$-overlap of $\chi$ and $\chi '$ as the new $(k+1)$-configuration given by (see figure 7)

\[ \begin{array}{rcl} \chi\boxplus_{\delta} \chi' \colon \mathcal{P}([k+1])\setminus \{\varnothing\} & \to & \{0, 1\} \\ I\, & \mapsto & \Bigg\{ \begin{array}{@{}lcl} (I)\chi & & \text{if } k+1\not\in I, \\ (I\setminus \{k+1\})\chi' & & \text{if } \{k+1\}\subsetneq I,\\ \delta & & \text{if } \{k+1\}=I. \end{array} \end{array} \]

Figure 7. Schematic representation for ${\chi }_{\scriptstyle {\{\{1\},\{1,2\}\}}} \boxplus _1 {\chi }_{\scriptstyle {\{\{1,2\}\}}} = {\chi }_{\scriptstyle {\{\{1\},\{3\},\{1,2\},\{1,2,3\}\}}}$.

Remark 3.5 Note that the join of two $k$-configurations is, again, a $k$-configuration whereas their $\delta$-overlap is a $(k+1)$-configuration. Moreover, the join is a commutative operator while, in general, the $\delta$-overlap is not.

Next, we define the related notion of intersection configuration, which is essential to state our results.

Definition 3.6 Let $G$ be a group, let $k\geq 1$, and let $\mathcal {H}=\{ H_i \}_{i\in [k]}$ be a family of $k$ subgroups of $G$ (with possible repetitions). For every nonempty $I\subseteq [k]$, we write $H_I =\bigcap _{\, i\in I} H_i$; note that $H_I \cap H_J = H_{I \cup J}$. We define the intersection configuration determined by $\mathcal {H}$, denoted by $\chi^\mathcal {H}$, as

\[ \begin{array}{rcl} \chi^\mathcal{H} \colon \mathcal{P}([k])\setminus \{\varnothing\} & \to & \{0, 1\} \\ I & \mapsto & \left\{ \begin{array}{@{}ll} 0 & \text{if } H_I \text{ is finitely generated,} \\ 1 & \text{if } H_I \text{ is not finitely generated.} \end{array}\right. \end{array} \]

We say that a $k$-configuration $\chi$ is realizable in $G$ if it is the intersection configuration of some family of $k$ subgroups of $G$; that is, if there exists a family $\mathcal {H}$ of $k$ subgroups of $G$ such that $\chi^{\mathcal {H}}=\chi$; in this case, we also say that ${\mathcal {H}}$ realizes $\chi$, and that $G$ admits a realization of $\chi$.

For example, the $\mathsf {0}$ $k$-configuration is always realizable in any group $G$ (realized, for instance, by the trivial $k$-family ${\mathcal {H}}=\{ \{1\} \}_{i\in [k]}$). On the contrary, the $\mathsf {1}$ $k$-configuration is realizable in a group $G$ if and only if $G$ contains a non-f.g. subgroup $H\leqslant G$; in this case, it is enough to take ${\mathcal {H}}=\{ H \}_{i\in [k]}$. As a third example, for a $k$-configuration $\chi$ to be realizable in a free group ${\mathbb {F}_{n}}$, a necessary condition is that it does not violate the Howson property, i.e. for every nonempty $I,J\subseteq [k]$, $(I)\chi =(J)\chi =0$ implies $(I\cup J)\chi =0$. That is, two white vertices never meet at a black vertex in the directed 2-coloured hypercube representing $\chi$. In § 6 we see that this condition indeed characterizes the realizable configurations in a free group ${\mathbb {F}_{n}}$, $n\geq 2$ (see theorem 6.7).

Of course, if $G_1\leqslant G_2$ then every $k$-configuration realizable in $G_1$ is also realizable in $G_2$. In particular since, for $2\leq r_1, r_2\leq \infty$, $\mathbb {F}_{\!r_1}\times \mathbb {Z}^m$ and $\mathbb {F}_{\!r_2}\times \mathbb {Z}^m$ are both subgroups of each other, the $k$-configurations realizable in $\mathbb {F}_{\!r_1}\times \mathbb {Z}^m$ coincide with those realizable in $\mathbb {F}_{\!r_2}\times \mathbb {Z}^m$; therefore, when considering FTFA groups, it is enough to restrict our attention to $\mathbb {F}_{2}\times \mathbb {Z}^m$. In contrast, as we see below, the abelian rank $m$ plays an important role in this respect: the set of $k$-configurations which are realizable in $\mathbb {F}_{2}\times \mathbb {Z}^m$ grows strictly with $m$ (see proposition 4.5).

A natural question in this context is whether there exist groups admitting realizations of any finite configuration.

Definition 3.7 A group $G$ is called intersection-saturated if every finite configuration is realizable in $G$.

In § 5 we use the results obtained for FTFA groups to exhibit explicit examples of finitely presented intersection-saturated groups.

4. Unrealizable configurations

The description obtained in [8] suggests a high degree of flexibility for the intersections of subgroups of FTFA groups: not only these groups are non-Howson, but it is not possible to bound the rank of the intersection of two finitely generated subgroups in terms of their ranks, even when it is finitely generated. In this section, we show that, despite this flexibility, there are indeed obstructions to the realizability of $k$-configurations in $\mathbb {F}_{n}\times \mathbb {Z}^m$, and that these obstructions are dictated by the ambient abelian rank $m$. The cornerstone result is the following easy lemma.

Lemma 4.1 Let $H_1,\ldots,H_k$ be $k\geq 2$ arbitrary subgroups of ${\mathbb {F}_{n}}\times \mathbb {Z}^m$. If, for some nonempty subsets $I,J\subseteq [k]$, $H_I = \bigcap _{i \in I} H_i$ and $H_J= \bigcap _{j \in J} H_j$ are finitely generated whereas $H_{I\cup J}=H_I\cap H_J$ is not, then there exist $i\in I$ and $j\in J$ such that $L_i = H_i \cap \mathbb {Z}^m$ and $L_j = H_j \cap \mathbb {Z}^m$ both have infinite index in $\mathbb {Z}^m$; that is, $L_i$ and $L_j$ are free-abelian groups of rank strictly smaller than $m$.

Proof. Consider the intersection diagram for the subgroups $H_I$ and $H_J$ (see figure 1, replacing $1,2$ with $I,J$, respectively). Since $H_I$ and $H_J$ are finitely generated, $H_I\pi$ and $H_J\pi$ are so and, by the Howson property of free groups, $H_I\pi \cap H_J\pi$ is finitely generated as well. On the contrary, $H_{I\cup J} = H_I \cap H_J$ (and hence $(H_I\cap H_J)\pi =(L_I+L_J)R^{{\boldsymbol {\leftarrow }}}\rho ^{{\boldsymbol {\leftarrow }}}$, which is a normal subgroup of $H_I \pi \cap H_J\pi$, see proposition 2.5) is not finitely generated. Therefore, $(H_{I}\cap H_{J})\pi$ must have infinite index in $H_I \pi \cap H_J\pi$, and $L_I+L_J$ (and so both $L_I$ and $L_J$) must also have infinite index in $\mathbb {Z}^m$. Since $L_I=\bigcap _{i\in I} L_i$, at least one of the $L_i$'s, $i\in I$, must have infinite index in $\mathbb {Z}^m$, i.e. $\mathrm {rk}(L_i)\leq m-1$; similarly for $J$.

Remark 4.2 We say that a collection of $r$ subsets $\mathcal {I}=\{I_1, \ldots,I_r\}\subseteq {\mathcal {P}}([k])$ is independent if, when considering all the $2^r$ possible unions among them, we obtain $2^r$ different results, i.e. whenever for every $S,T\subseteq \{1,\ldots,r\}$, $\bigcup _{s\in S} I_s =\bigcup _{t\in T} I_t$ implies $S=T$ (understanding that $\bigcup _{s\in \emptyset } I_s =\emptyset$). Note the following immediate properties of this notion: (i) any collection of sets containing the empty set $\varnothing$ is not independent; (ii) for $I\subseteq [k]$, $\{ I\}$ is independent if and only if $I\neq \varnothing$; (iii) if $\{I_1, \ldots,I_r\}$ is independent then $r\leq k$; (iv) if $\{I_1, \ldots,I_r\}$ is independent then any subset of it is also independent. Moreover, avoiding coincidences with the total union is enough to get independence: $\{I_1, \ldots,I_r\}$ is independent if and only if, for every $M\subseteq \{1,\ldots,r\}$ with $|M|=r-1$, we have $\bigcup _{m\in M} I_m \neq I_1\cup \cdots \cup I_r$. Indeed, the implication to the right is obvious; for the implication to the left, take $S,T\subseteq \{1,\ldots,r\}$ satisfying $\bigcup _{s\in S} I_s =\bigcup _{t\in T} I_t$; if $S\neq T$ then there is an index contained in one of them and not in the other, say $j\in S\setminus T$, and then (We use the standard notation putting a hat to denote a missing element.):

\begin{align*} I_1\cup I_2\cup \cdots \cup I_r & = \textstyle{I_1\cup \cdots \cup \widehat{I_j} \cup \cdots \cup I_r\cup \bigcup_{s\in S} I_s} \\ & = \textstyle{I_1\cup \cdots \cup \widehat{I_j}\cup \cdots \cup I_r \cup \bigcup_{t\in T} I_t = I_1\cup \cdots \cup \widehat{I_j}\cup \cdots \cup I_r,} \end{align*}

contradicting our assumption.

Proposition 4.3 Let $\chi$ be a $k$-configuration for which there is a (independent) collection of $r\geq 2$ nonempty subsets $I_1,\ldots,I_r\subseteq [k]$ such that, for every $j\in \{1,\ldots,r\}$, $(I_1\cup \cdots \cup \widehat {I_j}\cup \cdots \cup I_r)\chi =0$, but $(I_1\cup \cdots \cup I_r)\chi =1$. Then $\chi$ is not realizable in ${\mathbb {F}_{n}}\times \mathbb {Z}^{r-2}$.

Proof. Note that, by remark 4.2, the hypothesis on $\chi$ forces the collection of subsets $\{ I_1,\ldots,I_r\}$ to be independent; in particular, they are all nonempty and $2\leq r\leq k$.

We prove the non-realizability of $\chi$ in ${\mathbb {F}_{n}}\times \mathbb {Z}^{r-2}$, by induction on $r\geq 2$. In the case $r=2$, the statement is clearly true, as otherwise the Howson property for free groups ${\mathbb {F}_{n}} ={\mathbb {F}_{n}}\times \mathbb {Z}^{2-2}$ would be violated.

Now, assume the claim is true for $r-1 \geq 2$, and let us prove it for $r$. Let $\chi$ be a $k$-configuration with $I_1,\ldots,I_r$ satisfying the hypothesis, assume it is realizable in ${\mathbb {F}_{n}}\times \mathbb {Z}^{r-2}$, say by subgroups $H_1,\ldots,H_k\leqslant {\mathbb {F}_{n}}\times \mathbb {Z}^{r-2}$, and let us find a contradiction. We have that, for every $j\in \{1,\ldots,r\}$, $H_{I_1\cup \cdots \cup \widehat {I_j}\cup \cdots \cup I_r}= H_{I_1}\cap \cdots \cap \smash {\widehat {H_{I_j}}}\cap \cdots \cap H_{I_r}$ is finitely generated, while $H_{I_1\cup \cdots \cup I_r}=H_{I_1}\cap \cdots \cap H_{I_r}$ is not. Since both $H_{I_2\cup \cdots \cup I_r}$ and $H_{I_1\cup I_3\cup \cdots \cup I_r}$ are finitely generated but their intersection $H_{I_1\cup \cdots \cup I_r}$ is not, lemma 4.1 tells us that there exists $\ell \in I_1\cup \cdots \cup I_r$ such that $L_{\ell }$ has infinite index in $\mathbb {Z}^{r-2}$ and so, rank less than or equal to $r-3$. Up to renumbering the subsets, we can assume $\ell \in I_r$ and so, $L_{I_r}=\bigcap _{i\in I_r} L_i$ also has rank less than or equal to $r-3$. Note that, as a group, $H_{I_r}$ is then isomorphic to the direct product of a free group $F$, and $L_{I_r}\simeq \mathbb {Z}^{\mathrm {rk} (L_{I_r})}\leqslant \mathbb {Z}^{r-3}$.

Consider now $H'_i=H_i\cap H_{I_r}$, for $i=1,\ldots,k$. On the one hand, these are all subgroups of $H_{I_r}\simeq F\times \mathbb {Z}^{\mathrm {rk} (L_{I_r})}\leqslant \mathbb {F}_{n}\times \mathbb {Z}^{r-3}$. On the other, the (independent) collection of subsets $I_1,\ldots,I_{r-1}\subseteq [k]$ satisfy that, for every $j\in \{1,\ldots,r-1\}$:

\begin{align*} H'_{I_1\cup \cdots \cup \widehat{I_j}\cup\cdots \cup I_{r-1}} & = H'_{I_1}\cap \cdots \cap \widehat{H'_{I_j}}\cap \cdots \cap H'_{I_{r-1}}\\ & = (H_{I_1}\cap H_{I_r})\cap \cdots \cap \widehat{(H_{I_j}\cap H_{I_r})}\cap \cdots \cap (H_{I_{r-1}}\cap H_{I_r})\\ & = H_{I_1}\cap \cdots \cap \widehat{H_{I_j}}\cap \cdots \cap H_{I_r} = H_{I_1\cup \cdots \cup \widehat{I_j}\cup\cdots \cup I_r} \end{align*}

is finitely generated, whereas

\[ H'_{I_1\cup \cdots \cup I_{r-1}} = H'_{I_1}\cap \cdots \cap H'_{I_{r-1}}= H_{I_1}\cap \cdots \cap H_{I_{r-1}}\cap H_{I_r}=H_{I_1\cup \cdots \cup I_r} \]

is not. This contradicts the inductive hypothesis.

Example 4.4 This last result shows explicit restrictions in the lattice of subgroups of ${\mathbb {F}_{n}} \times \mathbb {Z}^m$. For example, for $k=r=3$, it tells us the following: if $H_1,H_2,H_3\leqslant {\mathbb {F}_{n}}\times \mathbb {Z}$ are arbitrary subgroups, and $H_1\cap H_2$, $H_1\cap H_3$, and $H_2\cap H_3$ are all finitely generated, then $H_1\cap H_2\cap H_3$ must be finitely generated as well.

The proposition below shows that, by strictly increasing the abelian rank $m$, the set of configurations realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ strictly increases as well.

Proposition 4.5 The $k$-configuration ${\chi }_{\scriptstyle {{[k]}}}$ is realizable in $\mathbb {F}_{2} \times \mathbb {Z}^{k-1}$, but not in $\mathbb {F}_{2} \times \mathbb {Z}^{k-2}$.

Proof. The second claim follows from proposition 4.3, taking $r=k$ and $I_1 = \{1\}, \ldots, I_k=\{k\}$.

Let us prove the first claim. For $k=1$ the statement is just saying that the $1$-configuration $\{1\}\mapsto 1$, namely $\mathsf {1}$, is realizable in $\mathbb {F}_{2}\times \mathbb {Z}^{1-1}=\mathbb {F}_{2}$. This is obviously true since it is enough to take $H_1\leqslant \mathbb {F}_{2}$ to be any non-f.g. subgroup.

Assume $k\geqslant 2$. We need to construct a family of subgroups $\mathcal {H} = \{ H_1,\ldots,H_k\}$ of $\mathbb {F}_{2} \times \mathbb {Z}^{k-1}$ such that all partial intersections $H_I$ (where $\varnothing \neq I\subsetneq [k]$) are finitely generated, while the total one $H_{[k]}$ is not. Let $\{x,y\}$ be two free letters generating $\mathbb {F}_{2}$, let $\{\mathbf {e_1}, \ldots,\mathbf {e_{k-1}}\}$ be the canonical free-abelian basis for $\mathbb {Z}^{k-1}$, and consider the following subgroups:

\begin{align*} H_1 & = \langle x, y; \mathrm{t}^\mathbf{e_2}, \ldots, \mathrm{t}^\mathbf{e_{k-1}} \rangle \,\leqslant\, \mathbb{F}_{2} \times \mathbb{Z}^{k-1}, \\ H_2 & = \langle x, y; \mathrm{t}^\mathbf{e_1}, \mathrm{t}^\mathbf{e_3}, \ldots, \mathrm{t}^\mathbf{e_{k-1}} \rangle \,\leqslant\, \mathbb{F}_{2} \times \mathbb{Z}^{k-1}, \\ & \vdots \\ H_{k-1} & = \langle x, y; \mathrm{t}^\mathbf{e_1}, \ldots, \mathrm{t}^\mathbf{e_{k-2}} \rangle \,\leqslant\, \mathbb{F}_{2} \times \mathbb{Z}^{k-1}, \\ H_k & = \langle x, y\mathrm{t}^\mathbf{e_1}; \mathrm{t}^\mathbf{e_2-e_1}, \ldots, \mathrm{t}^\mathbf{e_{k-1}-e_1} \rangle =\langle x, y\mathrm{t}^\mathbf{e_1}, \ldots, y\mathrm{t}^\mathbf{e_{k-1}} \rangle \,\leqslant\, \mathbb{F}_{2} \times \mathbb{Z}^{k-1}. \end{align*}

For a given nonempty set of indices $I\subseteq [k]$, let us compute $H_I$ by distinguishing the following three possible cases:

Case 1: $k\notin I$. In this case, clearly, $H_I=\langle x, y; \mathrm {t}^\mathbf {e_j} \text { for } j\notin I \rangle$, which is finitely generated.

Case 2: $k\in I\subsetneq [k]$. In this case, without loss of generality we may assume that $1\notin I$ and so, $H_I$ is again finitely generated:

\begin{align*} H_I& =H_{I\setminus \{k\}} \cap H_k =\langle x, y; \mathrm{t}^\mathbf{e_j} \text{ for } j\not\in I \rangle \cap \langle x, y\mathrm{t}^\mathbf{e_1}, y\mathrm{t}^\mathbf{e_2}, \ldots ,y\mathrm{t}^\mathbf{e_{k-1}} \rangle \\ & = \{w(x,y)\mathrm{t}^{\mathbf{a}} \mid a_j=0, \forall\ j\in I \setminus \{k\} \} \cap \{w(x,y)\mathrm{t}^{\mathbf{a}} \mid a_1+\cdots +a_{k-1}=|w|_y\} \\ & = \{w(x,y)\mathrm{t}^{\mathbf{a}} \mid a_1+\cdots +a_{k-1}=|w|_y \text{ and } a_j=0\, \forall j\in I \setminus \{k\}\}\\ & = \langle x, y\mathrm{t}^\mathbf{e_j} \text{ for } j\not\in I \rangle \\ & = \langle x, y\mathrm{t}^{\mathbf{e_1}}; \mathrm{t}^\mathbf{e_j-e_1} \text{ for } j\not\in I \rangle. \end{align*}

Case 3: $I=[k]$. In this case,

\[ H_I=(H_1\cap \cdots \cap H_{k-1})\cap H_k =\langle x, y \rangle \cap \langle x, y\mathrm{t}^\mathbf{e_1}; \mathrm{t}^\mathbf{e_2-e_1}, \ldots ,\mathrm{t}^\mathbf{e_{k-1}-e_1}\rangle = \langle \! \langle \hspace{1pt} x \hspace{1pt} \rangle \! \rangle_{\mathbb{F}_{2}}, \]

the normal closure of $x$ in $\mathbb {F}_{2}$, which is not finitely generated.

Apart from ${\chi }_{\scriptstyle {{[k]}}}$ being an explicit example of a $k$-configuration which is realizable in $\mathbb {F}_{2}\times \mathbb {Z}^{k-1}$ but not in $\mathbb {F}_{2}\times \mathbb {Z}^{k-2}$, we observe that there are strong restrictions which every realization of ${\chi }_{\scriptstyle {{[k]}}}$ in $\mathbb {F}_{2}\times \mathbb {Z}^{k-1}$ must satisfy. This supports the idea that finding an exact characterization of the $k$-configurations realizable in $\mathbb {F}_{2} \times \mathbb {Z}^{m}$ for a given value of $m$, may be a complicated task.

Corollary 4.6 Every realization of the $k$-configuration ${\chi }_{\scriptstyle {{[k]}}}$ in $\mathbb {F}_{2} \times \mathbb {Z}^{k-1}$ must mandatorily be with subgroups $H_1,\ldots,H_k\leqslant \mathbb {F}_{2} \times \mathbb {Z}^{k-1}$ satisfying $\mathrm {rk} (L_{H_i})\geq k-2$, $i=1,\ldots,k$.

Proof. Suppose that a certain family $\mathcal {H}=\{H_1,\ldots,H_k\}$ of subgroups of $\mathbb {F}_{2} \times \mathbb {Z}^{k-1}$ realizes ${\chi }_{\scriptstyle {{[k]}}}$. Then, clearly, the new family $\{H_1\cap H_i, \ldots, H_{i-1}\cap H_i, H_{i+1}\cap H_i, \ldots,H_k\cap H_i\}$ realizes ${\chi }_{\scriptstyle {{[k-1]}}}$. Since, for all $j=1,\ldots,\widehat {i}, \ldots,k$, $H_j\cap H_i\leqslant H_i \simeq \mathbb {F}_{\!r}\times L_{H_i}\simeq \mathbb {F}_{\!r}\times \mathbb {Z}^{\mathrm {rk} (L_{H_i})}$ for some $0\leq r\leq \infty$, proposition 4.5 tells us that $\mathrm {rk} (L_{H_i})\geq k-2$, for $i=1,\ldots,k$.

Remark 4.7 Any realization of a $k$-configuration ${\chi }_{\scriptstyle {\mathcal {I}}}$ in $\mathbb {F}_{n} \times \mathbb {Z}^{m}$ must be by subgroups $H_1,\ldots,H_k$ satisfying $\mathrm {rk} ( \bigcap _{i\in I} H_i\pi ) \geq 2$, for every $I\in \mathcal {I}$: since $\bigcap _{i\in I} H_i$ is not finitely generated, this follows immediately from theorem 2.9 applied to the subgroups $H_i$ with $i\in I$. Alternatively, since $(\bigcap _{i\in I} H_i)\pi$ is not finitely generated and it is contained in $\bigcap _{i\in I} H_i\pi$, this last subgroup must be free nonabelian.

5. Realizing $k$-configurations

Our goal in this section is to show that, for every $k\geq 1$, any $k$-configuration $\chi$ is realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, for large enough $m$. Note that, for this purpose, we can always assume $n=2$. Proposition 4.5 already shows an interesting family of realizable $k$-configurations. It is straightforward to see that, conveniently adding trivial subgroups, it can be restated as follows.

Lemma 5.1 Let $n\geq 2$. For every nonempty subset $I_0 \subseteq [k]$, the almost-$\mathsf {0}$ $k$-configuration ${\chi }_{\scriptstyle {I_0}}$ is realizable in $\mathbb {F}_{n}\times \mathbb {Z}^{|I_0|-1}$ by subgroups $H_1,\ldots,H_k$ further satisfying $\mathrm {rk} ( \bigcap _{i\in I} H_i\pi ) \neq 1$ for every nonempty $I\subseteq [k]$.

Proof. Without loss of generality, we may assume that $I_0=[r]=\{1,\ldots,r\}$, where $1\leq r=|I_0|\leq k$. By proposition 4.5, the $r$-configuration ${\chi }_{\scriptstyle {{I_0}}}$ is realizable in $\mathbb {F}_{2}\times \mathbb {Z}^{r-1}$ by subgroups $H_1,\ldots,H_r\leqslant \mathbb {F}_{2}\times \mathbb {Z}^{r-1}$ satisfying that $\mathrm {rk} ( \bigcap _{j=1}^r H_j\pi ) \geq 2$ (as it is mandatory according to remark 4.7). Let $H_{r+1}=\cdots =H_{k}= \{ 1 \}$. For any nonempty $I\subseteq [k]$ let us look at $H_I$ by distinguishing three cases:

Case 1: $I=[r]$. By construction, $H_I$ is not finitely generated.

Case 2: $I\subsetneq [r]$. By construction, $H_I$ is finitely generated.

Case 3: $I\not \subseteq [r]$. In this case, $H_I=H_{I\cap [r]}\cap \{1\}=\{1\}$ is obviously finitely generated.

Hence, we have realized the $k$-configuration ${\chi }_{\scriptstyle {I_0}}$ in $\mathbb {F}_{2}\times \mathbb {Z}^{r-1}\leqslant \mathbb {F}_{n}\times \mathbb {Z}^{|I_0|-1}$ by subgroups $H_1,\ldots,H_k$ such that, for every nonempty $I\subseteq [k]$, $\bigcap _{i\in I} H_i\pi$ is either trivial or has rank $\geq \! 2$; therefore, $\mathrm {rk} ( \bigcap _{i\in I} H_i\pi )\neq 1$, as required.

Note that, in order to realize $\chi \vee \chi '$ in a group $G$, we need to find $k$ subgroups $H_1,\ldots,H_k\leqslant G$ such that, for every nonempty $I\subseteq [k]$, $H_I$ is finitely generated whenever $(I)\chi =0$ and $(I)\chi '=0$, and it is not finitely generated whenever $(I)\chi =1$ or $(I)\chi '=1$. Equivalence (2.9) matches the intended purpose. Note, however, that in order to use it (theorem 2.14), we need to include the technical hypothesis $\min (r',r'')\neq 1$, since, as shown in example 2.16, equivalence (2.9) may fail if $\min (r',r'') = 1$. Taking this into account, the result below provides a way to realize in the family of FTFA groups the join of two already realizable configurations (at some abelian cost).

Proposition 5.2 Let $\chi '$ be a $k$-configuration realizable in $\mathbb {F}_{\!n'}\times \mathbb {Z}^{m'}$ by $H'_1,\ldots,H'_k$, and $\chi ''$ be a $k$-configuration realizable in $\mathbb {F}_{\!n''}\times \mathbb {Z}^{m''}\!$ by $H''_1,\ldots,H''_k$; and, for every nonempty $I\subseteq [k]$, let $r'_I=\mathrm {rk} ( \bigcap _{i\in I} H'_i\pi )$ and $r''_I=\mathrm {rk} ( \bigcap _{i\in I} H''_i\pi )$. If ${\min \{r'_I,r''_I\} \neq 1}$ for every $I\subseteq [k]$ with $|I|\geq 2$, then $\chi '\vee \chi ''$ is realizable in $\mathbb {F}_{\!n'+ n''} \times \mathbb {Z}^{m'+ m''}$.

Proof. Under the assumptions of the statement, consider the subgroups:

\begin{align*} H_1& =\langle H'_1, H''_1\rangle, \ldots ,H_k = \langle H'_k, H''_k\rangle \leqslant (\mathbb{F}_{\!n'}\times \mathbb{Z}^{m'})\circledast (\mathbb{F}_{\!n''}\times \mathbb{Z}^{m''})\\ & \simeq \mathbb{F}_{\!n'+n''}\times \mathbb{Z}^{m'+m''}. \end{align*}

For every singleton $I=\{i\}\subseteq [k]$, it is clear that $H_i$ is finitely generated if and only if both $H'_i$ and $H''_i$ are finitely generated. And, for each $I\subseteq [k]$ with $|I|\geq 2$, we apply theorem 2.14 to obtain that:

\[ \bigcap\nolimits_{i\in I} H_i \text{ is f.g.} \ \Leftrightarrow\ \text{both } \bigcap\nolimits_{i\in I} H'_i \quad\text{and}\quad \bigcap\nolimits_{i\in I} H''_i \text{ are f.g.} \]

This means that $H_1,\ldots,H_k$ realize the $k$-configuration $\chi '\vee \chi ''$ in the group $\mathbb {F}_{\!n'+n''}\times \mathbb {Z}^{m'+m''}$.

Corollary 5.3 Let $n\geq 2$, $k\geq 1$, and $i \in [k]$. If a $k$-configuration $\chi$ is realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, then $\chi \vee {\chi }_{\scriptstyle {\{i\}}}$ is also realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$; the converse is not true, in general.

Proof. Take two free nonabelian subgroups $F', F''\leqslant \mathbb {F}_{n}$ in free-factor position, $\langle F', F'' \rangle =F'*F''$. Let $H'_1,\ldots,H'_k \leqslant G'=F'\times \mathbb {Z}^m$ be a realization of $\chi$, and let $H''_i\leqslant G''=F''\times \mathbb {Z}^0$ be non-f.g. and $H''_j=1\leqslant G''$ for $j\neq i$ (of course, realizing ${\chi }_{\scriptstyle {\{i\}}}$). Since $\min \{r'_I,r''_I\}=0\neq 1$ for every $I\subseteq [k]$, $|I|\geq 2$, we can apply proposition 5.2 to obtain a realization of $\chi \vee {\chi }_{\scriptstyle {\{i\}}}$ in $G'\circledast G''\leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$.

The converse is not true since the 2-configuration ${\chi }_{\scriptstyle {\{\{1\}, \{1,2\}\}}}$ is realizable in ${\mathbb {F}_{n}}$, whereas ${\chi }_{\scriptstyle {\{1,2\}}}$ is not.

Below, we present a variation of proposition 5.2 which will be crucial in order to use this result inductively in the proof of theorem 5.5.

Corollary 5.4 Let $\chi '$ be realizable in $\mathbb {F}_{\!n'}\times \mathbb {Z}^{m'}$ by subgroups $H'_1,\ldots,H'_k$ satisfying $r'_I \neq 1$, for all $I\subseteq [k]$ with $|I|\geq 2$, and let $\chi ''$ be realizable in $\mathbb {F}_{\!n''}\times \mathbb {Z}^{m''}$ by subgroups $H''_1,\ldots,H''_k$ satisfying $r''_I \neq 1$, for all $I\subseteq [k]$ with $|I|\geq 2$. Then, $\chi '\vee \chi ''$ is realizable in $\mathbb {F}_{\!n'+n''}\times \mathbb {Z}^{m'+m''}$, by the subgroups $H_1=\langle H'_1,H''_1 \rangle,\ldots,H_k=\langle H'_k,H''_k \rangle$, satisfying (again) $r_I =\mathrm {rk} ( \bigcap _{i\in I} H_i\pi ) \neq 1$, for all $I\subseteq [k]$ with $|I|\geq 2$.

Proof. Note that we are under slightly stronger conditions that in proposition 5.2; hence, the realizability of $\chi '\vee \chi ''$ follows immediately. Moreover, by proposition 2.11, for each $I\subseteq [k]$ with $|I|\geq 2$, $\bigcap _{i\in I} H_i\pi =( \bigcap _{i\in I} H'_i\pi ) * ( \bigcap _{i\in I} H''_i\pi )$. Since, by hypothesis, $\mathrm {rk}( \bigcap _{i\in I} H'_i\pi ) \neq 1$ and $\mathrm {rk} ( \bigcap _{i\in I} H''_i\pi )\neq 1$, we conclude that $\mathrm {rk} ( \bigcap _{i\in I} H_i\pi )\neq 1$, as claimed.

Finally, iterating corollary 5.4, we obtain the main results from this section.

Theorem 5.5 Every finite configuration ${\chi }_{\scriptstyle {\mathcal {I}}}$ is realizable in ${\mathbb {F}_{n}}\times \mathbb {Z}^m$, for $m \geq \sum _{I\in \mathcal {I}} (|I|-1)$ and $n\geq 2$.

Proof. Let $\chi$ be a $k$-configuration. If $\chi$ is the $\mathsf {0}$ $k$-configuration ($\chi ={\chi }_{\scriptstyle {\varnothing }}$) then it can be realized by the trivial subgroups $H_1=\cdots =H_k=\{1\}\leqslant \mathbb {F}_{n}\times \mathbb {Z}^0$. If it is an almost-$\mathsf {0}$ $k$-configuration $\chi ={\chi }_{\scriptstyle {I_0}}$ then, by lemma 5.1, it can be realized by subgroups $H_1,\ldots,H_k \leqslant \mathbb {F}_{n}\times \mathbb {Z}^{|I_0|-1}$, further satisfying $\mathrm {rk} ( \bigcap _{i\in I} H_i\pi ) \neq 1$, for each nonempty $I\subseteq [k]$.

In any other case, let $(1)\chi^{{\boldsymbol {\leftarrow }}}=\{I_1, \ldots, I_r\}$ be the support of $\chi$, and we can decompose $\chi$ as the join of the corresponding almost-$\mathsf {0}$ $k$-configurations $\chi ={\chi }_{\scriptstyle {{I_1}}}\vee \cdots \vee {\chi }_{\scriptstyle {{I_r}}}$. Now, realize each ${\chi }_{\scriptstyle {{I_i}}}$ in $\mathbb {F}_{n}\times \mathbb {Z}^{|I_i|-1}$ as above, and repeatedly apply corollary 5.4, to get a realization of $\chi$ in $\mathbb {F}_{\!rn}\times \mathbb {Z}^{|I_1|+\cdots +|I_r|-r}\leqslant \mathbb {F}_{n}\times \mathbb {Z}^{m}$.

Remark 5.6 The proof of theorem 5.5 actually shows a bit more than the statement: any $k$-configuration $\chi$ is realizable in ${\mathbb {F}_{n}}\times \mathbb {Z}^m$, for every $n\geq 2$ and $m\geq \sum _{(I)\chi =1} (|I|-1)$, by subgroups $H_1,\ldots,H_k$ further satisfying that, for every $I\subseteq [k]$ with $|I|\geq 2$, $\mathrm {rk} ( \bigcap _{\, i\in I} H_i\pi ) \neq 1$.

Example 5.7 Let $\mathcal {I}=\{\{1\}, \{2,3\}, \{1,3,4\}, \{2,3,4\}\}$ and consider the 4-configuration $\chi ={\chi }_{\scriptstyle {\mathcal {I}}}$. Let us follow the previous inductive argument to realize $\chi$ in $\mathbb {F}_{2}\times \mathbb {Z}^m$ for large enough $m$. We have to find a family of four subgroups $\mathcal {H}=\{ H_1,H_2,H_3,H_4\}$ of $\mathbb {F}_{2}\times \mathbb {Z}^m$ such that $\chi^{\mathcal {H}}=\chi$.

Decomposing $\chi$ as the join of the corresponding almost-$\mathsf {0}$ $4$-configurations, we have

\[ \chi={\chi}_{\scriptstyle{{\{1\}}}}\textstyle{\vee} {\chi}_{\scriptstyle{{\{2,3\}}}}\textstyle{\vee} {\chi}_{\scriptstyle{{\{1,3,4\}}}}\textstyle{\vee} {\chi}_{\scriptstyle{{\{2,3,4\}}}}. \]

Let $\mathbb {F}_{2}=\langle x,y \mid -\rangle$ and consider the bi-infinite list of freely independent words $u_j=y^{-j}xy^j\in \mathbb {F}_{2}$, for $j\in \mathbb {Z}$. For the abelian part, take $m=0+1+2+2=5$ and let $\{\mathbf {e_1}, \mathbf {e_2}, \mathbf {e_3}, \mathbf {e_4}, \mathbf {e_5}\}$ be the canonical basis for $\mathbb {Z}^5$. Using lemma 5.1, we can realize the almost-$\mathsf {0}$ 4-configurations individually in the following way:

• • ${\chi }_{\scriptstyle {\{1\}}}$ as $H'_1=\langle \ldots, u_{-2}, u_{-1}\rangle$, $H'_2=\{1\}$, $H'_3=\{1\}$, $H'_4=\{1\}$, all viewed as subgroups of $G'=\langle...,u_{-2},u_{-1}; -\rangle \leqslant \mathbb {F}_{2}\times \mathbb {Z}^5$;

• • ${\chi }_{\scriptstyle {\{2,3\}}}$ as $H''_1=\{1\}$, $H''_2=\langle u_0, u_1 \rangle$, $H''_3=\langle u_0, u_1\mathrm {t}^\mathbf {e_1} \rangle$, $H''_4=\{1\}$, all viewed as subgroups of $G''=\langle u_0, u_1; \mathrm {t}^\mathbf {e_1}\rangle \leqslant \mathbb {F}_{2}\times \mathbb {Z}^5$;

• • ${\chi }_{\scriptstyle {\{1,3,4\}}}$ as $H'''_1=\langle u_2, u_3; \mathrm {t}^\mathbf {e_3}\rangle$, $H'''_2=\{1\}$, $H'''_3=\langle u_2, u_3; \mathrm {t}^\mathbf {e_2} \rangle$, $H'''_4=\langle u_2, u_3\mathrm {t}^\mathbf {e_2}; \mathrm {t}^\mathbf {e_3-e_2}\rangle$, all viewed as subgroups of $G'''=\langle u_2, u_3; \mathrm {t}^\mathbf {e_2}, \mathrm {t}^\mathbf {e_3}\rangle \leqslant \mathbb {F}_{2}\times \mathbb {Z}^5$;

• • ${\chi }_{\scriptstyle {\{2,3,4\}}}$ as $H''''_1=\{1\}$, $H''''_2=\langle u_4, u_5; \mathrm {t}^\mathbf {e_5}\rangle$, $H''''_3=\langle u_4, u_5; \mathrm {t}^\mathbf {e_4} \rangle$, $H''''_4=\langle u_4, u_5\mathrm {t}^\mathbf {e_4}; \mathrm {t}^\mathbf {e_5-e_4}\rangle$, all viewed as subgroups of $G''''=\langle u_4, u_5; \mathrm {t}^\mathbf {e_4}, \mathrm {t}^\mathbf {e_5}\rangle \leqslant \mathbb {F}_{2}\times \mathbb {Z}^5$.

Note that, as stated in lemma 5.1, each of these realizations is by subgroups whose intersections of projections to the free part are never cyclic; more precisely, for each nonempty $I\subseteq [k]$, we have $\mathrm {rk} ( \bigcap _{i\in I} H'_i\pi ) \neq 1$, $\mathrm {rk} ( \bigcap _{i\in I} H''_i\pi ) \neq 1$, $\mathrm {rk} ( \bigcap _{i\in I} H'''_i\pi ) \neq 1$, and $\mathrm {rk} ( \bigcap _{i\in I} H''''_i\pi ) \neq 1$. Moreover, we already took care to choose these realizations in strongly complementary subgroups of $\mathbb {F}_{2}\times \mathbb {Z}^5$, namely $G'$, $G''$, $G'''$ and $G''''$, respectively. Therefore, we can repeatedly apply corollary 5.4 to get the following realization of $\chi ={\chi }_{\scriptstyle {{\{1\}}}}\vee {\chi }_{\scriptstyle {{\{2,3\}}}}\vee {\chi }_{\scriptstyle {{\{1,3,4\}}}}\vee {\chi }_{\scriptstyle {{\{2,3,4\}}}}$ in $G'\circledast G''\circledast G'''\circledast G''''\leqslant \mathbb {F}_{2}\times \mathbb {Z}^5$:

\begin{align*} H_1 & = \langle \ldots, u_{{-}2}, u_{{-}1},u_{2}, u_3; \mathrm{t}^\mathbf{e_3}\rangle, \\ H_2 & = \langle u_0, u_1, u_4, u_5; \mathrm{t}^\mathbf{e_5}\rangle, \\ H_3 & = \langle u_0, u_1\mathrm{t}^\mathbf{e_1}, u_2, u_3, u_4, u_5; \mathrm{t}^\mathbf{e_2}, \mathrm{t}^\mathbf{e_4}\rangle, \\ H_4 & = \langle u_2, u_3\mathrm{t}^\mathbf{e_2}, u_4, u_5\mathrm{t}^\mathbf{e_4}; \mathrm{t}^\mathbf{e_3-e_2}, \mathrm{t}^\mathbf{e_5-e_4}\rangle. \end{align*}

□

This result tells us that every configuration is realizable collectively in the family of groups ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, i.e. in $\mathbb {F}_{2}\times \mathbb {Z}^m$ for $m$ large enough. Hence, in a group $G$ containing all of $\mathbb {F}_{2}\times \mathbb {Z}^m$ as subgroups it will be possible to realize any configuration.

Theorem 5.8 There exist finitely presented intersection-saturated groups.

Proof. Recall that we denote by $\mathbb {Z}^{\infty }$ the direct sum of countably many copies of $\mathbb {Z}$, namely $\mathbb {Z}^{\infty }=\bigoplus _{n=1}^{\infty } \mathbb {Z}$. From theorem 5.5, it is enough to construct a finitely presented group $G$ containing $\mathbb {F}_{2}\times \mathbb {Z}^{\infty }$.

Consider Thompson's group $F$: it is well known that $F$ is finitely presented (in fact, it admits a presentation with just two generators and two relations, see [4, Thm. 3.4]), and that it contains $\mathbb {Z}^{\infty }$, see [4, Thm. 4.8]. Therefore, $G=\mathbb {F}_{2}\times F$ is a finitely presented intersection-saturated group. (Note that Thomson's group contains no nonabelian free subgroup so, in order to get intersection-saturation via our arguments, it is necessary to take the direct product with $\mathbb {F}_{2}$.)

Alternatively, we can consider $\bigoplus _{n=-\infty }^{\infty } \mathbb {Z}\,{=}\,\langle \ldots,x_{-1}, x_0, x_1, \ldots \mid [x_i, x_j]\,{=}\,1, \forall \ i,j\in \mathbb {Z}\rangle$, take the automorphism $\varphi$ given by translation of coordinates, $x_i\mapsto x_{i+1}$, and take the semidirect product $G'=\mathbb {Z}^{\infty } \rtimes _{\varphi } \mathbb {Z}$. This group is finitely generated (in fact, by just $x_0$ and the stable letter $t$) and (not finitely but) recursively presented; so, by Higman's embedding theorem, it embeds in a finitely presented group $G'\hookrightarrow G$. Clearly, $\mathbb {F}_{2}\times G$ is finitely presented as well, and intersection-saturated.

6. Characterization for the free group case

In this section, we characterize the configurations which are realizable in a free group ${\mathbb {F}_{n}}$, $n\geq 2$. Roughly speaking, they are precisely those satisfying the Howson property; see theorem 6.7. That is, the Howson property is the only true obstacle for intersection realizability in a free nonabelian group. We first introduce a couple of notions convenient to state and prove our last result.

Definition 6.1 A $k$-configuration $\chi$ is said to be Howson if, for every nonempty $I,J\subseteq [k]$, we have $(I\cup J)\chi =0$ whenever $(I)\chi =(J)\chi =0$ (see figure 8).

Figure 8. Configuration is Howson if and only if it does not contain this pattern (where the snaked arrows denote directed paths, and the black vertex is where both paths first meet).

Definition 6.2 Let $\chi$ be a $k$-configuration with $k\geq 2$, and let $i\in [k]$. The restriction of $\chi$ to $\widehat {i} = [k]\setminus \{i\}$ is the $k-1$ configuration obtained from $\chi$ by removing index $i$ from the ambient, and restricting $\chi$ to the nonempty subsets of $[k]$ not containing $i$, i.e.

\[ \begin{array}{rcl} {\chi}_{\scriptstyle{|\widehat{i}}} \colon \mathcal{P}([k]\setminus \{i\})\setminus \{\varnothing\} & \to & \{0, 1\} \\ I\, & \mapsto & (I)\chi\,. \end{array} \]

Obviously, if $\chi$ is realizable in a group $G$ then so is ${\chi }_{\scriptstyle {|\hspace {1pt}\widehat {i}}}$.

Definition 6.3 Let $\chi$ be a $k$-configuration, and let $i\in [k]$. The index $i$ is said to be $\mathsf {0}$-chromatic (in $\chi$) if $(I)\chi =0$ for every $I\subseteq [k]$ containing $i$; in other words, if $\chi ={\chi }_{\scriptstyle {\mid \,\widehat {i}}} \,\boxplus _0 \mathsf {0}$. Similarly, the index $i$ is said to be $\mathsf {1}$-chromatic (in $\chi$) if $\chi = {\chi }_{\scriptstyle {\mid \,\widehat {i}}} \boxplus _1 \mathsf {1}$.

Below, we use a typical property of free groups to realize intersection configurations ‘as deep as desired’ into an FTFA group: any configuration realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$, can always be realized using only a subgroup of $\mathbb {F}_{n}$ of some desired rank (at least two), and admitting a free supplement of arbitrary rank.

Lemma 6.4 If a configuration $\chi$ is realizable in an FTFA group ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ with $n\geq 2$ then, for every $2\leq r\leq \infty$ and every $0\leq s\leq \infty$, there exist subgroups $F,K\leqslant \mathbb {F}_{n}$ such that $\mathrm {rk}(F)=r$, $\mathrm {rk}(K)=s$ and $\langle F, K \rangle =F*K\leqslant \mathbb {F}_{n}$, such that $\chi$ is also realizable in $F\times \mathbb {Z}^m \leqslant {\mathbb {F}_{n}} \times \mathbb {Z}^m$.

Proof. This is an immediate consequence of the fact that $\mathbb {F}_{\!\infty }$ embeds in ${\mathbb {F}_{n}}$, for all $n \geq 2$.

Observe that, in the particular case $m'= m''= 0$ (corresponding to free groups), the claim in proposition 5.2 follows immediately from proposition 2.11, without any hypothesis on the ranks of the subgroups.

Proposition 6.5 Let $\chi '$ be a $k$-configuration realizable in $\mathbb {F}_{\!n'}$ and $\chi ''$ be a $k$-configuration realizable in $\mathbb {F}_{\!n''}$. Then, $\chi '\vee \chi ''$ is realizable in $\mathbb {F}_{\!n'+n''}$.

Corollary 6.6 If a $k$-configuration $\chi$ is realizable in $\mathbb {F}_{n}$ with $n\geq 2$, then the $(k+1)$-configurations $\chi \boxplus _0 \mathsf {0}$, $\chi \boxplus _1 \mathsf {1}$, $\chi \boxplus _{0} \chi$, and $\chi \boxplus _{1} \chi$ are also realizable in $\mathbb {F}_{n}$.

Proof. Apply lemma 6.4 with $m=0$, $r=\infty$, and $s=2$. Let $\{u, v\}$ be a free basis for the subgroup $K$, and let $H_1,\ldots, H_k$ be a family of subgroups realizing $\chi$ in $F\leqslant \mathbb {F}_{n}$. Now, in order to realize:

• • $\chi \boxplus _0 \mathsf {0}$, it is enough to take the subgroups $\widetilde {H}_1=H_1,\ldots, \widetilde {H}_k=H_k$, and $\widetilde {H}_{k+1}= \{ 1 \}$;

• • $\chi \boxplus _1 \mathsf {1}$, it is enough to take $\widetilde {H}_1=H_1*\langle u,v \rangle,\ldots, \widetilde {H}_k=H_k*\langle u,v \rangle$ and $\widetilde {H}_{k+1}=\langle \! \langle \hspace {1pt} v \hspace {1pt} \rangle \! \rangle _K$: for every $i \neq k+1$, $\widetilde {H}_{k+1} \cap \widetilde {H}_i = \widetilde {H}_{k+1}$ which is non-f.g., and by proposition 6.5, $\widetilde {H}_1,\ldots,\widetilde {H}_k$ realize $\chi \vee \mathsf {0}=\chi$;

• • $\chi \boxplus _0 \chi$, it is enough to take $\widetilde {H}_1=H_1,\ldots, \widetilde {H}_k=H_k$, and $\widetilde {H}_{k+1}=\mathbb {F}_{n}$;

• • $\chi \boxplus _1 \chi$, it is enough to take $\widetilde {H}_1=H_1,\ldots, \widetilde {H}_k=H_k$, and $\widetilde {H}_{k+1}=F$.

This completes the proof.

Theorem 6.7 A finite configuration is realizable in ${\mathbb {F}_{n}}$, with $n\geq 2$, if and only if it is Howson.

Proof. For all the proof, we can assume $n=2$. Clearly, $\chi$ being Howson is a necessary condition. To show the converse, we will do induction on the cardinal of the support of $\chi$, say $s$ (regardless of its size $k$). If $s=0$ then $\chi$ is the $\mathsf {0}$ $k$-configuration, which is clearly realizable in $\mathbb {F}_{2}$ (in fact, in any group).

Suppose that every Howson configuration with support of size strictly less than $s\geq 1$ is realizable in $\mathbb {F}_{2}$. Let $\chi$ be a Howson $k$-configuration with support of cardinal $s$, and let us realize it in $\mathbb {F}_{2}$.

We define the cone of $\chi$ with vertex $I\subseteq [k]$, denoted by $c_{I}(\chi )$, as the $k$-configuration obtained after removing from the support of $\chi$ all the sets of indices not contained in $I$, if any; i.e.

\[ \begin{array}{rcl} c_{I}(\chi)\colon {\mathcal{P}}([k])\setminus \{\varnothing\} & \to & \{0, 1\} \\ J\, & \mapsto & \left\{ \begin{array}{@{}ll} 0 & \text{if } J\not\subseteq I, \\ (J)\chi & \text{if } J\subseteq I. \end{array}\right. \end{array} \]

Now let $I_1, \ldots,I_p\subseteq [k]$ be the maximal elements (w.r.t. inclusion) in the support of $\chi$. It is clear that $\chi =c_{I_1}(\chi )\vee \cdots \vee c_{I_p}(\chi )$. If $p\geq 2$, by the induction hypothesis we can realize each of $c_{I_1}(\chi ), \ldots,c_{I_p}(\chi )$ in $\mathbb {F}_{2}$, and by proposition 6.5, we can realize their join $\chi$, in $\mathbb {F}_{2}$ as well.

Hence, we are reduced to the case $p=1$, i.e. $\chi$ is a Howson $k$-configuration for which there is a nonempty set of indices $I_1 \subseteq [k]$ with $(I_1)\chi =1$, and $(J)\chi =0$ for every $J\not \subseteq I_1$. If $I_1\neq [k]$ then any index $j\in [k]\setminus I_1$ is $\mathsf {0}$-chromatic and, by corollary 6.6, in order to realize $\chi ={\chi }_{\scriptstyle {\mid \,\widehat {j}}} \boxplus _0 \mathsf {0}$ we are reduced to realize the restriction ${\chi }_{\scriptstyle {\mid \,\widehat {j}}}$ ; repeating this operation for all such indices, we are reduced to the case $I_1=[k]$. That is, $\chi$ is a Howson $k$-configuration such that $([k])\chi =1$.

If every nonempty $I\subseteq [k]$ satisfies $(I)\chi =1$ then $\chi =\mathsf {1}$ and so, it is realizable in $\mathbb {F}_{2}$. Otherwise, take $\varnothing \neq I_2\subseteq [k]$ with $(I_2)\chi =0$ and with maximal possible cardinal. Since $I_2 \neq [k]$, there exist indices $j\not \in I_2$. And any such index $j$ is $\mathsf {1}$-chromatic: in fact, any subset $J\subseteq [k]$ containing $j$ satisfies $|I_2\cup J|>|I_2|$ so $(I_2\cup J)\chi =1$ and, since $\chi$ is Howson and $(I_2)\chi = 0$, then $(J)\chi =1$. Hence, by induction hypothesis, ${\chi }_{\scriptstyle {\mid \, \widehat {j}}}$ is realizable in $\mathbb {F}_{2}$ and, by corollary 6.6, $\chi ={\chi }_{\scriptstyle {\mid \,\widehat {j}}} \boxplus _1 \mathsf {1}$ is also realizable in $\mathbb {F}_{2}$. This concludes the proof.

As it is clear from the previous argument, all the steps in the proof of theorem 6.7 are constructive. The result below follows.

Corollary 6.8 There is an algorithm which, on input a Howson $k$-configuration $\chi$, provides explicit generators for subgroups $H_1,\ldots,H_k\leqslant \mathbb {F}_{2}$ realizing $\chi$.

7. Open questions

We finish by asking three related natural questions.

Question 7.1 Is the obstruction in proposition 4.3 the only one for a configuration to be realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ for a particular abelian dimension $m$?

Question 7.2 Which $k$-configurations $\chi$ are realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ for any fixed $m$? Is it possible to give an explicit characterization in terms of $m$? Or at least an algorithm which, on input $\chi$ and $m$, decides whether $\chi$ is realizable in ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ (and, in the affirmative case, computes such a realization)?

Question 7.3 Is there a finitely presented intersection-saturated group $G$ which does not contain ${\mathbb {F}_{2} \times \mathbb {Z}^{m}}$, for some $m\in \mathbb {N}$?