The measurement of body composition is a central topic of current paediatric research because of its association with health and disease in infancy, childhood and adulthood(Reference Kriemler, Manse-Wenger and Zahner1–Reference Wells and Petrel3). Such an assessment is also important to investigate the effect of lifestyle interventions on fat and fat-free tissues(Reference Pietrobelli4).
Body fat is most commonly estimated from anthropometric measurement(Reference Wang, Thornton and Kolesnik5, Reference Himes6). BMI is often used as a surrogate marker but does not provide an accurate assessment of body fat, and this is especially true in children and adolescents(Reference Krebs, Himes and Jacobson7–Reference Prentice and Jebb9). Waist circumference is gaining popularity as an indicator of childhood obesity but it is more related to visceral fat than to total body fat(Reference Brambilla, Bedogni and Moreno10, Reference McCarthy11). Skinfold thicknesses have long been used as measures of subcutaneous fat and are usually more accurate than BMI at predicting body fat(Reference Durnin and Rahaman12). Although skinfolds are not recommended for routine clinical use in children(Reference Himes6, Reference Krebs, Himes and Jacobson7), they can be very useful in the epidemiological setting whenever a measure of body fat more accurate than BMI is needed to disentangle the effects of fat and fat-free tissues on health outcomes(Reference Ketel, Volman and Seidell13, Reference van Lenthe, van Mechelen and Kemper14).
The four-compartment model has been used to cross-validate portable techniques such as anthropometry and bioelectrical impedance analysis in small samples of children under laboratory conditions(Reference Wells and Petrel3). However, this reference model is not suitable for use in epidemiological studies because of its complexity and cost. Although not a ‘gold standard’ method for the assessment of body composition, dual-energy X-ray absorptiometry (DXA) compares well with the four-component model (i.e. adjusted regression between fat mass by the two methods does not deviate from the line of identity)(Reference Fields and Goran15, Reference Pintauro, Nagy and Duthie16), is more readily available and is being increasingly used for clinical and epidemiological applications(Reference Wells and Petrel3, Reference Helba and Binkovitz17, Reference Lohman and Going18). However, DXA is not portable and uses ionising radiation so that it is mainly used to validate indirect techniques that are then used to assess body composition(Reference Goran, Driscoll and Johnson19).
To date, most calibration studies of anthropometry have been performed in convenience samples of children(Reference Goran, Driscoll and Johnson19–Reference Sarría, García-Llop and Moreno22). Only one study has been performed in a representative sample of adolescents (aged 13–18 years) from the general population and it focused on the validation of external algorithms(Reference Rodriguez, Moreno and Blay23). Thus, there is a clear need of studies evaluating the accuracy of anthropometry as an index of body fat in representative samples of children.
The Kinder-Sportstudie (KISS) is a randomised controlled trial aimed to test whether a physical activity programme can improve body composition, physical activity, physical fitness and quality of life in a representative sample of 6- to 13-year-old Swiss children(Reference Zahner, Puder and Roth24). The baseline data of the KISS study offered the unique opportunity to cross-validate anthropometry against DXA in a representative sample of the general paediatric population. The aim of the present study was, therefore, to compare the accuracy of BMI, waist circumference and skinfold thicknesses for the assessment of percentage body fat (PBF) in the KISS children.
Methods
Study design
The study protocol of KISS (ISRCTN 15360785) is described in detail elsewhere(Reference Zahner, Puder and Roth24). Briefly, the KISS children were randomly selected and stratified by class, geographic area and ethnicity to be representative of Swiss children with respect to sex, sociodemographic status and BMI. The baseline data, collected in the summer of 2005, were used for the present analysis. Informed consent was obtained verbally from each child and written consent was obtained by at least one parent. The study was conducted according to the Declaration of Helsinki and was approved by the Ethical Committee of the University of Basel, the Cantonal Ethical Committee of Aargau and the Swiss Federal Institute of Technology.
Subjects
A total of 502 of 540 children agreed to participate. Complete data were available for 497 children and 372 of them (75 %) had both DXA and anthropometry measured and were evaluated for the present study. The lack of DXA measurements for 125 (25 %) of the children was due to the request of their parents that they were not exposed to ionising radiation. The option to refuse DXA measurements was explicitly recognised by the study protocol and systematically offered during the study. Anthropometry and DXA measurements were performed within 2 d as described below.
Anthropometric evaluation and pubertal assessment
Anthropometric measurements were performed by two experienced operators as described in detail elsewhere(Reference Zahner, Puder and Roth24). Briefly, body weight was measured to the nearest 5 g using an electronic scale (Seca, Basel, Switzerland) and standing height to the nearest 2 mm using a wall-mounted stadiometer (Seca). Waist circumference was measured to the nearest 1 mm using a flexible tape midway between the lowest rib and the iliac crest. Skinfold thickness was measured in triplicate to the nearest 1 mm using a Harpenden calliper (British Indicators, Burgess Hill, West Sussex, UK) at the triceps, biceps, subscapular and supra-iliac sites following the Anthropometric Standardization Reference Manual (Reference Lohman, Roche and Martorell25). The mean of the three measurements was used for analysis. The inter-operator technical error of measurement for skinfolds, as determined by a preliminary study performed by the two study operators on thirty-six children, was 1·0 mm for triceps skinfold, 1·1 mm for biceps skinfold, 1·4 mm for subscapular skinfold and 2·9 mm for supra-iliac skinfold, with corresponding coefficients of reliability ≥ 0·91. These values are within the suggested limits of tolerance and are in agreement with other paediatric studies(Reference Moreno, Joyanes and Mesana26, Reference Ulijaszek and Kerr27). BMI was calculated and transformed into standard deviation scores (SDS) using the 1990 UK reference data(Reference Cole, Freeman and Price28). Overweight and obesity were determined by the International Obesity Task Force classification system(Reference Cole, Bellizzi and Flegal29). The triceps and subscapular skinfolds were summed to obtain the sum of two skinfolds (SF2) and the biceps, triceps, subscapular and supra-iliac skinfolds were summed to obtain the sum of four skinfolds (SF4)(Reference Durnin and Rahaman12, Reference Bedogni, Iughetti and Ferrari30, Reference Frisancho31). Pubertal stage was self-assessed using Tanner's criteria(Reference Zahner, Puder and Roth24, Reference Tanner and Whitehouse32).
Dual-energy X-ray absorptiometry
The three-compartment DXA model separates body mass into lean tissue mass, fat mass and bone mineral content(Reference Pietrobelli, Formica and Wang33). DXA was performed by the same operator using an Hologic QDR-4500 densitometer (Hologic, Waltham, MA, USA) coupled with paediatric software. Head measurements were excluded from the calculation of body composition. The DXA scanner was calibrated daily against a standard phantom provided by the manufacturer. PBF was calculated as (fat mass/body weight) × 100.
Statistical analysis
Normally distributed variables are given as mean values and standard deviations, and minimum and maximum values. Variables that were not normally distributed (skinfolds) were log-transformed using natural logarithms to achieve or better approach the normal distribution (Shapiro–Wilk test) and are given as geometric mean and minimum and maximum values. Between-group comparisons of continuous variables were performed using unpaired Student's t tests on untransformed values for normally distributed variables and on log-transformed values for not normally distributed variables(Reference Bland and Altman34). Between-group comparisons of categorical variables were performed using Fisher's exact test. We selected eight potential predictors of PBF for evaluation: sex (male v. female), age (continuous), pubertal stage (Tanner stage 1 v. stages 2–5), BMI (continuous), waist circumference (continuous), log-transformed triceps skinfold (logTSF; continuous), log-transformed sum of triceps and subscapular skinfolds (logSF2; continuous) and log-transformed sum of triceps, biceps, subscapular and supra-iliac skinfolds (logSF4; continuous). Potential predictors were chosen on the basis of the following considerations: (1) sex, age and pubertal stage are major determinants of body composition(Reference Lohman and Going18); (2) triceps skinfold is easily accessible and does not require that the subject takes off her/his clothes (provided that the acromion and the olecranon can be properly localised), which is an important condition in the epidemiological setting, especially for girls; (3) logSF2 is expected to be more accurate than a single skinfold (logTSF) and is less burdensome than logSF4, which requires the measurement of four skinfolds(Reference Durnin and Rahaman12, Reference Frisancho31). The contribution of each predictor was evaluated by measuring its bootstrap inclusion fraction at multiple backward stepwise linear regression on 1000 random samples of 372 subjects (P value to enter = 0·05; P value to remove = 0·10)(Reference Royston and Sauerbrei35, Reference Steyerberg36). On the basis of the bootstrap analyses, we evaluated seven combinations of predictors. Age, sex and pubertal stage were included in all models, plus: (1) logTSF; (2) logTSF and waist circumference; (3) logSF2; (4) logSF4; (5) BMI; (6) waist circumference; (7) BMI and waist circumference. Standard diagnostic tests and plots were used to check model assumptions and fit(Reference Ryan37). The 95 % CI of regression coefficients and measures of model fit – adjusted determination coefficient (![]() ) and root mean square error of the estimate (RMSE) – were calculated on 1000 bootstrap samples of 372 subjects with bias correction. In other words, the bootstrap analysis provides an internal cross-calibration on 1000 samples.
) and root mean square error of the estimate (RMSE) – were calculated on 1000 bootstrap samples of 372 subjects with bias correction. In other words, the bootstrap analysis provides an internal cross-calibration on 1000 samples.
Multivariable fractional polynomials were used to test whether the fit could be improved by non-linear transformations(Reference Royston and Sauerbrei35). Because there was no gain in fit for any model, all continuous predictors were modelled as linear. Bland & Altman's method was used to calculate the fixed and proportional bias of the seven models(Reference Bland and Altman38). Lin's concordance correlation coefficient (CCC) was used as a further measure of agreement because of the presence of proportional bias(Reference Lin39, Reference Lin40). We also tested for the existence of a trend between the absolute inter-method difference and the quintiles of the average using the Jonckheere–Terpstra test for ordered alternatives (both ascending and descending). All statistical tests were two-tailed and statistical significance was set to a P value < 0·05. Statistical analysis was performed using STATA 11.0 (StataCorp, College Station, TX, USA).
Results
Of the 497 KISS children for whom age, weight and height were available, 372 (75 %) underwent anthropometry and DXA and were considered for the present study. The age of the children without DXA measurements was significantly lower than that of the children who had them available (8·6 (sd 2·2) v. 9·5 (sd 2·1) years; P < 0·001) but the distribution of sex (P = 0·520) and the SDS of weight (P = 0·238), height (P = 0·206) and BMI (P = 0·346) was not different between the two groups (data not shown).
Table 1 reports the anthropometric measurements of the 372 children. Of the children, 260 (70 %) were prepubertal (117 girls and 143 boys) and 112 (30 %) children were pubertal or postpubertal (seventy-seven girls and thirty-five boys). While there was no difference in age, weight, height and BMI between males and females, total body fat and PBF, as well as single skinfolds and their sums, were significantly higher in girls. Of the children 322 (87 %) had a normal weight, forty-one (11 %) were overweight and nine (2 %) were obese according to the International Obesity Task Force classification(Reference Cole, Bellizzi and Flegal29).
Table 1 Measurements of the 372 children
(Mean values, standard deviations and ranges)

Min, minimum value; Max, maximum value; SDS, standard deviation score; SF2, sum of triceps and subscapular skinfolds; SF4, sum of triceps, biceps, subscapular and supra-iliac skinfolds.
* Student's t test.
† Geometric mean (between-group comparison performed on log-transformed value).
Table 2 gives the bootstrap inclusion fraction, i.e. the number of times out of 1000 that the candidate predictors were selected for inclusion in the models. In model 1, sex, age and logTSF were selected 100 % of the time while waist was selected 93 %, BMI 57 % and pubertal stage 25 % of the time. In model 2, sex, age and logSF2 were selected 100 % of the time while waist was selected 41 %, pubertal stage 25 % and BMI 21 % of the time. Last, in model 3, sex, age and logSF4 were selected 100 % of the time while BMI was selected 49 %, pubertal stage 40 % and waist 17 % of the time. In other words, waist circumference improved the prediction of PBF in the model including logTSF, while neither BMI nor waist circumference improved the prediction of PBF in the models including logSF4 or logSF2.
Table 2 Bootstrap selection of predictors of percentage body fat (n 372)*
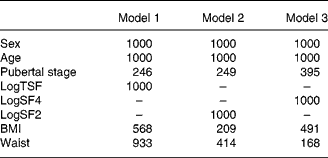
LogTSF, log-transformed triceps skinfold; logSF4, log-transformed sum of triceps, biceps, subscapular and supra-iliac skinfolds; logSF2, log-transformed sum of triceps and subscapular skinfolds.
* Values represent the bootstrap inclusion fraction, i.e. the number of times out of 1000 that the candidate predictors were selected as predictors at bootstrapped backward stepwise linear regression.
Table 3 gives the seven prediction models selected for further evaluation on the basis of the previous analysis. As determined by ![]() and RMSE, models 3 and 4 were similarly accurate and better than models 1, 2, 5, 6 and 7.
and RMSE, models 3 and 4 were similarly accurate and better than models 1, 2, 5, 6 and 7.
Table 3 Comparison of seven regression models for the prediction of percentage body fat (n 372)
(Regression coefficients or measures of model fit and 95 % bootstrapped confidence intervals†)

![]() , adjusted determination coefficient; logTSF, log-transformed triceps skinfold; logSF2, log-transformed sum of triceps and subscapular skinfolds; logSF4, log-transformed sum of triceps, biceps, subscapular and supra-iliac skinfolds; RMSE, root mean squared error.
, adjusted determination coefficient; logTSF, log-transformed triceps skinfold; logSF2, log-transformed sum of triceps and subscapular skinfolds; logSF4, log-transformed sum of triceps, biceps, subscapular and supra-iliac skinfolds; RMSE, root mean squared error.
* P < 0·001.
† 95 % CI were calculated using bootstrap in 1000 random samples.
Table 4 reports the fixed and proportional bias and the CCC for the seven prediction models. The fixed bias, i.e. the mean inter-method difference, was 0 % in all cases but the limits of agreement were narrower for models 3 and 4 than for the remaining models. Likewise, a negative proportional bias, i.e. a negative correlation between the inter-method difference and the average of the methods, was present in all cases but was lowest for models 3 and 4. Because the presence of a proportional bias makes the fixed bias an unreliable measure of agreement, we used CCC to evaluate agreement. CCC shows that models 3 and 4 are better than the other models at predicting PBF. The absolute inter-method difference for the respective models is shown in Fig. 1. The absolute inter-method difference showed an increasing trend for increasing quintile of the average of methods only for models 6 and 7.
Table 4 Bias and concordance of the seven models for the prediction of percentage body fat (n 372)
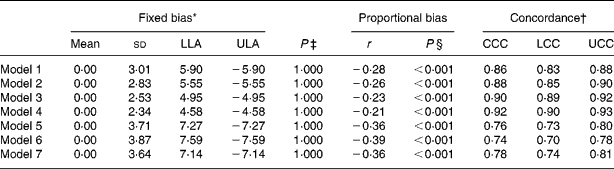
LLA, Bland & Altman's lower limit of agreement; ULA, Bland & Altman's upper limit of agreement; r, Pearson's correlation coefficient; CCC, Lin's concordance correlation coefficient; LCC, 95 % lower limit of agreement of CCC; UCC, 95 % upper limit of agreement of CCC.
* Calculated as (predicted − measured).
† P < 0·001 for all values of the CCC.
‡ Tests the null hypothesis that the mean bias equals 0.
§ Tests the null hypothesis of no association between the bias and the average.

Fig. 1 Relationship between the absolute inter-method difference (calculated as predicted − measured) and the quintiles of the average of the methods for the seven different models: (a) model 1 (P = 0·1984); (b) model 2 (P = 0·4930); (c) model 3 (P = 0·4936); (d) model 4 (P = 0·0684); (e) model 5 (P = 0·0373); (f) model 6 (P = 0·0159); (g) model 7 (P = 0·0062). The absolute inter-method difference showed an increasing trend for increasing quintile of the average of methods only for models 6 and 7. Box plots give the median value ( = ), 25th and 75th percentiles (lower and upper limits of the box) and lower and upper adjacent values (whiskers). ●, Outliers. The P values for trend were obtained from a Jonckheere–Terpstra test for ordered alternatives (both ascending and descending).
Discussion
KISS allowed us to perform a novel cross-calibration study of anthropometry for the prediction of PBF in a representative sample of the general paediatric population. To date, only the Alimentación y Valoración del Estado Nutricional de los Adolescentes (AVENA) study has performed a validation of anthropometry in a general population of children(Reference Rodriguez, Moreno and Blay23). However, the AVENA children were older (aged 13–18 years) than the KISS children and the main aim of the AVENA study was to validate external algorithms(Reference Rodriguez, Moreno and Blay23). In the present study, we showed that logSF2 is nearly as accurate as logSF4 and that both are better than BMI and waist circumference at estimating PBF in 6- to 13-year-old Swiss children. Although logTSF is less accurate than log2SF, it is still a better predictor of PBF than BMI, waist circumference and their combination. This has important implications for paediatric epidemiological research aiming to disentangle the effects of fat and fat-free tissues on health outcomes.
In recent years, it has been increasingly recognised that BMI and waist circumference are not accurate measures of body fat, especially in children(Reference Prentice and Jebb9, Reference Brambilla, Bedogni and Moreno10). The present results are in general agreement with other studies performed in non-representative samples of children showing that skinfolds are better than BMI at predicting PBF(Reference Himes6, Reference Goran, Driscoll and Johnson19–Reference Sarría, García-Llop and Moreno22, Reference Freedman, Wang and Ogden41). The present results are also in general agreement with the AVENA study, which shows that selected skinfolds offer reasonably accurate estimates of PBF at the population level in a representative sample of 13- to 18-year-old Spanish adolescents(Reference Rodriguez, Moreno and Blay23). The most accurate prediction of PBF in the AVENA study from the sum of triceps and subscapular skinfolds was obtained using the Slaughter equation in males. However, in the KISS study, this equation was less accurate than in the AVENA study. The Slaughter equation applied to KISS boys showed in fact a mean fixed bias of − 5·7 (sd 2·8) % (P < 0·001) v. one of 1·6 (sd 0·6)% in the AVENA study and, more importantly, a substantial proportional bias (r 0·87; P < 0·001) which was absent in the AVENA study (r 0·01; P>0·05). Despite these differences, which are likely to reflect differences in the study populations, the KISS and AVENA studies together suggest that skinfolds may be used for predicting PBF in children and adolescents.
The measurement of skinfolds is not recommended for routine evaluation of obese children(Reference Himes6, Reference Krebs, Himes and Jacobson7). This is because skinfolds do not add to the prediction of body fat in subjects with a BMI above the 95th percentile for age and, more importantly, to the prognostic value of BMI(Reference Krebs, Himes and Jacobson7, Reference Freedman, Wang and Ogden41–Reference Mei, Grummer-Strawn and Wang43). This is partially attributable to the higher error of measurement of skinfolds at high levels of adiposity. In this respect, the lack of an association between the absolute inter-method difference and the quintiles of the average for skinfolds has to be interpreted in light of the fact that just 2 % of our children were obese, so that the well-known lower reproducibility of skinfold measurements at higher values of adiposity had a minimal effect on the accuracy of the estimate of PBF in our population(Reference Ulijaszek and Kerr27).
On the other hand, epidemiologists are increasingly interested in evaluating the effects of fat and fat-free tissues on health outcomes using adiposity indexes rather than BMI(Reference Twisk, Kemper and van Mechelen44). The present study shows that log-transformed skinfolds are much better than BMI, waist circumference and their combination at estimating PBF in a general population of 6- to 13-year-old children, supporting their use as surrogate measures of body fat in epidemiological studies. The skinfolds measured in the present study were chosen because they are the most commonly employed(Reference Lohman and Going18, Reference Bedogni, Iughetti and Ferrari30, Reference Frisancho31). The modest increase of ![]() and the modest reduction of RMSE obtained by predicting PBF from logSF4 (RMSE 2·35; 95 % CI 2·14, 2·55 kg) as compared with logSF2 (RMSE 2·54; 95 % CI 2·34, 2·73 kg) is not enough to justify the measurement of four skinfolds in an epidemiological context where time is a significant constraint. Yet, for selected epidemiological applications, one may accept the lower R adj2 and the higher RMSE of logTSF (RMSE 3·02; 95 % CI 2·78, 3·26 kg) as compared with log2SF by considering that the triceps skinfold is simpler and less embarrassing to measure and offers a prediction of PBF that it still better than by the use of BMI and waist circumference.
and the modest reduction of RMSE obtained by predicting PBF from logSF4 (RMSE 2·35; 95 % CI 2·14, 2·55 kg) as compared with logSF2 (RMSE 2·54; 95 % CI 2·34, 2·73 kg) is not enough to justify the measurement of four skinfolds in an epidemiological context where time is a significant constraint. Yet, for selected epidemiological applications, one may accept the lower R adj2 and the higher RMSE of logTSF (RMSE 3·02; 95 % CI 2·78, 3·26 kg) as compared with log2SF by considering that the triceps skinfold is simpler and less embarrassing to measure and offers a prediction of PBF that it still better than by the use of BMI and waist circumference.
Although the present analysis of the KISS data provides novel information for the non-invasive assessment of body fat in paediatric epidemiological studies, it is not without limitations. First, 25 % of our children did not undergo DXA measurements. These children were younger than those with DXA, but they had the same SDS of weight, height and BMI. Thus, we are confident that the generalisability of our findings to the entire KISS population is not compromised. Second, our conclusions apply only to 6- to 13-year-old Swiss children. It is of interest, however, that the mean SDS of BMI is very close to the 50th percentile and its minimum and maximum values are within three SDS of the reference data, reflecting the distribution of anthropometry expected in the UK and possibly other Western populations. Third, DXA measurements are sensitive to soft tissue hydration. In particular, PBF estimates made by DXA tend to be higher when the hydration of the fat-free mass is low(Reference Roemmich, Clark and Weltman45). However, the magnitude of this error under normal conditions, as in the present study, is small and does not affect the validity of DXA(Reference Pietrobelli, Wang and Formica46). Fourth, a well-known limitation of DXA is that body composition estimates made by densitometers of different manufacturers are not comparable(Reference Plank47), which makes the external cross-validation of DXA-based prediction models potentially more difficult than with other methods.
In conclusion, the log-transformed sums of two and four skinfolds were found to be similarly accurate indices of PBF in a representative sample of 6- to 13-year-old Swiss children. Due to its simplicity and low cost, the sum of two skinfolds may be used to evaluate the association of PBF with health outcomes in epidemiological studies. Nevertheless, the KISS algorithms should be cross-validated in external samples before being employed in research.
Acknowledgements
We thank all children, parents and teachers for taking part in the study. KISS was funded by the Swiss Federal Office of Sports (grant no. SWI05-013) and the Swiss National Science Foundation (grant no. PMPDB-114401). The sponsors had no role in the design and conduct of the study, collection, management, analysis and interpretation of the data. There was no sponsoring from industry.All authors had full access to the data and take responsibility for the integrity of the data and the accuracy of the analysis. S. K., L. Z., R. R. and U. M. were responsible for the study concept, design and the acquisition of data. S. K. and G. B. were responsible for the analysis and interpretation of the data and drafted the manuscript. All authors took part in the critical revision of the manuscript for important intellectual content. S. K. and L. Z. obtained funding for the study. S. K. and G. B. are guarantors of the study.We declare that we have no conflict of interest.


 ) and the root mean squared error (RMSE; kg) were calculated for each model. LogSF4 (
) and the root mean squared error (RMSE; kg) were calculated for each model. LogSF4 (




