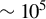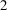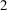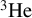Detailed characterization of kHz-rate laser-driven fusion at a thin liquid sheet with a neutron detection suite

Abstract

We present detailed characterization of laser-driven fusion and neutron production ($\sim {10}^5$/second) using 8 mJ, 40 fs laser pulses on a thin (<1 μm) D${}_2$O liquid sheet employing a measurement suite. At relativistic intensity ($\sim 5\times {10}^{18}$ W/cm${}^2$) and high repetition rate (1 kHz), the system produces deuterium–deuterium (D-D) fusion, allowing for consistent neutron generation. Evidence of D-D fusion neutron production is verified by a measurement suite with three independent detection systems: an EJ-309 organic scintillator with pulse-shape discrimination, a ${}^3\mathrm{He}$ proportional counter and a set of 36 bubble detectors. Time-of-flight analysis of the scintillator data shows the energy of the produced neutrons to be consistent with 2.45 MeV. Particle-in-cell simulations using the WarpX code support significant neutron production from D-D fusion events in the laser–target interaction region. This high-repetition-rate laser-driven neutron source could provide a low-cost, on-demand test bed for radiation hardening and imaging applications.

1. Introduction

The penetrating power and element-dependent cross-section of neutrons render them a useful tool for non-destructive evaluation of materials and structures^{[ 1]}. Consequently, portable neutron sources are in high demand for applications in the neutron radiography^{[ 2, 3]} of jet engine turbine blades, concrete structures for bridges and roads and also in the detection of sensitive nuclear^{[ 4]} and explosive^{[ 5]} materials for national security applications. Neutrons are also useful for cancer treatment^{[ 6]}. Typically, available neutron sources with high spatial resolution are not movable (e.g., nuclear reactors), and conventional portable neutron sources do not offer the high resolution required for many applications.

Ultra-intense laser-based neutron sources, first demonstrated by Pretzler et al. ^{[ 7]}, Norreys et al. ^{[ 8]} and thereafter by others^{[ 9, 10]}, offer both portability and the promise of high resolution, and have been studied for over two decades^{[ 11– 17]}. Such experiments have been mostly single shot in nature, typically offering ${10}^5$ – ${10}^6$ neutrons per joule per shot. One of the highest single shot yields to date was from an experiment involving the Trident laser system producing approximately ${10}^{10}$ neutrons per shot for 70 J laser pulse energy on target^{[ 18]}. Many applications require moderated thermal or epithermal neutrons with small source size^{[ 19]} or low divergence, necessitating fast neutron sources with at least ${10}^9$ neutrons/s, preferably more than ${10}^{12}$ neutrons/s rates^{[ 20]}. This level of production requires laser-based sources to operate at higher repetition rates than those in the existing literature. A 1-Hz laser-based neutron generator using flying pellets as targets was demonstrated by Komeda et al. ^{[ 21]}, and Hah et al. ^{[ 22, 23]} demonstrated neutron generation from vapor at 0.5 kHz. Here, we demonstrate a unique mJ-class, kHz-rate laser driving the fusion and neutron generation within approximately 500-nm thick flowing liquid sheet ${\mathrm{D}}_2\mathrm{O}$ targets that produced approximately ${10}^9$ neutrons with over 30 minutes of operation.

Furthermore, in the previous laser-based neutron generation studies, a plethora of neutron diagnostics in two broad categories are used: (1) energy resolving and (2) counting or measuring the total dose. For energy resolution, neutron-time-of-flight (nTOF) detectors are most common, among them scintillation detectors (plastic or liquid scintillators) coupled with photomultiplier tubes (PMTs), where the on-shot signal is captured with the aid of fast oscilloscopes^{[ 14]}. The typical lifetime of these events is multiple nanoseconds, with longer decay tails following the faster rise time^{[ 24]}. Since all laser–plasma interactions at ultrahigh intensities with solid density targets produce copious amounts of X-/gamma-rays, in TOF settings, the neutron signal observed in these detectors appears within the decay tail of the gamma signals, resulting in a poor signal-to-noise ratio (SNR). Therefore, to improve the SNR, one has to move the nTOF detectors farther away from the interaction region, thereby lowering the neutron signal due to the inverse r ${}^2$ law, causing significant SNR reduction. Complicating the problem further, such a detection setup does not guarantee linearity of the signal strength with the neutron dose, as there is no way to distinguish multiple neutron hits within the same laser shot event. In most of the referenced work, dose detection was performed using bubble detectors or CR-39 plastic track detectors. CR-39 detectors are sensitive not only to neutrons, but also to ions and electrons, so care has to be taken in positioning and shielding them near the interaction region. Furthermore, care has to be taken in etching the CR-39 pieces to develop the neutron etch pits inside them^{[ 14]}. Bubble detectors appear to be very popular in the field^{[ 18, 22]}, as they are apparently gamma-blind. However, they have inherent consistency problems, as they are strongly influenced by aging, ambient conditions and repeated exposure to radiation, among other things^{[ 25– 27]}.

In this paper, we address the detection issues by detailed characterization of the fusion source with a suite of neutron detectors: bubble detectors, liquid scintillators and a ${}^3\mathrm{He}$ proportional counter. In this way, we were able to corroborate the accuracy of dose measurements of the bubble detectors with those of the other two detectors. Furthermore, the liquid scintillator detector digitizer instrumentation employed the pulse-shape discrimination (PSD) technique, which allowed us not only to separate neutron and photon events, but also to achieve a more reliable and linear neutron energy spectrum.

2. Experimental setup for kHz-rate neutron generation and the detector suite

In this section, we discuss the experimental setup as well as the relevant nuclear physics and neutron detection principles. Laser and liquid target parameters are discussed in Section 2.1; for more details on the liquid sheet target system, see Ref. [28]. Earlier, this system was also used in ion acceleration experiments described by Morrison et al. ^{[ 29]} and Snyder et al. ^{[ 30]}. Section 2.2 provides a brief review of the underlying nuclear physics of the tabletop laser-induced fusion, and Section 2.3 explains the principles of operation of the neutron detectors.

Figure 1 Simplified overhead view of the target chamber and surrounding detectors. The main beam has a central wavelength of 780 nm with 8 mJ energy; the probe beam has a central wavelength of 420 nm with 80 μJ energy.

2.1. Liquid target chamber setup for neutron generation

A 1-kHz Ti:sapphire laser was incident on a sheet of room-temperature, free-flowing deuterium oxide ( ${\mathrm{D}}_2\mathrm{O}$ ). On-target intensities upwards of $5\times {10}^{18}$   $\mathrm{W}/{\mathrm{cm}}^2$ were reached with 8 mJ of energy in 40 fs and a 1.65 μm (full width at half maximum (FWHM)) spot size, focused with an f/1.0 gold-coated off-axis parabolic mirror (OAP, Aperture Optical Science). The laser has a central wavelength of 780 nm and is incident on the target s-polarized with an angle of incidence of approximately 45°.

The target is a sub-micrometer-thick liquid flowing sheet formed from two intersecting 25 μm diameter ${\mathrm{D}}_2\mathrm{O}$ cylindrical jets. As discussed by George et al. ^{[ 28]}, this sub-micrometer scale target is extremely stable and can operate at a kHz repetition rate or above. Two pumps, one for each jet, push the ${\mathrm{D}}_2\mathrm{O}$ through at a rate of 1 mL/minute. The approximately 65 mL size of the smaller of the two pumps thus limits the duration of an experiment to around an hour. Without this constraint, an experiment could run indefinitely. With roughly tens of nano-liters of ${\mathrm{D}}_2\mathrm{O}$ ionized per shot and the ability to recycle what remains, the target material costs roughly 2 US dollars per minute of run-time.

A second laser, temporally locked to the main laser, is used to image the interaction region in a pump–probe scheme. The energy in this frequency-shifted probe (80 μJ) is significantly lower than that of the main laser pulse. The probe has a 420 nm central wavelength and 80 fs pulse duration^{[ 31]}. A simplified chamber diagram can be seen in Figure 1 and a 3D rendering is shown in Figure 2. The probe beam passes through the target and the microscope objective to be imaged onto a camera, allowing real-time video diagnostics with temporal resolution of approximately 50 fs and spatial resolution of 1 μm. This video is the primary diagnostic that is used to align the laser–target system and maximize energy into the sheet.

Figure 2 Three-dimensional model of the interaction region. As in Figure 1, the main beam is shown in red and the probe beam is shown in blue. The jets are in white near the top of the image, and the size of the liquid sheet is exaggerated for illustration.

The 107-cm diameter stainless steel chamber is brought to a final vacuum of approximately 1 Torr, which is limited by the vapor pressure of heavy water and the tendency of the liquid target to freeze. This is below the approximately 7-Torr threshold for ion acceleration noted by Snyder et al. ^{[ 30]}. This pressure is measured at the edge of the chamber; it is expected that the pressure in the vicinity of the target may be significantly higher than the stated 1 Torr. The distance between the target and pressure transducer is approximately 53 cm.

2.2. Laser-induced deuterium–deuterium fusion

When ultra-intense laser pulses interact with a deuterium-rich target, two processes can give rise to neutron production^{[ 13]}, from the bulk and from a deuterium-rich catcher placed at the back of the target (the so-called pitcher–catcher scheme). Neutron production in the bulk may be categorized by two general processes. Firstly, as the absorbed laser energy is transferred from hot electrons to ions in the bulk, the local temperature at and near the focal region may become very high, which may cause deuterium–deuterium (D-D) fusion. Secondly, a significant portion of the hot target then explodes after some time, where the exploding high-energy deuterons collide with each other, causing D-D fusion events (a few nanoseconds after the pulse leaves the target; see, for example, the supplementary movie target explosion dynamics captured for a liquid target in Ref. [32] for similar intensities). At our laser intensities of high ${10}^{18}\;\mathrm{W}/{\mathrm{cm}}^2$ , energetic deuterons are accelerated outward from the surface primarily via target normal sheath acceleration (TNSA)^{[ 33, 34]}, which may then impinge on a nearby secondary deuteron-rich target. At energies of approximately keV and above, colliding deuterons can fuse together (D-D fusion), with half of the fusion reactions producing ${}^3\mathrm{He}$ and a neutron and the other half producing tritium and a proton:

(1) $$\begin{align}^2\mathrm{H}+{}^2\mathrm{H}\to {}^3\mathrm{H}\mathrm{e}+\mathrm{n}+3.27\ \mathrm{MeV},\nonumber\\^2\mathrm{H}+{}^2\mathrm{H}\to {}^3\mathrm{H}+{}^1\mathrm{H}+4.03\ \mathrm{MeV}.\end{align}$$

In the neutron producing branch, the 3.27 MeV Q-value is distributed as kinetic energy of the two products. With roughly a quarter of the total mass, the free neutron will take roughly three quarters of the energy, or 2.45 MeV. Our experiment is designed to detect neutrons from these D-D fusion events. We also provide evidence in Section 3.2.1 that the neutron energies are 2.45 MeV, as expected.

In the center-of-mass frame, neutrons are emitted without a directional bias. The approximately $5\times {10}^{18}\;\mathrm{W}/{\mathrm{cm}}^2$ average laser intensity of this experiment implies a maximum energy of accelerated deuterons in the 0.1–1 MeV range, which is not expected to produce significant anisotropy in the angular distribution of neutrons.

2.3. Suite of three neutron detection systems

Three independent detection systems are used to verify the generation of neutrons: an EJ-309 organic liquid scintillator (Eljen Technology) coupled to a photomultiplier tube (Hamamatsu, R7724), a ${}^3\mathrm{He}$ proportional counter (Reuter-Stokes) and a set of 36 bubble detectors (Bubble Tech Industries, BDS). The bubble detectors are the fastest to setup but have certain uncertainties in measurement, the EJ-309 has a fast response that could help in measuring the neutron energy and the ${}^3\mathrm{He}$ detector is highly efficient for thermal neutron detection and is inherently gamma-blind^{[ 35, 36]}. Our suite of the three detectors is utilized for high measurement confidence in neutron counts and the results are compared in Section 3.1.

EJ-309 organic scintillator: the EJ-309 scintillator consisted of a 5.08 cm right-hand circular cylindrical liquid cell in a thin aluminum housing. This cell was coupled to a 5.08-cm diameter PMT via a borosilicate glass window and EJ-550 silicone grease. The scintillator and PMT detector system, housed in 1.3-cm thick bismuth box with an additional 1.3-cm thick lead sheet at the front of the bismuth box, was placed 150 cm from the target interaction area. Both photons and neutrons were measured during laser operation even with the shielding in place, indicating an extremely active photon source. Photon and neutron events can be separated in the analysis via PSD due to the different scintillation decay profiles created by recoil electrons (corresponding to photon interactions) and recoil protons (corresponding to neutron interactions). The EJ-309 has good discrimination between photons and neutrons, even in a high gamma-ray environment^{[ 37]}. The detector was biased to –1300 V and events were analyzed with a waveform digitizer (CAEN Technologies, DT5730) and CoMPASS software.

In post-processing, typically a scintillation light-yield threshold is set, below which the neutrons and photons are indistinguishable. Such below-threshold events are discarded from the analysis. A GEometry ANd Tracking (Geant4)^{[ 38]} Monte Carlo radiation transport simulation of the experiment is used to determine the absolute neutron detection efficiency of the EJ-309 scintillator as a function of the light-yield threshold, accounting for geometric effects. In Geant4, the neutrons are modeled as coming from a point source with the scintillator at a distance of 150 cm. Neutrons are emitted isotropically in the Geant4 simulation. Figure 3 shows the simulated estimated absolute efficiency both with and without the environment modeled, highlighting negligible environmental scattering effects above a 0.4 MeVee (MeVee, MeV electron equivalent) light-yield threshold.

Figure 3 Absolute detection efficiency of the EJ-309 scintillator calculated via Geant4 simulation. The vertical axis indicates that roughly ${10}^5$ neutrons are produced for every neutron detected, and the shaded regions indicate error. Light-yield thresholds are equal to or more than 0.4 MeVee, and the difference in the two efficiencies is less than 0.5%. The units are defined such that 1 MeVee (MeV electron equivalent) equals the number of scintillation photons produced by a 1 MeV electron.

A ${}^{137}\mathrm{Cs}$ source is used for the energy calibration of the EJ-309, with a known Compton edge at 478 keV^{[ 39]}. This value is chosen as the light threshold for the detection efficiency: matching the calibration value minimizes error from an imperfect calibration, and environmental effects at this threshold are negligible. However, multiple-scatter events cloud the Compton edge, and without a Monte Carlo simulation as detailed by Dietze and Klein^{[ 40]}, its location cannot be precisely known. In addition, these calculations are based on the MeVee unit, which is flawed in the context of fast neutron detection in organic scintillators due to an inherent assumption of proportionality^{[ 41]}. In calibrating an organic scintillator based on the Compton edge of a known source, care must be taken to minimize these issues.

³He counter: this detector relies on thermal neutron capture on ${}^3\mathrm{He}$ , which creates a proton and a triton that carry the 764 keV Q-value of the reaction as kinetic energy in opposite directions, as given by the following:

(2) $$\begin{align}{}^3\mathrm{H}\mathrm{e}+{\mathrm{n}}_{\mathrm{th}}\to {}^1\mathrm{H}+{}^3\mathrm{H}+764\ \mathrm{keV}.\end{align}$$

A ${}^3\mathrm{He}$ proportional counter leverages the high cross-section of this thermal neutron capture reaction as well as the favorable properties of ${}^3\mathrm{He}$ as a fill gas. When neutron capture occurs, the proton and triton ionize the ${}^3\mathrm{He}$ gas and the created charge is collected via an electric field from an applied bias voltage. This results in a signal with energy that corresponds to the reaction Q-value. As the ${}^3\mathrm{He}$ counter is most sensitive to thermal neutrons (thermal neutron cross-section, 5330 barns^{[ 36]}), moderation is needed to detect fast neutrons with high efficiency. This moderation must then be carefully modeled in Geant4 to attain an accurate efficiency estimation. A 2.5 cm by 81.3 cm cylindrical ${}^3\mathrm{He}$ proportional counter was positioned approximately 140 cm from the target position. Blocks of paraffin wax were placed in front of the detector for neutron moderation. The detector was biased to 1100 V and signals were recorded using Maestro software.

The integral of the full-energy peak (FEP) at $Q=764$ keV gives the number of detected neutrons. Not all fast neutrons are moderated by the paraffin, and some may elastically scatter off of the ${}^3\mathrm{He}$ nuclei and deposit a wide range of energies. To eliminate these spurious counts, which underlie the FEP, the FEP region is fit to a Gaussian and exponential decay function. The integral of the Gaussian, corresponding to full-energy capture, yields the detected events. The counts in the exponential, corresponding to neutron scatter, are discarded. As the ${}^3\mathrm{He}$ tube is sensitive to neutrons generated by cosmic rays, each experiment is run alongside a natural background measurement, which is then subtracted from the main data, hereafter referred to as background-subtracted data. A Geant4 simulation is used to estimate the ${}^3\mathrm{He}$ absolute neutron detection efficiency, accounting for environmental scattering from the vacuum chamber, EJ-309 detection system, lead and bismuth shielding and low-Z moderating blocks. All other objects in the room were neglected; the model does not account for the room-return impact or additional moderation of the neglected objects. The Geant4 simulated absolute efficiency is $1.53\times {10}^{-4}\pm 0.3\%$ : for every neutron detected, $65,450\pm 170$ neutrons are emitted from the target into 4 $\pi$ .

Bubble detectors: the bubble detector spectrometer (BDS) is a set of 36 detectors rated to measure neutrons above six different energy thresholds: 0.01, 0.1, 0.6, 1, 2.5 and 10 MeV, with six detectors at each threshold. The bubble detectors boast no photon detection and minimal ion/electron sensitivity. In each detector, a polymer gel suspends millimeter-sized super-heated liquid droplets. As a neutron passes through the gel, it deposits its energy into recoil ions; these ions then may pass through a super-heated liquid drop, which quickly vaporizes and expands into a visible bubble^{[ 42]}.

One bubble detector of each energy threshold is placed in a group, with six groups attached at various positions directly to the outside of the chamber. After the experiment, bubbles were counted by eye as a measure of the neutron count, using the bubbles/neutron sensitivity measured by Lewis et al. ^{[ 42]}. The bubbles can then be compressed, allowing the detectors to be reused. The bubble detectors in these experiments were used 16 times over several months, although they had first been activated two years prior.

The measured data of the neutrons from the laser-driven fusion source and their comparisons are described in the following section.

3. Demonstration of kHz-rate neutron generation and its characterization

In this section we present the results of generation and characterization of the neutron flux from low-pulse-energy, high-repetition-rate tabletop fusion for the setup presented in Figure 1. Three independent detection systems and up to 40 individual detectors are used simultaneously, allowing full characterization of the neutron yield and direct comparison between detection systems. The results of the counting measurements are discussed below, in Section 3.1. Then, the neutron energy and angular distributions are characterized in Section 3.2.

3.1. Observation with neutron detection suite

EJ-309 organic scintillator: Figure 4 shows the 2D PSD histogram from the EJ-309 liquid scintillator. The PSD metric on the y-axis is the ratio between the integral of the tail of the scintillation event’s pulse to the total pulse integral from scintillation. The x-axis is given by the total pulse integral. Recoil protons from neutron interactions result in more delayed scintillation light compared to recoil electrons from photon interactions, and thus neutron counts have a higher PSD value than photon counts. As such, two separate features form in Figure 4, corresponding to neutrons at the higher-PSD cluster and photons in the lower-PSD cluster. The data in Figure 4 are mapped to a 1D histogram of PSD values in Figure 5. To mitigate environmental scattering effects and avoid misclassifying neutron and gamma-ray signals, a 478 keVee (keVee, keV electron equivalent) light-yield threshold is used for all experimental measurements.

As a control, natural (undeuterated) water is tested under the same conditions, as laser pulses on ${\mathrm{H}}_2\mathrm{O}$ should not produce neutrons. Figure 5 shows the PSD histogram of the ${\mathrm{H}}_2\mathrm{O}$ target in red. No significant neutron feature is present. The ${\mathrm{H}}_2\mathrm{O}$ experiment was half the duration of the ${\mathrm{D}}_2\mathrm{O}$ experiment, causing the size difference of the photon peaks.

Figure 4 Two-dimensional PSD histogram of neutrons and photons in the organic scintillator. The color scale denotes the number of events.

Figure 5 One-dimensional PSD histograms for the EJ-309 scintillator. The blue data are the same as in Figure 4; the red curve shows a shorter-duration experiment with ${\mathrm{H}}_2\mathrm{O}$ instead of ${\mathrm{D}}_2\mathrm{O}$ as a control.

³He counter: Figure 6 shows the background-subtracted data from the ${}^3\mathrm{He}$ proportional counter, comparing the ${\mathrm{D}}_2\mathrm{O}$ (blue) and ${\mathrm{H}}_2\mathrm{O}$ (red) experiments. For ${\mathrm{D}}_2\mathrm{O}$ , a sharp peak corresponding to the thermal neutron capture energy (764 keV) is seen along with a large number of counts at lower energies. For ${\mathrm{H}}_2\mathrm{O}$ , few total counts are recorded with no significant events near the thermal capture energy. Several hundred counts are seen at low energies, most likely due to the X-ray environment from the laser–plasma interactions. This large discrepancy in low-energy counts indicates that the signal at such energy in the ${\mathrm{D}}_2\mathrm{O}$ data is a result of neutron scatter, which is accounted for using the fitting method described in Section 2.3.

Figure 6 Background-subtracted data from the ${}^3\mathrm{He}$ tube. ${\mathrm{D}}_2\mathrm{O}$ (blue) and ${\mathrm{H}}_2\mathrm{O}$ (red) correspond to the same experiments shown in Figure 5.

Bubble detectors: in the analysis of the BDS, the 2.5 and 10 MeV bubble detectors were neglected, as their response to 2.45 MeV neutrons is not well characterized. With each individual detector typically exhibiting 15 or fewer bubbles over an hour of run-time, the set of 24 remaining bubble detectors showed hundreds of bubbles after an experiment with ${\mathrm{D}}_2\mathrm{O}$ . In contrast, over two separate ${\mathrm{H}}_2\mathrm{O}$ experiments totaling 102 minutes of run-time, only five bubbles in total were created. Normalizing by time, this corresponds to 0.05 bubbles/minute for ${\mathrm{H}}_2\mathrm{O}$ as opposed to 5.5 bubbles/minute from a representative ${\mathrm{D}}_2\mathrm{O}$ experiment.

Both the proportional counter and organic scintillator require analysis to eliminate spurious counts: the EJ-309 requires PSD to separate particle types, and the proportional counter requires fitting techniques to remove scattering events. With greater shielding on the EJ-309 and more moderation on the proportional counter, these unwanted events should be reduced, making analysis easier and more accurate. However, increased moderation may not be possible in all applications because of geometry constraints; for example, large amounts of wax are needed surrounding the 85-cm tube. By comparison, the EJ-309 (with PMT and Bi+Pb shielding) is small and additional lead shielding can easily be placed in front of the scintillator, blocking the line-of-sight from the source. Also, the ${}^3\mathrm{He}$ counter is more sensitive to unavoidable room-return effects from extraneous equipment, walls and the floor due to its dependence on thermal neutrons.

The BDS is convenient and easy to use because of its insensitivity to photons; hence, no analysis is needed to distinguish neutrons from other events. To obtain a neutron count from these bubbles even a non-expert can count the bubbles using calibration data provided by the manufacturer. Their small size allows them to be placed almost anywhere; also, they are inexpensive compared to the other two detectors. However, temperature has a significant effect: operating even a few degrees above the recommended temperature of 20 ${}^{\circ }$ C causes an increase in detection efficiency and a decrease in the energy threshold, an effect that is not well characterized in the literature^{[ 25]}. Several hours of compression were needed to reset the bubble detectors for reuse, which may limit how many experiments can be performed. In addition, the bubble detectors have a limited lifespan and their sensitivity shifts after repeated use^{[ 26]}. Ultimately, the bubble detectors need special care to obtain quantitative measurement of neutrons, especially, maintaining the temperature and keeping track of the measurement history.

The BDS typically measured neutrons in the high ${10}^5$ to low ${10}^6$ neutrons/second range. Due to the close proximity of bubble detectors within a group, it is possible that a neutron may be counted more than once as it scatters multiple times. This may be one reason for this high flux estimation by the BDS, which was significantly higher than the flux recorded by the other two detection systems: the ${}^3\mathrm{He}$ proportional counter typically saw neutrons/second in the low ${10}^5$ regime, with the EJ-309 in the high ${10}^4$ regime. Table 1 displays the neutron counts and uncertainties for a selection of two experiments when all detectors were used simultaneously. The reported error in the BDS is only the statistical (counting) uncertainty, whereas the error in the other two detectors includes both statistical uncertainty and the uncertainty in the Geant4 efficiency calculations.

Table 1 Comparison of neutrons/second and associated statistical errors from the three detection systems across two separate experiments. Note that other non-statistical errors contribute to the uncertainties and are not represented in this table, in particular for the ${}^3$ He detector and bubble detectors.

The unknown shifts in the efficiency of the BDS, not represented in the reported error of Table 1, make it unsurprising that the results do not closely match the results from the other two detectors. However, the scintillator and proportional counter should agree on neutron flux; instead, the ${}^3\mathrm{He}$ counter records a neutron flux two to four times higher than the EJ-309, depending on the experiment. The Geant4 modeling of the ${}^3\mathrm{He}$ counter is likely a large source of this discrepancy due to the detector’s sensitivity to thermal neutrons. Only modeled are the experiment chamber, detectors and wax moderation: all other equipment in the room that may contribute to neutron thermalization is neglected. The uncertainty introduced by not including these features is difficult to quantify and is not included in the error analysis above. Comprehensive modeling of the neutron thermalization process and subsequent thermal neutron scatters is known to be a challenge, in part due to the many possible contributions to thermalization and in part due to deficiencies in knowledge of relevant cross-sections^{[ 43]}. With a greater amount of thermalization in the experiment than what is modeled, the Geant4 analysis underestimates the absolute efficiency and thus overestimates the total neutrons emitted. Upon adding a thin floor and walls to the model, the estimated neutron emission by the ${}^3\mathrm{He}$ detector was reduced by roughly half, bringing it closer to the predicted flux of the EJ-309. The EJ-309 is insensitive to thermal neutrons and therefore does not depend so strongly on details of the Geant4 model.

Before detection efficiency and solid angle considerations, the proportional counter saw the highest number of raw counts, allowing for lower relative statistical error. However, the significant difference in relative error ( $\sim$ 0.5% for the proportional counter as opposed to $\sim$ 15% for the scintillator) is a result of different considerations being included. The uncertainty in the ${}^3\mathrm{He}$ efficiency only includes the statistical Monte Carlo uncertainty that is standard in Geant4, whereas the uncertainty in the EJ-309 efficiency also includes light-yield uncertainty, as detailed in the literature^{[ 44– 46]}. In addition, the uncertainty in the EJ-309 efficiency estimation overcomes thermalization uncertainty or environmental neutron scattering effects by using a light-yield threshold of 478 keVee, while the ${}^3\mathrm{He}$ detector response is unable to overcome this issue.

To summarize, the EJ-309 detector likely provides the most reliable measurement of neutron production. Although it is easiest to infer the neutron numbers from the BDS, the results are found to be inconsistent as the detectors have unknown dependencies on many parameters while suffering from poor counting statistics. The ${}^3\mathrm{He}$ proportional counter is too reliant on a detailed environmental model, which can be challenging to develop for a laboratory setup. In comparison, the EJ-309 detectors are well characterized in the literature and they have minimal environmental effects at energy thresholds above 0.4 MeVee.

3.2. Neutron characterization

Next, the neutron energy was measured using the time-of-flight (TOF) between the particle detection pulse at the EJ-309 scintillator and the laser pulse incident on the target. The expected energy is 2.45 MeV. Then, several experimental parameters are varied: the chamber pressure and pre-pulse effects on the neutron yield are studied, and the spatial distribution of the source is measured in a pitcher–catcher scheme.

3.2.1. 2.45 MeV neutrons

With a known distance from the neutron source to the scintillator, the time delay between the impingement of the pulse on the target and the arrival of neutrons can be used to determine the neutrons’ energies. The time at which the neutrons are produced is first estimated by the laser trigger signal, and then corrected with the arrival of the photons in the scintillator, as they travel at a known speed. This TOF analysis is shown in Figure 7. Relativistic forms of all equations are used. The detector electronics bin all events into 4-nanosecond windows, causing the discrete energy data in Figure 7. Still, a sharp peak in energies is seen around the expected 2.45 MeV, confirming D-D fusion.

Figure 7 Energy histogram of emitted neutrons, as measured by the organic scintillator via time-of-flight. Data were collected for 54 minutes with the scintillator subtending 0.0035 steradians, and counts are not scaled with detection efficiency. That is, only the raw counts are shown. The peak corresponds to the expected 2.45 MeV of D-D fusion neutrons.

Detected neutron counts with lower energy are likely a result of neutron scattering from laboratory surrounding features, such as the room’s floor and walls, as well as the nearby paraffin wax surrounding the ${}^3\mathrm{He}$ detector. The low-energy counts may also, in part, be due to deuteron breakup, as high-energy ( $\gtrsim$ 2.2 MeV) deuterons strike nearby materials. In addition, neutrons are emitted with 2.45 MeV in the center-of-momentum (COM) frame: if the initial deuterons have a bias in initial momentum, the scintillator in the lab frame will measure the neutron as faster or slower. Based on Figure 7 (for the configuration in Figure 1), our measurements strongly indicate that fusion neutrons are generated as the ${\mathrm{D}}_2\mathrm{O}$ liquid sheet target is expanding both in the forward and backward directions. The distribution of these COM frames gives a Gaussian profile to the neutron energy peak.

3.2.2. Anisotropy and spatial resolution

To further characterize our neutron source, we examine its angular distribution. Although the neutrons are expected to be produced isotropically, a catcher could introduce a directional bias; the deuterons in a solid ${\mathrm{D}}_2\mathrm{O}$ catcher should function as additional targets for the laser-accelerated deuterons. Placed immediately behind the liquid sheet, deuterons striking the catcher now have a bias in initial momentum, causing a potential bias in the direction of the overall neutron flux. However, as found by Willingale et al. ^{[ 13]} with a plastic target and a catcher, catchers are inefficient neutron sources: their low temperature increases the stopping power and makes fusion less likely. Our solid ${\mathrm{D}}_2\mathrm{O}$ catcher (heavy ice) did not significantly affect the isotropy.

Three identical EJ-309 detectors and PMTs were placed at different viewing angles around the chamber, all in the horizontal plane. Each scintillator was shielded from gamma-rays either with lead bricks or a bismuth container. The results are seen in Table 2: no detector measured significantly higher neutron generation than any other, indicating the catcher’s failure to contribute to neutron yield anisotropy. In addition, when compared to an identical experiment without a catcher, no significant difference in total neutron yield was observed. This is consistent with the observation of Ref. [13], where bulk neutron production was shown to exceed neutron production by the pitcher–catcher method for intensities near the range of intensities described here.

Table 2 Detector angles, estimated source counts and calculated uncertainties for the three-scintillator array. Detectors are named by their viewing angle, with ${0}^{\circ }$ defined as the laser propagation direction.

4. Simulation with WarpX

We ran proof-of-concept particle-in-cell (PIC) simulations using the WarpX code^{[ 47]} that recently implemented a fusion model using an algorithm developed by Higginson et al. ^{[ 48]}. These 2D3v simulations feature a laser modeled after the experiment with an energy of $7.7$ mJ and a peak intensity of $5.3\times {10}^{18}$ W cm ${}^{-2}$ . The 780-nm laser was modeled as Gaussian in space, sine squared in time (40 fs FWHM) and focused on the center of the target (1.8 μm FWHM spot size) with a 45 ${}^{\circ }$ angle of incidence. Simulations were performed with a cell size of 1.47 nm, 100 deuterium/25 electron macroparticles per cell and a time-step of 0.95 times the Courant–Friedrichs–Lewy (CFL) limit. The target was ionized deuterium with a density set by the number density of deuterium in heavy water. The target was 0.5-μm thick with a length of 20 μm. We did not include oxygen ions for simplicity and in line with the proof-of-concept goal of the simulations.

Particles were given an initial temperature of 100 eV. The fusion model includes a fusion multiplier parameter described by Higginson et al. ^{[ 48]}, which increases the probability of a fusion event occurring but proportionally decreases the weight of the neutron (and helium) macroparticles produced^{[ 48]}. The weight of a macroparticle refers to the number of physical particles it represents. Setting this parameter to ${10}^{12}$ allowed us to sufficiently sample the fusion products. As discussed by Higginson et al., this approach produces similar results to using orders of magnitude more particles per cell. No significant neutron production occurred without the laser irradiation, as expected.

Figure 8 2D3v PIC simulation results. The top figure shows neutron count data versus time and shows the difference between s- and p-polarization. The dashed line marks the time when the laser’s pulse envelope interacts with the target. Neutrons begin to leave the simulation starting around 800 fs. The bottom figure shows energy spectra of the simulation particles at 500 fs. Deuteron energies are shown with dotted lines and neutron energies are shown with solid lines. The p-polarized laser simulations show enhanced neutron generation and ion acceleration.

We simulated both an s-polarized laser (as in the experiments) and a p-polarized laser to explore the effect of polarization on neutron yield. Figure 8 shows the neutron yield from an s-polarized and p-polarized laser, with fusion primarily occurring after the pulse envelope of the laser finishes its interaction with the target. We found that p-polarization enhanced neutron production by a factor of 2.6.

Figure 8 shows the kinetic energy spectra of deuterons and neutrons at 500 fs after the start of the simulation. There were decreasing numbers of ions at higher energies, as expected for TNSA, which is the dominant ion acceleration mechanism at these intensities (e.g., see Refs. [29,49]). Also as expected, the p-polarized simulation has better laser absorption^{[ 50]} and higher maximum ion energies. These ion energies continue to increase after 500 fs, but we select this snapshot, which is after most of the neutrons are generated and before deuterons begin leaving the simulation boundaries. Neutron energies fall into a distribution around 2.45 MeV, the expected energy yield of a D-D neutron fusion event. The supplemental movie (see the Supplementary Material section) shows the time evolution of the deuterium density and neutron generation for the simulation with s-polarization. A snapshot of the movie, a few hundred femtoseconds after irradiation, is shown in Figure 9. The results clearly show neutron production from the center of the target where the laser-interaction region occurs, rather than uniformly along the length of the target. We have also carried out simulations with a catcher behind the target, and found negligible neutron contributions due to the catcher. This confirms our experimental observation that, in our case, most of the neutron production happened in the bulk, which is also consistent with Willingale et al.’s earlier work^{[ 13]}. Jiao et al. ^{[ 51]} also used the deuteron distributions from 2D PIC simulations to estimate neutron reaction rates and similarly found increased neutron generation from the target near the interaction region.

Figure 9 A frame of the 2D3v simulation with s-polarization at 600 fs after the start of the simulation, showing the deuterated sheet in black and neutrons in red. The supplemental movie (see the Supplementary Material section) shows the full evolution through 900 fs.

5. Comparison of our results to the literature

It should be noted that our experimental results demonstrate neutron generation even without a catcher, unlike most other experiments that required a catcher to achieve maximal neutron generation. We are only aware of a few other papers where ultra-intense lasers have produced D-D neutrons without a catcher. The following is an outline of the advances of our work as compared to the literature.

As mentioned earlier, the recent paper by Jiao et al. ^{[ 51]} inferred neutron generation directly from a solid deuterium target using only bubble detectors at the Texas Petawatt Laser. Furthermore, their neutron generation was accomplished at a rate of one shot per hour. However, their simulation results are qualitatively similar to ours but they used a higher intensity laser and a different PIC code. Finally, both efforts point to the interesting possibility of generating neutrons from a relatively small spot on the target, which is possible across a wide range of laser energies and repetition rates.

Hah et al. ^{[ 22, 23]} demonstrated neutron generation from ultra-intense laser irradiation of a 10-μm-diameter liquid column of heavy water (no catcher present). Similar to our work, a millijoule-class laser was used but with a 0.5-kHz repetition-rate neutron generation compared to our 1-kHz rate. Overall, Hah et al. generated similar numbers of neutrons per second to our experiment. Our effort leveraged a more extensive suite of neutron detectors and we provide more information about how these detectors were used (Section 2.3). An obvious difference between the two efforts is that we demonstrated neutron generation from a half-micrometer-thick liquid sheet, so our neutron source is potentially smaller. In future work, we can determine whether a heavy water sheet or a liquid column is more effective for producing neutrons.

Another key difference from our work is that Hah et al. ^{[ 22, 23]} performed experiments with 20-Torr background pressure to prevent the heavy water jet from freezing, whereas in our work we operated at 1 Torr. Neutron generation at this lower pressure implies that the neutrons originate within the target, but additional work is needed for verification.

6. Conclusion

Three independent detection systems confirm D-D fusion neutron generation at a kHz rate from laser–plasma interactions at our thin D ${}_2$ O sheet. Approximately ${10}^5$ neutrons/second were emitted in a 4 $\pi$ solid angle for up to an hour. The generated neutrons were found to carry 2.45 MeV of kinetic energy, providing evidence of D-D fusion. Simulations indicate that neutrons emerge from a relatively small volume in the laser-interaction region of the target.

Of the three detection systems employed, (1) the EJ-309 was found to have the highest precision, (2) the efficiency of the BDS is not well characterized beyond a narrow use case and (3) the efficiency of the proportional counter is reliant on a detailed environmental model, which cannot be easily obtained. As shown in Figure 3, environmental scattering has a negligible impact on the EJ-309’s efficiency at thresholds above 0.4 MeVee. Many other laser-based neutron studies exclusively use bubble detectors (or a BDS) for neutron flux measurements, and based on our finding those fluxes may be somewhat overestimated.

One of the potential application of our laser-driven system is the ability to generate high-repetition-rate mixed radiation. Our system has demonstrated MeV ions, electrons and X-rays at 1 kHz – the addition of neutrons allows for a sustained mixed radiation environment^{[ 29, 52, 53]} that could be useful for radiation hardening for nuclear or space weather testing. Furthermore, because of the small target volume where the neutron is generated, such a source would be ideal for neutron radiography.