1. Introduction
Ice shelves are of crucial importance for the overall behavior of the Antarctic ice sheet. They govern, to a large extent, the flux of inland ice to the ocean, and thus control the wastage of the entire ice mass of West and East Antarctica. It is obvious that the flow of inland ice into the ocean is hindered by their existence. In the context of climate dynamics, therefore, ice shelves constitute a crucial element in the interaction between climate and cryosphere. The mathematical description of iceshelf dynamics has a long history, beginning with Weertman’s paper in 1957 (Reference WeertmanWeertman, 1957) and including the works of Reference Weis, Greve and HutterWeis and others (1999) and Reference BaralBaral (1999). Perturbation techniques are used to develop a hierarchy of classes of theories of icesheet equations, which are dominated by shearing processes, and iceshelf equations, which are chiefly governed by extensional and compacting flows. To lowest order in the shallowness parameter of these flows (the ratio between depth scale and horizontal scale of these ice masses, ε =H/L), two limiting theories have been developed: the shallowice approximation (SIA) for sheets and the shallowshelf approximation (SSA) for shelves. We shall call these the zerothorder approximations. Recent work has concentrated on higherorder approximations and proper mathematical matching procedures between shelves and sheets across the groundingline region and, thus, proper transition rules from ice sheets to ice shelves (e.g. Reference SchoofSchoof, 2007; Reference Kirchner, Hutter, Jakobsson and GyllencreutzKirchner and others, 2011; Reference SatoSato, 2012; Reference Sato and GreveSato and Greve, 2012; Reference Ahlkrona, Kirchner and LöstedtAhlkrona and others, 2013a,Reference Ahlkrona, Kirchner and Löstedtb); they are not the focus of this paper.
Here we prefer to consider an SSA formulation in isolation. The great unsolved problem in iceshelf dynamics (perhaps in the whole of glaciology) is the treatment of the shelf front. Reference Weis, Greve and HutterWeis and others (1999) write:
To date we know of no (even just half way reasonable) proposal how to deal theoretically with this boundary condition. No response of an icesheet/iceshelf system to climate variations can be computationally forecasted, unless this boundary condition is properly parameterized. Kinematic, as well as dynamic, relations must be postulated… Dynamically, an equivalent description of the calving rate – the second condition – is the relevant climatological statement, describing the mass loss of the shelf, for which only first estimates exist … The difficulty with parameterizations of the calving rate is its intermittent nonsmooth occurrence in nature. Such discontinuous behavior of the mass loss by ice shelves is most likely not adequately parameterizable, but smeared over long time scales (of decades) a smooth parameterization may well be possible, and the study by Reference Van der VeenVan der Veen (1996) gives hints as to how a functional relation might look like, but validation of the proposed equation may even be more difficult as long term observations are not available. So, a proposed set of equations will … remain largely conjectural.
The situation now – almost 15 years later – is essentially the same, but our understanding has advanced. Reference AlleyAlley and others (2008) hypothesize that ‘alongflow ice shelf spreading is the dominant control on calving’. Their calving flux, c, is written as a power law of the variable ![]() wH, where
wH, where ![]() is the alongflow spreading rate, w the halfwidth of the ice front and H the ice front thickness. Whereas the proposed power law correlates reasonably well with inferences from data, the authors' parameterizations only involve external parameters, which express no explicit connection with material behavior.
is the alongflow spreading rate, w the halfwidth of the ice front and H the ice front thickness. Whereas the proposed power law correlates reasonably well with inferences from data, the authors' parameterizations only involve external parameters, which express no explicit connection with material behavior.
Today's approach is no longer to necessarily parameterize the calving rate (i.e. the rate of mass loss along the front boundary) or related terms. The present understanding is that the ice in the immediate vicinity of the shelf front is being weakened due to accumulating fractures (which may be transported from further inland), which finally leads to calving events. This calls for the incorporation of some kind of damage or fracture parameterization into iceshelf models, in order to predict/assess their stability and possible onsetting instabilities, which have been shown to fall apart on a surprisingly short timescale. Precursory steps to develop such a view of the calving processes have been undertaken by Reference Benn, Warren and MottramBenn and others (2007).
Damage concepts have been introduced in iceshelf dynamics only very recently. While we were preparing this paper, Reference Albrecht and LevermannAlbrecht and Levermann (2013) published work that incorporates an evolution equation of a scalar fracture density variable, 𝜙, with ![]() = f, where f is the fracture production rate which they parameterize. The variable φ enters into the stress/strainrate relation of their model via an additional ‘enhancement factor’ (their Eqn (6)), and this enhancement factor is treated in the SSA as a function of the inplane coordinates, x and y (their Eqn (5)).
= f, where f is the fracture production rate which they parameterize. The variable φ enters into the stress/strainrate relation of their model via an additional ‘enhancement factor’ (their Eqn (6)), and this enhancement factor is treated in the SSA as a function of the inplane coordinates, x and y (their Eqn (5)).
A similar formulation was used by Reference BorstadBorstad and others (2012). They inferred values of a damage variable from measured velocity fields, with the goal of finding a critical upper bound for this damage variable. In the same way as Reference Albrecht and LevermannAlbrecht and Levermann (2013), they implicitly assume the damage variable to be constant over depth.
Interesting work that describes calving has also been done by Reference BassisBassis (2011), using methods of statistical physics, and by Reference Bassis and JacobsBassis and Jacobs (2013), who introduced a granular material point of view. However, these methods are not readily applicable within the SSA framework.
It is known that stresses across the iceshelf thickness are strongly z- dependent and, consequently, a fracture criterion for the stresses, which relates the effective stress to the ‘ordinary’ Cauchy stress, must equally be z- dependent, so that an effective viscosity for the shelf must be defined by keeping the temperature and the damageeffect variable as fields in three dimensions: x, y and z.
This paper presents this crucial subtlety and demonstrates the strict conditions that must be observed when deriving a complete twodimensional (2-D) model. Section 2 presents the governing equations of ice shelf flow. Beyond the ‘classical’ field equations and their approximation for shallow floating masses, and the constitutive relations for the stress deviator, heat flux and internal energy, special attention is devoted to the derivation of the damageevolution equation and the parameterization of the damage production rate. It follows the Hayhurst criterion (as specified by Reference Pralong and FunkPralong and Funk, 2005), but needs to be altered for ice shelves, because of the flotation in ocean water. Section 3 is devoted to the SSA, first for damagefree ice; it demonstrates the strong z- dependence of the temperature. Subsequently, damaged ice is treated, showing that both the temperature and damage variable must be treated as threedimensional (3-D) fields, while only the velocities have a plugflow character. An attempt to derive a fully 2-D theory demonstrates the limitation of such an approximation to isothermal shelves. In Section 4, finally, a failure criterion is formulated, which suggests how the free fronts and, consequently, the evolution of the calving rates can be determined. Thus, if damage concepts govern the calving rate, these concepts also determine the growth and decline of the ice shelves and, therefore, the increase or decrease of buttressing of the inland ice and finally the climate impact.
2. Governing Equations of Iceshelf Flow
In the following, we formulate the continuummechanical framework for damaged ice shelves. The thermomechanically coupled initialboundaryvalue problem for undamaged ice was formulated by Reference Weis, Greve and HutterWeis and others (1999). We add to this a damage variable which keeps track of microcrack accumulation due to tensile stresses. We use a scalar damage theory, governed by a phenomenological damageevolution equation of the Kachanov–Rabotnov type (Reference KachanovKachanov, 1958; Reference RabotnovRabotnov, 1969), as used by Reference Pralong and FunkPralong and Funk (2005).
We assume that the ice shelf consists of purely meteoric ice, so we do not have the complication of distinguishing between meteoric and marine ice. Thus, the problem we consider is that of a floating layer of glacier ice of variable thickness, which is attached to and fed by an ice sheet or a tidewater glacier. Using the terminology of Reference Weis, Greve and HutterWeis and others (1999), the margins of the ice sheet are called
the ‘grounding line’ – the iceshelf/icesheet interface;
the ‘coastline’ – where the ice shelf reaches solid land and
the ‘calving front’ – the margin towards the ocean, subject to mass loss by calving.
Additionally, the ice/air interface on top of the ice shelf is referred to as the ‘iceshelf surface’ and the ice/ocean interface as the ‘base’. Boundary conditions have to be specified on each of these five boundaries.
2.1. Balance equations, free fields
The free fields which we consider are
pressure, p,
ice velocity, v,
absolute temperature, T,
damage density, Y.
For convenience, we postpone a precise definition of the damage variable, Y, to Section 2.2. For the moment, we simply consider this variable as a scalar field which allows us to keep track of the density of microcracks accumulated at a certain point in the material. This scalar description of damage accumulation ignores any anisotropic effect of damage, giving it the advantage of simplicity. More adequate tensorial formulations of damage could be made in future analyses.
The governing equations for these quantities are the balance equations for mass, momentum, energy and damage effect.
As far as kinematics (and not thermodynamics) are concerned, glacier ice can be assumed to be a densitypreserving fluid. The balance equations for mass, momentum and energy are thus (Reference HutterHutter, 1983)
where t is the time, ρ is the mass density of ice, D is the symmetric strainrate tensor and g is the gravitational force density. In these equations, we have used the constitutive quantities deviatoric Cauchy stress, t D, specific internal energy, u, and heat flux density, q. These quantities are given by the constitutive relations in Section 2.2. Furthermore, the time derivatives on the lefthand sides of Eqns (2) and (3) can be understood as material derivatives:

for any scalar or vector-valued field, φ.
The above relations can be found in any standard textbook on continuum physics; this is not the case for the damage balance. We assume the balance law of the damage variable, Y, to have neither a flux nor a supply term. The damage balance equation thus reads
where FY is the damage production rate density, which we refer to as the ‘damageevolution function’.
2.2. Constitutive equations
In the following, constitutive relations will be given for the heat flux density, the specific internal energy, the deviatoric Cauchy stress and the damage production rate.
These constitutive quantities will be assumed to be functions of the set
where k = ∇T is the temperature gradient and p w is the water pressure of the surrounding ocean at a certain depth. Thus, we consider a viscous heatconducting fluid subject to damage accumulation.
2.2.1. Heat flux and internal energy
Although heat flux and internal energy could depend on certain isotropic representations of the state space, S, we restrict our consideration to Fourier’s law for the heat flow density:
where k(T) > 0 is the thermal conductivity, and a temperaturedependent heat capacity, c(T) > 0, so the differential of specific internal energy reads
2.2.2. Deviatoric stress
Polycrystalline glacier ice behaves on geophysical timescales like a strainsoftening viscous fluid (Reference GlenGlen, 1952, Reference Glen1958; Reference SteinemannSteinemann, 1958). The presence of an accumulation of microcracks (i.e. damage) manifests itself in further softening of the material as it becomes increasingly damaged. We express this in the constitutive relation
where B (T) is the temperature-dependent rate factor, f( D) is a function describing the nonlinear rheology and 0 < Y ≤ 1 is the scalar damage variable. Equation (9) defines the constitutive meaning of the damage variable, Y: at Y = 1 the material behaves as it does in the absence of damage; as the material becomes increasingly damaged Y approaches 0. In the language of a mean-field approach, the damage variable, Y, can be seen as the ratio of the intact and the total area in a certain cross section of a reference volume of the material. (Y relates to the damage variables used by Reference Pralong and FunkPralong and Funk (2005) by Y = 1 – D = Z −1. Our choice of the damage variable is due to the convenient interpretation of Y as effective ice thickness, which will emerge below.)
For the rate factor, B (T), we adapt the usually assumed Arrhenius-type parameterization, and for the rheological function, f (D), we use the regularized isotropic generalization of Glen’s and Steinemann’s power law (Reference NyeNye, 1959),
where n is a phenomenological constant, is a small regularization constant and ![]() is the second isotropic invariant of a rank2 tensor.
is the second isotropic invariant of a rank2 tensor.
2.2.3. Damage evolution
The damage-evolution function parameterizes how damage accumulates in reaction to a certain level of tensile stress. Reference Pralong and FunkPralong and Funk (2005) formulated a Kachanov–Rabatonov damage-evolution law for glacier ice. Rewriting their result in terms of Y yields
where b, r, k and σ th are positive phenomenological constants, σ is called the ‘damage yield measure’ and

With positive b, non-trivial FY is negative, so with damage evolution the value of Y decreases.
Damage accumulation starts as soon as the damage yield measure, σ, (Eqn (11)) exceeds a certain threshold value, σ th. This stress function is a scalar function of the Cauchy stress tensor, giving a certain weight to its invariants. It is a nontrivial problem to find a suitable stress function that reflects the reaction of the material to multiaxial stress states. In order to find one, Reference Pralong and FunkPralong and Funk (2005) considered the experimental results of Reference HayhurstHayhurst (1972), who found the time to creep rupture in different alloys at high homologous temperatures was proportional to some negative power of the expression

where α, β and γ are positive constants normalized to unity, α + β + γ = 1, and t 1 is the maximum principal stress. (Note that the definitions of these constants that are used by Reference Pralong and FunkPralong and Funk (2005) are different from those used by Reference HayhurstHayhurst (1972), whose nomenclature we adopt here.) Reference Pralong and FunkPralong and Funk (2005) set the stress function,, equal to the expression in Eqn (13), with the Cauchy stress tensor replaced by the ‘effective Cauchy stress tensor’,
Equation (13) assigns three causes of damage inception and evolution to the scalar damage yield measure, σ > σ
th: (1) principal tensile stress, (2) mean isotropic stress and (3) shearing. These correspond to experiments under simple tension, volumetric extension and pure or simple shearing, respectively. The coefficients α, β and γ = 1 – α – β distribute these contributions to the three typical stress measures, ![]() such that for α = γ = 0 volumetric extension makes mean stress the critical failure mode. Similarly, for α = 1,γ = 0 (and thus β = 0), the principal tensile stress is the critical failure mode, and for α = 0, γ = 1 (→ β = 0) failure occurs due to octahedral shear stress.
such that for α = γ = 0 volumetric extension makes mean stress the critical failure mode. Similarly, for α = 1,γ = 0 (and thus β = 0), the principal tensile stress is the critical failure mode, and for α = 0, γ = 1 (→ β = 0) failure occurs due to octahedral shear stress.
The coefficients b, k, r,α, β, γ and σ th are material constants, and for glacier ice they take the values given in Table 1 (Reference Pralong and FunkPralong and Funk, 2005). They are determined by least-square procedures from laboratory tension experiments. (Note that we do not cite a value for parameter k. This is due to the fact that Pralong and Funk used a stress-dependent parameterization for this parameter, which is probably not appropriate for the case we consider here. Effectively, these authors mostly used a value of 3.5–4, which could perhaps be adopted for our purposes.)
For an ice mass subject to the conditions of the shallow-shelf approximation, we have to make some modifications to this theory. First, we have to take into account the influence of water penetrating into any crack which opens at the base of the ice shelf. This water, being at a pressure close to the ice overburden pressure, tends to counterbalance the action of the latter as an effect opposing crack opening. We thus propose to replace the pressure, p, in the Cauchy stress tensor by the effective pressure
where p w is the water pressure at a given depth (Fig. 1). This change accounts for the fact that the water pressure reduces the contribution to failure of the local mean pressure in ice near the base of the ice shelf that is exposed to crevasses. It assures that damage evolution in an ice shelf always starts at the top or base, not somewhere in between.

Fig. 1. Illustration of water and ice pressure on the ice shelf close to the calving front.
Furthermore, we have to carefully reevaluate Reference Pralong and FunkPralong and Funk’s (2005) idea of rescaling the entire Cauchy stress tensor by a factor Y −1. In the SSA limit, the hydrostatic stress is dominated by the ice overburden contribution, and, therefore, is mostly compressive. Assuming that volumetric effects act thus mainly in opposition to crack formation, we propose to apply Reference Pralong and FunkPralong and Funk’s (2005) rescaling principle only to the deviatoric stresses, t D. The resulting parameterization for the damage yield measure reads

However, close to the surface, there may also arise tensile hydrostatic stresses in the SSA. The damage evolution due to these may be underestimated by the parameterization (Eqn (16)). We estimate that this effect is fairly small. Nevertheless, future research should bear in mind that Eqn (16) is only a parameterization and nothing more. Different parameterizations, eventually applying a rescaling also to p, or even to p w or the contribution proportional to β, may be justified just as well.
The changes of the parameterization of σ motivated above likely imply that numerical values for α,β,γ and σ th may be slightly different than those given in Table 1. In an inverse approach, the values of Table 1 may be used as a starting set, possibly to be improved.
Considering the limit of FY as Y → 0, it is clear that the behavior of the proposed model is nonphysical. This may be striking at first glance; however, any damage mechanics theory is only strictly valid for comparably low damage accumulations. Therefore, as Y → 0, the damageevolution theory becomes meaningless at some point. This is a conceptual problem of continuum damage mechanics; however, in practice, this deficiency is simply ‘solved’ by freezing the evolution of Y at some small threshold value, Y min > 0. At Y = Y min, FY is consequently set to 0.
Table 1. Parameter values as given by Reference Pralong and FunkPralong and Funk (2005). The value L g is the characteristic size of the glacier fracture zone in the direction of the crevasse

2.3. Boundary conditions
The boundary conditions are:
vanishing shear stress at the free and basal surfaces, vanishing pressure at the free surface and given ocean water pressure at the basal surface according to
where h w is the level of the ocean surface;
prescribed surface temperature, T s = T atm, and T base = T ocean, where T ocean is the upper-ocean water temperature;
prescribed depth-averaged incoming horizontal velocity field at the grounding line and prescribed vertical temperature profile along the grounding line;
no-slip boundary condition and prescribed temperature distribution along solid boundaries;
kinematic boundary conditions for the motion of the free and basal surfaces, the iceshelf front line and the grounding line.
Note there are no boundary conditions for the damage variable, Y, because its evolution equation is simply a transport equation with no flux term, for which Eqn (5) is only an initialvalue problem. Y is nevertheless expected to influence the calvingfront boundary condition. This is a difficult problem, which will eventually determine the mass loss rate along the iceshelf front. The principal idea of this will be sketched below.
3. Shallow-shelf Approximation
Polar ice shelves typically have a horizontal extent, L, of several hundred kilometers, but a vertical extent, H, of only several hundred meters. This extremely shallow geometry, together with the fact that the ice thickness varies only very slowly horizontally, motivates a scaling of the governing equations of ice flow in powers of
This scaling suggests a regular perturbation scheme (Reference BaralBaral, 1999); the zeroth order of this perturbation scheme is the SSA. This scaling is rigorously discussed by Reference Weis, Greve and HutterWeis and others (1999); here, in Section 3.1, we outline only the most important points of ice-shelf dynamics in the SSA and in the absence of damage. We then discuss how a damage-evolution theory can be implemented into this framework.
>3.1. Shallowshelf ice mechanics in the absence of damage
The starting point of the SSA is the momentum balance with neglected acceleration terms (Stokes approximation), subject to the hydrostatic approximation. The latter assumes (Reference Greve and BlatterGreve and Blatter, 2009) that the z- component of the momentum balance (where the z- axis is collinear with gravity) reduces to a balance between the vertical gradient of the vertical diagonal stress and the gravity force:
where g = ‖g‖. The momentum balance (Eqn (2)) in this approximation reads


where h is the level of the ice surface. Notice that the occurrence of txz and tyz in Eqns (20) and (21) is crucial. These stress components can only be eliminated via z- integration and the imposition of stress boundary conditions at the free and basal surfaces.
A shallow ice shelf is always floating. Its flow regime is characterized mainly by plug flow, i.e.
where x and y are the horizontal coordinates and z is perpendicular to the ocean surface. The strain-rate tensor thus has the structure

and depends to lowest order only on the x and y coordinates. In addition, the zeroth-order Cauchy stress deviator reads

This structure of the deviatoric stresses in SSA, together with the zero-shear boundary conditions at the top and the base of the ice shelf motivate a vertical integration of the zeroth order of the momentum balance in the hydrostatic approximation (Eqns (20) and (21)). This yields


Where H is the thickness of the ice shelf, and

are the membrane stresses. (Membrane stresses are the 2-D equivalent of forces. They describe the force acting on a length increment within a plane membrane.)
In its vertically integrated form (ignoring the damage effect), the stress/strainrate relation (Eqn (9)) reads

As the strain-rate tensor in the SSA limit is constant along z, this relation can be written as
Where the quantities ‘effective viscosity’,

and ‘effective rate factor’

have been defined, as well as the ‘effective strain rate’

Ice mechanics for an isothermal ice shelf in the SSA limit is thus essentially a 2D model. However, as soon as the thermomechanically coupled problem is considered, we have to treat the temperature, T = T (x, y, z, t), as a field of three space dimensions evolving according to the boundary-value problem

Computationally the non-isothermal shelf equations are no more complicated than the corresponding equations in the SIA. In a forward-integration procedure with determined mechanical fields and temperature at time t, the temperature distribution at time t+Δt can be computed by forward-in-time integration of the spatially 3-D boundary-value problem (Eqns (34–38)) with given mechanical fields at time t.
In order to consider a simple, exclusively 2-D theory, we have to use the gross approximation of an isothermal ice shelf. As we will see in Section 3.2, the inclusion of a damage variable gives rise to a similar tradeoff; we can consider a completely 2-D theory but only at the cost of making certain, sometimes drastic, approximations.
3.2. Damage mechanics in the SSA
In order to include a damage variable in the SSA equations, we have to modify the constitutive equation for the deviatoric stresses, and include Eqn (11) as damage balance equation. We thus start from Eqn (9) and scale it:
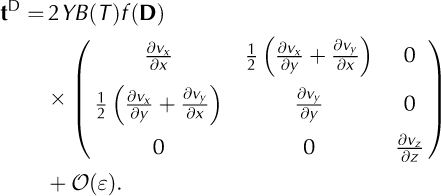
This shows that t D is strongly z- dependent, because B(T) and Y vary in general with z. The corresponding vertically integrated constitutive equation is (up to higher-order contributions)

where

is again an effective rate factor. This quantity obviously contains the softening effect of both damage and temperature. These two cannot be separated, as the integral in Eqn (40) cannot be written as two separate integrals.
The evolution of the damage variable, Y, is governed by Eqns (5), (11) and (16). It is a nontrivial task to write an SSA version of this equation, as it contains the Cauchy stresses, which in the SSA limits have been replaced by the membrane stresses. Equation (5) can be written as

From Eqns (39) and (40), we can see that the effective stress, ![]() = tD/Y, arising in the argument of FY
may be expressed as
= tD/Y, arising in the argument of FY
may be expressed as

where {i, j} ⊂ {x, y}. Using the deviatoric propery of ![]() , we can also calculate the z- component, and finally obtain
, we can also calculate the z- component, and finally obtain

Equation (44) can be used to evaluate the largest principal effective stress, ![]() and the second invariant,
and the second invariant, ![]() , for use in the evaluation of σ in Eqn (16) and FY
in Eqn (11). To this end we also use p(z) = pg(h – z) – txx
D – txy
D
, which is a consequence of the hydrostatic approximation.
, for use in the evaluation of σ in Eqn (16) and FY
in Eqn (11). To this end we also use p(z) = pg(h – z) – txx
D – txy
D
, which is a consequence of the hydrostatic approximation.
Obviously, it is possible to express the effective stress governing the evolution of Y in terms of the shallow-shelf quantities, N and β. This reflects the fact that the shallow-shelf velocity profile is constant over depth. As an effect, the effective stress is obtained by simply distributing the total membrane force, N, equally (up to temperature effects in B, which are absent for an isothermal theory) over the remaining depth profile. We conclude that, interestingly, a shallow-shelf damage theory is automatically a mean-field approximation.
It is equally possible to maintain the three-dimensionality for the determination of the damage-effect variable, Y, and the temperature field, T, while describing the mechanical membrane problem using Eqns (26), (27), (40) and (41) and computing Y from Eqns (42) and (44). To see this, assume that at time t the membrane forces, N, the velocity field, v, the temperature field, T, and the damage-effect field, Y, are known. With a forward-in-time integration the temperature distribution, T, and the damage-effect field, Y, at time t + Δt can then be computed using Eqns (5), (11), (16), (42), (44) and (3), (7), (8), as well as the velocity field and membrane forces at t þ t. This shows that, once the fields are initialized, forward integration is possible also when T and Y are z- dependent.
This will most likely be the integration procedure that will be used in realistic ice-shelf developments, when damage evolution is accounted for. In fact, the descriptions of the z- dependence of the temperature field, T, and the effective shear stress, ![]() , are important ingredients of a quantitatively correct evolution of damage.
, are important ingredients of a quantitatively correct evolution of damage.
3.3. Effectivethickness approximation
It would obviously be desirable to have a theory which only involves vertically integrated quantities. Even in the absence of damage, this can only be achieved for an isothermal ice shelf. Therefore, in the following we discuss how a 2-D damage-evolution theory can be implemented into the SSA for an isothermal ice shelf. It turns out that further approximations have to be made to accomplish this task.
3.3.1. Integrated damage as effective ice thickness
We assume the ice shelf to be isothermal, at a constant temperature, T. In this case, the vertically integrated stress/strainrate relation reads

The quantity ![]() is the vertical integral of the damage variable, Y. As the latter equals 1 if stress can be transmitted, and 0 if no stress can be transmitted due to damage, one can think of
is the vertical integral of the damage variable, Y. As the latter equals 1 if stress can be transmitted, and 0 if no stress can be transmitted due to damage, one can think of ![]() as the effective vertical profile, over which the membrane forces, N, are transmitted. We consequently call
as the effective vertical profile, over which the membrane forces, N, are transmitted. We consequently call ![]() the ‘effective ice thickness’. It is the goal now to establish a damage-evolution theory with
the ‘effective ice thickness’. It is the goal now to establish a damage-evolution theory with ![]() as the only dynamic variable.
as the only dynamic variable.
In order to study the time evolution of ![]() , we consider it at a Lagrangian point, X, which is thus moving along with the material (a Eulerian description works in basically the same way, but adds more complicated boundary terms). Using Eqn (42), we can write the exact time evolution of
, we consider it at a Lagrangian point, X, which is thus moving along with the material (a Eulerian description works in basically the same way, but adds more complicated boundary terms). Using Eqn (42), we can write the exact time evolution of ![]() as
as

where the Leibniz rule has been applied. From Eqn (42), it is clear that we cannot evaluate Eqn (46) when we only know ![]() : The damageevolution function, FY
, explicitly depends on the local value of Y as a function of z, which cannot be determined from its depth integral,
: The damageevolution function, FY
, explicitly depends on the local value of Y as a function of z, which cannot be determined from its depth integral, ![]() . Consequently, the only way to estimate the time evolution of the effective thickness is to make a reasonable assumption for the spatial distribution of Y over depth for a given value of
. Consequently, the only way to estimate the time evolution of the effective thickness is to make a reasonable assumption for the spatial distribution of Y over depth for a given value of ![]() .
.
By construction of FY as a function of p w, it is clear that damage nucleates at the surface and the base of the ice shelf. Furthermore, once damage evolution has started, the dependency on Y-k, k > 0, has Y evolving rather quickly towards 0 (strictly speaking, towards the lower boundary value Y min > 0, where we interrupt the damage evolution). Further evolution of the ‘crack’ towards the center of the ice profile is governed by the redistribution of the load, N, to the remaining profile.
With these ideas in mind, it seems straightforward to approximate Y (z) by a step function:

where h
w is the level of the ocean surface. This model for the spatial distribution of Y allows explicit evaluation of Eqn (46), and therefore allows us to estimate the evolution of ![]() by merely knowing vertically integrated quantities.
by merely knowing vertically integrated quantities.
Of course, this approximation needs to be justified. While this is hard to argue analytically, we will nevertheless provide a numerical example, showing that to a reasonable approximation, this very simple model for Y(z) approximately reflects the behavior of the ‘exact’ z- dependent theory. Such an example is shown in Figure 2. In this example, a one-dimensional situation has been considered, where a membrane stress, N, is equally redistributed over the intact part of the ice. The evolution of the damage variable is governed by a stress function:

Fig. 2. Temporal evolution of the effective ice thickness, ![]() (1) according to Eqns (42) and (44) (dotted curves), and (2) in the effective-thickness approximation according to Eqns (46) and (47) (solid curves). The total ice thickness H = 200 m, and the parameters have been set to k = 3.5, r = 0.43, σth
= 3 × 104 Pa, b = 1.7 × 10−9 Pa-r S−1. Values of the total membrane stress, N, in units of Hσ
th, are (a) 1.2 and 1.8, and (b) 2.1.
(1) according to Eqns (42) and (44) (dotted curves), and (2) in the effective-thickness approximation according to Eqns (46) and (47) (solid curves). The total ice thickness H = 200 m, and the parameters have been set to k = 3.5, r = 0.43, σth
= 3 × 104 Pa, b = 1.7 × 10−9 Pa-r S−1. Values of the total membrane stress, N, in units of Hσ
th, are (a) 1.2 and 1.8, and (b) 2.1.
Figure 2 shows the time evolution of the integrated damage variable (or effective thickness), ![]() .This has been calculated either using a depth-dependent theory (i.e. Y(z) evolves as governed by Eqns (42) and (44)), or using the effective-thickness approximation (i.e.
.This has been calculated either using a depth-dependent theory (i.e. Y(z) evolves as governed by Eqns (42) and (44)), or using the effective-thickness approximation (i.e. ![]() is treated as a free variable evolving according to Eqns (46) and (47), without allowing for a freely evolving field, Y(z). It turns out that the two results for Y are largely comparable for stresses close to the threshold stress; for larger stresses the approximation becomes less exact, and may even yield qualitatively different results (Fig. 2b). This should be seen as an argument that a 2-D membrane theory may be used as a computationally simple toy model, which may at best yield qualitative results. However, the exact z- dependent theory should always be preferred. This is particularly the case for a non-isothermal ice shelf, where any membrane approximation with 2-D temperature,
is treated as a free variable evolving according to Eqns (46) and (47), without allowing for a freely evolving field, Y(z). It turns out that the two results for Y are largely comparable for stresses close to the threshold stress; for larger stresses the approximation becomes less exact, and may even yield qualitatively different results (Fig. 2b). This should be seen as an argument that a 2-D membrane theory may be used as a computationally simple toy model, which may at best yield qualitative results. However, the exact z- dependent theory should always be preferred. This is particularly the case for a non-isothermal ice shelf, where any membrane approximation with 2-D temperature, ![]() , and damage variable,
, and damage variable, ![]() , is physically doubtful.
, is physically doubtful.
4. Where to cut off the ice shelf?
The above models allow the evolution of ice shelves including damage evolution to be computed, but do not yield information on the calving mechanism at, or close to, the ice front. In earlier theoretical and practical attempts, calving of ice at the ice-shelf front was introduced, for example, by stating that ice chunks thinner than 200 m would break off. The approach using continuum damage mechanics has the advantage that a rational criterion is applied to describe the deterioration of the ice in ice sheets; this is certainly closer to material physics. However, in the present description we still need a criterion to determine the break-off of ice from the shelf close to the ice front of the barrier.
A rather obvious criterion may be to use a lower bound of the effective ice thickness, ![]() , as the limit value,
, as the limit value, ![]() , at which calving of the frontal shelf ice may occur. However, such a threshold would likely depend on the actual ice thickness, H(x,y,t), so we instead impose a threshold condition on the dimensionless variable
, at which calving of the frontal shelf ice may occur. However, such a threshold would likely depend on the actual ice thickness, H(x,y,t), so we instead impose a threshold condition on the dimensionless variable

Thus, the curve in x-y space where Ỹ reaches a certain threshold value, Ỹmin,
determines the calving front at time t. When temperature, T, and damage variable, Y, evolve as 3-D functions, ![]() Otherwise,
Otherwise, ![]() evolves according to Eqns (46) and (47). The ice volume between Cγ(t-Δt) then determines the calving rate between t – Δt and t, and C
Y
(t) defines the new ice front. The innovative step is to now introduce numerical values for Ỹmin ∊ (0-1]. Superficially, one might think that Eqn (50) brings us nothing new, as Ỹmin is again a depth scale. This, however, ignores the fact that Ỹmin is a depth-integrated damage-effect variable, which encapsulates the severity of the damage. More explicitly, small values of Ỹ ∊ (0-1] indicate that the material deterioration is large. Or Ỹ = 0.2 indicates that damage has progressed more than with Ỹ = 0.25 These properties are expressions for damage with a degree of scale invariance.
evolves according to Eqns (46) and (47). The ice volume between Cγ(t-Δt) then determines the calving rate between t – Δt and t, and C
Y
(t) defines the new ice front. The innovative step is to now introduce numerical values for Ỹmin ∊ (0-1]. Superficially, one might think that Eqn (50) brings us nothing new, as Ỹmin is again a depth scale. This, however, ignores the fact that Ỹmin is a depth-integrated damage-effect variable, which encapsulates the severity of the damage. More explicitly, small values of Ỹ ∊ (0-1] indicate that the material deterioration is large. Or Ỹ = 0.2 indicates that damage has progressed more than with Ỹ = 0.25 These properties are expressions for damage with a degree of scale invariance.
Of course, expressions for the breaking-off of ice that are more complex and more flexible than Eqn (50) are possible, but, for the present, we refrain from proposing such variants.
5. Conclusion
In this paper, we have indicated how the problem of an ice shelf subject to deterioration due to the accumulation of microcracks can be addressed by implementing a continuum damage theory into the field equations of the shallowshelf theory. In order to consider the simplest possible example, we have used a scalar damage variable, subject to a Kachanov–Rabotnov evolution equation, as proposed by Reference Pralong and FunkPralong and Funk (2005). Although the scaling of the SSA does not alter the damageevolution equation as such, its functional structure still breaks down to a meanfield approximation in the SSA limit.
We have demonstrated that an exact upscaling of the mesoscale damage evolution requires the field, Y, to be 3-D; i.e. in addition to the temperature, T, there is another scalar field which cannot be considered in terms of a purely 2-D membrane theory. Nevertheless, an approximation could be found which allows us to construct a damage-dependent membrane theory.
It would be desirable to implement these damage theories into a numerical ice-shelf model, in order to see whether it can be used to formulate a reasonable model of the decay of polar ice shelves.
Finally, a word of warning to potential SSA modelers. First, our model is a proposal for calving which is based on a criterion that involves the resistance property of shelves, based on their toughness against breaking. We regard it as a first step towards an alternative to most existing calving models (Reference AlleyAlley and others, 2008), but we are certainly aware of its restrictions. Our model does not involve concepts which explicitly make use of boundary-layer effects at the shelf front. Such effects are observable as a very thin region close to the front where increased crevassing is evident. One might therefore be tempted to introduce, instead of Eqn (5), a balance law with a flux term, Y . However, such an alternative model formulation suffers from several disadvantages. It requires boundary conditions on Y or ∂Y/∂n or combinations thereof, which are not physically transparent, and it requires a constitutive relation for φY . This latter point implies that the thermodynamic theory and the compatibility of the SSA with damage evolution must be developed. We suggest that applying our simpler model to realistic ice shelves and studying the outcome of such computations is more promising.
There remains, however, a further complication. It is known that the thermomechanics of ice shelves using the secondorder SSA (SOSSA) is structurally a prestressed plate with strong membrane and weak bending effects (Reference BaralBaral, 1999), and these bending effects manifest themselves primarily at boundaries. It is physically obvious that the shelf front is exposed to ocean surface waves, which are likely to drive bending oscillations close to the shelf front. In the event that treating our above ideas on weakening of ice shelves with the SSA fails, then it would be inescapable that the calving processes need to be treated as a SOSSA. For simplicity we hope that this will not be the case.
Acknowledgements
We thank Martin Funk and the Laboratory of Hydraulics, Hydrology and Glaciology, ETH Zürich, for supporting the work of A.K. on this project. We also thank Nina Kirchner and an anonymous referee for detailed and constructive reviews, which helped to improve the paper.





