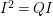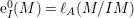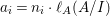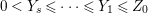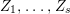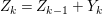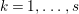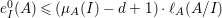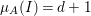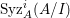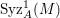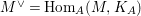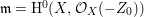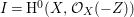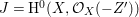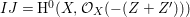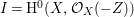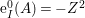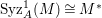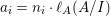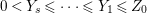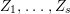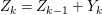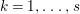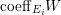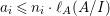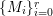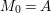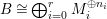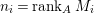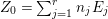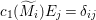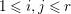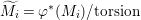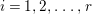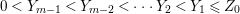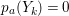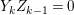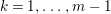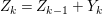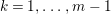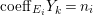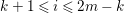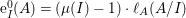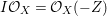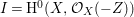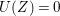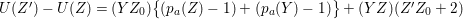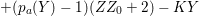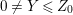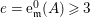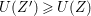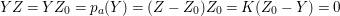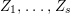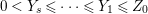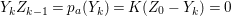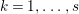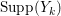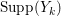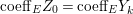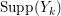1 Introduction
In the paper [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY] we established the theory of Ulrich ideals and modules with a generalized form. The classical concept of Ulrich modules, or maximally generated maximal Cohen–Macaulay modules (MGMCM modules), was introduced by [Reference UlrichU, Reference Brennan, Herzog and UlrichBHU]. In our language, MGMCM modules are just Ulrich modules with respect to the maximal ideal. For instance, any indecomposable nonfree maximal Cohen–Macaulay module over a hypersurface local ring of multiplicity (degree) ![]() $2$ is an MGMCM module. While they are very few MGMCM modules in general, our Ulrich modules include many more members than MGMCM modules.
$2$ is an MGMCM module. While they are very few MGMCM modules in general, our Ulrich modules include many more members than MGMCM modules.
To state the main results, let us begin with the definition of Ulrich ideals and modules. Let ![]() $A$ be a Cohen–Macaulay local ring with maximal ideal
$A$ be a Cohen–Macaulay local ring with maximal ideal ![]() $\mathfrak{m}$ and
$\mathfrak{m}$ and 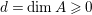 $d=\dim A\geqslant 0$, and let
$d=\dim A\geqslant 0$, and let ![]() $I\subset A$ be an
$I\subset A$ be an ![]() $\mathfrak{m}$-primary ideal. For simplicity, we assume that
$\mathfrak{m}$-primary ideal. For simplicity, we assume that ![]() $I$ contains a parameter ideal
$I$ contains a parameter ideal 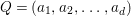 $Q=(a_{1},a_{2},\ldots ,a_{d})$ of
$Q=(a_{1},a_{2},\ldots ,a_{d})$ of ![]() $A$ as a reduction, that is,
$A$ as a reduction, that is, 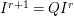 $I^{r+1}=QI^{r}$ for some integer
$I^{r+1}=QI^{r}$ for some integer ![]() $r\geqslant 1$.
$r\geqslant 1$.
Definition 1.1. We say that ![]() $I$ is an Ulrich ideal of
$I$ is an Ulrich ideal of ![]() $A$ if it satisfies the following conditions:
$A$ if it satisfies the following conditions:
(1)
 $I^{2}=QI$;
$I^{2}=QI$;(2)
 $I/I^{2}$ is a free
$I/I^{2}$ is a free  $A/I$-module.
$A/I$-module.
Let ![]() ${\mathcal{X}}_{A}$ denote the set of all Ulrich ideals that are not parameter ideals.
${\mathcal{X}}_{A}$ denote the set of all Ulrich ideals that are not parameter ideals.
For instance, ![]() $(A,\mathfrak{m})$ is a Cohen–Macaulay local ring of maximal embedding dimension [Reference SallySa] if and only if
$(A,\mathfrak{m})$ is a Cohen–Macaulay local ring of maximal embedding dimension [Reference SallySa] if and only if ![]() $\mathfrak{m}$ is an Ulrich ideal.
$\mathfrak{m}$ is an Ulrich ideal.
Definition 1.2. Let ![]() $M$ be a nonzero finitely generated
$M$ be a nonzero finitely generated ![]() $A$-module, and let
$A$-module, and let ![]() $I\subset A$ be an
$I\subset A$ be an ![]() $\mathfrak{m}$-primary ideal. Then we say that
$\mathfrak{m}$-primary ideal. Then we say that ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, if the following conditions are satisfied:
$I$, if the following conditions are satisfied:
(1)
 $M$ is a maximal Cohen–Macaulay
$M$ is a maximal Cohen–Macaulay  $A$-module;
$A$-module;(2)
 $\text{e}_{I}^{0}(M)=\ell _{A}(M/IM)$;
$\text{e}_{I}^{0}(M)=\ell _{A}(M/IM)$;(3)
 $M/IM$ is
$M/IM$ is  $A/I$-free.
$A/I$-free.
Here, ![]() $\text{e}_{I}^{0}(M)$ denotes the multiplicity of
$\text{e}_{I}^{0}(M)$ denotes the multiplicity of ![]() $M$ with respect to
$M$ with respect to ![]() $I$ and
$I$ and 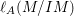 $\ell _{A}(M/IM)$ denotes the length of the
$\ell _{A}(M/IM)$ denotes the length of the ![]() $A$-module
$A$-module ![]() $M/IM$.
$M/IM$.
In [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY], we proved that all higher syzygy modules 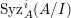 $\text{Syz}_{A}^{i}(A/I)$ of an Ulrich ideal
$\text{Syz}_{A}^{i}(A/I)$ of an Ulrich ideal ![]() $I$ are Ulrich modules with respect to
$I$ are Ulrich modules with respect to ![]() $I$. Moreover, if
$I$. Moreover, if ![]() $A$ is of finite Cohen Macaulay (CM) representation type, then
$A$ is of finite Cohen Macaulay (CM) representation type, then ![]() ${\mathcal{X}}_{A}$ is a finite set. Recall here that a Cohen–Macaulay local ring is said to be of finite CM-representation type if there are only a finite number of isomorphism classes of indecomposable maximal Cohen–Macaulay
${\mathcal{X}}_{A}$ is a finite set. Recall here that a Cohen–Macaulay local ring is said to be of finite CM-representation type if there are only a finite number of isomorphism classes of indecomposable maximal Cohen–Macaulay ![]() $A$-modules. Thus, we consider the following natural question.
$A$-modules. Thus, we consider the following natural question.
Problem 1.3. Let ![]() $(A,\mathfrak{m})$ be a Cohen–Macaulay local ring of finite CM-representation type.
$(A,\mathfrak{m})$ be a Cohen–Macaulay local ring of finite CM-representation type.
(1) Classify all Ulrich ideals
 $I$ of
$I$ of  $A$.
$A$.(2) Classify all Ulrich
 $A$-modules with respect to a given
$A$-modules with respect to a given  $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal  $I$.
$I$.(3) Determine all
 $\mathfrak{m}$-primary ideals
$\mathfrak{m}$-primary ideals  $I$ so that there exists an Ulrich
$I$ so that there exists an Ulrich  $A$-module with respect to
$A$-module with respect to  $I$.
$I$.
In [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Section 9], we gave an answer to the problem as above in the case of a one-dimensional Gorenstein local ring of finite CM-representation type by using techniques from representation theory of maximal Cohen–Macaulay modules. We want to give a complete answer to the question as above in the case of a two-dimensional Gorenstein local ring of finite CM-representation type. It is well known that two-dimensional Gorenstein local rings of finite CM-representation type (over an algebraically closed field of characteristic ![]() $0$) are two-dimensional Gorenstein rational singularities.
$0$) are two-dimensional Gorenstein rational singularities.
Let us explain the organization of the paper. In Section 3, we introduce the notion of weakly special Cohen–Macaulay modules; let ![]() $A$ be a Cohen–Macaulay local domain, and let
$A$ be a Cohen–Macaulay local domain, and let ![]() $I\subset A$ be an
$I\subset A$ be an ![]() $\mathfrak{m}$-primary ideal. A maximal Cohen–Macaulay
$\mathfrak{m}$-primary ideal. A maximal Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M$ is called a weakly special Cohen–Macaulay
$M$ is called a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ if
$I$ if 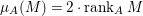 ${\it\mu}_{A}(M)=2\cdot \,\text{rank}_{A}\,M$ and
${\it\mu}_{A}(M)=2\cdot \,\text{rank}_{A}\,M$ and ![]() $M/IM$ is
$M/IM$ is ![]() $A/I$-free, where
$A/I$-free, where ![]() ${\it\mu}_{A}(M)$ denotes the cardinality of a minimal set of generators of
${\it\mu}_{A}(M)$ denotes the cardinality of a minimal set of generators of ![]() $M$; see Definition 3.1. Then we prove that
$M$; see Definition 3.1. Then we prove that ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ and
$I$ and ![]() $I$ is a good ideal (see Section 2) if and only if
$I$ is a good ideal (see Section 2) if and only if ![]() $M$ is a weakly special Cohen–Macaulay
$M$ is a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ for a Gorenstein local domain
$I$ for a Gorenstein local domain ![]() $A$ and a nonparameter
$A$ and a nonparameter ![]() $\mathfrak{m}$-primary stable ideal
$\mathfrak{m}$-primary stable ideal ![]() $I$; see Theorem 3.2 for details. As an application, we give a partial answer to the Problem 1.3(3). This implies that
$I$; see Theorem 3.2 for details. As an application, we give a partial answer to the Problem 1.3(3). This implies that ![]() $I$ is an Ulrich ideal if and only if there exists an Ulrich
$I$ is an Ulrich ideal if and only if there exists an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ for any two-dimensional Gorenstein rational singularity.
$I$ for any two-dimensional Gorenstein rational singularity.
In Section 4, we modify the notion of special Cohen–Macaulay ![]() $A$-modules introduced by Wunram [Reference WunramWu1] (see also [Reference ItoIto, Reference Iyama and WemyssIW]). Let
$A$-modules introduced by Wunram [Reference WunramWu1] (see also [Reference ItoIto, Reference Iyama and WemyssIW]). Let ![]() $A$ be a two-dimensional rational singularity, and let
$A$ be a two-dimensional rational singularity, and let ![]() $M$ be a maximal Cohen–Macaulay
$M$ be a maximal Cohen–Macaulay ![]() $A$-module without free summands. Then
$A$-module without free summands. Then ![]() $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ if and only if
$I$ if and only if 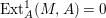 $\text{Ext}_{A}^{1}(M,A)=0$ and
$\text{Ext}_{A}^{1}(M,A)=0$ and ![]() $M/IM$ is
$M/IM$ is ![]() $A/I$-free; see Definition 4.5. Special Cohen–Macaulay
$A/I$-free; see Definition 4.5. Special Cohen–Macaulay ![]() $A$-modules are weakly special Cohen–Macaulay
$A$-modules are weakly special Cohen–Macaulay ![]() $A$-modules (but the converse is not true in general). The main result in this section is the following theorem, which gives a criterion for
$A$-modules (but the converse is not true in general). The main result in this section is the following theorem, which gives a criterion for ![]() $I$ (resp.
$I$ (resp. ![]() $Z$) to be a special ideal (resp. a special cycle) in terms of cycles.
$Z$) to be a special ideal (resp. a special cycle) in terms of cycles.
Theorem 4.10.
Let ![]() $(A,\mathfrak{m})$ be a two-dimensional complete local normal domain with rational singularity having the minimal resolution of singularities with the exceptional divisor
$(A,\mathfrak{m})$ be a two-dimensional complete local normal domain with rational singularity having the minimal resolution of singularities with the exceptional divisor 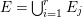 $E=\bigcup _{i=1}^{r}E_{j}$. Let
$E=\bigcup _{i=1}^{r}E_{j}$. Let 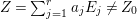 $Z=\sum _{j=1}^{r}a_{j}E_{j}\neq Z_{0}$ be an anti-nef cycle on the minimal resolution
$Z=\sum _{j=1}^{r}a_{j}E_{j}\neq Z_{0}$ be an anti-nef cycle on the minimal resolution 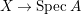 $X\rightarrow \,\text{Spec}\,A$, and put
$X\rightarrow \,\text{Spec}\,A$, and put ![]() $I=I_{Z}$. Let
$I=I_{Z}$. Let 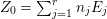 $Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$ denote the fundamental cycle on
$Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$ denote the fundamental cycle on ![]() $X$. Let
$X$. Let ![]() $M_{i}$ be an indecomposable maximal Cohen–Macaulay
$M_{i}$ be an indecomposable maximal Cohen–Macaulay ![]() $A$-module so that
$A$-module so that 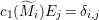 $c_{1}(\widetilde{M}_{i})E_{j}={\it\delta}_{i,j}$,
$c_{1}(\widetilde{M}_{i})E_{j}={\it\delta}_{i,j}$, 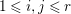 $1\leqslant i,j\leqslant r$; see Theorem–Definition 4 for details. Then the following conditions are equivalent for every
$1\leqslant i,j\leqslant r$; see Theorem–Definition 4 for details. Then the following conditions are equivalent for every 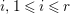 $i,1\leqslant i\leqslant r$.
$i,1\leqslant i\leqslant r$.
(1)
 $M_{i}$ is a special Cohen–Macaulay
$M_{i}$ is a special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$.
$I$.(2)
 $a_{i}=n_{i}\cdot \ell _{A}(A/I)$.
$a_{i}=n_{i}\cdot \ell _{A}(A/I)$.(3) There exist positive cycles
 $0<Y_{s}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$ and anti-nef cycles
$0<Y_{s}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$ and anti-nef cycles  $Z_{1},\ldots ,Z_{s}$ so that
$Z_{1},\ldots ,Z_{s}$ so that  $Z_{k}=Z_{k-1}+Y_{k}$ for each
$Z_{k}=Z_{k-1}+Y_{k}$ for each  $k=1,\ldots ,s$ and where
$k=1,\ldots ,s$ and where $$\begin{eqnarray}\displaystyle & & \displaystyle Z_{k-1}\cdot Y_{k}=0,\quad p_{a}(Y_{k})=0\quad \text{and}\quad \text{coeff}_{E_{i}}Y_{k}=n_{i}\nonumber\\ \displaystyle & & \displaystyle \quad \text{for every }k=1,2,\ldots ,s,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Z_{k-1}\cdot Y_{k}=0,\quad p_{a}(Y_{k})=0\quad \text{and}\quad \text{coeff}_{E_{i}}Y_{k}=n_{i}\nonumber\\ \displaystyle & & \displaystyle \quad \text{for every }k=1,2,\ldots ,s,\nonumber\end{eqnarray}$$ $\text{coeff}_{E_{i}}W$ stands for the coefficient of
$\text{coeff}_{E_{i}}W$ stands for the coefficient of  $E_{i}$ in a cycle
$E_{i}$ in a cycle  $W$.
$W$.
When this is the case, 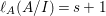 $\ell _{A}(A/I)=s+1$ and every
$\ell _{A}(A/I)=s+1$ and every 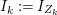 $I_{k}:=I_{Z_{k}}$ is a special ideal. Moreover, for every
$I_{k}:=I_{Z_{k}}$ is a special ideal. Moreover, for every 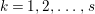 $k=1,2,\ldots ,s$, we obtain that
$k=1,2,\ldots ,s$, we obtain that 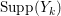 $\text{Supp}(Y_{k})$ is connected,
$\text{Supp}(Y_{k})$ is connected, 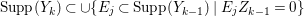 $\text{Supp}(Y_{k})\subset \cup \{E_{j}\subset \text{Supp}(Y_{k-1})\mid E_{j}Z_{k-1}=0\}$, and
$\text{Supp}(Y_{k})\subset \cup \{E_{j}\subset \text{Supp}(Y_{k-1})\mid E_{j}Z_{k-1}=0\}$, and ![]() $Y_{k}$ is the fundamental cycle on
$Y_{k}$ is the fundamental cycle on  $\text{Supp}(Y_{k})$.
$\text{Supp}(Y_{k})$.
In Section 5, we give a complete list of Ulrich ideals and Ulrich modules with respect to some ideal ![]() $I$ for any two-dimensional Gorenstein rational Cohen–Macaulay singularity. The main tools are the Riemann–Roch formula, the McKay correspondence and results in Section 4. The following theorem is the main result in this paper.
$I$ for any two-dimensional Gorenstein rational Cohen–Macaulay singularity. The main tools are the Riemann–Roch formula, the McKay correspondence and results in Section 4. The following theorem is the main result in this paper.
Theorem 1.4. Let ![]() $A$ be a two-dimensional Gorenstein rational singularity. Then the set
$A$ be a two-dimensional Gorenstein rational singularity. Then the set ![]() ${\mathcal{X}}_{A}$ of all nonparameter Ulrich ideals is given by the following.
${\mathcal{X}}_{A}$ of all nonparameter Ulrich ideals is given by the following.
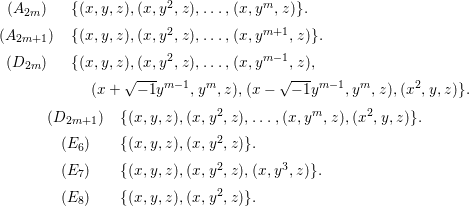
In Section 6, we discuss Ulrich ideals of two-dimensional non-Gorenstein rational singularities. We show that any Ulrich ideal is integrally closed and is represented on the minimal resolution of singularities, and also is a special ideal in the sense of Section 4. For instance, any non-Gorenstein cyclic quotient singularity admits a unique Ulrich ideal, that is, the maximal ideal (see also Section 7).
2 Preliminaries
2.1 Ulrich ideals and modules
First we recall the notion of good ideals in a Gorenstein local ring.
Definition 2.1. (See [Reference Goto, Iai and WatanabeGIW].)
Suppose that ![]() $A$ is a Gorenstein local ring. Let
$A$ is a Gorenstein local ring. Let ![]() $I\subset A$ be a nonparameter
$I\subset A$ be a nonparameter ![]() $\mathfrak{m}$-primary ideal. If
$\mathfrak{m}$-primary ideal. If 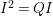 $I^{2}=QI$ holds for some minimal reduction
$I^{2}=QI$ holds for some minimal reduction ![]() $Q$ of
$Q$ of ![]() $I$, then
$I$, then ![]() $I$ is called a stable ideal. If
$I$ is called a stable ideal. If ![]() $I$ is stable and
$I$ is stable and 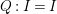 $Q:I=I$, then
$Q:I=I$, then ![]() $I$ is called a good ideal. An
$I$ is called a good ideal. An ![]() $\mathfrak{m}$-primary stable ideal
$\mathfrak{m}$-primary stable ideal ![]() $I$ is good if and only if
$I$ is good if and only if 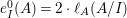 $e_{I}^{0}(A)=2\cdot \ell _{A}(A/I)$.
$e_{I}^{0}(A)=2\cdot \ell _{A}(A/I)$.
An Ulrich ideal in a Gorenstein local ring is always a good ideal.
Proposition 2.2. (See [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Lemma 2.3, Corollary 2.6].)
Let ![]() $A$ be a
$A$ be a ![]() $d$-dimensional Cohen–Macaulay local ring, and let
$d$-dimensional Cohen–Macaulay local ring, and let ![]() $I\subset A$ be a nonparameter
$I\subset A$ be a nonparameter ![]() $\mathfrak{m}$-primary ideal. Then we have the following.
$\mathfrak{m}$-primary ideal. Then we have the following.
(1) Suppose that
 $I$ is stable. Then
$I$ is stable. Then  $e_{I}^{0}(A)\leqslant ({\it\mu}_{A}(I)-d+1)\cdot \ell _{A}(A/I)$. Equality holds if and only if
$e_{I}^{0}(A)\leqslant ({\it\mu}_{A}(I)-d+1)\cdot \ell _{A}(A/I)$. Equality holds if and only if  $I$ is an Ulrich ideal.
$I$ is an Ulrich ideal.(2) Suppose that
 $A$ is Gorenstein. Then the following conditions are equivalent:
$A$ is Gorenstein. Then the following conditions are equivalent:(a)
 $I$ is an Ulrich ideal;
$I$ is an Ulrich ideal;(b)
 $I$ is a good ideal and
$I$ is a good ideal and  ${\it\mu}_{A}(I)=d+1$;
${\it\mu}_{A}(I)=d+1$;(c)
 $I$ is a good ideal and
$I$ is a good ideal and  $A/I$ is Gorenstein.
$A/I$ is Gorenstein.
Let us give two typical examples of Ulrich ideals.
Example 2.3. It is well known that 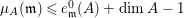 ${\it\mu}_{A}(\mathfrak{m})\leqslant e_{\mathfrak{m}}^{0}(A)+\dim A-1$ holds true [Reference AbhyankarAb]. Equality holds if and only if the maximal ideal
${\it\mu}_{A}(\mathfrak{m})\leqslant e_{\mathfrak{m}}^{0}(A)+\dim A-1$ holds true [Reference AbhyankarAb]. Equality holds if and only if the maximal ideal ![]() $\mathfrak{m}$ is stable (see [Reference SallySa]). Then
$\mathfrak{m}$ is stable (see [Reference SallySa]). Then ![]() $A$ is said to have maximal embedding dimension. By 2.2(1),
$A$ is said to have maximal embedding dimension. By 2.2(1), ![]() $\mathfrak{m}$ is an Ulrich ideal if and only if
$\mathfrak{m}$ is an Ulrich ideal if and only if ![]() $A$ has maximal embedding dimension.
$A$ has maximal embedding dimension.
Suppose that ![]() $A$ is a two-dimensional hypersurface of degree
$A$ is a two-dimensional hypersurface of degree ![]() $2$. Then the maximal ideal
$2$. Then the maximal ideal ![]() $\mathfrak{m}$ is an Ulrich ideal. Moreover, a power
$\mathfrak{m}$ is an Ulrich ideal. Moreover, a power ![]() $\mathfrak{m}^{k}$ is a good ideal but not an Ulrich ideal for all
$\mathfrak{m}^{k}$ is a good ideal but not an Ulrich ideal for all ![]() $k\geqslant 2$.
$k\geqslant 2$.
Example 2.4. Let 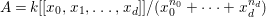 $A=k[[x_{0},x_{1},\ldots ,x_{d}]]/(x_{0}^{n_{0}}+\cdots +x_{d}^{n_{d}})$ be a diagonal hypersurface. Suppose that
$A=k[[x_{0},x_{1},\ldots ,x_{d}]]/(x_{0}^{n_{0}}+\cdots +x_{d}^{n_{d}})$ be a diagonal hypersurface. Suppose that 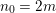 $n_{0}=2m$ is even. Then
$n_{0}=2m$ is even. Then 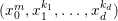 $(x_{0}^{m},x_{1}^{k_{1}},\ldots ,x_{d}^{k_{d}})$ is an Ulrich ideal for every
$(x_{0}^{m},x_{1}^{k_{1}},\ldots ,x_{d}^{k_{d}})$ is an Ulrich ideal for every 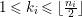 $1\leqslant k_{i}\leqslant \lfloor \frac{n_{i}}{2}\rfloor$
$1\leqslant k_{i}\leqslant \lfloor \frac{n_{i}}{2}\rfloor$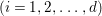 $(i=1,2,\ldots ,d)$.
$(i=1,2,\ldots ,d)$.
The following theorem gives a relationship between Ulrich ideals and Ulrich modules with respect to ideals.
Theorem 2.5. (Cf. [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Theorem 4.1].)
Let ![]() $A$ be a Cohen–Macaulay local ring of dimension
$A$ be a Cohen–Macaulay local ring of dimension ![]() $d$. Then the following conditions are equivalent:
$d$. Then the following conditions are equivalent:
(1)
 $I$ is a nonparameter Ulrich ideal;
$I$ is a nonparameter Ulrich ideal;(2)
 $\text{Syz}_{A}^{i}(A/I)$ is an Ulrich
$\text{Syz}_{A}^{i}(A/I)$ is an Ulrich  $A$-module with respect to
$A$-module with respect to  $I$ for all
$I$ for all  $i\geqslant d$.
$i\geqslant d$.
Note that there exists a non-Ulrich ideal ![]() $I$ so that
$I$ so that 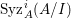 $\text{Syz}_{A}^{i}(A/I)$ is an Ulrich
$\text{Syz}_{A}^{i}(A/I)$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ (see, e.g., Examples 3.7, 3.8).
$I$ (see, e.g., Examples 3.7, 3.8).
On the other hand, we can construct new Ulrich modules from a given Ulrich module by the following theorem.
Theorem 2.6. (See also [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Lemma 4.2, Theorem 5.1].)
Suppose that ![]() $A$ is a Cohen–Macaulay local ring of dimension
$A$ is a Cohen–Macaulay local ring of dimension ![]() $d$ which admits a canonical module
$d$ which admits a canonical module ![]() $K_{A}$. Assume that
$K_{A}$. Assume that ![]() $I$ is an Ulrich ideal with
$I$ is an Ulrich ideal with 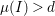 ${\it\mu}(I)>d$ and
${\it\mu}(I)>d$ and ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Then:
$I$. Then:
(1)
 $\text{Syz}_{A}^{1}(M)$ is an Ulrich
$\text{Syz}_{A}^{1}(M)$ is an Ulrich  $A$-module with respect to
$A$-module with respect to  $I$;
$I$;(2)
 $M^{\vee }=\text{Hom}_{A}(M,K_{A})$ is an Ulrich
$M^{\vee }=\text{Hom}_{A}(M,K_{A})$ is an Ulrich  $A$-module with respect to
$A$-module with respect to  $I$.
$I$.
2.2 Two-dimensional rational singularities
Throughout this subsection, let ![]() $A$ be a two-dimensional complete normal local domain with unique maximal ideal
$A$ be a two-dimensional complete normal local domain with unique maximal ideal ![]() $\mathfrak{m}$ containing an algebraically closed field
$\mathfrak{m}$ containing an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $0$, unless otherwise specified. (Many results in this paper hold true if
$0$, unless otherwise specified. (Many results in this paper hold true if ![]() $k$ is an algebraically closed field of positive characteristic. For simplicity, we assume that
$k$ is an algebraically closed field of positive characteristic. For simplicity, we assume that ![]() $k$ has characteristic
$k$ has characteristic ![]() $0$.) Moreover, assume that
$0$.) Moreover, assume that ![]() $A$ has a rational singularity, that is, there exists a resolution of singularities
$A$ has a rational singularity, that is, there exists a resolution of singularities 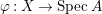 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ with
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ with 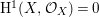 $\text{H}^{1}(X,{\mathcal{O}}_{X})=0$ (see [Reference LipmanLi1, Reference LipmanLi2]). A typical example of rational singularities is a quotient singularity. Moreover, (two-dimensional) Gorenstein rational singularities are called rational double points, which are hypersurfaces of degree
$\text{H}^{1}(X,{\mathcal{O}}_{X})=0$ (see [Reference LipmanLi1, Reference LipmanLi2]). A typical example of rational singularities is a quotient singularity. Moreover, (two-dimensional) Gorenstein rational singularities are called rational double points, which are hypersurfaces of degree ![]() $2$.
$2$.
Positive cycles, anti-nef cycles. In what follows, let 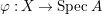 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be a resolution of singularities with
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be a resolution of singularities with 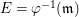 $E={\it\varphi}^{-1}(\mathfrak{m})$ the exceptional divisor. Let
$E={\it\varphi}^{-1}(\mathfrak{m})$ the exceptional divisor. Let 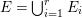 $E=\bigcup _{i=1}^{r}E_{i}$ be the decomposition into irreducible components of
$E=\bigcup _{i=1}^{r}E_{i}$ be the decomposition into irreducible components of ![]() $E$. In the set
$E$. In the set 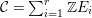 ${\mathcal{C}}=\sum _{i=1}^{r}\mathbb{Z}E_{i}$ of cycles supported on
${\mathcal{C}}=\sum _{i=1}^{r}\mathbb{Z}E_{i}$ of cycles supported on ![]() $E$, we define a partial order
$E$, we define a partial order ![]() ${\leqslant}$ as follows: for
${\leqslant}$ as follows: for ![]() $Z$,
$Z$, ![]() $Z^{\prime }\in {\mathcal{C}}$,
$Z^{\prime }\in {\mathcal{C}}$, ![]() $Z\leqslant Z^{\prime }$ if every coefficient of
$Z\leqslant Z^{\prime }$ if every coefficient of ![]() $E_{i}$ in
$E_{i}$ in ![]() $Z^{\prime }-Z$ is nonnegative. A cycle
$Z^{\prime }-Z$ is nonnegative. A cycle 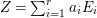 $Z=\sum _{i=1}^{r}a_{i}E_{i}$ is called positive, denoted by
$Z=\sum _{i=1}^{r}a_{i}E_{i}$ is called positive, denoted by ![]() $Z>0$, if
$Z>0$, if ![]() $0\leqslant Z$ and
$0\leqslant Z$ and ![]() $Z\neq 0$.
$Z\neq 0$.
On the other hand, a positive cycle 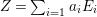 $Z=\sum _{i=1}a_{i}E_{i}$ is said to be anti-nef if
$Z=\sum _{i=1}a_{i}E_{i}$ is said to be anti-nef if 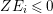 $ZE_{i}\leqslant 0$ for every
$ZE_{i}\leqslant 0$ for every 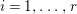 $i=1,\ldots ,r$, where
$i=1,\ldots ,r$, where ![]() $ZY$ denotes the intersection number of
$ZY$ denotes the intersection number of ![]() $Z$ and
$Z$ and ![]() $Y$.
$Y$.
Virtual genus. Since the intersection matrix 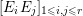 $[E_{i}E_{j}]_{1\leqslant i,j\leqslant r}$ is negative definite, there exists the unique
$[E_{i}E_{j}]_{1\leqslant i,j\leqslant r}$ is negative definite, there exists the unique ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $\text{K}_{X}$, the canonical divisor, so that the equation
$\text{K}_{X}$, the canonical divisor, so that the equation
 $$\begin{eqnarray}p_{a}(E_{i}):={\displaystyle \frac{E_{i}^{2}+\text{K}_{X}E_{i}}{2}}+1=0\end{eqnarray}$$
$$\begin{eqnarray}p_{a}(E_{i}):={\displaystyle \frac{E_{i}^{2}+\text{K}_{X}E_{i}}{2}}+1=0\end{eqnarray}$$ holds for every 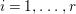 $i=1,\ldots ,r$. If
$i=1,\ldots ,r$. If 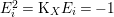 $E_{i}^{2}=\text{K}_{X}E_{i}=-1$, then
$E_{i}^{2}=\text{K}_{X}E_{i}=-1$, then ![]() $E_{i}\cong \mathbb{P}^{1}$ is called a
$E_{i}\cong \mathbb{P}^{1}$ is called a ![]() $(-1)$-curve. We say that
$(-1)$-curve. We say that ![]() $X$ is a minimal resolution if
$X$ is a minimal resolution if ![]() $X$ contains no
$X$ contains no ![]() $(-1)$-curve. Such a resolution is unique up to isomorphism. Moreover, for any positive cycle
$(-1)$-curve. Such a resolution is unique up to isomorphism. Moreover, for any positive cycle ![]() $Y>0$, we put
$Y>0$, we put
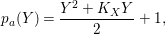 $$\begin{eqnarray}p_{a}(Y)={\displaystyle \frac{Y^{2}+K_{X}Y}{2}}+1,\end{eqnarray}$$
$$\begin{eqnarray}p_{a}(Y)={\displaystyle \frac{Y^{2}+K_{X}Y}{2}}+1,\end{eqnarray}$$ which is called the virtual genus of ![]() $Y$. One can easily see that
$Y$. One can easily see that
 $$\begin{eqnarray}p_{a}(Y+Y^{\prime })=p_{a}(Y)+p_{a}(Y^{\prime })+YY^{\prime }-1.\end{eqnarray}$$
$$\begin{eqnarray}p_{a}(Y+Y^{\prime })=p_{a}(Y)+p_{a}(Y^{\prime })+YY^{\prime }-1.\end{eqnarray}$$ Furthermore, it is well known that if ![]() $A$ is a rational singularity then
$A$ is a rational singularity then 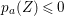 $p_{a}(Z)\leqslant 0$ holds true for every positive cycle
$p_{a}(Z)\leqslant 0$ holds true for every positive cycle ![]() $Z$ [Reference ArtinAr, Proposition 1].
$Z$ [Reference ArtinAr, Proposition 1].
Dual graph. In what follows, assume that 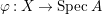 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ is the minimal resolution of singularities with
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ is the minimal resolution of singularities with 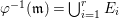 ${\it\varphi}^{-1}(\mathfrak{m})=\bigcup _{i=1}^{r}E_{i}$. Then the dual graph
${\it\varphi}^{-1}(\mathfrak{m})=\bigcup _{i=1}^{r}E_{i}$. Then the dual graph ![]() ${\rm\Gamma}$ of
${\rm\Gamma}$ of ![]() ${\it\varphi}$ is a simple graph with the vertex set
${\it\varphi}$ is a simple graph with the vertex set ![]() $\{E_{i}\}_{i=1}^{r}$ and the edge defined by the following:
$\{E_{i}\}_{i=1}^{r}$ and the edge defined by the following:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{the edge }E_{i}-E_{j}\text{ exists (resp. does not exist) if and only if}\nonumber\\ \displaystyle & & \displaystyle \quad E_{i}E_{j}=1~(\text{resp. }E_{i}E_{j}=0).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{the edge }E_{i}-E_{j}\text{ exists (resp. does not exist) if and only if}\nonumber\\ \displaystyle & & \displaystyle \quad E_{i}E_{j}=1~(\text{resp. }E_{i}E_{j}=0).\nonumber\end{eqnarray}$$For instance, we have the following example:

Let 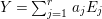 $Y=\sum _{j=1}^{r}a_{j}E_{j}$ be a positive cycle on
$Y=\sum _{j=1}^{r}a_{j}E_{j}$ be a positive cycle on ![]() $X$. Then we put
$X$. Then we put 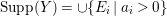 $\text{Supp}(Y)=\cup \{E_{i}\mid a_{i}>0\}$, the support of
$\text{Supp}(Y)=\cup \{E_{i}\mid a_{i}>0\}$, the support of ![]() $Y$. Such a set is called connected if the induced subgraph is connected. Note that if
$Y$. Such a set is called connected if the induced subgraph is connected. Note that if ![]() $Y$ is positive and
$Y$ is positive and 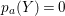 $p_{a}(Y)=0$ then
$p_{a}(Y)=0$ then ![]() $Y$ is connected.
$Y$ is connected.
Integrally closed ideal. Let ![]() $I$ be an
$I$ be an ![]() $\mathfrak{m}$-primary ideal of
$\mathfrak{m}$-primary ideal of ![]() $A$. An element
$A$. An element ![]() $z\in A$ is said to be integral over
$z\in A$ is said to be integral over ![]() $I$ if an equation
$I$ if an equation
 $$\begin{eqnarray}z^{n}+c_{1}z^{n-1}+\cdots +c^{n}=0\end{eqnarray}$$
$$\begin{eqnarray}z^{n}+c_{1}z^{n-1}+\cdots +c^{n}=0\end{eqnarray}$$ holds for some positive integer ![]() $n$ and
$n$ and ![]() $c_{i}\in I^{i}$ for each
$c_{i}\in I^{i}$ for each 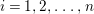 $i=1,2,\ldots ,n$. The set of all elements
$i=1,2,\ldots ,n$. The set of all elements ![]() $z$ that are integral over
$z$ that are integral over ![]() $I$ forms an ideal containing
$I$ forms an ideal containing ![]() $I$. This ideal is called the integral closure of
$I$. This ideal is called the integral closure of ![]() $I$ denoted by
$I$ denoted by ![]() $\overline{I}$. An ideal
$\overline{I}$. An ideal ![]() $I$ is said to be integrally closed if
$I$ is said to be integrally closed if ![]() $\overline{I}=I$.
$\overline{I}=I$.
Now suppose that ![]() $I$ is integrally closed. Then
$I$ is integrally closed. Then ![]() $I$ is said to be represented on
$I$ is said to be represented on ![]() $X$ if there exists an anti-nef cycle
$X$ if there exists an anti-nef cycle ![]() $Z$ with support in
$Z$ with support in ![]() $E$ so that
$E$ so that 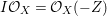 $I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ and
$I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ and 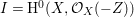 $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then we denote such an ideal
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then we denote such an ideal ![]() $I$ by
$I$ by ![]() $I=I_{Z}$. The product of two integrally closed ideals of
$I=I_{Z}$. The product of two integrally closed ideals of ![]() $A$ is also integrally closed [Reference LipmanLi1, Theorem 7.1]. There is a one-to-one correspondence between the set of integrally closed
$A$ is also integrally closed [Reference LipmanLi1, Theorem 7.1]. There is a one-to-one correspondence between the set of integrally closed ![]() $\mathfrak{m}$-primary ideals of
$\mathfrak{m}$-primary ideals of ![]() $A$ that are represented on
$A$ that are represented on ![]() $X$ and the set of anti-nef cycles
$X$ and the set of anti-nef cycles 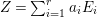 $Z=\sum _{i=1}^{r}a_{i}E_{i}$ on
$Z=\sum _{i=1}^{r}a_{i}E_{i}$ on ![]() $X$ (see, e.g., [Reference LipmanLi1, Section 18]).
$X$ (see, e.g., [Reference LipmanLi1, Section 18]).
Good ideal. Now we recall the notion of good ideals of rational singularities.
Definition 2.7. Let ![]() $I$ be an
$I$ be an ![]() $\mathfrak{m}$-primary ideal of
$\mathfrak{m}$-primary ideal of ![]() $A$. Then
$A$. Then ![]() $I$ is called good if
$I$ is called good if ![]() $I$ is represented on the minimal resolution of singularities.
$I$ is represented on the minimal resolution of singularities.
Notice that this definition is different from that of Definition 2.1. However, for any ![]() $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal ![]() $I$ of a two-dimensional Gorenstein rational singularity,
$I$ of a two-dimensional Gorenstein rational singularity, ![]() $I$ is good in the sense of Definition 2.1 if and only if it is good in the sense of Definition 2.7 (see also [Reference Goto, Iai and WatanabeGIW, Theorem 7.8] or [Reference Watanabe and YoshidaWY]).
$I$ is good in the sense of Definition 2.1 if and only if it is good in the sense of Definition 2.7 (see also [Reference Goto, Iai and WatanabeGIW, Theorem 7.8] or [Reference Watanabe and YoshidaWY]).
Notice that (1), (2) can be easily seen from the definition.
Lemma 2.8. (Cf. [Reference Goto, Iai and WatanabeGIW, Section 7].)
Let ![]() $A$ be a two-dimensional (not necessarily Gorenstein) rational singularity, and let
$A$ be a two-dimensional (not necessarily Gorenstein) rational singularity, and let 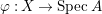 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ denote the minimal resolution of singularities. Then we have the following.
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ denote the minimal resolution of singularities. Then we have the following.
(1) The minimum element (say,
 $Z_{0}$) among all non-zero anti-nef cycles on
$Z_{0}$) among all non-zero anti-nef cycles on  $X$ exists. This cycle
$X$ exists. This cycle  $Z_{0}$ is called the fundamental cycle on
$Z_{0}$ is called the fundamental cycle on  $X$ which corresponds to the maximal ideal
$X$ which corresponds to the maximal ideal  $\mathfrak{m}$. In particular,
$\mathfrak{m}$. In particular,  $\mathfrak{m}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{0}))$ is a good ideal.
$\mathfrak{m}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{0}))$ is a good ideal.(2) If
 $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$ and
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$ and  $J=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z^{\prime }))$ are good ideals of
$J=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z^{\prime }))$ are good ideals of  $A$, then
$A$, then  $IJ=\text{H}^{0}(X,{\mathcal{O}}_{X}(-(Z+Z^{\prime })))$ is also a good ideal.
$IJ=\text{H}^{0}(X,{\mathcal{O}}_{X}(-(Z+Z^{\prime })))$ is also a good ideal.(3) Suppose that
 $Z$ is an anti-nef cycle on
$Z$ is an anti-nef cycle on  $X$. If
$X$. If  $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$, then
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$, then  $\text{e}_{I}^{0}(A)=-Z^{2}$.
$\text{e}_{I}^{0}(A)=-Z^{2}$.
The colength 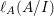 $\ell _{A}(A/I)$ can also be determined by the anti-nef cycle
$\ell _{A}(A/I)$ can also be determined by the anti-nef cycle ![]() $Z$ (see the Riemann–Roch formula (Lemma 4.12)).
$Z$ (see the Riemann–Roch formula (Lemma 4.12)).
3 Weakly special Cohen–Macaulay modules over Gorenstein local domains
Throughout this section, let ![]() $A$ be a Gorenstein local domain, and let
$A$ be a Gorenstein local domain, and let ![]() $I\subset A$ be a nonparameter
$I\subset A$ be a nonparameter ![]() $\mathfrak{m}$-primary ideal, unless otherwise specified. In this section, we introduce the notion of weakly special Cohen–Macaulay modules, which are closely related to Ulrich modules.
$\mathfrak{m}$-primary ideal, unless otherwise specified. In this section, we introduce the notion of weakly special Cohen–Macaulay modules, which are closely related to Ulrich modules.
Definition 3.1. (Weakly special CM module, ideal)
Let ![]() $A$ be a Cohen–Macaulay local domain, and let
$A$ be a Cohen–Macaulay local domain, and let ![]() $M$ be a maximal Cohen–Macaulay
$M$ be a maximal Cohen–Macaulay ![]() $A$-module. If
$A$-module. If ![]() $M$ satisfies
$M$ satisfies 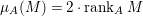 ${\it\mu}_{A}(M)=2\cdot \,\text{rank}_{A}\,M$ and
${\it\mu}_{A}(M)=2\cdot \,\text{rank}_{A}\,M$ and ![]() $M/IM$ is
$M/IM$ is ![]() $A/I$-free, then
$A/I$-free, then ![]() $M$ is called a weakly special Cohen–Macaulay
$M$ is called a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.
$I$.
Suppose that ![]() $I\subset A$ is a stable ideal. If there exists a weakly special Cohen–Macaulay
$I\subset A$ is a stable ideal. If there exists a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, then
$I$, then ![]() $I$ is called a weakly special ideal of
$I$ is called a weakly special ideal of ![]() $A$.
$A$.
Now suppose that ![]() $A$ is a Gorenstein local ring. Let
$A$ is a Gorenstein local ring. Let ![]() $I\subset A$ be a stable
$I\subset A$ be a stable ![]() $\mathfrak{m}$-primary ideal with minimal reduction
$\mathfrak{m}$-primary ideal with minimal reduction ![]() $Q$. Then as
$Q$. Then as 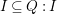 $I\subseteq Q:I$, we have
$I\subseteq Q:I$, we have 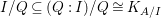 $I/Q\subseteq (Q:I)/Q\cong K_{A/I}$. Hence,
$I/Q\subseteq (Q:I)/Q\cong K_{A/I}$. Hence,
 $$\begin{eqnarray}e_{I}^{0}(A)=\ell _{A}(A/Q)\leqslant \ell _{A}(A/I)+\ell (K_{A/I})=2\cdot \ell _{A}(A/I),\end{eqnarray}$$
$$\begin{eqnarray}e_{I}^{0}(A)=\ell _{A}(A/Q)\leqslant \ell _{A}(A/I)+\ell (K_{A/I})=2\cdot \ell _{A}(A/I),\end{eqnarray}$$ where the last equality follows from the Matlis duality theorem. Note that equality holds if and only if ![]() $I$ is a good ideal.
$I$ is a good ideal.
The following theorem is the main result in this section.
Theorem 3.2. Suppose that ![]() $A$ is a Gorenstein local domain and
$A$ is a Gorenstein local domain and ![]() $I$ is a stable ideal of
$I$ is a stable ideal of ![]() $A$. Let
$A$. Let ![]() $M$ be a maximal Cohen–Macaulay
$M$ be a maximal Cohen–Macaulay ![]() $A$-module. Then the following condition are equivalent:
$A$-module. Then the following condition are equivalent:
(1)
 $M$ is an Ulrich
$M$ is an Ulrich  $A$-module with respect to
$A$-module with respect to  $I$, and
$I$, and  $I$ is a good ideal;
$I$ is a good ideal;(2)
 $M$ is a weakly special Cohen–Macaulay
$M$ is a weakly special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$.
$I$.
Proof of Theorem 3.2.
We may assume that ![]() $M/IM$ is
$M/IM$ is ![]() $A/I$-free. Thus,
$A/I$-free. Thus,
 $$\begin{eqnarray}\ell _{A}(M/IM)={\it\mu}_{A}(M)\cdot \ell _{A}(A/I).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M/IM)={\it\mu}_{A}(M)\cdot \ell _{A}(A/I).\end{eqnarray}$$ (1) ![]() $\Longrightarrow$ (2): By assumption we have
$\Longrightarrow$ (2): By assumption we have
 $$\begin{eqnarray}\ell _{A}(M/IM)=e_{I}^{0}(M)=e_{I}^{0}(A)\cdot \,\text{rank}_{A}M=2\cdot \ell _{A}(A/I)\cdot \,\text{rank}_{A}M,\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M/IM)=e_{I}^{0}(M)=e_{I}^{0}(A)\cdot \,\text{rank}_{A}M=2\cdot \ell _{A}(A/I)\cdot \,\text{rank}_{A}M,\end{eqnarray}$$ where the second equality follows from the associativity formula of multiplicities (e.g. [Reference MatsumuraMa, Theorem 14.8]). It follows from the above two equalities that 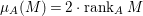 ${\it\mu}_{A}(M)=2\cdot \,\text{rank}_{A}\,M$. Thus,
${\it\mu}_{A}(M)=2\cdot \,\text{rank}_{A}\,M$. Thus, ![]() $M$ is a weakly special Cohen–Macaulay
$M$ is a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.
$I$.
(2) ![]() $\Longrightarrow$ (1): Since
$\Longrightarrow$ (1): Since ![]() $M$ is a maximal Cohen–Macaulay
$M$ is a maximal Cohen–Macaulay ![]() $A$-module, we have
$A$-module, we have
 $$\begin{eqnarray}\ell _{A}(M/IM)\leqslant e_{I}^{0}(M).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M/IM)\leqslant e_{I}^{0}(M).\end{eqnarray}$$On the other hand, by the observation and the equality described above, we get
 $$\begin{eqnarray}\displaystyle \ell _{A}(M/IM) & = & \displaystyle {\it\mu}_{A}(M)\cdot \ell _{A}(A/I)=2\cdot \,\text{rank}_{A}M\cdot \ell _{A}(A/I)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle e_{I}^{0}(A)\cdot \,\text{rank}_{A}M=e_{I}^{0}(M).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(M/IM) & = & \displaystyle {\it\mu}_{A}(M)\cdot \ell _{A}(A/I)=2\cdot \,\text{rank}_{A}M\cdot \ell _{A}(A/I)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle e_{I}^{0}(A)\cdot \,\text{rank}_{A}M=e_{I}^{0}(M).\nonumber\end{eqnarray}$$ Therefore, 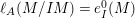 $\ell _{A}(M/IM)=e_{I}^{0}(M)$ and
$\ell _{A}(M/IM)=e_{I}^{0}(M)$ and 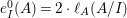 $e_{I}^{0}(A)=2\cdot \ell _{A}(A/I)$. That is,
$e_{I}^{0}(A)=2\cdot \ell _{A}(A/I)$. That is, ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ and
$I$ and ![]() $I$ is a good ideal.◻
$I$ is a good ideal.◻
Corollary 3.3. Suppose that ![]() $A$ is a Gorenstein local domain. If
$A$ is a Gorenstein local domain. If ![]() $I$ is an Ulrich ideal, then it is a weakly special ideal.
$I$ is an Ulrich ideal, then it is a weakly special ideal.
Proof. If ![]() $I$ is an Ulrich ideal, then it is a good ideal by Proposition 2.2, and
$I$ is an Ulrich ideal, then it is a good ideal by Proposition 2.2, and 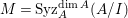 $M=\text{Syz}_{A}^{\dim A}(A/I)$ is an Ulrich
$M=\text{Syz}_{A}^{\dim A}(A/I)$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ by Theorem 2.5. By Theorem 3.2,
$I$ by Theorem 2.5. By Theorem 3.2, ![]() $M$ is a weakly special Cohen–Macaulay
$M$ is a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Hence,
$I$. Hence, ![]() $I$ is a weakly special ideal, as required.◻
$I$ is a weakly special ideal, as required.◻
Proposition 3.4. Suppose that ![]() $A$ is a hypersurface local domain. Then
$A$ is a hypersurface local domain. Then ![]() $I\subset A$ is an Ulrich ideal if and only if it is a weakly special ideal.
$I\subset A$ is an Ulrich ideal if and only if it is a weakly special ideal.
Proof. It suffices to prove the “if” part. Now suppose that ![]() $I$ is a weakly special ideal. Take a weakly special Cohen–Macaulay
$I$ is a weakly special ideal. Take a weakly special Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M$ with respect to
$M$ with respect to ![]() $I$. By Theorem 3.2,
$I$. By Theorem 3.2, ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Since
$I$. Since ![]() $A$ is a hypersurface and
$A$ is a hypersurface and ![]() $M$ is a maximal Cohen–Macaulay
$M$ is a maximal Cohen–Macaulay ![]() $A$-module without free summands, we have a minimal free presentation
$A$-module without free summands, we have a minimal free presentation 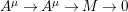 $A^{{\it\mu}}\rightarrow A^{{\it\mu}}\rightarrow M\rightarrow 0$, which induces an exact sequence
$A^{{\it\mu}}\rightarrow A^{{\it\mu}}\rightarrow M\rightarrow 0$, which induces an exact sequence
 $$\begin{eqnarray}(A/Q)^{{\it\mu}}\rightarrow (A/Q)^{{\it\mu}}\xrightarrow[]{f}M/QM\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}(A/Q)^{{\it\mu}}\rightarrow (A/Q)^{{\it\mu}}\xrightarrow[]{f}M/QM\rightarrow 0.\end{eqnarray}$$ As 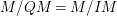 $M/QM=M/IM$ is
$M/QM=M/IM$ is ![]() $A/I$-free, we have
$A/I$-free, we have 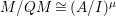 $M/QM\cong (A/I)^{{\it\mu}}$. It is easy to observe that the kernel of
$M/QM\cong (A/I)^{{\it\mu}}$. It is easy to observe that the kernel of ![]() $f$ is isomorphic to
$f$ is isomorphic to ![]() $(I/Q)^{{\it\mu}}$. Hence, there is a surjection
$(I/Q)^{{\it\mu}}$. Hence, there is a surjection 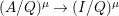 $(A/Q)^{{\it\mu}}\rightarrow (I/Q)^{{\it\mu}}$, which shows
$(A/Q)^{{\it\mu}}\rightarrow (I/Q)^{{\it\mu}}$, which shows 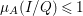 ${\it\mu}_{A}(I/Q)\leqslant 1$. Thus,
${\it\mu}_{A}(I/Q)\leqslant 1$. Thus, 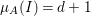 ${\it\mu}_{A}(I)=d+1$, and hence Proposition 2.2 implies that
${\it\mu}_{A}(I)=d+1$, and hence Proposition 2.2 implies that ![]() $I$ is an Ulrich ideal.◻
$I$ is an Ulrich ideal.◻
The following corollary gives a partial answer to Problem 1.3.
Corollary 3.5. Suppose that ![]() $A$ is a hypersurface local domain, and
$A$ is a hypersurface local domain, and ![]() $I\subset A$ is a good ideal. If there exists an Ulrich
$I\subset A$ is a good ideal. If there exists an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, then
$I$, then ![]() $I$ is an Ulrich ideal.
$I$ is an Ulrich ideal.
Question 3.6. Let ![]() $A$ be a Gorenstein local domain, and let
$A$ be a Gorenstein local domain, and let ![]() $I\subset A$ be a stable ideal. Suppose that there exists an Ulrich
$I\subset A$ be a stable ideal. Suppose that there exists an Ulrich ![]() $A$-module
$A$-module ![]() $M$ with respect to
$M$ with respect to ![]() $I$. Is then
$I$. Is then ![]() $I$ an Ulrich ideal (especially, a good ideal)?
$I$ an Ulrich ideal (especially, a good ideal)?
The next example shows that we cannot remove the assumption that ![]() $I$ is stable in Question 3.6.
$I$ is stable in Question 3.6.
Example 3.7. Let ![]() $k$ be a field, and let
$k$ be a field, and let ![]() $e\geqslant 3$ be an integer. Set
$e\geqslant 3$ be an integer. Set 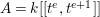 $A=k[[t^{e},t^{e+1}]]$ and
$A=k[[t^{e},t^{e+1}]]$ and 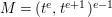 $M=(t^{e},t^{e+1})^{e-1}$. Then
$M=(t^{e},t^{e+1})^{e-1}$. Then ![]() $A$ is a hypersurface local domain and
$A$ is a hypersurface local domain and ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to 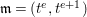 $\mathfrak{m}=(t^{e},t^{e+1})$, the maximal ideal of
$\mathfrak{m}=(t^{e},t^{e+1})$, the maximal ideal of ![]() $A$. However,
$A$. However, ![]() $\mathfrak{m}$ is not stable.
$\mathfrak{m}$ is not stable.
The next example shows that we cannot relax the assumption that ![]() $A$ is a local domain in Question 3.6.
$A$ is a local domain in Question 3.6.
Example 3.8. Let ![]() $k$ be a field, and let
$k$ be a field, and let ![]() $a$,
$a$, ![]() $e$ be integers with
$e$ be integers with 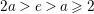 $2a>e>a\geqslant 2$. Set
$2a>e>a\geqslant 2$. Set 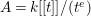 $A=k[[t]]/(t^{e})$, and
$A=k[[t]]/(t^{e})$, and 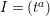 $I=(t^{a})$. Then
$I=(t^{a})$. Then ![]() $I^{2}=0$ but
$I^{2}=0$ but 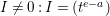 $I\neq 0:I=(t^{e-a})$. Hence,
$I\neq 0:I=(t^{e-a})$. Hence, ![]() $I$ is stable but not good. Then
$I$ is stable but not good. Then 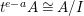 $t^{e-a}A\cong A/I$ is an Ulrich
$t^{e-a}A\cong A/I$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.
$I$.
4 Special Cohen–Macaulay modules over two-dimensional rational singularities
Throughout this section, let ![]() $(A,\mathfrak{m})$ be a two-dimensional complete normal local domain with an algebraically closed residue field
$(A,\mathfrak{m})$ be a two-dimensional complete normal local domain with an algebraically closed residue field ![]() $k$ of characteristic zero. Let
$k$ of characteristic zero. Let 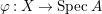 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities, with
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities, with 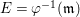 $E={\it\varphi}^{-1}(\mathfrak{m})$ the exceptional divisor. Let
$E={\it\varphi}^{-1}(\mathfrak{m})$ the exceptional divisor. Let 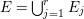 $E=\bigcup _{j=1}^{r}E_{j}$ be the decomposition into irreducible components of
$E=\bigcup _{j=1}^{r}E_{j}$ be the decomposition into irreducible components of ![]() $E$. Let
$E$. Let ![]() $I\subset A$ be an
$I\subset A$ be an ![]() $\mathfrak{m}$-primary ideal, and let
$\mathfrak{m}$-primary ideal, and let ![]() $Q$ be a minimal reduction of
$Q$ be a minimal reduction of ![]() $I$. For every maximal Cohen–Macaulay
$I$. For every maximal Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M$, we put
$M$, we put 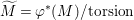 $\widetilde{M}={\it\varphi}^{\ast }(M)/\text{torsion}$.
$\widetilde{M}={\it\varphi}^{\ast }(M)/\text{torsion}$.
First, we recall the notion of special Cohen–Macaulay modules.
Theorem–Definition.
[Special McKay correspondence due to Wunram] Assume that ![]() $A$ is a rational singularity, and let
$A$ is a rational singularity, and let 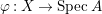 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be as above. For every
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be as above. For every ![]() $i$, there exists a unique indecomposable maximal Cohen–Macaulay
$i$, there exists a unique indecomposable maximal Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M_{i}$ (up to isomorphism) with
$M_{i}$ (up to isomorphism) with 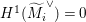 $H^{1}(\widetilde{M_{i}}^{\vee })=0$, so that
$H^{1}(\widetilde{M_{i}}^{\vee })=0$, so that
 $$\begin{eqnarray}c_{1}(\widetilde{M_{i}})E_{j}={\it\delta}_{ij}\end{eqnarray}$$
$$\begin{eqnarray}c_{1}(\widetilde{M_{i}})E_{j}={\it\delta}_{ij}\end{eqnarray}$$ for every 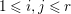 $1\leqslant i,j\leqslant r$ and
$1\leqslant i,j\leqslant r$ and 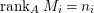 $\,\text{rank}_{A}\,M_{i}=n_{i}$, where
$\,\text{rank}_{A}\,M_{i}=n_{i}$, where ![]() $c_{1}(\widetilde{M})$ denotes the first Chern class of
$c_{1}(\widetilde{M})$ denotes the first Chern class of ![]() $\widetilde{M}$ and
$\widetilde{M}$ and 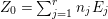 $Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$ denotes the fundamental cycle on
$Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$ denotes the fundamental cycle on ![]() $X$.
$X$.
Based upon this theorem, we define a (nontrivial) special Cohen–Macaulay ![]() $A$-module, which has been defined in more general settings.
$A$-module, which has been defined in more general settings.
Definition 4.1. (Special CM module)
Suppose that ![]() $A$ is a two-dimensional rational singularity. Let
$A$ is a two-dimensional rational singularity. Let ![]() $M$ be a maximal Cohen–Macaulay
$M$ be a maximal Cohen–Macaulay ![]() $A$-module. Then
$A$-module. Then ![]() $M$ is called a special Cohen–Macaulay
$M$ is called a special Cohen–Macaulay ![]() $A$-module if
$A$-module if ![]() $M$ is isomorphic to a finite direct sum of
$M$ is isomorphic to a finite direct sum of 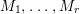 $M_{1},\ldots ,M_{r}$.
$M_{1},\ldots ,M_{r}$.
Remark 4.2. Let ![]() $K_{A}$ denote the canonical module of
$K_{A}$ denote the canonical module of ![]() $A$. A maximal Cohen–Macaulay
$A$. A maximal Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M$ is said to be a special Cohen–Macaulay
$M$ is said to be a special Cohen–Macaulay ![]() $A$-module if
$A$-module if 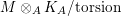 $M\otimes _{A}K_{A}/\text{torsion}$ is Cohen–Macaulay. This condition is equivalent to
$M\otimes _{A}K_{A}/\text{torsion}$ is Cohen–Macaulay. This condition is equivalent to 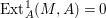 $\text{Ext}_{A}^{1}(M,A)=0$ (see [Reference Iyama and WemyssIW]). In particular, any free
$\text{Ext}_{A}^{1}(M,A)=0$ (see [Reference Iyama and WemyssIW]). In particular, any free ![]() $A$-module or any maximal Cohen–Macaulay module over a Gorenstein local domain
$A$-module or any maximal Cohen–Macaulay module over a Gorenstein local domain ![]() $A$ is a special Cohen–Macaulay
$A$ is a special Cohen–Macaulay ![]() $A$-module in this sense. However, in this paper, we use the notion of special Cohen–Macaulay modules for two-dimensional rational singularities only.
$A$-module in this sense. However, in this paper, we use the notion of special Cohen–Macaulay modules for two-dimensional rational singularities only.
Iyama and Wemyss [Reference Iyama and WemyssIW] proved the following characterization of special Cohen–Macaulay modules.
Proposition 4.3. (Cf. [Reference Iyama and WemyssIW, Theorem 3.6].)
Suppose that ![]() $A$ is a two-dimensional rational singularity. Let
$A$ is a two-dimensional rational singularity. Let ![]() $M$ be a maximal Cohen–Macaulay
$M$ be a maximal Cohen–Macaulay ![]() $A$-module without free summands. Then
$A$-module without free summands. Then ![]() $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay ![]() $A$-module if and only if
$A$-module if and only if 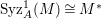 $\text{Syz}_{A}^{1}(M)\cong M^{\ast }$, where
$\text{Syz}_{A}^{1}(M)\cong M^{\ast }$, where 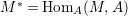 $M^{\ast }=\text{Hom}_{A}(M,A)$.
$M^{\ast }=\text{Hom}_{A}(M,A)$.
Remark 4.4. Suppose that ![]() $A$ is a Gorenstein rational singularity, that is,
$A$ is a Gorenstein rational singularity, that is, ![]() $A$ is a rational double point. Then any maximal Cohen–Macaulay
$A$ is a rational double point. Then any maximal Cohen–Macaulay ![]() $A$-module is a finite direct sum of free modules and special Cohen–Macaulay
$A$-module is a finite direct sum of free modules and special Cohen–Macaulay ![]() $A$-modules.
$A$-modules.
As in the case of Ulrich modules, we define a special CM module with respect to an Ulrich ideal ![]() $I$.
$I$.
Definition 4.5. (Special CM module with respect to  $I$)
$I$)
Suppose that ![]() $A$ is a two-dimensional rational singularity with unique maximal ideal
$A$ is a two-dimensional rational singularity with unique maximal ideal ![]() $\mathfrak{m}$, and let
$\mathfrak{m}$, and let ![]() $I\subset A$ be an
$I\subset A$ be an ![]() $\mathfrak{m}$-primary ideal. A finitely generated
$\mathfrak{m}$-primary ideal. A finitely generated ![]() $A$-module
$A$-module ![]() $M$ is called a special Cohen–Macaulay
$M$ is called a special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ if the following conditions are satisfied:
$I$ if the following conditions are satisfied:
(1)
 $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay  $A$-module, that is,
$A$-module, that is,  $\text{Syz}_{A}^{1}(M)\cong M^{\ast }$;
$\text{Syz}_{A}^{1}(M)\cong M^{\ast }$;(2)
 $M/IM$ is
$M/IM$ is  $A/I$-free.
$A/I$-free.
Any special Cohen–Macaulay ![]() $A$-module is a weakly special Cohen–Macaulay
$A$-module is a weakly special Cohen–Macaulay ![]() $A$-module in the sense of 2.1, but we believe that the converse is not true in general.
$A$-module in the sense of 2.1, but we believe that the converse is not true in general.
Lemma 4.6. Suppose that ![]() $A$ is a two-dimensional rational singularity. Let
$A$ is a two-dimensional rational singularity. Let ![]() $M$ be a maximal Cohen–Macaulay
$M$ be a maximal Cohen–Macaulay ![]() $A$-module. Then:
$A$-module. Then:
(1) if
 $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$, then it is a weakly special Cohen–Macaulay
$I$, then it is a weakly special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$;
$I$;(2) when
 $\,\text{rank}_{A}\,M=1$, the converse of
$\,\text{rank}_{A}\,M=1$, the converse of  $(1)$ holds true.
$(1)$ holds true.
Proof. (1) Suppose that ![]() $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay ![]() $A$-module. Then we have the following exact sequence:
$A$-module. Then we have the following exact sequence:
 $$\begin{eqnarray}0\rightarrow M^{\ast }\rightarrow A^{n}\rightarrow M\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M^{\ast }\rightarrow A^{n}\rightarrow M\rightarrow 0,\end{eqnarray}$$ where 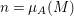 $n={\it\mu}_{A}(M)$. This yields
$n={\it\mu}_{A}(M)$. This yields 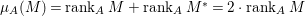 ${\it\mu}_{A}(M)=\,\text{rank}_{A}\,M+\,\text{rank}_{A}\,M^{\ast }=2\cdot \,\text{rank}_{A}\,M$.
${\it\mu}_{A}(M)=\,\text{rank}_{A}\,M+\,\text{rank}_{A}\,M^{\ast }=2\cdot \,\text{rank}_{A}\,M$.
(2) Take an ideal ![]() $J\subset A$ that is isomorphic to
$J\subset A$ that is isomorphic to ![]() $M$. Then
$M$. Then 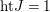 $\text{ht}J=1$ and
$\text{ht}J=1$ and ![]() $A/J$ is Cohen–Macaulay. It suffices to show that
$A/J$ is Cohen–Macaulay. It suffices to show that  $\text{Syz}_{A}^{1}(J)\cong J^{\ast }$.
$\text{Syz}_{A}^{1}(J)\cong J^{\ast }$.
As 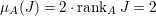 ${\it\mu}_{A}(J)=2\cdot \,\text{rank}_{A}\,J=2$, we can write
${\it\mu}_{A}(J)=2\cdot \,\text{rank}_{A}\,J=2$, we can write 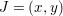 $J=(x,y)$. Then
$J=(x,y)$. Then
 $$\begin{eqnarray}\text{Syz}_{A}^{1}(J)\cong \left\{\left[\begin{array}{@{}c@{}}{\it\alpha}\\ {\it\beta}\end{array}\right]\in A^{2}\,\bigg|\,{\it\alpha}x+{\it\beta}y=0\right\}\cong (x):y\cong J^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\text{Syz}_{A}^{1}(J)\cong \left\{\left[\begin{array}{@{}c@{}}{\it\alpha}\\ {\it\beta}\end{array}\right]\in A^{2}\,\bigg|\,{\it\alpha}x+{\it\beta}y=0\right\}\cong (x):y\cong J^{\ast }.\end{eqnarray}$$ Hence, ![]() $M\cong J$ is a special Cohen–Macaulay
$M\cong J$ is a special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.◻
$I$.◻
[Reference WunramWu1, Example 1] is a weakly special Cohen–Macaulay ![]() $R$-module of rank
$R$-module of rank ![]() $2$ which is not special. After submitting the previous version of this paper, Yusuke Nakajima and the anonymous referee showed us such a concrete example [Reference NakajimaNa, Example 3.6, Example A.5]. See the example below.
$2$ which is not special. After submitting the previous version of this paper, Yusuke Nakajima and the anonymous referee showed us such a concrete example [Reference NakajimaNa, Example 3.6, Example A.5]. See the example below.
Remark 4.7. Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $0$, and let
$0$, and let ![]() $G$ be the group
$G$ be the group
 $$\begin{eqnarray}G=\left<\left(\begin{array}{@{}cc@{}}i & 0\\ 0 & -i\end{array}\right),\left(\begin{array}{@{}cc@{}}0 & i\\ i & 0\end{array}\right),\left(\begin{array}{@{}cc@{}}{\it\xi}_{6} & 0\\ 0 & {\it\xi}_{6}\end{array}\right)\right>=\mathbb{D}_{5,2}\subset \text{GL}(2,k),\end{eqnarray}$$
$$\begin{eqnarray}G=\left<\left(\begin{array}{@{}cc@{}}i & 0\\ 0 & -i\end{array}\right),\left(\begin{array}{@{}cc@{}}0 & i\\ i & 0\end{array}\right),\left(\begin{array}{@{}cc@{}}{\it\xi}_{6} & 0\\ 0 & {\it\xi}_{6}\end{array}\right)\right>=\mathbb{D}_{5,2}\subset \text{GL}(2,k),\end{eqnarray}$$ where ![]() $i$ (resp.
$i$ (resp. ![]() ${\it\xi}_{6}$) is a primitive fourth (resp. sixth) root of unity (see [Reference RiemenschneiderRi]).
${\it\xi}_{6}$) is a primitive fourth (resp. sixth) root of unity (see [Reference RiemenschneiderRi]).
Let 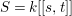 $S=k[[s,t]]$ be the formal power series ring over
$S=k[[s,t]]$ be the formal power series ring over ![]() $k$, and let
$k$, and let ![]() $A=S^{G}$ be the invariant subring of
$A=S^{G}$ be the invariant subring of ![]() $S$. Then the AR quiver of
$S$. Then the AR quiver of ![]() $A$ (see, e.g., [Reference YoshinoY]) is the following (see, e.g., [Reference Iyama and WemyssIW, Example 4.6] and [Reference NakajimaNa, Example 3.6]).
$A$ (see, e.g., [Reference YoshinoY]) is the following (see, e.g., [Reference Iyama and WemyssIW, Example 4.6] and [Reference NakajimaNa, Example 3.6]).

Then all indecomposable special Cohen–Macaulay modules of ![]() $A$ are
$A$ are ![]() $M_{02}$,
$M_{02}$, ![]() $M_{11}$,
$M_{11}$, ![]() $M_{31}$ and
$M_{31}$ and ![]() $M_{41}$ (see [Reference Iyama and WemyssIW, Example 4.6]). In particular,
$M_{41}$ (see [Reference Iyama and WemyssIW, Example 4.6]). In particular, ![]() $M_{2,2}$ is an indecomposable maximal Cohen–Macaulay
$M_{2,2}$ is an indecomposable maximal Cohen–Macaulay ![]() $A$-module which is not special. On the other hand,
$A$-module which is not special. On the other hand, 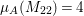 ${\it\mu}_{A}(M_{22})=4$ and
${\it\mu}_{A}(M_{22})=4$ and 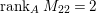 $\,\text{rank}_{A}\,M_{22}=2$ by [Reference NakajimaNa, Example A.5]. Hence,
$\,\text{rank}_{A}\,M_{22}=2$ by [Reference NakajimaNa, Example A.5]. Hence, ![]() $M_{22}$ is weakly special but not special (with respect to
$M_{22}$ is weakly special but not special (with respect to ![]() $\mathfrak{m}$).
$\mathfrak{m}$).
Next, we introduce the notion of special ideals.
Definition 4.8. (Special ideal)
An ![]() $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal ![]() $I\subset A$ is called a special ideal if it is a good ideal (cf. Definition 2.7) and there exists a special Cohen–Macaulay
$I\subset A$ is called a special ideal if it is a good ideal (cf. Definition 2.7) and there exists a special Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M$ (equivalently,
$M$ (equivalently, ![]() $M_{j}$ for some
$M_{j}$ for some ![]() $j$) with respect to
$j$) with respect to ![]() $I$. When this is the case, such a cycle
$I$. When this is the case, such a cycle ![]() $Z$ is called a special cycle.
$Z$ is called a special cycle.
In the rest of this section, we give a characterization of special ideals in terms of cycles. Before doing that, we need the following lemma, which also plays an important role in Section 6.
Let 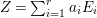 $Z=\sum _{i=1}^{r}a_{i}E_{i}$ and
$Z=\sum _{i=1}^{r}a_{i}E_{i}$ and 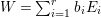 $W=\sum _{i=1}^{r}b_{i}E_{i}$ be anti-nef cycles on
$W=\sum _{i=1}^{r}b_{i}E_{i}$ be anti-nef cycles on ![]() $X$. Put
$X$. Put 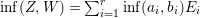 $\inf (Z,W)=\sum _{i=1}^{r}\inf (a_{i},b_{i})E_{i}$, then one can easily see that
$\inf (Z,W)=\sum _{i=1}^{r}\inf (a_{i},b_{i})E_{i}$, then one can easily see that 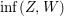 $\inf (Z,W)$ is also an anti-nef cycle on
$\inf (Z,W)$ is also an anti-nef cycle on ![]() $X$.
$X$.
Lemma 4.9. Assume that ![]() $Z\neq Z_{0}$ is an anti-nef cycle on
$Z\neq Z_{0}$ is an anti-nef cycle on ![]() $X$. Then we can find the following anti-nef cycles
$X$. Then we can find the following anti-nef cycles 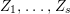 $Z_{1},\ldots ,Z_{s}$ and positive cycles
$Z_{1},\ldots ,Z_{s}$ and positive cycles 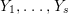 $Y_{1},\ldots ,Y_{s}$ so that
$Y_{1},\ldots ,Y_{s}$ so that 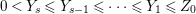 $0<Y_{s}\leqslant Y_{s-1}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$:
$0<Y_{s}\leqslant Y_{s-1}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$:
 $$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{2} & = & Z_{1}+Y_{2},\\ Z_{1} & = & Z_{0}+Y_{1},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{2} & = & Z_{1}+Y_{2},\\ Z_{1} & = & Z_{0}+Y_{1},\end{array}\right.\end{eqnarray}$$ where ![]() $Z_{0}$ denotes the fundamental cycle on
$Z_{0}$ denotes the fundamental cycle on ![]() $X$.
$X$.
Proof. We can take an integer ![]() $s\geqslant 1$ such that
$s\geqslant 1$ such that 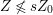 $Z\not \leqslant sZ_{0}$ and
$Z\not \leqslant sZ_{0}$ and 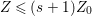 $Z\leqslant (s+1)Z_{0}$. Put
$Z\leqslant (s+1)Z_{0}$. Put 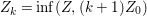 $Z_{k}=\inf (Z,(k+1)Z_{0})$ for every
$Z_{k}=\inf (Z,(k+1)Z_{0})$ for every 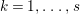 $k=1,\ldots ,s$. Then
$k=1,\ldots ,s$. Then 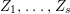 $Z_{1},\ldots ,Z_{s}$ are anti-nef cycles. In particular,
$Z_{1},\ldots ,Z_{s}$ are anti-nef cycles. In particular, 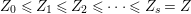 $Z_{0}\leqslant Z_{1}\leqslant Z_{2}\leqslant \cdots \leqslant Z_{s}=Z$. Moreover, if we put
$Z_{0}\leqslant Z_{1}\leqslant Z_{2}\leqslant \cdots \leqslant Z_{s}=Z$. Moreover, if we put 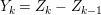 $Y_{k}=Z_{k}-Z_{k-1}$ for every
$Y_{k}=Z_{k}-Z_{k-1}$ for every 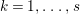 $k=1,\ldots ,s$, then we can obtain the required sequence.◻
$k=1,\ldots ,s$, then we can obtain the required sequence.◻
Under the notation as in Lemma 4.9, we put 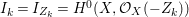 $I_{k}=I_{Z_{k}}=H^{0}(X,{\mathcal{O}}_{X}(-Z_{k}))$ for every
$I_{k}=I_{Z_{k}}=H^{0}(X,{\mathcal{O}}_{X}(-Z_{k}))$ for every 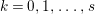 $k=0,1,\ldots ,s$. Then each
$k=0,1,\ldots ,s$. Then each ![]() $I_{k}$ is a good ideal and
$I_{k}$ is a good ideal and
 $$\begin{eqnarray}I=I_{s}\subset I_{s-1}\subset \cdots \subset I_{1}\subset I_{0}=\mathfrak{m}.\end{eqnarray}$$
$$\begin{eqnarray}I=I_{s}\subset I_{s-1}\subset \cdots \subset I_{1}\subset I_{0}=\mathfrak{m}.\end{eqnarray}$$ The following theorem is the main theorem in this section, which gives a criterion for ![]() $I=I_{Z}$ to be a special ideal in terms of cycles.
$I=I_{Z}$ to be a special ideal in terms of cycles.
Theorem 4.10. Let 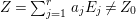 $Z=\sum _{j=1}^{r}a_{j}E_{j}\neq Z_{0}$ be an anti-nef cycle on the minimal resolution
$Z=\sum _{j=1}^{r}a_{j}E_{j}\neq Z_{0}$ be an anti-nef cycle on the minimal resolution 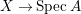 $X\rightarrow \,\text{Spec}\,A$, and put
$X\rightarrow \,\text{Spec}\,A$, and put ![]() $I=I_{Z}$. Let
$I=I_{Z}$. Let 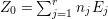 $Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$ denote the fundamental cycle on
$Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$ denote the fundamental cycle on ![]() $X$. Suppose that
$X$. Suppose that 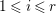 $1\leqslant i\leqslant r$. Then the following conditions are equivalent:
$1\leqslant i\leqslant r$. Then the following conditions are equivalent:
(1)
 $M_{i}$ is a special Cohen–Macaulay
$M_{i}$ is a special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$;
$I$;(2)
 $a_{i}=n_{i}\cdot \ell _{A}(A/I)$;
$a_{i}=n_{i}\cdot \ell _{A}(A/I)$;(3) there exist positive cycles
 $0<Y_{s}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$ and anti-nef cycles
$0<Y_{s}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$ and anti-nef cycles  $Z_{1},\ldots ,Z_{s}$ so that
$Z_{1},\ldots ,Z_{s}$ so that  $Z_{k}=Z_{k-1}+Y_{k}$ for each
$Z_{k}=Z_{k-1}+Y_{k}$ for each  $k=1,\ldots ,s$ and where
$k=1,\ldots ,s$ and where $$\begin{eqnarray}\displaystyle & & \displaystyle Z_{k-1}\cdot Y_{k}=0,\quad p_{a}(Y_{k})=0\quad \text{and}\quad \text{coeff}_{E_{i}}Y_{k}=n_{i}\nonumber\\ \displaystyle & & \displaystyle \quad \text{for every }k=1,2,\ldots ,s,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Z_{k-1}\cdot Y_{k}=0,\quad p_{a}(Y_{k})=0\quad \text{and}\quad \text{coeff}_{E_{i}}Y_{k}=n_{i}\nonumber\\ \displaystyle & & \displaystyle \quad \text{for every }k=1,2,\ldots ,s,\nonumber\end{eqnarray}$$ $\text{coeff}_{E_{i}}W$ stands for the coefficient of
$\text{coeff}_{E_{i}}W$ stands for the coefficient of  $E_{i}$ in a cycle
$E_{i}$ in a cycle  $W$.
$W$.
When this is the case, 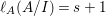 $\ell _{A}(A/I)=s+1$ and every
$\ell _{A}(A/I)=s+1$ and every 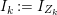 $I_{k}:=I_{Z_{k}}$ is a special ideal. Moreover, for every
$I_{k}:=I_{Z_{k}}$ is a special ideal. Moreover, for every 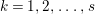 $k=1,2,\ldots ,s$, we obtain that
$k=1,2,\ldots ,s$, we obtain that 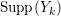 $\text{Supp}(Y_{k})$ is given as one of the connected components of
$\text{Supp}(Y_{k})$ is given as one of the connected components of 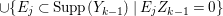 $\cup \{E_{j}\subset \text{Supp}(Y_{k-1})\mid E_{j}Z_{k-1}=0\}$, and
$\cup \{E_{j}\subset \text{Supp}(Y_{k-1})\mid E_{j}Z_{k-1}=0\}$, and ![]() $Y_{k}$ is the fundamental cycle on
$Y_{k}$ is the fundamental cycle on 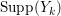 $\text{Supp}(Y_{k})$.
$\text{Supp}(Y_{k})$.
Remark 4.11. ![]() $Y+Z$ is not necessarily anti-nef even if
$Y+Z$ is not necessarily anti-nef even if ![]() $Y$ is the fundamental cycle on
$Y$ is the fundamental cycle on ![]() $X$ that satisfies
$X$ that satisfies 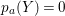 $p_{a}(Y)=0$ and
$p_{a}(Y)=0$ and ![]() $YZ=0$.
$YZ=0$.
Let us begin the proof of Theorem 4.10. The following formula is one of the main tools in this paper.
Lemma 4.12. (Kato’s Riemann–Roch formula; [Reference KatoKa, Reference Watanabe and YoshidaWY])
Let ![]() $Z$ be an anti-nef cycle on the minimal resolution of singularities
$Z$ be an anti-nef cycle on the minimal resolution of singularities ![]() $X$, and put
$X$, and put 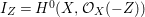 $I_{Z}=H^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then for any maximal Cohen–Macaulay
$I_{Z}=H^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then for any maximal Cohen–Macaulay ![]() $A$-module
$A$-module ![]() $M$, we have
$M$, we have
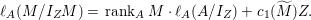 $$\begin{eqnarray}\ell _{A}(M/I_{Z}M)=\,\text{rank}_{A}M\cdot \ell _{A}(A/I_{Z})+c_{1}(\widetilde{M})Z.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M/I_{Z}M)=\,\text{rank}_{A}M\cdot \ell _{A}(A/I_{Z})+c_{1}(\widetilde{M})Z.\end{eqnarray}$$In particular,
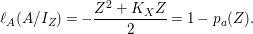 $$\begin{eqnarray}\ell _{A}(A/I_{Z})=-{\displaystyle \frac{Z^{2}+K_{X}Z}{2}}=1-p_{a}(Z).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(A/I_{Z})=-{\displaystyle \frac{Z^{2}+K_{X}Z}{2}}=1-p_{a}(Z).\end{eqnarray}$$The next lemma easily follows from Lemma 4.12.
Lemma 4.13. Under the notation as in Theorem 4.10, we have
 $$\begin{eqnarray}\ell _{A}(A/I_{k})=\ell _{A}(A/I_{k-1})-Y_{k}Z_{k-1}+1-p_{a}(Y_{k}).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(A/I_{k})=\ell _{A}(A/I_{k-1})-Y_{k}Z_{k-1}+1-p_{a}(Y_{k}).\end{eqnarray}$$Proof. By Lemma 4.12, we have
 $$\begin{eqnarray}\displaystyle \ell _{A}(A/I_{k}) & = & \displaystyle 1-p_{a}(Z_{k})=1-p_{a}(Z_{k-1}+Y_{k})\nonumber\\ \displaystyle & = & \displaystyle 1-p_{a}(Z_{k-1})-p_{a}(Y_{k})-Y_{k}Z_{k-1}+1\nonumber\\ \displaystyle & = & \displaystyle \ell _{A}(A/I_{k-1})-Y_{k}Z_{k-1}+1-p_{a}(Y_{k}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(A/I_{k}) & = & \displaystyle 1-p_{a}(Z_{k})=1-p_{a}(Z_{k-1}+Y_{k})\nonumber\\ \displaystyle & = & \displaystyle 1-p_{a}(Z_{k-1})-p_{a}(Y_{k})-Y_{k}Z_{k-1}+1\nonumber\\ \displaystyle & = & \displaystyle \ell _{A}(A/I_{k-1})-Y_{k}Z_{k-1}+1-p_{a}(Y_{k}),\nonumber\end{eqnarray}$$as required. ◻
The following lemma is a key lemma in the proof of the theorem.
Lemma 4.14. Under the notation as in Theorem 4.10, we have
(1)
 $a_{i}\leqslant n_{i}\cdot \ell _{A}(A/I)$;
$a_{i}\leqslant n_{i}\cdot \ell _{A}(A/I)$;(2) equality holds in (1) if and only if
 $M_{i}$ is a special Cohen–Macaulay
$M_{i}$ is a special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$.
$I$.
Proof. By Kato’s Riemann–Roch formula, we have
 $$\begin{eqnarray}\ell _{A}(M_{i}/IM_{i})=\,\text{rank}_{A}M_{i}\cdot \ell _{A}(A/I)+c_{1}(\widetilde{M_{i}})\cdot Z=n_{i}\cdot \ell _{A}(A/I)+a_{i}.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M_{i}/IM_{i})=\,\text{rank}_{A}M_{i}\cdot \ell _{A}(A/I)+c_{1}(\widetilde{M_{i}})\cdot Z=n_{i}\cdot \ell _{A}(A/I)+a_{i}.\end{eqnarray}$$ On the other hand, 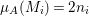 ${\it\mu}_{A}(M_{i})=2n_{i}$ because
${\it\mu}_{A}(M_{i})=2n_{i}$ because ![]() $M_{i}$ is a special Cohen–Macaulay
$M_{i}$ is a special Cohen–Macaulay ![]() $A$-module (with respect to
$A$-module (with respect to ![]() $\mathfrak{m}$). Hence,
$\mathfrak{m}$). Hence,
 $$\begin{eqnarray}\ell _{A}(M_{i}/IM_{i})\leqslant {\it\mu}_{A}(M_{i})\cdot \ell _{A}(A/I)=2n_{i}\cdot \ell _{A}(A/I).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M_{i}/IM_{i})\leqslant {\it\mu}_{A}(M_{i})\cdot \ell _{A}(A/I)=2n_{i}\cdot \ell _{A}(A/I).\end{eqnarray}$$ Therefore, 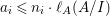 $a_{i}\leqslant n_{i}\cdot \ell _{A}(A/I)$ and equality holds true if and only if
$a_{i}\leqslant n_{i}\cdot \ell _{A}(A/I)$ and equality holds true if and only if 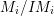 $M_{i}/IM_{i}$ is
$M_{i}/IM_{i}$ is ![]() $A/I$-free, which means that
$A/I$-free, which means that ![]() $M_{i}$ is a special Cohen–Macaulay
$M_{i}$ is a special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.◻
$I$.◻
Proof of Theorem 4.10.
(1) ![]() $\Longleftrightarrow$ (2) follows from Lemma 4.14.
$\Longleftrightarrow$ (2) follows from Lemma 4.14.
(2) ![]() $\Longrightarrow$ (3): Choose anti-nef cycles
$\Longrightarrow$ (3): Choose anti-nef cycles 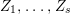 $Z_{1},\ldots ,Z_{s}$ and positive cycles
$Z_{1},\ldots ,Z_{s}$ and positive cycles 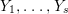 $Y_{1},\ldots ,Y_{s}$ that satisfy the condition of Lemma 4.9. For these
$Y_{1},\ldots ,Y_{s}$ that satisfy the condition of Lemma 4.9. For these ![]() $Y_{i}$s and
$Y_{i}$s and ![]() $Z_{i}$s, we use induction on
$Z_{i}$s, we use induction on ![]() $s$. By Lemma 4.13, we have
$s$. By Lemma 4.13, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle n_{i}\cdot \ell _{A}(A/I)-\text{coeff}_{E_{i}}Z\nonumber\\ \displaystyle & & \displaystyle \quad =n_{i}\left\{\ell _{A}(A/I_{s-1})-Y_{s}Z_{s-1}+1-p_{a}(Y_{s})\right\}-\text{coeff}_{E_{i}}Z_{s-1}-\text{coeff}_{E_{i}}Y_{s}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{n_{i}\cdot \ell _{A}(A/I_{s-1})-\text{coeff}_{E_{i}}Z_{s-1}\right\}+n_{i}(-Y_{s}Z_{s-1})+n_{i}(-p_{a}(Y_{s}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left\{n_{i}-\text{coeff}_{E_{i}}Y_{s}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle n_{i}\cdot \ell _{A}(A/I)-\text{coeff}_{E_{i}}Z\nonumber\\ \displaystyle & & \displaystyle \quad =n_{i}\left\{\ell _{A}(A/I_{s-1})-Y_{s}Z_{s-1}+1-p_{a}(Y_{s})\right\}-\text{coeff}_{E_{i}}Z_{s-1}-\text{coeff}_{E_{i}}Y_{s}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{n_{i}\cdot \ell _{A}(A/I_{s-1})-\text{coeff}_{E_{i}}Z_{s-1}\right\}+n_{i}(-Y_{s}Z_{s-1})+n_{i}(-p_{a}(Y_{s}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left\{n_{i}-\text{coeff}_{E_{i}}Y_{s}\right\}.\nonumber\end{eqnarray}$$ By the induction hypothesis, 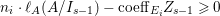 $n_{i}\cdot \ell _{A}(A/I_{s-1})-\text{coeff}_{E_{i}}Z_{s-1}\geqslant 0$. Since
$n_{i}\cdot \ell _{A}(A/I_{s-1})-\text{coeff}_{E_{i}}Z_{s-1}\geqslant 0$. Since ![]() $Z_{s-1}$ is anti-nef,
$Z_{s-1}$ is anti-nef, 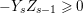 $-Y_{s}Z_{s-1}\geqslant 0$. As
$-Y_{s}Z_{s-1}\geqslant 0$. As ![]() $A$ is rational,
$A$ is rational, 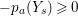 $-p_{a}(Y_{s})\geqslant 0$. By the choice of
$-p_{a}(Y_{s})\geqslant 0$. By the choice of ![]() $Y_{s}$,
$Y_{s}$, 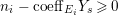 $n_{i}-\text{coeff}_{E_{i}}Y_{s}\geqslant 0$. Hence, we obtain the required inequality, and equality holds if and only if
$n_{i}-\text{coeff}_{E_{i}}Y_{s}\geqslant 0$. Hence, we obtain the required inequality, and equality holds if and only if
 $$\begin{eqnarray}\displaystyle & & \displaystyle n_{i}\cdot \ell _{A}(A/I_{s-1})=\text{coeff}_{E_{i}}Z_{s-1},\nonumber\\ \displaystyle & & \displaystyle Y_{s}Z_{s-1}=p_{a}(Y_{s})=0\quad \text{and}\quad n_{i}=\text{coeff}_{E_{i}}Y_{s}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle n_{i}\cdot \ell _{A}(A/I_{s-1})=\text{coeff}_{E_{i}}Z_{s-1},\nonumber\\ \displaystyle & & \displaystyle Y_{s}Z_{s-1}=p_{a}(Y_{s})=0\quad \text{and}\quad n_{i}=\text{coeff}_{E_{i}}Y_{s}.\nonumber\end{eqnarray}$$ Therefore, the assertion follows from the induction hypothesis. We can prove the converse 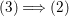 $(3)\Longrightarrow (2)$ similarly.
$(3)\Longrightarrow (2)$ similarly.
Now suppose that one of (1), (2), (3) holds. The induction hypothesis implies that ![]() $I_{s-1}$ is a special ideal with
$I_{s-1}$ is a special ideal with 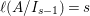 $\ell (A/I_{s-1})=s$,
$\ell (A/I_{s-1})=s$, 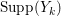 $\text{Supp}(Y_{k})$ is connected,
$\text{Supp}(Y_{k})$ is connected, 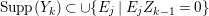 $\text{Supp}(Y_{k})\subset \cup \{E_{j}\mid E_{j}Z_{k-1}=0\}$ and
$\text{Supp}(Y_{k})\subset \cup \{E_{j}\mid E_{j}Z_{k-1}=0\}$ and ![]() $Y_{k}$ is the fundamental cycle on
$Y_{k}$ is the fundamental cycle on 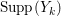 $\text{Supp}(Y_{k})$ for every
$\text{Supp}(Y_{k})$ for every  $k=1,\ldots ,s-1$. Then it follows from Lemma 4.13 that
$k=1,\ldots ,s-1$. Then it follows from Lemma 4.13 that 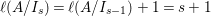 $\ell (A/I_{s})=\ell (A/I_{s-1})+1=s+1$. As
$\ell (A/I_{s})=\ell (A/I_{s-1})+1=s+1$. As 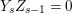 $Y_{s}Z_{s-1}=0$, it follows that
$Y_{s}Z_{s-1}=0$, it follows that 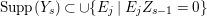 $\text{Supp}(Y_{s})\subset \cup \{E_{j}\mid E_{j}Z_{s-1}=0\}$. Moreover, since
$\text{Supp}(Y_{s})\subset \cup \{E_{j}\mid E_{j}Z_{s-1}=0\}$. Moreover, since 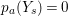 $p_{a}(Y_{s})=0$,
$p_{a}(Y_{s})=0$, ![]() $Y_{s}$ must be connected.
$Y_{s}$ must be connected.
Let us show that ![]() $Y_{s}$ is the fundamental cycle on
$Y_{s}$ is the fundamental cycle on 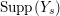 $\text{Supp}(Y_{s})$. For each
$\text{Supp}(Y_{s})$. For each 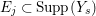 $E_{j}\subset \text{Supp}(Y_{s})$,
$E_{j}\subset \text{Supp}(Y_{s})$, 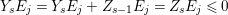 $Y_{s}E_{j}=Y_{s}E_{j}+Z_{s-1}E_{j}=Z_{s}E_{j}\leqslant 0$. Hence,
$Y_{s}E_{j}=Y_{s}E_{j}+Z_{s-1}E_{j}=Z_{s}E_{j}\leqslant 0$. Hence, ![]() $Y_{s}$ is anti-nef on
$Y_{s}$ is anti-nef on 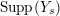 $\text{Supp}(Y_{s})$. If
$\text{Supp}(Y_{s})$. If ![]() $Y_{s}$ is not the fundamental cycle on
$Y_{s}$ is not the fundamental cycle on 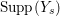 $\text{Supp}(Y_{s})$, then there exist an
$\text{Supp}(Y_{s})$, then there exist an 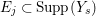 $E_{j}\subset \text{Supp}(Y_{s})$ and an anti-nef cycle
$E_{j}\subset \text{Supp}(Y_{s})$ and an anti-nef cycle ![]() $Y_{s}^{\prime }$ on
$Y_{s}^{\prime }$ on 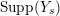 $\text{Supp}(Y_{s})$ so that
$\text{Supp}(Y_{s})$ so that 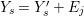 $Y_{s}=Y_{s}^{\prime }+E_{j}$. Then
$Y_{s}=Y_{s}^{\prime }+E_{j}$. Then
 $$\begin{eqnarray}0=p_{a}(Y_{s})=p_{a}(Y_{s}^{\prime })+p_{a}(E_{j})+Y_{s}^{\prime }E_{j}-1\leqslant p_{a}(Y_{s}^{\prime })-1\leqslant -1.\end{eqnarray}$$
$$\begin{eqnarray}0=p_{a}(Y_{s})=p_{a}(Y_{s}^{\prime })+p_{a}(E_{j})+Y_{s}^{\prime }E_{j}-1\leqslant p_{a}(Y_{s}^{\prime })-1\leqslant -1.\end{eqnarray}$$This is a contradiction. ◻
5 Ulrich ideals and modules over rational double points
The goal of this section is to classify Ulrich ideals of any two-dimensional Gorenstein rational singularity (rational double point) ![]() $A$, and to determine all of the Ulrich
$A$, and to determine all of the Ulrich ![]() $A$-modules with respect to those ideals.
$A$-modules with respect to those ideals.
First, we recall the definition of rational double points.
Definition 5.1. (Rational double point)
Let ![]() $A$ be a two-dimensional complete Noetherian local ring with unique maximal ideal
$A$ be a two-dimensional complete Noetherian local ring with unique maximal ideal ![]() $\mathfrak{m}$ containing an algebraically closed field
$\mathfrak{m}$ containing an algebraically closed field ![]() $k$. Then
$k$. Then ![]() $A$ is said to be a rational double point if it is isomorphic to the hypersurface
$A$ is said to be a rational double point if it is isomorphic to the hypersurface 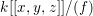 $k[[x,y,z]]/(f)$, where
$k[[x,y,z]]/(f)$, where ![]() $f$ is one of the following polynomials:
$f$ is one of the following polynomials:
 $$\begin{eqnarray}\begin{array}{@{}cll@{}}(A_{n}) & z^{2}+x^{2}+y^{n+1} & (n\geqslant 1),\\ (D_{n}) & z^{2}+x^{2}y+y^{n-1} & (n\geqslant 4),\\ (E_{6}) & z^{2}+x^{3}+y^{4}, & \\ (E_{7}) & z^{2}+x^{3}+xy^{3}, & \\ (E_{8}) & z^{2}+x^{3}+y^{5}. & \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cll@{}}(A_{n}) & z^{2}+x^{2}+y^{n+1} & (n\geqslant 1),\\ (D_{n}) & z^{2}+x^{2}y+y^{n-1} & (n\geqslant 4),\\ (E_{6}) & z^{2}+x^{3}+y^{4}, & \\ (E_{7}) & z^{2}+x^{3}+xy^{3}, & \\ (E_{8}) & z^{2}+x^{3}+y^{5}. & \end{array}\end{eqnarray}$$ By flat base change, it is known that ![]() $A$ is a two-dimensional local Gorenstein rational singularity (of characteristic
$A$ is a two-dimensional local Gorenstein rational singularity (of characteristic ![]() $0$) if and only if the
$0$) if and only if the ![]() $\mathfrak{m}$-adic completion
$\mathfrak{m}$-adic completion ![]() $\widehat{A}$ is a rational double point in the above sense [Reference ViehwegVi, Remarks p.1].
$\widehat{A}$ is a rational double point in the above sense [Reference ViehwegVi, Remarks p.1].
The following theorem is the first main result in this section. In the latter half of this section, we give the complete classification of Ulrich ideals and modules as an application of the theorem.
Theorem 5.2. (See also Theorem 3.2.)
Assume that ![]() $A$ is a rational double point of dimension
$A$ is a rational double point of dimension ![]() $2$, and let
$2$, and let ![]() $I\subset A$ be a nonparameter
$I\subset A$ be a nonparameter ![]() $\mathfrak{m}$-primary ideal. Suppose that
$\mathfrak{m}$-primary ideal. Suppose that ![]() $M$ is a maximal Cohen–Macaulay
$M$ is a maximal Cohen–Macaulay ![]() $A$-module. Then the following conditions are equivalent:
$A$-module. Then the following conditions are equivalent:
(1)
 $M$ is an Ulrich
$M$ is an Ulrich  $A$-module with respect to
$A$-module with respect to  $I$;
$I$;(2)
 $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$;
$I$;(3)
 $M$ is a weakly special Cohen–Macaulay
$M$ is a weakly special Cohen–Macaulay  $A$-module with respect to
$A$-module with respect to  $I$;
$I$;(4)
 $M/IM$ is
$M/IM$ is  $A/I$-free and
$A/I$-free and  $M$ has no free summands.
$M$ has no free summands.
When this is the case, ![]() $I$ is an Ulrich ideal and
$I$ is an Ulrich ideal and 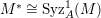 $M^{\ast }\cong \text{Syz}_{A}^{1}(M)$ is also an Ulrich
$M^{\ast }\cong \text{Syz}_{A}^{1}(M)$ is also an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.
$I$.
In what follows, we prove Theorem 5.2. We need several lemmas. Although the following lemma can be proved in a similar method to the proof of Theorem 3.2, we do not need to assume that ![]() $I$ is stable here.
$I$ is stable here.
Lemma 5.3. Assume that ![]() $A$ is a rational double point of dimension
$A$ is a rational double point of dimension ![]() $2$, and let
$2$, and let ![]() $I\subset A$ be an
$I\subset A$ be an ![]() $\mathfrak{m}$-primary ideal. Then
$\mathfrak{m}$-primary ideal. Then 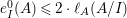 $e_{I}^{0}(A)\leqslant 2\cdot \ell _{A}(A/I)$ holds true and equality holds if and only if
$e_{I}^{0}(A)\leqslant 2\cdot \ell _{A}(A/I)$ holds true and equality holds if and only if ![]() $I$ is a good ideal.
$I$ is a good ideal.
Proof. The lemma is well known, but we give a proof here for the convenience of the reader. Let ![]() $\overline{I}$ denote the integral closure of
$\overline{I}$ denote the integral closure of ![]() $I$. Take a minimal reduction
$I$. Take a minimal reduction ![]() $Q$ of
$Q$ of ![]() $I$. Then since
$I$. Then since ![]() $Q$ is also a minimal reduction of
$Q$ is also a minimal reduction of ![]() $\overline{I}$ and
$\overline{I}$ and 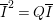 $\overline{I}^{2}=Q\overline{I}$, we have
$\overline{I}^{2}=Q\overline{I}$, we have
 $$\begin{eqnarray}I\subset \overline{I}\subset Q:\overline{I}\subset Q:I.\end{eqnarray}$$
$$\begin{eqnarray}I\subset \overline{I}\subset Q:\overline{I}\subset Q:I.\end{eqnarray}$$The Matlis duality theorem implies that
 $$\begin{eqnarray}\displaystyle e_{I}^{0}(A) & = & \displaystyle \ell _{A}(A/Q)=\ell _{A}(A/I)+\ell _{A}(I/Q)\leqslant \ell _{A}(A/I)+\ell _{A}(Q:I/Q)\nonumber\\ \displaystyle & = & \displaystyle 2\cdot \ell _{A}(A/I),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{I}^{0}(A) & = & \displaystyle \ell _{A}(A/Q)=\ell _{A}(A/I)+\ell _{A}(I/Q)\leqslant \ell _{A}(A/I)+\ell _{A}(Q:I/Q)\nonumber\\ \displaystyle & = & \displaystyle 2\cdot \ell _{A}(A/I),\nonumber\end{eqnarray}$$ and equality holds if and only if 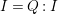 $I=Q:I$, that is,
$I=Q:I$, that is, ![]() $I$ is a good ideal.◻
$I$ is a good ideal.◻
Almost all of the maximal Cohen–Macaulay ![]() $A$-modules over a hypersurface of multiplicity
$A$-modules over a hypersurface of multiplicity ![]() $2$ can be regarded as Ulrich modules in the classical sense.
$2$ can be regarded as Ulrich modules in the classical sense.
Lemma 5.4. (Cf. [Reference Herzog and KühlHKuh, Corollary 1.4].)
Let ![]() $A$ be a hypersurface local domain of
$A$ be a hypersurface local domain of 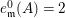 $e_{\mathfrak{m}}^{0}(A)=2$. Then every maximal Cohen–Macaulay
$e_{\mathfrak{m}}^{0}(A)=2$. Then every maximal Cohen–Macaulay ![]() $A$-module without free summands satisfies
$A$-module without free summands satisfies 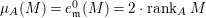 ${\it\mu}_{A}(M)=e_{\mathfrak{m}}^{0}(M)=2\cdot \,\text{rank}_{A}\,M$, that is,
${\it\mu}_{A}(M)=e_{\mathfrak{m}}^{0}(M)=2\cdot \,\text{rank}_{A}\,M$, that is, ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $\mathfrak{m}$.
$\mathfrak{m}$.
Any two-dimensional rational double point ![]() $A$ can be regarded as an invariant subring
$A$ can be regarded as an invariant subring ![]() $B^{G}$, where
$B^{G}$, where 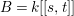 $B=k[[s,t]]$ is a formal power series ring over
$B=k[[s,t]]$ is a formal power series ring over ![]() $k$, and
$k$, and ![]() $G$ is a finite subgroup of
$G$ is a finite subgroup of 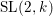 $\text{SL}(2,k)$. Thus, we can apply the so-called McKay correspondence, which is a special case of “special McKay correspondence” (see Section 4).
$\text{SL}(2,k)$. Thus, we can apply the so-called McKay correspondence, which is a special case of “special McKay correspondence” (see Section 4).
Lemma 5.5. (McKay correspondence)
Let 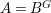 $A=B^{G}$ as above. Then we have the following.
$A=B^{G}$ as above. Then we have the following.
(1) The ring
 $A$ is of finite CM-representation type. Let
$A$ is of finite CM-representation type. Let  $\{M_{i}\}_{i=0}^{r}$ be the set of isomorphism classes of indecomposable maximal Cohen–Macaulay
$\{M_{i}\}_{i=0}^{r}$ be the set of isomorphism classes of indecomposable maximal Cohen–Macaulay  $A$-modules, where
$A$-modules, where  $M_{0}=A$. Then
$M_{0}=A$. Then  $B\cong \bigoplus _{i=0}^{r}M_{i}^{\oplus n_{i}}$, where
$B\cong \bigoplus _{i=0}^{r}M_{i}^{\oplus n_{i}}$, where  $n_{i}=\,\text{rank}_{A}\,M_{i}$.
$n_{i}=\,\text{rank}_{A}\,M_{i}$.(2) The fundamental cycle is given by
 $Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$, so that if we choose indices suitably, then
$Z_{0}=\sum _{j=1}^{r}n_{j}E_{j}$, so that if we choose indices suitably, then  $c_{1}(\widetilde{M_{i}})E_{j}={\it\delta}_{ij}$ for
$c_{1}(\widetilde{M_{i}})E_{j}={\it\delta}_{ij}$ for  $1\leqslant i,j\leqslant r$, where
$1\leqslant i,j\leqslant r$, where  $c_{1}(\ast )$ denotes the Chern class, and
$c_{1}(\ast )$ denotes the Chern class, and  $\widetilde{M_{i}}={\it\varphi}^{\ast }(M_{i})/\text{torsion}$. In particular,
$\widetilde{M_{i}}={\it\varphi}^{\ast }(M_{i})/\text{torsion}$. In particular,  $M_{i}$ is a special Cohen–Macaulay
$M_{i}$ is a special Cohen–Macaulay  $A$-module (with respect to
$A$-module (with respect to  $\mathfrak{m}$) for every
$\mathfrak{m}$) for every  $i=1,2,\ldots ,r$.
$i=1,2,\ldots ,r$.
We are now ready to prove Theorem 5.2.
Proof of Theorem 5.2.
 $(1)\Longrightarrow (2)$: Since
$(1)\Longrightarrow (2)$: Since ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, it has no free summands because no free module is an Ulrich
$I$, it has no free summands because no free module is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Thus,
$I$. Thus, ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $\mathfrak{m}$ by Lemma 5.4, and it is also a special Cohen–Macaulay
$\mathfrak{m}$ by Lemma 5.4, and it is also a special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $\mathfrak{m}$ by Lemma 5.5. Hence,
$\mathfrak{m}$ by Lemma 5.5. Hence, ![]() $M$ is a special Cohen–Macaulay
$M$ is a special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ because
$I$ because ![]() $M/IM$ is
$M/IM$ is ![]() $A/I$-free.
$A/I$-free.
 $(2)\Longrightarrow (3)$: See Lemma 4.6.
$(2)\Longrightarrow (3)$: See Lemma 4.6.
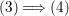 $(3)\Longrightarrow (4)$: Trivial.
$(3)\Longrightarrow (4)$: Trivial.
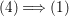 $(4)\Longrightarrow (1)$: By Lemma 5.4,
$(4)\Longrightarrow (1)$: By Lemma 5.4, ![]() $M$ is a weakly special Cohen–Macaulay
$M$ is a weakly special Cohen–Macaulay ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Note that
$I$. Note that 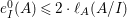 $e_{I}^{0}(A)\leqslant 2\cdot \ell _{A}(A/I)$ by Lemma 5.3. By a similar argument to the proof of Theorem 3.2, we have
$e_{I}^{0}(A)\leqslant 2\cdot \ell _{A}(A/I)$ by Lemma 5.3. By a similar argument to the proof of Theorem 3.2, we have
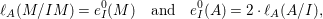 $$\begin{eqnarray}\ell _{A}(M/IM)=e_{I}^{0}(M)\quad \text{and}\quad e_{I}^{0}(A)=2\cdot \ell _{A}(A/I),\end{eqnarray}$$
$$\begin{eqnarray}\ell _{A}(M/IM)=e_{I}^{0}(M)\quad \text{and}\quad e_{I}^{0}(A)=2\cdot \ell _{A}(A/I),\end{eqnarray}$$ whence ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, and
$I$, and ![]() $I$ is a good ideal.
$I$ is a good ideal.
Since ![]() $A$ is a hypersurface local domain, Proposition 3.4 implies that
$A$ is a hypersurface local domain, Proposition 3.4 implies that ![]() $I$ is an Ulrich ideal. In particular,
$I$ is an Ulrich ideal. In particular, ![]() $A/I$ is Gorenstein. Thus, application of Theorem 2.6 yields that
$A/I$ is Gorenstein. Thus, application of Theorem 2.6 yields that 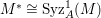 $M^{\ast }\cong \text{Syz}_{A}^{1}(M)$ is also an Ulrich
$M^{\ast }\cong \text{Syz}_{A}^{1}(M)$ is also an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$.◻
$I$.◻
The corollary below follows from Proposition 3.4 and Theorem 5.2.
Corollary 5.6. Assume that ![]() $A$ is a rational double point of dimension
$A$ is a rational double point of dimension ![]() $2$. Let
$2$. Let ![]() $I$ be an
$I$ be an ![]() $\mathfrak{m}$-primary ideal. Then the following conditions are equivalent:
$\mathfrak{m}$-primary ideal. Then the following conditions are equivalent:
(1)
 $I$ is an Ulrich ideal;
$I$ is an Ulrich ideal;(2)
 $I$ is a special ideal;
$I$ is a special ideal;(3)
 $I$ is a weakly special ideal;
$I$ is a weakly special ideal;(4) there exists an Ulrich
 $A$-module with respect to
$A$-module with respect to  $I$.
$I$.
In the rest of this section, we classify all Ulrich ideals and Ulrich modules over rational double points of dimension ![]() $2$ using the results in the previous section.
$2$ using the results in the previous section.
Let 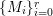 $\{M_{i}\}_{i=0}^{r}$ be the set of indecomposable maximal Cohen–Macaulay
$\{M_{i}\}_{i=0}^{r}$ be the set of indecomposable maximal Cohen–Macaulay ![]() $A$-modules, so that
$A$-modules, so that 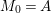 $M_{0}=A$ and
$M_{0}=A$ and 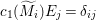 $c_{1}(\widetilde{M_{i}})E_{j}={\it\delta}_{ij}$ for all
$c_{1}(\widetilde{M_{i}})E_{j}={\it\delta}_{ij}$ for all 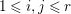 $1\leqslant i,j\leqslant r$.
$1\leqslant i,j\leqslant r$.
Now suppose that ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Then
$I$. Then ![]() $M$ is a finite direct sum of
$M$ is a finite direct sum of 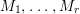 $M_{1},\ldots ,M_{r}$:
$M_{1},\ldots ,M_{r}$:
 $$\begin{eqnarray}M\cong M_{1}^{\oplus k_{1}}\oplus \cdots \oplus M_{r}^{\oplus k_{r}},\end{eqnarray}$$
$$\begin{eqnarray}M\cong M_{1}^{\oplus k_{1}}\oplus \cdots \oplus M_{r}^{\oplus k_{r}},\end{eqnarray}$$ because ![]() $M$ has no free summands. Whenever
$M$ has no free summands. Whenever ![]() $k_{i}>0$,
$k_{i}>0$, ![]() $M_{i}$ must be an Ulrich
$M_{i}$ must be an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$. Hence, it suffices to characterize all
$I$. Hence, it suffices to characterize all ![]() $M_{i}$ that are Ulrich
$M_{i}$ that are Ulrich ![]() $A$-modules with respect to
$A$-modules with respect to ![]() $I$. On the other hand, Theorem 5.2 implies that
$I$. On the other hand, Theorem 5.2 implies that ![]() $I$ is an Ulrich ideal, whence
$I$ is an Ulrich ideal, whence ![]() $I$ is a special ideal. Thus, those ideals
$I$ is a special ideal. Thus, those ideals ![]() $I$ (or cycles
$I$ (or cycles ![]() $Z$) are determined by Theorem 4.10. Moreover, it is not difficult to determine all
$Z$) are determined by Theorem 4.10. Moreover, it is not difficult to determine all ![]() $M_{i}$ that are Ulrich
$M_{i}$ that are Ulrich ![]() $A$-modules with respect to
$A$-modules with respect to ![]() $I_{Z}$ by Theorem 5.2.
$I_{Z}$ by Theorem 5.2.
Let ![]() $I$ be a good ideal of
$I$ be a good ideal of ![]() $A$, and let
$A$, and let ![]() $Z$ be an anti-nef cycle on the minimal resolution
$Z$ be an anti-nef cycle on the minimal resolution ![]() $X$ such that
$X$ such that 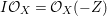 $I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ and
$I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ and 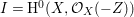 $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$, that is,
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$, that is, ![]() $I=I_{Z}$. Then we call
$I=I_{Z}$. Then we call ![]() $Z$ an Ulrich cycle if
$Z$ an Ulrich cycle if ![]() $I$ is an Ulrich ideal. Note that by Corollary 5.6,
$I$ is an Ulrich ideal. Note that by Corollary 5.6, ![]() $Z$ is an Ulrich cycle if and only if it is a special cycle.
$Z$ is an Ulrich cycle if and only if it is a special cycle.
Now let us illustrate the main theorem by the following example. Let 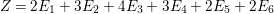 $Z=2E_{1}+3E_{2}+4E_{3}+3E_{4}+2E_{5}+2E_{6}$ be the cycle of the rational double point
$Z=2E_{1}+3E_{2}+4E_{3}+3E_{4}+2E_{5}+2E_{6}$ be the cycle of the rational double point 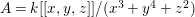 $A=k[[x,y,z]]/(x^{3}+y^{4}+z^{2})$, and put
$A=k[[x,y,z]]/(x^{3}+y^{4}+z^{2})$, and put 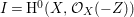 $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then since
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then since ![]() $Z$ is an anti-nef cycle on the minimal resolution
$Z$ is an anti-nef cycle on the minimal resolution 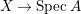 $X\rightarrow \,\text{Spec}\,A$ with support in
$X\rightarrow \,\text{Spec}\,A$ with support in 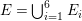 $E=\bigcup _{i=1}^{6}E_{i}$,
$E=\bigcup _{i=1}^{6}E_{i}$, ![]() $Z$ can be described as follows.
$Z$ can be described as follows.

Furthermore, by Theorem 4.10(2), ![]() $M_{i}$ is an Ulrich
$M_{i}$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ if and only if
$I$ if and only if ![]() $i=1$ or
$i=1$ or ![]() $5$, because
$5$, because 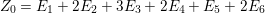 $Z_{0}=E_{1}+2E_{2}+3E_{3}+2E_{4}+E_{5}+2E_{6}$ and
$Z_{0}=E_{1}+2E_{2}+3E_{3}+2E_{4}+E_{5}+2E_{6}$ and 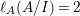 $\ell _{A}(A/I)=2$. In other words, any Ulrich
$\ell _{A}(A/I)=2$. In other words, any Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$ is given by
$I$ is given by  $M\cong M_{1}^{\oplus a}\oplus M_{5}^{\oplus b}$ for some integers
$M\cong M_{1}^{\oplus a}\oplus M_{5}^{\oplus b}$ for some integers ![]() $a,b\geqslant 0$. We can describe this by the following picture.
$a,b\geqslant 0$. We can describe this by the following picture.

We are now ready to state the main theorem in this section.
Theorem 5.7. Let ![]() $A$ be a two-dimensional rational double point. Let
$A$ be a two-dimensional rational double point. Let 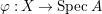 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities with
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities with 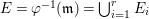 $E={\it\varphi}^{-1}(\mathfrak{m})=\bigcup _{i=1}^{r}E_{i}$, the exceptional divisor on
$E={\it\varphi}^{-1}(\mathfrak{m})=\bigcup _{i=1}^{r}E_{i}$, the exceptional divisor on ![]() $X$. Then all Ulrich cycles
$X$. Then all Ulrich cycles ![]() $Z_{k}$ of
$Z_{k}$ of ![]() $A$ and all indecomposable Ulrich
$A$ and all indecomposable Ulrich ![]() $A$-modules with respect to
$A$-modules with respect to 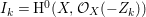 $I_{k}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{k}))$ are given by the following.
$I_{k}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{k}))$ are given by the following.
![]() $\bullet$
$\bullet$![]() $(A_{n})$
$(A_{n})$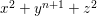 $x^{2}+y^{n+1}+z^{2}$
$x^{2}+y^{n+1}+z^{2}$
When ![]() $n=2m$, the complete list of all Ulrich cycles is given by the following:
$n=2m$, the complete list of all Ulrich cycles is given by the following:

for 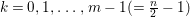 $k=0,1,\ldots ,m-1(=\frac{n}{2}-1)$. Then
$k=0,1,\ldots ,m-1(=\frac{n}{2}-1)$. Then 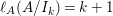 $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each  $k=0,1,\ldots ,m-1$.
$k=0,1,\ldots ,m-1$.
When 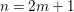 $n=2m+1$, the complete list of all Ulrich cycles is given by the following:
$n=2m+1$, the complete list of all Ulrich cycles is given by the following:

for 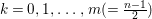 $k=0,1,\ldots ,m(=\frac{n-1}{2})$. Then
$k=0,1,\ldots ,m(=\frac{n-1}{2})$. Then 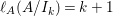 $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each 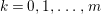 $k=0,1,\ldots ,m$.
$k=0,1,\ldots ,m$.
![]() $\bullet$
$\bullet$![]() $(D_{n})$
$(D_{n})$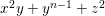 $x^{2}y+y^{n-1}+z^{2}$
$x^{2}y+y^{n-1}+z^{2}$![]() $(n\geqslant 4)$
$(n\geqslant 4)$
When ![]() $n=2m$, the complete list of all Ulrich cycles is given by the following:
$n=2m$, the complete list of all Ulrich cycles is given by the following:

for 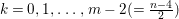 $k=0,1,\ldots ,m-2(=\frac{n-4}{2})$.
$k=0,1,\ldots ,m-2(=\frac{n-4}{2})$.



Then 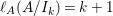 $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each 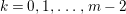 $k=0,1,\ldots ,m-2$,
$k=0,1,\ldots ,m-2$, 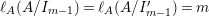 $\ell _{A}(A/I_{m-1})=\ell _{A}(A/I_{m-1}^{\prime })=m$ and
$\ell _{A}(A/I_{m-1})=\ell _{A}(A/I_{m-1}^{\prime })=m$ and 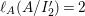 $\ell _{A}(A/I_{2}^{\prime })=2$, where
$\ell _{A}(A/I_{2}^{\prime })=2$, where ![]() $m=\frac{n}{2}$.
$m=\frac{n}{2}$.
When 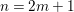 $n=2m+1$, the complete list of all Ulrich cycles is given by the following:
$n=2m+1$, the complete list of all Ulrich cycles is given by the following:

for 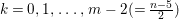 $k=0,1,\ldots ,m-2(=\frac{n-5}{2})$.
$k=0,1,\ldots ,m-2(=\frac{n-5}{2})$.

Then 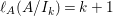 $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each 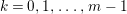 $k=0,1,\ldots ,m-1$, and
$k=0,1,\ldots ,m-1$, and 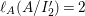 $\ell _{A}(A/I_{2}^{\prime })=2$.
$\ell _{A}(A/I_{2}^{\prime })=2$.
![]() $\bullet$
$\bullet$![]() $(E_{6})$
$(E_{6})$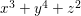 $x^{3}+y^{4}+z^{2}$
$x^{3}+y^{4}+z^{2}$
The Ulrich cycles of ![]() $A$ are the following
$A$ are the following ![]() $Z_{0}$ and
$Z_{0}$ and ![]() $Z_{1}$ with
$Z_{1}$ with 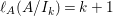 $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each ![]() $k=0,1$:
$k=0,1$:

![]() $\bullet$
$\bullet$![]() $(E_{7})$
$(E_{7})$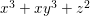 $x^{3}+xy^{3}+z^{2}$
$x^{3}+xy^{3}+z^{2}$
The Ulrich cycles of ![]() $A$ are the following
$A$ are the following ![]() $Z_{0}$,
$Z_{0}$, ![]() $Z_{1}$ and
$Z_{1}$ and ![]() $Z_{2}$ with
$Z_{2}$ with 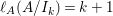 $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each  $k=0,1,2$:
$k=0,1,2$:

![]() $\bullet$
$\bullet$![]() $(E_{8})$
$(E_{8})$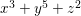 $x^{3}+y^{5}+z^{2}$
$x^{3}+y^{5}+z^{2}$
The Ulrich cycles of ![]() $A$ are the following
$A$ are the following ![]() $Z_{0}$ and
$Z_{0}$ and ![]() $Z_{1}$ with
$Z_{1}$ with  $\ell _{A}(A/I_{k})=k+1$ for each
$\ell _{A}(A/I_{k})=k+1$ for each ![]() $k=0,1$:
$k=0,1$:

In our previous paper [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Section 9], we gave a complete list of the nonparameter Ulrich ideals for one-dimensional simple singularities. We can also do this for two-dimensional simple singularities (rational double points).
Corollary 5.8. With the same notation as in Theorem 5.7, the set ![]() ${\mathcal{X}}_{A}$ is equal to the following.
${\mathcal{X}}_{A}$ is equal to the following.

Proof. One can easily see that any ideal ![]() $I$ appearing in the corollary has the form
$I$ appearing in the corollary has the form 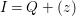 $I=Q+(z)$, where
$I=Q+(z)$, where ![]() $Q$ is a parameter ideal of
$Q$ is a parameter ideal of ![]() $A$ and
$A$ and 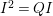 $I^{2}=QI$,
$I^{2}=QI$, 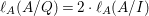 $\ell _{A}(A/Q)=2\cdot \ell _{A}(A/I)$ and
$\ell _{A}(A/Q)=2\cdot \ell _{A}(A/I)$ and 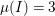 ${\it\mu}(I)=3$. Hence, those ideals
${\it\mu}(I)=3$. Hence, those ideals ![]() $I$ are Ulrich.
$I$ are Ulrich.
On the other hand, Theorem 5.7 implies that 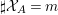 $\sharp {\mathcal{X}}_{A}=m$ (resp.
$\sharp {\mathcal{X}}_{A}=m$ (resp. ![]() $m+1$,
$m+1$, ![]() $m+2$,
$m+2$, ![]() $m+1$,
$m+1$, ![]() $2$,
$2$, ![]() $3$,
$3$, ![]() $2$) if
$2$) if ![]() $A$ is a rational double point of type
$A$ is a rational double point of type ![]() $(A_{2m})$ (resp.
$(A_{2m})$ (resp. 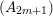 $(A_{2m+1})$,
$(A_{2m+1})$, ![]() $(D_{2m})$,
$(D_{2m})$, 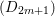 $(D_{2m+1})$,
$(D_{2m+1})$, ![]() $(E_{6})$,
$(E_{6})$, ![]() $(E_{7})$,
$(E_{7})$, ![]() $(E_{8})$). Hence, the set as above coincides with
$(E_{8})$). Hence, the set as above coincides with ![]() ${\mathcal{X}}_{A}$, respectively.◻
${\mathcal{X}}_{A}$, respectively.◻
Proof of Theorem 5.7.
We first consider the cases ![]() $(E_{6})$,
$(E_{6})$, ![]() $(E_{7})$,
$(E_{7})$, ![]() $(E_{8})$.
$(E_{8})$.
The case ![]() $(E_{6})$:
$(E_{6})$: 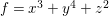 $f=x^{3}+y^{4}+z^{2}$. The fundamental cycle
$f=x^{3}+y^{4}+z^{2}$. The fundamental cycle ![]() $Z_{0}$ on the minimal resolution is given by
$Z_{0}$ on the minimal resolution is given by

Now suppose that ![]() $Z_{0}+Y$ is a special cycle for some positive cycle
$Z_{0}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Z_{0}$. Since
$Y\leqslant Z_{0}$. Since 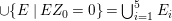 $\cup \{E\mid EZ_{0}=0\}=\bigcup _{i=1}^{5}E_{i}$ is connected, we have
$\cup \{E\mid EZ_{0}=0\}=\bigcup _{i=1}^{5}E_{i}$ is connected, we have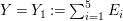 $Y=Y_{1}:=\sum _{i=1}^{5}E_{i}$ in Theorem 4.10(3). Conversely, if we put
$Y=Y_{1}:=\sum _{i=1}^{5}E_{i}$ in Theorem 4.10(3). Conversely, if we put

then ![]() $Z_{1}$ is anti-nef and
$Z_{1}$ is anti-nef and  $p(Y_{1})=0$ because
$p(Y_{1})=0$ because ![]() $Y_{1}$ can be regarded as the fundamental cycle on the dual graph (of the minimal resolution) of type
$Y_{1}$ can be regarded as the fundamental cycle on the dual graph (of the minimal resolution) of type ![]() $(A_{5})$. Hence,
$(A_{5})$. Hence, ![]() $Z_{1}$ is a special cycle and
$Z_{1}$ is a special cycle and ![]() $M$ is an Ulrich
$M$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I_{Z_{1}}$ if and only if it is a finite direct sum of
$I_{Z_{1}}$ if and only if it is a finite direct sum of ![]() $M_{1}$ and
$M_{1}$ and ![]() $M_{5}$, because
$M_{5}$, because 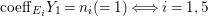 $\text{coeff}_{E_{i}}Y_{1}=n_{i}(=1)\Longleftrightarrow i=1,5$ (see Theorem 4.10).
$\text{coeff}_{E_{i}}Y_{1}=n_{i}(=1)\Longleftrightarrow i=1,5$ (see Theorem 4.10).
Suppose that 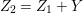 $Z_{2}=Z_{1}+Y$ is a special cycle for some positive cycle
$Z_{2}=Z_{1}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Y_{1}$. As
$Y\leqslant Y_{1}$. As 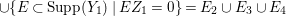 $\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}=E_{2}\cup E_{3}\cup E_{4}$ is connected, we have that
$\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}=E_{2}\cup E_{3}\cup E_{4}$ is connected, we have that 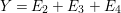 $Y=E_{2}+E_{3}+E_{4}$ as the fundamental cycle on
$Y=E_{2}+E_{3}+E_{4}$ as the fundamental cycle on 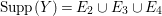 $\text{Supp}(Y)=E_{2}\cup E_{3}\cup E_{4}$. However,
$\text{Supp}(Y)=E_{2}\cup E_{3}\cup E_{4}$. However, 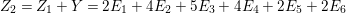 $Z_{2}=Z_{1}+Y=2E_{1}+4E_{2}+5E_{3}+4E_{4}+2E_{5}+2E_{6}$ is not anti-nef because
$Z_{2}=Z_{1}+Y=2E_{1}+4E_{2}+5E_{3}+4E_{4}+2E_{5}+2E_{6}$ is not anti-nef because 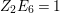 $Z_{2}E_{6}=1$. Therefore, the special cycles of
$Z_{2}E_{6}=1$. Therefore, the special cycles of ![]() $(E_{6})$ are
$(E_{6})$ are ![]() $Z_{0}$ and
$Z_{0}$ and ![]() $Z_{1}$.
$Z_{1}$.
The case ![]() $(E_{7})$:
$(E_{7})$: 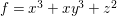 $f=x^{3}+xy^{3}+z^{2}$. The fundamental cycle
$f=x^{3}+xy^{3}+z^{2}$. The fundamental cycle ![]() $Z_{0}$ on the minimal resolution is given by
$Z_{0}$ on the minimal resolution is given by

Since 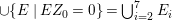 $\cup \{E\mid EZ_{0}=0\}=\bigcup _{i=2}^{7}E_{i}$ is isomorphic to the dual graph of
$\cup \{E\mid EZ_{0}=0\}=\bigcup _{i=2}^{7}E_{i}$ is isomorphic to the dual graph of ![]() $(D_{6})$, if
$(D_{6})$, if 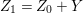 $Z_{1}=Z_{0}+Y$ is a special cycle for some positive cycle
$Z_{1}=Z_{0}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Z_{0}$, then we have
$Y\leqslant Z_{0}$, then we have

Conversely, one can easily see that the following ![]() $Z_{1}$ is a special cycle by Theorem 4.10.
$Z_{1}$ is a special cycle by Theorem 4.10.

Note that 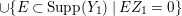 $\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}$ admits two connected components:
$\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}$ admits two connected components:

The fundamental cycles ![]() $Y_{2}$ of their components are
$Y_{2}$ of their components are 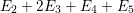 $E_{2}+2E_{3}+E_{4}+E_{5}$ and
$E_{2}+2E_{3}+E_{4}+E_{5}$ and ![]() $E_{6}$, respectively. Note that
$E_{6}$, respectively. Note that 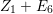 $Z_{1}+E_{6}$ is anti-nef but
$Z_{1}+E_{6}$ is anti-nef but 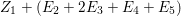 $Z_{1}+(E_{2}+2E_{3}+E_{4}+E_{5})$ is not anti-nef. Therefore, we are done.
$Z_{1}+(E_{2}+2E_{3}+E_{4}+E_{5})$ is not anti-nef. Therefore, we are done.
The case ![]() $(E_{8})$:
$(E_{8})$: 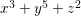 $x^{3}+y^{5}+z^{2}$. The fundamental cycle
$x^{3}+y^{5}+z^{2}$. The fundamental cycle ![]() $Z_{0}$ on the minimal resolution is given by
$Z_{0}$ on the minimal resolution is given by

Suppose that ![]() $Z_{0}+Y$ is a special cycle for some positive cycle
$Z_{0}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Z_{0}$. As
$Y\leqslant Z_{0}$. As  $\cup \{E\mid EZ_{0}=0\}=\bigcup _{i\neq 7}E_{i}$ is connected and the corresponding graph is isomorphic to the dual graph of
$\cup \{E\mid EZ_{0}=0\}=\bigcup _{i\neq 7}E_{i}$ is connected and the corresponding graph is isomorphic to the dual graph of ![]() $(E_{7})$, we have
$(E_{7})$, we have

Conversely, if we put

then ![]() $Z_{1}$ is a special cycle by Theorem 4.10.
$Z_{1}$ is a special cycle by Theorem 4.10.
Now suppose that ![]() $Z_{1}+Y$ is a special cycle for some positive cycle
$Z_{1}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Y_{1}$. Since
$Y\leqslant Y_{1}$. Since  $\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}=E_{2}\cup E_{3}\cup E_{4}\cup E_{5}\cup E_{6}\cup E_{8}$ is connected, we have
$\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}=E_{2}\cup E_{3}\cup E_{4}\cup E_{5}\cup E_{6}\cup E_{8}$ is connected, we have 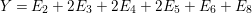 $Y=E_{2}+2E_{3}+2E_{4}+2E_{5}+E_{6}+E_{8}$. However,
$Y=E_{2}+2E_{3}+2E_{4}+2E_{5}+E_{6}+E_{8}$. However, ![]() $Z_{1}+Y$ is not anti-nef.
$Z_{1}+Y$ is not anti-nef.
We next consider the case ![]() $(A_{n})$.
$(A_{n})$.
The case ![]() $(A_{2m})$:
$(A_{2m})$: 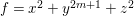 $f=x^{2}+y^{2m+1}+z^{2}$. The fundamental cycle
$f=x^{2}+y^{2m+1}+z^{2}$. The fundamental cycle ![]() $Z_{0}$ on the minimal resolution is given by
$Z_{0}$ on the minimal resolution is given by

That is, 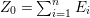 $Z_{0}=\sum _{i=1}^{n}E_{i}$.
$Z_{0}=\sum _{i=1}^{n}E_{i}$.
Now suppose that ![]() $Z_{0}+Y$ is a special cycle for some positive cycle
$Z_{0}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Z_{0}$. Since
$Y\leqslant Z_{0}$. Since 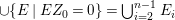 $\cup \{E\mid EZ_{0}=0\}=\bigcup _{i=2}^{n-1}E_{i}$ is connected,
$\cup \{E\mid EZ_{0}=0\}=\bigcup _{i=2}^{n-1}E_{i}$ is connected, ![]() $Y=Y_{1}$, where
$Y=Y_{1}$, where ![]() $Y_{1}$ is the fundamental cycle on
$Y_{1}$ is the fundamental cycle on 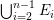 $\bigcup _{i=2}^{n-1}E_{i}$; that is,
$\bigcup _{i=2}^{n-1}E_{i}$; that is, 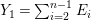 $Y_{1}=\sum _{i=2}^{n-1}E_{i}$. Conversely,
$Y_{1}=\sum _{i=2}^{n-1}E_{i}$. Conversely,

is a special cycle by Theorem 4.10. Similarly, if we put 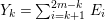 $Y_{k}=\sum _{i=k+1}^{2m-k}E_{i}$ for every
$Y_{k}=\sum _{i=k+1}^{2m-k}E_{i}$ for every 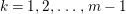 $k=1,2,\ldots ,m-1$, then we have:
$k=1,2,\ldots ,m-1$, then we have:
(a)
 $0<Y_{m-1}<Y_{m-2}<\cdots Y_{2}<Y_{1}\leqslant Z_{0}$;
$0<Y_{m-1}<Y_{m-2}<\cdots Y_{2}<Y_{1}\leqslant Z_{0}$;(b)
 $p_{a}(Y_{k})=0$ and
$p_{a}(Y_{k})=0$ and  $Y_{k}Z_{k-1}=0$ for every
$Y_{k}Z_{k-1}=0$ for every  $k=1,\ldots ,m-1$;
$k=1,\ldots ,m-1$;(c)
 $Z_{k}=Z_{k-1}+Y_{k}$ is anti-nef for every
$Z_{k}=Z_{k-1}+Y_{k}$ is anti-nef for every  $k=1,\ldots ,m-1$;
$k=1,\ldots ,m-1$;(d)
 $\text{coeff}_{E_{i}}Y_{k}=n_{i}$ if and only if
$\text{coeff}_{E_{i}}Y_{k}=n_{i}$ if and only if  $k+1\leqslant i\leqslant 2m-k$.
$k+1\leqslant i\leqslant 2m-k$.
This produces a sequence of Ulrich ideals:
 $$\begin{eqnarray}I_{Z_{m-1}}\subset I_{Z_{m-2}}\subset \cdots \subset I_{Z_{1}}=\mathfrak{m}.\end{eqnarray}$$
$$\begin{eqnarray}I_{Z_{m-1}}\subset I_{Z_{m-2}}\subset \cdots \subset I_{Z_{1}}=\mathfrak{m}.\end{eqnarray}$$ We can determine Ulrich ideals in the case of 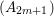 $(A_{2m+1})$ similarly.
$(A_{2m+1})$ similarly.
Finally, we consider the case ![]() $(D_{n})$:
$(D_{n})$: 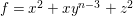 $f=x^{2}+xy^{n-3}+z^{2}$.
$f=x^{2}+xy^{n-3}+z^{2}$.
The case ![]() $(D_{2m})$:
$(D_{2m})$: 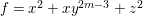 $f=x^{2}+xy^{2m-3}+z^{2}$. The fundamental cycle
$f=x^{2}+xy^{2m-3}+z^{2}$. The fundamental cycle ![]() $Z_{0}$ on the minimal resolution of singularities is given by
$Z_{0}$ on the minimal resolution of singularities is given by

That is, 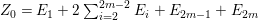 $Z_{0}=E_{1}+2\sum _{i=2}^{2m-2}E_{i}+E_{2m-1}+E_{2m}$.
$Z_{0}=E_{1}+2\sum _{i=2}^{2m-2}E_{i}+E_{2m-1}+E_{2m}$.
Now suppose that ![]() $Z_{0}+Y$ is a special cycle on
$Z_{0}+Y$ is a special cycle on ![]() $X$ for some positive cycle
$X$ for some positive cycle ![]() $Y\leqslant Z_{0}$. Since
$Y\leqslant Z_{0}$. Since 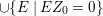 $\cup \{E\mid EZ_{0}=0\}$ has two connected components, we have that
$\cup \{E\mid EZ_{0}=0\}$ has two connected components, we have that ![]() $Y=E_{1}$ or
$Y=E_{1}$ or ![]() $Y=Y_{1}$:
$Y=Y_{1}$:

Conversely,

and

are special cycles by Theorem 4.10.
Suppose that ![]() $Z_{1}+Y$ is a special cycle for some positive cycle
$Z_{1}+Y$ is a special cycle for some positive cycle ![]() $Y\leqslant Y_{1}$. Since
$Y\leqslant Y_{1}$. Since 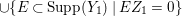 $\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}$ has two connected components, we have
$\cup \{E\subset \text{Supp}(Y_{1})\mid EZ_{1}=0\}$ has two connected components, we have ![]() $Y=E_{3}$ or
$Y=E_{3}$ or ![]() $Y=Y_{2}$, where
$Y=Y_{2}$, where

Then 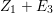 $Z_{1}+E_{3}$ is not anti-nef, but
$Z_{1}+E_{3}$ is not anti-nef, but

is a special cycle. Similarly, if we put
 $$\begin{eqnarray}Y_{k}=E_{2k+1}+2\mathop{\sum }_{i=2k+2}^{2m-2}E_{i}+E_{2m-1}+E_{2m},\qquad Z_{k}=Z_{k-1}+Y_{k},\end{eqnarray}$$
$$\begin{eqnarray}Y_{k}=E_{2k+1}+2\mathop{\sum }_{i=2k+2}^{2m-2}E_{i}+E_{2m-1}+E_{2m},\qquad Z_{k}=Z_{k-1}+Y_{k},\end{eqnarray}$$ for each  $k=1,2,\ldots ,m-2$, then we have a sequence of positive cycles
$k=1,2,\ldots ,m-2$, then we have a sequence of positive cycles
 $$\begin{eqnarray}0<Y_{m-2}<Y_{m-3}<\cdots <Y_{1}\leqslant Z_{0}.\end{eqnarray}$$
$$\begin{eqnarray}0<Y_{m-2}<Y_{m-3}<\cdots <Y_{1}\leqslant Z_{0}.\end{eqnarray}$$ By Theorem 4.10, ![]() $Z_{0}$,
$Z_{0}$, 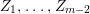 $Z_{1},\ldots ,Z_{m-2}$ are special cycles. Note that
$Z_{1},\ldots ,Z_{m-2}$ are special cycles. Note that
 $$\begin{eqnarray}\cup \{E\subset \text{Supp}(Y_{m-2})\mid EZ_{m-2}=0\}=E_{2m-3}\cup E_{2m-1}\cup E_{2m}\end{eqnarray}$$
$$\begin{eqnarray}\cup \{E\subset \text{Supp}(Y_{m-2})\mid EZ_{m-2}=0\}=E_{2m-3}\cup E_{2m-1}\cup E_{2m}\end{eqnarray}$$and

By a similar argument to that above, we obtain two minimal special cycles:


The case 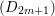 $(D_{2m+1})$. The fundamental cycle
$(D_{2m+1})$. The fundamental cycle ![]() $Z_{0}$ on the minimal resolution is given by
$Z_{0}$ on the minimal resolution is given by

If we put
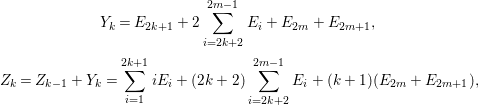 $$\begin{eqnarray}\displaystyle & \displaystyle Y_{k}=E_{2k+1}+2\mathop{\sum }_{i=2k+2}^{2m-1}E_{i}+E_{2m}+E_{2m+1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle Z_{k}=Z_{k-1}+Y_{k}=\mathop{\sum }_{i=1}^{2k+1}iE_{i}+(2k+2)\mathop{\sum }_{i=2k+2}^{2m-1}E_{i}+(k+1)(E_{2m}+E_{2m+1}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Y_{k}=E_{2k+1}+2\mathop{\sum }_{i=2k+2}^{2m-1}E_{i}+E_{2m}+E_{2m+1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle Z_{k}=Z_{k-1}+Y_{k}=\mathop{\sum }_{i=1}^{2k+1}iE_{i}+(2k+2)\mathop{\sum }_{i=2k+2}^{2m-1}E_{i}+(k+1)(E_{2m}+E_{2m+1}), & \displaystyle \nonumber\end{eqnarray}$$ for each 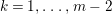 $k=1,\ldots ,m-2$, then
$k=1,\ldots ,m-2$, then 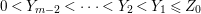 $0<Y_{m-2}<\cdots <Y_{2}<Y_{1}\leqslant Z_{0}$ are positive cycles and
$0<Y_{m-2}<\cdots <Y_{2}<Y_{1}\leqslant Z_{0}$ are positive cycles and 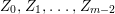 $Z_{0},Z_{1},\ldots ,Z_{m-2}$ are special cycles.
$Z_{0},Z_{1},\ldots ,Z_{m-2}$ are special cycles.
Now suppose that 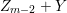 $Z_{m-2}+Y$ is a special cycle for some positive cycle
$Z_{m-2}+Y$ is a special cycle for some positive cycle 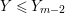 $Y\leqslant Y_{m-2}$. Since
$Y\leqslant Y_{m-2}$. Since
 $$\begin{eqnarray}\cup \{E\subset \text{Supp}(Y_{m-2})\mid EZ_{m-2}=0\}=E_{2m-1}\cup E_{2m}\cup E_{2m+1}\end{eqnarray}$$
$$\begin{eqnarray}\cup \{E\subset \text{Supp}(Y_{m-2})\mid EZ_{m-2}=0\}=E_{2m-1}\cup E_{2m}\cup E_{2m+1}\end{eqnarray}$$ is connected, we have that 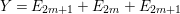 $Y=E_{2m+1}+E_{2m}+E_{2m+1}$.
$Y=E_{2m+1}+E_{2m}+E_{2m+1}$.
Set 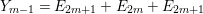 $Y_{m-1}=E_{2m+1}+E_{2m}+E_{2m+1}$. Conversely,
$Y_{m-1}=E_{2m+1}+E_{2m}+E_{2m+1}$. Conversely, 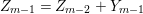 $Z_{m-1}=Z_{m-2}+Y_{m-1}$ is a special cycle by Theorem 4.10. Note that
$Z_{m-1}=Z_{m-2}+Y_{m-1}$ is a special cycle by Theorem 4.10. Note that ![]() $Z_{m-1}$ is the minimal one among those special cycles.◻
$Z_{m-1}$ is the minimal one among those special cycles.◻
6 Ulrich ideals of non-Gorenstein rational singularities
In this section, we study Ulrich ideals of two-dimensional non-Gorenstein rational singularities. Notice that the maximal ideal ![]() $\mathfrak{m}$ is always an Ulrich ideal of such a local ring.
$\mathfrak{m}$ is always an Ulrich ideal of such a local ring.
We first show that any Ulrich ideal of a two-dimensional rational singularity is a good ideal. In order to obtain a characterzation of Ulrich ideals, we need the following definition.
Throughout this section, let ![]() $(A,\mathfrak{m})$ be a two-dimensional non-Gorenstein rational singularity, and let
$(A,\mathfrak{m})$ be a two-dimensional non-Gorenstein rational singularity, and let 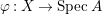 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities.
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities.
Definition 6.1. Let 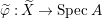 $\widetilde{{\it\varphi}}:\widetilde{X}\rightarrow \,\text{Spec}\,A$ be a resolution of singularities of
$\widetilde{{\it\varphi}}:\widetilde{X}\rightarrow \,\text{Spec}\,A$ be a resolution of singularities of ![]() $\,\text{Spec}\,A$. Decompose
$\,\text{Spec}\,A$. Decompose ![]() $\widetilde{{\it\varphi}}$ as
$\widetilde{{\it\varphi}}$ as 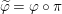 $\widetilde{{\it\varphi}}={\it\varphi}\circ {\it\pi}$, where
$\widetilde{{\it\varphi}}={\it\varphi}\circ {\it\pi}$, where 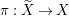 ${\it\pi}:\widetilde{X}\rightarrow X$. Let
${\it\pi}:\widetilde{X}\rightarrow X$. Let ![]() ${\it\pi}^{\ast }Z_{0}$ denote the pull-back of the fundamental cycle
${\it\pi}^{\ast }Z_{0}$ denote the pull-back of the fundamental cycle ![]() $Z_{0}$ on the minimal resoluition to
$Z_{0}$ on the minimal resoluition to ![]() $\widetilde{X}$. Then for any anti-nef cycle
$\widetilde{X}$. Then for any anti-nef cycle ![]() $Z$ on
$Z$ on ![]() $\widetilde{X}$, we put
$\widetilde{X}$, we put
 $$\begin{eqnarray}U(Z)=({\it\varphi}^{\ast }Z_{0}\cdot Z)(p_{a}(Z)-1)+Z^{2},\end{eqnarray}$$
$$\begin{eqnarray}U(Z)=({\it\varphi}^{\ast }Z_{0}\cdot Z)(p_{a}(Z)-1)+Z^{2},\end{eqnarray}$$ where ![]() $p_{a}(Z)$ denotes the virtual genus of
$p_{a}(Z)$ denotes the virtual genus of ![]() $Z$ (see the remark below).
$Z$ (see the remark below).
Theorem 6.2. Let ![]() $(A,\mathfrak{m})$ be a two-dimensional rational singularity. Let
$(A,\mathfrak{m})$ be a two-dimensional rational singularity. Let ![]() $I$ be an
$I$ be an ![]() $\mathfrak{m}$-primary ideal with
$\mathfrak{m}$-primary ideal with 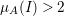 ${\it\mu}_{A}(I)>2$. Then the following conditions are equivalent:
${\it\mu}_{A}(I)>2$. Then the following conditions are equivalent:
(1)
 $I$ is an Ulrich ideal;
$I$ is an Ulrich ideal;(2)
 $\text{e}_{I}^{0}(A)=({\it\mu}(I)-1)\cdot \ell _{A}(A/I)$;
$\text{e}_{I}^{0}(A)=({\it\mu}(I)-1)\cdot \ell _{A}(A/I)$;(3)
 $I$ is an integrally closed ideal represented on the minimal resolution of singularities
$I$ is an integrally closed ideal represented on the minimal resolution of singularities  ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ such that
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ such that  $I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$,
$I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$,  $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$ and
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$ and  $U(Z)=0$.
$U(Z)=0$.
Proof. 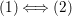 $(1)\Longleftrightarrow (2)$ follows from [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Lemma 2.3].
$(1)\Longleftrightarrow (2)$ follows from [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Lemma 2.3].
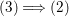 $(3)\Longrightarrow (2)$: Any integrally closed ideal
$(3)\Longrightarrow (2)$: Any integrally closed ideal ![]() $I$ in a two-dimensional rational singularity is stable. Moreover,
$I$ in a two-dimensional rational singularity is stable. Moreover, 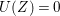 $U(Z)=0$ means that
$U(Z)=0$ means that 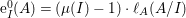 $\text{e}_{I}^{0}(A)=({\it\mu}(I)-1)\cdot \ell _{A}(A/I)$. Thus, the assertion immediately follows from this.
$\text{e}_{I}^{0}(A)=({\it\mu}(I)-1)\cdot \ell _{A}(A/I)$. Thus, the assertion immediately follows from this.
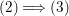 $(2)\Longrightarrow (3)$: Since
$(2)\Longrightarrow (3)$: Since ![]() $I$ is an Ulrich ideal by (1), we have that
$I$ is an Ulrich ideal by (1), we have that 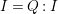 $I=Q:I$ for any minimal reduction
$I=Q:I$ for any minimal reduction ![]() $Q$ of
$Q$ of ![]() $I$ by [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Corollary 2.6]. Then as
$I$ by [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Corollary 2.6]. Then as 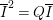 $\overline{I}^{2}=Q\overline{I}$, we get
$\overline{I}^{2}=Q\overline{I}$, we get 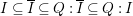 $I\subseteq \overline{I}\subseteq Q:\overline{I}\subseteq Q:I$. Hence,
$I\subseteq \overline{I}\subseteq Q:\overline{I}\subseteq Q:I$. Hence, ![]() $I=\overline{I}$ is integrally closed.
$I=\overline{I}$ is integrally closed.
Let 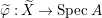 $\widetilde{{\it\varphi}}:\widetilde{X}\rightarrow \,\text{Spec}\,A$ be a resolution of singularities so that
$\widetilde{{\it\varphi}}:\widetilde{X}\rightarrow \,\text{Spec}\,A$ be a resolution of singularities so that 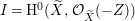 $I=\text{H}^{0}(\widetilde{X},{\mathcal{O}}_{\widetilde{X}}(-Z))$ and
$I=\text{H}^{0}(\widetilde{X},{\mathcal{O}}_{\widetilde{X}}(-Z))$ and 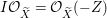 $I{\mathcal{O}}_{\widetilde{X}}={\mathcal{O}}_{\widetilde{X}}(-Z)$ is invertible for some anti-nef cycle
$I{\mathcal{O}}_{\widetilde{X}}={\mathcal{O}}_{\widetilde{X}}(-Z)$ is invertible for some anti-nef cycle ![]() $Z$ on
$Z$ on ![]() $\widetilde{X}$. Then (2) implies that
$\widetilde{X}$. Then (2) implies that 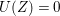 $U(Z)=0$.
$U(Z)=0$.
Now suppose that ![]() $I$ is not represented on the minimal resolution of singularities
$I$ is not represented on the minimal resolution of singularities  ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$. Then there exists a contraction
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$. Then there exists a contraction 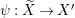 ${\it\psi}:\widetilde{X}\rightarrow X^{\prime }$ of a
${\it\psi}:\widetilde{X}\rightarrow X^{\prime }$ of a ![]() $(-1)$-curve
$(-1)$-curve ![]() $E$ on
$E$ on ![]() $\widetilde{X}$ such that
$\widetilde{X}$ such that ![]() $I$ is not represented on
$I$ is not represented on ![]() $X^{\prime }$. Consider the following commutative diagram:
$X^{\prime }$. Consider the following commutative diagram:

Then we may assume that 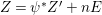 $Z={\it\psi}^{\ast }Z^{\prime }+nE$ for some anti-nef cycle
$Z={\it\psi}^{\ast }Z^{\prime }+nE$ for some anti-nef cycle ![]() $Z^{\prime }$ on
$Z^{\prime }$ on ![]() $X^{\prime }$ and an integer
$X^{\prime }$ and an integer ![]() $n\geqslant 1$. Note that
$n\geqslant 1$. Note that 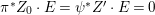 ${\it\pi}^{\ast }Z_{0}\cdot E={\it\psi}^{\ast }Z^{\prime }\cdot E=0$ (see, e.g., [Reference Goto, Iai and WatanabeGIW, Fact 7.7]). Then
${\it\pi}^{\ast }Z_{0}\cdot E={\it\psi}^{\ast }Z^{\prime }\cdot E=0$ (see, e.g., [Reference Goto, Iai and WatanabeGIW, Fact 7.7]). Then
 $$\begin{eqnarray}\displaystyle U(Z)-U(Z^{\prime }) & = & \displaystyle \left({\it\pi}^{\ast }Z_{0}\cdot ({\it\psi}^{\ast }Z^{\prime }+nE)\right)(p_{a}({\it\psi}^{\ast }Z^{\prime })+p_{a}(nE)+{\it\psi}^{\ast }Z^{\prime }\cdot nE-2)\nonumber\\ \displaystyle & & \displaystyle +\,({\it\psi}^{\ast }Z^{\prime }+nE)^{2}-({\it\pi}^{\ast }Z_{0}\cdot {\it\psi}^{\ast }Z^{\prime })\left(p_{a}({\it\psi}^{\ast }Z^{\prime })-1\right)-({\it\psi}^{\ast }Z^{\prime })^{2}\nonumber\\ \displaystyle & = & \displaystyle ({\it\pi}^{\ast }Z_{0}\cdot {\it\psi}^{\ast }Z^{\prime })(p_{a}(nE)-1)+(nE)^{2}\nonumber\\ \displaystyle & = & \displaystyle \left(({\it\pi}^{\prime })^{\ast }Z_{0}\cdot Z^{\prime }+2\right)\frac{(nE)^{2}}{2}+\frac{n(K_{X}\cdot E)}{2}\left(({\it\pi}^{\prime })^{\ast }Z_{0}\cdot Z^{\prime }\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U(Z)-U(Z^{\prime }) & = & \displaystyle \left({\it\pi}^{\ast }Z_{0}\cdot ({\it\psi}^{\ast }Z^{\prime }+nE)\right)(p_{a}({\it\psi}^{\ast }Z^{\prime })+p_{a}(nE)+{\it\psi}^{\ast }Z^{\prime }\cdot nE-2)\nonumber\\ \displaystyle & & \displaystyle +\,({\it\psi}^{\ast }Z^{\prime }+nE)^{2}-({\it\pi}^{\ast }Z_{0}\cdot {\it\psi}^{\ast }Z^{\prime })\left(p_{a}({\it\psi}^{\ast }Z^{\prime })-1\right)-({\it\psi}^{\ast }Z^{\prime })^{2}\nonumber\\ \displaystyle & = & \displaystyle ({\it\pi}^{\ast }Z_{0}\cdot {\it\psi}^{\ast }Z^{\prime })(p_{a}(nE)-1)+(nE)^{2}\nonumber\\ \displaystyle & = & \displaystyle \left(({\it\pi}^{\prime })^{\ast }Z_{0}\cdot Z^{\prime }+2\right)\frac{(nE)^{2}}{2}+\frac{n(K_{X}\cdot E)}{2}\left(({\it\pi}^{\prime })^{\ast }Z_{0}\cdot Z^{\prime }\right).\nonumber\end{eqnarray}$$ Since 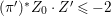 $({\it\pi}^{\prime })^{\ast }Z_{0}\cdot Z^{\prime }\leqslant -2$ and
$({\it\pi}^{\prime })^{\ast }Z_{0}\cdot Z^{\prime }\leqslant -2$ and 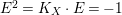 $E^{2}=K_{X}\cdot E=-1$, we get
$E^{2}=K_{X}\cdot E=-1$, we get 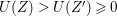 $U(Z)>U(Z^{\prime })\geqslant 0$. This is a contradiction.◻
$U(Z)>U(Z^{\prime })\geqslant 0$. This is a contradiction.◻
In what follows, we always assume that 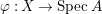 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ is the minimal resolution of singularities,
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ is the minimal resolution of singularities, 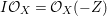 $I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ is invertible and
$I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ is invertible and 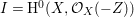 $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$ for some anti-nef cycle
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$ for some anti-nef cycle ![]() $Z$ on
$Z$ on ![]() $X$. Let
$X$. Let 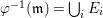 ${\it\varphi}^{-1}(\mathfrak{m})=\bigcup _{i}E_{i}$ denote the exceptional divisor on
${\it\varphi}^{-1}(\mathfrak{m})=\bigcup _{i}E_{i}$ denote the exceptional divisor on ![]() $X$ with the irreducible components
$X$ with the irreducible components 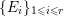 $\{E_{i}\}_{1\leqslant i\leqslant r}$. Let
$\{E_{i}\}_{1\leqslant i\leqslant r}$. Let ![]() $Z_{0}$ (resp.
$Z_{0}$ (resp. ![]() $K$) denote the fundamental cycle (resp. the canonical divisor) on
$K$) denote the fundamental cycle (resp. the canonical divisor) on ![]() $X$. Notice that
$X$. Notice that 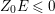 $Z_{0}E\leqslant 0$ and
$Z_{0}E\leqslant 0$ and 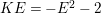 $KE=-E^{2}-2$ for all exceptional curves
$KE=-E^{2}-2$ for all exceptional curves ![]() $E$.
$E$.
The next target is to characterize Ulrich cycles in terms of dual graphs. In order to do that, we recall the sequence of anti-nef cycles introduced in Lemma 4.9. Assume that ![]() $Z\neq Z_{0}$ is an anti-nef cycle on
$Z\neq Z_{0}$ is an anti-nef cycle on ![]() $X$. Then we can find the following anti-nef cycles
$X$. Then we can find the following anti-nef cycles 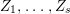 $Z_{1},\ldots ,Z_{s}$ and positive cycles
$Z_{1},\ldots ,Z_{s}$ and positive cycles 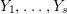 $Y_{1},\ldots ,Y_{s}$, so that
$Y_{1},\ldots ,Y_{s}$, so that 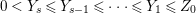 $0<Y_{s}\leqslant Y_{s-1}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$:
$0<Y_{s}\leqslant Y_{s-1}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$:
 $$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{2} & = & Z_{1}+Y_{2},\\ Z_{1} & = & Z_{0}+Y_{1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{2} & = & Z_{1}+Y_{2},\\ Z_{1} & = & Z_{0}+Y_{1}.\end{array}\right.\end{eqnarray}$$The following lemma plays a key role in the proof of the main theorem in this section.
Lemma 6.3. Let ![]() $Z$,
$Z$, ![]() $Z^{\prime }$ be anti-nef cycles on
$Z^{\prime }$ be anti-nef cycles on ![]() $X$ with
$X$ with 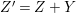 $Z^{\prime }=Z+Y$, where
$Z^{\prime }=Z+Y$, where ![]() $Y$ is a positive cycle. Then we have the following.
$Y$ is a positive cycle. Then we have the following.
(1)
 $U(Z^{\prime })-U(Z)=(YZ_{0})\big\{(p_{a}(Z)-1)+(p_{a}(Y)-1)\big\}+(YZ)(Z^{\prime }Z_{0}+2)$
$U(Z^{\prime })-U(Z)=(YZ_{0})\big\{(p_{a}(Z)-1)+(p_{a}(Y)-1)\big\}+(YZ)(Z^{\prime }Z_{0}+2)$ $+(p_{a}(Y)-1)(ZZ_{0}+2)-KY$.
$+(p_{a}(Y)-1)(ZZ_{0}+2)-KY$.(2) Assume that
 $0\neq Y\leqslant Z_{0}$ and
$0\neq Y\leqslant Z_{0}$ and  $e=\text{e}_{\mathfrak{m}}^{0}(A)\geqslant 3$. Then
$e=\text{e}_{\mathfrak{m}}^{0}(A)\geqslant 3$. Then  $U(Z^{\prime })\geqslant U(Z)$ holds true, and equality holds if and only if
$U(Z^{\prime })\geqslant U(Z)$ holds true, and equality holds if and only if  $YZ=YZ_{0}=p_{a}(Y)=(Z-Z_{0})Z_{0}=K(Z_{0}-Y)=0$.
$YZ=YZ_{0}=p_{a}(Y)=(Z-Z_{0})Z_{0}=K(Z_{0}-Y)=0$.
Proof. (1) Since 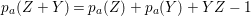 $p_{a}(Z+Y)=p_{a}(Z)+p_{a}(Y)+YZ-1$ by definition, we have
$p_{a}(Z+Y)=p_{a}(Z)+p_{a}(Y)+YZ-1$ by definition, we have
 $$\begin{eqnarray}\displaystyle U(Z^{\prime })-U(Z) & = & \displaystyle (ZZ_{0}+YZ_{0})(p_{a}(Z)-1+p_{a}(Y)-1+YZ)\nonumber\\ \displaystyle & & \displaystyle +\,(Z^{2}+2YZ+Y^{2})-(ZZ_{0})(p_{a}(Z)-1)-Z^{2}\nonumber\\ \displaystyle & = & \displaystyle (YZ_{0})\big\{(p_{a}(Z)-1)+(p_{a}(Y)-1)\big\}\nonumber\\ \displaystyle & & \displaystyle +\,(YZ)(ZZ_{0}+YZ_{0}+2)+(p_{a}(Y)-1)(ZZ_{0})+Y^{2}\nonumber\\ \displaystyle & = & \displaystyle (YZ_{0})\big\{(p_{a}(Z)-1)+(p_{a}(Y)-1)\big\}+(YZ)(Z^{\prime }Z_{0}+2)\nonumber\\ \displaystyle & & \displaystyle +\,(p_{a}(Y)-1)(ZZ_{0}+2)-KY,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U(Z^{\prime })-U(Z) & = & \displaystyle (ZZ_{0}+YZ_{0})(p_{a}(Z)-1+p_{a}(Y)-1+YZ)\nonumber\\ \displaystyle & & \displaystyle +\,(Z^{2}+2YZ+Y^{2})-(ZZ_{0})(p_{a}(Z)-1)-Z^{2}\nonumber\\ \displaystyle & = & \displaystyle (YZ_{0})\big\{(p_{a}(Z)-1)+(p_{a}(Y)-1)\big\}\nonumber\\ \displaystyle & & \displaystyle +\,(YZ)(ZZ_{0}+YZ_{0}+2)+(p_{a}(Y)-1)(ZZ_{0})+Y^{2}\nonumber\\ \displaystyle & = & \displaystyle (YZ_{0})\big\{(p_{a}(Z)-1)+(p_{a}(Y)-1)\big\}+(YZ)(Z^{\prime }Z_{0}+2)\nonumber\\ \displaystyle & & \displaystyle +\,(p_{a}(Y)-1)(ZZ_{0}+2)-KY,\nonumber\end{eqnarray}$$ where the last equality follows from 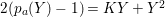 $2(p_{a}(Y)-1)=KY+Y^{2}$.
$2(p_{a}(Y)-1)=KY+Y^{2}$.
(2) Assume that ![]() $Y\leqslant Z_{0}$. As
$Y\leqslant Z_{0}$. As  $X\rightarrow \,\text{Spec}\,A$ is the minimal resolution, we have that
$X\rightarrow \,\text{Spec}\,A$ is the minimal resolution, we have that 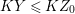 $KY\leqslant KZ_{0}$ because
$KY\leqslant KZ_{0}$ because 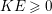 $KE\geqslant 0$ for all curves
$KE\geqslant 0$ for all curves ![]() $E$ on
$E$ on ![]() $X$. Since
$X$. Since ![]() $Z_{0}$ is anti-nef and
$Z_{0}$ is anti-nef and ![]() $Z-Z_{0}$,
$Z-Z_{0}$, ![]() $Y$ are positive, we get
$Y$ are positive, we get
 $$\begin{eqnarray}Z^{\prime }Z_{0}+2=(Z-Z_{0})Z_{0}+YZ_{0}+(Z_{0}^{2}+2)\leqslant Z_{0}^{2}+2=-e+2<0.\end{eqnarray}$$
$$\begin{eqnarray}Z^{\prime }Z_{0}+2=(Z-Z_{0})Z_{0}+YZ_{0}+(Z_{0}^{2}+2)\leqslant Z_{0}^{2}+2=-e+2<0.\end{eqnarray}$$ Moreover, 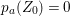 $p_{a}(Z_{0})=0$ implies that
$p_{a}(Z_{0})=0$ implies that
 $$\begin{eqnarray}\displaystyle & & \displaystyle (p_{a}(Y)-1)(ZZ_{0}+2)-KY\nonumber\\ \displaystyle & & \displaystyle \quad =p_{a}(Y)(ZZ_{0}+2)-(Z-Z_{0})Z_{0}-K(Y-Z_{0})\geqslant 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (p_{a}(Y)-1)(ZZ_{0}+2)-KY\nonumber\\ \displaystyle & & \displaystyle \quad =p_{a}(Y)(ZZ_{0}+2)-(Z-Z_{0})Z_{0}-K(Y-Z_{0})\geqslant 0,\nonumber\end{eqnarray}$$ and equality holds if and only if 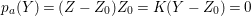 $p_{a}(Y)=(Z-Z_{0})Z_{0}=K(Y-Z_{0})=0$.
$p_{a}(Y)=(Z-Z_{0})Z_{0}=K(Y-Z_{0})=0$.
Note that ![]() $YZ_{0}$,
$YZ_{0}$, 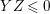 $YZ\leqslant 0$ and
$YZ\leqslant 0$ and 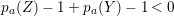 $p_{a}(Z)-1+p_{a}(Y)-1<0$. Hence,
$p_{a}(Z)-1+p_{a}(Y)-1<0$. Hence, 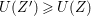 $U(Z^{\prime })\geqslant U(Z)$, and equality holds if and only if
$U(Z^{\prime })\geqslant U(Z)$, and equality holds if and only if 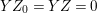 $YZ_{0}=YZ=0$ and
$YZ_{0}=YZ=0$ and 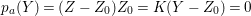 $p_{a}(Y)=(Z-Z_{0})Z_{0}=K(Y-Z_{0})=0$.◻
$p_{a}(Y)=(Z-Z_{0})Z_{0}=K(Y-Z_{0})=0$.◻
The main result in this section is the following theorem, which enables us to determine all Ulrich ideals of a two-dimensional (non-Gorenstein) rational singularity. For a positive cycle ![]() $Z$ on
$Z$ on ![]() $X$, we write
$X$, we write 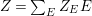 $Z=\sum _{E}Z_{E}E$, where
$Z=\sum _{E}Z_{E}E$, where ![]() $Z_{E}$ is a nonnegative integer.
$Z_{E}$ is a nonnegative integer.
Theorem 6.4. Let ![]() $(A,\mathfrak{m})$ be a two-dimensional rational singularity with
$(A,\mathfrak{m})$ be a two-dimensional rational singularity with 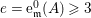 $e=\text{e}_{\mathfrak{m}}^{0}(A)\geqslant 3$, and let
$e=\text{e}_{\mathfrak{m}}^{0}(A)\geqslant 3$, and let 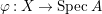 ${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities. Set
${\it\varphi}:X\rightarrow \,\text{Spec}\,A$ be the minimal resolution of singularities. Set 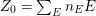 $Z_{0}=\sum _{E}n_{E}E$, the fundamental cycle on
$Z_{0}=\sum _{E}n_{E}E$, the fundamental cycle on ![]() $X$. Let
$X$. Let ![]() $Z$ be an anti-nef cycle on
$Z$ be an anti-nef cycle on ![]() $X$ with
$X$ with 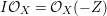 $I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ and
$I{\mathcal{O}}_{X}={\mathcal{O}}_{X}(-Z)$ and 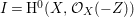 $I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then the following conditions are equivalent:
$I=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z))$. Then the following conditions are equivalent:
(1)
 $I$ is an Ulrich ideal, that is,
$I$ is an Ulrich ideal, that is,  $Z$ is an Ulrich cycle on
$Z$ is an Ulrich cycle on  $X$;
$X$;(2) there exist a sequence of anti-nef cycles
 $Z_{1},\ldots ,Z_{s}$ and a sequence of positive cycles
$Z_{1},\ldots ,Z_{s}$ and a sequence of positive cycles  $0<Y_{s}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$ for some
$0<Y_{s}\leqslant \cdots \leqslant Y_{1}\leqslant Z_{0}$ for some  $s\geqslant 1$ so that (6.4.3)and
$s\geqslant 1$ so that (6.4.3)and $$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{1} & = & Z_{0}+Y_{1},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{1} & = & Z_{0}+Y_{1},\end{array}\right.\end{eqnarray}$$ $Y_{k}Z_{k-1}=p_{a}(Y_{k})=K(Z_{0}-Y_{k})=0$ for every
$Y_{k}Z_{k-1}=p_{a}(Y_{k})=K(Z_{0}-Y_{k})=0$ for every  $k=1,\ldots ,s$.
$k=1,\ldots ,s$.
When this is the case, the following conditions are satisfied.
(a)
 $\{E\mid E^{2}\leqslant -3\}$ is contained in
$\{E\mid E^{2}\leqslant -3\}$ is contained in  $\text{Supp}(Y_{1})$.
$\text{Supp}(Y_{1})$.(b)
 $\text{Supp}(Y_{k})$ is given as one of the connected components of
$\text{Supp}(Y_{k})$ is given as one of the connected components of  $\{E\mid EZ_{k-1}=0\}$ in
$\{E\mid EZ_{k-1}=0\}$ in  $\{E\mid EZ_{0}=0\}$.
$\{E\mid EZ_{0}=0\}$.(c)
 $Y_{k}$ is the fundamental cycle on
$Y_{k}$ is the fundamental cycle on  $\text{Supp}(Y_{k})$.
$\text{Supp}(Y_{k})$.(d)
 $\text{coeff}_{E}Z_{0}=\text{coeff}_{E}Y_{k}$ for every
$\text{coeff}_{E}Z_{0}=\text{coeff}_{E}Y_{k}$ for every  $E$ with
$E$ with  $E^{2}\leqslant -3$.
$E^{2}\leqslant -3$.
If, in addition, we put 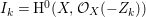 $I_{k}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{k}))$, then
$I_{k}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{k}))$, then ![]() $I_{k}$ is an Ulrich ideal, so that
$I_{k}$ is an Ulrich ideal, so that
 $$\begin{eqnarray}\mathfrak{m}=I_{0}\supseteq I_{1}\supseteq \cdots \supseteq I_{s}=I\quad \text{and}\quad \ell _{A}(A/I)=s+1.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}=I_{0}\supseteq I_{1}\supseteq \cdots \supseteq I_{s}=I\quad \text{and}\quad \ell _{A}(A/I)=s+1.\end{eqnarray}$$Proof. Take a sequence as in (2).
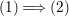 $(1)\Longrightarrow (2)$: Lemma 6.3 implies that
$(1)\Longrightarrow (2)$: Lemma 6.3 implies that
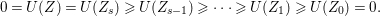 $$\begin{eqnarray}0=U(Z)=U(Z_{s})\geqslant U(Z_{s-1})\geqslant \cdots \geqslant U(Z_{1})\geqslant U(Z_{0})=0.\end{eqnarray}$$
$$\begin{eqnarray}0=U(Z)=U(Z_{s})\geqslant U(Z_{s-1})\geqslant \cdots \geqslant U(Z_{1})\geqslant U(Z_{0})=0.\end{eqnarray}$$ Hence, all ![]() $Z_{k}$ are Ulrich cycles and
$Z_{k}$ are Ulrich cycles and
 $$\begin{eqnarray}Y_{k}Z_{k-1}=Y_{k}Z_{0}=p_{a}(Y_{k})=(Z_{k}-Z_{0})Z_{0}=K(Z_{0}-Y_{k})=0\end{eqnarray}$$
$$\begin{eqnarray}Y_{k}Z_{k-1}=Y_{k}Z_{0}=p_{a}(Y_{k})=(Z_{k}-Z_{0})Z_{0}=K(Z_{0}-Y_{k})=0\end{eqnarray}$$ for every 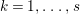 $k=1,\ldots ,s$. By a similar argument to that in the proof of Theorem 4.10, we have
$k=1,\ldots ,s$. By a similar argument to that in the proof of Theorem 4.10, we have 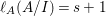 $\ell _{A}(A/I)=s+1$.
$\ell _{A}(A/I)=s+1$.
If 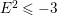 $E^{2}\leqslant -3$, then
$E^{2}\leqslant -3$, then 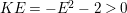 $KE=-E^{2}-2>0$. Thus,
$KE=-E^{2}-2>0$. Thus, 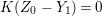 $K(Z_{0}-Y_{1})=0$ implies that
$K(Z_{0}-Y_{1})=0$ implies that 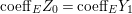 $\text{coeff}_{E}Z_{0}=\text{coeff}_{E}Y_{1}$ for every
$\text{coeff}_{E}Z_{0}=\text{coeff}_{E}Y_{1}$ for every ![]() $E$ with
$E$ with 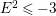 $E^{2}\leqslant -3$. In particular,
$E^{2}\leqslant -3$. In particular, 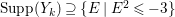 $\text{Supp}(Y_{k})\supseteq \{E\mid E^{2}\leqslant -3\}$. On the other hand,
$\text{Supp}(Y_{k})\supseteq \{E\mid E^{2}\leqslant -3\}$. On the other hand, 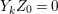 $Y_{k}Z_{0}=0$ implies that
$Y_{k}Z_{0}=0$ implies that 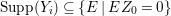 $\text{Supp}(Y_{i})\subseteq \{E\mid EZ_{0}=0\}$ because
$\text{Supp}(Y_{i})\subseteq \{E\mid EZ_{0}=0\}$ because ![]() $Z_{0}$ is an anti-nef cycle.
$Z_{0}$ is an anti-nef cycle.
Now suppose (2). Fix ![]() $i$ with
$i$ with 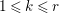 $1\leqslant k\leqslant r$. Since
$1\leqslant k\leqslant r$. Since ![]() $Z_{k-1}$ is anti-nef and
$Z_{k-1}$ is anti-nef and 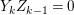 $Y_{k}Z_{k-1}=0$, a similar argument to the above yields that
$Y_{k}Z_{k-1}=0$, a similar argument to the above yields that 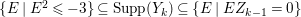 $\{E\mid E^{2}\leqslant -3\}\subseteq \text{Supp}(Y_{k})\subseteq \{E\mid EZ_{k-1}=0\}$.
$\{E\mid E^{2}\leqslant -3\}\subseteq \text{Supp}(Y_{k})\subseteq \{E\mid EZ_{k-1}=0\}$.
As 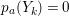 $p_{a}(Y_{k})=0$,
$p_{a}(Y_{k})=0$, 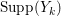 $\text{Supp}(Y_{k})$ is connected. Moreover,
$\text{Supp}(Y_{k})$ is connected. Moreover, 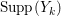 $\text{Supp}(Y_{k})$ is one of the connected components of
$\text{Supp}(Y_{k})$ is one of the connected components of 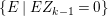 $\{E\mid EZ_{k-1}=0\}$. Indeed, if there exists a curve
$\{E\mid EZ_{k-1}=0\}$. Indeed, if there exists a curve 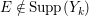 $E\notin \text{Supp}(Y_{k})$ such that
$E\notin \text{Supp}(Y_{k})$ such that 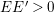 $EE^{\prime }>0$ for some
$EE^{\prime }>0$ for some 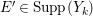 $E^{\prime }\in \text{Supp}(Y_{k})$, then
$E^{\prime }\in \text{Supp}(Y_{k})$, then 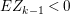 $EZ_{k-1}<0$ since
$EZ_{k-1}<0$ since 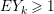 $EY_{k}\geqslant 1$ and
$EY_{k}\geqslant 1$ and 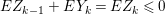 $EZ_{k-1}+EY_{k}=EZ_{k}\leqslant 0$.
$EZ_{k-1}+EY_{k}=EZ_{k}\leqslant 0$.
- Claim.
 $Y_{k}$ is the fundamental cycle on
$Y_{k}$ is the fundamental cycle on  $\text{Supp}(Y_{k})$.
$\text{Supp}(Y_{k})$.
Take 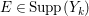 $E\in \text{Supp}(Y_{k})$. As
$E\in \text{Supp}(Y_{k})$. As 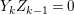 $Y_{k}Z_{k-1}=0$, we have
$Y_{k}Z_{k-1}=0$, we have 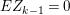 $EZ_{k-1}=0$. If
$EZ_{k-1}=0$. If 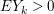 $EY_{k}>0$, then
$EY_{k}>0$, then 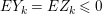 $EY_{k}=EZ_{k}\leqslant 0$. This is a contradiction. Hence,
$EY_{k}=EZ_{k}\leqslant 0$. This is a contradiction. Hence, 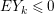 $EY_{k}\leqslant 0$. Namely,
$EY_{k}\leqslant 0$. Namely, ![]() $Y_{k}$ is anti-nef. Moreover, if
$Y_{k}$ is anti-nef. Moreover, if ![]() $Y_{k}$ is not the fundamental cycle on
$Y_{k}$ is not the fundamental cycle on 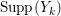 $\text{Supp}(Y_{k})$, then we know that
$\text{Supp}(Y_{k})$, then we know that 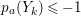 $p_{a}(Y_{k})\leqslant -1$. This contradicts the assumption
$p_{a}(Y_{k})\leqslant -1$. This contradicts the assumption 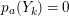 $p_{a}(Y_{k})=0$. Hence,
$p_{a}(Y_{k})=0$. Hence, ![]() $Y_{k}$ must be the fundamental cycle on
$Y_{k}$ must be the fundamental cycle on 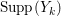 $\text{Supp}(Y_{k})$.
$\text{Supp}(Y_{k})$.
To see  $(2)\Longrightarrow (1)$, we notice that (c) implies that
$(2)\Longrightarrow (1)$, we notice that (c) implies that 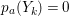 $p_{a}(Y_{k})=0$. Condition (b) means that
$p_{a}(Y_{k})=0$. Condition (b) means that 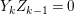 $Y_{k}Z_{k-1}=0$. Hence,
$Y_{k}Z_{k-1}=0$. Hence, 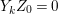 $Y_{k}Z_{0}=0$. Note that the equalities
$Y_{k}Z_{0}=0$. Note that the equalities 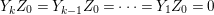 $Y_{k}Z_{0}=Y_{k-1}Z_{0}=\cdots =Y_{1}Z_{0}=0$ yield
$Y_{k}Z_{0}=Y_{k-1}Z_{0}=\cdots =Y_{1}Z_{0}=0$ yield 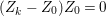 $(Z_{k}-Z_{0})Z_{0}=0$. Condition (d) implies that
$(Z_{k}-Z_{0})Z_{0}=0$. Condition (d) implies that  $K(Z_{0}-Y_{k})=0$. Therefore,
$K(Z_{0}-Y_{k})=0$. Therefore, 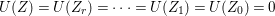 $U(Z)=U(Z_{r})=\cdots =U(Z_{1})=U(Z_{0})=0$, as required.◻
$U(Z)=U(Z_{r})=\cdots =U(Z_{1})=U(Z_{0})=0$, as required.◻
The following assertion does not hold true without the assumption that ![]() $A$ is rational (see [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Example 2.2]).
$A$ is rational (see [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Example 2.2]).
Corollary 6.5. Let ![]() $A$ be a two-dimensional rational singularity. If
$A$ be a two-dimensional rational singularity. If ![]() $I$ is an Ulrich ideal of
$I$ is an Ulrich ideal of ![]() $A$, then
$A$, then ![]() $I$ is a special ideal and
$I$ is a special ideal and ![]() $A/I$ is Gorenstein.
$A/I$ is Gorenstein.
Proof. Denote by ![]() $\mathfrak{m}$ the maximal ideal of
$\mathfrak{m}$ the maximal ideal of ![]() $R$. We may assume that
$R$. We may assume that ![]() $A$ is not Gorenstein, that is,
$A$ is not Gorenstein, that is, 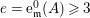 $e=\text{e}_{\mathfrak{m}}^{0}(A)\geqslant 3$. Then by Theorem 6.4, we can find a sequence of Ulrich cycles
$e=\text{e}_{\mathfrak{m}}^{0}(A)\geqslant 3$. Then by Theorem 6.4, we can find a sequence of Ulrich cycles 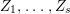 $Z_{1},\ldots ,Z_{s}$ and positive cycles
$Z_{1},\ldots ,Z_{s}$ and positive cycles 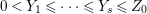 $0<Y_{1}\leqslant \cdots \leqslant Y_{s}\leqslant Z_{0}$ satisfying all conditions in Theorem 6.4, so that
$0<Y_{1}\leqslant \cdots \leqslant Y_{s}\leqslant Z_{0}$ satisfying all conditions in Theorem 6.4, so that
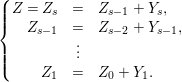 $$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{1} & = & Z_{0}+Y_{1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}rcl@{}}Z=Z_{s} & = & Z_{s-1}+Y_{s},\\ Z_{s-1} & = & Z_{s-2}+Y_{s-1},\\ & \vdots & \\ Z_{1} & = & Z_{0}+Y_{1}.\end{array}\right.\end{eqnarray}$$ Then 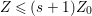 $Z\leqslant (s+1)Z_{0}$ and
$Z\leqslant (s+1)Z_{0}$ and 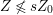 $Z\not \leqslant sZ_{0}$. In particular,
$Z\not \leqslant sZ_{0}$. In particular, ![]() $\mathfrak{m}^{s}\not \subseteq I$ and
$\mathfrak{m}^{s}\not \subseteq I$ and 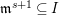 $\mathfrak{m}^{s+1}\subseteq I$. Moreover,
$\mathfrak{m}^{s+1}\subseteq I$. Moreover, ![]() $I$ is a special ideal by Theorem 4.10. We have only to show the following claim.
$I$ is a special ideal by Theorem 4.10. We have only to show the following claim.
- Claim.
There exists a minimal set of generators
 $\{u_{1},\ldots ,u_{p},t\}$ such that
$\{u_{1},\ldots ,u_{p},t\}$ such that  $I=(u_{1},\ldots ,u_{p},t^{s+1})$.
$I=(u_{1},\ldots ,u_{p},t^{s+1})$.
Set 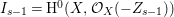 $I_{s-1}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{s-1}))$. Then
$I_{s-1}=\text{H}^{0}(X,{\mathcal{O}}_{X}(-Z_{s-1}))$. Then ![]() $I_{s-1}$ is also an Ulrich ideal. Therefore, we may assume that we can write
$I_{s-1}$ is also an Ulrich ideal. Therefore, we may assume that we can write 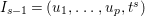 $I_{s-1}=(u_{1},\ldots ,u_{p},t^{s})$ for some minimal set of generators of
$I_{s-1}=(u_{1},\ldots ,u_{p},t^{s})$ for some minimal set of generators of ![]() $\mathfrak{m}$. Since
$\mathfrak{m}$. Since 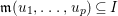 $\mathfrak{m}(u_{1},\ldots ,u_{p})\subseteq I$ and
$\mathfrak{m}(u_{1},\ldots ,u_{p})\subseteq I$ and ![]() $\mathfrak{m}^{s}\not \subseteq I$, we have that
$\mathfrak{m}^{s}\not \subseteq I$, we have that ![]() $t^{s}\notin I$. Hence, by
$t^{s}\notin I$. Hence, by 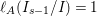 $\ell _{A}(I_{s-1}/I)=1$, we can choose an element
$\ell _{A}(I_{s-1}/I)=1$, we can choose an element ![]() $a_{i}\in A$ such that
$a_{i}\in A$ such that 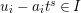 $u_{i}-a_{i}t^{s}\in I$ for every
$u_{i}-a_{i}t^{s}\in I$ for every ![]() $i$. By replacing
$i$. By replacing ![]() $u_{i}$ with
$u_{i}$ with 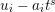 $u_{i}-a_{i}t^{s}$, we may assume that
$u_{i}-a_{i}t^{s}$, we may assume that 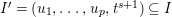 $I^{\prime }=(u_{1},\ldots ,u_{p},t^{s+1})\subseteq I$. As
$I^{\prime }=(u_{1},\ldots ,u_{p},t^{s+1})\subseteq I$. As 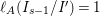 $\ell _{A}(I_{s-1}/I^{\prime })=1$ and
$\ell _{A}(I_{s-1}/I^{\prime })=1$ and  $I\neq I_{s-1}$, we can conclude that
$I\neq I_{s-1}$, we can conclude that ![]() $I=I^{\prime }$, as required.◻
$I=I^{\prime }$, as required.◻
7 Examples
Throughout this section, let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $0$. Let
$0$. Let ![]() ${\mathcal{X}}_{A}$ denote the set of nonparameter Ulrich ideals of
${\mathcal{X}}_{A}$ denote the set of nonparameter Ulrich ideals of ![]() $A$.
$A$.
Example 7.1. Let 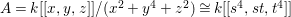 $A=k[[x,y,z]]/(x^{2}+y^{4}+z^{2})\cong k[[s^{4},st,t^{4}]]$ be a two-dimensional rational double point of type
$A=k[[x,y,z]]/(x^{2}+y^{4}+z^{2})\cong k[[s^{4},st,t^{4}]]$ be a two-dimensional rational double point of type ![]() $(A_{4})$. Theorem 5.7 implies that
$(A_{4})$. Theorem 5.7 implies that 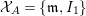 ${\mathcal{X}}_{A}=\{\mathfrak{m},I_{1}\}$, where
${\mathcal{X}}_{A}=\{\mathfrak{m},I_{1}\}$, where 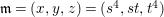 $\mathfrak{m}=(x,y,z)=(s^{4},st,t^{4})$ and
$\mathfrak{m}=(x,y,z)=(s^{4},st,t^{4})$ and 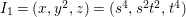 $I_{1}=(x,y^{2},z)=(s^{4},s^{2}t^{2},t^{4})$.
$I_{1}=(x,y^{2},z)=(s^{4},s^{2}t^{2},t^{4})$.
The corresponding anti-nef cycle to ![]() $\mathfrak{m}$ (resp.
$\mathfrak{m}$ (resp. ![]() $I_{1}$) on the minimal resolution is
$I_{1}$) on the minimal resolution is

Moreover, if we put
 $$\begin{eqnarray}M_{0}=A,\quad M_{1}=As+At^{3},\quad M_{2}=As^{2}+At^{2}\quad ~\text{and}\quad ~M_{3}=As^{3}+At,\end{eqnarray}$$
$$\begin{eqnarray}M_{0}=A,\quad M_{1}=As+At^{3},\quad M_{2}=As^{2}+At^{2}\quad ~\text{and}\quad ~M_{3}=As^{3}+At,\end{eqnarray}$$ then they are representatives of indecomposable maximal Cohen–Macaulay ![]() $A$-modules, and thus any maximal Cohen–Macaulay
$A$-modules, and thus any maximal Cohen–Macaulay ![]() $A$-module can be written as
$A$-module can be written as
 $$\begin{eqnarray}A^{\oplus k}\oplus M_{1}^{\oplus k_{1}}\oplus M_{2}^{\oplus k_{2}}\oplus M_{3}^{\oplus k_{3}}.\end{eqnarray}$$
$$\begin{eqnarray}A^{\oplus k}\oplus M_{1}^{\oplus k_{1}}\oplus M_{2}^{\oplus k_{2}}\oplus M_{3}^{\oplus k_{3}}.\end{eqnarray}$$ Note that 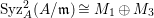 $\text{Syz}_{A}^{2}(A/\mathfrak{m})\cong M_{1}\oplus M_{3}$ and
$\text{Syz}_{A}^{2}(A/\mathfrak{m})\cong M_{1}\oplus M_{3}$ and 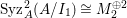 $\text{Syz}_{A}^{2}(A/I_{1})\cong M_{2}^{\oplus 2}$. Moreover, Theorem 5.7 says that any Ulrich
$\text{Syz}_{A}^{2}(A/I_{1})\cong M_{2}^{\oplus 2}$. Moreover, Theorem 5.7 says that any Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $\mathfrak{m}$ (resp.
$\mathfrak{m}$ (resp. ![]() $I_{1}$) can be written as
$I_{1}$) can be written as
 $$\begin{eqnarray}M_{1}^{\oplus k_{1}}\oplus M_{2}^{\oplus k_{2}}\oplus M_{3}^{\oplus k_{3}}\quad \big(\text{resp. }M_{2}^{\oplus k_{2}}\big).\end{eqnarray}$$
$$\begin{eqnarray}M_{1}^{\oplus k_{1}}\oplus M_{2}^{\oplus k_{2}}\oplus M_{3}^{\oplus k_{3}}\quad \big(\text{resp. }M_{2}^{\oplus k_{2}}\big).\end{eqnarray}$$ In general, there exists an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, but not a direct summand of
$I$, but not a direct summand of 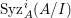 $\text{Syz}_{A}^{i}(A/I)$, which contradicts Example 7.1.
$\text{Syz}_{A}^{i}(A/I)$, which contradicts Example 7.1.
Example 7.2. Let 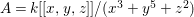 $A=k[[x,y,z]]/(x^{3}+y^{5}+z^{2})$ be a rational double point of type
$A=k[[x,y,z]]/(x^{3}+y^{5}+z^{2})$ be a rational double point of type ![]() $(E_{8})$. By Theorem 5.7 and Corollary 5.8, the set of Ulrich ideals is
$(E_{8})$. By Theorem 5.7 and Corollary 5.8, the set of Ulrich ideals is 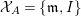 ${\mathcal{X}}_{A}=\{\mathfrak{m},I\}$, where
${\mathcal{X}}_{A}=\{\mathfrak{m},I\}$, where 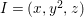 $I=(x,y^{2},z)$ with
$I=(x,y^{2},z)$ with 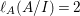 $\ell _{A}(A/I)=2$.
$\ell _{A}(A/I)=2$.

Let ![]() $M_{i}$ denote the indecomposable maximal Cohen–Macaulay
$M_{i}$ denote the indecomposable maximal Cohen–Macaulay ![]() $A$-module corresponding to
$A$-module corresponding to ![]() $E_{i}$ (up to equivalence) via the McKay correspondence for every
$E_{i}$ (up to equivalence) via the McKay correspondence for every 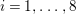 $i=1,\ldots ,8$. Then we have
$i=1,\ldots ,8$. Then we have 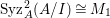 $\text{Syz}_{A}^{2}(A/I)\cong M_{1}$. Indeed, since
$\text{Syz}_{A}^{2}(A/I)\cong M_{1}$. Indeed, since 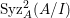 $\text{Syz}_{A}^{2}(A/I)$ is an Ulrich
$\text{Syz}_{A}^{2}(A/I)$ is an Ulrich ![]() $A$-module with respect to
$A$-module with respect to ![]() $I$, it is isomorphic to
$I$, it is isomorphic to ![]() $M_{1}^{\oplus k}$ for some
$M_{1}^{\oplus k}$ for some ![]() $k\geqslant 1$. Then
$k\geqslant 1$. Then ![]() $k=1$ because
$k=1$ because 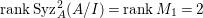 $\,\text{rank}\,\text{Syz}_{A}^{2}(A/I)=\,\text{rank}\,M_{1}=2$.
$\,\text{rank}\,\text{Syz}_{A}^{2}(A/I)=\,\text{rank}\,M_{1}=2$.
Next we see that 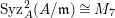 $\text{Syz}_{A}^{2}(A/\mathfrak{m})\cong M_{7}$. Set
$\text{Syz}_{A}^{2}(A/\mathfrak{m})\cong M_{7}$. Set 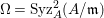 ${\rm\Omega}=\text{Syz}_{A}^{2}(A/\mathfrak{m})$. As
${\rm\Omega}=\text{Syz}_{A}^{2}(A/\mathfrak{m})$. As 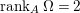 $\,\text{rank}_{A}\,{\rm\Omega}=2$, we have
$\,\text{rank}_{A}\,{\rm\Omega}=2$, we have 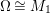 ${\rm\Omega}\cong M_{1}$ or
${\rm\Omega}\cong M_{1}$ or 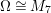 ${\rm\Omega}\cong M_{7}$. It follows from [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Corollary 7.7] that
${\rm\Omega}\cong M_{7}$. It follows from [Reference Goto, Ozeki, Takahashi, Watanabe and YoshidaGOTWY, Corollary 7.7] that 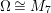 ${\rm\Omega}\cong M_{7}$.
${\rm\Omega}\cong M_{7}$.
Similarly, one can easily see that 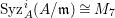 $\text{Syz}_{A}^{i}(A/\mathfrak{m})\cong M_{7}$ and
$\text{Syz}_{A}^{i}(A/\mathfrak{m})\cong M_{7}$ and 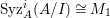 $\text{Syz}_{A}^{i}(A/I)\cong M_{1}$ for every
$\text{Syz}_{A}^{i}(A/I)\cong M_{1}$ for every ![]() $i\geqslant 2$. Hence,
$i\geqslant 2$. Hence, ![]() $M_{2}$ cannot be written as a direct summand of
$M_{2}$ cannot be written as a direct summand of 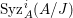 $\text{Syz}_{A}^{i}(A/J)$ for any Ulrich ideal
$\text{Syz}_{A}^{i}(A/J)$ for any Ulrich ideal ![]() $J$.
$J$.
Two-dimensional rational double points ![]() $(A_{n})$ (Gorenstein quotient singularities) admit a sequence of Ulrich ideals of length
$(A_{n})$ (Gorenstein quotient singularities) admit a sequence of Ulrich ideals of length 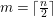 $m=\lceil \frac{n}{2}\rceil$:
$m=\lceil \frac{n}{2}\rceil$:
 $$\begin{eqnarray}(x,y^{m},z)\subset \cdots \subset (x,y^{2},z)\subset (x,y,z).\end{eqnarray}$$
$$\begin{eqnarray}(x,y^{m},z)\subset \cdots \subset (x,y^{2},z)\subset (x,y,z).\end{eqnarray}$$ However, the following example shows that each two-dimensional non-Gorenstein cyclic quotient singularity has a unique Ulrich ideal (that is, the maximal ideal ![]() $\mathfrak{m}$).
$\mathfrak{m}$).
Example 7.3. (Cyclic quotient singularity)
Let ![]() $A$ be a two-dimensional cyclic quotient singularity of type
$A$ be a two-dimensional cyclic quotient singularity of type ![]() $\frac{1}{n}(1,q)$, where
$\frac{1}{n}(1,q)$, where ![]() $q$ and
$q$ and ![]() $n$ are integers with
$n$ are integers with  $1<q<n$,
$1<q<n$, 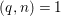 $(q,n)=1$. Namely,
$(q,n)=1$. Namely, ![]() $A$ is the invariant subring of the cyclic group generated by
$A$ is the invariant subring of the cyclic group generated by
 $$\begin{eqnarray}g=\left[\begin{array}{@{}cc@{}}{\it\varepsilon}_{n} & 0\\ 0 & {\it\varepsilon}_{n}^{q}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}g=\left[\begin{array}{@{}cc@{}}{\it\varepsilon}_{n} & 0\\ 0 & {\it\varepsilon}_{n}^{q}\end{array}\right],\end{eqnarray}$$ where ![]() ${\it\varepsilon}_{n}$ denotes the primitive
${\it\varepsilon}_{n}$ denotes the primitive ![]() $n$th root of
$n$th root of ![]() $1\in k$.
$1\in k$.
Now suppose that ![]() $A$ is not Gorenstein, that is,
$A$ is not Gorenstein, that is, ![]() $q+1$ is not divided by
$q+1$ is not divided by ![]() $n$. Then there exists an exceptional curve
$n$. Then there exists an exceptional curve ![]() $E_{i}$ so that
$E_{i}$ so that 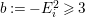 $b:=-E_{i}^{2}\geqslant 3$. In particular,
$b:=-E_{i}^{2}\geqslant 3$. In particular, 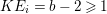 $KE_{i}=b-2\geqslant 1$. Let
$KE_{i}=b-2\geqslant 1$. Let ![]() ${\rm\Gamma}$ be the dual graph of the minimal resolution of singularities
${\rm\Gamma}$ be the dual graph of the minimal resolution of singularities 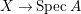 $X\rightarrow \,\text{Spec}\,A$.
$X\rightarrow \,\text{Spec}\,A$.

It is well known that ![]() $\mathfrak{m}$ is an Ulrich ideal. Now suppose that there exists an Ulrich ideal other than
$\mathfrak{m}$ is an Ulrich ideal. Now suppose that there exists an Ulrich ideal other than ![]() $\mathfrak{m}$. Then we can take
$\mathfrak{m}$. Then we can take ![]() $Y_{1}$ satisfying the conditions (a), (b) in Theorem 6.4. In particular,
$Y_{1}$ satisfying the conditions (a), (b) in Theorem 6.4. In particular, 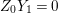 $Z_{0}Y_{1}=0$,
$Z_{0}Y_{1}=0$, 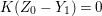 $K(Z_{0}-Y_{1})=0$ and
$K(Z_{0}-Y_{1})=0$ and 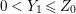 $0<Y_{1}\leqslant Z_{0}$. Set
$0<Y_{1}\leqslant Z_{0}$. Set 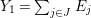 $Y_{1}=\sum _{j\in J}E_{j}$ for some non-empty subset
$Y_{1}=\sum _{j\in J}E_{j}$ for some non-empty subset ![]() $J$ of
$J$ of 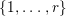 $\{1,\ldots ,r\}$.
$\{1,\ldots ,r\}$.
If ![]() $i\in J$, then
$i\in J$, then 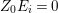 $Z_{0}E_{i}=0$ because
$Z_{0}E_{i}=0$ because 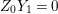 $Z_{0}Y_{1}=0$. On the other hand,
$Z_{0}Y_{1}=0$. On the other hand, 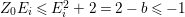 $Z_{0}E_{i}\leqslant E_{i}^{2}+2=2-b\leqslant -1$. This is a contradiction. Hence,
$Z_{0}E_{i}\leqslant E_{i}^{2}+2=2-b\leqslant -1$. This is a contradiction. Hence, ![]() $i\notin J$. Then
$i\notin J$. Then 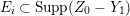 $E_{i}\subset \text{Supp}(Z_{0}-Y_{1})$. This implies that
$E_{i}\subset \text{Supp}(Z_{0}-Y_{1})$. This implies that 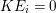 $KE_{i}=0$ because
$KE_{i}=0$ because 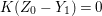 $K(Z_{0}-Y_{1})=0$, which contradicts the choice of
$K(Z_{0}-Y_{1})=0$, which contradicts the choice of ![]() $E_{i}$. Hence, the maximal ideal is the only Ulrich ideal of
$E_{i}$. Hence, the maximal ideal is the only Ulrich ideal of ![]() $A$.
$A$.
Remark 7.4. Let ![]() $A$ be a cyclic quotient singularity as above. Then one can obtain many examples of special cycles in general by a similar argument to the proof of Theorem 5.7.
$A$ be a cyclic quotient singularity as above. Then one can obtain many examples of special cycles in general by a similar argument to the proof of Theorem 5.7.
Example 7.5. (Rational triple points)
Let 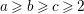 $a\geqslant b\geqslant c\geqslant 2$. If we set
$a\geqslant b\geqslant c\geqslant 2$. If we set 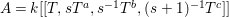 $A=k[[T,sT^{a},s^{-1}T^{b},(s+1)^{-1}T^{c}]]$, then it is a two-dimensional rational singularity with
$A=k[[T,sT^{a},s^{-1}T^{b},(s+1)^{-1}T^{c}]]$, then it is a two-dimensional rational singularity with 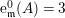 $\text{e}_{\mathfrak{m}}^{0}(A)=3$ and
$\text{e}_{\mathfrak{m}}^{0}(A)=3$ and
 $$\begin{eqnarray}\displaystyle A & \cong & \displaystyle k[[t,x,y,z]]/(xy-t^{a+b},xz-t^{a+c}+zt^{a},yz-yt^{c}+zt^{b})\nonumber\\ \displaystyle & \cong & \displaystyle k[[t,x,y,z]]\bigg/I_{2}\left(\begin{array}{@{}ccc@{}}x & t^{b} & t^{c}-z\\ t^{a} & y & z\end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & \cong & \displaystyle k[[t,x,y,z]]/(xy-t^{a+b},xz-t^{a+c}+zt^{a},yz-yt^{c}+zt^{b})\nonumber\\ \displaystyle & \cong & \displaystyle k[[t,x,y,z]]\bigg/I_{2}\left(\begin{array}{@{}ccc@{}}x & t^{b} & t^{c}-z\\ t^{a} & y & z\end{array}\right).\nonumber\end{eqnarray}$$ See [Reference WahlWah, 3.6] and the dual graph of the minimal resolution 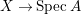 $X\rightarrow \,\text{Spec}\,A$ below.
$X\rightarrow \,\text{Spec}\,A$ below.
Put 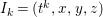 $I_{k}=(t^{k},x,y,z)$. Then
$I_{k}=(t^{k},x,y,z)$. Then ![]() $I_{k}$ is an Ulrich ideal of colength
$I_{k}$ is an Ulrich ideal of colength ![]() $k$ for every
$k$ for every ![]() $k$ with
$k$ with 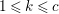 $1\leqslant k\leqslant c$. In fact, if we put
$1\leqslant k\leqslant c$. In fact, if we put 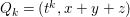 $Q_{k}=(t^{k},x+y+z)$, then
$Q_{k}=(t^{k},x+y+z)$, then 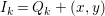 $I_{k}=Q_{k}+(x,y)$ and
$I_{k}=Q_{k}+(x,y)$ and 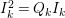 $I_{k}^{2}=Q_{k}I_{k}$. Furthermore, we have
$I_{k}^{2}=Q_{k}I_{k}$. Furthermore, we have 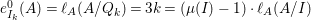 $e_{I_{k}}^{0}(A)=\ell _{A}(A/Q_{k})=3k=({\it\mu}(I)-1)\cdot \ell _{A}(A/I)$. Hence,
$e_{I_{k}}^{0}(A)=\ell _{A}(A/Q_{k})=3k=({\it\mu}(I)-1)\cdot \ell _{A}(A/I)$. Hence, ![]() $I_{k}$ is an Ulrich ideal.
$I_{k}$ is an Ulrich ideal.

Let 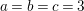 $a=b=c=3$. Now consider the corresponding cycles.
$a=b=c=3$. Now consider the corresponding cycles.

Note that all special cycles are Ulrich cycles.
Example 7.6. Let 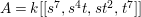 $A=k[[s^{7},s^{4}t,st^{2},t^{7}]]$. Then
$A=k[[s^{7},s^{4}t,st^{2},t^{7}]]$. Then ![]() $A$ is a two-dimensional cyclic quotient singularity, which is an invariant subring of a cyclic group generated by
$A$ is a two-dimensional cyclic quotient singularity, which is an invariant subring of a cyclic group generated by
 $$\begin{eqnarray}g=\left(\begin{array}{@{}cc@{}}{\it\varepsilon}_{7} & \\ & {\it\varepsilon}_{7}^{3}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}g=\left(\begin{array}{@{}cc@{}}{\it\varepsilon}_{7} & \\ & {\it\varepsilon}_{7}^{3}\end{array}\right).\end{eqnarray}$$ Since  ${\displaystyle \frac{7}{~3~}}=3-{\displaystyle \frac{1}{2-1/2}}$, the dual graph can be written as the following form (e.g. [Reference RiemenschneiderRi]):
${\displaystyle \frac{7}{~3~}}=3-{\displaystyle \frac{1}{2-1/2}}$, the dual graph can be written as the following form (e.g. [Reference RiemenschneiderRi]):

If we put 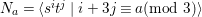 $N_{a}=\langle s^{i}t^{j}\mid i+3j\equiv a(\text{mod}~3)\rangle$ for
$N_{a}=\langle s^{i}t^{j}\mid i+3j\equiv a(\text{mod}~3)\rangle$ for 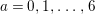 $a=0,1,\ldots ,6$, then
$a=0,1,\ldots ,6$, then 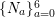 $\{N_{a}\}_{a=0}^{6}$ forms a representative of isomorphism classes of indecomposable maximal Cohen–Macaulay
$\{N_{a}\}_{a=0}^{6}$ forms a representative of isomorphism classes of indecomposable maximal Cohen–Macaulay ![]() $A$-modules. Then
$A$-modules. Then 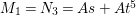 $M_{1}=N_{3}=As+At^{5}$,
$M_{1}=N_{3}=As+At^{5}$, 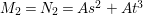 $M_{2}=N_{2}=As^{2}+At^{3}$ and
$M_{2}=N_{2}=As^{2}+At^{3}$ and 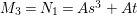 $M_{3}=N_{1}=As^{3}+At$ are indecomposable special Cohen–Macaulay
$M_{3}=N_{1}=As^{3}+At$ are indecomposable special Cohen–Macaulay ![]() $A$-modules. On the other hand,
$A$-modules. On the other hand, 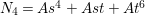 $N_{4}=As^{4}+Ast+At^{6}$,
$N_{4}=As^{4}+Ast+At^{6}$, 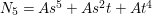 $N_{5}=As^{5}+As^{2}t+At^{4}$,
$N_{5}=As^{5}+As^{2}t+At^{4}$, 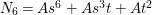 $N_{6}=As^{6}+As^{3}t+At^{2}$ are indecomposable Ulrich
$N_{6}=As^{6}+As^{3}t+At^{2}$ are indecomposable Ulrich ![]() $A$-modules with respect to the maximal ideal
$A$-modules with respect to the maximal ideal ![]() $\mathfrak{m}$. See also [Reference WunramWu2].
$\mathfrak{m}$. See also [Reference WunramWu2].
All special cycles are  $Z_{0}=E_{1}+E_{2}+E_{3}$ and
$Z_{0}=E_{1}+E_{2}+E_{3}$ and 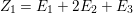 $Z_{1}=E_{1}+2E_{2}+E_{3}$. (Note that
$Z_{1}=E_{1}+2E_{2}+E_{3}$. (Note that ![]() $Z_{1}$ is not an Ulrich cycle (see Example 7.3).) Any special Cohen–Macaulay module with respect to
$Z_{1}$ is not an Ulrich cycle (see Example 7.3).) Any special Cohen–Macaulay module with respect to ![]() $I_{Z_{1}}$ is of the form
$I_{Z_{1}}$ is of the form ![]() $M_{2}^{\oplus k}$.
$M_{2}^{\oplus k}$.
However, we do not have the complete list of Ulrich modules with respect to some ideal.
Acknowledgements
The authors thank Yukari Ito, Osamu Iyama, Yusuke Nakajima and Michael Wemyss for valuable comments and conversations. The authors are also grateful to the referee for reading the paper carefully and giving many valuable suggestions. In particular, Remark 4.7 is due to his/her advice.