No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
The classical comparison and interlacing theorems of Sturm were originally proved for the equations
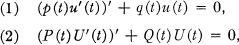
under the assumption that all coefficients are real-valued, continuous, and p > 0, P > 0. Atkinson [1, Chapter 8] has carried out the standard theory for eigenvalue problems involving (1), under the more general hypothesis
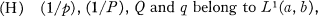
Please note a has been issued for this article.