1. Introduction
Inertial confinement fusion (ICF)[ Reference Atzeni and Meyer-ter-Vehn1] experiments have made astonishing progress, historically achieving a net energy gain[ Reference Zylstra, Hurricane, Callahan, Kritcher, Ralph, Robey, Ross, Young, Baker, Casey, Döppner, Divol, Hohenberger, Le Pape, Pak, Patel, Tommasini, Ali, Amendt, Atherton, Bachmann, Bailey, Benedetti, Berzak Hopkins, Betti, Bhandarkar, Biener, Bionta, Birge, Bond, Bradley, Braun, Briggs, Bruhn, Celliers, Chang, Chapman, Chen, Choate, Christopherson, Clark, Crippen, Dewald, Dittrich, Edwards, Farmer, Field, Fittinghoff, Frenje, Gaffney, Gatu Johnson, Glenzer, Grim, Haan, Hahn, Hall, Hammel, Harte, Hartouni, Heebner, Hernandez, Herrmann, Herrmann, Hinkel, Ho, Holder, Hsing, Huang, Humbird, Izumi, Jarrott, Jeet, Jones, Kerbel, Kerr, Khan, Kilkenny, Kim, Geppert Kleinrath, Geppert Kleinrath, Kong, Koning, Kroll, Kruse, Kustowski, Landen, Langer, Larson, Lemos, Lindl, Ma, MacDonald, MacGowan, Mackinnon, MacLaren, MacPhee, Marinak, Mariscal, Marley, Masse, Meaney, Meezan, Michel, Millot, Milovich, Moody, Moore, Morton, Murphy, Newman, Di Nicola, Nikroo, Nora, Patel, Pelz, Peterson, Ping, Pollock, Ratledge, Rice, Rinderknecht, Rosen, Rubery, Salmonson, Sater, Schiaffino, Schlossberg, Schneider, Schroeder, Scott, Sepke, Sequoia, Sherlock, Shin, Smalyuk, Spears, Springer, Stadermann, Stoupin, Strozzi, Suter, Thomas, Town, Tubman, Trosseille, Volegov, Weber, Widmann, Wild, Wilde, Van Wonterghem, Woods, Woodworth, Yamaguchi, Yang and Zimmerman2]. High-energy laser irradiation at the megajoule level can cause laser-induced damage (LID)[ Reference Bass, Vickers, Guss, Norton, Cross, Carr and Feigenbaum3] on the surface of the final optics assembly (FOA)[ Reference Zhao, Wu, Lin, Zhu and Wang4, Reference Baisden, Atherton, Hawley, Land, Menapace, Miller, Runkel, Spaeth, Stolz, Suratwala, Wegner and Wong5], limiting the long-term high-power operation of laser facilities. Online detection of the damage status of optics is essential for the safe and efficient operation of ICF facilities. The National Ignition Facility (NIF)[ Reference Zylstra, Kritcher, Hurricane, Callahan, Ralph, Casey, Pak, Landen, Bachmann, Baker, Hopkins, Bhandarkar, Biener, Bionta, Birge, Braun, Briggs, Celliers, Chen, Choate, Clark, Divol, Döppner, Fittinghoff, Edwards, Johnson, Gharibyan, Haan, Hahn, Hartouni, Hinkel, Ho, Hohenberger, Holder, Huang, Izumi, Jeet, Jones, Kerr, Khan, Kleinrath, Kleinrath, Kong, Lamb, Le Pape, Lemos, Lindl, MacGowan, Mackinnon, MacPhee, Marley, Meaney, Millot, Moore, Newman, Di Nicola, Nikroo, Nora, Patel, Rice, Rubery, Sater, Schlossberg, Sepke, Sequoia, Shin, Stadermann, Stoupin, Strozzi, Thomas, Tommasini, Trosseille, Tubman, Volegov, Weber, Wild, Woods, Yang and Young6, Reference Betti and Hurricane7], the Laser Megajoule (LMJ) in France[ Reference Miquel, Lion and Vivini8, Reference Guillaume, Chloé, Jérôme and François9] and the laser facility at the China Academy of Engineering Physics (CAEP)[ Reference Li, Wang, Jin, Huang, Wang, Su and Zhao10, Reference Zheng, Zhang, Wei, Jing, Sui, Zheng, Yuan, Jiang, Su, Zhou, Li, Wang, Hu, He, Xiang, Peng, Feng, Guo, Li, Zhu, Yu, You, Fan and Zhang11] have developed their final optics damage inspection (FODI) systems[ Reference Conder, Chang, Kegelmeyer, Spaeth and Whitman12– Reference Wei, Chen, Tang, Peng and Liu14] to capture damage images of optics online. After the ICF experiments, the imaging system is fed into the center of the target chamber by the support positioning system and captures images of the optics using dark-field imaging with edge illumination. Figure 1 shows the methodology.

Figure 1 Schematic diagram of the methodology for online capturing images of optics (FODI images) by the FODI system.
Dark-field imaging of damage with edge illumination appears as bright spots on a dark background. The damage status of the optics can be assessed by locating and segmenting these bright spots. Complex factors such as large differences in damage size, uneven illumination and stray light interference[ Reference Wei, Chen, Liu, Peng, Tang, Zhu, Hu, Xiang, Liu, Sun and Liu15] make accurate damage image segmentation more challenging, as shown in Figure 2.

Figure 2 An example of the FODI image. (a)–(c) Images of stray light interference. (d), (e) Images of large damage sites. (f), (g) Images of weak damage sites.
The Lawrence Livermore National Laboratory (LLNL) proposed a classical local area signal-to-noise ratio (LASNR) algorithm[ Reference Kegelmeyer, Fong, Glenn and Liebman16]. This algorithm highlights weak damage signals from its local neighborhood and has a high detection recall. However, its detection accuracy and robustness are largely limited by factors such as changing illumination conditions, stray light interference and noise.
Semantic segmentation algorithms based on deep convolutional neural networks do not require custom-built parameters for the above multifactor interference scenes and can automatically extract effective damage features and robustly segment damage sites. Chu et al. [ Reference Chu, Zhang, Tian, Zhang, Wang, Chen and Geng17] of CAEP constructed a fully convolutional network with a U-shaped architecture (U-Net). Through fully supervised training, this model achieves higher damage detection accuracy than conventional methods. However, producing large quantities of pixel-level labels requires specialist knowledge and a great deal of time and effort.
Weakly supervised learning methods can reduce the cost of manual annotation. Currently, state-of-the-art weakly supervised semantic segmentation algorithms are based on class activation maps, and the general procedures of these methods are shown in Figure 3. Relying on only image-level labels, deep learning models can generate pixel-level segmentation results. Zhou et al. [ Reference Zhou, Khosla, Lapedriza, Oliva and Torralba18] first proposed class activation mapping (CAM) to achieve target segmentation by visualizing feature points that play an important role in target classification. However, it is inconvenient to modify the network structure and retrain the model in practical applications. Later, gradient-weighted class activation mapping (Grad-CAM) and its variants[ Reference Selvaraju, Cogswell, Das, Vedantam, Parikh and Batra19– Reference Wang, Wang, Du, Yang, Zhang, Ding, Mardziel and Hu21] were proposed. They generate class activation maps using the average gradients of the target class score with respect to the feature maps of the final convolutional layer as class activation weights (global weight CAM). Limited by the spatial resolution of the final convolutional layer, Grad-CAM can only roughly locate the targets. Recently, Jiang et al. [ Reference Jiang, Zhang, Hou, Cheng and Wei22] proposed layer class activation mapping (LayerCAM). They use pixel-level weights to generate reliable class activation maps for each stage and combine them to obtain fine-grained segmentation results (pixel-level weight CAM). Figure 4 shows the typical results of Grad-CAM and LayerCAM on FODI images. LayerCAM has the potential to solve our segmentation problem.

Figure 3 The process of class activation mapping.

Figure 4 Examples of class activation maps generated by Grad-CAM and LayerCAM on FODI images. The red arrows point to scattered activated regions. The yellow arrows point to underactivated regions.
However, we found two problems with LayerCAM. One is that the discontinuous pixel-level class activation weights generate scattered class activation regions, resulting in a single damage object being segmented into multiple objects. The other is that large damage sites are underactivated in the class activation maps from shallow layers, leading to degradation in segmentation accuracy or even missed detections, as shown in Figure 4.
Based on the above analysis, we propose continuous gradient fusion CAM (CG-Fusion CAM) to generate more fine-grained class activation maps with an appropriate activation degree, enabling efficient and accurate detection and segmentation of damage sites with large size differences.
2. Methodology
Our CG-Fusion CAM method includes four parts: (1) a classification network, (2) continuous gradient CAM (CG-CAM), (3) nonlinear multiscale fusion (NM-Fusion) and (4) post-processing.
The overall pipeline is shown in Figure 5. The classification network is used to extract image features and determine their categories. CG-CAM is used to generate more fine-grained class activation maps with complete activated regions. Unlike the gradient-based CAM algorithms above, we propose a new method for backpropagating gradients. It distributes the feature point gradient in the low-resolution layer equally to each feature point (within the same pooling kernel) in the forward (taking the direction of forward propagation as positive) high-resolution layer. The scattered gradients of the high-resolution feature maps restore continuity, preserving the fine-grained information lost in down-sampling. NM-Fusion is used to further enhance the effect of class activation in CG-CAM. We propose an algorithm to nonlinearly activate multiscale fused heatmaps. On the basis of improving the fine granularity of class activation maps through linearly fusing multiscale heatmaps, the original image is used to compensate for the underactivation of large targets based on the complementarity of the target gray values. Subsequently, the high-level semantic information from deep layers is used to nonlinearly activate the target regions and suppress the stray light interference introduced by the original images. Post-processing is used to segment class activation maps and generate the overall damage segmentation results for large-aperture optics. We choose the dynamic threshold segmentation algorithm to obtain high-precision target regions.

Figure 5 The pipeline of CG-Fusion CAM.
2.1. Classification network
The selection of the classification network has an important impact on the effectiveness of feature extraction, the accuracy of the class activation weights and the localization performance of the class activation maps. Therefore, we choose the VGG-16 algorithm as our classification network with excellent classification ability, simple structure, fast training speed and easy deployment[ Reference Simonyan and Zisserman23]. VGG-16 contains two parts: a feature extraction layer and a classification layer. Among them, the feature extraction layer contains five stages. Each stage consists of several convolutional layers and a max-pooling layer. Each convolutional layer contains multiple channel outputs, also known as feature maps.
2.2. Continuous gradient CAM
2.2.1. Analysis
Inspired by LayerCAM, we use the class activation maps with higher spatial resolution generated from the shallow layers to increase the fine-grained information of targets. However, the typical phenomenon of scattered class activation regions is present at each stage of VGG-16, as shown in Figure 6. We further decompose the class activation map for each channel of each stage into its feature map and gradient map and find that the discontinuity of the gradients associated with the target regions leads to scattered class activation regions. Figure 6 randomly shows the partial channel results of Stage 5.

Figure 6 The class activation maps of LayerCAM from different stages. The red box shows the feature and gradient maps of some channels from Stage 5.
According to the chain rule[ Reference Goodfellow, Bengio and Courville24, Reference LeCun, Boser, Denker, Henderson, Howard, Hubbard and Jackel25], max-pooling layers are the cause of scattered gradients. This is because, in forward propagation, max-pooling layers retain only the largest feature value in each kernel to compress features and reduce computation. In backpropagation, each max-pooling layer passes its gradient to the maximum feature value (within the same pooling kernel) in the forward convolution layer, but the nonmaximum features have no gradients and are assigned zero. Figure 7(a) illustrates the method of backpropagating gradients from the max-pooling layer to the convolution layer.

Figure 7 The original and CG-CAM methods of backpropagating gradients from the max-pooling layer to the convolution layer.

Figure 8 Comparison of LayerCAM and CG-CAM results from different stages. (a), (d) Feature maps. (b), (e) Class activation gradient maps. (c), (f) Channel class activation maps.
The activation maps generated by LayerCAM using scattered gradients (Figure 7(a)) do not contain much more fine-grained information from high-resolution feature maps. They are the results of up-sampling the low-resolution class activation maps by interpolating zeros. To effectively preserve more fine-grained features, the CG-CAM proposed in this paper reassigns reliable gradients to them, generating continuous gradients for high-resolution feature maps.
2.2.2. Algorithm
Specifically, in backpropagation, our CG-CAM extracts the gradients of the last convolutional layer (the forward layer of the max-pooling layer) at each stage by the hook operation[
Reference Nakashima26]. Then, the average pooling operation and the up-sampling operation distribute the gradient equally to each feature point within the same pooling kernel, restoring the continuity of the scattered gradients, as shown in Figure 7(b). CG-CAM uses the modified gradients as pixel-level weights to activate corresponding feature points. Formally, the weight
![]() ${w}_{ij}^{kc}$
of the spatial position (
${w}_{ij}^{kc}$
of the spatial position (
![]() $i$
,
$i$
,
![]() $j$
) in the
$j$
) in the
![]() $k$
th channel feature map of a certain convolutional layer to the target class
$k$
th channel feature map of a certain convolutional layer to the target class
![]() $c$
can be written as follows:
$c$
can be written as follows:
where
![]() $\mathrm{upsample}$
is the up-sampling function,
$\mathrm{upsample}$
is the up-sampling function,
![]() $\mathrm{avgpool}2\mathrm{d}$
is the average pooling function and
$\mathrm{avgpool}2\mathrm{d}$
is the average pooling function and
![]() ${g}_{ij}^{kc}$
is the gradient of the predicted score
${g}_{ij}^{kc}$
is the gradient of the predicted score
![]() ${y}^c$
(before softmax) of the target class
${y}^c$
(before softmax) of the target class
![]() $c$
with respect to the feature map
$c$
with respect to the feature map
![]() ${A}_{ij}^k$
. Its formula is as follows:
${A}_{ij}^k$
. Its formula is as follows:
 $$\begin{align}{g}_{ij}^{kc}=\frac{\partial {y}^c}{\partial {A}_{ij}^k},\end{align}$$
$$\begin{align}{g}_{ij}^{kc}=\frac{\partial {y}^c}{\partial {A}_{ij}^k},\end{align}$$
where
![]() ${A}_{ij}^k$
is the feature value of the spatial position (
${A}_{ij}^k$
is the feature value of the spatial position (
![]() $i$
,
$i$
,
![]() $j$
) in the
$j$
) in the
![]() $k$
th channel of a certain convolutional layer. The class activation map
$k$
th channel of a certain convolutional layer. The class activation map
![]() ${M}^c$
of CG-CAM is calculated as follows:
${M}^c$
of CG-CAM is calculated as follows:
 $$\begin{align}{M}^c=\mathrm{ReLU}\left(\sum \limits_k{w}_{ij}^{kc}\cdot {A}_{ij}^k\right)=\mathrm{ReLU}\left(\sum \limits_k{\widehat{A}}^k\right),\end{align}$$
$$\begin{align}{M}^c=\mathrm{ReLU}\left(\sum \limits_k{w}_{ij}^{kc}\cdot {A}_{ij}^k\right)=\mathrm{ReLU}\left(\sum \limits_k{\widehat{A}}^k\right),\end{align}$$
where
![]() ${\widehat{A}}^k$
is the class activation map of the
${\widehat{A}}^k$
is the class activation map of the
![]() $k$
th channel. Linearly summing the
$k$
th channel. Linearly summing the
![]() ${\widehat{A}}^k$
of all channels, we obtain the
${\widehat{A}}^k$
of all channels, we obtain the
![]() ${M}^c$
of a certain convolutional layer. We also apply the rectified linear unit (ReLU) operation to remove the effect of negative gradients.
${M}^c$
of a certain convolutional layer. We also apply the rectified linear unit (ReLU) operation to remove the effect of negative gradients.
Figure 8 shows the visualization results of the gradients before and after the application of CG-CAM from randomly selected channels at each stage. Compared to the original scattered gradients of LayerCAM, the gradients generated by CG-CAM are continuous and smooth. This allows more semantic regions of the targets to be activated. Comparative experiments demonstrate that CG-CAM can effectively preserve high-resolution features, solve the problem of scattered class activation regions caused by the loss of fine-grained information gradients in LayerCAM and significantly improve the quality of class activation maps.
2.3. Nonlinear multiscale fusion algorithm
2.3.1. Analysis
LayerCAM further enhances the activation effect by combining shallow class activation maps, but introduces the problem of underactivation of large targets. As shown in Figure 9, small targets are well activated, but large targets are only activated at the edges in the class activation maps from shallow layers. The activation differences can be caused by the characteristics of the network itself. The receptive fields of the shallow layers are relatively small and tend to capture some detailed features, such as the edges and corners of the targets[ Reference Elyan, Vuttipittayamongkol, Johnston, Martin, McPherson, Moreno-García, Jayne and Sarker27]. As the depth increases, the receptive field of the network gradually expands, eventually capturing the entire contours of the targets[ Reference Simon and Rodner28].

Figure 9 Results of LayerCAM from each convolutional layer.
Underactivation degrades location accuracy or even leads to missed detections, requiring compensation for underactivated regions of large damage sites. Linearly fusing the overactivated results from deep layers (such as LayerCAM) can mitigate this underactivation to some extent, but also masks some of the fine-grained features in shallow layers, resulting in some loss of segmentation accuracy. We find that the gray values of the large targets are low in the class activation maps from the shallow layers but high in the original images. The opposite is true for small targets. Therefore, we propose a multiscale fusion method that uses the original images to compensate for the underactivation of large targets in CG-CAM.
2.3.2. Algorithm
Specifically, based on the complementary property of gray values, our NM-Fusion adds the gray values of the original image
![]() $I$
and those of the class activation map
$I$
and those of the class activation map
![]() ${M}_{\mathrm{CG}-\mathrm{CAM}}$
to generate a new class activation map
${M}_{\mathrm{CG}-\mathrm{CAM}}$
to generate a new class activation map
![]() ${M}_{\mathrm{multi}}$
. This operation is part of multiscale fusion and eliminates the negative impact of underactivation on segmentation, while high-resolution original images do not degrade the fine granularity of
${M}_{\mathrm{multi}}$
. This operation is part of multiscale fusion and eliminates the negative impact of underactivation on segmentation, while high-resolution original images do not degrade the fine granularity of
![]() ${M}_{\mathrm{multi}}$
. In addition, NM-Fusion extracts the foreground information of the class activation map generated from the final convolutional layer as its mask to filter out the stray light interference introduced by
${M}_{\mathrm{multi}}$
. In addition, NM-Fusion extracts the foreground information of the class activation map generated from the final convolutional layer as its mask to filter out the stray light interference introduced by
![]() $I$
. The class activation map of NM-Fusion
$I$
. The class activation map of NM-Fusion
![]() ${M}_{\mathrm{fusion}}$
is calculated as follows:
${M}_{\mathrm{fusion}}$
is calculated as follows:
 $$\begin{align} {M}_{\mathrm{fusion}}& =\left(I+{M}_{\mathrm{CG}-\mathrm{CAM}}\right)\times \mathrm{mask}\nonumber\\& ={M}_{\mathrm{multi}}\times \varepsilon \left({M}_{\mathrm{deep}}-{v}_{\mathrm{thr}}\right),\end{align}$$
$$\begin{align} {M}_{\mathrm{fusion}}& =\left(I+{M}_{\mathrm{CG}-\mathrm{CAM}}\right)\times \mathrm{mask}\nonumber\\& ={M}_{\mathrm{multi}}\times \varepsilon \left({M}_{\mathrm{deep}}-{v}_{\mathrm{thr}}\right),\end{align}$$
 $$\begin{align}\varepsilon \left(\mathrm{input}\right)=\left\{\begin{array}{ll}0& \mathrm{input}<0,\\ {}1& \mathrm{input}\ge 0,\end{array}\right.\ \qquad\end{align}$$
$$\begin{align}\varepsilon \left(\mathrm{input}\right)=\left\{\begin{array}{ll}0& \mathrm{input}<0,\\ {}1& \mathrm{input}\ge 0,\end{array}\right.\ \qquad\end{align}$$
where
![]() ${v}_{\mathrm{thr}}$
is a reasonable threshold and
${v}_{\mathrm{thr}}$
is a reasonable threshold and
![]() $\varepsilon$
(
$\varepsilon$
(
![]() $\cdot$
) is the step function for generating the mask. The class activation map
$\cdot$
) is the step function for generating the mask. The class activation map
![]() ${M}_{\mathrm{deep}}$
of the final convolutional layer has reliable high-level semantic information with a clean and low-noise background (Figure 4). Its overactivated foregrounds can nonlinearly activate high-resolution target regions in
${M}_{\mathrm{deep}}$
of the final convolutional layer has reliable high-level semantic information with a clean and low-noise background (Figure 4). Its overactivated foregrounds can nonlinearly activate high-resolution target regions in
![]() ${M}_{\mathrm{multi}}$
without losing fine-grained information, selectively filtering out stray light interference. This reflects the ‘nonlinear’ connotation of NM-Fusion.
${M}_{\mathrm{multi}}$
without losing fine-grained information, selectively filtering out stray light interference. This reflects the ‘nonlinear’ connotation of NM-Fusion.
![]() ${M}_{\mathrm{deep}}$
is calculated as follows:
${M}_{\mathrm{deep}}$
is calculated as follows:
 $$\begin{align} {M}_{\mathrm{deep}}& =\mathrm{ReLU}\left(\sum \limits_k{w}_k^c\cdot {A}_k\right)\nonumber\\& =\mathrm{ReLU}\left(\sum \limits_k\left(\frac{1}{N}\sum \limits_i\sum \limits_j{g}_{ij}^{kc}\right)\cdot {A}_k\right),\end{align}$$
$$\begin{align} {M}_{\mathrm{deep}}& =\mathrm{ReLU}\left(\sum \limits_k{w}_k^c\cdot {A}_k\right)\nonumber\\& =\mathrm{ReLU}\left(\sum \limits_k\left(\frac{1}{N}\sum \limits_i\sum \limits_j{g}_{ij}^{kc}\right)\cdot {A}_k\right),\end{align}$$
where N denotes the number of locations in the feature map
![]() ${A}_k$
. To further optimize the quality of
${A}_k$
. To further optimize the quality of
![]() ${M}_{\mathrm{CG}-\mathrm{CAM}}$
, we linearly fuse the multiscale class activation maps from multiple stages of CG-CAM. Together with the original image, they form the ‘multiscale fusion’ connotation of NM-Fusion.
${M}_{\mathrm{CG}-\mathrm{CAM}}$
, we linearly fuse the multiscale class activation maps from multiple stages of CG-CAM. Together with the original image, they form the ‘multiscale fusion’ connotation of NM-Fusion.
![]() ${M}_{\mathrm{CG}-\mathrm{CAM}}$
is calculated as follows:
${M}_{\mathrm{CG}-\mathrm{CAM}}$
is calculated as follows:
 $$\begin{align}{M}_{\mathrm{CG}-\mathrm{CAM}}=\sum \limits_{l=1}^4{M}_{\mathrm{Stage}\;l},\end{align}$$
$$\begin{align}{M}_{\mathrm{CG}-\mathrm{CAM}}=\sum \limits_{l=1}^4{M}_{\mathrm{Stage}\;l},\end{align}$$
where
![]() ${M}_{\mathrm{Stage}\;l}$
is the class activation map of CG-CAM generated from the last convolutional layer at the
${M}_{\mathrm{Stage}\;l}$
is the class activation map of CG-CAM generated from the last convolutional layer at the
![]() $l$
th stage. The results of CG-CAM differ at different stages. As the stage becomes shallower, the class activation maps tend to capture more fine-grained features, but the underactivation problem becomes more severe.
$l$
th stage. The results of CG-CAM differ at different stages. As the stage becomes shallower, the class activation maps tend to capture more fine-grained features, but the underactivation problem becomes more severe.
The comparison of the fusion results from different stages is shown in Figure 10. As the depth of the fusion stage increases, the fusion of the first four stages reaches the best state, with clear boundaries of the target activation regions. However, the addition of the last stage degrades the activation quality and the target boundaries become blurred. This is because the last stage is the deep layer of the network with low-resolution feature maps. Fusing the rough target position information from Stage 5 cannot improve the fine granularity. Thus,
![]() ${M}_{\mathrm{CG}-\mathrm{CAM}}$
is a linear fusion result of the first four stages.
${M}_{\mathrm{CG}-\mathrm{CAM}}$
is a linear fusion result of the first four stages.

Figure 10 Comparison of the multiscale fusion effect from different stages of CG-CAM. The red arrows point to blurred boundaries.

Figure 11 Examples of typical samples. (a) Background class samples. (b) Damage class samples. (c) Manually produced damage class samples.
2.4. Post-processing
Accurate segmentation of the foreground in the class activation maps is required to achieve precise localization and extraction of damage sites. Simple threshold segmentation cannot achieve ideal segmentation results, so we use the local dynamic threshold segmentation algorithm[
Reference Sauvola and Pietikäinen29] for post-processing. Using a sliding window to iterate through all image regions, an appropriate segmentation threshold
![]() $T\left(i,j\right)$
is determined based on the contrast of gray values in the local window. It is calculated as follows:
$T\left(i,j\right)$
is determined based on the contrast of gray values in the local window. It is calculated as follows:
 $$\begin{align}T\left(i,j\right)=\mu \left(i,j\right)\left(1+k\left(\frac{\sigma \left(i,j\right)}{R}-1\right)\right),\end{align}$$
$$\begin{align}T\left(i,j\right)=\mu \left(i,j\right)\left(1+k\left(\frac{\sigma \left(i,j\right)}{R}-1\right)\right),\end{align}$$
where (
![]() $i$
,
$i$
,
![]() $j$
) is the pixel position,
$j$
) is the pixel position,
![]() $\mu \left(i,j\right)$
is the local mean gray value within the window,
$\mu \left(i,j\right)$
is the local mean gray value within the window,
![]() $\sigma \left(i,j\right)$
denotes the corresponding standard deviation,
$\sigma \left(i,j\right)$
denotes the corresponding standard deviation,
![]() $R$
is the assumed maximum value of the standard deviation and
$R$
is the assumed maximum value of the standard deviation and
![]() $k$
is the sensitivity parameter. By setting appropriate parameters, the local dynamic threshold segmentation algorithm can adaptively segment damage sites in
$k$
is the sensitivity parameter. By setting appropriate parameters, the local dynamic threshold segmentation algorithm can adaptively segment damage sites in
![]() ${M}_{\mathrm{fusion}}$
.
${M}_{\mathrm{fusion}}$
.
Finally, the damage segmentation regions of all the sub-images are spliced back according to the corresponding positions. Then, a union operation is performed to combine the repeated segmentation results for each damage site in the overlapping regions into one region. The damage segmentation results for the large-aperture optics are shown in the following section.
3. Experiments
3.1. FODI damage dataset
We acquired images of large-aperture optics in the CAEP high-power laser facility online using the FODI system, and produced the FODI damage dataset through cropping processing and dataset enhancement.
3.1.1. Cropping processing
The resolution of large-aperture FODI images is 4096
![]() $\times$
4096, which is too large for the input of the neural network. We crop the images using a 128×128 sliding window with a step size of 64. The 50% window overlap ensures coherence of information between adjacent windows.
$\times$
4096, which is too large for the input of the neural network. We crop the images using a 128×128 sliding window with a step size of 64. The 50% window overlap ensures coherence of information between adjacent windows.
3.1.2. Dataset enhancement
To improve the ability of the classification network to extract effective features that distinguish between stray light interference and damage sites, we need to enhance the dataset. The limited occurrence of some stray light interference and large damage sites in ICF experiments make it difficult to collect large quantities of these samples. We artificially superimpose the damage image on the stray light interference image to produce a new damage image. Figure 11 shows the typical damage class samples, background class samples and manually produced damage class samples.
The FODI damage dataset we produced contains 1155 training samples and 512 test samples. The ratio of damage class samples to background class samples is approximately 1:1. The training samples include 175 manually produced damage class images and 118 background class images with various stray light interference selected for dataset enhancement. To objectively reflect the performance of the classification network, the test samples cover all types of stray light interference and damage sites.
3.2. Evaluation metrics
In the classification task, the accuracy, precision, recall, F1 and false positive rate (FPR) are used to evaluate the classification performance of the network (calculated from the damage class, excluding the background class). The statistical objects are images.
In the semantic segmentation task, we provide pixel recall (p-R), pixel precision (p-P), pixel F1 (p-F1) and pixel intersection over union (IoU) to evaluate the performance of the algorithms. The statistical objects are pixels. The IoU is defined as follows:
In addition, when faced with multiple targets, pixel-level evaluation metrics can mask the negative impact of incorrectly detecting small targets, resulting in a large number of false positive regions in the results. Therefore, we additionally provide a target-level metric, the false detection rate (FDR), to evaluate the target detection performance of the algorithm. It is defined as follows:
where TP is the number of objects correctly detected as damage sites and FP is the number of objects incorrectly detected as damage sites. Referring to the definition of evaluation metrics in the object localization task[ Reference Choe, Oh, Lee, Chun, Akata and Shim30], we use the pixel IoU to determine whether each detected connected domain is a real damage site or not. The determining formula is as follows:
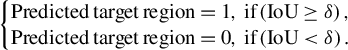 $$\begin{align}\left\{\begin{array}{@{}l}\mathrm{Predicted}\kern0.17em \mathrm{target}\kern0.17em \mathrm{region}=1,\ \mathrm{if}\left(\mathrm{IoU}\ge \delta \right),\\{}\mathrm{Predicted}\kern0.17em \mathrm{target}\kern0.17em \mathrm{region}=0,\ \mathrm{if}\left(\mathrm{IoU}<\delta \right).\end{array}\right.\end{align}$$
$$\begin{align}\left\{\begin{array}{@{}l}\mathrm{Predicted}\kern0.17em \mathrm{target}\kern0.17em \mathrm{region}=1,\ \mathrm{if}\left(\mathrm{IoU}\ge \delta \right),\\{}\mathrm{Predicted}\kern0.17em \mathrm{target}\kern0.17em \mathrm{region}=0,\ \mathrm{if}\left(\mathrm{IoU}<\delta \right).\end{array}\right.\end{align}$$
In this paper,
![]() $\delta$
is set to 0 (usually set to 0.5) to compare the false detection performance of the algorithms. Otherwise, Grad-CAM cannot reasonably calculate this metric due to the low IoU scores caused by the rough segmentation results.
$\delta$
is set to 0 (usually set to 0.5) to compare the false detection performance of the algorithms. Otherwise, Grad-CAM cannot reasonably calculate this metric due to the low IoU scores caused by the rough segmentation results.
Table 1 The classification performance of the VGG-16 model on our dataset.

Table 2 Comparison of baselines and our method under various evaluation metrics.

3.3. Classification experiment
In the experiments, only image-level labels are used to train the VGG-16 classification network. Each sample is flipped horizontally and vertically with a 50% probability before being fed into the network to increase the generalization ability of the network. The initial parameters are loaded with weights pretrained on ImageNet to avoid local optima or saddle points and to allow the network to converge quickly. The initial learning rate is set to
![]() $10^{-3}$
, and a decay strategy is implemented. The batch size is set to 32 and the training epoch is set to 30 for iterative training. The optimizer in this paper uses the SGD (stochastic gradient descent) optimizer to update the network weights.
$10^{-3}$
, and a decay strategy is implemented. The batch size is set to 32 and the training epoch is set to 30 for iterative training. The optimizer in this paper uses the SGD (stochastic gradient descent) optimizer to update the network weights.
In Table 1, we report the classification performance of the VGG-16 model trained on the enhanced dataset. The F1 of the classification network reaches 97.75%, with the ability to effectively identify damage sites.
3.4. Weakly supervised segmentation and target detection
To illustrate the semantic segmentation and target detection performance of the algorithms, we selected 338 damage class images containing typical stray light interference as the test set and manually produced their pixel-level labels (ground-truth). We compare the semantic segmentation and target detection results of five baseline algorithms, as shown in Table 2 and Figure 12. Among them, the LASNR belongs to the conventional methods. VGG16-Unet and DeepLabv3 (Resnet50 as the backbone) are fully supervised semantic segmentation methods. Grad-CAM and LayerCAM are weakly supervised semantic segmentation methods. Figure 13 shows the overall damage segmentation results of a large-aperture optic.

Figure 12 Comparison of the class activation maps and segmentation results between the baselines and our method. The green areas are the false positive segmentation results. The red areas are the segmentation results containing true damage sites.

Figure 13 The overall damage segmentation results of a large-aperture optic. (a)–(d) Enlarged local images.
The experimental results show that the LASNR has a strong segmentation capability with a pixel recall of 99.27%, but produces high false detection results. In comparison, Grad-CAM has a much lower FDR of 5.51%, but has rough class activation regions that are unable to segment multiple targets into independent individuals. The segmentation results from LayerCAM are much finer, with an IoU score of 41.82%, which is better than the results from the two baselines above. However, the underactivation of LayerCAM leads to missed detection of large damage sites with a recall of less than 90%. In addition, its scattered class activation regions result in a high FDR of 19.57%.
Our method produces more fine-grained class activation maps, and the class activation regions are activated appropriately for various sizes of damage sites. Our IoU score is up to 63.78%, an improvement of 56.68% and 21.96% over Grad-CAM and LayerCAM, respectively, which is comparable to that of fully supervised segmentation algorithms. In addition, our method can suppress stray light interference with the lowest FDR of all algorithms being only 0.90%.
3.5. Ablation experiment
We successively remove two algorithms from the pipeline, CG-CAM and NM-Fusion, and test the detection and segmentation performance of the remaining algorithms. This experiment demonstrates their respective effects on optimizing class activation maps and improving damage segmentation performance. The results are shown in Table 3 and Figures 14 and 15.
Table 3 Comparison of the baseline and our two core algorithms under various evaluation metrics.

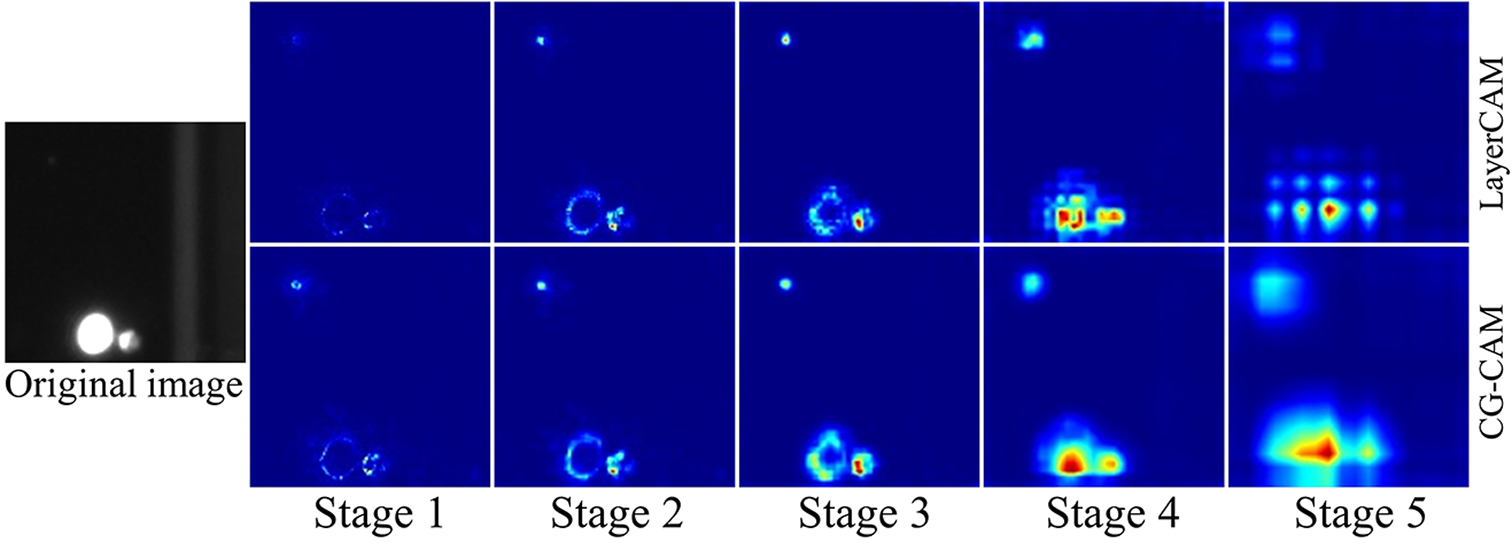
Figure 14 Comparison of the class activation maps between LayerCAM and CG-CAM from different stages.
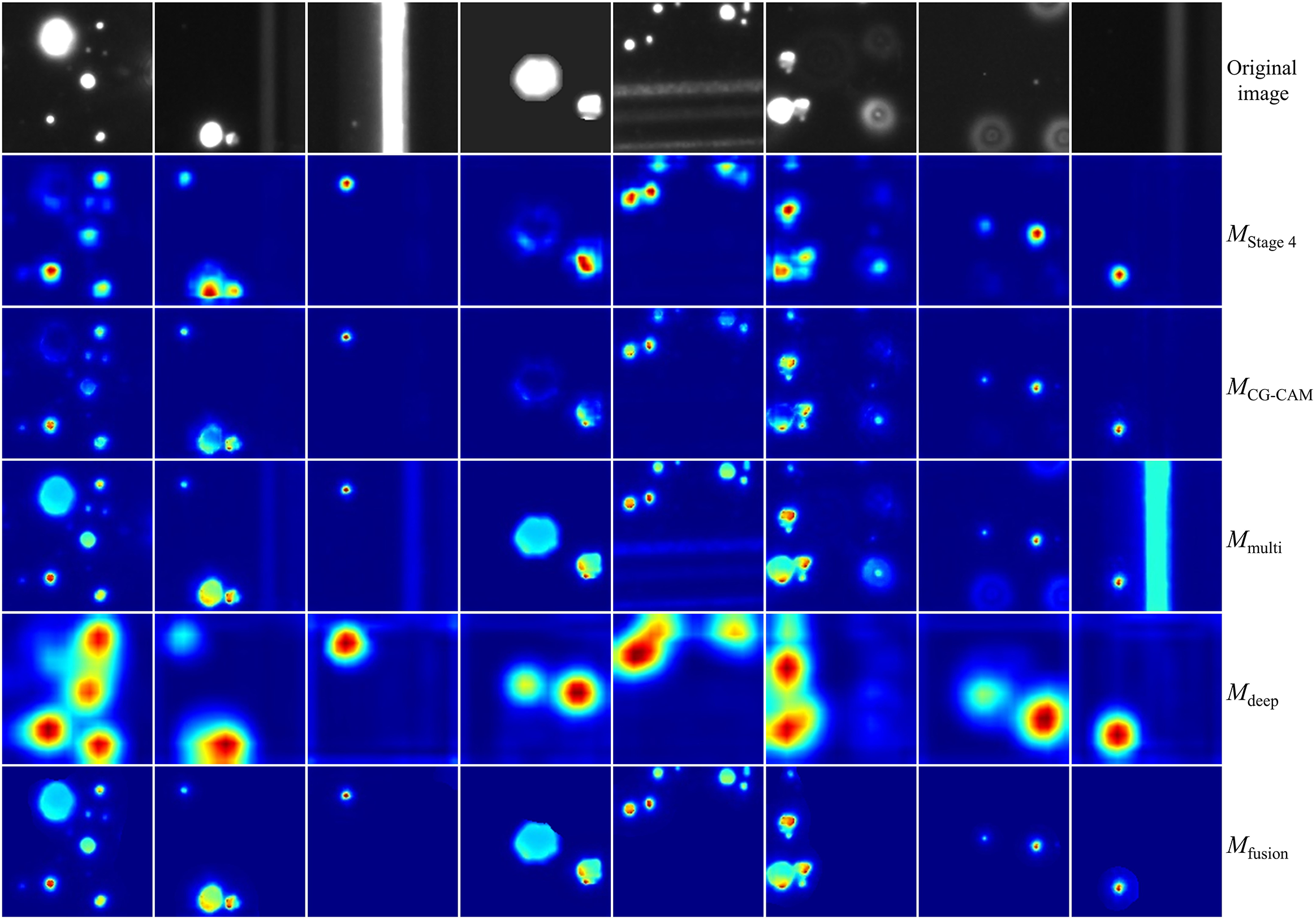
Figure 15 The effect of each step in the nonlinear multiscale fusion algorithm.
CG-CAM enables the scattered class activation regions of LayerCAM to form a whole with semantic meaning (Figure 14), preserving high-resolution features with rich detail information. The IoU score of CG-CAM is improved by 10.35% and the FDR is reduced by 10.89% compared to LayerCAM.
Based on the CG-CAM results, the effect of each step in NM-Fusion is shown in Figure 15. Compared to the results from a single stage, the fusion of multiscale heatmaps from shallow layers further improves the spatial resolution of class activation maps. Compensated by the original images, the underactivation of large damage sites is effectively improved. Finally, semantic class activation masks generated from the final convolutional layers nonlinearly activate target regions in the multiscale fusion images, filter out the stray light interference and produce more fine-grained class activation maps with an appropriate activation degree. After the addition of NM-Fusion, the IoU score is improved by 11.61% compared to CG-CAM and the FDR of the damage sites is significantly reduced by 7.78%. NM-Fusion solves the problem of underactivation of large targets caused by LayerCAM’s simple linear fusion of class activation maps from shallow layers to obtain more fine-grained information.
4. Conclusion
In this paper, a weakly supervised semantic segmentation method with CG-CAM and its NM-Fusion has been proposed for accurate segmentation of LID on large-aperture optics in ICF facilities in the face of complicated damage morphology, uneven illumination and stray light interference. The classification, detection and segmentation performance of our method has been tested on the FODI damage dataset. Experimental results show that our method can generate appropriately activated high-resolution class activation maps for damage targets of various sizes, with better target detection and segmentation capabilities than current CAM methods. Relying only on image-level labels and limited sample training, our method has achieved segmentation performance comparable to that of fully supervised algorithms, with an IoU score of 63.78%. False detection of damage sites has also been effectively suppressed, with an FDR of 0.90%. The proposed method has been applied to the large laser facility to detect the damage condition of the optics. In the future, we will delve deeper into the relationship between feature maps and class activation gradients to further improve the performance of weakly supervised semantic segmentation.





















