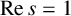1. Introduction
A classical problem in analytic number theory is to find explicit bounds for the Riemann zeta-function. In particular, bounds on the line
![]() $\mathrm {Re}\,{s}=1$
are of great interest, owing to their usefulness in estimations for the Möbius function and the von Mangoldt function. The main purpose of this paper is to obtain new bounds for the Riemann zeta-function in ranges where currently it is challenging to get computational verification.
$\mathrm {Re}\,{s}=1$
are of great interest, owing to their usefulness in estimations for the Möbius function and the von Mangoldt function. The main purpose of this paper is to obtain new bounds for the Riemann zeta-function in ranges where currently it is challenging to get computational verification.
1.1. Background
Let
![]() $\zeta (s)$
be the Riemann zeta-function. Unconditionally, it is known that, as
$\zeta (s)$
be the Riemann zeta-function. Unconditionally, it is known that, as
![]() $t\to \infty $
,
$t\to \infty $
,
 $$ \begin{align} \frac{1}{\zeta(1+it)} = O(\log t) \quad \mbox{and} \quad \frac{\zeta'(1+it)}{\zeta(1+it)} = O(\log t). \end{align} $$
$$ \begin{align} \frac{1}{\zeta(1+it)} = O(\log t) \quad \mbox{and} \quad \frac{\zeta'(1+it)}{\zeta(1+it)} = O(\log t). \end{align} $$
Currently, the best explicit bounds for
![]() $1/\zeta (1+it)$
and
$1/\zeta (1+it)$
and
![]() $\zeta '(1+it)/\zeta (1+it)$
are given by
$\zeta '(1+it)/\zeta (1+it)$
are given by
 $$ \begin{align} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq 42.9\log t \quad\mbox{and}\quad \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq 40.14\log t, \end{align} $$
$$ \begin{align} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq 42.9\log t \quad\mbox{and}\quad \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq 40.14\log t, \end{align} $$
for
![]() $t\geq 133$
. The first bound in (1.2) was established by Carneiro et al. in [Reference Carneiro, Chirre, Helfgott and Mejía-Cordero2, Proposition A.2], and the second bound was established by Trudgian in [Reference Trudgian15]. There are improvements in the orders of magnitude of the mentioned estimates (see, for example, [Reference Titchmarsh14, page 135]), but it appears that those bounds are better when t is astronomically large and then they will not be useful for computational purposes.
$t\geq 133$
. The first bound in (1.2) was established by Carneiro et al. in [Reference Carneiro, Chirre, Helfgott and Mejía-Cordero2, Proposition A.2], and the second bound was established by Trudgian in [Reference Trudgian15]. There are improvements in the orders of magnitude of the mentioned estimates (see, for example, [Reference Titchmarsh14, page 135]), but it appears that those bounds are better when t is astronomically large and then they will not be useful for computational purposes.
On the other hand, assuming the Riemann hypothesis (RH), Littlewood proved in [Reference Littlewood7] that, as
![]() $t\to \infty $
,
$t\to \infty $
,
 $$ \begin{align*} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq\bigg(\frac{12e^\gamma}{\pi^2}+o(1)\bigg) \log\log t, \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq\bigg(\frac{12e^\gamma}{\pi^2}+o(1)\bigg) \log\log t, \end{align*} $$
where
![]() $\gamma $
is the Euler–Mascheroni constant. An explicit version of this result has been given by Lamzouri et al. [Reference Lamzouri, Li and Soundararajan6, page 2394], establishing that
$\gamma $
is the Euler–Mascheroni constant. An explicit version of this result has been given by Lamzouri et al. [Reference Lamzouri, Li and Soundararajan6, page 2394], establishing that
 $$ \begin{align*} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq\frac{12e^\gamma}{\pi^2}\bigg(\log\log t - \log 2 + \frac{1}{2} + \frac{1}{\log \log t}+\frac{14\log\log t}{\log t}\bigg), \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq\frac{12e^\gamma}{\pi^2}\bigg(\log\log t - \log 2 + \frac{1}{2} + \frac{1}{\log \log t}+\frac{14\log\log t}{\log t}\bigg), \end{align*} $$
for
![]() $t\geq 10^{10}$
. Moreover, recently, Chirre et al. [Reference Chirre, Simonič and Valås Hagen3, Theorem 5] proved under RH that
$t\geq 10^{10}$
. Moreover, recently, Chirre et al. [Reference Chirre, Simonič and Valås Hagen3, Theorem 5] proved under RH that
 $$ \begin{align*} \left|\frac{\zeta'(1+it)}{\zeta(1+it)}\right|\leq 2\log\log t -0.4989 + \,5.35\,\frac{(\log\log t)^2}{\log t}, \end{align*} $$
$$ \begin{align*} \left|\frac{\zeta'(1+it)}{\zeta(1+it)}\right|\leq 2\log\log t -0.4989 + \,5.35\,\frac{(\log\log t)^2}{\log t}, \end{align*} $$
for
![]() $t\geq 10^{30}$
. Some generalisations of these estimates for families of L-functions can be found in [Reference Lumley8, Reference Palojärvi and Simonič10].
$t\geq 10^{30}$
. Some generalisations of these estimates for families of L-functions can be found in [Reference Lumley8, Reference Palojärvi and Simonič10].
1.2. Bounds for zeta under partial RH
We are interested in obtaining bounds for the Riemann zeta-function, but assuming only a partial verification of RH. For
![]() $T>0$
, we say that RH is true up to height T if all nontrivial zeros
$T>0$
, we say that RH is true up to height T if all nontrivial zeros
![]() $\rho =\beta +i\gamma $
of
$\rho =\beta +i\gamma $
of
![]() $\zeta (s)$
such that
$\zeta (s)$
such that
![]() $|\gamma |\leq T$
satisfy
$|\gamma |\leq T$
satisfy
![]() $\beta =1/2$
. The best current result of this type is given by Platt and Trudgian [Reference Platt and Trudgian12] who verified numerically, in a rigorous way using interval arithmetic, that RH is true up to height
$\beta =1/2$
. The best current result of this type is given by Platt and Trudgian [Reference Platt and Trudgian12] who verified numerically, in a rigorous way using interval arithmetic, that RH is true up to height
![]() $T=3\cdot 10^{12}$
.
$T=3\cdot 10^{12}$
.
Theorem 1.1. For a fixed
![]() $\delta $
with
$\delta $
with
![]() $0<\delta <1$
, define
$0<\delta <1$
, define
Assume RH up to height
![]() $T\geq 10^9$
. Then, for
$T\geq 10^9$
. Then, for
![]() $10^6\leq t\leq (1-\delta )T$
,
$10^6\leq t\leq (1-\delta )T$
,
 $$ \begin{align} \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq 2\log\log t+1.219 + \frac{16.108}{(\log\log t)^2}+1.057E_\delta(T) \end{align} $$
$$ \begin{align} \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq 2\log\log t+1.219 + \frac{16.108}{(\log\log t)^2}+1.057E_\delta(T) \end{align} $$
and
 $$ \begin{align} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq {2e^\gamma}\bigg(\log\log t +3.404 + \frac{9.378}{\log \log t}\bigg)\cdot\exp(0.793E_\delta(T)). \end{align} $$
$$ \begin{align} \bigg|\frac{1}{\zeta(1+it)}\bigg|\leq {2e^\gamma}\bigg(\log\log t +3.404 + \frac{9.378}{\log \log t}\bigg)\cdot\exp(0.793E_\delta(T)). \end{align} $$
From Theorem 1.1, we can also derive explicit versions of (1.1) in a finite but large range where computational verification is difficult. In fact, by Platt and Trudgian’s result, we can take
![]() $T=3\cdot 10^{12}$
and, letting
$T=3\cdot 10^{12}$
and, letting
![]() $\delta =10^{-5}$
, it follows unconditionally that
$\delta =10^{-5}$
, it follows unconditionally that
 $$ \begin{align*} \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq 0.639\cdot \log t \quad\mbox{and}\quad \frac{1}{|\zeta(1+it)|}\leq 2.506\cdot\log t, \end{align*} $$
$$ \begin{align*} \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq 0.639\cdot \log t \quad\mbox{and}\quad \frac{1}{|\zeta(1+it)|}\leq 2.506\cdot\log t, \end{align*} $$
for
![]() $10^6\leq t\leq 2.99997\cdot 10^{12}$
. This improves (1.2) in the range
$10^6\leq t\leq 2.99997\cdot 10^{12}$
. This improves (1.2) in the range
![]() $10^6\leq t\leq 2.99997\cdot 10^{12}$
.
$10^6\leq t\leq 2.99997\cdot 10^{12}$
.
We mention that (1.5) is derived from an upper bound for
![]() $|\!\log \zeta (1+it)|$
(see (3.4)), which allows us to deduce that
$|\!\log \zeta (1+it)|$
(see (3.4)), which allows us to deduce that
 $$ \begin{align} |\zeta(1+it)|\leq {2e^\gamma}\bigg(\log\log t +3.404 + \frac{9.378}{\log \log t}\bigg)\cdot\exp(0.793E_\delta(T)). \end{align} $$
$$ \begin{align} |\zeta(1+it)|\leq {2e^\gamma}\bigg(\log\log t +3.404 + \frac{9.378}{\log \log t}\bigg)\cdot\exp(0.793E_\delta(T)). \end{align} $$
Currently, the best unconditional explicit bound for
![]() $\zeta (1+it)$
is given by Patel, who proved in [Reference Patel11, Theorem 1.1] that, for
$\zeta (1+it)$
is given by Patel, who proved in [Reference Patel11, Theorem 1.1] that, for
![]() $t\geq 3$
,
$t\geq 3$
,
So, (1.6) improves (1.7) if RH is verified up to height T for T sufficiently large.
The proof of Theorem 1.1 is carried out in Section 3 and partly follows the conditional proofs of [Reference Montgomery and Vaughan9, Section 13.2]. Here, an explicit formula is used that relates the zeros of
![]() $\zeta (s)$
and the prime numbers. This formula is unconditional and contains a certain sum involving the nontrivial zeros. Assuming RH, this sum is bounded without much effort. In our case, the novelty is in bounding the contribution of the nontrivial zeros, since we only assume RH up to height T. We split this sum into two parts, the zeros with ordinates
$\zeta (s)$
and the prime numbers. This formula is unconditional and contains a certain sum involving the nontrivial zeros. Assuming RH, this sum is bounded without much effort. In our case, the novelty is in bounding the contribution of the nontrivial zeros, since we only assume RH up to height T. We split this sum into two parts, the zeros with ordinates
![]() $|\gamma |\leq T$
and
$|\gamma |\leq T$
and
![]() $|\gamma |>T$
, and analyse them separately. These sums are studied in Section 2. The proof of Theorem 1.1 is short, and the constants involved can be improved slightly.
$|\gamma |>T$
, and analyse them separately. These sums are studied in Section 2. The proof of Theorem 1.1 is short, and the constants involved can be improved slightly.
Throughout the paper, we use the notation
![]() $\alpha =O^*(\beta )$
, which means that
$\alpha =O^*(\beta )$
, which means that
![]() $|\alpha |\leq \beta $
.
$|\alpha |\leq \beta $
.
2. The sum over the nontrivial zeros
To bound the sum related to the nontrivial zeros of
![]() $\zeta (s)$
with ordinates
$\zeta (s)$
with ordinates
![]() $|\gamma |\leq T$
, we use the following lemma.
$|\gamma |\leq T$
, we use the following lemma.
Lemma 2.1. Assume RH up to height
![]() $T>0$
. Then, for
$T>0$
. Then, for
![]() $t\geq 10^6$
and
$t\geq 10^6$
and
![]() $1\leq \alpha \leq 3/2$
,
$1\leq \alpha \leq 3/2$
,
 $$ \begin{align*} \sum_{|\gamma|\leq T}\frac{\alpha-\tfrac{1}{2}}{(\alpha-\tfrac{1}{2})^2+(t-\gamma)^2} \leq \mathrm{Re}\,\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}+\frac{\log t}{2}. \end{align*} $$
$$ \begin{align*} \sum_{|\gamma|\leq T}\frac{\alpha-\tfrac{1}{2}}{(\alpha-\tfrac{1}{2})^2+(t-\gamma)^2} \leq \mathrm{Re}\,\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}+\frac{\log t}{2}. \end{align*} $$
Proof. Letting
![]() $s=\alpha +it$
and using the fractional decomposition of
$s=\alpha +it$
and using the fractional decomposition of
![]() $\zeta (s)$
(see [Reference Montgomery and Vaughan9, Corollary 10.14]), we get
$\zeta (s)$
(see [Reference Montgomery and Vaughan9, Corollary 10.14]), we get
 $$ \begin{align*} \sum_{\gamma}\frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} = \mathrm{Re}\,\frac{\zeta'(s)}{\zeta(s)}+\frac{1}{2}\,\mathrm{Re}\,\frac{\Gamma'}{\Gamma}\bigg(\frac{s}{2}+1\bigg)-\frac{\log \pi}{2} + \frac{\alpha-1}{(\alpha-1)^2+t^2}. \end{align*} $$
$$ \begin{align*} \sum_{\gamma}\frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} = \mathrm{Re}\,\frac{\zeta'(s)}{\zeta(s)}+\frac{1}{2}\,\mathrm{Re}\,\frac{\Gamma'}{\Gamma}\bigg(\frac{s}{2}+1\bigg)-\frac{\log \pi}{2} + \frac{\alpha-1}{(\alpha-1)^2+t^2}. \end{align*} $$
From the bound
 $$ \begin{align*} \frac{\Gamma'}{\Gamma}(z)= \log z -\frac{1}{2z}+ O^*\bigg(\frac{1}{4|z|^2}\bigg) \quad\mbox{for}\ \mathrm{Re}\,{z}\geq 0 \end{align*} $$
$$ \begin{align*} \frac{\Gamma'}{\Gamma}(z)= \log z -\frac{1}{2z}+ O^*\bigg(\frac{1}{4|z|^2}\bigg) \quad\mbox{for}\ \mathrm{Re}\,{z}\geq 0 \end{align*} $$
(see [Reference Helfgott4, Lemma 3.11, page 67]), it follows that
 $$ \begin{align} \sum_{\gamma}\frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} \leq \mathrm{Re}\,\frac{\zeta'(s)}{\zeta(s)}+\frac{\log t}{2}. \end{align} $$
$$ \begin{align} \sum_{\gamma}\frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} \leq \mathrm{Re}\,\frac{\zeta'(s)}{\zeta(s)}+\frac{\log t}{2}. \end{align} $$
On the other hand, splitting the sum over the zeros and using the fact that
![]() $\mathrm {Re}\,\rho <1$
, we get
$\mathrm {Re}\,\rho <1$
, we get
 $$ \begin{align} \sum_{\gamma} \frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} & = \sum_{|\gamma|\leq T}\frac{\alpha-\tfrac{1}{2}}{(\alpha-\frac{1}{2})^2+(t-\gamma)^2} + \sum_{|\gamma|>T}\frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} \notag \\ & \geq \sum_{|\gamma|\leq T}\frac{\alpha-\frac{1}{2}}{(\alpha-\frac{1}{2})^2+(t-\gamma)^2}. \end{align} $$
$$ \begin{align} \sum_{\gamma} \frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} & = \sum_{|\gamma|\leq T}\frac{\alpha-\tfrac{1}{2}}{(\alpha-\frac{1}{2})^2+(t-\gamma)^2} + \sum_{|\gamma|>T}\frac{\alpha-\mathrm{Re}\,{\rho}}{(\alpha-\mathrm{Re}\,{\rho})^2+(t-\gamma)^2} \notag \\ & \geq \sum_{|\gamma|\leq T}\frac{\alpha-\frac{1}{2}}{(\alpha-\frac{1}{2})^2+(t-\gamma)^2}. \end{align} $$
By combining (2.1) and (2.2), we arrive at the desired result.
To bound the sum related to the nontrivial zeros of
![]() $\zeta (s)$
with ordinates
$\zeta (s)$
with ordinates
![]() $|\gamma |>T$
, we use the auxiliary function
$|\gamma |>T$
, we use the auxiliary function
 $$ \begin{align*} E(t,T):=\sum_{|\gamma|>T}\frac{1}{(\gamma-t)^2}, \end{align*} $$
$$ \begin{align*} E(t,T):=\sum_{|\gamma|>T}\frac{1}{(\gamma-t)^2}, \end{align*} $$
where t does not coincide with an ordinate of a zero of
![]() $\zeta (s)$
. This function measures, in a certain sense, the difference between the bounds under RH up to height T and the bounds under RH. In fact, for a fixed
$\zeta (s)$
. This function measures, in a certain sense, the difference between the bounds under RH up to height T and the bounds under RH. In fact, for a fixed
![]() $t\geq 0$
, we see that
$t\geq 0$
, we see that
To estimate
![]() $E(t,T)$
, the parameter t must not be close to the ordinates of the zeros, and we need to take T sufficiently large to reduce the contribution. Here, we bound this term using a sum studied by Brent, Platt and Trudgian in [Reference Brent, Platt and Trudgian1].
$E(t,T)$
, the parameter t must not be close to the ordinates of the zeros, and we need to take T sufficiently large to reduce the contribution. Here, we bound this term using a sum studied by Brent, Platt and Trudgian in [Reference Brent, Platt and Trudgian1].
Lemma 2.2. Fix
![]() $0<\delta <1$
and
$0<\delta <1$
and
![]() $T\geq 10^9$
. Then, for
$T\geq 10^9$
. Then, for
![]() $0\leq t\leq (1-\delta )T$
,
$0\leq t\leq (1-\delta )T$
,
where
![]() $E_\delta (T)$
was defined in (1.3).
$E_\delta (T)$
was defined in (1.3).
Proof. Since
![]() $t\leq (1-\delta )T$
, we find that
$t\leq (1-\delta )T$
, we find that
 $$ \begin{align*} E(t,T)=\sum_{|\gamma|>T}\frac{1}{(\gamma-t)^2}= \sum_{\gamma>T}\frac{1}{(\gamma-t)^2}+\sum_{\gamma>T}\frac{1}{(\gamma+t)^2}\leq\bigg(\frac{1}{\delta^2}+1\bigg)\sum_{\gamma>T}\frac{1}{\gamma^2}. \end{align*} $$
$$ \begin{align*} E(t,T)=\sum_{|\gamma|>T}\frac{1}{(\gamma-t)^2}= \sum_{\gamma>T}\frac{1}{(\gamma-t)^2}+\sum_{\gamma>T}\frac{1}{(\gamma+t)^2}\leq\bigg(\frac{1}{\delta^2}+1\bigg)\sum_{\gamma>T}\frac{1}{\gamma^2}. \end{align*} $$
By [Reference Brent, Platt and Trudgian1, Theorem 1 and Example 1],
 $$ \begin{align*} \bigg| {\sum_{\gamma\geq T}}'\frac{1}{\gamma^2}-\frac{1}{2\pi}\int_{T}^\infty\frac{\log(t/2\pi)}{t^2}\,dt\bigg|\leq \frac{0.14 + 0.56\log T}{T^2}, \end{align*} $$
$$ \begin{align*} \bigg| {\sum_{\gamma\geq T}}'\frac{1}{\gamma^2}-\frac{1}{2\pi}\int_{T}^\infty\frac{\log(t/2\pi)}{t^2}\,dt\bigg|\leq \frac{0.14 + 0.56\log T}{T^2}, \end{align*} $$
where the prime symbol
![]() $'$
indicates that if
$'$
indicates that if
![]() $\gamma =T$
, then it is counted with weight
$\gamma =T$
, then it is counted with weight
![]() $1/2$
. Thus,
$1/2$
. Thus,
 $$ \begin{align*} \sum_{\gamma>T}\frac{1}{\gamma^2}\leq \frac{1}{2\pi T}\log\bigg(\frac{T}{2\pi}\bigg)+\frac{1}{2\pi T}+\frac{0.14 + 0.56\log T}{T^2}. \end{align*} $$
$$ \begin{align*} \sum_{\gamma>T}\frac{1}{\gamma^2}\leq \frac{1}{2\pi T}\log\bigg(\frac{T}{2\pi}\bigg)+\frac{1}{2\pi T}+\frac{0.14 + 0.56\log T}{T^2}. \end{align*} $$
Hence, using
![]() $T\geq 10^9$
concludes the proof.
$T\geq 10^9$
concludes the proof.
3. Proof of Theorem 1.1
3.1. Bounding
 $\zeta '(s)/\zeta (s)$
$\zeta '(s)/\zeta (s)$
Assume that RH is true up to height
![]() $T\geq 10^9$
. Let
$T\geq 10^9$
. Let
![]() ${t\geq 10^6}$
and
${t\geq 10^6}$
and
![]() $1\leq \alpha \leq 3/2$
. Given
$1\leq \alpha \leq 3/2$
. Given
![]() $x, y \geq 2$
and
$x, y \geq 2$
and
![]() $s=\alpha +it$
, the unconditional formula [Reference Montgomery and Vaughan9, Equation 13.35] states that
$s=\alpha +it$
, the unconditional formula [Reference Montgomery and Vaughan9, Equation 13.35] states that
![]() $\zeta '(s)/\zeta (s)$
is equal to
$\zeta '(s)/\zeta (s)$
is equal to
 $$ \begin{align} -\sum_{\rho}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}-\sum_{k=1}^\infty\frac{(xy)^{-2k-s}-x^{-2k-s}}{(2k+s)^2\log y}+\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}-\sum_{n\leq xy}\frac{\Lambda(n)}{n^s}w(n),\hfill \end{align} $$
$$ \begin{align} -\sum_{\rho}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}-\sum_{k=1}^\infty\frac{(xy)^{-2k-s}-x^{-2k-s}}{(2k+s)^2\log y}+\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}-\sum_{n\leq xy}\frac{\Lambda(n)}{n^s}w(n),\hfill \end{align} $$
where
![]() $w(n)$
is the function defined in [Reference Montgomery and Vaughan9, page 433] satisfying
$w(n)$
is the function defined in [Reference Montgomery and Vaughan9, page 433] satisfying
![]() $|w(n)|\leq 1$
. We bound each term of (3.1). Since
$|w(n)|\leq 1$
. We bound each term of (3.1). Since
![]() $|(xy)^{\rho -s}-x^{\rho -s}|\leq x^{\mathrm {Re}\,{\rho }-\alpha }(y^{\mathrm {Re}\,{\rho }-\alpha }+1)$
and
$|(xy)^{\rho -s}-x^{\rho -s}|\leq x^{\mathrm {Re}\,{\rho }-\alpha }(y^{\mathrm {Re}\,{\rho }-\alpha }+1)$
and
![]() $\mathrm {Re}\,{\rho }<1$
,
$\mathrm {Re}\,{\rho }<1$
,
 $$ \begin{align*} \bigg|\sum_{\rho} & \frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\bigg| =\bigg|\sum_{|\gamma|\leq T}\frac{(xy)^{\frac{1}{2}+i\gamma-s}-x^{\frac{1}{2}+i\gamma-s}}{(\frac{1}{2}+i\gamma-s)^2\log y} + \sum_{|\gamma|>T}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\bigg| \\ & \leq \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{\log y}\sum_{|\gamma|\leq T}\frac{1}{(\alpha-\frac{1}{2})^2+(t-\gamma)^2} + \frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\,E(t,T). \\ &\leq \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{(\alpha-\frac{1}{2})\log y}\cdot\mathrm{Re}\,\frac{\zeta'(s)}{\zeta(s)}+\frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)\log t}{2(\alpha-\frac{1}{2})\log y}+ \frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\,E_\delta(T), \end{align*} $$
$$ \begin{align*} \bigg|\sum_{\rho} & \frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\bigg| =\bigg|\sum_{|\gamma|\leq T}\frac{(xy)^{\frac{1}{2}+i\gamma-s}-x^{\frac{1}{2}+i\gamma-s}}{(\frac{1}{2}+i\gamma-s)^2\log y} + \sum_{|\gamma|>T}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\bigg| \\ & \leq \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{\log y}\sum_{|\gamma|\leq T}\frac{1}{(\alpha-\frac{1}{2})^2+(t-\gamma)^2} + \frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\,E(t,T). \\ &\leq \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{(\alpha-\frac{1}{2})\log y}\cdot\mathrm{Re}\,\frac{\zeta'(s)}{\zeta(s)}+\frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)\log t}{2(\alpha-\frac{1}{2})\log y}+ \frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\,E_\delta(T), \end{align*} $$
from the assumption that
![]() $10^6\leq t\leq (1-\delta )T$
and Lemmas 2.1 and 2.2. We estimate the next terms in (3.1) trivially as
$10^6\leq t\leq (1-\delta )T$
and Lemmas 2.1 and 2.2. We estimate the next terms in (3.1) trivially as
 $$ \begin{align*} \bigg|\sum_{k=1}^\infty\frac{(xy)^{-2k-s}-x^{-2k-s}}{(2k+s)^2\log y} \bigg|\leq \frac{0.3}{t^2}, \quad \bigg|\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}\bigg| \leq \frac{2.9}{t^2} \end{align*} $$
$$ \begin{align*} \bigg|\sum_{k=1}^\infty\frac{(xy)^{-2k-s}-x^{-2k-s}}{(2k+s)^2\log y} \bigg|\leq \frac{0.3}{t^2}, \quad \bigg|\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}\bigg| \leq \frac{2.9}{t^2} \end{align*} $$
and
 $$ \begin{align*} \bigg|\sum_{n\leq xy}\frac{\Lambda(n)}{n^s}w(n)\bigg|\leq \sum_{n\leq xy}\frac{\Lambda(n)}{n^\alpha}. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n\leq xy}\frac{\Lambda(n)}{n^s}w(n)\bigg|\leq \sum_{n\leq xy}\frac{\Lambda(n)}{n^\alpha}. \end{align*} $$
Inserting these bounds in (3.1), we arrive at
 $$ \begin{align*} \left|\frac{\zeta'(s)}{\zeta(s)}\right| &\leq \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{(\alpha-\frac{1}{2})\log y}{\bigg|\frac{\zeta'(s)}{\zeta(s)}\bigg|} \\ &\quad +\frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)\log t}{2(\alpha-\frac{1}{2})\log y} +\sum_{n\leq xy}\frac{\Lambda(n)}{n^\alpha}+\frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\,E_\delta(T)+\frac{3.2}{t^2}. \end{align*} $$
$$ \begin{align*} \left|\frac{\zeta'(s)}{\zeta(s)}\right| &\leq \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{(\alpha-\frac{1}{2})\log y}{\bigg|\frac{\zeta'(s)}{\zeta(s)}\bigg|} \\ &\quad +\frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)\log t}{2(\alpha-\frac{1}{2})\log y} +\sum_{n\leq xy}\frac{\Lambda(n)}{n^\alpha}+\frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\,E_\delta(T)+\frac{3.2}{t^2}. \end{align*} $$
Now, let
![]() $\lambda _0=1.2784\ldots $
be the point where the function
$\lambda _0=1.2784\ldots $
be the point where the function
![]() $\lambda \mapsto (1+e^\lambda )/\lambda $
reaches its minimum value
$\lambda \mapsto (1+e^\lambda )/\lambda $
reaches its minimum value
![]() $\mathcal {A}_0=3.5911\ldots $
in
$\mathcal {A}_0=3.5911\ldots $
in
![]() $(0,\infty )$
. Take
$(0,\infty )$
. Take
 $$ \begin{align*} y = \exp\bigg(\frac{\lambda_0}{\alpha-\frac{1}{2}}\bigg)\geq 2 \quad\mbox{and}\quad x= \frac{\log^2t}{y}\geq 2. \end{align*} $$
$$ \begin{align*} y = \exp\bigg(\frac{\lambda_0}{\alpha-\frac{1}{2}}\bigg)\geq 2 \quad\mbox{and}\quad x= \frac{\log^2t}{y}\geq 2. \end{align*} $$
Note that
 $$ \begin{align*} \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{(\alpha-\frac{1}{2})\log y}= \mathcal{A}_0(\log t)^{1-2\alpha}<1 \quad\mbox{and}\quad \frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\leq \frac{2}{\log y}=\frac{2\alpha-1}{\lambda_0}. \end{align*} $$
$$ \begin{align*} \frac{x^{\frac{1}{2}-\alpha}(y^{\frac{1}{2}-\alpha}+1)}{(\alpha-\frac{1}{2})\log y}= \mathcal{A}_0(\log t)^{1-2\alpha}<1 \quad\mbox{and}\quad \frac{x^{1-\alpha}(y^{1-\alpha}+1)}{\log y}\leq \frac{2}{\log y}=\frac{2\alpha-1}{\lambda_0}. \end{align*} $$
Therefore, we get
 $$ \begin{align} \bigg|\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}\bigg| \leq (1+ \epsilon(\alpha,t))\bigg[\frac{\mathcal{A}_0}{2}{(\log t)^{2-2\alpha}} +\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n^\alpha}+ \frac{(2\alpha-1)}{\lambda_0}E_\delta(T)+\frac{3.2}{t^2}\bigg], \end{align} $$
$$ \begin{align} \bigg|\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}\bigg| \leq (1+ \epsilon(\alpha,t))\bigg[\frac{\mathcal{A}_0}{2}{(\log t)^{2-2\alpha}} +\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n^\alpha}+ \frac{(2\alpha-1)}{\lambda_0}E_\delta(T)+\frac{3.2}{t^2}\bigg], \end{align} $$
where
![]() $\epsilon (\alpha ,t)$
is defined as
$\epsilon (\alpha ,t)$
is defined as
 $$ \begin{align*} \epsilon(\alpha,t):=\frac{1}{\mathcal{A}_0^{-1}(\log t)^{2\alpha-1}-1}. \end{align*} $$
$$ \begin{align*} \epsilon(\alpha,t):=\frac{1}{\mathcal{A}_0^{-1}(\log t)^{2\alpha-1}-1}. \end{align*} $$
3.2. Bounding
 $\zeta '(1+it)/\zeta (1+it)$
$\zeta '(1+it)/\zeta (1+it)$
Letting
![]() $\alpha =1$
in (3.2), it follows that
$\alpha =1$
in (3.2), it follows that
 $$ \begin{align*} \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq(1+ \epsilon(1,t))\bigg[\frac{\mathcal{A}_0}{2} +\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n}+ \frac{E_\delta(T)}{\lambda_0}+\frac{3.2}{t^2}\bigg]. \end{align*} $$
$$ \begin{align*} \bigg|\frac{\zeta'(1+it)}{\zeta(1+it)}\bigg|\leq(1+ \epsilon(1,t))\bigg[\frac{\mathcal{A}_0}{2} +\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n}+ \frac{E_\delta(T)}{\lambda_0}+\frac{3.2}{t^2}\bigg]. \end{align*} $$
To bound the sum over the primes in the above expression, we use the estimate (see [Reference Johnston, Ramaré and Trudgian5, Lemma 10])
 $$ \begin{align*} \sum_{n\leq X}\frac{\Lambda(n)}{n}\leq \log X - \gamma + \frac{1.3}{\log^2X} \quad \mbox{for all} \ X>1. \end{align*} $$
$$ \begin{align*} \sum_{n\leq X}\frac{\Lambda(n)}{n}\leq \log X - \gamma + \frac{1.3}{\log^2X} \quad \mbox{for all} \ X>1. \end{align*} $$
Finally, using
![]() $t\geq 10^6$
, we arrive at (1.4).
$t\geq 10^6$
, we arrive at (1.4).
3.3. Bounding log
 $\zeta (1+it)$
$\zeta (1+it)$
By the fundamental calculus theorem,
 $$ \begin{align*} \log\zeta(1+it) = \log\zeta\left(\frac{3}{2}+it\right) -\int_{1}^{{3}/{2}}\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}\,d\alpha. \end{align*} $$
$$ \begin{align*} \log\zeta(1+it) = \log\zeta\left(\frac{3}{2}+it\right) -\int_{1}^{{3}/{2}}\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}\,d\alpha. \end{align*} $$
Since
![]() $|\!\log \zeta (\tfrac {3}{2}+it)|\leq \log \zeta (\tfrac {3}{2})$
, we obtain
$|\!\log \zeta (\tfrac {3}{2}+it)|\leq \log \zeta (\tfrac {3}{2})$
, we obtain
 $$ \begin{align*} |\!\log\zeta(1+it)|\leq \int_{1}^{{3}/{2}}\bigg|\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}\bigg|\,d\alpha +\log\zeta\left(\frac{3}{2}\right). \end{align*} $$
$$ \begin{align*} |\!\log\zeta(1+it)|\leq \int_{1}^{{3}/{2}}\bigg|\frac{\zeta'(\alpha+it)}{\zeta(\alpha+it)}\bigg|\,d\alpha +\log\zeta\left(\frac{3}{2}\right). \end{align*} $$
To bound the right-hand side of this inequality, we use
![]() $\epsilon (\alpha ,t)\leq \epsilon (1,t)$
in
$\epsilon (\alpha ,t)\leq \epsilon (1,t)$
in
![]() $1\leq \alpha \leq 3/2$
and integrate (3.2) from
$1\leq \alpha \leq 3/2$
and integrate (3.2) from
![]() $1$
to
$1$
to
![]() $3/2$
to obtain
$3/2$
to obtain
 $$ \begin{align*} |\!\log\zeta(1+it)| &\leq (1+ \epsilon(1,t))\bigg[\frac{\mathcal{A}_0}{4\log\log t}+\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n\log n}-\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n} +\frac{3E_\delta(T)}{4\lambda_0}\bigg]\\ &\quad +\log\zeta\left(\frac{3}{2}\right), \end{align*} $$
$$ \begin{align*} |\!\log\zeta(1+it)| &\leq (1+ \epsilon(1,t))\bigg[\frac{\mathcal{A}_0}{4\log\log t}+\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n\log n}-\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n} +\frac{3E_\delta(T)}{4\lambda_0}\bigg]\\ &\quad +\log\zeta\left(\frac{3}{2}\right), \end{align*} $$
where we have used
![]() $-\mathcal {A}_0/(4\log t\log \log t)+1.6/t^2<0$
. Furthermore, since
$-\mathcal {A}_0/(4\log t\log \log t)+1.6/t^2<0$
. Furthermore, since
 $$ \begin{align*}\log\zeta\left(\frac{3}{2}\right)= \sum_{n\geq 1}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n}=0.960\ldots,\end{align*} $$
$$ \begin{align*}\log\zeta\left(\frac{3}{2}\right)= \sum_{n\geq 1}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n}=0.960\ldots,\end{align*} $$
we have
 $$ \begin{align*} \left(1+ \epsilon(1,t)\right)\sum_{n> \log^2t}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n}\leq \epsilon(1,t)\sum_{n\geq 1}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n}, \end{align*} $$
$$ \begin{align*} \left(1+ \epsilon(1,t)\right)\sum_{n> \log^2t}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n}\leq \epsilon(1,t)\sum_{n\geq 1}\frac{\Lambda(n)}{n^{\frac{3}{2}}\log n}, \end{align*} $$
for
![]() $t\geq 10^6$
. This implies that
$t\geq 10^6$
. This implies that
 $$ \begin{align} |\!\log\zeta(1+it)| \leq (1+ \epsilon(1,t))\bigg[\frac{\mathcal{A}_0}{4\log\log t}+\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n\log n} +\frac{3E_\delta(T)}{4\lambda_0}\bigg]. \end{align} $$
$$ \begin{align} |\!\log\zeta(1+it)| \leq (1+ \epsilon(1,t))\bigg[\frac{\mathcal{A}_0}{4\log\log t}+\sum_{n\leq \log^2t}\frac{\Lambda(n)}{n\log n} +\frac{3E_\delta(T)}{4\lambda_0}\bigg]. \end{align} $$
To bound the sum over the primes, we use [Reference Rosser and Schoenfeld13, Equation (3.30)] to see that, for
![]() $x>1$
,
$x>1$
,
 $$ \begin{align*} \sum_{n\leq x}\frac{\Lambda(n)}{n\log n}\leq \sum_{p\leq x}\sum_{k= 1}^{\infty}\frac{1}{kp^k}=\log\prod_{p\leq x}\bigg(1-\frac{1}{p}\bigg)^{-1}\leq \log\log x+\gamma + \frac{1}{\log^2x}. \end{align*} $$
$$ \begin{align*} \sum_{n\leq x}\frac{\Lambda(n)}{n\log n}\leq \sum_{p\leq x}\sum_{k= 1}^{\infty}\frac{1}{kp^k}=\log\prod_{p\leq x}\bigg(1-\frac{1}{p}\bigg)^{-1}\leq \log\log x+\gamma + \frac{1}{\log^2x}. \end{align*} $$
Inserting this in (3.3), we arrive at
 $$ \begin{align*} &|\!\log\zeta(1+it)| \\ &\quad \leq (1+ \epsilon(1,t))\bigg[\log\log\log t + \log(2e^\gamma)+\frac{\mathcal{A}_0}{4\log\log t}+\frac{1}{4(\log\log t)^2} +\frac{3E_\delta(T)}{4\lambda_0}\bigg]. \end{align*} $$
$$ \begin{align*} &|\!\log\zeta(1+it)| \\ &\quad \leq (1+ \epsilon(1,t))\bigg[\log\log\log t + \log(2e^\gamma)+\frac{\mathcal{A}_0}{4\log\log t}+\frac{1}{4(\log\log t)^2} +\frac{3E_\delta(T)}{4\lambda_0}\bigg]. \end{align*} $$
Thus,
 $$ \begin{align} |\!\log\zeta(1+it)|\leq \log\log\log t + \log(2e^\gamma)+\frac{3.404}{\log\log t}+0.793E_\delta(T). \end{align} $$
$$ \begin{align} |\!\log\zeta(1+it)|\leq \log\log\log t + \log(2e^\gamma)+\frac{3.404}{\log\log t}+0.793E_\delta(T). \end{align} $$
Taking exponentials in this inequality and using the estimate
![]() $e^x\leq 1+x+0.8093x^2$
for
$e^x\leq 1+x+0.8093x^2$
for
![]() $0\leq x\leq 1.297$
, we obtain
$0\leq x\leq 1.297$
, we obtain
 $$ \begin{align*} \exp(|\!\log\zeta(1+it)|)\leq {2e^\gamma}\bigg(\log\log t +3.404 + \frac{9.378}{\log \log t}\bigg)\cdot\exp(0.793E_\delta(T)). \end{align*} $$
$$ \begin{align*} \exp(|\!\log\zeta(1+it)|)\leq {2e^\gamma}\bigg(\log\log t +3.404 + \frac{9.378}{\log \log t}\bigg)\cdot\exp(0.793E_\delta(T)). \end{align*} $$
Since
![]() $\log |\zeta (1+it)|^{-1}\leq |\!\log \zeta (1+it)|$
and
$\log |\zeta (1+it)|^{-1}\leq |\!\log \zeta (1+it)|$
and
![]() $\log |\zeta (1+it)|\leq |\!\log \zeta (1+it)|$
, we deduce (1.5) and (1.6), respectively.
$\log |\zeta (1+it)|\leq |\!\log \zeta (1+it)|$
, we deduce (1.5) and (1.6), respectively.
Acknowledgement
I am grateful to Harald Helfgott for encouraging me in this project and for helpful discussions related to the material in this paper.