Shape- and scale-dependent coupling between spheroids and velocity gradients in turbulence

Abstract

Rotations of spheroidal particles immersed in turbulent flows reflect the combined effects of fluid strain and vorticity, as well as the time history of these quantities along the particle's trajectory. Conversely, particle rotation statistics in turbulence provide a way to characterise the Lagrangian properties of velocity gradients. Particle rotations are also important for a range of environmental and industrial processes where particles of various shapes and sizes are immersed in a turbulent flow. In this study, we investigate the rotations of inertialess spheroidal particles that follow Lagrangian fluid trajectories. We perform direct numerical simulations (DNS) of homogeneous isotropic turbulence and investigate the dynamics of different particle shapes at different scales in turbulence using a filtering approach. We find that the mean-square particle angular velocity is nearly independent of particle shape across all scales from the Kolmogorov scale to the integral scale. The particle shape does determine the relative split between different modes of rotation (spinning vs tumbling), but this split is also almost independent of the filter scale suggesting a Lagrangian scale-invariance in velocity gradients. We show how the split between spinning and tumbling can be quantitatively related to the particle's alignment with respect to the fluid vorticity.

1. Introduction

In the Lagrangian study of turbulence, a point-sized sphere is used to probe the flow since such a particle adopts the velocity and angular velocity of the fluid in its immediate vicinity. Extending this idea to spheroids (figure 1) offers a more intricate way to examine the Lagrangian flow structure since spheroids rotate due to both fluid rotation and strain, and thus the statistics of spheroid rotations reflect the Lagrangian dynamics of velocity gradients (Voth & Soldati 2017). Rotations of spheroidal particles and their coupling with velocity gradients are also important in applications where non-spherical particles are immersed in turbulent flows, such as microswimmers (Jumars et al. 2009; Guasto, Rusconi & Stocker 2012; Pujara, Koehl & Variano 2018; Borgnino et al. 2019; Bordoloi, Variano & Verhille 2020), atmospheric aerosol and sediment transport (Spurny 2000; Mehta 2013; Gustavsson & Mehlig 2016; Roy et al. 2019; Gustavsson et al. 2021; Li et al. 2021; Samant et al. 2021), process engineering (Clift, Grace & Weber 2005; Lundell, Söderberg & Alfredsson 2011; Ardekani et al. 2017; Ardekani & Brandt 2018; Schneiders et al. 2019; Will et al. 2021) and flow diagnostics (Rosti et al. 2018; Hejazi, Krellenstein & Voth 2019; Cavaiola, Olivieri & Mazzino 2020).

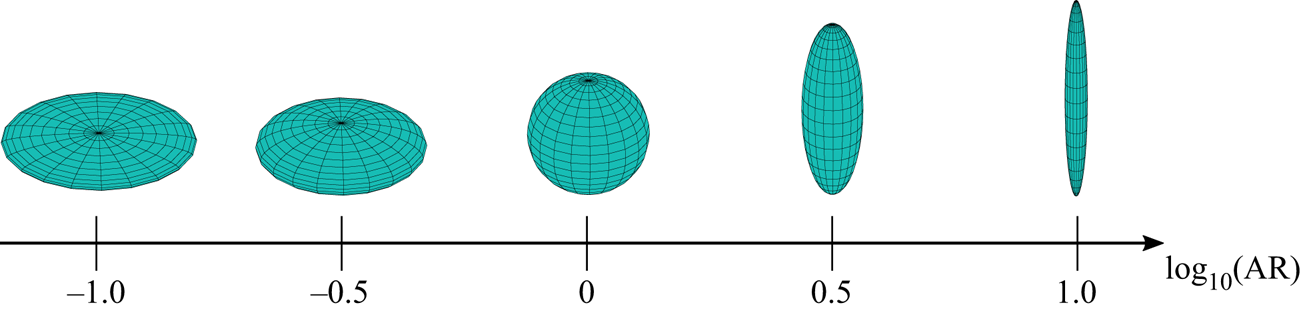
Figure 1. Spheroids as a function of aspect ratio (AR).

In this study, we examine how spheroids of different shapes rotate due to their coupling with velocity gradients at different scales in homogeneous and isotropic turbulence. The angular velocity of a spheroid due to local velocity gradients in the absence of inertia is given by Jeffery's (1922) equation:

(1.1)\begin{equation} \boldsymbol{\omega}_{\boldsymbol{p}} = \tfrac{1}{2}\boldsymbol{\omega} + \lambda \boldsymbol{p} \times \boldsymbol{\mathsf{S}}\boldsymbol{p}, \end{equation}

where $\boldsymbol {\omega }_{\boldsymbol {p}}$ is the particle angular velocity vector, $\boldsymbol {p}$ is the particle orientation vector and $\lambda = (\mathrm {AR}^2 - 1)/(\mathrm {AR}^2 + 1)$ is the shape factor with $\mathrm {AR}$ being the particle aspect ratio (figure 1). The velocity gradients are represented by the fluid vorticity vector $\boldsymbol {\omega }$ and the strain-rate tensor $\boldsymbol{\mathsf{S}}$, which relate to the velocity gradient tensor ${\mathsf{A}}_{ij} = \partial u_{i}/\partial x_j$ via ${{\mathsf{S}}_{ij}} = \tfrac {1}{2}({\mathsf{A}}_{ij} + {\mathsf{A}}_{ji})$ and $\omega _i = \varepsilon _{ijk}{\mathsf{A}}_{kj}$ with $\varepsilon _{ijk}$ being the alternating symbol. The first term of (1.1) shows that particles of all aspect ratios rotate at the local rotation rate of the fluid and the second term shows that non-spherical particles have additional rotation due to the local strain rate. Decomposing (1.1) into its spinning $(\boldsymbol {\omega _{p}} \boldsymbol {\cdot } \boldsymbol {p})$ and tumbling $(\mathrm {d}\boldsymbol {p}/\mathrm {d}t = \dot {\boldsymbol {p}} = \boldsymbol {\omega }_{\boldsymbol {p}} \times \boldsymbol {p})$ rates gives

(1.2a)$$\begin{gather} \boldsymbol{\omega}_{\boldsymbol{p}} \boldsymbol{\cdot} \boldsymbol{p} = \tfrac{1}{2}\boldsymbol{\omega}\boldsymbol{\cdot}\boldsymbol{p} \end{gather}$$

(1.2b)$$\begin{gather}\dot{\boldsymbol{p}} = \tfrac{1}{2} \boldsymbol{\omega} \times \boldsymbol{p} + \lambda [\boldsymbol{\mathsf{S}}\boldsymbol{p} - (\,{\boldsymbol{p}}^{T}\boldsymbol{\mathsf{S}}\boldsymbol{p})\boldsymbol{p} ], \end{gather}$$

where spinning is the particle rotation about its axis of symmetry and tumbling is the particle rotation of the axis of symmetry. Spinning and tumbling are related to the total particle angular velocity via the Pythagorean relation $\boldsymbol {\omega }_{\boldsymbol {p}}^2 = (\boldsymbol {\omega }_{\boldsymbol {p}} \boldsymbol {\cdot } \boldsymbol {p})^2 + \dot {\boldsymbol {p}}^2$.

When spheroids follow Lagrangian fluid trajectories and rotate in response to the velocity gradients along those trajectories, the mean-square spinning ($\langle (\boldsymbol {\omega }_{\boldsymbol {p}} \boldsymbol {\cdot } \boldsymbol {p})^2 \rangle$) and tumbling ($\langle \dot {\boldsymbol {p}}^2 \rangle$) rates reflect the distribution of particle orientations with respect to principal directions of the velocity gradients. Equation (1.2b) shows that the particle tumbling rate for a given shape in isotropic turbulence is a joint distribution in a seven-dimensional space (Ni et al. 2015): five scalar parameters characterise the velocity gradient tensor in isotropic turbulence (e.g. two to quantify the eigenvalues of the strain-rate tensor, two to specify the orientation of vorticity in the strain-rate eigenframe, and one to quantify the magnitude of vorticity) and an additional two parameters describe the particle orientation with respect to the velocity gradient tensor (e.g. two angles relative to the strain-rate eigenframe). Thus, the spinning and tumbling rates depend on the history of vorticity and strain along Lagrangian trajectories. Being able to predict these rotation rates is useful for the applications mentioned above and for benchmarking stochastic models of the velocity gradient tensor; for example, Chevillard & Meneveau (2013) showed that a model based on the recent fluid deformation approximation was able to correctly predict the tumbling of rods and Leppin & Wilczek (2020) showed that inclusion of strain-vorticity interactions and shorter autocorrelation time scales for the strain rate compared with the rotation rate were crucial for predicting the tumbling of discs.

Spinning and tumbling rates can be predicted analytically for particles randomly oriented with respect to the velocity gradient tensor, but results from experiments and direct numerical simulations (DNS) have shown that this does not provide an accurate prediction of particle rotation rates in turbulence (Shin & Koch 2005; Parsa et al. 2012; Chevillard & Meneveau 2013; Byron et al. 2015; Pujara & Variano 2017). For example, tumbling of small rods ($\textrm {AR} \gg 1$) and spinning of small discs ($\textrm {AR} \ll 1$) are suppressed relative to their values for random orientation. Qualitatively, this is understood to be because rods align with the vorticity causing them to spin more than they tumble and discs align perpendicularly to the vorticity causing them to tumble more than they spin (Pumir & Wilkinson 2011; Ni, Ouellette & Voth 2014; Byron et al. 2015). While this picture suggests that alignment with vorticity controls the dynamics of particle rotations, a quantitative understanding of this behaviour has not been found. For example, conditional averages of the seven-dimensional joint distribution showed that rod tumbling was equally strongly dependent on both the mean-square vorticity and strain rate and the problem could not be further simplified via a lower-dimensional projection (Ni et al. 2015). Here, we present a line of argument that allows us to quantitatively predict the spinning and tumbling rates of spheroids in isotropic turbulence based on their alignment with vorticity. We test this prediction against data from DNS and find good agreement.

Since spheroid rotation statistics reveal Lagrangian dynamics of velocity gradients, an understanding of the scale-dependency of these statistics can contribute to improving models of the turbulent energy cascade (Meneveau & Lund 1994; Chertkov, Pumir & Shraiman 1999; Luthi et al. 2007; Xu, Pumir & Bodenschatz 2011; Pumir, Bodenschatz & Xu 2013), subgrid-scale models for large-eddy simulations (Meneveau, Lund & Cabot 1996; van der Bos et al. 2002) and models of particle motion (Toschi & Bodenschatz 2009; Cisse, Homann & Bec 2013; Parsa & Voth 2014). As a way to characterise multiscale properties of Lagrangian turbulence, we investigate the scale-dependency in our simulations using a filtering approach where particle rotations are tracked along Lagrangian trajectories in turbulent velocity fields filtered at various scales. Our results show that particle rotation statistics are remarkably scale-independent when normalised appropriately and we are able to predict the spinning and tumbling rates for different shapes from the dissipation scales to the integral scale. We interpret this as a sign of fairly robust scale-invariance for velocity gradients across the complete scale spectrum of turbulence when examined in the Lagrangian frame.

2. Direct numerical simulations

2.1. Velocity gradients along Lagrangian trajectories

We use DNS of isotropic turbulence to generate data of velocity gradient time histories along Lagrangian trajectories. We do this in the fully resolved flow field and for the flow field filtered at various length scales.

The DNS are performed with a standard pseudo-spectral Navier–Stokes solver. A third-order Runge–Kutta method is used for time stepping the vorticity formulation of the equation, and a high-order Fourier smoothing (Hou & Li 2007) is used for reducing aliasing errors. Turbulence is maintained in a 3-D-periodic domain of $2{\rm \pi} \times 2{\rm \pi} \times 2{\rm \pi}$ (DNS units) by applying a fixed energy injection rate in the wavenumber interval $1 \leqslant k \leqslant 2$ (DNS units). We use a small-scale resolution of $k_M \eta = 3$ (where $k_M$ is the maximum wavenumber resolved and $\eta$ is the Kolmogorov length) for a fully developed turbulent flow with a Taylor-scale Reynolds number $R_\lambda \approx 200$ and a scale separation of $L / \eta \approx 140$ and $T / \tau _\eta \approx 20$. Using the root-mean-squared velocity component u and the energy spectrum $E(k)$, the integral length is defined as $L = {\rm \pi}\int \textrm {d}k E(k) / (2k u^2)$ and the large eddy turn-over time as $T = L / u$. To generate filtered flow fields, the velocity field is filtered at length scale $\ell$ using a Gaussian filter as detailed in Lalescu & Wilczek (2018). Values for $\ell$ vary from zero (no filtering) to $L$ (the integral scale). Preliminary datasets were generated using all three spherically symmetric filter types described in Lalescu & Wilczek (2018) (i.e. ball filter, Gaussian filter, sharp spectral filter), but the filter type resulted in only small changes in the results with the overall trend being insensitive to the precise filter type.

At each filter scale $\ell$, $10^4$ tracer trajectories are integrated in the flow using the corresponding velocity fields, and the velocity gradient tensor is sampled along these trajectories to generate a large database of Lagrangian time histories of velocity gradients along tracer trajectories.

To analyse particle rotations across different filter scales, we introduce a scale-local time scale defined by $\tau _{\ell } = \langle {\mathsf{A}}_{ij} {\mathsf{A}}_{ij} \rangle ^{-1/2}$, which varies smoothly from $\tau _\eta$ for the fully resolved flow to the expected Kolmogorov scaling $\tau _{\ell } \sim \ell ^{2/3}$ in the inertial subrange (figure 2a). Here $\tau _{\ell }$ is a quantitative measure of the correlation time and the inverse strength of the velocity gradients at scale $\ell$, making it ideally suited to compare particle rotations across a range of scales. Note that we do not explicitly distinguish between filtered and unfiltered quantities in our notation. The filtering is implicitly indicated wherever there is a variation with $\ell$.

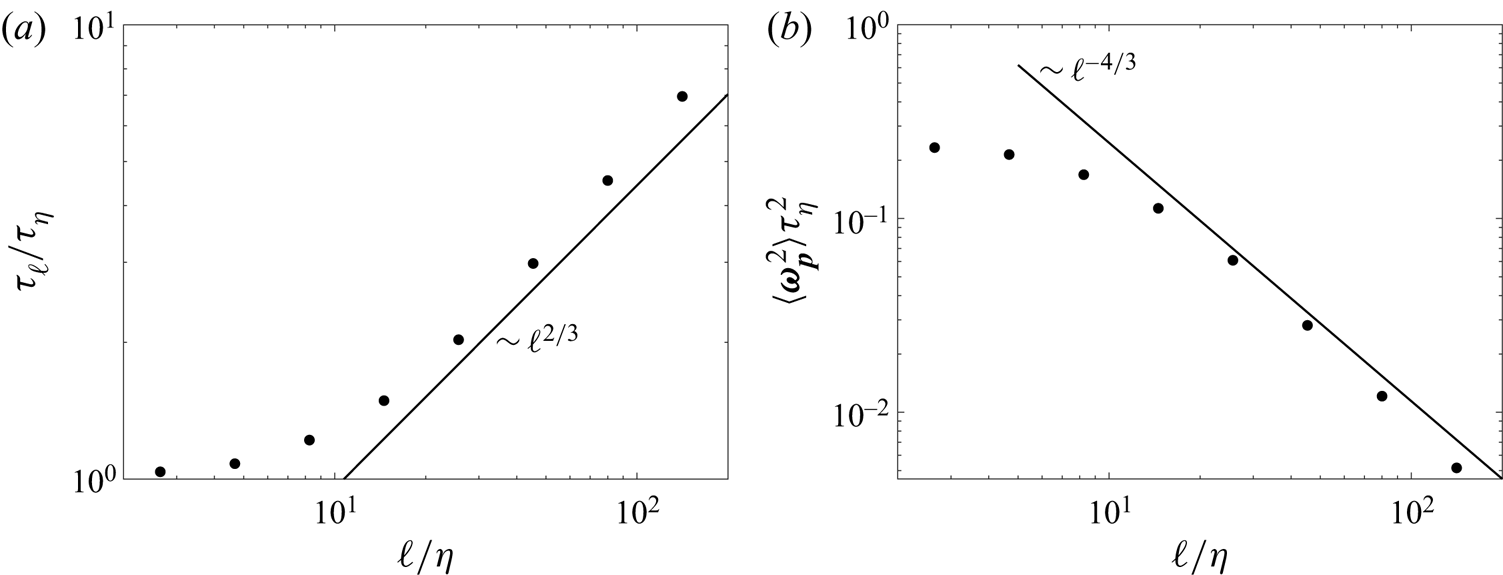
Figure 2. Variation of (a) scale-local time scale $\tau _{\ell } = \langle {\mathsf{A}}_{ij} {\mathsf{A}}_{ij} \rangle ^{-1/2}$ and (b) mean-square particle angular velocity $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle$ as functions of filter scale $\ell$. Data in panel (b) is for spherical particles.

2.2. Scale-dependency in particle rotation statistics

We use the database of Lagrangian time histories of velocity gradients to compute the orientations and rotations of spheroids by integrating Jeffery's (1922) equations (1.2b) using a fourth-order Runge–Kutta method. After an initial transient of several $\tau _{\ell }$, the statistics of particle rotations reach a stationary state. We calculate the statistical moments of particle rotations after this initial transient period.

Figure 2(b) shows that data for mean-square particle angular velocity follows a power law scaling in the inertial subrange $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle \sim \ell ^{-4/3}$. This scaling behaviour, which was first introduced in the context of tumbling rods by Parsa & Voth (2014) and found to be applicable in several other contexts since then (Bordoloi & Variano 2017; Bounoua, Bouchet & Verhille 2018; Pujara et al. 2018; Pujara, Voth & Variano 2019; Oehmke et al. 2021), can be derived based on the expectation that the particle rotation rate scales as the magnitude of the velocity gradients at a given scale $\boldsymbol {\omega }_{\boldsymbol {p}} \sim \tau _{\ell }^{-1} = \langle {\mathsf{A}}_{ij} {\mathsf{A}}_{ij} \rangle ^{1/2}$ and that the magnitude of the velocity gradients follow Kolmogorov scaling in the inertial range ${\mathsf{A}}_{ij} \sim \ell ^{-2/3}$.

When the mean-square particle angular velocity is examined in terms of the scale-local time scale $\tau _{\ell }$ in figure 3(a), we observe that the mean-square rotation rate for particles for all scales is almost shape-independent. Particles of all shapes have approximately the same rotation rate as spheres (or spherical fluid elements) at all scales of turbulence so that $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle \approx \tfrac {1}{4}\langle \boldsymbol {\omega }^2 \rangle$. Surprisingly, figure 3(a) also shows that the relationship between particle shape and their spinning and tumbling rates is qualitatively preserved as the filter scale increases, even up to the integral scale. Discs tumble much more than they spin and rods spin more than they tumble at all scales of turbulence. As the filter scale increases, there is a shift towards the spinning and tumbling rates becoming weaker functions of particle shape, but the main qualitative trend is preserved. Overall, the results in figure 3(a), which are normalised by the scale-local time scale $\tau _{\ell }$, reflect an unexpected scale-invariance in the Lagrangian dynamics of velocity gradients.

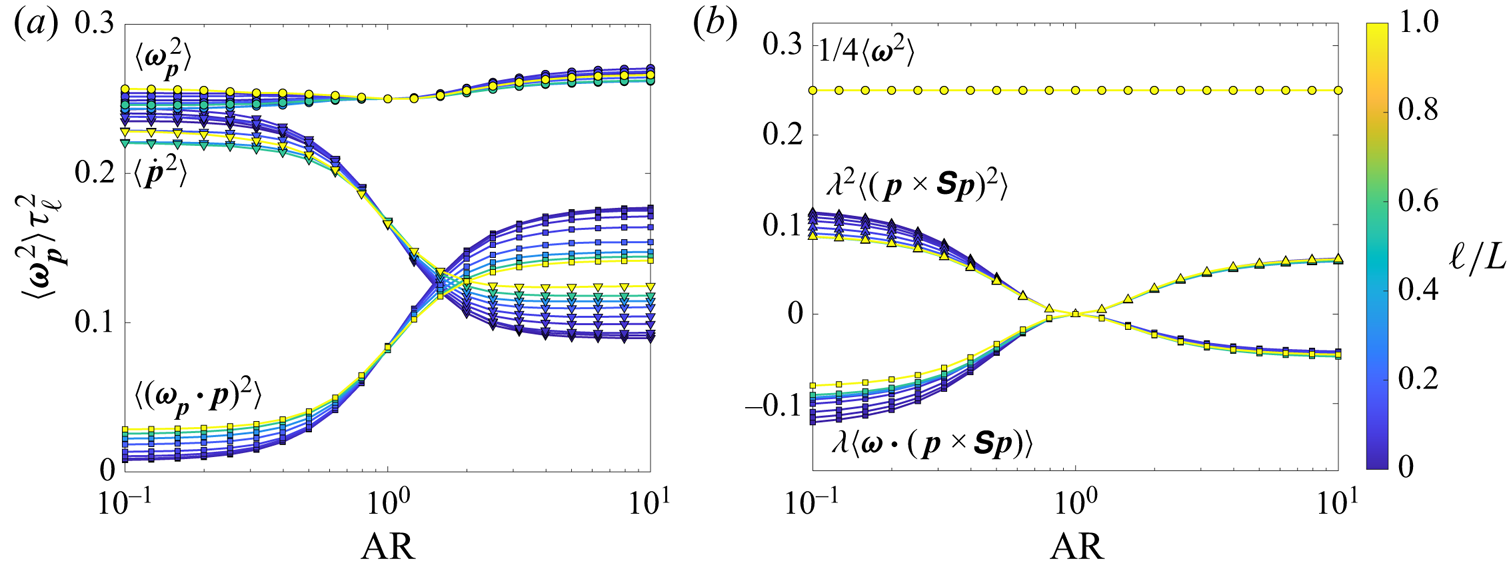
Figure 3. (a) Mean-square particle angular velocity and its decomposition into spinning and tumbling for spheroids of different aspect ratios in turbulence filtered at different length scales. (b) Mean-square particle angular velocity and its decomposition into vorticity-induced rotations ($\tfrac {1}{4}\langle \boldsymbol {\omega }^2 \rangle$), strain-induced rotations ($\lambda ^2 \langle (\,\boldsymbol {p} \times \boldsymbol{\mathsf{S}}\boldsymbol {p} )^2 \rangle$), and the cross-correlation of vorticity- and strain-induced rotations ($\lambda \langle \boldsymbol {\omega } \boldsymbol {\cdot } (\,\boldsymbol {p} \times \boldsymbol{\mathsf{S}}\boldsymbol {p} ) \rangle$).

To further examine the shape independence of the mean-square particle angular velocity $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle$, we take the mean square of (1.1) to analyse the situation in terms of rotations due to vorticity and strain. This shows that the mean-square particle angular velocity has contributions from vorticity, strain rate and a combination of vorticity and strain:

(2.1)\begin{equation} \langle \boldsymbol{\omega}_{\boldsymbol{p}}^2 \rangle = \tfrac{1}{4}\langle \boldsymbol{\omega}^2 \rangle + \lambda^2 \langle \left(\,\boldsymbol{p} \times \boldsymbol{\mathsf{S}}\boldsymbol{p} \right)^2 \rangle + \lambda \langle \boldsymbol{\omega} \boldsymbol{\cdot} \left(\,\boldsymbol{p} \times \boldsymbol{\mathsf{S}}\boldsymbol{p} \right) \rangle. \end{equation}

The particle shape only influences the second and third terms, which contain the strain-rate tensor. Figure 3(b) shows the particle rotation rates split into the three terms in (2.1). While the vorticity term is shape-independent and the strain term is always positive as expected, the cross term is almost exactly equal and opposite to the strain term. This near cancellation is the reason why $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle$ is nearly independent of particle shape at all scales in turbulence. We note that this behaviour is specific to Lagrangian trajectories and the mutual interactions between vorticity and strain-rate along these trajectories. The rotations of particles distributed at random positions and orientations within a snapshot of a turbulent velocity field do not show the same behaviour (as previously shown in Parsa et al. 2012; Chevillard & Meneveau 2013; Pujara & Variano 2017). While this property of vorticity-strain interactions in the Lagrangian dynamics of velocity gradients was previously noted for point-sized particles (Byron et al. 2015; Pujara & Variano 2017), the results in figure 3(b) show that this behaviour is scale-invariant.

2.3. Particle spinning and tumbling

In this section, we show how the particle spinning and tumbling rates observed in figure 3(a) can be quantitatively predicted in terms of particle alignment with vorticity. Starting from (2.1), we note that an (approximate) cancellation of the last two terms on the right-side leads to $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle \approx \tfrac {1}{4} \langle \boldsymbol {\omega }^2 \rangle$. In homogeneous isotropic turbulence, the mean-square fluid vorticity and the mean dissipation rate are related via $\langle \boldsymbol {\omega }^2 \rangle = 2 \langle {\mathsf{S}}_{ij}{\mathsf{S}}_{ij} \rangle = \tau _{\eta }^{-2}$, where $\tau _{\eta }$ is the Kolmogorov time scale that characterises the smallest scales of motion. In terms of $\tau _{\eta }$, the mean-square particle rotation rate would be

(2.2)\begin{equation} \langle \boldsymbol{\omega}_{\boldsymbol{p}}^2 \rangle \approx \tfrac{1}{4} \tau_{\eta}^{{-}2}. \end{equation}

To predict the spinning and tumbling rates of particles, we next consider the spinning equation. By taking the mean square of (1.2a), we get

(2.3)\begin{equation} \langle ( \boldsymbol{\omega_{p}} \boldsymbol{\cdot} \boldsymbol{p} )^2 \rangle = \tfrac{1}{4} \langle \boldsymbol{\omega}^2 \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle \approx \tfrac{1}{4} \langle \boldsymbol{\omega}^2 \rangle \langle \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle = \tfrac{1}{4} \tau_{\eta}^{{-}2} \langle \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle, \end{equation}

where we have assumed that the magnitude of vorticity and the degree of alignment between the particle and the vorticity are statistically independent. Here, e_ω is the unit vector that defines the direction of vorticity. Under this assumption, (2.3) gives a prediction for the mean-square spinning rate solely based on particle alignment with vorticity. We can also obtain a prediction for the tumbling rate in terms of the particle alignment with vorticity by combining (2.3) with (2.2) and using the Pythagorean relation $\langle \boldsymbol {\omega }_{\boldsymbol {p}}^2 \rangle = \langle (\boldsymbol {\omega }_{\boldsymbol {p}} \boldsymbol {\cdot } \boldsymbol {p})^2 \rangle + \langle \dot {\boldsymbol {p}}^2 \rangle$:

(2.4)\begin{equation} \langle \dot{\boldsymbol{p}}^2 \rangle \approx \tfrac{1}{4}\langle \boldsymbol{\omega}^2 \rangle (1 - \langle \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle ) = \tfrac{1}{4} \tau_{\eta}^{{-}2} \langle (1 - \langle \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle ). \end{equation}

Altogether, we have predictions of the particle rotation, tumbling and spinning rates solely in terms of the particle alignment with vorticity:

(2.5a)$$\begin{gather} \langle \boldsymbol{\omega}_{\boldsymbol{p}}^2 \rangle \tau_{\eta}^{2} \approx \tfrac{1}{4}, \end{gather}$$

(2.5b)$$\begin{gather}\langle \dot{\boldsymbol{p}}^2 \rangle \tau_{\eta}^{2} \approx \tfrac{1}{4}(1 - \langle \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle), \end{gather}$$

(2.5c)$$\begin{gather}\langle ( \boldsymbol{\omega_{p}} \boldsymbol{\cdot} \boldsymbol{p} )^2 \rangle \tau_{\eta}^{2} \approx \tfrac{1}{4}\langle \left( \boldsymbol{e}_{\omega} \boldsymbol{\cdot}\boldsymbol{p} \right)^2 \rangle. \end{gather}$$

We can now examine the predictions of (2.5) using data from our simulations. By replacing $\tau _{\eta }$ with $\tau _{\ell }$, we can also extend these predictions to all scales of turbulence. Since these predictions are based on the mean-square particle alignment with vorticity, we first show this quantity in figure 4. We see that while discs tend to be perpendicular to the vorticity and rods tend to be parallel to the vorticity, particles of all shapes become more randomly aligned with respect to vorticity as the filter scale increases. Particle alignment with vorticity can be understood as the longest particle axis and the vorticity vector both independently coming to align with the direction of Lagrangian stretching (Ni et al. 2014). The data in figure 4 show that this effect weakens with increasing filter scale due to the effects of subfilter-scale motions on the velocity gradient dynamics (Chertkov et al. 1999; Pujara et al. 2019).

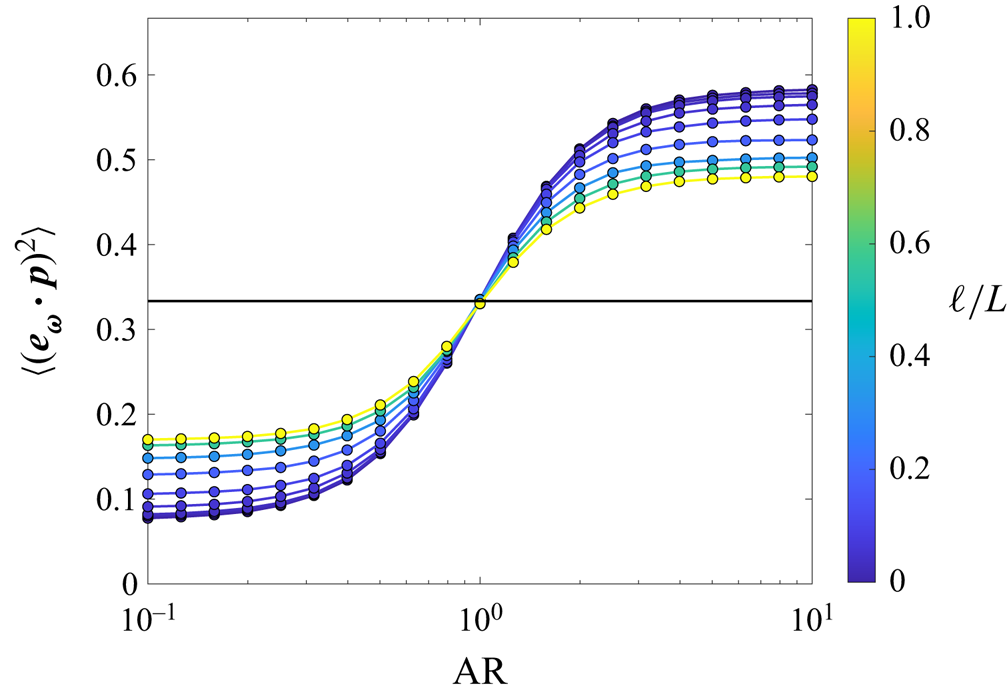
Figure 4. Mean-square particle alignment with vorticity as a function of particle shape and filter scale. Random alignment corresponds to a value of 1/3 (solid black line).

Next, we examine the assumption made in deriving (2.5), namely that particle alignment with vorticity is independent of the vorticity magnitude. Figure 5(a) shows the particle-vorticity alignment conditioned on the square of the vorticity magnitude for high-aspect-ratio rods and discs. We see that particle alignment with vorticity is stronger as the vorticity magnitude is increased, which likely reflects a recent history of Lagrangian stretching, but this variation does not stray too far from the overall mean-square alignment (shown by the thin horizontal coloured lines in figure 5). Examined in this way, our assumption is only partially supported by the data. However, in figure 5(b), we show a more direct evaluation of the assumption made in (2.3), namely that particle spinning can be related to particle alignment with vorticity via the relation $\langle ( \boldsymbol {\omega } \boldsymbol {\cdot }\boldsymbol {p} )^2 \rangle \approx \langle \boldsymbol {\omega }^2 \rangle \langle ( \boldsymbol {e}_{\omega } \boldsymbol {\cdot }\boldsymbol {p} )^2 \rangle$. The data show that this assumption has a less than 20 % error for moderately oblate to highly prolate particles with aspect ratios in the range $0.6 \le \mathrm{AR} \le 10$. It is interesting that for prolate particles, the mean-square particle spinning can be accurately estimated by assuming independence between vorticity magnitude and particle alignment with vorticity and that the error in this approximation is independent of filter scale. For highly oblate particles ($\mathrm{AR} \le 0.6$), the error in this approximation can be large and depends on the filter scale.

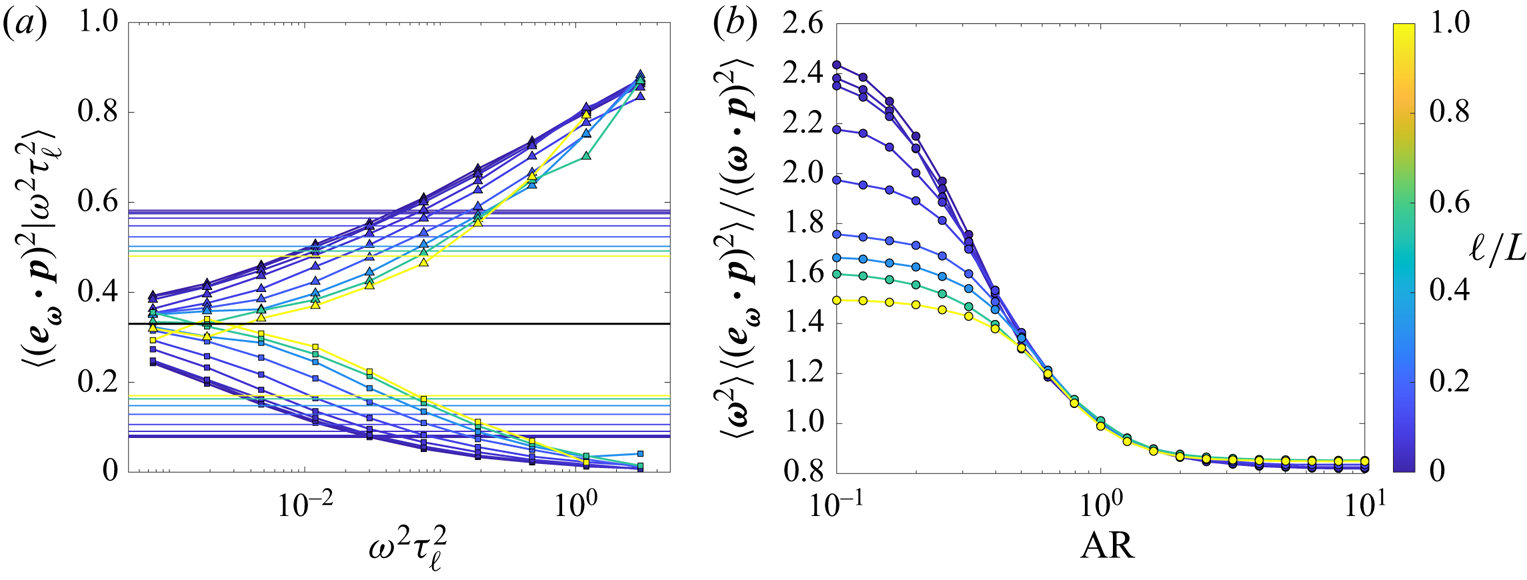
Figure 5. (a) Mean-square particle alignment with vorticity conditioned on the mean-square fluid vorticity. Symbols are data for high-aspect-ratio rods ($\mathrm {AR} = 10^1$; triangles and top lines) and discs ($\mathrm {AR} = 10^{-1}$; squares and bottom lines). Thin horizontal lines correspond to the unconditional mean-square particle alignment with vorticity ($\langle ( \boldsymbol {e}_{\omega } \boldsymbol {\cdot }\boldsymbol {p} )^2 \rangle$). Random alignment corresponds to a value of 1/3 (solid black line). (b) A direct evaluation of the independence between vorticity magnitude and particle alignment assumed in (2.3).

Finally, we show how the predictions of (2.5) compare against data in figure 6. The data lie close to the 1-to-1 lines (figure 6a,b), regardless of the filter scale and particle aspect ratio. Thus, (2.5) provide reasonable predictions of spinning and tumbling rates, despite invoking the approximation that particle alignment is independent of the strength of local vorticity. The error induced by this approximation does not greatly affect the quality of predictions from (2.5) because the error is either small in relative terms (prolate and moderately oblate particles) or because even when the error is large in relative terms it only leads to a small error in absolute terms (highly oblate particles). For highly oblate particles, the prediction of particle spinning has a large relative error, but small absolute error because such particles have low spinning rates. In fact, while the relative error is larger for oblate particles compared with prolate particles in figure 5(b), the absolute error is actually slightly smaller for the oblate particles compared with prolate particles in figure 6(a). In figures 6(c) and 6(d), we can see that these predictions fare well against data for different particle shapes for fully resolved data ($\ell /L = 0$) and for data at the largest filter scale ($\ell /L = 1$), respectively.

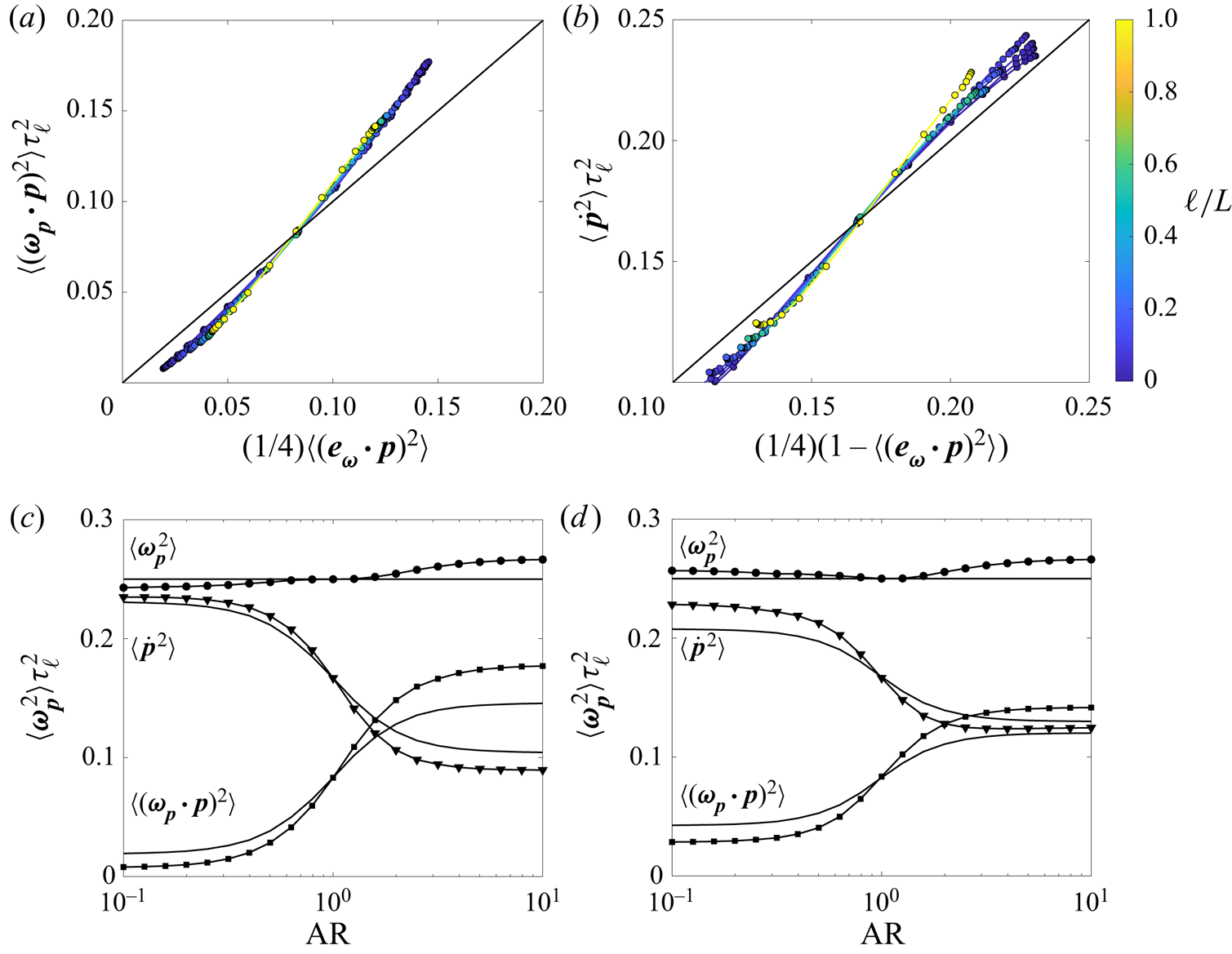
Figure 6. Spinning (a) and tumbling (b) rates compared against the predictions from (2.5) for all shapes across all scales with the solid black line showing the 1 : 1 correspondence. (c,d) Predictions from (2.5) (solid black lines) and DNS data (symbols) across all shapes for unfiltered DNS data ($\ell /L = 0$) (c) and DNS data filtered at the integral scale ($\ell /L = 1$) (d).

3. Discussion

We have conducted DNS to examine the statistics of the shape- and scale-dependent coupling between velocity gradients and spheroids in turbulence. By applying a filter that progressively removes small scales from the fully resolved simulations, we have obtained Lagrangian trajectories of tracer particles in filtered fields and calculated spheroid rotations along these trajectories using Jeffery's equation. Our focus has been on the particle rotation rates and on the decomposition of rotations in the particle frame into the spinning and tumbling rates.

Particle rotation rates decrease as the filter scale increases following a power law that is consistent with Kolmogorov scaling in the inertial subrange. When normalised by scale-local time scales, we find that the mean-square particle rotation rates are independent of the particle shape. Even though the spinning and tumbling rates are a function of particle shape, surprisingly, there is little additional dependency on scale. Moreover, we have also shown that relative rates of spinning and tumbling can be reasonably predicted solely from knowledge of particle alignment with the vorticity vector even though the full dependency of these rotation rates is a function of seven variables that quantify the velocity gradient tensor and particle orientation within its axes.

Our results consistently show that the dynamics of the velocity gradient tensor has scale-invariant properties in the Lagrangian frame that are not observed in the Eulerian frame. While Eulerian statistics of vorticity alignment with the strain eigenframe and flow topologies are known to exhibit qualitative differences in the inertial range relative to the dissipation (viscous) range (van der Bos et al. 2002; Danish & Meneveau 2018), no such changes are observed as a function of scale when velocity gradient dynamics is examined in the Lagrangian frame through the lens of coupling between velocity gradients and spheroids. Our results also suggest that spinning and tumbling rates of large anisotropic particles where particle inertia due to density differences with the fluid can be assumed small (e.g. Parsa & Voth 2014; Bordoloi & Variano 2017; Pujara et al. 2019) are likely to follow the same trends with particle shape previously observed in small particles (Voth & Soldati 2017). While a refined understanding of the detailed flow-particle interactions may still require laboratory experiments or particle-resolved simulations, our results show that it is possible to predict rotation statistics for subgrid-scale particles in large-eddy simulations in principle. For example, particle orientations and rotations at the smallest scale resolved in the simulations could be used to predict particle statistics at subgrid scales based on the scaling arguments provided herein. The scale-invariance of spinning and tumbling rates of spheroids also motivate future work on extending stochastic models of the Lagrangian velocity gradient tensor (Meneveau 2011; Chevillard & Meneveau 2013; Johnson & Meneveau 2018; Leppin & Wilczek 2020) to the inertial range. Finally, it would also be interesting to test our predictive framework for particle spinning and tumbling in other canonical turbulent flows such as channel flow where interesting similarities and differences have been observed in terms of how particles align compared with isotropic turbulence (Zhao & Andersson 2016).